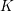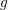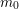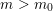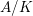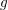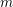Fix a number field
![]() $K$
, a prime
$K$
, a prime
![]() $p$
and a positive integer
$p$
and a positive integer
![]() $g$
. Assuming Lang’s conjecture, we showed in [Reference Abramovich and Várilly-AlvaradoAV16] that there exists an integer
$g$
. Assuming Lang’s conjecture, we showed in [Reference Abramovich and Várilly-AlvaradoAV16] that there exists an integer
![]() $r$
such that no principally polarized abelian variety
$r$
such that no principally polarized abelian variety
![]() $A/K$
has full level-
$A/K$
has full level-
![]() $p^{r}$
structure. Recall that, for a positive integer
$p^{r}$
structure. Recall that, for a positive integer
![]() $m$
, a full level-
$m$
, a full level-
![]() $m$
structure on an abelian variety
$m$
structure on an abelian variety
![]() $A/K$
is an isomorphism of group schemes on the
$A/K$
is an isomorphism of group schemes on the
![]() $m$
-torsion subgroup
$m$
-torsion subgroup
Our goal in this note is to show how to dispose of the dependency on a fixed prime
![]() $p$
, at the cost of assuming Vojta’s conjecture (see [Reference VojtaVoj98, Conjecture 2.3] and Conjecture 3.1 below).
$p$
, at the cost of assuming Vojta’s conjecture (see [Reference VojtaVoj98, Conjecture 2.3] and Conjecture 3.1 below).
Theorem A. Let
![]() $K$
be a number field and let
$K$
be a number field and let
![]() $g$
be a positive integer. Assume Vojta’s conjecture. Then there is an integer
$g$
be a positive integer. Assume Vojta’s conjecture. Then there is an integer
![]() $m_{0}$
such that for any
$m_{0}$
such that for any
![]() $m>m_{0}$
no principally polarized abelian variety
$m>m_{0}$
no principally polarized abelian variety
![]() $A/K$
of dimension
$A/K$
of dimension
![]() $g$
has full level-
$g$
has full level-
![]() $m$
structure.
$m$
structure.
Theorem A follows from combining [Reference Abramovich and Várilly-AlvaradoAV16, Theorem 1.1] and a new result in this note, as follows.
Theorem B. Let
![]() $K$
be a number field and let
$K$
be a number field and let
![]() $g$
be a positive integer. Assume Vojta’s conjecture. Then there is an integer
$g$
be a positive integer. Assume Vojta’s conjecture. Then there is an integer
![]() $m_{0}$
such that for any prime
$m_{0}$
such that for any prime
![]() $p>m_{0}$
no principally polarized abelian variety
$p>m_{0}$
no principally polarized abelian variety
![]() $A/K$
of dimension
$A/K$
of dimension
![]() $g$
has full level-
$g$
has full level-
![]() $p$
structure.
$p$
structure.
1 Introduction
1.1 Vojta’s conjecture for varieties
Before Merel proved that torsion on elliptic curves over number fields is uniformly bounded [Reference MerelMer96], it was known that statements related to Masser–Oesterlé’s
![]() $abc$
conjecture [Reference FreyFre89, Conjecture A-B-C] or Szpiro’s conjecture [Reference SzpiroSzp90, Conjecture 1] imply such bounds; see Frey [Reference FreyFre89, Corollary 2.2], Hindry–Silverman [Reference Hindry and SilvermanHS88, Theorem 7.1] and Flexor–Oesterlé [Reference Flexor and OesterléFO90]. In this paper, we use Vojta’s conjecture [Reference VojtaVoj98, Conjecture 2.3] as a higher-dimensional analogue of the
$abc$
conjecture [Reference FreyFre89, Conjecture A-B-C] or Szpiro’s conjecture [Reference SzpiroSzp90, Conjecture 1] imply such bounds; see Frey [Reference FreyFre89, Corollary 2.2], Hindry–Silverman [Reference Hindry and SilvermanHS88, Theorem 7.1] and Flexor–Oesterlé [Reference Flexor and OesterléFO90]. In this paper, we use Vojta’s conjecture [Reference VojtaVoj98, Conjecture 2.3] as a higher-dimensional analogue of the
![]() $abc$
conjecture to study level structures on abelian varieties of dimension
$abc$
conjecture to study level structures on abelian varieties of dimension
![]() ${>}1$
.
${>}1$
.
Vojta’s conjecture is a quantitative statement, comparing heights
![]() $h_{K_{X}(D)}(x)$
, with respect to the log canonical divisor
$h_{K_{X}(D)}(x)$
, with respect to the log canonical divisor
![]() $K_{X}(D)$
, of rational points
$K_{X}(D)$
, of rational points
![]() $x$
in general position on a smooth projective variety
$x$
in general position on a smooth projective variety
![]() $X$
over a number field
$X$
over a number field
![]() $K$
, with the truncated counting function
$K$
, with the truncated counting function
![]() $N_{K}^{(1)}(D,x)$
of such points (see (2.4)) with respect to a normal crossings divisor
$N_{K}^{(1)}(D,x)$
of such points (see (2.4)) with respect to a normal crossings divisor
![]() $D$
. The simplest statement, for
$D$
. The simplest statement, for
![]() $K$
-rational points, says that if
$K$
-rational points, says that if
![]() $K_{X}(D)$
is big, then, for small
$K_{X}(D)$
is big, then, for small
![]() $\unicode[STIX]{x1D6FF}$
,
$\unicode[STIX]{x1D6FF}$
,
for all rational points
![]() $x\in X(K)$
outside a Zariski-closed proper subset.
$x\in X(K)$
outside a Zariski-closed proper subset.
The general notation is, unfortunately, involved, and explained in §2. The conjecture does have qualitative corollaries, which are easier to explain. The truncated counting function
![]() $N_{K}^{(1)}(D,x)$
measures how often the point
$N_{K}^{(1)}(D,x)$
measures how often the point
![]() $x$
reduces to a point on
$x$
reduces to a point on
![]() $D$
modulo primes of
$D$
modulo primes of
![]() $K$
. In particular, when
$K$
. In particular, when
![]() $D$
is empty, then
$D$
is empty, then
![]() $N_{K}^{(1)}(D,x)=0$
, in which case the statement says that the height
$N_{K}^{(1)}(D,x)=0$
, in which case the statement says that the height
![]() $h_{K_{X}(D)}(x)$
is bounded. Since the height of a big divisor is a counting function outside a Zariski-closed subvariety, this implies that rational points are not Zariski dense. So, Vojta’s conjecture implies Lang’s conjecture: the rational points on a positive-dimensional variety of general type are not Zariski dense. More generally,
$h_{K_{X}(D)}(x)$
is bounded. Since the height of a big divisor is a counting function outside a Zariski-closed subvariety, this implies that rational points are not Zariski dense. So, Vojta’s conjecture implies Lang’s conjecture: the rational points on a positive-dimensional variety of general type are not Zariski dense. More generally,
![]() $N_{K}^{(1)}(D,x)=0$
whenever
$N_{K}^{(1)}(D,x)=0$
whenever
![]() $x$
extends to an integral point on
$x$
extends to an integral point on
![]() $X\smallsetminus D$
. This recovers the statement of the Lang–Vojta conjecture: the integral points on a positive-dimensional variety of logarithmic general type are not Zariski dense.
$X\smallsetminus D$
. This recovers the statement of the Lang–Vojta conjecture: the integral points on a positive-dimensional variety of logarithmic general type are not Zariski dense.
Campana studied varieties where divisors between
![]() $K_{X}$
and
$K_{X}$
and
![]() $K_{X}+D$
are big and, for algebraic curves, stated qualitative conjectures interpolating between Faltings’ and Siegel’s theorems. We will study these intermediate conjectures in higher dimensions in a follow-up note. These statements are qualitative consequences of Vojta’s conjecture.
$K_{X}+D$
are big and, for algebraic curves, stated qualitative conjectures interpolating between Faltings’ and Siegel’s theorems. We will study these intermediate conjectures in higher dimensions in a follow-up note. These statements are qualitative consequences of Vojta’s conjecture.
Our arguments below use Vojta’s conjecture for points of bounded degree, which requires an additional discriminant term
![]() $d_{K}(K(x))$
: for small
$d_{K}(K(x))$
: for small
![]() $\unicode[STIX]{x1D6FF}$
the inequality
$\unicode[STIX]{x1D6FF}$
the inequality
is conjectured to hold, away from a Zariski-closed subset, where
![]() $H$
is a big divisor. Note that when
$H$
is a big divisor. Note that when
![]() $x\in X(K)$
, we have
$x\in X(K)$
, we have
![]() $d_{K}(K(x))=0$
.
$d_{K}(K(x))=0$
.
1.2 Vojta’s conjecture for stacks
Theorem B is decidedly about rational points on stacks, not varieties. Specifically, an abelian variety
![]() $A/K$
corresponds to a rational point on the moduli stack
$A/K$
corresponds to a rational point on the moduli stack
![]() $\widetilde{{\mathcal{A}}}_{g}$
of principally polarized abelian varieties. It should thus come as no surprise that, to prove Theorem B, we require a version of Vojta’s conjecture for Deligne–Mumford stacks (Proposition 3.2), which we deduce from Vojta’s original conjecture.
$\widetilde{{\mathcal{A}}}_{g}$
of principally polarized abelian varieties. It should thus come as no surprise that, to prove Theorem B, we require a version of Vojta’s conjecture for Deligne–Mumford stacks (Proposition 3.2), which we deduce from Vojta’s original conjecture.
Surprisingly, unlike the case of varieties, Vojta’s conjecture for stacks requires a discriminant term even for a
![]() $K$
-rational point: the image of such a point
$K$
-rational point: the image of such a point
![]() $x$
in
$x$
in
![]() $X$
is naturally a stack
$X$
is naturally a stack
![]() ${\mathcal{T}}_{x}$
that is in general ramified over the ring of integers
${\mathcal{T}}_{x}$
that is in general ramified over the ring of integers
![]() ${\mathcal{O}}_{K}$
. The corresponding inequality
${\mathcal{O}}_{K}$
. The corresponding inequality
holds away from a Zariski-closed proper subset, conditional on Vojta’s conjecture for varieties.
Proposition 3.2 is proved by passing to a branched covering
![]() $Y\rightarrow X$
by a variety. Such a covering was constructed by Kresch and Vistoli in [Reference Kresch and VistoliKV04, Theorem 1]; we adapt their construction to stacks with normal crossings divisors in Proposition 2.3.
$Y\rightarrow X$
by a variety. Such a covering was constructed by Kresch and Vistoli in [Reference Kresch and VistoliKV04, Theorem 1]; we adapt their construction to stacks with normal crossings divisors in Proposition 2.3.
While the discriminant term comes naturally from Vojta’s statement for points of bounded degree, one might contemplate doing away with it. It is, however, indispensable, at least if one is to state a conjecture that is not patently false. Consider the root stack
![]() $X=\mathbb{P}^{2}(\sqrt{C})$
, where
$X=\mathbb{P}^{2}(\sqrt{C})$
, where
![]() $C$
is a curve of degree
$C$
is a curve of degree
![]() ${\geqslant}7$
, and let
${\geqslant}7$
, and let
![]() $D=\emptyset$
. Then
$D=\emptyset$
. Then
![]() $K_{X}$
is ample,
$K_{X}$
is ample,
![]() $N_{K}^{(1)}(D,x)\equiv 0$
and yet there is a dense collection of rational points on the open subset
$N_{K}^{(1)}(D,x)\equiv 0$
and yet there is a dense collection of rational points on the open subset
![]() $\mathbb{P}^{2}\smallsetminus C\subset X$
.
$\mathbb{P}^{2}\smallsetminus C\subset X$
.
1.3 Abelian varieties, counting functions and discriminants
Fix an integer
![]() $m_{0}$
and consider the set
$m_{0}$
and consider the set
![]() $\widetilde{{\mathcal{A}}}_{g}(K)_{p\geqslant m_{0}}$
of points corresponding to abelian varieties admitting full level-
$\widetilde{{\mathcal{A}}}_{g}(K)_{p\geqslant m_{0}}$
of points corresponding to abelian varieties admitting full level-
![]() $p$
structures for primes
$p$
structures for primes
![]() $p\geqslant m_{0}$
. Our task is to show that for large
$p\geqslant m_{0}$
. Our task is to show that for large
![]() $m_{0}$
this set is empty. To this end, it is natural to focus on an irreducible component
$m_{0}$
this set is empty. To this end, it is natural to focus on an irreducible component
![]() $X\subset \overline{\widetilde{{\mathcal{A}}}_{g}(K)_{p\geqslant m_{0}}}$
of the Zariski closure. This leads to the following setup: consider a closed substack
$X\subset \overline{\widetilde{{\mathcal{A}}}_{g}(K)_{p\geqslant m_{0}}}$
of the Zariski closure. This leads to the following setup: consider a closed substack
![]() $X\subset \widetilde{{\mathcal{A}}}_{g}$
, a resolution of singularities
$X\subset \widetilde{{\mathcal{A}}}_{g}$
, a resolution of singularities
![]() $X^{\prime }\rightarrow X$
and a normal crossings compactification
$X^{\prime }\rightarrow X$
and a normal crossings compactification
![]() $\overline{X}^{\prime }$
with boundary divisor
$\overline{X}^{\prime }$
with boundary divisor
![]() $D$
. Following Zuo [Reference ZuoZuo00, Theorem 0.1(ii)], we showed in [Reference Abramovich and Várilly-AlvaradoAV16, Theorem 1.9] that
$D$
. Following Zuo [Reference ZuoZuo00, Theorem 0.1(ii)], we showed in [Reference Abramovich and Várilly-AlvaradoAV16, Theorem 1.9] that
![]() $K_{\overline{X}^{\prime }}(D)$
is big.
$K_{\overline{X}^{\prime }}(D)$
is big.
With a version of Vojta’s conjecture for stacks in hand, the key to proving Theorem B is to show that, for points
![]() $x\in X^{\prime }(K)$
corresponding to abelian varieties with full level-
$x\in X^{\prime }(K)$
corresponding to abelian varieties with full level-
![]() $p$
structure, the terms
$p$
structure, the terms
![]() $N_{K}^{(1)}(D,x)$
and
$N_{K}^{(1)}(D,x)$
and
![]() $d_{K}({\mathcal{T}}_{x})$
on the left-hand side of (1.1) are small compared to the height
$d_{K}({\mathcal{T}}_{x})$
on the left-hand side of (1.1) are small compared to the height
![]() $h_{K_{\overline{X}^{\prime }}(D)}(x)$
, as soon as
$h_{K_{\overline{X}^{\prime }}(D)}(x)$
, as soon as
![]() $p$
is large enough.
$p$
is large enough.
To this end, we show that each one of these terms is bounded by a small fraction of the height
![]() $h_{D}(x)$
; see Lemmas 4.4 and 4.5. First, to bound the truncated counting function
$h_{D}(x)$
; see Lemmas 4.4 and 4.5. First, to bound the truncated counting function
![]() $N_{K}^{(1)}(D,x)$
, we use the fact that the compactified moduli space
$N_{K}^{(1)}(D,x)$
, we use the fact that the compactified moduli space
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}^{[p]}$
of abelian varieties with full level-
$\overline{\widetilde{{\mathcal{A}}}}_{g}^{[p]}$
of abelian varieties with full level-
![]() $p$
structure is highly ramified over the compactification
$p$
structure is highly ramified over the compactification
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}$
along the boundary. This is well known away from characteristic
$\overline{\widetilde{{\mathcal{A}}}}_{g}$
along the boundary. This is well known away from characteristic
![]() $p$
; see [Reference Abramovich and Várilly-AlvaradoAV16, Proposition 4.1]. The remaining case of characteristic
$p$
; see [Reference Abramovich and Várilly-AlvaradoAV16, Proposition 4.1]. The remaining case of characteristic
![]() $p$
is proven in Proposition A.4 as part of the Appendix by Madapusi Pera, where the structure of the boundary is described using Mumford’s construction.
$p$
is proven in Proposition A.4 as part of the Appendix by Madapusi Pera, where the structure of the boundary is described using Mumford’s construction.
Second, using standard discriminant bounds, we show that the discriminant term
![]() $d_{k}({\mathcal{T}}_{x})$
grows at most like
$d_{k}({\mathcal{T}}_{x})$
grows at most like
![]() $\log p$
. Meanwhile, the height
$\log p$
. Meanwhile, the height
![]() $h_{D}(x)$
grows at least linearly in
$h_{D}(x)$
grows at least linearly in
![]() $p$
. For this we use a point-counting argument of Flexor–Oesterlé [Reference Flexor and OesterléFO90, Théorème 3] and Silverberg [Reference SilverbergSil92, Theorem 3.3] (see also Kamienny [Reference KamiennyKam82, §6(2a)]) to show that
$p$
. For this we use a point-counting argument of Flexor–Oesterlé [Reference Flexor and OesterléFO90, Théorème 3] and Silverberg [Reference SilverbergSil92, Theorem 3.3] (see also Kamienny [Reference KamiennyKam82, §6(2a)]) to show that
![]() $x$
reduces to
$x$
reduces to
![]() $D$
modulo a small prime, whose contribution to
$D$
modulo a small prime, whose contribution to
![]() $h_{D}(x)$
is at least proportional to
$h_{D}(x)$
is at least proportional to
![]() $p$
, since
$p$
, since
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}^{[p]}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
is highly ramified.
$\overline{\widetilde{{\mathcal{A}}}}_{g}^{[p]}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
is highly ramified.
Together, these two bounds can be leveraged to show that the totality of points
![]() $x\in X^{\prime }(K)$
corresponding to abelian varieties over
$x\in X^{\prime }(K)$
corresponding to abelian varieties over
![]() $K$
with full level-
$K$
with full level-
![]() $p$
structure for
$p$
structure for
![]() $p\gg 0$
is contained in a Zariski-closed proper subset of
$p\gg 0$
is contained in a Zariski-closed proper subset of
![]() $X^{\prime }$
. A Noetherian induction argument allows us to deduce Theorem B from this result.
$X^{\prime }$
. A Noetherian induction argument allows us to deduce Theorem B from this result.
2 Preliminaries
In this section, we set up notation that will remain in force throughout. Let
![]() $K$
be a number field and let
$K$
be a number field and let
![]() $\overline{K}$
be a fixed algebraic closure of
$\overline{K}$
be a fixed algebraic closure of
![]() $K$
. We write
$K$
. We write
![]() ${\mathcal{O}}_{K}$
for the ring of integers of
${\mathcal{O}}_{K}$
for the ring of integers of
![]() $K$
and
$K$
and
![]() $\operatorname{Disc}({\mathcal{O}}_{K})$
for its discriminant. We denote by
$\operatorname{Disc}({\mathcal{O}}_{K})$
for its discriminant. We denote by
![]() $M_{K}^{0}$
the set of non-zero primes of
$M_{K}^{0}$
the set of non-zero primes of
![]() ${\mathcal{O}}_{K}$
; for
${\mathcal{O}}_{K}$
; for
![]() $p\in M_{K}^{0}$
, we write
$p\in M_{K}^{0}$
, we write
![]() ${\mathcal{O}}_{K,p}$
for the localization of
${\mathcal{O}}_{K,p}$
for the localization of
![]() ${\mathcal{O}}_{K}$
at
${\mathcal{O}}_{K}$
at
![]() $p$
and
$p$
and
![]() $\unicode[STIX]{x1D705}(p)$
for the residue field. We use
$\unicode[STIX]{x1D705}(p)$
for the residue field. We use
![]() $S$
to denote a finite set of places of
$S$
to denote a finite set of places of
![]() $K$
that includes the infinite places, and
$K$
that includes the infinite places, and
![]() ${\mathcal{O}}_{K,S}$
for the ring of
${\mathcal{O}}_{K,S}$
for the ring of
![]() $S$
-integers of
$S$
-integers of
![]() $K$
.
$K$
.
For a finite extension
![]() $L/K$
, we write
$L/K$
, we write
![]() $\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{L}/{\mathcal{O}}_{K}}$
for the module of Kähler differentials.
$\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{L}/{\mathcal{O}}_{K}}$
for the module of Kähler differentials.
2.1 Discriminants of fields
For a finite extension
![]() $E/K$
, following Vojta, define the relative logarithmic discriminant as
$E/K$
, following Vojta, define the relative logarithmic discriminant as
Noting that
![]() $(\operatorname{Disc}({\mathcal{O}}_{K}))=N_{K/\mathbb{Q}}\det \unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{K}/\mathbb{Z}}$
as ideals, we have
$(\operatorname{Disc}({\mathcal{O}}_{K}))=N_{K/\mathbb{Q}}\det \unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{K}/\mathbb{Z}}$
as ideals, we have
see [Reference VojtaVoj98, p. 1106]. The right-hand side can be decomposed into a sum of local contributions
For
![]() $p\in M_{K}^{0}$
, we write
$p\in M_{K}^{0}$
, we write
for the contribution of the primes above
![]() $p$
, so that
$p$
, so that
![]() $d_{K}(E)=\sum _{p\in M_{K}^{0}}d_{K}(E)_{p}$
.
$d_{K}(E)=\sum _{p\in M_{K}^{0}}d_{K}(E)_{p}$
.
If
![]() $L/E$
is a further finite extension, the formula for discriminants in the tower
$L/E$
is a further finite extension, the formula for discriminants in the tower
![]() $L/E/K$
gives
$L/E/K$
gives
In particular, if
![]() $L/E$
is unramified above
$L/E$
is unramified above
![]() $p\in M_{K}^{0}$
, then
$p\in M_{K}^{0}$
, then
![]() $d_{K}(L)_{p}=d_{K}(E)_{p}.$
$d_{K}(L)_{p}=d_{K}(E)_{p}.$
2.2 Discriminants of stacks
We shall need analogous definitions where
![]() $\operatorname{Spec}{\mathcal{O}}_{E}$
is replaced by a normal separated Deligne–Mumford stack
$\operatorname{Spec}{\mathcal{O}}_{E}$
is replaced by a normal separated Deligne–Mumford stack
![]() ${\mathcal{T}}$
with coarse moduli scheme
${\mathcal{T}}$
with coarse moduli scheme
![]() $\operatorname{Spec}{\mathcal{O}}_{E}$
:
$\operatorname{Spec}{\mathcal{O}}_{E}$
:
 $$\begin{eqnarray}\displaystyle d_{K}({\mathcal{T}}) & = & \displaystyle \frac{1}{\deg ({\mathcal{T}}/{\mathcal{O}}_{K})}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{T}}})-\log |\!\operatorname{Disc}({\mathcal{O}}_{K})|=\frac{1}{\deg ({\mathcal{T}}/{\mathcal{O}}_{K})}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{T}}/\operatorname{Spec}{\mathcal{O}}_{K}}),\nonumber\\ \displaystyle d_{K}({\mathcal{T}})_{p} & = & \displaystyle \frac{1}{\deg ({\mathcal{T}}/{\mathcal{O}}_{K})}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{T}}_{p}})-\log |\!\operatorname{Disc}({\mathcal{O}}_{K})|=\frac{1}{\deg ({\mathcal{T}}/{\mathcal{O}}_{K})}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{T}}_{p}/\operatorname{Spec}{\mathcal{O}}_{K,p}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{K}({\mathcal{T}}) & = & \displaystyle \frac{1}{\deg ({\mathcal{T}}/{\mathcal{O}}_{K})}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{T}}})-\log |\!\operatorname{Disc}({\mathcal{O}}_{K})|=\frac{1}{\deg ({\mathcal{T}}/{\mathcal{O}}_{K})}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{T}}/\operatorname{Spec}{\mathcal{O}}_{K}}),\nonumber\\ \displaystyle d_{K}({\mathcal{T}})_{p} & = & \displaystyle \frac{1}{\deg ({\mathcal{T}}/{\mathcal{O}}_{K})}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{T}}_{p}})-\log |\!\operatorname{Disc}({\mathcal{O}}_{K})|=\frac{1}{\deg ({\mathcal{T}}/{\mathcal{O}}_{K})}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{T}}_{p}/\operatorname{Spec}{\mathcal{O}}_{K,p}}).\nonumber\end{eqnarray}$$
The quantity
![]() $\deg ({\mathcal{T}}/{\mathcal{O}}_{K})$
is in general rational, as the fiber over
$\deg ({\mathcal{T}}/{\mathcal{O}}_{K})$
is in general rational, as the fiber over
![]() $\operatorname{Spec}K$
might be a gerbe over
$\operatorname{Spec}K$
might be a gerbe over
![]() $\operatorname{Spec}E$
.Footnote
1
However, we still have
$\operatorname{Spec}E$
.Footnote
1
However, we still have
![]() $d_{K}({\mathcal{T}})=\sum _{p\in M_{K}^{0}}d_{K}({\mathcal{T}})_{p}$
.
$d_{K}({\mathcal{T}})=\sum _{p\in M_{K}^{0}}d_{K}({\mathcal{T}})_{p}$
.
Choose a morphism
![]() $\operatorname{Spec}{\mathcal{O}}_{F}\rightarrow {\mathcal{T}}$
unramified above
$\operatorname{Spec}{\mathcal{O}}_{F}\rightarrow {\mathcal{T}}$
unramified above
![]() $p$
, so that
$p$
, so that
![]() $(\unicode[STIX]{x1D6FA}_{{\mathcal{T}}/\operatorname{Spec}{\mathcal{O}}_{K}})_{\operatorname{Spec}{\mathcal{O}}_{F,p}}=\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{F,p}/{\mathcal{O}}_{K,p}}.$
Since
$(\unicode[STIX]{x1D6FA}_{{\mathcal{T}}/\operatorname{Spec}{\mathcal{O}}_{K}})_{\operatorname{Spec}{\mathcal{O}}_{F,p}}=\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{F,p}/{\mathcal{O}}_{K,p}}.$
Since
![]() $[F:K]=\deg ({\mathcal{T}}/{\mathcal{O}}_{K})\cdot \deg (\operatorname{Spec}{\mathcal{O}}_{F}/{\mathcal{T}})$
, we can compute
$[F:K]=\deg ({\mathcal{T}}/{\mathcal{O}}_{K})\cdot \deg (\operatorname{Spec}{\mathcal{O}}_{F}/{\mathcal{T}})$
, we can compute
![]() $d_{K}({\mathcal{T}})_{p}$
entirely with schemes.
$d_{K}({\mathcal{T}})_{p}$
entirely with schemes.
Lemma 2.1. For
![]() $\operatorname{Spec}{\mathcal{O}}_{F}\rightarrow {\mathcal{T}}$
unramified above
$\operatorname{Spec}{\mathcal{O}}_{F}\rightarrow {\mathcal{T}}$
unramified above
![]() $p$
, we have
$p$
, we have
![]() $d_{K}({\mathcal{T}})_{p}=d_{K}(F)_{p}.$
$d_{K}({\mathcal{T}})_{p}=d_{K}(F)_{p}.$
We deduce analogues of (2.1) and (2.2).
Lemma 2.2. Let
![]() $L/E$
be a finite extension field and
$L/E$
be a finite extension field and
![]() $\unicode[STIX]{x1D70B}:\operatorname{Spec}{\mathcal{O}}_{L}\rightarrow {\mathcal{T}}$
a morphism. Then
$\unicode[STIX]{x1D70B}:\operatorname{Spec}{\mathcal{O}}_{L}\rightarrow {\mathcal{T}}$
a morphism. Then
and
Proof. To prove the local statement, choose
![]() $\unicode[STIX]{x1D713}:\operatorname{Spec}{\mathcal{O}}_{F}\rightarrow {\mathcal{T}}$
unramified above
$\unicode[STIX]{x1D713}:\operatorname{Spec}{\mathcal{O}}_{F}\rightarrow {\mathcal{T}}$
unramified above
![]() $p$
, and let
$p$
, and let
![]() ${\mathcal{U}}=\operatorname{Spec}({\mathcal{O}}_{F})\times _{{\mathcal{T}}}\operatorname{Spec}({\mathcal{O}}_{L})$
with projection
${\mathcal{U}}=\operatorname{Spec}({\mathcal{O}}_{F})\times _{{\mathcal{T}}}\operatorname{Spec}({\mathcal{O}}_{L})$
with projection
![]() $\unicode[STIX]{x1D719}:{\mathcal{U}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{L})$
. These objects fit together in the commutative diagram
$\unicode[STIX]{x1D719}:{\mathcal{U}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{L})$
. These objects fit together in the commutative diagram

We have
and
The projection formula gives
and finally
 $$\begin{eqnarray}\displaystyle d_{K}(L)_{p} & = & \displaystyle \frac{1}{[L:K]}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{L,p}/{\mathcal{O}}_{K,p}})=\frac{1}{[L:K]\deg \unicode[STIX]{x1D713}}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{U}}_{p}/\operatorname{Spec}({\mathcal{O}}_{K,p})})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[L:K]\deg \unicode[STIX]{x1D713}}(\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{U}}_{p}/\operatorname{Spec}({\mathcal{O}}_{F,p})})+(\deg \unicode[STIX]{x1D70B})\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{F,p}/{\mathcal{O}}_{K,p}}))\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[L:K]\deg \unicode[STIX]{x1D713}}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{U}}_{p}/{\mathcal{T}}_{p}})+\frac{1}{\deg ({\mathcal{T}}/\operatorname{Spec}{\mathcal{O}}_{K})}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{T}}_{p}/\operatorname{Spec}({\mathcal{O}}_{K,p})})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[L:K]}\deg (\unicode[STIX]{x1D6FA}_{\operatorname{Spec}({\mathcal{O}}_{L,p})/{\mathcal{T}}_{p}})+d_{K}({\mathcal{T}})_{p},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{K}(L)_{p} & = & \displaystyle \frac{1}{[L:K]}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{L,p}/{\mathcal{O}}_{K,p}})=\frac{1}{[L:K]\deg \unicode[STIX]{x1D713}}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{U}}_{p}/\operatorname{Spec}({\mathcal{O}}_{K,p})})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[L:K]\deg \unicode[STIX]{x1D713}}(\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{U}}_{p}/\operatorname{Spec}({\mathcal{O}}_{F,p})})+(\deg \unicode[STIX]{x1D70B})\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{O}}_{F,p}/{\mathcal{O}}_{K,p}}))\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[L:K]\deg \unicode[STIX]{x1D713}}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{U}}_{p}/{\mathcal{T}}_{p}})+\frac{1}{\deg ({\mathcal{T}}/\operatorname{Spec}{\mathcal{O}}_{K})}\deg (\unicode[STIX]{x1D6FA}_{{\mathcal{T}}_{p}/\operatorname{Spec}({\mathcal{O}}_{K,p})})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[L:K]}\deg (\unicode[STIX]{x1D6FA}_{\operatorname{Spec}({\mathcal{O}}_{L,p})/{\mathcal{T}}_{p}})+d_{K}({\mathcal{T}})_{p},\nonumber\end{eqnarray}$$
as required. The global formula follows by summing over
![]() $p\in M_{K}^{0}$
.◻
$p\in M_{K}^{0}$
.◻
2.3 Heights on stacks
For a divisor
![]() $H$
on a smooth projective scheme
$H$
on a smooth projective scheme
![]() $Y$
, we denote by
$Y$
, we denote by
![]() $h_{H}(x)$
the Weil height of
$h_{H}(x)$
the Weil height of
![]() $x$
with respect to
$x$
with respect to
![]() $H$
, which is well defined up to a bounded function on
$H$
, which is well defined up to a bounded function on
![]() $Y(\overline{K})$
. To define a notion of height on a Deligne–Mumford stack, we pull back to a cover by a scheme and work there instead. Let
$Y(\overline{K})$
. To define a notion of height on a Deligne–Mumford stack, we pull back to a cover by a scheme and work there instead. Let
![]() $X/K$
be a smooth proper Deligne–Mumford stack with projective coarse moduli scheme and let
$X/K$
be a smooth proper Deligne–Mumford stack with projective coarse moduli scheme and let
![]() $H\subset X$
be a divisor. Let
$H\subset X$
be a divisor. Let
![]() $f:Y\rightarrow X$
be the finite flat surjective morphism from a smooth projective scheme
$f:Y\rightarrow X$
be the finite flat surjective morphism from a smooth projective scheme
![]() $Y$
guaranteed by [Reference Kresch and VistoliKV04, Theorem 1] or Proposition 2.3 below. For a point
$Y$
guaranteed by [Reference Kresch and VistoliKV04, Theorem 1] or Proposition 2.3 below. For a point
![]() $x\in X(\overline{K})$
, let
$x\in X(\overline{K})$
, let
![]() $y\in Y(\overline{K})$
be a point over
$y\in Y(\overline{K})$
be a point over
![]() $x$
and define
$x$
and define
This definition has the advantage of having functoriality properties of heights built into it. It is also compatible with passing to the coarse moduli space, at the price of working with
![]() $\mathbb{Q}$
-Cartier divisors on slightly singular schemes: any divisor
$\mathbb{Q}$
-Cartier divisors on slightly singular schemes: any divisor
![]() $H$
on
$H$
on
![]() $X$
is the pullback of a
$X$
is the pullback of a
![]() $\mathbb{Q}$
-Cartier divisor
$\mathbb{Q}$
-Cartier divisor
![]() $\text{}\underline{H}$
on the coarse moduli space
$\text{}\underline{H}$
on the coarse moduli space
![]() $\text{}\underline{X}$
and, if
$\text{}\underline{X}$
and, if
![]() $\text{}\underline{x}\in \text{}\underline{X}$
is the image of
$\text{}\underline{x}\in \text{}\underline{X}$
is the image of
![]() $x$
, then
$x$
, then
Our definition has the disadvantage that there can be infinitely many rational points (with the same image in
![]() $\text{}\underline{X}$
) with the same height. In a forthcoming paper, Ellenberg et al. construct an alternative notion of height on a stack, with the property that there are only finitely many non-isomorphic points with bounded height.
$\text{}\underline{X}$
) with the same height. In a forthcoming paper, Ellenberg et al. construct an alternative notion of height on a stack, with the property that there are only finitely many non-isomorphic points with bounded height.
2.4 Normal crossings models
Let
![]() $(\mathscr{X},\mathscr{D})$
be a pair with
$(\mathscr{X},\mathscr{D})$
be a pair with
![]() $\mathscr{X}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K,S}$
a smooth proper morphism from a scheme or a Deligne–Mumford stack, and
$\mathscr{X}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K,S}$
a smooth proper morphism from a scheme or a Deligne–Mumford stack, and
![]() $\mathscr{D}$
a fiber-wise normal crossings divisor on
$\mathscr{D}$
a fiber-wise normal crossings divisor on
![]() $\mathscr{X}$
. Let
$\mathscr{X}$
. Let
![]() $(X,D)$
be the generic fiber of the pair
$(X,D)$
be the generic fiber of the pair
![]() $(\mathscr{X},\mathscr{D})$
; we say that
$(\mathscr{X},\mathscr{D})$
; we say that
![]() $(\mathscr{X},\mathscr{D})$
is a normal crossings model of the pair
$(\mathscr{X},\mathscr{D})$
is a normal crossings model of the pair
![]() $(X,D)$
. Write
$(X,D)$
. Write
![]() $\mathscr{D}=\sum _{i}\mathscr{D}_{i}$
and let
$\mathscr{D}=\sum _{i}\mathscr{D}_{i}$
and let
![]() $D_{i}$
be the generic fiber of
$D_{i}$
be the generic fiber of
![]() $\mathscr{D}_{i}$
.
$\mathscr{D}_{i}$
.
2.5 Intersection multiplicities on schemes and stacks
For
![]() $R$
an integral extension of
$R$
an integral extension of
![]() ${\mathcal{O}}_{K,S}$
, and
${\mathcal{O}}_{K,S}$
, and
![]() $q\subset R$
a non-zero prime ideal, let
$q\subset R$
a non-zero prime ideal, let
![]() $R_{q}$
be the localization of
$R_{q}$
be the localization of
![]() $R$
at
$R$
at
![]() $q$
, with maximal ideal
$q$
, with maximal ideal
![]() $\mathfrak{m}_{q}$
and residue field
$\mathfrak{m}_{q}$
and residue field
![]() $\unicode[STIX]{x1D705}(q)$
.
$\unicode[STIX]{x1D705}(q)$
.
We first define multiplicities for integral points. Let
![]() $x\in \mathscr{X}(R_{q})$
, and define
$x\in \mathscr{X}(R_{q})$
, and define
![]() $n_{q}(\mathscr{D}_{i},x)$
as the intersection multiplicity of
$n_{q}(\mathscr{D}_{i},x)$
as the intersection multiplicity of
![]() $x$
and
$x$
and
![]() $\mathscr{D}_{i}$
. In other words, letting
$\mathscr{D}_{i}$
. In other words, letting
![]() $I_{\mathscr{D}_{i}}$
denote the ideal of
$I_{\mathscr{D}_{i}}$
denote the ideal of
![]() $\mathscr{D}_{i}$
, we have an equality of ideals in
$\mathscr{D}_{i}$
, we have an equality of ideals in
![]() $R_{q}$
:
$R_{q}$
:
Note that if
![]() $R^{\prime }$
is an integral extension of
$R^{\prime }$
is an integral extension of
![]() $R$
, with maximal ideal
$R$
, with maximal ideal
![]() $\mathfrak{q}\mid q$
, and if
$\mathfrak{q}\mid q$
, and if
![]() $y\in \mathscr{X}(R_{\mathfrak{q}}^{\prime })$
is the composite of
$y\in \mathscr{X}(R_{\mathfrak{q}}^{\prime })$
is the composite of
![]() $\operatorname{Spec}R_{\mathfrak{q}}^{\prime }\rightarrow \operatorname{Spec}R_{q}\rightarrow \mathscr{X}$
, then we have
$\operatorname{Spec}R_{\mathfrak{q}}^{\prime }\rightarrow \operatorname{Spec}R_{q}\rightarrow \mathscr{X}$
, then we have
![]() $n_{\mathfrak{q}}(\mathscr{D}_{i},y)=e(\mathfrak{q}\mid q)n_{q}(\mathscr{D}_{i},x)$
, where
$n_{\mathfrak{q}}(\mathscr{D}_{i},y)=e(\mathfrak{q}\mid q)n_{q}(\mathscr{D}_{i},x)$
, where
![]() $e(\mathfrak{q}\mid q)$
is the ramification index of
$e(\mathfrak{q}\mid q)$
is the ramification index of
![]() $\mathfrak{q}$
over
$\mathfrak{q}$
over
![]() $q$
.
$q$
.
This observation prompts the following extension of the definition of
![]() $n_{q}(\mathscr{D}_{i},x)$
to a rational point
$n_{q}(\mathscr{D}_{i},x)$
to a rational point
![]() $x$
of
$x$
of
![]() $\mathscr{X}$
. Denoting by
$\mathscr{X}$
. Denoting by
![]() $K(R)$
and
$K(R)$
and
![]() $K(R^{\prime })$
the respective fraction fields of
$K(R^{\prime })$
the respective fraction fields of
![]() $R$
and
$R$
and
![]() $R^{\prime }$
, if
$R^{\prime }$
, if
![]() $x\in \mathscr{X}(K(R))$
and if
$x\in \mathscr{X}(K(R))$
and if
![]() $y\in \mathscr{X}(R^{\prime })$
is an integral point over
$y\in \mathscr{X}(R^{\prime })$
is an integral point over
![]() $x$
, then the quantity
$x$
, then the quantity
is well defined.
Finally, define
![]() $n_{q}(\sum a_{i}\mathscr{D}_{i},x):=\sum _{i}a_{i}n_{q}(\mathscr{D}_{i},x)$
.
$n_{q}(\sum a_{i}\mathscr{D}_{i},x):=\sum _{i}a_{i}n_{q}(\mathscr{D}_{i},x)$
.
2.6 Counting functions
Following Vojta [Reference VojtaVoj98, p. 1106], for
![]() $x\in \mathscr{X}(\overline{K})$
, with residue field
$x\in \mathscr{X}(\overline{K})$
, with residue field
![]() $K(x)$
, define the truncated counting function
$K(x)$
, define the truncated counting function
 $$\begin{eqnarray}N_{K}^{(1)}(D,x)=\frac{1}{[K(x):K]}\mathop{\sum }_{\substack{ q\in \operatorname{Spec}{\mathcal{O}}_{K(x),S} \\ n_{q}(\mathscr{D},x)>0}}\log |\unicode[STIX]{x1D705}(q)|.\end{eqnarray}$$
$$\begin{eqnarray}N_{K}^{(1)}(D,x)=\frac{1}{[K(x):K]}\mathop{\sum }_{\substack{ q\in \operatorname{Spec}{\mathcal{O}}_{K(x),S} \\ n_{q}(\mathscr{D},x)>0}}\log |\unicode[STIX]{x1D705}(q)|.\end{eqnarray}$$
The quantity on the right-hand side of (2.4) depends on the model
![]() $(\mathscr{X},\mathscr{D})$
and the finite set
$(\mathscr{X},\mathscr{D})$
and the finite set
![]() $S$
only up to a bounded function on
$S$
only up to a bounded function on
![]() $X(\overline{K})$
. However, we are interested in this quantity only up to such functions. Hence, the notation
$X(\overline{K})$
. However, we are interested in this quantity only up to such functions. Hence, the notation
![]() $N_{K}^{(1)}(D,x)$
does not reflect the model
$N_{K}^{(1)}(D,x)$
does not reflect the model
![]() $(\mathscr{X},\mathscr{D})$
or the finite set
$(\mathscr{X},\mathscr{D})$
or the finite set
![]() $S$
.
$S$
.
By [Reference VojtaVoj98, p. 1113] or [Reference Hindry and SilvermanHS00, Theorem B.8.1(e)], we have the bound
which can be further improved whenever we bound the multiplicities
![]() $n_{\mathfrak{q}}(D,x)$
from below.
$n_{\mathfrak{q}}(D,x)$
from below.
2.7 Coverings of stacks
We require the following version of [Reference Kresch and VistoliKV04, Theorem 1], due to Kresch and Vistoli, adapted to the case of a stack with a normal crossings divisor.
Proposition 2.3. Suppose that
![]() $X/K$
is a smooth proper Deligne–Mumford stack with projective moduli scheme, with a normal crossings divisor
$X/K$
is a smooth proper Deligne–Mumford stack with projective moduli scheme, with a normal crossings divisor
![]() $D\subset X$
. Then there exists a finite surjective morphism
$D\subset X$
. Then there exists a finite surjective morphism
![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$
such that
$\unicode[STIX]{x1D70B}:Y\rightarrow X$
such that
![]() $Y$
is a smooth projective irreducible scheme,
$Y$
is a smooth projective irreducible scheme,
![]() $D_{Y}:=\unicode[STIX]{x1D70B}^{\ast }D\subset Y$
is a normal crossings divisor and the ramification divisor
$D_{Y}:=\unicode[STIX]{x1D70B}^{\ast }D\subset Y$
is a normal crossings divisor and the ramification divisor
![]() $R$
of
$R$
of
![]() $Y\rightarrow X$
meets every stratum of
$Y\rightarrow X$
meets every stratum of
![]() $D_{Y}$
properly.
$D_{Y}$
properly.
The proof of this proposition requires the following slicing lemma.
Lemma 2.4 (See [Reference Kresch and VistoliKV04, Lemma 1]).
Let
![]() $f:U\rightarrow V$
be a morphism of quasi-projective varieties over an infinite field, with constant fiber dimension
$f:U\rightarrow V$
be a morphism of quasi-projective varieties over an infinite field, with constant fiber dimension
![]() $r>0$
; let
$r>0$
; let
![]() $D\subset V$
be a divisor. Assume that
$D\subset V$
be a divisor. Assume that
![]() $U$
is smooth and
$U$
is smooth and
![]() $D_{U}=f^{-1}D$
is a simple normal crossings divisor. Let
$D_{U}=f^{-1}D$
is a simple normal crossings divisor. Let
![]() $U\subset \mathbb{P}^{N}$
be a projective embedding. Denote by
$U\subset \mathbb{P}^{N}$
be a projective embedding. Denote by
![]() $D_{U}^{I}$
the closed strata of
$D_{U}^{I}$
the closed strata of
![]() $(U,D_{U})$
, and assume further that
$(U,D_{U})$
, and assume further that
![]() $D_{U}^{I}\rightarrow D^{I}:=f(D_{U}^{I})$
is generically smooth for each
$D_{U}^{I}\rightarrow D^{I}:=f(D_{U}^{I})$
is generically smooth for each
![]() $I$
. Then, for sufficiently high
$I$
. Then, for sufficiently high
![]() $d$
, the intersection
$d$
, the intersection
![]() $D_{U}^{I}\cap H^{(d)}$
of each stratum
$D_{U}^{I}\cap H^{(d)}$
of each stratum
![]() $D_{U}^{I}$
with a general hypersurface
$D_{U}^{I}$
with a general hypersurface
![]() $H^{(d)}\subset \mathbb{P}^{N}$
of degree
$H^{(d)}\subset \mathbb{P}^{N}$
of degree
![]() $d$
is a smooth Cartier divisor in
$d$
is a smooth Cartier divisor in
![]() $D_{U}^{I}$
, generically smooth and of constant fiber dimension
$D_{U}^{I}$
, generically smooth and of constant fiber dimension
![]() $r-1$
over
$r-1$
over
![]() $D^{I}$
.
$D^{I}$
.
Proof of the lemma.
For each
![]() $I$
, [Reference Kresch and VistoliKV04, Lemma 1] applied to
$I$
, [Reference Kresch and VistoliKV04, Lemma 1] applied to
![]() $U\rightarrow V$
replaced by
$U\rightarrow V$
replaced by
![]() $D_{U}^{I}\rightarrow D^{I}$
provides an integer
$D_{U}^{I}\rightarrow D^{I}$
provides an integer
![]() $d_{I}$
and, for each
$d_{I}$
and, for each
![]() $d\geqslant d_{I}$
, an open subset of
$d\geqslant d_{I}$
, an open subset of
![]() $\unicode[STIX]{x1D6E4}(\mathbb{P}^{N},{\mathcal{O}}(d))$
, where
$\unicode[STIX]{x1D6E4}(\mathbb{P}^{N},{\mathcal{O}}(d))$
, where
![]() $D_{U}^{I}\cap H^{(d)}$
is a smooth Cartier divisor in
$D_{U}^{I}\cap H^{(d)}$
is a smooth Cartier divisor in
![]() $D_{U}^{I}$
of constant fiber dimension
$D_{U}^{I}$
of constant fiber dimension
![]() $r-1$
over
$r-1$
over
![]() $D^{I}$
. By Bertini’s theorem, after possibly enlarging
$D^{I}$
. By Bertini’s theorem, after possibly enlarging
![]() $d_{I}$
we may replace it by a smaller open subset, where
$d_{I}$
we may replace it by a smaller open subset, where
![]() $D_{U}^{I}\cap H^{(d)}\rightarrow D^{I}$
is also generically smooth. Take
$D_{U}^{I}\cap H^{(d)}\rightarrow D^{I}$
is also generically smooth. Take
![]() $d\geqslant \max _{I}d_{I}$
.◻
$d\geqslant \max _{I}d_{I}$
.◻
Proof of Proposition 2.3.
First, we note that
![]() $X$
is a quotient stack: to see this, one combines [Reference Kresch and VistoliKV04, Theorem 2] together with a result of Gabber implying that the Azumaya–Brauer group of a quasi-projective scheme over a field coincides with the cohomological Brauer group [Reference de JongdJon]. Next, proceeding as in the proof of [Reference Kresch and VistoliKV04, Theorem 1], one can construct a smooth projective morphism of stacks
$X$
is a quotient stack: to see this, one combines [Reference Kresch and VistoliKV04, Theorem 2] together with a result of Gabber implying that the Azumaya–Brauer group of a quasi-projective scheme over a field coincides with the cohomological Brauer group [Reference de JongdJon]. Next, proceeding as in the proof of [Reference Kresch and VistoliKV04, Theorem 1], one can construct a smooth projective morphism of stacks
![]() $\unicode[STIX]{x1D70B}:P\rightarrow X$
with a representable open substack
$\unicode[STIX]{x1D70B}:P\rightarrow X$
with a representable open substack
![]() $Q\subset P$
, whose fiber dimension is greater than
$Q\subset P$
, whose fiber dimension is greater than
![]() $\dim (P\smallsetminus Q)$
. The induced morphism on coarse moduli spaces
$\dim (P\smallsetminus Q)$
. The induced morphism on coarse moduli spaces
![]() $U\rightarrow \text{}\underline{X}$
is surjective, and
$U\rightarrow \text{}\underline{X}$
is surjective, and
![]() $U$
is quasi-projective by [Reference Kresch and VistoliKV04, Lemma 2].
$U$
is quasi-projective by [Reference Kresch and VistoliKV04, Lemma 2].
Beginning with the map
![]() $U\rightarrow \text{}\underline{X}$
and the image of
$U\rightarrow \text{}\underline{X}$
and the image of
![]() $D$
via
$D$
via
![]() $X\rightarrow \text{}\underline{X}$
, repeated applications of Lemma 2.4 yield a closed subscheme
$X\rightarrow \text{}\underline{X}$
, repeated applications of Lemma 2.4 yield a closed subscheme
![]() $Y\subset U$
such that the map
$Y\subset U$
such that the map
![]() $Y\rightarrow \text{}\underline{X}$
is finite and surjective, and such that
$Y\rightarrow \text{}\underline{X}$
is finite and surjective, and such that
![]() $D_{Y}$
is a normal crossings divisor whose strata meet the ramification divisor of
$D_{Y}$
is a normal crossings divisor whose strata meet the ramification divisor of
![]() $Y\rightarrow \text{}\underline{X}$
properly. We can assume that
$Y\rightarrow \text{}\underline{X}$
properly. We can assume that
![]() $Y$
is disjoint from the image of
$Y$
is disjoint from the image of
![]() $P\smallsetminus Q$
in
$P\smallsetminus Q$
in
![]() $U$
, by dimension reasons. We can thus lift
$U$
, by dimension reasons. We can thus lift
![]() $Y$
to a representable substack of
$Y$
to a representable substack of
![]() $Q$
, because
$Q$
, because
![]() $Q$
is representable, and get the desired morphism
$Q$
is representable, and get the desired morphism
![]() $Y\rightarrow X$
.◻
$Y\rightarrow X$
.◻
2.8 Rational and integral points on stacks
We will make use of the following standard observations.
Lemma 2.5. Let
![]() $R$
be a Dedekind domain with fraction field
$R$
be a Dedekind domain with fraction field
![]() $K$
.
$K$
.
-
(1) Let
 $f:Y\rightarrow X$
be a proper representable morphism of algebraic stacks over
$f:Y\rightarrow X$
be a proper representable morphism of algebraic stacks over
 $R$
. Let
$R$
. Let
 $y\in Y(K)$
and
$y\in Y(K)$
and
 $x=f(y)$
. Then
$x=f(y)$
. Then
 $y$
extends to a point
$y$
extends to a point
 $\unicode[STIX]{x1D702}\in Y(R)$
if and only if
$\unicode[STIX]{x1D702}\in Y(R)$
if and only if
 $x$
extends to a point
$x$
extends to a point
 $\unicode[STIX]{x1D709}\in X(R)$
.
$\unicode[STIX]{x1D709}\in X(R)$
. -
(2) Let
 $X/R$
be an algebraic stack,
$X/R$
be an algebraic stack,
 $Y/R$
a proper scheme and
$Y/R$
a proper scheme and
 $Y\rightarrow X$
a morphism. If
$Y\rightarrow X$
a morphism. If
 $x\in X(K)$
is the image of
$x\in X(K)$
is the image of
 $y\in Y(K)$
, then it extends to
$y\in Y(K)$
, then it extends to
 $\unicode[STIX]{x1D709}\in X(R)$
.
$\unicode[STIX]{x1D709}\in X(R)$
. -
(3) Let
 $X/R$
be a proper algebraic stack,
$X/R$
be a proper algebraic stack,
 $Y/R$
a proper scheme and
$Y/R$
a proper scheme and
 $Y\rightarrow X$
a flat surjective morphism of degree
$Y\rightarrow X$
a flat surjective morphism of degree
 $M$
. Let
$M$
. Let
 $x\in X(K)$
. There are a finite extension
$x\in X(K)$
. There are a finite extension
 $L/K$
, with
$L/K$
, with
 $[L:K]\leqslant M$
and
$[L:K]\leqslant M$
and
 $R_{L}\subset L$
the integral closure of
$R_{L}\subset L$
the integral closure of
 $R$
, and a point
$R$
, and a point
 $\unicode[STIX]{x1D709}\in X(R_{L})$
lifting
$\unicode[STIX]{x1D709}\in X(R_{L})$
lifting
 $x$
.
$x$
.
Proof. (1) Given
![]() $\unicode[STIX]{x1D702}\in Y(R)$
, we have
$\unicode[STIX]{x1D702}\in Y(R)$
, we have
![]() $f(\unicode[STIX]{x1D702})=\unicode[STIX]{x1D709}\in X(R)$
. If
$f(\unicode[STIX]{x1D702})=\unicode[STIX]{x1D709}\in X(R)$
. If
![]() $\unicode[STIX]{x1D709}\in X(R)$
, consider the fibered product
$\unicode[STIX]{x1D709}\in X(R)$
, consider the fibered product
![]() $Z=\operatorname{Spec}R\times _{X}Y$
defined by
$Z=\operatorname{Spec}R\times _{X}Y$
defined by
![]() $\unicode[STIX]{x1D709}$
, which is representable and proper over
$\unicode[STIX]{x1D709}$
, which is representable and proper over
![]() $R$
. Then
$R$
. Then
![]() $y$
gives a point of
$y$
gives a point of
![]() $Z(K)$
, which extends to
$Z(K)$
, which extends to
![]() $R$
by the valuative criterion of properness.
$R$
by the valuative criterion of properness.
(2) By the valuative criterion for properness,
![]() $y$
extends to
$y$
extends to
![]() $\unicode[STIX]{x1D702}\in Y(R)$
, whose composition with
$\unicode[STIX]{x1D702}\in Y(R)$
, whose composition with
![]() $Y\rightarrow X$
gives
$Y\rightarrow X$
gives
![]() $\unicode[STIX]{x1D709}\in X(R)$
.
$\unicode[STIX]{x1D709}\in X(R)$
.
(3) The
![]() $K$
-scheme
$K$
-scheme
![]() $Z=\operatorname{Spec}K\times _{X}Y$
is finite of degree
$Z=\operatorname{Spec}K\times _{X}Y$
is finite of degree
![]() $M$
and hence admits a rational point
$M$
and hence admits a rational point
![]() $y\in Z(L)$
with
$y\in Z(L)$
with
![]() $[L:K]\leqslant M$
. The composition
$[L:K]\leqslant M$
. The composition
![]() $\operatorname{Spec}L\rightarrow Z\rightarrow Y$
extends to
$\operatorname{Spec}L\rightarrow Z\rightarrow Y$
extends to
![]() $\unicode[STIX]{x1D702}\in Y(R_{L})$
by the valuative criterion for properness, and its composition with
$\unicode[STIX]{x1D702}\in Y(R_{L})$
by the valuative criterion for properness, and its composition with
![]() $f$
is a point
$f$
is a point
![]() $\unicode[STIX]{x1D709}\in X(R_{L})$
lifting
$\unicode[STIX]{x1D709}\in X(R_{L})$
lifting
![]() $x$
.◻
$x$
.◻
3 Vojta’s conjecture for varieties and stacks
We write
![]() $K_{X}$
for the canonical divisor class of a smooth variety or smooth Deligne–Mumford stack
$K_{X}$
for the canonical divisor class of a smooth variety or smooth Deligne–Mumford stack
![]() $X$
.
$X$
.
Conjecture 3.1 (Vojta [Reference VojtaVoj98, Conjecture 2.3]).
Let
![]() $X$
be a smooth projective variety over a number field
$X$
be a smooth projective variety over a number field
![]() $K$
,
$K$
,
![]() $D$
a normal crossings divisor on
$D$
a normal crossings divisor on
![]() $X$
and
$X$
and
![]() $H$
a big line bundle on
$H$
a big line bundle on
![]() $X$
. Let
$X$
. Let
![]() $r$
be a positive integer and fix
$r$
be a positive integer and fix
![]() $\unicode[STIX]{x1D6FF}>0$
. Then there is a proper Zariski-closed subset
$\unicode[STIX]{x1D6FF}>0$
. Then there is a proper Zariski-closed subset
![]() $Z\subset X$
containing
$Z\subset X$
containing
![]() $D$
such that
$D$
such that
for all
![]() $x\in X(\overline{K})\smallsetminus Z(\overline{K})$
with
$x\in X(\overline{K})\smallsetminus Z(\overline{K})$
with
![]() $[K(x):K]\leqslant r$
.
$[K(x):K]\leqslant r$
.
We note that variants of the conjecture above have been stated, involving the counting function
![]() $N_{K}(D,x)=(1/[K(x):K])\sum _{\mathfrak{q}}n_{\mathfrak{q}}(D,x)\log |\unicode[STIX]{x1D705}(\mathfrak{q})|$
and a different coefficient in front of the discriminant term
$N_{K}(D,x)=(1/[K(x):K])\sum _{\mathfrak{q}}n_{\mathfrak{q}}(D,x)\log |\unicode[STIX]{x1D705}(\mathfrak{q})|$
and a different coefficient in front of the discriminant term
![]() $d_{K}(K(x))$
. It may be possible to deduce results similar to Theorem B from these variants; we do not do so here.
$d_{K}(K(x))$
. It may be possible to deduce results similar to Theorem B from these variants; we do not do so here.
We shall need a version of Vojta’s conjecture for Deligne–Mumford stacks. For a smooth proper Deligne–Mumford stack
![]() $\mathscr{X}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K,S}$
, we write
$\mathscr{X}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K,S}$
, we write
![]() $X=\mathscr{X}_{K}$
for the generic fiber, which we assume is irreducible, and
$X=\mathscr{X}_{K}$
for the generic fiber, which we assume is irreducible, and
![]() $\text{}\underline{X}$
for the coarse moduli space of
$\text{}\underline{X}$
for the coarse moduli space of
![]() $X$
. Similarly, for a normal crossings divisor
$X$
. Similarly, for a normal crossings divisor
![]() $\mathscr{D}$
of
$\mathscr{D}$
of
![]() $\mathscr{X}$
, we write
$\mathscr{X}$
, we write
![]() $D$
for its generic fiber.
$D$
for its generic fiber.
Given a point
![]() $x\in \mathscr{X}(\overline{K})$
, we take the Zariski closure and normalization of its image, and extend it uniquely to a morphism, denoted
$x\in \mathscr{X}(\overline{K})$
, we take the Zariski closure and normalization of its image, and extend it uniquely to a morphism, denoted
![]() ${\mathcal{T}}_{x}\rightarrow \mathscr{X}$
, where
${\mathcal{T}}_{x}\rightarrow \mathscr{X}$
, where
![]() ${\mathcal{T}}_{x}$
is a normal stack with coarse moduli scheme
${\mathcal{T}}_{x}$
is a normal stack with coarse moduli scheme
![]() $\operatorname{Spec}{\mathcal{O}}_{K(x),S}$
. We thus have the relative discriminant
$\operatorname{Spec}{\mathcal{O}}_{K(x),S}$
. We thus have the relative discriminant
![]() $d_{K}({\mathcal{T}}_{x})$
defined in §2.2.
$d_{K}({\mathcal{T}}_{x})$
defined in §2.2.
Proposition 3.2 (Vojta for stacks).
Assume that Vojta’s conjecture 3.1 holds. Let
![]() $\mathscr{X}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K,S}$
,
$\mathscr{X}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K,S}$
,
![]() $X$
,
$X$
,
![]() $\text{}\underline{X}$
and
$\text{}\underline{X}$
and
![]() $D$
be as above. Suppose that
$D$
be as above. Suppose that
![]() $\text{}\underline{X}$
is projective and let
$\text{}\underline{X}$
is projective and let
![]() $H$
be a big line bundle on it. Let
$H$
be a big line bundle on it. Let
![]() $r$
be a positive integer and fix
$r$
be a positive integer and fix
![]() $\unicode[STIX]{x1D6FF}>0$
. Then there is a proper Zariski-closed subset
$\unicode[STIX]{x1D6FF}>0$
. Then there is a proper Zariski-closed subset
![]() $Z\subset X$
containing
$Z\subset X$
containing
![]() $D$
such that
$D$
such that
for all
![]() $x\in X(\overline{K})\smallsetminus Z(\overline{K})$
with
$x\in X(\overline{K})\smallsetminus Z(\overline{K})$
with
![]() $[K(x):K]\leqslant r$
.
$[K(x):K]\leqslant r$
.
Proof. Let
![]() $Y\rightarrow X$
be the finite cover of
$Y\rightarrow X$
be the finite cover of
![]() $X$
guaranteed by Proposition 2.3. Possibly after enlarging
$X$
guaranteed by Proposition 2.3. Possibly after enlarging
![]() $S$
, we may assume that
$S$
, we may assume that
![]() $Y\rightarrow X$
extends to
$Y\rightarrow X$
extends to
![]() $\unicode[STIX]{x1D70B}:\mathscr{Y}\rightarrow \mathscr{X}$
for some model
$\unicode[STIX]{x1D70B}:\mathscr{Y}\rightarrow \mathscr{X}$
for some model
![]() $\mathscr{Y}$
of
$\mathscr{Y}$
of
![]() $Y$
, so a point
$Y$
, so a point
![]() $y\in Y(K(y))$
extends to
$y\in Y(K(y))$
extends to
![]() $\operatorname{Spec}{\mathcal{O}}_{K(y),S}\rightarrow \mathscr{Y}$
, and composes to
$\operatorname{Spec}{\mathcal{O}}_{K(y),S}\rightarrow \mathscr{Y}$
, and composes to
![]() $\operatorname{Spec}{\mathcal{O}}_{K(y),S}\rightarrow \mathscr{X}$
. We denote
$\operatorname{Spec}{\mathcal{O}}_{K(y),S}\rightarrow \mathscr{X}$
. We denote
![]() $\unicode[STIX]{x1D70B}(y)=x$
, and its extension as a stack by
$\unicode[STIX]{x1D70B}(y)=x$
, and its extension as a stack by
![]() ${\mathcal{T}}:={\mathcal{T}}_{x}\rightarrow \mathscr{X}$
.
${\mathcal{T}}:={\mathcal{T}}_{x}\rightarrow \mathscr{X}$
.
By Riemann–Hurwitz, we have
Thus, for
![]() $y\in Y(\overline{K})$
with
$y\in Y(\overline{K})$
with
![]() $\unicode[STIX]{x1D70B}(y)=x$
outside a proper Zariski-closed subset of
$\unicode[STIX]{x1D70B}(y)=x$
outside a proper Zariski-closed subset of
![]() $Y$
, we have
$Y$
, we have
Let
![]() $\text{}\underline{\unicode[STIX]{x1D70B}}:Y\rightarrow \text{}\underline{X}$
be the composition of
$\text{}\underline{\unicode[STIX]{x1D70B}}:Y\rightarrow \text{}\underline{X}$
be the composition of
![]() $\unicode[STIX]{x1D70B}$
with the natural map
$\unicode[STIX]{x1D70B}$
with the natural map
![]() $X\rightarrow \text{}\underline{X}$
. Let
$X\rightarrow \text{}\underline{X}$
. Let
![]() $B=\text{}\underline{\unicode[STIX]{x1D70B}}^{\ast }(H)$
; then
$B=\text{}\underline{\unicode[STIX]{x1D70B}}^{\ast }(H)$
; then
![]() $B$
is big and, by functoriality of heights, we have
$B$
is big and, by functoriality of heights, we have
for all
![]() $y\in Y(\overline{K})$
. Let
$y\in Y(\overline{K})$
. Let
![]() $\mathscr{D}_{Y}=\unicode[STIX]{x1D70B}^{\ast }\mathscr{D}$
.
$\mathscr{D}_{Y}=\unicode[STIX]{x1D70B}^{\ast }\mathscr{D}$
.
Lemma 3.3. We have
![]() $N_{K}^{(1)}(D_{Y},y)\leqslant N_{K}^{(1)}(D,x)$
.
$N_{K}^{(1)}(D_{Y},y)\leqslant N_{K}^{(1)}(D,x)$
.
Proof. Note that
![]() $n_{q}(\mathscr{D}_{Y},y)>0$
if and only if
$n_{q}(\mathscr{D}_{Y},y)>0$
if and only if
![]() $n_{q}(\mathscr{D},x)>0$
. Then
$n_{q}(\mathscr{D},x)>0$
. Then
 $$\begin{eqnarray}\displaystyle N_{K}^{(1)}(D_{Y},y) & = & \displaystyle \frac{1}{[K(y):K]}\mathop{\sum }_{\substack{ \mathfrak{q}\in \operatorname{Spec}{\mathcal{O}}_{K(y),S} \\ n_{\mathfrak{q}}(\mathscr{D}_{Y},y)>0}}\log |\unicode[STIX]{x1D705}(\mathfrak{q})|\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[K(y):K]}\mathop{\sum }_{q:n_{q}(\mathscr{D},x)>0}\mathop{\sum }_{\mathfrak{q}\mid q}\log |\unicode[STIX]{x1D705}(\mathfrak{q})|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{[K(y):K]}\mathop{\sum }_{q:n_{q}(\mathscr{D},x)>0}\mathop{\sum }_{\mathfrak{q}\mid q}e(\mathfrak{q}\mid q)\log |\unicode[STIX]{x1D705}(\mathfrak{q})|\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[K(y):K]}\mathop{\sum }_{q:n_{q}(\mathscr{D},x)>0}[K(y):K(x)]\log |\unicode[STIX]{x1D705}(q)|\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[K(x):K]}\mathop{\sum }_{q:n_{q}(\mathscr{D},x)>0}\log |\unicode[STIX]{x1D705}(q)|=N_{K}^{(1)}(D,x).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{K}^{(1)}(D_{Y},y) & = & \displaystyle \frac{1}{[K(y):K]}\mathop{\sum }_{\substack{ \mathfrak{q}\in \operatorname{Spec}{\mathcal{O}}_{K(y),S} \\ n_{\mathfrak{q}}(\mathscr{D}_{Y},y)>0}}\log |\unicode[STIX]{x1D705}(\mathfrak{q})|\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[K(y):K]}\mathop{\sum }_{q:n_{q}(\mathscr{D},x)>0}\mathop{\sum }_{\mathfrak{q}\mid q}\log |\unicode[STIX]{x1D705}(\mathfrak{q})|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{[K(y):K]}\mathop{\sum }_{q:n_{q}(\mathscr{D},x)>0}\mathop{\sum }_{\mathfrak{q}\mid q}e(\mathfrak{q}\mid q)\log |\unicode[STIX]{x1D705}(\mathfrak{q})|\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[K(y):K]}\mathop{\sum }_{q:n_{q}(\mathscr{D},x)>0}[K(y):K(x)]\log |\unicode[STIX]{x1D705}(q)|\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{[K(x):K]}\mathop{\sum }_{q:n_{q}(\mathscr{D},x)>0}\log |\unicode[STIX]{x1D705}(q)|=N_{K}^{(1)}(D,x).\nonumber\end{eqnarray}$$
◻
Lemma 3.4. We have
Proof. Write
![]() $\mathscr{Y}_{{\mathcal{T}}}=\mathscr{Y}\times _{\mathscr{X}}{\mathcal{T}}$
. The morphism
$\mathscr{Y}_{{\mathcal{T}}}=\mathscr{Y}\times _{\mathscr{X}}{\mathcal{T}}$
. The morphism
![]() ${\mathcal{T}}\rightarrow \mathscr{X}$
is representable, since it is the normalization of a substack. It follows that
${\mathcal{T}}\rightarrow \mathscr{X}$
is representable, since it is the normalization of a substack. It follows that
![]() $\mathscr{Y}_{{\mathcal{T}}}$
is a scheme. Also,
$\mathscr{Y}_{{\mathcal{T}}}$
is a scheme. Also,
![]() $\operatorname{Spec}{\mathcal{O}}_{K(y)}\rightarrow \mathscr{Y}_{{\mathcal{T}}}$
is the normalization of the image subscheme
$\operatorname{Spec}{\mathcal{O}}_{K(y)}\rightarrow \mathscr{Y}_{{\mathcal{T}}}$
is the normalization of the image subscheme
![]() $\overline{\text{Im}(y)}$
.
$\overline{\text{Im}(y)}$
.
Therefore,
(since
![]() $\deg \unicode[STIX]{x1D6FA}$
drops when passing to normalization, subscheme or pullback)
$\deg \unicode[STIX]{x1D6FA}$
drops when passing to normalization, subscheme or pullback)
as needed.◻
Continuing with the proof of Proposition 3.2, Conjecture 3.1 for
![]() $Y$
gives
$Y$
gives
for
![]() $y$
away from a proper closed subset. By Lemma 2.2, we have
$y$
away from a proper closed subset. By Lemma 2.2, we have
By Lemmas 3.3 and 3.4, the left-hand side of (3.1) is majorized by
On the other hand, for the right-hand side of (3.1), we have
All together, we obtain
which, after canceling
![]() $h_{R}(y)$
, gives
$h_{R}(y)$
, gives
A point
![]() $x$
with
$x$
with
![]() $[K(x):K]\leqslant r$
is the image of a point
$[K(x):K]\leqslant r$
is the image of a point
![]() $y$
with
$y$
with
![]() $[K(y):K]\leqslant r\cdot \deg \unicode[STIX]{x1D70B}$
. Thus, the proposition for
$[K(y):K]\leqslant r\cdot \deg \unicode[STIX]{x1D70B}$
. Thus, the proposition for
![]() $\mathscr{X}$
,
$\mathscr{X}$
,
![]() $\mathscr{D}$
,
$\mathscr{D}$
,
![]() $H$
,
$H$
,
![]() $r$
and
$r$
and
![]() $\unicode[STIX]{x1D6FF}$
follows from Conjecture 3.1 applied to
$\unicode[STIX]{x1D6FF}$
follows from Conjecture 3.1 applied to
![]() $Y$
,
$Y$
,
![]() $\unicode[STIX]{x1D70B}^{\ast }\mathscr{D}$
,
$\unicode[STIX]{x1D70B}^{\ast }\mathscr{D}$
,
![]() $B$
,
$B$
,
![]() $r\cdot \deg \unicode[STIX]{x1D70B}$
and
$r\cdot \deg \unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D6FF}$
.◻
$\unicode[STIX]{x1D6FF}$
.◻
4 Proof of the main result
4.1 Moduli spaces and toroidal compactifications
We follow the notation of [Reference Abramovich and Várilly-AlvaradoAV16]. However, we work over
![]() $\operatorname{Spec}\mathbb{Z}$
:
$\operatorname{Spec}\mathbb{Z}$
:

The construction of
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
by Faltings and Chai [Reference Faltings and ChaiFC90, p. 128] yields a stack smooth over
$\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
by Faltings and Chai [Reference Faltings and ChaiFC90, p. 128] yields a stack smooth over
![]() $\operatorname{Spec}\mathbb{Z}[\unicode[STIX]{x1D701}_{m},1/m]$
, where
$\operatorname{Spec}\mathbb{Z}[\unicode[STIX]{x1D701}_{m},1/m]$
, where
![]() $\unicode[STIX]{x1D701}_{m}$
is a primitive
$\unicode[STIX]{x1D701}_{m}$
is a primitive
![]() $m$
th root of unity. Its boundary is a normal crossings divisor. However, their definition of full level-
$m$
th root of unity. Its boundary is a normal crossings divisor. However, their definition of full level-
![]() $m$
structure requires a symplectic isomorphism
$m$
structure requires a symplectic isomorphism
![]() $A[m]\xrightarrow[{}]{{\sim}}(\mathbb{Z}/m\mathbb{Z})^{2g}$
. In [Reference Faltings and ChaiFC90, IV, Remark 6.12], they relaxed the requirement that the isomorphism be symplectic, giving a stack smooth over
$A[m]\xrightarrow[{}]{{\sim}}(\mathbb{Z}/m\mathbb{Z})^{2g}$
. In [Reference Faltings and ChaiFC90, IV, Remark 6.12], they relaxed the requirement that the isomorphism be symplectic, giving a stack smooth over
![]() $\operatorname{Spec}\mathbb{Z}[1/m]$
; in [Reference Faltings and ChaiFC90, I, Definition 1.8], they also considered full level structures in our sense (albeit still requiring the isomorphism (0.1) to be symplectic). Combining these remarks, we obtain a stack we denote
$\operatorname{Spec}\mathbb{Z}[1/m]$
; in [Reference Faltings and ChaiFC90, I, Definition 1.8], they also considered full level structures in our sense (albeit still requiring the isomorphism (0.1) to be symplectic). Combining these remarks, we obtain a stack we denote
![]() $(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m]}$
, smooth over
$(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m]}$
, smooth over
![]() $\mathbb{Z}[1/m]$
. If
$\mathbb{Z}[1/m]$
. If
![]() $m\geqslant 3$
, this stack is a scheme [Reference Faltings and ChaiFC90, IV.6.9].
$m\geqslant 3$
, this stack is a scheme [Reference Faltings and ChaiFC90, IV.6.9].
We extend the construction to
![]() $\operatorname{Spec}\mathbb{Z}$
by defining
$\operatorname{Spec}\mathbb{Z}$
by defining
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
to be the normalization of
$\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
to be the normalization of
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}$
in
$\overline{\widetilde{{\mathcal{A}}}}_{g}$
in
![]() $(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m]}$
. The resulting stack is not smooth over primes dividing
$(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m]}$
. The resulting stack is not smooth over primes dividing
![]() $m$
, and even the interior of the stack over such primes does not have a modular interpretation. However, the boundary structure of this stack at primes dividing
$m$
, and even the interior of the stack over such primes does not have a modular interpretation. However, the boundary structure of this stack at primes dividing
![]() $m$
is described in the Appendix.
$m$
is described in the Appendix.
The natural morphism
![]() ${\mathcal{A}}_{g}^{[m]}\rightarrow {\mathcal{A}}_{g}$
that ‘forgets the level structure’ is finite and, since we chose compatible compactifications, it extends to a finite morphism
${\mathcal{A}}_{g}^{[m]}\rightarrow {\mathcal{A}}_{g}$
that ‘forgets the level structure’ is finite and, since we chose compatible compactifications, it extends to a finite morphism
![]() $\unicode[STIX]{x1D70B}_{m}:\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
; see [Reference Faltings and ChaiFC90, Theorem IV.6.7(1)].
$\unicode[STIX]{x1D70B}_{m}:\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
; see [Reference Faltings and ChaiFC90, Theorem IV.6.7(1)].
4.2 Rational points and covers of bounded degree
The stack
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}$
is proper, but a rational point
$\overline{\widetilde{{\mathcal{A}}}}_{g}$
is proper, but a rational point
![]() $x\in \overline{\widetilde{{\mathcal{A}}}}_{g}$
might not extend to an integral point: it might correspond to an abelian variety with potentially semistable, but not semistable, reduction. In this section, we explain how one can use an integral extension of bounded degree to lift
$x\in \overline{\widetilde{{\mathcal{A}}}}_{g}$
might not extend to an integral point: it might correspond to an abelian variety with potentially semistable, but not semistable, reduction. In this section, we explain how one can use an integral extension of bounded degree to lift
![]() $x$
to a finite cover of
$x$
to a finite cover of
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}$
that is a scheme, where the lift of
$\overline{\widetilde{{\mathcal{A}}}}_{g}$
that is a scheme, where the lift of
![]() $x$
can be extended to an integral point.
$x$
can be extended to an integral point.
We apply Lemma 2.5(3), which requires a covering
![]() $Y\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
by a scheme. This can be achieved using [Reference Kresch and VistoliKV04, Theorem 1], but a more explicit construction in our situation is given in the following well-known lemma.
$Y\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
by a scheme. This can be achieved using [Reference Kresch and VistoliKV04, Theorem 1], but a more explicit construction in our situation is given in the following well-known lemma.
Lemma 4.1. Let
![]() $m=m_{1}m_{2}$
be a product of two coprime integers each
$m=m_{1}m_{2}$
be a product of two coprime integers each
![]() ${\geqslant}3$
. Then the stack
${\geqslant}3$
. Then the stack
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
is a scheme.
$\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
is a scheme.
Proof. First, recall that if
![]() $d\geqslant 3$
is an integer, the stack
$d\geqslant 3$
is an integer, the stack
![]() $(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[d]})_{\mathbb{Z}[1/d]}$
is a scheme. It suffices to show that
$(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[d]})_{\mathbb{Z}[1/d]}$
is a scheme. It suffices to show that
![]() $(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m_{1}]}$
and
$(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m_{1}]}$
and
![]() $(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m_{2}]}$
are schemes. This in turn follows because for
$(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m_{2}]}$
are schemes. This in turn follows because for
![]() $i=1$
and
$i=1$
and
![]() $2$
, the stack
$2$
, the stack
![]() $(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m_{i}]}$
is the normalization of the scheme
$(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m_{i}]}$
is the normalization of the scheme
![]() $(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m_{i}]})_{\mathbb{Z}[1/m_{i}]}$
in the scheme
$(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m_{i}]})_{\mathbb{Z}[1/m_{i}]}$
in the scheme
![]() $(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m]}$
.◻
$(\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{\mathbb{Z}[1/m]}$
.◻
Since
![]() $12=3\cdot 4$
is the product of two relatively prime integers each
$12=3\cdot 4$
is the product of two relatively prime integers each
![]() ${\geqslant}3$
, it follows that
${\geqslant}3$
, it follows that
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}^{[12]}$
is a scheme. Let
$\overline{\widetilde{{\mathcal{A}}}}_{g}^{[12]}$
is a scheme. Let
![]() $M=\deg \unicode[STIX]{x1D70B}_{12}:\overline{\widetilde{{\mathcal{A}}}}_{g}^{[12]}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
. We obtain the following result.
$M=\deg \unicode[STIX]{x1D70B}_{12}:\overline{\widetilde{{\mathcal{A}}}}_{g}^{[12]}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
. We obtain the following result.
Proposition 4.2. Let
![]() $R$
be a Dedekind domain with field of fractions
$R$
be a Dedekind domain with field of fractions
![]() $K$
. Fix a point
$K$
. Fix a point
![]() $y\in \overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}(K)$
. There are a finite extension
$y\in \overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}(K)$
. There are a finite extension
![]() $L/K$
, with
$L/K$
, with
![]() $[L:K]\leqslant M$
and
$[L:K]\leqslant M$
and
![]() $R_{L}\subset L$
the integral closure of
$R_{L}\subset L$
the integral closure of
![]() $R$
, and a point
$R$
, and a point
![]() $\unicode[STIX]{x1D702}\in \overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}(R_{L})$
lifting
$\unicode[STIX]{x1D702}\in \overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}(R_{L})$
lifting
![]() $y$
.
$y$
.
Proof. Applying Lemma 2.5(3) to the point
![]() $\unicode[STIX]{x1D70B}_{m}(y)\in \overline{\widetilde{{\mathcal{A}}}}_{g}$
, we have a point
$\unicode[STIX]{x1D70B}_{m}(y)\in \overline{\widetilde{{\mathcal{A}}}}_{g}$
, we have a point
![]() $\unicode[STIX]{x1D709}\in \overline{\widetilde{{\mathcal{A}}}}_{g}(R_{L})$
lifting
$\unicode[STIX]{x1D709}\in \overline{\widetilde{{\mathcal{A}}}}_{g}(R_{L})$
lifting
![]() $\unicode[STIX]{x1D70B}_{m}(y)$
. Applying Lemma 2.5(1) to the representable morphism
$\unicode[STIX]{x1D70B}_{m}(y)$
. Applying Lemma 2.5(1) to the representable morphism
![]() $\unicode[STIX]{x1D70B}_{m}$
, the point lifts to
$\unicode[STIX]{x1D70B}_{m}$
, the point lifts to
![]() $\unicode[STIX]{x1D702}\in \overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}(R_{L})$
.◻
$\unicode[STIX]{x1D702}\in \overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}(R_{L})$
.◻
4.3 Substacks
Let
![]() $X\subseteq (\widetilde{{\mathcal{A}}}_{g})_{K}$
be a closed substack, let
$X\subseteq (\widetilde{{\mathcal{A}}}_{g})_{K}$
be a closed substack, let
![]() $X^{\prime }\rightarrow X$
be a resolution of singularities and
$X^{\prime }\rightarrow X$
be a resolution of singularities and
![]() $X^{\prime }\subset \overline{X}^{\prime }$
a smooth compactification with
$X^{\prime }\subset \overline{X}^{\prime }$
a smooth compactification with
![]() $D=\overline{X}^{\prime }\smallsetminus X^{\prime }$
a normal crossings divisor. Assume that the rational map
$D=\overline{X}^{\prime }\smallsetminus X^{\prime }$
a normal crossings divisor. Assume that the rational map
![]() $f:\overline{X}^{\prime }\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
is a morphism. Let
$f:\overline{X}^{\prime }\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
is a morphism. Let
![]() $X_{m}^{\prime }=X^{\prime }\times _{\widetilde{{\mathcal{A}}}_{g}}\widetilde{{\mathcal{A}}}_{g}^{[m]}$
, and let
$X_{m}^{\prime }=X^{\prime }\times _{\widetilde{{\mathcal{A}}}_{g}}\widetilde{{\mathcal{A}}}_{g}^{[m]}$
, and let
![]() $\overline{X}_{m}^{\prime }\rightarrow \overline{X}^{\prime }\times _{\overline{\widetilde{{\mathcal{A}}}}_{g}}\overline{{\mathcal{A}}}_{g}^{[m]}$
be a resolution of singularities with projections
$\overline{X}_{m}^{\prime }\rightarrow \overline{X}^{\prime }\times _{\overline{\widetilde{{\mathcal{A}}}}_{g}}\overline{{\mathcal{A}}}_{g}^{[m]}$
be a resolution of singularities with projections
![]() $\unicode[STIX]{x1D70B}_{m}^{X}:\overline{X}_{m}^{\prime }\rightarrow \overline{X}^{\prime }$
and
$\unicode[STIX]{x1D70B}_{m}^{X}:\overline{X}_{m}^{\prime }\rightarrow \overline{X}^{\prime }$
and
![]() $f_{m}:\overline{X}_{m}^{\prime }\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
.
$f_{m}:\overline{X}_{m}^{\prime }\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
.
We now spread these objects over
![]() ${\mathcal{O}}_{K,S}$
for a suitable finite set of places
${\mathcal{O}}_{K,S}$
for a suitable finite set of places
![]() $S$
containing the archimedean places. Let
$S$
containing the archimedean places. Let
![]() $(\mathscr{X},\mathscr{D})$
be a normal crossings model of
$(\mathscr{X},\mathscr{D})$
be a normal crossings model of
![]() $(\overline{X}^{\prime },D)$
over
$(\overline{X}^{\prime },D)$
over
![]() $\operatorname{Spec}{\mathcal{O}}_{K,S}$
. As above, write
$\operatorname{Spec}{\mathcal{O}}_{K,S}$
. As above, write
![]() $\mathscr{D}=\sum _{i}\mathscr{D}_{i}$
. Such a model exists, even for Deligne–Mumford stacks, by [Reference OlssonOls06, Proposition 2.2].
$\mathscr{D}=\sum _{i}\mathscr{D}_{i}$
. Such a model exists, even for Deligne–Mumford stacks, by [Reference OlssonOls06, Proposition 2.2].
Let
![]() $X(K)_{[m]}$
be the set of
$X(K)_{[m]}$
be the set of
![]() $K$
-rational points of
$K$
-rational points of
![]() $X$
corresponding to abelian varieties
$X$
corresponding to abelian varieties
![]() $A/K$
admitting full level-
$A/K$
admitting full level-
![]() $m$
structure. Define
$m$
structure. Define
4.4 Intersection multiplicities for integral and rational points
Write
![]() $E$
for the boundary divisors of
$E$
for the boundary divisors of
![]() $(\overline{\widetilde{{\mathcal{A}}}}_{g})_{K}$
, and
$(\overline{\widetilde{{\mathcal{A}}}}_{g})_{K}$
, and
![]() $\mathscr{E}$
for its closure in
$\mathscr{E}$
for its closure in
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}$
, which is a Cartier divisor. We have an equality of divisors on
$\overline{\widetilde{{\mathcal{A}}}}_{g}$
, which is a Cartier divisor. We have an equality of divisors on
![]() $\overline{X}^{\prime }$
:
$\overline{X}^{\prime }$
:
where each
![]() $a_{i}>0$
; see [Reference Abramovich and Várilly-AlvaradoAV16, (4.3)]. This equality extends over
$a_{i}>0$
; see [Reference Abramovich and Várilly-AlvaradoAV16, (4.3)]. This equality extends over
![]() $\operatorname{Spec}{\mathcal{O}}_{K,S}$
to
$\operatorname{Spec}{\mathcal{O}}_{K,S}$
to
By [Reference Abramovich and Várilly-AlvaradoAV16, Proposition 4.1 or Equation (4.1)], we have that
![]() $\unicode[STIX]{x1D70B}_{m}^{\ast }E=mE_{m}$
for some Cartier divisor
$\unicode[STIX]{x1D70B}_{m}^{\ast }E=mE_{m}$
for some Cartier divisor
![]() $E_{m}\subset (\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{K}$
. Spreading out
$E_{m}\subset (\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]})_{K}$
. Spreading out
![]() $E_{m}$
to
$E_{m}$
to
![]() $\mathscr{E}_{m}$
in
$\mathscr{E}_{m}$
in
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
, we obtain
$\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
, we obtain
![]() $\unicode[STIX]{x1D70B}_{m}^{\ast }\mathscr{E}=m\mathscr{E}_{m}$
; moreover, by Proposition A.4 in the Appendix,
$\unicode[STIX]{x1D70B}_{m}^{\ast }\mathscr{E}=m\mathscr{E}_{m}$
; moreover, by Proposition A.4 in the Appendix,
![]() $\mathscr{E}_{m}$
is a Cartier divisor.
$\mathscr{E}_{m}$
is a Cartier divisor.
Let
![]() $q\subset {\mathcal{O}}_{K,S}$
be a non-zero prime ideal. Assume that there are maps
$q\subset {\mathcal{O}}_{K,S}$
be a non-zero prime ideal. Assume that there are maps
![]() $\unicode[STIX]{x1D709}:\operatorname{Spec}{\mathcal{O}}_{K,q}\rightarrow \mathscr{X}$
and
$\unicode[STIX]{x1D709}:\operatorname{Spec}{\mathcal{O}}_{K,q}\rightarrow \mathscr{X}$
and
![]() $\unicode[STIX]{x1D709}_{m}:\operatorname{Spec}{\mathcal{O}}_{K,q}\rightarrow \mathscr{X}_{m}$
such that
$\unicode[STIX]{x1D709}_{m}:\operatorname{Spec}{\mathcal{O}}_{K,q}\rightarrow \mathscr{X}_{m}$
such that
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D70B}_{m}^{X}\circ \unicode[STIX]{x1D709}_{m}$
, and write
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D70B}_{m}^{X}\circ \unicode[STIX]{x1D709}_{m}$
, and write
![]() $x\in \mathscr{X}({\mathcal{O}}_{K,q})$
and
$x\in \mathscr{X}({\mathcal{O}}_{K,q})$
and
![]() $x_{m}\in \mathscr{X}_{m}({\mathcal{O}}_{K,q})$
for the respective integral points corresponding to
$x_{m}\in \mathscr{X}_{m}({\mathcal{O}}_{K,q})$
for the respective integral points corresponding to
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $\unicode[STIX]{x1D709}_{m}$
. These objects and arrows fit together in the commutative diagram
$\unicode[STIX]{x1D709}_{m}$
. These objects and arrows fit together in the commutative diagram

We have an equality of divisors on
![]() $\operatorname{Spec}{\mathcal{O}}_{K,q}$
:
$\operatorname{Spec}{\mathcal{O}}_{K,q}$
:
which translates to
The divisor on the left has multiplicity
![]() $\sum a_{i}n_{q}(\mathscr{D}_{i},x)$
. If
$\sum a_{i}n_{q}(\mathscr{D}_{i},x)$
. If
![]() $x\in \mathscr{X}({\mathcal{O}}_{K,q})$
, then the intersection multiplicities
$x\in \mathscr{X}({\mathcal{O}}_{K,q})$
, then the intersection multiplicities
![]() $n_{q}(\mathscr{D}_{i},x)$
are integers, and we deduce that
$n_{q}(\mathscr{D}_{i},x)$
are integers, and we deduce that
If the quantity
![]() $\sum a_{i}n_{q}(\mathscr{D}_{i},x)$
is non-zero, then
$\sum a_{i}n_{q}(\mathscr{D}_{i},x)$
is non-zero, then
![]() $m\leqslant \sum a_{i}n_{q}(\mathscr{D}_{i},x)$
, and thus
$m\leqslant \sum a_{i}n_{q}(\mathscr{D}_{i},x)$
, and thus
in other words,
Given a rational point
![]() $x\in \mathscr{X}(K)$
, we apply Proposition 4.2 and obtain an extension field
$x\in \mathscr{X}(K)$
, we apply Proposition 4.2 and obtain an extension field
![]() $L/K$
with
$L/K$
with
![]() $[L:K]\leqslant M$
and an integral extension
$[L:K]\leqslant M$
and an integral extension
![]() ${\mathcal{O}}_{L,q}$
with a point
${\mathcal{O}}_{L,q}$
with a point
![]() $\unicode[STIX]{x1D709}\in \mathscr{X}({\mathcal{O}}_{L,q})$
lifting
$\unicode[STIX]{x1D709}\in \mathscr{X}({\mathcal{O}}_{L,q})$
lifting
![]() $x$
. Since for any
$x$
. Since for any
![]() $\mathfrak{q}\mid q$
we have
$\mathfrak{q}\mid q$
we have
![]() $e(\mathfrak{q}\mid q)\leqslant M$
, (2.3) gives
$e(\mathfrak{q}\mid q)\leqslant M$
, (2.3) gives
We summarize this discussion in the following proposition.
Proposition 4.3. With notation as in §4.3, write
![]() $\unicode[STIX]{x1D6FC}(X):=(M\cdot \max \{a_{i}\})^{-1}>0$
, which depends
$\unicode[STIX]{x1D6FC}(X):=(M\cdot \max \{a_{i}\})^{-1}>0$
, which depends
![]() $X$
, but not on
$X$
, but not on
![]() $x$
. Let
$x$
. Let
![]() $x_{m}\in X_{m}^{\prime }(K)$
be a rational point in
$x_{m}\in X_{m}^{\prime }(K)$
be a rational point in
![]() $X_{m}^{\prime }$
with image
$X_{m}^{\prime }$
with image
![]() $x\in X^{\prime }(K)$
. Suppose that
$x\in X^{\prime }(K)$
. Suppose that
![]() $n_{q}(\mathscr{D},x)>0$
. Then
$n_{q}(\mathscr{D},x)>0$
. Then
4.5 Proof of Theorem B
Lemma 4.4. Fix
![]() $\unicode[STIX]{x1D716}^{\prime }>0$
. Then there is an integer
$\unicode[STIX]{x1D716}^{\prime }>0$
. Then there is an integer
![]() $m_{0}:=m_{0}(\unicode[STIX]{x1D716}^{\prime },K,X)$
such that for all primes
$m_{0}:=m_{0}(\unicode[STIX]{x1D716}^{\prime },K,X)$
such that for all primes
![]() $p\geqslant m_{0}$
and
$p\geqslant m_{0}$
and
![]() $x\in X(K)_{[p]}$
we have
$x\in X(K)_{[p]}$
we have
Proof. Let
![]() $A/K$
be the abelian variety of dimension
$A/K$
be the abelian variety of dimension
![]() $g$
associated with
$g$
associated with
![]() $x\in X(K)_{[p]}$
. Since
$x\in X(K)_{[p]}$
. Since
![]() $A$
has full level-
$A$
has full level-
![]() $p$
structure, we know that
$p$
structure, we know that
![]() $\#A[p](K)\geqslant p^{g}$
. Thus, if
$\#A[p](K)\geqslant p^{g}$
. Thus, if
![]() $\mathfrak{q}$
is a prime ideal of
$\mathfrak{q}$
is a prime ideal of
![]() $K$
that does not divide
$K$
that does not divide
![]() $p$
, then
$p$
, then
![]() $\#A[p](\unicode[STIX]{x1D705}(\mathfrak{q}))\geqslant p^{g}$
(see [Reference Hindry and SilvermanHS00, C.1.4]). We choose
$\#A[p](\unicode[STIX]{x1D705}(\mathfrak{q}))\geqslant p^{g}$
(see [Reference Hindry and SilvermanHS00, C.1.4]). We choose
![]() $m_{0}\geqslant 8$
, so
$m_{0}\geqslant 8$
, so
![]() $p\neq 2$
, freeing us to pick
$p\neq 2$
, freeing us to pick
![]() $\mathfrak{q}\mid 2$
. This implies that
$\mathfrak{q}\mid 2$
. This implies that
![]() $\unicode[STIX]{x1D705}(\mathfrak{q})=2^{f(\mathfrak{q}|q)}\leqslant 2^{[K:\mathbb{Q}]}$
.
$\unicode[STIX]{x1D705}(\mathfrak{q})=2^{f(\mathfrak{q}|q)}\leqslant 2^{[K:\mathbb{Q}]}$
.
We follow Flexor–Oesterlé [Reference Flexor and OesterléFO90, Théorème 3] and Silverberg [Reference SilverbergSil92, Theorem 3.3]; see also Kamienny [Reference KamiennyKam82, §6(2a)]. Suppose now that
![]() $A$
has good reduction at
$A$
has good reduction at
![]() $\mathfrak{q}$
, so that, by the Lang–Weil estimates, we have
$\mathfrak{q}$
, so that, by the Lang–Weil estimates, we have
Thus, if
![]() $A$
has good reduction at
$A$
has good reduction at
![]() $\mathfrak{q}\mid 2$
, we have
$\mathfrak{q}\mid 2$
, we have
In other words, if
![]() $p>\unicode[STIX]{x1D6FE}$
, then
$p>\unicode[STIX]{x1D6FE}$
, then
![]() $A$
must have bad reduction at primes
$A$
must have bad reduction at primes
![]() $\mathfrak{q}\mid 2$
, so
$\mathfrak{q}\mid 2$
, so
![]() $n_{\mathfrak{q}}(\mathscr{D},x)>0$
. By Proposition 4.3, the stronger inequality (4.1) holds with
$n_{\mathfrak{q}}(\mathscr{D},x)>0$
. By Proposition 4.3, the stronger inequality (4.1) holds with
![]() $m=p$
. We use this to see that if
$m=p$
. We use this to see that if
![]() $p>\unicode[STIX]{x1D6FE}$
, then as in the estimate (2.5) we have
$p>\unicode[STIX]{x1D6FE}$
, then as in the estimate (2.5) we have
so
![]() $h_{\unicode[STIX]{x1D716}^{\prime }D}(x)$
grows at least linearly in
$h_{\unicode[STIX]{x1D716}^{\prime }D}(x)$
grows at least linearly in
![]() $p$
.
$p$
.
Now we crudely bound
![]() $d_{K}({\mathcal{T}}_{x})$
from above. Note that
$d_{K}({\mathcal{T}}_{x})$
from above. Note that
![]() $x$
is an integral point away from
$x$
is an integral point away from
![]() $p$
. As in §4.4, passing to a cover of finite bounded degree
$p$
. As in §4.4, passing to a cover of finite bounded degree
![]() ${\leqslant}M=M(g)$
, we may replace
${\leqslant}M=M(g)$
, we may replace
![]() $x$
with an integral point
$x$
with an integral point
![]() $y$
in such a way that
$y$
in such a way that
![]() $[K(y):K]\leqslant M$
. The discriminant ideal of
$[K(y):K]\leqslant M$
. The discriminant ideal of
![]() ${\mathcal{T}}_{x}$
divides the discriminant ideal of the extension
${\mathcal{T}}_{x}$
divides the discriminant ideal of the extension
![]() $K(y)/K$
; we compare their factors at
$K(y)/K$
; we compare their factors at
![]() $p$
. Let
$p$
. Let
![]() $d_{K}(K(y))_{p}$
denote the contribution at
$d_{K}(K(y))_{p}$
denote the contribution at
![]() $p$
of
$p$
of
![]() $d_{K}(K(y))$
; ignoring negative terms coming from the discriminant of
$d_{K}(K(y))$
; ignoring negative terms coming from the discriminant of
![]() ${\mathcal{O}}_{K}$
, we have the estimate
${\mathcal{O}}_{K}$
, we have the estimate
where
![]() $v_{p}$
denotes the usual
$v_{p}$
denotes the usual
![]() $p$
-adic valuation. By [Reference NeukirchNeu99, Proof of III.2.13], we have
$p$
-adic valuation. By [Reference NeukirchNeu99, Proof of III.2.13], we have
Hence,
grows at most linearly in
![]() $\log p$
, and the result follows.◻
$\log p$
, and the result follows.◻
Lemma 4.5. Fix
![]() $\unicode[STIX]{x1D716}^{\prime }>0$
. Then there is an integer
$\unicode[STIX]{x1D716}^{\prime }>0$
. Then there is an integer
![]() $m_{0}:=m_{0}(\unicode[STIX]{x1D716}^{\prime },K,X)$
such that for all primes
$m_{0}:=m_{0}(\unicode[STIX]{x1D716}^{\prime },K,X)$
such that for all primes
![]() $p\geqslant m_{0}$
, if
$p\geqslant m_{0}$
, if
![]() $x\in X(K)_{[p]}$
, then
$x\in X(K)_{[p]}$
, then
Proof. If
![]() $x\in X(K)_{[p]}$
, then whenever
$x\in X(K)_{[p]}$
, then whenever
![]() $n_{q}(\mathscr{D},x)>0$
, Proposition 4.3 implies that the stronger inequality (4.1) holds. Hence,
$n_{q}(\mathscr{D},x)>0$
, Proposition 4.3 implies that the stronger inequality (4.1) holds. Hence,
 $$\begin{eqnarray}\displaystyle p\unicode[STIX]{x1D6FC}(X)N_{K}^{(1)}(D,x) & = & \displaystyle \mathop{\sum }_{n_{q}(\mathscr{D},x)>0}p\unicode[STIX]{x1D6FC}(X)\log |\unicode[STIX]{x1D705}(q)|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{n_{q}(\mathscr{D},x)>0}n_{q}(\mathscr{D},x)\log |\unicode[STIX]{x1D705}(q)|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle h_{D}(x)+O(1),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p\unicode[STIX]{x1D6FC}(X)N_{K}^{(1)}(D,x) & = & \displaystyle \mathop{\sum }_{n_{q}(\mathscr{D},x)>0}p\unicode[STIX]{x1D6FC}(X)\log |\unicode[STIX]{x1D705}(q)|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{n_{q}(\mathscr{D},x)>0}n_{q}(\mathscr{D},x)\log |\unicode[STIX]{x1D705}(q)|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle h_{D}(x)+O(1),\nonumber\end{eqnarray}$$
where in the last inequality we use the estimate (2.5). Taking
![]() $m_{0}>1/(\unicode[STIX]{x1D716}^{\prime }\unicode[STIX]{x1D6FC}(X))$
, we have
$m_{0}>1/(\unicode[STIX]{x1D716}^{\prime }\unicode[STIX]{x1D6FC}(X))$
, we have
![]() $p\unicode[STIX]{x1D6FC}(X)>1/\unicode[STIX]{x1D716}^{\prime }$
and hence
$p\unicode[STIX]{x1D6FC}(X)>1/\unicode[STIX]{x1D716}^{\prime }$
and hence
![]() $N_{K}^{(1)}(D,x)\leqslant h_{\unicode[STIX]{x1D716}^{\prime }D}(x)+O(1)$
.◻
$N_{K}^{(1)}(D,x)\leqslant h_{\unicode[STIX]{x1D716}^{\prime }D}(x)+O(1)$
.◻
Proof of Theorem B.
We proceed by Noetherian induction. For each integer
![]() $i\geqslant 1$
, let
$i\geqslant 1$
, let
Note that
![]() $W_{i}$
is a closed subset of
$W_{i}$
is a closed subset of
![]() ${\mathcal{A}}_{g}$
, and that
${\mathcal{A}}_{g}$
, and that
![]() $W_{i}\supseteq W_{i+1}$
for every
$W_{i}\supseteq W_{i+1}$
for every
![]() $i$
. The chain of
$i$
. The chain of
![]() $W_{i}$
must stabilize by the Noetherian property of the Zariski topology of
$W_{i}$
must stabilize by the Noetherian property of the Zariski topology of
![]() ${\mathcal{A}}_{g}$
. Say
${\mathcal{A}}_{g}$
. Say
![]() $W_{n}=W_{n+1}=\cdots \,$
.
$W_{n}=W_{n+1}=\cdots \,$
.
We claim that
![]() $W_{n}$
has dimension
$W_{n}$
has dimension
![]() ${\leqslant}0$
. Suppose not, and let
${\leqslant}0$
. Suppose not, and let
![]() $X\subseteq W_{n}$
be an irreducible component of positive dimension. Fix
$X\subseteq W_{n}$
be an irreducible component of positive dimension. Fix
![]() $\unicode[STIX]{x1D716}>0$
so that
$\unicode[STIX]{x1D716}>0$
so that
![]() $K_{X}+(1-\unicode[STIX]{x1D716})D$
is big: such an
$K_{X}+(1-\unicode[STIX]{x1D716})D$
is big: such an
![]() $\unicode[STIX]{x1D716}$
exists by [Reference Abramovich and Várilly-AlvaradoAV16, Corollary 1.10]. Next, choose a
$\unicode[STIX]{x1D716}$
exists by [Reference Abramovich and Várilly-AlvaradoAV16, Corollary 1.10]. Next, choose a
![]() $\mathbb{Q}$
-ample divisor
$\mathbb{Q}$
-ample divisor
![]() $H$
such that
$H$
such that
![]() $K_{X}+(1-\unicode[STIX]{x1D716})D-H$
is effective, and apply Proposition 3.2, with
$K_{X}+(1-\unicode[STIX]{x1D716})D-H$
is effective, and apply Proposition 3.2, with
![]() $r=1$
, to conclude that there is a Zariski-closed proper subset
$r=1$
, to conclude that there is a Zariski-closed proper subset
![]() $Z\subset X$
such that if
$Z\subset X$
such that if
![]() $x\in X(K)\smallsetminus Z(K)$
, then
$x\in X(K)\smallsetminus Z(K)$
, then
By Lemma 4.5, for all primes
![]() $p>m_{0}$
, any
$p>m_{0}$
, any
![]() $x\in X(K)_{[p]}$
satisfies
$x\in X(K)_{[p]}$
satisfies
![]() $N_{K}^{(1)}(D,x)\leqslant h_{(\unicode[STIX]{x1D716}/2)D}(x)+O(1)$
. On the other hand, Lemma 4.4 guarantees that, after possibly enlarging
$N_{K}^{(1)}(D,x)\leqslant h_{(\unicode[STIX]{x1D716}/2)D}(x)+O(1)$
. On the other hand, Lemma 4.4 guarantees that, after possibly enlarging
![]() $m_{0}$
, for all primes
$m_{0}$
, for all primes
![]() $p\geqslant m_{0}$
, any
$p\geqslant m_{0}$
, any
![]() $x\in X(K)_{[p]}$
satisfies
$x\in X(K)_{[p]}$
satisfies
![]() $h_{(\unicode[STIX]{x1D716}/2)D}(x)+O(1)\geqslant d_{K}({\mathcal{T}}_{x})$
. If also
$h_{(\unicode[STIX]{x1D716}/2)D}(x)+O(1)\geqslant d_{K}({\mathcal{T}}_{x})$
. If also
![]() $x\notin Z(K)$
, we deduce that
$x\notin Z(K)$
, we deduce that
By our choice of
![]() $H$
and [Reference Hindry and SilvermanHS00, Theorem B.3.2(e)], we obtain
$H$
and [Reference Hindry and SilvermanHS00, Theorem B.3.2(e)], we obtain
Using [Reference Hindry and SilvermanHS00, Theorem B.3.2(e,g)], we conclude that the set of
![]() $x\in X(K)_{p\geqslant m_{0}}$
outside
$x\in X(K)_{p\geqslant m_{0}}$
outside
![]() $Z(K)$
is not dense, and thus
$Z(K)$
is not dense, and thus
![]() $X(K)_{p\geqslant m_{0}}$
is contained in a Zariski-closed proper subset of
$X(K)_{p\geqslant m_{0}}$
is contained in a Zariski-closed proper subset of
![]() $X$
. On the other hand, if
$X$
. On the other hand, if
![]() $m_{0}>n$
, then
$m_{0}>n$
, then
![]() $W_{m_{0}}=W_{n}$
, so
$W_{m_{0}}=W_{n}$
, so
![]() $X$
is also an irreducible component of
$X$
is also an irreducible component of
![]() $W_{m_{0}}$
and hence
$W_{m_{0}}$
and hence
![]() $\overline{X(K)_{p\geqslant m_{0}}}=X$
, which is a contradiction. This proves that
$\overline{X(K)_{p\geqslant m_{0}}}=X$
, which is a contradiction. This proves that
![]() $\dim W_{n}\leqslant 0$
.
$\dim W_{n}\leqslant 0$
.
Finally, if
![]() $W_{n}$
is a finite set of points, then it is well known that the full level structures that can possibly appear in any of the corresponding finitely many geometric isomorphism classes are bounded. Indeed, if
$W_{n}$
is a finite set of points, then it is well known that the full level structures that can possibly appear in any of the corresponding finitely many geometric isomorphism classes are bounded. Indeed, if
![]() $\mathfrak{q}\in M_{K}^{0}$
is a fixed prime of potential good reduction, all twists with full level-
$\mathfrak{q}\in M_{K}^{0}$
is a fixed prime of potential good reduction, all twists with full level-
![]() $p$
structure with
$p$
structure with
![]() $p>2,\mathfrak{q}\nmid p$
have good reduction at
$p>2,\mathfrak{q}\nmid p$
have good reduction at
![]() $\mathfrak{q}$
. Since the
$\mathfrak{q}$
. Since the
![]() $p$
-torsion points inject modulo
$p$
-torsion points inject modulo
![]() $\mathfrak{q}$
, we have
$\mathfrak{q}$
, we have
![]() $p\leqslant (1+N\mathfrak{q}^{1/2})^{2}.$
Alternatively, following Manin [Reference ManinMan69, §3], there are only finitely many isomorphism classes over
$p\leqslant (1+N\mathfrak{q}^{1/2})^{2}.$
Alternatively, following Manin [Reference ManinMan69, §3], there are only finitely many isomorphism classes over
![]() $K_{\mathfrak{q}}$
and, for each, the torsion subgroup is finite.◻
$K_{\mathfrak{q}}$
and, for each, the torsion subgroup is finite.◻
Acknowledgements
This paper originated at the workshop ‘Explicit methods for modularity of K3 surfaces and other higher weight motives’ held at ICERM in October 2015. We thank the organizers of the workshop and the staff at ICERM for creating the conditions that sparked this project. We thank Jordan Ellenberg, Aaron Levin, Bjorn Poonen, Joseph Silverman, Doug Ulmer and Yu Yasufuku for useful discussions and Mark Kisin for comments and for instigating the Appendix. This paper is posted as arXiv:1604.04571.
Appendix. Compactifications with full level structure
Keerthi Madapusi Pera
The purpose of this appendix is to lay out certain facts about toroidal compactifications of the moduli of principally polarized abelian varieties with full level structure at ‘bad’ primes. This is a straightforward extension of the theory of [Reference Faltings and ChaiFC90] and could possibly also be extracted from the work of Lan [Reference LanLan16].
A.1
Equip
![]() $\mathbb{Z}^{2g}=\mathbb{Z}^{g}\oplus \mathbb{Z}^{g}$
with the standard non-degenerate symplectic pairing
$\mathbb{Z}^{2g}=\mathbb{Z}^{g}\oplus \mathbb{Z}^{g}$
with the standard non-degenerate symplectic pairing
For every integer
![]() $m\in \mathbb{Z}_{{>}0}$
, equip
$m\in \mathbb{Z}_{{>}0}$
, equip
![]() $(\mathbb{Z}/m\mathbb{Z})^{2g}$
with the non-degenerate pairing
$(\mathbb{Z}/m\mathbb{Z})^{2g}$
with the non-degenerate pairing
![]() $\unicode[STIX]{x1D713}_{m}$
inherited from
$\unicode[STIX]{x1D713}_{m}$
inherited from
![]() $\unicode[STIX]{x1D713}$
. A symplectic level-
$\unicode[STIX]{x1D713}$
. A symplectic level-
![]() $m$
structure on a principally polarized abelian scheme
$m$
structure on a principally polarized abelian scheme
![]() $(A,\unicode[STIX]{x1D706})$
over a base
$(A,\unicode[STIX]{x1D706})$
over a base
![]() $S$
will consist of a pair
$S$
will consist of a pair
![]() $(\unicode[STIX]{x1D702},\unicode[STIX]{x1D719})$
, where
$(\unicode[STIX]{x1D702},\unicode[STIX]{x1D719})$
, where
are isomorphisms of group schemes over
![]() $S$
such that
$S$
such that
![]() $\unicode[STIX]{x1D702}$
carries the pairing
$\unicode[STIX]{x1D702}$
carries the pairing
![]() $\unicode[STIX]{x1D713}_{m}$
to the pairing
$\unicode[STIX]{x1D713}_{m}$
to the pairing
![]() $\unicode[STIX]{x1D719}\circ e_{\unicode[STIX]{x1D706}}$
on
$\unicode[STIX]{x1D719}\circ e_{\unicode[STIX]{x1D706}}$
on
![]() $A[m]$
. Here
$A[m]$
. Here
is the symplectic Weil pairing induced by the polarization
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
A.2
Let
![]() $\widetilde{{\mathcal{A}}}_{g}$
be the algebraic stack over
$\widetilde{{\mathcal{A}}}_{g}$
be the algebraic stack over
![]() $\mathbb{Z}$
parameterizing principally polarized abelian varieties of dimension
$\mathbb{Z}$
parameterizing principally polarized abelian varieties of dimension
![]() $g$
. Over
$g$
. Over
![]() $\mathbb{Z}[1/m]$
, we have a finite étale morphism of algebraic stacks
$\mathbb{Z}[1/m]$
, we have a finite étale morphism of algebraic stacks
parameterizing symplectic level-
![]() $m$
structures on the universal abelian scheme over
$m$
structures on the universal abelian scheme over
![]() $\widetilde{{\mathcal{A}}}_{g}[1/m]$
. By a classical argument of Serre, points of
$\widetilde{{\mathcal{A}}}_{g}[1/m]$
. By a classical argument of Serre, points of
![]() $\widetilde{{\mathcal{A}}}_{g,m}[1/m]$
have trivial automorphism schemes as soon as
$\widetilde{{\mathcal{A}}}_{g,m}[1/m]$
have trivial automorphism schemes as soon as
![]() $m\geqslant 3$
; see e.g. [Reference Faltings and ChaiFC90, ch. IV, Remark 6.2(c) or Corollary 6.9].
$m\geqslant 3$
; see e.g. [Reference Faltings and ChaiFC90, ch. IV, Remark 6.2(c) or Corollary 6.9].
Fix any toroidal compactification
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}$
of
$\overline{\widetilde{{\mathcal{A}}}}_{g}$
of
![]() $\widetilde{{\mathcal{A}}}_{g}$
(see [Reference Faltings and ChaiFC90, ch. IV]). We now obtain an open immersion
$\widetilde{{\mathcal{A}}}_{g}$
(see [Reference Faltings and ChaiFC90, ch. IV]). We now obtain an open immersion
of algebraic stacks over
![]() $\mathbb{Z}$
by taking the normalization of the open immersion
$\mathbb{Z}$
by taking the normalization of the open immersion
in
![]() $\widetilde{{\mathcal{A}}}_{g,m}[1/m]$
.
$\widetilde{{\mathcal{A}}}_{g,m}[1/m]$
.
The stack
![]() $\widetilde{{\mathcal{A}}}_{g,m}$
has no obvious moduli interpretation over
$\widetilde{{\mathcal{A}}}_{g,m}$
has no obvious moduli interpretation over
![]() $\mathbb{Z}$
, and we know little about the singularities of its fibers over primes dividing
$\mathbb{Z}$
, and we know little about the singularities of its fibers over primes dividing
![]() $m$
. However, this is not an obstruction to studying its general structure at the boundary. For this, we will need some information about the stratification of the boundary.
$m$
. However, this is not an obstruction to studying its general structure at the boundary. For this, we will need some information about the stratification of the boundary.
A.3
We direct the reader to [Reference Madapusi PeraMad15, §1] for the notion of a principally polarized 1-motif
![]() $(Q,\unicode[STIX]{x1D706})$
over a base
$(Q,\unicode[STIX]{x1D706})$
over a base
![]() $S$
. Here we will note that it consists of a
$S$
. Here we will note that it consists of a
![]() $1$
-motif
$1$
-motif
![]() $Q$
, that is, a two-term complex
$Q$
, that is, a two-term complex
![]() $u:X\rightarrow J$
, where
$u:X\rightarrow J$
, where
![]() $J$
is a semi-abelian scheme over
$J$
is a semi-abelian scheme over
![]() $S$
that is an extension of an abelian scheme by a torus, and
$S$
that is an extension of an abelian scheme by a torus, and
![]() $X$
is a locally constant sheaf of finite free abelian groups, and an isomorphism
$X$
is a locally constant sheaf of finite free abelian groups, and an isomorphism
![]() $\unicode[STIX]{x1D706}:Q\xrightarrow[{}]{\simeq }Q^{\vee }$
to its dual
$\unicode[STIX]{x1D706}:Q\xrightarrow[{}]{\simeq }Q^{\vee }$
to its dual
![]() $1$
-motif
$1$
-motif
![]() $Q^{\vee }$
.
$Q^{\vee }$
.
We will say that
![]() $(Q,\unicode[STIX]{x1D706})$
is of type
$(Q,\unicode[STIX]{x1D706})$
is of type
![]() $(r,s)$
for
$(r,s)$
for
![]() $r,s\in \mathbb{Z}_{{\geqslant}0}$
if the abelian part of
$r,s\in \mathbb{Z}_{{\geqslant}0}$
if the abelian part of
![]() $J$
has dimension
$J$
has dimension
![]() $s$
and if
$s$
and if
![]() $X=\text{}\underline{\mathbb{Z}}^{r}$
. The polarization
$X=\text{}\underline{\mathbb{Z}}^{r}$
. The polarization
![]() $\unicode[STIX]{x1D706}$
then canonically identifies the toric part of
$\unicode[STIX]{x1D706}$
then canonically identifies the toric part of
![]() $J$
with
$J$
with
![]() $\mathbb{G}_{m}^{r}$
.
$\mathbb{G}_{m}^{r}$
.
Suppose that
![]() $(Q,\unicode[STIX]{x1D706})$
is of type
$(Q,\unicode[STIX]{x1D706})$
is of type
![]() $(r,s)$
, and set
$(r,s)$
, and set
![]() $g=r+s$
. Given
$g=r+s$
. Given
![]() $m\in \mathbb{Z}_{{>}0}$
, one has the
$m\in \mathbb{Z}_{{>}0}$
, one has the
![]() $m$
-torsion
$m$
-torsion
![]() $Q[m]$
of the
$Q[m]$
of the
![]() $1$
-motif
$1$
-motif
![]() $Q$
: this is a finite flat group scheme over
$Q$
: this is a finite flat group scheme over
![]() $S$
of rank
$S$
of rank
![]() $2g$
, and the polarization equips it with a non-degenerate Weil pairing
$2g$
, and the polarization equips it with a non-degenerate Weil pairing
![]() $e_{\unicode[STIX]{x1D706}}$
with values in
$e_{\unicode[STIX]{x1D706}}$
with values in
![]() $\unicode[STIX]{x1D707}_{m}$
.
$\unicode[STIX]{x1D707}_{m}$
.
Let
![]() $B$
be the abelian part of
$B$
be the abelian part of
![]() $J$
. Then there is a natural ascending three-step filtration
$J$
. Then there is a natural ascending three-step filtration
where
![]() $W_{-2}Q[m]$
is isotropic for the Weil pairing,
$W_{-2}Q[m]$
is isotropic for the Weil pairing,
![]() $W_{-1}Q[m]$
is its orthogonal complement,
$W_{-1}Q[m]$
is its orthogonal complement,
![]() $\text{gr}_{-1}^{W}Q[m]$
is identified with
$\text{gr}_{-1}^{W}Q[m]$
is identified with
![]() $B[m]$
, compatibly with Weil pairings, and
$B[m]$
, compatibly with Weil pairings, and
![]() $\text{gr}_{0}^{W}Q[m]$
is identified with
$\text{gr}_{0}^{W}Q[m]$
is identified with
![]() $(\mathbb{Z}/m\mathbb{Z})^{r}$
. The induced pairing
$(\mathbb{Z}/m\mathbb{Z})^{r}$
. The induced pairing
is the canonical one.
Let
![]() $I_{r}\subset \mathbb{Z}^{2g}$
be the isotropic subspace spanned by the first
$I_{r}\subset \mathbb{Z}^{2g}$
be the isotropic subspace spanned by the first
![]() $r$
basis vectors of the first copy of
$r$
basis vectors of the first copy of
![]() $\mathbb{Z}^{g}$
. We have identifications
$\mathbb{Z}^{g}$
. We have identifications
so that the induced non-degenerate pairing
is the standard symmetric pairing
![]() $(u,v)\mapsto uv^{t}$
.
$(u,v)\mapsto uv^{t}$
.
A symplectic level-
![]() $m$
structure on
$m$
structure on
![]() $(Q,\unicode[STIX]{x1D706})$
is a pair
$(Q,\unicode[STIX]{x1D706})$
is a pair
![]() $(\unicode[STIX]{x1D702},\unicode[STIX]{x1D719})$
, where
$(\unicode[STIX]{x1D702},\unicode[STIX]{x1D719})$
, where
are isomorphisms of group schemes over
![]() $S$
such that
$S$
such that
![]() $\unicode[STIX]{x1D702}$
carries the pairing
$\unicode[STIX]{x1D702}$
carries the pairing
![]() $\unicode[STIX]{x1D713}_{m}$
to the pairing
$\unicode[STIX]{x1D713}_{m}$
to the pairing
![]() $\unicode[STIX]{x1D719}\circ e_{\unicode[STIX]{x1D706}}$
on
$\unicode[STIX]{x1D719}\circ e_{\unicode[STIX]{x1D706}}$
on
![]() $Q[m]$
and the subspace
$Q[m]$
and the subspace
![]() $I_{r}/mI_{r}$
onto
$I_{r}/mI_{r}$
onto
![]() $W_{-2}Q[m]$
, so that the induced isomorphism
$W_{-2}Q[m]$
, so that the induced isomorphism
is the identity.
We now obtain a moduli stack
![]() $\widetilde{{\mathcal{Y}}}_{r,s}$
over
$\widetilde{{\mathcal{Y}}}_{r,s}$
over
![]() $\mathbb{Z}$
of principally polarized
$\mathbb{Z}$
of principally polarized
![]() $1$
-motifs, and a finite étale cover
$1$
-motifs, and a finite étale cover
over
![]() $\mathbb{Z}[1/m]$
, parameterizing symplectic level-
$\mathbb{Z}[1/m]$
, parameterizing symplectic level-
![]() $m$
structures on the universal principally polarized
$m$
structures on the universal principally polarized
![]() $1$
-motif.
$1$
-motif.
A.4
Consider the moduli stack
![]() $\widetilde{{\mathcal{Y}}}_{r,0}$
: this parameterizes principally polarized
$\widetilde{{\mathcal{Y}}}_{r,0}$
: this parameterizes principally polarized
![]() $1$
-motifs of the form
$1$
-motifs of the form
![]() $u:\mathbb{Z}^{r}\rightarrow \mathbb{G}_{m}^{r}$
. Alternatively, it parameterizes symmetric pairings
$u:\mathbb{Z}^{r}\rightarrow \mathbb{G}_{m}^{r}$
. Alternatively, it parameterizes symmetric pairings
![]() $\mathbb{Z}^{r}\times \mathbb{Z}^{r}\rightarrow \mathbb{G}_{m}$
. As such, it is represented over
$\mathbb{Z}^{r}\times \mathbb{Z}^{r}\rightarrow \mathbb{G}_{m}$
. As such, it is represented over
![]() $\mathbb{Z}$
by the torus with character group
$\mathbb{Z}$
by the torus with character group
![]() $\mathsf{S}_{r}=\text{Sym}^{2}\mathbb{Z}^{r}$
.
$\mathsf{S}_{r}=\text{Sym}^{2}\mathbb{Z}^{r}$
.
Similarly, by the discussion in [Reference Faltings and ChaiFC90, ch. IV, §6.5], the morphism
parameterizes lifts
![]() $(1/m)\mathbb{Z}^{r}\rightarrow \mathbb{G}_{m}^{r}$
of the universal homomorphism
$(1/m)\mathbb{Z}^{r}\rightarrow \mathbb{G}_{m}^{r}$
of the universal homomorphism
![]() $\mathbb{Z}^{r}\rightarrow \mathbb{G}_{m}^{r}$
, and so is represented over
$\mathbb{Z}^{r}\rightarrow \mathbb{G}_{m}^{r}$
, and so is represented over
![]() $\mathbb{Z}[1/m]$
by the torus with character group
$\mathbb{Z}[1/m]$
by the torus with character group
![]() $(1/m)\mathsf{S}_{r}$
. The natural map
$(1/m)\mathsf{S}_{r}$
. The natural map
corresponds to the map of tori induced by the inclusion
![]() $\mathsf{S}_{r}{\hookrightarrow}(1/m)\mathsf{S}_{r}$
of character groups.
$\mathsf{S}_{r}{\hookrightarrow}(1/m)\mathsf{S}_{r}$
of character groups.
Therefore, the normalization
![]() $\widetilde{{\mathcal{Y}}}_{r,0,m}$
of
$\widetilde{{\mathcal{Y}}}_{r,0,m}$
of
![]() $\widetilde{{\mathcal{Y}}}_{r,0}$
in
$\widetilde{{\mathcal{Y}}}_{r,0}$
in
![]() $\widetilde{{\mathcal{Y}}}_{r,0,m}[1/m]$
is represented over
$\widetilde{{\mathcal{Y}}}_{r,0,m}[1/m]$
is represented over
![]() $\mathbb{Z}$
by the torus with character group
$\mathbb{Z}$
by the torus with character group
![]() $(1/m)\mathsf{S}_{r}$
, and is in particular smooth over
$(1/m)\mathsf{S}_{r}$
, and is in particular smooth over
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
A.5
When
![]() $s>0$
,
$s>0$
,
![]() $\widetilde{{\mathcal{Y}}}_{r,s}$
permits a similar, but slightly more elaborate, description. We have the obvious map
$\widetilde{{\mathcal{Y}}}_{r,s}$
permits a similar, but slightly more elaborate, description. We have the obvious map
![]() $\widetilde{{\mathcal{Y}}}_{r,s}\rightarrow \widetilde{{\mathcal{A}}}_{s}$
assigning to a polarized
$\widetilde{{\mathcal{Y}}}_{r,s}\rightarrow \widetilde{{\mathcal{A}}}_{s}$
assigning to a polarized
![]() $1$
-motif
$1$
-motif
![]() $(Q,\unicode[STIX]{x1D706})$
of type
$(Q,\unicode[STIX]{x1D706})$
of type
![]() $(r,s)$
the abelian part of the semi-abelian scheme
$(r,s)$
the abelian part of the semi-abelian scheme
![]() $J$
.
$J$
.
There is a natural action of the torus
![]() ${\mathcal{Y}}_{r,0}$
on
${\mathcal{Y}}_{r,0}$
on
![]() ${\mathcal{Y}}_{r,s}$
: given a polarized
${\mathcal{Y}}_{r,s}$
: given a polarized
![]() $1$
-motif
$1$
-motif
![]() $(Q_{0},\unicode[STIX]{x1D706}_{0})$
of type
$(Q_{0},\unicode[STIX]{x1D706}_{0})$
of type
![]() $(r,0)$
associated with a homomorphism
$(r,0)$
associated with a homomorphism
![]() $u_{0}:\text{}\underline{\mathbb{Z}}^{r}\rightarrow \mathbb{G}_{m}^{r}$
and a polarized
$u_{0}:\text{}\underline{\mathbb{Z}}^{r}\rightarrow \mathbb{G}_{m}^{r}$
and a polarized
![]() $1$
-motif
$1$
-motif
![]() $(Q,\unicode[STIX]{x1D706})$
of type
$(Q,\unicode[STIX]{x1D706})$
of type
![]() $(r,s)$
associated with
$(r,s)$
associated with
![]() $u:\text{}\underline{\mathbb{Z}}^{r}\rightarrow J$
, the product
$u:\text{}\underline{\mathbb{Z}}^{r}\rightarrow J$
, the product
![]() $u_{0}\cdot u:\text{}\underline{\mathbb{Z}}^{r}\rightarrow J$
corresponds to another principally polarized
$u_{0}\cdot u:\text{}\underline{\mathbb{Z}}^{r}\rightarrow J$
corresponds to another principally polarized
![]() $1$
-motif of type
$1$
-motif of type
![]() $(r,s)$
.
$(r,s)$
.
The quotient of
![]() $\widetilde{{\mathcal{Y}}}_{r,s}$
by this action is naturally identified with the abelian scheme
$\widetilde{{\mathcal{Y}}}_{r,s}$
by this action is naturally identified with the abelian scheme
![]() $\widetilde{{\mathcal{C}}}_{r,s}\rightarrow \widetilde{{\mathcal{A}}}_{s}$
that parameterizes homomorphisms
$\widetilde{{\mathcal{C}}}_{r,s}\rightarrow \widetilde{{\mathcal{A}}}_{s}$
that parameterizes homomorphisms
where
![]() $B$
is the universal abelian scheme over
$B$
is the universal abelian scheme over
![]() $\widetilde{{\mathcal{A}}}_{s}$
. So, we obtain a tower of algebraic stacks:
$\widetilde{{\mathcal{A}}}_{s}$
. So, we obtain a tower of algebraic stacks:
where the first morphism is a
![]() $\widetilde{{\mathcal{Y}}}_{r,0}$
-torsor, and the second is an abelian scheme.
$\widetilde{{\mathcal{Y}}}_{r,0}$
-torsor, and the second is an abelian scheme.
From the discussion in [Reference Faltings and ChaiFC90, ch. IV, §6.5], we find that the stack
![]() $\widetilde{{\mathcal{Y}}}_{r,s,m}[1/m]$
admits a compatible tower structure:
$\widetilde{{\mathcal{Y}}}_{r,s,m}[1/m]$
admits a compatible tower structure:
Here
![]() $\widetilde{{\mathcal{C}}}_{r,s,m}[1/m]$
parameterizes homomorphisms
$\widetilde{{\mathcal{C}}}_{r,s,m}[1/m]$
parameterizes homomorphisms
where
![]() $B$
is the universal abelian scheme over
$B$
is the universal abelian scheme over
![]() $\widetilde{{\mathcal{A}}}_{s,m}[1/m]$
, and
$\widetilde{{\mathcal{A}}}_{s,m}[1/m]$
, and
![]() $\widetilde{{\mathcal{Y}}}_{r,s,m}[1/m]$
parameterizes homomorphisms
$\widetilde{{\mathcal{Y}}}_{r,s,m}[1/m]$
parameterizes homomorphisms
lifting
![]() $v_{m}$
, where
$v_{m}$
, where
![]() $J$
is the universal semi-abelian scheme over
$J$
is the universal semi-abelian scheme over
![]() $\widetilde{{\mathcal{C}}}_{r,s,m}[1/m]$
parameterized by the homomorphism
$\widetilde{{\mathcal{C}}}_{r,s,m}[1/m]$
parameterized by the homomorphism
It is therefore naturally a
![]() $\widetilde{{\mathcal{Y}}}_{r,0,m}[1/m]$
-torsor over
$\widetilde{{\mathcal{Y}}}_{r,0,m}[1/m]$
-torsor over
![]() $\widetilde{{\mathcal{C}}}_{r,s,m}[1/m]$
.
$\widetilde{{\mathcal{C}}}_{r,s,m}[1/m]$
.
From this description, it is clear that the normalization of the tower (A.1) in the tower (A.2) gives us a tower
where
is still an abelian scheme parameterizing homomorphisms
![]() $v_{m}:(1/m)\mathbb{Z}^{r}\rightarrow B$
(with
$v_{m}:(1/m)\mathbb{Z}^{r}\rightarrow B$
(with
![]() $B$
the universal abelian scheme over
$B$
the universal abelian scheme over
![]() $\widetilde{{\mathcal{A}}}_{s,m}$
), and
$\widetilde{{\mathcal{A}}}_{s,m}$
), and
is once again a
![]() $\widetilde{{\mathcal{Y}}}_{r,0,m}$
-torsor parameterizing lifts
$\widetilde{{\mathcal{Y}}}_{r,0,m}$
-torsor parameterizing lifts
![]() $u_{m}:(1/m)\mathbb{Z}^{r}\rightarrow J$
of
$u_{m}:(1/m)\mathbb{Z}^{r}\rightarrow J$
of
![]() $v_{m}$
, where
$v_{m}$
, where
![]() $J$
is still classified by
$J$
is still classified by
![]() $v=m\cdot v_{m}$
.
$v=m\cdot v_{m}$
.
In particular, the morphism
is obtained via pushforward of torsors along the morphism
of tori, which is of course canonically isomorphic to the multiplication-by-
![]() $m$
map
$m$
map
A.6
Fix a rational polyhedral cone
![]() $\unicode[STIX]{x1D70E}\subset (\mathsf{S}_{r})_{\mathbb{Q}}$
: this gives us twisted toric embeddings
$\unicode[STIX]{x1D70E}\subset (\mathsf{S}_{r})_{\mathbb{Q}}$
: this gives us twisted toric embeddings
The complements of these embeddings admit a natural stratification with a unique closed stratum, which we denote by
![]() ${\mathcal{Z}}_{r,s}(\unicode[STIX]{x1D70E})$
and
${\mathcal{Z}}_{r,s}(\unicode[STIX]{x1D70E})$
and
![]() ${\mathcal{Z}}_{r,s,m}(\unicode[STIX]{x1D70E})$
, respectively.
${\mathcal{Z}}_{r,s,m}(\unicode[STIX]{x1D70E})$
, respectively.
Let
![]() $\widehat{\widetilde{{\mathcal{Y}}}}_{r,s}(\unicode[STIX]{x1D70E})$
and
$\widehat{\widetilde{{\mathcal{Y}}}}_{r,s}(\unicode[STIX]{x1D70E})$
and
![]() $\widehat{\widetilde{{\mathcal{Y}}}}_{r,s}(\unicode[STIX]{x1D70E})$
be the formal completions of
$\widehat{\widetilde{{\mathcal{Y}}}}_{r,s}(\unicode[STIX]{x1D70E})$
be the formal completions of
![]() $\widetilde{{\mathcal{Y}}}_{r,s}(\unicode[STIX]{x1D70E})$
and
$\widetilde{{\mathcal{Y}}}_{r,s}(\unicode[STIX]{x1D70E})$
and
![]() $\widetilde{{\mathcal{Y}}}_{r,s,m}(\unicode[STIX]{x1D70E})$
, respectively, along their closed strata. By abuse of notation, write
$\widetilde{{\mathcal{Y}}}_{r,s,m}(\unicode[STIX]{x1D70E})$
, respectively, along their closed strata. By abuse of notation, write
![]() $\widehat{\widetilde{{\mathcal{Y}}}}_{r,s,m}(\unicode[STIX]{x1D70E})[1/m]$
for the completion of
$\widehat{\widetilde{{\mathcal{Y}}}}_{r,s,m}(\unicode[STIX]{x1D70E})[1/m]$
for the completion of
![]() $\widetilde{{\mathcal{Y}}}_{r,s,m}(\unicode[STIX]{x1D70E})[1/m]$
along its closed stratum.
$\widetilde{{\mathcal{Y}}}_{r,s,m}(\unicode[STIX]{x1D70E})[1/m]$
along its closed stratum.
Note that the morphism
is obtained via contraction along the multiplication-by-
![]() $m$
map on
$m$
map on
![]() $\widetilde{{\mathcal{Y}}}_{r,0}$
.
$\widetilde{{\mathcal{Y}}}_{r,0}$
.
A.7
Let
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70E})\subset \text{GL}_{r}(\mathbb{Z})$
be the stabilizer of
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70E})\subset \text{GL}_{r}(\mathbb{Z})$
be the stabilizer of
![]() $\unicode[STIX]{x1D70E}$
, and let
$\unicode[STIX]{x1D70E}$
, and let
![]() $\unicode[STIX]{x1D6E4}_{m}(\unicode[STIX]{x1D70E})\leqslant \unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70E})$
be the subgroup of matrices that are trivial mod
$\unicode[STIX]{x1D6E4}_{m}(\unicode[STIX]{x1D70E})\leqslant \unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70E})$
be the subgroup of matrices that are trivial mod
![]() $m$
: these are both finite groups, and
$m$
: these are both finite groups, and
![]() $\unicode[STIX]{x1D6E4}_{m}(\unicode[STIX]{x1D70E})$
is trivial as soon as
$\unicode[STIX]{x1D6E4}_{m}(\unicode[STIX]{x1D70E})$
is trivial as soon as
![]() $m\geqslant 3$
.
$m\geqslant 3$
.
By the main results of [Reference Faltings and ChaiFC90, ch. IV], the toroidal compactification
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}$
admits a stratification by locally closed substacks
$\overline{\widetilde{{\mathcal{A}}}}_{g}$
admits a stratification by locally closed substacks
![]() ${\mathcal{Z}}(r,\unicode[STIX]{x1D70E})$
equipped with an isomorphism to
${\mathcal{Z}}(r,\unicode[STIX]{x1D70E})$
equipped with an isomorphism to
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70E})\backslash {\mathcal{Z}}_{r,g-r}(\unicode[STIX]{x1D70E})$
for some
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70E})\backslash {\mathcal{Z}}_{r,g-r}(\unicode[STIX]{x1D70E})$
for some
![]() $r\leqslant g$
and some
$r\leqslant g$
and some
![]() $\unicode[STIX]{x1D70E}\subset (\mathsf{S}_{r})_{\mathbb{Q}}$
, and such that this isomorphism extends to one of formal completions
$\unicode[STIX]{x1D70E}\subset (\mathsf{S}_{r})_{\mathbb{Q}}$
, and such that this isomorphism extends to one of formal completions
Faltings and Chai use the language of degeneration data. For a formulation using our language of
![]() $1$
-motifs, we guide the reader to [Reference StrohStr10, §3.1.5].
$1$
-motifs, we guide the reader to [Reference StrohStr10, §3.1.5].
The main idea is that, on every formally étale affine chart
one obtains a principally polarized
![]() $1$
-motif
$1$
-motif
![]() $(Q,\unicode[STIX]{x1D706})$
of type
$(Q,\unicode[STIX]{x1D706})$
of type
![]() $(r,g-r)$
over the fraction field
$(r,g-r)$
over the fraction field
![]() $K(R)$
of
$K(R)$
of
![]() $R$
associated with a semi-abelian scheme
$R$
associated with a semi-abelian scheme
![]() $J\rightarrow \operatorname{Spec}R$
, and a period map
$J\rightarrow \operatorname{Spec}R$
, and a period map
![]() $u:\mathbb{Z}^{r}\rightarrow J(K(R))$
. This period map ‘degenerates’ along
$u:\mathbb{Z}^{r}\rightarrow J(K(R))$
. This period map ‘degenerates’ along
![]() $\operatorname{Spec}R/I$
, and a construction of Mumford, explained in [Reference Faltings and ChaiFC90, ch. III], now gives us a principally polarized abelian scheme
$\operatorname{Spec}R/I$
, and a construction of Mumford, explained in [Reference Faltings and ChaiFC90, ch. III], now gives us a principally polarized abelian scheme
![]() $(A,\unicode[STIX]{x1D713})$
over
$(A,\unicode[STIX]{x1D713})$
over
![]() $K(R)$
with semi-abelian degeneration over
$K(R)$
with semi-abelian degeneration over
![]() $R$
, and equipped with a canonical symplectic identification
$R$
, and equipped with a canonical symplectic identification
![]() $Q[m]\xrightarrow[{}]{\simeq }A[m]$
for every integer
$Q[m]\xrightarrow[{}]{\simeq }A[m]$
for every integer
![]() $m$
. The pair
$m$
. The pair
![]() $(A,\unicode[STIX]{x1D713})$
now gives a map
$(A,\unicode[STIX]{x1D713})$
now gives a map
![]() $\operatorname{Spec}K(R)\rightarrow \widetilde{{\mathcal{A}}}_{g}$
, which extends to a map
$\operatorname{Spec}K(R)\rightarrow \widetilde{{\mathcal{A}}}_{g}$
, which extends to a map
which in turn induces a map
of formal algebraic stacks. These maps are now glued together to give the inverse of the desired isomorphism of formal neighborhoods.
Similarly,
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g,m}[1/m]$
admits a compatible stratification by locally closed substacks
$\overline{\widetilde{{\mathcal{A}}}}_{g,m}[1/m]$
admits a compatible stratification by locally closed substacks
![]() ${\mathcal{Z}}_{m}(r,\unicode[STIX]{x1D70E})[1/m]$
equipped with an isomorphism to
${\mathcal{Z}}_{m}(r,\unicode[STIX]{x1D70E})[1/m]$
equipped with an isomorphism to
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70E})\backslash {\mathcal{Z}}_{r,g-r,m}(\unicode[STIX]{x1D70E})[1/m]$
, and such that this isomorphism extends to one of formal completions
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D70E})\backslash {\mathcal{Z}}_{r,g-r,m}(\unicode[STIX]{x1D70E})[1/m]$
, and such that this isomorphism extends to one of formal completions
Proposition A.1. The stratification on
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g,m}[1/m]$
extends to one of
$\overline{\widetilde{{\mathcal{A}}}}_{g,m}[1/m]$
extends to one of
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g,m}$
by substacks
$\overline{\widetilde{{\mathcal{A}}}}_{g,m}$
by substacks
![]() ${\mathcal{Z}}_{m}(r,\unicode[STIX]{x1D70E})$
equipped with an isomorphism to
${\mathcal{Z}}_{m}(r,\unicode[STIX]{x1D70E})$
equipped with an isomorphism to
![]() ${\mathcal{Z}}_{r,g-r,m}(\unicode[STIX]{x1D70E})$
, extending to an isomorphism
${\mathcal{Z}}_{r,g-r,m}(\unicode[STIX]{x1D70E})$
, extending to an isomorphism
Proof. Let
be a formally étale affine chart. The tautological principally polarized
![]() $1$
-motif
$1$
-motif
![]() $(Q,\unicode[STIX]{x1D706})$
over
$(Q,\unicode[STIX]{x1D706})$
over
![]() $\operatorname{Spec}K(R)$
is now equipped with a canonical symplectic level-
$\operatorname{Spec}K(R)$
is now equipped with a canonical symplectic level-
![]() $m$
structure, which in turn also equips the principally polarized abelian scheme
$m$
structure, which in turn also equips the principally polarized abelian scheme
![]() $(A,\unicode[STIX]{x1D713})$
, obtained from it via Mumford’s construction, with a symplectic level-
$(A,\unicode[STIX]{x1D713})$
, obtained from it via Mumford’s construction, with a symplectic level-
![]() $m$
structure.
$m$
structure.
This implies that the associated map
![]() $\operatorname{Spec}K(R)\rightarrow \widetilde{{\mathcal{A}}}_{g}$
has a canonical lift
$\operatorname{Spec}K(R)\rightarrow \widetilde{{\mathcal{A}}}_{g}$
has a canonical lift
which then extends to a map
![]() $\operatorname{Spec}R\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g,m}$
.
$\operatorname{Spec}R\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g,m}$
.
Assume now that
![]() $R$
is a complete local ring of
$R$
is a complete local ring of
![]() $\widetilde{{\mathcal{Y}}}_{r,g-r,m}(\unicode[STIX]{x1D70E})$
with maximal ideal
$\widetilde{{\mathcal{Y}}}_{r,g-r,m}(\unicode[STIX]{x1D70E})$
with maximal ideal
![]() $I$
and algebraically closed residue field, and let
$I$
and algebraically closed residue field, and let
![]() $R^{\prime }$
be the complete local ring of
$R^{\prime }$
be the complete local ring of
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g,m}$
at the image of the geometric closed point of
$\overline{\widetilde{{\mathcal{A}}}}_{g,m}$
at the image of the geometric closed point of
![]() $\operatorname{Spec}R$
. We claim that the induced map
$\operatorname{Spec}R$
. We claim that the induced map
![]() $R^{\prime }\rightarrow R$
is an isomorphism. This follows from two observations: first, it is a finite map of normal local rings. Second, by the description of the stratification in characteristic
$R^{\prime }\rightarrow R$
is an isomorphism. This follows from two observations: first, it is a finite map of normal local rings. Second, by the description of the stratification in characteristic
![]() $0$
, if
$0$
, if
![]() $p$
is the residue characteristic of
$p$
is the residue characteristic of
![]() $R$
, then, for any maximal ideal
$R$
, then, for any maximal ideal
![]() $\mathfrak{m}^{\prime }\subset R^{\prime }[1/p]$
, the ideal
$\mathfrak{m}^{\prime }\subset R^{\prime }[1/p]$
, the ideal
![]() $\mathfrak{m}=\mathfrak{m}^{\prime }R[1/p]$
is once again maximal, and the induced map
$\mathfrak{m}=\mathfrak{m}^{\prime }R[1/p]$
is once again maximal, and the induced map
is an isomorphism. The second assertion shows, via faithfully flat descent, that every element of
![]() $R$
is contained in
$R$
is contained in
![]() $R^{\prime }[1/p]$
, and the first shows that it must already be contained in
$R^{\prime }[1/p]$
, and the first shows that it must already be contained in
![]() $R^{\prime }$
.
$R^{\prime }$
.
Let
![]() $\unicode[STIX]{x1D702}_{m}:\overline{\widetilde{{\mathcal{A}}}}_{g,m}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
be the natural finite map. Combining the previous paragraph with Artin approximation, we find that
$\unicode[STIX]{x1D702}_{m}:\overline{\widetilde{{\mathcal{A}}}}_{g,m}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
be the natural finite map. Combining the previous paragraph with Artin approximation, we find that
![]() $\unicode[STIX]{x1D702}_{m}$
is étale locally isomorphic to the finite map
$\unicode[STIX]{x1D702}_{m}$
is étale locally isomorphic to the finite map
for varying choices of
![]() $r$
and
$r$
and
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
We claim that the reduced stack
![]() ${\mathcal{Z}}_{m}(r,\unicode[STIX]{x1D70E})$
underlying the locally closed substack
${\mathcal{Z}}_{m}(r,\unicode[STIX]{x1D70E})$
underlying the locally closed substack
![]() $\unicode[STIX]{x1D702}_{m}^{-1}({\mathcal{Z}}(r,\unicode[STIX]{x1D70E}))\subset \overline{\widetilde{{\mathcal{A}}}}_{g,m}$
is normal. This can be checked on complete local rings using the observation that the reduced substack underlying the pre-image of
$\unicode[STIX]{x1D702}_{m}^{-1}({\mathcal{Z}}(r,\unicode[STIX]{x1D70E}))\subset \overline{\widetilde{{\mathcal{A}}}}_{g,m}$
is normal. This can be checked on complete local rings using the observation that the reduced substack underlying the pre-image of
![]() ${\mathcal{Z}}_{r,g-r}(\unicode[STIX]{x1D70E})$
under the map (A.5) is normal.
${\mathcal{Z}}_{r,g-r}(\unicode[STIX]{x1D70E})$
under the map (A.5) is normal.
Moreover, from this and the fact that the locally closed substacks
![]() ${\mathcal{Z}}(r,\unicode[STIX]{x1D70E})$
stratify
${\mathcal{Z}}(r,\unicode[STIX]{x1D70E})$
stratify
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}$
, one can deduce that the locally closed substacks
$\overline{\widetilde{{\mathcal{A}}}}_{g}$
, one can deduce that the locally closed substacks
![]() ${\mathcal{Z}}_{m}(r,\unicode[STIX]{x1D70E})$
stratify
${\mathcal{Z}}_{m}(r,\unicode[STIX]{x1D70E})$
stratify
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g,m}$
.
$\overline{\widetilde{{\mathcal{A}}}}_{g,m}$
.
By normality of the target, the map
extends uniquely to a map
lifting the composition
This extension necessarily factors through a finite map
which is an isomorphism in the generic fiber. By looking at complete local rings, it is seen to be a finite étale map and hence an isomorphism.
The last assertion about the formal completions now follows from [Reference Madapusi PeraMad15, (A.3.2)]. ◻
From this and the explicit nature of the map (A.4), we immediately obtain the following result.
Proposition A.2. Let
![]() $\unicode[STIX]{x1D702}_{m}:\overline{\widetilde{{\mathcal{A}}}}_{g,m}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
be the natural finite map, and let
$\unicode[STIX]{x1D702}_{m}:\overline{\widetilde{{\mathcal{A}}}}_{g,m}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
be the natural finite map, and let
![]() ${\mathcal{D}}_{m}\subset \overline{\widetilde{{\mathcal{A}}}}_{g,m}$
be the complement of
${\mathcal{D}}_{m}\subset \overline{\widetilde{{\mathcal{A}}}}_{g,m}$
be the complement of
![]() $\widetilde{{\mathcal{A}}}_{g,m}$
, equipped with its reduced scheme structure.
$\widetilde{{\mathcal{A}}}_{g,m}$
, equipped with its reduced scheme structure.
Then
![]() ${\mathcal{D}}_{m}$
is a relative Cartier divisor over
${\mathcal{D}}_{m}$
is a relative Cartier divisor over
![]() $\mathbb{Z}$
. Moreover, if
$\mathbb{Z}$
. Moreover, if
![]() ${\mathcal{D}}\subset \overline{\widetilde{{\mathcal{A}}}}_{g}$
is the boundary divisor with its reduced scheme structure, then we have an equality of Cartier divisors
${\mathcal{D}}\subset \overline{\widetilde{{\mathcal{A}}}}_{g}$
is the boundary divisor with its reduced scheme structure, then we have an equality of Cartier divisors
![]() $\unicode[STIX]{x1D702}_{m}^{\ast }{\mathcal{D}}=m\cdot {\mathcal{D}}_{m}$
.
$\unicode[STIX]{x1D702}_{m}^{\ast }{\mathcal{D}}=m\cdot {\mathcal{D}}_{m}$
.
Remark A.3. Note that the above proposition remains true if we replace
![]() $\widetilde{{\mathcal{A}}}_{g,m}$
and its compactification with the normalizations of their base change over
$\widetilde{{\mathcal{A}}}_{g,m}$
and its compactification with the normalizations of their base change over
![]() ${\mathcal{O}}_{K}$
, for any number field
${\mathcal{O}}_{K}$
, for any number field
![]() $K/\mathbb{Q}$
.
$K/\mathbb{Q}$
.
Proposition A.4. Let
![]() $\widetilde{{\mathcal{A}}}_{g}^{[m]}$
and
$\widetilde{{\mathcal{A}}}_{g}^{[m]}$
and
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
be as in §4. Let
$\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
be as in §4. Let
![]() $\unicode[STIX]{x1D70B}_{m}:\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
be the natural finite map, and let
$\unicode[STIX]{x1D70B}_{m}:\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}\rightarrow \overline{\widetilde{{\mathcal{A}}}}_{g}$
be the natural finite map, and let
![]() ${\mathcal{D}}^{[m]}\subset \overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
be the complement of
${\mathcal{D}}^{[m]}\subset \overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
be the complement of
![]() $\widetilde{{\mathcal{A}}}_{g}^{[m]}$
, equipped with its reduced scheme structure.
$\widetilde{{\mathcal{A}}}_{g}^{[m]}$
, equipped with its reduced scheme structure.
Then
![]() ${\mathcal{D}}^{[m]}$
is a relative effective Cartier divisor over
${\mathcal{D}}^{[m]}$
is a relative effective Cartier divisor over
![]() $\mathbb{Z}$
.Footnote
2
Moreover, we have
$\mathbb{Z}$
.Footnote
2
Moreover, we have
![]() $\unicode[STIX]{x1D70B}_{m}^{\ast }{\mathcal{D}}=m\cdot {\mathcal{D}}^{[m]}$
.
$\unicode[STIX]{x1D70B}_{m}^{\ast }{\mathcal{D}}=m\cdot {\mathcal{D}}^{[m]}$
.
Proof. Over
![]() $\mathbb{Z}[1/m,\unicode[STIX]{x1D707}_{m}]$
,
$\mathbb{Z}[1/m,\unicode[STIX]{x1D707}_{m}]$
,
![]() $\widetilde{{\mathcal{A}}}_{g}^{[m]}$
and
$\widetilde{{\mathcal{A}}}_{g}^{[m]}$
and
![]() $\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
can be identified with a disjoint union of copies of
$\overline{\widetilde{{\mathcal{A}}}}_{g}^{[m]}$
can be identified with a disjoint union of copies of
![]() $(\widetilde{{\mathcal{A}}}_{g,m})_{\mathbb{Z}[1/m,\unicode[STIX]{x1D707}_{m}]}$
and
$(\widetilde{{\mathcal{A}}}_{g,m})_{\mathbb{Z}[1/m,\unicode[STIX]{x1D707}_{m}]}$
and
![]() $(\overline{\widetilde{{\mathcal{A}}}}_{g,m})_{\mathbb{Z}[1/m,\unicode[STIX]{x1D707}_{m}]}$
, respectively. So, the result is true over
$(\overline{\widetilde{{\mathcal{A}}}}_{g,m})_{\mathbb{Z}[1/m,\unicode[STIX]{x1D707}_{m}]}$
, respectively. So, the result is true over
![]() $\mathbb{Z}[1/m]$
. Moreover, by Proposition A.2 and Remark A.3, it is true after a change of scalars to
$\mathbb{Z}[1/m]$
. Moreover, by Proposition A.2 and Remark A.3, it is true after a change of scalars to
![]() $\mathbb{Z}[\unicode[STIX]{x1D707}_{m}]$
followed by normalization. Combining the two, we find that the result is already true over
$\mathbb{Z}[\unicode[STIX]{x1D707}_{m}]$
followed by normalization. Combining the two, we find that the result is already true over
![]() $\mathbb{Z}$
.◻
$\mathbb{Z}$
.◻