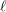Constraints on the cohomological correspondence associated to a self map

Abstract

In this paper we establish some constraints on the eigenvalues for the action of a self map of a proper variety on its $\ell$-adic cohomology. The essential ingredients are a trace formula due to Fujiwara, and the theory of weights.

1 Introduction

Let $X$ be a smooth projective variety over a field $k$ and $f:X\rightarrow X$ a dominant self map of  $X$ . When $k=\mathbb{C}$ one can look at the topological entropy of the dynamical system $(X(\mathbb{C}),f)$ , which has been shown to be equal to the logarithm of the spectral radius of $f^{\ast }$ acting on the Betti cohomology of $X(\mathbb{C})$  [Gro03, Yom87]. When $k$ is an arbitrary field, there is no obvious and useful notion of a topological entropy; however, it still makes sense to look at the action of $f^{\ast }$ on suitable cohomology theories.

Esnault and Srinivas studied this question for automorphisms of surfaces over finite fields [ES13]. They looked at the action of $f^{\ast }$ on the $\ell$ -adic cohomology of a smooth proper surface defined over an algebraic closure of a finite field. In this case they showed that the spectral radius on $H_{\acute{\text{e}}\text{t}}^{\ast }(X,\mathbb{Q}_{\ell })$ coincides with the spectral radius on the smallest $f^{\ast }$ stable sub-algebra generated by any ample class $\unicode[STIX]{x1D714}\in H_{\acute{\text{e}}\text{t}}^{2}(X,\mathbb{Q}_{\ell })$ . Since such a sub-space of the cohomology is stable under specialization, this at once proves the result for automorphisms of surfaces over arbitrary base fields. This in particular leads naturally to the question of whether the spectral radius restricted to the even degree cohomology is the same as that on the entire cohomology (see [ES13, § 6.3]).

From an arithmetical viewpoint there is an abundance of self maps arising from the Galois group of the base field. The corresponding action on cohomology gives rise to interesting Galois representations. These Galois representations are often hard to understand and contain information about the variety itself. We combine these arithmetical and dynamical points of view to define a zeta function associated to a self map of a variety over a finite field (see Definition 2.12). We obtain the principal result of this paper by studying the analytical properties of this zeta function, which we now state.

Let $k$ be either an algebraic closure of a finite field or the field of complex numbers $\mathbb{C}$ . Fix a prime $\ell$ invertible in $k$ (if $\text{char}(k)>0$ ), and an embedding

(1.1) $$\begin{eqnarray}\unicode[STIX]{x1D70F}:\mathbb{Q}_{\ell }{\hookrightarrow}\mathbb{C}.\end{eqnarray}$$

Suppose $X$ is a proper scheme over $k$ . Let $H^{\ast }(X)$ be the $\ell$ -adic cohomology of $X$ (when $\text{char}(k)>0$ ) with its increasing weight filtration [Del80, § 5.3.6], or the singular cohomology $H^{\ast }(X(\mathbb{C}),\mathbb{Q})$ (when $k=\mathbb{C}$ ) with its mixed Hodge structure [Del74b, Proposition 8.1.20]. Let $W_{k}H^{\ast }(X)$ be the associated weight filtration.

Let $f:X\rightarrow X$ be a self map of $X$ .

Let $\unicode[STIX]{x1D706}_{\text{odd}}$ (respectively, $\unicode[STIX]{x1D706}_{\text{even}}$ ) be the spectral radius (with respect to $\unicode[STIX]{x1D70F}$ if $\text{char}(k)>0$ ) for the action of $f^{\ast }$ on $\bigoplus _{i\geqslant 0}H^{2i+1}(X)$ (respectively, $\bigoplus _{i\geqslant 0}H^{2i}(X)$ ). Let $k_{\text{odd}}$ be the maximum among integers $k$ with the property that the spectral radius for the action of $f^{\ast }$ on $\text{Gr}_{W}^{k}H^{i}(X)$ is $\unicode[STIX]{x1D706}_{\text{odd}}$ , where $i$ is an odd integer. Similarly define $k_{\text{even}}$ .

Theorem 1.1. Using the above notation, we have the following statements.

1. (1) $\unicode[STIX]{x1D706}_{\text{even}}\geqslant \unicode[STIX]{x1D706}_{\text{odd}}$ .

2. (2) If equality holds in $(1)$ , then $k_{\text{even}}\geqslant k_{\text{odd}}$ .

The inequality in $(2)$ seems to be previously unknown even for smooth projective varieties over $\mathbb{C}$ . The inequality in $(1)$ extends what was previously known for smooth projective varieties over $\mathbb{C}$ using analytical techniques (via the Gromov–Yomdin theory) to arbitrary proper varieties over $\mathbb{C}$ . However, the properness assumption is necessary, as shown by Example 3.6.

Theorem 1.1 immediately allows us to deduce the following corollary.

Corollary 1.2. Let $f:X\rightarrow X$ be a self map of a proper scheme over an arbitrary field $k$ . Let $\ell$ be a prime invertible in $k$ and $\bar{k}$ an algebraic closure of $k$ . Fix an embedding $\unicode[STIX]{x1D70F}:\mathbb{Q}_{\ell }{\hookrightarrow}\mathbb{C}$ . Then the spectral radius (with respect to $\unicode[STIX]{x1D70F}$ ) for the action of $f_{\bar{k}}^{\ast }$ on the entire $\ell$ -adic cohomology $H^{\ast }(X_{\bar{k}},\mathbb{Q}_{\ell })$ is equal to the spectral radius for its action on $\bigoplus _{i\geqslant 0}H^{2i}(X_{\bar{k}},\mathbb{Q}_{\ell })$ .

These constraints on the eigenvalues can be seen as a consequence of a positivity condition. When the base field is finite, and the variety is proper, the logarithm of the zeta function (see Definition 2.12) is a power series with positive coefficients and it is this positivity that we exploit (via Lemma 3.1). The geometric Frobenius plays a dual role here: on the one hand, it ensures the above positivity (see Proposition 2.10); and on the other hand, we can ‘distinguish’ cohomology classes using their weights.

In a recent work, Truong [Tru16] has shown among other things that for a dominant self map of a smooth projective variety over an arbitrary base field the spectral radius on the $\ell$ -adic cohomology is bounded above by its spectral radius on the ring of algebraic cycles mod numerical equivalence, thus implying that the spectral radius on the even degree cohomology and the entire cohomology are the same. We believe that the point of view taken in this paper is different from that in [Tru16].

2 A zeta function associated to a self map

In this section we shall introduce a zeta function associated to a proper self map of a separated scheme of finite type over $\mathbb{F}_{q}$ . The analytic properties of this zeta function will be central to the results in § 3.

Let $\mathbb{F}_{q}$ be a finite field with $q$ elements of characteristic $p$ . Let $k$ be an algebraic closure of  $\mathbb{F}_{q}$ . Let $\ell$ be a prime co-prime to $p$ .

Schemes over $\mathbb{F}_{q}$ will be denoted by a subscript $0$ ( $X_{0},~Y_{0}$ , etc.). Similarly, morphisms of schemes over $\mathbb{F}_{q}$ will be denoted by $f_{0},~g_{0}$ , etc. The corresponding object over $k$ will be denoted without a subscript ( $X,~f$ , etc.).

Let $X$ be a separated scheme of finite type over $k$ . Let $H^{i}(X,\mathbb{Q}_{\ell })$ and $H_{c}^{i}(X,\mathbb{Q}_{\ell })$ respectively denote the $i$ th usual and compactly supported $\ell$ -adic étale cohomology of $X$ .

For any self map $f:X\rightarrow X$ , we define

(2.1) $$\begin{eqnarray}\text{Tr}(f^{\ast },H^{\ast }(X,\mathbb{Q}_{\ell })):=\mathop{\sum }_{i=0}^{2\,\text{dim}(X)}(-1)^{i}\text{Tr}(f^{\ast };H^{i}(X,\mathbb{Q}_{\ell }))\in \mathbb{Q}_{\ell }.\end{eqnarray}$$

Similarly, when $f$ is proper, we define

(2.2) $$\begin{eqnarray}\text{Tr}(f^{\ast },H_{c}^{\ast }(X,\mathbb{Q}_{\ell })):=\mathop{\sum }_{i=0}^{2\,\text{dim}(X)}(-1)^{i}\text{Tr}(f^{\ast };H_{c}^{i}(X,\mathbb{Q}_{\ell }))\in \mathbb{Q}_{\ell }.\end{eqnarray}$$

Definition 2.1 (Absolute Frobenius).

For any scheme $X_{0}/\mathbb{F}_{q}$ , the absolute Frobenius (with respect to $\mathbb{F}_{q}$ )  $F_{X_{0},q}:X_{0}\rightarrow X_{0}$ is the morphism which is the identity on the underlying topological space, and for any open affine sub-scheme $U_{0}\subseteq X_{0}$ ,  $F_{X_{0},q}|_{U_{0}}$ corresponds to the ring endomorphism of $\unicode[STIX]{x1D6E4}(U_{0},{\mathcal{O}}_{U_{0}})$ given by $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x1D6FC}^{q}$ .

Remark 2.2. The absolute Frobenius is a morphism over $\mathbb{F}_{q}$ .

The following lemma is standard, and we state it without a proof.

Lemma 2.3. Let $X_{0}$ be separated scheme of finite type over $\mathbb{F}_{q}$ . Then $X_{0}/\mathbb{F}_{q}$ is unramified (and hence étale) if and only if $F_{X_{0},q}$ is an unramified morphism.

Definition 2.4 (Geometric Frobenius).

For a scheme $X_{0}/\mathbb{F}_{q}$ let $X$ denote the base change of $X_{0}$ to $k$ . The geometric Frobenius (with respect to $\mathbb{F}_{q}$ ) is the morphism $F_{X,q}:X\rightarrow X$ induced from $F_{X_{0},q}:X_{0}\rightarrow X_{0}$ by base change.

Remark 2.5. The geometric Frobenius morphism is a morphism over $k$ .

A scheme $X/k$ is said to be defined over $\mathbb{F}_{q}$ if there exist a scheme $X_{0}/\mathbb{F}_{q}$ and an isomorphism of $k$ -schemes between $X$ and $X_{0}\times _{\mathbb{F}_{q}}k$ . Given any such scheme $X/k$ defined over $\mathbb{F}_{q}$ and a choice of a $\mathbb{F}_{q}$ structure as above, the geometric Frobenius morphism $F_{X_{0}\times _{\mathbb{F}_{q}}k}$ induces a self map of $X/k$ . We call this the geometric Frobenius (with respect to $\mathbb{F}_{q}$ and $X_{0}$ ) and denote it by $F_{X,q}$ .

In a similar vein, a diagram of schemes over $k$ is said to be defined over $\mathbb{F}_{q}$ if it is obtained as a base change of a diagram over $\mathbb{F}_{q}$ .

Now suppose $f_{0}:X_{0}\rightarrow X_{0}$ is a self map of a separated scheme of finite type over $\mathbb{F}_{q}$ . Let $(X,f)$ be the corresponding pair over $k$ , obtained by base change. Let $\unicode[STIX]{x1D6E4}_{f_{0}\circ F_{X_{0},q}}^{t}$ be the transpose of the graph of $f_{0}\circ F_{X_{0},q}$ and $\unicode[STIX]{x1D6E5}_{X_{0}}$ denote the diagonal embedding of $X_{0}$ in $X_{0}\times _{\mathbb{F}_{q}}X_{0}$ . Note that $f_{0}$ and $F_{X_{0},q}$ commute.

Lemma 2.6. With notation as above, the scheme $\unicode[STIX]{x1D6E4}_{f_{0}\circ (F_{X_{0},q})^{m}}^{t}\,\cap \,\unicode[STIX]{x1D6E5}_{X_{0}}$ is étale over $\mathbb{F}_{q}$ for all $m\geqslant 1$ .

Proof. If $m$ is greater than $1$ , by replacing $f_{0}$ by $f_{0}\circ (F_{X_{0},q})^{m-1}$ we reduce to the case $m=1$ .

Let $Z_{0}:=\unicode[STIX]{x1D6E4}_{f_{0}\circ F_{X_{0},q}}^{t}\,\cap \,\unicode[STIX]{x1D6E5}_{X_{0}}$ and $g_{0}:=f_{0}\circ F_{X_{0},q}$ . We have a cartesian diagram

Here the morphism $\unicode[STIX]{x1D6E4}_{g_{0}}^{t}$ is the transpose of the graph of $g_{0}$ and $\text{pr}_{i}$ , $i=1,2$ , are the projections. The commutativity of the above diagram implies that $(f_{0}\circ i)\circ F_{Z_{0},q}=(f_{0}\circ F_{X_{0},q})\circ i$ is a closed immersion. Hence $F_{Z_{0},q}$ is a closed immersion and thus an unramified morphism. Lemma 2.3 now implies that $Z_{0}$ is unramfied (and hence étale) over $\mathbb{F}_{q}$ .◻

Let $f:X\rightarrow X$ be a self map of a finite type scheme over $k$ .

Definition 2.7 (Fixed point).

A closed point $x\in X$ is said to be a fixed point of $f$ if $f(x)=x$ .

Proposition 2.8. Let $f_{0}:X_{0}\rightarrow X_{0}$ be a self map of a smooth, proper scheme over $\mathbb{F}_{q}$ . Then $\text{Tr}((f^{m}\circ F_{X,q}^{n})^{\ast },H^{\ast }(X,\mathbb{Q}_{\ell }))$ is the number of fixed points of $f^{m}\circ F_{X,q}^{n}$ acting on $X$ .

Proof. This is an immediate consequence of Lemma 2.6 and the trace formula in [SGA4½, ch. 4, Corollaire 3.7]. ◻

The above proposition naturally leads to the following questions for an arbitrary $X_{0}$ , a proper $f_{0}$ and integers $m\geqslant 1$ .

Question 2.9. Is the $\ell$ -adic number $\text{Tr}((f\circ F_{X,q}^{m})^{\ast },H_{c}^{\ast }(X,\mathbb{Q}_{\ell }))$ an integer? If yes, then is it equal to the number of fixed points of $f\circ F_{X,q}^{m}$ acting on $X$ ?

A trace formula by Fujiwara sheds some light on these questions.

Proposition 2.10. Both parts of Question 2.9 have a positive answer if $m$ is sufficiently large. Moreover, when $X_{0}$ is proper any $m\geqslant 1$ would do.

Proof. This is an immediate consequence of Fujiwara’s trace formula (see [Fuj97, Corollary 5.4.5]; cf. [Ill06, § 3.5(b)]). ◻

Proposition 2.10 motivates the following definition.

Definition 2.11. Let $n_{0}(f)$ be the least integer $m$ such that both parts of Question 2.9 have a positive answer.

Now we are in a position to define the zeta function and study its analytical properties.

Let $X_{0}$ be a separated scheme of finite type over $\mathbb{F}_{q}$ , and $f_{0}:X_{0}\rightarrow X_{0}$ a proper self map (also defined over $\mathbb{F}_{q}$ ). Let $\ell$ be a prime invertible in $\mathbb{F}_{q}$ .

For any field $K$ , let $K[[t]]$ and $K((t))$ respectively be the ring of formal power series and the field of formal Laurent series with coefficients in $K$ .

Definition 2.12. The zeta function $Z(X_{0},f_{0},t)$ corresponding to $(X_{0},f_{0})$ is defined to be

$$\begin{eqnarray}Z(X_{0},f_{0},t)=\exp \biggl(\mathop{\sum }_{n\geqslant 1}{\displaystyle \frac{\text{Tr}((f\circ F_{X,q})^{n\ast },H_{c}^{\ast }(X,\mathbb{Q}_{\ell }))t^{n}}{n}}\biggr)\in \mathbb{Q}_{\ell }[[t]]\subset \mathbb{Q}_{\ell }((t)).\end{eqnarray}$$

Remark 2.13. When $f_{0}$ is the identity, one recovers the Hasse–Weil zeta function of the scheme  $X_{0}$ .

Lemma 2.14. The zeta function $Z(X_{0},f_{0},t)$ belongs to $\mathbb{Q}(t)\,\cap \,\mathbb{Q}_{\ell }[[t]]\subseteq \mathbb{Q}_{\ell }((t))$ and is independent of $\ell$ .

Proof. The result in [Ill06, § 3.5(b)] implies that the above power series is actually in $\mathbb{Q}[[t]]$ and is independent of $\ell$ . The trace–determinant relation [Del74a, 1.5.3] implies that $Z(X_{0},f_{0},t)$ is a rational function in $\mathbb{Q}_{\ell }$ . Hence $Z(X_{0},f_{0},t)\in \mathbb{Q}_{\ell }(t)\,\cap \,\mathbb{Q}[[t]]\subset \mathbb{Q}_{\ell }[[t]]$ and hence in $\mathbb{Q}(t)$ (see [Del74a, Lemme 1.7]). Thus $Z(X_{0},f_{0},t)\in \mathbb{Q}(t)$ and is independent of $\ell$ .◻

Corollary 2.15. The formal power series $Z(X_{0},f_{0},t)\in \mathbb{Q}[[t]]\subseteq \mathbb{C}[[t]]$ has a non-trivial radius of convergence about the origin in the complex plane and has a meromorphic continuation onto the entire complex plane as a rational function.

Proof. It follows from Lemma 2.14 that the formal power series $Z(X_{0},f_{0},t)$ coincides with the power series expansion (about the origin) of a rational function with coefficients in $\mathbb{Q}$ , as elements of $\mathbb{Q}[[t]]$ . Hence the result.◻

Remark 2.16. Suppose $X_{0}$ is geometrically connected and $f_{0}:X_{0}\rightarrow X_{0}$ a constant map (necessarily mapping to a $\mathbb{F}_{q}$ -valued point). The associated zeta function $Z(X_{0},f_{0},t)$ is $1/(1-t)\in \mathbb{Q}[[t]]$ . We shall see in the next section that even when $f_{0}$ is not dominant, the zeta function associated to it still carries enough information for us to use. This is in contrast to the techniques in [ES13], where $f_{0}$ being an automorphism was crucially used.

3 Some new constraints on the eigenvalues

In this section we establish some new constraints on the eigenvalues for the action of a self map of a proper variety on its $\ell$ -adic cohomology.

We retain the notation and conventions of § 2.

Lemma 3.1. Let $G(t)\in t\mathbb{Q}[[t]]$ be a formal power series with non-negative coefficients and with no constant term. Then the formal power series $\exp (G(t))\in \mathbb{Q}[[t]]$ and $G(t)$ have the same radius of convergence about the origin in the complex plane. In particular, in the disc of its convergence, the formal power series $\exp (G(t))$ , considered as a holomorphic function, coincides with the exponential (in the analytic sense) of a holomorphic function.

Proof. It is clear that the radius of convergence of the formal power series $\exp (G(t))$ is at least as large as that of the formal power series $G(t)$ , subject to the latter having a non-trivial radius of convergence. To complete the proof it suffices to show that the radius of convergence of the formal power series $\exp (G(t))$ is bounded above by the radius of convergence of $G(t)$ .

Using the comparison test for convergence, it suffices to show that

$$\begin{eqnarray}\frac{d^{n}}{dt^{n}}(\exp (G(t)))|_{t=0}\geqslant G^{(n)}(0),\end{eqnarray}$$

where $G^{(n)}(t)$ is the $n$ th formal derivative of $G(t)$  [Rud87, 10.6, (8)]. We shall show by induction on $n$ that

$$\begin{eqnarray}\frac{d^{n}}{dt^{n}}(\exp (G(t)))=P_{n}(G^{(1)}(t),G^{(2)}(t),\ldots ,G^{(n)}(t))\exp (G(t))\quad \text{in }\mathbb{Q}[[t]],\end{eqnarray}$$

where $P_{n}(x_{1},x_{2},\ldots ,x_{n})$ is a polynomial with positive integral coefficients and is of the form $P_{n}(x_{1},x_{2},\ldots ,x_{n})=x_{n}+\widetilde{P}_{n}(x_{1},x_{2},\ldots ,x_{n-1})$ for some polynomial $\widetilde{P}_{n}$ in one variable fewer.

For $n=1$ the statement is obviously true. Assume now that the statement is true with $n=k$ . The chain rule of differentiation then implies the statement for $n=k+1$ . In particular, one observes that

$$\begin{eqnarray}\frac{d^{n}}{dt^{n}}(\exp (G(t)))|_{t=0}=G^{(n)}(0)+\widetilde{P}_{n}(G^{(1)}(0),G^{(2)}(0),\ldots ,G^{(n-1)}(0)).\end{eqnarray}$$

The non-negativity of the coefficients of $G(t)$ implies the non-negativity of $G^{(n)}(0)$ . Since the coefficients of the polynomial $\widetilde{P}_{n}$ are positive, we are done.◻

Lemma 3.2. Let $R(t),Q(t)\in \mathbb{C}[t]$ be polynomials with complex coefficients. Let $G(t)\in t\mathbb{Q}[[t]]$ be a formal power series with non-negative coefficients and with no constant term such that

(3.1) $$\begin{eqnarray}\exp (G(t))=\frac{R(t)}{Q(t)},\end{eqnarray}$$

as elements in $\mathbb{C}[[t]]$ . Then any closed disc around the origin in the complex plane containing a root of $R(t)$ necessarily contains a root of $Q(t)$ .

Proof. First note that (3.1) implies that $\exp (G(t))$ has a non-trivial radius of convergence. Let $\unicode[STIX]{x1D6E5}$ be a closed disc around the origin not containing a root of $Q(t)$ . Then the equality in (3.1) implies that $\exp (G(t))$ is convergent in an open neighbourhood of $\unicode[STIX]{x1D6E5}$ .

Moreover, since $G(t)$ has non-negative coefficients, Lemma 3.1 and (3.1) together imply that the rational function $R(t)/Q(t)$ equals the exponential of a holomorphic function on $\unicode[STIX]{x1D6E5}$ , and hence $R(t)$ cannot have a root in $\unicode[STIX]{x1D6E5}$ .◻

Let $k$ be either an algebraic closure of a finite field or the field of complex numbers $\mathbb{C}$ . Let $X/k$ be a proper scheme.

Fix a prime $\ell$ invertible in $k$ (if $\text{char}(k)>0$ ), and an embedding

(3.2) $$\begin{eqnarray}\unicode[STIX]{x1D70F}:\mathbb{Q}_{\ell }{\hookrightarrow}\mathbb{C}.\end{eqnarray}$$

Let $f:X\rightarrow X$ be a self map of $X$ (over $k$ ). Let $\unicode[STIX]{x1D706}_{\text{even}},\unicode[STIX]{x1D706}_{\text{odd}}$ , $k_{\text{even}}$ , $k_{\text{odd}}$ be as defined in the introduction. Then one has the following result.

Theorem 3.3.

1. (1) $\unicode[STIX]{x1D706}_{\text{even}}\geqslant \unicode[STIX]{x1D706}_{\text{odd}}$ .

2. (2) If equality holds in $(1)$ , then $k_{\text{even}}\geqslant k_{\text{odd}}$ .

Proof. Using a standard spreading-out argument, we can reduce to the case where $k$ is an algebraic closure of a finite field. Moreover, we fix a model $(X_{0},f_{0})$ for the pair $(X,f)$ over a finite sub-field $\mathbb{F}_{q}$ of $k$ .

Note that for any positive integer $r$ , the spectral radius (with respect to $\unicode[STIX]{x1D70F}$ ) of $f^{r\ast }$ acting on the odd and even degree cohomology is $\unicode[STIX]{x1D706}_{\text{odd}}^{r}$ and $\unicode[STIX]{x1D706}_{\text{even}}^{r}$ , respectively. There exists an iterate of $f$ which maps a connected component of $X$ into itself. Hence $f^{\ast }$ acting on $H^{0}(X,\mathbb{Q}_{\ell })$ has at least one eigenvalue of modulus $1$ (with respect to any $\unicode[STIX]{x1D70F}$ ). Thus $\unicode[STIX]{x1D706}_{\text{even}}\geqslant 1$ . If $\unicode[STIX]{x1D706}_{\text{odd}}=0$ we are done, hence we can assume that $\unicode[STIX]{x1D706}_{\text{odd}}\neq 0$ .

Fix a positive integer $r$ and consider the zeta function (see Definition 2.12) of the pair $(X_{0},f_{0}^{r})$ . It follows from Corollary 2.15 that this zeta function is defined as a holomorphic function in a non-trivial neighbourhood of the origin, and has a meromorphic continuation onto the entire complex plane as a rational function. Suppose that $R(t)/Q(t)$ is the meromorphic continuation, where $R(t)$ and $Q(t)$ are co-prime rational polynomials in $t$ . Moreover, using the trace–determinant relation (see [Del74a, 1.5.3]), one has

(3.3) $$\begin{eqnarray}Z(X_{0},f_{0}^{r},t)=\mathop{\prod }_{i=0}^{2\,\text{dim}(X)}P_{i}(t)^{(-1)^{i+1}}\quad \text{in}\;\mathbb{Q}_{\ell }[[t]]\subset \mathbb{C}[[t]](\text{via}\;\unicode[STIX]{x1D70F}),\end{eqnarray}$$

where $P_{i}(t)=\text{det}(1-t(F_{X,q}\circ f^{r})^{\ast },H^{i}(X,\mathbb{Q}_{\ell }))$ , $0\leqslant i\leqslant 2\,\text{dim}(X)$ .

Moreover, one also has

(3.4) $$\begin{eqnarray}Z(X_{0},f_{0}^{r},t)=\frac{R(t)}{Q(t)}\quad \text{in}\;\mathbb{Q}[[t]].\end{eqnarray}$$

Hence (3.3) and (3.4) imply that the complex roots of $R(t)$ and $Q(t)$ are a subset of the inverse eigenvalues of $(F_{X,q}\circ f^{r})^{\ast }$ acting on the odd and even degree cohomology, respectively. In particular, they are non-zero. Also note that $f^{\ast }$ and $F_{X,q}^{\ast }$ commute and hence can be simultaneously brought into a Jordan canonical form. Hence any eigenvalue of $F_{X,q}^{\ast }\circ f^{r\ast }$ acting on any $H^{i}(X,\mathbb{Q}_{\ell })$ is a product of an eigenvalue of $F_{X,q}^{\ast }$ and one of $f^{r\ast }$ acting on the same $H^{i}(X,\mathbb{Q}_{\ell })$ .

Let $\unicode[STIX]{x1D6FC}$ be any complex root of $\prod _{0\leqslant i\leqslant \text{dim}(X)}P_{2i}(t)\in \mathbb{C}[t]$ (via $\unicode[STIX]{x1D70F}$ in (3.2)). Since the $i$ th compactly supported $\ell$ -adic cohomology is of weight less than or equal to $i$  [Del80, Théorème 1 (3.3.1)], one has

(3.5) $$\begin{eqnarray}\frac{1}{|\unicode[STIX]{x1D6FC}|}\leqslant \unicode[STIX]{x1D706}_{\text{even}}^{r}q^{\text{dim}(X)}.\end{eqnarray}$$

In particular, $Q(t)$ has no roots on the closed disc of radius $1/(q^{\text{dim}(X)}\unicode[STIX]{x1D706}_{\text{even}}^{r})$ .

Since $\unicode[STIX]{x1D706}_{\text{odd}}^{r}$ is the spectral radius (with respect to $\unicode[STIX]{x1D70F}$ ) for $f^{r\ast }$ acting on the oddly graded cohomology, there exist an odd index $2i+1$ and a complex root $\unicode[STIX]{x1D6FD}$ of $P_{2i+1}(t)$ such that

(3.6) $$\begin{eqnarray}|\unicode[STIX]{x1D6FD}|=\frac{1}{\unicode[STIX]{x1D706}_{\text{odd}}^{r}q^{m(\unicode[STIX]{x1D6FD})}}\leqslant \frac{1}{\unicode[STIX]{x1D706}_{\text{odd}}^{r}},\end{eqnarray}$$

where $2m(\unicode[STIX]{x1D6FD})$ is a non-negative integer (corresponding to the weight of the Frobenius). In particular, $\unicode[STIX]{x1D6FD}$ is not a root of $\prod _{0\leqslant i\leqslant \text{dim}(X)}P_{2i}(t)\in \mathbb{C}[t]$ . Hence $\unicode[STIX]{x1D6FD}$ is a root of $R(t)$ . Thus $R(t)$ has a root in the closed disc of radius $1/\unicode[STIX]{x1D706}_{\text{odd}}^{r}$ .

It follows from Proposition 2.10 that the zeta function $Z(X_{0},f_{0}^{k},t)$ is of the form $\exp (G(t))$ , where $G(t)\in t\mathbb{Q}[[t]]$ has non-negative coefficients. Thus Lemma 3.2 implies that

$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D706}_{\text{odd}}^{r}}\geqslant \frac{1}{q^{\text{dim}(X)}\unicode[STIX]{x1D706}_{\text{even}}^{r}},\end{eqnarray}$$

and hence

$$\begin{eqnarray}\unicode[STIX]{x1D706}_{\text{even}}^{r}q^{\text{dim}(X)}\geqslant \unicode[STIX]{x1D706}_{\text{odd}}^{r}.\end{eqnarray}$$

Since $r$ was an arbitrary positive integer, this implies

$$\begin{eqnarray}\unicode[STIX]{x1D706}_{\text{even}}\geqslant \unicode[STIX]{x1D706}_{\text{odd}}.\end{eqnarray}$$

Now suppose $\unicode[STIX]{x1D706}_{\text{even}}=\unicode[STIX]{x1D706}_{\text{odd}}$ . We shall prove that $k_{\text{even}}\geqslant k_{\text{odd}}$ .

Let $\unicode[STIX]{x1D707}_{i}$ be the spectral radius (with respect to $\unicode[STIX]{x1D70F}$ in (3.2)) for the action of $f^{\ast }$ on $H^{2i}(X,\mathbb{Q}_{\ell })$ for each $0\leqslant i\leqslant \text{dim}(X)$ . Then there exists an integer $r\gg 0$ such that for any integer $i\in [0,\text{dim}(X)]$ with $\unicode[STIX]{x1D707}_{i}\neq \unicode[STIX]{x1D706}_{\text{even}}$ , we have

(3.7) $$\begin{eqnarray}\unicode[STIX]{x1D707}_{i}^{r}q^{\text{dim}(X)}<\unicode[STIX]{x1D706}_{\text{even}}^{r}\leqslant \unicode[STIX]{x1D706}_{\text{even}}^{r}q^{k_{\text{even}}/2}.\end{eqnarray}$$

As before, Lemma 2.14 and Corollary 2.15 imply that the zeta function $Z(X_{0},f_{0}^{r},t)$ has a non-trivial radius of convergence about the origin and has a meromorphic continuation of the form $R(t)/Q(t)$ onto the entire complex plane, with $R(t)$ and $Q(t)$ being co-prime rational polynomials. Also the zeros of $R(t)$ and $Q(t)$ are a subset of the inverse eigenvalues of $(F_{X,q}\circ f^{r})^{\ast }$ acting on the odd and even degree cohomology respectively.

Since the $i$ th compactly supported $\ell$ -adic cohomology is of weight less than or equal to $i$  [Del80, Théorème 1 (3.3.1)]), the weight filtration on $H^{i}(X,\mathbb{Q}_{\ell })$ satisfies $W_{k}H^{i}(X,\mathbb{Q}_{\ell })=H^{i}(X,\mathbb{Q}_{\ell })$ for $k\geqslant i$ .

Let

$$\begin{eqnarray}P_{i,k}(t):=\text{det}(1-t(F_{X,q}\circ f^{r})^{\ast },\text{Gr}_{W}^{k}H^{i}(X,\mathbb{Q}_{\ell })),\quad 0\leqslant k\leqslant i,~0\leqslant i\leqslant 2\,\text{dim}(X).\end{eqnarray}$$

As before,

$$\begin{eqnarray}P_{i}(t):=\text{det}(1-t(F_{X,q}\circ f^{r})^{\ast },H^{i}(X,\mathbb{Q}_{\ell })),\quad 0\leqslant i\leqslant 2\,\text{dim}(X).\end{eqnarray}$$

Since the weight filtration is respected by the action of $F_{X,q}^{\ast }\circ f^{r\ast }$ (see [Del80, § 5.3.6]), one has an equality

$$\begin{eqnarray}\mathop{\prod }_{i=0}^{\text{dim}(X)}\mathop{\prod }_{k=0}^{2i}P_{2i,k}(t)=\mathop{\prod }_{0\leqslant i\leqslant \text{dim}(X)}P_{2i}(t)\in \mathbb{C}[t]\quad (\text{via}\;\unicode[STIX]{x1D70F}\;\text{in (3.2)}).\end{eqnarray}$$

Let $\unicode[STIX]{x1D6FC}$ be any complex zero of $\prod _{0\leqslant i\leqslant \text{dim}(X)}P_{2i}(t)\in \mathbb{C}[t]$ . Then $\unicode[STIX]{x1D6FC}$ is a zero of $P_{2i,k}(t)$ for some integer $i\in [0,\text{dim}(X)]$ and $0\leqslant k\leqslant 2i$ . If $\unicode[STIX]{x1D707}_{i}\neq \unicode[STIX]{x1D706}_{\text{even}}$ , then (3.7) implies

(3.8) $$\begin{eqnarray}\frac{1}{|\unicode[STIX]{x1D6FC}|}\leqslant \unicode[STIX]{x1D707}_{i}^{r}q^{k/2}\leqslant \unicode[STIX]{x1D707}_{i}^{r}q^{\text{dim}(X)}.\end{eqnarray}$$

On the other hand, the definition of $k_{\text{even}}$ implies that if $\unicode[STIX]{x1D707}_{i}=\unicode[STIX]{x1D706}_{\text{even}}$ , then $k\leqslant k_{\text{even}}$ . Thus (3.7) implies that for any complex root $\unicode[STIX]{x1D6FC}$ of $\prod _{0\leqslant i\leqslant \text{dim}(X)}P_{2i}(t)$ ,

(3.9) $$\begin{eqnarray}\frac{1}{|\unicode[STIX]{x1D6FC}|}\leqslant \unicode[STIX]{x1D706}_{\text{even}}^{r}q^{k/2}\leqslant \unicode[STIX]{x1D706}_{\text{even}}^{r}q^{k_{\text{even}}/2}.\end{eqnarray}$$

In particular, the same holds true for any complex root of $Q(t)$ .

Moreover, from the definition of $k_{\text{odd}}$ it follows that there exist an odd index $2i+1$ and a complex root $\unicode[STIX]{x1D6FD}$ of $P_{2i+1,k_{\text{odd}}}(t)$ such that $1/|\unicode[STIX]{x1D6FD}|=\unicode[STIX]{x1D706}_{\text{odd}}^{r}q^{k_{\text{odd}}/2}=\unicode[STIX]{x1D706}_{\text{even}}^{r}q^{k_{\text{odd}}/2}$ . If $k_{\text{odd}}\neq k_{\text{even}}$ ,  $\unicode[STIX]{x1D6FD}$ is not a root of $\prod _{0\leqslant i\leqslant \text{dim}(X)}P_{2i}(t)$ , and thus is necessarily a root of $R(t)$ . Thus $R(t)$ has a root on the closed disc of radius $1/(\unicode[STIX]{x1D706}_{\text{odd}}^{r}q^{k_{\text{odd}}/2})$ . Arguing as before using Proposition 2.10 and Lemma 3.2, we conclude that

$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D706}_{\text{odd}}^{r}q^{k_{\text{odd}}/2}}\geqslant \frac{1}{\unicode[STIX]{x1D706}_{\text{even}}^{r}q^{k_{\text{even}}/2}}.\end{eqnarray}$$

Hence $k_{\text{even}}\geqslant k_{\text{odd}}$ .◻

Corollary 3.4. Let $f:X\rightarrow X$ be a self map of a proper scheme over an arbitrary field $k$ . Let $\ell$ be a prime invertible in $k$ and $\bar{k}$ an algebraic closure of $k$ . Fix an embedding $\unicode[STIX]{x1D70F}:\mathbb{Q}_{\ell }{\hookrightarrow}\mathbb{C}$ . Then the spectral radius (with respect to $\unicode[STIX]{x1D70F}$ ) for the action of $f_{\bar{k}}^{\ast }$ on the entire $\ell$ -adic cohomology $H^{\ast }(X_{\bar{k}},\mathbb{Q}_{\ell })$ is equal to the spectral radius for its action on $\bigoplus _{i\geqslant 0}H^{2i}(X_{\bar{k}},\mathbb{Q}_{\ell })$ .

The following simple example shows that inequality $(1)$ in Theorem 3.3 need not be strict.

Example 3.5. Let $k=\mathbb{C}$ and $X=E\times E\times E$ where $E$ is any elliptic curve over $\mathbb{C}$ .

Let $f$ be the automorphism of $X$ given by $f(x,y,z)=(2x+3y,x+2y,z)$ . We have $f=g\times 1_{E}$ , where $g:E\rightarrow E$ is the automorphism $(x,y)\mapsto (2x+3y,x+2y)$ , and $1_{E}$ is the identity map on $E$ . Let $\unicode[STIX]{x1D706}_{\text{even}},\unicode[STIX]{x1D706}_{\text{odd}},k_{\text{even}},k_{\text{odd}}$ be as defined in the previous section for the action of $f^{\ast }$ on $H^{\ast }(X(\mathbb{C}),\mathbb{Q})$ . One can easily show that $\unicode[STIX]{x1D706}_{\text{even}}=\unicode[STIX]{x1D706}_{\text{odd}}=(2+\sqrt{3})^{2}$ , while $k_{\text{even}}=4$ and $k_{\text{odd}}=3$ .

The following example shows that Theorem 3.3 is false without the properness hypothesis, even for smooth varieties.

Example 3.6. Let $T/k$ be a rank- $2$ torus (split over $\mathbb{F}_{q}$ ) and $f:T\rightarrow T$ any group automorphism of $T$ . Then $\text{ker}(f\circ F_{T,q}^{n}-1_{T})$ is a finite étale group scheme. Since it is a subgroup scheme of a torus, its order (or rank) is co-prime to $p$ , the characteristic of $\mathbb{F}_{q}$ . For any integer $n\in \mathbb{N}$ , let $\text{Fix}(f\circ F_{T,q}^{n})$ be the number of fixed points of $f\circ F_{T,q}^{n}$ acting on $T$ . Then

$$\begin{eqnarray}\text{Fix}(f\circ F_{T,q}^{n})=|P_{f}(q^{n})|,\end{eqnarray}$$

where $P_{f}(t):=\text{det}(1-tM_{f};X^{\ast }(T))$ , in which $M_{f}$ is the linear map on the co-character lattice $X^{\ast }(T)$ induced by $f$ .

Let $\ell$ be a prime different from $p$ . The only non-trivial compactly supported $\ell$ -adic cohomology groups of $T$ are $H_{c}^{2}(T,\mathbb{Q}_{\ell })\simeq \mathbb{Q}_{\ell }$ ,  $H_{c}^{3}(T,\mathbb{Q}_{\ell })\simeq X^{\ast }(T)\otimes _{\mathbb{Q}_{\ell }}\mathbb{Q}_{\ell }(-1)$ and $H_{c}^{4}(T,\mathbb{Q}_{\ell })\simeq \bigwedge ^{2}X^{\ast }(T)\otimes _{\mathbb{Q}_{\ell }}\mathbb{Q}_{\ell }(-2)$ . Thus for all integers $n\geqslant 1$ ,

$$\begin{eqnarray}\text{Tr}((f\circ F_{T,q}^{n})^{\ast },H_{c}^{\ast }(T,\mathbb{Q}_{\ell }))=P_{f}(q^{n}).\end{eqnarray}$$

Let $f$ be chosen such that $|\text{Tr}(M_{f})|>2$ and $\text{det}(M_{f})=1$ . Note that the eigenvalues of $f^{\ast }$ acting on the compactly supported $\ell$ -adic cohomology are algebraic integers independent of  $\ell$ . Since $\text{Tr}((f\circ F_{T,q}^{n})^{\ast },H_{c}^{\ast }(T,\mathbb{Q}_{\ell }))=P_{f}(q^{n})$ , it follows that, for any embedding $\unicode[STIX]{x1D70F}:\mathbb{Q}_{\ell }{\hookrightarrow}\mathbb{C}$ :

1. (1) $f^{\ast }$ acting on $H_{c}^{3}(T,\mathbb{Q}_{\ell })$ has at least one eigenvalue of modulus greater than $1$ ;

2. (2) $f^{\ast }$ acts as identity on $H_{c}^{2}(T,\mathbb{Q}_{\ell })$ and $H_{c}^{4}(T,\mathbb{Q}_{\ell })$ .

Hence $\unicode[STIX]{x1D706}_{\text{odd}}>\unicode[STIX]{x1D706}_{\text{even}}$ .

A careful look at the proof of Theorem 3.3 shows that the failure of Theorem 3.3 without the properness hypothesis (as in Example 3.6), can be attributed to $n_{0}(f^{r})$ (see Definition 2.11) being strictly greater than $1$ . This motivates us to consider the growth of an upper bound for $n_{0}(f^{r})$ with respect to $r$ for non-proper varieties. In a future work it will be shown that there exists an upper bound which grows at most linearly with $r$ .