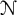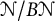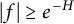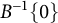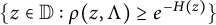Invertibility Threshold for Nevanlinna Quotient Algebras

Abstract

Let $\mathcal {N}$ be the Nevanlinna class, and let B be a Blaschke product. It is shown that the natural invertibility criterion in the quotient algebra $\mathcal {N} / B \mathcal {N}$ , that is, $|f| \ge e^{-H} $ on the set $B^{-1}\{0\}$ for some positive harmonic function H, holds if and only if the function $- \log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ , at least for large enough functions H. We also study the corresponding class of positive harmonic functions H on the unit disc such that the latter condition holds. We also discuss the analogous invertibility problem in quotients of the Smirnov class.

1 Introduction

The Nevanlinna class $\mathcal {N}$ is the algebra of analytic functions f in $\mathbb {D}$ , the unit disc of the complex plane, such that $\log |f|$ has a positive harmonic majorant in $\mathbb {D}$ . Any $f\in \mathcal {N}$ factors as $f=B F$ , where B is a Blaschke product and $F\in \mathcal {N}$ is invertible, as are all zero-free functions in the Nevanlinna class. Any principal ideal in $\mathcal {N}$ is thus of the form $B\mathcal {N}$ , and if the zero set of B is $\Lambda =(\lambda _k)_k$ , this ideal is the set of functions in $\mathcal {N}$ which vanish at $\Lambda $ . If there are m distinct indices k such that $\lambda _k=a$ , B is understood to vanish at a with order m. Fix a Blaschke product B and $f\in \mathcal {N}$ . It is clear that the class $[f]=\{f+Bh:h\in \mathcal {N}\}$ is uniquely determined by the restriction of f to $\Lambda $ . If $[f]$ is invertible in the quotient algebra $\mathcal {N} \big / B\mathcal {N}$ , then there exists a positive harmonic function H such that $|f(\lambda _k)|\geq e^{-H(\lambda _k)}$ , $k=1,2,\dots $ . However, the converse is not true in general. For a given Blaschke product B, we would like to find out which positive harmonic functions H will make the converse true.

The analogous problem for the algebra $H^\infty $ of bounded analytic functions f on the unit disc, with the obvious necessary condition for invertibility $|f(\lambda _k)|\geq \varepsilon>0$ , was studied in [6] in connection with the Corona Theorem and interpolating sequences. We first need to give some background on the classical $H^\infty $ theory. Recall that $H^\infty $ is endowed with the norm $||f||_\infty :=\sup \{|f(z)|:z\in \mathbb {D} \}$ .

We will use the standard pseudohyperbolic distance on $\mathbb {D}$ given by

$$ \begin{align*} \rho(a_1 , a_2 ) := |a_1 - a_2| |1 - \overline{a_2} a_1|^{-1} , \end{align*} $$

for $a_1, a_2 \in \mathbb {D}$ .

We now recall two classical results of Carleson. A sequence of (necessarily) distinct points $\Lambda =(\lambda _k)_k$ in $\mathbb {D}$ is called an $ {H}^\infty $ -interpolating sequence if for any bounded sequence of complex values $\{w_k\}$ there exists $f\in H^\infty $ such that $f(\lambda _k)=w_k$ , $k=1,2,\ldots $ . A celebrated result of Carleson states that $\Lambda =(\lambda _k)_k$ is $\textbf {H}^\infty $ -interpolating if and only if there exists a constant $\delta>0$ such that

$$ \begin{align*} (1-|{\lambda}_k|^2) |B'(\lambda_k)| \geq \delta ,\quad k =1,2, \ldots , \end{align*} $$

where B is the Blaschke product with zeros $(\lambda _k)_k$ . Observe that

$$ \begin{align*}(1-|\lambda_k|^2)|B'(\lambda_k)| = \prod_{j:j\neq k} \rho(\lambda_k,\lambda_j) .\end{align*} $$

The classical Corona Theorem states that the ideal generated by the functions $f_1,\ldots ,f_n\in H^\infty $ is the whole algebra $H^\infty $ if and only if $\inf \{|f_1(z)|+\cdots +|f_n(z)|:z\in \mathbb {D} \}>0$ . See [3, 4] or Chapters VII and VIII of [5].

A function $I\in H^\infty $ is called inner if $\left |\lim _{r\to 1} I(r\xi )\right |=1$ for almost every $\xi $ in the unit circle $\partial \mathbb {D}$ . Any inner function I factors as $I=B S$ , where B is a Blaschke product and S is an inner function without zeros. It follows from the classical Theorem of Beurling on the invariant subspaces of the shift operator, that any weak* closed ideal in $H^\infty $ is of the form $I H^\infty = \{Ih : h \in H^\infty \}$ for some inner function I. See [5, p. 82]. Fix an inner function I, and consider the quotient Banach algebra $H^\infty \big / IH^\infty $ with the norm

$$ \begin{align*} ||[f]||_{H^\infty \big/ IH^\infty}=\inf\{||f+Ih||_\infty:h\in H^\infty\},\hspace{0.5cm}f\in H^\infty. \end{align*} $$

Let $\Lambda =(\lambda _k)_k$ be the zero set of I. It is clear that if $[f]$ is invertible in $H^\infty \big / IH^\infty $ , then $\inf |f(\lambda _k)|>0$ . This condition is not always sufficient, as one can observe considering the extreme situation where I is zero-free.

Let I be an inner function with zeros $\Lambda = (\lambda _k )_k$ . Let $\delta =\delta (I)$ be the infimum of the positive numbers $\gamma>0$ such that if $f\in H^\infty $ , $||f||_\infty \leq 1$ satisfies $\inf _k|f(\lambda _k)|\geq \gamma $ , then $[f]$ is invertible in $H^\infty \big / IH^\infty $ , or equivalently, there exist $g,h\in H^\infty $ such that $fg=1+Ih$ . If I is a nontrivial inner function without zeros in $\mathbb {D}$ , we set $\delta (I)=1$ . Hence, if $\gamma>\delta (I)$ , for any $f\in H^\infty $ , $||f||_\infty \leq 1$ with $\inf _k|f(\lambda _k)|\geq \gamma $ , we have that $[f]$ is invertible in $H^\infty \big / IH^\infty $ ; while if $0<\gamma <\delta (I)$ , there exists $f\in H^\infty $ , $||f||_\infty \leq 1$ with $\inf _k|f(\lambda _k)|\geq \gamma $ such that $[f]$ is not invertible in $H^\infty \big / IH^\infty $ .

Gorkin, Mortini, and Nikolski proved in [6] that $\delta (I)=0$ if and only if I satisfies, for any $\varepsilon>0$ , the condition

(1.1) $$ \begin{align} \inf\{|I(z)|:\rho(z, \Lambda )>\varepsilon\} >0. \end{align} $$

If I is a Blaschke product whose zeros $\Lambda $ are a finite union of $\textbf {H}^\infty $ -interpolating sequences (or, equivalently, if $\sum _k(1-|\lambda _k|)\delta (\lambda _k)$ is a Carleson measure), then condition (1.1) is satisfied. Here, $\delta (\lambda _k)$ denotes the Dirac mass at the point $\lambda _k$ . However, there are Blaschke products I satisfying (1.1) whose zeros are not a finite union of $\textbf {H}^\infty $ -interpolating sequences. See [1, 6]. For this reason, the authors of [6] called property (1.1) the weak embedding property (WEP). It would be interesting to describe the Blaschke products I satisfying the WEP in terms of the location of their zeros. Some further results and questions on inner functions satisfying the WEP can be found in [2].

The study of the invertibility in $H^\infty \big / IH^\infty $ was continued by Nikolskii and Vasyunin in [11], where it was proved that for any $0<\delta <1$ , there exists a Blaschke product I such that $\delta (I)=\delta $ . In other words, one can find an invertibility threshold at any level, by choosing the Blaschke product appropriately. The main purpose of this paper is to discuss the analogous problem in the Nevanlinna class.

We now turn to the analogues in the Nevanlinna class of the above results. In many of those, positive harmonic functions will play the role that was played by positive constants in the $H^\infty $ setting. We begin with interpolating sequences.

Let Har $_+(\mathbb {D})$ denote the cone of positive harmonic functions on $\mathbb {D}$ . Given a sequence of distinct points $\Lambda =(\lambda _k)_k\subset \mathbb {D}$ , let $W(\Lambda )$ be the set of sequences of complex numbers $\{w_k\}$ such that there exists $H\in $ Har $_+(\mathbb {D})$ with $\log ^+|w_k|\leq H(\lambda _k)$ , $k=1,2,\ldots $ . Observe that $\{f(\lambda _k)\}\subset W(\Lambda )$ for any $f\in \mathcal {N}$ . A sequence of points $\Lambda =(\lambda _k)_k\subset \mathbb {D}$ is called an interpolating sequence for $\mathcal {N}$ if for any sequence of values $\{w_k\}\subset W(\Lambda )$ there exists $f\in \mathcal {N}$ such that $f(\lambda _k)=w_k, k=1,2,\dots $ . It was proved in [7] that $\Lambda =(\lambda _k)_k$ is an interpolating sequence for $\mathcal {N}$ if and only if there exists $H\in $ Har $_+$ ( $\mathbb {D}$ ) such that

(1.2) $$ \begin{align} (1-|\lambda_k|^2)|B'(\lambda_k)|\geq e^{-H(\lambda_k)},\hspace{0.5cm} k=1,2,\ldots, \end{align} $$

where B is the Blaschke product with zeros $(\lambda _k)_k$ .

Using a result of Wolff, Mortini proved the following version of the Corona Theorem for $\mathcal {N}$ . Let $f_1,\ldots ,f_n\in \mathcal {N}$ . Then there exist $g_1,\ldots ,g_n\in \mathcal {N}$ such that $f_1g_1+\cdots +f_ng_n=1$ if and only if the function $-\log (|f_1|+\cdots +|f_n|)$ has a harmonic majorant in $\mathbb {D}$ . See [10] or [8].

The analogue of the WEP in the Nevanlinna class was introduced in [9] where it was proved that invertible classes $[f]$ in $\mathcal {N} \big / B\mathcal {N}$ are precisely the classes for which there exists $H=H(f)\in $ Har $_+(\mathbb {D})$ such that $|f(\lambda _k)|\geq e^{-H(\lambda _k)}$ , $k=1,2,\ldots $ , if and only if B satisfies the following analogue of the WEP: for any $H_1\in $ Har $_+(\mathbb {D})$ , there exists $H_2\in $ Har $_+(\mathbb {D})$ such that

$$ \begin{align*} |B(z)|\geq e^{-H_2(z)}\hspace{0.5cm}\text{ if }\hspace{0.5cm}\rho(z, \Lambda )\geq e^{-H_1(z)}. \end{align*} $$

In contrast with the situation in $H^\infty $ , the main result in [9] states that this property holds if and only if the zeros of B are a finite union (or, more properly, superposition) of interpolating sequences in the Nevanlinna class.

As we said, the main purpose of the present paper is to discuss an analogue in the Nevanlinna class of the result of Nikolski and Vasyunin [11] described above. Let B be the Blaschke product with zero set $\Lambda =\{\lambda _k\}$ . Consider the Nevanlinna quotient algebra $\mathcal {N} \big / B\mathcal {N}$ . Fix $f\in \mathcal {N}$ . As mentioned above, a necessary condition for the class $[f]$ to be invertible in $\mathcal {N} \big / B\mathcal {N}$ is that there exists $H\in $ Har $_+(\mathbb {D})$ such that

(1.3) $$ \begin{align} |f(\lambda_k)|\geq e^{-H(\lambda_k)}, \hspace{0.5cm} k=1,2,\ldots. \end{align} $$

In analogy with the definition of $\delta (B)$ in the context of $H^\infty $ , we are interested in which functions $H\in $ Har $_+(\mathbb {D})$ have the property that (1.3) guarantees that the class $[f]$ is invertible in $\mathcal {N} \big / B\mathcal {N}$ .

Because functions without zeros are invertible in $\mathcal {N}$ , to study the invertibility of $[f]$ in $\mathcal {N} \big / B\mathcal {N}$ , we can assume that f is a Blaschke product. Multiplying f by a constant, we may also assume that H is bigger than any prescribed positive constant. So we normalize our study of the “threshold” inside the cone of harmonic functions by assuming $f\in H^\infty $ , $||f||_\infty \leq 1$ , and $H \ge c_0>0$ .

Our first result says that the invertibility problem is roughly equivalent to the existence of a harmonic majorant of $-\log |B|$ restricted to a certain subset of $\mathbb {D}$ .

Definition 1.1 A function $F\colon \mathbb {D}\longrightarrow [0,+\infty )$ has a harmonic majorant on the set $E\subset \mathbb {D}$ if there exists $H\in $ Har $_+(\mathbb {D})$ such that $F(z)\leq H(z)$ for any $z\in E$ .

We will need an auxiliary function associated to any Blaschke sequence.

Definition 1.2 Given a Blaschke sequence $\Lambda =(\lambda _k)_k$ , let $H_\Lambda $ denote the positive harmonic function defined by

(1.4) $$ \begin{align} H_\Lambda(z)=\sum_k\int_{I_k}\frac{1-|z|^2}{|\xi-z|^2}|\mathrm{d}\,\xi|,\hspace{0.5cm}z\in\mathbb{D}, \end{align} $$

where $I_k:=\{\xi \in \partial \mathbb {D}:|\xi -\lambda _k / |\lambda _k||\leq 1-|\lambda _k|\}$ denotes the Privalov shadow of $\lambda _k$ .

Theorem 1.1 Let B be a Blaschke product with zero set $\Lambda =(\lambda _k)_k$ .

1. (1) For any $C\in (0,1)$ , the following statement holds. Let $H\in $ Har $_+(\mathbb {D})$ , and assume that the function $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ . Then, for any $f\in H^\infty $ , $||f||_\infty \leq 1$ such that

   (1.5) $$ \begin{align} |f(\lambda_k)|> e^{-CH(\lambda_k)}, \quad k=1,2, \ldots , \end{align} $$
   there exist $g,h\in \mathcal {N}$ such that $fg=1+Bh$ .

2. (2) For any $C>1$ , there exists a constant $C_0>0$ such that the following statement holds. Let $H\in $ Har $_+(\mathbb {D})$ with $H\geq C_0 H_\Lambda $ . Assume that for any $f\in H^\infty $ , $||f||_\infty \leq 1$ such that

   $$ \begin{align*} |f(\lambda_k)|> e^{-CH(\lambda_k)}, \quad k=1,2, \ldots , \end{align*} $$
   there exist $g,h\in \mathcal {N}$ such that $fg=1+Bh$ . Then, the function $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}\, : \rho (z,\Lambda )\geq e^{-H(z)}\}$ .

In Corollary 2.4, after the proof of this theorem in Section 2, we show how the result can be extended to Bézout equations with any number of generators.

Observe that Theorem 1.1 is analogous to the equivalence of (a) and (b) in [9, Theorem A]. Hence, given a Blaschke product B with zero set $\Lambda $ , and for large enough positive harmonic functions H, the invertibility problem in the quotient algebra $\mathcal {N } / B \mathcal {N}$ can be reduced to the study of the following class.

Definition 1.3 Given a Blaschke product B, let $\mathcal {H}(B)$ be the set of functions $H\in $ Har $_+(\mathbb {D})$ such that $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}\,:\rho (z,\Lambda )\geq e^{-H(z)}\}$ .

It is easy to see that constant functions are always in $\mathcal {H}(B)$ (see Proposition 4.1 of [7] or Lemma 2.1 below), and that if $H_1\in \mathcal {H}(B)$ and $H_2 \in \mbox {Har}_+(\mathbb {D})$ , $H_2 \le H_1$ , then $H_2\in \mathcal {H}(B)$ . In this language, the main result of [9] reads as follows: $\mathcal {H}(B)=$ Har $_+(\mathbb {D})$ if and only if $\Lambda $ is a finite union of interpolating sequences for $\mathcal {N}$ .

Our next result says that for any Blaschke product B, $\mathcal {H}(B)$ does contain unbounded functions.

Theorem 1.2 Let B be a Blaschke product with zero set $\Lambda =(\lambda _k)_k$ . Then,

1. (1) there exists a function $H\in $ Har $_+(\mathbb {D})$ with $\limsup _{k\to \infty } H(\lambda _k)=+\infty $ , such that $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}\,:\rho (z,\Lambda )\geq e^{-H(z)}\}$ .

2. (2) there exists a function $H\in $ Har $_+(\mathbb {D})$ with $\limsup _{k\to \infty } H(\lambda _k)=+\infty $ such that if $f\in H^\infty $ , $||f||_\infty \leq 1$ satisfies $|f(\lambda _k)|\geq e^{-H(\lambda _k)}$ , $k=1,2,\ldots $ , then there exist $g,h\in \mathcal {N}$ such that $fg=1+Bh$ .

Conversely, given two positive harmonic functions $H_1, H_2$ , where the condition $H_1 \le H_2$ does not hold, we would like to see whether there exists a Blaschke product that discriminates between them, that is to say, such that $H_2\in \mathcal {H}(B)$ but $H_1\notin \mathcal {H}(B)$ . We obtain such a Blaschke product in two different cases.

Theorem 1.3

1. (1) Let $H_1,H_2\in $ Har $_+(\mathbb {D})$ such that

   $$ \begin{align*} \limsup_{|z|\to1}\;\frac{H_1(z)}{H_2(z)}=+\infty. \end{align*} $$
   Then, there exists a Blaschke product B with zero set $\Lambda $ such that $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H_2(z)}\}$ but has no harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H_1(z)}\}$ .

2. (2) For any $\eta _0>0$ , and any unbounded positive harmonic function H, there exists a Blaschke product B such that $H \in \mathcal H(B)$ but $(1+\eta _0)H \notin \mathcal H(B)$ .

The first part of the theorem can be applied, in particular, when $H_2=1$ , which means that for any unbounded $H_1 \in \mbox {Har}_+(\mathbb {D})$ , there exists a Blaschke product B, so that $H_1 \notin \mathcal H(B)$ . It should be noted that in the second part of the theorem, the Blaschke product B has zeros concentrated in a way controlled by the size of the harmonic function H we started from. The next result involves this critical size. In order to state it, we need more notation.

Consider the usual dyadic Whitney squares

$$ \begin{align*} Q_{k,j}=\{re^{i\theta}\in\mathbb{D}\,:2^{-k}\leq1-r<2^{-k+1}, j 2\pi 2^{-k}\leq\theta<(j+1)2\pi 2^{-k}\}, \end{align*} $$

where $k\geq 0$ and $j=0,\ldots ,2^k-1$ . Consider also the corresponding projections on $\partial \mathbb {D}$ given by

$$ \begin{align*} I_{k,j}=\{e^{i\theta}\in\partial\mathbb{D} : j 2\pi 2^{-k}\leq\theta<(j+1)2\pi 2^{-k}\}. \end{align*} $$

Given a Blaschke sequence $\Lambda =(\lambda _k)_k$ and a dyadic Whitney square Q, let $N(Q)=\#(\Lambda \cap Q)$ be the number of indices k such that $\lambda _k \in Q$ . Observe that there exists a universal constant $C>0$ such that for any dyadic Whitney square Q and any $z \in Q$ , we have $H_ \Lambda (z) \geq C N(Q)$ .

In connection to part 2 of Theorem 1.3, it is interesting to observe that for functions $H\in $ Har $_+(\mathbb {D})$ growing sufficiently fast with respect to the number of zeros of B, we have $H\in \mathcal {H}(B)$ if and only if $CH\in \mathcal {H}(B)$ for some (all) constants $C>0$ .

Theorem 1.4 Let B be a Blaschke product with zero set $\Lambda $ . Let $H\in $ Har $_+(\mathbb {D})$ such that

(1.6) $$ \begin{align} \inf\{e^{H(z)}:z\in Q\}\geq N(Q), \end{align} $$

for any dyadic Whitney square Q. Assume that the function $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ . Then, for any $C>1$ , the function $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-CH(z)}\}$ .

Part (2) of Theorem 1.3 shows that the above result no longer holds when condition (1.6) is not satisfied.

Our last result provides a sufficient condition for a function $H\in $ Har $_+(\mathbb {D})$ to belong to $\mathcal {H}(B)$ . Given a dyadic Whitney square Q, let $z(Q)$ denote its center.

Theorem 1.5 Let B be a Blaschke product with zero set $\Lambda $ . Let $\mathcal {A}$ be the collection of dyadic Whitney squares Q such that $N(Q)=\#(\Lambda \cap Q)>0$ . Let $H\in $ Har $_+(\mathbb {D})$ . Assume that there exists $H_1\in $ Har $_+(\mathbb {D})$ such that $N(Q)H(z(Q))\leq H_1(z(Q))$ for any $Q\in \mathcal {A}$ . Then, the function $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ .

Notice that we impose no direct restriction on the values of H in the dyadic squares where no zero of B is present. Moreover, we will introduce a class of Blaschke products for which this sufficient condition is also necessary. This is done at the end of Section 2. In Section 4, we study the corresponding invertibility problem in quotients of the Smirnov class.

In this paper, $C_0, C_1, C_2, \ldots $ will denote absolute constants, whereas $C(\delta )$ will denote a constant which depends on the parameter $\delta>0$ .

2 Proofs of Theorems 1.1 and 1.2

Recall that if $\Lambda $ is a Blaschke sequence, $H_\Lambda $ denotes the positive harmonic function defined in (1.4). The proof of Theorem 1.1 uses two auxiliary results. The first one is Proposition 4.1 of [7].

Lemma 2.1 Let B be a Blaschke product with zero set $\Lambda $ . Then, for any $\delta>0$ , there exists $C_\delta>0$ such that $-\log |B(z)|\leq C_\delta H_\Lambda (z)$ if $\rho (z,\Lambda )\geq \delta $ .

Lemma 2.2 Let $\Lambda $ be a Blaschke sequence, and let A be a sequence of points in $\mathbb {D}$ satisfying that there exist a constant $0<\gamma <1$ and a natural number k such that for any $a\in A$ , there is $\lambda (a)\in \Lambda $ with $\rho (a,\lambda (a))\leq \gamma $ and $\#\{a\in A:\lambda (a)=\lambda \}\leq k$ for any $\lambda \in \Lambda $ . Then, A is a Blaschke sequence, and for any $\delta>0$ , there is a constant $C=C(\gamma ,\delta ,k)>0$ such that

$$ \begin{align*} \sum_{a\in A:\rho(a,z)>\delta} \log\left|\frac{a-z}{1-\overline{a}z}\right|{}^{-1}\leq CH_\Lambda(z),\hspace{0.5cm}z\in\mathbb{D}. \end{align*} $$

Proof Because $\rho (a,z)>\delta $ , there is a constant $C_1=C_1(\delta )>0$ such that

$$ \begin{align*} \log\left|\frac{a-z}{1-\overline{a}z}\right|{}^{-1}\leq C_1 \hspace{1pt}\left(1-\left|\frac{a-z}{1-\overline{a}z}\right|{}^{2}\right)=C_1 \hspace{1pt}\frac{(1-|a|^2)(1-|z|^2)}{|1-\overline{a}z|^2}. \end{align*} $$

Observe that because $\rho (a, \lambda (a))\leq \gamma $ , there is a constant $C_2=C_2(\gamma )>0$ such that

$$ \begin{align*} \int_{I(\lambda(a))}\frac{1-|z|^2}{|\xi-z|^2}\,|\mathrm{d}\xi|\geq C_2\hspace{1pt}\frac{(1-|a|^2)(1-|z|^2)}{|1-\overline{a}z|^2}. \end{align*} $$

Recall that $I(\lambda (a)) = \{ \xi \in \partial \mathbb {D} : |\xi - \lambda (a) / |\lambda (a)| | \leq 1- |\lambda (a)| \}$ is the Privalov shadow of $\lambda (a)$ . We add up these inequalities, and, because any $\lambda \in \Lambda $ will be repeated at most k times, we get the result.▪

A sequence $A= (a_k )_k$ of (necessarily distinct) points in $\mathbb {D}$ is called separated if $\eta (A) = \inf \{ \rho (a_k , a_j ) : j,k \in \mathbb {N}, j \neq k \}>0$ . The number $\eta (A)$ is called the separation constant of A.

Corollary 2.3 Let $\Lambda $ be a Blaschke sequence, and let A be a separated sequence of points in $\mathbb {D}$ with separation constant $\eta = \eta (A) $ . Assume that there exists $0<\gamma <1$ such that for any $a\in A$ , there is $\lambda (a)\in \Lambda $ with $\rho (a,\lambda (a))\leq \gamma $ . Then, A is a Blaschke sequence, and for any $0<\delta <1$ , there is a constant $C=C(\eta ,\gamma ,\delta )>0$ such that

$$ \begin{align*} \sum_{a\in A:\rho(a,z)>\delta}\log\left|\frac{a-z}{1-\overline{a}z}\right|{}^{-1} \leq CH_\Lambda(z),\hspace{0.5cm}z\in\mathbb{D}. \end{align*} $$

Proof Because A is a separated sequence, there exists a constant $k=k(\gamma ,\eta )>0$ such that $\#\{a\in A:\lambda (a)=\lambda \}\leq k$ . Then, the result follows from Lemma 2.2.▪

We are now ready to prove Theorem 1.1.

Proof of Theorem 1.1 (1) We first show that for any $C\in (0,1)$ , for any $f\in H^\infty $ , $||f||_\infty \leq 1$ satisfying (1.5), there exists $H_1=H_1(f, B)\in \mbox {Har}_+(\mathbb {D})$ such that

(2.1) $$ \begin{align} -\log(|B(z)|+|f(z)|)\leq \min\left( -\log |B(z)|,-\log|f(z)| \right) \leq H_1(z),\hspace{0.5cm}z\in\mathbb{D}. \end{align} $$

It will be enough to split $ \mathbb {D} $ into subsets and find positive harmonic functions on $\mathbb {D}$ that are majorants for one of the two terms over each subset. There will be four cases. First, we need to choose $\delta>0$ such that $\delta$ verifies $\delta < \frac {1-C}{1+C}$ , or equivalently, $C<\frac {1-\delta }{1+\delta } $ .

For any $z\in \mathbb {D}$ , let $\lambda _z \in \Lambda $ be a point such that $\rho (z, \Lambda )=\rho (z, \lambda _z)$ .

Case 1. $\delta \le \rho (z, \Lambda ) $ . Then, Lemma 2.1 yields $-\log |B(z)|\leq C_\delta H_\Lambda (z)$ .

Case 2. $e^{-H(z)} \le \rho (z, \Lambda ) \le \delta $ . Then, the assumption of the theorem yields a harmonic majorant for $-\log |B(z)|$ .

Case 3. $\rho (z, \Lambda ) \le \min (e^{-H(z)}, \delta )$ , and $H(\lambda _z) \le 1$ . Then, $|f(\lambda _z)|\ge e^{-CH(\lambda _z) } \ge e^{-C}$ ; because by the Schwarz–Pick lemma, $\rho (f(z),f(\lambda _z))\le \delta $ , then [5, Chapter 1, equation (1.8)]

$$ \begin{align*}|f(z)| \ge \frac{|f(\lambda_z)|-\delta}{1-\delta |f(\lambda_z)|} \ge \frac{e^{-C}-\delta}{1-e^{-C}\delta}>0, \end{align*} $$

so $-\log |f(z)|$ is bounded by a constant.

Case 4. $\rho (z, \Lambda ) \le \min (e^{-H(z)}, \delta )$ , and $H(\lambda _z) \ge 1$ . Then, Harnack’s inequality implies

$$ \begin{align*} H(z) \ge \frac{1-\delta}{1+\delta} H(\lambda_z). \end{align*} $$

Then, another application of the Schwarz–Pick lemma yields

$$ \begin{align*} |f(z)| &\ge \frac{e^{-CH(\lambda_z)}- \rho(z, \Lambda)}{1-\rho(z, \Lambda)e^{-CH(\lambda_z)}} \ge e^{-CH(\lambda_z)}- e^{-H(z)} \\ &\ge e^{-CH(\lambda_z)}- e^{-\frac{1-\delta}{1+\delta} H(\lambda_z)} \ge e^{-CH(\lambda_z)} \left( 1- \exp \left( C- \frac{1-\delta}{1+\delta} \right)\right). \end{align*} $$

By another application of Harnack’s inequality, $-\log |f(z)| \le C_2 H(z) + C_3$ .

Having established (2.1), we can apply the Corona Theorem for the Nevanlinna class to obtain functions $g,h\in \mathcal {N}$ such that $fg=1+Bh$ .

(2) Let $\delta _1 \in (0,1)$ , to be chosen later, and define $U_1=\{z\in \mathbb {D}:\rho (z,\Lambda )<\delta _1\}$ . By construction, there is an absolute constant $C_1>0$ such that $H_\Lambda (\lambda ) \ge C_1$ for any $\lambda \in \Lambda $ , so by Harnack’s inequality, $H_\Lambda (z)\ge \frac {1-\delta _1}{1+\delta _1}C_1$ for all $z\in U_1$ .

Consider the set $E=\{z\in \mathbb {D}:\rho (z,\Lambda )< e^{-H(z)}\}$ . Taking $C_0$ large enough so that $C_0 \frac {1-\delta _1}{1+\delta _1}C_1> \log \delta _1^{-1}$ , we ensure $E \Subset U_1$ . Let $U_2:= U_1 \setminus E$ .

We will construct a separated sequence A such that the values of $\log |B|^{-1}$ on A control its values on $U_2$ .

There are constants $0<\delta _3<\delta _2<1$ such that the $\rho $ -diameter of each Whitney square does not exceed $\delta _2$ , and any disk $D_\rho (z,\delta _3)$ intersects at most four Whitney squares. In each Whitney square q such that $\overline q \cap \overline {U_2} \neq \emptyset $ , choose a point $a = a(q) \in \overline q \cap \overline {U_2} $ such that

$$ \begin{align*} \log|B(a(q))|^{-1}=\max\{\log|B(z)|^{-1}:z \in \overline q \cap \overline{U_2} \}. \end{align*} $$

Let $A_0:= \{ a(q) : \overline q \cap \overline {U_2} \neq \emptyset \}$ . Define an equivalence relation on $A_0$ by $a(q) \sim a(q')$ if there exists a finite chain of squares $q_i$ such that $q_1=q$ , $q_m=q'$ , and $\rho (a(q_{i+1}),a(q_{i}) )< \delta _3/4$ , $ 1\le i \le m-1$ . Then, we always have $m\le 4$ for any class. Define A by selecting one element a in each class by

$$ \begin{align*} \log|B(a(q))|^{-1}=\max\{\log|B(a(q'))|^{-1}: a(q) \sim a(q') \}. \end{align*} $$

Therefore, A is $(\delta _3/4)$ -separated, and for any $z \in U_2$ , there exists $a \in A$ such that $\rho (z,a)\le \frac {\delta _3+\delta _2}{1+\delta _3\delta _2} := \delta _4<1 $ and $ \log |B(z)|^{-1} \le \log |B(a)|^{-1}$ .

Because A is a separated sequence, Corollary 2.3 gives that A is a Blaschke sequence, and, if $B_A$ denotes the Blaschke product with zero set A, there exists a constant $C_2=C_2 (\delta _3)>0$ such that

(2.2) $$ \begin{align} \log|B_A (z)|^{-1}\leq C_2 H_{\Lambda} (z)+\log\rho(z,A)^{-1},\hspace{0.5cm}z\in\mathbb{D}. \end{align} $$

Fix $\lambda _k\in \Lambda $ , and $a_k\in A$ such that $\rho (\lambda _k, a_k)=\rho (\lambda _k,A)$ . Recall that $a_k \in \overline {U_2}$ , so $e^{-H(a_k)} \le \rho (\lambda _k, a_k) \le \delta _1$ . Then,

$$ \begin{align*} \log|B_A (\lambda_k)|^{-1}\leq C_2 H_\Lambda(\lambda_k)&+ \log\rho(\lambda_k,a_k)^{-1}\\ &\leq \frac{C_2}{C_0} H(\lambda_k)+ H(a_k) \leq \left(\frac{C_2}{C_0}+ \frac{1+\delta_1}{1-\delta_1}\right) H(\lambda_k). \end{align*} $$

We can choose $C_0$ and $\delta _1$ so that $\left (\frac {C_2}{C_0}+ \frac {1+\delta _1}{1-\delta _1}\right )<C$ , then the function $f=B_A$ satisfies estimate (1.5) with the constant C. By assumption, there exist $g,h\in \mathcal {N}$ such that $Bg+B_Ah=1$ . We deduce that there exists $H_1\in $ Har $_+(\mathbb {D})$ such that $-\log |B(a_k)|\leq H_1(a_k)$ , $k=1, 2, \ldots $ .

For any $z\in U_2$ , there exists $a\in A$ such that $ \log |B(z)|^{-1} \le \log |B(a)|^{-1}$ and $H_1(a) \le \frac {1+\delta _4}{1-\delta _4} H_1(z)$ . Hence, $-\log |B|$ has a harmonic majorant in $U_2$ . Because, by Lemma 2.1, $-\log |B|$ has a harmonic majorant on $\mathbb {D} \setminus U_1$ ; the proof is complete. ▪

The proof of part (1) can be easily adapted to show the following more general fact.

Corollary 2.4 Let B be a Blaschke product with zero set $\Lambda = \{\lambda _k \}$ . Then, for any constant $C<1$ , the following statement holds. Let $H\in $ Har $_+(\mathbb {D})$ , and assume that the function $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ . Then, for any $f_1 , \ldots , f_n \in H^\infty $ , $||f_i||_\infty \leq 1$ , $i=1, \ldots , n$ , such that

$$ \begin{align*} \sum_{i=1}^n |f_i (\lambda_k)|> e^{-CH(\lambda_k)}, \quad k=1,2, \ldots , \end{align*} $$

there exist $g_1, \ldots , g_n,h\in \mathcal {N}$ such that $\sum _i f_ig_i=1+Bh$ .

On the other hand, the n-tuple analogue of part 2 trivially holds, because the hypothesis for $n\ge 1$ implies the hypothesis for $n=1$ which is the one used in Theorem 1.1.

The proof of Theorem 1.2 uses the following auxiliary result.

Lemma 2.5 Let $\{Q_j\}$ be an infinite sequence of different dyadic Whitney squares, and let $\{M_j\}$ be a sequence of positive numbers with $\lim _{j \to \infty } M_j=\infty $ . Then, there exist $H\in $ Har $_+(\mathbb {D})$ and a constant $C_0>0$ such that $H_j=\sup \{H(z):z\in Q_j\}$ satisfies $H_j\leq M_j+C_0$ for any $j=1, 2, \ldots $ , and $\limsup _{j \to \infty } H_j=\infty $ .

Proof The idea is to construct by induction a variant of the function $H_\Lambda $ . For any Whitney cube Q, let us set

(2.3) $$ \begin{align} h_Q(z):= \int_{I(Q)} \frac{1-|z|^2}{|e^{i\theta}-z|^2} \frac{d\theta}{2\pi}, \end{align} $$

where $I(Q)$ is the radial projection of Q onto $\partial \mathbb {D}$ .

Note that there exists an absolute constant $c>0$ such that the function $h_Q$ has the following properties:

(2.4) $$ \begin{align} 0\le h_Q (z) \le 1, \forall z \in \mathbb{D}; \quad h_Q (z) \leq \frac{l(Q)}{c(1-|z|)}, \forall z \in \mathbb{D}; \quad 0 < c \le h_Q (z), \forall z \in Q. \end{align} $$

We will construct inductively a sequence of coefficients $\mu _m$ and an increasing sequence of integers $(j_m)$ , so that $H:=\sum _m \mu _m h_{Q_{j_m}}$ satisfies the conclusion of the lemma. There is no loss of generality in assuming that $l(Q_{j+1})\le l(Q_{j})$ for all j. Let $H_0:=0$ . For any $k>0$ , let us denote $H^{(k)}:=\sum _{m=1}^k \mu _m h_{Q_{j_m}}$ . Let $H^{(k)}_j:=\sup _{Q_j} H^{(k)}$ . We want to prove by induction on k that:

(2.5) $$ \begin{align} H^{(k)}_j \le M_j + \sum_{m=1}^k 2^{-m/2}, j=1,2,\ldots. \end{align} $$

In particular, this will show that $\sup _k H^{(k)}$ will be bounded on any square $Q_j$ ; therefore, $H:= \sum _{j=1}^\infty \mu _m h_{Q_{j_m}}$ will be well defined and will satisfy $H_j\le M_j +C_0$ , for all $j \in \mathbb {Z}_+$ .

For $k=0$ , the property (2.5) is vacuously true. Suppose it is satisfied for k. Because $H^{(k)}$ is bounded and $M_j \to \infty $ , there exists $R \in (0, l(Q_{j_k}) )$ such that for any $j \in \mathbb {Z}_+$ such that $l(Q_j) \le R$ , then $M_j - H^{(k)}_j \ge 2^{(k+1)/2}$ . Now, there exists $R'<R$ such that for all z such that $|z| \le 1-R/2$ (in particular, for $z\in Q_j$ with $j\le j_k$ ) and for all Q such that $l(Q) \le R'$ , $h_Q(z) < 2^{-k-1}$ . Pick $j_{k+1}$ to be the smallest j such that $l(Q_j) \le R'$ , and $\mu _{k+1}:=2^{(k+1)/2}$ . Then, for all j such that $l(Q_j)\ge R$ , by the induction hypothesis,

$$ \begin{align*} H^{(k+1)}_j = H^{(k)}_j + \mu_{k+1} h_{Q_{j_{k+1}}} \le H^{(k)}_j + 2^{(k+1)/2} 2^{-k-1} \le M_j + \sum_{m=1}^{k+1} 2^{-m/2}. \end{align*} $$

On the other hand, for all j such that $l(Q_j)\le R$ ,

$$ \begin{align*} H^{(k+1)}_j = H^{(k)}_j + \mu_{k+1} h_{Q_{j_{k+1}}} \le H^{(k)}_j + \mu_{k+1} = H^{(k)}_j + 2^{(k+1)/2} \le M_j, \end{align*} $$

by the choice of R. The inductive condition (2.5) is satisfied. Finally, notice that for $z \in Q_j$ so that $j=j_m$ for some m,

$$ \begin{align*} H(z) \ge \mu_m h_{Q_{j_m}} \ge c 2^{m/2} \to \infty \mbox{ as } m\to \infty. \\[-36pt]\end{align*} $$

▪

Proof of Theorem 1.2 (1) For each dyadic Whitney square Q, recall ${N(Q)=\#(Q\cap \Lambda )}$ , and let $\mathcal {U}(Q)$ be the collection of at most nine dyadic Whitney squares $Q_1$ such that $\overline {Q_1}\cap \overline {Q}\neq \emptyset $ . Observe that there exists an absolute constant $\delta>0$ such that

$$ \begin{align*} \delta\;\leq\;\rho(Q,\mathbb{D}\;\backslash\;\mathcal{U}(Q)) := \inf \{\rho (z, w): z \in Q , w \in \mathbb{D}\;\backslash\;\mathcal{U}(Q) \} \end{align*} $$

for any dyadic Whitney square Q. Consider also $M(Q)=\#(\mathcal {U}(Q)\cap \Lambda )$ . Let $\{Q_j\}$ be the collection of dyadic Whitney squares such that $M(Q_j)>0$ . The Blaschke condition gives that

Then, there exists a sequence $\{\tilde {M_j}\}$ , $\tilde {M_j} \geq M(Q_j)$ for any $j \geq 1$ , with

$$ \begin{align*} \lim_{j\to\infty} \tilde{M_j} \big/ M(Q_j)=+\infty \text { and } \sum\tilde{M_j} l(Q_j)<\infty. \end{align*} $$

Lemma 2.5 provides $H\in $ Har $_+(\mathbb {D})$ such that $H(z) \leq \tilde {M_j}\big / M(Q_j) +C_0$ for any $z\in Q_j$ and $\limsup _{j\to \infty }\sup \{H(z):z\in Q_j\}=+\infty $ . Because the sequence $\Lambda $ is contained in $\cup Q_j $ , Harnack’s inequality gives that $\limsup _{k\to \infty } H(\lambda _k)=+\infty $ . We will now show that the function $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ . Because $\rho (\Lambda ,\mathbb {D}\backslash \cup Q_j)\geq \delta>0$ , Lemma 2.1 gives that $-\log |B|$ has a harmonic majorant on $\mathbb {D}\backslash \cup Q_j$ . Now, fix $z\in Q_j$ with $\rho (z,\Lambda )\geq e^{-H(z)}$ and split $\Lambda =\Lambda _1\cup \Lambda _2$ , where $\Lambda _1=\{\lambda _k:\rho (\lambda _k,z)\leq \delta \}$ and $\Lambda _2=\{\lambda _k:\rho (\lambda _k,z)>\delta \}$ . By Lemma 2.1, there exists a constant $C=C(\delta )>0$ such that

On the other hand, because $\rho (\lambda _k,z)\geq e^{-H(z)}$ , we have

Consider the harmonic function $H_1:=\sum _j\tilde {M_j} h_{Q_j}$ , where $h_Q$ is as in (2.3). By the last estimate in (2.4), $H_1(z)\geq c\tilde {M_j}$ for any $z\in Q_j$ . We deduce that

$$ \begin{align*} \log|B(z)|^{-1}\leq CH_\Lambda(z)+ c^{-1} (1+ C_0) H_1(z), \end{align*} $$

and this finishes the proof of part (1).

To prove part (2), let C be as in Theorem 1.1(1), and $\tilde H$ a function as in part (1). If we set $H:=C\tilde H$ , applying Theorem 1.1(1) yields our result.▪

We now present a family of Blaschke products B for which the family $\mathcal {H}(B)$ can be easily described. Let $\Lambda =(\lambda _k)_k$ be a separated sequence in $\mathbb {D}$ , that is, assume $\eta =\inf \{\rho (\lambda _k,\lambda _j):k\neq j\}>0$ . Let $N =\{N_j\}$ be a sequence of positive integers tending to infinity such that

$$ \begin{align*} \sum N_j(1-|\lambda_j|)<\infty. \end{align*} $$

Consider the Blaschke product $B(\Lambda , N)$ defined as

(2.6) $$ \begin{align} B(\Lambda,N)(z)=\prod_j\left(\frac{\overline{\lambda_j}}{|\lambda_j|}\frac{\lambda_j-z}{1-\overline{\lambda_j}z}\right)^{N_j},\hspace{0.5cm}z\in\mathbb{D}. \end{align} $$

Consider the pairwise disjoint pseudohyperbolic disks $D_j=\{z\in \mathbb {D}:\rho (z,\lambda _j)\leq \eta / 4\}$ , $j=1, 2, \ldots $ . By Lemma 2.1, $-\log |B(\Lambda , N)|$ has a harmonic majorant on $\mathbb {D}\backslash \cup _j D_j$ . Again, by Lemma 2.1, there exists a constant $C>0$ and a function $H_1 \in $ Har $_+(\mathbb {D})$ such that

Fix $H\in $ Har $_+(\mathbb {D})$ . Then, $-\log |B(\Lambda , N)|$ has a harmonic majorant on $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ if and only if there exists $H_2\in $ Har $_+(\mathbb {D})$ such that

$$ \begin{align*} N_j\log\rho(z,a_j)^{-1}\leq H_2(a_j),\hspace{0.5cm}j=1, 2, \ldots, \end{align*} $$

whenever $\rho (z,a_j)\geq e^{-H(z)}$ . Hence, $-\log |B(\Lambda , N)|$ has a harmonic majorant on $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ if and only if the mapping $a_j\rightarrow N_jH(a_j)$ has a harmonic majorant. Hence, for the Blaschke products $B(\Lambda , N)$ , the sufficient condition given in Theorem 1.5 is also necessary. In other words, we have $H \in \mathcal {H} (B(\Lambda , N))$ if and only there exists $H_2 \in $ Har $_+(\mathbb {D})$ such that $N_j H(a_j) \leq H_2 (a_j)$ , for any j.

The examples of $B_\Lambda $ given here do not have simple zeros, in fact the multiplicities are unbounded. However, one easily gets a similar example by replacing each point $a_j$ with multiplicity $N_j$ by $N_j$ distinct points contained in a hyperbolic disc centered at $a_j$ of radius, say, $10^{-3}\eta $ .

3 Proofs of Theorems 1.3–1.5

We start with the proof of part (1) of Theorem 1.3.

Proof of Theorem 1.3 (1)

Let $a_j\in \mathbb {D}$ with

$$ \begin{align*} \lim_{j\to\infty}\frac{H_1(a_j)}{H_2(a_j)} = \infty. \end{align*} $$

Considering a subsequence if necessary, we can assume that $\rho (a_j,a_k)\geq 1/2$ if $k\neq j$ . Because $H_1 (a_j) (1 - |a_j|) \leq 2 H_1 (0)$ for any j, we have $\lim _{j \to \infty } (1-|a_j|) H_2 (a_j) =0$ . Pick a sequence $\{N_j\}$ of positive integers such that $\lim _{j \to \infty } N_j(1-|a_j|)H_2(a_j)=0$ and $\lim _{j \to \infty } N_j(1-|a_j|)H_1(a_j)=+\infty $ . Considering a subsequence of $\{a_j\}$ again if necessary, we may assume that

(3.1) $$ \begin{align} \sum N_j(1-|a_j|)H_2(a_j)<\infty. \end{align} $$

Now, let B be the Blaschke product defined by

As discussed at the end of the previous section, for any $H\in $ Har $_+(\mathbb {D})$ , the function $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\{a_j\})\geq e^{-H(z)}\}$ if and only if the mapping $F(H)$ defined by $F(H)(a_j)=N_jH(a_j)$ , $j\geq 1$ , and $F(H)(z)=0$ if $z \notin \{a_j \}$ , has a harmonic majorant. Because $\lim _{j \to \infty } N_j H_1(a_j)(1-|a_j|)=+\infty $ , the mapping $F(H_1)$ cannot have a harmonic majorant. Consider the function

where $Q_j$ is the dyadic Whitney square containing $a_j$ . Here, $h_Q$ is the function defined in (2.3). Because $l(Q_j)$ is comparable to $ 1-|a_j|$ , the above sum converges by (3.1). Observe that last estimate of (2.4) gives that there exists an absolute constant $C_1>0$ such that

$$ \begin{align*} H_3(a_j)\geq C_1N_jH_2(a_j),\hspace{0.5cm} j=1, 2, \ldots. \end{align*} $$

Hence, $F(H_2)$ has a harmonic majorant. ▪

Proof of Theorem 1.3 (2)

By Harnack’s inequality, there is a constant $\gamma \in (0,1)$ such that for any dyadic Whitney square Q, any positive harmonic function H, any $z,z'\in Q$ , we have $\gamma H(z') \le H(z) \le \gamma ^{-1} H(z')$ . Pick $\eta \in (0,\eta _0)$ .

Given an unbounded positive harmonic function H, we can choose a sequence of dyadic Whitney squares $\{Q_j\}$ such that

1. (1) $l(Q_{j}) = 2^{-j}$ , $j \geq 1$ .

2. (2) If $z_j$ denotes the center of $Q_j$ ,

   $$ \begin{align*} H(z_{j}) \to \infty \mbox{ and } H(z_j) \le \frac{\gamma}{2(1+\eta)} j. \end{align*} $$

To prove that we can satisfy the second condition, in the case where

$$ \begin{align*}\max_{z:|z|=1- 2^{-j}} H(z) \le \frac{\gamma}{2(1+\eta)} j, \end{align*} $$

it is enough to choose $Q_j$ to be the dyadic Whitney square with $l(Q_j) = 2^{-j}$ , where the maximum is attained; otherwise,

$$ \begin{align*}\max_{z:|z|=1-2^{-j}} H(z) \geq \frac{\gamma}{2(1+\eta)} j. \end{align*} $$

Because $H(0) \geq \min \{H(z) : |z|=1- 2^{-j} \}$ , for j large enough, we can find a point z, $|z|=1- 2^{-j} $ , such that

$$ \begin{align*}H(z)= \frac{{\gamma}^3}{2(1+\eta)} j. \end{align*} $$

We choose $Q_j$ to be the dyadic Whitney square containing z. Then,

(3.2) $$ \begin{align} \frac{\gamma^4}{2(1+\eta)} j \le H(z_j) \le \frac{\gamma^2}{2(1+\eta)} j. \end{align} $$

Note that because H is unbounded, we have $\max \{H(z): |z|= 1- 2^{-j} \} \to \infty $ as $j \to \infty $ . Hence, the estimate (3.2) gives that $\lim _{j \to \infty } H(z_j) = \infty $ . We shall need to take subsequences of $\{Q_j \}$ , while keeping the same name for the sequence. Choose a sequence $R_j\to 0$ such that

(3.3) $$ \begin{align} \lim_{j\to\infty} \frac{\log R_j^{-1}}{H(z_j)} =0. \end{align} $$

Observe that $\lim _{j\to \infty } l(Q_j)^2 H(z_j) \log \frac 1{R_j} =0$ . Indeed, for j large enough, we have

$$ \begin{align*} 0 < l(Q_j)^2 H(z_j) \log \frac1{R_j} \le l(Q_j)^2 H(z_j)^2 \le \left( l(Q_j) \frac{\gamma}{2(1+\eta)} \log \frac1{l(Q_j)} \right)^2. \end{align*} $$

Now, with $[\cdot ]$ denoting the integer part of a real number, define the sequence of integers

(3.4) $$ \begin{align} N_j:= \left[ \frac1{l(Q_j) \left(H(z_j) \log \frac1{R_j}\right)^{1/2}} \right]. \end{align} $$

For $z_0\in \mathbb {D}$ and $t>0$ , let $D_\rho (z_0,t)=\{z\in \mathbb {D}:\rho (z,z_0)\leq t\}$ denote the pseudohyperbolic disk of radius t centered at $z_0$ . We define the sequence $\Lambda $ as the union of finite sequences $\Lambda ^{(k)} \subset Q_k$ . For each k, $\Lambda ^{(k)}$ is the union of

1. (1) the point $z_k$ with multiplicity $N_k$ and

2. (2) a maximal subset of points $\lambda _j = \lambda _j (k)$ contained in the pseudohyperbolic disc $D_\rho (z_k, R_k)$ such that for any $i\neq j$ , $ \rho (\lambda _i,\lambda _j) \ge e^{-(1+\eta )H(z_k)}$ .

Here, maximal means that for any $z \in D_\rho (z_k, R_k)$ , there exists $\lambda _j$ such that $\rho (z , \lambda _j) \leq e^{-(1+ \eta ) H (z_k)} $ . Observe that the number of points $\{ \lambda _j \}$ is of the order of $R_k^2 e^{2(1+ \eta ) H (z_k)}$ . See page 3 of [5]. Note that we are adding to the multiple zero $z_k$ a set of points $\lambda _j$ with a cardinality on the order of $R_k^2 e^{2(1+\eta )H(z_k)}$ , which tends to infinity by (3.3). We proceed to take a subsequence of $\Lambda $ (still denoted by the same letter) that will make it, among other things, a Blaschke sequence.

First observe that

(3.5) $$ \begin{align} \lim_{j\to\infty} l(Q_j) N_j \log \frac1{R_j} = \lim_{j\to\infty} \left( \frac{\log \frac1{R_j}}{H(z_j)} \right)^{1/2} =0, \end{align} $$

and

(3.6) $$ \begin{align} \lim_{j\to\infty} l(Q_j) N_j H(z_j) = \lim_{j\to\infty} \left( \frac{H(z_j)}{ \log \frac1{R_j} } \right)^{1/2} = \infty. \end{align} $$

On the other hand, applying the second inequality in (3.2) and passing to logarithms, one gets

(3.7) $$ \begin{align} \lim_{j\to\infty} \left( l(Q_j) e^{2(1+\eta)H(z_j)} R_j^2 \log \frac1{R_j} \right)=0. \end{align} $$

We now complete the definition of $\Lambda $ by restricting to a subsequence again denoted by $(Q_j)$ such that $\rho (Q_k , Q_j) \geq 1/2$ if $k \neq j$ and such that

(3.8) $$ \begin{align} \sum_{j=1}^\infty l(Q_j) \left(N_j \log \frac1{R_j}+ e^{2(1+\eta)H(z_j)} R_j^2 \log \frac1{R_j} \right) < \infty, \end{align} $$

which is possible by (3.5) and (3.7). Let $\Lambda = \cup \Lambda ^{(k)}$ be the resulting sequence.

Observe that an immediate consequence of this is that $\Lambda $ is now a Blaschke sequence, because

$$ \begin{align*} \sum_{j=1}^\infty l(Q_j) \left(N_j + e^{2(1+\eta)H(z_j)} R_j^2 \right) < \infty. \end{align*} $$

Note that the estimate (3.8) is stronger. Actually, the extra factor $\log (1/R_j)$ will be needed later.

Claim 1. For k large enough,

$$ \begin{align*} \{ \zeta \in Q_k: \rho(\zeta, \Lambda) \ge e^{-H(\zeta)} \} \cap D_\rho (z_k,R_k) =\emptyset. \end{align*} $$

Proof For any $\zeta \in D(z_k,R_k)$ , there is a $\lambda _j$ such that $\rho (\zeta ,\lambda _j)< e^{-(1+\eta )H(z_k)}$ . Because $\lim _{k \to \infty } R_k =0$ , by Harnack’s inequality, there is a number $\gamma _k <1$ with $\lim _{k\to \infty } \gamma _k=1$ , such that $\gamma _k H(z_k) \le H(z) \le \gamma _k^{-1} H(z_k)$ for any $z\in D(z_k,R_k)$ . Then, for k large enough,

$$ \begin{align*} \log \rho(\zeta,\lambda_j) < -(1+\eta)H(z_k) \le - \gamma_k^{-1} H(z_k) \le - H(\zeta). \\[-36pt]\end{align*} $$

▪

We henceforth restrict attention to the tail of the sequence where the conclusion of Claim 1 holds.

Claim 2. $H \in \mathcal H(B)$ .

Proof Because $\rho (Q_k , Q_j ) \geq 1/2$ if $k \neq j$ , it is enough to majorize, on each $Q_k$ , the part of the product corresponding to the local zeros, that is, to find $H_1 \in $ Har $_+(\mathbb {D})$ such that

$$ \begin{align*} \sum_{\lambda \in \Lambda \cap Q_k} \log\frac1{\rho(\zeta,\lambda)} \leq H_1 (z_k), \quad \zeta \in Q_k, k =1,2,\ldots, \end{align*} $$

if $\rho (\zeta , \Lambda ) \geq e^{- H (\zeta )}$ . By the previous claim, this only occurs when $\zeta \notin D_\rho (z_k , R_k)$ . Then, the above sum breaks into two terms: those corresponding to $\lambda = z_k$ can be estimated by $- N_k \log R_k$ , and those admit a harmonic majorant of the form $C' \sum _j N_j \log \frac 1{R_j} h_{Q_j}$ , because by (3.8),

$$ \begin{align*}\sum_{j=1}^\infty l(Q_j) N_j \log \frac1{R_j} <\infty .\end{align*} $$

The second term corresponds to the points $\lambda = \lambda _j \in \Lambda ^{(k)} \setminus \{z_k \}$ . After applying an automorphism of the disc mapping $\lambda _k$ to $0$ , the corresponding sum

$$ \begin{align*}\sum_{\lambda_ j \in \Lambda^{(k)} \setminus \{z_k \} } \log\frac1{\rho(\zeta,\lambda)} \end{align*} $$

reduces to a Riemann sum for the area integral of $\log \frac 1{|z|}$ , with disks of (Euclidean) radius $e^{-(1+\eta )H(z_k)}$ . The integral is convergent, and after an elementary computation, one finds that the second term is bounded by a fixed multiple of $e^{2(1+\eta )H(z_k)} R_k^2 \log \frac 1{R_k} $ . Again by (3.8), this term also admits a harmonic majorant.▪

We now want to show that $-\log |B|$ has no harmonic majorant on the set $\{z: \rho (z,\Lambda )> e^{-(1+\eta _0)H(z)}\}$ .

Claim 3. For k large enough,

$$ \begin{align*} \{ \zeta \in Q_k: \rho(\zeta, \Lambda) \ge e^{-(1+\eta_0 )H(\zeta)} \} \cap \overline D(z_k,e^{-(1+\eta)H(z_k)}) \neq \emptyset. \\[-36pt]\end{align*} $$

▪

Proof The choice of the points $\{\lambda _j \}$ gives that there is a point $\zeta $ such that $\rho (z_k,\zeta )= e^{-(1+\eta )H(z_k)}$ and for any $\lambda _j \in \Lambda ^{(k)} \setminus \{z_k \}$ , we have $\rho (\zeta ,\lambda _j)\ge \frac 12 e^{-(1+\eta )H(z_k)}$ . Therefore, because $\eta < \eta _0$ , for k large enough,

$$ \begin{align*} \log \rho(\zeta, \Lambda) \ge -\log 2 -(1+\eta)H(z_k) &\ge -\log 2 -\gamma_k^{-1}(1+\eta)H(\zeta) \\ &\ge -(1+\eta_0)H(\zeta). \\[-36pt]\end{align*} $$

▪

Let $\zeta $ be a point in the nonempty intersection given by Claim 3. Because B has a zero at $z_k$ of multiplicity $N_k$ ,

$$ \begin{align*} \log \frac1{|B(\zeta)|} \ge N_k (1+\eta )H(z_k), \end{align*} $$

and (3.6) implies that this cannot admit a harmonic majorant, because any majorizing function would have to grow faster than $1/l(Q_k)$ at the points $z_k$ . ▪

The proof of Theorem 1.4 uses the following variant of Lemma 1.1 of [9].

Lemma 3.1 There exists a universal constant $C_0\geq 1$ such that the following statement holds. Let $\Lambda $ be a Blaschke sequence and $H\in $ Har $_+(\mathbb {D})$ . Let $z\in \mathbb {D}$ with $e^{H(z)}\geq \max \{C_0,\#\{\lambda \in \Lambda :\rho (\lambda ,z)\leq \frac {1}{2}\}\}$ . Then, there exists $\tilde {z}\in \mathbb {D}$ with $\rho (\tilde {z},\Lambda )\geq e^{ - H (\tilde {z} )}$ and $\rho (\tilde {z},z)\leq e^{-H(z)/C_0}$ .

Proof We can assume that $H(z)\geq 100$ . A calculation shows that there exists a constant $C_1>1$ such that

$$ \begin{align*} C_1^{-1}t^2(1-|z|)^2\leq \text{ Area }D_\rho(z,t)\leq C_1t^2(1-|z|)^2. \end{align*} $$

See page 3 of [5]. Using these estimates and the fact that $H(z)\geq 100$ , one can show that there exists a sufficiently large universal constant $C_0>0$ such that the pseudohyperbolic disk $D_\rho (z,e^{-H(z)/C_0})$ contains more than $e^{3H(z)/2}$ pairwise disjoint pseudohyperbolic disks $D_j$ of pseudohyperbolic radius $e^{-H(z_j)}$ . Here, $z_j$ denotes the center of $D_j$ . Because $e^{H(z)}\geq \#(\Lambda \cap D_\rho (z,\frac {1}{2}))$ , there exists at least one $D_j$ with $D_j\cap \Lambda =\emptyset $ , and we can take as $\tilde {z}$ the center of $D_j$ .▪

Proof of Theorem 1.4 Let $C_0\geq 1$ be the constant appearing in Lemma 3.1. Fix $C>1$ . We will show that there exists a constant $C_1=C_1 (C)>0$ such that for any $z\in \mathbb {D}$ with $C_0^{-1}\geq \rho (z,\Lambda )\geq e^{-CH(z)}$ , there exists $\tilde {z}\in \mathbb {D}$ with $\rho (\tilde {z},\Lambda )\geq e^{-H(\tilde {z})}$ and

(3.9) $$ \begin{align} \log|B(z)|^{-1}\leq C_1 (\log|B(\tilde{z})|^{-1}+H_\Lambda(\tilde{z})). \end{align} $$

Fix $z\in \mathbb {D}$ with $C_0^{-1}\geq \rho (z,\Lambda )\geq e^{-CH(z)}$ . Apply Lemma 3.1 to find $\tilde {z}\in \mathbb {D}$ with $\rho (\tilde {z},z)\leq e^{-H(z)/C_0}$ such that $\rho (\tilde {z},\Lambda )\geq e^{-H(\tilde {z})}$ . Let $\Lambda = (\lambda _k)_k$ and split $\Lambda =\Lambda _1\cup \Lambda _2\cup \Lambda _3$ where $\Lambda _1=\{\lambda _k:\rho (z,\lambda _k)\leq e^{-H(z)/2C_0}\}$ , $\Lambda _2=\{\lambda _k: e^{-H(z)/2C_0}<\rho (z,\lambda _k)\leq 1/2 \}$ , and $\Lambda _3=\{\lambda _k:\rho (z,\lambda _k ) \geq 1/2 \}$ . By lemma 2.1, there exists a constant $C_2>0$ such that

$$ \begin{align*} \sum_{\lambda_k\in\Lambda_3}\log\rho(z,\lambda_k)^{-1}\leq C_2 H_\Lambda(z). \end{align*} $$

If $\lambda _k\in \Lambda _2$ , we have $\rho (\tilde {z},\lambda _k)\leq \rho (z,\tilde {z})+\rho (z,\lambda _k)\leq 2\rho (z,\lambda _k)$ . Using the obvious estimate $2x\leq x^{1/2}$ , which holds for $0\leq x\leq 1/\sqrt {2}$ , we deduce $\rho (\tilde {z},\lambda _k)\leq \rho (z,\lambda _k)^{1/2}$ . Hence,

$$ \begin{align*} \sum_{\lambda_k\in\Lambda_2}\log\rho(z,\lambda_k)^{-1}\leq 2 \sum_{\lambda_k\in\Lambda_2}\log\rho(\tilde{z},\lambda_k)^{-1}\leq 2\log|B(\tilde{z})|^{-1}. \end{align*} $$

Finally, because $\rho (z,\Lambda )\geq e^{-CH(z)}$ , we have that

$$ \begin{align*} \sum_{\lambda_k\in\Lambda_1}\log\rho(z,\lambda_k)^{-1}\leq CH(z)\#\Lambda_1. \end{align*} $$

Observe that if $\lambda _k\in \Lambda _1$ , then $\rho (\tilde {z},\lambda _k)\leq \rho (z,\tilde {z})+\rho (z,\lambda _k)\leq 2e^{-H(z)/2C_0}$ , and we deduce that there exists a universal constant $C_3>0$ such that

$$ \begin{align*} \log|B(\tilde{z})|^{-1}\geq \sum_{\lambda_k\in\Lambda_1}\log\rho(\tilde{z},\lambda_k)^{-1}\geq C_3 \frac{H(z)}{C_0}\#\Lambda_1. \end{align*} $$

Hence, there exists a constant $C_4>0$ such that

$$ \begin{align*} \sum_{\lambda_k\in\Lambda_1}\log\rho(z,\lambda_k)^{-1}\leq C_4\log|B(\tilde{z})|^{-1}. \end{align*} $$

Collecting these estimates, one finds a constant $C_5>0$ such that

$$ \begin{align*} \log|B(z)|^{-1}\leq C_5 (\log|B(\tilde{z})|^{-1}+H_\Lambda (z)). \end{align*} $$

Because by Harnack’s inequality $H_\Lambda (z)$ and $H_\Lambda (\tilde {z})$ are comparable, this proves (3.9). Now, (3.9), the assumption, and another application of Harnack’s inequality give that $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}: C_0^{-1} \geq \rho (z,\Lambda )\geq e^{-CH(z)}\}$ . By Lemma 2.1, there exists a constant $C_6>0$ such that $-\log |B(z)|\leq C_6 H_\Lambda (z)$ if $\rho (z,\Lambda )\geq C_0^{-1}$ . This completes the proof. ▪

Proof of Theorem 1.5 Fix $z\in \mathbb {D}$ with $\rho (z,\Lambda )\geq e^{-H(z)}$ . Consider $\Lambda _1=\{\lambda _k:\rho (\lambda _k,z)\leq 1/2 \}$ and $\Lambda _2=\{\lambda _k:\rho (\lambda _k,z)> 1/2 \}$ . By Lemma 2.1, there exists an absolute constant $C_1>0$ such that

$$ \begin{align*} \sum_{\lambda_k\in\Lambda_2}\log\rho(\lambda_k,z)^{-1}\leq C_1H_\Lambda(z). \end{align*} $$

On the other hand, because $\rho (z,\Lambda )\geq e^{-H(z)}$ , we have

$$ \begin{align*} \sum_{\lambda_k\in\Lambda_1}\log\rho(\lambda_k,z)^{-1}\leq H(z)\#\Lambda_1. \end{align*} $$

Let Q be the dyadic Whitney square containing z. Because there exists a universal constant $0<C_2<1$ such that each point $\lambda _k\in \Lambda _1$ satisfies $\rho (\lambda _k,z(Q))\leq C_2$ , we deduce that there exists a constant $C_3>0$ such that $H(z)\#\Lambda _1 \leq C_3H_1(z)$ . Hence, $C_1H_\Lambda +C_3H_1$ is a harmonic majorant of $-\log |B|$ on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ . ▪

Corollary 3.2 Let B be a Blaschke product with zero set $\Lambda $ . Let $H\in $ Har $_+(\mathbb {D})$ such that

$$ \begin{align*} \sum N(Q)H(z(Q))l(Q)<\infty, \end{align*} $$

where the sum is taken over all dyadic Whitney squares Q such that $N(Q)>0$ . Then, $-\log |B|$ has a harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ .

Proof of Corollary 3.2 Consider the harmonic function $H_1\in $ Har $_+(\mathbb {D})$ defined by

$$ \begin{align*} H_1(z)=\sum N(Q)H(z(Q)) h_Q, \quad z \in \mathbb{D} , \end{align*} $$

where the sum is taken over all dyadic Whitney squares Q with $N(Q)>0$ . Observe that by (2.4), there exists a positive constant $C>0$ such that $H_1(z(Q))\geq C N(Q)H(z(Q))$ for any Q with $N(Q)>0$ . Now, the result follows from Theorem 1.5.▪

4 Smirnov quotient algebras

A quasibounded harmonic function is a harmonic function on the unit disc which is the Poisson integral of an integrable function on the unit circle. We denote by $QB_+(\mathbb {D})$ the cone of positive quasibounded harmonic functions on $\mathbb {D}$ . An analytic function f on $\mathbb {D}$ is in the Smirnov class $\mathcal {N}^+$ if the function $\log ^+|f|$ has a quasibounded harmonic majorant in $\mathbb {D}$ . A function in the Nevanlinna class is in the Smirnov class if and only if its canonical inner–outer factorization has no singular function in the denominator. Hence, the Smirnov class $\mathcal {N}^+$ is an algebra where the invertible functions are exactly the outer functions. Interpolating sequences in $\mathcal {N}^+$ were described as those sequences $\{z_n \}$ of points in $\mathbb {D}$ for which there exists $H \in QB_+(\mathbb {D})$ such that condition (1.2) holds. See Theorem 1.3 of [7]. Mortini proved in [10, Satz 4] the following Corona-Type Theorem in the Smirnov class. Given $f_1,\ldots ,f_n\in \mathcal {N}^+$ , the Bézout equation $f_1g_1+\cdots +f_ng_n\equiv 1$ can be solved with functions $g_1,\ldots ,g_n\in \mathcal {N}^+$ if and only if there exists $H\in QB_+(\mathbb {D})$ such that

$$ \begin{align*}\sum_{i=1}^n |f_i (z)| \geq e^{-H(z)}, \quad z \in \mathbb{D}. \end{align*} $$

Given an inner function I with zero set $\Lambda = \{\lambda _k \}$ , we want to study invertibility in the quotient algebra $\mathcal {N}^+/I\mathcal {N}^+$ . Let $f\in \mathcal {N}^+$ and assume that the class $[f]$ is invertible in $\mathcal {N}^+ \big / I\mathcal {N}^+$ , that is, there exist $g,h \in \mathcal {N}^+ $ such that $fg=1 + Ih$ . Then, there exists $H\in QB_+(\mathbb {D})$ such that

(4.1) $$ \begin{align} |f(\lambda_k)|\geq e^{-H(\lambda_k)}, \hspace{0.5cm} k=1,2,\ldots. \end{align} $$

We are interested on studying the converse statement. Observe that if I had a nonconstant singular inner factor, then for any $h \in \mathcal {N}^+$ , there would exist $\xi \in \partial \mathbb {D}$ such that $I(z)h(z)$ would tend to zero when z approaches $\xi $ nontangentially. Actually, let S be a nonconstant singular inner factor of I. Then, $\min \{|S(z)h(z)| : z \in \mathbb {D} \} =0$ , because otherwise S would be invertible in $\mathcal {N}^+$ . Hence, if I has a nonconstant singular inner factor, we cannot expect that condition (4.1) implies that $[f]$ is invertible in $\mathcal {N}^+ \big / I\mathcal {N}^+$ . When I is a Blaschke product, we have the following analogue of Theorem 1.1.

Theorem 4.1 Let B be a Blaschke product with zero set $\Lambda =(\lambda _k)_k$ .

1. (1) For any $C\in (0,1)$ , the following statement holds. Let $H\in QB_+ (\mathbb {D})$ , and assume that the function $-\log |B|$ has a quasibounded harmonic majorant on the set $\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ . Then, for any $f\in H^\infty $ , $||f||_\infty \leq 1$ such that

   $$ \begin{align*} |f(\lambda_k)|> e^{-CH(\lambda_k)}, \quad k=1,2, \ldots , \end{align*} $$
   there exist $g,h\in \mathcal {N}^+$ such that $fg=1+Bh$ .

2. (2) For any $C>1$ , there exists a constant $C_0>0$ such that the following statement holds. Let $H\in QB_+ (\mathbb {D})$ with $H\geq C_0 H_\Lambda $ . Assume that for any $f\in H^\infty $ , $||f||_\infty \leq 1$ such that

   $$ \begin{align*} |f(\lambda_k)|> e^{-CH(\lambda_k)}, \quad k=1,2, \ldots , \end{align*} $$
   there exist $g,h\in \mathcal {N}^+$ such that $fg=1+Bh$ . Then, the function $-\log |B|$ has a quasibounded harmonic majorant on the set $\{z\in \mathbb {D}\, : \rho (z,\Lambda )\geq e^{-H(z)}\}$ .

The proof is the same as that of Theorem 1.1, taking into account the fact that $H_\Lambda $ is a quasibounded positive harmonic function.

Hence, as in the case of the Nevanlinna class, the invertibility problem in $\mathcal {N}^+ / B \mathcal {N}^+$ roughly reduces to studying the set of functions $H\in QB_+ (\mathbb {D})$ such that $-\log |B|$ has a quasibounded harmonic majorant on the set $\{z\in \mathbb {D}\,:\rho (z,\Lambda )\geq e^{-H(z)}\}$ . So, given an inner function I with zero set $\Lambda $ , it is natural to consider the set $\mathcal {H}_{QB} (I)$ of functions $H\in QB_+ (\mathbb {D})$ such that $-\log |I|$ has a quasibounded harmonic majorant on the set $\{z\in \mathbb {D}\,:\rho (z,\Lambda )\geq e^{-H(z)}\}$ . Our next result says that if I has a nonconstant singular inner factor, then $\mathcal {H}_{QB} (I)$ does not contain large functions.

Lemma 4.2 Let I be an inner function with zero set $\Lambda $ and nonconstant singular inner factor S. Then, for any $H \in Har_+(\mathbb {D})$ with $H>H_\Lambda $ , the function $-\log |I|$ has no quasibounded harmonic majorant on the set $\{z\in \mathbb {D}\,:\rho (z,\Lambda )\geq e^{-H(z)}\}$ .

Proof We argue by contradiction. So assume that $H, H_1$ are quasibounded positive harmonic functions such that

(4.2) $$ \begin{align} - \log |S(z)| \leq - \log |I(z)| \leq H_1(z) \, \text{ if } \,\rho(z,\Lambda)\geq e^{-H(z)}. \end{align} $$

We want to show that $- \log |S(z)| \leq H_1(z) $ for any $z \in \mathbb {D}$ . Assume that $H(z)> 10$ . Let $N(z)$ be the number of points $\lambda \in \Lambda $ with $\rho (\lambda , z ) \leq e^{-H(z) / 10}$ . Note that in the pseudohyperbolic disc $\{w \in \mathbb {D} : \rho (w, z) \leq e^{-H(z) / 10} \}$ , there are at least $ e^{ C H(z) }$ pairwise disjoint pseudohyperbolic discs $\{D_j \}$ of pseudohyperbolic radius $ e^{- H(z) }$ . Here, $C>0$ denotes a small positive constant. We deduce that there exists $D_j$ such that $D_j \cap \Lambda = \emptyset $ . Otherwise, we would have a point of $\Lambda $ in each $D_j$ and then $N(z) \geq e^{C H(z)}$ which contradicts the assumption $H \geq H_\Lambda $ . Pick $\tilde z \in D_j$ , and note that $\rho (z, \tilde z) \leq e^{- H(z)/10}$ and $\rho (\tilde z , \Lambda ) \geq e^{- H(z)} $ . Hence, (4.2) gives

$$ \begin{align*}- \log |S(\tilde z)| \leq H_1(\tilde z). \end{align*} $$

By Harnack’s inequality, there exists an absolute constant $C>0$ such that $-\log |S(z)| \leq C H_1 (z)$ . Because $-\log |S|$ is the Poisson integral of a nontrivial singular measure on the unit circle, this is a contradiction.▪

If I has a nonconstant singular inner factor and finitely many or very sparse zeros, the set $\mathcal {H}_{QB} (I)$ is empty. On the other hand, if I satisfies the WEP, then $\mathcal {H}_{QB} (I)$ contains the constants. When I is a Blaschke product, $\mathcal {H}_{QB} (I)$ is the whole cone of positive quasiharmonic functions if and only if the zeros of I are a finite union of interpolating sequences in the Smirnov class. See [9]. We have not explored the analogues of our Theorems 1.1–1.5 for the class $\mathcal {H}_{QB} (B)$ .