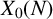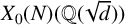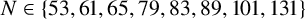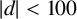1 Introduction
There has been a lot of recent interest in computing low-degree points on modular curves and, in particular, in computing quadratic points on the curves
![]() $X_0(N)$
. Computing such points gives much insight into the arithmetic of elliptic curves and has direct applications in the resolution of Diophantine equations (see [Reference Freitas and Siksek8, page 888] or [Reference Michaud-Jacobs10] for such examples).
$X_0(N)$
. Computing such points gives much insight into the arithmetic of elliptic curves and has direct applications in the resolution of Diophantine equations (see [Reference Freitas and Siksek8, page 888] or [Reference Michaud-Jacobs10] for such examples).
As we range over all quadratic fields, a curve
![]() $X_0(N)$
will either have finitely many or infinitely many quadratic points. For those curves
$X_0(N)$
will either have finitely many or infinitely many quadratic points. For those curves
![]() $X_0(N)$
that have finitely many quadratic points, these points have been computed in many cases, such as when the genus of
$X_0(N)$
that have finitely many quadratic points, these points have been computed in many cases, such as when the genus of
![]() $X_0(N)$
is
$X_0(N)$
is
![]() $\leq 5$
, or when
$\leq 5$
, or when
![]() $X_0(N)$
is bielliptic [Reference Box5, Reference Najman and Vukorepa12, Reference Ozman and Siksek14]. If
$X_0(N)$
is bielliptic [Reference Box5, Reference Najman and Vukorepa12, Reference Ozman and Siksek14]. If
![]() $X_0(N)$
has genus
$X_0(N)$
has genus
![]() $ \geq 2$
and has infinitely many quadratic points (so that
$ \geq 2$
and has infinitely many quadratic points (so that
![]() $X_0(N)$
is either hyperelliptic, or bielliptic with an elliptic quotient of positive rank over
$X_0(N)$
is either hyperelliptic, or bielliptic with an elliptic quotient of positive rank over
![]() $\mathbb {Q}$
), a geometric description of all the quadratic points has been given in these cases [Reference Box5, Reference Bruin and Najman6, Reference Najman and Vukorepa12].
$\mathbb {Q}$
), a geometric description of all the quadratic points has been given in these cases [Reference Box5, Reference Bruin and Najman6, Reference Najman and Vukorepa12].
There are precisely
![]() $10$
values of N such that the modular curve
$10$
values of N such that the modular curve
![]() $X_0(N)$
is bielliptic with an elliptic quotient of positive rank [Reference Bars3, pages 26–28]. For two of these values of N, namely
$X_0(N)$
is bielliptic with an elliptic quotient of positive rank [Reference Bars3, pages 26–28]. For two of these values of N, namely
![]() $37$
and
$37$
and
![]() $43$
, the methods we present will not work (see Remark 2.2), and so we will consider the remaining eight values of N, which are
$43$
, the methods we present will not work (see Remark 2.2), and so we will consider the remaining eight values of N, which are
For each
![]() $N \in \mathcal {N}$
, the elliptic curve
$N \in \mathcal {N}$
, the elliptic curve
![]() $X_0^+(N) = X_0(N) / w_N$
has rank
$X_0^+(N) = X_0(N) / w_N$
has rank
![]() $1$
over
$1$
over
![]() $\mathbb {Q}$
. In [Reference Box5, Reference Najman and Vukorepa12], it is proven that every quadratic point on
$\mathbb {Q}$
. In [Reference Box5, Reference Najman and Vukorepa12], it is proven that every quadratic point on
![]() $X_0(N)$
arises as the pullback of a rational point on
$X_0(N)$
arises as the pullback of a rational point on
![]() $X_0^+(N)$
(via the natural degree
$X_0^+(N)$
(via the natural degree
![]() $2$
quotient map). However, this classification does not describe
$2$
quotient map). However, this classification does not describe
![]() $X_0(N)(K)$
for a given quadratic field K. The purpose of this paper is to introduce a Mordell–Weil sieve that can be used to check, for
$X_0(N)(K)$
for a given quadratic field K. The purpose of this paper is to introduce a Mordell–Weil sieve that can be used to check, for
![]() $N \in \mathcal {N}$
, whether
$N \in \mathcal {N}$
, whether
![]() $X_0(N)(K) = X_0(N)(\mathbb {Q})$
for a given quadratic field K. The sieve uses information on the splitting behaviour of primes in K together with the structure of the Mordell–Weil group of
$X_0(N)(K) = X_0(N)(\mathbb {Q})$
for a given quadratic field K. The sieve uses information on the splitting behaviour of primes in K together with the structure of the Mordell–Weil group of
![]() $X_0^+(N)(\mathbb {Q})$
modulo these primes. The sieve builds on ideas present in the author’s work in [Reference Michaud-Jacobs10, pages 338–340]. We prove the following result.
$X_0^+(N)(\mathbb {Q})$
modulo these primes. The sieve builds on ideas present in the author’s work in [Reference Michaud-Jacobs10, pages 338–340]. We prove the following result.
Theorem 1.1. Let
![]() $N \in \{53,61,65,79,83,89,101,131\}$
and let
$N \in \{53,61,65,79,83,89,101,131\}$
and let
![]() $d \in \mathbb {Z}$
such that
$d \in \mathbb {Z}$
such that
![]() ${\lvert d \rvert < 100}$
. Then,
${\lvert d \rvert < 100}$
. Then,
![]() $X_0(N)(\mathbb {Q}(\sqrt {d})) \ne X_0(N)(\mathbb {Q})$
if and only if
$X_0(N)(\mathbb {Q}(\sqrt {d})) \ne X_0(N)(\mathbb {Q})$
if and only if
![]() $d \in \mathcal {D}_N$
, where
$d \in \mathcal {D}_N$
, where
 $$ \begin{align*} \mathcal{D}_{53} & = \{ -43, -11, -7, -1 \}, \\ \mathcal{D}_{61} & = \{ -19, -3, -1, 61 \}, \\ \mathcal{D}_{65} & = \{ -79, -1 \}, \\ \mathcal{D}_{79} & = \{ -43, -7, -3 \}, \\ \mathcal{D}_{83} & = \{ -67, -43, -19, -2 \}, \\ \mathcal{D}_{89} & = \{ -67, -11, -2, -1, 89 \}, \\ \mathcal{D}_{101} & = \{ -43, -19, -1 \}, \\ \mathcal{D}_{131} & = \{ -67, -19, -2 \}. \end{align*} $$
$$ \begin{align*} \mathcal{D}_{53} & = \{ -43, -11, -7, -1 \}, \\ \mathcal{D}_{61} & = \{ -19, -3, -1, 61 \}, \\ \mathcal{D}_{65} & = \{ -79, -1 \}, \\ \mathcal{D}_{79} & = \{ -43, -7, -3 \}, \\ \mathcal{D}_{83} & = \{ -67, -43, -19, -2 \}, \\ \mathcal{D}_{89} & = \{ -67, -11, -2, -1, 89 \}, \\ \mathcal{D}_{101} & = \{ -43, -19, -1 \}, \\ \mathcal{D}_{131} & = \{ -67, -19, -2 \}. \end{align*} $$
Although we have considered integers d satisfying
![]() $\lvert d \rvert < 100$
here, there are no apparent obstructions to proving analogous results for any integer d.
$\lvert d \rvert < 100$
here, there are no apparent obstructions to proving analogous results for any integer d.
For certain (but not all) integers d, the results of Theorem 1.1 could be achieved by applying [Reference Ozman13, Theorem 1.1] or some of the techniques described in [Reference Banwait, Najman and Padurariu2]. In Section 3, we compare (for
![]() $N = 53$
) our results with those one can obtain by applying [Reference Ozman13, Theorem 1.1], and use this to provide an example of a curve that violates the Hasse principle.
$N = 53$
) our results with those one can obtain by applying [Reference Ozman13, Theorem 1.1], and use this to provide an example of a curve that violates the Hasse principle.
We note that results of a similar nature to Theorem 1.1 (obtained using different techniques) are proven in [Reference Najman and Trbović11] for hyperelliptic curves
![]() $X_0(N)$
.
$X_0(N)$
.
The Magma [Reference Bosma, Cannon and Playoust4] code used to support the computations in this paper is available at https://github.com/michaud-jacobs/bielliptic.
2 A Mordell–Weil sieve
In this section, we present a Mordell–Weil sieve and apply it to prove Theorem 1.1.
We first describe how to obtain a suitable model for
![]() $X_0(N)$
for
$X_0(N)$
for
![]() $N \in \mathcal {N}$
. Let g denote the genus of the modular curve
$N \in \mathcal {N}$
. Let g denote the genus of the modular curve
![]() $X_0(N)$
. We start by computing a basis
$X_0(N)$
. We start by computing a basis
![]() $f_1, \ldots , f_g$
of cusp forms for
$f_1, \ldots , f_g$
of cusp forms for
![]() $S_2(\Gamma _0(N))$
with integer Fourier coefficients such that the Atkin–Lehner involution
$S_2(\Gamma _0(N))$
with integer Fourier coefficients such that the Atkin–Lehner involution
![]() $w_N$
satisfies
$w_N$
satisfies
![]() $w_N(f_1) = f_1$
and
$w_N(f_1) = f_1$
and
![]() $w_N(f_i) = -f_i$
for
$w_N(f_i) = -f_i$
for
![]() $2 \leq i \leq g$
(we refer to such a basis as a diagonalised basis). For each
$2 \leq i \leq g$
(we refer to such a basis as a diagonalised basis). For each
![]() $N \in \mathcal {N}$
, the curve
$N \in \mathcal {N}$
, the curve
![]() $X_0(N)$
is nonhyperelliptic of genus
$X_0(N)$
is nonhyperelliptic of genus
![]() $>2$
and we may obtain a nonsingular model for
$>2$
and we may obtain a nonsingular model for
![]() $X_0(N)$
over
$X_0(N)$
over
![]() $\mathbb {Q}$
in
$\mathbb {Q}$
in
![]() $\mathbb {P}^{g-1}_{x_1, \ldots , x_g}$
as the image of the canonical embedding on the cusp forms
$\mathbb {P}^{g-1}_{x_1, \ldots , x_g}$
as the image of the canonical embedding on the cusp forms
![]() $f_1, \ldots , f_g$
. The details of this (standard) procedure are described in [Reference Galbraith9, pages 17–38], and the Magma code we used to do this is adapted from [Reference Ozman and Siksek14].
$f_1, \ldots , f_g$
. The details of this (standard) procedure are described in [Reference Galbraith9, pages 17–38], and the Magma code we used to do this is adapted from [Reference Ozman and Siksek14].
With this procedure, the Atkin–Lehner involution
![]() $w_N$
on this model is given by the map
$w_N$
on this model is given by the map
![]() $(x_1 : x_2 : \cdots : x_g) \mapsto (-x_1 : x_2 : \cdots : x_g)$
. We denote by
$(x_1 : x_2 : \cdots : x_g) \mapsto (-x_1 : x_2 : \cdots : x_g)$
. We denote by
![]() $ \psi : X_0(N) \rightarrow X_0^+(N) $
the degree
$ \psi : X_0(N) \rightarrow X_0^+(N) $
the degree
![]() $2$
map induced by quotienting by
$2$
map induced by quotienting by
![]() $w_N$
. In each case, we found that the projection map onto the coordinates
$w_N$
. In each case, we found that the projection map onto the coordinates
![]() $x_2, \ldots , x_g$
had degree
$x_2, \ldots , x_g$
had degree
![]() $2$
and image
$2$
and image
![]() $X_0^+(N)$
(and not some quotient of
$X_0^+(N)$
(and not some quotient of
![]() $X_0^+(N)$
), so that the map
$X_0^+(N)$
), so that the map
![]() $\psi $
is given by
$\psi $
is given by
 $$ \begin{align*} \psi : X_0(N) & \longrightarrow X_0^+(N) \\ (x_1 : x_2 : \cdots : x_g) & \longmapsto (x_2 : \cdots : x_g). \end{align*} $$
$$ \begin{align*} \psi : X_0(N) & \longrightarrow X_0^+(N) \\ (x_1 : x_2 : \cdots : x_g) & \longmapsto (x_2 : \cdots : x_g). \end{align*} $$
In fact, we then obtained a Weierstrass model for
![]() $X_0^+(N)$
and composed
$X_0^+(N)$
and composed
![]() $\psi $
with this transformation (see the example in Section 3). The reason for using a diagonalised model for
$\psi $
with this transformation (see the example in Section 3). The reason for using a diagonalised model for
![]() $X_0(N)$
is twofold. First, it forces the coordinates of a quadratic point to be of a certain shape, as we see below. Second, it greatly speeds up the computations we perform in the sieving step.
$X_0(N)$
is twofold. First, it forces the coordinates of a quadratic point to be of a certain shape, as we see below. Second, it greatly speeds up the computations we perform in the sieving step.
Let
![]() $K = \mathbb {Q}(\sqrt {d})$
be a quadratic field and write
$K = \mathbb {Q}(\sqrt {d})$
be a quadratic field and write
![]() $\sigma $
for the generator of
$\sigma $
for the generator of
![]() $\mathrm {Gal}(K/\mathbb {Q})$
. Suppose that
$\mathrm {Gal}(K/\mathbb {Q})$
. Suppose that
![]() $P \in X_0(N)(K) \backslash X_0(N)(\mathbb {Q})$
(equivalently, P is a noncuspidal quadratic point). In projective coordinates, we may write
$P \in X_0(N)(K) \backslash X_0(N)(\mathbb {Q})$
(equivalently, P is a noncuspidal quadratic point). In projective coordinates, we may write
 $$ \begin{align*} P & = (a_1 + b_1\sqrt{d} : a_2 + b_2 \sqrt{d} : \cdots : a_g + b_g \sqrt{d}), \\ w_N(P) & = (-a_1 - b_1\sqrt{d} : a_2 + b_2\sqrt{d} : \cdots : a_g + b_g \sqrt{d}), \quad\text{and} \\ P^\sigma & = (a_1 - b_1\sqrt{d} : a_2 - b_2 \sqrt{d} : \cdots : a_g - b_g \sqrt{d}), \end{align*} $$
$$ \begin{align*} P & = (a_1 + b_1\sqrt{d} : a_2 + b_2 \sqrt{d} : \cdots : a_g + b_g \sqrt{d}), \\ w_N(P) & = (-a_1 - b_1\sqrt{d} : a_2 + b_2\sqrt{d} : \cdots : a_g + b_g \sqrt{d}), \quad\text{and} \\ P^\sigma & = (a_1 - b_1\sqrt{d} : a_2 - b_2 \sqrt{d} : \cdots : a_g - b_g \sqrt{d}), \end{align*} $$
where
![]() $a_i, b_i \in \mathbb {Z}$
for
$a_i, b_i \in \mathbb {Z}$
for
![]() $1 \leq i \leq g$
.
$1 \leq i \leq g$
.
As discussed in the introduction, thanks to the work of Box, and Najman and Vukorepa in [Reference Box5, Reference Najman and Vukorepa12], we know that
![]() $\psi (P) = \psi (P^\sigma ) \in X_0^+(N)(\mathbb {Q})$
, or equivalently,
$\psi (P) = \psi (P^\sigma ) \in X_0^+(N)(\mathbb {Q})$
, or equivalently,
![]() ${w_N(P) = P^\sigma }$
. It follows that
${w_N(P) = P^\sigma }$
. It follows that
with
![]() $b_1 \neq 0$
, and we may assume that
$b_1 \neq 0$
, and we may assume that
![]() $\gcd (b_1,a_2, \ldots , a_g) = 1$
by rescaling if necessary.
$\gcd (b_1,a_2, \ldots , a_g) = 1$
by rescaling if necessary.
We now present the sieve in the case that
![]() $N \neq 65$
. In the case where
$N \neq 65$
. In the case where
![]() $N = 65$
, we will need to adapt the sieve slightly, and we discuss this case in the proof of Theorem 1.1. For each
$N = 65$
, we will need to adapt the sieve slightly, and we discuss this case in the proof of Theorem 1.1. For each
![]() $N \neq 65$
, we have
$N \neq 65$
, we have
![]() $X_0^+(N)(\mathbb {Q}) \cong \mathbb {Z}$
, and we let R denote a generator of the Mordell–Weil group, so that
$X_0^+(N)(\mathbb {Q}) \cong \mathbb {Z}$
, and we let R denote a generator of the Mordell–Weil group, so that
Let
![]() $\ell $
be a prime of good reduction for our models of
$\ell $
be a prime of good reduction for our models of
![]() $X_0(N)$
and
$X_0(N)$
and
![]() $X_0^+(N)$
, and consider the following commutative diagram, where
$X_0^+(N)$
, and consider the following commutative diagram, where
![]() $\sim $
denotes reduction mod
$\sim $
denotes reduction mod
![]() $\ell $
, or a prime of K above
$\ell $
, or a prime of K above
![]() $\ell $
:
$\ell $
:

By commutativity,
![]() $\psi _\ell (\widetilde {P}) = m \cdot \widetilde {R}$
, so that
$\psi _\ell (\widetilde {P}) = m \cdot \widetilde {R}$
, so that
![]() $\widetilde {P} \in \psi _\ell ^{-1}(m \cdot \widetilde {R})$
. Write
$\widetilde {P} \in \psi _\ell ^{-1}(m \cdot \widetilde {R})$
. Write
![]() $G_\ell $
for the order of
$G_\ell $
for the order of
![]() $\widetilde {R}$
in the group
$\widetilde {R}$
in the group
![]() $\widetilde {X}_0^+(N)(\mathbb {F}_\ell )$
. Then,
$\widetilde {X}_0^+(N)(\mathbb {F}_\ell )$
. Then,
for some integer
![]() $m_0$
satisfying
$m_0$
satisfying
![]() $0 \leq m_0 < G_\ell $
and
$0 \leq m_0 < G_\ell $
and
![]() $m \equiv m_0 \pmod {G_\ell }$
. We note that
$m \equiv m_0 \pmod {G_\ell }$
. We note that
![]() $\psi _\ell ^{-1}(m \cdot \widetilde {R}) = \psi _\ell ^{-1}(m_0 \cdot \widetilde {R})$
. For each integer
$\psi _\ell ^{-1}(m \cdot \widetilde {R}) = \psi _\ell ^{-1}(m_0 \cdot \widetilde {R})$
. For each integer
![]() $m_1$
with
$m_1$
with
![]() $0 \leq m_1 < G_\ell $
, we explicitly compute the set
$0 \leq m_1 < G_\ell $
, we explicitly compute the set
![]() $\psi _\ell ^{-1}(m_1 \cdot \widetilde {R}) \subset \widetilde {X}_0(N)(\mathbb {F}_{\ell ^2})$
. There are three cases.
$\psi _\ell ^{-1}(m_1 \cdot \widetilde {R}) \subset \widetilde {X}_0(N)(\mathbb {F}_{\ell ^2})$
. There are three cases.
-
(i) The set
 $\psi _\ell ^{-1}(m_1 \cdot \widetilde {R})$
consists of a pair of distinct points defined over
$\psi _\ell ^{-1}(m_1 \cdot \widetilde {R})$
consists of a pair of distinct points defined over
 $\mathbb {F}_\ell $
.
$\mathbb {F}_\ell $
.If
 $\ell $
is inert or ramifies in K, then
$\ell $
is inert or ramifies in K, then
 $\psi _\ell ^{-1}(m \cdot \widetilde {R})$
will not consist of a pair of distinct points defined over
$\psi _\ell ^{-1}(m \cdot \widetilde {R})$
will not consist of a pair of distinct points defined over
 $\mathbb {F}_{\ell }$
, and so
$\mathbb {F}_{\ell }$
, and so
 $ m \not \equiv m_1 \pmod {G_\ell }$
.
$ m \not \equiv m_1 \pmod {G_\ell }$
. -
(ii) The set
 $\psi _\ell ^{-1}(m_1 \cdot \widetilde {R})$
consists of a pair of points defined over
$\psi _\ell ^{-1}(m_1 \cdot \widetilde {R})$
consists of a pair of points defined over
 $\mathbb {F}_{\ell ^2}$
(with each point not defined over
$\mathbb {F}_{\ell ^2}$
(with each point not defined over
 $\mathbb {F}_\ell $
).
$\mathbb {F}_\ell $
).If
 $\ell $
splits or ramifies in K, then
$\ell $
splits or ramifies in K, then
 $\psi _\ell ^{-1}(m \cdot \widetilde {R})$
will not consist of a pair of points defined over
$\psi _\ell ^{-1}(m \cdot \widetilde {R})$
will not consist of a pair of points defined over
 $\mathbb {F}_{\ell ^2}$
, and so
$\mathbb {F}_{\ell ^2}$
, and so
 $ m \not \equiv m_1 \pmod {G_\ell }$
.
$ m \not \equiv m_1 \pmod {G_\ell }$
. -
(iii) The set
 $\psi _\ell ^{-1}(m_1 \cdot \widetilde {R})$
consists of a single point defined over
$\psi _\ell ^{-1}(m_1 \cdot \widetilde {R})$
consists of a single point defined over
 $\mathbb {F}_\ell $
.
$\mathbb {F}_\ell $
.
Verifying the splitting behaviour of the prime
![]() $\ell $
in cases (i) and (ii) leaves us with a list of possible values for
$\ell $
in cases (i) and (ii) leaves us with a list of possible values for
![]() $m \pmod {G_\ell }$
.
$m \pmod {G_\ell }$
.
We may then repeat this process with a list of primes
![]() $\ell _1, \ldots , \ell _s$
. For each i with
$\ell _1, \ldots , \ell _s$
. For each i with
![]() $1 \leq i \leq s$
, we obtain a list of possibilities for
$1 \leq i \leq s$
, we obtain a list of possibilities for
![]() $m \pmod {G_{\ell _i}}$
. This gives a system of congruences that we may solve using the Chinese remainder theorem to obtain a list of possibilities for
$m \pmod {G_{\ell _i}}$
. This gives a system of congruences that we may solve using the Chinese remainder theorem to obtain a list of possibilities for
![]() $m \pmod {\mathrm {lcm}(G_{\ell _i})_{1 \leq i \leq s)}}$
. If no solution exists to this system of congruences, then we obtain a contradiction and conclude that
$m \pmod {\mathrm {lcm}(G_{\ell _i})_{1 \leq i \leq s)}}$
. If no solution exists to this system of congruences, then we obtain a contradiction and conclude that
![]() $X_0(N)(K) = X_0(N)(\mathbb {Q})$
.
$X_0(N)(K) = X_0(N)(\mathbb {Q})$
.
Proof of Theorem 1.1 for
 $N \ne 65$
.
$N \ne 65$
.
Let
![]() $N \in \mathcal {N} \backslash \{65\}$
. We start by proving that if
$N \in \mathcal {N} \backslash \{65\}$
. We start by proving that if
![]() $d \in \mathcal {D}_N$
, then
$d \in \mathcal {D}_N$
, then
![]() $X_0(N)(\mathbb {Q}(\sqrt {d})) \ne X_0(N)(\mathbb {Q})$
. We computed the preimages
$X_0(N)(\mathbb {Q}(\sqrt {d})) \ne X_0(N)(\mathbb {Q})$
. We computed the preimages
![]() $\psi ^{-1}(t \cdot R)$
for
$\psi ^{-1}(t \cdot R)$
for
![]() $t \in \mathbb {Z}$
with
$t \in \mathbb {Z}$
with
![]() $\lvert t \rvert \leq 5$
and verified the field of definition of the points we obtained. For each
$\lvert t \rvert \leq 5$
and verified the field of definition of the points we obtained. For each
![]() $d \in \mathcal {D}_N$
, we found a pair of quadratic points in
$d \in \mathcal {D}_N$
, we found a pair of quadratic points in
![]() $X_0(N)(\mathbb {Q}(\sqrt {d}))$
.
$X_0(N)(\mathbb {Q}(\sqrt {d}))$
.
For the converse, we suppose that
![]() $\lvert d \rvert < 100$
with
$\lvert d \rvert < 100$
with
![]() $d \notin \mathcal {D}_N$
and aim to prove that
$d \notin \mathcal {D}_N$
and aim to prove that
![]() $X_0(N)(\mathbb {Q}(\sqrt {d})) = X_0(N)(\mathbb {Q})$
. We note that this is immediate if
$X_0(N)(\mathbb {Q}(\sqrt {d})) = X_0(N)(\mathbb {Q})$
. We note that this is immediate if
![]() $\mathbb {Q}(\sqrt {d}) = \mathbb {Q}$
, so we assume that
$\mathbb {Q}(\sqrt {d}) = \mathbb {Q}$
, so we assume that
![]() $\mathbb {Q}(\sqrt {d})$
is a quadratic field. Suppose, for a contradiction, that
$\mathbb {Q}(\sqrt {d})$
is a quadratic field. Suppose, for a contradiction, that
![]() ${P \in X_0(N)(\mathbb {Q}(\sqrt {d})) \backslash X_0(N)(\mathbb {Q})}$
. We applied the Mordell–Weil sieve described above with the following (ordered) choice of primes (we discuss this choice in Remark 2.1):
${P \in X_0(N)(\mathbb {Q}(\sqrt {d})) \backslash X_0(N)(\mathbb {Q})}$
. We applied the Mordell–Weil sieve described above with the following (ordered) choice of primes (we discuss this choice in Remark 2.1):
In each case, this led to a contradiction.
Proof of Theorem 1.1 for
 $N = 65$
.
$N = 65$
.
The proof of the theorem in this case is very similar to the case where
![]() $N \neq 65$
. The key difference is that
$N \neq 65$
. The key difference is that
![]() $X_0^+(N)(\mathbb {Q}) \cong \mathbb {Z} \oplus \mathbb {Z} / 2\mathbb {Z}$
. We write Q for the
$X_0^+(N)(\mathbb {Q}) \cong \mathbb {Z} \oplus \mathbb {Z} / 2\mathbb {Z}$
. We write Q for the
![]() $2$
-torsion point and choose a point R such that any point in
$2$
-torsion point and choose a point R such that any point in
![]() $X_0^+(N)(\mathbb {Q})$
may be expressed as
$X_0^+(N)(\mathbb {Q})$
may be expressed as
![]() $m \cdot R + n \cdot Q$
for some
$m \cdot R + n \cdot Q$
for some
![]() $m \in \mathbb {Z}$
and
$m \in \mathbb {Z}$
and
![]() $n = 0$
or
$n = 0$
or
![]() $1$
. For our choice of R, we found that
$1$
. For our choice of R, we found that
![]() $\psi ^{-1}(-R)$
and
$\psi ^{-1}(-R)$
and
![]() $\psi ^{-1}(-2R)$
consisted of pairs of quadratic points defined over
$\psi ^{-1}(-2R)$
consisted of pairs of quadratic points defined over
![]() $\mathbb {Q}(\sqrt {-1})$
and
$\mathbb {Q}(\sqrt {-1})$
and
![]() $\mathbb {Q}(\sqrt {-79})$
, respectively, proving one direction of the theorem.
$\mathbb {Q}(\sqrt {-79})$
, respectively, proving one direction of the theorem.
For the converse, let
![]() $d \notin \mathcal {D}_N$
be such that
$d \notin \mathcal {D}_N$
be such that
![]() $\mathbb {Q}(\sqrt {d})$
is a quadratic field and
$\mathbb {Q}(\sqrt {d})$
is a quadratic field and
![]() $\lvert d \rvert < 100$
. Suppose, for a contradiction, that there exists a point
$\lvert d \rvert < 100$
. Suppose, for a contradiction, that there exists a point
![]() $P \in X_0(N)(\mathbb {Q}(\sqrt {d})) \backslash X_0(N)(\mathbb {Q})$
. Either
$P \in X_0(N)(\mathbb {Q}(\sqrt {d})) \backslash X_0(N)(\mathbb {Q})$
. Either
![]() $\psi (P) = m \cdot R$
or
$\psi (P) = m \cdot R$
or
![]() $m \cdot R + Q$
. In the first case, we apply the sieve exactly as in the proof for
$m \cdot R + Q$
. In the first case, we apply the sieve exactly as in the proof for
![]() $N \neq 65$
(with the same choice of primes) to achieve a contradiction. In the second case, we again apply the sieve in the same way, except that we work with the point
$N \neq 65$
(with the same choice of primes) to achieve a contradiction. In the second case, we again apply the sieve in the same way, except that we work with the point
![]() $m \cdot R + Q$
instead. To be precise, for each prime
$m \cdot R + Q$
instead. To be precise, for each prime
![]() $\ell $
, we have
$\ell $
, we have
![]() $\widetilde {P} \in \psi _\ell ^{-1}(m \cdot \widetilde {R} + \widetilde {Q})$
, and so we compute
$\widetilde {P} \in \psi _\ell ^{-1}(m \cdot \widetilde {R} + \widetilde {Q})$
, and so we compute
![]() $\psi _\ell ^{-1}(m_1 \cdot \widetilde {R} + \widetilde {Q})$
for
$\psi _\ell ^{-1}(m_1 \cdot \widetilde {R} + \widetilde {Q})$
for
![]() $0 \leq m_1 < G_\ell $
. By considering each preimage and the splitting behaviour of
$0 \leq m_1 < G_\ell $
. By considering each preimage and the splitting behaviour of
![]() $\ell $
in the quadratic field
$\ell $
in the quadratic field
![]() $\mathbb {Q}(\sqrt {d})$
, we obtain a list of possibilities for
$\mathbb {Q}(\sqrt {d})$
, we obtain a list of possibilities for
![]() $m \pmod {G_\ell }$
. As in the previous case, we achieved a contradiction for each d.
$m \pmod {G_\ell }$
. As in the previous case, we achieved a contradiction for each d.
The total computation time for the proof of Theorem 1.1 was 2500 seconds running on a 2200 MHz AMD Opteron.
Remark 2.1. We discuss the choice of primes
![]() $\mathcal {L}$
used in the proof of the theorem. We start by choosing the primes that ramify as these usually eliminate the greatest number of possibilities for
$\mathcal {L}$
used in the proof of the theorem. We start by choosing the primes that ramify as these usually eliminate the greatest number of possibilities for
![]() $m \pmod {G_\ell }$
. We then choose primes
$m \pmod {G_\ell }$
. We then choose primes
![]() $\ell $
such that the values
$\ell $
such that the values
![]() $G_\ell $
are small and share many prime factors. There are two reasons for doing this. First, when solving each system of congruences, we are more likely to obtain fewer solutions and ultimately a contradiction. Second, we avoid (or reduce the likelihood) of a combinatorial explosion, since the lowest common multiple of the
$G_\ell $
are small and share many prime factors. There are two reasons for doing this. First, when solving each system of congruences, we are more likely to obtain fewer solutions and ultimately a contradiction. Second, we avoid (or reduce the likelihood) of a combinatorial explosion, since the lowest common multiple of the
![]() $G_\ell $
can grow very quickly if the primes
$G_\ell $
can grow very quickly if the primes
![]() $\ell $
are not chosen carefully. We note that the largest prime
$\ell $
are not chosen carefully. We note that the largest prime
![]() $\ell $
we in fact ended up reaching was
$\ell $
we in fact ended up reaching was
![]() $\ell = 593$
in the case where
$\ell = 593$
in the case where
![]() $N = 101$
and
$N = 101$
and
![]() $d = 31$
.
$d = 31$
.
Remark 2.2. As discussed in the introduction, we have not considered the curves
![]() $X_0(37)$
or
$X_0(37)$
or
![]() $X_0(43)$
. The curve
$X_0(43)$
. The curve
![]() $X_0(37)$
is bielliptic with an elliptic quotient of positive rank, but it is also hyperelliptic, and therefore has two sources of infinitely many quadratic points, meaning the sieve we have presented would not work. The reason the sieve does not work for the curve
$X_0(37)$
is bielliptic with an elliptic quotient of positive rank, but it is also hyperelliptic, and therefore has two sources of infinitely many quadratic points, meaning the sieve we have presented would not work. The reason the sieve does not work for the curve
![]() $X_0(43)$
is due to the fact that
$X_0(43)$
is due to the fact that
![]() $X_0(43)$
has a noncuspidal rational point that is fixed by the Atkin–Lehner involution
$X_0(43)$
has a noncuspidal rational point that is fixed by the Atkin–Lehner involution
![]() $w_{43}$
. The sieve cannot distinguish between this rational point and a putative quadratic point.
$w_{43}$
. The sieve cannot distinguish between this rational point and a putative quadratic point.
Although we have presented this sieve for certain specific bielliptic modular curves
![]() $X_0(N)$
, the sieve could be suitably adapted to compute quadratic points on a wider range of curves. Indeed, it should even be possible to apply a similar sieve to compute quadratic points on any curve X with a degree
$X_0(N)$
, the sieve could be suitably adapted to compute quadratic points on a wider range of curves. Indeed, it should even be possible to apply a similar sieve to compute quadratic points on any curve X with a degree
![]() $2$
quotient of genus
$2$
quotient of genus
![]() $\geq 1$
, if there are finitely many quadratic points on X not arising as pullbacks of rational points on this quotient, and that these have all been computed. Although, as in the
$\geq 1$
, if there are finitely many quadratic points on X not arising as pullbacks of rational points on this quotient, and that these have all been computed. Although, as in the
![]() $X_0(43)$
case discussed above, there may be obstructions to the sieving process succeeding.
$X_0(43)$
case discussed above, there may be obstructions to the sieving process succeeding.
3 Example computations
In this section, we provide some details of computations in the case where
![]() $N = 53$
. We start by obtaining a model for the genus
$N = 53$
. We start by obtaining a model for the genus
![]() $4$
curve
$4$
curve
![]() $X_0(53)$
on which the Atkin–Lehner involution acts diagonally. By searching for relations between a diagonalised basis of cusp forms, we obtain the following model in
$X_0(53)$
on which the Atkin–Lehner involution acts diagonally. By searching for relations between a diagonalised basis of cusp forms, we obtain the following model in
![]() $\mathbb {P}^3_{x_1,x_2,x_3,x_4}$
:
$\mathbb {P}^3_{x_1,x_2,x_3,x_4}$
:
 $$ \begin{align*} & x_1^2 - x_2^2 + 2x_2x_3 - 6x_2x_4 + 11x_3^2 - 6x_3x_4 - x_4^2 = 0, \\ & x_1^3 - x_1x_2^2 + 2x_1x_2x_3 - 6x_1x_2x_4 + 11x_1x_3^2 - 6x_1x_3x_4 - x_1x_4^2 = 0, \\ & x_1^2x_2 - x_2^3 + 2x_2^2x_3 + 5x_2x_3^2 + 5x_2x_4^2 - 6x_3^2x_4 + 6x_4^3 = 0, \\ & x_1^2x_3 - x_2^2x_3 + 2x_2x_3^2 - 6x_2x_3x_4 + 11x_3^3 - 6x_3^2x_4 - x_3x_4^2 = 0, \\ & x_1^2x_4 - x_2x_3^2 + 3x_2x_3x_4 - 5x_2x_4^2 + 10x_3^2x_4 - 6x_3x_4^2 = 0, \\ & x_2^2x_4 - x_2x_3^2 + x_2x_3x_4 + x_2x_4^2 - x_3^2x_4 + x_4^3 = 0. \end{align*} $$
$$ \begin{align*} & x_1^2 - x_2^2 + 2x_2x_3 - 6x_2x_4 + 11x_3^2 - 6x_3x_4 - x_4^2 = 0, \\ & x_1^3 - x_1x_2^2 + 2x_1x_2x_3 - 6x_1x_2x_4 + 11x_1x_3^2 - 6x_1x_3x_4 - x_1x_4^2 = 0, \\ & x_1^2x_2 - x_2^3 + 2x_2^2x_3 + 5x_2x_3^2 + 5x_2x_4^2 - 6x_3^2x_4 + 6x_4^3 = 0, \\ & x_1^2x_3 - x_2^2x_3 + 2x_2x_3^2 - 6x_2x_3x_4 + 11x_3^3 - 6x_3^2x_4 - x_3x_4^2 = 0, \\ & x_1^2x_4 - x_2x_3^2 + 3x_2x_3x_4 - 5x_2x_4^2 + 10x_3^2x_4 - 6x_3x_4^2 = 0, \\ & x_2^2x_4 - x_2x_3^2 + x_2x_3x_4 + x_2x_4^2 - x_3^2x_4 + x_4^3 = 0. \end{align*} $$
The equations for the Atkin–Lehner involution on this particular model are given by
![]() $w_{53} : (x_1 : x_2 : x_3 : x_4) \mapsto (-x_1 : x_2 : x_3 : x_4)$
. The degree
$w_{53} : (x_1 : x_2 : x_3 : x_4) \mapsto (-x_1 : x_2 : x_3 : x_4)$
. The degree
![]() $2$
map to the elliptic curve
$2$
map to the elliptic curve
![]() $X_0^+(53)$
is then simply given by the projection map
$X_0^+(53)$
is then simply given by the projection map
![]() $(x_1 : x_2 : x_3 : x_4) \mapsto (x_2 : x_3 : x_4)$
. We then apply a transformation to take the image of this projection map to the following Weierstrass form:
$(x_1 : x_2 : x_3 : x_4) \mapsto (x_2 : x_3 : x_4)$
. We then apply a transformation to take the image of this projection map to the following Weierstrass form:
The map
![]() $\psi $
is given by
$\psi $
is given by
 $$ \begin{align*} \psi: X_0(53) & \longrightarrow X_0^+(53) \\ (x_1 : x_2 : x_3 : x_4) & \longmapsto (x_2x_3 + x_3x_4 : x_2^2 + x_2x_4 - x_3x_4 + x_4^2 : x_3x_4). \end{align*} $$
$$ \begin{align*} \psi: X_0(53) & \longrightarrow X_0^+(53) \\ (x_1 : x_2 : x_3 : x_4) & \longmapsto (x_2x_3 + x_3x_4 : x_2^2 + x_2x_4 - x_3x_4 + x_4^2 : x_3x_4). \end{align*} $$
We choose
![]() $R = (0 : -1 : 1) \in X_0^+(53)(\mathbb {Q})$
as a generator of the Mordell–Weil group.
$R = (0 : -1 : 1) \in X_0^+(53)(\mathbb {Q})$
as a generator of the Mordell–Weil group.
We now exhibit some steps in the sieving process for
![]() $d = -47$
. As in the previous section, we will assume that
$d = -47$
. As in the previous section, we will assume that
![]() $P \in X_0(53)(\mathbb {Q}(\sqrt {d})) \backslash X_0(53)(\mathbb {Q})$
and write
$P \in X_0(53)(\mathbb {Q}(\sqrt {d})) \backslash X_0(53)(\mathbb {Q})$
and write
![]() $\psi (P) = m \cdot R$
. We apply the sieve with the primes
$\psi (P) = m \cdot R$
. We apply the sieve with the primes
![]() $ \ell = 5,7$
and
$ \ell = 5,7$
and
![]() $11$
. The prime
$11$
. The prime
![]() $\ell = 5$
is inert in
$\ell = 5$
is inert in
![]() $\mathbb {Q}(\sqrt {d})$
and we find that
$\mathbb {Q}(\sqrt {d})$
and we find that
![]() $m \equiv 3$
or
$m \equiv 3$
or
![]() $5 \pmod {6}$
. Next,
$5 \pmod {6}$
. Next,
![]() $\ell = 7$
splits and we find that
$\ell = 7$
splits and we find that
![]() $m \equiv 0, 3, 4, 7$
or
$m \equiv 0, 3, 4, 7$
or
![]() $11 \pmod {12}$
. Combining this with the previous condition, we have
$11 \pmod {12}$
. Combining this with the previous condition, we have
![]() $m \equiv 3$
or
$m \equiv 3$
or
![]() $11 \pmod {12}$
. Finally, the prime
$11 \pmod {12}$
. Finally, the prime
![]() $\ell = 11$
is inert and we find that
$\ell = 11$
is inert and we find that
![]() $m \equiv 1, 2, 5, 7$
or
$m \equiv 1, 2, 5, 7$
or
![]() $10 \pmod {12}$
, which is a contradiction. We conclude that
$10 \pmod {12}$
, which is a contradiction. We conclude that
![]() $X_0(53)(\mathbb {Q}(\sqrt {-47})) = X_0(53)(\mathbb {Q})$
.
$X_0(53)(\mathbb {Q}(\sqrt {-47})) = X_0(53)(\mathbb {Q})$
.
We have in fact proven that
![]() $X_0(53)(K) = X_0(53)(\mathbb {Q})$
for any quadratic field K in which
$X_0(53)(K) = X_0(53)(\mathbb {Q})$
for any quadratic field K in which
![]() $5$
and
$5$
and
![]() $11$
are inert and
$11$
are inert and
![]() $7$
splits. In a similar vein, when
$7$
splits. In a similar vein, when
![]() $d = 3$
, we achieved a contradiction using only the prime
$d = 3$
, we achieved a contradiction using only the prime
![]() $\ell = 3$
, and this proves that
$\ell = 3$
, and this proves that
![]() $X_0(53)(K) = X_0(53)(\mathbb {Q})$
for any quadratic field K in which
$X_0(53)(K) = X_0(53)(\mathbb {Q})$
for any quadratic field K in which
![]() $3$
ramifies. This type of result is similar to those appearing in [Reference Najman and Trbović11], and we could seek to prove more results along these lines, but we do not pursue this here.
$3$
ramifies. This type of result is similar to those appearing in [Reference Najman and Trbović11], and we could seek to prove more results along these lines, but we do not pursue this here.
To verify that the sieve is working as expected, we can try applying it for a value
![]() ${d \in \mathcal {D}_{53}}$
. For example, applying the sieve with
${d \in \mathcal {D}_{53}}$
. For example, applying the sieve with
![]() $d = -11 \in \mathcal {D}_{53}$
and the primes in
$d = -11 \in \mathcal {D}_{53}$
and the primes in
![]() $\mathcal {L}$
(defined as in (2.1)) outputs a list of possibilities for
$\mathcal {L}$
(defined as in (2.1)) outputs a list of possibilities for
![]() $m \pmod {\mathrm {lcm}(G_\ell )_{\ell \in \mathcal {L}}}$
, where
$m \pmod {\mathrm {lcm}(G_\ell )_{\ell \in \mathcal {L}}}$
, where
![]() $\mathrm {lcm}(G_\ell )_{\ell \in \mathcal {L}} = 63504000$
. We find that either
$\mathrm {lcm}(G_\ell )_{\ell \in \mathcal {L}} = 63504000$
. We find that either
![]() $m = 1$
or that
$m = 1$
or that
![]() $m \ge 1905121$
. The fact that
$m \ge 1905121$
. The fact that
![]() $m = 1$
remains as a possibility is because
$m = 1$
remains as a possibility is because
![]() $\psi ^{-1}(1 \cdot R)$
consists of a pair of quadratic points defined over
$\psi ^{-1}(1 \cdot R)$
consists of a pair of quadratic points defined over
![]() $\mathbb {Q}(\sqrt {-11})$
.
$\mathbb {Q}(\sqrt {-11})$
.
It is interesting to consider how the results of Theorem 1.1 overlap with the results one may obtain by applying the techniques of [Reference Ozman13], which give a criterion for testing whether
![]() $X_0(N)(\mathbb {Q}(\sqrt {d})) = X_0(N)(\mathbb {Q})$
by checking local points on the curve
$X_0(N)(\mathbb {Q}(\sqrt {d})) = X_0(N)(\mathbb {Q})$
by checking local points on the curve
![]() $X_0^{(d)}(N)$
. This curve is the quadratic twist of
$X_0^{(d)}(N)$
. This curve is the quadratic twist of
![]() $X_0(N)$
by the Atkin–Lehner involution
$X_0(N)$
by the Atkin–Lehner involution
![]() $w_N$
and the quadratic extension
$w_N$
and the quadratic extension
![]() $\mathbb {Q}(\sqrt {d}) / \mathbb {Q}$
(see [Reference Clark7, page 628] for a precise definition). For
$\mathbb {Q}(\sqrt {d}) / \mathbb {Q}$
(see [Reference Clark7, page 628] for a precise definition). For
![]() $N = 53$
, in Theorem 1.1, we prove that
$N = 53$
, in Theorem 1.1, we prove that
![]() $X_0(N)(\mathbb {Q}(\sqrt {d})) = X_0(N)(\mathbb {Q})$
for
$X_0(N)(\mathbb {Q}(\sqrt {d})) = X_0(N)(\mathbb {Q})$
for
![]() $117$
values of d, with d squarefree and
$117$
values of d, with d squarefree and
![]() $\lvert d \rvert < 100$
. Applying [Reference Ozman13, Theorem 1.1], we reproduced these results for
$\lvert d \rvert < 100$
. Applying [Reference Ozman13, Theorem 1.1], we reproduced these results for
![]() $94$
of these values. (As discussed in [Reference Banwait1, page 39], some care is needed to interpret correctly parts (5) and (6) of [Reference Ozman13, Theorem 1.1].) For some values of d, where our sieving method works, but applying [Reference Ozman13, Theorem 1.1] fails, we can often obtain examples of curves that violate the Hasse principle. Continuing our example with
$94$
of these values. (As discussed in [Reference Banwait1, page 39], some care is needed to interpret correctly parts (5) and (6) of [Reference Ozman13, Theorem 1.1].) For some values of d, where our sieving method works, but applying [Reference Ozman13, Theorem 1.1] fails, we can often obtain examples of curves that violate the Hasse principle. Continuing our example with
![]() $d = -47$
, we find that
$d = -47$
, we find that
![]() $X_0^{(-47)}(53)(\mathbb {Q})$
has points everywhere locally by applying [Reference Ozman13, Theorem 1.1]. However,
$X_0^{(-47)}(53)(\mathbb {Q})$
has points everywhere locally by applying [Reference Ozman13, Theorem 1.1]. However,
![]() $X_0^{(-47)}(53)(\mathbb {Q}) = \emptyset $
, as proven above. Similar examples are considered in [Reference Ozman13, pages 344–346], where a standard Mordell–Weil sieve is applied to twists of a hyperelliptic curve.
$X_0^{(-47)}(53)(\mathbb {Q}) = \emptyset $
, as proven above. Similar examples are considered in [Reference Ozman13, pages 344–346], where a standard Mordell–Weil sieve is applied to twists of a hyperelliptic curve.
Acknowledgement
I would like to thank the anonymous referee for a careful reading of the paper.