Published online by Cambridge University Press: 22 September 2020
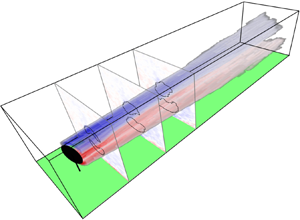
A quantitative understanding of the dominant mechanisms that govern the generation and decay of the counter-rotating vortex pair (CVP) produced by yawed wind turbines is needed to fully realize the potential of yawing for wind farm power maximization and regulation. Observations from large eddy simulations (LES) of yawed wind turbines in the turbulent atmospheric boundary layer and concepts from the aircraft trailing vortex literature inform a model for the shed vorticity and circulation. The model is formed through analytical integration of simplified forms of the vorticity transport equation. Based on an eddy viscosity approach, it uses the boundary-layer friction velocity as the velocity scale and the width of the vorticity distribution itself as the length scale. As with the widely used Jensen model for wake deficit evolution in wind farms, our analytical expressions do not require costly numerical integration of differential equations. The predicted downstream decay of maximum vorticity and total circulation agree well with LES results. We also show that the vorticity length scale grows linearly with downstream distance and find several power laws for the decay of maximum vorticity. These results support the notion that the decay of the CVP is dominated by gradual cancellation of the vorticity at the line of symmetry of the wake through cross-diffusion.