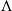An experimental investigation on the aerodynamic characteristics and vortex dynamics of a flying wing

Abstract

In this paper, we present a detailed experimental investigation mainly on the vortical flow fields and the associated vortex breakdown phenomena over a non-slender flying wing (sweep angle, ${\rm{\Lambda }}$ = 53°). In the process, the aerodynamic coefficients were also determined using a six-component force balance. Surface oil flow visualisation, surface pressure measurements and particle image velocimetry (PIV) measurements, in various crossflow planes and in a longitudinal plane passing through the leading-edge vortex core, were carried out at various Reynolds numbers to understand the flow field over the non-slender flying wing. Aerodynamic characteristics of the flying wing show local peaks and valleys in the pitching moment coefficient. The surface flow visualisation reveals that the nonlinearity of the pitching moment curve is due to the complex nature of vortical flow structures. The flow visualisation also demonstrates the presence of a wave-like surface pattern, and its size is found to reduce with increasing Reynolds numbers. The present PIV measurements confirm that this wave-like surface pattern is associated with vortex breakdown phenomena. These measurements also reveal that the vortex breakdown has not reached the apex of the wing, even at post-stall angle-of-attack. For pre-stall ($\alpha $ = 20°) flow regimes, it is observed that the location of the vortex breakdown moves downstream as the Reynolds number increases, but this influence is minimised at near-stall ($\alpha $ = 25°) and post-stall ($\alpha $ = 30°) flow regimes. Reconstructed velocity field using the first 10 dominant proper orthogonal decomposition (POD) modes reveals that the nature of the vortex breakdown over the flying wing is a spiral-type vortex breakdown.

Nomenclature

${\rm{\Lambda }}$

sweep angle, deg

${U_\infty }$

free stream velocity, m/s

$\alpha \;$

angle-of-attack, deg

${q_\infty }$

dynamic pressure (= $\rho U_\infty ^2/2$ )

$X,Y,Z\;$

coordinate measured along the streamwise, spanwise direction and normal to surface, respectively, mm, with respect to the origin located at the apex

$C,b,S$

root chord, maximum wing span and planform area

${b^2}/S,X/C$

aspect ratio, and non-dimensional chordwise location along streamwise direction

Re

Reynolds number based on the root chord

${C_L}$

lift coefficient (= $L/\left( {{q_\infty }S} \right)$ )

${C_D}$

drag coefficient (= $D/\left( {{q_\infty }S} \right)$ )

${C_{PM}}$

pitching moment coefficient (= $PM/\left( {{q_\infty }SC} \right)$ ) (pitching moment positive for nose up)

${X_{cg}}$

non-dimensional distance of centre of gravity from apex of model

${X_{cp}}$

non-dimensional distance of centre of pressure from apex of model

${C_p}$

coefficient of mean pressure (= $p - {p_\infty }/\left( {\rho U_\infty ^2/2} \right))$

${C_{p,{\rm{\;\;}}RMS}}$

coefficient of root-mean-squared pressure

${Y_{max}}$

maximum spanwise distance from root chord

$\eta = Y/{Y_{max}}$

normalised spanwise distance

$dt$

time step

${X_{VB}}$

vortex breakdown location normalised with root-chord of the flying wing, along streamwise direction

${X_{f,{\rm{\;\;}}RMS}}$

root-mean-squared of the fluctuation of the Vortex breakdown location, normalised with root-chord of the flying wing, along streamwise direction

${X_{vc}}$

coordinate along the longitudinal plane passing through the trajectory of vortex core

${\omega _X},{\rm{\;\;}}{\omega _{vc}}$

ensemble-averaged axial vorticity and azimuthal vorticity

${\bar u_{vc}},u'_{\!\!vc},{u_I},{u_{RMS}}$

mean velocity, velocity fluctuation and instantaneous velocity, m/s along vortex core and Root mean squared velocity

Abbreviation and Subscripts

vc

vortex core

VB

vortex breakdown

MRP

moment reference point from apex of the flying wing

LEV

leading-edge vortex

PIV

proper image velocitimetry

POD

proper orthogonal decomposition

$\infty $

freestream conditions

RMS

root-mean-squared

UCAV

unmanned combat aerial vehicle

1.0 Introduction

In the past decades, aerodynamic characteristics and leading-edge vortical flow field have been a field of interest over non-slender flying wing [1–5]. A slender/non-slender flying wing is defined based on the leading-edge sweep angle [5, 6]; if the sweep angle ( ${\rm{\Lambda }}$ ) is greater than 55°, the wing is called a slender wing; otherwise, it is termed as a non-slender wing ( ${\rm{\Lambda }} \le $ 55°), as can be seen in Fig. 1. A flying wing is a type of aircraft that has no tail, and its wings make up most of the structure. The wings are connected to the fuselage. This design allows the aircraft to generate most of its aerodynamic forces and moments from the wings alone [7, 8]. At high angles of attack, the leading-edge primary vortex (LEV) of a flying wing experiences a phenomenon called vortex breakdown. This is characterised by sudden expansion of the vortex core, presence of a stagnation point on the vortex axis and an increase in adverse pressure gradient and turbulence levels [9–13]. Vortex breakdown can affect both the steady and unsteady aerodynamics of the flying wing, which in turn can cause a loss of lift [10, 11, 14, 15]. It is, therefore, critical to study the behaviour of the leading-edge vortices and understand the vortex breakdown phenomenon in order to develop safe and effective flying wing designs.

Peckham and Atkinson [16] found the existence of a vortex breakdown at the trailing edge of a Gothic wing, whereas Werlé [17, 18] was the first to point out the sudden bursting of the leading-edge vortex using the flow visualisation technique on a slender delta wing. Following that, various theoretical and experimental aspects of vortex breakdown are explained based on instability, wave propagation and flow stagnation over cylindrical tubes and slender delta wings (Harvey [19]; Lambourne [9]; Benjamin [20]; Sarpkaya [21]; Hall [10]; Leibovich [22]; Escudier [23]; Brown and Lopez [24]; Lopez and Perry [25]; Delery [26]). Over a delta wing, there exist two primary forms of vortex breakdown: a bubble type, which has an axisymmetric shape, and a spiral type, which has a non-axisymmetric spiral/corkscrew type shape [9, 11]. The vortex breakdown also causes buffeting, unsteadiness and poor control of flying vehicles [27]. Subsequently, experimental investigations were focused on the characteristics and unsteady nature of the vortex breakdown, as well as its onset criterion [12, 14, 28–30]. Some studies reported that the bubble type and the spiral type can interchange each other from time to time. Additionally, the spiral type occurs more frequently than the bubble type over a slender delta wing [31, 32].

Figure 1. The schematic shows the (a) Isometric view, (b) Side view, (c) Front view, and (d) Top view of the Catia design of the non-slender flying wing model for the present investigation.

Recently, the NATO RTO/AVT-113 Task group [33] investigated various aspects of flow topology, including the formation of vortical flow at different angles of attack, the influence of Reynolds and Mach numbers, transition behaviour on vortex dynamics, vortex breakdown and boundary layer flow over a delta wing with a round leading edge. These extensive tests served to validate numerical findings based on inviscid CFD simulations of a delta wing ( ${\rm{\Lambda }}$ = 65°) with a sharp leading edge.

These studies indicate that vortex structure and vortex breakdown phenomena were extensively studied in the past for a slender delta wing configuration. However, it is equally important to investigate the flow field over a non-slender delta wing for the next-generation micro-air vehicles and unmanned combat air vehicles [5]. The three-dimensional complex flow field resulting from the vortex breakdown and its associated flow structures at the pre-stall, near-stall and post-stall over a non-slender flying wing configuration are not fully understood. Also, as compared to the slender delta wing, there is a limited amount of literature available on the vortical flow and vortex breakdown phenomena over a non-slender delta wing [3–5, 32, 34–36].

However, some studies have recently been performed on an actual non-slender flying wing with variable leading-edge geometries using UCAV 1303 [37] and UCAV stability and control configuration (SACCON) [38–40] to explain the aerodynamic behaviour and vortex dynamics. However, the leading-edge radius varies along the longitudinal direction for the SACCON configuration, with a sharp LE around the nose, a decreasing LE radius at mid-section, and a decreasing radius along with thickness up to the wingtip. A twist (0–5°) on the leading edge of the wings is also present in this case. Both the experimental and numerical approaches were used to understand the vortical flow physics in connection with the non-linear aerodynamic behaviour over the SACCON ( ${\rm{\Lambda }}$ = 53°) configuration. Similarly, Kumar et al. [15] considered a non-slender flying wing and found that the lift curve is non-linear and the slope of the lift curve is gradual at higher angles of attack, as compared to the slender delta wing. Their experiments also indicate presence of a vortical flow without and with vortex breakdown. But the type of the vortex breakdown, and the associated flow physics, as well as its effects on the aerodynamic characteristics for the non-slender flying wing configurations are hardly available in the literature. Therefore, the flow field associated with vortex breakdown over a non-slender flying wing is worth studying.

Specifically, we make an effort here to address the following questions: What is the relation between the surface flow topology over the flying wing and the pitching moment characteristics? How does a vortex breakdown manifest in the surface flow visualisation? How do its location and size change with Reynolds number and angle-of-attack? What is the type of vortex breakdown for a flying wing?

To investigate these aspects, surface oil flow visualisations, surface pressure measurements and the entire flow field measurements using the particle image velocimetry (PIV) technique are carried out at different angles of attack and Reynolds numbers. The PIV measurements were carried out at different cross-flow planes as well as in a longitudinal plane. The present article has been organised as follows: the experimental details and methodology are described in Section 2, results and discussions are presented in Section 3, followed by the summary and concluding remarks in Section 4.

2.0 Experimental setup and methodology

2.1 Wind tunnel and flying wing model

The present experimental work was carried out in a low-speed tunnel. It is a closed-circuit tunnel with a test section size of 1.68 m $ \times $ 0.9 m $ \times $ 0.6 m (length $ \times $ width $ \times $ height), and the ratio of its contraction cone is 6.5. It is equipped with a speed controller made by Siemens to control the wind speed in the test section. The maximum speed of the tunnel is 35 m/s, and the turbulence level in the test section was measured to be 0.3% of the freestream velocity.

A flying wing configuration with a complex geometrical profile was used for the present investigation. The Trust for Applied Aerodynamics in India (TAAI) proposed this configuration at the event of the Symposium for Promotion of Indigenous CFD Process in Engineering Sciences (SPICES-2013). The geometrical profile of this flying wing that blends delta and lambda wing shapes has a rounded leading edge with decreasing thickness and radius along the chordwise direction from its apex to the wingtip without control surfaces, as shown in Fig. 1. A sting was used to mount the model inside the tunnel test section. The sting was attached with a pitching mechanism, which was used to change the angle-of-attack. In the current study, apex of the flying wing model is considered as the origin of the axis system, as shown in Fig. 1; here, $X$ and $Y$ denote the streamwise direction and the spanwise direction, respectively, whereas $Z$ indicates the normal to the surface. The selective laser sintering process was used to manufacture the flying wing model with the help of micron-sized polymer powder (PA 2200), as this provides a smooth surface finish to the wing model. The polymer, which is thermoplastic in nature, has a high tensile strength ( $ \approx $ 48 MPa), high melting point ( $ \approx $ 172–180°C), good chemical resistance, lightweight (bulk density $ \approx $ 0.45 g/cm $^3$ ) and excellent long-term constant behaviour. This ensures that the fabricated model considered in the present study is rigid enough with a smooth surface finish.

The fabricated flying wing model has a leading-edge sweep angle, ${\rm{\Lambda }} = 53$ °; it can be considered as a non-slender flying wing [5]. The model has a root chord ( $C$ ) of 0.39 m and a maximum span ( $b$ ) of 0.551 m. The planform area ( $S$ ) is defined as the area of the geometric shape seen in the top view (Fig. 1(d)), and it is found to be 0.1074 m $^2$ . The aspect ratio of the model is defined as ${b^2}/S$ , and it is found to be 2.84. The blockage ratio is defined as the ratio of the frontal area of the flying wing model at a particular angle-of-attack to the area of the test section, and it is found to be 9.65 ${\rm{\% }}$ at $\alpha $ = 30° (Barlow et al. [41]).

2.2 Force measurement and oil flow visualisation technique

A six-component strain-gauge balance was used to measure the aerodynamic forces and moment coefficients. This balance was first calibrated in a calibration rig. However, the voltage signals from the force balance were acquired at a rate of 300 samples per second. These signals were then converted to the force and moment data using the calibration matrix. These force and moment data were acquired for 10 seconds duration to calculate an average of these quantities. It should also be noted that the force balance data were corrected for the tunnel blockage effect using the simple tunnel correction approach, as reported by Shindo [42]. This force balance was used in many of our previous works e.g. Kumar et al. [15].

Surface oil flow visualisation is often used to depict the surface flow pattern, as it is easy and inexpensive (Lu [43]; Bisgood [44]). This qualitative technique was used here for surface flow patterns over the flying wing. For oil flow visualisation, surface of the model was painted using a mixture of titanium dioxide powder, transformer oil and oleic acid. A halogen lamp was used to illuminate the painted surface for imaging purposes. A streaky deposit of the mixture marked the direction of the flow while air flowed over the surface. Further, using a DSLR camera (Nikon, D750, in monochromatic mode) with a lens (Nikkor, 24–120 mm focal range), the surface oil pattern was imaged at different angles of attack, as shown in Fig. 2.

Figure 2. Schematic view showing the arrangement of the flying wing model and DSLR cameras in the test section for oil flow visualisation.

2.3 Pressure measurement technique

In order to measure pressure on the surface of the model, various static pressure ports were made on the surface of the model along the spanwise direction (i.e. $Y$ direction) at various chordwise locations ( $X/C$ ), as shown in Fig. 3; here, $X$ denotes the chordwise distance from the apex of the flying wing model along the streamwise direction. Measurements were carried out at different spanwise locations, $Y/{Y_{max}}$ (see Fig. 3); here $Y$ is the spanwise distance from the root chord of the flying wing model, and ${Y_{max}}$ is the local semi-span of the flying wing model. A total of 109 pressure ports on the upper surface of the flying wing model were utilised. It may be noted that the pressure ports/taps on the port side of the flying wing model at $X/C$ = 0.6 were used to ensure the symmetric nature of the pressure distribution. Many pressure ports were made between the leading edge and 75% ${Y_{max}}$ line, and the number of ports was made coarser beyond 75% ${Y_{max}}$ , as shown in Fig. 3. This pressure port distribution was chosen to capture the steep pressure gradient near the leading edge of the flying wing.

Figure 3. A diagrammatic representation of pressure port distribution on the flying wing.

For surface pressure measurement, electronically scanned pressure (ESP) scanners were used. Measurements at 32 ports can be carried out using a single ESP, which is a differential pressure scanner. Other than the ESP, the pressure measurement system consists of a multiplexer unit, a high-speed 14-bit DAQ module (PXI-6133) with a PXI system and a workstation with an interface board (PCI-8336). A total of four scanners were used: three scanners with a 20-inch water column range and one scanner with a 10-inch water column. While conducting the measurements, these scanners were kept inside the flying wing. Reference pressure was measured using a Pitot-static tube, which was mounted on the wall of the test section. Applying the unique binary address to the multiplexers, the output of each ESP was selectively routed to the DAQ module (PXI- 6133). These multiplexers can switch between ports at maximum rates of up to 20,000 ports/s. However, in the present measurements, the pressure was scanned at the rate of 19,520 ports/s, yielding a sampling rate of 610 samples/s/port. The voltage output from the pressure scanners was converted to pressure data using the calibration coefficients with the help of Labview-based virtual instrumentation.

2.4 Particle image velocimetry (PIV) technique

Two-dimensional PIV measurements (2D-PIV) were carried out in both the crossflow plane and the longitudinal plane. Two CCD cameras were used for simultaneous PIV measurements on the starboard side and the port side of the flying wing, as shown in Fig. 4(a); here, the light sheet, which was perpendicular to the surface, was aligned in crossflow plane. The measurements in the longitudinal plane were carried out along the trajectory of vortex core around the before and after vortex breakdown region and perpendicular to the surface of the flying wing model, as shown in Fig. 4(b); here, the trajectory of vortex core was identified using surface oil flow visualisation. In this case, only one CCD camera was used, as shown in Fig. 4(b). Illumination of the measurement plane was achieved using a dual-head Nd-YAG laser (Quantel Evergreen, 200 mJ/pulse, 15 Hz) with an acquisition rate of 10 Hz. The laser pulses were controlled by a synchroniser (IDTvision) with a suitable time delay. A commercial fog generator (Antari Z1500II-R) was used for seeding particles in the flow. It was placed near the diffuser section of the closed-circuit wind tunnel to allow better mixing of the seeding particles (dia. $\sim $ 1–2 $\mu $ m) before entering the test section.

Figure 4. Schematic diagram of the experimental setups for particle image velocimetry (PIV) measurements in (a) the crossflow plane, and (b) the longitudinal plane passing through the trajectory of vortex core.

Images of the seeding particles were acquired using the MicroVec software (Vision Asia, Singapore) with a CCD camera (8 MP resolution, pixel array 3,312 $ \times $ 2,488, 8 bit, Imprex), which was equipped with a suitable lens (50 mm/85 mm focal length). At each measurement location, 1,000 pairs of images were acquired for data analysis. Using the Provision XS package (IDTvision, USA), these images were then processed with a correlation window size of 32 $ \times $ 32 pixels. It should be noted that this PIV processing package includes a mesh-free second-order algorithm and a high spatial resolution feature (Lourenco and Krothapalli [45]). This package was also used in previous works (Kumar et al. [15]).

In addition, the time-resolved PIV (TR-PIV) technique was also used in the longitudinal plane to measure the time sequence of the flow field along the trajectory of vortex core. Raw images were acquired using a CMOS camera (PCO Dimax HS4 camera, 4 MP resolution, pixel array 2,000 $ \times $ 2,000) equipped with 85 mm lens. The flow field was illuminated using a Nd-YLF dual-head laser (Photonic Industries, USA), which can provide 40 mJ/pulse at 1 kHz. Motion-Pro timing hub (IDTvision, USA) was used to synchronise both the laser and the camera. In the case of TR-PIV measurements, Safex fog generator (procured through Dantec Dynamics) was used to seed the flow. PIV images were acquired at 1 kHz (i.e. 1,000 image pairs per second) on the starboard side of the flying wing, as shown in Fig. 4(b). In one experimental run, 6,000 image pairs were acquired. These images were then processed using the PIVlab software with a correlation window of 32 $\; \times {\rm{\;}}$ 32 pixels and an overlap of 50% (Thielicke [46]; Thielicke and Sonntag [76]).

Based on the above PIV processing parameters, the effective region of interest, number of vectors, vector spacing, etc., are given in Table 1. In the crossflow plane, these quantities are given for the maximum and minimum regions of interest. It should be noted here that the effective region of interest means the area of the acquired image that was processed for velocity fields.

Table 1. PIV processing parameters for various cases

2.5 Uncertainty analysis

Uncertainty analyses were carried out to estimate the uncertainties of various measured quantities reported here. The maximum uncertainty values for the lift coefficient ( ${C_L}$ ), drag coefficient ( ${C_D}$ ) and the pitching moment coefficient ( ${C_{PM}}$ ) are found to be $ \approx $ 1 ${\rm{\% }}$ , $ \approx $ 2 ${\rm{\% }}$ , and $ \approx $ 1.5 ${\rm{\% }}$ , respectively. The uncertainty of the pressure measurements mainly depends on the maximum errors of the ESP scanner and the manometer. The maximum uncertainties of both the ESP scanners and the manometer used in this experimental work are 0.05% of the full-scale pressure range. Based on these factors, uncertainty in the pressure coefficient is found to be 0.07%. Uncertainty in the PIV measurements mainly depends on the seeding particles, optical setup, calibration, image acquisition, image processing software and timing error (Gui and Wereley [47]; Raffel et al. [48]; Sciacchitano [49]; Balamurugan and Mandal [50]). The maximum uncertainty in the velocity measurements reported here is found to be $ \approx $ 2.5% of the freestream velocity.

3.0 Results and discussion

Here, we present the results based on our force measurements, surface flow visualisations, surface pressure measurements and PIV measurements at different angles of attack. Measurements were carried out at different Reynolds numbers based on the root chord of the flying wing.

3.1 Aerodynamic characteristics and surface flow features

Characteristics of the pitching moment coefficient ( ${C_{PM}}$ ) along with the lift ( ${C_L}$ ) and drag ( ${C_D}$ ) coefficients are shown in Fig. 5, for different Reynolds numbers. Peaks and valleys in the pitching moment curve clearly appear to be associated with the change of slope of the lift curve; we may note that ${C_L}$ and ${C_D}$ data for Re = 7.5 $\; \times \;$ 10 $^5$ are reproduced from Kumar et al. [15], for comparison purpose. However, using the surface flow visualisation and the lift curve, we make an effort to explain the variation of the pitching moment coefficient. While doing so, we utilise the leading-edge suction analogy (Polhamus [51, 52]; Traub [53]). The total lift of the flying wing can be considered as a summation of the potential lift that is generated due to the pressure distribution over the surface of the wing in the absence of the leading-edge vortex and the vortex-assisted lift, which is generated due to the leading-edge vortex assisted pressure distribution. However, considering the normal force ( $N$ ) is approximately equal to the lift force ( $L$ ), the pitching moment about the centre of gravity or equivalently the pitching moment coefficient ( ${C_{PM}}$ ) about the centre of gravity can approximately be written as ${C_{PM}} \approx A{C_L}\!\left( {{X_{cg}} - {X_{cp}}} \right)$ ; here, $A$ is a constant, ${X_{cg}}$ and ${X_{cp}}$ denote the distances of the centre of gravity and the centre of pressure from the nose of the model, respectively. Negative values of ${C_{PM}}$ about ${X_{cg}}$ (i.e. nose down moment) for $\alpha \gt $ 0°, as seen in Fig. 5, indicates that ${X_{cp}}$ is always behind ${X_{cg}}$ .

Figure 5. Aerodynamic coefficients of the flying wing for Re = 3.5 $ \times {\rm{\;}}$ 10 $^5$ , 4.3 $\; \times {\rm{\;}}$ 10 $^5$ and 7.5 $\; \times {\rm{\;}}$ 10 $^5$ ; lift, ${C_L}$ , and drag, ${C_D}$ , coefficients at Re = 7.5 $ \times {\rm{\;}}$ 10 $^5$ are reproduced from Kumar et al. [15].

Figure 6. Surface oil flow visualisation on the upper surface of the flying wing at (a) $\alpha $ = 6°, (b) $\alpha $ = 8°, (c) $\alpha $ = 12°, and (d) $\alpha $ = 17° for Re = 7.5 $ \times $ 10 $^5$ .

Figure 5 shows that the pitching moment coefficient decreases almost linearly for 0° $ \le \alpha \le $ 6°, while the lift and the lift curve slope increase. Enhancement of lift is certainly due to the enhanced pressure difference between the upper and the lower surface. The lift in this range of $\alpha $ consists of both potential lift, as indicated by surface flow visualisation showing mostly attached flow over the surface of the flying wing, and lift (loss) resulting from flow separation at the rear portion of the flying wing, as observed at rear portion in Fig. 6(a). The small change in the lift coefficient within the range of 0° $ \le \alpha \le $ 6° is attributed to these small separated regions, which, as expected, are found to reduce with increasing Reynolds numbers. Therefore, the rapid decrease of the moment coefficient, ${C_{PM}}$ , about the centre of gravity can mainly be attributed to a rapid increase of ${C_L}$ , as compared to the expected decrease of the moment arm $\left( {\left| {{X_{cg}} - {X_{cp}}} \right|} \right)$ . Though the lift coefficient continues to increase, the lift curve slope starts to reduce at $\alpha \approx $ 6° and continues to do so until $\alpha \approx $ 10°. Interestingly, the pitching moment coefficient starts to increase within 6° $ \le \alpha \le $ 10°, before it starts to reduce at about $\alpha \approx $ 10°. This may be associated with a possible rapid decrease of the moment arm, as compared to the slower increase of ${C_L}$ . The flow visualisation indicates that the decrease of lift curve slop (for 6° $ \le \alpha \le $ 10°) is due to the presence of a small separated flow region along the leading edge before a fully developed leading-edge vortex (primary vortex) originates along the leading edge (see Fig. 6(b)). Further, an increase of the lift curve slope can clearly be noticed for 10° $ \le \alpha \le $ 14° in Fig. 5. This increase can be attributed to the generation of the fully developed leading-edge vortex (primary vortex) that produces the vortex-generated lift. The flow visualisation in Fig. 6(c) shows the presence of a leading-edge vortex. The reduction in the pitching moment coefficient within this $\alpha $ range may again be attributed to the rapid increase of ${C_L}$ . Further reduction of the lift curve slope and an increase of the pitching moment coefficient for 14° $ \le \alpha \le $ 24° may again be attributed to the reduction of lift curve slope, mainly due to the flow separation and the vortex breakdown over the wing (Figs. 6(d) and 7), and the expected decrease of the moment arm, respectively. A similar drop in the pitching moment curve was also reported for the SACCON geometry for Re = 1.6 $\; \times {\rm{\;}}$ 10 $^6$ [39, 54].

Figure 7. Surface oil flow visualisation on the upper surface of the flying wing at pre-stall angle, $\alpha $ = 20° for (a) Re = 2.5 $ \times $ 10 $^5$ , and (b) for Re = 7.5 $ \times $ 10 $^5$ .

Figure 8. Mean velocity vectors over the contours of the normalised ensemble averaged axial vorticity, ${\omega _X}C/{U_\infty }$ at $X/C$ = 0.45, 0.5, 0.6, 0.8 and 1.0 at $\alpha $ = 20° (pre-stall flow field) for both the (a) starboard, (b) port sides of the flying wing, respectively. Additionally, (c) shows the perspective view at $X/C$ = 1 for the starboard side of the flying wing.

For a better understanding of the leading-edge vortex and its eventual breakdown at different Reynolds numbers, the surface flow visualisations at $\alpha $ = 20°, for Re = 2.5 $ \times {\rm{\;}}$ 10 $^5$ and 7.5 $\; \times {\rm{\;}}$ 10 $^5$ , are shown in Fig. 7(a) and (b), respectively. The signature of the leading-edge vortex, which is often mentioned as the leading-edge primary vortex in the literature, can clearly be identified from these surface flow visualisations. This leading-edge vortex is the result of the primary separation of the shear layer emanating from the leading edge and its roll-up. The separated shear layer finally reattaches with the upper surface of the flying wing. However, Fig. 7(a) also shows two wave-like surface patterns near the leading edge followed by a kink within the chordwise distance, 0.3 $ \le X/C \le $ 0.6 on the starboard and port sides of the flying wing, respectively. In the range of chordwise distance, 0.4 $ \le X/C \le $ 0.5, a sudden expansion of the skin friction lines on the flying wing appears to indicate the onset of the vortex breakdown, which is adjacent to the wave-like surface pattern over the upper surface of the flying wing configuration, as shown in Fig. 7(a). The white lines over the starboard side of the flying wing in Fig. 7(a) indicate the centreline or trajectory of the primary vortex. Along the vortex centreline, $X1$ , ${X_{vb}}$ , and $X3$ in the enlarged view in Fig. 7(a), denotes the starting of the wave-like surface pattern and the onset of vortex breakdown location and the ending of the wave-like surface pattern, respectively. These wave-like patterns move upstream with increasing angle-of-attack, as shown in Figs. 6(d) and 7(b) for $\alpha $ = 17° and 20°, respectively, at Re = 7.5 $\; \times $ 10 $^5$ . The size of the wave-like surface flow pattern reduces as the Reynolds number increases (from Re = 2.5 $ \times $ 10 $^5$ to 7.5 $ \times $ 10 $^5$ ) at pre-stall flow region ( $\alpha $ = 20°), as seen in Fig. 7. Further quantitative assessments of these flow features are discussed in the following.

3.2 Mean vortical flow field in the crossflow plane

For further investigation, the two-dimensional (2D) PIV measurements were carried out at different crossflow planes, which are perpendicular to the vortex axis. The measurements were carried out at five different chordwise locations ( $X/C$ ) for both the starboard and the port sides of the flying wing model for Re = 2.5 $ \times {\rm{\;}}$ 10 $^5$ at angles of attack, $\alpha $ = 20°, 25° and 30°, as shown in Figs. 8, 9 and 10, respectively.

Figure 9. Mean velocity vectors over the contours of the normalised ensemble averaged axial vorticity, ${\omega _X}C/{U_\infty }$ at $X/C$ = 0.2, 0.3, 0.4, 0.8 and 1.0 at $\alpha $ = 25° (near-stall flow field) for both the (a) starboard and (b) port sides of the flying wing, respectively.

Figure 10. Mean velocity vectors over the contours of the normalised ensemble averaged axial vorticity, ${\omega _X}C/{U_\infty }$ at $X/C$ = 0.1, 0.2, 0.3, 0.8 and 1.0 at $\alpha $ = 30° (post-stall flow field) for both the (a) starboard and (b) port sides of the flying wing, respectively.

For the pre-stall flow regime at $\alpha $ = 20°, Fig. 8 shows the mean velocity vectors over the normalised contours of the mean axial vorticity, ${\omega _X}C/{U_\infty }$ at chordwise locations, $X/C$ = 0.45, 0.5, 0.6, 0.8 and 1.0 for starboard and port sides of the flying model; here ${\omega _X}$ is the ensemble-averaged axial vorticity and ${U_\infty }$ is freestream velocity. Figure 8 shows that the averaged vorticity values are concentrated in a smaller area and higher at $X/C$ = 0.45, as compared to the locations, $X/C \geq $ 0.45. The velocity vectors, normalised with their respective magnitude for clarity and overlaid with the vorticity contours, reveal the vortical structure over the flying wing. A symmetric nature of the leading-edge vortices can clearly be noticed in this figure. The leading-edge vortices are found to be oval shaped over the flying wing. Moreover, the vortical structure is found to be associated with diffused vorticity in the vortex core, and its size appears to increase rather gradually in the chordwise distance, 0.45 $ \le X/C \le $ 0.5, as compared to the sudden increase in vortex size for the case of a slender delta wing [5, 11, 55–57]. At downstream locations, i.e. at $X/C$ = 0.8 and 1.0, the vorticity is found to be diffused within the vortex core in both sides of the flying wing. Interestingly, two counter-rotating vortices are observed at $X/C$ = 1.0, an elongated one in size as the leading-edge vortex and another one small in size as the trailing-edge vortex on either side of the flying wing. Various authors reported presence of multiple vortices on the surface of a delta/double delta wing [58–61]. However, these works on a delta/double delta wing indicate that the trailing edge does not play any role in the generation of these multiple vortices. But the present flying wing configuration has two swept wing-like portions near $X/C$ = 1 (see Fig. 1). Due to the pressure difference between the upper and lower surfaces, the shear layers from both the surfaces of the wing roll up to generate two counter-rotating vortices, as clearly seen in the perspective view in Fig. 8(c). Therefore, the present counter rotating vortices at $X/C$ = 1 are actually generated due to the leading and trailing edges of the flying wing (see Fig. 8(c)).

For the near-stall flow regime at $\alpha $ = 25°, Fig. 9 shows the mean velocity vectors over the normalised contours of the mean axial vorticity, ${\omega _X}C/{U_\infty }$ , at chordwise locations $X/C$ = 0.2, 0.3, 0.4, 0.8 and 1.0, for the starboard and the port sides of the flying wing. At this higher angle-of-attack, $\alpha $ = 25°, the normalised vorticity values are seen to be higher up to the chordwise location, $X/C$ = 0.3, for both sides of the flying wing. Similar to the pre-stall flow regime, the symmetric nature of the oval-shaped leading-edge vortices can be seen even at a near-stall angle-of-attack over the flying wing. However, the vortices are found to be comparatively larger in size at the corresponding $X/C$ locations. Similar to the pre-stall case, two counter-rotating vorticities are observed on either side of the flying wing at the chordwise location at $X/C$ = 1.0, and the trailing-edge vortices also increase in size.

Furthermore, for the post-stall flow regime at $\alpha $ = 30°, Fig. 10 shows that the mean velocity vectors and axial vorticity patterns still exist at chordwise locations, $X/C$ = 0.1, 0.2, 0.3, 0.8 and 1.0 for both sides of the flying wing. The normalised vorticity values are seen to be higher till the chordwise location, $X/C$ = 0.2, beyond which the vorticity values are found to be highly diffused within the increasing sizes of the vortices.

Sudden changes from the concentrated vorticity values to the diffused vorticity along the vortex core, as seen in the above PIV measurements (Figs. 8, 9 and 10), indicate the presence of the vortex breakdown phenomena in the range of the chordwise distance, 0.45 $ \le X/C \le $ 0.5, 0.3 $ \le X/C \le $ 0.4 and 0.2 $ \le X/C \le $ 0.3 over the flying wing, for $\alpha $ = 20°, 25° and 30°, respectively. The concentrated vorticity in the primary vortex core, which diffuses while moving downstream, is found to be similar to the observation of Ol and Gharib [3] on a non-slender delta wing. However, the present observation also indicates that the onset of vortex breakdown moves towards the apex with increasing angle-of-attack, and it has not reached the apex even at the post-stall angle-of-attack, $\alpha $ = 30°. Vortices are also found to be larger in size with increasing angle-of-attack.

3.3 Surface pressure measurements

For further analysis, the surface pressure measurements at various chordwise locations were carried out on the starboard side of the flying wing configuration at $\alpha $ = 20°, 25° and 30°, for Re = 2.5 $ \times $ 10 $^5$ . The coefficient of mean pressure variations along the normalised spanwise distance, $\eta $ = $Y/{Y_{max}}$ , are displayed in Fig. 11; here $Y$ is the spanwise distance and ${Y_{max}}$ is the maximum local half-span from the root chord of the flying wing, as mentioned earlier. Therefore, the locations of the root chord and the leading edge are given by $\eta \left( { = Y/{Y_{max}}} \right)$ = 0 and 1, respectively.

Figure 11. Surface pressure distribution ( ${C_p}$ ) at cross-sections, $X/C$ = 0.2, 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8 on the starboard side of the flying wing along the span-wise distance at $\alpha $ = 20°, 25° and 30°. The grey color shaded region in the first panel shows a representative front view of the starboard side of the flying wing.

Figure 11 shows that there exists a strong suction in the range of 0.2 $ \le X/C \le $ 0.4 at $\alpha $ = 20°, that is, for the pre-stall flow regime. This, in turn, indicates that the leading-edge primary vortex is strong up to $X/C$ = 0.4. Beyond $X/C$ = 0.4, a gradual decrease in suction can be noticed in Fig. 11, which clearly indicates the onset of vortex breakdown in between the chordwise locations 0.4 $ \le X/C \le $ 0.5. The suction peak in between 0.2 $ \le X/C \le $ 0.5 is seen to move toward the root chord of the flying wing. However, at $\alpha $ = 25°, that is, in the near-stall regime, the suction is seen to be strong within 0.2 $ \le X/C \le $ 0.3, and beyond $X/C$ = 0.3, a gradual decrease in suction can be noticed indicating the onset of vortex breakdown, which has moved upstream (0.3 $ \le X/C \le $ 0.4), as compared to the one at $\alpha $ = 20°. It can be noticed that the vortex breakdown is yet to reach the apex of the flying wing, even at this near-stall flow regime. This observation is consistent with the PIV data shown in Fig. 9. At $\alpha $ = 30°, that is, at the post-stall flow regime, the pressure distribution indicates that the primary vortex is strong till $X/C$ = 0.2. After this, a gradual decrease in suction is observed within the chordwise location, 0.2 $ \le X/C \le $ 0.3. This, in turn, indicates that the onset of vortex breakdown is further shifted upstream, as compared to the previous two cases. It is also interesting to note that the leading-edge primary vortex still exists even after the stall has occurred on the flying wing. This is also consistent with the cross-plane PIV measurements for this case, as shown in Fig. 10.

Figure 12 shows the coefficient of root-mean-squared (RMS) values of pressure fluctuation, ${C_{p,{\rm{\;\;}}RMS}}$ , along the spanwise direction, $\eta $ , at angles of attack, $\alpha $ = 20°, 25° and 30°, for the various chordwise locations. The peak in ${C_{p,{\rm{\;\;}}RMS}}$ starts to appear nearly at the onset of the wave-like pattern, as shown in Fig. 7(a), and then it continues to be present in all the downstream locations presented here. Further, it is observed that the peak in ${C_{p,{\rm{\;\;}}RMS}}$ moves towards the root chord while moving downstream. After carefully checking the crossflow PIV data, we found that the vortex core region over the surface of the flying wing is associated with the maximum RMS pressure peaks for all $\alpha $ . This aspect along with PIV and pressure data (Fig. 13) has further been elaborated in the following paragraph. Therefore, shifting of maximum ${C_{p,{\rm{\;\;}}RMS}}$ towards the root chord can be attributed to the shifting of the vortex core towards the root chord. Gursul et al. [5] reported a similar observation based on the ${u_{RMS}}$ for a delta wing. However, the pressure (fluctuation is also seen to be maximum in the range of chordwise location, 0.3 $ \le X/C \le $ 0.6, 0.3 $ \le X/C \le $ 0.4 and 0.2 $ \le X/C \le $ 0.3, for $\alpha $ = 20°, 25°, 30°, respectively. Interestingly, the wave-like pattern is also seen to be present in these chordwise locations for respective $\alpha $ , as can be seen in Fig. 7(a) for $\alpha $ = 20°. This indicates that the leading-edge vortex is highly unsteady around the wave-like pattern. Also, the maximum RMS pressure fluctuation is found at the near-stall flow regime, at $\alpha $ = 25°, as compared to the pre-stall and the post-stall flow regimes.

Figure 12. Surface pressure fluctuation intensities ( ${C_{p,{\rm{\;\;}}RMS}}$ ) at cross-sections $X/C$ = 0.2, 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8 on the starboard side of the flying wing along the spanwise distance at $\alpha $ = 20°, 25° and 30°. The grey color shaded region in the first panel shows a representative front view of the starboard side of the flying wing.

Figure 13. Effect of Reynolds number on the surface mean pressure ( ${C_p}$ ) and RMS pressure ( ${C_{p,{\rm{\;\;}}RMS}}$ ) distributions at $\alpha $ = 20° (Panels $a,b,c,d$ ) and $\alpha $ = 30° (Panels $b,c,d,e$ ). Color contours of the averaged axial vorticity ( ${\omega _X}C/{U_\infty }$ ) and the velocity vectors obtained from the PIV measurements at the corresponding locations are shown for Re = 2.5 $ \times $ 10 $^5$ . For $\alpha $ = 20°, $X/C$ = 0.4 corresponds to the location before the breakdown and $X/C$ = 0.5 corresponds to the location after the breakdown. Similarly, for $\alpha $ = 20°, $X/C$ = 0.2 corresponds to the location before the breakdown and $X/C$ = 0.3 corresponds to the location after the breakdown.

To find the effect of Reynolds number on the peak suction pressure and the RMS ( ${C_{p,RMS}}$ ) pressure, we have plotted the pressure distributions in Fig. 13 at the locations just before and after the vortex breakdown, for three different Reynolds number, named as Re = 2.5 $\; \times {\rm{\;}}$ 10 $^5$ , 5.0 $ \times {\rm{\;}}$ 10 $^5$ and 6.2 $\; \times {\rm{\;}}$ 10 $^5$ . For better understanding, the pressure distributions have been displayed over the vorticity contours and velocity vectors at the corresponding location for Re = 2.5 $\; \times \;$ 10 $^5$ . The panels in the left column in Fig. 13 refer to $\alpha = 20$ °, and those in the right column refer to $\alpha = 30$ °. The first two panels (one mean pressure and one RMS pressure) in the left column correspond to the location just before the vortex breakdown, and the next two panels (one mean pressure and one RMS pressure) in the left column correspond to the location after the vortex breakdown. Similarly, the panels in the right column correspond to the locations before and after the vortex breakdown at $\alpha = $ 30°. Figure 13(a, e, c, and g) shows that the minimum suction pressure, i.e. minimum mean $ - {C_p}$ values, occurs near the reattachment location, as indicated by the velocity vectors of the flow field, similar to a swept delta wing [62], whereas the peak suction pressure (mean $-{C_p}$ ) occurs near the vortex core, albeit with slight offset towards the leading edge. On the other hand, Fig. 13(b, f, d and h) shows that the peak RMS ( ${C_{p,RMS}}$ ) pressure occurs in-between the vortex core and the reattachment around the vortex breakdown region for both the pre-stall and post-stall angles of attack. Further, the peak RMS pressure appears to move toward the leading edge with increasing Reynolds number.

3.4 Mean flow field in the longitudinal plane along the vortex core

For further investigation of the above unsteadiness, the 2D-PIV measurements were carried out in a longitudinal plane, perpendicular to the surface along the trajectory of vortex core, i.e. along the white line, as shown in Fig. 7(a); it may be noted that ${X_{vc}}$ denotes the coordinate along this plane. The PIV measurements were performed at $\alpha $ = 20°, 25° and 30° for Re = 2.5 $ \times {\rm{\;}}$ 10 $^5$ . The mean velocity contours and the associated streamlines are shown in Fig. 14(a), (b) and (c), respectively. It should be noted that the mean quantities are obtained based on an ensemble average of 1,000 PIV realisations. The mean velocity along the vortex core is denoted by $\overline {{u_{vc}}} $ and the corresponding fluctuating velocity is $u'_{\!\!vc}\!\left( { = {u_I} - \overline {{u_{vc}}} } \right)$ ; here, ${u_I}$ is the instantaneous velocity along the vortex core.

Figure 14. Contours of normalised ensemble averaged axial velocity, $\overline {{u_{vc}}} /{U_\infty }$ and the associated streamlines pattern with critical points; sectional streamlines are multicolored by normalised ensemble averaged axial velocity, $\overline {{u_{vc}}} /{U_\infty }$ at (a) $\alpha $ = 20°, (b) $\alpha $ = 25°, (c) $\alpha $ = 30°.

The normalised mean velocity contours, $\overline {{u_{vc}}} /{U_\infty }$ , in Fig. 14, show that the value of the mean velocity reduces gradually followed by a reverse flow regime, $\overline {{u_{vc}}} /{U_\infty }$ $ \le $ 0. The corresponding streamline patterns, which are also shown in these figures, clearly reveal the existence of a stagnation point ( $\overline {{u_{vc}}} /{U_\infty }$ = 0) along the vortex core. Since existence of a stagnation point along the vortex core indicates the onset of vortex breakdown [23, 36, 63] $\overline {{u_{vc}}} /{U_\infty }$ = 0 is considered here as the criterion for vortex breakdown. It should be noted that, similar to a non-slender delta wing [13, 64], a jet-like profile before the vortex breakdown and a wake-like profile after the breakdown are found even in the present study, but not shown for brevity.

However, based on the above breakdown criterion, the onset of vortex breakdown is found to start at chordwise locations, $X/C \approx $ 0.48, 0.35 and 0.23 for $\alpha $ = 20°, 25° and 30°, respectively. These exact values of the breakdown location corroborate well with the ranges estimated from the coefficient of pressure distribution (see Fig. 11). Interestingly, the onset of vortex breakdown is found to be associated with the wave-like structures, as seen in flow visualisations for the corresponding angle-of-attack.

For a better understanding of the flow field downstream of the onset of vortex breakdown, the selected regions of the mean flow streamlines are shown in enlarged views in Fig. 14(a), (b) and (c), for $\alpha $ = 20°, 25° and 30°, respectively. Following the work of Perry and Chong [65], Chong et al. [66] and Rockwell [67], we find that there exist three unstable foci (denoted by F ${\rm{\;}}_1^ - $ , F ${\rm{\;}}_2^ - $ and F ${\rm{\;}}_3^ - $ ), as the streamlines are seen to spiral out from the centre, and two saddle nodes (S ${\rm{\;}}_1^ + $ and S ${\rm{\;}}_2^ + $ ), as there exist incoming and outgoing streamlines at those nodes, for $\alpha $ = 20°. On the other hand, only one unstable focus is found to exist for $\alpha $ = 25° and 30°. Further, these unstable nodes and foci indicate that the nature of the vortex breakdown may be spiral-type, as the streamlines are asymmetric about the vortex core after the onset of vortex breakdown.

Another interesting phenomenon that has been observed is the oscillation of the vortex breakdown location in the streamwise direction over the surface of the flying wing, similar to those seen on a delta wing [14, 68]. Here, we investigate this oscillating phenomenon at different Reynolds numbers and angles of attack. Mean and root-mean-squared values of the vortex breakdown location ( ${X_{VB}}$ ) have been estimated from the acquired PIV realisations in the longitudinal plane. Remarkably, our findings, as shown in Fig. 15(a), reveal a compelling trend. In particular, for the pre-stall angle-of-attack ( $\alpha $ = 20°), our quantitative measurements show a downstream shift in the mean breakdown location as the Reynolds number increases, whereas no significant changes in the breakdown location can be noticed for the near-stall ( $\alpha $ = 25°) and post-stall ( $\alpha $ = 30°) angles of attack. To find out the unsteady nature of the breakdown location, we have also estimated the RMS values of the breakdown location ( ${X_{f,{\rm{\;\;}}RMS}}$ ), as shown in Fig. 15(b). One may notice that ${X_{f,{\rm{\;\;}}RMS}}$ values increase with Reynolds number for the pre-stall $\alpha $ = 20°, whereas the values for the near stall and post-stall angles of attack seem to arrive at some constant magnitudes after an initial drop. This result suggests that the breakdown location is more unsteady for the pre-stall angle-of-attack than the near-stall and post-stall angles of attack. Further, the unsteadiness increases with the Reynolds number for the pre-stall angle-of-attack, whereas it does not significantly change with the Reynolds number for the near-stall and post-stall angles of attack.

Figure 15. Reynolds number effects on variations of (a) the mean vortex breakdown location ( ${X_{VB}}$ ) and (b) the root-mean-squared (RMS) of fluctuation of the breakdown location ( ${X_{f,{\rm{\;\;}}RMS}}$ ) for $\alpha $ = 20°, 25° and 30°.

3.5 Proper orthogonal decomposition of the flow field

Proper orthogonal decomposition (POD) analysis along the longitudinal plane has been performed to investigate the low-dimensional nature of the vortical flows over the flying wing. Since its introduction to fluid mechanics by Lumley [69], this decomposition technique is often used to extract the coherent structures from an unsteady flow field [70]. The PIV measurements in a flow field provide a large volume of data, and therefore, it is useful to use such a tool to extract the dominant flow structures. The method of snapshot, proposed by Sirovich [70], has been used here to calculate the POD modes and the associated energy. The present POD methodology is adapted from the work of Mandal et al. [71], as briefly discussed below.

The fluctuating velocity field ( ${\bf{u}}{\rm{'}} = {{\bf{u}}_{\bf{I}}} - \bar{\bf{u}}$ ) has been obtained by subtracting the ensemble mean ( $\bar{\bf{u}}$ ) from each instantaneous PIV realisation ( ${\bf{u}}$ ). The covariance matrix is then obtained as ${R_{ij}} = \left( {{\bf{u}}{{\rm{'}}_{\!\!i}},{\bf{u}}{{\rm{'}}_{\!\!j}}} \right)$ , where $i = 1,2, \ldots ,M$ and $j = 1,2, \ldots ,M$ . Here, $M$ is the total number of PIV realisations. The covariance matrix ${R_{ij}}$ is symmetric and its non-negative eigenvalues, ${\lambda _i}$ , indicate the relative importance of each POD mode. The summation of all the eigenvalues can be considered as the total energy, ${\rm{E}}\left( { = \mathop \sum \nolimits_{i = 1}^M {\lambda _i}} \right)$ , and the relative energy of each POD mode can be defined as ${{\rm{E}}_k} = {\lambda _k}/{\rm{E}}$ [71]. The eigenfunctions or POD modes are defined as

(1) \begin{align} {{\rm{\Phi }}^k} = \mathop \sum \limits_{i = 1}^M \,\phi _i^k{\bf{u}}{{\rm{'}}_{\!i}},{\rm{\;\;\;\;\;\;\;\;}}k = 1,2,....,M\end{align}

where ${\phi ^k}$ are orthogonal eigenvectors, which form a complete set, and $\phi _i^k$ indicates the ${i^{th}}$ component of the ${k^{th}}$ eigenvector. The eigenfunctions, ${{\rm{\Phi }}^k}$ , are normalised such that

(2) \begin{align}\left( {{{\rm{\Phi }}_i},{{\rm{\Phi }}_j}} \right) = 1.\end{align}

3.5.1 POD analysis in the longitudinal plane

The POD analysis has been performed on time-resolved PIV data, which were acquired in the longitudinal plane of the leading-edge vortex on the starboard side of the flying wing. For this analysis, 6,000 TR-PIV realisations were used. The relative and cumulative energy distributions of the first 30 POD modes are shown in Fig. 16(a) and (b), for $\alpha $ = 20° and $\alpha $ = 30°, respectively. A rapid decrease of the relative energy and rapid increase of the cumulative energy with mode numbers can be noticed for both $\alpha $ = 20° and 30°. Four dominant POD modes are also shown in Fig. 16(a) and (b), for $\alpha $ = 20° and 30°, respectively. The first mode contains 4.67% of total energy at $\alpha $ = 20°, whereas the next three modes carry approximately 1.9%, 1.53% and 1.3%, respectively. Similarly, the first dominant mode contains 2.5% of total energy at $\alpha $ = 30°, and the following three modes contain approximately 1.21%, 1.03% and 0.85%, respectively. The cumulative energy distribution, in Fig. 16(a), shows that the first 30 POD modes contain 21.76% energy, whereas 378 POD modes are required to capture 50.03% energy at $\alpha $ = 20°. Similarly, the first 30 POD modes carry 14.1% energy, and one needs 563 POD modes to capture 50.03% energy at $\alpha $ = 30°. This indicates that the small scales are generated as we increase the angle-of-attack.

Figure 16. Relative and cumulative energies along with four POD modes in a plane passing through the trajectory of vortex core. (a) $\alpha $ = 20°, and (b) $\alpha $ = 30°.

Figure 16(a) and (b) also show the first four dominant POD modes at $\alpha $ = 20° (pre-stall regime) and $\alpha $ = 30° (post-stall regime). At both angles of attack, the first mode shows large velocity fluctuations around the vortex breakdown location, indicating highly unsteady flow phenomena around that location. In fact, fluctuation of the breakdown location about the mean location is also estimated from the entire PIV realisations. The RMS values of these fluctuations about the mean locations, for $\alpha $ = 20° and 30°, are found to be 1.62% and 1.68% of the root chord, respectively.

Further, Fig. 16 shows that the first POD mode in the longitudinal plane is involved either with negative or positive $u$ fluctuations. A non-axisymmetric nature of these velocity fluctuations with considerable magnitude along the vortex core can also be noticed. Higher modes (i.e. from mode 2 onward) represent smaller flow structures with similar non-axisymmetric velocity fluctuations. A POD mode itself can be different from a coherent structure; that is, it does not necessarily represent a structure that needs to evolve coherently in the flow field [72, 73]. A coherent structure may be composed of a few POD modes confined in some spatial domain [73]. Since a POD mode itself does not clearly reveal whether the vortex breakdown is associated with spiral-type breakdown or bubble-type breakdown, we have reconstructed the instantaneous flow fields using the first ten dominant POD modes for a clear understanding of the type of vortex breakdown. Figure 17 shows the reconstructed time sequence of the flow fields. We can clearly see in Fig. 17 that all the reconstructed velocity fields are associated with some counter-rotating vortex pairs along the axis of the leading-edge vortex, together with some patches of positive and negative $u$ fluctuations. These flow features indicate a spiral-type flow breakdown, as schematically detailed in the following.

Figure 17. Time sequence of the reconstructed fluctuating velocity field over the contours of $u{{\rm{'}}_{vc}}$ . Ten POD modes are used for reconstruction at $\alpha $ = 20°.

Flow field inside a bubble type breakdown is often seen to be symmetric about the mid-plane of the vortex axis, as compared to the spiral breakdown, which is highly asymmetric about the midplane of the vortex axis [74, 75]. A simple sketch of a spiral-type vortex breakdown is shown in Fig. 18(a). During a PIV measurement in the midplane of the vortex axis, a laser sheet can cut a spiral vortex at some specific locations, for example, at locations L1, L2, L3, L4 and L5, as schematically shown in Fig. 18(b), which will appear as counter-rotating vortex pairs in the laser plane (i.e. in the measurement plane). This is exactly what we can observe in Figure 18. Therefore, the POD analysis clearly indicates that there exists a spiral-type vortex breakdown.

Figure 18. (a) A simple schematic depicting spiral vortex breakdown and (b) The PIV measurement plane along the midplane of the leading-edge vortex core.

4.0 Summary and concluding remarks

An experimental study at some pre-stall, near-stall and post-stall angles of attack has been carried out to understand better some non-linear aerodynamic characteristics of a non-slender flying wing configuration. To achieve this, various measurements, i.e. force, surface pressure and whole flow field measurements, including surface flow visualisation, were conducted in both the cross-flow and longitudinal planes. The findings of this study are summarised as follows.

1. 1. The present study clearly reveals that changes in flow patterns at particular angles of attack over the surface of the flying wing lead to highly non-linear lift curve behaviour and associated peaks and valleys in the pitching moment coefficient. Additionally, surface flow visualisation showed a wave-like surface pattern followed by a kink, symmetric about the root chord at $\alpha $ = 20° for Re $ = $ 2.5 $\; \times {\rm{\;}}$ 10 $^5$ . The wave-like pattern is found to move upstream with an increasing angle-of-attack, and its size is reduced with increasing Reynolds number.

2. 2. The PIV measurements in the crossflow plane reveal symmetrical vortices about the root chord, which increase in size after the wave-like pattern. A sudden enlargement of the vortex size after the wave-like pattern, accompanied by diffused axial vorticity, indicates vortex breakdown over the flying wing. Additionally, our measurements at $X/C = $ 0.1 demonstrate two counter-rotating vortices, one primary leading-edge vortex, and another trailing-edge vortex. Interestingly, we also observe that a primary leading-edge vortex can persist even at a post-stall angle-of-attack ( $\alpha = $ 30°), and the vortex breakdown can still occur at some downstream location of the apex of the wing.

3. 3. The PIV measurements in the longitudinal plane clearly reveal the existence of a stagnation point ( ${\bar u_{vc}}/{U_\infty } = $ 0) followed by a reverse flow region ( ${\bar u_{vc}}/{U_\infty }$ $ \le $ 0). The stagnation point shifts towards the upstream with an increasing angle-of-attack. However, the PIV measurements, along with the pressure distribution, confirm that the wave-like surface flow pattern is associated with the vortex breakdown, as the location of the stagnation point is found to correspond to the wave-like structure, as seen in the flow visualisation image. This is further supported by the fact that ${C_{p,{\rm{\;\;}}RMS}}$ increases on the onset of a wave-like pattern, as one can expect a highly unsteady flow field after the vortex breakdown. The maximum unsteadiness ( ${C_{p,{\rm{\;\;}}RMS}}$ ) is found near-stall angle-of-attack. The mean location of the vortex breakdown moves in the downstream direction with increasing Reynolds number at a pre-stall ( $\alpha = $ 20°) angle-of-attack, whereas it does not change significantly with Reynolds number for the near-stall ( $\alpha = $ 25°) and the post-stall ( $\alpha = $ 30°) angles of attack.

4. 4. Existence of unstable nodes and foci in the streamline topology indicates a spiral-type vortex breakdown. To confirm this, the velocity fields obtained from the TR-PIV measurements in the longitudinal plane are reconstructed using the first 10 POD modes to remove the high-frequency noise from the data. A time sequence of the reconstructed velocity fields reveals the wiggling nature of the velocity fluctuations with considerable magnitude along the vortex core. These results suggest that the vortex breakdown is a spiral-type breakdown.

On the whole, the present investigation clearly reveals that a spiral-type vortex breakdown on a flying wing configuration manifests as a wave-like surface pattern, which moves upstream with an increasing angle-of-attack. This pattern moves downstream and shrinks in size with an increasing Reynolds number.