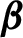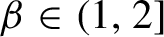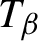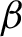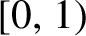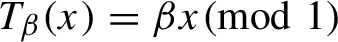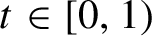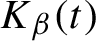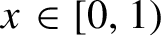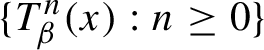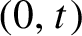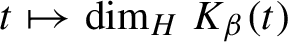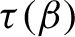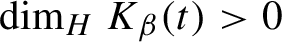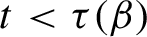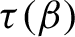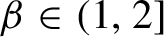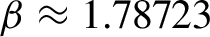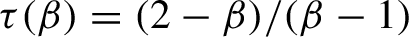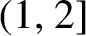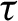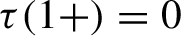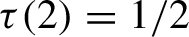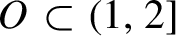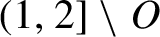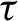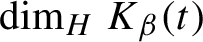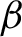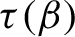1 Introduction
The mathematical study of dynamical systems with holes, called open dynamical systems, was first proposed by Pianigiani and Yorke [Reference Pianigiani and Yorke27] in 1979. In recent years, open dynamical systems have received considerable attention from both theoretical and applied perspectives (cf. [Reference Demers, Wright and Young13–Reference Demers and Young15]). In the general setting, one considers a discrete dynamical system
![]() $(X, T)$
, where X is a compact metric space and
$(X, T)$
, where X is a compact metric space and
![]() $T: X\to X$
is a continuous map having positive topological entropy. Let
$T: X\to X$
is a continuous map having positive topological entropy. Let
![]() $H\subset X$
be an open connected set, called the hole. It is interesting to study the set of points
$H\subset X$
be an open connected set, called the hole. It is interesting to study the set of points
![]() $x\in X$
whose orbit
$x\in X$
whose orbit
![]() $\{T^{n}(x): n\ge 0\}$
never hits the hole H. In other words, we are interested in the survivor set
$\{T^{n}(x): n\ge 0\}$
never hits the hole H. In other words, we are interested in the survivor set
 $$ \begin{align*} K(H)=\{x\in X: T^{n}(x)\notin H \text{ for all } n\ge 0\}=X\setminus\bigcup_{n=0}^{\infty} T^{-n}(H). \end{align*} $$
$$ \begin{align*} K(H)=\{x\in X: T^{n}(x)\notin H \text{ for all } n\ge 0\}=X\setminus\bigcup_{n=0}^{\infty} T^{-n}(H). \end{align*} $$
It is known that the size of
![]() ${K}(H)$
depends not only on the size but also on the position of the hole H (cf. [Reference Bunimovich and Yurchenko7]). In [Reference Urbański29, Reference Urbański30], Urbański considered
${K}(H)$
depends not only on the size but also on the position of the hole H (cf. [Reference Bunimovich and Yurchenko7]). In [Reference Urbański29, Reference Urbański30], Urbański considered
![]() $C^{2}$
-expanding, orientation-preserving circle maps with a hole of the form
$C^{2}$
-expanding, orientation-preserving circle maps with a hole of the form
![]() $(0,t)$
. In particular, he proved that for the doubling map
$(0,t)$
. In particular, he proved that for the doubling map
![]() $T_{2}$
on the circle
$T_{2}$
on the circle
![]() $\mathbb R/\mathbb Z\sim [0,1)$
, that is,
$\mathbb R/\mathbb Z\sim [0,1)$
, that is,
![]() $T_{2}:[0,1)\to [0,1); x\mapsto 2x\pmod 1$
, the Hausdorff dimension of the survivor set
$T_{2}:[0,1)\to [0,1); x\mapsto 2x\pmod 1$
, the Hausdorff dimension of the survivor set
![]() $ K_{2}(t):=\{x\in [0,1): T_{2}^{n}(x)\notin (0,t) \text { for all } n\ge 0\} $
depends continuously on the parameter
$ K_{2}(t):=\{x\in [0,1): T_{2}^{n}(x)\notin (0,t) \text { for all } n\ge 0\} $
depends continuously on the parameter
![]() $t\in [0,1)$
. Furthermore, he showed that the dimension function
$t\in [0,1)$
. Furthermore, he showed that the dimension function
![]() $\eta _{2}: t\mapsto \dim _{H} K_{2}(t)$
is a devil’s staircase, and studied its bifurcation set. Carminati and Tiozzo [Reference Carminati and Tiozzo9] showed that the function
$\eta _{2}: t\mapsto \dim _{H} K_{2}(t)$
is a devil’s staircase, and studied its bifurcation set. Carminati and Tiozzo [Reference Carminati and Tiozzo9] showed that the function
![]() $\eta _{2}$
has an interesting analytic property: the local Hölder exponent of
$\eta _{2}$
has an interesting analytic property: the local Hölder exponent of
![]() $\eta _{2}$
at any bifurcation point t is equal to
$\eta _{2}$
at any bifurcation point t is equal to
![]() $\eta _{2}(t)$
. For the doubling map
$\eta _{2}(t)$
. For the doubling map
![]() $T_{2}$
with an arbitrary hole
$T_{2}$
with an arbitrary hole
![]() $(a,b)\subset [0,1)$
, Glendinning and Sidorov [Reference Glendinning and Sidorov18] studied (i) when the survivor set
$(a,b)\subset [0,1)$
, Glendinning and Sidorov [Reference Glendinning and Sidorov18] studied (i) when the survivor set
![]() $K_{2}(a,b)=\{x\in [0,1): T_{2}^{n} (x)\notin (a,b) \text { for all } n\ge 0\}$
is non-empty; (ii) when
$K_{2}(a,b)=\{x\in [0,1): T_{2}^{n} (x)\notin (a,b) \text { for all } n\ge 0\}$
is non-empty; (ii) when
![]() $K_{2}(a,b)$
is infinite; and (iii) when
$K_{2}(a,b)$
is infinite; and (iii) when
![]() $K_{2}(a,b)$
has positive Hausdorff dimension. They proved that when the size of the hole
$K_{2}(a,b)$
has positive Hausdorff dimension. They proved that when the size of the hole
![]() $(a,b)$
is strictly smaller than
$(a,b)$
is strictly smaller than
![]() $0.175092$
, the survivor set
$0.175092$
, the survivor set
![]() $K_{2}(a,b)$
has positive Hausdorff dimension. The work of Glendinning and Sidorov was partially extended by Clark [Reference Clark10] to the
$K_{2}(a,b)$
has positive Hausdorff dimension. The work of Glendinning and Sidorov was partially extended by Clark [Reference Clark10] to the
![]() $\beta $
-dynamical system
$\beta $
-dynamical system
![]() $([0,1), T_{\beta })$
with a hole
$([0,1), T_{\beta })$
with a hole
![]() $(a,b)$
, where
$(a,b)$
, where
![]() $\beta \in (1,2]$
and
$\beta \in (1,2]$
and
![]() $T_{\beta }(x):=\beta x\pmod 1$
.
$T_{\beta }(x):=\beta x\pmod 1$
.
Motivated by the above works, Kalle et al [Reference Kalle, Kong, Langeveld and Li20] considered the survivor set in the
![]() $\beta $
-dynamical system
$\beta $
-dynamical system
![]() $([0, 1), T_{\beta })$
with a hole at zero. More precisely, for
$([0, 1), T_{\beta })$
with a hole at zero. More precisely, for
![]() $t\in [0,1)$
, they determined the Hausdorff dimension of the survivor set
$t\in [0,1)$
, they determined the Hausdorff dimension of the survivor set
 $$ \begin{align*} K_{\beta}(t)=\{x\in[0,1): T_{\beta}^{n} (x)\notin (0,t) \text{ for all } n\ge 0\}, \end{align*} $$
$$ \begin{align*} K_{\beta}(t)=\{x\in[0,1): T_{\beta}^{n} (x)\notin (0,t) \text{ for all } n\ge 0\}, \end{align*} $$
and showed that the dimension function
![]() $\eta _{\beta }: t\mapsto \dim _{H} K_{\beta }(t)$
is a non-increasing Devil’s staircase. So there exists a critical value
$\eta _{\beta }: t\mapsto \dim _{H} K_{\beta }(t)$
is a non-increasing Devil’s staircase. So there exists a critical value
![]() $\tau (\beta )\in [0,1)$
such that
$\tau (\beta )\in [0,1)$
such that
![]() $\dim _{H} K_{\beta }(t)>0$
if and only if
$\dim _{H} K_{\beta }(t)>0$
if and only if
![]() $t<\tau (\beta )$
. Kalle et al [Reference Kalle, Kong, Langeveld and Li20] gave general lower and upper bounds for
$t<\tau (\beta )$
. Kalle et al [Reference Kalle, Kong, Langeveld and Li20] gave general lower and upper bounds for
![]() $\tau (\beta )$
. In particular, they showed that
$\tau (\beta )$
. In particular, they showed that
![]() $\tau (\beta )\le 1-{1}/{\beta }$
for all
$\tau (\beta )\le 1-{1}/{\beta }$
for all
![]() $\beta \in (1,2]$
, and the equality
$\beta \in (1,2]$
, and the equality
![]() $\tau (\beta )=1-{1}/{\beta }$
holds for infinitely many
$\tau (\beta )=1-{1}/{\beta }$
holds for infinitely many
![]() $\beta \in (1,2]$
. They left open the interesting question to determine
$\beta \in (1,2]$
. They left open the interesting question to determine
![]() $\tau (\beta )$
for all
$\tau (\beta )$
for all
![]() $\beta \in (1,2]$
. In this paper, we give a complete description of the critical value
$\beta \in (1,2]$
. In this paper, we give a complete description of the critical value
for each
![]() $\beta \in (1,2]$
. Qualitatively, our main result is the following.
$\beta \in (1,2]$
. Qualitatively, our main result is the following.
Theorem 1.
-
(i) The function
 $\tau : \beta \mapsto \tau (\beta )$
is left continuous on
$\tau : \beta \mapsto \tau (\beta )$
is left continuous on
 $(1,2]$
with right-hand limits everywhere (càdlàg), and, as a result, has only countably many discontinuities.
$(1,2]$
with right-hand limits everywhere (càdlàg), and, as a result, has only countably many discontinuities. -
(ii)
 $\tau $
has no downward jumps.
$\tau $
has no downward jumps. -
(iii) There is an open set
 $O\subset (1,2]$
, whose complement
$O\subset (1,2]$
, whose complement
 $(1,2]\setminus O$
has zero Hausdorff dimension, such that
$(1,2]\setminus O$
has zero Hausdorff dimension, such that
 $\tau $
is real-analytic, convex, and strictly decreasing on each connected component of O.
$\tau $
is real-analytic, convex, and strictly decreasing on each connected component of O.
Quantitatively, the main results are Theorem 2 and Propositions 6.2 and 6.3. Together with Proposition 1.12, they specify the value of
![]() $\tau (\beta )$
for all
$\tau (\beta )$
for all
![]() $\beta \in (1,2]$
. In Proposition 1.9 below, we give an explicit description of the discontinuities of the map
$\beta \in (1,2]$
. In Proposition 1.9 below, we give an explicit description of the discontinuities of the map
![]() $\tau $
, which shows that the dimension
$\tau $
, which shows that the dimension
![]() $\dim _{H} K_{\beta }(t)$
is not jointly continuous in
$\dim _{H} K_{\beta }(t)$
is not jointly continuous in
![]() $\beta $
and t. The closures of the connected components of the set O in Theorem 1(iii) form a pairwise disjoint collection
$\beta $
and t. The closures of the connected components of the set O in Theorem 1(iii) form a pairwise disjoint collection
![]() $\{I_{\alpha }\}$
of closed intervals which we call basic intervals (see Definition 1.5). In the remainder of this introduction, we describe these basic intervals by using certain substitutions on Farey words. We then give a formula for
$\{I_{\alpha }\}$
of closed intervals which we call basic intervals (see Definition 1.5). In the remainder of this introduction, we describe these basic intervals by using certain substitutions on Farey words. We then give a formula for
![]() $\tau (\beta )$
on each basic interval (see Theorem 2) and decompose the complement
$\tau (\beta )$
on each basic interval (see Theorem 2) and decompose the complement
![]() $(1,2]\backslash \bigcup _{\alpha } I_{\alpha }$
into countably many disjoint subsets (see Theorem 3), which are of two essentially different types. We then calculate
$(1,2]\backslash \bigcup _{\alpha } I_{\alpha }$
into countably many disjoint subsets (see Theorem 3), which are of two essentially different types. We then calculate
![]() $\tau (\beta )$
on each subset.
$\tau (\beta )$
on each subset.
To describe the critical value
![]() $\tau (\beta )$
, we first introduce the Farey words, also called standard words (see [Reference Lothaire24, Ch. 2.2]). Following a recent paper of Carminati, Isola, and Tiozzo [Reference Carminati, Isola and Tiozzo8], we define recursively a sequence of ordered sets
$\tau (\beta )$
, we first introduce the Farey words, also called standard words (see [Reference Lothaire24, Ch. 2.2]). Following a recent paper of Carminati, Isola, and Tiozzo [Reference Carminati, Isola and Tiozzo8], we define recursively a sequence of ordered sets
![]() $(F_{n})_{n=0}^{\infty }$
. Let
$(F_{n})_{n=0}^{\infty }$
. Let
![]() $F_{0}=(0,1)$
, and for
$F_{0}=(0,1)$
, and for
![]() $n\ge 0$
, the ordered set
$n\ge 0$
, the ordered set
![]() $F_{n+1}=(v_{1},\ldots , v_{2^{n+1}+1})$
is obtained from
$F_{n+1}=(v_{1},\ldots , v_{2^{n+1}+1})$
is obtained from
![]() $F_{n}=(w_{1},\ldots , w_{2^{n}+1})$
by inserting for each
$F_{n}=(w_{1},\ldots , w_{2^{n}+1})$
by inserting for each
![]() $1\le j\le 2^{n}$
the new word
$1\le j\le 2^{n}$
the new word
![]() $w_{j}w_{j+1}$
between the two neighboring words
$w_{j}w_{j+1}$
between the two neighboring words
![]() $w_{j}$
and
$w_{j}$
and
![]() $w_{j+1}$
. So,
$w_{j+1}$
. So,
 $$ \begin{align} &F_{1}=(0,01,1),\quad F_{2}=(0,001,01,011,1),\nonumber\\[3pt] F_{3}&=(0,0001,001,00101,01,01011,011,0111,1), \end{align} $$
$$ \begin{align} &F_{1}=(0,01,1),\quad F_{2}=(0,001,01,011,1),\nonumber\\[3pt] F_{3}&=(0,0001,001,00101,01,01011,011,0111,1), \end{align} $$
and so on (see §2 for more details on Farey words). Set
![]() $\Omega _{F}^{*}:=\bigcup _{n=1}^{\infty } F_{n}\setminus F_{0}$
. Then each word in
$\Omega _{F}^{*}:=\bigcup _{n=1}^{\infty } F_{n}\setminus F_{0}$
. Then each word in
![]() $\Omega _{F}^{*}$
is called a non-degenerate Farey word. Note that any word in
$\Omega _{F}^{*}$
is called a non-degenerate Farey word. Note that any word in
![]() $\Omega _{F}^{*}$
has length at least two, and begins with digit
$\Omega _{F}^{*}$
has length at least two, and begins with digit
![]() $0$
and ends with digit
$0$
and ends with digit
![]() $1$
. We will use the Farey words as basic bricks to construct infinitely many pairwise disjoint closed intervals so that we can explicitly determine
$1$
. We will use the Farey words as basic bricks to construct infinitely many pairwise disjoint closed intervals so that we can explicitly determine
![]() $\tau (\beta )$
for
$\tau (\beta )$
for
![]() $\beta $
in each of these intervals. Furthermore, we will show that these closed intervals cover
$\beta $
in each of these intervals. Furthermore, we will show that these closed intervals cover
![]() $(1,2]$
up to a set of zero Hausdorff dimension.
$(1,2]$
up to a set of zero Hausdorff dimension.
The construction of these basic intervals depends on certain substitutions of Farey words. For this reason, we need to introduce a larger class of words, called Lyndon words; see [Reference Kalle, Kong, Langeveld and Li20, Lemma 3.2].
Definition 1.1. A word
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}\in \{0,1\}^{*}$
is Lyndon if
$ {\mathbf {s}}=s_{1}\ldots s_{m}\in \{0,1\}^{*}$
is Lyndon if
Here and throughout the paper, we use lexicographical order
![]() $\succ $
between sequences and words; see §2. The words
$\succ $
between sequences and words; see §2. The words
![]() $0$
and
$0$
and
![]() $1$
are (vacuously) Lyndon. Let
$1$
are (vacuously) Lyndon. Let
![]() $\Omega _{L}^{*}$
denote the set of all Lyndon words of length at least two. Then by Definition 1.1, each
$\Omega _{L}^{*}$
denote the set of all Lyndon words of length at least two. Then by Definition 1.1, each
![]() $ {\mathbf {s}}\in \Omega _{L}^{*}$
has a prefix
$ {\mathbf {s}}\in \Omega _{L}^{*}$
has a prefix
![]() $0$
and a suffix
$0$
and a suffix
![]() $1$
. It is well known that each Farey word is Lyndon (cf. [Reference Carminati, Isola and Tiozzo8, Proposition 2.8]). Thus
$1$
. It is well known that each Farey word is Lyndon (cf. [Reference Carminati, Isola and Tiozzo8, Proposition 2.8]). Thus
![]() $\Omega _{F}^{*}\subset \Omega _{L}^{*}$
.
$\Omega _{F}^{*}\subset \Omega _{L}^{*}$
.
Now we define a substitution operator
![]() $\bullet $
in
$\bullet $
in
![]() $\Omega _{L}^{*}$
. This requires the following notation. By a word we mean a finite string of zeros and ones. For any two words,
$\Omega _{L}^{*}$
. This requires the following notation. By a word we mean a finite string of zeros and ones. For any two words,
![]() $\mathbf u=u_{1}\ldots u_{m}, \mathbf v=v_{1}\ldots v_{n}$
, we denote by
$\mathbf u=u_{1}\ldots u_{m}, \mathbf v=v_{1}\ldots v_{n}$
, we denote by
![]() $\mathbf u\mathbf v=u_{1}\ldots u_{m} v_{1}\ldots v_{n}$
their concatenation. Furthermore, we write
$\mathbf u\mathbf v=u_{1}\ldots u_{m} v_{1}\ldots v_{n}$
their concatenation. Furthermore, we write
![]() $\mathbf u^{\infty }$
for the periodic sequence with periodic block
$\mathbf u^{\infty }$
for the periodic sequence with periodic block
![]() $\mathbf u$
. For a word
$\mathbf u$
. For a word
![]() $\mathbf w=w_{1}\ldots w_{n}\in \{0,1\}^{n}$
, we denote
$\mathbf w=w_{1}\ldots w_{n}\in \{0,1\}^{n}$
, we denote
![]() $\mathbf w^{-}:=w_{1}\ldots w_{n-1}{0}$
if
$\mathbf w^{-}:=w_{1}\ldots w_{n-1}{0}$
if
![]() $w_{n}=1$
, and
$w_{n}=1$
, and
![]() $\mathbf w^{+}:=w_{1}\ldots w_{n-1}{1}$
if
$\mathbf w^{+}:=w_{1}\ldots w_{n-1}{1}$
if
![]() $w_{n}=0$
. Furthermore, we denote by
$w_{n}=0$
. Furthermore, we denote by
![]() $\mathbb {L}(\mathbf w)$
the lexicographically largest cyclic permutation of
$\mathbb {L}(\mathbf w)$
the lexicographically largest cyclic permutation of
![]() $\mathbf w$
. Now for two words
$\mathbf w$
. Now for two words
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{L}^{*}$
and
$ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{L}^{*}$
and
![]() $ {\mathbf {r}}=r_{1}\ldots r_{\ell }\in \{0,1\}^{\ell }$
, we define
$ {\mathbf {r}}=r_{1}\ldots r_{\ell }\in \{0,1\}^{\ell }$
, we define
where
 $$ \begin{align*}c_{1}\ldots c_{m}=\left\{\begin{array} {@{}lll} {\mathbf{s}}^{-}&\textrm{if } r_{1}=0,\\[3pt] \mathbb{L}( {\mathbf{s}})^{+}&\textrm{if } r_{1}=1, \end{array} \right.\end{align*} $$
$$ \begin{align*}c_{1}\ldots c_{m}=\left\{\begin{array} {@{}lll} {\mathbf{s}}^{-}&\textrm{if } r_{1}=0,\\[3pt] \mathbb{L}( {\mathbf{s}})^{+}&\textrm{if } r_{1}=1, \end{array} \right.\end{align*} $$
and for
![]() $1\le j<\ell $
,
$1\le j<\ell $
,
 $$ \begin{align*} c_{jm+1}\ldots c_{(j+1)m}=\left\{\begin{array} {@{}lll} \mathbb{L}( {\mathbf{s}})&\textrm{if } r_{j}r_{j+1}=00,\\[3pt] \mathbb{L}( {\mathbf{s}})^{+}&\textrm{if } r_{j}r_{j+1}=01,\\[3pt] {\mathbf{s}}^{-}&\textrm{if } r_{j}r_{j+1}=10,\\[3pt] {\mathbf{s}} &\textrm{if } r_{j}r_{j+1}=11. \end{array} \right. \end{align*} $$
$$ \begin{align*} c_{jm+1}\ldots c_{(j+1)m}=\left\{\begin{array} {@{}lll} \mathbb{L}( {\mathbf{s}})&\textrm{if } r_{j}r_{j+1}=00,\\[3pt] \mathbb{L}( {\mathbf{s}})^{+}&\textrm{if } r_{j}r_{j+1}=01,\\[3pt] {\mathbf{s}}^{-}&\textrm{if } r_{j}r_{j+1}=10,\\[3pt] {\mathbf{s}} &\textrm{if } r_{j}r_{j+1}=11. \end{array} \right. \end{align*} $$
For an equivalent definition of the substitution operator
![]() $\bullet $
, see §3.
$\bullet $
, see §3.
Example 1.2. Let
![]() $ {\mathbf {r}}=01, {\mathbf {s}}=001$
, and
$ {\mathbf {r}}=01, {\mathbf {s}}=001$
, and
![]() $ {\mathbf {t}}=011$
be three words in
$ {\mathbf {t}}=011$
be three words in
![]() $\Omega _{F}^{*}$
. Then
$\Omega _{F}^{*}$
. Then
![]() $\mathbb {L}( {\mathbf {r}})=10$
and
$\mathbb {L}( {\mathbf {r}})=10$
and
![]() $\mathbb {L}( {\mathbf {s}})=100$
. So, by equation (1.3), it follows that
$\mathbb {L}( {\mathbf {s}})=100$
. So, by equation (1.3), it follows that
 $$ \begin{align*} {\mathbf{r}}\bullet {\mathbf{s}}&= {\mathbf{r}}\bullet 001= {\mathbf{r}}^{-}\mathbb{L}( {\mathbf{r}})\mathbb{L}( {\mathbf{r}})^{+}=001011\in\Omega_{L}^{*},\\[3pt] {\mathbf{s}}\bullet {\mathbf{t}}&= {\mathbf{s}}\bullet 011= {\mathbf{s}}^{-}\mathbb{L}( {\mathbf{s}})^{+} {\mathbf{s}}=000\,101\,001\in\Omega_{L}^{*}. \end{align*} $$
$$ \begin{align*} {\mathbf{r}}\bullet {\mathbf{s}}&= {\mathbf{r}}\bullet 001= {\mathbf{r}}^{-}\mathbb{L}( {\mathbf{r}})\mathbb{L}( {\mathbf{r}})^{+}=001011\in\Omega_{L}^{*},\\[3pt] {\mathbf{s}}\bullet {\mathbf{t}}&= {\mathbf{s}}\bullet 011= {\mathbf{s}}^{-}\mathbb{L}( {\mathbf{s}})^{+} {\mathbf{s}}=000\,101\,001\in\Omega_{L}^{*}. \end{align*} $$
Then
![]() $\mathbb {L}( {\mathbf {r}}\bullet {\mathbf {s}})=110010$
, and thus
$\mathbb {L}( {\mathbf {r}}\bullet {\mathbf {s}})=110010$
, and thus
and
 $$ \begin{align*} {\mathbf{r}}\bullet( {\mathbf{s}}\bullet {\mathbf{t}})&= {\mathbf{r}}\bullet 000101001 \\[3pt] &= {\mathbf{r}}^{-}\mathbb{L}( {\mathbf{r}})\mathbb{L}( {\mathbf{r}})\mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{-}\mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{-}\mathbb{L}( {\mathbf{r}})\mathbb{L}( {\mathbf{r}})^{+}=00\,10\,10\,11\,00\,11\,00\,10\,11. \end{align*} $$
$$ \begin{align*} {\mathbf{r}}\bullet( {\mathbf{s}}\bullet {\mathbf{t}})&= {\mathbf{r}}\bullet 000101001 \\[3pt] &= {\mathbf{r}}^{-}\mathbb{L}( {\mathbf{r}})\mathbb{L}( {\mathbf{r}})\mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{-}\mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{-}\mathbb{L}( {\mathbf{r}})\mathbb{L}( {\mathbf{r}})^{+}=00\,10\,10\,11\,00\,11\,00\,10\,11. \end{align*} $$
Hence,
![]() $( {\mathbf {r}}\bullet {\mathbf {s}})\bullet {\mathbf {t}}= {\mathbf {r}}\bullet ( {\mathbf {s}}\bullet {\mathbf {t}})$
, suggesting that the operator
$( {\mathbf {r}}\bullet {\mathbf {s}})\bullet {\mathbf {t}}= {\mathbf {r}}\bullet ( {\mathbf {s}}\bullet {\mathbf {t}})$
, suggesting that the operator
![]() $\bullet $
is associative. However, observe that
$\bullet $
is associative. However, observe that
![]() $ {\mathbf {r}}\bullet {\mathbf {s}}=00\, 10\, 11\ne 000\,101= {\mathbf {s}}\bullet {\mathbf {r}}$
. So
$ {\mathbf {r}}\bullet {\mathbf {s}}=00\, 10\, 11\ne 000\,101= {\mathbf {s}}\bullet {\mathbf {r}}$
. So
![]() $\bullet $
is not commutative.
$\bullet $
is not commutative.
From Example 1.2, we see that
![]() $\Omega _{F}^{*}$
is not closed under the substitution operator
$\Omega _{F}^{*}$
is not closed under the substitution operator
![]() $\bullet $
, since
$\bullet $
, since
![]() $ {\mathbf {r}}\bullet {\mathbf {s}}=001011\not \in \Omega _{F}^{*}$
. Hence we need the larger collection
$ {\mathbf {r}}\bullet {\mathbf {s}}=001011\not \in \Omega _{F}^{*}$
. Hence we need the larger collection
![]() $\Omega _{L}^{*}$
. It turns out that
$\Omega _{L}^{*}$
. It turns out that
![]() $\Omega _{L}^{*}$
is a non-Abelian semi-group under the substitution operator
$\Omega _{L}^{*}$
is a non-Abelian semi-group under the substitution operator
![]() $\bullet $
.
$\bullet $
.
Proposition 1.3.
![]() $(\Omega _{L}^{*},\bullet )$
forms a non-Abelian semi-group.
$(\Omega _{L}^{*},\bullet )$
forms a non-Abelian semi-group.
Remark 1.4. The substitution operator
![]() $\bullet $
defined in equation (1.3) is similar to that introduced by Allaart [Reference Allaart1], who used it to study the entropy plateaus in unique q-expansions.
$\bullet $
defined in equation (1.3) is similar to that introduced by Allaart [Reference Allaart1], who used it to study the entropy plateaus in unique q-expansions.
Let
be the set of all substitutions of Farey words from
![]() $\Omega _{F}^{*}$
. Then by Proposition 1.3 it follows that
$\Omega _{F}^{*}$
. Then by Proposition 1.3 it follows that
![]() $\Omega _{F}^{*}\subset \Lambda \subset \Omega _{L}^{*}$
. Moreover, both inclusions are strict. For instance,
$\Omega _{F}^{*}\subset \Lambda \subset \Omega _{L}^{*}$
. Moreover, both inclusions are strict. For instance,
![]() $001011=01\bullet 001\in \Lambda \backslash \Omega _{F}^{*}$
by Example 1.2 and Proposition 2.4 below, and
$001011=01\bullet 001\in \Lambda \backslash \Omega _{F}^{*}$
by Example 1.2 and Proposition 2.4 below, and
![]() $0010111\in \Omega _{L}^{*}\backslash \Lambda $
.
$0010111\in \Omega _{L}^{*}\backslash \Lambda $
.
Given
![]() $\beta \in (1,2]$
, for a sequence
$\beta \in (1,2]$
, for a sequence
![]() $(c_{i})\in \{0,1\}^{\mathbb {N}}$
, we write
$(c_{i})\in \{0,1\}^{\mathbb {N}}$
, we write
 $$ \begin{align*} ((c_{i}))_{\beta}:=\sum_{i=1}^{\infty}\frac{c_{i}}{\beta^{i}}. \end{align*} $$
$$ \begin{align*} ((c_{i}))_{\beta}:=\sum_{i=1}^{\infty}\frac{c_{i}}{\beta^{i}}. \end{align*} $$
Now we define the basic intervals.
Definition 1.5. A closed interval
![]() $I=[\beta _{\ell },\beta _{*}]\subset (1,2]$
is called a basic interval if there exists a word
$I=[\beta _{\ell },\beta _{*}]\subset (1,2]$
is called a basic interval if there exists a word
![]() $ {\mathbf {S}}\in \Lambda $
such that
$ {\mathbf {S}}\in \Lambda $
such that
 $$ \begin{align*} (\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta_{\ell}}=1\quad\textrm{and}\quad (\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta_{*}}=1. \end{align*} $$
$$ \begin{align*} (\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta_{\ell}}=1\quad\textrm{and}\quad (\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta_{*}}=1. \end{align*} $$
The interval
![]() $I=I^ {\mathbf {S}}$
is also called a basic interval generated by
$I=I^ {\mathbf {S}}$
is also called a basic interval generated by
![]() $ {\mathbf {S}}$
.
$ {\mathbf {S}}$
.
The subscripts for the endpoints
![]() $\beta _{\ell }$
and
$\beta _{\ell }$
and
![]() $\beta _{*}$
of a basic interval will be clarified when we define the Lyndon intervals (see Definition 1.8 below). Our second main result gives a formula for
$\beta _{*}$
of a basic interval will be clarified when we define the Lyndon intervals (see Definition 1.8 below). Our second main result gives a formula for
![]() $\tau (\beta )$
when
$\tau (\beta )$
when
![]() $\beta $
lies in a basic interval
$\beta $
lies in a basic interval
![]() $I^ {\mathbf {S}}$
.
$I^ {\mathbf {S}}$
.
Theorem 2.
-
(i) The basic intervals
 $I^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
are pairwise disjoint.
$I^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
are pairwise disjoint. -
(ii) If
 $I^ {\mathbf {S}}$
is a basic interval generated by
$I^ {\mathbf {S}}$
is a basic interval generated by
 $ {\mathbf {S}}\in \Lambda $
, then (1.5)
$ {\mathbf {S}}\in \Lambda $
, then (1.5) $$ \begin{align} \tau(\beta)=( {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta}\quad\textrm{for {every} } \beta\in I^ {\mathbf{S}}. \end{align} $$
$$ \begin{align} \tau(\beta)=( {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta}\quad\textrm{for {every} } \beta\in I^ {\mathbf{S}}. \end{align} $$
-
(iii) The function
 $\tau $
is strictly decreasing on
$\tau $
is strictly decreasing on
 $I^ {\mathbf {S}}$
, and is real-analytic and strictly convex in the interior of
$I^ {\mathbf {S}}$
, and is real-analytic and strictly convex in the interior of
 $I^ {\mathbf {S}}$
.
$I^ {\mathbf {S}}$
.
Remark 1.6. Note that (iii) follows immediately from (ii). For the special case when
![]() $ {\mathbf {S}}\in \Omega _{F}^{*}$
, the formula (1.5) was stated without proof by Kalle et al [Reference Kalle, Kong, Langeveld and Li20].
$ {\mathbf {S}}\in \Omega _{F}^{*}$
, the formula (1.5) was stated without proof by Kalle et al [Reference Kalle, Kong, Langeveld and Li20].
Example 1.7.
-
(i) Let
 $ {\mathbf {s}}=01\in \Omega _{F}^{*}$
. Then by Definition 1.5, the basic interval
$ {\mathbf {s}}=01\in \Omega _{F}^{*}$
. Then by Definition 1.5, the basic interval
 $I^{01}=[\beta _{\ell },\beta _{*}]$
satisfies By numerical calculation, we get
$I^{01}=[\beta _{\ell },\beta _{*}]$
satisfies By numerical calculation, we get $$ \begin{align*} & (\mathbb{L}(01)^{\kern-0.1pt\infty})_{\beta_{\ell}}\kern1.5pt{=}\kern1.5pt((10)^{\kern-0.1pt\infty})_{\beta_{\ell}} \kern1.5pt{=}\kern1.5pt 1 \!\quad\textrm{and}\quad\! (\mathbb{L}(01)^{\kern-0.1pt+}(01)^{\kern-0.1pt-}\mathbb{L}(01)^{\kern-0.1pt\infty})_{\beta_{*}}\kern1.5pt{=}\kern1.5pt(1100(10)^{\infty})_{\beta_{*}}\kern1.5pt{=}\kern1.5pt1. \end{align*} $$
$$ \begin{align*} & (\mathbb{L}(01)^{\kern-0.1pt\infty})_{\beta_{\ell}}\kern1.5pt{=}\kern1.5pt((10)^{\kern-0.1pt\infty})_{\beta_{\ell}} \kern1.5pt{=}\kern1.5pt 1 \!\quad\textrm{and}\quad\! (\mathbb{L}(01)^{\kern-0.1pt+}(01)^{\kern-0.1pt-}\mathbb{L}(01)^{\kern-0.1pt\infty})_{\beta_{*}}\kern1.5pt{=}\kern1.5pt(1100(10)^{\infty})_{\beta_{*}}\kern1.5pt{=}\kern1.5pt1. \end{align*} $$
 $I^{01} \approx [1.61803, 1.73867]$
(see Figure 1). In fact,
$I^{01} \approx [1.61803, 1.73867]$
(see Figure 1). In fact,
 $\beta _{\ell }=(1+\sqrt {5})/2$
. Theorem 2 yields that
$\beta _{\ell }=(1+\sqrt {5})/2$
. Theorem 2 yields that  $$ \begin{align*} \tau(\beta)=(00(10)^{\infty})_{\beta}=\frac{1}{\beta(\beta^{2}-1)}\quad\text{for all }\beta\in I^{01}. \end{align*} $$
$$ \begin{align*} \tau(\beta)=(00(10)^{\infty})_{\beta}=\frac{1}{\beta(\beta^{2}-1)}\quad\text{for all }\beta\in I^{01}. \end{align*} $$
-
(ii) Let
 $ {\mathbf {s}}_{1}= {\mathbf {s}}_{2}=01\in \Omega _{F}^{*}$
. Then
$ {\mathbf {s}}_{1}= {\mathbf {s}}_{2}=01\in \Omega _{F}^{*}$
. Then
 $ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet {\mathbf {s}}_{2}=01\bullet 01=0011$
. By Definition 1.5, the basic interval
$ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet {\mathbf {s}}_{2}=01\bullet 01=0011$
. By Definition 1.5, the basic interval
 $I^{ {\mathbf {s}}_{1}\bullet {\mathbf {s}}_{2}}=I^{0011}=[\beta _{\ell },\beta _{*}]$
is given implicitly by Numerical calculation gives
$I^{ {\mathbf {s}}_{1}\bullet {\mathbf {s}}_{2}}=I^{0011}=[\beta _{\ell },\beta _{*}]$
is given implicitly by Numerical calculation gives $$ \begin{align*} (\mathbb{L}(0011)^{\infty})_{\beta_{\ell}}&=((1100)^{\infty})_{\beta_{\ell}}=1,\\[3pt] \quad (\mathbb{L}(0011)^{+}(0011)^{-}\mathbb{L}(0011)^{\infty})_{\beta_{*}}&=(11010010(1100)^{\infty})_{\beta_{*}}=1. \end{align*} $$
$$ \begin{align*} (\mathbb{L}(0011)^{\infty})_{\beta_{\ell}}&=((1100)^{\infty})_{\beta_{\ell}}=1,\\[3pt] \quad (\mathbb{L}(0011)^{+}(0011)^{-}\mathbb{L}(0011)^{\infty})_{\beta_{*}}&=(11010010(1100)^{\infty})_{\beta_{*}}=1. \end{align*} $$
 $I^{0011}\approx [1.75488, 1.78431]$
(see Figure 1), and Theorem 2 implies
$I^{0011}\approx [1.75488, 1.78431]$
(see Figure 1), and Theorem 2 implies  $$ \begin{align*} \tau(\beta)=( {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta}=(0010(1100)^{\infty})_{\beta}=\frac{1}{\beta^{3}}+\frac{1+\beta}{\beta^{2}(\beta^{4}-1)}\quad\text{for all }\beta\in I^{0011}. \end{align*} $$
$$ \begin{align*} \tau(\beta)=( {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta}=(0010(1100)^{\infty})_{\beta}=\frac{1}{\beta^{3}}+\frac{1+\beta}{\beta^{2}(\beta^{4}-1)}\quad\text{for all }\beta\in I^{0011}. \end{align*} $$

Figure 1 Graph of the critical value function
![]() $\tau (\beta )$
for
$\tau (\beta )$
for
![]() $\beta \in (1,2]$
. We see that
$\beta \in (1,2]$
. We see that
![]() $\tau (\beta )\le 1-1/\beta $
for all
$\tau (\beta )\le 1-1/\beta $
for all
![]() $\beta \in (1,2]$
, and the function
$\beta \in (1,2]$
, and the function
![]() $\tau $
is strictly decreasing in each basic interval
$\tau $
is strictly decreasing in each basic interval
![]() $I^ {\mathbf {S}}$
. For example, the basic interval generated by the Farey word
$I^ {\mathbf {S}}$
. For example, the basic interval generated by the Farey word
![]() $01$
is given by
$01$
is given by
![]() $I^{01}=[\beta _{\ell }, \beta _{*}]\approx [1.61803,1.73867]$
with
$I^{01}=[\beta _{\ell }, \beta _{*}]\approx [1.61803,1.73867]$
with
![]() ${((10)^{\infty })_{\beta _{\ell }}=(1100(10)^{\infty })_{\beta _{*}}=1}$
. Furthermore, for any
${((10)^{\infty })_{\beta _{\ell }}=(1100(10)^{\infty })_{\beta _{*}}=1}$
. Furthermore, for any
![]() $\beta \in I^{01}$
, we have
$\beta \in I^{01}$
, we have
 $\tau (\beta )=(00(10)^{\infty })_{\beta }={1}/{\beta (\beta ^{2}-1)}$
; see Example 1.7 for more details.
$\tau (\beta )=(00(10)^{\infty })_{\beta }={1}/{\beta (\beta ^{2}-1)}$
; see Example 1.7 for more details.
Next, we introduce the Lyndon intervals.
Definition 1.8. For each Lyndon word
![]() $ {\mathbf {S}}\in \Omega _{L}^{*}$
, the interval
$ {\mathbf {S}}\in \Omega _{L}^{*}$
, the interval
 $J^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}},\beta _{r}^ {\mathbf {S}}]\subset (1,2]$
is called a Lyndon interval generated by
$J^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}},\beta _{r}^ {\mathbf {S}}]\subset (1,2]$
is called a Lyndon interval generated by
![]() $ {\mathbf {S}}$
if
$ {\mathbf {S}}$
if
 $$ \begin{align*} (\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta_{\ell}^ {\mathbf{S}}}=1\quad\textrm{and}\quad (\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty})_{\beta_{r}^ {\mathbf{S}}}=1. \end{align*} $$
$$ \begin{align*} (\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta_{\ell}^ {\mathbf{S}}}=1\quad\textrm{and}\quad (\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty})_{\beta_{r}^ {\mathbf{S}}}=1. \end{align*} $$
If in particular
![]() $ {\mathbf {S}}\in \Omega _{F}^{*}$
, we call
$ {\mathbf {S}}\in \Omega _{F}^{*}$
, we call
![]() $J^ {\mathbf {S}}$
a Farey interval.
$J^ {\mathbf {S}}$
a Farey interval.
We remark that the Farey intervals defined in [Reference Kalle, Kong, Langeveld and Li20, Definition 4.5] are half-open intervals, which is slightly different from our definition. It turns out that the discontinuity points of
![]() $\tau $
are precisely the right endpoints of the Lyndon intervals
$\tau $
are precisely the right endpoints of the Lyndon intervals
![]() $J^ {\mathbf {S}}$
with
$J^ {\mathbf {S}}$
with
![]() $ {\mathbf {S}}\in \Lambda $
.
$ {\mathbf {S}}\in \Lambda $
.
Proposition 1.9. The function
![]() $\tau $
is continuous on
$\tau $
is continuous on
![]() $(1,2]\backslash \{\beta _{r}^ {\mathbf {S}}: {\mathbf {S}}\in \Lambda \}$
. However, for each
$(1,2]\backslash \{\beta _{r}^ {\mathbf {S}}: {\mathbf {S}}\in \Lambda \}$
. However, for each
![]() $ {\mathbf {S}}\in \Lambda $
, we have
$ {\mathbf {S}}\in \Lambda $
, we have
 $$ \begin{align} \lim_{\beta\searrow\beta_{r}^ {\mathbf{S}}}\tau(\beta)=( {\mathbf{S}}^{\infty})_{\beta_{r}^ {\mathbf{S}}}>( {\mathbf{S}} 0^{\infty})_{\beta_{r}^ {\mathbf{S}}}=\tau(\beta_{r}^ {\mathbf{S}}). \end{align} $$
$$ \begin{align} \lim_{\beta\searrow\beta_{r}^ {\mathbf{S}}}\tau(\beta)=( {\mathbf{S}}^{\infty})_{\beta_{r}^ {\mathbf{S}}}>( {\mathbf{S}} 0^{\infty})_{\beta_{r}^ {\mathbf{S}}}=\tau(\beta_{r}^ {\mathbf{S}}). \end{align} $$
Remark 1.10. Proposition 1.9 implies that although the dimension
![]() $\dim _{H} K_{\beta }(t)$
is continuous in t for fixed
$\dim _{H} K_{\beta }(t)$
is continuous in t for fixed
![]() $\beta $
, it is not jointly continuous in
$\beta $
, it is not jointly continuous in
![]() $\beta $
and t. In particular, when
$\beta $
and t. In particular, when
![]() $t=\tau (\beta _{r}^ {\mathbf {S}})$
for
$t=\tau (\beta _{r}^ {\mathbf {S}})$
for
![]() $ {\mathbf {S}}\in \Lambda $
, the function
$ {\mathbf {S}}\in \Lambda $
, the function
![]() $\beta \mapsto \dim _{H} K_{\beta }(t)$
has a jump at
$\beta \mapsto \dim _{H} K_{\beta }(t)$
has a jump at
![]() $\beta _{r}^ {\mathbf {S}}$
.
$\beta _{r}^ {\mathbf {S}}$
.
It was shown in [Reference Kalle, Kong, Langeveld and Li20, §4] that the Farey intervals
![]() $J^ {\mathbf {s}}, {\mathbf {s}}\in \Omega _{F}^{*}$
are pairwise disjoint, and the exceptional set
$J^ {\mathbf {s}}, {\mathbf {s}}\in \Omega _{F}^{*}$
are pairwise disjoint, and the exceptional set
 $$ \begin{align*} E:=(1,2]\setminus\bigcup_{ {\mathbf{s}}\in\Omega_{F}^{*}}J^ {\mathbf{s}} \end{align*} $$
$$ \begin{align*} E:=(1,2]\setminus\bigcup_{ {\mathbf{s}}\in\Omega_{F}^{*}}J^ {\mathbf{s}} \end{align*} $$
has zero Hausdorff dimension. We strengthen this result slightly and show in Proposition 5.6(i) that E is uncountable and has zero packing dimension.
From Definitions 1.5 and 1.8, it follows that
![]() $I^ {\mathbf {S}}\subset J^{ {\mathbf {S}}}$
for any
$I^ {\mathbf {S}}\subset J^{ {\mathbf {S}}}$
for any
![]() $ {\mathbf {S}}\in \Lambda $
, and the two intervals
$ {\mathbf {S}}\in \Lambda $
, and the two intervals
![]() $I^ {\mathbf {S}}$
and
$I^ {\mathbf {S}}$
and
![]() $J^ {\mathbf {S}}$
have the same left endpoint (see Proposition 5.1.) In Proposition 5.6(ii), we show that for any
$J^ {\mathbf {S}}$
have the same left endpoint (see Proposition 5.1.) In Proposition 5.6(ii), we show that for any
![]() $ {\mathbf {S}}\in {\Lambda }$
, the Lyndon intervals
$ {\mathbf {S}}\in {\Lambda }$
, the Lyndon intervals
 $J^{ {\mathbf {S}}\bullet {\mathbf {r}}}, {\mathbf {r}}\in \Omega _{F}^{*}$
are pairwise disjoint subsets of
$J^{ {\mathbf {S}}\bullet {\mathbf {r}}}, {\mathbf {r}}\in \Omega _{F}^{*}$
are pairwise disjoint subsets of
![]() $J^ {\mathbf {S}}\setminus I^ {\mathbf {S}}$
, and the relative exceptional set
$J^ {\mathbf {S}}\setminus I^ {\mathbf {S}}$
, and the relative exceptional set
 $$ \begin{align*} E^ {\mathbf{S}}:=(J^ {\mathbf{S}}\setminus I^ {\mathbf{S}})\setminus\bigcup_{ {\mathbf{r}}\in\Omega_{F}^{*}}J^{ {\mathbf{S}}\bullet {\mathbf{r}}} \end{align*} $$
$$ \begin{align*} E^ {\mathbf{S}}:=(J^ {\mathbf{S}}\setminus I^ {\mathbf{S}})\setminus\bigcup_{ {\mathbf{r}}\in\Omega_{F}^{*}}J^{ {\mathbf{S}}\bullet {\mathbf{r}}} \end{align*} $$
is also uncountable and has zero box-counting dimension. In Proposition 5.1, we show that the Lyndon intervals
![]() $J^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
have a tree structure. This gives rise to the set
$J^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
have a tree structure. This gives rise to the set
 $$ \begin{align} E_{\infty}:=\bigcap_{k=1}^{\infty}\bigcup_{ {\mathbf{S}}\in\Lambda(k)}J^{ {\mathbf{S}}}, \end{align} $$
$$ \begin{align} E_{\infty}:=\bigcap_{k=1}^{\infty}\bigcup_{ {\mathbf{S}}\in\Lambda(k)}J^{ {\mathbf{S}}}, \end{align} $$
where
![]() $\Lambda (k):=\{ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}:~ {\mathbf {s}}_{i}\in \Omega _{F}^{*} \text { for all } 1\le i\le k\}$
. We call
$\Lambda (k):=\{ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}:~ {\mathbf {s}}_{i}\in \Omega _{F}^{*} \text { for all } 1\le i\le k\}$
. We call
![]() $E_{\infty }$
the infinitely Farey set, because its elements arise from substitutions of an infinite sequence of Farey words. It follows at once that
$E_{\infty }$
the infinitely Farey set, because its elements arise from substitutions of an infinite sequence of Farey words. It follows at once that
![]() $E_{\infty }$
is uncountable; we show in Proposition 5.8 that it has zero Hausdorff dimension.
$E_{\infty }$
is uncountable; we show in Proposition 5.8 that it has zero Hausdorff dimension.
Combining the above results, we obtain our last main theorem.
Theorem 3. The interval
![]() $(1,2]$
can be partitioned as
$(1,2]$
can be partitioned as
 $$ \begin{align*} (1,2]=E\cup E_{\infty}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}E^{ {\mathbf{S}}}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}I^{ {\mathbf{S}}}, \end{align*} $$
$$ \begin{align*} (1,2]=E\cup E_{\infty}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}E^{ {\mathbf{S}}}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}I^{ {\mathbf{S}}}, \end{align*} $$
and the basic intervals
![]() $\{I^{ {\mathbf {S}}}: {\mathbf {S}}\in \Lambda \}$
cover
$\{I^{ {\mathbf {S}}}: {\mathbf {S}}\in \Lambda \}$
cover
![]() $(1,2]$
up to a set of zero Hausdorff dimension.
$(1,2]$
up to a set of zero Hausdorff dimension.
Remark 1.11. It is worth mentioning that the Lyndon intervals
![]() $J^ {\mathbf {S}}$
and the relative exceptional sets
$J^ {\mathbf {S}}$
and the relative exceptional sets
![]() $E^ {\mathbf {S}}$
constructed in our paper have similar geometrical structure as the relative entropy plateaus and relative bifurcation sets studied in [Reference Allaart and Kong2], where they were used to describe the local dimension of the set of univoque bases.
$E^ {\mathbf {S}}$
constructed in our paper have similar geometrical structure as the relative entropy plateaus and relative bifurcation sets studied in [Reference Allaart and Kong2], where they were used to describe the local dimension of the set of univoque bases.
The following result was established in the proof of [Reference Kalle, Kong, Langeveld and Li20, Theorem D].
Proposition 1.12. For any
![]() $\beta \in (1,2]$
, we have
$\beta \in (1,2]$
, we have
![]() $\tau (\beta )\le 1-{1}/{\beta }$
. Furthermore,
$\tau (\beta )\le 1-{1}/{\beta }$
. Furthermore,
 $$ \begin{align*} \tau(\beta)=1-\frac{1}{\beta}\quad\textrm{for any } \beta\in E. \end{align*} $$
$$ \begin{align*} \tau(\beta)=1-\frac{1}{\beta}\quad\textrm{for any } \beta\in E. \end{align*} $$
Thus, in view of Theorem 3, it remains to determine
![]() $\tau (\beta )$
for
$\tau (\beta )$
for
![]() $\beta \in E^ {\mathbf {S}}$
with
$\beta \in E^ {\mathbf {S}}$
with
![]() $ {\mathbf {S}}\in \Lambda $
and for
$ {\mathbf {S}}\in \Lambda $
and for
![]() $\beta \in E_{\infty }$
. In Proposition 6.2, we compute
$\beta \in E_{\infty }$
. In Proposition 6.2, we compute
![]() $\tau (\beta )$
for
$\tau (\beta )$
for
![]() $\beta \in E^ {\mathbf {S}}$
by relating the relative exceptional set
$\beta \in E^ {\mathbf {S}}$
by relating the relative exceptional set
![]() $E^ {\mathbf {S}}$
to the exceptional set E via a renormalization map
$E^ {\mathbf {S}}$
to the exceptional set E via a renormalization map
![]() $\Psi _ {\mathbf {S}}$
. Proposition 6.3 gives an expression for
$\Psi _ {\mathbf {S}}$
. Proposition 6.3 gives an expression for
![]() $\tau (\beta )$
when
$\tau (\beta )$
when
![]() $\beta \in E_{\infty }$
. As an illustration of the latter, in Proposition 6.4, we construct in each Farey interval
$\beta \in E_{\infty }$
. As an illustration of the latter, in Proposition 6.4, we construct in each Farey interval
![]() $J^ {\mathbf {s}}$
a transcendental base
$J^ {\mathbf {s}}$
a transcendental base
![]() $\beta _{\infty }^ {\mathbf {s}}\in E_{\infty }$
and give an explicit formula for
$\beta _{\infty }^ {\mathbf {s}}\in E_{\infty }$
and give an explicit formula for
![]() $\tau (\beta _{\infty }^ {\mathbf {s}})$
. Here we point out an interesting connection with unique
$\tau (\beta _{\infty }^ {\mathbf {s}})$
. Here we point out an interesting connection with unique
![]() $\beta $
-expansions: Let
$\beta $
-expansions: Let
![]() $\beta \approx 1.78723$
be the Komornik–Loreti constant (cf. [Reference Komornik and Loreti21]); that is,
$\beta \approx 1.78723$
be the Komornik–Loreti constant (cf. [Reference Komornik and Loreti21]); that is,
![]() $\beta $
is the smallest base in which 1 has a unique expansion. Then it follows from Proposition 6.4 that
$\beta $
is the smallest base in which 1 has a unique expansion. Then it follows from Proposition 6.4 that
![]() $\beta =\beta _{\infty }^{01}\in E_{\infty }$
, and
$\beta =\beta _{\infty }^{01}\in E_{\infty }$
, and
![]() $\tau (\beta )=({2-\beta })/({\beta -1})\approx 0.270274$
.
$\tau (\beta )=({2-\beta })/({\beta -1})\approx 0.270274$
.
The rest of the paper is organized as follows. In §2, we recall some properties of Farey words and Farey intervals, as well as greedy and quasi-greedy
![]() $\beta $
-expansions. In §3, we give an equivalent definition of the substitution operator
$\beta $
-expansions. In §3, we give an equivalent definition of the substitution operator
![]() $\bullet $
, and prove Proposition 1.3. The proof of Theorem 2 is given in §4. At the heart of the argument is Proposition 4.1, which clarifies the role of the special Lyndon words
$\bullet $
, and prove Proposition 1.3. The proof of Theorem 2 is given in §4. At the heart of the argument is Proposition 4.1, which clarifies the role of the special Lyndon words
![]() $ {\mathbf {S}}\in \Lambda $
and is used in several settings to derive the upper bound for
$ {\mathbf {S}}\in \Lambda $
and is used in several settings to derive the upper bound for
![]() $\tau (\beta )$
. The relative exceptional sets
$\tau (\beta )$
. The relative exceptional sets
![]() $E^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
and the infinitely Farey set
$E^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
and the infinitely Farey set
![]() $E_{\infty }$
are studied in detail in §5, where we show that all of these sets have zero Hausdorff dimension, proving Theorem 3. In §6, we determine the critical value
$E_{\infty }$
are studied in detail in §5, where we show that all of these sets have zero Hausdorff dimension, proving Theorem 3. In §6, we determine the critical value
![]() $\tau (\beta )$
for
$\tau (\beta )$
for
![]() $\beta $
in the relative exceptional sets
$\beta $
in the relative exceptional sets
![]() $E^ {\mathbf {S}}$
and the infinitely Farey set
$E^ {\mathbf {S}}$
and the infinitely Farey set
![]() $E_{\infty }$
. Finally, in §7, we show that the function
$E_{\infty }$
. Finally, in §7, we show that the function
![]() $\beta \mapsto \tau (\beta )$
is càdlàg, and prove Proposition 1.9 and Theorem 1.
$\beta \mapsto \tau (\beta )$
is càdlàg, and prove Proposition 1.9 and Theorem 1.
2 Farey words and Farey intervals
In this section, we recall some properties of Farey words, which are vital in determining the critical value
![]() $\tau (\beta )$
. We also recall from [Reference Kalle, Kong, Langeveld and Li20] the Farey intervals, and review basic properties of greedy and quasi-greedy
$\tau (\beta )$
. We also recall from [Reference Kalle, Kong, Langeveld and Li20] the Farey intervals, and review basic properties of greedy and quasi-greedy
![]() $\beta $
-expansions.
$\beta $
-expansions.
First we introduce some terminology from symbolic dynamics (cf. [Reference Lind and Marcus23]). Let
![]() $\{0,1\}^{\mathbb {N}}$
be the set of all infinite sequences of zeros and ones. Denote by
$\{0,1\}^{\mathbb {N}}$
be the set of all infinite sequences of zeros and ones. Denote by
![]() $\sigma $
the left shift map. Then
$\sigma $
the left shift map. Then
![]() $(\{0,1\}^{\mathbb {N}}, \sigma )$
is a full shift. By a word we mean a finite string of zeros and ones. Let
$(\{0,1\}^{\mathbb {N}}, \sigma )$
is a full shift. By a word we mean a finite string of zeros and ones. Let
![]() $\{0, 1\}^{*}$
be the set of all words over the alphabet
$\{0, 1\}^{*}$
be the set of all words over the alphabet
![]() $\{0,1\}$
together with the empty word
$\{0,1\}$
together with the empty word
![]() $\epsilon $
. For a word
$\epsilon $
. For a word
![]() $ {\mathbf {c}}\in \{0,1\}^{*}$
, we denote its length by
$ {\mathbf {c}}\in \{0,1\}^{*}$
, we denote its length by
![]() $| {\mathbf {c}}|$
, and for a digit
$| {\mathbf {c}}|$
, and for a digit
![]() $a\in \{0,1\}$
, we denote by
$a\in \{0,1\}$
, we denote by
![]() $| {\mathbf {c}}|_{a}$
the number of occurrences of a in the word
$| {\mathbf {c}}|_{a}$
the number of occurrences of a in the word
![]() $ {\mathbf {c}}$
. For two words
$ {\mathbf {c}}$
. For two words
![]() $\mathbf c=c_{1}\ldots c_{m}$
and
$\mathbf c=c_{1}\ldots c_{m}$
and
![]() $\mathbf d=d_{1}\ldots d_{n}$
in
$\mathbf d=d_{1}\ldots d_{n}$
in
![]() $\{0,1\}^{*}$
, we write
$\{0,1\}^{*}$
, we write
![]() $\mathbf {cd}=c_{1}\ldots c_{m}d_{1}\ldots d_{n}$
for their concatenation. For
$\mathbf {cd}=c_{1}\ldots c_{m}d_{1}\ldots d_{n}$
for their concatenation. For
![]() $n\in \mathbb {N}$
, we denote by
$n\in \mathbb {N}$
, we denote by
![]() $\mathbf c^{n}$
the n-fold concatenation of
$\mathbf c^{n}$
the n-fold concatenation of
![]() $\mathbf c$
with itself, and by
$\mathbf c$
with itself, and by
![]() $\mathbf c^{\infty }$
the periodic sequence with period block
$\mathbf c^{\infty }$
the periodic sequence with period block
![]() $\mathbf c$
.
$\mathbf c$
.
Throughout the paper, we will use the lexicographical order ‘
![]() $\prec , \preccurlyeq , \succ $
’ or ‘
$\prec , \preccurlyeq , \succ $
’ or ‘
![]() $\succcurlyeq $
’ between sequences and words. For example, for two sequences
$\succcurlyeq $
’ between sequences and words. For example, for two sequences
![]() $(c_{i}), (d_{i})\in \{0,1\}^{\mathbb {N}}$
, we say
$(c_{i}), (d_{i})\in \{0,1\}^{\mathbb {N}}$
, we say
![]() $(c_{i})\prec (d_{i})$
if
$(c_{i})\prec (d_{i})$
if
![]() $c_{1}<d_{1}$
, or there exists
$c_{1}<d_{1}$
, or there exists
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $c_{1}\ldots c_{n}=d_{1}\ldots d_{n}$
and
$c_{1}\ldots c_{n}=d_{1}\ldots d_{n}$
and
![]() $c_{n+1}<d_{n+1}$
. For two words
$c_{n+1}<d_{n+1}$
. For two words
![]() $\mathbf c, \mathbf d$
, we say
$\mathbf c, \mathbf d$
, we say
![]() $\mathbf c\prec \mathbf d$
if
$\mathbf c\prec \mathbf d$
if
![]() $\mathbf c 0^{\infty }\prec \mathbf d 0^{\infty }$
. We also recall from §1 that if
$\mathbf c 0^{\infty }\prec \mathbf d 0^{\infty }$
. We also recall from §1 that if
![]() $\mathbf c=c_{1}\ldots c_{m}$
with
$\mathbf c=c_{1}\ldots c_{m}$
with
![]() $c_{m}=0$
, then
$c_{m}=0$
, then
![]() $\mathbf c^{+} =c_{1}\ldots c_{m-1}1$
; and if
$\mathbf c^{+} =c_{1}\ldots c_{m-1}1$
; and if
![]() $\mathbf c=c_{1}\ldots c_{m}$
with
$\mathbf c=c_{1}\ldots c_{m}$
with
![]() $c_{m}=1$
, then
$c_{m}=1$
, then
![]() $\mathbf c^{-} =c_{1}\ldots c_{m-1}0$
. Finally, for a word
$\mathbf c^{-} =c_{1}\ldots c_{m-1}0$
. Finally, for a word
![]() $\mathbf {c}=c_{1} c_{2}\ldots c_{n}$
, we denote its reflection by
$\mathbf {c}=c_{1} c_{2}\ldots c_{n}$
, we denote its reflection by
![]() $\overline {\mathbf {c}}:=(1-c_{1})(1-c_{2})\ldots (1-c_{n})$
.
$\overline {\mathbf {c}}:=(1-c_{1})(1-c_{2})\ldots (1-c_{n})$
.
2.1 Farey words
Farey words have attracted much attention in the literature due to their intimate connection with rational rotations on the circle (see [Reference Lothaire24, Ch. 2]) and their one-to-one correspondence with the rational numbers in
![]() $[0,1]$
(see equation (2.1) below). In the following, we adopt the definition from a recent paper of Carminati, Isola, and Tiozzo [Reference Carminati, Isola and Tiozzo8].
$[0,1]$
(see equation (2.1) below). In the following, we adopt the definition from a recent paper of Carminati, Isola, and Tiozzo [Reference Carminati, Isola and Tiozzo8].
First we recursively define a sequence of ordered sets
![]() $F_{n}, n=0,1,2,\ldots $
. Let
$F_{n}, n=0,1,2,\ldots $
. Let
![]() $F_{0}=(0,1)$
; and for
$F_{0}=(0,1)$
; and for
![]() $n\ge 0$
, the ordered set
$n\ge 0$
, the ordered set
![]() $F_{n+1}=(v_{1}, \ldots , v_{2^{n+1}+1})$
is obtained from
$F_{n+1}=(v_{1}, \ldots , v_{2^{n+1}+1})$
is obtained from
![]() $F_{n}=(w_{1},\ldots , w_{2^{n}+1})$
by
$F_{n}=(w_{1},\ldots , w_{2^{n}+1})$
by
 $$ \begin{align*} \left\{ \begin{array} {@{}ll} v_{2i-1}=w_{i}&\textrm{for } 1\le i\le 2^{n}+1,\\[3pt] v_{2i}=w_{i}w_{i+1}&\textrm{for } 1\le i\le 2^{n}. \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array} {@{}ll} v_{2i-1}=w_{i}&\textrm{for } 1\le i\le 2^{n}+1,\\[3pt] v_{2i}=w_{i}w_{i+1}&\textrm{for } 1\le i\le 2^{n}. \end{array} \right. \end{align*} $$
In other words,
![]() $F_{n+1}$
is obtained from
$F_{n+1}$
is obtained from
![]() $F_{n}$
by inserting for each
$F_{n}$
by inserting for each
![]() $1\le j\le 2^{n}$
the new word
$1\le j\le 2^{n}$
the new word
![]() $w_{j}w_{j+1}$
between the two neighboring words
$w_{j}w_{j+1}$
between the two neighboring words
![]() $w_{j}$
and
$w_{j}$
and
![]() $w_{j+1}$
. See equation (1.2) for examples. Note that for each
$w_{j+1}$
. See equation (1.2) for examples. Note that for each
![]() $n\ge 0$
, the ordered set
$n\ge 0$
, the ordered set
![]() $F_{n}$
consists of
$F_{n}$
consists of
![]() $2^{n}+1$
words which are listed from the left to the right in lexicographically increasing order. We call
$2^{n}+1$
words which are listed from the left to the right in lexicographically increasing order. We call
![]() $w\in \{0,1\}^{*}$
a Farey word if
$w\in \{0,1\}^{*}$
a Farey word if
![]() $w\in F_{n}$
for some
$w\in F_{n}$
for some
![]() $n\ge 0$
, and we denote by
$n\ge 0$
, and we denote by
![]() $\Omega _{F}:=\bigcup _{n=1}^{\infty } F_{n}$
the set of all Farey words. As shown in [Reference Carminati, Isola and Tiozzo8, Proposition 2.3], the set
$\Omega _{F}:=\bigcup _{n=1}^{\infty } F_{n}$
the set of all Farey words. As shown in [Reference Carminati, Isola and Tiozzo8, Proposition 2.3], the set
![]() $\Omega _{F}$
can be bijectively mapped to
$\Omega _{F}$
can be bijectively mapped to
![]() $\mathbb {Q}\cap [0,1]$
via the map
$\mathbb {Q}\cap [0,1]$
via the map
 $$ \begin{align} \xi: \Omega_{F}\to\mathbb Q\cap[0,1];\quad {\mathbf{s}}\mapsto\frac{| {\mathbf{s}}|_{1}}{| {\mathbf{s}}|}. \end{align} $$
$$ \begin{align} \xi: \Omega_{F}\to\mathbb Q\cap[0,1];\quad {\mathbf{s}}\mapsto\frac{| {\mathbf{s}}|_{1}}{| {\mathbf{s}}|}. \end{align} $$
So,
![]() $\xi ( {\mathbf {s}})$
is the frequency of the digit
$\xi ( {\mathbf {s}})$
is the frequency of the digit
![]() $1$
in
$1$
in
![]() $ {\mathbf {s}}$
.
$ {\mathbf {s}}$
.
For each
![]() $n\ge 1$
, set
$n\ge 1$
, set
and
 $$ \begin{align*} F_{n}^{0}:=\{w\in F_{n}^{*}: |w|_{0}>|w|_{1}\},\quad F_{n}^{1}:=\{w\in F_{n}^{*}: |w|_{1}>|w|_{0}\}. \end{align*} $$
$$ \begin{align*} F_{n}^{0}:=\{w\in F_{n}^{*}: |w|_{0}>|w|_{1}\},\quad F_{n}^{1}:=\{w\in F_{n}^{*}: |w|_{1}>|w|_{0}\}. \end{align*} $$
For example,
![]() $F_{1}^{*}=(01), F_{2}^{*}=(001, 01, 011)$
, and
$F_{1}^{*}=(01), F_{2}^{*}=(001, 01, 011)$
, and
 $F_{2}^{0}=(001), F_{2}^{1}=(011)$
. The following decomposition can be deduced from [Reference Carminati, Isola and Tiozzo8, Proposition 2.3].
$F_{2}^{0}=(001), F_{2}^{1}=(011)$
. The following decomposition can be deduced from [Reference Carminati, Isola and Tiozzo8, Proposition 2.3].
Lemma 2.1. For any
![]() $n\ge 2$
, we have
$n\ge 2$
, we have
 $F_{n}^{*}=F_{n}^{0}\cup F_{1}^{*}\cup F_{n}^{1}$
.
$F_{n}^{*}=F_{n}^{0}\cup F_{1}^{*}\cup F_{n}^{1}$
.
The ordered sets
![]() $F_{n}^{*},n\ge 1$
can also be obtained via substitutions. We define the two substitution operators by
$F_{n}^{*},n\ge 1$
can also be obtained via substitutions. We define the two substitution operators by
 $$ \begin{align} U_{0}:\left\{\begin{array}{@{}l} 0 \mapsto 0,\\[3pt] 1\mapsto 01, \end{array} \right.\textrm{ and }\quad U_{1}:\left\{ \begin{array}{@{}l} 0 \mapsto 01,\\[3pt] 1 \mapsto 1. \end{array} \right. \end{align} $$
$$ \begin{align} U_{0}:\left\{\begin{array}{@{}l} 0 \mapsto 0,\\[3pt] 1\mapsto 01, \end{array} \right.\textrm{ and }\quad U_{1}:\left\{ \begin{array}{@{}l} 0 \mapsto 01,\\[3pt] 1 \mapsto 1. \end{array} \right. \end{align} $$
Then
![]() $U_{0}$
and
$U_{0}$
and
![]() $U_{1}$
naturally induce a map on
$U_{1}$
naturally induce a map on
![]() $\{0,1\}^{*}$
or
$\{0,1\}^{*}$
or
![]() $\{0,1\}^{\mathbb {N}}$
. For example,
$\{0,1\}^{\mathbb {N}}$
. For example,
The following result was proven in [Reference Carminati, Isola and Tiozzo8, Proposition 2.9].
Lemma 2.2. For each
![]() $a\in \{0,1\}$
, the map
$a\in \{0,1\}$
, the map
![]() $U_{a}: F_{n}^{*}\to F_{n+1}^{a}$
is bijective.
$U_{a}: F_{n}^{*}\to F_{n+1}^{a}$
is bijective.
By Lemmas 2.1 and 2.2, it follows that the ordered sets
![]() $F_{n}^{*}$
can be obtained by the substitution operators
$F_{n}^{*}$
can be obtained by the substitution operators
![]() $U_{0}$
and
$U_{0}$
and
![]() $U_{1}$
on the set
$U_{1}$
on the set
![]() $F_{1}^{*}=(01)$
. We will clarify this in the next proposition. Let
$F_{1}^{*}=(01)$
. We will clarify this in the next proposition. Let
![]() $\Omega _{F}^{*}$
be the set of all non-degenerate Farey words, that is,
$\Omega _{F}^{*}$
be the set of all non-degenerate Farey words, that is,
 $$ \begin{align*} \Omega_{F}^{*}=\bigcup_{n=1}^{\infty} F_{n}^{*}. \end{align*} $$
$$ \begin{align*} \Omega_{F}^{*}=\bigcup_{n=1}^{\infty} F_{n}^{*}. \end{align*} $$
For a word
![]() $\mathbf c=c_{1}\ldots c_{m}\in \{0,1\}^{*}$
, let
$\mathbf c=c_{1}\ldots c_{m}\in \{0,1\}^{*}$
, let
![]() $\mathbb {S}(\mathbf c)$
and
$\mathbb {S}(\mathbf c)$
and
![]() $\mathbb {L}(\mathbf c)$
be the lexicographically smallest and largest cyclic permutations of
$\mathbb {L}(\mathbf c)$
be the lexicographically smallest and largest cyclic permutations of
![]() $\mathbf c$
, respectively. In other words,
$\mathbf c$
, respectively. In other words,
![]() $\mathbb {S}(\mathbf c)$
is the lexicographically smallest word among
$\mathbb {S}(\mathbf c)$
is the lexicographically smallest word among
and
![]() $\mathbb {L}(\mathbf c)$
is the lexicographically largest word in the above list. The following properties of Farey words are well known (see, e.g., [Reference Carminati, Isola and Tiozzo8, Proposition 2.5]).
$\mathbb {L}(\mathbf c)$
is the lexicographically largest word in the above list. The following properties of Farey words are well known (see, e.g., [Reference Carminati, Isola and Tiozzo8, Proposition 2.5]).
Lemma 2.3. Let
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{F}^{*}$
. Then the following hold.
$ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{F}^{*}$
. Then the following hold.
-
(i)
 $\mathbb {S}( {\mathbf {s}})= {\mathbf {s}}$
and
$\mathbb {S}( {\mathbf {s}})= {\mathbf {s}}$
and
 $\mathbb {L}( {\mathbf {s}})=s_{m}s_{m-1}\ldots s_{1}$
.
$\mathbb {L}( {\mathbf {s}})=s_{m}s_{m-1}\ldots s_{1}$
. -
(ii)
 ${ {\mathbf {s}}^{-}}$
is a palindrome; that is,
${ {\mathbf {s}}^{-}}$
is a palindrome; that is,
 $s_{1}\ldots s_{m-1}(s_{m}-1)=(s_{m}-1)s_{m-1}s_{m-2}\ldots s_{1}$
.
$s_{1}\ldots s_{m-1}(s_{m}-1)=(s_{m}-1)s_{m-1}s_{m-2}\ldots s_{1}$
. -
(iii) The word
 $ {\mathbf {s}}$
has a conjugate
$ {\mathbf {s}}$
has a conjugate
 $\tilde { {\mathbf {s}}}\in \Omega _{F}^{*}$
, given by (2.3)
$\tilde { {\mathbf {s}}}\in \Omega _{F}^{*}$
, given by (2.3) $$ \begin{align} \tilde{ {\mathbf{s}}}:=\overline{\mathbb{L}( {\mathbf{s}})}=0\,\overline{s_{2}\ldots s_{m-1}}\,1. \end{align} $$
$$ \begin{align} \tilde{ {\mathbf{s}}}:=\overline{\mathbb{L}( {\mathbf{s}})}=0\,\overline{s_{2}\ldots s_{m-1}}\,1. \end{align} $$
The last equality in equation (2.3) follows from statements (i) and (ii). In terms of the correspondence equation (2.1), if
![]() $\xi ( {\mathbf {s}})=r\in \mathbb {Q}\cap [0,1]$
, then
$\xi ( {\mathbf {s}})=r\in \mathbb {Q}\cap [0,1]$
, then
![]() $\xi (\tilde { {\mathbf {s}}})=1-r$
. Note also that the conjugate of
$\xi (\tilde { {\mathbf {s}}})=1-r$
. Note also that the conjugate of
![]() $\tilde { {\mathbf {s}}}$
is simply
$\tilde { {\mathbf {s}}}$
is simply
![]() $ {\mathbf {s}}$
itself.
$ {\mathbf {s}}$
itself.
The following explicit description of
![]() $\Omega _{F}^{*}$
will be useful in §4 to prove the upper bound for
$\Omega _{F}^{*}$
will be useful in §4 to prove the upper bound for
![]() $\tau (\beta )$
.
$\tau (\beta )$
.
Proposition 2.4.
![]() $\Omega _{F}^{*}$
consists of all words in one of the following forms:
$\Omega _{F}^{*}$
consists of all words in one of the following forms:
-
(i)
 $01^{p}$
or
$01^{p}$
or
 $0^{p} 1$
for some
$0^{p} 1$
for some
 $p\in \mathbb {N}$
;
$p\in \mathbb {N}$
; -
(ii)
 $01^{p} 01^{p+t_{1}}\ldots 01^{p+t_{N}}01^{p+1}$
for some
$01^{p} 01^{p+t_{1}}\ldots 01^{p+t_{N}}01^{p+1}$
for some
 $p\in \mathbb {N}$
and Farey word
$p\in \mathbb {N}$
and Farey word
 $0 t_{1}\ldots t_{N}1\in \Omega _{F}^{*}$
;
$0 t_{1}\ldots t_{N}1\in \Omega _{F}^{*}$
; -
(iii)
 $0^{p+1}10^{p+t_{1}}1\ldots 0^{p+t_{N}}10^{p} 1$
for some
$0^{p+1}10^{p+t_{1}}1\ldots 0^{p+t_{N}}10^{p} 1$
for some
 $p\in \mathbb {N}$
and Farey word
$p\in \mathbb {N}$
and Farey word
 $0 t_{1}\ldots t_{N}1\in \Omega _{F}^{*}$
.
$0 t_{1}\ldots t_{N}1\in \Omega _{F}^{*}$
.
Proof. Note that
![]() $01=U_{1}(0)=U_{0}(1)\in F_{1}^{*}\subset \Omega _{F}^{*}$
. Furthermore, for
$01=U_{1}(0)=U_{0}(1)\in F_{1}^{*}\subset \Omega _{F}^{*}$
. Furthermore, for
![]() $p\in \mathbb {N}$
and
$p\in \mathbb {N}$
and
![]() $0 t_{1}\ldots t_{N}1\in \Omega _{F}^{*}$
, we have
$0 t_{1}\ldots t_{N}1\in \Omega _{F}^{*}$
, we have
 $$ \begin{align*} 01^{p}=U_{1}(01^{p-1})&=U_{1}^{p-1}(U_{0}(1)),\\[3pt] 0^{p}1=U_{0}(0^{p-1}1)&=U_{0}^{p-1}(U_{1}(0)),\\[3pt] 01^{p} 01^{p+t_{1}}\ldots 01^{p+t_{N}}01^{p+1}&=U_{1}^{p}(U_{0}(0t_{1}\ldots t_{N}1)),\\[3pt] 0^{p+1}10^{p+t_{1}}1\ldots 0^{p+t_{N}}10^{p} 1&=U_{0}^{p}(U_{1}(0\,\overline{t_{1}\ldots t_{N}}\,1)). \end{align*} $$
$$ \begin{align*} 01^{p}=U_{1}(01^{p-1})&=U_{1}^{p-1}(U_{0}(1)),\\[3pt] 0^{p}1=U_{0}(0^{p-1}1)&=U_{0}^{p-1}(U_{1}(0)),\\[3pt] 01^{p} 01^{p+t_{1}}\ldots 01^{p+t_{N}}01^{p+1}&=U_{1}^{p}(U_{0}(0t_{1}\ldots t_{N}1)),\\[3pt] 0^{p+1}10^{p+t_{1}}1\ldots 0^{p+t_{N}}10^{p} 1&=U_{0}^{p}(U_{1}(0\,\overline{t_{1}\ldots t_{N}}\,1)). \end{align*} $$
By Lemma 2.3(iii), if
![]() $0 t_{1}\ldots t_{N}1\in \Omega _{F}^{*}$
, then
$0 t_{1}\ldots t_{N}1\in \Omega _{F}^{*}$
, then
![]() $0\,\overline {t_{1}\ldots t_{N}}\,1\in \Omega _{F}^{*}$
as well. Hence by Lemma 2.2, all the above words lie in
$0\,\overline {t_{1}\ldots t_{N}}\,1\in \Omega _{F}^{*}$
as well. Hence by Lemma 2.2, all the above words lie in
![]() $\Omega _{F}^{*}$
.
$\Omega _{F}^{*}$
.
To prove the converse, it suffices to show that each word in
![]() $\Omega _{F}^{*}$
is of the form
$\Omega _{F}^{*}$
is of the form
 $U_{0}^{p}(U_{1}( {\mathbf {t}}))$
or
$U_{0}^{p}(U_{1}( {\mathbf {t}}))$
or
![]() $U_{1}^{p}(U_{0}( {\mathbf {t}}))$
for some
$U_{1}^{p}(U_{0}( {\mathbf {t}}))$
for some
![]() $p\geq 0$
and Farey word
$p\geq 0$
and Farey word
![]() $ {\mathbf {t}}\in \Omega _{F}$
. This is clearly true for
$ {\mathbf {t}}\in \Omega _{F}$
. This is clearly true for
 $01=U_{0}^{0}(U_{1}(0))$
, where
$01=U_{0}^{0}(U_{1}(0))$
, where
![]() $U_{0}^{0}$
denotes the identity map. Let
$U_{0}^{0}$
denotes the identity map. Let
![]() $n\geq 1$
and suppose the statement is true for all Farey words in
$n\geq 1$
and suppose the statement is true for all Farey words in
![]() $F_{n}^{*}$
. Take
$F_{n}^{*}$
. Take
![]() $ {\mathbf {s}}\in F_{n+1}^{*}$
with
$ {\mathbf {s}}\in F_{n+1}^{*}$
with
![]() $ {\mathbf {s}}\neq 01$
. By Lemmas 2.1 and 2.2,
$ {\mathbf {s}}\neq 01$
. By Lemmas 2.1 and 2.2,
![]() $ {\mathbf {s}}=U_{0}( {\mathbf {t}})$
or
$ {\mathbf {s}}=U_{0}( {\mathbf {t}})$
or
![]() $ {\mathbf {s}}=U_{1}( {\mathbf {t}})$
for some Farey word
$ {\mathbf {s}}=U_{1}( {\mathbf {t}})$
for some Farey word
![]() $ {\mathbf {t}}\in F_{n}^{*}$
. We assume the former, as the argument for the second case is similar. By the induction hypothesis, either
$ {\mathbf {t}}\in F_{n}^{*}$
. We assume the former, as the argument for the second case is similar. By the induction hypothesis, either
 $ {\mathbf {t}}=U_{0}^{p}(U_{1}(\mathbf {u}))$
for some
$ {\mathbf {t}}=U_{0}^{p}(U_{1}(\mathbf {u}))$
for some
![]() $\mathbf {u}\in \Omega _{F}$
and
$\mathbf {u}\in \Omega _{F}$
and
![]() $p\geq 0$
, in which case
$p\geq 0$
, in which case
 $ {\mathbf {s}}=U_{0}^{p+1}(U_{1}(\mathbf {u}))$
; or
$ {\mathbf {s}}=U_{0}^{p+1}(U_{1}(\mathbf {u}))$
; or
![]() $ {\mathbf {t}}=U_{1}^{p}(U_{0}(\mathbf {u}))$
for some
$ {\mathbf {t}}=U_{1}^{p}(U_{0}(\mathbf {u}))$
for some
![]() $\mathbf {u}\in \Omega _{F}$
and
$\mathbf {u}\in \Omega _{F}$
and
![]() $p\geq 1$
, in which case
$p\geq 1$
, in which case
![]() $ {\mathbf {s}}=U_{0}(U_{1}(\mathbf {v}))$
, where
$ {\mathbf {s}}=U_{0}(U_{1}(\mathbf {v}))$
, where
 $\mathbf {v}=U_{1}^{p-1}(U_{0}(\mathbf {u}))\in \Omega _{F}$
. In both cases,
$\mathbf {v}=U_{1}^{p-1}(U_{0}(\mathbf {u}))\in \Omega _{F}$
. In both cases,
![]() $ {\mathbf {s}}$
is of the required form.
$ {\mathbf {s}}$
is of the required form.
Observe that the two types of words in Proposition 2.4(i) are each others conjugates, and the conjugate of a Farey word of type (ii) is a Farey word of type (iii), and vice versa. For more properties of Farey words, we refer to the book of Lothaire [Reference Lothaire24] and the references therein.
2.2 Quasi-greedy expansions, Farey intervals, and Lyndon intervals
Given
![]() $\beta \in (1,2]$
, let
$\beta \in (1,2]$
, let
![]() $\delta (\beta )=\delta _{1}(\beta )\delta _{2}(\beta )\ldots \in \{0,1\}^{\mathbb {N}}$
be the quasi-greedy
$\delta (\beta )=\delta _{1}(\beta )\delta _{2}(\beta )\ldots \in \{0,1\}^{\mathbb {N}}$
be the quasi-greedy
![]() $\beta $
-expansion of
$\beta $
-expansion of
![]() $1$
(cf. [Reference Daróczy and Kátai11]), that is,
$1$
(cf. [Reference Daróczy and Kátai11]), that is,
![]() $\delta (\beta )$
is the lexicographically largest sequence not ending with
$\delta (\beta )$
is the lexicographically largest sequence not ending with
![]() $0^{\infty }$
such that
$0^{\infty }$
such that
![]() ${(\delta _{i}(\beta ))_{\beta }=1}$
. The following property of
${(\delta _{i}(\beta ))_{\beta }=1}$
. The following property of
![]() $\delta (\beta )$
is well known (cf. [Reference Baiocchi and Komornik6]).
$\delta (\beta )$
is well known (cf. [Reference Baiocchi and Komornik6]).
Lemma 2.5.
-
(i) The map
 $\beta \mapsto \delta (\beta )$
is an increasing bijection from
$\beta \mapsto \delta (\beta )$
is an increasing bijection from
 $\beta \in (1,2]$
to the set of sequences
$\beta \in (1,2]$
to the set of sequences
 $(a_{i})\in \{0,1\}^{\mathbb {N}}$
not ending with
$(a_{i})\in \{0,1\}^{\mathbb {N}}$
not ending with
 $0^{\infty }$
and satisfying
$0^{\infty }$
and satisfying  $$ \begin{align*} \sigma^{n}((a_{i}))\preccurlyeq (a_{i})\quad\text{for all } n\ge 0. \end{align*} $$
$$ \begin{align*} \sigma^{n}((a_{i}))\preccurlyeq (a_{i})\quad\text{for all } n\ge 0. \end{align*} $$
-
(ii) The map
 $\beta \mapsto \delta (\beta )$
is left continuous everywhere on
$\beta \mapsto \delta (\beta )$
is left continuous everywhere on
 $(1,2]$
with respect to the order topology, and it is right continuous at
$(1,2]$
with respect to the order topology, and it is right continuous at
 $\beta _{0}\in (1,2)$
if and only if
$\beta _{0}\in (1,2)$
if and only if
 $\delta (\beta _{0})$
is not periodic. Furthermore, if
$\delta (\beta _{0})$
is not periodic. Furthermore, if
 $\delta (\beta _{0})=(a_{1}\ldots a_{m})^{\infty }$
with minimal period m, then
$\delta (\beta _{0})=(a_{1}\ldots a_{m})^{\infty }$
with minimal period m, then
 $\delta (\beta )\searrow a_{1}\ldots a_{m}^{+} 0^{\infty }$
as
$\delta (\beta )\searrow a_{1}\ldots a_{m}^{+} 0^{\infty }$
as
 $\beta \searrow \beta _{0}$
.
$\beta \searrow \beta _{0}$
.
Recall from Definition 1.1 that for a word
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m} \in \Omega _{L}^{*}$
, we have
$ {\mathbf {s}}=s_{1}\ldots s_{m} \in \Omega _{L}^{*}$
, we have
![]() $s_{i+1}\ldots s_{m}\succ s_{1}\ldots s_{m-i}$
for all
$s_{i+1}\ldots s_{m}\succ s_{1}\ldots s_{m-i}$
for all
![]() $1\le i<m$
. The following basic fact can be found in [Reference Allouche and Shallit5, Theorem 1.5.3].
$1\le i<m$
. The following basic fact can be found in [Reference Allouche and Shallit5, Theorem 1.5.3].
Lemma 2.6. Let
![]() $ {\mathbf {c}}=c_{1}\ldots c_{m}\in \{0,1\}^{*}$
, and suppose two cyclic permutations of
$ {\mathbf {c}}=c_{1}\ldots c_{m}\in \{0,1\}^{*}$
, and suppose two cyclic permutations of
![]() $ {\mathbf {c}}$
are equal (that is,
$ {\mathbf {c}}$
are equal (that is,
![]() $c_{i+1}\ldots c_{m} c_{1}\ldots c_{i}=c_{j+1}\ldots c_{m} c_{1}\ldots c_{j}$
, where
$c_{i+1}\ldots c_{m} c_{1}\ldots c_{i}=c_{j+1}\ldots c_{m} c_{1}\ldots c_{j}$
, where
![]() $i\neq j$
). Then
$i\neq j$
). Then
![]() $ {\mathbf {c}}$
is periodic; in other words,
$ {\mathbf {c}}$
is periodic; in other words,
![]() $ {\mathbf {c}}= {\mathbf {b}}^{k}$
for some word
$ {\mathbf {c}}= {\mathbf {b}}^{k}$
for some word
![]() $ {\mathbf {b}}$
and
$ {\mathbf {b}}$
and
![]() $k\geq 2$
.
$k\geq 2$
.
In fact, the length of
![]() $ {\mathbf {b}}$
in Lemma 2.6 can be taken to equal
$ {\mathbf {b}}$
in Lemma 2.6 can be taken to equal
![]() $\gcd (|i-j|,m)$
.
$\gcd (|i-j|,m)$
.
Lemma 2.7. Let
![]() $ {\mathbf {s}} \in \Omega _{L}^{*}$
and
$ {\mathbf {s}} \in \Omega _{L}^{*}$
and
![]() $ \mathbf {a}=\mathbb {L}( {\mathbf {s}})=a_{1}\ldots a_{m}$
. Then
$ \mathbf {a}=\mathbb {L}( {\mathbf {s}})=a_{1}\ldots a_{m}$
. Then
Furthermore,
Proof. First we prove equation (2.4). Since
![]() $ {\mathbf {s}}$
is Lyndon, it is not periodic. Hence
$ {\mathbf {s}}$
is Lyndon, it is not periodic. Hence
![]() $ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
is not periodic, because any cyclic permutation of a periodic word is periodic. Since
$ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
is not periodic, because any cyclic permutation of a periodic word is periodic. Since
![]() $ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
, we have
$ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
, we have
Suppose equality holds for some i. Then
so
![]() $a_{i+1}\ldots a_{m} a_{1}\ldots a_{i}=\mathbb {L}( {\mathbf {s}})= \mathbf {a}$
by definition of
$a_{i+1}\ldots a_{m} a_{1}\ldots a_{i}=\mathbb {L}( {\mathbf {s}})= \mathbf {a}$
by definition of
![]() $\mathbb {L}( {\mathbf {s}})$
. By Lemma 2.6, this cannot happen, since
$\mathbb {L}( {\mathbf {s}})$
. By Lemma 2.6, this cannot happen, since
![]() $ \mathbf {a}$
is not periodic.
$ \mathbf {a}$
is not periodic.
Next we prove equation (2.5). Since
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}$
is a Lyndon word, any word of length
$ {\mathbf {s}}=s_{1}\ldots s_{m}$
is a Lyndon word, any word of length
![]() $k\in \{1, \ldots , m-1\}$
occurring in
$k\in \{1, \ldots , m-1\}$
occurring in
![]() $ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
is lexicographically larger than or equal to
$ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
is lexicographically larger than or equal to
![]() $s_{1}\ldots s_{k}$
. By equation (2.4), it follows that
$s_{1}\ldots s_{k}$
. By equation (2.4), it follows that
for all
![]() $0<k<m$
. Hence, by equations (2.6) and (2.4), we conclude that
$0<k<m$
. Hence, by equations (2.6) and (2.4), we conclude that
![]() $\sigma ^{n}( \mathbf {a}^{+}{ {\mathbf {s}}^{-}} \mathbf {a}^{\infty })\prec \mathbf {a}^{+}{ {\mathbf {s}}^{-}} \mathbf {a}^{\infty }$
for all
$\sigma ^{n}( \mathbf {a}^{+}{ {\mathbf {s}}^{-}} \mathbf {a}^{\infty })\prec \mathbf {a}^{+}{ {\mathbf {s}}^{-}} \mathbf {a}^{\infty }$
for all
![]() $n\ge 1$
. This completes the proof.
$n\ge 1$
. This completes the proof.
Lemma 2.8. Let
![]() $\beta \in (1,2)$
. Then
$\beta \in (1,2)$
. Then
![]() $\delta (\beta )$
is periodic if and only if
$\delta (\beta )$
is periodic if and only if
![]() $\delta (\beta )=\mathbb {L}( {\mathbf {s}})^{\infty }$
for some Lyndon word
$\delta (\beta )=\mathbb {L}( {\mathbf {s}})^{\infty }$
for some Lyndon word
![]() $ {\mathbf {s}}$
of length at least two.
$ {\mathbf {s}}$
of length at least two.
Proof. Suppose
![]() $\delta (\beta )=(a_{1}\ldots a_{m})^{\infty }$
with minimal period block
$\delta (\beta )=(a_{1}\ldots a_{m})^{\infty }$
with minimal period block
![]() $ \mathbf {a}=a_{1}\ldots a_{m}$
. Then
$ \mathbf {a}=a_{1}\ldots a_{m}$
. Then
![]() $m\ge 2$
since
$m\ge 2$
since
![]() $\beta <2$
. Take
$\beta <2$
. Take
![]() $ {\mathbf {s}}:=\mathbb {S}( \mathbf {a})$
. Then
$ {\mathbf {s}}:=\mathbb {S}( \mathbf {a})$
. Then
![]() $ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
, and
$ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
, and
If equality holds for some i, then we deduce just as in the proof of Lemma 2.7 that
![]() $ {\mathbf {s}}$
is periodic. However, then
$ {\mathbf {s}}$
is periodic. However, then
![]() $ \mathbf {a}$
is also periodic, contradicting that m is the minimal period of
$ \mathbf {a}$
is also periodic, contradicting that m is the minimal period of
![]() $\delta (\beta )$
. Hence, strict inequality holds in equation (2.7), and
$\delta (\beta )$
. Hence, strict inequality holds in equation (2.7), and
![]() $ {\mathbf {s}}$
is Lyndon. The converse is trivial.
$ {\mathbf {s}}$
is Lyndon. The converse is trivial.
Recall the Farey intervals and Lyndon intervals from Definition 1.8. The following properties of Lyndon intervals and Farey intervals were established in the proof of [Reference Kalle, Kong, Langeveld and Li20, Theorem C].
Lemma 2.9.
-
(i) The Farey intervals
 $J^ {\mathbf {s}}, {\mathbf {s}}\in \Omega _{F}^{*}$
are pairwise disjoint, and their union is dense in
$J^ {\mathbf {s}}, {\mathbf {s}}\in \Omega _{F}^{*}$
are pairwise disjoint, and their union is dense in
 $(1,2]$
.
$(1,2]$
. -
(ii) Any two Lyndon intervals are either disjoint or one is contained in the other.
-
(iii) For any Lyndon interval
 $J^ {\mathbf {S}}, {\mathbf {S}}\in \Omega _{L}^{*}$
, there exists a unique Farey interval
$J^ {\mathbf {S}}, {\mathbf {S}}\in \Omega _{L}^{*}$
, there exists a unique Farey interval
 $J^ {\mathbf {r}}$
such that
$J^ {\mathbf {r}}$
such that
 $J^ {\mathbf {S}}\subset {J^ {\mathbf {r}}}$
.
$J^ {\mathbf {S}}\subset {J^ {\mathbf {r}}}$
.
Note that (iii) follows immediately from (i) and (ii).
2.3 Greedy expansions and the symbolic survivor set
Given
![]() $\beta \in (1,2]$
and
$\beta \in (1,2]$
and
![]() $t\in [0,1)$
, we call the sequence
$t\in [0,1)$
, we call the sequence
![]() $(d_{i})\in \{0,1\}^{\mathbb {N}}$
a
$(d_{i})\in \{0,1\}^{\mathbb {N}}$
a
![]() $\beta $
-expansion of t if
$\beta $
-expansion of t if
![]() $((d_{i}))_{\beta }=t$
. Note that a point
$((d_{i}))_{\beta }=t$
. Note that a point
![]() $t\in [0,1)$
may have multiple
$t\in [0,1)$
may have multiple
![]() $\beta $
-expansions. We denote by
$\beta $
-expansions. We denote by
![]() $b(t,\beta )=(b_{i}(t,\beta ))\in \{0,1\}^{\mathbb {N}}$
the greedy
$b(t,\beta )=(b_{i}(t,\beta ))\in \{0,1\}^{\mathbb {N}}$
the greedy
![]() $\beta $
-expansion of t, which is the lexicographically largest expansion of t in base
$\beta $
-expansion of t, which is the lexicographically largest expansion of t in base
![]() $\beta $
. Since
$\beta $
. Since
![]() $T_{\beta }(t)=\beta t\pmod 1$
, it follows that
$T_{\beta }(t)=\beta t\pmod 1$
, it follows that
 $b(T_{\beta }^{n}(t), \beta )=\sigma ^{n}(b(t,\beta ))=b_{n+1}(t,\beta )b_{n+2}(t,\beta )\ldots $
. The following result was established by Parry [Reference Parry26] and de Vries and Komornik [Reference de Vries and Komornik12, Lemma 2.5 and Proposition 2.6].
$b(T_{\beta }^{n}(t), \beta )=\sigma ^{n}(b(t,\beta ))=b_{n+1}(t,\beta )b_{n+2}(t,\beta )\ldots $
. The following result was established by Parry [Reference Parry26] and de Vries and Komornik [Reference de Vries and Komornik12, Lemma 2.5 and Proposition 2.6].
Lemma 2.10. Let
![]() $\beta \in (1,2]$
. The map
$\beta \in (1,2]$
. The map
![]() $t\mapsto b(t,\beta )$
is an increasing bijection from
$t\mapsto b(t,\beta )$
is an increasing bijection from
![]() $[0,1)$
to
$[0,1)$
to
Furthermore:
-
(i) the map
 $t\mapsto b(t,\beta )$
is right-continuous everywhere in
$t\mapsto b(t,\beta )$
is right-continuous everywhere in
 $[0,1)$
with respect to the order topology in
$[0,1)$
with respect to the order topology in
 $\{0,1\}^{\mathbb {N}}$
;
$\{0,1\}^{\mathbb {N}}$
; -
(ii) if
 $b(t_{0},\beta )$
does not end with
$b(t_{0},\beta )$
does not end with
 $0^{\infty }$
, then the map
$0^{\infty }$
, then the map
 $t\mapsto b(t,\beta )$
is continuous at
$t\mapsto b(t,\beta )$
is continuous at
 $t_{0}$
;
$t_{0}$
; -
(iii) if
 $b(t_{0},\beta )=b_{1}\ldots b_{m} 0^{\infty }$
with
$b(t_{0},\beta )=b_{1}\ldots b_{m} 0^{\infty }$
with
 $b_{m}=1$
, then
$b_{m}=1$
, then
 $b(t, \beta )\nearrow b_{1}\ldots b_{m}^{-}\delta (\beta )$
as
$b(t, \beta )\nearrow b_{1}\ldots b_{m}^{-}\delta (\beta )$
as
 $t\nearrow t_{0}$
.
$t\nearrow t_{0}$
.
Recall that the survivor set
![]() $K_{\beta }(t)$
consists of all
$K_{\beta }(t)$
consists of all
![]() $x\in [0,1)$
whose orbit
$x\in [0,1)$
whose orbit
 $\{T^{n}_{\beta }(x): n\ge 0\}$
avoids the hole
$\{T^{n}_{\beta }(x): n\ge 0\}$
avoids the hole
![]() $(0,t)$
. To describe the dimension of
$(0,t)$
. To describe the dimension of
![]() $K_{\beta }(t)$
, we introduce the topological entropy of a symbolic set. For a subset
$K_{\beta }(t)$
, we introduce the topological entropy of a symbolic set. For a subset
![]() $X\subset \{0,1\}^{\mathbb {N}}$
, its topological entropy
$X\subset \{0,1\}^{\mathbb {N}}$
, its topological entropy
![]() $h_{\mathrm {top}}(X)$
is defined by
$h_{\mathrm {top}}(X)$
is defined by
 $$ \begin{align*} h_{\mathrm{top}}(X):=\liminf_{n\to\infty}\frac{\log\#B_{n}(X)}{n}, \end{align*} $$
$$ \begin{align*} h_{\mathrm{top}}(X):=\liminf_{n\to\infty}\frac{\log\#B_{n}(X)}{n}, \end{align*} $$
where
![]() $\#B_{n}(X)$
denotes the number of all length n words occurring in sequences of X. The following result for the Hausdorff dimension of
$\#B_{n}(X)$
denotes the number of all length n words occurring in sequences of X. The following result for the Hausdorff dimension of
![]() $K_{\beta }(t)$
can be essentially deduced from Raith [Reference Raith28] (see also [Reference Kalle, Kong, Langeveld and Li20]).
$K_{\beta }(t)$
can be essentially deduced from Raith [Reference Raith28] (see also [Reference Kalle, Kong, Langeveld and Li20]).
Lemma 2.11. Given
![]() $\beta \in (1,2]$
and
$\beta \in (1,2]$
and
![]() $t\in [0,1)$
, the Hausdorff dimension of
$t\in [0,1)$
, the Hausdorff dimension of
![]() $K_{\beta }(t)$
is given by
$K_{\beta }(t)$
is given by
 $$ \begin{align*} \dim_{H} K_{\beta}(t) =\frac{h_{\mathrm{top}}(\mathbf K_{\beta}(t))}{\log\beta}, \end{align*} $$
$$ \begin{align*} \dim_{H} K_{\beta}(t) =\frac{h_{\mathrm{top}}(\mathbf K_{\beta}(t))}{\log\beta}, \end{align*} $$
where
 $$ \begin{align*} \mathbf K_{\beta}(t)=\{(d_{i})\in\{0,1\}^{\mathbb{N}}: b(t,\beta)\preccurlyeq\sigma^{n}((d_{i}))\prec \delta(\beta) \text{ for all } n\ge 0\}. \end{align*} $$
$$ \begin{align*} \mathbf K_{\beta}(t)=\{(d_{i})\in\{0,1\}^{\mathbb{N}}: b(t,\beta)\preccurlyeq\sigma^{n}((d_{i}))\prec \delta(\beta) \text{ for all } n\ge 0\}. \end{align*} $$
To determine the critical value
![]() $\tau (\beta )$
for
$\tau (\beta )$
for
![]() $\beta $
inside any Farey interval
$\beta $
inside any Farey interval
![]() $J^ {\mathbf {s}}$
, we first need to develop some properties of the substitution operator
$J^ {\mathbf {s}}$
, we first need to develop some properties of the substitution operator
![]() $\bullet $
from equation (1.3). We do this in the next section.
$\bullet $
from equation (1.3). We do this in the next section.
3 Substitution of Lyndon words
In this section, we give an equivalent definition of the substitution operator in
![]() $\Omega _{L}^{*}$
introduced in equation (1.3), and prove that
$\Omega _{L}^{*}$
introduced in equation (1.3), and prove that
![]() $\Omega _{L}^{*}$
forms a semi-group under this substitution operator. This will play a crucial role in the rest of the paper.
$\Omega _{L}^{*}$
forms a semi-group under this substitution operator. This will play a crucial role in the rest of the paper.
3.1 An equivalent definition of the substitution
Given a Lyndon word
![]() $ {\mathbf {s}}\in \Omega _{L}^{*}$
with
$ {\mathbf {s}}\in \Omega _{L}^{*}$
with
![]() $ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
, we construct a directed graph
$ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
, we construct a directed graph
![]() $G=(V, E)$
as in Figure 2. The directed graph G has two starting vertices ‘Start-
$G=(V, E)$
as in Figure 2. The directed graph G has two starting vertices ‘Start-
![]() $0$
’ and ‘Start-
$0$
’ and ‘Start-
![]() $1$
’. The directed edges in the graph G take labels from
$1$
’. The directed edges in the graph G take labels from
![]() $\{0,1\}$
, and the vertices in G take labels from
$\{0,1\}$
, and the vertices in G take labels from
![]() $\{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. Denote by
$\{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. Denote by
![]() $\mathcal L^{E}$
the edge labeling and by
$\mathcal L^{E}$
the edge labeling and by
![]() $\mathcal L^{V}$
the vertex labeling. Then for each directed edge
$\mathcal L^{V}$
the vertex labeling. Then for each directed edge
![]() $e\in E(G)$
, we have
$e\in E(G)$
, we have
![]() $\mathcal L^{E}(e)\in \{0,1\}$
, and for each vertex
$\mathcal L^{E}(e)\in \{0,1\}$
, and for each vertex
![]() $v\in V(G)$
, we have
$v\in V(G)$
, we have
![]() $\mathcal L^{V}(v)\in \{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. The labeling maps
$\mathcal L^{V}(v)\in \{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. The labeling maps
![]() $\mathcal L^{E}$
and
$\mathcal L^{E}$
and
![]() $\mathcal L^{V}$
naturally induce the maps on the infinite edge paths and infinite vertex paths in G, respectively. For example, for an infinite edge path
$\mathcal L^{V}$
naturally induce the maps on the infinite edge paths and infinite vertex paths in G, respectively. For example, for an infinite edge path
![]() $e_{1}e_{2}\ldots $
, we have
$e_{1}e_{2}\ldots $
, we have
Here we call
![]() $e_{1}e_{2}\ldots $
an infinite edge path in G if the initial vertex of
$e_{1}e_{2}\ldots $
an infinite edge path in G if the initial vertex of
![]() $e_{1}$
is one of the starting vertices and for any
$e_{1}$
is one of the starting vertices and for any
![]() $i\ge 1$
, the terminal vertex
$i\ge 1$
, the terminal vertex
![]() $t(e_{i})$
equals the initial vertex
$t(e_{i})$
equals the initial vertex
![]() $i(e_{i+1})$
. Similarly, for an infinite vertex path
$i(e_{i+1})$
. Similarly, for an infinite vertex path
![]() $v=v_{1}v_{2}\ldots $
, we have
$v=v_{1}v_{2}\ldots $
, we have
where we call
![]() $v_{1}v_{2}\ldots $
an infinite vertex path in G if
$v_{1}v_{2}\ldots $
an infinite vertex path in G if
![]() $v_{1}$
is one of the starting vertices and for any
$v_{1}$
is one of the starting vertices and for any
![]() $i\ge 1$
, there exists a directed edge
$i\ge 1$
, there exists a directed edge
![]() $e\in E(G)$
such that
$e\in E(G)$
such that
![]() $i(e)=v_{i}$
and
$i(e)=v_{i}$
and
![]() $t(e)=v_{i+1}$
.
$t(e)=v_{i+1}$
.

Figure 2 The directed graph
![]() $G=(V, E)$
with the edge labels from
$G=(V, E)$
with the edge labels from
![]() $\{0, 1\}$
and vertex labels from
$\{0, 1\}$
and vertex labels from
![]() $\{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
, where
$\{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
, where
![]() $ {\mathbf {s}}\in \Omega _{L}^{*}$
and
$ {\mathbf {s}}\in \Omega _{L}^{*}$
and
![]() $ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
.
$ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
.
Let
![]() $X_{E}=X_{E}(G)$
be the edge shift consisting of all labelings of infinite edge paths in G, that is,
$X_{E}=X_{E}(G)$
be the edge shift consisting of all labelings of infinite edge paths in G, that is,
One can verify easily that
![]() ${X_{E}=\{0,1\}^{\mathbb {N}}}$
. Also, let
${X_{E}=\{0,1\}^{\mathbb {N}}}$
. Also, let
![]() $X_{V}=X_{V}(G)$
be the vertex shift which consists of all labelings of infinite vertex paths in G, that is,
$X_{V}=X_{V}(G)$
be the vertex shift which consists of all labelings of infinite vertex paths in G, that is,
Then any sequence in
![]() $X_{V}$
is an infinite concatenation of words from
$X_{V}$
is an infinite concatenation of words from
![]() $\{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. Observe that the edge shift
$\{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. Observe that the edge shift
![]() $X_{E}$
is right-resolving, which means that out-going edges from the same vertex have different labels (cf. [Reference Lind and Marcus23]). Moreover, different vertices have different labels. So for each
$X_{E}$
is right-resolving, which means that out-going edges from the same vertex have different labels (cf. [Reference Lind and Marcus23]). Moreover, different vertices have different labels. So for each
![]() $(d_{i})\in X_{E}$
, there is a unique infinite edge path
$(d_{i})\in X_{E}$
, there is a unique infinite edge path
![]() $e_{1}e_{2}\ldots $
in G such that
$e_{1}e_{2}\ldots $
in G such that
![]() $d_{1}d_{2}\ldots =\mathcal L^{E}(e_{1}e_{2}\ldots ).$
$d_{1}d_{2}\ldots =\mathcal L^{E}(e_{1}e_{2}\ldots ).$
Definition 3.1. The substitution map
![]() $\Phi _ {\mathbf {s}}$
from
$\Phi _ {\mathbf {s}}$
from
![]() $X_{E}$
to
$X_{E}$
to
![]() $X_{V}$
is defined by
$X_{V}$
is defined by
where
![]() $t(e_{i})$
denotes the terminal vertex of the directed edge
$t(e_{i})$
denotes the terminal vertex of the directed edge
![]() $e_{i}$
.
$e_{i}$
.
We can extend the substitution map
![]() $\Phi _ {\mathbf {s}}$
to a map from
$\Phi _ {\mathbf {s}}$
to a map from
![]() $B_{*}(X_{E})$
to
$B_{*}(X_{E})$
to
![]() $B_{*}(X_{V})$
by
$B_{*}(X_{V})$
by
where
![]() $B_{*}(X_{E})$
consists of all labelings of finite edge paths in G and
$B_{*}(X_{E})$
consists of all labelings of finite edge paths in G and
![]() $B_{*}(X_{V})$
consists of all labelings of finite vertex paths in G. So, by equations (1.3) and (3.1), it follows that for any two words
$B_{*}(X_{V})$
consists of all labelings of finite vertex paths in G. So, by equations (1.3) and (3.1), it follows that for any two words
![]() $ {\mathbf {s}}\in \Omega _{L}^{*}$
and
$ {\mathbf {s}}\in \Omega _{L}^{*}$
and
![]() $ {\mathbf {r}}\in \{0,1\}^{*}$
, we have
$ {\mathbf {r}}\in \{0,1\}^{*}$
, we have
Example 3.2. Let
![]() $ {\mathbf {s}}=01$
and
$ {\mathbf {s}}=01$
and
![]() $ {\mathbf {r}}=001011$
. Then
$ {\mathbf {r}}=001011$
. Then
![]() $ {\mathbf {s}}\in \Omega _{F}^{*}$
and
$ {\mathbf {s}}\in \Omega _{F}^{*}$
and
![]() $ {\mathbf {r}}\in \Omega _{L}^{*}\setminus \Omega _{F}^{*}$
. Furthermore,
$ {\mathbf {r}}\in \Omega _{L}^{*}\setminus \Omega _{F}^{*}$
. Furthermore,
![]() ${ {\mathbf {s}}^{-}}=00, \mathbf {a}=\mathbb {L}( {\mathbf {s}})=10, \mathbf {a}^{+}=11$
. So by the definition of
${ {\mathbf {s}}^{-}}=00, \mathbf {a}=\mathbb {L}( {\mathbf {s}})=10, \mathbf {a}^{+}=11$
. So by the definition of
![]() $\Phi _ {\mathbf {s}}$
, it follows that
$\Phi _ {\mathbf {s}}$
, it follows that
 $$ \begin{align*} \Phi_ {\mathbf{s}}( {\mathbf{r}})&=\Phi_ {\mathbf{s}}( 001011 )={ {\mathbf{s}}^{-}} \mathbf{a} \mathbf{a}^{+}{ {\mathbf{s}}^{-}} \mathbf{a}^{+} {\mathbf{s}}=001011001101, \\[3pt] \Phi_ {\mathbf{s}}( {\mathbf{r}}^{-})&= \Phi_ {\mathbf{s}}( 001010)={ {\mathbf{s}}^{-}} \mathbf{a} \mathbf{a}^{+}{ {\mathbf{s}}^{-}} \mathbf{a}^{+}{ {\mathbf{s}}^{-}}=001011001100. \end{align*} $$
$$ \begin{align*} \Phi_ {\mathbf{s}}( {\mathbf{r}})&=\Phi_ {\mathbf{s}}( 001011 )={ {\mathbf{s}}^{-}} \mathbf{a} \mathbf{a}^{+}{ {\mathbf{s}}^{-}} \mathbf{a}^{+} {\mathbf{s}}=001011001101, \\[3pt] \Phi_ {\mathbf{s}}( {\mathbf{r}}^{-})&= \Phi_ {\mathbf{s}}( 001010)={ {\mathbf{s}}^{-}} \mathbf{a} \mathbf{a}^{+}{ {\mathbf{s}}^{-}} \mathbf{a}^{+}{ {\mathbf{s}}^{-}}=001011001100. \end{align*} $$
Observe that
![]() $\Phi _ {\mathbf {s}}( {\mathbf {r}}^{-})=\Phi _ {\mathbf {s}}( {\mathbf {r}})^{-}$
. By Definition 1.1, one can check that
$\Phi _ {\mathbf {s}}( {\mathbf {r}}^{-})=\Phi _ {\mathbf {s}}( {\mathbf {r}})^{-}$
. By Definition 1.1, one can check that
![]() $\Phi _ {\mathbf {s}}( {\mathbf {r}})\in \Omega _{L}^{*}$
. Furthermore,
$\Phi _ {\mathbf {s}}( {\mathbf {r}})\in \Omega _{L}^{*}$
. Furthermore,
and
3.2 Properties of the substitution
Motivated by Examples 1.2 and 3.2, we study the properties of the substitution
![]() $\Phi _ {\mathbf {s}}$
. We will show that
$\Phi _ {\mathbf {s}}$
. We will show that
![]() $\Omega _{L}^{*}$
forms a semi-group under the substitution operator defined in Definition 3.1. First we prove the monotonicity of
$\Omega _{L}^{*}$
forms a semi-group under the substitution operator defined in Definition 3.1. First we prove the monotonicity of
![]() $\Phi _ {\mathbf {s}}$
.
$\Phi _ {\mathbf {s}}$
.
Lemma 3.3. Let
![]() $ {\mathbf {s}}\in \Omega _{L}^{*}$
. Then the map
$ {\mathbf {s}}\in \Omega _{L}^{*}$
. Then the map
![]() $\Phi _ {\mathbf {s}}$
is strictly increasing in
$\Phi _ {\mathbf {s}}$
is strictly increasing in
![]() $X_{E}=\{0,1\}^{\mathbb {N}}$
.
$X_{E}=\{0,1\}^{\mathbb {N}}$
.
Proof. Let
![]() $(d_{i})$
and
$(d_{i})$
and
![]() $(d_{i}^{\prime })$
be two sequences in
$(d_{i}^{\prime })$
be two sequences in
![]() $X_{E}$
, and let
$X_{E}$
, and let
![]() $(e_{i}), (e_{i}^{\prime })$
be their corresponding edge paths; thus,
$(e_{i}), (e_{i}^{\prime })$
be their corresponding edge paths; thus,
![]() $(d_{i})=\mathcal L^{E}((e_{i}))$
and
$(d_{i})=\mathcal L^{E}((e_{i}))$
and
 $(d_{i}^{\prime })=\mathcal L^{E}((e_{i}^{\prime }))$
. Suppose
$(d_{i}^{\prime })=\mathcal L^{E}((e_{i}^{\prime }))$
. Suppose
![]() $(d_{i})\prec (d_{i}^{\prime })$
. Then there exists
$(d_{i})\prec (d_{i}^{\prime })$
. Then there exists
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $d_{1}\ldots d_{k-1}=d_{1}^{\prime }\ldots d_{k-1}^{\prime }$
and
$d_{1}\ldots d_{k-1}=d_{1}^{\prime }\ldots d_{k-1}^{\prime }$
and
![]() $d_{k}<d_{k}^{\prime }$
. If
$d_{k}<d_{k}^{\prime }$
. If
![]() $k=1$
, then
$k=1$
, then
![]() $d_{1}=0$
and
$d_{1}=0$
and
![]() $d_{1}^{\prime }=1$
. So,
$d_{1}^{\prime }=1$
. So,
![]() $\mathcal L^{V}(t(e_{1}))={ {\mathbf {s}}^{-}}$
and
$\mathcal L^{V}(t(e_{1}))={ {\mathbf {s}}^{-}}$
and
 $\mathcal L^{V}(t(e_{1}^{\prime }))= \mathbf {a}^{+}$
. By Definition 3.1, it follows that
$\mathcal L^{V}(t(e_{1}^{\prime }))= \mathbf {a}^{+}$
. By Definition 3.1, it follows that
![]() $\Phi _ {\mathbf {s}}((d_{i}))\prec \Phi _ {\mathbf {s}}((d_{i}^{\prime }))$
.
$\Phi _ {\mathbf {s}}((d_{i}))\prec \Phi _ {\mathbf {s}}((d_{i}^{\prime }))$
.
If
![]() $k>1$
, then
$k>1$
, then
![]() $e_{1}\ldots e_{k-1}=e_{1}^{\prime }\ldots e_{k-1}^{\prime }$
, which implies that the initial vertices of
$e_{1}\ldots e_{k-1}=e_{1}^{\prime }\ldots e_{k-1}^{\prime }$
, which implies that the initial vertices of
![]() $e_{k}$
and
$e_{k}$
and
![]() $e_{k}^{\prime }$
coincide. Since
$e_{k}^{\prime }$
coincide. Since
![]() $d_{k}<d_{k}^{\prime }$
, by the definition of
$d_{k}<d_{k}^{\prime }$
, by the definition of
![]() $\mathcal L^{V}$
, it follows that (see Figure 2)
$\mathcal L^{V}$
, it follows that (see Figure 2)
 $$ \begin{align*} \mathcal L^{V}(t(e_{k}))\prec\mathcal L^{V}(t(e_{k}^{\prime})). \end{align*} $$
$$ \begin{align*} \mathcal L^{V}(t(e_{k}))\prec\mathcal L^{V}(t(e_{k}^{\prime})). \end{align*} $$
By Definition 3.1, we also have
![]() $\Phi _ {\mathbf {s}}((d_{i}))\prec \Phi _ {\mathbf {s}}((d_{i}^{\prime }))$
. This completes the proof.
$\Phi _ {\mathbf {s}}((d_{i}))\prec \Phi _ {\mathbf {s}}((d_{i}^{\prime }))$
. This completes the proof.
Lemma 3.4. Let
![]() $ {\mathbf {s}}\in \Omega _{L}^{*}$
. Then for any word
$ {\mathbf {s}}\in \Omega _{L}^{*}$
. Then for any word
![]() $ {\mathbf {d}}=d_{1}\ldots d_{k}\in B_{*}(X_{E})$
with
$ {\mathbf {d}}=d_{1}\ldots d_{k}\in B_{*}(X_{E})$
with
![]() $k\ge 2$
, we have
$k\ge 2$
, we have
 $$ \begin{align*} \left\{ \begin{array}{@{}ll} \Phi_ {\mathbf{s}}( {\mathbf{d}}^{-})=\Phi_ {\mathbf{s}}( {\mathbf{d}})^{-}&\textrm{if } d_{k}=1,\\[3pt] \Phi_ {\mathbf{s}}( {\mathbf{d}}^{+})=\Phi_ {\mathbf{s}}( {\mathbf{d}})^{+}&\textrm{if } d_{k}=0. \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{@{}ll} \Phi_ {\mathbf{s}}( {\mathbf{d}}^{-})=\Phi_ {\mathbf{s}}( {\mathbf{d}})^{-}&\textrm{if } d_{k}=1,\\[3pt] \Phi_ {\mathbf{s}}( {\mathbf{d}}^{+})=\Phi_ {\mathbf{s}}( {\mathbf{d}})^{+}&\textrm{if } d_{k}=0. \end{array} \right. \end{align*} $$
Proof. Since
![]() $ {\mathbf {d}}=d_{1}\ldots d_{k}\in B_{*}(X_{E})$
, there exists a unique finite edge path
$ {\mathbf {d}}=d_{1}\ldots d_{k}\in B_{*}(X_{E})$
, there exists a unique finite edge path
![]() $e_{1}\ldots e_{k}$
such that
$e_{1}\ldots e_{k}$
such that
![]() $\mathcal L^{E}(e_{1}\ldots e_{k})= {\mathbf {d}}$
. If
$\mathcal L^{E}(e_{1}\ldots e_{k})= {\mathbf {d}}$
. If
![]() $d_{k}=1$
, then
$d_{k}=1$
, then
![]() $ {\mathbf {d}}^{-}=d_{1}\ldots d_{k-1}0$
can be represented by a unique finite edge path
$ {\mathbf {d}}^{-}=d_{1}\ldots d_{k-1}0$
can be represented by a unique finite edge path
![]() $e_{1}^{\prime }\ldots e_{k}^{\prime }$
with
$e_{1}^{\prime }\ldots e_{k}^{\prime }$
with
![]() $e_{1}^{\prime }\ldots e_{k-1}^{\prime }=e_{1}\ldots e_{k-1}$
. By the definition of
$e_{1}^{\prime }\ldots e_{k-1}^{\prime }=e_{1}\ldots e_{k-1}$
. By the definition of
![]() $\mathcal L^{V}$
, it follows that
$\mathcal L^{V}$
, it follows that
 $\mathcal L^{V}(t(e_{k}^{\prime }))=\mathcal L^{V}(t(e_{k}))^{-}$
. Therefore, by Definition 3.1, it follows that
$\mathcal L^{V}(t(e_{k}^{\prime }))=\mathcal L^{V}(t(e_{k}))^{-}$
. Therefore, by Definition 3.1, it follows that
 $$ \begin{align*} \Phi_ {\mathbf{s}}( {\mathbf{d}}^{-})=\Phi_ {\mathbf{s}}(\mathcal L^{E}(e_{1}^{\prime}\ldots e_{k}^{\prime})) &= \Phi_ {\mathbf{s}}(\mathcal L^{E}(e_{1}\ldots e_{k-1}e_{k}^{\prime}))\\[3pt] &=\mathcal L^{V}(t(e_{1})\ldots t(e_{k-1})t(e_{k}^{\prime})) \\[3pt] &=\mathcal L^{V}(t(e_{1})\ldots t(e_{k}))^{-}=\Phi_ {\mathbf{s}}( {\mathbf{d}})^{-}. \end{align*} $$
$$ \begin{align*} \Phi_ {\mathbf{s}}( {\mathbf{d}}^{-})=\Phi_ {\mathbf{s}}(\mathcal L^{E}(e_{1}^{\prime}\ldots e_{k}^{\prime})) &= \Phi_ {\mathbf{s}}(\mathcal L^{E}(e_{1}\ldots e_{k-1}e_{k}^{\prime}))\\[3pt] &=\mathcal L^{V}(t(e_{1})\ldots t(e_{k-1})t(e_{k}^{\prime})) \\[3pt] &=\mathcal L^{V}(t(e_{1})\ldots t(e_{k}))^{-}=\Phi_ {\mathbf{s}}( {\mathbf{d}})^{-}. \end{align*} $$
This proves the first equality of the lemma. The second equality follows analogously.
Recall the operator
![]() $\bullet $
from equation (3.2). In the following, we prove Proposition 1.3 by showing that
$\bullet $
from equation (3.2). In the following, we prove Proposition 1.3 by showing that
![]() $\Omega _{L}^{*}$
is closed under
$\Omega _{L}^{*}$
is closed under
![]() $\bullet $
and that
$\bullet $
and that
![]() $\bullet $
is associative. The proof will be split into a sequence of lemmas. First we prove that
$\bullet $
is associative. The proof will be split into a sequence of lemmas. First we prove that
![]() $\Omega _{L}^{*}$
is closed under
$\Omega _{L}^{*}$
is closed under
![]() $\bullet $
.
$\bullet $
.
Lemma 3.5. For any
![]() $ {\mathbf {s}}, {\mathbf {r}}\in \Omega _{L}^{*}$
, we have
$ {\mathbf {s}}, {\mathbf {r}}\in \Omega _{L}^{*}$
, we have
![]() $ {\mathbf {s}}\bullet {\mathbf {r}}\in \Omega _{L}^{*}$
.
$ {\mathbf {s}}\bullet {\mathbf {r}}\in \Omega _{L}^{*}$
.
Proof. Let
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{L}^{*}$
and
$ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{L}^{*}$
and
![]() $ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
. Then there exists
$ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
. Then there exists
![]() $j\in \{1,\ldots ,m-1\}$
such that
$j\in \{1,\ldots ,m-1\}$
such that
Let
![]() $ {\mathbf {r}}=r_{1}\ldots r_{\ell }\in \Omega _{L}^{*}$
. Then we can write
$ {\mathbf {r}}=r_{1}\ldots r_{\ell }\in \Omega _{L}^{*}$
. Then we can write
![]() $ {\mathbf {s}}\bullet {\mathbf {r}}=\Phi _ {\mathbf {s}}( {\mathbf {r}})=b_{1}\ldots b_{m\ell }$
. Furthermore, there exists a finite edge path
$ {\mathbf {s}}\bullet {\mathbf {r}}=\Phi _ {\mathbf {s}}( {\mathbf {r}})=b_{1}\ldots b_{m\ell }$
. Furthermore, there exists a finite edge path
![]() $e_{1}\ldots e_{\ell }$
representing
$e_{1}\ldots e_{\ell }$
representing
![]() $ {\mathbf {r}}$
such that
$ {\mathbf {r}}$
such that
where each block
![]() $ {\mathbf {b}}_{i}\in \{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. Note that
$ {\mathbf {b}}_{i}\in \{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. Note that
![]() $ {\mathbf {b}}_{1}={ {\mathbf {s}}^{-}}$
since the block
$ {\mathbf {b}}_{1}={ {\mathbf {s}}^{-}}$
since the block
![]() $ {\mathbf {r}}$
begins with
$ {\mathbf {r}}$
begins with
![]() $r_{1}=0$
. By Definition 1.1, it suffices to prove
$r_{1}=0$
. By Definition 1.1, it suffices to prove
We split the proof of equation (3.4) into two cases.
Case I.
![]() $i=km$
for some
$i=km$
for some
![]() $k\in \{1, 2,\ldots , \ell -1\}$
. Then
$k\in \{1, 2,\ldots , \ell -1\}$
. Then
![]() $b_{i+1}\ldots b_{m\ell }= {\mathbf {b}}_{k+1}\ldots {\mathbf {b}}_{\ell }$
. Since
$b_{i+1}\ldots b_{m\ell }= {\mathbf {b}}_{k+1}\ldots {\mathbf {b}}_{\ell }$
. Since
![]() $ {\mathbf {r}}$
is a Lyndon word, we have
$ {\mathbf {r}}$
is a Lyndon word, we have
![]() $r_{k+1}\ldots r_{\ell }\succ r_{1}\ldots r_{\ell -k}$
. So, equation (3.4) follows directly by Lemma 3.3.
$r_{k+1}\ldots r_{\ell }\succ r_{1}\ldots r_{\ell -k}$
. So, equation (3.4) follows directly by Lemma 3.3.
Case II.
![]() $i=km+p$
for some
$i=km+p$
for some
![]() $k\in \{0,1,\ldots , \ell -1\}$
and
$k\in \{0,1,\ldots , \ell -1\}$
and
![]() $p\in \{1,\ldots , m-1\}$
. Then
$p\in \{1,\ldots , m-1\}$
. Then
![]() $b_{i+1}\ldots b_{m\ell }=b_{i+1}\ldots b_{i+m-p} {\mathbf {b}}_{k+2}\ldots {\mathbf {b}}_{\ell }$
. In the following, we prove equation (3.4) by considering the four possible choices of
$b_{i+1}\ldots b_{m\ell }=b_{i+1}\ldots b_{i+m-p} {\mathbf {b}}_{k+2}\ldots {\mathbf {b}}_{\ell }$
. In the following, we prove equation (3.4) by considering the four possible choices of
![]() $ {\mathbf {b}}_{k+1}\in \{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. If
$ {\mathbf {b}}_{k+1}\in \{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. If
![]() $ {\mathbf {b}}_{k+1}= {\mathbf {s}}$
, then by using that
$ {\mathbf {b}}_{k+1}= {\mathbf {s}}$
, then by using that
![]() $ {\mathbf {s}}\in \Omega _{L}^{*}$
, we conclude that
$ {\mathbf {s}}\in \Omega _{L}^{*}$
, we conclude that
proving equation (3.4). Similarly, if
![]() $ {\mathbf {b}}_{k+1}= \mathbf {a}^{+}$
, then by equation (3.3), one can also prove that
$ {\mathbf {b}}_{k+1}= \mathbf {a}^{+}$
, then by equation (3.3), one can also prove that
![]() $b_{i+1}\ldots b_{i+m-p} \succ b_{1}\ldots b_{m-p}$
. Now we assume
$b_{i+1}\ldots b_{i+m-p} \succ b_{1}\ldots b_{m-p}$
. Now we assume
![]() $ {\mathbf {b}}_{k+1}={ {\mathbf {s}}^{-}}$
. Then by using
$ {\mathbf {b}}_{k+1}={ {\mathbf {s}}^{-}}$
. Then by using
![]() $ {\mathbf {s}}\in \Omega _{L}^{*}$
, it follows that
$ {\mathbf {s}}\in \Omega _{L}^{*}$
, it follows that
Observe that the word
![]() ${ {\mathbf {s}}^{-}}$
can only be followed by
${ {\mathbf {s}}^{-}}$
can only be followed by
![]() $ \mathbf {a}$
or
$ \mathbf {a}$
or
![]() $ \mathbf {a}^{+}$
in G (see Figure 2). So
$ \mathbf {a}^{+}$
in G (see Figure 2). So
![]() $ {\mathbf {b}}_{k+2}\in \{ \mathbf {a}, \mathbf {a}^{+}\}$
. Since
$ {\mathbf {b}}_{k+2}\in \{ \mathbf {a}, \mathbf {a}^{+}\}$
. Since
![]() $ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
, we obtain that
$ \mathbf {a}=\mathbb {L}( {\mathbf {s}})$
, we obtain that
Thus, by equations (3.5) and (3.6), we conclude that
![]() $b_{i+1}\ldots b_{i+m}\succ b_{1}\ldots b_{m}$
, proving equation (3.4). Finally, suppose
$b_{i+1}\ldots b_{i+m}\succ b_{1}\ldots b_{m}$
, proving equation (3.4). Finally, suppose
![]() $ {\mathbf {b}}_{k+1}= \mathbf {a}$
. Note that the word
$ {\mathbf {b}}_{k+1}= \mathbf {a}$
. Note that the word
![]() $ \mathbf {a}$
can only be followed by
$ \mathbf {a}$
can only be followed by
![]() $ \mathbf {a}$
or
$ \mathbf {a}$
or
![]() $ \mathbf {a}^{+}$
in G. Then by equation (3.3) and using
$ \mathbf {a}^{+}$
in G. Then by equation (3.3) and using
![]() $ {\mathbf {s}}\in \Omega _{L}^{*}$
, we have
$ {\mathbf {s}}\in \Omega _{L}^{*}$
, we have
This completes the proof.
Say a finite or infinite sequence of words
![]() $ {\mathbf {b}}_{1},\ldots , {\mathbf {b}}_{n}$
or
$ {\mathbf {b}}_{1},\ldots , {\mathbf {b}}_{n}$
or
![]() $ {\mathbf {b}}_{1}, {\mathbf {b}}_{2},\ldots $
is connectible if for each i, the last digit of
$ {\mathbf {b}}_{1}, {\mathbf {b}}_{2},\ldots $
is connectible if for each i, the last digit of
![]() $ {\mathbf {b}}_{i}$
differs from the first digit of
$ {\mathbf {b}}_{i}$
differs from the first digit of
![]() $ {\mathbf {b}}_{i+1}$
. Thus, for instance, the sequence
$ {\mathbf {b}}_{i+1}$
. Thus, for instance, the sequence
![]() $1101, 00111$
is connectible whereas the sequence
$1101, 00111$
is connectible whereas the sequence
![]() $11010, 0111$
is not.
$11010, 0111$
is not.
Lemma 3.6.
-
(i) Let
 $ {\mathbf {b}}_{1}, {\mathbf {b}}_{2},\ldots $
be a (finite or infinite) connectible sequence of words. Then for any
$ {\mathbf {b}}_{1}, {\mathbf {b}}_{2},\ldots $
be a (finite or infinite) connectible sequence of words. Then for any
 $ {\mathbf {s}}\in \Omega _{L}^{*}$
,
$ {\mathbf {s}}\in \Omega _{L}^{*}$
,  $$ \begin{align*} \Phi_ {\mathbf{s}}( {\mathbf{b}}_{1} {\mathbf{b}}_{2}\ldots)=\Phi_ {\mathbf{s}}( {\mathbf{b}}_{1})\Phi_ {\mathbf{s}}( {\mathbf{b}}_{2})\ldots. \end{align*} $$
$$ \begin{align*} \Phi_ {\mathbf{s}}( {\mathbf{b}}_{1} {\mathbf{b}}_{2}\ldots)=\Phi_ {\mathbf{s}}( {\mathbf{b}}_{1})\Phi_ {\mathbf{s}}( {\mathbf{b}}_{2})\ldots. \end{align*} $$
-
(ii) Let
 $ {\mathbf {s}}, {\mathbf {r}}\in \Omega _{L}^{*}$
. Then
$ {\mathbf {s}}, {\mathbf {r}}\in \Omega _{L}^{*}$
. Then
 $\Phi _ {\mathbf {s}}( {\mathbf {r}}^{\infty })=\Phi _ {\mathbf {s}}( {\mathbf {r}})^{\infty }$
and
$\Phi _ {\mathbf {s}}( {\mathbf {r}}^{\infty })=\Phi _ {\mathbf {s}}( {\mathbf {r}})^{\infty }$
and
 $\Phi _ {\mathbf {s}}(\mathbb {L}( {\mathbf {r}})^{\infty })=\Phi _ {\mathbf {s}}(\mathbb {L}( {\mathbf {r}}))^{\infty }$
.
$\Phi _ {\mathbf {s}}(\mathbb {L}( {\mathbf {r}})^{\infty })=\Phi _ {\mathbf {s}}(\mathbb {L}( {\mathbf {r}}))^{\infty }$
.
Proof. To prove (i), it suffices to show that if
![]() $ {\mathbf {b}}_{1}, {\mathbf {b}}_{2}$
is a connectible sequence, then
$ {\mathbf {b}}_{1}, {\mathbf {b}}_{2}$
is a connectible sequence, then
![]() $\Phi _ {\mathbf {s}}( {\mathbf {b}}_{1} {\mathbf {b}}_{2})=\Phi _ {\mathbf {s}}( {\mathbf {b}}_{1})\Phi _ {\mathbf {s}}( {\mathbf {b}}_{2})$
; the statement then extends to arbitrary connectible sequences by induction.
$\Phi _ {\mathbf {s}}( {\mathbf {b}}_{1} {\mathbf {b}}_{2})=\Phi _ {\mathbf {s}}( {\mathbf {b}}_{1})\Phi _ {\mathbf {s}}( {\mathbf {b}}_{2})$
; the statement then extends to arbitrary connectible sequences by induction.
Without loss of generality, by the symmetry of the edge-labels in Figure 2, we may assume that
![]() $ {\mathbf {b}}_{1}$
ends in the digit 0 and
$ {\mathbf {b}}_{1}$
ends in the digit 0 and
![]() $ {\mathbf {b}}_{2}$
begins with the digit 1. However, note that in the directed graph in Figure 2, if we travel along an edge labeled 0 followed by an edge labeled 1, we always end up at the vertex labeled
$ {\mathbf {b}}_{2}$
begins with the digit 1. However, note that in the directed graph in Figure 2, if we travel along an edge labeled 0 followed by an edge labeled 1, we always end up at the vertex labeled
![]() $ \mathbf {a}^{+}$
, which is also the first vertex visited after traveling along an edge labeled 1 from the ‘Start-1’ vertex. Thus,
$ \mathbf {a}^{+}$
, which is also the first vertex visited after traveling along an edge labeled 1 from the ‘Start-1’ vertex. Thus,
![]() $\Phi _ {\mathbf {s}}( {\mathbf {b}}_{1} {\mathbf {b}}_{2})=\Phi _ {\mathbf {s}}( {\mathbf {b}}_{1})\Phi _ {\mathbf {s}}( {\mathbf {b}}_{2})$
.
$\Phi _ {\mathbf {s}}( {\mathbf {b}}_{1} {\mathbf {b}}_{2})=\Phi _ {\mathbf {s}}( {\mathbf {b}}_{1})\Phi _ {\mathbf {s}}( {\mathbf {b}}_{2})$
.
Statement (ii) follows from (i) since
![]() $ {\mathbf {r}}$
begins with digit 0 and ends with digit 1, so
$ {\mathbf {r}}$
begins with digit 0 and ends with digit 1, so
![]() $ {\mathbf {r}}$
is connectible to itself; and similarly,
$ {\mathbf {r}}$
is connectible to itself; and similarly,
![]() $\mathbb {L}( {\mathbf {r}})$
begins with digit 1 and ends with digit 0, so
$\mathbb {L}( {\mathbf {r}})$
begins with digit 1 and ends with digit 0, so
![]() $\mathbb {L}( {\mathbf {r}})$
is connectible to itself.
$\mathbb {L}( {\mathbf {r}})$
is connectible to itself.
To prove that
![]() $\bullet $
is associative, we need the following result, which says that the two operators
$\bullet $
is associative, we need the following result, which says that the two operators
![]() $\bullet $
and
$\bullet $
and
![]() $\mathbb {L}$
commute.
$\mathbb {L}$
commute.
Lemma 3.7. For any
![]() $ {\mathbf {s}}, {\mathbf {r}}\in \Omega _{L}^{*}$
, we have
$ {\mathbf {s}}, {\mathbf {r}}\in \Omega _{L}^{*}$
, we have
![]() $\mathbb {L}( {\mathbf {s}}\bullet {\mathbf {r}})= {\mathbf {s}}\bullet \mathbb {L}( {\mathbf {r}})$
.
$\mathbb {L}( {\mathbf {s}}\bullet {\mathbf {r}})= {\mathbf {s}}\bullet \mathbb {L}( {\mathbf {r}})$
.
Proof. The proof is similar to that of Lemma 3.5. Let
![]() $ {\mathbf {r}}=r_{1}\ldots r_{\ell }\in \Omega _{L}^{*}$
. First we show that
$ {\mathbf {r}}=r_{1}\ldots r_{\ell }\in \Omega _{L}^{*}$
. First we show that
![]() $ {\mathbf {s}}\bullet \mathbb {L}( {\mathbf {r}})$
is a cyclic permutation of
$ {\mathbf {s}}\bullet \mathbb {L}( {\mathbf {r}})$
is a cyclic permutation of
![]() $ {\mathbf {s}}\bullet {\mathbf {r}}$
. Note that
$ {\mathbf {s}}\bullet {\mathbf {r}}$
. Note that
![]() $\mathbb {L}( {\mathbf {r}})=r_{j+1}\ldots r_{\ell } r_{1}\ldots r_{j}$
for some
$\mathbb {L}( {\mathbf {r}})=r_{j+1}\ldots r_{\ell } r_{1}\ldots r_{j}$
for some
![]() $1<j<\ell $
. Then
$1<j<\ell $
. Then
![]() $r_{j}=0$
and
$r_{j}=0$
and
![]() $r_{j+1}=1$
, so Lemma 3.6(i) implies that
$r_{j+1}=1$
, so Lemma 3.6(i) implies that
However, since
![]() $ {\mathbf {r}}\in \Omega _{L}^{*}$
, we have
$ {\mathbf {r}}\in \Omega _{L}^{*}$
, we have
![]() $r_{\ell }=1$
and
$r_{\ell }=1$
and
![]() $r_{1}=0$
, so by Lemma 3.6(i), we obtain that
$r_{1}=0$
, so by Lemma 3.6(i), we obtain that
This, together with equation (3.7), proves that
![]() $ {\mathbf {s}}\bullet \mathbb {L}( {\mathbf {r}})$
is indeed a cyclic permutation of
$ {\mathbf {s}}\bullet \mathbb {L}( {\mathbf {r}})$
is indeed a cyclic permutation of
![]() $ {\mathbf {s}}\bullet {\mathbf {r}}$
. It remains to prove that
$ {\mathbf {s}}\bullet {\mathbf {r}}$
. It remains to prove that
![]() $ {\mathbf {s}}\bullet \mathbb {L}( {\mathbf {r}})$
is the lexicographically largest cyclic permutation of itself.
$ {\mathbf {s}}\bullet \mathbb {L}( {\mathbf {r}})$
is the lexicographically largest cyclic permutation of itself.
Write
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{L}^{*}$
with
$ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{L}^{*}$
with
![]() $ \mathbf {a}=\mathbb {L}( {\mathbf {s}})=a_{1}\ldots a_{m}$
, and write
$ \mathbf {a}=\mathbb {L}( {\mathbf {s}})=a_{1}\ldots a_{m}$
, and write
![]() $\mathbb {L}( {\mathbf {r}})=c_{1}\ldots c_{\ell }$
. Then by Lemma 2.7, it follows that
$\mathbb {L}( {\mathbf {r}})=c_{1}\ldots c_{\ell }$
. Then by Lemma 2.7, it follows that
 $$ \begin{align} a_{i+1}\ldots a_{m}&\prec a_{1}\ldots a_{m-i}\quad\text{for all } 0<i<m;\nonumber\\[5pt] c_{i+1}\ldots c_{\ell}&\prec c_{1}\ldots c_{\ell-i}\quad \text{for all } 0<i<\ell. \end{align} $$
$$ \begin{align} a_{i+1}\ldots a_{m}&\prec a_{1}\ldots a_{m-i}\quad\text{for all } 0<i<m;\nonumber\\[5pt] c_{i+1}\ldots c_{\ell}&\prec c_{1}\ldots c_{\ell-i}\quad \text{for all } 0<i<\ell. \end{align} $$
Write
![]() $ {\mathbf {s}}\bullet \mathbb {L}( {\mathbf {r}})= {\mathbf {b}}_{1}\ldots {\mathbf {b}}_{\ell }=b_{1}\ldots b_{m\ell }$
, where each
$ {\mathbf {s}}\bullet \mathbb {L}( {\mathbf {r}})= {\mathbf {b}}_{1}\ldots {\mathbf {b}}_{\ell }=b_{1}\ldots b_{m\ell }$
, where each
![]() $ {\mathbf {b}}_{i}\in \{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. Then it suffices to prove that
$ {\mathbf {b}}_{i}\in \{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbf {a}, \mathbf {a}^{+}\}$
. Then it suffices to prove that
Since
![]() $\mathbb {L}( {\mathbf {r}})$
has a prefix
$\mathbb {L}( {\mathbf {r}})$
has a prefix
![]() $c_{1}=1$
, we see that
$c_{1}=1$
, we see that
![]() $b_{1}\ldots b_{m}= {\mathbf {b}}_{1}= \mathbf {a}^{+}$
. So, by using equation (3.8) and the same argument as in the proof of Lemma 3.5, we can prove equation (3.9).
$b_{1}\ldots b_{m}= {\mathbf {b}}_{1}= \mathbf {a}^{+}$
. So, by using equation (3.8) and the same argument as in the proof of Lemma 3.5, we can prove equation (3.9).
The next lemma will be used in the proof of Lemma 5.3 and Proposition 6.2.
Lemma 3.8. Let
![]() $ {\mathbf {s}}\in \Omega _{L}^{*}$
, and take two sequences
$ {\mathbf {s}}\in \Omega _{L}^{*}$
, and take two sequences
![]() $(c_{i}), (d_{i})\in \{0,1\}^{\mathbb {N}}$
.
$(c_{i}), (d_{i})\in \{0,1\}^{\mathbb {N}}$
.
-
(i) If
 $d_{1}=1$
, then
$d_{1}=1$
, then $$ \begin{align*} \sigma^{n}((c_{i}))\prec (d_{i}) \quad\text{for all } n\ge 0\quad\Longrightarrow\quad \sigma^{n}(\Phi_ {\mathbf{s}}((c_{i})))\prec \Phi_ {\mathbf{s}}((d_{i})) \quad\text{for all } n\ge 0. \end{align*} $$
$$ \begin{align*} \sigma^{n}((c_{i}))\prec (d_{i}) \quad\text{for all } n\ge 0\quad\Longrightarrow\quad \sigma^{n}(\Phi_ {\mathbf{s}}((c_{i})))\prec \Phi_ {\mathbf{s}}((d_{i})) \quad\text{for all } n\ge 0. \end{align*} $$
-
(ii) If
 $d_{1}=0$
, then
$d_{1}=0$
, then  $$ \begin{align*} \sigma^{n}((c_{i}))\succ (d_{i}) \quad\text{for all } n\ge 0\quad\Longrightarrow\quad \sigma^{n}(\Phi_ {\mathbf{s}}((c_{i})))\succ \Phi_ {\mathbf{s}}((d_{i})) \quad\text{for all } n\ge 0. \end{align*} $$
$$ \begin{align*} \sigma^{n}((c_{i}))\succ (d_{i}) \quad\text{for all } n\ge 0\quad\Longrightarrow\quad \sigma^{n}(\Phi_ {\mathbf{s}}((c_{i})))\succ \Phi_ {\mathbf{s}}((d_{i})) \quad\text{for all } n\ge 0. \end{align*} $$
Proof. (i) Suppose
![]() $d_{1}=1$
and
$d_{1}=1$
and
![]() $\sigma ^{n}((c_{i}))\prec (d_{i})$
for all
$\sigma ^{n}((c_{i}))\prec (d_{i})$
for all
![]() $n\ge 0$
. Then
$n\ge 0$
. Then
![]() $\Phi _{ {\mathbf {s}}}((d_{i}))$
begins with
$\Phi _{ {\mathbf {s}}}((d_{i}))$
begins with
![]() $\mathbb {L}( {\mathbf {s}})^{+}$
. If
$\mathbb {L}( {\mathbf {s}})^{+}$
. If
![]() $n\equiv 0\pmod {| {\mathbf {s}}|}$
, then by Lemma 3.3, it follows that
$n\equiv 0\pmod {| {\mathbf {s}}|}$
, then by Lemma 3.3, it follows that
![]() $\sigma ^{n}(\Phi _ {\mathbf {s}}((c_{i})))\prec \Phi _ {\mathbf {s}}((d_{i}))$
. If
$\sigma ^{n}(\Phi _ {\mathbf {s}}((c_{i})))\prec \Phi _ {\mathbf {s}}((d_{i}))$
. If
![]() $n\ne 0\pmod {| {\mathbf {s}}|}$
, then by using
$n\ne 0\pmod {| {\mathbf {s}}|}$
, then by using
![]() $\Phi _ {\mathbf {s}}(d_{1})=\mathbb {L}( {\mathbf {s}})^{+}$
and the same argument as in the proof of Lemma 3.7, one can verify that
$\Phi _ {\mathbf {s}}(d_{1})=\mathbb {L}( {\mathbf {s}})^{+}$
and the same argument as in the proof of Lemma 3.7, one can verify that
![]() $\sigma ^{n}(\Phi _ {\mathbf {s}}((c_{i})))\prec \Phi _ {\mathbf {s}}((d_{i}))$
. The proof of (ii) is similar.
$\sigma ^{n}(\Phi _ {\mathbf {s}}((c_{i})))\prec \Phi _ {\mathbf {s}}((d_{i}))$
. The proof of (ii) is similar.
Finally, we show that
![]() $\bullet $
is associative.
$\bullet $
is associative.
Lemma 3.9. For any three words
![]() $ {\mathbf {r}}, {\mathbf {s}}, {\mathbf {t}}\in \Omega _{L}^{*}$
, we have
$ {\mathbf {r}}, {\mathbf {s}}, {\mathbf {t}}\in \Omega _{L}^{*}$
, we have
![]() $( {\mathbf {r}}\bullet {\mathbf {s}})\bullet {\mathbf {t}}= {\mathbf {r}}\bullet ( {\mathbf {s}}\bullet {\mathbf {t}})$
.
$( {\mathbf {r}}\bullet {\mathbf {s}})\bullet {\mathbf {t}}= {\mathbf {r}}\bullet ( {\mathbf {s}}\bullet {\mathbf {t}})$
.
Proof. Let
![]() $ {\mathbf {r}}=r_{1}\ldots r_{m}, {\mathbf {s}}=s_{1}\ldots s_{n}$
, and
$ {\mathbf {r}}=r_{1}\ldots r_{m}, {\mathbf {s}}=s_{1}\ldots s_{n}$
, and
![]() $ {\mathbf {t}}=t_{1}\ldots t_{\ell }$
. Then we can write
$ {\mathbf {t}}=t_{1}\ldots t_{\ell }$
. Then we can write
![]() $( {\mathbf {r}}\bullet {\mathbf {s}})\bullet {\mathbf {t}}$
as
$( {\mathbf {r}}\bullet {\mathbf {s}})\bullet {\mathbf {t}}$
as
where each
![]() $\mathbf B_{i}\in \{( {\mathbf {r}}\bullet {\mathbf {s}})^{-}, {\mathbf {r}}\bullet {\mathbf {s}}, \mathbb {L}( {\mathbf {r}}\bullet {\mathbf {s}}), \mathbb {L}( {\mathbf {r}}\bullet {\mathbf {s}})^{+}\}$
. Since
$\mathbf B_{i}\in \{( {\mathbf {r}}\bullet {\mathbf {s}})^{-}, {\mathbf {r}}\bullet {\mathbf {s}}, \mathbb {L}( {\mathbf {r}}\bullet {\mathbf {s}}), \mathbb {L}( {\mathbf {r}}\bullet {\mathbf {s}})^{+}\}$
. Since
![]() $t_{1}=0$
, we have
$t_{1}=0$
, we have
![]() ${\mathbf B_{1}=( {\mathbf {r}}\bullet {\mathbf {s}})^{-}}$
. Furthermore, by the definition of
${\mathbf B_{1}=( {\mathbf {r}}\bullet {\mathbf {s}})^{-}}$
. Furthermore, by the definition of
![]() $\Phi _{ {\mathbf {r}}\bullet {\mathbf {s}}}$
it follows that for
$\Phi _{ {\mathbf {r}}\bullet {\mathbf {s}}}$
it follows that for
![]() $1<i\le \ell $
,
$1<i\le \ell $
,
 $$ \begin{align} \mathbf B_{i}=\left\{ \begin{array} {@{}ll} \mathbb{L}( {\mathbf{r}}\bullet {\mathbf{s}})&\textrm{if } t_{i-1}t_{i}=00,\\[3pt] \mathbb{L}( {\mathbf{r}}\bullet {\mathbf{s}})^{+}&\textrm{if } t_{i-1}t_{i}=01,\\[3pt] ( {\mathbf{r}}\bullet {\mathbf{s}})^{-}&\textrm{if } t_{i-1}t_{i}=10,\\[3pt] {\mathbf{r}}\bullet {\mathbf{s}}&\textrm{if } t_{i-1}t_{i}=11. \end{array} \right. \end{align} $$
$$ \begin{align} \mathbf B_{i}=\left\{ \begin{array} {@{}ll} \mathbb{L}( {\mathbf{r}}\bullet {\mathbf{s}})&\textrm{if } t_{i-1}t_{i}=00,\\[3pt] \mathbb{L}( {\mathbf{r}}\bullet {\mathbf{s}})^{+}&\textrm{if } t_{i-1}t_{i}=01,\\[3pt] ( {\mathbf{r}}\bullet {\mathbf{s}})^{-}&\textrm{if } t_{i-1}t_{i}=10,\\[3pt] {\mathbf{r}}\bullet {\mathbf{s}}&\textrm{if } t_{i-1}t_{i}=11. \end{array} \right. \end{align} $$
Similarly, we can write
where each
![]() $ {\mathbf {b}}_{i}\in \{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbb {L}( {\mathbf {s}}), \mathbb {L}( {\mathbf {s}})^{+}\}$
, and it follows from the definition of
$ {\mathbf {b}}_{i}\in \{{ {\mathbf {s}}^{-}}, {\mathbf {s}}, \mathbb {L}( {\mathbf {s}}), \mathbb {L}( {\mathbf {s}})^{+}\}$
, and it follows from the definition of
![]() $\Phi _ {\mathbf {s}}$
that
$\Phi _ {\mathbf {s}}$
that
 $$ \begin{align} {\mathbf{b}}_{i}=\left\{ \begin{array} {@{}ll} \mathbb{L}( {\mathbf{s}})&\textrm{if } t_{i-1}t_{i}=00,\\[3pt] \mathbb{L}( {\mathbf{s}})^{+}&\textrm{if } t_{i-1}t_{i}=01,\\[3pt] { {\mathbf{s}}^{-}}&\textrm{if } t_{i-1}t_{i}=10,\\[3pt] {\mathbf{s}}&\textrm{if } t_{i-1}t_{i}=11, \end{array} \right. \end{align} $$
$$ \begin{align} {\mathbf{b}}_{i}=\left\{ \begin{array} {@{}ll} \mathbb{L}( {\mathbf{s}})&\textrm{if } t_{i-1}t_{i}=00,\\[3pt] \mathbb{L}( {\mathbf{s}})^{+}&\textrm{if } t_{i-1}t_{i}=01,\\[3pt] { {\mathbf{s}}^{-}}&\textrm{if } t_{i-1}t_{i}=10,\\[3pt] {\mathbf{s}}&\textrm{if } t_{i-1}t_{i}=11, \end{array} \right. \end{align} $$
for
![]() $1<i\le \ell $
. Comparing equations (3.11) and (3.12) and using Lemmas 3.4 and 3.7, it follows that
$1<i\le \ell $
. Comparing equations (3.11) and (3.12) and using Lemmas 3.4 and 3.7, it follows that
Moreover, the sequence
![]() $ {\mathbf {b}}_{1}, {\mathbf {b}}_{2},\ldots , {\mathbf {b}}_{\ell }$
is connectible because
$ {\mathbf {b}}_{1}, {\mathbf {b}}_{2},\ldots , {\mathbf {b}}_{\ell }$
is connectible because
![]() $ {\mathbf {b}}_{1} {\mathbf {b}}_{2}\ldots {\mathbf {b}}_{\ell }=\Phi _ {\mathbf {s}}( {\mathbf {t}})$
arises from a walk along the directed graph in Figure 2. Hence, Lemma 3.6 and equation (3.10) yield
$ {\mathbf {b}}_{1} {\mathbf {b}}_{2}\ldots {\mathbf {b}}_{\ell }=\Phi _ {\mathbf {s}}( {\mathbf {t}})$
arises from a walk along the directed graph in Figure 2. Hence, Lemma 3.6 and equation (3.10) yield
as desired.
4 Critical values in a basic interval
In this section, we will prove Theorem 2. Recall from equation (1.4) that
![]() $\Lambda $
consists of all words
$\Lambda $
consists of all words
![]() $ {\mathbf {S}}$
of the form
$ {\mathbf {S}}$
of the form
where each
![]() $ {\mathbf {s}}_{i}\in \Omega _{F}^{*}$
. By Proposition 1.3, it follows that
$ {\mathbf {s}}_{i}\in \Omega _{F}^{*}$
. By Proposition 1.3, it follows that
![]() $\Lambda \subset \Omega _{L}^{*}$
, and each
$\Lambda \subset \Omega _{L}^{*}$
, and each
![]() $ {\mathbf {S}}\in \Lambda $
can be uniquely represented in the above form. Take
$ {\mathbf {S}}\in \Lambda $
can be uniquely represented in the above form. Take
![]() $ {\mathbf {S}}\in \Lambda $
. As in Definition 1.5, we let
$ {\mathbf {S}}\in \Lambda $
. As in Definition 1.5, we let
 $I^ {\mathbf {S}}:=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
be the basic interval generated by
$I^ {\mathbf {S}}:=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
be the basic interval generated by
![]() $ {\mathbf {S}}$
. Then by Lemmas 2.5 and 2.7, it follows that
$ {\mathbf {S}}$
. Then by Lemmas 2.5 and 2.7, it follows that
 $$ \begin{align} \delta(\beta_{\ell}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{\infty}\quad\textrm{and}\quad \delta(\beta_{*}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty}. \end{align} $$
$$ \begin{align} \delta(\beta_{\ell}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{\infty}\quad\textrm{and}\quad \delta(\beta_{*}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty}. \end{align} $$
To prove Theorem 2, we first prove the following proposition, which provides one of the key tools in this paper and will be used again in §6.
Proposition 4.1. For any
![]() $ {\mathbf {S}}\in \Lambda $
, the set
$ {\mathbf {S}}\in \Lambda $
, the set
is countable.
We point out that the specific form of
![]() $ {\mathbf {S}}$
is essential in this proposition: it is not enough to merely assume that
$ {\mathbf {S}}$
is essential in this proposition: it is not enough to merely assume that
![]() $ {\mathbf {S}}$
is a Lyndon word. For instance, take
$ {\mathbf {S}}$
is a Lyndon word. For instance, take
![]() $ {\mathbf {S}}=0010111\in \Omega _{L}^{*}$
. Then
$ {\mathbf {S}}=0010111\in \Omega _{L}^{*}$
. Then
![]() $\mathbb {L}( {\mathbf {S}})=1110010$
, and it is easy to see that
$\mathbb {L}( {\mathbf {S}})=1110010$
, and it is easy to see that
![]() $\Gamma ( {\mathbf {S}})\supset \{10,110\}^{\mathbb {N}}$
.
$\Gamma ( {\mathbf {S}})\supset \{10,110\}^{\mathbb {N}}$
.
For
![]() $ {\mathbf {S}}= {\mathbf {s}}\in \Omega _{F}^{*}$
, Proposition 4.1 follows from the following stronger result, proved in [Reference Kalle, Kong, Langeveld and Li20, Proposition 4.4].
$ {\mathbf {S}}= {\mathbf {s}}\in \Omega _{F}^{*}$
, Proposition 4.1 follows from the following stronger result, proved in [Reference Kalle, Kong, Langeveld and Li20, Proposition 4.4].
Lemma 4.2. For any
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{F}^{*}$
, the set
$ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{F}^{*}$
, the set
consists of exactly m different elements.
To reduce the technicalities in the proof of Proposition 4.1, we extend the definition from Lemma 2.3(iii) and define the conjugate of any word
![]() $ {\mathbf {S}}\in \Lambda $
by
$ {\mathbf {S}}\in \Lambda $
by
Lemma 4.3. The function
![]() $\varphi :\Lambda \to \{0,1\}^{*};\ {\mathbf {S}}\mapsto \varphi ( {\mathbf {S}})$
is a semigroup automorphism on
$\varphi :\Lambda \to \{0,1\}^{*};\ {\mathbf {S}}\mapsto \varphi ( {\mathbf {S}})$
is a semigroup automorphism on
![]() $(\Lambda ,\bullet )$
. That is,
$(\Lambda ,\bullet )$
. That is,
![]() $\varphi $
maps
$\varphi $
maps
![]() $\Lambda $
bijectively onto itself, and
$\Lambda $
bijectively onto itself, and
Furthermore,
![]() $\varphi $
is its own inverse:
$\varphi $
is its own inverse:
Proof. We prove equations (4.3) and (4.4) simultaneously by induction on the degree k of
![]() $ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}$
. For
$ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}$
. For
![]() $k=1$
, equation (4.3) is trivial and equation (4.4) follows from Lemma 2.3(iii). Now suppose equations (4.3) and (4.4) both hold for any word
$k=1$
, equation (4.3) is trivial and equation (4.4) follows from Lemma 2.3(iii). Now suppose equations (4.3) and (4.4) both hold for any word
![]() $ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}$
of degree k, and consider
$ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}$
of degree k, and consider
![]() $ {\mathbf {S}}\bullet {\mathbf {r}}$
with
$ {\mathbf {S}}\bullet {\mathbf {r}}$
with
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
. Set
$ {\mathbf {r}}\in \Omega _{F}^{*}$
. Set
 $\widetilde { {\mathbf {S}}}:=\varphi ( {\mathbf {S}})$
. We claim first that for any word
$\widetilde { {\mathbf {S}}}:=\varphi ( {\mathbf {S}})$
. We claim first that for any word
![]() $ {\mathbf {t}}\in \{0,1\}^{*}$
,
$ {\mathbf {t}}\in \{0,1\}^{*}$
,
 $$ \begin{align} \Phi_ {\mathbf{S}}(\overline{ {\mathbf{t}}})=\overline{\Phi_{\widetilde{ {\mathbf{S}}}}( {\mathbf{t}})}. \end{align} $$
$$ \begin{align} \Phi_ {\mathbf{S}}(\overline{ {\mathbf{t}}})=\overline{\Phi_{\widetilde{ {\mathbf{S}}}}( {\mathbf{t}})}. \end{align} $$
The expression on the right is well defined since, by equation (4.3),
 $\widetilde { {\mathbf {S}}}=\varphi ( {\mathbf {s}}_{1})\bullet \cdots \bullet \varphi ( {\mathbf {s}}_{k})\in \Omega _{L}^{*}$
.
$\widetilde { {\mathbf {S}}}=\varphi ( {\mathbf {s}}_{1})\bullet \cdots \bullet \varphi ( {\mathbf {s}}_{k})\in \Omega _{L}^{*}$
.
Write
![]() $ {\mathbf {A}}:=\mathbb {L}( {\mathbf {S}})$
and
$ {\mathbf {A}}:=\mathbb {L}( {\mathbf {S}})$
and
![]() $\widetilde { {\mathbf {A}}}:=\mathbb {L}(\widetilde { {\mathbf {S}}})$
. By equation (4.4),
$\widetilde { {\mathbf {A}}}:=\mathbb {L}(\widetilde { {\mathbf {S}}})$
. By equation (4.4),
 $\varphi (\widetilde { {\mathbf {S}}})= {\mathbf {S}}$
, so we have
$\varphi (\widetilde { {\mathbf {S}}})= {\mathbf {S}}$
, so we have
Now note the rotational skew-symmetry in the edge labels of the directed graph in Figure 2. The edge path corresponding to the word
![]() $\overline { {\mathbf {t}}}$
is just the
$\overline { {\mathbf {t}}}$
is just the
![]() $180^{\circ }$
rotation about the center of the figure of the edge path corresponding to
$180^{\circ }$
rotation about the center of the figure of the edge path corresponding to
![]() $ {\mathbf {t}}$
. However, replacing the vertex labels
$ {\mathbf {t}}$
. However, replacing the vertex labels
![]() $ {\mathbf {S}}, {\mathbf {S}}^{-}, {\mathbf {A}}$
, and
$ {\mathbf {S}}, {\mathbf {S}}^{-}, {\mathbf {A}}$
, and
![]() $ {\mathbf {A}}^{+}$
by
$ {\mathbf {A}}^{+}$
by
![]() $\widetilde { {\mathbf {S}}}=\overline { {\mathbf {A}}}$
,
$\widetilde { {\mathbf {S}}}=\overline { {\mathbf {A}}}$
,
![]() $\widetilde { {\mathbf {S}}}^{-}=\overline { {\mathbf {A}}^{+}}$
,
$\widetilde { {\mathbf {S}}}^{-}=\overline { {\mathbf {A}}^{+}}$
,
![]() $\widetilde { {\mathbf {A}}}=\overline { {\mathbf {S}}}$
, and
$\widetilde { {\mathbf {A}}}=\overline { {\mathbf {S}}}$
, and
![]() $\widetilde { {\mathbf {A}}}^{+}=\overline { {\mathbf {S}}^{-}}$
, respectively, and rotating the whole graph by
$\widetilde { {\mathbf {A}}}^{+}=\overline { {\mathbf {S}}^{-}}$
, respectively, and rotating the whole graph by
![]() $180^{\circ }$
, we get the original graph back except that all the vertex labels and edge labels are reflected. This implies equation (4.5).
$180^{\circ }$
, we get the original graph back except that all the vertex labels and edge labels are reflected. This implies equation (4.5).
Now we can apply equation (4.5) to
![]() $ {\mathbf {t}}=\overline {\mathbb {L}( {\mathbf {r}})}$
and obtain:
$ {\mathbf {t}}=\overline {\mathbb {L}( {\mathbf {r}})}$
and obtain:
 $$ \begin{align} \varphi( {\mathbf{S}})\bullet \varphi( {\mathbf{r}})=\widetilde{ {\mathbf{S}}}\bullet\varphi( {\mathbf{r}})=\Phi_{\widetilde{ {\mathbf{S}}}}(\overline{\mathbb{L}( {\mathbf{r}})})=\overline{\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}}))} =\overline{ {\mathbf{S}}\bullet\mathbb{L}( {\mathbf{r}})}=\overline{\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})}=\varphi( {\mathbf{S}}\bullet {\mathbf{r}}). \end{align} $$
$$ \begin{align} \varphi( {\mathbf{S}})\bullet \varphi( {\mathbf{r}})=\widetilde{ {\mathbf{S}}}\bullet\varphi( {\mathbf{r}})=\Phi_{\widetilde{ {\mathbf{S}}}}(\overline{\mathbb{L}( {\mathbf{r}})})=\overline{\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}}))} =\overline{ {\mathbf{S}}\bullet\mathbb{L}( {\mathbf{r}})}=\overline{\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})}=\varphi( {\mathbf{S}}\bullet {\mathbf{r}}). \end{align} $$
Since
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
was arbitrary, the induction hypothesis of equations (4.3) and (4.7) give
$ {\mathbf {r}}\in \Omega _{F}^{*}$
was arbitrary, the induction hypothesis of equations (4.3) and (4.7) give
Thus, equation (4.3) holds for
![]() $k+1$
in place of k. Next, by Lemma 2.3(iii),
$k+1$
in place of k. Next, by Lemma 2.3(iii),
![]() $\varphi ( {\mathbf {s}}_{i})\in \Omega _{F}^{*}$
and
$\varphi ( {\mathbf {s}}_{i})\in \Omega _{F}^{*}$
and
![]() $\varphi (\varphi ( {\mathbf {s}}_{i}))= {\mathbf {s}}_{i}$
for each i, so applying equation (4.8) with
$\varphi (\varphi ( {\mathbf {s}}_{i}))= {\mathbf {s}}_{i}$
for each i, so applying equation (4.8) with
![]() $\varphi ( {\mathbf {s}}_{i})$
in place of
$\varphi ( {\mathbf {s}}_{i})$
in place of
![]() $ {\mathbf {s}}_{i}$
for each i, we conclude that
$ {\mathbf {s}}_{i}$
for each i, we conclude that
![]() $\varphi (\varphi ( {\mathbf {S}}^{\prime }))= {\mathbf {S}}^{\prime }$
for every
$\varphi (\varphi ( {\mathbf {S}}^{\prime }))= {\mathbf {S}}^{\prime }$
for every
![]() $ {\mathbf {S}}^{\prime }\in \Lambda $
of degree
$ {\mathbf {S}}^{\prime }\in \Lambda $
of degree
![]() $k+1$
also.
$k+1$
also.
Thus, we have proved equations (4.3) and (4.4) by induction. Now the remaining statements of the lemma follow immediately: by equation (4.3), Lemma 2.3(iii), and Proposition 1.3, it follows that
![]() $\varphi ( {\mathbf {S}})\in \Lambda $
for every
$\varphi ( {\mathbf {S}})\in \Lambda $
for every
![]() $ {\mathbf {S}}\in \Lambda $
, whereas equation (4.4) implies that
$ {\mathbf {S}}\in \Lambda $
, whereas equation (4.4) implies that
![]() $\varphi : \Lambda \to \Lambda $
is bijective. Therefore,
$\varphi : \Lambda \to \Lambda $
is bijective. Therefore,
![]() $\varphi $
is an automorphism of
$\varphi $
is an automorphism of
![]() $(\Lambda ,\bullet )$
.
$(\Lambda ,\bullet )$
.
Define
It is clear that
![]() $\overline {\Gamma ( {\mathbf {S}})}$
has the same cardinality as
$\overline {\Gamma ( {\mathbf {S}})}$
has the same cardinality as
![]() $\Gamma ( {\mathbf {S}})$
. Observe also by equation (4.6) that
$\Gamma ( {\mathbf {S}})$
. Observe also by equation (4.6) that
 $$ \begin{align} \overline{\Gamma( {\mathbf{S}})}&=\{(y_{i}): {\mathbf{S}}^{\infty}\preccurlyeq \sigma^{n}(\overline{(y_{i})})\preccurlyeq \mathbb{L}( {\mathbf{S}})^{\infty}\ \text{ for all } n\geq 0\}\nonumber\\[3pt] &=\{(y_{i}): \overline{ {\mathbf{S}}}^{\infty}\succcurlyeq \sigma^{n}((y_{i}))\succcurlyeq \overline{\mathbb{L}( {\mathbf{S}})}^{\infty}\ \text{ for all } n\geq 0\}\nonumber\\[3pt] &=\{(y_{i}): \mathbb{L}(\varphi( {\mathbf{S}}))^{\infty} \succcurlyeq \sigma^{n}((y_{i}))\succcurlyeq \varphi( {\mathbf{S}})^{\infty}\ \text{ for all } n\geq 0\}\nonumber\\[3pt] &=\Gamma(\varphi( {\mathbf{S}})). \end{align} $$
$$ \begin{align} \overline{\Gamma( {\mathbf{S}})}&=\{(y_{i}): {\mathbf{S}}^{\infty}\preccurlyeq \sigma^{n}(\overline{(y_{i})})\preccurlyeq \mathbb{L}( {\mathbf{S}})^{\infty}\ \text{ for all } n\geq 0\}\nonumber\\[3pt] &=\{(y_{i}): \overline{ {\mathbf{S}}}^{\infty}\succcurlyeq \sigma^{n}((y_{i}))\succcurlyeq \overline{\mathbb{L}( {\mathbf{S}})}^{\infty}\ \text{ for all } n\geq 0\}\nonumber\\[3pt] &=\{(y_{i}): \mathbb{L}(\varphi( {\mathbf{S}}))^{\infty} \succcurlyeq \sigma^{n}((y_{i}))\succcurlyeq \varphi( {\mathbf{S}})^{\infty}\ \text{ for all } n\geq 0\}\nonumber\\[3pt] &=\Gamma(\varphi( {\mathbf{S}})). \end{align} $$
Proof of Proposition 4.1
For
![]() $ {\mathbf {S}}= {\mathbf {s}}\in \Omega _{F}^{*}$
, the proposition follows from Lemma 4.2. So it suffices to prove that if
$ {\mathbf {S}}= {\mathbf {s}}\in \Omega _{F}^{*}$
, the proposition follows from Lemma 4.2. So it suffices to prove that if
![]() $\Gamma ( {\mathbf {S}})$
is countable for an
$\Gamma ( {\mathbf {S}})$
is countable for an
![]() $ {\mathbf {S}}\in \Lambda $
, then
$ {\mathbf {S}}\in \Lambda $
, then
![]() $\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
is also countable for any
$\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
is also countable for any
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
.
$ {\mathbf {r}}\in \Omega _{F}^{*}$
.
Fix
![]() $ {\mathbf {S}}\in \Lambda $
with
$ {\mathbf {S}}\in \Lambda $
with
![]() $\Gamma ( {\mathbf {S}})$
countable; fix
$\Gamma ( {\mathbf {S}})$
countable; fix
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
, and note that
$ {\mathbf {r}}\in \Omega _{F}^{*}$
, and note that
![]() $ {\mathbf {r}}$
begins with
$ {\mathbf {r}}$
begins with
![]() $0$
and
$0$
and
![]() $\mathbb {L}( {\mathbf {r}})$
begins with
$\mathbb {L}( {\mathbf {r}})$
begins with
![]() $1$
. Therefore,
$1$
. Therefore,
![]() $ {\mathbf {S}}\bullet {\mathbf {r}}$
begins with
$ {\mathbf {S}}\bullet {\mathbf {r}}$
begins with
![]() $ {\mathbf {S}}^{-}$
and
$ {\mathbf {S}}^{-}$
and
![]() $\mathbb {L}( {\mathbf {S}}\bullet {\mathbf {r}})= {\mathbf {S}}\bullet \mathbb {L}( {\mathbf {r}})$
begins with
$\mathbb {L}( {\mathbf {S}}\bullet {\mathbf {r}})= {\mathbf {S}}\bullet \mathbb {L}( {\mathbf {r}})$
begins with
![]() $\mathbb {L}( {\mathbf {S}})^{+}$
. So
$\mathbb {L}( {\mathbf {S}})^{+}$
. So
By equations (4.2) and (4.10), it follows that
Since
![]() $\Gamma ( {\mathbf {S}})$
is countable, it suffices to prove that the difference set
$\Gamma ( {\mathbf {S}})$
is countable, it suffices to prove that the difference set
![]() $\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})\setminus \Gamma ( {\mathbf {S}})$
is countable. By Proposition 2.4, the word
$\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})\setminus \Gamma ( {\mathbf {S}})$
is countable. By Proposition 2.4, the word
![]() $ {\mathbf {r}}$
must be of one of the following four types:
$ {\mathbf {r}}$
must be of one of the following four types:
-
(I)
 $ {\mathbf {r}}=01^{p}$
for some
$ {\mathbf {r}}=01^{p}$
for some
 $p\in \mathbb {N}$
;
$p\in \mathbb {N}$
; -
(II)
 $ {\mathbf {r}}=0^{p} 1$
for some
$ {\mathbf {r}}=0^{p} 1$
for some
 $p\in \mathbb {N}$
;
$p\in \mathbb {N}$
; -
(III)
 $ {\mathbf {r}}=01^{p}01^{p+t_{1}}\ldots 01^{p+t_{N}}01^{p+1}$
for some
$ {\mathbf {r}}=01^{p}01^{p+t_{1}}\ldots 01^{p+t_{N}}01^{p+1}$
for some
 $p\in \mathbb {N}$
and
$p\in \mathbb {N}$
and
 $0t_{1}\ldots t_{N} 1\in \Omega _{F}^{*}$
;
$0t_{1}\ldots t_{N} 1\in \Omega _{F}^{*}$
; -
(IV)
 $ {\mathbf {r}}=0^{p+1}10^{p+t_{1}}1\ldots 0^{p+t_{N}}10^{p}1$
for some
$ {\mathbf {r}}=0^{p+1}10^{p+t_{1}}1\ldots 0^{p+t_{N}}10^{p}1$
for some
 $p\in \mathbb {N}$
and
$p\in \mathbb {N}$
and
 $0t_{1}\ldots t_{N} 1\in \Omega _{F}^{*}$
;
$0t_{1}\ldots t_{N} 1\in \Omega _{F}^{*}$
;
Since the words in (II) and (IV) are the conjugates of the words in (I) and (III), respectively, it suffices by Lemma 4.3 and the relationship of equation (4.9) to consider cases (I) and (III). Let
![]() $ {\mathbf {A}}:=\mathbb {L}( {\mathbf {S}})$
.
$ {\mathbf {A}}:=\mathbb {L}( {\mathbf {S}})$
.
Case I.
![]() $ {\mathbf {r}}=01^{p}$
for some
$ {\mathbf {r}}=01^{p}$
for some
![]() $p\in \mathbb {N}$
. Note that
$p\in \mathbb {N}$
. Note that
![]() $ {\mathbf {S}}\bullet {\mathbf {r}}=\Phi _ {\mathbf {S}}(01^{p})= {\mathbf {S}}^{-} {\mathbf {A}}^{+} {\mathbf {S}}^{p-1}$
and
$ {\mathbf {S}}\bullet {\mathbf {r}}=\Phi _ {\mathbf {S}}(01^{p})= {\mathbf {S}}^{-} {\mathbf {A}}^{+} {\mathbf {S}}^{p-1}$
and
![]() $\mathbb {L}( {\mathbf {S}}\bullet {\mathbf {r}})= {\mathbf {S}}\bullet \mathbb {L}( {\mathbf {r}})=\Phi _ {\mathbf {S}}(1^{p} 0)= {\mathbf {A}}^{+} {\mathbf {S}}^{p-1} {\mathbf {S}}^{-}$
. Then
$\mathbb {L}( {\mathbf {S}}\bullet {\mathbf {r}})= {\mathbf {S}}\bullet \mathbb {L}( {\mathbf {r}})=\Phi _ {\mathbf {S}}(1^{p} 0)= {\mathbf {A}}^{+} {\mathbf {S}}^{p-1} {\mathbf {S}}^{-}$
. Then
![]() $\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
consists of all sequences
$\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
consists of all sequences
![]() $(x_{i})\in \{0,1\}^{\mathbb {N}}$
satisfying
$(x_{i})\in \{0,1\}^{\mathbb {N}}$
satisfying
Take a sequence
![]() $(x_{i})\in \Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})\setminus \Gamma ( {\mathbf {S}})$
. Then by equations (4.2) and (4.11), it follows that
$(x_{i})\in \Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})\setminus \Gamma ( {\mathbf {S}})$
. Then by equations (4.2) and (4.11), it follows that
![]() $x_{k+1}\ldots x_{k+m}= {\mathbf {S}}^{-}$
or
$x_{k+1}\ldots x_{k+m}= {\mathbf {S}}^{-}$
or
![]() $ {\mathbf {A}}^{+}$
for some
$ {\mathbf {A}}^{+}$
for some
![]() $k\ge 0$
. If
$k\ge 0$
. If
![]() $x_{k+1}\ldots x_{k+m}= {\mathbf {S}}^{-}$
, then by taking
$x_{k+1}\ldots x_{k+m}= {\mathbf {S}}^{-}$
, then by taking
![]() $n=k$
in equation (4.11), we obtain
$n=k$
in equation (4.11), we obtain
However, by taking
![]() $n=k+m$
in equation (4.11), we see that the above inequality is indeed an equality. So,
$n=k+m$
in equation (4.11), we see that the above inequality is indeed an equality. So,
![]() $x_{k+1}x_{k+2}\ldots =( {\mathbf {S}}^{-} {\mathbf {A}}^{+} {\mathbf {S}}^{p-1})^{\infty }$
.
$x_{k+1}x_{k+2}\ldots =( {\mathbf {S}}^{-} {\mathbf {A}}^{+} {\mathbf {S}}^{p-1})^{\infty }$
.
If
![]() $x_{k+1}\ldots x_{k+m}= {\mathbf {A}}^{+}$
, then by taking
$x_{k+1}\ldots x_{k+m}= {\mathbf {A}}^{+}$
, then by taking
![]() $n=k$
in equation (4.11), we have
$n=k$
in equation (4.11), we have
Note by equation (4.11) that
![]() $x_{i+1}\ldots x_{i+m}\succcurlyeq {\mathbf {S}}^{-}$
for all
$x_{i+1}\ldots x_{i+m}\succcurlyeq {\mathbf {S}}^{-}$
for all
![]() $i\ge 0$
. So by equation (4.12), there must exist a
$i\ge 0$
. So by equation (4.12), there must exist a
![]() $j\in \{k+m, k+2m, \ldots , k+pm\}$
such that
$j\in \{k+m, k+2m, \ldots , k+pm\}$
such that
![]() $x_{j+1}\ldots x_{j+m}= {\mathbf {S}}^{-}$
. Then by the same argument as above, we conclude that
$x_{j+1}\ldots x_{j+m}= {\mathbf {S}}^{-}$
. Then by the same argument as above, we conclude that
 $x_{j+1}x_{j+2}\ldots =( {\mathbf {S}}^{-} {\mathbf {A}}^{+} {\mathbf {S}}^{p-1})^{\infty }$
. So,
$x_{j+1}x_{j+2}\ldots =( {\mathbf {S}}^{-} {\mathbf {A}}^{+} {\mathbf {S}}^{p-1})^{\infty }$
. So,
![]() $\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})\setminus \Gamma ( {\mathbf {S}})$
is at most countable.
$\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})\setminus \Gamma ( {\mathbf {S}})$
is at most countable.
Case III.
![]() $ {\mathbf {r}}=01^{p}01^{p+t_{1}}\ldots 01^{p+t_{N}}01^{p+1}$
, where
$ {\mathbf {r}}=01^{p}01^{p+t_{1}}\ldots 01^{p+t_{N}}01^{p+1}$
, where
![]() $p\in \mathbb {N}$
and
$p\in \mathbb {N}$
and
![]() $\hat {\mathbf {r}}:=0 t_{1}\ldots t_{N} 1\in \Omega _{F}^{*}$
. Consider the substitution
$\hat {\mathbf {r}}:=0 t_{1}\ldots t_{N} 1\in \Omega _{F}^{*}$
. Consider the substitution
 $$ \begin{align*} \eta_{p}:=U_{1}^{p}\circ U_{0}: 0\mapsto 01^{p};\quad 1\mapsto 01^{p+1}. \end{align*} $$
$$ \begin{align*} \eta_{p}:=U_{1}^{p}\circ U_{0}: 0\mapsto 01^{p};\quad 1\mapsto 01^{p+1}. \end{align*} $$
Then
![]() $ {\mathbf {r}}=\eta _{p}(\hat {\mathbf {r}})$
, as shown in the proof of Proposition 2.4. Note by Lemma 2.3 that
$ {\mathbf {r}}=\eta _{p}(\hat {\mathbf {r}})$
, as shown in the proof of Proposition 2.4. Note by Lemma 2.3 that
![]() $ \mathbb {L}( {\mathbf {r}})=1^{p+1}01^{p+t_{1}}01^{p+t_{2}}\ldots 01^{p+t_{N}}01^{p}0$
and
$ \mathbb {L}( {\mathbf {r}})=1^{p+1}01^{p+t_{1}}01^{p+t_{2}}\ldots 01^{p+t_{N}}01^{p}0$
and
![]() $\mathbb {L}(\hat {\mathbf {r}})=1 t_{1}\ldots t_{N} 0$
. Then
$\mathbb {L}(\hat {\mathbf {r}})=1 t_{1}\ldots t_{N} 0$
. Then
 $$ \begin{align} \mathbb{L}( {\mathbf{r}})^{\infty}&=\sigma((01^{p+1}01^{p+t_{1}}{{\kern-1.5pt}\ldots{\kern-1.5pt}} 01^{p+t_{N}}01^{p})^{\infty}) =\sigma(\eta_{p}((1t_{1} {{\kern-1.5pt}\ldots{\kern-1.5pt}} t_{N} 0)^{\infty}))=\sigma(\eta_{p}(\mathbb{L}(\hat {\mathbf{r}})^{\infty})). \end{align} $$
$$ \begin{align} \mathbb{L}( {\mathbf{r}})^{\infty}&=\sigma((01^{p+1}01^{p+t_{1}}{{\kern-1.5pt}\ldots{\kern-1.5pt}} 01^{p+t_{N}}01^{p})^{\infty}) =\sigma(\eta_{p}((1t_{1} {{\kern-1.5pt}\ldots{\kern-1.5pt}} t_{N} 0)^{\infty}))=\sigma(\eta_{p}(\mathbb{L}(\hat {\mathbf{r}})^{\infty})). \end{align} $$
Claim. If
![]() $(x_{i})\in \Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
begins with
$(x_{i})\in \Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
begins with
![]() $x_{1}\ldots x_{m}= {\mathbf {S}}^{-}$
, then there exists a unique sequence
$x_{1}\ldots x_{m}= {\mathbf {S}}^{-}$
, then there exists a unique sequence
![]() $(z_{i})\in \{0,1\}^{\mathbb {N}}$
such that
$(z_{i})\in \{0,1\}^{\mathbb {N}}$
such that
![]() $(x_{i})=\Phi _ {\mathbf {S}}(\eta _{p}(z_{1}z_{2}\ldots ))$
.
$(x_{i})=\Phi _ {\mathbf {S}}(\eta _{p}(z_{1}z_{2}\ldots ))$
.
Note that
![]() $ {\mathbf {r}}$
begins with
$ {\mathbf {r}}$
begins with
![]() $01^{p}0$
and
$01^{p}0$
and
![]() $\mathbb {L}( {\mathbf {r}})$
begins with
$\mathbb {L}( {\mathbf {r}})$
begins with
![]() $1^{p+1}0$
. Then
$1^{p+1}0$
. Then
![]() $ {\mathbf {S}}\bullet {\mathbf {r}}$
begins with
$ {\mathbf {S}}\bullet {\mathbf {r}}$
begins with
![]() $\Phi _ {\mathbf {S}}(01^{p}0)= {\mathbf {S}}^{-} {\mathbf {A}}^{+} {\mathbf {S}}^{p-1} {\mathbf {S}}^{-}$
and
$\Phi _ {\mathbf {S}}(01^{p}0)= {\mathbf {S}}^{-} {\mathbf {A}}^{+} {\mathbf {S}}^{p-1} {\mathbf {S}}^{-}$
and
![]() $\mathbb {L}( {\mathbf {S}}\bullet {\mathbf {r}})= {\mathbf {S}}\bullet \mathbb {L}( {\mathbf {r}})$
begins with
$\mathbb {L}( {\mathbf {S}}\bullet {\mathbf {r}})= {\mathbf {S}}\bullet \mathbb {L}( {\mathbf {r}})$
begins with
![]() $\Phi _ {\mathbf {S}}(1^{p+1}0)= {\mathbf {A}}^{+} {\mathbf {S}}^{p} {\mathbf {S}}^{-}$
. Let
$\Phi _ {\mathbf {S}}(1^{p+1}0)= {\mathbf {A}}^{+} {\mathbf {S}}^{p} {\mathbf {S}}^{-}$
. Let
![]() $(x_{i})\in \Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
with
$(x_{i})\in \Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
with
![]() $x_{1}\ldots x_{m}= {\mathbf {S}}^{-}$
. Then
$x_{1}\ldots x_{m}= {\mathbf {S}}^{-}$
. Then
 $$ \begin{align} {\mathbf{S}}^{-} {\mathbf{A}}^{+} {\mathbf{S}}^{p-1} {\mathbf{S}}^{-}\preccurlyeq x_{n+1}\ldots x_{n+m(p+2)}\preccurlyeq {\mathbf{A}}^{+} {\mathbf{S}}^{p} {\mathbf{S}}^{-}\quad\text{for all } n\ge 0. \end{align} $$
$$ \begin{align} {\mathbf{S}}^{-} {\mathbf{A}}^{+} {\mathbf{S}}^{p-1} {\mathbf{S}}^{-}\preccurlyeq x_{n+1}\ldots x_{n+m(p+2)}\preccurlyeq {\mathbf{A}}^{+} {\mathbf{S}}^{p} {\mathbf{S}}^{-}\quad\text{for all } n\ge 0. \end{align} $$
By taking
![]() $n=0$
in equation (4.14), it follows that
$n=0$
in equation (4.14), it follows that
 $$ \begin{align} x_{m+1}\ldots x_{m(p+2)}\succcurlyeq {\mathbf{A}}^{+} {\mathbf{S}}^{p-1} {\mathbf{S}}^{-}. \end{align} $$
$$ \begin{align} x_{m+1}\ldots x_{m(p+2)}\succcurlyeq {\mathbf{A}}^{+} {\mathbf{S}}^{p-1} {\mathbf{S}}^{-}. \end{align} $$
However, by taking
![]() $n=m$
in equation (4.14), we have
$n=m$
in equation (4.14), we have
 $$ \begin{align} x_{m+1}\ldots x_{m(p+3)}\preccurlyeq {\mathbf{A}}^{+} {\mathbf{S}}^{p} {\mathbf{S}}^{-}. \end{align} $$
$$ \begin{align} x_{m+1}\ldots x_{m(p+3)}\preccurlyeq {\mathbf{A}}^{+} {\mathbf{S}}^{p} {\mathbf{S}}^{-}. \end{align} $$
By equations (4.14)–(4.16), it follows that
 $$ \begin{align*} \textrm{either}\quad x_{m+1}\ldots x_{m(p+2)}= {\mathbf{A}}^{+} {\mathbf{S}}^{p-1} {\mathbf{S}}^{-}\quad\textrm{or}\quad x_{m+1}\ldots x_{m(p+3)}= {\mathbf{A}}^{+} {\mathbf{S}}^{p} {\mathbf{S}}^{-}. \end{align*} $$
$$ \begin{align*} \textrm{either}\quad x_{m+1}\ldots x_{m(p+2)}= {\mathbf{A}}^{+} {\mathbf{S}}^{p-1} {\mathbf{S}}^{-}\quad\textrm{or}\quad x_{m+1}\ldots x_{m(p+3)}= {\mathbf{A}}^{+} {\mathbf{S}}^{p} {\mathbf{S}}^{-}. \end{align*} $$
Observe that in both cases, we obtain a block ending with
![]() $ {\mathbf {S}}^{-}$
. Then we can repeat the above argument indefinitely, and conclude that
$ {\mathbf {S}}^{-}$
. Then we can repeat the above argument indefinitely, and conclude that
 $$ \begin{align} (x_{i})\in\{ {\mathbf{S}}^{-} {\mathbf{A}}^{+} {\mathbf{S}}^{p-1}, {\mathbf{S}}^{-} {\mathbf{A}}^{+} {\mathbf{S}}^{p}\}^{\mathbb{N}}=\{\Phi_ {\mathbf{S}}(\eta_{p}(0)), \Phi_ {\mathbf{S}}(\eta_{p}(1))\}^{\mathbb{N}}. \end{align} $$
$$ \begin{align} (x_{i})\in\{ {\mathbf{S}}^{-} {\mathbf{A}}^{+} {\mathbf{S}}^{p-1}, {\mathbf{S}}^{-} {\mathbf{A}}^{+} {\mathbf{S}}^{p}\}^{\mathbb{N}}=\{\Phi_ {\mathbf{S}}(\eta_{p}(0)), \Phi_ {\mathbf{S}}(\eta_{p}(1))\}^{\mathbb{N}}. \end{align} $$
Since
![]() $\eta _{p}(0)=01^{p}$
and
$\eta _{p}(0)=01^{p}$
and
 $\eta _{p}(1)=01^{p+1}$
, it follows from equation (4.17) and Lemma 3.6 that
$\eta _{p}(1)=01^{p+1}$
, it follows from equation (4.17) and Lemma 3.6 that
for some sequence
![]() $(z_{i})\in \{0,1\}^{\mathbb {N}}$
. The uniqueness of
$(z_{i})\in \{0,1\}^{\mathbb {N}}$
. The uniqueness of
![]() $(z_{i})$
follows by the definition of the substitutions
$(z_{i})$
follows by the definition of the substitutions
![]() $\eta _{p}$
and
$\eta _{p}$
and
![]() $\Phi _ {\mathbf {S}}$
. This proves the claim.
$\Phi _ {\mathbf {S}}$
. This proves the claim.
Now take a sequence
![]() $(x_{i})\in \Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})\setminus \Gamma ( {\mathbf {S}})$
. Then by equations (4.2) and (4.14), we can find an
$(x_{i})\in \Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})\setminus \Gamma ( {\mathbf {S}})$
. Then by equations (4.2) and (4.14), we can find an
![]() $n_{0}\ge 0$
such that
$n_{0}\ge 0$
such that
![]() $x_{n_{0}+1}\ldots x_{n_{0}+m}= {\mathbf {S}}^{-}$
or
$x_{n_{0}+1}\ldots x_{n_{0}+m}= {\mathbf {S}}^{-}$
or
![]() $ {\mathbf {A}}^{+}$
. If
$ {\mathbf {A}}^{+}$
. If
![]() $x_{n_{0}+1}\ldots x_{n_{0}+m}= {\mathbf {A}}^{+}$
, then by equation (4.14), there must exist
$x_{n_{0}+1}\ldots x_{n_{0}+m}= {\mathbf {A}}^{+}$
, then by equation (4.14), there must exist
![]() $n_{1}>n_{0}$
such that
$n_{1}>n_{0}$
such that
![]() $x_{n_{1}+1}\ldots x_{n_{1}+m}= {\mathbf {S}}^{-}$
. So, without loss of generality, we may assume
$x_{n_{1}+1}\ldots x_{n_{1}+m}= {\mathbf {S}}^{-}$
. So, without loss of generality, we may assume
![]() $x_{n_{0}+1}\ldots x_{n_{0}+m}= {\mathbf {S}}^{-}$
. Then by the claim there is a unique sequence
$x_{n_{0}+1}\ldots x_{n_{0}+m}= {\mathbf {S}}^{-}$
. Then by the claim there is a unique sequence
![]() $(z_{i})\in \{0,1\}^{\mathbb {N}}$
that
$(z_{i})\in \{0,1\}^{\mathbb {N}}$
that
![]() $x_{n_{0}+1}x_{n_{0}+2}\ldots =\Phi _ {\mathbf {S}}(\eta _{p}(z_{1}z_{2}\ldots ))\in \Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
. By the definition of
$x_{n_{0}+1}x_{n_{0}+2}\ldots =\Phi _ {\mathbf {S}}(\eta _{p}(z_{1}z_{2}\ldots ))\in \Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
. By the definition of
![]() $\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
, it follows that
$\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})$
, it follows that
Note by
![]() $ {\mathbf {r}}=\eta _{p}(\hat { {\mathbf {r}}})$
and Lemma 3.6(ii) that
$ {\mathbf {r}}=\eta _{p}(\hat { {\mathbf {r}}})$
and Lemma 3.6(ii) that
![]() $( {\mathbf {S}}\bullet {\mathbf {r}})^{\infty }=\Phi _ {\mathbf {S}}( {\mathbf {r}}^{\infty })=\Phi _ {\mathbf {S}}(\eta _{p}(\hat {\mathbf {r}}^{\infty }))$
. Similarly, by Lemmas 3.6(ii), 3.7, and equation (4.13), it follows that
$( {\mathbf {S}}\bullet {\mathbf {r}})^{\infty }=\Phi _ {\mathbf {S}}( {\mathbf {r}}^{\infty })=\Phi _ {\mathbf {S}}(\eta _{p}(\hat {\mathbf {r}}^{\infty }))$
. Similarly, by Lemmas 3.6(ii), 3.7, and equation (4.13), it follows that
![]() $\mathbb {L}( {\mathbf {S}}\bullet {\mathbf {r}})^{\infty }=\Phi _ {\mathbf {S}}(\mathbb {L}( {\mathbf {r}})^{\infty })=\Phi _ {\mathbf {S}}(\sigma (\eta _{p}(\mathbb {L}(\hat {\mathbf {r}})^{\infty })))$
. Thus, equation (4.19) can be rewritten as
$\mathbb {L}( {\mathbf {S}}\bullet {\mathbf {r}})^{\infty }=\Phi _ {\mathbf {S}}(\mathbb {L}( {\mathbf {r}})^{\infty })=\Phi _ {\mathbf {S}}(\sigma (\eta _{p}(\mathbb {L}(\hat {\mathbf {r}})^{\infty })))$
. Thus, equation (4.19) can be rewritten as
By Lemma 3.3, this implies that
 $$ \begin{align} \eta_{p}(\hat {\mathbf{r}}^{\infty})\preccurlyeq \sigma^{n}(\eta_{p}(z_{1}z_{2}\ldots))\preccurlyeq \sigma(\eta_{p}(\mathbb{L}(\hat {\mathbf{r}})^{\infty})\big)\quad\text{for all } n\ge 0. \end{align} $$
$$ \begin{align} \eta_{p}(\hat {\mathbf{r}}^{\infty})\preccurlyeq \sigma^{n}(\eta_{p}(z_{1}z_{2}\ldots))\preccurlyeq \sigma(\eta_{p}(\mathbb{L}(\hat {\mathbf{r}})^{\infty})\big)\quad\text{for all } n\ge 0. \end{align} $$
Note
![]() $(c_{i})\prec (d_{i})$
is equivalent to
$(c_{i})\prec (d_{i})$
is equivalent to
![]() $\eta _{p}((c_{i}))\prec \eta _{p}((d_{i}))$
. So, by equation (4.20) and the definition of
$\eta _{p}((c_{i}))\prec \eta _{p}((d_{i}))$
. So, by equation (4.20) and the definition of
![]() $\eta _{p}$
, it follows that
$\eta _{p}$
, it follows that
and hence
![]() $(z_{i})\in \Gamma (\hat {\mathbf {r}})$
. Since
$(z_{i})\in \Gamma (\hat {\mathbf {r}})$
. Since
![]() $\hat {\mathbf {r}}\in \Omega _{F}^{*}$
, we know that
$\hat {\mathbf {r}}\in \Omega _{F}^{*}$
, we know that
![]() $\Gamma (\hat {\mathbf {r}})$
is finite by Lemma 4.2. Hence there are only countably many choices for the sequence
$\Gamma (\hat {\mathbf {r}})$
is finite by Lemma 4.2. Hence there are only countably many choices for the sequence
![]() $(z_{i})$
, and thus by the claim, there are only countably many choices for the tail sequence of
$(z_{i})$
, and thus by the claim, there are only countably many choices for the tail sequence of
![]() $(x_{i})$
. Therefore,
$(x_{i})$
. Therefore,
![]() $\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})\setminus \Gamma ( {\mathbf {S}})$
is at most countable.
$\Gamma ( {\mathbf {S}}\bullet {\mathbf {r}})\setminus \Gamma ( {\mathbf {S}})$
is at most countable.
Recall from Lemma 2.11 the symbolic survivor set
![]() $\mathbf K_{\beta }(t)$
. To prove Theorem 2, we also recall the following result from [Reference Kalle, Kong, Langeveld and Li20, Lemma 3.7].
$\mathbf K_{\beta }(t)$
. To prove Theorem 2, we also recall the following result from [Reference Kalle, Kong, Langeveld and Li20, Lemma 3.7].
Lemma 4.4. Let
![]() $\beta \in (1,2]$
and
$\beta \in (1,2]$
and
![]() $t\in [0,1)$
. If
$t\in [0,1)$
. If
![]() $\sigma ^{m}(\delta (\beta ))\preccurlyeq b(t,\beta )$
, then
$\sigma ^{m}(\delta (\beta ))\preccurlyeq b(t,\beta )$
, then
Proof of Theorem 2
That the basic intervals
![]() $I^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
are pairwise disjoint will be shown in Proposition 5.1 below. In what follows, we fix a basic interval
$I^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
are pairwise disjoint will be shown in Proposition 5.1 below. In what follows, we fix a basic interval
 $I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
. Take
$I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
. Take
![]() $\beta \in I^ {\mathbf {S}}$
, and let
$\beta \in I^ {\mathbf {S}}$
, and let
![]() $t^{*}=(\Phi _ {\mathbf {S}}(0^{\infty }))_{\beta }= ( {\mathbf {S}}^{-} {\mathbf {A}}^{\infty })_{\beta }$
, where
$t^{*}=(\Phi _ {\mathbf {S}}(0^{\infty }))_{\beta }= ( {\mathbf {S}}^{-} {\mathbf {A}}^{\infty })_{\beta }$
, where
![]() $ {\mathbf {A}}=\mathbb {L}( {\mathbf {S}})=A_{1}\ldots A_{m}$
. Then by equation (4.1) and Lemma 2.5, it follows that
$ {\mathbf {A}}=\mathbb {L}( {\mathbf {S}})=A_{1}\ldots A_{m}$
. Then by equation (4.1) and Lemma 2.5, it follows that
 $$ \begin{align} {\mathbf{A}}^{\infty}=\delta(\beta_{\ell}^ {\mathbf{S}})\preccurlyeq \delta(\beta)\preccurlyeq \delta(\beta_{*}^ {\mathbf{S}})= {\mathbf{A}}^{+} {\mathbf{S}}^{-} {\mathbf{A}}^{\infty}. \end{align} $$
$$ \begin{align} {\mathbf{A}}^{\infty}=\delta(\beta_{\ell}^ {\mathbf{S}})\preccurlyeq \delta(\beta)\preccurlyeq \delta(\beta_{*}^ {\mathbf{S}})= {\mathbf{A}}^{+} {\mathbf{S}}^{-} {\mathbf{A}}^{\infty}. \end{align} $$
Since
![]() $ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}$
with each
$ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}$
with each
![]() $ {\mathbf {s}}_{i}\in \Omega _{F}^{*}$
, by Proposition 1.3, we have
$ {\mathbf {s}}_{i}\in \Omega _{F}^{*}$
, by Proposition 1.3, we have
![]() $ {\mathbf {S}}\in \Omega _{L}^{*}$
. If
$ {\mathbf {S}}\in \Omega _{L}^{*}$
. If
 $\beta \in (\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
, then by Lemma 2.7, we have
$\beta \in (\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
, then by Lemma 2.7, we have
and by Lemma 2.10, it follows that
![]() $ {\mathbf {S}}^{-} {\mathbf {A}}^{\infty }$
is the greedy
$ {\mathbf {S}}^{-} {\mathbf {A}}^{\infty }$
is the greedy
![]() $\beta $
-expansion of
$\beta $
-expansion of
![]() $t^{*}$
, that is,
$t^{*}$
, that is,
![]() $b(t^{*}, \beta )= {\mathbf {S}}^{-} {\mathbf {A}}^{\infty }$
. If
$b(t^{*}, \beta )= {\mathbf {S}}^{-} {\mathbf {A}}^{\infty }$
. If
 $\beta =\beta _{\ell }^ {\mathbf {S}}$
, then
$\beta =\beta _{\ell }^ {\mathbf {S}}$
, then
![]() $\sigma ^{n}( {\mathbf {S}}^{-} {\mathbf {A}}^{\infty })\preccurlyeq {\mathbf {A}}^{\infty }=\delta (\beta )$
for all
$\sigma ^{n}( {\mathbf {S}}^{-} {\mathbf {A}}^{\infty })\preccurlyeq {\mathbf {A}}^{\infty }=\delta (\beta )$
for all
![]() $n\ge 0$
; and in this case, one can verify that the greedy
$n\ge 0$
; and in this case, one can verify that the greedy
![]() $\beta $
-expansion of
$\beta $
-expansion of
![]() $t^{*}$
is given by
$t^{*}$
is given by
![]() $b(t^{*}, \beta )= {\mathbf {S}}0^{\infty }$
.
$b(t^{*}, \beta )= {\mathbf {S}}0^{\infty }$
.
First we prove
![]() $\tau (\beta )\ge t^{*}$
. Note that
$\tau (\beta )\ge t^{*}$
. Note that
![]() $ {\mathbf {A}}=A_{1}\ldots A_{m}$
. Let
$ {\mathbf {A}}=A_{1}\ldots A_{m}$
. Let
![]() $t_{N}:= (( {\mathbf {S}}^{-} {\mathbf {A}}^{N} A_{1}\ldots A_{j})^{\infty })_{\beta },$
where the index
$t_{N}:= (( {\mathbf {S}}^{-} {\mathbf {A}}^{N} A_{1}\ldots A_{j})^{\infty })_{\beta },$
where the index
![]() $j\in \{1,\ldots , m\}$
satisfies
$j\in \{1,\ldots , m\}$
satisfies
![]() $ {\mathbf {S}}=\mathbb {S}( {\mathbf {A}})=A_{j+1}\ldots A_{m} A_{1}\ldots A_{j}.$
Note by Lemma 2.7 that
$ {\mathbf {S}}=\mathbb {S}( {\mathbf {A}})=A_{j+1}\ldots A_{m} A_{1}\ldots A_{j}.$
Note by Lemma 2.7 that
![]() $A_{i+1}\ldots A_{m}\prec A_{1}\ldots A_{m-i}$
for any
$A_{i+1}\ldots A_{m}\prec A_{1}\ldots A_{m-i}$
for any
![]() $0<i<m$
. Then by equation (4.21), one can verify that
$0<i<m$
. Then by equation (4.21), one can verify that
 $$ \begin{align*} \sigma^{n}(( {\mathbf{S}}^{-} {\mathbf{A}}^{N} A_{1}\ldots A_{j})^{\infty})&=\sigma^{n}( {\mathbf{S}}^{-} {\mathbf{A}}^{N+1}(A_{1}\ldots A_{j}^{-} {\mathbf{A}}^{N+1})^{\infty})\\[3pt] &\prec {\mathbf{A}}^{\infty}\preccurlyeq\delta(\beta)\quad \text{for all } n\ge 0. \end{align*} $$
$$ \begin{align*} \sigma^{n}(( {\mathbf{S}}^{-} {\mathbf{A}}^{N} A_{1}\ldots A_{j})^{\infty})&=\sigma^{n}( {\mathbf{S}}^{-} {\mathbf{A}}^{N+1}(A_{1}\ldots A_{j}^{-} {\mathbf{A}}^{N+1})^{\infty})\\[3pt] &\prec {\mathbf{A}}^{\infty}\preccurlyeq\delta(\beta)\quad \text{for all } n\ge 0. \end{align*} $$
So,
![]() $b(t_{N}, \beta )=( {\mathbf {S}}^{-} {\mathbf {A}}^{N} A_{1}\ldots A_{j})^{\infty }$
. This implies that any sequence
$b(t_{N}, \beta )=( {\mathbf {S}}^{-} {\mathbf {A}}^{N} A_{1}\ldots A_{j})^{\infty }$
. This implies that any sequence
![]() $(x_{i})$
constructed by arbitrarily concatenating blocks of the form
$(x_{i})$
constructed by arbitrarily concatenating blocks of the form
 $$ \begin{align*} {\mathbf{S}}^{-} {\mathbf{A}}^{k} A_{1}\ldots A_{j},\quad k>N \end{align*} $$
$$ \begin{align*} {\mathbf{S}}^{-} {\mathbf{A}}^{k} A_{1}\ldots A_{j},\quad k>N \end{align*} $$
satisfies
![]() $( {\mathbf {S}}^{-} {\mathbf {A}}^{N} A_{1}\ldots A_{j})^{\infty }\preccurlyeq \sigma ^{n}((x_{i}))\prec \delta (\beta )$
for all
$( {\mathbf {S}}^{-} {\mathbf {A}}^{N} A_{1}\ldots A_{j})^{\infty }\preccurlyeq \sigma ^{n}((x_{i}))\prec \delta (\beta )$
for all
![]() $n\ge 0$
. So,
$n\ge 0$
. So,
 $$ \begin{align*} \{ {\mathbf{S}}^{-} {\mathbf{A}}^{N+1}A_{1}\ldots A_{j}, {\mathbf{S}}^{-} {\mathbf{A}}^{N+2}A_{1}\ldots A_{j}\}^{\mathbb{N}}\subset\mathbf K_{\beta}(t_{N}). \end{align*} $$
$$ \begin{align*} \{ {\mathbf{S}}^{-} {\mathbf{A}}^{N+1}A_{1}\ldots A_{j}, {\mathbf{S}}^{-} {\mathbf{A}}^{N+2}A_{1}\ldots A_{j}\}^{\mathbb{N}}\subset\mathbf K_{\beta}(t_{N}). \end{align*} $$
By Lemma 2.11, this implies that
![]() $\dim _{H} K_{\beta }(t_{N})>0$
for all
$\dim _{H} K_{\beta }(t_{N})>0$
for all
![]() $N\ge 1$
. Thus,
$N\ge 1$
. Thus,
![]() $\tau (\beta )\ge t_{N}$
for all
$\tau (\beta )\ge t_{N}$
for all
![]() $N\ge 1$
. Note that
$N\ge 1$
. Note that
![]() $t_{N}\nearrow t^{*}$
as
$t_{N}\nearrow t^{*}$
as
![]() $N\to \infty $
. We then conclude that
$N\to \infty $
. We then conclude that
![]() $\tau (\beta )\ge t^{*}$
.
$\tau (\beta )\ge t^{*}$
.
Next we prove
![]() $\tau (\beta )\le t^{*}$
. By equation (4.21) and Lemma 4.4, it follows that
$\tau (\beta )\le t^{*}$
. By equation (4.21) and Lemma 4.4, it follows that
 $$ \begin{align} \mathbf K_{\beta}(t^{*})&\subset\{(x_{i}): {\mathbf{S}}^{-} {\mathbf{A}}^{\infty}\preccurlyeq \sigma^{n}((x_{i}))\prec {\mathbf{A}}^{+} {\mathbf{S}}^{-} {\mathbf{A}}^{\infty} \text{ for all } n\ge 0\}\nonumber\\[3pt] &=\{(x_{i}): {\mathbf{S}}^{-} {\mathbf{A}}^{\infty}\preccurlyeq \sigma^{n}((x_{i}))\preccurlyeq {\mathbf{A}}^{\infty} \text{ for all } n\ge 0\}=:\Gamma. \end{align} $$
$$ \begin{align} \mathbf K_{\beta}(t^{*})&\subset\{(x_{i}): {\mathbf{S}}^{-} {\mathbf{A}}^{\infty}\preccurlyeq \sigma^{n}((x_{i}))\prec {\mathbf{A}}^{+} {\mathbf{S}}^{-} {\mathbf{A}}^{\infty} \text{ for all } n\ge 0\}\nonumber\\[3pt] &=\{(x_{i}): {\mathbf{S}}^{-} {\mathbf{A}}^{\infty}\preccurlyeq \sigma^{n}((x_{i}))\preccurlyeq {\mathbf{A}}^{\infty} \text{ for all } n\ge 0\}=:\Gamma. \end{align} $$
Note by Proposition 4.1 that
![]() $\Gamma ( {\mathbf {S}})=\{(x_{i}): {\mathbf {S}}^{\infty }\preccurlyeq \sigma ^{n}((x_{i}))\preccurlyeq {\mathbf {A}}^{\infty } \text { for all } n\ge 0\}$
is a countable subset of
$\Gamma ( {\mathbf {S}})=\{(x_{i}): {\mathbf {S}}^{\infty }\preccurlyeq \sigma ^{n}((x_{i}))\preccurlyeq {\mathbf {A}}^{\infty } \text { for all } n\ge 0\}$
is a countable subset of
![]() $\Gamma $
. Furthermore, any sequence in the difference set
$\Gamma $
. Furthermore, any sequence in the difference set
![]() $\Gamma \setminus \Gamma ( {\mathbf {S}})$
must end with
$\Gamma \setminus \Gamma ( {\mathbf {S}})$
must end with
![]() $ {\mathbf {S}}^{-} {\mathbf {A}}^{\infty }$
. As a result,
$ {\mathbf {S}}^{-} {\mathbf {A}}^{\infty }$
. As a result,
![]() $\Gamma $
is also countable. By equation (4.22), this implies that
$\Gamma $
is also countable. By equation (4.22), this implies that
![]() $\dim _{H} K_{\beta }(t^{*})=0$
, and thus
$\dim _{H} K_{\beta }(t^{*})=0$
, and thus
![]() $\tau (\beta )\le t^{*}$
. This completes the proof.
$\tau (\beta )\le t^{*}$
. This completes the proof.
5 Geometrical structure of the basic intervals and exceptional sets
In this section, we will prove Theorem 3. The proof will be split into two subsections. In §5.1, we demonstrate the tree structure of the Lyndon intervals
![]() $J^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
, and the relative exceptional sets
$J^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
, and the relative exceptional sets
![]() $E^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
, from which it follows that the basic intervals
$E^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
, from which it follows that the basic intervals
 $I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
,
$I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
,
![]() $ {\mathbf {S}}\in \Lambda $
are pairwise disjoint. We show that each relative exceptional set
$ {\mathbf {S}}\in \Lambda $
are pairwise disjoint. We show that each relative exceptional set
![]() $E^ {\mathbf {S}}$
has zero box-counting dimension, and the exceptional set E has zero packing dimension. In §5.2, we prove that the infinitely Farey set
$E^ {\mathbf {S}}$
has zero box-counting dimension, and the exceptional set E has zero packing dimension. In §5.2, we prove that the infinitely Farey set
![]() $E_{\infty }$
has zero Hausdorff dimension.
$E_{\infty }$
has zero Hausdorff dimension.
5.1 Tree structure of the Lyndon intervals and relative exceptional sets
Given
![]() $ {\mathbf {S}}\in \Lambda $
, recall from Definitions 1.5 and 1.8 the basic interval
$ {\mathbf {S}}\in \Lambda $
, recall from Definitions 1.5 and 1.8 the basic interval
 $I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}},\beta _{*}^ {\mathbf {S}}]$
and the Lyndon interval
$I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}},\beta _{*}^ {\mathbf {S}}]$
and the Lyndon interval
 $J^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]$
generated by
$J^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]$
generated by
![]() $ {\mathbf {S}}$
, respectively. Then by Lemmas 2.5 and 2.7, it follows that
$ {\mathbf {S}}$
, respectively. Then by Lemmas 2.5 and 2.7, it follows that
 $$ \begin{align} \delta(\beta_{\ell}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{\infty},\quad \delta(\beta_{*}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty}\quad\textrm{and}\quad \delta(\beta_{r}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty}. \end{align} $$
$$ \begin{align} \delta(\beta_{\ell}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{\infty},\quad \delta(\beta_{*}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty}\quad\textrm{and}\quad \delta(\beta_{r}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty}. \end{align} $$
First we show that the Lyndon intervals
![]() $J^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
have a tree structure.
$J^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
have a tree structure.
Proposition 5.1. Let
![]() $ {\mathbf {S}}\in {\Lambda }$
. Then
$ {\mathbf {S}}\in {\Lambda }$
. Then
![]() $I^ {\mathbf {S}}\subset J^{ {\mathbf {S}}}$
. Furthermore,
$I^ {\mathbf {S}}\subset J^{ {\mathbf {S}}}$
. Furthermore,
-
(i) for any
 $ {\mathbf {r}}\in \Omega _{F}^{*}$
, we have
$ {\mathbf {r}}\in \Omega _{F}^{*}$
, we have
 $J^{ {\mathbf {S}}\bullet {\mathbf {r}}}\subset J^ {\mathbf {S}}\setminus I^ {\mathbf {S}}$
;
$J^{ {\mathbf {S}}\bullet {\mathbf {r}}}\subset J^ {\mathbf {S}}\setminus I^ {\mathbf {S}}$
; -
(ii) for any two different words
 $ {\mathbf {r}}, {\mathbf {r}}^{\prime }\in \Omega _{F}^{*}$
, we have
$ {\mathbf {r}}, {\mathbf {r}}^{\prime }\in \Omega _{F}^{*}$
, we have
 $J^{ {\mathbf {S}}\bullet {\mathbf {r}}}\cap J^{ {\mathbf {S}}\bullet {\mathbf {r}}^{\prime }}=\emptyset $
.
$J^{ {\mathbf {S}}\bullet {\mathbf {r}}}\cap J^{ {\mathbf {S}}\bullet {\mathbf {r}}^{\prime }}=\emptyset $
.
Proof. Let
 $I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
and
$I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
and
 $J^{ {\mathbf {S}}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]$
. Then by equation (5.1), it follows that
$J^{ {\mathbf {S}}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]$
. Then by equation (5.1), it follows that
 $$ \begin{align*} \delta(\beta_{*}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty}\prec \mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty}=\delta(\beta_{r}^ {\mathbf{S}}), \end{align*} $$
$$ \begin{align*} \delta(\beta_{*}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty}\prec \mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty}=\delta(\beta_{r}^ {\mathbf{S}}), \end{align*} $$
which implies
![]() $\beta _{*}^ {\mathbf {S}}<\beta _{r}^ {\mathbf {S}}$
by Lemma 2.5. So
$\beta _{*}^ {\mathbf {S}}<\beta _{r}^ {\mathbf {S}}$
by Lemma 2.5. So
![]() $I^ {\mathbf {S}} \subset J^ {\mathbf {S}}$
.
$I^ {\mathbf {S}} \subset J^ {\mathbf {S}}$
.
For (i), let
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
. Then
$ {\mathbf {r}}\in \Omega _{F}^{*}$
. Then
![]() $ {\mathbf {r}}$
begins with digit
$ {\mathbf {r}}$
begins with digit
![]() $0$
and ends with digit
$0$
and ends with digit
![]() $1$
. By Lemmas 3.6(ii) and 3.7, this implies that
$1$
. By Lemmas 3.6(ii) and 3.7, this implies that
 $$ \begin{align*} \delta(\beta_{\ell}^{ {\mathbf{S}}\bullet {\mathbf{r}}})&= \mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{\infty}=( {\mathbf{S}}\bullet\mathbb{L}( {\mathbf{r}}))^{\infty}=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{\infty})\\[3pt] &\succ \Phi_ {\mathbf{S}}(10^{\infty})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty}=\delta(\beta_{*}^ {\mathbf{S}}). \end{align*} $$
$$ \begin{align*} \delta(\beta_{\ell}^{ {\mathbf{S}}\bullet {\mathbf{r}}})&= \mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{\infty}=( {\mathbf{S}}\bullet\mathbb{L}( {\mathbf{r}}))^{\infty}=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{\infty})\\[3pt] &\succ \Phi_ {\mathbf{S}}(10^{\infty})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty}=\delta(\beta_{*}^ {\mathbf{S}}). \end{align*} $$
So,
 $\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}}>{\beta _{*}^ {\mathbf {S}}}$
. Furthermore, by Lemmas 3.4, 3.6(ii), and 3.7, it follows that
$\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}}>{\beta _{*}^ {\mathbf {S}}}$
. Furthermore, by Lemmas 3.4, 3.6(ii), and 3.7, it follows that
 $$ \begin{align*} \delta(\beta_{r}^{ {\mathbf{S}}\bullet {\mathbf{r}}})&=\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{+}( {\mathbf{S}}\bullet {\mathbf{r}})^{\infty}\\[3pt] &=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{+})\Phi_ {\mathbf{S}}( {\mathbf{r}}^{\infty})=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{\infty})\\[3pt] &\prec \Phi_ {\mathbf{S}}(1^{\infty})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty}=\delta(\beta_{r}^ {\mathbf{S}}). \end{align*} $$
$$ \begin{align*} \delta(\beta_{r}^{ {\mathbf{S}}\bullet {\mathbf{r}}})&=\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{+}( {\mathbf{S}}\bullet {\mathbf{r}})^{\infty}\\[3pt] &=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{+})\Phi_ {\mathbf{S}}( {\mathbf{r}}^{\infty})=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{\infty})\\[3pt] &\prec \Phi_ {\mathbf{S}}(1^{\infty})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty}=\delta(\beta_{r}^ {\mathbf{S}}). \end{align*} $$
This proves
![]() $\beta _{r}^{ {\mathbf {S}}\bullet {\mathbf {r}}}<\beta _{r}^ {\mathbf {S}}$
. Hence,
$\beta _{r}^{ {\mathbf {S}}\bullet {\mathbf {r}}}<\beta _{r}^ {\mathbf {S}}$
. Hence,
 $J^{ {\mathbf {S}}\bullet {\mathbf {r}}}=[\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}}, \beta _{r}^{ {\mathbf {S}}\bullet {\mathbf {r}}}]\subset (\beta _{*}^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]=J^ {\mathbf {S}}\setminus I^ {\mathbf {S}}$
.
$J^{ {\mathbf {S}}\bullet {\mathbf {r}}}=[\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}}, \beta _{r}^{ {\mathbf {S}}\bullet {\mathbf {r}}}]\subset (\beta _{*}^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]=J^ {\mathbf {S}}\setminus I^ {\mathbf {S}}$
.
Next we prove (ii). Let
![]() $ {\mathbf {r}}, {\mathbf {r}}^{\prime }$
be two different Farey words in
$ {\mathbf {r}}, {\mathbf {r}}^{\prime }$
be two different Farey words in
![]() $\Omega _{F}^{*}$
. By Lemma 2.9(i), it follows that
$\Omega _{F}^{*}$
. By Lemma 2.9(i), it follows that
![]() $J^{ {\mathbf {r}}}\cap J^{ {\mathbf {r}}^{\prime }}=\emptyset $
. Write
$J^{ {\mathbf {r}}}\cap J^{ {\mathbf {r}}^{\prime }}=\emptyset $
. Write
![]() $J^{ {\mathbf {r}}}=[\beta _{\ell }^ {\mathbf {r}}, \beta _{r}^ {\mathbf {r}}]$
and
$J^{ {\mathbf {r}}}=[\beta _{\ell }^ {\mathbf {r}}, \beta _{r}^ {\mathbf {r}}]$
and
 $J^{ {\mathbf {r}}^{\prime }}=[\beta _{\ell }^{ {\mathbf {r}}^{\prime }}, \beta _{r}^{ {\mathbf {r}}^{\prime }}]$
. Since
$J^{ {\mathbf {r}}^{\prime }}=[\beta _{\ell }^{ {\mathbf {r}}^{\prime }}, \beta _{r}^{ {\mathbf {r}}^{\prime }}]$
. Since
![]() $J^ {\mathbf {r}}$
and
$J^ {\mathbf {r}}$
and
![]() $J^{ {\mathbf {r}}^{\prime }}$
are disjoint, we may assume
$J^{ {\mathbf {r}}^{\prime }}$
are disjoint, we may assume
 $\beta _{r}^ {\mathbf {r}}<\beta _{\ell }^{ {\mathbf {r}}^{\prime }}$
. By equation (5.1) and Lemma 2.5, it follows that
$\beta _{r}^ {\mathbf {r}}<\beta _{\ell }^{ {\mathbf {r}}^{\prime }}$
. By equation (5.1) and Lemma 2.5, it follows that
 $$ \begin{align} \mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{\infty}=\delta(\beta_{r}^ {\mathbf{r}})\prec \delta(\beta_{\ell}^{ {\mathbf{r}}^{\prime}})=\mathbb{L}( {\mathbf{r}}^{\prime})^{\infty}. \end{align} $$
$$ \begin{align} \mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{\infty}=\delta(\beta_{r}^ {\mathbf{r}})\prec \delta(\beta_{\ell}^{ {\mathbf{r}}^{\prime}})=\mathbb{L}( {\mathbf{r}}^{\prime})^{\infty}. \end{align} $$
Then by equations (5.1), (5.2), and Lemma 3.3, we obtain that
 $$ \begin{align*} \delta(\beta_{r}^{ {\mathbf{S}}\bullet {\mathbf{r}}})&=\mathbb{L}(S\bullet {\mathbf{r}})^{+}(S\bullet {\mathbf{r}})^{\infty}=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{\infty})\\[3pt] &\prec\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}}^{\prime})^{\infty})=\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}}^{\prime})^{\infty}=\delta(\beta_{\ell}^{ {\mathbf{S}}\bullet {\mathbf{r}}^{\prime}}). \end{align*} $$
$$ \begin{align*} \delta(\beta_{r}^{ {\mathbf{S}}\bullet {\mathbf{r}}})&=\mathbb{L}(S\bullet {\mathbf{r}})^{+}(S\bullet {\mathbf{r}})^{\infty}=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{\infty})\\[3pt] &\prec\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}}^{\prime})^{\infty})=\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}}^{\prime})^{\infty}=\delta(\beta_{\ell}^{ {\mathbf{S}}\bullet {\mathbf{r}}^{\prime}}). \end{align*} $$
It follows that
 $\beta _{r}^{ {\mathbf {S}}\bullet {\mathbf {r}}}<\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}^{\prime }}$
, and hence
$\beta _{r}^{ {\mathbf {S}}\bullet {\mathbf {r}}}<\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}^{\prime }}$
, and hence
![]() $J^{ {\mathbf {S}}\bullet {\mathbf {r}}}\cap J^{ {\mathbf {S}}\bullet {\mathbf {r}}^{\prime }}=\emptyset $
.
$J^{ {\mathbf {S}}\bullet {\mathbf {r}}}\cap J^{ {\mathbf {S}}\bullet {\mathbf {r}}^{\prime }}=\emptyset $
.
Remark 5.2. Proposition 5.1 implies that the Lyndon intervals
![]() $J^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
have a tree structure. More precisely, we say
$J^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
have a tree structure. More precisely, we say
![]() $J^{\mathbf R}$
is an offspring of
$J^{\mathbf R}$
is an offspring of
![]() $J^ {\mathbf {S}}$
if there exists a word
$J^ {\mathbf {S}}$
if there exists a word
![]() $\mathbf T\in \Lambda $
such that
$\mathbf T\in \Lambda $
such that
![]() $\mathbf R= {\mathbf {S}}\bullet \mathbf T$
. Then any offspring of
$\mathbf R= {\mathbf {S}}\bullet \mathbf T$
. Then any offspring of
![]() $J^ {\mathbf {S}}$
is a subset of
$J^ {\mathbf {S}}$
is a subset of
![]() $J^ {\mathbf {S}}$
. Furthermore, if
$J^ {\mathbf {S}}$
. Furthermore, if
![]() $J^{ {\mathbf {S}}^{\prime }}$
is not an offspring of
$J^{ {\mathbf {S}}^{\prime }}$
is not an offspring of
![]() $J^ {\mathbf {S}}$
and
$J^ {\mathbf {S}}$
and
![]() $J^ {\mathbf {S}}$
is not an offspring of
$J^ {\mathbf {S}}$
is not an offspring of
![]() $J^{ {\mathbf {S}}^{\prime }}$
, then Proposition 5.1 implies that
$J^{ {\mathbf {S}}^{\prime }}$
, then Proposition 5.1 implies that
![]() $J^{ {\mathbf {S}}^{\prime }}\cap J^ {\mathbf {S}}=\emptyset $
. Consequently, the basic intervals
$J^{ {\mathbf {S}}^{\prime }}\cap J^ {\mathbf {S}}=\emptyset $
. Consequently, the basic intervals
![]() $I^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
are pairwise disjoint.
$I^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
are pairwise disjoint.
Recall from §1 the exceptional set
 $E=(1,2]\setminus \bigcup _{ {\mathbf {r}}\in \Omega _{F}^{*}}J^ {\mathbf {r}}$
and the relative exceptional sets
$E=(1,2]\setminus \bigcup _{ {\mathbf {r}}\in \Omega _{F}^{*}}J^ {\mathbf {r}}$
and the relative exceptional sets
 $E^ {\mathbf {S}}=(J^ {\mathbf {S}}\setminus I^ {\mathbf {S}})\setminus \bigcup _{ {\mathbf {r}}\in \Omega _{F}^{*}}J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
with
$E^ {\mathbf {S}}=(J^ {\mathbf {S}}\setminus I^ {\mathbf {S}})\setminus \bigcup _{ {\mathbf {r}}\in \Omega _{F}^{*}}J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
with
![]() $ {\mathbf {S}}\in \Lambda $
. Next we will show that E is bijectively mapped to
$ {\mathbf {S}}\in \Lambda $
. Next we will show that E is bijectively mapped to
![]() $E^ {\mathbf {S}}$
via the map
$E^ {\mathbf {S}}$
via the map
 $$ \begin{align} \Psi_ {\mathbf{S}}: (1,2]\to J^ {\mathbf{S}}\setminus I^ {\mathbf{S}}=(\beta_{*}^ {\mathbf{S}}, \beta_{r}^ {\mathbf{S}}];\quad \beta\mapsto \delta^{-1}\circ\Phi_ {\mathbf{S}}\circ\delta(\beta), \end{align} $$
$$ \begin{align} \Psi_ {\mathbf{S}}: (1,2]\to J^ {\mathbf{S}}\setminus I^ {\mathbf{S}}=(\beta_{*}^ {\mathbf{S}}, \beta_{r}^ {\mathbf{S}}];\quad \beta\mapsto \delta^{-1}\circ\Phi_ {\mathbf{S}}\circ\delta(\beta), \end{align} $$
where
![]() $\delta (\beta )$
is the quasi-greedy
$\delta (\beta )$
is the quasi-greedy
![]() $\beta $
-expansion of
$\beta $
-expansion of
![]() $1$
.
$1$
.
We mention that
![]() $\Psi _ {\mathbf {S}}$
is not surjective, which somewhat complicates the proof of Proposition 5.4 below. For example, let
$\Psi _ {\mathbf {S}}$
is not surjective, which somewhat complicates the proof of Proposition 5.4 below. For example, let
![]() $ {\mathbf {S}}=011$
. Then
$ {\mathbf {S}}=011$
. Then
![]() $\delta (\beta _{*}^ {\mathbf {S}})=111010(110)^{\infty }$
and
$\delta (\beta _{*}^ {\mathbf {S}})=111010(110)^{\infty }$
and
![]() $\delta (\beta _{r}^ {\mathbf {S}})=111(011)^{\infty }$
. Take
$\delta (\beta _{r}^ {\mathbf {S}})=111(011)^{\infty }$
. Take
![]() $\beta \in (\beta _{*}^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]$
such that
$\beta \in (\beta _{*}^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]$
such that
![]() $\delta (\beta )=1110110^{\infty }$
. One can verify that
$\delta (\beta )=1110110^{\infty }$
. One can verify that
![]() $\beta \notin \Psi _ {\mathbf {S}}((1,2])$
, since
$\beta \notin \Psi _ {\mathbf {S}}((1,2])$
, since
![]() $\delta (\beta )$
cannot be written as a concatenation of words from
$\delta (\beta )$
cannot be written as a concatenation of words from
![]() $\{ {\mathbf {S}}, {\mathbf {S}}^{-},\mathbb {L}( {\mathbf {S}}),\mathbb {L}( {\mathbf {S}})^{+}\}$
.
$\{ {\mathbf {S}}, {\mathbf {S}}^{-},\mathbb {L}( {\mathbf {S}}),\mathbb {L}( {\mathbf {S}})^{+}\}$
.
Lemma 5.3. For any
![]() $ {\mathbf {S}}\in \Lambda $
, the map
$ {\mathbf {S}}\in \Lambda $
, the map
![]() $\Psi _ {\mathbf {S}}$
is well defined and strictly increasing.
$\Psi _ {\mathbf {S}}$
is well defined and strictly increasing.
Proof. Let
![]() $ {\mathbf {S}}\in \Lambda $
with
$ {\mathbf {S}}\in \Lambda $
with
![]() $ {\mathbf {A}}=\mathbb {L}( {\mathbf {S}})$
. First we show that the map
$ {\mathbf {A}}=\mathbb {L}( {\mathbf {S}})$
. First we show that the map
![]() $\Psi _ {\mathbf {S}}: (1,2]\to J^ {\mathbf {S}}\setminus I^ {\mathbf {S}}=(\beta _{*}^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]$
is well defined. Note that
$\Psi _ {\mathbf {S}}: (1,2]\to J^ {\mathbf {S}}\setminus I^ {\mathbf {S}}=(\beta _{*}^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]$
is well defined. Note that
 $$ \begin{align} \delta(\beta_{*}^ {\mathbf{S}})= {\mathbf{A}}^{+} {\mathbf{S}}^{-} {\mathbf{A}}^{\infty}=\Phi_ {\mathbf{S}}(10^{\infty})\quad\textrm{and}\quad \delta(\beta_{r}^ {\mathbf{S}})= {\mathbf{A}}^{+} {\mathbf{S}}^{\infty}=\Phi_ {\mathbf{S}}(1^{\infty}). \end{align} $$
$$ \begin{align} \delta(\beta_{*}^ {\mathbf{S}})= {\mathbf{A}}^{+} {\mathbf{S}}^{-} {\mathbf{A}}^{\infty}=\Phi_ {\mathbf{S}}(10^{\infty})\quad\textrm{and}\quad \delta(\beta_{r}^ {\mathbf{S}})= {\mathbf{A}}^{+} {\mathbf{S}}^{\infty}=\Phi_ {\mathbf{S}}(1^{\infty}). \end{align} $$
Take
![]() $\beta \in (1,2]$
. Then
$\beta \in (1,2]$
. Then
![]() $10^{\infty }\prec \delta (\beta )\preccurlyeq 1^{\infty }$
. By Lemma 3.3 and equation (5.4), it follows that
$10^{\infty }\prec \delta (\beta )\preccurlyeq 1^{\infty }$
. By Lemma 3.3 and equation (5.4), it follows that
 $$ \begin{align*} \delta(\beta_{*}^ {\mathbf{S}})\prec\Phi_ {\mathbf{S}}(\delta(\beta))\preccurlyeq \delta(\beta_{r}^ {\mathbf{S}}). \end{align*} $$
$$ \begin{align*} \delta(\beta_{*}^ {\mathbf{S}})\prec\Phi_ {\mathbf{S}}(\delta(\beta))\preccurlyeq \delta(\beta_{r}^ {\mathbf{S}}). \end{align*} $$
Thus, by Lemma 2.5, it suffices to prove that
Note by Lemma 2.5 that
![]() $\sigma ^{n}(\delta (\beta ))\preccurlyeq \delta (\beta )$
for all
$\sigma ^{n}(\delta (\beta ))\preccurlyeq \delta (\beta )$
for all
![]() $n\ge 0$
, and
$n\ge 0$
, and
![]() $\delta (\beta )$
begins with digit
$\delta (\beta )$
begins with digit
![]() $1$
. Thus, equation (5.5) follows by Lemma 3.8(i), and we conclude that the map
$1$
. Thus, equation (5.5) follows by Lemma 3.8(i), and we conclude that the map
![]() $\Psi _ {\mathbf {S}}$
is well defined.
$\Psi _ {\mathbf {S}}$
is well defined.
The monotonicity of
![]() $\Psi _ {\mathbf {S}} =\delta ^{-1}\circ \Phi _ {\mathbf {S}}\circ \delta $
follows since both maps
$\Psi _ {\mathbf {S}} =\delta ^{-1}\circ \Phi _ {\mathbf {S}}\circ \delta $
follows since both maps
![]() $\delta $
and
$\delta $
and
![]() $\Phi _ {\mathbf {S}}$
are strictly increasing by Lemmas 2.5 and 3.3, respectively. This completes the proof.
$\Phi _ {\mathbf {S}}$
are strictly increasing by Lemmas 2.5 and 3.3, respectively. This completes the proof.
Proposition 5.4. For any
![]() $ {\mathbf {S}}\in \Lambda $
, we have
$ {\mathbf {S}}\in \Lambda $
, we have
![]() $\Psi _ {\mathbf {S}}(E)=E^ {\mathbf {S}}$
.
$\Psi _ {\mathbf {S}}(E)=E^ {\mathbf {S}}$
.
Proof. We first prove that
 $$ \begin{align} \Psi_ {\mathbf{S}}(\beta_{\ell}^ {\mathbf{r}})=\beta_{\ell}^{ {\mathbf{S}}\bullet {\mathbf{r}}}\quad\textrm{and}\quad \Psi_ {\mathbf{S}}(\beta_{r}^ {\mathbf{r}})=\beta_{r}^{ {\mathbf{S}}\bullet {\mathbf{r}}} \quad\text{for all } {\mathbf{r}}\in{\Omega_{L}^{*}}. \end{align} $$
$$ \begin{align} \Psi_ {\mathbf{S}}(\beta_{\ell}^ {\mathbf{r}})=\beta_{\ell}^{ {\mathbf{S}}\bullet {\mathbf{r}}}\quad\textrm{and}\quad \Psi_ {\mathbf{S}}(\beta_{r}^ {\mathbf{r}})=\beta_{r}^{ {\mathbf{S}}\bullet {\mathbf{r}}} \quad\text{for all } {\mathbf{r}}\in{\Omega_{L}^{*}}. \end{align} $$
Observe that
![]() $\delta (\beta _{\ell }^ {\mathbf {r}})=\mathbb {L}( {\mathbf {r}})^{\infty }$
. Then by Lemmas 3.6(ii) and 3.7, it follows that
$\delta (\beta _{\ell }^ {\mathbf {r}})=\mathbb {L}( {\mathbf {r}})^{\infty }$
. Then by Lemmas 3.6(ii) and 3.7, it follows that
 $$ \begin{align*} \Phi_ {\mathbf{S}}(\delta(\beta_{\ell}^ {\mathbf{r}}))=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{\infty})=( {\mathbf{S}}\bullet\mathbb{L}( {\mathbf{r}}))^{\infty}=\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{\infty}=\delta(\beta_{\ell}^{ {\mathbf{S}}\bullet {\mathbf{r}}}), \end{align*} $$
$$ \begin{align*} \Phi_ {\mathbf{S}}(\delta(\beta_{\ell}^ {\mathbf{r}}))=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{\infty})=( {\mathbf{S}}\bullet\mathbb{L}( {\mathbf{r}}))^{\infty}=\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{\infty}=\delta(\beta_{\ell}^{ {\mathbf{S}}\bullet {\mathbf{r}}}), \end{align*} $$
so
 $\Psi _ {\mathbf {S}}(\beta _{\ell }^ {\mathbf {r}})=\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
. Similarly, since
$\Psi _ {\mathbf {S}}(\beta _{\ell }^ {\mathbf {r}})=\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
. Similarly, since
![]() $\delta (\beta _{r}^ {\mathbf {r}})=\mathbb {L}( {\mathbf {r}})^{+} {\mathbf {r}}^{\infty }$
, Lemmas 3.4, 3.6(ii), and 3.7 imply that
$\delta (\beta _{r}^ {\mathbf {r}})=\mathbb {L}( {\mathbf {r}})^{+} {\mathbf {r}}^{\infty }$
, Lemmas 3.4, 3.6(ii), and 3.7 imply that
 $$ \begin{align*} \Phi_ {\mathbf{S}}(\delta(\beta_{r}^ {\mathbf{r}}))&=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{\infty})=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{+})\Phi_ {\mathbf{S}}( {\mathbf{r}}^{\infty})\\[3pt] &=( {\mathbf{S}}\bullet\mathbb{L}( {\mathbf{r}}))^{+}\Phi_ {\mathbf{S}}( {\mathbf{r}})^{\infty}=\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{+}( {\mathbf{S}}\bullet {\mathbf{r}})^{\infty}=\delta(\beta_{r}^{ {\mathbf{S}}\bullet {\mathbf{r}}}). \end{align*} $$
$$ \begin{align*} \Phi_ {\mathbf{S}}(\delta(\beta_{r}^ {\mathbf{r}}))&=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{+} {\mathbf{r}}^{\infty})=\Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}})^{+})\Phi_ {\mathbf{S}}( {\mathbf{r}}^{\infty})\\[3pt] &=( {\mathbf{S}}\bullet\mathbb{L}( {\mathbf{r}}))^{+}\Phi_ {\mathbf{S}}( {\mathbf{r}})^{\infty}=\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{+}( {\mathbf{S}}\bullet {\mathbf{r}})^{\infty}=\delta(\beta_{r}^{ {\mathbf{S}}\bullet {\mathbf{r}}}). \end{align*} $$
We conclude that
![]() $\Psi _ {\mathbf {S}}(\beta _{r}^{ {\mathbf {r}}})=\beta _{r}^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
. This proves equation (5.6).
$\Psi _ {\mathbf {S}}(\beta _{r}^{ {\mathbf {r}}})=\beta _{r}^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
. This proves equation (5.6).
Note by Lemma 2.5(ii) that the map
![]() $\beta \mapsto \delta (\beta )$
is left continuous in
$\beta \mapsto \delta (\beta )$
is left continuous in
![]() $(1,2]$
, and is right continuous at a point
$(1,2]$
, and is right continuous at a point
![]() $\beta _{0}$
if and only if
$\beta _{0}$
if and only if
![]() $\delta (\beta _{0})$
is not periodic. Hence by Lemma 2.8, it follows that the map
$\delta (\beta _{0})$
is not periodic. Hence by Lemma 2.8, it follows that the map
![]() $\beta \mapsto \delta (\beta )$
is continuous at
$\beta \mapsto \delta (\beta )$
is continuous at
![]() $\beta _{0}$
if and only if
$\beta _{0}$
if and only if
![]() $\delta (\beta _{0})$
is not of the form
$\delta (\beta _{0})$
is not of the form
![]() $\mathbb {L}( {\mathbf {r}})^{\infty }$
for a Lyndon word
$\mathbb {L}( {\mathbf {r}})^{\infty }$
for a Lyndon word
![]() $ {\mathbf {r}}$
. Since
$ {\mathbf {r}}$
. Since
![]() $\Phi _ {\mathbf {S}}$
is clearly continuous with respect to the order topology and the map
$\Phi _ {\mathbf {S}}$
is clearly continuous with respect to the order topology and the map
![]() $\delta ^{-1}$
is continuous, it follows that
$\delta ^{-1}$
is continuous, it follows that
![]() $\Psi _ {\mathbf {S}}$
is continuous at
$\Psi _ {\mathbf {S}}$
is continuous at
![]() $\beta _{0}$
if and only if
$\beta _{0}$
if and only if
![]() $\delta (\beta _{0})$
is not of the form
$\delta (\beta _{0})$
is not of the form
![]() $\mathbb {L}( {\mathbf {r}})^{\infty }$
for a Lyndon word
$\mathbb {L}( {\mathbf {r}})^{\infty }$
for a Lyndon word
![]() $ {\mathbf {r}}$
. Moreover,
$ {\mathbf {r}}$
. Moreover,
![]() $\Psi _ {\mathbf {S}}$
is left continuous everywhere.
$\Psi _ {\mathbf {S}}$
is left continuous everywhere.
Note that if
![]() $\delta (\beta _{0})=\mathbb {L}( {\mathbf {r}})^{\infty }$
, then by Lemma 2.5(ii), it follows that as
$\delta (\beta _{0})=\mathbb {L}( {\mathbf {r}})^{\infty }$
, then by Lemma 2.5(ii), it follows that as
![]() $\beta $
decreases to
$\beta $
decreases to
![]() $\beta _{0}$
, the sequence
$\beta _{0}$
, the sequence
![]() $\delta (\beta )$
converges to
$\delta (\beta )$
converges to
![]() $\mathbb {L}( {\mathbf {r}})^{+}0^{\infty }$
with respect to the order topology, that is,
$\mathbb {L}( {\mathbf {r}})^{+}0^{\infty }$
with respect to the order topology, that is,
![]() $\lim _{\beta \searrow \beta _{0}}\delta (\beta )=\mathbb {L}( {\mathbf {r}})^{+}0^{\infty }$
. Since
$\lim _{\beta \searrow \beta _{0}}\delta (\beta )=\mathbb {L}( {\mathbf {r}})^{+}0^{\infty }$
. Since
![]() $\Psi _ {\mathbf {S}}$
is increasing, it follows that
$\Psi _ {\mathbf {S}}$
is increasing, it follows that
 $$ \begin{align*} \Psi_ {\mathbf{S}}((1,2])=(J^ {\mathbf{S}}\backslash I^ {\mathbf{S}})\backslash \bigcup_{ {\mathbf{r}}\in\Omega_{L}^{*}} (p^{ {\mathbf{r}}},q^{ {\mathbf{r}}}], \end{align*} $$
$$ \begin{align*} \Psi_ {\mathbf{S}}((1,2])=(J^ {\mathbf{S}}\backslash I^ {\mathbf{S}})\backslash \bigcup_{ {\mathbf{r}}\in\Omega_{L}^{*}} (p^{ {\mathbf{r}}},q^{ {\mathbf{r}}}], \end{align*} $$
where
![]() $\delta (p^ {\mathbf {r}})=\Phi _ {\mathbf {S}}(\mathbb {L}( {\mathbf {r}})^{\infty })$
and
$\delta (p^ {\mathbf {r}})=\Phi _ {\mathbf {S}}(\mathbb {L}( {\mathbf {r}})^{\infty })$
and
![]() $\delta (q^ {\mathbf {r}})=\Phi _ {\mathbf {S}}(\mathbb {L}( {\mathbf {r}})^{+}0^{\infty })$
. Note that
$\delta (q^ {\mathbf {r}})=\Phi _ {\mathbf {S}}(\mathbb {L}( {\mathbf {r}})^{+}0^{\infty })$
. Note that
![]() $(p^ {\mathbf {r}},q^ {\mathbf {r}}]\subset J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
. By Lemma 2.9(iii), there is a (unique) Farey word
$(p^ {\mathbf {r}},q^ {\mathbf {r}}]\subset J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
. By Lemma 2.9(iii), there is a (unique) Farey word
![]() $\hat { {\mathbf {r}}}$
such that
$\hat { {\mathbf {r}}}$
such that
![]() $J^ {\mathbf {r}}\subset J^{\hat r}$
. Applying equation (5.6) to both
$J^ {\mathbf {r}}\subset J^{\hat r}$
. Applying equation (5.6) to both
![]() $ {\mathbf {r}}$
and
$ {\mathbf {r}}$
and
![]() $\hat { {\mathbf {r}}}$
, and using Lemma 5.3, we conclude that
$\hat { {\mathbf {r}}}$
, and using Lemma 5.3, we conclude that
![]() $J^{ {\mathbf {S}}\bullet {\mathbf {r}}}\subset J^{ {\mathbf {S}}\bullet \hat { {\mathbf {r}}}}$
. Hence,
$J^{ {\mathbf {S}}\bullet {\mathbf {r}}}\subset J^{ {\mathbf {S}}\bullet \hat { {\mathbf {r}}}}$
. Hence,
![]() $(p^ {\mathbf {r}},q^ {\mathbf {r}}]\subset J^{ {\mathbf {S}}\bullet \hat { {\mathbf {r}}}}$
. Therefore, if
$(p^ {\mathbf {r}},q^ {\mathbf {r}}]\subset J^{ {\mathbf {S}}\bullet \hat { {\mathbf {r}}}}$
. Therefore, if
 $\beta \in E^ {\mathbf {S}}=(J^ {\mathbf {S}}\backslash I^ {\mathbf {S}})\backslash \bigcup _{ {\mathbf {r}}\in \Omega _{F}^{*}} J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
, then
$\beta \in E^ {\mathbf {S}}=(J^ {\mathbf {S}}\backslash I^ {\mathbf {S}})\backslash \bigcup _{ {\mathbf {r}}\in \Omega _{F}^{*}} J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
, then
![]() $\beta $
lies in the range of
$\beta $
lies in the range of
![]() $\Psi _ {\mathbf {S}}$
. This implies that
$\Psi _ {\mathbf {S}}$
. This implies that
Now assume first that
![]() $\beta \in \Psi _ {\mathbf {S}}(E)$
. Then
$\beta \in \Psi _ {\mathbf {S}}(E)$
. Then
![]() $\beta =\Psi _ {\mathbf {S}}({\hat \beta })$
, where
$\beta =\Psi _ {\mathbf {S}}({\hat \beta })$
, where
![]() ${\hat \beta }\not \in J^ {\mathbf {r}}$
for any
${\hat \beta }\not \in J^ {\mathbf {r}}$
for any
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
. Hence,
$ {\mathbf {r}}\in \Omega _{F}^{*}$
. Hence,
![]() $\beta \not \in J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
for any
$\beta \not \in J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
for any
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
by equation (5.6) and since
$ {\mathbf {r}}\in \Omega _{F}^{*}$
by equation (5.6) and since
![]() $\Psi _ {\mathbf {S}}$
is increasing. Therefore,
$\Psi _ {\mathbf {S}}$
is increasing. Therefore,
![]() $\beta \in E^ {\mathbf {S}}$
.
$\beta \in E^ {\mathbf {S}}$
.
Conversely, suppose
![]() $\beta \in E^ {\mathbf {S}}$
. By equation (5.7),
$\beta \in E^ {\mathbf {S}}$
. By equation (5.7),
![]() $\beta =\Psi _ {\mathbf {S}}({\hat \beta })$
for some
$\beta =\Psi _ {\mathbf {S}}({\hat \beta })$
for some
![]() ${\hat \beta }\in (1,2]$
. If
${\hat \beta }\in (1,2]$
. If
![]() ${\hat \beta }\in J^ {\mathbf {r}}$
for some
${\hat \beta }\in J^ {\mathbf {r}}$
for some
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
, then
$ {\mathbf {r}}\in \Omega _{F}^{*}$
, then
![]() $\beta \in \Psi _ {\mathbf {S}}(J^ {\mathbf {r}})\subset J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
by equation (5.6), contradicting that
$\beta \in \Psi _ {\mathbf {S}}(J^ {\mathbf {r}})\subset J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
by equation (5.6), contradicting that
![]() $\beta \in E^ {\mathbf {S}}$
. Hence,
$\beta \in E^ {\mathbf {S}}$
. Hence,
![]() ${\hat \beta }\in E$
and then
${\hat \beta }\in E$
and then
![]() $\beta \in \Psi _ {\mathbf {S}}(E)$
. This completes the proof.
$\beta \in \Psi _ {\mathbf {S}}(E)$
. This completes the proof.
Kalle et al proved in [Reference Kalle, Kong, Langeveld and Li20, Theorem C] that the Farey intervals
![]() $J^ {\mathbf {r}}, {\mathbf {r}}\in \Omega _{F}^{*}$
cover the whole interval
$J^ {\mathbf {r}}, {\mathbf {r}}\in \Omega _{F}^{*}$
cover the whole interval
![]() $(1,2]$
up to a set of zero Hausdorff dimension. Here we strengthen this result and show that the exceptional set E is uncountable and has zero packing dimension. Furthermore, we show that each relative exceptional set
$(1,2]$
up to a set of zero Hausdorff dimension. Here we strengthen this result and show that the exceptional set E is uncountable and has zero packing dimension. Furthermore, we show that each relative exceptional set
![]() $E^ {\mathbf {S}}$
is uncountable and has zero box-counting dimension. The proof uses the following simple lemma.
$E^ {\mathbf {S}}$
is uncountable and has zero box-counting dimension. The proof uses the following simple lemma.
Lemma 5.5. Let
 $J^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}},\beta _{r}^ {\mathbf {S}}]=:[p,q]$
be any Lyndon interval. Then the length of
$J^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}},\beta _{r}^ {\mathbf {S}}]=:[p,q]$
be any Lyndon interval. Then the length of
![]() $J^ {\mathbf {S}}$
satisfies
$J^ {\mathbf {S}}$
satisfies
 $$ \begin{align*} |J^ {\mathbf{S}}|\leq \frac{q}{q-1}q^{-| {\mathbf{S}}|}. \end{align*} $$
$$ \begin{align*} |J^ {\mathbf{S}}|\leq \frac{q}{q-1}q^{-| {\mathbf{S}}|}. \end{align*} $$
Proof. Since
![]() $\delta (p)=\mathbb {L}( {\mathbf {S}})^{\infty }$
and
$\delta (p)=\mathbb {L}( {\mathbf {S}})^{\infty }$
and
![]() $\delta (q)=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty }$
, we have
$\delta (q)=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty }$
, we have
 $$ \begin{align*} (\mathbb{L}( {\mathbf{S}})^{+}0^{\infty})_{p}=1=(\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty})_{q}=:((c_{i}))_{q}. \end{align*} $$
$$ \begin{align*} (\mathbb{L}( {\mathbf{S}})^{+}0^{\infty})_{p}=1=(\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty})_{q}=:((c_{i}))_{q}. \end{align*} $$
It follows that
 $$ \begin{align*} |J^ {\mathbf{S}}|=q-p=\sum_{i=1}^{| {\mathbf{S}}|}\frac{c_{i}}{q^{i-1}}+\sum_{i=| {\mathbf{S}}|+1}^{\infty}\frac{c_{i}}{q^{i-1}}-\sum_{i=1}^{| {\mathbf{S}}|}\frac{c_{i}}{p^{i-1}} \le\sum_{i=| {\mathbf{S}}|+1}^{\infty}\frac{1}{q^{i-1}}=\frac{q}{q-1}q^{-| {\mathbf{S}}|}, \end{align*} $$
$$ \begin{align*} |J^ {\mathbf{S}}|=q-p=\sum_{i=1}^{| {\mathbf{S}}|}\frac{c_{i}}{q^{i-1}}+\sum_{i=| {\mathbf{S}}|+1}^{\infty}\frac{c_{i}}{q^{i-1}}-\sum_{i=1}^{| {\mathbf{S}}|}\frac{c_{i}}{p^{i-1}} \le\sum_{i=| {\mathbf{S}}|+1}^{\infty}\frac{1}{q^{i-1}}=\frac{q}{q-1}q^{-| {\mathbf{S}}|}, \end{align*} $$
as required.
Proposition 5.6.
-
(i) The exceptional set
is uncountable and has zero packing dimension. $$ \begin{align*} E=(1,2]\setminus\bigcup_{ {\mathbf{r}}\in\Omega_{F}^{*}}J^{ {\mathbf{r}}} \end{align*} $$
$$ \begin{align*} E=(1,2]\setminus\bigcup_{ {\mathbf{r}}\in\Omega_{F}^{*}}J^{ {\mathbf{r}}} \end{align*} $$
-
(ii) For any
 $ {\mathbf {S}}\in \Lambda $
, the relative exceptional set is uncountable and has zero box-counting dimension.
$ {\mathbf {S}}\in \Lambda $
, the relative exceptional set is uncountable and has zero box-counting dimension. $$ \begin{align*} E^ {\mathbf{S}}=(J^ {\mathbf{S}}\setminus I^ {\mathbf{S}})\setminus \bigcup_{ {\mathbf{r}}\in\Omega_{F}^{*}}J^{ {\mathbf{S}}\bullet {\mathbf{r}}} \end{align*} $$
$$ \begin{align*} E^ {\mathbf{S}}=(J^ {\mathbf{S}}\setminus I^ {\mathbf{S}})\setminus \bigcup_{ {\mathbf{r}}\in\Omega_{F}^{*}}J^{ {\mathbf{S}}\bullet {\mathbf{r}}} \end{align*} $$
Proof. (i) First we prove
![]() $\dim _{P} E=0$
. Let
$\dim _{P} E=0$
. Let
![]() $\rho _{N}\in (1,2]$
such that
$\rho _{N}\in (1,2]$
such that
![]() $\delta (\rho _{N})=(10^{N-1})^{\infty }$
. Then by Lemma 2.5, it follows that
$\delta (\rho _{N})=(10^{N-1})^{\infty }$
. Then by Lemma 2.5, it follows that
![]() $\rho _{N}\searrow 1$
as
$\rho _{N}\searrow 1$
as
![]() $N\to \infty $
. Thus
$N\to \infty $
. Thus
![]() $E=\bigcup _{N=1}^{\infty }(E\cap [\rho _{N},2])$
. By the countable stability of packing dimension (cf. [Reference Falconer16]), it suffices to prove that
$E=\bigcup _{N=1}^{\infty }(E\cap [\rho _{N},2])$
. By the countable stability of packing dimension (cf. [Reference Falconer16]), it suffices to prove that
Let
![]() $N\in \mathbb {N}$
. Take a Farey interval
$N\in \mathbb {N}$
. Take a Farey interval
![]() $J^ {\mathbf {s}}:=[p, q]\subset [\rho _{N}, 2]$
with
$J^ {\mathbf {s}}:=[p, q]\subset [\rho _{N}, 2]$
with
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{F}^{*}$
such that
$ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{F}^{*}$
such that
Write
![]() $\mathbb {L}( {\mathbf {s}})=a_{1}\ldots a_{m}$
. Then
$\mathbb {L}( {\mathbf {s}})=a_{1}\ldots a_{m}$
. Then
![]() $\delta (p)=(a_{1}\ldots a_{m})^{\infty }$
. Since
$\delta (p)=(a_{1}\ldots a_{m})^{\infty }$
. Since
![]() $p\ge \rho _{N}$
, by Lemma 2.5, we have
$p\ge \rho _{N}$
, by Lemma 2.5, we have
![]() $(a_{1}\ldots a_{m})^{\infty }=\delta (p)\succcurlyeq \delta (\rho _{N})=(10^{N-1})^{\infty }$
, which implies that
$(a_{1}\ldots a_{m})^{\infty }=\delta (p)\succcurlyeq \delta (\rho _{N})=(10^{N-1})^{\infty }$
, which implies that
![]() $a_{1}\ldots a_{N+1}\succcurlyeq 10^{N-1}1$
. Then by Proposition 2.4, we conclude that
$a_{1}\ldots a_{N+1}\succcurlyeq 10^{N-1}1$
. Then by Proposition 2.4, we conclude that
Note that
 $$ \begin{align*} (\mathbb{L}( {\mathbf{s}})^{+} 0^{\infty})_{p}=1=(\mathbb{L}( {\mathbf{s}})^{+}{ {\mathbf{s}}^{\infty}})_{q}=:((c_{i}))_{q}. \end{align*} $$
$$ \begin{align*} (\mathbb{L}( {\mathbf{s}})^{+} 0^{\infty})_{p}=1=(\mathbb{L}( {\mathbf{s}})^{+}{ {\mathbf{s}}^{\infty}})_{q}=:((c_{i}))_{q}. \end{align*} $$
So, by equation (5.10), it follows that
 $$ \begin{align*} \sum_{i=1}^{m}\frac{c_{i}}{p^{i}}=1=\sum_{i=1}^{m}\frac{c_{i}}{q^{i}}+\sum_{i=m+1}^{\infty}\frac{c_{i}}{q^{i}}>\sum_{i=1}^{m} \frac{c_{i}}{q^{i}}+\frac{1}{q^{m+N+1}}, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{m}\frac{c_{i}}{p^{i}}=1=\sum_{i=1}^{m}\frac{c_{i}}{q^{i}}+\sum_{i=m+1}^{\infty}\frac{c_{i}}{q^{i}}>\sum_{i=1}^{m} \frac{c_{i}}{q^{i}}+\frac{1}{q^{m+N+1}}, \end{align*} $$
which implies
 $$ \begin{align*} \frac{1}{q^{m+N+1}}<\sum_{i=1}^{\infty}\bigg(\frac{1}{p^{i}}-\frac{1}{q^{i}}\bigg)=\frac{q-p}{(p-1)(q-1)}. \end{align*} $$
$$ \begin{align*} \frac{1}{q^{m+N+1}}<\sum_{i=1}^{\infty}\bigg(\frac{1}{p^{i}}-\frac{1}{q^{i}}\bigg)=\frac{q-p}{(p-1)(q-1)}. \end{align*} $$
Whence,
 $$ \begin{align} |J^ {\mathbf{s}}|=q-p>\frac{(p-1)(q-1)}{q^{N+1}}q^{-m}\ge \frac{(\rho_{N}-1)^{2}}{2^{N+1}}q^{-m}. \end{align} $$
$$ \begin{align} |J^ {\mathbf{s}}|=q-p>\frac{(p-1)(q-1)}{q^{N+1}}q^{-m}\ge \frac{(\rho_{N}-1)^{2}}{2^{N+1}}q^{-m}. \end{align} $$
However, by Lemma 5.5, it follows that
 $$ \begin{align} |J^ {\mathbf{s}}|\le \frac{q}{q-1}q^{-m}\le\frac{2}{\rho_{N}-1}q^{-m} {\leq \frac{2}{\rho_{N}-1}\rho_{N}^{-m}}. \end{align} $$
$$ \begin{align} |J^ {\mathbf{s}}|\le \frac{q}{q-1}q^{-m}\le\frac{2}{\rho_{N}-1}q^{-m} {\leq \frac{2}{\rho_{N}-1}\rho_{N}^{-m}}. \end{align} $$
Now we list all of the Farey intervals in
![]() $[\rho _{N},2]$
in a decreasing order according to their length, say
$[\rho _{N},2]$
in a decreasing order according to their length, say
![]() $J^{ {\mathbf {s}}_{1}}, J^{ {\mathbf {s}}_{2}}, \ldots $
. In other words,
$J^{ {\mathbf {s}}_{1}}, J^{ {\mathbf {s}}_{2}}, \ldots $
. In other words,
![]() $|J^{ {\mathbf {s}}_{i}}|\ge |J^{ {\mathbf {s}}_{j}}|$
for any
$|J^{ {\mathbf {s}}_{i}}|\ge |J^{ {\mathbf {s}}_{j}}|$
for any
![]() $i<j$
. For a Farey interval
$i<j$
. For a Farey interval
![]() $J^ {\mathbf {s}}$
, if
$J^ {\mathbf {s}}$
, if
![]() $J^ {\mathbf {s}}=J^{ {\mathbf {s}}_{k}}$
, we then define its order index as
$J^ {\mathbf {s}}=J^{ {\mathbf {s}}_{k}}$
, we then define its order index as
![]() $o(J^ {\mathbf {s}})=k$
.
$o(J^ {\mathbf {s}})=k$
.
Set
![]() $C_{N}:=2\log 2/\log \rho _{N}$
. Let
$C_{N}:=2\log 2/\log \rho _{N}$
. Let
![]() $J^{ {\mathbf {s}}^{\prime }}$
be a Farey interval with
$J^{ {\mathbf {s}}^{\prime }}$
be a Farey interval with
![]() $| {\mathbf {s}}^{\prime }|>C_{N} m$
. Then by equations (5.9), (5.11), and (5.12), it follows that
$| {\mathbf {s}}^{\prime }|>C_{N} m$
. Then by equations (5.9), (5.11), and (5.12), it follows that
 $$ \begin{align*} |J^{ {\mathbf{s}}^{\prime}}|\le\frac{2}{\rho_{N}-1}\rho_{N}^{-C_{N} m}=\frac{2}{\rho_{N}-1}2^{-2m}<\frac{(\rho_{N}-1)^{2}}{2^{N+1}}2^{-m}\le |J^ {\mathbf{s}}|. \end{align*} $$
$$ \begin{align*} |J^{ {\mathbf{s}}^{\prime}}|\le\frac{2}{\rho_{N}-1}\rho_{N}^{-C_{N} m}=\frac{2}{\rho_{N}-1}2^{-2m}<\frac{(\rho_{N}-1)^{2}}{2^{N+1}}2^{-m}\le |J^ {\mathbf{s}}|. \end{align*} $$
This implies that
 $$ \begin{align} o(J^ {\mathbf{s}})\le\sum_{k=1}^{\lfloor C_{N} m\rfloor}\#\{ {\mathbf{s}}^{\prime}\in\Omega_{F}^{*}: | {\mathbf{s}}^{\prime}|=k\}\le\sum_{k=1}^{\lfloor C_{N} m\rfloor}(k-1)< C_{N}^{2} m^{2}, \end{align} $$
$$ \begin{align} o(J^ {\mathbf{s}})\le\sum_{k=1}^{\lfloor C_{N} m\rfloor}\#\{ {\mathbf{s}}^{\prime}\in\Omega_{F}^{*}: | {\mathbf{s}}^{\prime}|=k\}\le\sum_{k=1}^{\lfloor C_{N} m\rfloor}(k-1)< C_{N}^{2} m^{2}, \end{align} $$
where the second inequality follows by equation (2.1) since the number of non-degenerate Farey words of length k is at most
![]() $k-1$
(see [Reference Carminati, Isola and Tiozzo8, Proposition 2.3]). Together with equation (5.12), equation (5.13) implies that
$k-1$
(see [Reference Carminati, Isola and Tiozzo8, Proposition 2.3]). Together with equation (5.12), equation (5.13) implies that
 $$ \begin{align*} \liminf_{i\to\infty}\frac{-\log|J^{ {\mathbf{s}}_{i}}|}{o(J^{ {\mathbf{s}}_{i}})}&=+\infty. \end{align*} $$
$$ \begin{align*} \liminf_{i\to\infty}\frac{-\log|J^{ {\mathbf{s}}_{i}}|}{o(J^{ {\mathbf{s}}_{i}})}&=+\infty. \end{align*} $$
Note that
 $[\rho _{N},2]\cap E=[\rho _{N},2]\setminus \bigcup _{ {\mathbf {s}}\in \Omega _{F}^{*}}J^ {\mathbf {s}}$
. So, by [Reference Falconer17, Proposition 3.6], we conclude equation (5.8). This proves
$[\rho _{N},2]\cap E=[\rho _{N},2]\setminus \bigcup _{ {\mathbf {s}}\in \Omega _{F}^{*}}J^ {\mathbf {s}}$
. So, by [Reference Falconer17, Proposition 3.6], we conclude equation (5.8). This proves
![]() $\dim _{P} E=0$
.
$\dim _{P} E=0$
.
Next we prove that E is uncountable. For
![]() $ {\mathbf {s}}\in \Omega _{F}^{*}$
, let
$ {\mathbf {s}}\in \Omega _{F}^{*}$
, let
 $\hat J^ {\mathbf {s}}=(\beta _{\ell }^ {\mathbf {s}}, \beta _{r}^ {\mathbf {s}})$
be the interior of the Farey interval
$\hat J^ {\mathbf {s}}=(\beta _{\ell }^ {\mathbf {s}}, \beta _{r}^ {\mathbf {s}})$
be the interior of the Farey interval
![]() $J^ {\mathbf {s}}=[\beta _{\ell }^ {\mathbf {s}},\beta _{r}^ {\mathbf {s}}]$
. By Lemma 2.9(i), it follows that the compact set
$J^ {\mathbf {s}}=[\beta _{\ell }^ {\mathbf {s}},\beta _{r}^ {\mathbf {s}}]$
. By Lemma 2.9(i), it follows that the compact set
 $$ \begin{align*} \hat E:=[1,2]\setminus\bigcup_{ {\mathbf{s}}\in\Omega_{F}^{*}}\hat J^ {\mathbf{s}} \end{align*} $$
$$ \begin{align*} \hat E:=[1,2]\setminus\bigcup_{ {\mathbf{s}}\in\Omega_{F}^{*}}\hat J^ {\mathbf{s}} \end{align*} $$
is non-empty and has no isolated points. Hence,
![]() $\hat E$
is a perfect set and is therefore uncountable. Since
$\hat E$
is a perfect set and is therefore uncountable. Since
![]() $\hat {E}\backslash E$
is countable, it follows that E is uncountable as well.
$\hat {E}\backslash E$
is countable, it follows that E is uncountable as well.
(ii) In a similar way, we prove
![]() $\dim _{B} E^ {\mathbf {S}}=0$
. Note that
$\dim _{B} E^ {\mathbf {S}}=0$
. Note that
 $E^ {\mathbf {S}}=(\beta _{*}^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]\setminus \bigcup _{ {\mathbf {r}}\in \Omega _{F}^{*}}J^{S\bullet {\mathbf {r}}}$
. Fix a Farey word
$E^ {\mathbf {S}}=(\beta _{*}^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}}]\setminus \bigcup _{ {\mathbf {r}}\in \Omega _{F}^{*}}J^{S\bullet {\mathbf {r}}}$
. Fix a Farey word
![]() $ {\mathbf {r}}=r_{1}\ldots r_{m}$
. Then the Lyndon interval
$ {\mathbf {r}}=r_{1}\ldots r_{m}$
. Then the Lyndon interval
 $J^{ {\mathbf {S}}\bullet {\mathbf {r}}}=[\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}}, \beta _{r}^{ {\mathbf {S}}\bullet {\mathbf {r}}}]=:[p_ {\mathbf {r}}, q_ {\mathbf {r}}]$
satisfies
$J^{ {\mathbf {S}}\bullet {\mathbf {r}}}=[\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}}, \beta _{r}^{ {\mathbf {S}}\bullet {\mathbf {r}}}]=:[p_ {\mathbf {r}}, q_ {\mathbf {r}}]$
satisfies
 $$ \begin{align*} {(\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{+} 0^{\infty})_{p_ {\mathbf{r}}}=1=(\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{+} \; ( {\mathbf{S}}\bullet {\mathbf{r}})^{\infty})_{q_ {\mathbf{r}}}=:((d_{i}))_{q_ {\mathbf{r}}}.} \end{align*} $$
$$ \begin{align*} {(\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{+} 0^{\infty})_{p_ {\mathbf{r}}}=1=(\mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}})^{+} \; ( {\mathbf{S}}\bullet {\mathbf{r}})^{\infty})_{q_ {\mathbf{r}}}=:((d_{i}))_{q_ {\mathbf{r}}}.} \end{align*} $$
So,
 $$ \begin{align*} \sum_{i=1}^{m| {\mathbf{S}}|}\frac{d_{i}}{p_ {\mathbf{r}}^{i}}=1=\sum_{i=1}^{m| {\mathbf{S}}|}\frac{d_{i}}{q_ {\mathbf{r}}^{i}}+\sum_{i=m| {\mathbf{S}}|+1}^{\infty}\frac{d_{i}}{q_ {\mathbf{r}}^{i}}>\sum_{i=1}^{m| {\mathbf{S}}|}\frac{d_{i}}{q_ {\mathbf{r}}^{i}}+\frac{1}{q_ {\mathbf{r}}^{(m+1)| {\mathbf{S}}|+1}}, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{m| {\mathbf{S}}|}\frac{d_{i}}{p_ {\mathbf{r}}^{i}}=1=\sum_{i=1}^{m| {\mathbf{S}}|}\frac{d_{i}}{q_ {\mathbf{r}}^{i}}+\sum_{i=m| {\mathbf{S}}|+1}^{\infty}\frac{d_{i}}{q_ {\mathbf{r}}^{i}}>\sum_{i=1}^{m| {\mathbf{S}}|}\frac{d_{i}}{q_ {\mathbf{r}}^{i}}+\frac{1}{q_ {\mathbf{r}}^{(m+1)| {\mathbf{S}}|+1}}, \end{align*} $$
where the inequality follows by observing that
![]() $ {\mathbf {S}}\in \Omega _{L}^{*}$
and thus
$ {\mathbf {S}}\in \Omega _{L}^{*}$
and thus
![]() $ {\mathbf {S}}\bullet {\mathbf {r}}^{\infty }\succcurlyeq 0^{| {\mathbf {S}}|}10^{\infty }$
. Therefore,
$ {\mathbf {S}}\bullet {\mathbf {r}}^{\infty }\succcurlyeq 0^{| {\mathbf {S}}|}10^{\infty }$
. Therefore,
 $$ \begin{align*} \frac{1}{q_ {\mathbf{r}}^{(m+1)| {\mathbf{S}}|+1}}\le \sum_{i=1}^{\infty}\bigg(\frac{1}{p_ {\mathbf{r}}^{i}}-\frac{1}{q_ {\mathbf{r}}^{i}}\bigg)=\frac{q_ {\mathbf{r}}-p_ {\mathbf{r}}}{(p_ {\mathbf{r}}-1)(q_ {\mathbf{r}}-1)}, \end{align*} $$
$$ \begin{align*} \frac{1}{q_ {\mathbf{r}}^{(m+1)| {\mathbf{S}}|+1}}\le \sum_{i=1}^{\infty}\bigg(\frac{1}{p_ {\mathbf{r}}^{i}}-\frac{1}{q_ {\mathbf{r}}^{i}}\bigg)=\frac{q_ {\mathbf{r}}-p_ {\mathbf{r}}}{(p_ {\mathbf{r}}-1)(q_ {\mathbf{r}}-1)}, \end{align*} $$
which implies
 $$ \begin{align*} |J^{ {\mathbf{S}}\bullet {\mathbf{r}}}|=q_ {\mathbf{r}}-p_ {\mathbf{r}}\ge \frac{(p_ {\mathbf{r}}-1)(q_ {\mathbf{r}}-1)}{q_ {\mathbf{r}}^{| {\mathbf{S}}|+1}}q_ {\mathbf{r}}^{-| {\mathbf{S}}\bullet {\mathbf{r}}|}>\frac{(\beta_{*}^ {\mathbf{S}}-1)^{2}}{2^{| {\mathbf{S}}|+1}}q_ {\mathbf{r}}^{-| {\mathbf{S}}\bullet {\mathbf{r}}|}. \end{align*} $$
$$ \begin{align*} |J^{ {\mathbf{S}}\bullet {\mathbf{r}}}|=q_ {\mathbf{r}}-p_ {\mathbf{r}}\ge \frac{(p_ {\mathbf{r}}-1)(q_ {\mathbf{r}}-1)}{q_ {\mathbf{r}}^{| {\mathbf{S}}|+1}}q_ {\mathbf{r}}^{-| {\mathbf{S}}\bullet {\mathbf{r}}|}>\frac{(\beta_{*}^ {\mathbf{S}}-1)^{2}}{2^{| {\mathbf{S}}|+1}}q_ {\mathbf{r}}^{-| {\mathbf{S}}\bullet {\mathbf{r}}|}. \end{align*} $$
However, by Lemma 5.5, it follows that
 $$ \begin{align*} |J^{ {\mathbf{S}}\bullet {\mathbf{r}}}|\leq \frac{q_ {\mathbf{r}}}{q_ {\mathbf{r}}-1}q_ {\mathbf{r}}^{-m| {\mathbf{S}}|}\le\frac{2}{\beta_{*}^ {\mathbf{S}}-1}q_ {\mathbf{r}}^{-| {\mathbf{S}}\bullet {\mathbf{r}}|}. \end{align*} $$
$$ \begin{align*} |J^{ {\mathbf{S}}\bullet {\mathbf{r}}}|\leq \frac{q_ {\mathbf{r}}}{q_ {\mathbf{r}}-1}q_ {\mathbf{r}}^{-m| {\mathbf{S}}|}\le\frac{2}{\beta_{*}^ {\mathbf{S}}-1}q_ {\mathbf{r}}^{-| {\mathbf{S}}\bullet {\mathbf{r}}|}. \end{align*} $$
Now let
![]() $(J^{ {\mathbf {S}}\bullet {\mathbf {r}}_{i}})$
be an enumeration of the intervals
$(J^{ {\mathbf {S}}\bullet {\mathbf {r}}_{i}})$
be an enumeration of the intervals
![]() $J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
,
$J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
,
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
, arranged in order by decreasing length. Then by a similar argument as in (i) above, we obtain
$ {\mathbf {r}}\in \Omega _{F}^{*}$
, arranged in order by decreasing length. Then by a similar argument as in (i) above, we obtain
 $$ \begin{align*} \liminf_{i\to\infty}\frac{-\log|J^{ {\mathbf{S}}\bullet {\mathbf{r}}_{i}}|}{\log o(J^{ {\mathbf{S}}\bullet {\mathbf{r}}_{i}})}{=+\infty}. \end{align*} $$
$$ \begin{align*} \liminf_{i\to\infty}\frac{-\log|J^{ {\mathbf{S}}\bullet {\mathbf{r}}_{i}}|}{\log o(J^{ {\mathbf{S}}\bullet {\mathbf{r}}_{i}})}{=+\infty}. \end{align*} $$
Thus,
![]() $\dim _{B} E^ {\mathbf {S}}=0$
.
$\dim _{B} E^ {\mathbf {S}}=0$
.
Finally, since we showed in (i) that E is uncountable, we conclude by Lemma 5.3 and Proposition 5.4 that
![]() $E^ {\mathbf {S}}=\Psi _ {\mathbf {S}}(E)$
is also uncountable. This completes the proof.
$E^ {\mathbf {S}}=\Psi _ {\mathbf {S}}(E)$
is also uncountable. This completes the proof.
5.2 The infinitely Farey set
Recall from equation (1.7) that
 $$ \begin{align*} E_{\infty}=\bigcap_{n=1}^{\infty}\bigcup_{ {\mathbf{S}}\in\Lambda(n)}J^ {\mathbf{S}}, \end{align*} $$
$$ \begin{align*} E_{\infty}=\bigcap_{n=1}^{\infty}\bigcup_{ {\mathbf{S}}\in\Lambda(n)}J^ {\mathbf{S}}, \end{align*} $$
where
In particular,
![]() $\Lambda (1)=\Omega _{F}^{*}$
and
$\Lambda (1)=\Omega _{F}^{*}$
and
![]() $\Lambda =\bigcup _{n=1}^{\infty }\Lambda (n)$
. Note that
$\Lambda =\bigcup _{n=1}^{\infty }\Lambda (n)$
. Note that
 $(1,2]=E\cup \bigcup _{ {\mathbf {s}}\in \Omega _{F}^{*}}J^ {\mathbf {s}}$
. Furthermore, for each word
$(1,2]=E\cup \bigcup _{ {\mathbf {s}}\in \Omega _{F}^{*}}J^ {\mathbf {s}}$
. Furthermore, for each word
![]() $ {\mathbf {S}}\in \Lambda $
, we have
$ {\mathbf {S}}\in \Lambda $
, we have
 $$ \begin{align*} J^ {\mathbf{S}}\setminus I^ {\mathbf{S}}=E^ {\mathbf{S}}\cup\bigcup_{ {\mathbf{r}}\in\Omega_{F}^{*}}J^{ {\mathbf{S}}\bullet {\mathbf{r}}}. \end{align*} $$
$$ \begin{align*} J^ {\mathbf{S}}\setminus I^ {\mathbf{S}}=E^ {\mathbf{S}}\cup\bigcup_{ {\mathbf{r}}\in\Omega_{F}^{*}}J^{ {\mathbf{S}}\bullet {\mathbf{r}}}. \end{align*} $$
By iteration of the above equation, we obtain the following partition of the interval
![]() $(1,2]$
.
$(1,2]$
.
Lemma 5.7. The interval
![]() $(1,2]$
can be partitioned as
$(1,2]$
can be partitioned as
 $$ \begin{align*} (1,2]=E\cup E_{\infty}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}E^ {\mathbf{S}}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}I^ {\mathbf{S}}. \end{align*} $$
$$ \begin{align*} (1,2]=E\cup E_{\infty}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}E^ {\mathbf{S}}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}I^ {\mathbf{S}}. \end{align*} $$
To complete the proof of Theorem 3, we still need the following dimension result for
![]() $E_{\infty }$
.
$E_{\infty }$
.
Proposition 5.8. We have
![]() $\dim _{H} E_{\infty }=0$
.
$\dim _{H} E_{\infty }=0$
.
Proof. Note by equation (1.7) that
 $$ \begin{align} E_{\infty}=\bigcap_{n=1}^{\infty}\bigcup_{ {\mathbf{S}}\in\Lambda(n)}J^ {\mathbf{S}} \subset \bigcap_{n=1}^{\infty}\bigcup_{ {\mathbf{S}}\in\Lambda:| {\mathbf{S}}|\geq n}J^ {\mathbf{S}}. \end{align} $$
$$ \begin{align} E_{\infty}=\bigcap_{n=1}^{\infty}\bigcup_{ {\mathbf{S}}\in\Lambda(n)}J^ {\mathbf{S}} \subset \bigcap_{n=1}^{\infty}\bigcup_{ {\mathbf{S}}\in\Lambda:| {\mathbf{S}}|\geq n}J^ {\mathbf{S}}. \end{align} $$
This suggests covering
![]() $E_{\infty }$
by the intervals
$E_{\infty }$
by the intervals
![]() $J^ {\mathbf {S}}$
for
$J^ {\mathbf {S}}$
for
![]() $ {\mathbf {S}}\in \Lambda $
with
$ {\mathbf {S}}\in \Lambda $
with
![]() $| {\mathbf {S}}|\geq n$
for a sufficiently large n. To this end, we first estimate the diameter of
$| {\mathbf {S}}|\geq n$
for a sufficiently large n. To this end, we first estimate the diameter of
![]() $J^ {\mathbf {S}}$
. Take
$J^ {\mathbf {S}}$
. Take
![]() $ {\mathbf {S}}\in \Lambda $
with
$ {\mathbf {S}}\in \Lambda $
with
![]() $| {\mathbf {S}}|=m$
, and write
$| {\mathbf {S}}|=m$
, and write
![]() $J^ {\mathbf {S}}=[p,q]$
. Then
$J^ {\mathbf {S}}=[p,q]$
. Then
![]() $\delta (p)=\mathbb {L}( {\mathbf {S}})^{\infty }$
and
$\delta (p)=\mathbb {L}( {\mathbf {S}})^{\infty }$
and
![]() $\delta (q)=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty }$
, and it follows from Lemma 5.5 that
$\delta (q)=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty }$
, and it follows from Lemma 5.5 that
 $$ \begin{align} {|J^ {\mathbf{S}}|\leq \frac{q}{q-1}\cdot q^{-m}.} \end{align} $$
$$ \begin{align} {|J^ {\mathbf{S}}|\leq \frac{q}{q-1}\cdot q^{-m}.} \end{align} $$
Let
![]() $(\beta _{n})$
be an arbitrary sequence in
$(\beta _{n})$
be an arbitrary sequence in
![]() $(1,2)$
decreasing to
$(1,2)$
decreasing to
![]() $1$
. We will use equation (5.15) to show that
$1$
. We will use equation (5.15) to show that
![]() $\dim _{H} (E_{\infty }\cap (\beta _{n},2])=0$
for all
$\dim _{H} (E_{\infty }\cap (\beta _{n},2])=0$
for all
![]() $n\in \mathbb {N}$
, so the result will follow from the countable stability of Hausdorff dimension (cf. [Reference Falconer16]). Fix
$n\in \mathbb {N}$
, so the result will follow from the countable stability of Hausdorff dimension (cf. [Reference Falconer16]). Fix
![]() $n\in \mathbb {N}$
. Observe that if
$n\in \mathbb {N}$
. Observe that if
![]() $J^ {\mathbf {S}}=[p,q]$
intersects
$J^ {\mathbf {S}}=[p,q]$
intersects
![]() $(\beta _{n},2]$
, then
$(\beta _{n},2]$
, then
![]() $q>\beta _{n}$
and so by equation (5.15),
$q>\beta _{n}$
and so by equation (5.15),
 $$ \begin{align} |J^ {\mathbf{S}}|\leq \frac{2}{\beta_{n}-1}\beta_{n}^{-m}=:C_{n}\beta_{n}^{-m}. \end{align} $$
$$ \begin{align} |J^ {\mathbf{S}}|\leq \frac{2}{\beta_{n}-1}\beta_{n}^{-m}=:C_{n}\beta_{n}^{-m}. \end{align} $$
Next, we count how many words
![]() $ {\mathbf {S}}\in \Lambda $
there are with
$ {\mathbf {S}}\in \Lambda $
there are with
![]() $| {\mathbf {S}}|=m$
. Call this number
$| {\mathbf {S}}|=m$
. Call this number
![]() $N_{m}$
. Observe that if
$N_{m}$
. Observe that if
![]() $ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet {\mathbf {s}}_{2}\bullet \cdots \bullet {\mathbf {s}}_{k}$
and
$ {\mathbf {S}}= {\mathbf {s}}_{1}\bullet {\mathbf {s}}_{2}\bullet \cdots \bullet {\mathbf {s}}_{k}$
and
![]() $| {\mathbf {s}}_{i}|=l_{i}$
for
$| {\mathbf {s}}_{i}|=l_{i}$
for
![]() $i=1,\ldots ,k$
, then
$i=1,\ldots ,k$
, then
![]() $| {\mathbf {S}}|=l_{1} l_{2}\ldots l_{k}$
. Note by [Reference Carminati, Isola and Tiozzo8, Proposition 2.3] that
$| {\mathbf {S}}|=l_{1} l_{2}\ldots l_{k}$
. Note by [Reference Carminati, Isola and Tiozzo8, Proposition 2.3] that
![]() $\#\{ {\mathbf {r}}\in \Omega _{F}^{*}: | {\mathbf {r}}|=l\}\le l-1$
for any
$\#\{ {\mathbf {r}}\in \Omega _{F}^{*}: | {\mathbf {r}}|=l\}\le l-1$
for any
![]() $l\ge 2$
. Thus, for any given tuple
$l\ge 2$
. Thus, for any given tuple
![]() $(l_{1},\ldots ,l_{k})$
, the number of possible choices for the words
$(l_{1},\ldots ,l_{k})$
, the number of possible choices for the words
![]() $ {\mathbf {s}}_{1},\ldots , {\mathbf {s}}_{k}$
is at most
$ {\mathbf {s}}_{1},\ldots , {\mathbf {s}}_{k}$
is at most
![]() $l_{1} l_{2}\ldots l_{k}=| {\mathbf {S}}|=m$
. It remains to estimate how many ordered factorizations of m there are, that is, to estimate the number
$l_{1} l_{2}\ldots l_{k}=| {\mathbf {S}}|=m$
. It remains to estimate how many ordered factorizations of m there are, that is, to estimate the number
By considering the possible values of
![]() $l_{1}$
, it is easy to see that
$l_{1}$
, it is easy to see that
![]() $f_{m}$
satisfies the recursion
$f_{m}$
satisfies the recursion
 $$ \begin{align*} f_{m}=\sum_{d|m, d>1}f_{m/d}, \end{align*} $$
$$ \begin{align*} f_{m}=\sum_{d|m, d>1}f_{m/d}, \end{align*} $$
where we set
![]() $f_{1}:=1$
. (See [Reference Hille19].) We claim that
$f_{1}:=1$
. (See [Reference Hille19].) We claim that
![]() $f_{m}\leq m^{2}$
. This is trivial for
$f_{m}\leq m^{2}$
. This is trivial for
![]() $m=1$
, so let
$m=1$
, so let
![]() $m\geq 2$
and assume
$m\geq 2$
and assume
![]() $f_{n}\leq n^{2}$
for all
$f_{n}\leq n^{2}$
for all
![]() $n<m$
; then
$n<m$
; then
 $$ \begin{align*} f_{m}=\sum_{d|m, d>1}f_{m/d}\leq \sum_{d|m, d>1}\bigg(\frac{m}{d}\bigg)^{2} \leq m^{2}\sum_{d=2}^{\infty} \frac{1}{d^{2}}=m^{2}\bigg(\frac{\pi^{2}}{6}-1\bigg)<m^{2}. \end{align*} $$
$$ \begin{align*} f_{m}=\sum_{d|m, d>1}f_{m/d}\leq \sum_{d|m, d>1}\bigg(\frac{m}{d}\bigg)^{2} \leq m^{2}\sum_{d=2}^{\infty} \frac{1}{d^{2}}=m^{2}\bigg(\frac{\pi^{2}}{6}-1\bigg)<m^{2}. \end{align*} $$
This proves the claim, and we thus conclude that
![]() $N_{m}\leq m^{3}$
. Now, given
$N_{m}\leq m^{3}$
. Now, given
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() ${\delta>0}$
, choose N large enough so that
${\delta>0}$
, choose N large enough so that
![]() $C_{n} (\beta _{n})^{-N}<\delta $
. Using equations (5.14) and (5.16), we obtain
$C_{n} (\beta _{n})^{-N}<\delta $
. Using equations (5.14) and (5.16), we obtain
 $$ \begin{align*} \mathcal H_{\delta}^{\varepsilon}(E_{\infty{\cap(\beta_{n},2]}})\leq \sum_{ {\mathbf{S}}\in\Lambda: | {\mathbf{S}}|\geq N,\ J^ {\mathbf{S}}\cap(\beta_{n},2]\neq\emptyset} |J^ {\mathbf{S}}|^{\varepsilon}\leq \sum_{m=N}^{\infty} m^{3} {C_{n}^{\varepsilon}\beta_{n}^{-m\varepsilon}}\to 0 \end{align*} $$
$$ \begin{align*} \mathcal H_{\delta}^{\varepsilon}(E_{\infty{\cap(\beta_{n},2]}})\leq \sum_{ {\mathbf{S}}\in\Lambda: | {\mathbf{S}}|\geq N,\ J^ {\mathbf{S}}\cap(\beta_{n},2]\neq\emptyset} |J^ {\mathbf{S}}|^{\varepsilon}\leq \sum_{m=N}^{\infty} m^{3} {C_{n}^{\varepsilon}\beta_{n}^{-m\varepsilon}}\to 0 \end{align*} $$
as
![]() $N\to \infty $
. This shows that
$N\to \infty $
. This shows that
![]() $\dim _{H} {(E_{\infty }\cap (\beta _{n},2])}=0$
, as desired.
$\dim _{H} {(E_{\infty }\cap (\beta _{n},2])}=0$
, as desired.
6 Critical values in the exceptional sets
By Proposition 1.12, Theorem 2, and Theorem 3, it suffices to determine the critical value
![]() $\tau (\beta )$
for
$\tau (\beta )$
for
 $$ \begin{align*} \beta\in \bigcup_{ {\mathbf{S}}\in\Lambda}E^ {\mathbf{S}}\cup E_{\infty}. \end{align*} $$
$$ \begin{align*} \beta\in \bigcup_{ {\mathbf{S}}\in\Lambda}E^ {\mathbf{S}}\cup E_{\infty}. \end{align*} $$
First we compute
![]() $\tau (\beta )$
for
$\tau (\beta )$
for
 $\beta \in \bigcup _{ {\mathbf {S}}\in \Lambda }E^ {\mathbf {S}}$
. Recall from Lemma 5.3 and Proposition 5.4 that for each
$\beta \in \bigcup _{ {\mathbf {S}}\in \Lambda }E^ {\mathbf {S}}$
. Recall from Lemma 5.3 and Proposition 5.4 that for each
![]() $ {\mathbf {S}}\in \Lambda $
, the map
$ {\mathbf {S}}\in \Lambda $
, the map
![]() $\Psi _ {\mathbf {S}}$
bijectively maps the exceptional set
$\Psi _ {\mathbf {S}}$
bijectively maps the exceptional set
 $E=(1,2]\setminus \bigcup _{ {\mathbf {s}}\in \Omega _{F}^{*}}J^ {\mathbf {s}}$
to the relative exceptional set
$E=(1,2]\setminus \bigcup _{ {\mathbf {s}}\in \Omega _{F}^{*}}J^ {\mathbf {s}}$
to the relative exceptional set
 $E^ {\mathbf {S}}= (J^ {\mathbf {S}}\setminus I^ {\mathbf {S}})\setminus \bigcup _{ {\mathbf {r}}\in \Omega _{F}^{*}}J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
.
$E^ {\mathbf {S}}= (J^ {\mathbf {S}}\setminus I^ {\mathbf {S}})\setminus \bigcup _{ {\mathbf {r}}\in \Omega _{F}^{*}}J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
.
Lemma 6.1. Let
![]() $\hat {\beta }\in E\backslash \{2\}$
with
$\hat {\beta }\in E\backslash \{2\}$
with
![]() $\delta (\hat {\beta })=\delta _{1}\delta _{2}\ldots .$
Also let
$\delta (\hat {\beta })=\delta _{1}\delta _{2}\ldots .$
Also let
![]() $ {\mathbf {S}}\in \Lambda $
, and set
$ {\mathbf {S}}\in \Lambda $
, and set
![]() $\beta :=\Psi _ {\mathbf {S}}(\hat {\beta })$
. Then
$\beta :=\Psi _ {\mathbf {S}}(\hat {\beta })$
. Then
-
(i)
 $b(\tau (\hat {\beta }),\hat {\beta })=0\delta _{2}\delta _{3}\ldots ;$
and
$b(\tau (\hat {\beta }),\hat {\beta })=0\delta _{2}\delta _{3}\ldots ;$
and -
(ii) the map
 $\hat {t}\mapsto (\Phi _ {\mathbf {S}}(b(\hat {t},\hat {\beta })))_{\beta }$
is continuous at
$\hat {t}\mapsto (\Phi _ {\mathbf {S}}(b(\hat {t},\hat {\beta })))_{\beta }$
is continuous at
 $\tau (\hat {\beta })$
.
$\tau (\hat {\beta })$
.
Proof. First we prove (i). Note by Proposition 1.12 that
 $\tau (\hat \beta )=1-{1/\hat \beta }=(0\delta _{2}\delta _{3}\ldots )_{\hat \beta }$
. So by Lemma 2.10, it suffices to verify that
$\tau (\hat \beta )=1-{1/\hat \beta }=(0\delta _{2}\delta _{3}\ldots )_{\hat \beta }$
. So by Lemma 2.10, it suffices to verify that
By Lemma 2.5, it is immediate that
![]() $\sigma ^{n}(0\delta _{2}\delta _{3}\ldots )\preccurlyeq {(\delta _{i})}$
for all
$\sigma ^{n}(0\delta _{2}\delta _{3}\ldots )\preccurlyeq {(\delta _{i})}$
for all
![]() $n\geq 0$
. If equality holds for some n, then
$n\geq 0$
. If equality holds for some n, then
![]() $\delta (\hat {\beta }){=(\delta _{i})}$
is periodic with period
$\delta (\hat {\beta }){=(\delta _{i})}$
is periodic with period
![]() $m\geq 2$
(since
$m\geq 2$
(since
![]() $\hat {\beta }\neq 2$
), so by Lemma 2.8,
$\hat {\beta }\neq 2$
), so by Lemma 2.8,
![]() $\delta (\hat {\beta })=\mathbb {L}( {\mathbf {r}})^{\infty }$
for some Lyndon word
$\delta (\hat {\beta })=\mathbb {L}( {\mathbf {r}})^{\infty }$
for some Lyndon word
![]() $ {\mathbf {r}}$
. This implies
$ {\mathbf {r}}$
. This implies
 $\hat {\beta }={\beta _{\ell }^{ {\mathbf {r}}}}\in J^{ {\mathbf {r}}}$
. However, then by Lemma 2.9,
$\hat {\beta }={\beta _{\ell }^{ {\mathbf {r}}}}\in J^{ {\mathbf {r}}}$
. However, then by Lemma 2.9,
![]() $\hat {\beta }\in J^ {\mathbf {s}}$
for some Farey word
$\hat {\beta }\in J^ {\mathbf {s}}$
for some Farey word
![]() $ {\mathbf {s}}$
, and so
$ {\mathbf {s}}$
, and so
![]() $\hat {\beta }\not \in E$
, a contradiction. This proves equation (6.1), and then yields statement (i).
$\hat {\beta }\not \in E$
, a contradiction. This proves equation (6.1), and then yields statement (i).
For (ii), note by Lemma 2.10(ii) that the map
![]() $\hat {t}\mapsto b(\hat {t},\hat {\beta })$
is continuous at all points
$\hat {t}\mapsto b(\hat {t},\hat {\beta })$
is continuous at all points
![]() $\hat {t}$
for which
$\hat {t}$
for which
![]() $b(\hat t,\hat \beta )$
does not end with
$b(\hat t,\hat \beta )$
does not end with
![]() $0^{\infty }$
. Furthermore, the map
$0^{\infty }$
. Furthermore, the map
![]() $\Phi _ {\mathbf {S}}$
is continuous with respect to the order topology. So, by statement (i), it follows that the map
$\Phi _ {\mathbf {S}}$
is continuous with respect to the order topology. So, by statement (i), it follows that the map
 $\hat {t}\mapsto (\Phi _ {\mathbf {S}}(b(\hat {t},\hat {\beta })))_{\beta }$
is continuous at
$\hat {t}\mapsto (\Phi _ {\mathbf {S}}(b(\hat {t},\hat {\beta })))_{\beta }$
is continuous at
![]() $\tau (\hat {\beta })$
, completing the proof.
$\tau (\hat {\beta })$
, completing the proof.
Proposition 6.2. Let
![]() $ {\mathbf {S}}\in \Lambda $
. Then for any
$ {\mathbf {S}}\in \Lambda $
. Then for any
![]() $\beta \in E^ {\mathbf {S}}$
, we have
$\beta \in E^ {\mathbf {S}}$
, we have
where
![]() $1\delta _{2}\delta _{3}\ldots $
is the quasi-greedy expansion of
$1\delta _{2}\delta _{3}\ldots $
is the quasi-greedy expansion of
![]() $1$
in base
$1$
in base
 $\hat \beta :=\Psi _ {\mathbf {S}}^{-1}(\beta )$
.
$\hat \beta :=\Psi _ {\mathbf {S}}^{-1}(\beta )$
.
Proof. Let
![]() $\beta \in E^ {\mathbf {S}}$
. Then by Lemma 5.3 and Proposition 5.4, there exists a unique
$\beta \in E^ {\mathbf {S}}$
. Then by Lemma 5.3 and Proposition 5.4, there exists a unique
![]() $\hat \beta \in E$
such that
$\hat \beta \in E$
such that
 ${\hat \beta }=\Psi _ {\mathbf {S}}^{-1}(\beta )\in E$
, in other words,
${\hat \beta }=\Psi _ {\mathbf {S}}^{-1}(\beta )\in E$
, in other words,
![]() $\delta (\beta )=\Phi _ {\mathbf {S}}(\delta ({\hat \beta }))$
. Write
$\delta (\beta )=\Phi _ {\mathbf {S}}(\delta ({\hat \beta }))$
. Write
![]() $\delta ({\hat \beta })=\delta _{1}\delta _{2}\ldots $
and set
$\delta ({\hat \beta })=\delta _{1}\delta _{2}\ldots $
and set
![]() $t^{*}:=(\Phi _ {\mathbf {S}}(0\delta _{2}\delta _{3}\ldots ))_{\beta }$
. We will show that
$t^{*}:=(\Phi _ {\mathbf {S}}(0\delta _{2}\delta _{3}\ldots ))_{\beta }$
. We will show that
![]() $\tau (\beta )=t^{*}$
, by proving that
$\tau (\beta )=t^{*}$
, by proving that
![]() $h_{\mathrm {top}}(\mathbf K_{\beta }(t))>0$
for
$h_{\mathrm {top}}(\mathbf K_{\beta }(t))>0$
for
![]() $t<t^{*}$
, and
$t<t^{*}$
, and
![]() $\mathbf K_{\beta }(t)$
is countable for
$\mathbf K_{\beta }(t)$
is countable for
![]() $t>t^{*}$
. We consider separately the two cases: (i)
$t>t^{*}$
. We consider separately the two cases: (i)
![]() $\hat {\beta }<2$
and (ii)
$\hat {\beta }<2$
and (ii)
![]() $\hat {\beta }=2$
.
$\hat {\beta }=2$
.
Case I.
![]() $\hat {\beta }<2$
. First, for notational convenience, we define the map
$\hat {\beta }<2$
. First, for notational convenience, we define the map
 $$ \begin{align*} \Theta_{ {\mathbf{S}},\hat{\beta}}: (0,1)\to (0,1); \quad \hat{t}\mapsto (\Phi_ {\mathbf{S}}(b(\hat{t},\hat{\beta})))_{\beta}. \end{align*} $$
$$ \begin{align*} \Theta_{ {\mathbf{S}},\hat{\beta}}: (0,1)\to (0,1); \quad \hat{t}\mapsto (\Phi_ {\mathbf{S}}(b(\hat{t},\hat{\beta})))_{\beta}. \end{align*} $$
Since by Lemma 6.1 the map
 $\Theta _{ {\mathbf {S}},\hat {\beta }}$
is continuous at
$\Theta _{ {\mathbf {S}},\hat {\beta }}$
is continuous at
![]() $\tau (\hat {\beta })$
and
$\tau (\hat {\beta })$
and
 $t^{*}=\Theta _{ {\mathbf {S}},\hat {\beta }}(\tau (\hat \beta ))=(\Phi _ {\mathbf {S}}(0\delta _{2}\delta _{3}\ldots ))_{\beta }$
, it is, by the monotonicity of the set-valued map
$t^{*}=\Theta _{ {\mathbf {S}},\hat {\beta }}(\tau (\hat \beta ))=(\Phi _ {\mathbf {S}}(0\delta _{2}\delta _{3}\ldots ))_{\beta }$
, it is, by the monotonicity of the set-valued map
![]() $t\mapsto \mathbf K_{\beta }(t)$
, sufficient to prove the following two things:
$t\mapsto \mathbf K_{\beta }(t)$
, sufficient to prove the following two things:
 $$ \begin{align} \hat{t}<\tau(\hat{\beta}) \quad \Longrightarrow \quad h_{\mathrm{top}}(\mathbf K_{\beta}(\Theta_{ {\mathbf{S}},\hat{\beta}}(\hat{t})))>0, \end{align} $$
$$ \begin{align} \hat{t}<\tau(\hat{\beta}) \quad \Longrightarrow \quad h_{\mathrm{top}}(\mathbf K_{\beta}(\Theta_{ {\mathbf{S}},\hat{\beta}}(\hat{t})))>0, \end{align} $$
and
 $$ \begin{align} \hat{t}>\tau(\hat{\beta}) \quad \Longrightarrow \quad \mathbf K_{\beta}(\Theta_{ {\mathbf{S}},\hat{\beta}}(\hat{t}))\ \mbox{is countable}. \end{align} $$
$$ \begin{align} \hat{t}>\tau(\hat{\beta}) \quad \Longrightarrow \quad \mathbf K_{\beta}(\Theta_{ {\mathbf{S}},\hat{\beta}}(\hat{t}))\ \mbox{is countable}. \end{align} $$
First, take
![]() $\hat {t}<\tau (\hat {\beta })$
and set
$\hat {t}<\tau (\hat {\beta })$
and set
 $t:=\Theta _{ {\mathbf {S}},\hat {\beta }}(\hat {t})=(\Phi _ {\mathbf {S}}(b(\hat t, \hat \beta )))_{\beta }$
. Since
$t:=\Theta _{ {\mathbf {S}},\hat {\beta }}(\hat {t})=(\Phi _ {\mathbf {S}}(b(\hat t, \hat \beta )))_{\beta }$
. Since
![]() $\sigma ^{n}(b(\hat {t},\hat {\beta }))\prec \delta (\hat {\beta })$
for all
$\sigma ^{n}(b(\hat {t},\hat {\beta }))\prec \delta (\hat {\beta })$
for all
![]() $n\geq 0$
, Lemma 3.8 implies that
$n\geq 0$
, Lemma 3.8 implies that
Hence,
![]() $b(t,\beta )=\Phi _ {\mathbf {S}}(b(\hat {t},\hat {\beta }))$
. Now
$b(t,\beta )=\Phi _ {\mathbf {S}}(b(\hat {t},\hat {\beta }))$
. Now
 $$ \begin{align*} \Phi_ {\mathbf{S}}(\mathbf K_{\hat\beta}(\hat{t}))&=\{\Phi_ {\mathbf{S}}((x_{i})): b(\hat{t},\hat{\beta})\preccurlyeq \sigma^{n}((x_{i}))\prec\delta(\hat{\beta}) \text{ for all } n\geq 0\}\\[3pt] &\subset \{\Phi_ {\mathbf{S}}((x_{i})): \Phi_ {\mathbf{S}}(b(\hat{t},\hat{\beta}))\preccurlyeq \sigma^{n}(\Phi_ {\mathbf{S}}((x_{i})))\prec\Phi_ {\mathbf{S}}(\delta(\hat{\beta})) \text{ for all } n\geq 0\}\\[3pt] &=\{\Phi_ {\mathbf{S}}((x_{i})): b(t,\beta)\preccurlyeq \sigma^{n}(\Phi_ {\mathbf{S}}((x_{i})))\prec \delta(\beta) \text{ for all } n\geq 0\}\\[3pt] &\subset \{(y_{i}): b(t,\beta)\preccurlyeq \sigma^{n}((y_{i})) \prec \delta(\beta) \text{ for all } n\geq 0\}=\mathbf K_{\beta}(t), \end{align*} $$
$$ \begin{align*} \Phi_ {\mathbf{S}}(\mathbf K_{\hat\beta}(\hat{t}))&=\{\Phi_ {\mathbf{S}}((x_{i})): b(\hat{t},\hat{\beta})\preccurlyeq \sigma^{n}((x_{i}))\prec\delta(\hat{\beta}) \text{ for all } n\geq 0\}\\[3pt] &\subset \{\Phi_ {\mathbf{S}}((x_{i})): \Phi_ {\mathbf{S}}(b(\hat{t},\hat{\beta}))\preccurlyeq \sigma^{n}(\Phi_ {\mathbf{S}}((x_{i})))\prec\Phi_ {\mathbf{S}}(\delta(\hat{\beta})) \text{ for all } n\geq 0\}\\[3pt] &=\{\Phi_ {\mathbf{S}}((x_{i})): b(t,\beta)\preccurlyeq \sigma^{n}(\Phi_ {\mathbf{S}}((x_{i})))\prec \delta(\beta) \text{ for all } n\geq 0\}\\[3pt] &\subset \{(y_{i}): b(t,\beta)\preccurlyeq \sigma^{n}((y_{i})) \prec \delta(\beta) \text{ for all } n\geq 0\}=\mathbf K_{\beta}(t), \end{align*} $$
where the first inclusion again follows by Lemma 3.8. We deduce that
 $$ \begin{align*} h_{\mathrm{top}}(\mathbf K_{\beta}(t))\geq h_{\mathrm{top}}(\Phi_ {\mathbf{S}}(\mathbf K_{\hat\beta}(\hat{t})))=| {\mathbf{S}}|^{-1}h_{\mathrm{top}}(\mathbf K_{\hat\beta}(\hat{t}))>0, \end{align*} $$
$$ \begin{align*} h_{\mathrm{top}}(\mathbf K_{\beta}(t))\geq h_{\mathrm{top}}(\Phi_ {\mathbf{S}}(\mathbf K_{\hat\beta}(\hat{t})))=| {\mathbf{S}}|^{-1}h_{\mathrm{top}}(\mathbf K_{\hat\beta}(\hat{t}))>0, \end{align*} $$
where the last inequality follows since
![]() $\hat {t}<\tau (\hat {\beta })$
. This gives equation (6.2).
$\hat {t}<\tau (\hat {\beta })$
. This gives equation (6.2).
Next, let
![]() $\hat {t}>\tau (\hat {\beta })$
and set
$\hat {t}>\tau (\hat {\beta })$
and set
 $t:=\Theta _{ {\mathbf {S}},\hat {\beta }}(\hat {t})$
. Then, by the same argument as above, we have
$t:=\Theta _{ {\mathbf {S}},\hat {\beta }}(\hat {t})$
. Then, by the same argument as above, we have
![]() $b(t,\beta )=\Phi _ {\mathbf {S}}(b(\hat t,\hat \beta ))$
. Since
$b(t,\beta )=\Phi _ {\mathbf {S}}(b(\hat t,\hat \beta ))$
. Since
![]() $\hat {\beta }\in E$
, there exists a sequence of Farey intervals
$\hat {\beta }\in E$
, there exists a sequence of Farey intervals
 $J^{ {\mathbf {r}}_{k}}=[\beta _{\ell }^{ {\mathbf {r}}_{k}}, \beta _{r}^{ {\mathbf {r}}_{k}}]$
with
$J^{ {\mathbf {r}}_{k}}=[\beta _{\ell }^{ {\mathbf {r}}_{k}}, \beta _{r}^{ {\mathbf {r}}_{k}}]$
with
![]() $ {\mathbf {r}}_{k}\in \Omega _{F}^{*}$
such that
$ {\mathbf {r}}_{k}\in \Omega _{F}^{*}$
such that
 $\hat q_{k}:=\beta _{\ell }^{ {\mathbf {r}}_{k}}\searrow \hat \beta $
as
$\hat q_{k}:=\beta _{\ell }^{ {\mathbf {r}}_{k}}\searrow \hat \beta $
as
![]() $k\to \infty $
.
$k\to \infty $
.
We claim that
![]() $b(\hat {t},\hat {\beta })\succ ( {\mathbf {r}}_{k})^{\infty }$
for all sufficiently large k. This can be seen as follows. As explained in the proof of Lemma 6.1,
$b(\hat {t},\hat {\beta })\succ ( {\mathbf {r}}_{k})^{\infty }$
for all sufficiently large k. This can be seen as follows. As explained in the proof of Lemma 6.1,
![]() $\delta (\hat {\beta })$
is not periodic, and therefore by Lemma 2.5(ii), the map
$\delta (\hat {\beta })$
is not periodic, and therefore by Lemma 2.5(ii), the map
![]() $\beta ^{\prime }\mapsto \delta (\beta ^{\prime })$
is continuous at
$\beta ^{\prime }\mapsto \delta (\beta ^{\prime })$
is continuous at
![]() $\hat {\beta }$
(where we use
$\hat {\beta }$
(where we use
![]() $\beta ^{\prime }$
to denote a generic base). This implies
$\beta ^{\prime }$
to denote a generic base). This implies
![]() $\delta (\hat {q}_{k})\searrow \delta (\hat {\beta })=1\delta _{2}\delta _{3}\ldots $
as
$\delta (\hat {q}_{k})\searrow \delta (\hat {\beta })=1\delta _{2}\delta _{3}\ldots $
as
![]() $k\to \infty $
. However,
$k\to \infty $
. However,
 $\delta (\hat {q}_{k})=\delta (\beta _{\ell }^{ {\mathbf {r}}_{k}})=\mathbb {L}( {\mathbf {r}}_{k})^{\infty }$
, and by Lemma 2.3,
$\delta (\hat {q}_{k})=\delta (\beta _{\ell }^{ {\mathbf {r}}_{k}})=\mathbb {L}( {\mathbf {r}}_{k})^{\infty }$
, and by Lemma 2.3,
![]() $\mathbb {L}( {\mathbf {r}}_{k})$
is the word obtained from
$\mathbb {L}( {\mathbf {r}}_{k})$
is the word obtained from
![]() $ {\mathbf {r}}_{k}$
by flipping the first and last digits. Thus,
$ {\mathbf {r}}_{k}$
by flipping the first and last digits. Thus,
![]() $( {\mathbf {r}}_{k})^{\infty }$
converges to
$( {\mathbf {r}}_{k})^{\infty }$
converges to
![]() $0\delta _{2}\delta _{3}\ldots $
in the order topology. Since
$0\delta _{2}\delta _{3}\ldots $
in the order topology. Since
![]() $\hat {t}>\tau (\hat {\beta })$
implies
$\hat {t}>\tau (\hat {\beta })$
implies
![]() $b(\hat {t},\hat {\beta })\succ b(\tau (\hat {\beta }),\hat {\beta })=0\delta _{2}\delta _{3}\ldots $
, the claim follows.
$b(\hat {t},\hat {\beta })\succ b(\tau (\hat {\beta }),\hat {\beta })=0\delta _{2}\delta _{3}\ldots $
, the claim follows.
We can now deduce that for all sufficiently large k,
 $$ \begin{align*} \mathbf K_{\beta}(t)&=\{(y_{i}):b(t,\beta)\preccurlyeq\sigma^{n}((y_{i}))\prec \delta(\beta) \text{ for all } n\ge 0\}\\[3pt] &=\{(y_{i}):\Phi_ {\mathbf{S}}(b(\hat t, \hat\beta))\preccurlyeq\sigma^{n}((y_{i}))\prec \Phi_ {\mathbf{S}}(\delta(\hat\beta)) \text{ for all } n\ge 0\}\\[3pt] &\subset \{(y_{i}): \Phi_ {\mathbf{S}}(( {\mathbf{r}}_{k})^{\infty})\preccurlyeq \sigma^{n}((y_{i}))\prec \Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}}_{k})^{\infty}) \text{ for all } n\ge 0\}\\[3pt] &=\{(y_{i}): ( {\mathbf{S}}\bullet {\mathbf{r}}_{k})^{\infty}\preccurlyeq \sigma^{n}((y_{i}))\prec \mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}}_{k})^{\infty} \text{ for all } n\ge 0\}, \end{align*} $$
$$ \begin{align*} \mathbf K_{\beta}(t)&=\{(y_{i}):b(t,\beta)\preccurlyeq\sigma^{n}((y_{i}))\prec \delta(\beta) \text{ for all } n\ge 0\}\\[3pt] &=\{(y_{i}):\Phi_ {\mathbf{S}}(b(\hat t, \hat\beta))\preccurlyeq\sigma^{n}((y_{i}))\prec \Phi_ {\mathbf{S}}(\delta(\hat\beta)) \text{ for all } n\ge 0\}\\[3pt] &\subset \{(y_{i}): \Phi_ {\mathbf{S}}(( {\mathbf{r}}_{k})^{\infty})\preccurlyeq \sigma^{n}((y_{i}))\prec \Phi_ {\mathbf{S}}(\mathbb{L}( {\mathbf{r}}_{k})^{\infty}) \text{ for all } n\ge 0\}\\[3pt] &=\{(y_{i}): ( {\mathbf{S}}\bullet {\mathbf{r}}_{k})^{\infty}\preccurlyeq \sigma^{n}((y_{i}))\prec \mathbb{L}( {\mathbf{S}}\bullet {\mathbf{r}}_{k})^{\infty} \text{ for all } n\ge 0\}, \end{align*} $$
where the inclusion follows using the claim and
![]() $\delta (\hat {\beta })\prec \delta (\hat {q}_{k})=\mathbb {L}( {\mathbf {r}}_{k})^{\infty }$
. Hence,
$\delta (\hat {\beta })\prec \delta (\hat {q}_{k})=\mathbb {L}( {\mathbf {r}}_{k})^{\infty }$
. Hence,
![]() $\mathbf K_{\beta }(t)$
is countable by Proposition 4.1. This establishes equation (6.3).
$\mathbf K_{\beta }(t)$
is countable by Proposition 4.1. This establishes equation (6.3).
Case II.
![]() $\hat {\beta }=2$
. In this case,
$\hat {\beta }=2$
. In this case,
![]() $\delta (\hat {\beta })=1^{\infty }$
, so
$\delta (\hat {\beta })=1^{\infty }$
, so
![]() $\delta (\beta )=\Phi _ {\mathbf {S}}(\delta (\hat {\beta }))=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty }$
and
$\delta (\beta )=\Phi _ {\mathbf {S}}(\delta (\hat {\beta }))=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty }$
and
![]() $t^{*}=(\Phi _ {\mathbf {S}}(01^{\infty }))_{\beta }=( {\mathbf {S}}^{-}\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty })_{\beta }=( {\mathbf {S}} 0^{\infty })_{\beta }$
. Recall that
$t^{*}=(\Phi _ {\mathbf {S}}(01^{\infty }))_{\beta }=( {\mathbf {S}}^{-}\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty })_{\beta }=( {\mathbf {S}} 0^{\infty })_{\beta }$
. Recall that
![]() $\beta =\beta _{r}^ {\mathbf {S}}$
is the right endpoint of the Lyndon interval
$\beta =\beta _{r}^ {\mathbf {S}}$
is the right endpoint of the Lyndon interval
![]() $J^ {\mathbf {S}}$
.
$J^ {\mathbf {S}}$
.
If
![]() $t<t^{*}$
, then
$t<t^{*}$
, then
![]() $b(t,\beta )\prec b(t^{*},\beta )= {\mathbf {S}} 0^{\infty }$
, so by Lemma 2.10(iii), there exists
$b(t,\beta )\prec b(t^{*},\beta )= {\mathbf {S}} 0^{\infty }$
, so by Lemma 2.10(iii), there exists
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $b(t,\beta )\preccurlyeq {\mathbf {S}}^{-}\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{k} 0^{\infty }$
. It follows that
$b(t,\beta )\preccurlyeq {\mathbf {S}}^{-}\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{k} 0^{\infty }$
. It follows that
 $$ \begin{align*} \mathbf K_{\beta}(t)&=\{(x_{i}): b(t,\beta)\preccurlyeq \sigma^{n}((x_{i}))\prec\delta(\beta) \text{ for all } n\geq 0\}\\[3pt] &\supset \{\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{k} {\mathbf{S}}^{-},\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{k+1} {\mathbf{S}}^{-}\}^{\mathbb{N}}, \end{align*} $$
$$ \begin{align*} \mathbf K_{\beta}(t)&=\{(x_{i}): b(t,\beta)\preccurlyeq \sigma^{n}((x_{i}))\prec\delta(\beta) \text{ for all } n\geq 0\}\\[3pt] &\supset \{\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{k} {\mathbf{S}}^{-},\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{k+1} {\mathbf{S}}^{-}\}^{\mathbb{N}}, \end{align*} $$
and hence
![]() $h_{\mathrm {top}}(\mathbf K_{\beta }(t))>0$
.
$h_{\mathrm {top}}(\mathbf K_{\beta }(t))>0$
.
Now suppose
![]() $t>t^{*}$
. Then
$t>t^{*}$
. Then
![]() $b(t,\beta )\succ b(t^{*},\beta )= {\mathbf {S}} 0^{\infty }$
, so by Lemma 4.4,
$b(t,\beta )\succ b(t^{*},\beta )= {\mathbf {S}} 0^{\infty }$
, so by Lemma 4.4,
 $$ \begin{align*} \mathbf K_{\beta}(t)&=\{(x_{i}): b(t,\beta)\preccurlyeq \sigma^{n}((x_{i}))\prec\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty} \text{ for all } n\geq 0\}\\[3pt] &\subset \{(x_{i}): {\mathbf{S}} 0^{\infty}\preccurlyeq \sigma^{n}((x_{i})){\prec} \mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty} \text{ for all } n\geq 0\}\\[3pt] &=\{(x_{i}): {\mathbf{S}}^{\infty}\preccurlyeq \sigma^{n}((x_{i}))\preccurlyeq \mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty} \text{ for all } n\geq 0\}\\[3pt] &= \{(x_{i}): {\mathbf{S}}^{\infty}\preccurlyeq \sigma^{n}((x_{i}))\preccurlyeq \mathbb{L}( {\mathbf{S}})^{\infty} \text{ for all } n\geq 0\}, \end{align*} $$
$$ \begin{align*} \mathbf K_{\beta}(t)&=\{(x_{i}): b(t,\beta)\preccurlyeq \sigma^{n}((x_{i}))\prec\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty} \text{ for all } n\geq 0\}\\[3pt] &\subset \{(x_{i}): {\mathbf{S}} 0^{\infty}\preccurlyeq \sigma^{n}((x_{i})){\prec} \mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty} \text{ for all } n\geq 0\}\\[3pt] &=\{(x_{i}): {\mathbf{S}}^{\infty}\preccurlyeq \sigma^{n}((x_{i}))\preccurlyeq \mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{\infty} \text{ for all } n\geq 0\}\\[3pt] &= \{(x_{i}): {\mathbf{S}}^{\infty}\preccurlyeq \sigma^{n}((x_{i}))\preccurlyeq \mathbb{L}( {\mathbf{S}})^{\infty} \text{ for all } n\geq 0\}, \end{align*} $$
where the second equality follows by using
![]() $ {\mathbf {S}}\in \Omega _{L}^{*}$
, so
$ {\mathbf {S}}\in \Omega _{L}^{*}$
, so
![]() $\sigma ^{n}((x_{i}))\succcurlyeq {\mathbf {S}} 0^{\infty }$
for all
$\sigma ^{n}((x_{i}))\succcurlyeq {\mathbf {S}} 0^{\infty }$
for all
![]() $n\ge 0$
if and only if
$n\ge 0$
if and only if
![]() $\sigma ^{n}((x_{i}))\succcurlyeq {\mathbf {S}}^{\infty }$
for all
$\sigma ^{n}((x_{i}))\succcurlyeq {\mathbf {S}}^{\infty }$
for all
![]() $n\ge 0$
. Therefore,
$n\ge 0$
. Therefore,
![]() $\mathbf K_{\beta }(t)$
is countable by Proposition 4.1. This completes the proof.
$\mathbf K_{\beta }(t)$
is countable by Proposition 4.1. This completes the proof.
Next we will determine the critical value
![]() $\tau (\beta )$
for
$\tau (\beta )$
for
![]() $\beta \in {E_{\infty }}$
. Recall from equation (1.7) that
$\beta \in {E_{\infty }}$
. Recall from equation (1.7) that
 $$ \begin{align*} {E_{\infty}=\bigcap_{n=1}^{\infty}\bigcup_{ {\mathbf{S}}\in\Lambda(n)}J^ {\mathbf{S}},} \end{align*} $$
$$ \begin{align*} {E_{\infty}=\bigcap_{n=1}^{\infty}\bigcup_{ {\mathbf{S}}\in\Lambda(n)}J^ {\mathbf{S}},} \end{align*} $$
where for each
![]() $n\in \mathbb {N}$
, the Lyndon intervals
$n\in \mathbb {N}$
, the Lyndon intervals
![]() $J^ {\mathbf {S}}, {\mathbf {S}}\in {\Lambda }(n)$
are pairwise disjoint. Thus, for any
$J^ {\mathbf {S}}, {\mathbf {S}}\in {\Lambda }(n)$
are pairwise disjoint. Thus, for any
![]() $\beta \in {E_{\infty }}$
, there exists a unique sequence of words
$\beta \in {E_{\infty }}$
, there exists a unique sequence of words
![]() $( {\mathbf {s}}_{k})$
with each
$( {\mathbf {s}}_{k})$
with each
![]() $ {\mathbf {s}}_{k}\in \Omega _{F}^{*}$
such that
$ {\mathbf {s}}_{k}\in \Omega _{F}^{*}$
such that
 $$ \begin{align*} \{\beta\}=\bigcap_{n=1}^{\infty} J^{ {\mathbf{s}}_{1}\bullet\cdots\bullet {\mathbf{s}}_{n}}. \end{align*} $$
$$ \begin{align*} \{\beta\}=\bigcap_{n=1}^{\infty} J^{ {\mathbf{s}}_{1}\bullet\cdots\bullet {\mathbf{s}}_{n}}. \end{align*} $$
We call
![]() $( {\mathbf {s}}_{k})$
the coding of
$( {\mathbf {s}}_{k})$
the coding of
![]() $\beta $
.
$\beta $
.
Proposition 6.3. For any
![]() $\beta \in {E_{\infty }}$
with its coding
$\beta \in {E_{\infty }}$
with its coding
![]() $( {\mathbf {s}}_{k})$
, we have
$( {\mathbf {s}}_{k})$
, we have
 $$ \begin{align*} \tau(\beta) =\lim_{n\to\infty} ( {\mathbf{s}}_{1}\bullet\cdots\bullet {\mathbf{s}}_{n} 0^{\infty})_{\beta}. \end{align*} $$
$$ \begin{align*} \tau(\beta) =\lim_{n\to\infty} ( {\mathbf{s}}_{1}\bullet\cdots\bullet {\mathbf{s}}_{n} 0^{\infty})_{\beta}. \end{align*} $$
Proof. Take
![]() $\beta \in E_{\infty }$
. For
$\beta \in E_{\infty }$
. For
![]() $k\ge 1$
, let
$k\ge 1$
, let
![]() $ {\mathbf {S}}_{k}:= {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}$
and write
$ {\mathbf {S}}_{k}:= {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}$
and write
![]() $t_{k}:=( {\mathbf {S}}_{k} 0^{\infty })_{\beta }$
. Note that
$t_{k}:=( {\mathbf {S}}_{k} 0^{\infty })_{\beta }$
. Note that
 $\beta \in J^{ {\mathbf {S}}_{k}}=[\beta _{\ell }^{ {\mathbf {S}}_{k}}, \beta _{r}^{ {\mathbf {S}}_{k}}]$
for all
$\beta \in J^{ {\mathbf {S}}_{k}}=[\beta _{\ell }^{ {\mathbf {S}}_{k}}, \beta _{r}^{ {\mathbf {S}}_{k}}]$
for all
![]() $k\ge 1$
. Hence,
$k\ge 1$
. Hence,
 $$ \begin{align} \delta(\beta)\succ\delta(\beta_{\ell}^{ {\mathbf{S}}_{k}})=\mathbb{L}( {\mathbf{S}}_{k})^{\infty}, \end{align} $$
$$ \begin{align} \delta(\beta)\succ\delta(\beta_{\ell}^{ {\mathbf{S}}_{k}})=\mathbb{L}( {\mathbf{S}}_{k})^{\infty}, \end{align} $$
which implies that
![]() $b(t_{k},\beta )= {\mathbf {S}}_{k} 0^{\infty }$
for all
$b(t_{k},\beta )= {\mathbf {S}}_{k} 0^{\infty }$
for all
![]() $k\ge 1$
. Observe that
$k\ge 1$
. Observe that
![]() $ {\mathbf {S}}_{k+1}= {\mathbf {S}}_{k}\bullet {\mathbf {s}}_{k+1}$
begins with
$ {\mathbf {S}}_{k+1}= {\mathbf {S}}_{k}\bullet {\mathbf {s}}_{k+1}$
begins with
![]() $ {\mathbf {S}}_{k}^{-}$
. Therefore,
$ {\mathbf {S}}_{k}^{-}$
. Therefore,
so the sequence
![]() $(t_{k})$
is decreasing. Since
$(t_{k})$
is decreasing. Since
![]() $t_{k}\ge 0$
for all
$t_{k}\ge 0$
for all
![]() $k\ge 1$
, the limit
$k\ge 1$
, the limit
![]() $t^{*}:=\lim _{k\to \infty }t_{k}$
exists. We will now show that
$t^{*}:=\lim _{k\to \infty }t_{k}$
exists. We will now show that
![]() $\tau (\beta )=t^{*}$
.
$\tau (\beta )=t^{*}$
.
First we prove
![]() $\tau (\beta )\le t^{*}$
. Since
$\tau (\beta )\le t^{*}$
. Since
![]() $t_{k}$
decreases to
$t_{k}$
decreases to
![]() $t^{*}$
as
$t^{*}$
as
![]() $k\to \infty $
, it suffices to prove that
$k\to \infty $
, it suffices to prove that
![]() $\tau (\beta )\le t_{k}$
for all
$\tau (\beta )\le t_{k}$
for all
![]() $k\ge 1$
. Let
$k\ge 1$
. Let
 $q_{k}:=\beta _{r}^{ {\mathbf {S}}_{k}}$
for all
$q_{k}:=\beta _{r}^{ {\mathbf {S}}_{k}}$
for all
![]() $k\geq 1$
. Then
$k\geq 1$
. Then
![]() $q_{k}>\beta $
since
$q_{k}>\beta $
since
![]() $\beta \in J^{ {\mathbf {S}}_{k}}$
, and
$\beta \in J^{ {\mathbf {S}}_{k}}$
, and
![]() $q_{k}\searrow \beta $
as
$q_{k}\searrow \beta $
as
![]() $k\to \infty $
. Set
$k\to \infty $
. Set
![]() $t_{k}^{\prime }:=( {\mathbf {S}}_{k} 0^{\infty })_{q_{k}}$
. Since
$t_{k}^{\prime }:=( {\mathbf {S}}_{k} 0^{\infty })_{q_{k}}$
. Since
![]() $q_{k}>\beta $
, one can verify that
$q_{k}>\beta $
, one can verify that
![]() $b(t_{k}^{\prime }, q_{k})= {\mathbf {S}}_{k}0^{\infty }=b(t_{k},\beta )$
. So,
$b(t_{k}^{\prime }, q_{k})= {\mathbf {S}}_{k}0^{\infty }=b(t_{k},\beta )$
. So,
 $$ \begin{align} \mathbf K_{\beta}(t_{k})&=\{(x_{i}):b(t_{k},\beta)\preccurlyeq\sigma^{n}((x_{i}))\prec \delta(\beta) \text{ for all } n\ge 0\}\nonumber\\[3pt] &\subset\{(x_{i}): {\mathbf{S}}_{k} 0^{\infty} \preccurlyeq\sigma^{n}((x_{i}))\prec \delta(q_{k}) \text{ for all } n\ge 0\}=\mathbf K_{q_{k}}(t_{k}^{\prime}). \end{align} $$
$$ \begin{align} \mathbf K_{\beta}(t_{k})&=\{(x_{i}):b(t_{k},\beta)\preccurlyeq\sigma^{n}((x_{i}))\prec \delta(\beta) \text{ for all } n\ge 0\}\nonumber\\[3pt] &\subset\{(x_{i}): {\mathbf{S}}_{k} 0^{\infty} \preccurlyeq\sigma^{n}((x_{i}))\prec \delta(q_{k}) \text{ for all } n\ge 0\}=\mathbf K_{q_{k}}(t_{k}^{\prime}). \end{align} $$
Note by Proposition 6.2 and Case II of its proof that
![]() $\tau (q_{k})=( {\mathbf {S}}_{k} 0^{\infty })_{q_{k}}=t_{k}^{\prime }$
. This implies that
$\tau (q_{k})=( {\mathbf {S}}_{k} 0^{\infty })_{q_{k}}=t_{k}^{\prime }$
. This implies that
![]() $\dim _{H} K_{q_{k}}(t_{k}^{\prime })=0$
, and thus by equation (6.5), we have
$\dim _{H} K_{q_{k}}(t_{k}^{\prime })=0$
, and thus by equation (6.5), we have
![]() $\dim _{H} K_{\beta }(t_{k})=0$
. Hence,
$\dim _{H} K_{\beta }(t_{k})=0$
. Hence,
![]() $\tau (\beta )\le t_{k}$
for any
$\tau (\beta )\le t_{k}$
for any
![]() $k\ge 1$
. Letting
$k\ge 1$
. Letting
![]() $k\to \infty $
, we obtain that
$k\to \infty $
, we obtain that
![]() $\tau (\beta )\le t^{*}$
.
$\tau (\beta )\le t^{*}$
.
Next we prove
![]() $\tau (\beta )\ge t^{*}$
. Note that
$\tau (\beta )\ge t^{*}$
. Note that
![]() $\beta =\Psi _{ {\mathbf {S}}_{k}}(\beta _{k})$
, where
$\beta =\Psi _{ {\mathbf {S}}_{k}}(\beta _{k})$
, where
![]() $\beta _{k}\in E_{\infty }$
has coding
$\beta _{k}\in E_{\infty }$
has coding
![]() $( {\mathbf {s}}_{k+1}, {\mathbf {s}}_{k+2},\ldots )$
. Let
$( {\mathbf {s}}_{k+1}, {\mathbf {s}}_{k+2},\ldots )$
. Let
![]() $a(\hat t,\beta _{k})$
denote the quasi-greedy expansion of
$a(\hat t,\beta _{k})$
denote the quasi-greedy expansion of
![]() $\hat t$
in base
$\hat t$
in base
![]() $\beta _{k}$
(cf. [Reference de Vries and Komornik12, Lemma 2.3]). Observe that the map
$\beta _{k}$
(cf. [Reference de Vries and Komornik12, Lemma 2.3]). Observe that the map
![]() $\hat t\mapsto a(\hat t, \beta _{k})$
is strictly increasing and left continuous everywhere in
$\hat t\mapsto a(\hat t, \beta _{k})$
is strictly increasing and left continuous everywhere in
![]() $(0,1)$
, and thus the map
$(0,1)$
, and thus the map
![]() $\hat t\mapsto (\Phi _{ {\mathbf {S}}_{k}}(a(\hat t,\beta _{k})))_{\beta }$
is also left continuous in
$\hat t\mapsto (\Phi _{ {\mathbf {S}}_{k}}(a(\hat t,\beta _{k})))_{\beta }$
is also left continuous in
![]() $(0,1)$
. So, by the same argument as in the proof of equation (6.2), it follows that
$(0,1)$
. So, by the same argument as in the proof of equation (6.2), it follows that
for every
![]() $k\in \mathbb {N}$
, and letting
$k\in \mathbb {N}$
, and letting
![]() $k\to \infty $
gives
$k\to \infty $
gives
![]() $\tau (\beta )\geq t^{*}$
.
$\tau (\beta )\geq t^{*}$
.
To illustrate Proposition 6.3, we construct in each Farey interval
![]() $J^ {\mathbf {s}}$
a transcendental base
$J^ {\mathbf {s}}$
a transcendental base
![]() $\beta \in E_{\infty }$
and give an explicit formula for the critical value
$\beta \in E_{\infty }$
and give an explicit formula for the critical value
![]() $\tau (\beta )$
. Recall from [Reference Allouche and Shallit4] that the classical Thue–Morse sequence
$\tau (\beta )$
. Recall from [Reference Allouche and Shallit4] that the classical Thue–Morse sequence
![]() $(\theta _{i})_{i=0}^{\infty }=01101001\ldots $
is defined recursively as follows. Let
$(\theta _{i})_{i=0}^{\infty }=01101001\ldots $
is defined recursively as follows. Let
![]() $\theta _{0}=0$
; and if
$\theta _{0}=0$
; and if
![]() $\theta _{0}\ldots \theta _{2^{n}-1}$
is defined for some
$\theta _{0}\ldots \theta _{2^{n}-1}$
is defined for some
![]() $n\ge 0$
, then
$n\ge 0$
, then
By the definition of
![]() $(\theta _{i})$
, it follows that
$(\theta _{i})$
, it follows that
Komornik and Loreti [Reference Komornik and Loreti21] showed that
Proposition 6.4. Given
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}=0 {\mathbf {c}} 1\in \Omega _{F}^{*}$
, let
$ {\mathbf {s}}=s_{1}\ldots s_{m}=0 {\mathbf {c}} 1\in \Omega _{F}^{*}$
, let
![]() $\beta :=\beta _{\infty }^ {\mathbf {s}}\in (1,2]$
such that
$\beta :=\beta _{\infty }^ {\mathbf {s}}\in (1,2]$
such that
Then
![]() $\beta \in E_{\infty }\cap J^ {\mathbf {s}}$
is transcendental, and
$\beta \in E_{\infty }\cap J^ {\mathbf {s}}$
is transcendental, and
 $$ \begin{align*} \tau(\beta)=\frac{2\sum_{j=2}^{m} s_{j}\beta^{m-j}+\beta^{m-1}-\beta^{m}}{\beta^{m}-1}. \end{align*} $$
$$ \begin{align*} \tau(\beta)=\frac{2\sum_{j=2}^{m} s_{j}\beta^{m-j}+\beta^{m-1}-\beta^{m}}{\beta^{m}-1}. \end{align*} $$
We point out that in the above proposition,
![]() $ {\mathbf {c}}$
may be the empty word. To prove the transcendence of
$ {\mathbf {c}}$
may be the empty word. To prove the transcendence of
![]() $\beta $
, we recall the following result due to Mahler [Reference Mahler25].
$\beta $
, we recall the following result due to Mahler [Reference Mahler25].
Lemma 6.5. (Mahler, 1976)
If z is an algebraic number in the open unit disc, then the number
![]() $ Z:=\sum _{i=1}^{\infty }\theta _{i} z^{i} $
is transcendental.
$ Z:=\sum _{i=1}^{\infty }\theta _{i} z^{i} $
is transcendental.
Proof of Proposition 6.4
Let
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}=0 {\mathbf {c}} 1\in \Omega _{F}^{*}$
. First we prove that
$ {\mathbf {s}}=s_{1}\ldots s_{m}=0 {\mathbf {c}} 1\in \Omega _{F}^{*}$
. First we prove that
By Lemma 2.5, it suffices to prove that
![]() $\sigma ^{n}((\delta _{i}))\preccurlyeq (\delta _{i})$
for all
$\sigma ^{n}((\delta _{i}))\preccurlyeq (\delta _{i})$
for all
![]() $n\ge 1$
. Note by Lemma 2.3 that
$n\ge 1$
. Note by Lemma 2.3 that
![]() $\delta _{1}\ldots \delta _{m}=1 {\mathbf {c}} 1=\mathbb {L}( {\mathbf {s}})^{+}=:{a_{1}\ldots a_{m}^{+}}$
. Take
$\delta _{1}\ldots \delta _{m}=1 {\mathbf {c}} 1=\mathbb {L}( {\mathbf {s}})^{+}=:{a_{1}\ldots a_{m}^{+}}$
. Take
![]() $n\in \mathbb {N}$
, and write
$n\in \mathbb {N}$
, and write
![]() $n=mk+j$
with
$n=mk+j$
with
![]() $k\in \mathbb {N}\cup \{0\}$
and
$k\in \mathbb {N}\cup \{0\}$
and
![]() $j\in \{1,2,\ldots ,m\}$
. We will prove
$j\in \{1,2,\ldots ,m\}$
. We will prove
![]() $\sigma ^{n}((\delta _{i}))\prec (\delta _{i})$
in the following three cases.
$\sigma ^{n}((\delta _{i}))\prec (\delta _{i})$
in the following three cases.
Case I.
![]() $j\in \{1,2,\ldots , m-2\}$
. Note by equation (6.7) that
$j\in \{1,2,\ldots , m-2\}$
. Note by equation (6.7) that
![]() $\theta _{2k}=1-\theta _{2k+1}$
. This implies that
$\theta _{2k}=1-\theta _{2k+1}$
. This implies that
![]() $\sigma ^{n}((\delta _{i}))$
begins with either
$\sigma ^{n}((\delta _{i}))$
begins with either
![]() $a_{j+1}\ldots a_{m}$
or
$a_{j+1}\ldots a_{m}$
or
![]() $a_{j+1}\ldots a_{m}^{+}s_{1}\ldots s_{m-1}$
. By Lemma 2.7, it follows that
$a_{j+1}\ldots a_{m}^{+}s_{1}\ldots s_{m-1}$
. By Lemma 2.7, it follows that
![]() $\sigma ^{n}((\delta _{i}))\prec (\delta _{i})$
.
$\sigma ^{n}((\delta _{i}))\prec (\delta _{i})$
.
Case II.
![]() $j=m-1$
. Then
$j=m-1$
. Then
![]() $\sigma ^{n}((\delta _{i}))$
begins with
$\sigma ^{n}((\delta _{i}))$
begins with
![]() $\theta _{2k}\theta _{2k+1} {\mathbf {c}}$
for some
$\theta _{2k}\theta _{2k+1} {\mathbf {c}}$
for some
![]() $k\in \mathbb {N}$
. If
$k\in \mathbb {N}$
. If
![]() $\theta _{2k}=0$
, then it is clear that
$\theta _{2k}=0$
, then it is clear that
![]() $\sigma ^{n}((\delta _{i}))\prec (\delta _{i})$
since
$\sigma ^{n}((\delta _{i}))\prec (\delta _{i})$
since
![]() $\delta _{1}=1$
. Otherwise, equation (6.7) implies that
$\delta _{1}=1$
. Otherwise, equation (6.7) implies that
![]() $\theta _{2k}\theta _{2k+1} {\mathbf {c}}=10 {\mathbf {c}}=1 s_{1}\ldots s_{m-1}$
. Hence,
$\theta _{2k}\theta _{2k+1} {\mathbf {c}}=10 {\mathbf {c}}=1 s_{1}\ldots s_{m-1}$
. Hence,
where the strict inequality follows since
![]() $s_{1}\ldots s_{m-1}\preccurlyeq a_{2}\ldots a_{m}$
.
$s_{1}\ldots s_{m-1}\preccurlyeq a_{2}\ldots a_{m}$
.
Case III.
![]() $j=m$
. Then
$j=m$
. Then
where the strict inequality is a consequence of equation (6.8).
Therefore, by Cases I–III, we establish equation (6.9). Next we show that
![]() $\beta \in E_{\infty }$
. For
$\beta \in E_{\infty }$
. For
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $ {\mathbf {S}}_{k}:= {\mathbf {s}}_{1}\bullet {\mathbf {s}}_{2}\bullet \cdots \bullet {\mathbf {s}}_{k}$
with
$ {\mathbf {S}}_{k}:= {\mathbf {s}}_{1}\bullet {\mathbf {s}}_{2}\bullet \cdots \bullet {\mathbf {s}}_{k}$
with
![]() $ {\mathbf {s}}_{1}= {\mathbf {s}}$
and
$ {\mathbf {s}}_{1}= {\mathbf {s}}$
and
![]() $ {\mathbf {s}}_{i}=01$
for all
$ {\mathbf {s}}_{i}=01$
for all
![]() $2\le i\le k$
. Then
$2\le i\le k$
. Then
![]() $ {\mathbf {S}}_{k}\in \Lambda $
for all
$ {\mathbf {S}}_{k}\in \Lambda $
for all
![]() $k\in \mathbb {N}$
. So it suffices to show that
$k\in \mathbb {N}$
. So it suffices to show that
![]() $\beta \in J^{ {\mathbf {S}}_{k}}$
for all
$\beta \in J^{ {\mathbf {S}}_{k}}$
for all
![]() $k\ge 1$
. First we claim that
$k\ge 1$
. First we claim that
 $$ \begin{align} {\mathbf{S}}_{k}=\overline{\theta_{1}} {\mathbf{c}}\overline{\theta_{2}}\,\overline{\theta_{3}} {\mathbf{c}}\overline{\theta_{4}}\ldots \overline{\theta_{2^{k}-1}} {\mathbf{c}}\overline{\theta_{2^{k}}}^{+},\quad \mathbb{L}({ {\mathbf{S}}_{k}})=\theta_{1} {\mathbf{c}}\theta_{2}\,\theta_{3} {\mathbf{c}}\theta_{4}\,\ldots\theta_{2^{k}-1} {\mathbf{c}}\theta_{2^{k}}^{-} \end{align} $$
$$ \begin{align} {\mathbf{S}}_{k}=\overline{\theta_{1}} {\mathbf{c}}\overline{\theta_{2}}\,\overline{\theta_{3}} {\mathbf{c}}\overline{\theta_{4}}\ldots \overline{\theta_{2^{k}-1}} {\mathbf{c}}\overline{\theta_{2^{k}}}^{+},\quad \mathbb{L}({ {\mathbf{S}}_{k}})=\theta_{1} {\mathbf{c}}\theta_{2}\,\theta_{3} {\mathbf{c}}\theta_{4}\,\ldots\theta_{2^{k}-1} {\mathbf{c}}\theta_{2^{k}}^{-} \end{align} $$
for all
![]() $k\ge 1$
.
$k\ge 1$
.
Since
 $ {\mathbf {S}}_{1}= {\mathbf {s}}=0 {\mathbf {c}} 1=\overline {\theta _{1}} {\mathbf {c}}\overline {\theta _{2}}^{+}$
and
$ {\mathbf {S}}_{1}= {\mathbf {s}}=0 {\mathbf {c}} 1=\overline {\theta _{1}} {\mathbf {c}}\overline {\theta _{2}}^{+}$
and
![]() $\mathbb {L}( {\mathbf {S}}_{1})=1 {\mathbf {c}} 0=\theta _{1} {\mathbf {c}}\theta _{2}^{-}$
, equation (6.10) holds for
$\mathbb {L}( {\mathbf {S}}_{1})=1 {\mathbf {c}} 0=\theta _{1} {\mathbf {c}}\theta _{2}^{-}$
, equation (6.10) holds for
![]() ${k=1}$
. Now suppose equation (6.10) holds for a given
${k=1}$
. Now suppose equation (6.10) holds for a given
![]() $k\in \mathbb {N}$
. Then
$k\in \mathbb {N}$
. Then
 $$ \begin{align*} {\mathbf{S}}_{k+1}= {\mathbf{S}}_{k}\bullet(01) = {\mathbf{S}}_{k}^{-}\mathbb{L}( {\mathbf{S}}_{k})^{+}&=\overline{\theta_{1}} {\mathbf{c}}\overline{\theta_{2}}\ldots \overline{\theta_{2^{k}-1}} {\mathbf{c}}\overline{\theta_{2^{k}}}\;\theta_{1} {\mathbf{c}}\theta_{2}\,\ldots\theta_{2^{k}-1} {\mathbf{c}}\theta_{2^{k}}\\[3pt] &=\overline{\theta_{1}} {\mathbf{c}}\overline{\theta_{2}}\ldots\overline{\theta_{2^{k+1}-1}} {\mathbf{c}}\overline{\theta_{2^{k+1}}}^{+}, \end{align*} $$
$$ \begin{align*} {\mathbf{S}}_{k+1}= {\mathbf{S}}_{k}\bullet(01) = {\mathbf{S}}_{k}^{-}\mathbb{L}( {\mathbf{S}}_{k})^{+}&=\overline{\theta_{1}} {\mathbf{c}}\overline{\theta_{2}}\ldots \overline{\theta_{2^{k}-1}} {\mathbf{c}}\overline{\theta_{2^{k}}}\;\theta_{1} {\mathbf{c}}\theta_{2}\,\ldots\theta_{2^{k}-1} {\mathbf{c}}\theta_{2^{k}}\\[3pt] &=\overline{\theta_{1}} {\mathbf{c}}\overline{\theta_{2}}\ldots\overline{\theta_{2^{k+1}-1}} {\mathbf{c}}\overline{\theta_{2^{k+1}}}^{+}, \end{align*} $$
where the last equality follows since, by the definition of
![]() $(\theta _{i})$
in equation (6.6),
$(\theta _{i})$
in equation (6.6),
 $\theta _{2^{k}+1}\ldots \theta _{2^{k+1}}=\overline {\theta _{1}\ldots \theta _{2^{k}}}^{+}$
. Similarly, by the induction hypothesis and Lemma 3.7, we obtain
$\theta _{2^{k}+1}\ldots \theta _{2^{k+1}}=\overline {\theta _{1}\ldots \theta _{2^{k}}}^{+}$
. Similarly, by the induction hypothesis and Lemma 3.7, we obtain
 $$ \begin{align*} \mathbb{L}( {\mathbf{S}}_{k+1})=\mathbb{L}( {\mathbf{S}}_{k}\bullet (01))= {\mathbf{S}}_{k}\bullet\mathbb{L}(01)&= {\mathbf{S}}_{k}\bullet(10)=\mathbb{L}( {\mathbf{S}}_{k})^{+} {\mathbf{S}}_{k}^{-}\\[3pt] &=\theta_{1} {\mathbf{c}}\theta_{2}\,\ldots\theta_{2^{k}-1} {\mathbf{c}}\theta_{2^{k}}\,\overline{\theta_{1}} {\mathbf{c}}\overline{\theta_{2}}\ldots \overline{\theta_{2^{k}-1}} {\mathbf{c}}\overline{\theta_{2^{k}}}\\[3pt] &=\theta_{1} {\mathbf{c}}\theta_{2}\,\ldots\theta_{2^{k+1}-1} {\mathbf{c}}\theta_{2^{k+1}}^{-}. \end{align*} $$
$$ \begin{align*} \mathbb{L}( {\mathbf{S}}_{k+1})=\mathbb{L}( {\mathbf{S}}_{k}\bullet (01))= {\mathbf{S}}_{k}\bullet\mathbb{L}(01)&= {\mathbf{S}}_{k}\bullet(10)=\mathbb{L}( {\mathbf{S}}_{k})^{+} {\mathbf{S}}_{k}^{-}\\[3pt] &=\theta_{1} {\mathbf{c}}\theta_{2}\,\ldots\theta_{2^{k}-1} {\mathbf{c}}\theta_{2^{k}}\,\overline{\theta_{1}} {\mathbf{c}}\overline{\theta_{2}}\ldots \overline{\theta_{2^{k}-1}} {\mathbf{c}}\overline{\theta_{2^{k}}}\\[3pt] &=\theta_{1} {\mathbf{c}}\theta_{2}\,\ldots\theta_{2^{k+1}-1} {\mathbf{c}}\theta_{2^{k+1}}^{-}. \end{align*} $$
Hence, by induction, equation (6.10) holds for all
![]() $k\ge 1$
.
$k\ge 1$
.
Next, recall that the Lyndon interval
 $J^{ {\mathbf {S}}_{k}}=[\beta _{\ell }^{ {\mathbf {S}}_{k}}, \beta _{r}^{ {\mathbf {S}}_{k}}]$
satisfies
$J^{ {\mathbf {S}}_{k}}=[\beta _{\ell }^{ {\mathbf {S}}_{k}}, \beta _{r}^{ {\mathbf {S}}_{k}}]$
satisfies
 $$ \begin{align} \delta(\beta_{\ell}^{ {\mathbf{S}}_{k}})=\mathbb{L}( {\mathbf{S}}_{k})^{\infty}\quad\textrm{and}\quad \delta(\beta_{r}^{ {\mathbf{S}}_{k}})=\mathbb{L}( {\mathbf{S}}_{k})^{+} {\mathbf{S}}_{k}^{\infty}. \end{align} $$
$$ \begin{align} \delta(\beta_{\ell}^{ {\mathbf{S}}_{k}})=\mathbb{L}( {\mathbf{S}}_{k})^{\infty}\quad\textrm{and}\quad \delta(\beta_{r}^{ {\mathbf{S}}_{k}})=\mathbb{L}( {\mathbf{S}}_{k})^{+} {\mathbf{S}}_{k}^{\infty}. \end{align} $$
By equations (6.9) and (6.10), it follows that
![]() $\delta (\beta )$
begins with
$\delta (\beta )$
begins with
![]() $\mathbb {L}( {\mathbf {S}}_{k})^{+}$
, so by equation (6.11),
$\mathbb {L}( {\mathbf {S}}_{k})^{+}$
, so by equation (6.11),
 $\delta (\beta )\succ \mathbb {L}( {\mathbf {S}}_{k})^{\infty }=\delta (\beta _{\ell }^{ {\mathbf {S}}_{k}})$
. Thus,
$\delta (\beta )\succ \mathbb {L}( {\mathbf {S}}_{k})^{\infty }=\delta (\beta _{\ell }^{ {\mathbf {S}}_{k}})$
. Thus,
 $\beta>\beta _{\ell }^{ {\mathbf {S}}_{k}}$
for all
$\beta>\beta _{\ell }^{ {\mathbf {S}}_{k}}$
for all
![]() $k\ge 1$
. However, by equations (6.9), (6.10), and Lemmas 3.7 and 3.9, we see that
$k\ge 1$
. However, by equations (6.9), (6.10), and Lemmas 3.7 and 3.9, we see that
![]() $\delta (\beta )$
also begins with
$\delta (\beta )$
also begins with
 $$ \begin{align*} \mathbb{L}( {\mathbf{S}}_{k+2})^{+}&=\mathbb{L}( {\mathbf{S}}_{k}\bullet(01\bullet 01))^{+}=\mathbb{L}( {\mathbf{S}}_{k}\bullet(0011))^{+}\\[3pt] &=( {\mathbf{S}}_{k}\bullet\mathbb{L}(0011))^{+}=( {\mathbf{S}}_{k}\bullet (1100))^{+} =\mathbb{L}( {\mathbf{S}}_{k})^{+} {\mathbf{S}}_{k} {\mathbf{S}}_{k}^{-}\mathbb{L}( {\mathbf{S}}_{k})^{+}, \end{align*} $$
$$ \begin{align*} \mathbb{L}( {\mathbf{S}}_{k+2})^{+}&=\mathbb{L}( {\mathbf{S}}_{k}\bullet(01\bullet 01))^{+}=\mathbb{L}( {\mathbf{S}}_{k}\bullet(0011))^{+}\\[3pt] &=( {\mathbf{S}}_{k}\bullet\mathbb{L}(0011))^{+}=( {\mathbf{S}}_{k}\bullet (1100))^{+} =\mathbb{L}( {\mathbf{S}}_{k})^{+} {\mathbf{S}}_{k} {\mathbf{S}}_{k}^{-}\mathbb{L}( {\mathbf{S}}_{k})^{+}, \end{align*} $$
which is strictly smaller than a prefix of
 $\delta (\beta _{r}^{ {\mathbf {S}}_{k}})^{+}={\mathbb {L}( {\mathbf {S}}_{k})^{+}} {\mathbf {S}}_{k}^{\infty }$
. This implies that
$\delta (\beta _{r}^{ {\mathbf {S}}_{k}})^{+}={\mathbb {L}( {\mathbf {S}}_{k})^{+}} {\mathbf {S}}_{k}^{\infty }$
. This implies that
 $\beta <\beta _{r}^{ {\mathbf {S}}_{k}}$
for all
$\beta <\beta _{r}^{ {\mathbf {S}}_{k}}$
for all
![]() $k\ge 1$
. Hence,
$k\ge 1$
. Hence,
![]() $\beta \in J^{ {\mathbf {S}}_{k}}$
for all
$\beta \in J^{ {\mathbf {S}}_{k}}$
for all
![]() $k\ge 1$
, and thus
$k\ge 1$
, and thus
![]() $\beta \in E_{\infty }\cap J^ {\mathbf {s}}$
. Furthermore, by equations (6.9), (6.10), and Proposition 6.3, it follows that
$\beta \in E_{\infty }\cap J^ {\mathbf {s}}$
. Furthermore, by equations (6.9), (6.10), and Proposition 6.3, it follows that
 $$ \begin{align*} \tau({\beta})&=\lim_{k\to\infty}( {\mathbf{S}}_{k} 0^{\infty})_{\beta}=(\overline{\theta_{1}} {\mathbf{c}}\overline{\theta_{2}}\,\overline{\theta_{3}} {\mathbf{c}}\overline{\theta_{4}}\ldots)_{\beta}\\[3pt] &=\sum_{k=0}^{\infty}\bigg(\frac{1}{\beta^{m k+1}}+2\sum_{j=2}^{m-1}\frac{s_{j}}{\beta^{m k+j}}+\frac{1}{\beta^{m k+m}}\bigg)-({\theta_{1}} {\mathbf{c}}{\theta_{2}}{\theta_{3}} {\mathbf{c}}\theta_{4}\ldots)_{\beta}\\[3pt] &=\frac{\beta^{m-1}+2\sum_{j=2}^{m-1}s_{j}\beta^{m-j}+1}{\beta^{m}-1}-1\\[3pt] &=\frac{2\sum_{j=2}^{m} s_{j}\beta^{m-j}+\beta^{m-1}-\beta^{m}}{\beta^{m}-1}, \end{align*} $$
$$ \begin{align*} \tau({\beta})&=\lim_{k\to\infty}( {\mathbf{S}}_{k} 0^{\infty})_{\beta}=(\overline{\theta_{1}} {\mathbf{c}}\overline{\theta_{2}}\,\overline{\theta_{3}} {\mathbf{c}}\overline{\theta_{4}}\ldots)_{\beta}\\[3pt] &=\sum_{k=0}^{\infty}\bigg(\frac{1}{\beta^{m k+1}}+2\sum_{j=2}^{m-1}\frac{s_{j}}{\beta^{m k+j}}+\frac{1}{\beta^{m k+m}}\bigg)-({\theta_{1}} {\mathbf{c}}{\theta_{2}}{\theta_{3}} {\mathbf{c}}\theta_{4}\ldots)_{\beta}\\[3pt] &=\frac{\beta^{m-1}+2\sum_{j=2}^{m-1}s_{j}\beta^{m-j}+1}{\beta^{m}-1}-1\\[3pt] &=\frac{2\sum_{j=2}^{m} s_{j}\beta^{m-j}+\beta^{m-1}-\beta^{m}}{\beta^{m}-1}, \end{align*} $$
where we recall that
![]() $ {\mathbf {c}}=s_{2}\ldots s_{m-1}$
, and the last equality uses that
$ {\mathbf {c}}=s_{2}\ldots s_{m-1}$
, and the last equality uses that
![]() $s_{m}=1$
.
$s_{m}=1$
.
Finally, the transcendence of
![]() $\beta $
follows by using equation (6.9), Lemma 6.5, and a similar argument as in the proof of [Reference Kong and Li22, Proposition 5.2].
$\beta $
follows by using equation (6.9), Lemma 6.5, and a similar argument as in the proof of [Reference Kong and Li22, Proposition 5.2].
Remark 6.6.
-
(i) When
 $ {\mathbf {s}}=01$
, the base
$ {\mathbf {s}}=01$
, the base
 $\beta _{\infty }^{01}\approx 1.78723$
given in Proposition 6.4 is the Komornik–Loreti constant (cf. [Reference Komornik and Loreti21]), whose transcendence was first proved by Allouche and Cosnard [Reference Allouche and Cosnard3]. In this case, we obtain
$\beta _{\infty }^{01}\approx 1.78723$
given in Proposition 6.4 is the Komornik–Loreti constant (cf. [Reference Komornik and Loreti21]), whose transcendence was first proved by Allouche and Cosnard [Reference Allouche and Cosnard3]. In this case, we obtain
 $\tau (\beta _{\infty }^{01})=(2-\beta _{\infty }^{01})/(\beta _{\infty }^{01}-1)\approx 0.270274$
.
$\tau (\beta _{\infty }^{01})=(2-\beta _{\infty }^{01})/(\beta _{\infty }^{01}-1)\approx 0.270274$
. -
(ii) When
 $ {\mathbf {s}}=001$
, the base
$ {\mathbf {s}}=001$
, the base
 $\beta _{\infty }^{001}\approx 1.55356$
is a critical value for the fat Sierpinski gaskets studied by Li and the second author in [Reference Kong and Li22]. In this case, we have
$\beta _{\infty }^{001}\approx 1.55356$
is a critical value for the fat Sierpinski gaskets studied by Li and the second author in [Reference Kong and Li22]. In this case, we have
 $\tau (\beta _{\infty }^{001})\approx 0.241471$
.
$\tau (\beta _{\infty }^{001})\approx 0.241471$
.
By Proposition 6.4 and numerical calculation, we give in Table 1 the triples
![]() $( {\mathbf {s}}, \beta _{\infty }^ {\mathbf {s}}, \tau (\beta _{\infty }^ {\mathbf {s}}))$
for all
$( {\mathbf {s}}, \beta _{\infty }^ {\mathbf {s}}, \tau (\beta _{\infty }^ {\mathbf {s}}))$
for all
![]() $ {\mathbf {s}}\in F_{3}^{*}\subset \Omega _{F}^{*}$
. Based on Proposition 6.4, we conjecture that each base
$ {\mathbf {s}}\in F_{3}^{*}\subset \Omega _{F}^{*}$
. Based on Proposition 6.4, we conjecture that each base
![]() $\beta \in E_{\infty }$
is transcendental.
$\beta \in E_{\infty }$
is transcendental.
Table 1 The triples
![]() $( {\mathbf {s}}, \beta _{\infty }^ {\mathbf {s}}, \tau (\beta _{\infty }^ {\mathbf {s}}))$
with
$( {\mathbf {s}}, \beta _{\infty }^ {\mathbf {s}}, \tau (\beta _{\infty }^ {\mathbf {s}}))$
with
![]() $ {\mathbf {s}}\in F_{3}^{*}\subset \Omega _{F}^{*}$
.
$ {\mathbf {s}}\in F_{3}^{*}\subset \Omega _{F}^{*}$
.

7 Càdlàg property of the critical value function
In this section, we prove Proposition 1.9 and Theorem 1. Recall by Lemma 5.7 that the interval
![]() $(1,2]$
can be partitioned as
$(1,2]$
can be partitioned as
 $$ \begin{align} (1,2]=E\cup\bigcup_{ {\mathbf{s}}\in\Omega_{F}^{*}}J^ {\mathbf{s}}=E \cup E_{\infty}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}E^ {\mathbf{S}}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}I^ {\mathbf{S}}. \end{align} $$
$$ \begin{align} (1,2]=E\cup\bigcup_{ {\mathbf{s}}\in\Omega_{F}^{*}}J^ {\mathbf{s}}=E \cup E_{\infty}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}E^ {\mathbf{S}}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}I^ {\mathbf{S}}. \end{align} $$
Here we emphasize that the exceptional set E, the relative exceptional sets
![]() $E^ {\mathbf {S}}$
and the infinitely Farey set
$E^ {\mathbf {S}}$
and the infinitely Farey set
![]() $E_{\infty }$
featuring in equation (7.1) all have Lebesgue measure zero in view of Propositions 5.6 and 5.8. Hence the basic intervals
$E_{\infty }$
featuring in equation (7.1) all have Lebesgue measure zero in view of Propositions 5.6 and 5.8. Hence the basic intervals
![]() $I^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
, and then certainly the Lyndon intervals
$I^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
, and then certainly the Lyndon intervals
![]() $J^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
, are dense in
$J^ {\mathbf {S}}, {\mathbf {S}}\in \Lambda $
, are dense in
![]() $(1,2]$
. This allows for approximation of points in
$(1,2]$
. This allows for approximation of points in
![]() $E, E^ {\mathbf {S}}$
, and
$E, E^ {\mathbf {S}}$
, and
![]() $E_{\infty }$
by left and/or right endpoints of such Lyndon intervals. We also recall from Theorem 2 that for any basic interval
$E_{\infty }$
by left and/or right endpoints of such Lyndon intervals. We also recall from Theorem 2 that for any basic interval
 $I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
with
$I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
with
 $\delta (\beta _{\ell }^ {\mathbf {S}})=\mathbb {L}( {\mathbf {S}})^{\infty }$
and
$\delta (\beta _{\ell }^ {\mathbf {S}})=\mathbb {L}( {\mathbf {S}})^{\infty }$
and
![]() $\delta (\beta _{*}^ {\mathbf {S}})=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{-}\mathbb {L}( {\mathbf {S}})^{\infty }$
, the critical value is given by
$\delta (\beta _{*}^ {\mathbf {S}})=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{-}\mathbb {L}( {\mathbf {S}})^{\infty }$
, the critical value is given by
 $$ \begin{align} \tau(\beta)=(\Phi_ {\mathbf{S}}(0^{\infty}))_{\beta}=( {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta}\quad\textrm{for any } \beta\in I^ {\mathbf{S}}. \end{align} $$
$$ \begin{align} \tau(\beta)=(\Phi_ {\mathbf{S}}(0^{\infty}))_{\beta}=( {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta}\quad\textrm{for any } \beta\in I^ {\mathbf{S}}. \end{align} $$
Moreover, by Proposition 6.2, it follows that for each
![]() $\beta \in E^ {\mathbf {S}}$
, we have
$\beta \in E^ {\mathbf {S}}$
, we have
where
![]() $1\delta _{2}\delta _{3}\ldots =\delta ({\hat \beta })$
with
$1\delta _{2}\delta _{3}\ldots =\delta ({\hat \beta })$
with
![]() ${\hat \beta }={\Psi _ {\mathbf {S}}}^{-1}(\beta )\in E$
. In particular, when
${\hat \beta }={\Psi _ {\mathbf {S}}}^{-1}(\beta )\in E$
. In particular, when
![]() $\beta \in E$
, we have
$\beta \in E$
, we have
![]() $\tau (\beta )=1-{1}/{\beta }$
(see Proposition 1.12). When
$\tau (\beta )=1-{1}/{\beta }$
(see Proposition 1.12). When
![]() $\beta \in E_{\infty }$
, it follows by Proposition 6.3 that
$\beta \in E_{\infty }$
, it follows by Proposition 6.3 that
 $$ \begin{align} \tau(\beta)=\lim_{n\to\infty}( {\mathbf{s}}_{1}\bullet {\mathbf{s}}_{2}\bullet\cdots\bullet {\mathbf{s}}_{n} 0^{\infty})_{\beta}, \end{align} $$
$$ \begin{align} \tau(\beta)=\lim_{n\to\infty}( {\mathbf{s}}_{1}\bullet {\mathbf{s}}_{2}\bullet\cdots\bullet {\mathbf{s}}_{n} 0^{\infty})_{\beta}, \end{align} $$
where
![]() $( {\mathbf {s}}_{k})$
is the unique coding of
$( {\mathbf {s}}_{k})$
is the unique coding of
![]() $\beta $
(that is,
$\beta $
(that is,
![]() $\beta \in J^{ {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}}$
for all
$\beta \in J^{ {\mathbf {s}}_{1}\bullet \cdots \bullet {\mathbf {s}}_{k}}$
for all
![]() $k\in \mathbb {N}$
).
$k\in \mathbb {N}$
).
From equation (7.2), it is clear that the critical value function
![]() $\tau $
is continuous inside each basic interval
$\tau $
is continuous inside each basic interval
 $I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
. So, in view of equation (7.1), we still need to consider the continuity of
$I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}}, \beta _{*}^ {\mathbf {S}}]$
. So, in view of equation (7.1), we still need to consider the continuity of
![]() $\tau $
for
$\tau $
for
 $\beta \in {E\cup E_{\infty }\cup \bigcup _{ {\mathbf {S}}\in \Lambda }(E^ {\mathbf {S}}\setminus \{\beta _{r}^ {\mathbf {S}}\})}$
, the left continuity of
$\beta \in {E\cup E_{\infty }\cup \bigcup _{ {\mathbf {S}}\in \Lambda }(E^ {\mathbf {S}}\setminus \{\beta _{r}^ {\mathbf {S}}\})}$
, the left continuity of
![]() $\tau $
at
$\tau $
at
 $\beta =\beta _{\ell }^ {\mathbf {S}}$
and
$\beta =\beta _{\ell }^ {\mathbf {S}}$
and
![]() $\beta =\beta _{r}^ {\mathbf {S}}$
, and the right continuity of
$\beta =\beta _{r}^ {\mathbf {S}}$
, and the right continuity of
![]() $\tau $
at
$\tau $
at
![]() $\beta =\beta _{*}^ {\mathbf {S}}$
. We need the following lemma.
$\beta =\beta _{*}^ {\mathbf {S}}$
. We need the following lemma.
Lemma 7.1. If
![]() $\beta \in (1,2)$
and
$\beta \in (1,2)$
and
![]() $\delta (\beta )$
is periodic, then
$\delta (\beta )$
is periodic, then
 $\beta \in \bigcup _{ {\mathbf {S}}\in \Lambda } I^ {\mathbf {S}}$
.
$\beta \in \bigcup _{ {\mathbf {S}}\in \Lambda } I^ {\mathbf {S}}$
.
Proof. Assume
![]() $\delta (\beta )$
is periodic. In view of equation (7.1), it suffices to prove
$\delta (\beta )$
is periodic. In view of equation (7.1), it suffices to prove
 $$ \begin{align*} \beta\notin E\cup E_{\infty}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}E^ {\mathbf{S}}. \end{align*} $$
$$ \begin{align*} \beta\notin E\cup E_{\infty}\cup\bigcup_{ {\mathbf{S}}\in\Lambda}E^ {\mathbf{S}}. \end{align*} $$
First we prove
![]() $\beta \notin E$
. By Lemma 2.8,
$\beta \notin E$
. By Lemma 2.8,
![]() $\delta (\beta )=\mathbb {L}( {\mathbf {S}}^{\prime })^{\infty }$
for some Lyndon word
$\delta (\beta )=\mathbb {L}( {\mathbf {S}}^{\prime })^{\infty }$
for some Lyndon word
![]() $ {\mathbf {S}}^{\prime }$
. This means
$ {\mathbf {S}}^{\prime }$
. This means
![]() $\beta $
is the left endpoint of a Lyndon interval, so by Lemma 2.9,
$\beta $
is the left endpoint of a Lyndon interval, so by Lemma 2.9,
![]() $\beta \in J^ {\mathbf {s}}$
for some Farey word
$\beta \in J^ {\mathbf {s}}$
for some Farey word
![]() $ {\mathbf {s}}$
. Hence,
$ {\mathbf {s}}$
. Hence,
![]() $\beta \not \in E$
.
$\beta \not \in E$
.
Next, suppose
![]() $\beta \in E^ {\mathbf {S}}$
for some
$\beta \in E^ {\mathbf {S}}$
for some
![]() $ {\mathbf {S}}\in \Lambda $
. Clearly,
$ {\mathbf {S}}\in \Lambda $
. Clearly,
![]() $\beta \ne \beta _{r}^ {\mathbf {S}}$
since
$\beta \ne \beta _{r}^ {\mathbf {S}}$
since
![]() $\delta (\beta _{r}^ {\mathbf {S}})=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty }$
is not periodic. Thus
$\delta (\beta _{r}^ {\mathbf {S}})=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty }$
is not periodic. Thus
 $\beta \in (\beta _{*}^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}})\setminus \bigcup _{r\in \Omega _{F}^{*}}J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
. So, by Proposition 5.6, there is a sequence
$\beta \in (\beta _{*}^ {\mathbf {S}}, \beta _{r}^ {\mathbf {S}})\setminus \bigcup _{r\in \Omega _{F}^{*}}J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
. So, by Proposition 5.6, there is a sequence
![]() $( {\mathbf {r}}_{k})$
of Farey words such that
$( {\mathbf {r}}_{k})$
of Farey words such that
 $\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}}\searrow \beta $
. Write
$\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}}\searrow \beta $
. Write
![]() $\delta (\beta )=(a_{1}\ldots a_{n})^{\infty }$
with minimal period n. Then by Lemma 2.5, it follows that
$\delta (\beta )=(a_{1}\ldots a_{n})^{\infty }$
with minimal period n. Then by Lemma 2.5, it follows that
 $\delta (\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}})\searrow a_{1}\ldots a_{n}^{+} 0^{\infty }$
, so for all sufficiently large k,
$\delta (\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}})\searrow a_{1}\ldots a_{n}^{+} 0^{\infty }$
, so for all sufficiently large k,
 $\delta (\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}})$
contains a block of more than
$\delta (\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}})$
contains a block of more than
![]() $2m$
zeros, where
$2m$
zeros, where
![]() $m:=| {\mathbf {S}}|$
. However, this is impossible, since
$m:=| {\mathbf {S}}|$
. However, this is impossible, since
 $\delta (\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}})=\mathbb {L}( {\mathbf {S}}\bullet {\mathbf {r}}_{k})^{\infty }$
is a concatenation of blocks from
$\delta (\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}})=\mathbb {L}( {\mathbf {S}}\bullet {\mathbf {r}}_{k})^{\infty }$
is a concatenation of blocks from
![]() $ {\mathbf {S}}, {\mathbf {S}}^{-}, \mathbb {L}( {\mathbf {S}})$
, and
$ {\mathbf {S}}, {\mathbf {S}}^{-}, \mathbb {L}( {\mathbf {S}})$
, and
![]() $\mathbb {L}( {\mathbf {S}})^{+}$
. These blocks all have length m, and only
$\mathbb {L}( {\mathbf {S}})^{+}$
. These blocks all have length m, and only
![]() $ {\mathbf {S}}^{-}$
could possibly consist of all zeros, while
$ {\mathbf {S}}^{-}$
could possibly consist of all zeros, while
![]() $ {\mathbf {S}}^{-}$
can only be followed by
$ {\mathbf {S}}^{-}$
can only be followed by
![]() $\mathbb {L}( {\mathbf {S}})$
or
$\mathbb {L}( {\mathbf {S}})$
or
![]() $\mathbb {L}( {\mathbf {S}})^{+}$
. Thus,
$\mathbb {L}( {\mathbf {S}})^{+}$
. Thus,
 $\delta (\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}})$
cannot contain a block of
$\delta (\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}})$
cannot contain a block of
![]() $2m$
zeros. This contradiction shows that
$2m$
zeros. This contradiction shows that
![]() $\beta \not \in E^ {\mathbf {S}}$
.
$\beta \not \in E^ {\mathbf {S}}$
.
Finally, suppose
![]() $\beta \in E_{\infty }$
. Then there is a sequence
$\beta \in E_{\infty }$
. Then there is a sequence
![]() $( {\mathbf {S}}_{k})$
of words in
$( {\mathbf {S}}_{k})$
of words in
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\beta $
lies in the interior of
$\beta $
lies in the interior of
![]() $J^{ {\mathbf {S}}_{k}}$
for each k. Note that
$J^{ {\mathbf {S}}_{k}}$
for each k. Note that
 $\beta =\beta _{\ell }^{ {\mathbf {S}}^{\prime }}$
is the left endpoint of
$\beta =\beta _{\ell }^{ {\mathbf {S}}^{\prime }}$
is the left endpoint of
![]() $J^{ {\mathbf {S}}^{\prime }}$
. Thus,
$J^{ {\mathbf {S}}^{\prime }}$
. Thus,
![]() $J^{ {\mathbf {S}}^{\prime }}\cap J^{ {\mathbf {S}}_{k}}\neq \emptyset $
, and therefore by Lemma 2.9, it must be the case that
$J^{ {\mathbf {S}}^{\prime }}\cap J^{ {\mathbf {S}}_{k}}\neq \emptyset $
, and therefore by Lemma 2.9, it must be the case that
![]() $J^{ {\mathbf {S}}^{\prime }}\subset J^{ {\mathbf {S}}_{k}}$
for all k. However this is impossible, since
$J^{ {\mathbf {S}}^{\prime }}\subset J^{ {\mathbf {S}}_{k}}$
for all k. However this is impossible, since
![]() $|J^{ {\mathbf {S}}_{k}}|\to 0$
. Hence,
$|J^{ {\mathbf {S}}_{k}}|\to 0$
. Hence,
![]() $\beta \not \in E_{\infty }$
.
$\beta \not \in E_{\infty }$
.
Proof of Proposition 1.9
First fix
![]() $\beta _{0}\in (1,2]\setminus \{\beta _{r}^ {\mathbf {S}}: {\mathbf {S}}\in \Lambda \}$
. It is sufficient to prove that
$\beta _{0}\in (1,2]\setminus \{\beta _{r}^ {\mathbf {S}}: {\mathbf {S}}\in \Lambda \}$
. It is sufficient to prove that
-
(*) for each
 $N\in \mathbb {N}$
, there exists
$N\in \mathbb {N}$
, there exists
 $r>0$
such that if
$r>0$
such that if
 $\beta \in (1,2]$
satisfies
$\beta \in (1,2]$
satisfies
 $|\beta -\beta _{0}|<r$
, then there is a word
$|\beta -\beta _{0}|<r$
, then there is a word
 $s_{1}\ldots s_{N}$
such that
$s_{1}\ldots s_{N}$
such that
 $\tau (\beta )$
has a
$\tau (\beta )$
has a
 $\beta $
-expansion beginning with
$\beta $
-expansion beginning with
 $s_{1}\ldots s_{N}$
, and
$s_{1}\ldots s_{N}$
, and
 $\tau (\beta _{0})$
has a
$\tau (\beta _{0})$
has a
 $\beta _{0}$
-expansion beginning with
$\beta _{0}$
-expansion beginning with
 $s_{1}\ldots s_{N}$
.
$s_{1}\ldots s_{N}$
.
For, if
![]() $\tau (\beta )=(s_{1}\ldots s_{N} c_{1} c_{2}\ldots )_{\beta }$
and
$\tau (\beta )=(s_{1}\ldots s_{N} c_{1} c_{2}\ldots )_{\beta }$
and
![]() $\tau (\beta _{0})=(s_{1}\ldots s_{N} d_{1} d_{2}\ldots )_{\beta _{0}}$
, then
$\tau (\beta _{0})=(s_{1}\ldots s_{N} d_{1} d_{2}\ldots )_{\beta _{0}}$
, then
 $$ \begin{align*} |\tau(\beta)-\tau(\beta_{0})|&\leq |(s_{1}\ldots s_{N} c_{1} c_{2}\ldots)_{\beta}-(s_{1}\ldots s_{N} c_{1} c_{2}\ldots)_{\beta_{0}}|\\[3pt] &\quad + |(s_{1}\ldots s_{N} c_{1} c_{2}\ldots)_{\beta_{0}}-(s_{1}\ldots s_{N} d_{1} d_{2}\ldots)_{\beta_{0}}|\\[3pt] &\leq \sum_{i=1}^{\infty} \bigg|\frac{1}{\beta^{i}}-\frac{1}{\beta_{0}^{i}}\bigg|+\sum_{i=N+1}^{\infty} \frac{1}{\beta_{0}^{i}}\\[3pt] &=\frac{|\beta-\beta_{0}|}{(\beta-1)(\beta_{0}-1)}+\frac{1}{(\beta_{0}-1)\beta_{0}^{N}}\\[3pt] &<\frac{r}{(\beta-1)(\beta_{0}-1)}+\frac{1}{(\beta_{0}-1)\beta_{0}^{N}}, \end{align*} $$
$$ \begin{align*} |\tau(\beta)-\tau(\beta_{0})|&\leq |(s_{1}\ldots s_{N} c_{1} c_{2}\ldots)_{\beta}-(s_{1}\ldots s_{N} c_{1} c_{2}\ldots)_{\beta_{0}}|\\[3pt] &\quad + |(s_{1}\ldots s_{N} c_{1} c_{2}\ldots)_{\beta_{0}}-(s_{1}\ldots s_{N} d_{1} d_{2}\ldots)_{\beta_{0}}|\\[3pt] &\leq \sum_{i=1}^{\infty} \bigg|\frac{1}{\beta^{i}}-\frac{1}{\beta_{0}^{i}}\bigg|+\sum_{i=N+1}^{\infty} \frac{1}{\beta_{0}^{i}}\\[3pt] &=\frac{|\beta-\beta_{0}|}{(\beta-1)(\beta_{0}-1)}+\frac{1}{(\beta_{0}-1)\beta_{0}^{N}}\\[3pt] &<\frac{r}{(\beta-1)(\beta_{0}-1)}+\frac{1}{(\beta_{0}-1)\beta_{0}^{N}}, \end{align*} $$
and this can be made as small as desired by choosing N sufficiently large and r sufficiently small. In view of equation (7.1), we prove
![]() $(*)$
by considering several cases.
$(*)$
by considering several cases.
Case I.
 $\beta _{0}\in (\beta _{\ell }^ {\mathbf {S}},\beta _{*}^ {\mathbf {S}})$
for some basic interval
$\beta _{0}\in (\beta _{\ell }^ {\mathbf {S}},\beta _{*}^ {\mathbf {S}})$
for some basic interval
 $I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}},\beta _{*}^ {\mathbf {S}}]$
with
$I^ {\mathbf {S}}=[\beta _{\ell }^ {\mathbf {S}},\beta _{*}^ {\mathbf {S}}]$
with
![]() $ {\mathbf {S}}\in \Lambda $
. It is clear from Theorem 2 that
$ {\mathbf {S}}\in \Lambda $
. It is clear from Theorem 2 that
![]() $(*)$
holds in this case.
$(*)$
holds in this case.
Case II.
![]() $\beta _{0}\in E$
. Then by Proposition 5.6, there exists a sequence of Farey intervals
$\beta _{0}\in E$
. Then by Proposition 5.6, there exists a sequence of Farey intervals
 $J^{ {\mathbf {s}}_{k}}=[\beta _{\ell }^{ {\mathbf {s}}_{k}}, \beta _{r}^{ {\mathbf {s}}_{k}}]$
such that
$J^{ {\mathbf {s}}_{k}}=[\beta _{\ell }^{ {\mathbf {s}}_{k}}, \beta _{r}^{ {\mathbf {s}}_{k}}]$
such that
 $\beta _{\ell }^{ {\mathbf {s}}_{k}}\to \beta _{0}$
as
$\beta _{\ell }^{ {\mathbf {s}}_{k}}\to \beta _{0}$
as
![]() $k\to \infty $
. Furthermore,
$k\to \infty $
. Furthermore,
![]() $|J^{ {\mathbf {s}}_{k}}|\to 0$
as
$|J^{ {\mathbf {s}}_{k}}|\to 0$
as
![]() $k\to \infty $
. This implies that the length
$k\to \infty $
. This implies that the length
![]() $| {\mathbf {s}}_{k}|$
of the Farey word
$| {\mathbf {s}}_{k}|$
of the Farey word
![]() $ {\mathbf {s}}_{k}$
goes to infinity as
$ {\mathbf {s}}_{k}$
goes to infinity as
![]() $k\to \infty $
. Let
$k\to \infty $
. Let
![]() $N\in \mathbb {N}$
be given. We can choose
$N\in \mathbb {N}$
be given. We can choose
![]() $r>0$
small enough so that if a Farey interval
$r>0$
small enough so that if a Farey interval
![]() $J^ {\mathbf {s}}$
intersects
$J^ {\mathbf {s}}$
intersects
![]() ${(\beta _{0}-r,\beta _{0}+r)}$
, then
${(\beta _{0}-r,\beta _{0}+r)}$
, then
![]() $| {\mathbf {s}}|>N$
and
$| {\mathbf {s}}|>N$
and
We can guarantee equation (7.5) because for
![]() $\beta _{0}\in E\setminus \{2\}$
, the expansion
$\beta _{0}\in E\setminus \{2\}$
, the expansion
![]() $\delta (\beta _{0})$
is not periodic by Lemma 7.1, so by Lemma 2.5, the map
$\delta (\beta _{0})$
is not periodic by Lemma 7.1, so by Lemma 2.5, the map
![]() $\beta \mapsto \delta (\beta )$
is continuous at
$\beta \mapsto \delta (\beta )$
is continuous at
![]() $\beta _{0}$
. Furthermore, for
$\beta _{0}$
. Furthermore, for
![]() $\beta _{0}=2$
, the map
$\beta _{0}=2$
, the map
![]() $\beta \mapsto \delta (\beta )$
is left continuous at
$\beta \mapsto \delta (\beta )$
is left continuous at
![]() $\beta _{0}$
.
$\beta _{0}$
.
Let
![]() $\beta \in (\beta _{0}-r, \beta _{0}+r)$
. By equation (7.1), we have either
$\beta \in (\beta _{0}-r, \beta _{0}+r)$
. By equation (7.1), we have either
![]() $\beta \in E$
or
$\beta \in E$
or
![]() $\beta \in J^ {\mathbf {s}}$
for some
$\beta \in J^ {\mathbf {s}}$
for some
![]() $ {\mathbf {s}}\in \Omega _{F}^{*}$
. If
$ {\mathbf {s}}\in \Omega _{F}^{*}$
. If
![]() $\beta \in E$
, then by Proposition 1.12, it follows that
$\beta \in E$
, then by Proposition 1.12, it follows that
![]() $\tau (\beta )=1-{1}/{\beta }=(0\delta _{2}(\beta )\delta _{3}(\beta )\ldots )_{\beta }$
and
$\tau (\beta )=1-{1}/{\beta }=(0\delta _{2}(\beta )\delta _{3}(\beta )\ldots )_{\beta }$
and
 $$ \begin{align} \tau(\beta_{0})=1-\frac{1}{\beta_{0}}=(0\delta_{2}(\beta_{0})\delta_{3}(\beta_{0})\ldots)_{\beta_{0}}, \end{align} $$
$$ \begin{align} \tau(\beta_{0})=1-\frac{1}{\beta_{0}}=(0\delta_{2}(\beta_{0})\delta_{3}(\beta_{0})\ldots)_{\beta_{0}}, \end{align} $$
so
![]() $(*)$
holds by equation (7.5).
$(*)$
holds by equation (7.5).
Next we assume
![]() $\beta \in J^ {\mathbf {s}}$
with
$\beta \in J^ {\mathbf {s}}$
with
![]() $ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{F}^{*}$
. By our choice of r, it follows that
$ {\mathbf {s}}=s_{1}\ldots s_{m}\in \Omega _{F}^{*}$
. By our choice of r, it follows that
![]() $m=| {\mathbf {s}}|>N$
, and equation (7.5) holds. Since
$m=| {\mathbf {s}}|>N$
, and equation (7.5) holds. Since
![]() $\beta \in J^ {\mathbf {s}}=[\beta _{\ell }^ {\mathbf {s}}, \beta _{r}^ {\mathbf {s}}]$
, we have
$\beta \in J^ {\mathbf {s}}=[\beta _{\ell }^ {\mathbf {s}}, \beta _{r}^ {\mathbf {s}}]$
, we have
![]() $\mathbb {L}( {\mathbf {s}})^{\infty }\preccurlyeq \delta (\beta )\preccurlyeq \mathbb {L}( {\mathbf {s}})^{+}{ {\mathbf {s}}^{\infty }}$
. Write
$\mathbb {L}( {\mathbf {s}})^{\infty }\preccurlyeq \delta (\beta )\preccurlyeq \mathbb {L}( {\mathbf {s}})^{+}{ {\mathbf {s}}^{\infty }}$
. Write
![]() $\mathbb {L}( {\mathbf {s}})=a_{1}\ldots a_{m}$
; then by equation (7.5), it follows that
$\mathbb {L}( {\mathbf {s}})=a_{1}\ldots a_{m}$
; then by equation (7.5), it follows that
Observe by equations (7.1)–(7.4) and Lemma 2.3 that
![]() $\tau (\beta )$
has a
$\tau (\beta )$
has a
![]() $\beta $
expansion beginning with
$\beta $
expansion beginning with
![]() ${ {\mathbf {s}}^{-}}=0a_{2}\ldots a_{m}$
. Hence, by equation (7.7),
${ {\mathbf {s}}^{-}}=0a_{2}\ldots a_{m}$
. Hence, by equation (7.7),
![]() $\tau (\beta )$
has a
$\tau (\beta )$
has a
![]() $\beta $
-expansion with prefix
$\beta $
-expansion with prefix
This, together with equation (7.6), gives
![]() $(*)$
.
$(*)$
.
Case III.
![]() $\beta _{0}\in E^ {\mathbf {S}}\backslash \{\beta _{r}^ {\mathbf {S}}\}$
for some
$\beta _{0}\in E^ {\mathbf {S}}\backslash \{\beta _{r}^ {\mathbf {S}}\}$
for some
![]() $ {\mathbf {S}}\in \Lambda $
. The proof is similar to that of Case II, but there are some extra details involving the substitution operator. By Proposition 5.6, it follows that
$ {\mathbf {S}}\in \Lambda $
. The proof is similar to that of Case II, but there are some extra details involving the substitution operator. By Proposition 5.6, it follows that
 $$ \begin{align} {\beta_{0}}\in(\beta_{*}^ {\mathbf{S}}, \beta_{r}^ {\mathbf{S}})\setminus\bigcup_{ {\mathbf{r}}\in\Omega_{F}^{*}}J^{ {\mathbf{S}}\bullet {\mathbf{r}}}, \end{align} $$
$$ \begin{align} {\beta_{0}}\in(\beta_{*}^ {\mathbf{S}}, \beta_{r}^ {\mathbf{S}})\setminus\bigcup_{ {\mathbf{r}}\in\Omega_{F}^{*}}J^{ {\mathbf{S}}\bullet {\mathbf{r}}}, \end{align} $$
and there exists a sequence
![]() $( {\mathbf {r}}_{k})$
of Farey words such that
$( {\mathbf {r}}_{k})$
of Farey words such that
 $\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}}\to {\beta _{0}}$
as
$\beta _{\ell }^{ {\mathbf {S}}\bullet {\mathbf {r}}_{k}}\to {\beta _{0}}$
as
![]() $k\to \infty $
. This implies that
$k\to \infty $
. This implies that
![]() $| {\mathbf {r}}_{k}|\to \infty $
as
$| {\mathbf {r}}_{k}|\to \infty $
as
![]() $k\to \infty $
.
$k\to \infty $
.
Let
![]() $N\in \mathbb {N}$
be given; without loss of generality, we may assume that
$N\in \mathbb {N}$
be given; without loss of generality, we may assume that
![]() $N=N^{\prime }| {\mathbf {S}}|$
for some integer
$N=N^{\prime }| {\mathbf {S}}|$
for some integer
![]() $N^{\prime }$
. By Lemma 7.1, we can choose
$N^{\prime }$
. By Lemma 7.1, we can choose
![]() $r>0$
sufficiently small so that if a Lyndon interval
$r>0$
sufficiently small so that if a Lyndon interval
![]() $J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
intersects
$J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
intersects
![]() $(\beta _{0}-r,\beta _{0}+r)$
, then
$(\beta _{0}-r,\beta _{0}+r)$
, then
![]() $| {\mathbf {r}}|>N^{\prime }$
and
$| {\mathbf {r}}|>N^{\prime }$
and
 $$ \begin{align} \delta_{1}(\beta)\ldots \delta_{N^{\prime}| {\mathbf{S}}|}(\beta)=\delta_{1}(\beta_{0})\ldots\delta_{N^{\prime}| {\mathbf{S}}|}(\beta_{0})= {\mathbf{S}}\bullet(\delta_{1}({\hat\beta_{0}})\ldots\delta_{N^{\prime}}({\hat\beta_{0}})) \end{align} $$
$$ \begin{align} \delta_{1}(\beta)\ldots \delta_{N^{\prime}| {\mathbf{S}}|}(\beta)=\delta_{1}(\beta_{0})\ldots\delta_{N^{\prime}| {\mathbf{S}}|}(\beta_{0})= {\mathbf{S}}\bullet(\delta_{1}({\hat\beta_{0}})\ldots\delta_{N^{\prime}}({\hat\beta_{0}})) \end{align} $$
for any
![]() $\beta \in (\beta _{0}-r,\beta _{0}+r)$
, where
$\beta \in (\beta _{0}-r,\beta _{0}+r)$
, where
 ${\hat \beta _{0}}=\Psi _ {\mathbf {S}}^{-1}(\beta _{0})\in E$
.
${\hat \beta _{0}}=\Psi _ {\mathbf {S}}^{-1}(\beta _{0})\in E$
.
Now take
![]() $\beta \in (\beta _{0}-r, \beta _{0}+r)$
. By equation (7.9), it follows that either
$\beta \in (\beta _{0}-r, \beta _{0}+r)$
. By equation (7.9), it follows that either
![]() $\beta \in E^ {\mathbf {S}}$
or
$\beta \in E^ {\mathbf {S}}$
or
![]() $\beta \in J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
for some
$\beta \in J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
for some
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
. If
$ {\mathbf {r}}\in \Omega _{F}^{*}$
. If
![]() $\beta \in E^ {\mathbf {S}}$
, we let
$\beta \in E^ {\mathbf {S}}$
, we let
 ${\hat \beta }=\Psi _ {\mathbf {S}}^{-1}(\beta )$
. Then equation (7.10) yields
${\hat \beta }=\Psi _ {\mathbf {S}}^{-1}(\beta )$
. Then equation (7.10) yields
 $$ \begin{align*} {\mathbf{S}}\bullet(\delta_{1}(\hat\beta)\ldots\delta_{N^{\prime}}(\hat\beta))=\delta_{1}(\beta)\ldots\delta_{N^{\prime}| {\mathbf{S}}|}(\beta) = {\mathbf{S}}\bullet(\delta_{1}(\hat{\beta}_{0})\ldots\delta_{N^{\prime}}(\hat{\beta}_{0})), \end{align*} $$
$$ \begin{align*} {\mathbf{S}}\bullet(\delta_{1}(\hat\beta)\ldots\delta_{N^{\prime}}(\hat\beta))=\delta_{1}(\beta)\ldots\delta_{N^{\prime}| {\mathbf{S}}|}(\beta) = {\mathbf{S}}\bullet(\delta_{1}(\hat{\beta}_{0})\ldots\delta_{N^{\prime}}(\hat{\beta}_{0})), \end{align*} $$
which implies
![]() $\delta _{1}(\hat \beta )\ldots \delta _{N^{\prime }}(\hat \beta )=\delta _{1}(\hat {\beta }_{0})\ldots \delta _{N^{\prime }}(\hat {\beta }_{0})$
. So, by equation (7.3), it follows that
$\delta _{1}(\hat \beta )\ldots \delta _{N^{\prime }}(\hat \beta )=\delta _{1}(\hat {\beta }_{0})\ldots \delta _{N^{\prime }}(\hat {\beta }_{0})$
. So, by equation (7.3), it follows that
![]() $\tau (\beta )$
has a
$\tau (\beta )$
has a
![]() $\beta $
-expansion with a prefix
$\beta $
-expansion with a prefix
which coincides with a prefix of a
![]() $\beta _{0}$
-expansion of
$\beta _{0}$
-expansion of
![]() $\tau (\beta _{0})$
. This gives
$\tau (\beta _{0})$
. This gives
![]() $(*)$
.
$(*)$
.
If
![]() $\beta \in J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
for some
$\beta \in J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
for some
![]() $ {\mathbf {r}}=r_{1}\ldots r_{m}\in \Omega _{F}^{*}$
, then by our assumption on r, we have
$ {\mathbf {r}}=r_{1}\ldots r_{m}\in \Omega _{F}^{*}$
, then by our assumption on r, we have
![]() $m>N^{\prime }$
. Furthermore,
$m>N^{\prime }$
. Furthermore,
Therefore, writing
![]() $\mathbb {L}( {\mathbf {r}})=b_{1}\ldots b_{m}$
, it follows from equation (7.10) that
$\mathbb {L}( {\mathbf {r}})=b_{1}\ldots b_{m}$
, it follows from equation (7.10) that
 $$ \begin{align} {\mathbf{S}}\bullet(b_{1}\ldots b_{N^{\prime}})=\delta_{1}(\beta)\ldots\delta_{N^{\prime}| {\mathbf{S}}|}(\beta)= {\mathbf{S}}\bullet(\delta_{1}(\hat{\beta}_{0})\ldots \delta_{N^{\prime}}(\hat{\beta}_{0})). \end{align} $$
$$ \begin{align} {\mathbf{S}}\bullet(b_{1}\ldots b_{N^{\prime}})=\delta_{1}(\beta)\ldots\delta_{N^{\prime}| {\mathbf{S}}|}(\beta)= {\mathbf{S}}\bullet(\delta_{1}(\hat{\beta}_{0})\ldots \delta_{N^{\prime}}(\hat{\beta}_{0})). \end{align} $$
This shows that
![]() $b_{1}\ldots b_{N^{\prime }}=\delta _{1}(\hat {\beta }_{0})\ldots \delta _{N^{\prime }}(\hat {\beta }_{0})$
. Now observe by equations (7.1)–(7.4) and Lemma 2.3 that
$b_{1}\ldots b_{N^{\prime }}=\delta _{1}(\hat {\beta }_{0})\ldots \delta _{N^{\prime }}(\hat {\beta }_{0})$
. Now observe by equations (7.1)–(7.4) and Lemma 2.3 that
![]() $\tau (\beta )$
has a
$\tau (\beta )$
has a
![]() $\beta $
-expansion beginning with
$\beta $
-expansion beginning with
![]() $( {\mathbf {S}}\bullet {\mathbf {r}})^{-}= {\mathbf {S}}\bullet (0 b_{2}\ldots b_{m})$
. So, by equations (7.3) and (7.11), it follows that
$( {\mathbf {S}}\bullet {\mathbf {r}})^{-}= {\mathbf {S}}\bullet (0 b_{2}\ldots b_{m})$
. So, by equations (7.3) and (7.11), it follows that
![]() $\tau (\beta )$
has a
$\tau (\beta )$
has a
![]() $\beta $
-expansion with a prefix
$\beta $
-expansion with a prefix
of length N, which is also a prefix of a
![]() $\beta _{0}$
-expansion of
$\beta _{0}$
-expansion of
![]() $\tau (\beta _{0})$
. This again gives
$\tau (\beta _{0})$
. This again gives
![]() $(*)$
.
$(*)$
.
Case IV.
 $\beta _{0}=\beta _{\ell }^ {\mathbf {S}}$
for some
$\beta _{0}=\beta _{\ell }^ {\mathbf {S}}$
for some
![]() $ {\mathbf {S}}\in \Lambda $
. Here the right continuity of
$ {\mathbf {S}}\in \Lambda $
. Here the right continuity of
![]() $\tau $
at
$\tau $
at
![]() $\beta _{0}$
follows from Theorem 2. The left continuity can be seen as follows. If
$\beta _{0}$
follows from Theorem 2. The left continuity can be seen as follows. If
![]() $ {\mathbf {S}}\in \Omega _{F}^{*}$
, then
$ {\mathbf {S}}\in \Omega _{F}^{*}$
, then
![]() $\tau (\beta _{0})$
has a
$\tau (\beta _{0})$
has a
![]() $\beta _{0}$
-expansion
$\beta _{0}$
-expansion
 $0\delta _{2}(\beta _{\ell }^ {\mathbf {S}})\delta _{3}(\beta _{\ell }^ {\mathbf {S}})\ldots $
, and the left continuity follows by the argument in Case II, using the left continuity of the map
$0\delta _{2}(\beta _{\ell }^ {\mathbf {S}})\delta _{3}(\beta _{\ell }^ {\mathbf {S}})\ldots $
, and the left continuity follows by the argument in Case II, using the left continuity of the map
![]() $\beta \mapsto \delta (\beta )$
at
$\beta \mapsto \delta (\beta )$
at
![]() $\beta _{0}$
. Otherwise,
$\beta _{0}$
. Otherwise,
![]() $ {\mathbf {S}}= {\mathbf {S}}^{\prime }\bullet {\mathbf {r}}$
for some
$ {\mathbf {S}}= {\mathbf {S}}^{\prime }\bullet {\mathbf {r}}$
for some
![]() $ {\mathbf {S}}^{\prime }\in \Lambda $
and
$ {\mathbf {S}}^{\prime }\in \Lambda $
and
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
, and
$ {\mathbf {r}}\in \Omega _{F}^{*}$
, and
![]() $\tau (\beta _{0})$
has a
$\tau (\beta _{0})$
has a
![]() $\beta _{0}$
-expansion
$\beta _{0}$
-expansion
![]() $\Phi _{ {\mathbf {S}}^{\prime }}(0\delta _{2}(\beta _{\ell }^ {\mathbf {r}})\delta _{3}(\beta _{\ell }^ {\mathbf {r}})\ldots )$
. In this case the left continuity follows from the argument in Case III.
$\Phi _{ {\mathbf {S}}^{\prime }}(0\delta _{2}(\beta _{\ell }^ {\mathbf {r}})\delta _{3}(\beta _{\ell }^ {\mathbf {r}})\ldots )$
. In this case the left continuity follows from the argument in Case III.
Case V.
![]() $\beta _{0}=\beta _{*}^ {\mathbf {S}}$
for some
$\beta _{0}=\beta _{*}^ {\mathbf {S}}$
for some
![]() $ {\mathbf {S}}\in \Lambda $
. Here the left continuity at
$ {\mathbf {S}}\in \Lambda $
. Here the left continuity at
![]() $\beta _{0}$
follows from Theorem 2. The right continuity can be seen as follows. First note that
$\beta _{0}$
follows from Theorem 2. The right continuity can be seen as follows. First note that
 $$ \begin{align*} \delta(\beta_{*}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty} \quad\mbox{and}\quad \tau(\beta_{*}^ {\mathbf{S}})=({\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta_{*}^ {\mathbf{S}}}. \end{align*} $$
$$ \begin{align*} \delta(\beta_{*}^ {\mathbf{S}})=\mathbb{L}( {\mathbf{S}})^{+} {\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty} \quad\mbox{and}\quad \tau(\beta_{*}^ {\mathbf{S}})=({\mathbf{S}}^{-}\mathbb{L}( {\mathbf{S}})^{\infty})_{\beta_{*}^ {\mathbf{S}}}. \end{align*} $$
Observe also that
 $\beta _{*}^ {\mathbf {S}}=\lim _{\hat {\beta }\searrow 1}\Psi _ {\mathbf {S}}(\hat {\beta })$
, so by Lemma 2.5,
$\beta _{*}^ {\mathbf {S}}=\lim _{\hat {\beta }\searrow 1}\Psi _ {\mathbf {S}}(\hat {\beta })$
, so by Lemma 2.5,
 $\Phi _ {\mathbf {S}}(\delta (\hat {\beta }))\searrow \delta (\beta _{*}^ {\mathbf {S}})$
as
$\Phi _ {\mathbf {S}}(\delta (\hat {\beta }))\searrow \delta (\beta _{*}^ {\mathbf {S}})$
as
![]() $\hat {\beta }\searrow 1$
.
$\hat {\beta }\searrow 1$
.
Now let
![]() $N\in \mathbb {N}$
be given. As in Case III, we may assume that
$N\in \mathbb {N}$
be given. As in Case III, we may assume that
![]() $N=N^{\prime }| {\mathbf {S}}|$
for some integer
$N=N^{\prime }| {\mathbf {S}}|$
for some integer
![]() $N^{\prime }$
. We choose
$N^{\prime }$
. We choose
![]() $r>0$
small enough so that if
$r>0$
small enough so that if
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
and
$ {\mathbf {r}}\in \Omega _{F}^{*}$
and
![]() $J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
intersects
$J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
intersects
![]() ${(\beta _{0},\beta _{0}+r)}$
, then
${(\beta _{0},\beta _{0}+r)}$
, then
![]() $| {\mathbf {r}}|>N^{\prime }$
. Now take
$| {\mathbf {r}}|>N^{\prime }$
. Now take
![]() $\beta \in (\beta _{0},\beta _{0}+r)$
. If
$\beta \in (\beta _{0},\beta _{0}+r)$
. If
![]() $\beta \in E^ {\mathbf {S}}$
, then
$\beta \in E^ {\mathbf {S}}$
, then
![]() $\beta =\Psi _ {\mathbf {S}}(\hat {\beta })$
for some
$\beta =\Psi _ {\mathbf {S}}(\hat {\beta })$
for some
![]() $\hat {\beta }\in E$
, and
$\hat {\beta }\in E$
, and
![]() $\delta (\beta )=\Phi _ {\mathbf {S}}(\delta (\hat {\beta }))$
. Note that if
$\delta (\beta )=\Phi _ {\mathbf {S}}(\delta (\hat {\beta }))$
. Note that if
![]() $\beta \searrow \beta _{0}$
, then
$\beta \searrow \beta _{0}$
, then
![]() $\hat {\beta }\searrow 1$
and so
$\hat {\beta }\searrow 1$
and so
![]() $\delta (\hat {\beta })\searrow 10^{\infty }$
. Thus, we may also assume r is small enough so that
$\delta (\hat {\beta })\searrow 10^{\infty }$
. Thus, we may also assume r is small enough so that
![]() $\delta (\hat {\beta })$
begins with
$\delta (\hat {\beta })$
begins with
![]() $10^{N^{\prime }-1}$
. Then
$10^{N^{\prime }-1}$
. Then
![]() $\tau (\beta )$
has a
$\tau (\beta )$
has a
![]() $\beta $
-expansion beginning with
$\beta $
-expansion beginning with
![]() $\Phi _ {\mathbf {S}}(0^{N^{\prime }})= {\mathbf {S}}^{-}\mathbb {L}( {\mathbf {S}})^{N^{\prime }-1}$
, which is also a prefix of length N of a
$\Phi _ {\mathbf {S}}(0^{N^{\prime }})= {\mathbf {S}}^{-}\mathbb {L}( {\mathbf {S}})^{N^{\prime }-1}$
, which is also a prefix of length N of a
![]() $\beta _{0}$
-expansion of
$\beta _{0}$
-expansion of
![]() $\tau (\beta _{0})$
.
$\tau (\beta _{0})$
.
Similarly, if
![]() $\beta \in J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
, then we may assume r is small enough so that
$\beta \in J^{ {\mathbf {S}}\bullet {\mathbf {r}}}$
, then we may assume r is small enough so that
![]() $ {\mathbf {r}}$
begins with
$ {\mathbf {r}}$
begins with
![]() $0^{N^{\prime }-1}$
. Then
$0^{N^{\prime }-1}$
. Then
![]() $\tau (\beta )$
has a
$\tau (\beta )$
has a
![]() $\beta $
-expansion beginning with
$\beta $
-expansion beginning with
![]() $( {\mathbf {S}}\bullet {\mathbf {r}})^{-}$
, and therefore beginning with
$( {\mathbf {S}}\bullet {\mathbf {r}})^{-}$
, and therefore beginning with
![]() $ {\mathbf {S}}^{-}\mathbb {L}( {\mathbf {S}})^{N^{\prime }-1}$
, and we conclude as above.
$ {\mathbf {S}}^{-}\mathbb {L}( {\mathbf {S}})^{N^{\prime }-1}$
, and we conclude as above.
Case VI.
![]() $\beta _{0}\in E_{\infty }$
. Then there exists a sequence
$\beta _{0}\in E_{\infty }$
. Then there exists a sequence
![]() $( {\mathbf {s}}_{k})$
of Farey words such that
$( {\mathbf {s}}_{k})$
of Farey words such that
 $$ \begin{align*} \{\beta\} =\bigcap_{k=1}^{\infty} J^{ {\mathbf{S}}_{k}}, \end{align*} $$
$$ \begin{align*} \{\beta\} =\bigcap_{k=1}^{\infty} J^{ {\mathbf{S}}_{k}}, \end{align*} $$
where
![]() $ {\mathbf {S}}_{k}:= {\mathbf {s}}_{1}\bullet {\mathbf {s}}_{2}\bullet \cdots \bullet {\mathbf {s}}_{k}$
. Note that
$ {\mathbf {S}}_{k}:= {\mathbf {s}}_{1}\bullet {\mathbf {s}}_{2}\bullet \cdots \bullet {\mathbf {s}}_{k}$
. Note that
![]() $J^{ {\mathbf {S}}_{k}}\supset J^{ {\mathbf {S}}_{k+1}}$
for all
$J^{ {\mathbf {S}}_{k}}\supset J^{ {\mathbf {S}}_{k+1}}$
for all
![]() $k\ge 1$
, and
$k\ge 1$
, and
![]() $| {\mathbf {S}}_{k}|\to \infty $
as
$| {\mathbf {S}}_{k}|\to \infty $
as
![]() $k\to \infty $
.
$k\to \infty $
.
Let
![]() $N\in \mathbb {N}$
be given, and choose k so large that
$N\in \mathbb {N}$
be given, and choose k so large that
![]() $| {\mathbf {S}}_{k}|>N$
. Choose
$| {\mathbf {S}}_{k}|>N$
. Choose
![]() $r>0$
sufficiently small so that
$r>0$
sufficiently small so that
![]() $(\beta _{0}-r, \beta _{0}+r)\subset J^{ {\mathbf {S}}_{k}}$
. Take
$(\beta _{0}-r, \beta _{0}+r)\subset J^{ {\mathbf {S}}_{k}}$
. Take
![]() $\beta \in (\beta _{0}-r, \beta _{0}+r)$
. Then
$\beta \in (\beta _{0}-r, \beta _{0}+r)$
. Then
![]() $\beta \in J^{ {\mathbf {S}}_{k}}$
, so by equations (7.1)–(7.4), it follows that
$\beta \in J^{ {\mathbf {S}}_{k}}$
, so by equations (7.1)–(7.4), it follows that
![]() $\tau (\beta )$
has a
$\tau (\beta )$
has a
![]() $\beta $
-expansion beginning with
$\beta $
-expansion beginning with
![]() $ {\mathbf {S}}_{k}^{-}$
, which is also a prefix (of length at least N) of a
$ {\mathbf {S}}_{k}^{-}$
, which is also a prefix (of length at least N) of a
![]() $\beta _{0}$
-expansion of
$\beta _{0}$
-expansion of
![]() $\tau (\beta _{0})$
. Hence, we obtain
$\tau (\beta _{0})$
. Hence, we obtain
![]() $(*)$
.
$(*)$
.
Finally, we consider
![]() $\beta _{0}=\beta _{r}^ {\mathbf {S}}$
for
$\beta _{0}=\beta _{r}^ {\mathbf {S}}$
for
![]() $ {\mathbf {S}}\in \Lambda $
. The left continuity at
$ {\mathbf {S}}\in \Lambda $
. The left continuity at
![]() $\beta _{0}$
(that is, the analog of
$\beta _{0}$
(that is, the analog of
![]() $(*)$
for
$(*)$
for
![]() $\beta \in (\beta _{0}-r,\beta _{0})$
) follows just as in Case III. The jump at
$\beta \in (\beta _{0}-r,\beta _{0})$
) follows just as in Case III. The jump at
![]() $\beta _{0}$
(that is, equation (1.6)) can be seen as follows. Since
$\beta _{0}$
(that is, equation (1.6)) can be seen as follows. Since
![]() $\tau (\beta _{0})=( {\mathbf {S}} 0^{\infty })_{\beta _{0}}<( {\mathbf {S}}^{\infty })_{\beta _{0}}$
by Proposition 6.2 (or rather, Case II of its proof), it suffices to show that
$\tau (\beta _{0})=( {\mathbf {S}} 0^{\infty })_{\beta _{0}}<( {\mathbf {S}}^{\infty })_{\beta _{0}}$
by Proposition 6.2 (or rather, Case II of its proof), it suffices to show that
 $$ \begin{align} \lim_{\beta\searrow\beta_{0}}\tau(\beta)=( {\mathbf{S}}^{\infty})_{\beta_{0}}. \end{align} $$
$$ \begin{align} \lim_{\beta\searrow\beta_{0}}\tau(\beta)=( {\mathbf{S}}^{\infty})_{\beta_{0}}. \end{align} $$
First assume
![]() $ {\mathbf {S}}\in \Omega _{F}^{*}$
. Then
$ {\mathbf {S}}\in \Omega _{F}^{*}$
. Then
![]() $\delta (\beta _{0})=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty }$
, and by Lemma 2.3, it follows that
$\delta (\beta _{0})=\mathbb {L}( {\mathbf {S}})^{+} {\mathbf {S}}^{\infty }$
, and by Lemma 2.3, it follows that
![]() $ {\mathbf {S}}^{\infty }=0\delta _{2}(\beta _{0})\delta _{3}(\beta _{0})\ldots $
. So, by the same argument as in Case II, we obtain equation (7.12).
$ {\mathbf {S}}^{\infty }=0\delta _{2}(\beta _{0})\delta _{3}(\beta _{0})\ldots $
. So, by the same argument as in Case II, we obtain equation (7.12).
Next suppose
![]() $ {\mathbf {S}}= {\mathbf {S}}^{\prime }\bullet {\mathbf {r}}$
for some
$ {\mathbf {S}}= {\mathbf {S}}^{\prime }\bullet {\mathbf {r}}$
for some
![]() $ {\mathbf {S}}^{\prime }\in \Lambda $
and
$ {\mathbf {S}}^{\prime }\in \Lambda $
and
![]() $ {\mathbf {r}}\in \Omega _{F}^{*}$
. Then
$ {\mathbf {r}}\in \Omega _{F}^{*}$
. Then
where
 $\hat \beta _{0}=\Psi _{ {\mathbf {S}}^{\prime }}^{-1}(\beta _{0})\in E$
. This implies that
$\hat \beta _{0}=\Psi _{ {\mathbf {S}}^{\prime }}^{-1}(\beta _{0})\in E$
. This implies that
The same argument as in Case III then yields equation (7.12).
Acknowledgements
The authors thank the anonymous referee for several helpful comments. P.A. is partially supported by Simons Foundation grant # 709869. D.K. thanks Charlene Kalle for some useful discussions when she visited Chongqing University in November 2019. He is supported by NSFC No. 11971079 and the Fundamental and Frontier Research Project of Chongqing No. cstc2019jcyj-msxmX0338 and No. cx2019067. Derong Kong is the corresponding author.