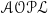An ASP Framework for the Refinement of Authorization and Obligation Policies

Abstract

This paper introduces a framework for assisting policy authors in refining and improving their policies. In particular, we focus on authorization and obligation policies that can be encoded in Gelfond and Lobo’s $\mathscr{AOPL}$ language for policy specification. We propose a framework that detects the statements that make a policy inconsistent, underspecified, or ambiguous with respect to an action being executed in a given state. We also give attention to issues that arise at the intersection of authorization and obligation policies, for instance when the policy requires an unauthorized action to be executed. The framework is encoded in Answer Set Programming.

1 Introduction

This paper introduces a framework for assisting policy authors in refining and improving the policies they elaborate. Here, by a policy we mean a collection of statements that describe the permissions and obligations related to an agent’s actions.

In particular, we focus on authorization and obligation policies that can be encoded in the policy specification language $\mathscr{AOPL}$ by Gelfond and Lobo Gelfond and Lobo (2008). $\mathscr{AOPL}$ allows an author to specify policies for an autonomous agent acting in a changing environment. A description of the dynamic domain in terms of sorts of the domain, relevant fluents, and actions is assumed to be available to the policy writer. Policy rules of $\mathscr{AOPL}$ may be of two kinds: authorization rules specifying what actions are permitted/ not permitted and in which situations, and obligation rules indicating what actions an agent must perform or not perform under certain conditions. Rules can either be strict or defeasible, and preferences between defeasible rules can be set by the policy author. The semantics of $\mathscr{AOPL}$ is defined via a translation into Answer Set Programming (ASP) (Gelfond and Lifschitz 1991). Gelfond and Lobo define policy properties such as consistency and categoricity. However, there is a gap in analyzing what happens at the intersection between authorization and obligation policies, for instance when a policy requires an unauthorized action to be executed, which is called a modality conflict by Craven et al. Craven et al. (2009).

We propose a framework that detects the rules that make a policy inconsistent, underspecified, or ambiguous with respect to an action and a given state. The goal is to notify the policy author about the natural language statements in the policy that may be causing an issue and explain why that is the case for the particular action and state.

Given rapid advancements in AI in the past years, the importance of setting and enforcing policies on intelligent agents has become paramount. At the same time, policy specifications can become large and intricate. Thus, assisting policy authors and knowledge engineers with policy refinement by automatically detecting issues in a provably correct way and highlighting conflicting policy statements is of great importance. The contributions of our work are as follows:

• We define a new translation of $\mathscr{AOPL}$ policies into ASP by reifying policy rules.

• We formally define issues that may arise in $\mathscr{AOPL}$ policies and describe how to detect the causing policy statements, using the reified ASP translation.

• We define means for explaining the root causes for issues like inconsistency, underspecification, ambiguity, and modality conflicts.

In what follows, we provide a short description of language $\mathscr{AOPL}$ in Section 2 and give a motivating example in Section 3. We describe our new translation of $\mathscr{AOPL}$ policies into ASP in Section 4 and introduce our framework in Section 5. We discuss related work in Section 6 and end with conclusions and future work.

2 Background: Language $\boldsymbol{\mathscr{AOPL}}$

Let us now briefly present the $\mathscr{AOPL}$ language. We direct the unfamiliar reader to outside resources on ASP (Gelfond and Lifschitz 1991; Marek and Truszczynski 1999) and action language $\mathscr{AL}_d$ (Gelfond and Inclezan 2013; Gelfond and Kahl 2014), which are also relevant to this work.

Gelfond and Lobo Gelfond and Lobo (2008) ¹ introduced the Authorization and Obligation Policy Language $\mathscr{AOPL}$ for specifying policies for an intelligent agent acting in a dynamic environment. A policy is a collection of authorization and obligation statements, which we simply call authorizations and obligations, respectively. An authorization indicates whether an agent’s action is permitted or not, and under which conditions. An obligation describes whether an agent is obligated or not obligated to perform a specific action under certain conditions. An $\mathscr{AOPL}$ policy works in conjunction with a dynamic system description of the agent’s environment written in an action language such as $\mathscr{AL}_d$ . The signature of the dynamic system description includes predicates denoting sorts for the elements in the domain; fluents (i.e. properties of the domain that may be changed by actions); and actions. As in $\mathscr{AL}_d$ , we consider dynamic systems that can be represented by a directed graph, called a transition diagram, containing a finite number of nodes representing physically possible states of the dynamic domain. A state is a complete and consistent set of fluent literals. Arcs in the transition diagram are labeled by action atoms (shortly actions) that take the system from one state to another. Actions can be elementary or compound, where a compound action is a set of elementary actions executed simultaneously.

The signature of an $\mathscr{AOPL}$ policy includes the signature of the associated dynamic system and additional predicates permitted for authorizations, obl for obligations, and prefer for establishing preferences between authorizations or obligations. A prefer atom is created from the predicate prefer; similarly for permitted and obl atoms.

Definition 1 (Policy)

An $\mathscr{AOPL}$ policy $\mathscr{P}$ is a finite collection of statements of the form:

(1a) \begin{align} & \ \ permitted\left(e\right) & \textbf{ if } \ cond \end{align}

(1b) \begin{align} & \neg permitted\left(e\right) & \textbf{ if } \ cond \end{align}

(1c) \begin{align}& \ \ obl\left(h\right) & \textbf{ if } \ cond \end{align}

(1d) \begin{align}& \neg obl\left(h\right) & \textbf{ if } \ cond\end{align}

(1e) \begin{align}d: \textbf{normally } & \ \ permitted(e) & \textbf{ if } \ cond\end{align}

(1f) \begin{align}d: \textbf{normally } & \neg permitted(e) & \textbf{ if } \ cond\end{align}

(1g) \begin{align}d: \textbf{normally } & \ \ obl(h) & \textbf{ if } \ cond\end{align}

(1h) \begin{align}d: \textbf{normally } & \neg obl(h) & \textbf{ if } \ cond\end{align}

(1i) \begin{align}& \ \ {\textit{prefer}}(d_i, d_j) & \end{align}

where e is an elementary action; h is a happening (i.e. an elementary action or its negation ² ); cond is a (possibly empty) collection of atoms of the signature, except for atoms containing the predicate prefer; d appearing in (1e)–(1h) denotes a defeasible rule label; and $d_i$ , $d_j$ in (1i) refer to two distinct rule labels from $\mathscr{P}$ . Rules (1a)–(1d) encode strict policy statements, while rules (1e)–(1h) encode defeasible statements (i.e. statements that may have exceptions). Rule (1i) captures priorities between defeasible statements.

In deontic terms, rules (1a) and (1e) denote permissions; rules (1b) and (1f) denote prohibitions; rules (1c) and (1g) denote obligations; and rules (1d) and (1h) denote dispensations.

The semantics of an $\mathscr{AOPL}$ policy determine a mapping $\textbf{P}(\sigma)$ from states of a transition diagram $\mathscr{T}$ into a collection of permitted and obl literals. To formally describe the semantics of $\mathscr{AOPL}$ , a translation of a policy and transition diagram into ASP is defined.

Definition 2 (ASP Translation of a Policy and State)

The translation lp is defined as:

• If x is a fluent literal, action literal, permitted, or obl literal, then $lp(x) =_{def} x$ .

• If L is a set of literals, then $lp(L) =_{def} \{lp(l) : l \in L\}$

• If $r = \unicode{x201C}l \ \textbf{if} \ cond\unicode{x201D}$ is a strict rule like the ones in (1a)–(1d), then $lp(r) =_{def} lp(l) \leftarrow lp(cond)$

• If r is a defeasible rule like (1e) or (1f), or a preference rule “prefer $(d_i, d_j)$ ” like the one in (1i), then lp(r) is obtained using standard ASP techniques for encoding defaults, as shown in equations (2a), (2b), and (2c) respectively:

  (2a) \begin{align} permitted(e) & \leftarrow \ lp(cond), \mbox{not}\ ab(d), \mbox{not}\ \neg permitted(e) \end{align}
  (2b) \begin{align} \neg permitted(e) & \leftarrow \ lp(cond), \mbox{not}\ ab(d), \mbox{not}\ permitted(e) \end{align}
  (2c) \begin{align} ab(d_j) & \leftarrow \ lp(cond_i) \end{align}
  where $cond_i$ is the condition of $d_i$ . Similarly for defeasible obligations (1g) and (1h).

• If $\mathscr{P}$ is a policy, then $lp(\mathscr{P}) =_{def} \{lp(st) : st \in \mathscr{P}\}$ .

• If $\mathscr{P}$ is a policy and $\sigma$ is a state of the (transition diagram associated with the) dynamic system description $\mathscr{T}$ ,

$$lp(\mathscr{P}, \sigma) =_{def} lp(\mathscr{P}) \cup lp(\sigma)$$

Properties of an $\mathscr{AOPL}$ policy $\mathscr{P}$ are defined in terms of the answer sets of the logic program $lp(\mathscr{P}, \sigma)$ expanded with appropriate rules.

The following definitions by Gelfond and Lobo are relevant to our work (original definition numbers in parenthesis). In what follows a denotes a (possibly) compound action (i.e. a set of simultaneously executed elementary actions), while e refers to an elementary action. An event $\langle \sigma, a \rangle$ is a pair consisting of a state $\sigma$ and a (possibly) compound action a executed in $\sigma$ . ³

Definition 3 (Consistency – Def. 3)

A policy $\mathscr{P}$ for $\mathscr{T}$ is called consistent if for every state $\sigma$ of $\mathscr{T}$ , the logic program $lp(\mathscr{P}, \sigma)$ is consistent, that is, it has an answer set.

Definition 4 (Policy Compliance for Authorizations – Defs. 4 and 5)

• An event $\langle \sigma, a \rangle$ is strongly compliant with authorization policy $\mathscr{P}$ if for every $e \in a$ we have that $permitted(e) \in$ $\textbf{P}(\sigma)$ (i.e. the logic program $lp(\mathscr{P}, \sigma)$ entails permitted(e)).

• An event $\langle \sigma, a \rangle$ is weakly compliant with authorization policy $\mathscr{P}$ if for every $e \in a$ we have that $\neg permitted(e) \notin$ $\textbf{P}(\sigma)$ (i.e. the logic program $lp(\mathscr{P}, \sigma)$ does not entail $\neg permitted(e)$ ).

• An event $\langle \sigma, a \rangle$ is non-compliant with authorization policy $\mathscr{P}$ if for every $e \in a$ we have that $\neg permitted(e) \in$ $\textbf{P}(\sigma)$ (i.e. the logic program $lp(\mathscr{P}, \sigma)$ entails $\neg permitted(e)$ ).

Definition 5 (Policy Compliance for Obligations – Def. 9)

An event $\langle \sigma, a \rangle$ is compliant with obligation policy $\mathscr{P}$ if

• For every $obl(e) \in$ $\textbf{P}(\sigma)$ we have that $e \in a$ , and

• For every $obl(\neg e) \in$ $\textbf{P}(\sigma)$ we have that $e \notin a$ .

Definition 6 (Categoricity – Def. 6)

A policy $\mathscr{P}$ for $\mathscr{T}$ is called categorical if for every state $\sigma$ of $\mathscr{T}$ the logic program $lp(\mathscr{P}, \sigma)$ is categorical, that is, has exactly one answer set.

Note that $\mathscr{AOPL}$ does not discuss interactions between authorizations and obligations referring to the same action, for instance situations when both obl(e) and $\neg permitted(e)$ are part of the answer set of $lp(\mathscr{P}, \sigma)$ for some state $\sigma$ .

3 Motivating example

To illustrate the policy refinement process that we want to facilitate, let’s consider an example provided by Gelfond and Lobo, expanded with an additional rule (4):

Example 1 (Authorization Policy Example)

1. (1) A military officer is not allowed to command a mission they authorized.

2. (2) A colonel is allowed to command a mission they authorized.

3. (3) A military observer can never authorize a mission.

4. (4) A military officer must command a mission if ordered by their superior to do so.

Before discussing the encoding of this policy, let us assume that the description of this domain includes actions $assume\_comm(C, M)$ and $authorize\_comm(C, M)$ ; fluents authorized(C, M) and $ordered\_by\_superior(C, M)$ ; and sorts colonel(C) and observer(C), where C is a commander and M is a mission.

In the English description of the policy in Example 1, note that statements (1) and (2) are phrased as strict rules and thus an automated translation process into $\mathscr{AOPL}$ would produce the policy:

(3a) \begin{align} \neg permitted(assume\_comm(C, M)) & \textbf{ if } authorized(C, M) \end{align}

(3b) \begin{align} permitted(assume\_comm(C, M)) & \textbf{ if } colonel(C) \end{align}

(3c) \begin{align} \neg permitted(authorize\_comm(C, M)) & \textbf{ if } observer(C) \end{align}

(3d) \begin{align} obl(assume\_comm(C, M)) & \textbf{ if } ordered\_by\_superior(C, M) \end{align}

Such a policy is inconsistent in a state in which authorized(c, m) and colonel(c) both hold, due to rules (3a) and (3b). Gelfond and Lobo indicate that “[s]ince the nature of the first two authorization policy statements of our example are contradictory we naturally assume them to be defeasible” and replace the encoding in rules (3a) and (3b) with

$$ \begin{array}{ll} d_1(C, M)\ : & {\bf normally} \ \neg permitted(assume\_comm(C, M)) \ \textbf{ if } authorized(C, M) \\ d_2(C, M)\ : & {\bf normally} \ \ \ permitted(assume\_comm(C, M)) \ \textbf{ if } colonel(C) \\ & prefer(d_2(C, M), d_1(C, M)) \end{array}$$

while leaving rule (3c) as it is. Rule (3d) is unaffected, as it corresponds to the new policy statement (4) that we added to the original example by Gelfond and Lobo, to illustrate obligations.

This approach has several drawbacks: (a) it puts the burden on the knowledge engineer, who may have a more limited knowledge of the domain than the policy author and thus may make false assumptions; (b) it does not scale for large and intricate policies; and (c) it would be difficult to automate. Instead, we propose a framework that detects inconsistencies like the one above, alerts the policy author of the conflicting policy statements and the conditions that cause them, and allows the policy author to refine the policy (with options for refinement possibly suggested, in the future). In particular, for Example 1, we expect our framework to indicate that statements (1) and (2) are in conflict in a state in which both colonel(c) and authorized(c, m) are true. Similarly, our framework should flag the contradiction between the obligation in rule (4) and rule (1) in a state in which authorized(c, m) and $ordered\_by\_superior(c, m)$ both hold.

To achieve this goal, we modify $\mathscr{AOPL}$ by introducing labels for all rules (including strict and preference rules) ⁴ and connecting rules of $\mathscr{AOPL}$ with natural language statements of the original policy via a new predicate text as in the following example for the strict policy rule in (3c) where $s_1$ is the label for the strict authorization rule:

$$\begin{array}{ll}s_1 :& \neg permitted(authorize\_command(C, M)) \textbf{ if } observer(C) \\& text(s_1, ``\mbox{A military observer can never authorize a mission.}")\end{array}$$

Additionally, we define a different translation of $\mathscr{AOPL}$ into ASP, which we will denote by $rei\_lp$ as it reifies policy rules. We define the $rei\_lp$ translation in the next section.

4 Reification of policy rules

The new translation of $\mathscr{AOPL}$ into ASP that we propose follows previous methods for the reification of rules in other domains, such as reasoning about prioritized defaults (Gelfond and Son 1997) or belief states (Balduccini et al. 2020). Similar to the definition of the lp translation function, the signature of $rei\_lp(\mathscr{P})$ for a policy $\mathscr{P}$ applying in a dynamic domain described by $\mathscr{T}$ contains the sorts, fluents, and actions of $\mathscr{T}$ . To simplify the presentation, we limit ourselves to boolean fluents and use the general syntax

(4) \begin{equation}r : [{\bf normally}] \ hd \ {\bf if} \ cond\end{equation}

to refer to both strict and defeasible, authorization and obligation rules from $\mathscr{P}$ . We use the term head of rule r to refer to the hd part in (4), where $hd \in HD$ ,

$$HD = \bigcup\limits_{e \in E}\{permitted(e), \neg permitted(e), obl(e), obl(\neg e), \neg obl(e), \neg obl(\neg e)\}$$

and E is the set of all elementary actions in $\mathscr{T}$ . The signature of $rei\_lp(\mathscr{P})$ also includes the elements of HD and the following predicates:

• rule(r) – where r is a rule label (referred shortly as “rule” below)

• type(r, ty) – where $ty \in \{strict,$ defeasible, prefer $\}$ is the type of rule r

• text(r, t) – to denote that rule r corresponds to policy statement t

• head(r, hd) – to denote the head hd of rule r

• body(r, b(r)) – where b(r) denotes the condition cond in rule r and b is a new function added to the signature of $rei\_lp(\mathscr{P})$

• mbr(b(r), l) – for every l in the condition cond of rule r (mbr stands for “member”)

• ab(r) – for every defeasible rule r

• holds(x) – where x may be a rule r, the head hd of a rule, function b(r) representing the cond of a rule r, literal l of $\mathscr{T}$ , or ab(r) from above

• $opp(r, \overline{hd})$ – where r is a defeasible rule and $\overline{hd} \in HD$ (opp stands for “opposite”)

• prefer $(d_1, d_2)$ – where $d_1$ and $d_2$ are defeasible rule labels

The predicate holds helps determine which policy rules are applicable, based on what fluents are true/false in a state and the interactions between policy rules. The predicate $opp(r, \overline{hd})$ indicates that $\overline{hd}$ is the logical complement of r’s head hd.

The translation $rei\_lp(\mathscr{P})$ consists of facts encoding the rules in $\mathscr{P}$ using the predicates rule, type, head, mbr, and prefer, as well as the set of policy-independent rules below, which define predicates holds and opp, where L is a fluent literal, E an elementary action, and H a happening (i.e. an elementary action or its negation).

$$\begin{array}{lll}\displaystyle body(R, b(R)) & \leftarrow & rule(R)\\ holds(R) & \leftarrow & type(R, strict), holds(b(R))\\ holds(R) & \leftarrow & type(R, defeasible), holds(b(R)), \\ & & opp(R, O), \mbox{not } holds(O), \mbox{not } holds(ab(R))\end{array}$$

$$\begin{array}{lll}\displaystyle holds(B) & \leftarrow & body(R, B), N = \#count\{L : mbr(B, L)\},\\ & & N = \#count\{L : mbr(B, L), holds(L)\}\\ holds(ab(R2)) & \leftarrow & {\textit{prefer}}(R1, R2), holds(b(R1)) \\ holds(Hd) & \leftarrow & rule(R), holds(R), head(R, Hd)\\ opp(R, permitted(E)) & \leftarrow & head(R, \neg permitted(E))\\ opp(R, \neg permitted(E)) & \leftarrow & head(R, permitted(E))\\ opp(R, obl(H)) & \leftarrow & head(R, \neg obl(H))\\ opp(R, \neg obl(H)) & \leftarrow & head(R, obl(H))\end{array}$$

Definition 7 (Reified ASP Translation of a Policy and State)

Given a state $\sigma$ of $\mathscr{T}$ , $rei\_lp(\mathscr{P}, \sigma)$ $=_{def} $ $rei\_lp(\mathscr{P})$ $\cup \ \{ holds(l) : l \in \sigma \ \}$ .

This definition will be used in conducting various policy analysis tasks in Section 5.

Proposition 1 (Relationship between the Original and Reified ASP Translations)

Given a state $\sigma$ of $\mathscr{T}$ , there is a one-to-one correspondence $map : {\cal A} \rightarrow {\cal B}$ between the collection of answer sets ${\cal A}$ of $lp(\mathscr{P}, \sigma)$ and the collection of answer sets ${\cal B}$ of $rei\_lp(\mathscr{P}, \sigma)$ such that if $map (A) = B$ then $\forall hd \in HD \cap A, \exists holds(hd) \in B$ .

5 Policy analysis

In what follows, we assume that the cond part of a policy rule cannot include atoms from the set HD (i.e. atoms obtained from predicates permitted and obl). We plan to consider more general policies in future work. Lifting this restriction complicates the task of finding explanations beyond the goal of the current work.

5.1 Analyzing authorization policies

Our goal in analyzing policies is to assist a policy author in refining their policies by indicating to them the rules that cause concern. Thus, when analyzing an authorization policy $\mathscr{P}$ with respect to an elementary action e in a state $\sigma$ , we focus on the tasks:

• Explain the causes of inconsistencies – determining the rules that cause a policy to derive both holds(permitted(e)) and $holds(\neg permitted(e))$ when using the $rei\_lp$ translation

• Detect and explain underspecification – determining whether rules about e exist or not, and, if they exist, explain why they do not fire. (Craven et al. 2009) call this situation coverage gaps.)

• Detect and explain ambiguity – determining whether there are conflicting defeasible rules that produce holds(permitted(e)) in some answer sets and $holds(\neg permitted(e))$ in others, and indicating which rules these are.

5.1.1 Inconsistency

To detect and explain inconsistencies with respect to an elementary action e and state $\sigma$ we introduce the following predicates:

• $inconsistency(e, r_1, r_2)$ – indicates that the pair of rules $r_1$ and $r_2$ both fire and cause the inconsistency; $r_1$ produces permitted(e) and $r_2$ produces $\neg permitted(e)$

• $inconsistency\_expl(e, t_1, t_2)$ – does the same but indicates the natural language texts of the corresponding policy statements

• $inconsistency\_expl\_pos(e, l)$ – indicates that l is a fluent/static that holds in $\sigma$ and contributes to the inconsistency in a rule that produces permitted(e)

• $inconsistency\_expl\_neg(e, l)$ – similar to the previous predicate, but for rules that produce $\neg permitted(e)$

We define a logic program I consisting of the rules below:

$$\begin{array}{lll}inconsistency(E, R1, R2) & \leftarrow & holds(permitted(E)), holds(\neg permitted(E)),\\ & & holds(R1), head(R1, permitted(E)), \\ & & holds(R2), head(R2, \neg permitted(E))\\inconsistency\_expl(E, T1, T2) & \leftarrow & inconsistency(E, R1, R2),\\ & & text(R1, T1), text(R2, T2)\end{array}$$

$$\begin{array}{lll}inconsistency\_expl\_pos(E, L) & \leftarrow & inconsistency(E, R1, \_), head(R1, permitted(E)), \\ & & mbr(b(R1), L), holds(L)\\inconsistency\_expl\_neg(E, L) & \leftarrow & inconsistency(E, \_, R2), head(R2, \neg permitted(E)),\\ & & mbr(b(R2), L), holds(L) \end{array}$$

We restate Definition 3 in terms of the $rei\_lp(\mathscr{P}, \sigma)$ translation.

Definition 8 (Inconsistency Redefined)

An authorization policy $\mathscr{P}$ is inconsistent with respect to an elementary action e and a state $\sigma$ if the answer set of $rei\_lp(\mathscr{P}, \sigma)$ $\cup$ I contains $inconsistency(e, r_1, r_2)$ for a pair of rules $r_1$ and $r_2$ .

Definition 9 (Explaining the Causes of Inconsistency)

• An explanation for the inconsistency of e in $\sigma$ is the set of pairs of strings $\{(t_1, t_2) : inconsistency\_expl(e, t_1, t_2) \in $ $rei\_lp(\mathscr{P}, \sigma)$ $\cup$ I $\}$ .

• A fluent literal l contributes positively (or negatively) to the inconsistency of e in $\sigma$ if the answer set of $rei\_lp(\mathscr{P}, \sigma)$ $\cup$ I contains $inconsistency\_expl\_pos(e, l)$ (or $inconsistency\_expl\_neg(e, l)$ , respectively).

The collection of atoms identified in Definition 9 can be collected from the answer set of $rei\_lp(\mathscr{P}, \sigma)$ $\cup$ I and post-processed to provide more human-friendly output.

5.1.2 Underspecification

We define the notion of underspecification of an elementary action e in a state $\sigma$ as the lack of explicit information as to whether e is permitted or not permitted in that state, similar to the concept of coverage gap defined by Craven et al. (2009). Note that underspecification is different from non-categoricity, where a policy may be ambiguous because e is deemed permitted in some answer sets and not permitted in others.

Definition 10 (Categoricity and Underspecification of an Action in a State)

A consistent authorization policy $\mathscr{P}$ is categorical with respect to an elementary action e and state $\sigma$ if one of the following cases is true:

1. 1. $rei\_lp(\mathscr{P}, \sigma)$ entails holds(permitted(e)), or

2. 2. $rei\_lp(\mathscr{P}, \sigma)$ entails $holds(\neg permitted(e))$ , or

3. 3. For every answer set S of $rei\_lp(\mathscr{P}, \sigma)$ ,

   $$\{holds(permitted(e)), holds(\neg permitted(e))\}\cap \ S = \emptyset$$

In this last case, we say that e is underspecified in state $\sigma$ .

Underspecification is important because it may reflect an oversight from the policy author. If it’s unintended, it can have negative consequences in planning domains for example, when an agent may want to choose the most compliant plan and thus actions that are mistakenly underspecified may never be selected. To test whether an action e is underspecified in a state, we define the set of rules $Check_{und}(e)$ consisting of the set of constraints:

$$\begin{array}{ll}\{ & \leftarrow holds(permitted(e)), \\ & \leftarrow \ holds(\neg permitted(e))\ \ \}\end{array}$$

Definition 11 (Detecting Underspecification)

Action e is underspecified in $\sigma$ if the logic program $lp(\mathscr{P}, \sigma) \cup Check_{und}(e)$ is consistent.

Whenever an elementary action is underspecified in a state, there may be two explanations: (Case 1) the authorization policy contains no rules about e, or (Case 2) rules about e exist in the policy but none of them apply in state $\sigma$ . Once we establish that an elementary action is underspecified, we want to explain to the policy author why that is the case. For the first case, we just want to inform the policy author about the situation. In the second case, we want to report, for each authorization rule about e, which fluents make the rule non-applicable. Note that a defeasible rule r with head hd (see (4)) cannot be made unapplicable by the complement $\overline{hd}$ , as the complement is underivable as well in an underspecified policy. Similarly, a preference rule cannot disable a defeasible rule either, as this can only be the case when the complement $\overline{hd}$ can be inferred.

Let U be the logic program

$$\begin{array}{lll}rules\_exist(E) & \leftarrow & head(R, \ permitted(E); \neg permitted(E))\\underspec\_1(E) & \leftarrow & \mbox{not } rules\_exist(E)\\underspec\_1\_expl({\unicode{x201C}Case 1,\unicode{x201D}} E) & \leftarrow & underspec\_1(E)\\underspec\_2(E) & \leftarrow & rules\_exist(E)\\underspec\_2(E, R, L) & \leftarrow & underspec\_2(E), rule(R),\\ & & head(R,\ permitted(E); \neg permitted(E)), \\ & & mbr(b(R), L), \\ & & \mbox{not } holds(L) \\underspec\_2\_expl({\unicode{x201C}Case 2,\unicode{x201D}} E, R, L, T) & \leftarrow & underspec\_2(E, R, L),\\& & text(R, T)\end{array}$$

Definition 12 (Explaining the Causes of Underspecification)

An explanation for the underspecification of e in $\sigma$ is the set of atoms formed by predicates $underspec\_1\_expl$ and $underspec\_2\_expl$ found in the answer set of $rei\_lp(\mathscr{P}, \sigma)$ $\cup$ U.

For a more human-friendly explanation, an atom $underspec\_1\_expl({\unicode{x201C}Case 1,\unicode{x201D}} e)$ in the answer set can be replaced with an explanation of the form “There are no authorization rules about e” in the post-processing phase. A collection of atoms of the form

$$\{underspec\_2\_expl({\unicode{x201C}Case 2,\unicode{x201D}} e, r, l_1, t), \dots, underspec\_2\_expl({\unicode{x201C}Case 2,\unicode{x201D}} e, r, l_n, t)\}$$

can be replaced with the explanation “Rule r about action e (stating that ‘t’) is rendered inapplicable by the fact that fluent(s) $l_1, \dots, l_n$ do not hold in this state.”

5.1.3 Ambiguity

We define ambiguity as the case when the policy allows a choice between permitted(e) and $\neg permitted(e)$ . This notion of ambiguity overlaps with that of a non-categorical policy. However, given our assumption that permitted atoms are not included in the condition cond of policy rules, ambiguity is a much more specific case. We claim that, if $\mathscr{P}$ is a consistent, non-categorical policy with respect to e in $\sigma$ (see Definition 10), then holds(permitted(e)) will be in some answer sets of $rei\_lp(\mathscr{P}, \sigma)$ and $holds(\neg permitted(e))$ will be in others, but it cannot be the case that an answer set does not contain either. ⁵

The justification is that the body cond of policy rules is fully determined by the unique values of fluents in $\sigma$ . Hence, strict rules either fire or do not. If a strict ruled fired, it would automatically override the defeasible rules with the complementary head, and thus lead either to inconsistency (depending on which other strict rules fire) or categoricity. The only source of non-categoricity can be the presence of defeasible rules with complementary heads and satisfied conditions, and which are not overridden by preference rules.

Definition 13 (Ambiguity of an Action in a State)

Let $\mathscr{P}$ be a policy that is consistent and non-categorical with respect to elementary action e and state $\sigma$ . Let $rei\_lp(\mathscr{P}, \sigma)$ have n answer sets, out of which $n_p$ answer sets contain holds(permitted(e)) and $n_{np}$ contain $holds(\neg permitted(e))$ .

$\mathscr{P}$ is ambiguous with respect to e and $\sigma$ if $n \neq n_p$ , $n \neq n_{np}$ and $n = n_p + n_{np}$ .

Next, let’s describe how we detect ambiguity.

Definition 14 (Detecting Ambiguity)

Action e is ambiguous in $\sigma$ if holds(permitted(e)) and $holds(\neg permitted(e))$ are not entailed by $rei\_lp(\mathscr{P}, \sigma)$ and e is not underspecified in $\sigma$ .

Once ambiguity is established, an explanation for ambiguity is needed. To produce it, we define the logic program A consisting of the rules:

$$\begin{array}{lll}ambiguous(E, R1, R2) & \leftarrow & defeasible\_rule(R1), head(R1, permitted(E)),\\ & & defeasible\_rule(R2), head(R2, \neg permitted(E)),\\ & & holds(b(R1)), holds(b(R2)),\\ & & \mbox{not } holds(ab(R1)), \mbox{not } holds(ab(R2))\\ambiguity\_expl(E, T1, T2)& \leftarrow & ambiguous(E, R1, R2), text(R1, T2), text(R2, T2)\\\end{array}$$

Definition 15 (Explaining the Causes of Ambiguity)

An explanation for the ambiguity of e in $\sigma$ is the set of pairs of strings:

$$\{(t_1, t_2) : ambiguity\_expl(e, t_1, t_2) \in rei\_lp(\mathscr{P}, \sigma) \cup { \textbf{ A}} \}$$

5.1.4 Observation about strongly vs weakly compliant policies

Gelfond and Lobo distinguish between actions that are strongly compliant in a state versus weakly compliant (see Definition 4). In planning, as shown by Meyer and Inclezan Meyer and Inclezan (2021), it seems reasonable to prefer strongly compliant actions over weakly compliant ones. However, in the theorem below we show that the class of weakly compliant actions includes strongly compliant ones. What we really need for planning purposes is distinguishing between strongly compliant and underspecified actions in a state, so that we can create a preference order between actions.

Theorem 1 (Strongly vs Weakly Compliant Actions)

All elementary actions that are strongly compliant in a state $\sigma$ are also weakly compliant.

Proof Note that, in this proof, we consider the original lp translation of $\mathscr{AOPL}$ , which is equivalent with, but more convenient to use here than, the reified translation $rei\_lp$ as stated in Proposition 1. According to Definition 4 borrowed from Gelfond and Lobo’s work, elementary action e is strongly compliant with authorization policy $\mathscr{P}$ if $lp(\mathscr{P}, \sigma)$ entails permitted(e), and it is weakly compliant if $lp(\mathscr{P}, \sigma)$ does not entail $\neg permitted(e)$ . For consistent policies, the latter condition is obviously true if e is strongly compliant in $\sigma$ , as having permitted(e) in every answer set of $lp(\mathscr{P}, \sigma)$ implies that $\neg permitted(e)$ must be absent from each such answer set. If the policy is inconsistent, the theorem is vacuously true.

Given our assumption that permitted (and obl) atoms cannot appear in the cond part of policy rules, an elementary action e can only be either strongly compliant in $\sigma$ or underspecified. ⁶

We formulate the following proposition, which is useful in creating an ordering of actions based on compliance (relevant in planning).

Proposition 2 (Properties of Authorization Policies)

• If condition cond of authorization rules is not allowed to contain permitted (or obl) atoms and $\mathscr{P}$ is categorical with respect to e and $\sigma$ , then e is either strongly compliant, non-compliant, or underspecified in $\sigma$ .

• If condition cond of authorization rules is not allowed to contain permitted (or obl) atoms and $\mathscr{P}$ is non-categorical with respect to e and $\sigma$ , then e is neither strongly compliant nor non-compliant; it may be either underspecified or ambiguous.

5.2 Obligation policy analysis

The techniques from Section 5.1 for determining rules that create inconsistencies, underspecification, and ambiguity with respect to an elementary action and a state can be easily adapted to obligation policies as well. Obligation policies apply to happenings, which are actions or their negations. For instance, given an elementary action e, the following literals are part of the signature of the policy: obl(e), $obl(\neg e)$ , $\neg obl(e)$ , and $\neg obl(\neg e)$ . Inconsistencies between obl(e) and $\neg obl(e)$ on one hand, or between $obl(\neg e)$ and $\neg obl(\neg e)$ are easy to detect. However, there are additional incongruencies that may decrease the quality of a policy, and we may want to alert the policy writer about them as well.

For instance, if a policy $\mathscr{P}$ entails both obl(e) and $obl(\neg e)$ in a state $\sigma$ , then any event $\langle \sigma, a\rangle$ will be non-compliant, no matter whether $e \in a$ or $e \notin a$ . In actuality, it means that the policy does not allow for the agent to be compliant with respect to obligations in state $\sigma$ . Thus the notions of inconsistency and ambiguity should be adapted or expanded to include this situation. We propose the following definition:

Definition 16 (Conflicting Policy)

Given a consistent obligation policy $\mathscr{P}$ , a state $\sigma$ and an elementary action e, we call $\mathscr{P}$ a conflicting obligation policy with respect to $\sigma$ and e if the logic program $rei\_lp(\mathscr{P}, \sigma)$ entails both holds(obl(e)) and $holds(obl(\neg e))$ .

Explanations for conflicting obligation policies can be found using techniques similar to the ones in Section 5.1.

5.3 The intersection between authorization and obligation policies

When combining an authorization policy with an obligation policy, there are a few cases that, while not necessarily inconsistent, certainly seem to require non-compliant behavior from the agent. This is especially the case when an event $\langle \sigma, e\rangle$ is strongly compliant with the obligation policy but non-compliant with the authorization policy (i.e. in terms of the original translation lp of $\mathscr{AOPL}$ into ASP, $lp(\mathscr{P}, \sigma)$ entails both obl(e) and $\neg permitted(e)$ according to Definitions 4 and 5). Other situations that may require the policy authors’ attention, though to a lesser degree, are when an action is permitted but the agent is obligated not to execute it (i.e. $lp(\mathscr{P}, \sigma)$ entails both permitted(e) and $obl(\neg e)$ ) or when the agent is obligated to execute an action that is underspecified in that state. We indicate the level of urgency of each of these situations by adding a number from 1 to 3, with 1 being the most needing of re-consideration and 3 being the least urgent.

Once it has been established that the policies are strongly compliant, non-compliant, or underspecified with respect to the state and elementary action, the following ASP rules determine which policy rules need to be re-visited.

$$\begin{array}{lll}require\_cons(E, R1, R2, 1) & \leftarrow & holds(R1), head(R1, obl(E)), \\ & & holds(R2), head(R2, \neg permitted(E))\\require\_cons(E, R1, R2, 2) & \leftarrow & holds(R1), head(R1, obl(\neg E)), \\ & & holds(R2), head(R2, permitted(E))\\require\_cons(E, R1, R2, 3) & \leftarrow & holds(R1), head(R1, obl(E)), \\ & & \mbox{not } holds(permitted(E)),\\ & & \mbox{not } holds(\neg permitted(E))\\require\_cons\_expl(E, T1, T2, N) & \leftarrow & require\_cons(E, R1, R2, N), \\ & & text(R1, T1), text(R2, T2).\end{array}$$

6 Related work

Meyer and Inclezan (2021) developed an architecture for policy-aware intentional agents ( $\mathscr{APIA}$ ) by leveraging Blount et al.’s theory of intentions (2015). An agent’s behavior was ensured to be compliant with authorization and obligation policies specified in $\mathscr{AOPL}$ and translated into ASP. Meyer and Inclezan’s work first highlighted the issues that may arise at the intersection between $\mathscr{AOPL}$ authorization and obligation and policies. In the $\mathscr{APIA}$ architecture, conflicts of this nature were resolved by modifying the policy’s ASP encoding to state that such conflicts render a policy inconsistent. In the current work our intention is to alert policy authors about such situations and provide them with the opportunity to decide which policy statements to modify in order to restore consistency. Additionally, in the current work we delve deeper into the tasks associated with policy analysis and look at underspecification and ambiguity as well. We also focus on providing explanations as to why such issues arise.

Craven et al.’s work (2009) is the closest to ours in its intent. The authors define language $\mathscr{L}$ for policy specification and include both authorization and obligation policies. They define a solid set of tasks that an automated analysis of a policy should accomplish, such as discovering modality conflicts and coverage gaps, which we target in our work as well. Their research assumes that the underlying dynamic domain is specified in Event Calculus (Kowalski and Sergot 1989). Explanations are found via an abductive constraint logic programming proof procedure. Given the absence of a comparison between languages $\mathscr{L}$ and $\mathscr{AOPL}$ , it is important to study the problem of policy analysis with respect to language $\mathscr{AOPL}$ as well. $\mathscr{AOPL}$ has clear advantages, including its ability to express defeasible policies and preferences between policies. Moreover, $\mathscr{AOPL}$ can be seamlessly integrated with ASP-based dynamic system descriptions, as different properties of $\mathscr{AOPL}$ policies can be checked by finding the answer sets of an ASP program. This would allow coupling policies with system descriptions specified in higher-level action languages that translate into ASP, such as the modular action language $\mathscr{ALM}$ (Inclezan and Gelfond 2016), and associated libraries about action and change (Inclezan 2016; 2019).

Other research on policy modeling or analysis using ASP exists, but the goals tend to be different from ours. Corapi et al. (2011) use inductive logic programming and software engineering-inspired processes to assist policy authors with policy refinement. In their work, refinement suggestions are provided, but this process is driven by use cases that need to be manually created. As a result, the quality of the resulting policy depends on the quality and coverage of the use cases that are provided as an input. In turn, our approach is meant to be more comprehensive and transparent, as it is guided by the policy rules themselves. Another work that uses ASP for policy modeling is that of De Vos et al. (2019). Their work encompasses the same types of policies as $\mathscr{AOPL}$ , but their focus is on compliance checking and providing explanations for the compliance or non-compliance of events. In contrast, we focus on policy analysis, not compliance checking; our explanations highlight potential problems with a policy and indicate statements that need to be refined. Havur et al. (2021) present a framework called DALICC for comparing and resolving compatibility issues with licenses. The goal of their framework is more narrow than ours in the sense that it only focuses on licences and not normative statements in general. For a survey on other policy analysis methods and tools, not necessarily ASP-related, we direct the reader to the paper by Jabal et al. (2019).

In general, in the policy specification and analysis community, there is a intense focus on access control policies, which may involve the Role-Based Access Control (RBAC) model outlined by Ferraiolo et al. (2001); the Attribute-Based Access Control Model (ABAC) explored for instance by Davari and Zulkernine (2021) and Xu et al. (2016); or the Category-based Access Control Model explored by Alves and Fernández (2014). A secondary focus falls on policies for the management of computer systems. In contrast, $\mathscr{AOPL}$ is more general and could be used to represent social norms, for example.

Finally, our work touches upon explainability and finding the causes of issues encountered in $\mathscr{AOPL}$ policies. To find even deeper causes that reside in the inner-workings of the dynamic system, we can leverage existing work on explainability in reasoning about action and change, such as the research by LeBlanc et al. (2019); planning domains, as in the work by Vasileiou et al. (2022); or logic programming in general, including research by Fandinno and Schultz (2019) or Cabalar et al. (2020).

7 Conclusions

In this paper we introduced a framework for analyzing policies described in the language $\mathscr{AOPL}$ with respect to inconsistencies, underspecification, ambiguity, and modality conflict. We reified policy rules in order to detect which policy statements cause the particular issue and (if relevant), which fluents of the domain contribute to such problems. In doing so, we defined new properties of $\mathscr{AOPL}$ policies and took a special look at what happens at the intersection of authorization and obligation policies.

As part of future work, we plan to create a system that implements this framework in a way that is user-friendly for policy writers and knowledge engineers. We also intend to extend the framework by lifting some of the simplifying restrictions that we imposed here, for instance by studying the case when there is incomplete information about a state or allowing permitted and obl atoms in the conditions of policy rules.