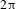1 Introduction
Phase is one of the most important parameters to describe the laser beam. There are special requirements for this parameter in many cases. Therefore, a variety of techniques have been developed to control it. From the point of view of whether they can be adjusted in real time, there are mainly two types: passive and active. The passive device is usually constructed according to the desired special phase distribution. But there is a high demand for measurement and manufacturing precision. Once the element is finished, it cannot be adjusted. However, the phase modulation generated by the active device can be adjusted in real time. This means that the phase distribution can be optimized if the shaped result does not meet the requirements. To a certain extent, the active phase modulation scheme can reduce the requirements for the accuracy of phase measurement and manufacturing. As the device can generate arbitrary phase distribution according to the demand, it has been applied in many fields, including dynamic wavefront compensation, femtosecond pulse shaping, optical information processing and so on[Reference Davis, McNamara, Cottrell and Sonehara1–Reference Sanner, Huot, Audouard, Larat, Huignard and Loiseaux8].
Active phase-type devices include deformable mirrors, micro-electro-mechanical system devices, liquid crystal spatial light modulators and so on. By comparison, the liquid crystal spatial light modulator has a high spatial resolution and requires low driving voltage. Two of the most common are liquid crystal on silicon (LCOS) and optically addressed types[Reference Davis, McNamara, Cottrell and Sonehara1–Reference Vaughan, Hornung, Feurer and Nelson6, Reference Igasaki, Li, Yoshida, Toyoda, Inoue, Mukohzaka, Kobayashi and Hara9–Reference Huang, Fan, Zhang, Li, Tang, Guo, Li and Lin14]. The energy efficiencies of both types are higher than 80%. But the LCOS type is a reflective and electrically addressed type, which means it is easy to cause spectral distortion because of Fabry–Perot interference. And the black-matrix effect generated by the two-dimensional periodic opaque electrodes can make the beam quality worse. However, the optically addressed device can avoid this problem as its two-dimensional electrode is not discrete, but continuous. The filling factor of this type reaches 100%, which means the generated phase distribution is continuous, not multi-step. Although the liquid crystal light valve proposed by Lawrence Livermore National Laboratory is an amplitude-type device, the basic principle is same and it has overcome the above two problems. Because of the high transmittance and the flexible shaping ability for 1053 nm coherent light, this technology won the R&D 100 award in 2012[10, Reference Heebner, Borden, Miller, Stolz, Suratwala, Wegner, Hermann, Henesian, Haynam, Hunter, Christensen, Wong, Seppala, Brunton, Tse, Awwal, Franks, Marley, Williams, Scanlan, Budge, Monticelli, Walmer, Dixit, Widmayer, Wolfe, Bude, McCarty and DiNicola11]. Although the modulator mentioned in this paper is the phase type, not the amplitude type, it has all the advantages of optically addressed devices compared with the traditional liquid crystal modulator such as the LCOS modulator; it avoids the problems of spectral distortion and black-matrix effect.
We have also carried out some work in optically addressed liquid crystal devices driven by the light-emitting diode (LED). Both the online performance test and engineering verification of the device have been realized in recent years[Reference Huang, Fan, Li and Lin12–Reference Huang, Fan, Zhang, Li, Tang, Guo, Li and Lin14]. So far, our home-made devices have been used in the SGXX facility for more than a year, fully demonstrating the reliability of these devices. In this paper, a newly developed phase-type optically addressed modulator driven by the blue LED is reported. Its working principle, control method and phase modulation capability are mainly introduced. A new method of measuring the relationship between gray level and phase retardation is proposed. The accuracy of the curve is further confirmed by designing special experiments. According to the curve, several special phase distributions have been realized by this device. The results show that, not only the maximum phase retardation is larger than
![]() $2\unicode[STIX]{x03C0}$
for 1053 nm wavelength, but also the control accuracy is high.
$2\unicode[STIX]{x03C0}$
for 1053 nm wavelength, but also the control accuracy is high.

Figure 1. (a) The device and (b) its working principle.

Figure 2. The optical setup for testing the optically addressed spatial light modulator (SLM). CW, continuous-wave; PBS, polarizing beam splitter.

Figure 3. The measured phase distribution with the shape ‘
2 Working principle
In addition to the liquid crystal material, the working principle of this phase type device is the same as the amplitude type device[Reference Heebner, Borden, Miller, Stolz, Suratwala, Wegner, Hermann, Henesian, Haynam, Hunter, Christensen, Wong, Seppala, Brunton, Tse, Awwal, Franks, Marley, Williams, Scanlan, Budge, Monticelli, Walmer, Dixit, Widmayer, Wolfe, Bude, McCarty and DiNicola11–Reference Huang, Fan, Zhang, Li, Tang, Guo, Li and Lin14]. Because of the photoconductive effect of BSO (
![]() $\text{Bi}_{12}\text{SiO}_{20}$
) crystal, the voltage on the crystal will change when the projected blue light intensity changes. It will also lead to the change of voltage on the liquid crystal layer. Different modes of the liquid crystal result in different kinds of modulators. The amplitude-type device usually adopts the twisted nematic mode, while the phase-type device usually adopts the nematic mode. For the phase-type modulator in this paper, different voltages on the liquid crystal layer will lead to different phase delays. This means that the phase delay will change when the blue light intensity on the modulator changes. As a result, we can control the wavefront of 1053 nm laser beam if the blue light intensity distribution can be adjusted precisely.
$\text{Bi}_{12}\text{SiO}_{20}$
) crystal, the voltage on the crystal will change when the projected blue light intensity changes. It will also lead to the change of voltage on the liquid crystal layer. Different modes of the liquid crystal result in different kinds of modulators. The amplitude-type device usually adopts the twisted nematic mode, while the phase-type device usually adopts the nematic mode. For the phase-type modulator in this paper, different voltages on the liquid crystal layer will lead to different phase delays. This means that the phase delay will change when the blue light intensity on the modulator changes. As a result, we can control the wavefront of 1053 nm laser beam if the blue light intensity distribution can be adjusted precisely.

Figure 4. (a) The gray bitmap, (b) the measured phase distribution, and (c) the relationship of both when
![]() $G_{0}=0$
.
$G_{0}=0$
.

Figure 5. The relationships of gray level and measured phase delay when the parameter
![]() $G_{0}$
is (a) 0.1, (b) 0.2, (c) 0.3, (d) 0.4, (e) 0.5, and (f) 0.6, respectively.
$G_{0}$
is (a) 0.1, (b) 0.2, (c) 0.3, (d) 0.4, (e) 0.5, and (f) 0.6, respectively.

Figure 6. The gray-phase curves obtained from experiments when the parameter
![]() $G_{0}$
is different.
$G_{0}$
is different.
Both the device and its working principle have been shown in Figure 1. Bitmapped blue light from the LCOS modulator is projected onto the photoconductive BSO layer. As a result, we can control the intensity distribution of blue light by setting corresponding bitmaps. The high-definition multimedia interface (HDMI) port in Figure 1(a) is connected to the computer which can adjust the bitmap setting in the internal LCOS modulator. This means that the wavefront of 1053 nm laser beam will be controlled by the computer. The maximum effective area is about
![]() $15~\text{mm}\times 15~\text{mm}$
, which can be divided into
$15~\text{mm}\times 15~\text{mm}$
, which can be divided into
![]() $768~\text{pixel}\times 768~\text{pixel}$
. Its maximum transmittance is about 90% for 1053 nm wavelength and the damage threshold of this device is estimated to be
$768~\text{pixel}\times 768~\text{pixel}$
. Its maximum transmittance is about 90% for 1053 nm wavelength and the damage threshold of this device is estimated to be
![]() $200~\text{mJ}/\text{cm}^{2}$
for 12 ns@1 Hz laser pulse.
$200~\text{mJ}/\text{cm}^{2}$
for 12 ns@1 Hz laser pulse.
3 Measurement and verification of the gray-phase curve
The optical setup has been shown in Figure 2. The wavefront sensor SID4-HR from Phasics is located on the image plane of the modulator. To demonstrate the phase modulation capability of this device, we set the special phase distribution with the shape ‘
Based on the result mentioned above, the device can generate different phase modulations by loading the corresponding bitmap. As a result, in order to accurately control the phase distribution, we must know the relationship between the gray level of bitmap and the phase delay of the device. Since the wavefront sensor can only measure the phase distribution, not the absolute value of the phase, we design the method as described below.
The loaded bitmap is set according to the formula
The two-dimensional distribution when
![]() $G_{0}=0$
has been shown in Figure 4(a). Figure 4(b) shows the corresponding phase delay distribution measured with the wavefront sensor. According to these two figures, we can get the relationship between gray level and phase delay as shown in Figure 4(c).
$G_{0}=0$
has been shown in Figure 4(a). Figure 4(b) shows the corresponding phase delay distribution measured with the wavefront sensor. According to these two figures, we can get the relationship between gray level and phase delay as shown in Figure 4(c).

Figure 7. One-dimensional comparisons of designed phase distribution and measured phase distribution when the parameter
![]() $T$
is (a) 1.86 mm, (b) 3.72 mm, and (c) 5.58 mm, respectively.
$T$
is (a) 1.86 mm, (b) 3.72 mm, and (c) 5.58 mm, respectively.
In order to verify the accuracy of the curve shown in Figure 4(c), we set different bitmaps and measure the corresponding phase delay distributions, according to which we can get some other gray-phase curves. The two-dimensional gray distributions will be set according to Equation (1), but the parameter
![]() $G_{0}$
will be different. When the parameter
$G_{0}$
will be different. When the parameter
![]() $G_{0}$
changes, the phase difference between the edge and the central region will change. Different parameter
$G_{0}$
changes, the phase difference between the edge and the central region will change. Different parameter
![]() $G_{0}$
means different range of gray level in the gray-phase curve. Theoretically, when the parameter
$G_{0}$
means different range of gray level in the gray-phase curve. Theoretically, when the parameter
![]() $G_{0}$
increases, the range of the gray-phase curve will become shorter, but it should always be part of the curve shown in Figure 4(c). Different results have been shown in Figure 5 when the parameter
$G_{0}$
increases, the range of the gray-phase curve will become shorter, but it should always be part of the curve shown in Figure 4(c). Different results have been shown in Figure 5 when the parameter
![]() $G_{0}$
is 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6, respectively.
$G_{0}$
is 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6, respectively.
Figure 6 shows the gray-phase curves in one picture obtained from experiments when the parameter
![]() $G_{0}$
is different. These curves are basically coincident, which fully proves the accuracy of the gray-phase curve shown in Figure 4. As a result, this device can generate the desired phase distribution according to the green curve in Figure 6, which is also the curve in Figure 4(c).
$G_{0}$
is different. These curves are basically coincident, which fully proves the accuracy of the gray-phase curve shown in Figure 4. As a result, this device can generate the desired phase distribution according to the green curve in Figure 6, which is also the curve in Figure 4(c).
4 Realization of special phase distribution
Two-dimensional phase distribution will be designed according to the formula
Designed and measured phase distributions in three cases with different parameter
![]() $T$
have been shown in Figure 7. The results show that the actual loaded phase is basically consistent with the setting value.
$T$
have been shown in Figure 7. The results show that the actual loaded phase is basically consistent with the setting value.
5 Conclusion
The above-mentioned experimental results show that the phase shaping accuracy of this device is high. If further feedback control is carried out, the actual modulation effect can be more ideal. At present, the maximum phase delay is about
![]() $1.2\unicode[STIX]{x1D706}$
for 1053 nm wavelength and the maximum region is
$1.2\unicode[STIX]{x1D706}$
for 1053 nm wavelength and the maximum region is
![]() $15~\text{mm}\times 15~\text{mm}$
. Our next goal is to develop a phase-type spatial light modulator with larger phase delay and larger region.
$15~\text{mm}\times 15~\text{mm}$
. Our next goal is to develop a phase-type spatial light modulator with larger phase delay and larger region.