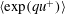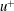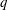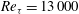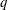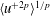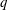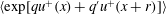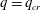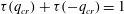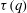1 Introduction and definitions
The topic of turbulent boundary layers has been one of the centrepieces of research in turbulent flows for many decades (Cebeci & Bradshaw Reference Cebeci and Bradshaw1977; Pope Reference Pope2000; Schultz & Flack Reference Schultz and Flack2007; Smits, McKeon & Marusic Reference Smits, Mckeon and Marusic2011; Marusic et al.
Reference Marusic, Monty, Hultmark and Smits2013). An important feature of wall boundary-layer flows is the logarithmic law (Prandtl Reference Prandtl1925; von Kármán Reference von Kármán1930) for the mean velocity profile
![]() $U/u_{{\it\tau}}\equiv U^{+}={\it\kappa}^{-1}\ln (zu_{{\it\tau}}/{\it\nu})+B$
valid in the inertial region, where
$U/u_{{\it\tau}}\equiv U^{+}={\it\kappa}^{-1}\ln (zu_{{\it\tau}}/{\it\nu})+B$
valid in the inertial region, where
![]() $z$
is the distance to the wall,
$z$
is the distance to the wall,
![]() $u_{{\it\tau}}$
is the friction velocity based on the wall stress
$u_{{\it\tau}}$
is the friction velocity based on the wall stress
![]() ${\it\tau}_{w}$
(
${\it\tau}_{w}$
(
![]() $u_{{\it\tau}}=\sqrt{{\it\tau}_{w}/{\it\rho}}$
,
$u_{{\it\tau}}=\sqrt{{\it\tau}_{w}/{\it\rho}}$
,
![]() ${\it\rho}$
is the fluid density),
${\it\rho}$
is the fluid density),
![]() ${\it\nu}$
is the kinematic viscosity,
${\it\nu}$
is the kinematic viscosity,
![]() ${\it\kappa}$
is the von Kármán constant, and
${\it\kappa}$
is the von Kármán constant, and
![]() $B$
is another constant (see results in Smits et al. (Reference Smits, Mckeon and Marusic2011), Jiménez (Reference Jiménez2013), Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013), Lee & Moser (Reference Lee and Moser2015) for recent empirical evidence for logarithmic scaling of the mean velocity). Even if only approximately valid under realistic conditions, such a basic property of wall-bounded turbulent flows continues to provide predictions in many practical applications, and it helps to test models, calibrate parameters, and guide the development of theories.
$B$
is another constant (see results in Smits et al. (Reference Smits, Mckeon and Marusic2011), Jiménez (Reference Jiménez2013), Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013), Lee & Moser (Reference Lee and Moser2015) for recent empirical evidence for logarithmic scaling of the mean velocity). Even if only approximately valid under realistic conditions, such a basic property of wall-bounded turbulent flows continues to provide predictions in many practical applications, and it helps to test models, calibrate parameters, and guide the development of theories.
Recently, a logarithmic behaviour has also been observed in the inertial region for the variance of the fluctuations in the streamwise velocity component. Such behaviour can be motivated by model predictions based on the ‘attached eddy hypothesis’ by Townsend (Reference Townsend1976) and Perry, Henbest & Chong (Reference Perry, Henbest and Chong1986). There has been growing evidence (Marusic & Kunkel Reference Marusic and Kunkel2003; Hultmark et al.
Reference Hultmark, Vallikivi, Bailey and Smits2012) for a logarithmic behaviour of the form
![]() $\langle {u^{+}}^{2}\rangle =B_{1}-A_{1}\ln (z/{\it\delta})$
, where
$\langle {u^{+}}^{2}\rangle =B_{1}-A_{1}\ln (z/{\it\delta})$
, where
![]() $u^{+}$
is the normalized streamwise velocity fluctuation and
$u^{+}$
is the normalized streamwise velocity fluctuation and
![]() ${\it\delta}$
is an outer length scale. For developing boundary layers the outer scale is the boundary-layer thickness, while it is the radius for pipes, and the half-height for plane channels. Empirical data are mostly consistent with a value of
${\it\delta}$
is an outer length scale. For developing boundary layers the outer scale is the boundary-layer thickness, while it is the radius for pipes, and the half-height for plane channels. Empirical data are mostly consistent with a value of
![]() $A_{1}\approx 1.25$
(the Townsend–Perry constant), whereas
$A_{1}\approx 1.25$
(the Townsend–Perry constant), whereas
![]() $B_{1}$
is flow-dependent and thus not universal. The logarithmic structure extends to higher-order moments (Meneveau & Marusic Reference Meneveau and Marusic2013), and high-order structure functions also exhibit logarithmic behaviour in the relevant range of streamwise separation between two points (de Silva et al.
Reference de Silva, Marusic, Woodcock and Meneveau2015). Davidson, Nickels & Krogstad (Reference Davidson, Nickels and Krogstad2006) and Davidson & Krogstad (Reference Davidson and Krogstad2014) describe relevant prior work on logarithmic scaling of second-order structure functions.
$B_{1}$
is flow-dependent and thus not universal. The logarithmic structure extends to higher-order moments (Meneveau & Marusic Reference Meneveau and Marusic2013), and high-order structure functions also exhibit logarithmic behaviour in the relevant range of streamwise separation between two points (de Silva et al.
Reference de Silva, Marusic, Woodcock and Meneveau2015). Davidson, Nickels & Krogstad (Reference Davidson, Nickels and Krogstad2006) and Davidson & Krogstad (Reference Davidson and Krogstad2014) describe relevant prior work on logarithmic scaling of second-order structure functions.
From the perspective of statistical descriptions of wall-bounded turbulence, high positive moments emphasize those intense events that deviate significantly from the mean. In fact, the most extreme value can be obtained from the limit of very high-order moments, since
![]() $\max (u)=\lim _{p\rightarrow +\infty }\langle u^{p}\rangle ^{1/p}$
. Those intense events, from a phenomenological perspective, can indicate the presence of certain flow structures, for example, high- and low-velocity streak structures that are known to be important in momentum transport in wall turbulence. However, moments do not provide a natural way to distinguish between the positive and negative fluctuations. Even-order moments mix the contributions from both positive and negative sides of the distribution. Odd-order moments emphasize the difference between the contributions of positive and negative fluctuations, which does not facilitate emphasizing positive and negative contributions separately. Conditional moments can be used for such discrimination, but they depend on both the threshold and the order of the moment, increasing complexity.
$\max (u)=\lim _{p\rightarrow +\infty }\langle u^{p}\rangle ^{1/p}$
. Those intense events, from a phenomenological perspective, can indicate the presence of certain flow structures, for example, high- and low-velocity streak structures that are known to be important in momentum transport in wall turbulence. However, moments do not provide a natural way to distinguish between the positive and negative fluctuations. Even-order moments mix the contributions from both positive and negative sides of the distribution. Odd-order moments emphasize the difference between the contributions of positive and negative fluctuations, which does not facilitate emphasizing positive and negative contributions separately. Conditional moments can be used for such discrimination, but they depend on both the threshold and the order of the moment, increasing complexity.
Another option to be explored here is provided by the exponential of the random variable of interest, and then considering various moments of this new random variable. More specifically, considering streamwise velocity fluctuations in a boundary layer at a height
![]() $z$
, and point-pair distances
$z$
, and point-pair distances
![]() $r$
in the streamwise direction, we consider the following statistical objects:
$r$
in the streamwise direction, we consider the following statistical objects:
These are the single- and two-point moment generating functions (MGFs), respectively. The parameter
![]() $q$
, a real number, serves as a ‘dial’ to emphasize different parts of the signal, such as high- and low-speed regions, for positive and negative values of
$q$
, a real number, serves as a ‘dial’ to emphasize different parts of the signal, such as high- and low-speed regions, for positive and negative values of
![]() $q$
, respectively. For two-point statistics, choosing different values of
$q$
, respectively. For two-point statistics, choosing different values of
![]() $q$
and
$q$
and
![]() $q^{\prime }$
enables one to emphasize particular behaviours at points separated by a distance
$q^{\prime }$
enables one to emphasize particular behaviours at points separated by a distance
![]() $r$
. One natural consequence of the definition of MGFs is that single- and two-point moments can be directly computed from the curvatures of the MGFs at the origin, according to
$r$
. One natural consequence of the definition of MGFs is that single- and two-point moments can be directly computed from the curvatures of the MGFs at the origin, according to
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \langle u^{+p}\rangle =\left.{\displaystyle \frac{\partial ^{p}W(q;z)}{\partial q^{p}}}\right|_{q=0},\\ \displaystyle \langle {u^{+}(x)}^{p}{u^{+}(x+r)}^{p^{\prime }}\rangle =\left.{\displaystyle \frac{\partial ^{p^{\prime }}}{\partial q^{\prime p^{\prime }}}}{\displaystyle \frac{\partial ^{p}}{\partial q^{p}}}W(q,q^{\prime };z,r)\right|_{q=0,q^{\prime }=0}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \langle u^{+p}\rangle =\left.{\displaystyle \frac{\partial ^{p}W(q;z)}{\partial q^{p}}}\right|_{q=0},\\ \displaystyle \langle {u^{+}(x)}^{p}{u^{+}(x+r)}^{p^{\prime }}\rangle =\left.{\displaystyle \frac{\partial ^{p^{\prime }}}{\partial q^{\prime p^{\prime }}}}{\displaystyle \frac{\partial ^{p}}{\partial q^{p}}}W(q,q^{\prime };z,r)\right|_{q=0,q^{\prime }=0}.\end{array}\right\}\end{eqnarray}$$
It is worth noting here that central moments are solely determined by the moment generating function at
![]() $q=0$
.
$q=0$
.
It is also useful to mention that
![]() $W(q;z)$
as defined corresponds to a highly simplified and real-valued subset of the more general object described by the Hopf equation (Hopf Reference Hopf1952; Monin & Yaglom Reference Monin and Yaglom2007). This equation describes the full
$W(q;z)$
as defined corresponds to a highly simplified and real-valued subset of the more general object described by the Hopf equation (Hopf Reference Hopf1952; Monin & Yaglom Reference Monin and Yaglom2007). This equation describes the full
![]() $N$
-point joint PDF of velocity fluctuations, where
$N$
-point joint PDF of velocity fluctuations, where
![]() $N$
is the total number of different spatial points needed to describe the flow. Basic interest in the Hopf equation follows from the fact that it is a linear equation, and therefore self-contained, requiring no closure. It describes the time evolution of the generalized moment generating function
$N$
is the total number of different spatial points needed to describe the flow. Basic interest in the Hopf equation follows from the fact that it is a linear equation, and therefore self-contained, requiring no closure. It describes the time evolution of the generalized moment generating function
![]() ${\it\Psi}({\bf\theta})=\langle \text{exp}(\text{i}\!\int \!{\bf\theta}(\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{u}(\boldsymbol{x})\,\text{d}^{3}\boldsymbol{x})\rangle$
, where
${\it\Psi}({\bf\theta})=\langle \text{exp}(\text{i}\!\int \!{\bf\theta}(\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{u}(\boldsymbol{x})\,\text{d}^{3}\boldsymbol{x})\rangle$
, where
![]() $\boldsymbol{u}$
is the velocity field,
$\boldsymbol{u}$
is the velocity field,
![]() $\text{i}{\bf\theta}(\boldsymbol{x})$
is a complex ‘test field’ which serves as a (very high-dimensional) independent variable taking on specified values at every point in the flow. As mentioned before, the Hopf equation is a linear equation for
$\text{i}{\bf\theta}(\boldsymbol{x})$
is a complex ‘test field’ which serves as a (very high-dimensional) independent variable taking on specified values at every point in the flow. As mentioned before, the Hopf equation is a linear equation for
![]() ${\it\Psi}({\bf\theta})$
. However, it includes functional derivatives with respect to the entire test field
${\it\Psi}({\bf\theta})$
. However, it includes functional derivatives with respect to the entire test field
![]() ${\bf\theta}(\boldsymbol{x})$
, and solving such functional equations remains an unattainable theoretical goal. The new quantity
${\bf\theta}(\boldsymbol{x})$
, and solving such functional equations remains an unattainable theoretical goal. The new quantity
![]() $W(q;z)$
may be considered to be a highly simplified version, a ‘subset’, of
$W(q;z)$
may be considered to be a highly simplified version, a ‘subset’, of
![]() ${\it\Psi}({\bf\theta})$
in which we take a special-case test field
${\it\Psi}({\bf\theta})$
in which we take a special-case test field
![]() $\text{i}{\it\theta}_{j}(\boldsymbol{x})=q{\it\delta}(\boldsymbol{x}-z\hat{\boldsymbol{k}}){\it\delta}_{j1}$
, and similarly for the two-point MGF
$\text{i}{\it\theta}_{j}(\boldsymbol{x})=q{\it\delta}(\boldsymbol{x}-z\hat{\boldsymbol{k}}){\it\delta}_{j1}$
, and similarly for the two-point MGF
![]() $\text{i}{\it\theta}_{j}(\boldsymbol{x})=q{\it\delta}(\boldsymbol{x}-z\hat{\boldsymbol{k}}){\it\delta}_{j1}+q^{\prime }{\it\delta}(\boldsymbol{x}-r\hat{\boldsymbol{i}}-z\hat{\boldsymbol{k}}){\it\delta}_{j1}$
(where
$\text{i}{\it\theta}_{j}(\boldsymbol{x})=q{\it\delta}(\boldsymbol{x}-z\hat{\boldsymbol{k}}){\it\delta}_{j1}+q^{\prime }{\it\delta}(\boldsymbol{x}-r\hat{\boldsymbol{i}}-z\hat{\boldsymbol{k}}){\it\delta}_{j1}$
(where
![]() $\hat{\boldsymbol{k}}$
and
$\hat{\boldsymbol{k}}$
and
![]() $\hat{\boldsymbol{i}}$
are the unit vectors in the wall-normal and streamwise directions, respectively).
$\hat{\boldsymbol{i}}$
are the unit vectors in the wall-normal and streamwise directions, respectively).
Another connection with prior approaches can be highlighted. In the study of small-scale intermittency and anomalous scaling, high-order moments of turbulent kinetic energy dissipation normalized by its mean,
![]() ${\it\varepsilon}/\langle {\it\varepsilon}\rangle$
, such as
${\it\varepsilon}/\langle {\it\varepsilon}\rangle$
, such as
![]() $\langle ({\it\varepsilon}/\langle {\it\varepsilon}\rangle )^{q}\rangle$
with
$\langle ({\it\varepsilon}/\langle {\it\varepsilon}\rangle )^{q}\rangle$
with
![]() $q>0$
, are used to emphasize the highly intermittent peaks in dissipation, while the low-dissipation regions can be highlighted by moments of negative order
$q>0$
, are used to emphasize the highly intermittent peaks in dissipation, while the low-dissipation regions can be highlighted by moments of negative order
![]() $q<0$
(see e.g. Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1991; O’Neil & Meneveau Reference O’Neil and Meneveau1993; Frish Reference Frish1995). The analogy is then between
$q<0$
(see e.g. Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1991; O’Neil & Meneveau Reference O’Neil and Meneveau1993; Frish Reference Frish1995). The analogy is then between
![]() $u^{+}$
and the variable
$u^{+}$
and the variable
![]() $\ln ({\it\varepsilon}/\langle {\it\varepsilon}\rangle )$
. As will be seen in the discussion in §§ 2 and 3, an analogy between the momentum cascade and the energy cascade can be formally made, providing helpful insights for the study of wall-bounded flows (see also Jiménez Reference Jiménez2011).
$\ln ({\it\varepsilon}/\langle {\it\varepsilon}\rangle )$
. As will be seen in the discussion in §§ 2 and 3, an analogy between the momentum cascade and the energy cascade can be formally made, providing helpful insights for the study of wall-bounded flows (see also Jiménez Reference Jiménez2011).
The discussion here focuses on boundary-layer flows. For the variance of the streamwise velocity fluctuations to exhibit logarithmic scaling one may hypothesize that
![]() $\langle \text{exp}(qu^{+})\rangle$
exhibits power-law scaling with respect to
$\langle \text{exp}(qu^{+})\rangle$
exhibits power-law scaling with respect to
![]() $z$
near
$z$
near
![]() $q=0$
, since
$q=0$
, since
However, the known logarithmic behaviour of
![]() $\langle u^{+2}\rangle$
does not imply power-law scaling of
$\langle u^{+2}\rangle$
does not imply power-law scaling of
![]() $W(q;z)$
for
$W(q;z)$
for
![]() $q$
values away from
$q$
values away from
![]() $q=0$
, so this must be tested based on data.
$q=0$
, so this must be tested based on data.
The rest of the paper is organized as follows: the scaling behaviour of the single-point MGF is investigated in § 2, including empirical evidence of power-law scaling as a function of height
![]() $z$
, for
$z$
, for
![]() $q$
both positive and negative. Experimental measurements of flow at
$q$
both positive and negative. Experimental measurements of flow at
![]() $Re_{{\it\tau}}\approx 13\,000$
from the Melbourne High Reynolds Number Boundary Layer Wind Tunnel (HRNBLWT) are considered for this purpose. In § 3, we consider two-point MGFs and, in particular, provide an ‘attached eddy’ model based prediction of a scaling transition for
$Re_{{\it\tau}}\approx 13\,000$
from the Melbourne High Reynolds Number Boundary Layer Wind Tunnel (HRNBLWT) are considered for this purpose. In § 3, we consider two-point MGFs and, in particular, provide an ‘attached eddy’ model based prediction of a scaling transition for
![]() $W(q,-q;z,r)$
. This behaviour is confirmed by analysis of experimental data. Statistical convergence of the data is examined in § 4, and conclusions are provided in § 5. Throughout the paper,
$W(q,-q;z,r)$
. This behaviour is confirmed by analysis of experimental data. Statistical convergence of the data is examined in § 4, and conclusions are provided in § 5. Throughout the paper,
![]() $u^{+}$
is the streamwise velocity fluctuation normalized by friction velocity and
$u^{+}$
is the streamwise velocity fluctuation normalized by friction velocity and
![]() $z$
is the wall-normal coordinate. The overall picture of wall-bounded flows provided by the Townsend attached eddy hypothesis (Townsend Reference Townsend1976) is found useful in the discussion and is often invoked (or implied). In Townsend (Reference Townsend1976), as well as in Perry & Chong (Reference Perry and Chong1982) and Woodcock & Marusic (Reference Woodcock and Marusic2015), the boundary layer is hypothesized to consist of attached eddies whose sizes scale with their distance from the wall and whose population density scales inversely with distance from the wall.
$z$
is the wall-normal coordinate. The overall picture of wall-bounded flows provided by the Townsend attached eddy hypothesis (Townsend Reference Townsend1976) is found useful in the discussion and is often invoked (or implied). In Townsend (Reference Townsend1976), as well as in Perry & Chong (Reference Perry and Chong1982) and Woodcock & Marusic (Reference Woodcock and Marusic2015), the boundary layer is hypothesized to consist of attached eddies whose sizes scale with their distance from the wall and whose population density scales inversely with distance from the wall.
2 Scaling of single-point MGFs
We present results of the MGFs from high-Reynolds-number boundary-layer turbulence. Hot-wire streamwise velocity measurements at
![]() $Re_{{\it\tau}}=13\,000$
from the Melbourne HRNBLWT are analysed (with
$Re_{{\it\tau}}=13\,000$
from the Melbourne HRNBLWT are analysed (with
![]() $U_{\infty }=20$
(
$U_{\infty }=20$
(
![]() $\text{m s}^{-1}$
),
$\text{m s}^{-1}$
),
![]() $u_{{\it\tau}}=0.639$
(
$u_{{\it\tau}}=0.639$
(
![]() $\text{m s}^{-1}$
) and
$\text{m s}^{-1}$
) and
![]() ${\it\delta}=0.319$
(m), see Marusic et al. (Reference Marusic, Chauhan, Kulandaivelu and Hutchins2015) for further details of the dataset). The MGFs are computed for various
${\it\delta}=0.319$
(m), see Marusic et al. (Reference Marusic, Chauhan, Kulandaivelu and Hutchins2015) for further details of the dataset). The MGFs are computed for various
![]() $q$
values in a range between
$q$
values in a range between
![]() $\pm 2$
. Statistics are evaluated at the 50 measurement heights averaging over a time interval of approximately
$\pm 2$
. Statistics are evaluated at the 50 measurement heights averaging over a time interval of approximately
![]() $T_{\mathit{data}}=11\,200{\it\delta}/U_{\infty }$
. The measured MGFs as function of wall distance in inner units are shown in figure 1(a) for representative values of
$T_{\mathit{data}}=11\,200{\it\delta}/U_{\infty }$
. The measured MGFs as function of wall distance in inner units are shown in figure 1(a) for representative values of
![]() $q$
. In the range
$q$
. In the range
![]() $610<z^{+}$
,
$610<z^{+}$
,
![]() $z<0.2{\it\delta}$
(see Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) for detailed discussion on the range of the log layer), power-law behaviour is observed. Moreover, there is significant difference in the scaling exponents of
$z<0.2{\it\delta}$
(see Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) for detailed discussion on the range of the log layer), power-law behaviour is observed. Moreover, there is significant difference in the scaling exponents of
![]() $W(q;z)$
for positive and negative
$W(q;z)$
for positive and negative
![]() $q$
values of the same magnitude. This is especially the case for high
$q$
values of the same magnitude. This is especially the case for high
![]() $|q|$
. The respective scaling ranges differ depending on the sign of
$|q|$
. The respective scaling ranges differ depending on the sign of
![]() $q$
: for
$q$
: for
![]() $q>0$
, the power-law region extends down to heights
$q>0$
, the power-law region extends down to heights
![]() $z^{+}\approx 400$
, while for
$z^{+}\approx 400$
, while for
![]() $q<0$
, the power-law region is shorter, down only to wall distances of about
$q<0$
, the power-law region is shorter, down only to wall distances of about
![]() $z^{+}\approx 600$
. Note that
$z^{+}\approx 600$
. Note that
![]() $z^{+}\approx 400$
corresponds nominally to the lower limit
$z^{+}\approx 400$
corresponds nominally to the lower limit
![]() $3Re_{{\it\tau}}^{0.5}$
identified in Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) as appropriate for the logarithmic scaling range of the variance. This appears appropriate for the
$3Re_{{\it\tau}}^{0.5}$
identified in Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) as appropriate for the logarithmic scaling range of the variance. This appears appropriate for the
![]() $q>0$
cases, but for
$q>0$
cases, but for
![]() $q<0$
, the range is more consistent with
$q<0$
, the range is more consistent with
![]() $z^{+}=600$
. Since negative
$z^{+}=600$
. Since negative
![]() $q$
emphasizes the scaling behaviour of the low-speed regions of the flow, it is concluded that these are affected by wall and viscous effects up to larger distances from the wall, consistent with those regions being associated more prevalently with positive vertical velocities.
$q$
emphasizes the scaling behaviour of the low-speed regions of the flow, it is concluded that these are affected by wall and viscous effects up to larger distances from the wall, consistent with those regions being associated more prevalently with positive vertical velocities.

Figure 1. (a) Log–log plot of
![]() $\langle \text{exp}(qu^{+})\rangle$
against
$\langle \text{exp}(qu^{+})\rangle$
against
![]() $z^{+}$
for
$z^{+}$
for
![]() $q=\pm 0.5,\pm 1,\pm 1.5,\pm 2$
. Solid symbols are used for positive
$q=\pm 0.5,\pm 1,\pm 1.5,\pm 2$
. Solid symbols are used for positive
![]() $q$
values and hollow symbols are used for negative
$q$
values and hollow symbols are used for negative
![]() $q$
values. The extent of the scaling regions,
$q$
values. The extent of the scaling regions,
![]() $375<z^{+}$
,
$375<z^{+}$
,
![]() $z<0.2{\it\delta}$
for
$z<0.2{\it\delta}$
for
![]() $q>0$
and
$q>0$
and
![]() $610<z^{+}$
,
$610<z^{+}$
,
![]() $z<0.2{\it\delta}$
for
$z<0.2{\it\delta}$
for
![]() $q<0$
are indicated by vertical dashed lines. (b) Premultiplied single-point MGF,
$q<0$
are indicated by vertical dashed lines. (b) Premultiplied single-point MGF,
![]() $C(q){z^{+}}^{{\it\tau}(q)}\cdot \langle \text{exp}(qu^{+})\rangle$
. The prefactor
$C(q){z^{+}}^{{\it\tau}(q)}\cdot \langle \text{exp}(qu^{+})\rangle$
. The prefactor
![]() $C(q)$
is determined from the power-law fitting (such that in the fitted range
$C(q)$
is determined from the power-law fitting (such that in the fitted range
![]() $C(q){z^{+}}^{-{\it\tau}(q)}\approx \langle \text{exp}(qu^{+})\rangle$
). Values of
$C(q){z^{+}}^{-{\it\tau}(q)}\approx \langle \text{exp}(qu^{+})\rangle$
). Values of
![]() ${\it\tau}(q)$
used in the premultiplied quantities are
${\it\tau}(q)$
used in the premultiplied quantities are
![]() ${\it\tau}=0.17$
, 0.54, 0.91, 1.18 for
${\it\tau}=0.17$
, 0.54, 0.91, 1.18 for
![]() $q=-0.5$
,
$q=-0.5$
,
![]() $-1$
,
$-1$
,
![]() $-1.5$
,
$-1.5$
,
![]() $-2$
and
$-2$
and
![]() ${\it\tau}=0.17$
, 0.63, 1.27, 2.04 for
${\it\tau}=0.17$
, 0.63, 1.27, 2.04 for
![]() $q=0.5$
, 1, 1.5, 2.
$q=0.5$
, 1, 1.5, 2.
Equation (1.3) suggests power scaling of
![]() $W(q;z)$
near
$W(q;z)$
near
![]() $q=0$
and for
$q=0$
and for
![]() $z$
values where the
$z$
values where the
![]() $\langle u^{+2}\rangle$
has logarithmic scaling. Such scaling can also be obtained by considering the velocity fluctuations as resulting from a sum of discrete random contributions from attached eddies:
$\langle u^{+2}\rangle$
has logarithmic scaling. Such scaling can also be obtained by considering the velocity fluctuations as resulting from a sum of discrete random contributions from attached eddies:
Here the
![]() $a_{i}$
are random additives, assumed to be identically and independently distributed, each associated with an attached eddy of size
$a_{i}$
are random additives, assumed to be identically and independently distributed, each associated with an attached eddy of size
![]() ${\sim}{\it\delta}/2^{i}$
if for simplicity we choose a scale ratio of 2. The number of additives
${\sim}{\it\delta}/2^{i}$
if for simplicity we choose a scale ratio of 2. The number of additives
![]() $N_{z}$
is taken to be proportional to the number of attached eddies at any given height
$N_{z}$
is taken to be proportional to the number of attached eddies at any given height
![]() $z$
. If the eddy population density is inversely proportional to
$z$
. If the eddy population density is inversely proportional to
![]() $z$
according to the attached eddy hypothesis (Townsend Reference Townsend1976), then
$z$
according to the attached eddy hypothesis (Townsend Reference Townsend1976), then
![]() $N_{z}$
is proportional to:
$N_{z}$
is proportional to:
As a result, the exponential moment can be evaluated
where
![]() $C_{e}$
is some constant. Equation (2.3) provides a prediction for the scaling exponents
$C_{e}$
is some constant. Equation (2.3) provides a prediction for the scaling exponents
![]() ${\it\tau}(q)$
:
${\it\tau}(q)$
:
![]() ${\it\tau}(q)$
is determined by the probability density function (p.d.f.) of the random additives
${\it\tau}(q)$
is determined by the probability density function (p.d.f.) of the random additives
![]() $a$
, representing the velocity field induced by a typical attached eddy. If these eddies are assumed to be purely inertial without dependence on viscosity, then
$a$
, representing the velocity field induced by a typical attached eddy. If these eddies are assumed to be purely inertial without dependence on viscosity, then
![]() ${\it\tau}(q)$
would be expected to be independent of Reynolds number. Furthermore, if
${\it\tau}(q)$
would be expected to be independent of Reynolds number. Furthermore, if
![]() $a$
is assumed to be a Gaussian variable, then (2.4) leads to the quadratic law
$a$
is assumed to be a Gaussian variable, then (2.4) leads to the quadratic law
where
![]() $C$
is another constant. In order to compare this behaviour with measurements, we fit
$C$
is another constant. In order to compare this behaviour with measurements, we fit
![]() ${\it\tau}(q)$
from data (as shown in figure 1
a) in the relatively narrow and conservative range
${\it\tau}(q)$
from data (as shown in figure 1
a) in the relatively narrow and conservative range
![]() $600<z^{+}$
,
$600<z^{+}$
,
![]() $z<0.2{\it\delta}$
, the common range where both positive and negative
$z<0.2{\it\delta}$
, the common range where both positive and negative
![]() $q$
display good scaling. The quality of the power-law fitting is further examined in figure 1(b), where the premultiplied single-point MGFs are plotted against the wall-normal distance. The fitted
$q$
display good scaling. The quality of the power-law fitting is further examined in figure 1(b), where the premultiplied single-point MGFs are plotted against the wall-normal distance. The fitted
![]() ${\it\tau}(q)$
curve is plotted against
${\it\tau}(q)$
curve is plotted against
![]() $q$
in figure 2, including error bars determined by the ratio of the root mean square of the variation in
$q$
in figure 2, including error bars determined by the ratio of the root mean square of the variation in
![]() $\log (\exp (qu^{+}))-{\it\tau}(q)\log (z^{+})$
in the fitted range of
$\log (\exp (qu^{+}))-{\it\tau}(q)\log (z^{+})$
in the fitted range of
![]() $z^{+}$
to the corresponding expected increase (or decrease) in
$z^{+}$
to the corresponding expected increase (or decrease) in
![]() $\langle \text{exp}(qu^{+})\rangle$
indicated by the fitted parameter. Due to statistical convergence issues, evaluation of
$\langle \text{exp}(qu^{+})\rangle$
indicated by the fitted parameter. Due to statistical convergence issues, evaluation of
![]() ${\it\tau}(q)$
is limited to
${\it\tau}(q)$
is limited to
![]() $|q|<2$
. A quadratic fit around
$|q|<2$
. A quadratic fit around
![]() $q=0$
is shown with the solid line in figure 2. The fit yields
$q=0$
is shown with the solid line in figure 2. The fit yields
![]() ${\it\tau}(q)=0.63q^{2}$
. According to (1.3),
${\it\tau}(q)=0.63q^{2}$
. According to (1.3),
This is consistent with the prior measurements of the ‘Perry–Townsend’ constant
![]() $A_{1}\approx 1.25$
(Hultmark et al.
Reference Hultmark, Vallikivi, Bailey and Smits2012; Marusic et al.
Reference Marusic, Monty, Hultmark and Smits2013; Meneveau & Marusic Reference Meneveau and Marusic2013). Studying possible Reynolds number effects falls beyond the scope of this paper.
$A_{1}\approx 1.25$
(Hultmark et al.
Reference Hultmark, Vallikivi, Bailey and Smits2012; Marusic et al.
Reference Marusic, Monty, Hultmark and Smits2013; Meneveau & Marusic Reference Meneveau and Marusic2013). Studying possible Reynolds number effects falls beyond the scope of this paper.

Figure 2. Measured scaling exponents
![]() ${\it\tau}(q)$
(symbols), obtained from fitting
${\it\tau}(q)$
(symbols), obtained from fitting
![]() $W(q;z)$
as a function of
$W(q;z)$
as a function of
![]() $z$
, in the range
$z$
, in the range
![]() $610<z^{+}$
and
$610<z^{+}$
and
![]() $z<0.2{\it\delta}$
. Error bars show the uncertainty in the obtained exponents. A quadratic fit around the origin yields
$z<0.2{\it\delta}$
. Error bars show the uncertainty in the obtained exponents. A quadratic fit around the origin yields
![]() ${\it\tau}(q)=0.63q^{2}$
(blue solid line).
${\it\tau}(q)=0.63q^{2}$
(blue solid line).
We can also compute
![]() $\langle {u^{+}}^{2p}\rangle ^{1/p}$
using the single-point MGF
$\langle {u^{+}}^{2p}\rangle ^{1/p}$
using the single-point MGF
![]() $\langle \text{exp}(qu^{+})\rangle$
. Equations (1.2), (1.3) and (2.5) lead to
$\langle \text{exp}(qu^{+})\rangle$
. Equations (1.2), (1.3) and (2.5) lead to
![]() $\langle {u^{+}}^{2}\rangle =1\times 2C\log ({\it\delta}/z)$
,
$\langle {u^{+}}^{2}\rangle =1\times 2C\log ({\it\delta}/z)$
,
![]() $\langle {u^{+}}^{4}\rangle ^{1/2}=3^{1/2}\times 2C\log ({\it\delta}/z)$
,
$\langle {u^{+}}^{4}\rangle ^{1/2}=3^{1/2}\times 2C\log ({\it\delta}/z)$
,
![]() $\langle {u^{+}}^{6}\rangle ^{1/3}=15^{1/3}\times 2C\log ({\it\delta}/z)$
and
$\langle {u^{+}}^{6}\rangle ^{1/3}=15^{1/3}\times 2C\log ({\it\delta}/z)$
and
![]() $\langle {u^{+}}^{8}\rangle ^{1/4}=105^{1/4}\times 2C\log ({\it\delta}/z)$
, recovering the scaling of generalized logarithmic laws (Meneveau & Marusic Reference Meneveau and Marusic2013). Because of the Gaussianity that underlies (2.5), it is not surprising that
$\langle {u^{+}}^{8}\rangle ^{1/4}=105^{1/4}\times 2C\log ({\it\delta}/z)$
, recovering the scaling of generalized logarithmic laws (Meneveau & Marusic Reference Meneveau and Marusic2013). Because of the Gaussianity that underlies (2.5), it is not surprising that
![]() $A_{p}/A_{1}=[(2p-1)!!]^{1/p}$
(see Meneveau & Marusic Reference Meneveau and Marusic2013; Woodcock & Marusic Reference Woodcock and Marusic2015). But, as can be discerned in figure 2, the quadratic fit becomes highly inaccurate away from
$A_{p}/A_{1}=[(2p-1)!!]^{1/p}$
(see Meneveau & Marusic Reference Meneveau and Marusic2013; Woodcock & Marusic Reference Woodcock and Marusic2015). But, as can be discerned in figure 2, the quadratic fit becomes highly inaccurate away from
![]() $q=0$
, consistent with known deviations from Gaussian behaviour of velocity fluctuations in wall boundary-layer turbulence. Also the data are asymmetric, showing significantly stronger deviations from the Gaussian prediction for
$q=0$
, consistent with known deviations from Gaussian behaviour of velocity fluctuations in wall boundary-layer turbulence. Also the data are asymmetric, showing significantly stronger deviations from the Gaussian prediction for
![]() $q<0$
than for
$q<0$
than for
![]() $q>0$
. These results constitute new information about the flow and may prove important in comparing with models.
$q>0$
. These results constitute new information about the flow and may prove important in comparing with models.
3 Two-point MGFs and scaling transition
In this section, the scaling behaviour of the two-point moment generating function
![]() $W(q,q^{\prime };z,r)=\langle \exp [qu^{+}(x,z)+q^{\prime }u^{+}(x+r,z)]\rangle$
in the logarithmic region (for moments as function of
$W(q,q^{\prime };z,r)=\langle \exp [qu^{+}(x,z)+q^{\prime }u^{+}(x+r,z)]\rangle$
in the logarithmic region (for moments as function of
![]() $z$
) and in the relevant range of the two-point separation distance
$z$
) and in the relevant range of the two-point separation distance
![]() $r$
is investigated. Note that here we indicate
$r$
is investigated. Note that here we indicate
![]() $z$
explicitly to avoid confusion. Before analysing the data, predictions of scaling behaviour exploiting the assumed hierarchical tree structure of attached eddies are presented. Figure 3 shows a sketch of attached eddies. We consider two points at a wall distance
$z$
explicitly to avoid confusion. Before analysing the data, predictions of scaling behaviour exploiting the assumed hierarchical tree structure of attached eddies are presented. Figure 3 shows a sketch of attached eddies. We consider two points at a wall distance
![]() $z$
that are separated by a distance
$z$
that are separated by a distance
![]() $r$
in the flow (
$r$
in the flow (
![]() $x$
) direction. Velocity fluctuations at the two points are given by the random additives
$x$
) direction. Velocity fluctuations at the two points are given by the random additives
![]() $a_{i}$
corresponding to all the eddies ‘above’ a given point. As a result, two points at a distance
$a_{i}$
corresponding to all the eddies ‘above’ a given point. As a result, two points at a distance
![]() $r$
will share a subset of common additives from the larger eddies that contain both points, while each contains independent additives from eddies that are not common to both points. This consideration then enables one to factor the exponentials to separate common and separate contributions. The approach follows that of Meneveau & Chhabra (Reference Meneveau and Chhabra1990) and O’Neil & Meneveau (Reference O’Neil and Meneveau1993) who considered such factorizations of two-point moments of dissipation rate, and a crucial concept is that of the size of the smallest common eddy,
$r$
will share a subset of common additives from the larger eddies that contain both points, while each contains independent additives from eddies that are not common to both points. This consideration then enables one to factor the exponentials to separate common and separate contributions. The approach follows that of Meneveau & Chhabra (Reference Meneveau and Chhabra1990) and O’Neil & Meneveau (Reference O’Neil and Meneveau1993) who considered such factorizations of two-point moments of dissipation rate, and a crucial concept is that of the size of the smallest common eddy,
![]() $r_{c}$
. To find the scaling for
$r_{c}$
. To find the scaling for
![]() $W(q,q^{\prime };z,r)$
, the quantity
$W(q,q^{\prime };z,r)$
, the quantity
![]() $\exp (qu^{+}(x,z)+q^{\prime }u^{+}(x+r,z))$
is conditioned based on the size of the smallest common eddy
$\exp (qu^{+}(x,z)+q^{\prime }u^{+}(x+r,z))$
is conditioned based on the size of the smallest common eddy
![]() $r_{c}$
of the points under consideration, and the final result is given by the sum over all possible common eddy sizes
$r_{c}$
of the points under consideration, and the final result is given by the sum over all possible common eddy sizes
![]() $r_{c}$
:
$r_{c}$
:
where
![]() $P_{r_{c}}$
is the probability that the smallest common eddy shared by the two points
$P_{r_{c}}$
is the probability that the smallest common eddy shared by the two points
![]() $(x,z)$
,
$(x,z)$
,
![]() $(x+r,z)$
is of size
$(x+r,z)$
is of size
![]() $r_{c}$
. Eddies of size larger than
$r_{c}$
. Eddies of size larger than
![]() $r_{c}$
affect both points equally.
$r_{c}$
affect both points equally.

Figure 3. Conceptual sketch of a boundary layer with three hierarchies of attached eddies (I, II, III).
![]() ${\it\theta}\approx 17^{\circ }$
is the inclination angle of a typical attached eddy; consistent with a packet structure (Woodcock & Marusic Reference Woodcock and Marusic2015). Both points in set A as well as in set B are at a height
${\it\theta}\approx 17^{\circ }$
is the inclination angle of a typical attached eddy; consistent with a packet structure (Woodcock & Marusic Reference Woodcock and Marusic2015). Both points in set A as well as in set B are at a height
![]() $z$
above the wall and are separated by a distance
$z$
above the wall and are separated by a distance
![]() $r$
in the flow direction. An attached eddy affects the region beneath it, as is indicated by the shaded region (Townsend Reference Townsend1976).
$r$
in the flow direction. An attached eddy affects the region beneath it, as is indicated by the shaded region (Townsend Reference Townsend1976).
Also, we make the association that an eddy size of
![]() $r_{c}$
in the horizontal direction has a height
$r_{c}$
in the horizontal direction has a height
![]() $z_{c}=r_{c}\tan {\it\theta}$
. Factorizing the exponential at both points to contributions from eddies of size larger than
$z_{c}=r_{c}\tan {\it\theta}$
. Factorizing the exponential at both points to contributions from eddies of size larger than
![]() $r_{c}$
(heights above
$r_{c}$
(heights above
![]() $z_{c}$
) and eddies smaller than
$z_{c}$
) and eddies smaller than
![]() $r_{c}$
(heights less than
$r_{c}$
(heights less than
![]() $z_{c}$
) leads to
$z_{c}$
) leads to
Eddies of size smaller than
![]() $r_{c}$
cannot affect both points at the same time, therefore the differences
$r_{c}$
cannot affect both points at the same time, therefore the differences
![]() $u^{+}(x,z)-u^{+}(x,z_{c})$
and
$u^{+}(x,z)-u^{+}(x,z_{c})$
and
![]() $u^{+}(x+r,z)-u^{+}(x+r,z_{c})$
(or the ratio of the exponentials), which according to the random additive ansatz (2.1) contain only contributions (additives) from eddies of size smaller than
$u^{+}(x+r,z)-u^{+}(x+r,z_{c})$
(or the ratio of the exponentials), which according to the random additive ansatz (2.1) contain only contributions (additives) from eddies of size smaller than
![]() $r_{c}$
, can be assumed to be statistically independent. Also, they are independent of the additives corresponding to the velocity difference
$r_{c}$
, can be assumed to be statistically independent. Also, they are independent of the additives corresponding to the velocity difference
![]() $u^{+}(x,{\it\delta})-u^{+}(x,z_{c})$
. These arguments lead to
$u^{+}(x,{\it\delta})-u^{+}(x,z_{c})$
. These arguments lead to
Following the same arguments that lead to (2.3), we have
and similarly at
![]() $x+r$
involving
$x+r$
involving
![]() ${\it\tau}(q^{\prime })$
. Substituting (3.4) into (3.2) leads to
${\it\tau}(q^{\prime })$
. Substituting (3.4) into (3.2) leads to
To estimate
![]() $P_{r_{c}}$
for some height
$P_{r_{c}}$
for some height
![]() $z$
, we follow Meneveau & Chhabra (Reference Meneveau and Chhabra1990) and O’Neil & Meneveau (Reference O’Neil and Meneveau1993), and argue that
$z$
, we follow Meneveau & Chhabra (Reference Meneveau and Chhabra1990) and O’Neil & Meneveau (Reference O’Neil and Meneveau1993), and argue that
![]() $P_{r_{c}}$
is proportional to the area of a strip of thickness
$P_{r_{c}}$
is proportional to the area of a strip of thickness
![]() $r$
along the perimeter of an eddy of size
$r$
along the perimeter of an eddy of size
![]() $r_{c}$
(area
$r_{c}$
(area
![]() ${\sim}r\,r_{c}$
), divided by the total area of such an eddy in the plane (
${\sim}r\,r_{c}$
), divided by the total area of such an eddy in the plane (
![]() ${\sim}r_{c}^{2}$
). For point pairs falling within such a strip, the two points typically pertain to different eddies of size
${\sim}r_{c}^{2}$
). For point pairs falling within such a strip, the two points typically pertain to different eddies of size
![]() $r_{c}$
. Hence
$r_{c}$
. Hence
![]() $P_{r_{c}}\sim r/r_{c}$
, and after replacing
$P_{r_{c}}\sim r/r_{c}$
, and after replacing
![]() $z_{c}=r_{c}\tan {\it\theta}$
, we can write
$z_{c}=r_{c}\tan {\it\theta}$
, we can write
where a prefactor depending on
![]() $\tan {\it\theta}$
has been omitted for simplicity. At high Reynolds numbers, we can consider the situation
$\tan {\it\theta}$
has been omitted for simplicity. At high Reynolds numbers, we can consider the situation
![]() ${\it\delta}/\text{tan}\,{\it\theta}\gg r$
. Thinking in terms of a discrete hierarchy of eddies, the sum in (3.6) becomes a geometric one. It is dominated either by the value at small scales
${\it\delta}/\text{tan}\,{\it\theta}\gg r$
. Thinking in terms of a discrete hierarchy of eddies, the sum in (3.6) becomes a geometric one. It is dominated either by the value at small scales
![]() $r_{c}\sim r$
or at large scales
$r_{c}\sim r$
or at large scales
![]() $r_{c}\sim {\it\delta}/\text{tan}\,{\it\theta}$
, depending on the sign of the exponent. Therefore, two asymptotic regimes can then be identified:
$r_{c}\sim {\it\delta}/\text{tan}\,{\it\theta}$
, depending on the sign of the exponent. Therefore, two asymptotic regimes can then be identified:
indicating a ‘scaling transition’ with respect to
![]() $r$
when
$r$
when
![]() $q$
and
$q$
and
![]() $q^{\prime }$
are such that
$q^{\prime }$
are such that
![]() ${\it\tau}(q)+{\it\tau}(q^{\prime })-{\it\tau}(q+q^{\prime })-1=0$
.
${\it\tau}(q)+{\it\tau}(q^{\prime })-{\it\tau}(q+q^{\prime })-1=0$
.
To examine whether such a scaling transition exists in the measurements, we consider the specific case
![]() $q^{\prime }=-q$
, for which the predicted scaling behaviour with respect to
$q^{\prime }=-q$
, for which the predicted scaling behaviour with respect to
![]() $r$
is:
$r$
is:
since
![]() ${\it\tau}(0)=0$
by construction. It is worth noting here that such a scaling transition is indicative of the ‘tree-like’ or hierarchical and space-filling structure on which the attached eddies are organized and, since the transition occurs away from
${\it\tau}(0)=0$
by construction. It is worth noting here that such a scaling transition is indicative of the ‘tree-like’ or hierarchical and space-filling structure on which the attached eddies are organized and, since the transition occurs away from
![]() $q=0$
, it cannot be diagnosed using traditional two-point moments.
$q=0$
, it cannot be diagnosed using traditional two-point moments.
Based on the dataset described before,
![]() $W(q,-q;z,r)$
is evaluated and plotted against
$W(q,-q;z,r)$
is evaluated and plotted against
![]() $r^{+}$
in figure 4(a) for a specific wall-normal position in the log region (here taken at
$r^{+}$
in figure 4(a) for a specific wall-normal position in the log region (here taken at
![]() $z^{+}=600$
) and for various values of
$z^{+}=600$
) and for various values of
![]() $q$
. We evaluate two-point correlations using direct summation (and checked that FFT gives essentially the same results). The relevant range in
$q$
. We evaluate two-point correlations using direct summation (and checked that FFT gives essentially the same results). The relevant range in
![]() $r$
for the scaling predicted in (3.7) is between
$r$
for the scaling predicted in (3.7) is between
![]() $r=z/\text{tan}({\it\theta})$
(any
$r=z/\text{tan}({\it\theta})$
(any
![]() $r$
below this value corresponds to eddies of size smaller than
$r$
below this value corresponds to eddies of size smaller than
![]() $z$
and is thus not relevant) and
$z$
and is thus not relevant) and
![]() $0.15{\it\delta}/\text{tan}\,{\it\theta}$
(this is more conservative compared to
$0.15{\it\delta}/\text{tan}\,{\it\theta}$
(this is more conservative compared to
![]() $0.2{\it\delta}/\text{tan}\,{\it\theta}$
). For the specific height considered in figure 4, this range corresponds to
$0.2{\it\delta}/\text{tan}\,{\it\theta}$
). For the specific height considered in figure 4, this range corresponds to
![]() $2000<r^{+}<6500$
and is indicated by the dashed vertical lines. As can be seen,
$2000<r^{+}<6500$
and is indicated by the dashed vertical lines. As can be seen,
![]() $W(q,-q;z,r)$
does exhibit power-law scaling in the relevant range of
$W(q,-q;z,r)$
does exhibit power-law scaling in the relevant range of
![]() $r$
. The quality of the power-law fitting is further examined in figure 4(b), where the premultiplied two-point MGFs are plotted against the two-point distance
$r$
. The quality of the power-law fitting is further examined in figure 4(b), where the premultiplied two-point MGFs are plotted against the two-point distance
![]() $r^{+}$
. Moreover, as is already clear in figure 4(a), the scaling exponent gradually increases as
$r^{+}$
. Moreover, as is already clear in figure 4(a), the scaling exponent gradually increases as
![]() $q$
increases, but then the slope ceases to increase further with increasing
$q$
increases, but then the slope ceases to increase further with increasing
![]() $q$
. We fit for
$q$
. We fit for
![]() ${\it\Phi}(q)$
in the range of
${\it\Phi}(q)$
in the range of
![]() $r$
indicated by the two vertical dashed lines in figure 4. Figure 5 compares the measured
$r$
indicated by the two vertical dashed lines in figure 4. Figure 5 compares the measured
![]() ${\it\Phi}(q)$
and the prediction made in (3.8). Measured values for
${\it\Phi}(q)$
and the prediction made in (3.8). Measured values for
![]() ${\it\tau}(q)$
and
${\it\tau}(q)$
and
![]() ${\it\tau}(-q)$
are used in (3.8). As can be seen from figure 5, a scaling transition exists and it appears to be correctly predicted by the scaling analysis leading to (3.7). The error bars for the fitted slopes are estimated as the ratio of the root mean square of the variations in
${\it\tau}(-q)$
are used in (3.8). As can be seen from figure 5, a scaling transition exists and it appears to be correctly predicted by the scaling analysis leading to (3.7). The error bars for the fitted slopes are estimated as the ratio of the root mean square of the variations in
![]() $\log (W(q,-q;z,r))-{\it\Phi}(q)\log (r)$
in the fitting range of
$\log (W(q,-q;z,r))-{\it\Phi}(q)\log (r)$
in the fitting range of
![]() $r$
to the expected change indicated by the fitted parameter, i.e.
$r$
to the expected change indicated by the fitted parameter, i.e.
![]() $\text{error}=\text{r.m.s.}[\log (W(q,-q;z,r))-{\it\Phi}(q)\log (r)]/({\it\Phi}(q)\log ({\rm\Delta}r))$
, where
$\text{error}=\text{r.m.s.}[\log (W(q,-q;z,r))-{\it\Phi}(q)\log (r)]/({\it\Phi}(q)\log ({\rm\Delta}r))$
, where
![]() ${\rm\Delta}r$
is range of
${\rm\Delta}r$
is range of
![]() $r$
used in fitting.
$r$
used in fitting.

Figure 4. Log–log plot of
![]() $W(q,-q;z,r)$
against
$W(q,-q;z,r)$
against
![]() $r$
at
$r$
at
![]() $z^{+}=600$
, for nine values of
$z^{+}=600$
, for nine values of
![]() $q$
ranging from 0 to 1.5 (shown values are
$q$
ranging from 0 to 1.5 (shown values are
![]() $q=0$
, 0.188, 0.375, 0.563, 0.75, 0.938, 1.125, 1.313 and 1.5). The range of
$q=0$
, 0.188, 0.375, 0.563, 0.75, 0.938, 1.125, 1.313 and 1.5). The range of
![]() $r$
chosen to determine the power-law scaling exponent (relevant for the log region) is
$r$
chosen to determine the power-law scaling exponent (relevant for the log region) is
![]() $z/\text{tan}\,{\it\theta}$
, to
$z/\text{tan}\,{\it\theta}$
, to
![]() $0.15{\it\delta}/\text{tan}\,{\it\theta}$
. At
$0.15{\it\delta}/\text{tan}\,{\it\theta}$
. At
![]() $z^{+}=600$
, this range corresponds to (approximately)
$z^{+}=600$
, this range corresponds to (approximately)
![]() $2000<r^{+}<6500$
. This range is indicated by two thin dashed vertical lines. The fits are indicated by solid lines. (b) Premultiplied two-point MGFs
$2000<r^{+}<6500$
. This range is indicated by two thin dashed vertical lines. The fits are indicated by solid lines. (b) Premultiplied two-point MGFs
![]() $C(q){r^{+}}^{-{\it\Phi}(q)}W(q,-q;z,r)$
for representative
$C(q){r^{+}}^{-{\it\Phi}(q)}W(q,-q;z,r)$
for representative
![]() $q$
values. The prefactor
$q$
values. The prefactor
![]() $C(q)$
is determined from the power-law fitting.
$C(q)$
is determined from the power-law fitting.
![]() ${\it\Phi}(q)$
used in the premultiplied quantities are 0.18, 0.61, 1.04 for
${\it\Phi}(q)$
used in the premultiplied quantities are 0.18, 0.61, 1.04 for
![]() $q$
being 0.375, 0.75, 1.313.
$q$
being 0.375, 0.75, 1.313.

Figure 5. A comparison of the experimental measurements and model predictions of
![]() ${\it\Phi}(q)$
(symbols and solid line) against
${\it\Phi}(q)$
(symbols and solid line) against
![]() $q$
.
$q$
.
![]() ${\it\Phi}(q)$
is the exponent on
${\it\Phi}(q)$
is the exponent on
![]() $r$
in the predicted scaling behaviour of
$r$
in the predicted scaling behaviour of
![]() $W(q,-q;z,r)$
.
$W(q,-q;z,r)$
.
Furthermore, the scaling of
![]() $W(q,q^{\prime };z,r)$
can be used to compute general moments such as
$W(q,q^{\prime };z,r)$
can be used to compute general moments such as
![]() $\langle u^{m}(x,z)u^{n}(x+r,z)\rangle$
and
$\langle u^{m}(x,z)u^{n}(x+r,z)\rangle$
and
![]() $\langle (u(x,z)-u(x+r,z))^{2n}\rangle$
(the latter are simply combinations of
$\langle (u(x,z)-u(x+r,z))^{2n}\rangle$
(the latter are simply combinations of
![]() $\langle u_{z}^{m}(x)u_{z}^{n}(x+r)\rangle$
). As an example, we compute
$\langle u_{z}^{m}(x)u_{z}^{n}(x+r)\rangle$
). As an example, we compute
![]() $\langle u^{+}(x)u^{+}(x+r)\rangle$
using (1.2), (3.7):
$\langle u^{+}(x)u^{+}(x+r)\rangle$
using (1.2), (3.7):
This logarithmic scaling is not unexpected since it is consistent with the
![]() $-1$
power law in the energy spectrum. With
$-1$
power law in the energy spectrum. With
![]() $\langle u^{+}(x)u^{+}(x+r)\rangle$
known, we can compute the structure function as
$\langle u^{+}(x)u^{+}(x+r)\rangle$
known, we can compute the structure function as
This recovers the observation made in de Silva et al. (Reference de Silva, Marusic, Woodcock and Meneveau2015). Higher-order structure functions can be calculated and logarithmic scalings can be recovered within in this framework (not shown here for succinctness).
4 Data convergence
Statistical convergence of the statistical moments measured in this work can be verified by examining the premultiplied probability density function (p.d.f.). In particular, we examine
![]() $\text{e}^{\pm u^{+}}P(u^{+})$
and
$\text{e}^{\pm u^{+}}P(u^{+})$
and
![]() $\text{e}^{\pm 2u^{+}}P(u^{+})$
, where
$\text{e}^{\pm 2u^{+}}P(u^{+})$
, where
![]() $P(u^{+})$
is the single-point p.d.f. of the velocity at a representative wall-normal height
$P(u^{+})$
is the single-point p.d.f. of the velocity at a representative wall-normal height
![]() $z^{+}=610$
(which is above
$z^{+}=610$
(which is above
![]() $3Re^{0.5}$
and is still deep into the log region). For the two-point MGF considered in § 3, we evaluate the two-point joint p.d.f.
$3Re^{0.5}$
and is still deep into the log region). For the two-point MGF considered in § 3, we evaluate the two-point joint p.d.f.
![]() $P(u_{1},u_{2})$
where
$P(u_{1},u_{2})$
where
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{2}$
are velocities at two points
$u_{2}$
are velocities at two points
![]() $x$
and
$x$
and
![]() $x+r$
, and examine the quantity
$x+r$
, and examine the quantity
![]() $L(u_{1})$
defined as
$L(u_{1})$
defined as
Since
![]() $W(q,-q;z,r)=\int L(u_{1})\,\text{d}u_{1}$
, examination of the tails of
$W(q,-q;z,r)=\int L(u_{1})\,\text{d}u_{1}$
, examination of the tails of
![]() $L(u_{1})$
provides information about statistical convergence in measurements of
$L(u_{1})$
provides information about statistical convergence in measurements of
![]() $W(q,-q;z,r)$
. We examine
$W(q,-q;z,r)$
. We examine
![]() $L(u_{1})$
at the same wall-normal height
$L(u_{1})$
at the same wall-normal height
![]() $z^{+}=610$
and a representative
$z^{+}=610$
and a representative
![]() $r^{+}=2500$
(which is within the relevant range
$r^{+}=2500$
(which is within the relevant range
![]() $z/\text{tan}\,{\it\theta}<r<0.15{\it\delta}/\text{tan}\,{\it\theta}$
).
$z/\text{tan}\,{\it\theta}<r<0.15{\it\delta}/\text{tan}\,{\it\theta}$
).
As can be seen in figure 6, the quantities of interest, i.e.
![]() $\langle \text{e}^{qu^{+}}\rangle$
and
$\langle \text{e}^{qu^{+}}\rangle$
and
![]() $\langle \text{e}^{q(u^{+}(x)-u^{+}(x+r))}\rangle$
, which are equal to the area under these curves, are well captured by the data available, at least for those
$\langle \text{e}^{q(u^{+}(x)-u^{+}(x+r))}\rangle$
, which are equal to the area under these curves, are well captured by the data available, at least for those
![]() $q$
values considered in §§ 2 and 3. Additionally, these figures illustrate the properties of MGFs that, by raising
$q$
values considered in §§ 2 and 3. Additionally, these figures illustrate the properties of MGFs that, by raising
![]() $\exp (u^{+})$
to positive or negative powers, regions of high or low velocity are highlighted respectively (as is seen in figure 6
a) and show distinctly asymmetric behaviour.
$\exp (u^{+})$
to positive or negative powers, regions of high or low velocity are highlighted respectively (as is seen in figure 6
a) and show distinctly asymmetric behaviour.

Figure 6. Premultiplied p.d.f.
![]() $\exp (u^{+})P(u^{+})$
(a) and
$\exp (u^{+})P(u^{+})$
(a) and
![]() $L(u)$
(b).
$L(u)$
(b).
5 Conclusions
Introducing a new framework for the study of turbulence statistics in the logarithmic region in boundary layers, basic properties of the single-point and two-point moment generating function have been investigated. Power-law behaviours are observed in relevant ranges of
![]() $z$
and
$z$
and
![]() $r$
(the latter for two-point moment generating functions) during analysis of experimental measurements. By taking negative or positive values of the parameter
$r$
(the latter for two-point moment generating functions) during analysis of experimental measurements. By taking negative or positive values of the parameter
![]() $q$
, the single-point moment generating function
$q$
, the single-point moment generating function
![]() $W(q;z)$
can be used to investigate separately the properties of low-velocity regions and high-velocity regions. Such distinctions are not easily accessible when using traditional moments. A scaling transition in the two-point MGF,
$W(q;z)$
can be used to investigate separately the properties of low-velocity regions and high-velocity regions. Such distinctions are not easily accessible when using traditional moments. A scaling transition in the two-point MGF,
![]() $W(q,-q;z,r)$
, is predicted based on a simplified model inspired by the attached eddy hypothesis. Such a transition is indeed observed in the measurements and provides quantifiable evidence that the attached eddies through the log region are organized in a ‘tree-like’ or hierarchical and space-filling manner. Such an organization was assumed in previous attached eddy modelling efforts (Woodcock & Marusic Reference Woodcock and Marusic2015). Deviations from Gaussian statistics are visible in the scaling behaviour of the MGFs for
$W(q,-q;z,r)$
, is predicted based on a simplified model inspired by the attached eddy hypothesis. Such a transition is indeed observed in the measurements and provides quantifiable evidence that the attached eddies through the log region are organized in a ‘tree-like’ or hierarchical and space-filling manner. Such an organization was assumed in previous attached eddy modelling efforts (Woodcock & Marusic Reference Woodcock and Marusic2015). Deviations from Gaussian statistics are visible in the scaling behaviour of the MGFs for
![]() $q$
away from
$q$
away from
![]() $q=0$
. Various turbulence statistics can be derived from the MGFs and known logarithmic scaling laws in single-point even-order moments and structure functions can be recovered.
$q=0$
. Various turbulence statistics can be derived from the MGFs and known logarithmic scaling laws in single-point even-order moments and structure functions can be recovered.
Acknowledgements
The authors gratefully acknowledge the financial support of the Office of Naval Research, the National Science Foundation, and the Australian Research Council.