1 Introduction
In recent years, technical lightweight design has become increasingly important in technology to save energy and resources as well as to provide functional advantages. The aim of lightweight design is the minimization of mass by making full use of the structural load-bearing capacity without weakening the stiffness and other functions of the structure. Due to the reduction of material, resources can be saved, resulting in functional and economic advantages. On the other hand, the development of lightweight constructions leads to higher costs, e.g., due to more complex development and manufacturing processes. In this context, lightweight constructions represent a compromise between costs and benefits under given boundary conditions (Wiedemann Reference Wiedemann2007; Klein Reference Klein2013).
In order to solve this conflict of objectives, the adaptation of biological lightweight design principles has established itself as a common procedure for the development of lightweight designs (Nachtigall & Wisser Reference Nachtigall and Wisser2013). Biological constructions are always subject to selection pressures within the framework of evolution, where the design using a minimum of resources under given boundary conditions prevails. Therefore, biological lightweight constructions are an important source of ideas to solve technical lightweight problems with minimal mass and energy requirements (Degischer & Lüftl Reference Degischer and Lüftl2009; VDI 6224-1 2012). An important source is the human musculoskeletal system, whereby some lightweight principles are already being applied in technology and others have not yet been implemented.
The lightweight construction of the musculoskeletal system is not achieved through the action of individual lightweight design principles, but above all through their coordinated interaction. In addition to a hierarchical bone structure that increases bone strength (Weiner & Wagner Reference Weiner and Wagner1998; Fratzl-Zelman, Misof & Roschger Reference Fratzl-Zelman, Misof and Roschger2011), the lightweight design of the musculoskeletal system mainly results from the interplay of a minimization of bending loads through tension chording, a functional adaptation through bone remodeling and a bending-minimized motion control by the sensorimotor system (Pauwels Reference Pauwels1965). The biological control and optimization strategies, which describe the interaction of these principles, run simultaneously in nature. Prevailing bionic solutions that use the lightweight design principles neglect the coordinated interplay of these principles. Moreover, transfer is limited to isolated principles, e.g., in the context of structure optimization as simultaneous implementation of bone remodeling processes (Mattheck Reference Mattheck1997; Witzel & Preuschoft Reference Witzel and Preuschoft2005; VDI 6224-3 2017) or the use of tension chords and passive elements to minimize bending (Witte et al. Reference Witte, Fischer, Schilling, Ilg, Dillmann, Eckert and Wittenburg2000; Möhl Reference Möhl2003; Klug et al. Reference Klug, Möhl, Stryk and Barth2005; Ananthanarayanan, Azadi & Kim Reference Ananthanarayanan, Azadi and Kim2012). Therefore, further potential for lightweight design can be expected.
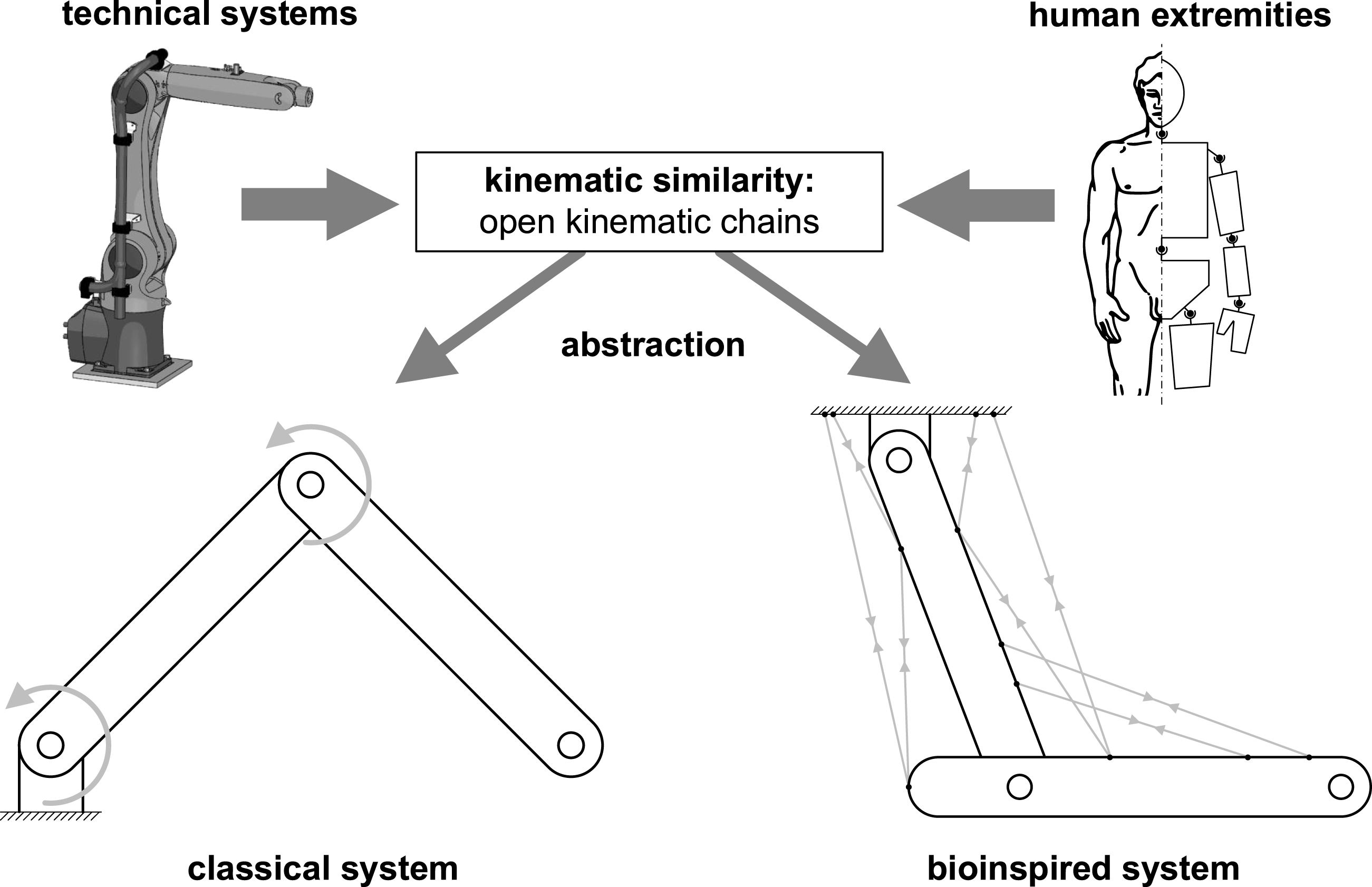
Figure 1. Comparison of the human extremities and an articulated arm robot to demonstrate the kinematic similarity. Difference in the principle of motion generation: Motion due to joint moments in the classic system (left); Drive by tension chords in the bioinspired system (right) (adjusted according to Bartz, Remus & Bender Reference Bartz, Remus and Bender2018b ; Bartz Reference Bartz2019).
In this paper, the lightweight design potential for technology is examined, which arises from the interaction of the lightweight design principles of the musculoskeletal system, which has not been considered so far. Due to the kinematic similarity of the human extremities to technical systems that can be understood as open kinematic chains, e.g., articulated arm robots, shown in Figure 1, the examinations are carried out on such systems. In general, kinematic chains can be found in robot systems, mechanical linkages, construction machinery and humanoid robots. These systems each have different requirements, e.g., with regard to control characteristics, robustness, reliability, durability and safety. In addition to these application-specific requirements, these systems have in common that they benefit from lower mass of the moving parts and less required energy. The fundamental examinations in this paper are carried out on an abstract level for systems of this type by applying the aforementioned lightweight design principles of the musculoskeletal system regarding only on lightweight design properties. For this purpose, two systems are compared, the classical and bioinspired systems shown in Figure 1. In the bioinspired system the application of the interplay of lightweight design principles should be applied. On this abstract level, the drive mainly differ in the principle of motion generation. While motion in the classical system is generated kinematically determined by joint moments, motion in the bioinspired system is generated kinematically overdetermined by a variety of muscle forces. Through this redundant motion generation in the bioinspired system, a functional integration according to a biological role model takes place, in which the muscle forces enable further tasks in particular the compensation of bending loads during motion. Before the examinations are presented, the lightweight design principles and their interaction that are applied in the bioinspired system and technical solutions already implemented are presented.
2 Musculoskeletal lightweight design and state of research in technical implementation
The lightweight design of the musculoskeletal system is based on a coordinated interplay of various lightweight design principles, which act on different morphological levels. At the micro level, bone strength results from hierarchical bone formation by combining hard and tough materials (Weiner & Wagner Reference Weiner and Wagner1998; Fratzl-Zelman et al. Reference Fratzl-Zelman, Misof and Roschger2011). This well-known lightweight construction principle is already used in the development of technical composite materials (Degischer & Lüftl Reference Degischer and Lüftl2009). In addition to this material-related lightweight construction through composite construction, the lightweight design of the musculoskeletal system is mainly achieved through the interplay of the three aforementioned lightweight design principles that can be considered on a macroscopic system level. The aim of the interaction is to minimize bending stresses and to homogenize the mechanical stress spatially and over time, which can save mass and resources (Pauwels Reference Pauwels1965). The three lightweight design principles used in this paper are:
(i) functional adaptation through remodeling of bone mass along main stress trajectories;
(ii) active and passive tension chording of the bones by muscles and ligaments;
(iii) bending-minimized motion control of the extremities by the sensorimotor system.
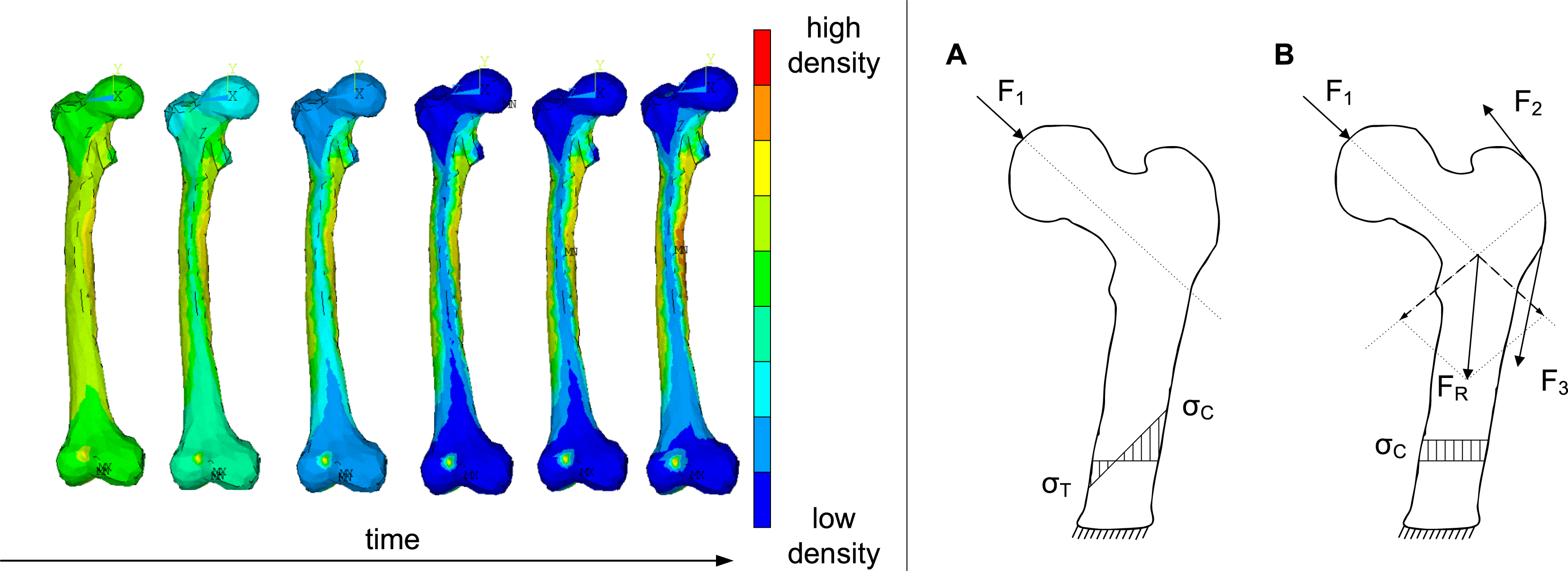
Figure 2. Functional adaption (left) and tension chording of a femur bone (right) (Gößling et al. Reference Gößling, Herzog, Witzel, Bender, Marjanović, Štorga, Škec, Bojčetić and Pavković2014; Bartz et al. Reference Bartz, Waschinsky, Gößling, Bender and Ricken2016).
Functional adaptation describes the adaptation of the structure and density of the bone to the mechanical stress and the resulting minimization of stress peaks (von Meyer & Culmann Reference von Meyer and Culmann1867; Wolff Reference Wolff1892; Roux Reference Roux1895; Frost Reference Frost2003). This enables an efficient use of material and resources (Turner Reference Turner1998; Sugiyama et al. Reference Sugiyama, Meakin, Browne, Galea, Price and Lanyon2012). The left part of Figure 2 shows the stress-controlled remodeling of bone mass of a femur over time, which is loaded by a human gait. In the outer areas bone material is deposited (represented by a high density) and in the inner area material is degraded (represented by a low density). The principle of functional adaptations is used in various technical solutions for structural optimization. Methods derived from functional adaptation can be found in computer-aided methods for structural optimization and synthesis of technical components such as the Soft-Kill-Option and Computer-Aided-Optimization (Mattheck Reference Mattheck1997; VDI 6224-3 2017), finite element structure synthesis (Witzel & Preuschoft Reference Witzel and Preuschoft2005; Gößling Reference Gößling2010) and in evolutionary structure optimization methods based on the theory of porous media (Ricken, Schwarz & Bluhm Reference Ricken, Schwarz and Bluhm2007; Bartz et al. Reference Bartz, Waschinsky, Gößling, Bender and Ricken2016). These methods are based on algorithms that simulate a stress-controlled material remodeling and thus enable a synthesis of stress-compliant component structures.
The lightweight design principle of tension chording of the bones by muscles and ligaments was first described by Pauwels (Reference Pauwels1965). This tension chording is used to transform external bending loads into physiological compressive loads through the active introduction of muscle forces (or passive introduction through ligaments) (Pauwels Reference Pauwels1965; Richard & Kullmer Reference Richard and Kullmer2014). The compensation of bending loads by conversion into compressive loads is advantageous, since bone has a higher compressive strength than tensile strength due to its microscopic structure (Kummer Reference Kummer2005). The principle of tension chording is shown in a simplified way in the right part of Figure 2 on a bone loaded by a part of the weight force of a human
![]() $F_{1}$
. Without tension chording, bending stresses would occur in the bone, represented in case A by tensile stress
$F_{1}$
. Without tension chording, bending stresses would occur in the bone, represented in case A by tensile stress
![]() $\unicode[STIX]{x1D70E}_{T}$
in the left region and compressive stress
$\unicode[STIX]{x1D70E}_{T}$
in the left region and compressive stress
![]() $\unicode[STIX]{x1D70E}_{C}$
in the right region of the bone. In the musculoskeletal system, a ligament, the so-called Tractus iliotibialis, runs along the right side of the femur, which introduces the forces
$\unicode[STIX]{x1D70E}_{C}$
in the right region of the bone. In the musculoskeletal system, a ligament, the so-called Tractus iliotibialis, runs along the right side of the femur, which introduces the forces
![]() $F_{2}$
and
$F_{2}$
and
![]() $F_{3}$
in order to produce the resulting force
$F_{3}$
in order to produce the resulting force
![]() $F_{R}$
, shown in case B. The force
$F_{R}$
, shown in case B. The force
![]() $F_{R}$
is approximately collinear to the central axis of the bone, so that bending stress is minimized and a relatively homogeneous compressive load can arise. In addition to this simplified example, numerous muscles act as tension chords in case of motions. The muscle forces have a multifunctional effect, because, in addition to generating motion of the bone, they compensate bending loads by actively introducing forces. Though a functional integration takes place. Through this simultaneous compensation of bending loads, resources and weight can be saved with the same load-bearing capacity (Pauwels Reference Pauwels1965). The tension chording is technically used, detached from the biological motivation, in static constructions, e.g., cranes. In dynamic constructions, e.g., bionic robots, passive and active tension chords are used to generate motion and damping with minimal bending (Witte et al.
Reference Witte, Fischer, Schilling, Ilg, Dillmann, Eckert and Wittenburg2000; Möhl Reference Möhl2003; Klug et al.
Reference Klug, Möhl, Stryk and Barth2005; Ananthanarayanan et al.
Reference Ananthanarayanan, Azadi and Kim2012). However, the redundant motion generation described above is not applied and an interaction with functional adaptation, as it exists in the musculoskeletal system, has not yet been taken into account.
$F_{R}$
is approximately collinear to the central axis of the bone, so that bending stress is minimized and a relatively homogeneous compressive load can arise. In addition to this simplified example, numerous muscles act as tension chords in case of motions. The muscle forces have a multifunctional effect, because, in addition to generating motion of the bone, they compensate bending loads by actively introducing forces. Though a functional integration takes place. Through this simultaneous compensation of bending loads, resources and weight can be saved with the same load-bearing capacity (Pauwels Reference Pauwels1965). The tension chording is technically used, detached from the biological motivation, in static constructions, e.g., cranes. In dynamic constructions, e.g., bionic robots, passive and active tension chords are used to generate motion and damping with minimal bending (Witte et al.
Reference Witte, Fischer, Schilling, Ilg, Dillmann, Eckert and Wittenburg2000; Möhl Reference Möhl2003; Klug et al.
Reference Klug, Möhl, Stryk and Barth2005; Ananthanarayanan et al.
Reference Ananthanarayanan, Azadi and Kim2012). However, the redundant motion generation described above is not applied and an interaction with functional adaptation, as it exists in the musculoskeletal system, has not yet been taken into account.
In addition, the musculoskeletal system uses an active, bending-minimized motion control of the extremities. The sensorimotor system of the body endeavors to avoid unfavorable lever ratios and accelerations that lead to bending loads (Pauwels Reference Pauwels1965). Motion control is used in many technical applications, e.g., for path planning of industrial robots (Weber Reference Weber2017) or for bioinspired control of humanoid robots (El Khoury, Lamiraux & Taix Reference El Khoury, Lamiraux and Taix2013; Mombaur, Koch & Felis Reference Mombaur, Koch and Felis2014). However, the aim is not to minimize bending as in the human musculoskeletal system, but rather e.g., to minimize the energy used and stabilization of the movement.
In summary, it can be stated that the lightweight design principles mentioned above are used isolated in technical applications. However, the principles are adapted individually and are not considered in their interplay. In the musculoskeletal system the lightweight design principles are in a state of flow equilibrium, the so-called homeostasis. It is assumed that the biological system is thus in an optimal state of energy consumption with structural use (Flechtner Reference Flechtner1972; Borck Reference Borck2014). The adaptation of the structure takes place in a coordinated (synchronous) interaction with the muscle forces. This interaction of forces and structures, or of form and function, is not yet used in the technical design process. The application of the interaction of the lightweight design principles of the musculoskeletal system therefore has lightweight design potential for technical products.
In the following, a new approach is proposed with which the interplay of the biological lightweight design principles can be examined for the abstract consideration of technical kinematic chains mentioned in the introduction and applied to a technical system.
3 Overarching goals and methods for the examination of musculoskeletal lightweight potentials
The overarching goal of the examinations presented in this paper is to study and apply the lightweight design potential of the interplay of the lightweight principles of the musculoskeletal system to technical systems. The examinations are carried out at the abstraction level described in the introduction with a focus on the lightweight design properties of the mass and deformation without taking application-specific requirements into account. Most of the examinations presented in this paper are based on the work of Bartz (Reference Bartz2019). The quantification of the influence of the interplay of the lightweight design principles is done by comparing a bioinspired system with a classical system, shown in Figure 3.
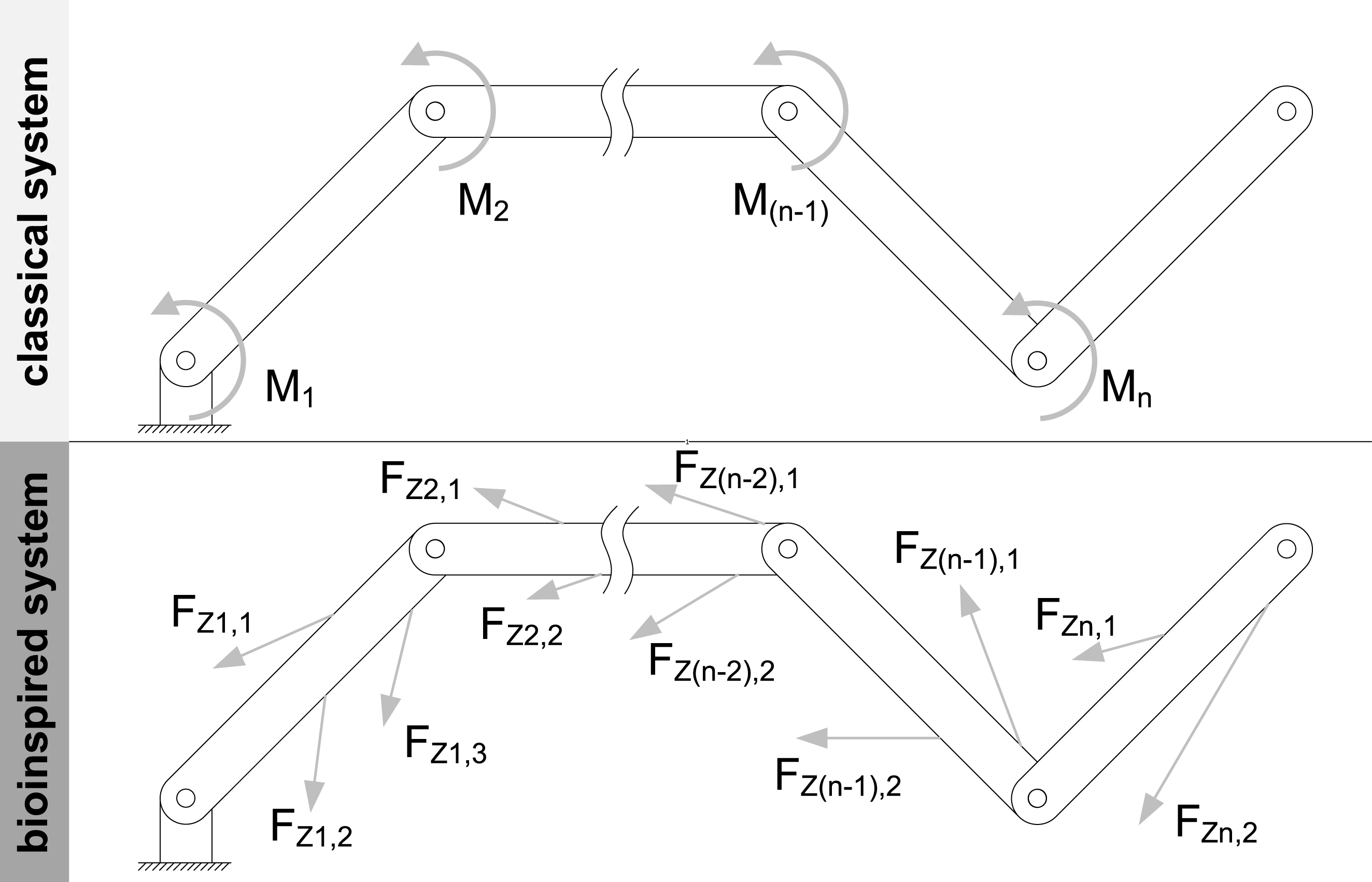
Figure 3. The systems examined in this paper: classical system (top); bioinspired system (bottom) (adjusted according to Bartz Reference Bartz2019).
Both systems are open kinematic chains with generally
![]() $n$
elements and
$n$
elements and
![]() $n$
joints. Both systems have the same kinematics, but the kinetics differs due to a different principle of motion generation. In the classical system, the movement of an element
$n$
joints. Both systems have the same kinematics, but the kinetics differs due to a different principle of motion generation. In the classical system, the movement of an element
![]() $i$
takes place via the direct initiation of a joint moment
$i$
takes place via the direct initiation of a joint moment
![]() $\mathbf{M}_{i}$
at the joint point, e.g., via an articulated motor. The movement is kinematically determined. The precondition for the application of the lightweight design principles of the musculoskeletal system is the realization of redundancies in the generation of motion in the form of kinematic over-determination. Therefore, in the bioinspired system, the motion of an element
$\mathbf{M}_{i}$
at the joint point, e.g., via an articulated motor. The movement is kinematically determined. The precondition for the application of the lightweight design principles of the musculoskeletal system is the realization of redundancies in the generation of motion in the form of kinematic over-determination. Therefore, in the bioinspired system, the motion of an element
![]() $i$
is realized by the interaction of
$i$
is realized by the interaction of
![]() $m$
-different tension chords with the tension forces
$m$
-different tension chords with the tension forces
![]() $\mathbf{F}_{Zi,j}$
, which have lever arms
$\mathbf{F}_{Zi,j}$
, which have lever arms
![]() $\mathbf{r}_{j}$
to a joint
$\mathbf{r}_{j}$
to a joint
![]() $n_{i}$
. In sum, they replace the joint moment
$n_{i}$
. In sum, they replace the joint moment
![]() $\mathbf{M}_{i}$
of the classical systems (according to Bartz Reference Bartz2019):
$\mathbf{M}_{i}$
of the classical systems (according to Bartz Reference Bartz2019):
In order to compare the classical and bioinspired system with regard to lightweight design properties, two different design approaches are used as examination methods, shown in Figure 4. The classical design procedure is sequential, i.e., the forces and moments required for the movements are determined at the beginning of the development process and then an adapted geometry is determined. The forces and moments are determined within the framework of a multibody simulation, the structural optimization through topology optimization within the framework of a finite element calculation. In order to use the unknown synchronous interplay of the lightweight design principles of the musculoskeletal system in a sequential process for technology, this paper proposes an iterative approach for the bioinspired system, represented by the dashed lines in Figure 4. Thus, the classical determination of forces is extended by the lightweight design principles of the tension chording and the bending-minimized motion control according to Pauwels (Reference Pauwels1965). By considering bending minimization as a further optimization goal, the classical multibody simulation is transformed into a multicriteria optimization problem. The structure optimization takes place after the multibody simulation, so that two separate optimizations are carried out. The classical sequential procedure is to be converted into an iterative procedure by a feedback of the topology optimization to the multibody simulation.
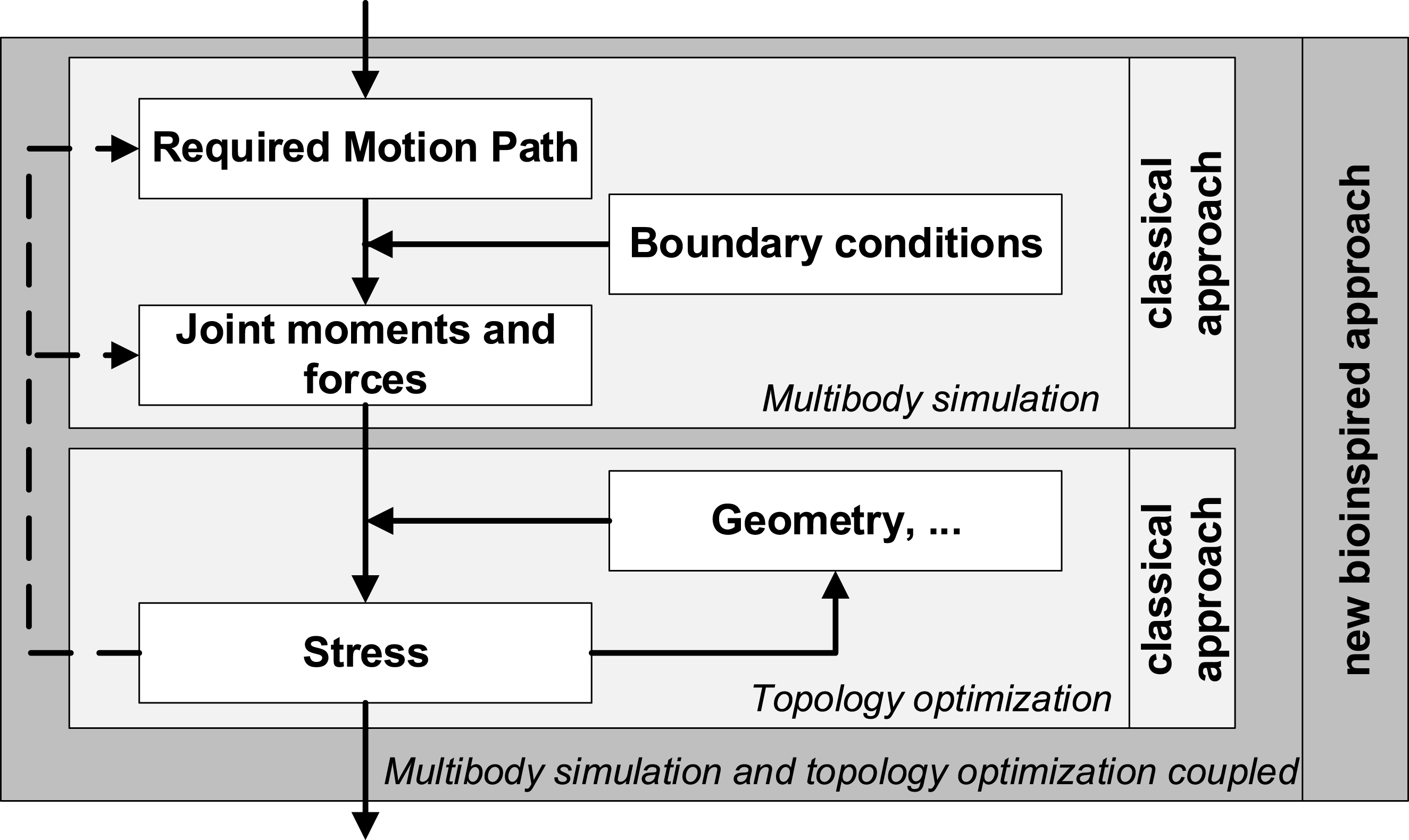
Figure 4. Extension of the classical to a bioinspired approach: The classical approach is supplemented by an iterative procedure by coupling topology optimization and multibody simulation (represented by the dashed arrows) (adjusted according to Bartz et al. Reference Bartz, Remus and Bender2018b and Bartz Reference Bartz2019).
On the basis of the presented modeling for the classical and bioinspired system as well as the design approaches, the main research question, whether technical kinematic chains can be improved by applying the interplay of the lightweight design principles of the musculoskeletal system with regard to lightweight design properties, is examined. The examination of the hypothesis that the application of musculoskeletal lightweight design principles in technology achieves a similar lightweight design effect as in the musculoskeletal system is further carried out by two studies: a theoretical examination of a simple beam system (Section 4) and a practical application on an articulated arm robot with two arm segments (Section 5). The results of the two studies can contribute to apply the lightweight design of the musculoskeletal system to specific technical fields of application.
4 Theoretical studies on simple technical beams
The theoretical examination of the lightweight design potential of the musculoskeletal system is carried out on a dynamically loaded technical beam system, shown in the left part of Figure 5. The beam of length
![]() $l$
is pivoted at pivot point
$l$
is pivoted at pivot point
![]() $S_{0}$
and is accelerated by moment
$S_{0}$
and is accelerated by moment
![]() $M_{1}$
. The continuous mass distribution
$M_{1}$
. The continuous mass distribution
![]() $m$
has a load effect. The moment of inertia around the pivot point
$m$
has a load effect. The moment of inertia around the pivot point
![]() $S_{0}$
is
$S_{0}$
is
![]() $J_{0}$
. The running variable of the rotation is
$J_{0}$
. The running variable of the rotation is
![]() $\unicode[STIX]{x1D711}$
. All calculations take place within the framework of Bernoulli’s beam theory in relative units. The beam as described is used to analyze the aforementioned classical system under the acceleration of the moment
$\unicode[STIX]{x1D711}$
. All calculations take place within the framework of Bernoulli’s beam theory in relative units. The beam as described is used to analyze the aforementioned classical system under the acceleration of the moment
![]() $M_{1}$
.
$M_{1}$
.
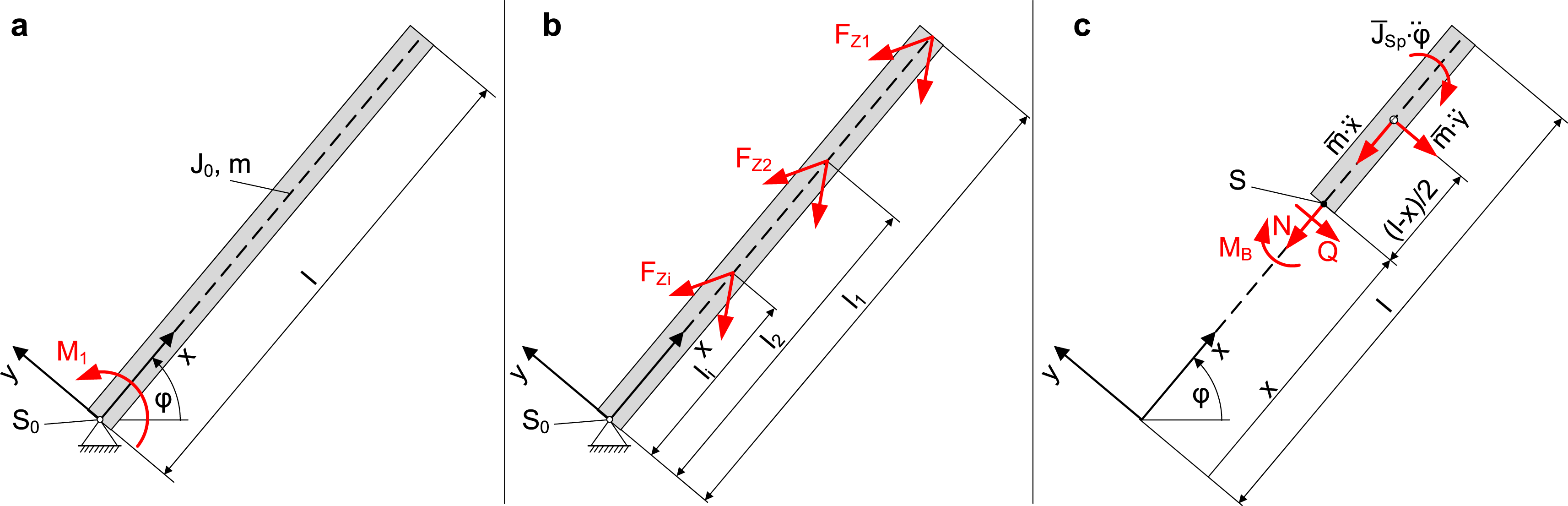
Figure 5.
(a) Articulated beam with acceleration moment
![]() $M_{1}$
;
(b) beam with tensile forces induced by tension chords; (c) internal forces on the right section of beam (Bartz Reference Bartz2019).
$M_{1}$
;
(b) beam with tensile forces induced by tension chords; (c) internal forces on the right section of beam (Bartz Reference Bartz2019).
In order to analyze the influence of the lightweight design principles of the musculoskeletal system, the classical system is compared to the bioinspired system shown in the middle of Figure 5. In this system the movement
![]() $\unicode[STIX]{x1D711}$
is realized by
$\unicode[STIX]{x1D711}$
is realized by
![]() $n$
tension chords with the forces
$n$
tension chords with the forces
![]() $F_{Zi}$
and lever arms to pivot point
$F_{Zi}$
and lever arms to pivot point
![]() $l_{i}$
(summarized in the vectors
$l_{i}$
(summarized in the vectors
![]() $\mathbf{F}_{Z}$
and
$\mathbf{F}_{Z}$
and
![]() $\mathbf{l}$
). The angle of the tension chords to the beam axis is assumed to be
$\mathbf{l}$
). The angle of the tension chords to the beam axis is assumed to be
![]() $10^{\circ }$
. The angles occurring in the musculoskeletal system are often larger (Pietak et al.
Reference Pietak, Ma, Beck and Stringer2013), which leads to lower normal loads and is more advantageous for lightweight design (Pauwels Reference Pauwels1965). However, for the theoretical examination, the worst case is assumed and it is examined whether lightweight design advantages arise despite conservative considerations.
$10^{\circ }$
. The angles occurring in the musculoskeletal system are often larger (Pietak et al.
Reference Pietak, Ma, Beck and Stringer2013), which leads to lower normal loads and is more advantageous for lightweight design (Pauwels Reference Pauwels1965). However, for the theoretical examination, the worst case is assumed and it is examined whether lightweight design advantages arise despite conservative considerations.
For the examination and evaluation, the internal forces as shown in the sectional view on the right of Figure 5 are used. Here,
![]() $N$
describes the normal force distribution,
$N$
describes the normal force distribution,
![]() $Q$
the shear force distribution and
$Q$
the shear force distribution and
![]() $M_{B}$
the bending moment distribution. The calculation of the loads and the determination of the beam geometry is carried out for the classical system according to the procedure shown in Figure 5. The determination of the tension chord forces
$M_{B}$
the bending moment distribution. The calculation of the loads and the determination of the beam geometry is carried out for the classical system according to the procedure shown in Figure 5. The determination of the tension chord forces
![]() $\mathbf{F}_{Z}$
in the bioinspired system is done by an optimization calculation under two conditions. Following the lightweight design principle of the tension chording of the musculoskeletal system, it is formulated as objective function
$\mathbf{F}_{Z}$
in the bioinspired system is done by an optimization calculation under two conditions. Following the lightweight design principle of the tension chording of the musculoskeletal system, it is formulated as objective function
![]() $f(\mathbf{F}_{Z})$
that the integral of the bending moment
$f(\mathbf{F}_{Z})$
that the integral of the bending moment
![]() $M_{B}(x)$
along the beam axis
$M_{B}(x)$
along the beam axis
![]() $x$
is minimal (according to Bartz Reference Bartz2019):
$x$
is minimal (according to Bartz Reference Bartz2019):
The forces of the tension chords
![]() $\mathbf{F}_{Z}$
should enable the same motion of the beam as the moment
$\mathbf{F}_{Z}$
should enable the same motion of the beam as the moment
![]() $M_{1}$
in the classical system (see formula from last section). This kinematic boundary condition is formulated in a secondary condition
$M_{1}$
in the classical system (see formula from last section). This kinematic boundary condition is formulated in a secondary condition
![]() $g(\mathbf{F}_{Z})$
:
$g(\mathbf{F}_{Z})$
:
The procedure for calculating the bioinspired system is as shown in Figure 4. The optimization problem is solved using the method of Lagrange multipliers. The arrangement of the tension chords attachments along the beam axis is done by an algorithm, which positions the attachments optimally in order to minimize the bending moment maxima. The results of the calculations for both systems are shown in Figure 6. The classical system is compared with three bioinspired systems with one, two and four pairs of tension chords each. In the left part of the figure, the bending moment distribution is plotted over the beam axis. The bending moments are scaled to the maximum bending moment
![]() $M_{\max }$
in the classical system. The right part of the figure shows the resulting masses of the bioinspired systems as well as the strain energy in relation to the mass and strain energy of the classical system.
$M_{\max }$
in the classical system. The right part of the figure shows the resulting masses of the bioinspired systems as well as the strain energy in relation to the mass and strain energy of the classical system.
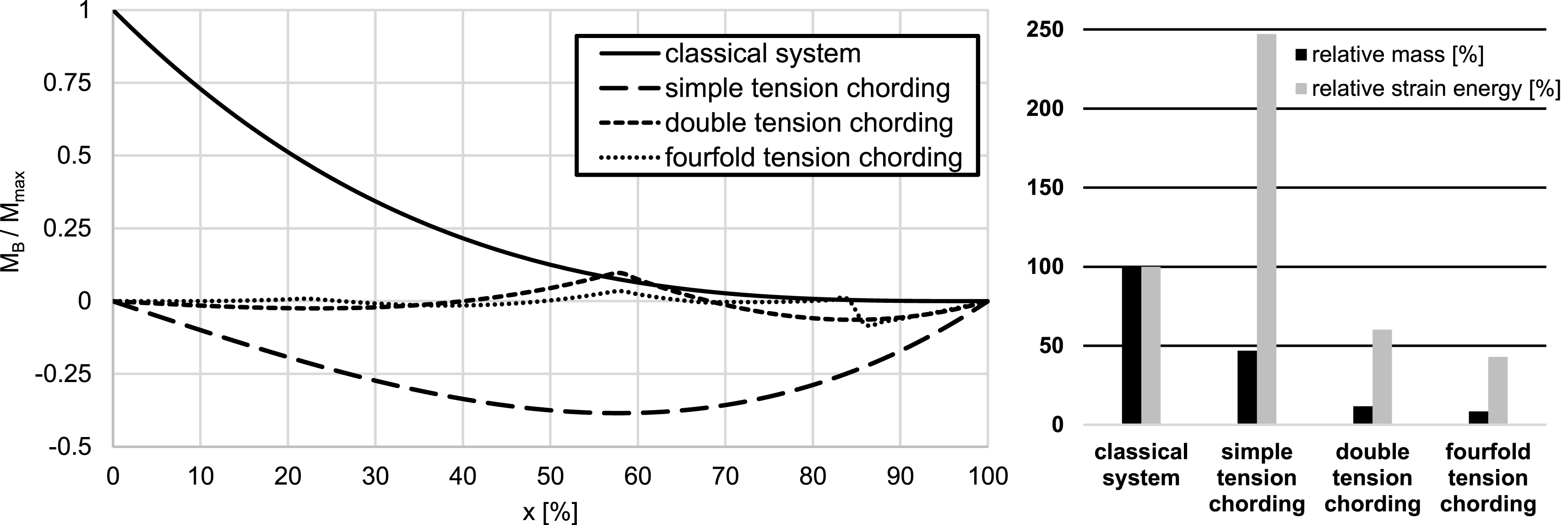
Figure 6. Bending moments along the beam axis (left); comparison of the mass and strain energy (right) (adjusted according to Bartz Reference Bartz2019).
It can be seen that by using the tension chording in the bioinspired system the bending moment distribution can be influenced and minimized (left part of Figure 6). Already by using simple tension chording the maximum bending moment can be reduced more than 50%. However, due to a lack of redundancies while using simple tension chording, the bending moment curve cannot be actively influenced. The effect of the active influence of the bending moment distribution is apparent in the systems with double and fourfold tension chording. The use of double tension chording reduces the maximum bending moment to almost 90% and the use of fourfold tension chording reduces the maximum bending moment to just over 90%. The difference between double and fourfold tension chording is no longer as great as the difference between single and double tension chording.
The influence of bending minimization is shown in the mass of the systems (right part of Figure 6). The mass of the classic system is reduced by more than 50% using simple tension chording, by almost 90% using double tension chording and by more than 90% using fourfold tension chording. Once again, it is shown that two tension chords are sufficient to achieve a light structure in this simple beam system. To evaluate the lightweight design potential, the deformation behavior is considered using the strain energy. The lightweight design and the resulting possible changes in the stiffness of the bioinspired systems should maintain the functionality. In the system under simple tension chording, the strain energy is higher than in the classical system. The reason for this is that only the magnitude of the bending moment can be minimized by simple tension chording, but not the distribution. Thus high bending moment remains in the middle of the beam axis which results in a higher deformation due to lower stiffness. This disadvantage is compensated by using double tension chording, which reduces the stain energy to almost 50% of the strain energy of the classical system. The influence of the fourfold tension chording on the strain energy is small compared to double tension chording, as the bending moment over the beam axis can already be highly reduced by the double tension chording.
In the bioinspired system, additional normal forces are induced by the tension chording, which is necessary to minimize the bending moment. The normal load increases with the reduction of the bending load. The distribution of the normal load along the beam axis scaled to the maximum normal load
![]() $N_{\max }$
of the classical system is shown in Figure 7. It shows that the normal load in the bioinspired system is between five and almost twenty times greater than in the classical system, depending on the number of tension chords. The increasing normal load therefore represents an upper limit with regard to the number of tension chords. Therefore, multiple tension chords are not necessary to minimize bending. In addition, the risk of buckling increases due to the normal load.
$N_{\max }$
of the classical system is shown in Figure 7. It shows that the normal load in the bioinspired system is between five and almost twenty times greater than in the classical system, depending on the number of tension chords. The increasing normal load therefore represents an upper limit with regard to the number of tension chords. Therefore, multiple tension chords are not necessary to minimize bending. In addition, the risk of buckling increases due to the normal load.
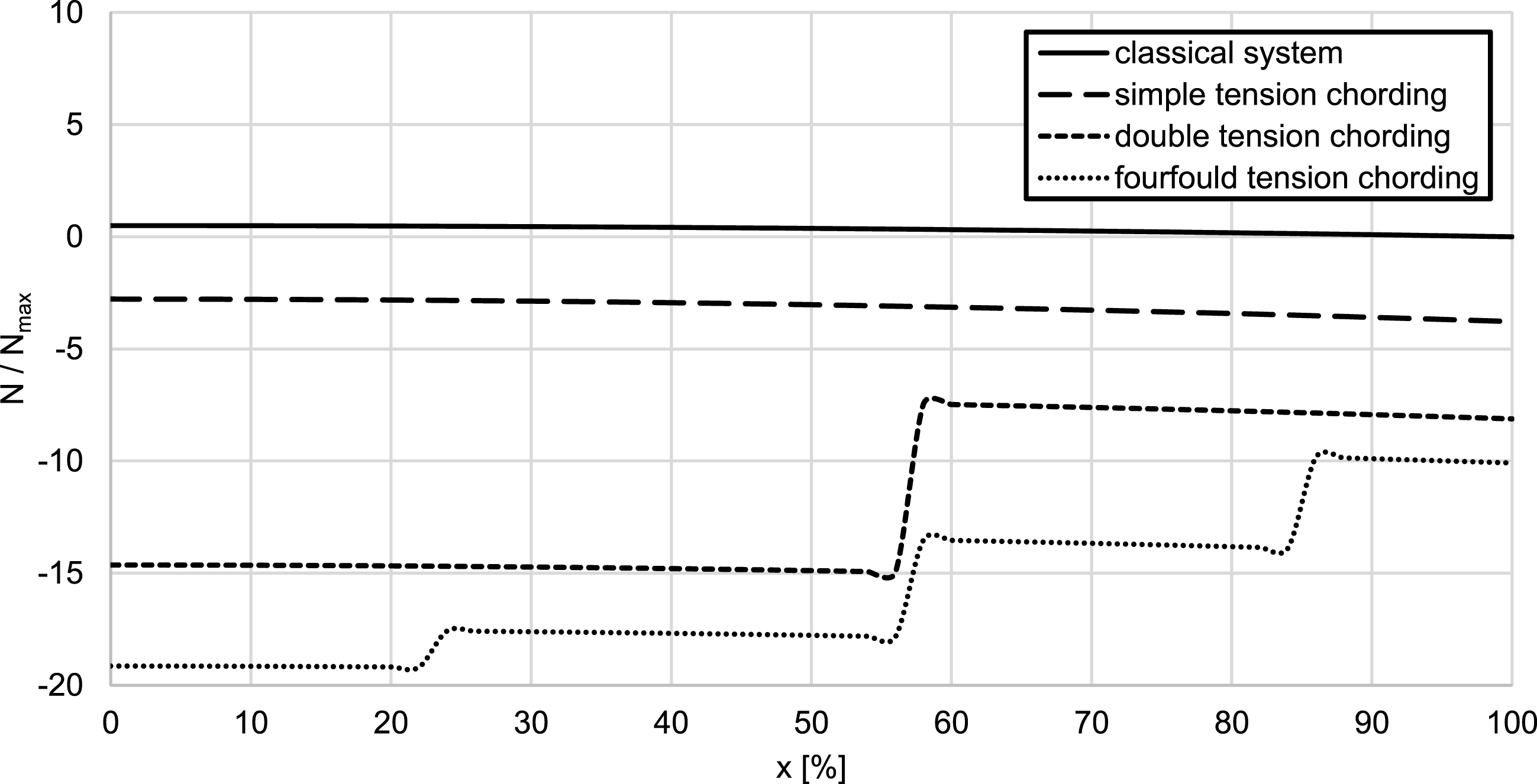
Figure 7. Normal load distribution along the beam axis (adjusted according to Bartz Reference Bartz2019).
Conclusion and evaluation of the theoretical studies:
The theoretical studies show that the application of the interaction of the lightweight design principles of the musculoskeletal system to the example of a simple beam system can lead to a lower mass than classical lightweight design strategies for structural design. The theoretical considerations thus support the research hypothesis that a combination of tension chording with functional adaptation can have an advantage in terms of weight and energy for a technical system. It can be seen that double tension chording already achieves good lightweight design results by actively influencing the bending moment distribution. The results, however, are only derived from an isolated analysis of a simple beam system. For different load cases, more tension chords can be advantageous. However, the number of tension chords required for a technical implementation also depends on the drive scheme and its implementation. For further practical examination, the following studies are carried out on an articulated arm robot as a practical example.
5 Practical studies by application on an articulated arm robot
In order to study the new bioinspired approach using a practical example, the approach is used to design an articulated arm robot (according to Bartz Reference Bartz2019). The examined articulated arm robot is oriented to the kinematics and dimensions of the human extremities and therefore has two arm segments and two joints each. The preliminary designs of the classical and bioinspired system of the robot with drive scheme are shown in Figure 8. For the studies, the dimensions of the articulated arm robot are based on the dimensions of the human upper arm (humerus) and the two forearm bones (ulna and radius) according to DIN 33402-2 (2005) and Pietak et al. (Reference Pietak, Ma, Beck and Stringer2013). This ensures that the proportions of lengths to diameters and assumed loads and speeds fit together well without prior diameter and length determination. However, the values and results can be scaled to other geometries. For the length of the first arm segment 315 mm is selected and for the second arm segment 270 mm. The profile height of the arm segments determines the design space in which the arm structures can synthesize. The height of the arm segment profiles is set at 100 mm for an average length/diameter ratio for one arm bone with an uplift for topology optimization. A quenched and tempered steel with isotropic material properties is selected as the material. Since lightweight material design is not considered in this study, however, the selection can be applied to other materials.
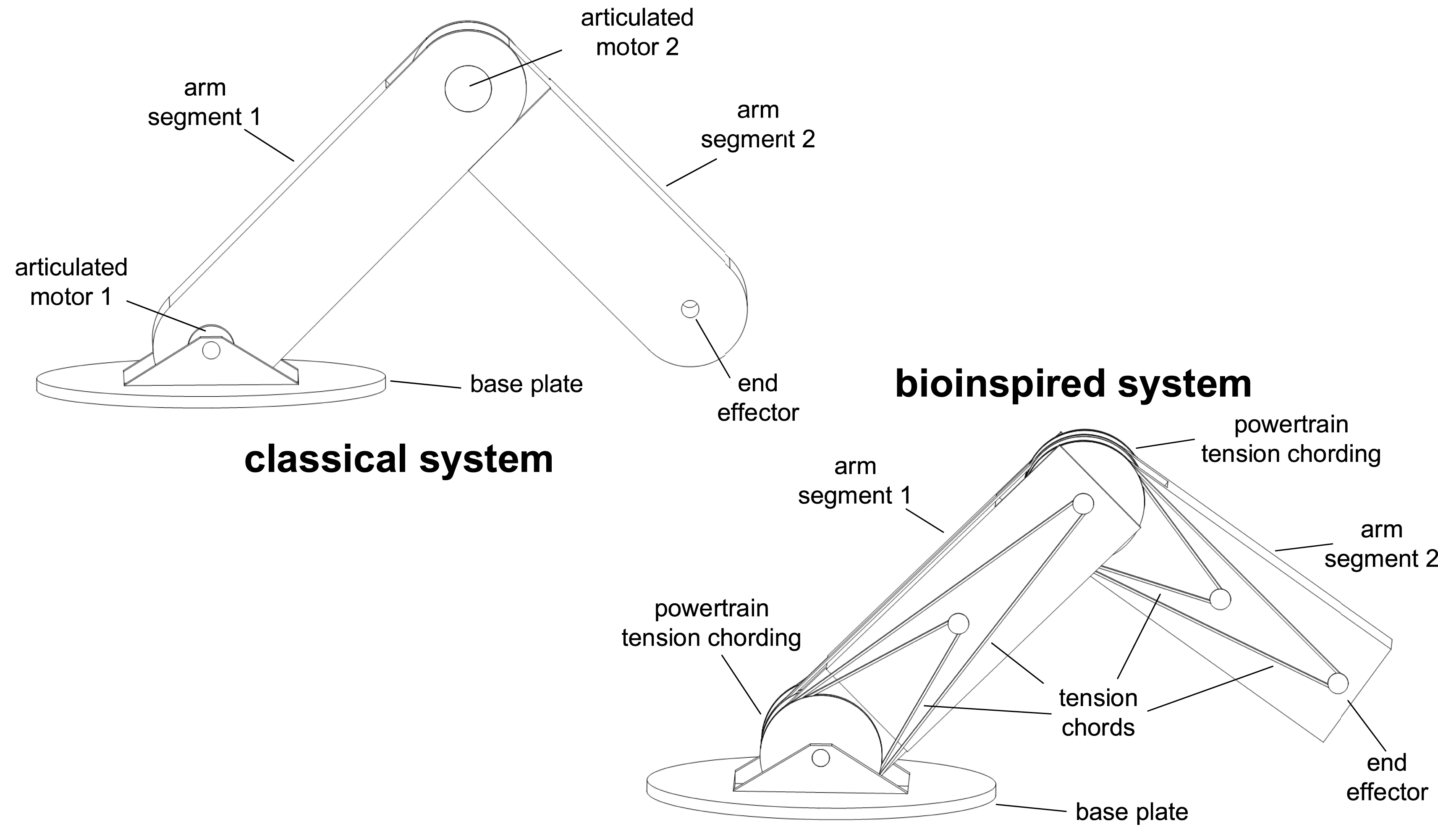
Figure 8. Preliminary designs of the articulated arm robots before applying the classical and the bioinspired design approach (adjusted according to Bartz Reference Bartz2019).
The classical and bioinspired systems shown in Figure 8 will each be designed to move a mass of 15 kg at the end effector. In the classical system the movement of the arm segments takes place by articulated motors. Articulated motor 1 connects the arm segment 1 with the base plate. The connection and the drive between arm segments 1 and 2 are realized by the articulated motor 2. In the bioinspired system, each two pairs of tension chords are used instead of the articulated motors for the movement of the arm segments. One pair of tension chord is engaged at the end of each segment, the other at the dynamic center of mass of the system. The limitation to double tension chording is made on the one hand due to the increasing complexity of the drive concept with an increasing number of tension chords and on the other hand due to the results of the theoretical investigations that already double tension chording considerably reduce the bending moment distribution.
The design calculation is generally carried out according to the procedure shown in Figure 4. A detailed comparison of the simulation process of the classical and bioinspired system is shown in Figure 9. At the beginning of the procedure there is the already described exchange of the principle of motion generation. This enables the bioinspired system to have redundancies by the movement forces that can be used to influence the bending load.

Figure 9. Flow chart of the design calculation: Classical approach (left) with extensions of the bioinspired approach (right) (adjusted according to Bartz et al. Reference Bartz, Gößling, Remus, Bender, Marjanović, Štorga, Škec, Bojčetić and Pavković2018a ; Bartz et al. Reference Bartz, Remus and Bender2018b and Bartz Reference Bartz2019).
With the classical and bioinspired system described in Figure 8, a multibody simulation is carried out at the beginning to determine the path and loads. While in the classical approach the path determination is carried out with classical path control approaches, in the bioinspired approach the path control is supplemented to such an extent that a path is determined on which the bending moment distribution is minimized. Thus, the lightweight design principle of the musculoskeletal system of the bending-minimized motion control of the sensomotoric system is implemented. The determination of the motion loads is carried out in the classical approach using a classical multibody simulation calculation. In the bioinspired approach the calculation of the redundant motion forces is done by an inverse dynamic calculation with the aim to find an optimal force interplay that minimizes the bending load. Both the motion control and the determination of the motion loads are implemented in Matlab. The determination of a bending minimizing path and loads is done with the help of multicriteria optimization calculations using the MatlabOptimizationToolbox. Both in the classical and in the bioinspired approach, a topology optimization takes place after the multibody simulation. In contrast to the classical approach, the bioinspired approach involves an iteration back to multibody simulation after topology optimization. Due to the changed mass, the bending moment distribution changes, so that new tension chord forces and a different path for bending minimization may be necessary. This loop iteratively reproduces the interaction of the lightweight design principles of the tension chording and bending-minimized motion control with the functional adaptation. If the mass does not change anymore and therefore the calculation converges, a finite element analysis is carried out as in the classical approach in order to perform a strength verification. If the strength is not given, in the classic approach the geometry can be worked up, while in the bioinspired approach the principle of tension chording can also be improved.
For the practical examinations of the lightweight design potential of the musculoskeletal system for technology, the classical and bioinspired articulated arm robots are calculated and designed with the described approaches. The simulation is carried out for a defined pick-and-place task from point
![]() $P_{\text{start}}$
to point
$P_{\text{start}}$
to point
![]() $P_{\text{end}}$
, starting at the angle position shown in Figure 8 to the same angle position mirrored to the vertical. As motion time two seconds are given at a maximum angular acceleration of
$P_{\text{end}}$
, starting at the angle position shown in Figure 8 to the same angle position mirrored to the vertical. As motion time two seconds are given at a maximum angular acceleration of
![]() $5~\text{s}^{-2}$
. Figure 10 shows the path curves of both systems after convergence of the simulation. In the classical system, a fully synchronous point-to-point path control is used, which has the advantage of minimizing accelerations and thus minimizing the loads caused by inertial forces (Weber Reference Weber2017). This results in a symmetrical path to the middle position in the classical system, in which both arm segments are in the same angular position. In the bioinspired system, however, the movement path is asymmetrical. The reason for this is the path control used, inspired on the human sensorimotor system. The path control avoids unfavorable lever arms, so that at the start the first arm segment is moved faster than the second arm segment in order to keep the lever arm of the mass at the end effector point to the bearing joint low.
$5~\text{s}^{-2}$
. Figure 10 shows the path curves of both systems after convergence of the simulation. In the classical system, a fully synchronous point-to-point path control is used, which has the advantage of minimizing accelerations and thus minimizing the loads caused by inertial forces (Weber Reference Weber2017). This results in a symmetrical path to the middle position in the classical system, in which both arm segments are in the same angular position. In the bioinspired system, however, the movement path is asymmetrical. The reason for this is the path control used, inspired on the human sensorimotor system. The path control avoids unfavorable lever arms, so that at the start the first arm segment is moved faster than the second arm segment in order to keep the lever arm of the mass at the end effector point to the bearing joint low.
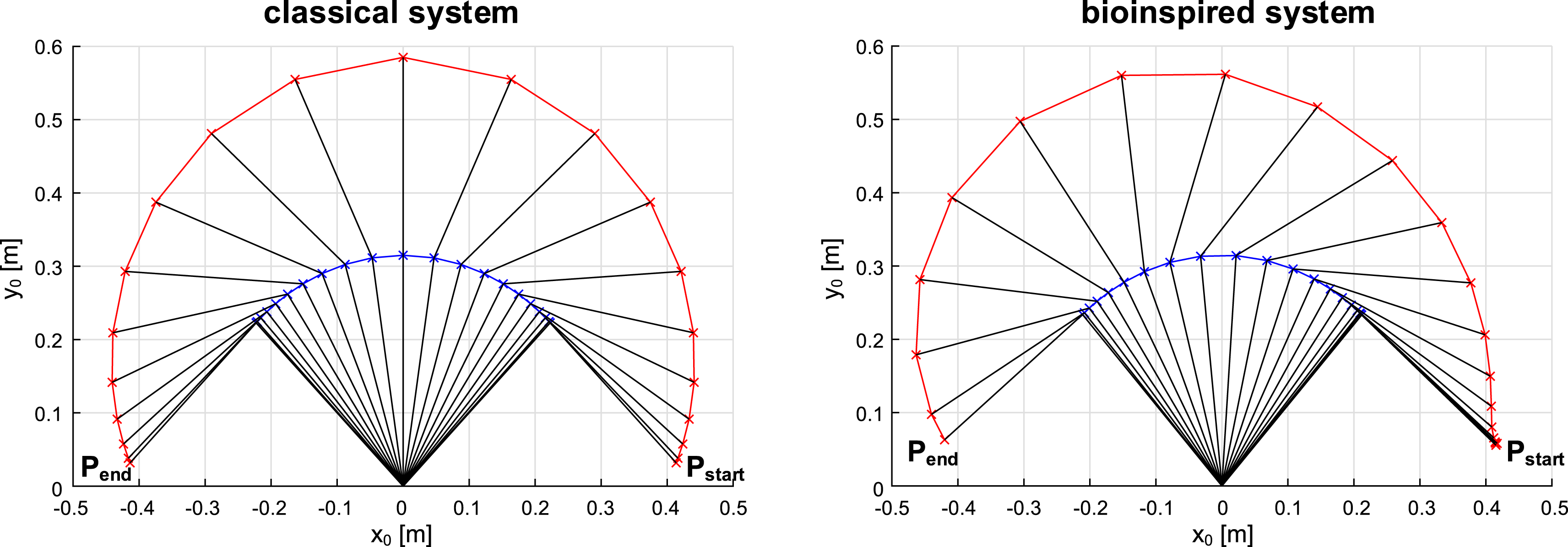
Figure 10. Comparison of the movement paths of the classical (left) and the bioinspired system (right). The angular positions of the arm segments are shown in time steps of 0.1 seconds (adjusted according to Bartz Reference Bartz2019).
For topology optimization, the highest load cases for start and end phases and additionally a time-averaged load case are selected. These load cases are used to perform a topology optimization in Ansys Workbench. The load cases are weighted equally. The load cases for the bioinspired system are qualitatively similar over time, so that the average load of the structure is covered by the selection and the same weighting. In the classical case, the load changes from the positive to the negative maximum over time with the maximum load cases. By selecting the extremes, the load cases cover the entire load spectrum and by considering the mean load case at mean angular position with the same weighting, the mean component load can be covered. The goal of topology optimization is to minimize mass while maximizing stiffness. Further boundary conditions are symmetry of the geometry to the vertical and horizontal planes. The reason for this is that the articulated arm robot should also reverse the path and no loads act in spatial direction. The post-processing of geometry after topology optimization is done in SpaceClaim and SolidWorks. The prepared results after convergence of the entire simulation of both systems are shown in Figure 11.

Figure 11. Assembly of synthesized articulated arm robots: classical system (left); bioinspired system (right) (Bartz Reference Bartz2019).
The arm segments of the classical system have a structure optimized for bending load, in which the material is positioned far from the beam axis in order to increase the section modulus against bending. The stiffness is achieved by the belts running at the top and bottom. More material remains near the joints due to the maximum bending moment to provide bending and shear stiffness. The structure of the arm segments of the bioinspired system differs fundamentally from that of the classical system. Due to the minimized bending load, the shear force-absorbing structures in the upper and lower boundary areas of the segments are omitted. For this purpose, a full load-bearing compression structure develops in the area near the beam axis due to the normal force acting mainly in the beam axis. Since the tension chording forces are applied at the edges of the segments, material can be saved in the middle of the beam. In contrast to the classical system, the material required for stiffness is also required for load-bearing capacity, which leads to better utilization of the structure.
The advantages of the compressive structure of the bioinspired system compared to the bending optimized structure of the classical system are shown by a comparison of the masses of the arm segments. The masses of the arm segments 1 and 2 are 5.61 kg and 4.83 kg in the classical system and 3.44 kg and 3.06 kg in the bioinspired system. By using the tension chords, more than 36% of the mass of the classic system can be saved for both arm segments. The mass of the chords and pulleys in the bioinspired system and the mass of the articulated motor in the classical system are not taken into account. A rough calculation of the drive indicates that the lighter chords and pulleys result in an additional weight advantage compared to an articulated motor.
Conclusion and evaluation of the practical studies:
The application of the bioinspired approach to an articulated arm robot shows that the design according to the lightweight design principles of the musculoskeletal system enables a lighter and more bending reduced system than the classical design. The exchange of the principle of motion generation leads to different structures in the classical and the bioinspired system. In the classical system, bending stiff structures develop, in the bioinspired system compression stiff structures are generated. By maintaining the stiffness, the structures in the classical system are not fully load-bearing, which requires a larger volume, resulting in a higher mass. However, a finite element analysis shows that the deflection of the tension chords via the second joint has a negative effect on the first arm segment in the bioinspired system. The additional joint force caused by the deflection must be compensated by the tension chording of the first arm segment. This results in higher loads in the first arm segment, which means that further lightweight potential is lost. In this work, a concept from Feyerabend (Reference Feyerabend1991) was used for the drive, who among other things examined different drive concepts for articulated arm robots with regard to lightweight design properties. Here a concept was chosen in which the tension chords are driven by motors below the base plate by means of chords and deflection pulleys in the joints. The advantage of this is that the moving mass is lower due to the lack of articulated motors. However, the results show that this drive concept in combination with the tension chording principle generates high joint loads. It is also unsuitable for numerous tension chords. More advantageous is a concept without joint deflecting tension chords, in which, for example, the tension chords of the segment are attached directly between each other similar to the arrangement of muscles and bones in the musculoskeletal system. Thus the tension chords have not to be transferred into the base plate and can contribute bending minimization of both arm segments.
6 Conclusions and outlook regarding to specific technical applications
The theoretical and practical studies presented in this paper support the research hypothesis that the application of the interplay of lightweight design principles of the musculoskeletal system in a bioinspired approach can lead to lighter technical systems than a classical design. By applying the interplay of musculoskeletal lightweight design principles in an iterative method by coupling multibody simulation and topology optimization, the mass can be reduced by minimizing the bending stress. In addition to pure mass savings, higher accelerations and thus shorter movement times due to lower inertia and further advantages arise from the bioinspired approach. Depending on the application, saving material and energy can have advantages in terms of sustainability and costs. The compressive structures resulting from the lower bending stress are easier to manufacture than bending stiff structures due to their less complex geometry. The reduction of the bending stiffness does not have a negative effect as long as the bending is always minimized by the tension chords and a nearly homogeneous compressive load is achieved. The structure is optimally adapted to this compressive stress.
Discussion and outlook on technical system properties:
According to the results of the studies in this paper, it is sufficient to design the structure once for the maximum load cases. However, the design was carried out for known and simple load cases. There are no studies available for unknown and more complex load cases. Whether it is possible to always achieve the same qualitative load distribution with two pairs of tension chords and whether a homogeneous compressive distribution is more advantageous than, for example, a temporally homogeneous bending moment distribution set by tension chording, should therefore be investigated in further work. More influence can be taken on the load distribution by further tension chords. Due to the increasing number of tension chords, the degree of redundancy in the system also increases, so that the advantage of the principle of redundant motion generation through function integration comes to bear further. By using several tension chords, there are more configurations to perpetuate a qualitatively similar load distribution for different load cases. Thereby the iterative coupling of the multibody simulation with the structure optimization could perhaps be omitted, since the structure is adapted only once to the qualitatively same load case, which would be an advantage. In contrast to the approach presented in this paper, this implementation requires a control system with sensors. Further work must be carried out on control behavior and the generation of qualitatively similar load distributions.
However, the increasing number of tension chords also causes problems. On the one hand, an increasing number of tension chords increases the control effort of the actuators. On the other hand, the complexity of the drive scheme for the tension chords increases. In the examinations of the articulated arm robots, two pairs of tension chords per arm segment already show that the drive becomes complex and that additional high loads are created in the system by the chords running around the joints. A possible solution to the problem of the drive of the tension chording and the high loads caused by deflection is the use of tension chords that connect one segment directly to another, inspired by the muscles attachment in the musculoskeletal system. Individual tension chords can thus be controlled directly without deflection, e.g., electronically, pneumatically or hydraulically, and equipped with sensors, which is advantageous for control. Tension chording according to this concept can be realized by technical linear actuators. The requirements for these linear actuators are that they must allow long ranges of positioning, act quickly and precisely and have a low mass. A low mass is important in order not to lose the advantage of the lack of mass of articulated motors. In the sense of the biological model, the use of artificial muscles is conceivable, the development of which is the subject of current research (Li et al. Reference Li, Vog, Rus and Wood2017; Acome et al. Reference Acome, Mitchell, Morrissey, Emmett, Benjamin, King, Radakovitz and Keplinger2018; Kellaris et al. Reference Kellaris, Gopaluni Venkata, Smith, Mitchell and Keplinger2018). Other possible linear actuators are shape memory actuators or pneumatic and hydraulic cylinders. Electromagnetic drives, which are too heavy according to the current state of research, are unsuitable. Current artificial muscles are not yet precise enough in positioning and control times. Shape memory actuators have short positioning ranges and require a path amplifier. With pneumatic and hydraulic cylinders, additional compressive forces can be used in the system to adjust the load, but the weight must also be taken into account here. There is a need for further research in order to implement a suitable actuator system.
Furthermore, no studies have been carried out to determine the dynamic behavior resulting from the exchange of the principle of motion generation. Due to the increased elasticity of the form-fit driving tension chords, an expansion slip occurs when forces are applied, which articulated motors in classical systems do not exhibit. This results in a fundamentally different and more complex dynamic control and response behavior. Furthermore, the biological lightweight design principle of passive tension chording was not investigated in this examination. This could lead to further advantages in terms of dynamic properties. Finally, the externally guided tension chords also change the safety requirements of the system, since the drive is no longer completely locked to the outside.
Discussion and outlook on technical fields of application:
The questions about technical system properties should be investigated in further work in order to apply the musculoskeletal lightweight potential to specific applications with different technical requirements. In addition to the discussed technical properties, further work is needed to find out which specific technical systems can be supported by the new bioinspired approach and in which form. The discussion of technical advantages and disadvantages shows that for complex systems and different load cases, additional requirements are placed on the system with regard to control and the drive concept. Depending on the application, a slow and smooth control or a fast and precise positioning control is desired. It therefore depends on a specific application whether one of the properties discussed in this paper is an advantage or a disadvantage. The advantage of mass saving is basically something every technical system can benefit from. However, for special technical applications the question arises as to whether, in addition to mass savings, the new system properties resulting from the use of musculoskeletal lightweight design principles are beneficial, or whether the cost of compensating possible disadvantages is greater than the benefit for the system. Therefore, two possibilities can be considered: first, systems that are kinematically similar to the musculoskeletal system and that benefit from the new characteristics, and second, systems in which the expense of high additional costs is tolerated.
Kinematically similar systems to the musculoskeletal system are mainly found in robotics. According to studies by Frutig (Reference Frutig2013) and Hansmersmann et al. (Reference Hansmersmann, Birenbaum, Burkhardt, Schneider and Stroka2016) there is a trend in industry toward lightweight robot systems and collaboration robots, where higher flexibility and modified dynamic properties are desired. Low inertial forces are advantageous for human–machine interaction and for unintended contact. In addition, the field of humanoid robots can be examined, which are kinematically and dynamically similar to the musculoskeletal system. Additionally to the lightweight design properties, a benefit can arise from the combination of a passive tension belt and inertial control for stability (Lipfert et al. Reference Lipfert, Günther, Renjewski, Grimmer and Seyfarth2012; Renjewski et al. Reference Renjewski, Spröwitz, Peekema, Jones and Hurst2015). On the other hand, there is also a trend in classical mechanical and plant engineering, e.g., manufacturing robot, to increase motion and cycle times and thus output quantities by lightweight design (Hansmersmann et al. Reference Hansmersmann, Birenbaum, Burkhardt, Schneider and Stroka2016). In order to support this field of application with the lightweight design of the musculoskeletal system, it is essential that the stiffness and dynamic properties are not impaired and that the development effort remains low. The ideal case is given when the technical effort is low and the planned additional costs or the profit from the lightweight design are high.
Systems in which the systems functions and properties are prioritized higher than cost are found mainly in aerospace technology. There are various applications, e.g., in the field of drive technology, which could benefit from musculoskeletal lightweight design. However, further work is needed to find out which areas of specific application there are. The discussion shows the need for further research on the applicability of the interaction of the lightweight design principles of the musculoskeletal system to specific technical systems.
Finally, it must be examined how the new approach is integrated into the product development process and how it should be used for new developments or only for adjustments or generational developments. Further methods should be developed which can support the developer, e.g., in finding and implementing the new principle of motion generation through tension chording.













