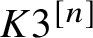0 Introduction
0.1 K3 surfaces
Gromov–Witten theory is the intersection theory of the moduli space
 ${\overline M}_{g,n}(X,\beta )$
of stable maps to a target X in degree
${\overline M}_{g,n}(X,\beta )$
of stable maps to a target X in degree
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
. If X carries a holomorphic symplectic form, the virtual fundamental class of the moduli space vanishes. Instead Gromov–Witten theory is defined through the reduced virtual fundamental class
$\beta \in H_{2}(X,{\mathbb {Z}})$
. If X carries a holomorphic symplectic form, the virtual fundamental class of the moduli space vanishes. Instead Gromov–Witten theory is defined through the reduced virtual fundamental class
 $$ \begin{align*} [ {\overline M}_{g,n}(X,\beta) ]^{\text{red}} \in A_{\ast}({\overline M}_{g,n}(X,\beta)). \end{align*} $$
$$ \begin{align*} [ {\overline M}_{g,n}(X,\beta) ]^{\text{red}} \in A_{\ast}({\overline M}_{g,n}(X,\beta)). \end{align*} $$
When working with reduced Gromov–Witten invariants, one observes in many examples the following dichotomy:
-
1. The invariants are notoriously difficult to compute, in particular if the class
 $\beta $
is not primitive.
$\beta $
is not primitive. -
2. The structure of the invariants is simpler than for general target X. That is, the invariants have additional nongeometric symmetries such as the independence (understood correctly) from the divisibility of the curve class.
Physicists would say that X has additional super-symmetry, which should explain this phenomenon. A mathematical explanation is unfortunately very much missing so far.
As an example, let us consider a K3 surface S and the Hodge integral
 $$ \begin{align*} R_{g,\beta} = \int_{ [ {\overline M}_{g,n}(S,\beta) ]^{\text{red}} } (-1)^{g} \lambda_{g}. \end{align*} $$
$$ \begin{align*} R_{g,\beta} = \int_{ [ {\overline M}_{g,n}(S,\beta) ]^{\text{red}} } (-1)^{g} \lambda_{g}. \end{align*} $$
We can formally subtract “multiple cover contributions” from
![]() $\beta $
byFootnote
1
$\beta $
byFootnote
1
 $$ \begin{align*} \widetilde{r}_{g,\beta} = \sum_{k | \beta} k^{2g-3} \mu(k) R_{g, \beta/k} \end{align*} $$
$$ \begin{align*} \widetilde{r}_{g,\beta} = \sum_{k | \beta} k^{2g-3} \mu(k) R_{g, \beta/k} \end{align*} $$
where we have used the Möbius function
 $$ \begin{align*} \mu(k) = \begin{cases} (-1)^{\ell} & \text{ if } k = p_{1} \cdots p_{\ell} \text{ for distinct primes } p_{i} \\ 0 & \text{ else}. \end{cases} \end{align*} $$
$$ \begin{align*} \mu(k) = \begin{cases} (-1)^{\ell} & \text{ if } k = p_{1} \cdots p_{\ell} \text{ for distinct primes } p_{i} \\ 0 & \text{ else}. \end{cases} \end{align*} $$
By deformation invariance,
![]() $\widetilde {r}_{g,\beta }$
depends on
$\widetilde {r}_{g,\beta }$
depends on
![]() $(S,\beta )$
only through the divisibility
$(S,\beta )$
only through the divisibility
![]() $m = \mathsf {div}(\beta )$
and the square
$m = \mathsf {div}(\beta )$
and the square
![]() $s = \beta \cdot \beta $
. One writes
$s = \beta \cdot \beta $
. One writes
The following remarkable result by Pandharipande and Thomas shows that the invariants
![]() $\widetilde {r}_{g,\beta }$
do not depend on the divisibility.
$\widetilde {r}_{g,\beta }$
do not depend on the divisibility.
Theorem 1 [Reference Pandharipande and Thomas49]
For all
![]() $g,m,s$
we have:
$g,m,s$
we have:
![]() $\widetilde {r}_{g,m,s} = \widetilde {r}_{g,1,s}$
.
$\widetilde {r}_{g,m,s} = \widetilde {r}_{g,1,s}$
.
The calculation of the primitive invariants
![]() $\widetilde {r}_{g,1,s}$
is much easier compared to the imprimitive case and was performed first in [Reference Maulik, Pandharipande and Thomas38]. Several other proofs are available in the literature by now. Together with the theorem, this yields a complete determination of
$\widetilde {r}_{g,1,s}$
is much easier compared to the imprimitive case and was performed first in [Reference Maulik, Pandharipande and Thomas38]. Several other proofs are available in the literature by now. Together with the theorem, this yields a complete determination of
![]() $\widetilde {r}_{g, \beta }$
, called the Katz–Klemm–Vafa formula [Reference Katz, Klemm and Vafa25].
$\widetilde {r}_{g, \beta }$
, called the Katz–Klemm–Vafa formula [Reference Katz, Klemm and Vafa25].
In [Reference Oberdieck, Pandharipande, Faber, Farkas and van der Geer45], it was conjectured that more generally any Gromov–Witten invariant of a K3 surface is independent of the divisibility after subtracting multiple covers. The divisibility
![]() $2$
case was solved recently [Reference Bae and Buelles1], but the general case remains a challenge.
$2$
case was solved recently [Reference Bae and Buelles1], but the general case remains a challenge.
0.2 Holomorphic-symplectic varieties
A smooth projective variety X is (irreducible) holomorphic-symplectic if it is simply connected and the space of holomorphic
![]() $2$
-forms
$2$
-forms
 $H^{0}(X,\Omega _{X}^{2})$
is spanned by a symplectic form. These varieties can be viewed as higher-dimensional analogues of K3 surfaces. For example, the cohomology
$H^{0}(X,\Omega _{X}^{2})$
is spanned by a symplectic form. These varieties can be viewed as higher-dimensional analogues of K3 surfaces. For example, the cohomology
![]() $H^{2}(X,{\mathbb {Z}})$
carries a canonical nondegenerate integer-valued quadratic form. The prime example of a holomorphic-symplectic variety is the Hilbert scheme of n points of a K3 surface and its deformations, which we call varieties of
$H^{2}(X,{\mathbb {Z}})$
carries a canonical nondegenerate integer-valued quadratic form. The prime example of a holomorphic-symplectic variety is the Hilbert scheme of n points of a K3 surface and its deformations, which we call varieties of
![]() $K3^{[n]}$
type.Footnote
2
$K3^{[n]}$
type.Footnote
2
We conjecture in this paper that the Gromov–Witten theory of
![]() $K3^{[n]}$
-type varieties is independent of the divisibility of the curve class, made precise in the following sense: Let
$K3^{[n]}$
-type varieties is independent of the divisibility of the curve class, made precise in the following sense: Let
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
be an effective (hence, nonzero) curve class, and consider the Gromov–Witten class
$\beta \in H_{2}(X,{\mathbb {Z}})$
be an effective (hence, nonzero) curve class, and consider the Gromov–Witten class
 $$ \begin{align*} {\mathcal C}_{g,N,\beta}(\alpha) = \operatorname{ev}_{\ast}\left( \tau^{\ast}(\alpha) \cap [ {\overline M}_{g,N}(X,\beta) ]^{\text{red}} \right) \in H^{\ast}(X^{N}) \end{align*} $$
$$ \begin{align*} {\mathcal C}_{g,N,\beta}(\alpha) = \operatorname{ev}_{\ast}\left( \tau^{\ast}(\alpha) \cap [ {\overline M}_{g,N}(X,\beta) ]^{\text{red}} \right) \in H^{\ast}(X^{N}) \end{align*} $$
where
 $\tau : {\overline M}_{g,N}(X,\beta ) \to {\overline M}_{g,N}$
is the forgetful morphism to the moduli space of curves, and
$\tau : {\overline M}_{g,N}(X,\beta ) \to {\overline M}_{g,N}$
is the forgetful morphism to the moduli space of curves, and
 $\alpha \in H^{\ast }({\overline M}_{g,N})$
is a tautological class [Reference Faber and Pandharipande16]. The classes
$\alpha \in H^{\ast }({\overline M}_{g,N})$
is a tautological class [Reference Faber and Pandharipande16]. The classes
![]() ${\mathcal C}_{g,N,\beta }(\alpha )$
encode the full numerical Gromov–Witten theory of X.
${\mathcal C}_{g,N,\beta }(\alpha )$
encode the full numerical Gromov–Witten theory of X.
We formally subtract the multiple cover contributions from this class:
 $$ \begin{align} \mathsf{c}_{g,N,\beta}(\alpha) = \sum_{k|\beta} \mu(k) k^{3g-3+N-\deg(\alpha)} (-1)^{[\beta] + [\beta/k]} {\mathcal C}_{g,N,\beta/k}(\alpha) \end{align} $$
$$ \begin{align} \mathsf{c}_{g,N,\beta}(\alpha) = \sum_{k|\beta} \mu(k) k^{3g-3+N-\deg(\alpha)} (-1)^{[\beta] + [\beta/k]} {\mathcal C}_{g,N,\beta/k}(\alpha) \end{align} $$
where we use that the residue of
![]() $\beta $
with respect to the quadratic form
$\beta $
with respect to the quadratic form
can be canonically identified up to multiplication by
![]() $\pm 1$
with an element of
$\pm 1$
with an element of
![]() ${\mathbb {Z}} / (2n-2) {\mathbb {Z}}$
; see Section 1.5.
${\mathbb {Z}} / (2n-2) {\mathbb {Z}}$
; see Section 1.5.
Let
![]() $X^{\prime }$
be any variety of
$X^{\prime }$
be any variety of
![]() $K3^{[n]}$
-type, and let
$K3^{[n]}$
-type, and let
be any real isometry such that
![]() $\varphi (\beta ) \in H_{2}(X^{\prime },{\mathbb {Z}})$
is a primitive effective curve class satisfying
$\varphi (\beta ) \in H_{2}(X^{\prime },{\mathbb {Z}})$
is a primitive effective curve class satisfying
Extend
![]() $\varphi $
to the full cohomology as a parallel transport lift (Section 1.6)
$\varphi $
to the full cohomology as a parallel transport lift (Section 1.6)
The following is the main conjecture.
Conjecture A.
 $$ \begin{align*} \mathsf{c}_{g,N,\beta}(\alpha) = \varphi^{-1}\left( {\mathcal C}_{g,N,\varphi(\beta)}(\alpha) \right) \end{align*} $$
$$ \begin{align*} \mathsf{c}_{g,N,\beta}(\alpha) = \varphi^{-1}\left( {\mathcal C}_{g,N,\varphi(\beta)}(\alpha) \right) \end{align*} $$
The right-hand side of the conjecture is given by the Gromov–Witten theory for a primitive class. Hence, the conjecture reduces calculations in imprimitive classes (which are hard) to those for primitive ones (which are easier). A different but equivalent version of the conjecture is formulated in Section 2.3. The equivalent version shows that the above reduces for K3 surfaces to the conjecture [Reference Oberdieck, Pandharipande, Faber, Farkas and van der Geer45, Conj.C2].
The moduli space
 ${\overline M}_{g,0}(X,\beta )$
is of reduced virtual dimension
${\overline M}_{g,0}(X,\beta )$
is of reduced virtual dimension
Hence, the Gromov–Witten theory of X of
![]() $K3^{[n]}$
-type vanishes for
$K3^{[n]}$
-type vanishes for
![]() $g>1$
if
$g>1$
if
![]() $n \geq 3$
, and for
$n \geq 3$
, and for
![]() $g> 2$
if
$g> 2$
if
![]() $n=2$
. Moreover, for
$n=2$
. Moreover, for
![]() $g=1$
the virtual dimension (2) is always one-dimensional, so relatively small. Hence, in dimension
$g=1$
the virtual dimension (2) is always one-dimensional, so relatively small. Hence, in dimension
![]() $>2$
, Conjecture A mainly concerns the genus zero theory. Our main evidence in genus
$>2$
, Conjecture A mainly concerns the genus zero theory. Our main evidence in genus
![]() $g>0$
comes from the case of K3 surfaces [Reference Pandharipande and Thomas49, Reference Bae and Buelles1, Reference Oberdieck, Pandharipande, Faber, Farkas and van der Geer45] and the remarkable fact that there is a single formula which governs all
$g>0$
comes from the case of K3 surfaces [Reference Pandharipande and Thomas49, Reference Bae and Buelles1, Reference Oberdieck, Pandharipande, Faber, Farkas and van der Geer45] and the remarkable fact that there is a single formula which governs all
![]() $K3^{[n]}$
at the same time.
$K3^{[n]}$
at the same time.
In genus
![]() $0$
, up to the sign
$0$
, up to the sign
![]() $(-1)^{[\beta ]+[\beta /k]}$
, equation (22) is precisely the formula that defines the BPS numbers of a Calabi–Yau manifold in terms of Gromov–Witten invariants. However, the appearence of the sign is a new feature, particular to the holomorphic-symplectic case. For example, it does not appear in the definition of genus
$(-1)^{[\beta ]+[\beta /k]}$
, equation (22) is precisely the formula that defines the BPS numbers of a Calabi–Yau manifold in terms of Gromov–Witten invariants. However, the appearence of the sign is a new feature, particular to the holomorphic-symplectic case. For example, it does not appear in the definition of genus
![]() $0$
BPS numbers of Calabi–Yau fourfolds as given by Klemm–Pandharipande [Reference Klemm and Pandharipande27]. We expect a similar multiple cover formula to hold for all holomorphic-symplectic varieties. What stops us from formulating it is that the precise term that generalizes the sign is not clear (aside from that there would be no evidence available at all).
$0$
BPS numbers of Calabi–Yau fourfolds as given by Klemm–Pandharipande [Reference Klemm and Pandharipande27]. We expect a similar multiple cover formula to hold for all holomorphic-symplectic varieties. What stops us from formulating it is that the precise term that generalizes the sign is not clear (aside from that there would be no evidence available at all).
In the appendix, we also formulate a multiple cover rule for abelian surfaces, extending a proposal for abelian varieties in [Reference Bryan, Oberdieck, Pandharipande and Yin7].
0.3 Noether–Lefschetz theory
There are three types of invariants associated to a one-parameter family
![]() $\pi : {\mathcal X} \to C$
of quasi-polarized holomorphic-symplectic varieties:
$\pi : {\mathcal X} \to C$
of quasi-polarized holomorphic-symplectic varieties:
-
(i) the Noether–Lefschetz numbers of
 $\pi $
,
$\pi $
, -
(ii) the Gromov–Witten invariants of
 ${\mathcal X}$
in fiber classes,
${\mathcal X}$
in fiber classes, -
(iii) the reduced Gromov–Witten invariants of a holomorphic-symplectic fiber of the family.
We refer to Section 3 for the definition of a one-parameter family of quasi-polarized holomorphic-symplectic varieties and its Noether–Lefschetz numbers. By a result of Maulik and Pandharipande [Reference Maulik and Pandharipande37], there is a geometric relation intertwining these three invariants. This relation (for a carefully selected family
![]() $\pi $
) was used in [Reference Klemm, Maulik, Pandharipande and Scheidegger26] to prove Theorem 1 in genus
$\pi $
) was used in [Reference Klemm, Maulik, Pandharipande and Scheidegger26] to prove Theorem 1 in genus
![]() $0$
and then later in [Reference Pandharipande and Thomas49] in the general case. Roughly, for a nice family, the relation becomes invertible and reduces the problem to considering ordinary Gromov–Witten invariants of a K3-fibered threefold which then can be attacked by more standard methods.
$0$
and then later in [Reference Pandharipande and Thomas49] in the general case. Roughly, for a nice family, the relation becomes invertible and reduces the problem to considering ordinary Gromov–Witten invariants of a K3-fibered threefold which then can be attacked by more standard methods.
In this paper, we follow the same strategy for holomorphic symplectic varieties of
![]() $K3^{[n]}$
-type. We first discuss the Maulik–Pandharipande relation in this case (Section 4) and then apply it in two cases:
$K3^{[n]}$
-type. We first discuss the Maulik–Pandharipande relation in this case (Section 4) and then apply it in two cases:
-
(i) A generic pencil of Fano varieties of a cubic fourfold [Reference Beauville and Donagi2]:
 $$ \begin{align*} {\mathcal X} \subset \operatorname{Gr}(2,6) \times \mathbb{P}^{1}, \quad \pi : {\mathcal X} \to \mathbb{P}^{1}. \end{align*} $$
$$ \begin{align*} {\mathcal X} \subset \operatorname{Gr}(2,6) \times \mathbb{P}^{1}, \quad \pi : {\mathcal X} \to \mathbb{P}^{1}. \end{align*} $$
-
(ii) A generic pencil of Debarre–Voisin varieties [Reference Debarre and Voisin15]:
 $$ \begin{align*} {\mathcal X} \subset \operatorname{Gr}(6,10) \times \mathbb{P}^{1}, \quad \pi : {\mathcal X} \to \mathbb{P}^{1}. \end{align*} $$
$$ \begin{align*} {\mathcal X} \subset \operatorname{Gr}(6,10) \times \mathbb{P}^{1}, \quad \pi : {\mathcal X} \to \mathbb{P}^{1}. \end{align*} $$
The examples are choosen such that the Gromov–Witten invariants of
![]() ${\mathcal X}$
can be computed using mirror symmetry [Reference Ciocan-Fontanine and Kim11]. For the family of Fano varieties, the Noether–Lefschetz numbers have already been computed by Li and Zhang [Reference Li and Zhang31]. The Gromov–Witten/Noether–Lefschetz relation for the Fano family then yields an explicit infinite family of relations that need to hold for Conjecture A to be true. Using a computer, we checked that these relations are satisfied up to degree
${\mathcal X}$
can be computed using mirror symmetry [Reference Ciocan-Fontanine and Kim11]. For the family of Fano varieties, the Noether–Lefschetz numbers have already been computed by Li and Zhang [Reference Li and Zhang31]. The Gromov–Witten/Noether–Lefschetz relation for the Fano family then yields an explicit infinite family of relations that need to hold for Conjecture A to be true. Using a computer, we checked that these relations are satisfied up to degree
![]() $d \leq 38$
(with respect to the Plücker polarization). The relations involve curve classes of both high self-intersection and high divisibility. Together with previously known cases, we also obtain the following.
$d \leq 38$
(with respect to the Plücker polarization). The relations involve curve classes of both high self-intersection and high divisibility. Together with previously known cases, we also obtain the following.
Proposition 1. In genus
![]() $0$
and
$0$
and
![]() $K3^{[2]}$
-type Conjecture A holds for
$K3^{[2]}$
-type Conjecture A holds for
![]() $\beta = m \cdot \alpha $
, where
$\beta = m \cdot \alpha $
, where
![]() $\alpha $
is primitive whenever:
$\alpha $
is primitive whenever:
-
○
 $(\alpha , \alpha ) < 0$
, or
$(\alpha , \alpha ) < 0$
, or -
○
 $(\alpha , \alpha ) = 0$
and (
$(\alpha , \alpha ) = 0$
and (
 $m=2$
or
$m=2$
or
 $N=1$
), or
$N=1$
), or -
○
 $(\alpha , \alpha ) = 3/2$
and
$(\alpha , \alpha ) = 3/2$
and
 $m \in \{ 2,3,5 \}$
.
$m \in \{ 2,3,5 \}$
.
Ideally, we would like to apply our methods to other families. However, it is quite difficult to find appropriate one-parameter families. They must be (a) a zero section of a homogeneous vector bundle on the geometric invariant theory (GIT) quotient of a vector space by a reductive group, and (b) their singular fibers must have mild singularieties. A promising candidate seemed to be a generic pencil of Iliev–Manivel fourfolds [Reference Iliev and Manivel24],
but unfortunately, the singular fibers appear to be too singular.Footnote 3
0.4 Debarre–Voisin fourfolds
For the generic pencil
![]() $\pi : {\mathcal X} \to \mathbb {P}^{1}$
of Debarre–Voisin fourfolds, the Noether–Lefschetz numbers have not yet been determined. Instead, we use the known cases of Conjecture A and the mirror symmetry calculations for the total space
$\pi : {\mathcal X} \to \mathbb {P}^{1}$
of Debarre–Voisin fourfolds, the Noether–Lefschetz numbers have not yet been determined. Instead, we use the known cases of Conjecture A and the mirror symmetry calculations for the total space
![]() ${\mathcal X}$
to obtain constraints for the Noether–Lefschetz numbers. By using the modularity of the generating series of Noether–Lefschetz numbers due to Borcherds and McGraw [Reference Borcherds5, Reference McGraw39], we can then determine the full series.
${\mathcal X}$
to obtain constraints for the Noether–Lefschetz numbers. By using the modularity of the generating series of Noether–Lefschetz numbers due to Borcherds and McGraw [Reference Borcherds5, Reference McGraw39], we can then determine the full series.
Consider the generating series of Noether–Lefschetz numbers of
![]() $\pi $
as defined in Section 3.8.1,
$\pi $
as defined in Section 3.8.1,
 $$ \begin{align*} \varphi(q) = \sum_{D \geq 0} q^{D/11} \mathsf{NL}^{\pi}(D), \end{align*} $$
$$ \begin{align*} \varphi(q) = \sum_{D \geq 0} q^{D/11} \mathsf{NL}^{\pi}(D), \end{align*} $$
where D runs over all squares modulo
![]() $11$
.
$11$
.
Define the weight
![]() $1,2,3$
modular forms
$1,2,3$
modular forms
 $$ \begin{gather*} E_{1}(\tau) = 1 + 2 \sum_{n \geq 1} q^{n} \sum_{d|n} \chi_{p}\left( \frac{n}{d} \right), \quad \ \Delta_{11}(\tau) = \eta(\tau)^{2} \eta(11 \tau)^{2} \\ E_{3}(\tau) = \sum_{n \geq 1} q^{n} \sum_{d|n} d^{2} \chi_{p}\left( \frac{n}{d} \right), \end{gather*} $$
$$ \begin{gather*} E_{1}(\tau) = 1 + 2 \sum_{n \geq 1} q^{n} \sum_{d|n} \chi_{p}\left( \frac{n}{d} \right), \quad \ \Delta_{11}(\tau) = \eta(\tau)^{2} \eta(11 \tau)^{2} \\ E_{3}(\tau) = \sum_{n \geq 1} q^{n} \sum_{d|n} d^{2} \chi_{p}\left( \frac{n}{d} \right), \end{gather*} $$
where
![]() $\eta (\tau ) = q^{1/24} \prod _{n \geq 1} (1-q^{n})$
is the Dirichlet eta function,
$\eta (\tau ) = q^{1/24} \prod _{n \geq 1} (1-q^{n})$
is the Dirichlet eta function,
![]() $q = e^{2 \pi i \tau }$
and
$q = e^{2 \pi i \tau }$
and
![]() $\chi _{11}$
is the Dirichlet character given by the Legendre symbol
$\chi _{11}$
is the Dirichlet character given by the Legendre symbol
![]() $\left (\frac { \cdot }{11} \right )$
. Consider the following weight
$\left (\frac { \cdot }{11} \right )$
. Consider the following weight
![]() $11$
modular forms for
$11$
modular forms for
![]() $\Gamma _{0}(11)$
and character
$\Gamma _{0}(11)$
and character
![]() $\chi _{11}$
:
$\chi _{11}$
:
 $$ \begin{align*} \varphi_{0}(q) & = -5 \, E_{1}^{11} + 430 \, E_{1}^{8} E_{3} + \frac{5,199,920}{9} \, \Delta_{11}^{3} E_{1}^{5} - \frac{35,407,490}{27} \, \Delta_{11}^{4} E_{1}^{3} \\ &\ \ \ + \frac{49,194,440}{9} \, \Delta_{11}^{2} E_{1}^{4} E_{3} + 248,350 \, E_{1}^{5} E_{3}^{2} - \frac{596,661,440}{27} \, \Delta_{11}^{3} E_{1}^{2} E_{3} \\ &\ \ \ - \frac{306,631,760}{9} \, \Delta_{11} E_{1}^{3} E_{3}^{2} + \frac{51,243,500}{3} \, \Delta_{11}^{4} E_{3} + \frac{1,331,452,540}{27} \, \Delta_{11}^{2} E_{1} E_{3}^{2}\\ &\ \ \ + \frac{349,019,440}{9} \, E_{1}^{2} E_{3}^{3} \\ & = -5 + 320q + 255,420q^{2} + 14,793,440q^{3} + 262,345,260q^{4} + \ldots \\ \varphi_{1}(q) & = -5 \, E_{1}^{11} + 110 \, E_{1}^{8} E_{3} + \frac{722,740}{3,993} \, \Delta_{11}^{3} E_{1}^{5} - \frac{1,805,750}{3993} \, \Delta_{11}^{4} E_{1}^{3} \\ &\ \ \ - \frac{12,660,620}{11979} \Delta_{11}^{2} E_{1}^{4} E_{3} - 990 E_{1}^{5} E_{3}^{2} + \frac{118,940}{363} \Delta_{11}^{5} E_{1} + \frac{5,609,180}{3,993} \Delta_{11}^{3} E_{1}^{2} E_{3} \\ &\ \ \ + \frac{29,208,460}{11,979} \, \Delta_{11} E_{1}^{3} E_{3}^{2} + \frac{3,500}{33} \, \Delta_{11}^{4} E_{3} + \frac{2,610,980}{1,089} \, E_{1}^{2} E_{3}^{3} \\ & = -5 + 320q^{11} + 990q^{12} + 5,500q^{14} + 11,440q^{15} + \ldots \end{align*} $$
$$ \begin{align*} \varphi_{0}(q) & = -5 \, E_{1}^{11} + 430 \, E_{1}^{8} E_{3} + \frac{5,199,920}{9} \, \Delta_{11}^{3} E_{1}^{5} - \frac{35,407,490}{27} \, \Delta_{11}^{4} E_{1}^{3} \\ &\ \ \ + \frac{49,194,440}{9} \, \Delta_{11}^{2} E_{1}^{4} E_{3} + 248,350 \, E_{1}^{5} E_{3}^{2} - \frac{596,661,440}{27} \, \Delta_{11}^{3} E_{1}^{2} E_{3} \\ &\ \ \ - \frac{306,631,760}{9} \, \Delta_{11} E_{1}^{3} E_{3}^{2} + \frac{51,243,500}{3} \, \Delta_{11}^{4} E_{3} + \frac{1,331,452,540}{27} \, \Delta_{11}^{2} E_{1} E_{3}^{2}\\ &\ \ \ + \frac{349,019,440}{9} \, E_{1}^{2} E_{3}^{3} \\ & = -5 + 320q + 255,420q^{2} + 14,793,440q^{3} + 262,345,260q^{4} + \ldots \\ \varphi_{1}(q) & = -5 \, E_{1}^{11} + 110 \, E_{1}^{8} E_{3} + \frac{722,740}{3,993} \, \Delta_{11}^{3} E_{1}^{5} - \frac{1,805,750}{3993} \, \Delta_{11}^{4} E_{1}^{3} \\ &\ \ \ - \frac{12,660,620}{11979} \Delta_{11}^{2} E_{1}^{4} E_{3} - 990 E_{1}^{5} E_{3}^{2} + \frac{118,940}{363} \Delta_{11}^{5} E_{1} + \frac{5,609,180}{3,993} \Delta_{11}^{3} E_{1}^{2} E_{3} \\ &\ \ \ + \frac{29,208,460}{11,979} \, \Delta_{11} E_{1}^{3} E_{3}^{2} + \frac{3,500}{33} \, \Delta_{11}^{4} E_{3} + \frac{2,610,980}{1,089} \, E_{1}^{2} E_{3}^{3} \\ & = -5 + 320q^{11} + 990q^{12} + 5,500q^{14} + 11,440q^{15} + \ldots \end{align*} $$
Theorem 2. Let
![]() $\pi : {\mathcal X} \to \mathbb {P}^{1}$
be a generic pencil of Debarre–Voisin fourfolds. Then the generating series of its Noether–Lefschetz numbers is
$\pi : {\mathcal X} \to \mathbb {P}^{1}$
be a generic pencil of Debarre–Voisin fourfolds. Then the generating series of its Noether–Lefschetz numbers is
 $$ \begin{align*} \varphi(q^{11}) = \varphi_{0}(q^{11}) + \varphi_{1}(q) = -10 + 640 q^{11} + 990 q^{12} + 5,500 q^{14} + 11,440 q^{15} \\ + 21,450 q^{16} + 198,770 q^{20} + 510,840 q^{22} + \ldots \end{align*} $$
$$ \begin{align*} \varphi(q^{11}) = \varphi_{0}(q^{11}) + \varphi_{1}(q) = -10 + 640 q^{11} + 990 q^{12} + 5,500 q^{14} + 11,440 q^{15} \\ + 21,450 q^{16} + 198,770 q^{20} + 510,840 q^{22} + \ldots \end{align*} $$
Debarre–Voisin varieties are parametrized by a
![]() $20$
-dimensional projective irreducible GIT quotient
$20$
-dimensional projective irreducible GIT quotient
 $$ \begin{align*} {\mathcal M}_{\text{DV}} = \mathbb{P}( \wedge^{3} V_{10}^{\vee} )// \mathrm{SL}(V_{10}), \end{align*} $$
$$ \begin{align*} {\mathcal M}_{\text{DV}} = \mathbb{P}( \wedge^{3} V_{10}^{\vee} )// \mathrm{SL}(V_{10}), \end{align*} $$
where
![]() $V_{10}$
is a vector space of dimension
$V_{10}$
is a vector space of dimension
![]() $10$
. The period map from this moduli space to the moduli space of holomorphic-symplectic varieties
$10$
. The period map from this moduli space to the moduli space of holomorphic-symplectic varieties
is birational [Reference O’Grady41] and regular on the open locus corresponding to smooth Debarre–Voisin varieties of dimension four. When passing to the Baily–Borel compactification
![]() $\overline {{\mathcal M}_{H}}$
, this birational map can be resolved. An Hassett–Looijenga–Shah (HLS) divisor in
$\overline {{\mathcal M}_{H}}$
, this birational map can be resolved. An Hassett–Looijenga–Shah (HLS) divisor in
![]() ${\mathcal M}_{H}$
is the image of an exceptional divisor under this resolved map. These divisors reflect a difference between the GIT and the Baily–Borel compactification as they parametrize holomorphic-symplectic fourfolds of the same polarization type as a Debarre–Voisin fourfold, but for which the generic member is not a Debarre–Voisin fourfold.
${\mathcal M}_{H}$
is the image of an exceptional divisor under this resolved map. These divisors reflect a difference between the GIT and the Baily–Borel compactification as they parametrize holomorphic-symplectic fourfolds of the same polarization type as a Debarre–Voisin fourfold, but for which the generic member is not a Debarre–Voisin fourfold.
Let e be a square modulo
![]() $11$
, and let
$11$
, and let
be the Noether–Lefschetz divisor of the first type of discriminant e; see Section 3.8.2 for the precise definition. Observe that there is a natural gapFootnote
4
in the modular form
![]() $\varphi (q)$
:
$\varphi (q)$
:
 $$ \begin{align*} \varphi(q^{11}) = -10 + \underbrace{ 0 \cdot q^{1} + 0 \cdot q^{3} + \ldots + 0 \cdot q^{9} }_{\text{gap}} + 640 q^{11} + 990 q^{12} + 5500 q^{14} + \ldots \end{align*} $$
$$ \begin{align*} \varphi(q^{11}) = -10 + \underbrace{ 0 \cdot q^{1} + 0 \cdot q^{3} + \ldots + 0 \cdot q^{9} }_{\text{gap}} + 640 q^{11} + 990 q^{12} + 5500 q^{14} + \ldots \end{align*} $$
Translating from Heegner divisors to the irreducible divisors
![]() ${\mathcal C}_{2e}$
, this gap yields the following.
${\mathcal C}_{2e}$
, this gap yields the following.
Corollary 1. The divisors
![]() ${\mathcal C}_{2}, {\mathcal C}_{6}, {\mathcal C}_{8}, {\mathcal C}_{10}, {\mathcal C}_{18}$
are HLS divisors of the moduli space of Debarre–Voisin fourfolds. The divisor
${\mathcal C}_{2}, {\mathcal C}_{6}, {\mathcal C}_{8}, {\mathcal C}_{10}, {\mathcal C}_{18}$
are HLS divisors of the moduli space of Debarre–Voisin fourfolds. The divisor
![]() ${\mathcal C}_{30}$
is not HLS.
${\mathcal C}_{30}$
is not HLS.
The statement that
![]() ${\mathcal C}_{2}, {\mathcal C}_{6}, {\mathcal C}_{10}, {\mathcal C}_{18}$
are HLS is the main result of [Reference Debarre, Han, O’Grady and Voisin13]. The argument here gives an independent and mostly formal proof of the main result of [Reference Debarre, Han, O’Grady and Voisin13]. The only geometric input lies in describing in understanding the geometry of the singular fibers (a result of J. Song, see C). The result that
${\mathcal C}_{2}, {\mathcal C}_{6}, {\mathcal C}_{10}, {\mathcal C}_{18}$
are HLS is the main result of [Reference Debarre, Han, O’Grady and Voisin13]. The argument here gives an independent and mostly formal proof of the main result of [Reference Debarre, Han, O’Grady and Voisin13]. The only geometric input lies in describing in understanding the geometry of the singular fibers (a result of J. Song, see C). The result that
![]() ${\mathcal C}_{30}$
is not a HLS divisor answers a question of [Reference Debarre, Han, O’Grady and Voisin13]. The fact that
${\mathcal C}_{30}$
is not a HLS divisor answers a question of [Reference Debarre, Han, O’Grady and Voisin13]. The fact that
![]() ${\mathcal C}_{8}$
is HLS seems to be new, and it would be interesting to understand the geometry of these loci, as is done in [Reference Debarre, Han, O’Grady and Voisin13] for the other cases. In principle, Theorem 2 can be used to show that the divisors listed in Corollary 1 are the only Noether–Lefschetz divisors
${\mathcal C}_{8}$
is HLS seems to be new, and it would be interesting to understand the geometry of these loci, as is done in [Reference Debarre, Han, O’Grady and Voisin13] for the other cases. In principle, Theorem 2 can be used to show that the divisors listed in Corollary 1 are the only Noether–Lefschetz divisors
![]() ${\mathcal C}_{2e}$
which are HLS.
${\mathcal C}_{2e}$
which are HLS.
Remark 1. After the first version of this paper appeared online, I learned that Theorem 2 and Corollary 1 was independently obtained by Calla Tschanz based on the results of [Reference Debarre, Han, O’Grady and Voisin13].
0.5 Convention
If
![]() $\gamma \in H^{i}(X,{\mathbb {Q}})$
is a cohomology class, we write
$\gamma \in H^{i}(X,{\mathbb {Q}})$
is a cohomology class, we write
![]() $\deg (\gamma ) = i/2$
for the complex cohomological degree of
$\deg (\gamma ) = i/2$
for the complex cohomological degree of
![]() $\gamma $
. For X holomorphic-symplectic, we identify
$\gamma $
. For X holomorphic-symplectic, we identify
![]() $\mathop {\text {Pic}}\nolimits (X)$
with its image in
$\mathop {\text {Pic}}\nolimits (X)$
with its image in
![]() $H^{2}(X,{\mathbb {Z}})$
under the map taking the first Chern class. Let
$H^{2}(X,{\mathbb {Z}})$
under the map taking the first Chern class. Let
![]() $\mathsf {Hilb}_{n}(S)$
be the Hilbert scheme of points of a K3 surface. Given
$\mathsf {Hilb}_{n}(S)$
be the Hilbert scheme of points of a K3 surface. Given
![]() $\alpha \in H^{\ast }(S,{\mathbb {Q}})$
and
$\alpha \in H^{\ast }(S,{\mathbb {Q}})$
and
![]() $i> 0$
, we let
$i> 0$
, we let
be the i-th Nakajima operator [Reference Nakajima40] given by adding a i-fat point on a cycle with class
![]() $\alpha $
; we use the convention of [Reference Oberdieck46]. We write
$\alpha $
; we use the convention of [Reference Oberdieck46]. We write
![]() $A \in H_{2}(\mathsf {Hilb}_{n}(S))$
for the class of a generic fiber of the singular locus of the Hilbert Chow morphism, and we let
$A \in H_{2}(\mathsf {Hilb}_{n}(S))$
for the class of a generic fiber of the singular locus of the Hilbert Chow morphism, and we let
![]() $-2 \delta $
be the class of the diagonal. We identify
$-2 \delta $
be the class of the diagonal. We identify
using the Nakajima operators [Reference Oberdieck42].
0.6 Subsequent work
In [Reference Oberdieck43], the main conjecture of this paper (Conjecture A) is proven for all
![]() $K3^{[n]}$
in genus
$K3^{[n]}$
in genus
![]() $0$
and for
$0$
and for
![]() $N \leq 3$
markings.
$N \leq 3$
markings.
1 The monodromy in
 $K3^{[n]}$
-type
$K3^{[n]}$
-type
1.1 Overview
Let X be a (irreducible) holomorphic-symplectic variety. The lattice
![]() $H^{2}(X,{\mathbb {Z}})$
is equipped with the integral and nondegenerate Beauville–Bogomolov–Fujiki quadratic form. We will also equip
$H^{2}(X,{\mathbb {Z}})$
is equipped with the integral and nondegenerate Beauville–Bogomolov–Fujiki quadratic form. We will also equip
![]() $H^{\ast }(X,{\mathbb {Z}})$
with the usual Poincaré pairing. Both pairings are extended to the
$H^{\ast }(X,{\mathbb {Z}})$
with the usual Poincaré pairing. Both pairings are extended to the
![]() ${\mathbb {C}}$
-valued cohomology groups by linearity. Let
${\mathbb {C}}$
-valued cohomology groups by linearity. Let
![]() $\mathsf {Mon}(X)$
be the subgroup of
$\mathsf {Mon}(X)$
be the subgroup of
![]() $O(H^{\ast }(X,{\mathbb {Z}}))$
generated by all monodromy operators, and let
$O(H^{\ast }(X,{\mathbb {Z}}))$
generated by all monodromy operators, and let
![]() $\mathsf {Mon}^{2}(X)$
be its image in
$\mathsf {Mon}^{2}(X)$
be its image in
![]() $O(H^{2}(X,{\mathbb {Z}}))$
.
$O(H^{2}(X,{\mathbb {Z}}))$
.
The goal of this section is to describe the monodromy group in the case that X is of
![]() $K3^{[n]}$
-type, and we will assume so from now on. The main references for the sections are Markman’s papers [Reference Markman33, Reference Markman34].
$K3^{[n]}$
-type, and we will assume so from now on. The main references for the sections are Markman’s papers [Reference Markman33, Reference Markman34].
1.2 Monodromy
Let X be of
![]() $K3^{[n]}$
-type. By work of Markman [Reference Markman34, Thm.1.3], [Reference Markman35, Lemma 2.1], we have that
$K3^{[n]}$
-type. By work of Markman [Reference Markman34, Thm.1.3], [Reference Markman35, Lemma 2.1], we have that
where the first isomorphism is the restriction map and
![]() $\widetilde {O}^{+}(H^{2}(X,{\mathbb {Z}}))$
is the subgroup of
$\widetilde {O}^{+}(H^{2}(X,{\mathbb {Z}}))$
is the subgroup of
![]() $O(H^{2}(X,{\mathbb {Z}}))$
of orientation preserving lattice automorphisms which act by
$O(H^{2}(X,{\mathbb {Z}}))$
of orientation preserving lattice automorphisms which act by
![]() $\pm 1$
on the discriminant.Footnote
5
The first isomorpism implies that any parallel transport operator
$\pm 1$
on the discriminant.Footnote
5
The first isomorpism implies that any parallel transport operator
![]() $H^{\ast }(X_{1}, {\mathbb {Z}}) \to H^{\ast }(X_{2}, {\mathbb {Z}})$
between two
$H^{\ast }(X_{1}, {\mathbb {Z}}) \to H^{\ast }(X_{2}, {\mathbb {Z}})$
between two
![]() $K3^{[n]}$
-type varieties is uniquely determined by its restriction to
$K3^{[n]}$
-type varieties is uniquely determined by its restriction to
![]() $H^{2}(X_{1},{\mathbb {Z}})$
.
$H^{2}(X_{1},{\mathbb {Z}})$
.
If
![]() $g \in \mathsf {Mon}^{2}(X)$
, we let
$g \in \mathsf {Mon}^{2}(X)$
, we let
![]() $\tau (g) \in \{ \pm 1 \}$
be the sign by which g acts on the discriminant lattice. This defines a character
$\tau (g) \in \{ \pm 1 \}$
be the sign by which g acts on the discriminant lattice. This defines a character
1.3 Zariski closure
By [Reference Markman33, Lemma 4.11] if
![]() $n \geq 3$
, the Zariski closure of
$n \geq 3$
, the Zariski closure of
![]() $\mathsf {Mon}(X)$
in
$\mathsf {Mon}(X)$
in
![]() $O(H^{\ast }(X,{\mathbb {C}}))$
is
$O(H^{\ast }(X,{\mathbb {C}}))$
is
![]() $O(H^{2}(X,{\mathbb {C}})) \times {\mathbb {Z}}_{2}$
. The inclusion yields the representation
$O(H^{2}(X,{\mathbb {C}})) \times {\mathbb {Z}}_{2}$
. The inclusion yields the representation
which acts by degree-preserving orthogonal ring isomorphism. There is a natural embedding
under which
![]() $\rho $
restricts to the monodromy representation. In case
$\rho $
restricts to the monodromy representation. In case
![]() $n \in \{ 1 ,2 \}$
, the Zariski closure is
$n \in \{ 1 ,2 \}$
, the Zariski closure is
![]() $O(H^{2}(X,{\mathbb {C}}))$
. In this case, we define the representation (4) by letting it act through
$O(H^{2}(X,{\mathbb {C}}))$
. In this case, we define the representation (4) by letting it act through
![]() $O(H^{2}(X,{\mathbb {C}}))$
.
$O(H^{2}(X,{\mathbb {C}}))$
.
The representation
![]() $\rho $
is determined by the following properties.
$\rho $
is determined by the following properties.
Property 0. For any
![]() $(g, \tau ) \in O(H^{2}(X,{\mathbb {C}})) \times {\mathbb {Z}}_{2}$
, we have
$(g, \tau ) \in O(H^{2}(X,{\mathbb {C}})) \times {\mathbb {Z}}_{2}$
, we have
Property 1. The restriction of
![]() $\rho $
to
$\rho $
to
![]() $\mathrm {SO}(H^{2}(X,{\mathbb {C}})) \times \{ 0 \}$
is the integrated action of the Looijenga–Lunts–Verbitsky algebra [Reference Looijenga and Lunts32, Reference Verbitsky51].
$\mathrm {SO}(H^{2}(X,{\mathbb {C}})) \times \{ 0 \}$
is the integrated action of the Looijenga–Lunts–Verbitsky algebra [Reference Looijenga and Lunts32, Reference Verbitsky51].
Property 2. We have
where D acts on
![]() $H^{2i}(X,{\mathbb {C}})$
by multiplication by
$H^{2i}(X,{\mathbb {C}})$
by multiplication by
![]() $(-1)^{i}$
.
$(-1)^{i}$
.
Property 3. Assume that
![]() $X = \mathsf {Hilb}_{n}(S)$
, and identify
$X = \mathsf {Hilb}_{n}(S)$
, and identify
![]() $H^{2}(X,{\mathbb {Z}})$
with
$H^{2}(X,{\mathbb {Z}})$
with
![]() $H^{2}(S,{\mathbb {Z}}) \oplus {\mathbb {Z}} \delta $
. Then the restriction of
$H^{2}(S,{\mathbb {Z}}) \oplus {\mathbb {Z}} \delta $
. Then the restriction of
![]() $\rho $
to
$\rho $
to
![]() $O(H^{2}(X,{\mathbb {C}}))_{\delta } \times 1$
(identified naturally with
$O(H^{2}(X,{\mathbb {C}}))_{\delta } \times 1$
(identified naturally with
![]() $O(H^{2}(S,{\mathbb {C}}))$
) is the Zariski closure of the induced action on the Hilbert scheme by the monodromy representation of S.
$O(H^{2}(S,{\mathbb {C}}))$
) is the Zariski closure of the induced action on the Hilbert scheme by the monodromy representation of S.
In particular, the action is equivariant with respect to the Nakajima operators: For
![]() $g \in O(H^{2}(X,{\mathbb {C}}))_{\delta }$
let
$g \in O(H^{2}(X,{\mathbb {C}}))_{\delta }$
let
![]() $\tilde {g} = g|_{H^{2}(S,{\mathbb {C}}))} \oplus \mathrm {id}_{H^{0}(S,{\mathbb {Z}}) \oplus H^{4}(S,{\mathbb {Z}})}$
. Then
$\tilde {g} = g|_{H^{2}(S,{\mathbb {C}}))} \oplus \mathrm {id}_{H^{0}(S,{\mathbb {Z}}) \oplus H^{4}(S,{\mathbb {Z}})}$
. Then
 $$ \begin{align*} \rho(g, 1) \left( \prod_{i} {\mathfrak{q}}_{k_{i}}(\alpha_{i}) 1 \right) = \prod_{i} {\mathfrak{q}}_{k_{i}}( \tilde{g} \alpha_{i} ) 1. \end{align*} $$
$$ \begin{align*} \rho(g, 1) \left( \prod_{i} {\mathfrak{q}}_{k_{i}}(\alpha_{i}) 1 \right) = \prod_{i} {\mathfrak{q}}_{k_{i}}( \tilde{g} \alpha_{i} ) 1. \end{align*} $$
Property 4. Let
![]() $P_{\psi } : H^{\ast }(X_{1}, {\mathbb {Z}}) \to H^{\ast }(X_{2}, {\mathbb {Z}})$
be a parallel transport operator with
$P_{\psi } : H^{\ast }(X_{1}, {\mathbb {Z}}) \to H^{\ast }(X_{2}, {\mathbb {Z}})$
be a parallel transport operator with
![]() $\psi = P_{\psi }|_{H^{2}(X_{1},{\mathbb {Z}})}$
. Then
$\psi = P_{\psi }|_{H^{2}(X_{1},{\mathbb {Z}})}$
. Then
 $$ \begin{align*} P_{\psi}^{-1} \circ \rho(g, \tau) \circ P_{\psi} = \rho( \psi^{-1} g \psi, \tau). \end{align*} $$
$$ \begin{align*} P_{\psi}^{-1} \circ \rho(g, \tau) \circ P_{\psi} = \rho( \psi^{-1} g \psi, \tau). \end{align*} $$
Property 1 follows by [Reference Markman33, Lemma 4.13]. The other properties also follow from the results of [Reference Markman33]. Properties 1–3 determine the action
![]() $\rho $
completely in the Hilbert scheme case. Moreover, by [Reference Oberdieck46], this description is explicit in the Nakajima basis. The last condition extends this presentation then to arbitrary X. The parallel transport operator between different moduli spaces of stable sheaves can also be described more explicitly [Reference Markman33].
$\rho $
completely in the Hilbert scheme case. Moreover, by [Reference Oberdieck46], this description is explicit in the Nakajima basis. The last condition extends this presentation then to arbitrary X. The parallel transport operator between different moduli spaces of stable sheaves can also be described more explicitly [Reference Markman33].
1.4 Parallel transport
Let
be the Mukai lattice. For
![]() $n \geq 2$
, any holomorphic-symplectic variety of
$n \geq 2$
, any holomorphic-symplectic variety of
![]() $K3[n]$
-type is equipped with a canonical choice of a primitive embedding
$K3[n]$
-type is equipped with a canonical choice of a primitive embedding
unique up to composition by an element by
![]() $O(\Lambda )$
; see [Reference Markman34, Cor.9.4].
$O(\Lambda )$
; see [Reference Markman34, Cor.9.4].
Theorem 3 [Reference Markman34, Thm.9.8]
An isometry
![]() $\psi : H^{2}(X_{1}, {\mathbb {Z}}) \to H^{2}(X_{1}, {\mathbb {Z}})$
is the restriction of a parallel transport operator if and only if it is orientation preserving and there exists an
$\psi : H^{2}(X_{1}, {\mathbb {Z}}) \to H^{2}(X_{1}, {\mathbb {Z}})$
is the restriction of a parallel transport operator if and only if it is orientation preserving and there exists an
![]() $\eta \in O(\Lambda )$
such that
$\eta \in O(\Lambda )$
such that
Orientation preserving is here defined with respect to the canonical choice of orientation of the positive cone of
![]() $X_{i}$
given by the real and imaginary part of the symplectic form and a Kähler class. If
$X_{i}$
given by the real and imaginary part of the symplectic form and a Kähler class. If
![]() $X_{1} = X_{2}$
, the theorem reduces to the second isomorphism in equation (3).
$X_{1} = X_{2}$
, the theorem reduces to the second isomorphism in equation (3).
1.5 Curve classes
By Eichler’s criterion [Reference Gritsenko, Hulek and Sankaran19, Lemma 3.5], Theorem 3 yields a complete set of deformation invariants of curve classes in
![]() $K3^{[n]}$
-type. To state the result we need the following constriction:
$K3^{[n]}$
-type. To state the result we need the following constriction:
The orthogonal complement
is isomorphic to the lattice
![]() ${\mathbb {Z}}$
with intersection form
${\mathbb {Z}}$
with intersection form
![]() $(2n-2)$
. Let
$(2n-2)$
. Let
![]() $v \in L$
be a generator, and consider the isomorphism of abelian groups
$v \in L$
be a generator, and consider the isomorphism of abelian groups
 $$ \begin{align} L^{\vee} / L \xrightarrow{\cong} {\mathbb{Z}} / (2n-2){\mathbb{Z}} \end{align} $$
$$ \begin{align} L^{\vee} / L \xrightarrow{\cong} {\mathbb{Z}} / (2n-2){\mathbb{Z}} \end{align} $$
determined by sending
![]() $v/(2n-2)$
to the residue class of
$v/(2n-2)$
to the residue class of
![]() $1$
. Since the generators of L are
$1$
. Since the generators of L are
![]() $\pm v$
, equation (5) is canonical up to multiplication by
$\pm v$
, equation (5) is canonical up to multiplication by
![]() $1$
.
$1$
.
Since
![]() $\Lambda $
is unimodular, there exists a natural isomorphism ([Reference Huybrechts22, Sec.14])
$\Lambda $
is unimodular, there exists a natural isomorphism ([Reference Huybrechts22, Sec.14])
 $$ \begin{align*} H^{2}(X,{\mathbb{Z}})^{\vee} / H^{2}(X,{\mathbb{Z}}) \xrightarrow{\cong} L^{\vee}/L. \end{align*} $$
$$ \begin{align*} H^{2}(X,{\mathbb{Z}})^{\vee} / H^{2}(X,{\mathbb{Z}}) \xrightarrow{\cong} L^{\vee}/L. \end{align*} $$
If we use Poincaré duality to identify
![]() $H_{2}(X,{\mathbb {Z}})$
with
$H_{2}(X,{\mathbb {Z}})$
with
![]() $H^{2}(X,{\mathbb {Z}})^{\vee }$
, this yields the residue map
$H^{2}(X,{\mathbb {Z}})^{\vee }$
, this yields the residue map
 $$ \begin{align*} r_{X}:H_{2}(X,{\mathbb{Z}})/H^{2}(X,{\mathbb{Z}}) \xrightarrow{\cong} L^{\vee}/L \xrightarrow{\cong} {\mathbb{Z}}/(2n-2) {\mathbb{Z}}. \end{align*} $$
$$ \begin{align*} r_{X}:H_{2}(X,{\mathbb{Z}})/H^{2}(X,{\mathbb{Z}}) \xrightarrow{\cong} L^{\vee}/L \xrightarrow{\cong} {\mathbb{Z}}/(2n-2) {\mathbb{Z}}. \end{align*} $$
The map depends on the choice of the generator v and, hence, is unique up to multiplication by
![]() $\pm 1$
.
$\pm 1$
.
Definition 1. The residue set of a class
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
is defined by
$\beta \in H_{2}(X,{\mathbb {Z}})$
is defined by
if
![]() $n \geq 2$
and by
$n \geq 2$
and by
![]() $\pm [\beta ]=0$
otherwise.
$\pm [\beta ]=0$
otherwise.
Note that, since
![]() $r_{X}$
is canonical up to sign, the residue set is independent of the choice of map
$r_{X}$
is canonical up to sign, the residue set is independent of the choice of map
![]() $r_{X}$
.
$r_{X}$
.
Remark 2. (i) Since parallel transport operators respect the embedding
![]() $i_{X}$
up to composing with an isomorphism of
$i_{X}$
up to composing with an isomorphism of
![]() $\Lambda $
, the residue set
$\Lambda $
, the residue set
![]() $[\beta ]$
is preserved under deformation. (This is also reflected in the fact that the monodromy acts by
$[\beta ]$
is preserved under deformation. (This is also reflected in the fact that the monodromy acts by
![]() $\pm 1$
on the discriminant.) (ii) In the case of the Hilbert scheme
$\pm 1$
on the discriminant.) (ii) In the case of the Hilbert scheme
![]() $X = \mathsf {Hilb}_{n}(S)$
of a K3 surface, let
$X = \mathsf {Hilb}_{n}(S)$
of a K3 surface, let
![]() $A \in H_{2}(X)$
be the class of an exceptional curve, that is, the class of a fiber of the Hilbert–Chow morphism
$A \in H_{2}(X)$
be the class of an exceptional curve, that is, the class of a fiber of the Hilbert–Chow morphism
![]() $\mathsf {Hilb}_{n}(S) \to \mathrm {Sym}^{n}(S)$
over a generic point in the singular locus. We have a natural identification
$\mathsf {Hilb}_{n}(S) \to \mathrm {Sym}^{n}(S)$
over a generic point in the singular locus. We have a natural identification
The morphism
![]() $r_{X}$
then sends (up to sign) the class
$r_{X}$
then sends (up to sign) the class
![]() $[A]$
to
$[A]$
to
![]() $1 \in {\mathbb {Z}}_{2n-2}$
. (iii) In other words, we could have defined the residue class also by first deforming to the Hilbert scheme and then taking the coefficient of A modulo
$1 \in {\mathbb {Z}}_{2n-2}$
. (iii) In other words, we could have defined the residue class also by first deforming to the Hilbert scheme and then taking the coefficient of A modulo
![]() $2n-2$
. This is usually the practical way to compute the residue class.□
$2n-2$
. This is usually the practical way to compute the residue class.□
Let
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
be a class. The class
$\beta \in H_{2}(X,{\mathbb {Z}})$
be a class. The class
![]() $\beta $
has then the following deformation invariants:
$\beta $
has then the following deformation invariants:
-
(i) the divisibility
 $\mathsf {div}(\beta )$
in
$\mathsf {div}(\beta )$
in
 $H_{2}(X,{\mathbb {Z}})$
,
$H_{2}(X,{\mathbb {Z}})$
, -
(ii) the Beauville–Bogomolov norm
 $(\beta , \beta ) \in {\mathbb {Q}}$
, and
$(\beta , \beta ) \in {\mathbb {Q}}$
, and -
(iii) the residue set
 $\pm \left [ \frac {\beta }{\mathsf {div}(\beta )} \right ] \in {\mathbb {Z}} / (2n-2) {\mathbb {Z}}$
.
$\pm \left [ \frac {\beta }{\mathsf {div}(\beta )} \right ] \in {\mathbb {Z}} / (2n-2) {\mathbb {Z}}$
.
The global Torelli theorem and Eichler’s criterion yields the following.
Corollary 2. Two pairs
![]() $(X,\beta )$
and
$(X,\beta )$
and
![]() $(X^{\prime },\beta ^{\prime })$
of a
$(X^{\prime },\beta ^{\prime })$
of a
![]() $K3^{[n]}$
-type variety and a class in
$K3^{[n]}$
-type variety and a class in
![]() $H_{2}(X,{\mathbb {Z}})$
which pairs positively with a Kähler class are deformation equivalent if and only if the invariants (i–iii) agree.
$H_{2}(X,{\mathbb {Z}})$
which pairs positively with a Kähler class are deformation equivalent if and only if the invariants (i–iii) agree.
Remark 3. By the global Torelli theorem, if
![]() $\beta $
and
$\beta $
and
![]() $\beta ^{\prime }$
are both of Hodge type, the deformation in the corollary can be chosen such that the curve class stays of Hodge type.
$\beta ^{\prime }$
are both of Hodge type, the deformation in the corollary can be chosen such that the curve class stays of Hodge type.
1.6 Lifts of isometries of
 $H^{2}$
$H^{2}$
Let
![]() $X_{1}, X_{2}$
be of
$X_{1}, X_{2}$
be of
![]() $K3^{[n]}$
-type, and let
$K3^{[n]}$
-type, and let
be an isometry. An operator
![]() $\widetilde {g} : H^{\ast }(X_{1},{\mathbb {C}}) \to H^{\ast }(X_{2},{\mathbb {C}})$
is a parallel transport lift of g if it is of the form
$\widetilde {g} : H^{\ast }(X_{1},{\mathbb {C}}) \to H^{\ast }(X_{2},{\mathbb {C}})$
is a parallel transport lift of g if it is of the form
 $$ \begin{align*} \widetilde{g} = \rho(g \circ \psi^{-1}, 1) \circ P_{\psi} \end{align*} $$
$$ \begin{align*} \widetilde{g} = \rho(g \circ \psi^{-1}, 1) \circ P_{\psi} \end{align*} $$
for a parallel transport operator
![]() $P_{\psi } : H^{\ast }(X_{1}, {\mathbb {Z}}) \to H^{\ast }(X_{2},{\mathbb {Z}})$
with restriction
$P_{\psi } : H^{\ast }(X_{1}, {\mathbb {Z}}) \to H^{\ast }(X_{2},{\mathbb {Z}})$
with restriction
![]() $\psi = P|_{H^{2}(X_{1},{\mathbb {Z}})}$
. In particular, any parallel transport lift is a degree-preserving orthogonal ring isomorphism.
$\psi = P|_{H^{2}(X_{1},{\mathbb {Z}})}$
. In particular, any parallel transport lift is a degree-preserving orthogonal ring isomorphism.
Recall from Section 1.3, Property 2, the operator
 $$ \begin{align*} \widetilde{D} = \rho(\mathrm{id}, -1) = D \circ \rho(-\mathrm{id}_{H^{2}(X_{2},{\mathbb{Z}})}, 1). \end{align*} $$
$$ \begin{align*} \widetilde{D} = \rho(\mathrm{id}, -1) = D \circ \rho(-\mathrm{id}_{H^{2}(X_{2},{\mathbb{Z}})}, 1). \end{align*} $$
Lemma 1. A parallel transport lift of g is unique up to composition by
![]() $\widetilde {D}$
.
$\widetilde {D}$
.
Proof. Consider two parallel transport lifts of g,
 $$ \begin{align*} \widetilde{g_{i}} = \gamma(g \circ \psi_{i}^{-1}) \circ P_{\psi_{i}}, \quad i=1,2 \end{align*} $$
$$ \begin{align*} \widetilde{g_{i}} = \gamma(g \circ \psi_{i}^{-1}) \circ P_{\psi_{i}}, \quad i=1,2 \end{align*} $$
for parallel transport operators
![]() $P_{\psi _{1}}, P_{\psi _{2}}$
. We will show that
$P_{\psi _{1}}, P_{\psi _{2}}$
. We will show that
Let
![]() $\gamma (h) = \rho (h, 1)$
. If
$\gamma (h) = \rho (h, 1)$
. If
 $\tau (\psi _{1} \circ \psi _{2}^{-1}) = 1$
, then
$\tau (\psi _{1} \circ \psi _{2}^{-1}) = 1$
, then
 $$ \begin{align*} \gamma(g \circ \psi_{1}^{-1}) \circ P_{\psi_{1}} \circ P_{\psi_{2}}^{-1} = \gamma(g \psi_{1}^{-1}) \circ \gamma(\psi_{1} \circ \psi_{2}^{-1}) = \gamma( g \psi_{2}^{-1}). \end{align*} $$
$$ \begin{align*} \gamma(g \circ \psi_{1}^{-1}) \circ P_{\psi_{1}} \circ P_{\psi_{2}}^{-1} = \gamma(g \psi_{1}^{-1}) \circ \gamma(\psi_{1} \circ \psi_{2}^{-1}) = \gamma( g \psi_{2}^{-1}). \end{align*} $$
If
 $\tau (\psi _{1} \circ \psi _{2}^{-1}) = -1$
, then
$\tau (\psi _{1} \circ \psi _{2}^{-1}) = -1$
, then
 $$ \begin{align*} \gamma(g \circ \psi_{1}^{-1}) \circ P_{\psi_{1}} \circ P_{\psi_{2}}^{-1} = \gamma(g \psi_{1}^{-1}) \circ D \circ \gamma(-\psi_{1} \circ \psi_{2}^{-1}) = \widetilde{D} \circ \gamma( g \psi_{2}^{-1}) \end{align*} $$
$$ \begin{align*} \gamma(g \circ \psi_{1}^{-1}) \circ P_{\psi_{1}} \circ P_{\psi_{2}}^{-1} = \gamma(g \psi_{1}^{-1}) \circ D \circ \gamma(-\psi_{1} \circ \psi_{2}^{-1}) = \widetilde{D} \circ \gamma( g \psi_{2}^{-1}) \end{align*} $$
2 The multiple cover conjecture
2.1 Overview
Let X be a variety of
![]() $K3^{[n]}$
-type, and let
$K3^{[n]}$
-type, and let
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
be an effective curve class. The moduli space
$\beta \in H_{2}(X,{\mathbb {Z}})$
be an effective curve class. The moduli space
 ${\overline M}_{g,N}(X,\beta )$
of N-marked genus g stable maps to X in class
${\overline M}_{g,N}(X,\beta )$
of N-marked genus g stable maps to X in class
![]() $\beta $
carries a reduced virtual fundamental class
$\beta $
carries a reduced virtual fundamental class
 $[ {\overline M}_{g,N}(X,\beta ) ]^{\text {red}}$
of dimension
$[ {\overline M}_{g,N}(X,\beta ) ]^{\text {red}}$
of dimension
![]() $(2n-3)(1-g)+N+1$
. Gromov–Witten invariants of X are defined by pairing with this class:
$(2n-3)(1-g)+N+1$
. Gromov–Witten invariants of X are defined by pairing with this class:
 $$ \begin{align} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{n} \big\rangle^{X}_{g,\beta} := \int_{ [ {\overline M}_{g,n}(X,\beta) ]^{\text{red}} } \pi^{\ast}(\alpha) \cup \prod_{i} \operatorname{ev}_{i}^{\ast}(\gamma_{i}), \end{align} $$
$$ \begin{align} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{n} \big\rangle^{X}_{g,\beta} := \int_{ [ {\overline M}_{g,n}(X,\beta) ]^{\text{red}} } \pi^{\ast}(\alpha) \cup \prod_{i} \operatorname{ev}_{i}^{\ast}(\gamma_{i}), \end{align} $$
where
 $\operatorname {ev}_{i} : {\overline M}_{g,n}(X,\beta ) \to X$
are the evaluation maps,
$\operatorname {ev}_{i} : {\overline M}_{g,n}(X,\beta ) \to X$
are the evaluation maps,
 $\tau : {\overline M}_{g,n}(X,\beta ) \to {\overline M}_{g,n}$
is the forgetful map and
$\tau : {\overline M}_{g,n}(X,\beta ) \to {\overline M}_{g,n}$
is the forgetful map and
 $\alpha \in H^{\ast }({\overline M}_{g,n})$
is a tautological class [Reference Faber and Pandharipande16].
$\alpha \in H^{\ast }({\overline M}_{g,n})$
is a tautological class [Reference Faber and Pandharipande16].
In this section, we state a conjecture to express the invariants (6) for
![]() $\beta $
an arbitrary class in terms of invariants where
$\beta $
an arbitrary class in terms of invariants where
![]() $\beta $
is primitive.
$\beta $
is primitive.
2.2 Invariance
Let
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
be an effective curve class, and let
$\beta \in H_{2}(X,{\mathbb {Z}})$
be an effective curve class, and let
 $$ \begin{align*} \widetilde{O}^{+}(H^{2}(X,{\mathbb{Z}}))_{\beta} \subset \widetilde{O}^{+}(H^{2}(X,{\mathbb{Z}})) \end{align*} $$
$$ \begin{align*} \widetilde{O}^{+}(H^{2}(X,{\mathbb{Z}}))_{\beta} \subset \widetilde{O}^{+}(H^{2}(X,{\mathbb{Z}})) \end{align*} $$
be the subgroup fixing
![]() $\beta $
(either via the monodromy representation or equivalently, via the dual action on
$\beta $
(either via the monodromy representation or equivalently, via the dual action on
![]() $H^{2}(X,{\mathbb {Z}})^{\vee } \cong H_{2}(X,{\mathbb {Z}})$
under the Beauville–Bogomolov form). Applying Remark 3 and the deformation invariance of the reduced Gromov–Witten invariants, we find that
$H^{2}(X,{\mathbb {Z}})^{\vee } \cong H_{2}(X,{\mathbb {Z}})$
under the Beauville–Bogomolov form). Applying Remark 3 and the deformation invariance of the reduced Gromov–Witten invariants, we find that
 $$ \begin{align*} \Big\langle \alpha\, ;\, \gamma_{1}, \ldots, \gamma_{n} \Big\rangle^{X}_{g,\beta} = \Big\langle \alpha\, ;\, \mu(\varphi) \gamma_{1},\ \ldots,\ \mu(\varphi) \gamma_{n} \Big\rangle^{X}_{g,\beta} \end{align*} $$
$$ \begin{align*} \Big\langle \alpha\, ;\, \gamma_{1}, \ldots, \gamma_{n} \Big\rangle^{X}_{g,\beta} = \Big\langle \alpha\, ;\, \mu(\varphi) \gamma_{1},\ \ldots,\ \mu(\varphi) \gamma_{n} \Big\rangle^{X}_{g,\beta} \end{align*} $$
for all
 $\varphi \in \widetilde {O}^{+}(H^{2}(X,{\mathbb {Z}}))_{\beta }$
, where we have used
$\varphi \in \widetilde {O}^{+}(H^{2}(X,{\mathbb {Z}}))_{\beta }$
, where we have used
to denote the monodromy representation (defined by the isomorphism (3) composed with the inclusion
![]() $\mathsf {Mon}(X) \subset O(H^{\ast }(X,{\mathbb {Z}}))$
).
$\mathsf {Mon}(X) \subset O(H^{\ast }(X,{\mathbb {Z}}))$
).
The image of
 $\widetilde {O}^{+}(H^{2}(X,{\mathbb {Z}}))_{\beta }$
is Zariski dense in
$\widetilde {O}^{+}(H^{2}(X,{\mathbb {Z}}))_{\beta }$
is Zariski dense in
 $$ \begin{align*} G_{\beta} &= (O(H^{2}(X,{\mathbb{C}})) \times {\mathbb{Z}}/2)_{\beta} \\ &\kern-3pt:= \{ g \in O(H^{2}(X,{\mathbb{C}})) \times {\mathbb{Z}}/2 {\mathbb{Z}}\ |\ \rho(g) \beta = \beta \}. \end{align*} $$
$$ \begin{align*} G_{\beta} &= (O(H^{2}(X,{\mathbb{C}})) \times {\mathbb{Z}}/2)_{\beta} \\ &\kern-3pt:= \{ g \in O(H^{2}(X,{\mathbb{C}})) \times {\mathbb{Z}}/2 {\mathbb{Z}}\ |\ \rho(g) \beta = \beta \}. \end{align*} $$
It follows that for all
![]() $g \in G_{\beta }$
we have
$g \in G_{\beta }$
we have
 $$ \begin{align} \Big\langle \alpha\, ;\, \gamma_{1}, \ldots, \gamma_{n} \Big\rangle^{X}_{g,\beta} = \Big\langle \alpha\, ;\, \rho(g) \gamma_{1},\ \ldots,\ \rho(g) \gamma_{n} \Big\rangle^{X}_{g,\beta}. \end{align} $$
$$ \begin{align} \Big\langle \alpha\, ;\, \gamma_{1}, \ldots, \gamma_{n} \Big\rangle^{X}_{g,\beta} = \Big\langle \alpha\, ;\, \rho(g) \gamma_{1},\ \ldots,\ \rho(g) \gamma_{n} \Big\rangle^{X}_{g,\beta}. \end{align} $$
Equivalently, the pushforward of the reduced virtual class lies in the invariant part of the diagonal
![]() $G_{\beta }$
action:
$G_{\beta }$
action:
 $$ \begin{align*} \operatorname{ev}_{\ast} \left( \tau^{\ast}(\alpha) \cap [{\overline M}_{g,n}(X,\beta)]^{\text{red}} \right) \in H^{\ast}(X^{n}, {\mathbb{Q}})^{G_{\beta}}. \end{align*} $$
$$ \begin{align*} \operatorname{ev}_{\ast} \left( \tau^{\ast}(\alpha) \cap [{\overline M}_{g,n}(X,\beta)]^{\text{red}} \right) \in H^{\ast}(X^{n}, {\mathbb{Q}})^{G_{\beta}}. \end{align*} $$
The representation
![]() $\rho $
restricted to
$\rho $
restricted to
![]() $\{ \mathrm {id} \} \times {\mathbb {Z}}_{2}$
acts trivially on
$\{ \mathrm {id} \} \times {\mathbb {Z}}_{2}$
acts trivially on
![]() $H^{2}(X,{\mathbb {C}})$
. Hence, for X a K3 surface, we obtain the invariance of the Gromov–Witten class under the group
$H^{2}(X,{\mathbb {C}})$
. Hence, for X a K3 surface, we obtain the invariance of the Gromov–Witten class under the group
![]() $O(H^{2}(X,{\mathbb {C}}))_{\beta }$
. This matches what was conjectured in [Reference Oberdieck, Pandharipande, Faber, Farkas and van der Geer45, Conj.C1] and then proven along the above lines in [Reference Buelles9].
$O(H^{2}(X,{\mathbb {C}}))_{\beta }$
. This matches what was conjectured in [Reference Oberdieck, Pandharipande, Faber, Farkas and van der Geer45, Conj.C1] and then proven along the above lines in [Reference Buelles9].
2.3 Multiple-cover conjecture
The main conjecture is the following: Let
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
be any effective curve class. For every divisor
$\beta \in H_{2}(X,{\mathbb {Z}})$
be any effective curve class. For every divisor
![]() $k | \beta $
, let
$k | \beta $
, let
![]() $X_{k}$
be a variety of
$X_{k}$
be a variety of
![]() $K3^{[n]}$
type and let
$K3^{[n]}$
type and let
be a real isometry such that:
-
○
 $\varphi _{k}(\beta /k)$
is a primitive curve class
$\varphi _{k}(\beta /k)$
is a primitive curve class -
○
 $\pm \left [ \varphi _{k}(\beta /k) \right ] = \pm [\beta /k]$
.
$\pm \left [ \varphi _{k}(\beta /k) \right ] = \pm [\beta /k]$
.
We extend
![]() $\varphi _{k}$
as a parallel transport lift (Section 1.6) to the full cohomology:
$\varphi _{k}$
as a parallel transport lift (Section 1.6) to the full cohomology:
By Section 2.6 below, pairs
![]() $(X_{k}, \varphi _{k})$
satisfying these properties can always be found.
$(X_{k}, \varphi _{k})$
satisfying these properties can always be found.
Conjecture B. For any effective curve class
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
, we have
$\beta \in H_{2}(X,{\mathbb {Z}})$
, we have
 $$ \begin{align*} &\Big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \Big\rangle^{X}_{g,\beta} \\ &\qquad= \sum_{k | \beta} k^{3g-3+N - \deg(\alpha)} (-1)^{[\beta] + [\beta/k]} \Big\langle \alpha; \varphi_{k}(\gamma_{1}), \ldots, \varphi_{k}(\gamma_{N}) \Big\rangle^{X_{k}}_{g,\varphi_{k}(\beta/k)}. \end{align*} $$
$$ \begin{align*} &\Big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \Big\rangle^{X}_{g,\beta} \\ &\qquad= \sum_{k | \beta} k^{3g-3+N - \deg(\alpha)} (-1)^{[\beta] + [\beta/k]} \Big\langle \alpha; \varphi_{k}(\gamma_{1}), \ldots, \varphi_{k}(\gamma_{N}) \Big\rangle^{X_{k}}_{g,\varphi_{k}(\beta/k)}. \end{align*} $$
The invariance property discussed in Section 7 and Property 4 of Section 1.3 imply that the right-hand side of the conjecture is independent of the choice of
![]() $(X_{k},\varphi _{k})$
. Using that
$(X_{k},\varphi _{k})$
. Using that
![]() $\sum _{k|a} \mu (k) = \delta _{a1}$
, Conjecture B is also seen to be equivalent to Conjecture A of the introduction.
$\sum _{k|a} \mu (k) = \delta _{a1}$
, Conjecture B is also seen to be equivalent to Conjecture A of the introduction.
The reduced Gromov–Witten invariants of X can only be nonzero if the dimension constraint
 $$ \begin{align*} (\dim X - 3)(1-g) + N + 1 = \deg(\alpha) + \sum_{i} \deg(\gamma_{i}) \end{align*} $$
$$ \begin{align*} (\dim X - 3)(1-g) + N + 1 = \deg(\alpha) + \sum_{i} \deg(\gamma_{i}) \end{align*} $$
is satisfied. Hence, the conjecture can also be rewritten as
 $$ \begin{align*} \Big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \Big\rangle^{X}_{g,\beta} = \sum_{k | \beta} k^{\dim(X)(g-1) - 1 + \sum_{i} \deg(\gamma_{i})} (-1)^{[\beta] + [\beta/k]} \Big\langle \alpha; \varphi_{k}(\gamma_{1}), \ldots, \varphi_{k}(\gamma_{N}) \Big\rangle^{X}_{g,\varphi_{k}(\beta/k)}. \end{align*} $$
$$ \begin{align*} \Big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \Big\rangle^{X}_{g,\beta} = \sum_{k | \beta} k^{\dim(X)(g-1) - 1 + \sum_{i} \deg(\gamma_{i})} (-1)^{[\beta] + [\beta/k]} \Big\langle \alpha; \varphi_{k}(\gamma_{1}), \ldots, \varphi_{k}(\gamma_{N}) \Big\rangle^{X}_{g,\varphi_{k}(\beta/k)}. \end{align*} $$
Since for K3 surfaces the residue always vanishes, Conjecture B specializes for K3 surfaces to the conjecture made in [Reference Oberdieck, Pandharipande, Faber, Farkas and van der Geer45, Conj C2].
Remark 4. The condition that we ask of the residue, i.e.,
![]() $\pm \left [ \varphi _{k}(\beta /k) \right ] = \pm [\beta /k]$
, is necessary for the conjecture to hold. For example, consider X of
$\pm \left [ \varphi _{k}(\beta /k) \right ] = \pm [\beta /k]$
, is necessary for the conjecture to hold. For example, consider X of
![]() $K3^{[5]}$
-type and two primitive classes
$K3^{[5]}$
-type and two primitive classes
![]() $\beta _{1}, \beta _{2}$
with
$\beta _{1}, \beta _{2}$
with
![]() $(\beta _{1} \cdot \beta _{1}) = (\beta _{2} \cdot \beta _{2}) = 16$
but
$(\beta _{1} \cdot \beta _{1}) = (\beta _{2} \cdot \beta _{2}) = 16$
but
![]() $[\beta _{1}]=0$
and
$[\beta _{1}]=0$
and
![]() $[\beta _{2}] = 4$
in
$[\beta _{2}] = 4$
in
![]() ${\mathbb {Z}}/8 {\mathbb {Z}}$
. Then by [Reference Oberdieck42] one has
${\mathbb {Z}}/8 {\mathbb {Z}}$
. Then by [Reference Oberdieck42] one has
 $$ \begin{align*} \operatorname{ev}_{\ast}[{\overline M}_{0,1}(X,\beta_{1})]^{\text{red}} = 1464 \beta_{1}^{\vee}, \quad \operatorname{ev}_{\ast}[{\overline M}_{0,1}(X,\beta_{2})]^{\text{red}} = 480 \beta_{2}^{\vee}, \end{align*} $$
$$ \begin{align*} \operatorname{ev}_{\ast}[{\overline M}_{0,1}(X,\beta_{1})]^{\text{red}} = 1464 \beta_{1}^{\vee}, \quad \operatorname{ev}_{\ast}[{\overline M}_{0,1}(X,\beta_{2})]^{\text{red}} = 480 \beta_{2}^{\vee}, \end{align*} $$
so an isometry taking
![]() $\beta _{1}$
to
$\beta _{1}$
to
![]() $\beta _{2}$
does not preserve Gromov–Witten invariants.
$\beta _{2}$
does not preserve Gromov–Witten invariants.
2.4 Uniruled divisors
An uniruled divisor
![]() $D \subset X$
which is swept out by a rational curve in class
$D \subset X$
which is swept out by a rational curve in class
![]() $\beta $
is a component of the image of
$\beta $
is a component of the image of
![]() $\operatorname {ev}:{\overline M}_{0,1}(X,\beta ) \to X$
. The virtual class of these uniruled divisors is given by the pushforward
$\operatorname {ev}:{\overline M}_{0,1}(X,\beta ) \to X$
. The virtual class of these uniruled divisors is given by the pushforward
![]() $\operatorname {ev}_{\ast } [{\overline M}_{0,1}(X,\beta )]^{\text {red}}$
. For
$\operatorname {ev}_{\ast } [{\overline M}_{0,1}(X,\beta )]^{\text {red}}$
. For
![]() $\beta $
primitive and
$\beta $
primitive and
![]() $(X,\beta )$
very generally, the virtual class is closely related to the actual class [Reference Oberdieck, Shen and Yin47].
$(X,\beta )$
very generally, the virtual class is closely related to the actual class [Reference Oberdieck, Shen and Yin47].
By monodromy invariance (e.g., [Reference Oberdieck, Shen and Yin47, Section 2.6]), there exists
![]() $N_{\beta } \in {\mathbb {Q}}$
such that
$N_{\beta } \in {\mathbb {Q}}$
such that
 $$ \begin{align} \operatorname{ev}_{\ast} [{\overline M}_{0,1}(X,\beta)]^{\text{red}} = N_{\beta} \cdot h , \end{align} $$
$$ \begin{align} \operatorname{ev}_{\ast} [{\overline M}_{0,1}(X,\beta)]^{\text{red}} = N_{\beta} \cdot h , \end{align} $$
where
![]() $h = ( \beta , - ) \in H_{2}(X,{\mathbb {Q}})^{\vee } \cong H^{2}(X,{\mathbb {Q}})$
is the dual of
$h = ( \beta , - ) \in H_{2}(X,{\mathbb {Q}})^{\vee } \cong H^{2}(X,{\mathbb {Q}})$
is the dual of
![]() $\beta $
with respect to the Beauville–Bogomolov–Fujiki form. Since by deformation invariance
$\beta $
with respect to the Beauville–Bogomolov–Fujiki form. Since by deformation invariance
![]() $N_{\beta }$
only depends on the divisibility
$N_{\beta }$
only depends on the divisibility
![]() $m = \mathsf {div}(\beta )$
, the square
$m = \mathsf {div}(\beta )$
, the square
![]() $s = (\beta , \beta )$
and the residue
$s = (\beta , \beta )$
and the residue
![]() $r = [\beta / \mathsf {div}(\beta )]$
we write
$r = [\beta / \mathsf {div}(\beta )]$
we write
Conjecture B then says that
 $$ \begin{align} N_{m,s,r} = \sum_{k | \beta} \frac{1}{k^{3}} (-1)^{mr + \frac{m}{k} r} N_{1, \frac{s}{k^{2}}, \frac{mr}{k}}. \end{align} $$
$$ \begin{align} N_{m,s,r} = \sum_{k | \beta} \frac{1}{k^{3}} (-1)^{mr + \frac{m}{k} r} N_{1, \frac{s}{k^{2}}, \frac{mr}{k}}. \end{align} $$
The primitive numbers
![]() $N_{1,s,r}$
have been determined in [Reference Oberdieck42].
$N_{1,s,r}$
have been determined in [Reference Oberdieck42].
Example 1. Let
![]() $X = \mathsf {Hilb}_{2}(S)$
, and let
$X = \mathsf {Hilb}_{2}(S)$
, and let
![]() $A \in H_{2}(X,{\mathbb {Z}})$
be the class of the exceptional curve. We have
$A \in H_{2}(X,{\mathbb {Z}})$
be the class of the exceptional curve. We have
 $$ \begin{align*} \operatorname{ev}_{\ast} [{\overline M}_{0,1}(X,\beta)]^{\text{red}} = \Delta_{\mathsf{Hilb}_{2}(S)} = -2 \delta. \end{align*} $$
$$ \begin{align*} \operatorname{ev}_{\ast} [{\overline M}_{0,1}(X,\beta)]^{\text{red}} = \Delta_{\mathsf{Hilb}_{2}(S)} = -2 \delta. \end{align*} $$
Since
 $A^{\vee } = -\frac {1}{2} \delta $
, we see
$A^{\vee } = -\frac {1}{2} \delta $
, we see
 $N_{1,-\frac {1}{2},1} = 4$
. The multiple cover formula then predicts that for even
$N_{1,-\frac {1}{2},1} = 4$
. The multiple cover formula then predicts that for even
![]() $\ell \in {\mathbb {Z}}_{\geq 1}$
we have
$\ell \in {\mathbb {Z}}_{\geq 1}$
we have
 $$ \begin{align*} N_{\ell A} = -\frac{1}{\ell^{3}} N_{1,-\frac{1}{2},1} + \frac{1}{(\ell/2)^{3}} N_{1,-2,0} = \frac{-4}{\ell^{3}} + \frac{8}{\ell^{3}} = \frac{4}{\ell^{3}}, \end{align*} $$
$$ \begin{align*} N_{\ell A} = -\frac{1}{\ell^{3}} N_{1,-\frac{1}{2},1} + \frac{1}{(\ell/2)^{3}} N_{1,-2,0} = \frac{-4}{\ell^{3}} + \frac{8}{\ell^{3}} = \frac{4}{\ell^{3}}, \end{align*} $$
where we have used
![]() $N_{1,-2,0} = 1$
. This matches the degree-scaling property discussed in [Reference Maulik and Oblomkov36, Reference Okounkov and Pandharipande48].
$N_{1,-2,0} = 1$
. This matches the degree-scaling property discussed in [Reference Maulik and Oblomkov36, Reference Okounkov and Pandharipande48].
2.5 Fourfolds
We consider genus
![]() $0$
Gromov–Witten invariants of a variety X of
$0$
Gromov–Witten invariants of a variety X of
![]() $K3^{[2]}$
-type. By dimension considerations, all genus
$K3^{[2]}$
-type. By dimension considerations, all genus
![]() $0$
Gromov–Witten invariants are determined by the two-point class:
$0$
Gromov–Witten invariants are determined by the two-point class:
 $$ \begin{align*} \operatorname{ev}_{\ast} [{\overline M}_{0,2}(X,\beta)]^{\text{red}} \in H^{\ast}(X \times X). \end{align*} $$
$$ \begin{align*} \operatorname{ev}_{\ast} [{\overline M}_{0,2}(X,\beta)]^{\text{red}} \in H^{\ast}(X \times X). \end{align*} $$
Following the arguments of [Reference Oberdieck, Shen and Yin47, Sec.2]Footnote
6
, for every effective
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
there exist constantsFootnote
7
$\beta \in H_{2}(X,{\mathbb {Z}})$
there exist constantsFootnote
7
![]() $F_{\beta }, G_{\beta } \in {\mathbb {Q}}$
such that
$F_{\beta }, G_{\beta } \in {\mathbb {Q}}$
such that
 $$ \begin{align*} \operatorname{ev}_{\ast}[{\overline M}_{0,2}(X,\beta)]^{\text{red}} &= F_{\beta} (h^{2} \otimes h^{2}) + G_{\beta} \big(h \otimes \beta + \beta \otimes h + (h \otimes h) \cdot c_{BB} \big) \\ & \quad + \left( -\frac{1}{30} (h^{2} \otimes c_{2} + c_{2} \otimes h^{2}) + \frac{1}{900} (\beta, \beta) c_{2} \otimes c_{2} \right) (G_{\beta} + (\beta, \beta) F_{\beta} ), \end{align*} $$
$$ \begin{align*} \operatorname{ev}_{\ast}[{\overline M}_{0,2}(X,\beta)]^{\text{red}} &= F_{\beta} (h^{2} \otimes h^{2}) + G_{\beta} \big(h \otimes \beta + \beta \otimes h + (h \otimes h) \cdot c_{BB} \big) \\ & \quad + \left( -\frac{1}{30} (h^{2} \otimes c_{2} + c_{2} \otimes h^{2}) + \frac{1}{900} (\beta, \beta) c_{2} \otimes c_{2} \right) (G_{\beta} + (\beta, \beta) F_{\beta} ), \end{align*} $$
where
-
○
 $h = ( \beta , - ) \in H^{2}(X,{\mathbb {Q}})$
is the dual of the curve class,
$h = ( \beta , - ) \in H^{2}(X,{\mathbb {Q}})$
is the dual of the curve class, -
○
 $c_{2} = c_{2}(X)$
is the second Chern class, and
$c_{2} = c_{2}(X)$
is the second Chern class, and -
○
 $c_{BB} \in H^{2}(X) \otimes H^{2}(X)$
is the inverse of the Beauville–Bogomolov–Fujiki form.
$c_{BB} \in H^{2}(X) \otimes H^{2}(X)$
is the inverse of the Beauville–Bogomolov–Fujiki form.
In
![]() $K3^{[2]}$
-type, the residue
$K3^{[2]}$
-type, the residue
![]() $r = [\beta ]$
of a curve class is determined by
$r = [\beta ]$
of a curve class is determined by
![]() $s = (\beta ,\beta )$
via
$s = (\beta ,\beta )$
via
![]() $r = 2 s \text { mod } 2$
. So we can write
$r = 2 s \text { mod } 2$
. So we can write
![]() $F_{\beta } = F_{m,s}$
and
$F_{\beta } = F_{m,s}$
and
![]() $G_{\beta } = G_{m,s}$
. The multiple cover conjecture for
$G_{\beta } = G_{m,s}$
. The multiple cover conjecture for
![]() $K3^{[2]}$
-type in genus
$K3^{[2]}$
-type in genus
![]() $0$
is then equivalent to
$0$
is then equivalent to
 $$ \begin{gather*} F_{m,s} = \sum_{k|m} \frac{1}{k^{5}} (-1)^{2 (s+s/k^{2})} F_{1,\frac{s}{k^{2}}} \\ G_{m,s} = \sum_{k|m} \frac{1}{k^{3}} (-1)^{2 (s+s/k^{2})} G_{1,\frac{s}{k^{2}}}. \end{gather*} $$
$$ \begin{gather*} F_{m,s} = \sum_{k|m} \frac{1}{k^{5}} (-1)^{2 (s+s/k^{2})} F_{1,\frac{s}{k^{2}}} \\ G_{m,s} = \sum_{k|m} \frac{1}{k^{3}} (-1)^{2 (s+s/k^{2})} G_{1,\frac{s}{k^{2}}}. \end{gather*} $$
We can also define
 $$ \begin{gather*} f_{m,s} = \sum_{k|m} \frac{\mu(k)}{k^{5}} (-1)^{2(s + s/k^{2})} F_{\frac{m}{k},\frac{s}{k^{2}}} \\ g_{m,s} = \sum_{k|m} \frac{\mu(k)}{k^{3}} (-1)^{2(s + s/k^{2})} G_{\frac{m}{k},\frac{s}{k^{2}}}. \end{gather*} $$
$$ \begin{gather*} f_{m,s} = \sum_{k|m} \frac{\mu(k)}{k^{5}} (-1)^{2(s + s/k^{2})} F_{\frac{m}{k},\frac{s}{k^{2}}} \\ g_{m,s} = \sum_{k|m} \frac{\mu(k)}{k^{3}} (-1)^{2(s + s/k^{2})} G_{\frac{m}{k},\frac{s}{k^{2}}}. \end{gather*} $$
and arrive at the following.
Lemma 2. Conjecture B in
![]() $K3^{[2]}$
-type and genus
$K3^{[2]}$
-type and genus
![]() $0$
is equivalent to
$0$
is equivalent to
The first few cases are known.
Proposition 2. Conjecture B in
![]() $K3^{[2]}$
-type and genus
$K3^{[2]}$
-type and genus
![]() $0$
holds for all classes
$0$
holds for all classes
![]() $\beta $
such that (i)
$\beta $
such that (i)
![]() $(\beta , \beta ) < 0$
or (ii)
$(\beta , \beta ) < 0$
or (ii)
![]() $(\beta , \beta ) = 0$
and
$(\beta , \beta ) = 0$
and
![]() $N=1$
.
$N=1$
.
Proof. The case
![]() $(\beta , \beta ) < 0$
follows from [Reference Maulik and Oblomkov36, Reference Okounkov and Pandharipande48]. In case
$(\beta , \beta ) < 0$
follows from [Reference Maulik and Oblomkov36, Reference Okounkov and Pandharipande48]. In case
![]() $(\beta , \beta ) = 0$
, the series
$(\beta , \beta ) = 0$
, the series
![]() $g_{m,s}$
is determined by intersecting the one-pointed class with a curve, and then using the methods of [Reference Oberdieck42] to reduce to
$g_{m,s}$
is determined by intersecting the one-pointed class with a curve, and then using the methods of [Reference Oberdieck42] to reduce to
![]() $\mathsf {Hilb}_{2}(\mathbb {P}^{1} \times E)$
. The resulting series is evaluated by T in [Reference Oberdieck42, Thm.9].
$\mathsf {Hilb}_{2}(\mathbb {P}^{1} \times E)$
. The resulting series is evaluated by T in [Reference Oberdieck42, Thm.9].
For later use, we will also need to following expression for one-pointed descendence invariants:
 $$ \begin{align*} \operatorname{ev}_{\ast} [{\overline M}_{0,1}(X,\beta) ] & = G_{\beta} \beta^{\vee} \\ \operatorname{ev}_{\ast} \left( \psi_{1} \cdot [{\overline M}_{0,1}(X,\beta) ] \right) & = 2 F_{\beta} h^{2} - \frac{1}{15} \left( G_{\beta} + (\beta, \beta) F_{\beta} \right) c_{2}(X) \\ \operatorname{ev}_{\ast} \left( \psi_{1}^{2} \cdot [{\overline M}_{0,1}(X,\beta) ] \right) & = -12 F_{\beta} \\ \operatorname{ev}_{\ast} \left( \psi_{1}^{3} \cdot [{\overline M}_{0,1}(X,\beta) ] \right) & = 24 F_{\beta}. \end{align*} $$
$$ \begin{align*} \operatorname{ev}_{\ast} [{\overline M}_{0,1}(X,\beta) ] & = G_{\beta} \beta^{\vee} \\ \operatorname{ev}_{\ast} \left( \psi_{1} \cdot [{\overline M}_{0,1}(X,\beta) ] \right) & = 2 F_{\beta} h^{2} - \frac{1}{15} \left( G_{\beta} + (\beta, \beta) F_{\beta} \right) c_{2}(X) \\ \operatorname{ev}_{\ast} \left( \psi_{1}^{2} \cdot [{\overline M}_{0,1}(X,\beta) ] \right) & = -12 F_{\beta} \\ \operatorname{ev}_{\ast} \left( \psi_{1}^{3} \cdot [{\overline M}_{0,1}(X,\beta) ] \right) & = 24 F_{\beta}. \end{align*} $$
This follows by monodromy invariance and topological recursions. In particular, to check the multiple cover formula in
![]() $K3^{[2]}$
-type and genus
$K3^{[2]}$
-type and genus
![]() $0$
it is enough to consider one-point descendent invariants.
$0$
it is enough to consider one-point descendent invariants.
Remark 5. For convenience, we recall the evaluation of
![]() $f_{1,m,s}$
and
$f_{1,m,s}$
and
![]() $g_{1,m,s}$
. Let
$g_{1,m,s}$
. Let
 $$ \begin{gather*} \vartheta(q) = \sum_{n \in {\mathbb{Z}}} q^{n^{2}}, \quad \alpha(q) = \sum_{\substack{\text{odd }n> 0 \\ d|n}} d q^{n}, \\ G_{2}(q) = -\frac{1}{24} + \sum_{n \geq 1} \sum_{d|n} d q^{n}, \quad \Delta(q) = q \prod_{n \geq 1} (1-q^{n})^{24}. \end{gather*} $$
$$ \begin{gather*} \vartheta(q) = \sum_{n \in {\mathbb{Z}}} q^{n^{2}}, \quad \alpha(q) = \sum_{\substack{\text{odd }n> 0 \\ d|n}} d q^{n}, \\ G_{2}(q) = -\frac{1}{24} + \sum_{n \geq 1} \sum_{d|n} d q^{n}, \quad \Delta(q) = q \prod_{n \geq 1} (1-q^{n})^{24}. \end{gather*} $$
Then by [Reference Oberdieck42] one has
 $$ \begin{align*} \sum_{s} f_{1,s} (-q)^{4s} &= \frac{1}{4} \frac{-1}{\vartheta(q) \alpha(q) \Delta(q^{4})} \\ \sum_{s} g_{1,s} (-q)^{4s} &= \frac{1}{12} \frac{\vartheta^{4}(q) + 4 \alpha(q) + 24 G_{2}(q^{4})}{\vartheta(q) \alpha(q) \Delta(q^{4})}. \end{align*} $$
$$ \begin{align*} \sum_{s} f_{1,s} (-q)^{4s} &= \frac{1}{4} \frac{-1}{\vartheta(q) \alpha(q) \Delta(q^{4})} \\ \sum_{s} g_{1,s} (-q)^{4s} &= \frac{1}{12} \frac{\vartheta^{4}(q) + 4 \alpha(q) + 24 G_{2}(q^{4})}{\vartheta(q) \alpha(q) \Delta(q^{4})}. \end{align*} $$
2.6 Hilbert schemes of elliptic K3 surfaces
Let
be an elliptic K3 surface with a section. Let
![]() $B, F \in H^{2}(S,{\mathbb {Z}})$
be the class of the section and a fiber, respectively, and let
$B, F \in H^{2}(S,{\mathbb {Z}})$
be the class of the section and a fiber, respectively, and let
We consider the Hilbert scheme
![]() $X = \mathsf {Hilb}_{n} S$
and the generating series of Gromov–Witten invariants
$X = \mathsf {Hilb}_{n} S$
and the generating series of Gromov–Witten invariants
 $$ \begin{align*} F_{g,m}(\alpha; \gamma_{1}, \ldots, \gamma_{N}) = \sum_{d = -m}^{\infty} \sum_{r \in {\mathbb{Z}}} \left\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \right\rangle^{\mathsf{Hilb}_{n} S}_{g, mW+dF+rA} q^{d} (-p)^{r}. \end{align*} $$
$$ \begin{align*} F_{g,m}(\alpha; \gamma_{1}, \ldots, \gamma_{N}) = \sum_{d = -m}^{\infty} \sum_{r \in {\mathbb{Z}}} \left\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \right\rangle^{\mathsf{Hilb}_{n} S}_{g, mW+dF+rA} q^{d} (-p)^{r}. \end{align*} $$
We state a characterization of the multiple cover formula:
Consider the basis of
![]() $H^{\ast }(S,{\mathbb {R}})$
defined by
$H^{\ast }(S,{\mathbb {R}})$
defined by
where
![]() ${\mathsf {p}}$
is the class of a point and
${\mathsf {p}}$
is the class of a point and
![]() $e_{3}, \ldots , e_{22}$
is a basis of
$e_{3}, \ldots , e_{22}$
is a basis of
![]() ${\mathbb {Q}}\langle W,F \rangle ^{\perp }$
in
${\mathbb {Q}}\langle W,F \rangle ^{\perp }$
in
![]() $H^{2}(S,{\mathbb {R}})$
. An element
$H^{2}(S,{\mathbb {R}})$
. An element
![]() $\gamma \in H^{\ast }(X,{\mathbb {R}})$
is in the Nakajima basis with respect to
$\gamma \in H^{\ast }(X,{\mathbb {R}})$
is in the Nakajima basis with respect to
![]() ${\mathcal B}$
if it is of the form
${\mathcal B}$
if it is of the form
 $$ \begin{align*} \gamma = \prod_{i} {\mathfrak{q}}_{k_{i}}(\alpha_{i})1, \quad \alpha_{i} \in {\mathcal B}. \end{align*} $$
$$ \begin{align*} \gamma = \prod_{i} {\mathfrak{q}}_{k_{i}}(\alpha_{i})1, \quad \alpha_{i} \in {\mathcal B}. \end{align*} $$
Let
![]() $w(\gamma )$
and
$w(\gamma )$
and
![]() $f(\gamma )$
be the number of classes
$f(\gamma )$
be the number of classes
![]() $\alpha _{i}$
which are equal to W and F, respectively, and define a modified degree grading
$\alpha _{i}$
which are equal to W and F, respectively, and define a modified degree grading
![]() $\underline {\deg }$
by:
$\underline {\deg }$
by:
For a series
 $f = \sum _{d,r} c(d,r) q^{d} p^{r}$
, define the formal Hecke operator by
$f = \sum _{d,r} c(d,r) q^{d} p^{r}$
, define the formal Hecke operator by
 $$ \begin{align*} T_{m,\ell} f = \sum_{d,r} \left( \sum_{k|(m,d,r)} k^{\ell-1} c\left( \frac{md}{k^{2}}, \frac{r}{k} \right) \right) q^{d} p^{r}. \end{align*} $$
$$ \begin{align*} T_{m,\ell} f = \sum_{d,r} \left( \sum_{k|(m,d,r)} k^{\ell-1} c\left( \frac{md}{k^{2}}, \frac{r}{k} \right) \right) q^{d} p^{r}. \end{align*} $$
Lemma 3. Conjecture B holds if and only if for all
![]() $m>0$
, all
$m>0$
, all
![]() $g, N, \alpha $
and all
$g, N, \alpha $
and all
![]() $(\deg , \underline {\deg })$
-bihomogeneous classes
$(\deg , \underline {\deg })$
-bihomogeneous classes
![]() $\gamma _{i}$
we have
$\gamma _{i}$
we have
 $$ \begin{align} F_{g,m}(\alpha; \gamma_{1}, \ldots, \gamma_{N}) = m^{\sum_{i} \deg(\gamma_{i}) - \underline{\deg}(\gamma_{i})} \cdot T_{m,\ell} F_{g,1}(\alpha; \gamma_{1}, \ldots, \gamma_{N}) \end{align} $$
$$ \begin{align} F_{g,m}(\alpha; \gamma_{1}, \ldots, \gamma_{N}) = m^{\sum_{i} \deg(\gamma_{i}) - \underline{\deg}(\gamma_{i})} \cdot T_{m,\ell} F_{g,1}(\alpha; \gamma_{1}, \ldots, \gamma_{N}) \end{align} $$
where
![]() $\ell = 2n(g-1) + \sum _{i} \underline {\deg }(\gamma _{i})$
.
$\ell = 2n(g-1) + \sum _{i} \underline {\deg }(\gamma _{i})$
.
Proof. Given the class
![]() $\beta = mW + dF + rA$
and a divisor
$\beta = mW + dF + rA$
and a divisor
![]() $k | \beta $
, consider the real isometry
$k | \beta $
, consider the real isometry
![]() $\varphi _{k} : H^{2}(X,{\mathbb {R}}) \to H^{2}(X,{\mathbb {R}})$
defined by
$\varphi _{k} : H^{2}(X,{\mathbb {R}}) \to H^{2}(X,{\mathbb {R}})$
defined by
 $$ \begin{align*} W & \mapsto \frac{k}{m} W \\ F & \mapsto \frac{m}{k} F \\ \gamma & \mapsto \gamma \text{ for all } \gamma \perp W,F. \end{align*} $$
$$ \begin{align*} W & \mapsto \frac{k}{m} W \\ F & \mapsto \frac{m}{k} F \\ \gamma & \mapsto \gamma \text{ for all } \gamma \perp W,F. \end{align*} $$
We extend this map to the full cohomology by
![]() $\varphi _{k} = \rho (\phi _{k},0): H^{\ast }(X,{\mathbb {R}}) \to H^{\ast }(X,{\mathbb {R}})$
. We then have
$\varphi _{k} = \rho (\phi _{k},0): H^{\ast }(X,{\mathbb {R}}) \to H^{\ast }(X,{\mathbb {R}})$
. We then have
 $$ \begin{align*} \varphi_{k}\left( \frac{\beta}{k} \right) = W + \frac{dm}{k^{2}} F + \frac{r}{k} A. \end{align*} $$
$$ \begin{align*} \varphi_{k}\left( \frac{\beta}{k} \right) = W + \frac{dm}{k^{2}} F + \frac{r}{k} A. \end{align*} $$
The Nakajima operators are equivariant with respect to the action of
![]() $\varphi _{k}$
, and the isometry of
$\varphi _{k}$
, and the isometry of
![]() $H^{\ast }(S,{\mathbb {R}})$
given by
$H^{\ast }(S,{\mathbb {R}})$
given by
see Property 3 of Section 1.3.
Let
![]() $\gamma _{i} \in H^{\ast }(X,{\mathbb {Q}})$
be elements in the Nakajima basis with respect to
$\gamma _{i} \in H^{\ast }(X,{\mathbb {Q}})$
be elements in the Nakajima basis with respect to
![]() ${\mathcal B}$
. If Conjecture B holds, then its application with respect to
${\mathcal B}$
. If Conjecture B holds, then its application with respect to
![]() $\varphi _{k}$
yields:
$\varphi _{k}$
yields:
 $$ \begin{align} F_{g,m}(\alpha; \gamma_{1}, \ldots, \gamma_{N}) &= \sum_{d,r} q^{d} p^{r} \sum_{k|(m,d,r)} (-1)^{r/k} k^{3g-3+N-\deg(\alpha)} \nonumber\\ &\quad \times \left( \frac{m}{k} \right)^{\sum_{i} f(\gamma_{i}) -w(\gamma_{i})} \left\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \right\rangle^{\mathsf{Hilb}_{n}}_{g, W + \frac{md}{k^{2}} F + \frac{r}{k} A}. \end{align} $$
$$ \begin{align} F_{g,m}(\alpha; \gamma_{1}, \ldots, \gamma_{N}) &= \sum_{d,r} q^{d} p^{r} \sum_{k|(m,d,r)} (-1)^{r/k} k^{3g-3+N-\deg(\alpha)} \nonumber\\ &\quad \times \left( \frac{m}{k} \right)^{\sum_{i} f(\gamma_{i}) -w(\gamma_{i})} \left\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \right\rangle^{\mathsf{Hilb}_{n}}_{g, W + \frac{md}{k^{2}} F + \frac{r}{k} A}. \end{align} $$
Using the dimension constraint, our modified degree function and the formal Hecke operators this becomes: Define the weight of a cohomology class in the Nakajima basis with respect to
![]() ${\mathcal B}$
by
${\mathcal B}$
by
 $$ \begin{align*} {\mathsf{wt}}\left( \prod_{i} {\mathfrak{q}}_{a_{i}}(\alpha_{i}) 1 \right) = \sum_{i} {\mathsf{wt}}(\alpha_{i}), \end{align*} $$
$$ \begin{align*} {\mathsf{wt}}\left( \prod_{i} {\mathfrak{q}}_{a_{i}}(\alpha_{i}) 1 \right) = \sum_{i} {\mathsf{wt}}(\alpha_{i}), \end{align*} $$
where
 $$ \begin{align*} {\mathsf{wt}}(\alpha) = \begin{cases} 1 & \text{ if } \alpha \in \{ {\mathsf{p}}, W \} \\ -1 & \text{ if } \alpha \in \{ 1, F \} \\ 0 & \text{ if } \alpha \in \{ 1,F,W,{\mathsf{p}} \}^{\perp}. \end{cases} \end{align*} $$
$$ \begin{align*} {\mathsf{wt}}(\alpha) = \begin{cases} 1 & \text{ if } \alpha \in \{ {\mathsf{p}}, W \} \\ -1 & \text{ if } \alpha \in \{ 1, F \} \\ 0 & \text{ if } \alpha \in \{ 1,F,W,{\mathsf{p}} \}^{\perp}. \end{cases} \end{align*} $$
For a homogeneous
![]() $\gamma \in H^{\ast }(\mathsf {Hilb}_{n}(S))$
, we then set
$\gamma \in H^{\ast }(\mathsf {Hilb}_{n}(S))$
, we then set
![]() $\underline {\deg }(\gamma ) = {\mathsf {wt}}(\gamma ) + n$
.
$\underline {\deg }(\gamma ) = {\mathsf {wt}}(\gamma ) + n$
.
Since the Nakajima operator
![]() ${\mathfrak {q}}_{i}(\alpha )$
has degree
${\mathfrak {q}}_{i}(\alpha )$
has degree
![]() $i-1 + \deg (\alpha )$
, we have for
$i-1 + \deg (\alpha )$
, we have for
 $\gamma = \prod _{i=1}^{\ell } {\mathfrak {q}}_{i}(\alpha _{i}) 1 \in H^{\ast }(\mathsf {Hilb}_{n} S )$
that
$\gamma = \prod _{i=1}^{\ell } {\mathfrak {q}}_{i}(\alpha _{i}) 1 \in H^{\ast }(\mathsf {Hilb}_{n} S )$
that
 $$ \begin{align*} \deg( \gamma ) = n - \ell + \sum_{i} \deg(\alpha_{i}). \end{align*} $$
$$ \begin{align*} \deg( \gamma ) = n - \ell + \sum_{i} \deg(\alpha_{i}). \end{align*} $$
Hence, we can rewrite
 $$ \begin{align*} \sum_{i=1}^{n} \deg(\gamma_{i}) + w - f & = n N - \sum_{i} \ell(\gamma_{i}) + \sum_{i,j} \deg(\alpha_{ij}) + w - f \\ & = n M + \sum_{i} {\mathsf{wt}}(\gamma_{i}) \\ & = \sum_{i} \underline{\deg}(\gamma_{i}) \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{n} \deg(\gamma_{i}) + w - f & = n N - \sum_{i} \ell(\gamma_{i}) + \sum_{i,j} \deg(\alpha_{ij}) + w - f \\ & = n M + \sum_{i} {\mathsf{wt}}(\gamma_{i}) \\ & = \sum_{i} \underline{\deg}(\gamma_{i}) \end{align*} $$
 $$ \begin{align} F_{g,m}(\alpha; \gamma_{1}, \ldots, \gamma_{N}) &= m^{\sum_{i} \deg(\gamma_{i}) - \underline{\deg}(\gamma_{i})} \nonumber\\ &\quad \times \sum_{d,r} q^{d} p^{r} \sum_{k|(m,d,r)} (-1)^{r/k} k^{2n(g-1)-1 + \sum_{i} \underline{\deg}(\gamma_{i})} \left\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \right\rangle^{\mathsf{Hilb}_{n}}_{g, W + \frac{md}{k^{2}} F + \frac{r}{k} A} \end{align} $$
$$ \begin{align} F_{g,m}(\alpha; \gamma_{1}, \ldots, \gamma_{N}) &= m^{\sum_{i} \deg(\gamma_{i}) - \underline{\deg}(\gamma_{i})} \nonumber\\ &\quad \times \sum_{d,r} q^{d} p^{r} \sum_{k|(m,d,r)} (-1)^{r/k} k^{2n(g-1)-1 + \sum_{i} \underline{\deg}(\gamma_{i})} \left\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \right\rangle^{\mathsf{Hilb}_{n}}_{g, W + \frac{md}{k^{2}} F + \frac{r}{k} A} \end{align} $$
which is equation (10).
Conversely, equality (10) implies Conjecture B since any pair
![]() $(X,\beta )$
is deformation equivalent to some
$(X,\beta )$
is deformation equivalent to some
![]() $(\mathsf {Hilb}_{n}(S), \widetilde {\beta } = mW+dF+kA)$
with
$(\mathsf {Hilb}_{n}(S), \widetilde {\beta } = mW+dF+kA)$
with
![]() $m>0$
, and the right-hand side of Conjecture B is independent of choices.
$m>0$
, and the right-hand side of Conjecture B is independent of choices.
We will reinterpret the lemma in terms of Jacobi forms in [Reference Oberdieck44]. See also [Reference Bae and Buelles1] for a parallel discussion in the case of K3 surfaces.
3 Noether–Lefschetz theory
3.1 Lattice polarized holomorphic-symplectic varieties
Let V be the abstract lattice, and let
![]() $L \subset V$
be a primitive nondegenerate sublatticeFootnote
8
.
$L \subset V$
be a primitive nondegenerate sublatticeFootnote
8
.
An L-polarization of a holomorphic-symplectic variety X is a primitive embedding
such that
-
○ there exists an isometry
 $\varphi : V \xrightarrow {\cong } H^{2}(X,{\mathbb {Z}})$
with
$\varphi : V \xrightarrow {\cong } H^{2}(X,{\mathbb {Z}})$
with
 $\varphi |_{L} = j$
, and
$\varphi |_{L} = j$
, and -
○ the image
 $j(L)$
contains an ample class.
$j(L)$
contains an ample class.
We call the isometry
![]() $\varphi $
as above a marking of
$\varphi $
as above a marking of
![]() $(X,j)$
. If the image
$(X,j)$
. If the image
![]() $j(L)$
only contains a big and nef line bundle, we say that X is L-quasipolarized. Let
$j(L)$
only contains a big and nef line bundle, we say that X is L-quasipolarized. Let
![]() ${\mathcal M}_{L}$
be the moduli space of L-quasipolarized holomorphic-symplectic varieties of a given fixed deformation type.
${\mathcal M}_{L}$
be the moduli space of L-quasipolarized holomorphic-symplectic varieties of a given fixed deformation type.
The period domain associated to
![]() $L \subset V$
is
$L \subset V$
is
and has two connected components. Let
![]() ${\mathcal D}_{L}^{+}$
be one of these components. Consider the subgroup
${\mathcal D}_{L}^{+}$
be one of these components. Consider the subgroup
which, for some choice of marking
![]() $\varphi : V \to H^{2}(X,{\mathbb {Z}})$
for some
$\varphi : V \to H^{2}(X,{\mathbb {Z}})$
for some
![]() $(X,j)$
defining a point in
$(X,j)$
defining a point in
![]() ${\mathcal M}_{L}$
, can be identified with the monodromy group
${\mathcal M}_{L}$
, can be identified with the monodromy group
![]() $\mathsf {Mon}^{2}(X)$
of X.Footnote
9
Let
$\mathsf {Mon}^{2}(X)$
of X.Footnote
9
Let
![]() $\mathsf {Mon}(V)_{L}$
be the subgroup of
$\mathsf {Mon}(V)_{L}$
be the subgroup of
![]() $\mathsf {Mon}(V)$
that acts trivially on L. Then the global Torelli theorem says that the period mapping
$\mathsf {Mon}(V)$
that acts trivially on L. Then the global Torelli theorem says that the period mapping
is surjective, restricts to an open embedding on the open locus of L-polarized holomorphic symplectic varieties and any fiber consists of birational holomorphic symplectic varieties; see [Reference Markman34] for a survey and references.
3.2 One-parameter families
Let
![]() $L_{i}, i = 1, \ldots , \ell $
be an integral basis of L.
$L_{i}, i = 1, \ldots , \ell $
be an integral basis of L.
Given a compact complex manifold
![]() ${\mathcal X}$
of dimension
${\mathcal X}$
of dimension
![]() $2n+1$
, line bundles
$2n+1$
, line bundles
and a morphism
![]() $\pi : {\mathcal X} \to C$
to a smooth proper curve, following [Reference Klemm, Maulik, Pandharipande and Scheidegger26, 0.2.2], we call the tuple
$\pi : {\mathcal X} \to C$
to a smooth proper curve, following [Reference Klemm, Maulik, Pandharipande and Scheidegger26, 0.2.2], we call the tuple
![]() $({\mathcal X}, {\mathcal L}_{1}, \ldots , {\mathcal L}_{\ell }, \pi )$
a one-parameter family of L-quasipolarized holomorphic-symplectic varieties if the following holds:
$({\mathcal X}, {\mathcal L}_{1}, \ldots , {\mathcal L}_{\ell }, \pi )$
a one-parameter family of L-quasipolarized holomorphic-symplectic varieties if the following holds:
-
(i) For every
 $t \in C$
, the fiber
$t \in C$
, the fiber
 $(X_{t}, L_{i} \mapsto {\mathcal L}_{i}|_{X_{t}})$
is a L-quasipolarized holomorphic-symplectic variety.
$(X_{t}, L_{i} \mapsto {\mathcal L}_{i}|_{X_{t}})$
is a L-quasipolarized holomorphic-symplectic variety. -
(ii) There exists an vector
 $h \in L$
which yields a quasi-polarization on all fibers of
$h \in L$
which yields a quasi-polarization on all fibers of
 $\pi $
simultaneously.
$\pi $
simultaneously.
Any one-parameter family as above defines a morphism
![]() $\iota _{\pi } : C \to {\mathcal M}_{L}$
into the moduli space of L-quasipolarized holomorphic-symplectic varieties (of the deformation type specified by a fiber).
$\iota _{\pi } : C \to {\mathcal M}_{L}$
into the moduli space of L-quasipolarized holomorphic-symplectic varieties (of the deformation type specified by a fiber).
3.3 Noether–Lefschetz cycles
Given primitive sublattices
![]() $L \subset \widetilde {L} \subset V$
, consider the open substack
$L \subset \widetilde {L} \subset V$
, consider the open substack
 $$ \begin{align*} {\mathcal M}_{\widetilde{L}}^{\prime} \subset {\mathcal M}_{\widetilde{L}} \end{align*} $$
$$ \begin{align*} {\mathcal M}_{\widetilde{L}}^{\prime} \subset {\mathcal M}_{\widetilde{L}} \end{align*} $$
parametrizing pairs
![]() $(X, j : \widetilde {L} \hookrightarrow \mathop {\text {Pic}}\nolimits (X))$
such that
$(X, j : \widetilde {L} \hookrightarrow \mathop {\text {Pic}}\nolimits (X))$
such that
![]() $j(L)$
contains a quasi-polarization. There exists a natural proper morphism
$j(L)$
contains a quasi-polarization. There exists a natural proper morphism
 $\iota : {\mathcal M}_{\widetilde {L}}^{\prime } \to {\mathcal M}_{L}$
defined by restricting j to L. The Noether–Lefschetz cycle associated to
$\iota : {\mathcal M}_{\widetilde {L}}^{\prime } \to {\mathcal M}_{L}$
defined by restricting j to L. The Noether–Lefschetz cycle associated to
![]() $\widetilde {L}$
is the class of the reduced image of this map:
$\widetilde {L}$
is the class of the reduced image of this map:
 $$ \begin{align*} \mathsf{NL}_{\widetilde{L}} = [ \iota( {\mathcal M}_{\widetilde{L}}^{\prime} ) ] \in A^{c}({\mathcal M}_{L}). \end{align*} $$
$$ \begin{align*} \mathsf{NL}_{\widetilde{L}} = [ \iota( {\mathcal M}_{\widetilde{L}}^{\prime} ) ] \in A^{c}({\mathcal M}_{L}). \end{align*} $$
The codimension c of the cycle is given by
![]() $\mathrm {rank}(\widetilde {L}) - \mathrm {rank}(L)$
. For
$\mathrm {rank}(\widetilde {L}) - \mathrm {rank}(L)$
. For
![]() $c=1$
, we call
$c=1$
, we call
![]() $\mathsf {NL}_{\widetilde {L}}$
a Noether–Lefschetz divisor of the first type.
$\mathsf {NL}_{\widetilde {L}}$
a Noether–Lefschetz divisor of the first type.
3.4 Heegner divisors
We review the construction of Heegner divisors. Their relation to Noether–Lefschetz divisors will yield modularity results for intersection numbers with Noether–Lefschetz divisors.
Consider the lattice
and the subgroup
where
![]() $O^{+}(M)$
stands for those automorphisms which preserve the orientation, or equivalently, the component
$O^{+}(M)$
stands for those automorphisms which preserve the orientation, or equivalently, the component
![]() ${\mathcal D}_{L}^{+}$
. We consider the quotient
${\mathcal D}_{L}^{+}$
. We consider the quotient
For every
![]() $n \in {\mathbb {Q}}_{<0}$
and
$n \in {\mathbb {Q}}_{<0}$
and
![]() $\gamma \in M^{\vee }/M$
, the associated Heegner divisor is:
$\gamma \in M^{\vee }/M$
, the associated Heegner divisor is:
 $$ \begin{align*} y_{n,\gamma} = \left( \sum_{\substack{ v \in M^{\vee} \\ \frac{1}{2} v \cdot v = n,\, [v] = \gamma } } v^{\perp} \right) / \Gamma_{M}. \end{align*} $$
$$ \begin{align*} y_{n,\gamma} = \left( \sum_{\substack{ v \in M^{\vee} \\ \frac{1}{2} v \cdot v = n,\, [v] = \gamma } } v^{\perp} \right) / \Gamma_{M}. \end{align*} $$
For
![]() $n=0$
, we define
$n=0$
, we define
![]() $y_{n,\gamma }$
by the descent
$y_{n,\gamma }$
by the descent
![]() ${\mathcal K}$
of the tautological line bundle
${\mathcal K}$
of the tautological line bundle
![]() ${\mathcal O}(-1)$
on
${\mathcal O}(-1)$
on
![]() ${\mathcal D}_{L}$
equipped with the natural
${\mathcal D}_{L}$
equipped with the natural
![]() $\Gamma _{M}$
-action. Concretely, we set
$\Gamma _{M}$
-action. Concretely, we set
 $$ \begin{align*} y_{0,\gamma} = \begin{cases} c_{1}({\mathcal K}^{\ast}) & \text{ if } \gamma = 0 \\ 0 & \text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} y_{0,\gamma} = \begin{cases} c_{1}({\mathcal K}^{\ast}) & \text{ if } \gamma = 0 \\ 0 & \text{ otherwise.} \end{cases} \end{align*} $$
In case
![]() $n>0$
, we set
$n>0$
, we set
![]() $y_{n,\gamma } = 0$
in all cases.
$y_{n,\gamma } = 0$
in all cases.
Define the formal power series of Heegner divisors
 $$ \begin{align*} \Phi(q) = \sum_{n \in {\mathbb{Q}}_{\leq 0}} \sum_{\gamma \in M^{\vee}/M} y_{n,\gamma} q^{-n} e_{\gamma} \end{align*} $$
$$ \begin{align*} \Phi(q) = \sum_{n \in {\mathbb{Q}}_{\leq 0}} \sum_{\gamma \in M^{\vee}/M} y_{n,\gamma} q^{-n} e_{\gamma} \end{align*} $$
which is an element of
 $\mathop {\text {Pic}}\nolimits ({\mathcal D}_{L}^{+} / \Gamma _{M})[[q^{1/N}]] \otimes {\mathbb {C}}[M^{\vee }/M]$
, where
$\mathop {\text {Pic}}\nolimits ({\mathcal D}_{L}^{+} / \Gamma _{M})[[q^{1/N}]] \otimes {\mathbb {C}}[M^{\vee }/M]$
, where
![]() $e_{\gamma }$
are the elements of the group ring
$e_{\gamma }$
are the elements of the group ring
![]() ${\mathbb {C}}[M^{\vee }/M]$
indexed by
${\mathbb {C}}[M^{\vee }/M]$
indexed by
![]() $\gamma $
and N is the smallest integer for which
$\gamma $
and N is the smallest integer for which
![]() $M^{\vee }(N)$
is an even lattice.
$M^{\vee }(N)$
is an even lattice.
We recall the modularity result of Borcherds in the formulation of [Reference Maulik and Pandharipande37].
Theorem 4. ([Reference Borcherds5, Reference McGraw39]) The generating series
![]() $\Phi (q)$
is the Fourier-expansion of a modular form of weight
$\Phi (q)$
is the Fourier-expansion of a modular form of weight
![]() $\mathrm {rank}(M)/2$
for the dual of the Weil representation
$\mathrm {rank}(M)/2$
for the dual of the Weil representation
![]() $\rho _{M}^{\vee }$
of the metaplectic group
$\rho _{M}^{\vee }$
of the metaplectic group
![]() $\mathrm {Mp}_{2}({\mathbb {Z}})$
:
$\mathrm {Mp}_{2}({\mathbb {Z}})$
:
The modular forms for the dual of the Weil representations can be computed easily by a Sage program of Brandon Williams [Reference Williams53].
3.5 Noether–Lefschetz divisors of the second type
The precise relationship between Noether–Lefschetz and Heegner divisors for arbitrary holomorphic-symplectic varieties is somewhat painful to state. For once the monodromy group
![]() $\mathsf {Mon}^{2}(X)$
is not known in general, and even if it is known it usually does not contain
$\mathsf {Mon}^{2}(X)$
is not known in general, and even if it is known it usually does not contain
![]() $\Gamma _{M}$
or is contained in
$\Gamma _{M}$
or is contained in
![]() $\Gamma _{M}$
. To simplify the situation, we from now on restrict to the case of
$\Gamma _{M}$
. To simplify the situation, we from now on restrict to the case of
![]() $K3[n]$
-type for
$K3[n]$
-type for
![]() $n \geq 2$
. Hence, we let
$n \geq 2$
. Hence, we let
and we fix an identification
![]() $V^{\vee }/V = {\mathbb {Z}}/(2n-2){\mathbb {Z}}$
.
$V^{\vee }/V = {\mathbb {Z}}/(2n-2){\mathbb {Z}}$
.
We define the Noether–Lefschetz divisors of second type:
 $$ \begin{align*} \mathsf{NL}_{s,d, \pm r} \in A^{1}({\mathcal M}_{L}), \end{align*} $$
$$ \begin{align*} \mathsf{NL}_{s,d, \pm r} \in A^{1}({\mathcal M}_{L}), \end{align*} $$
where
![]() $d = (d_{1}, \ldots , d_{\ell }) \in {\mathbb {Z}}^{\ell }$
,
$d = (d_{1}, \ldots , d_{\ell }) \in {\mathbb {Z}}^{\ell }$
,
![]() $s \in {\mathbb {Q}}$
and
$s \in {\mathbb {Q}}$
and
![]() $r \in {\mathbb {Z}}/(2n-2){\mathbb {Z}}$
are given. Consider the intersection matrix of the basis
$r \in {\mathbb {Z}}/(2n-2){\mathbb {Z}}$
are given. Consider the intersection matrix of the basis
![]() $L_{i}$
:
$L_{i}$
:
 $$ \begin{align*} \mathsf{a} = \big( a_{ij} \big)_{i,j=1}^{\ell} = \big( L_{i} \cdot L_{j} \big)_{i,j=1}^{\ell}. \end{align*} $$
$$ \begin{align*} \mathsf{a} = \big( a_{ij} \big)_{i,j=1}^{\ell} = \big( L_{i} \cdot L_{j} \big)_{i,j=1}^{\ell}. \end{align*} $$
We set
 $$ \begin{align*} \Delta(s, d) = \det \begin{pmatrix} a & d^{t} \\ d & s \end{pmatrix} = \det \begin{pmatrix} a_{11} & \cdots & a_{1 \ell} & d_{1} \\ \vdots & & \vdots & \vdots \\ a_{\ell 1} & \cdots & a_{\ell \ell} & d_{\ell} \\ d_{1} & \cdots & d_{\ell} & s \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \Delta(s, d) = \det \begin{pmatrix} a & d^{t} \\ d & s \end{pmatrix} = \det \begin{pmatrix} a_{11} & \cdots & a_{1 \ell} & d_{1} \\ \vdots & & \vdots & \vdots \\ a_{\ell 1} & \cdots & a_{\ell \ell} & d_{\ell} \\ d_{1} & \cdots & d_{\ell} & s \end{pmatrix}. \end{align*} $$
Case:
![]() $\Delta (s, d) \neq 0$
. We define
$\Delta (s, d) \neq 0$
. We define
 $$ \begin{align*} \mathsf{NL}_{s,d, \pm r} = \sum_{L\subset \tilde{L} \subset V} \mu(s,d, r | L\subset \tilde{L} \subset V ) \cdot \mathsf{NL}_{\tilde{L}}, \end{align*} $$
$$ \begin{align*} \mathsf{NL}_{s,d, \pm r} = \sum_{L\subset \tilde{L} \subset V} \mu(s,d, r | L\subset \tilde{L} \subset V ) \cdot \mathsf{NL}_{\tilde{L}}, \end{align*} $$
where the sum runs over all isomorphism classes of primitive embeddings
![]() $L \subset \tilde {L} \subset V$
with
$L \subset \tilde {L} \subset V$
with
![]() $\mathrm {rank}(\tilde {L}) = \ell +1$
. The multiplicityFootnote
10
$\mathrm {rank}(\tilde {L}) = \ell +1$
. The multiplicityFootnote
10
![]() $\mu (s,d, r | L\subset \tilde {L} \subset V )$
is the number of elements
$\mu (s,d, r | L\subset \tilde {L} \subset V )$
is the number of elements
![]() $\beta \in V^{\vee }$
which are contained in
$\beta \in V^{\vee }$
which are contained in
![]() $\widetilde {L} \otimes {\mathbb {Q}}$
and satisfy:
$\widetilde {L} \otimes {\mathbb {Q}}$
and satisfy:
Here we have used the canonical embeddings
![]() $V^{\vee } \subset V \otimes {\mathbb {Q}}$
and
$V^{\vee } \subset V \otimes {\mathbb {Q}}$
and
![]() $\widetilde {L} \otimes {\mathbb {Q}} \subset V \otimes {\mathbb {Q}}$
.
$\widetilde {L} \otimes {\mathbb {Q}} \subset V \otimes {\mathbb {Q}}$
.
Case:
![]() $\Delta (s, d) = 0$
. In this case, any curve class with these invariants has to lie in
$\Delta (s, d) = 0$
. In this case, any curve class with these invariants has to lie in
![]() $L \otimes {\mathbb {Q}}$
and is uniquely determined by the degree d. Hence, we let
$L \otimes {\mathbb {Q}}$
and is uniquely determined by the degree d. Hence, we let
![]() $\beta \in L \otimes {\mathbb {Q}}$
be the unique class so that
$\beta \in L \otimes {\mathbb {Q}}$
be the unique class so that
![]() $\beta \cdot L_{i} = d_{i}$
for all i.Footnote
11
If
$\beta \cdot L_{i} = d_{i}$
for all i.Footnote
11
If
![]() $\beta $
lies in
$\beta $
lies in
![]() $V^{\vee }$
and has residue
$V^{\vee }$
and has residue
![]() $[\beta ] = \pm r$
, we define
$[\beta ] = \pm r$
, we define
and we define
![]() $\mathsf {NL}_{s,d, \pm r} = 0$
otherwise.
$\mathsf {NL}_{s,d, \pm r} = 0$
otherwise.
Remark 6. Often the residue set
![]() $\pm [\beta ]$
of a class
$\pm [\beta ]$
of a class
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
is determined by the degrees
$\beta \in H_{2}(X,{\mathbb {Z}})$
is determined by the degrees
![]() $d_{i} = \beta \cdot L_{i}$
. For example, if L contains a class
$d_{i} = \beta \cdot L_{i}$
. For example, if L contains a class
![]() $\ell $
such that
$\ell $
such that
we may define a natural isomorphism by cupping with
![]() $\ell $
:
$\ell $
:
 $$ \begin{align*} H_{2}(X,{\mathbb{Z}}) / H^{2}(X,{\mathbb{Z}}) \xrightarrow{\cong} {\mathbb{Z}} / (2n-2){\mathbb{Z}}, \gamma \mapsto \gamma \cdot \ell. \end{align*} $$
$$ \begin{align*} H_{2}(X,{\mathbb{Z}}) / H^{2}(X,{\mathbb{Z}}) \xrightarrow{\cong} {\mathbb{Z}} / (2n-2){\mathbb{Z}}, \gamma \mapsto \gamma \cdot \ell. \end{align*} $$
(Not every polarization is of that form, for example the case of double covers of EPW sextics.) In other cases, the residue set is determined by the norm
![]() $\beta \cdot \beta $
, for example in
$\beta \cdot \beta $
, for example in
![]() $K3^{[2]}$
-type. When the residue is determined by s and d, we will drop it from the notation of Noether–Lefschetz divisors.□
$K3^{[2]}$
-type. When the residue is determined by s and d, we will drop it from the notation of Noether–Lefschetz divisors.□
3.6 Heegner and Noether–Lefschetz divisors
By the result of Markman,
![]() $\mathsf {Mon}(V) \subset O(V)$
is the subgroup of orientation-preserving isometries which act by
$\mathsf {Mon}(V) \subset O(V)$
is the subgroup of orientation-preserving isometries which act by
![]() $\pm \mathrm {id}$
on the discriminant. Hence, we have the inclusion
$\pm \mathrm {id}$
on the discriminant. Hence, we have the inclusion
![]() $\Gamma _{M} \subset \mathsf {Mon}(V)_{L}$
of index
$\Gamma _{M} \subset \mathsf {Mon}(V)_{L}$
of index
![]() $1$
or
$1$
or
![]() $2$
. This yields the diagram
$2$
. This yields the diagram

where
![]() $\pi $
is either an isomorphism or of degree
$\pi $
is either an isomorphism or of degree
![]() $2$
.
$2$
.
Let
![]() $C \subset {\mathcal M}_{L}$
be a complete curve, and define the modular form
$C \subset {\mathcal M}_{L}$
be a complete curve, and define the modular form
We write
![]() $\Phi _{C}[n,\gamma ]$
for the coefficient of
$\Phi _{C}[n,\gamma ]$
for the coefficient of
![]() $q^{n} e^{\gamma }$
in the Fourier-expansion of
$q^{n} e^{\gamma }$
in the Fourier-expansion of
![]() $\Phi _{C}$
.
$\Phi _{C}$
.
We will need also
 $$ \begin{align*} \widetilde{\Delta}(s, d) := -\frac{1}{2} \cdot \frac{1}{\det(a)} \det \begin{pmatrix} a & d^{t} \\ d & s \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \widetilde{\Delta}(s, d) := -\frac{1}{2} \cdot \frac{1}{\det(a)} \det \begin{pmatrix} a & d^{t} \\ d & s \end{pmatrix}. \end{align*} $$
The following gives the main connection between the Noether–Lefschetz divisors of the second type and the Heegner divisors.
Proposition 3. There exists a canonically defined class
![]() $\gamma (s,d,r) \in M^{\vee }/M$
(abbreviated also by
$\gamma (s,d,r) \in M^{\vee }/M$
(abbreviated also by
![]() $\gamma (r)$
) such that we have the following:
$\gamma (r)$
) such that we have the following:
-
(a) If
 $\pi $
is an isomorphism,
$\pi $
is an isomorphism,  $$ \begin{align*} C \cdot \mathsf{NL}_{s,d, \pm r} = \Phi_{C}\left[ \widetilde{\Delta}(s,d) , \gamma(r)\right]. \end{align*} $$
$$ \begin{align*} C \cdot \mathsf{NL}_{s,d, \pm r} = \Phi_{C}\left[ \widetilde{\Delta}(s,d) , \gamma(r)\right]. \end{align*} $$
-
(b) If
 $\pi $
is of degree
$\pi $
is of degree
 $2$
,
$2$
,  $$ \begin{align*} C \cdot \mathsf{NL}_{s,d, \pm r} = \begin{cases} \frac{1}{2} \Phi_{C}\left[ \widetilde{\Delta}(s,d), \gamma(r) \right] & \text{ if } r=-r \\[10pt] \frac{1}{2} \left( \Phi_{C}\left[ \widetilde{\Delta}(s,d), \gamma(r) \right] + \Phi_{C}\left[ \widetilde{\Delta}(s,d), \gamma(-r) \right] \right) & \text{ otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*} C \cdot \mathsf{NL}_{s,d, \pm r} = \begin{cases} \frac{1}{2} \Phi_{C}\left[ \widetilde{\Delta}(s,d), \gamma(r) \right] & \text{ if } r=-r \\[10pt] \frac{1}{2} \left( \Phi_{C}\left[ \widetilde{\Delta}(s,d), \gamma(r) \right] + \Phi_{C}\left[ \widetilde{\Delta}(s,d), \gamma(-r) \right] \right) & \text{ otherwise. } \end{cases} \end{align*} $$
In
![]() $K3^{[2]}$
-type, we have
$K3^{[2]}$
-type, we have
![]() $V^{\vee }/V = {\mathbb {Z}}_{2}$
so that
$V^{\vee }/V = {\mathbb {Z}}_{2}$
so that
![]() $\pi $
is an isomorphism. Moreover, the residue r of any
$\pi $
is an isomorphism. Moreover, the residue r of any
![]() $\beta \in V^{\vee }$
is determined by its norm
$\beta \in V^{\vee }$
is determined by its norm
![]() $s= \beta \cdot \beta $
. Hence, omitting r from the notation we find the following.
$s= \beta \cdot \beta $
. Hence, omitting r from the notation we find the following.
Corollary 3. In
![]() $K3^{[2]}$
type, there exists a canonical class
$K3^{[2]}$
type, there exists a canonical class
![]() $\gamma = \gamma (d,s)$
with
$\gamma = \gamma (d,s)$
with
 $$ \begin{align*} C \cdot \mathsf{NL}_{s,d} = \Phi_{C}[ \widetilde{\Delta}(s,d), \gamma ]. \end{align*} $$
$$ \begin{align*} C \cdot \mathsf{NL}_{s,d} = \Phi_{C}[ \widetilde{\Delta}(s,d), \gamma ]. \end{align*} $$
Remark 7. In fact, in
![]() $K3^{[2]}$
type, the proof below will imply the equality of divisors
$K3^{[2]}$
type, the proof below will imply the equality of divisors
 $$ \begin{align*} \mathsf{NL}_{s,d} = \Phi[ \widetilde{\Delta}(s,d), \gamma ] = y_{-\tilde{\Delta}(s,d), \gamma} \end{align*} $$
$$ \begin{align*} \mathsf{NL}_{s,d} = \Phi[ \widetilde{\Delta}(s,d), \gamma ] = y_{-\tilde{\Delta}(s,d), \gamma} \end{align*} $$
on
![]() ${\mathcal M}_{L}$
, where we have omitted the pullback by the period map
${\mathcal M}_{L}$
, where we have omitted the pullback by the period map
![]() $\mathrm {Per}$
on the right-hand side.
$\mathrm {Per}$
on the right-hand side.
For the proof of Proposition 3, we will repeatedly use the following basic linear algebra fact whose proof we skip.
Lemma 4. Consider an
![]() ${\mathbb {R}}$
-vector space
${\mathbb {R}}$
-vector space
![]() $\Lambda $
with inner product
$\Lambda $
with inner product
![]() $\langle -, - \rangle $
and an orthogonal decomposition
$\langle -, - \rangle $
and an orthogonal decomposition
![]() $L \oplus M = \Lambda $
. Let
$L \oplus M = \Lambda $
. Let
![]() $L_{i}$
be a basis of L with intersection matrix
$L_{i}$
be a basis of L with intersection matrix
![]() $a_{ij} = L_{i} \cdot L_{j}$
. For
$a_{ij} = L_{i} \cdot L_{j}$
. For
![]() $\beta \in \Lambda $
with
$\beta \in \Lambda $
with
![]() $d_{i} = \beta \cdot L_{i}$
, let
$d_{i} = \beta \cdot L_{i}$
, let
 $v = \beta - \sum _{i,j} d_{i} a^{ij} L_{j}$
be the projection of
$v = \beta - \sum _{i,j} d_{i} a^{ij} L_{j}$
be the projection of
![]() $\beta $
onto M, where
$\beta $
onto M, where
![]() $a^{ij}$
are the entries of
$a^{ij}$
are the entries of
![]() $a^{-1}$
. Then we have
$a^{-1}$
. Then we have
 $$ \begin{align*} \langle v,v \rangle = \frac{1}{\det(a)} \det \begin{pmatrix} a & d^{t} \\ d & \langle \beta, \beta \rangle \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \langle v,v \rangle = \frac{1}{\det(a)} \det \begin{pmatrix} a & d^{t} \\ d & \langle \beta, \beta \rangle \end{pmatrix}, \end{align*} $$
where
![]() $d = (d_{1}, \ldots , d_{\ell })$
.
$d = (d_{1}, \ldots , d_{\ell })$
.
The main step in the proof of the proposition is given by the following lemma: For fixed
![]() $d = (d_{1}, \ldots , d_{\ell }), s$
and
$d = (d_{1}, \ldots , d_{\ell }), s$
and
![]() $r \in {\mathbb {Z}}_{2n-2}$
consider the divisor on
$r \in {\mathbb {Z}}_{2n-2}$
consider the divisor on
![]() ${\mathcal D}_{L} / \Gamma _{M}$
given by
${\mathcal D}_{L} / \Gamma _{M}$
given by
 $$ \begin{align*} \mathsf{NL}_{s, d,r} = \left( \sum_{\beta} \beta^{\perp} \right)/\Gamma_{M}, \end{align*} $$
$$ \begin{align*} \mathsf{NL}_{s, d,r} = \left( \sum_{\beta} \beta^{\perp} \right)/\Gamma_{M}, \end{align*} $$
where the sum is over all classes
![]() $\beta \in V^{\vee }$
such that
$\beta \in V^{\vee }$
such that
Moreover,
![]() $\beta ^{\perp }$
stands for the hyperplane in
$\beta ^{\perp }$
stands for the hyperplane in
![]() $\mathbb {P}(V)$
orthogonal to
$\mathbb {P}(V)$
orthogonal to
![]() $\beta $
intersected with the period domain
$\beta $
intersected with the period domain
![]() $D_{L}$
.
$D_{L}$
.
Lemma 5. There exists a canonically defined class
![]() $\gamma = \gamma (s,d, r) \in M^{\vee }/M$
such that
$\gamma = \gamma (s,d, r) \in M^{\vee }/M$
such that
 $$ \begin{align*} \mathsf{NL}_{s, d,r} = y_{n,\gamma} \ \in A^{1}({\mathcal D}_{L}/\Gamma_{M}), \end{align*} $$
$$ \begin{align*} \mathsf{NL}_{s, d,r} = y_{n,\gamma} \ \in A^{1}({\mathcal D}_{L}/\Gamma_{M}), \end{align*} $$
where
 $n = \frac {1}{2} \frac {1}{\det (a)} \det \binom {a\ d}{d\ s}$
.
$n = \frac {1}{2} \frac {1}{\det (a)} \det \binom {a\ d}{d\ s}$
.
Proof. In view of the definition of both sides of the claimed equation, it is enough to establish a bijection between
-
(a) the set of classes
 $\beta \in V^{\vee }$
satisfying (13), and
$\beta \in V^{\vee }$
satisfying (13), and -
(b) the set of classes
 $v \in M^{\vee }$
satisfying
$v \in M^{\vee }$
satisfying
 $v^{2} = \frac {1}{\det (a)} \det \binom {a\ d}{d\ s}$
and
$v^{2} = \frac {1}{\det (a)} \det \binom {a\ d}{d\ s}$
and
 $[v]=\gamma $
for an appropriately defined
$[v]=\gamma $
for an appropriately defined
 $\gamma $
.
$\gamma $
.
Consider a primitive embedding
![]() $V \subset \Lambda $
into the Mukai lattice
$V \subset \Lambda $
into the Mukai lattice
Let
![]() $e,f$
be a symplectic basis of one summand of U. We choose the embedding such that
$e,f$
be a symplectic basis of one summand of U. We choose the embedding such that
![]() $V^{\perp } = {\mathbb {Z}} L_{0}$
, where
$V^{\perp } = {\mathbb {Z}} L_{0}$
, where
![]() $L_{0} = e+(n-1)f$
. Since
$L_{0} = e+(n-1)f$
. Since
![]() $\Lambda $
is unimodular, there exists a canonical isomorphism
$\Lambda $
is unimodular, there exists a canonical isomorphism
and we may assume that under this isomorphism the class
![]() $L_{0}/(2n-2)$
mod
$L_{0}/(2n-2)$
mod
![]() ${\mathbb {Z}} L_{0}$
corresponds to
${\mathbb {Z}} L_{0}$
corresponds to
![]() $1 \in {\mathbb {Z}}/(2n-2) {\mathbb {Z}}$
.
$1 \in {\mathbb {Z}}/(2n-2) {\mathbb {Z}}$
.
Step 1. Let
![]() $d_{0} \in {\mathbb {Z}}$
be any integer such that
$d_{0} \in {\mathbb {Z}}$
be any integer such that
![]() $d_{0} \equiv r$
modulo
$d_{0} \equiv r$
modulo
![]() $2n-2$
, and let
$2n-2$
, and let
![]() $\widetilde {s} \in 2 {\mathbb {Z}}$
such that
$\widetilde {s} \in 2 {\mathbb {Z}}$
such that
 $$ \begin{align*} s = \frac{1}{2n-2} \det \begin{pmatrix} 2n-2 & d_{0} \\ d_{0} & \widetilde{s} \end{pmatrix} \ \Longleftrightarrow \ \widetilde{s} = s + \frac{d_{0}^{2}}{2n-2}. \end{align*} $$
$$ \begin{align*} s = \frac{1}{2n-2} \det \begin{pmatrix} 2n-2 & d_{0} \\ d_{0} & \widetilde{s} \end{pmatrix} \ \Longleftrightarrow \ \widetilde{s} = s + \frac{d_{0}^{2}}{2n-2}. \end{align*} $$
(We may assume such
![]() $\widetilde {s}$
exists: Otherwise, the set in (a) is empty and by the argument below also the set in (b)). Then we claim that there exists a bijection between the set in (a) and
$\widetilde {s}$
exists: Otherwise, the set in (a) is empty and by the argument below also the set in (b)). Then we claim that there exists a bijection between the set in (a) and
-
(c) the set of classes
 $\widetilde {\beta } \in \Lambda $
such that
$\widetilde {\beta } \in \Lambda $
such that
 $\widetilde {\beta } \cdot L_{i} = d_{i}$
for all
$\widetilde {\beta } \cdot L_{i} = d_{i}$
for all
 $i=0,\ldots , \ell $
and
$i=0,\ldots , \ell $
and
 $\widetilde {\beta } \cdot \widetilde {\beta } = \widetilde {s}$
.
$\widetilde {\beta } \cdot \widetilde {\beta } = \widetilde {s}$
.
Proof of Step 1
Given
![]() $\widetilde {\beta }$
satisfying the conditions in (c), then
$\widetilde {\beta }$
satisfying the conditions in (c), then
 $$ \begin{align*} \beta = \widetilde{\beta} - \frac{d_{0}}{2n-2} L_{0} \end{align*} $$
$$ \begin{align*} \beta = \widetilde{\beta} - \frac{d_{0}}{2n-2} L_{0} \end{align*} $$
lies in
![]() $V^{\vee }$
. Moreover,
$V^{\vee }$
. Moreover,
![]() $[\beta ]$
is the class in
$[\beta ]$
is the class in
![]() $V^{\vee }/V$
corresponding to
$V^{\vee }/V$
corresponding to
![]() $d_{0}/(2n-2)$
in
$d_{0}/(2n-2)$
in
![]() $({\mathbb {Z}} L_{0})^{\vee } / {\mathbb {Z}} L_{0}$
under (14); hence,
$({\mathbb {Z}} L_{0})^{\vee } / {\mathbb {Z}} L_{0}$
under (14); hence,
![]() $[\beta ] = r$
. Also,
$[\beta ] = r$
. Also,
![]() $\beta \cdot L_{i}=d_{i}$
for
$\beta \cdot L_{i}=d_{i}$
for
![]() $i=1,\ldots , \ell $
. The equality
$i=1,\ldots , \ell $
. The equality
![]() $\beta \cdot \beta = s$
is by definition of
$\beta \cdot \beta = s$
is by definition of
![]() $\widetilde {s}$
and Lemma 4.
$\widetilde {s}$
and Lemma 4.
Conversely, let
![]() $\delta = -e + (n-1) f$
, and observe that
$\delta = -e + (n-1) f$
, and observe that
![]() $L_{0} \cdot \delta = 0$
and
$L_{0} \cdot \delta = 0$
and
![]() $L_{0} / (2n-2) + \delta /(2n-2) = f$
. Hence, if
$L_{0} / (2n-2) + \delta /(2n-2) = f$
. Hence, if
![]() $\beta $
satisfies (a) then
$\beta $
satisfies (a) then
![]() $\beta $
is an element of
$\beta $
is an element of
 $d_{0} \cdot \frac {\delta }{2n-2} + V$
, and hence,
$d_{0} \cdot \frac {\delta }{2n-2} + V$
, and hence,
 $$ \begin{align*} \beta \mapsto \beta + \frac{d_{0}}{2n-2} L_{0} \in \Lambda \end{align*} $$
$$ \begin{align*} \beta \mapsto \beta + \frac{d_{0}}{2n-2} L_{0} \in \Lambda \end{align*} $$
defines the required inverse.
We consider now the embedding
![]() $M \subset \Lambda $
and the orthogonal complement
$M \subset \Lambda $
and the orthogonal complement
Since
![]() $\Lambda $
is unimodular, we have an isomorphism
$\Lambda $
is unimodular, we have an isomorphism
We specify the class
![]() $\gamma $
via this isomorphism. Concretely, we set
$\gamma $
via this isomorphism. Concretely, we set
 $$ \begin{align*} \gamma := \left[ \sum_{i,j = 0}^{\ell} d_{i} a^{ij} L_{j} \right] \in \widehat{L}^{\vee} / \widehat{L}, \end{align*} $$
$$ \begin{align*} \gamma := \left[ \sum_{i,j = 0}^{\ell} d_{i} a^{ij} L_{j} \right] \in \widehat{L}^{\vee} / \widehat{L}, \end{align*} $$
where we let
![]() $a^{ij}$
denote the entries of the inverse of the extended intersection matrix
$a^{ij}$
denote the entries of the inverse of the extended intersection matrix
![]() $\hat {a} = ( L_{i} \cdot L_{j} )_{i,j=0, \ldots , \ell }$
.
$\hat {a} = ( L_{i} \cdot L_{j} )_{i,j=0, \ldots , \ell }$
.
If we replace
![]() $d_{0}$
by
$d_{0}$
by
![]() $d_{0} + (2n-2)$
, then since
$d_{0} + (2n-2)$
, then since
![]() $a^{00} = 1/(2n-2)$
and
$a^{00} = 1/(2n-2)$
and
![]() $a^{0j} = 0$
for
$a^{0j} = 0$
for
![]() $j \neq 0$
, the expression
$j \neq 0$
, the expression
![]() $\sum d_{i} a^{ij} L_{j}$
gets replaced by the same expression plus
$\sum d_{i} a^{ij} L_{j}$
gets replaced by the same expression plus
![]() $L_{0}$
. Hence, the class
$L_{0}$
. Hence, the class
![]() $\gamma $
only depends on
$\gamma $
only depends on
![]() $s,(d_{1}, \ldots , d_{\ell }),r$
.
$s,(d_{1}, \ldots , d_{\ell }),r$
.
Step 2. There exists a bijection between the classes in (c) and (b).
Proof of Step 2
We have the bijection
 $$ \begin{align*} \widetilde{\beta} \mapsto \widetilde{\beta} - \sum_{i,j=0}^{r} d_{i} a^{ij} L_{j} \in M^{\vee}. \end{align*} $$
$$ \begin{align*} \widetilde{\beta} \mapsto \widetilde{\beta} - \sum_{i,j=0}^{r} d_{i} a^{ij} L_{j} \in M^{\vee}. \end{align*} $$
Combining Step 1 and 2 finished the proof of the lemma.
Proof of Proposition 3
By definition we have:
 $$ \begin{align*} \mathsf{NL}_{s,d_{1}, \ldots, d_{r}, \pm r} = \mathrm{Per}^{\ast}\left[ \left( \sum_{\beta} \beta^{\perp} \right) / \mathsf{Mon}(V)_{L} \right], \end{align*} $$
$$ \begin{align*} \mathsf{NL}_{s,d_{1}, \ldots, d_{r}, \pm r} = \mathrm{Per}^{\ast}\left[ \left( \sum_{\beta} \beta^{\perp} \right) / \mathsf{Mon}(V)_{L} \right], \end{align*} $$
where the sum is over all
![]() $\beta \in V^{\vee }$
such that
$\beta \in V^{\vee }$
such that
Hence, if
![]() $\pi $
is an isomorphism, the result follows from this by Lemma 5.
$\pi $
is an isomorphism, the result follows from this by Lemma 5.
Hence, assume now
![]() $\pi $
is of degree
$\pi $
is of degree
![]() $2$
, and let
$2$
, and let
![]() $\widetilde {C} = \mathrm {Per}(C)$
.
$\widetilde {C} = \mathrm {Per}(C)$
.
If
![]() $-r = r$
, then the morphism
$-r = r$
, then the morphism
![]() $\mathsf {NL}_{s,d, r} \to \mathsf {NL}_{s,d, \pm r}$
given by restriction of
$\mathsf {NL}_{s,d, r} \to \mathsf {NL}_{s,d, \pm r}$
given by restriction of
![]() $\pi $
is of degree
$\pi $
is of degree
![]() $2$
. Therefore,
$2$
. Therefore,
 $$ \begin{align*} C \cdot \mathsf{NL}_{s,d, \pm r} = \frac{1}{2} \widetilde{C} \cdot \pi_{\ast} \mathsf{NL}_{s,d, r} = \frac{1}{2} \pi^{\ast}[\widetilde{C}] \cdot \mathsf{NL}_{s,d, r} \end{align*} $$
$$ \begin{align*} C \cdot \mathsf{NL}_{s,d, \pm r} = \frac{1}{2} \widetilde{C} \cdot \pi_{\ast} \mathsf{NL}_{s,d, r} = \frac{1}{2} \pi^{\ast}[\widetilde{C}] \cdot \mathsf{NL}_{s,d, r} \end{align*} $$
which then implies the claim by Lemma 5. If
![]() $r \neq -r$
, then we have
$r \neq -r$
, then we have
![]() $\pi _{\ast } \mathsf {NL}_{s,d, r} = \mathsf {NL}_{s,d, \pm r}$
from which the result follows.
$\pi _{\ast } \mathsf {NL}_{s,d, r} = \mathsf {NL}_{s,d, \pm r}$
from which the result follows.
3.7 Noether–Lefschetz numbers
Let
![]() $({\mathcal X}, {\mathcal L}_{1}, \ldots , {\mathcal L}_{\ell }, \pi )$
be a one-parameter family of L-quasipolarized holomorphic-symplectic varieties of
$({\mathcal X}, {\mathcal L}_{1}, \ldots , {\mathcal L}_{\ell }, \pi )$
be a one-parameter family of L-quasipolarized holomorphic-symplectic varieties of
![]() $K3^{[n]}$
-type. We have the associated classifying morphism
$K3^{[n]}$
-type. We have the associated classifying morphism
We define the Noether–Lefschetz numbers of the family by
 $$ \begin{align*} \mathsf{NL}^{\pi}_{s,d, \pm r} = \int_{C} \iota_{\pi}^{\ast}\mathsf{NL}^{\pi}_{s,d, \pm r}. \end{align*} $$
$$ \begin{align*} \mathsf{NL}^{\pi}_{s,d, \pm r} = \int_{C} \iota_{\pi}^{\ast}\mathsf{NL}^{\pi}_{s,d, \pm r}. \end{align*} $$
Intuitively, the Noether–Lefschetz numbers are the number of fibers of
![]() $\pi $
for which there exists a Hodge class
$\pi $
for which there exists a Hodge class
![]() $\beta $
with prescribed norm
$\beta $
with prescribed norm
![]() $\beta \cdot \beta = s$
, degree
$\beta \cdot \beta = s$
, degree
![]() $\beta \cdot L_{i} = d_{i}$
and residue
$\beta \cdot L_{i} = d_{i}$
and residue
![]() $[\beta ] = \pm r$
.
$[\beta ] = \pm r$
.
In
![]() $K3^{[2]}$
-type we will also often write
$K3^{[2]}$
-type we will also often write
![]() $\Phi ^{\pi }(q) = \iota _{\pi }^{\ast } \Phi (q)$
.
$\Phi ^{\pi }(q) = \iota _{\pi }^{\ast } \Phi (q)$
.
The families of holomorphic-symplectic varieties we will encounter in geometric constructions often come with mildly singular fibers. The definition of Noether–Lefschetz numbers can be extended to these families as follows. Let
![]() $\pi : {\mathcal X} \to C$
be a projective flat morphism to a smooth curve, and let
$\pi : {\mathcal X} \to C$
be a projective flat morphism to a smooth curve, and let
![]() ${\mathcal L}_{1}, \ldots , {\mathcal L}_{\ell } \in \mathop {\text {Pic}}\nolimits ({\mathcal X})$
. We assume that over a nonempty open subset of C this defines a one-parameter family of L-quasipolarized holomorphic-symplectic varieties of
${\mathcal L}_{1}, \ldots , {\mathcal L}_{\ell } \in \mathop {\text {Pic}}\nolimits ({\mathcal X})$
. We assume that over a nonempty open subset of C this defines a one-parameter family of L-quasipolarized holomorphic-symplectic varieties of
![]() $K3^{[n]}$
type. We also assume that around every singular point the monodromy is finite. Then there exists a cover
$K3^{[n]}$
type. We also assume that around every singular point the monodromy is finite. Then there exists a cover
such that the pullback family
![]() $f^{\ast } {\mathcal X} \to \widetilde {C}$
is bimeromorphic to a one-parameter family of L-quasipolarized holomorphic-symplectic varieties of
$f^{\ast } {\mathcal X} \to \widetilde {C}$
is bimeromorphic to a one-parameter family of L-quasipolarized holomorphic-symplectic varieties of
![]() $K3^{[n]}$
-type,
$K3^{[n]}$
-type,
See, for example, [Reference Kollár, Laza, Saccà and Voisin28]. Concretely, around each basepoint of a singular fiber, after a cover that trivializes the monodromy, the rational map
![]() $C \dashrightarrow {\mathcal M}_{L}$
can be extended. (In the examples we will consider, we can construct the cover
$C \dashrightarrow {\mathcal M}_{L}$
can be extended. (In the examples we will consider, we can construct the cover
![]() $\tilde {C} \to C$
and the birational model
$\tilde {C} \to C$
and the birational model
![]() $\tilde {{\mathcal X}}$
explicitly). We define the Noether–Lefschetz numbers of
$\tilde {{\mathcal X}}$
explicitly). We define the Noether–Lefschetz numbers of
![]() $\pi $
by
$\pi $
by
 $$ \begin{align*} \mathsf{NL}^{\pi}_{s,d,\pm r} := \frac{1}{k} \mathsf{NL}^{\widetilde{\pi}}_{s,d,\pm}, \end{align*} $$
$$ \begin{align*} \mathsf{NL}^{\pi}_{s,d,\pm r} := \frac{1}{k} \mathsf{NL}^{\widetilde{\pi}}_{s,d,\pm}, \end{align*} $$
where k is the degree of the cover
![]() $\widetilde {C} \to C$
. Since the Noether–Lefschetz divisors are pulled back from the separated period domain, the definition is independent of the choice of cover.
$\widetilde {C} \to C$
. Since the Noether–Lefschetz divisors are pulled back from the separated period domain, the definition is independent of the choice of cover.
3.8 Example: Prime discriminant in
 $K3^{[2]}$
-type
$K3^{[2]}$
-type
Let
be the
![]() $K3^{[2]}$
-lattice and consider a primitive vector
$K3^{[2]}$
-lattice and consider a primitive vector
![]() $H \in V$
satisfying
$H \in V$
satisfying
-
○
 $H \cdot H = 2p$
for a prime p with
$H \cdot H = 2p$
for a prime p with
 $p \equiv 3$
mod
$p \equiv 3$
mod
 $4$
,
$4$
, -
○
 $\langle H, V \rangle = 2 {\mathbb {Z}}$
.
$\langle H, V \rangle = 2 {\mathbb {Z}}$
.
Equivalently,
![]() $H/2$
defines a primitive vector in
$H/2$
defines a primitive vector in
![]() $V^{\vee }$
and has norm
$V^{\vee }$
and has norm
![]() $p/2$
. By Eichler’s criterion [Reference Gritsenko, Hulek and Sankaran19, Lemma 3.5], there exists a unique
$p/2$
. By Eichler’s criterion [Reference Gritsenko, Hulek and Sankaran19, Lemma 3.5], there exists a unique
![]() $O(V)$
orbit of vectors H satisfying these condition. To be concrete, we choose
$O(V)$
orbit of vectors H satisfying these condition. To be concrete, we choose
 $$ \begin{align*} H = 2\left( e^{\prime} + \frac{p+1}{4} f^{\prime} \right) + \delta, \end{align*} $$
$$ \begin{align*} H = 2\left( e^{\prime} + \frac{p+1}{4} f^{\prime} \right) + \delta, \end{align*} $$
where
![]() $e^{\prime },f^{\prime }$
is a basis of one of the summands U. In V one then has
$e^{\prime },f^{\prime }$
is a basis of one of the summands U. In V one then has
 $$ \begin{align*} M = H^{\perp} \cong E_{8}(-1)^{\oplus 2} \oplus U^{\oplus 2} \oplus \begin{pmatrix} -2 & -1 \\ -1 & -\frac{p+1}{2} \end{pmatrix}, \end{align*} $$
$$ \begin{align*} M = H^{\perp} \cong E_{8}(-1)^{\oplus 2} \oplus U^{\oplus 2} \oplus \begin{pmatrix} -2 & -1 \\ -1 & -\frac{p+1}{2} \end{pmatrix}, \end{align*} $$
a lattice of discriminant group
![]() ${\mathbb {Z}}/p {\mathbb {Z}}$
.
${\mathbb {Z}}/p {\mathbb {Z}}$
.
We consider H-quasipolarized holomorphic-symplectic varieties X of
![]() $K3^{[2]}$
-type. Examples are the Fano varieties of lines (
$K3^{[2]}$
-type. Examples are the Fano varieties of lines (
![]() $p=3$
) or the Debarre–Voisin fourfolds (
$p=3$
) or the Debarre–Voisin fourfolds (
![]() $p=11$
); see below. For these varieties, the Borcherds modular forms and the relationship between between Noether–Lefschetz divisors of first and second type can be described very explicitly.
$p=11$
); see below. For these varieties, the Borcherds modular forms and the relationship between between Noether–Lefschetz divisors of first and second type can be described very explicitly.
3.8.1 The Borcherds modular forms
Consider the series of Noether–Lefschetz numbers of second type
 $$ \begin{align*} \Phi^{\pi}(q) = \sum_{\gamma} \Phi^{\pi}_{\gamma}(q) e_{\gamma} \end{align*} $$
$$ \begin{align*} \Phi^{\pi}(q) = \sum_{\gamma} \Phi^{\pi}_{\gamma}(q) e_{\gamma} \end{align*} $$
for a one-parameter family
![]() $\pi $
of holomorphic-symplectic varieties of this polarization type. This is a modular form of weight
$\pi $
of holomorphic-symplectic varieties of this polarization type. This is a modular form of weight
![]() $11$
for the Weil representation on
$11$
for the Weil representation on
![]() $M^{\vee }/M$
. The space of such forms is easily computed through [Reference Williams53], and the first values are given in the following table.
$M^{\vee }/M$
. The space of such forms is easily computed through [Reference Williams53], and the first values are given in the following table.
Table 1 The dimension of the space of modular forms of weight
![]() $11$
for the Weil representation associated to M.
$11$
for the Weil representation associated to M.

If we write
![]() $y_{1}, y_{2}$
for the standard basis of the lattice
$y_{1}, y_{2}$
for the standard basis of the lattice
 $\begin {pmatrix} -2 & -1 \\ -1 & -\frac {p+1}{2} \end {pmatrix}$
, then the discrimimant of M is generated by
$\begin {pmatrix} -2 & -1 \\ -1 & -\frac {p+1}{2} \end {pmatrix}$
, then the discrimimant of M is generated by
 $$ \begin{align*} y^{\prime} = \frac{1}{p} (2 y_{2}-y_{1}) \end{align*} $$
$$ \begin{align*} y^{\prime} = \frac{1}{p} (2 y_{2}-y_{1}) \end{align*} $$
which has norm
![]() $y^{\prime } \cdot y^{\prime } = -2/p$
. Hence, for any element v of
$y^{\prime } \cdot y^{\prime } = -2/p$
. Hence, for any element v of
![]() $M^{\vee }$
, written as
$M^{\vee }$
, written as
we have
 $-\frac {1}{2} p v \cdot v = k^{2}$
modulo p. In particular, this determines
$-\frac {1}{2} p v \cdot v = k^{2}$
modulo p. In particular, this determines
![]() $[v] \in {\mathbb {Z}}/p{\mathbb {Z}}$
up to multiplication by
$[v] \in {\mathbb {Z}}/p{\mathbb {Z}}$
up to multiplication by
![]() $\pm 1$
. Thus, for any
$\pm 1$
. Thus, for any
![]() $v \in M^{\vee }$
, we see that
$v \in M^{\vee }$
, we see that
-
(i)
 $D := -\frac {p}{2} v \cdot v$
is a square modulo p, and
$D := -\frac {p}{2} v \cdot v$
is a square modulo p, and -
(ii)
 $r=[v]$
is determined from D via
$r=[v]$
is determined from D via
 $r^{2} \equiv D$
mod p, up to multiplication by
$r^{2} \equiv D$
mod p, up to multiplication by
 $\pm 1$
.
$\pm 1$
.
By the redundancy of Heegner divisors
![]() $y_{n,\gamma } = y_{n,-\gamma }$
, the coefficient
$y_{n,\gamma } = y_{n,-\gamma }$
, the coefficient
![]() $q^{n} e_{\gamma }$
of
$q^{n} e_{\gamma }$
of
![]() $\Phi (q)$
is thus determined by n alone. It is, hence, enough to consider
$\Phi (q)$
is thus determined by n alone. It is, hence, enough to consider
 $$ \begin{align} \varphi^{\pi}(q) = \frac{1}{2} \Phi^{\pi}_{0}(q) + \frac{1}{2} \sum_{\gamma \in M^{\vee}/M} \Phi^{\pi}_{\gamma}(q). \end{align} $$
$$ \begin{align} \varphi^{\pi}(q) = \frac{1}{2} \Phi^{\pi}_{0}(q) + \frac{1}{2} \sum_{\gamma \in M^{\vee}/M} \Phi^{\pi}_{\gamma}(q). \end{align} $$
Let
![]() $\chi _{p}$
be the Dirichlet character given by the Legendre symbol
$\chi _{p}$
be the Dirichlet character given by the Legendre symbol
 $\left ( \frac { \cdot }{p} \right )$
.
$\left ( \frac { \cdot }{p} \right )$
.
Proposition 4. The series
![]() $\Phi ^{\pi }_{0}(q)$
and
$\Phi ^{\pi }_{0}(q)$
and
![]() $\sum _{\gamma \in M^{\vee }/M} \Phi ^{\pi }_{\gamma }(q^{p})$
are modular forms of weight
$\sum _{\gamma \in M^{\vee }/M} \Phi ^{\pi }_{\gamma }(q^{p})$
are modular forms of weight
![]() $11$
and character
$11$
and character
![]() $\chi _{p}$
for the congruence subgroup
$\chi _{p}$
for the congruence subgroup
![]() $\Gamma _{0}(p)$
.
$\Gamma _{0}(p)$
.
Proof. The modularity of the first series is well-known [Reference Borcherds4]. The second is one direction of the Bruinier–Bundschuh isomorphism [Reference Bruinier and Bundschuh6].
The generators of the ring of modular forms for the character
![]() $\chi _{p}$
is easily computable (see, e.g., [Reference Borcherds4, Sec.12]) which yields explicit formulas for
$\chi _{p}$
is easily computable (see, e.g., [Reference Borcherds4, Sec.12]) which yields explicit formulas for
![]() $\varphi ^{\pi }$
. One example for Fano varieties can be found in [Reference Li and Zhang31]. We will consider the case of Debarre–Voisin fourfolds below.
$\varphi ^{\pi }$
. One example for Fano varieties can be found in [Reference Li and Zhang31]. We will consider the case of Debarre–Voisin fourfolds below.
Finally, the Noether–Lefschetz numbers of the family are given by
 $$ \begin{align*} \mathsf{NL}^{\pi}_{s,d} = \varphi^{\pi}\left[ -\frac{1}{4p} \det \begin{pmatrix} 2p & d \\ d & s \end{pmatrix} \right]. \end{align*} $$
$$ \begin{align*} \mathsf{NL}^{\pi}_{s,d} = \varphi^{\pi}\left[ -\frac{1}{4p} \det \begin{pmatrix} 2p & d \\ d & s \end{pmatrix} \right]. \end{align*} $$
3.8.2 Noether–Lefschetz divisors the first type
The relationship between Noether–Lefschetz divisors of the first and second type is not so easy to state in general. However, here the situation simplifies. For any
![]() $w \in H^{\perp } \subset V$
, we consider the intersection of
$w \in H^{\perp } \subset V$
, we consider the intersection of
![]() $w^{\perp }$
with the period domain
$w^{\perp }$
with the period domain
![]() ${\mathcal D}_{H}$
,
${\mathcal D}_{H}$
,
The image of this divisor under the quotient map
![]() ${\mathcal D}_{H} \to {\mathcal D}_{H}/\Gamma _{M}$
defines an irreducible divisor that by a result of Debarre and Macrì [Reference Debarre and Macrì14] only depends on the discriminant
${\mathcal D}_{H} \to {\mathcal D}_{H}/\Gamma _{M}$
defines an irreducible divisor that by a result of Debarre and Macrì [Reference Debarre and Macrì14] only depends on the discriminant
Moreover, e is a square modulo p. We write
![]() ${\mathcal C}_{2e}$
for this divisor.
${\mathcal C}_{2e}$
for this divisor.
The relationship between Noether–Lefschetz divisors of first and second type is given as follows.
Proposition 5. Let
![]() $D \geq 1$
be a square modulo p, and let
$D \geq 1$
be a square modulo p, and let
![]() $\alpha \in {\mathbb {Z}}/p {\mathbb {Z}}$
such that
$\alpha \in {\mathbb {Z}}/p {\mathbb {Z}}$
such that
![]() $\alpha ^{2} \equiv D$
mod p. The associated Heegner divisor
$\alpha ^{2} \equiv D$
mod p. The associated Heegner divisor
![]() $y_{-D/p,\alpha }$
, denoted also by
$y_{-D/p,\alpha }$
, denoted also by
![]() $\mathsf {NL}(D)$
, is given by
$\mathsf {NL}(D)$
, is given by
 $$ \begin{align*} \mathsf{NL}(D) = \sum_{\substack{a_{0} \geq 0, k \in \{ 0, \ldots, \lfloor \frac{p}{2} \rfloor \} \\ e = p a_{0} + k^{2} \geq 1}} \left| \left\{ c \in {\mathbb{Z}}\, \middle|\, c^{2} = \frac{D}{e},\ kc \equiv \alpha \text{mod } p \right\} \right| {\mathcal C}_{2e}. \end{align*} $$
$$ \begin{align*} \mathsf{NL}(D) = \sum_{\substack{a_{0} \geq 0, k \in \{ 0, \ldots, \lfloor \frac{p}{2} \rfloor \} \\ e = p a_{0} + k^{2} \geq 1}} \left| \left\{ c \in {\mathbb{Z}}\, \middle|\, c^{2} = \frac{D}{e},\ kc \equiv \alpha \text{mod } p \right\} \right| {\mathcal C}_{2e}. \end{align*} $$
In particular, we have
 $$ \begin{align*} \mathsf{NL}(D) = \begin{cases} {\mathcal C}_{2D} + \ldots & \text{ if } D \neq 0 \text{ mod } 11 \\ 2 {\mathcal C}_{2D} + \ldots & \text{ if } D = 0 \text{ mod } 11, \end{cases} \end{align*} $$
$$ \begin{align*} \mathsf{NL}(D) = \begin{cases} {\mathcal C}_{2D} + \ldots & \text{ if } D \neq 0 \text{ mod } 11 \\ 2 {\mathcal C}_{2D} + \ldots & \text{ if } D = 0 \text{ mod } 11, \end{cases} \end{align*} $$
where
![]() $\ldots $
stands for terms
$\ldots $
stands for terms
![]() ${\mathcal C}_{2e}$
with
${\mathcal C}_{2e}$
with
![]() $e<D$
. This shows that the Noether–Lefschetz divisors of the first type are related to the Heegner divisors by an invertible upper triangular matrx. If D is square free, then
$e<D$
. This shows that the Noether–Lefschetz divisors of the first type are related to the Heegner divisors by an invertible upper triangular matrx. If D is square free, then
![]() $\mathsf {NL}(D)$
and
$\mathsf {NL}(D)$
and
![]() ${\mathcal C}_{2D}$
agree up to a constant.
${\mathcal C}_{2D}$
agree up to a constant.
Proof. For any positive
![]() $e = p a_{0} + k^{2}$
with
$e = p a_{0} + k^{2}$
with
![]() $k \in \{ 0, 1 \ldots , \lfloor \frac {p}{2} \rfloor \}$
and
$k \in \{ 0, 1 \ldots , \lfloor \frac {p}{2} \rfloor \}$
and
![]() $a \geq 1$
, we choose a lattice
$a \geq 1$
, we choose a lattice
![]() $K_{e} \subset V$
containing H and such that
$K_{e} \subset V$
containing H and such that
![]() $\mathrm {disc}(K_{e}^{\perp }) = -2e$
. The lattice is unique up to an automorphism of V that fixes H [Reference Debarre and Macrì14]. Fix
$\mathrm {disc}(K_{e}^{\perp }) = -2e$
. The lattice is unique up to an automorphism of V that fixes H [Reference Debarre and Macrì14]. Fix
 $s \in \frac {1}{2} {\mathbb {Z}}$
with
$s \in \frac {1}{2} {\mathbb {Z}}$
with
![]() $2s \equiv 3 (4)$
and
$2s \equiv 3 (4)$
and
![]() $d \geq 1$
such that
$d \geq 1$
such that
 $D = -\frac {1}{4} \det \binom {2p\ d}{d\ s} = \frac {1}{4}( d^{2} - 2ps )$
. Then by Proposition 3, Remark 7 and the definition we have
$D = -\frac {1}{4} \det \binom {2p\ d}{d\ s} = \frac {1}{4}( d^{2} - 2ps )$
. Then by Proposition 3, Remark 7 and the definition we have
 $$ \begin{align*} \mathsf{NL}(D) = \mathsf{NL}_{s,d} = \sum_{e} \mu(K_{e}, s, d) {\mathcal C}_{2e}, \end{align*} $$
$$ \begin{align*} \mathsf{NL}(D) = \mathsf{NL}_{s,d} = \sum_{e} \mu(K_{e}, s, d) {\mathcal C}_{2e}, \end{align*} $$
where the multiplicity is given by
It remains to calculate the multiplicity. We first embed V into the Mukai lattice
![]() $\Lambda $
as the orthogonal of
$\Lambda $
as the orthogonal of
![]() $e+f$
such that
$e+f$
such that
![]() $\delta = -e+f$
. Here,
$\delta = -e+f$
. Here,
![]() $e,f$
is a symplectic basis of a not previously used copy of U. One finds that
$e,f$
is a symplectic basis of a not previously used copy of U. One finds that
 $$ \begin{align*} \widehat{L} = (M^{\perp} \subset \Lambda) \cong \begin{pmatrix} 2 & 1 \\ 1 & \frac{p+1}{2} \end{pmatrix} \end{align*} $$
$$ \begin{align*} \widehat{L} = (M^{\perp} \subset \Lambda) \cong \begin{pmatrix} 2 & 1 \\ 1 & \frac{p+1}{2} \end{pmatrix} \end{align*} $$
which has the integral basis
 $$ \begin{align*} x_{1} = e+f, \quad x_{2} = e^{\prime} + \frac{p+1}{4} f^{\prime} + f. \end{align*} $$
$$ \begin{align*} x_{1} = e+f, \quad x_{2} = e^{\prime} + \frac{p+1}{4} f^{\prime} + f. \end{align*} $$
Let us next choose
where
![]() $e^{\prime \prime }, f^{\prime \prime }$
is a symplectic basis of a third copy of U. The saturation of
$e^{\prime \prime }, f^{\prime \prime }$
is a symplectic basis of a third copy of U. The saturation of
![]() $K_{e} \oplus {\mathbb {Z}} (e+f)$
inside
$K_{e} \oplus {\mathbb {Z}} (e+f)$
inside
![]() $\Lambda $
is then given by
$\Lambda $
is then given by
 $$ \begin{align*} \widetilde{K}_{e} \cong \begin{pmatrix} 2 & 1 & 0 \\ 1 & \frac{p+1}{2} & k \\ 0 & k & -2 a_{0} \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \widetilde{K}_{e} \cong \begin{pmatrix} 2 & 1 & 0 \\ 1 & \frac{p+1}{2} & k \\ 0 & k & -2 a_{0} \end{pmatrix}, \end{align*} $$
where the lattice is generated by
![]() $x_{1}, x_{2}$
and
$x_{1}, x_{2}$
and
![]() $x_{3} = k f^{\prime } + e^{\prime \prime } - a_{0} f^{\prime \prime }$
.
$x_{3} = k f^{\prime } + e^{\prime \prime } - a_{0} f^{\prime \prime }$
.
We follow the recipe of the proof of Lemma 5, that is we compare the multiplicity (16) with a simpler multiplicity for
![]() $\tilde {K}_{e}$
. If
$\tilde {K}_{e}$
. If
![]() $s \in 2 {\mathbb {Z}}$
, then for D to be an integer, we must have d even. Then as in Lemma 5, one gets
$s \in 2 {\mathbb {Z}}$
, then for D to be an integer, we must have d even. Then as in Lemma 5, one gets
 $$ \begin{align*} \mu(K_{e}, s, d) = \left| \left\{ \beta \in \widetilde{K}_{e} \middle| \beta \cdot x_{1} = 0,\ \beta \cdot x_{2} = \frac{d}{2}, \ \beta \cdot \beta = s \right\} \right|. \end{align*} $$
$$ \begin{align*} \mu(K_{e}, s, d) = \left| \left\{ \beta \in \widetilde{K}_{e} \middle| \beta \cdot x_{1} = 0,\ \beta \cdot x_{2} = \frac{d}{2}, \ \beta \cdot \beta = s \right\} \right|. \end{align*} $$
If
 $s+\frac {1}{2} \in {\mathbb {Z}}$
, then d is odd, and
$s+\frac {1}{2} \in {\mathbb {Z}}$
, then d is odd, and
 $$ \begin{align*} \mu(K_{e}, s, d) = \left| \left\{ \beta \in \widetilde{K}_{e} \middle| \beta \cdot x_{1} = 1,\ \beta \cdot x_{2} = \frac{d+1}{2}, \ \beta \cdot \beta = s+\frac{1}{2} \right\} \right|. \end{align*} $$
$$ \begin{align*} \mu(K_{e}, s, d) = \left| \left\{ \beta \in \widetilde{K}_{e} \middle| \beta \cdot x_{1} = 1,\ \beta \cdot x_{2} = \frac{d+1}{2}, \ \beta \cdot \beta = s+\frac{1}{2} \right\} \right|. \end{align*} $$
The result follows from this by a direct calculation. For exposition, we evaluate the multiplicity in the first case. Using that
![]() $\beta \cdot x_{1} = 0$
, any element
$\beta \cdot x_{1} = 0$
, any element
![]() $\beta \in \tilde {K}_{e}$
as on the right-hand side is given by
$\beta \in \tilde {K}_{e}$
as on the right-hand side is given by
Let
![]() $\tilde {d} = d/2$
. The condition
$\tilde {d} = d/2$
. The condition
![]() $\beta \cdot x_{2} = \tilde {d}$
yields
$\beta \cdot x_{2} = \tilde {d}$
yields
![]() $a p + kc = \tilde {d}$
which can be solved if and only if
$a p + kc = \tilde {d}$
which can be solved if and only if
![]() $kc \equiv \tilde {d}$
mod p, in which case
$kc \equiv \tilde {d}$
mod p, in which case
![]() $a = (\tilde {d}-kc)/p$
. Inserting this expression into
$a = (\tilde {d}-kc)/p$
. Inserting this expression into
![]() $\beta \cdot \beta $
yields
$\beta \cdot \beta $
yields
 $$ \begin{align*} c^{2} e = \tilde{d}^{2} - \frac{p}{2} s = -\frac{1}{4}(2ps-d^{2}) = D. \end{align*} $$
$$ \begin{align*} c^{2} e = \tilde{d}^{2} - \frac{p}{2} s = -\frac{1}{4}(2ps-d^{2}) = D. \end{align*} $$
Finally,
![]() $D = \tilde {d}^{2}$
mod p, and hence, if
$D = \tilde {d}^{2}$
mod p, and hence, if
![]() $\alpha ^{2} = D$
mod p, then
$\alpha ^{2} = D$
mod p, then
![]() $\alpha = \pm \tilde {d}$
. If
$\alpha = \pm \tilde {d}$
. If
![]() $\alpha \equiv 0$
mod p, then the result follows. In the other case, among
$\alpha \equiv 0$
mod p, then the result follows. In the other case, among
 $c \in \{ \pm \sqrt {D/e} \}$
, there is precisely one solution to
$c \in \{ \pm \sqrt {D/e} \}$
, there is precisely one solution to
![]() $kc \equiv \tilde {d}$
mod p if and only if there is precisely one solution to
$kc \equiv \tilde {d}$
mod p if and only if there is precisely one solution to
![]() $kc \equiv \alpha $
mod p.
$kc \equiv \alpha $
mod p.
3.9 Example: Cubic fourfolds
We consider Fano varieties of lines
of a cubic fourfold. By [Reference Beauville and Donagi2], the Plücker polarization is of square
![]() $6$
and pairs evenly with any class in
$6$
and pairs evenly with any class in
![]() $H^{2}(X,{\mathbb {Z}})$
. Hence, their deformation type is governed by the discussion in Section 3.8 for
$H^{2}(X,{\mathbb {Z}})$
. Hence, their deformation type is governed by the discussion in Section 3.8 for
![]() $p=3$
. The Borcherds modular form for the generic pencil of Fano varieties is computed in [Reference Li and Zhang31].
$p=3$
. The Borcherds modular form for the generic pencil of Fano varieties is computed in [Reference Li and Zhang31].
Let
![]() $U \subset \mathbb {P}( H^{0}(\mathbb {P}^{5}, {\mathcal O}(3)))$
be the open locus corresponding to cubic fourfolds with at worst ADE singularities. There is a period mapping
$U \subset \mathbb {P}( H^{0}(\mathbb {P}^{5}, {\mathcal O}(3)))$
be the open locus corresponding to cubic fourfolds with at worst ADE singularities. There is a period mapping
to the corresponding moduli space. The pullback of the divisors
![]() ${\mathcal C}_{2e}$
under this mapping are the special cubic fourfolds of discriminant
${\mathcal C}_{2e}$
under this mapping are the special cubic fourfolds of discriminant
![]() $d=2e$
; see [Reference Hassett21, Reference Li and Zhang31]. (A cubic fourfold
$d=2e$
; see [Reference Hassett21, Reference Li and Zhang31]. (A cubic fourfold
![]() $Y \subset \mathbb {P}^{5}$
is special if it contains an algebraic surface S such that the saturation of
$Y \subset \mathbb {P}^{5}$
is special if it contains an algebraic surface S such that the saturation of
![]() $[S]$
and
$[S]$
and
![]() $h^{2}$
is of discriminant d).
$h^{2}$
is of discriminant d).
For the one-parameter family
![]() $\pi $
of Fano varieties of lines of a generic pencil of cubic fourfolds, the Noether–Lefschetz numbers of the second type
$\pi $
of Fano varieties of lines of a generic pencil of cubic fourfolds, the Noether–Lefschetz numbers of the second type
![]() $\mathsf {NL}_{s,d}^{\pi }$
and of first type
$\mathsf {NL}_{s,d}^{\pi }$
and of first type
are then related to the classical geometry of special cubic fourfolds. For example,
 $$ \begin{gather*} \mathsf{NL}^{\pi}_{-2,0} = \mathsf{NL}^{\pi}(D = 3) = 192 \\ \mathsf{NL}^{\pi}_{-2,4} = \mathsf{NL}^{\pi}(D = 7) = 917,568 \end{gather*} $$
$$ \begin{gather*} \mathsf{NL}^{\pi}_{-2,0} = \mathsf{NL}^{\pi}(D = 3) = 192 \\ \mathsf{NL}^{\pi}_{-2,4} = \mathsf{NL}^{\pi}(D = 7) = 917,568 \end{gather*} $$
are the degrees of the (closure of the) divisors in
![]() $\mathbb {P}( H^{0}(\mathbb {P}^{5}, {\mathcal O}(3)))$
parametrizing nodal and Pfaffian cubics, respectively. The locus of determinantal cubic fourfolds
$\mathbb {P}( H^{0}(\mathbb {P}^{5}, {\mathcal O}(3)))$
parametrizing nodal and Pfaffian cubics, respectively. The locus of determinantal cubic fourfolds
![]() $p^{-1} {\mathcal C}_{2}$
is of codimension
$p^{-1} {\mathcal C}_{2}$
is of codimension
![]() $\geq 2$
; see, e.g., [Reference Huybrechts23, Rmk 3.23], and hence,
$\geq 2$
; see, e.g., [Reference Huybrechts23, Rmk 3.23], and hence,
 $$ \begin{align*} \mathsf{NL}^{\pi}_{-1/2,1} = \mathsf{NL}^{\pi}(D=1) = 0. \end{align*} $$
$$ \begin{align*} \mathsf{NL}^{\pi}_{-1/2,1} = \mathsf{NL}^{\pi}(D=1) = 0. \end{align*} $$
Thus, one gets that
 $$ \begin{align*} \mathsf{NL}^{\pi}_{-5/2,1} = \mathsf{NL}^{\pi}(D = 4) = 3402 \end{align*} $$
$$ \begin{align*} \mathsf{NL}^{\pi}_{-5/2,1} = \mathsf{NL}^{\pi}(D = 4) = 3402 \end{align*} $$
which is the degree of the locus
![]() $p^{-1} {\mathcal C}_{8}$
of cubics containing a plane. The equalities of the Noether–Lefschetz numbers of first and second type above follow from Proposition 5: In the first three cases, since D is square free, and in the last case we use that
$p^{-1} {\mathcal C}_{8}$
of cubics containing a plane. The equalities of the Noether–Lefschetz numbers of first and second type above follow from Proposition 5: In the first three cases, since D is square free, and in the last case we use that
![]() ${\mathcal C}_{2}$
does not meet the curve defined by
${\mathcal C}_{2}$
does not meet the curve defined by
![]() $\pi $
.
$\pi $
.
3.10 Example II: Debarre–Voisin fourfolds
A Debarre–Voisin fourfold [Reference Debarre and Voisin15] is the holomorphic-symplectic variety
given as the vanishing locus of a section of
![]() $\Lambda ^{3} {\mathcal U}^{\vee }$
, where
$\Lambda ^{3} {\mathcal U}^{\vee }$
, where
![]() ${\mathcal U} \subset {\mathbb {C}}^{10} \otimes {\mathcal O}$
is the universal subbundle on the Grassmannian. These varieties are of
${\mathcal U} \subset {\mathbb {C}}^{10} \otimes {\mathcal O}$
is the universal subbundle on the Grassmannian. These varieties are of
![]() $K3^{[2]}$
-type, and the Plücker polarization is of degree
$K3^{[2]}$
-type, and the Plücker polarization is of degree
![]() $H^{2} = 22$
and pairs evenly with any class in
$H^{2} = 22$
and pairs evenly with any class in
![]() $H^{2}(X,{\mathbb {Z}})$
. Hence, we are in the situation of Section 3.8 for
$H^{2}(X,{\mathbb {Z}})$
. Hence, we are in the situation of Section 3.8 for
![]() $p=11$
. The Noether–Lefschetz numbers for a generic pencil of these varieties will be computed below.
$p=11$
. The Noether–Lefschetz numbers for a generic pencil of these varieties will be computed below.
3.11 Refined Noether–Lefschetz divisors
We will need refined Noether–Lefschetz divisors which also depend on the divisibility
![]() $m \geq 1$
of the curve class. Refined Noether–Lefschetz numbers are then defined as usually by intersection with Noether–Lefschetz divisors. As before, we assume that we are in
$m \geq 1$
of the curve class. Refined Noether–Lefschetz numbers are then defined as usually by intersection with Noether–Lefschetz divisors. As before, we assume that we are in
![]() $K3^{[n]}$
-type. Let
$K3^{[n]}$
-type. Let
![]() $s \in {\mathbb {Q}}$
,
$s \in {\mathbb {Q}}$
,
![]() $d = (d_{1}, \ldots , d_{\ell }) \in {\mathbb {Z}}^{\ell }$
and
$d = (d_{1}, \ldots , d_{\ell }) \in {\mathbb {Z}}^{\ell }$
and
![]() $r \in {\mathbb {Z}}_{2n-2}$
be fixed.
$r \in {\mathbb {Z}}_{2n-2}$
be fixed.
If
![]() $\Delta (s, d) \neq 0$
, we set
$\Delta (s, d) \neq 0$
, we set
 $$ \begin{align*} \mathsf{NL}_{m, s,d, \pm r} = \sum_{L\subset \tilde{L} \subset V} \mu(m, s,d, r | L\subset \tilde{L} \subset V ) \cdot \mathsf{NL}_{\tilde{L}}, \end{align*} $$
$$ \begin{align*} \mathsf{NL}_{m, s,d, \pm r} = \sum_{L\subset \tilde{L} \subset V} \mu(m, s,d, r | L\subset \tilde{L} \subset V ) \cdot \mathsf{NL}_{\tilde{L}}, \end{align*} $$
where the refined multiplicity
![]() $\mu ( \ldots )$
is the number of classes
$\mu ( \ldots )$
is the number of classes
![]() $\beta \in V^{\vee }$
which are contained in
$\beta \in V^{\vee }$
which are contained in
![]() $\widetilde {L} \otimes {\mathbb {Q}}$
, satisfy
$\widetilde {L} \otimes {\mathbb {Q}}$
, satisfy
![]() $\beta \cdot \beta = s$
,
$\beta \cdot \beta = s$
,
![]() $\beta \cdot L_{i} = d_{i}$
and such that the following new conditions hold:
$\beta \cdot L_{i} = d_{i}$
and such that the following new conditions hold:
 $$ \begin{align*} \mathsf{div}(\beta) = m, \quad \left[ \frac{\beta}{\mathsf{div}(\beta)} \right] = \pm r \in {\mathbb{Z}}/(2n-2){\mathbb{Z}}. \end{align*} $$
$$ \begin{align*} \mathsf{div}(\beta) = m, \quad \left[ \frac{\beta}{\mathsf{div}(\beta)} \right] = \pm r \in {\mathbb{Z}}/(2n-2){\mathbb{Z}}. \end{align*} $$
Note that we treat the residue different from the nonrefined case.
If
![]() $\Delta (s, d) = 0$
, we define
$\Delta (s, d) = 0$
, we define
if m is the gcd of
![]() $d_{1}, \ldots , d_{r}$
and the unique class
$d_{1}, \ldots , d_{r}$
and the unique class
![]() $\beta \in L \otimes {\mathbb {Q}}$
with
$\beta \in L \otimes {\mathbb {Q}}$
with
![]() $\beta \cdot L_{i} = d_{i}/m$
lies in
$\beta \cdot L_{i} = d_{i}/m$
lies in
![]() $V^{\vee }$
and has residue
$V^{\vee }$
and has residue
![]() $[\beta ] = \pm r$
. Otherwise, we set
$[\beta ] = \pm r$
. Otherwise, we set
![]() $\mathsf {NL}_{m, s,d, \pm r} = 0$
.
$\mathsf {NL}_{m, s,d, \pm r} = 0$
.
We then have
 $$ \begin{align} \mathsf{NL}_{s,d, \pm r} = \sum_{m \geq 1} \sum_{\substack{\pm r^{\prime}\\ \pm m \cdot r^{\prime} = \pm r}} \mathsf{NL}_{m, s,d, \pm r^{\prime}} \end{align} $$
$$ \begin{align} \mathsf{NL}_{s,d, \pm r} = \sum_{m \geq 1} \sum_{\substack{\pm r^{\prime}\\ \pm m \cdot r^{\prime} = \pm r}} \mathsf{NL}_{m, s,d, \pm r^{\prime}} \end{align} $$
and
By a simple induction argument as in [Reference Klemm, Maulik, Pandharipande and Scheidegger26, Lemma 1], these two equations show that the data of the unrefined Noether–Lefschetz numbers are equivalent to the the data of the refined Noether–Lefschetz numbers/divisors.
Remark 8. If the residue of a class is determined by d and s, the inverse relation between refined and unrefined is easy to state. We simply have
 $$ \begin{align*} \mathsf{NL}_{1,s,d} = \sum_{k|\mathrm{gcd}(d_{1}, \ldots, d_{\ell})} \mu(k) \cdot \mathsf{NL}_{s/k^{2}, d/k}, \end{align*} $$
$$ \begin{align*} \mathsf{NL}_{1,s,d} = \sum_{k|\mathrm{gcd}(d_{1}, \ldots, d_{\ell})} \mu(k) \cdot \mathsf{NL}_{s/k^{2}, d/k}, \end{align*} $$
parallel to the multiple cover rule we study in this paper.
4 Gromov–Witten theory and Noether–Lefschetz theory
Let V be the
![]() $K3^{[n]}$
-lattice, and let
$K3^{[n]}$
-lattice, and let
![]() $L \subset V$
be a fixed primitive sublattice with integral basis
$L \subset V$
be a fixed primitive sublattice with integral basis
![]() $L_{i}$
. We consider a one-parameter family
$L_{i}$
. We consider a one-parameter family
of L-quasipolarized holomorphic-symplectic varieties of
![]() $K3^{[n]}$
-type.
$K3^{[n]}$
-type.
The goal of this section is to relate Gromov–Witten invariants of
![]() ${\mathcal X}$
in fiber classes to the Noether–Lefschetz numbers of the family and the reduced Gromov–Witten invariants in
${\mathcal X}$
in fiber classes to the Noether–Lefschetz numbers of the family and the reduced Gromov–Witten invariants in
![]() $K3^{[n]}$
-type.
$K3^{[n]}$
-type.
4.1 Gromov–Witten invariants of the family
Let
![]() $\gamma _{i} \in H^{\ast }({\mathcal X})$
be cohomology classes which can be written in terms of polynomials
$\gamma _{i} \in H^{\ast }({\mathcal X})$
be cohomology classes which can be written in terms of polynomials
![]() $p_{i}$
in the Chern classes of
$p_{i}$
in the Chern classes of
![]() ${\mathcal L}_{i}$
,
${\mathcal L}_{i}$
,
Let
 ${\overline M}_{g,N}({\mathcal X}, d)$
for
${\overline M}_{g,N}({\mathcal X}, d)$
for
![]() $d \in {\mathbb {Z}}^{\ell }$
be the moduli space of N-marked genus g stable maps
$d \in {\mathbb {Z}}^{\ell }$
be the moduli space of N-marked genus g stable maps
![]() $f : C \to {\mathcal X}$
such that
$f : C \to {\mathcal X}$
such that
-
○ f maps into the fibers of
 ${\mathcal X}$
, that is
${\mathcal X}$
, that is
 $\pi _{\ast } f_{\ast }[C] = 0$
, and
$\pi _{\ast } f_{\ast }[C] = 0$
, and -
○ f is of degree
 $d_{i}$
against
$d_{i}$
against
 $L_{i}$
,
$L_{i}$
,  $$ \begin{align*} \int_{[C]} f^{\ast}(c_{1}({\mathcal L}_{i})) = d_{i}. \end{align*} $$
$$ \begin{align*} \int_{[C]} f^{\ast}(c_{1}({\mathcal L}_{i})) = d_{i}. \end{align*} $$
We consider the invariants
 $$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}}_{g,d} = \int_{[{\overline M}_{g,n}({\mathcal X}, d)]} \tau^{\ast}(\alpha) \operatorname{ev}_{1}^{\ast}(\gamma_{1}) \cdots \operatorname{ev}_{N}^{\ast}(\gamma_{N}), \end{align*} $$
$$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}}_{g,d} = \int_{[{\overline M}_{g,n}({\mathcal X}, d)]} \tau^{\ast}(\alpha) \operatorname{ev}_{1}^{\ast}(\gamma_{1}) \cdots \operatorname{ev}_{N}^{\ast}(\gamma_{N}), \end{align*} $$
where
 $\alpha \in H^{\ast }({\overline M}_{g,n})$
is tautological and
$\alpha \in H^{\ast }({\overline M}_{g,n})$
is tautological and
![]() $\tau $
is the forgetful map.
$\tau $
is the forgetful map.
4.2 Gromov–Witten invariants of the fiber
Let X be any holomorphic-symplectic variety of
![]() $K3^{[n]}$
-type, and let
$K3^{[n]}$
-type, and let
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
be an effective curve class. Assume there exists an embedding
$\beta \in H_{2}(X,{\mathbb {Z}})$
be an effective curve class. Assume there exists an embedding
which is an isometry onto its image such that
![]() $\beta \cdot L_{i} = d_{i}$
for all i. As usual, we let
$\beta \cdot L_{i} = d_{i}$
for all i. As usual, we let
![]() $L_{i} \in H^{2}(X,{\mathbb {R}})$
denote the image of
$L_{i} \in H^{2}(X,{\mathbb {R}})$
denote the image of
![]() $L_{i} \in L$
under this map. Let also
$L_{i} \in L$
under this map. Let also
By deformation invariance and the invariance property of Section 2.2, the reduced Gromov–Witten invariant
 $\big \langle \alpha; \gamma _{1}, \ldots , \gamma _{N} \big \rangle ^{X}_{g,\beta }$
only depends on the degree
$\big \langle \alpha; \gamma _{1}, \ldots , \gamma _{N} \big \rangle ^{X}_{g,\beta }$
only depends on the degree
![]() $d = (d_{1}, \ldots , d_{\ell })$
, the polynomials
$d = (d_{1}, \ldots , d_{\ell })$
, the polynomials
![]() $p_{i}$
,
$p_{i}$
,
![]() $s = \beta \cdot \beta $
and the curve invariants
$s = \beta \cdot \beta $
and the curve invariants
![]() $m = \mathsf {div}(\beta )$
and the residue set
$m = \mathsf {div}(\beta )$
and the residue set
![]() $\pm r = \pm [ \beta / \mathsf {div}(\beta ) ]$
. We write
$\pm r = \pm [ \beta / \mathsf {div}(\beta ) ]$
. We write
 $$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{X}_{g,\beta} = \big\langle \alpha; p_{1}, \ldots, p_{N} \big\rangle^{X}_{g,m,s,d,\pm r}. \end{align*} $$
$$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{X}_{g,\beta} = \big\langle \alpha; p_{1}, \ldots, p_{N} \big\rangle^{X}_{g,m,s,d,\pm r}. \end{align*} $$
4.3 The relation
Consider the refined Noether–Lefschetz numbers of
![]() $\pi $
,
$\pi $
,
 $$ \begin{align*} \mathsf{NL}^{\pi}_{m, s,d, \pm r} := \int_{C} \iota_{\pi}^{\ast} \mathsf{NL}_{m, s,d, \pm r^{\prime}}, \end{align*} $$
$$ \begin{align*} \mathsf{NL}^{\pi}_{m, s,d, \pm r} := \int_{C} \iota_{\pi}^{\ast} \mathsf{NL}_{m, s,d, \pm r^{\prime}}, \end{align*} $$
where
![]() $\iota _{\pi }: C \to {\mathcal M}_{L}$
is the morphism defined by the family.
$\iota _{\pi }: C \to {\mathcal M}_{L}$
is the morphism defined by the family.
Proposition 6. Let
![]() $\gamma _{i} = p_{i}({\mathcal L}_{1}, \ldots , {\mathcal L}_{\ell }) \in H^{\ast }({\mathcal X})$
. Then we have
$\gamma _{i} = p_{i}({\mathcal L}_{1}, \ldots , {\mathcal L}_{\ell }) \in H^{\ast }({\mathcal X})$
. Then we have
 $$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}}_{g,d} = \sum_{m,s, \pm r} \mathsf{NL}^{\pi}_{m,s, d, \pm r} \cdot \big\langle \alpha \cdot (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X}_{g,m,s,d,\pm r}. \end{align*} $$
$$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}}_{g,d} = \sum_{m,s, \pm r} \mathsf{NL}^{\pi}_{m,s, d, \pm r} \cdot \big\langle \alpha \cdot (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X}_{g,m,s,d,\pm r}. \end{align*} $$
Here,
![]() $\lambda _{i}$
are the i-th Chern classes of the Hodge bundle on the moduli space of stable curves. The proposition can be extended to more general classes
$\lambda _{i}$
are the i-th Chern classes of the Hodge bundle on the moduli space of stable curves. The proposition can be extended to more general classes
![]() $\gamma _{i}$
. It is enough to assume that
$\gamma _{i}$
. It is enough to assume that
![]() $\gamma _{i}$
is the product of some polynomial in the
$\gamma _{i}$
is the product of some polynomial in the
![]() ${\mathcal L}_{i}$
and a class which restricts to a monodromy invariant class on each fiber, for example, a Chern class.
${\mathcal L}_{i}$
and a class which restricts to a monodromy invariant class on each fiber, for example, a Chern class.
Proof. The proof follows by the identical argument as for the K3 surfaces, as discussed in [Reference Maulik and Pandharipande37, Section 3.2]. The above equality in the K3 case is [Reference Maulik and Pandharipande37, Eqn. (17)]. As in [Reference Maulik and Pandharipande37], for each
![]() $\xi \in C$
, we want to group together all curve classes in
$\xi \in C$
, we want to group together all curve classes in
![]() $H_{2}({\mathcal X}_{\xi },{\mathbb {Z}})$
of degree d which have the same Gromov–Witten invariants. By Corollary 2, we, hence, may group together classes of the same square, the same divisibility and the same residue. Thus, we replace the set
$H_{2}({\mathcal X}_{\xi },{\mathbb {Z}})$
of degree d which have the same Gromov–Witten invariants. By Corollary 2, we, hence, may group together classes of the same square, the same divisibility and the same residue. Thus, we replace the set
![]() $B_{\xi }(m,h,d)$
of [Reference Maulik and Pandharipande37, Sec.3.2] by
$B_{\xi }(m,h,d)$
of [Reference Maulik and Pandharipande37, Sec.3.2] by
 $$ \begin{align*} B_{\xi}(m,s,d, \pm r) = \left\{ \beta \in H_{2}({\mathcal X}_{\xi},{\mathbb{Z}}) \middle| \begin{array}{c} (\beta,\beta)=s,\ \mathsf{div}(\beta) = m, \\ {[} \beta/\mathsf{div}(\beta)] = \pm r,\ \beta \cdot L_{i} = d_{i} \\ \beta \perp H^{2,0}({\mathcal X}_{\xi},{\mathbb{C}}) \end{array} \right\}. \end{align*} $$
$$ \begin{align*} B_{\xi}(m,s,d, \pm r) = \left\{ \beta \in H_{2}({\mathcal X}_{\xi},{\mathbb{Z}}) \middle| \begin{array}{c} (\beta,\beta)=s,\ \mathsf{div}(\beta) = m, \\ {[} \beta/\mathsf{div}(\beta)] = \pm r,\ \beta \cdot L_{i} = d_{i} \\ \beta \perp H^{2,0}({\mathcal X}_{\xi},{\mathbb{C}}) \end{array} \right\}. \end{align*} $$
The rest of the argument of [Reference Maulik and Pandharipande37, Sec.3] goes through without change.
4.4 Reformulation
We can rewrite Proposition 6 in terms of invariants where we have formally subtracted multiple cover contrubtions. For simplicity, assume that for
![]() $\beta \in H_{2}(X,{\mathbb {Z}})$
the residue
$\beta \in H_{2}(X,{\mathbb {Z}})$
the residue
![]() $r([\beta ])$
is determined by the degrees
$r([\beta ])$
is determined by the degrees
![]() $d_{i} = \beta \cdot L_{i}$
. Write
$d_{i} = \beta \cdot L_{i}$
. Write
![]() $r(d)$
for the residue. Proposition 6 then says that
$r(d)$
for the residue. Proposition 6 then says that
 $$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}}_{g,d} = \sum_{m,s} \mathsf{NL}^{\pi}_{m,s, d} \cdot \big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X}_{g,m,s,d}. \end{align*} $$
$$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}}_{g,d} = \sum_{m,s} \mathsf{NL}^{\pi}_{m,s, d} \cdot \big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X}_{g,m,s,d}. \end{align*} $$
Let us subtract formally the multiple cover contributions from the invariants of
![]() ${\mathcal X}$
,
${\mathcal X}$
,
 $$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}, \text{mc}}_{g,d} := \sum_{k|d} (-1)^{r(d) + r(d/k)} \mu(k) k^{2g-3+N-\deg(\alpha)} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}}_{g,d/k} \end{align*} $$
$$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}, \text{mc}}_{g,d} := \sum_{k|d} (-1)^{r(d) + r(d/k)} \mu(k) k^{2g-3+N-\deg(\alpha)} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}}_{g,d/k} \end{align*} $$
as well as from the the reduced Gromov–Witten invariants,
 $$ \begin{align*} &\kern-6pt\big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X,\text{mc}}_{g,m,s,d} \\ &\quad := \sum_{k|m} (-1)^{r(d) + r(d/k)} k^{2g-3+N-\deg(\alpha)} \mu(k) \big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X}_{g,m/k,s/k^{2},d/k}. \end{align*} $$
$$ \begin{align*} &\kern-6pt\big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X,\text{mc}}_{g,m,s,d} \\ &\quad := \sum_{k|m} (-1)^{r(d) + r(d/k)} k^{2g-3+N-\deg(\alpha)} \mu(k) \big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X}_{g,m/k,s/k^{2},d/k}. \end{align*} $$
The following is the result of a short calculation.
Lemma 6. We have
 $$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}, \text{mc}}_{g,d} = \sum_{m,s} \mathsf{NL}_{m,s,d} \cdot \big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X,\text{mc}}_{g,m,s,d}. \end{align*} $$
$$ \begin{align*} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}, \text{mc}}_{g,d} = \sum_{m,s} \mathsf{NL}_{m,s,d} \cdot \big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X,\text{mc}}_{g,m,s,d}. \end{align*} $$
In particular, if the multiple cover conjecture (Conjecture B) holds, after subtracting the multiple cover contributions, the invariants of X do not depend on the divisibility m, and so with equation (18), we obtain
 $$ \begin{align} \begin{aligned} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}, \text{mc}}_{g,d} & = \sum_{s} \big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X,\text{mc}}_{g,1,s,d} \sum_{m,s} \mathsf{NL}_{m,s,d} \\ & = \sum_{s} \mathsf{NL}_{s,d} \cdot \big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X,\text{mc}}_{g,1,s,d}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big\langle \alpha; \gamma_{1}, \ldots, \gamma_{N} \big\rangle^{{\mathcal X}, \text{mc}}_{g,d} & = \sum_{s} \big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X,\text{mc}}_{g,1,s,d} \sum_{m,s} \mathsf{NL}_{m,s,d} \\ & = \sum_{s} \mathsf{NL}_{s,d} \cdot \big\langle \alpha (-1)^{g} \lambda_{g}; p_{1}, \ldots, p_{N} \big\rangle^{X,\text{mc}}_{g,1,s,d}. \end{aligned} \end{align} $$
5 Mirror symmetry
5.1 Overview
In this section, we review how to use mirror symmetry formulas to compute the genus
![]() $0$
Gromov–Witten invariants for the total space
$0$
Gromov–Witten invariants for the total space
![]() ${\mathcal X}$
of generic pencils of Fano varieties of lines of cubic fourfolds and of Debarre–Voisin varieties.
${\mathcal X}$
of generic pencils of Fano varieties of lines of cubic fourfolds and of Debarre–Voisin varieties.
Mirror symmetry here means an application of the following results: Givental’s description of the I-function for complete intersections in toric varieties [Reference Givental18], the proof of the abelian/nonabelian correspondence by Webb that relates the I-function of a GIT quotient with that of its abelian quotient [Reference Webb52] and the genus
![]() $0$
wallcrossing formula between quasi-maps and Gromov–Witten invariants for GIT quotients by Ciocan-Fontanine and Kim [Reference Ciocan-Fontanine and Kim11].
$0$
wallcrossing formula between quasi-maps and Gromov–Witten invariants for GIT quotients by Ciocan-Fontanine and Kim [Reference Ciocan-Fontanine and Kim11].
We first determine the small I-function for the cases we are interested in, then we shortly recall how to relate the I and J functions. We assume basic familiarity with the language of [Reference Ciocan-Fontanine and Kim11, Reference Webb52] throughout.
5.2 I-functions
We work in the following setup: Let V be a vector space over
![]() ${\mathbb {C}}$
, and let G be a connected reductive group acting faithfully on V on the left. We also fix a character of G for which we assume that the semistable and stable locus, denoted by
${\mathbb {C}}$
, and let G be a connected reductive group acting faithfully on V on the left. We also fix a character of G for which we assume that the semistable and stable locus, denoted by
![]() $V^{s}(G)$
, agrees. For simplicity, we also assume that the G-action on the stable locus is free. We consider the GIT quotient
$V^{s}(G)$
, agrees. For simplicity, we also assume that the G-action on the stable locus is free. We consider the GIT quotient
Let
![]() $T \subset G$
be a maximal torus, and consider also the abelian quotient
$T \subset G$
be a maximal torus, and consider also the abelian quotient
![]() $V^{s}(T)/T$
. We have then the following diagram relating the abelian and nonabelian quotients:
$V^{s}(T)/T$
. We have then the following diagram relating the abelian and nonabelian quotients:

The Weyl group W of G acts naturally on the cohomology of
![]() $V^{s}(G)/T$
, and one has the isomorphism
$V^{s}(G)/T$
, and one has the isomorphism
 $$ \begin{align*} \xi^{\ast} : H^{\ast}(V^{s}(G)/G , {\mathbb{Q}}) \xrightarrow{\cong} H^{\ast}( V^{s}(G)/T, {\mathbb{Q}} )^{W}. \end{align*} $$
$$ \begin{align*} \xi^{\ast} : H^{\ast}(V^{s}(G)/G , {\mathbb{Q}}) \xrightarrow{\cong} H^{\ast}( V^{s}(G)/T, {\mathbb{Q}} )^{W}. \end{align*} $$
Let E be a G-representation, and consider a smooth zero locus of the associated homogeneous bundle E on Y,
The small I-function of X in Y is a formal series
 $$ \begin{align*} I^{X} = I^{Y,E} = 1 + \sum_{\beta \neq 0} q^{\beta} I_{\beta}(z), \end{align*} $$
$$ \begin{align*} I^{X} = I^{Y,E} = 1 + \sum_{\beta \neq 0} q^{\beta} I_{\beta}(z), \end{align*} $$
where
![]() $\beta \in H_{2}(Y,{\mathbb {Z}})$
runs over all curve classes,
$\beta \in H_{2}(Y,{\mathbb {Z}})$
runs over all curve classes,
![]() $q^{\beta }$
is a formal variable and
$q^{\beta }$
is a formal variable and
![]() $I_{\beta }(z)$
is a formal series in
$I_{\beta }(z)$
is a formal series in
![]() $z^{\pm 1}$
with coefficients in
$z^{\pm 1}$
with coefficients in
![]() $H^{\ast }(Y,{\mathbb {Q}})$
. It can then be determined in the following steps.
$H^{\ast }(Y,{\mathbb {Q}})$
. It can then be determined in the following steps.
Abelian/Nonabelian correspondence ([Reference Webb52]).
 $$ \begin{align*} \xi^{\ast} I_{\beta}^{Y,E} = j^{\ast} \sum_{\tilde{\beta} \mapsto \beta} \left( \prod_{\alpha} \frac{\prod_{k=-\infty}^{\tilde{\beta} \cdot c_{1}(L_{\alpha})} (c_{1}(L_{\alpha}) + kz)}{\prod_{k=-\infty}^{0} (c_{1}(L_{\alpha}) + kz)} \right) I_{\tilde{\beta}}^{V//T,E}, \end{align*} $$
$$ \begin{align*} \xi^{\ast} I_{\beta}^{Y,E} = j^{\ast} \sum_{\tilde{\beta} \mapsto \beta} \left( \prod_{\alpha} \frac{\prod_{k=-\infty}^{\tilde{\beta} \cdot c_{1}(L_{\alpha})} (c_{1}(L_{\alpha}) + kz)}{\prod_{k=-\infty}^{0} (c_{1}(L_{\alpha}) + kz)} \right) I_{\tilde{\beta}}^{V//T,E}, \end{align*} $$
where
![]() $\alpha $
runs over the roots of G and
$\alpha $
runs over the roots of G and
![]() $L_{\alpha }$
is the associated line bundle on the abelian quotient,
$L_{\alpha }$
is the associated line bundle on the abelian quotient,
![]() $\tilde {\beta } \in H_{2}(V//T,{\mathbb {Z}}) = \operatorname {Hom}(\chi (T),{\mathbb {Z}})$
runs over the characters of T that restrict to the given character
$\tilde {\beta } \in H_{2}(V//T,{\mathbb {Z}}) = \operatorname {Hom}(\chi (T),{\mathbb {Z}})$
runs over the characters of T that restrict to the given character
![]() $\beta \in H_{2}(Y,{\mathbb {Z}}) = \operatorname {Hom}(\chi (G),{\mathbb {Z}})$
under the map induced by
$\beta \in H_{2}(Y,{\mathbb {Z}}) = \operatorname {Hom}(\chi (G),{\mathbb {Z}})$
under the map induced by
![]() $\chi (G) \to \chi (T)$
. When it is clear from context, we will often omit the pullbacks
$\chi (G) \to \chi (T)$
. When it is clear from context, we will often omit the pullbacks
![]() $\xi ^{\ast }$
and
$\xi ^{\ast }$
and
![]() $j^{\ast }$
from the notation.
$j^{\ast }$
from the notation.
Twisting ([Reference Givental18]). When restricting the G-representation E to T, it decomposes into a direct sum of one-dimensional representations
![]() $M_{i}$
. We write
$M_{i}$
. We write
![]() $M_{i}$
also for the associated line bundles on
$M_{i}$
also for the associated line bundles on
![]() $V//T$
. Then
$V//T$
. Then
 $$ \begin{align*} I^{V//T,E}_{\beta} = \left( \prod_{i=1}^{\mathrm{rk}(E)} \prod_{k=1}^{c_{1}(M_{i}) \cdot \beta} (c_{1}(M_{i}) + kz) \right) \cdot I^{X}_{\beta}. \end{align*} $$
$$ \begin{align*} I^{V//T,E}_{\beta} = \left( \prod_{i=1}^{\mathrm{rk}(E)} \prod_{k=1}^{c_{1}(M_{i}) \cdot \beta} (c_{1}(M_{i}) + kz) \right) \cdot I^{X}_{\beta}. \end{align*} $$
Toric varieties ([Reference Givental18]). Let
![]() $D_{i}, i=1, \ldots , n$
be the torus invariant divisors on the toric variety
$D_{i}, i=1, \ldots , n$
be the torus invariant divisors on the toric variety
![]() $V//T$
.
$V//T$
.
 $$ \begin{align*} I_{\beta}^{V//T} = \prod_{i=1}^{n} \frac{ \prod_{k=-\infty}^{0} (D_{i} + kz) }{ \prod_{k=-\infty}^{D_{i} \cdot \beta} (D_{i} + kz) }. \end{align*} $$
$$ \begin{align*} I_{\beta}^{V//T} = \prod_{i=1}^{n} \frac{ \prod_{k=-\infty}^{0} (D_{i} + kz) }{ \prod_{k=-\infty}^{D_{i} \cdot \beta} (D_{i} + kz) }. \end{align*} $$
Example 2. (Projective space
![]() $\mathbb {P}^{n-1}$
) We have
$\mathbb {P}^{n-1}$
) We have
 $I^{\mathbb {P}^{n-1}}_{d} = ( \prod _{k=1}^{d} (H + kz)^{n} )^{-1}$
.
$I^{\mathbb {P}^{n-1}}_{d} = ( \prod _{k=1}^{d} (H + kz)^{n} )^{-1}$
.
Example 3. (Grassmannian) Let
![]() $M_{k \times n}$
be the space of
$M_{k \times n}$
be the space of
![]() $k \times n$
-matrices acted on by
$k \times n$
-matrices acted on by
![]() $\mathrm {GL}(k)$
on the left. Taking the determinant character, the stable locus is the locus of matrices of full rank and the associated GIT quotient is the Grassmannian
$\mathrm {GL}(k)$
on the left. Taking the determinant character, the stable locus is the locus of matrices of full rank and the associated GIT quotient is the Grassmannian
The stable locus for the maximal torus
![]() $T \subset \mathrm {GL}(k)$
of diagonal matrices is given by matrices where each row is nonzero. The abelian quotient is
$T \subset \mathrm {GL}(k)$
of diagonal matrices is given by matrices where each row is nonzero. The abelian quotient is
 $$ \begin{align*} M_{k \times n} // T = \underbrace{\mathbb{P}^{n-1} \times \ldots \times \mathbb{P}^{n-1}}_{k \text{ times }}. \end{align*} $$
$$ \begin{align*} M_{k \times n} // T = \underbrace{\mathbb{P}^{n-1} \times \ldots \times \mathbb{P}^{n-1}}_{k \text{ times }}. \end{align*} $$
The roots of
![]() $\mathrm {GL}(k)$
are
$\mathrm {GL}(k)$
are
 $e_{i}^{\ast } - e_{j}^{\ast }$
and correspond to
$e_{i}^{\ast } - e_{j}^{\ast }$
and correspond to
![]() ${\mathcal O}(H_{i} - H_{j})$
, where
${\mathcal O}(H_{i} - H_{j})$
, where
![]() $H_{i}$
is the hyperplane class pulled back from the i-th factor.
$H_{i}$
is the hyperplane class pulled back from the i-th factor.
The universal subbundle
![]() ${\mathcal U} \to {\mathbb {C}}^{n} \otimes {\mathcal O}_{\operatorname {Gr}}$
on the Grassmannian corresponds to the inclusion of G-representations
${\mathcal U} \to {\mathbb {C}}^{n} \otimes {\mathcal O}_{\operatorname {Gr}}$
on the Grassmannian corresponds to the inclusion of G-representations
where a column vector
![]() $w \in {\mathbb {C}}^{k}$
is acting on by
$w \in {\mathbb {C}}^{k}$
is acting on by
![]() $g \cdot w := (g^{t})^{-1} w$
, and
$g \cdot w := (g^{t})^{-1} w$
, and
![]() ${\mathbb {C}}^{n}$
carries the trivial representation. The Plücker polarization on
${\mathbb {C}}^{n}$
carries the trivial representation. The Plücker polarization on
![]() $\operatorname {Gr}(k,n)$
thus corresponds to the line bundle
$\operatorname {Gr}(k,n)$
thus corresponds to the line bundle
![]() ${\mathcal O}(H_{1} + \ldots + H_{k})$
on
${\mathcal O}(H_{1} + \ldots + H_{k})$
on
![]() $(\mathbb {P}^{n-1})^{k}$
. Hence, if we consider degree d curves on the Grassmannian, in the abelian/nonabelian correspondence we have to sum over
$(\mathbb {P}^{n-1})^{k}$
. Hence, if we consider degree d curves on the Grassmannian, in the abelian/nonabelian correspondence we have to sum over
![]() $(d_{1}, \ldots , d_{k})$
adding up to d.
$(d_{1}, \ldots , d_{k})$
adding up to d.
Calculating the I-function is then easy. For example, for
![]() $k=2$
(and dropping the pullbacks
$k=2$
(and dropping the pullbacks
![]() $\xi ^{\ast }$
,
$\xi ^{\ast }$
,
![]() $j^{\ast }$
from notation), one obtains
$j^{\ast }$
from notation), one obtains
 $$ \begin{align*} I^{\operatorname{Gr}(2,n)}_{d} = \sum_{d=d_{1} + d_{2}} (-1)^{d} \frac{ H_{1} - H_{2} + (d_{1} - d_{2})z }{H_{1} - H_{2}} \frac{1}{ \prod_{k=1}^{d_{1}} (H_{1} + kz)^{n} \prod_{k=1}^{d_{2}} (H_{2} + kz)^{n} }, \end{align*} $$
$$ \begin{align*} I^{\operatorname{Gr}(2,n)}_{d} = \sum_{d=d_{1} + d_{2}} (-1)^{d} \frac{ H_{1} - H_{2} + (d_{1} - d_{2})z }{H_{1} - H_{2}} \frac{1}{ \prod_{k=1}^{d_{1}} (H_{1} + kz)^{n} \prod_{k=1}^{d_{2}} (H_{2} + kz)^{n} }, \end{align*} $$
where the division by
![]() $H_{1} - H_{2}$
is to take place formally.
$H_{1} - H_{2}$
is to take place formally.
Example 4. (Fano variety of a cubic fourfold) The Fano variety of a cubic fourfold
![]() $X \subset \operatorname {Gr}(2,6)$
is a zero locus of a section of
$X \subset \operatorname {Gr}(2,6)$
is a zero locus of a section of
![]() $\mathrm {Sym}^{3}(U^{\vee })$
. On the abelian quotient
$\mathrm {Sym}^{3}(U^{\vee })$
. On the abelian quotient
![]() $\mathbb {P}^{5} \times \mathbb {P}^{5}$
, this vector bundle corresponds to
$\mathbb {P}^{5} \times \mathbb {P}^{5}$
, this vector bundle corresponds to
We find the I-function
 $$ \begin{align*} I^{X \subset \operatorname{Gr}(2,6)} = I^{\operatorname{Gr}(2,6)}_{d} \cdot \prod_{\substack{3 = i_{1} + i_{2} \\ i_{1}, i_{2} \geq 0}} \prod_{k=1}^{i_{1} d_{1} + i_{2} d_{2}} (i_{1} H_{1} + i_{2} H_{2} + kz). \end{align*} $$
$$ \begin{align*} I^{X \subset \operatorname{Gr}(2,6)} = I^{\operatorname{Gr}(2,6)}_{d} \cdot \prod_{\substack{3 = i_{1} + i_{2} \\ i_{1}, i_{2} \geq 0}} \prod_{k=1}^{i_{1} d_{1} + i_{2} d_{2}} (i_{1} H_{1} + i_{2} H_{2} + kz). \end{align*} $$
Example 5. (A pencil of cubic fourfolds) We consider a generic pencil of cubic fourfolds
![]() ${\mathcal X} \subset \operatorname {Gr}(2,6) \times \mathbb {P}^{1}$
. Since
${\mathcal X} \subset \operatorname {Gr}(2,6) \times \mathbb {P}^{1}$
. Since
![]() ${\mathcal X}$
is the zero locus of a generic section of the globally generated bundle
${\mathcal X}$
is the zero locus of a generic section of the globally generated bundle
![]() $\mathrm {Sym}^{3}(U^{\vee }) \otimes {\mathcal O}_{\mathbb {P}^{1}}(1)$
, it is smooth by a Bertini type argument. The abelian quotient is
$\mathrm {Sym}^{3}(U^{\vee }) \otimes {\mathcal O}_{\mathbb {P}^{1}}(1)$
, it is smooth by a Bertini type argument. The abelian quotient is
![]() $\mathbb {P}^{5} \times \mathbb {P}^{5} \times \mathbb {P}^{1}$
. Let h be the hyperplane class on
$\mathbb {P}^{5} \times \mathbb {P}^{5} \times \mathbb {P}^{1}$
. Let h be the hyperplane class on
![]() $\mathbb {P}^{1}$
. Then the I-function for the fiber part reads:
$\mathbb {P}^{1}$
. Then the I-function for the fiber part reads:
 $$ \begin{align*} &\quad I^{{\mathcal X}}_{(d,0)} = (-1)^{d} \sum_{d=d_{1} + d_{2}} \frac{ H_{1} - H_{2} + (d_{1} - d_{2})z }{H_{1} - H_{2}} \cdot \\ &\frac{1}{ \prod_{k=1}^{d_{1}} (H_{1} + kz)^{6} \prod_{k=1}^{d_{2}} (H_{2} + kz)^{6} } \prod_{\substack{3 = i_{1} + i_{2} \\ i_{1}, i_{2} \geq 0}} \prod_{k=1}^{i_{1} d_{1} + i_{2} d_{2}} (i_{1} H_{1} + i_{2} H_{2} + h + kz). \end{align*} $$
$$ \begin{align*} &\quad I^{{\mathcal X}}_{(d,0)} = (-1)^{d} \sum_{d=d_{1} + d_{2}} \frac{ H_{1} - H_{2} + (d_{1} - d_{2})z }{H_{1} - H_{2}} \cdot \\ &\frac{1}{ \prod_{k=1}^{d_{1}} (H_{1} + kz)^{6} \prod_{k=1}^{d_{2}} (H_{2} + kz)^{6} } \prod_{\substack{3 = i_{1} + i_{2} \\ i_{1}, i_{2} \geq 0}} \prod_{k=1}^{i_{1} d_{1} + i_{2} d_{2}} (i_{1} H_{1} + i_{2} H_{2} + h + kz). \end{align*} $$
Example 6. (A pencil of Debarre–Voisin fourfolds) We consider a pencil
![]() ${\mathcal X} \subset \operatorname {Gr}(6,10) \times \mathbb {P}^{1}$
of DV fourfolds which is cut out by
${\mathcal X} \subset \operatorname {Gr}(6,10) \times \mathbb {P}^{1}$
of DV fourfolds which is cut out by
![]() $\wedge ^{3} {\mathcal U}^{\vee } \otimes {\mathcal O}(1)$
. The abelian quotient is
$\wedge ^{3} {\mathcal U}^{\vee } \otimes {\mathcal O}(1)$
. The abelian quotient is
![]() $(\mathbb {P}^{9})^{6} \times \mathbb {P}^{1}$
. We let h be the hyperplane class of
$(\mathbb {P}^{9})^{6} \times \mathbb {P}^{1}$
. We let h be the hyperplane class of
![]() $\mathbb {P}^{1}$
and
$\mathbb {P}^{1}$
and
![]() $H_{i}$
be the hyperplane class pulled back from the i-th copy of
$H_{i}$
be the hyperplane class pulled back from the i-th copy of
![]() $\mathbb {P}^{9}$
. Then the I-function in the fiber class is
$\mathbb {P}^{9}$
. Then the I-function in the fiber class is
 $$ \begin{align*} I^{{\mathcal X}}_{(d,0)} &= (-1)^{d} \sum_{d=d_{1} + \ldots + d_{6}} \left( \prod_{1 \leq i < j \leq 6} \frac{ H_{i} - H_{j} + (d_{i} - d_{j})z }{H_{i} - H_{j}} \right) \\ &\quad \times \prod_{i=1}^{6} \prod_{k=1}^{d_{i}} \frac{1}{ (H_{i} + kz)^{10} } \\ & \quad\times \prod_{1 \leq i_{1} < i_{2} < i_{3} \leq 6} \prod_{k=1}^{d_{i_{1}} + d_{i_{2}} + d_{i_{3}}} (H_{i_{1}} + H_{i_{2}} + H_{i_{3}} + h + kz). \end{align*} $$
$$ \begin{align*} I^{{\mathcal X}}_{(d,0)} &= (-1)^{d} \sum_{d=d_{1} + \ldots + d_{6}} \left( \prod_{1 \leq i < j \leq 6} \frac{ H_{i} - H_{j} + (d_{i} - d_{j})z }{H_{i} - H_{j}} \right) \\ &\quad \times \prod_{i=1}^{6} \prod_{k=1}^{d_{i}} \frac{1}{ (H_{i} + kz)^{10} } \\ & \quad\times \prod_{1 \leq i_{1} < i_{2} < i_{3} \leq 6} \prod_{k=1}^{d_{i_{1}} + d_{i_{2}} + d_{i_{3}}} (H_{i_{1}} + H_{i_{2}} + H_{i_{3}} + h + kz). \end{align*} $$
5.3 I and J functions
Given a GIT quotient X as before, let
![]() $t \in H^{2}(X,{\mathbb {C}})$
be any element (or a formal variable). The big J-function (at
$t \in H^{2}(X,{\mathbb {C}})$
be any element (or a formal variable). The big J-function (at
![]() $\epsilon = \infty $
) with insertion t is
$\epsilon = \infty $
) with insertion t is
 $$ \begin{align*} J^{\infty}(q,t,z) = e^{\frac{t}{z}} \left[ 1 + \sum_{\beta \neq 0} e^{\beta \cdot t} q^{\beta} \operatorname{ev}_{\ast}\left( \frac{ [ {\overline M}_{0,1}( X, \beta) ]^{\text{vir}} }{z (z-\psi)} \right) \right]. \end{align*} $$
$$ \begin{align*} J^{\infty}(q,t,z) = e^{\frac{t}{z}} \left[ 1 + \sum_{\beta \neq 0} e^{\beta \cdot t} q^{\beta} \operatorname{ev}_{\ast}\left( \frac{ [ {\overline M}_{0,1}( X, \beta) ]^{\text{vir}} }{z (z-\psi)} \right) \right]. \end{align*} $$
Expand the small I-function according to degree:
 $$ \begin{align*} I = I_{0}(q) + \frac{I_{1}(q)}{z} + \frac{I_{2}(q)}{z^{2}} + \ldots \,. \end{align*} $$
$$ \begin{align*} I = I_{0}(q) + \frac{I_{1}(q)}{z} + \frac{I_{2}(q)}{z^{2}} + \ldots \,. \end{align*} $$
Then the mirror theorem [Reference Ciocan-Fontanine and Kim11] states that
 $$ \begin{align*} J^{\infty}\left( q, \frac{I_{1}(q)}{I_{0}(q)} ,z \right) = \frac{I(q,z)}{I_{0}(q)}. \end{align*} $$
$$ \begin{align*} J^{\infty}\left( q, \frac{I_{1}(q)}{I_{0}(q)} ,z \right) = \frac{I(q,z)}{I_{0}(q)}. \end{align*} $$
By inverting this relation, we can compute the descendent one-point invariants of X. We sketch the details for the case of the Lefschetz pencil
![]() ${\mathcal X} \subset \operatorname {Gr}(2,6) \times \mathbb {P}^{1}$
of Fano’s. In this case (with H the Plücker polarization on
${\mathcal X} \subset \operatorname {Gr}(2,6) \times \mathbb {P}^{1}$
of Fano’s. In this case (with H the Plücker polarization on
![]() $\operatorname {Gr}(2,6)$
), let us write
$\operatorname {Gr}(2,6)$
), let us write
Then with
![]() $t = I_{1}(q)/I_{0}(q)$
and since
$t = I_{1}(q)/I_{0}(q)$
and since
![]() $\beta $
is fiber we get
$\beta $
is fiber we get
 $$ \begin{align*} e^{\beta \cdot t} q^{d} = \left( q e^{ \frac{f_{1}(q)}{f_{0}(q)} } \right)^{d} = Q^{d}, \end{align*} $$
$$ \begin{align*} e^{\beta \cdot t} q^{d} = \left( q e^{ \frac{f_{1}(q)}{f_{0}(q)} } \right)^{d} = Q^{d}, \end{align*} $$
where we have identified
![]() $q^{\beta } = q^{d}$
and used the variable
$q^{\beta } = q^{d}$
and used the variable
 $$ \begin{align*} Q = q \exp\left( \frac{f_{1}(q)}{f_{0}(q)} \right). \end{align*} $$
$$ \begin{align*} Q = q \exp\left( \frac{f_{1}(q)}{f_{0}(q)} \right). \end{align*} $$
Then we obtain the relation
 $$ \begin{align*} \exp\left( -\frac{I_{1}(q)}{I_{0}(q)} \frac{1}{z} \right) \frac{I^{\text{fib}}(q,z)}{I_{0}(q)} = 1 + \sum_{\beta \neq 0} Q^{\beta} \operatorname{ev}_{\ast}\left( \frac{ [ {\overline M}_{0,1}( X, \beta) ]^{\text{vir}} }{z (z-\psi)} \right), \end{align*} $$
$$ \begin{align*} \exp\left( -\frac{I_{1}(q)}{I_{0}(q)} \frac{1}{z} \right) \frac{I^{\text{fib}}(q,z)}{I_{0}(q)} = 1 + \sum_{\beta \neq 0} Q^{\beta} \operatorname{ev}_{\ast}\left( \frac{ [ {\overline M}_{0,1}( X, \beta) ]^{\text{vir}} }{z (z-\psi)} \right), \end{align*} $$
where
![]() $I^{\text {fib}}(q,z)$
stands for the I-functions involving only fiber classes
$I^{\text {fib}}(q,z)$
stands for the I-functions involving only fiber classes
![]() $\beta $
.
$\beta $
.
6 Results
6.1 Cubic fourfolds
We consider a generic pencil of Fano varieties of cubic fourfolds
This defines a one-parameter family
![]() $\pi : {\mathcal X} \to \mathbb {P}^{1}$
polarized by the Plücker embeddings. The family has precisely
$\pi : {\mathcal X} \to \mathbb {P}^{1}$
polarized by the Plücker embeddings. The family has precisely
![]() $192$
singular fibers
$192$
singular fibers
![]() ${\mathcal X}_{t}$
, which are irreducible varieties with ordinary double point singularities along a smooth K3 surface (and smooth elsewhere) [Reference Clemens and Griffiths12]. The blowup
${\mathcal X}_{t}$
, which are irreducible varieties with ordinary double point singularities along a smooth K3 surface (and smooth elsewhere) [Reference Clemens and Griffiths12]. The blowup
![]() $\mathrm {Bl}_{S} {\mathcal X}_{t}$
along the singular locus is isomorphic to the Hilbert scheme
$\mathrm {Bl}_{S} {\mathcal X}_{t}$
along the singular locus is isomorphic to the Hilbert scheme
![]() $\mathsf {Hilb}_{2}(S)$
, and the blowdown map contracts a
$\mathsf {Hilb}_{2}(S)$
, and the blowdown map contracts a
![]() $\mathbb {P}^{1}$
-bundle over S along its fibers which are
$\mathbb {P}^{1}$
-bundle over S along its fibers which are
![]() $(-2)$
-curves [Reference Hassett21, Sec.6.3]. The map
$(-2)$
-curves [Reference Hassett21, Sec.6.3]. The map
![]() ${\mathcal X} \to \mathbb {P}^{1}$
is a ordinary double point degeneration to
${\mathcal X} \to \mathbb {P}^{1}$
is a ordinary double point degeneration to
![]() ${\mathcal X}_{t}$
.
${\mathcal X}_{t}$
.
To obtain a family of smooth holomorphic-symplectic manifolds, we follow the arguments of Maulik and Pandharipande [Reference Maulik and Pandharipande37, Sec.5.1]. We choose a double cover
which is ramified along the
![]() $192$
base points of nodal fibers. The family
$192$
base points of nodal fibers. The family
then has double point singularities along the surfaces S which can be resolved by a small resolution
The family
![]() $\tilde {\pi }$
is a one-parameter family of quasi-polarized
$\tilde {\pi }$
is a one-parameter family of quasi-polarized
![]() $K3^{[2]}$
-type varieties, polarized by the pullback of the Plücker polarization.
$K3^{[2]}$
-type varieties, polarized by the pullback of the Plücker polarization.
The Noether–Lefschetz numbers of the family
![]() $\pi $
in terms of
$\pi $
in terms of
![]() $\tilde {\pi }$
are then
$\tilde {\pi }$
are then
 $$ \begin{align*} \mathsf{NL}_{s,d}^{\pi} = \frac{1}{2} \mathsf{NL}_{s,d}^{\tilde{\pi}}. \end{align*} $$
$$ \begin{align*} \mathsf{NL}_{s,d}^{\pi} = \frac{1}{2} \mathsf{NL}_{s,d}^{\tilde{\pi}}. \end{align*} $$
We also have the following comparison of Gromov–Witten invariants of the total spaces of
![]() ${\mathcal X}$
and
${\mathcal X}$
and
![]() $\tilde {{\mathcal X}}$
in fiber classes. We consider one-pointed invariants to simplify the notation.
$\tilde {{\mathcal X}}$
in fiber classes. We consider one-pointed invariants to simplify the notation.
Lemma 7. For any
![]() $i, \alpha $
,
$i, \alpha $
,
 $$ \begin{align*} \langle \alpha; H^{i} \rangle^{{\mathcal X}, \text{mc}}_{g,d} = \frac{1}{2} \langle \alpha; H^{i} \rangle^{\widetilde{{\mathcal X}}, \text{mc}}_{g,d}. \end{align*} $$
$$ \begin{align*} \langle \alpha; H^{i} \rangle^{{\mathcal X}, \text{mc}}_{g,d} = \frac{1}{2} \langle \alpha; H^{i} \rangle^{\widetilde{{\mathcal X}}, \text{mc}}_{g,d}. \end{align*} $$
Proof. We need to prove that
 $$ \begin{align*} \langle \alpha; H^{i} \rangle^{{\mathcal X}}_{g,d} = \frac{1}{2} \langle \alpha; H^{i} \rangle^{\widetilde{{\mathcal X}}}_{g,d}. \end{align*} $$
$$ \begin{align*} \langle \alpha; H^{i} \rangle^{{\mathcal X}}_{g,d} = \frac{1}{2} \langle \alpha; H^{i} \rangle^{\widetilde{{\mathcal X}}}_{g,d}. \end{align*} $$
This follows from the same argument as in [Reference Maulik and Pandharipande37, Lem. 4]: The conifold transition is taken relative to the K3 surface S. The extra components which appear in the degeneration argument is a bundle (with fiber
![]() $\mathbb {P}({\mathcal O}_{\mathbb {P}^{1}}(-1) \oplus {\mathcal O}_{\mathbb {P}^{1}}(-1) \oplus {\mathcal O}_{\mathbb {P}^{1}})$
or a quadric in
$\mathbb {P}({\mathcal O}_{\mathbb {P}^{1}}(-1) \oplus {\mathcal O}_{\mathbb {P}^{1}}(-1) \oplus {\mathcal O}_{\mathbb {P}^{1}})$
or a quadric in
![]() $\mathbb {P}^{4}$
) over the K3 surface S. Because of the existence of the symplectic form, it follows that the curve classes which may contribute nontrivially have to be fiber classes. The argument of [Reference Li and Ruan30] then goes through without change.
$\mathbb {P}^{4}$
) over the K3 surface S. Because of the existence of the symplectic form, it follows that the curve classes which may contribute nontrivially have to be fiber classes. The argument of [Reference Li and Ruan30] then goes through without change.
By the lemma the Gromov–Witten/Noether–Lefschetz relation of Propsition 6 extends to the family
![]() $\pi $
. Specializing to genus
$\pi $
. Specializing to genus
![]() $0$
we obtain that
$0$
we obtain that
 $$ \begin{align} \big\langle \alpha; H^{i} \big\rangle^{{\mathcal X}, \text{mc}}_{0,d} = \sum_{m,s} \big\langle \alpha; H^{i} \big\rangle^{X,\text{mc}}_{0,m,s,d} \mathsf{NL}^{\pi}_{m,s,d}. \end{align} $$
$$ \begin{align} \big\langle \alpha; H^{i} \big\rangle^{{\mathcal X}, \text{mc}}_{0,d} = \sum_{m,s} \big\langle \alpha; H^{i} \big\rangle^{X,\text{mc}}_{0,m,s,d} \mathsf{NL}^{\pi}_{m,s,d}. \end{align} $$
The left-hand side can be computed using the mirror symmetry formulas of Section 5. The primitive invariants appearing on the right-hand side are given by Remark 5. The Noether–Lefschetz numbers
![]() $\mathsf {NL}_{s,d}$
, and hence, their refinements
$\mathsf {NL}_{s,d}$
, and hence, their refinements
![]() $\mathsf {NL}_{m,s,d}$
are determined by [Reference Li and Zhang31] and the formulas in Section 3.11. By using a computer (see the author’s website for the code), one finds that for degree
$\mathsf {NL}_{m,s,d}$
are determined by [Reference Li and Zhang31] and the formulas in Section 3.11. By using a computer (see the author’s website for the code), one finds that for degree
![]() $6, 8, 9, 15$
this equation uniquely determines the invariants
$6, 8, 9, 15$
this equation uniquely determines the invariants
![]() $f_{\beta }, g_{\beta }$
for
$f_{\beta }, g_{\beta }$
for
![]() $\beta = m \alpha $
in cases
$\beta = m \alpha $
in cases
![]() $(m,\alpha ) \in \{ (2,0), (2,3/2), (3,3/2), (5,3/2) \}$
. Moreover, one checks then that for these degrees we have
$(m,\alpha ) \in \{ (2,0), (2,3/2), (3,3/2), (5,3/2) \}$
. Moreover, one checks then that for these degrees we have
 $$ \begin{align} \big\langle \alpha; H^{i} \big\rangle^{{\mathcal X}, \text{mc}}_{0,d} = \sum_{s} \mathsf{NL}_{s,d} \cdot \big\langle \alpha; H^{i} \big\rangle^{X,\text{mc}}_{0,1,s,d}. \end{align} $$
$$ \begin{align} \big\langle \alpha; H^{i} \big\rangle^{{\mathcal X}, \text{mc}}_{0,d} = \sum_{s} \mathsf{NL}_{s,d} \cdot \big\langle \alpha; H^{i} \big\rangle^{X,\text{mc}}_{0,1,s,d}. \end{align} $$
which implies that Conjecture A holds in these cases. Together with Proposition 2 this proves Proposition 1. (As mentioned in the introduction, we have checked equation (21) up to degree
![]() $38$
, which provides plenty of evidence for Conjecture A.)
$38$
, which provides plenty of evidence for Conjecture A.)
6.2 Debarre–Voisin fourfolds
We consider a generic pencil of Debarre–Voisin fourfolds
The case is very similar to the case of cubic fourfolds. As shown in C (by J. Song), we have the same description of the singular fibers as in the Fano case. In particular, we may use the same double cover construction and conclude the Gromov–Witten/Noether–Lefschetz relation (20) for
![]() $\pi $
.
$\pi $
.
We want to determine the generating series of Noether–Lefschetz numbers
 $$ \begin{align*} \varphi(q) = \sum_{D \geq 0} q^{D/11} \mathsf{NL}^{\pi}(D), \end{align*} $$
$$ \begin{align*} \varphi(q) = \sum_{D \geq 0} q^{D/11} \mathsf{NL}^{\pi}(D), \end{align*} $$
where D runs over squares modulo
![]() $11$
, and we used the notation of Section 3.8. Recall that we have
$11$
, and we used the notation of Section 3.8. Recall that we have
 $$ \begin{align*} \mathsf{NL}^{\pi}_{s,d} = \mathsf{NL}^{\pi}\left(D \right), \ \text{ where }\ D = -\frac{1}{4} \det \begin{pmatrix} 22 & d \\ d & s \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \mathsf{NL}^{\pi}_{s,d} = \mathsf{NL}^{\pi}\left(D \right), \ \text{ where }\ D = -\frac{1}{4} \det \begin{pmatrix} 22 & d \\ d & s \end{pmatrix}. \end{align*} $$
We first prove the following basic invariants.
Lemma 8.
![]() $\mathsf {NL}^{\pi }(0) = -10$
and
$\mathsf {NL}^{\pi }(0) = -10$
and
![]() $\mathsf {NL}^{\pi }(11) = 640$
.
$\mathsf {NL}^{\pi }(11) = 640$
.
Proof. We have
 $$ \begin{align*} \mathsf{NL}^{\pi}(0) = \int_{\mathbb{P}^{1}} \iota_{\pi}^{\ast} c_{1}({\mathcal K}^{\ast}), \end{align*} $$
$$ \begin{align*} \mathsf{NL}^{\pi}(0) = \int_{\mathbb{P}^{1}} \iota_{\pi}^{\ast} c_{1}({\mathcal K}^{\ast}), \end{align*} $$
where
![]() ${\mathcal K} \to {\mathcal D}_{L} / \Gamma _{M}$
is the descent of the tautological bundle
${\mathcal K} \to {\mathcal D}_{L} / \Gamma _{M}$
is the descent of the tautological bundle
![]() ${\mathcal O}(-1)$
. It is well-known that
${\mathcal O}(-1)$
. It is well-known that
![]() $\iota _{\pi }^{\ast } {\mathcal K}$
corresponds to the Hodge bundle
$\iota _{\pi }^{\ast } {\mathcal K}$
corresponds to the Hodge bundle
![]() $\pi _{\ast } \Omega ^{2}_{\pi }$
. Hence,
$\pi _{\ast } \Omega ^{2}_{\pi }$
. Hence,
![]() $\iota _{\pi }^{\ast } {\mathcal K}^{\ast }$
is isomorphic to
$\iota _{\pi }^{\ast } {\mathcal K}^{\ast }$
is isomorphic to
which has fiber
![]() $H^{2}({\mathcal X}_{t},{\mathcal O}_{{\mathcal X}_{t}})$
over
$H^{2}({\mathcal X}_{t},{\mathcal O}_{{\mathcal X}_{t}})$
over
![]() $t \in \mathbb {P}^{1}$
. In K-theory we have
$t \in \mathbb {P}^{1}$
. In K-theory we have
By a Riemann–Roch calculation (using the software package [Reference Lehn and Sorger29]), we find that
 $$ \begin{align*} 3 c_{1}({\mathcal L}) = \int {\mathrm{ch}}_{1}( R \pi_{\ast} {\mathcal O} ) = \int \pi_{\ast}( {\mathrm{td}}_{{\mathcal X}} / {\mathrm{td}}_{\mathbb{P}^{1}} ) = -30. \end{align*} $$
$$ \begin{align*} 3 c_{1}({\mathcal L}) = \int {\mathrm{ch}}_{1}( R \pi_{\ast} {\mathcal O} ) = \int \pi_{\ast}( {\mathrm{td}}_{{\mathcal X}} / {\mathrm{td}}_{\mathbb{P}^{1}} ) = -30. \end{align*} $$
The number
![]() $\mathsf {NL}^{\pi }(11) = \mathsf {NL}_{-2,0}$
is the number of singular fibers. To compute these, we recall that the singular locus of every singular fiber is a smooth K3 surface and the blowup along the singular locus has exceptional divisor a
$\mathsf {NL}^{\pi }(11) = \mathsf {NL}_{-2,0}$
is the number of singular fibers. To compute these, we recall that the singular locus of every singular fiber is a smooth K3 surface and the blowup along the singular locus has exceptional divisor a
![]() $\mathbb {P}^{1}$
-bundle over the K3 surface. Hence, the topological Euler characteristic of a singular fiber is
$\mathbb {P}^{1}$
-bundle over the K3 surface. Hence, the topological Euler characteristic of a singular fiber is
![]() $300$
. By a standard computation (using [Reference Lehn and Sorger29]), the topological Euler number of the total family is
$300$
. By a standard computation (using [Reference Lehn and Sorger29]), the topological Euler number of the total family is
![]() $e({\mathcal X}) = -147,{12}$
. Hence, if
$e({\mathcal X}) = -147,{12}$
. Hence, if
![]() $\delta $
is the number of singular fibers we get
$\delta $
is the number of singular fibers we get
The last part also follows from [Reference Debarre and Voisin15, Proof of Prop.3.1].
To further constrain the Noether–Lefschetz numbers, we argue as follows. By a computer check (see again the author’s webpage), the Gromov–Witten/Noether–Lefschetz relation
 $$ \begin{align} \big\langle H^{3} \big\rangle^{{\mathcal X}, \text{mc}}_{0,d} = \sum_{m, s} \big\langle H^{3} \big\rangle^{X,\text{mc}}_{0,m,s,d} \mathsf{NL}^{\pi}_{m,s,d} \end{align} $$
$$ \begin{align} \big\langle H^{3} \big\rangle^{{\mathcal X}, \text{mc}}_{0,d} = \sum_{m, s} \big\langle H^{3} \big\rangle^{X,\text{mc}}_{0,m,s,d} \mathsf{NL}^{\pi}_{m,s,d} \end{align} $$
involves for
![]() $d \leq 13$
only terms for which the multiple cover conjecture is known by Proposition 2. Hence, for
$d \leq 13$
only terms for which the multiple cover conjecture is known by Proposition 2. Hence, for
![]() $d \leq 13$
we may rewrite it
$d \leq 13$
we may rewrite it
 $$ \begin{align*} \big\langle H^{3} \big\rangle^{{\mathcal X}, \text{mc}}_{0,d} = \sum_{s} \mathsf{NL}_{s,d} \cdot \big\langle H^{3} \big\rangle^{X,\text{mc}}_{0,1,s,d}. \end{align*} $$
$$ \begin{align*} \big\langle H^{3} \big\rangle^{{\mathcal X}, \text{mc}}_{0,d} = \sum_{s} \mathsf{NL}_{s,d} \cdot \big\langle H^{3} \big\rangle^{X,\text{mc}}_{0,1,s,d}. \end{align*} $$
The left-hand side can be computed using the mirror symmetry formalism. The primitive invariants on the right are given in Remark 5. For
![]() $1 \leq d \leq 5$
one obtains
$1 \leq d \leq 5$
one obtains
 $$ \begin{align} \begin{aligned} 0 & = 264 \mathsf{NL}(3) \\ 130,680 & = 3,960 \mathsf{NL}(1) + 132 \mathsf{NL}(12) \\ 0 & = 792 \mathsf{NL}(5) \\ 3,020,160 & = 264 \mathsf{NL}(15) + 7,920 \mathsf{NL}(4) \\ 0 & = 1,320 \mathsf{NL}(9) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 0 & = 264 \mathsf{NL}(3) \\ 130,680 & = 3,960 \mathsf{NL}(1) + 132 \mathsf{NL}(12) \\ 0 & = 792 \mathsf{NL}(5) \\ 3,020,160 & = 264 \mathsf{NL}(15) + 7,920 \mathsf{NL}(4) \\ 0 & = 1,320 \mathsf{NL}(9) \end{aligned} \end{align} $$
Using equations (23) and
![]() $\mathsf {NL}(0) = -10$
and employing Williams’ program [Reference Williams53], we find that:
$\mathsf {NL}(0) = -10$
and employing Williams’ program [Reference Williams53], we find that:
This in turn determines the modular form
![]() $\Phi ^{\pi }$
uniquely. (One independently checks that indeed
$\Phi ^{\pi }$
uniquely. (One independently checks that indeed
![]() $\mathsf {NL}(11) = 640$
matches the second result of Lemma 8.)
$\mathsf {NL}(11) = 640$
matches the second result of Lemma 8.)
Theorem 2 follows from this, from Proposition 4 and straightforward linear algebra (by [Reference Borcherds4, Sec.12], we have that
![]() $E_{1}, \Delta _{11}, E_{3}$
generate the ring of modular forms for character
$E_{1}, \Delta _{11}, E_{3}$
generate the ring of modular forms for character
![]() $\chi _{11}$
:
$\chi _{11}$
:
 $$ \begin{align*} \bigoplus_{k \geq 0} \mathrm{Mod}_{k}(\Gamma_{0}(11), \chi_{11}^{k}) = {\mathbb{C}}[ E_{1}, \Delta_{11}, E_{3} ] / (\text{relations})). \end{align*} $$
$$ \begin{align*} \bigoplus_{k \geq 0} \mathrm{Mod}_{k}(\Gamma_{0}(11), \chi_{11}^{k}) = {\mathbb{C}}[ E_{1}, \Delta_{11}, E_{3} ] / (\text{relations})). \end{align*} $$
Proof of Corollary 1
Define the Noether–Lefschetz numbers of first type:
 $$ \begin{align*} {\mathcal C}^{\pi}_{2e} = \frac{1}{2} \int_{C} \iota_{\tilde{\pi}}^{\ast} {\mathcal C}_{2e}. \end{align*} $$
$$ \begin{align*} {\mathcal C}^{\pi}_{2e} = \frac{1}{2} \int_{C} \iota_{\tilde{\pi}}^{\ast} {\mathcal C}_{2e}. \end{align*} $$
These are related to the
![]() $\mathsf {NL}^{\pi }(D)$
by Proposition 5. The proof, hence, follows from equation (24) and Lemma 9 below.
$\mathsf {NL}^{\pi }(D)$
by Proposition 5. The proof, hence, follows from equation (24) and Lemma 9 below.
Lemma 9.
![]() ${\mathcal C}_{2e}$
is HLS if and only if
${\mathcal C}_{2e}$
is HLS if and only if
![]() ${\mathcal C}^{\pi }_{2e} = 0$
.
${\mathcal C}^{\pi }_{2e} = 0$
.
Proof. Let
![]() ${\mathcal M}_{DV}^{\prime } \subset {\mathcal M}_{DV}$
be the open locus consisting of Debarre–Voisin varieties which are either smooth or singular with ordinary double point singularity along a smooth K3 surface (which holds on an open subset of the irreducible discriminant divisor [Reference Benedetti and Song3]). By [Reference Debarre and Voisin15], the complement of
${\mathcal M}_{DV}^{\prime } \subset {\mathcal M}_{DV}$
be the open locus consisting of Debarre–Voisin varieties which are either smooth or singular with ordinary double point singularity along a smooth K3 surface (which holds on an open subset of the irreducible discriminant divisor [Reference Benedetti and Song3]). By [Reference Debarre and Voisin15], the complement of
![]() ${\mathcal M}_{DV}^{\prime }$
has codimension
${\mathcal M}_{DV}^{\prime }$
has codimension
![]() $2$
. The period map extends to a morphism
$2$
. The period map extends to a morphism
 $p : {\mathcal M}_{DV}^{\prime } \to {\mathcal M}_{H} \subset \overline {{\mathcal M}}_{H}$
. Let also
$p : {\mathcal M}_{DV}^{\prime } \to {\mathcal M}_{H} \subset \overline {{\mathcal M}}_{H}$
. Let also
 $\tilde {p} : \widetilde {{\mathcal M}}_{DV} \to \overline {{\mathcal M}}_{H}$
be the resolution of the rational period map
$\tilde {p} : \widetilde {{\mathcal M}}_{DV} \to \overline {{\mathcal M}}_{H}$
be the resolution of the rational period map
![]() ${\mathcal M}_{DV} \dashrightarrow \overline {{\mathcal M}}_{H}$
. We view
${\mathcal M}_{DV} \dashrightarrow \overline {{\mathcal M}}_{H}$
. We view
![]() ${\mathcal M}_{DV}^{\prime }$
as a open subvariety of
${\mathcal M}_{DV}^{\prime }$
as a open subvariety of
![]() $\widetilde {{\mathcal M}}_{DV}$
,
$\widetilde {{\mathcal M}}_{DV}$
,
 $$ \begin{align*} {\mathcal M}_{DV}^{\prime} \overset{j}{\hookrightarrow} \widetilde{{\mathcal M}}_{DV} \xrightarrow{\tilde{p}} \overline{{\mathcal M}}_{H}. \end{align*} $$
$$ \begin{align*} {\mathcal M}_{DV}^{\prime} \overset{j}{\hookrightarrow} \widetilde{{\mathcal M}}_{DV} \xrightarrow{\tilde{p}} \overline{{\mathcal M}}_{H}. \end{align*} $$
We need the following basic fact: Assume
![]() $D = \tilde {p}_{\ast } E$
for some irreducible divisor
$D = \tilde {p}_{\ast } E$
for some irreducible divisor
![]() $E \subset \widetilde {{\mathcal M}}_{DV}$
. Since
$E \subset \widetilde {{\mathcal M}}_{DV}$
. Since
![]() $\tilde {p}$
is birational [Reference O’Grady41], by Zariski’s main theorem [Reference Hartshorne20, Cor.11.4], E is the unique irreducible divisor in
$\tilde {p}$
is birational [Reference O’Grady41], by Zariski’s main theorem [Reference Hartshorne20, Cor.11.4], E is the unique irreducible divisor in
![]() $\widetilde {{\mathcal M}}_{DV}$
which maps to D (otherwise, the generic point of the image would have more than two preimages; hence, the fiber would not be connected), and by the same argument, the map
$\widetilde {{\mathcal M}}_{DV}$
which maps to D (otherwise, the generic point of the image would have more than two preimages; hence, the fiber would not be connected), and by the same argument, the map
![]() $E \to D$
is birational. Hence,
$E \to D$
is birational. Hence,
![]() $\tilde {p}^{\ast } \tilde {p}_{\ast } E = E$
. This yields
$\tilde {p}^{\ast } \tilde {p}_{\ast } E = E$
. This yields
We find that D is HLS (term on the right vanishes for some necessarily unique E) if and only if
![]() $p^{\ast } D = 0$
in
$p^{\ast } D = 0$
in
 $A^{1}({\mathcal M}_{DV}^{\prime })$
.
$A^{1}({\mathcal M}_{DV}^{\prime })$
.
There is a
![]() $\mathrm {SL}(V_{10})$
-bundle
$\mathrm {SL}(V_{10})$
-bundle
![]() $\pi : U \to {\mathcal M}_{DV}^{\prime }$
for an open
$\pi : U \to {\mathcal M}_{DV}^{\prime }$
for an open
 $U \subset \mathbb {P}(\wedge ^{3} V_{10}^{\ast })$
with complement of codimension
$U \subset \mathbb {P}(\wedge ^{3} V_{10}^{\ast })$
with complement of codimension
![]() $\geq 2$
. Hence, we also have
$\geq 2$
. Hence, we also have
![]() $p^{\ast } D = 0$
if and only if
$p^{\ast } D = 0$
if and only if
![]() $\pi ^{\ast } p^{\ast } D = 0$
if and only if
$\pi ^{\ast } p^{\ast } D = 0$
if and only if
![]() $\pi ^{\ast } p^{\ast } D \cdot L = 0$
for a generic line L in U.
$\pi ^{\ast } p^{\ast } D \cdot L = 0$
for a generic line L in U.
Appendix A A multiple cover rule for abelian surfaces
In this appendix, we state a conjectural rule that expressed reduced Gromov–Witten invariants of an abelian surfaces for any curve class
![]() $\beta $
in terms of invariants for which
$\beta $
in terms of invariants for which
![]() $\beta $
is primitive. The conjectural formula extends a proposal of [Reference Bryan, Oberdieck, Pandharipande and Yin7] for the abelian surface analogue of the Katz–Klemm–Vafa formula. As in the hyperkähler case, the conjecture can be reinterpreted as saying that, after subtracting multiple covers, the Gromov–Witten invariants are independent of the divisibility.
$\beta $
is primitive. The conjectural formula extends a proposal of [Reference Bryan, Oberdieck, Pandharipande and Yin7] for the abelian surface analogue of the Katz–Klemm–Vafa formula. As in the hyperkähler case, the conjecture can be reinterpreted as saying that, after subtracting multiple covers, the Gromov–Witten invariants are independent of the divisibility.
A.1 Monodromy
Recall that the cohomology of an abelian surface is described by
 $$ \begin{align*} H^{i}(A,{\mathbb{Q}}) = \bigwedge^{i} H^{1}(A,{\mathbb{Q}}). \end{align*} $$
$$ \begin{align*} H^{i}(A,{\mathbb{Q}}) = \bigwedge^{i} H^{1}(A,{\mathbb{Q}}). \end{align*} $$
The class of a point
![]() ${\mathsf {p}} \in H^{4}(A,{\mathbb {Z}})$
thus defines a canonical element
${\mathsf {p}} \in H^{4}(A,{\mathbb {Z}})$
thus defines a canonical element
 $$ \begin{align*} {\mathsf{p}} \in \bigwedge^{4} H^{1}(A,{\mathbb{Q}}). \end{align*} $$
$$ \begin{align*} {\mathsf{p}} \in \bigwedge^{4} H^{1}(A,{\mathbb{Q}}). \end{align*} $$
An isomorphism of abelian groups
![]() $\varphi : H^{1}(A,{\mathbb {Z}}) \to H^{1}(A^{\prime },{\mathbb {Z}})$
extends naturally to a morphism of the full cohomology
$\varphi : H^{1}(A,{\mathbb {Z}}) \to H^{1}(A^{\prime },{\mathbb {Z}})$
extends naturally to a morphism of the full cohomology
![]() $H^{\ast }(A,{\mathbb {Z}})$
by setting
$H^{\ast }(A,{\mathbb {Z}})$
by setting
 $\varphi |_{H^{i}(A,{\mathbb {Z}})} = \wedge ^{i} \varphi $
. One has that
$\varphi |_{H^{i}(A,{\mathbb {Z}})} = \wedge ^{i} \varphi $
. One has that
![]() $\varphi $
is a parallel transport operator (i.e., the parallel transport along a deformation from A to
$\varphi $
is a parallel transport operator (i.e., the parallel transport along a deformation from A to
![]() $A^{\prime }$
through complex tori) if and only if
$A^{\prime }$
through complex tori) if and only if
![]() $\varphi $
preserves the canonical element [Reference Birkenhake and Lange8, Sec.1.10].
$\varphi $
preserves the canonical element [Reference Birkenhake and Lange8, Sec.1.10].
The Zariski closure of the space of parallel transport operators is the set of
![]() ${\mathbb {C}}$
-vector spaces homomorphisms:
${\mathbb {C}}$
-vector spaces homomorphisms:
 $$ \begin{align*} M_{A,A^{\prime}} = \{ \varphi : H^{1}(A,{\mathbb{C}}) \to H^{1}(A^{\prime},{\mathbb{C}}) | \varphi({\mathsf{p}}) = {\mathsf{p}}^{\prime} \}. \end{align*} $$
$$ \begin{align*} M_{A,A^{\prime}} = \{ \varphi : H^{1}(A,{\mathbb{C}}) \to H^{1}(A^{\prime},{\mathbb{C}}) | \varphi({\mathsf{p}}) = {\mathsf{p}}^{\prime} \}. \end{align*} $$
It follows that the induced map
![]() $\wedge ^{2} \varphi : H^{2}(A,{\mathbb {C}}) \to H^{2}(A^{\prime },{\mathbb {C}})$
preserves the canonical inner product. If
$\wedge ^{2} \varphi : H^{2}(A,{\mathbb {C}}) \to H^{2}(A^{\prime },{\mathbb {C}})$
preserves the canonical inner product. If
![]() $A^{\prime }=A$
, the above just says that the monodromy group is
$A^{\prime }=A$
, the above just says that the monodromy group is
![]() $\mathrm {SL}(H^{1}(A,{\mathbb {Z}}))$
and its Zariski closure
$\mathrm {SL}(H^{1}(A,{\mathbb {Z}}))$
and its Zariski closure
![]() $\mathrm {SL}(H^{1}(A,{\mathbb {C}}))$
.
$\mathrm {SL}(H^{1}(A,{\mathbb {C}}))$
.
A.2 Multiple cover rule
Let
![]() $\beta \in H_{2}(A,{\mathbb {Z}})$
be an effective curve class. For any divisor
$\beta \in H_{2}(A,{\mathbb {Z}})$
be an effective curve class. For any divisor
![]() $k | \beta $
, choose an abelian variety
$k | \beta $
, choose an abelian variety
![]() $A_{k}$
and a morphism
$A_{k}$
and a morphism
![]() $\varphi _{k} : H^{1}(A,{\mathbb {R}}) \to H^{1}(A_{k},{\mathbb {R}})$
preserving the canonical element such that the induced morphism
$\varphi _{k} : H^{1}(A,{\mathbb {R}}) \to H^{1}(A_{k},{\mathbb {R}})$
preserving the canonical element such that the induced morphism
 $$ \begin{align*} \varphi_{k} = \bigoplus_{i} \wedge^{i} \varphi_{k} : H^{\ast}(A,{\mathbb{R}}) \to H^{\ast}(A_{k}, {\mathbb{R}}) \end{align*} $$
$$ \begin{align*} \varphi_{k} = \bigoplus_{i} \wedge^{i} \varphi_{k} : H^{\ast}(A,{\mathbb{R}}) \to H^{\ast}(A_{k}, {\mathbb{R}}) \end{align*} $$
takes
![]() $\beta /k$
to a primitive effective curve class.
$\beta /k$
to a primitive effective curve class.
Let also
 $\alpha \in H^{\ast }({\overline M}_{g,n})$
be a tautological class and
$\alpha \in H^{\ast }({\overline M}_{g,n})$
be a tautological class and
![]() $\gamma _{i} \in H^{\ast }(A,{\mathbb {R}})$
be arbitrary insertions.
$\gamma _{i} \in H^{\ast }(A,{\mathbb {R}})$
be arbitrary insertions.
Conjecture C. For any effective curve class
![]() $\beta \in H_{2}(A,{\mathbb {Z}})$
,
$\beta \in H_{2}(A,{\mathbb {Z}})$
,
 $$ \begin{align*} \Big\langle \alpha; \gamma_{1}, \ldots, \gamma_{n} \Big\rangle^{A}_{g,\beta} = \sum_{k | \beta} k^{3g-3+n - \deg(\alpha)} \Big\langle \alpha; \varphi_{k}(\gamma_{1}), \ldots, \varphi_{k}(\gamma_{n}) \Big\rangle^{A_{k}}_{g,\varphi_{k}(\beta/k)}. \end{align*} $$
$$ \begin{align*} \Big\langle \alpha; \gamma_{1}, \ldots, \gamma_{n} \Big\rangle^{A}_{g,\beta} = \sum_{k | \beta} k^{3g-3+n - \deg(\alpha)} \Big\langle \alpha; \varphi_{k}(\gamma_{1}), \ldots, \varphi_{k}(\gamma_{n}) \Big\rangle^{A_{k}}_{g,\varphi_{k}(\beta/k)}. \end{align*} $$
A.3 Example
We apply the conjectural multiple cover formula to the analogue of the Katz–Klemm–Vafa formula for abelian surfaces which is the integral
 $$ \begin{align*} N^{\text{FLS}}_{g,\beta} = \int_{ [ {\overline M}_{g,n}(A,\beta)^{\text{FLS}} ]^{\text{red}}} (-1)^{g-2} \lambda_{g-2}, \end{align*} $$
$$ \begin{align*} N^{\text{FLS}}_{g,\beta} = \int_{ [ {\overline M}_{g,n}(A,\beta)^{\text{FLS}} ]^{\text{red}}} (-1)^{g-2} \lambda_{g-2}, \end{align*} $$
where
 ${\overline M}_{g,n}(A,\beta )^{\text {FLS}}$
is the substack of
${\overline M}_{g,n}(A,\beta )^{\text {FLS}}$
is the substack of
 ${\overline M}_{g,n}(A,\beta )$
that maps with image in a fixed linear system (FLS); see [Reference Bryan, Oberdieck, Pandharipande and Yin7].
${\overline M}_{g,n}(A,\beta )$
that maps with image in a fixed linear system (FLS); see [Reference Bryan, Oberdieck, Pandharipande and Yin7].
To apply the multiple cover rule, we specialize to
![]() $A = E \times E^{\prime }$
. Consider symplectic bases
$A = E \times E^{\prime }$
. Consider symplectic bases
which give a basis of
![]() $H^{1}(A,{\mathbb {Z}})$
(we omit the pullback), and let
$H^{1}(A,{\mathbb {Z}})$
(we omit the pullback), and let
We take
![]() $\beta = (d_{1},d_{2}) := d_{1} \omega _{1} + d_{2} \omega _{2}$
. For every
$\beta = (d_{1},d_{2}) := d_{1} \omega _{1} + d_{2} \omega _{2}$
. For every
![]() $k | \mathrm {gcd}(d_{1},d_{2})$
, define
$k | \mathrm {gcd}(d_{1},d_{2})$
, define
![]() $\varphi _{k} \in \mathrm {SL}(H^{1}(A,{\mathbb {Q}}))$
by
$\varphi _{k} \in \mathrm {SL}(H^{1}(A,{\mathbb {Q}}))$
by
 $$ \begin{align*} \alpha_{1} \mapsto \alpha_{1},\quad \beta_{1} \mapsto \frac{k}{d_{1}} \beta_{1},\quad \alpha_{2} \mapsto \alpha_{2},\quad \beta_{2} \mapsto \frac{d_{1}}{k} \beta_{2}. \end{align*} $$
$$ \begin{align*} \alpha_{1} \mapsto \alpha_{1},\quad \beta_{1} \mapsto \frac{k}{d_{1}} \beta_{1},\quad \alpha_{2} \mapsto \alpha_{2},\quad \beta_{2} \mapsto \frac{d_{1}}{k} \beta_{2}. \end{align*} $$
The extension to the full cohomology satisfies
 $$ \begin{align*} \varphi_{k}( \beta/k ) = \omega_{1} + \frac{d_{1} d_{2}}{k^{2}} \omega_{2} = (1, d_{1} d_{2}/k^{2}). \end{align*} $$
$$ \begin{align*} \varphi_{k}( \beta/k ) = \omega_{1} + \frac{d_{1} d_{2}}{k^{2}} \omega_{2} = (1, d_{1} d_{2}/k^{2}). \end{align*} $$
Recall the result of Bryan ([Reference Bryan, Oberdieck, Pandharipande and Yin7, Sec.3.2]) that
 $$ \begin{align*} N^{\text{FLS}}_{g,\beta} = \Big\langle (-1)^{g-2} \lambda_{g-2}; \prod_{i=1}^{4} \xi_{i} \Big\rangle^{A}_{g,\beta}, \end{align*} $$
$$ \begin{align*} N^{\text{FLS}}_{g,\beta} = \Big\langle (-1)^{g-2} \lambda_{g-2}; \prod_{i=1}^{4} \xi_{i} \Big\rangle^{A}_{g,\beta}, \end{align*} $$
where we can take
Conjecture C then implies
 $$ \begin{align*} N^{\text{FLS}}_{g,(d,d^{\prime})} & = \sum_{k|\beta} k^{2g-3+6} \big\langle (-1)^{g-2} \lambda_{g-2}; \prod_{i=1}^{4} \varphi_{k}(\xi_{i}) \big\rangle_{g, (1, dd^{\prime}/k^{2})} \\ & = \sum_{k|\beta} k^{2g+3} N^{\text{FLS}}_{g,(1,dd^{\prime}/k^{2})} \end{align*} $$
$$ \begin{align*} N^{\text{FLS}}_{g,(d,d^{\prime})} & = \sum_{k|\beta} k^{2g-3+6} \big\langle (-1)^{g-2} \lambda_{g-2}; \prod_{i=1}^{4} \varphi_{k}(\xi_{i}) \big\rangle_{g, (1, dd^{\prime}/k^{2})} \\ & = \sum_{k|\beta} k^{2g+3} N^{\text{FLS}}_{g,(1,dd^{\prime}/k^{2})} \end{align*} $$
which matches precisely Conjecture A in [Reference Bryan, Oberdieck, Pandharipande and Yin7].
Appenidx B Comparision with Gopakumar–Vafa invariants
For a K3 surface S and effective curve class
![]() $\beta \in H_{2}(S,{\mathbb {Z}})$
, consider the Gromov–Witten invariant
$\beta \in H_{2}(S,{\mathbb {Z}})$
, consider the Gromov–Witten invariant
 $$ \begin{align*} R_{g,\beta} = \int_{ [ {\overline M}_{g,n}(S,\beta) ]^{\text{red}} } (-1)^{g} \lambda_{g}. \end{align*} $$
$$ \begin{align*} R_{g,\beta} = \int_{ [ {\overline M}_{g,n}(S,\beta) ]^{\text{red}} } (-1)^{g} \lambda_{g}. \end{align*} $$
Fix any primitive effective class
![]() $\alpha \in H_{2}(S,{\mathbb {Z}})$
. Define the generating series
$\alpha \in H_{2}(S,{\mathbb {Z}})$
. Define the generating series
 $$ \begin{align*} F_{\alpha} = \sum_{g \geq 0} \sum_{m>0} R_{g, m \alpha} u^{2g-2} v^{m}, \end{align*} $$
$$ \begin{align*} F_{\alpha} = \sum_{g \geq 0} \sum_{m>0} R_{g, m \alpha} u^{2g-2} v^{m}, \end{align*} $$
where
![]() $u,v$
are formal variables. Following [Reference Pandharipande and Thomas49], the Gopakumar–Vafa invariants
$u,v$
are formal variables. Following [Reference Pandharipande and Thomas49], the Gopakumar–Vafa invariants
![]() $r_{g,m \alpha } \in {\mathbb {Q}}$
of the K3 surface S are defined by the equality
$r_{g,m \alpha } \in {\mathbb {Q}}$
of the K3 surface S are defined by the equality
 $$ \begin{align} F_{\alpha} = \sum_{g \geq 0} \sum_{m> 0} r_{g,m \alpha} \sum_{k>0} \frac{1}{k} \left( \frac{ \sin(ku/2) }{2} \right)^{2g-2} v^{km}. \end{align} $$
$$ \begin{align} F_{\alpha} = \sum_{g \geq 0} \sum_{m> 0} r_{g,m \alpha} \sum_{k>0} \frac{1}{k} \left( \frac{ \sin(ku/2) }{2} \right)^{2g-2} v^{km}. \end{align} $$
Recall from the introduction (Section 0.1) the numbers
 $$ \begin{align*} \widetilde{r}_{g,\beta} = \sum_{k | \beta} k^{2g-3} \mu(k) R_{g, \beta/k}. \end{align*} $$
$$ \begin{align*} \widetilde{r}_{g,\beta} = \sum_{k | \beta} k^{2g-3} \mu(k) R_{g, \beta/k}. \end{align*} $$
We have the following connection between the invariants
![]() $r_{g,\beta }$
and
$r_{g,\beta }$
and
![]() $\widetilde {r}_{g, \beta }$
: For any g, consider the expansion
$\widetilde {r}_{g, \beta }$
: For any g, consider the expansion
 $$ \begin{align} \left( \frac{1}{2} \sin(u/2) \right)^{2g-2} = \sum_{\tilde{g}} a_{g, \tilde{g}} u^{2 \tilde{g}-2}. \end{align} $$
$$ \begin{align} \left( \frac{1}{2} \sin(u/2) \right)^{2g-2} = \sum_{\tilde{g}} a_{g, \tilde{g}} u^{2 \tilde{g}-2}. \end{align} $$
Lemma 10. For any
![]() $g \geq 0$
, we have the upper-triangular relation
$g \geq 0$
, we have the upper-triangular relation
 $$ \begin{align} \tilde{r}_{\tilde{g},\beta} = \sum_{\tilde{g}} a_{g, \tilde{g}} r_{g, \beta}. \end{align} $$
$$ \begin{align} \tilde{r}_{\tilde{g},\beta} = \sum_{\tilde{g}} a_{g, \tilde{g}} r_{g, \beta}. \end{align} $$
In [Reference Pandharipande and Thomas49], it was shown that the
![]() $r_{g,\beta }$
do not depend on the divisibility of the curve class
$r_{g,\beta }$
do not depend on the divisibility of the curve class
![]() $\beta $
. By equation (27), we find that also
$\beta $
. By equation (27), we find that also
![]() $\tilde {r}_{g,\beta }$
does not depend on the divisibility, as claimed in Theorem 1. Since (27) is upper-triangular, we see that also the converse holds, i.e.,
$\tilde {r}_{g,\beta }$
does not depend on the divisibility, as claimed in Theorem 1. Since (27) is upper-triangular, we see that also the converse holds, i.e.,
![]() $r_{g,\beta }$
does not depend on the divisibility if and only if the same holds for
$r_{g,\beta }$
does not depend on the divisibility if and only if the same holds for
![]() $\tilde {r}_{g,\beta }$
.
$\tilde {r}_{g,\beta }$
.
Proof of Lemma 10
Let us define
 $$ \begin{align*} \hat{r}_{\tilde{g},\beta} := \sum_{\tilde{g}} a_{g, \tilde{g}} r_{g, \beta}. \end{align*} $$
$$ \begin{align*} \hat{r}_{\tilde{g},\beta} := \sum_{\tilde{g}} a_{g, \tilde{g}} r_{g, \beta}. \end{align*} $$
Inserting equation (26) into equation (25), we get
 $$ \begin{align*} F_{\alpha} &= \sum_{g \geq 0} \sum_{m> 0} r_{g,m \alpha} \sum_{k>0} \frac{1}{k} \sum_{\tilde{g}} a_{g,\tilde{g}} k^{2 \tilde{g}-2} u^{2 \tilde{g}-2} v^{km} \\ &= \sum_{\tilde{g} \geq 0} \sum_{m > 0} \sum_{k>0} k^{2 \tilde{g}-3} \hat{r}_{g, m \alpha} u^{2 \tilde{g}-2} v^{km}. \end{align*} $$
$$ \begin{align*} F_{\alpha} &= \sum_{g \geq 0} \sum_{m> 0} r_{g,m \alpha} \sum_{k>0} \frac{1}{k} \sum_{\tilde{g}} a_{g,\tilde{g}} k^{2 \tilde{g}-2} u^{2 \tilde{g}-2} v^{km} \\ &= \sum_{\tilde{g} \geq 0} \sum_{m > 0} \sum_{k>0} k^{2 \tilde{g}-3} \hat{r}_{g, m \alpha} u^{2 \tilde{g}-2} v^{km}. \end{align*} $$
Taking the
![]() $v^{n} u^{2g-2}$
coefficient, this shows that
$v^{n} u^{2g-2}$
coefficient, this shows that
 $$ \begin{align*} R_{g, n\alpha} = \sum_{k|n} k^{2 g-3} \hat{r}_{g,n/k \alpha}. \end{align*} $$
$$ \begin{align*} R_{g, n\alpha} = \sum_{k|n} k^{2 g-3} \hat{r}_{g,n/k \alpha}. \end{align*} $$
By Möbius inversion (i.e., using the identity
![]() $\sum _{d|n, d>0} \mu (d) = \delta _{n1}$
), we get
$\sum _{d|n, d>0} \mu (d) = \delta _{n1}$
), we get
 $\hat {r}_{g,n \alpha } = \sum _{k | n} k^{2g-3} \mu (k) R_{g, n \alpha /k}$
, so
$\hat {r}_{g,n \alpha } = \sum _{k | n} k^{2g-3} \mu (k) R_{g, n \alpha /k}$
, so
![]() $\widetilde {r}_{g, n\alpha } = \hat {r}_{g, n \alpha }$
.
$\widetilde {r}_{g, n\alpha } = \hat {r}_{g, n \alpha }$
.
By [Reference Pandharipande and Thomas49], all the
![]() $r_{g,\beta }$
are integers. It would be interesting to find integer-invariants which underlie the Gromov–Witten invariants of hyperkähler varieties in dimension
$r_{g,\beta }$
are integers. It would be interesting to find integer-invariants which underlie the Gromov–Witten invariants of hyperkähler varieties in dimension
![]() $>2$
. For hyperkähler fourfolds, a partial proposal is discussed in [Reference Cao, Oberdieck and Toda10].
$>2$
. For hyperkähler fourfolds, a partial proposal is discussed in [Reference Cao, Oberdieck and Toda10].
Appendix C Geometry of a general singular Debarre–Voisin fourfold by Jieao Song
We give a description for the singularities of a general singular Debarre–Voisin variety. In the notation of [Reference Benedetti and Song3], the class of the trivector
![]() $\sigma $
defining a general such Debarre–Voisin variety
$\sigma $
defining a general such Debarre–Voisin variety
![]() $X_{6}^{\sigma }$
lies in the divisor
$X_{6}^{\sigma }$
lies in the divisor
![]() ${\mathcal {D}}^{3,3,10}$
: There exists a unique three-dimensional subspace
${\mathcal {D}}^{3,3,10}$
: There exists a unique three-dimensional subspace
![]() $V_{3}\subset V_{10}$
such that
$V_{3}\subset V_{10}$
such that
![]() $\sigma $
satisfies the degeneracy condition
$\sigma $
satisfies the degeneracy condition
![]() $\sigma (V_{3},V_{3},V_{10})=0$
. Under the period map, this divisor corresponds to the Heegner divisorFootnote
12
$\sigma (V_{3},V_{3},V_{10})=0$
. Under the period map, this divisor corresponds to the Heegner divisorFootnote
12
![]() ${\mathcal {D}}_{22}$
in the period domain. We obtained the following description for the set-theoretical singular locus of
${\mathcal {D}}_{22}$
in the period domain. We obtained the following description for the set-theoretical singular locus of
![]() $X_{6}^{\sigma }$
in [Reference Benedetti and Song3, Proposition 2.4].
$X_{6}^{\sigma }$
in [Reference Benedetti and Song3, Proposition 2.4].
Proposition 7. Let
![]() $[\sigma ]\in {\mathcal {D}}^{3,3,10}$
be general so that there exists a unique three-dimensional subspace
$[\sigma ]\in {\mathcal {D}}^{3,3,10}$
be general so that there exists a unique three-dimensional subspace
![]() $V_{3}\subset V_{10}$
with
$V_{3}\subset V_{10}$
with
![]() $\sigma (V_{3},V_{3},V_{10})=0$
. Set-theoretically, the singular locus of
$\sigma (V_{3},V_{3},V_{10})=0$
. Set-theoretically, the singular locus of
![]() $X_{6}^{\sigma }$
is
$X_{6}^{\sigma }$
is
 $$ \begin{align*} S:={\left\{{[V_{6}]\in X_{6}^{\sigma}}\;\middle|\;{V_{6}\supset V_{3}}\right\}}, \end{align*} $$
$$ \begin{align*} S:={\left\{{[V_{6}]\in X_{6}^{\sigma}}\;\middle|\;{V_{6}\supset V_{3}}\right\}}, \end{align*} $$
which is a K3 surface of degree
![]() $22$
.
$22$
.
We prove the following stronger result, following the idea in [Reference Hassett21, Lemma 6.3.1], where a similar result is proved for the variety of lines of a nodal cubic hypersurface. We shall see that the two cases share some surprising similarities.
Proposition 8. Let
![]() $\sigma $
be as in the previous proposition. For the associated Debarre–Voisin variety
$\sigma $
be as in the previous proposition. For the associated Debarre–Voisin variety
![]() $X_{6}^{\sigma }$
, the singularities along the degree-
$X_{6}^{\sigma }$
, the singularities along the degree-
![]() $22$
K3 surface S are codimension-
$22$
K3 surface S are codimension-
![]() $2$
ordinary double points. More precisely, by blowing up the singular locus S, we get a smooth hyperkähler fourfold of
$2$
ordinary double points. More precisely, by blowing up the singular locus S, we get a smooth hyperkähler fourfold of
![]() $\mathrm {K3}^{[2]}$
-type, and the exceptional divisor is a conic fibration over S.
$\mathrm {K3}^{[2]}$
-type, and the exceptional divisor is a conic fibration over S.
Proof. We briefly recall the argument for the nodal cubic: For a cubic
![]() $X\subset {\mathbf {P}}^{5}={\mathbf {P}}(V_{6})$
containing a node
$X\subset {\mathbf {P}}^{5}={\mathbf {P}}(V_{6})$
containing a node
![]() $p:= [V_{1}]$
, the projectivized normal cone
$p:= [V_{1}]$
, the projectivized normal cone
![]() ${\mathbf {P}} C_{p} X$
is a quadric hypersurface Q in
${\mathbf {P}} C_{p} X$
is a quadric hypersurface Q in
![]() ${\mathbf {P}} T_{p} {\mathbf {P}}^{5}={\mathbf {P}}(V_{6}/V_{1})$
, and the varieties of lines
${\mathbf {P}} T_{p} {\mathbf {P}}^{5}={\mathbf {P}}(V_{6}/V_{1})$
, and the varieties of lines
![]() $F\subset \operatorname {Gr}(2,V_{6})$
are singular along a K3 surface S parametrizing lines in X passing through p. Instead of blowing up S in F, Hassett considered studying the ambient Grassmannian
$F\subset \operatorname {Gr}(2,V_{6})$
are singular along a K3 surface S parametrizing lines in X passing through p. Instead of blowing up S in F, Hassett considered studying the ambient Grassmannian
![]() $\operatorname {Gr}(2,V_{6})$
and blowing up the Schubert variety
$\operatorname {Gr}(2,V_{6})$
and blowing up the Schubert variety
![]() $\Sigma := {\mathbf {P}}(V_{6}/V_{1})\subset \operatorname {Gr}(2,V_{6})$
, which parametrizes all lines in
$\Sigma := {\mathbf {P}}(V_{6}/V_{1})\subset \operatorname {Gr}(2,V_{6})$
, which parametrizes all lines in
![]() ${\mathbf {P}}(V_{6})$
passing through p. This gives the following Cartesian diagram
${\mathbf {P}}(V_{6})$
passing through p. This gives the following Cartesian diagram

For a given point
![]() $x:= [V_{2}]\in S$
, we get one distinguished point
$x:= [V_{2}]\in S$
, we get one distinguished point
![]() $y:= [V_{2}/V_{1}]$
in
$y:= [V_{2}/V_{1}]$
in
![]() ${\mathbf {P}}^{4}={\mathbf {P}}(V_{6}/V_{1})$
that lies on the quadric Q. The projectivized normal space
${\mathbf {P}}^{4}={\mathbf {P}}(V_{6}/V_{1})$
that lies on the quadric Q. The projectivized normal space
![]() ${\mathbf {P}}{\mathcal {N}}_{\Sigma /\operatorname {Gr}(2,V_{6}),x}$
can be identified with
${\mathbf {P}}{\mathcal {N}}_{\Sigma /\operatorname {Gr}(2,V_{6}),x}$
can be identified with
![]() ${\mathbf {P}}(V_{6}/V_{2})$
, which parametrizes lines in
${\mathbf {P}}(V_{6}/V_{2})$
, which parametrizes lines in
![]() ${\mathbf {P}}^{4}={\mathbf {P}}(V_{6}/V_{1})$
passing through the point y, and the projectivized normal cone
${\mathbf {P}}^{4}={\mathbf {P}}(V_{6}/V_{1})$
passing through the point y, and the projectivized normal cone
![]() ${\mathbf {P}} C_{S,x}F$
is given by the subscheme parametrizing such lines that are also entirely contained in the quadric threefold Q, in other words, lines in Q passing through a given point. This condition gives a smooth conic curve, so the singularities of F along S are indeed codimension-2 ordinary double points.
${\mathbf {P}} C_{S,x}F$
is given by the subscheme parametrizing such lines that are also entirely contained in the quadric threefold Q, in other words, lines in Q passing through a given point. This condition gives a smooth conic curve, so the singularities of F along S are indeed codimension-2 ordinary double points.
We use a similar argument to study the singular Debarre–Voisin variety
![]() $X_{6}^{\sigma }$
. By assumption, the hyperplane section
$X_{6}^{\sigma }$
. By assumption, the hyperplane section
![]() $X_{3}^{\sigma }$
admits an ordinary double point at
$X_{3}^{\sigma }$
admits an ordinary double point at
![]() $[V_{3}]$
, so its tangent cone at
$[V_{3}]$
, so its tangent cone at
![]() $[V_{3}]$
is a smooth quadric hypersurface Q in the projectivization of the tangent space
$[V_{3}]$
is a smooth quadric hypersurface Q in the projectivization of the tangent space
 $$ \begin{align*}{\mathbf{P}} T_{[V_{3}]}\operatorname{Gr}(3,V_{10})\simeq{\mathbf{P}}\operatorname{Hom}(V_{3},V_{10}/V_{3})=: {\mathbf{P}}(T_{21})={\mathbf{P}}^{20}.\end{align*} $$
$$ \begin{align*}{\mathbf{P}} T_{[V_{3}]}\operatorname{Gr}(3,V_{10})\simeq{\mathbf{P}}\operatorname{Hom}(V_{3},V_{10}/V_{3})=: {\mathbf{P}}(T_{21})={\mathbf{P}}^{20}.\end{align*} $$
For a given
![]() $x:= [V_{6}]\in S$
, the projective space
$x:= [V_{6}]\in S$
, the projective space
![]() ${\mathbf {P}}\operatorname {Hom}(V_{3},V_{6}/V_{3})=:{\mathbf {P}}(T_{9})={\mathbf {P}}^{8}$
gives a distinguished linear subspace contained in Q.
${\mathbf {P}}\operatorname {Hom}(V_{3},V_{6}/V_{3})=:{\mathbf {P}}(T_{9})={\mathbf {P}}^{8}$
gives a distinguished linear subspace contained in Q.
Following the proof of Hassett, instead of blowing up S in
![]() $X_{6}^{\sigma }$
, we consider the ambient Grassmannian
$X_{6}^{\sigma }$
, we consider the ambient Grassmannian
![]() $\operatorname {Gr}(6,V_{10})$
and blow up the entire Schubert variety
$\operatorname {Gr}(6,V_{10})$
and blow up the entire Schubert variety
which is smooth of codimension 12. We have the following description for its normal bundle in
![]() $\operatorname {Gr}(6,V_{10})$
:
$\operatorname {Gr}(6,V_{10})$
:
where we denote by
![]() ${\mathcal {U}}_{6}$
and
${\mathcal {U}}_{6}$
and
![]() ${\mathcal {Q}}_{10/6}$
the restrictions to
${\mathcal {Q}}_{10/6}$
the restrictions to
![]() $\Sigma $
of the two tautological bundles on
$\Sigma $
of the two tautological bundles on
![]() $\operatorname {Gr}(6,V_{10})$
. For the given point
$\operatorname {Gr}(6,V_{10})$
. For the given point
![]() $x\in S$
, the projectivization of the normal space is therefore an 11-dimensional projective space
$x\in S$
, the projectivization of the normal space is therefore an 11-dimensional projective space
where we recall that
![]() $T_{21}$
is the tangent space of
$T_{21}$
is the tangent space of
![]() $\operatorname {Gr}(3,V_{10})$
at
$\operatorname {Gr}(3,V_{10})$
at
![]() $[V_{3}]$
, and
$[V_{3}]$
, and
![]() $T_{9}$
is the tangent space of
$T_{9}$
is the tangent space of
![]() $\operatorname {Gr}(3,V_{6})$
at
$\operatorname {Gr}(3,V_{6})$
at
![]() $[V_{3}]$
, viewed as a subspace of
$[V_{3}]$
, viewed as a subspace of
![]() $T_{21}$
.
$T_{21}$
.
Consider the proper transform of
![]() $X_{6}^{\sigma }$
denoted by
$X_{6}^{\sigma }$
denoted by
 $\tilde X_{6}^{\sigma }$
. We have the following Cartesian diagram
$\tilde X_{6}^{\sigma }$
. We have the following Cartesian diagram

Consequently, we get a natural closed embedding of the projectivized normal cone
The total projective space
![]() ${\mathbf {P}}(T_{21}/T_{9})$
parametrizes nine-dimensional linear subspaces of
${\mathbf {P}}(T_{21}/T_{9})$
parametrizes nine-dimensional linear subspaces of
![]() ${\mathbf {P}}(T_{21})$
that contain the distinguished
${\mathbf {P}}(T_{21})$
that contain the distinguished
![]() ${\mathbf {P}}^{8}={\mathbf {P}}(T_{9})$
, and the projectivized normal cone
${\mathbf {P}}^{8}={\mathbf {P}}(T_{9})$
, and the projectivized normal cone
![]() ${\mathbf {P}} C_{S,x} X_{6}^{\sigma }$
can then be identified with the subscheme that parametrizes such
${\mathbf {P}} C_{S,x} X_{6}^{\sigma }$
can then be identified with the subscheme that parametrizes such
![]() ${\mathbf {P}}^{9}$
that are also contained in the quadric Q. In other words, it parametrizes nine-dimensional linear subspaces in a 19-dimensional quadric containing a fixed
${\mathbf {P}}^{9}$
that are also contained in the quadric Q. In other words, it parametrizes nine-dimensional linear subspaces in a 19-dimensional quadric containing a fixed
![]() ${\mathbf {P}}^{8}$
. This is again a smooth conic curve, just like in the nodal cubic case. Thus, the singularities of
${\mathbf {P}}^{8}$
. This is again a smooth conic curve, just like in the nodal cubic case. Thus, the singularities of
![]() $X_{6}^{\sigma }$
along S are indeed codimension-2 ordinary double points, and
$X_{6}^{\sigma }$
along S are indeed codimension-2 ordinary double points, and
 $\tilde X_{6}^{\sigma }$
is smooth.
$\tilde X_{6}^{\sigma }$
is smooth.
Finally, we show that the resolution
 $\tilde X_{6}^{\sigma }$
that we obtained has trivial canonical class. Since
$\tilde X_{6}^{\sigma }$
that we obtained has trivial canonical class. Since
![]() $X_{6}^{\sigma }$
is birational to the Hilbert square
$X_{6}^{\sigma }$
is birational to the Hilbert square
![]() $S^{[2]}$
, this will then force
$S^{[2]}$
, this will then force
 $\tilde X_{6}^{\sigma }$
to be a smooth hyperkähler fourfold of
$\tilde X_{6}^{\sigma }$
to be a smooth hyperkähler fourfold of
![]() $\mathrm {K3}^{[2]}$
-type.
$\mathrm {K3}^{[2]}$
-type.
We denote by E the exceptional divisor for the blowup
![]() $\operatorname {Bl}_{\Sigma }\operatorname {Gr}(6,V_{10})\to \operatorname {Gr}(6,V_{10})$
, and by D the exceptional divisor for the blowup
$\operatorname {Bl}_{\Sigma }\operatorname {Gr}(6,V_{10})\to \operatorname {Gr}(6,V_{10})$
, and by D the exceptional divisor for the blowup
 $\tilde X_{6}^{\sigma }\to X_{6}^{\sigma }$
. The divisor D can be identified with the projectivized normal cone
$\tilde X_{6}^{\sigma }\to X_{6}^{\sigma }$
. The divisor D can be identified with the projectivized normal cone
![]() ${\mathbf {P}} C_{S} X_{6}^{\sigma }$
, so the morphism
${\mathbf {P}} C_{S} X_{6}^{\sigma }$
, so the morphism
![]() $D\to S$
is a conic fibration by the above analysis. By construction, the Zariski open subset
$D\to S$
is a conic fibration by the above analysis. By construction, the Zariski open subset
 $\tilde X_{6}^{\sigma }\setminus D$
is isomorphic to the smooth locus
$\tilde X_{6}^{\sigma }\setminus D$
is isomorphic to the smooth locus
![]() $X_{6}^{\sigma }\setminus S$
. The latter has trivial canonical class since it is the regular zero-locus of
$X_{6}^{\sigma }\setminus S$
. The latter has trivial canonical class since it is the regular zero-locus of
![]() $\sigma $
viewed as a section of the vector bundle
$\sigma $
viewed as a section of the vector bundle
 $\bigwedge ^{3}{\mathcal {U}}_{6}^{\vee }$
. Therefore, the canonical divisor
$\bigwedge ^{3}{\mathcal {U}}_{6}^{\vee }$
. Therefore, the canonical divisor
 $K_{\tilde X_{6}^{\sigma }}$
is linearly equivalent to some multiple of D. We write
$K_{\tilde X_{6}^{\sigma }}$
is linearly equivalent to some multiple of D. We write
 $K_{\tilde X_{6}^{\sigma }}=m D$
, and it remains to show that
$K_{\tilde X_{6}^{\sigma }}=m D$
, and it remains to show that
![]() $m=0$
.
$m=0$
.
Since
![]() $D\to S$
is a smooth conic fibration in the projectivized normal bundle
$D\to S$
is a smooth conic fibration in the projectivized normal bundle
![]() $E\to \Sigma $
, the relative
$E\to \Sigma $
, the relative
![]() ${\mathcal {O}}(-1)$
of
${\mathcal {O}}(-1)$
of
![]() $E\to \Sigma $
restricts to the relative canonical bundle of
$E\to \Sigma $
restricts to the relative canonical bundle of
![]() $D\to S$
. Note that by the Leray–Hirsch theorem, this bundle is necessarily nontrivial. Since E is the exceptional divisor, the relative
$D\to S$
. Note that by the Leray–Hirsch theorem, this bundle is necessarily nontrivial. Since E is the exceptional divisor, the relative
![]() ${\mathcal {O}}(-1)$
on E is given by
${\mathcal {O}}(-1)$
on E is given by
![]() ${\mathcal {O}}_{E}(E)$
, so we have
${\mathcal {O}}_{E}(E)$
, so we have
Using the fact that S is a K3 surface and that
 ${\mathcal {O}}_{E}(E)|_{\tilde X_{6}^{\sigma }}\simeq {\mathcal {O}}_{\tilde X_{6}^{\sigma }}(D)$
, this gives
${\mathcal {O}}_{E}(E)|_{\tilde X_{6}^{\sigma }}\simeq {\mathcal {O}}_{\tilde X_{6}^{\sigma }}(D)$
, this gives
 $$ \begin{align*} \omega_{D}\simeq\omega_{D/S}\simeq{\mathcal{O}}_{\tilde X_{6}^{\sigma}}(D)|_{D},\quad\text{hence} \quad K_{D}=D|_{D}, \end{align*} $$
$$ \begin{align*} \omega_{D}\simeq\omega_{D/S}\simeq{\mathcal{O}}_{\tilde X_{6}^{\sigma}}(D)|_{D},\quad\text{hence} \quad K_{D}=D|_{D}, \end{align*} $$
which in particular must be nontrivial.
On the other hand, by the adjunction formula, we have
 $$ \begin{align*} K_{D}\simeq(K_{\tilde X_{6}^{\sigma}}+D)|_{D}=(m+1)D|_{D}. \end{align*} $$
$$ \begin{align*} K_{D}\simeq(K_{\tilde X_{6}^{\sigma}}+D)|_{D}=(m+1)D|_{D}. \end{align*} $$
Thus, we may conclude that
![]() $m=0$
, and
$m=0$
, and
 $K_{\tilde X_{6}^{\sigma }}$
is indeed trivial.
$K_{\tilde X_{6}^{\sigma }}$
is indeed trivial.
Remark 9. Contrary to the nodal cubic case, the resolution
 $\tilde X_{6}^{\sigma }$
obtained is not isomorphic to the Hilbert scheme
$\tilde X_{6}^{\sigma }$
obtained is not isomorphic to the Hilbert scheme
![]() $S^{[2]}$
, even for a generic member of the family. This can be seen by studying the chamber decomposition for a generic
$S^{[2]}$
, even for a generic member of the family. This can be seen by studying the chamber decomposition for a generic
![]() $S^{[2]}$
with Picard rank 2: One may find exactly two chambers in the movable cone, corresponding to
$S^{[2]}$
with Picard rank 2: One may find exactly two chambers in the movable cone, corresponding to
![]() $S^{[2]}$
and a second birational model; the Plücker polarization pulled back to
$S^{[2]}$
and a second birational model; the Plücker polarization pulled back to
![]() $S^{[2]}$
via the birational map is equal to
$S^{[2]}$
via the birational map is equal to
![]() $10H-33\delta $
and not nef (see, for example, [Reference Debarre, Han, O’Grady and Voisin13, Table 1]), so we may conclude that
$10H-33\delta $
and not nef (see, for example, [Reference Debarre, Han, O’Grady and Voisin13, Table 1]), so we may conclude that
 $\tilde X_{6}^{\sigma }$
is the second birational model. The two models are related by a Mukai flop, and it would be interesting to see this geometrically.
$\tilde X_{6}^{\sigma }$
is the second birational model. The two models are related by a Mukai flop, and it would be interesting to see this geometrically.
Acknowledgements
The idea to use Noether–Lefschetz theory for the Gromov–Witten theory of
![]() $K3^{[2]}$
-type varieties is due to E. Scheidegger and quite old [Reference Scheidegger50]. I also owe a great debt to the beautiful paper on Noether–Lefschetz theory by D. Maulik and R. Pandharipande [Reference Maulik and Pandharipande37]. I further thank T. Beckmann, J. Bryan, T. H. Buelles, O. Debarre, E. Markman, G. Mongardi, R. Mboro and J. Song for useful comments and the referees for a careful reading and helpful remarks.
$K3^{[2]}$
-type varieties is due to E. Scheidegger and quite old [Reference Scheidegger50]. I also owe a great debt to the beautiful paper on Noether–Lefschetz theory by D. Maulik and R. Pandharipande [Reference Maulik and Pandharipande37]. I further thank T. Beckmann, J. Bryan, T. H. Buelles, O. Debarre, E. Markman, G. Mongardi, R. Mboro and J. Song for useful comments and the referees for a careful reading and helpful remarks.
Conflicts of Interest
None.
Financial Support
The author was funded by the Deutsche Forschungsgemeinschaft (DFG)–OB 512/1-1.