A Practical Guide to Deconvolution of Fluorescence Microscope Imagery

Introduction

Over the past decade, deconvolution of 3D light optical microscopy data has advanced from an obscure technique employed by only a few dedicated souls to a routine method that is now available with all modern microscope systems. Dramatic increases in computer power, algorithm sophistication, and software ease of use have brought the power of deconvolution to the general microscope user, and processing large 3D datasets is no longer a rate-limiting step in the imaging process.

Deconvolution is a computational technique that is applied to digital imagery to compensate for the optical limitations of the imaging instrument by reducing out-of-focus blurring or haze [1]. The increased contrast and resolution of the restored data improves not only the visual quality but also the ability to quantify both object dimensions and image intensity. Deconvolution algorithms have been particularly effective in processing 3D fluorescence microscopy data from the following modalities: widefield epi-fluorescence, transmitted light brightfield, spinning disk confocal, laser scanning confocal, and multi-photon fluorescence [2, 3, 4, 5].

Diffraction in a standard epi-fluorescence microscope limits the smallest lateral resolvable feature to about half the emission wavelength with high numerical-aperture (NA) objective lenses, and the axial resolution is about 3 times worse. The aberrations inherent in the microscope are modeled by the characteristic point-spread-function (PSF), which describes how every point of light emitted by the specimen is observed by the user or camera. The PSF can be easily observed by imaging sub-resolution fluorescence microspheres and focusing through the sample to observe the characteristic hourglass shape [4].

Mathematically, the image observed at the CCD camera can be modeled as a convolution between the true 3D light distribution of the specimen and the spatially invariant 3D PSF of the instrument, which is contaminated with Poisson-distributed noise due to photon counting. The ability to restore an accurate representation of the true specimen is limited by the accuracy of the PSF model and the amount of noise contamination. The process to improve the quality of the observed imagery is termed deblurring or deconvolution, depending on the type of algorithm.

Collecting the dataset

In order to deconvolve 3D microscope data there are hardware, software, and dataset requirements. Considering epi-fluorescence imaging, a modern research-grade light optical microscope with computer-controlled Z-focusing mechanism and a digital CCD camera are essential for most applications. The algorithms require a 3D dataset with evenly spaced optical slices that can be as fine as 250 nm apart, so the Z-focusing mechanism must have high accuracy and repeatability (hand focusing is not suitable). The CCD camera should be optimized for low-light imaging, with low readout and background noise, and may be cooled to achieve this.

Correct data sampling is essential for proper deconvolution, and each objective lens has an optimal lateral (Δ_XY) and axial (Δ_Z) spacing that is determined by the Nyquist sampling rate:

See Table 1 for recommended lateral and axial Nyquist spacings. In practice, spacings up to 1.5 times larger can be successfully used for deconvolution.

Table 1: Recommended lateral and axial sample spacing for different objective lenses with widefield microscopy (520 nm emission).

Note: Spacings up to 1.5 times larger can be successfully used with deconvolution.

When setting up the 3D image acquisition, the exposure time should be minimized to reduce photo-damage and bleaching, while maintaining sufficient signal levels to overcome the inherent noise. Large saturated regions should be avoided as they cannot be accurately restored. Consider using a modality such as brightfield, phase contrast, or DIC to initially find and focus on the region of interest prior to using fluorescence to minimize the amount light exposure.

Ideally the optical slices should extend above and below the specimen until the defocused features are blurred to a uniform haze. If this is excessive, consider a Z region that is up to twice the apparent specimen thickness (for example, for a 10-μm thick specimen, take additional slices 3–5 μm above and below).

The microscope control and acquisition software should record all the appropriate information about the optical setup and pixel/slice spacing with the image meta-data. This is essential for proper post processing, whether doing deconvolution, image analysis, or visualization. This information should also be recorded in the lab notebook for verification purposes or if the meta-data is lost when converting file formats.

The Algorithms

There are a variety of deblurring and deconvolution algorithms available that may be either integrated into the image acquisition software, be a commercial standalone package, or even be free open-source alternatives.

Deblurring Algoritms

In the context of this article, deblurring algorithms refer to methods that attempt to remove the blur and haze from the observed dataset. The most well-known deblurring techniques are the nearest neighbors and no-neighbors algorithms, and these were some of the earliest methods used due to their low computational and memory requirements [4].

The nearest-neighbors method uses 3 optical slices and attempts to remove the blur contribution in the center focal plane by subtracting defocused versions of the adjacent slices, leaving only the sharp features. This process is repeated through the whole 3D stack of slices. The result is a visual improvement, but it is non-quantitative because 90–99% of the captured photons are removed. The no-neighbors method is similar but only considers a single slice at a time and is equivalent to an un-sharp masking that is often used in photography. These algorithms should only be used for a quick visual inspection of the collected data prior to using a deconvolution algorithm.

Deconvolution Algorithms—Linear Filtering

In contrast to deblurring methods, deconvolution algorithms attempt to restore the true image intensities from the observed data and are either linear or iterative (non-linear) in nature.

Image formation in a light optical microscope can be modeled as a convolution between the true specimen light distribution and the PSF. Mathematically, this convolution process can be efficiently described as a multiplication between the frequency domain representations of the specimen and the PSF. In the frequency domain the PSF is described by the 3D optical transfer function (OTF) and is usually computed using the Fast Fourier Transform (FFT).

If the image blur is caused by multiplication with the OTF, then it stands that this process could be reversible by dividing by the OTF, which is the basis for inverse filtering. In reality this is not possible because the OTF contains zero components, and the high frequency image components with very small magnitudes are easily corrupted by noise contamination. In practice the Wiener filter is used, which takes into account the noise to perform a stable filtering. The Wiener filter uses a full 3D OTF, is executed in a single processing step, and is an example of linear filtering. There is no inherent limitation on negative pixel values, which prevents accurate intensity quantification. Also, the Wiener filter can only restore frequency components inside the bandlimit of the OTF [3, 4].

Deconvolution Algorithms—Iterative Restoration

The most advanced deconvolution algorithms are iterative, requiring multiple cycles to converge towards a desired solution. The iterative algorithms impose non-negativity on the solution, can suppress noise, and can even recover frequencies beyond the bandwidth limit. They come at the cost of increased memory requirements and computational processing [3, 4].

Rather than trying to directly reverse the blurring process (for example, by Wiener filtering), iterative algorithms make an estimate of the object, then create a blurred version using the PSF, and finally compare the result with the actual observed data. An optimization procedure is then used to produce an improved estimate, and the process is iterated until the desired solution is converged. The algorithms impose constraints such as non-negative pixel intensities, leading to the term constrained iterative deconvolution. The algorithm may run until a convergence criterion has been reached or simply for a user-defined number of iterations. The optimal number of iterations will balance blur removal with noise amplification that often occurs.

Typical iterative algorithms are based on measures such as least squares and maximum likelihood (ML). The least-squares optimization seeks to minimize the square error between the observed data and the reblurred estimate and assumes Gaussian-distributed noise contamination. Maximum likelihood is a probabilistic approach that seeks to find the statistically most likely solution given the observed data, the PSF model, and the noise probability distribution [3, 5]. The maximum likelihood solution can be found using the expectation-maximization (EM) process, and, in the case of Poisson distributed noise, one popular implementation is the Richardson-Lucy (RL) iterative algorithm [3]. The RL iterations are multiplicative in nature, which inherently imposes a non-negativity constraint.

Figure 1 shows the maximum-intensity projection of a 3D widefield fluorescence image of spirogyra collected with a 0.75 NA objective lens at 540 nm and 1μm-spaced Z slices (original data courtesy of Olympus Soft Imaging Solutions, Münster, Germany). The results after processing using nearest neighbors deblurring, Wiener filtering, and 10 iterations of ML-based deconvolution are also shown. The iterative deconvolution has increased the dynamic range by a factor of 16 and minimized the residual blur that is still visible with the other algorithms. The nearest neighbors used a 95% haze removal factor, leaving only 5% of the original photons and reducing the dynamic range by a factor of 5. The iterative deconvolution also shows improved restoration of the axial features compared to the other algorithms.

Figure 1: Maximum intensity projections from original 3D spirogyra specimen (collected with 0.75 NA air objective lens, 1 μm Z slices), and following different post-processing algorithms. XY, XZ and ZY views are shown. The axial views have been stretched by a factor of 3 to ensure cubic voxels. The volume dimensions (XYZ) are approximately 108 x 88 x 25 μm. (A) Original (maximum intensity = 4095), (B) Nearest neighbors at 95% (max = 881), (C) Wiener filter (max = 32803), and (D) ML deconvolution, 10 iterations (max = 65540). Dataset from Olympus SIS (Munster, Germany).

Figure 2 illustrates the ML iterative deconvolution of a multi-channel cellular dataset with a high NA objective lens (1.42 NA oil) and wide-field fluorescence. The original dataset resolves no clear structures; however, after 20 iterations of deconvolution, the cellular components are well-defined. The result would likely be further improved with finer Z sampling, as 0.79 μm is under-sampling for the objective lens used. Despite this, the algorithm is still able to extract useful information.

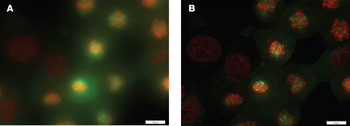
Figure 2: (A) Maximum intensity projection of multi-channel widefield fluorescence dataset, and (B) following iterative ML deconvolution (20 iterations). The objective lens was a 1.42 NA oil with 13 Z slices 0.79 μm apart (under-sampled in Z). Specimen: a LLC-PK1 (kidney proximal tubule) cell line from a pig kidney. Staining is with mCherry H2B-18 (red channel) and mEGFP Tublin-6 (green channel).The image dimensions (XY) are approximately 92.2 x 69.6 μm. Dataset from Olympus SIS (Munster, Germany).

PSF Estimation

The quality of the restoration is directly based on the accuracy of the PSF model applied, and estimating an accurate PSF can be difficult. Three typical methods are theoretical calculation using microscope parameters, empirical measurement using sub-resolution beads, and blind or adaptive deconvolution that estimates the PSF directly from the observed data. Each approach has different effects on restoration accuracy, imaging protocol, user effort, and computational requirements [3, 4].

Historically, imaging sub-resolution fluorescent microspheres (100–200 nm diameter) was the most often used approach. This involves preparing a separate slide of beads with the same embedding medium as the specimen and capturing a thru-focus 3D dataset of an isolated bead to approximate the optical PSF for each emission wavelength.

Even without collecting PSFs for deconvolution, observing a bead slide is very useful for assessing the alignment and optimal operation of the microscope. When focusing up and down through the beads, the defocused regions should look equivalent both above and below the in-focus plane. If rings are observed on one side and blobs on the other, then spherical aberration is likely a problem, which should be minimized by matching the specimen embedding and objective lens immersion medium refractive indexes and by using the proper coverslip thickness (measured using a micrometer) [4]. An objective lens correction collar is designed to correct spherical aberration, though optimizing the setting can be tricky as the plane of focus changes with the collar position, requiring constant refocusing.

Blind Deconvolution

One of the more recent algorithm developments in the restoration of blurred images is the ability to determine both the underlying object and the PSF from the observed image. This process is termed blind deconvolution, and although initially it may not seem possible, there is a wide body of research and practical implementations that support the technique [3, 4, 5]. The key is that there are additional physical constraints that can be imposed on the solution, such as non-negative pixel intensities and additional a priori knowledge, including frequency band limits on the estimated PSF, which make the problem tractable [3].

The advantage of blind deconvolution is that it reduces the need for a highly accurate PSF to be provided to the deconvolution algorithm. In regular non-blind deconvolution the PSF is fixed, and the algorithm attempts to fit the solution to the model, even if the PSF isn't accurate, which can lead to restoration artifacts. With blind deconvolution, both the image and PSF estimates are adapted during each iteration to find the best fit to the observed data. This adaptability can reduce potential artifacts and also makes deconvolution easier for microscope users because they don't have to be concerned with collecting exact PSFs as part of their imaging experiment. Most algorithms that employ blind deconvolution use a calculated PSF as the starting point for the PSF. Blind deconvolution requires about twice the computational time to estimate both the image and PSF, but it should not be relied upon to compensate for poor imaging setup or excessive optical aberrations. Figure 3 shows blind deconvolution of a widefield fluorescence dataset (brine shrimp) for 20 iterations. The Z dimension is under-sampled, so a finer spacing would likely improve the result further.

Figure 3: Maximum intensity projections of brine shrimp specimen, (A) original widefield fluorescence dataset, and (B) following blind deconvolution (20 iterations). Imaging parameters: 40x 0.9 NA Air lens, 535 nm emission, 0.16 μm pixel spacing, 1 μm slices, 16 slices with 1344 x 1024 pixels. Original dataset courtesy of Olympus SIS (Center Valley, PA).

Other Microscope Modalities

Deconvolution processing is most often associated with wide-field epi-fluorescence microscopy, but the algorithms can be successfully applied to other optical microscope modalities, providing suitable PSF information is provided. Even laser scanning confocal and multi-photon modalities can benefit from deconvolution processing by reducing the inherent axial smearing and suppressing the noise contamination from low photon counts. With confocal microscopy, the imaging efficiency can be improved by opening the pinhole to collect more light, increasing the signal level at the cost of some increased blur, but then relying on the deconvolution to correct for this in post-processing [6].

Transmitted light brightfield datasets can be processed, providing that the image formation can be modeled by the specimen absorbing light and not contrast resulting from phase interference [3]. Spinning-disk confocal-based systems can also benefit from deconvolution, particularly when using blind deconvolution, because the haze is not as severe as wide-field, but the detection efficiency is higher than with laser-scanning confocal. Figure 4 shows an example of a spinning disk dataset that is processed using blind deconvolution, which was necessary because the model for the spinning disk PSF was not known. The result shows excellent contrast of features and cells.

Figure 4: Maximum intensity projections of brine shrimp specimen, (A) original spinning disk confocal (Olympus DSU) dataset, and (B) following blind deconvolution (20 iterations). Same imaging parameters and specimen as Figure 3. Original dataset courtesy of Olympus SIS (Center Valley, PA).

Employing deconvolution algorithms will not enable a wide-field microscope to have the depth penetration of a confocal system or enable a confocal to achieve the high overall detection efficiency that is possible with widefield. Deconvolution will not make poorly acquired data good but, rather, make good data better. In fact, deconvolved data will often show many imaging problems that were previously obscured by the out-of-focus blur.

Analyzing the Results

When analyzing the deconvolution results, the original and processed datasets should be compared by observing individual optical slices as well as maximum intensity and other projections. Features that now appear clearly in the deconvolved data should also being present in the original imagery but may have been obscured by out-of-focus blur and noise. Be cautious of fine texture that may just be the result of amplified noise. The software should display the optical slice intensities scaled relative to the brightest features in the whole 3D volume. Although it may appear that the resulting data is “dimmer” than the original imagery, this is simply because the deconvolution has dramatically increased the dynamic range of the dataset, which must now be scaled down to fit the 8-bit range of the display monitor.

Residual out-of-focus haze may be an indication of either spherical aberration that hasn't been accounted for or the use of a PSF that does not accurately match the blur in the original dataset. Other imaging artifacts such as flicker between slices may also be more apparent and should be compensated for prior to deconvolution. Boundary or edge artifacts can be expected if parts of the specimen extend beyond the field of view.

Once the data has been accurately restored, closely spaced features should be more easily resolvable, object borders should be more defined, the apparent brightness of the specimen should increase, background noise should be suppressed, and total image intensity should be preserved. Deconvolved datasets should result in better 3D visualization and easier segmentation in subsequent image analysis by clearly revealing the objects of interest.

Summary

Deconvolution algorithms can now be routinely applied to 3D optical microscope imagery collected from a variety of modalities. It is important to understand the issues involved in properly setting up the instrument for acquisition, minimizing aberrations, and correct image sampling. This is essential for all microscope imaging, not just deconvolution; however, deconvolution will reveal the full imaging capabilities of the instrument and extract more information about the specimen. For more in-depth reading see the references [1] [1, 2, 3, 4, 5, 6].