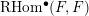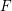1 Introduction
A differential graded (DG) algebra is said to be formal if it is quasi-isomorphic to its homology algebra. Formality is a central concept with roots in real homotopy theory [Reference Deligne, Griffiths, Morgan and SullivanDGMS75], deformation quantization [Reference KontsevichKon03], and deformation theory [Reference Goldman and MillsonGM88]. The presence of formality is in general difficult to prove and has important consequences: in topology, formality implies vanishing of all Massey products; in deformation quantization, it implies that every Poisson manifold has a deformation quantization; in deformation theory, it implies that the underlying derived, or non-commutatively thickened, moduli spaces are locally defined by cup products, leading to a linear-algebraic (quiver) interpretation. The following conjecture was made by Kaledin and Lehn in [Reference Kaledin and LehnKL07].
Conjecture 1.1. For a projective K3 surface
![]() $X$
with a generic polarization
$X$
with a generic polarization
![]() $H$
, let
$H$
, let
![]() $F$
be a
$F$
be a
![]() $H$
-polystable coherent sheaf on
$H$
-polystable coherent sheaf on
![]() $X$
. Then the DG algebra
$X$
. Then the DG algebra
![]() $\operatorname{RHom}^{\bullet }(F,F)$
is formal.
$\operatorname{RHom}^{\bullet }(F,F)$
is formal.
In this paper we prove two generalizations of this conjecture.
Theorem 1.2. For a projective K3 surface
![]() $X$
with an arbitrary polarization
$X$
with an arbitrary polarization
![]() $H$
, let
$H$
, let
![]() $F$
be an
$F$
be an
![]() $H$
-polystable coherent sheaf on
$H$
-polystable coherent sheaf on
![]() $X$
. Then the DG algebra
$X$
. Then the DG algebra
![]() $\operatorname{RHom}^{\bullet }(F,F)$
is formal.
$\operatorname{RHom}^{\bullet }(F,F)$
is formal.
Theorem 1.3. Let
![]() $X$
be a projective K3 surface,
$X$
be a projective K3 surface,
![]() $\mathbf{v}$
a Mukai vector, and
$\mathbf{v}$
a Mukai vector, and
![]() $\unicode[STIX]{x1D70E}\in \operatorname{Stab}^{\dagger }(X)$
a Bridgeland stability condition that is generic with respect to
$\unicode[STIX]{x1D70E}\in \operatorname{Stab}^{\dagger }(X)$
a Bridgeland stability condition that is generic with respect to
![]() $\mathbf{v}$
. For any
$\mathbf{v}$
. For any
![]() $\unicode[STIX]{x1D70E}$
-polystable derived object
$\unicode[STIX]{x1D70E}$
-polystable derived object
![]() $F$
of Mukai vector
$F$
of Mukai vector
![]() $\mathbf{v}$
, the DG algebra
$\mathbf{v}$
, the DG algebra
![]() $\operatorname{RHom}^{\bullet }(F,F)$
is formal.
$\operatorname{RHom}^{\bullet }(F,F)$
is formal.
Conjecture 1.1 was proved in [Reference Kaledin and LehnKL07] for
![]() $F={\mathcal{I}}_{Z}^{\oplus n}$
, where
$F={\mathcal{I}}_{Z}^{\oplus n}$
, where
![]() ${\mathcal{I}}_{Z}$
is the ideal sheaf of a zero-dimensional closed subscheme. In [Reference ZhangZha12], the conjecture was proved in a few more cases; see Proposition 3.1. It was also pointed out in [Reference ZhangZha12] that the technique from [Reference Kaledin and LehnKL07] is no longer enough for tackling the remaining cases. In this paper we explore the following new idea.
${\mathcal{I}}_{Z}$
is the ideal sheaf of a zero-dimensional closed subscheme. In [Reference ZhangZha12], the conjecture was proved in a few more cases; see Proposition 3.1. It was also pointed out in [Reference ZhangZha12] that the technique from [Reference Kaledin and LehnKL07] is no longer enough for tackling the remaining cases. In this paper we explore the following new idea.
Proposition 1.4. For smooth projective varieties
![]() $X$
and
$X$
and
![]() $Y$
, let
$Y$
, let
be a derived equivalence. Then for any object
![]() $F\in D^{b}(\operatorname{Coh}(X))$
, the DG algebra
$F\in D^{b}(\operatorname{Coh}(X))$
, the DG algebra
![]() $\operatorname{RHom}^{\bullet }(F,F)$
is formal if and only if
$\operatorname{RHom}^{\bullet }(F,F)$
is formal if and only if
![]() $\operatorname{RHom}^{\bullet }(\unicode[STIX]{x1D6F7}(F),\unicode[STIX]{x1D6F7}(F))$
is formal.
$\operatorname{RHom}^{\bullet }(\unicode[STIX]{x1D6F7}(F),\unicode[STIX]{x1D6F7}(F))$
is formal.
The main ingredient in the proof of Proposition 1.4 is a theorem of Lunts and Orlov [Reference Lunts and OrlovLO10, Theorem 2.14] stating that, for a smooth projective variety
![]() $X$
,
$X$
,
![]() $D^{b}(\operatorname{Coh}(X))$
admits a strongly unique DG enhancement. The proof of Theorem 1.2 follows easily from Proposition 1.4: given any polystable sheaf
$D^{b}(\operatorname{Coh}(X))$
admits a strongly unique DG enhancement. The proof of Theorem 1.2 follows easily from Proposition 1.4: given any polystable sheaf
![]() $F$
, there exists some Fourier–Mukai transform
$F$
, there exists some Fourier–Mukai transform
![]() $\unicode[STIX]{x1D6F7}$
by [Reference YoshiokaYos09, Theorem 1.7], such that
$\unicode[STIX]{x1D6F7}$
by [Reference YoshiokaYos09, Theorem 1.7], such that
![]() $\unicode[STIX]{x1D6F7}(F)$
is a polystable sheaf and satisfies the assumption required in [Reference ZhangZha12]. Similarly, Theorem 1.3 is reduced to Theorem 1.2 by applying autoequivalences of
$\unicode[STIX]{x1D6F7}(F)$
is a polystable sheaf and satisfies the assumption required in [Reference ZhangZha12]. Similarly, Theorem 1.3 is reduced to Theorem 1.2 by applying autoequivalences of
![]() $D^{b}(\operatorname{Coh}(X))$
constructed using [Reference BridgelandBri08, Reference YoshiokaYos09, Reference Bayer and MacrìBM14a, Reference Bayer and MacrìBM14b].
$D^{b}(\operatorname{Coh}(X))$
constructed using [Reference BridgelandBri08, Reference YoshiokaYos09, Reference Bayer and MacrìBM14a, Reference Bayer and MacrìBM14b].
For the relation between Conjecture 1.1 and non-commutative deformation theory see, for example, [Reference TodaTod17]; for the relation to derived deformation theory see [Reference ToënToe17]. Formality implies that all non-trivial analogs of the higher Massey products on
![]() $\operatorname{Ext}^{\bullet }(F,F)$
are zero. Thus our results imply immediately the local quadraticity of the Kuranishi spaces of polystable sheaves on K3 surfaces obtained by [Reference YoshiokaYos16, Corollary 0.6], and in a particular case by [Reference Arbarello and SaccàAS18, Theorem 3.7]. Our approach of reducing everything to [Reference ZhangZha12] is inspired by their approaches.
$\operatorname{Ext}^{\bullet }(F,F)$
are zero. Thus our results imply immediately the local quadraticity of the Kuranishi spaces of polystable sheaves on K3 surfaces obtained by [Reference YoshiokaYos16, Corollary 0.6], and in a particular case by [Reference Arbarello and SaccàAS18, Theorem 3.7]. Our approach of reducing everything to [Reference ZhangZha12] is inspired by their approaches.
Our results have several other immediate implications. We can recover the main theorem of [Reference Arbarello and SaccàAS18, Theorem 1.1] on symplectic resolutions of moduli spaces
![]() ${\mathcal{M}}_{X,H}(\mathbf{v})$
of
${\mathcal{M}}_{X,H}(\mathbf{v})$
of
![]() $H$
-semistable sheaves on K3 surfaces via variations of geometric invariant theory quotients of quiver varieties, by combining Theorem 1.2 and [Reference TodaTod18, Theorem 1.3], as explained in [Reference TodaTod18]. We can also obtain that
$H$
-semistable sheaves on K3 surfaces via variations of geometric invariant theory quotients of quiver varieties, by combining Theorem 1.2 and [Reference TodaTod18, Theorem 1.3], as explained in [Reference TodaTod18]. We can also obtain that
![]() ${\mathcal{M}}_{X,H}(\mathbf{v})$
has symplectic singularities for arbitrary polarizations
${\mathcal{M}}_{X,H}(\mathbf{v})$
has symplectic singularities for arbitrary polarizations
![]() $H$
, by combining Theorem 1.2 and [Reference Bellamy and SchedlerBS16, Proposition 1.2], which generalizes slightly [Reference Kaledin, Lehn and SorgerKLS06, Theorem 6.2]. Moreover, our results and the recent [Reference BudurBud18] imply immediately that the Kuranishi spaces of polystable sheaves have rational singularities; see [Reference BudurBud18, Remarks 3.5 and 4.5].
$H$
, by combining Theorem 1.2 and [Reference Bellamy and SchedlerBS16, Proposition 1.2], which generalizes slightly [Reference Kaledin, Lehn and SorgerKLS06, Theorem 6.2]. Moreover, our results and the recent [Reference BudurBud18] imply immediately that the Kuranishi spaces of polystable sheaves have rational singularities; see [Reference BudurBud18, Remarks 3.5 and 4.5].
It is worth noting that Theorem 1.2 fails if
![]() $F$
is not polystable. In [Reference Lekili and UedaLU18] several families of K3 surfaces
$F$
is not polystable. In [Reference Lekili and UedaLU18] several families of K3 surfaces
![]() $X$
are exhibited, on which the formality of
$X$
are exhibited, on which the formality of
![]() $\operatorname{RHom}^{\bullet }(F,F)$
fails for a split generator
$\operatorname{RHom}^{\bullet }(F,F)$
fails for a split generator
![]() $F$
of
$F$
of
![]() $D^{b}(\operatorname{Coh}(X))$
.
$D^{b}(\operatorname{Coh}(X))$
.
Our results should have a symplectic counterpart. Kontsevich’s homological mirror symmetry conjecture says that
![]() $D^{b}(\operatorname{Coh}(X))$
is equivalent to a triangulated category constructed from the symplectic geometry of the mirror of a Calabi–Yau manifold
$D^{b}(\operatorname{Coh}(X))$
is equivalent to a triangulated category constructed from the symplectic geometry of the mirror of a Calabi–Yau manifold
![]() $X$
. Our Corollary 2.15 below guarantees that formality would be mirrored. However, before any mirror conclusions can be drawn, a technical hurdle must be passed: we use
$X$
. Our Corollary 2.15 below guarantees that formality would be mirrored. However, before any mirror conclusions can be drawn, a technical hurdle must be passed: we use
![]() $\mathbb{C}$
coefficients, whereas homological mirror symmetry uses Novikov rings; see [Reference SeidelSei15].
$\mathbb{C}$
coefficients, whereas homological mirror symmetry uses Novikov rings; see [Reference SeidelSei15].
Throughout this paper, the ground field is
![]() $\mathbb{C}$
, except in § 2 and in Proposition 1.4 where we can allow an arbitrary ground field
$\mathbb{C}$
, except in § 2 and in Proposition 1.4 where we can allow an arbitrary ground field
![]() $\Bbbk$
. In § 2 we prove Proposition 1.4, while the proofs of Theorems 1.2 and 1.3 are given in § 3.
$\Bbbk$
. In § 2 we prove Proposition 1.4, while the proofs of Theorems 1.2 and 1.3 are given in § 3.
At the request of the referees, we have removed in this version some material known to experts. The considerably more detailed earlier version [Reference Budur and ZhangBZ18] of this paper remains available on arXiv.
2 Formality via uniqueness of DG enhancement
2.1 Generalities on DG categories
We gather together some classical concepts mainly following [Reference Lunts and OrlovLO10]. We work over a fixed field
![]() $\Bbbk$
. All categories are assumed to be small and
$\Bbbk$
. All categories are assumed to be small and
![]() $\Bbbk$
-linear.
$\Bbbk$
-linear.
Definition 2.1. A DG category is a
![]() $\Bbbk$
-linear category
$\Bbbk$
-linear category
![]() $\mathscr{A}$
whose morphism spaces
$\mathscr{A}$
whose morphism spaces
![]() $\operatorname{Hom}(A_{1},A_{2})$
are DG
$\operatorname{Hom}(A_{1},A_{2})$
are DG
![]() $\Bbbk$
-modules (also known as complexes of
$\Bbbk$
-modules (also known as complexes of
![]() $\Bbbk$
-vector spaces), such that
$\Bbbk$
-vector spaces), such that
are morphisms of DG
![]() $\Bbbk$
-modules for any objects
$\Bbbk$
-modules for any objects
![]() $A_{1},A_{2},A_{3}\in \operatorname{Ob}(\mathscr{A})$
. Moreover, for any
$A_{1},A_{2},A_{3}\in \operatorname{Ob}(\mathscr{A})$
. Moreover, for any
![]() $A\in \operatorname{Ob}(\mathscr{A})$
, there is an identity morphism
$A\in \operatorname{Ob}(\mathscr{A})$
, there is an identity morphism
![]() $1_{A}\in \operatorname{Hom}_{\mathscr{A}}(A,A)$
which is closed of degree
$1_{A}\in \operatorname{Hom}_{\mathscr{A}}(A,A)$
which is closed of degree
![]() $0$
and compatible with the composition.
$0$
and compatible with the composition.
Remark 2.2. The definition implies that the graded Leibniz rule holds and
![]() $\operatorname{Hom}_{\mathscr{A}}(A,A)$
is a DG algebra for any
$\operatorname{Hom}_{\mathscr{A}}(A,A)$
is a DG algebra for any
![]() $A\in \operatorname{Ob}(\mathscr{A})$
.
$A\in \operatorname{Ob}(\mathscr{A})$
.
Definition 2.3. The homotopy category
![]() $H^{0}(\mathscr{A})$
of a DG category
$H^{0}(\mathscr{A})$
of a DG category
![]() $\mathscr{A}$
is a
$\mathscr{A}$
is a
![]() $\Bbbk$
-linear category with the same objects as in
$\Bbbk$
-linear category with the same objects as in
![]() $\mathscr{A}$
and morphism spaces
$\mathscr{A}$
and morphism spaces
for any
![]() $A_{1},A_{2}\in \operatorname{Ob}(\mathscr{A})$
.
$A_{1},A_{2}\in \operatorname{Ob}(\mathscr{A})$
.
Definition 2.4. A DG functor
![]() ${\mathcal{F}}:\mathscr{A}\rightarrow \mathscr{B}$
between two DG categories is given by a map of sets
${\mathcal{F}}:\mathscr{A}\rightarrow \mathscr{B}$
between two DG categories is given by a map of sets
and morphisms of DG
![]() $\Bbbk$
-modules
$\Bbbk$
-modules
for any
![]() $A_{1},A_{2}\in \operatorname{Ob}(\mathscr{A})$
, compatible with compositions (1) and units.
$A_{1},A_{2}\in \operatorname{Ob}(\mathscr{A})$
, compatible with compositions (1) and units.
Definition 2.5. A DG functor
![]() ${\mathcal{F}}:\mathscr{A}\rightarrow \mathscr{B}$
is called a quasi-equivalence if
${\mathcal{F}}:\mathscr{A}\rightarrow \mathscr{B}$
is called a quasi-equivalence if
![]() ${\mathcal{F}}(X,Y)$
is a quasi-isomorphism for any
${\mathcal{F}}(X,Y)$
is a quasi-isomorphism for any
![]() $X,Y\in \operatorname{Ob}(\mathscr{A})$
and the induced functor on the homotopy categories
$X,Y\in \operatorname{Ob}(\mathscr{A})$
and the induced functor on the homotopy categories
is an equivalence of categories.
Remark 2.6. In fact, instead of requiring
![]() $H^{0}({\mathcal{F}})$
to be an equivalence, it is sufficient to require it to be essentially surjective, as the full faithfulness is already encoded in the quasi-isomorphisms of morphism spaces. See, for example, [Reference ToënToe11, Definition 2, § 2.3].
$H^{0}({\mathcal{F}})$
to be an equivalence, it is sufficient to require it to be essentially surjective, as the full faithfulness is already encoded in the quasi-isomorphisms of morphism spaces. See, for example, [Reference ToënToe11, Definition 2, § 2.3].
We denote the category of small DG categories with DG functors as morphisms by dgCat, and its localization with respect to quasi-equivalences by Hqe. It was proven in [Reference TabuadaTab05] that dgCat has the structure of a model category, with quasi-equivalences being the weak equivalences in the model structure. Then Hqe is the homotopy category of this model category. One special property of this model structure on dgCat is that every small DG category is a fibrant object.
Definition 2.7. A morphism between two DG categories in Hqe is called a quasi-functor. We say that two DG categories are quasi-equivalent if they are isomorphic in Hqe.
By this definition, two quasi-equivalent DG categories can be connected by a zigzag chain of DG functors with alternative arrow directions. In fact, one has the following simpler presentation for a quasi-functor (see [Reference Lunts and OrlovLO10, p. 858]; we supply a proof for the sake of completeness).
Lemma 2.8. Let
![]() $\mathscr{A}$
and
$\mathscr{A}$
and
![]() $\mathscr{B}$
be DG categories. Any quasi-functor from
$\mathscr{B}$
be DG categories. Any quasi-functor from
![]() $\mathscr{A}$
to
$\mathscr{A}$
to
![]() $\mathscr{B}$
can be represented by the diagram
$\mathscr{B}$
can be represented by the diagram
where
![]() $\mathscr{C}$
is a DG category,
$\mathscr{C}$
is a DG category,
![]() $f$
and
$f$
and
![]() $g$
are DG functors, with
$g$
are DG functors, with
![]() $f$
being a quasi-equivalence. Moreover,
$f$
being a quasi-equivalence. Moreover,
![]() $\mathscr{A}$
and
$\mathscr{A}$
and
![]() $\mathscr{B}$
are quasi-equivalent if and only if
$\mathscr{B}$
are quasi-equivalent if and only if
![]() $g$
is also a quasi-equivalence.
$g$
is also a quasi-equivalence.
Proof. By the fundamental theorem of model categories [Reference HoveyHov99, Theorem 1.2.10(ii)], we can represent a quasi-functor from
![]() $\mathscr{A}$
to
$\mathscr{A}$
to
![]() $\mathscr{B}$
by a DG functor
$\mathscr{B}$
by a DG functor
![]() $\mathscr{C}\stackrel{g}{\longrightarrow }\mathscr{D}$
, where
$\mathscr{C}\stackrel{g}{\longrightarrow }\mathscr{D}$
, where
![]() $\mathscr{C}\stackrel{f}{\longrightarrow }\mathscr{A}$
is a cofibrant replacement of
$\mathscr{C}\stackrel{f}{\longrightarrow }\mathscr{A}$
is a cofibrant replacement of
![]() $\mathscr{A}$
, and
$\mathscr{A}$
, and
![]() $\mathscr{B}\stackrel{h}{\longrightarrow }\mathscr{D}$
is a fibrant replacement of
$\mathscr{B}\stackrel{h}{\longrightarrow }\mathscr{D}$
is a fibrant replacement of
![]() $\mathscr{B}$
. Since
$\mathscr{B}$
. Since
![]() $\mathscr{B}$
itself is a fibrant object, we can choose
$\mathscr{B}$
itself is a fibrant object, we can choose
![]() $\mathscr{D}=\mathscr{B}$
and
$\mathscr{D}=\mathscr{B}$
and
![]() $h$
the identity functor. Hence we get (2). The other statement follows from [Reference HoveyHov99, Theorem 1.2.10(iv)].◻
$h$
the identity functor. Hence we get (2). The other statement follows from [Reference HoveyHov99, Theorem 1.2.10(iv)].◻
For any DG category
![]() $\mathscr{A}$
, the pre-triangulated hull
$\mathscr{A}$
, the pre-triangulated hull
![]() $\mathscr{A}^{\text{pre\text{-}tr}}$
of
$\mathscr{A}^{\text{pre\text{-}tr}}$
of
![]() $\mathscr{A}$
was constructed in [Reference Bondal and KapranovBK91] by formally adding to
$\mathscr{A}$
was constructed in [Reference Bondal and KapranovBK91] by formally adding to
![]() $\mathscr{A}$
all shifts, all cones of morphisms, and cones of morphisms between cones, etc. There is a canonical embedding of DG categories
$\mathscr{A}$
all shifts, all cones of morphisms, and cones of morphisms between cones, etc. There is a canonical embedding of DG categories
![]() $\mathscr{A}{\hookrightarrow}\mathscr{A}^{\text{pre\text{-}tr}}$
.
$\mathscr{A}{\hookrightarrow}\mathscr{A}^{\text{pre\text{-}tr}}$
.
Definition 2.9. A DG category
![]() $\mathscr{A}$
is said to be pre-triangulated if, for every object
$\mathscr{A}$
is said to be pre-triangulated if, for every object
![]() $A\in \mathscr{A}$
and
$A\in \mathscr{A}$
and
![]() $n\in \mathbb{Z}$
, the object
$n\in \mathbb{Z}$
, the object
![]() $A[n]\in \mathscr{A}^{\text{pre\text{-}tr}}$
is homotopy equivalent to an object in
$A[n]\in \mathscr{A}^{\text{pre\text{-}tr}}$
is homotopy equivalent to an object in
![]() $\mathscr{A}$
, and for every closed morphism
$\mathscr{A}$
, and for every closed morphism
![]() $f$
in
$f$
in
![]() $\mathscr{A}$
of degree
$\mathscr{A}$
of degree
![]() $0$
, the object
$0$
, the object
![]() $\operatorname{Cone}(f)\in \mathscr{A}^{\text{pre\text{-}tr}}$
is homotopy equivalent to an object in
$\operatorname{Cone}(f)\in \mathscr{A}^{\text{pre\text{-}tr}}$
is homotopy equivalent to an object in
![]() $\mathscr{A}$
.
$\mathscr{A}$
.
Remark 2.10. In other words, a DG category
![]() $\mathscr{A}$
is pre-triangulated if and only if the DG functor
$\mathscr{A}$
is pre-triangulated if and only if the DG functor
![]() $\mathscr{A}{\hookrightarrow}\mathscr{A}^{\text{pre\text{-}tr}}$
is a quasi-equivalence; equivalently, the embedding of the homotopy categories
$\mathscr{A}{\hookrightarrow}\mathscr{A}^{\text{pre\text{-}tr}}$
is a quasi-equivalence; equivalently, the embedding of the homotopy categories
![]() $H^{0}(\mathscr{A}){\hookrightarrow}H^{0}(\mathscr{A}^{\text{pre-tr}})$
is an equivalence. In such a case,
$H^{0}(\mathscr{A}){\hookrightarrow}H^{0}(\mathscr{A}^{\text{pre-tr}})$
is an equivalence. In such a case,
![]() $H^{0}(\mathscr{A})$
is naturally a triangulated category.
$H^{0}(\mathscr{A})$
is naturally a triangulated category.
Definition 2.11. A DG enhancement of a triangulated category
![]() $\mathscr{T}$
is a pair
$\mathscr{T}$
is a pair
![]() $(\mathscr{B},e)$
, where
$(\mathscr{B},e)$
, where
![]() $\mathscr{B}$
is a pre-triangulated DG category and
$\mathscr{B}$
is a pre-triangulated DG category and
![]() $e:H^{0}(\mathscr{B})\rightarrow \mathscr{T}$
is an equivalence of triangulated categories.
$e:H^{0}(\mathscr{B})\rightarrow \mathscr{T}$
is an equivalence of triangulated categories.
Definition 2.12. We say that a triangulated category
![]() $\mathscr{T}$
has a unique DG enhancement if, given two DG enhancements
$\mathscr{T}$
has a unique DG enhancement if, given two DG enhancements
![]() $(\mathscr{B},e)$
and
$(\mathscr{B},e)$
and
![]() $(\mathscr{B}^{\prime },e^{\prime })$
of
$(\mathscr{B}^{\prime },e^{\prime })$
of
![]() $\mathscr{T}$
, there exists a quasi-functor
$\mathscr{T}$
, there exists a quasi-functor
![]() ${\mathcal{F}}:\mathscr{B}\rightarrow \mathscr{B}^{\prime }$
such that
${\mathcal{F}}:\mathscr{B}\rightarrow \mathscr{B}^{\prime }$
such that
![]() $H^{0}({\mathcal{F}}):H^{0}(\mathscr{B})\rightarrow H^{0}(\mathscr{B}^{\prime })$
is an equivalence of triangulated categories. We say that
$H^{0}({\mathcal{F}}):H^{0}(\mathscr{B})\rightarrow H^{0}(\mathscr{B}^{\prime })$
is an equivalence of triangulated categories. We say that
![]() $\mathscr{T}$
has a strongly unique DG enhancement if, moreover,
$\mathscr{T}$
has a strongly unique DG enhancement if, moreover,
![]() ${\mathcal{F}}$
can be chosen so that the functors
${\mathcal{F}}$
can be chosen so that the functors
![]() $e$
and
$e$
and
![]() $e^{\prime }\circ H^{0}({\mathcal{F}})$
are isomorphic.
$e^{\prime }\circ H^{0}({\mathcal{F}})$
are isomorphic.
2.2 Preservation of formality
We explain now why the uniqueness of the DG enhancement of a triangulated category helps with formality problems. The key is the following result. Although it might be known to experts, we nevertheless supply a proof since we do not know of any in the literature.
Proposition 2.13. Let
![]() $(\mathscr{B}_{1},e_{1})$
and
$(\mathscr{B}_{1},e_{1})$
and
![]() $(\mathscr{B}_{2},e_{2})$
be DG enhancements of a triangulated category
$(\mathscr{B}_{2},e_{2})$
be DG enhancements of a triangulated category
![]() $\mathscr{T}$
. Let
$\mathscr{T}$
. Let
![]() $T\in \operatorname{Ob}(\mathscr{T})$
,
$T\in \operatorname{Ob}(\mathscr{T})$
,
![]() $B_{1}\in \operatorname{Ob}(\mathscr{B}_{1})$
,
$B_{1}\in \operatorname{Ob}(\mathscr{B}_{1})$
,
![]() $B_{2}\in \operatorname{Ob}(\mathscr{B}_{2})$
, such that
$B_{2}\in \operatorname{Ob}(\mathscr{B}_{2})$
, such that
![]() $T$
,
$T$
,
![]() $e_{1}(B_{1})$
and
$e_{1}(B_{1})$
and
![]() $e_{2}(B_{2})$
are isomorphic in
$e_{2}(B_{2})$
are isomorphic in
![]() $\mathscr{T}$
. Assume that
$\mathscr{T}$
. Assume that
![]() $\mathscr{T}$
has a strongly unique DG enhancement. Then
$\mathscr{T}$
has a strongly unique DG enhancement. Then
![]() $\operatorname{Hom}_{\mathscr{B}_{1}}(B_{1},B_{1})$
and
$\operatorname{Hom}_{\mathscr{B}_{1}}(B_{1},B_{1})$
and
![]() $\operatorname{Hom}_{\mathscr{B}_{2}}(B_{2},B_{2})$
are quasi-isomorphic DG algebras.
$\operatorname{Hom}_{\mathscr{B}_{2}}(B_{2},B_{2})$
are quasi-isomorphic DG algebras.
Proof. For
![]() $i=1$
and
$i=1$
and
![]() $2$
, we construct a full subcategory
$2$
, we construct a full subcategory
![]() $\mathscr{C}_{i}$
of
$\mathscr{C}_{i}$
of
![]() $\mathscr{B}_{i}$
, whose objects are given by
$\mathscr{B}_{i}$
, whose objects are given by
Clearly
![]() $\mathscr{C}_{i}$
is also a DG category. We claim it is pre-triangulated. Indeed, let
$\mathscr{C}_{i}$
is also a DG category. We claim it is pre-triangulated. Indeed, let
![]() $\mathscr{B}_{i}^{\text{pre\text{-}tr}}$
and
$\mathscr{B}_{i}^{\text{pre\text{-}tr}}$
and
![]() $\mathscr{C}_{i}^{\text{pre\text{-}tr}}$
be the pre-triangulated hulls of
$\mathscr{C}_{i}^{\text{pre\text{-}tr}}$
be the pre-triangulated hulls of
![]() $\mathscr{B}_{i}$
and
$\mathscr{B}_{i}$
and
![]() $\mathscr{C}_{i}$
respectively. Then all functors in the commutative diagram
$\mathscr{C}_{i}$
respectively. Then all functors in the commutative diagram

are fully faithful. By the assumption that
![]() $\mathscr{B}_{i}$
is pre-triangulated, the upper horizontal arrow is an equivalence. By the construction of
$\mathscr{B}_{i}$
is pre-triangulated, the upper horizontal arrow is an equivalence. By the construction of
![]() $\mathscr{C}_{i}$
, the left vertical arrow is also an equivalence. In particular, they are essentially surjective. Hence the bottom horizontal arrow must be essentially surjective, hence an equivalence, which proves that
$\mathscr{C}_{i}$
, the left vertical arrow is also an equivalence. In particular, they are essentially surjective. Hence the bottom horizontal arrow must be essentially surjective, hence an equivalence, which proves that
![]() $\mathscr{C}_{i}$
is a pre-triangulated DG category. Moreover, since the composition
$\mathscr{C}_{i}$
is a pre-triangulated DG category. Moreover, since the composition
is an equivalence of categories, we conclude that
![]() $\mathscr{C}_{i}$
is a DG enhancement of
$\mathscr{C}_{i}$
is a DG enhancement of
![]() $\mathscr{T}$
.
$\mathscr{T}$
.
By assumption,
![]() $\mathscr{T}$
has a strongly unique DG enhancement. Therefore, by Lemma 2.8, there exists some DG category
$\mathscr{T}$
has a strongly unique DG enhancement. Therefore, by Lemma 2.8, there exists some DG category
![]() $\mathscr{C}_{0}$
such that both functors
$\mathscr{C}_{0}$
such that both functors
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
in the roof
$f_{2}$
in the roof
are quasi-equivalences. In particular, all functors in the diagram

are equivalences of categories, and the diagram is
![]() $2$
-commutative (the two compositions from
$2$
-commutative (the two compositions from
![]() $H^{0}(\mathscr{C}_{0})$
to
$H^{0}(\mathscr{C}_{0})$
to
![]() $\mathscr{T}$
are isomorphic functors).
$\mathscr{T}$
are isomorphic functors).
By the essential surjectivity of
![]() $f_{1}$
, there exists some
$f_{1}$
, there exists some
![]() $B_{0}\in \operatorname{Ob}(\mathscr{C}_{0})$
, such that
$B_{0}\in \operatorname{Ob}(\mathscr{C}_{0})$
, such that
![]() $f_{1}(B_{0})\cong B_{1}$
in
$f_{1}(B_{0})\cong B_{1}$
in
![]() $H^{0}(\mathscr{C}_{1})$
. By the construction of
$H^{0}(\mathscr{C}_{1})$
. By the construction of
![]() $\mathscr{C}_{1}$
, we know that
$\mathscr{C}_{1}$
, we know that
![]() $B_{1}$
is the only object in its isomorphism class of objects in
$B_{1}$
is the only object in its isomorphism class of objects in
![]() $H^{0}(\mathscr{C}_{1})$
, hence
$H^{0}(\mathscr{C}_{1})$
, hence
![]() $f_{1}(B_{0})=B_{1}$
. By the
$f_{1}(B_{0})=B_{1}$
. By the
![]() $2$
-commutativity of the diagram, the images of
$2$
-commutativity of the diagram, the images of
![]() $f_{2}(B_{0})$
and
$f_{2}(B_{0})$
and
![]() $B_{2}$
are both isomorphic to
$B_{2}$
are both isomorphic to
![]() $T$
in
$T$
in
![]() $\mathscr{T}$
, hence
$\mathscr{T}$
, hence
![]() $f_{2}(B_{0})$
and
$f_{2}(B_{0})$
and
![]() $B_{2}$
themselves are in the same isomorphism class of objects in
$B_{2}$
themselves are in the same isomorphism class of objects in
![]() $H^{0}(\mathscr{C}_{2})$
, which implies
$H^{0}(\mathscr{C}_{2})$
, which implies
![]() $f_{2}(B_{0})=B_{2}$
by the construction of the category
$f_{2}(B_{0})=B_{2}$
by the construction of the category
![]() $\mathscr{C}_{2}$
.
$\mathscr{C}_{2}$
.
Since
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
are quasi-equivalences, the morphism
$f_{2}$
are quasi-equivalences, the morphism
is a quasi-isomorphism of DG algebras for
![]() $i=1$
and
$i=1$
and
![]() $2$
. Since
$2$
. Since
![]() $\mathscr{C}_{i}$
is a full subcategory of
$\mathscr{C}_{i}$
is a full subcategory of
![]() $\mathscr{B}_{i}$
for
$\mathscr{B}_{i}$
for
![]() $i=1$
and
$i=1$
and
![]() $2$
, we conclude that
$2$
, we conclude that
![]() $\operatorname{Hom}_{\mathscr{B}_{1}}(B_{1},B_{1})$
and
$\operatorname{Hom}_{\mathscr{B}_{1}}(B_{1},B_{1})$
and
![]() $\operatorname{Hom}_{\mathscr{B}_{2}}(B_{2},B_{2})$
are quasi-isomorphic DG algebras.◻
$\operatorname{Hom}_{\mathscr{B}_{2}}(B_{2},B_{2})$
are quasi-isomorphic DG algebras.◻
Remark 2.14. Under the assumption of the above proposition, we can associate canonically to any
![]() $T\in \operatorname{Ob}(\mathscr{T})$
a DG algebra
$T\in \operatorname{Ob}(\mathscr{T})$
a DG algebra
![]() $\operatorname{Hom}_{\mathscr{B}_{1}}(B_{1},B_{1})$
(for any lift
$\operatorname{Hom}_{\mathscr{B}_{1}}(B_{1},B_{1})$
(for any lift
![]() $B_{1}$
of
$B_{1}$
of
![]() $T$
in any DG enhancement
$T$
in any DG enhancement
![]() $\mathscr{B}_{1}$
of
$\mathscr{B}_{1}$
of
![]() $\mathscr{T}$
), which is well defined up to quasi-isomorphisms. For convenience, we will denote this (quasi-isomorphism class of) DG algebra by
$\mathscr{T}$
), which is well defined up to quasi-isomorphisms. For convenience, we will denote this (quasi-isomorphism class of) DG algebra by
![]() $\operatorname{RHom}^{\bullet }(T,T)$
.
$\operatorname{RHom}^{\bullet }(T,T)$
.
The following alternative formulation of the proposition is useful.
Corollary 2.15. Let
![]() $\unicode[STIX]{x1D6F7}:\mathscr{T}_{1}\rightarrow \mathscr{T}_{2}$
be an equivalence of triangulated categories. Assume that
$\unicode[STIX]{x1D6F7}:\mathscr{T}_{1}\rightarrow \mathscr{T}_{2}$
be an equivalence of triangulated categories. Assume that
![]() $\mathscr{T}_{2}$
(hence
$\mathscr{T}_{2}$
(hence
![]() $\mathscr{T}_{1}$
) has a strongly unique DG enhancement. Then, for any object
$\mathscr{T}_{1}$
) has a strongly unique DG enhancement. Then, for any object
![]() $T\in \operatorname{Ob}(\mathscr{T}_{1})$
, the DG algebras
$T\in \operatorname{Ob}(\mathscr{T}_{1})$
, the DG algebras
![]() $\operatorname{RHom}^{\bullet }(T,T)$
and
$\operatorname{RHom}^{\bullet }(T,T)$
and
![]() $\operatorname{RHom}^{\bullet }(\unicode[STIX]{x1D6F7}(T),\unicode[STIX]{x1D6F7}(T))$
are quasi-isomorphic. In particular,
$\operatorname{RHom}^{\bullet }(\unicode[STIX]{x1D6F7}(T),\unicode[STIX]{x1D6F7}(T))$
are quasi-isomorphic. In particular,
![]() $\operatorname{RHom}(T,T)$
is formal if and only if
$\operatorname{RHom}(T,T)$
is formal if and only if
![]() $\operatorname{RHom}(\unicode[STIX]{x1D6F7}(T),\unicode[STIX]{x1D6F7}(T))$
is formal. ◻
$\operatorname{RHom}(\unicode[STIX]{x1D6F7}(T),\unicode[STIX]{x1D6F7}(T))$
is formal. ◻
Proof of Proposition 1.4.
The proposition follows immediately from Corollary 2.15 and [Reference Lunts and OrlovLO10, Theorem 2.14] which states that
![]() $D^{b}(\operatorname{Coh}(X))$
has a strongly unique DG enhancement for a smooth projective variety
$D^{b}(\operatorname{Coh}(X))$
has a strongly unique DG enhancement for a smooth projective variety
![]() $X$
.◻
$X$
.◻
3 Formality on K3 surfaces
3.1 Formality for coherent sheaves
From now on,
![]() $(X,H)$
is a complex projective K3 surface and
$(X,H)$
is a complex projective K3 surface and
![]() $\Bbbk =\mathbb{C}$
. Let
$\Bbbk =\mathbb{C}$
. Let
![]() $F$
be a coherent sheaf on
$F$
be a coherent sheaf on
![]() $X$
. The Mukai vector of
$X$
. The Mukai vector of
![]() $F$
is
$F$
is
If we write
![]() $\mathbf{v}=(\mathbf{v}_{0},\mathbf{v}_{1},\mathbf{v}_{2})$
, then the dual of
$\mathbf{v}=(\mathbf{v}_{0},\mathbf{v}_{1},\mathbf{v}_{2})$
, then the dual of
![]() $\mathbf{v}$
is defined by
$\mathbf{v}$
is defined by
![]() $\mathbf{v}^{\vee }=(\mathbf{v}_{0},-\mathbf{v}_{1},\mathbf{v}_{2})$
. The Mukai pairing on
$\mathbf{v}^{\vee }=(\mathbf{v}_{0},-\mathbf{v}_{1},\mathbf{v}_{2})$
. The Mukai pairing on
![]() $H_{\text{alg}}^{\ast }(X,\mathbb{Z})$
is defined by
$H_{\text{alg}}^{\ast }(X,\mathbb{Z})$
is defined by
where the products on the right-hand side are Poincaré pairings.
Recall from [Reference Huybrechts and LehnHL10] that for a coherent sheaf one has the notions of
![]() $H$
-(semi)stability (Gieseker) and
$H$
-(semi)stability (Gieseker) and
![]() $\unicode[STIX]{x1D707}_{H}$
-(semi)stability (slope). An
$\unicode[STIX]{x1D707}_{H}$
-(semi)stability (slope). An
![]() $H$
-semistable sheaf
$H$
-semistable sheaf
![]() $F$
is
$F$
is
![]() $H$
-polystable if it can be written in the form
$H$
-polystable if it can be written in the form
where
![]() $F_{1},\ldots ,F_{k}$
are pairwise non-isomorphic
$F_{1},\ldots ,F_{k}$
are pairwise non-isomorphic
![]() $H$
-stable summands, and
$H$
-stable summands, and
![]() $n_{1},\ldots ,n_{k}$
are strictly positive integers.
$n_{1},\ldots ,n_{k}$
are strictly positive integers.
The moduli space of
![]() $H$
-semistable coherent sheaves on
$H$
-semistable coherent sheaves on
![]() $X$
of Mukai vector
$X$
of Mukai vector
![]() $\mathbf{v}$
is denoted by
$\mathbf{v}$
is denoted by
![]() ${\mathcal{M}}_{X,H}(\mathbf{v})$
. The closed points of
${\mathcal{M}}_{X,H}(\mathbf{v})$
. The closed points of
![]() ${\mathcal{M}}_{X,H}(\mathbf{v})$
are in one-to-one correspondence with the
${\mathcal{M}}_{X,H}(\mathbf{v})$
are in one-to-one correspondence with the
![]() $H$
-polystable sheaves, and with the
$H$
-polystable sheaves, and with the
![]() $S$
-equivalence classes of semistable sheaves.
$S$
-equivalence classes of semistable sheaves.
The following result generalized a special case proved in [Reference Kaledin and LehnKL07, Proposition 3.1].
Proposition 3.1 [Reference ZhangZha12, Proposition 1.3].
Let
![]() $(X,H)$
be a projective K3 surface, and
$(X,H)$
be a projective K3 surface, and
![]() $\mathbf{v}$
a Mukai vector of positive rank. Assume
$\mathbf{v}$
a Mukai vector of positive rank. Assume
![]() $H$
is generic with respect to
$H$
is generic with respect to
![]() $\mathbf{v}$
, and there is at least one
$\mathbf{v}$
, and there is at least one
![]() $\unicode[STIX]{x1D707}_{H}$
-stable sheaf of Mukai vector
$\unicode[STIX]{x1D707}_{H}$
-stable sheaf of Mukai vector
![]() $\mathbf{v}$
. Let
$\mathbf{v}$
. Let
![]() $F$
be a
$F$
be a
![]() $H$
-polystable sheaf with a decomposition given by (3). Assume either:
$H$
-polystable sheaf with a decomposition given by (3). Assume either:
(i)
 $\operatorname{rk}F_{i}=1$
for all
$\operatorname{rk}F_{i}=1$
for all
 $i=1,\ldots ,k$
; or
$i=1,\ldots ,k$
; or(ii)
 $\operatorname{rk}F_{i}\geqslant 2$
for all
$\operatorname{rk}F_{i}\geqslant 2$
for all
 $i=1,\ldots ,k$
.
$i=1,\ldots ,k$
.
Then the DG algebra
![]() $\operatorname{RHom}^{\bullet }(F,F)$
is formal.
$\operatorname{RHom}^{\bullet }(F,F)$
is formal.
Remark 3.2. By [Reference Arbarello and SaccàAS18, Remark 3.4(2)], the assumption of
![]() $H$
being generic with respect to
$H$
being generic with respect to
![]() $\mathbf{v}$
is not necessary for case (ii). However, case (i) does require it.
$\mathbf{v}$
is not necessary for case (ii). However, case (i) does require it.
Remark 3.3. As explained in [Reference ZhangZha12, § 2], instead of requiring the existence of a
![]() $\unicode[STIX]{x1D707}_{H}$
-stable sheaf of Mukai vector
$\unicode[STIX]{x1D707}_{H}$
-stable sheaf of Mukai vector
![]() $\mathbf{v}$
, it suffices to require that each stable summand
$\mathbf{v}$
, it suffices to require that each stable summand
![]() $F_{i}$
has a
$F_{i}$
has a
![]() $\unicode[STIX]{x1D707}_{H}$
-stable deformation in its own moduli.
$\unicode[STIX]{x1D707}_{H}$
-stable deformation in its own moduli.
Define the integral functor
where
![]() $p$
and
$p$
and
![]() $q$
are the first and the second projection from
$q$
are the first and the second projection from
![]() $X\times X$
, and
$X\times X$
, and
![]() ${\mathcal{I}}_{\unicode[STIX]{x1D6E5}}$
is the ideal sheaf of the diagonal embedding
${\mathcal{I}}_{\unicode[STIX]{x1D6E5}}$
is the ideal sheaf of the diagonal embedding
![]() $X{\hookrightarrow}X\times X$
. It is an autoequivalence [Reference HuybrechtsHuy06, Examples 10.9]. The following result of Yoshioka is crucial.
$X{\hookrightarrow}X\times X$
. It is an autoequivalence [Reference HuybrechtsHuy06, Examples 10.9]. The following result of Yoshioka is crucial.
Theorem 3.4 [Reference YoshiokaYos09, Proposition 1.5, Theorem 1.7].
Let
![]() $(X,H)$
be a projective K3 surface. Then, for any
$(X,H)$
be a projective K3 surface. Then, for any
![]() $F\in D^{b}(\operatorname{Coh}(X))$
with Mukai vector
$F\in D^{b}(\operatorname{Coh}(X))$
with Mukai vector
for some
![]() $r,a\in \mathbb{Z}$
,
$r,a\in \mathbb{Z}$
,
![]() $d\in \mathbb{Q}$
and
$d\in \mathbb{Q}$
and
![]() $D\in \operatorname{NS}(X)_{\mathbb{Q}}\cap H^{\bot }$
, the Mukai vector of
$D\in \operatorname{NS}(X)_{\mathbb{Q}}\cap H^{\bot }$
, the Mukai vector of
![]() $\unicode[STIX]{x1D6F7}(F)$
can be given by
$\unicode[STIX]{x1D6F7}(F)$
can be given by
for some
![]() $\widehat{D}\in \operatorname{NS}(X)_{\mathbb{Q}}\cap H^{\bot }$
. Moreover, in either of the two cases
$\widehat{D}\in \operatorname{NS}(X)_{\mathbb{Q}}\cap H^{\bot }$
. Moreover, in either of the two cases
(1)
 $r>0$
,
$r>0$
,
 $a>0$
, and
$a>0$
, and
 $d>\max \{4r^{2}+1/H^{2},~2r(\mathbf{v}^{2}-D^{2})\}$
,
$d>\max \{4r^{2}+1/H^{2},~2r(\mathbf{v}^{2}-D^{2})\}$
,(2)
 $r=0$
, and
$r=0$
, and
 $a>\max \left\{3,~(\mathbf{v}^{2}-D^{2})/2+1\right\}$
,
$a>\max \left\{3,~(\mathbf{v}^{2}-D^{2})/2+1\right\}$
,
![]() $\unicode[STIX]{x1D6F7}$
induces an isomorphism
$\unicode[STIX]{x1D6F7}$
induces an isomorphism
![]() ${\mathcal{M}}_{X,H}(\mathbf{v})\cong {\mathcal{M}}_{X,H}(\widehat{\mathbf{v}})$
preserving
${\mathcal{M}}_{X,H}(\mathbf{v})\cong {\mathcal{M}}_{X,H}(\widehat{\mathbf{v}})$
preserving
![]() $H$
-polystability, such that, for every
$H$
-polystability, such that, for every
![]() $H$
-polystable sheaf
$H$
-polystable sheaf
![]() $F$
,
$F$
,
![]() $\unicode[STIX]{x1D6F7}(F_{i})$
is
$\unicode[STIX]{x1D6F7}(F_{i})$
is
![]() $\unicode[STIX]{x1D707}_{H}$
-stable for each
$\unicode[STIX]{x1D707}_{H}$
-stable for each
![]() $H$
-stable summand
$H$
-stable summand
![]() $F_{i}$
of
$F_{i}$
of
![]() $F$
.
$F$
.
In fact, by [Reference HuybrechtsHuy06, Examples 10.9, (ii)] one has
![]() $D=\widehat{D}$
in the above theorem.
$D=\widehat{D}$
in the above theorem.
Proof of Theorem 1.2.
We write
![]() $\mathbf{v}=(r,dH+D,a)$
for the Mukai vector of
$\mathbf{v}=(r,dH+D,a)$
for the Mukai vector of
![]() $F$
as above. Suppose that
$F$
as above. Suppose that
![]() $(r,dH+D)\neq (0,0)$
. Then
$(r,dH+D)\neq (0,0)$
. Then
![]() $r\geqslant 0$
, and
$r\geqslant 0$
, and
![]() $r=0$
would imply
$r=0$
would imply
![]() $d>0$
since otherwise
$d>0$
since otherwise
![]() $dH+D$
is not effective. Then for any positive integer
$dH+D$
is not effective. Then for any positive integer
![]() $m$
,
$m$
,
Denote the right-hand side of (5) by
![]() $\mathbf{v}^{\prime }=(\mathbf{v}_{0}^{\prime },\mathbf{v}_{1}^{\prime },\mathbf{v}_{2}^{\prime })$
. For
$\mathbf{v}^{\prime }=(\mathbf{v}_{0}^{\prime },\mathbf{v}_{1}^{\prime },\mathbf{v}_{2}^{\prime })$
. For
![]() $m\gg 0$
, the following two conditions hold.
$m\gg 0$
, the following two conditions hold.
- (
 $\dagger$
)
$\dagger$
) The vector
 $\mathbf{v}^{\prime }$
satisfies (either of) the conditions in Theorem 3.4 (depending on whether the rank of
$\mathbf{v}^{\prime }$
satisfies (either of) the conditions in Theorem 3.4 (depending on whether the rank of
 $\mathbf{v}$
is positive or zero); cf. [Reference YoshiokaYos09, Remark 1.4].
$\mathbf{v}$
is positive or zero); cf. [Reference YoshiokaYos09, Remark 1.4].- (
 $\ddagger$
)
$\ddagger$
) Either
 $0<\mathbf{v}_{0}^{\prime }<\mathbf{v}_{2}^{\prime }$
or
$0<\mathbf{v}_{0}^{\prime }<\mathbf{v}_{2}^{\prime }$
or
 $0<H\cdot \mathbf{v}_{1}^{\prime }<\mathbf{v}_{2}^{\prime }$
(depending on whether the rank of
$0<H\cdot \mathbf{v}_{1}^{\prime }<\mathbf{v}_{2}^{\prime }$
(depending on whether the rank of
 $\mathbf{v}$
is positive or zero).
$\mathbf{v}$
is positive or zero).
Consider the composition of autoequivalences
For an
![]() $H$
-polystable sheaf
$H$
-polystable sheaf
![]() $F$
with a decomposition (3), the Mukai vector of
$F$
with a decomposition (3), the Mukai vector of
![]() $F\,\otimes \,H^{m}$
is
$F\,\otimes \,H^{m}$
is
![]() $\mathbf{v}^{\prime }=\mathbf{v}\cdot e^{mH}$
. The condition
$\mathbf{v}^{\prime }=\mathbf{v}\cdot e^{mH}$
. The condition
![]() $(\dagger )$
guarantees that
$(\dagger )$
guarantees that
![]() $\unicode[STIX]{x1D6F7}(F\,\otimes \,H^{m})$
is an
$\unicode[STIX]{x1D6F7}(F\,\otimes \,H^{m})$
is an
![]() $H$
-polystable sheaf by Theorem 3.4, which can be decomposed into stable summands in the form
$H$
-polystable sheaf by Theorem 3.4, which can be decomposed into stable summands in the form
For each
![]() $i$
, the condition
$i$
, the condition
![]() $(\ddagger )$
guarantees that the last component of the Mukai vector of
$(\ddagger )$
guarantees that the last component of the Mukai vector of
![]() $F_{i}\,\otimes \,H^{m}$
is at least
$F_{i}\,\otimes \,H^{m}$
is at least
![]() $2$
, which implies that the rank of
$2$
, which implies that the rank of
![]() $\unicode[STIX]{x1D6F7}(F_{i}\,\otimes \,H^{m})$
is at least
$\unicode[STIX]{x1D6F7}(F_{i}\,\otimes \,H^{m})$
is at least
![]() $2$
, hence
$2$
, hence
![]() $\unicode[STIX]{x1D6F7}(F\,\otimes \,H^{m})$
satisfies condition (ii) in Proposition 3.1. Moreover, each
$\unicode[STIX]{x1D6F7}(F\,\otimes \,H^{m})$
satisfies condition (ii) in Proposition 3.1. Moreover, each
![]() $\unicode[STIX]{x1D6F7}(F_{i})$
is
$\unicode[STIX]{x1D6F7}(F_{i})$
is
![]() $\unicode[STIX]{x1D707}_{H}$
-stable. By Proposition 3.1 and Remarks 3.2 and 3.3, the DG algebra
$\unicode[STIX]{x1D707}_{H}$
-stable. By Proposition 3.1 and Remarks 3.2 and 3.3, the DG algebra
![]() $\operatorname{RHom}^{\bullet }(\unicode[STIX]{x1D6F7}(F\,\otimes \,H^{m}),\unicode[STIX]{x1D6F7}(F\,\otimes \,H^{m}))$
is formal, hence
$\operatorname{RHom}^{\bullet }(\unicode[STIX]{x1D6F7}(F\,\otimes \,H^{m}),\unicode[STIX]{x1D6F7}(F\,\otimes \,H^{m}))$
is formal, hence
![]() $\operatorname{RHom}^{\bullet }(F,F)$
is also formal by Proposition 1.4.
$\operatorname{RHom}^{\bullet }(F,F)$
is also formal by Proposition 1.4.
The case of
![]() $(r,dH+D)=(0,0)$
is reduced to Proposition 3.1(i) by applying (4).◻
$(r,dH+D)=(0,0)$
is reduced to Proposition 3.1(i) by applying (4).◻
3.2 Formality for derived objects
Let
![]() $\operatorname{Stab}^{\dagger }(X)$
be the connected component of the space of stability conditions on
$\operatorname{Stab}^{\dagger }(X)$
be the connected component of the space of stability conditions on
![]() $X$
which contains the geometric ones; see [Reference BridgelandBri08, Definition 11.4]. The following proposition was communicated to us by Yoshioka and Bayer. Since it is well known to experts, on the advice of the referees we leave out the details. The reader can, however, find a full proof in an earlier version of this paper [Reference Budur and ZhangBZ18].
$X$
which contains the geometric ones; see [Reference BridgelandBri08, Definition 11.4]. The following proposition was communicated to us by Yoshioka and Bayer. Since it is well known to experts, on the advice of the referees we leave out the details. The reader can, however, find a full proof in an earlier version of this paper [Reference Budur and ZhangBZ18].
Proposition 3.5. Let
![]() $X$
be a projective K3 surface,
$X$
be a projective K3 surface,
![]() $\mathbf{v}$
a Mukai vector, and
$\mathbf{v}$
a Mukai vector, and
![]() $\unicode[STIX]{x1D70E}\in \operatorname{Stab}^{\dagger }(X)$
generic with respect to
$\unicode[STIX]{x1D70E}\in \operatorname{Stab}^{\dagger }(X)$
generic with respect to
![]() $\mathbf{v}$
. Then there exists an autoequivalence
$\mathbf{v}$
. Then there exists an autoequivalence
which induces an isomorphism
![]() ${\mathcal{M}}_{X,\unicode[STIX]{x1D70E}}(\mathbf{v})\cong {\mathcal{M}}_{X,\unicode[STIX]{x1D714}}(\mathbf{u})$
preserving S-equivalence classes, between the moduli space of
${\mathcal{M}}_{X,\unicode[STIX]{x1D70E}}(\mathbf{v})\cong {\mathcal{M}}_{X,\unicode[STIX]{x1D714}}(\mathbf{u})$
preserving S-equivalence classes, between the moduli space of
![]() $\unicode[STIX]{x1D70E}$
-semistable objects of class
$\unicode[STIX]{x1D70E}$
-semistable objects of class
![]() $\mathbf{v}$
, and the moduli space of
$\mathbf{v}$
, and the moduli space of
![]() $\unicode[STIX]{x1D714}$
-semistable sheaves of class
$\unicode[STIX]{x1D714}$
-semistable sheaves of class
![]() $\mathbf{u}$
for some generic ample class
$\mathbf{u}$
for some generic ample class
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() $X$
.
$X$
.
Proof. For
![]() $\mathbf{v}^{2}>0$
, this is essentially [Reference Bayer and MacrìBM14a, Lemma 7.3], generalized to the current form by an idea of Yoshioka; see [Reference Meachan and ZhangMZ16, Remark 3.15].
$\mathbf{v}^{2}>0$
, this is essentially [Reference Bayer and MacrìBM14a, Lemma 7.3], generalized to the current form by an idea of Yoshioka; see [Reference Meachan and ZhangMZ16, Remark 3.15].
For
![]() $\mathbf{v}^{2}\leqslant 0$
, the idea of the proof is due to Bayer. By [Reference Bayer and MacrìBM14a, Lemmas 7.1 and 7.2(b)], we can assume
$\mathbf{v}^{2}\leqslant 0$
, the idea of the proof is due to Bayer. By [Reference Bayer and MacrìBM14a, Lemmas 7.1 and 7.2(b)], we can assume
![]() $\mathbf{v}$
is primitive. We can also assume the leading component
$\mathbf{v}$
is primitive. We can also assume the leading component
![]() $\mathbf{v}_{0}>0$
. Indeed, if
$\mathbf{v}_{0}>0$
. Indeed, if
![]() $\mathbf{v}_{0}<0$
, we can apply the shift functor
$\mathbf{v}_{0}<0$
, we can apply the shift functor
![]() $[1]$
, so that
$[1]$
, so that
![]() $\mathbf{v}$
gets replaced by
$\mathbf{v}$
gets replaced by
![]() $-\mathbf{v}$
. If
$-\mathbf{v}$
. If
![]() $\mathbf{v}_{0}=0$
, after tensoring with a line bundle if necessary, we can assume
$\mathbf{v}_{0}=0$
, after tensoring with a line bundle if necessary, we can assume
![]() $\mathbf{v}_{2}\neq 0$
. Then one applies (4) to obtain
$\mathbf{v}_{2}\neq 0$
. Then one applies (4) to obtain
![]() $\widehat{\mathbf{v}}$
whose leading component is non-zero.
$\widehat{\mathbf{v}}$
whose leading component is non-zero.
The rest of the proof makes use of the wall-crossing technique. By [Reference BridgelandBri08, § 9],
![]() $\operatorname{Stab}^{\dagger }(X)$
admits a wall and chamber structure. There is one chamber which contains
$\operatorname{Stab}^{\dagger }(X)$
admits a wall and chamber structure. There is one chamber which contains
![]() $\unicode[STIX]{x1D70E}$
as an interior point, and another ‘Gieseker chamber’ in which we can pick a stability condition
$\unicode[STIX]{x1D70E}$
as an interior point, and another ‘Gieseker chamber’ in which we can pick a stability condition
![]() $\unicode[STIX]{x1D70F}$
, such that the
$\unicode[STIX]{x1D70F}$
, such that the
![]() $\unicode[STIX]{x1D70F}$
-stability for class
$\unicode[STIX]{x1D70F}$
-stability for class
![]() $\mathbf{v}$
is the same as the Gieseker
$\mathbf{v}$
is the same as the Gieseker
![]() $\unicode[STIX]{x1D6FD}$
-twisted
$\unicode[STIX]{x1D6FD}$
-twisted
![]() $\unicode[STIX]{x1D714}$
-stability for some generic
$\unicode[STIX]{x1D714}$
-stability for some generic
![]() $\unicode[STIX]{x1D6FD}\in \operatorname{NS}(X)_{\mathbb{Q}}$
and
$\unicode[STIX]{x1D6FD}\in \operatorname{NS}(X)_{\mathbb{Q}}$
and
![]() $\unicode[STIX]{x1D714}\in \operatorname{Amp}(X)_{\mathbb{Q}}$
; see [Reference BridgelandBri08, § 14]. The assumptions
$\unicode[STIX]{x1D714}\in \operatorname{Amp}(X)_{\mathbb{Q}}$
; see [Reference BridgelandBri08, § 14]. The assumptions
![]() $\mathbf{v}_{0}>0$
and
$\mathbf{v}_{0}>0$
and
![]() $\unicode[STIX]{x1D714}$
being generic imply further that the
$\unicode[STIX]{x1D714}$
being generic imply further that the
![]() $\unicode[STIX]{x1D6FD}$
-twisted
$\unicode[STIX]{x1D6FD}$
-twisted
![]() $\unicode[STIX]{x1D714}$
-stability for class
$\unicode[STIX]{x1D714}$
-stability for class
![]() $\mathbf{v}$
is the same as the untwisted
$\mathbf{v}$
is the same as the untwisted
![]() $\unicode[STIX]{x1D714}$
-stability by an argument similar to [Reference YoshiokaYos01, Lemma 1.1]. We can move
$\unicode[STIX]{x1D714}$
-stability by an argument similar to [Reference YoshiokaYos01, Lemma 1.1]. We can move
![]() $\unicode[STIX]{x1D70E}$
to
$\unicode[STIX]{x1D70E}$
to
![]() $\unicode[STIX]{x1D70F}$
in
$\unicode[STIX]{x1D70F}$
in
![]() $\operatorname{Stab}^{\dagger }(X)$
along a path that never meets two walls simultaneously. For each wall-crossing, we can construct an explicit autoequivalence of
$\operatorname{Stab}^{\dagger }(X)$
along a path that never meets two walls simultaneously. For each wall-crossing, we can construct an explicit autoequivalence of
![]() $D^{b}(\operatorname{Coh}(X))$
which induces an isomorphism of the moduli spaces of stable objects with respect to generic stability conditions in the neighboring chambers separated by the wall. The idea of its explicit construction in the case of
$D^{b}(\operatorname{Coh}(X))$
which induces an isomorphism of the moduli spaces of stable objects with respect to generic stability conditions in the neighboring chambers separated by the wall. The idea of its explicit construction in the case of
![]() $\mathbf{v}^{2}<0$
is essentially contained in [Reference Bayer and MacrìBM14b, Proposition 6.8], and in the case of
$\mathbf{v}^{2}<0$
is essentially contained in [Reference Bayer and MacrìBM14b, Proposition 6.8], and in the case of
![]() $\mathbf{v}^{2}=0$
it is a combination of [Reference Bayer and MacrìBM14a, Lemma 7.2(a)] and the twisted K3 surface version of [Reference BridgelandBri08, Theorem 12.1] which can be found in [Reference Huybrechts, Macrì and StellariHMS08, § 3.1]; see [Reference Bayer and MacrìBM14a, Remark 6.4].◻
$\mathbf{v}^{2}=0$
it is a combination of [Reference Bayer and MacrìBM14a, Lemma 7.2(a)] and the twisted K3 surface version of [Reference BridgelandBri08, Theorem 12.1] which can be found in [Reference Huybrechts, Macrì and StellariHMS08, § 3.1]; see [Reference Bayer and MacrìBM14a, Remark 6.4].◻
Proof of Theorem 1.3.
By Proposition 3.5,
![]() $\unicode[STIX]{x1D6E9}(F)$
is an
$\unicode[STIX]{x1D6E9}(F)$
is an
![]() $L$
-polystable coherent sheaf on
$L$
-polystable coherent sheaf on
![]() $X$
. By Theorem 1.2, the DG algebra
$X$
. By Theorem 1.2, the DG algebra
![]() $\operatorname{RHom}^{\bullet }(\unicode[STIX]{x1D6E9}(F),\unicode[STIX]{x1D6E9}(F))$
is formal, which implies that
$\operatorname{RHom}^{\bullet }(\unicode[STIX]{x1D6E9}(F),\unicode[STIX]{x1D6E9}(F))$
is formal, which implies that
![]() $\operatorname{RHom}^{\bullet }(F,F)$
is formal by Proposition 1.4.◻
$\operatorname{RHom}^{\bullet }(F,F)$
is formal by Proposition 1.4.◻
Acknowledgements
We thank T. Bridgeland for pointing out to us the relevance of [Reference Lunts and OrlovLO10] to the formality conjecture. We also thank E. Arbarello, A. Bayer, A. King, A. Krug, Y. Lekili, G. Saccà and K. Yoshioka for their help with questions and for inspiring discussions. The second named author thanks the organizers of the School on Deformation Theory (University of Turin, July 2017) for the stimulating atmosphere and excellent lectures related to this topic. The first named author was partly supported by KU Leuven OT, FWO, and Methusalem grants.