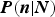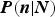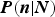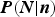1. INTRODUCTION
One difficulty in reconstructing the history of glaciations in a given area is that a moraine deposited by a glacial advance can be destroyed by a subsequent glacial advance. The paper by Gibbons and others (Reference Gibbons, Megeath and Pierce1984) (we will refer to this paper of Gibbons, Megeath and Pierce as GMP) refers to this as ‘obliterative overlap.’ For example, if there have been ten glacial advances in a given valley, there may be only three moraines left at the present time. In order to analyze such situations, GMP formulated an elegant model, in which the key quantity of interest is
![]() $P(n\vert N)$
, the probability that n moraines are preserved, given that N glacial advances have occurred. Note that within the GMP model we have 1 ≤ n ≤ N, since the most recent moraine is always preserved, and one particular scenario results in all N moraines left intact. For a recent application of the model see, for example, Young and others (Reference Young, Schweinsberg, Briner and Schaefer2015).
$P(n\vert N)$
, the probability that n moraines are preserved, given that N glacial advances have occurred. Note that within the GMP model we have 1 ≤ n ≤ N, since the most recent moraine is always preserved, and one particular scenario results in all N moraines left intact. For a recent application of the model see, for example, Young and others (Reference Young, Schweinsberg, Briner and Schaefer2015).
The key assumptions of the GMP model are: (1) all N! possible orderings of the extents of the glacial advances are equally likely; or, to quote GMP, ‘moraines were deposited at various distances from their glacial source areas randomly over time.’ (2) A given glacial advance obliterates the moraines of all previous advances of lesser extent.
The degree to which this model fits a given situation depends on many factors. Detailed, careful studies have shown that glacial advances and retreats occur on many timescales, as the glaciers respond to both climate fluctuations, and to more systematic, long-term changes (Reichert and others, Reference Reichert, Bengtsson and Oerlemans2002; Roe and O'Neal, Reference Roe and O'Neal2009; Roe, Reference Roe2011; Anderson and others, Reference Anderson, Roe and Anderson2014). If the net effect of these complicated processes is that the average of L (the length of an advance) is both time-independent and not correlated with the length of other advances, then the GMP model will be suitable. If, however, the statistics of L is time dependent, the GMP model may miss important features of the situation. For example, if the mean value of L decreases gradually with time, we have a long-term glacial retreat scenario, and as GMP point out, their model will underestimate n. A more subtle complication would be the following: even if the average length of an advance had no long-term trend, there could be shorter-term correlations between the successive values of L.
The preceding paragraph discusses assumption (1). We should also note the following: while it may not be very likely, if an overrun moraine is not obliterated, assumption (2) is violated. The judgment of the field geologist can be important in such a case. If a moraine survives, but in a degraded form, which strongly indicates it was overrun by a later one, then it should not be counted as contributing toward n, if the GMP model is being applied.
In this paper, we take the view that the GMP model provides a very useful basic description, and captures important real-world features of the obliterative-overlap phenomenon. Thus, it is worth elucidating in more detail the actual predictions of the model. Here, we will concentrate on deriving explicit formulae, which embody the predictions of the model.
2. CALCULATION OF THE GENERATING FUNCTION
Given the assumptions of their model, GMP were able to derive a recursion equation satisfied by
![]() $P(n\vert N)$
(for n ≥ 2):
$P(n\vert N)$
(for n ≥ 2):
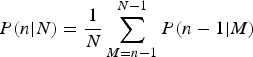 $$P(n \vert N) = \displaystyle{1 \over N}\sum\limits_{M = n - 1}^{N - 1} P(n - 1 \vert M)$$
$$P(n \vert N) = \displaystyle{1 \over N}\sum\limits_{M = n - 1}^{N - 1} P(n - 1 \vert M)$$
Note that
![]() $P(1\vert N) = 1/N$
. To gain insight into Eqn (1), note that if n moraines are to survive, the length of the very last glacial advance can have N − n + 1 possible positions, relative to the lengths of the other advances. That is, its length can be the shortest, the second shortest, the third shortest and up to the
$P(1\vert N) = 1/N$
. To gain insight into Eqn (1), note that if n moraines are to survive, the length of the very last glacial advance can have N − n + 1 possible positions, relative to the lengths of the other advances. That is, its length can be the shortest, the second shortest, the third shortest and up to the
![]() $(N - n + 1)$
th shortest. For each of these cases, if we compute how many ways there can be a total of n surviving moraines, divide by N!, and then combine, we arrive at Eqn (1). The authors then used this equation to generate a table of values for
$(N - n + 1)$
th shortest. For each of these cases, if we compute how many ways there can be a total of n surviving moraines, divide by N!, and then combine, we arrive at Eqn (1). The authors then used this equation to generate a table of values for
![]() $P(n\vert N)$
. The calculations revealed, perhaps surprisingly, that the number of surviving moraines would probably be quite small. For example, when N = 20, the most likely value for n is n = 3. The authors did not present a closed form solution for
$P(n\vert N)$
. The calculations revealed, perhaps surprisingly, that the number of surviving moraines would probably be quite small. For example, when N = 20, the most likely value for n is n = 3. The authors did not present a closed form solution for
![]() $P(n\vert N)$
, or for quantities such as 〈n〉 or
$P(n\vert N)$
, or for quantities such as 〈n〉 or
![]() $\sigma _n^2 = \langle (n - \langle n\rangle )^2\rangle $
.
$\sigma _n^2 = \langle (n - \langle n\rangle )^2\rangle $
.
In order to make progress in analyzing the GMP model, we rely on a widely used approach: we compute the generating function (see, e.g., chapter 7 of Wallace, Reference Wallace1972). The generating function for
![]() $P(n\vert N)$
uses a real-valued auxiliary variable x, and is defined as follows:
$P(n\vert N)$
uses a real-valued auxiliary variable x, and is defined as follows:
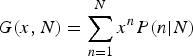 $$G(x,N) = \sum\limits_{n = 1}^N x^nP(n \vert N)$$
$$G(x,N) = \sum\limits_{n = 1}^N x^nP(n \vert N)$$
Once we have an explicit form for G(x,N), we may determine
![]() $P(n\vert N)$
from the coefficient of x
n
; we also have:
$P(n\vert N)$
from the coefficient of x
n
; we also have:
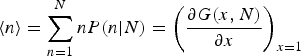 $$\langle n\rangle = \sum\limits_{n = 1}^N nP(n \vert N) = \left( {\displaystyle{{\partial G(x,N)} \over {\partial x}}} \right)_{x = 1}$$
$$\langle n\rangle = \sum\limits_{n = 1}^N nP(n \vert N) = \left( {\displaystyle{{\partial G(x,N)} \over {\partial x}}} \right)_{x = 1}$$
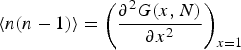 $$\langle n(n - 1)\rangle = \left( {\displaystyle{{\partial ^2G(x,N)} \over {\partial x^2}}} \right)_{x = 1}$$
$$\langle n(n - 1)\rangle = \left( {\displaystyle{{\partial ^2G(x,N)} \over {\partial x^2}}} \right)_{x = 1}$$
Equations (3) and (4) may be used to calculate
![]() $\sigma _n^2 $
.
$\sigma _n^2 $
.
To compute the generating function, we use the result derived by GMP, Eqn (1):
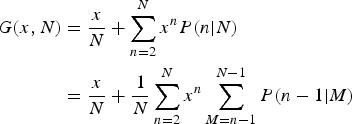 $$\eqalign{G(x,N) & = \displaystyle{x \over N} + \sum\limits_{n = 2}^N x^nP(n \vert N) \cr & = \displaystyle{x \over N} + \displaystyle{1 \over N}\sum\limits_{n = 2}^N x^n\sum\limits_{M = n - 1}^{N - 1} P(n - 1 \vert M)}$$
$$\eqalign{G(x,N) & = \displaystyle{x \over N} + \sum\limits_{n = 2}^N x^nP(n \vert N) \cr & = \displaystyle{x \over N} + \displaystyle{1 \over N}\sum\limits_{n = 2}^N x^n\sum\limits_{M = n - 1}^{N - 1} P(n - 1 \vert M)}$$
By rearranging the sums in the preceding equation, we may rewrite it as
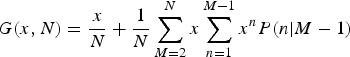 $$G(x,N) = \displaystyle{x \over N} + \displaystyle{1 \over N}\sum\limits_{M = 2}^N x\sum\limits_{n = 1}^{M - 1} x^nP(n \vert M - 1)$$
$$G(x,N) = \displaystyle{x \over N} + \displaystyle{1 \over N}\sum\limits_{M = 2}^N x\sum\limits_{n = 1}^{M - 1} x^nP(n \vert M - 1)$$
or
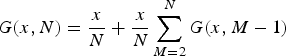 $$G(x,N) = \displaystyle{x \over N} + \displaystyle{x \over N}\sum\limits_{M = 2}^N G(x,M - 1)$$
$$G(x,N) = \displaystyle{x \over N} + \displaystyle{x \over N}\sum\limits_{M = 2}^N G(x,M - 1)$$
Using the previous equation, we can derive an iterative formula:
This allows us to write down the solution for the generating function:
The numerator in the previous equation is a known mathematical function called Pochhammer's symbol:
where
![]() $\Gamma (x)$
is the Gamma function (see Abramowitz and Stegun, Reference Abramowitz and Stegun1965).
$\Gamma (x)$
is the Gamma function (see Abramowitz and Stegun, Reference Abramowitz and Stegun1965).
3. RESULTS
The fact that the numerator of the expression given for G(x,N) in Eqn (10) is actually a well-known mathematical function is very useful. The coefficient of x
n
gives us
![]() $P(n\vert N)$
, and is known to be:
$P(n\vert N)$
, and is known to be:
Let us explain what this equation means. The function s(N,n) is known as a Stirling number of the first kind, and arises in certain areas of mathematics. The book by Abramowitz and Stegun (Reference Abramowitz and Stegun1965) contains information on these numbers, and they are available as built-in functions in programs such as Maple and Mathematica. The website Wolfram MathWorld also contains useful information on both the Pochhammer symbols and the Stirling numbers. As usually defined some of the Stirling numbers are negative, so the magnitude (|s|) is a necessary part of the answer.
In Figure 1, we plot this distribution for several values of N. We reproduce the numerical results of GMP, and can see that even as N grows, the distribution has significant statistical weight only at rather small values of n.

Fig. 1. Plots of
![]() $P(n\vert N)$
, the probability that n moraines are preserved, given that N glacial advances have occurred, for various values of N. The exact result, Eqn (12), is used to construct the plots. (a) N = 5. (b) N = 10. (c) N = 30.
$P(n\vert N)$
, the probability that n moraines are preserved, given that N glacial advances have occurred, for various values of N. The exact result, Eqn (12), is used to construct the plots. (a) N = 5. (b) N = 10. (c) N = 30.
Next, the generating function (10) can be used to compute important properties of the distribution given by (12). These results are presented, for example, in the paper by Louchard (Reference Louchard2010), who considers exactly this problem. The average value of n is
Here
![]() $\psi (x)$
is the digamma function, and γ is Euler's constant, γ = 0.57721, …. The variance is given by
$\psi (x)$
is the digamma function, and γ is Euler's constant, γ = 0.57721, …. The variance is given by
Here
![]() $\psi (1,x)$
is the first polygamma function. The digamma function, for integer values of its argument, is defined by
$\psi (1,x)$
is the first polygamma function. The digamma function, for integer values of its argument, is defined by
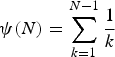 $$\psi (N) = \sum\limits_{k = 1}^{N - 1} \displaystyle{1 \over k}$$
$$\psi (N) = \sum\limits_{k = 1}^{N - 1} \displaystyle{1 \over k}$$
The first polygamma function is defined by
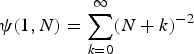 $$\psi (1,N) = \sum\limits_{k = 0}^\infty (N + k)^{ - 2}$$
$$\psi (1,N) = \sum\limits_{k = 0}^\infty (N + k)^{ - 2}$$
For more information on the digamma and polygamma functions, see Abramowitz and Stegun (Reference Abramowitz and Stegun1965).
In Figure 2, we plot both 〈n〉 and σ n as functions of N. We can see how slowly 〈n〉 grows as N increases, and that σ n is smaller than 〈n〉. In Figure 3, we show the ratio σ n /〈n〉 as a function of N. It has a quite narrow range of values, and for N greater than about five, this ratio has a value in the range 0.38–0.40 over a wide range of N.

Fig. 3. Plot of the ratio σ/〈n〉 as a function of N.
In Figure 4, we plot 〈n〉, 〈n〉 + σ n and 〈n〉 − σ n as functions of N, to see the band of likely values for n, the number of preserved moraines. We see, for example, that for N = 10, n is likely to be between 1 and 4, and even for N = 20, n is likely to be in the range of 2–5.

Fig. 4. Plot of 〈n〉, 〈n〉 + σ and 〈n〉 − σ, as functions of N. This illustrates the range of likely values of n, the number of preserved moraines.
A very nice, simplifying result is presented by Louchard (Reference Louchard2010), for the large-N behavior of the average value of n:
If we plot the exact answer, Eqn (13) and the approximation (17), it turns out that they agree remarkably well even for N as small as N = 2. Thus, the simple, accurate approximation in Eqn (17) conveys the key idea that 〈n〉 grows as ln(N), which of course is much smaller than N as N becomes large. Louchard (Reference Louchard2010) also presents a simple result for the large-N behavior of the variance:
This is not quite as accurate as the previous equation at N = 2 or 3, but is still very good. Thus, the spread in values of n goes as
![]() $\surd \ln (N)$
as N gets large.
$\surd \ln (N)$
as N gets large.
4. DISCUSSION
Gibbons and others (Reference Gibbons, Megeath and Pierce1984) invented an elegant probabilistic model to describe glacial moraine preservation in the presence of obliterative overlap. Their scenario captures important features of the geological situation, and is an interesting statistical model in its own right. As their calculations revealed, the typical number of surviving moraines is surprisingly small. We presented explicit, analytic solutions for key quantities of their model, including
![]() $P(n\vert N)$
, the mean value 〈n〉 and the variance
$P(n\vert N)$
, the mean value 〈n〉 and the variance
![]() $\sigma _n^2 $
. The probability distribution is given in terms of the Stirling numbers of the first kind. These explicit results help in understanding the consequences of the GMP model. In particular, the large-N estimates, that 〈n〉 goes as ln(N) and that σ
n
goes as
$\sigma _n^2 $
. The probability distribution is given in terms of the Stirling numbers of the first kind. These explicit results help in understanding the consequences of the GMP model. In particular, the large-N estimates, that 〈n〉 goes as ln(N) and that σ
n
goes as
![]() $\surd \ln (N)$
, make clear just how small the typical number of preserved moraines will be.
$\surd \ln (N)$
, make clear just how small the typical number of preserved moraines will be.
As GMP point out, the observed value of n can serve as a guide to the value of N. One way to do this is to study
![]() $P(N\vert n)$
, the probability that there were N glacial advances, given that we now observe n preserved moraines. We will conclude with a discussion of how to do this.
$P(N\vert n)$
, the probability that there were N glacial advances, given that we now observe n preserved moraines. We will conclude with a discussion of how to do this.
If we have a theory for
![]() $P(n\vert N)$
, such as that invented by GMP, but we are interested in
$P(n\vert N)$
, such as that invented by GMP, but we are interested in
![]() $P(N\vert n)$
, it is natural to use Bayes' theorem (see, e.g., D'Agostini, Reference D'Agostini2003) to write
$P(N\vert n)$
, it is natural to use Bayes' theorem (see, e.g., D'Agostini, Reference D'Agostini2003) to write
In this equation,
![]() $P_0(N)$
is called the prior; it gives the probability we assign to various values of N, before we have the information on n. Since P(n) is not a function of N, we may write
$P_0(N)$
is called the prior; it gives the probability we assign to various values of N, before we have the information on n. Since P(n) is not a function of N, we may write
where we select the constant c to normalize
![]() $P(N\vert n)$
on N.
$P(N\vert n)$
on N.
To see how this works in a simple example, we can use the explicit result, Eqn (12). Suppose that we have three surviving moraines, so that n = 3. Then
To complete the analysis, we need to choose a prior. For simplicity, we will assume our background knowledge tells us that N is between 2 and 12, and take
![]() $P_0(N)$
to be constant for 2 ≤ N ≤ 12, and zero otherwise. We stress that, by using expert knowledge about the behavior of glaciers, this simple prior could be replaced by a more detailed one. Figure 5 shows a plot of
$P_0(N)$
to be constant for 2 ≤ N ≤ 12, and zero otherwise. We stress that, by using expert knowledge about the behavior of glaciers, this simple prior could be replaced by a more detailed one. Figure 5 shows a plot of
![]() $P(N\vert3)$
, with our simple choice of prior. We can see that it has a broad peak with a maximum at N = 8. Note that the Bayesian approach, embodied in Eqn (20), is not restricted to the GMP model; a more sophisticated model for
$P(N\vert3)$
, with our simple choice of prior. We can see that it has a broad peak with a maximum at N = 8. Note that the Bayesian approach, embodied in Eqn (20), is not restricted to the GMP model; a more sophisticated model for
![]() $P(n\vert N)$
could be used.
$P(n\vert N)$
could be used.

Fig. 5. Plot of
![]() $P(N\vert3)$
, the probability that there were N glacial advances, given that three moraines have survived. Equation (21) was used.
$P(N\vert3)$
, the probability that there were N glacial advances, given that three moraines have survived. Equation (21) was used.
ACKNOWLEDGEMENTS
The author would like to thank Andrew Mugler for helpful discussions. This work was supported by the National Science Foundation (grant no. EAR 0112480).