Published online by Cambridge University Press: 22 June 2022
We study the complexity of isomorphism of classes of metric structures using methods from infinitary continuous logic. For Borel classes of locally compact structures, we prove that if the equivalence relation of isomorphism is potentially 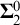 $\mathbf {\Sigma }^0_2$, then it is essentially countable. We also provide an equivalent model-theoretic condition that is easy to check in practice. This theorem is a common generalization of a result of Hjorth about pseudo-connected metric spaces and a result of Hjorth–Kechris about discrete structures. As a different application, we also give a new proof of Kechris’s theorem that orbit equivalence relations of actions of Polish locally compact groups are essentially countable.
$\mathbf {\Sigma }^0_2$, then it is essentially countable. We also provide an equivalent model-theoretic condition that is easy to check in practice. This theorem is a common generalization of a result of Hjorth about pseudo-connected metric spaces and a result of Hjorth–Kechris about discrete structures. As a different application, we also give a new proof of Kechris’s theorem that orbit equivalence relations of actions of Polish locally compact groups are essentially countable.