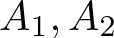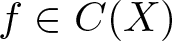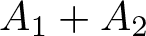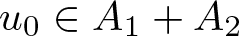1. Introduction
The classical Chebyshev alternation theorem gives a criterion for a polynomial P of degree not greater than n to be the best uniform approximation to a continuous real-valued function f, using the oscillating nature of the difference f − P. More precisely, the theorem asserts that P is the best uniform approximation to f on ![]() $[0,1]$ if and only if there exist n + 2 points ti in
$[0,1]$ if and only if there exist n + 2 points ti in ![]() $[0,1]$ such that
$[0,1]$ such that
 \begin{equation*}
f(t_{k})-P(t_{k})=(-1)^{k}\max_{t\in \lbrack 0,1]}\left\vert
f(t)-P(t)\right\vert ,\quad \text{}k=1,\ldots,n+2.
\end{equation*}
\begin{equation*}
f(t_{k})-P(t_{k})=(-1)^{k}\max_{t\in \lbrack 0,1]}\left\vert
f(t)-P(t)\right\vert ,\quad \text{}k=1,\ldots,n+2.
\end{equation*} See the monograph of Natanson [Reference Natanson and Obolensky14] for a comprehensive commentary on this theorem. Several general alternation theorems applying to an arbitrary finite dimensional subspace M of C(X) for X, a cell in ![]() $\mathbb{R}^{d}$ , may be found in Buck [Reference Buck4]. For the history and various variants of the Chebyshev alternation theorem, consult [Reference Brosowski and da Silva3].
$\mathbb{R}^{d}$ , may be found in Buck [Reference Buck4]. For the history and various variants of the Chebyshev alternation theorem, consult [Reference Brosowski and da Silva3].
In this paper, we prove a Chebyshev-type alternation theorem for a best approximation of a continuous function, defined on a compact metric space, by sums of two algebras. To make the problem more precise, assume X is a compact metric space, C(X) is the space of real-valued continuous functions on X, A 1 and A 2 are closed subalgebras of C(X) containing constants. For a given function ![]() $f\in C(X)$, consider the approximation of f by elements of
$f\in C(X)$, consider the approximation of f by elements of ![]() $A_{1}+A_{2}$. We ask and answer the following question: which conditions imposed on
$A_{1}+A_{2}$. We ask and answer the following question: which conditions imposed on ![]() $u_{0}\in A_{1}+A_{2}$ are necessary and sufficient for the equality
$u_{0}\in A_{1}+A_{2}$ are necessary and sufficient for the equality
 \begin{equation}
\left\Vert f-u_{{0}}\right\Vert =\inf_{u\in A_{1}+A_{2}}\left\Vert
f-u\right\Vert ?
\end{equation}
\begin{equation}
\left\Vert f-u_{{0}}\right\Vert =\inf_{u\in A_{1}+A_{2}}\left\Vert
f-u\right\Vert ?
\end{equation} Here ![]() $\left\Vert \cdot \right\Vert $ denotes the standard uniform norm in C(X). Recall that a function u 0 satisfying Equation (1.1) is called a best approximation to
$\left\Vert \cdot \right\Vert $ denotes the standard uniform norm in C(X). Recall that a function u 0 satisfying Equation (1.1) is called a best approximation to ![]() $f.$
$f.$
It should be remarked that approximation problems concerning sums of algebras were studied in many papers (see Khavinson’s monograph [Reference Khavinson and Khavinson10] for an extensive discussion). The history of this subject goes back to 1937 and 1948 papers by M.H. Stone [Reference Stone19, Reference Stone20]. He considered the most particular case of the approximation by sums of algebras, namely the case when only one algebra is involved. A version of the corresponding famous result, known as the Stone–Weierstrass theorem, states that a subalgebra ![]() $
A\subset C(X)$, which contains a non-zero constant function, is dense in the whole space C(X) if and only if A separates points of X (i.e., for any two different points x and y in X, there exists a function
$
A\subset C(X)$, which contains a non-zero constant function, is dense in the whole space C(X) if and only if A separates points of X (i.e., for any two different points x and y in X, there exists a function ![]() $g\in A$ with
$g\in A$ with ![]() $g(x)\neq g(y)$). Density of the sum of two subalgebras A 1 and A 2 in C(X) (for a compact Hausdorff X) was extensively studied in Marshall and O’Farrell [Reference Marshall and O’Farrell12, Reference Marshall and O’Farrell13]. In [Reference Marshall and O’Farrell13], they gave a complete description of measures on X orthogonal to the sum
$g(x)\neq g(y)$). Density of the sum of two subalgebras A 1 and A 2 in C(X) (for a compact Hausdorff X) was extensively studied in Marshall and O’Farrell [Reference Marshall and O’Farrell12, Reference Marshall and O’Farrell13]. In [Reference Marshall and O’Farrell13], they gave a complete description of measures on X orthogonal to the sum ![]() $A_{1}+A_{2}$. From this description, they obtained a geometrical condition, which is equivalent to the density of
$A_{1}+A_{2}$. From this description, they obtained a geometrical condition, which is equivalent to the density of ![]() $A_{1}+A_{2}$ in C(X). The paper [Reference Marshall and O’Farrell13] also indicates main difficulties with the sum of more than two algebras.
$A_{1}+A_{2}$ in C(X). The paper [Reference Marshall and O’Farrell13] also indicates main difficulties with the sum of more than two algebras.
This paper exploits the same mathematical and geometrically explicit objects from Marshall and O’Farrell [Reference Marshall and O’Farrell12, Reference Marshall and O’Farrell13] for characterization of a best approximation by a sum of two algebras. To prove our main result, we use various results and ideas of Functional Analysis and General Topology.
Note that the algebras Ai, in particular cases, turn into algebras of univariate functions, ridge functions and radial functions. The literature abounds with the use of ridge functions and radial functions. Ridge functions and radial functions are defined as multivariate functions of the form ![]() $g(\mathbf{a}\cdot \mathbf{x})$ and
$g(\mathbf{a}\cdot \mathbf{x})$ and ![]() $g(\left\vert \mathbf{x}-\mathbf{a
}\right\vert _{e})$, respectively, where
$g(\left\vert \mathbf{x}-\mathbf{a
}\right\vert _{e})$, respectively, where ![]() $\mathbf{a}\in \mathbb{R}^{d}$ is a fixed vector,
$\mathbf{a}\in \mathbb{R}^{d}$ is a fixed vector, ![]() $\mathbf{x}\in \mathbb{R}^{d}$ is the variable,
$\mathbf{x}\in \mathbb{R}^{d}$ is the variable, ![]() $\mathbf{a}
\cdot \mathbf{x}$ is the usual inner product,
$\mathbf{a}
\cdot \mathbf{x}$ is the usual inner product, ![]() $\left\vert \mathbf{x-a}
\right\vert _{e}$ is the Euclidean distance between x and a and g is a univariate function.
$\left\vert \mathbf{x-a}
\right\vert _{e}$ is the Euclidean distance between x and a and g is a univariate function.
2. The main result
Let X be a compact metric space, C(X) be the space of real-valued continuous functions on X and ![]() $A_{1}\subset C(X),$
$A_{1}\subset C(X),$ ![]() $A_{2}\subset C(X)$ be two closed algebras that contain the constants. Define the equivalence relation
$A_{2}\subset C(X)$ be two closed algebras that contain the constants. Define the equivalence relation ![]() $R_{i},$
$R_{i},$ ![]() $i=1,2,$ for elements in X by setting
$i=1,2,$ for elements in X by setting
 \begin{equation*}
a\overset{R_{i}}{\sim }b\quad \text{if }f(a)=f(b)\ \text{for all }f\in A_{i}.
\end{equation*}
\begin{equation*}
a\overset{R_{i}}{\sim }b\quad \text{if }f(a)=f(b)\ \text{for all }f\in A_{i}.
\end{equation*} Then, for each ![]() $i=1,2,$ the quotient space
$i=1,2,$ the quotient space ![]() $X_{i}=X/R_{i}$ with respect to the relation Ri, equipped with the quotient space topology, is compact and the natural projections
$X_{i}=X/R_{i}$ with respect to the relation Ri, equipped with the quotient space topology, is compact and the natural projections ![]() $s:X\rightarrow X_{1}$ and
$s:X\rightarrow X_{1}$ and ![]() $p:X\rightarrow X_{2}$ are continuous. Note that the quotient spaces X 1 and X 2 are not only compact but also Hausdorff (see, e.g., [Reference Khavinson and Khavinson10, p.54]). In view of the Stone–Weierstrass theorem, the algebras A 1 and A 2 have the following set representations:
$p:X\rightarrow X_{2}$ are continuous. Note that the quotient spaces X 1 and X 2 are not only compact but also Hausdorff (see, e.g., [Reference Khavinson and Khavinson10, p.54]). In view of the Stone–Weierstrass theorem, the algebras A 1 and A 2 have the following set representations:
 \begin{eqnarray*}
A_{1} &=&\{g(s(x)):g\in C(X_{1})\}, \\
A_{2} &=&\{h(p(x)):h\in C(X_{2})\}.
\end{eqnarray*}
\begin{eqnarray*}
A_{1} &=&\{g(s(x)):g\in C(X_{1})\}, \\
A_{2} &=&\{h(p(x)):h\in C(X_{2})\}.
\end{eqnarray*}We proceed with the definition of lightning bolts with respect to two algebras. These objects are essential for our further analysis.
Definition 2.1. (see [Reference Marshall and O’Farrell13])
A finite or infinite ordered set ![]() $l=\{x_{1},x_{2},\ldots\}\subset X$, where
$l=\{x_{1},x_{2},\ldots\}\subset X$, where ![]() $x_{i}\neq x_{i+1}$, with either
$x_{i}\neq x_{i+1}$, with either ![]() $s(x_{1})=s(x_{2}),\ p(x_{2})=p(x_{3}),\ s(x_{3})=s(x_{4}),\ \ldots$ or
$s(x_{1})=s(x_{2}),\ p(x_{2})=p(x_{3}),\ s(x_{3})=s(x_{4}),\ \ldots$ or ![]() $p(x_{1})=p(x_{2}),\ s(x_{2})=s(x_{3}),\ p(x_{3})=p(x_{4}),\ldots$ is called a lightning bolt with respect to the algebras A 1 and A 2.
$p(x_{1})=p(x_{2}),\ s(x_{2})=s(x_{3}),\ p(x_{3})=p(x_{4}),\ldots$ is called a lightning bolt with respect to the algebras A 1 and A 2.
In the sequel, we will simply use the term “bolt” instead of the expression “lightning bolt with respect to the algebras A 1 and A 2”. If in a finite bolt ![]() $\{x_{1},\ldots,x_{n},x_{n+1}\}$,
$\{x_{1},\ldots,x_{n},x_{n+1}\}$, ![]() $
x_{n+1}=x_{1}$ and n is an even number, then the bolt
$
x_{n+1}=x_{1}$ and n is an even number, then the bolt ![]() $\{x_{1},\ldots,x_{n}\}$ is said to be closed.
$\{x_{1},\ldots,x_{n}\}$ is said to be closed.
Bolts, in the special case when ![]() $X\subset \mathbb{R}^{2}$, and
$X\subset \mathbb{R}^{2}$, and ![]() $
A_{1}=\{g(x)\}$ and
$
A_{1}=\{g(x)\}$ and ![]() $A_{2}=\{h(y)\}$ are geometrically explicit objects. In this case, a bolt is an ordered set
$A_{2}=\{h(y)\}$ are geometrically explicit objects. In this case, a bolt is an ordered set ![]() $\{x_{1},x_{2},\ldots\}$ in
$\{x_{1},x_{2},\ldots\}$ in ![]() $\mathbb{R}^{2}$ with the line segments
$\mathbb{R}^{2}$ with the line segments ![]() $[x_{i},x_{i+1}],$
$[x_{i},x_{i+1}],$ ![]() $i=1,\ldots,n,$ perpendicular alternatively to the x and y axes. Bolts, in this particular and simplest case, were first introduced by Diliberto and Straus in [Reference Diliberto and Straus6]. They were further used in many works devoted to the approximation of multivariate functions by sums of univariate functions (see [Reference Khavinson and Khavinson10]). Bolts appeared in a number of papers with several different names such as permissible lines (see [Reference Diliberto and Straus6]), paths (see, e.g., [Reference Light and Cheney11]), trips (see, e.g., [Reference Marshall and O’Farrell12]) and links (see, e.g., [Reference Cowsik, Klopotowski and Nadkarni5]). The term bolt of lightning is due to Arnold [Reference Arnold1]. Marshall and O’Farrell [Reference Marshall and O’Farrell13] generalized these objects to the case of two abstract subalgebras of the space of continuous functions defined on a compact Hausdorff space. They gave many central properties of bolts and functionals associated with them.
$i=1,\ldots,n,$ perpendicular alternatively to the x and y axes. Bolts, in this particular and simplest case, were first introduced by Diliberto and Straus in [Reference Diliberto and Straus6]. They were further used in many works devoted to the approximation of multivariate functions by sums of univariate functions (see [Reference Khavinson and Khavinson10]). Bolts appeared in a number of papers with several different names such as permissible lines (see [Reference Diliberto and Straus6]), paths (see, e.g., [Reference Light and Cheney11]), trips (see, e.g., [Reference Marshall and O’Farrell12]) and links (see, e.g., [Reference Cowsik, Klopotowski and Nadkarni5]). The term bolt of lightning is due to Arnold [Reference Arnold1]. Marshall and O’Farrell [Reference Marshall and O’Farrell13] generalized these objects to the case of two abstract subalgebras of the space of continuous functions defined on a compact Hausdorff space. They gave many central properties of bolts and functionals associated with them.
Let us now define extremal bolts.
Definition 2.2. A finite or infinite bolt ![]() $\{x_{1},x_{2},\ldots\}$ is said to be extremal for a function
$\{x_{1},x_{2},\ldots\}$ is said to be extremal for a function ![]() $f\in C(X)$ if
$f\in C(X)$ if ![]() $
f(x_{i})=(-1)^{i}\left\Vert f\right\Vert$,
$
f(x_{i})=(-1)^{i}\left\Vert f\right\Vert$, ![]() $i=1,2,\ldots$, or
$i=1,2,\ldots$, or ![]() $f(x_{i})=(-1)^{i+1}
\left\Vert f\right\Vert ,$
$f(x_{i})=(-1)^{i+1}
\left\Vert f\right\Vert ,$ ![]() $i=1,2,\ldots$.
$i=1,2,\ldots$.
We continue with the notion of image of a finite signed measure µ and a measure space ![]() $(U,\mathcal{A},\mu ).$ Let F be a mapping from the set U to the set
$(U,\mathcal{A},\mu ).$ Let F be a mapping from the set U to the set ![]() $T.$ Then a measure space
$T.$ Then a measure space ![]() $(T,\mathcal{B},\nu )$ is called an image of the measure space
$(T,\mathcal{B},\nu )$ is called an image of the measure space ![]() $(U,\mathcal{A},\mu )$ if the measurable sets
$(U,\mathcal{A},\mu )$ if the measurable sets ![]() $
B\in \mathcal{B}$ are the subsets of T such that
$
B\in \mathcal{B}$ are the subsets of T such that ![]() $F^{-1}(B)\in \mathcal{A}$ and
$F^{-1}(B)\in \mathcal{A}$ and
The measure ν is called an image of µ and denoted by ![]() $F\circ \mu $. Clearly,
$F\circ \mu $. Clearly,
since under mapping F, there is a possibility of mixing up the images of those sets on which µ is positive with those where it is negative. Besides, note that if a bounded function ![]() $g:T\rightarrow $
$g:T\rightarrow $ ![]() $\mathbb{R}$ is
$\mathbb{R}$ is ![]() $
F\circ \mu $-measurable, then the composite function
$
F\circ \mu $-measurable, then the composite function ![]() $[g\circ
F]:U\rightarrow $
$[g\circ
F]:U\rightarrow $ ![]() $\mathbb{R}$ is µ-measurable and
$\mathbb{R}$ is µ-measurable and
 \begin{equation}
\int_{U}[g\circ F]\,{\rm d}\mu =\int_{T}gd[F\circ \mu ].
\end{equation}
\begin{equation}
\int_{U}[g\circ F]\,{\rm d}\mu =\int_{T}gd[F\circ \mu ].
\end{equation} To prove our main result, we need the following auxiliary lemmas and Singer’s theorem on characterization of a best approximation from a subspace of C(X). By ![]() $C^{\ast }(X)$, we denote the class of regular real-valued measures of finite total variation defined on Borel subsets of
$C^{\ast }(X)$, we denote the class of regular real-valued measures of finite total variation defined on Borel subsets of ![]() $X.$
$X.$
Lemma 2.1. A measure ![]() $\mu \in C^{\ast }(X)$ is orthogonal to
$\mu \in C^{\ast }(X)$ is orthogonal to ![]() $A_{1}+A_{2}$ if and only if
$A_{1}+A_{2}$ if and only if
That is, for any Borel subsets ![]() $E_{i}\subset X_{i}$,
$E_{i}\subset X_{i}$, ![]() $i=1,2$,
$i=1,2$, ![]() $\mu
(s^{-1}(E_{1}))=0$ and
$\mu
(s^{-1}(E_{1}))=0$ and ![]() $\mu (p^{-1}(E_{2}))=0$.
$\mu (p^{-1}(E_{2}))=0$.
The proof of this lemma easily follows from Equation (2.1).
Lemma 2.2. The quotient spaces X 1 and X 2 are metrizable.
This lemma is a consequence of the following two facts:
(1) Let A be a family of functions continuous on a compact space X and r an equivalence relation defined by A:
 \begin{equation*}
x\overset{r}{\sim }y\quad \text{if }f(x)=f(y)\quad \text{for all }f\in A.
\end{equation*}
\begin{equation*}
x\overset{r}{\sim }y\quad \text{if }f(x)=f(y)\quad \text{for all }f\in A.
\end{equation*}Then the saturation r(F) of any closed set
 $F\subset X$ (
$F\subset X$ ( $r(F)\overset{def}
{=}\bigcup\nolimits_{x\in F}r(x)$; r(x) is the equivalence class of x) is closed, and hence the canonical projection
$r(F)\overset{def}
{=}\bigcup\nolimits_{x\in F}r(x)$; r(x) is the equivalence class of x) is closed, and hence the canonical projection  $\pi :X\rightarrow X/r$ is a closed mapping (see [Reference Khavinson and Khavinson10, p. 54]).
$\pi :X\rightarrow X/r$ is a closed mapping (see [Reference Khavinson and Khavinson10, p. 54]).(2) Let π be a closed continuous mapping of a metric space X onto a topological space Y. Then the following statements are all equivalent (see [Reference Stone18] and [Reference Herman7, Theorem 5.5]):
(a) Y satisfies the first countability axiom.
(b)
 $\mathbf{bd}(\pi ^{-1}(y))$ is compact for each
$\mathbf{bd}(\pi ^{-1}(y))$ is compact for each  $y\in Y$ (here
$y\in Y$ (here  $\mathbf{
bd}(\pi ^{-1}(y))$ denotes the boundary of
$\mathbf{
bd}(\pi ^{-1}(y))$ denotes the boundary of  $\pi ^{-1}(y)$).
$\pi ^{-1}(y)$).(c) Y is metrizable.
The following theorem plays an essential role in the proof of our main result.
Theorem 2.1. (see Singer [Reference Singer16])
Let X be a compact space, M be a linear subspace of C(X), ![]() $f\in C(X)\backslash M$ and
$f\in C(X)\backslash M$ and ![]() $
u_{0}\in M.$ Then u 0 is a best approximation in M to f if and only if there exists a regular Borel measure µ on X such that
$
u_{0}\in M.$ Then u 0 is a best approximation in M to f if and only if there exists a regular Borel measure µ on X such that
(1) The total variation
 $\left\Vert \mu \right\Vert =1$;
$\left\Vert \mu \right\Vert =1$;(2) µ is orthogonal to the subspace M, that is,
 $
\int_{X}u\,{\rm d}\mu =0$ for all
$
\int_{X}u\,{\rm d}\mu =0$ for all  $u\in M$;
$u\in M$;(3) For the Jordan decomposition
 $\mu =\mu ^{+}-\mu ^{-}$,
$\mu =\mu ^{+}-\mu ^{-}$,
 \begin{equation*}
f(x)-u_{0}(x)=\left\{
\begin{array}{c}
\left\Vert f-u_{0}\right\Vert\ \text{for }x\in \text{supp}(\mu ^{+})\text{,}
\\
-\left\Vert f-u_{0}\right\Vert\ \text{for }x\in \text{supp}(\mu ^{-})\text{,}
\end{array}
\right.
\end{equation*}
\begin{equation*}
f(x)-u_{0}(x)=\left\{
\begin{array}{c}
\left\Vert f-u_{0}\right\Vert\ \text{for }x\in \text{supp}(\mu ^{+})\text{,}
\\
-\left\Vert f-u_{0}\right\Vert\ \text{for }x\in \text{supp}(\mu ^{-})\text{,}
\end{array}
\right.
\end{equation*}
where supp![]() $(\mu ^{+})$ and supp
$(\mu ^{+})$ and supp![]() $(\mu ^{-})$ are closed supports of the positive measures
$(\mu ^{-})$ are closed supports of the positive measures ![]() $\mu ^{+}$ and µ −, respectively.
$\mu ^{+}$ and µ −, respectively.
Our main result is the following theorem.
Theorem 2.2. Assume X is a compact metric space. A function ![]() $u_{0}\in A_{1}+A_{2}$ is a best approximation to a function
$u_{0}\in A_{1}+A_{2}$ is a best approximation to a function ![]() $f\in
C(X)$ if and only if there exists a closed or infinite bolt extremal for the function
$f\in
C(X)$ if and only if there exists a closed or infinite bolt extremal for the function ![]() $f-u_{0}$.
$f-u_{0}$.
Proof. Necessity. Assume u 0 is a best approximation from ![]() $A_{1}+A_{2}$ to f. Since
$A_{1}+A_{2}$ to f. Since ![]() $A_{1}+A_{2}$ is a subspace of C(X), we have a regular Borel measure µ satisfying the conditions (1)–(3) of Theorem 2.1.
$A_{1}+A_{2}$ is a subspace of C(X), we have a regular Borel measure µ satisfying the conditions (1)–(3) of Theorem 2.1.
Take any point x 0 in supp![]() $(\mu ^{+})$ and consider the point
$(\mu ^{+})$ and consider the point ![]() $
y_{0}=s(x_{0})$ in X 1. Since by Lemma 2.2, X 1 is metrizable (hence first countable), there is a nested countable open neighbourhood basis at y 0. Denote this basis by
$
y_{0}=s(x_{0})$ in X 1. Since by Lemma 2.2, X 1 is metrizable (hence first countable), there is a nested countable open neighbourhood basis at y 0. Denote this basis by ![]() $\{O_{n}(y_{0})\}_{n=1}^{\infty }$. For each n,
$\{O_{n}(y_{0})\}_{n=1}^{\infty }$. For each n, ![]() $\mu ^{+}\left[ s^{-1}(O_{n}(y_{0}))\right] \gt 0$, since
$\mu ^{+}\left[ s^{-1}(O_{n}(y_{0}))\right] \gt 0$, since ![]() $
s^{-1}(O_{n}(y_{0}))$ is an open set containing x 0. By Lemma 2.1,
$
s^{-1}(O_{n}(y_{0}))$ is an open set containing x 0. By Lemma 2.1, ![]() $\mu
\left[ s^{-1}(O_{n}(y_{0}))\right] =0$. Therefore,
$\mu
\left[ s^{-1}(O_{n}(y_{0}))\right] =0$. Therefore, ![]() $\mu ^{-}\left[
s^{-1}(O_{n}(y_{0}))\right] \gt 0$. It follows that for each n, the intersection
$\mu ^{-}\left[
s^{-1}(O_{n}(y_{0}))\right] \gt 0$. It follows that for each n, the intersection ![]() $s^{-1}(O_{n}(y_{0}))\cap \text{supp}(\mu ^{-})$ is not empty. Take now any points
$s^{-1}(O_{n}(y_{0}))\cap \text{supp}(\mu ^{-})$ is not empty. Take now any points ![]() $z_{n}\in s^{-1}(O_{n}(y_{0}))\cap \text{supp}(\mu ^{-})$,
$z_{n}\in s^{-1}(O_{n}(y_{0}))\cap \text{supp}(\mu ^{-})$, ![]() $
n=1,2,\ldots$. Since supp
$
n=1,2,\ldots$. Since supp![]() $(\mu ^{-})$ is sequentially compact (as a closed set in a compact metric space), the sequence
$(\mu ^{-})$ is sequentially compact (as a closed set in a compact metric space), the sequence ![]() $\{z_{n}\}_{n=1}^{\infty }$ or a subsequence of it converges to a point x 1 in supp
$\{z_{n}\}_{n=1}^{\infty }$ or a subsequence of it converges to a point x 1 in supp![]() $(\mu ^{-})$. We may assume without loss of generality that
$(\mu ^{-})$. We may assume without loss of generality that ![]() $z_{n}\rightarrow x_{1}$, as
$z_{n}\rightarrow x_{1}$, as ![]() $
n\rightarrow \infty $. Since for any n,
$
n\rightarrow \infty $. Since for any n, ![]() $s(z_{n})\in O_{n}(y_{0})$ and
$s(z_{n})\in O_{n}(y_{0})$ and ![]() $
\{O_{n}(y_{0})\}_{n=1}^{\infty }$ is a nested neighbourhood basis, we obtain that
$
\{O_{n}(y_{0})\}_{n=1}^{\infty }$ is a nested neighbourhood basis, we obtain that ![]() $s(z_{n})\rightarrow y_{0}$, as
$s(z_{n})\rightarrow y_{0}$, as ![]() $n\rightarrow \infty $. On the other hand, since s is continuous,
$n\rightarrow \infty $. On the other hand, since s is continuous, ![]() $s(z_{n})\rightarrow s(x_{1})$, as
$s(z_{n})\rightarrow s(x_{1})$, as ![]() $
n\rightarrow \infty $. It follows that
$
n\rightarrow \infty $. It follows that ![]() $s(x_{1})=y_{0}=s(x_{0})$. Note that
$s(x_{1})=y_{0}=s(x_{0})$. Note that ![]() $
x_{0}\in \text{supp}(\mu ^{+})$ and
$
x_{0}\in \text{supp}(\mu ^{+})$ and ![]() $x_{1}\in \text{supp}(\mu ^{-})$.
$x_{1}\in \text{supp}(\mu ^{-})$.
Changing s and ![]() $\mu ^{+}$ to p and µ −, correspondingly, repeat the above process with the point
$\mu ^{+}$ to p and µ −, correspondingly, repeat the above process with the point ![]() $y_{1}=p(x_{1})$ and a nested countable neighbourhood basis at y 1. Then we obtain a point
$y_{1}=p(x_{1})$ and a nested countable neighbourhood basis at y 1. Then we obtain a point ![]() $x_{2}\in \text{supp}(\mu
^{+})$ such that
$x_{2}\in \text{supp}(\mu
^{+})$ such that ![]() $p(x_{2})=p(x_{1}).$ Continuing this process, we can construct points
$p(x_{2})=p(x_{1}).$ Continuing this process, we can construct points ![]() $x_{3}\in \text{supp}(\mu ^{-})$ ,
$x_{3}\in \text{supp}(\mu ^{-})$ , ![]() $x_{4}\in $supp
$x_{4}\in $supp![]() $(\mu ^{+})$, and so on. Note that the set of all constructed points xi,
$(\mu ^{+})$, and so on. Note that the set of all constructed points xi, ![]() $
i=0,1,\ldots, $ forms a bolt. By Theorem 2.1, this bolt is extremal for the function
$
i=0,1,\ldots, $ forms a bolt. By Theorem 2.1, this bolt is extremal for the function ![]() $f-u_{0}$.
$f-u_{0}$.
Sufficiency. The main idea in this part is the application of the Banach–Alaoglu theorem on weak![]() $^{\text{*}}$ sequential compactness of the closed unit ball in
$^{\text{*}}$ sequential compactness of the closed unit ball in ![]() $E^{\ast }$ for a separable Banach space E (see, e.g., Rudin [Reference Rudin15, p. 66]). Note that since X is a compact metric space, the space C(X) is separable. Thus, the closed unit ball B of the continuous dual of C(X) is sequentially compact, which means that any sequence in B has a convergent subsequence converging to a point in B.
$E^{\ast }$ for a separable Banach space E (see, e.g., Rudin [Reference Rudin15, p. 66]). Note that since X is a compact metric space, the space C(X) is separable. Thus, the closed unit ball B of the continuous dual of C(X) is sequentially compact, which means that any sequence in B has a convergent subsequence converging to a point in B.
With each bolt ![]() $l=\{x_{1},\ldots,x_{n}\}$ with respect to A 1 and A 2, we associate the following bolt functional
$l=\{x_{1},\ldots,x_{n}\}$ with respect to A 1 and A 2, we associate the following bolt functional
 \begin{equation*}
r_{l}(F)=\frac{1}{n}\sum_{i=1}^{n}(-1)^{n+1}F(x_{i}).
\end{equation*}
\begin{equation*}
r_{l}(F)=\frac{1}{n}\sum_{i=1}^{n}(-1)^{n+1}F(x_{i}).
\end{equation*} It is an exercise to check that rl is a linear bounded functional on C(X) with the norm ![]() $\left\Vert r_{l}\right\Vert \leq 1$ and
$\left\Vert r_{l}\right\Vert \leq 1$ and ![]() $\left\Vert
r_{l}\right\Vert =1$ if and only if the set of points xi with odd indices i does not intersect with the set of points with even indices. Besides, if l is closed, then
$\left\Vert
r_{l}\right\Vert =1$ if and only if the set of points xi with odd indices i does not intersect with the set of points with even indices. Besides, if l is closed, then ![]() $r_{l}\in (A_{1}+A_{2})^{\perp },$ where
$r_{l}\in (A_{1}+A_{2})^{\perp },$ where ![]() $
(A_{1}+A_{2})^{\perp }$ is the annihilator of the subspace
$
(A_{1}+A_{2})^{\perp }$ is the annihilator of the subspace ![]() $
A_{1}+A_{2}\subset C(X).$ If l is not closed, then rl is generally not an annihilating functional. However, it satisfies the following important inequality
$
A_{1}+A_{2}\subset C(X).$ If l is not closed, then rl is generally not an annihilating functional. However, it satisfies the following important inequality
 \begin{equation}
\left\vert r_{l}(v_{i})\right\vert \leq \frac{2}{n}\left\Vert
v_{i}\right\Vert ,
\end{equation}
\begin{equation}
\left\vert r_{l}(v_{i})\right\vert \leq \frac{2}{n}\left\Vert
v_{i}\right\Vert ,
\end{equation}for all ![]() $v_{i}\in A_{i}$,
$v_{i}\in A_{i}$, ![]() $i=1,2$. This inequality means that for bolts l with sufficiently large number of points, rl behaves like an annihilating functional on each Ai, and hence on
$i=1,2$. This inequality means that for bolts l with sufficiently large number of points, rl behaves like an annihilating functional on each Ai, and hence on ![]() $A_{1}+A_{2}$. To see the validity of Equation (2.2), it is enough to recall that
$A_{1}+A_{2}$. To see the validity of Equation (2.2), it is enough to recall that ![]() $v_{1}=$
$v_{1}=$ ![]() $g\circ s$,
$g\circ s$, ![]() $
v_{2}=$
$
v_{2}=$ ![]() $h\circ p$ and consider the chain of equalities
$h\circ p$ and consider the chain of equalities ![]() $
g(s(x_{1}))=g(s(x_{2})),$
$
g(s(x_{1}))=g(s(x_{2})),$ ![]() $g(s(x_{3}))=g(s(x_{4})),\ldots$ (or
$g(s(x_{3}))=g(s(x_{4})),\ldots$ (or ![]() $g(s(x_{2}))=g(s(x_{3})),$
$g(s(x_{2}))=g(s(x_{3})),$ ![]() $g(s(x_{4}))=g(s(x_{5})),\ldots$) for
$g(s(x_{4}))=g(s(x_{5})),\ldots$) for ![]() $v_{1}(x)=g(s(x))$ and similar equalities for
$v_{1}(x)=g(s(x))$ and similar equalities for ![]() $v_{2}(x)=h(p(x))$.
$v_{2}(x)=h(p(x))$.
Returning to the sufficiency part of the theorem, note that there may be two cases. The first case happens when there exists a closed bolt ![]() $
l=\{x_{1},\ldots,x_{2n}\}$ extremal for
$
l=\{x_{1},\ldots,x_{2n}\}$ extremal for ![]() $f-u_{0}.$ In this case, it is not difficult to verify that u 0 is a best approximation. Indeed, on the one hand, the following equalities are valid:
$f-u_{0}.$ In this case, it is not difficult to verify that u 0 is a best approximation. Indeed, on the one hand, the following equalities are valid:
On the other hand, for any function ![]() $u\in A_{1}+A_{2}$, we have
$u\in A_{1}+A_{2}$, we have
Thus, ![]() $\left\Vert f-u_{0}\right\Vert \leq \left\Vert f-u\right\Vert $ for any
$\left\Vert f-u_{0}\right\Vert \leq \left\Vert f-u\right\Vert $ for any ![]() $u\in A_{1}+A_{2}$. That is, u 0 is a best approximation.
$u\in A_{1}+A_{2}$. That is, u 0 is a best approximation.
The second case is the existence of an infinite bolt ![]() $l=\{x_{1},x_{2},\ldots\}$ extremal for
$l=\{x_{1},x_{2},\ldots\}$ extremal for ![]() $f-u_{0}$. In this case, we proceed as follows. From l, we form the finite bolts
$f-u_{0}$. In this case, we proceed as follows. From l, we form the finite bolts ![]() $l_{k}=\{x_{1},\ldots,x_{k}\},$
$l_{k}=\{x_{1},\ldots,x_{k}\},$ ![]() $k=1,2,\ldots$, and consider the bolt functionals
$k=1,2,\ldots$, and consider the bolt functionals ![]() $r_{l_{k}}$. For the ease of notation, let us put
$r_{l_{k}}$. For the ease of notation, let us put ![]() $r_{k}=r_{l_{k}}.$ The sequence
$r_{k}=r_{l_{k}}.$ The sequence ![]() $\{r_{_{k}}\}_{k=1}^{\infty }$ is contained in the closed unit ball of the dual space
$\{r_{_{k}}\}_{k=1}^{\infty }$ is contained in the closed unit ball of the dual space ![]() $C^{\ast }(X).$ By the Banach–Alaoglu theorem, the sequence
$C^{\ast }(X).$ By the Banach–Alaoglu theorem, the sequence ![]() $\{r_{_{k}}\}_{k=1}^{\infty }$ must have weak
$\{r_{_{k}}\}_{k=1}^{\infty }$ must have weak![]() $^{\text{*}}$ cluster points. Assume
$^{\text{*}}$ cluster points. Assume ![]() $r^{\ast }$ is one of them. Without loss of generality, we may assume that
$r^{\ast }$ is one of them. Without loss of generality, we may assume that  $r_{k}\overset{{\textrm weak}^{\ast }}{
\longrightarrow }r^{\ast },$ as
$r_{k}\overset{{\textrm weak}^{\ast }}{
\longrightarrow }r^{\ast },$ as ![]() $k\rightarrow \infty .$ From Equation (2.2) it follows that
$k\rightarrow \infty .$ From Equation (2.2) it follows that ![]() $r^{\ast }(v_{1}+v_{2})=0,$ for any
$r^{\ast }(v_{1}+v_{2})=0,$ for any ![]() $v_{i}\in A_{i},$
$v_{i}\in A_{i},$ ![]() $i=1,2$. That is,
$i=1,2$. That is, ![]() $r^{\ast }$ belongs to the annihilator of the subspace
$r^{\ast }$ belongs to the annihilator of the subspace ![]() $A_{1}+A_{2}$. Since we have also
$A_{1}+A_{2}$. Since we have also ![]() $\left\Vert r^{\ast }\right\Vert \leq 1,$ it follows that
$\left\Vert r^{\ast }\right\Vert \leq 1,$ it follows that
for all functions ![]() $u\in A_{1}+A_{2}.$ On the other hand, since the infinite bolt
$u\in A_{1}+A_{2}.$ On the other hand, since the infinite bolt ![]() $\{x_{1},x_{2},\ldots\}$ is extremal for
$\{x_{1},x_{2},\ldots\}$ is extremal for ![]() $f-u_{0},$
$f-u_{0},$
Hence,
From Equations (2.3) and (2.4), we obtain that
for all ![]() $u\in A_{1}+A_{2}.$ This means that u 0 is a best approximation to f.
$u\in A_{1}+A_{2}.$ This means that u 0 is a best approximation to f.
Remark 1. In [Reference Asgarova and Ismailov2], Theorem 2.2 was proved under additional assumption that the algebras have the C-property, that is, for any ![]() $w\in
C(X)$, the functions
$w\in
C(X)$, the functions
 \begin{eqnarray*}
g_{1}(a) &=&\max_{\substack{x\in X \\ s(x)=a}}w(x),\text{}g_{2}(a)=\min
_{\substack{x\in X \\ s(x)=a}}w(x),\text{}a\in X_{1}, \\
h_{1}(b) &=&\max_{\substack{x\in X \\ p(x)=b}}w(x),\text{}h_{2}(b)=\min
_{\substack{x\in X \\ p(x)=b}}w(x),\text{}b\in X_{2}
\end{eqnarray*}
\begin{eqnarray*}
g_{1}(a) &=&\max_{\substack{x\in X \\ s(x)=a}}w(x),\text{}g_{2}(a)=\min
_{\substack{x\in X \\ s(x)=a}}w(x),\text{}a\in X_{1}, \\
h_{1}(b) &=&\max_{\substack{x\in X \\ p(x)=b}}w(x),\text{}h_{2}(b)=\min
_{\substack{x\in X \\ p(x)=b}}w(x),\text{}b\in X_{2}
\end{eqnarray*}are continuous.
Remark 2. Note that in the special case when ![]() $X\subset \mathbb{R}^{2}$ and
$X\subset \mathbb{R}^{2}$ and ![]() $s,p$ are the coordinate functions, a Chebyshev-type alternation theorem was first obtained by Havinson [Reference Havinson9]. In [Reference Ismailov8], similar alternation theorems were proved for ridge functions and certain function compositions.
$s,p$ are the coordinate functions, a Chebyshev-type alternation theorem was first obtained by Havinson [Reference Havinson9]. In [Reference Ismailov8], similar alternation theorems were proved for ridge functions and certain function compositions.
Remark 3. Note that characterization of a best approximation from a sum of more than two subalgebras ![]() $A_{1},\ldots,A_{k}$ of C(X) seems to be beyond the scope of the methods discussed herein. A bolt with respect to two algebras A 1 and A 2 is constructed as a sequence of points
$A_{1},\ldots,A_{k}$ of C(X) seems to be beyond the scope of the methods discussed herein. A bolt with respect to two algebras A 1 and A 2 is constructed as a sequence of points ![]() $
\{x_{1},x_{2},\ldots\}$ with the links
$
\{x_{1},x_{2},\ldots\}$ with the links ![]() $x_{i}x_{i+1}$ travelling alternatively in equivalence classes of the relations R 1 and R 2 (see above). In this case, the bolt functional rl has important property (2.2), which leads to the functional
$x_{i}x_{i+1}$ travelling alternatively in equivalence classes of the relations R 1 and R 2 (see above). In this case, the bolt functional rl has important property (2.2), which leads to the functional ![]() $r^{\ast }$ annihilating all elements of the sum
$r^{\ast }$ annihilating all elements of the sum ![]() $
A_{1}+A_{2}$. The problem becomes complicated when the number of summands in the sum
$
A_{1}+A_{2}$. The problem becomes complicated when the number of summands in the sum ![]() $A_{1}+\cdots +A_{k}$ is more than two. The simple generalization of bolts demands a sequence of points
$A_{1}+\cdots +A_{k}$ is more than two. The simple generalization of bolts demands a sequence of points ![]() $\{x_{1},x_{2},\ldots\}$ with the links
$\{x_{1},x_{2},\ldots\}$ with the links ![]() $x_{i}x_{i+1}$ travelling in three or more alternating equivalence classes. But in this case, the number 2 in Equation (2.2) grows unboundedly as n tends to infinity, and we cannot arrive at any annihilating functional like
$x_{i}x_{i+1}$ travelling in three or more alternating equivalence classes. But in this case, the number 2 in Equation (2.2) grows unboundedly as n tends to infinity, and we cannot arrive at any annihilating functional like ![]() $r^{\ast }$. For
$r^{\ast }$. For ![]() $k\geq 3$, we do not know a reasonable description of a sequence of points
$k\geq 3$, we do not know a reasonable description of a sequence of points ![]() $\{x_{1},x_{2},\ldots\}$ and functionals
$\{x_{1},x_{2},\ldots\}$ and functionals ![]() $r_{l_{n}}$, associated with the first n points
$r_{l_{n}}$, associated with the first n points ![]() $
x_{1},\ldots,x_{n}$, such that any weak
$
x_{1},\ldots,x_{n}$, such that any weak![]() $^{\text{*}}$ cluster point of the sequence
$^{\text{*}}$ cluster point of the sequence ![]() $\{r_{l_{n}}\}_{n=1}^{\infty }$ is orthogonal to the sum
$\{r_{l_{n}}\}_{n=1}^{\infty }$ is orthogonal to the sum ![]() $
A_{1}+\cdots +A_{k}$. We refer the interested reader to Sternfeld [Reference Sternfeld17] for discussions on differences between the cases of two and more than two algebras.
$
A_{1}+\cdots +A_{k}$. We refer the interested reader to Sternfeld [Reference Sternfeld17] for discussions on differences between the cases of two and more than two algebras.
Competing interests
The authors declare none.