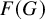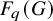1 Introduction
1.1 Categorical approach to quantum groups
Let G be an affine algebraic group over a field k. The Tannaka duality theorems [Reference Rivano71, Reference Deligne25] imply that one can uniquely reconstruct G from the data of a symmetric monoidal category
![]() $\operatorname {\mathrm {Rep}}(G)$
of G-representations and the forgetful symmetric monoidal functor
$\operatorname {\mathrm {Rep}}(G)$
of G-representations and the forgetful symmetric monoidal functor
Namely, F admits a right adjoint
![]() $F^{\mathrm {R}}\colon \mathrm {Vect}\rightarrow \operatorname {\mathrm {Rep}}(G)$
, and the algebra
$F^{\mathrm {R}}\colon \mathrm {Vect}\rightarrow \operatorname {\mathrm {Rep}}(G)$
, and the algebra
![]() $\mathcal {O}(G)$
of polynomial functions on G can be reconstructed as
$\mathcal {O}(G)$
of polynomial functions on G can be reconstructed as
where the Hopf algebra structure on
![]() $\mathcal {O}(G)$
is reconstructed from the monoidal structure on F.
$\mathcal {O}(G)$
is reconstructed from the monoidal structure on F.
Suppose G is a reductive algebraic group,
![]() $q\in \mathbf {C}^\times $
, and consider the category
$q\in \mathbf {C}^\times $
, and consider the category
![]() $\operatorname {\mathrm {Rep}}_q(G)$
of representations of the quantum group with divided powers [Reference Lusztig62, Reference Chari and Pressley21]. Then
$\operatorname {\mathrm {Rep}}_q(G)$
of representations of the quantum group with divided powers [Reference Lusztig62, Reference Chari and Pressley21]. Then
![]() $\operatorname {\mathrm {Rep}}_q(G)$
carries a natural braided monoidal structure, and the forgetful functor
$\operatorname {\mathrm {Rep}}_q(G)$
carries a natural braided monoidal structure, and the forgetful functor
is merely monoidal. In the same way, the Hopf algebra
![]() $\mathcal {O}_q(G)$
of functions on the quantum group is reconstructed as
$\mathcal {O}_q(G)$
of functions on the quantum group is reconstructed as
![]() $FF^{\mathrm {R}}(k)$
.
$FF^{\mathrm {R}}(k)$
.
The failure of the forgetful functor to preserve the braiding is captured by the R-matrix (see Theorem 2.27): that is, a collection of maps
for two representations
![]() $V,W\in \operatorname {\mathrm {Rep}}_q(G)$
. Moreover, for three representations
$V,W\in \operatorname {\mathrm {Rep}}_q(G)$
. Moreover, for three representations
![]() $U,V,W\in \operatorname {\mathrm {Rep}}_q(G)$
, the R-matrix satisfies the Yang–Baxter equation
$U,V,W\in \operatorname {\mathrm {Rep}}_q(G)$
, the R-matrix satisfies the Yang–Baxter equation
in
![]() $\mathrm {End}(U\otimes V\otimes W)$
.
$\mathrm {End}(U\otimes V\otimes W)$
.
1.2 Dynamical quantum groups
In several areas of mathematical physics, a version of the above equation has appeared for a dynamical R-matrix
![]() $R_{V, W}(\lambda )\colon V\otimes W\rightarrow V\otimes W$
, which depends on a parameter
$R_{V, W}(\lambda )\colon V\otimes W\rightarrow V\otimes W$
, which depends on a parameter
![]() $\lambda \in \mathfrak {h}^*$
(dual space of the Cartan subalgebra
$\lambda \in \mathfrak {h}^*$
(dual space of the Cartan subalgebra
![]() $\mathfrak {h}\subset \mathfrak {g}$
); the corresponding dynamical Yang–Baxter equation is
$\mathfrak {h}\subset \mathfrak {g}$
); the corresponding dynamical Yang–Baxter equation is
where the shifts refer to the
![]() $\mathfrak {h}$
-weights of the corresponding elements of
$\mathfrak {h}$
-weights of the corresponding elements of
![]() $U\otimes V\otimes W$
. We refer to
$U\otimes V\otimes W$
. We refer to
![]() $\mathrm {U}\mathfrak {h}\cong \mathcal {O}(\mathfrak {h}^*)$
as the base of the dynamical quantum group. As explained by Felder [Reference Felder41], equation (4) is closely related to the star-triangle relation for face-type statistical mechanical models [Reference Baxter6]. Moreover, it naturally appears in the description of the exchange algebra in the Liouville and Toda conformal field theories [Reference Gervais and Neveu43]. The study of the dynamical R-matrix gave rise to the theory of dynamical quantum groups; see [Reference Etingof and Schiffmann35, Reference Etingof33] for reviews.
$\mathrm {U}\mathfrak {h}\cong \mathcal {O}(\mathfrak {h}^*)$
as the base of the dynamical quantum group. As explained by Felder [Reference Felder41], equation (4) is closely related to the star-triangle relation for face-type statistical mechanical models [Reference Baxter6]. Moreover, it naturally appears in the description of the exchange algebra in the Liouville and Toda conformal field theories [Reference Gervais and Neveu43]. The study of the dynamical R-matrix gave rise to the theory of dynamical quantum groups; see [Reference Etingof and Schiffmann35, Reference Etingof33] for reviews.
On the classical level, ordinary quantum groups correspond to Poisson-Lie structures on G [Reference Drinfeld30]. Similarly, dynamical quantum groups correspond to dynamical Poisson groupoid structures on the trivial groupoid
![]() $\mathfrak {h}^*\times G\times \mathfrak {h}^*\rightrightarrows \mathfrak {h}^*$
(see [Reference Laurent-Gengoux, Stiénon and Ping59] for Poisson groupoids and [Reference Etingof and Varchenko36] for the dynamical version). After quantisation, ordinary quantum groups become Hopf algebras, while dynamical quantum groups become bialgebroids or Hopf algebroids (see [Reference Takeuchi82] for the original definition of bialgebroids, [Reference Jiang-Hua61, Reference Ping92] for Hopf algebroids and [Reference Etingof and Varchenko37] for the dynamical version).
$\mathfrak {h}^*\times G\times \mathfrak {h}^*\rightrightarrows \mathfrak {h}^*$
(see [Reference Laurent-Gengoux, Stiénon and Ping59] for Poisson groupoids and [Reference Etingof and Varchenko36] for the dynamical version). After quantisation, ordinary quantum groups become Hopf algebras, while dynamical quantum groups become bialgebroids or Hopf algebroids (see [Reference Takeuchi82] for the original definition of bialgebroids, [Reference Jiang-Hua61, Reference Ping92] for Hopf algebroids and [Reference Etingof and Varchenko37] for the dynamical version).
One is naturally led to wonder about the categorical interpretation of dynamical quantum groups similar to the categorical interpretation in equation (2) of ordinary quantum groups explained above. Our first goal is to develop such an approach (inspired by a previous work by Donin and Mudrov [Reference Donin and Mudrov28, Reference Donin and Mudrov29]) and prove Tannaka-type reconstruction statements.
1.3 Dynamical quantum groups via Harish-Chandra bimodules
An important object in representation theory is the category
![]() $\mathrm {HC}(G)$
of Harish-Chandra bimodules: the monoidal category of
$\mathrm {HC}(G)$
of Harish-Chandra bimodules: the monoidal category of
![]() $\mathrm {U}\mathfrak {g}$
-bimodules with an integrable diagonal action. As we will explain shortly, the theory of dynamical quantum groups turns out to be closely related to the category
$\mathrm {U}\mathfrak {g}$
-bimodules with an integrable diagonal action. As we will explain shortly, the theory of dynamical quantum groups turns out to be closely related to the category
![]() $\mathrm {HC}(H)$
of Harish-Chandra bimodules for a torus H. In the main body of the paper (see section 3.1), we present a general formalism that incorporates classical and quantum examples as well as nonabelian bases (following [Reference Safronov73]), but for simplicity here we stick to the case of
$\mathrm {HC}(H)$
of Harish-Chandra bimodules for a torus H. In the main body of the paper (see section 3.1), we present a general formalism that incorporates classical and quantum examples as well as nonabelian bases (following [Reference Safronov73]), but for simplicity here we stick to the case of
![]() $\mathrm {HC}(H)$
.
$\mathrm {HC}(H)$
.
First, we introduce the notion of a Harish-Chandra bialgebroid, which is an
![]() $\mathfrak {h}$
-bialgebroid introduced in [Reference Etingof and Varchenko37, Section 4.1] with certain integrability assumptions; see Theorem 3.29 for the general definition and Theorem 3.30 for the case of
$\mathfrak {h}$
-bialgebroid introduced in [Reference Etingof and Varchenko37, Section 4.1] with certain integrability assumptions; see Theorem 3.29 for the general definition and Theorem 3.30 for the case of
![]() $\mathrm {HC}(H)$
. Namely, it is a bigraded algebra
$\mathrm {HC}(H)$
. Namely, it is a bigraded algebra
![]() $B=\oplus _{\alpha , \beta \in \Lambda } B_{\alpha \beta }$
, where
$B=\oplus _{\alpha , \beta \in \Lambda } B_{\alpha \beta }$
, where
![]() $\Lambda $
is the character lattice of H, together with two quantum moment maps
$\Lambda $
is the character lattice of H, together with two quantum moment maps
![]() $s,t\colon \mathcal {O}(\mathfrak {h}^*)\rightarrow B$
, a coproduct
$s,t\colon \mathcal {O}(\mathfrak {h}^*)\rightarrow B$
, a coproduct
![]() $\Delta \colon B\rightarrow B\times _{\mathrm {U}\mathfrak {h}} B$
, where the Takeuchi product introduced in [Reference Takeuchi82] is
$\Delta \colon B\rightarrow B\times _{\mathrm {U}\mathfrak {h}} B$
, where the Takeuchi product introduced in [Reference Takeuchi82] is
and a counit
![]() $\epsilon \colon B\rightarrow \mathrm {D}(H)$
into the algebra of differential operators on H. We prove the following equivalent characterisation of Harish-Chandra bialgebroids (see Theorem 3.32).
$\epsilon \colon B\rightarrow \mathrm {D}(H)$
into the algebra of differential operators on H. We prove the following equivalent characterisation of Harish-Chandra bialgebroids (see Theorem 3.32).
Theorem. A colimit-preserving lax monoidal comonad
![]() $\bot \colon \mathrm {HC}(H)\rightarrow \mathrm {HC}(H)$
is the same as a Harish-Chandra bialgebroid B, so
$\bot \colon \mathrm {HC}(H)\rightarrow \mathrm {HC}(H)$
is the same as a Harish-Chandra bialgebroid B, so
![]() $\bot (M) = B\times _{\mathrm {U}\mathfrak {h}} M$
.
$\bot (M) = B\times _{\mathrm {U}\mathfrak {h}} M$
.
We may similarly define comodules over a Harish-Chandra bialgebroid in terms of a
![]() $\Lambda $
-graded
$\Lambda $
-graded
![]() $\mathcal {O}(\mathfrak {h}^*)$
-module
$\mathcal {O}(\mathfrak {h}^*)$
-module
![]() $M=\oplus _{\alpha \in \Lambda } M_\alpha $
together with a coaction map
$M=\oplus _{\alpha \in \Lambda } M_\alpha $
together with a coaction map
![]() $M\rightarrow B\times _{\mathrm {U}\mathfrak {h}} M$
. We prove the following Tannaka reconstruction theorem (see Theorem 3.35).
$M\rightarrow B\times _{\mathrm {U}\mathfrak {h}} M$
. We prove the following Tannaka reconstruction theorem (see Theorem 3.35).
Theorem. Suppose
![]() $\mathcal {D}$
is a monoidal category with a monoidal functor
$\mathcal {D}$
is a monoidal category with a monoidal functor
![]() $F\colon \mathcal {D} \rightarrow \mathrm {HC}(H)$
that admits a colimit-preserving right adjoint
$F\colon \mathcal {D} \rightarrow \mathrm {HC}(H)$
that admits a colimit-preserving right adjoint
![]() $F^{\mathrm {R}}\colon \mathrm {HC}(H)\rightarrow \mathcal {D}$
. Then there is a Harish-Chandra bialgebroid B such that
$F^{\mathrm {R}}\colon \mathrm {HC}(H)\rightarrow \mathcal {D}$
. Then there is a Harish-Chandra bialgebroid B such that
![]() $(F\circ F^{\mathrm {R}})(-)\cong B\times _{\mathrm {U}\mathfrak {h}}(-)$
and F factors through a monoidal functor
$(F\circ F^{\mathrm {R}})(-)\cong B\times _{\mathrm {U}\mathfrak {h}}(-)$
and F factors through a monoidal functor
If F is conservative and preserves equalisers, the above functor is an equivalence.
Let us now explain the origin of dynamical R-matrices. Assume that
![]() $\mathcal {D}$
, in addition, has a braided monoidal structure. Moreover, assume that the functor
$\mathcal {D}$
, in addition, has a braided monoidal structure. Moreover, assume that the functor
![]() $F\colon \mathcal {D}\rightarrow \mathrm {HC}(H)$
lands in free Harish-Chandra bimodules: that is, there is a functor
$F\colon \mathcal {D}\rightarrow \mathrm {HC}(H)$
lands in free Harish-Chandra bimodules: that is, there is a functor
![]() $F'\colon \mathcal {D}\rightarrow \operatorname {\mathrm {Rep}}(H)$
and an equivalence
$F'\colon \mathcal {D}\rightarrow \operatorname {\mathrm {Rep}}(H)$
and an equivalence
![]() $F(x)\cong \mathrm {U}\mathfrak {h}\otimes F'(x)$
for any object
$F(x)\cong \mathrm {U}\mathfrak {h}\otimes F'(x)$
for any object
![]() $x\in \mathcal {D}$
. The following is Theorem 4.11.
$x\in \mathcal {D}$
. The following is Theorem 4.11.
Proposition. Under the above assumptions, the image of the braiding under
![]() $F\colon \mathcal {D}\rightarrow \mathrm {HC}(H)$
gives rise to dynamical R-matrices
$F\colon \mathcal {D}\rightarrow \mathrm {HC}(H)$
gives rise to dynamical R-matrices
![]() $R\colon \mathfrak {h}^*\rightarrow \mathrm {End}(F'(x)\otimes F'(y))$
satisfying the dynamical Yang–Baxter equation (4).
$R\colon \mathfrak {h}^*\rightarrow \mathrm {End}(F'(x)\otimes F'(y))$
satisfying the dynamical Yang–Baxter equation (4).
The above proposition is a direct quantum analogue of an interpretation of classical dynamical r-matrices in terms of 1-shifted Poisson morphisms (see [Reference Calaque, Pantev, Toën, Vaquié and Vezzosi20] for what this means)
![]() $[\mathfrak {h}^*/H]\rightarrow \mathrm {B} G$
; see [Reference Safronov74, Proposition 5.7].
$[\mathfrak {h}^*/H]\rightarrow \mathrm {B} G$
; see [Reference Safronov74, Proposition 5.7].
Let us compare these results to Tannaka reconstruction results for bialgebroids proven in [Reference Szlachányi81, Reference Shimizu77]. Suppose R is a ring. It is shown in [Reference Szlachányi81, Theorem 5.4] that a colimit-preserving oplax monoidal monad on the category
![]() ${}_{R}\mathrm {BMod}_{R}$
of R-bimodules is the same as a bialgebroid over R. Comparing it to our Theorem 3.32, the difference is that we work with lax monoidal comonads instead, replace
${}_{R}\mathrm {BMod}_{R}$
of R-bimodules is the same as a bialgebroid over R. Comparing it to our Theorem 3.32, the difference is that we work with lax monoidal comonads instead, replace
![]() ${}_{\mathrm {U}\mathfrak {h}}\mathrm {BMod}_{\mathrm {U}\mathfrak {h}}$
by the full subcategory
${}_{\mathrm {U}\mathfrak {h}}\mathrm {BMod}_{\mathrm {U}\mathfrak {h}}$
by the full subcategory
![]() $\mathrm {HC}(H)$
of Harish-Chandra bimodules and replace Takeuchi’s bialgebroids by Harish-Chandra bialgebroids (i.e., adding an extra integrability assumption).
$\mathrm {HC}(H)$
of Harish-Chandra bimodules and replace Takeuchi’s bialgebroids by Harish-Chandra bialgebroids (i.e., adding an extra integrability assumption).
Szlachányi [Reference Szlachányi81, Theorem 3.6] has proven a Tannaka-type reconstruction result for monoidal functors
![]() $F\colon \mathcal {D}\rightarrow {}_{R}\mathrm {BMod}_{R}$
admitting left adjoints in terms of modules over the corresponding bialgebroid. Shimizu has also proven a version of such a Tannaka reconstruction result in terms of comodules over the bialgebroid (see [Reference Shimizu77, Theorem 4.3, Lemma 4.18]).
$F\colon \mathcal {D}\rightarrow {}_{R}\mathrm {BMod}_{R}$
admitting left adjoints in terms of modules over the corresponding bialgebroid. Shimizu has also proven a version of such a Tannaka reconstruction result in terms of comodules over the bialgebroid (see [Reference Shimizu77, Theorem 4.3, Lemma 4.18]).
1.4 Parabolic restriction
Two standard dynamical quantum groups
![]() $F(G)$
and
$F(G)$
and
![]() $F_q(G)$
are introduced in [Reference Etingof and Varchenko31, Section 5] in terms of the so-called exchange construction. Here
$F_q(G)$
are introduced in [Reference Etingof and Varchenko31, Section 5] in terms of the so-called exchange construction. Here
![]() $F(G)$
quantises the standard rational dynamical r-matrix and
$F(G)$
quantises the standard rational dynamical r-matrix and
![]() $F_q(G)$
quantises the standard trigonometric dynamical r-matrix (see [Reference Etingof and Schiffmann35, Section 4]). Our second goal of the paper is to relate these dynamical quantum groups to objects in geometric representation theory.
$F_q(G)$
quantises the standard trigonometric dynamical r-matrix (see [Reference Etingof and Schiffmann35, Section 4]). Our second goal of the paper is to relate these dynamical quantum groups to objects in geometric representation theory.
Let G be a split reductive algebraic group over a characteristic zero field k,
![]() $B\subset G$
a Borel subgroup and
$B\subset G$
a Borel subgroup and
![]() $H=B/[B, B]$
the abstract Cartan subgroup; we denote by
$H=B/[B, B]$
the abstract Cartan subgroup; we denote by
![]() $\mathfrak {g},\mathfrak {b},\mathfrak {h}$
their Lie algebras. Consider the correspondence of algebraic stacks
$\mathfrak {g},\mathfrak {b},\mathfrak {h}$
their Lie algebras. Consider the correspondence of algebraic stacks

It appears in many areas of symplectic geometry and geometric representation theory:
-
○ Let
 $\tilde {\mathfrak {g}}$
be the variety parametrising Borel subgroups of G together with an element
$\tilde {\mathfrak {g}}$
be the variety parametrising Borel subgroups of G together with an element
 $x\in \mathfrak {g}$
contained in the Lie algebra of the corresponding Borel subgroup. The projection
$x\in \mathfrak {g}$
contained in the Lie algebra of the corresponding Borel subgroup. The projection
 $\tilde {\mathfrak {g}}\rightarrow \mathfrak {g}$
is known as the Grothendieck–Springer resolution (see [Reference Chriss and Ginzburg22, Section 3.1.31]). We may identify
$\tilde {\mathfrak {g}}\rightarrow \mathfrak {g}$
is known as the Grothendieck–Springer resolution (see [Reference Chriss and Ginzburg22, Section 3.1.31]). We may identify
 $[\tilde {\mathfrak {g}}/G]\cong [\mathfrak {b}/B]$
so that the projection
$[\tilde {\mathfrak {g}}/G]\cong [\mathfrak {b}/B]$
so that the projection
 $[\mathfrak {b}/B]\rightarrow [\mathfrak {g}^*/G]$
is identified with the Grothendieck–Springer resolution
$[\mathfrak {b}/B]\rightarrow [\mathfrak {g}^*/G]$
is identified with the Grothendieck–Springer resolution
 $[\tilde {\mathfrak {g}}/G]\rightarrow [\mathfrak {g}/G]$
. The study of the categories of
$[\tilde {\mathfrak {g}}/G]\rightarrow [\mathfrak {g}/G]$
. The study of the categories of
 $\mathrm {D}$
-modules on this correspondence is closely related to Springer theory (see [Reference Gunningham46] and references there).
$\mathrm {D}$
-modules on this correspondence is closely related to Springer theory (see [Reference Gunningham46] and references there). -
○ Let
 $N\subset B$
be the unipotent radical. Then we may identify where
$N\subset B$
be the unipotent radical. Then we may identify where $$\begin{align*}[\mathfrak{b}/B]\cong [G\backslash \mathrm{T}^*(G/N) / H],\end{align*}$$
$$\begin{align*}[\mathfrak{b}/B]\cong [G\backslash \mathrm{T}^*(G/N) / H],\end{align*}$$
 $\mathrm {T}^*(G/N)/H\rightarrow G/B$
is the universal family of twisted cotangent bundles over the flag variety parametrised by
$\mathrm {T}^*(G/N)/H\rightarrow G/B$
is the universal family of twisted cotangent bundles over the flag variety parametrised by
 $\lambda \in \mathfrak {h}^*$
. In particular, quantisation of this correspondence is closely related to the Beilinson–Bernstein localisation theorem [Reference Beilinson and Bernstein7] (see [Reference Ben-Zvi and Nadler9]).
$\lambda \in \mathfrak {h}^*$
. In particular, quantisation of this correspondence is closely related to the Beilinson–Bernstein localisation theorem [Reference Beilinson and Bernstein7] (see [Reference Ben-Zvi and Nadler9]).
-
○ The stacks
 $[\mathfrak {g}^*/G],[\mathfrak {h}^*/H]$
have 1-shifted symplectic structures in the sense of [Reference Pantev, Toën, Vaquié and Vezzosi69]; moreover, equation (5) is a 1-shifted Lagrangian correspondence. It is shown in [Reference Calaque19, Section 2.2.1] that a Lagrangian L in
$[\mathfrak {g}^*/G],[\mathfrak {h}^*/H]$
have 1-shifted symplectic structures in the sense of [Reference Pantev, Toën, Vaquié and Vezzosi69]; moreover, equation (5) is a 1-shifted Lagrangian correspondence. It is shown in [Reference Calaque19, Section 2.2.1] that a Lagrangian L in
 $[\mathfrak {g}^*/G]$
is the same as a Hamiltonian G-space: that is, an algebraic symplectic variety X equipped with a symplectic G-action and a moment map
$[\mathfrak {g}^*/G]$
is the same as a Hamiltonian G-space: that is, an algebraic symplectic variety X equipped with a symplectic G-action and a moment map
 $X\rightarrow \mathfrak {g}^*$
. Composing the Lagrangian
$X\rightarrow \mathfrak {g}^*$
. Composing the Lagrangian
 $L\rightarrow [\mathfrak {g}^*/G]$
with the correspondence equation (5), we obtain a Lagrangian in
$L\rightarrow [\mathfrak {g}^*/G]$
with the correspondence equation (5), we obtain a Lagrangian in
 $[\mathfrak {h}^*/H]$
: that is, a Hamiltonian H-space. It is shown in [Reference Safronov72] that this procedure coincides with the procedure of symplectic implosion [Reference Guillemin, Jeffrey and Sjamaar45, Reference Dancer, Kirwan and Swann23].
$[\mathfrak {h}^*/H]$
: that is, a Hamiltonian H-space. It is shown in [Reference Safronov72] that this procedure coincides with the procedure of symplectic implosion [Reference Guillemin, Jeffrey and Sjamaar45, Reference Dancer, Kirwan and Swann23]. -
○ One may replace Lie algebras by the corresponding groups: that is, one may consider the correspondence
 $[G/G]\leftarrow [B/B]\rightarrow [H/H]$
. It is shown in [Reference Boalch14, Theorem A] that this correspondence (and its analogue for a parabolic subgroup) appears in the description of logarithmic connections on a disk.
$[G/G]\leftarrow [B/B]\rightarrow [H/H]$
. It is shown in [Reference Boalch14, Theorem A] that this correspondence (and its analogue for a parabolic subgroup) appears in the description of logarithmic connections on a disk.
Consider the induced bimodule category
where
![]() $\mathrm {QCoh}([\mathfrak {g}^*/G])$
is the symmetric monoidal category of quasi-coherent sheaves on the stack
$\mathrm {QCoh}([\mathfrak {g}^*/G])$
is the symmetric monoidal category of quasi-coherent sheaves on the stack
![]() $[\mathfrak {g}^*/G]$
. Explicitly, it can be identified as
$[\mathfrak {g}^*/G]$
. Explicitly, it can be identified as
and similarly for H.
In section 3.3, we study a quantum version of the bimodule given by equation (6):
Here, as before,
![]() $\mathrm {HC}(G)$
is the monoidal category of Harish-Chandra bimodules: that is,
$\mathrm {HC}(G)$
is the monoidal category of Harish-Chandra bimodules: that is,
![]() $\mathrm {U}\mathfrak {g}$
-bimodules with an integrable diagonal action.
$\mathrm {U}\mathfrak {g}$
-bimodules with an integrable diagonal action.
![]() $\mathcal {O}^{\mathrm {univ}}$
is a universal version of category
$\mathcal {O}^{\mathrm {univ}}$
is a universal version of category
![]() $\mathcal {O}$
: it is the category of
$\mathcal {O}$
: it is the category of
![]() $\mathrm {U}\mathfrak {g}$
-modules internal to the category
$\mathrm {U}\mathfrak {g}$
-modules internal to the category
![]() $\operatorname {\mathrm {Rep}}(H)$
whose
$\operatorname {\mathrm {Rep}}(H)$
whose
![]() $\mathfrak {n}$
-action is locally nilpotent. Equivalently, it is the category of
$\mathfrak {n}$
-action is locally nilpotent. Equivalently, it is the category of
![]() $(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {h})$
-bimodules whose diagonal B-action is integrable. The module structure on either side is given by the tensor product of bimodules using the latter description of
$(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {h})$
-bimodules whose diagonal B-action is integrable. The module structure on either side is given by the tensor product of bimodules using the latter description of
![]() $\mathcal {O}^{\mathrm {univ}}$
. The universal Verma module
$\mathcal {O}^{\mathrm {univ}}$
. The universal Verma module
![]() $M^{\mathrm {univ}} = \mathrm {U}\mathfrak {g}\otimes _{\mathrm {U}\mathfrak {b}}\mathrm {U}\mathfrak {h}$
is naturally an object of
$M^{\mathrm {univ}} = \mathrm {U}\mathfrak {g}\otimes _{\mathrm {U}\mathfrak {b}}\mathrm {U}\mathfrak {h}$
is naturally an object of
![]() $\mathcal {O}^{\mathrm {univ}}$
.
$\mathcal {O}^{\mathrm {univ}}$
.
Let us explain how it relates to the classical picture. The algebra
![]() $\mathrm {U}\mathfrak {g}$
has a natural PBW filtration; consider the corresponding Rees algebra over
$\mathrm {U}\mathfrak {g}$
has a natural PBW filtration; consider the corresponding Rees algebra over
![]() $k[\hbar ]$
. The above constructions can be repeated to produce
$k[\hbar ]$
. The above constructions can be repeated to produce
![]() $k[\hbar ]$
-linear categories so that at
$k[\hbar ]$
-linear categories so that at
![]() $\hbar =0$
, the bimodule given by equation (7) reduces to the bimodule given by equation (6).
$\hbar =0$
, the bimodule given by equation (7) reduces to the bimodule given by equation (6).
Passing to the right adjoint of the action functor
![]() $\mathrm {HC}(H)\rightarrow \mathcal {O}^{\mathrm {univ}}$
on the universal Verma module
$\mathrm {HC}(H)\rightarrow \mathcal {O}^{\mathrm {univ}}$
on the universal Verma module
![]() $M^{\mathrm {univ}}$
, one obtains the parabolic restriction functor
$M^{\mathrm {univ}}$
, one obtains the parabolic restriction functor
given by
![]() $\mathrm {res}(X) = (X/X\mathfrak {n})^N$
, which is naturally lax monoidal. The following statement combines Theorem 3.10 and Theorem 5.7 and provides a quantisation of symplectic implosion.
$\mathrm {res}(X) = (X/X\mathfrak {n})^N$
, which is naturally lax monoidal. The following statement combines Theorem 3.10 and Theorem 5.7 and provides a quantisation of symplectic implosion.
Proposition. An algebra in
![]() $\mathrm {HC}(G)$
is a G-equivariant algebra A with a quantum moment map
$\mathrm {HC}(G)$
is a G-equivariant algebra A with a quantum moment map
![]() $\mathrm {U}\mathfrak {g}\rightarrow A$
. We have an isomorphism of algebras
$\mathrm {U}\mathfrak {g}\rightarrow A$
. We have an isomorphism of algebras
![]() $\mathrm {res}(A)\cong A/\!\!/ N$
, where
$\mathrm {res}(A)\cong A/\!\!/ N$
, where
![]() $A/\!\!/ N$
is the quantum Hamiltonian reduction by N.
$A/\!\!/ N$
is the quantum Hamiltonian reduction by N.
For a generic central character
![]() $\chi \colon \mathrm {Z}(\mathrm {U}\mathfrak {g})\rightarrow \mathbf {C}$
, the BGG category
$\chi \colon \mathrm {Z}(\mathrm {U}\mathfrak {g})\rightarrow \mathbf {C}$
, the BGG category
![]() $\mathcal {O}_\chi $
with that central character is semisimple with simple objects given by Verma modules. We prove an analogous statement in the universal case. The following statement combines Theorem 5.17 and Theorem 5.18.
$\mathcal {O}_\chi $
with that central character is semisimple with simple objects given by Verma modules. We prove an analogous statement in the universal case. The following statement combines Theorem 5.17 and Theorem 5.18.
Theorem. Consider the subcategories
![]() $\mathrm {HC}(H)^{\mathrm {gen}}\subset \mathrm {HC}(H)$
and
$\mathrm {HC}(H)^{\mathrm {gen}}\subset \mathrm {HC}(H)$
and
![]() $\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}\subset \mathcal {O}^{\mathrm {univ}}$
of modules with generic
$\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}\subset \mathcal {O}^{\mathrm {univ}}$
of modules with generic
![]() $\mathfrak {h}$
-weights. Then the functor
$\mathfrak {h}$
-weights. Then the functor
![]() $\mathrm {HC}(H)^{\mathrm {gen}}\rightarrow \mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is an equivalence. In particular,
$\mathrm {HC}(H)^{\mathrm {gen}}\rightarrow \mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is an equivalence. In particular,
is strongly monoidal and colimit-preserving.
The key step in the above statement is to prove that the Verma module for generic highest weights is projective; in the universal setting, this is captured by the existence of the extremal projector [Reference Asherova, Smirnov and Tolstoy4] (see Theorem 5.14), which splits the projection
![]() $\mathrm {U}\mathfrak {g}\rightarrow M^{\mathrm {univ}}$
for generic
$\mathrm {U}\mathfrak {g}\rightarrow M^{\mathrm {univ}}$
for generic
![]() $\mathfrak {h}$
-weights.
$\mathfrak {h}$
-weights.
There is a natural monoidal functor
![]() $\mathrm {free}\colon \operatorname {\mathrm {Rep}}(G)\rightarrow \mathrm {HC}(G)$
given by
$\mathrm {free}\colon \operatorname {\mathrm {Rep}}(G)\rightarrow \mathrm {HC}(G)$
given by
![]() $V\mapsto \mathrm {U}\mathfrak {g}\otimes V$
, so we get a monoidal functor
$V\mapsto \mathrm {U}\mathfrak {g}\otimes V$
, so we get a monoidal functor
Moreover, we show in Theorem 5.23 that the Harish-Chandra bialgebroid reconstructed from
![]() $\operatorname {\mathrm {Rep}}(G) \rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
is isomorphic to
$\operatorname {\mathrm {Rep}}(G) \rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
is isomorphic to
![]() $F(G)$
(as an
$F(G)$
(as an
![]() $\mathfrak {h}$
-bialgebroid) so that
$\mathfrak {h}$
-bialgebroid) so that
![]() $\operatorname {\mathrm {Rep}}(G)$
is equivalent to
$\operatorname {\mathrm {Rep}}(G)$
is equivalent to
![]() $F(G)$
-comodules. We also prove analogous statements in the setting of quantum groups in Section 5.2.
$F(G)$
-comodules. We also prove analogous statements in the setting of quantum groups in Section 5.2.
These results have the following interpretation. The same braided monoidal category
![]() $\operatorname {\mathrm {Rep}}_q(G)$
has different monoidal functors
$\operatorname {\mathrm {Rep}}_q(G)$
has different monoidal functors
![]() $\operatorname {\mathrm {Rep}}_q(G)\rightarrow \mathrm {Vect}$
corresponding to different choices of the classical r-matrix; by Tannaka duality, this corresponds to nonstandard quantum groups, such as the Cremmer–Gervais quantum group in the case
$\operatorname {\mathrm {Rep}}_q(G)\rightarrow \mathrm {Vect}$
corresponding to different choices of the classical r-matrix; by Tannaka duality, this corresponds to nonstandard quantum groups, such as the Cremmer–Gervais quantum group in the case
![]() $G=\mathrm {SL}_n$
. In this paper, we study the monoidal functors
$G=\mathrm {SL}_n$
. In this paper, we study the monoidal functors
![]() $\operatorname {\mathrm {Rep}}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}}$
, which give rise to dynamical quantum groups. Note that these are different ways to study the same braided monoidal category.
$\operatorname {\mathrm {Rep}}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}}$
, which give rise to dynamical quantum groups. Note that these are different ways to study the same braided monoidal category.
We also expect that the approach to dynamical quantum groups
![]() $F(G)$
and
$F(G)$
and
![]() $F_q(G)$
presented here in terms of the correspondence in equation (5) might be useful to have an interpretation of Felder’s dynamical quantum group [Reference Felder41] in terms of the 1-shifted Lagrangian correspondence
$F_q(G)$
presented here in terms of the correspondence in equation (5) might be useful to have an interpretation of Felder’s dynamical quantum group [Reference Felder41] in terms of the 1-shifted Lagrangian correspondence
![]() $\mathrm {Bun}_G(E)\leftarrow \mathrm {Bun}_B(E)\rightarrow \mathrm {Bun}_H(E)$
of moduli stacks of bundles on an elliptic curve E. It is interesting to note that the same correspondence is closely related to Feigin–Odesskii algebras [Reference Feigin and Odesskii40] (in particular, Sklyanin algebras [Reference Sklyanin79]); see [Reference Safronov74, Example 4.11] and [Reference Hua and Polishchuk48].
$\mathrm {Bun}_G(E)\leftarrow \mathrm {Bun}_B(E)\rightarrow \mathrm {Bun}_H(E)$
of moduli stacks of bundles on an elliptic curve E. It is interesting to note that the same correspondence is closely related to Feigin–Odesskii algebras [Reference Feigin and Odesskii40] (in particular, Sklyanin algebras [Reference Sklyanin79]); see [Reference Safronov74, Example 4.11] and [Reference Hua and Polishchuk48].
It is shown in [Reference Ben-Zvi, Brochier and Jordan8, Theorem 3.11] that
![]() $\mathrm {HC}_q(G)$
-module categories are the same as
$\mathrm {HC}_q(G)$
-module categories are the same as
![]() $\operatorname {\mathrm {Rep}}_q(G)$
-braided module categories [Reference Brochier17, Section 5.1]. In particular, the monoidal functor
$\operatorname {\mathrm {Rep}}_q(G)$
-braided module categories [Reference Brochier17, Section 5.1]. In particular, the monoidal functor
![]() $\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}}$
allows one to transfer
$\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}}$
allows one to transfer
![]() $\operatorname {\mathrm {Rep}}_q(H)$
-braided module categories to
$\operatorname {\mathrm {Rep}}_q(H)$
-braided module categories to
![]() $\operatorname {\mathrm {Rep}}_q(G)$
-braided module categories.
$\operatorname {\mathrm {Rep}}_q(G)$
-braided module categories.
1.5 Dynamical Weyl group
Let
![]() $W=\mathrm {N}(H)/H$
be the Weyl group and
$W=\mathrm {N}(H)/H$
be the Weyl group and
![]() $\hat {W}$
the braid group covering W. The group W naturally acts on the symmetric monoidal category
$\hat {W}$
the braid group covering W. The group W naturally acts on the symmetric monoidal category
![]() $\operatorname {\mathrm {Rep}}(H)$
, so we may consider the category of W-invariants
$\operatorname {\mathrm {Rep}}(H)$
, so we may consider the category of W-invariants
![]() $\operatorname {\mathrm {Rep}}(H)^W$
. Moreover, there exists a map
$\operatorname {\mathrm {Rep}}(H)^W$
. Moreover, there exists a map
![]() $\hat {W}\rightarrow \mathrm {N}(H)$
lifting
$\hat {W}\rightarrow \mathrm {N}(H)$
lifting
![]() $\hat {W}\rightarrow W$
[Reference Tits84], so the forgetful functor
$\hat {W}\rightarrow W$
[Reference Tits84], so the forgetful functor
![]() $\operatorname {\mathrm {Rep}}(G)\rightarrow \operatorname {\mathrm {Rep}}(H)$
factors through a symmetric monoidal functor
$\operatorname {\mathrm {Rep}}(G)\rightarrow \operatorname {\mathrm {Rep}}(H)$
factors through a symmetric monoidal functor
Our third goal of the paper is to exhibit Weyl symmetry of the parabolic restriction functor for Harish-Chandra bimodules. A similar setup works for quantum groups using the quantum Weyl group [Reference Lusztig62, Reference Soibelman80, Reference Kirillov and Reshetikhin57]. Note, however, that the resulting functor
is not monoidal: in fact, the failure of the quantum Weyl group to be monoidal is related to the failure of the functor
![]() $\operatorname {\mathrm {Rep}}_q(G)\rightarrow \operatorname {\mathrm {Rep}}_q(H)$
to be braided; this can be encapsulated in the notion of a braided Coxeter category [Reference Appel and Laredo3].
$\operatorname {\mathrm {Rep}}_q(G)\rightarrow \operatorname {\mathrm {Rep}}_q(H)$
to be braided; this can be encapsulated in the notion of a braided Coxeter category [Reference Appel and Laredo3].
Zhelobenko [Reference Zhelobenko93], in the study of Mickelsson algebras, has introduced a collection of Zhelobenko operators
![]() $q_w\colon \mathrm {U}\mathfrak {g}\rightarrow \mathrm {U}\mathfrak {g}$
for every element of the Weyl group
$q_w\colon \mathrm {U}\mathfrak {g}\rightarrow \mathrm {U}\mathfrak {g}$
for every element of the Weyl group
![]() $w\in W$
satisfying the braid relations (see Theorem 6.1). It was realised in [Reference Khoroshkin and Ogievetsky53] that these operators give an action of the braid group
$w\in W$
satisfying the braid relations (see Theorem 6.1). It was realised in [Reference Khoroshkin and Ogievetsky53] that these operators give an action of the braid group
![]() $\hat {W}$
on a localised Mickelsson algebra.
$\hat {W}$
on a localised Mickelsson algebra.
Consider the W-action on
![]() $\mathrm {HC}(H)$
, where W acts on
$\mathrm {HC}(H)$
, where W acts on
![]() $\mathrm {U}\mathfrak {h}$
via the dot action (the usual W-action shifted by the half-sum of positive roots
$\mathrm {U}\mathfrak {h}$
via the dot action (the usual W-action shifted by the half-sum of positive roots
![]() $\rho $
) and on H via the usual action. The above results directly imply the following statement (see Theorem 6.5).
$\rho $
) and on H via the usual action. The above results directly imply the following statement (see Theorem 6.5).
Theorem. The Zhelobenko operators define a monoidal functor
lifting
![]() $\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
.
$\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
.
Suppose
![]() $V\in \operatorname {\mathrm {Rep}}(G)$
. Then
$V\in \operatorname {\mathrm {Rep}}(G)$
. Then
![]() $\mathrm {res}^{\mathrm {gen}}(\mathrm {U}\mathfrak {g}\otimes V)\cong (\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\otimes V$
, where
$\mathrm {res}^{\mathrm {gen}}(\mathrm {U}\mathfrak {g}\otimes V)\cong (\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\otimes V$
, where
![]() $(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\supset \mathrm {U}\mathfrak {h}$
is a certain localisation (see Theorem 5.12). In particular, the
$(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\supset \mathrm {U}\mathfrak {h}$
is a certain localisation (see Theorem 5.12). In particular, the
![]() $\hat {W}$
-symmetry is captured by certain rational maps
$\hat {W}$
-symmetry is captured by certain rational maps
![]() $A_{w, V}\colon \mathfrak {h}^*\rightarrow \mathrm {End}(V)$
satisfying the braid relation. We prove in Theorem 6.8 that these coincide with the dynamical Weyl group operators introduced in [Reference Tarasov and Varchenko83, Reference Etingof and Varchenko32].
$A_{w, V}\colon \mathfrak {h}^*\rightarrow \mathrm {End}(V)$
satisfying the braid relation. We prove in Theorem 6.8 that these coincide with the dynamical Weyl group operators introduced in [Reference Tarasov and Varchenko83, Reference Etingof and Varchenko32].
Let us mention a relationship between these results and the generalised Harish–Chandra isomorphism [Reference Khoroshkin, Nazarov and Vinberg56]. Consider the functor
![]() $\widetilde {\mathrm {res}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)$
given by
$\widetilde {\mathrm {res}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)$
given by
![]() $\tilde {\mathrm {res}}(X) = \mathfrak {n}_- X \backslash X / X\mathfrak {n}_+$
. There is a natural transformation
$\tilde {\mathrm {res}}(X) = \mathfrak {n}_- X \backslash X / X\mathfrak {n}_+$
. There is a natural transformation
![]() $\mathrm {res}(X)\rightarrow \widetilde {\mathrm {res}}(X)$
, which becomes an isomorphism in
$\mathrm {res}(X)\rightarrow \widetilde {\mathrm {res}}(X)$
, which becomes an isomorphism in
![]() $\mathrm {HC}(H)^{\mathrm {gen}}$
(see Theorem 5.16). We obtain a restriction map
$\mathrm {HC}(H)^{\mathrm {gen}}$
(see Theorem 5.16). We obtain a restriction map

The object
![]() $(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\in \mathrm {HC}(H)^{\mathrm {gen}}$
has a canonical
$(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\in \mathrm {HC}(H)^{\mathrm {gen}}$
has a canonical
![]() $\hat {W}$
-equivariance structure given by the dot action of W on
$\hat {W}$
-equivariance structure given by the dot action of W on
![]() $\mathrm {U}\mathfrak {h}$
. In particular, Zhelobenko operators define maps
$\mathrm {U}\mathfrak {h}$
. In particular, Zhelobenko operators define maps
![]() $\mathrm {U}\mathfrak {h}\otimes V^H\rightarrow (\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\otimes V^H$
and, in fact, the action factors through the action of the Weyl group. The resulting homomorphism
$\mathrm {U}\mathfrak {h}\otimes V^H\rightarrow (\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\otimes V^H$
and, in fact, the action factors through the action of the Weyl group. The resulting homomorphism
is shown in [Reference Khoroshkin, Nazarov and Vinberg56] to be an isomorphism. It generalises the usual Harish-Chandra isomorphism (see, e.g., [Reference Humphreys49, Theorem 1.10]), which is obtained for
![]() $V=k$
the trivial one-dimensional representation.
$V=k$
the trivial one-dimensional representation.
The papers [Reference Braverman and Finkelberg16, Reference Ginzburg and Riche44] gave an interpretation of the dynamical Weyl group in terms of equivariant cohomology of the affine Grassmannian of the Langlands dual group, using the geometric Satake equivalence. It would be interesting to see the appearance of the Zhelobenko operators using the Langlands dual interpretation of Harish-Chandra bimodules from [Reference Bezrukavnikov and Finkelberg12].
Let us mention a categorical point of view on the Weyl symmetry of the parabolic restriction functor
![]() $\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)$
. By abstract reasons, the action functor
$\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)$
. By abstract reasons, the action functor
![]() $\mathrm {HC}(G)\rightarrow \mathcal {O}^{\mathrm {univ}}$
factors through the category of coalgebras over a comonad
$\mathrm {HC}(G)\rightarrow \mathcal {O}^{\mathrm {univ}}$
factors through the category of coalgebras over a comonad
![]() $\mathrm {St}\colon \mathcal {O}^{\mathrm {univ}}\rightarrow \mathcal {O}^{\mathrm {univ}}$
obtained from the right adjoint of the action functor. In particular, for generic weights, parabolic restriction factors through the category of
$\mathrm {St}\colon \mathcal {O}^{\mathrm {univ}}\rightarrow \mathcal {O}^{\mathrm {univ}}$
obtained from the right adjoint of the action functor. In particular, for generic weights, parabolic restriction factors through the category of
![]() $\mathrm {St}$
-coalgebras in
$\mathrm {St}$
-coalgebras in
![]() $\mathrm {HC}(H)^{\mathrm {gen}}$
. We expect that there is an equivalence between
$\mathrm {HC}(H)^{\mathrm {gen}}$
. We expect that there is an equivalence between
![]() $\mathrm {St}$
and the comonad corresponding to the W-action on
$\mathrm {St}$
and the comonad corresponding to the W-action on
![]() $\mathrm {HC}(H)^{\mathrm {gen}}$
. We refer to [Reference Ben-Zvi and Nadler9], where it is called the Weyl comonad, and [Reference Gunningham46, Theorem 4.6] for an analogous theorem in the setting of
$\mathrm {HC}(H)^{\mathrm {gen}}$
. We refer to [Reference Ben-Zvi and Nadler9], where it is called the Weyl comonad, and [Reference Gunningham46, Theorem 4.6] for an analogous theorem in the setting of
![]() $\mathrm {D}$
-modules.
$\mathrm {D}$
-modules.
2 Background
In this section, we recall some facts about locally presentable categories, cp-rigid monoidal categories and Tannaka reconstruction for bialgebras.
2.1 Locally presentable categories
Let k be a field. All categories and functors we will consider are k-linear. Throughout this paper, we work with locally presentable categories (refer to [Reference Adámek and Rosický1] and [Reference Brandenburg, Chirvasitu and Johnson-Freyd15, Section 2] for more details). Here are the main examples:
-
○ If
 $\mathcal {C}$
is a small category, the category of presheaves
$\mathcal {C}$
is a small category, the category of presheaves
 $\mathrm {Fun}(\mathcal {C}^{\mathrm {op}}, \mathrm {Vect})$
is locally presentable. For instance, this applies to the category
$\mathrm {Fun}(\mathcal {C}^{\mathrm {op}}, \mathrm {Vect})$
is locally presentable. For instance, this applies to the category
 $\mathrm {LMod}_A$
of (left) modules over a k-algebra A.
$\mathrm {LMod}_A$
of (left) modules over a k-algebra A. -
○ If
 $\mathcal {C}$
is a small category that admits finite colimits, the ind-completion
$\mathcal {C}$
is a small category that admits finite colimits, the ind-completion
 $\mathrm {Ind}(\mathcal {C})$
(see [Reference Kashiwara and Schapira51, Chapter 6] for what it means) is locally presentable.
$\mathrm {Ind}(\mathcal {C})$
(see [Reference Kashiwara and Schapira51, Chapter 6] for what it means) is locally presentable. -
○ If C is a k-coalgebra, the category of C-comodules
 $\mathrm {CoMod}_C$
is locally presentable (see [Reference Wischnewsky91, Corollary 9], noting that a Grothendieck category is locally presentable). In fact,
$\mathrm {CoMod}_C$
is locally presentable (see [Reference Wischnewsky91, Corollary 9], noting that a Grothendieck category is locally presentable). In fact,
 $\mathrm {CoMod}_C$
is the ind-completion of the category of finite-dimensional C-comodules (see [Reference Rivano71, Corollaire 2.2.2.3]).
$\mathrm {CoMod}_C$
is the ind-completion of the category of finite-dimensional C-comodules (see [Reference Rivano71, Corollaire 2.2.2.3]). -
○ If
 $\mathcal {C}, \mathcal {D}$
are locally presentable categories, the category
$\mathcal {C}, \mathcal {D}$
are locally presentable categories, the category
 $\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {D})$
of colimit-preserving functors from
$\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {D})$
of colimit-preserving functors from
 $\mathcal {C}$
to
$\mathcal {C}$
to
 $\mathcal {D}$
is locally presentable.
$\mathcal {D}$
is locally presentable.
It turns out that many examples of locally presentable categories are, in fact, presheaf categories.
Definition 2.1. Let
![]() $\mathcal {C}$
be a locally presentable category. An object
$\mathcal {C}$
be a locally presentable category. An object
![]() $x\in \mathcal {C}$
is
compact projective
if
$x\in \mathcal {C}$
is
compact projective
if
![]() $\mathrm {Hom}_{\mathcal {C}}(x, -)\colon \mathcal {C}\rightarrow \mathrm {Vect}$
preserves colimits.
$\mathrm {Hom}_{\mathcal {C}}(x, -)\colon \mathcal {C}\rightarrow \mathrm {Vect}$
preserves colimits.
![]() $\mathcal {C}$
has
enough compact projectives
if every object receives a nonzero morphism from a compact projective.
$\mathcal {C}$
has
enough compact projectives
if every object receives a nonzero morphism from a compact projective.
We denote by
![]() $\mathcal {C}^{\mathrm {cp}}\subset \mathcal {C}$
the full subcategory of compact projective objects.
$\mathcal {C}^{\mathrm {cp}}\subset \mathcal {C}$
the full subcategory of compact projective objects.
Proposition 2.2. Suppose
![]() $\mathcal {C}$
has enough compact projectives. Then the functor
$\mathcal {C}$
has enough compact projectives. Then the functor
given by
![]() $x\mapsto (y\mapsto \mathrm {Hom}_{\mathcal {C}}(y, x))$
is an equivalence.
$x\mapsto (y\mapsto \mathrm {Hom}_{\mathcal {C}}(y, x))$
is an equivalence.
Locally presentable categories naturally form a symmetric monoidal 2-category
![]() $\mathrm {Pr}^{\mathrm {L}}$
[Reference Bird13]:
$\mathrm {Pr}^{\mathrm {L}}$
[Reference Bird13]:
-
○ Its objects are locally presentable categories.
-
○ Its 1-morphisms are colimit-preserving functors.
-
○ Its 2-morphisms are natural transformations.
-
○ The tensor product is uniquely determined by the following property: for
 $\mathcal {C},\mathcal {D},\mathcal {E}\in \mathrm {Pr}^{\mathrm {L}}$
a colimit-preserving functor
$\mathcal {C},\mathcal {D},\mathcal {E}\in \mathrm {Pr}^{\mathrm {L}}$
a colimit-preserving functor
 $\mathcal {C}\otimes \mathcal {D}\rightarrow \mathcal {E}$
is the same as a bifunctor
$\mathcal {C}\otimes \mathcal {D}\rightarrow \mathcal {E}$
is the same as a bifunctor
 $\mathcal {C}\times \mathcal {D}\rightarrow \mathcal {E}$
preserving colimits in each variables.
$\mathcal {C}\times \mathcal {D}\rightarrow \mathcal {E}$
preserving colimits in each variables. -
○ The unit is
 $\mathrm {Vect}\in \mathrm {Pr}^{\mathrm {L}}$
.
$\mathrm {Vect}\in \mathrm {Pr}^{\mathrm {L}}$
.
An important fact about locally presentable categories is that a colimit-preserving functor between locally presentable categories admits a right adjoint. We will now write a formula for the adjoint, assuming the source category has enough compact projectives. Let us first recall the notion of a coend (see [Reference Loregian60] for more details on coends).
Definition 2.3. Suppose
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {D}$
are locally presentable categories. The
coend
of a bifunctor
$\mathcal {D}$
are locally presentable categories. The
coend
of a bifunctor
![]() $F\colon \mathcal {C}\times \mathcal {C}^{\mathrm {op}}\rightarrow \mathcal {D}$
is the coequaliser
$F\colon \mathcal {C}\times \mathcal {C}^{\mathrm {op}}\rightarrow \mathcal {D}$
is the coequaliser

We will use the following Yoneda-like property of coends (see [Reference Loregian60, Proposition 2.2.1]).
Proposition 2.4. For any functors
![]() $F\colon \mathcal {C}\rightarrow \mathcal {D}, G\colon \mathcal {C}^{\mathrm {op}}\rightarrow \mathcal {D}$
, we have natural isomorphisms
$F\colon \mathcal {C}\rightarrow \mathcal {D}, G\colon \mathcal {C}^{\mathrm {op}}\rightarrow \mathcal {D}$
, we have natural isomorphisms
 $$\begin{align*}\int^{x\in\mathcal{C}} \mathrm{Hom}_{\mathcal{C}}(x, y)\otimes F(x)\cong F(y),\qquad \int^{x\in\mathcal{C}} \mathrm{Hom}_{\mathcal{C}}(y, x)\otimes G(x)\cong G(y).\end{align*}$$
$$\begin{align*}\int^{x\in\mathcal{C}} \mathrm{Hom}_{\mathcal{C}}(x, y)\otimes F(x)\cong F(y),\qquad \int^{x\in\mathcal{C}} \mathrm{Hom}_{\mathcal{C}}(y, x)\otimes G(x)\cong G(y).\end{align*}$$
The following is an immediate corollary.
Proposition 2.5. Suppose
![]() $F\colon \mathcal {C}\rightarrow \mathcal {D}$
is a colimit-preserving functor of locally presentable categories, where
$F\colon \mathcal {C}\rightarrow \mathcal {D}$
is a colimit-preserving functor of locally presentable categories, where
![]() $\mathcal {C}$
has enough compact projectives. Then the right adjoint is given by the coend
$\mathcal {C}$
has enough compact projectives. Then the right adjoint is given by the coend
 $$\begin{align*}F^{\mathrm{R}}(x) = \int^{y\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{D}}(F(y), x)\otimes y.\end{align*}$$
$$\begin{align*}F^{\mathrm{R}}(x) = \int^{y\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{D}}(F(y), x)\otimes y.\end{align*}$$
The counit of the adjunction
![]() $FF^{\mathrm {R}}(x)\rightarrow x$
is given by the evaluation map
$FF^{\mathrm {R}}(x)\rightarrow x$
is given by the evaluation map
![]() $\mathrm {Hom}_{\mathcal {D}}(F(y), x)\otimes F(y)\rightarrow x$
; the unit of the adjunction
$\mathrm {Hom}_{\mathcal {D}}(F(y), x)\otimes F(y)\rightarrow x$
; the unit of the adjunction
![]() $z\rightarrow F^{\mathrm {R}} F(z)$
is given by including the identity map
$z\rightarrow F^{\mathrm {R}} F(z)$
is given by including the identity map
![]() $\mathrm {id}\colon F(z)\rightarrow F(z)$
in the coend.
$\mathrm {id}\colon F(z)\rightarrow F(z)$
in the coend.
2.2 Cp-rigidity
By convention, all monoidal categories
![]() $\mathcal {C}$
that we consider in this paper are locally presentable such that the tensor product bifunctor
$\mathcal {C}$
that we consider in this paper are locally presentable such that the tensor product bifunctor
![]() $\mathcal {C}\times \mathcal {C}\rightarrow \mathcal {C}$
preserves colimits in each variable. So, by the universal property of the tensor product in
$\mathcal {C}\times \mathcal {C}\rightarrow \mathcal {C}$
preserves colimits in each variable. So, by the universal property of the tensor product in
![]() $\mathrm {Pr}^{\mathrm {L}}$
, it descends to a colimit-preserving functor
$\mathrm {Pr}^{\mathrm {L}}$
, it descends to a colimit-preserving functor
We denote by
![]() $\mathcal {C}^{\otimes \mathrm {op}}$
the same category with the opposite monoidal structure.
$\mathcal {C}^{\otimes \mathrm {op}}$
the same category with the opposite monoidal structure.
We will consider rigid monoidal categories in the text. Since we work with large categories, we cannot expect all objects to be dualisable (as in the category of all vector spaces); instead, we will restrict our attention to compact projective objects.
Definition 2.6. Let
![]() $\mathcal {C}$
be a monoidal category with enough compact projectives. It is
cp-rigid
if every compact projective object admits left and right duals.
$\mathcal {C}$
be a monoidal category with enough compact projectives. It is
cp-rigid
if every compact projective object admits left and right duals.
Lemma 2.7. Suppose
![]() $\mathcal {C}$
is a cp-rigid monoidal category and
$\mathcal {C}$
is a cp-rigid monoidal category and
![]() $x,y\in \mathcal {C}$
are compact projective objects. Then
$x,y\in \mathcal {C}$
are compact projective objects. Then
![]() $x\otimes y$
is also compact projective.
$x\otimes y$
is also compact projective.
Proof. We have
By assumption, the tensor product preserves colimits in each variable, so
![]() $(-)\otimes y^\vee $
is colimit-preserving. Since x is compact projective,
$(-)\otimes y^\vee $
is colimit-preserving. Since x is compact projective,
![]() $\mathrm {Hom}_{\mathcal {C}}(x, -)$
is colimit-preserving. Therefore,
$\mathrm {Hom}_{\mathcal {C}}(x, -)$
is colimit-preserving. Therefore,
![]() $\mathrm {Hom}_{\mathcal {C}}(x\otimes y, -)$
is also colimit-preserving.
$\mathrm {Hom}_{\mathcal {C}}(x\otimes y, -)$
is also colimit-preserving.
If
![]() $\mathcal {C}$
is cp-rigid, the tensor product functor
$\mathcal {C}$
is cp-rigid, the tensor product functor
![]() $T\colon \mathcal {C}\otimes \mathcal {C}\rightarrow \mathcal {C}$
admits a colimit-preserving right adjoint
$T\colon \mathcal {C}\otimes \mathcal {C}\rightarrow \mathcal {C}$
admits a colimit-preserving right adjoint
![]() $T^{\mathrm {R}}\colon \mathcal {C}\rightarrow \mathcal {C}\otimes \mathcal {C}$
(see, e.g., [Reference Brochier, Jordan and Snyder18, Section 5.3]). It has the following explicit formula.
$T^{\mathrm {R}}\colon \mathcal {C}\rightarrow \mathcal {C}\otimes \mathcal {C}$
(see, e.g., [Reference Brochier, Jordan and Snyder18, Section 5.3]). It has the following explicit formula.
Proposition 2.8. Suppose
![]() $\mathcal {C}$
is a cp-rigid monoidal category. Then
$\mathcal {C}$
is a cp-rigid monoidal category. Then
 $$\begin{align*}T^{\mathrm{R}}(y) \cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} (y\otimes x^\vee)\boxtimes x.\end{align*}$$
$$\begin{align*}T^{\mathrm{R}}(y) \cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} (y\otimes x^\vee)\boxtimes x.\end{align*}$$
Proof. By Theorem 2.5, the right adjoint is
 $$\begin{align*}T^{\mathrm{R}}(y) \cong \int^{x_1,x_2\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{C}}(x_1\otimes x_2, y)\otimes (x_1\boxtimes x_2).\end{align*}$$
$$\begin{align*}T^{\mathrm{R}}(y) \cong \int^{x_1,x_2\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{C}}(x_1\otimes x_2, y)\otimes (x_1\boxtimes x_2).\end{align*}$$
Since compact projective objects in
![]() $\mathcal {C}$
are dualisable, we can rewrite it as
$\mathcal {C}$
are dualisable, we can rewrite it as
 $$ \begin{align*} T^{\mathrm{R}}(y)&\cong \int^{x_1,x_2\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{C}}(x_1, y\otimes x_2^\vee)\otimes (x_1\boxtimes x_2) \\ &\cong \int^{x_2\in\mathcal{C}^{\mathrm{cp}}} (y\otimes x_2^\vee)\boxtimes x_2, \end{align*} $$
$$ \begin{align*} T^{\mathrm{R}}(y)&\cong \int^{x_1,x_2\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{C}}(x_1, y\otimes x_2^\vee)\otimes (x_1\boxtimes x_2) \\ &\cong \int^{x_2\in\mathcal{C}^{\mathrm{cp}}} (y\otimes x_2^\vee)\boxtimes x_2, \end{align*} $$
where in the last isomorphism, we have used Theorem 2.4.
Consider
![]() $\mathcal {C}\otimes \mathcal {C}$
as a
$\mathcal {C}\otimes \mathcal {C}$
as a
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
-module category via the left action on the first factor and the right action on the second factor. By [Reference Brochier, Jordan and Snyder18, Proposition 4.1],
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
-module category via the left action on the first factor and the right action on the second factor. By [Reference Brochier, Jordan and Snyder18, Proposition 4.1],
![]() $T^{\mathrm {R}}$
is a functor of
$T^{\mathrm {R}}$
is a functor of
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
-module categories. This can be expressed in the following isomorphism.
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
-module categories. This can be expressed in the following isomorphism.
Proposition 2.9. Suppose
![]() $\mathcal {C}$
is as before. Then
$\mathcal {C}$
is as before. Then
![]() $T^{\mathrm {R}}\colon \mathcal {C}\rightarrow \mathcal {C}\otimes \mathcal {C}$
is a functor of
$T^{\mathrm {R}}\colon \mathcal {C}\rightarrow \mathcal {C}\otimes \mathcal {C}$
is a functor of
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
-module categories. Concretely, for any object
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
-module categories. Concretely, for any object
![]() $y\in \mathcal {C}$
, there is a natural isomorphism
$y\in \mathcal {C}$
, there is a natural isomorphism
 $$\begin{align*}\int^{x\in\mathcal{C}^{\mathrm{cp}}} (y\otimes x^\vee)\boxtimes x\cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} x^\vee\boxtimes (x\otimes y)\end{align*}$$
$$\begin{align*}\int^{x\in\mathcal{C}^{\mathrm{cp}}} (y\otimes x^\vee)\boxtimes x\cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} x^\vee\boxtimes (x\otimes y)\end{align*}$$
that is given for a compact projective
![]() $y\in \mathcal {C}$
by
$y\in \mathcal {C}$
by
 $$\begin{align*}x^\vee\boxtimes(x\otimes y)\xrightarrow{\mathrm{coev}_y\otimes \mathrm{id}} (y\otimes y^\vee\otimes x^\vee)\boxtimes (x\otimes y)\xrightarrow{\pi_{x\otimes y}} \int^{x\in\mathcal{C}^{\mathrm{cp}}} (y\otimes x^\vee)\boxtimes x.\end{align*}$$
$$\begin{align*}x^\vee\boxtimes(x\otimes y)\xrightarrow{\mathrm{coev}_y\otimes \mathrm{id}} (y\otimes y^\vee\otimes x^\vee)\boxtimes (x\otimes y)\xrightarrow{\pi_{x\otimes y}} \int^{x\in\mathcal{C}^{\mathrm{cp}}} (y\otimes x^\vee)\boxtimes x.\end{align*}$$
Corollary 2.10. The object
![]() $T^{\mathrm {R}}(\mathbf {1})\in \mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
has a natural algebra structure.
$T^{\mathrm {R}}(\mathbf {1})\in \mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
has a natural algebra structure.
Proof.
![]() $T^{\mathrm {R}} T$
is naturally a monad on
$T^{\mathrm {R}} T$
is naturally a monad on
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
. By definition,
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
. By definition,
![]() $T\colon \mathcal {C}\otimes \mathcal {C}\rightarrow \mathcal {C}$
is a functor of
$T\colon \mathcal {C}\otimes \mathcal {C}\rightarrow \mathcal {C}$
is a functor of
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
-module categories. By Theorem 2.9
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
-module categories. By Theorem 2.9
![]() $T^{\mathrm {R}}\colon \mathcal {C}\rightarrow \mathcal {C}\otimes \mathcal {C}$
is also a functor of
$T^{\mathrm {R}}\colon \mathcal {C}\rightarrow \mathcal {C}\otimes \mathcal {C}$
is also a functor of
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
-module categories. Therefore,
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
-module categories. Therefore,
![]() $(T^{\mathrm {R}} T)(\mathbf {1}_{\mathcal {C}\otimes \mathcal {C}})$
has a natural algebra structure.
$(T^{\mathrm {R}} T)(\mathbf {1}_{\mathcal {C}\otimes \mathcal {C}})$
has a natural algebra structure.
The key property of cp-rigid monoidal categories is that they are canonically self-dual objects of
![]() $\mathrm {Pr}^{\mathrm {L}}$
.
$\mathrm {Pr}^{\mathrm {L}}$
.
Theorem 2.11. Let
![]() $\mathcal {C}$
be a cp-rigid monoidal category with a compact projective unit. The evaluation and coevaluation pairings
$\mathcal {C}$
be a cp-rigid monoidal category with a compact projective unit. The evaluation and coevaluation pairings
establish the self-duality of
![]() $\mathcal {C}$
as an object of the symmetric monoidal bicategory
$\mathcal {C}$
as an object of the symmetric monoidal bicategory
![]() $\mathrm {Pr}^{\mathrm {L}}$
.
$\mathrm {Pr}^{\mathrm {L}}$
.
Proof. See [Reference Hoyois, Safronov, Scherotzke and Sibilla47, Proposition 2.16] for an analogous statement on the level of
![]() $\infty $
-categories.
$\infty $
-categories.
Remark 2.12. The conclusion of the theorem remains true if we drop the assumption that the unit of
![]() $\mathcal {C}$
is compact and projective and replace
$\mathcal {C}$
is compact and projective and replace
![]() $\mathrm {Hom}_{\mathcal {C}}(\mathbf {1}, -)\colon \mathcal {C}\rightarrow \mathrm {Vect}$
by the colimit-preserving functor that coincides with
$\mathrm {Hom}_{\mathcal {C}}(\mathbf {1}, -)\colon \mathcal {C}\rightarrow \mathrm {Vect}$
by the colimit-preserving functor that coincides with
![]() $\mathrm {Hom}_{\mathcal {C}}(\mathbf {1}, -)$
on compact projective objects.
$\mathrm {Hom}_{\mathcal {C}}(\mathbf {1}, -)$
on compact projective objects.
Corollary 2.13. Let
![]() $\mathcal {C}$
be a cp-rigid monoidal category with a compact projective unit and
$\mathcal {C}$
be a cp-rigid monoidal category with a compact projective unit and
![]() $\mathcal {D}$
any monoidal category. Then the functor
$\mathcal {D}$
any monoidal category. Then the functor
given by
is an equivalence.
2.3 Duoidal categories
Let us now study the monoidal properties of the equivalence given by equation (13). The functor category
![]() $\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {D})$
has a natural monoidal structure given by the Day convolution [Reference Day24] defined by
$\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {D})$
has a natural monoidal structure given by the Day convolution [Reference Day24] defined by
 $$ \begin{align} (F\otimes_{\mathrm{Day}} G)(x) = \int^{x_1,x_2\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{C}}(x_1\otimes x_2, x)\otimes F(x_1)\otimes G(x_2) \end{align} $$
$$ \begin{align} (F\otimes_{\mathrm{Day}} G)(x) = \int^{x_1,x_2\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{C}}(x_1\otimes x_2, x)\otimes F(x_1)\otimes G(x_2) \end{align} $$
with the unit functor
Proposition 2.14. The equivalence given by equation (13) upgrades to a monoidal equivalence
where we equip
![]() $\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {D})$
with the Day convolution monoidal structure.
$\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {D})$
with the Day convolution monoidal structure.
Proof. Clearly, the units are compatible since
![]() $\mathbf {1}_{\mathcal {D}}\boxtimes \mathbf {1}_{\mathcal {C}}$
is sent to the functor
$\mathbf {1}_{\mathcal {D}}\boxtimes \mathbf {1}_{\mathcal {C}}$
is sent to the functor
![]() $(x\mapsto \mathrm {ev}(\mathbf {1}_{\mathcal {C}}, x)\otimes \mathbf {1}_{\mathcal {D}})$
.
$(x\mapsto \mathrm {ev}(\mathbf {1}_{\mathcal {C}}, x)\otimes \mathbf {1}_{\mathcal {D}})$
.
Now consider two objects
![]() $d_1\boxtimes c_1, d_2\boxtimes c_2\in \mathcal {D}\otimes \mathcal {C}$
. Their Day convolution is computed by
$d_1\boxtimes c_1, d_2\boxtimes c_2\in \mathcal {D}\otimes \mathcal {C}$
. Their Day convolution is computed by
 $$ \begin{align*} &((d_1\boxtimes c_1)\otimes_{\mathrm{Day}} (d_2\boxtimes c_2))(x) \\ = &\int^{x_1,x_2\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{C}}(x_1\otimes x_2, x)\otimes (d_1\otimes d_2)\otimes \mathrm{Hom}_{\mathcal{C}}(\mathbf{1}, c_1\otimes x_1)\otimes \mathrm{Hom}_{\mathcal{C}}(\mathbf{1}, c_2\otimes x_2). \end{align*} $$
$$ \begin{align*} &((d_1\boxtimes c_1)\otimes_{\mathrm{Day}} (d_2\boxtimes c_2))(x) \\ = &\int^{x_1,x_2\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{C}}(x_1\otimes x_2, x)\otimes (d_1\otimes d_2)\otimes \mathrm{Hom}_{\mathcal{C}}(\mathbf{1}, c_1\otimes x_1)\otimes \mathrm{Hom}_{\mathcal{C}}(\mathbf{1}, c_2\otimes x_2). \end{align*} $$
So, we have to exhibit a natural isomorphism
 $$\begin{align*}\mathrm{Hom}_{\mathcal{C}}(\mathbf{1}, c_2\otimes c_1\otimes x)\cong \int^{x_1,x_2\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{C}}(x_1\otimes x_2, x)\otimes \mathrm{Hom}_{\mathcal{C}}(\mathbf{1}, c_1\otimes x_1)\otimes \mathrm{Hom}_{\mathcal{C}}(\mathbf{1}, c_2\otimes x_2).\end{align*}$$
$$\begin{align*}\mathrm{Hom}_{\mathcal{C}}(\mathbf{1}, c_2\otimes c_1\otimes x)\cong \int^{x_1,x_2\in\mathcal{C}^{\mathrm{cp}}} \mathrm{Hom}_{\mathcal{C}}(x_1\otimes x_2, x)\otimes \mathrm{Hom}_{\mathcal{C}}(\mathbf{1}, c_1\otimes x_1)\otimes \mathrm{Hom}_{\mathcal{C}}(\mathbf{1}, c_2\otimes x_2).\end{align*}$$
By assumption,
![]() $\mathcal {C}$
is generated by compact projectives, so it is enough to define this isomorphism on those.
$\mathcal {C}$
is generated by compact projectives, so it is enough to define this isomorphism on those.
The right-hand side is
 $$ \begin{align*} &\quad \int^{x_1,x_2} \mathrm{Hom}(x_1\otimes x_2, x)\otimes \mathrm{Hom}(\mathbf{1}, c_1\otimes x_1)\otimes \mathrm{Hom}(\mathbf{1}, c_2\otimes x_2) \\ &\cong \int^{x_1,x_2} \mathrm{Hom}(x_1\otimes x_2, x)\otimes \mathrm{Hom}(c_1^\vee, x_1)\otimes \mathrm{Hom}(c_2^\vee, x_2) \\ &\cong \mathrm{Hom}(c_1^\vee\otimes c_2^\vee, x) \\ &\cong \mathrm{Hom}(\mathbf{1}, c_2\otimes c_1\otimes x), \end{align*} $$
$$ \begin{align*} &\quad \int^{x_1,x_2} \mathrm{Hom}(x_1\otimes x_2, x)\otimes \mathrm{Hom}(\mathbf{1}, c_1\otimes x_1)\otimes \mathrm{Hom}(\mathbf{1}, c_2\otimes x_2) \\ &\cong \int^{x_1,x_2} \mathrm{Hom}(x_1\otimes x_2, x)\otimes \mathrm{Hom}(c_1^\vee, x_1)\otimes \mathrm{Hom}(c_2^\vee, x_2) \\ &\cong \mathrm{Hom}(c_1^\vee\otimes c_2^\vee, x) \\ &\cong \mathrm{Hom}(\mathbf{1}, c_2\otimes c_1\otimes x), \end{align*} $$
where we have used Theorem 2.4 in the third line.
We will now examine the monoidal properties of the self-duality pairings given by equations (11) and (12).
Proposition 2.15. The functors
have a natural lax monoidal structure.
Proof. We begin with the evaluation functor. The unit map
![]() $k\rightarrow \mathrm {ev}(\mathbf {1}, \mathbf {1})=\mathrm {Hom}_{\mathcal {C}}(\mathbf {1}, \mathbf {1})$
is given by the inclusion of the identity. Suppose
$k\rightarrow \mathrm {ev}(\mathbf {1}, \mathbf {1})=\mathrm {Hom}_{\mathcal {C}}(\mathbf {1}, \mathbf {1})$
is given by the inclusion of the identity. Suppose
![]() $c_1\boxtimes c_2,d_1\boxtimes d_2\in \mathcal {C}^{\otimes \mathrm {op}}\otimes \mathcal {C}$
are two compact projective objects. Then we define
$c_1\boxtimes c_2,d_1\boxtimes d_2\in \mathcal {C}^{\otimes \mathrm {op}}\otimes \mathcal {C}$
are two compact projective objects. Then we define
![]() $\mathrm {ev}(c_1, c_2)\otimes \mathrm {ev}(d_1, d_2)\rightarrow \mathrm {ev}(d_1\otimes c_1, c_2\otimes d_2)$
via the commutative diagram
$\mathrm {ev}(c_1, c_2)\otimes \mathrm {ev}(d_1, d_2)\rightarrow \mathrm {ev}(d_1\otimes c_1, c_2\otimes d_2)$
via the commutative diagram

Next we consider the coevaluation functor. A lax monoidal structure on
![]() $\mathrm {coev}$
is the same as an algebra structure on
$\mathrm {coev}$
is the same as an algebra structure on
![]() $\mathrm {coev}(k)=T^{\mathrm {R}}(\mathbf {1})$
, which, in turn, is provided by Theorem 2.10.
$\mathrm {coev}(k)=T^{\mathrm {R}}(\mathbf {1})$
, which, in turn, is provided by Theorem 2.10.
Now suppose
![]() $\mathcal {C},\mathcal {D}$
are cp-rigid monoidal categories with compact projective units and
$\mathcal {C},\mathcal {D}$
are cp-rigid monoidal categories with compact projective units and
![]() $\mathcal {E}$
any monoidal category. Then the composition functor
$\mathcal {E}$
any monoidal category. Then the composition functor
has a natural lax monoidal structure with respect to the Day convolution.
Proposition 2.16. Suppose
![]() $\mathcal {C},\mathcal {D},\mathcal {E}$
are as above. The diagrams
$\mathcal {C},\mathcal {D},\mathcal {E}$
are as above. The diagrams

and

of lax monoidal functors with respect to the Day convolution commute up to a monoidal natural isomorphism.
Recall the following notion (see [Reference Aguiar and Mahajan2, Definition 6.1], where it is called a 2-monoidal category).
Definition 2.17. A
duoidal category
is a category
![]() $\mathcal {C}$
equipped with two monoidal structures
$\mathcal {C}$
equipped with two monoidal structures
![]() $(\mathcal {C}, \circ , I)$
and
$(\mathcal {C}, \circ , I)$
and
![]() $(\mathcal {C}, \otimes , J)$
such that the functors
$(\mathcal {C}, \otimes , J)$
such that the functors
![]() $\circ \colon \mathcal {C}\times \mathcal {C}\rightarrow \mathcal {C}$
and
$\circ \colon \mathcal {C}\times \mathcal {C}\rightarrow \mathcal {C}$
and
![]() $I\colon \mathrm {Vect}\rightarrow \mathcal {C}$
are lax monoidal with respect to
$I\colon \mathrm {Vect}\rightarrow \mathcal {C}$
are lax monoidal with respect to
![]() $(\otimes , J)$
.
$(\otimes , J)$
.
Example 2.18. Consider the category
![]() $\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {C})$
. It carries a monoidal structure
$\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {C})$
. It carries a monoidal structure
![]() $\circ $
given by the composition of functors whose unit I is the identity functor. It also carries the Day convolution monoidal structure
$\circ $
given by the composition of functors whose unit I is the identity functor. It also carries the Day convolution monoidal structure
![]() $\otimes _{Day}$
. It is shown in [Reference Garner and Franco42, Proposition 50] that the two are compatible so that
$\otimes _{Day}$
. It is shown in [Reference Garner and Franco42, Proposition 50] that the two are compatible so that
![]() $\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {C})$
is a duoidal category.
$\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {C})$
is a duoidal category.
Example 2.19. Consider the category
![]() $\mathcal {C}\otimes \mathcal {C}$
. It carries a convolution monoidal structure
$\mathcal {C}\otimes \mathcal {C}$
. It carries a convolution monoidal structure
![]() $\circ $
defined by
$\circ $
defined by
whose unit is
![]() $I = \mathrm {coev}(k)\in \mathcal {C}\otimes \mathcal {C}$
. It also carries a pointwise monoidal structure
$I = \mathrm {coev}(k)\in \mathcal {C}\otimes \mathcal {C}$
. It also carries a pointwise monoidal structure
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
whose unit is
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
whose unit is
![]() $J = \mathbf {1}_{\mathcal {C}}\boxtimes \mathbf {1}_{\mathcal {C}}$
. It follows from Theorem 2.15 that the two monoidal structures are compatible, so
$J = \mathbf {1}_{\mathcal {C}}\boxtimes \mathbf {1}_{\mathcal {C}}$
. It follows from Theorem 2.15 that the two monoidal structures are compatible, so
![]() $\mathcal {C}\otimes \mathcal {C}$
becomes a duoidal category. Moreover,
$\mathcal {C}\otimes \mathcal {C}$
becomes a duoidal category. Moreover,
![]() $\mathcal {C}$
is naturally a module category over
$\mathcal {C}$
is naturally a module category over
![]() $\mathcal {C}\otimes \mathcal {C}$
with respect to convolution
$\mathcal {C}\otimes \mathcal {C}$
with respect to convolution
and is given by
We are now ready to relate the two duoidal structures. The following statement combines Theorems 2.14 and 2.16.
Theorem 2.20. Suppose
![]() $\mathcal {C}$
is a cp-rigid monoidal category with a compact projective unit. The equivalence given by equation (13)
$\mathcal {C}$
is a cp-rigid monoidal category with a compact projective unit. The equivalence given by equation (13)
given by
![]() $c_1\boxtimes c_2\mapsto (d\mapsto \mathrm {ev}(c_2, d)\otimes c_1)$
upgrades to an equivalence of duoidal categories, where the two monoidal structures are the convolution product and the pointwise monoidal structure on
$c_1\boxtimes c_2\mapsto (d\mapsto \mathrm {ev}(c_2, d)\otimes c_1)$
upgrades to an equivalence of duoidal categories, where the two monoidal structures are the convolution product and the pointwise monoidal structure on
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
while the two monoidal structures on
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
while the two monoidal structures on
![]() $\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {C})$
are the composition of functors and Day convolution. This equivalence intertwines
$\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {C})$
are the composition of functors and Day convolution. This equivalence intertwines
![]() $\mathcal {C}$
as a
$\mathcal {C}$
as a
![]() $\mathcal {C}\otimes \mathcal {C}$
-module category with respect to convolution and
$\mathcal {C}\otimes \mathcal {C}$
-module category with respect to convolution and
![]() $\mathcal {C}$
as a
$\mathcal {C}$
as a
![]() $\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {C})$
-module category with respect to composition of functors.
$\mathrm {Fun}^{\mathrm {L}}(\mathcal {C}, \mathcal {C})$
-module category with respect to composition of functors.
2.4 Bimodules and lax monoidal functors
Suppose
![]() $f\colon A\rightarrow B$
is a homomorphism of algebras. Then B becomes an
$f\colon A\rightarrow B$
is a homomorphism of algebras. Then B becomes an
![]() $(A, B)$
-bimodule with a distinguished element given by
$(A, B)$
-bimodule with a distinguished element given by
![]() $1\in B$
. Conversely, the data of an
$1\in B$
. Conversely, the data of an
![]() $(A, B)$
-bimodule M with a distinguished element
$(A, B)$
-bimodule M with a distinguished element
![]() $1_M\in M$
such that the action map
$1_M\in M$
such that the action map
![]() $B\rightarrow M$
is an isomorphism, is the same as the data of a homomorphism
$B\rightarrow M$
is an isomorphism, is the same as the data of a homomorphism
![]() $A\rightarrow B$
. In this section, we will describe a similar construction on the categorical level. Recall from [Reference Etingof, Gelaki, Nikshych and Ostrik34, Chapters 7.1,7.2] the notion of a module category over a monoidal category.
$A\rightarrow B$
. In this section, we will describe a similar construction on the categorical level. Recall from [Reference Etingof, Gelaki, Nikshych and Ostrik34, Chapters 7.1,7.2] the notion of a module category over a monoidal category.
Suppose
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {D}$
are monoidal categories and
$\mathcal {D}$
are monoidal categories and
![]() $\mathcal {M}$
a
$\mathcal {M}$
a
![]() $(\mathcal {C}, \mathcal {D})$
bimodule category together with a distinguished object
$(\mathcal {C}, \mathcal {D})$
bimodule category together with a distinguished object
![]() $\mathrm {Dist}\in \mathcal {M}$
. The action functors of
$\mathrm {Dist}\in \mathcal {M}$
. The action functors of
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {D}$
on
$\mathcal {D}$
on
![]() $\mathrm {Dist}\in \mathcal {M}$
define colimit-preserving functors
$\mathrm {Dist}\in \mathcal {M}$
define colimit-preserving functors
which we write as
![]() $x\mapsto x\otimes \mathrm {Dist}$
and
$x\mapsto x\otimes \mathrm {Dist}$
and
![]() $y\mapsto \mathrm {Dist}\otimes y$
, respectively. By the adjoint functor theorem, these admit right adjoints that we denote by
$y\mapsto \mathrm {Dist}\otimes y$
, respectively. By the adjoint functor theorem, these admit right adjoints that we denote by
![]() $\mathrm {act}^{\mathrm {R}}_{\mathcal {C}}$
and
$\mathrm {act}^{\mathrm {R}}_{\mathcal {C}}$
and
![]() $\mathrm {act}^{\mathrm {R}}_{\mathcal {D}}$
. The counit of the adjunction defines a natural morphism
$\mathrm {act}^{\mathrm {R}}_{\mathcal {D}}$
. The counit of the adjunction defines a natural morphism
for
![]() $m\in \mathcal {M}$
. Moreover,
$m\in \mathcal {M}$
. Moreover,
![]() $\mathrm {act}_{\mathcal {D}}\colon \mathcal {D}\rightarrow \mathcal {M}$
is a functor of right
$\mathrm {act}_{\mathcal {D}}\colon \mathcal {D}\rightarrow \mathcal {M}$
is a functor of right
![]() $\mathcal {D}$
-module categories, so
$\mathcal {D}$
-module categories, so
![]() $\mathrm {act}^{\mathrm {R}}_{\mathcal {D}}\colon \mathcal {M}\rightarrow \mathcal {D}$
is a lax
$\mathrm {act}^{\mathrm {R}}_{\mathcal {D}}\colon \mathcal {M}\rightarrow \mathcal {D}$
is a lax
![]() $\mathcal {D}$
-module functor: that is, we have a natural morphism
$\mathcal {D}$
-module functor: that is, we have a natural morphism
satisfying an associativity axiom.
Consider the functor
Proposition 2.21. The morphisms
and
 $$ \begin{align*} \mathrm{act}^{\mathrm{R}}_{\mathcal{D}}(x\otimes\mathrm{Dist})\otimes\mathrm{act}^{\mathrm{R}}_{\mathcal{D}}(y\otimes\mathrm{Dist})&\rightarrow \mathrm{act}^{\mathrm{R}}_{\mathcal{D}}(x\otimes \mathrm{Dist}\otimes \mathrm{act}^{\mathrm{R}}_{\mathcal{D}}(y\otimes \mathrm{Dist})) \\ &\rightarrow \mathrm{act}^{\mathrm{R}}_{\mathcal{D}}(x\otimes y\otimes \mathrm{Dist}) \end{align*} $$
$$ \begin{align*} \mathrm{act}^{\mathrm{R}}_{\mathcal{D}}(x\otimes\mathrm{Dist})\otimes\mathrm{act}^{\mathrm{R}}_{\mathcal{D}}(y\otimes\mathrm{Dist})&\rightarrow \mathrm{act}^{\mathrm{R}}_{\mathcal{D}}(x\otimes \mathrm{Dist}\otimes \mathrm{act}^{\mathrm{R}}_{\mathcal{D}}(y\otimes \mathrm{Dist})) \\ &\rightarrow \mathrm{act}^{\mathrm{R}}_{\mathcal{D}}(x\otimes y\otimes \mathrm{Dist}) \end{align*} $$
define the structure of a lax monoidal functor on
![]() $F_{\mathcal {C}\mathcal {D}}$
.
$F_{\mathcal {C}\mathcal {D}}$
.
Proof. Let us prove the associativity condition. For brevity, denote
![]() $a^{\mathrm {R}}=\mathrm {act}^{\mathrm {R}}_{\mathcal {D}}$
,
$a^{\mathrm {R}}=\mathrm {act}^{\mathrm {R}}_{\mathcal {D}}$
,
![]() $D=\mathrm {Dist}$
. We have to show that the diagram
$D=\mathrm {Dist}$
. We have to show that the diagram

is commutative. Using naturality and the associativity condition for the lax module structure on
![]() $\mathrm {act}^{\mathrm {R}}$
, the above diagram is reduced to
$\mathrm {act}^{\mathrm {R}}$
, the above diagram is reduced to

The top segment commutes by naturality of
![]() $\phi $
. The middle segment commutes since
$\phi $
. The middle segment commutes since
![]() $\epsilon $
is a natural transformation of
$\epsilon $
is a natural transformation of
![]() $\mathcal {D}$
-module functors. The bottom segment commutes by naturality of
$\mathcal {D}$
-module functors. The bottom segment commutes by naturality of
![]() $\epsilon $
.
$\epsilon $
.
Unitality is proven analogously.
Note that in the above construction, we may freely replace
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {D}$
, so we similarly obtain a lax monoidal functor
$\mathcal {D}$
, so we similarly obtain a lax monoidal functor
Definition 2.22. Suppose
![]() $\mathcal {D}$
is a monoidal category and
$\mathcal {D}$
is a monoidal category and
![]() $\mathcal {M}$
a
$\mathcal {M}$
a
![]() $\mathcal {D}$
-module category with a distinguished object.
$\mathcal {D}$
-module category with a distinguished object.
![]() $\mathcal {M}$
is
free of rank 1
if the action functor
$\mathcal {M}$
is
free of rank 1
if the action functor
![]() $\mathrm {act}_{\mathcal {D}}\colon \mathcal {D}\rightarrow \mathcal {M}$
is an equivalence.
$\mathrm {act}_{\mathcal {D}}\colon \mathcal {D}\rightarrow \mathcal {M}$
is an equivalence.
Proposition 2.23. Suppose
![]() $\mathcal {M}$
is free of rank 1 over
$\mathcal {M}$
is free of rank 1 over
![]() $\mathcal {D}$
. Then the lax monoidal functor
$\mathcal {D}$
. Then the lax monoidal functor
![]() $F_{\mathcal {C}\mathcal {D}}\colon \mathcal {C}\rightarrow \mathcal {D}$
is strongly monoidal and preserves colimits.
$F_{\mathcal {C}\mathcal {D}}\colon \mathcal {C}\rightarrow \mathcal {D}$
is strongly monoidal and preserves colimits.
Proof. Since
![]() $\mathrm {act}_{\mathcal {D}}$
is an equivalence, both the counit
$\mathrm {act}_{\mathcal {D}}$
is an equivalence, both the counit
![]() $\epsilon \colon \mathrm {Dist}\otimes \mathrm {act}^{\mathrm {R}}_{\mathcal {D}}(m)\rightarrow m$
and the structure of a lax module functor
$\epsilon \colon \mathrm {Dist}\otimes \mathrm {act}^{\mathrm {R}}_{\mathcal {D}}(m)\rightarrow m$
and the structure of a lax module functor
![]() $\phi \colon \mathrm {act}^{\mathrm {R}}_{\mathcal {D}}(m)\otimes y\rightarrow \mathrm {act}^{\mathrm {R}}_{\mathcal {D}}(m\otimes y)$
are isomorphisms. In particular,
$\phi \colon \mathrm {act}^{\mathrm {R}}_{\mathcal {D}}(m)\otimes y\rightarrow \mathrm {act}^{\mathrm {R}}_{\mathcal {D}}(m\otimes y)$
are isomorphisms. In particular,
![]() $F_{\mathcal {C}\mathcal {D}}$
is strongly monoidal.
$F_{\mathcal {C}\mathcal {D}}$
is strongly monoidal.
Moreover,
![]() $\mathrm {act}_{\mathcal {D}}^{\mathrm {R}}$
is the inverse to
$\mathrm {act}_{\mathcal {D}}^{\mathrm {R}}$
is the inverse to
![]() $\mathrm {act}_{\mathcal {D}}$
, so it preserves colimits.
$\mathrm {act}_{\mathcal {D}}$
, so it preserves colimits.
2.5 Tannaka reconstruction for bialgebras
Recall the Tannaka reconstruction results for bialgebras; refer to [Reference Deligne25, Reference Rivano71] for the commutative case and [Reference Ulbrich85, Reference Ulbrich86, Reference Schauenburg75] for the general case.
Let
![]() $B\in \mathrm {Vect}$
be a bialgebra. Then
$B\in \mathrm {Vect}$
be a bialgebra. Then
![]() $\mathcal {C}=\mathrm {CoMod}_B$
, the category of (left) B-comodules, is locally presentable. Moreover, it is equipped with a conservative and colimit-preserving monoidal forgetful functor
$\mathcal {C}=\mathrm {CoMod}_B$
, the category of (left) B-comodules, is locally presentable. Moreover, it is equipped with a conservative and colimit-preserving monoidal forgetful functor
![]() $F\colon \mathcal {C}\rightarrow \mathrm {Vect}$
, which admits a colimit-preserving right adjoint
$F\colon \mathcal {C}\rightarrow \mathrm {Vect}$
, which admits a colimit-preserving right adjoint
![]() $F^{\mathrm {R}}\colon \mathrm {Vect}\rightarrow \mathcal {C}$
sending V to the cofree B-comodule
$F^{\mathrm {R}}\colon \mathrm {Vect}\rightarrow \mathcal {C}$
sending V to the cofree B-comodule
![]() $B\otimes V$
cogenerated by V. There is a converse to this statement.
$B\otimes V$
cogenerated by V. There is a converse to this statement.
Proposition 2.24. Suppose
![]() $\mathcal {C}$
is a monoidal category with a colimit-preserving monoidal forgetful functor
$\mathcal {C}$
is a monoidal category with a colimit-preserving monoidal forgetful functor
![]() $F\colon \mathcal {C}\rightarrow \mathrm {Vect}$
, which admits a colimit-preserving right adjoint
$F\colon \mathcal {C}\rightarrow \mathrm {Vect}$
, which admits a colimit-preserving right adjoint
![]() $F^{\mathrm {R}}\colon \mathrm {Vect}\rightarrow \mathcal {C}$
. Then
$F^{\mathrm {R}}\colon \mathrm {Vect}\rightarrow \mathcal {C}$
. Then
![]() $B=FF^{\mathrm {R}}(k)$
is a bialgebra and F factors as
$B=FF^{\mathrm {R}}(k)$
is a bialgebra and F factors as
Moreover, the latter functor is an equivalence if and only if F is conservative and preserves equalisers.
Remark 2.25. A more familiar statement of Tannaka reconstruction is obtained by passing to compact objects in the above statement. Namely, for a small abelian monoidal category
![]() $\mathcal {C}^{\mathrm {c}}$
with a biexact tensor product and a monoidal functor
$\mathcal {C}^{\mathrm {c}}$
with a biexact tensor product and a monoidal functor
to the category of finite-dimensional vector spaces, there is a canonical bialgebra B (the bialgebra of coendomorphisms of F; see [Reference Etingof, Gelaki, Nikshych and Ostrik34, Section 1.10]) such that F factors through
through the category of finite-dimensional B-comodules. Moreover, the latter functor is an equivalence if and only if F is exact and faithful. Refer to [Reference Etingof, Gelaki, Nikshych and Ostrik34, Section 5.4] for more details.
Let us now be more explicit. Consider the setup of Theorem 2.24, where
![]() $\mathcal {C}$
is a monoidal category with enough compact projectives and a compact projective unit. Since
$\mathcal {C}$
is a monoidal category with enough compact projectives and a compact projective unit. Since
![]() $F^{\mathrm {R}}$
preserves colimits, F preserves compact projective objects. In particular, for
$F^{\mathrm {R}}$
preserves colimits, F preserves compact projective objects. In particular, for
![]() $y\in \mathcal {C}^{\mathrm {cp}}$
, the vector space
$y\in \mathcal {C}^{\mathrm {cp}}$
, the vector space
![]() $F(y)$
is finite-dimensional. So, by Theorem 2.5, the bialgebra B is
$F(y)$
is finite-dimensional. So, by Theorem 2.5, the bialgebra B is
 $$ \begin{align} B = \int^{y\in\mathcal{C}^{\mathrm{cp}}} F(y)^\vee\otimes F(y). \end{align} $$
$$ \begin{align} B = \int^{y\in\mathcal{C}^{\mathrm{cp}}} F(y)^\vee\otimes F(y). \end{align} $$
For
![]() $y\in \mathcal {C}^{\mathrm {cp}}$
let us denote by
$y\in \mathcal {C}^{\mathrm {cp}}$
let us denote by
the natural projection. For
![]() $y,z\in \mathcal {C}$
, denote by
$y,z\in \mathcal {C}$
, denote by
the monoidal structure on F (the unit isomorphism will be implicit). The bialgebra structure on B is given on generators as follows:
-
○ The coproduct is
 $$\begin{align*}F(y)^\vee\otimes F(y)\xrightarrow{\mathrm{id}\otimes\mathrm{coev}_{F(y)}\otimes \mathrm{id}}F(y)^\vee\otimes F(y)\otimes F(y)^\vee\otimes F(y)\xrightarrow{\pi_y\otimes \pi_y} B\otimes B.\end{align*}$$
$$\begin{align*}F(y)^\vee\otimes F(y)\xrightarrow{\mathrm{id}\otimes\mathrm{coev}_{F(y)}\otimes \mathrm{id}}F(y)^\vee\otimes F(y)\otimes F(y)^\vee\otimes F(y)\xrightarrow{\pi_y\otimes \pi_y} B\otimes B.\end{align*}$$
-
○ The counit is
 $$\begin{align*}F(y)^\vee\otimes F(y)\xrightarrow{\mathrm{ev}_{F(y)}} k.\end{align*}$$
$$\begin{align*}F(y)^\vee\otimes F(y)\xrightarrow{\mathrm{ev}_{F(y)}} k.\end{align*}$$
-
○ The product is
 $$ \begin{align*} (F(y)^\vee\otimes F(y))\otimes (F(z)^\vee\otimes F(z))&\cong (F(y)\otimes F(z))^\vee\otimes F(y)\otimes F(z)\\ &\xrightarrow{(J_{y,z}^{-1})^\vee\otimes J_{y,z}} F(y\otimes z)^\vee\otimes F(y\otimes z)\\ &\xrightarrow{\pi_{y\otimes z}} B. \end{align*} $$
$$ \begin{align*} (F(y)^\vee\otimes F(y))\otimes (F(z)^\vee\otimes F(z))&\cong (F(y)\otimes F(z))^\vee\otimes F(y)\otimes F(z)\\ &\xrightarrow{(J_{y,z}^{-1})^\vee\otimes J_{y,z}} F(y\otimes z)^\vee\otimes F(y\otimes z)\\ &\xrightarrow{\pi_{y\otimes z}} B. \end{align*} $$
-
○ The unit is
 $$\begin{align*}k\cong F(\mathbf{1})^\vee\otimes F(\mathbf{1})\xrightarrow{\pi_{\mathbf{1}}} B.\end{align*}$$
$$\begin{align*}k\cong F(\mathbf{1})^\vee\otimes F(\mathbf{1})\xrightarrow{\pi_{\mathbf{1}}} B.\end{align*}$$
It will also be useful to think about
![]() $\pi _y$
as elements
$\pi _y$
as elements
The following statement is immediate from the above formulas.
Theorem 2.26. The bialgebra B is spanned, as a k-vector space, by the matrix coefficients of
![]() $T_y$
for
$T_y$
for
![]() $y\in \mathcal {C}^{\mathrm {cp}}$
, subject to the relation
$y\in \mathcal {C}^{\mathrm {cp}}$
, subject to the relation
for every
![]() $f\colon x\rightarrow y$
. Moreover:
$f\colon x\rightarrow y$
. Moreover:
-
○ For
 $y\in \mathcal {C}^{\mathrm {cp}}$
, we have (17)
$y\in \mathcal {C}^{\mathrm {cp}}$
, we have (17) $$ \begin{align} \Delta(T_y) = T_y\otimes T_y. \end{align} $$
$$ \begin{align} \Delta(T_y) = T_y\otimes T_y. \end{align} $$
-
○ For
 $y\in \mathcal {C}^{\mathrm {cp}}$
, we have (18)
$y\in \mathcal {C}^{\mathrm {cp}}$
, we have (18) $$ \begin{align} \epsilon(T_y) = \mathrm{id}_{F(y)}\in\mathrm{End}(F(y)). \end{align} $$
$$ \begin{align} \epsilon(T_y) = \mathrm{id}_{F(y)}\in\mathrm{End}(F(y)). \end{align} $$
-
○ Suppose
 $x,y\in \mathcal {C}^{\mathrm {cp}}$
are two objects. Then (19)as elements of
$x,y\in \mathcal {C}^{\mathrm {cp}}$
are two objects. Then (19)as elements of $$ \begin{align} J^{-1}_{x,y}T_{x\otimes y}J_{x,y}=(T_x\otimes \mathrm{id}_{F(y)})(\mathrm{id}_{F(x)}\otimes T_y) \end{align} $$
$$ \begin{align} J^{-1}_{x,y}T_{x\otimes y}J_{x,y}=(T_x\otimes \mathrm{id}_{F(y)})(\mathrm{id}_{F(x)}\otimes T_y) \end{align} $$
 $B\otimes \mathrm {End}(F(x\otimes y))\cong B\otimes \mathrm {End}(F(x)\otimes F(y))$
.
$B\otimes \mathrm {End}(F(x\otimes y))\cong B\otimes \mathrm {End}(F(x)\otimes F(y))$
.
-
○
 $T_{\mathbf {1}}\in B\otimes \mathrm {End}(F(\mathbf {1}))\cong B$
is the unit.
$T_{\mathbf {1}}\in B\otimes \mathrm {End}(F(\mathbf {1}))\cong B$
is the unit.
Let us now study what happens when
![]() $\mathcal {C}$
is in addition equipped with a braiding.
$\mathcal {C}$
is in addition equipped with a braiding.
Definition 2.27. Suppose
![]() $\mathcal {C}$
is a braided monoidal category and
$\mathcal {C}$
is a braided monoidal category and
![]() $F\colon \mathcal {C}\rightarrow \mathrm {Vect}$
a monoidal functor. For
$F\colon \mathcal {C}\rightarrow \mathrm {Vect}$
a monoidal functor. For
![]() $x,y\in \mathcal {C}$
, the
$x,y\in \mathcal {C}$
, the
![]() $\boldsymbol {R}$
-matrix
is
$\boldsymbol {R}$
-matrix
is
It will be convenient to use the standard matrix notation for R-matrices acting on several variables: given
![]() $x,y,z\in \mathcal {C}$
, we denote
$x,y,z\in \mathcal {C}$
, we denote
as an element of
![]() $\mathrm {End}(F(x)\otimes F(y)\otimes F(z))$
and similarly for
$\mathrm {End}(F(x)\otimes F(y)\otimes F(z))$
and similarly for
![]() $R_{13}$
and
$R_{13}$
and
![]() $R_{23}$
. We let the transposed R-matrix
$R_{23}$
. We let the transposed R-matrix
![]() $R_{21}$
be
$R_{21}$
be
We also denote
as elements of
![]() $B\otimes \mathrm {End}(F(x)\otimes F(y))$
.
$B\otimes \mathrm {End}(F(x)\otimes F(y))$
.
Proposition 2.28. Suppose
![]() $x,y,z\in \mathcal {C}$
. Then the R-matrix satisfies the Yang–Baxter equation
$x,y,z\in \mathcal {C}$
. Then the R-matrix satisfies the Yang–Baxter equation
in
![]() $\mathrm {End}(F(x)\otimes F(y)\otimes F(z))$
. Moreover, T satisfies the FRT relation
$\mathrm {End}(F(x)\otimes F(y)\otimes F(z))$
. Moreover, T satisfies the FRT relation
in
![]() $B\otimes \mathrm {End}(F(x)\otimes F(y))$
.
$B\otimes \mathrm {End}(F(x)\otimes F(y))$
.
Proof. Denote
Then the Yang–Baxter equation (20) is equivalent to the braid equation
which holds in any braided monoidal category.
By equation (16), we have
![]() $F(\sigma _{x,y})T_{x\otimes y} = T_{y\otimes x} F(\sigma _{x,y})$
. The relation given by (19) and the equality
$F(\sigma _{x,y})T_{x\otimes y} = T_{y\otimes x} F(\sigma _{x,y})$
. The relation given by (19) and the equality
imply equation (21).
Remark 2.29. Quantum groups were originally introduced in [Reference Faddeev, Skljanin and Tahtadžjan39, Reference Faddeev, Reshetikhin and Takhtadzhyan38] as bialgebras as in Theorem 2.26 satisfying the FRT relation in equation (21). The above statements show, conversely, that this relation naturally follows from the categorical framework.
2.6 Coend algebras and reflection equation
Let
![]() $\mathcal {C}$
be a cp-rigid monoidal category. Recall the formula for the right adjoint
$\mathcal {C}$
be a cp-rigid monoidal category. Recall the formula for the right adjoint
![]() $T^{\mathrm {R}}\colon \mathcal {C}\rightarrow \mathcal {C}\otimes \mathcal {C}$
for the tensor product functor
$T^{\mathrm {R}}\colon \mathcal {C}\rightarrow \mathcal {C}\otimes \mathcal {C}$
for the tensor product functor
![]() $\mathcal {C}\otimes \mathcal {C}\rightarrow \mathcal {C}$
from Theorem 2.8.
$\mathcal {C}\otimes \mathcal {C}\rightarrow \mathcal {C}$
from Theorem 2.8.
Definition 2.30. The
canonical coend
is the object
![]() $\mathcal {F}\in \mathcal {C}$
defined by
$\mathcal {F}\in \mathcal {C}$
defined by
 $$ \begin{align} \mathcal{F} = T T^{\mathrm{R}}(\mathbf{1}) = \int^{x\in\mathcal{C}^{\mathrm{cp}}} x^\vee\otimes x. \end{align} $$
$$ \begin{align} \mathcal{F} = T T^{\mathrm{R}}(\mathbf{1}) = \int^{x\in\mathcal{C}^{\mathrm{cp}}} x^\vee\otimes x. \end{align} $$
For
![]() $x\in \mathcal {C}^{\mathrm {cp}}$
, let us denote by
$x\in \mathcal {C}^{\mathrm {cp}}$
, let us denote by
the natural projection.
Now, suppose in addition that
![]() $\mathcal {C}$
is braided monoidal. Then
$\mathcal {C}$
is braided monoidal. Then
![]() $\mathcal {F}$
admits a structure of a braided Hopf algebra (see, e.g., [Reference Lyubashenko and Majid64, Reference Lyubashenko63, Reference Shimizu78]). Explicitly, the algebra structure is given on generators as follows:
$\mathcal {F}$
admits a structure of a braided Hopf algebra (see, e.g., [Reference Lyubashenko and Majid64, Reference Lyubashenko63, Reference Shimizu78]). Explicitly, the algebra structure is given on generators as follows:
-
○ The product is
 $$ \begin{align*} (x^\vee\otimes x)\otimes (y^\vee\otimes y)&\xrightarrow{\sigma_{x^\vee\otimes x, y^\vee}} y^\vee\otimes x^\vee\otimes x\otimes y\\ &\cong (x\otimes y)^\vee\otimes x\otimes y\\ &\xrightarrow{\pi_{x\otimes y}}\mathcal{F}. \end{align*} $$
$$ \begin{align*} (x^\vee\otimes x)\otimes (y^\vee\otimes y)&\xrightarrow{\sigma_{x^\vee\otimes x, y^\vee}} y^\vee\otimes x^\vee\otimes x\otimes y\\ &\cong (x\otimes y)^\vee\otimes x\otimes y\\ &\xrightarrow{\pi_{x\otimes y}}\mathcal{F}. \end{align*} $$
-
○ The unit is
 $$\begin{align*}\mathbf{1}\xrightarrow{\pi_{\mathbf{1}}} \mathcal{F}.\end{align*}$$
$$\begin{align*}\mathbf{1}\xrightarrow{\pi_{\mathbf{1}}} \mathcal{F}.\end{align*}$$
Consider a monoidal functor
![]() $F\colon \mathcal {C}\rightarrow \mathrm {Vect}$
. The projections
$F\colon \mathcal {C}\rightarrow \mathrm {Vect}$
. The projections
![]() $\pi _x$
give rise to elements
$\pi _x$
give rise to elements
Comparing the formulas in equations (15) and (22), we see that there is an isomorphism of vector spaces
In particular, as before,
![]() $F(\mathcal {F})$
is spanned, as a k-vector space, by the matrix coefficients of
$F(\mathcal {F})$
is spanned, as a k-vector space, by the matrix coefficients of
![]() $K_x$
for
$K_x$
for
![]() $x\in \mathcal {C}^{\mathrm {cp}}$
subject to the relation in equation (16) for every
$x\in \mathcal {C}^{\mathrm {cp}}$
subject to the relation in equation (16) for every
![]() $f\colon x\rightarrow y$
. As before,
$f\colon x\rightarrow y$
. As before,
![]() $K_{\mathbf {1}}\in F(\mathcal {F})$
is the unit. However, the multiplication is different. The following was proved in [Reference Majid66, Reference Donin, Kulish and Mudrov26].
$K_{\mathbf {1}}\in F(\mathcal {F})$
is the unit. However, the multiplication is different. The following was proved in [Reference Majid66, Reference Donin, Kulish and Mudrov26].
Proposition 2.31. Suppose
![]() $x,y\in \mathcal {C}^{\mathrm {cp}}$
are two objects. Then the reflection equation
$x,y\in \mathcal {C}^{\mathrm {cp}}$
are two objects. Then the reflection equation
holds in
![]() $F(\mathcal {F})\otimes \mathrm {End}(F(x)\otimes F(y))$
.
$F(\mathcal {F})\otimes \mathrm {End}(F(x)\otimes F(y))$
.
Remark 2.32. The reflection equation algebra in the theory of quantum groups was introduced in [Reference Kulish and Sklyanin58] as the algebra generated by the matrix elements of K satisfying the reflection equation (23). We see that it coincides with
![]() $F(\mathcal {F})$
. So,
$F(\mathcal {F})$
. So,
![]() $\mathcal {F}$
is also sometimes known as the reflection equation algebra.
$\mathcal {F}$
is also sometimes known as the reflection equation algebra.
Example 2.33. Suppose H is a Hopf algebra and consider
![]() $\mathcal {C}=\mathrm {LMod}_H$
. Then the coend algebra
$\mathcal {C}=\mathrm {LMod}_H$
. Then the coend algebra
![]() $\mathcal {F}$
is a Drinfeld twist of the restricted dual Hopf algebra
$\mathcal {F}$
is a Drinfeld twist of the restricted dual Hopf algebra
 $$\begin{align*}H^\circ=\int^{V\in\mathrm{LMod}_H^{\mathrm{cp}}} V^\vee\otimes V;\end{align*}$$
$$\begin{align*}H^\circ=\int^{V\in\mathrm{LMod}_H^{\mathrm{cp}}} V^\vee\otimes V;\end{align*}$$
see [Reference Donin and Mudrov27, Definition 4.12].
3 Harish-Chandra bimodules
In this section, we study categories of classical and quantum Harish-Chandra bimodules as well as introduce Harish-Chandra bialgebroids.
3.1 General definition
We will now present a general categorical definition that encompasses categories of both classical and quantum Harish-Chandra bimodules. We refer to section 3.3 for a relationship to the usual Harish-Chandra bimodules. This formalism is closely related to the theory of dynamical extensions of monoidal categories introduced in [Reference Donin and Mudrov28]; see Theorem 3.2.
Throughout this section, we fix a cp-rigid monoidal category
![]() $\mathcal {C}$
. Recall from [Reference Etingof, Gelaki, Nikshych and Ostrik34, Definition 7.13.1] that the Drinfeld centre
$\mathcal {C}$
. Recall from [Reference Etingof, Gelaki, Nikshych and Ostrik34, Definition 7.13.1] that the Drinfeld centre
![]() $\mathrm {Z}_{\mathrm {Dr}}(\mathcal {C})$
is the braided monoidal category consisting of pairs
$\mathrm {Z}_{\mathrm {Dr}}(\mathcal {C})$
is the braided monoidal category consisting of pairs
![]() $(z, \tau )$
, where
$(z, \tau )$
, where
![]() $z\in \mathcal {C}$
and
$z\in \mathcal {C}$
and
is a natural isomorphism satisfying standard compatibilities. The monoidal structure is given by
where
![]() $\tilde {\tau }$
is the composite
$\tilde {\tau }$
is the composite
where we omit associators. We refer to [Reference Etingof, Gelaki, Nikshych and Ostrik34, Proposition 8.5.1] for the braided monoidal structure on
![]() $\mathrm {Z}_{\mathrm {Dr}}(\mathcal {C})$
.
$\mathrm {Z}_{\mathrm {Dr}}(\mathcal {C})$
.
Definition 3.1. Let
![]() $(\mathcal {L}, \tau )$
be a commutative algebra in
$(\mathcal {L}, \tau )$
be a commutative algebra in
![]() $\mathrm {Z}_{\mathrm {Dr}}(\mathcal {C})$
. The
category of Harish-Chandra bimodules
is
$\mathrm {Z}_{\mathrm {Dr}}(\mathcal {C})$
. The
category of Harish-Chandra bimodules
is
When there is no confusion, we simply denote
![]() $\mathrm {HC}=\mathrm {HC}(\mathcal {C}, \mathcal {L})$
.
$\mathrm {HC}=\mathrm {HC}(\mathcal {C}, \mathcal {L})$
.
Remark 3.2. A commutative algebra in the Drinfeld centre is called a base algebra in [Reference Donin and Mudrov28, Definition 4.1]. The full subcategory of
![]() $\mathrm {HC}(\mathcal {C}, \mathcal {L})$
consisting of free left
$\mathrm {HC}(\mathcal {C}, \mathcal {L})$
consisting of free left
![]() $\mathcal {L}$
-modules is called a dynamical extension of
$\mathcal {L}$
-modules is called a dynamical extension of
![]() $\mathcal {C}$
over
$\mathcal {C}$
over
![]() $\mathcal {L}$
in [Reference Donin and Mudrov28, Section 4.2].
$\mathcal {L}$
in [Reference Donin and Mudrov28, Section 4.2].
If H is a Hopf algebra, recall that the Drinfeld centre
![]() $\mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
is equivalent to the category of Yetter–Drinfeld modules over H (see [Reference Kassel52, Section XIII.5]). This gives rise to the following important example.
$\mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
is equivalent to the category of Yetter–Drinfeld modules over H (see [Reference Kassel52, Section XIII.5]). This gives rise to the following important example.
Proposition 3.3. Suppose H is a Hopf algebra, and consider
![]() $\mathcal {C}=\mathrm {LMod}_H$
. A commutative algebra
$\mathcal {C}=\mathrm {LMod}_H$
. A commutative algebra
![]() $\mathcal {L}$
in
$\mathcal {L}$
in
![]() $\mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
is the same as an H-algebra
$\mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
is the same as an H-algebra
![]() $\mathcal {L}$
equipped with a left H-coaction
$\mathcal {L}$
equipped with a left H-coaction
![]() $\delta \colon \mathcal {L}\rightarrow H\otimes \mathcal {L}$
, a map of H-algebras, denoted by
$\delta \colon \mathcal {L}\rightarrow H\otimes \mathcal {L}$
, a map of H-algebras, denoted by
![]() $x\mapsto x_{(-1)}\otimes x_{(0)}$
satisfying
$x\mapsto x_{(-1)}\otimes x_{(0)}$
satisfying
The corresponding isomorphism
![]() $\tau _M\colon M\otimes \mathcal {L}\rightarrow \mathcal {L}\otimes M$
is given by
$\tau _M\colon M\otimes \mathcal {L}\rightarrow \mathcal {L}\otimes M$
is given by
Proof. The compatibility of
![]() $\tau _M$
with the monoidal structure on
$\tau _M$
with the monoidal structure on
![]() $\mathrm {LMod}_H$
follows from the coassociativity and counitality of the H-coaction. The compatibility of
$\mathrm {LMod}_H$
follows from the coassociativity and counitality of the H-coaction. The compatibility of
![]() $\tau _M$
with the algebra structure on
$\tau _M$
with the algebra structure on
![]() $\mathcal {L}$
is equivalent to the equation
$\mathcal {L}$
is equivalent to the equation
which follows from the condition that
![]() $\mathcal {L}\rightarrow H\otimes \mathcal {L}$
is an algebra map. The commutativity of the multiplication on
$\mathcal {L}\rightarrow H\otimes \mathcal {L}$
is an algebra map. The commutativity of the multiplication on
![]() $\mathcal {L}\in \mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
is
$\mathcal {L}\in \mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
is
Remark 3.4. The inverse morphism
![]() $\mathcal {L}\otimes M\rightarrow M\otimes \mathcal {L}$
is given by
$\mathcal {L}\otimes M\rightarrow M\otimes \mathcal {L}$
is given by
Example 3.5. Consider a Hopf algebra H, and let
![]() $\mathcal {L}=H$
. Consider the adjoint action of H on
$\mathcal {L}=H$
. Consider the adjoint action of H on
![]() $\mathcal {L}$
$\mathcal {L}$
for
![]() $h\in H$
and
$h\in H$
and
![]() $x\in \mathcal {L}$
. Consider the H-coaction
$x\in \mathcal {L}$
. Consider the H-coaction
![]() $\mathcal {L}\rightarrow H\otimes \mathcal {L}$
given by the coproduct on H. Then
$\mathcal {L}\rightarrow H\otimes \mathcal {L}$
given by the coproduct on H. Then
In particular,
 $$ \begin{align*} y_{(2)} (S^{-1}(y_{(1)}))\triangleright x &= y_{(3)} S^{-1}(y_{(2)})x y_{(1)} \\ &= \epsilon(y_{(2)}) x y_{(1)} \\ &= xy, \end{align*} $$
$$ \begin{align*} y_{(2)} (S^{-1}(y_{(1)}))\triangleright x &= y_{(3)} S^{-1}(y_{(2)})x y_{(1)} \\ &= \epsilon(y_{(2)}) x y_{(1)} \\ &= xy, \end{align*} $$
which shows that
![]() $(\mathcal {L}, \tau )$
is a commutative algebra in
$(\mathcal {L}, \tau )$
is a commutative algebra in
![]() $\mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
.
$\mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
.
Since
![]() $\mathcal {L}$
is a commutative algebra in
$\mathcal {L}$
is a commutative algebra in
![]() $\mathrm {Z}_{\mathrm {Dr}}(\mathcal {C})$
, the category
$\mathrm {Z}_{\mathrm {Dr}}(\mathcal {C})$
, the category
![]() $\mathrm {HC}$
has a natural monoidal structure given by the relative tensor product: given left
$\mathrm {HC}$
has a natural monoidal structure given by the relative tensor product: given left
![]() $\mathcal {L}$
-modules
$\mathcal {L}$
-modules
![]() $M,N\in \mathcal {C}$
, we may turn M into a right
$M,N\in \mathcal {C}$
, we may turn M into a right
![]() $\mathcal {L}$
-module using
$\mathcal {L}$
-module using
![]() $\tau _M$
, and then the tensor product is given by
$\tau _M$
, and then the tensor product is given by
![]() $M\otimes _{\mathcal {L}} N$
. We also have an adjunction
$M\otimes _{\mathcal {L}} N$
. We also have an adjunction
where
![]() $\mathrm {free}\colon \mathcal {C}\rightarrow \mathrm {HC}$
is the monoidal functor
$\mathrm {free}\colon \mathcal {C}\rightarrow \mathrm {HC}$
is the monoidal functor
![]() $x\mapsto \mathcal {L}\otimes x$
given by the free left
$x\mapsto \mathcal {L}\otimes x$
given by the free left
![]() $\mathcal {L}$
-module and
$\mathcal {L}$
-module and
![]() $\mathrm {forget}\colon \mathrm {HC}\rightarrow \mathcal {C}$
is given by forgetting the
$\mathrm {forget}\colon \mathrm {HC}\rightarrow \mathcal {C}$
is given by forgetting the
![]() $\mathcal {L}$
-module structure.
$\mathcal {L}$
-module structure.
Observe that
![]() $\mathcal {L}^{\mathrm {op}}$
is an algebra in
$\mathcal {L}^{\mathrm {op}}$
is an algebra in
![]() $\mathcal {C}^{\otimes \mathrm {op}}$
. Moreover, it lifts to a commutative algebra in
$\mathcal {C}^{\otimes \mathrm {op}}$
. Moreover, it lifts to a commutative algebra in
![]() $\mathrm {Z}_{\mathrm {Dr}}(\mathcal {C}^{\otimes \mathrm {op}})$
if we consider the inverse isomorphism
$\mathrm {Z}_{\mathrm {Dr}}(\mathcal {C}^{\otimes \mathrm {op}})$
if we consider the inverse isomorphism
![]() $\tau _x$
.
$\tau _x$
.
Lemma 3.6. There is a natural monoidal equivalence
![]() $\mathrm {HC}(\mathcal {C}, \mathcal {L})^{\otimes \mathrm {op}}\cong \mathrm {HC}(\mathcal {C}^{\otimes \mathrm {op}}, \mathcal {L}^{\mathrm {op}})$
.
$\mathrm {HC}(\mathcal {C}, \mathcal {L})^{\otimes \mathrm {op}}\cong \mathrm {HC}(\mathcal {C}^{\otimes \mathrm {op}}, \mathcal {L}^{\mathrm {op}})$
.
The following construction explains why
![]() $\mathrm {HC}$
deserves to be called the category of bimodules. There is a natural monoidal functor
$\mathrm {HC}$
deserves to be called the category of bimodules. There is a natural monoidal functor
given by sending a left
![]() $\mathcal {L}$
-module M to the
$\mathcal {L}$
-module M to the
![]() $\mathcal {L}$
-bimodule, where the right
$\mathcal {L}$
-bimodule, where the right
![]() $\mathcal {L}$
-action is obtained via
$\mathcal {L}$
-action is obtained via
![]() $\tau _M$
. It realises
$\tau _M$
. It realises
![]() $\mathrm {HC}$
as a full subcategory of
$\mathrm {HC}$
as a full subcategory of
![]() ${}_{\mathcal {L}}\mathrm {BMod}_{\mathcal {L}}(\mathcal {C})$
consisting of objects
${}_{\mathcal {L}}\mathrm {BMod}_{\mathcal {L}}(\mathcal {C})$
consisting of objects
![]() $M\in {}_{\mathcal {L}}\mathrm {BMod}_{\mathcal {L}}(\mathcal {C})$
such that the right and left actions are related by
$M\in {}_{\mathcal {L}}\mathrm {BMod}_{\mathcal {L}}(\mathcal {C})$
such that the right and left actions are related by
![]() $\tau _M$
.
$\tau _M$
.
Let us now analyse the categorical properties of
![]() $\mathrm {HC}$
.
$\mathrm {HC}$
.
Proposition 3.7. The category
![]() $\mathrm {HC}$
is cp-rigid. Moreover, we may take
$\mathrm {HC}$
is cp-rigid. Moreover, we may take
![]() $\mathrm {free}(V)\in \mathrm {HC}$
for all
$\mathrm {free}(V)\in \mathrm {HC}$
for all
![]() $V\in \mathcal {C}^{\mathrm {cp}}$
as the generating set of compact projective objects. If the unit of
$V\in \mathcal {C}^{\mathrm {cp}}$
as the generating set of compact projective objects. If the unit of
![]() $\mathcal {C}$
is compact projective, so is the unit in
$\mathcal {C}$
is compact projective, so is the unit in
![]() $\mathrm {HC}$
.
$\mathrm {HC}$
.
Proof. The functor
![]() $\mathrm {free}\colon \mathcal {C}\rightarrow \mathrm {HC}$
has a colimit-preserving right adjoint
$\mathrm {free}\colon \mathcal {C}\rightarrow \mathrm {HC}$
has a colimit-preserving right adjoint
![]() $\mathrm {forget}\colon \mathrm {HC}\rightarrow \mathcal {C}$
. So,
$\mathrm {forget}\colon \mathrm {HC}\rightarrow \mathcal {C}$
. So,
![]() $\mathrm {free}(V)\in \mathrm {HC}$
is compact projective if
$\mathrm {free}(V)\in \mathrm {HC}$
is compact projective if
![]() $V\in \mathcal {C}^{\mathrm {cp}}$
.
$V\in \mathcal {C}^{\mathrm {cp}}$
.
The category
![]() $\mathrm {HC}$
is generated by
$\mathrm {HC}$
is generated by
![]() $\mathrm {free}(V)$
for
$\mathrm {free}(V)$
for
![]() $V\in \mathcal {C}$
since
$V\in \mathcal {C}$
since
![]() $\mathrm {forget}$
is conservative. But since
$\mathrm {forget}$
is conservative. But since
![]() $\mathcal {C}$
has enough compact projectives, we may restrict to
$\mathcal {C}$
has enough compact projectives, we may restrict to
![]() $V\in \mathcal {C}^{\mathrm {cp}}$
.
$V\in \mathcal {C}^{\mathrm {cp}}$
.
Since
![]() $\mathcal {C}$
is cp-rigid, the objects
$\mathcal {C}$
is cp-rigid, the objects
![]() $V\in \mathcal {C}^{\mathrm {cp}}$
are dualisable. Since
$V\in \mathcal {C}^{\mathrm {cp}}$
are dualisable. Since
![]() $\mathrm {free}\colon \mathcal {C}\rightarrow \mathrm {HC}$
is monoidal, the objects
$\mathrm {free}\colon \mathcal {C}\rightarrow \mathrm {HC}$
is monoidal, the objects
![]() $\mathrm {free}(V)\in \mathrm {HC}$
are also dualisable. But we have just shown that such objects are the generating compact projective objects, while by [Reference Brochier, Jordan and Snyder18, Proposition 4.1], it is enough to check cp-rigidity on the generating compact projective objects.
$\mathrm {free}(V)\in \mathrm {HC}$
are also dualisable. But we have just shown that such objects are the generating compact projective objects, while by [Reference Brochier, Jordan and Snyder18, Proposition 4.1], it is enough to check cp-rigidity on the generating compact projective objects.
The unit of
![]() $\mathrm {HC}$
is
$\mathrm {HC}$
is
![]() $\mathcal {L}$
viewed as a free left
$\mathcal {L}$
viewed as a free left
![]() $\mathcal {L}$
-module of rank 1, so
$\mathcal {L}$
-module of rank 1, so
which shows that
![]() $\mathcal {L}$
is compact projective if and only if
$\mathcal {L}$
is compact projective if and only if
![]() $\mathbf {1}_{\mathcal {C}}\in \mathcal {C}$
is.
$\mathbf {1}_{\mathcal {C}}\in \mathcal {C}$
is.
3.2 Quantum moment maps
Recall that for an algebra
![]() $A\in \operatorname {\mathrm {Rep}}(G)$
, a quantum moment map is a map
$A\in \operatorname {\mathrm {Rep}}(G)$
, a quantum moment map is a map
![]() $\mu \colon \mathrm {U}\mathfrak {g}\rightarrow A$
such that the infinitesimal
$\mu \colon \mathrm {U}\mathfrak {g}\rightarrow A$
such that the infinitesimal
![]() $\mathfrak {g}$
-action on A is given by
$\mathfrak {g}$
-action on A is given by
![]() $[\mu (x), -]$
for
$[\mu (x), -]$
for
![]() $x\in \mathfrak {g}$
. The following version of this definition in our setting was introduced in [Reference Safronov73, Definition 3.1].
$x\in \mathfrak {g}$
. The following version of this definition in our setting was introduced in [Reference Safronov73, Definition 3.1].
Definition 3.8. Let
![]() $A\in \mathcal {C}$
be an algebra. A
quantum moment map
is an algebra map
$A\in \mathcal {C}$
be an algebra. A
quantum moment map
is an algebra map
![]() $\mu \colon \mathcal {L}\rightarrow A$
such that the diagram
$\mu \colon \mathcal {L}\rightarrow A$
such that the diagram

commutes.
Remark 3.9. Recall that
![]() $\mathcal {L}\in \mathrm {Z}_{\mathrm {Dr}}(\mathcal {C})$
is a commutative algebra. The quantum moment map condition expressed by equation (25) says that
$\mathcal {L}\in \mathrm {Z}_{\mathrm {Dr}}(\mathcal {C})$
is a commutative algebra. The quantum moment map condition expressed by equation (25) says that
![]() $\mu \colon \mathcal {L}\rightarrow A$
is a central map.
$\mu \colon \mathcal {L}\rightarrow A$
is a central map.
Proposition 3.10. An algebra in
![]() $\mathrm {HC}$
is an algebra in
$\mathrm {HC}$
is an algebra in
![]() $\mathcal {C}$
equipped with a quantum moment map.
$\mathcal {C}$
equipped with a quantum moment map.
Proof. Via the embedding
![]() $\mathrm {bimod}\colon \mathrm {HC}\rightarrow {}_{\mathcal {L}}\mathrm {BMod}_{\mathcal {L}}(\mathcal {C})$
of equation (24), an algebra
$\mathrm {bimod}\colon \mathrm {HC}\rightarrow {}_{\mathcal {L}}\mathrm {BMod}_{\mathcal {L}}(\mathcal {C})$
of equation (24), an algebra
![]() $A\in \mathrm {HC}$
gives rise to an algebra in
$A\in \mathrm {HC}$
gives rise to an algebra in
![]() ${}_{\mathcal {L}}\mathrm {BMod}_{\mathcal {L}}(\mathcal {C})$
. An algebra in the category of bimodules is the same as an algebra
${}_{\mathcal {L}}\mathrm {BMod}_{\mathcal {L}}(\mathcal {C})$
. An algebra in the category of bimodules is the same as an algebra
![]() $A\in \mathcal {C}$
equipped with an algebra map
$A\in \mathcal {C}$
equipped with an algebra map
![]() $\mu \colon \mathcal {L}\rightarrow A$
. The condition that it lands in
$\mu \colon \mathcal {L}\rightarrow A$
. The condition that it lands in
![]() $\mathrm {HC}\subset {}_{\mathcal {L}}\mathrm {BMod}_{\mathcal {L}}(\mathcal {C})$
is precisely the quantum moment map equation (25).
$\mathrm {HC}\subset {}_{\mathcal {L}}\mathrm {BMod}_{\mathcal {L}}(\mathcal {C})$
is precisely the quantum moment map equation (25).
The following is [Reference Safronov73, Definition 3.10].
Definition 3.11. Suppose
![]() $\epsilon \colon \mathcal {L}\rightarrow \mathbf {1}_{\mathcal {C}}$
is a morphism of algebras in
$\epsilon \colon \mathcal {L}\rightarrow \mathbf {1}_{\mathcal {C}}$
is a morphism of algebras in
![]() $\mathcal {C}$
and A is an algebra equipped with a quantum moment map. The
Hamiltonian reduction of
$\mathcal {C}$
and A is an algebra equipped with a quantum moment map. The
Hamiltonian reduction of
![]() $\boldsymbol {A}$
is
$\boldsymbol {A}$
is
A canonical example of an algebra with a quantum moment map we will use is the following. Let
![]() $T_{\mathrm {HC}}\colon \mathrm {HC}\otimes \mathrm {HC}\rightarrow \mathrm {HC}$
be the tensor product functor. By Theorem 2.15, the object
$T_{\mathrm {HC}}\colon \mathrm {HC}\otimes \mathrm {HC}\rightarrow \mathrm {HC}$
be the tensor product functor. By Theorem 2.15, the object
![]() $T^{\mathrm {R}}(\mathbf {1}_{\mathrm {HC}})\in \mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
is an algebra. Identifying
$T^{\mathrm {R}}(\mathbf {1}_{\mathrm {HC}})\in \mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
is an algebra. Identifying
![]() $\mathrm {HC}(\mathcal {C}, \mathcal {L})^{\otimes \mathrm {op}}\cong \mathrm {HC}(\mathcal {C}^{\otimes \mathrm {op}}, \mathcal {L}^{\mathrm {op}})$
using Theorem 3.6, we see that
$\mathrm {HC}(\mathcal {C}, \mathcal {L})^{\otimes \mathrm {op}}\cong \mathrm {HC}(\mathcal {C}^{\otimes \mathrm {op}}, \mathcal {L}^{\mathrm {op}})$
using Theorem 3.6, we see that
is an algebra equipped with a quantum moment map from
![]() $\mathcal {L}\boxtimes \mathcal {L}^{\mathrm {op}}$
.
$\mathcal {L}\boxtimes \mathcal {L}^{\mathrm {op}}$
.
Definition 3.12. Let
![]() $\mathcal {C}, \mathrm {HC}$
be as before. The algebra
$\mathcal {C}, \mathrm {HC}$
be as before. The algebra
![]() $\mathcal {D}\in \mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
is
$\mathcal {D}\in \mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
is
We denote the canonical quantum moment map by
Proposition 3.13. We have an equivalence
 $$\begin{align*}\mathcal{D}\cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} (\mathcal{L}\otimes x^\vee)\boxtimes x\cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} x^\vee\boxtimes (x\otimes \mathcal{L}),\end{align*}$$
$$\begin{align*}\mathcal{D}\cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} (\mathcal{L}\otimes x^\vee)\boxtimes x\cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} x^\vee\boxtimes (x\otimes \mathcal{L}),\end{align*}$$
where the latter isomorphism is provided by Theorem 2.9. The algebra structure is given by
 $$ \begin{align*} ((\mathcal{L}\otimes x^\vee)\boxtimes x)\otimes((\mathcal{L}\otimes y^\vee)\boxtimes y)&\cong (\mathcal{L}\otimes x^\vee\otimes \mathcal{L}\otimes y^\vee)\boxtimes (y\otimes x) \\ &\xrightarrow{\mathrm{id}\otimes \tau_{x^\vee}\otimes \mathrm{id}} (\mathcal{L}\otimes \mathcal{L}\otimes x^\vee\otimes y^\vee)\boxtimes (y\otimes x) \\ &\xrightarrow{m\otimes \mathrm{id}} (\mathcal{L}\otimes (y\otimes x)^\vee)\boxtimes (y\otimes x) \\ &\xrightarrow{\pi_{y\otimes x}} \int^{x\in\mathcal{C}^{\mathrm{cp}}} (\mathcal{L}\otimes x^\vee)\boxtimes x. \end{align*} $$
$$ \begin{align*} ((\mathcal{L}\otimes x^\vee)\boxtimes x)\otimes((\mathcal{L}\otimes y^\vee)\boxtimes y)&\cong (\mathcal{L}\otimes x^\vee\otimes \mathcal{L}\otimes y^\vee)\boxtimes (y\otimes x) \\ &\xrightarrow{\mathrm{id}\otimes \tau_{x^\vee}\otimes \mathrm{id}} (\mathcal{L}\otimes \mathcal{L}\otimes x^\vee\otimes y^\vee)\boxtimes (y\otimes x) \\ &\xrightarrow{m\otimes \mathrm{id}} (\mathcal{L}\otimes (y\otimes x)^\vee)\boxtimes (y\otimes x) \\ &\xrightarrow{\pi_{y\otimes x}} \int^{x\in\mathcal{C}^{\mathrm{cp}}} (\mathcal{L}\otimes x^\vee)\boxtimes x. \end{align*} $$
The two quantum moment maps
![]() $\mathcal {L},\mathcal {L}^{\mathrm {op}}\rightarrow \mathcal {D}$
are given by
$\mathcal {L},\mathcal {L}^{\mathrm {op}}\rightarrow \mathcal {D}$
are given by
and
Proof. Since
![]() $\mathrm {free}\colon \mathcal {C}\rightarrow \mathrm {HC}$
is a monoidal functor, by adjunction, we get a natural isomorphism
$\mathrm {free}\colon \mathcal {C}\rightarrow \mathrm {HC}$
is a monoidal functor, by adjunction, we get a natural isomorphism
where
![]() $T_{\mathcal {C}}\colon \mathcal {C}\otimes \mathcal {C}\rightarrow \mathcal {C}$
is the tensor product functor. In particular, applying equation (27) to
$T_{\mathcal {C}}\colon \mathcal {C}\otimes \mathcal {C}\rightarrow \mathcal {C}$
is the tensor product functor. In particular, applying equation (27) to
![]() $\mathbf {1}_{\mathrm {HC}}$
, we get isomorphisms
$\mathbf {1}_{\mathrm {HC}}$
, we get isomorphisms
 $$\begin{align*}\mathcal{D}\cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} (\mathcal{L}\otimes x^\vee)\boxtimes x\cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} x^\vee\boxtimes (x\otimes \mathcal{L})\end{align*}$$
$$\begin{align*}\mathcal{D}\cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} (\mathcal{L}\otimes x^\vee)\boxtimes x\cong \int^{x\in\mathcal{C}^{\mathrm{cp}}} x^\vee\boxtimes (x\otimes \mathcal{L})\end{align*}$$
using Theorem 2.8.
We have a natural isomorphism
given by Theorem 2.9 that gives rise to an algebra isomorphism
which gives the required formula.
Example 3.14. Suppose H is a Hopf algebra,
![]() $\mathcal {L}$
is a commutative algebra in
$\mathcal {L}$
is a commutative algebra in
![]() $\mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
(see Theorem 3.3) and
$\mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
(see Theorem 3.3) and
![]() $\mathcal {C}=\mathrm {LMod}_H$
. Let
$\mathcal {C}=\mathrm {LMod}_H$
. Let
 $$\begin{align*}H^\circ = \int^{V\in\mathrm{LMod}_H^{\mathrm{cp}}} V^\vee\otimes V\end{align*}$$
$$\begin{align*}H^\circ = \int^{V\in\mathrm{LMod}_H^{\mathrm{cp}}} V^\vee\otimes V\end{align*}$$
be the restricted dual Hopf algebra. By construction,
![]() $\mathcal {L}$
is an H-comodule algebra, and
$\mathcal {L}$
is an H-comodule algebra, and
![]() $H^\circ $
is an H-module algebra (via the left H-action). Then
$H^\circ $
is an H-module algebra (via the left H-action). Then
![]() $\mathcal {D}$
is the smash product algebra generated by
$\mathcal {D}$
is the smash product algebra generated by
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $H^\circ $
with the additional relation
$H^\circ $
with the additional relation
for
![]() $h\in H^\circ $
and
$h\in H^\circ $
and
![]() $l\in \mathcal {L}$
.
$l\in \mathcal {L}$
.
3.3 Classical Harish-Chandra bimodules
Let G be a reductive group over a characteristic zero field k, and denote by
![]() $\mathfrak {g}$
its Lie algebra. Let
$\mathfrak {g}$
its Lie algebra. Let
![]() $\operatorname {\mathrm {Rep}}(G)$
be the ind-completion of the category of finite-dimensional representations. The category
$\operatorname {\mathrm {Rep}}(G)$
be the ind-completion of the category of finite-dimensional representations. The category
![]() $\operatorname {\mathrm {Rep}}(G)$
is semisimple, so it has enough compact projectives and its unit is compact projective.
$\operatorname {\mathrm {Rep}}(G)$
is semisimple, so it has enough compact projectives and its unit is compact projective.
Suppose
![]() $V\in \operatorname {\mathrm {Rep}}(G)$
is a G-representation. For
$V\in \operatorname {\mathrm {Rep}}(G)$
is a G-representation. For
![]() $x\in \mathrm {U}\mathfrak {g}$
and
$x\in \mathrm {U}\mathfrak {g}$
and
![]() $v\in V$
, we denote by
$v\in V$
, we denote by
![]() $x\triangleright v$
the induced
$x\triangleright v$
the induced
![]() $\mathrm {U}\mathfrak {g}$
-action on V. Consider the natural isomorphism
$\mathrm {U}\mathfrak {g}$
-action on V. Consider the natural isomorphism
given by
for
![]() $x\in \mathfrak {g}$
. It follows from Theorem 3.3 that
$x\in \mathfrak {g}$
. It follows from Theorem 3.3 that
![]() $(\mathrm {U}\mathfrak {g}, \tau )$
defines a commutative algebra in
$(\mathrm {U}\mathfrak {g}, \tau )$
defines a commutative algebra in
![]() $\mathrm {Z}_{\mathrm {Dr}}(\operatorname {\mathrm {Rep}}(G))$
.
$\mathrm {Z}_{\mathrm {Dr}}(\operatorname {\mathrm {Rep}}(G))$
.
Definition 3.15. The category of classical Harish-Chandra bimodules is
Remark 3.16. The embedding in equation (24) realises
![]() $\mathrm {HC}(G)$
as the category of
$\mathrm {HC}(G)$
as the category of
![]() $\mathrm {U}\mathfrak {g}$
-bimodules whose diagonal
$\mathrm {U}\mathfrak {g}$
-bimodules whose diagonal
![]() $\mathfrak {g}$
-action is integrable (see [Reference Bernstein and Gelfand11, Definition 5.2] for the original definition of Harish-Chandra bimodules).
$\mathfrak {g}$
-action is integrable (see [Reference Bernstein and Gelfand11, Definition 5.2] for the original definition of Harish-Chandra bimodules).
The following easy lemma (see [Reference Safronov73, Example 3.4]) shows that the definition of a quantum moment map we gave in Theorem 3.8 coincides with the classical notion of a quantum moment map.
Lemma 3.17. Let
![]() $A\in \operatorname {\mathrm {Rep}}(G)$
be an algebra. A quantum moment map
$A\in \operatorname {\mathrm {Rep}}(G)$
be an algebra. A quantum moment map
![]() $\mu \colon \mathrm {U}\mathfrak {g}\rightarrow A$
is the same as an algebra map such that for every
$\mu \colon \mathrm {U}\mathfrak {g}\rightarrow A$
is the same as an algebra map such that for every
![]() $x\in \mathfrak {g}$
the commutator
$x\in \mathfrak {g}$
the commutator
![]() $[\mu (x), -]$
coincides with the differential of the G-action.
$[\mu (x), -]$
coincides with the differential of the G-action.
In the same way, the quantum Hamiltonian reduction from Theorem 3.11 coincides with the usual definition
of the reduced algebra.
Given a variety X equipped with a G-action, the algebra of differential operators
![]() $\mathrm {D}(X)$
carries a quantum moment map
$\mathrm {D}(X)$
carries a quantum moment map
![]() $\mu \colon \mathrm {U}\mathfrak {g}\rightarrow \mathrm {D}(X)$
, which sends
$\mu \colon \mathrm {U}\mathfrak {g}\rightarrow \mathrm {D}(X)$
, which sends
![]() $\mathfrak {g}\subset \mathrm {U}\mathfrak {g}$
to vector fields on X generating the infinitesimal action. For instance,
$\mathfrak {g}\subset \mathrm {U}\mathfrak {g}$
to vector fields on X generating the infinitesimal action. For instance,
![]() $\mathrm {D}(G)$
carries a moment map
$\mathrm {D}(G)$
carries a moment map
coming from the left and right G-action on itself. Let us explain how it arises in our context.
By the Peter–Weyl theorem, we have an isomorphism of algebras
 $$\begin{align*}\mathcal{O}(G)\cong \int^{V\in\operatorname{\mathrm{Rep}}^{\mathrm{fd}}(G)} V^\vee\boxtimes V\in\operatorname{\mathrm{Rep}}(G)\otimes \operatorname{\mathrm{Rep}}(G),\end{align*}$$
$$\begin{align*}\mathcal{O}(G)\cong \int^{V\in\operatorname{\mathrm{Rep}}^{\mathrm{fd}}(G)} V^\vee\boxtimes V\in\operatorname{\mathrm{Rep}}(G)\otimes \operatorname{\mathrm{Rep}}(G),\end{align*}$$
where
![]() $\mathcal {O}(G)$
carries a
$\mathcal {O}(G)$
carries a
![]() $G\times G$
-action coming from the left and right G-action on itself. Using this, we can also describe the algebra
$G\times G$
-action coming from the left and right G-action on itself. Using this, we can also describe the algebra
![]() $\mathcal {D}$
from Theorem 3.12.
$\mathcal {D}$
from Theorem 3.12.
Proposition 3.18. The algebra
![]() $\mathcal {D}\in \mathrm {HC}(G)\otimes \mathrm {HC}(G)^{\otimes \mathrm {op}}$
is isomorphic to
$\mathcal {D}\in \mathrm {HC}(G)\otimes \mathrm {HC}(G)^{\otimes \mathrm {op}}$
is isomorphic to
![]() $\mathrm {D}(G)\cong \mathrm {U}\mathfrak {g}\otimes \mathcal {O}(G)$
equipped with the
$\mathrm {D}(G)\cong \mathrm {U}\mathfrak {g}\otimes \mathcal {O}(G)$
equipped with the
![]() $G\times G$
-action and the quantum moment map given by equation (29).
$G\times G$
-action and the quantum moment map given by equation (29).
In the abelian case, the category of Harish-Chandra bimodules has a straightforward description. Suppose H is a split torus; let
![]() $\mathfrak {h}$
be its Lie algebra and
$\mathfrak {h}$
be its Lie algebra and
![]() $\Lambda =\mathrm {Hom}(H, \mathbb {G}_{\mathrm {m}})$
the character lattice. Then
$\Lambda =\mathrm {Hom}(H, \mathbb {G}_{\mathrm {m}})$
the character lattice. Then
![]() $\operatorname {\mathrm {Rep}}(H)$
is equivalent to the category of
$\operatorname {\mathrm {Rep}}(H)$
is equivalent to the category of
![]() $\Lambda $
-graded vector spaces, and
$\Lambda $
-graded vector spaces, and
![]() $\mathrm {HC}(H)$
is equivalent to the category of
$\mathrm {HC}(H)$
is equivalent to the category of
![]() $\Lambda $
-graded
$\Lambda $
-graded
![]() $\mathrm {Sym}(\mathfrak {h})$
-modules
$\mathrm {Sym}(\mathfrak {h})$
-modules
![]() $\oplus _{\lambda \in \Lambda } M(\lambda )$
.
$\oplus _{\lambda \in \Lambda } M(\lambda )$
.
Given
![]() $\lambda \in \Lambda $
, we consider the translation functor
$\lambda \in \Lambda $
, we consider the translation functor
![]() $\lambda ^*\colon \mathrm {LMod}_{\mathrm {Sym}(\mathfrak {h})}\rightarrow \mathrm {LMod}_{\mathrm {Sym}(\mathfrak {h})}$
. Then the monoidal structure
$\lambda ^*\colon \mathrm {LMod}_{\mathrm {Sym}(\mathfrak {h})}\rightarrow \mathrm {LMod}_{\mathrm {Sym}(\mathfrak {h})}$
. Then the monoidal structure
![]() $\otimes ^{\mathrm {HC}}$
on
$\otimes ^{\mathrm {HC}}$
on
![]() $\mathrm {HC}(H)$
is given by
$\mathrm {HC}(H)$
is given by
Suppose
![]() $V\in \operatorname {\mathrm {Rep}}(H)$
. Given a vector
$V\in \operatorname {\mathrm {Rep}}(H)$
. Given a vector
![]() $v\in V$
of weight
$v\in V$
of weight
![]() $\mu \in \Lambda $
and
$\mu \in \Lambda $
and
![]() $f\in \mathcal {O}(\mathfrak {h}^*)\cong \mathrm {U}\mathfrak {h}$
, the map given by equation (28) is given by
$f\in \mathcal {O}(\mathfrak {h}^*)\cong \mathrm {U}\mathfrak {h}$
, the map given by equation (28) is given by
for
![]() $\lambda \in \mathfrak {h}^*$
. It is convenient to write it as
$\lambda \in \mathfrak {h}^*$
. It is convenient to write it as
where h is understood as acting on
![]() $v\in V$
. Similarly, given a collection of representations
$v\in V$
. Similarly, given a collection of representations
![]() $V_1, \dots , V_n\in \operatorname {\mathrm {Rep}}(H)$
and vectors
$V_1, \dots , V_n\in \operatorname {\mathrm {Rep}}(H)$
and vectors
![]() $v_i\in V_i$
, we denote
$v_i\in V_i$
, we denote
if
![]() $v_i$
has weight
$v_i$
has weight
![]() $\mu _i\in \Lambda $
.
$\mu _i\in \Lambda $
.
3.4 Quantum groups
In this section, we fix our conventions for quantum groups. Fix
![]() $k=\mathbf {C}$
. Let G be a connected reductive group,
$k=\mathbf {C}$
. Let G be a connected reductive group,
![]() $B, B_-\subset G$
a pair of opposite Borel subgroups and
$B, B_-\subset G$
a pair of opposite Borel subgroups and
![]() $H=B\cap B_-$
a Cartan subgroup. Denote by
$H=B\cap B_-$
a Cartan subgroup. Denote by
![]() $\Lambda =\mathrm {Hom}(H, \mathbb {G}_{\mathrm {m}})$
its weight lattice and
$\Lambda =\mathrm {Hom}(H, \mathbb {G}_{\mathrm {m}})$
its weight lattice and
![]() $\Lambda ^\vee =\mathrm {Hom}(\mathbb {G}_{\mathrm {m}}, H)$
the coweight lattice; we denote by
$\Lambda ^\vee =\mathrm {Hom}(\mathbb {G}_{\mathrm {m}}, H)$
the coweight lattice; we denote by
![]() $\langle -, -\rangle \colon \Lambda ^\vee \times \Lambda \rightarrow \mathbf {Z}$
the canonical pairing. For two simple roots
$\langle -, -\rangle \colon \Lambda ^\vee \times \Lambda \rightarrow \mathbf {Z}$
the canonical pairing. For two simple roots
![]() $\alpha _i,\alpha _j\in \Lambda $
, denote by
$\alpha _i,\alpha _j\in \Lambda $
, denote by
![]() $\alpha _i\cdot \alpha _j\in \mathbf {Z}$
the corresponding entry of the symmetrised Cartan matrix. Choose an integer
$\alpha _i\cdot \alpha _j\in \mathbf {Z}$
the corresponding entry of the symmetrised Cartan matrix. Choose an integer
![]() $d\in \mathbf {Z}$
and a symmetric bilinear form
$d\in \mathbf {Z}$
and a symmetric bilinear form
![]() $(-, -)\colon \Lambda \times \Lambda \rightarrow \frac {1}{d}\mathbf {Z}$
such that
$(-, -)\colon \Lambda \times \Lambda \rightarrow \frac {1}{d}\mathbf {Z}$
such that
![]() $(\alpha _i, \alpha _j) = \alpha _i\cdot \alpha _j$
. Given a complex number
$(\alpha _i, \alpha _j) = \alpha _i\cdot \alpha _j$
. Given a complex number
![]() $q^{1/d}\in \mathbf {C}^\times $
, we have the exponentiated pairing
$q^{1/d}\in \mathbf {C}^\times $
, we have the exponentiated pairing
given by
![]() $\lambda ,\mu \mapsto q^{-(\lambda , \mu )}$
. Our assumption is that
$\lambda ,\mu \mapsto q^{-(\lambda , \mu )}$
. Our assumption is that
![]() $q^{1/d}$
is not a root of unity.
$q^{1/d}$
is not a root of unity.
We denote by
![]() $\mathrm {U}_q(\mathfrak {g})$
the quantum group defined as in [Reference Lusztig62] with a slight modification that its Cartan part is
$\mathrm {U}_q(\mathfrak {g})$
the quantum group defined as in [Reference Lusztig62] with a slight modification that its Cartan part is
![]() $\mathrm {U}_q(\mathfrak {h})=k[\Lambda ]$
with Cartan generators
$\mathrm {U}_q(\mathfrak {h})=k[\Lambda ]$
with Cartan generators
![]() $K_\mu $
for
$K_\mu $
for
![]() $\mu \in \Lambda $
(note that the Cartan part in [Reference Lusztig62] is
$\mu \in \Lambda $
(note that the Cartan part in [Reference Lusztig62] is
![]() $k[\Lambda ^\vee ]$
). We denote by
$k[\Lambda ^\vee ]$
). We denote by
![]() $\mathrm {U}_q(\mathfrak {b})\subset \mathrm {U}_q(\mathfrak {g})$
the quantum Borel subalgebra,
$\mathrm {U}_q(\mathfrak {b})\subset \mathrm {U}_q(\mathfrak {g})$
the quantum Borel subalgebra,
![]() $\mathrm {U}_q(\mathfrak {n}), \mathrm {U}_q(\mathfrak {n}_-)\subset \mathrm {U}_q(\mathfrak {g})$
the quantum nilpotent subalgebras and
$\mathrm {U}_q(\mathfrak {n}), \mathrm {U}_q(\mathfrak {n}_-)\subset \mathrm {U}_q(\mathfrak {g})$
the quantum nilpotent subalgebras and
![]() $\mathrm {U}_q^{>0}(\mathfrak {n}),\mathrm {U}_q^{<0}(\mathfrak {n}_-)$
their augmentation ideals. For each simple root
$\mathrm {U}_q^{>0}(\mathfrak {n}),\mathrm {U}_q^{<0}(\mathfrak {n}_-)$
their augmentation ideals. For each simple root
![]() $\alpha $
, we denote by
$\alpha $
, we denote by
![]() $\{E_\alpha , K_\alpha , F_\alpha \}$
the corresponding generators of the
$\{E_\alpha , K_\alpha , F_\alpha \}$
the corresponding generators of the
![]() $\mathrm {U}_q(\mathfrak {sl}_2)$
-subalgebra (they are denoted by
$\mathrm {U}_q(\mathfrak {sl}_2)$
-subalgebra (they are denoted by
![]() $E_i, \tilde {K}_i, F_i$
in [Reference Lusztig62, Section 3.1.1]).
$E_i, \tilde {K}_i, F_i$
in [Reference Lusztig62, Section 3.1.1]).
We have the corresponding categories obtained from this data:
-
○
 $\operatorname {\mathrm {Rep}}_q(H)$
is the braided monoidal category of
$\operatorname {\mathrm {Rep}}_q(H)$
is the braided monoidal category of
 $\Lambda $
-graded vector spaces with the braiding given by
$\Lambda $
-graded vector spaces with the braiding given by
 $\Pi \tau $
, where
$\Pi \tau $
, where
 $\tau $
is the map exchanging the tensor factors.
$\tau $
is the map exchanging the tensor factors. -
○
 $\operatorname {\mathrm {Rep}}_q(G)$
is the ind-completion of the braided monoidal category of finite-dimensional
$\operatorname {\mathrm {Rep}}_q(G)$
is the ind-completion of the braided monoidal category of finite-dimensional
 $\Lambda $
-graded vector spaces with a
$\Lambda $
-graded vector spaces with a
 $\mathrm {U}_q(\mathfrak {g})$
-module structure such that for every vector
$\mathrm {U}_q(\mathfrak {g})$
-module structure such that for every vector
 $x_\lambda $
of weight
$x_\lambda $
of weight
 $\lambda \in \Lambda $
, we have
$\lambda \in \Lambda $
, we have
 $K_\mu x_\lambda = q^{(\mu , \lambda )} x_\lambda $
. The braiding is given by
$K_\mu x_\lambda = q^{(\mu , \lambda )} x_\lambda $
. The braiding is given by
 $\Theta \circ \Pi \circ \tau $
, where
$\Theta \circ \Pi \circ \tau $
, where
 $\Theta \in \mathrm {U}_q(\mathfrak {n}_-)\widehat {\otimes }\mathrm {U}_q(\mathfrak {n})$
is the so-called quasi R-matrix. Refer to [Reference Lusztig62, Section 32] for more details.
$\Theta \in \mathrm {U}_q(\mathfrak {n}_-)\widehat {\otimes }\mathrm {U}_q(\mathfrak {n})$
is the so-called quasi R-matrix. Refer to [Reference Lusztig62, Section 32] for more details. -
○
 $\operatorname {\mathrm {Rep}}_q(B)$
is the ind-completion of the monoidal category of finite-dimensional
$\operatorname {\mathrm {Rep}}_q(B)$
is the ind-completion of the monoidal category of finite-dimensional
 $\Lambda $
-graded vector spaces with a compatible
$\Lambda $
-graded vector spaces with a compatible
 $\mathrm {U}_q(\mathfrak {b})$
-module structure.
$\mathrm {U}_q(\mathfrak {b})$
-module structure.
Definition 3.19. A
![]() $\mathrm {U}_q(\mathfrak {g})$
-module M is
integrable
if it lies in the image of the forgetful functor
$\mathrm {U}_q(\mathfrak {g})$
-module M is
integrable
if it lies in the image of the forgetful functor
Equivalently, an integrable
![]() $\mathrm {U}_q(\mathfrak {g})$
-module is a locally finite type 1
$\mathrm {U}_q(\mathfrak {g})$
-module is a locally finite type 1
![]() $\mathrm {U}_q(\mathfrak {g})$
-module. We introduce an analogous definition for
$\mathrm {U}_q(\mathfrak {g})$
-module. We introduce an analogous definition for
![]() $\mathrm {U}_q(\mathfrak {b})$
-modules.
$\mathrm {U}_q(\mathfrak {b})$
-modules.
Denote by
![]() $\mathcal {O}_q(G)\in \operatorname {\mathrm {Rep}}_q(G)$
the coend algebra from Theorem 2.30.
$\mathcal {O}_q(G)\in \operatorname {\mathrm {Rep}}_q(G)$
the coend algebra from Theorem 2.30.
Definition 3.20. A
![]() $\mathrm {U}_q(\mathfrak {g})$
-module M is
locally finite
if for every
$\mathrm {U}_q(\mathfrak {g})$
-module M is
locally finite
if for every
![]() $m\in M$
, the vector space
$m\in M$
, the vector space
![]() $\mathrm {U}_q(\mathfrak {g})m$
is finite-dimensional.
$\mathrm {U}_q(\mathfrak {g})m$
is finite-dimensional.
The algebra
![]() $\mathrm {U}_q(\mathfrak {g})$
with respect to the adjoint
$\mathrm {U}_q(\mathfrak {g})$
with respect to the adjoint
![]() $\mathrm {U}_q(\mathfrak {g})$
-action on itself
$\mathrm {U}_q(\mathfrak {g})$
-action on itself
![]() $x, y\mapsto x_{(1)}yS(x_{(2)})$
is not locally finite, and we denote by
$x, y\mapsto x_{(1)}yS(x_{(2)})$
is not locally finite, and we denote by
the largest locally finite submodule.
Example 3.21. Consider
![]() $\mathrm {U}_q(\mathfrak {sl}_2)$
with the generators
$\mathrm {U}_q(\mathfrak {sl}_2)$
with the generators
![]() $E,K,F$
and relations
$E,K,F$
and relations
 $$\begin{align*}KE = q^2 EK,\qquad KF = q^{-2} FK,\qquad EF-FE=\frac{K-K^{-1}}{q-q^{-1}}.\end{align*}$$
$$\begin{align*}KE = q^2 EK,\qquad KF = q^{-2} FK,\qquad EF-FE=\frac{K-K^{-1}}{q-q^{-1}}.\end{align*}$$
Then
![]() $\mathrm {U}_q(\mathfrak {sl}_2)^{\mathrm {lf}}$
is the subalgebra generated by
$\mathrm {U}_q(\mathfrak {sl}_2)^{\mathrm {lf}}$
is the subalgebra generated by
![]() $EK^{-1}$
, F and
$EK^{-1}$
, F and
![]() $K^{-1}$
.
$K^{-1}$
.
It is easy to see that
![]() $\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}\subset \mathrm {U}_q(\mathfrak {g})$
is a subalgebra, but note that it is not a subcoalgebra. Nevertheless, the following is shown in [Reference Joseph50, Theorem 7.1.6].
$\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}\subset \mathrm {U}_q(\mathfrak {g})$
is a subalgebra, but note that it is not a subcoalgebra. Nevertheless, the following is shown in [Reference Joseph50, Theorem 7.1.6].
Proposition 3.22.
![]() $\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}\subset \mathrm {U}_q(\mathfrak {g})$
is a left coideal: that is, the coproduct restricts to a map
$\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}\subset \mathrm {U}_q(\mathfrak {g})$
is a left coideal: that is, the coproduct restricts to a map
Remark 3.23. There is a close relationship between the algebras
![]() $\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
and
$\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
and
![]() $\mathcal {O}_q(G)$
, which can be established using the quantum Killing form [Reference Rosso70]. If G is semisimple simply-connected,
$\mathcal {O}_q(G)$
, which can be established using the quantum Killing form [Reference Rosso70]. If G is semisimple simply-connected,
![]() $\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}\cong \mathcal {O}_q(G)$
; see [Reference Joseph50, Proposition 7.1.23] and [Reference Voigt and Yuncken89, Theorem 2.113].
$\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}\cong \mathcal {O}_q(G)$
; see [Reference Joseph50, Proposition 7.1.23] and [Reference Voigt and Yuncken89, Theorem 2.113].
3.5 Quantum Harish-Chandra bimodules
For
![]() $V\in \operatorname {\mathrm {Rep}}_q(G)$
,
$V\in \operatorname {\mathrm {Rep}}_q(G)$
,
![]() $v\in V$
an
$v\in V$
an
![]() $x\in \mathrm {U}_q(\mathfrak {g})$
, we denote by
$x\in \mathrm {U}_q(\mathfrak {g})$
, we denote by
![]() $x\triangleright v$
the
$x\triangleright v$
the
![]() $\mathrm {U}_q(\mathfrak {g})$
-action. For
$\mathrm {U}_q(\mathfrak {g})$
-action. For
![]() $x\in \mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
, we denote by
$x\in \mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
, we denote by
![]() $\Delta (x) = x_{(1)}\otimes x_{(2)}$
the coproduct on
$\Delta (x) = x_{(1)}\otimes x_{(2)}$
the coproduct on
![]() $\mathrm {U}_q(\mathfrak {g})$
, where we note that
$\mathrm {U}_q(\mathfrak {g})$
, where we note that
![]() $x_{(2)}\in \mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
by Theorem 3.22. We define the natural isomorphism
$x_{(2)}\in \mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
by Theorem 3.22. We define the natural isomorphism
by
Consider
![]() $\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}\in \operatorname {\mathrm {Rep}}_q(G)$
with respect to the adjoint action. It follows from Theorem 3.3 that
$\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}\in \operatorname {\mathrm {Rep}}_q(G)$
with respect to the adjoint action. It follows from Theorem 3.3 that
![]() $(\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}, \tau )$
is a commutative algebra in
$(\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}, \tau )$
is a commutative algebra in
![]() $\mathrm {Z}_{\mathrm {Dr}}(\operatorname {\mathrm {Rep}}_q(G))$
.
$\mathrm {Z}_{\mathrm {Dr}}(\operatorname {\mathrm {Rep}}_q(G))$
.
Definition 3.24. The category of quantum Harish-Chandra bimodules is
Remark 3.25. A similar definition of the category of quantum Harish-Chandra bimodules is given in [Reference Voigt and Yuncken89, Definition 5.26].
Remark 3.26. By [Reference Safronov73, Theorem 3.10], the notion of quantum moment maps in this setting coincides with the quantum moment maps for quantum group actions introduced in [Reference Varagnolo and Vasserot88, Section 1.5].
In this case, the algebra
![]() $\mathcal {D}$
from Theorem 3.12 is the algebra of quantum differential operators
$\mathcal {D}$
from Theorem 3.12 is the algebra of quantum differential operators
![]() $\mathcal {D}_q(G)$
on G (see [Reference Backelin and Kremnizer5, Section 4.1], where it is denoted by
$\mathcal {D}_q(G)$
on G (see [Reference Backelin and Kremnizer5, Section 4.1], where it is denoted by
![]() $\mathcal {D}_q^{fin}$
).
$\mathcal {D}_q^{fin}$
).
As in the case of classical Harish-Chandra bimodules, in the abelian case, the category
![]() $\mathrm {HC}_q(G)$
has a straightforward description. Let H be a torus and
$\mathrm {HC}_q(G)$
has a straightforward description. Let H be a torus and
![]() $\Lambda $
its weight lattice. Then
$\Lambda $
its weight lattice. Then
![]() $\mathrm {U}_q(\mathfrak {h})^{\mathrm {lf}} = \mathrm {U}_q(\mathfrak {h}) = \mathcal {O}(H)$
and
$\mathrm {U}_q(\mathfrak {h})^{\mathrm {lf}} = \mathrm {U}_q(\mathfrak {h}) = \mathcal {O}(H)$
and
![]() $\mathrm {HC}_q(H)$
is equivalent to the category of
$\mathrm {HC}_q(H)$
is equivalent to the category of
![]() $\Lambda $
-graded
$\Lambda $
-graded
![]() $\mathcal {O}(H)$
-modules. There is a homomorphism
$\mathcal {O}(H)$
-modules. There is a homomorphism
whose dual map
![]() $\mathcal {O}(H)=k[\Lambda ]\rightarrow \mathcal {O}(\Lambda )$
on the level of functions is
$\mathcal {O}(H)=k[\Lambda ]\rightarrow \mathcal {O}(\Lambda )$
on the level of functions is
for
![]() $\mu ,\lambda \in \Lambda $
. In particular,
$\mu ,\lambda \in \Lambda $
. In particular,
![]() $\Lambda $
acts by translations on H, and we denote the induced functor by
$\Lambda $
acts by translations on H, and we denote the induced functor by
The monoidal structure
![]() $\otimes ^{\mathrm {HC}}$
on
$\otimes ^{\mathrm {HC}}$
on
![]() $\mathrm {HC}_q(H)$
is given by
$\mathrm {HC}_q(H)$
is given by
Suppose
![]() $V\in \operatorname {\mathrm {Rep}}(H)$
,
$V\in \operatorname {\mathrm {Rep}}(H)$
,
![]() $v\in V$
and
$v\in V$
and
![]() $f\in \mathcal {O}(H)\cong \mathrm {U}_q(\mathfrak {h})$
. Then the map given by equation (30) is
$f\in \mathcal {O}(H)\cong \mathrm {U}_q(\mathfrak {h})$
. Then the map given by equation (30) is
for
![]() $\lambda \in H$
.
$\lambda \in H$
.
3.6 Harish-Chandra bimodules and bialgebroids
Let us again consider the general setup of section 3.1, where
![]() $\mathcal {C}$
is a cp-rigid monoidal category with a compact projective unit. In particular,
$\mathcal {C}$
is a cp-rigid monoidal category with a compact projective unit. In particular,
![]() $\mathrm {HC}$
is also a cp-rigid monoidal category with a compact projective unit. Our goal in this section is to describe a Tannaka reconstruction result for monoidal forgetful functors to
$\mathrm {HC}$
is also a cp-rigid monoidal category with a compact projective unit. Our goal in this section is to describe a Tannaka reconstruction result for monoidal forgetful functors to
![]() $\mathrm {HC}$
.
$\mathrm {HC}$
.
Recall from Theorem 2.19 that the category
![]() $\mathrm {HC}\otimes \mathrm {HC}$
carries two monoidal structures: the pointwise monoidal structure on
$\mathrm {HC}\otimes \mathrm {HC}$
carries two monoidal structures: the pointwise monoidal structure on
![]() $\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
and the convolution product. We will call the latter the Takeuchi product in this setting.
$\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
and the convolution product. We will call the latter the Takeuchi product in this setting.
Definition 3.27. The
Takeuchi product
![]() $\times _{\mathcal {L}}$
is the monoidal structure on
$\times _{\mathcal {L}}$
is the monoidal structure on
![]() $\mathrm {HC}\otimes \mathrm {HC}$
given by
$\mathrm {HC}\otimes \mathrm {HC}$
given by
with the unit
![]() $\mathrm {coev}(k)=\mathcal {D}\in \mathrm {HC}\otimes \mathrm {HC}$
.
$\mathrm {coev}(k)=\mathcal {D}\in \mathrm {HC}\otimes \mathrm {HC}$
.
Example 3.28. Consider the setup of Theorem 3.15. An object of
![]() $\mathrm {HC}(G)\otimes \mathrm {HC}(G)\cong \mathrm {HC}(G\times G)$
is a
$\mathrm {HC}(G)\otimes \mathrm {HC}(G)\cong \mathrm {HC}(G\times G)$
is a
![]() $\mathrm {U}\mathfrak {g}\otimes (\mathrm {U}\mathfrak {g})^{\mathrm {op}}$
-bimodule with a certain integrability condition. For a
$\mathrm {U}\mathfrak {g}\otimes (\mathrm {U}\mathfrak {g})^{\mathrm {op}}$
-bimodule with a certain integrability condition. For a
![]() $(\mathrm {U}\mathfrak {g})^{\mathrm {op}}$
-bimodule M and a
$(\mathrm {U}\mathfrak {g})^{\mathrm {op}}$
-bimodule M and a
![]() $\mathrm {U}\mathfrak {g}$
-bimodule N, the Takeuchi product is the subspace
$\mathrm {U}\mathfrak {g}$
-bimodule N, the Takeuchi product is the subspace
of elements
![]() $\sum _i m_i\otimes n_i$
satisfying
$\sum _i m_i\otimes n_i$
satisfying
for every
![]() $x\in \mathrm {U}\mathfrak {g}$
; see [Reference Takeuchi82].
$x\in \mathrm {U}\mathfrak {g}$
; see [Reference Takeuchi82].
We will now formulate the notion of bialgebroids in the category of Harish-Chandra bimodules. Recall that the algebra
![]() $\mathcal {D}\cong T^{\mathrm {R}}(\mathcal {L})\in \mathcal {C}\otimes \mathcal {C}^{\mathrm {op}}$
carries a natural quantum moment map given by equation (26).
$\mathcal {D}\cong T^{\mathrm {R}}(\mathcal {L})\in \mathcal {C}\otimes \mathcal {C}^{\mathrm {op}}$
carries a natural quantum moment map given by equation (26).
Definition 3.29. A
Harish-Chandra bialgebroid
is an algebra
![]() $B\in \mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
equipped with a quantum moment map
$B\in \mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
equipped with a quantum moment map
![]() $s\otimes t\colon \mathcal {L}\boxtimes \mathcal {L}^{\mathrm {op}}\rightarrow B$
, which allows us to regard B as an algebra in
$s\otimes t\colon \mathcal {L}\boxtimes \mathcal {L}^{\mathrm {op}}\rightarrow B$
, which allows us to regard B as an algebra in
![]() $\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
, together with a coassociative coproduct
$\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
, together with a coassociative coproduct
![]() $\Delta \colon B\rightarrow B\times _{\mathcal {L}} B$
, a map of algebras in
$\Delta \colon B\rightarrow B\times _{\mathcal {L}} B$
, a map of algebras in
![]() $\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
, and a counit map
$\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
, and a counit map
![]() $\varepsilon \colon B\rightarrow \mathcal {D}$
, a map of algebras in
$\varepsilon \colon B\rightarrow \mathcal {D}$
, a map of algebras in
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
compatible with quantum moment maps.
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
compatible with quantum moment maps.
Example 3.30. Let H be a split torus and
![]() $\Lambda =\mathrm {Hom}(H, \mathbb {G}_{\mathrm {m}})$
its weight lattice, and consider the category of Harish-Chandra bimodules
$\Lambda =\mathrm {Hom}(H, \mathbb {G}_{\mathrm {m}})$
its weight lattice, and consider the category of Harish-Chandra bimodules
![]() $\mathrm {HC}(H)$
. A bialgebroid in
$\mathrm {HC}(H)$
. A bialgebroid in
![]() $\mathrm {HC}(H)$
is given by the following data:
$\mathrm {HC}(H)$
is given by the following data:
-
○ An algebra with a bigrading
 $$\begin{align*}B = \bigoplus_{\alpha,\beta\in\Lambda} B_{\alpha\beta}.\end{align*}$$
$$\begin{align*}B = \bigoplus_{\alpha,\beta\in\Lambda} B_{\alpha\beta}.\end{align*}$$
-
○ Algebra maps
that satisfy the quantum moment map equations $$\begin{align*}s, t\colon \mathcal{O}(\mathfrak{h}^*)\longrightarrow B\end{align*}$$
for
$$\begin{align*}s, t\colon \mathcal{O}(\mathfrak{h}^*)\longrightarrow B\end{align*}$$
for $$\begin{align*}s(f(\lambda)) a = a s(f(\lambda + \alpha)),\qquad t(f(\lambda)) a = a t(f(\lambda+\beta))\end{align*}$$
$$\begin{align*}s(f(\lambda)) a = a s(f(\lambda + \alpha)),\qquad t(f(\lambda)) a = a t(f(\lambda+\beta))\end{align*}$$
 $f\in \mathcal {O}(\mathfrak {h}^*)$
and
$f\in \mathcal {O}(\mathfrak {h}^*)$
and
 $a\in B_{\alpha \beta }$
.
$a\in B_{\alpha \beta }$
.
-
○ The coproduct
 $\Delta \colon B\rightarrow B\times _{\mathrm {U}\mathfrak {h}} B$
, a map of algebras compatible with the grading and quantum moment maps. Here the Takeuchi product is where the relative tensor product is the quotient of the k-linear tensor product modulo the relations
$\Delta \colon B\rightarrow B\times _{\mathrm {U}\mathfrak {h}} B$
, a map of algebras compatible with the grading and quantum moment maps. Here the Takeuchi product is where the relative tensor product is the quotient of the k-linear tensor product modulo the relations $$\begin{align*}(B\times_{\mathrm{U}\mathfrak{h}} B)_{\alpha\beta} = \bigoplus_{\delta\in\Lambda} B_{\alpha\delta}\otimes_{\mathcal{O}(\mathfrak{h}^*)} B_{\delta\beta},\end{align*}$$
$$\begin{align*}(B\times_{\mathrm{U}\mathfrak{h}} B)_{\alpha\beta} = \bigoplus_{\delta\in\Lambda} B_{\alpha\delta}\otimes_{\mathcal{O}(\mathfrak{h}^*)} B_{\delta\beta},\end{align*}$$
 $t(f)a\otimes b\sim a\otimes s(f) b$
for
$t(f)a\otimes b\sim a\otimes s(f) b$
for
 $a\otimes b\in B_{\alpha \delta }\otimes B_{\delta \beta }$
and
$a\otimes b\in B_{\alpha \delta }\otimes B_{\delta \beta }$
and
 $f\in \mathcal {O}(\mathfrak {h}^*)$
.
$f\in \mathcal {O}(\mathfrak {h}^*)$
.
-
○ The counit
 $\epsilon \colon B\rightarrow \mathrm {D}(H)$
, a map of algebras compatible with the grading and quantum moment maps.
$\epsilon \colon B\rightarrow \mathrm {D}(H)$
, a map of algebras compatible with the grading and quantum moment maps.
Remark 3.31. Essentially, this data is an
![]() $\mathfrak {h}$
-bialgebroid in the sense of [Reference Etingof and Varchenko37, Section 4.1]. The differences are as follows:
$\mathfrak {h}$
-bialgebroid in the sense of [Reference Etingof and Varchenko37, Section 4.1]. The differences are as follows:
-
○ For an
 $\mathfrak {h}$
-bialgebroid, the weights
$\mathfrak {h}$
-bialgebroid, the weights
 $\alpha ,\beta $
are not necessarily integral.
$\alpha ,\beta $
are not necessarily integral. -
○ The counit of an
 $\mathfrak {h}$
-bialgebroid takes values in the algebra of difference operators on
$\mathfrak {h}$
-bialgebroid takes values in the algebra of difference operators on
 $\mathfrak {h}^*$
. However, it contains the subalgebra of difference operators with integral shifts (i.e., in
$\mathfrak {h}^*$
. However, it contains the subalgebra of difference operators with integral shifts (i.e., in
 $\Lambda \subset \mathfrak {h}^*$
), which is equivalent to
$\Lambda \subset \mathfrak {h}^*$
), which is equivalent to
 $\mathrm {D}(H)$
via the so-called Mellin transform; see, for instance, [Reference Ben-Zvi and Nadler10, Section 2.1].
$\mathrm {D}(H)$
via the so-called Mellin transform; see, for instance, [Reference Ben-Zvi and Nadler10, Section 2.1].
So, a Harish-Chandra bialgebroid in
![]() $\mathrm {HC}(H)$
is an
$\mathrm {HC}(H)$
is an
![]() $\mathfrak {h}$
-bialgebroid with certain integrability assumptions.
$\mathfrak {h}$
-bialgebroid with certain integrability assumptions.
Theorem 3.32. Suppose B is a Harish-Chandra bialgebroid. The functor
![]() $\bot \colon \mathrm {HC}\rightarrow \mathrm {HC}$
given by
$\bot \colon \mathrm {HC}\rightarrow \mathrm {HC}$
given by
defines a lax monoidal comonad. Conversely, let
![]() $\bot \colon \mathrm {HC}\rightarrow \mathrm {HC}$
be a colimit-preserving lax monoidal comonad on
$\bot \colon \mathrm {HC}\rightarrow \mathrm {HC}$
be a colimit-preserving lax monoidal comonad on
![]() $\mathrm {HC}$
. Then
$\mathrm {HC}$
. Then
![]() $\bot (-)\cong B\times _{\mathcal {L}}(-)$
for some Harish-Chandra bialgebroid B.
$\bot (-)\cong B\times _{\mathcal {L}}(-)$
for some Harish-Chandra bialgebroid B.
Proof. Recall from [Reference Aguiar and Mahajan2, Definition 6.25] that a bimonoid in a duoidal category is an algebra with respect to one monoidal structure and a coalgebra with respect to the other monoidal structure, both compatible in a natural way. A coalgebra in
![]() $(\mathrm {Fun}^{\mathrm {L}}(\mathrm {HC}, \mathrm {HC}), \circ )$
is a colimit-preserving comonad on
$(\mathrm {Fun}^{\mathrm {L}}(\mathrm {HC}, \mathrm {HC}), \circ )$
is a colimit-preserving comonad on
![]() $\mathrm {HC}$
, and a bimonoid in
$\mathrm {HC}$
, and a bimonoid in
![]() $\mathrm {Fun}^{\mathrm {L}}(\mathrm {HC}, \mathrm {HC})$
is the same as lax monoidal comonad on
$\mathrm {Fun}^{\mathrm {L}}(\mathrm {HC}, \mathrm {HC})$
is the same as lax monoidal comonad on
![]() $\mathrm {HC}$
.
$\mathrm {HC}$
.
A colimit-preserving lax monoidal comonad on
![]() $\mathrm {HC}$
is the same as a bimonoid in the duoidal category
$\mathrm {HC}$
is the same as a bimonoid in the duoidal category
![]() $\mathrm {Fun}^{\mathrm {L}}(\mathrm {HC}, \mathrm {HC})$
. By Theorem 2.20, we have an equivalence of duoidal categories
$\mathrm {Fun}^{\mathrm {L}}(\mathrm {HC}, \mathrm {HC})$
. By Theorem 2.20, we have an equivalence of duoidal categories
![]() $\mathrm {HC}\otimes \mathrm {HC}\cong \mathrm {Fun}^{\mathrm {L}}(\mathrm {HC}, \mathrm {HC})$
. So,
$\mathrm {HC}\otimes \mathrm {HC}\cong \mathrm {Fun}^{\mathrm {L}}(\mathrm {HC}, \mathrm {HC})$
. So,
![]() $\bot $
corresponds to an object
$\bot $
corresponds to an object
![]() $B\in \mathrm {HC}\otimes \mathrm {HC}$
, which is both an algebra in
$B\in \mathrm {HC}\otimes \mathrm {HC}$
, which is both an algebra in
![]() $\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
as well as a coalgebra in
$\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
as well as a coalgebra in
![]() $(\mathrm {HC}\otimes \mathrm {HC}, \times _{\mathcal {L}})$
, both in a compatible way.
$(\mathrm {HC}\otimes \mathrm {HC}, \times _{\mathcal {L}})$
, both in a compatible way.
By Theorem 3.6, we have an equivalence of monoidal categories
so by Theorem 3.10, the data of an algebra
![]() $B\in \mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
boils down to an algebra
$B\in \mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
boils down to an algebra
![]() $B\in \mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
equipped with a quantum moment map
$B\in \mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
equipped with a quantum moment map
![]() $\mathcal {L}\boxtimes \mathcal {L}^{\mathrm {op}}\rightarrow B$
.
$\mathcal {L}\boxtimes \mathcal {L}^{\mathrm {op}}\rightarrow B$
.
The data of a comonad boils down to a coalgebra
![]() $(B, \Delta , \epsilon )$
in
$(B, \Delta , \epsilon )$
in
![]() $(\mathrm {HC}\otimes \mathrm {HC}, \times _{\mathcal {L}})$
. The counit is given by a map of algebras
$(\mathrm {HC}\otimes \mathrm {HC}, \times _{\mathcal {L}})$
. The counit is given by a map of algebras
![]() $\epsilon \colon B\rightarrow \mathrm {coev}(k)$
in
$\epsilon \colon B\rightarrow \mathrm {coev}(k)$
in
![]() $\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
. Identifying algebras in
$\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
. Identifying algebras in
![]() $\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
with algebras in
$\mathrm {HC}\otimes \mathrm {HC}^{\otimes \mathrm {op}}$
with algebras in
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
equipped with quantum moment maps by Theorem 3.10, the counit is the same as a map
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
equipped with quantum moment maps by Theorem 3.10, the counit is the same as a map
![]() $\varepsilon \colon B\rightarrow T^{\mathrm {R}}(\mathcal {L})\cong \mathcal {D}$
of algebras in
$\varepsilon \colon B\rightarrow T^{\mathrm {R}}(\mathcal {L})\cong \mathcal {D}$
of algebras in
![]() $\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
compatible with quantum moment maps from
$\mathcal {C}\otimes \mathcal {C}^{\otimes \mathrm {op}}$
compatible with quantum moment maps from
![]() $\mathcal {L}\boxtimes \mathcal {L}^{\mathrm {op}}$
.
$\mathcal {L}\boxtimes \mathcal {L}^{\mathrm {op}}$
.
The definition of representations of Harish-Chandra bialgebroids is straightforward.
Definition 3.33. Suppose
![]() $B\in \mathrm {HC}\otimes \mathrm {HC}$
is a Harish-Chandra bialgebroid. A
$B\in \mathrm {HC}\otimes \mathrm {HC}$
is a Harish-Chandra bialgebroid. A
![]() $\boldsymbol {B}$
-comodule
is an object
$\boldsymbol {B}$
-comodule
is an object
![]() $M\in \mathrm {HC}$
together with a coassociative and counital coaction
$M\in \mathrm {HC}$
together with a coassociative and counital coaction
![]() $M\rightarrow B\times _{\mathcal {L}} M$
.
$M\rightarrow B\times _{\mathcal {L}} M$
.
Equivalently, by Theorem 3.32 a B-comodule is a coalgebra over the comonad
![]() $\bot (M) = B\times _{\mathcal {L}} M$
.
$\bot (M) = B\times _{\mathcal {L}} M$
.
Example 3.34. Consider the category of Harish-Chandra bimodules
![]() $\mathrm {HC}(H)$
for a split torus H as in Theorem 3.30, and let B be a Harish-Chandra bialgebroid in
$\mathrm {HC}(H)$
for a split torus H as in Theorem 3.30, and let B be a Harish-Chandra bialgebroid in
![]() $\mathrm {HC}(H)$
. Then a B-comodule is a
$\mathrm {HC}(H)$
. Then a B-comodule is a
![]() $\mathcal {O}(\mathfrak {h}^*)$
-module
$\mathcal {O}(\mathfrak {h}^*)$
-module
together with a coaction map
 $$\begin{align*}M_\alpha\longrightarrow \bigoplus_{\beta\in\Lambda} B_{\alpha\beta}\otimes_{\mathcal{O}(\mathfrak{h}^*)} M_\beta,\end{align*}$$
$$\begin{align*}M_\alpha\longrightarrow \bigoplus_{\beta\in\Lambda} B_{\alpha\beta}\otimes_{\mathcal{O}(\mathfrak{h}^*)} M_\beta,\end{align*}$$
where B is considered a right
![]() $\mathcal {O}(\mathfrak {h}^*)$
-module via the left action of
$\mathcal {O}(\mathfrak {h}^*)$
-module via the left action of
![]() $t\colon \mathcal {O}(\mathfrak {h}^*)\rightarrow B$
. We require this coaction map to be compatible with the
$t\colon \mathcal {O}(\mathfrak {h}^*)\rightarrow B$
. We require this coaction map to be compatible with the
![]() $\mathcal {O}(\mathfrak {h}^*)$
-actions on both sides, where the
$\mathcal {O}(\mathfrak {h}^*)$
-actions on both sides, where the
![]() $\mathcal {O}(\mathfrak {h}^*)$
-action on the right is via the left multiplication by
$\mathcal {O}(\mathfrak {h}^*)$
-action on the right is via the left multiplication by
![]() $s\colon \mathcal {O}(\mathfrak {h}^*)\rightarrow B$
and coassociative and counital in the obvious way.
$s\colon \mathcal {O}(\mathfrak {h}^*)\rightarrow B$
and coassociative and counital in the obvious way.
We obtain a Tannaka recognition statement for Harish-Chandra bialgebroids.
Theorem 3.35. Suppose
![]() $\mathcal {D}$
is a monoidal category with a monoidal functor
$\mathcal {D}$
is a monoidal category with a monoidal functor
![]() $F\colon \mathcal {D}\rightarrow \mathrm {HC}$
, which admits a colimit-preserving right adjoint
$F\colon \mathcal {D}\rightarrow \mathrm {HC}$
, which admits a colimit-preserving right adjoint
![]() $F^{\mathrm {R}}\colon \mathrm {HC}\rightarrow \mathcal {D}$
. Then there is a Harish-Chandra bialgebroid B such that
$F^{\mathrm {R}}\colon \mathrm {HC}\rightarrow \mathcal {D}$
. Then there is a Harish-Chandra bialgebroid B such that
![]() $(F\circ F^{\mathrm {R}})(-)\cong B\times _{\mathcal {L}}(-)$
and F factors through a monoidal functor
$(F\circ F^{\mathrm {R}})(-)\cong B\times _{\mathcal {L}}(-)$
and F factors through a monoidal functor
If F is conservative and preserves equalisers, the above functor is an equivalence.
Proof. Since F is monoidal,
![]() $F^{\mathrm {R}}$
is lax monoidal. Therefore,
$F^{\mathrm {R}}$
is lax monoidal. Therefore,
![]() $\bot = FF^{\mathrm {R}}$
is a colimit-preserving lax monoidal comonad on
$\bot = FF^{\mathrm {R}}$
is a colimit-preserving lax monoidal comonad on
![]() $\mathrm {HC}$
. By Theorem 3.32, there is a Harish-Chandra bialgebroid B such that
$\mathrm {HC}$
. By Theorem 3.32, there is a Harish-Chandra bialgebroid B such that
![]() $\bot (-)\cong B\times _{\mathcal {L}}(-)$
. By the standard monadic arguments, F factors through
$\bot (-)\cong B\times _{\mathcal {L}}(-)$
. By the standard monadic arguments, F factors through
which is monoidal (see [Reference Szlachányi81, Proposition 3.5] for the dual statement). If F is conservative and preserves equalisers, by the Barr–Beck theorem [Reference MacLane65, Theorem VI.7.1] the above functor is an equivalence.
4 Dynamical R-matrices
In this section, we explain how the dynamical twists and dynamical R-matrices arise from the categorical formalism explained in this paper.
4.1 Dynamical twists
Consider a Hopf algebra H, a commutative algebra
![]() $\mathcal {L}\in \mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
(see Theorem 3.3) with a coaction map
$\mathcal {L}\in \mathrm {Z}_{\mathrm {Dr}}(\mathrm {LMod}_H)$
(see Theorem 3.3) with a coaction map
![]() $\delta \colon \mathcal {L}\rightarrow H\otimes \mathcal {L}$
(denoted by
$\delta \colon \mathcal {L}\rightarrow H\otimes \mathcal {L}$
(denoted by
![]() $x\mapsto x_{(-1)}\otimes x_{(0)}$
) and a cp-rigid monoidal category
$x\mapsto x_{(-1)}\otimes x_{(0)}$
) and a cp-rigid monoidal category
![]() $\mathcal {C}$
together with a forgetful functor
$\mathcal {C}$
together with a forgetful functor
![]() $F\colon \mathcal {C}\rightarrow \mathrm {LMod}_H$
, which we assume sends compact projective objects in
$F\colon \mathcal {C}\rightarrow \mathrm {LMod}_H$
, which we assume sends compact projective objects in
![]() $\mathcal {C}$
to finite-dimensional H-modules. It will be convenient to introduce the right H-coaction
$\mathcal {C}$
to finite-dimensional H-modules. It will be convenient to introduce the right H-coaction
by
Proposition 4.1. A monoidal structure with a strict unit map on the composite
is the same as a natural collection of elements
![]() $J_{X, Y}\in \mathcal {L}\otimes \mathrm {Hom}(F(X)\otimes F(Y), F(X\otimes Y))$
for
$J_{X, Y}\in \mathcal {L}\otimes \mathrm {Hom}(F(X)\otimes F(Y), F(X\otimes Y))$
for
![]() $X,Y\in \mathcal {C}^{\mathrm {cp}}$
satisfying
$X,Y\in \mathcal {C}^{\mathrm {cp}}$
satisfying
-
○ The elements
 $J_{X, Y}$
are H-invariant.
$J_{X, Y}$
are H-invariant. -
○ For a triple
 $X,Y,Z\in \mathcal {C}^{\mathrm {cp}}$
, the equation holds, where
$X,Y,Z\in \mathcal {C}^{\mathrm {cp}}$
, the equation holds, where $$\begin{align*}J_{X\otimes Y, Z}\circ(J_{X, Y}\otimes \mathrm{id}_Z) = J_{X, Y\otimes Z}\circ \delta^R_X(J_{Y, Z})\end{align*}$$
$$\begin{align*}J_{X\otimes Y, Z}\circ(J_{X, Y}\otimes \mathrm{id}_Z) = J_{X, Y\otimes Z}\circ \delta^R_X(J_{Y, Z})\end{align*}$$
 $\delta ^R_X$
means the H-factor in
$\delta ^R_X$
means the H-factor in
 $\delta ^R$
acts on X.
$\delta ^R$
acts on X.
-
○ For any
 $X\in \mathcal {C}^{\mathrm {cp}}$
, we have
$X\in \mathcal {C}^{\mathrm {cp}}$
, we have
 $J_{\mathbf {1}, X}=J_{X, \mathbf {1}} = 1\otimes \mathrm {id}_{F(X)}$
.
$J_{\mathbf {1}, X}=J_{X, \mathbf {1}} = 1\otimes \mathrm {id}_{F(X)}$
.
Proof. Recall that the monoidal structure on the functor
![]() $\mathrm {free}\colon \mathrm {LMod}_H \rightarrow \mathrm {HC}(\mathrm {LMod}_H, \mathcal {L})$
is given by the natural isomorphism
$\mathrm {free}\colon \mathrm {LMod}_H \rightarrow \mathrm {HC}(\mathrm {LMod}_H, \mathcal {L})$
is given by the natural isomorphism
 $$ \begin{align*} (\mathcal{L}\otimes X) \otimes_{\mathcal{L}} (\mathcal{L}\otimes Y) &\xrightarrow{\sim} \mathcal{L}\otimes X \otimes Y\\ a\otimes x \otimes b \otimes y &\mapsto ab_{(0)} \otimes S^{-1}(b_{(-1)}) \triangleright x \otimes y \end{align*} $$
$$ \begin{align*} (\mathcal{L}\otimes X) \otimes_{\mathcal{L}} (\mathcal{L}\otimes Y) &\xrightarrow{\sim} \mathcal{L}\otimes X \otimes Y\\ a\otimes x \otimes b \otimes y &\mapsto ab_{(0)} \otimes S^{-1}(b_{(-1)}) \triangleright x \otimes y \end{align*} $$
for any
![]() $X,Y\in \mathrm {LMod}_H$
. So, the monoidal structure on
$X,Y\in \mathrm {LMod}_H$
. So, the monoidal structure on
![]() $\mathcal {C}\rightarrow \mathrm {HC}(\mathrm {LMod}_H, \mathcal {L})$
is given by
$\mathcal {C}\rightarrow \mathrm {HC}(\mathrm {LMod}_H, \mathcal {L})$
is given by
where the first isomorphism is given by the monoidal structure on
![]() $\mathrm {free}$
and the second isomorphism is
$\mathrm {free}$
and the second isomorphism is
The composite is automatically a map of
![]() $\mathcal {L}$
-modules, and the compatibility with the H-action is the H-invariance condition on
$\mathcal {L}$
-modules, and the compatibility with the H-action is the H-invariance condition on
![]() $J_{X, Y}$
.
$J_{X, Y}$
.
The associativity condition for the monoidal structure on F is that for compact projective objects
![]() $X,Y,Z\in \mathcal {C}^{\mathrm {cp}}$
, the diagram
$X,Y,Z\in \mathcal {C}^{\mathrm {cp}}$
, the diagram

commutes. Considering the image of
![]() $(1\otimes a)\otimes (1\otimes b)\otimes (1\otimes c)$
under these maps, we get the second equation.
$(1\otimes a)\otimes (1\otimes b)\otimes (1\otimes c)$
under these maps, we get the second equation.
The unitality condition for the monoidal structure on F is equivalent to the last equation.
Let us now introduce a universal version of the previous statement. Suppose A is another Hopf algebra with a map of algebras
![]() $H\rightarrow A$
. We assume
$H\rightarrow A$
. We assume
![]() $\mathcal {C}=\mathrm {LMod}_A$
, and the forgetful functor
$\mathcal {C}=\mathrm {LMod}_A$
, and the forgetful functor
is given by restriction of modules. Denote by
![]() $(A, \Delta , \varepsilon )$
the coalgebra structure on A.
$(A, \Delta , \varepsilon )$
the coalgebra structure on A.
Definition 4.2. A dynamical twist is an invertible element
satisfying
-
1. The invariance condition
for every $$\begin{align*}h_{(1)} \triangleright J^0 \otimes h_{(2)} J^1 \otimes h_{(3)} J^2 = J^0\otimes J^1 h_{(1)} \otimes J^2 h_{(2)}\end{align*}$$
$$\begin{align*}h_{(1)} \triangleright J^0 \otimes h_{(2)} J^1 \otimes h_{(3)} J^2 = J^0\otimes J^1 h_{(1)} \otimes J^2 h_{(2)}\end{align*}$$
 $h\in H$
;
$h\in H$
;
-
2. The shifted cocycle equation
 $$\begin{align*}((\mathrm{id}\otimes \Delta \otimes \mathrm{id})J) (J \otimes 1) = ((\mathrm{id} \otimes \mathrm{id}\otimes \Delta)J)(J_{(0)}^0 \otimes S^{-1}(J_{(-1)}^0) \otimes J^1 \otimes J^2); \end{align*}$$
$$\begin{align*}((\mathrm{id}\otimes \Delta \otimes \mathrm{id})J) (J \otimes 1) = ((\mathrm{id} \otimes \mathrm{id}\otimes \Delta)J)(J_{(0)}^0 \otimes S^{-1}(J_{(-1)}^0) \otimes J^1 \otimes J^2); \end{align*}$$
-
3. The normalisation condition
 $$\begin{align*}(\mathrm{id} \otimes \varepsilon \otimes \mathrm{id}) J = 1\otimes 1\otimes 1 = (\mathrm{id} \otimes \mathrm{id} \otimes \varepsilon) J.\end{align*}$$
$$\begin{align*}(\mathrm{id} \otimes \varepsilon \otimes \mathrm{id}) J = 1\otimes 1\otimes 1 = (\mathrm{id} \otimes \mathrm{id} \otimes \varepsilon) J.\end{align*}$$
Example 4.3. Consider the trivial pair
![]() $H=\mathcal {L}=k$
given by the ground field. The invariance condition is empty, while the cocycle equation and the normalisation condition imply that
$H=\mathcal {L}=k$
given by the ground field. The invariance condition is empty, while the cocycle equation and the normalisation condition imply that
![]() $J\in A\otimes A$
is a (constant) twist for the Hopf algebra in the sense of [Reference Chari and Pressley21, Proposition 4.2.13].
$J\in A\otimes A$
is a (constant) twist for the Hopf algebra in the sense of [Reference Chari and Pressley21, Proposition 4.2.13].
Example 4.4. Suppose
![]() $\mathfrak {h}$
is an abelian Lie algebra, and consider
$\mathfrak {h}$
is an abelian Lie algebra, and consider
![]() $H=\mathcal {L}=\mathrm {U}\mathfrak {h}$
as in section 3.3. Then a dynamical twist is a function
$H=\mathcal {L}=\mathrm {U}\mathfrak {h}$
as in section 3.3. Then a dynamical twist is a function
![]() $J\colon \mathfrak {h}^*\rightarrow A\otimes A$
. The invariance condition is that
$J\colon \mathfrak {h}^*\rightarrow A\otimes A$
. The invariance condition is that
![]() $J(\lambda )$
is
$J(\lambda )$
is
![]() $\mathfrak {h}$
-invariant with respect to the adjoint action (the zero-weight condition). The shifted cocycle equation is
$\mathfrak {h}$
-invariant with respect to the adjoint action (the zero-weight condition). The shifted cocycle equation is
Proposition 4.5. The data of a dynamical twist is equivalent to the data of a monoidal structure on
![]() $\mathrm {LMod}_A \rightarrow \mathrm {HC}(\mathrm {LMod}_H, \mathcal {L})$
with a strict unit map.
$\mathrm {LMod}_A \rightarrow \mathrm {HC}(\mathrm {LMod}_H, \mathcal {L})$
with a strict unit map.
Proof. By Theorem 4.1, the monoidal structure is specified by a collection of elements
By naturality, these are uniquely determined by the elements
Two dynamical twists may be related by a gauge transformation.
Definition 4.6. A
gauge transformation
is an invertible H-invariant element
![]() $G\in \mathcal {L} \otimes A$
satisfying the normalisation condition
$G\in \mathcal {L} \otimes A$
satisfying the normalisation condition
Given a dynamical twist J and a gauge transformation G, we obtain a new dynamical twist by the formula
Example 4.7. Consider the pair
![]() $H=\mathcal {L}=\mathrm {U}\mathfrak {h}$
, as in Theorem 4.4. Then a gauge transformation is a zero-weight function
$H=\mathcal {L}=\mathrm {U}\mathfrak {h}$
, as in Theorem 4.4. Then a gauge transformation is a zero-weight function
![]() $G\colon \mathfrak {h}^*\rightarrow A^\times $
satisfying
$G\colon \mathfrak {h}^*\rightarrow A^\times $
satisfying
![]() $\varepsilon (G(\lambda )) = 1$
. Given a dynamical twist
$\varepsilon (G(\lambda )) = 1$
. Given a dynamical twist
![]() $J\colon \mathfrak {h}^*\rightarrow A\otimes A$
, its gauge transformation is
$J\colon \mathfrak {h}^*\rightarrow A\otimes A$
, its gauge transformation is
Proposition 4.8. Suppose
![]() $J_1, J_2$
are two dynamical twists that give rise to monoidal structures on the functor
$J_1, J_2$
are two dynamical twists that give rise to monoidal structures on the functor
![]() $\mathrm {LMod}_A\rightarrow \mathrm {HC}(\mathrm {LMod}_H, \mathcal {L})$
by Theorem 4.5. The data of a gauge transformation between them is a monoidal natural isomorphism
$\mathrm {LMod}_A\rightarrow \mathrm {HC}(\mathrm {LMod}_H, \mathcal {L})$
by Theorem 4.5. The data of a gauge transformation between them is a monoidal natural isomorphism

4.2 Dynamical FRT and reflection equation algebras
Let us describe the Harish-Chandra bialgebroid B from Theorem 3.35 explicitly. Let
![]() $\mathcal {D}$
be a cp-rigid monoidal category and
$\mathcal {D}$
be a cp-rigid monoidal category and
![]() $F\colon \mathcal {D}\rightarrow \mathrm {HC}$
a monoidal functor that admits a colimit-preserving right adjoint
$F\colon \mathcal {D}\rightarrow \mathrm {HC}$
a monoidal functor that admits a colimit-preserving right adjoint
![]() $F^{\mathrm {R}}$
.
$F^{\mathrm {R}}$
.
By Theorem 2.5, the functor
![]() $FF^{\mathrm {R}}$
can be calculated as
$FF^{\mathrm {R}}$
can be calculated as
 $$ \begin{align*} FF^{\mathrm{R}}(x) &= \int^{y\in \mathcal{D}^{\mathrm{cp}}} \mathrm{Hom}_{\mathrm{HC}}(F(y)^\vee, x) \otimes F(y)^\vee \\ &\cong \int^{y\in\mathcal{D}^{\mathrm{cp}}} \mathrm{Hom}_{\mathrm{HC}}(\mathcal{L}, F(y)\otimes_{\mathcal{L}} x)\otimes F(y)^\vee. \end{align*} $$
$$ \begin{align*} FF^{\mathrm{R}}(x) &= \int^{y\in \mathcal{D}^{\mathrm{cp}}} \mathrm{Hom}_{\mathrm{HC}}(F(y)^\vee, x) \otimes F(y)^\vee \\ &\cong \int^{y\in\mathcal{D}^{\mathrm{cp}}} \mathrm{Hom}_{\mathrm{HC}}(\mathcal{L}, F(y)\otimes_{\mathcal{L}} x)\otimes F(y)^\vee. \end{align*} $$
Recalling the definition of the Takeuchi product from Theorem 3.27, we obtain that
![]() $FF^{\mathrm {R}}(x)\cong B\times _{\mathcal {L}} x$
, where the Harish-Chandra bialgebroid B is
$FF^{\mathrm {R}}(x)\cong B\times _{\mathcal {L}} x$
, where the Harish-Chandra bialgebroid B is
 $$\begin{align*}B\cong \int^{y\in\mathcal{D}^{\mathrm{cp}}} F(y)^\vee\boxtimes F(y)\in\mathrm{HC}\otimes\mathrm{HC}.\end{align*}$$
$$\begin{align*}B\cong \int^{y\in\mathcal{D}^{\mathrm{cp}}} F(y)^\vee\boxtimes F(y)\in\mathrm{HC}\otimes\mathrm{HC}.\end{align*}$$
As in section 2.5, denote by
the natural projections. The Harish-Chandra bialgebroid structure is given on generators as follows:
-
1. The coproduct
is $$\begin{align*}B\longrightarrow B\times_{\mathcal{L}} B\cong \int^{(y,z)\in \mathcal{D}^{\mathrm{cp}} \times \mathcal{D}^{\mathrm{cp}}} \mathrm{Hom}_{\mathrm{HC}}(\mathcal{L}, F(y)\otimes_{\mathcal{L}} F(z)^\vee)\otimes F(y)^\vee\boxtimes F(z)\end{align*}$$
$$\begin{align*}B\longrightarrow B\times_{\mathcal{L}} B\cong \int^{(y,z)\in \mathcal{D}^{\mathrm{cp}} \times \mathcal{D}^{\mathrm{cp}}} \mathrm{Hom}_{\mathrm{HC}}(\mathcal{L}, F(y)\otimes_{\mathcal{L}} F(z)^\vee)\otimes F(y)^\vee\boxtimes F(z)\end{align*}$$
 $$\begin{align*}F(y)^\vee\boxtimes F(y)\xrightarrow{\mathrm{coev}\otimes \mathrm{id}} \mathrm{Hom}_{\mathrm{HC}}(\mathcal{L}, F(y)\otimes_{\mathcal{L}} F(y)^\vee)\otimes F(y)^\vee\boxtimes F(y)\xrightarrow{\pi_{y, y}} B\times_{\mathcal{L}} B.\end{align*}$$
$$\begin{align*}F(y)^\vee\boxtimes F(y)\xrightarrow{\mathrm{coev}\otimes \mathrm{id}} \mathrm{Hom}_{\mathrm{HC}}(\mathcal{L}, F(y)\otimes_{\mathcal{L}} F(y)^\vee)\otimes F(y)^\vee\boxtimes F(y)\xrightarrow{\pi_{y, y}} B\times_{\mathcal{L}} B.\end{align*}$$
-
2. The counit
is the projection $$\begin{align*}B\longrightarrow T^{\mathrm{R}}_{\mathrm{HC}}(\mathcal{L}) = \int^{P\in\mathrm{HC}^{\mathrm{cp}}} P^\vee\boxtimes P\end{align*}$$
$$\begin{align*}B\longrightarrow T^{\mathrm{R}}_{\mathrm{HC}}(\mathcal{L}) = \int^{P\in\mathrm{HC}^{\mathrm{cp}}} P^\vee\boxtimes P\end{align*}$$
 $$\begin{align*}F(y)^\vee\boxtimes F(y) \rightarrow T^{\mathrm{R}}_{\mathrm{HC}}(\mathcal{L}).\end{align*}$$
$$\begin{align*}F(y)^\vee\boxtimes F(y) \rightarrow T^{\mathrm{R}}_{\mathrm{HC}}(\mathcal{L}).\end{align*}$$
-
3. The product is the composite
 $$ \begin{align*} (F(y)^\vee \boxtimes F(y)) \otimes_{\mathcal{L}\otimes \mathcal{L}} (F(z)^\vee \boxtimes F(z)) &= (F(y)^\vee\otimes_{\mathcal{L}} F(z)^\vee)\boxtimes (F(z)\otimes_{\mathcal{L}} F(y)) \\ &\cong (F(z)\otimes_{\mathcal{L}} F(y))^\vee\boxtimes (F(z)\otimes_{\mathcal{L}} F(y)) \\ &\xrightarrow{(J^{-1}_{z,y})^\vee\boxtimes J_{z,y}} F(z\otimes y)^\vee\boxtimes F(z\otimes y) \\ &\xrightarrow{\pi_{z\otimes y}} B. \end{align*} $$
$$ \begin{align*} (F(y)^\vee \boxtimes F(y)) \otimes_{\mathcal{L}\otimes \mathcal{L}} (F(z)^\vee \boxtimes F(z)) &= (F(y)^\vee\otimes_{\mathcal{L}} F(z)^\vee)\boxtimes (F(z)\otimes_{\mathcal{L}} F(y)) \\ &\cong (F(z)\otimes_{\mathcal{L}} F(y))^\vee\boxtimes (F(z)\otimes_{\mathcal{L}} F(y)) \\ &\xrightarrow{(J^{-1}_{z,y})^\vee\boxtimes J_{z,y}} F(z\otimes y)^\vee\boxtimes F(z\otimes y) \\ &\xrightarrow{\pi_{z\otimes y}} B. \end{align*} $$
-
4. The quantum moment map is
 $$\begin{align*}\mathcal{L} \boxtimes \mathcal{L}^{\mathrm{op}} \cong F(\mathbf{1}) \boxtimes F(\mathbf{1}) \xrightarrow{\pi_{\mathbf{1}}} B. \end{align*}$$
$$\begin{align*}\mathcal{L} \boxtimes \mathcal{L}^{\mathrm{op}} \cong F(\mathbf{1}) \boxtimes F(\mathbf{1}) \xrightarrow{\pi_{\mathbf{1}}} B. \end{align*}$$
We will now concentrate on the case
![]() $\mathcal {C}=\operatorname {\mathrm {Rep}}(H)$
for H a split torus with weight lattice
$\mathcal {C}=\operatorname {\mathrm {Rep}}(H)$
for H a split torus with weight lattice
![]() $\Lambda $
and
$\Lambda $
and
![]() $\mathcal {L}=\mathrm {U}\mathfrak {h}$
, so
$\mathcal {L}=\mathrm {U}\mathfrak {h}$
, so
![]() $\mathrm {HC}=\mathrm {HC}(H)$
. Moreover, we assume that the functor
$\mathrm {HC}=\mathrm {HC}(H)$
. Moreover, we assume that the functor
![]() $F\colon \mathcal {D}\rightarrow \mathrm {HC}(H)$
factors as the composite
$F\colon \mathcal {D}\rightarrow \mathrm {HC}(H)$
factors as the composite
For an object
![]() $y\in \mathcal {D}$
, we denote its image in
$y\in \mathcal {D}$
, we denote its image in
![]() $\operatorname {\mathrm {Rep}}(H)$
by the same letter. In this case, the monoidal structure is given by a dynamical twist
$\operatorname {\mathrm {Rep}}(H)$
by the same letter. In this case, the monoidal structure is given by a dynamical twist
as in Theorem 4.1.
The projections
in
![]() $\mathrm {HC}(H\times H)$
may be encoded in elements
$\mathrm {HC}(H\times H)$
may be encoded in elements
Analogously to Theorem 2.26, we obtain the following explicit description of the bialgebroid B.
Theorem 4.9. The bialgebroid B is spanned, as an
![]() $\mathcal {O}(\mathfrak {h}^*)$
-bimodule, by the matrix coefficients of
$\mathcal {O}(\mathfrak {h}^*)$
-bimodule, by the matrix coefficients of
![]() $T_y$
for
$T_y$
for
![]() $y\in \mathcal {D}^{\mathrm {cp}}$
subject to the relation
$y\in \mathcal {D}^{\mathrm {cp}}$
subject to the relation
for every
![]() $j\colon x\rightarrow y$
. Moreover, we have:
$j\colon x\rightarrow y$
. Moreover, we have:
-
1.
 $\Delta (T_y) = T_y\otimes T_y$
for every
$\Delta (T_y) = T_y\otimes T_y$
for every
 $y\in \mathcal {D}^{cp}$
.
$y\in \mathcal {D}^{cp}$
. -
2.
 $\epsilon (T_y) = 1\otimes \mathrm {id}_y\in \mathrm {D}(H)\otimes \mathrm {End}(y)$
for every
$\epsilon (T_y) = 1\otimes \mathrm {id}_y\in \mathrm {D}(H)\otimes \mathrm {End}(y)$
for every
 $y\in \mathcal {D}^{\mathrm {cp}}$
.
$y\in \mathcal {D}^{\mathrm {cp}}$
. -
3. For every
 $f\in \mathcal {O}(\mathfrak {h}^*)$
and
$f\in \mathcal {O}(\mathfrak {h}^*)$
and
 $y\in \mathcal {D}^{\mathrm {cp}}$
,
$y\in \mathcal {D}^{\mathrm {cp}}$
,  $$ \begin{align*} s(f(\lambda)) T_y &= T_y s(f(\lambda + h)) \\ t(f(\lambda+h)) T_y &= T_y t(f(\lambda )). \end{align*} $$
$$ \begin{align*} s(f(\lambda)) T_y &= T_y s(f(\lambda + h)) \\ t(f(\lambda+h)) T_y &= T_y t(f(\lambda )). \end{align*} $$
-
4.
 $J^t_{y, z}(\lambda )^{-1} T_{y\otimes z} J^s_{y, z}(\lambda ) = (T_y\otimes \mathrm {id})(\mathrm {id}\otimes T_z)$
, where by the superscripts, we mean the left multiplication with the
$J^t_{y, z}(\lambda )^{-1} T_{y\otimes z} J^s_{y, z}(\lambda ) = (T_y\otimes \mathrm {id})(\mathrm {id}\otimes T_z)$
, where by the superscripts, we mean the left multiplication with the
 $\mathcal {O}(\mathfrak {h}^*)$
-part by either the source
$\mathcal {O}(\mathfrak {h}^*)$
-part by either the source
 $(s)$
or the target
$(s)$
or the target
 $(t)$
map.
$(t)$
map. -
5.
 $T_{\mathbf {1}}\in B$
is the unit.
$T_{\mathbf {1}}\in B$
is the unit.
Definition 4.10. Suppose
![]() $\mathcal {D}$
is a braided monoidal category together with a forgetful functor
$\mathcal {D}$
is a braided monoidal category together with a forgetful functor
![]() $\mathcal {D}\rightarrow \operatorname {\mathrm {Rep}}(H)$
and a monoidal structure on the composite
$\mathcal {D}\rightarrow \operatorname {\mathrm {Rep}}(H)$
and a monoidal structure on the composite
![]() $\mathcal {D}\rightarrow \operatorname {\mathrm {Rep}}(H)\xrightarrow {\mathrm {free}} \mathrm {HC}(H)$
. For
$\mathcal {D}\rightarrow \operatorname {\mathrm {Rep}}(H)\xrightarrow {\mathrm {free}} \mathrm {HC}(H)$
. For
![]() $x,y\in \mathcal {D}$
, define the morphism
$x,y\in \mathcal {D}$
, define the morphism
![]() $\mathrm {U}\mathfrak {h}\otimes x\otimes y\rightarrow \mathrm {U}\mathfrak {h}\otimes y\otimes x$
by
$\mathrm {U}\mathfrak {h}\otimes x\otimes y\rightarrow \mathrm {U}\mathfrak {h}\otimes y\otimes x$
by
The
dynamical
![]() $\boldsymbol {R}$
-matrix
is the map
$\boldsymbol {R}$
-matrix
is the map
![]() $R_{x, y}\colon \mathfrak {h}^*\rightarrow \mathrm {End}(x\otimes y)$
given by
$R_{x, y}\colon \mathfrak {h}^*\rightarrow \mathrm {End}(x\otimes y)$
given by
As in section 2.5, we use the standard notation
![]() $T_1 = T_x \otimes \mathrm {id}$
and
$T_1 = T_x \otimes \mathrm {id}$
and
![]() $T_2=\mathrm {id}\otimes T_y$
and similarly for the R-matrix.
$T_2=\mathrm {id}\otimes T_y$
and similarly for the R-matrix.
Proposition 4.11. Let
![]() $x,y,z\in \mathcal {D}^{\mathrm {cp}}$
.
$x,y,z\in \mathcal {D}^{\mathrm {cp}}$
.
-
1. The dynamical R-matrix satisfies the dynamical Yang-Baxter equation
in $$\begin{align*}R_{23}(\lambda)R_{13}(\lambda-h^{(2)}) R_{12}(\lambda) = R_{12}(\lambda-h^{(3)}) R_{13}(\lambda) R_{23}(\lambda-h^{(1)})\end{align*}$$
$$\begin{align*}R_{23}(\lambda)R_{13}(\lambda-h^{(2)}) R_{12}(\lambda) = R_{12}(\lambda-h^{(3)}) R_{13}(\lambda) R_{23}(\lambda-h^{(1)})\end{align*}$$
 $\mathrm {End}(x\otimes y\otimes z)$
.
$\mathrm {End}(x\otimes y\otimes z)$
.
-
2. The element T satisfies the dynamical FRT relation
in $$\begin{align*}R^t(\lambda) T_1 T_2 = T_2 T_1 R^s(\lambda)\end{align*}$$
$$\begin{align*}R^t(\lambda) T_1 T_2 = T_2 T_1 R^s(\lambda)\end{align*}$$
 $B\otimes \mathrm {End}(x\otimes y)$
.
$B\otimes \mathrm {End}(x\otimes y)$
.
Proof. As in the proof of Theorem 2.28, the element
![]() $\hat {R}$
satisfies the braid relation
$\hat {R}$
satisfies the braid relation
in
![]() $\mathrm {U}\mathfrak {h}\otimes \mathrm {End}(x\otimes y\otimes z)$
. Observing that
$\mathrm {U}\mathfrak {h}\otimes \mathrm {End}(x\otimes y\otimes z)$
. Observing that
![]() $\check {R} = \sigma \circ R$
, we get the dynamical Yang–Baxter equation.
$\check {R} = \sigma \circ R$
, we get the dynamical Yang–Baxter equation.
To show the second part, recall from Theorem 4.9 that
Decomposing
![]() $T_{x\otimes y}$
and
$T_{x\otimes y}$
and
![]() $T_{y\otimes x}$
into
$T_{y\otimes x}$
into
![]() $T_x$
and
$T_x$
and
![]() $T_y$
using property
$T_y$
using property
![]() $(4)$
of the same theorem, we get the result.
$(4)$
of the same theorem, we get the result.
5 Fusion of Verma modules
In this section, we construct standard dynamical twists for
![]() $\mathrm {U}\mathfrak {g}$
and
$\mathrm {U}\mathfrak {g}$
and
![]() $\mathrm {U}_q(\mathfrak {g})$
using the so-called exchange construction introduced in [Reference Etingof and Varchenko31].
$\mathrm {U}_q(\mathfrak {g})$
using the so-called exchange construction introduced in [Reference Etingof and Varchenko31].
5.1 Classical parabolic restriction
Let G be a reductive group over an algebraically closed field k of characteristic zero and
![]() $\mathfrak {g}$
its Lie algebra. Fix a Borel subgroup
$\mathfrak {g}$
its Lie algebra. Fix a Borel subgroup
![]() $B\subset G$
and denote
$B\subset G$
and denote
![]() $H = B / [B, B]$
; their Lie algebras are denoted by
$H = B / [B, B]$
; their Lie algebras are denoted by
![]() $\mathfrak {b}$
and
$\mathfrak {b}$
and
![]() $\mathfrak {h}$
. We denote by N the kernel of
$\mathfrak {h}$
. We denote by N the kernel of
![]() $B\rightarrow H$
with Lie algebra
$B\rightarrow H$
with Lie algebra
![]() $\mathfrak {n}$
. Let W be the Weyl group.
$\mathfrak {n}$
. Let W be the Weyl group.
We will later use the Harish-Chandra isomorphism; see [Reference Humphreys49, Theorem 1.10].
Theorem 5.1. There is a unique homomorphism of algebras
the Harish-Chandra homomorphism, such that for any
![]() $z\in \mathrm {Z}(\mathrm {U}\mathfrak {g})$
and
$z\in \mathrm {Z}(\mathrm {U}\mathfrak {g})$
and
![]() $m\in M^{\mathrm {univ}}$
, we have
$m\in M^{\mathrm {univ}}$
, we have
Definition 5.2. The
universal category
![]() $\mathcal {O}$
is the category
$\mathcal {O}$
is the category
![]() $\mathcal {O}^{\mathrm {univ}}$
of
$\mathcal {O}^{\mathrm {univ}}$
of
![]() $(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {h})$
-bimodules whose diagonal
$(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {h})$
-bimodules whose diagonal
![]() $\mathfrak {b}$
-action integrates to a B-action. The
universal Verma module
is
$\mathfrak {b}$
-action integrates to a B-action. The
universal Verma module
is
Remark 5.3. Just like the usual category
![]() $\mathcal {O}$
is constructed to contain objects like Verma modules, we define
$\mathcal {O}$
is constructed to contain objects like Verma modules, we define
![]() $\mathcal {O}^{\mathrm {univ}}$
to contain objects like universal Verma modules.
$\mathcal {O}^{\mathrm {univ}}$
to contain objects like universal Verma modules.
Remark 5.4. We may identify
![]() $\mathcal {O}^{\mathrm {univ}}$
with the category of
$\mathcal {O}^{\mathrm {univ}}$
with the category of
![]() $\mathrm {U}\mathfrak {g}$
-modules in the category
$\mathrm {U}\mathfrak {g}$
-modules in the category
![]() $\operatorname {\mathrm {Rep}}(H)$
whose
$\operatorname {\mathrm {Rep}}(H)$
whose
![]() $\mathfrak {n}$
-action is locally nilpotent.
$\mathfrak {n}$
-action is locally nilpotent.
We will now define an important bimodule structure on
![]() $\mathcal {O}^{\mathrm {univ}}$
:
$\mathcal {O}^{\mathrm {univ}}$
:
Both actions are given by the relative tensor products of bimodules. Given a
![]() $\mathrm {U}\mathfrak {g}$
-bimodule
$\mathrm {U}\mathfrak {g}$
-bimodule
![]() $X\in \mathrm {HC}(G)$
and a
$X\in \mathrm {HC}(G)$
and a
![]() $(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {h})$
-bimodule
$(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {h})$
-bimodule
![]() $M\in \mathcal {O}^{\mathrm {univ}}$
,
$M\in \mathcal {O}^{\mathrm {univ}}$
,
![]() $X\otimes _{\mathrm {U}\mathfrak {g}} M$
is an
$X\otimes _{\mathrm {U}\mathfrak {g}} M$
is an
![]() $(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {h})$
-bimodule. Since the diagonal
$(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {h})$
-bimodule. Since the diagonal
![]() $\mathfrak {g}$
-action on X is integrable, so is the diagonal
$\mathfrak {g}$
-action on X is integrable, so is the diagonal
![]() $\mathfrak {b}$
-action. Therefore, the diagonal
$\mathfrak {b}$
-action. Therefore, the diagonal
![]() $\mathfrak {b}$
-action on
$\mathfrak {b}$
-action on
![]() $X\otimes _{\mathrm {U}\mathfrak {g}} M$
is integrable. The
$X\otimes _{\mathrm {U}\mathfrak {g}} M$
is integrable. The
![]() $\mathrm {HC}(H)$
action is defined similarly.
$\mathrm {HC}(H)$
action is defined similarly.
Let
be the actions of
![]() $\mathrm {HC}(G)$
and
$\mathrm {HC}(G)$
and
![]() $\mathrm {HC}(H)$
on the universal Verma module
$\mathrm {HC}(H)$
on the universal Verma module
![]() $M^{\mathrm {univ}}\in \mathcal {O}^{\mathrm {univ}}$
. Using Theorem 2.21, we obtain the following lax monoidal functors.
$M^{\mathrm {univ}}\in \mathcal {O}^{\mathrm {univ}}$
. Using Theorem 2.21, we obtain the following lax monoidal functors.
Definition 5.5. The parabolic restriction is the lax monoidal functor
The parabolic induction is the lax monoidal functor
Let us now make these functors more explicit. Consider the functor
which sends a
![]() $(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {h})$
-bimodule to the subspace of highest-weight vectors with respect to the
$(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {h})$
-bimodule to the subspace of highest-weight vectors with respect to the
![]() $\mathrm {U}\mathfrak {g}$
-action. It still has a remaining
$\mathrm {U}\mathfrak {g}$
-action. It still has a remaining
![]() $\mathrm {U}\mathfrak {h}$
-bimodule structure, so it defines an object of
$\mathrm {U}\mathfrak {h}$
-bimodule structure, so it defines an object of
![]() $\mathrm {HC}(H)$
.
$\mathrm {HC}(H)$
.
Proposition 5.6. The functor
![]() $(-)^N\colon \mathcal {O}^{\mathrm {univ}}\rightarrow \mathrm {HC}(H)$
is right adjoint to
$(-)^N\colon \mathcal {O}^{\mathrm {univ}}\rightarrow \mathrm {HC}(H)$
is right adjoint to
![]() $\mathrm {act}_H\colon \mathrm {HC}(H)\rightarrow \mathcal {O}^{\mathrm {univ}}$
.
$\mathrm {act}_H\colon \mathrm {HC}(H)\rightarrow \mathcal {O}^{\mathrm {univ}}$
.
Proof. Identify
![]() $\mathcal {O}^{\mathrm {univ}}$
with the highest-weight
$\mathcal {O}^{\mathrm {univ}}$
with the highest-weight
![]() $\mathrm {U}\mathfrak {g}$
-modules in the category
$\mathrm {U}\mathfrak {g}$
-modules in the category
![]() $\operatorname {\mathrm {Rep}}(H)$
following Theorem 5.4. For
$\operatorname {\mathrm {Rep}}(H)$
following Theorem 5.4. For
![]() $M\in \mathcal {O}^{\mathrm {univ}}$
and
$M\in \mathcal {O}^{\mathrm {univ}}$
and
![]() $X\in \mathrm {HC}(H)$
, we have
$X\in \mathrm {HC}(H)$
, we have
 $$ \begin{align*} \mathrm{Hom}_{\mathcal{O}^{\mathrm{univ}}}(\mathrm{act}_H(X), M) &= \mathrm{Hom}_{\mathcal{O}^{\mathrm{univ}}}(\mathrm{U}\mathfrak{g}\otimes_{\mathrm{U}\mathfrak{b}} X, M) \\ &\cong \mathrm{Hom}_{{}_{\mathrm{U}\mathfrak{b}}\mathrm{BMod}_{\mathrm{U}\mathfrak{h}}}(X, M) \\ &\cong \mathrm{Hom}_{\mathrm{HC}(H)}(X, M^N). \end{align*} $$
$$ \begin{align*} \mathrm{Hom}_{\mathcal{O}^{\mathrm{univ}}}(\mathrm{act}_H(X), M) &= \mathrm{Hom}_{\mathcal{O}^{\mathrm{univ}}}(\mathrm{U}\mathfrak{g}\otimes_{\mathrm{U}\mathfrak{b}} X, M) \\ &\cong \mathrm{Hom}_{{}_{\mathrm{U}\mathfrak{b}}\mathrm{BMod}_{\mathrm{U}\mathfrak{h}}}(X, M) \\ &\cong \mathrm{Hom}_{\mathrm{HC}(H)}(X, M^N). \end{align*} $$
So,
The lax monoidal structure on
![]() $\mathrm {res}$
can be described explicitly as follows. For
$\mathrm {res}$
can be described explicitly as follows. For
![]() $X,Y\in \mathrm {HC}(G)$
, the morphism
$X,Y\in \mathrm {HC}(G)$
, the morphism
is given by
![]() $[x] \otimes [y] \mapsto [x \otimes y]$
. This assignment is independent of the choice of a representative of
$[x] \otimes [y] \mapsto [x \otimes y]$
. This assignment is independent of the choice of a representative of
![]() $[x]$
since
$[x]$
since
![]() $[y]$
is N-invariant.
$[y]$
is N-invariant.
Remark 5.7. Since
![]() $\mathrm {res}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)$
is lax monoidal, it sends algebras in
$\mathrm {res}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)$
is lax monoidal, it sends algebras in
![]() $\mathrm {HC}(G)$
to algebras in
$\mathrm {HC}(G)$
to algebras in
![]() $\mathrm {HC}(H)$
. By Theorem 3.10, an algebra in
$\mathrm {HC}(H)$
. By Theorem 3.10, an algebra in
![]() $\mathrm {HC}(G)$
is a G-algebra equipped with a quantum moment map
$\mathrm {HC}(G)$
is a G-algebra equipped with a quantum moment map
![]() $\mu \colon \mathrm {U}\mathfrak {g}\rightarrow A$
. It is easy to see that
$\mu \colon \mathrm {U}\mathfrak {g}\rightarrow A$
. It is easy to see that
![]() $\mathrm {res}(A)$
is the quantum Hamiltonian reduction
$\mathrm {res}(A)$
is the quantum Hamiltonian reduction
![]() $A/\!\!/ N$
. This algebra is known as the Mickelsson algebra [Reference Mickelsson67]; refer to [Reference Zhelobenko94] for more details.
$A/\!\!/ N$
. This algebra is known as the Mickelsson algebra [Reference Mickelsson67]; refer to [Reference Zhelobenko94] for more details.
Recall that the coinduction functor
is right adjoint to the obvious restriction functor
![]() $\operatorname {\mathrm {Rep}}(G)\rightarrow \operatorname {\mathrm {Rep}}(B)$
. Denote in the same way the functor
$\operatorname {\mathrm {Rep}}(G)\rightarrow \operatorname {\mathrm {Rep}}(B)$
. Denote in the same way the functor
of coinduction from B to G using the diagonal B-action.
Proposition 5.8. The functor
![]() $\mathrm {coind}_B^G\colon \mathcal {O}^{\mathrm {univ}}\rightarrow \mathrm {HC}(G)$
is right adjoint to
$\mathrm {coind}_B^G\colon \mathcal {O}^{\mathrm {univ}}\rightarrow \mathrm {HC}(G)$
is right adjoint to
![]() $\mathrm {act}_G\colon \mathrm {HC}(G)\rightarrow \mathcal {O}^{\mathrm {univ}}$
.
$\mathrm {act}_G\colon \mathrm {HC}(G)\rightarrow \mathcal {O}^{\mathrm {univ}}$
.
Proof. For
![]() $M\in \mathcal {O}^{\mathrm {univ}}$
and
$M\in \mathcal {O}^{\mathrm {univ}}$
and
![]() $X\in \mathrm {HC}(G)$
, we have
$X\in \mathrm {HC}(G)$
, we have
 $$ \begin{align*} \mathrm{Hom}_{\mathcal{O}^{\mathrm{univ}}}(\mathrm{act}_G(X), M) &= \mathrm{Hom}_{\mathcal{O}^{\mathrm{univ}}}(X\otimes_{\mathrm{U}\mathfrak{b}} \mathrm{U}\mathfrak{h}, M) \\ &\cong \mathrm{Hom}_{{}_{\mathrm{U}\mathfrak{g}}\mathrm{BMod}_{\mathrm{U}\mathfrak{b}}}(X, M). \end{align*} $$
$$ \begin{align*} \mathrm{Hom}_{\mathcal{O}^{\mathrm{univ}}}(\mathrm{act}_G(X), M) &= \mathrm{Hom}_{\mathcal{O}^{\mathrm{univ}}}(X\otimes_{\mathrm{U}\mathfrak{b}} \mathrm{U}\mathfrak{h}, M) \\ &\cong \mathrm{Hom}_{{}_{\mathrm{U}\mathfrak{g}}\mathrm{BMod}_{\mathrm{U}\mathfrak{b}}}(X, M). \end{align*} $$
Both X and M are
![]() $(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {b})$
-bimodules whose diagonal
$(\mathrm {U}\mathfrak {g}, \mathrm {U}\mathfrak {b})$
-bimodules whose diagonal
![]() $\mathfrak {b}$
-action integrates to a B-action: that is, they are objects of
$\mathfrak {b}$
-action integrates to a B-action: that is, they are objects of
![]() $\mathrm {LMod}_{\mathrm {U}\mathfrak {g}}(\operatorname {\mathrm {Rep}} B)$
. Moreover, X lies in the image of the forgetful functor
$\mathrm {LMod}_{\mathrm {U}\mathfrak {g}}(\operatorname {\mathrm {Rep}} B)$
. Moreover, X lies in the image of the forgetful functor
But by definition,
![]() $\mathrm {coind}_B^G$
is the right adjoint to the forgetful functor
$\mathrm {coind}_B^G$
is the right adjoint to the forgetful functor
![]() $\operatorname {\mathrm {Rep}} G\rightarrow \operatorname {\mathrm {Rep}} B$
.
$\operatorname {\mathrm {Rep}} G\rightarrow \operatorname {\mathrm {Rep}} B$
.
Let us now compute the values of
![]() $\mathrm {res}$
and
$\mathrm {res}$
and
![]() $\mathrm {ind}$
on the units.
$\mathrm {ind}$
on the units.
Proposition 5.9. The natural morphism
![]() $\mathrm {U}\mathfrak {h}\rightarrow \mathrm {res}(\mathrm {U}\mathfrak {g})$
is an isomorphism.
$\mathrm {U}\mathfrak {h}\rightarrow \mathrm {res}(\mathrm {U}\mathfrak {g})$
is an isomorphism.
Proof. By Theorem 5.6,
![]() $\mathrm {res}(\mathrm {U}\mathfrak {g}) \cong (M^{\mathrm {univ}})^N$
, and we have to show that
$\mathrm {res}(\mathrm {U}\mathfrak {g}) \cong (M^{\mathrm {univ}})^N$
, and we have to show that
is an isomorphism. Let
where
![]() $\mathrm {Frac}(\mathrm {U}\mathfrak {h})$
is the fraction field of
$\mathrm {Frac}(\mathrm {U}\mathfrak {h})$
is the fraction field of
![]() $\mathrm {U}\mathfrak {h}$
. The map
$\mathrm {U}\mathfrak {h}$
. The map
![]() $M^{\mathrm {univ}}\rightarrow M^{\mathrm {univ}, \mathrm {gen}}$
is injective, and
$M^{\mathrm {univ}}\rightarrow M^{\mathrm {univ}, \mathrm {gen}}$
is injective, and
![]() $(-)^N$
is left exact, so
$(-)^N$
is left exact, so
![]() $(M^{\mathrm {univ}})^N\longrightarrow (M^{\mathrm {univ}, \mathrm {gen}})^N$
is injective. But the Verma module for generic highest weights is irreducible (see [Reference Humphreys49, Theorem 4.4]), so
$(M^{\mathrm {univ}})^N\longrightarrow (M^{\mathrm {univ}, \mathrm {gen}})^N$
is injective. But the Verma module for generic highest weights is irreducible (see [Reference Humphreys49, Theorem 4.4]), so
is an isomorphism. This implies the claim.
Corollary 5.10. The induced map
coincides with the Harish-Chandra homomorphism
![]() $\mathrm {hc}\colon \mathrm {Z}(\mathrm {U}\mathfrak {g})\rightarrow \mathrm {U}\mathfrak {h}$
.
$\mathrm {hc}\colon \mathrm {Z}(\mathrm {U}\mathfrak {g})\rightarrow \mathrm {U}\mathfrak {h}$
.
Proof. The map
sends a central element
![]() $z\in \mathrm {Z}(\mathrm {U}\mathfrak {g})$
to the left action of
$z\in \mathrm {Z}(\mathrm {U}\mathfrak {g})$
to the left action of
![]() $z\in \mathrm {Z}(\mathrm {U}\mathfrak {g})$
on
$z\in \mathrm {Z}(\mathrm {U}\mathfrak {g})$
on
![]() $M^{\mathrm {univ}}$
. By Theorem 5.1, it is equal to the right action of
$M^{\mathrm {univ}}$
. By Theorem 5.1, it is equal to the right action of
![]() $\mathrm {hc}(z)\in \mathrm {U}\mathfrak {h}$
on
$\mathrm {hc}(z)\in \mathrm {U}\mathfrak {h}$
on
![]() $M^{\mathrm {univ}}$
. To conclude, observe that the map
$M^{\mathrm {univ}}$
. To conclude, observe that the map
is an isomorphism of right
![]() $\mathrm {U}\mathfrak {h}$
-modules.
$\mathrm {U}\mathfrak {h}$
-modules.
Proposition 5.11. Suppose G is connected and simply connected. Then there is an isomorphism
where the
![]() $\mathrm {Z}(\mathrm {U}\mathfrak {g})$
-action on
$\mathrm {Z}(\mathrm {U}\mathfrak {g})$
-action on
![]() $\mathrm {U}\mathfrak {h}$
is via the Harish-Chandra homomorphism
$\mathrm {U}\mathfrak {h}$
is via the Harish-Chandra homomorphism
![]() $\mathrm {hc}$
.
$\mathrm {hc}$
.
Proof. By Theorem 5.8,
![]() $\mathrm {ind}(\mathrm {U}\mathfrak {h})\cong \mathrm {coind}_B^G(M^{\mathrm {univ}})$
. Identifying B-representations with G-equivariant quasi-coherent sheaves on
$\mathrm {ind}(\mathrm {U}\mathfrak {h})\cong \mathrm {coind}_B^G(M^{\mathrm {univ}})$
. Identifying B-representations with G-equivariant quasi-coherent sheaves on
![]() $G/B$
,
$G/B$
,
![]() $M^{\mathrm {univ}}$
is sent to
$M^{\mathrm {univ}}$
is sent to
![]() $(\pi _* \mathrm {D}_{G/N})^H$
, where
$(\pi _* \mathrm {D}_{G/N})^H$
, where
![]() $\pi \colon G/N\rightarrow G/B$
. Therefore,
$\pi \colon G/N\rightarrow G/B$
. Therefore,
The claim then follows from [Reference Šapovalov90, Reference van den Hombergh and de Vries87]; see also [Reference Miličić68, Lemma 3.1].
Note that the functor
![]() $\mathrm {res}$
preserves neither limits nor colimits, and it is merely lax monoidal. We will now show that after a localisation, it becomes exact and monoidal.
$\mathrm {res}$
preserves neither limits nor colimits, and it is merely lax monoidal. We will now show that after a localisation, it becomes exact and monoidal.
Definition 5.12. A weight
![]() $\lambda \in \mathfrak {h}^*$
is
generic
if
$\lambda \in \mathfrak {h}^*$
is
generic
if
![]() $\langle \lambda , \alpha ^\vee \rangle \not \in \mathbb {Z}$
for every root
$\langle \lambda , \alpha ^\vee \rangle \not \in \mathbb {Z}$
for every root
![]() $\alpha $
. Denote by
$\alpha $
. Denote by
![]() $\mathfrak {h}^{*, \mathrm {gen}}\subset \mathfrak {h}^*$
the subset of generic weights. Let
$\mathfrak {h}^{*, \mathrm {gen}}\subset \mathfrak {h}^*$
the subset of generic weights. Let
![]() $\mathrm {HC}(H)^{\mathrm {gen}}\subset \mathrm {HC}(H)$
and
$\mathrm {HC}(H)^{\mathrm {gen}}\subset \mathrm {HC}(H)$
and
![]() $\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}\subset \mathcal {O}^{\mathrm {univ}}$
be the full subcategories of right
$\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}\subset \mathcal {O}^{\mathrm {univ}}$
be the full subcategories of right
![]() $\mathrm {U}\mathfrak {h}$
-modules supported on generic weights. Let
$\mathrm {U}\mathfrak {h}$
-modules supported on generic weights. Let
![]() $(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\subset \mathrm {Frac}(\mathrm {U}\mathfrak {h})$
be the subspace of rational functions on
$(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\subset \mathrm {Frac}(\mathrm {U}\mathfrak {h})$
be the subspace of rational functions on
![]() $\mathfrak {h}^*$
regular on
$\mathfrak {h}^*$
regular on
![]() $\mathfrak {h}^{*, \mathrm {gen}}$
.
$\mathfrak {h}^{*, \mathrm {gen}}$
.
By construction,
and similarly for
![]() $\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
. Moreover, both
$\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
. Moreover, both
![]() $\mathrm {HC}(H)^{\mathrm {gen}}\subset \mathrm {HC}(H)$
and
$\mathrm {HC}(H)^{\mathrm {gen}}\subset \mathrm {HC}(H)$
and
![]() $\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}\subset \mathcal {O}^{\mathrm {univ}}$
admit left adjoints given by localisation. Let
$\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}\subset \mathcal {O}^{\mathrm {univ}}$
admit left adjoints given by localisation. Let
be the universal Verma module with generic highest weights.
Choose a Borel subgroup
![]() $B_-\subset G$
opposite to B, with Lie algebra
$B_-\subset G$
opposite to B, with Lie algebra
![]() $\mathfrak {b}_-$
. Let
$\mathfrak {b}_-$
. Let
be the opposite universal Verma module.
Definition 5.13. The functor of
![]() $\mathfrak {n}_-$
-coinvariants
$\mathfrak {n}_-$
-coinvariants
is
![]() $M_{\mathfrak {n}_-} = M^{\mathrm {univ}}_-\otimes _{\mathrm {U}\mathfrak {g}} M$
.
$M_{\mathfrak {n}_-} = M^{\mathrm {univ}}_-\otimes _{\mathrm {U}\mathfrak {g}} M$
.
We will now recall the extremal projector introduced in [Reference Asherova, Smirnov and Tolstoy4]; see also [Reference Zhelobenko94].
Theorem 5.14. An extension
![]() $T(\mathfrak {g})$
of
$T(\mathfrak {g})$
of
![]() $\mathrm {U}\mathfrak {g}$
is obtained by replacing
$\mathrm {U}\mathfrak {g}$
is obtained by replacing
![]() $\mathrm {U}\mathfrak {h}\subset \mathrm {U}\mathfrak {g}$
with
$\mathrm {U}\mathfrak {h}\subset \mathrm {U}\mathfrak {g}$
with
![]() $\mathrm {Frac}(\mathrm {U}\mathfrak {h})$
and considering certain power series. There is an element
$\mathrm {Frac}(\mathrm {U}\mathfrak {h})$
and considering certain power series. There is an element
![]() $P\in T(\mathfrak {g})$
satisfying the following properties:
$P\in T(\mathfrak {g})$
satisfying the following properties:
-
1.
 $\mathfrak {n} P = P\mathfrak {n}_- = 0$
.
$\mathfrak {n} P = P\mathfrak {n}_- = 0$
. -
2.
 $P-1\in T(\mathfrak {g})\mathfrak {n}\cap \mathfrak {n}_- T(\mathfrak {g})$
.
$P-1\in T(\mathfrak {g})\mathfrak {n}\cap \mathfrak {n}_- T(\mathfrak {g})$
.
The action of P is well-defined on left
![]() $\mathrm {U}\mathfrak {g}$
-modules whose
$\mathrm {U}\mathfrak {g}$
-modules whose
![]() $\mathfrak {n}$
-action is locally nilpotent and that have generic
$\mathfrak {n}$
-action is locally nilpotent and that have generic
![]() $\mathfrak {h}$
-weights.
$\mathfrak {h}$
-weights.
Example 5.15. Suppose
![]() $\mathfrak {g}=\mathfrak {sl}_2$
. The extremal projector in this case is (see, e.g., [Reference Khoroshkin and Ogievetsky53])
$\mathfrak {g}=\mathfrak {sl}_2$
. The extremal projector in this case is (see, e.g., [Reference Khoroshkin and Ogievetsky53])
 $$\begin{align*}P = \sum_{n=0}^\infty \frac{(-1)^n}{n!} g_n^{-1} f^n e^n,\end{align*}$$
$$\begin{align*}P = \sum_{n=0}^\infty \frac{(-1)^n}{n!} g_n^{-1} f^n e^n,\end{align*}$$
where
 $$\begin{align*}g_n = \prod_{j=1}^n (h+j+1).\end{align*}$$
$$\begin{align*}g_n = \prod_{j=1}^n (h+j+1).\end{align*}$$
We will now describe some applications of extremal projectors.
Proposition 5.16. There is a natural isomorphism of functors
![]() $(-)_{\mathfrak {n}_-}\cong (-)^N\colon \mathcal {O}^{\mathrm {univ},\mathrm {gen}}\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
. In particular, they are exact.
$(-)_{\mathfrak {n}_-}\cong (-)^N\colon \mathcal {O}^{\mathrm {univ},\mathrm {gen}}\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
. In particular, they are exact.
Proof. Take
![]() $M\in \mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
, and consider the composite
$M\in \mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
, and consider the composite
We will prove that it is an isomorphism.
Since the weights of the right
![]() $\mathrm {U}\mathfrak {h}$
-action on M are generic and the weights of the diagonal
$\mathrm {U}\mathfrak {h}$
-action on M are generic and the weights of the diagonal
![]() $\mathrm {U}\mathfrak {h}$
-action are integral, the weights of the left
$\mathrm {U}\mathfrak {h}$
-action are integral, the weights of the left
![]() $\mathrm {U}\mathfrak {h}$
-action are also generic. Moreover, the left
$\mathrm {U}\mathfrak {h}$
-action are also generic. Moreover, the left
![]() $\mathrm {U}\mathfrak {n}$
-action is locally nilpotent. In particular, the action of the extremal projector from Theorem 5.14
$\mathrm {U}\mathfrak {n}$
-action is locally nilpotent. In particular, the action of the extremal projector from Theorem 5.14
is well-defined. It lands in N-invariants by the property
![]() $\mathfrak {n} P = 0$
. It factors through
$\mathfrak {n} P = 0$
. It factors through
![]() $\mathfrak {n}_-$
-coinvariants by the property
$\mathfrak {n}_-$
-coinvariants by the property
![]() $P\mathfrak {n}_- = 0$
. So, it gives a map
$P\mathfrak {n}_- = 0$
. So, it gives a map
For
![]() $m\in M^N$
, we have
$m\in M^N$
, we have
![]() $Pm = m$
since
$Pm = m$
since
![]() $P-1\in T(\mathfrak {g})\mathfrak {n}$
. In particular,
$P-1\in T(\mathfrak {g})\mathfrak {n}$
. In particular,
![]() $P\circ \pi = \mathrm {id}$
. For
$P\circ \pi = \mathrm {id}$
. For
![]() $m\in M$
,
$m\in M$
,
![]() $[m] = [Pm]$
in
$[m] = [Pm]$
in
![]() $M_{\mathfrak {n}_-}$
since
$M_{\mathfrak {n}_-}$
since
![]() $P-1\in \mathfrak {n}_- T(\mathfrak {g})$
. In particular,
$P-1\in \mathfrak {n}_- T(\mathfrak {g})$
. In particular,
![]() $\pi \circ P = \mathrm {id}$
.
$\pi \circ P = \mathrm {id}$
.
Theorem 5.17. The category
![]() $\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is free of rank 1 as a
$\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is free of rank 1 as a
![]() $\mathrm {HC}(H)^{\mathrm {gen}}$
-module category in the sense of Theorem 2.22.
$\mathrm {HC}(H)^{\mathrm {gen}}$
-module category in the sense of Theorem 2.22.
Proof. The unit of the adjunction
![]() $\mathrm {act}_H\dashv (-)^N$
between
$\mathrm {act}_H\dashv (-)^N$
between
![]() $\mathrm {HC}(H)^{\mathrm {gen}}$
and
$\mathrm {HC}(H)^{\mathrm {gen}}$
and
![]() $\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is
$\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is
By the PBW isomorphism, this map is an isomorphism. In particular,
![]() $\mathrm {act}_H\colon \mathrm {HC}(H)^{\mathrm {gen}}\rightarrow \mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is fully faithful.
$\mathrm {act}_H\colon \mathrm {HC}(H)^{\mathrm {gen}}\rightarrow \mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is fully faithful.
Since the
![]() $\mathfrak {n}$
-action on
$\mathfrak {n}$
-action on
![]() $M\in \mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is locally nilpotent,
$M\in \mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is locally nilpotent,
![]() $M^N = 0$
if and only if
$M^N = 0$
if and only if
![]() $M=0$
. But
$M=0$
. But
![]() $(-)^N\colon \mathcal {O}^{\mathrm {univ}, \mathrm {gen}}\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
is exact by Theorem 5.16. Therefore, it is conservative. Since its left adjoint
$(-)^N\colon \mathcal {O}^{\mathrm {univ}, \mathrm {gen}}\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
is exact by Theorem 5.16. Therefore, it is conservative. Since its left adjoint
![]() $\mathrm {act}_H$
is fully faithful, it is an equivalence.
$\mathrm {act}_H$
is fully faithful, it is an equivalence.
Corollary 5.18. The composite
is strongly monoidal and colimit-preserving.
Proof. By Theorem 5.17,
![]() $\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is free of rank 1 as a
$\mathcal {O}^{\mathrm {univ}, \mathrm {gen}}$
is free of rank 1 as a
![]() $\mathrm {HC}(H)^{\mathrm {gen}}$
-module category. The claim then follows from Theorem 2.23.
$\mathrm {HC}(H)^{\mathrm {gen}}$
-module category. The claim then follows from Theorem 2.23.
Remark 5.19. Consider the morphism of stacks
![]() $p\colon [\mathfrak {b}/B]\rightarrow [\mathfrak {h}/H]$
. It admits a section
$p\colon [\mathfrak {b}/B]\rightarrow [\mathfrak {h}/H]$
. It admits a section
![]() $s\colon [\mathfrak {h}/H]\rightarrow [\mathfrak {b}/B]$
, so
$s\colon [\mathfrak {h}/H]\rightarrow [\mathfrak {b}/B]$
, so
![]() $p\circ s=\mathrm {id}_{[\mathfrak {h}/H]}$
. It is shown in [Reference Sevostyanov76] that, restricting to generic weights, there is a homotopy
$p\circ s=\mathrm {id}_{[\mathfrak {h}/H]}$
. It is shown in [Reference Sevostyanov76] that, restricting to generic weights, there is a homotopy
![]() $s\circ p\sim \mathrm {id}_{[\mathfrak {b}/B]}$
given by the classical limit of the extremal projector. The proof of Theorem 5.17 gives an analogous interpretation of the extremal projector on the quantum level.
$s\circ p\sim \mathrm {id}_{[\mathfrak {b}/B]}$
given by the classical limit of the extremal projector. The proof of Theorem 5.17 gives an analogous interpretation of the extremal projector on the quantum level.
We will now show that
![]() $\mathrm {res}^{\mathrm {gen}}$
gives rise to a dynamical twist. For this, according to Theorem 4.1, we have to show that
$\mathrm {res}^{\mathrm {gen}}$
gives rise to a dynamical twist. For this, according to Theorem 4.1, we have to show that
![]() $\mathrm {res}^{\mathrm {gen}}$
of a free Harish–Chandra bimodule is free: that is, we have to establish an isomorphism between
$\mathrm {res}^{\mathrm {gen}}$
of a free Harish–Chandra bimodule is free: that is, we have to establish an isomorphism between
![]() $(V\otimes M^{\mathrm {univ}})^N$
and
$(V\otimes M^{\mathrm {univ}})^N$
and
![]() $V\otimes (\mathrm {U}\mathfrak {h})^{\mathrm {gen}}$
in
$V\otimes (\mathrm {U}\mathfrak {h})^{\mathrm {gen}}$
in
![]() $\mathrm {HC}(H)^{\mathrm {gen}}$
, for every
$\mathrm {HC}(H)^{\mathrm {gen}}$
, for every
![]() $V\in \operatorname {\mathrm {Rep}}(G)$
.
$V\in \operatorname {\mathrm {Rep}}(G)$
.
Theorem 5.20. The morphism
where the second morphism is induced by the projection
![]() $M^{\mathrm {univ}, \mathrm {gen}}\rightarrow (\mathrm {U}\mathfrak {h})^{\mathrm {gen}}$
onto the highest weights, defines a natural isomorphism witnessing commutativity of the diagram
$M^{\mathrm {univ}, \mathrm {gen}}\rightarrow (\mathrm {U}\mathfrak {h})^{\mathrm {gen}}$
onto the highest weights, defines a natural isomorphism witnessing commutativity of the diagram

Proof. Let
![]() $M_\lambda $
be the Verma module of a generic highest weight
$M_\lambda $
be the Verma module of a generic highest weight
![]() $\lambda \in \mathfrak {h}^*$
, and denote by
$\lambda \in \mathfrak {h}^*$
, and denote by
![]() $x_\lambda \in M_\lambda $
the highest-weight vector. We have to show that the map
$x_\lambda \in M_\lambda $
the highest-weight vector. We have to show that the map
![]() $(V\otimes M_\lambda )^N\rightarrow V$
given by
$(V\otimes M_\lambda )^N\rightarrow V$
given by
where
![]() $\dots $
contain elements of
$\dots $
contain elements of
![]() $M_\lambda $
of weight less than
$M_\lambda $
of weight less than
![]() $\lambda $
, is an isomorphism. This is the content of [Reference Etingof and Varchenko31, Theorem 8].
$\lambda $
, is an isomorphism. This is the content of [Reference Etingof and Varchenko31, Theorem 8].
Remark 5.21. The
![]() $(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}$
-module
$(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}$
-module
![]() $\mathrm {res}^{\mathrm {gen}}(V\otimes \mathrm {U}\mathfrak {g})$
admits another natural basis constructed in [Reference Khoroshkin54].
$\mathrm {res}^{\mathrm {gen}}(V\otimes \mathrm {U}\mathfrak {g})$
admits another natural basis constructed in [Reference Khoroshkin54].
Consider
![]() $V,W\in \operatorname {\mathrm {Rep}}(G)$
. Let us recall that Etingof and Varchenko [Reference Etingof and Varchenko31] have introduced the
fusion matrix
$V,W\in \operatorname {\mathrm {Rep}}(G)$
. Let us recall that Etingof and Varchenko [Reference Etingof and Varchenko31] have introduced the
fusion matrix
depending rationally on a parameter
![]() $\lambda \in \mathfrak {h}^*$
as follows. Consider the Verma module
$\lambda \in \mathfrak {h}^*$
as follows. Consider the Verma module
![]() $M_\lambda $
with highest-weight
$M_\lambda $
with highest-weight
![]() $\lambda \in \mathfrak {h}^*$
. For
$\lambda \in \mathfrak {h}^*$
. For
![]() $V\in \operatorname {\mathrm {Rep}}(G)$
denote by
$V\in \operatorname {\mathrm {Rep}}(G)$
denote by
![]() $V=\oplus _{\lambda \in \Lambda } V[\lambda ]$
its weight decomposition. Consider a morphism
$V=\oplus _{\lambda \in \Lambda } V[\lambda ]$
its weight decomposition. Consider a morphism
![]() $M_\lambda \rightarrow M_\mu \otimes V$
. The image of a highest-weight vector
$M_\lambda \rightarrow M_\mu \otimes V$
. The image of a highest-weight vector
![]() $x_\lambda \in M_\lambda $
has the form
$x_\lambda \in M_\lambda $
has the form
where
![]() $\dots $
denote terms containing elements of
$\dots $
denote terms containing elements of
![]() $M_\mu $
of lower weight. This determines a morphism
$M_\mu $
of lower weight. This determines a morphism
For generic
![]() $\mu $
, it is an isomorphism, and for
$\mu $
, it is an isomorphism, and for
![]() $v\in V[\lambda -\mu ]$
, we denote by
$v\in V[\lambda -\mu ]$
, we denote by
![]() $\Phi ^v_\lambda \in \mathrm {Hom}_{\mathrm {U}\mathfrak {g}}(M_\lambda , M_\mu \otimes V)$
the preimage of v under this map.
$\Phi ^v_\lambda \in \mathrm {Hom}_{\mathrm {U}\mathfrak {g}}(M_\lambda , M_\mu \otimes V)$
the preimage of v under this map.
For
![]() $v\in V$
and
$v\in V$
and
![]() $w\in W$
of weights
$w\in W$
of weights
![]() $\mathrm {wt}(v)$
and
$\mathrm {wt}(v)$
and
![]() $\mathrm {wt}(w)$
, consider the composite
$\mathrm {wt}(w)$
, consider the composite
The fusion matrix is defined so that this composite is
![]() $\Phi ^{J^{EV}_{W, V}(\lambda )(w\otimes v)}_\lambda $
. By [Reference Etingof and Varchenko31, Theorem 48],
$\Phi ^{J^{EV}_{W, V}(\lambda )(w\otimes v)}_\lambda $
. By [Reference Etingof and Varchenko31, Theorem 48],
![]() $J^{EV}_{W, V}(\lambda )$
quantises the standard rational solution of the dynamical Yang–Baxter equation (see [Reference Etingof and Varchenko36, Theorem 3.2]).
$J^{EV}_{W, V}(\lambda )$
quantises the standard rational solution of the dynamical Yang–Baxter equation (see [Reference Etingof and Varchenko36, Theorem 3.2]).
Combining Theorem 5.18 and Theorem 5.20, we obtain a monoidal structure on the composite
In particular, as in Theorem 4.1, this gives rise to linear maps
depending rationally on
![]() $\lambda \in \mathfrak {h}^*$
.
$\lambda \in \mathfrak {h}^*$
.
Proposition 5.22. Let
![]() $V,W\in \operatorname {\mathrm {Rep}}(G)$
. The map
$V,W\in \operatorname {\mathrm {Rep}}(G)$
. The map
![]() $J_{V, W}(\lambda )\colon V\otimes W\rightarrow V\otimes W$
coincides with a permutation of the fusion matrix
$J_{V, W}(\lambda )\colon V\otimes W\rightarrow V\otimes W$
coincides with a permutation of the fusion matrix
where
![]() $\tau $
is the flip of tensor factors.
$\tau $
is the flip of tensor factors.
Proof. Let
![]() $x^{\mathrm {univ}}\in M^{\mathrm {univ}}$
be the generator of the universal Verma module and
$x^{\mathrm {univ}}\in M^{\mathrm {univ}}$
be the generator of the universal Verma module and
![]() $x_\lambda \in M_\lambda $
be the generator of the Verma module of highest weight
$x_\lambda \in M_\lambda $
be the generator of the Verma module of highest weight
![]() $\lambda $
. Using the PBW identification
$\lambda $
. Using the PBW identification
![]() $M^{\mathrm {univ}}\cong \mathrm {U}\mathfrak {n}_-\otimes \mathrm {U}\mathfrak {h}$
, we identify elements of
$M^{\mathrm {univ}}\cong \mathrm {U}\mathfrak {n}_-\otimes \mathrm {U}\mathfrak {h}$
, we identify elements of
![]() $M^{\mathrm {univ}}$
with functions
$M^{\mathrm {univ}}$
with functions
![]() $\mathfrak {h}^*\rightarrow \mathrm {U}\mathfrak {n}_-$
.
$\mathfrak {h}^*\rightarrow \mathrm {U}\mathfrak {n}_-$
.
For
![]() $v\in V$
, we denote by
$v\in V$
, we denote by
![]() $\sum v_i\otimes a_i x^{\mathrm {univ}}$
the unique highest-weight element of
$\sum v_i\otimes a_i x^{\mathrm {univ}}$
the unique highest-weight element of
![]() $V\otimes M^{\mathrm {univ}}$
, which has an expansion
$V\otimes M^{\mathrm {univ}}$
, which has an expansion
![]() $v\otimes x^{\mathrm {univ}}+\dots $
. Similarly, for
$v\otimes x^{\mathrm {univ}}+\dots $
. Similarly, for
![]() $w\in W$
, we denote by
$w\in W$
, we denote by
![]() $\sum w_i\otimes b_i x^{\mathrm {univ}} = w\otimes x^{\mathrm {univ}} + \dots $
the highest-weight element of
$\sum w_i\otimes b_i x^{\mathrm {univ}} = w\otimes x^{\mathrm {univ}} + \dots $
the highest-weight element of
![]() $W\otimes M^{\mathrm {univ}}$
.
$W\otimes M^{\mathrm {univ}}$
.
Under the morphism given by equation (33)
we have
It is then easy to see that
Using the same notations, the map
![]() $\Phi _\lambda ^v\colon M_\lambda \rightarrow M_{\lambda -\mathrm {wt}(v)} \otimes V$
is
$\Phi _\lambda ^v\colon M_\lambda \rightarrow M_{\lambda -\mathrm {wt}(v)} \otimes V$
is
Therefore, the composite given by equation (35) is
 $$ \begin{align*} x_\lambda &\mapsto \sum_i a_i(\lambda-\mathrm{wt}(v)) x_{\lambda-\mathrm{wt}(v)}\otimes v_i\\ &\mapsto \sum_{i,j} a_i(\lambda-\mathrm{wt}(v))_{(1)} b_j(\lambda-\mathrm{wt}(v)-\mathrm{wt}(w))x_{\lambda-\mathrm{wt}(v)-\mathrm{wt}(w)}\otimes a_i(\lambda-\mathrm{wt}(v))_{(2)} w_j\otimes v_i. \end{align*} $$
$$ \begin{align*} x_\lambda &\mapsto \sum_i a_i(\lambda-\mathrm{wt}(v)) x_{\lambda-\mathrm{wt}(v)}\otimes v_i\\ &\mapsto \sum_{i,j} a_i(\lambda-\mathrm{wt}(v))_{(1)} b_j(\lambda-\mathrm{wt}(v)-\mathrm{wt}(w))x_{\lambda-\mathrm{wt}(v)-\mathrm{wt}(w)}\otimes a_i(\lambda-\mathrm{wt}(v))_{(2)} w_j\otimes v_i. \end{align*} $$
The resulting element of
![]() $M_{\lambda -\mathrm {wt}(v)-\mathrm {wt}(w)}\otimes W\otimes V$
is
$M_{\lambda -\mathrm {wt}(v)-\mathrm {wt}(w)}\otimes W\otimes V$
is
which proves the claim.
Moreover, in [Reference Etingof and Varchenko31, Section 5], Etingof and Varchenko have introduced an
![]() $\mathfrak {h}$
-bialgebroid
$\mathfrak {h}$
-bialgebroid
![]() $F(G)$
.
$F(G)$
.
Theorem 5.23. Consider the monoidal functor
It admits a colimit-preserving right adjoint; denote by
![]() $B\in \mathrm {HC}(H)^{\mathrm {gen}}\otimes \mathrm {HC}(H)^{\mathrm {gen}}$
the Harish-Chandra bialgebroid corresponding to this monoidal functor constructed in Theorem 3.35. Then we have an isomorphism of
$B\in \mathrm {HC}(H)^{\mathrm {gen}}\otimes \mathrm {HC}(H)^{\mathrm {gen}}$
the Harish-Chandra bialgebroid corresponding to this monoidal functor constructed in Theorem 3.35. Then we have an isomorphism of
![]() $\mathfrak {h}$
-bialgebroids
$\mathfrak {h}$
-bialgebroids
Proof. By Theorem 5.20, the functor
![]() $\operatorname {\mathrm {Rep}}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
factors as
$\operatorname {\mathrm {Rep}}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
factors as
Under this composite, a finite-dimensional G-representation
![]() $V\in \operatorname {\mathrm {Rep}}(G)$
is sent to a compact projective object
$V\in \operatorname {\mathrm {Rep}}(G)$
is sent to a compact projective object
![]() $(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\otimes V\in \mathrm {HC}(H)^{\mathrm {gen}}$
, so this functor admits a colimit-preserving right adjoint.
$(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\otimes V\in \mathrm {HC}(H)^{\mathrm {gen}}$
, so this functor admits a colimit-preserving right adjoint.
Since G is semisimple, by Theorem 4.9, the Harish-Chandra bialgebroid B is isomorphic to
where the sum is over isomorphism classes of irreducible finite-dimensional G-representations. In particular, we get an isomorphism of
![]() $(\mathrm {Frac}(\mathrm {U}\mathfrak {h}),\mathrm {Frac}(\mathrm {U}\mathfrak {h}))$
-bimodules
$(\mathrm {Frac}(\mathrm {U}\mathfrak {h}),\mathrm {Frac}(\mathrm {U}\mathfrak {h}))$
-bimodules
In the notations of Theorem 4.9 and [Reference Etingof and Varchenko31, Section 5], the isomorphism is given by
 $$ \begin{align*} T_V & \mapsto L^V, \\ t(f(\lambda)) & \mapsto f(\lambda^1), \\ s(f(\lambda)) & \mapsto f(\lambda^2). \end{align*} $$
$$ \begin{align*} T_V & \mapsto L^V, \\ t(f(\lambda)) & \mapsto f(\lambda^1), \\ s(f(\lambda)) & \mapsto f(\lambda^2). \end{align*} $$
It is clear that this isomorphism preserves coproduct, counit and unit and the only nontrivial check is that the product is preserved as well. The relations
![]() $(18),(19)$
in Reference Etingof and Varchenko31 are clearly satisfied. For
$(18),(19)$
in Reference Etingof and Varchenko31 are clearly satisfied. For
![]() $(20)$
, the claim follows from Theorem 5.22.
$(20)$
, the claim follows from Theorem 5.22.
5.2 Quantum parabolic restriction
In this section, we define a parabolic restriction in the setting of quantum groups; we use the notation from section 3.4.
Definition 5.24. The
universal quantum category
![]() $\mathcal {O}$
is the category
$\mathcal {O}$
is the category
![]() $\mathcal {O}_q^{\mathrm {univ}}$
of
$\mathcal {O}_q^{\mathrm {univ}}$
of
![]() $(\mathrm {U}_q(\mathfrak {g}),\mathrm {U}_q(\mathfrak {h}))$
-bimodules whose diagonal
$(\mathrm {U}_q(\mathfrak {g}),\mathrm {U}_q(\mathfrak {h}))$
-bimodules whose diagonal
![]() $\mathrm {U}_q(\mathfrak {b})$
-action is integrable. The
universal quantum Verma module
is the object
$\mathrm {U}_q(\mathfrak {b})$
-action is integrable. The
universal quantum Verma module
is the object
Remark 5.25. As in the classical case, we may identify
![]() $\mathcal {O}_q^{\mathrm {univ}}$
with the full subcategory of
$\mathcal {O}_q^{\mathrm {univ}}$
with the full subcategory of
![]() $\mathrm {LMod}_{\mathrm {U}_q(\mathfrak {g})}(\operatorname {\mathrm {Rep}}_q(H))$
of
$\mathrm {LMod}_{\mathrm {U}_q(\mathfrak {g})}(\operatorname {\mathrm {Rep}}_q(H))$
of
![]() $\mathrm {U}_q(\mathfrak {g})$
-modules whose
$\mathrm {U}_q(\mathfrak {g})$
-modules whose
![]() $\mathrm {U}_q(\mathfrak {n})$
-action is locally finite.
$\mathrm {U}_q(\mathfrak {n})$
-action is locally finite.
We will now define a quantum analogue of the bimodules given by equation (32):
Lemma 5.26. Suppose
![]() $X\in \mathrm {HC}_q(G)$
. The left
$X\in \mathrm {HC}_q(G)$
. The left
![]() $\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
-module structure on
$\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
-module structure on
![]() $X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} \mathrm {U}_q(\mathfrak {g})$
has a canonically extension to a
$X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} \mathrm {U}_q(\mathfrak {g})$
has a canonically extension to a
![]() $\mathrm {U}_q(\mathfrak {g})$
-module structure. Moreover, the left
$\mathrm {U}_q(\mathfrak {g})$
-module structure. Moreover, the left
![]() $\mathrm {U}_q(\mathfrak {n})$
-action on
$\mathrm {U}_q(\mathfrak {n})$
-action on
![]() $X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} M^{\mathrm {univ}}$
is locally finite.
$X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} M^{\mathrm {univ}}$
is locally finite.
Proof. Recall from Theorem 3.4 that the left action of
![]() $a\in \mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
on
$a\in \mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
on
![]() $x\in X$
is
$x\in X$
is
where
![]() $\operatorname {\mathrm {ad}}$
refers to the diagonal
$\operatorname {\mathrm {ad}}$
refers to the diagonal
![]() $\mathrm {U}_q(\mathfrak {g})$
-action on X. So, we may extend the left
$\mathrm {U}_q(\mathfrak {g})$
-action on X. So, we may extend the left
![]() $\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
-action on the relative tensor product
$\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
-action on the relative tensor product
![]() $X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} \mathrm {U}_q(\mathfrak {g})$
to a
$X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} \mathrm {U}_q(\mathfrak {g})$
to a
![]() $\mathrm {U}_q(\mathfrak {g})$
-action by the formula
$\mathrm {U}_q(\mathfrak {g})$
-action by the formula
for
![]() $a\in \mathrm {U}_q(\mathfrak {g})$
an
$a\in \mathrm {U}_q(\mathfrak {g})$
an
![]() $x\otimes h\in X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} \mathrm {U}_q(\mathfrak {g})$
. It is well-defined (i.e., descends to the relative tensor product) using the formula
$x\otimes h\in X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} \mathrm {U}_q(\mathfrak {g})$
. It is well-defined (i.e., descends to the relative tensor product) using the formula
![]() $(\operatorname {\mathrm {ad}} a_{(1)})(l)a_{(2)} = al$
for any
$(\operatorname {\mathrm {ad}} a_{(1)})(l)a_{(2)} = al$
for any
![]() $a\in \mathrm {U}_q(\mathfrak {g})$
and
$a\in \mathrm {U}_q(\mathfrak {g})$
and
![]() $l\in \mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
.
$l\in \mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
.
The diagonal
![]() $\mathrm {U}_q(\mathfrak {n})$
-action on
$\mathrm {U}_q(\mathfrak {n})$
-action on
![]() $X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} M^{\mathrm {univ}}$
is locally finite since it is so on X and
$X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} M^{\mathrm {univ}}$
is locally finite since it is so on X and
![]() $M^{\mathrm {univ}}$
.
$M^{\mathrm {univ}}$
.
A
![]() $\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
-bimodule
$\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}$
-bimodule
![]() $X\in \mathrm {HC}_q(G)$
acts on a
$X\in \mathrm {HC}_q(G)$
acts on a
![]() $(\mathrm {U}_q(\mathfrak {g}), \mathrm {U}_q(\mathfrak {h}))$
-bimodule
$(\mathrm {U}_q(\mathfrak {g}), \mathrm {U}_q(\mathfrak {h}))$
-bimodule
![]() $M\in \mathcal {O}_q^{\mathrm {univ}}$
via
$M\in \mathcal {O}_q^{\mathrm {univ}}$
via
By construction, it is a
![]() $(\mathrm {U}_q(\mathfrak {g}), \mathrm {U}_q(\mathfrak {h}))$
-bimodule. Since the diagonal
$(\mathrm {U}_q(\mathfrak {g}), \mathrm {U}_q(\mathfrak {h}))$
-bimodule. Since the diagonal
![]() $\mathrm {U}_q(\mathfrak {n})$
-action on X and the left
$\mathrm {U}_q(\mathfrak {n})$
-action on X and the left
![]() $\mathrm {U}_q(\mathfrak {n})$
-action on M are locally finite, so is the left
$\mathrm {U}_q(\mathfrak {n})$
-action on M are locally finite, so is the left
![]() $\mathrm {U}_q(\mathfrak {n})$
-action on this bimodule. In particular, it lies in
$\mathrm {U}_q(\mathfrak {n})$
-action on this bimodule. In particular, it lies in
![]() $\mathcal {O}_q^{\mathrm {univ}}$
.
$\mathcal {O}_q^{\mathrm {univ}}$
.
For a
![]() $\mathrm {U}_q(\mathfrak {h})$
-bimodule
$\mathrm {U}_q(\mathfrak {h})$
-bimodule
![]() $X\in \mathrm {HC}_q(H)$
and a
$X\in \mathrm {HC}_q(H)$
and a
![]() $(\mathrm {U}_q(\mathfrak {g}), \mathrm {U}_q(\mathfrak {h}))$
-bimodule
$(\mathrm {U}_q(\mathfrak {g}), \mathrm {U}_q(\mathfrak {h}))$
-bimodule
![]() $M\in \mathcal {O}_q^{\mathrm {univ}}$
, the action is
$M\in \mathcal {O}_q^{\mathrm {univ}}$
, the action is
Let
be the actions of
![]() $\mathrm {HC}_q(G)$
and
$\mathrm {HC}_q(G)$
and
![]() $\mathrm {HC}_q(H)$
on the universal Verma module
$\mathrm {HC}_q(H)$
on the universal Verma module
![]() $M^{\mathrm {univ}}$
.
$M^{\mathrm {univ}}$
.
Definition 5.27. The parabolic restriction and parabolic induction are the lax monoidal functors
 $$ \begin{align*} \mathrm{res}&=\mathrm{act}^{\mathrm{R}}_H\circ \mathrm{act}_G\colon \mathrm{HC}_q(G)\longrightarrow \mathrm{HC}_q(H) \\ \mathrm{ind}&=\mathrm{act}^{\mathrm{R}}_G\circ \mathrm{act}_H\colon \mathrm{HC}_q(H)\longrightarrow \mathrm{HC}_q(G). \end{align*} $$
$$ \begin{align*} \mathrm{res}&=\mathrm{act}^{\mathrm{R}}_H\circ \mathrm{act}_G\colon \mathrm{HC}_q(G)\longrightarrow \mathrm{HC}_q(H) \\ \mathrm{ind}&=\mathrm{act}^{\mathrm{R}}_G\circ \mathrm{act}_H\colon \mathrm{HC}_q(H)\longrightarrow \mathrm{HC}_q(G). \end{align*} $$
We have a functor
of
![]() $\mathrm {U}_q(\mathfrak {n})$
-invariants.
$\mathrm {U}_q(\mathfrak {n})$
-invariants.
Proposition 5.28. The functor
![]() $(-)^{\mathrm {U}_q(\mathfrak {n})}\colon \mathcal {O}_q^{\mathrm {univ}}\rightarrow \mathrm {HC}_q(H)$
is right adjoint to
$(-)^{\mathrm {U}_q(\mathfrak {n})}\colon \mathcal {O}_q^{\mathrm {univ}}\rightarrow \mathrm {HC}_q(H)$
is right adjoint to
![]() $\mathrm {act}_H\colon \mathrm {HC}_q(H)\rightarrow \mathcal {O}_q^{\mathrm {univ}}$
.
$\mathrm {act}_H\colon \mathrm {HC}_q(H)\rightarrow \mathcal {O}_q^{\mathrm {univ}}$
.
Proof. For
![]() $M\in \mathcal {O}_q^{\mathrm {univ}}$
and
$M\in \mathcal {O}_q^{\mathrm {univ}}$
and
![]() $X\in \mathrm {HC}_q(H)$
, we have
$X\in \mathrm {HC}_q(H)$
, we have
 $$ \begin{align*} \mathrm{Hom}_{\mathcal{O}_q^{\mathrm{univ}}}(\mathrm{act}_H(X), M)&= \mathrm{Hom}_{\mathcal{O}_q^{\mathrm{univ}}}(\mathrm{U}_q(\mathfrak{g})\otimes_{\mathrm{U}_q(\mathfrak{b})} X, M) \\ &\cong \mathrm{Hom}_{{}_{\mathrm{U}_q(\mathfrak{b})}\mathrm{BMod}_{\mathrm{U}_q(\mathfrak{h})}}(X, M) \\ &\cong \mathrm{Hom}_{\mathrm{HC}_q(H)}(X, M^{\mathrm{U}_q(n)}). \end{align*} $$
$$ \begin{align*} \mathrm{Hom}_{\mathcal{O}_q^{\mathrm{univ}}}(\mathrm{act}_H(X), M)&= \mathrm{Hom}_{\mathcal{O}_q^{\mathrm{univ}}}(\mathrm{U}_q(\mathfrak{g})\otimes_{\mathrm{U}_q(\mathfrak{b})} X, M) \\ &\cong \mathrm{Hom}_{{}_{\mathrm{U}_q(\mathfrak{b})}\mathrm{BMod}_{\mathrm{U}_q(\mathfrak{h})}}(X, M) \\ &\cong \mathrm{Hom}_{\mathrm{HC}_q(H)}(X, M^{\mathrm{U}_q(n)}). \end{align*} $$
Proposition 5.29. The natural morphism
![]() $\mathrm {U}_q(\mathfrak {h})\rightarrow \mathrm {res}(\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}})$
is an isomorphism.
$\mathrm {U}_q(\mathfrak {h})\rightarrow \mathrm {res}(\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}})$
is an isomorphism.
Proof. The proof is similar to the proof of Theorem 5.9, where we again use the fact that the quantum Verma module is irreducible for generic parameters [Reference Voigt and Yuncken89, Theorem 4.15].
A weight for a
![]() $\mathrm {U}_q(\mathfrak {g})$
-module is specified by an element of
$\mathrm {U}_q(\mathfrak {g})$
-module is specified by an element of
![]() $H(k)\cong \mathrm {Hom}(\Lambda , k^\times )$
. We will use an additive notation for weights, so a vector v of weight
$H(k)\cong \mathrm {Hom}(\Lambda , k^\times )$
. We will use an additive notation for weights, so a vector v of weight
![]() $\lambda $
satisfies
$\lambda $
satisfies
![]() $K_\mu v= q^{(\lambda , \mu )} v$
. For a root
$K_\mu v= q^{(\lambda , \mu )} v$
. For a root
![]() $\alpha $
, we denote
$\alpha $
, we denote
![]() $q_\alpha = q^{(\alpha , \alpha )/2}$
.
$q_\alpha = q^{(\alpha , \alpha )/2}$
.
Definition 5.30. A weight
![]() $\lambda $
is
generic
if
$\lambda $
is
generic
if
![]() $q^{(\alpha , \lambda )}\not \in \pm q_\alpha ^{\mathbf {Z}}$
for every root
$q^{(\alpha , \lambda )}\not \in \pm q_\alpha ^{\mathbf {Z}}$
for every root
![]() $\alpha $
. Denote by
$\alpha $
. Denote by
![]() $H^{\mathrm {gen}}\subset H$
the subset of generic weights. We denote by
$H^{\mathrm {gen}}\subset H$
the subset of generic weights. We denote by
![]() $\mathrm {HC}_q^{\mathrm {gen}}(H)\subset \mathrm {HC}_q(H)$
and
$\mathrm {HC}_q^{\mathrm {gen}}(H)\subset \mathrm {HC}_q(H)$
and
![]() $\mathcal {O}_q^{\mathrm {univ},\mathrm {gen}}\subset \mathcal {O}_q^{\mathrm {univ}}$
the full subcategories of modules with generic
$\mathcal {O}_q^{\mathrm {univ},\mathrm {gen}}\subset \mathcal {O}_q^{\mathrm {univ}}$
the full subcategories of modules with generic
![]() $\mathrm {U}_q(\mathfrak {h})$
-weights. Let
$\mathrm {U}_q(\mathfrak {h})$
-weights. Let
![]() $\mathrm {U}_q(\mathfrak {h})^{\mathrm {gen}}\subset \mathrm {Frac}(\mathrm {U}_q(\mathfrak {h}))$
be the subspace of rational functions on H regular on
$\mathrm {U}_q(\mathfrak {h})^{\mathrm {gen}}\subset \mathrm {Frac}(\mathrm {U}_q(\mathfrak {h}))$
be the subspace of rational functions on H regular on
![]() $H^{\mathrm {gen}}$
.
$H^{\mathrm {gen}}$
.
We denote by
the universal quantum Verma module with generic highest weights.
A generalisation of the extremal projector to quantum groups was introduced in [Reference Khoroshkin and Tolstoy55].
Theorem 5.31. An extension
![]() $T_q(\mathfrak {g})$
of
$T_q(\mathfrak {g})$
of
![]() $\mathrm {U}_q(\mathfrak {g})$
is obtained by replacing
$\mathrm {U}_q(\mathfrak {g})$
is obtained by replacing
![]() $\mathrm {U}_q(\mathfrak {h})\subset \mathrm {U}_q(\mathfrak {g})$
with
$\mathrm {U}_q(\mathfrak {h})\subset \mathrm {U}_q(\mathfrak {g})$
with
![]() $\mathrm {Frac}(\mathrm {U}_q(\mathfrak {h}))$
and considering certain power series. There is an element
$\mathrm {Frac}(\mathrm {U}_q(\mathfrak {h}))$
and considering certain power series. There is an element
![]() $P\in T_q(\mathfrak {g})$
satisfying the following properties:
$P\in T_q(\mathfrak {g})$
satisfying the following properties:
-
1.
 $\mathrm {U}_q^{>0}(\mathfrak {n}) P = P \mathrm {U}_q^{>0}(\mathfrak {n}_-) = 0$
.
$\mathrm {U}_q^{>0}(\mathfrak {n}) P = P \mathrm {U}_q^{>0}(\mathfrak {n}_-) = 0$
. -
2.
 $P-1\in T_q(\mathfrak {g})\mathrm {U}_q^{>0}(\mathfrak {n})\cap \mathrm {U}_q^{>0}(\mathfrak {n}_-) T_q(\mathfrak {g})$
.
$P-1\in T_q(\mathfrak {g})\mathrm {U}_q^{>0}(\mathfrak {n})\cap \mathrm {U}_q^{>0}(\mathfrak {n}_-) T_q(\mathfrak {g})$
.
The action of P is well-defined on left
![]() $\mathrm {U}_q(\mathfrak {g})$
-modules whose
$\mathrm {U}_q(\mathfrak {g})$
-modules whose
![]() $\mathrm {U}_q(\mathfrak {n})$
-action is locally nilpotent and that have generic
$\mathrm {U}_q(\mathfrak {n})$
-action is locally nilpotent and that have generic
![]() $\mathrm {U}_q(\mathfrak {h})$
-weights.
$\mathrm {U}_q(\mathfrak {h})$
-weights.
Example 5.32. Consider
![]() $\mathrm {U}_q(\mathfrak {sl}_2)$
with generators
$\mathrm {U}_q(\mathfrak {sl}_2)$
with generators
![]() $E,K,F$
as in Theorem 3.21. Let
$E,K,F$
as in Theorem 3.21. Let
![]() $[n] = \frac {q^n-q^{-n}}{q-q^{-1}}$
be the quantum integer,
$[n] = \frac {q^n-q^{-n}}{q-q^{-1}}$
be the quantum integer,
![]() $[n]! = \prod _{j=1}^n [j]!$
the quantum factorial and
$[n]! = \prod _{j=1}^n [j]!$
the quantum factorial and
 $$\begin{align*}[h+n] = \frac{Kq^n-K^{-1}q^{-n}}{q-q^{-1}}\in\mathrm{U}_q(\mathfrak{sl}_2)\end{align*}$$
$$\begin{align*}[h+n] = \frac{Kq^n-K^{-1}q^{-n}}{q-q^{-1}}\in\mathrm{U}_q(\mathfrak{sl}_2)\end{align*}$$
for
![]() $n\in \mathbf {Z}$
. Then the extremal projector is (see, e.g., [Reference Khoroshkin and Ogievetsky53, Section 9])
$n\in \mathbf {Z}$
. Then the extremal projector is (see, e.g., [Reference Khoroshkin and Ogievetsky53, Section 9])
 $$\begin{align*}P = \sum_{n=0}^\infty \frac{(-1)^n}{[n]!} g_n^{-1} F^n E^n,\end{align*}$$
$$\begin{align*}P = \sum_{n=0}^\infty \frac{(-1)^n}{[n]!} g_n^{-1} F^n E^n,\end{align*}$$
where
![]() $g_n = \prod _{j=1}^n [h+j+1]$
.
$g_n = \prod _{j=1}^n [h+j+1]$
.
Completely analogously to the proof of Theorem 5.17, one proves the following statement.
Theorem 5.33. The category
![]() $\mathcal {O}_q^{\mathrm {univ}, \mathrm {gen}}$
is free of rank
$\mathcal {O}_q^{\mathrm {univ}, \mathrm {gen}}$
is free of rank
![]() $1$
as a
$1$
as a
![]() $\mathrm {HC}_q(H)^{\mathrm {gen}}$
-module category.
$\mathrm {HC}_q(H)^{\mathrm {gen}}$
-module category.
Corollary 5.34. The functor
![]() $\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}}$
is strongly monoidal and colimit-preserving.
$\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}}$
is strongly monoidal and colimit-preserving.
Similar to the classical case, the parabolic restriction of a free Harish-Chandra bimodule is free.
Theorem 5.35. For every
![]() $V\in \operatorname {\mathrm {Rep}}_q(G)$
, the morphism
$V\in \operatorname {\mathrm {Rep}}_q(G)$
, the morphism
where the second morphism is induced by the projection
![]() $M^{\mathrm {univ}, \mathrm {gen}}\rightarrow \mathrm {U}_q(\mathfrak {h})^{\mathrm {gen}}$
onto highest weights, defines a natural isomorphism witnessing commutativity of the diagram
$M^{\mathrm {univ}, \mathrm {gen}}\rightarrow \mathrm {U}_q(\mathfrak {h})^{\mathrm {gen}}$
onto highest weights, defines a natural isomorphism witnessing commutativity of the diagram

Combining Theorem 5.34 and Theorem 5.35, we obtain a monoidal structure on the composite
In particular, by Theorem 4.1, this gives rise to linear maps
rational functions on H.
Example 5.36. Consider
![]() $G=\mathrm {SL}_2$
and
$G=\mathrm {SL}_2$
and
![]() $V\in \operatorname {\mathrm {Rep}}_q(\mathrm {SL}_2)$
the irreducible two-dimensional representation with the basis
$V\in \operatorname {\mathrm {Rep}}_q(\mathrm {SL}_2)$
the irreducible two-dimensional representation with the basis
![]() $\{v_+,v_- \}$
such that
$\{v_+,v_- \}$
such that
The isomorphism
![]() $\mathrm {U}_q(\mathfrak {h})^{\mathrm {gen}} \otimes V \rightarrow (V \otimes M^{\mathrm {univ},\mathrm {gen}})^{\mathrm {U}_q(\mathfrak {n})}$
is given by
$\mathrm {U}_q(\mathfrak {h})^{\mathrm {gen}} \otimes V \rightarrow (V \otimes M^{\mathrm {univ},\mathrm {gen}})^{\mathrm {U}_q(\mathfrak {n})}$
is given by
 $$ \begin{align*} 1 \otimes v_+ & \mapsto v_+ \otimes 1, \\ 1 \otimes v_- & \mapsto v_- \otimes 1 - q^{-1} v_+ \otimes F\cdot [h]^{-1} x^{\mathrm{univ}}. \end{align*} $$
$$ \begin{align*} 1 \otimes v_+ & \mapsto v_+ \otimes 1, \\ 1 \otimes v_- & \mapsto v_- \otimes 1 - q^{-1} v_+ \otimes F\cdot [h]^{-1} x^{\mathrm{univ}}. \end{align*} $$
Then the matrix of
![]() $J_{V,V}(\lambda )$
in the basis
$J_{V,V}(\lambda )$
in the basis
![]() $\{ v_+ \otimes v_+,v_+ \otimes v_-, v_- \otimes v_+, v_- \otimes v_- \}$
is given by
$\{ v_+ \otimes v_+,v_+ \otimes v_-, v_- \otimes v_+, v_- \otimes v_- \}$
is given by
 $$\begin{align*}\left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & -q^{-\lambda-1}[\lambda+1]^{-1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right).\end{align*}$$
$$\begin{align*}\left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & -q^{-\lambda-1}[\lambda+1]^{-1} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right).\end{align*}$$
Our convention for the coproduct on
![]() $\mathrm {U}_q(\mathfrak {g})$
follows [Reference Lusztig62, Lemma 3.1.4]. For two
$\mathrm {U}_q(\mathfrak {g})$
follows [Reference Lusztig62, Lemma 3.1.4]. For two
![]() $\mathrm {U}_q(\mathfrak {g})$
-modules
$\mathrm {U}_q(\mathfrak {g})$
-modules
![]() $V,W$
, we denote by
$V,W$
, we denote by
![]() $V\overline {\otimes } W$
the vector space
$V\overline {\otimes } W$
the vector space
![]() $V\otimes W$
equipped with the
$V\otimes W$
equipped with the
![]() $\mathrm {U}_q(\mathfrak {g})$
-module structure via the opposite coproduct:
$\mathrm {U}_q(\mathfrak {g})$
-module structure via the opposite coproduct:
Consider
![]() $V,W\in \operatorname {\mathrm {Rep}}_q(G)$
. Similarly to the classical case, Etingof and Varchenko [Reference Etingof and Varchenko31] have introduced the
fusion matrix
$V,W\in \operatorname {\mathrm {Rep}}_q(G)$
. Similarly to the classical case, Etingof and Varchenko [Reference Etingof and Varchenko31] have introduced the
fusion matrix
![]() $J^{EV}_{V, W}(\lambda )\colon V\otimes W\rightarrow V\otimes W$
, a rational function on H, using intertwiners of quantum Verma modules. Note, however, that in our notations, they are considering maps
$J^{EV}_{V, W}(\lambda )\colon V\otimes W\rightarrow V\otimes W$
, a rational function on H, using intertwiners of quantum Verma modules. Note, however, that in our notations, they are considering maps
with the property that
![]() $\Phi ^v_{\lambda }(x_\lambda ) = x_\lambda \otimes v + \dots $
. Analogously to Theorem 5.22, we have the following statement.
$\Phi ^v_{\lambda }(x_\lambda ) = x_\lambda \otimes v + \dots $
. Analogously to Theorem 5.22, we have the following statement.
Proposition 5.37. Let
![]() $V,W\in \operatorname {\mathrm {Rep}}_q(G)$
. The maps
$V,W\in \operatorname {\mathrm {Rep}}_q(G)$
. The maps
![]() $J_{V, W}$
and
$J_{V, W}$
and
![]() $J^{EV}_{W, V}$
are related as follows:
$J^{EV}_{W, V}$
are related as follows:
In [Reference Etingof and Varchenko31, Section 5], Etingof and Varchenko have introduced an
![]() $\mathfrak {h}$
-bialgebroid
$\mathfrak {h}$
-bialgebroid
![]() $F_q(G)$
. Analogously to Theorem 5.23, we obtain the following statement.
$F_q(G)$
. Analogously to Theorem 5.23, we obtain the following statement.
Theorem 5.38. Consider the monoidal functor
It admits a colimit-preserving right adjoint; denote by
![]() $B\in \mathrm {HC}_q(H)^{\mathrm {gen}}\otimes \mathrm {HC}_q(H)^{\mathrm {gen}}$
the Harish-Chandra bialgebroid corresponding to this monoidal functor constructed in Theorem 3.35. Then we have an isomorphism of
$B\in \mathrm {HC}_q(H)^{\mathrm {gen}}\otimes \mathrm {HC}_q(H)^{\mathrm {gen}}$
the Harish-Chandra bialgebroid corresponding to this monoidal functor constructed in Theorem 3.35. Then we have an isomorphism of
![]() $\mathfrak {h}$
-algebroids
$\mathfrak {h}$
-algebroids
6 Dynamical Weyl groups
In this section, we introduce a Weyl symmetry of the parabolic restriction functors
![]() $\mathrm {res}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)$
and
$\mathrm {res}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)$
and
![]() $\mathrm {res}\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)$
introduced in section 5 and relate it to dynamical Weyl groups.
$\mathrm {res}\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)$
introduced in section 5 and relate it to dynamical Weyl groups.
6.1 Classical Zhelobenko operators
Fix a group G and its Lie algebra
![]() $\mathfrak {g}$
as in section 5.1. Recall that the Weyl group is
$\mathfrak {g}$
as in section 5.1. Recall that the Weyl group is
where
![]() $\mathrm {N}(H)$
is the normaliser of H in G. Denote by
$\mathrm {N}(H)$
is the normaliser of H in G. Denote by
![]() $\hat {W}$
the corresponding braid group generated by simple reflections
$\hat {W}$
the corresponding braid group generated by simple reflections
![]() $s_\alpha \in W$
with the relation (for
$s_\alpha \in W$
with the relation (for
![]() $\alpha \neq \beta $
)
$\alpha \neq \beta $
)
 $$\begin{align*}\underbrace{s_\alpha s_\beta s_\alpha \dots}_{m_{\alpha\beta}} = \underbrace{s_\beta s_\alpha s_\beta \dots}_{m_{\alpha\beta}},\end{align*}$$
$$\begin{align*}\underbrace{s_\alpha s_\beta s_\alpha \dots}_{m_{\alpha\beta}} = \underbrace{s_\beta s_\alpha s_\beta \dots}_{m_{\alpha\beta}},\end{align*}$$
where
![]() $m_{\alpha \beta }$
is the Coxeter matrix. There is a canonical map
$m_{\alpha \beta }$
is the Coxeter matrix. There is a canonical map
![]() $W\rightarrow \hat {W}$
, which sends a reduced expression
$W\rightarrow \hat {W}$
, which sends a reduced expression
![]() $w=s_1\cdot \dots \cdot s_n\in W$
to the corresponding element in
$w=s_1\cdot \dots \cdot s_n\in W$
to the corresponding element in
![]() $\hat {W}$
.
$\hat {W}$
.
We may lift
![]() $w\in W$
to elements
$w\in W$
to elements
![]() $T_w\in \mathrm {N}(H)$
satisfying the braid relations. Moreover, for a simple reflection
$T_w\in \mathrm {N}(H)$
satisfying the braid relations. Moreover, for a simple reflection
![]() $s_\alpha \in W$
, the element
$s_\alpha \in W$
, the element
![]() $T_{s_\alpha }^2\in H$
has order at most 2 [Reference Tits84]. For concreteness, we assume that the elements
$T_{s_\alpha }^2\in H$
has order at most 2 [Reference Tits84]. For concreteness, we assume that the elements
![]() $T_w$
act via the
$T_w$
act via the
![]() $q=1$
version of Lusztig’s operators
$q=1$
version of Lusztig’s operators
![]() $T^{\prime }_{w, 1}$
as in [Reference Lusztig62, Section 5.2.1].
$T^{\prime }_{w, 1}$
as in [Reference Lusztig62, Section 5.2.1].
Denote by
![]() $\rho \in \mathfrak {h}^*$
the half-sum of positive roots. For an element
$\rho \in \mathfrak {h}^*$
the half-sum of positive roots. For an element
![]() $w\in W$
and
$w\in W$
and
![]() $\lambda \in \mathfrak {h}^*$
, denote by
$\lambda \in \mathfrak {h}^*$
, denote by
![]() $w\cdot \lambda \in \mathfrak {h}^*$
the
dot action
:
$w\cdot \lambda \in \mathfrak {h}^*$
the
dot action
:
The induced action on
![]() $h\in \mathfrak {h}\subset \mathrm {U}\mathfrak {h}$
is denoted by
$h\in \mathfrak {h}\subset \mathrm {U}\mathfrak {h}$
is denoted by
where the usual W action on
![]() $\mathrm {U}\mathfrak {h}$
is simply denoted by
$\mathrm {U}\mathfrak {h}$
is simply denoted by
![]() $w(d)$
for
$w(d)$
for
![]() $d\in \mathrm {U}\mathfrak {h}$
.
$d\in \mathrm {U}\mathfrak {h}$
.
Recall that for a right
![]() $\mathrm {U}\mathfrak {g}$
-module X,
$\mathrm {U}\mathfrak {g}$
-module X,
![]() $X\otimes _{\mathrm {U}\mathfrak {g}} M^{\mathrm {univ}}\cong X/X\mathfrak {n}$
. In the study of Mickelsson algebras, Zhelobenko [Reference Zhelobenko93] has introduced a collection of operators acting on
$X\otimes _{\mathrm {U}\mathfrak {g}} M^{\mathrm {univ}}\cong X/X\mathfrak {n}$
. In the study of Mickelsson algebras, Zhelobenko [Reference Zhelobenko93] has introduced a collection of operators acting on
![]() $\mathrm {U}\mathfrak {g}$
-bimodules for each element of the Weyl group. Refer to [Reference Khoroshkin and Ogievetsky53, Section 6] for the proof of the following results.
$\mathrm {U}\mathfrak {g}$
-bimodules for each element of the Weyl group. Refer to [Reference Khoroshkin and Ogievetsky53, Section 6] for the proof of the following results.
Theorem 6.1. Suppose
![]() $X\in \mathrm {HC}(G)$
. Suppose
$X\in \mathrm {HC}(G)$
. Suppose
![]() $\alpha $
is a simple root, and denote by
$\alpha $
is a simple root, and denote by
![]() $\{e_\alpha , h_\alpha , f_\alpha \}$
the standard generators of the corresponding
$\{e_\alpha , h_\alpha , f_\alpha \}$
the standard generators of the corresponding
![]() $\mathfrak {sl}_2$
subalgebra
$\mathfrak {sl}_2$
subalgebra
![]() $\mathfrak {g}_\alpha \subset \mathfrak {g}$
. Consider the
Zhelobenko operator
$\mathfrak {g}_\alpha \subset \mathfrak {g}$
. Consider the
Zhelobenko operator
![]() $\breve {q}_\alpha \colon X\rightarrow X$
given by an infinite series
$\breve {q}_\alpha \colon X\rightarrow X$
given by an infinite series
 $$\begin{align*}\breve{q}_\alpha(x) = \sum_{n=0}^\infty \frac{(-1)^n}{n!} (\operatorname{\mathrm{ad}} e_\alpha)^n(T_{s_\alpha}(x)) f_\alpha^n g_{n, \alpha}^{-1},\end{align*}$$
$$\begin{align*}\breve{q}_\alpha(x) = \sum_{n=0}^\infty \frac{(-1)^n}{n!} (\operatorname{\mathrm{ad}} e_\alpha)^n(T_{s_\alpha}(x)) f_\alpha^n g_{n, \alpha}^{-1},\end{align*}$$
where
 $$\begin{align*}g_{n,\alpha} = \prod_{j=1}^n (h_\alpha-j+1)\end{align*}$$
$$\begin{align*}g_{n,\alpha} = \prod_{j=1}^n (h_\alpha-j+1)\end{align*}$$
and
![]() $\operatorname {\mathrm {ad}} e_\alpha $
refers to the diagonal
$\operatorname {\mathrm {ad}} e_\alpha $
refers to the diagonal
![]() $\mathfrak {g}$
-action on X. Then the operators
$\mathfrak {g}$
-action on X. Then the operators
![]() $\breve {q}_\alpha $
descend to well-defined linear isomorphisms
$\breve {q}_\alpha $
descend to well-defined linear isomorphisms
which satisfy the following relations:
-
1.
 $\breve {q}_\alpha ((\operatorname {\mathrm {ad}} d)(x)) = (\operatorname {\mathrm {ad}} s_\alpha (d))(\breve {q}_\alpha (x))$
for every
$\breve {q}_\alpha ((\operatorname {\mathrm {ad}} d)(x)) = (\operatorname {\mathrm {ad}} s_\alpha (d))(\breve {q}_\alpha (x))$
for every
 $d\in \mathfrak {h}$
and
$d\in \mathfrak {h}$
and
 $x\in X$
.
$x\in X$
. -
2.
 $\breve {q}_\alpha (dx) = (s_\alpha \cdot d)\breve {q}_\alpha (x)$
for every
$\breve {q}_\alpha (dx) = (s_\alpha \cdot d)\breve {q}_\alpha (x)$
for every
 $d\in \mathfrak {h}$
and
$d\in \mathfrak {h}$
and
 $x\in X$
.
$x\in X$
. -
3.
 $\underbrace {\breve {q}_\alpha \breve {q}_\beta \breve {q}_\alpha \dots }_{m_{\alpha \beta }} = \underbrace {\breve {q}_\beta \breve {q}_\alpha \breve {q}_\beta \dots }_{m_{\alpha \beta }}$
for
$\underbrace {\breve {q}_\alpha \breve {q}_\beta \breve {q}_\alpha \dots }_{m_{\alpha \beta }} = \underbrace {\breve {q}_\beta \breve {q}_\alpha \breve {q}_\beta \dots }_{m_{\alpha \beta }}$
for
 $\alpha \neq \beta $
.
$\alpha \neq \beta $
. -
4.
 $\breve {q}_\alpha ^2(x) = (h_\alpha +1)^{-1}T_{s_\alpha }^2(x) (h_{\alpha }+1)$
for every
$\breve {q}_\alpha ^2(x) = (h_\alpha +1)^{-1}T_{s_\alpha }^2(x) (h_{\alpha }+1)$
for every
 $x\in X$
.
$x\in X$
.
For an element
![]() $w\in W$
with a reduced decomposition
$w\in W$
with a reduced decomposition
![]() $w=s_{\alpha _1}\dots s_{\alpha _n}$
, we define
$w=s_{\alpha _1}\dots s_{\alpha _n}$
, we define
The third relation in Theorem 6.1 shows that
![]() $\breve {q}_w$
is independent of the chosen decomposition.
$\breve {q}_w$
is independent of the chosen decomposition.
In addition, we have the following important multiplicativity property of the Zhelobenko operators proven in [Reference Khoroshkin and Ogievetsky53, Theorem 3].
Theorem 6.2. Let
![]() $X,Y\in \mathrm {HC}(G)$
, and take
$X,Y\in \mathrm {HC}(G)$
, and take
![]() $x\in X$
and
$x\in X$
and
![]() $y\in Y$
, where
$y\in Y$
, where
![]() $\mathfrak {n} y\in Y\mathfrak {n}$
. Then we have an equality
$\mathfrak {n} y\in Y\mathfrak {n}$
. Then we have an equality
in
![]() $X\otimes _{\mathrm {U}\mathfrak {g}} Y\otimes _{\mathrm {U}\mathfrak {g}} M^{\mathrm {univ}, \mathrm {gen}}$
.
$X\otimes _{\mathrm {U}\mathfrak {g}} Y\otimes _{\mathrm {U}\mathfrak {g}} M^{\mathrm {univ}, \mathrm {gen}}$
.
6.2 Classical dynamical Weyl group
Given a group G, we may regard it as a discrete monoidal category
![]() $\mathrm {Cat}(G)$
. Let us recall the notion of a G-action on a monoidal category and the category of G-equivariant objects (see, e.g., [Reference Etingof, Gelaki, Nikshych and Ostrik34, Section 2.7]).
$\mathrm {Cat}(G)$
. Let us recall the notion of a G-action on a monoidal category and the category of G-equivariant objects (see, e.g., [Reference Etingof, Gelaki, Nikshych and Ostrik34, Section 2.7]).
Definition 6.3. Let
![]() $\mathcal {C}\in \mathrm {Pr}^{\mathrm {L}}$
be a monoidal category. A
$\mathcal {C}\in \mathrm {Pr}^{\mathrm {L}}$
be a monoidal category. A
![]() $\boldsymbol {G}$
-action on
$\boldsymbol {G}$
-action on
![]() $\mathcal {C}$
is a monoidal functor
$\mathcal {C}$
is a monoidal functor
to the monoidal category of monoidal colimit-preserving endofunctors on
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Explicitly, for every element
![]() $g\in G$
, we have a monoidal functor
$g\in G$
, we have a monoidal functor
![]() $S_g\colon \mathcal {C}\rightarrow \mathcal {C}$
together with a natural isomorphism
$S_g\colon \mathcal {C}\rightarrow \mathcal {C}$
together with a natural isomorphism
![]() $S_e\cong \mathrm {id}$
and natural isomorphisms
$S_e\cong \mathrm {id}$
and natural isomorphisms
![]() $S_{gh}\cong S_g\circ S_h$
for a pair of elements
$S_{gh}\cong S_g\circ S_h$
for a pair of elements
![]() $g,h\in G$
satisfying an associativity axiom.
$g,h\in G$
satisfying an associativity axiom.
Definition 6.4. Suppose
![]() $\mathcal {C}$
is a monoidal category with a G-action. A
$\mathcal {C}$
is a monoidal category with a G-action. A
![]() $\boldsymbol {G}$
-equivariant object
is an object
$\boldsymbol {G}$
-equivariant object
is an object
![]() $x\in \mathcal {C}$
equipped with isomorphisms
$x\in \mathcal {C}$
equipped with isomorphisms
![]() $S_g(x)\cong x$
compatible with the isomorphisms
$S_g(x)\cong x$
compatible with the isomorphisms
![]() $S_{gh}\cong S_g\circ S_h$
and
$S_{gh}\cong S_g\circ S_h$
and
![]() $S_e\cong \mathrm {id}$
. We denote by
$S_e\cong \mathrm {id}$
. We denote by
![]() $\mathcal {C}^G$
the category of G-equivariant objects.
$\mathcal {C}^G$
the category of G-equivariant objects.
The category
![]() $\mathrm {HC}(H)\cong \mathrm {LMod}_{\mathrm {U}\mathfrak {h}}(\operatorname {\mathrm {Rep}} H)$
carries a natural action of the Weyl group W defined as follows. Let us regard
$\mathrm {HC}(H)\cong \mathrm {LMod}_{\mathrm {U}\mathfrak {h}}(\operatorname {\mathrm {Rep}} H)$
carries a natural action of the Weyl group W defined as follows. Let us regard
![]() $X\in \mathrm {HC}(H)$
as a
$X\in \mathrm {HC}(H)$
as a
![]() $\mathrm {U}\mathfrak {h}$
-bimodule. Then the action of
$\mathrm {U}\mathfrak {h}$
-bimodule. Then the action of
![]() $w\in W$
twists the left and right
$w\in W$
twists the left and right
![]() $\mathrm {U}\mathfrak {h}$
-actions by the dot action:
$\mathrm {U}\mathfrak {h}$
-actions by the dot action:
![]() $S_w(X) = X$
as a plain vector space with the
$S_w(X) = X$
as a plain vector space with the
![]() $\mathrm {U}\mathfrak {h}$
-bimodule structure given by
$\mathrm {U}\mathfrak {h}$
-bimodule structure given by
for
![]() $x\in X$
and
$x\in X$
and
![]() $d\in \mathrm {U}\mathfrak {h}$
. The dot action of W on
$d\in \mathrm {U}\mathfrak {h}$
. The dot action of W on
![]() $\mathfrak {h}$
is given by affine transformations, so the corresponding diagonal
$\mathfrak {h}$
is given by affine transformations, so the corresponding diagonal
![]() $\mathfrak {h}$
-action on
$\mathfrak {h}$
-action on
![]() $S_w(X)$
is given by its linear part: that is, we twist the diagonal
$S_w(X)$
is given by its linear part: that is, we twist the diagonal
![]() $\mathfrak {h}$
-action on X by the usual W-action. By construction,
$\mathfrak {h}$
-action on X by the usual W-action. By construction,
![]() $S_e=\mathrm {id}$
and
$S_e=\mathrm {id}$
and
![]() $S_{w_1w_2} = S_{w_1}\circ S_{w_2}$
. Moreover, the identity map of vector spaces
$S_{w_1w_2} = S_{w_1}\circ S_{w_2}$
. Moreover, the identity map of vector spaces
together with the dot action
define a monoidal structure on the collection
![]() $\{S_w\}_{w\in W}$
.
$\{S_w\}_{w\in W}$
.
The functor
is naturally W-equivariant, where the maps
are given by the dot action on the
![]() $\mathrm {U}\mathfrak {h}$
factor.
$\mathrm {U}\mathfrak {h}$
factor.
Restricting the W-action on
![]() $\mathrm {HC}(H)$
under the quotient map
$\mathrm {HC}(H)$
under the quotient map
![]() $\hat {W}\rightarrow W$
from the braid group, we obtain a natural action of
$\hat {W}\rightarrow W$
from the braid group, we obtain a natural action of
![]() $\hat {W}$
on
$\hat {W}$
on
![]() $\mathrm {HC}(H)$
.
$\mathrm {HC}(H)$
.
Recall that by Theorem 5.18, the parabolic restriction functor
given by
![]() $X\mapsto (X\otimes _{\mathrm {U}\mathfrak {g}} M^{\mathrm {univ}})^N$
is monoidal. We will now show that it factors through
$X\mapsto (X\otimes _{\mathrm {U}\mathfrak {g}} M^{\mathrm {univ}})^N$
is monoidal. We will now show that it factors through
![]() $\hat {W}$
-invariants.
$\hat {W}$
-invariants.
Theorem 6.5. The Zhelobenko operators define a factorisation

of
![]() $\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
through a monoidal functor
$\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
through a monoidal functor
![]() $\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}, \hat {W}}$
.
$\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}, \hat {W}}$
.
Proof. Let us first construct a factorisation of
![]() $\mathrm {res}^{\mathrm {gen}}$
through
$\mathrm {res}^{\mathrm {gen}}$
through
![]() $\mathrm {HC}(H)^{\mathrm {gen}, \hat {W}}\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
as a plain (nonmonoidal) functor. Since the braid group
$\mathrm {HC}(H)^{\mathrm {gen}, \hat {W}}\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
as a plain (nonmonoidal) functor. Since the braid group
![]() $\hat {W}$
is generated by simple reflections
$\hat {W}$
is generated by simple reflections
![]() $\{s_\alpha \}$
, for
$\{s_\alpha \}$
, for
![]() $X\in \mathrm {HC}(G)$
, we have to specify natural isomorphisms
$X\in \mathrm {HC}(G)$
, we have to specify natural isomorphisms
satisfying the braid relations. We define them to be the Zhelobenko operators
![]() $\breve {q}_\alpha $
. The compatibility with the
$\breve {q}_\alpha $
. The compatibility with the
![]() $\mathrm {U}\mathfrak {h}$
-bimodule action follows from parts (1) and (2) of Theorem 6.1. The braid relations follow from part (3) of the same theorem.
$\mathrm {U}\mathfrak {h}$
-bimodule action follows from parts (1) and (2) of Theorem 6.1. The braid relations follow from part (3) of the same theorem.
Next, we have to construct a monoidal structure on
![]() $\mathrm {HC}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}, \hat {W}}$
compatible with the one on
$\mathrm {HC}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}, \hat {W}}$
compatible with the one on
![]() $\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
, which we recall is given by equation (33). The unit map is the natural inclusion
$\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}(G)\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
, which we recall is given by equation (33). The unit map is the natural inclusion
![]() $\mathrm {U}\mathfrak {h}\hookrightarrow (M^{\mathrm {univ}})^N$
.
$\mathrm {U}\mathfrak {h}\hookrightarrow (M^{\mathrm {univ}})^N$
.
We begin by showing compatibility with the tensor products. By Theorem 5.16, the functor of N-invariants
![]() $\mathcal {O}^{\mathrm {univ}}\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
is exact. In particular, we may exchange the order of left N-invariants and right
$\mathcal {O}^{\mathrm {univ}}\rightarrow \mathrm {HC}(H)^{\mathrm {gen}}$
is exact. In particular, we may exchange the order of left N-invariants and right
![]() $\mathfrak {n}$
-coinvariants in the definition of
$\mathfrak {n}$
-coinvariants in the definition of
![]() $\mathrm {res}(X) = (X/X\mathfrak {n})^N$
. But then the diagram
$\mathrm {res}(X) = (X/X\mathfrak {n})^N$
. But then the diagram

is commutative by Theorem 6.2.
Next, we have to show compatibility with the unit maps. Consider the diagram

To show that it is commutative, we have to compute the action of
![]() $\breve {q}_{\alpha }$
on
$\breve {q}_{\alpha }$
on
![]() $\mathrm {U}\mathfrak {h}\hookrightarrow M^{\mathrm {univ}}$
. By part (2) of Theorem 6.1,
$\mathrm {U}\mathfrak {h}\hookrightarrow M^{\mathrm {univ}}$
. By part (2) of Theorem 6.1,
![]() $\breve {q}_{\alpha }(d\cdot 1) = (s_\alpha \cdot d) \breve {q}_{\alpha }(1)$
, where
$\breve {q}_{\alpha }(d\cdot 1) = (s_\alpha \cdot d) \breve {q}_{\alpha }(1)$
, where
![]() $d\in \mathrm {U}\mathfrak {h}$
and
$d\in \mathrm {U}\mathfrak {h}$
and
![]() $1\in \mathrm {U}\mathfrak {g}$
is the unit. But it is obvious from the explicit formula for
$1\in \mathrm {U}\mathfrak {g}$
is the unit. But it is obvious from the explicit formula for
![]() $\breve {q}_{\alpha }$
that
$\breve {q}_{\alpha }$
that
![]() $\breve {q}_{\alpha }(1)=1$
.
$\breve {q}_{\alpha }(1)=1$
.
Let us now analyse the composite monoidal functor
Recall that by Theorem 5.20, we have a commutative diagram

of plain (nonmonoidal) categories.
Consider
![]() $V\in \operatorname {\mathrm {Rep}}(G)$
. Using the natural isomorphism
$V\in \operatorname {\mathrm {Rep}}(G)$
. Using the natural isomorphism
in
![]() $\mathrm {HC}(H)^{\mathrm {gen}}$
provided by the above diagram, we obtain that the
$\mathrm {HC}(H)^{\mathrm {gen}}$
provided by the above diagram, we obtain that the
![]() $\hat {W}$
-invariance of
$\hat {W}$
-invariance of
![]() $\mathrm {res}^{\mathrm {gen}}(\mathrm {U}\mathfrak {g}\otimes V)$
boils down to maps
$\mathrm {res}^{\mathrm {gen}}(\mathrm {U}\mathfrak {g}\otimes V)$
boils down to maps
![]() $(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\otimes V\rightarrow (\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\otimes S_w(V)$
obtained via the composite
$(\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\otimes V\rightarrow (\mathrm {U}\mathfrak {h})^{\mathrm {gen}}\otimes S_w(V)$
obtained via the composite
Such maps are uniquely determined by their value on
![]() $1\otimes v$
, which gives linear maps
$1\otimes v$
, which gives linear maps
depending rationally on a parameter
![]() $\lambda \in \mathfrak {h}^*$
.
$\lambda \in \mathfrak {h}^*$
.
Let
![]() $V,U\in \operatorname {\mathrm {Rep}}(G)$
, and recall the matrix
$V,U\in \operatorname {\mathrm {Rep}}(G)$
, and recall the matrix
![]() $J_{V, U}(\lambda )\colon V\otimes U\rightarrow V\otimes U$
defined in section 5.1, which controls the monoidal structure on the composite
$J_{V, U}(\lambda )\colon V\otimes U\rightarrow V\otimes U$
defined in section 5.1, which controls the monoidal structure on the composite
![]() $\operatorname {\mathrm {Rep}}(G)\rightarrow \operatorname {\mathrm {Rep}}(H)\xrightarrow {\mathrm {free}_H} \mathrm {HC}(H)^{\mathrm {gen}}$
.
$\operatorname {\mathrm {Rep}}(G)\rightarrow \operatorname {\mathrm {Rep}}(H)\xrightarrow {\mathrm {free}_H} \mathrm {HC}(H)^{\mathrm {gen}}$
.
Proposition 6.6. For any simple reflection
![]() $s_\alpha $
and
$s_\alpha $
and
![]() $V,U\in \operatorname {\mathrm {Rep}}(G)$
, we have an equality
$V,U\in \operatorname {\mathrm {Rep}}(G)$
, we have an equality
of rational functions
![]() $\mathfrak {h}^*\rightarrow \mathrm {End}(V\otimes U)$
, where
$\mathfrak {h}^*\rightarrow \mathrm {End}(V\otimes U)$
, where
![]() $A^{(1)}$
denotes
$A^{(1)}$
denotes
![]() $A\otimes 1$
and
$A\otimes 1$
and
![]() $A^{(2)}$
denotes
$A^{(2)}$
denotes
![]() $1\otimes A$
.
$1\otimes A$
.
Proof. Consider the diagram

where the middle square is given by equation (38).
The left vertical arrow is
![]() $A_{s_\alpha , V}^{(1)}(\lambda )A_{s_\alpha , U}^{(2)}(\lambda -h^{(1)}) $
, and the right vertical arrow is
$A_{s_\alpha , V}^{(1)}(\lambda )A_{s_\alpha , U}^{(2)}(\lambda -h^{(1)}) $
, and the right vertical arrow is
![]() $A_{s_\alpha , V\otimes U}(\lambda )$
. Using the isomorphism given by equation (37), the bottom horizontal arrow is
$A_{s_\alpha , V\otimes U}(\lambda )$
. Using the isomorphism given by equation (37), the bottom horizontal arrow is
![]() $J_{V,U}(s_{\alpha }\cdot \lambda )$
.
$J_{V,U}(s_{\alpha }\cdot \lambda )$
.
Let us now compute a particular example of the operators
![]() $A_{w, V}(\lambda )$
. Consider
$A_{w, V}(\lambda )$
. Consider
![]() $G=\mathrm {SL}_2$
, V the two-dimensional irreducible representation,
$G=\mathrm {SL}_2$
, V the two-dimensional irreducible representation,
![]() $H\subset G$
the subgroup of diagonal matrices and w the unique simple reflection. We can lift it to the matrix
$H\subset G$
the subgroup of diagonal matrices and w the unique simple reflection. We can lift it to the matrix
![]() $T\in \mathrm {N}(H)$
given by
$T\in \mathrm {N}(H)$
given by
 $$\begin{align*}T = \left(\begin{array}{cc} 0 & -1 \\ 1 & 0\end{array}\right). \end{align*}$$
$$\begin{align*}T = \left(\begin{array}{cc} 0 & -1 \\ 1 & 0\end{array}\right). \end{align*}$$
Let
![]() $\{e, h, f\}$
be the standard basis of
$\{e, h, f\}$
be the standard basis of
![]() $\mathfrak {sl}_2$
. Let
$\mathfrak {sl}_2$
. Let
![]() $\{v_+, v_-\}$
be the basis of V such that
$\{v_+, v_-\}$
be the basis of V such that
Proposition 6.7. The action of
![]() $A_{w, V}(\lambda )$
is given as follows:
$A_{w, V}(\lambda )$
is given as follows:
 $$ \begin{align*} A_{w, V}(\lambda) v_+ &= v_- \\ A_{w, V}(\lambda) v_- &= -\frac{\lambda+2}{\lambda+1} v_+. \end{align*} $$
$$ \begin{align*} A_{w, V}(\lambda) v_+ &= v_- \\ A_{w, V}(\lambda) v_- &= -\frac{\lambda+2}{\lambda+1} v_+. \end{align*} $$
Proof. The isomorphism
![]() $(\mathrm {U}\mathfrak {h})^{\mathrm {gen}} \otimes V \rightarrow (V \otimes M^{\mathrm {univ},\mathrm {gen}})^N$
is given by
$(\mathrm {U}\mathfrak {h})^{\mathrm {gen}} \otimes V \rightarrow (V \otimes M^{\mathrm {univ},\mathrm {gen}})^N$
is given by
 $$ \begin{align*} 1 \otimes v_+ & \mapsto v_+ \otimes x^{\mathrm{univ}}, \\ 1 \otimes v_- & \mapsto v_- \otimes x^{\mathrm{univ}} - v_+ \otimes fh^{-1} x^{\mathrm{univ}}, \end{align*} $$
$$ \begin{align*} 1 \otimes v_+ & \mapsto v_+ \otimes x^{\mathrm{univ}}, \\ 1 \otimes v_- & \mapsto v_- \otimes x^{\mathrm{univ}} - v_+ \otimes fh^{-1} x^{\mathrm{univ}}, \end{align*} $$
where
![]() $x^{\mathrm {univ}}\in M^{\mathrm {univ},\mathrm {gen}}$
is the generator. We have
$x^{\mathrm {univ}}\in M^{\mathrm {univ},\mathrm {gen}}$
is the generator. We have
 $$\begin{align*}\breve{q}_w(v_+ \otimes 1) = \sum\limits_n \frac{(-1)^n}{n!} \operatorname{\mathrm{ad}}_e^n(v_- \otimes 1) f^n g_n^{-1} = v_- \otimes 1 - v_+ \otimes fh^{-1}, \end{align*}$$
$$\begin{align*}\breve{q}_w(v_+ \otimes 1) = \sum\limits_n \frac{(-1)^n}{n!} \operatorname{\mathrm{ad}}_e^n(v_- \otimes 1) f^n g_n^{-1} = v_- \otimes 1 - v_+ \otimes fh^{-1}, \end{align*}$$
hence
![]() $A_{w,V}(\lambda )(v_+) = v_-$
. To compute
$A_{w,V}(\lambda )(v_+) = v_-$
. To compute
![]() $A_{w,V}(\lambda )(v_-)$
, we use the property in (4) from Theorem 6.1, namely,
$A_{w,V}(\lambda )(v_-)$
, we use the property in (4) from Theorem 6.1, namely,
Under identification
![]() $S_w(\mathrm {res}^{\mathrm {gen}} (V \otimes \mathrm {U}\mathfrak {g})) \cong (\mathrm {U}\mathfrak {h})^{\mathrm {gen}} \otimes S_w(V)$
, we have
$S_w(\mathrm {res}^{\mathrm {gen}} (V \otimes \mathrm {U}\mathfrak {g})) \cong (\mathrm {U}\mathfrak {h})^{\mathrm {gen}} \otimes S_w(V)$
, we have
and the claim follows.
We return to the case of arbitrary G. Recall that Tarasov and Varchenko [Reference Tarasov and Varchenko83] have introduced the dynamical Weyl group: that is, a collection of operators
![]() $A^{TV}_{w, V}(\lambda )\colon V\rightarrow V$
for every finite-dimensional
$A^{TV}_{w, V}(\lambda )\colon V\rightarrow V$
for every finite-dimensional
![]() $\mathfrak {g}$
-representation V and
$\mathfrak {g}$
-representation V and
![]() $w\in W$
depending rationally on the parameter
$w\in W$
depending rationally on the parameter
![]() $\lambda \in \mathfrak {h}^*$
. We will now prove that the operators
$\lambda \in \mathfrak {h}^*$
. We will now prove that the operators
![]() $A_{w, V}$
constructed from the Zhelobenko operators coincide with the dynamical Weyl group.
$A_{w, V}$
constructed from the Zhelobenko operators coincide with the dynamical Weyl group.
Theorem 6.8. For any
![]() $V\in \operatorname {\mathrm {Rep}}(G)$
and
$V\in \operatorname {\mathrm {Rep}}(G)$
and
![]() $w\in W$
, we have an equality of rational functions
$w\in W$
, we have an equality of rational functions
Proof. Both
![]() $A^{TV}_{w, V}(\lambda )$
and
$A^{TV}_{w, V}(\lambda )$
and
![]() $A_{w, V}(\lambda )$
are given by products in terms of simple reflections, so it is enough to establish the fact for a simple reflection
$A_{w, V}(\lambda )$
are given by products in terms of simple reflections, so it is enough to establish the fact for a simple reflection
![]() $w=s_\alpha $
along a simple root
$w=s_\alpha $
along a simple root
![]() $\alpha $
.
$\alpha $
.
In turn, both
![]() $A^{TV}_{s_\alpha , V}(\lambda )$
and
$A^{TV}_{s_\alpha , V}(\lambda )$
and
![]() $A_{s_\alpha , V}(\lambda )$
are defined by considering the corresponding
$A_{s_\alpha , V}(\lambda )$
are defined by considering the corresponding
![]() $\mathfrak {sl}_2$
-subalgebra
$\mathfrak {sl}_2$
-subalgebra
![]() $\mathfrak {g}_\alpha \subset \mathfrak {g}$
generated by
$\mathfrak {g}_\alpha \subset \mathfrak {g}$
generated by
![]() $\{e_\alpha , h_\alpha , f_\alpha \}$
. So, it is enough to prove the claim for
$\{e_\alpha , h_\alpha , f_\alpha \}$
. So, it is enough to prove the claim for
![]() $G=\mathrm {SL}_2$
.
$G=\mathrm {SL}_2$
.
For a tensor product of representations,
![]() $A_{w, V}(\lambda )$
satisfies a multiplicativity property given by Theorem 6.6, and so does
$A_{w, V}(\lambda )$
satisfies a multiplicativity property given by Theorem 6.6, and so does
![]() $A^{TV}_{w, V}(\lambda )$
(see [Reference Tarasov and Varchenko83, Lemma 7], where the relationship between
$A^{TV}_{w, V}(\lambda )$
(see [Reference Tarasov and Varchenko83, Lemma 7], where the relationship between
![]() $J_{V, U}(\lambda )$
and
$J_{V, U}(\lambda )$
and
![]() $J^{EV}_{V, U}(\lambda )$
is given by Theorem 5.22). Therefore, it is enough to check the equality on the 2-dimensional irreducible representation of
$J^{EV}_{V, U}(\lambda )$
is given by Theorem 5.22). Therefore, it is enough to check the equality on the 2-dimensional irreducible representation of
![]() $\mathfrak {sl}_2$
, which follows by comparing the expressions given in Theorem 6.7 with the explicit expressions given in [Reference Tarasov and Varchenko83, Section 2.5] (see also [Reference Etingof and Varchenko32, Lemma 5] for an explicit description of the dynamical Weyl group in the 2-dimensional representation of quantum
$\mathfrak {sl}_2$
, which follows by comparing the expressions given in Theorem 6.7 with the explicit expressions given in [Reference Tarasov and Varchenko83, Section 2.5] (see also [Reference Etingof and Varchenko32, Lemma 5] for an explicit description of the dynamical Weyl group in the 2-dimensional representation of quantum
![]() $\mathfrak {sl}_2$
).
$\mathfrak {sl}_2$
).
6.3 Quantum Zhelobenko operators
We continue to use notations for quantum groups from section 5.2. It was shown by Lusztig [Reference Lusztig62], Soibelman [Reference Soibelman80] and Kirillov–Reshetikhin [Reference Kirillov and Reshetikhin57] that one can introduce an action of the braid group
![]() $\hat {W}$
on modules in
$\hat {W}$
on modules in
![]() $\operatorname {\mathrm {Rep}}_q(G)$
. For
$\operatorname {\mathrm {Rep}}_q(G)$
. For
![]() $V\in \operatorname {\mathrm {Rep}}_q(G)$
and
$V\in \operatorname {\mathrm {Rep}}_q(G)$
and
![]() $w\in W$
, we denote by
$w\in W$
, we denote by
![]() $T_w\colon V\rightarrow V$
the corresponding operator of the quantum Weyl group (for definitiveness, we consider
$T_w\colon V\rightarrow V$
the corresponding operator of the quantum Weyl group (for definitiveness, we consider
![]() $T^{\prime }_{w, +1}$
in the notation of [Reference Lusztig62, Chapter 5]).
$T^{\prime }_{w, +1}$
in the notation of [Reference Lusztig62, Chapter 5]).
Example 6.9. Consider
![]() $\mathrm {U}_q(\mathfrak {sl}_2)$
with generators
$\mathrm {U}_q(\mathfrak {sl}_2)$
with generators
![]() $E,K,F$
, as in Theorem 3.21,
$E,K,F$
, as in Theorem 3.21,
![]() $V\in \operatorname {\mathrm {Rep}}_q(\mathrm {SL}_2)$
and
$V\in \operatorname {\mathrm {Rep}}_q(\mathrm {SL}_2)$
and
![]() $v\in V$
a vector of weight n. Then
$v\in V$
a vector of weight n. Then
 $$\begin{align*}T_w(v) = \sum_{a,b,c;a-b+c=n} (-1)^b q^{-ac+b} \frac{F^a E^b F^c}{[a]![b]![c]!} v\end{align*}$$
$$\begin{align*}T_w(v) = \sum_{a,b,c;a-b+c=n} (-1)^b q^{-ac+b} \frac{F^a E^b F^c}{[a]![b]![c]!} v\end{align*}$$
for the unique nontrivial element
![]() $w\in W$
.
$w\in W$
.
The Weyl group W acts in the standard way on the weight lattice
![]() $\Lambda $
. We introduce the dot action of W on
$\Lambda $
. We introduce the dot action of W on
![]() $\mathrm {U}_q(\mathfrak {h})=k[\Lambda ]$
by
$\mathrm {U}_q(\mathfrak {h})=k[\Lambda ]$
by
for every
![]() $\mu \in \Lambda $
.
$\mu \in \Lambda $
.
Recall that for a root
![]() $\alpha $
, we denote
$\alpha $
, we denote
![]() $q_\alpha = q^{(\alpha , \alpha )/2}$
. The quantum integer is
$q_\alpha = q^{(\alpha , \alpha )/2}$
. The quantum integer is
 $$\begin{align*}[n]_\alpha = \frac{q_\alpha^n - q_\alpha^{-n}}{q_\alpha-q_\alpha^{-1}}\end{align*}$$
$$\begin{align*}[n]_\alpha = \frac{q_\alpha^n - q_\alpha^{-n}}{q_\alpha-q_\alpha^{-1}}\end{align*}$$
and the quantum factorial is defined similarly. The quantum Zhelobenko operators were introduced in [Reference Khoroshkin and Ogievetsky53, Section 9]. For the following statement, recall Theorem 5.26, which explains that the infinite sums in the quantum Zhelobenko operators are well-defined.
Theorem 6.10. Suppose
![]() $X\in \mathrm {HC}_q(G)$
. For a simple root
$X\in \mathrm {HC}_q(G)$
. For a simple root
![]() $\alpha $
, we denote by
$\alpha $
, we denote by
![]() $\{E_\alpha , K_\alpha , F_\alpha \}$
the corresponding subset of generators of
$\{E_\alpha , K_\alpha , F_\alpha \}$
the corresponding subset of generators of
![]() $\mathrm {U}_q(\mathfrak {g})$
. Consider the
quantum Zhelobenko operator
on X given by
$\mathrm {U}_q(\mathfrak {g})$
. Consider the
quantum Zhelobenko operator
on X given by
 $$\begin{align*}\breve{q}_\alpha(x) = \sum_{n=0}^\infty \frac{(-1)^n}{[n]_\alpha!} (\operatorname{\mathrm{ad}} (K_\alpha^{-1}E_\alpha))^n((\operatorname{\mathrm{ad}} T_{s_\alpha})(x)) F_\alpha^n g_{n,\alpha}^{-1},\end{align*}$$
$$\begin{align*}\breve{q}_\alpha(x) = \sum_{n=0}^\infty \frac{(-1)^n}{[n]_\alpha!} (\operatorname{\mathrm{ad}} (K_\alpha^{-1}E_\alpha))^n((\operatorname{\mathrm{ad}} T_{s_\alpha})(x)) F_\alpha^n g_{n,\alpha}^{-1},\end{align*}$$
where
 $$\begin{align*}g_{n,\alpha} = \prod_{j=1}^n [h_\alpha-j+1]_\alpha\end{align*}$$
$$\begin{align*}g_{n,\alpha} = \prod_{j=1}^n [h_\alpha-j+1]_\alpha\end{align*}$$
and
![]() $\operatorname {\mathrm {ad}} (K_{\alpha }^{-1} E_\alpha )$
refers to the diagonal
$\operatorname {\mathrm {ad}} (K_{\alpha }^{-1} E_\alpha )$
refers to the diagonal
![]() $\mathrm {U}_q(\mathfrak {g})$
-action. Then the operators
$\mathrm {U}_q(\mathfrak {g})$
-action. Then the operators
![]() $\breve {q}_\alpha $
descend to linear isomorphisms
$\breve {q}_\alpha $
descend to linear isomorphisms
which satisfy the following relations:
-
1.
 $\breve {q}_\alpha ((\operatorname {\mathrm {ad}} d)(x)) = (\operatorname {\mathrm {ad}} s_\alpha (d))(\breve {q}_\alpha (x))$
for every
$\breve {q}_\alpha ((\operatorname {\mathrm {ad}} d)(x)) = (\operatorname {\mathrm {ad}} s_\alpha (d))(\breve {q}_\alpha (x))$
for every
 $d\in \mathrm {U}_q(\mathfrak {h})$
and
$d\in \mathrm {U}_q(\mathfrak {h})$
and
 $x\in X$
.
$x\in X$
. -
2.
 $\breve {q}_\alpha (dx) = (s_\alpha \cdot d)\breve {q}_\alpha (x)$
for every
$\breve {q}_\alpha (dx) = (s_\alpha \cdot d)\breve {q}_\alpha (x)$
for every
 $d\in \mathrm {U}_q(\mathfrak {h})$
and
$d\in \mathrm {U}_q(\mathfrak {h})$
and
 $x\in X$
.
$x\in X$
. -
3.
 $\underbrace {\breve {q}_\alpha \breve {q}_\beta \breve {q}_\alpha \dots }_{m_{\alpha \beta }} = \underbrace {\breve {q}_\beta \breve {q}_\alpha \breve {q}_\beta \dots }_{m_{\alpha \beta }}$
for
$\underbrace {\breve {q}_\alpha \breve {q}_\beta \breve {q}_\alpha \dots }_{m_{\alpha \beta }} = \underbrace {\breve {q}_\beta \breve {q}_\alpha \breve {q}_\beta \dots }_{m_{\alpha \beta }}$
for
 $\alpha \neq \beta $
.
$\alpha \neq \beta $
.
The third property allows us to define
![]() $\breve {q}_w$
for any element
$\breve {q}_w$
for any element
![]() $w\in \hat {W}$
. We also have a multiplicativity property.
$w\in \hat {W}$
. We also have a multiplicativity property.
Theorem 6.11. Let
![]() $X,Y\in \mathrm {HC}_q(G)$
, and take
$X,Y\in \mathrm {HC}_q(G)$
, and take
![]() $x\in X$
and
$x\in X$
and
![]() $y\in Y$
, where
$y\in Y$
, where
![]() $\mathrm {U}_q^{>0}(\mathfrak {n})y\in Y\mathrm {U}_q^{>0}(\mathfrak {n})$
. Then we have an equality
$\mathrm {U}_q^{>0}(\mathfrak {n})y\in Y\mathrm {U}_q^{>0}(\mathfrak {n})$
. Then we have an equality
in
![]() $X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} Y\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} M_q^{\mathrm {univ}, \mathrm {gen}}$
.
$X\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} Y\otimes _{\mathrm {U}_q(\mathfrak {g})^{\mathrm {lf}}} M_q^{\mathrm {univ}, \mathrm {gen}}$
.
6.4 Quantum dynamical Weyl group
As in section 6.2, quantum Zhelobenko operators define the Weyl symmetry of the parabolic restriction functor
![]() $\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}}$
.
$\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}}$
.
The W-action on
![]() $\mathrm {HC}_q(H)$
is defined similarly to the W-action on
$\mathrm {HC}_q(H)$
is defined similarly to the W-action on
![]() $\mathrm {HC}(H)$
. An element
$\mathrm {HC}(H)$
. An element
![]() $w\in W$
gives rise to a functor
$w\in W$
gives rise to a functor
![]() $S_w\colon \mathrm {HC}_q(H)\rightarrow \mathrm {HC}_q(H)$
given as follows. For
$S_w\colon \mathrm {HC}_q(H)\rightarrow \mathrm {HC}_q(H)$
given as follows. For
![]() $X\in \mathrm {HC}_q(H)$
, we set
$X\in \mathrm {HC}_q(H)$
, we set
![]() $S_w(X) = X$
as a vector space with the
$S_w(X) = X$
as a vector space with the
![]() $\mathrm {U}_q(\mathfrak {h})$
-bimodule structure given by
$\mathrm {U}_q(\mathfrak {h})$
-bimodule structure given by
where
![]() $d\in \mathrm {U}_q(\mathfrak {h})$
and
$d\in \mathrm {U}_q(\mathfrak {h})$
and
![]() $x\in X$
. The functors
$x\in X$
. The functors
![]() $\{S_w\}$
have obvious monoidal structures.
$\{S_w\}$
have obvious monoidal structures.
Consider the action of the quantum Zhelobenko operators
Theorem 6.12. The quantum Zhelobenko operators define a factorisation

of
![]() $\mathrm {res}^{\mathrm {gen}}_q\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}}$
through a monoidal functor
$\mathrm {res}^{\mathrm {gen}}_q\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}}$
through a monoidal functor
![]() $\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}, \hat {W}}$
.
$\mathrm {res}^{\mathrm {gen}}\colon \mathrm {HC}_q(G)\rightarrow \mathrm {HC}_q(H)^{\mathrm {gen}, \hat {W}}$
.
By Theorem 5.35, we have a commutative diagram

which gives rise to a monoidal structure on the composite
As in section 6.2, we obtain linear maps
![]() $A_{w, V}(\lambda )\colon V\rightarrow V$
for every
$A_{w, V}(\lambda )\colon V\rightarrow V$
for every
![]() $V\in \operatorname {\mathrm {Rep}}_q(G)$
, which are rational functions on H. For
$V\in \operatorname {\mathrm {Rep}}_q(G)$
, which are rational functions on H. For
![]() $V,U\in \operatorname {\mathrm {Rep}}_q(G)$
, recall the matrix
$V,U\in \operatorname {\mathrm {Rep}}_q(G)$
, recall the matrix
![]() $J_{V, U}(\lambda )\colon V\otimes U\rightarrow V\otimes U$
defined in section 5.2.
$J_{V, U}(\lambda )\colon V\otimes U\rightarrow V\otimes U$
defined in section 5.2.
Proposition 6.13. For any simple reflection
![]() $s_\alpha $
and
$s_\alpha $
and
![]() $V,U\in \operatorname {\mathrm {Rep}}_q(G)$
, we have an equality
$V,U\in \operatorname {\mathrm {Rep}}_q(G)$
, we have an equality
of rational functions
![]() $H\rightarrow \mathrm {End}(V\otimes U)$
.
$H\rightarrow \mathrm {End}(V\otimes U)$
.
Let us now compute the operators
![]() $A_{w, V}$
for
$A_{w, V}$
for
![]() $G=\mathrm {SL}_2$
. Consider the irreducible two-dimensional representation
$G=\mathrm {SL}_2$
. Consider the irreducible two-dimensional representation
![]() $V\in \operatorname {\mathrm {Rep}}_q(G)$
with the basis
$V\in \operatorname {\mathrm {Rep}}_q(G)$
with the basis
![]() $\{v_+, v_-\}$
such that
$\{v_+, v_-\}$
such that
Proposition 6.14. The action of
![]() $A_{w, V}(\lambda )$
is given as follows:
$A_{w, V}(\lambda )$
is given as follows:
 $$ \begin{align*} A_{w, V}(\lambda) v_+ &= v_- \\ A_{w, V}(\lambda) v_- &= -\frac{[\lambda+2]}{[\lambda+1]} v_+. \end{align*} $$
$$ \begin{align*} A_{w, V}(\lambda) v_+ &= v_- \\ A_{w, V}(\lambda) v_- &= -\frac{[\lambda+2]}{[\lambda+1]} v_+. \end{align*} $$
Proof. The isomorphism
![]() $\mathrm {U}_q(\mathfrak {h})^{\mathrm {gen}} \otimes V \rightarrow (V \otimes M^{\mathrm {univ},\mathrm {gen}})^N$
is given by
$\mathrm {U}_q(\mathfrak {h})^{\mathrm {gen}} \otimes V \rightarrow (V \otimes M^{\mathrm {univ},\mathrm {gen}})^N$
is given by
 $$ \begin{align*} 1 \otimes v_+ & \mapsto v_+ \otimes x^{\mathrm{univ}}, \\ 1 \otimes v_- & \mapsto v_- \otimes 1 - q^{-1} v_+ \otimes F\cdot [h]^{-1} \cdot x^{\mathrm{univ}}. \end{align*} $$
$$ \begin{align*} 1 \otimes v_+ & \mapsto v_+ \otimes x^{\mathrm{univ}}, \\ 1 \otimes v_- & \mapsto v_- \otimes 1 - q^{-1} v_+ \otimes F\cdot [h]^{-1} \cdot x^{\mathrm{univ}}. \end{align*} $$
By [Reference Lusztig62, Proposition 5.2.2], we have
Therefore,
 $$\begin{align*}\breve{q}_w(v_+\otimes 1) = \sum_{n=0}^\infty \frac{(-1)^n}{[n]!} (\operatorname{\mathrm{ad}} (K^{-1}E))^n(v_-\otimes 1) F^n g_{n}^{-1} = v_-\otimes 1 - q^{-1} v_+\otimes F[h]^{-1},\end{align*}$$
$$\begin{align*}\breve{q}_w(v_+\otimes 1) = \sum_{n=0}^\infty \frac{(-1)^n}{[n]!} (\operatorname{\mathrm{ad}} (K^{-1}E))^n(v_-\otimes 1) F^n g_{n}^{-1} = v_-\otimes 1 - q^{-1} v_+\otimes F[h]^{-1},\end{align*}$$
which implies that
Using the formula for the square of the quantum Zhelobenko operator [Reference Khoroshkin and Ogievetsky53, Corollary 9.6], we obtain
which implies that
Remark 6.15. The formulas (9.10) and (9.11) in [Reference Khoroshkin and Ogievetsky53] are missing a sign; see [Reference Lusztig62, Proposition 5.2.2].
Etingof and Varchenko [Reference Etingof and Varchenko32] have introduced a quantum analogue of the dynamical Weyl group: that is, a collection of rational functions
![]() $A^{EV}_{w, V}(\lambda )\colon V\rightarrow V$
for every
$A^{EV}_{w, V}(\lambda )\colon V\rightarrow V$
for every
![]() $V\in \operatorname {\mathrm {Rep}}_q(G)$
and
$V\in \operatorname {\mathrm {Rep}}_q(G)$
and
![]() $w\in W$
. We are now ready to relate
$w\in W$
. We are now ready to relate
![]() $A_{w, V}$
and
$A_{w, V}$
and
![]() $A^{EV}_{w, V}$
.
$A^{EV}_{w, V}$
.
Theorem 6.16. For any
![]() $V\in \operatorname {\mathrm {Rep}}_q(G)$
an
$V\in \operatorname {\mathrm {Rep}}_q(G)$
an
![]() $w\in W$
, we have an equality of rational functions
$w\in W$
, we have an equality of rational functions
Proof. The proof is analogous to the proof of Theorem 6.8. Both
![]() $A^{EV}_{w, V}$
and
$A^{EV}_{w, V}$
and
![]() $A_{w, V}$
are given by a product over simple reflections, so it is enough to establish this equality for a simple reflection
$A_{w, V}$
are given by a product over simple reflections, so it is enough to establish this equality for a simple reflection
![]() $w=s_\alpha $
.
$w=s_\alpha $
.
We have
![]() $s_\alpha (\rho ) = \rho - \alpha $
, so
$s_\alpha (\rho ) = \rho - \alpha $
, so
In particular, both sides of the equality given by equation (39) are defined in terms of the corresponding
![]() $\mathrm {U}_q(\mathfrak {sl}_2)$
-subalgebra, so it is enough to restrict our attention to
$\mathrm {U}_q(\mathfrak {sl}_2)$
-subalgebra, so it is enough to restrict our attention to
![]() $G=\mathrm {SL}_2$
. Using the multiplicativity property of
$G=\mathrm {SL}_2$
. Using the multiplicativity property of
![]() $A^{EV}_{w, V}$
and
$A^{EV}_{w, V}$
and
![]() $A_{w, V}$
given by [Reference Etingof and Varchenko32, Lemma 4] and Theorem 6.13, we reduce to the case of the defining representation. The equality on the defining representation of
$A_{w, V}$
given by [Reference Etingof and Varchenko32, Lemma 4] and Theorem 6.13, we reduce to the case of the defining representation. The equality on the defining representation of
![]() $\mathrm {SL}_2$
follows from comparing the formulas in [Reference Etingof and Varchenko32, Lemma 5] and Theorem 6.14.
$\mathrm {SL}_2$
follows from comparing the formulas in [Reference Etingof and Varchenko32, Lemma 5] and Theorem 6.14.
Acknowledgements
We would like to thank Adrien Brochier, Damien Calaque, Sam Gunningham and David Jordan for useful discussions.
Conflicts of Interest
None.
Financial support
The authors were supported by the NCCR SwissMAP grant of the Swiss National Science Foundation.