1 Introduction
Many relationships that political scientists are interested in are conditional. Political scientists frequently specify models to test whether the effect of a variable of interest, the treatment, is conditional upon a moderating variable. Starting with Brambor, Clark, and Golder (Reference Brambor, Clark and Golder2006), a number of publications have focused on improving practice and inference in the use of interaction models (e.g., Beiser-McGrath and Beiser-McGrath Reference Beiser-McGrath and Beiser-McGrath2020; Berry, DeMeritt, and Esarey Reference Berry, DeMeritt and Esarey2010, Reference Berry, DeMeritt and Esarey2016; Blackwell and Olson Reference Blackwell and Olson2021; Esarey and Sumner Reference Esarey and Sumner2018; Hainmueller, Mummolo, and Xu Reference Hainmueller, Mummolo and Xu2019).
Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) identify a key issue stemming from the uncritical application of the assumption that the marginal effect of the treatment linearly changes with changing values of the moderating variable (they refer to this as the linear interaction effect [LIE] assumption). When this assumption does not hold, inferences based on a linear interaction model will be biased. Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) introduce a binning estimator and a kernel estimator that relax the LIE assumption and allow researchers to uncover nonlinear interactive relationships. The authors suggest two ways of diagnosing when the LIE assumption does not hold and scholars should use one of those estimators instead of a linear interaction model: (a) a Wald test based on the comparison of the binning estimator and a linear interaction specification and (b) graphical methods investigating the raw data.
However, the methods Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) propose for diagnosing violations of the LIE assumption do not prevent other forms of bias to enter. In particular, the binning estimator for modeling nonlinear interactions can pick up unmodeled nonlinearities in control variables which are correlated with the moderator. When relevant nonlinear terms of control variables are omitted from the model, truly linear interactions can be misidentified as nonlinear. Moreover, graphical diagnostic tools are of limited use for uncovering the true relationship in these cases.
In this letter, we demonstrate this problem using simulations. The simulations show that the Wald test based on the binning estimator misdiagnoses violations of the LIE assumption when relevant quadratic terms of control variables are omitted. Moreover, we demonstrate the inability of graphical diagnostics to detect this problem.
The results suggest that while moving beyond linearity as a default in the estimation of interaction effects can expand our knowledge of political processes, it needs to be coupled with a broader consideration of nonlinearities, both independent and interactive, in model specification (Beiser-McGrath and Beiser-McGrath Reference Beiser-McGrath and Beiser-McGrath2020). Allowing for a nonlinear interaction effect, without accounting for other potential nonlinearities, leaves this interaction effect open to absorbing these unmodeled effects, thus causing bias.
We propose two approaches to assess the robustness of a specified nonlinear interaction effect to misspecification bias. First, we suggest using methods for variable selection to identify nonlinearities and interactions among the variables used for covariate adjustment (Z) that have the potential to cause bias in the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) binning estimator, and thus should be included. Second, we propose more general machine learning methods that allow for a full set of nonlinearities, interactions, and nonlinear interactions while avoiding overfitting, in order to minimize this problem (Beiser-McGrath and Beiser-McGrath Reference Beiser-McGrath and Beiser-McGrath2020; Blackwell and Olson Reference Blackwell and Olson2021; Hainmueller and Hazlett Reference Hainmueller and Hazlett2014; Kenkel and Signorino Reference Kenkel and Signorino2013).
2 The Problem
In this section, we show how the approach to modeling nonlinear interaction effects proposed by Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) can suffer from misspecification bias. For diagnosis and as one option for analysis, Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) introduce a binning estimatorFootnote 1 where
![]() $G_J$
are dummies associated with different bins across the range of X
$G_J$
are dummies associated with different bins across the range of X
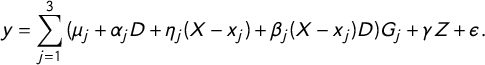 $$ \begin{align} y = \sum_{j=1}^{3}{(\mu_j + \alpha_j D + \eta_j (X - x_j ) + \beta_j (X - x_j )D)G_j + \gamma Z+ \epsilon}. \end{align} $$
$$ \begin{align} y = \sum_{j=1}^{3}{(\mu_j + \alpha_j D + \eta_j (X - x_j ) + \beta_j (X - x_j )D)G_j + \gamma Z+ \epsilon}. \end{align} $$
This specification allows for the relationship between y and a treatment D to vary nonlinearly with the values of a moderator X. Moreover, the interflex R package that implements this estimator allows researchers to specify whether to use a functional form referred to as fully moderated that interacts all control variables with the moderator X (but not the treatment D). Importantly, however, the binning estimator, fully moderated or not, does not account for nonlinearities in variables used for covariate adjustment (Z). This is problematic as unmodeled nonlinear functions of Z can be picked up by the more flexible functional form allowed for X when moderating D, thus potentially incorrectly implying that X moderates D nonlinearly.
2.1 Simulation Evidence
We show the potential for this to occur with a Monte Carlo simulation. In our data generating process, the true effect of D is conditional on X with a linear functional form (i.e., a linear and not a nonlinear interaction effect), that is,
We draw X and Z jointly from a multivariate normal distribution with mean zero, variance one, and covariance
![]() $\rho = 0.5$
and D and
$\rho = 0.5$
and D and
![]() $\epsilon $
from a standard normal distribution.
$\epsilon $
from a standard normal distribution.
To assess whether a nonlinear interaction effect is supported by the estimator, we examine the p-value from the Wald test proposed by Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) that is based on the binning estimator. Under the null hypothesis, there is no nonlinear interaction effect, and thus the p-values of the Wald test from our simulations should be distributed uniformly given the null is true. In the simulations, the binning estimator splits X into three bins at the terciles using the default settings of the interflex R package, as this is how we expect applied researchers typically engage with modeling nonlinear interaction effects.Footnote 2
We estimate four models 1,000 times each using the binning estimator. The first set of models includes D, X, and Z as proposed by Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019). The second also adjusts for the inclusion of
![]() $D^2$
,
$D^2$
,
![]() $X^2$
, and
$X^2$
, and
![]() $Z^2$
. By doing so, we can assess how model misspecification, in terms of failure to account for other possible nonlinearities, affects inferences about the presence of nonlinear interaction effects. Within each set of models, we use the fully moderated version of the binning estimator that interacts X with all control variables (Z) (Blackwell and Olson Reference Blackwell and Olson2021) and a version that is not fully moderated, that is, does not include any interactions between X and control variables.
$Z^2$
. By doing so, we can assess how model misspecification, in terms of failure to account for other possible nonlinearities, affects inferences about the presence of nonlinear interaction effects. Within each set of models, we use the fully moderated version of the binning estimator that interacts X with all control variables (Z) (Blackwell and Olson Reference Blackwell and Olson2021) and a version that is not fully moderated, that is, does not include any interactions between X and control variables.
Figure 1 displays the results of our simulations.Footnote 3 The models in each panel use the binning estimator, with one curve showing results from the fully moderated version that interacts X with all control variables and one curve showing the not fully moderated version. In addition, the models in panel (b) include squared terms of all variables in the model: D, X, and Z. Thus, the models in panel (b) include the term
![]() $Z^2$
from the data generating process, whereas the models in panel (a) do not.
$Z^2$
from the data generating process, whereas the models in panel (a) do not.
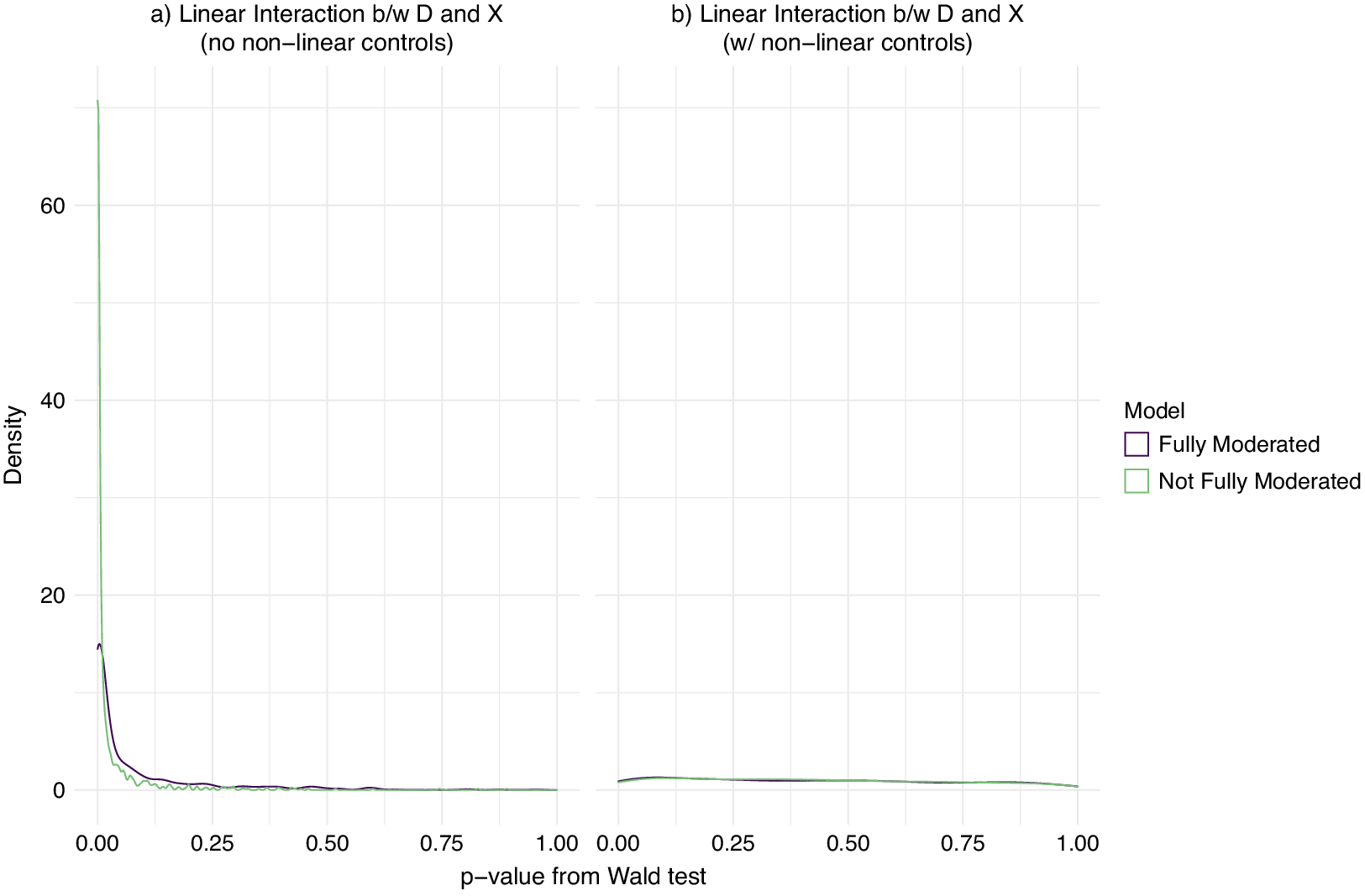
Figure 1 Distribution of p-values from the Wald test of whether the linear interaction model can be rejected in favor of the more flexible binning estimator model that relaxes the linear interaction effect assumption.
The models in panel (b) that include additional squared terms correctly identify that there is no nonlinear interaction in the data, with a uniform distribution of p-values as expected if the null were true. In panel (a), on the other hand, both specifications identify a nonlinear interaction in the data even though there is only a linear interaction in the data generating process. The not fully moderated specification that is the default option in the most recent version of the interflex R package (Version 1.2.6) is particularly prone to do so and returns a Wald test with a p-value less than 0.05 in 86.5% of simulated datasets, whereas the moderated version does so in 66% of simulated datasets. Thus, researchers using the binning estimator in its default specification are likely to incorrectly mistake a linear interaction for a nonlinear one if a quadratic term of a control variable that is correlated with the moderator is omitted from the model.Footnote 4
2.2 Binning Estimator Results
We now turn to examining the substantive inferences from the binning estimator applied to this case. Figure 2 shows results from the fully moderated binning estimator on one of the datasets simulated under the data generating process described above.Footnote 5 Even though the relationship between D and Y is moderated linearly by X, the results based on the binning estimator suggest that X non-linearly moderates the relationship between D and Y, both in the fully moderated form in panel (a) and in the unmoderated form in panel (b).
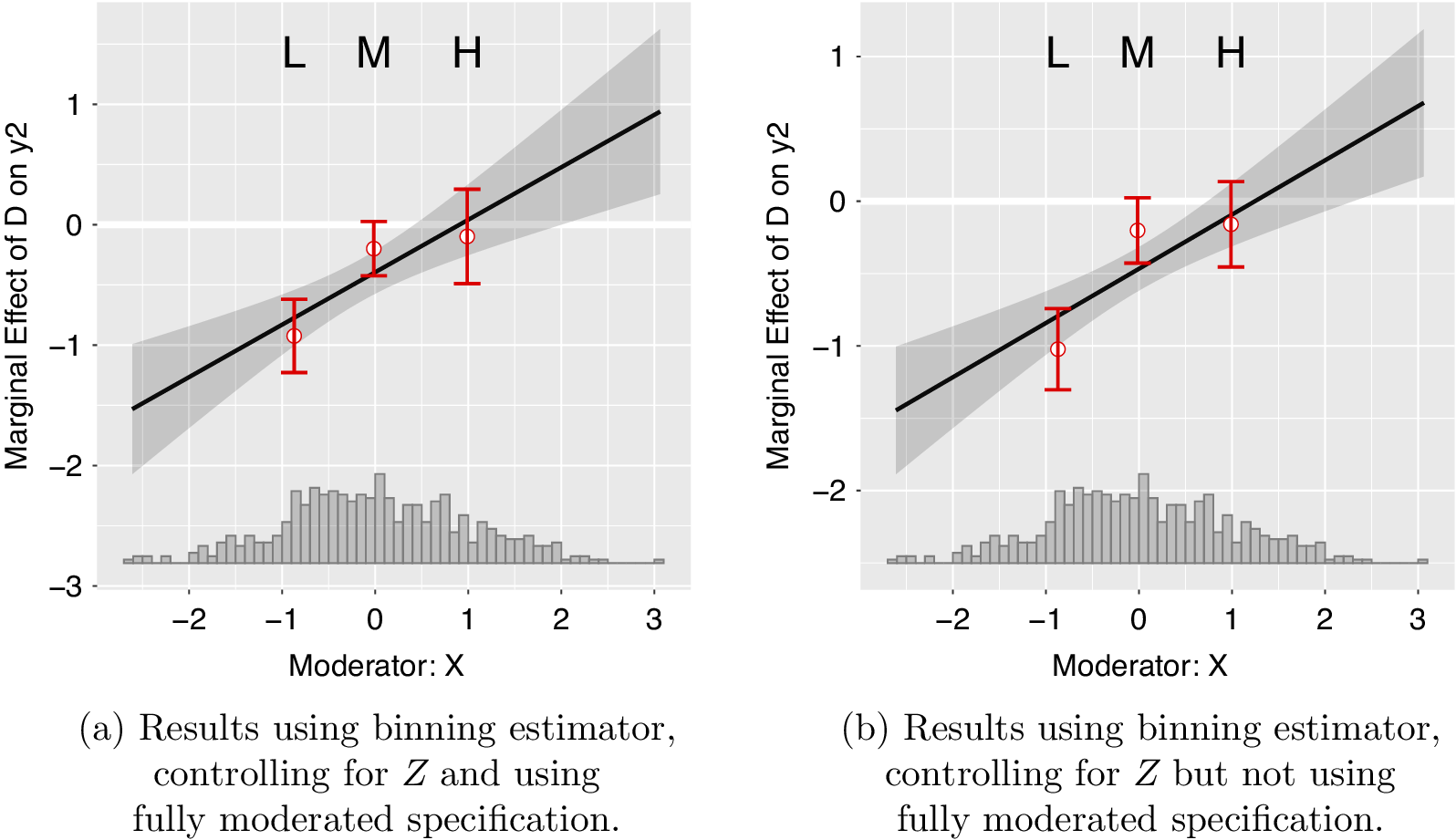
Figure 2 Estimated nonlinear interaction effects from the Binning estimator.
3 Solutions
Our simulation evidence of the best practice for diagnosing nonlinear interactions as suggested by Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) shows that researchers can incorrectly identify a nonlinear interaction when a relevant squared term in a control variable correlated with its constitutive terms is omitted. How should researchers avoid this issue? As this issue occurs when relevant squared terms are omitted (see Figure 1), researchers need to make sure that all relevant nonlinearities are included in the model.
In the first step, this means that when considering whether there are nonlinear interaction effects in a model, scholars also need to think carefully about whether there are theoretical reasons that suggest that one of the control variables may have a nonlinear effect. In a first instance, scholars can include polynomials of those variables to model their expectations.
In the second step, we suggest using methods for variable selection to identify nonlinearities and interactions in the set of variables used for covariate adjustment (Z) with the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) binning estimator. A common method for doing so is the use of the adaptive Lasso, which explicitly sets small parameter estimates to zero. Such an approach has been used by applied researchers when faced with specification uncertainty generally (e.g., Bosancianu et al. Reference Bosancianu, Hilbig, Humphreys, Sampada, Lieber and Scacco2020) but also for the estimation of interaction effects (e.g., Belloni, Chernozhukov, and Hansen Reference Belloni, Chernozhukov and Hansen2013; Blackwell and Olson Reference Blackwell and Olson2021). This approach retains the ease of interpretation, post-estimation, provided by the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) binning estimator. Using the adaptive Lasso to select control terms will help researchers identify relevant nonlinearities among control variables that they did not consider in the first step.
In the third step, we suggest basing inference on machine learning methods that allow for flexible functional forms and complex interactions while at the same time penalizing against unnecessary complexity. This approach also has the advantage of easily incorporating additional nonlinear interactions between the D and X terms with the covariates Z, reducing the possibility of the specified nonlinear interaction picking up an alternative unspecified nonlinear interaction. Beiser-McGrath and Beiser-McGrath (Reference Beiser-McGrath and Beiser-McGrath2020) show in Monte Carlo analyses that the adaptive Lasso, kernel regularized least squares (KRLS), and Bayesian additive regression trees (BARTs) are good at identifying linear interactions in the presence of additional nonlinearities and interactions among other correlated variables in the data generating process. However, there is the potential drawback of these methods being more complex, both computationally and in terms of post-estimation inference, thereby placing a greater burden on applied researchers. Additionally, while such methods do not result in “false positives” (Beiser-McGrath and Beiser-McGrath Reference Beiser-McGrath and Beiser-McGrath2020), that is, incorrectly suggesting the presence of interaction effects, they are conservative as penalization can lead to “false negatives”, that is, setting true interaction effects to zero (Blackwell and Olson Reference Blackwell and Olson2021).Footnote 6 Despite these potential drawbacks, the third step is necessary to identify nonlinear interactions between variables of interest and other control variables in the model.
In sum, we suggest researchers follow the following three steps. We consider these three steps as providing an increasing degree of robustness when evaluating nonlinear interaction effects. This process allows researchers to assess how confident they can be about the presence of a nonlinear interaction effect originally identified using the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) binning estimator, as each step increases the robustness of their estimation to nonlinearities and unmodeled nonlinear interaction effects.
-
• Step 1: Think theoretically about whether any nonlineariti among control variables are plausible and if so, include terms to model them as control variables when using the binning estimator.
-
• Step 2: Use the adaptive Lasso to select nonlinearities among control variables and include those as control variables in the binning estimator.
-
• Step 3: Use the adaptive Lasso to estimate a fully interactive and nonlinear model.
To demonstrate the relevance of the proposed technical solutions we propose in Steps 2 and 3, we reanalyze the previous example using the solutions we propose. Figure 3 finds that both of our proposed solutions suggest a linear interaction effect over the majority of the support for X. In contrast, the nonlinear interaction binning estimator finds a significant nonlinear interaction effect. While the marginal effect increases comparing the first and second bin estimates, from this point, it remains constant when comparing the second and third bin estimats. Additionally, the kernel estimator proposed by Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) also displays nonlinearities, even though the true marginal effect is linear. This example shows that by allowing for a broader range of nonlinearities, both independent and interactive, than the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) estimators, the methods we propose are able to avoid the bias that arises from model misspecification due to unmodeled nonlinearities.
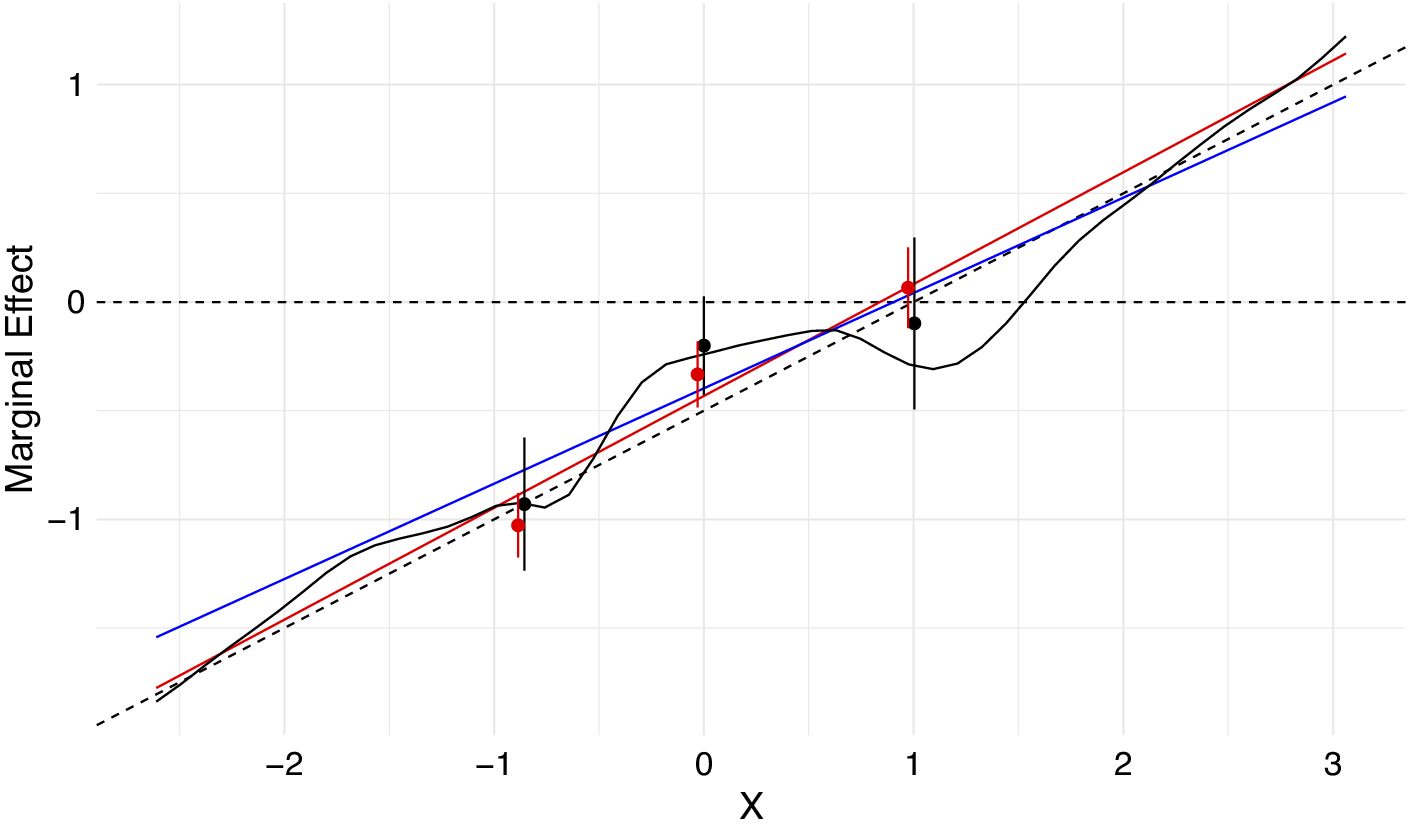
Figure 3 Nonlinear interaction effect estimators incorrectly identify a nonlinear interaction effect, when the true interaction effect is linear and covariates have nonlinear effects. The dashed line presents the true marginal effect. The blue line presents the marginal effect from a standard linear interaction model. Point estimates with 95% confidence intervals from the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) binning estimator are also displayed in black, and from the binning estimator with adaptive Lasso selected nonlinearities and interactions for covariate adjustment in red. The black line presents the marginal effect from the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) kernel estimator. The red line presents the marginal effect from a fully nonlinear interactive adaptive Lasso.
4 Reanalysis of Previous Studies
We also provide a broader replication of previous studies, to demonstrate how our proposals for increasing the robustness of nonlinear interaction effects affect inferences more generally. To do so, we use the replications of previous research presented in Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019). From this set of studies, we focus on those that do not suffer from the issue of common support, which was also discussed by Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019). Additionally, we do not replicate studies that do not have additional covariates (Z) beyond the moderator (
![]() $X)$
, and that suffer from computational issues.Footnote 7 This leaves us with 17 studies with 23 estimated interaction effects that we reanalyze.Footnote 8 Figure 4 illustrates the findings of our reanalysis. In each panel, the black line shows the marginal effect from a standard linear interaction model, the black point estimates derive from the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) binning estimator, the red point estimates derive from the binning estimator with adaptive Lasso selected nonlinearities and interactions for covariate adjustment, and the red line presents the marginal effect from a fully nonlinear interactive adaptive Lasso.
$X)$
, and that suffer from computational issues.Footnote 7 This leaves us with 17 studies with 23 estimated interaction effects that we reanalyze.Footnote 8 Figure 4 illustrates the findings of our reanalysis. In each panel, the black line shows the marginal effect from a standard linear interaction model, the black point estimates derive from the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) binning estimator, the red point estimates derive from the binning estimator with adaptive Lasso selected nonlinearities and interactions for covariate adjustment, and the red line presents the marginal effect from a fully nonlinear interactive adaptive Lasso.
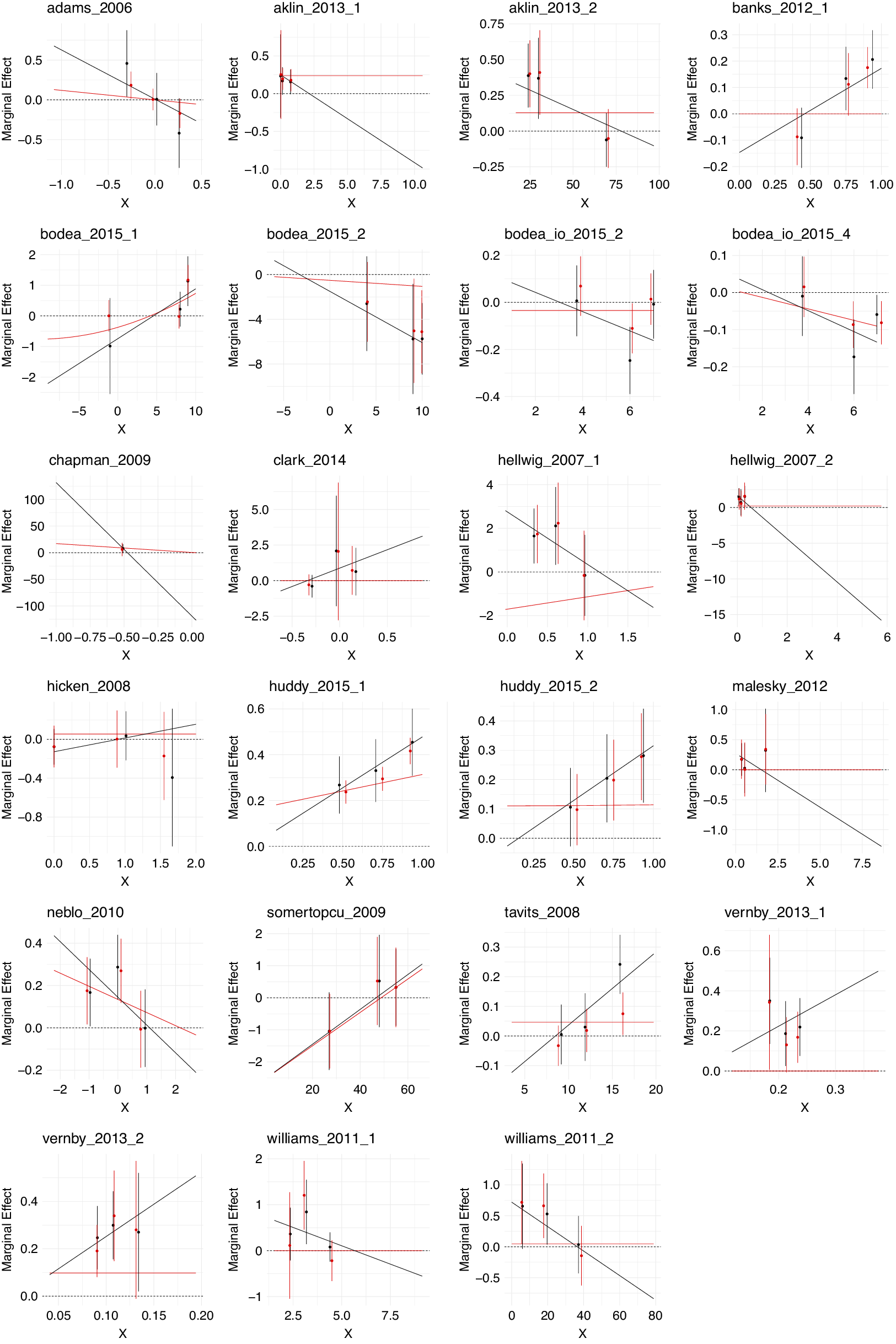
Figure 4 Reanalysis of 23 nonlinear interaction effects from 17 studies. The black line shows the marginal effect from a standard linear interaction model, the black point estimates derive from the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) binning estimator, the red point estimates from the binning estimator with adaptive Lasso selected nonlinearities and interactions for covariate adjustment, and the red line presents the marginal effect from a fully nonlinear interactive adaptive Lasso.
We now summarize the findings from Figure 4.Footnote 9 First, we examine the results from the original binning estimator (black point estimates in Figure 4). Using this estimator, we find a clear nonlinear relationship with the point estimates of the marginal effects changing nonmonotonically between terciles for 13 of the interactions. In addition, five of the interactions where marginal effects do not change nonmonotonically are visibly nonlinear.Footnote 10
We now compare these inferences from the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) binning estimator to our proposed solutions. First, comparing these findings to a version of the binning estimator which accounts for nonlinearities and interactions among the set of variables used for covariate adjustment (Z), selected by the adaptive Lasso, the findings (red point estimates in Figure 4) are very similar. In one of the cases where the marginal effects between terciles change nonmonotonically when using the original binning estimator this is no longer the case using Lasso-selected control variables (bodea_2015_2), even though the interactive relationship is still visibly nonlinear. In addition, only one of the interactions that were found to be visibly nonlinear without changing nonmonotonically using the original binning estimator is no longer at least visibly nonlinear when including Lasso-selected controls (tavits_2008).
Second, using the more severe robustness check of the fully nonlinear interactive adaptive Lasso, we find that the adaptive Lasso only finds a weakly nonlinear interaction in one of the 18 cases that were identified by the binning estimator as substantively nonlinear interactions (bodea_2015_1). Instead, in 12 of these cases, the Lasso suggests that there is no interaction between the two variables of interest at all (the slope of the marginal effect is zero, i.e., a horizontal line). In the remaining five cases that were identified as substantively nonlinear interactions by the binning estimator, the Lasso suggests a linear interaction.
In the Supplementary Material, we conduct additional analyses for those interaction effects where the fully specified adaptive Lasso returns a noninteractive effect, that is, a constant marginal effect. For those cases we also estimate BARTs (Green and Kern Reference Green and Kern2012), to ensure that these results are not purely a function of potential penalization bias from the Lasso. For 10 of the 14 interaction effects, we find that BART also leads to the inference that there is no substantive interaction effect, and for all studies, no statistically significant interaction effect, increasing our confidence that these inferences are not due to the choice of estimator.
One concern may be that the lack of interaction effects identified is a product of regularization bias, where meaningful interactions are over-regularized and set to zero in this high-dimensional setting. However, we do find many nonlinearities and nonlinear interactions for other variables in Section 5 of the Supplementary Material. This suggests that regularization bias is not a problem per se, rather the nonlinear interactions specified are absorbing other important nonlinearities and nonlinear interactions that are not specified in the typical application of the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) estimator. Thus, in practice, omitted interaction bias is a larger concern than regularization bias.
In summary, our results suggest that the estimation of nonlinear interaction effects is sensitive to the problem of unmodeled nonlinearities discussed in this paper as well as the broader issue of omitted interaction bias discussed in previous research (Beiser-McGrath and Beiser-McGrath Reference Beiser-McGrath and Beiser-McGrath2020; Blackwell and Olson Reference Blackwell and Olson2021). The solutions we propose in this paper thus provide researchers with approaches to evaluate the sensitivity of their chosen nonlinear interaction effects which can help demonstrate the strength and robustness of their findings.
5 Conclusion
Interaction effects are commonly used in Applied Political Science (Brambor et al. Reference Brambor, Clark and Golder2006). Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) have convincingly demonstrated that an incorrect assumption of a linear functional form of moderating effects can lead to bias. They have also provided essential tools for researches to estimate a nonlinear interaction effect and provided a code of the best practice to enable researchers to diagnose when the linear interaction effect assumption does not hold.
We have shown in this research note, however, that by relaxing this functional form assumption, there is the risk of unmodeled nonlinearities among variables used for covariate adjustment (Z) biasing interaction effect estimates. This can result in researchers finding evidence for a nonlinear interaction effect, even though the true interaction effect is likely linear. Moreover, the diagnostic tools suggested by Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) are not able to identify this potential bias, leaving researchers vulnerable to omitted nonlinearities in correlated control variables. Additionally, allowing for a fuller set of nonlinear interactions, including D and X, finds that many interaction effects are likely zero, as they are absorbing other nonmodeled nonlinear additive and interaction effects.
The results suggest that while moving beyond linearity as a default in the estimation of interaction effects is crucial for ensuring robust inferences, it needs to be coupled with a broader consideration of nonlinearities, both independent and interactive, in model specification (Beiser-McGrath and Beiser-McGrath Reference Beiser-McGrath and Beiser-McGrath2020). Methods such as the adaptive Lasso (Blackwell and Olson Reference Blackwell and Olson2021; Kenkel and Signorino Reference Kenkel and Signorino2013), KRLS (Hainmueller and Hazlett Reference Hainmueller and Hazlett2014), and BARTs (Green and Kern Reference Green and Kern2012) thus serve as an important step in establishing the robustness of nonlinear interaction effects identified through the Hainmueller et al. (Reference Hainmueller, Mummolo and Xu2019) estimator.
Acknowledgments
This paper has been previously presented at the 2021 EPSA Conference and the 2021 PSA Conference and has benefitted from those participants questions and comments. Particular thanks go to Vera Troeger, the anonymous reviewers, and the Editor for their insights and suggestions.
Data Availability Statement
Replication code for this article is available in Beiser-McGrath and Beiser-McGrath (Reference Beiser-McGrath and Beiser-McGrath2022) at https://doi.org/10.7910/DVN/S44D0E.
Supplementary Material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2022.25.






