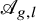1 Introduction
We work over the field of complex numbers throughout this paper.
Syzygies of abelian varieties have attracted lots of attention in recent years. Recall the following question asked by Ito for
![]() $p\geq 0$
and by Lozovanu for
$p\geq 0$
and by Lozovanu for
![]() $p=-1$
as well (see [Reference ItoIto1] and [Reference LozovanuLoz]).
$p=-1$
as well (see [Reference ItoIto1] and [Reference LozovanuLoz]).
Conjecture 1.1. Let
![]() $(A, L)$
be a polarized abelian variety of dimension g and
$(A, L)$
be a polarized abelian variety of dimension g and
![]() $p\geq -1$
an integer. If
$p\geq -1$
an integer. If
![]() $(L^g)>(g(p+2)))^g$
and
$(L^g)>(g(p+2)))^g$
and
![]() $(L^d\cdot B)>(d(p+2))^d$
for any abelian subvariety B of A of dimension
$(L^d\cdot B)>(d(p+2))^d$
for any abelian subvariety B of A of dimension
![]() $0<d<g$
, then L satisfies Property
$0<d<g$
, then L satisfies Property
![]() $(N_p)$
.
$(N_p)$
.
We summarize recent progress towards this conjecture.
1.1
 $\mathbb Q$
-twisted sheaves
$\mathbb Q$
-twisted sheaves
Given a coherent sheaf
![]() $\mathcal {F}$
on A and a rational number
$\mathcal {F}$
on A and a rational number
![]() $t\in \mathbb Q$
, following [Reference Jiang and PareschiJP], we formally define the
$t\in \mathbb Q$
, following [Reference Jiang and PareschiJP], we formally define the
![]() $\mathbb Q$
-twisted sheaves
$\mathbb Q$
-twisted sheaves
![]() $\mathcal {F}\langle tL \rangle $
. We say that
$\mathcal {F}\langle tL \rangle $
. We say that
![]() $\mathcal {F}\langle tL\rangle $
is IT
$\mathcal {F}\langle tL\rangle $
is IT
![]() $^0$
if the i-th cohomological support loci
$^0$
if the i-th cohomological support loci
![]() $V^i(\mu _b^*\mathcal {F}\otimes L^{\otimes b^2t})$
is empty for each
$V^i(\mu _b^*\mathcal {F}\otimes L^{\otimes b^2t})$
is empty for each
![]() $i>0$
, where b is an integer such that
$i>0$
, where b is an integer such that
![]() $b^2t\in \mathbb Z$
. Note that this definition does not depend on the choice of b. Assume that D is an effective
$b^2t\in \mathbb Z$
. Note that this definition does not depend on the choice of b. Assume that D is an effective
![]() $\mathbb Q$
-divisor on A such that D is
$\mathbb Q$
-divisor on A such that D is
![]() $\mathbb Q$
-equivalent to
$\mathbb Q$
-equivalent to
![]() $tL$
. We will also write
$tL$
. We will also write
![]() $\mathcal {F}\langle D\rangle =\mathcal {F}\langle tL \rangle $
.
$\mathcal {F}\langle D\rangle =\mathcal {F}\langle tL \rangle $
.
Similarly, we say that
![]() $\mathcal {F}\langle tL \rangle $
is M-regular (resp. GV) if
$\mathcal {F}\langle tL \rangle $
is M-regular (resp. GV) if
(resp.
![]() $\operatorname {\mathrm {codim}}_{\operatorname {\mathrm {Pic}}^0(A)}V^i(\mu _b^*\mathcal {F}\otimes L^{\otimes (b^2t)})\geq i$
) for all
$\operatorname {\mathrm {codim}}_{\operatorname {\mathrm {Pic}}^0(A)}V^i(\mu _b^*\mathcal {F}\otimes L^{\otimes (b^2t)})\geq i$
) for all
![]() $i>0$
. We can similarly define the cohomology ranks of
$i>0$
. We can similarly define the cohomology ranks of
![]() $\mathcal {F}\langle tL\rangle $
:
$\mathcal {F}\langle tL\rangle $
:
where
![]() $Q\in \operatorname {\mathrm {Pic}}^0(A)$
is general. The main result of [Reference Jiang and PareschiJP] says that the function
$Q\in \operatorname {\mathrm {Pic}}^0(A)$
is general. The main result of [Reference Jiang and PareschiJP] says that the function
![]() $t\rightarrow h^i(A, \mathcal {F}\langle tL\rangle )$
is locally polynomial on a left or right neighborhood of a rational number and can be extended to a continuous function from
$t\rightarrow h^i(A, \mathcal {F}\langle tL\rangle )$
is locally polynomial on a left or right neighborhood of a rational number and can be extended to a continuous function from
![]() $\mathbb R$
to
$\mathbb R$
to
![]() $\mathbb R$
. We call this function the i-th cohomological rank function of
$\mathbb R$
. We call this function the i-th cohomological rank function of
![]() $\mathcal {F}$
and denote it by
$\mathcal {F}$
and denote it by
![]() $h^i_{\mathcal {F}, L}(t)$
.
$h^i_{\mathcal {F}, L}(t)$
.
Let
![]() $\mathcal {I}_o$
be the ideal sheaf of the neutral element o of A. The basepoint freeness threshold
$\mathcal {I}_o$
be the ideal sheaf of the neutral element o of A. The basepoint freeness threshold
![]() $\beta (L)$
is defined to be
$\beta (L)$
is defined to be
By the main theorem of [Reference HaconHac],
![]() $\beta (L)$
is also equal to
$\beta (L)$
is also equal to
It was observed in [Reference Jiang and PareschiJP] that
![]() $\beta (L)\leq 1$
and equality holds iff
$\beta (L)\leq 1$
and equality holds iff
![]() $|L|$
has a basepoint. This shows that
$|L|$
has a basepoint. This shows that
![]() $\beta (L)$
may vary in families. More generally, if for some rational number
$\beta (L)$
may vary in families. More generally, if for some rational number
![]() $t=\frac {a}{b}$
,
$t=\frac {a}{b}$
,
![]() $V^i(\mu _b^*\mathcal {I}_o\otimes L^{\otimes (ab)})$
is a nonempty proper subset of
$V^i(\mu _b^*\mathcal {I}_o\otimes L^{\otimes (ab)})$
is a nonempty proper subset of
![]() $\operatorname {\mathrm {Pic}}^0(A)$
,
$\operatorname {\mathrm {Pic}}^0(A)$
,
![]() $\beta (L)=t$
. However, there is, by far, no general way to determine
$\beta (L)=t$
. However, there is, by far, no general way to determine
![]() $\beta (L)$
. It is also not clear whether or not
$\beta (L)$
. It is also not clear whether or not
![]() $\beta (L)$
is always a rational number.
$\beta (L)$
is always a rational number.
By [Reference Jiang and PareschiJP, Section 8] and [Reference CaucciC, Theorem 1.1], knowing the exact number of the basepoint freeness threshold
![]() $\beta (L)$
helps to understand the syzygies of L.
$\beta (L)$
helps to understand the syzygies of L.
Theorem 1.2. For
![]() $p\geq -1$
, if
$p\geq -1$
, if
![]() $\beta (L)<\frac {1}{p+2}$
, L satisfies Property
$\beta (L)<\frac {1}{p+2}$
, L satisfies Property
![]() $(N_p)$
.
$(N_p)$
.
Remark 1.3. Ito refined this criteria in [Reference ItoIto4, Theorem 1.5] by showing that if
![]() $\mathcal {I}_o\langle \frac {1}{p+2}L\rangle $
is M-regular for some integer
$\mathcal {I}_o\langle \frac {1}{p+2}L\rangle $
is M-regular for some integer
![]() $p> 0$
, L satisfies Property
$p> 0$
, L satisfies Property
![]() $(N_p)$
.
$(N_p)$
.
Caucci then asked the following question, which would imply Conjecture 1.1.
Conjecture 1.4. Let
![]() $(A, L)$
be a polarized abelian variety of dimension g and
$(A, L)$
be a polarized abelian variety of dimension g and
![]() $p\geq -1$
an integer. If
$p\geq -1$
an integer. If
![]() $(L^g)>(g(p+2)))^g$
and
$(L^g)>(g(p+2)))^g$
and
![]() $(L^d\cdot B)>(d(p+2))^d$
for any abelian subvariety B of A of dimension
$(L^d\cdot B)>(d(p+2))^d$
for any abelian subvariety B of A of dimension
![]() $0<d<g$
, then
$0<d<g$
, then
![]() $\beta (L)<\frac {1}{p+2}$
.
$\beta (L)<\frac {1}{p+2}$
.
1.2 Known results
By Theorem 1.2, in order to solve Conjecture 1.1 and Conjecture 1.4, it suffices to prove that
 $$ \begin{align} &\beta(L)\leq n(L):=\\ \nonumber \mathrm{inf}\{\frac{d}{\sqrt[d]{(L^d\cdot B)}}\mid\qquad & B \text{ is an abelian subvariety of dimension}\; 1\leq d \leq g\}. \end{align} $$
$$ \begin{align} &\beta(L)\leq n(L):=\\ \nonumber \mathrm{inf}\{\frac{d}{\sqrt[d]{(L^d\cdot B)}}\mid\qquad & B \text{ is an abelian subvariety of dimension}\; 1\leq d \leq g\}. \end{align} $$
There are various ways to estimate
![]() $\beta (L)$
. In [Reference ItoIto2], Ito showed that the Angehrn-Siu method (see [Reference Angehrn and SiuAS, Reference HelmkeHel, Reference KawamataK]), which was initially applied to attack Fujita’s basepoint-freeness conjecture, can also be used to estimate
$\beta (L)$
. In [Reference ItoIto2], Ito showed that the Angehrn-Siu method (see [Reference Angehrn and SiuAS, Reference HelmkeHel, Reference KawamataK]), which was initially applied to attack Fujita’s basepoint-freeness conjecture, can also be used to estimate
![]() $\beta (L)$
. To be more precise, let
$\beta (L)$
. To be more precise, let
 $$ \begin{align*} &\quad r'(L):=\mathrm{inf}\{t\in \mathbb Q\mid \text{ there exists a } \mathbb{Q}\text{-divisor}\; D\sim_{\mathbb Q}tL \\ &\text{such that }\; o\; \text{is an isolated component of}\; \mathrm{Nklt}(A, D)\}, \end{align*} $$
$$ \begin{align*} &\quad r'(L):=\mathrm{inf}\{t\in \mathbb Q\mid \text{ there exists a } \mathbb{Q}\text{-divisor}\; D\sim_{\mathbb Q}tL \\ &\text{such that }\; o\; \text{is an isolated component of}\; \mathrm{Nklt}(A, D)\}, \end{align*} $$
where the non-klt locus
![]() $\mathrm {Nklt}(A, D)$
is the subscheme of A defined by the multiplier ideal
$\mathrm {Nklt}(A, D)$
is the subscheme of A defined by the multiplier ideal
![]() $\mathcal {J}(A, D)$
(see, for instance, [Reference LazarsfeldLaz2, Section 9 and 10]). Ito proved in [Reference ItoIto2] that we always have
$\mathcal {J}(A, D)$
(see, for instance, [Reference LazarsfeldLaz2, Section 9 and 10]). Ito proved in [Reference ItoIto2] that we always have
![]() $\beta (L)\leq r'(L)$
,
$\beta (L)\leq r'(L)$
,
![]() $ r'(L)\leq n(L)$
when
$ r'(L)\leq n(L)$
when
![]() $(A, L)$
is a polarized simple abelian 3-fold, and Conjecture 1.1 and Conjecture 1.4 hold for any polarized abelian 3-fold.
$(A, L)$
is a polarized simple abelian 3-fold, and Conjecture 1.1 and Conjecture 1.4 hold for any polarized abelian 3-fold.
In higher dimensions, we have proved in [Reference JiangJz] via generic vanishing that
![]() $\beta (L)\leq 2n(L).$
This implies that given a polarized abelian variety
$\beta (L)\leq 2n(L).$
This implies that given a polarized abelian variety
![]() $(A, L)$
, if
$(A, L)$
, if
![]() $(L^d\cdot B)>(2(p+2)d)^d$
for any abelian subvariety B of dimension
$(L^d\cdot B)>(2(p+2)d)^d$
for any abelian subvariety B of dimension
![]() $1\leq d\leq g$
, L satisfies Property
$1\leq d\leq g$
, L satisfies Property
![]() $(N_p)$
.
$(N_p)$
.
Based on Bridgeland’s stability condition on surfaces, Lahoz-Rojas [Reference Lahoz and RojasLR] and Rojas [Reference RojasR] almost determined the cohomological rank functions
![]() $h^i_{\mathcal {I}_o, L}$
for any polarized abelian surface
$h^i_{\mathcal {I}_o, L}$
for any polarized abelian surface
![]() $(A, L)$
of Picard number
$(A, L)$
of Picard number
![]() $1$
. When L is of polarization type
$1$
. When L is of polarization type
![]() $(1, d)$
, Rojas proved that
$(1, d)$
, Rojas proved that
![]() $\beta (L)=\frac {1}{\sqrt {d}}$
when d is a perfect square or
$\beta (L)=\frac {1}{\sqrt {d}}$
when d is a perfect square or
![]() $\beta (L)=\frac {2y}{x-1}$
where
$\beta (L)=\frac {2y}{x-1}$
where
![]() $(x, y)$
is the minimal or the second minimal positive solution of the Pell’s equation
$(x, y)$
is the minimal or the second minimal positive solution of the Pell’s equation
![]() $X^2-4dY^2=1$
when d is not a perfect square. In either case, we have
$X^2-4dY^2=1$
when d is not a perfect square. In either case, we have
![]() $\beta (L)< \frac {\sqrt {d}+1}{d}<\frac {\sqrt {2}}{\sqrt {d}}=n(L)$
when
$\beta (L)< \frac {\sqrt {d}+1}{d}<\frac {\sqrt {2}}{\sqrt {d}}=n(L)$
when
![]() $d\geq 6$
.
$d\geq 6$
.
Via a degeneration method, Ito studied in [Reference ItoIto3] the syzygies of general polarized abelian varieties of type
![]() $(1,\ldots ,1, d)$
. He proved that when
$(1,\ldots ,1, d)$
. He proved that when
![]() $d\geq \frac {(p+2)^{g+1}-1}{p+1}$
, L satisfies Property
$d\geq \frac {(p+2)^{g+1}-1}{p+1}$
, L satisfies Property
![]() $(N_p)$
.
$(N_p)$
.
Inspired by the results of Ito and Rojas, one may believe that
![]() $\beta (L)$
should be quite close to
$\beta (L)$
should be quite close to
 $\displaystyle\frac {1}{\sqrt[g]{h^0(A, L)}}=\frac {\sqrt[g]{g!}}{\sqrt[g]{(L^g)}}$
for general polarized abelian variety
$\displaystyle\frac {1}{\sqrt[g]{h^0(A, L)}}=\frac {\sqrt[g]{g!}}{\sqrt[g]{(L^g)}}$
for general polarized abelian variety
![]() $(A, L)$
of dimension g.
$(A, L)$
of dimension g.
1.3 Main results
In this paper, we follow Ito’s approach to apply the Angehrn-Siu method to estimate
![]() $\beta (L)$
for polarized abelian varieties. We improve the known upper bounds for
$\beta (L)$
for polarized abelian varieties. We improve the known upper bounds for
![]() $\beta (L)$
for higher dimensional polarized abelian varieties.
$\beta (L)$
for higher dimensional polarized abelian varieties.
We denote, respectively, by g and l the dimension and the polarization type of a polarized abelian variety
![]() $(A, L)$
. There is a quasi-projective variety
$(A, L)$
. There is a quasi-projective variety
![]() $\mathcal {A}_{g, l}$
parametrizing such polarized abelian varieties. We may assume that l is primitive.
$\mathcal {A}_{g, l}$
parametrizing such polarized abelian varieties. We may assume that l is primitive.
Theorem 1.5. Let
![]() $(A, L)$
be a very general polarized abelian variety in
$(A, L)$
be a very general polarized abelian variety in
![]() $\mathcal {A}_{g, l}$
. When
$\mathcal {A}_{g, l}$
. When
![]() $g=4$
or
$g=4$
or
![]() $5$
or
$5$
or
![]() $6$
, we have
$6$
, we have
![]() $\beta (L)\leq n(L)$
. When
$\beta (L)\leq n(L)$
. When
![]() $g\geq 7$
, we also have
$g\geq 7$
, we also have
![]() $\beta (L)\leq n(L)$
, except for possibly finitely many primitive polarization types l in each dimension g.
$\beta (L)\leq n(L)$
, except for possibly finitely many primitive polarization types l in each dimension g.
Theorem 1.6. Let
![]() $(A, L)$
be a polarized abelian
$(A, L)$
be a polarized abelian
![]() $4$
-fold. Assume that
$4$
-fold. Assume that
![]() $(L^4)>((2+\frac {4}{\sqrt {3}})(p+2))^4$
and
$(L^4)>((2+\frac {4}{\sqrt {3}})(p+2))^4$
and
![]() $(L^d\cdot B)>((p+2)d)^d$
for any abelian subvariety B of dimension
$(L^d\cdot B)>((p+2)d)^d$
for any abelian subvariety B of dimension
![]() $1\leq d\leq 3$
. Then,
$1\leq d\leq 3$
. Then,
![]() $\beta (L)<\frac {1}{p+2}$
.
$\beta (L)<\frac {1}{p+2}$
.
Remark 1.7. Note that
![]() $2+\frac {4}{\sqrt {3}}\approx 4.31$
. Thus, Theorem 1.6 is quite close to Conjecture 1.4 for abelian 4-folds.
$2+\frac {4}{\sqrt {3}}\approx 4.31$
. Thus, Theorem 1.6 is quite close to Conjecture 1.4 for abelian 4-folds.
Theorem 1.8. Let
![]() $(A, L)$
be a polarized abelian
$(A, L)$
be a polarized abelian
![]() $5$
-fold. Assume that A is simple and
$5$
-fold. Assume that A is simple and
![]() $(L^5)>(8(p+2))^5$
. Then,
$(L^5)>(8(p+2))^5$
. Then,
![]() $\beta (L)< \frac {1}{p+2}$
.
$\beta (L)< \frac {1}{p+2}$
.
In higher dimensions, we also have slight improvements of
![]() $\beta (L)$
. For
$\beta (L)$
. For
![]() $g\geq 6$
, we define
$g\geq 6$
, we define
![]() $\alpha _{g, g-2}=\sqrt [g-2]{\frac {15(g-3)!}{g-1}}$
,
$\alpha _{g, g-2}=\sqrt [g-2]{\frac {15(g-3)!}{g-1}}$
,
![]() $\alpha _{g, 2}=\sqrt {\frac {5(g-2)+1}{g-1}}$
. For
$\alpha _{g, 2}=\sqrt {\frac {5(g-2)+1}{g-1}}$
. For
![]() $3\leq d\leq g-3$
,
$3\leq d\leq g-3$
,
 $$ \begin{align*}\alpha_{g,d}=\sqrt[d]{\frac{\frac{5}{2}d!(g-d)}{\binom{g-1}{g-d}}},\end{align*} $$
$$ \begin{align*}\alpha_{g,d}=\sqrt[d]{\frac{\frac{5}{2}d!(g-d)}{\binom{g-1}{g-d}}},\end{align*} $$
and let
Theorem 1.9. Let
![]() $(A, L)$
be a polarized abelian variety of dimension
$(A, L)$
be a polarized abelian variety of dimension
![]() $g\geq 6$
. Assume that A is simple and
$g\geq 6$
. Assume that A is simple and
![]() $(L^g)>((2g-\alpha _g)(p+2))^g$
,
$(L^g)>((2g-\alpha _g)(p+2))^g$
,
![]() $\beta (L)< \frac {1}{p+2}$
.
$\beta (L)< \frac {1}{p+2}$
.
Note that
![]() $\alpha _6=\alpha _{6,3}=\sqrt [3]{\frac {9}{2}}$
,
$\alpha _6=\alpha _{6,3}=\sqrt [3]{\frac {9}{2}}$
,
![]() $\alpha _7=\alpha _{7, 3}=\sqrt [3]{4}$
,
$\alpha _7=\alpha _{7, 3}=\sqrt [3]{4}$
,
![]() $\alpha _8=\alpha _{8, 3}=\sqrt [3]{\frac {25}{7}}$
.
$\alpha _8=\alpha _{8, 3}=\sqrt [3]{\frac {25}{7}}$
.
2 Preliminaries
2.1 Log canonical centers
Let X be a smooth projective variety and
![]() $\Delta $
be an effective
$\Delta $
be an effective
![]() $\mathbb Q$
-divisor on X. We take
$\mathbb Q$
-divisor on X. We take
![]() $\mu : Y\rightarrow X$
a log resolution of
$\mu : Y\rightarrow X$
a log resolution of
![]() $(X, \Delta )$
, and we write
$(X, \Delta )$
, and we write
where E runs through prime divisors of Y and
![]() $\mu _*(\sum _Ea(E, X, \Delta )E)=-\Delta $
.
$\mu _*(\sum _Ea(E, X, \Delta )E)=-\Delta $
.
We say that
![]() $(X, \Delta )$
is log canonical at x if
$(X, \Delta )$
is log canonical at x if
![]() $a(E, X, \Delta )\geq -1$
for all prime divisors E on Y such that
$a(E, X, \Delta )\geq -1$
for all prime divisors E on Y such that
![]() $x\in \mu (E)$
. For a prime divisor E on Y, if
$x\in \mu (E)$
. For a prime divisor E on Y, if
![]() $(X, \Delta )$
is log canonical at the generic point of
$(X, \Delta )$
is log canonical at the generic point of
![]() $\mu (E)$
and the discrepancy
$\mu (E)$
and the discrepancy
![]() $a(E, X, \Delta )=-1$
, we call
$a(E, X, \Delta )=-1$
, we call
![]() $\mu (E)$
a log canonical center of
$\mu (E)$
a log canonical center of
![]() $(X, \Delta )$
.
$(X, \Delta )$
.
When
![]() $(X, \Delta )$
is log canonical at x, there are finitely many log canonical centers containing x, and the intersection of two such log canonical centers is the union of certain log canonical centers containing x (see, for instance, [Reference KawamataK, Proposition 1.5] or [Reference FujinoF, Theorem 9.1]). Thus, there exists a unique minimal log canonical center Z of
$(X, \Delta )$
is log canonical at x, there are finitely many log canonical centers containing x, and the intersection of two such log canonical centers is the union of certain log canonical centers containing x (see, for instance, [Reference KawamataK, Proposition 1.5] or [Reference FujinoF, Theorem 9.1]). Thus, there exists a unique minimal log canonical center Z of
![]() $(X, \Delta )$
through x. Moreover, Z is normal and has rational singularities around x. More precisely, locally around x, there exists a
$(X, \Delta )$
through x. Moreover, Z is normal and has rational singularities around x. More precisely, locally around x, there exists a
![]() $\mathbb Q$
-effective divisor
$\mathbb Q$
-effective divisor
![]() $\Delta _Z$
such that
$\Delta _Z$
such that
![]() $(Z, \Delta _Z)$
is klt (see, for instance, [Reference Fujino and YoshinoriFG, Theorem 7.1]). However, the singularities of Z away from x cannot be controlled in general. The following result due to Xiaodong Jiang from [Reference JiangJx, Proposition 5.1] will be applied later.
$(Z, \Delta _Z)$
is klt (see, for instance, [Reference Fujino and YoshinoriFG, Theorem 7.1]). However, the singularities of Z away from x cannot be controlled in general. The following result due to Xiaodong Jiang from [Reference JiangJx, Proposition 5.1] will be applied later.
Proposition 2.1. Let X be a smooth projective variety and
![]() $\Delta $
an effective
$\Delta $
an effective
![]() $\mathbb Q$
-divisor on X with Z a log canonical center of
$\mathbb Q$
-divisor on X with Z a log canonical center of
![]() $(X, \Delta )$
Footnote
1
. Let
$(X, \Delta )$
Footnote
1
. Let
![]() $\nu : \overline {Z}\rightarrow Z$
be the normalization. Then, there exists an effective
$\nu : \overline {Z}\rightarrow Z$
be the normalization. Then, there exists an effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $\Delta _{\overline {Z}}$
on
$\Delta _{\overline {Z}}$
on
![]() $\overline {Z}$
such that
$\overline {Z}$
such that
![]() $\nu ^*(K_X+\Delta )\sim _{\mathbb Q} K_{\overline {Z}}+\Delta _{\overline {Z}}$
.
$\nu ^*(K_X+\Delta )\sim _{\mathbb Q} K_{\overline {Z}}+\Delta _{\overline {Z}}$
.
We then have the immediate corollary.
Corollary 2.2. Under the above assumption, we have
where
![]() $Z'$
is any
$Z'$
is any
![]() $\mathbb Q$
-Gorenstein partial resolution of
$\mathbb Q$
-Gorenstein partial resolution of
![]() $\overline {Z}$
.
$\overline {Z}$
.
Proof. Let
![]() $\rho : Z'\rightarrow \overline {Z}$
be a
$\rho : Z'\rightarrow \overline {Z}$
be a
![]() $\mathbb Q$
-Gorenstein partial resolution and let
$\mathbb Q$
-Gorenstein partial resolution and let
![]() $\mu : \tilde {Z}\xrightarrow {\sigma }Z'\xrightarrow {\rho } \overline {Z}$
be a log resolution of
$\mu : \tilde {Z}\xrightarrow {\sigma }Z'\xrightarrow {\rho } \overline {Z}$
be a log resolution of
![]() $(\overline {Z}, \Delta _{\overline {Z}})$
. Let
$(\overline {Z}, \Delta _{\overline {Z}})$
. Let
![]() $\Delta _{\tilde {Z}}=\mu _*^{-1}(\Delta _{\overline {Z}})$
. We then have
$\Delta _{\tilde {Z}}=\mu _*^{-1}(\Delta _{\overline {Z}})$
. We then have
![]() $K_{\tilde {Z}}+\Delta _{\tilde {Z}}+E_1=\mu ^*(K_{\overline {Z}}+\Delta _{\overline {Z}})+E_2$
and
$K_{\tilde {Z}}+\Delta _{\tilde {Z}}+E_1=\mu ^*(K_{\overline {Z}}+\Delta _{\overline {Z}})+E_2$
and
![]() $K_{\tilde {Z}}+E_3=\sigma ^*K_{Z'}+E_4$
, where
$K_{\tilde {Z}}+E_3=\sigma ^*K_{Z'}+E_4$
, where
![]() $E_i$
are
$E_i$
are
![]() $\mathbb Q$
-effective
$\mathbb Q$
-effective
![]() $\mu $
-exceptional divisors for
$\mu $
-exceptional divisors for
![]() $1\leq i\leq 4$
. Thus,
$1\leq i\leq 4$
. Thus,
![]() $ \operatorname {\mathrm {vol}}(\overline {Z}, K_{\overline {Z}}+\Delta _{\overline {Z}})=\operatorname {\mathrm {vol}}(\tilde {Z}, \mu ^*(K_{\overline {Z}}+\Delta _{\overline {Z}})+E_2+E_3)=\operatorname {\mathrm {vol}}(\tilde {Z}, K_{\tilde {Z}}+\Delta _{\tilde {Z}}+E_1+E_3)\geq \operatorname {\mathrm {vol}}(Z', K_{Z'})$
.
$ \operatorname {\mathrm {vol}}(\overline {Z}, K_{\overline {Z}}+\Delta _{\overline {Z}})=\operatorname {\mathrm {vol}}(\tilde {Z}, \mu ^*(K_{\overline {Z}}+\Delta _{\overline {Z}})+E_2+E_3)=\operatorname {\mathrm {vol}}(\tilde {Z}, K_{\tilde {Z}}+\Delta _{\tilde {Z}}+E_1+E_3)\geq \operatorname {\mathrm {vol}}(Z', K_{Z'})$
.
The reason that we are interested to know the lower bound of the restricted volume is that we like to apply Helmke’s induction to cut down log canonical centers.
We briefly recall Helmke’s work [Reference HelmkeHel]. Let D be an ample effective
![]() $\mathbb Q$
-divisor on a smooth projective variety X of dimension n. We assume that
$\mathbb Q$
-divisor on a smooth projective variety X of dimension n. We assume that
![]() $x\in D$
and
$x\in D$
and
![]() $\mathrm {mult}_xD=m>0$
. Let
$\mathrm {mult}_xD=m>0$
. Let
![]() $c:=\mathrm {lct}(D, x)$
be the log canonical threshold of D at x; namely, c is the maximal rational number such that
$c:=\mathrm {lct}(D, x)$
be the log canonical threshold of D at x; namely, c is the maximal rational number such that
![]() $(X, cD)$
is log canonical at x. Let Z be the minimal log canonical center of
$(X, cD)$
is log canonical at x. Let Z be the minimal log canonical center of
![]() $(X, cD)$
through x and denote
$(X, cD)$
through x and denote
![]() $d=\dim Z$
. Helmke and Ein independently introduced the local discrepancyFootnote
2
$d=\dim Z$
. Helmke and Ein independently introduced the local discrepancyFootnote
2
![]() $b_x(X, cD)$
of
$b_x(X, cD)$
of
![]() $(X, cD)$
at x, which is the rational number
$(X, cD)$
at x, which is the rational number
 $$ \begin{align*} \mathrm{max}\{\mathrm{mult}_x E\mid\qquad & E\;\text{ is an effective}\; \mathbb Q\text{-divisor}\; \\ & \text{such that}\; (X, cD+E) \;\text{is log canonical at}\; x\}. \end{align*} $$
$$ \begin{align*} \mathrm{max}\{\mathrm{mult}_x E\mid\qquad & E\;\text{ is an effective}\; \mathbb Q\text{-divisor}\; \\ & \text{such that}\; (X, cD+E) \;\text{is log canonical at}\; x\}. \end{align*} $$
It is known that
![]() $0\leq b_x(X, cD)\leq n-cm$
,
$0\leq b_x(X, cD)\leq n-cm$
,
![]() $b_x(X, cD)\leq d$
and
$b_x(X, cD)\leq d$
and
![]() $b_x(X, cD)=0$
iff
$b_x(X, cD)=0$
iff
![]() $Z=\{x\}$
(see [Reference HelmkeHel] and [Reference EinE]).
$Z=\{x\}$
(see [Reference HelmkeHel] and [Reference EinE]).
Helmke’s induction can be summarized as follows (see [Reference HelmkeHel, Proposition 3.2 and Theorem 4.3]).
Proposition 2.3. Under the above assumption, assume that
![]() $c<1$
.
$c<1$
.
-
(1) If
 $(D^{\dim Z}\cdot Z)>(\frac {b_x(X, cD)}{1-c})^{\dim Z}\mathrm {mult}_xZ$
, there exists a rational number
$(D^{\dim Z}\cdot Z)>(\frac {b_x(X, cD)}{1-c})^{\dim Z}\mathrm {mult}_xZ$
, there exists a rational number
 $0<c'<1-c$
, an effective
$0<c'<1-c$
, an effective
 $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
 $D'\sim _{\mathbb Q}c'D$
, such that
$D'\sim _{\mathbb Q}c'D$
, such that
 $(X, cD+D')$
is log canonical at x and the minimal log canonical center
$(X, cD+D')$
is log canonical at x and the minimal log canonical center
 $Z'$
of
$Z'$
of
 $(X, cD+D')$
through x is a proper subset of Z.
$(X, cD+D')$
through x is a proper subset of Z. -
(2) If
 $m\geq n$
, let
$m\geq n$
, let
 $c_1=c+c'$
and
$c_1=c+c'$
and
 $D_1=cD+D'$
. Then,
$D_1=cD+D'$
. Then,
 $\frac {b_x(X, D_1)}{1-c_1}<\frac {b_x(X, cD)}{1-c}\leq n$
.
$\frac {b_x(X, D_1)}{1-c_1}<\frac {b_x(X, cD)}{1-c}\leq n$
. -
(3)
 $\mathrm {mult}_xZ\leq \binom {n-\lceil b_x(X, cD) \rceil }{n-d}$
.
$\mathrm {mult}_xZ\leq \binom {n-\lceil b_x(X, cD) \rceil }{n-d}$
.
Remark 2.4. Let
![]() $(A, L)$
be a polarized abelian variety. Assume that an effective
$(A, L)$
be a polarized abelian variety. Assume that an effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $D\sim _{\mathbb Q}tL$
such that
$D\sim _{\mathbb Q}tL$
such that
![]() $(X, D)$
is log canonical around the neutral element o, and Z is the minimal log canonical center through o. Choose an integer
$(X, D)$
is log canonical around the neutral element o, and Z is the minimal log canonical center through o. Choose an integer
![]() $m\geq 1$
such that
$m\geq 1$
such that
![]() $\mathcal {I}_Z\otimes L^{\otimes m}$
is globally generated. Then, by a standard argument (see, for instance, [Reference KawamataK, Proposition 2.3]), we know that for a small perturbation
$\mathcal {I}_Z\otimes L^{\otimes m}$
is globally generated. Then, by a standard argument (see, for instance, [Reference KawamataK, Proposition 2.3]), we know that for a small perturbation
![]() $D'=(1-\epsilon )D+\eta H$
of D, where
$D'=(1-\epsilon )D+\eta H$
of D, where
![]() $0<\epsilon , \eta \ll 1$
and
$0<\epsilon , \eta \ll 1$
and
![]() $H\in |\mathcal {I}_Z\otimes L^{\otimes m}|$
general, Z is an irreducible component of
$H\in |\mathcal {I}_Z\otimes L^{\otimes m}|$
general, Z is an irreducible component of
![]() $\mathrm {Nklt}(A, D')$
. In particular, if
$\mathrm {Nklt}(A, D')$
. In particular, if
![]() $Z=\{o\}$
, we have
$Z=\{o\}$
, we have
![]() $\beta (L)\leq r'(L)\leq t$
. When Z is an abelian subvariety of A and
$\beta (L)\leq r'(L)\leq t$
. When Z is an abelian subvariety of A and
![]() $\beta (L|_Z)\leq t$
, we also have
$\beta (L|_Z)\leq t$
, we also have
![]() $\beta (L)\leq t$
by Ito’s work [Reference ItoIto2, Proposition 6.6].
$\beta (L)\leq t$
by Ito’s work [Reference ItoIto2, Proposition 6.6].
2.2 A generic vanishing approach
We recall some results from [Reference JiangJz].
Lemma 2.5. Let
![]() $(A, L)$
be a polarized abelian variety. Assume that
$(A, L)$
be a polarized abelian variety. Assume that
![]() $D\sim _{\mathbb Q} tL$
is an effective
$D\sim _{\mathbb Q} tL$
is an effective
![]() $\mathbb Q$
-divisor such that there exists an effective divisor
$\mathbb Q$
-divisor such that there exists an effective divisor
![]() $H\preceq D$
. Then,
$H\preceq D$
. Then,
![]() $\mathcal {I}_{K}\langle tL\rangle $
is GV, where K is the neutral component of the kernel of the morphism
$\mathcal {I}_{K}\langle tL\rangle $
is GV, where K is the neutral component of the kernel of the morphism
 $$ \begin{align*} &\varphi_H: A\rightarrow \operatorname{\mathrm{Pic}}^0(A)\\ & x\rightarrow t_x^*\mathcal{O}_A(H)\otimes \mathcal{O}_A(-H). \end{align*} $$
$$ \begin{align*} &\varphi_H: A\rightarrow \operatorname{\mathrm{Pic}}^0(A)\\ & x\rightarrow t_x^*\mathcal{O}_A(H)\otimes \mathcal{O}_A(-H). \end{align*} $$
In particular, when H is ample,
![]() $\mathcal {I}_o\langle tL\rangle $
is GV and thus,
$\mathcal {I}_o\langle tL\rangle $
is GV and thus,
![]() $\beta (L)\leq t$
.
$\beta (L)\leq t$
.
Proof. This follows directly from the proof of (1) of [Reference JiangJz, Proposition 4.1].
The following theorem is essentially the main result of [Reference JiangJz].
Theorem 2.6. Let
![]() $(A, L)$
be a polarized abelian variety. Assume that
$(A, L)$
be a polarized abelian variety. Assume that
-
○ there exists an irreducible normal subvariety Z of A such that
 $\mathcal {I}_Z\langle t_0L\rangle $
is IT
$\mathcal {I}_Z\langle t_0L\rangle $
is IT
 $^0$
for some positive rational number
$^0$
for some positive rational number
 $t_0$
and a smooth model of Z is of general type;
$t_0$
and a smooth model of Z is of general type; -
○ and there exists an effective
 $\mathbb Q$
-Weil divisor
$\mathbb Q$
-Weil divisor
 $D_Z$
on Z and a big
$D_Z$
on Z and a big
 $\mathbb Q$
-Cartier divisor
$\mathbb Q$
-Cartier divisor
 $V_Z$
such that
$V_Z$
such that
 $K_Z+D_Z$
is
$K_Z+D_Z$
is
 $\mathbb Q$
-Cartier and
$\mathbb Q$
-Cartier and
 $t_0L|_Z\sim _{\mathbb Q}2(K_Z+D_Z)+V_Z$
.
$t_0L|_Z\sim _{\mathbb Q}2(K_Z+D_Z)+V_Z$
.
We have
![]() $\beta (L)\leq t_0$
.
$\beta (L)\leq t_0$
.
Since [Reference JiangJz, Theorem 1.4] is not stated in this way, let’s briefly recall the proof for the readers’ convenience.
Proof. It suffices to show that
![]() $\mathcal {I}_0\langle t_0L\rangle $
is GV. After a translation, we may assume that
$\mathcal {I}_0\langle t_0L\rangle $
is GV. After a translation, we may assume that
![]() $o\in Z$
is a smooth point of Z. We have the short exact sequence
$o\in Z$
is a smooth point of Z. We have the short exact sequence
By the first condition, it suffices to show that
![]() $\mathcal {I}_{o, Z}\langle t_0L\rangle $
is GV.
$\mathcal {I}_{o, Z}\langle t_0L\rangle $
is GV.
We may also assume that Z is smooth (one may check [Reference JiangJz, Subsection 5.1] for the full argument). Then, since Z is of general type,
![]() $\omega _Z\otimes \mathcal {I}_{o, Z}$
is GV (see [Reference JiangJz, Lemma 2.6]). Then, one can take an integer M sufficiently divisible such that
$\omega _Z\otimes \mathcal {I}_{o, Z}$
is GV (see [Reference JiangJz, Lemma 2.6]). Then, one can take an integer M sufficiently divisible such that
![]() $Mt_0\in \mathbb Z$
and consider the multiplication-by-M map
$Mt_0\in \mathbb Z$
and consider the multiplication-by-M map
![]() $\pi _M: A\rightarrow A$
and denote by
$\pi _M: A\rightarrow A$
and denote by
![]() $Z^M$
the inverse image
$Z^M$
the inverse image
![]() $\pi _M^{-1}(Z)$
. By the second condition,
$\pi _M^{-1}(Z)$
. By the second condition,
![]() $\mathcal {O}_{Z^M}(M^2t_0L-K_{Z^M})$
has a nontrivial section s. Indeed, the second condition implies that
$\mathcal {O}_{Z^M}(M^2t_0L-K_{Z^M})$
has a nontrivial section s. Indeed, the second condition implies that
![]() $M^2t_0L|_{Z^M}-K_{Z^M}$
is
$M^2t_0L|_{Z^M}-K_{Z^M}$
is
![]() $\mathbb Q$
-equivalent to the sum of
$\mathbb Q$
-equivalent to the sum of
![]() $K_{Z^M}$
and a big divisor, and one can conclude by Nadel’s vanishing and generic vanishing that
$K_{Z^M}$
and a big divisor, and one can conclude by Nadel’s vanishing and generic vanishing that
![]() $M^2t_0L|_{Z^M}-K_{Z^M}$
has a global section.Footnote
3
$M^2t_0L|_{Z^M}-K_{Z^M}$
has a global section.Footnote
3
Via this section, we have a short exact sequence
We then check that all terms in this short exact sequence are GV. We may assume that the zero locus of s does not intersect with
![]() $o_M:=\pi _M^{-1}(o)$
. Then, we have another short exact sequence
$o_M:=\pi _M^{-1}(o)$
. Then, we have another short exact sequence
Note that
![]() $\mathcal {I}_{o_M}\otimes K_{Z^M}=\pi _M^{*}(\mathcal {I}_o\otimes K_Z)$
is GV. Hence,
$\mathcal {I}_{o_M}\otimes K_{Z^M}=\pi _M^{*}(\mathcal {I}_o\otimes K_Z)$
is GV. Hence,
![]() $\mathcal {I}_{o_M}\otimes \mathcal {O}_{Z^M}(M^2t_0L)$
is also GV. This implies that
$\mathcal {I}_{o_M}\otimes \mathcal {O}_{Z^M}(M^2t_0L)$
is also GV. This implies that
![]() $\mathcal {I}_{o,Z}\langle t_0L\rangle $
is GV.
$\mathcal {I}_{o,Z}\langle t_0L\rangle $
is GV.
We shall apply Theorem 2.6 in the following way.
Proposition 2.7. Let
![]() $(A, L)$
be a polarized simple abelian variety. Assume that an effective
$(A, L)$
be a polarized simple abelian variety. Assume that an effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $D\sim _{\mathbb Q}t_0L$
and
$D\sim _{\mathbb Q}t_0L$
and
![]() $\mathrm {lct}(D, o)<\frac {1}{2}$
. Then,
$\mathrm {lct}(D, o)<\frac {1}{2}$
. Then,
![]() $\beta (L)\leq 2\mathrm {lct}(D, o)t_0<t_0$
.
$\beta (L)\leq 2\mathrm {lct}(D, o)t_0<t_0$
.
Proof. We take
![]() $c=\mathrm {lct}(D)$
the global log canonical threshold of D (i.e., c is the maximal rational number such that
$c=\mathrm {lct}(D)$
the global log canonical threshold of D (i.e., c is the maximal rational number such that
![]() $(A, cD)$
is a log canonical pair). Then,
$(A, cD)$
is a log canonical pair). Then,
![]() $c\leq \mathrm {lct}(D, o)<\frac {1}{2}$
. After a small perturbation of
$c\leq \mathrm {lct}(D, o)<\frac {1}{2}$
. After a small perturbation of
![]() $cD$
and taking a translation, we may assume that the log canonical pair
$cD$
and taking a translation, we may assume that the log canonical pair
![]() $(A, cD)$
has only one log canonical center Z, which is thus an irreducible normal subvariety of A and
$(A, cD)$
has only one log canonical center Z, which is thus an irreducible normal subvariety of A and
![]() $o\in Z$
. Therefore, the multiplier ideal sheaf
$o\in Z$
. Therefore, the multiplier ideal sheaf
![]() $\mathcal {J}(A, cD)=\mathcal {I}_Z$
, and by Nadel’s vanishing, we have
$\mathcal {J}(A, cD)=\mathcal {I}_Z$
, and by Nadel’s vanishing, we have
![]() $\mathcal {I}_Z\langle 2ct_0L\rangle $
is IT
$\mathcal {I}_Z\langle 2ct_0L\rangle $
is IT
![]() $^0$
. Since A is simple, a smooth model of Z is of general type.
$^0$
. Since A is simple, a smooth model of Z is of general type.
However, by the main theorem of [Reference Fujino and YoshinoriFG], we know that there exists an effective
![]() $\mathbb Q$
-Weil divisor
$\mathbb Q$
-Weil divisor
![]() $D_Z$
on Z such that
$D_Z$
on Z such that
![]() $K_Z+D_Z$
is
$K_Z+D_Z$
is
![]() $\mathbb Q$
-Cartier and
$\mathbb Q$
-Cartier and
![]() $cD|_Z\sim _{\mathbb Q}K_Z+D_Z$
. Thus, for any rational number
$cD|_Z\sim _{\mathbb Q}K_Z+D_Z$
. Thus, for any rational number
![]() $0<\epsilon \ll 1$
,
$0<\epsilon \ll 1$
,
![]() $(2ct_0+\epsilon )L|_Z\sim _{\mathbb Q} 2(K_Z+D_Z)+\epsilon L|_Z$
. Therefore, by Theorem 2.6,
$(2ct_0+\epsilon )L|_Z\sim _{\mathbb Q} 2(K_Z+D_Z)+\epsilon L|_Z$
. Therefore, by Theorem 2.6,
![]() $ \beta (L)\leq 2ct_0+\epsilon $
for any rational number
$ \beta (L)\leq 2ct_0+\epsilon $
for any rational number
![]() $0<\epsilon \ll 1$
. We then have
$0<\epsilon \ll 1$
. We then have
![]() $\beta (L)\leq 2\mathrm {lct}(D, o)t_0<t_0.$
$\beta (L)\leq 2\mathrm {lct}(D, o)t_0<t_0.$
2.3 Canonical volumes of subvarieties of abelian varieties
Barja, Pardini and Stoppino studied higher dimensional Severi type inequalities for varieties of maximal Albanese dimension in [Reference Barja, Pardini and StoppinoBPS]. One of their main results is the following (see [Reference Barja, Pardini and StoppinoBPS, Corollary 6.12]).
Theorem 2.8. Let
![]() $a: X\rightarrow A$
be a morphism from a smooth projective variety of general type of dimension
$a: X\rightarrow A$
be a morphism from a smooth projective variety of general type of dimension
![]() $d\geq 2$
to an abelian variety A. Assume that
$d\geq 2$
to an abelian variety A. Assume that
![]() $a: X\rightarrow a(X)$
is of degree
$a: X\rightarrow a(X)$
is of degree
![]() $1$
. Then,
$1$
. Then,
![]() $\operatorname {\mathrm {vol}}(K_X)\geq \frac {5}{2}d!\chi (\omega _X) .$
$\operatorname {\mathrm {vol}}(K_X)\geq \frac {5}{2}d!\chi (\omega _X) .$
However, Pareschi and Popa generalized the Castelnuovo-De Franchis inequality in [Reference Pareschi Giuseppe and PopaPP]. The following result is a simple corollary of [Reference Pareschi Giuseppe and PopaPP, Theorem 3.3].
Theorem 2.9. Let
![]() $a: X\rightarrow A$
be a morphism from a smooth projective variety of general type of dimension
$a: X\rightarrow A$
be a morphism from a smooth projective variety of general type of dimension
![]() $d\geq 2$
to an abelian variety A of dimension g. Assume that A is simple and a is generically finite from X onto its image. Then,
$d\geq 2$
to an abelian variety A of dimension g. Assume that A is simple and a is generically finite from X onto its image. Then,
![]() $\chi (\omega _X)\geq g-d$
.
$\chi (\omega _X)\geq g-d$
.
Proof. Since a is generically finite onto its image, we have
and for each
![]() $i\geq 0$
,
$i\geq 0$
,
by Grauert-Riemenschneider vanishing (see for instance [Reference LazarsfeldLaz1, Theorem 4.3.9]. In particular, each irreducible component of
![]() $V^i(a_*\omega _X)$
is a translation of an abelian subvariety of
$V^i(a_*\omega _X)$
is a translation of an abelian subvariety of
![]() $\operatorname {\mathrm {Pic}}^0(A)$
by the main result of [Reference Green and LazarsfeldGL].
$\operatorname {\mathrm {Pic}}^0(A)$
by the main result of [Reference Green and LazarsfeldGL].
However, by the main result of [Reference HaconHac],
![]() $a_*\omega _X$
is GV. Thus,
$a_*\omega _X$
is GV. Thus,
![]() $V^i(a_*\omega _X)$
is a union of translations of proper abelian subvariety of
$V^i(a_*\omega _X)$
is a union of translations of proper abelian subvariety of
![]() $\operatorname {\mathrm {Pic}}^0(A)$
for each
$\operatorname {\mathrm {Pic}}^0(A)$
for each
![]() $i\geq 1$
. Since A is simple by assumption, so is
$i\geq 1$
. Since A is simple by assumption, so is
![]() $\operatorname {\mathrm {Pic}}^0(A)$
. Thus,
$\operatorname {\mathrm {Pic}}^0(A)$
. Thus,
![]() $V^i(a_*\omega _X)$
consists of finitely many points for each
$V^i(a_*\omega _X)$
consists of finitely many points for each
![]() $i\geq 1$
. In particular, the neutral element
$i\geq 1$
. In particular, the neutral element
![]() $\mathcal {O}_A$
is an isolated component of
$\mathcal {O}_A$
is an isolated component of
![]() $V^i(a_*\omega _X)$
for each
$V^i(a_*\omega _X)$
for each
![]() $i\geq 1$
. According to [Reference Pareschi Giuseppe and PopaPP, Definition 3.1], the generic vanishing index of
$i\geq 1$
. According to [Reference Pareschi Giuseppe and PopaPP, Definition 3.1], the generic vanishing index of
![]() $a_*\omega _X$
is
$a_*\omega _X$
is
![]() $g-d$
. By [Reference Pareschi Giuseppe and PopaPP, Theorem 3.3], we have
$g-d$
. By [Reference Pareschi Giuseppe and PopaPP, Theorem 3.3], we have
![]() $\chi (\omega _X)=\chi (a_*\omega _X)\geq g-d $
.
$\chi (\omega _X)=\chi (a_*\omega _X)\geq g-d $
.
Remark 2.10. In [Reference Lazarsfeld Robert and PopaLP], Lazarsfeld and Popa conjectured that under that assumption of Theorem 2.9,
![]() $\chi (\omega _X)> g-d$
when g is large compared to
$\chi (\omega _X)> g-d$
when g is large compared to
![]() $\chi (\omega _X)$
. Coandă verified that
$\chi (\omega _X)$
. Coandă verified that
![]() $\chi (\omega _X)\geq 3$
when
$\chi (\omega _X)\geq 3$
when
![]() $g\geq 5$
and
$g\geq 5$
and
![]() $g-d=2$
([Reference Lazarsfeld Robert and PopaLP, Proposition 4.10])
$g-d=2$
([Reference Lazarsfeld Robert and PopaLP, Proposition 4.10])
Combining Theorem 2.8 and 2.9, we have an estimation of the canonical volume of irreducible subvarieties of simple abelian varieties.
Corollary 2.11. Let Z be an irreducible subvariety of dimension d of a simple abelian variety A of dimension g. Let
![]() $\rho : X\rightarrow Z$
be a desingularization. Then,
$\rho : X\rightarrow Z$
be a desingularization. Then,
![]() $\operatorname {\mathrm {vol}}(K_X)\geq \frac {5}{2}d!(g-d)$
.
$\operatorname {\mathrm {vol}}(K_X)\geq \frac {5}{2}d!(g-d)$
.
When X is a surface, we can slightly improve Theorem 2.8.
Proposition 2.12. Let
![]() $a: S\rightarrow A$
be a morphism from a smooth projective surface of general type to an abelian variety A of dimension
$a: S\rightarrow A$
be a morphism from a smooth projective surface of general type to an abelian variety A of dimension
![]() $g\geq 3$
. Assume that
$g\geq 3$
. Assume that
![]() $a: S\rightarrow a(S)$
is of degree
$a: S\rightarrow a(S)$
is of degree
![]() $1$
. Then,
$1$
. Then,
![]() $\operatorname {\mathrm {vol}}(K_S)\geq 5\chi (\omega _S)+1$
.
$\operatorname {\mathrm {vol}}(K_S)\geq 5\chi (\omega _S)+1$
.
Proof. We follow the proof of [Reference Barja, Pardini and StoppinoBPS, Theorem 5.5 and Corollary 5.6], where it was proved that
![]() $\operatorname {\mathrm {vol}}(K_S)\geq 5\chi (\omega _S)$
. It suffices to show that the equality can never hold.
$\operatorname {\mathrm {vol}}(K_S)\geq 5\chi (\omega _S)$
. It suffices to show that the equality can never hold.
We may assume that S is minimal and
![]() $a^*: \operatorname {\mathrm {Pic}}^0(A)\rightarrow \operatorname {\mathrm {Pic}}^0(S)$
is injective.
$a^*: \operatorname {\mathrm {Pic}}^0(A)\rightarrow \operatorname {\mathrm {Pic}}^0(S)$
is injective.
Fix an ample divisor H on A. Following [Reference Barja, Pardini and StoppinoBPS], we consider the continuous rank functions:
![]() $F(t):=h^0_a(A, a_*\omega _S\otimes H^t)$
and
$F(t):=h^0_a(A, a_*\omega _S\otimes H^t)$
and
![]() $G(t):=h^0_a(A, a_*(\omega _S^{\otimes 2})\otimes H^{2t})$
. By definition, continuous rank functions are the
$G(t):=h^0_a(A, a_*(\omega _S^{\otimes 2})\otimes H^{2t})$
. By definition, continuous rank functions are the
![]() $0$
-th cohomological rank functions. Thus, in our terminology,
$0$
-th cohomological rank functions. Thus, in our terminology,
![]() $F(t)=h^0_{a_*\omega _S, H}(t)$
and
$F(t)=h^0_{a_*\omega _S, H}(t)$
and
![]() $G(t)=h^0_{a_*(\omega _S^{\otimes 2}), H}(2t)$
.
$G(t)=h^0_{a_*(\omega _S^{\otimes 2}), H}(2t)$
.
Following the proof in [Reference Barja, Pardini and StoppinoBPS, Theorem 5.5], we know that
![]() $D^{-1}G(t)\geq 6 D^{-1}F(t)$
for
$D^{-1}G(t)\geq 6 D^{-1}F(t)$
for
![]() $t\leq 0$
, where
$t\leq 0$
, where
![]() $D^{-1}G(t)$
and
$D^{-1}G(t)$
and
![]() $D^{-1}F(t)$
are, respectively, the left derivative of the functions F and G at t. We also observe that
$D^{-1}F(t)$
are, respectively, the left derivative of the functions F and G at t. We also observe that
![]() $G(t)=F(t)=0$
when
$G(t)=F(t)=0$
when
![]() $t\ll 0$
. Hence, if
$t\ll 0$
. Hence, if
![]() $G(0)=6F(0)$
(i.e.,
$G(0)=6F(0)$
(i.e.,
![]() $\operatorname {\mathrm {vol}}(K_S)= 5\chi (\omega _S)$
),
$\operatorname {\mathrm {vol}}(K_S)= 5\chi (\omega _S)$
),
![]() $G(t)=6F(t)$
for all
$G(t)=6F(t)$
for all
![]() $t\leq 0$
.
$t\leq 0$
.
Since
![]() $a_*(\omega _S^{\otimes 2})$
is an IT
$a_*(\omega _S^{\otimes 2})$
is an IT
![]() $^0$
sheaf on A, for
$^0$
sheaf on A, for
![]() $-1\ll t<0$
,
$-1\ll t<0$
,
![]() $a_*(\omega _S^{\otimes 2})\langle 2tH\rangle $
remains to be IT
$a_*(\omega _S^{\otimes 2})\langle 2tH\rangle $
remains to be IT
![]() $^0$
(see [Reference Jiang and PareschiJP, Theorem 5.2]). Thus,
$^0$
(see [Reference Jiang and PareschiJP, Theorem 5.2]). Thus,
is a degree
![]() $2 $
polynomial function for
$2 $
polynomial function for
![]() $-1\ll t<0.$
$-1\ll t<0.$
However,
 $$ \begin{align*} F(t)&=\chi(S, K_S+tH)+h^1_{a_*\omega_S, H}(t)-h^2_{a_*\omega_S, H}(t)\\ &=\frac{1}{2}(H^2)_St^2+\frac{1}{2}(K_S\cdot H)_St+\chi(\omega_S)+h^1_{a_*\omega_S, H}(t)\\ &\quad - h^2_{a_*\omega_S, H}(t). \end{align*} $$
$$ \begin{align*} F(t)&=\chi(S, K_S+tH)+h^1_{a_*\omega_S, H}(t)-h^2_{a_*\omega_S, H}(t)\\ &=\frac{1}{2}(H^2)_St^2+\frac{1}{2}(K_S\cdot H)_St+\chi(\omega_S)+h^1_{a_*\omega_S, H}(t)\\ &\quad - h^2_{a_*\omega_S, H}(t). \end{align*} $$
We recall the formula in [Reference Jiang and PareschiJP, Proposition 2.3]:
for
![]() $-1\ll t<0.$
$-1\ll t<0.$
Since
![]() $a^*: \operatorname {\mathrm {Pic}}^0(A)\rightarrow \operatorname {\mathrm {Pic}}^0(S)$
is injective, we know that
$a^*: \operatorname {\mathrm {Pic}}^0(A)\rightarrow \operatorname {\mathrm {Pic}}^0(S)$
is injective, we know that
![]() $R^2\Phi _{\mathcal {P}}(a_*\omega _S)$
is the skyscraper sheaf at
$R^2\Phi _{\mathcal {P}}(a_*\omega _S)$
is the skyscraper sheaf at
![]() $o_{\hat {A}}$
. Hence,
$o_{\hat {A}}$
. Hence,
![]() $h^2_{a_*\omega _S, H}(t)=\chi (H)(-t)^g$
for
$h^2_{a_*\omega _S, H}(t)=\chi (H)(-t)^g$
for
![]() $-1\ll t<0.$
$-1\ll t<0.$
Similarly, since S is of general type,
![]() $a_*\omega _S$
is a M-regular sheaf on A (see Subsection 2.3). Then,
$a_*\omega _S$
is a M-regular sheaf on A (see Subsection 2.3). Then,
![]() $\operatorname {\mathrm {codim}}_{\operatorname {\mathrm {Pic}}^0(A)}V^1(a_*\omega _S)\geq 2$
. We also know that the support of
$\operatorname {\mathrm {codim}}_{\operatorname {\mathrm {Pic}}^0(A)}V^1(a_*\omega _S)\geq 2$
. We also know that the support of
![]() $R^1\Phi _{\mathcal {P}}(a_*\omega _S)$
is contained in
$R^1\Phi _{\mathcal {P}}(a_*\omega _S)$
is contained in
![]() $V^1(a_*\omega _S)$
. Consider the Chern characters of
$V^1(a_*\omega _S)$
. Consider the Chern characters of
![]() $R^1\Phi _{\mathcal {P}}(a_*\omega _S)$
. We have
$R^1\Phi _{\mathcal {P}}(a_*\omega _S)$
. We have
![]() $\mathrm {ch}_i(\varphi _H^*R^1\Phi _{\mathcal {P}}(a_*\omega _S))=0\in H^{2i}(A, \mathbb Q)$
for
$\mathrm {ch}_i(\varphi _H^*R^1\Phi _{\mathcal {P}}(a_*\omega _S))=0\in H^{2i}(A, \mathbb Q)$
for
![]() $i=0, 1$
. If the codimension of the support of
$i=0, 1$
. If the codimension of the support of
![]() $R^1\Phi _{\mathcal {P}}(a_*\omega _S)$
is equal to
$R^1\Phi _{\mathcal {P}}(a_*\omega _S)$
is equal to
![]() $2$
, we may assume that
$2$
, we may assume that
![]() $\mathcal {Z}_1,\ldots , \mathcal {Z}_s$
are the codimension-
$\mathcal {Z}_1,\ldots , \mathcal {Z}_s$
are the codimension-
![]() $2$
components of its support and
$2$
components of its support and
![]() $a_i>0$
is the rank of
$a_i>0$
is the rank of
![]() $R^1\Phi _{\mathcal {P}}(a_*\omega _S)$
at the generic point of
$R^1\Phi _{\mathcal {P}}(a_*\omega _S)$
at the generic point of
![]() $\mathcal {Z}_i$
. Then,
$\mathcal {Z}_i$
. Then,
![]() $\mathrm {ch}_2(\varphi _H^*R^1\Phi _{\mathcal {P}}(a_*\omega _S))=\sum _ia_i[\varphi _H^{-1}\mathcal {Z}_i]$
. Hence,
$\mathrm {ch}_2(\varphi _H^*R^1\Phi _{\mathcal {P}}(a_*\omega _S))=\sum _ia_i[\varphi _H^{-1}\mathcal {Z}_i]$
. Hence,
 $$ \begin{align*}h^1_{a_*\omega_S, H}(t)=\alpha_{2}t^2+\sum_{3\leq i\leq g}\alpha_it^i\end{align*} $$
$$ \begin{align*}h^1_{a_*\omega_S, H}(t)=\alpha_{2}t^2+\sum_{3\leq i\leq g}\alpha_it^i\end{align*} $$
for
![]() $-1\ll t<0,$
where
$-1\ll t<0,$
where
![]() $\alpha _2\geq 0$
.
$\alpha _2\geq 0$
.
We compare the coefficient of
![]() $t^2$
for
$t^2$
for
![]() $F(t)$
and
$F(t)$
and
![]() $G(t)$
, which are, respectively,
$G(t)$
, which are, respectively,
![]() $\frac {1}{2}(H^2)_S+\alpha _2$
and
$\frac {1}{2}(H^2)_S+\alpha _2$
and
![]() $2(H^2)_S$
and conclude that
$2(H^2)_S$
and conclude that
![]() $G(t)\neq 6F(t)$
.
$G(t)\neq 6F(t)$
.
The following corollary seems to be new, and it would be interesting to characterize the surfaces where the equality holds.
Corollary 2.13. Let Z be a smooth projective surface of general type. Assume that
![]() $q(Z)\geq 4$
and Z is of maximal Albanese dimension, and either Z is birational to a product of two smooth projective curves of genus
$q(Z)\geq 4$
and Z is of maximal Albanese dimension, and either Z is birational to a product of two smooth projective curves of genus
![]() $2$
or
$2$
or
![]() $\operatorname {\mathrm {vol}}(Z, K_Z)\geq 16$
.
$\operatorname {\mathrm {vol}}(Z, K_Z)\geq 16$
.
Proof. We first assume that Z is a minimal surface of general type. Then,
![]() $\chi (\omega _Z)\geq 1$
and
$\chi (\omega _Z)\geq 1$
and
![]() $\operatorname {\mathrm {vol}}(Z, K_Z)=K_Z^2>0$
.
$\operatorname {\mathrm {vol}}(Z, K_Z)=K_Z^2>0$
.
When
![]() $\chi (\omega _Z)=1$
, by the main result of [Reference Hacon and PardiniHP] (see also [Reference Jiang, Lahoz and TirabassiJLT]) and the assumption that
$\chi (\omega _Z)=1$
, by the main result of [Reference Hacon and PardiniHP] (see also [Reference Jiang, Lahoz and TirabassiJLT]) and the assumption that
![]() $q(Z)\geq 4$
, we know that
$q(Z)\geq 4$
, we know that
![]() $q(Z)=4$
and Z is birational to a product of two smooth projective curves of genus
$q(Z)=4$
and Z is birational to a product of two smooth projective curves of genus
![]() $2$
.
$2$
.
We now consider the case
![]() $\chi (\omega _{Z})= 2$
and
$\chi (\omega _{Z})= 2$
and
![]() $q(Z)\geq 4$
. When
$q(Z)\geq 4$
. When
![]() $q(Z)\geq 5$
, then
$q(Z)\geq 5$
, then
![]() $\chi (\omega _Z)<q(Z)-2$
. By the Castelnuovo-de Francis theorem (see, for instance, [Reference Pareschi Giuseppe and PopaPP, Theorem A]), there exists a fibration
$\chi (\omega _Z)<q(Z)-2$
. By the Castelnuovo-de Francis theorem (see, for instance, [Reference Pareschi Giuseppe and PopaPP, Theorem A]), there exists a fibration
![]() $f: Z\rightarrow C$
from Z to a smooth projective curve of genus
$f: Z\rightarrow C$
from Z to a smooth projective curve of genus
![]() $\geq 2$
. We denote by F a general fiber of f. Then,
$\geq 2$
. We denote by F a general fiber of f. Then,
![]() $g(C)+g(F)\geq q(Z)\geq 5$
(see, for instance, [Reference DebarreD2, the Lemme in the appendix]). We then have
$g(C)+g(F)\geq q(Z)\geq 5$
(see, for instance, [Reference DebarreD2, the Lemme in the appendix]). We then have
(see, for instance, [Reference DebarreD2, the Corollaire in the appendix]). When
![]() $q(Z)=4$
, then
$q(Z)=4$
, then
![]() $p_g(Z)=5$
. By the main result of [Reference Barja, Naranjo and PirolaBNP], we have
$p_g(Z)=5$
. By the main result of [Reference Barja, Naranjo and PirolaBNP], we have
![]() $16\leq \operatorname {\mathrm {vol}}(Z, K_Z)\leq 18$
.
$16\leq \operatorname {\mathrm {vol}}(Z, K_Z)\leq 18$
.
When
![]() $\chi (\omega _Z)\geq 3$
, let
$\chi (\omega _Z)\geq 3$
, let
![]() $Z'$
be the smooth minimal model of the Albanese image
$Z'$
be the smooth minimal model of the Albanese image
![]() $a_Z(Z)$
. After birational modifications of Z, we have the factorization of the Albanese morphism of Z
$a_Z(Z)$
. After birational modifications of Z, we have the factorization of the Albanese morphism of Z
where
![]() $\rho $
is birational.
$\rho $
is birational.
If
![]() $a_Z$
is birational onto its image, we apply Proposition 2.12 to conclude that
$a_Z$
is birational onto its image, we apply Proposition 2.12 to conclude that
We then assume that
![]() $\deg \tau>1$
. If
$\deg \tau>1$
. If
![]() $Z'$
is of general type, we have
$Z'$
is of general type, we have
![]() $\operatorname {\mathrm {vol}}(Z, K_Z)\geq (\deg \tau ) K_{Z'}^2\geq 2(K_{Z'}^2)$
by the ramification formula. By the previous discussions, we have already seen that either
$\operatorname {\mathrm {vol}}(Z, K_Z)\geq (\deg \tau ) K_{Z'}^2\geq 2(K_{Z'}^2)$
by the ramification formula. By the previous discussions, we have already seen that either
![]() $Z'$
is birational to a product of two smooth projective curves of genus
$Z'$
is birational to a product of two smooth projective curves of genus
![]() $2$
or
$2$
or
![]() $K_{Z'}^2\geq 16$
. In either case,
$K_{Z'}^2\geq 16$
. In either case,
![]() $\operatorname {\mathrm {vol}}(Z, K_Z)\geq 16$
. Finally, we consider the case that
$\operatorname {\mathrm {vol}}(Z, K_Z)\geq 16$
. Finally, we consider the case that
![]() $Z'$
is not of general type. Since
$Z'$
is not of general type. Since
![]() $a_Z(Z)$
generates
$a_Z(Z)$
generates
![]() $A_Z$
, we see easily that
$A_Z$
, we see easily that
![]() $\rho $
is an isomorphism and
$\rho $
is an isomorphism and
![]() $Z'$
is fibred by an elliptic curve E in
$Z'$
is fibred by an elliptic curve E in
![]() $A_Z$
, and the quotient
$A_Z$
, and the quotient
![]() $C':=Z'/E$
is a smooth projective curve of genus
$C':=Z'/E$
is a smooth projective curve of genus
![]() $\geq q(Z)-1\geq 3$
. We then have a surjective morphism
$\geq q(Z)-1\geq 3$
. We then have a surjective morphism
![]() $Z\rightarrow C'$
from Z to
$Z\rightarrow C'$
from Z to
![]() $C'$
. We conclude again by [Reference DebarreD2, the Corollaire in the appendix] that
$C'$
. We conclude again by [Reference DebarreD2, the Corollaire in the appendix] that
![]() $\operatorname {\mathrm {vol}}(Z, K_Z)\geq 16$
.
$\operatorname {\mathrm {vol}}(Z, K_Z)\geq 16$
.
2.4 Intersections with abelian subvarieties
When we apply Ito’s approach to study basepoint freeness thresholds of polarized abelian varieties
![]() $(A, L)$
, it may happen that the log canonical center Z of a pair
$(A, L)$
, it may happen that the log canonical center Z of a pair
![]() $(A, D)$
is an abelian subvariety of A or is a subvariety fibred by an abelian subvariety of A.
$(A, D)$
is an abelian subvariety of A or is a subvariety fibred by an abelian subvariety of A.
Ito realized that one can deal with these cases with Poincaré’s reducibility theorem for polarized abelian varieties. When Z is an abelian subvariety, we have the following result [Reference ItoIto2, Proposition 6.6].
Proposition 2.14. Let
![]() $(A, L) $
be a polarized abelian variety. Assume that there exists an effective
$(A, L) $
be a polarized abelian variety. Assume that there exists an effective
![]() $\mathbb Q$
-divisor D such that an abelian subvariety B is an irreducible component of
$\mathbb Q$
-divisor D such that an abelian subvariety B is an irreducible component of
![]() $\mathrm {Nklt}(A, D)$
and
$\mathrm {Nklt}(A, D)$
and
![]() $tL-D$
is an ample
$tL-D$
is an ample
![]() $\mathbb Q$
-divisor. Assume, furthermore, that
$\mathbb Q$
-divisor. Assume, furthermore, that
![]() $\beta (L|_B)<t$
. Then,
$\beta (L|_B)<t$
. Then,
![]() $\beta (L)<t$
.
$\beta (L)<t$
.
When Z is fibred by an abelian subvariety B, it is important to estimate the intersection number
![]() $(L^{\dim B}\cdot B)$
. The author learned the following result from a private communication with Atsushi Ito.
$(L^{\dim B}\cdot B)$
. The author learned the following result from a private communication with Atsushi Ito.
Lemma 2.15. Let D be an ample
![]() $\mathbb Q$
-divisor on A and let B be a abelian subvariety of A of dimension d. Let
$\mathbb Q$
-divisor on A and let B be a abelian subvariety of A of dimension d. Let
![]() $\varphi : A\rightarrow A/B$
be the quotient morphism. Then, there exists an ample
$\varphi : A\rightarrow A/B$
be the quotient morphism. Then, there exists an ample
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $H_B$
on
$H_B$
on
![]() $A/B$
such that
$A/B$
such that
![]() $D-\varphi ^*H_B$
is a nef
$D-\varphi ^*H_B$
is a nef
![]() $\mathbb Q$
-divisor and
$\mathbb Q$
-divisor and
![]() $D^g=\binom {g}{d}(D^d\cdot B)(H_B^{g-d})_{A/B}$
.
$D^g=\binom {g}{d}(D^d\cdot B)(H_B^{g-d})_{A/B}$
.
Proof. Let M be a positive sufficiently divisible integer such that
![]() $MD$
is an integral divisor and
$MD$
is an integral divisor and
![]() $L=\mathcal {O}_A(MD)$
is an ample line bundle on A. By Poincaré’s reducibility (see, for instance, [Reference Birkenhake and LangeBL, Corollary 5.3.6]), there exists an abelian subvariety K of A such that the natural morphism
$L=\mathcal {O}_A(MD)$
is an ample line bundle on A. By Poincaré’s reducibility (see, for instance, [Reference Birkenhake and LangeBL, Corollary 5.3.6]), there exists an abelian subvariety K of A such that the natural morphism
![]() $K\rightarrow A/B$
is an isogeny and the addition morphism
$K\rightarrow A/B$
is an isogeny and the addition morphism
![]() $\pi : K\times B\rightarrow A$
induces an isogeny of polarized abelian varieties
$\pi : K\times B\rightarrow A$
induces an isogeny of polarized abelian varieties
![]() $(K, L_K)\times (B, L_B)\rightarrow (A, L)$
, where
$(K, L_K)\times (B, L_B)\rightarrow (A, L)$
, where
![]() $L_K$
and
$L_K$
and
![]() $L_B$
are, respectively, the restriction of L on K and B. Then, one can consider the natural isogeny
$L_B$
are, respectively, the restriction of L on K and B. Then, one can consider the natural isogeny
![]() $\mu _K: K\rightarrow A/B$
. Note that
$\mu _K: K\rightarrow A/B$
. Note that
![]() $L|_K$
cannot descend to
$L|_K$
cannot descend to
![]() $A/B$
in general, but there exists an effective
$A/B$
in general, but there exists an effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $D_B$
on
$D_B$
on
![]() $A/B$
such that
$A/B$
such that
![]() $L|_K$
is algebraically equivalent to
$L|_K$
is algebraically equivalent to
![]() $\mu _K^*D_B$
as
$\mu _K^*D_B$
as
![]() $\mathbb Q$
-divisors. Let
$\mathbb Q$
-divisors. Let
![]() $H_B=\frac {1}{M}D_B$
, and it is easy to check that
$H_B=\frac {1}{M}D_B$
, and it is easy to check that
![]() $H_B$
satisfies the desired properties.
$H_B$
satisfies the desired properties.
Corollary 2.16. Let
![]() $(A, L)$
be a polarized abelian variety of dimension g with
$(A, L)$
be a polarized abelian variety of dimension g with
![]() $n(L)<\frac {1}{p+2}$
. Assume that Conjecture 1.4 holds in dimension
$n(L)<\frac {1}{p+2}$
. Assume that Conjecture 1.4 holds in dimension
![]() $\leq g-1$
. Let
$\leq g-1$
. Let
![]() $D=\frac {1}{p+2}L$
. Then, either
$D=\frac {1}{p+2}L$
. Then, either
 $$ \begin{align} (D^d\cdot B)\geq \frac{(D^g)}{\binom{g}{d}(g-d)^{g-d}} \end{align} $$
$$ \begin{align} (D^d\cdot B)\geq \frac{(D^g)}{\binom{g}{d}(g-d)^{g-d}} \end{align} $$
for all abelian subvariety B of dimension
![]() $1\leq d\leq g-1$
or
$1\leq d\leq g-1$
or
![]() $\beta (L)<\frac {1}{p+2}$
.
$\beta (L)<\frac {1}{p+2}$
.
Remark 2.17. Let
![]() $0<d<g$
be positive integers. Then,
$0<d<g$
be positive integers. Then,
 $$ \begin{align*}\frac{g^g}{d^d\binom{g}{d}}>(g-d)^{g-d}.\end{align*} $$
$$ \begin{align*}\frac{g^g}{d^d\binom{g}{d}}>(g-d)^{g-d}.\end{align*} $$
More precisely, by Stirling’s formula, for any positive integer n, we have
Thus,
 $$ \begin{align*}\frac{g^g}{d^d\binom{g}{d}}>(g-d)^{g-d}\sqrt{\frac{2\pi d(g-d)}{g}}.\end{align*} $$
$$ \begin{align*}\frac{g^g}{d^d\binom{g}{d}}>(g-d)^{g-d}\sqrt{\frac{2\pi d(g-d)}{g}}.\end{align*} $$
Proof. If the inequalities (2) fail for some abelian subvarieties, we pick B such that
![]() $\dim B=d$
is maximal and
$\dim B=d$
is maximal and
![]() $(D^d\cdot B)< \frac {(D^g)}{\binom {g}{d}(g-d)^{g-d}}$
. By Lemma 2.15, there exists an ample
$(D^d\cdot B)< \frac {(D^g)}{\binom {g}{d}(g-d)^{g-d}}$
. By Lemma 2.15, there exists an ample
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $H_{B}$
such that
$H_{B}$
such that
![]() $D-\varphi ^*H_{B}$
is a nef
$D-\varphi ^*H_{B}$
is a nef
![]() $\mathbb Q$
-divisor and
$\mathbb Q$
-divisor and
 $$ \begin{align*}(H_{B}^{g-d})_{A/B}=\frac{(D^g)}{\binom{g}{d}(D^d\cdot B)}>(g-d)^{g-d}.\end{align*} $$
$$ \begin{align*}(H_{B}^{g-d})_{A/B}=\frac{(D^g)}{\binom{g}{d}(D^d\cdot B)}>(g-d)^{g-d}.\end{align*} $$
Moreover, by the argument of Lemma 2.15, for each abelian subvariety C of
![]() $A/B$
of dimension
$A/B$
of dimension
![]() $r>0$
,
$r>0$
,
![]() $(H_{B}^r\cdot C)_{A/B}=\frac {(D^{d+r}\cdot \varphi ^{-1}(C))}{\binom {d+r}{d}(D^d\cdot B)}$
. By the maximality of B, we conclude that
$(H_{B}^r\cdot C)_{A/B}=\frac {(D^{d+r}\cdot \varphi ^{-1}(C))}{\binom {d+r}{d}(D^d\cdot B)}$
. By the maximality of B, we conclude that
 $$ \begin{align*} (H_{B}^r\cdot C)_{A/B}=\frac{(D^{d+r}\cdot \varphi^{-1}(C))}{\binom{d+r}{d}(D^d\cdot B)}>\qquad &\frac{ \binom{g}{d}(g-d)^{g-d}}{\binom{d+r}{d}\binom{g}{d+r}(g-d-r)^{g-d-r}}\\ &=\frac{ (g-d)^{g-d}}{(g-d-r)^{g-d-r}\binom{g-d}{r}}\\ & >r^r. \end{align*} $$
$$ \begin{align*} (H_{B}^r\cdot C)_{A/B}=\frac{(D^{d+r}\cdot \varphi^{-1}(C))}{\binom{d+r}{d}(D^d\cdot B)}>\qquad &\frac{ \binom{g}{d}(g-d)^{g-d}}{\binom{d+r}{d}\binom{g}{d+r}(g-d-r)^{g-d-r}}\\ &=\frac{ (g-d)^{g-d}}{(g-d-r)^{g-d-r}\binom{g-d}{r}}\\ & >r^r. \end{align*} $$
Since Conjecture 1.4 holds in dimension
![]() $g-d$
,
$g-d$
,
![]() $\mathcal {I}_{o_{A/B}}\langle (1-\epsilon )H_B\rangle $
is GV for some
$\mathcal {I}_{o_{A/B}}\langle (1-\epsilon )H_B\rangle $
is GV for some
![]() $0<\epsilon \ll 1$
. Thus,
$0<\epsilon \ll 1$
. Thus,
![]() $\mathcal {I}_B\langle (1-\epsilon )\varphi ^*H_B\rangle $
is also GV. Since
$\mathcal {I}_B\langle (1-\epsilon )\varphi ^*H_B\rangle $
is also GV. Since
![]() $D-\varphi ^*H_B$
is a nef
$D-\varphi ^*H_B$
is a nef
![]() $\mathbb Q$
-divisor,
$\mathbb Q$
-divisor,
![]() $\mathcal {I}_B\langle (1-\epsilon )D\rangle $
is GV. We then consider the short exact sequence
$\mathcal {I}_B\langle (1-\epsilon )D\rangle $
is GV. We then consider the short exact sequence
Since by the assumption that Conjecture 1.4 holds in dimension d,
![]() $\mathcal {I}_{o, B}\langle (1-\epsilon )D\rangle $
is also GV and hence,
$\mathcal {I}_{o, B}\langle (1-\epsilon )D\rangle $
is also GV and hence,
![]() $\mathcal {I}_o\langle (1-\epsilon )D\rangle $
is GV. Thus,
$\mathcal {I}_o\langle (1-\epsilon )D\rangle $
is GV. Thus,
![]() $\beta (L)<\frac {1}{p+2}$
.
$\beta (L)<\frac {1}{p+2}$
.
Lemma 2.18. Let D be an effective ample
![]() $\mathbb Q$
-divisor on an abelian variety A. Assume that
$\mathbb Q$
-divisor on an abelian variety A. Assume that
![]() $(A, D)$
is log canonical at o, and the minimal log canonical center Z through o is a subvariety of dimension d fibred by an abelian subvariety B of dimension
$(A, D)$
is log canonical at o, and the minimal log canonical center Z through o is a subvariety of dimension d fibred by an abelian subvariety B of dimension
![]() $d'$
such that the desingularization of
$d'$
such that the desingularization of
![]() $Z/B$
is of general type. Then,
$Z/B$
is of general type. Then,
 $$ \begin{align*}(D^d\cdot Z)\geq \binom{d}{d'}(D^{d'}\cdot B)\operatorname{\mathrm{vol}}(K_{(Z/B)'}),\end{align*} $$
$$ \begin{align*}(D^d\cdot Z)\geq \binom{d}{d'}(D^{d'}\cdot B)\operatorname{\mathrm{vol}}(K_{(Z/B)'}),\end{align*} $$
where
![]() $(Z/B)'$
is a smooth model of the quotient
$(Z/B)'$
is a smooth model of the quotient
![]() $Z/B$
.
$Z/B$
.
Proof. We consider the quotient morphism
![]() $A\rightarrow A/B$
. We may assume that
$A\rightarrow A/B$
. We may assume that
![]() $MD$
is an integral divisor corresponding to a line bundle L for some integer
$MD$
is an integral divisor corresponding to a line bundle L for some integer
![]() $M>0$
. By Poincaré’s reducibility theorem (see, for instance, [Reference Birkenhake and LangeBL, Corollary 5.3.6]), there exists an abelian subvariety K of A such that the natural morphism
$M>0$
. By Poincaré’s reducibility theorem (see, for instance, [Reference Birkenhake and LangeBL, Corollary 5.3.6]), there exists an abelian subvariety K of A such that the natural morphism
![]() $K\rightarrow A/B$
is an isogeny, and the addition morphism
$K\rightarrow A/B$
is an isogeny, and the addition morphism
![]() $\pi : K\times B\rightarrow A$
induces an isogeny of polarized abelian varieties
$\pi : K\times B\rightarrow A$
induces an isogeny of polarized abelian varieties
![]() $(K, L_K)\times (B, L_B)\rightarrow (A, L)$
, where
$(K, L_K)\times (B, L_B)\rightarrow (A, L)$
, where
![]() $L_K$
and
$L_K$
and
![]() $L_B$
are, respectively, the restriction of L on K and B.
$L_B$
are, respectively, the restriction of L on K and B.
Note that
![]() $\tilde {Z}:=Z\times _A(K\times B)$
is isomorphic to the product
$\tilde {Z}:=Z\times _A(K\times B)$
is isomorphic to the product
![]() $\tilde {Z/B}\times B$
, where
$\tilde {Z/B}\times B$
, where
![]() $\tilde {Z/B}=(Z/B)\times _{A/B}K$
. Thus,
$\tilde {Z/B}=(Z/B)\times _{A/B}K$
. Thus,
 $$ \begin{align*} (D^d\cdot Z)&=\frac{1}{M^d}(L^d\cdot Z)=\frac{1}{M^d\deg\pi}((L_K\boxtimes L_B)^d\cdot\tilde{Z})\\ &=\frac{1}{M^d\deg\pi}\big((L_K\boxtimes L_B)^d\cdot(\tilde{Z/B}\times B)\big)\\ &=\frac{\binom{d}{d'}}{M^{d-d'}\deg\pi}(D^{d'}\cdot B)(L_K^{d-d'}\cdot \tilde{Z/B}). \end{align*} $$
$$ \begin{align*} (D^d\cdot Z)&=\frac{1}{M^d}(L^d\cdot Z)=\frac{1}{M^d\deg\pi}((L_K\boxtimes L_B)^d\cdot\tilde{Z})\\ &=\frac{1}{M^d\deg\pi}\big((L_K\boxtimes L_B)^d\cdot(\tilde{Z/B}\times B)\big)\\ &=\frac{\binom{d}{d'}}{M^{d-d'}\deg\pi}(D^{d'}\cdot B)(L_K^{d-d'}\cdot \tilde{Z/B}). \end{align*} $$
Let
![]() $\nu : \overline {Z}\rightarrow Z$
be its normalization. By Proposition 2.1,
$\nu : \overline {Z}\rightarrow Z$
be its normalization. By Proposition 2.1,
![]() $\nu ^*D\sim _{\mathbb Q}K_{\overline {Z}}+V_{\overline {Z}}$
for some effective
$\nu ^*D\sim _{\mathbb Q}K_{\overline {Z}}+V_{\overline {Z}}$
for some effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $V_{\overline {Z}}$
. Consider the pullback of this
$V_{\overline {Z}}$
. Consider the pullback of this
![]() $\mathbb Q$
-linear equivalence on the normalization
$\mathbb Q$
-linear equivalence on the normalization
![]() $ \overline {\tilde {Z}}$
of
$ \overline {\tilde {Z}}$
of
![]() $\tilde {Z}$
and then restricting it to a general fiber of
$\tilde {Z}$
and then restricting it to a general fiber of
![]() $ \overline {\tilde {Z}}\rightarrow B$
. We see that
$ \overline {\tilde {Z}}\rightarrow B$
. We see that
![]() $\varsigma ^*(\frac {1}{M}L_{K})\sim _{\mathbb Q}K_{\widehat {Z/B}}+V_{\widehat {Z/B}} $
, where
$\varsigma ^*(\frac {1}{M}L_{K})\sim _{\mathbb Q}K_{\widehat {Z/B}}+V_{\widehat {Z/B}} $
, where
![]() $\varsigma :\widehat {Z/B}\rightarrow \tilde {Z/B}$
is the normalization and
$\varsigma :\widehat {Z/B}\rightarrow \tilde {Z/B}$
is the normalization and
![]() $V_{\widehat {Z/B}}$
is an effective
$V_{\widehat {Z/B}}$
is an effective
![]() $\mathbb Q$
-divisor on
$\mathbb Q$
-divisor on
![]() $\widehat {Z/B}$
. Thus,
$\widehat {Z/B}$
. Thus,
![]() $(L_K^{d-d'}\cdot \tilde {Z/B})= M^{d-d'}\operatorname {\mathrm {vol}}(\widehat {Z/B}, K_{\widehat {Z/B}}+V_{\widehat {Z/B}})\geq (\deg \pi )M^{d-d'}\operatorname {\mathrm {vol}}(K_{(Z/B)'})$
.
$(L_K^{d-d'}\cdot \tilde {Z/B})= M^{d-d'}\operatorname {\mathrm {vol}}(\widehat {Z/B}, K_{\widehat {Z/B}}+V_{\widehat {Z/B}})\geq (\deg \pi )M^{d-d'}\operatorname {\mathrm {vol}}(K_{(Z/B)'})$
.
3 Very general polarized abelian varieties
In [Reference JiangJz], we applied Helmke’s induction to confirm that Conjecture 1.4 holds for Hodge theoretically very general polarized abelian varieties with special polarizations. We now show that the calculation indeed implies that Conjecture 1.4 holds for almost all generic polarized abelian varieties in fixed dimensions.
Recall that we say a polarized abelian variety
![]() $(A, L)$
is Hodge theoretically very general if
$(A, L)$
is Hodge theoretically very general if
![]() $\dim _{\mathbb Q}H^{k,k}(A, \mathbb Q)=1$
for all
$\dim _{\mathbb Q}H^{k,k}(A, \mathbb Q)=1$
for all
![]() $1\leq k\leq g-1$
. We observe that by Hard Lefschetz and Poincaré duality,
$1\leq k\leq g-1$
. We observe that by Hard Lefschetz and Poincaré duality,
![]() $(A, L)$
is Hodge theoretically very general iff
$(A, L)$
is Hodge theoretically very general iff
![]() $\dim _{\mathbb Q}H^{\lfloor \frac {g}{2}\rfloor ,\lfloor \frac {g}{2}\rfloor }(A, \mathbb Q)=1$
. We also observe that when
$\dim _{\mathbb Q}H^{\lfloor \frac {g}{2}\rfloor ,\lfloor \frac {g}{2}\rfloor }(A, \mathbb Q)=1$
. We also observe that when
![]() $(A, L)$
is Hodge theoretically very general, A is a simple abelian variety and hence,
$(A, L)$
is Hodge theoretically very general, A is a simple abelian variety and hence,
![]() $n(L)=\displaystyle\frac {g}{\sqrt [g]{(L^g)}}$
. Note that in order to compare
$n(L)=\displaystyle\frac {g}{\sqrt [g]{(L^g)}}$
. Note that in order to compare
![]() $\beta (L)$
and
$\beta (L)$
and
![]() $n(L)$
, we can assume that L is primitive.
$n(L)$
, we can assume that L is primitive.
Theorem 3.1. Let
![]() $(A, L)$
be a Hodge theoretically very general polarized abelian variety of type
$(A, L)$
be a Hodge theoretically very general polarized abelian variety of type
![]() $l=(1,\delta _2,\ldots ,\delta _g)$
. Assume that
$l=(1,\delta _2,\ldots ,\delta _g)$
. Assume that
 $$ \begin{align*} \delta:=\delta_2\cdots\delta_g\geq \mathrm{ max}\big\{\frac{(k(k+1)\cdots(g-1))^{\frac{g(g-1)}{k}}}{(g!)^{\frac{(g-1)(g-k)}{k}}}\mid 2\leq k\leq g-2\big\}. \end{align*} $$
$$ \begin{align*} \delta:=\delta_2\cdots\delta_g\geq \mathrm{ max}\big\{\frac{(k(k+1)\cdots(g-1))^{\frac{g(g-1)}{k}}}{(g!)^{\frac{(g-1)(g-k)}{k}}}\mid 2\leq k\leq g-2\big\}. \end{align*} $$
Then,
![]() $\beta (L) \leq n(L).$
$\beta (L) \leq n(L).$
Proof. We apply Ito’s strategy that it suffices to show
![]() $r'(L)\leq n(L)$
. Let
$r'(L)\leq n(L)$
. Let
![]() $t\in (n(L), n(L)+\epsilon )$
be a rational number, where
$t\in (n(L), n(L)+\epsilon )$
be a rational number, where
![]() $0<\epsilon \ll 1$
and denote by
$0<\epsilon \ll 1$
and denote by
![]() $D\sim _{\mathbb Q} tL$
an effective rational number such that
$D\sim _{\mathbb Q} tL$
an effective rational number such that
![]() $\mathrm {mult}_0D>g$
(there exists such D since
$\mathrm {mult}_0D>g$
(there exists such D since
![]() $((tL)^g)>g^g$
). We then just need to apply Proposition 2.3 to get a divisor
$((tL)^g)>g^g$
). We then just need to apply Proposition 2.3 to get a divisor
![]() $D'\sim _{\mathbb Q}cD$
with
$D'\sim _{\mathbb Q}cD$
with
![]() $0<c<1$
, and the neutral element o of A is a minimal log canonical center of
$0<c<1$
, and the neutral element o of A is a minimal log canonical center of
![]() $(A, D')$
. By Proposition 2.3, it suffices to verify that
$(A, D')$
. By Proposition 2.3, it suffices to verify that
![]() $(D^{k}\cdot Z)>\binom {g-1}{g-k}g^k$
for any irreducible subvariety Z of dimension k for
$(D^{k}\cdot Z)>\binom {g-1}{g-k}g^k$
for any irreducible subvariety Z of dimension k for
![]() $1\leq k\leq g-1$
.
$1\leq k\leq g-1$
.
Recall that
![]() $\beta (L)\leq 1$
and equality holds if and only if
$\beta (L)\leq 1$
and equality holds if and only if
![]() $|L|$
has a basepoint. Thus, we may assume that
$|L|$
has a basepoint. Thus, we may assume that
![]() $(L^g)>g^g$
(i.e.,
$(L^g)>g^g$
(i.e.,
![]() $n(L)<1$
). Then, since the class
$n(L)<1$
). Then, since the class
![]() $[L]$
is the generator of
$[L]$
is the generator of
![]() $\mathrm {NS}(A)=\operatorname {\mathrm {Pic}}(A)/\operatorname {\mathrm {Pic}}^0(A)$
, we can assume that Z is of codimension
$\mathrm {NS}(A)=\operatorname {\mathrm {Pic}}(A)/\operatorname {\mathrm {Pic}}^0(A)$
, we can assume that Z is of codimension
![]() $\geq 2$
. Since A is simple, by the main result of [Reference DebarreD1], for any irreducible curve Z of A,
$\geq 2$
. Since A is simple, by the main result of [Reference DebarreD1], for any irreducible curve Z of A,
![]() $(L\cdot Z)>\sqrt [g]{(L^g)}>g$
. Thus, it suffices to verify that
$(L\cdot Z)>\sqrt [g]{(L^g)}>g$
. Thus, it suffices to verify that
![]() $(D^{k}\cdot Z)>\binom {g-1}{g-k}g^k$
for any irreducible subvariety Z of dimension k, where
$(D^{k}\cdot Z)>\binom {g-1}{g-k}g^k$
for any irreducible subvariety Z of dimension k, where
![]() $2\leq k\leq g-2$
.
$2\leq k\leq g-2$
.
For any irreducible subvariety Z of dimension k, we denote by
![]() $[Z]\in H^{g-k, g-k}(A, \mathbb Z)\subset H^{2g-2k}(A, \mathbb C)$
its cohomology class. Then,
$[Z]\in H^{g-k, g-k}(A, \mathbb Z)\subset H^{2g-2k}(A, \mathbb C)$
its cohomology class. Then,
![]() $[Z]$
is a positive integral multiple of
$[Z]$
is a positive integral multiple of
![]() $\frac {L^{g-k}}{(g-k)!\delta _2\cdots \delta _{g-k}}$
by the assumption that A is Hodge theoretically very general. Thus,
$\frac {L^{g-k}}{(g-k)!\delta _2\cdots \delta _{g-k}}$
by the assumption that A is Hodge theoretically very general. Thus,
 $$ \begin{align*} (D^k\cdot Z)> \frac{g^k}{(L^g)^{\frac{k}{g}}}(L^k\cdot Z) \geq g^k\frac{(L^g)^{\frac{g-k}{g}}}{(g-k)!\delta_2\cdots\delta_{g-k}}. \end{align*} $$
$$ \begin{align*} (D^k\cdot Z)> \frac{g^k}{(L^g)^{\frac{k}{g}}}(L^k\cdot Z) \geq g^k\frac{(L^g)^{\frac{g-k}{g}}}{(g-k)!\delta_2\cdots\delta_{g-k}}. \end{align*} $$
We just need to verify that
 $$ \begin{align} \frac{(L^g)^{\frac{g-k}{g}}}{(g-k)!\delta_2\cdots\delta_{g-k}}\geq \binom{g-1}{g-k}. \end{align} $$
$$ \begin{align} \frac{(L^g)^{\frac{g-k}{g}}}{(g-k)!\delta_2\cdots\delta_{g-k}}\geq \binom{g-1}{g-k}. \end{align} $$
Note that
![]() $\delta _2\cdots \delta _{g-k}\leq \delta ^{\frac {g-k-1}{g-1}}$
. Thus,
$\delta _2\cdots \delta _{g-k}\leq \delta ^{\frac {g-k-1}{g-1}}$
. Thus,
 $$ \begin{align*} \frac{ (L^g)^{\frac{g-k}{g}}}{(g-k)!\delta_2\cdots\delta_{g-k}} \geq &\delta^{\frac{g-k}{g}-\frac{g-k-1}{g-1}}\frac{ (g!)^{\frac{g-k}{g}}}{(g-k)!}\\ &\ \ =\delta^{\frac{k}{g(g-1)}}\frac{ (g!)^{\frac{g-k}{g}}}{(g-k)!}. \end{align*} $$
$$ \begin{align*} \frac{ (L^g)^{\frac{g-k}{g}}}{(g-k)!\delta_2\cdots\delta_{g-k}} \geq &\delta^{\frac{g-k}{g}-\frac{g-k-1}{g-1}}\frac{ (g!)^{\frac{g-k}{g}}}{(g-k)!}\\ &\ \ =\delta^{\frac{k}{g(g-1)}}\frac{ (g!)^{\frac{g-k}{g}}}{(g-k)!}. \end{align*} $$
The assumption on
![]() $\delta $
makes sure that
$\delta $
makes sure that
![]() $ \frac {(L^g)^{\frac {g-k}{g}}}{(g-k)!\delta _2\cdots \delta _{g-k}}\geq \binom {g-1}{g-k}$
for
$ \frac {(L^g)^{\frac {g-k}{g}}}{(g-k)!\delta _2\cdots \delta _{g-k}}\geq \binom {g-1}{g-k}$
for
![]() $2\leq k\leq g-2$
.
$2\leq k\leq g-2$
.
By the above theorem, we see that in order to verify Conjecture 1.1 and Conjecture 1.4 for very general polarized abelian varieties, it suffices to check finitely many families in each dimension. By the same computation with some extra efforts, we finish the proof of Theorem 1.5.
Proof. When
![]() $g=4$
, the assumption in Theorem 3.1 is simply that
$g=4$
, the assumption in Theorem 3.1 is simply that
![]() $\delta =h^0(A, L)\geq \frac {6^6}{24^3}=\frac {27}{8}$
. However, for
$\delta =h^0(A, L)\geq \frac {6^6}{24^3}=\frac {27}{8}$
. However, for
![]() $\delta \leq 3$
,
$\delta \leq 3$
,
![]() $n(L)=\frac {4}{\sqrt [4]{24\delta }}>1$
we know that
$n(L)=\frac {4}{\sqrt [4]{24\delta }}>1$
we know that
![]() $|L|$
has basepoints and
$|L|$
has basepoints and
![]() $\beta (L)=1$
.
$\beta (L)=1$
.
When
![]() $g=5$
, we repeat the argument in the proof of Theorem 3.1. We first check (3) for
$g=5$
, we repeat the argument in the proof of Theorem 3.1. We first check (3) for
![]() $g=5$
and
$g=5$
and
![]() $k=2$
or
$k=2$
or
![]() $3$
, which are
$3$
, which are
![]() $(L^5)^{\frac {3}{5}}\geq 24\delta _2\delta _3$
and
$(L^5)^{\frac {3}{5}}\geq 24\delta _2\delta _3$
and
![]() $(L^5)^{\frac {2}{5}}\geq 12\delta _2$
. It is easy to verify that both inequalities hold when
$(L^5)^{\frac {2}{5}}\geq 12\delta _2$
. It is easy to verify that both inequalities hold when
![]() $\delta _5\geq 5$
or
$\delta _5\geq 5$
or
![]() $\delta _2\geq 3$
. When
$\delta _2\geq 3$
. When
![]() $\delta _2=1$
,
$\delta _2=1$
,
![]() $\delta \geq 5$
implies that both inequalities hold and if
$\delta \geq 5$
implies that both inequalities hold and if
![]() $\delta <5$
,
$\delta <5$
,
![]() $\beta (L)=1$
. When
$\beta (L)=1$
. When
![]() $\delta _2=2$
and
$\delta _2=2$
and
![]() $\delta _5\leq 4$
, the above inequalities fail only when the polarization type is
$\delta _5\leq 4$
, the above inequalities fail only when the polarization type is
![]() $(1,2,2,2,2)$
. But in this case,
$(1,2,2,2,2)$
. But in this case,
 $n(L)=\displaystyle\frac {5}{\sqrt [5]{120\delta (L)}}>1$
. Thus, we still have
$n(L)=\displaystyle\frac {5}{\sqrt [5]{120\delta (L)}}>1$
. Thus, we still have
![]() $\beta (L)\leq 1<n(L)$
.
$\beta (L)\leq 1<n(L)$
.
When
![]() $g=6$
, we first remark that we may assume that l is not of the form
$g=6$
, we first remark that we may assume that l is not of the form
![]() $(1,\ldots , 1, \delta _6)$
. If l is of the form
$(1,\ldots , 1, \delta _6)$
. If l is of the form
![]() $(1,\ldots , 1, \delta _6)$
, since
$(1,\ldots , 1, \delta _6)$
, since
![]() $(A, L)$
is very general, by [Reference ItoIto3, Theorem 1.5],
$(A, L)$
is very general, by [Reference ItoIto3, Theorem 1.5],
 $\beta (L)\leq \displaystyle\frac {1}{\lfloor \sqrt [6]{\delta _6}\rfloor }<\frac {6}{\sqrt [6]{720\delta _6}}$
. Thus, we will assume that
$\beta (L)\leq \displaystyle\frac {1}{\lfloor \sqrt [6]{\delta _6}\rfloor }<\frac {6}{\sqrt [6]{720\delta _6}}$
. Thus, we will assume that
![]() $\delta _5\geq 2$
. We then check (3) for
$\delta _5\geq 2$
. We then check (3) for
![]() $k=2$
,
$k=2$
,
![]() $3$
and
$3$
and
![]() $4$
, which are
$4$
, which are
![]() $(L^6)\geq (20\delta _2)^3$
,
$(L^6)\geq (20\delta _2)^3$
,
![]() $(L^6)\geq (60\delta _2\delta _3)^2$
and
$(L^6)\geq (60\delta _2\delta _3)^2$
and
![]() $(L^6)^{\frac {2}{3}}\geq 120\delta _2\delta _3\delta _4$
. Since
$(L^6)^{\frac {2}{3}}\geq 120\delta _2\delta _3\delta _4$
. Since
![]() $\delta _5\geq 2$
, we see that these inequalities hold when
$\delta _5\geq 2$
, we see that these inequalities hold when
![]() $\delta _6\geq 5$
. When
$\delta _6\geq 5$
. When
![]() $\delta _6=4$
, one can verify that these inequalities hold, except the polarization types
$\delta _6=4$
, one can verify that these inequalities hold, except the polarization types
![]() $(1,4,4,4,4,4)$
or
$(1,4,4,4,4,4)$
or
![]() $(1,1, 1,1,2,4)$
or
$(1,1, 1,1,2,4)$
or
![]() $(1, 2, 2, 2, 2, 2, 4)$
. When
$(1, 2, 2, 2, 2, 2, 4)$
. When
![]() $\delta _6=3$
, these inequalities hold, except the polarization types
$\delta _6=3$
, these inequalities hold, except the polarization types
![]() $(1,3,3,3,3,3)$
. Note that for the polarization types
$(1,3,3,3,3,3)$
. Note that for the polarization types
![]() $(1, 1, 1,1, 2,4)$
, or
$(1, 1, 1,1, 2,4)$
, or
![]() $(1,2,2,2,2,4)$
or with
$(1,2,2,2,2,4)$
or with
![]() $\delta _6\leq 2$
,
$\delta _6\leq 2$
,
![]() $n(L)>1$
and thus,
$n(L)>1$
and thus,
![]() $\beta (L)<n(L)$
. We finally need to consider the polarization types
$\beta (L)<n(L)$
. We finally need to consider the polarization types
![]() $(1,4,4,4,4,4)$
and
$(1,4,4,4,4,4)$
and
![]() $(1,3,3,3,3,3)$
. These two cases can be dealt by a result of Ito. When
$(1,3,3,3,3,3)$
. These two cases can be dealt by a result of Ito. When
![]() $(A, L)$
is a polarized abelian sixfold of polarization type
$(A, L)$
is a polarized abelian sixfold of polarization type
![]() $(1,4,4,4,4,4)$
(resp.
$(1,4,4,4,4,4)$
(resp.
![]() $(1,3,3,3,3,3)$
), let
$(1,3,3,3,3,3)$
), let
![]() $(S, L')$
be a very general polarized abelian surface of polarization type
$(S, L')$
be a very general polarized abelian surface of polarization type
![]() $(1, 4)$
(resp.
$(1, 4)$
(resp.
![]() $(1, 3)$
). By [Reference ItoIto5, Proposition 5.1], we always have
$(1, 3)$
). By [Reference ItoIto5, Proposition 5.1], we always have
![]() $\beta (L)\leq \beta (L')$
. It is known that
$\beta (L)\leq \beta (L')$
. It is known that
![]() $\beta (L')=\frac {1}{2}$
(resp.
$\beta (L')=\frac {1}{2}$
(resp.
![]() $\frac {2}{3}$
) (see [Reference ItoIto3, Proposition 4.3 and Lemma A.4]). We then still have
$\frac {2}{3}$
) (see [Reference ItoIto3, Proposition 4.3 and Lemma A.4]). We then still have
![]() $\beta (L)<n(L)$
for the polarization types
$\beta (L)<n(L)$
for the polarization types
![]() $(1,4,4,4,4,4)$
and
$(1,4,4,4,4,4)$
and
![]() $(1,3,3,3,3,3)$
.
$(1,3,3,3,3,3)$
.
Remark 3.2. The last paragraph of the above proof is due to the anonymous referee.
4 Abelian fourfolds
4.1 The proof of Theorem 1.6
Proof. It suffices to show that
![]() $\beta (L)<\frac {1}{p+2}$
or equivalently
$\beta (L)<\frac {1}{p+2}$
or equivalently
![]() $\mathcal {I}_o\langle \frac {1}{p+2}L\rangle $
is IT
$\mathcal {I}_o\langle \frac {1}{p+2}L\rangle $
is IT
![]() $^0$
, where o is the neutral element of A.
$^0$
, where o is the neutral element of A.
Since
![]() $(L^4)>((2+\frac {4}{\sqrt {3}})(p+2))^4$
, there exists an effective
$(L^4)>((2+\frac {4}{\sqrt {3}})(p+2))^4$
, there exists an effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $D\sim _{\mathbb Q}\frac {1}{p+2}L$
such that
$D\sim _{\mathbb Q}\frac {1}{p+2}L$
such that
![]() $\mathrm {mult}_o(D)=m>2+\frac {4}{\sqrt {3}}$
. Let
$\mathrm {mult}_o(D)=m>2+\frac {4}{\sqrt {3}}$
. Let
![]() $c=\mathrm {lct}(D, o)\leq \frac {4}{m}$
be the log canonical threshold of D at o and let Z be the minimal log canonical center of
$c=\mathrm {lct}(D, o)\leq \frac {4}{m}$
be the log canonical threshold of D at o and let Z be the minimal log canonical center of
![]() $(A, cD)$
through o. By Proposition 2.7, we may assume that
$(A, cD)$
through o. By Proposition 2.7, we may assume that
![]() $c\geq \frac {1}{2}$
.
$c\geq \frac {1}{2}$
.
Step 1. We first deal with the case that Z is a divisor. By Lemma 2.5,
![]() $\mathcal {I}_K\langle \frac {c}{p+2}L\rangle $
is GV, where K is the kernel of
$\mathcal {I}_K\langle \frac {c}{p+2}L\rangle $
is GV, where K is the kernel of
![]() $\varphi _{Z}$
. If K is a point, we are done. Otherwise, by the assumption that
$\varphi _{Z}$
. If K is a point, we are done. Otherwise, by the assumption that
![]() $(L^d\cdot B)>(d(p+2))^d$
for any abelian subvariety B of dimension
$(L^d\cdot B)>(d(p+2))^d$
for any abelian subvariety B of dimension
![]() $1\leq d\leq 3$
and Ito’s results [Reference ItoIto1, Reference ItoIto2],
$1\leq d\leq 3$
and Ito’s results [Reference ItoIto1, Reference ItoIto2],
![]() $\mathcal {I}_{o,K}\langle \frac {1}{p+2}L\rangle $
is IT
$\mathcal {I}_{o,K}\langle \frac {1}{p+2}L\rangle $
is IT
![]() $^0$
. Thus, from the short exact sequence
$^0$
. Thus, from the short exact sequence
we conclude that
![]() $\mathcal {I}_o\langle \frac {1}{p+2}L\rangle $
is IT
$\mathcal {I}_o\langle \frac {1}{p+2}L\rangle $
is IT
![]() $^0$
.
$^0$
.
Step 2. If Z is a curve, by Proposition 2.3, Z is smooth at o and as soon as
![]() $(D\cdot Z)>4\geq \frac {b_o(A, cD)}{1-c}$
, there exists
$(D\cdot Z)>4\geq \frac {b_o(A, cD)}{1-c}$
, there exists
![]() $D_1\sim _{\mathbb Q}c_1D$
with
$D_1\sim _{\mathbb Q}c_1D$
with
![]() $c<c_1<1$
such that
$c<c_1<1$
such that
![]() $(A, D_1)$
is log canonical at o and
$(A, D_1)$
is log canonical at o and
![]() $\{o\}$
is a minimal log canonical center. Then, we have by Remark 2.4 that
$\{o\}$
is a minimal log canonical center. Then, we have by Remark 2.4 that
![]() $\beta (L)\leq r'(L)\leq \frac {c_1}{p+2}<\frac {1}{p+2}$
.
$\beta (L)\leq r'(L)\leq \frac {c_1}{p+2}<\frac {1}{p+2}$
.
By Corollary 2.2, we know that
where
![]() $\nu : \overline {Z}\rightarrow Z$
is the normalization. Thus, we are done once
$\nu : \overline {Z}\rightarrow Z$
is the normalization. Thus, we are done once
![]() $g(\overline {Z})\geq 3$
.
$g(\overline {Z})\geq 3$
.
When
![]() $g(\overline {Z})=1$
,
$g(\overline {Z})=1$
,
![]() $Z=\overline {Z}$
is an elliptic curve. We conclude again by Proposition 2.14, Remark 2.4 and the assumption that
$Z=\overline {Z}$
is an elliptic curve. We conclude again by Proposition 2.14, Remark 2.4 and the assumption that
![]() $(L\cdot Z)>p+2$
and thus,
$(L\cdot Z)>p+2$
and thus,
![]() $\beta (L|_Z)<\frac {1}{p+2}$
.
$\beta (L|_Z)<\frac {1}{p+2}$
.
If
![]() $g(\overline {Z})=2$
, Z generates an abelian surface B of A. By Corollary 2.16, we may assume that
$g(\overline {Z})=2$
, Z generates an abelian surface B of A. By Corollary 2.16, we may assume that
![]() $(D^2\cdot B)\geq \frac {4^4}{\binom {4}{2}2^2}= \frac {32}{3}$
. Then, by Hodge index theorem,
$(D^2\cdot B)\geq \frac {4^4}{\binom {4}{2}2^2}= \frac {32}{3}$
. Then, by Hodge index theorem,
Step 3. When Z is a surface, we need to apply Helmke’s induction. We may assume that Z is not an abelian surface. Otherwise, we conclude directly by Proposition 2.14 and Ito’s work in [Reference ItoIto1]. We know that
![]() $\mathrm {mult}_oZ\leq 3$
by Proposition 2.3. Let
$\mathrm {mult}_oZ\leq 3$
by Proposition 2.3. Let
![]() $\mu : \tilde {Z}\rightarrow \overline {Z}\rightarrow Z$
be the minimal resolution of the normalization
$\mu : \tilde {Z}\rightarrow \overline {Z}\rightarrow Z$
be the minimal resolution of the normalization
![]() $\overline {Z}$
of Z. Since Z is not an abelian variety,
$\overline {Z}$
of Z. Since Z is not an abelian variety,
![]() $\tilde {Z}$
is a surface of maximal Albanese dimension of Kodaira dimension
$\tilde {Z}$
is a surface of maximal Albanese dimension of Kodaira dimension
![]() $\geq 1$
. Since there exist no rational curves on
$\geq 1$
. Since there exist no rational curves on
![]() $\overline {Z}$
,
$\overline {Z}$
,
![]() $\tilde {Z}$
is minimal.
$\tilde {Z}$
is minimal.
Claim.
![]() $((cD)^2\cdot Z)\geq 16$
when
$((cD)^2\cdot Z)\geq 16$
when
![]() $\mathrm {mult}_oZ=3$
;
$\mathrm {mult}_oZ=3$
;
![]() $((cD)^2\cdot Z)\geq 16$
or
$((cD)^2\cdot Z)\geq 16$
or
![]() $(D^2\cdot Z)\geq 16\sqrt [3]{6}$
when
$(D^2\cdot Z)\geq 16\sqrt [3]{6}$
when
![]() $\mathrm {mult}_oZ=2$
;
$\mathrm {mult}_oZ=2$
;
![]() $(D^2\cdot Z)>16$
when Z is smooth at o.
$(D^2\cdot Z)>16$
when Z is smooth at o.
When
![]() $\tilde {Z}$
is not of general type, Z is fibred by an elliptic curve E, and since Z has rational singularities around o, Z is indeed smooth at o. We need to show that
$\tilde {Z}$
is not of general type, Z is fibred by an elliptic curve E, and since Z has rational singularities around o, Z is indeed smooth at o. We need to show that
![]() $(D^2\cdot Z)>16$
. Let
$(D^2\cdot Z)>16$
. Let
![]() $C=Z/E$
be the quotient and
$C=Z/E$
be the quotient and
![]() $\tilde {C}$
be the normalization of C. By Corollary 2.16, we may assume
$\tilde {C}$
be the normalization of C. By Corollary 2.16, we may assume
![]() $(D\cdot E)\geq \frac {64}{27}$
and by Lemma 2.18, we have
$(D\cdot E)\geq \frac {64}{27}$
and by Lemma 2.18, we have
Thus, we are done when
![]() $g(\tilde {C})\geq 3$
. When
$g(\tilde {C})\geq 3$
. When
![]() $g(\tilde {C})=2$
, Z generates an abelian
$g(\tilde {C})=2$
, Z generates an abelian
![]() $3$
-fold B of A and
$3$
-fold B of A and
![]() $C\hookrightarrow B/E$
is an ample divisor. Thus,
$C\hookrightarrow B/E$
is an ample divisor. Thus,
![]() $(C^2)_{B/E}=a\geq 2$
and hence,
$(C^2)_{B/E}=a\geq 2$
and hence,
![]() $Z^2$
is algebraically equivalent to
$Z^2$
is algebraically equivalent to
![]() $aE$
as
$aE$
as
![]() $1$
-cycles of B. By Corollary 2.16, we may assume that
$1$
-cycles of B. By Corollary 2.16, we may assume that
![]() $(D^3\cdot B)\geq 4^3$
. Then, by Hodge index,
$(D^3\cdot B)\geq 4^3$
. Then, by Hodge index,
 $$ \begin{align*} (D^2\cdot Z)=((D|_B)^2\cdot Z)_B\quad &\geq \sqrt{(D^3)_B(D|_B\cdot Z^2)_B}\\ & \geq \sqrt{4^3\cdot a\cdot \frac{64}{27}}\geq 16\sqrt{\frac{32}{27}}>16. \end{align*} $$
$$ \begin{align*} (D^2\cdot Z)=((D|_B)^2\cdot Z)_B\quad &\geq \sqrt{(D^3)_B(D|_B\cdot Z^2)_B}\\ & \geq \sqrt{4^3\cdot a\cdot \frac{64}{27}}\geq 16\sqrt{\frac{32}{27}}>16. \end{align*} $$
We now assume that
![]() $\tilde {Z}$
is of general type.
$\tilde {Z}$
is of general type.
If
![]() $q(\tilde {Z})\geq 4$
, by Corollary 2.13,
$q(\tilde {Z})\geq 4$
, by Corollary 2.13,
![]() $\operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq 16$
or
$\operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq 16$
or
![]() $\tilde {Z}\simeq C_1\times C_2$
, where
$\tilde {Z}\simeq C_1\times C_2$
, where
![]() $C_i$
is a smooth projective curve of genus
$C_i$
is a smooth projective curve of genus
![]() $2$
. In the latter case
$2$
. In the latter case
![]() $\mu $
is the normalization of Z, and since Z is normal at o, it is smooth at o. We apply Proposition 2.1 and conclude that
$\mu $
is the normalization of Z, and since Z is normal at o, it is smooth at o. We apply Proposition 2.1 and conclude that
 $$ \begin{align*} (D^2\cdot Z)=(\mu^*(D)^2)_{\tilde{Z}}\quad & \geq (K_{\tilde{Z}}\cdot \mu^*D)_{\tilde{Z}} \\ &=2(C_1\cdot \mu^*D)_{\tilde{Z}} +2(C_2\cdot \mu^*D)_{\tilde{Z}}. \end{align*} $$
$$ \begin{align*} (D^2\cdot Z)=(\mu^*(D)^2)_{\tilde{Z}}\quad & \geq (K_{\tilde{Z}}\cdot \mu^*D)_{\tilde{Z}} \\ &=2(C_1\cdot \mu^*D)_{\tilde{Z}} +2(C_2\cdot \mu^*D)_{\tilde{Z}}. \end{align*} $$
Note that the image of
![]() $C_i$
generates an abelian surface
$C_i$
generates an abelian surface
![]() $B_i$
of A. By Corollary 2.16, we may assume that
$B_i$
of A. By Corollary 2.16, we may assume that
![]() $(D^2\cdot B_i)\geq \frac {32}{3}$
. Thus, by Hodge index,
$(D^2\cdot B_i)\geq \frac {32}{3}$
. Thus, by Hodge index,
![]() $(C_i\cdot \mu ^*D)_{\tilde {Z}}\geq 8/\sqrt {3}$
. Therefore, we have
$(C_i\cdot \mu ^*D)_{\tilde {Z}}\geq 8/\sqrt {3}$
. Therefore, we have
![]() $(D^2\cdot Z)\geq 32/\sqrt {3}>16$
. In the former case,
$(D^2\cdot Z)\geq 32/\sqrt {3}>16$
. In the former case,
![]() $ ((cD)^2\cdot Z)=\operatorname {\mathrm {vol}}(Z, cD)\geq \operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq 16$
by Corollary 2.2.
$ ((cD)^2\cdot Z)=\operatorname {\mathrm {vol}}(Z, cD)\geq \operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq 16$
by Corollary 2.2.
If
![]() $q(\tilde {Z})=3$
, Z generates an abelian 3-fold
$q(\tilde {Z})=3$
, Z generates an abelian 3-fold
![]() $B\subset A$
. Then, Z is an ample divisor of B. Moreover, in this case, the embedded dimension of Z at o is at most
$B\subset A$
. Then, Z is an ample divisor of B. Moreover, in this case, the embedded dimension of Z at o is at most
![]() $3$
. Thus,
$3$
. Thus,
![]() $\mathrm {mult}_o(Z)\leq 2$
by the well-known facts about isolated rational surface singularities (see [Reference ArtinA, Corollary 6]). As before, by Corollary 2.16, we may assume that
$\mathrm {mult}_o(Z)\leq 2$
by the well-known facts about isolated rational surface singularities (see [Reference ArtinA, Corollary 6]). As before, by Corollary 2.16, we may assume that
![]() $(D^3\cdot B)\geq 4^3$
. Since Z is an ample divisor of B,
$(D^3\cdot B)\geq 4^3$
. Since Z is an ample divisor of B,
![]() $(Z^3)_B\geq 6$
. Thus,
$(Z^3)_B\geq 6$
. Thus,
Step 4.
If Z is smooth at o, we have shown that
![]() $(D^2\cdot Z)>16$
. Thus, by Proposition 2.3, there exists an effective
$(D^2\cdot Z)>16$
. Thus, by Proposition 2.3, there exists an effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $D_1\sim _{\mathbb Q} c_1D$
with
$D_1\sim _{\mathbb Q} c_1D$
with
![]() $c_1<1$
such that
$c_1<1$
such that
![]() $(A, D_1)$
is log canonical at o whose minimal log canonical center
$(A, D_1)$
is log canonical at o whose minimal log canonical center
![]() $Z_1$
through o is a proper subset of Z and
$Z_1$
through o is a proper subset of Z and
![]() $\frac {b_o(A, D_1)}{1-c_1}\leq \frac {b_o(A, cD)}{1-c}\leq 4$
. We then finish the proof by going back to Step 2.
$\frac {b_o(A, D_1)}{1-c_1}\leq \frac {b_o(A, cD)}{1-c}\leq 4$
. We then finish the proof by going back to Step 2.
If
![]() $\mathrm {mult}_oZ= 3$
, we have already seen that
$\mathrm {mult}_oZ= 3$
, we have already seen that
![]() $((cD)^2\cdot Z)\geq 16$
. In order to apply Helmke’s induction, we need to verify that
$((cD)^2\cdot Z)\geq 16$
. In order to apply Helmke’s induction, we need to verify that
Note that
![]() $b_o(A, cD)\leq 4-cm<4-(2+\frac {4}{\sqrt {3}})c$
. It is elementary to verify that
$b_o(A, cD)\leq 4-cm<4-(2+\frac {4}{\sqrt {3}})c$
. It is elementary to verify that
 $$ \begin{align*}\frac{16}{c^2}\geq 3\big(\frac{4-(2+\frac{4}{\sqrt{3}})c}{1-c}\big)^2\end{align*} $$
$$ \begin{align*}\frac{16}{c^2}\geq 3\big(\frac{4-(2+\frac{4}{\sqrt{3}})c}{1-c}\big)^2\end{align*} $$
always holds. We then finish the proof as before.
If
![]() $\mathrm {mult}_oZ=2$
and
$\mathrm {mult}_oZ=2$
and
![]() $((cD)^2\cdot Z)\geq 16$
, we conclude as the multiplicity
$((cD)^2\cdot Z)\geq 16$
, we conclude as the multiplicity
![]() $3$
case. If
$3$
case. If
![]() $\mathrm {mult}_oZ=2$
and
$\mathrm {mult}_oZ=2$
and
![]() $(D^2\cdot Z)\geq 16\sqrt [3]{6}$
, we need to verify that
$(D^2\cdot Z)\geq 16\sqrt [3]{6}$
, we need to verify that
Since
![]() $c\geq \frac {1}{2}$
, we have
$c\geq \frac {1}{2}$
, we have
![]() $\frac {b_o(A, cD)}{1-c}<4-\frac {(\frac {4}{\sqrt {3}}-2)c}{1-c}\leq 6-\frac {4}{\sqrt {3}}$
. We then check that
$\frac {b_o(A, cD)}{1-c}<4-\frac {(\frac {4}{\sqrt {3}}-2)c}{1-c}\leq 6-\frac {4}{\sqrt {3}}$
. We then check that
![]() $16\sqrt [3]{6}>2(6-\frac {4}{\sqrt {3}})^2$
.
$16\sqrt [3]{6}>2(6-\frac {4}{\sqrt {3}})^2$
.
4.2 The proof of Theorem 1.8
We apply the same strategy as in the proof of Theorem 1.6.
Fix an effective
![]() $\mathbb Q$
-divisor such that
$\mathbb Q$
-divisor such that
![]() $D\sim _{\mathbb Q}\frac {1}{p+2}L$
, such that
$D\sim _{\mathbb Q}\frac {1}{p+2}L$
, such that
![]() $\mathrm {mult}_oD>8$
. Let
$\mathrm {mult}_oD>8$
. Let
![]() $c_1=\mathrm {lct}(D, o)<\frac {5}{8}$
be the log canonical threshold of D at o and let
$c_1=\mathrm {lct}(D, o)<\frac {5}{8}$
be the log canonical threshold of D at o and let
![]() $Z_1$
be the minimal log canonical center of
$Z_1$
be the minimal log canonical center of
![]() $(A, c_1D)$
at o. By Proposition 2.7, we may assume that
$(A, c_1D)$
at o. By Proposition 2.7, we may assume that
![]() $c_1\geq \frac {1}{2}$
. Thus,
$c_1\geq \frac {1}{2}$
. Thus,
If
![]() $Z_1$
is a divisor, we conclude by Lemma 2.5.
$Z_1$
is a divisor, we conclude by Lemma 2.5.
If
![]() $Z_1$
is a threefold, we apply Helmke’s induction. Let
$Z_1$
is a threefold, we apply Helmke’s induction. Let
![]() $\rho : \tilde {Z_1}\rightarrow Z_1$
be a desingularization. Then,
$\rho : \tilde {Z_1}\rightarrow Z_1$
be a desingularization. Then,
![]() $\operatorname {\mathrm {vol}}(K_{\tilde {Z_1}})\geq \frac {5}{2}\times 3!\times 3=45$
by Theorem 2.8, Theorem 2.9 and Remark 2.10. We also note that
$\operatorname {\mathrm {vol}}(K_{\tilde {Z_1}})\geq \frac {5}{2}\times 3!\times 3=45$
by Theorem 2.8, Theorem 2.9 and Remark 2.10. We also note that
![]() $\mathrm {mult}_oZ_1\leq 6$
. Note that
$\mathrm {mult}_oZ_1\leq 6$
. Note that
 $$ \begin{align*}(D^3\cdot Z_1)\geq \operatorname{\mathrm{vol}}(K_{\tilde{Z_1}})/c_1^3>\frac{45}{(\frac{5}{8})^3}\geq 48>\big(\frac{b_o(A, c_1D)}{1-c_1}\big)^3\mathrm{mult}_{o}(Z_1).\end{align*} $$
$$ \begin{align*}(D^3\cdot Z_1)\geq \operatorname{\mathrm{vol}}(K_{\tilde{Z_1}})/c_1^3>\frac{45}{(\frac{5}{8})^3}\geq 48>\big(\frac{b_o(A, c_1D)}{1-c_1}\big)^3\mathrm{mult}_{o}(Z_1).\end{align*} $$
Thus, there exists an effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $ D_2\sim _{\mathbb Q}c_2D$
such that
$ D_2\sim _{\mathbb Q}c_2D$
such that
![]() $c_1<c_2<1$
, such that
$c_1<c_2<1$
, such that
![]() $(A, D_2)$
is log canonical at o, whose minimal lc center through o is a proper subvariety
$(A, D_2)$
is log canonical at o, whose minimal lc center through o is a proper subvariety
![]() $Z_2$
contained in
$Z_2$
contained in
![]() $Z_1$
, and
$Z_1$
, and
![]() $\frac {b_o(A, D_2)}{1-c_2}<\frac {b_o(A, c_1D)}{1-c_1}<2$
.
$\frac {b_o(A, D_2)}{1-c_2}<\frac {b_o(A, c_1D)}{1-c_1}<2$
.
When
![]() $Z_2$
is a surface, we have
$Z_2$
is a surface, we have
![]() $\mathrm {mult}_oZ_2\leq 4$
. Let
$\mathrm {mult}_oZ_2\leq 4$
. Let
![]() $\tilde {Z}_2$
be its smooth model. Since A is simple,
$\tilde {Z}_2$
be its smooth model. Since A is simple,
![]() $\tilde {Z}_2$
is of general type and hence,
$\tilde {Z}_2$
is of general type and hence,
![]() $\operatorname {\mathrm {vol}}(K_{\tilde {Z_2}})\geq 16$
by Corollary 2.13. We then have
$\operatorname {\mathrm {vol}}(K_{\tilde {Z_2}})\geq 16$
by Corollary 2.13. We then have
Thus, by Helmke’s induction, we may assume that
![]() $Z_2$
is a curve. In this case, we verify easily that
$Z_2$
is a curve. In this case, we verify easily that
![]() $(D\cdot Z_2)>\frac {b_o(A, D_2)}{1-c_2}$
. Therefore, there exists an effective
$(D\cdot Z_2)>\frac {b_o(A, D_2)}{1-c_2}$
. Therefore, there exists an effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $D_3\sim _{\mathbb Q}c_3L$
with
$D_3\sim _{\mathbb Q}c_3L$
with
![]() $c_2<c_3<1$
such that
$c_2<c_3<1$
such that
![]() $(A, D_3)$
is log canonical at o and o is a minimal log canonical center of
$(A, D_3)$
is log canonical at o and o is a minimal log canonical center of
![]() $(A, D_3)$
. We then finish the proof of Theorem 1.8.
$(A, D_3)$
. We then finish the proof of Theorem 1.8.
4.3 The proof of Theorem 1.9
The proof of Theorem 1.9 is identical to that of Theorem 1.8. We first observe that
![]() $\alpha _g\leq \alpha _{g,2}=\sqrt {\frac {5(g-2)+1}{g-1}}<\sqrt {5}$
. We then fix an effective
$\alpha _g\leq \alpha _{g,2}=\sqrt {\frac {5(g-2)+1}{g-1}}<\sqrt {5}$
. We then fix an effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $D\sim \frac {1}{p+2}L$
such that
$D\sim \frac {1}{p+2}L$
such that
![]() $\mathrm {mult}_oD>2g-\alpha _g$
and thus let
$\mathrm {mult}_oD>2g-\alpha _g$
and thus let
![]() $c<\frac {g}{2g-\sqrt {5}}$
be the log canonical threshold of
$c<\frac {g}{2g-\sqrt {5}}$
be the log canonical threshold of
![]() $(A, D)$
at o. We may assume that
$(A, D)$
at o. We may assume that
![]() $c\geq \frac {1}{2}$
by Proposition 2.7. Then
$c\geq \frac {1}{2}$
by Proposition 2.7. Then
Let Z be the minimal log canonical threshold of
![]() $(A, cD)$
through o. Let
$(A, cD)$
through o. Let
![]() $d=\dim Z$
. Then,
$d=\dim Z$
. Then,
![]() $\mathrm {mult}_oD\leq \binom {g-1}{g-d}$
.
$\mathrm {mult}_oD\leq \binom {g-1}{g-d}$
.
If
![]() $d=g-1$
, we conclude by Lemma 2.5. Thus, we may assume that
$d=g-1$
, we conclude by Lemma 2.5. Thus, we may assume that
![]() $1\leq d\leq g-2$
.
$1\leq d\leq g-2$
.
For a smooth model
![]() $\tilde {Z}$
of Z, by Theorem 2.8, Theorem 2.9, Remark 2.10 and Proposition 2.12, we have
$\tilde {Z}$
of Z, by Theorem 2.8, Theorem 2.9, Remark 2.10 and Proposition 2.12, we have
![]() $\operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq \frac {15}{2}(g-2)!$
when
$\operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq \frac {15}{2}(g-2)!$
when
![]() $d=g-2$
,
$d=g-2$
,
![]() $\operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq \frac {5}{2}d!(g-d)$
when
$\operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq \frac {5}{2}d!(g-d)$
when
![]() $3\leq d\leq g-3$
,
$3\leq d\leq g-3$
,
![]() $\operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq 5(g-2)+1$
when
$\operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq 5(g-2)+1$
when
![]() $d=2$
and
$d=2$
and
![]() $\operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq 2(g-1)$
when
$\operatorname {\mathrm {vol}}(K_{\tilde {Z}})\geq 2(g-1)$
when
![]() $d=1$
. By Corollary 2.2,
$d=1$
. By Corollary 2.2,
![]() $(D^d\cdot Z)\geq \frac {1}{c^d}\operatorname {\mathrm {vol}}(K_{\tilde {Z}})>\operatorname {\mathrm {vol}}(K_{\tilde {Z}})$
. We then have
$(D^d\cdot Z)\geq \frac {1}{c^d}\operatorname {\mathrm {vol}}(K_{\tilde {Z}})>\operatorname {\mathrm {vol}}(K_{\tilde {Z}})$
. We then have
We then repeatedly apply Helmke’s induction and the above calculation to cut down the log canonical centers and finish the proof.
Acknowledgements
The author thanks Atsushi Ito for helpful communications and, in particular, Lemma 2.15 is due to him. The author is grateful to the anonymous referee who provides an argument to improve Theorem 1.5 and many helpful comments. The author also thanks Chen Jiang for helpful conversations and Federico Caucci for helpful comments.
Competing interest
The authors have no competing interest to declare.
Financial support
The author is supported by NSFC for Innovative Research Groups (No. 12121001), by the National Key Research and Development Program of China (No. 2020YFA0713200), by the Natural Science Foundation of China (No. 11871155 and No. 11731004) and by the Natural Science Foundation of Shanghai (No. 21ZR1404500).