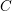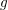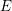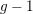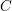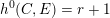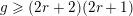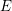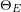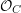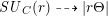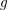1 Introduction
Let
![]() $C$
be a nonhyperelliptic curve of genus
$C$
be a nonhyperelliptic curve of genus
![]() $g$
and
$g$
and
![]() $L\in \operatorname{Pic}^{g-1}(C)$
a line bundle with
$L\in \operatorname{Pic}^{g-1}(C)$
a line bundle with
![]() $h^{0}(C,L)=2$
corresponding to a general double point of the Riemann theta divisor
$h^{0}(C,L)=2$
corresponding to a general double point of the Riemann theta divisor
![]() $\unicode[STIX]{x1D6E9}$
. It is well known that the projectivised tangent cone to
$\unicode[STIX]{x1D6E9}$
. It is well known that the projectivised tangent cone to
![]() $\unicode[STIX]{x1D6E9}$
at
$\unicode[STIX]{x1D6E9}$
at
![]() $L$
is a quadric hypersurface
$L$
is a quadric hypersurface
![]() $R_{L}$
of rank less than or equal to
$R_{L}$
of rank less than or equal to
![]() $4$
in the canonical space
$4$
in the canonical space
![]() $|K_{C}|^{\ast }$
, which contains the canonically embedded curve.
$|K_{C}|^{\ast }$
, which contains the canonically embedded curve.
Quadrics arising from tangent cones in this way have been much studied: Green [Reference GreenGre84] showed that the
![]() $R_{L}$
span the space of all quadrics in
$R_{L}$
span the space of all quadrics in
![]() $|K_{C}|^{\ast }$
containing
$|K_{C}|^{\ast }$
containing
![]() $C$
; and both Kempf and Schreyer [Reference Kempf and SchreyerKS88] and Ciliberto and Sernesi [Reference Ciliberto and SernesiCS92] have used the quadrics
$C$
; and both Kempf and Schreyer [Reference Kempf and SchreyerKS88] and Ciliberto and Sernesi [Reference Ciliberto and SernesiCS92] have used the quadrics
![]() $R_{L}$
in various ways to give new proofs of Torelli’s theorem.
$R_{L}$
in various ways to give new proofs of Torelli’s theorem.
In another direction: via the Riemann–Kempf singularity theorem [Reference KempfKem73], one sees that the rulings on
![]() $R_{L}$
cut out the linear series
$R_{L}$
cut out the linear series
![]() $|L|$
and
$|L|$
and
![]() $|K_{C}L^{-1}|$
on the canonical curve. Thus the data of the tangent cone and the canonical curve allow one to reconstruct the line bundle
$|K_{C}L^{-1}|$
on the canonical curve. Thus the data of the tangent cone and the canonical curve allow one to reconstruct the line bundle
![]() $L$
. In this paper we study a related construction for vector bundles of higher rank.
$L$
. In this paper we study a related construction for vector bundles of higher rank.
Let
![]() $V\rightarrow C$
be a semistable vector bundle of rank
$V\rightarrow C$
be a semistable vector bundle of rank
![]() $r$
and integral slope
$r$
and integral slope
![]() $h$
. We consider the set
$h$
. We consider the set
It is by now well known that for general
![]() $V$
, this is the support of a divisor
$V$
, this is the support of a divisor
![]() $\unicode[STIX]{x1D6E9}_{V}$
algebraically equivalent to a translate of
$\unicode[STIX]{x1D6E9}_{V}$
algebraically equivalent to a translate of
![]() $r\cdot \unicode[STIX]{x1D6E9}$
. If
$r\cdot \unicode[STIX]{x1D6E9}$
. If
![]() $V$
has trivial determinant, then in fact
$V$
has trivial determinant, then in fact
![]() $\unicode[STIX]{x1D6E9}_{V}$
, when it exists, belongs to
$\unicode[STIX]{x1D6E9}_{V}$
, when it exists, belongs to
![]() $|r\unicode[STIX]{x1D6E9}|$
.
$|r\unicode[STIX]{x1D6E9}|$
.
For general
![]() $V$
, the projectivised tangent cone
$V$
, the projectivised tangent cone
![]() ${\mathcal{T}}_{M}(\unicode[STIX]{x1D6E9}_{V})$
to
${\mathcal{T}}_{M}(\unicode[STIX]{x1D6E9}_{V})$
to
![]() $\unicode[STIX]{x1D6E9}_{V}$
at a point
$\unicode[STIX]{x1D6E9}_{V}$
at a point
![]() $M$
of multiplicity
$M$
of multiplicity
![]() $r+1$
is a determinantal hypersurface of degree
$r+1$
is a determinantal hypersurface of degree
![]() $r+1$
in
$r+1$
in
![]() $|K_{C}|^{\ast }$
(see, for example, Casalaina-Martin and Teixidor i Bigas [Reference Casalaina-Martin and Teixidor i BigasCT11]). Our first main result (§ 3.2) is a construction which from
$|K_{C}|^{\ast }$
(see, for example, Casalaina-Martin and Teixidor i Bigas [Reference Casalaina-Martin and Teixidor i BigasCT11]). Our first main result (§ 3.2) is a construction which from
![]() ${\mathcal{T}}_{M}(\unicode[STIX]{x1D6E9}_{V})$
recovers the bundle
${\mathcal{T}}_{M}(\unicode[STIX]{x1D6E9}_{V})$
recovers the bundle
![]() $V\otimes M$
, up to the involution
$V\otimes M$
, up to the involution
![]() $V\otimes M\mapsto K_{C}\otimes M^{-1}\otimes V^{\ast }$
. This is valid whenever
$V\otimes M\mapsto K_{C}\otimes M^{-1}\otimes V^{\ast }$
. This is valid whenever
![]() $V\otimes M$
and
$V\otimes M$
and
![]() $K_{C}\otimes M^{-1}\otimes V^{\ast }$
are globally generated.
$K_{C}\otimes M^{-1}\otimes V^{\ast }$
are globally generated.
We apply this construction to give an improvement of a result of Brivio and Verra [Reference Brivio and VerraBV12]. To describe this application, we need to recall some more objects. Write
![]() $\mathit{SU}_{C}(r)$
for the moduli space of semistable bundles of rank
$\mathit{SU}_{C}(r)$
for the moduli space of semistable bundles of rank
![]() $r$
and trivial determinant over
$r$
and trivial determinant over
![]() $C$
. The association
$C$
. The association
![]() $V\mapsto \unicode[STIX]{x1D6E9}_{V}$
defines a map
$V\mapsto \unicode[STIX]{x1D6E9}_{V}$
defines a map
called the theta map. Drezet and Narasimhan [Reference Drezet and NarasimhanDN89] showed that the line bundle associated to the theta map is the ample generator of the Picard group of
![]() $\mathit{SU}_{C}(r)$
. Moreover, the indeterminacy locus of
$\mathit{SU}_{C}(r)$
. Moreover, the indeterminacy locus of
![]() ${\mathcal{D}}$
consists of those bundles
${\mathcal{D}}$
consists of those bundles
![]() $V\in \mathit{SU}_{C}(r)$
for which (1) is the whole Picard variety. This has been much studied; see, for example, Pauly [Reference PaulyPau10], Popa [Reference PopaPop99] and Raynaud [Reference RaynaudRay82].
$V\in \mathit{SU}_{C}(r)$
for which (1) is the whole Picard variety. This has been much studied; see, for example, Pauly [Reference PaulyPau10], Popa [Reference PopaPop99] and Raynaud [Reference RaynaudRay82].
Brivio and Verra [Reference Brivio and VerraBV12] showed that
![]() ${\mathcal{D}}$
is generically injective for a general curve of genus
${\mathcal{D}}$
is generically injective for a general curve of genus
![]() $g\geqslant \binom{3r}{r}-2r-1$
, partially answering a conjecture of Beauville [Reference BeauvilleBea06, §6]. We apply the aforementioned construction to give the following sharpening of Brivio and Verra’s result.
$g\geqslant \binom{3r}{r}-2r-1$
, partially answering a conjecture of Beauville [Reference BeauvilleBea06, §6]. We apply the aforementioned construction to give the following sharpening of Brivio and Verra’s result.
Theorem 1.1. For
![]() $r\geqslant 2$
and
$r\geqslant 2$
and
![]() $C$
a Petri general curve of genus
$C$
a Petri general curve of genus
![]() $g\geqslant (2r+2)(2r+1)$
, the theta map (2) is generically injective.
$g\geqslant (2r+2)(2r+1)$
, the theta map (2) is generically injective.
In addition to giving the statement for several new values of
![]() $g$
when
$g$
when
![]() $r\geqslant 3$
(our lower bound for
$r\geqslant 3$
(our lower bound for
![]() $g$
depends quadratically on
$g$
depends quadratically on
![]() $r$
rather than exponentially), our proof is constructive, based on the method mentioned above for explicitly recovering the bundle
$r$
rather than exponentially), our proof is constructive, based on the method mentioned above for explicitly recovering the bundle
![]() $V$
from the tangent cone to the theta divisor at a point of multiplicity
$V$
from the tangent cone to the theta divisor at a point of multiplicity
![]() $r+1$
. This gives a new example, in the context of vector bundles, of the principle apparent in [Reference Kempf and SchreyerKS88] and [Reference Ciliberto and SernesiCS92] that the geometry of a theta divisor at a sufficiently singular point can encode essentially all the information of the bundle and/or the curve.
$r+1$
. This gives a new example, in the context of vector bundles, of the principle apparent in [Reference Kempf and SchreyerKS88] and [Reference Ciliberto and SernesiCS92] that the geometry of a theta divisor at a sufficiently singular point can encode essentially all the information of the bundle and/or the curve.
Our method works for
![]() $r=2$
, but in this case much more is already known: Narasimhan and Ramanan [Reference Narasimhan and RamananNR69] showed, for
$r=2$
, but in this case much more is already known: Narasimhan and Ramanan [Reference Narasimhan and RamananNR69] showed, for
![]() $g=2$
and
$g=2$
and
![]() $r=2$
, that
$r=2$
, that
![]() ${\mathcal{D}}$
is an isomorphism
${\mathcal{D}}$
is an isomorphism
![]() $\mathit{SU}_{C}(2)\xrightarrow[{}]{{\sim}}\mathbb{P}^{3}$
, and van Geemen and Izadi [Reference van Geemen and IzadivGI01] generalised this statement to nonhyperelliptic curves of higher genus. Note that our proof of Theorem 4.1 is not valid for hyperelliptic curves (see Remark 4.3).
$\mathit{SU}_{C}(2)\xrightarrow[{}]{{\sim}}\mathbb{P}^{3}$
, and van Geemen and Izadi [Reference van Geemen and IzadivGI01] generalised this statement to nonhyperelliptic curves of higher genus. Note that our proof of Theorem 4.1 is not valid for hyperelliptic curves (see Remark 4.3).
Here is a more detailed summary of the paper. In § 2, we study semistable bundles
![]() $E$
of slope
$E$
of slope
![]() $g-1$
for which the Petri trace map
$g-1$
for which the Petri trace map
is injective. A bundle
![]() $E$
with this property will be called Petri trace injective. We prove that for large enough genus, the theta divisor of a generic
$E$
with this property will be called Petri trace injective. We prove that for large enough genus, the theta divisor of a generic
![]() $V\in \mathit{SU}_{C}(r)$
contains a point
$V\in \mathit{SU}_{C}(r)$
contains a point
![]() $M$
of multiplicity
$M$
of multiplicity
![]() $r+1$
such that
$r+1$
such that
![]() $V\otimes M$
and
$V\otimes M$
and
![]() $K_{C}\otimes M^{-1}\otimes V^{\ast }$
are Petri trace injective and globally generated.
$K_{C}\otimes M^{-1}\otimes V^{\ast }$
are Petri trace injective and globally generated.
Now suppose that
![]() $E$
is a vector bundle of slope
$E$
is a vector bundle of slope
![]() $g-1$
with
$g-1$
with
![]() $h^{0}(C,E)\geqslant r+1$
. If
$h^{0}(C,E)\geqslant r+1$
. If
![]() $\unicode[STIX]{x1D6E9}_{E}$
is defined, then the tangent cone to
$\unicode[STIX]{x1D6E9}_{E}$
is defined, then the tangent cone to
![]() $\unicode[STIX]{x1D6E9}_{E}$
at
$\unicode[STIX]{x1D6E9}_{E}$
at
![]() ${\mathcal{O}}_{C}$
is a determinantal hypersurface in
${\mathcal{O}}_{C}$
is a determinantal hypersurface in
![]() $|K_{C}|^{\ast }=\mathbb{P}^{g-1}$
containing the canonical embedding of
$|K_{C}|^{\ast }=\mathbb{P}^{g-1}$
containing the canonical embedding of
![]() $C$
. We prove (Proposition 3.3 and Corollary 3.5) that if
$C$
. We prove (Proposition 3.3 and Corollary 3.5) that if
![]() $C$
is a general curve of genus
$C$
is a general curve of genus
![]() $g\geqslant (2r+2)(2r+1)$
, and
$g\geqslant (2r+2)(2r+1)$
, and
![]() $E$
a globally generated Petri trace injective bundle of rank
$E$
a globally generated Petri trace injective bundle of rank
![]() $r$
and slope
$r$
and slope
![]() $g-1$
with
$g-1$
with
![]() $h^{0}(C,E)=r+1$
, then the bundle
$h^{0}(C,E)=r+1$
, then the bundle
![]() $E$
can be reconstructed up to the involution
$E$
can be reconstructed up to the involution
![]() $E\mapsto K_{C}\otimes E^{\ast }$
from a certain determinantal representation of the tangent cone to
$E\mapsto K_{C}\otimes E^{\ast }$
from a certain determinantal representation of the tangent cone to
![]() $\unicode[STIX]{x1D6E9}_{E}$
at
$\unicode[STIX]{x1D6E9}_{E}$
at
![]() ${\mathcal{O}}_{C}$
. By a classical result of Frobenius (whose proof we sketch in Proposition 3.7), any two such representations are equivalent up to transpose. The generic injectivity of the theta map for a Petri general curve (Theorem 4.1) can then be deduced by combining these facts and the statement in § 2 that the theta divisor of a general
${\mathcal{O}}_{C}$
. By a classical result of Frobenius (whose proof we sketch in Proposition 3.7), any two such representations are equivalent up to transpose. The generic injectivity of the theta map for a Petri general curve (Theorem 4.1) can then be deduced by combining these facts and the statement in § 2 that the theta divisor of a general
![]() $V\in \mathit{SU}_{C}(r)$
contains a suitable point of multiplicity
$V\in \mathit{SU}_{C}(r)$
contains a suitable point of multiplicity
![]() $r+1$
.
$r+1$
.
We assume throughout that the ground field is
![]() $\mathbb{C}$
. The reconstruction of
$\mathbb{C}$
. The reconstruction of
![]() $E$
from its tangent cone in § 3.2 is valid for an algebraically closed field of characteristic zero or
$E$
from its tangent cone in § 3.2 is valid for an algebraically closed field of characteristic zero or
![]() $p>0$
not dividing
$p>0$
not dividing
![]() $r+1$
.
$r+1$
.
2 Singularities of theta divisors of vector bundles
2.1 Petri trace injective bundles
Let
![]() $C$
be a projective smooth curve of genus
$C$
be a projective smooth curve of genus
![]() $g\geqslant 2$
. Let
$g\geqslant 2$
. Let
![]() $V\rightarrow C$
be a stable vector bundle of rank
$V\rightarrow C$
be a stable vector bundle of rank
![]() $r\geqslant 2$
and integral slope
$r\geqslant 2$
and integral slope
![]() $h$
, and consider the locus
$h$
, and consider the locus
If this is not the whole of
![]() $\operatorname{Pic}^{g-1-h}(C)$
, then it is the support of the theta divisor
$\operatorname{Pic}^{g-1-h}(C)$
, then it is the support of the theta divisor
![]() $\unicode[STIX]{x1D6E9}_{V}$
.
$\unicode[STIX]{x1D6E9}_{V}$
.
The theta divisor of a vector bundle is a special case of a twisted Brill–Noether locus
The following is central in the study of these loci (see, for example, Teixidor i Bigas [Reference Teixidor i BigasTiB14, §1]): For
![]() $E\rightarrow C$
a stable vector bundle, we consider the Petri trace map:
$E\rightarrow C$
a stable vector bundle, we consider the Petri trace map:
Then for
![]() $E=V\otimes M$
and
$E=V\otimes M$
and
![]() $M\in B_{1,g-1-h}^{n}(V)\backslash B_{1,g-1-h}^{n+1}(V)$
, the Zariski tangent space to the twisted Brill–Noether locus
$M\in B_{1,g-1-h}^{n}(V)\backslash B_{1,g-1-h}^{n+1}(V)$
, the Zariski tangent space to the twisted Brill–Noether locus
![]() $B_{1,g-1-h}^{n}(V)$
at
$B_{1,g-1-h}^{n}(V)$
at
![]() $M$
is exactly
$M$
is exactly
![]() $\operatorname{Im}(\bar{\unicode[STIX]{x1D707}})^{\bot }$
. This motivates the following definition.
$\operatorname{Im}(\bar{\unicode[STIX]{x1D707}})^{\bot }$
. This motivates the following definition.
Definition 2.1. Suppose
![]() $E\rightarrow C$
is a vector bundle with
$E\rightarrow C$
is a vector bundle with
![]() $h^{0}(C,E)=n\geqslant 1$
. If the map
$h^{0}(C,E)=n\geqslant 1$
. If the map
![]() $\unicode[STIX]{x1D707}$
above is injective, we will say that
$\unicode[STIX]{x1D707}$
above is injective, we will say that
![]() $E$
is Petri injective. If the composed map
$E$
is Petri injective. If the composed map
![]() $\bar{\unicode[STIX]{x1D707}}$
is injective, we will say that
$\bar{\unicode[STIX]{x1D707}}$
is injective, we will say that
![]() $E$
is Petri trace injective.
$E$
is Petri trace injective.
Remark 2.2. (1) Clearly, a Petri trace injective bundle is Petri injective. For line bundles, the two notions coincide.
(2) Suppose
![]() $V\in \mathit{U}_{C}(r,d)$
where
$V\in \mathit{U}_{C}(r,d)$
where
![]() $\mathit{U}_{C}(r,d)$
is the moduli space of semistable rank
$\mathit{U}_{C}(r,d)$
is the moduli space of semistable rank
![]() $r$
vector bundles of degree
$r$
vector bundles of degree
![]() $d$
. If
$d$
. If
![]() $E=V\otimes M$
is Petri trace injective for
$E=V\otimes M$
is Petri trace injective for
![]() $M\in \operatorname{Pic}^{e}(C)$
, then
$M\in \operatorname{Pic}^{e}(C)$
, then
![]() $B_{1,e}^{n}(V)$
is smooth at
$B_{1,e}^{n}(V)$
is smooth at
![]() $M$
and of the expected dimension
$M$
and of the expected dimension
(3) We will also need to refer to the usual generalised Brill–Noether locus
If
![]() $E$
is Petri injective then this is smooth and of the expected dimension
$E$
is Petri injective then this is smooth and of the expected dimension
at
![]() $E$
. See, for example, Grzegorczyk and Teixidor i Bigas [Reference Grzegorczyk and Teixidor i BigasGT09, §2].
$E$
. See, for example, Grzegorczyk and Teixidor i Bigas [Reference Grzegorczyk and Teixidor i BigasGT09, §2].
(4) Petri injectivity and Petri trace injectivity are open conditions on families of bundles
![]() ${\mathcal{E}}\rightarrow C\times B$
with
${\mathcal{E}}\rightarrow C\times B$
with
![]() $h^{0}(C,{\mathcal{E}}_{b})$
constant. Later, we will discuss the sense in which these properties are ‘open’ when
$h^{0}(C,{\mathcal{E}}_{b})$
constant. Later, we will discuss the sense in which these properties are ‘open’ when
![]() $h^{0}(C,{\mathcal{E}}_{b})$
may vary.
$h^{0}(C,{\mathcal{E}}_{b})$
may vary.
We will also need the notion of a Petri general curve.
Definition 2.3. A curve
![]() $C$
is called Petri general if every line bundle on
$C$
is called Petri general if every line bundle on
![]() $C$
is Petri injective.
$C$
is Petri injective.
By [Reference GiesekerGie82], the locus of curves which are not Petri general is a proper subset of the moduli space
![]() $M_{g}$
of curves of genus
$M_{g}$
of curves of genus
![]() $g$
, the so-called Gieseker–Petri locus. The hyperelliptic locus is contained in the Gieseker–Petri locus. Apart from this, in general not much is known about the components of the Gieseker–Petri locus and their dimensions. For an overview of known results, we refer to [Reference Teixidor i BigasTiB88, Reference FarkasFar05, Reference Bruno and SernesiBS11] and the references cited therein.
$g$
, the so-called Gieseker–Petri locus. The hyperelliptic locus is contained in the Gieseker–Petri locus. Apart from this, in general not much is known about the components of the Gieseker–Petri locus and their dimensions. For an overview of known results, we refer to [Reference Teixidor i BigasTiB88, Reference FarkasFar05, Reference Bruno and SernesiBS11] and the references cited therein.
Proposition 2.4. Suppose
![]() $V$
is a stable bundle of rank
$V$
is a stable bundle of rank
![]() $r$
and integral slope
$r$
and integral slope
![]() $h$
. Suppose
$h$
. Suppose
![]() $M_{0}\in \operatorname{Pic}^{g-1-h}(C)$
satisfies
$M_{0}\in \operatorname{Pic}^{g-1-h}(C)$
satisfies
![]() $h^{0}(C,V\otimes M_{0})\geqslant 1$
, and furthermore that
$h^{0}(C,V\otimes M_{0})\geqslant 1$
, and furthermore that
![]() $V\otimes M_{0}$
is Petri trace injective. Then the theta divisor
$V\otimes M_{0}$
is Petri trace injective. Then the theta divisor
![]() $\unicode[STIX]{x1D6E9}_{V}\subset \operatorname{Pic}^{g-1-h}(C)$
is defined. Furthermore, we have equality
$\unicode[STIX]{x1D6E9}_{V}\subset \operatorname{Pic}^{g-1-h}(C)$
is defined. Furthermore, we have equality
![]() $\operatorname{mult}_{M_{0}}\unicode[STIX]{x1D6E9}_{V}=h^{0}(C,V\otimes M_{0})$
.
$\operatorname{mult}_{M_{0}}\unicode[STIX]{x1D6E9}_{V}=h^{0}(C,V\otimes M_{0})$
.
Proof. Write
![]() $E:=V\otimes M_{0}$
. It is well known that via Serre duality,
$E:=V\otimes M_{0}$
. It is well known that via Serre duality,
![]() $\bar{\unicode[STIX]{x1D707}}$
is dual to the cup product map
$\bar{\unicode[STIX]{x1D707}}$
is dual to the cup product map
By hypothesis, therefore,
![]() $\bigcup$
is surjective. Since
$\bigcup$
is surjective. Since
![]() $E$
has Euler characteristic zero,
$E$
has Euler characteristic zero,
![]() $h^{0}(C,E)=h^{1}(C,E)$
. Hence there exists
$h^{0}(C,E)=h^{1}(C,E)$
. Hence there exists
![]() $b\in H^{1}(C,{\mathcal{O}}_{C})$
such that
$b\in H^{1}(C,{\mathcal{O}}_{C})$
such that
![]() $\cdot \cup b:H^{0}(C,E)\rightarrow H^{1}(C,E)$
is injective. The tangent vector
$\cdot \cup b:H^{0}(C,E)\rightarrow H^{1}(C,E)$
is injective. The tangent vector
![]() $b$
induces a deformation of
$b$
induces a deformation of
![]() $M_{0}$
and hence of
$M_{0}$
and hence of
![]() $E$
, which does not preserve any nonzero section of
$E$
, which does not preserve any nonzero section of
![]() $E$
. Therefore, the locus
$E$
. Therefore, the locus
is a proper sublocus of
![]() $\operatorname{Pic}^{g-1-h}(C)$
, so
$\operatorname{Pic}^{g-1-h}(C)$
, so
![]() $\unicode[STIX]{x1D6E9}_{V}$
is defined. Now we can apply Casalaina-Martin and Teixidor i Bigas [Reference Casalaina-Martin and Teixidor i BigasCT11, Proposition 4.1] to obtain the desired equality
$\unicode[STIX]{x1D6E9}_{V}$
is defined. Now we can apply Casalaina-Martin and Teixidor i Bigas [Reference Casalaina-Martin and Teixidor i BigasCT11, Proposition 4.1] to obtain the desired equality
![]() $\operatorname{mult}_{M_{0}}\unicode[STIX]{x1D6E9}_{V}=h^{0}(C,V\otimes M_{0})$
.◻
$\operatorname{mult}_{M_{0}}\unicode[STIX]{x1D6E9}_{V}=h^{0}(C,V\otimes M_{0})$
.◻
2.2 Existence of good singular points
In this section, we study global generatedness and Petri trace injectivity of the bundles
![]() $V\otimes M$
for
$V\otimes M$
for
![]() $M\in B_{1,g-1}^{r+1}(V)$
for general
$M\in B_{1,g-1}^{r+1}(V)$
for general
![]() $C$
and
$C$
and
![]() $V$
. The main result of this section is the following theorem.
$V$
. The main result of this section is the following theorem.
Theorem 2.5. Suppose
![]() $C$
is a Petri general curve of genus
$C$
is a Petri general curve of genus
![]() $g\geqslant (2r+2)(2r+1)$
and
$g\geqslant (2r+2)(2r+1)$
and
![]() $V\in \mathit{SU}_{C}(r)$
a general bundle. Then there exists
$V\in \mathit{SU}_{C}(r)$
a general bundle. Then there exists
![]() $M\in \unicode[STIX]{x1D6E9}_{V}$
such that
$M\in \unicode[STIX]{x1D6E9}_{V}$
such that
![]() $h^{0}(C,V\otimes M)=r+1$
, and both
$h^{0}(C,V\otimes M)=r+1$
, and both
![]() $V\otimes M$
and
$V\otimes M$
and
![]() $K_{C}\otimes M^{-1}\otimes V^{\ast }$
are globally generated and Petri trace injective.
$K_{C}\otimes M^{-1}\otimes V^{\ast }$
are globally generated and Petri trace injective.
The proof of this theorem has several ingredients. We begin by constructing a stable bundle
![]() $E_{0}$
with some of the properties we are interested in. Let
$E_{0}$
with some of the properties we are interested in. Let
![]() $F$
be a semistable bundle of rank
$F$
be a semistable bundle of rank
![]() $r-1$
and degree
$r-1$
and degree
![]() $(r-1)(g-1)-1$
, and let
$(r-1)(g-1)-1$
, and let
![]() $N$
be a line bundle of degree
$N$
be a line bundle of degree
![]() $g$
.
$g$
.
Lemma 2.6. A general extension
![]() $0\rightarrow F\rightarrow E\rightarrow N\rightarrow 0$
is a stable vector bundle.
$0\rightarrow F\rightarrow E\rightarrow N\rightarrow 0$
is a stable vector bundle.
Proof. Any subbundle
![]() $G$
of
$G$
of
![]() $E$
fits into an exact diagram
$E$
fits into an exact diagram
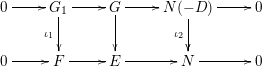
where
![]() $D$
is an effective divisor on
$D$
is an effective divisor on
![]() $C$
. If
$C$
. If
![]() $\unicode[STIX]{x1D704}_{2}=0$
, then
$\unicode[STIX]{x1D704}_{2}=0$
, then
![]() $\unicode[STIX]{x1D707}(G)=\unicode[STIX]{x1D707}(G_{1})\leqslant \unicode[STIX]{x1D707}(F)<\unicode[STIX]{x1D707}(E)$
. Suppose
$\unicode[STIX]{x1D707}(G)=\unicode[STIX]{x1D707}(G_{1})\leqslant \unicode[STIX]{x1D707}(F)<\unicode[STIX]{x1D707}(E)$
. Suppose
![]() $\unicode[STIX]{x1D704}_{2}\neq 0$
, and write
$\unicode[STIX]{x1D704}_{2}\neq 0$
, and write
![]() $s:=\operatorname{rk}(G_{1})$
. If
$s:=\operatorname{rk}(G_{1})$
. If
![]() $s\neq 0$
, the semistability of
$s\neq 0$
, the semistability of
![]() $F$
implies that
$F$
implies that
so in fact
![]() $\deg (G_{1})\leqslant s(g-1)-1$
. As
$\deg (G_{1})\leqslant s(g-1)-1$
. As
![]() $\deg (N)=g$
, we have
$\deg (N)=g$
, we have
![]() $\deg (G)\leqslant (s+1)(g-1)$
. Thus we need only exclude the case where
$\deg (G)\leqslant (s+1)(g-1)$
. Thus we need only exclude the case where
![]() $\deg (G_{1})=s(g-1)-1$
and
$\deg (G_{1})=s(g-1)-1$
and
![]() $D=0$
, so
$D=0$
, so
![]() $\unicode[STIX]{x1D704}_{2}=\operatorname{Id}_{N}$
. In this case, the existence of the above diagram is equivalent to
$\unicode[STIX]{x1D704}_{2}=\operatorname{Id}_{N}$
. In this case, the existence of the above diagram is equivalent to
![]() $[E]=(\unicode[STIX]{x1D704}_{1})_{\ast }[G]$
for some extension
$[E]=(\unicode[STIX]{x1D704}_{1})_{\ast }[G]$
for some extension
![]() $G$
, that is,
$G$
, that is,
![]() $[E]\in \operatorname{Im}((\unicode[STIX]{x1D704}_{1})_{\ast })$
.
$[E]\in \operatorname{Im}((\unicode[STIX]{x1D704}_{1})_{\ast })$
.
It therefore suffices to check that
is not surjective. This follows from the fact, easily shown by a Riemann–Roch calculation, that
![]() $h^{1}(C,\operatorname{Hom}(N,F/G_{1}))>0$
.
$h^{1}(C,\operatorname{Hom}(N,F/G_{1}))>0$
.
If
![]() $s=0$
, then we need to exclude the lifting of
$s=0$
, then we need to exclude the lifting of
![]() $G=N(-p)$
for all
$G=N(-p)$
for all
![]() $p\in C$
, that is,
$p\in C$
, that is,
A dimension count shows that this locus is not dense in
![]() $H^{1}(C,\operatorname{Hom}(N,F))$
.◻
$H^{1}(C,\operatorname{Hom}(N,F))$
.◻
Lemma 2.7. Suppose
![]() $h^{0}(C,N)\geqslant h^{1}(C,F)$
. Then for a general extension
$h^{0}(C,N)\geqslant h^{1}(C,F)$
. Then for a general extension
![]() $0\rightarrow F\rightarrow E\rightarrow N\rightarrow 0$
, the coboundary map is surjective.
$0\rightarrow F\rightarrow E\rightarrow N\rightarrow 0$
, the coboundary map is surjective.
Proof. Clearly it suffices to exhibit one extension
![]() $E_{0}$
with the required property. We write
$E_{0}$
with the required property. We write
![]() $n:=h^{1}(C,F)$
for brevity.
$n:=h^{1}(C,F)$
for brevity.
Let
![]() $0\rightarrow F\rightarrow \tilde{F}\rightarrow \unicode[STIX]{x1D70F}\rightarrow 0$
be an elementary transformation with
$0\rightarrow F\rightarrow \tilde{F}\rightarrow \unicode[STIX]{x1D70F}\rightarrow 0$
be an elementary transformation with
![]() $\deg (\unicode[STIX]{x1D70F})=n$
and such that the image of
$\deg (\unicode[STIX]{x1D70F})=n$
and such that the image of
![]() $\unicode[STIX]{x1D6E4}(C,\unicode[STIX]{x1D70F})$
generates
$\unicode[STIX]{x1D6E4}(C,\unicode[STIX]{x1D70F})$
generates
![]() $H^{1}(C,F)$
. We may assume that
$H^{1}(C,F)$
. We may assume that
![]() $\unicode[STIX]{x1D70F}$
is supported along
$\unicode[STIX]{x1D70F}$
is supported along
![]() $n$
general points
$n$
general points
![]() $p_{1},\ldots ,p_{n}$
of
$p_{1},\ldots ,p_{n}$
of
![]() $C$
which are not base points of
$C$
which are not base points of
![]() $|N|$
. Then
$|N|$
. Then
![]() $\unicode[STIX]{x1D70F}_{p_{i}}$
is generated by an element
$\unicode[STIX]{x1D70F}_{p_{i}}$
is generated by an element
defined up to nonzero scalar multiple. We write
![]() $[\unicode[STIX]{x1D719}_{i}]$
for the class in
$[\unicode[STIX]{x1D719}_{i}]$
for the class in
![]() $H^{1}(C,F)$
defined by
$H^{1}(C,F)$
defined by
![]() $\unicode[STIX]{x1D719}_{i}$
.
$\unicode[STIX]{x1D719}_{i}$
.
Now
![]() $h^{0}(C,N)\geqslant n$
and the image of
$h^{0}(C,N)\geqslant n$
and the image of
![]() $C$
is nondegenerate in
$C$
is nondegenerate in
![]() $|N|^{\ast }$
. As the
$|N|^{\ast }$
. As the
![]() $p_{i}$
can be assumed to be general, they impose independent conditions on sections of
$p_{i}$
can be assumed to be general, they impose independent conditions on sections of
![]() $N$
. We choose sections
$N$
. We choose sections
![]() $s_{1},\ldots ,s_{n}\in H^{0}(C,N)$
such that
$s_{1},\ldots ,s_{n}\in H^{0}(C,N)$
such that
![]() $s_{i}(p_{i})\neq 0$
but
$s_{i}(p_{i})\neq 0$
but
![]() $s_{i}(p_{j})=0$
for
$s_{i}(p_{j})=0$
for
![]() $j\neq i$
. For
$j\neq i$
. For
![]() $1\leqslant i\leqslant n$
, let
$1\leqslant i\leqslant n$
, let
![]() $\unicode[STIX]{x1D702}_{i}$
be a local section of
$\unicode[STIX]{x1D702}_{i}$
be a local section of
![]() $N^{-1}$
such that
$N^{-1}$
such that
![]() $\unicode[STIX]{x1D702}_{i}(s_{i}(p_{i}))=1$
.
$\unicode[STIX]{x1D702}_{i}(s_{i}(p_{i}))=1$
.
Let
![]() $0\rightarrow F\rightarrow E_{0}\rightarrow N\rightarrow 0$
be the extension with class
$0\rightarrow F\rightarrow E_{0}\rightarrow N\rightarrow 0$
be the extension with class
![]() $[E_{0}]$
defined by the image of
$[E_{0}]$
defined by the image of
by the coboundary map
![]() $\unicode[STIX]{x1D6E4}(C,N^{-1}\otimes \unicode[STIX]{x1D70F})\rightarrow H^{1}(C,N^{-1}\otimes F)$
. Then
$\unicode[STIX]{x1D6E4}(C,N^{-1}\otimes \unicode[STIX]{x1D70F})\rightarrow H^{1}(C,N^{-1}\otimes F)$
. Then
![]() $s_{i}\cup [E_{0}]=[\unicode[STIX]{x1D719}_{i}]$
for
$s_{i}\cup [E_{0}]=[\unicode[STIX]{x1D719}_{i}]$
for
![]() $1\leqslant i\leqslant n$
. Hence the image of
$1\leqslant i\leqslant n$
. Hence the image of
![]() $\cdot \cup [E_{0}]$
spans
$\cdot \cup [E_{0}]$
spans
![]() $H^{1}(C,F)$
.◻
$H^{1}(C,F)$
.◻
We now make further assumptions on
![]() $F$
and
$F$
and
![]() $N$
. If
$N$
. If
![]() $r=2$
, then
$r=2$
, then
![]() $g\geqslant (2r+2)(2r+1)=30$
. Hence by the Brill–Noether theory of line bundles on
$g\geqslant (2r+2)(2r+1)=30$
. Hence by the Brill–Noether theory of line bundles on
![]() $C$
, we may choose a line bundle
$C$
, we may choose a line bundle
![]() $F$
of degree
$F$
of degree
![]() $g-2$
with
$g-2$
with
![]() $h^{0}(C,F)=2$
and
$h^{0}(C,F)=2$
and
![]() $|F|$
base point free. If
$|F|$
base point free. If
![]() $r\geqslant 3$
: since
$r\geqslant 3$
: since
![]() $g\geqslant 3$
, we have
$g\geqslant 3$
, we have
![]() $(r-1)(g-1)-1\geqslant r$
. Therefore, by [Reference Bhosle, Brambila-Paz and NewsteadBBN15, Theorem 5.1] we may choose a semistable bundle
$(r-1)(g-1)-1\geqslant r$
. Therefore, by [Reference Bhosle, Brambila-Paz and NewsteadBBN15, Theorem 5.1] we may choose a semistable bundle
![]() $F$
of rank
$F$
of rank
![]() $r-1$
and degree
$r-1$
and degree
![]() $(r-1)(g-1)-1$
which is globally generated and satisfies
$(r-1)(g-1)-1$
which is globally generated and satisfies
![]() $h^{0}(C,F)=r$
, so
$h^{0}(C,F)=r$
, so
![]() $h^{1}(C,F)=r+1$
.
$h^{1}(C,F)=r+1$
.
Furthermore, again by Brill–Noether theory, since
![]() $g\geqslant (2r+2)(2r+1)$
we may choose
$g\geqslant (2r+2)(2r+1)$
we may choose
![]() $N\in \operatorname{Pic}^{g}(C)$
such that
$N\in \operatorname{Pic}^{g}(C)$
such that
![]() $h^{0}(C,N)=2r+2$
and
$h^{0}(C,N)=2r+2$
and
![]() $|N|$
is base point free. By Lemma 2.7, we may choose an
$|N|$
is base point free. By Lemma 2.7, we may choose an
![]() $(r+1)$
-dimensional subspace
$(r+1)$
-dimensional subspace
![]() $\unicode[STIX]{x1D6F1}\subset H^{0}(C,E)$
lifting from
$\unicode[STIX]{x1D6F1}\subset H^{0}(C,E)$
lifting from
![]() $H^{0}(C,N)$
.
$H^{0}(C,N)$
.
Proposition 2.8. Let
![]() $F$
,
$F$
,
![]() $N$
and
$N$
and
![]() $\unicode[STIX]{x1D6F1}$
be as above, and let
$\unicode[STIX]{x1D6F1}$
be as above, and let
![]() $0\rightarrow F\rightarrow E\rightarrow N\rightarrow 0$
be a general extension. Then the restricted Petri trace map
$0\rightarrow F\rightarrow E\rightarrow N\rightarrow 0$
be a general extension. Then the restricted Petri trace map
![]() $\unicode[STIX]{x1D6F1}\otimes H^{0}(C,K_{C}\otimes E^{\ast })\rightarrow H^{0}(C,K_{C})$
is injective.
$\unicode[STIX]{x1D6F1}\otimes H^{0}(C,K_{C}\otimes E^{\ast })\rightarrow H^{0}(C,K_{C})$
is injective.
Proof. Choose a basis
![]() $\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{r+1}$
for
$\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{r+1}$
for
![]() $\unicode[STIX]{x1D6F1}$
. For each
$\unicode[STIX]{x1D6F1}$
. For each
![]() $i$
, write
$i$
, write
![]() $\widetilde{\unicode[STIX]{x1D70E}_{i}}$
for the image of
$\widetilde{\unicode[STIX]{x1D70E}_{i}}$
for the image of
![]() $\unicode[STIX]{x1D70E}_{i}$
in
$\unicode[STIX]{x1D70E}_{i}$
in
![]() $H^{0}(C,N)$
.
$H^{0}(C,N)$
.
By Lemma 2.7, there is an isomorphism
![]() $H^{1}(C,E)\xrightarrow[{}]{{\sim}}H^{1}(C,N)$
. Hence, by Serre duality, the injection
$H^{1}(C,E)\xrightarrow[{}]{{\sim}}H^{1}(C,N)$
. Hence, by Serre duality, the injection
![]() $K_{C}\otimes N^{-1}{\hookrightarrow}K_{C}\otimes E^{\ast }$
induces an isomorphism on global sections. Choose a basis
$K_{C}\otimes N^{-1}{\hookrightarrow}K_{C}\otimes E^{\ast }$
induces an isomorphism on global sections. Choose a basis
![]() $\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{2r+1}$
for
$\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{2r+1}$
for
![]() $H^{0}(C,K_{C}\otimes E^{\ast })$
. For each
$H^{0}(C,K_{C}\otimes E^{\ast })$
. For each
![]() $j$
, write
$j$
, write
![]() $\widetilde{\unicode[STIX]{x1D70F}_{j}}$
for the preimage of
$\widetilde{\unicode[STIX]{x1D70F}_{j}}$
for the preimage of
![]() $\unicode[STIX]{x1D70F}_{j}$
by the aforementioned isomorphism.
$\unicode[STIX]{x1D70F}_{j}$
by the aforementioned isomorphism.
For each
![]() $i$
and
$i$
and
![]() $j$
we have a commutative diagram
$j$
we have a commutative diagram

where the top row defines the twisted endomorphism
Clearly this has rank one. As it factorises via
![]() $K_{C}\otimes N^{-1}$
, at a general point of
$K_{C}\otimes N^{-1}$
, at a general point of
![]() $C$
the eigenspace corresponding to the single nonzero eigenvalue is identified with the fibre of
$C$
the eigenspace corresponding to the single nonzero eigenvalue is identified with the fibre of
![]() $N^{-1}$
in
$N^{-1}$
in
![]() $E^{\ast }$
. Hence the Petri trace
$E^{\ast }$
. Hence the Petri trace
![]() $\bar{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70E}_{i}\otimes \unicode[STIX]{x1D70F}_{j})$
may be identified with the restriction to
$\bar{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70E}_{i}\otimes \unicode[STIX]{x1D70F}_{j})$
may be identified with the restriction to
![]() $N^{-1}$
. By the diagram, we may identify this restriction with
$N^{-1}$
. By the diagram, we may identify this restriction with
where
![]() $\unicode[STIX]{x1D707}_{N}$
is the Petri map of the line bundle
$\unicode[STIX]{x1D707}_{N}$
is the Petri map of the line bundle
![]() $N$
. Since
$N$
. Since
![]() $C$
is Petri,
$C$
is Petri,
![]() $\unicode[STIX]{x1D707}_{N}$
is injective. Hence the elements
$\unicode[STIX]{x1D707}_{N}$
is injective. Hence the elements
![]() $\bar{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70E}_{i}\otimes \unicode[STIX]{x1D70F}_{j})=\unicode[STIX]{x1D707}_{N}(\widetilde{\unicode[STIX]{x1D70E}_{i}}\otimes \widetilde{\unicode[STIX]{x1D70F}_{j}})$
are independent in
$\bar{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70E}_{i}\otimes \unicode[STIX]{x1D70F}_{j})=\unicode[STIX]{x1D707}_{N}(\widetilde{\unicode[STIX]{x1D70E}_{i}}\otimes \widetilde{\unicode[STIX]{x1D70F}_{j}})$
are independent in
![]() $H^{0}(C,K_{C})$
. This proves the statement.◻
$H^{0}(C,K_{C})$
. This proves the statement.◻
Before proceeding, we need to recall some background on coherent systems (see [Reference Bhosle, Brambila-Paz and NewsteadBBN08, §2] for an overview and [Reference Bradlow, García-Prada, Muñoz and NewsteadBGMN03] for more detail). We recall that a coherent system of type
![]() $(r,d,k)$
is a pair
$(r,d,k)$
is a pair
![]() $(W,\unicode[STIX]{x1D6F1})$
where
$(W,\unicode[STIX]{x1D6F1})$
where
![]() $W$
is a vector bundle of rank
$W$
is a vector bundle of rank
![]() $r$
and degree
$r$
and degree
![]() $d$
over
$d$
over
![]() $C$
, and
$C$
, and
![]() $\unicode[STIX]{x1D6F1}\subseteq H^{0}(C,W)$
is a subspace of dimension
$\unicode[STIX]{x1D6F1}\subseteq H^{0}(C,W)$
is a subspace of dimension
![]() $k$
. There is a stability condition for coherent systems depending on a real parameter
$k$
. There is a stability condition for coherent systems depending on a real parameter
![]() $\unicode[STIX]{x1D6FC}$
, and a moduli space
$\unicode[STIX]{x1D6FC}$
, and a moduli space
![]() $G(\unicode[STIX]{x1D6FC};r,d,k)$
for equivalence classes of
$G(\unicode[STIX]{x1D6FC};r,d,k)$
for equivalence classes of
![]() $\unicode[STIX]{x1D6FC}$
-semistable coherent systems of type
$\unicode[STIX]{x1D6FC}$
-semistable coherent systems of type
![]() $(r,d,k)$
. If
$(r,d,k)$
. If
![]() $k\geqslant r$
, then by [Reference Bradlow, García-Prada, Muñoz and NewsteadBGMN03, Proposition 4.6] there exists
$k\geqslant r$
, then by [Reference Bradlow, García-Prada, Muñoz and NewsteadBGMN03, Proposition 4.6] there exists
![]() $\unicode[STIX]{x1D6FC}_{L}\in \mathbb{R}$
such that
$\unicode[STIX]{x1D6FC}_{L}\in \mathbb{R}$
such that
![]() $G(\unicode[STIX]{x1D6FC};r,d,k)$
is independent of
$G(\unicode[STIX]{x1D6FC};r,d,k)$
is independent of
![]() $\unicode[STIX]{x1D6FC}$
for
$\unicode[STIX]{x1D6FC}$
for
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{L}$
. This ‘terminal’ moduli space is denoted
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{L}$
. This ‘terminal’ moduli space is denoted
![]() $G_{L}$
. Moreover, the locus
$G_{L}$
. Moreover, the locus
is an open subset of
![]() $G_{L}$
. For us,
$G_{L}$
. For us,
![]() $d=r(g-1)$
and
$d=r(g-1)$
and
![]() $k=r+1$
. To ease notation, we write
$k=r+1$
. To ease notation, we write
![]() $U:=U(r,r(g-1),r+1)$
.
$U:=U(r,r(g-1),r+1)$
.
Now let
![]() $N_{1}$
be a line bundle of degree
$N_{1}$
be a line bundle of degree
![]() $g$
with
$g$
with
![]() $h^{0}(C,N_{1})\geqslant r+2$
. Let
$h^{0}(C,N_{1})\geqslant r+2$
. Let
![]() $F$
be as above, and let
$F$
be as above, and let
![]() $0\rightarrow F\rightarrow E\rightarrow N_{1}\rightarrow 0$
be a general extension.
$0\rightarrow F\rightarrow E\rightarrow N_{1}\rightarrow 0$
be a general extension.
Lemma 2.9. For a general subspace
![]() $\unicode[STIX]{x1D6F1}\subset H^{0}(C,E)$
of dimension
$\unicode[STIX]{x1D6F1}\subset H^{0}(C,E)$
of dimension
![]() $r+1$
, the coherent system
$r+1$
, the coherent system
![]() $(E,\unicode[STIX]{x1D6F1})$
defines an element of
$(E,\unicode[STIX]{x1D6F1})$
defines an element of
![]() $U$
.
$U$
.
Proof. Recall the bundle
![]() $E_{0}$
defined in Lemma 2.7, which clearly is generically generated. Let us describe the subsheaf
$E_{0}$
defined in Lemma 2.7, which clearly is generically generated. Let us describe the subsheaf
![]() $E_{0}^{\prime }$
generated by
$E_{0}^{\prime }$
generated by
![]() $H^{0}(C,E_{0})$
.
$H^{0}(C,E_{0})$
.
Write
![]() $p_{1}+\cdots +p_{r+1}=:D$
. Clearly
$p_{1}+\cdots +p_{r+1}=:D$
. Clearly
![]() $s\cup [E_{0}]=0$
for any
$s\cup [E_{0}]=0$
for any
![]() $s\in H^{0}(C,N_{1}(-D))$
. Since the
$s\in H^{0}(C,N_{1}(-D))$
. Since the
![]() $p_{i}$
are general points,
$p_{i}$
are general points,
Therefore, the image of
![]() $H^{0}(C,E_{0})$
in
$H^{0}(C,E_{0})$
in
![]() $H^{0}(C,N_{1})$
is exactly
$H^{0}(C,N_{1})$
is exactly
![]() $H^{0}(C,N_{1}(-D))$
. As the subbundle
$H^{0}(C,N_{1}(-D))$
. As the subbundle
![]() $F\subset E_{0}$
is globally generated,
$F\subset E_{0}$
is globally generated,
![]() $E_{0}^{\prime }$
is an extension
$E_{0}^{\prime }$
is an extension
![]() $0\rightarrow F\rightarrow E_{0}^{\prime }\rightarrow N_{1}(-D)\rightarrow 0$
. Dualising and taking global sections, we obtain
$0\rightarrow F\rightarrow E_{0}^{\prime }\rightarrow N_{1}(-D)\rightarrow 0$
. Dualising and taking global sections, we obtain
Since both
![]() $N_{1}^{-1}(D)$
and
$N_{1}^{-1}(D)$
and
![]() $F^{\ast }$
are semistable of negative degree,
$F^{\ast }$
are semistable of negative degree,
![]() $h^{0}(C,N_{1}^{-1}(-D))=h^{0}(C,F^{\ast })=0$
, so
$h^{0}(C,N_{1}^{-1}(-D))=h^{0}(C,F^{\ast })=0$
, so
![]() $h^{0}(C,(E_{0}^{\prime })^{\ast })=0$
.
$h^{0}(C,(E_{0}^{\prime })^{\ast })=0$
.
Now let
![]() $\unicode[STIX]{x1D6F1}_{1}\subset H^{0}(C,E_{0})$
be any subspace of dimension
$\unicode[STIX]{x1D6F1}_{1}\subset H^{0}(C,E_{0})$
be any subspace of dimension
![]() $r+1$
generically generating
$r+1$
generically generating
![]() $E_{0}$
. Since
$E_{0}$
. Since
![]() $h^{0}(C,(E_{0}^{\prime })^{\ast })=0$
, by [Reference Bhosle, Brambila-Paz and NewsteadBBN08, Theorem 3.1(3)] the coherent system
$h^{0}(C,(E_{0}^{\prime })^{\ast })=0$
, by [Reference Bhosle, Brambila-Paz and NewsteadBBN08, Theorem 3.1(3)] the coherent system
![]() $(E_{0},\unicode[STIX]{x1D6F1}_{1})$
defines a point of
$(E_{0},\unicode[STIX]{x1D6F1}_{1})$
defines a point of
![]() $G_{L}$
. Since generic generatedness and vanishing of
$G_{L}$
. Since generic generatedness and vanishing of
![]() $h^{0}(C,(E^{\prime })^{\ast })$
are open conditions on families of bundles with a fixed number of sections, the same is true for a generic
$h^{0}(C,(E^{\prime })^{\ast })$
are open conditions on families of bundles with a fixed number of sections, the same is true for a generic
![]() $(E,\unicode[STIX]{x1D6F1})$
where
$(E,\unicode[STIX]{x1D6F1})$
where
![]() $E$
is an extension
$E$
is an extension
![]() $0\rightarrow F\rightarrow E\rightarrow N_{1}\rightarrow 0$
. By Lemma 2.6, in fact
$0\rightarrow F\rightarrow E\rightarrow N_{1}\rightarrow 0$
. By Lemma 2.6, in fact
![]() $(E,\unicode[STIX]{x1D6F1})$
belongs to
$(E,\unicode[STIX]{x1D6F1})$
belongs to
![]() $U$
.◻
$U$
.◻
Lemma 2.10. For generic
![]() $E$
represented in
$E$
represented in
![]() $U$
, we have
$U$
, we have
![]() $h^{0}(C,E)=h^{0}(C,K_{C}\otimes E^{\ast })=r+1$
.
$h^{0}(C,E)=h^{0}(C,K_{C}\otimes E^{\ast })=r+1$
.
Proof. Since
![]() $C$
is Petri general,
$C$
is Petri general,
![]() $B_{1,g}^{r+2}$
is irreducible in
$B_{1,g}^{r+2}$
is irreducible in
![]() $\operatorname{Pic}^{g}(C)$
. Thus there exists an irreducible family parametrising extensions of the form
$\operatorname{Pic}^{g}(C)$
. Thus there exists an irreducible family parametrising extensions of the form
![]() $0\rightarrow F\rightarrow E\rightarrow N_{1}\rightarrow 0$
where
$0\rightarrow F\rightarrow E\rightarrow N_{1}\rightarrow 0$
where
![]() $F$
is as above and
$F$
is as above and
![]() $N_{1}$
ranges over
$N_{1}$
ranges over
![]() $B_{1,g}^{r+2}$
. This contains the extension
$B_{1,g}^{r+2}$
. This contains the extension
![]() $E_{0}$
constructed above. By Lemma 2.7, a general element
$E_{0}$
constructed above. By Lemma 2.7, a general element
![]() $E_{1}$
of the family satisfies
$E_{1}$
of the family satisfies
![]() $h^{0}(C,E_{1})=r+1$
. By semicontinuity, the same is true for general
$h^{0}(C,E_{1})=r+1$
. By semicontinuity, the same is true for general
![]() $E$
represented in
$E$
represented in
![]() $U$
.◻
$U$
.◻
Now by [Reference Bhosle, Brambila-Paz and NewsteadBBN08, Theorem 3.1(4) and Remark 6.2], the locus
![]() $U$
is irreducible. Write
$U$
is irreducible. Write
![]() $B$
for the component of
$B$
for the component of
![]() $B_{r,r(g-1)}^{r+1}$
containing the image of
$B_{r,r(g-1)}^{r+1}$
containing the image of
![]() $U$
, and
$U$
, and
![]() $B^{\prime }$
for the sublocus
$B^{\prime }$
for the sublocus
![]() $\{E\in B:h^{0}(C,E)=r+1\}$
. Set
$\{E\in B:h^{0}(C,E)=r+1\}$
. Set
![]() $U^{\prime }:=U\times _{B}B^{\prime }$
; clearly
$U^{\prime }:=U\times _{B}B^{\prime }$
; clearly
![]() $U^{\prime }\cong B^{\prime }$
.
$U^{\prime }\cong B^{\prime }$
.
Let
![]() $\tilde{B}\rightarrow B$
be an étale cover such that there is a Poincaré bundle
$\tilde{B}\rightarrow B$
be an étale cover such that there is a Poincaré bundle
![]() ${\mathcal{E}}\rightarrow \tilde{B}\times C$
. In a natural way we obtain a commutative cube
${\mathcal{E}}\rightarrow \tilde{B}\times C$
. In a natural way we obtain a commutative cube

where all faces are fibre product diagrams. By a standard construction, we can find a complex of bundles
![]() $\unicode[STIX]{x1D6FC}:K^{0}\rightarrow K^{1}$
over
$\unicode[STIX]{x1D6FC}:K^{0}\rightarrow K^{1}$
over
![]() $\tilde{B}$
such that
$\tilde{B}$
such that
![]() $\operatorname{Ker}(\unicode[STIX]{x1D6FC}_{b})\cong H^{0}(C,K_{C}\otimes {\mathcal{E}}_{b}^{\ast })$
for each
$\operatorname{Ker}(\unicode[STIX]{x1D6FC}_{b})\cong H^{0}(C,K_{C}\otimes {\mathcal{E}}_{b}^{\ast })$
for each
![]() $b\in \tilde{B}$
. Following [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, ch. IV], we consider the Grassmann bundle
$b\in \tilde{B}$
. Following [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, ch. IV], we consider the Grassmann bundle
![]() $\operatorname{Gr}(r+1,K^{0})$
over
$\operatorname{Gr}(r+1,K^{0})$
over
![]() $\tilde{B}$
and the sublocus
$\tilde{B}$
and the sublocus
Write
![]() ${\mathcal{G}}_{1}:={\mathcal{G}}\times _{\tilde{B}}\tilde{U}$
. The fibre of
${\mathcal{G}}_{1}:={\mathcal{G}}\times _{\tilde{B}}\tilde{U}$
. The fibre of
![]() ${\mathcal{G}}_{1}$
over
${\mathcal{G}}_{1}$
over
![]() $({\mathcal{E}}_{b},\unicode[STIX]{x1D6F1})\in \tilde{U}$
is then
$({\mathcal{E}}_{b},\unicode[STIX]{x1D6F1})\in \tilde{U}$
is then
![]() $\operatorname{Gr}(r+1,H^{0}(C,K_{C}\otimes {\mathcal{E}}_{b}^{\ast }))$
.
$\operatorname{Gr}(r+1,H^{0}(C,K_{C}\otimes {\mathcal{E}}_{b}^{\ast }))$
.
Now let
![]() $E_{0}$
be a bundle as constructed in Lemma 2.7 with
$E_{0}$
be a bundle as constructed in Lemma 2.7 with
![]() $h^{0}(C,E_{0})=2r+2$
, and let
$h^{0}(C,E_{0})=2r+2$
, and let
![]() $\unicode[STIX]{x1D6F1}_{0}$
be a generic choice of
$\unicode[STIX]{x1D6F1}_{0}$
be a generic choice of
![]() $(r+1)$
-dimensional subspace of
$(r+1)$
-dimensional subspace of
![]() $H^{0}(C,E_{0})$
. We may assume
$H^{0}(C,E_{0})$
. We may assume
![]() $\tilde{U}$
is irreducible since
$\tilde{U}$
is irreducible since
![]() $U$
is. Since
$U$
is. Since
![]() $\tilde{U} \rightarrow U$
is étale, by Lemma 2.8 in fact
$\tilde{U} \rightarrow U$
is étale, by Lemma 2.8 in fact
![]() $U$
is also smooth at
$U$
is also smooth at
![]() $(E_{0},\unicode[STIX]{x1D6F1}_{0})$
(cf. [Reference Bradlow, García-Prada, Muñoz and NewsteadBGMN03, Proposition 3.10]). Therefore, we may choose a one-parameter family
$(E_{0},\unicode[STIX]{x1D6F1}_{0})$
(cf. [Reference Bradlow, García-Prada, Muñoz and NewsteadBGMN03, Proposition 3.10]). Therefore, we may choose a one-parameter family
![]() $\{(E_{t},\unicode[STIX]{x1D6F1}_{t}):t\in T\}$
in
$\{(E_{t},\unicode[STIX]{x1D6F1}_{t}):t\in T\}$
in
![]() $\tilde{U}$
such that
$\tilde{U}$
such that
![]() $(E_{t_{0}},\unicode[STIX]{x1D6F1}_{t_{0}})=(E_{0},\unicode[STIX]{x1D6F1}_{0})$
while
$(E_{t_{0}},\unicode[STIX]{x1D6F1}_{t_{0}})=(E_{0},\unicode[STIX]{x1D6F1}_{0})$
while
![]() $(E_{t},\unicode[STIX]{x1D6F1}_{t})$
belongs to
$(E_{t},\unicode[STIX]{x1D6F1}_{t})$
belongs to
![]() $\tilde{U} ^{\prime }$
for generic
$\tilde{U} ^{\prime }$
for generic
![]() $t\in T$
. Since the bundles have Euler characteristic zero, for generic
$t\in T$
. Since the bundles have Euler characteristic zero, for generic
![]() $t\in T$
there is exactly one choice of
$t\in T$
there is exactly one choice of
![]() $\unicode[STIX]{x1D6EC}\in {\mathcal{G}}_{1}|_{(E_{t},\unicode[STIX]{x1D6F1}_{t})}$
. Thus we obtain a section
$\unicode[STIX]{x1D6EC}\in {\mathcal{G}}_{1}|_{(E_{t},\unicode[STIX]{x1D6F1}_{t})}$
. Thus we obtain a section
![]() $T\backslash \{0\}\rightarrow {\mathcal{G}}_{1}$
. As
$T\backslash \{0\}\rightarrow {\mathcal{G}}_{1}$
. As
![]() $\dim T=1$
, this section can be extended uniquely to
$\dim T=1$
, this section can be extended uniquely to
![]() $0$
. We thus obtain a triple
$0$
. We thus obtain a triple
![]() $(E_{0},\unicode[STIX]{x1D6F1}_{0},\unicode[STIX]{x1D6EC}_{0})$
where
$(E_{0},\unicode[STIX]{x1D6F1}_{0},\unicode[STIX]{x1D6EC}_{0})$
where
![]() $\unicode[STIX]{x1D6EC}\subset H^{0}(C,K_{C}\otimes E_{0}^{\ast })$
has dimension
$\unicode[STIX]{x1D6EC}\subset H^{0}(C,K_{C}\otimes E_{0}^{\ast })$
has dimension
![]() $r+1$
. By Lemma 2.8, this triple is Petri trace injective. Hence
$r+1$
. By Lemma 2.8, this triple is Petri trace injective. Hence
is Petri trace injective for generic
![]() $t\in T$
. Thus a general bundle
$t\in T$
. Thus a general bundle
![]() $E$
represented in
$E$
represented in
![]() $\tilde{U} ^{\prime }$
is Petri trace injective.
$\tilde{U} ^{\prime }$
is Petri trace injective.
Furthermore, by [Reference Bhosle, Brambila-Paz and NewsteadBBN08, Theorem 3.1(4)], a general
![]() $(E,\unicode[STIX]{x1D6F1})\in U$
is globally generated (not just generically). Thus we obtain the following proposition.
$(E,\unicode[STIX]{x1D6F1})\in U$
is globally generated (not just generically). Thus we obtain the following proposition.
Proposition 2.11. A general element
![]() $E$
of the irreducible component
$E$
of the irreducible component
![]() $B\subseteq B_{r,r(g-1)}^{r+1}$
is Petri trace injective and globally generated with
$B\subseteq B_{r,r(g-1)}^{r+1}$
is Petri trace injective and globally generated with
![]() $h^{0}(C,E)=r+1$
.
$h^{0}(C,E)=r+1$
.
We can now prove the theorem.
Proof of Theorem 2.5.
Consider the map
![]() $a:\mathit{SU}_{C}(r)\times \operatorname{Pic}^{g-1}(C)\rightarrow \mathit{U}_{C}(r,r(g-1))$
given by
$a:\mathit{SU}_{C}(r)\times \operatorname{Pic}^{g-1}(C)\rightarrow \mathit{U}_{C}(r,r(g-1))$
given by
![]() $(V,M)\mapsto V\otimes M$
. This is an étale cover of degree
$(V,M)\mapsto V\otimes M$
. This is an étale cover of degree
![]() $r^{2g}$
. We write
$r^{2g}$
. We write
![]() $\overline{B}$
for the inverse image
$\overline{B}$
for the inverse image
![]() $a^{-1}(B)$
. Since
$a^{-1}(B)$
. Since
![]() $a$
is étale, we have
$a$
is étale, we have
![]() $T_{(V,M)}\overline{B}\cong T_{V\otimes M}B$
for each
$T_{(V,M)}\overline{B}\cong T_{V\otimes M}B$
for each
![]() $(V,M)\in B$
. In particular,
$(V,M)\in B$
. In particular,
We write
![]() $p$
for the projection
$p$
for the projection
![]() $\mathit{SU}_{C}(r)\times \operatorname{Pic}^{g-1}(C)\rightarrow \mathit{SU}_{C}(r)$
, and
$\mathit{SU}_{C}(r)\times \operatorname{Pic}^{g-1}(C)\rightarrow \mathit{SU}_{C}(r)$
, and
![]() $p_{1}$
for the restriction
$p_{1}$
for the restriction
![]() $p|_{\overline{B}}:\overline{B}\rightarrow \mathit{SU}_{C}(r)$
.
$p|_{\overline{B}}:\overline{B}\rightarrow \mathit{SU}_{C}(r)$
.
Claim.
![]() $p_{1}$
is dominant.
$p_{1}$
is dominant.
To see this: for
![]() $(V,M)\in \overline{B}$
, the locus
$(V,M)\in \overline{B}$
, the locus
![]() $p_{1}^{-1}(V)$
is identified with an open subset of the twisted Brill–Noether locus
$p_{1}^{-1}(V)$
is identified with an open subset of the twisted Brill–Noether locus
Moreover, for each such
![]() $(V,M)$
, we have
$(V,M)$
, we have
Since
![]() $V\otimes M$
is Petri trace injective, this dimension is
$V\otimes M$
is Petri trace injective, this dimension is
![]() $g-(r+1)^{2}$
. By semicontinuity, a general fibre of
$g-(r+1)^{2}$
. By semicontinuity, a general fibre of
![]() $p_{1}$
has dimension at most
$p_{1}$
has dimension at most
![]() $g-(r+1)^{2}$
. Therefore, in view of (6), the image of
$g-(r+1)^{2}$
. Therefore, in view of (6), the image of
![]() $p_{1}$
has dimension at least
$p_{1}$
has dimension at least
As
![]() $\mathit{SU}_{C}(r)$
is irreducible, the claim follows.
$\mathit{SU}_{C}(r)$
is irreducible, the claim follows.
We can now conclude the proof. Let
![]() $V\in \mathit{SU}_{C}(r)$
be general. By the claim, we can find
$V\in \mathit{SU}_{C}(r)$
be general. By the claim, we can find
![]() $(V,M)\in \tilde{P}$
such that
$(V,M)\in \tilde{P}$
such that
![]() $h^{0}(C,V\otimes M)=r+1$
and
$h^{0}(C,V\otimes M)=r+1$
and
![]() $V\otimes M$
is globally generated and Petri trace injective. By Proposition 2.4, the theta divisor
$V\otimes M$
is globally generated and Petri trace injective. By Proposition 2.4, the theta divisor
![]() $\unicode[STIX]{x1D6E9}_{V}$
exists and satisfies
$\unicode[STIX]{x1D6E9}_{V}$
exists and satisfies
![]() $\operatorname{mult}_{M}\unicode[STIX]{x1D6E9}_{V}=h^{0}(C,V\otimes M)=r+1$
. Finally, by considering a suitable sum of line bundles, we see that the involution
$\operatorname{mult}_{M}\unicode[STIX]{x1D6E9}_{V}=h^{0}(C,V\otimes M)=r+1$
. Finally, by considering a suitable sum of line bundles, we see that the involution
![]() $E\mapsto K_{C}\otimes E^{\ast }$
preserves the component
$E\mapsto K_{C}\otimes E^{\ast }$
preserves the component
![]() $\overline{B}$
. Since a general element of
$\overline{B}$
. Since a general element of
![]() $\overline{B}$
is globally generated, in general both
$\overline{B}$
is globally generated, in general both
![]() $V\otimes M$
and
$V\otimes M$
and
![]() $K_{C}\otimes M^{-1}\otimes V^{\ast }$
are globally generated. ◻
$K_{C}\otimes M^{-1}\otimes V^{\ast }$
are globally generated. ◻
3 Reconstruction of bundles from tangent cones to theta divisors
3.1 Tangent cones
Let
![]() $Y$
be a normal variety and
$Y$
be a normal variety and
![]() $Z\subset Y$
a divisor. Let
$Z\subset Y$
a divisor. Let
![]() $p$
be a smooth point of
$p$
be a smooth point of
![]() $Y$
which is a point of multiplicity
$Y$
which is a point of multiplicity
![]() $n\geqslant 1$
of
$n\geqslant 1$
of
![]() $Z$
. A local equation
$Z$
. A local equation
![]() $f$
for
$f$
for
![]() $Z$
near
$Z$
near
![]() $p$
has the form
$p$
has the form
![]() $f_{n}+f_{n+1}+\cdots \,$
, where the
$f_{n}+f_{n+1}+\cdots \,$
, where the
![]() $f_{i}$
are homogeneous polynomials of degree
$f_{i}$
are homogeneous polynomials of degree
![]() $i$
in local coordinates centred at
$i$
in local coordinates centred at
![]() $p$
. The projectivised tangent cone
$p$
. The projectivised tangent cone
![]() ${\mathcal{T}}_{p}(Z)$
to
${\mathcal{T}}_{p}(Z)$
to
![]() $Z$
at
$Z$
at
![]() $p$
is the hypersurface in
$p$
is the hypersurface in
![]() $\mathbb{P}T_{p}Y$
defined by the first nonzero component
$\mathbb{P}T_{p}Y$
defined by the first nonzero component
![]() $f_{n}$
of
$f_{n}$
of
![]() $f$
. (For a more intrinsic description, see [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, ch. II.1].)
$f$
. (For a more intrinsic description, see [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, ch. II.1].)
Now let
![]() $C$
be a curve of genus
$C$
be a curve of genus
![]() $g\geqslant (r+1)^{2}$
. Let
$g\geqslant (r+1)^{2}$
. Let
![]() $E$
be a Petri trace injective bundle of rank
$E$
be a Petri trace injective bundle of rank
![]() $r$
and degree
$r$
and degree
![]() $r(g-1)$
, with
$r(g-1)$
, with
![]() $h^{0}(C,E)=r+1$
. By Proposition 2.4 (with
$h^{0}(C,E)=r+1$
. By Proposition 2.4 (with
![]() $h=g-1$
), the theta divisor
$h=g-1$
), the theta divisor
![]() $\unicode[STIX]{x1D6E9}_{E}$
is defined and contains the origin
$\unicode[STIX]{x1D6E9}_{E}$
is defined and contains the origin
![]() ${\mathcal{O}}_{C}$
of
${\mathcal{O}}_{C}$
of
![]() $\text{Pic}^{0}(C)$
with multiplicity
$\text{Pic}^{0}(C)$
with multiplicity
![]() $h^{0}(C,E)=r+1$
.
$h^{0}(C,E)=r+1$
.
By [Reference Casalaina-Martin and Teixidor i BigasCT11, Theorem 3.4 and Remark 3.8] (see also Kempf [Reference KempfKem73]), the tangent cone
![]() ${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
to
${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
to
![]() $\unicode[STIX]{x1D6E9}_{E}$
at
$\unicode[STIX]{x1D6E9}_{E}$
at
![]() ${\mathcal{O}}_{C}$
is given by the determinant of an
${\mathcal{O}}_{C}$
is given by the determinant of an
![]() $(r+1)\times (r+1)$
matrix
$(r+1)\times (r+1)$
matrix
![]() $\unicode[STIX]{x1D6EC}=(l_{ij})$
of linear forms
$\unicode[STIX]{x1D6EC}=(l_{ij})$
of linear forms
![]() $l_{ij}$
on
$l_{ij}$
on
![]() $H^{1}(C,{\mathcal{O}}_{C})$
, which is related to the multiplication map
$H^{1}(C,{\mathcal{O}}_{C})$
, which is related to the multiplication map
![]() $\bar{\unicode[STIX]{x1D707}}$
as follows: in appropriate bases
$\bar{\unicode[STIX]{x1D707}}$
as follows: in appropriate bases
![]() $(s_{i})$
and
$(s_{i})$
and
![]() $(t_{j})$
of
$(t_{j})$
of
![]() $H^{0}(C,E)$
and
$H^{0}(C,E)$
and
![]() $H^{0}(C,K_{C}\otimes E^{\ast })$
respectively,
$H^{0}(C,K_{C}\otimes E^{\ast })$
respectively,
![]() $\unicode[STIX]{x1D6EC}$
is given by
$\unicode[STIX]{x1D6EC}$
is given by
Hence, via Serre duality,
![]() $\unicode[STIX]{x1D6EC}$
coincides with the cup product map
$\unicode[STIX]{x1D6EC}$
coincides with the cup product map
Thus the matrix
![]() $\unicode[STIX]{x1D6EC}=(l_{ij})$
is a matrix of linear forms on the canonical space
$\unicode[STIX]{x1D6EC}=(l_{ij})$
is a matrix of linear forms on the canonical space
![]() $|K_{C}|^{\ast }$
.
$|K_{C}|^{\ast }$
.
In the following two subsections, we will show on the one hand that one can recover the bundle
![]() $E$
from the determinantal representation of the tangent cone
$E$
from the determinantal representation of the tangent cone
![]() ${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
given by the matrix
${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
given by the matrix
![]() $\unicode[STIX]{x1D6EC}$
. On the other hand, up to changing bases in
$\unicode[STIX]{x1D6EC}$
. On the other hand, up to changing bases in
![]() $H^{0}(C,E)$
and
$H^{0}(C,E)$
and
![]() $H^{1}(C,E)$
there are only two determinantal representations of the tangent cone, namely
$H^{1}(C,E)$
there are only two determinantal representations of the tangent cone, namely
![]() $\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D6EC}$
and
![]() $\unicode[STIX]{x1D6EC}^{t}$
. Thus the tangent cone determines
$\unicode[STIX]{x1D6EC}^{t}$
. Thus the tangent cone determines
![]() $E$
up to an involution.
$E$
up to an involution.
We will denote by
![]() $\mathbb{P}=|K_{C}|^{\ast }$
the canonical space and by
$\mathbb{P}=|K_{C}|^{\ast }$
the canonical space and by
![]() $\unicode[STIX]{x1D711}$
the canonical embedding
$\unicode[STIX]{x1D711}$
the canonical embedding
![]() $C{\hookrightarrow}\mathbb{P}$
.
$C{\hookrightarrow}\mathbb{P}$
.
3.2 Reconstruction of the bundle from the tangent cone
As above, let
![]() $\unicode[STIX]{x1D6EC}=(l_{ij})$
be the determinantal representation of the tangent cone given by the cup product mapping. We identify the source of
$\unicode[STIX]{x1D6EC}=(l_{ij})$
be the determinantal representation of the tangent cone given by the cup product mapping. We identify the source of
![]() $\unicode[STIX]{x1D6EC}$
with
$\unicode[STIX]{x1D6EC}$
with
![]() $H^{0}(C,E)$
and the target with
$H^{0}(C,E)$
and the target with
![]() $H^{1}(C,E)$
:
$H^{1}(C,E)$
:
We recall that the Serre duality isomorphism sends
![]() $b\in H^{1}(C,E)$
to the linear form
$b\in H^{1}(C,E)$
to the linear form
In the following proofs, we will use principal parts in order to represent cohomology classes of certain bundles. We refer to [Reference KempfKem83] or [Reference PaulyPau03, §3.2] for the necessary background. See also Kempf and Schreyer [Reference Kempf and SchreyerKS88].
Lemma 3.1. Suppose that
![]() $h^{0}(C,E)=r+1$
and
$h^{0}(C,E)=r+1$
and
![]() $E$
and
$E$
and
![]() $K_{C}\otimes E^{\ast }$
are globally generated. Then the rank of
$K_{C}\otimes E^{\ast }$
are globally generated. Then the rank of
![]() $\unicode[STIX]{x1D6EC}|_{C}=\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6EC}$
is equal to
$\unicode[STIX]{x1D6EC}|_{C}=\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6EC}$
is equal to
![]() $r=\operatorname{rk}\,E$
at all points of
$r=\operatorname{rk}\,E$
at all points of
![]() $C$
. In particular, the canonical curve is contained in
$C$
. In particular, the canonical curve is contained in
![]() ${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
.
${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
.
Proof. For each
![]() $p\in C$
, write
$p\in C$
, write
![]() $\unicode[STIX]{x1D6FD}_{p}$
for a principal part with a simple pole supported at
$\unicode[STIX]{x1D6FD}_{p}$
for a principal part with a simple pole supported at
![]() $p$
. Then (see [Reference Kempf and SchreyerKS88]) the cohomology class
$p$
. Then (see [Reference Kempf and SchreyerKS88]) the cohomology class
![]() $[\unicode[STIX]{x1D6FD}_{p}]$
is identified with the image of
$[\unicode[STIX]{x1D6FD}_{p}]$
is identified with the image of
![]() $p$
by
$p$
by
![]() $\unicode[STIX]{x1D711}$
. Therefore, at
$\unicode[STIX]{x1D711}$
. Therefore, at
![]() $p\in C$
, the pullback
$p\in C$
, the pullback
![]() $\unicode[STIX]{x1D6EC}|_{C}$
is identified with the cup product map
$\unicode[STIX]{x1D6EC}|_{C}$
is identified with the cup product map
The kernel of
![]() $[\unicode[STIX]{x1D6FD}_{p}]\cup \cdot$
contains the subspace
$[\unicode[STIX]{x1D6FD}_{p}]\cup \cdot$
contains the subspace
![]() $H^{0}(C,E(-p))$
, which is one-dimensional since
$H^{0}(C,E(-p))$
, which is one-dimensional since
![]() $E$
is globally generated and
$E$
is globally generated and
![]() $h^{0}(C,E)=r+1$
. If
$h^{0}(C,E)=r+1$
. If
![]() $\operatorname{Ker}([\unicode[STIX]{x1D6FD}_{p}]\cup \cdot )$
has dimension greater than 1, then there is a section
$\operatorname{Ker}([\unicode[STIX]{x1D6FD}_{p}]\cup \cdot )$
has dimension greater than 1, then there is a section
![]() $s^{\prime }\in H^{0}(C,E)$
not vanishing at
$s^{\prime }\in H^{0}(C,E)$
not vanishing at
![]() $p$
such that
$p$
such that
By Serre duality, this means that
is zero in
![]() $H^{1}(C,K_{C})$
for all
$H^{1}(C,K_{C})$
for all
![]() $t\in H^{0}(C,K_{C}\otimes E^{\ast })$
. Hence the values at
$t\in H^{0}(C,K_{C}\otimes E^{\ast })$
. Hence the values at
![]() $p$
of all global sections of
$p$
of all global sections of
![]() $K_{C}\otimes E^{\ast }$
belong to the hyperplane in
$K_{C}\otimes E^{\ast }$
belong to the hyperplane in
![]() $(K_{C}\otimes E^{\ast })|_{p}$
defined by contraction with the nonzero vector
$(K_{C}\otimes E^{\ast })|_{p}$
defined by contraction with the nonzero vector
![]() $s^{\prime }(p)\in E|_{p}$
. Thus
$s^{\prime }(p)\in E|_{p}$
. Thus
![]() $K_{C}\otimes E^{\ast }$
is not globally generated, contrary to our hypothesis.◻
$K_{C}\otimes E^{\ast }$
is not globally generated, contrary to our hypothesis.◻
Remark 3.2. Casalaina-Martin and Teixidor i Bigas in [Reference Casalaina-Martin and Teixidor i BigasCT11, §6] prove more generally that if
![]() $E$
is a general vector bundle with
$E$
is a general vector bundle with
![]() $h^{0}(C,E)>kr$
, then the
$h^{0}(C,E)>kr$
, then the
![]() $k$
th secant variety of the canonical image
$k$
th secant variety of the canonical image
![]() $\unicode[STIX]{x1D711}(C)$
of
$\unicode[STIX]{x1D711}(C)$
of
![]() $C$
is contained in
$C$
is contained in
![]() ${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
.
${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
.
Proposition 3.3. Let
![]() $E$
be a vector bundle with
$E$
be a vector bundle with
![]() $h^{0}(C,E)=r+1$
, such that both
$h^{0}(C,E)=r+1$
, such that both
![]() $E$
and
$E$
and
![]() $K_{C}\otimes E^{\ast }$
are globally generated. Then the image of
$K_{C}\otimes E^{\ast }$
are globally generated. Then the image of
![]() $\unicode[STIX]{x1D6EC}|_{C}$
is isomorphic to
$\unicode[STIX]{x1D6EC}|_{C}$
is isomorphic to
![]() $T_{C}\otimes E$
.
$T_{C}\otimes E$
.
Proof. As
![]() $\unicode[STIX]{x1D711}^{\ast }{\mathcal{O}}_{\mathbb{P}^{g-1}}(-1)\cong T_{C}$
, the pullback
$\unicode[STIX]{x1D711}^{\ast }{\mathcal{O}}_{\mathbb{P}^{g-1}}(-1)\cong T_{C}$
, the pullback
![]() $\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}|_{C}$
is a map
$\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}|_{C}$
is a map
Write
![]() $L:=\det (E)$
, a line bundle of degree
$L:=\det (E)$
, a line bundle of degree
![]() $r(g-1)$
. Then
$r(g-1)$
. Then
![]() $\det (K_{C}\otimes E^{\ast })=K_{C}^{r}\otimes L^{-1}$
. As
$\det (K_{C}\otimes E^{\ast })=K_{C}^{r}\otimes L^{-1}$
. As
![]() $K_{C}\otimes E^{\ast }$
is globally generated, the evaluation sequence
$K_{C}\otimes E^{\ast }$
is globally generated, the evaluation sequence
is exact. For each
![]() $p\in C$
, the image of
$p\in C$
, the image of
![]() $(K_{C}^{-r}\otimes L)|_{p}$
in
$(K_{C}^{-r}\otimes L)|_{p}$
in
![]() $H^{0}(C,K_{C}\otimes E^{\ast })$
is exactly
$H^{0}(C,K_{C}\otimes E^{\ast })$
is exactly
![]() $\mathbb{C}\cdot t_{p}$
, where
$\mathbb{C}\cdot t_{p}$
, where
![]() $t_{p}$
is the unique section, up to scalar, of
$t_{p}$
is the unique section, up to scalar, of
![]() $K_{C}\otimes E^{\ast }$
vanishing at
$K_{C}\otimes E^{\ast }$
vanishing at
![]() $p$
.
$p$
.
Dualising, we obtain a diagram

Here
![]() $e_{p}$
can be identified up to scalar with the map
$e_{p}$
can be identified up to scalar with the map
![]() $f\mapsto f(t_{p})$
where
$f\mapsto f(t_{p})$
where
![]() $t_{p}$
is as above.
$t_{p}$
is as above.
Now for each
![]() $p\in C$
, the image
$p\in C$
, the image
annihilates
![]() $t_{p}\in H^{0}(C,K_{C}\otimes E^{\ast })$
, since the principal part
$t_{p}\in H^{0}(C,K_{C}\otimes E^{\ast })$
, since the principal part
![]() $\unicode[STIX]{x1D6FD}_{p}\cdot t_{p}$
is everywhere regular. Therefore,
$\unicode[STIX]{x1D6FD}_{p}\cdot t_{p}$
is everywhere regular. Therefore,
![]() $\unicode[STIX]{x1D6EC}|_{C}$
factorises via
$\unicode[STIX]{x1D6EC}|_{C}$
factorises via
![]() $\operatorname{Ker}(e)=T_{C}\otimes E$
. Since
$\operatorname{Ker}(e)=T_{C}\otimes E$
. Since
![]() $\operatorname{rk}(\unicode[STIX]{x1D6EC}|_{C})\equiv r$
by Lemma 3.1, we have
$\operatorname{rk}(\unicode[STIX]{x1D6EC}|_{C})\equiv r$
by Lemma 3.1, we have
![]() $\operatorname{Im}(\unicode[STIX]{x1D6EC}|_{C})\cong T_{C}\otimes E$
.◻
$\operatorname{Im}(\unicode[STIX]{x1D6EC}|_{C})\cong T_{C}\otimes E$
.◻
Remark 3.4. A straightforward computation shows also that
We will also want to study the transpose
![]() $\unicode[STIX]{x1D6EC}^{t}$
, which we will consider as a map
$\unicode[STIX]{x1D6EC}^{t}$
, which we will consider as a map
The proof of Proposition 3.3 also shows the following corollary.
Corollary 3.5. Let
![]() $E$
and
$E$
and
![]() $\unicode[STIX]{x1D6EC}$
be as above. Then the image of
$\unicode[STIX]{x1D6EC}$
be as above. Then the image of
![]() $\unicode[STIX]{x1D6EC}^{t}|_{C}$
is isomorphic to
$\unicode[STIX]{x1D6EC}^{t}|_{C}$
is isomorphic to
![]() $E^{\ast }$
.
$E^{\ast }$
.
Remark 3.6. In order to describe the cokernel of
![]() $\unicode[STIX]{x1D6EC}|_{C}$
, it is also enough to know at which points of
$\unicode[STIX]{x1D6EC}|_{C}$
, it is also enough to know at which points of
![]() $C$
a row of
$C$
a row of
![]() $\unicode[STIX]{x1D6EC}|_{C}$
vanishes. Dualising the sequence
$\unicode[STIX]{x1D6EC}|_{C}$
vanishes. Dualising the sequence
we see that
![]() $H^{0}(C,K_{C}\otimes E^{\ast })^{\ast }$
is canonically identified with a subspace of
$H^{0}(C,K_{C}\otimes E^{\ast })^{\ast }$
is canonically identified with a subspace of
![]() $H^{0}(C,K_{C}^{r}\otimes L^{-1})$
. Using the description of
$H^{0}(C,K_{C}^{r}\otimes L^{-1})$
. Using the description of
as in the above proof, we see that a row vanishes exactly in a divisor associated to
![]() $K_{C}^{r}\otimes L^{-1}$
. Hence, the cokernel is isomorphic to
$K_{C}^{r}\otimes L^{-1}$
. Hence, the cokernel is isomorphic to
![]() $K_{C}^{r}\otimes L^{-1}$
.
$K_{C}^{r}\otimes L^{-1}$
.
3.3 Uniqueness of the linear determinantal representation of the tangent cone
In order to show the desired uniqueness of the determinantal representation of the tangent cone, we use a classical result of Frobenius. See [Reference FrobeniusFro97] and also for a modern proof [Reference DieudonnéDie49, Reference WaterhouseWat87] and the references therein. For the sake of completeness we will give a sketch of a proof following Frobenius.
Proposition 3.7. Suppose
![]() $r\geqslant 1$
. Let
$r\geqslant 1$
. Let
![]() $A$
and
$A$
and
![]() $B$
be
$B$
be
![]() $(r+1)\times (r+1)$
matrices of independent linear forms, such that the entries of
$(r+1)\times (r+1)$
matrices of independent linear forms, such that the entries of
![]() $A$
are linear combinations of the entries of
$A$
are linear combinations of the entries of
![]() $B$
and
$B$
and
![]() $\det (A)=c\cdot \det (B)$
for a nonzero constant
$\det (A)=c\cdot \det (B)$
for a nonzero constant
![]() $k\in \mathbb{C}$
. Then, there exist invertible matrices
$k\in \mathbb{C}$
. Then, there exist invertible matrices
![]() $S,T\in \operatorname{Gl}(r+1,\mathbb{C})$
, unique up to scalar, such that
$S,T\in \operatorname{Gl}(r+1,\mathbb{C})$
, unique up to scalar, such that
![]() $A=S\cdot B\cdot T$
or
$A=S\cdot B\cdot T$
or
![]() $A=S\cdot B^{t}\cdot T$
.
$A=S\cdot B^{t}\cdot T$
.
Proof by Frobenius [Reference FrobeniusFro97, pp. 1011–1013].
Note that for
![]() $r\geqslant 1$
only one of the above cases can occur and the matrices
$r\geqslant 1$
only one of the above cases can occur and the matrices
![]() $S$
and
$S$
and
![]() $T$
are unique up to scalar. Indeed, let
$T$
are unique up to scalar. Indeed, let
![]() $A=SBT=S^{\prime }BT^{\prime }$
and set
$A=SBT=S^{\prime }BT^{\prime }$
and set
![]() $b_{ii}=1$
and
$b_{ii}=1$
and
![]() $b_{ij}=0$
if
$b_{ij}=0$
if
![]() $i\neq j$
; then
$i\neq j$
; then
![]() $ST=S^{\prime }T^{\prime }$
. Set
$ST=S^{\prime }T^{\prime }$
. Set
![]() $U=T({T^{\prime }}^{-1})=S({S^{\prime }}^{-1})$
; thus
$U=T({T^{\prime }}^{-1})=S({S^{\prime }}^{-1})$
; thus
![]() $UB=BU$
. Since
$UB=BU$
. Since
![]() $U$
commutes with every matrix, we have
$U$
commutes with every matrix, we have
![]() $U=k\cdot E_{r}$
and hence
$U=k\cdot E_{r}$
and hence
![]() $S^{\prime }=k\cdot S$
and
$S^{\prime }=k\cdot S$
and
![]() $T^{\prime }=1/k\cdot T$
. Similarly, one can show that
$T^{\prime }=1/k\cdot T$
. Similarly, one can show that
![]() $B^{t}$
is not equivalent to
$B^{t}$
is not equivalent to
![]() $B$
. Note also that there is no relation between any minors of
$B$
. Note also that there is no relation between any minors of
![]() $A$
or
$A$
or
![]() $B$
.
$B$
.
For
![]() $l=0,\ldots ,r$
, let
$l=0,\ldots ,r$
, let
![]() $c_{ij}^{l}$
be the coefficient of
$c_{ij}^{l}$
be the coefficient of
![]() $b_{ll}$
in
$b_{ll}$
in
![]() $a_{ij}$
and let
$a_{ij}$
and let
![]() $y$
be a new variable. We substitute
$y$
be a new variable. We substitute
![]() $b_{ll}$
with
$b_{ll}$
with
![]() $b_{ll}+y$
in
$b_{ll}+y$
in
![]() $A$
and
$A$
and
![]() $B$
and get new matrices, denoted by
$B$
and get new matrices, denoted by
![]() $(a_{ij}+y\cdot c_{ij}^{l})$
and
$(a_{ij}+y\cdot c_{ij}^{l})$
and
![]() $B^{l}$
, respectively. Since
$B^{l}$
, respectively. Since
![]() $\det B^{l}$
is linear in
$\det B^{l}$
is linear in
![]() $y$
, the coefficient of
$y$
, the coefficient of
![]() $y^{2}$
in
$y^{2}$
in
![]() $\det (a_{ij}+y\cdot c_{ij}^{l})=\det B^{l}$
has to vanish. But the coefficient is the sum of products of
$\det (a_{ij}+y\cdot c_{ij}^{l})=\det B^{l}$
has to vanish. But the coefficient is the sum of products of
![]() $2\times 2$
minors of
$2\times 2$
minors of
![]() $(c_{ij}^{l})$
and
$(c_{ij}^{l})$
and
![]() $(r-1)\times (r-1)$
minors of
$(r-1)\times (r-1)$
minors of
![]() $A$
. Since there are no relations between any minors of
$A$
. Since there are no relations between any minors of
![]() $A$
, all
$A$
, all
![]() $2\times 2$
minors of
$2\times 2$
minors of
![]() $(c_{ij}^{l})$
vanish. Hence,
$(c_{ij}^{l})$
vanish. Hence,
![]() $(c_{ij}^{l})$
has rank one for any
$(c_{ij}^{l})$
has rank one for any
![]() $l$
and we can write
$l$
and we can write
![]() $c_{ij}^{l}=p_{i}^{l}q_{j}^{l}$
where
$c_{ij}^{l}=p_{i}^{l}q_{j}^{l}$
where
![]() $p^{l}$
and
$p^{l}$
and
![]() $q^{l}$
are column and row vectors, respectively.
$q^{l}$
are column and row vectors, respectively.
Let
![]() $B_{0}=B|_{\{b_{ij}=0,i\neq j\}}$
and
$B_{0}=B|_{\{b_{ij}=0,i\neq j\}}$
and
![]() $A_{0}=A|_{\{b_{ij}=0,i\neq j\}}$
. Then
$A_{0}=A|_{\{b_{ij}=0,i\neq j\}}$
. Then
where
![]() $P=(p_{i}^{l})_{0\leqslant i,l\leqslant r}$
and
$P=(p_{i}^{l})_{0\leqslant i,l\leqslant r}$
and
![]() $Q=(q_{j}^{l})_{0\leqslant l,j\leqslant r}$
. Since
$Q=(q_{j}^{l})_{0\leqslant l,j\leqslant r}$
. Since
![]() $\det (A_{0})=c\cdot \det (B_{0})=c\cdot b_{00}\cdot \ldots \cdot b_{rr}$
, we get
$\det (A_{0})=c\cdot \det (B_{0})=c\cdot b_{00}\cdot \ldots \cdot b_{rr}$
, we get
![]() $\det (P)\cdot \det (Q)=c$
, hence
$\det (P)\cdot \det (Q)=c$
, hence
![]() $P$
and
$P$
and
![]() $Q$
are invertible.
$Q$
are invertible.
Let
![]() $\widetilde{B}=P^{-1}AQ^{-1}$
. By definition
$\widetilde{B}=P^{-1}AQ^{-1}$
. By definition
![]() $\widetilde{B}|_{\{b_{ij}=0,i\neq j\}}=B_{0}$
. Thus, the entries
$\widetilde{B}|_{\{b_{ij}=0,i\neq j\}}=B_{0}$
. Thus, the entries
![]() $\widetilde{b_{ij}}$
for
$\widetilde{b_{ij}}$
for
![]() $i\neq j$
and
$i\neq j$
and
![]() $v_{i}=\widetilde{b_{ii}}-b_{ii}$
are linear functions in
$v_{i}=\widetilde{b_{ii}}-b_{ii}$
are linear functions in
![]() $b_{ij}$
for
$b_{ij}$
for
![]() $i\neq j$
. Furthermore, we have
$i\neq j$
. Furthermore, we have
Comparing the coefficients of
![]() $b_{11}b_{22}\cdots b_{rr}$
in
$b_{11}b_{22}\cdots b_{rr}$
in
![]() $\det (\widetilde{B})$
and
$\det (\widetilde{B})$
and
![]() $\det (B)$
, we get
$\det (B)$
, we get
![]() $v_{0}=0$
. Similarly,
$v_{0}=0$
. Similarly,
![]() $v_{i}=0$
for
$v_{i}=0$
for
![]() $0\leqslant i\leqslant r$
. Comparing the coefficients of
$0\leqslant i\leqslant r$
. Comparing the coefficients of
![]() $b_{22}\cdots b_{rr}$
, we get
$b_{22}\cdots b_{rr}$
, we get
![]() $b_{12}b_{21}=\widetilde{b_{12}}\widetilde{b_{21}}$
and in general
$b_{12}b_{21}=\widetilde{b_{12}}\widetilde{b_{21}}$
and in general
Comparing the coefficients of
![]() $b_{33}\cdots b_{rr}$
, we get
$b_{33}\cdots b_{rr}$
, we get
![]() $b_{12}b_{23}b_{31}+b_{21}b_{13}b_{32}=\widetilde{b_{12}}\widetilde{b_{23}}\widetilde{b_{31}}+\widetilde{b_{21}}\widetilde{b_{13}}\widetilde{b_{32}}$
and in general
$b_{12}b_{23}b_{31}+b_{21}b_{13}b_{32}=\widetilde{b_{12}}\widetilde{b_{23}}\widetilde{b_{31}}+\widetilde{b_{21}}\widetilde{b_{13}}\widetilde{b_{32}}$
and in general
A careful study of these equations shows that either
where
![]() $K=(k_{i}\unicode[STIX]{x1D6FF}_{ij})_{0\leqslant i,j\leqslant r}$
. The claim follows.◻
$K=(k_{i}\unicode[STIX]{x1D6FF}_{ij})_{0\leqslant i,j\leqslant r}$
. The claim follows.◻
We now assume that
![]() $E$
is a Petri trace injective bundle. Let
$E$
is a Petri trace injective bundle. Let
![]() $\unicode[STIX]{x1D6EC}=(l_{ij})$
be a determinantal representation of the tangent cone
$\unicode[STIX]{x1D6EC}=(l_{ij})$
be a determinantal representation of the tangent cone
![]() ${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
as above. By Petri trace injectivity, the matrix
${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
as above. By Petri trace injectivity, the matrix
![]() $\unicode[STIX]{x1D6EC}$
is
$\unicode[STIX]{x1D6EC}$
is
![]() $(r+1)$
-generic (see [Reference EisenbudEis88] for a definition), that is, there are no relations between the entries
$(r+1)$
-generic (see [Reference EisenbudEis88] for a definition), that is, there are no relations between the entries
![]() $l_{ij}$
or any subminors of
$l_{ij}$
or any subminors of
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
Corollary 3.8. For a curve of genus
![]() $g\geqslant (r+1)^{2}$
and a Petri trace injective bundle
$g\geqslant (r+1)^{2}$
and a Petri trace injective bundle
![]() $E$
with
$E$
with
![]() $r+1$
global sections of degree
$r+1$
global sections of degree
![]() $r(g-1)$
, any determinantal representation of the tangent cone
$r(g-1)$
, any determinantal representation of the tangent cone
![]() ${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})\subset |K_{C}|^{\ast }$
is equivalent to
${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})\subset |K_{C}|^{\ast }$
is equivalent to
![]() $\unicode[STIX]{x1D6EC}$
or
$\unicode[STIX]{x1D6EC}$
or
![]() $\unicode[STIX]{x1D6EC}^{t}$
.
$\unicode[STIX]{x1D6EC}^{t}$
.
Proof. Let
![]() $\unicode[STIX]{x1D6FC}$
be any determinantal representation of the tangent cone
$\unicode[STIX]{x1D6FC}$
be any determinantal representation of the tangent cone
![]() ${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
in
${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
in
![]() $|K_{C}|^{\ast }$
. Then,
$|K_{C}|^{\ast }$
. Then,
![]() $\unicode[STIX]{x1D6FC}$
is an
$\unicode[STIX]{x1D6FC}$
is an
![]() $(r+1)\times (r+1)$
matrix of linear entries, since the degree of the tangent cone is
$(r+1)\times (r+1)$
matrix of linear entries, since the degree of the tangent cone is
![]() $r+1$
. Furthermore, the entries
$r+1$
. Furthermore, the entries
![]() $\unicode[STIX]{x1D6FC}_{ij}$
of
$\unicode[STIX]{x1D6FC}_{ij}$
of
![]() $\unicode[STIX]{x1D6FC}$
are linear combinations of the entries
$\unicode[STIX]{x1D6FC}$
are linear combinations of the entries
![]() $l_{ij}$
of
$l_{ij}$
of
![]() $\unicode[STIX]{x1D6EC}$
. Indeed, assume for some
$\unicode[STIX]{x1D6EC}$
. Indeed, assume for some
![]() $k,l$
that
$k,l$
that
![]() $\unicode[STIX]{x1D6FC}_{kl}$
is not a linear combination of the
$\unicode[STIX]{x1D6FC}_{kl}$
is not a linear combination of the
![]() $l_{ij}$
. Then
$l_{ij}$
. Then
![]() ${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
would be the cone over
${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
would be the cone over
![]() $V(\unicode[STIX]{x1D6FC}_{kl})\cap {\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
. Hence, the vertex of
$V(\unicode[STIX]{x1D6FC}_{kl})\cap {\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
. Hence, the vertex of
![]() ${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
defined by the entries
${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
defined by the entries
![]() $l_{ij}$
would have codimension strictly less than
$l_{ij}$
would have codimension strictly less than
![]() $(r+1)^{2}$
, a contradiction to the independence of the
$(r+1)^{2}$
, a contradiction to the independence of the
![]() $l_{ij}$
. The corollary follows from Proposition 3.7.◻
$l_{ij}$
. The corollary follows from Proposition 3.7.◻
4 Injectivity of the theta map
Theorem 4.1. Suppose
![]() $r\geqslant 2$
. Let
$r\geqslant 2$
. Let
![]() $C$
be a Petri general curve of genus
$C$
be a Petri general curve of genus
![]() $g\geqslant (2r+2)(2r+1)$
. Then the theta map
$g\geqslant (2r+2)(2r+1)$
. Then the theta map
![]() ${\mathcal{D}}:\mathit{SU}_{C}(r){\dashrightarrow}|r\unicode[STIX]{x1D6E9}|$
is generically injective.
${\mathcal{D}}:\mathit{SU}_{C}(r){\dashrightarrow}|r\unicode[STIX]{x1D6E9}|$
is generically injective.
Proof. Let
![]() $V\in \mathit{SU}_{C}(r)$
be a general stable bundle. By Theorem 2.5, there exists
$V\in \mathit{SU}_{C}(r)$
be a general stable bundle. By Theorem 2.5, there exists
![]() $M\in \unicode[STIX]{x1D6E9}_{V}$
such that
$M\in \unicode[STIX]{x1D6E9}_{V}$
such that
![]() $h^{0}(C,V\otimes M)=r+1$
, the bundle
$h^{0}(C,V\otimes M)=r+1$
, the bundle
![]() $V\otimes M=:E$
is Petri trace injective, and
$V\otimes M=:E$
is Petri trace injective, and
![]() $E$
and
$E$
and
![]() $K_{C}\otimes E^{\ast }$
are globally generated.
$K_{C}\otimes E^{\ast }$
are globally generated.
Note that tensoring by
![]() $M^{-1}$
defines an isomorphism
$M^{-1}$
defines an isomorphism
![]() $\unicode[STIX]{x1D6E9}_{V}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6E9}_{E}$
inducing an isomorphism
$\unicode[STIX]{x1D6E9}_{V}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6E9}_{E}$
inducing an isomorphism
![]() ${\mathcal{T}}_{M}(\unicode[STIX]{x1D6E9}_{V})\xrightarrow[{}]{{\sim}}{\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
. In order to use the results of the previous sections, we will work with
${\mathcal{T}}_{M}(\unicode[STIX]{x1D6E9}_{V})\xrightarrow[{}]{{\sim}}{\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
. In order to use the results of the previous sections, we will work with
![]() $\unicode[STIX]{x1D6E9}_{E}$
.
$\unicode[STIX]{x1D6E9}_{E}$
.
Now let
be a map of bundles of rank
![]() $r+1$
over
$r+1$
over
![]() $\mathbb{P}^{g-1}$
whose determinant defines the tangent cone
$\mathbb{P}^{g-1}$
whose determinant defines the tangent cone
![]() ${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
. By Corollary 3.8, the map
${\mathcal{T}}_{{\mathcal{O}}_{C}}(\unicode[STIX]{x1D6E9}_{E})$
. By Corollary 3.8, the map
![]() $\unicode[STIX]{x1D6FC}$
is equivalent either to
$\unicode[STIX]{x1D6FC}$
is equivalent either to
![]() $\unicode[STIX]{x1D6EC}$
or
$\unicode[STIX]{x1D6EC}$
or
![]() $\unicode[STIX]{x1D6EC}^{t}$
, where
$\unicode[STIX]{x1D6EC}^{t}$
, where
![]() $\unicode[STIX]{x1D6EC}$
is the representation given by the cup product mapping as defined in § 3. Therefore, by Proposition 3.3 and Corollary 3.5, the image
$\unicode[STIX]{x1D6EC}$
is the representation given by the cup product mapping as defined in § 3. Therefore, by Proposition 3.3 and Corollary 3.5, the image
![]() $E^{\prime }$
of
$E^{\prime }$
of
![]() $\unicode[STIX]{x1D6FC}|_{C}$
is isomorphic either to
$\unicode[STIX]{x1D6FC}|_{C}$
is isomorphic either to
![]() $T_{C}\otimes E=V\otimes M\otimes T_{C}$
or to
$T_{C}\otimes E=V\otimes M\otimes T_{C}$
or to
![]() $E^{\ast }=V^{\ast }\otimes M^{-1}$
. Thus
$E^{\ast }=V^{\ast }\otimes M^{-1}$
. Thus
![]() $V$
is isomorphic either to
$V$
is isomorphic either to
Now since in particular
![]() $g>(r+1)^{2}$
, the open subset
$g>(r+1)^{2}$
, the open subset
![]() $\{M\in \operatorname{Pic}^{g-1}(C):h^{0}(C,V\otimes M)=r+1\}\subseteq B_{1,g-1}^{r+1}(V)$
has a component of dimension
$\{M\in \operatorname{Pic}^{g-1}(C):h^{0}(C,V\otimes M)=r+1\}\subseteq B_{1,g-1}^{r+1}(V)$
has a component of dimension
![]() $g-(r+1)^{2}\geqslant 1$
. Therefore, we may assume that
$g-(r+1)^{2}\geqslant 1$
. Therefore, we may assume that
![]() $M^{2r}\not \cong K_{C}^{r}$
. Thus only one of the bundles in (7) can have trivial determinant. Hence there is only one possibility for
$M^{2r}\not \cong K_{C}^{r}$
. Thus only one of the bundles in (7) can have trivial determinant. Hence there is only one possibility for
![]() $V$
.
$V$
.
In summary, the data of the tangent cone
![]() ${\mathcal{T}}_{M}(\unicode[STIX]{x1D6E9}_{V})$
and the point
${\mathcal{T}}_{M}(\unicode[STIX]{x1D6E9}_{V})$
and the point
![]() $M$
, together with the property
$M$
, together with the property
![]() $\det (V)={\mathcal{O}}_{C}$
, determine the bundle
$\det (V)={\mathcal{O}}_{C}$
, determine the bundle
![]() $V$
up to isomorphism. In particular,
$V$
up to isomorphism. In particular,
![]() $\unicode[STIX]{x1D6E9}_{V}$
determines
$\unicode[STIX]{x1D6E9}_{V}$
determines
![]() $V$
.◻
$V$
.◻
Remark 4.2. The involution
![]() $M\mapsto K_{C}\otimes M^{-1}$
defines an isomorphism of varieties
$M\mapsto K_{C}\otimes M^{-1}$
defines an isomorphism of varieties
![]() $\unicode[STIX]{x1D6E9}_{V}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6E9}_{V^{\ast }}$
. We observe that the transposed map
$\unicode[STIX]{x1D6E9}_{V}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6E9}_{V^{\ast }}$
. We observe that the transposed map
![]() $\unicode[STIX]{x1D6EC}^{t}$
occurs naturally as the cup product map defining the tangent cone
$\unicode[STIX]{x1D6EC}^{t}$
occurs naturally as the cup product map defining the tangent cone
![]() ${\mathcal{T}}_{K_{C}\otimes M^{-1}}(\unicode[STIX]{x1D6E9}_{V^{\ast }})$
.
${\mathcal{T}}_{K_{C}\otimes M^{-1}}(\unicode[STIX]{x1D6E9}_{V^{\ast }})$
.
Remark 4.3. If
![]() $C$
is hyperelliptic, then the canonical map factorises via the hyperelliptic involution
$C$
is hyperelliptic, then the canonical map factorises via the hyperelliptic involution
![]() $\unicode[STIX]{x1D704}$
. Thus the construction in Proposition 3.3 can never give bundles over
$\unicode[STIX]{x1D704}$
. Thus the construction in Proposition 3.3 can never give bundles over
![]() $C$
which are not
$C$
which are not
![]() $\unicode[STIX]{x1D704}$
-invariant. We note that Beauville [Reference BeauvilleBea88] showed that in rank two, if
$\unicode[STIX]{x1D704}$
-invariant. We note that Beauville [Reference BeauvilleBea88] showed that in rank two, if
![]() $C$
is hyperelliptic then the bundles
$C$
is hyperelliptic then the bundles
![]() $V$
and
$V$
and
![]() $\unicode[STIX]{x1D704}^{\ast }V$
have the same theta divisor.
$\unicode[STIX]{x1D704}^{\ast }V$
have the same theta divisor.
Acknowledgements
The authors would like to thank Ciro Ciliberto, Peter Newstead, Christian Pauly, Frank-Olaf Schreyer and Edoardo Sernesi for helpful discussions and comments on this work.