1. Introduction
As an analytical tool for studies of the reaction of the Alpine water balance to climatic changes, a hydrometeorological model has been developed at the Institut für Meteorologie und Geophysik (Reference Kuhn, Nickus and PelletKuhn and others, 1982; Reference Kuhn, Pellet and SevrukKuhn and Pellet, 1989; Reference Kuhn and BatloggKuhn and Batlogg, 1998,Reference Kuhn and Batlogg1999). While it was originally designed to determine basin precipitation, it was obviously well suited for the analysis of the development of seasonal snow covers and glacier mass balance at basin scale using temperature and precipitation records of reference stations. For the resolution of the synoptic or daily time-scale a model with daily or hourly data input has to be used such as the HBV-ETH described by Reference Braun and RennerBraun and Renner (1992) and applied by Reference Braun, Weber and SchulzBraun and others (2000).
With a resolution of monthly values of the four components of the water balance of which only runoff is directly measured, only 12 of 48 variables are known and the remaining 36 have to be inferred by the model from additional information. The model results thus stand on shaky ground and need to be verified under a variety of climatic conditions and applications. The purpose of this paper is to reproduce two plausibility tests by comparing modeled and observed runoff at annual and decadal scales, where decadal refers to periods of approximately 10 years. The five basins selected for these tests are situated close enough to one another to ensure equal synoptic weather conditions, while differing strongly in topography and glacier cover.
2. Test Area
The basins are situated in the Silvretta mountains in Vorarl-berg and Tirol, Austria, centered around 46°55’ N, 10° 10’ E. The runoff flowing past Paznaun, Verwall and Illbache gauging stations is collected from several individual catchments; Kleinvermunt is a nearly ice-free sub-basin of Paznaun that is topographically and hydrologically different from the main basin. Some topographic characteristics are given in Table 1. Hydrological and glaciological conditions of the area have been treated in detail by Reference StueferStuefer (1994) and Reference BatloggBatlogg (1995).
Table 1. Topographic characteristics of the test basins
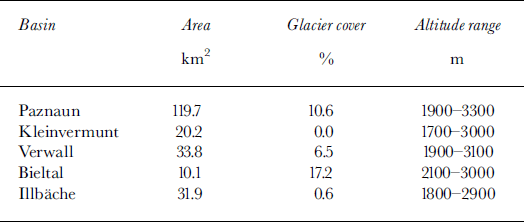
All basins are situated essentially above timberline, and display grass cover up to about 2600 m a.s.l. They have predominantly northerly aspect except Kleinvermunt which runs east to west. Verwall, Bieltal and Illbache are open to the advection of moist air from the northwest, while Kleinvermunt and Paznaun are better screened and drier, as is apparent in Table 2.
Table 2. Mean water-balance components, 1968/69–91/92, and range of runoff coefficients in that period
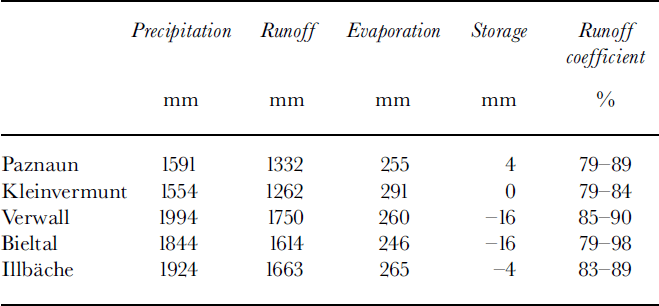
The range of runoff coefficients reflects the degree of glacienzation: the highest values arise in the basin with the largest ice-covered fraction, and the lowest maximum value in the ice-free Kleinvermunt basin. Similarly, in Table 3 the glacierized basins Paznaun, Verwall and Bieltal have runoff maxima in July, while in the nearly ice-free basins Illbache and Kleinvermunt the maximum is reached in June. Basin precipitation has maximum monthly values in July and August and minima in the late-fall and winter months.
Table 3. Seasonal course of runoff expressed in parts per thousand of annual suns

3. Model Structure and Input
In view of its climatological application, the model uses monthly time-steps and resolves altitude at 100 m intervals for which the total area a(h) and glacier-covered area g(h) are entered as initial input.
Hydrological variables are approximated in two steps: first, the annual balance of precipitation P, runoff Q, evaporation E and storage S for the basin is closed by using measured values of Q and a first estimate ofE, and by transferring S from the nearest glacier with actual mass-balance measurements, which yields annual basin precipitation in a first approximation. The next step consists of several iterations using monthly runoff data Q(mo), basin precipitation P(mo) constructed in analogy to the monthly course of station precipitation, and estimates of E(mo).
The transfer of mass balance is based on specific balance b(h), measured in a distant basin, applied to the local basin with area altitude distribution of glaciers g(h) and total area a(h).
Evaporation is approximated with a crude model that uses 0.5 mm d–1 over snow and 2 mmd-’ over snow-free vegetation, the snow cover being estimated initially The actual snow cover is generally reached after two iterations of the model.
This yields the first approximation of the annual basin precipitation P. Monthly values of basin precipitation P(mo) are then calculated in analogy to the relative monthly values of reference stations
All precipitation records are corrected for errors due to snowfall according to Sevruk (Reference Sevruk1983). The monthly storage is then calculated as
The altitudinal gradient of precipitation is estimated from meteorological stations in the basin or its surroundings. As is often observed in central Alpine stations, the precipitation gradient increases with altitude. In the Paznaun basin, for instance, a value of 30 mm (100m)–16 was adopted up to an altitude of 2500 m, and a value of 40 mm (100m)–1 above. In the simplest version of the model these gradients were kept constant throughout the year. Based on the monthly reference values of precipitation, a matrix of relative contributions Pτεl(mo,h) was constructed for all altitudes under the condition that its area-weighted integral over all altitudes and all months equalled the annual basin precipitation determined from the annual water balance. This matrix was kept constant in all years.
The distinction between snowfall and rain was made on the basis of observations on surrounding stations of various altitudes, from which the following relation between the temperature and the fraction τ of snow in the total monthly precipitation was found:
Being based on monthly mean temperatures, this kind of parameterization generally requires different coefficients than that based on actual temperatures during precipitation, which are expected to be below monthly average in summer and above monthly average in winter.
Temperatures T(mo,h) were extrapolated from the average T(mo) of two or three reference stations using values of dT/dh(mo) determined from the nearest mountain observatories for each month, keeping gradients constant at all altitudes. Degree days were counted using positive T(mo,h) only, which neglects individual positive daily means in a month with negative mean temperature. This deficiency was partly compensated by the introduction of a factor f(mo) ≤ 1.0, indicating the fraction of the area a(h) that was snow-covered in that month, as is necessary for the computation of monthly snowmelt. Degree-day factors D = 4 or 5mm deg d–1 were used for the basins in this study. Adjustment of both D and f(mo) must ensure that S(mo,h) in September is equal to the glacier mass balance inferred from reference glaciers.
At this stage it is possible to simulate the build-up and decay of the snow cover 5(mo,h) in a first approximation. As the evaporation was parameterized in terms of snow-covered/ snow-free ground, this delivers the second approximation of E(mo,h) and basin evaporation E which in turn serves as input to the second approximation of the basin balance. With Q being measured and S being transferred from outside, any change in E directly affects basin precipitation P.
4. Calibration and Tuning of the Model: The Need for Verification
After further iteration, the convergence was considered satisfactory when the simulated values of monthly basin runoff Q(mo) agreed by better than ±20 mm with the observed ones. In order to reach this agreement, the liquid-water fraction of 5(mo) had to be explicitly treated. This was done without altitude resolution, based on the condition that winter runoff of the order of 10–30 mm per month generated at times without any snowmelt had to be stored in summer, and that temporary retention of meltwater in the spring snow cover must not exceed 100 mm or 10% of the snow water equivalent, whichever was lower. Both of these manipulations affect the monthly course of components only, and have a sum of zero over the entire year.
At this point it is worth repeating what information has been transferred from outside the basin and what kind of internal calibration and tuning has been applied.
The basic input of Q(mo) has been assumed to be true, although it may be off by several per cent due to moving bed load and other changes of the cross-section.
The profiles of specific glacier mass balance b(h) have been imported from reference glaciers.
The zero-order approximation of monthly evaporation has been guessed from snow-cover data of the basin.
The seasonal course of T(mo, h) and P(mo, h) has been taken from P and T records of reference stations, with monthly values of dT/dh but constant dP/dh. (In other applications of the model a time variance of dP/dh was introduced to distinguish between advective and convective situations.)
The rain/snow transition was mapped from records at reference stations as r(mo,h). The shape of this matrix and the precipitation gradient dP/dh have been tuned to the amount of autumn runoff and the build-up of the winter snow cover, the latter being controlled also by the total amount of melt possible. That amount is controlled by dT/dh(mo) and by the degree-day factor D, while the relative snow-cover area f(mo) determines the progression of meltwater in spring and summer.
The tuning of the model has been performed with average data of 1952–92 for Paznaun, Kleinvermunt and Bieltal, and of 1969–92 for Verwall and Illbache. Before the model calibration can be verified by the simulation of individual years, the sensitivity of the simulated runoff with respect to temperature and precipitation must be established as follows.
5. Model Sensitivity to T and P
Table 4 summarizes the sensitivities determined by the following experiment: The basin precipitation was increased by 300 mm, all other parameters were left unchanged and the resulting change in monthly runoff was noted. When basin temperature was increased by PC, the new degree-day sums were automatically produced, while the rain/ snow transition, being stored as a matrix r(mo,h) without explicit reference to T, needed manual adjustment. This was accomplished by shifting the matrix upward by 160 m, equivalent to a 1°C warming and a mean lapse rate of 0.6°C(100m)–1. The respective changes in glacier mass balance S were generated by the model from the initially imported reference balance.
Table 4. Model sensitivity of annual evaporation E, glacier mass balance S and runoff Q to changes in temperature and precipitation
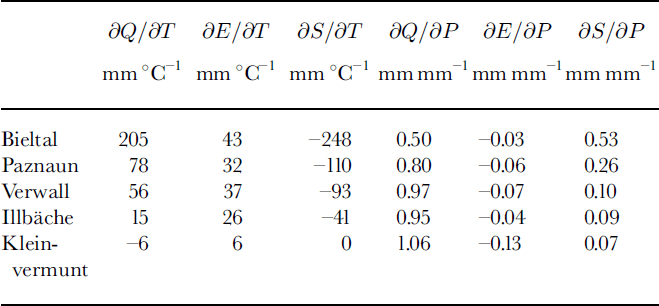
It is apparent that the most glacierized basin reacts most strongly to the prescribed warming with strongest melting and increased evaporation. Ice-free Kleinvermunt increases evaporation at the expense of runoff. In the highest basins the prescribed precipitation increase is mostly deposited as snow, while at the lowest basin it decreases evaporation to the extent that runoff increases by ≥ 1 mm per mm of precipitation.
6. Verification and Conclusion
While the model was calibrated with, and sensitivities were determined from, annual long-term averages, the test of the model will be using (1) individual years and (2) two periods of approximately 10 years that differ in temperature by approximately 1°C.
6.1. Annual values
The deviation of the runoff measured in the year i from the mean of 1952–92, ΔQi = Qi ― Qmean, was compared to the calculated
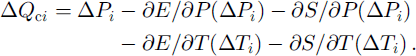
The correlation coefficients R(Qi, Qci) and the standard deviations σr(Q0 and σr(Qct) as well as σr(Qct ― Qt) are given in Table 5 for three basins. These quantities can be interpreted as a quality proof for the simulation Qci.
The correlation of simulated with observed annual runoff is poor in two basins and acceptable in Verwall, the only possible explanation being the representative of the reference stations for the basin. On the other hand, all three basins have comparable rms differences between observed and simulated runoff, indicating that if these differences display normal distribution, approximately two-thirds of them fall within the bracket of ±200 m or roughly ±15%.
Table 5. Correlation coefficients R and standard deviations s of simulated annual runoff Qcl and observed runoff QK in mm, for the time series indicated

6.2. Comparison of three periods
In order to test the model with longer-term averages, three periods were selected which had significant differences in temperature and varying differences in precipitation. The temperatures of four reference stations are given in Table 6, followed by the differences of P and Q for the two periods with record in all basins. The table indicates good performance of the model in four of the five basins, the reasons for the failure in the case of Bieltal remaining unknown.
Table 6. Averages of temperature T, precipitation P and runoff Q in three test periods. Values in lower part of this table are for third minus second period
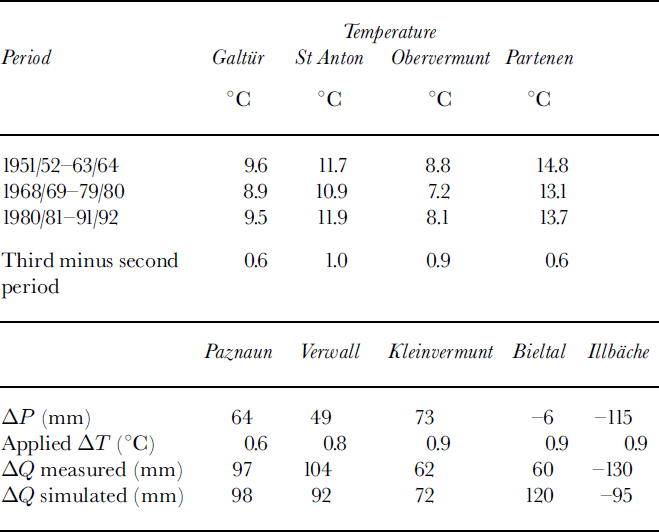
Compared to the variance analysis of annual values, it seems that deviations from the model assumptions or from the mean calibration conditions occurring in individual years are smoothed even when relatively short periods of the order of one decade are used. Thus, while the model is far from perfect for individual years, it seems safe to use it for clilmatological purposes.








