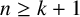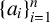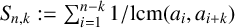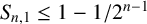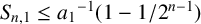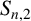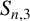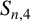1 Introduction
Chebyshev [Reference Chebyshev4] investigated the least common multiple of consecutive positive integers when he made the first important attempt to prove the prime number theorem stating that
![]() $\log \mathrm {lcm}(1, 2, \ldots , n)\sim n$
as n goes to infinity (see, for example, [Reference Ireland and Rosen13]). Hanson [Reference Hanson8] and Nair [Reference Nair14] gave upper and lower bounds for
$\log \mathrm {lcm}(1, 2, \ldots , n)\sim n$
as n goes to infinity (see, for example, [Reference Ireland and Rosen13]). Hanson [Reference Hanson8] and Nair [Reference Nair14] gave upper and lower bounds for
![]() $\mathrm {lcm}(1,2,\ldots ,n)$
and Nair’s lower bound was extended in [Reference Farhi6, Reference Hong, Luo, Qian and Wang11]. Goutziers [Reference Goutziers7] studied the asymptotic behaviour of the least common multiple of a set of integers not exceeding N. Bateman et al. [Reference Bateman, Kalb and Stenger1] obtained an asymptotic estimate for the least common multiple of arithmetic progressions that is generalised in [Reference Hong, Qian and Tan12] to products of linear polynomials. In another direction, Behrend [Reference Behrend2] strengthened an inequality of Heilbronn [Reference Heilbronn9] and Rohrbach [Reference Rohrbach15]. Erdős and Selfridge [Reference Erdős and Selfridge5] proved a remarkable old conjecture that predicts that the product of any two or more consecutive positive integers is never a perfect power.
$\mathrm {lcm}(1,2,\ldots ,n)$
and Nair’s lower bound was extended in [Reference Farhi6, Reference Hong, Luo, Qian and Wang11]. Goutziers [Reference Goutziers7] studied the asymptotic behaviour of the least common multiple of a set of integers not exceeding N. Bateman et al. [Reference Bateman, Kalb and Stenger1] obtained an asymptotic estimate for the least common multiple of arithmetic progressions that is generalised in [Reference Hong, Qian and Tan12] to products of linear polynomials. In another direction, Behrend [Reference Behrend2] strengthened an inequality of Heilbronn [Reference Heilbronn9] and Rohrbach [Reference Rohrbach15]. Erdős and Selfridge [Reference Erdős and Selfridge5] proved a remarkable old conjecture that predicts that the product of any two or more consecutive positive integers is never a perfect power.
Erdős observed another interesting phenomena related to least common multiples. Let n and k be positive integers with
![]() $n\ge k+1$
and let
$n\ge k+1$
and let
![]() $\{a_i\}_{i=1}^n$
be a strictly increasing sequence of positive integers. Let
$\{a_i\}_{i=1}^n$
be a strictly increasing sequence of positive integers. Let
 $$ \begin{align*} S_{n, k}:=\sum_{i=1}^{n-k}\frac{1}{\mathrm{lcm}(a_{i},a_{i+k})}. \end{align*} $$
$$ \begin{align*} S_{n, k}:=\sum_{i=1}^{n-k}\frac{1}{\mathrm{lcm}(a_{i},a_{i+k})}. \end{align*} $$
In 1978, Borwein [Reference Borwein3] confirmed a conjecture of Erdős by showing that
![]() $S_{n, 1}\le 1-{1}/{2^{n-1}}$
with equality if and only if
$S_{n, 1}\le 1-{1}/{2^{n-1}}$
with equality if and only if
![]() $a_{i}=2^{i-1}$
for
$a_{i}=2^{i-1}$
for
![]() $1\le i \le n$
. Recently, Hong [Reference Hong10] improved this upper bound and used the new result to get sharp upper bounds for
$1\le i \le n$
. Recently, Hong [Reference Hong10] improved this upper bound and used the new result to get sharp upper bounds for
![]() $S_{n, 2}$
and
$S_{n, 2}$
and
![]() $S_{n, 3}$
. He also characterised the sequences
$S_{n, 3}$
. He also characterised the sequences
![]() $\{a_i\}_{i=1}^\infty $
for which these upper bounds are attained. In this paper, we concentrate on
$\{a_i\}_{i=1}^\infty $
for which these upper bounds are attained. In this paper, we concentrate on
![]() $S_{n,4}$
. We will present an optimal upper bound for
$S_{n,4}$
. We will present an optimal upper bound for
![]() $S_{n, 4}$
and characterise the sequences
$S_{n, 4}$
and characterise the sequences
![]() $\{a_i\}_{i=1}^n$
for which this upper bound is attained.
$\{a_i\}_{i=1}^n$
for which this upper bound is attained.
As usual, for any real number x, we denote by
![]() $\lfloor x\rfloor $
and
$\lfloor x\rfloor $
and
![]() $\lceil x\rceil $
respectively the largest integer no more than x and the smallest integer no less than x. For brevity, we write
$\lceil x\rceil $
respectively the largest integer no more than x and the smallest integer no less than x. For brevity, we write
![]() $S_n :=S_{n, 4}$
.
$S_n :=S_{n, 4}$
.
The main result of this paper can be stated as follows.
Theorem 1.1. Let n be an integer with
![]() $n\ge 5$
and let
$n\ge 5$
and let
![]() $\{a_i\}_{i=1}^n$
be a strictly increasing sequence of positive integers. Then:
$\{a_i\}_{i=1}^n$
be a strictly increasing sequence of positive integers. Then:
-
(i)
 $S_{5}\le 1/5$
with equality if and only if
$S_{5}\le 1/5$
with equality if and only if
 $a_i=i$
for all
$a_i=i$
for all
 $i\in \{1, 2, 3, 4, 5\}$
;
$i\in \{1, 2, 3, 4, 5\}$
; -
(ii)
 $S_{6}\le {11}/{30}$
with equality if and only if
$S_{6}\le {11}/{30}$
with equality if and only if
 $a_i=i$
for all
$a_i=i$
for all
 $i\in \{1, 2, 3, 4, 5, 6\}$
;
$i\in \{1, 2, 3, 4, 5, 6\}$
; -
(iii)
 $S_{7}\le {43}/{90}$
with equality if and only if
$S_{7}\le {43}/{90}$
with equality if and only if
 $a_i=i$
for all
$a_i=i$
for all
 $i\in \{1, 2, 3, 4, 5, 6\}$
and
$i\in \{1, 2, 3, 4, 5, 6\}$
and
 $a_7=9$
;
$a_7=9$
; -
(vi)
 $S_{8}\le {101}/{180}$
with equality if and only if
$S_{8}\le {101}/{180}$
with equality if and only if
 $a_i=i$
for all
$a_i=i$
for all
 $i\in \{1, 2, 3, 4, 5, 6\}$
,
$i\in \{1, 2, 3, 4, 5, 6\}$
,
 $a_7=9$
and
$a_7=9$
and
 $a_8=12$
;
$a_8=12$
; -
(v) if
 $n\ge 9$
, then (1.1)where
$n\ge 9$
, then (1.1)where $$ \begin{align} S_{n}\le \frac{493}{420}-\frac{533}{105}\cdot\frac{1} {2^{\lfloor{n}/{4}\rfloor+1}} +\frac{\epsilon_{n}}{2^{\lfloor{n}/{4}\rfloor}}, \end{align} $$
and equality in (1.1) occurs if and only if
$$ \begin{align} S_{n}\le \frac{493}{420}-\frac{533}{105}\cdot\frac{1} {2^{\lfloor{n}/{4}\rfloor+1}} +\frac{\epsilon_{n}}{2^{\lfloor{n}/{4}\rfloor}}, \end{align} $$
and equality in (1.1) occurs if and only if $$ \begin{align*} \epsilon_n:= {\left\{\begin{array}{rl} 0 & \text{if} \ n\equiv 0\pmod 4,\\[5pt] \frac{2}{5} & \text{if} \ n\equiv 1\pmod 4,\\[5pt] \frac{11}{15} & \text{if} \ n\equiv 2\pmod 4,\\[5pt] \frac{107}{105} & \text{if} \ n\equiv 3\pmod 4, \end{array} \right.} \end{align*} $$
$$ \begin{align*} \epsilon_n:= {\left\{\begin{array}{rl} 0 & \text{if} \ n\equiv 0\pmod 4,\\[5pt] \frac{2}{5} & \text{if} \ n\equiv 1\pmod 4,\\[5pt] \frac{11}{15} & \text{if} \ n\equiv 2\pmod 4,\\[5pt] \frac{107}{105} & \text{if} \ n\equiv 3\pmod 4, \end{array} \right.} \end{align*} $$
 $a_i=i$
for all
$a_i=i$
for all
 $i\in \{1, 2, 3, 4\}$
and
$i\in \{1, 2, 3, 4\}$
and
 $a_{4i+1}=5\times 2^{i-1} \ (1\le i\le \lfloor {(n-1)}/{4}\rfloor ), a_{4i+2}= 3\times 2^{i} \ (1\le i\le \lfloor {(n-2)}/{4}\rfloor )$
,
$a_{4i+1}=5\times 2^{i-1} \ (1\le i\le \lfloor {(n-1)}/{4}\rfloor ), a_{4i+2}= 3\times 2^{i} \ (1\le i\le \lfloor {(n-2)}/{4}\rfloor )$
,
 $a_{4i+3}=7\times 2^{i-1} \ (1\le i\le \lfloor {(n-3)}/{4}\rfloor )$
and
$a_{4i+3}=7\times 2^{i-1} \ (1\le i\le \lfloor {(n-3)}/{4}\rfloor )$
and
 $a_{4i+4}=2^{i+2} \ (1\le i\le \lfloor {n}/{4}\rfloor -1)$
.
$a_{4i+4}=2^{i+2} \ (1\le i\le \lfloor {n}/{4}\rfloor -1)$
.
The rest of the paper is organised as follows. In Section 2, we prove several preliminary lemmas. In Section 3, we provide a proof for our main result.
2 Auxiliary lemmas
In this section, we supply several auxiliary lemmas that are needed in the proof of Theorem 1.1. The first is Hong’s upper bound [Reference Hong10, Theorem 1.2] which improves Borwein’s upper bound [Reference Borwein3].
Lemma 2.1 [Reference Hong10, Theorem 1.2]
Let n be an integer with
![]() $n\ge 2$
and let
$n\ge 2$
and let
![]() $\{a_i\}_{i=1}^n$
be a strictly increasing sequence of positive integers. Then
$\{a_i\}_{i=1}^n$
be a strictly increasing sequence of positive integers. Then
 $$ \begin{align} \sum_{i=1}^{n-1} \frac{1}{\mathrm{lcm}(a_{i},a_{i+1})} \le \frac{1}{a_{1}}\bigg(1-\frac{1}{2^{n-1}}\bigg) \end{align} $$
$$ \begin{align} \sum_{i=1}^{n-1} \frac{1}{\mathrm{lcm}(a_{i},a_{i+1})} \le \frac{1}{a_{1}}\bigg(1-\frac{1}{2^{n-1}}\bigg) \end{align} $$
with equality in (2.1) if and only if
![]() $a_{i}=2^{i-1}a_{1}$
for all integers i with
$a_{i}=2^{i-1}a_{1}$
for all integers i with
![]() $1 \le i \le n$
.
$1 \le i \le n$
.
Lemma 2.2. Let m be an integer with
![]() $m\ge 3$
. Then
$m\ge 3$
. Then
and
Proof. Since
![]() $m\ge 3$
, a direct computation gives the desired inequalities.
$m\ge 3$
, a direct computation gives the desired inequalities.
Lemma 2.3. Let
![]() $S_n$
be given as above. Then:
$S_n$
be given as above. Then:
-
(i)
 $S_5\le 1/5$
with equality if and only if
$S_5\le 1/5$
with equality if and only if
 $a_i=i$
for all
$a_i=i$
for all
 $i\in \{1, 2, 3, 4, 5\}$
;
$i\in \{1, 2, 3, 4, 5\}$
; -
(ii)
 $S_6\le {11}/{30}$
with equality if and only if
$S_6\le {11}/{30}$
with equality if and only if
 $a_i=i$
for all
$a_i=i$
for all
 $i\in \{1, 2, 3, 4, 5, 6\}$
;
$i\in \{1, 2, 3, 4, 5, 6\}$
; -
(iii)
 $S_7\le {43}/{90}$
with equality if and only if
$S_7\le {43}/{90}$
with equality if and only if
 $a_i=i$
for all
$a_i=i$
for all
 $i\in \{1, 2, 3, 4, 5, 6\}$
and
$i\in \{1, 2, 3, 4, 5, 6\}$
and
 $a_7=9$
.
$a_7=9$
.
Proof. We first deal with
![]() $S_5$
. Since
$S_5$
. Since
![]() $\mathrm {lcm}(a_1, a_{4})\ge a_{5}\ge 5$
,
$\mathrm {lcm}(a_1, a_{4})\ge a_{5}\ge 5$
,
The equality in (2.2) holds if and only if
![]() $\mathrm {lcm}(a_1, a_{5})=5$
, which is true if and only if
$\mathrm {lcm}(a_1, a_{5})=5$
, which is true if and only if
![]() $a_1=1$
and
$a_1=1$
and
![]() $a_5=5$
. However,
$a_5=5$
. However,
![]() $a_1<a_2<a_3<a_4<a_5$
. So the equality in (2.2) holds if and only if
$a_1<a_2<a_3<a_4<a_5$
. So the equality in (2.2) holds if and only if
![]() $a_i=i$
for all
$a_i=i$
for all
![]() $i\in \{1,2,3,4,5\}$
.
$i\in \{1,2,3,4,5\}$
.
Now consider
![]() $S_6$
. Since
$S_6$
. Since
![]() $a_2\ge 2, a_2\mid \mathrm {lcm}(a_2, a_{6})$
and
$a_2\ge 2, a_2\mid \mathrm {lcm}(a_2, a_{6})$
and
![]() $\mathrm {lcm}(a_2, a_{6})\ge a_6\ge 6$
, we deduce that
$\mathrm {lcm}(a_2, a_{6})\ge a_6\ge 6$
, we deduce that
![]() $\mathrm {lcm}(a_2, a_{6})\ge 6$
with equality if and only if
$\mathrm {lcm}(a_2, a_{6})\ge 6$
with equality if and only if
![]() $a_2=2$
and
$a_2=2$
and
![]() $a_6=6$
. So
$a_6=6$
. So
with equality in (2.3) if and only if
![]() $\mathrm {lcm}(a_1, a_{5})=5$
and
$\mathrm {lcm}(a_1, a_{5})=5$
and
![]() $\mathrm {lcm}(a_2, a_{6})=6$
, which is true if and only if
$\mathrm {lcm}(a_2, a_{6})=6$
, which is true if and only if
![]() $a_1=1, a_2=2, a_5=5$
and
$a_1=1, a_2=2, a_5=5$
and
![]() $a_6=6$
, which is true if and only if
$a_6=6$
, which is true if and only if
![]() $a_i=i$
for all
$a_i=i$
for all
![]() $i\in \{1,2,3,4, 5, 6\}$
.
$i\in \{1,2,3,4, 5, 6\}$
.
Finally, we consider
![]() $S_7$
. Since
$S_7$
. Since
![]() $a_3\ge 3, a_3\mid \mathrm {lcm}(a_3, a_{7})$
and
$a_3\ge 3, a_3\mid \mathrm {lcm}(a_3, a_{7})$
and
![]() $\mathrm {lcm}(a_3, a_{7})\ge a_7\ge 7$
, we deduce that either
$\mathrm {lcm}(a_3, a_{7})\ge a_7\ge 7$
, we deduce that either
![]() $\mathrm {lcm}(a_3, a_{7})=8$
which is true if and only if
$\mathrm {lcm}(a_3, a_{7})=8$
which is true if and only if
![]() $a_3=4$
and
$a_3=4$
and
![]() $a_7=8$
, or
$a_7=8$
, or
![]() $\mathrm {lcm}(a_3, a_{7})=9$
which is true if and only if
$\mathrm {lcm}(a_3, a_{7})=9$
which is true if and only if
![]() $a_3=3$
and
$a_3=3$
and
![]() $a_7=9$
, or
$a_7=9$
, or
![]() $\mathrm {lcm}(a_3, a_{7})\ge 10$
. We divide the rest of the proof into three cases.
$\mathrm {lcm}(a_3, a_{7})\ge 10$
. We divide the rest of the proof into three cases.
If
![]() $\mathrm {lcm}(a_3, a_{7})\ge 10$
, then
$\mathrm {lcm}(a_3, a_{7})\ge 10$
, then
as desired.
If
![]() $\mathrm {lcm}(a_3, a_{7})=8$
, then
$\mathrm {lcm}(a_3, a_{7})=8$
, then
![]() $a_3=4$
and
$a_3=4$
and
![]() $a_7=8$
. This implies that
$a_7=8$
. This implies that
![]() $a_4=5, a_5=6$
and
$a_4=5, a_5=6$
and
![]() $a_6=7$
. Since
$a_6=7$
. Since
![]() $(a_1, a_2)\in \{(1,2), (1,3), (2,3)\}$
, we have
$(a_1, a_2)\in \{(1,2), (1,3), (2,3)\}$
, we have
![]() $\mathrm {lcm}(a_1, a_{5})=6$
and
$\mathrm {lcm}(a_1, a_{5})=6$
and
![]() $\mathrm {lcm}(a_2, a_{6})\in \{14, 21\}$
. It then follows that
$\mathrm {lcm}(a_2, a_{6})\in \{14, 21\}$
. It then follows that
If
![]() $\mathrm {lcm}(a_3, a_{7})=9$
, then we must have
$\mathrm {lcm}(a_3, a_{7})=9$
, then we must have
![]() $a_3=3$
and
$a_3=3$
and
![]() $a_7=9$
. So
$a_7=9$
. So
![]() $\mathrm {lcm}(a_3, a_{7})=9$
. It then follows that
$\mathrm {lcm}(a_3, a_{7})=9$
. It then follows that
with equality in (2.4) if and only if
![]() $a_i=i$
for all
$a_i=i$
for all
![]() $i\in \{1,2,3,4,5,6\}$
and
$i\in \{1,2,3,4,5,6\}$
and
![]() $\mathrm {lcm}(a_3, a_{7})=9$
, if and only if
$\mathrm {lcm}(a_3, a_{7})=9$
, if and only if
![]() $a_i=i$
for all
$a_i=i$
for all
![]() $i\in \{1,2,3,4,5,6\}$
and
$i\in \{1,2,3,4,5,6\}$
and
![]() $a_7=9$
as required.
$a_7=9$
as required.
This completes the proof of Lemma 2.3.
Lemma 2.4. Let m be a positive integer with
![]() $m\ge 2$
and
$m\ge 2$
and
![]() $\mathcal {A}=\{a_i\}_{i=1}^8$
a strictly increasing sequence of eight positive integers. Let
$\mathcal {A}=\{a_i\}_{i=1}^8$
a strictly increasing sequence of eight positive integers. Let
 $$ \begin{align} \Box_m=\Box_m(\mathcal {A}):=\sum_{i=1}^4 \bigg(\frac{1}{\mathrm{lcm}(a_i, a_{i+4})} +\frac{1}{a_{i+4}}\bigg(1-\frac{1}{2^{m-2}}\bigg)\bigg). \end{align} $$
$$ \begin{align} \Box_m=\Box_m(\mathcal {A}):=\sum_{i=1}^4 \bigg(\frac{1}{\mathrm{lcm}(a_i, a_{i+4})} +\frac{1}{a_{i+4}}\bigg(1-\frac{1}{2^{m-2}}\bigg)\bigg). \end{align} $$
Then both of the following statements are true.
-
(i) Either
 $\Box _2= {101}/{180}$
which is true if and only if
$\Box _2= {101}/{180}$
which is true if and only if
 $a_i=i$
for all
$a_i=i$
for all
 $i\in \{1,2,3,4,5,6\}$
,
$i\in \{1,2,3,4,5,6\}$
,
 $a_7=9$
and
$a_7=9$
and
 $a_8=12$
, or
$a_8=12$
, or
 $\Box _2= {389}/{720}$
which holds if and only if
$\Box _2= {389}/{720}$
which holds if and only if
 $a_i=i$
for all integers
$a_i=i$
for all integers
 $i\in \{1,2,3,4,5,6\}$
,
$i\in \{1,2,3,4,5,6\}$
,
 $a_7=9$
and
$a_7=9$
and
 $a_8=16$
, or
$a_8=16$
, or
 $\Box _2= {453}/{840}$
which is true if and only if
$\Box _2= {453}/{840}$
which is true if and only if
 $a_i=i$
for all integers
$a_i=i$
for all integers
 $i\in \{1,2,3,4,5,6,7,8\}$
, or
$i\in \{1,2,3,4,5,6,7,8\}$
, or
 $\Box _2 < {453}/{840}$
.
$\Box _2 < {453}/{840}$
. -
(ii) If
 $m\ge 3$
, then (2.6)with equality in (2.6) if and only if
$m\ge 3$
, then (2.6)with equality in (2.6) if and only if $$ \begin{align} \Box_m\le\frac{493}{420}-\frac{533}{105}\cdot\frac{1}{2^{m+1}}, \end{align} $$
$$ \begin{align} \Box_m\le\frac{493}{420}-\frac{533}{105}\cdot\frac{1}{2^{m+1}}, \end{align} $$
 $a_i=i$
for all integers i with
$a_i=i$
for all integers i with
 $1\le i\le 8$
.
$1\le i\le 8$
.
Proof (i). Evidently,
![]() $\Box _2=\sum _{i=1}^4 {1}/{\mathrm {lcm}(a_i, a_{i+4})}.$
We consider the following cases.
$\Box _2=\sum _{i=1}^4 {1}/{\mathrm {lcm}(a_i, a_{i+4})}.$
We consider the following cases.
Case 1:
![]() $a_5\ge 6$
. Then
$a_5\ge 6$
. Then
![]() $a_8\ge 9$
. If
$a_8\ge 9$
. If
![]() $a_8\ge 10$
, then by the fact
$a_8\ge 10$
, then by the fact
![]() $\mathrm {lcm}(a_i, a_{i+4})\ge a_{i+4}$
for all
$\mathrm {lcm}(a_i, a_{i+4})\ge a_{i+4}$
for all
![]() $i\in \{1,2,3,4\}$
, we derive
$i\in \{1,2,3,4\}$
, we derive
If
![]() $a_8=9$
, then
$a_8=9$
, then
![]() $a_5=6$
,
$a_5=6$
,
![]() $a_6=7$
and
$a_6=7$
and
![]() $a_7=8$
. This implies that
$a_7=8$
. This implies that
![]() $a_1\in \{1,2\}$
,
$a_1\in \{1,2\}$
,
![]() $a_2\in \{2, 3\}, a_3\in \{3, 4\}$
and
$a_2\in \{2, 3\}, a_3\in \{3, 4\}$
and
![]() $a_4\in \{4,5\}$
. It follows that
$a_4\in \{4,5\}$
. It follows that
![]() $\mathrm {lcm}(a_1, a_5)=6$
,
$\mathrm {lcm}(a_1, a_5)=6$
,
![]() $\mathrm {lcm}(a_2, a_6)\in \{14, 21\}, \mathrm {lcm}(a_3, a_7)=\mathrm {lcm}(a_3, 8)\in \{8, 24\}$
and
$\mathrm {lcm}(a_2, a_6)\in \{14, 21\}, \mathrm {lcm}(a_3, a_7)=\mathrm {lcm}(a_3, 8)\in \{8, 24\}$
and
![]() $\mathrm {lcm}(a_4, a_8)=\mathrm {lcm}(a_4, 9)\in \{36, 45\}$
. So
$\mathrm {lcm}(a_4, a_8)=\mathrm {lcm}(a_4, 9)\in \{36, 45\}$
. So
Case 2:
![]() $a_5=5$
. Then
$a_5=5$
. Then
![]() $a_i=i$
for all integers i with
$a_i=i$
for all integers i with
![]() $1\le i\le 4$
. If
$1\le i\le 4$
. If
![]() $a_6\ge 7$
, then
$a_6\ge 7$
, then
![]() $a_7\ge 8$
and
$a_7\ge 8$
and
![]() $a_8\ge 9$
. So
$a_8\ge 9$
. So
![]() $\mathrm {lcm}(a_1, a_5)=5, \mathrm {lcm}(a_2, a_6)\ge 8, \mathrm {lcm}(a_3, a_7)\ge 9$
and
$\mathrm {lcm}(a_1, a_5)=5, \mathrm {lcm}(a_2, a_6)\ge 8, \mathrm {lcm}(a_3, a_7)\ge 9$
and
![]() $\mathrm {lcm}(a_4, a_8)\ge 12$
. However,
$\mathrm {lcm}(a_4, a_8)\ge 12$
. However,
![]() $1/9+ {1}/{12} < 1/6 + {1}/{21}$
. Thus
$1/9+ {1}/{12} < 1/6 + {1}/{21}$
. Thus
In what follows, we let
![]() $a_6=6$
. If
$a_6=6$
. If
![]() $a_7\ge 10$
, then
$a_7\ge 10$
, then
![]() $a_8\ge 11$
. It follows that
$a_8\ge 11$
. It follows that
![]() $\mathrm {lcm}(a_3, a_7)\ge 12$
with equality holding if and only if
$\mathrm {lcm}(a_3, a_7)\ge 12$
with equality holding if and only if
![]() $a_7=12$
, and
$a_7=12$
, and
![]() $\mathrm {lcm}(a_4, a_8)\ge 12$
with equality occurring if and only if
$\mathrm {lcm}(a_4, a_8)\ge 12$
with equality occurring if and only if
![]() $a_8=12$
. Since
$a_8=12$
. Since
![]() $a_7<a_8$
,
$a_7<a_8$
,
It remains to consider the case
![]() $a_7\in \{7, 8, 9\}$
. We consider three subcases.
$a_7\in \{7, 8, 9\}$
. We consider three subcases.
Subcase 2.1:
![]() $a_7=7$
. Then
$a_7=7$
. Then
![]() $\mathrm {lcm}(a_3, a_7)=21$
and
$\mathrm {lcm}(a_3, a_7)=21$
and
![]() $\mathrm {lcm}(a_4, a_8)=\mathrm {lcm}(4, a_8)\ge 8$
with equality if and only if
$\mathrm {lcm}(a_4, a_8)=\mathrm {lcm}(4, a_8)\ge 8$
with equality if and only if
![]() $a_8=8$
. So
$a_8=8$
. So
with equality if and only if
![]() $a_i=i$
for all integers i with
$a_i=i$
for all integers i with
![]() $1\le i\le 8$
.
$1\le i\le 8$
.
Subcase 2.2:
![]() $a_7=8$
. Then
$a_7=8$
. Then
![]() $a_8\ge 9$
. Hence
$a_8\ge 9$
. Hence
Subcase 2.3:
![]() $a_7=9$
. Then
$a_7=9$
. Then
![]() $a_8\ge 10$
. It follows that either
$a_8\ge 10$
. It follows that either
![]() $\mathrm {lcm}(a_4, a_8)=12$
which is true if and only if
$\mathrm {lcm}(a_4, a_8)=12$
which is true if and only if
![]() $a_8=12$
, or
$a_8=12$
, or
![]() $\mathrm {lcm}(a_4, a_8)=16$
which is true if and only if
$\mathrm {lcm}(a_4, a_8)=16$
which is true if and only if
![]() $a_8=16$
, or
$a_8=16$
, or
![]() $\mathrm {lcm}(a_4, a_8)\ge 20$
. We then deduce that either
$\mathrm {lcm}(a_4, a_8)\ge 20$
. We then deduce that either
which is true if and only if
![]() $a_i=i$
for all
$a_i=i$
for all
![]() $i\in \{1,2,3,4,5,6\}$
,
$i\in \{1,2,3,4,5,6\}$
,
![]() $a_7=9$
and
$a_7=9$
and
![]() $a_8=12$
, or
$a_8=12$
, or
which holds if and only if
![]() $a_i=i$
for all
$a_i=i$
for all
![]() $i\in \{1,2,3,4,5,6\}$
,
$i\in \{1,2,3,4,5,6\}$
,
![]() $a_7=9$
and
$a_7=9$
and
![]() $a_8=16$
, or
$a_8=16$
, or
as expected. This completes the proof of part (i).
(ii). Let
![]() $m\ge 3$
. Since
$m\ge 3$
. Since
![]() $\mathrm {lcm}(a_i, a_{i+4})\ge a_{i+4}$
for all integers i with
$\mathrm {lcm}(a_i, a_{i+4})\ge a_{i+4}$
for all integers i with
![]() $1\le i\le 4$
,
$1\le i\le 4$
,
 $$ \begin{align} \Box_m &\le\sum_{i=1}^4\bigg(\frac{1}{a_{i+4}}+\frac{1}{a_{i+4}} \bigg(1-\frac{1}{2^{m-2}}\bigg)\bigg) =\bigg(2-\frac{1}{2^{m-2}}\bigg)\sum_{i=5}^8\frac{1}{a_i} \end{align} $$
$$ \begin{align} \Box_m &\le\sum_{i=1}^4\bigg(\frac{1}{a_{i+4}}+\frac{1}{a_{i+4}} \bigg(1-\frac{1}{2^{m-2}}\bigg)\bigg) =\bigg(2-\frac{1}{2^{m-2}}\bigg)\sum_{i=5}^8\frac{1}{a_i} \end{align} $$
with equality in (2.7) if and only if
![]() $a_i\mid a_{i+4}$
for all integers
$a_i\mid a_{i+4}$
for all integers
![]() $i\in \{1, 2, 3, 4\}$
. Let
$i\in \{1, 2, 3, 4\}$
. Let
![]() $S_0:= {493}/{420} - {533}/{105} \cdot {1}/({2^{m+1}})$
. We divide the rest of the proof into two cases.
$S_0:= {493}/{420} - {533}/{105} \cdot {1}/({2^{m+1}})$
. We divide the rest of the proof into two cases.
Case 1:
![]() $a_5\ge 6$
. Then
$a_5\ge 6$
. Then
![]() $a_6\ge 7, a_7\ge 8$
and
$a_6\ge 7, a_7\ge 8$
and
![]() $a_8\ge 9$
. So by (2.7) and Lemma 2.2,
$a_8\ge 9$
. So by (2.7) and Lemma 2.2,
 $$ \begin{align*} \Box_m & \le \bigg(2-\frac{1}{2^{m-2}}\bigg)\sum_{i=5}^8\frac{1}{a_i} \le \bigg(\frac{1}{6}+\frac{1}{7}+\frac{1}{8} +\frac{1}{9}\bigg)\bigg(2-\frac{1}{2^{m-2}}\bigg)\nonumber\\[4pt] & <\frac{1}{5}+\frac{1}{6}+\frac{1}{8}+\frac{1}{21} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{7} +\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) =S_0 \end{align*} $$
$$ \begin{align*} \Box_m & \le \bigg(2-\frac{1}{2^{m-2}}\bigg)\sum_{i=5}^8\frac{1}{a_i} \le \bigg(\frac{1}{6}+\frac{1}{7}+\frac{1}{8} +\frac{1}{9}\bigg)\bigg(2-\frac{1}{2^{m-2}}\bigg)\nonumber\\[4pt] & <\frac{1}{5}+\frac{1}{6}+\frac{1}{8}+\frac{1}{21} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{7} +\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) =S_0 \end{align*} $$
since
![]() $m\ge 3$
. This gives the desired result for Case 1.
$m\ge 3$
. This gives the desired result for Case 1.
Case 2:
![]() $a_5=5$
. Then
$a_5=5$
. Then
![]() $a_i=i$
for all
$a_i=i$
for all
![]() $i\in \{1, 2, 3, 4\}$
. We consider three subcases.
$i\in \{1, 2, 3, 4\}$
. We consider three subcases.
Subcase 2.1:
![]() $a_6=6$
. Then
$a_6=6$
. Then
![]() $a_7\ge 7$
and
$a_7\ge 7$
and
![]() $\mathrm {lcm}(a_3, a_7)=\mathrm {lcm}(3, a_7)\ge 9$
. So
$\mathrm {lcm}(a_3, a_7)=\mathrm {lcm}(3, a_7)\ge 9$
. So
 $$ \begin{align} \Box_m & = \frac{1}{\mathrm{lcm}(1, 5)}+\frac{1}{\mathrm{lcm}(2, 6)} +\frac{1}{\mathrm{lcm}(3, a_{7})}+\frac{1}{\mathrm{lcm}(4, a_8)}\nonumber\\[6pt] &\quad +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{a_7}+\frac{1}{a_8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg). \end{align} $$
$$ \begin{align} \Box_m & = \frac{1}{\mathrm{lcm}(1, 5)}+\frac{1}{\mathrm{lcm}(2, 6)} +\frac{1}{\mathrm{lcm}(3, a_{7})}+\frac{1}{\mathrm{lcm}(4, a_8)}\nonumber\\[6pt] &\quad +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{a_7}+\frac{1}{a_8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg). \end{align} $$
If
![]() $a_7=7$
, then it follows from
$a_7=7$
, then it follows from
![]() $a_8\ge 8$
that
$a_8\ge 8$
that
![]() $\mathrm {lcm}(4, a_8)\ge 8$
with equality if and only if
$\mathrm {lcm}(4, a_8)\ge 8$
with equality if and only if
![]() $a_8=8$
. Therefore,
$a_8=8$
. Therefore,
 $$ \begin{align*} \Box_m & = \frac{1}{5}+\frac{1}{6}+\frac{1}{21}+\frac{1}{\mathrm{lcm}(4, a_8)}+\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{a_8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)\\[4pt] & \le \frac{1}{5}+\frac{1}{6}+\frac{1}{21}+\frac{1}{8}+\bigg(\frac{1}{5} +\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)=S_0 \end{align*} $$
$$ \begin{align*} \Box_m & = \frac{1}{5}+\frac{1}{6}+\frac{1}{21}+\frac{1}{\mathrm{lcm}(4, a_8)}+\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{a_8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)\\[4pt] & \le \frac{1}{5}+\frac{1}{6}+\frac{1}{21}+\frac{1}{8}+\bigg(\frac{1}{5} +\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)=S_0 \end{align*} $$
with equality if and only if
![]() $a_i=i$
for all integers i with
$a_i=i$
for all integers i with
![]() $1\le i\le 8$
.
$1\le i\le 8$
.
If
![]() $a_7=8$
, then
$a_7=8$
, then
![]() $a_8\ge 9$
and so
$a_8\ge 9$
and so
![]() $\mathrm {lcm}(4, a_8)\ge 12$
. Thus by (2.8),
$\mathrm {lcm}(4, a_8)\ge 12$
. Thus by (2.8),
If
![]() $a_7=9$
, then
$a_7=9$
, then
![]() $\mathrm {lcm}(3, a_7)=9$
,
$\mathrm {lcm}(3, a_7)=9$
,
![]() $a_8\ge 10$
and so
$a_8\ge 10$
and so
![]() $\mathrm {lcm}(4, a_8)\ge 12$
. Since
$\mathrm {lcm}(4, a_8)\ge 12$
. Since
![]() $m\ge 3$
and by Lemma 2.2,
$m\ge 3$
and by Lemma 2.2,
 $$ \begin{align*} \Box_m & <\frac{1}{5}+\frac{1}{6}+\frac{1}{9}+\frac{1}{12} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{9}+\frac{1}{10}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) \\[4pt] & <\frac{1}{5}+\frac{1}{6}+\frac{1}{8}+\frac{1}{21} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) =S_0. \end{align*} $$
$$ \begin{align*} \Box_m & <\frac{1}{5}+\frac{1}{6}+\frac{1}{9}+\frac{1}{12} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{9}+\frac{1}{10}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) \\[4pt] & <\frac{1}{5}+\frac{1}{6}+\frac{1}{8}+\frac{1}{21} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) =S_0. \end{align*} $$
If
![]() $a_7\ge 10$
, then
$a_7\ge 10$
, then
![]() $a_8\ge 11$
. Hence
$a_8\ge 11$
. Hence
![]() $\mathrm {lcm}(3, a_7)\ge 12$
with equality holding if and only if
$\mathrm {lcm}(3, a_7)\ge 12$
with equality holding if and only if
![]() $a_7=12$
, and
$a_7=12$
, and
![]() $\mathrm {lcm}(4, a_8)\ge 12$
with equality occurring if and only if
$\mathrm {lcm}(4, a_8)\ge 12$
with equality occurring if and only if
![]() $a_8=12$
. Since
$a_8=12$
. Since
![]() $a_7<a_8$
and
$a_7<a_8$
and
![]() $m\ge 3$
,
$m\ge 3$
,
 $$ \begin{align*} \Box_m & <\frac{1}{5}+\frac{1}{6}+\frac{1}{12}+\frac{1}{12} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{10}+\frac{1}{11}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) \\[4pt] & <\frac{1}{5}+\frac{1}{6}+\frac{1}{21}+\frac{1}{8}+\bigg(\frac{1}{5} +\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) =S_0. \end{align*} $$
$$ \begin{align*} \Box_m & <\frac{1}{5}+\frac{1}{6}+\frac{1}{12}+\frac{1}{12} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{10}+\frac{1}{11}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) \\[4pt] & <\frac{1}{5}+\frac{1}{6}+\frac{1}{21}+\frac{1}{8}+\bigg(\frac{1}{5} +\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) =S_0. \end{align*} $$
Subcase 2.2:
![]() $a_6=7$
. Then
$a_6=7$
. Then
![]() $a_7\ge 8$
and
$a_7\ge 8$
and
![]() $a_8\ge 9$
. So
$a_8\ge 9$
. So
![]() $\mathrm {lcm}(3, a_7)\ge 9$
with equality if and only if
$\mathrm {lcm}(3, a_7)\ge 9$
with equality if and only if
![]() $a_7=9$
, and
$a_7=9$
, and
![]() $\mathrm {lcm}(4, a_8)\ge 12$
with equality if and only if
$\mathrm {lcm}(4, a_8)\ge 12$
with equality if and only if
![]() $a_8=12$
. Since
$a_8=12$
. Since
![]() ${1}/{14} + 1/9 + {1}/{12} < 1/6 + 1/8 + {1}/{21}$
, it then follows immediately that
${1}/{14} + 1/9 + {1}/{12} < 1/6 + 1/8 + {1}/{21}$
, it then follows immediately that
 $$ \begin{align*} \Box_m & =\frac{1}{\mathrm{lcm}(1, 5)}+\frac{1} {\mathrm{lcm}(2, 7)}+\frac{1}{\mathrm{lcm}(3, a_{7})} +\frac{1}{\mathrm{lcm}(4, a_{8})}\nonumber\\[4pt] &\quad +\bigg(\frac{1}{5}+\frac{1}{7}+\frac{1}{a_7}+ \frac{1}{a_8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)\nonumber\\[4pt] & <\frac{1}{5}+\frac{1}{14}+\frac{1}{9} +\frac{1}{12}+\bigg(\frac{1}{5}+\frac{1}{7}+\frac{1}{8}+ \frac{1}{9}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)\nonumber\\[4pt] & <\frac{1}{5}+\frac{1}{6}+\frac{1}{21}+\frac{1}{8} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{7} +\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)=S_0. \end{align*} $$
$$ \begin{align*} \Box_m & =\frac{1}{\mathrm{lcm}(1, 5)}+\frac{1} {\mathrm{lcm}(2, 7)}+\frac{1}{\mathrm{lcm}(3, a_{7})} +\frac{1}{\mathrm{lcm}(4, a_{8})}\nonumber\\[4pt] &\quad +\bigg(\frac{1}{5}+\frac{1}{7}+\frac{1}{a_7}+ \frac{1}{a_8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)\nonumber\\[4pt] & <\frac{1}{5}+\frac{1}{14}+\frac{1}{9} +\frac{1}{12}+\bigg(\frac{1}{5}+\frac{1}{7}+\frac{1}{8}+ \frac{1}{9}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)\nonumber\\[4pt] & <\frac{1}{5}+\frac{1}{6}+\frac{1}{21}+\frac{1}{8} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{7} +\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)=S_0. \end{align*} $$
Subcase 2.3:
![]() $a_6\ge 8$
. Then
$a_6\ge 8$
. Then
![]() $a_7\ge 9$
and
$a_7\ge 9$
and
![]() $a_8\ge 10$
. Thus
$a_8\ge 10$
. Thus
![]() $\mathrm {lcm}(a_2, a_6)=\mathrm {lcm}(2, a_6)\ge 8$
,
$\mathrm {lcm}(a_2, a_6)=\mathrm {lcm}(2, a_6)\ge 8$
,
![]() $\mathrm {lcm}(a_3, a_7) =\mathrm {lcm}(3, a_7)\ge 9$
and
$\mathrm {lcm}(a_3, a_7) =\mathrm {lcm}(3, a_7)\ge 9$
and
![]() $\mathrm {lcm}(a_4, a_8)=\mathrm {lcm}(4, a_8)\ge a_8\ge 10$
which implies that
$\mathrm {lcm}(a_4, a_8)=\mathrm {lcm}(4, a_8)\ge a_8\ge 10$
which implies that
![]() $\mathrm {lcm}(a_4, a_8)\ge 12$
since
$\mathrm {lcm}(a_4, a_8)\ge 12$
since
![]() $4\mid \mathrm {lcm}(a_4, a_8)$
. It then follows from the inequality
$4\mid \mathrm {lcm}(a_4, a_8)$
. It then follows from the inequality
![]() $ 1/9 + {1}/{12} < 1/6 + {1}/{21}$
that
$ 1/9 + {1}/{12} < 1/6 + {1}/{21}$
that
 $$ \begin{align*} \Box_m & =\frac{1}{\mathrm{lcm}(1, 5)}+\frac{1} {\mathrm{lcm}(2, a_6)}+\frac{1}{\mathrm{lcm}(3, a_{7})} +\frac{1}{\mathrm{lcm}(4, a_{8})} \\[4pt] &\quad +\bigg(\frac{1}{5}+\frac{1}{a_6}+\frac{1}{a_7}+ \frac{1}{a_8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) \\& \le \frac{1}{5}+\frac{1}{8}+\frac{1}{9}+\frac{1}{12}+\bigg(\frac{1}{5}+\frac{1}{8} +\frac{1}{9}+\frac{1}{10}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)\nonumber\\[4pt] & <\frac{1}{5}+\frac{1}{6}+\frac{1}{21}+\frac{1}{8}+\bigg(\frac{1}{5}+\frac{1}{6} +\frac{1}{7}+\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)=S_0. \end{align*} $$
$$ \begin{align*} \Box_m & =\frac{1}{\mathrm{lcm}(1, 5)}+\frac{1} {\mathrm{lcm}(2, a_6)}+\frac{1}{\mathrm{lcm}(3, a_{7})} +\frac{1}{\mathrm{lcm}(4, a_{8})} \\[4pt] &\quad +\bigg(\frac{1}{5}+\frac{1}{a_6}+\frac{1}{a_7}+ \frac{1}{a_8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg) \\& \le \frac{1}{5}+\frac{1}{8}+\frac{1}{9}+\frac{1}{12}+\bigg(\frac{1}{5}+\frac{1}{8} +\frac{1}{9}+\frac{1}{10}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)\nonumber\\[4pt] & <\frac{1}{5}+\frac{1}{6}+\frac{1}{21}+\frac{1}{8}+\bigg(\frac{1}{5}+\frac{1}{6} +\frac{1}{7}+\frac{1}{8}\bigg)\bigg(1-\frac{1}{2^{m-2}}\bigg)=S_0. \end{align*} $$
This completes the proof of part (ii).
3 Proof of Theorem 1.1
Let
![]() $m\ge 2$
be an integer and let
$m\ge 2$
be an integer and let
![]() $\Box _m$
be defined as in (2.5). Then
$\Box _m$
be defined as in (2.5). Then
![]() $\Box _2=S_8$
, so the results for parts (i) to (iv) follow from Lemmas 2.3 and 2.4. It remains to prove (v).
$\Box _2=S_8$
, so the results for parts (i) to (iv) follow from Lemmas 2.3 and 2.4. It remains to prove (v).
We first deal with the upper bounds for
![]() $S_9, S_{10}$
and
$S_9, S_{10}$
and
![]() $S_{11}$
. For
$S_{11}$
. For
![]() $r\in \{1,2,3\}$
,
$r\in \{1,2,3\}$
,
 $$ \begin{align*} S_{8+r}=\Box_2+\sum_{i=1}^r\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})}. \end{align*} $$
$$ \begin{align*} S_{8+r}=\Box_2+\sum_{i=1}^r\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})}. \end{align*} $$
By Lemma 2.4, either
![]() $\Box _2= {101}/{180}$
which is true if and only if
$\Box _2= {101}/{180}$
which is true if and only if
![]() $a_i=i$
for all
$a_i=i$
for all
![]() $i\in \{1,2,3,4,5,6\}$
,
$i\in \{1,2,3,4,5,6\}$
,
![]() $a_7=9$
and
$a_7=9$
and
![]() $a_8=12$
, or
$a_8=12$
, or
![]() $\Box _2= {389}/{720}$
which holds if and only if
$\Box _2= {389}/{720}$
which holds if and only if
![]() $a_i=i$
for all integers
$a_i=i$
for all integers
![]() $i\in \{1,2,3,4,5,6\}$
,
$i\in \{1,2,3,4,5,6\}$
,
![]() $a_7=9$
and
$a_7=9$
and
![]() $a_8=16$
, or
$a_8=16$
, or
![]() $\Box _2= {453}/{840}$
which is true if and only if
$\Box _2= {453}/{840}$
which is true if and only if
![]() $a_i=i$
for all integers
$a_i=i$
for all integers
![]() $i\in \{1,2,3,4,5,6,7,8\}$
, or
$i\in \{1,2,3,4,5,6,7,8\}$
, or
![]() $\Box _2 < {453}/{840}$
.
$\Box _2 < {453}/{840}$
.
If
![]() $\Box _2 < {453}/{840}$
, then it follows from
$\Box _2 < {453}/{840}$
, then it follows from
![]() $\mathrm {lcm}(a_5, a_9)\ge 10, \mathrm {lcm}(a_6, a_{10})\ge 12$
and
$\mathrm {lcm}(a_5, a_9)\ge 10, \mathrm {lcm}(a_6, a_{10})\ge 12$
and
![]() $\mathrm {lcm}(a_7, a_{11})\ge 14$
that
$\mathrm {lcm}(a_7, a_{11})\ge 14$
that
 $$ \begin{align*} S_9 & <\frac{453}{840}+\frac{1}{\mathrm{lcm}(a_5, a_9)} \le \frac{453}{840}+\frac{1}{10}=\frac{537}{840}, \\[3pt] S_{10} & <\frac{453}{840}+\sum_{i=1}^2\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le \frac{453}{840}+\frac{1}{10}+\frac{1}{12}=\frac{607}{840}, \\[3pt] S_{11} & <\frac{453}{840}+\sum_{i=1}^3\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le \frac{453}{840}+\frac{1}{10}+\frac{1}{12}+\frac{1}{14}=\frac{667}{840}. \end{align*} $$
$$ \begin{align*} S_9 & <\frac{453}{840}+\frac{1}{\mathrm{lcm}(a_5, a_9)} \le \frac{453}{840}+\frac{1}{10}=\frac{537}{840}, \\[3pt] S_{10} & <\frac{453}{840}+\sum_{i=1}^2\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le \frac{453}{840}+\frac{1}{10}+\frac{1}{12}=\frac{607}{840}, \\[3pt] S_{11} & <\frac{453}{840}+\sum_{i=1}^3\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le \frac{453}{840}+\frac{1}{10}+\frac{1}{12}+\frac{1}{14}=\frac{667}{840}. \end{align*} $$
If
![]() $\Box _2= {101}/{180}$
, then by Lemma 2.4, we must have
$\Box _2= {101}/{180}$
, then by Lemma 2.4, we must have
![]() $a_i=i$
for all integers i with
$a_i=i$
for all integers i with
![]() $1\le i\le 6$
,
$1\le i\le 6$
,
![]() $a_7=9$
and
$a_7=9$
and
![]() $a_8=12$
. So
$a_8=12$
. So
![]() $a_9\ge 13$
,
$a_9\ge 13$
,
![]() $a_{10}\ge 14$
and
$a_{10}\ge 14$
and
![]() $a_{11}\ge 15$
. This implies that
$a_{11}\ge 15$
. This implies that
![]() $\mathrm {lcm}(a_5, a_9)=\mathrm {lcm}(5, a_9)\ge 15$
with equality if and only if
$\mathrm {lcm}(a_5, a_9)=\mathrm {lcm}(5, a_9)\ge 15$
with equality if and only if
![]() $a_9=15$
,
$a_9=15$
,
![]() $\mathrm {lcm}(a_6, a_{10})=\mathrm {lcm}(6, a_{10})\ge 18$
with equality if and only if
$\mathrm {lcm}(a_6, a_{10})=\mathrm {lcm}(6, a_{10})\ge 18$
with equality if and only if
![]() $a_{10}=18$
, and
$a_{10}=18$
, and
![]() $\mathrm {lcm}(a_7, a_{11})=\mathrm {lcm}(9, a_{11})\ge 18$
with equality if and only if
$\mathrm {lcm}(a_7, a_{11})=\mathrm {lcm}(9, a_{11})\ge 18$
with equality if and only if
![]() $a_{11}=18$
. Hence
$a_{11}=18$
. Hence
 $$ \begin{align*} S_9 & =\frac{101}{180}+\frac{1}{\mathrm{lcm}(a_5, a_9)} \le\frac{101}{180}+\frac{1}{15}=\frac{113}{180}<\frac{537}{840}, \\[3pt] S_{10} & =\frac{101}{180}+\sum_{i=1}^2\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le\frac{101}{180}+\frac{1}{15}+\frac{1}{18}=\frac{123}{180}<\frac{607}{840}, \\S_{11} & =\frac{101}{180}+\sum_{i=1}^3\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} <\frac{101}{180}+\frac{1}{15}+\frac{1}{18} +\frac{1}{18}=\frac{133}{180}<\frac{667}{840} \end{align*} $$
$$ \begin{align*} S_9 & =\frac{101}{180}+\frac{1}{\mathrm{lcm}(a_5, a_9)} \le\frac{101}{180}+\frac{1}{15}=\frac{113}{180}<\frac{537}{840}, \\[3pt] S_{10} & =\frac{101}{180}+\sum_{i=1}^2\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le\frac{101}{180}+\frac{1}{15}+\frac{1}{18}=\frac{123}{180}<\frac{607}{840}, \\S_{11} & =\frac{101}{180}+\sum_{i=1}^3\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} <\frac{101}{180}+\frac{1}{15}+\frac{1}{18} +\frac{1}{18}=\frac{133}{180}<\frac{667}{840} \end{align*} $$
as desired.
If
![]() $\Box _2= {389}/{720}$
, then by Lemma 2.4, we must have
$\Box _2= {389}/{720}$
, then by Lemma 2.4, we must have
![]() $a_i=i$
for all integers i with
$a_i=i$
for all integers i with
![]() $1\le i\le 6$
,
$1\le i\le 6$
,
![]() $a_7=9$
and
$a_7=9$
and
![]() $a_8=16$
. So
$a_8=16$
. So
![]() $a_9\ge 17$
,
$a_9\ge 17$
,
![]() $a_{10}\ge 18$
and
$a_{10}\ge 18$
and
![]() $a_{11}\ge 19$
which implies that
$a_{11}\ge 19$
which implies that
![]() $\mathrm {lcm}(a_5, a_9)=\mathrm {lcm}(5, a_9)\ge 20$
with equality if and only if
$\mathrm {lcm}(a_5, a_9)=\mathrm {lcm}(5, a_9)\ge 20$
with equality if and only if
![]() $a_9=20$
,
$a_9=20$
,
![]() $\mathrm {lcm}(a_6, a_{10})=\mathrm {lcm}(6, a_{10})\ge 18$
with equality if and only if
$\mathrm {lcm}(a_6, a_{10})=\mathrm {lcm}(6, a_{10})\ge 18$
with equality if and only if
![]() $a_{10}=18$
and
$a_{10}=18$
and
![]() $\mathrm {lcm}(a_7, a_{11})=\mathrm {lcm}(9, a_{11})\ge 27$
with equality if and only if
$\mathrm {lcm}(a_7, a_{11})=\mathrm {lcm}(9, a_{11})\ge 27$
with equality if and only if
![]() $a_{11}=27$
. One then deduces that
$a_{11}=27$
. One then deduces that
 $$ \begin{align*} S_9 & =\frac{389}{720}+\frac{1}{\mathrm{lcm}(a_5, a_9)} \le\frac{389}{720}+\frac{1}{20}=\frac{425}{720}<\frac{537}{840}, \\[4pt] S_{10}& =\frac{389}{720}+\sum_{i=1}^2\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} <\frac{389}{720}+\frac{1}{20}+\frac{1}{18}=\frac{465}{720}<\frac{607}{840}, \\[4pt] S_{11} & =\frac{389}{720}+\sum_{i=1}^3\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le\frac{389}{720}+\frac{1}{20}+\frac{1}{18} +\frac{1}{27}=\frac{465}{720}+\frac{1}{27}<\frac{667}{840} \end{align*} $$
$$ \begin{align*} S_9 & =\frac{389}{720}+\frac{1}{\mathrm{lcm}(a_5, a_9)} \le\frac{389}{720}+\frac{1}{20}=\frac{425}{720}<\frac{537}{840}, \\[4pt] S_{10}& =\frac{389}{720}+\sum_{i=1}^2\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} <\frac{389}{720}+\frac{1}{20}+\frac{1}{18}=\frac{465}{720}<\frac{607}{840}, \\[4pt] S_{11} & =\frac{389}{720}+\sum_{i=1}^3\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le\frac{389}{720}+\frac{1}{20}+\frac{1}{18} +\frac{1}{27}=\frac{465}{720}+\frac{1}{27}<\frac{667}{840} \end{align*} $$
as desired.
If
![]() $\Box _2 = {453}/{840}$
, then by Lemma 2.4, we must have
$\Box _2 = {453}/{840}$
, then by Lemma 2.4, we must have
![]() $a_i=i$
for all integers i with
$a_i=i$
for all integers i with
![]() $1\le i\le 8$
. So
$1\le i\le 8$
. So
![]() $a_9\ge 9$
which implies that
$a_9\ge 9$
which implies that
![]() $\mathrm {lcm}(a_5, a_9)\ge 10$
with equality if and only if
$\mathrm {lcm}(a_5, a_9)\ge 10$
with equality if and only if
![]() $a_9=10$
. Furthermore,
$a_9=10$
. Furthermore,
![]() $\mathrm {lcm}(a_6, a_{10})\ge 12$
with equality if and only if
$\mathrm {lcm}(a_6, a_{10})\ge 12$
with equality if and only if
![]() $a_{10}=12$
and
$a_{10}=12$
and
![]() $\mathrm {lcm}(a_7, a_{11})\ge 14$
with equality if and only if
$\mathrm {lcm}(a_7, a_{11})\ge 14$
with equality if and only if
![]() $a_{11}=14$
. Thus
$a_{11}=14$
. Thus
 $$ \begin{align} \hspace{-34pt}\ \ \ S_{10} =\frac{453}{840}+\sum_{i=1}^2\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le\frac{453}{840}+\frac{1}{10}+\frac{1}{12}=\frac{607}{840}, \end{align} $$
$$ \begin{align} \hspace{-34pt}\ \ \ S_{10} =\frac{453}{840}+\sum_{i=1}^2\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le\frac{453}{840}+\frac{1}{10}+\frac{1}{12}=\frac{607}{840}, \end{align} $$
 $$ \begin{align} S_{11} & =\frac{453}{840}+\sum_{i=1}^3\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le\frac{453}{840}+\frac{1}{10}+\frac{1}{12}+\frac{1}{14}=\frac{667}{840}, \end{align} $$
$$ \begin{align} S_{11} & =\frac{453}{840}+\sum_{i=1}^3\frac{1}{\mathrm{lcm}(a_{4+i}, a_{8+i})} \le\frac{453}{840}+\frac{1}{10}+\frac{1}{12}+\frac{1}{14}=\frac{667}{840}, \end{align} $$
where each equality in (3.1) to (3.3) holds if and only if
![]() $a_i=i$
for all integers i with
$a_i=i$
for all integers i with
![]() $1\le i\le 8$
,
$1\le i\le 8$
,
![]() $a_9=10$
,
$a_9=10$
,
![]() $a_{10}=12$
and
$a_{10}=12$
and
![]() $a_{11}=14$
. So part (v) is true when
$a_{11}=14$
. So part (v) is true when
![]() $9\le n\le 11$
.
$9\le n\le 11$
.
In what follows, we always assume that
![]() $n\ge 12$
. Then we can write
$n\ge 12$
. Then we can write
![]() $n=4m$
or
$n=4m$
or
![]() $n=4m+r$
for some integers m and r with
$n=4m+r$
for some integers m and r with
![]() $m\ge 3$
and
$m\ge 3$
and
![]() $1\le r\le 3$
. For any integer i with
$1\le r\le 3$
. For any integer i with
![]() $1\le i\le 4$
, we define
$1\le i\le 4$
, we define
 $$ \begin{align*} S_m^{(i)}:=\sum_{j=1}^{m-2}\frac{1}{\mathrm{lcm}(a_{4j+i}, a_{4j+4+i})}. \end{align*} $$
$$ \begin{align*} S_m^{(i)}:=\sum_{j=1}^{m-2}\frac{1}{\mathrm{lcm}(a_{4j+i}, a_{4j+4+i})}. \end{align*} $$
Then
 $$ \begin{align} S_{4m}&=\sum_{i=1}^4\bigg(\frac{1}{\mathrm{lcm}(a_i, a_{i+4})}+S_m^{(i)}\bigg) \end{align} $$
$$ \begin{align} S_{4m}&=\sum_{i=1}^4\bigg(\frac{1}{\mathrm{lcm}(a_i, a_{i+4})}+S_m^{(i)}\bigg) \end{align} $$
and
 $$ \begin{align} S_{4m+r}=S_{4m}+\sum_{i=1}^r\frac{1}{\mathrm{lcm}(a_{4m-4+i}, a_{4m+i})}. \end{align} $$
$$ \begin{align} S_{4m+r}=S_{4m}+\sum_{i=1}^r\frac{1}{\mathrm{lcm}(a_{4m-4+i}, a_{4m+i})}. \end{align} $$
For any integer i with
![]() $1\le i\le 4$
, applying Lemma 2.1 to the subsequence
$1\le i\le 4$
, applying Lemma 2.1 to the subsequence
![]() $\{a_{i+4}, a_{i+8},\ldots , a_{i+4(m-1)}\}$
yields
$\{a_{i+4}, a_{i+8},\ldots , a_{i+4(m-1)}\}$
yields
 $$ \begin{align} S_m^{(i)}=\sum_{j=1}^{m-2}\frac{1}{\mathrm{lcm}(a_{i+4j}, a_{i+4j+4})} \le \frac{1}{a_{i+4}}\bigg(1-\frac{1}{2^{m-2}}\bigg) \end{align} $$
$$ \begin{align} S_m^{(i)}=\sum_{j=1}^{m-2}\frac{1}{\mathrm{lcm}(a_{i+4j}, a_{i+4j+4})} \le \frac{1}{a_{i+4}}\bigg(1-\frac{1}{2^{m-2}}\bigg) \end{align} $$
with equality in (3.6) if and only if
![]() $a_{i+4j}=a_{i+4}\times 2^{j-1}$
for all integers j with
$a_{i+4j}=a_{i+4}\times 2^{j-1}$
for all integers j with
![]() $1\le j\le m-1$
. Further, for any integer i with
$1\le j\le m-1$
. Further, for any integer i with
![]() $1\le i\le r$
, applying Lemma 2.1 to the subsequence
$1\le i\le r$
, applying Lemma 2.1 to the subsequence
![]() $\{a_{4+i}, a_{8+i},\ldots , a_{4m+i}\}$
gives
$\{a_{4+i}, a_{8+i},\ldots , a_{4m+i}\}$
gives
 $$ \begin{align} S_m^{(i)}+\frac{1}{\mathrm{lcm}(a_{4m-4+i}, a_{4m+i})} =\sum_{j=1}^{m-1}\frac{1}{\mathrm{lcm}(a_{4j+i}, a_{4j+4+i})} \le \frac{1}{a_{4+i}}\bigg(1-\frac{1}{2^{m-1}}\bigg) \end{align} $$
$$ \begin{align} S_m^{(i)}+\frac{1}{\mathrm{lcm}(a_{4m-4+i}, a_{4m+i})} =\sum_{j=1}^{m-1}\frac{1}{\mathrm{lcm}(a_{4j+i}, a_{4j+4+i})} \le \frac{1}{a_{4+i}}\bigg(1-\frac{1}{2^{m-1}}\bigg) \end{align} $$
with equality in (3.7) if and only if
![]() $a_{4j+i}=a_{4+i}\times 2^{j-1}$
for all integers j with
$a_{4j+i}=a_{4+i}\times 2^{j-1}$
for all integers j with
![]() $1\le j\le m$
. Then by (3.4) and (3.6),
$1\le j\le m$
. Then by (3.4) and (3.6),
 $$ \begin{align} S_{4m} & \le \sum_{i=1}^4\bigg(\frac{1}{\mathrm{lcm}(a_i, a_{i+4})} +\frac{1}{a_{i+4}}\bigg(1-\frac{1}{2^{m-2}}\bigg)\bigg)=\Box_m \end{align} $$
$$ \begin{align} S_{4m} & \le \sum_{i=1}^4\bigg(\frac{1}{\mathrm{lcm}(a_i, a_{i+4})} +\frac{1}{a_{i+4}}\bigg(1-\frac{1}{2^{m-2}}\bigg)\bigg)=\Box_m \end{align} $$
with equality in (3.8) if and only if
![]() $a_{4j+i}=a_{4+i}\times 2^{j-1}$
for all integers i and j with
$a_{4j+i}=a_{4+i}\times 2^{j-1}$
for all integers i and j with
![]() $1\le j\le m-1$
and
$1\le j\le m-1$
and
![]() $1\le i\le 4$
. By (3.5), (3.6) and (3.7),
$1\le i\le 4$
. By (3.5), (3.6) and (3.7),
 $$ \begin{align} S_{4m+r}&=\sum_{i=1}^4\frac{1}{\mathrm{lcm}(a_i, a_{i+4})} +\sum_{i=1}^r\bigg(S_m^{(i)}+\frac{1}{\mathrm{lcm}(a_{4m-4+i}, a_{4m+i})}\bigg)+\sum_{i=r+1}^4 S_m^{(i)}\nonumber\\ &\le \sum_{i=1}^4\frac{1}{\mathrm{lcm}(a_i, a_{i+4})} +\sum_{i=1}^r \frac{1}{a_{4+i}}\bigg(1-\frac{1}{2^{m-1}}\bigg) +\sum_{i=r+1}^4 \frac{1}{a_{4+i}}\bigg(1-\frac{1}{2^{m-2}}\bigg)\nonumber \\ &=\sum_{i=1}^4\bigg(\frac{1}{\mathrm{lcm}(a_i, a_{i+4})}+\frac{1}{a_{i+4}}\bigg(1-\frac{1}{2^{m-2}}\bigg)\bigg) +\frac{1}{2^{m-1}}\sum_{i=1}^r \frac{1}{a_{4+i}}\nonumber\\ &=\Box_m+\frac{1}{2^{m-1}}\sum_{i=1}^r\frac{1}{a_{4+i}}, \end{align} $$
$$ \begin{align} S_{4m+r}&=\sum_{i=1}^4\frac{1}{\mathrm{lcm}(a_i, a_{i+4})} +\sum_{i=1}^r\bigg(S_m^{(i)}+\frac{1}{\mathrm{lcm}(a_{4m-4+i}, a_{4m+i})}\bigg)+\sum_{i=r+1}^4 S_m^{(i)}\nonumber\\ &\le \sum_{i=1}^4\frac{1}{\mathrm{lcm}(a_i, a_{i+4})} +\sum_{i=1}^r \frac{1}{a_{4+i}}\bigg(1-\frac{1}{2^{m-1}}\bigg) +\sum_{i=r+1}^4 \frac{1}{a_{4+i}}\bigg(1-\frac{1}{2^{m-2}}\bigg)\nonumber \\ &=\sum_{i=1}^4\bigg(\frac{1}{\mathrm{lcm}(a_i, a_{i+4})}+\frac{1}{a_{i+4}}\bigg(1-\frac{1}{2^{m-2}}\bigg)\bigg) +\frac{1}{2^{m-1}}\sum_{i=1}^r \frac{1}{a_{4+i}}\nonumber\\ &=\Box_m+\frac{1}{2^{m-1}}\sum_{i=1}^r\frac{1}{a_{4+i}}, \end{align} $$
and equality in (3.9) holds if and only if
![]() $a_{4j+i}=a_{4+i}\times 2^{j-1}$
for all integers i and j with
$a_{4j+i}=a_{4+i}\times 2^{j-1}$
for all integers i and j with
![]() $1\le j\le m-1$
and
$1\le j\le m-1$
and
![]() $1\le i\le 4$
and
$1\le i\le 4$
and
![]() $a_{4m+i}=a_{4+i}\times 2^{m-1}$
for all integers i with
$a_{4m+i}=a_{4+i}\times 2^{m-1}$
for all integers i with
![]() $1\le i\le r$
. Now by Lemma 2.4, if
$1\le i\le r$
. Now by Lemma 2.4, if
![]() $m\ge 3$
, then
$m\ge 3$
, then
 $$ \begin{align} \Box_m\le &\frac{1}{5}+\frac{1}{6}+\frac{1}{8}+\frac{1}{21} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\bigg) \bigg(1-\frac{1}{2^{m-2}}\bigg)\notag\\[4pt] =&\frac{493}{420}-\frac{533}{105}\cdot\frac{1}{2^{m+1}}:=S_0, \end{align} $$
$$ \begin{align} \Box_m\le &\frac{1}{5}+\frac{1}{6}+\frac{1}{8}+\frac{1}{21} +\bigg(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\bigg) \bigg(1-\frac{1}{2^{m-2}}\bigg)\notag\\[4pt] =&\frac{493}{420}-\frac{533}{105}\cdot\frac{1}{2^{m+1}}:=S_0, \end{align} $$
with equality in (3.10) if and only if
![]() $a_i=i$
for all integers i with
$a_i=i$
for all integers i with
![]() $1\le i\le 8$
. Notice that
$1\le i\le 8$
. Notice that
 $$ \begin{align} \sum_{i=1}^r\frac{1}{a_{4+i}}\le\sum_{i=1}^r\frac{1}{4+i} \end{align} $$
$$ \begin{align} \sum_{i=1}^r\frac{1}{a_{4+i}}\le\sum_{i=1}^r\frac{1}{4+i} \end{align} $$
with equality in (3.11) if and only if
![]() $a_{4+i}=4+i$
for all
$a_{4+i}=4+i$
for all
![]() $1\le i\le r$
. Therefore, by (3.8) and (3.10),
$1\le i\le r$
. Therefore, by (3.8) and (3.10),
![]() $S_{4m}\le S_0$
with equality if and only if
$S_{4m}\le S_0$
with equality if and only if
![]() $a_i=i$
for all
$a_i=i$
for all
![]() $i\in \{1, 2, 3, 4\}$
and
$i\in \{1, 2, 3, 4\}$
and
![]() $a_{4j+i}=(4+i)\times 2^{j-1}$
for all integers i and j with
$a_{4j+i}=(4+i)\times 2^{j-1}$
for all integers i and j with
![]() $1\le j\le m-1$
and
$1\le j\le m-1$
and
![]() $1\le i\le 4$
. It follows from (3.9) and (3.11) that
$1\le i\le 4$
. It follows from (3.9) and (3.11) that
 $$ \begin{align} S_{4m+r}\le S_0+\frac{1}{2^{m-1}}\sum_{i=1}^r\frac{1}{4+i} =\frac{493}{420}-\frac{533}{105}\cdot\frac{1}{2^{m+1}} +\frac{1}{2^{m-1}}\sum_{i=1}^r\frac{1}{4+i}, \end{align} $$
$$ \begin{align} S_{4m+r}\le S_0+\frac{1}{2^{m-1}}\sum_{i=1}^r\frac{1}{4+i} =\frac{493}{420}-\frac{533}{105}\cdot\frac{1}{2^{m+1}} +\frac{1}{2^{m-1}}\sum_{i=1}^r\frac{1}{4+i}, \end{align} $$
with equality in (3.12) if and only if
![]() $a_i=i$
for all
$a_i=i$
for all
![]() $i\in \{1, 2, 3, 4\}$
,
$i\in \{1, 2, 3, 4\}$
,
![]() $a_{4j+i}=(4+i)\times 2^{j-1}$
for all integers i and j with
$a_{4j+i}=(4+i)\times 2^{j-1}$
for all integers i and j with
![]() $1\le j\le m-1$
and
$1\le j\le m-1$
and
![]() $1\le i\le 4$
and
$1\le i\le 4$
and
![]() $a_{4m+i}=(4+i)\times 2^{m-1}$
for
$a_{4m+i}=(4+i)\times 2^{m-1}$
for
![]() $1\le i\le r$
. So part (v) is proved when
$1\le i\le r$
. So part (v) is proved when
![]() $n\ge 12$
.
$n\ge 12$
.
This completes the proof of Theorem 1.1.
Acknowledgement
This work was carried out during a visit by the first author to Brock University as a postdoctoral fellow. He would like to sincerely thank the host institution for its hospitality and for providing an excellent atmosphere for research.