1. Introduction
For the simulation and modeling of the water balance of glacierized basins, the specific mass balance, b, and its distribution on the glacier area, b(x, y), or with altitude, b(h), needs to be known. In most cases this requirement is not fulfilled so that mass-balance values from a measured reference glacier, b ref(h), are transferred to the unmeasured glaciers of the basin. Then
and
where the index u refers to the unmeasured glacier, s(h) is the area of an elevation band h, S is the total glacier area and the angled brackets hi indicate a time average. The transfer function f is more than a constant factor and may be meaningfully approximated if the unmeasured glacier has topographic and climatic conditions similar to those of the reference glacier, similarity depending on topography (width, length, slope, exposure to sun and wind, steepness and height of surrounding ridges) and regional climate (temperature at equilibrium-line altitude (ELA), precipitation, cloudiness). In the case that these are indeed similar, it is likely that both b u(h) and b ref(h) have similar shapes that are determined by local topography and energy-balance gradients. Examples of this similarity are given by Reference OerlemansOerlemans 2001, (figs 4.4 and 4.5) and Reference KuhnKuhn (1984). In this paper, we propose that the transfer may be accomplished by the shift of the reference profile b ref(h) along the altitude axis of the unmeasured glacier,
where the shift D is determined by the difference of area median elevations, M, of the two glaciers. The area median elevation of a glacier is that elevation both above and below which there is 50% of the glacier surface (in map projection). If the ELA were at that elevation, the accumulation-area ratio (AAR) would be 0.5. We decided to use the value 0.5 (rather than 0.67 which is often given for glaciers in equilibrium state) because it is closer to the AAR observed on alpine glaciers in recent years.
The procedure is summarized in Figure 1.

Fig. 1. Transfer procedure starting with the area profile of the reference glacier, s ref, and area median elevation, M ref, establishing M u from s u (a) and adjusting b u to M u (b).
The ELA would be a better reference, but it is known only for the reference glacier. The area median elevation of the unmeasured glacier, M u, on the other hand, can be determined from a map or digital model. In recent years ELA and M were close together on alpine glaciers, and even if there is not necessarily a linear relation between the two, this may be accepted as a useful approximation in view of other uncertainties.
In support of these simplifying assumptions we first present values of ELA, M, 〈b〉 and balance gradients, ∂b/∂h, for ten well-investigated alpine glaciers. They show a spread of values that is indicative of the influence of topographic setting and of the limitations of the proposed method.
We then apply the median transfer to a total of 19 basins in the eastern Alps that span a range of median differences, D, from –10 to +430 m, for two periods of different mean specific mass balance, to demonstrate the influence of topography, s(h).
Next, the s(h) and b(h) profiles of two well-measured glaciers are mutually exchanged, showing the effects of differences in aspect and altitude. If one of them is treated as the reference glacier and the other as the unknown, the success of shifting b(h) along the h axis can be quantified.
Finally, the results of mass-balance transfer from three reference glaciers to four unmeasured basins is verified with the difference in glacier surface elevation from 1969 to 1997 given by the Austrian Glacier Inventory (Reference Lambrecht and KuhnLambrecht and Kuhn, 2007).
2. Area Median Elevation And Ela
Of various indirect methods of mass-balance determination, the respective correlations of b with ELA and AAR are known to yield reasonable results for time series on individual glaciers. However, when comparing mean values of glaciers far apart, as are some of the glaciers in Table 1, the correlation is less reliable, as the glaciers may differ in local climate, surrounding topography and exposure to sun and wind.
Table 1. Area median elevation (M), equilibrium-line altitude (ELA), altitude range (R), specific balance (b) and mean balance gradient (db/dh) of ten alpine glaciers, 1990/91–1999/2000. All values are rounded. The ELA of Careser Glacier was extrapolated beyond the upper end of the glacier. Source: http://www.geo.unizh.ch/wgms/
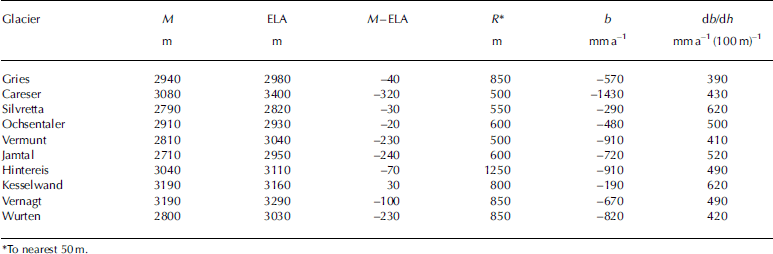
These factors also determine or disturb the relation between ELA and the area median elevation, M, on an intermediate timescale. The ELA reacts to climatic forcing on an annual timescale and, if averaged over one decade, as in Table 1, it reflects the climatic conditions of that decade. The area median elevation, M, on the other hand, expresses the geometry of a slowly changing ice body and is largely independent of the mass balance of single years. If, in the decade 1991–2000, some glaciers in Table 1 have a large difference in M–ELA this is an indication of their state of decay or of the slow reaction of their areal extent to changing climatic conditions. Those that have low values of M–ELA, like Silvretta or Kesselwand, must have been the fastest to react to changing climate, which is also in agreement with these glaciers having the least negative mass balances and the strongest mass-balance gradients.
We believe that M and ELA are known to three significant digits; all other values are known only to two significant digits.
From these considerations, two facts support the use of the area median elevation, M, as a basis for the transfer of mass-balance profiles: (1) M can be determined for unmeasured glaciers; and (2) M is a slowly changing reference that also may be used for decadal changes.
However, it is obvious from the values in Table 1 that even among eastern Alpine glaciers the reaction to climate may be so divergent that the transfer of b(h) is questionable, in particular if the balance gradients, db/dh, the balance, b, or the difference, M–ELA, are expected to be largely different in the unmeasured glacier compared with the reference glacier.
The success of a transfer is limited by the local topography which is expressed in the shape of the balance profile. For a straight linear balance profile like
which was found by Reference RasmussenRasmussen (2004) for several Scandinavian glaciers, topography obviously has little influence and it does not matter whether the b(h) profile is shifted along the h axis or the b axis. If the profile is hook-shaped with a topography-induced maximum in the firn basin, as for Hintereisferner and many other glaciers, there are two choices for a shift:
1. The shift along the b axis maintains the relation of b(h) to the given topography and changes b and ELA for given years at that glacier. This was dealt with in earlier studies, among them Reference Meier and TangbornMeier and Tangborn (1965), Reference HoinkesHoinkes (1970), Reference KuhnKuhn (1984) and Reference Rasmussen and ConwayRasmussen and Conway (2001).
2. The shift along the h axis (Equation (3)) transfers both ELA and the maximum of b to a new altitude. This is the shift we need for a transfer from a reference glacier to an unmeasured glacier. We note, however, that the topography of the unmeasured glacier may require individual adjustments of the b ref(h+D) that are dependent on the skill of the investigator.
There are also limitations in the mass-balance transfer that come from insufficient accuracy of either M or ELA. Using altitudinal profiles of mass balance, it is convenient to express an error in mass balance, Σb, which results from inaccurate specification of altitude, ΣM, as
If either M ref or Mu is off by 10m and db/dh is 500mm(100 m)–1, as in Table 1, then the error in b is 50 mm, and a mistake, ΣM, of the order of 100m makes a transfer questionable.
The transfer is inappropriate if it concerns the remnants of a decaying glacier the M of which used to be at a higher elevation than that of the remaining ice body. In that respect, the procedure should be applied only to glaciers of several hundreds of meters vertical extent, and to Mu from group mean values of s u(h) or from the largest glaciers of a group.
3. Application of The Transfer to Tyrolean Basins
We used the mean b(h) of three well-measured glaciers in the southern Ötztal Alps (Hintereisferner, Kesselwandferner and Vernagtferner) as mass-balance reference and applied it to 21 basins extending from the Arlberg region, about 60 km to the northwest, to the Hohe Tauern, about 100 km to the east. A subset of these basins is shown in Figure 2.

Fig. 2. A set of glacierized basins in the Ötztal and Stubai Alps. The reference glaciers are: H – Hintereis (46°47’ N, 10°45’ E); K – Kesselwand (46°51’ N, 10°47’ E); V – Vernagt (46°52’ N, 10°49’ E). The names of the gauging stations are given in Table 2 except Huben (HU), which is essentially the sum of RO, NT and OG. Graphic by L. Rastner.
Table 2. Adjustment of mean b(h) of Hintereis, Kesselwand and Vernagt to glacierized basins in the Austrian Alps (Fig. 2) for the periods 1967–84 and 1985–2003. D is the difference in median elevation of the reference glaciers (M ref = 3133 m) and unmeasured glaciers (M u) (Equation (4)). The last four glaciers are >60km away from the reference glaciers
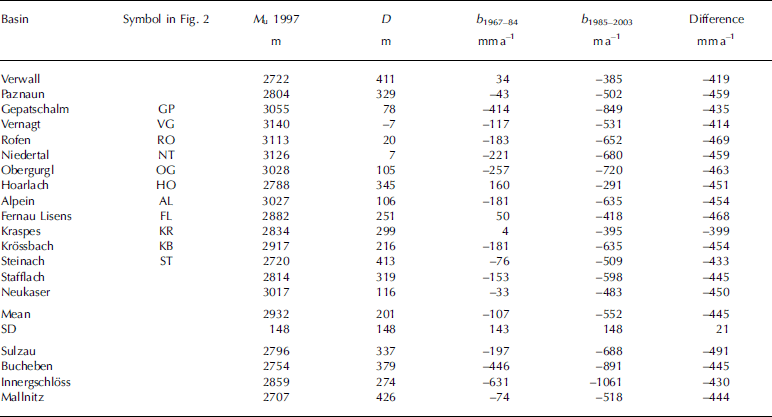
Table 2 presents the results of the adjustment of the reference balance to the area median glacier elevations of the respective basins for the periods 1967–84 and 1985–2003, as well as the resulting differences between these periods.
The most negative balances in Table 2 appear on those glaciers that have very low termini: Gepatsch (2100ma.s.l), Innergschlöss (2200ma.s.l.), Bucheben (2300ma.s.l.). The least negative, partly positive balances appear on the glaciers that are close to the northern margin of the Alps: Verwall, Paznaun, Hoarlach, Kraspes and Fernau Lisens. The variance of the differences in the last column indicates that b ref(h1985–2003) is not simply a shift of b ref(h1967α84) along the b axis but that the shape of b(h) differs in the two periods. The periods were chosen to stress the change in mass balance associated with the change in the North Atlantic Oscillation in the early 1980s. Between these periods mean annual temperature in Innsbruck increased by 0.9°C and mean summer temperature by 1.0°C.
4. Transfer Among Well-Measured Glaciers
Both Hintereisferner and Vernagtferner have a long history of glaciological investigations (Reference Kuhn, Dreiseitl, Hofinger, Markl, Span and KaserKuhn and others, 1999; Reference Reinwarth and Escher-VetterReinwarth and Escher-Vetter, 1999; Reference Markl, Matzi and PelletMarkl and others, 2008). As the glaciers are about 10 km distance from one another, they are influenced by the same regional climate. We used b(h) and s(h) of these two well-measured glaciers for the period 1990/91–1999/2000 to show the limits of b(h) transfer under optimum conditions. Data were restricted to the common altitude range, 2800–3600 m, the index V referring to Vernagtferner and H to Hintereisferner. The standard procedure of mass-balance determination was used:
and resulted in
Mutual exchange of s and b yielded
A shift of the reference curve b(h) by 100 m, applied to the area of the reference glacier, results in the difference in the two, +548 mm, being the weighted mean balance gradient per 100 m.
Applying the difference of median elevations of 150m from Table 1,
compared with the results of the direct mass-balance determination in that period
The difference of 150mm may be considered as representative of the accuracy of the transfer method.
5. An Independent Check With Volume Changes
For all glaciers treated here, there are digital elevation models in the Austrian Glacier Inventories of 1969 and 1998 (the original survey of Ötztal and Stubai glaciers was made in September 1997 (Reference Lambrecht and KuhnLambrecht and Kuhn, 2007)). Thus the mean change of surface elevation, ΔH, from September 1969 to September 1997 can be converted to mean specific balance assuming a suitable density (900 kgm–3 in the present case). This value serves to verify the 28 year mean value of 〈b〉 obtained by the direct glaciological method, which we consider less reliable than ΔH from a 28 year volume change.
Agreement of the two methods is expected to be limited. In the worst cases, photogrammetry of glacier surfaces is off by more than 1 m (Reference Abermann, Schneider and LambrechtAbermann and others (2007), studied one of the reference glaciers). Adding up 28 years of b by the direct glaciological method may even out random errors, but will propagate systematic errors. We may therefore be satisfied with the first check of the methods, which is shown in Table 3.
Table 3. Comparison of mean specific balance determined from volume change (ΔH) and by the direct glaciological method (〈b〉) for the period 1969–97
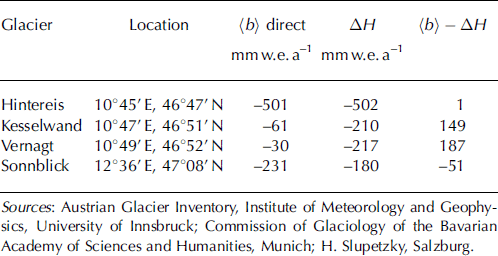
The agreement of the two methods for Hintereisferner is fortuitous, it is not the result of tuning. Part of the disagreement in the last column of Table 3 may be due to the significant change in glacier area from 1969 to 1997. This is also evident when the 1969–97 mean values of b(h) are applied once to the s(h) profiles of 1969 and once to those of 1997 for all glaciers of the Rofen valley:
1969: total glacier area = 43.5 km–2; 〈b〉 calculated with b(h)(1969–97) = –208mma–1
1997: total glacier area = 37.7 km–2; 〈b〉 calculated with b(h)(1969–97) = –96mma–1
These results highlight the importance of area changes which must be taken into account in all transfer exercises. At the same time the results show how these glaciers have adapted to the warmer environment by reducing the surface area and consequently the mean specific mass loss. This effect was reported by Reference Rasmussen and ConwayRasmussen and Conway (2001), among others.
When the surface-elevation changes of four of the glaciers in Table 2 are converted to water equivalent with an ice density of 900 kgm–3 (Table 4), the glaciers show ‘fairly’ homogeneous changes, i.e. they have similar mean specific mass balances in spite of significantly different median elevation.
Table 4. Surface elevation changes (ΔH 1969 – 97) of glaciers in four basins in the Stubai and Ötztal Alps, converted to mmw.e. –1
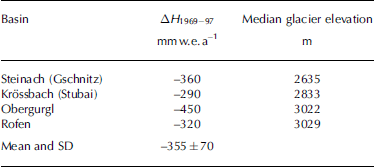
Table 4 shows that the resulting standard deviation of ΔH is less than the error expected in the transfer of b(h). While the distance of these basins from one another is <50 km, the median glacier elevations differ by nearly 400 m, and yet they have fairly homogeneous mass-balance conditions. We take this as confirmation of our view that topography on a basin scale changes the altitudinal distribution of accumulation and ablation in a given regional climate and that the median elevation of a glacier is an important key to these.
6. Transfer Vs Volume Change
We selected the basin of Gurgler Ache at Obergurgl (OG in Fig. 2; gauge at 1880 ma.s.l., 11°01’25’ E, 46˚52’16’ N, with 27 glaciers covering a total area of 23.5 km2 in 1997) to compare three methods of mass-balance transfer:
1. Direct transfer of the reference b(h). Using the 1970–97 mean b(h) of Hintereisferner as reference, we applied it to the glacier area, s(h), of the Gurgler Ache basin, which resulted in 〈b〉 = – 496 mm.
2. Transfer of b(h) with a shift according to median glacier elevation M GurglerAche = 3022 m, M Hintereisferner = 3040m with a sensitivity of 440mm per 100m shift of the reference curve, which is less than the valueof 548 mm(100 m)–1 found for Vernagtferner in section 4. This resulted in 〈b〉 = – 417 mm.
3. Converting surface-elevation changes of the glacier inventories of 1969 and 1997 (Reference Lambrecht and KuhnLambrecht and Kuhn, 2007) to mass balance with a mean ice density of 900 kgm–3 yielded a mean specific balance 〈b〉 = –448 mm.
The differences between the three values may be smaller than their respective errors, so the transfer between the two areas is a very positive example of this method. Part of the success was our decision to use only Hintereisferner as a reference, as this glacier has a similar topography and aspect to the glaciers in the basin of Gurgler Ache.
7. Conclusions
1. The transfer of b(h) from well-measured to unmeasured glaciers is a necessary procedure when studying local and regional climate–glacier relationships.
2. Although glaciers in one region often have a typically shaped profile, b(h), this profile cannot be transferred directly but must be adjusted to the altitude of the unmeasured glacier. Selected glacier basins in the Ötztal and Stubai Alps have glacier median elevations ranging from 2720 to 3140 m (Table 2).
3. While the median elevations and ELAs of fast-responding glaciers differed by only tens of meters in the period 1991–2000 (Table 1), they may be several hundreds of meters apart on decaying glaciers.
4. Using area median elevations of reference and unmeasured glaciers as a benchmark for the transfer of b(h) is a suboptimal compromise between the desirable and the feasible. It is feasible since M can be determined easily for unmeasured glaciers.
5. The transfer of b u(h) = b ref(h + D) is an extrapolation and is less reliable than the conversion of ΔH of two digital elevation models; however, these are not always available. Taking ±100mma–1 as a realistic accuracy of the direct glaciological method, the errors that may occur when transferring b(h) among ‘similar’ glaciers are more likely to be of the order of ±200mma–1.
6. When transferring b(h) from reference to unmeasured glaciers, care should be taken that datasets are consistent in time since both b(h) and s(h) change with time. Transfer should be restricted to glaciers of similar size and aspect. Manual adjustment to the topography of the unmeasured glacier may be required.
Acknowledgements
We thank F. Pellet for providing the data from the Glaciological Data Base of the Institute of Meteorology and Geophysics at the University of Innsbruck. The study was supported by Hydrographischer Dienst Tirol, the Commission of Geophysical Research of the Austrian Academy of Sciences and Project 4.1 AC of AlpS Zentrum für Naturgefahren Management, Innsbruck.








