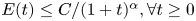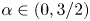Decay of weak solutions to Vlasov equation coupled with a shear thickening fluid

Abstract

We show that the energy norm of weak solutions to Vlasov equation coupled with a shear thickening fluid on the whole space has a decay rate the energy norm $E(t) \leq {C}/{(1+t)^{\alpha }}, \forall t \geq 0$ for $\alpha \in (0,3/2)$.

1. Introduction

In this paper, we study Vlasov equation coupled with a shear thickening fluid (see e.g. [7, 10])

(1.1)\begin{equation} \left\{\begin{array}{rcl} \partial_t f + v\cdot \nabla_x f+\nabla\cdot [(u-v)f] & = & 0,\\ \partial_t u - \nabla \cdot S(Du)+ (u\cdot\nabla_x)u + \nabla_x\pi & = & -\int_{{{\mathbb{R}}}^{3}} (u-v) f\,{\rm d}v,\\ \nabla \cdot u & = & 0. \end{array} \right. \end{equation}

Here $u:{{\mathbb {R}}}^{3}\times (0, T)\rightarrow {{\mathbb {R}}}^{3}$ is the flow velocity vector, $b:{{\mathbb {R}}}^{3}\times (0, T)\rightarrow {{\mathbb {R}}}^{3}$ is the magnetic vector, $\pi :{{\mathbb {R}}}^{3}\times (0, T)\rightarrow {{\mathbb {R}}}$ is the total pressure and $Du$ is the symmetric part of the velocity gradient, i.e.

\[ Du = D_{ij}u:= \frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right), \quad i,j=1,2,3. \]

To motivate the conditions on the stress tensor $S$, we recall the following examples of constitutive laws

(1.2)\begin{equation} S(Du) = (\mu_0+\mu_1|Du|^{p-2})Du \end{equation}

where $\mu _0\geq 0$ and $\mu _1>0$ are constants (see e.g. [1, 12]). The system is completed by the initial data:

(1.3)\begin{equation} u|_{t=0}=u_0,\quad \nabla_x\cdot u_0=0,\quad f|_{t=0}=f_0. \end{equation}

We recall some known results for the Newtonian case. Hamdache [8] proved the global existence of weak solutions to the time-dependent Stokes system coupled with the Vlasov equation in a bounded domain. Later, existence of weak solution was extended to the Vlasov–Navier–Stokes system by Boudin et al. [3] in a periodic domain (refer also to [4, 5] for hydrodynamic limit problems). When the fluid is inviscid, Baranger and Desvillettes established the local existence of solutions to the compressible Vlasov–Euler equations [2].

On the other hand, recently, Mucha et al. in [10] considered (1.1) and $S(Du)=(1+|Du|^{p-2})Du$ with $p\geq \frac {11}{5}$ for the case of a periodic domain, and they established the existence of solutions $(f,u)$ for a large initial data (see also [7]). Moreover, a divergence free vector $u$ and nonnegative function $f$ satisfy

\begin{equation*} \begin{aligned} u & \in L^{\infty}(0,T;\dot{W}^{1,p}_{div}(\mathbb{T}^{3}))\cap C([0,T];L^{2}_{div}(\mathbb{T}^{3}))\cap L^{2}(0,T;W^{2,2}(\mathbb{T}^{3}))\cap \\ & \quad\cap L^{\infty}(0,T;W^{1,2}({{\mathbb{R}}}^{3})) \cap L^{p}(0,T;\dot W^{1,3p}(\mathbb{T}^{3})),\quad \partial_t u\in L^{2}(0,T;L^{2}(\mathbb{T}^{3})),\\ f & \in L^{\infty}((0,T)\times\mathbb{T}^{3}\times{{\mathbb{R}}}^{3})\cap L^{\infty}(0,T;L^{1}(\mathbb{T}^{3}\times{{\mathbb{R}}}^{3})),\quad M_2 f\in L^{\infty}([0,T]). \end{aligned} \end{equation*}

Here, for non-negative and integrable functions $f$, we denote

\[ M_\alpha f(t):=\int_{\mathbb{T}^{3}\times{{\mathbb{R}}}^{3}}|v|^{\alpha} f(t,x,v)\,{\rm d}x\,{\rm d}v, \quad M_0f = \|f\|_{L^{1}} = 1. \]

Recently, Han-Kwan [9] showed the large time behaviour of small data solutions to the Vlasov–Navier–Stokes system, that is $p=2$ in (1.1) on ${{\mathbb {R}}}^{3} \times {{\mathbb {R}}}^{3}$. More speaking, he proved that for all $t \geq 0$ and $\alpha \in (0,3/2)$

(1.4)\begin{equation} E(t) \leq \frac{\varphi_\alpha(E(0))}{(1+t)^{\alpha}},\quad E(t):=\frac 12\left(\int_{{{\mathbb{R}}}^{3}\times{{\mathbb{R}}}^{3}} |v|^{2}f\,{\rm d}x\,{\rm d}v + \int_{{{\mathbb{R}}}^{3}} |u|^{2} \,{\rm d}x\right). \end{equation}

In this direction, we focus that Han-Kwan'a result extends to (1.1)–(1.3). Precisely, the solutions $(f,u)$ for Vlasov equation coupled with a shear thickening fluid (1.1)–(1.3) with a large initial data on ${{\mathbb {R}}}^{3} \times {{\mathbb {R}}}^{3}$ have the decay rate (1.4) under some assumptions. Unlike Han's results, we cannot use characteristic method (see [9, § 3] for the fluid equations, and thus, we give additional conditions. Our analysis is based on Han's approach, however to deal with the non-Newtonian case, we focus on the control of the stress tensor. Now, we present the main result of the paper.

Theorem 1.1 Let $p\geq \frac {11}{5}$ and

(1.5)\begin{equation} \|\rho_f\|_{L^{\infty}((0,T)\times {{\mathbb{R}}}^{3})}<\infty, \quad \rho_f(t,x):=\int_{{{\mathbb{R}}}^{3}}f(t,x,v)\,dv. \end{equation}

Suppose that the initial data $(f_0,u_0)$ satisfy

1. (i) $0\leq f_0\in (L^{1}\cap L^{\infty })({{\mathbb {R}}}^{3}\times {{\mathbb {R}}}^{3})$, $\textrm {supp}f_0(x,\cdot )\subset B(R)$ for some $R>0$ and a.a. $x\in {{\mathbb {R}}}^{3}$, where $B(R)$ is a ball centred at $0$ with radius $R$,

2. (ii) $u_0\in (L^{p}\cap W^{1,2}_{div})({{\mathbb {R}}}^{3})$ with $1\leq p<2$.

Then, there exists a constant $C$ (independent of $t$) such that global strong solutions $(f,u)$ to (1.1)–(1.3) satisfies

(1.6)\begin{equation} E(t) \leq \frac{C}{(1+t)^{\alpha}}, \quad \forall t \geq 0,\quad \alpha \in (0,3/2). \end{equation}

Remark 1.2 The result in [10] is also hold on the whole space. If the density function $f$ is ignored, the system (1.1) becomes to the Navier–Stokes equation of non-Newtonian type:

(1.7)\begin{equation} \partial_t u - \nabla \cdot (1+|Du|^{p-2})Du+ (u\cdot\nabla x)u + \nabla \pi=0. \end{equation}

For this equations, we knew that the solution for (1.7) satisfies the optimal temporal decay rate, that is, $\|u(t)\|_{L^{2}}\leq C(1+t)^{-{3}/{4}}$ for $p\geq 11/5$, which is the same result to Navier–Stokes equations (see also [6, 11]).

Remark 1.3 In light of the arguments in [9], using the characteristic method (see § 3 in [9]), it is possible to remove the condition (1.5) of $\rho _f$ for Vlasov–Navise–Stokes equation. Since this approach is not working for (1.1) due to strong stress tensor, the condition (1.5) in theorem 1.1 is necessary to control the drag force in the fluid equation for (1.1)–(1.3).

2. Preliminary

We first introduce some notations. Let $(X,\|\cdot \|)$ be a normed space. By $L^{q}(0,T;X)$, we denote the space of all Bochner measurable functions $\varphi :(0,T)\rightarrow X$ such that

\[ \left\{\begin{array}{ll} \|\varphi\|_{L^{q}(0,T;X)}:=\left(\displaystyle\int_0^{T} \|\varphi(t)\|^{q}\,{\rm d}t\right)^{{1}/{q}}<\infty & \mbox{if} \ 1\leq q<\infty,\\ \|\varphi\|_{L^{\infty}(0,T;X)}:=\displaystyle\sup_{t\in (0,T)}\|\varphi(t)\|<\infty & \mbox{if} \ q=\infty. \end{array}\right. \]

For $1\leq q\leq \infty$, we mean by $W^{k,q}(\mathbb {R}^{3})$ the usual Sobolev space. $A=(a_{ij})_{i,j=1}^{3}$ and $B=(b_{ij})_{i,j=1}^{3}$ be matrix valued maps and we then denote $A : B = \sum _{i,j=1}^{3} a_{ij}b_{ij}$. For vector fields $u, v$ we write $(u_iv_j)_{i,j=1,2,3}$ as $u\otimes v$. Unless specifically mentioned, the letter $C$ is used to represent a generic constant, which may change from line to line. And also, we denote by $A\lesssim B$ an estimate of the form $A\leq C B$ with some absolute constant $C$.

We first provide estimates of conservation laws and total energy dissipation in the lemma below.

Lemma 2.1 Let $(f,u)$ be a solution to (1.1)–(1.3) with sufficient integrability. Then we have the following estimates:

1. (i) (Mass conservation) The total mass of $f$ is conserved in time:

   \[ \int_{{{\mathbb{R}}}^{3}\times{{\mathbb{R}}}^{3}} f(x,v,t)\,{\rm d}x\,{\rm d}v = \int_{{{\mathbb{R}}}^{3}\times{{\mathbb{R}}}^{3}} f_0(x,v)\,{\rm d}x\,{\rm d}v \quad \forall \,t \geq 0. \]

2. (ii) (Momentum conservation) The total momentum is conserved in time: for all $t \geq 0$

   \begin{align*} & \int_{{{\mathbb{R}}}^{3}\times{{\mathbb{R}}}^{3}} vf(x,v,t)\,{\rm d}x\,{\rm d}v + \int_{{{\mathbb{R}}}^{3}} u(x,t)\,{\rm d}x\\ & \quad = \int_{{{\mathbb{R}}}^{3}\times{{\mathbb{R}}}^{3}} vf_0(x,v)\,{\rm d}x\,{\rm d}v + \int_{{{\mathbb{R}}}^{3}}u_0(x)\,{\rm d}x. \end{align*}

3. (iii) (Total energy conservation) The total energy is not increasing in time:

   \[ \frac{{\rm d}}{{\rm d}t} E(t)+ D(t) \leq 0. \]
   Here,
   \[ E(t):=\frac 12\left(\int_{{{\mathbb{R}}}^{3}\times{{\mathbb{R}}}^{3}} |v|^{2}f\,{\rm d}x\,{\rm d}v + \int_{{{\mathbb{R}}}^{3}} |u|^{2} \,{\rm d}x\right), \]
   and
   \[ D(t):=C_K\int_{{{\mathbb{R}}}^{3}} |D u|^{2}\,{\rm d}x+\int_{{{\mathbb{R}}}^{3}} |\nabla u|^{2}\,{\rm d}x + \int_{{{\mathbb{R}}}^{3}\times{{\mathbb{R}}}^{3}} |u-v|^{2} f\,{\rm d}x\,{\rm d}v, \]
   where $C_K$ is Korn's constant.

Lemma 2.2 Let $(f,u)$ be a solution to ( 1.1)–( 1.3). Then we have

\begin{align*} \int_{|\xi|\leq g(\tau)} |u(\tau) |^{2} \, \mathrm{d} \xi & \lesssim \left( \int_0^{\tau} \| U_0\|_{\text{L}^{2}({{\mathbb{R}}}^{3})}\right)^{2}\\ & \quad +g^{5}(\tau)\left(\left( \int_0^{\tau} \| u(s)\|_{\text{L}^{2}({{\mathbb{R}}}^{3})}^{2} \, \mathrm{d} s\right)^{2}\right.\\ & \quad \left.+\left(\int^{t}_0\|u(s)\|_{L^{2}({{\mathbb{R}}}^{3})} ^{({14-2p})/({19-5p})}\,{\rm d}s\right)^{({19-5p})/{8}}\right) \\ & \left.\quad + g^{3}(\tau) \left( \int_0^{\tau} \| (j_f - \rho_f u) (s)\|_{\text{L}^{1}({{\mathbb{R}}}^{3})} \, \mathrm{d} s\right)^{2}\right). \end{align*}

Here, $U_0$ is a solution of heat equation in ${{\mathbb {R}}}^{3}$, that is,

\[ \partial_tU_0-\Delta U_0 = 0,\quad U_0|_{t=0} = u_0. \]

Proof. We rewrite the fluid equation as

(2.1)\begin{equation} u_t - \triangle u- \nabla \cdot |Du|^{p-2}Du +(u \cdot \nabla) u +\nabla \pi=j_f-\rho_f u. \end{equation}

Applying the Fourier transformation of (2.1), we have

(2.2)\begin{equation} \hat{u}_t+|{\xi}|^{2}\hat{u} =:F(\xi, t),\quad \hat{u}_0(\xi):=\hat{u}(\xi,0)=\widehat{U_0}, \end{equation}

where

\[ F(\xi,t):=\widehat{\nabla\cdot |Du|^{p-2}Du}(\xi,t) -\widehat{(u\cdot\nabla)u}(\xi,t)-\widehat{\nabla P}(\xi,t)+\widehat{j_f-\rho_f}. \]

First of all, we note that for the divergence free vectors $v,w \in L^{\infty }(0,T; L^{2}(\mathbb {R}^{3}))$

\begin{align*} |\widehat{(v\cdot\nabla)w}(\xi,t)|& \cong\left| {\int_{{{\mathbb{R}}}^{3}}{\rm e}^{-{\rm i}x\cdot\xi}\nabla\cdot(u\otimes v)\,{\rm d}x} \right|\\ & \lesssim |\xi|\|v\otimes w\|_{L^{1}} \leq |\xi|(||v(t)||^{2}_{L^{2}}+||w(t)||^{2}_{L^{2}}), \end{align*}

and thus, we have

(2.3)\begin{equation} |\widehat{(u\cdot\nabla)u}(\xi,t)|\leq |\xi|||u(t)||^{2}_{L^{2}}, \end{equation}

Integrating (2.3) with respect to $\xi$ on the ball $\{ |\xi | \leq g(\tau )\}$, we obtain

\begin{align*} \int_{|\xi|\leq g(\tau)} \left(\int_0^{t} \left| \widehat{(u\cdot \nabla) u} \right| \mathrm{d} \tau \right)^{2} \mathrm{d} \xi & \lesssim \int_{|\xi|\leq g(\tau)} |\xi|^{2} \left(\int_0^{t} \left| \widehat{u \otimes u} \right| (\tau,\xi) \, \mathrm{d} \tau \right)^{2} \mathrm{d} \xi \\ & \lesssim g(\tau)^{5} \left(\int_0^{t} \left\| {u \otimes u} \right\|_{\text{L}^{1}} (\tau) \, \mathrm{d} \tau \right)^{2}. \end{align*}

To deal with $F$, taking the divergence operator for the fluid equation, we know that for all $\xi \in {{\mathbb {R}}}^{3}$,

\[ \widehat{\nabla P} = \frac{\xi \cdot \left( \widehat{\nabla\cdot(|Du|^{p-2}Du}(\xi,t)- \widehat{u\cdot \nabla u} + \widehat{j_f-\rho_f u} \right)}{|\xi|^{2}} \xi, \]

so that

\[ |\widehat{\nabla P} (\xi)| \leq |\xi|\left(|||Du(t)|^{p-1}||_{L^{1}}+||u(t)||^{2}_{L^{2}}\right)+\|j_f-\rho_f\|_{L^{1}}\quad \forall \ \xi \in {{\mathbb{R}}}^{3}. \]

With aid of the estimates above, $F(\xi, t)$ is bounded by

\[ |\hat{F}(\xi,t)| \leq |\xi|\left(||Du(t)||^{p-1}_{L^{p-1}}+||u(t)||^{2}_{L^{2}}\right)+\|j_f-\rho_f\|_{L^{1}}. \]

and thus

\begin{align*} \int_{|\xi|\leq g(\tau)} \left(\int_0^{t} \left| \hat{F} (\tau,\xi)\right| \mathrm{d} \tau \right)^{2} \,\mathrm{d} \xi & \lesssim g^{5}(\tau)\left(\left( \int_0^{\tau} \| u(s)\|_{\text{L}^{2}}^{2} \, \mathrm{d} s\right)^{2}\right.\\ & \quad \left.+\left(\int^{t}_0\|u(s)\|_{L^{2}} ^{({14-2p})/({19-5p})}\,{\rm d}s\right)^{({19-5p})/{8}}\right) \\ & \left.\quad + g^{3}(\tau) \left( \int_0^{\tau} \| (j_f - \rho_f u) (s)\|_{\text{L}^{1}} \, \mathrm{d} s\right)^{2}\right). \end{align*}

It follows from (2.2) that

\[ \hat{u}(\xi,t)= {\rm e}^{-|\xi|^{2}t}\hat{U}_0(\xi) +\int_0^{t}F(\xi,t){\rm e}^{-|\xi|^{2}(t-s)}\,{\rm d}s. \]

From the estimates above, the outcome we give is

\begin{align*} \int_{|\xi|\leq g(\tau)} |\hat{u}(\tau) |^{2} \, \mathrm{d} \xi & \lesssim \left( \int_0^{\tau} \| U_0\|_{\text{L}^{2}}\right)^{2} +g^{5}(\tau)\left(\left( \int_0^{\tau} \| u(s)\|_{\text{L}^{2}}^{2} \, \mathrm{d} s\right)^{2}\right.\\ & \quad \left.+\left(\int^{t}_0\|u(s)\|_{L^{2}} ^{({14-2p})/({19-5p})}\,{\rm d}s\right)^{({19-5p})/{8}}\right) \\ & \left.\quad + g^{3}(\tau) \left( \int_0^{\tau} \| (j_f - \rho_f u) (s)\|_{\text{L}^{1}} \, \mathrm{d} s\right)^{2}\right). \end{align*}

where we use the following estimates

\[ \int_0^{t}\|j_f-\rho_f\|_{L^{1}}\,{\rm d}s \leq \int_0^{t} \left(\int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} \, {\rm d}v \, {\rm d}x \right)^{1/2}\,{\rm d}s, \]

and also

\begin{align*} & \int_0^{t}\|\nabla u(s)\|^{p-1}_{L^{p-1}}\,{\rm d}s\\ & \quad \leq \int^{t}_0\|u(s)\|_{L^{2}}^{({7-p})/{4}}\|\nabla^{2} u(s)\|_{L^{2}}^{({5p-11})/{4}}\,{\rm d}s\\ & \quad \leq C\left(\int^{t}_0\|u(s)\|_{L^{2}} ^{({14-2p})/({19-5p})}\,{\rm d}s\right)^{({19-5p})/{8}} \left(\int_0^{\infty}\|\nabla^{2} u(t)\|_{L^{2}}^{2}\,{\rm d}t\right)^{({5p-11})/{8}}\\ & \quad \leq C\left(\int^{t}_0\|u(s)\|_{L^{2}} ^{({14-2p})/({19-5p})}\,{\rm d}s\right)^{({19-5p})/{8}},\quad \frac{5}{2}\leq p < 3, \end{align*}

and

\[ \int_0^{t}\|\nabla u(s)\|^{p-1}_{L^{p-1}}\,{\rm d}s\leq C \left\Vert {\nabla u} \right\Vert_{L^{2}((0,t)\times{{\mathbb{R}}}^{3})}^{{2}/({p-2})}\left\Vert {\nabla u} \right\Vert_{L^{p}((0,t);L^{p})}^{{p(p-3)}/({p-2})}<\infty,\quad p\geq 3, \]

thus this completes the proof.

Lemma 2.3 Gronwall inequality

Let $y(t)$ satisfy the following differential inequality. For almost all $s \geq 0$ and all $s \leq t \leq T$,

\[ y(t) + \int_s^{t} \tilde{g}^{2} (\tau) y(\tau) \, \mathrm{d} \tau \leq y(s) + \int_s^{t} \beta(\tau) \, \mathrm{d} \tau. \]

Then for almost all $t \in [0,T]$,

\[ y(t) \leq y(0) \exp\left( - \int_0^{t} \tilde{g}^{2} (\tau) \, \mathrm{d} \tau\right) + \int_0^{t} \exp\left( - \int_\tau^{t} \tilde{g}^{2} (r) \, \mathrm{d} r\right) \beta(\tau) \, \mathrm{d} \tau. \]

Proof of theorem 1.1. Following the idea in [13], let $g(t)$ be given a time-dependent cut-off function, determined later. Observe that

\begin{align*} \int_{{{\mathbb{R}}}^{3}}|Du|^{2}\,{\rm d}x\geq C_K\int_{{{\mathbb{R}}}^{3}} | \nabla_x u |^{2} \, {\rm d} x & = \int_{{{\mathbb{R}}}^{3}} | \xi|^{2} | \hat{u} |^{2} \, \xi \\ & \geq \int_{|\xi|\geq g(t)} | \xi|^{2} | \hat{u} |^{2} \, {\rm d} \xi \\ & \geq g^{2}(t) \| u\|_{L^{2}}^{2} - g^{2}(t) \int_{|\xi|\leq g(t)} | \hat{u} |^{2} \, {\rm d}\xi, \end{align*}

where $C_K$ is Korn's inequality. On the other hand, we note that

\[ \int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} \, {\rm d} v \, {\rm d} x\geq \frac{1}{2} \int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v|^{2} \, {\rm d} v \, {\rm d} x - {\|\rho_f\|_{L^{\infty}(0,T; L^{\infty})}} \| u\|_{L^{2}}^{2}. \]

Choose now $C_0>0$ large enough so that ${\|\rho _f\|_{L^{\infty }(0,T; L^{\infty })}}/({1+ C_0})\leq 1/2$. We will also ensure that for all $t \in [0,T]$, ${g^{2}(t)}/({1+ C_0})\leq 1/2$. Following the argument in [9, p. 6], we can know

\begin{align*} & C_K\int_{{{\mathbb{R}}}^{3}} | \nabla_x u |^{2} \, {\rm d} x + \int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} \, {\rm d} v \, {\rm d} x \\ & \quad \geq\frac{1}{2} \int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} + \frac{1}{2} \frac{g^{2}(t)}{1+ C_0} \left[ \int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v|^{2} \, {\rm d} v \, {\rm d} x + \| u\|_{L^{2}}^{2}\right] \\ & \qquad - g^{2}(t) \int_{|\xi|\leq g(t)} | \hat{u} |^{2} \, {\rm d} \xi. \end{align*}

Applying lemma 2.3 by the estimate above, we obtain

(2.4)\begin{align} \text{E}(t) & \exp\left(\int_0^{t} \tilde{g}^{2}(s) \, \mathrm{d} s \right) + \frac{1}{2} \int_0^{t} \left(\int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} \, \mathrm{d} v \, \mathrm{d} x\right) \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau \nonumber\\ & \leq \text{E}(0)+ \text{C} \int_0^{t} g^{2}(\tau) \| U_0 \|_{\text{L}^{2}}^{2} \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau \nonumber\\ & \quad + \text{C} \int_0^{t} g^{7}(\tau)\left( \int_0^{\tau} \| u(r)\|_{\text{L}^{2}}^{2} \, \mathrm{d} r\right)^{2} \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau\nonumber\\ & \quad + \text{C} \int_0^{t} g^{7}(\tau)\left( \left(\int^{\tau}_0\|u(s)\|_{L^{2}} ^{({14-2p})/({19-5p})}\,{\rm d}s\right)^{({19-5p})/{8}}\right)\notag\\ & \quad\times \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau \nonumber\\ & \quad + \text{C} \int_0^{t} g^{5}(\tau)\left( \int_0^{\tau} \left(\int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} \, \mathrm{d} v \, \mathrm{d} x \right)^{1/2} \, \mathrm{d} r \right)^{2}\notag\\ & \quad\times \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau. \end{align}

\[ g^{2}(t) = \frac{4\alpha (1+C_0)}{1+t}, \quad \mbox{i.e.,} \ \tilde{g}^{2}(t) = \frac{\alpha}{10+t}, \]

where $\alpha \in [1, 3/2)$ to be determined later. This gives

\[ \exp\left(\int_0^{\tau} \tilde{g}^{2}(r)\,{\rm d}r\right) = (10+\tau)^{\alpha}, \]

Note that we have, as $\alpha <3/2$,

(2.5)\begin{align} \text{E}(0)+ \int_0^{t} g^{2}(\tau) \| U_0(\tau) \|_{\text{L}^{2}}^{2} \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau & \lesssim \text{E}(0)+ \int_0^{t} \frac{\mathrm{d} \tau}{(1+ \tau)^{1+ 3/2 -\alpha}} \nonumber\\ & \lesssim 1. \end{align}

The remaining terms are now estimated sequentially. Assume that on $[0,T]$,

(2.6)\begin{equation} \text{E}(t) \lesssim \frac{1}{(1+t)^{\beta}}, \end{equation}

with $0\leq \beta <3/2$. Assuming (2.6), we have

(2.7)\begin{align} & \int_0^{t} g^{7}(\tau)\left( \int_0^{\tau} \| u(r)\|_{\text{L}^{2}}^{2} \, \mathrm{d} r\right)^{2} \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau \nonumber\\ & \quad \lesssim (1+t)^{\alpha-2\beta-1/2} \quad \text{if}\ \beta<1, \quad \alpha -2 \beta-3/2>{-}1,\nonumber\\ & \quad \lesssim 1 \quad \text{if}\ \beta<1, \quad \alpha -2 \beta-3/2<{-}1,\nonumber\\ & \quad \lesssim 1 \quad \text{if}\ \beta>1. \end{align}

On the other hand, by Hölder's inequality, we note that

(2.8)\begin{align} & \left( \left(\int^{\tau}_0\|u(s)\|_{L^{2}} ^{({14-2p})/({19-5p})}\,{\rm d}s\right)^{({19-5p})/{8}}\right)^{2}\notag\\ & \quad \leq \left(\int^{\tau}_0\|u(s)\|_{L^{2}} ^{({28-4p})/({19-5p})}\,{\rm d}s\tau\right)^{({19-5p})/{8}}\nonumber\\ & \quad \leq C\left(\int^{\tau}_0\|u(s)\|_{L^{2}}^{2}\,{\rm d}s\tau\right)+C. \end{align}

Here, we use the relation $({28-4p})/({19-5p})>2$ and $u \in L^{\infty }(0,\tau ; L^{2})$ by the energy estimate. Using (2.8), we have

(2.9)\begin{align} & \int_0^{t} g^{7}(\tau)\left( \left(\int^{\tau}_0\|u(s)\|_{L^{2}} ^{({14-2p})/({19-5p})}\,{\rm d}s\right)^{({19-5p})/{8}}\right)^{2} \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau\nonumber\\ & \quad \leq \int_0^{t} g^{7}(\tau)C\left(\int^{\tau}_0\|u(s)\|_{L^{2}}^{2}\,{\rm d}s\tau+C\right) \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau\nonumber\\ & \quad \leq C\int_0^{t} g^{7}(\tau)\left(\int^{\tau}_0\|u(s)\|_{L^{2}}^{2}\,{\rm d}s\tau\right) \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau\nonumber\\ & \qquad +C\int_0^{t} g^{7}(\tau) \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau\nonumber\\ & \quad \lesssim (1+t)^{\alpha-\beta-1/2}+(1+t)^{\alpha-3/2} \quad \text{if} \ \beta<1, \quad \alpha -\beta-3/2>{-}1, \nonumber\\ & \quad \lesssim 1 \quad \text{if}\ \beta<1, \quad \alpha -2 \beta-3/2<{-}1, \nonumber\\ & \quad \lesssim 1 \quad \text{if}\ \beta>1. \end{align}

Let us assume as well that on $[0,T]$,

(2.10)\begin{equation} \int_0^{t} \left(\int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} \, \mathrm{d} v \, \mathrm{d} x\right) (10+\tau)^{\alpha} \mathrm{d} \tau \lesssim \frac{(10+t)^{\alpha}}{(1+t)^{\beta}}. \end{equation}

Observe that if (2.10) holds for some $\alpha$, then it holds as well for all $\widetilde \alpha \geq \alpha$. Assuming (2.10) we have

(2.11)\begin{align} & \int_0^{t} g^{5}(\tau)\left( \int_0^{\tau} \left(\int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} \, \mathrm{d} v \, \mathrm{d} x \right)^{1/2} \, \mathrm{d} r \right)^{2} \exp\left(\int_0^{\tau} \tilde{g}^{2}(r) \, \mathrm{d} r \right) \mathrm{d} \tau \nonumber\\ & \quad \lesssim (1+t)^{2\alpha-\beta-3/2} \quad \text{if}\ 2\alpha - \beta-3/2>0, \nonumber\\ & \quad \lesssim 1 \quad \text{if}\ 2 \alpha - \beta-3/2<0. \end{align}

Now we argue by induction in order to increase the admissible values of $\beta$. Start with $\beta =0$, and take $\alpha =1$. The a priori estimates (2.6) and (2.10) are indeed satisfied since by the energy inequality

\[ \text{E}(t) + \int_0^{t} \left(\int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} \, \mathrm{d} v \, \mathrm{d} x\right) \mathrm{d} \tau \lesssim 1, \]

so that

\[ \int_0^{t} \left(\int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} (10+ \tau) \, \mathrm{d} v \, \mathrm{d} x\right) \mathrm{d} \tau \lesssim (10+t). \]

Using (2.4) together with (2.5), (2.7), (2.9) and (2.11), we obtain

\begin{align*} & {(10+t)} \text{E}(t) + \int_0^{t} \left(\int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} \, \mathrm{d} v \, \mathrm{d} x\right) (10+\tau) \,\mathrm{d} \tau\\ & \quad \lesssim 1+ (1+t)^{1/2} + (1+t)^{{-}1/2}, \end{align*}

so that

\[ \text{E}(t) + \frac{1}{(10+t)} \int_0^{t} \left(\int_{{{\mathbb{R}}}^{3}\times {{\mathbb{R}}}^{3}} f |v-u|^{2} \, \mathrm{d} v \, \mathrm{d} x\right) (10+\tau) \,\mathrm{d} \tau \lesssim \frac{1}{(1+t)^{1/2}}. \]

From now on, through the procedure method based on the inductive scheme in [9, p. 10], we can get the desired results. This completes the proof.