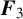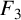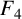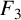A GENERALISATION OF A SUPERCONGRUENCE ON THE TRUNCATED APPELL SERIES $\boldsymbol F_3$

Abstract

Recently, Lin and Liu [‘Congruences for the truncated Appell series $F_3$ and $F_4$ ’, Integral Transforms Spec. Funct. 31(1) (2020), 10–17] confirmed a supercongruence on the truncated Appell series $F_3$ . Motivated by their work, we give a generalisation of this supercongruence by establishing a q-supercongruence modulo the fourth power of a cyclotomic polynomial.

1 Introduction

In 1880, Appell defined four kinds of double series $F_1$ , $F_2$ , $F_3$ , $F_4$ in two variables (see [13, pages 210–211]) by generalising the Gauss hypergeometric $_{2}F_1$ -series [1, (1.2.1)]. These four series, called Appell series, are famous in the field of double hypergeometric functions and play an important role in mathematical physics.

Based on the definition of the truncated hypergeometric series, Liu [8] introduced the truncated Appell series, defined by

$$ \begin{align*} F_1[a;b,b';c;x,y]_n &= \sum_{i=0}^{n}\sum_{j=0}^{n}\frac{(a)_{i+j}(b)_i(b')_j}{(c)_{i+j}}\cdot \frac{x^iy^j}{i!j!};\\[-3pt] F_2[a;b,b';c,c';x,y]_n &= \sum_{i=0}^{n}\sum_{j=0}^{n}\frac{(a)_{i+j}(b)_i(b')_j}{(c)_{i}(c')_{j}}\cdot \frac{x^iy^j}{i!j!};\\[-3pt] F_3[a,a';b,b';c;x,y]_n &= \sum_{i=0}^{n}\sum_{j=0}^{n}\frac{(a)_{i}(a')_{j}(b)_i(b')_j}{(c)_{i+j}}\cdot \frac{x^iy^j}{i!j!};\\[-3pt] F_4[a;b;c,c';x,y]_n &= \sum_{i=0}^{n}\sum_{j=0}^{n}\frac{(a)_{i+j}(b)_{i+j}}{(c)_{i}(c')_{j}}\cdot \frac{x^iy^j}{i!j!}, \end{align*} $$

where $(a)_n=a(a+1)\cdots (a+n-1),\ n\in \mathbb {Z}^{+}$ , with $(a)_0=1$ , is the shifted factorial.

Liu [8] confirmed two congruences for $F_1$ and $F_2$ by using some combinatorial identities. Later, Lin and Liu [7] studied congruence properties of the truncated Appell series $F_3$ and $F_4$ and found the following interesting result: for any odd prime p,

(1.1) $$ \begin{align} F_3[\tfrac12,\tfrac12;\tfrac12,\tfrac12;1;1,1]_{(p-1)/2} \equiv (-1)^{(p-1)/2} \pmod{p^2}. \end{align} $$

Motivated by the works of Lin and Liu and the recent progress on congruences and q-congruences (see [2–6, 9–12, 14–18]), we continue the study of congruence relations for the truncated Appell series. The goal of this paper is to give the following generalisation of (1.1).

Theorem 1.1. Let p be an odd prime. Then

$$ \begin{align*} F_3[\tfrac12,\tfrac12;\tfrac12,\tfrac12;1;1,1]_{(p-1)/2} \equiv (-1)^{(p-1)/2} \pmod{p^4}. \end{align*} $$

In fact, Theorem 1.1 can be verified by establishing the following more general q-supercongruence, which is the principal goal of this paper. To state the theorem, we need some q-notation. The q-shifted factorial is given by

$$ \begin{align*} (a;q)_n= \left \{ \begin{array}{@{}ll} (1-a)(1-aq)\cdots (1-aq^{n-1}) & n \in \mathbb {Z}^{+}, \\ 1 &n = 0, \end{array} \right. \end{align*} $$

and the q-binomial coefficients are defined by

$$ \begin{align*} {x\brack k}={x\brack k}_{q} = \left \{ \begin{array}{@{}ll} \dfrac{(q^{1+x-k};q)_k}{(q;q)_k} & k \geq 0, \\ \ 0 & k < 0. \end{array} \right. \end{align*} $$

Furthermore, $ [n]=[n]_q=(1-q^n)/(1-q)=1+q+\cdots +q^{n-1} $ denotes the q-integer, and $\Phi _n(q)$ stands for the nth cyclotomic polynomial in q, which is given by

$$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\leqslant k\leqslant n\\ \gcd(n,k)=1}}(q-\zeta^k) \end{align*} $$

with $\zeta $ a primitive nth root of unity.

Theorem 1.2. Let n be a positive odd integer and d an integer and suppose that $n\geq \max \{2d+1,1-2d\}$ . Then, modulo $\Phi _n(q)^4$ ,

(1.2) $$ \begin{align} &\sum_{i=0}^{{(n-1)}/{2}-d}\sum_{j=0}^{{(n-1)}/{2}+d}\frac{(q^{2d+1};q^2)_{i}^2(q^{1-2d};q^2)_{j}^2}{(q^2;q^2)_i(q^2;q^2)_j(q^2;q^2)_{i+j}} q^{2ij-4di+4dj} \nonumber\\ &\equiv \left \{ \begin{aligned} & (-1)^{{(n-1)}/{2}}q^{{(1-n^2)}/{4}} &d = 0, \\ & (1-q^n)^2q^{|d|(2+3|d|-n)-n+{(1-n^2)}/{4}}\sum_{k=1}^{2|d|}(-1)^{k-|d|+{(n-1)}/{2}}q^{k^2-k}H_k(-2|d|-1)\\ &\quad\quad\times\frac{(q^{n+2|d|-2k+1};q^2)_k(q^{4|d|-2k+2};q^2)_{(n-2|d|-1)/2}}{(q^2;q^2)_k(q^2;q^2)_{(n-2|d|-1)/2}} &d\neq 0, \end{aligned} \right. \end{align} $$

where

$$ \begin{align*} H_k(x)=\sum_{t=1}^{k}\frac{q^{2t+x}}{(1-q^{2t+x})^2}, \end{align*} $$

with $H_k(x)=0$ for any integer $k<1$ .

Clearly, letting $d=0$ , $q \rightarrow 1$ and $n=p$ , an odd prime, in Theorem 1.2, we immediately achieve Theorem 1.1. Additionally, the cases $d=\pm 1$ of Theorem 1.2 yield the following conclusion.

Corollary 1.3. Let $n\geq 3$ be a positive odd integer. Then, modulo $\Phi _n(q)^4$ ,

$$ \begin{align*} &\sum_{i=0}^{{(n-3)}/{2}}\sum_{j=0}^{{(n+1)}/{2}} \frac{(q^{3};q^2)_{i}^2(q^{-1};q^2)_{j}^2}{(q^2;q^2)_i(q^2;q^2)_j(q^2;q^2)_{i+j}}q^{2ij-4i+4j} \notag \\ &\quad \equiv (-1)^{{(n-1)}/{2}}[n]^2\frac{(q^{n-1};q^2)_2}{(1-q^4)}q^{6-2n+{(1-n^2)}/{4}}. \end{align*} $$

Setting $n=p$ , an odd prime, and then letting $q\rightarrow 1$ in Corollary 1.3, we instantly arrive at

(1.3) $$ \begin{align} \sum_{i=0}^{{(p-3)}/{2}}\sum_{j=0}^{{(p+1)}/{2}}\frac{(\frac32)_i^2(-\frac12)_j^2 }{(1)_i(1)_j(1)_{i+j}} \equiv 0 \pmod{p^4}. \end{align} $$

Numerical calculation indicates that the following generalisation of (1.3) should be true.

Conjecture 1.4. Let p be an odd prime and d an integer with $0<d\leq {(p-1)}/{2}$ . Then

(1.4) $$ \begin{align} \sum_{i=0}^{{(p-1)}/{2}-d}\sum_{j=0}^{{(p-1)}/{2}+d}\frac{(\frac{1}{2}+d)_i^2(\frac{1}{2}-d)_j^2 }{(1)_i(1)_j(1)_{i+j}} \equiv 0 \pmod{p^4}. \end{align} $$

2 Proof of Theorem 1.2

The q-Chu–Vandermonde identity [1, (1.5.2)] can be written as

(2.1) $$ \begin{align} {m+n\brack k}= \sum_{j=0}^{k}q^{\,j(m-k+j)} {m\brack k-j} {n\brack j}, \end{align} $$

which is useful in combinatorics and number theory and will play a key role in our proof of Theorem 1.2. Another preliminary result we require is as follows.

Lemma 2.1. Let n be a positive odd integer and d an integer with $n\geq 1-2d$ . Then

$$ \begin{align*} \begin{split} \sum_{j=0}^{{(n-1)}/{2}+d}(-1)^{\,j}q^{ij+{(\,j+2d-n)}j/{2}} {\frac{n-1}{2}+d\brack j} {\frac{n-1}{2}-d+j\brack j} {i+j\brack i}^{-1}= {i+2d-1\brack \frac{n-1}{2}+d} {\frac{n-1}{2}+d+i\brack i}^{-1}. \end{split} \end{align*} $$

Proof. It is routine to verify that

(2.2) $$ \begin{align} {\frac{n-1}{2}+d \brack j} {i+j\brack i}^{-1} &={\frac{n-1}{2}+d+i\brack\frac{n-1}{2}+d-j} {\frac{n-1}{2}+d+i\brack i}^{-1}, \end{align} $$

(2.3) $$ \begin{align} \hspace{-13.5pt}(-1)^{\,j} {\frac{n-1}{2}-d+j\brack j} &={-\frac{n-1}{2}+d-1\brack j} q^{{(n-2d+j)j}/{2}}. \end{align} $$

In view of the two simple relations (2.2) and (2.3), we immediately conclude that

$$ \begin{align*} \begin{split} &\sum_{j=0}^{{(n-1)}/{2}+d} (-1)^{\,j}q^{ij+{(\,j+2d-n)j}/{2}}{\frac{n-1}{2}-d+j\brack j} {\frac{n-1}{2}+d\brack j} {i+j\brack i}^{-1}\\ &\quad ={\frac{n-1}{2}+d+i\brack i}^{-1}\sum_{j=0}^{{(n-1)}/{2}+d}q^{\,j^2+ij} {\frac{n-1}{2}+d+i\brack \frac{n-1}{2}+d-j} {-\frac{n-1}{2}+d-1\brack j}\\ &\quad = {\frac{n-1}{2}+d+i\brack i}^{-1} {i+2d-1\brack \frac{n-1}{2}+d}, \end{split} \end{align*} $$

where the last step follows from the q-Chu–Vandermonde identity (2.1). This gives the desired result.

Proof of Theorem 1.2. It is not hard to see that

$$ \begin{align*} (1-q^{n+(2t+2d-1)})(1-q^{n-(2t+2d-1)})+(1-q^{2t+2d-1})^2q^{n-(2t+2d-1)}=(1-q^n)^2. \end{align*} $$

With the help of the above relation, we find that

$$ \begin{align*} \begin{split} &{\frac{n-1}{2}-d\brack k}_{q^2} {\frac{n-1}{2}+d+k\brack k}_{q^2}\\ &\quad =\frac{1}{(q^2;q^2)_k^2}\prod_{t=1}^{k}(1-q^{n+(2t+2d-1)})(1-q^{n-(2t+2d-1 )})\\ &\quad =\frac{1}{(q^2;q^2)_k^2}\prod_{t=1}^{k}\{(1-q^{n})^2-(1-q^{2t+2d-1})^2q^{n-(2t+2d-1)}\}\\ &\quad \equiv (-1)^k\frac{(q^{2d+1};q^2)_k^2}{(q^2;q^2)_k^2}q^{(n-k-2d)k}\{1-q^{-n}(1-q^n)^2H_k(2d-1)\} \pmod{\Phi_n(q)^4}, \end{split} \end{align*} $$

which implies that, modulo $\Phi _n(q)^4$ ,

(2.4) $$ \begin{align} \frac{(q^{2d+1};q^2)_k^2}{(q^2;q^2)_k^2} \equiv (-1)^kq^{(k+2d-n)k} {\frac{n-1}{2}-d\brack k}_{q^2} {\frac{n-1}{2}+d+k\brack k}_{q^2} \{1+q^{-n}(1-q^n)^2H_k(2d-1)\}. \end{align} $$

However, replacing d by $-d$ in the q-supercongruence (2.4), we easily get

(2.5) $$ \begin{align} \frac{(q^{1-2d};q^2)_k^2}{(q^2;q^2)_k^2} & \equiv (-1)^kq^{(k-2d-n)k} {\frac{n-1}{2}+d\brack k}_{q^2} {\frac{n-1}{2}-d+k\brack k}_{q^2} \notag \\[6pt] &\quad \times\{1+q^{-n}(1-q^n)^2H_k(-2d-1)\} \pmod{\Phi_n(q)^4}. \end{align} $$

Substituting the q-supercongruences (2.4) and (2.5) into the left-hand side of (1.2) in Theorem 1.2 gives: modulo $\Phi _n(q)^4$ ,

(2.6) $$ \begin{align} &\sum_{i=0}^{{(n-1)}/{2}-d} \sum_{j=0}^{{(n-1)}/{2}+d} \frac{(q^{2d+1};q^2)_{i}^2(q^{1-2d};q^2)_{j}^2}{(q^2;q^2)_i(q^2;q^2)_j(q^2;q^2)_{i+j}}q^{2ij-4di+4dj} \notag \\[6pt] &\quad\equiv\sum_{i=0}^{{(n-1)}/{2}-d} \sum_{j=0}^{{(n-1)}/{2}+d} (-1)^{i+j}q^{2ij+(i-2d-n)i+(\,j+2d-n)j} {\frac{n-1}{2}-d\brack i}_{q^2} {\frac{n-1}{2}+d+i\brack i}_{q^2} {\frac{n-1}{2}+d\brack j}_{q^2} \notag\\[6pt] &\qquad\times {\frac{n-1}{2}-d+j\brack j}_{q^2} {i+j\brack i}_{q^2}^{-1} \{1+q^{-n}(1-q^n)^2(H_i(2d-1)+H_j(-2d-1))\}. \end{align} $$

To simplify (2.6), we divide the right-hand side of (2.6) into three parts. Let L stand for the right-hand side of (2.6) and write

$$ \begin{align*}L=L_1+(1-q^n)^2(L_2(d)+L_2(-d)),\end{align*} $$

where

$$ \begin{align*} L_1 & := \sum_{i=0}^{{(n-1)}/{2}-d} \sum_{j=0}^{{(n-1)}/{2}+d} (-1)^{i+j}q^{2ij+(i-2d-n)i+(j+2d-n)j} {\frac{n-1}{2}-d\brack i}_{q^2} {\frac{n-1}{2}+d+i\brack i}_{q^2}\\[6pt] &\quad \times {\frac{n-1}{2}+d\brack j}_{q^2} {\frac{n-1}{2}-d+j\brack j}_{q^2} {i+j\brack i}_{q^2}^{-1}, \\[6pt] L_2(d)&:= \sum_{i=0}^{{(n-1)}/{2}-d}\sum_{j=0}^{{(n-1)}/{2}+d}(-1)^{i+j}q^{2ij+(i-2d-n)i+(\,j+2d-n)j-n} {\frac{n-1}{2}-d\brack i}_{q^2} {\frac{n-1}{2}+d+i\brack i}_{q^2}\\[6pt] &\quad \times{\frac{n-1}{2}+d\brack j}_{q^2} {\frac{n-1}{2}-d+j\brack j}_{q^2} {i+j\brack i}_{q^2}^{-1} H_i(2d-1). \end{align*} $$

We first consider the part $L_1$ . Applying the case $q\rightarrow q^2$ of Lemma 2.1, we can simplify $L_1$ by first calculating the terms indexed j as

(2.7) $$ \begin{align} L_1&=\sum_{i=0}^{{(n-1)}/{2}-d}(-1)^{i}q^{(i-2d-n)i} {\frac{n-1}{2}-d\brack i}_{q^2} {\frac{n-1}{2}+d+i\brack i}_{q^2}\nonumber\\ &\quad \times\sum_{j=0}^{{(n-1)}/{2}+d}(-1)^{\,j}q^{2ij+(\,j+2d-n)j} {\frac{n-1}{2}+d\brack j}_{q^2} {\frac{n-1}{2}-d+j\brack j}_{q^2} {i+j\brack i}_{q^2}^{-1}\nonumber\\ & = \sum_{i=0}^{{(n-1)}/{2}-d}(-1)^iq^{(i-2d-n)i} {\frac{n-1}{2}-d\brack i}_{q^2} {i+2d-1\brack \frac{n-1}{2}+d}_{q^2}. \end{align} $$

In fact, changing the summation order of i and j, $L_1$ can also be expressed as

(2.8) $$ \begin{align} L_1=\sum_{j=0}^{{(n-1)}/{2}+d}(-1)^{\kern1.3pt j}q^{(\,j+2d-n)j} {\frac{n-1}{2}+d\brack j}_{q^2} {j-2d-1\brack \frac{n-1}{2}-d}_{q^2}. \end{align} $$

Next, we shall discuss the evaluation of $L_1$ under three cases.

Case (i): $d=0$ . It is easy to check that

$$ \begin{align*} {i-1\brack \frac{n-1}{2}}_{q^2}=0 \quad\text{for } 1 \leq i \leq \frac{n-1}{2}, \end{align*} $$

which implies (2.7) equals $0$ except for $i=0$ . Thus (2.7) reduces to $(-1)^{(n-1)/2}q^{(1-n^2)/4}$ .

Case (ii): $d\geq 1$ . It is obvious that

$$ \begin{align*} {i+2d-1\brack \frac{n-1}{2}+d}_{q^2}=0 \quad\text{for } 0 \leq i \leq \frac{n-1}{2}-d, \end{align*} $$

which means (2.7) equals $0$ .

Case (iii): $d\leq -1$ . Similarly to case (ii),

$$ \begin{align*} {j-2d-1\brack \frac{n-1}{2}-d}_{q^2}=0 \quad\text{for } 0 \leq j \leq \frac{n-1}{2}+d. \end{align*} $$

It follows that (2.8) equals $0$ .

These considerations show that

(2.9) $$ \begin{align} L_1 = \left \{ \begin{aligned} &(-1)^{(n-1)/2}q^{(1-n^2)/4} &d = 0, & \\[2mm] & 0 &d \neq 0.& \end{aligned} \right. \end{align} $$

At the same time, recalling Lemma 2.1 with $q\rightarrow q^2$ again, we have shown

(2.10) $$ \begin{align} \begin{split} L_2(d) = \sum_{i=0}^{{(n-1)}/{2}-d}(-1)^iq^{(i-2d-n)i-n} {\frac{n-1}{2}-d\brack i}_{q^2} {i+2d-1\brack \frac{n-1}{2}+d}_{q^2}H_i(2d-1). \end{split} \end{align} $$

Likewise, we consider (2.10) in three cases. Following from the assumption that $H_k(x)=0$ for any integer $k<1$ , we thus attain

(2.11) $$ \begin{align} L_2(d)= \left \{ \begin{aligned} & \sum_{i=1}^{-2d}(-1)^iq^{(i-2d-n)i-n} {\frac{n-1}{2}-d\brack i}_{q^2} {i+2d-1\brack \frac{n-1}{2}+d}_{q^2} H_i(2d-1) &d \leq -1, \\ & \ 0 &d \geq 0.\ \ \end{aligned} \right. \end{align} $$

The detailed proof of (2.11) follows the proof of (2.9) and is omitted here. Now it remains to consider $L_2(-d)$ . Taking $d=-d$ in (2.11),

(2.12) $$ \begin{align} L_2(-d)= \left \{ \begin{aligned} &\ 0 &d \leq 0, & \\ & \sum_{j=1}^{2d}(-1)^jq^{(\,j+2d-n)j-n} {\frac{n-1}{2}+d\brack j}_{q^2} {j-2d-1\brack \frac{n-1}{2}-d}_{q^2} H_j(-2d-1) &d \geq 1.& \end{aligned} \right. \end{align} $$

Substituting the three formulas (2.9), (2.11) and (2.12) into (2.6), we arrive at

$$ \begin{align*} \begin{split} &\sum_{i=0}^{{(n-1)}/{2}-d}\sum_{j=0}^{{(n-1)}/{2}+d} \frac{(q^{2d+1};q^2)_{i}^2(q^{1-2d};q^2)_{j}^2}{(q^2;q^2)_i(q^2;q^2)_j(q^2;q^2)_{i+j}}q^{2ij-4di+4dj} \\ &\quad \equiv \left \{ \begin{aligned} & (1-q^n)^2\sum_{i=1}^{-2d}(-1)^iq^{(i-2d-n)i-n} {\frac{n-1}{2}-d\brack i}_{q^2} {i+2d-1\brack \frac{n-1}{2}+d}_{q^2} H_i(2d-1) &d \leq -1, & \\ & (-1)^{(n-1)/2}q^{(1-n^2)/4} &d = 0,& \\ & (1-q^n)^2\sum_{j=1}^{2d}(-1)^jq^{(\,j+2d-n)j-n} {\frac{n-1}{2}+d\brack j}_{q^2} {j-2d-1\brack \frac{n-1}{2}-d}_{q^2}H_j(-2d-1) &d \geq 1.& \end{aligned} \right. \end{split} \end{align*} $$

The cases $d \geq 1$ and $d \leq -1$ can be compactly combined into

$$ \begin{align*} &(1-q^n)^2q^{|d|(2+3|d|-n)-n+{(1-n^2)}/{4}}\\ &\quad\times \sum_{k=1}^{2|d|}(-1)^{k-|d|+(n-1)/2}q^{k^2-k}H_k(-2|d|-1) \frac{(q^{n+2|d|-2k+1};q^2)_k(q^{4|d|-2k+2};q^2)_{(n-2|d|-1)/2}}{(q^2;q^2)_k(q^2;q^2)_{(n-2|d|-1)/2}}. \end{align*} $$

As explained above, this completes the proof of Theorem 1.2.