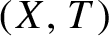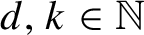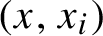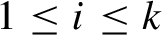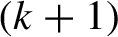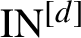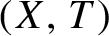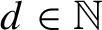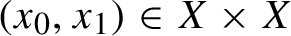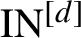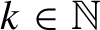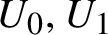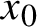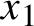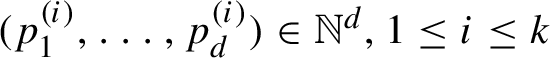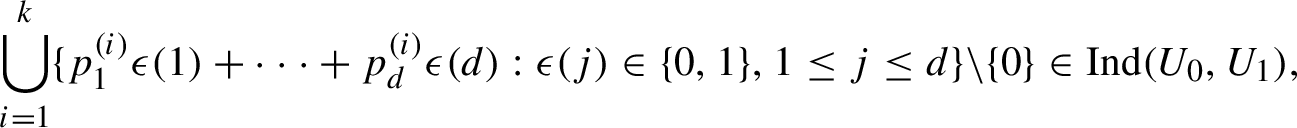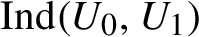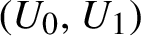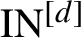1 Introduction
By a topological dynamical system or just a dynamical system, we mean a pair
![]() $(X,T)$
, where X is a compact metric space with a metric
$(X,T)$
, where X is a compact metric space with a metric
![]() $\rho $
and
$\rho $
and
![]() $T:X\to X$
is a homeomorphism.
$T:X\to X$
is a homeomorphism.
In recent years, the study of the dynamics of rotations on nilmanifolds and inverse limits of this kind of dynamics has drawn much interest, since it relates to many dynamical properties and has important applications in number theory. We refer to [Reference Host and Kra12] and the references therein for a systematic treatment on the subject.
In a pioneer work, Host, Kra and Maass [Reference Host, Kra and Maass13] introduced the notion of regionally proximal relation of order d for a dynamical system
![]() $(X,T)$
, denoted by
$(X,T)$
, denoted by
![]() $\mathbf {RP}^{[d]}(X)$
. For
$\mathbf {RP}^{[d]}(X)$
. For
![]() $d\in \mathbb {N}$
, we say that a minimal system is a system of order d if
$d\in \mathbb {N}$
, we say that a minimal system is a system of order d if
![]() $\mathbf {RP}^{[d]}(X)=\Delta $
, and this is equivalent for
$\mathbf {RP}^{[d]}(X)=\Delta $
, and this is equivalent for
![]() $(X,T)$
to an inverse limit of nilrotations on d-step nilsystems (see [Reference Host, Kra and Maass13, Theorem 2.8]). For a minimal distal system
$(X,T)$
to an inverse limit of nilrotations on d-step nilsystems (see [Reference Host, Kra and Maass13, Theorem 2.8]). For a minimal distal system
![]() $(X,T)$
, it was proved that
$(X,T)$
, it was proved that
![]() $\mathbf {RP}^{[d]}(X)$
is an equivalence relation and
$\mathbf {RP}^{[d]}(X)$
is an equivalence relation and
![]() $X/\mathbf {RP}^{[d]}(X)$
is the maximal factor of order d [Reference Host, Kra and Maass13]. Then Shao and Ye [Reference Shao and Ye22] showed that in fact for any minimal system,
$X/\mathbf {RP}^{[d]}(X)$
is the maximal factor of order d [Reference Host, Kra and Maass13]. Then Shao and Ye [Reference Shao and Ye22] showed that in fact for any minimal system,
![]() $\mathbf {RP}^{[d]}(X)$
is an equivalence relation and
$\mathbf {RP}^{[d]}(X)$
is an equivalence relation and
![]() $\mathbf {RP}^{[d]}(X)$
has the so-called lifting property.
$\mathbf {RP}^{[d]}(X)$
has the so-called lifting property.
The notion of k-regional proximal relation was introduced in [Reference Huang, Lu and Ye16]. It was shown that for a minimal system
![]() $(X,T)$
and
$(X,T)$
and
![]() $k\geq 2$
, if
$k\geq 2$
, if
![]() $(x,x_{i})$
is regionally proximal for all
$(x,x_{i})$
is regionally proximal for all
![]() $1\leq i\leq k$
, then
$1\leq i\leq k$
, then
![]() $(x_{1},\ldots ,x_{k})$
is k-regionally proximal, that is, for every
$(x_{1},\ldots ,x_{k})$
is k-regionally proximal, that is, for every
![]() $\delta>0$
, there exist
$\delta>0$
, there exist
![]() $x_{i}^{\prime }\in X$
,
$x_{i}^{\prime }\in X$
,
![]() $1\leq i\leq k$
, and
$1\leq i\leq k$
, and
![]() $n\in \mathbb {Z}$
such that
$n\in \mathbb {Z}$
such that
![]() $\rho (x_{i},x_{i}^{\prime })<\delta $
and
$\rho (x_{i},x_{i}^{\prime })<\delta $
and
![]() $ \rho (T^{n} x_{1}^{\prime },T^{n}x_{i}^{\prime })<\delta $
,
$ \rho (T^{n} x_{1}^{\prime },T^{n}x_{i}^{\prime })<\delta $
,
![]() $1\leq i\leq k$
. In this paper we extend this result to higher order (Theorem 3.2).
$1\leq i\leq k$
. In this paper we extend this result to higher order (Theorem 3.2).
Following the local entropy theory (for a survey see [Reference Glasner and Ye11]), each dynamical system admits a maximal zero topological entropy factor, and this factor is induced by the smallest closed invariant equivalence relation containing entropy pairs [Reference Blanchard and Lacroix3]. In [Reference Huang and Ye19], entropy pairs are characterized as those pairs that admit an interpolating set of positive density. Later on, the notions of sequence entropy pairs [Reference Huang, Li, Shao and Ye15] and untame pairs (called scrambled pairs in [Reference Huang14]) were introduced. In [Reference Kerr and Li20] the concept of independence was extensively studied and used to unify the aforementioned notions. Let
![]() $(X,T)$
be a dynamical system and
$(X,T)$
be a dynamical system and
![]() $\mathcal {A}=(U_{0},U_{1},\ldots ,U_{k})$
be a tuple of subsets of X. We say that a subset
$\mathcal {A}=(U_{0},U_{1},\ldots ,U_{k})$
be a tuple of subsets of X. We say that a subset
![]() $F\subset \mathbb {Z}$
is an independence set for
$F\subset \mathbb {Z}$
is an independence set for
![]() $\mathcal {A}$
if for any non-empty finite subset
$\mathcal {A}$
if for any non-empty finite subset
![]() $J\subset F$
and any
$J\subset F$
and any
![]() $s=(s(j):j\in J)\in \{0,1,\ldots ,k\}^{J}$
we have
$s=(s(j):j\in J)\in \{0,1,\ldots ,k\}^{J}$
we have
 $\bigcap _{j\in J}T^{-j}U_{s(j)}\neq \emptyset $
. It was shown that a pair of points
$\bigcap _{j\in J}T^{-j}U_{s(j)}\neq \emptyset $
. It was shown that a pair of points
![]() $x_{0},x_{1}$
in X is a sequence entropy pair if and only if each
$x_{0},x_{1}$
in X is a sequence entropy pair if and only if each
![]() $\mathcal {A}=(U_{0},U_{1})$
, where
$\mathcal {A}=(U_{0},U_{1})$
, where
![]() $U_{0}$
and
$U_{0}$
and
![]() $U_{1}$
are neighborhoods of
$U_{1}$
are neighborhoods of
![]() $x_{0}$
and
$x_{0}$
and
![]() $x_{1}$
respectively, has arbitrarily long finite independence sets. Also, the pair is an untame pair if and only if each
$x_{1}$
respectively, has arbitrarily long finite independence sets. Also, the pair is an untame pair if and only if each
![]() $\mathcal {A} = (U_{0} ,U_{1} )$
as before has infinite independence sets. It was shown [Reference Glasner8, Reference Huang, Li, Shao and Ye15, Reference Kerr and Li20] that a minimal null (respectively, tame) system is an almost one-to-one extension of its maximal equicontinuous factor and is uniquelyergodic.
$\mathcal {A} = (U_{0} ,U_{1} )$
as before has infinite independence sets. It was shown [Reference Glasner8, Reference Huang, Li, Shao and Ye15, Reference Kerr and Li20] that a minimal null (respectively, tame) system is an almost one-to-one extension of its maximal equicontinuous factor and is uniquelyergodic.
For
![]() $d\in \mathbb {N}$
and
$d\in \mathbb {N}$
and
![]() $p_{1},\ldots ,p_{d}\in \mathbb {Z}$
, we call the set
$p_{1},\ldots ,p_{d}\in \mathbb {Z}$
, we call the set
![]() $\{p_{1}\epsilon (1)+\cdots +p_{d}\epsilon (d):\epsilon (j)\in \{0,1\},1\leq j\leq d\}\backslash \{0\}$
an
$\{p_{1}\epsilon (1)+\cdots +p_{d}\epsilon (d):\epsilon (j)\in \{0,1\},1\leq j\leq d\}\backslash \{0\}$
an
![]() $IP_{d}$
-set. The notion of
$IP_{d}$
-set. The notion of
![]() $Ind_{fip}$
-pair was studied in [Reference Dong, Donoso, Maass, Shao and Ye4]: a pair of points
$Ind_{fip}$
-pair was studied in [Reference Dong, Donoso, Maass, Shao and Ye4]: a pair of points
![]() $x_{0},x_{1}$
in X is an
$x_{0},x_{1}$
in X is an
![]() $\text {Ind}_{fip}$
-pair if and only if the independence sets for each
$\text {Ind}_{fip}$
-pair if and only if the independence sets for each
![]() $\mathcal {A}=(U_{0},U_{1})$
as before contain an
$\mathcal {A}=(U_{0},U_{1})$
as before contain an
![]() $\mathrm {IP}_{d}$
-set for any
$\mathrm {IP}_{d}$
-set for any
![]() $d\in \mathbb {N}$
. It was shown that a minimal system without any non-trivial
$d\in \mathbb {N}$
. It was shown that a minimal system without any non-trivial
![]() $\mathrm {Ind}_{fip}$
-pair is an almost one-to-one extension of its maximal factor of order
$\mathrm {Ind}_{fip}$
-pair is an almost one-to-one extension of its maximal factor of order
![]() $\infty $
.
$\infty $
.
So, it is natural to ask: can we give a finer classification of almost automorphy of higher order (see Definition 2.7) using independence?
In this paper we introduce the notion of
![]() $IN^{[d]}$
-pair. A pair of points
$IN^{[d]}$
-pair. A pair of points
![]() $x_{0},x_{1}$
in X is an
$x_{0},x_{1}$
in X is an
![]() $\mathrm {IN}^{[d]}$
-pair if and only if the independence sets for each
$\mathrm {IN}^{[d]}$
-pair if and only if the independence sets for each
![]() $\mathcal {A} = (U_{0} ,U_{1} )$
as before contain a union of arbitrarily finitely many
$\mathcal {A} = (U_{0} ,U_{1} )$
as before contain a union of arbitrarily finitely many
![]() $\mathrm {IP}_{d}$
-sets. Using dynamical cubespaces, we first provide a characterization of
$\mathrm {IP}_{d}$
-sets. Using dynamical cubespaces, we first provide a characterization of
![]() $\mathrm {IN}^{[d]}$
-pairs for minimal systems (Lemma 2.12). By [Reference Host and Kra12, Ch. 6], the dynamical cubespaces of minimal nilsystems can also be viewed as nilsystems. Following this, it is shown that for minimal nilsystems, non-trivial regionally proximal of order d pairs are
$\mathrm {IN}^{[d]}$
-pairs for minimal systems (Lemma 2.12). By [Reference Host and Kra12, Ch. 6], the dynamical cubespaces of minimal nilsystems can also be viewed as nilsystems. Following this, it is shown that for minimal nilsystems, non-trivial regionally proximal of order d pairs are
![]() $\mathrm {IN}^{[d]}$
-pairs (Theorem 4.5). Moreover, this property also holds for inverse limits of minimal nilsystems.
$\mathrm {IN}^{[d]}$
-pairs (Theorem 4.5). Moreover, this property also holds for inverse limits of minimal nilsystems.
For a minimal system and
![]() $d\in \mathbb {N}$
, by reducing to the maximal factor of order
$d\in \mathbb {N}$
, by reducing to the maximal factor of order
![]() $\infty $
which is an inverse limit of minimal nilsystems [Reference Dong, Donoso, Maass, Shao and Ye4], we can show that any non-trivial regionally proximal of order d pair is an
$\infty $
which is an inverse limit of minimal nilsystems [Reference Dong, Donoso, Maass, Shao and Ye4], we can show that any non-trivial regionally proximal of order d pair is an
![]() $\mathrm {IN}^{[d]}$
-pair if it is minimal in the product system (Lemma5.4). Among other things, it turns out that for a minimal system, if it does not contain any non-trivial
$\mathrm {IN}^{[d]}$
-pair if it is minimal in the product system (Lemma5.4). Among other things, it turns out that for a minimal system, if it does not contain any non-trivial
![]() $\mathrm {IN}^{[d]}$
-pair, then it is an almost one-to-one extension of its maximal factor of order d (Theorem 5.7).
$\mathrm {IN}^{[d]}$
-pair, then it is an almost one-to-one extension of its maximal factor of order d (Theorem 5.7).
This paper is organized as follows. In §2 the basic notions used in the paper are introduced. In §3 we discuss the k-regionally proximal relation of higher order (Theorem3.2). In §4 it is shown that for a minimal nilsystem any regionally proximal of order d pair is an
![]() $\mathrm {IN}^{[d]}$
-pair (Theorem 4.5). In §5, among other things, we show that for any minimal system, if it does not contain any non-trivial
$\mathrm {IN}^{[d]}$
-pair (Theorem 4.5). In §5, among other things, we show that for any minimal system, if it does not contain any non-trivial
![]() $\mathrm {IN}^{[d]}$
-pair, then it is an almost one-to-one extension of its maximal factor of order d (Theorem 5.7). In the final section we construct a minimal system with trivial
$\mathrm {IN}^{[d]}$
-pair, then it is an almost one-to-one extension of its maximal factor of order d (Theorem 5.7). In the final section we construct a minimal system with trivial
![]() $\mathrm {IN}^{[d]}$
-pairs, and a non-trivial regionally proximal relation of order d (Example 6.1).
$\mathrm {IN}^{[d]}$
-pairs, and a non-trivial regionally proximal relation of order d (Example 6.1).
2 Preliminaries
In this section we gather definitions and preliminary results that will be necessary later on. Let
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $\mathbb {Z}$
be the sets of all positive integers and integers, respectively.
$\mathbb {Z}$
be the sets of all positive integers and integers, respectively.
2.1 Topological dynamical systems
A topological dynamical system (or dynamical system) is a pair
![]() $(X,T)$
, where X is a compact metric space with a metric
$(X,T)$
, where X is a compact metric space with a metric
![]() $\rho $
and
$\rho $
and
![]() $T : X \to X$
is a homeomorphism. If A is a non-empty closed subset of X and
$T : X \to X$
is a homeomorphism. If A is a non-empty closed subset of X and
![]() $TA\subset A$
, then
$TA\subset A$
, then
![]() $(A,T|_{A})$
is called a subsystem of
$(A,T|_{A})$
is called a subsystem of
![]() $(X,T)$
, where
$(X,T)$
, where
![]() $T|_{A}$
is the restriction of T on A. If there is no ambiguity, we use the notation T instead of
$T|_{A}$
is the restriction of T on A. If there is no ambiguity, we use the notation T instead of
![]() $T|_{A}$
. For
$T|_{A}$
. For
![]() $x\in X,\mathcal {O}(x,T)=\{T^{n}x: n\in \mathbb {Z}\}$
denotes the orbit of x. A dynamical system
$x\in X,\mathcal {O}(x,T)=\{T^{n}x: n\in \mathbb {Z}\}$
denotes the orbit of x. A dynamical system
![]() $(X,T)$
is called minimal if every point has dense orbit in X. A subset Y of X is called minimal if
$(X,T)$
is called minimal if every point has dense orbit in X. A subset Y of X is called minimal if
![]() $(Y,T)$
is a minimal subsystem of
$(Y,T)$
is a minimal subsystem of
![]() $(X,T)$
. A point
$(X,T)$
. A point
![]() $x\in X$
is called minimal if it is contained in a minimal set Y or, equivalently, if the subsystem
$x\in X$
is called minimal if it is contained in a minimal set Y or, equivalently, if the subsystem
![]() $(\overline {\mathcal {O}(x,T)},T)$
is minimal.
$(\overline {\mathcal {O}(x,T)},T)$
is minimal.
A homomorphism between the dynamical systems
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y,T)$
is a continuous onto map
$(Y,T)$
is a continuous onto map
![]() $\pi :X\to Y$
which intertwines the actions; one says that
$\pi :X\to Y$
which intertwines the actions; one says that
![]() $(Y,T)$
is a factor of
$(Y,T)$
is a factor of
![]() $(X,T)$
and that
$(X,T)$
and that
![]() $(X,T)$
is an extension of
$(X,T)$
is an extension of
![]() $(Y,T)$
. One also refers to
$(Y,T)$
. One also refers to
![]() $\pi $
as a factor map or an extension and one uses the notation
$\pi $
as a factor map or an extension and one uses the notation
![]() $\pi : (X,T) \to (Y,T)$
. The systems are said to be conjugate if
$\pi : (X,T) \to (Y,T)$
. The systems are said to be conjugate if
![]() $\pi $
is a bijection. An extension
$\pi $
is a bijection. An extension
![]() $\pi $
is determined by the corresponding closed invariant equivalence relation
$\pi $
is determined by the corresponding closed invariant equivalence relation
![]() $R_{\pi }=\{(x,x^{\prime })\in X\times X\colon \pi (x)=\pi (x^{\prime })\}$
. An extension
$R_{\pi }=\{(x,x^{\prime })\in X\times X\colon \pi (x)=\pi (x^{\prime })\}$
. An extension
![]() $\pi : (X,T) \to (Y,T)$
is almost one-to-one if the
$\pi : (X,T) \to (Y,T)$
is almost one-to-one if the
![]() $G_{\delta }$
set
$G_{\delta }$
set
![]() $X_{0}=\{x\in X:\pi ^{-1}(\pi (x))=\{x\}\}$
is dense.
$X_{0}=\{x\in X:\pi ^{-1}(\pi (x))=\{x\}\}$
is dense.
2.2 Discrete cubes and faces
Let X be a set and let
![]() $d\ge 1$
be an integer. We view the element
$d\ge 1$
be an integer. We view the element
![]() $\epsilon \in \{0, 1\}^{d}$
as a sequence
$\epsilon \in \{0, 1\}^{d}$
as a sequence
![]() $\epsilon =(\epsilon (1),\ldots , \epsilon (d))$
, where
$\epsilon =(\epsilon (1),\ldots , \epsilon (d))$
, where
![]() $\epsilon (i)\in \{0,1\}, 1\leq i \leq d$
. If
$\epsilon (i)\in \{0,1\}, 1\leq i \leq d$
. If
![]() $\vec {n} = (n_{1},\ldots , n_{d})\in \mathbb {Z}^{d}$
and
$\vec {n} = (n_{1},\ldots , n_{d})\in \mathbb {Z}^{d}$
and
![]() $\epsilon \in \{0,1\}^{d}$
, we define
$\epsilon \in \{0,1\}^{d}$
, we define
 $$ \begin{align*} \vec{n}\cdot \epsilon = \sum_{i=1}^{d} n_{i}\epsilon(i). \end{align*} $$
$$ \begin{align*} \vec{n}\cdot \epsilon = \sum_{i=1}^{d} n_{i}\epsilon(i). \end{align*} $$
We denote the set of maps
![]() $\{0,1\}^{d}\to X$
by
$\{0,1\}^{d}\to X$
by
![]() $X^{[d]}$
. For
$X^{[d]}$
. For
![]() $\epsilon \in \{0,1\}^{d}$
and
$\epsilon \in \{0,1\}^{d}$
and
![]() $\mathbf {x}\in X^{[d]}$
,
$\mathbf {x}\in X^{[d]}$
,
![]() $\mathbf {x}(\epsilon )$
will be used to denote the
$\mathbf {x}(\epsilon )$
will be used to denote the
![]() $\epsilon $
-component of
$\epsilon $
-component of
![]() $\mathbf {x}$
. For
$\mathbf {x}$
. For
![]() $x\in X$
, write
$x\in X$
, write
![]() $x^{[d]}=(x,x,\ldots ,x)\in X^{[d]}$
. The diagonal of
$x^{[d]}=(x,x,\ldots ,x)\in X^{[d]}$
. The diagonal of
![]() $X^{[d]}$
is
$X^{[d]}$
is
![]() $\Delta ^{[d]}=\Delta ^{[d]}(X)=\{ x^{[d]}:x\in X\}$
. Usually, when
$\Delta ^{[d]}=\Delta ^{[d]}(X)=\{ x^{[d]}:x\in X\}$
. Usually, when
![]() $d=1$
, we denote the diagonal by
$d=1$
, we denote the diagonal by
![]() $\Delta _{X}$
or
$\Delta _{X}$
or
![]() $\Delta $
instead of
$\Delta $
instead of
![]() $\Delta ^{[1]}$
. We can isolate the first coordinate, writing
$\Delta ^{[1]}$
. We can isolate the first coordinate, writing
 $X^{[d]}_{*}=X^{2^{d}-1}$
and writing
$X^{[d]}_{*}=X^{2^{d}-1}$
and writing
![]() $\mathbf {x}\in X^{[d]}$
as
$\mathbf {x}\in X^{[d]}$
as
 $\mathbf {x}=(\mathbf {x}(\vec {0}),\mathbf {x}_{*})$
, where
$\mathbf {x}=(\mathbf {x}(\vec {0}),\mathbf {x}_{*})$
, where
 $\mathbf {x}_{*}=(\mathbf {x}(\epsilon ):\epsilon \in \{0,1\}^{d}\backslash \{ \vec {0}\})\in X^{[d]}_{*}$
.
$\mathbf {x}_{*}=(\mathbf {x}(\epsilon ):\epsilon \in \{0,1\}^{d}\backslash \{ \vec {0}\})\in X^{[d]}_{*}$
.
Identifying
![]() $\{0,1\}^{d}$
with the set of vertices of the Euclidean unit cube, a Euclidean isometry of the unit cube permutes the vertices of the cube and thus the coordinates of a point
$\{0,1\}^{d}$
with the set of vertices of the Euclidean unit cube, a Euclidean isometry of the unit cube permutes the vertices of the cube and thus the coordinates of a point
![]() $\mathbf {x}\in X^{[d]}$
. These permutations are the Euclidean permutations of
$\mathbf {x}\in X^{[d]}$
. These permutations are the Euclidean permutations of
![]() $X^{[d]}$
.
$X^{[d]}$
.
A set of the form
for some
![]() $k\geq 0$
,
$k\geq 0$
,
![]() $1\leq i_{1}<\cdots <i_{k}\leq d$
and
$1\leq i_{1}<\cdots <i_{k}\leq d$
and
![]() $a_{i}\in \{0,1\}$
is called a face of codimension k of the discrete cube
$a_{i}\in \{0,1\}$
is called a face of codimension k of the discrete cube
![]() $\{0,1\}^{d}$
. (The case
$\{0,1\}^{d}$
. (The case
![]() $k=0$
corresponds to
$k=0$
corresponds to
![]() $\{0,1\}^{d}$
.) A face of codimension
$\{0,1\}^{d}$
.) A face of codimension
![]() $1$
is called a hyperface. If all
$1$
is called a hyperface. If all
![]() $a_{i}=1$
we say that the face is upper. Note all upper faces contain
$a_{i}=1$
we say that the face is upper. Note all upper faces contain
![]() $\vec {1}$
and there are exactly
$\vec {1}$
and there are exactly
![]() $2^{d}$
upper faces.
$2^{d}$
upper faces.
For
![]() $\epsilon ,\epsilon ^{\prime }\in \{0,1\}^{d}$
, we say that
$\epsilon ,\epsilon ^{\prime }\in \{0,1\}^{d}$
, we say that
![]() $\epsilon \geq \epsilon ^{\prime }$
if
$\epsilon \geq \epsilon ^{\prime }$
if
![]() $\epsilon (i)\geq \epsilon ^{\prime }(i)$
for all
$\epsilon (i)\geq \epsilon ^{\prime }(i)$
for all
![]() $1\leq i\leq d$
. Let F be a face of
$1\leq i\leq d$
. Let F be a face of
![]() $\{0,1\}^{d}$
. The smallest element of the face F is defined by
$\{0,1\}^{d}$
. The smallest element of the face F is defined by
![]() $\min F$
, meaning that
$\min F$
, meaning that
![]() $\min F\in F$
and
$\min F\in F$
and
![]() $\epsilon \geq \min F$
for all
$\epsilon \geq \min F$
for all
![]() $\epsilon \in F$
. Indeed, if a face F has form (1), then
$\epsilon \in F$
. Indeed, if a face F has form (1), then
![]() $\min F(i_{j})=a_{j}$
for
$\min F(i_{j})=a_{j}$
for
![]() $1\leq j\leq k$
, and
$1\leq j\leq k$
, and
![]() $\min F(i)=0$
for
$\min F(i)=0$
for
![]() $i\in \{1,\ldots ,d\}\backslash \{i_{1},\ldots ,i_{k}\}$
.
$i\in \{1,\ldots ,d\}\backslash \{i_{1},\ldots ,i_{k}\}$
.
2.3 Dynamical cubespaces
Let
![]() $(X,T)$
be a dynamical system and
$(X,T)$
be a dynamical system and
![]() $d\in \mathbb {N}$
. We define
$d\in \mathbb {N}$
. We define
![]() $\mathbf {Q}^{[d]}(X)$
to be the closure in
$\mathbf {Q}^{[d]}(X)$
to be the closure in
![]() $X^{[d]}$
of elements of the form
$X^{[d]}$
of elements of the form
 $$ \begin{align*} (T^{\vec{n}\cdot\epsilon}x=T^{n_{1}\epsilon(1)+\cdots+n_{d}\epsilon(d)}x:\epsilon\in\{0,1\}^{d}), \end{align*} $$
$$ \begin{align*} (T^{\vec{n}\cdot\epsilon}x=T^{n_{1}\epsilon(1)+\cdots+n_{d}\epsilon(d)}x:\epsilon\in\{0,1\}^{d}), \end{align*} $$
where
![]() $\vec {n}=(n_{1},\ldots ,n_{d})\in \mathbb {Z}^{d}$
and
$\vec {n}=(n_{1},\ldots ,n_{d})\in \mathbb {Z}^{d}$
and
![]() $x\in X$
. We call this set the dynamical cubespace of dimension d of the system.
$x\in X$
. We call this set the dynamical cubespace of dimension d of the system.
It is important to note that
![]() $\mathbf {Q}^{[d]}(X)$
is invariant under the Euclidean permutations of
$\mathbf {Q}^{[d]}(X)$
is invariant under the Euclidean permutations of
![]() $X^{[d]}$
.
$X^{[d]}$
.
Definition 2.1. Face transformations are defined inductively as follows. Let
 $T^{[1]}_{1}= \mathrm {id} \times T$
. If
$T^{[1]}_{1}= \mathrm {id} \times T$
. If
 $\{T^{[d-1]}_{j}\}_{j=1}^{d-1}$
is already defined, then set
$\{T^{[d-1]}_{j}\}_{j=1}^{d-1}$
is already defined, then set
 $$ \begin{align*} T^{[d]}_{j} & =T^{[d-1]}_{j}\times T^{[d-1]}_{j},\quad 1\leq j\leq d-1, \\[3pt] T^{[d]}_{d} & =\mathrm{id} {}^{[d-1]}\times T^{[d-1]}. \end{align*} $$
$$ \begin{align*} T^{[d]}_{j} & =T^{[d-1]}_{j}\times T^{[d-1]}_{j},\quad 1\leq j\leq d-1, \\[3pt] T^{[d]}_{d} & =\mathrm{id} {}^{[d-1]}\times T^{[d-1]}. \end{align*} $$
It is easy to see that for
![]() $1\leq j\leq d$
, the face transformation
$1\leq j\leq d$
, the face transformation
 $T^{[d]}_{j} : X^{[d]}\rightarrow X^{[d]}$
can be defined, for every
$T^{[d]}_{j} : X^{[d]}\rightarrow X^{[d]}$
can be defined, for every
![]() $\mathbf {x} \in X^{[d]}$
and
$\mathbf {x} \in X^{[d]}$
and
![]() $\epsilon \in \{0,1\}^{d} $
, by
$\epsilon \in \{0,1\}^{d} $
, by
 $$ \begin{align*} T^{[d]}_{j}\textbf{x}= \left\{ \begin{array}{@{}ll} (T^{[d]}_{j}\textbf{x})(\epsilon)=T\mathbf{x}(\epsilon), & \epsilon(j)=1{,} \\[3pt] (T^{[d]}_{j}\textbf{x})(\epsilon)=\mathbf{x}(\epsilon), & \epsilon(j)=0{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} T^{[d]}_{j}\textbf{x}= \left\{ \begin{array}{@{}ll} (T^{[d]}_{j}\textbf{x})(\epsilon)=T\mathbf{x}(\epsilon), & \epsilon(j)=1{,} \\[3pt] (T^{[d]}_{j}\textbf{x})(\epsilon)=\mathbf{x}(\epsilon), & \epsilon(j)=0{.} \end{array} \right. \end{align*} $$
The face group of dimension d is the group
![]() $\mathcal {F}^{[d]}(X)$
of transformations of
$\mathcal {F}^{[d]}(X)$
of transformations of
![]() $X^{[d]}$
spanned by the face transformations. The parallelepiped group of dimension d is the group
$X^{[d]}$
spanned by the face transformations. The parallelepiped group of dimension d is the group
![]() $\mathcal {G}^{[d]}(X)$
spanned by the diagonal transformation and the face transformations. We often write
$\mathcal {G}^{[d]}(X)$
spanned by the diagonal transformation and the face transformations. We often write
![]() $\mathcal {F}^{\hspace{2pt}[d]}$
and
$\mathcal {F}^{\hspace{2pt}[d]}$
and
![]() $\mathcal {G}^{[d]}$
instead of
$\mathcal {G}^{[d]}$
instead of
![]() $\mathcal {F}^{\hspace{2pt}[d]}(X)$
and
$\mathcal {F}^{\hspace{2pt}[d]}(X)$
and
![]() $\mathcal {G}^{[d]}(X)$
, respectively. For convenience, we denote the orbit closure of
$\mathcal {G}^{[d]}(X)$
, respectively. For convenience, we denote the orbit closure of
![]() $\mathbf {x}\in X^{[d]}$
under
$\mathbf {x}\in X^{[d]}$
under
![]() $\mathcal {F}^{\hspace{2pt}[d]}$
by
$\mathcal {F}^{\hspace{2pt}[d]}$
by
 $\overline {\mathcal {F}^{\hspace{2pt}[d]}}(\mathbf {x})$
, instead of
$\overline {\mathcal {F}^{\hspace{2pt}[d]}}(\mathbf {x})$
, instead of
 $\overline {\mathcal {O}(\mathbf {x},\mathcal {F}^{\hspace{2pt}[d]})}$
. Let
$\overline {\mathcal {O}(\mathbf {x},\mathcal {F}^{\hspace{2pt}[d]})}$
. Let
 $\mathbf {Q}^{[d]}_{x}(X)=\mathbf {Q}^{[d]}(X)\cap (\{x\}\times X^{2^{d}-1})$
.
$\mathbf {Q}^{[d]}_{x}(X)=\mathbf {Q}^{[d]}(X)\cap (\{x\}\times X^{2^{d}-1})$
.
Theorem 2.2. [Reference Shao and Ye22]
Let
![]() $(X,T)$
be a minimal system and
$(X,T)$
be a minimal system and
![]() $d\in \mathbb {N}$
. Then:
$d\in \mathbb {N}$
. Then:
-
(1)
 $(\mathbf {Q}^{[d]}(X),\mathcal {G}^{[d]})$
is a minimal system;
$(\mathbf {Q}^{[d]}(X),\mathcal {G}^{[d]})$
is a minimal system; -
(2)
 $(\overline {\mathcal {F}^{\hspace{2pt}[d]}}(x^{[d]}),\mathcal {F}^{\hspace{2pt}[d]})$
is minimal for all
$(\overline {\mathcal {F}^{\hspace{2pt}[d]}}(x^{[d]}),\mathcal {F}^{\hspace{2pt}[d]})$
is minimal for all
 $x\in X$
;
$x\in X$
; -
(3)
 $\overline {\mathcal {F}^{\hspace{2pt}[d]}}(x^{[d]})$
is the unique
$\overline {\mathcal {F}^{\hspace{2pt}[d]}}(x^{[d]})$
is the unique
 $\mathcal {F}^{\hspace{2pt}[d]}$
-minimal subset in
$\mathcal {F}^{\hspace{2pt}[d]}$
-minimal subset in
 $\mathbf {Q}^{[d]}_{x}(X)$
for all
$\mathbf {Q}^{[d]}_{x}(X)$
for all
 $x\in X$
.
$x\in X$
.
2.4 Proximality and regional proximality of higher order
Let
![]() $(X,T)$
be a dynamical system. A pair
$(X,T)$
be a dynamical system. A pair
![]() $(x,y)\in X\times X$
is proximal if
$(x,y)\in X\times X$
is proximal if
 $$ \begin{align*} \inf_{n\in \mathbb{Z}}\rho(T^{n}x,T^{n}y)=0, \end{align*} $$
$$ \begin{align*} \inf_{n\in \mathbb{Z}}\rho(T^{n}x,T^{n}y)=0, \end{align*} $$
and distal if it is not proximal. Denote by
![]() $\mathbf {P}(X)$
the set of all proximal pairs of X. The dynamical system
$\mathbf {P}(X)$
the set of all proximal pairs of X. The dynamical system
![]() $(X,T)$
is distal if
$(X,T)$
is distal if
![]() $(x,y)$
is a distal pair whenever
$(x,y)$
is a distal pair whenever
![]() $x,y\in X$
are distinct.
$x,y\in X$
are distinct.
An extension
![]() $\pi :(X,T)\to (Y,T)$
is proximal if
$\pi :(X,T)\to (Y,T)$
is proximal if
![]() $R_{\pi }\subset \mathbf {P}(X)$
.
$R_{\pi }\subset \mathbf {P}(X)$
.
Definition 2.3. Let
![]() $(X,T)$
be a dynamical system and
$(X,T)$
be a dynamical system and
![]() $d\in \mathbb {N}$
. The regionally proximal relation of order d is the relation
$d\in \mathbb {N}$
. The regionally proximal relation of order d is the relation
![]() $\textbf {RP}^{[d]} (X)$
defined by:
$\textbf {RP}^{[d]} (X)$
defined by:
![]() $(x,y)\in \textbf {RP}^{[d]}(X)$
if and only if for every
$(x,y)\in \textbf {RP}^{[d]}(X)$
if and only if for every
![]() $\delta>0$
, there exist
$\delta>0$
, there exist
![]() $x^{\prime },y^{\prime }\in X$
and
$x^{\prime },y^{\prime }\in X$
and
![]() $\vec {n}\in \mathbb {N}^{d}$
such that
$\vec {n}\in \mathbb {N}^{d}$
such that
![]() $\rho (x,x^{\prime })<\delta ,\rho (y,y^{\prime })<\delta $
, and
$\rho (x,x^{\prime })<\delta ,\rho (y,y^{\prime })<\delta $
, and
 $$ \begin{align*} \rho( T^{\vec{n}\cdot\epsilon} x^{\prime}, T^{\vec{n}\cdot\epsilon} y^{\prime})<\delta\quad\text{for all } \epsilon\in \{0,1\}^{d}\backslash\{ \vec{0}\}. \end{align*} $$
$$ \begin{align*} \rho( T^{\vec{n}\cdot\epsilon} x^{\prime}, T^{\vec{n}\cdot\epsilon} y^{\prime})<\delta\quad\text{for all } \epsilon\in \{0,1\}^{d}\backslash\{ \vec{0}\}. \end{align*} $$
We say that
![]() $(X,T)$
is a system of order d if
$(X,T)$
is a system of order d if
![]() $\mathbf {RP}^{[d]}(X)$
is trivial.
$\mathbf {RP}^{[d]}(X)$
is trivial.
It follows from [Reference Shao and Ye22, Lemma 3.5] that
Theorem 2.4. [Reference Shao and Ye22]
Let
![]() $(X,T)$
be a minimal system and
$(X,T)$
be a minimal system and
![]() $d\in \mathbb {N}$
. Then:
$d\in \mathbb {N}$
. Then:
-
(1)
 $(x,y)\in \mathbf {RP}^{[d]}(X)$
if and only if
$(x,y)\in \mathbf {RP}^{[d]}(X)$
if and only if
 $(x,y,\ldots ,y)=(x,y^{[d+1]}_{*})\in \mathbf {Q}^{[d+1]}(X)$
if and only if
$(x,y,\ldots ,y)=(x,y^{[d+1]}_{*})\in \mathbf {Q}^{[d+1]}(X)$
if and only if
 $(x,y,\ldots ,y)=(x,y^{[d+1]}_{*})\in \overline {\mathcal {F}^{[d+1]}}(x^{[d+1]})$
;
$(x,y,\ldots ,y)=(x,y^{[d+1]}_{*})\in \overline {\mathcal {F}^{[d+1]}}(x^{[d+1]})$
; -
(2)
 $\mathbf {RP}^{[d]}(X)$
is an equivalence relation.
$\mathbf {RP}^{[d]}(X)$
is an equivalence relation.
The regionally proximal relation of order d allows us to construct the maximal factor of order d of a minimal system. That is, any factor of order d factorizes through this system.
Theorem 2.5. [Reference Shao and Ye22]
Let
![]() $\pi :(X,T)\to (Y,T)$
be the factor map between minimal systems and
$\pi :(X,T)\to (Y,T)$
be the factor map between minimal systems and
![]() $d\in \mathbb {N}$
. Then:
$d\in \mathbb {N}$
. Then:
-
(1)
 $(\pi \times \pi ) \mathbf {RP}^{[d]}(X)=\mathbf {RP}^{[d]}(Y)$
;
$(\pi \times \pi ) \mathbf {RP}^{[d]}(X)=\mathbf {RP}^{[d]}(Y)$
; -
(2)
 $(Y,T)$
is a system of order d if and only if
$(Y,T)$
is a system of order d if and only if
 $\mathbf {RP}^{[d]}(X)\subset R_{\pi }$
.
$\mathbf {RP}^{[d]}(X)\subset R_{\pi }$
.
In particular, the quotient of
![]() $(X,T)$
under
$(X,T)$
under
![]() $\mathbf {RP}^{[d]}(X)$
is the maximal factor of order d of X.
$\mathbf {RP}^{[d]}(X)$
is the maximal factor of order d of X.
It follows that for any minimal system
![]() $(X,T)$
,
$(X,T)$
,
 $$ \begin{align*} \mathbf{RP}^{[\infty]}(X)=\bigcap_{d\geq1}\mathbf{RP}^{[d]}(X) \end{align*} $$
$$ \begin{align*} \mathbf{RP}^{[\infty]}(X)=\bigcap_{d\geq1}\mathbf{RP}^{[d]}(X) \end{align*} $$
is a closed invariant equivalence relation.
We now formulate the definition of systems of order
![]() $\infty $
.
$\infty $
.
Definition 2.6. A minimal system
![]() $(X,T)$
is a system of order
$(X,T)$
is a system of order
![]() $\infty $
if the equivalence relation
$\infty $
if the equivalence relation
![]() $\mathbf {RP}^{[\infty ]}(X)$
is trivial, that is, coincides with the diagonal.
$\mathbf {RP}^{[\infty ]}(X)$
is trivial, that is, coincides with the diagonal.
Let
![]() $(X,T)$
be a minimal system and
$(X,T)$
be a minimal system and
![]() $d\in \mathbb {N}\cup \{\infty \}$
. Set
$d\in \mathbb {N}\cup \{\infty \}$
. Set
Definition 2.7. Let
![]() $(X,T)$
be a minimal system and
$(X,T)$
be a minimal system and
![]() $d\in \mathbb {N}\cup \{\infty \}$
. A point
$d\in \mathbb {N}\cup \{\infty \}$
. A point
![]() $x\in X$
is called a d-step almost automorphic point if
$x\in X$
is called a d-step almost automorphic point if
![]() $\mathbf {RP}^{[d]}[x] = \{x\}.$
$\mathbf {RP}^{[d]}[x] = \{x\}.$
A minimal system
![]() $(X,T)$
is called d-step almost automorphic if it has a d-step almost automorphic point.
$(X,T)$
is called d-step almost automorphic if it has a d-step almost automorphic point.
Almost automorphic systems of higher order were studied systematically in [Reference Huang, Shao and Ye18]. Inparticular, we have the following proposition.
Proposition 2.8. [Reference Huang, Shao and Ye18, Theorem 8.13]
Let
![]() $(X,T)$
be a minimal system. Then
$(X,T)$
be a minimal system. Then
![]() $(X,T)$
is a d-step almost automorphic system for some
$(X,T)$
is a d-step almost automorphic system for some
![]() $d\in \mathbb {N}\cup \{\infty \}$
if and only if it is an almost one-to-one extension of its maximal factor of order d.
$d\in \mathbb {N}\cup \{\infty \}$
if and only if it is an almost one-to-one extension of its maximal factor of order d.
2.5 Independence
The notion of independence was firstly introduced and studied in[Reference Kerr and Li20]. It corresponds to a modification of the notion of interpolating set studied in[Reference Glasner and Weiss10,Reference Huang and Ye19].
Definition 2.9. Let
![]() $(X,T)$
be a dynamical system. Given a tuple
$(X,T)$
be a dynamical system. Given a tuple
![]() $\mathcal {A} = (U_{0},U_{1},\ldots ,U_{k} )$
of subsets of X, we say that a subset
$\mathcal {A} = (U_{0},U_{1},\ldots ,U_{k} )$
of subsets of X, we say that a subset
![]() $F\subset \mathbb {Z}$
is an independence set for
$F\subset \mathbb {Z}$
is an independence set for
![]() $\mathcal {A}$
if for any non-empty finite subset
$\mathcal {A}$
if for any non-empty finite subset
![]() $ J\subset F$
and any
$ J\subset F$
and any
![]() $s=(s(j):j\in J)\in \{0,1,\ldots ,k\}^{J}$
we have
$s=(s(j):j\in J)\in \{0,1,\ldots ,k\}^{J}$
we have
 $$ \begin{align*} \bigcap_{j\in J}T^{-j}U_{s(j)}\neq \emptyset. \end{align*} $$
$$ \begin{align*} \bigcap_{j\in J}T^{-j}U_{s(j)}\neq \emptyset. \end{align*} $$
We shall denote the collection of all independence sets for
![]() $\mathcal {A}$
by
$\mathcal {A}$
by
![]() $\mathrm {Ind}(U_{0},U_{1} ,\ldots ,U_{k} )$
.
$\mathrm {Ind}(U_{0},U_{1} ,\ldots ,U_{k} )$
.
We now define
![]() $\text {IN}^{[d]}$
-pairs.
$\text {IN}^{[d]}$
-pairs.
Definition 2.10. Let
![]() $(X,T)$
be a dynamical system and
$(X,T)$
be a dynamical system and
![]() $d\in \mathbb {N}$
. A pair
$d\in \mathbb {N}$
. A pair
![]() $(x_{0} ,x_{1} ) \in X \times X$
is called an
$(x_{0} ,x_{1} ) \in X \times X$
is called an
![]() $\text {IN}^{[d]}$
-pair if for any
$\text {IN}^{[d]}$
-pair if for any
![]() $k\in \mathbb {N}$
and any neighborhoods
$k\in \mathbb {N}$
and any neighborhoods
![]() $U_{0},U_{1}$
of
$U_{0},U_{1}$
of
![]() $x_{0}$
and
$x_{0}$
and
![]() $x_{1}$
respectively, there exist different
$x_{1}$
respectively, there exist different
 $(p_{1}^{(i)},\ldots ,p_{d}^{(i)})\in \mathbb {N}^{d}$
,
$(p_{1}^{(i)},\ldots ,p_{d}^{(i)})\in \mathbb {N}^{d}$
,
![]() $1\leq i\leq k$
, such that
$1\leq i\leq k$
, such that
 $$ \begin{align*} \bigcup_{i=1}^{k}\{ p_{1}^{(i)}\epsilon(1)+\cdots+p_{d}^{(i)}\epsilon(d):\epsilon\in \{0,1\}^{d}\}\backslash \{0\}\in \mathrm{Ind}(U_{0},U_{1}). \end{align*} $$
$$ \begin{align*} \bigcup_{i=1}^{k}\{ p_{1}^{(i)}\epsilon(1)+\cdots+p_{d}^{(i)}\epsilon(d):\epsilon\in \{0,1\}^{d}\}\backslash \{0\}\in \mathrm{Ind}(U_{0},U_{1}). \end{align*} $$
Denote by
![]() $\mathrm {IN}^{[d]} (X)$
the set of all
$\mathrm {IN}^{[d]} (X)$
the set of all
![]() $\mathrm {IN}^{[d]}$
-pairs of
$\mathrm {IN}^{[d]}$
-pairs of
![]() $(X,T)$
.
$(X,T)$
.
Remark 2.11. It is easy to see that for a dynamical system, any
![]() $\mathrm {IN}^{[d]}$
-pair is regionally proximal of order d, sequence entropy pairs coincide with
$\mathrm {IN}^{[d]}$
-pair is regionally proximal of order d, sequence entropy pairs coincide with
![]() $\mathrm {IN}^{[1]}$
-pairs and any
$\mathrm {IN}^{[1]}$
-pairs and any
![]() $\mathrm {Ind}_{fip}$
-pair is an
$\mathrm {Ind}_{fip}$
-pair is an
![]() $\mathrm {IN}^{[d]}$
-pair for every
$\mathrm {IN}^{[d]}$
-pair for every
![]() $d\in \mathbb {N}$
.
$d\in \mathbb {N}$
.
2.6 A criterion for being an
 $\mathrm {IN}^{[d]}$
-pair
$\mathrm {IN}^{[d]}$
-pair
We characterize
![]() $\mathrm {IN}^{[d]}$
-pairs using dynamical cubespaces.
$\mathrm {IN}^{[d]}$
-pairs using dynamical cubespaces.
Let
![]() $d,k\in \mathbb {N}$
. We fix an enumeration
$d,k\in \mathbb {N}$
. We fix an enumeration
![]() $\omega _{1},\ldots ,\omega _{2^{d}-1}$
of all elements of
$\omega _{1},\ldots ,\omega _{2^{d}-1}$
of all elements of
 $\{0,1\}^{d}\backslash \{\vec {0}\}$
. For
$\{0,1\}^{d}\backslash \{\vec {0}\}$
. For
![]() $1\leq i\leq k$
,
$1\leq i\leq k$
,
![]() $1\leq j\leq 2^{d}-1$
, let
$1\leq j\leq 2^{d}-1$
, let
 $$ \begin{align*} F_{ij}= \left\{ \epsilon\in \{0,1\}^{k(2^{d}+d)}: \begin{gathered} \epsilon({k(i-1)+j})=1, \text{ and } \\ \epsilon({k2^{d}+d(i-1)+s})=\omega_{j}(s),\;1\leq s\leq d \end{gathered} \right\}. \end{align*} $$
$$ \begin{align*} F_{ij}= \left\{ \epsilon\in \{0,1\}^{k(2^{d}+d)}: \begin{gathered} \epsilon({k(i-1)+j})=1, \text{ and } \\ \epsilon({k2^{d}+d(i-1)+s})=\omega_{j}(s),\;1\leq s\leq d \end{gathered} \right\}. \end{align*} $$
For
 $t_{j}\in \{0,1\}^{2^{d}-1},1\leq j\leq k$
, let
$t_{j}\in \{0,1\}^{2^{d}-1},1\leq j\leq k$
, let
 $\hat {\theta }=\hat {\theta }(t_{1},\ldots ,t_{k})\in \{0,1\}^{k(2^{d}+d)}$
such that
$\hat {\theta }=\hat {\theta }(t_{1},\ldots ,t_{k})\in \{0,1\}^{k(2^{d}+d)}$
such that
 $$ \begin{align*} \hat{\theta}(n)= \begin{cases} t_{i}(j), &n=k(i-1)+j,\;1\leq i\leq k,1\leq j\leq 2^{d}-1, \\ 0& \mathrm{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \hat{\theta}(n)= \begin{cases} t_{i}(j), &n=k(i-1)+j,\;1\leq i\leq k,1\leq j\leq 2^{d}-1, \\ 0& \mathrm{otherwise}. \end{cases} \end{align*} $$
For
![]() $1\leq a\leq k,1\leq b\leq 2^{d}-1$
, let
$1\leq a\leq k,1\leq b\leq 2^{d}-1$
, let
 $\theta =\theta (t_{1},\ldots ,t_{k},a,b)\in \{0,1\}^{k(2^{d}+d)}$
such that
$\theta =\theta (t_{1},\ldots ,t_{k},a,b)\in \{0,1\}^{k(2^{d}+d)}$
such that
 $$ \begin{align*} \theta(n)= \begin{cases} t_{i}(j), &n=k(i-1)+j,\;1\leq i\leq k,1\leq j\leq 2^{d}-1, \\ \omega_{b}(s), & n=k2^{d}+d(a-1)+s, \;1\leq s\leq d,\\ 0& \mathrm{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \theta(n)= \begin{cases} t_{i}(j), &n=k(i-1)+j,\;1\leq i\leq k,1\leq j\leq 2^{d}-1, \\ \omega_{b}(s), & n=k2^{d}+d(a-1)+s, \;1\leq s\leq d,\\ 0& \mathrm{otherwise}. \end{cases} \end{align*} $$
Let
 $$ \begin{align*} \Theta_{k,d}= \left\{\theta=\theta(t_{1},\ldots,t_{k},a,b): \begin{gathered} 1\leq a\leq k,1\leq b\leq 2^{d}-1, \\ t_{j}\in \{0,1\}^{2^{d}-1},1\leq j\leq k \end{gathered} \right\}. \end{align*} $$
$$ \begin{align*} \Theta_{k,d}= \left\{\theta=\theta(t_{1},\ldots,t_{k},a,b): \begin{gathered} 1\leq a\leq k,1\leq b\leq 2^{d}-1, \\ t_{j}\in \{0,1\}^{2^{d}-1},1\leq j\leq k \end{gathered} \right\}. \end{align*} $$
It is easy to check that
![]() $\theta =\theta (t_{1},\ldots ,t_{k},a,b)\in F_{ij}$
if and only if
$\theta =\theta (t_{1},\ldots ,t_{k},a,b)\in F_{ij}$
if and only if
![]() $a=i,b=j$
and
$a=i,b=j$
and
![]() $t_{a}(b)=1$
.
$t_{a}(b)=1$
.
Lemma 2.12. Let
![]() $(X,T)$
be a minimal system and
$(X,T)$
be a minimal system and
![]() $d\in \mathbb {N},x_{0},x_{1}\in X$
with
$d\in \mathbb {N},x_{0},x_{1}\in X$
with
![]() $x_{0}\neq x_{1}$
. For any
$x_{0}\neq x_{1}$
. For any
![]() $k\in \mathbb {N}$
, if there is some
$k\in \mathbb {N}$
, if there is some
 $\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
$\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
![]() $\mathbf {x}(\theta )=x_{t_{a}(b)}$
for any
$\mathbf {x}(\theta )=x_{t_{a}(b)}$
for any
![]() $\theta \in \Theta _{k,d}$
, then
$\theta \in \Theta _{k,d}$
, then
![]() $(x_{0},x_{1})$
is an
$(x_{0},x_{1})$
is an
![]() $\mathrm {IN}^{[d]}$
-pair.
$\mathrm {IN}^{[d]}$
-pair.
Proof. For
![]() $i=0,1$
, let
$i=0,1$
, let
![]() $U_{i}$
be a neighborhood of
$U_{i}$
be a neighborhood of
![]() $x_{i}$
and choose
$x_{i}$
and choose
![]() $\delta>0$
with
$\delta>0$
with
![]() $B(x_{i},\delta )=\{y\in X\colon \rho (x_{i},y)<\delta \}\subset U_{i}$
.
$B(x_{i},\delta )=\{y\in X\colon \rho (x_{i},y)<\delta \}\subset U_{i}$
.
Let
![]() $k\in \mathbb {N}$
and let
$k\in \mathbb {N}$
and let
 $\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
$\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
![]() $\mathbf {x}(\theta )=x_{t_{a}(b)}$
for any
$\mathbf {x}(\theta )=x_{t_{a}(b)}$
for any
![]() $\theta \in \Theta _{k,d}$
.
$\theta \in \Theta _{k,d}$
.
By Theorem 2.2, there exist
 $$ \begin{align*}\vec{n}=(n_{1},\ldots,n_{k2^{d}},m_{1}^{(1)}, \ldots,m_{d}^{(1)},\ldots,m_{1}^{(k)},\ldots,m_{d}^{(k)})\in \mathbb{N}^{k(2^{d}+d)}, \end{align*} $$
$$ \begin{align*}\vec{n}=(n_{1},\ldots,n_{k2^{d}},m_{1}^{(1)}, \ldots,m_{d}^{(1)},\ldots,m_{1}^{(k)},\ldots,m_{d}^{(k)})\in \mathbb{N}^{k(2^{d}+d)}, \end{align*} $$
![]() $n\in \mathbb {N} $
and
$n\in \mathbb {N} $
and
![]() $x\in X$
such that
$x\in X$
such that
 $$ \begin{align} \rho(T^{n+\vec{n}\cdot \epsilon}x,\mathbf{x}(\epsilon)) <\delta\quad\text{for all } \epsilon\in \{0,1\}^{k(2^{d}+d)}. \end{align} $$
$$ \begin{align} \rho(T^{n+\vec{n}\cdot \epsilon}x,\mathbf{x}(\epsilon)) <\delta\quad\text{for all } \epsilon\in \{0,1\}^{k(2^{d}+d)}. \end{align} $$
For
![]() $1\leq i\leq k$
, set
$1\leq i\leq k$
, set
 $\vec {m}_{i}=(m_{1}^{(i)},\ldots ,m_{d}^{(i)})$
. Recall that
$\vec {m}_{i}=(m_{1}^{(i)},\ldots ,m_{d}^{(i)})$
. Recall that
![]() $\mathbf {x}(\theta )=x_{t_{a}(b)}$
and
$\mathbf {x}(\theta )=x_{t_{a}(b)}$
and
![]() $\vec {n}\cdot \theta = \vec {n}\cdot \hat {\theta }+\vec {m}_{a}\cdot \omega _{b}$
. Thus by (3) we get that
$\vec {n}\cdot \theta = \vec {n}\cdot \hat {\theta }+\vec {m}_{a}\cdot \omega _{b}$
. Thus by (3) we get that
 $$ \begin{align*} T^{n+ \vec{n}\cdot\hat{\theta}}x\in T^{-\vec{m}_{a}\cdot \omega_{b}} U_{t_{a}(b)}. \end{align*} $$
$$ \begin{align*} T^{n+ \vec{n}\cdot\hat{\theta}}x\in T^{-\vec{m}_{a}\cdot \omega_{b}} U_{t_{a}(b)}. \end{align*} $$
Moreover,
 $$ \begin{align*} T^{ n+\vec{n}\cdot\hat{\theta}}x\in \bigcap_{i=1}^{k} \bigcap_{j=1}^{2^{d}-1} T^{-\vec{m}_{i}\cdot \omega_{j}} U_{t_{i}(j)}, \end{align*} $$
$$ \begin{align*} T^{ n+\vec{n}\cdot\hat{\theta}}x\in \bigcap_{i=1}^{k} \bigcap_{j=1}^{2^{d}-1} T^{-\vec{m}_{i}\cdot \omega_{j}} U_{t_{i}(j)}, \end{align*} $$
which implies that
 $$ \begin{align*} \bigcup_{i=1}^{k}\{ \vec{m}_{i}\cdot \epsilon:\epsilon\in \{0,1\}^{d}\}\backslash \{0\}\in \mathrm{ Ind}(U_{0},U_{1}). \end{align*} $$
$$ \begin{align*} \bigcup_{i=1}^{k}\{ \vec{m}_{i}\cdot \epsilon:\epsilon\in \{0,1\}^{d}\}\backslash \{0\}\in \mathrm{ Ind}(U_{0},U_{1}). \end{align*} $$
As k is arbitrary, we conclude that
![]() $(x_{0},x_{1})$
is an
$(x_{0},x_{1})$
is an
![]() $\mathrm {IN}^{[d]}$
-pair.
$\mathrm {IN}^{[d]}$
-pair.
2.7 Nilpotent groups, nilmanifolds and nilsystems
Let L be a group. For
![]() $g,h\in L$
, we write
$g,h\in L$
, we write
![]() $[g,h]=ghg^{-1}h^{-1}$
for the commutator of g and h. We write
$[g,h]=ghg^{-1}h^{-1}$
for the commutator of g and h. We write
![]() $[A,B]$
for the subgroup spanned by
$[A,B]$
for the subgroup spanned by
![]() $\{[a,b]:a\in A,b\in B\}$
. The commutator subgroups
$\{[a,b]:a\in A,b\in B\}$
. The commutator subgroups
![]() $L_{j}$
,
$L_{j}$
,
![]() $j\geq 1$
, are defined inductively by setting
$j\geq 1$
, are defined inductively by setting
![]() $L_{1}=L$
and
$L_{1}=L$
and
![]() $L_{j+1}=[L_{j},L]$
. Let
$L_{j+1}=[L_{j},L]$
. Let
![]() $k\geq 1$
be an integer. We say that L is k-step nilpotent if
$k\geq 1$
be an integer. We say that L is k-step nilpotent if
![]() $L_{k+1}$
is the trivial subgroup.
$L_{k+1}$
is the trivial subgroup.
Let L be a k-step nilpotent Lie group and
![]() $\Gamma $
a discrete cocompact subgroup of L. The compact manifold
$\Gamma $
a discrete cocompact subgroup of L. The compact manifold
![]() $X=L/\Gamma $
is called a k-step nilmanifold. The group L acts on X by left translations, and we write this action as
$X=L/\Gamma $
is called a k-step nilmanifold. The group L acts on X by left translations, and we write this action as
![]() $(g,x)\mapsto gx$
. Let
$(g,x)\mapsto gx$
. Let
![]() $\tau \in L$
and T be the transformation
$\tau \in L$
and T be the transformation
![]() $x\mapsto \tau x$
of X. Then
$x\mapsto \tau x$
of X. Then
![]() $(X,T)$
is called a k-step nilsystem.
$(X,T)$
is called a k-step nilsystem.
We also make use of inverse limits of nilsystems, and so we recall the definition of an inverse limit of systems (restricting ourselves to the case of sequential inverse limits). If
![]() $\{(X_{i},T_{i})\}_{i\in \mathbb {N}}$
are systems with
$\{(X_{i},T_{i})\}_{i\in \mathbb {N}}$
are systems with
![]() $\text {diam}(X_{i})\leq 1$
and
$\text {diam}(X_{i})\leq 1$
and
![]() $\phi _{i}:X_{i+1}\to X_{i}$
are factor maps, the inverse limit of the systems is defined to be the compact subset of
$\phi _{i}:X_{i+1}\to X_{i}$
are factor maps, the inverse limit of the systems is defined to be the compact subset of
![]() $\prod _{i\in \mathbb {N}}X_{i}$
given by
$\prod _{i\in \mathbb {N}}X_{i}$
given by
![]() $\{(x_{i})_{i\in \mathbb {N}}:\phi _{i}(x_{i+1})=x_{i},i\in \mathbb {N}\}$
, which is denoted by
$\{(x_{i})_{i\in \mathbb {N}}:\phi _{i}(x_{i+1})=x_{i},i\in \mathbb {N}\}$
, which is denoted by
![]() $\lim \nolimits _{\longleftarrow }\{ X_{i}\}_{i\in \mathbb {N}}$
. It is a compact metric space endowed with the distance
$\lim \nolimits _{\longleftarrow }\{ X_{i}\}_{i\in \mathbb {N}}$
. It is a compact metric space endowed with the distance
![]() $\rho (x,y)=\sum _{i\in \mathbb {N}}1/ 2^{i} \rho _{i}(x_{i},y_{i})$
. We note that the maps
$\rho (x,y)=\sum _{i\in \mathbb {N}}1/ 2^{i} \rho _{i}(x_{i},y_{i})$
. We note that the maps
![]() $\{T_{i}\}$
induce a transformation T on the inverse limit.
$\{T_{i}\}$
induce a transformation T on the inverse limit.
The following structure theorem characterizes inverse limits of nilsystems using dynamical cubespaces.
Theorem 2.13. (Host, Kra and Maass [Reference Host, Kra and Maass13, Theorem 1.2])
Assume that
![]() $(X,T)$
is a minimal system and let
$(X,T)$
is a minimal system and let
![]() $d\geq 2$
be an integer. The following properties are equivalent.
$d\geq 2$
be an integer. The following properties are equivalent.
-
(1) If
 $\mathbf {x},\mathbf {y}\in \mathbf {Q}^{[d]}(X)$
have
$\mathbf {x},\mathbf {y}\in \mathbf {Q}^{[d]}(X)$
have
 $2^{d}-1$
coordinates in common, then
$2^{d}-1$
coordinates in common, then
 $\mathbf {x}=\mathbf {y}$
.
$\mathbf {x}=\mathbf {y}$
. -
(2) If
 $x,y\in X$
are such that
$x,y\in X$
are such that
 $(x,y,\ldots ,y)\in \mathbf {Q}^{[d]}(X)$
, then
$(x,y,\ldots ,y)\in \mathbf {Q}^{[d]}(X)$
, then
 $x=y$
.
$x=y$
. -
(3) The system
 $(X,T)$
is an inverse limit of
$(X,T)$
is an inverse limit of
 $(d-1)$
-step minimal nilsystems.
$(d-1)$
-step minimal nilsystems.
This result shows that a minimal system is a system of order d if and only if it is an inverse limit of minimal d-step nilsystems.
Theorem 2.14. [Reference Dong, Donoso, Maass, Shao and Ye4, Theorem 3.6]
A minimal system
![]() $(X,T)$
is a system of order
$(X,T)$
is a system of order
![]() $\infty $
if and only if it is an inverse limit of minimal nilsystems.
$\infty $
if and only if it is an inverse limit of minimal nilsystems.
3 k-regionally proximal relation of higher order
In this section we discuss the k-regionally proximal relation of higher order.
Definition 3.1. Let
![]() $(X,T)$
be a dynamical system and
$(X,T)$
be a dynamical system and
![]() $d\in \mathbb {N}$
. For
$d\in \mathbb {N}$
. For
![]() $k\geq 2$
, a k-tuple
$k\geq 2$
, a k-tuple
![]() $(x_{1},\ldots ,x_{k})\in X^{k}$
is said to be k-regionally proximal of order d if for any
$(x_{1},\ldots ,x_{k})\in X^{k}$
is said to be k-regionally proximal of order d if for any
![]() $\delta>0$
, there exist
$\delta>0$
, there exist
![]() $x_{i}^{\prime }\in X$
,
$x_{i}^{\prime }\in X$
,
![]() $1\leq i\leq k$
, and
$1\leq i\leq k$
, and
![]() $\vec {n}\in \mathbb {N}^{d}$
such that
$\vec {n}\in \mathbb {N}^{d}$
such that
![]() $\rho (x_{i},x_{i}^{\prime })<\delta $
,
$\rho (x_{i},x_{i}^{\prime })<\delta $
,
![]() $1\leq i\leq k$
, and
$1\leq i\leq k$
, and
 $$ \begin{align*} \max_{1\leq i<j\leq k} \rho(T^{\vec{n}\cdot \epsilon}x_{i}^{\prime},T^{\vec{n}\cdot \epsilon}x_{j}^{\prime})<\delta\quad\text{for all } \epsilon\in \{0,1\}^{d}\backslash \{\vec{0}\}. \end{align*} $$
$$ \begin{align*} \max_{1\leq i<j\leq k} \rho(T^{\vec{n}\cdot \epsilon}x_{i}^{\prime},T^{\vec{n}\cdot \epsilon}x_{j}^{\prime})<\delta\quad\text{for all } \epsilon\in \{0,1\}^{d}\backslash \{\vec{0}\}. \end{align*} $$
In the proof of the following theorem, we will use enveloping semigroups in abstract topological dynamical systems. For more details, see Appendix A.
Theorem 3.2. Let
![]() $(X,T)$
be a minimal system and let
$(X,T)$
be a minimal system and let
![]() $d,k\in \mathbb {N}$
with
$d,k\in \mathbb {N}$
with
![]() $k\geq 2$
. For points
$k\geq 2$
. For points
![]() $x,x_{i}\in X$
,
$x,x_{i}\in X$
,
![]() $1\leq i\leq k$
, if
$1\leq i\leq k$
, if
![]() $(x,x_{i})$
is regionally proximal of order d for all i, then
$(x,x_{i})$
is regionally proximal of order d for all i, then
![]() $(x_{1},\ldots ,x_{k})$
is k-regionally proximal of order d.
$(x_{1},\ldots ,x_{k})$
is k-regionally proximal of order d.
Proof. Let
![]() $d,k\in \mathbb {N}$
with
$d,k\in \mathbb {N}$
with
![]() $k\geq 2$
. Fix
$k\geq 2$
. Fix
![]() $x\in X$
and let
$x\in X$
and let
![]() $x_{i}\in \mathbf {RP}^{[d]}[x]$
,
$x_{i}\in \mathbf {RP}^{[d]}[x]$
,
![]() $1\leq i\leq k$
.
$1\leq i\leq k$
.
We will show that
![]() $(x_{1},\ldots ,x_{k})$
is k-regionally proximal of order d.
$(x_{1},\ldots ,x_{k})$
is k-regionally proximal of order d.
Claim 1. Let
![]() $y\in \mathbf {RP}^{[d]}[x]$
and let
$y\in \mathbf {RP}^{[d]}[x]$
and let
![]() $\mathbf {y}\in X^{[d+1]}$
such that
$\mathbf {y}\in X^{[d+1]}$
such that
 $$ \begin{align*} \mathbf{y}(\epsilon)= \begin{cases} y, & \epsilon=(0,\ldots,0,1),\\ x & \mbox{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \mathbf{y}(\epsilon)= \begin{cases} y, & \epsilon=(0,\ldots,0,1),\\ x & \mbox{otherwise.} \end{cases} \end{align*} $$
Then
 $\mathbf {y} \in \overline {\mathcal {F}^{[d+1]}}(x^{[d+1]})$
.
$\mathbf {y} \in \overline {\mathcal {F}^{[d+1]}}(x^{[d+1]})$
.
Proof of Claim 1
As
![]() $(x,y)\in \mathbf {RP}^{[d]}(X)\subset \mathbf {RP}^{[d-1]}(X)$
, we have
$(x,y)\in \mathbf {RP}^{[d]}(X)\subset \mathbf {RP}^{[d-1]}(X)$
, we have
 $(x,y^{[d]}_{*})\in \overline {\mathcal {F}^{\hspace{2pt}[d]}}(x^{[d]})$
by Theorem 2.4. Notice that
$(x,y^{[d]}_{*})\in \overline {\mathcal {F}^{\hspace{2pt}[d]}}(x^{[d]})$
by Theorem 2.4. Notice that
 $(\overline {\mathcal {F}^{\hspace{2pt}[d]}}(x^{[d]}),\mathcal {F}^{\hspace{2pt}[d]})$
is minimal by Theorem 2.2. Then there is some sequence
$(\overline {\mathcal {F}^{\hspace{2pt}[d]}}(x^{[d]}),\mathcal {F}^{\hspace{2pt}[d]})$
is minimal by Theorem 2.2. Then there is some sequence
 $\{\vec {n}_{j}\}_{j\in \mathbb {N}}\subset \mathbb {Z}^{d}$
such that
$\{\vec {n}_{j}\}_{j\in \mathbb {N}}\subset \mathbb {Z}^{d}$
such that
 $$ \begin{align} (T^{\vec{n}_{j}\cdot \epsilon}:\epsilon\in \{0,1\}^{d})(x,y^{[d]}_{*})\to x^{[d]}, \end{align} $$
$$ \begin{align} (T^{\vec{n}_{j}\cdot \epsilon}:\epsilon\in \{0,1\}^{d})(x,y^{[d]}_{*})\to x^{[d]}, \end{align} $$
as
![]() $j\to \infty $
. Let
$j\to \infty $
. Let
![]() $\sigma $
be the map from
$\sigma $
be the map from
![]() $\mathbb {Z}^{d}$
to
$\mathbb {Z}^{d}$
to
![]() $\mathbb {Z}^{d+1}$
such that
$\mathbb {Z}^{d+1}$
such that
Again by Theorem 2.4,
 $(x,y^{[d+1]}_{*})\in \overline {\mathcal {F}^{[d+1]}}(x^{[d+1]})$
. Then by (4) we have
$(x,y^{[d+1]}_{*})\in \overline {\mathcal {F}^{[d+1]}}(x^{[d+1]})$
. Then by (4) we have
 $$ \begin{align*} (T^{\sigma( \vec{n}_{j})\cdot \omega}:\omega\in \{0,1\}^{d+1})(x,y^{[d+1]}_{*}) \to \mathbf{y}, \end{align*} $$
$$ \begin{align*} (T^{\sigma( \vec{n}_{j})\cdot \omega}:\omega\in \{0,1\}^{d+1})(x,y^{[d+1]}_{*}) \to \mathbf{y}, \end{align*} $$
as
![]() $j\to \infty $
, which implies that
$j\to \infty $
, which implies that
 $\mathbf {y}\in \overline {\mathcal {F}^{[d+1]}}(x^{[d+1]})$
.
$\mathbf {y}\in \overline {\mathcal {F}^{[d+1]}}(x^{[d+1]})$
.
For
![]() $1\leq i\leq k$
and
$1\leq i\leq k$
and
![]() $s=0,1$
, let
$s=0,1$
, let
 $$ \begin{align*} F_{i}^{s}=\{\epsilon\in\{0,1\}^{d+k}:\epsilon(j)=0,1\leq j\leq d,\;\epsilon(d+i)=s\}. \end{align*} $$
$$ \begin{align*} F_{i}^{s}=\{\epsilon\in\{0,1\}^{d+k}:\epsilon(j)=0,1\leq j\leq d,\;\epsilon(d+i)=s\}. \end{align*} $$
Claim 2. For every
![]() $1\leq i\leq k$
, there is
$1\leq i\leq k$
, there is
 $\mathbf {p}_{i}\in E(\overline {\mathcal {F}^{[d+k]}}(x^{[d+k]}),\mathcal {F}^{[d+k]})$
such that:
$\mathbf {p}_{i}\in E(\overline {\mathcal {F}^{[d+k]}}(x^{[d+k]}),\mathcal {F}^{[d+k]})$
such that:
-
(1)
 $\mathbf {p}_{i}(\epsilon )=\mathrm {id},\epsilon \in F_{i}^{0}$
;
$\mathbf {p}_{i}(\epsilon )=\mathrm {id},\epsilon \in F_{i}^{0}$
; -
(2)
 $\mathbf {p}_{i}(\epsilon )x=x_{i},\epsilon \in F_{i}^{1}$
;
$\mathbf {p}_{i}(\epsilon )x=x_{i},\epsilon \in F_{i}^{1}$
; -
(3)
 $\mathbf {p}_{i}(\epsilon )x=x,\epsilon \in \{0,1\}^{d+k}\backslash F_{i}^{1}$
.
$\mathbf {p}_{i}(\epsilon )x=x,\epsilon \in \{0,1\}^{d+k}\backslash F_{i}^{1}$
.
Proof of Claim 2
Let
![]() $i\in \{1,\ldots ,k\}$
and let
$i\in \{1,\ldots ,k\}$
and let
![]() $\mathbf {a}_{i}\in X^{[d+1]}$
such that
$\mathbf {a}_{i}\in X^{[d+1]}$
such that
 $$ \begin{align*} \mathbf{a}_{i}(\epsilon)= \begin{cases} x_{i}, & \epsilon=(0,\ldots,0,1),\\ x & \mbox{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \mathbf{a}_{i}(\epsilon)= \begin{cases} x_{i}, & \epsilon=(0,\ldots,0,1),\\ x & \mbox{otherwise.} \end{cases} \end{align*} $$
Then
 $\mathbf {a}_{i}\in \overline {\mathcal {F}^{[d+1]}}(x^{[d+1]})$
by Claim 1. Notice that
$\mathbf {a}_{i}\in \overline {\mathcal {F}^{[d+1]}}(x^{[d+1]})$
by Claim 1. Notice that
 $(\overline {\mathcal {F}^{[d+1]}}(x^{[d+1]}),\mathcal {F}^{[d+1]})$
is minimal. Then there is some sequence
$(\overline {\mathcal {F}^{[d+1]}}(x^{[d+1]}),\mathcal {F}^{[d+1]})$
is minimal. Then there is some sequence
 $\{\vec {n}^{(l)}=(n_{1}^{(l)},\ldots ,n_{d+1}^{(l)})\}_{l\in \mathbb {N}} \subset \mathbb {Z}^{d+1}$
such that
$\{\vec {n}^{(l)}=(n_{1}^{(l)},\ldots ,n_{d+1}^{(l)})\}_{l\in \mathbb {N}} \subset \mathbb {Z}^{d+1}$
such that
 $$ \begin{align} (T^{\vec{n}^{(l)}\cdot \epsilon}x:\epsilon\in \{0,1\}^{d+1})\to \mathbf{a}_{i}, \end{align} $$
$$ \begin{align} (T^{\vec{n}^{(l)}\cdot \epsilon}x:\epsilon\in \{0,1\}^{d+1})\to \mathbf{a}_{i}, \end{align} $$
as
![]() $ l\to \infty $
. For
$ l\to \infty $
. For
![]() $l\in \mathbb {N}$
, let
$l\in \mathbb {N}$
, let
 $\vec {m}^{(l)}=(m_{1}^{(l)},\ldots ,m_{d+k}^{(l)})\in \mathbb {Z}^{d+k}$
such that
$\vec {m}^{(l)}=(m_{1}^{(l)},\ldots ,m_{d+k}^{(l)})\in \mathbb {Z}^{d+k}$
such that
 $$ \begin{align*} m_{j}^{(l)}= \left\{ \begin{array}{ll} n_{j}^{(l)}, & j=1,\ldots,d{,} \\[3pt] n_{d+1}^{(l)}, & j=d+i{,}\\[3pt] 0& \mbox{otherwise.} \end{array} \right. \end{align*} $$
$$ \begin{align*} m_{j}^{(l)}= \left\{ \begin{array}{ll} n_{j}^{(l)}, & j=1,\ldots,d{,} \\[3pt] n_{d+1}^{(l)}, & j=d+i{,}\\[3pt] 0& \mbox{otherwise.} \end{array} \right. \end{align*} $$
Then by (5) we have that:
-
(1) for
 $\epsilon \in F_{i}^{0}$
,
$\epsilon \in F_{i}^{0}$
,
 $T^{\vec {m}^{(l)}\cdot \epsilon }=T^{0}=\mathrm {id}$
;
$T^{\vec {m}^{(l)}\cdot \epsilon }=T^{0}=\mathrm {id}$
; -
(2) for
 $\epsilon \in F_{i}^{1}$
,
$\epsilon \in F_{i}^{1}$
,
 $T^{\vec {m}^{(l)}\cdot \epsilon }x=T^{n_{d+1}^{(l)}}x\to x_{i}$
, as
$T^{\vec {m}^{(l)}\cdot \epsilon }x=T^{n_{d+1}^{(l)}}x\to x_{i}$
, as
 $l\to \infty $
;
$l\to \infty $
; -
(3) for
 $\epsilon \in \{0,1\}^{d+k}\backslash F_{i}^{1}$
,
$\epsilon \in \{0,1\}^{d+k}\backslash F_{i}^{1}$
,
 $T^{\vec {m}^{(l)}\cdot \epsilon }x= T^{\vec {n}^{(l)}\cdot \tilde {\epsilon }}x\to x$
, as
$T^{\vec {m}^{(l)}\cdot \epsilon }x= T^{\vec {n}^{(l)}\cdot \tilde {\epsilon }}x\to x$
, as
 $l\to \infty $
, where
$l\to \infty $
, where
 $\tilde {\epsilon }\in \{0,1\}^{d+1}$
with
$\tilde {\epsilon }\in \{0,1\}^{d+1}$
with
 $\tilde {\epsilon }(i)=\epsilon (i)$
,
$\tilde {\epsilon }(i)=\epsilon (i)$
,
 $1\leq i\leq d$
, and
$1\leq i\leq d$
, and
 $\tilde {\epsilon }(d+1)=\epsilon (d+i)$
.
$\tilde {\epsilon }(d+1)=\epsilon (d+i)$
.
Now assume that
 $$ \begin{align*} (T^{\vec{m}^{(l)}\cdot \epsilon}:\epsilon\in \{0,1\}^{d+k})\to \mathbf{p}_{i} \end{align*} $$
$$ \begin{align*} (T^{\vec{m}^{(l)}\cdot \epsilon}:\epsilon\in \{0,1\}^{d+k})\to \mathbf{p}_{i} \end{align*} $$
in
 $E(\overline {\mathcal {F}^{[d+k]}}(x^{[d+k]}),\mathcal {F}^{[d+k]})$
pointwise. It is easy to check that
$E(\overline {\mathcal {F}^{[d+k]}}(x^{[d+k]}),\mathcal {F}^{[d+k]})$
pointwise. It is easy to check that
![]() $\mathbf {p}_{i}$
meets the requirement.
$\mathbf {p}_{i}$
meets the requirement.
Now let
![]() $\mathbf {y}=\mathbf {p}_{k}\cdots \mathbf {p}_{1} x^{[d+k]}$
. For
$\mathbf {y}=\mathbf {p}_{k}\cdots \mathbf {p}_{1} x^{[d+k]}$
. For
![]() $1\leq i\leq k$
, let
$1\leq i\leq k$
, let
 $\omega _{i}=\min F_{i}^{1}$
and let
$\omega _{i}=\min F_{i}^{1}$
and let
 $$ \begin{align*} F=\bigg\{\epsilon\in \{0,1\}^{d+k}:\sum_{j=1}^{d}\epsilon(j)>0\bigg\}. \end{align*} $$
$$ \begin{align*} F=\bigg\{\epsilon\in \{0,1\}^{d+k}:\sum_{j=1}^{d}\epsilon(j)>0\bigg\}. \end{align*} $$
Claim 3.
 $\mathbf {y}\in \overline {\mathcal {F}^{[d+k]}}(x^{[d+k]})$
and:
$\mathbf {y}\in \overline {\mathcal {F}^{[d+k]}}(x^{[d+k]})$
and:
-
(1)
 $\mathbf {y}(\omega _{i})=x_{i},\; 1\leq i\leq k$
;
$\mathbf {y}(\omega _{i})=x_{i},\; 1\leq i\leq k$
; -
(2)
 $\mathbf {y}(\epsilon )=x,\epsilon \in F$
.
$\mathbf {y}(\epsilon )=x,\epsilon \in F$
.
Proof of Claim 3
Notice that
 $\omega _{i}\in F_{j}^{0}$
for any
$\omega _{i}\in F_{j}^{0}$
for any
![]() $i\neq j$
. Thus
$i\neq j$
. Thus
![]() $\mathbf {p}_{j}(\omega _{i})=\mathrm {id}$
by property (1) of Claim 2. By property (2) of Claim 2, we have
$\mathbf {p}_{j}(\omega _{i})=\mathrm {id}$
by property (1) of Claim 2. By property (2) of Claim 2, we have
![]() $\mathbf {p}_{i}(\omega _{i})x=x_{i}$
. This shows that
$\mathbf {p}_{i}(\omega _{i})x=x_{i}$
. This shows that
Let
![]() $\epsilon \in F$
. Then
$\epsilon \in F$
. Then
 $\epsilon \notin \bigcup _{i=1}^{k} F_{i}^{1}$
. By property (3) of Claim 2,
$\epsilon \notin \bigcup _{i=1}^{k} F_{i}^{1}$
. By property (3) of Claim 2,
![]() $\mathbf {p}_{i}(\epsilon )x=x$
for every i and thus we get that
$\mathbf {p}_{i}(\epsilon )x=x$
for every i and thus we get that
This shows Claim 3.
Fix
![]() $\delta>0$
. As
$\delta>0$
. As
 $\mathbf {y}\in \overline {\mathcal {F}^{[d+k]}}(x^{[d+k]})$
, there is some
$\mathbf {y}\in \overline {\mathcal {F}^{[d+k]}}(x^{[d+k]})$
, there is some
![]() $\vec {m}=(m_{1},\ldots ,m_{d+k})\in \mathbb {N}^{d+k}$
such that for all
$\vec {m}=(m_{1},\ldots ,m_{d+k})\in \mathbb {N}^{d+k}$
such that for all
![]() $\epsilon \in \{0,1\}^{d+k}$
,
$\epsilon \in \{0,1\}^{d+k}$
,
 $$ \begin{align} \rho(T^{\vec{m}\cdot \epsilon}x,\mathbf{y}(\epsilon))<\delta. \end{align} $$
$$ \begin{align} \rho(T^{\vec{m}\cdot \epsilon}x,\mathbf{y}(\epsilon))<\delta. \end{align} $$
Let
 $x_{i}^{\prime }=T^{\vec {m}\cdot \omega _{i}}x$
,
$x_{i}^{\prime }=T^{\vec {m}\cdot \omega _{i}}x$
,
![]() $1\leq i\leq k$
, and
$1\leq i\leq k$
, and
![]() $\vec {n}=(m_{1},\ldots ,m_{d})$
. By (6) and property (1) of Claim3, for
$\vec {n}=(m_{1},\ldots ,m_{d})$
. By (6) and property (1) of Claim3, for
![]() $1\leq i\leq k$
, we have
$1\leq i\leq k$
, we have
 $$ \begin{align*} \rho(x_{i}^{\prime},x_{i})=\rho(T^{\vec{m}\cdot \omega_{i}}x,\mathbf{y}(\omega_{i}))<\delta. \end{align*} $$
$$ \begin{align*} \rho(x_{i}^{\prime},x_{i})=\rho(T^{\vec{m}\cdot \omega_{i}}x,\mathbf{y}(\omega_{i}))<\delta. \end{align*} $$
For
 $\epsilon \in \{0,1\}^{d}\backslash \{\vec {0}\}$
, put
$\epsilon \in \{0,1\}^{d}\backslash \{\vec {0}\}$
, put
![]() $\hat {\epsilon }\in \{0,1\}^{d+k}$
such that
$\hat {\epsilon }\in \{0,1\}^{d+k}$
such that
 $$ \begin{align*} \hat{\epsilon}(j)= \begin{cases} \epsilon(j) & 1\leq j\leq d,\\ 0 & d+1\leq j\leq d+k. \end{cases} \end{align*} $$
$$ \begin{align*} \hat{\epsilon}(j)= \begin{cases} \epsilon(j) & 1\leq j\leq d,\\ 0 & d+1\leq j\leq d+k. \end{cases} \end{align*} $$
Then
![]() $\hat {\epsilon }+\omega _{i}\in F$
for
$\hat {\epsilon }+\omega _{i}\in F$
for
![]() $1\leq i\leq k$
. Moreover, we have that
$1\leq i\leq k$
. Moreover, we have that
 $$ \begin{align*} \rho(T^{\vec{n}\cdot \epsilon}x_{i}^{\prime},x)= \rho(T^{\vec{n}\cdot \epsilon+\vec{m}\cdot \omega_{i}}x,x)=\rho(T^{\vec{m}\cdot (\hat{\epsilon}+\omega_{i})}x, \mathbf{y}(\hat{\epsilon}+\omega_{i}))<\delta , \end{align*} $$
$$ \begin{align*} \rho(T^{\vec{n}\cdot \epsilon}x_{i}^{\prime},x)= \rho(T^{\vec{n}\cdot \epsilon+\vec{m}\cdot \omega_{i}}x,x)=\rho(T^{\vec{m}\cdot (\hat{\epsilon}+\omega_{i})}x, \mathbf{y}(\hat{\epsilon}+\omega_{i}))<\delta , \end{align*} $$
by (6) and property (2) of Claim 3 which implies that
![]() $(x_{1},\ldots ,x_{k})$
is k-regionally proximal of order d.
$(x_{1},\ldots ,x_{k})$
is k-regionally proximal of order d.
The proof is complete.□
4 Independence and minimal nilsystems
The main aim of this section is to study
![]() $\mathrm {IN}^{[d]}$
-pairs in minimal nilsystems. It turns out that for a minimal nilsystem, any regionally proximal of order d pair is an
$\mathrm {IN}^{[d]}$
-pairs in minimal nilsystems. It turns out that for a minimal nilsystem, any regionally proximal of order d pair is an
![]() $\mathrm {IN}^{[d]}$
-pair. We start by recalling some basic results in nilsystems. For more details and proofs, see [Reference Auslander, Green and Hahn2, Reference Parry21].
$\mathrm {IN}^{[d]}$
-pair. We start by recalling some basic results in nilsystems. For more details and proofs, see [Reference Auslander, Green and Hahn2, Reference Parry21].
If G is a nilpotent Lie group, let
![]() $G^{0}$
denote the connected component of its unit element
$G^{0}$
denote the connected component of its unit element
![]() $1_{G}$
. In the sequel,
$1_{G}$
. In the sequel,
![]() $s\geq 2$
is an integer and
$s\geq 2$
is an integer and
![]() $(X=G/\Gamma ,T)$
is a minimal s-step nilsystem. We let
$(X=G/\Gamma ,T)$
is a minimal s-step nilsystem. We let
![]() $\tau $
denote the element of G defining the transformation T. If
$\tau $
denote the element of G defining the transformation T. If
![]() $(X,T)$
is minimal, let
$(X,T)$
is minimal, let
![]() $G^{\prime }$
be the subgroup of G spanned by
$G^{\prime }$
be the subgroup of G spanned by
![]() $G^{0}$
and
$G^{0}$
and
![]() $\tau $
and let
$\tau $
and let
![]() $\Gamma ^{\prime }=\Gamma \cap G^{\prime }$
. Then we have that
$\Gamma ^{\prime }=\Gamma \cap G^{\prime }$
. Then we have that
![]() $G=G^{\prime }\Gamma $
. Thus the system
$G=G^{\prime }\Gamma $
. Thus the system
![]() $(X,T)$
is conjugate to the system
$(X,T)$
is conjugate to the system
![]() $(X^{\prime },T^{\prime })$
, where
$(X^{\prime },T^{\prime })$
, where
![]() $X^{\prime }=G^{\prime }/\Gamma ^{\prime }$
and
$X^{\prime }=G^{\prime }/\Gamma ^{\prime }$
and
![]() $T^{\prime }$
is the translation by
$T^{\prime }$
is the translation by
![]() $\tau $
on
$\tau $
on
![]() $X^{\prime }$
. Therefore, without loss of generality, we can restrict to the case G is spanned by
$X^{\prime }$
. Therefore, without loss of generality, we can restrict to the case G is spanned by
![]() $G^{0}$
and
$G^{0}$
and
![]() $\tau $
.
$\tau $
.
We fix an enumeration
![]() $F_{1},F_{2},\ldots ,F_{2^{d}}$
of all upper faces of
$F_{1},F_{2},\ldots ,F_{2^{d}}$
of all upper faces of
![]() $\{0,1\}^{d}$
, ordered such that codim
$\{0,1\}^{d}$
, ordered such that codim
![]() $(F_{i})$
is non-decreasing with i. Then
$(F_{i})$
is non-decreasing with i. Then
![]() $F_{1}=\{0,1\}^{d}$
, and the upper faces of codimension
$F_{1}=\{0,1\}^{d}$
, and the upper faces of codimension
![]() $1$
are
$1$
are
![]() $F_{2},\ldots ,F_{d+1}$
.
$F_{2},\ldots ,F_{d+1}$
.
If F is a face of
![]() $\{0,1\}^{d}$
, for
$\{0,1\}^{d}$
, for
![]() $g\in G$
we define
$g\in G$
we define
![]() $g^{(F)}\in G^{[d]}$
by
$g^{(F)}\in G^{[d]}$
by
 $$ \begin{align*} (g^{(F)})(\epsilon)= \begin{cases} g, & \epsilon\in F, \\ 1_{G}, & \epsilon\not\in F. \end{cases} \end{align*} $$
$$ \begin{align*} (g^{(F)})(\epsilon)= \begin{cases} g, & \epsilon\in F, \\ 1_{G}, & \epsilon\not\in F. \end{cases} \end{align*} $$
Denote by
![]() $\mathcal {HK}^{\hspace{2pt}[d]}$
the subgroup of
$\mathcal {HK}^{\hspace{2pt}[d]}$
the subgroup of
![]() $G^{[d]}$
spanned by
$G^{[d]}$
spanned by
Lemma 4.1. [Reference Host and Kra12, Ch. 12]
![]() $\mathcal {HK}^{\hspace{2pt}[d]}$
is a rational subgroup of
$\mathcal {HK}^{\hspace{2pt}[d]}$
is a rational subgroup of
![]() $G^{[d]}$
.
$G^{[d]}$
.
Lemma 4.1 means that
![]() $\Gamma ^{[d]}\cap \mathcal {HK}^{\hspace{2pt}[d]}$
is cocompact in
$\Gamma ^{[d]}\cap \mathcal {HK}^{\hspace{2pt}[d]}$
is cocompact in
![]() $\mathcal {HK}^{\hspace{2pt}[d]}$
, allowing us to define an s-step nilmanifold
$\mathcal {HK}^{\hspace{2pt}[d]}$
, allowing us to define an s-step nilmanifold
 $$ \begin{align*} \widetilde{X}^{[d]}= \frac{\mathcal{HK}^{[d]}}{\Gamma^{[d]}\cap \mathcal{HK}^{[d]}}. \end{align*} $$
$$ \begin{align*} \widetilde{X}^{[d]}= \frac{\mathcal{HK}^{[d]}}{\Gamma^{[d]}\cap \mathcal{HK}^{[d]}}. \end{align*} $$
Lemma 4.2. [Reference Host and Kra12, Ch. 12]
The nilmanifold
![]() $\widetilde {X}^{[d]}$
is equal to
$\widetilde {X}^{[d]}$
is equal to
![]() $\mathbf {Q}^{[d}(X)$
.
$\mathbf {Q}^{[d}(X)$
.
By Lemma 4.2 we can view
![]() $\mathbf {Q}^{[d]}(X)$
as a nilsystem, and it is also
$\mathbf {Q}^{[d]}(X)$
as a nilsystem, and it is also
![]() $\mathcal {HK}^{\hspace{2pt}[d]}$
-invariant.
$\mathcal {HK}^{\hspace{2pt}[d]}$
-invariant.
Lemma 4.3. [Reference Host and Kra12, Ch. 12]
Let F be a face of
![]() $\{0,1\}^{d}$
and let
$\{0,1\}^{d}$
and let
![]() $g\in G_{\mathrm {codim}(F)}$
. Then
$g\in G_{\mathrm {codim}(F)}$
. Then
![]() $g^{(F)}\in \mathcal {HK}^{\hspace{2pt}[d]}$
.
$g^{(F)}\in \mathcal {HK}^{\hspace{2pt}[d]}$
.
The following corollary is an immediate consequence of Lemmas 4.2 and 4.3.
Corollary 4.4. Let F be a face of
![]() $\{0,1\}^{d}$
and let
$\{0,1\}^{d}$
and let
![]() $g\in G_{\mathrm {codim}(F)}$
. Then
$g\in G_{\mathrm {codim}(F)}$
. Then
![]() $g^{(F)}\mathbf {x}\in \mathbf {Q}^{[d]}(X)$
for every
$g^{(F)}\mathbf {x}\in \mathbf {Q}^{[d]}(X)$
for every
![]() $\mathbf {x}\in \mathbf {Q}^{[d]}(X)$
.
$\mathbf {x}\in \mathbf {Q}^{[d]}(X)$
.
We are now in a position to show the main result of this section. In it proof we omit the nilpotency class as it is not important.
Theorem 4.5. Let
![]() $(X=G/\Gamma ,T)$
be a minimal nilsystem. For
$(X=G/\Gamma ,T)$
be a minimal nilsystem. For
![]() $x\in X$
and
$x\in X$
and
![]() $g\in G_{d+1}$
, if
$g\in G_{d+1}$
, if
![]() $x\neq gx$
, then
$x\neq gx$
, then
![]() $(x,gx)$
is an
$(x,gx)$
is an
![]() $\mathrm {IN}^{[d]}$
-pair.
$\mathrm {IN}^{[d]}$
-pair.
Proof. Let
![]() $x\in X$
and
$x\in X$
and
![]() $g\in G_{d+1}$
with
$g\in G_{d+1}$
with
![]() $x\neq gx$
. Put
$x\neq gx$
. Put
![]() $x_{0}=x$
and
$x_{0}=x$
and
![]() $x_{1}=gx$
. For
$x_{1}=gx$
. For
![]() $i=0,1$
, let
$i=0,1$
, let
![]() $U_{i}$
be a neighborhood of
$U_{i}$
be a neighborhood of
![]() $x_{i}$
and choose
$x_{i}$
and choose
![]() $\delta>0$
with
$\delta>0$
with
![]() $B(x_{i},\delta )\subset U_{i}$
.
$B(x_{i},\delta )\subset U_{i}$
.
We fix an enumeration
![]() $\omega _{1},\ldots ,\omega _{2^{d}-1}$
of all elements of
$\omega _{1},\ldots ,\omega _{2^{d}-1}$
of all elements of
 $\{0,1\}^{d}\backslash \{\vec {0}\}$
.
$\{0,1\}^{d}\backslash \{\vec {0}\}$
.
Let
![]() $k\in \mathbb {N}$
. For
$k\in \mathbb {N}$
. For
![]() $1\leq i\leq k$
,
$1\leq i\leq k$
,
![]() $1\leq j\leq 2^{d}-1$
, let
$1\leq j\leq 2^{d}-1$
, let
 $$ \begin{align*} F_{ij}= \left\{ \epsilon\in \{0,1\}^{k(2^{d}+d)}: \begin{gathered} \epsilon({k(i-1)+j})=1, \text{ and } \\ \epsilon({k2^{d}+d(i-1)+s})=\omega_{j}(s),\;1\leq s\leq d \end{gathered} \right\}\hspace{-3pt}. \end{align*} $$
$$ \begin{align*} F_{ij}= \left\{ \epsilon\in \{0,1\}^{k(2^{d}+d)}: \begin{gathered} \epsilon({k(i-1)+j})=1, \text{ and } \\ \epsilon({k2^{d}+d(i-1)+s})=\omega_{j}(s),\;1\leq s\leq d \end{gathered} \right\}\hspace{-3pt}. \end{align*} $$
Notice that
![]() $F_{ij}$
is a face of
$F_{ij}$
is a face of
 $\{0,1\}^{k(2^{d}+d)}$
of codimension
$\{0,1\}^{k(2^{d}+d)}$
of codimension
![]() $d+1$
for any
$d+1$
for any
![]() $i,j$
. It follows from Lemma 4.3 that
$i,j$
. It follows from Lemma 4.3 that
 $g^{(F_{ij})} \in \mathcal {HK}^{\hspace{2pt}[k(2^{d}+d)]}$
. Thus by Corollary 4.4 we have that
$g^{(F_{ij})} \in \mathcal {HK}^{\hspace{2pt}[k(2^{d}+d)]}$
. Thus by Corollary 4.4 we have that
 $$ \begin{align} \mathbf{x}= \bigg(\prod_{i=1}^{k}\prod_{j=1}^{2^{d}-1}g^{(F_{ij})}\bigg)x^{[k(2^{d}+d)]}\in \mathbf{Q}^{[k(2^{d}+d)]}(X). \end{align} $$
$$ \begin{align} \mathbf{x}= \bigg(\prod_{i=1}^{k}\prod_{j=1}^{2^{d}-1}g^{(F_{ij})}\bigg)x^{[k(2^{d}+d)]}\in \mathbf{Q}^{[k(2^{d}+d)]}(X). \end{align} $$
Recall that for any
![]() $\theta =\theta (t_{1},\ldots ,t_{k},a,b)\in \Theta _{k,d}$
, we have
$\theta =\theta (t_{1},\ldots ,t_{k},a,b)\in \Theta _{k,d}$
, we have
![]() $\theta \in F_{ij}$
if and only if
$\theta \in F_{ij}$
if and only if
![]() $a=i,b=j$
and
$a=i,b=j$
and
![]() $t_{a}(b)=1$
(see §2.6). Thus by (7) we get that
$t_{a}(b)=1$
(see §2.6). Thus by (7) we get that
 $$ \begin{align*} \mathbf{x}(\theta)= \bigg(\prod_{\substack{ 1\leq i\leq k,1\leq j\leq 2^{d} -1 \\ \theta\in F_{ij} \;}}g\bigg)x=x_{t_{a}(b)}. \end{align*} $$
$$ \begin{align*} \mathbf{x}(\theta)= \bigg(\prod_{\substack{ 1\leq i\leq k,1\leq j\leq 2^{d} -1 \\ \theta\in F_{ij} \;}}g\bigg)x=x_{t_{a}(b)}. \end{align*} $$
By Lemma 2.12, we deduce that
![]() $(x,gx)=(x_{0},x_{1})$
is an
$(x,gx)=(x_{0},x_{1})$
is an
![]() $\mathrm {IN}^{[d]}$
-pair.
$\mathrm {IN}^{[d]}$
-pair.
We refer to [Reference Dong, Donoso, Maass, Shao and Ye4] for the following description of maximal factors of higher order of minimal nilsystems.
Lemma 4.6. For
![]() $1\leq r\leq s$
, if
$1\leq r\leq s$
, if
![]() $X_{r}$
is the maximal factor of order r of X, then
$X_{r}$
is the maximal factor of order r of X, then
![]() $X_{r}$
has the form
$X_{r}$
has the form
![]() $G/(G_{r+1}\Gamma )$
, endowed with the translation by the projection of
$G/(G_{r+1}\Gamma )$
, endowed with the translation by the projection of
![]() $\tau $
on
$\tau $
on
![]() $G/G_{r+1}$
.
$G/G_{r+1}$
.
The following corollary is an immediate consequence of Theorem 4.5 and Lemma 4.6.
Corollary 4.7. Let
![]() $(X,T)$
be a minimal nilsystem and
$(X,T)$
be a minimal nilsystem and
![]() $d\in \mathbb {N}$
. Then
$d\in \mathbb {N}$
. Then
![]() $(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
if and only if
$(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
if and only if
![]() $(x_{0},x_{1})\in \mathbf {RP}^{[d]}(X)$
.
$(x_{0},x_{1})\in \mathbf {RP}^{[d]}(X)$
.
Corollary 4.8. Let
![]() $(X,T)$
be an inverse limit of minimal nilsystems and
$(X,T)$
be an inverse limit of minimal nilsystems and
![]() $d\in \mathbb {N}$
. Then
$d\in \mathbb {N}$
. Then
![]() $(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
if and only if
$(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
if and only if
![]() $(x_{0},x_{1})\in \mathbf {RP}^{[d]}(X)$
.
$(x_{0},x_{1})\in \mathbf {RP}^{[d]}(X)$
.
Proof. Let
![]() $(x_{0},x_{1})\in \mathbf {RP}^{[d]}(X)\backslash \Delta _{X} $
. By the definition of
$(x_{0},x_{1})\in \mathbf {RP}^{[d]}(X)\backslash \Delta _{X} $
. By the definition of
![]() $\mathrm {IN}^{[d]}$
-pairs, it suffices to show that
$\mathrm {IN}^{[d]}$
-pairs, it suffices to show that
![]() $(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
.
$(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
.
Assume that
![]() $X_{i}$
is a minimal nilsystem for every
$X_{i}$
is a minimal nilsystem for every
![]() $i\in \mathbb {N}$
, set
$i\in \mathbb {N}$
, set
![]() $X=\lim \nolimits _{\longleftarrow }\{X_{i}\}_{i\in \mathbb {N}}$
and assume that
$X=\lim \nolimits _{\longleftarrow }\{X_{i}\}_{i\in \mathbb {N}}$
and assume that
![]() $\pi _{i} :X\to X_{i}$
and
$\pi _{i} :X\to X_{i}$
and
![]() $\pi _{i,j}:X_{j}\to X_{i}$
are the factor maps.
$\pi _{i,j}:X_{j}\to X_{i}$
are the factor maps.
Set
![]() $x_{s}^{i}=\pi _{i}(x_{s})$
,
$x_{s}^{i}=\pi _{i}(x_{s})$
,
![]() $i\in \mathbb {N}$
,
$i\in \mathbb {N}$
,
![]() $s=0,1$
. Then
$s=0,1$
. Then
 $\pi _{i,j}(x_{s}^{j})=x_{s}^{i}$
and there is some
$\pi _{i,j}(x_{s}^{j})=x_{s}^{i}$
and there is some
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $x_{0}^{n}\neq x_{1}^{n}$
. For
$x_{0}^{n}\neq x_{1}^{n}$
. For
![]() $j\geq n$
and
$j\geq n$
and
![]() $s=0,1$
, we have
$s=0,1$
, we have
 $x_{s}^{n}=\pi _{n,j}(x_{s}^{j})$
which implies
$x_{s}^{n}=\pi _{n,j}(x_{s}^{j})$
which implies
 $x_{0}^{j}\neq x_{1}^{j}$
. Without loss of generality, we may assume
$x_{0}^{j}\neq x_{1}^{j}$
. Without loss of generality, we may assume
 $x_{0}^{i}\neq x_{1}^{i}$
for all
$x_{0}^{i}\neq x_{1}^{i}$
for all
![]() $i\in \mathbb {N}$
.
$i\in \mathbb {N}$
.
Let
![]() $k\in \mathbb {N}$
. It follows from Theorem 2.5 that
$k\in \mathbb {N}$
. It follows from Theorem 2.5 that
 $(x_{0}^{i},x_{1}^{i})\in \mathbf {RP}^{[d]}(X_{i}) $
for all
$(x_{0}^{i},x_{1}^{i})\in \mathbf {RP}^{[d]}(X_{i}) $
for all
![]() $i\in \mathbb {N}$
. By Theorem 4.5 and Lemma 4.6, for every
$i\in \mathbb {N}$
. By Theorem 4.5 and Lemma 4.6, for every
![]() $i\in \mathbb {N}$
there exists some
$i\in \mathbb {N}$
there exists some
 $\mathbf {x}_{i}\in \mathbf {Q}^{[k(2^{d}+d)]}(X_{i})$
such that
$\mathbf {x}_{i}\in \mathbf {Q}^{[k(2^{d}+d)]}(X_{i})$
such that
 $\mathbf {x}_{i}(\theta )=x_{t_{a}(b)}^{i}$
for all
$\mathbf {x}_{i}(\theta )=x_{t_{a}(b)}^{i}$
for all
![]() $\theta \in \Theta _{k,d}$
. Notice that
$\theta \in \Theta _{k,d}$
. Notice that
 $\mathbf {Q}^{[k(2^{d}+d)]}(X)$
is an inverse limit of the sequence
$\mathbf {Q}^{[k(2^{d}+d)]}(X)$
is an inverse limit of the sequence
 $\{\mathbf {Q}^{[k(2^{d}+d)]}(X_{i})\}_{i\in \mathbb {N}}$
. Thus for every
$\{\mathbf {Q}^{[k(2^{d}+d)]}(X_{i})\}_{i\in \mathbb {N}}$
. Thus for every
![]() $i\in \mathbb {N}$
there exists some
$i\in \mathbb {N}$
there exists some
 $\widetilde {\mathbf {x}}_{i}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
$\widetilde {\mathbf {x}}_{i}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
 $$ \begin{align*} \pi_{i}^{[k(2^{d}+d)]}(\widetilde{\mathbf{x}}_{i})=\mathbf{x}_{i}. \end{align*} $$
$$ \begin{align*} \pi_{i}^{[k(2^{d}+d)]}(\widetilde{\mathbf{x}}_{i})=\mathbf{x}_{i}. \end{align*} $$
Without loss of generality, assume that
![]() $\widetilde {\mathbf {x}}_{i} \to \mathbf {x}$
as
$\widetilde {\mathbf {x}}_{i} \to \mathbf {x}$
as
![]() $i\to \infty $
for some
$i\to \infty $
for some
 $\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
.
$\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
.
We claim that
![]() $\mathbf {x}(\theta )=x_{t_{a}(b)}$
for all
$\mathbf {x}(\theta )=x_{t_{a}(b)}$
for all
![]() $\theta \in \Theta _{k,d}$
.
$\theta \in \Theta _{k,d}$
.
Actually, for any
![]() $\theta \in \Theta _{k,d}$
and
$\theta \in \Theta _{k,d}$
and
![]() $i\leq j$
we have
$i\leq j$
we have
 $$ \begin{align*} \pi_{i}(\widetilde{\mathbf{x}}_{j}(\theta))=\pi_{i,j}\circ \pi_{j}(\widetilde{\mathbf{x}}_{j}(\theta)) =\pi_{i,j}( \mathbf{x}_{j}(\theta))=\pi_{i,j}( x_{t_{a}(b)}^{j})=x_{t_{a}(b)}^{i}. \end{align*} $$
$$ \begin{align*} \pi_{i}(\widetilde{\mathbf{x}}_{j}(\theta))=\pi_{i,j}\circ \pi_{j}(\widetilde{\mathbf{x}}_{j}(\theta)) =\pi_{i,j}( \mathbf{x}_{j}(\theta))=\pi_{i,j}( x_{t_{a}(b)}^{j})=x_{t_{a}(b)}^{i}. \end{align*} $$
By letting j go to infinity and the continuity of
![]() $\pi _{i}$
, we get
$\pi _{i}$
, we get
 $\pi _{i}(\mathbf {x}(\theta ))=x_{t_{a}(b)}^{i}$
for all
$\pi _{i}(\mathbf {x}(\theta ))=x_{t_{a}(b)}^{i}$
for all
![]() $i\in \mathbb {N}$
. This shows the claim and thus
$i\in \mathbb {N}$
. This shows the claim and thus
![]() $(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
by Lemma 2.12.
$(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
by Lemma 2.12.
This completes the proof.
5 The structure of minimal systems without non-trivial
 $\mathrm {IN}^{[d]}$
-pairs
$\mathrm {IN}^{[d]}$
-pairs
In this section we discuss the structure of minimal systems without non-trivial
![]() $\mathrm {IN}^{[d]}$
-pairs. We will show that such systems are almost one-to-one extensions of their maximal factors of order d.
$\mathrm {IN}^{[d]}$
-pairs. We will show that such systems are almost one-to-one extensions of their maximal factors of order d.
We start with the following useful lemma which can be found in the proof of [Reference Shao and Ye22, Theorem 3.1].
Lemma 5.1. Let
![]() $(X,T)$
be a dynamical system and
$(X,T)$
be a dynamical system and
![]() $d\in \mathbb {N}$
. If
$d\in \mathbb {N}$
. If
![]() $\mathbf {x}\in X^{[d]}$
is an
$\mathbf {x}\in X^{[d]}$
is an
![]() $\mathrm {id }\times T^{[d]}_{*}$
-minimal point, then it is an
$\mathrm {id }\times T^{[d]}_{*}$
-minimal point, then it is an
![]() $\mathcal {F}^{\hspace{2pt}[d]}$
-minimal point.
$\mathcal {F}^{\hspace{2pt}[d]}$
-minimal point.
Lemma 5.2. Let
![]() $(X,T)$
be a minimal system and
$(X,T)$
be a minimal system and
![]() $d\in \mathbb {N}$
. For
$d\in \mathbb {N}$
. For
![]() $\omega \in \{0,1\}^{d}$
and
$\omega \in \{0,1\}^{d}$
and
![]() $\mathbf {x}\in \mathbf {Q}^{[d]}(X)$
, let
$\mathbf {x}\in \mathbf {Q}^{[d]}(X)$
, let
![]() $\mathbf {y}\in X^{[d]}$
such that
$\mathbf {y}\in X^{[d]}$
such that
![]() $\mathbf {y}(\epsilon )=\mathbf {x}(\epsilon )$
if
$\mathbf {y}(\epsilon )=\mathbf {x}(\epsilon )$
if
![]() $\epsilon \in \{0,1\}^{d}\backslash \{\omega \}$
and
$\epsilon \in \{0,1\}^{d}\backslash \{\omega \}$
and
![]() $(\mathbf {x}(\omega ),\mathbf {y}(\omega ))\in \mathbf {RP}^{[\infty ]}(X)$
. If
$(\mathbf {x}(\omega ),\mathbf {y}(\omega ))\in \mathbf {RP}^{[\infty ]}(X)$
. If
![]() $\mathbf {y}$
is a
$\mathbf {y}$
is a
![]() $T^{[d]}$
-minimal point, then
$T^{[d]}$
-minimal point, then
![]() $\mathbf {y}\in \mathbf {Q}^{[d]}(X)$
.
$\mathbf {y}\in \mathbf {Q}^{[d]}(X)$
.
Proof. Let
![]() $\mathbf {x}(\omega )=x$
,
$\mathbf {x}(\omega )=x$
,
![]() $\mathbf {y}(\omega )=y$
and
$\mathbf {y}(\omega )=y$
and
![]() $(x,y)\in \mathbf {RP}^{[\infty ]}(X)$
.
$(x,y)\in \mathbf {RP}^{[\infty ]}(X)$
.
Case 1:
![]() $\omega =\vec {0}$
. As
$\omega =\vec {0}$
. As
![]() $\mathbf {x}\in \mathbf {Q}^{[d]}(X)$
, there exists some sequence
$\mathbf {x}\in \mathbf {Q}^{[d]}(X)$
, there exists some sequence
![]() $\{S_{i}\}_{i\in \mathbb {N}}\subset \mathcal {F}^{\hspace{2pt}[d]}$
such that
$\{S_{i}\}_{i\in \mathbb {N}}\subset \mathcal {F}^{\hspace{2pt}[d]}$
such that
![]() $S_{i} \mathbf {x}\to x^{[d]}$
as
$S_{i} \mathbf {x}\to x^{[d]}$
as
![]() $i\to \infty $
by Theorem 2.2. At the same time, we have that
$i\to \infty $
by Theorem 2.2. At the same time, we have that
 $S_{i}\mathbf {y}\to (y,x^{[d]}_{*})\in \mathbf {Q}^{[d]}(X)$
as
$S_{i}\mathbf {y}\to (y,x^{[d]}_{*})\in \mathbf {Q}^{[d]}(X)$
as
![]() $i\to \infty $
. By our hypothesis,
$i\to \infty $
. By our hypothesis,
![]() $\mathbf {y}$
is a
$\mathbf {y}$
is a
![]() $T^{[d]}$
-minimal point, so
$T^{[d]}$
-minimal point, so
![]() $\mathbf {y}$
is also an
$\mathbf {y}$
is also an
![]() $\mathrm {id }\times T^{[d]}_{*}$
-minimal point. Thus by Lemma 5.1,
$\mathrm {id }\times T^{[d]}_{*}$
-minimal point. Thus by Lemma 5.1,
![]() $\mathbf {y}$
is an
$\mathbf {y}$
is an
![]() $\mathcal {F}^{\hspace{2pt}[d]}$
-minimal point which implies that
$\mathcal {F}^{\hspace{2pt}[d]}$
-minimal point which implies that
![]() $\mathbf {y}$
also belongs to the orbit closure of
$\mathbf {y}$
also belongs to the orbit closure of
 $(y,x^{[d]}_{*})$
under the
$(y,x^{[d]}_{*})$
under the
![]() $\mathcal {F}^{\hspace{2pt}[d]}$
-action, and thus
$\mathcal {F}^{\hspace{2pt}[d]}$
-action, and thus
![]() $\mathbf {y}\in \mathbf {Q}^{[d]}(X)$
.
$\mathbf {y}\in \mathbf {Q}^{[d]}(X)$
.
Case 2:
 $\omega \neq \vec {0}$
. Recall that
$\omega \neq \vec {0}$
. Recall that
![]() $\mathbf {Q}^{[d]}(X)$
is invariant under the Euclidean permutations of
$\mathbf {Q}^{[d]}(X)$
is invariant under the Euclidean permutations of
![]() $X^{[d]}$
. We can choose some Euclidean permutation f such that
$X^{[d]}$
. We can choose some Euclidean permutation f such that
 $f(\mathbf {y})(\vec {0})=\mathbf {y}(\omega )$
.
$f(\mathbf {y})(\vec {0})=\mathbf {y}(\omega )$
.
Now we have
![]() $f(\mathbf {x})(\epsilon )=f(\mathbf {y})(\epsilon )$
for any
$f(\mathbf {x})(\epsilon )=f(\mathbf {y})(\epsilon )$
for any
 $\epsilon \in \{0,1\}^{d}\backslash \{\vec {0}\}$
and
$\epsilon \in \{0,1\}^{d}\backslash \{\vec {0}\}$
and
 $(f(\mathbf {x})(\vec {0}),f(\mathbf {y})(\vec {0}))\in \mathbf {RP}^{[\infty ]}(X)$
. Moreover,
$(f(\mathbf {x})(\vec {0}),f(\mathbf {y})(\vec {0}))\in \mathbf {RP}^{[\infty ]}(X)$
. Moreover,
![]() $f(\mathbf {y})$
is also a
$f(\mathbf {y})$
is also a
![]() $T^{[d]}$
-minimal point. By Case 1, we get that
$T^{[d]}$
-minimal point. By Case 1, we get that
![]() $f(\mathbf {y})\in \mathbf {Q}^{[d]}(X)$
and thus
$f(\mathbf {y})\in \mathbf {Q}^{[d]}(X)$
and thus
![]() $\mathbf {y}\in \mathbf {Q}^{[d]}(X)$
.
$\mathbf {y}\in \mathbf {Q}^{[d]}(X)$
.
Recall a characterization of
![]() $\mathrm {Ind}_{fip}$
-pairs in [Reference Dong, Donoso, Maass, Shao and Ye4, Corollary 4.4].
$\mathrm {Ind}_{fip}$
-pairs in [Reference Dong, Donoso, Maass, Shao and Ye4, Corollary 4.4].
Lemma 5.3. Let
![]() $(X,T)$
be a minimal system and
$(X,T)$
be a minimal system and
![]() $(x_{0},x_{1})\in \mathbf {RP}^{[\infty ]}(X)\backslash \Delta $
. If
$(x_{0},x_{1})\in \mathbf {RP}^{[\infty ]}(X)\backslash \Delta $
. If
![]() $(x_{0},x_{1}) $
is a
$(x_{0},x_{1}) $
is a
![]() $T\times T$
-minimal point, then
$T\times T$
-minimal point, then
![]() $(x_{0},x_{1})$
is an
$(x_{0},x_{1})$
is an
![]() $\mathrm {Ind}_{fip}$
-pair.
$\mathrm {Ind}_{fip}$
-pair.
Analogously to Lemma 5.3, we provide a characterization of
![]() $\mathrm {IN}^{[d]}$
-pairs.
$\mathrm {IN}^{[d]}$
-pairs.
Lemma 5.4. Let
![]() $(X,T)$
be a minimal system and
$(X,T)$
be a minimal system and
![]() $d\in \mathbb {N},(x_{0},x_{1})\in \mathbf {RP}^{[d]}(X)\backslash \Delta $
. If
$d\in \mathbb {N},(x_{0},x_{1})\in \mathbf {RP}^{[d]}(X)\backslash \Delta $
. If
![]() $(x_{0},x_{1})$
is a
$(x_{0},x_{1})$
is a
![]() $T\times T$
-minimal point, then
$T\times T$
-minimal point, then
![]() $(x_{0},x_{1})$
is an
$(x_{0},x_{1})$
is an
![]() $\mathrm {IN}^{[d]}$
-pair.
$\mathrm {IN}^{[d]}$
-pair.
Proof. Let
![]() $\pi :X\to X_{\infty }=X/\mathbf {RP}^{[\infty ]}(X)$
be the factor map and let
$\pi :X\to X_{\infty }=X/\mathbf {RP}^{[\infty ]}(X)$
be the factor map and let
![]() $u_{j}=\pi (x_{j})$
,
$u_{j}=\pi (x_{j})$
,
![]() $j=0,1$
. If
$j=0,1$
. If
![]() $u_{0}=u_{1}$
, then
$u_{0}=u_{1}$
, then
![]() $(x_{0},x_{1})\in \mathbf {RP}^{[\infty ]}(X)$
and thus
$(x_{0},x_{1})\in \mathbf {RP}^{[\infty ]}(X)$
and thus
![]() $(x_{0},x_{1})\in \mathrm {Ind}_{fip}(X)$
by Lemma 5.3. In particular, we have
$(x_{0},x_{1})\in \mathrm {Ind}_{fip}(X)$
by Lemma 5.3. In particular, we have
![]() $(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
.
$(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
.
Now assume that
![]() $u_{0}\neq u_{1}$
. Then
$u_{0}\neq u_{1}$
. Then
 $(u_{0},u_{1})\in \mathbf {RP}^{[d]}(X_{\infty })\backslash \Delta _{X_{\infty }}$
by Theorem 2.5 and
$(u_{0},u_{1})\in \mathbf {RP}^{[d]}(X_{\infty })\backslash \Delta _{X_{\infty }}$
by Theorem 2.5 and
![]() $(u_{0},u_{1})$
is a
$(u_{0},u_{1})$
is a
![]() $T\times T$
-minimal point as
$T\times T$
-minimal point as
![]() $(x_{0},x_{1})$
is a
$(x_{0},x_{1})$
is a
![]() $T\times T$
-minimal point.
$T\times T$
-minimal point.
Fix
![]() $k\in \mathbb {N}$
. By Lemma 2.12, it suffices to show that there is some
$k\in \mathbb {N}$
. By Lemma 2.12, it suffices to show that there is some
 $\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
$\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
![]() $\mathbf {x}(\theta )=x_{t_{a}(b)}$
for all
$\mathbf {x}(\theta )=x_{t_{a}(b)}$
for all
![]() $\theta \in \Theta _{k,d}$
.
$\theta \in \Theta _{k,d}$
.
Step 1: Reduction to the maximal factor of order
![]() $\infty $
. It follows from Theorem 2.14 that
$\infty $
. It follows from Theorem 2.14 that
![]() $X_{\infty }$
is an inverse limit of minimal nilsystems. By the argument in Corollary 4.8, there exists some
$X_{\infty }$
is an inverse limit of minimal nilsystems. By the argument in Corollary 4.8, there exists some
 $\mathbf {u}\in \mathbf {Q}^{[k(2^{d}+d)]}(X_{\infty })$
such that
$\mathbf {u}\in \mathbf {Q}^{[k(2^{d}+d)]}(X_{\infty })$
such that
![]() $\mathbf {u}(\theta )=u_{t_{a}(b)}$
for all
$\mathbf {u}(\theta )=u_{t_{a}(b)}$
for all
![]() $\theta \in \Theta _{k,d}$
.
$\theta \in \Theta _{k,d}$
.
Step 2: Lifting to X. Notice that
![]() $\pi ^{[l]}:(\mathbf {Q}^{[l]}(X),\mathcal {G}^{[l]})\to (\mathbf {Q}^{[l]}(X_{\infty }),\mathcal {G}^{[l]})$
is a factor map for every
$\pi ^{[l]}:(\mathbf {Q}^{[l]}(X),\mathcal {G}^{[l]})\to (\mathbf {Q}^{[l]}(X_{\infty }),\mathcal {G}^{[l]})$
is a factor map for every
![]() $l\in \mathbb {N}$
, where
$l\in \mathbb {N}$
, where
 $\pi ^{[l]}: X^{[l]}\rightarrow X_{\infty }^{[l]}$
is defined from
$\pi ^{[l]}: X^{[l]}\rightarrow X_{\infty }^{[l]}$
is defined from
![]() $\pi $
coordinatewise.
$\pi $
coordinatewise.
We note that Theorem 2.5 also holds for general abelian group actions. Thus there is some
 $\mathbf {w}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
$\mathbf {w}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
 $$ \begin{align*} \pi^{[k(2^{d}+d)]}(\mathbf{w})=\mathbf{u}, \end{align*} $$
$$ \begin{align*} \pi^{[k(2^{d}+d)]}(\mathbf{w})=\mathbf{u}, \end{align*} $$
which implies that
 $\mathbf {w}(\theta )\in \mathbf {RP}^{[\infty ]}[x_{t_{a}(b)}] $
for all
$\mathbf {w}(\theta )\in \mathbf {RP}^{[\infty ]}[x_{t_{a}(b)}] $
for all
![]() $\theta \in \Theta _{k,d}$
.
$\theta \in \Theta _{k,d}$
.
Step 3: Transformations.
Case 1:
![]() $(x_{0},x_{1},\mathbf {w})$
is a
$(x_{0},x_{1},\mathbf {w})$
is a
![]() $T^{[k(2^{d}+d)]+2}$
-minimal point. By Lemma 5.2, we can replace
$T^{[k(2^{d}+d)]+2}$
-minimal point. By Lemma 5.2, we can replace
![]() $\mathbf {w}(\theta )$
by
$\mathbf {w}(\theta )$
by
![]() $x_{t_{a}(b)}$
for all
$x_{t_{a}(b)}$
for all
![]() $\theta \in \Theta _{k,d}$
which implies that there is some
$\theta \in \Theta _{k,d}$
which implies that there is some
 $\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
$\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
such that
![]() $\mathbf {x}(\theta )=x_{t_{a}(b)}$
for all
$\mathbf {x}(\theta )=x_{t_{a}(b)}$
for all
![]() $\theta \in \Theta _{k,d}$
.
$\theta \in \Theta _{k,d}$
.
Case 2: General cases. By property (3) of Proposition A.2, there is a minimal point
 $$ \begin{align} (x_{0}^{\prime},x_{1}^{\prime},\mathbf{w}^{\prime}) \in \overline{\mathcal{O}((x_{0},x_{1},\mathbf{w}),T^{[k(2^{d}+d)]+2})} \end{align} $$
$$ \begin{align} (x_{0}^{\prime},x_{1}^{\prime},\mathbf{w}^{\prime}) \in \overline{\mathcal{O}((x_{0},x_{1},\mathbf{w}),T^{[k(2^{d}+d)]+2})} \end{align} $$
such that they are also proximal. Note that
 $\mathbf {Q}^{[k(2^{d}+d)]}(X)$
is
$\mathbf {Q}^{[k(2^{d}+d)]}(X)$
is
![]() $T^{[k(2^{d}+d)]}$
-invariant, and we get
$T^{[k(2^{d}+d)]}$
-invariant, and we get
 $\mathbf {w}^{\prime }\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
.
$\mathbf {w}^{\prime }\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
.
Now by (8),
![]() $(x_{i},x_{i}^{\prime }),(\mathbf {w}(\epsilon ),\mathbf {w}^{\prime }(\epsilon ))\in \mathbf {P}(X) $
for all
$(x_{i},x_{i}^{\prime }),(\mathbf {w}(\epsilon ),\mathbf {w}^{\prime }(\epsilon ))\in \mathbf {P}(X) $
for all
![]() $i=0,1$
and
$i=0,1$
and
 $\epsilon \in \{0,1\}^{[k(2^{d}+d)]}$
. As
$\epsilon \in \{0,1\}^{[k(2^{d}+d)]}$
. As
![]() $\mathbf {P}(X)\subset \mathbf {RP}^{[\infty ]}(X)$
and
$\mathbf {P}(X)\subset \mathbf {RP}^{[\infty ]}(X)$
and
 $\mathbf {w}(\theta )\in \mathbf {RP}^{[\infty ]}[x_{t_{a}(b)}]$
for all
$\mathbf {w}(\theta )\in \mathbf {RP}^{[\infty ]}[x_{t_{a}(b)}]$
for all
![]() $\theta \in \Theta _{k,d}$
, by equivalence of
$\theta \in \Theta _{k,d}$
, by equivalence of
![]() $\mathbf {RP}^{[\infty ]}(X)$
we get that
$\mathbf {RP}^{[\infty ]}(X)$
we get that
 $$ \begin{align*} \mathbf{w}^{\prime}(\theta)\in \mathbf{RP}^{[\infty]}[x^{\prime}_{t_{a}(b)}], \end{align*} $$
$$ \begin{align*} \mathbf{w}^{\prime}(\theta)\in \mathbf{RP}^{[\infty]}[x^{\prime}_{t_{a}(b)}], \end{align*} $$
which implies
 $\mathbf {w}^{\prime }\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
by Case 1.
$\mathbf {w}^{\prime }\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
by Case 1.
Recall that
![]() $(x_{0},x_{1})$
is a
$(x_{0},x_{1})$
is a
![]() $T\times T$
-minimal point and
$T\times T$
-minimal point and
 $ (x_{0}^{\prime },x_{1}^{\prime })\in \overline {\mathcal {O}((x_{0},x_{1}),T\times T)}$
. There exists some sequence
$ (x_{0}^{\prime },x_{1}^{\prime })\in \overline {\mathcal {O}((x_{0},x_{1}),T\times T)}$
. There exists some sequence
![]() $\{n_{i}\}_{i\in \mathbb {N}}\subset \mathbb {Z}$
such that
$\{n_{i}\}_{i\in \mathbb {N}}\subset \mathbb {Z}$
such that
as
![]() $i\to \infty $
. Let
$i\to \infty $
. Let
![]() $\mathbf {x}$
be some limit point of the sequence
$\mathbf {x}$
be some limit point of the sequence
 $\{ (T^{n_{i}})^{[k(2^{d}+d)]} \mathbf {w}^{\prime }\}_{i\in \mathbb {N}}$
. Then we have
$\{ (T^{n_{i}})^{[k(2^{d}+d)]} \mathbf {w}^{\prime }\}_{i\in \mathbb {N}}$
. Then we have
 $\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
and
$\mathbf {x}\in \mathbf {Q}^{[k(2^{d}+d)]}(X)$
and
![]() $\mathbf {x}(\theta )=x_{t_{a}(b)}$
for all
$\mathbf {x}(\theta )=x_{t_{a}(b)}$
for all
![]() $\theta \in \Theta _{k,d}$
.
$\theta \in \Theta _{k,d}$
.
As a consequence, we get the following corollary.
Corollary 5.5. Let
![]() $(X,T)$
be a minimal distal system and
$(X,T)$
be a minimal distal system and
![]() $d\in \mathbb {N}$
. Then
$d\in \mathbb {N}$
. Then
![]() $(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
if and only if
$(x_{0},x_{1})\in \mathrm {IN}^{[d]}(X)$
if and only if
![]() $(x_{0},x_{1})\in \mathbf {RP}^{[d]}(X)$
.
$(x_{0},x_{1})\in \mathbf {RP}^{[d]}(X)$
.
We are now able to show the main result of this section. We need the following theorem.
Theorem 5.6. [Reference Dong, Donoso, Maass, Shao and Ye4, Theorem 4.5]
Let
![]() $(X,T)$
be a minimal system. If X does not contain any non-trivial
$(X,T)$
be a minimal system. If X does not contain any non-trivial
![]() $\mathrm {Ind}_{fip}$
-pair, then it is an almost one-to-one extension of its maximal factor of order
$\mathrm {Ind}_{fip}$
-pair, then it is an almost one-to-one extension of its maximal factor of order
![]() $\infty $
.
$\infty $
.
Theorem 5.7. Let
![]() $(X,T)$
be a minimal system and
$(X,T)$
be a minimal system and
![]() $d\in \mathbb {N}$
. If X does not contain any non-trivial
$d\in \mathbb {N}$
. If X does not contain any non-trivial
![]() $\mathrm {IN}^{[d]}$
-pair, then it is an almost one-to-one extension of its maximal factor of order d.
$\mathrm {IN}^{[d]}$
-pair, then it is an almost one-to-one extension of its maximal factor of order d.
Proof. Let
![]() $(X,T)$
be a minimal system without non-trivial
$(X,T)$
be a minimal system without non-trivial
![]() $\mathrm {IN}^{[d]}$
-pairs, where
$\mathrm {IN}^{[d]}$
-pairs, where
![]() $d\in \mathbb {N}$
. Let
$d\in \mathbb {N}$
. Let
![]() $\pi :X\to X/\mathbf {RP}^{[d]}(X)$
be the factor map.
$\pi :X\to X/\mathbf {RP}^{[d]}(X)$
be the factor map.
We first show that
![]() $\pi $
is a proximal extension.
$\pi $
is a proximal extension.
Remark that if
![]() $(x,y)\in R_{\pi }=\mathbf {RP}^{[d]}(X)$
is a
$(x,y)\in R_{\pi }=\mathbf {RP}^{[d]}(X)$
is a
![]() $T\times T$
-minimal point, then by Lemma5.4 we have that
$T\times T$
-minimal point, then by Lemma5.4 we have that
![]() $(x,y)$
is an
$(x,y)$
is an
![]() $\mathrm {IN}^{[d]}$
-pair and thus we get that
$\mathrm {IN}^{[d]}$
-pair and thus we get that
![]() $x=y$
. Now consider any
$x=y$
. Now consider any
![]() $(x,y)\in R_{\pi }$
and
$(x,y)\in R_{\pi }$
and
![]() $u\in E(X,T)$
a minimal idempotent. As
$u\in E(X,T)$
a minimal idempotent. As
![]() $(ux,uy)$
is a
$(ux,uy)$
is a
![]() $T\times T$
-minimal point, we have from previous observation that
$T\times T$
-minimal point, we have from previous observation that
![]() $ux=uy$
, which implies that
$ux=uy$
, which implies that
![]() $(x,y)$
is a proximal pair.
$(x,y)$
is a proximal pair.
This shows that
![]() $\mathbf {P}(X)=\mathbf {RP}^{[\infty ]}(X)=\mathbf {RP}^{[d]}(X)$
, which implies that the maximal factor of order
$\mathbf {P}(X)=\mathbf {RP}^{[\infty ]}(X)=\mathbf {RP}^{[d]}(X)$
, which implies that the maximal factor of order
![]() $\infty $
of X is
$\infty $
of X is
![]() $X/\mathbf {RP}^{[d]}(X)$
.
$X/\mathbf {RP}^{[d]}(X)$
.
As X does not contain any non-trivial
![]() $\mathrm {IN}^{[d]}$
-pair, we get that
$\mathrm {IN}^{[d]}$
-pair, we get that
![]() $\mathrm {Ind}_{fip}(X)$
is trivial. By Theorem 5.6, X is an almost one-to-one extension of its maximal factor of order
$\mathrm {Ind}_{fip}(X)$
is trivial. By Theorem 5.6, X is an almost one-to-one extension of its maximal factor of order
![]() $\infty $
. From this, we deduce that X is an almost one-to-one extension of its maximal factor of order d.
$\infty $
. From this, we deduce that X is an almost one-to-one extension of its maximal factor of order d.
This completes the proof.
To end this section, we pose a question which we cannot solve in this paper.
Question 5.8. Let
![]() $(X,T)$
be a minimal system without any non-trivial
$(X,T)$
be a minimal system without any non-trivial
![]() $\mathrm {IN}^{[d]}$
-pair, where
$\mathrm {IN}^{[d]}$
-pair, where
![]() $d\in \mathbb {N}$
. Is
$d\in \mathbb {N}$
. Is
![]() $(X,T)$
uniquely ergodic?
$(X,T)$
uniquely ergodic?
6 An example
In the last part of this paper, we give the example which is mentioned in the introduction.
Example 6.1. For
![]() $d\in \mathbb {N}$
, there is a minimal system
$d\in \mathbb {N}$
, there is a minimal system
![]() $(X,T)$
such that
$(X,T)$
such that
![]() $\mathrm {IN}^{[d]}(X)$
is trivial but
$\mathrm {IN}^{[d]}(X)$
is trivial but
![]() $\mathbf {RP}^{[d]}(X)$
is non-trivial.
$\mathbf {RP}^{[d]}(X)$
is non-trivial.
We start with the following classical example. Let
![]() $\mathbb {T}=\mathbb {R}/\mathbb {Z}$
be the one-dimensional torus. Consider an irrational rotation
$\mathbb {T}=\mathbb {R}/\mathbb {Z}$
be the one-dimensional torus. Consider an irrational rotation
![]() $(\mathbb {T},R_{\alpha })$
. Choose
$(\mathbb {T},R_{\alpha })$
. Choose
![]() $x_{0}\in \mathbb {T}$
and split each point of the orbit
$x_{0}\in \mathbb {T}$
and split each point of the orbit
![]() $x_{n}=x_{0}+n\alpha $
into two points
$x_{n}=x_{0}+n\alpha $
into two points
![]() $x_{n}^{+},x_{n}^{-}$
. This procedure results is a Sturmian symbolic dynamical system
$x_{n}^{+},x_{n}^{-}$
. This procedure results is a Sturmian symbolic dynamical system
![]() $(X_{0},\sigma )$
which is a minimal almost one-to-one extension of
$(X_{0},\sigma )$
which is a minimal almost one-to-one extension of
![]() $(\mathbb {T},R_{\alpha })$
, and we denote this extension by
$(\mathbb {T},R_{\alpha })$
, and we denote this extension by
![]() $\pi $
. The minimal system
$\pi $
. The minimal system
![]() $(X_{0},\sigma )$
is null, which implies
$(X_{0},\sigma )$
is null, which implies
 $\mathrm {IN}^{[1]}(X_{0})=\Delta _{X_{0}}$
. For more details, see [Reference Glasner and Megrelishvili9, Example 14.4].
$\mathrm {IN}^{[1]}(X_{0})=\Delta _{X_{0}}$
. For more details, see [Reference Glasner and Megrelishvili9, Example 14.4].
For
![]() $d\geq 2$
, let
$d\geq 2$
, let
![]() $X=X_{0}\times \mathbb {T}^{d-1}$
. Define a continuous map
$X=X_{0}\times \mathbb {T}^{d-1}$
. Define a continuous map
![]() $T:X\to X$
by
$T:X\to X$
by
We next show that the system
![]() $(X,T)$
meets our requirement.
$(X,T)$
meets our requirement.
Let
![]() $T_{\alpha }:\mathbb {T}^{d}\to \mathbb {T}^{d}$
such that
$T_{\alpha }:\mathbb {T}^{d}\to \mathbb {T}^{d}$
such that
Then
![]() $(\mathbb {T}^{d},T_{\alpha })$
is a minimal d-step nilsystem (see, for example, [Reference Ye and Yu23, Example 5.22]). There is a continuous map from X to
$(\mathbb {T}^{d},T_{\alpha })$
is a minimal d-step nilsystem (see, for example, [Reference Ye and Yu23, Example 5.22]). There is a continuous map from X to
![]() $\mathbb {T}^{d}$
induced by
$\mathbb {T}^{d}$
induced by
![]() $\pi $
which will be denoted by
$\pi $
which will be denoted by
![]() $\widetilde {\pi }$
:
$\widetilde {\pi }$
:
Moreover,
![]() $\widetilde {\pi }$
induces a non-trivial extension
$\widetilde {\pi }$
induces a non-trivial extension
![]() $\widetilde {\pi }:(X,T)\to (\mathbb {T}^{d},T_{\alpha })$
. Notice that the factor map
$\widetilde {\pi }:(X,T)\to (\mathbb {T}^{d},T_{\alpha })$
. Notice that the factor map
![]() $\pi $
is almost one-to-one; a simple observation shows that the factor map
$\pi $
is almost one-to-one; a simple observation shows that the factor map
![]() $\widetilde {\pi }$
is also almost one-to-one. From this, we deduce that the system
$\widetilde {\pi }$
is also almost one-to-one. From this, we deduce that the system
![]() $(X,T)$
is minimal.
$(X,T)$
is minimal.
Claim 1.
![]() $\mathbf {RP}^{[d]}(X)=R_{\widetilde {\pi }}$
.
$\mathbf {RP}^{[d]}(X)=R_{\widetilde {\pi }}$
.
Proof of Claim 1
Write
![]() $z_{1}=\pi (x_{m}^{+})\in \mathbb {T}$
and
$z_{1}=\pi (x_{m}^{+})\in \mathbb {T}$
and
![]() $z_{0}=\alpha $
. A simple computation yields
$z_{0}=\alpha $
. A simple computation yields
 $$ \begin{align*} T^{n}(x_{m}^{*},z_{2},\ldots,z_{d}) =\bigg(\sigma^{n}x_{m}^{*},z_{2}+nz_{1}+\frac{n(n-1)}{2}z_{0},\ldots,\sum_{i=0}^{d}\binom{n}{d-i}z_{i}\bigg), \end{align*} $$
$$ \begin{align*} T^{n}(x_{m}^{*},z_{2},\ldots,z_{d}) =\bigg(\sigma^{n}x_{m}^{*},z_{2}+nz_{1}+\frac{n(n-1)}{2}z_{0},\ldots,\sum_{i=0}^{d}\binom{n}{d-i}z_{i}\bigg), \end{align*} $$
where
![]() $*\in \{+,-\},n\in \mathbb {Z}$
and
$*\in \{+,-\},n\in \mathbb {Z}$
and
 $\binom {n}{0}=1,\binom {n}{i}={n\cdot \cdots \cdot (n-i+1)}/{i !}$
for
$\binom {n}{0}=1,\binom {n}{i}={n\cdot \cdots \cdot (n-i+1)}/{i !}$
for
![]() $i=1,\ldots ,d$
.
$i=1,\ldots ,d$
.
From this, we get that for any
![]() $z_{2},\ldots ,z_{d}\in \mathbb {T}$
and
$z_{2},\ldots ,z_{d}\in \mathbb {T}$
and
![]() $m\in \mathbb {Z}$
, the points
$m\in \mathbb {Z}$
, the points
![]() $(x_{m}^{+},z_{2},\ldots ,z_{d})$
and
$(x_{m}^{+},z_{2},\ldots ,z_{d})$
and
![]() $(x_{m}^{-},z_{2},\ldots ,z_{d})$
can be close enough, which implies that two such points are proximal, and also are regionally proximal of order d by (2). It follows that
$(x_{m}^{-},z_{2},\ldots ,z_{d})$
can be close enough, which implies that two such points are proximal, and also are regionally proximal of order d by (2). It follows that
![]() $R_{\widetilde {\pi }}\subset \mathbf {RP}^{[d]}(X)$
.
$R_{\widetilde {\pi }}\subset \mathbf {RP}^{[d]}(X)$
.
On the other hand, by Theorem 2.5, one has that
 $$ \begin{align*} (\widetilde{\pi }\times\widetilde{ \pi}) \mathbf{RP}^{[d]}(X)=\mathbf{RP}^{[d]}(\mathbb{T}^{d})=\Delta_{\mathbb{T}^{d}}, \end{align*} $$
$$ \begin{align*} (\widetilde{\pi }\times\widetilde{ \pi}) \mathbf{RP}^{[d]}(X)=\mathbf{RP}^{[d]}(\mathbb{T}^{d})=\Delta_{\mathbb{T}^{d}}, \end{align*} $$
which implies
![]() $\mathbf {RP}^{[d]}(X)\subset R_{\widetilde {\pi }}$
.
$\mathbf {RP}^{[d]}(X)\subset R_{\widetilde {\pi }}$
.
This shows Claim 1 and thus
![]() $\mathbf {RP}^{[d]}(X)$
is non-trivial.
$\mathbf {RP}^{[d]}(X)$
is non-trivial.
Claim 2.
![]() $\mathrm {IN}^{[d]}(X)=\Delta $
.
$\mathrm {IN}^{[d]}(X)=\Delta $
.
To show this claim, we need the following proposition.
Proposition 6.2. [Reference Huang, Maass and Ye17, Proposition 3.2]
Let
![]() $\pi :(Y,T) \longrightarrow (Z,T)$
be a factor map of dynamical systems. If
$\pi :(Y,T) \longrightarrow (Z,T)$
be a factor map of dynamical systems. If
![]() $(y_{1},y_{2})\in \mathrm {IN}^{[1]}(Y)$
, then
$(y_{1},y_{2})\in \mathrm {IN}^{[1]}(Y)$
, then
![]() $(\pi (y_{1}),\pi (y_{2}))\in \mathrm {IN}^{[1]}(Z)$
.
$(\pi (y_{1}),\pi (y_{2}))\in \mathrm {IN}^{[1]}(Z)$
.
Proof of Claim 2
Let
![]() $\mathbf {x}=(x_{1},\ldots ,x_{d}),\mathbf {y}=(y_{1},\ldots ,y_{d})\in X$
with
$\mathbf {x}=(x_{1},\ldots ,x_{d}),\mathbf {y}=(y_{1},\ldots ,y_{d})\in X$
with
![]() $(\mathbf {x},\mathbf {y})\in \mathrm {IN}^{[d]}(X)$
. By the definition of the
$(\mathbf {x},\mathbf {y})\in \mathrm {IN}^{[d]}(X)$
. By the definition of the
![]() $ \mathrm {IN}^{[d]}$
-pair, we get that
$ \mathrm {IN}^{[d]}$
-pair, we get that
![]() $ \mathrm {IN}^{[d]}(X)\subset \mathbf {RP}^{[d]}(X)$
, which implies
$ \mathrm {IN}^{[d]}(X)\subset \mathbf {RP}^{[d]}(X)$
, which implies
![]() $x_{2}=y_{2},\ldots ,x_{d}=y_{d}$
by Claim 1.
$x_{2}=y_{2},\ldots ,x_{d}=y_{d}$
by Claim 1.
Let
![]() $\theta $
be the projection from X to
$\theta $
be the projection from X to
![]() $X_{0}$
. It is easy to see
$X_{0}$
. It is easy to see
![]() $\theta $
induces a factor map
$\theta $
induces a factor map
![]() $\theta :(X,T)\to (X_{0},\sigma )$
. Notice that
$\theta :(X,T)\to (X_{0},\sigma )$
. Notice that
![]() $(\mathbf {x},\mathbf {y})\in \mathrm {IN}^{[d]}(X)\subset \mathrm {IN}^{[1]}(X)$
. Thus by Proposition 6.2, one has
$(\mathbf {x},\mathbf {y})\in \mathrm {IN}^{[d]}(X)\subset \mathrm {IN}^{[1]}(X)$
. Thus by Proposition 6.2, one has
![]() $(x_{1},y_{1})=(\theta (\mathbf {x}),\theta (\mathbf {y})) \in \mathrm {IN}^{[d]}(X_{0})=\Delta _{X_{0}}$
, which implies
$(x_{1},y_{1})=(\theta (\mathbf {x}),\theta (\mathbf {y})) \in \mathrm {IN}^{[d]}(X_{0})=\Delta _{X_{0}}$
, which implies
![]() $x_{1}=y_{1}$
.
$x_{1}=y_{1}$
.
This shows that
![]() $\mathrm {IN}^{[d]}(X)=\Delta $
.
$\mathrm {IN}^{[d]}(X)=\Delta $
.
Acknowledgements
The author would like to thank Professors Wen Huang, Song Shao and Xiangdong Ye for helping discussions. The author was supported by NNSF of China (11431012,11971455).
A Appendix. Basic facts about abstract topological dynamics
We recall some basic definitions and results in abstract topological dynamical systems. For more details, see [Reference Auslander1, Reference Ellis6].
A.1 Topological transformation groups
A topological dynamical system is a triple
![]() $\mathcal {X}=(X,\mathcal {T},\Pi )$
, where X is a compact metrizable space,
$\mathcal {X}=(X,\mathcal {T},\Pi )$
, where X is a compact metrizable space,
![]() $\mathcal {T}$
is a
$\mathcal {T}$
is a
![]() $T_{2}$
topological group and
$T_{2}$
topological group and
![]() $\Pi :T\times X\to X$
is a continuous map such that
$\Pi :T\times X\to X$
is a continuous map such that
![]() $\Pi (e,x)=x$
and
$\Pi (e,x)=x$
and
![]() $\Pi (s,\Pi (t,x))=\Pi (st,x)$
. We shall fix
$\Pi (s,\Pi (t,x))=\Pi (st,x)$
. We shall fix
![]() $\mathcal {T}$
and suppress the action symbol.
$\mathcal {T}$
and suppress the action symbol.
![]() $\mathcal {X}$
is widely also called a topological transformation group or a flow. Usually we omit
$\mathcal {X}$
is widely also called a topological transformation group or a flow. Usually we omit
![]() $\Pi $
and denote a system by
$\Pi $
and denote a system by
![]() $(X,\mathcal {T}\hspace{2pt})$
.
$(X,\mathcal {T}\hspace{2pt})$
.
Let
![]() $(X,\mathcal {T}\hspace{2pt})$
be a system and
$(X,\mathcal {T}\hspace{2pt})$
be a system and
![]() $x\in X$
. Then
$x\in X$
. Then
![]() $\mathcal {O}(x,\mathcal {T}\hspace{2pt})$
denotes the orbit of x, which is also denoted by
$\mathcal {O}(x,\mathcal {T}\hspace{2pt})$
denotes the orbit of x, which is also denoted by
![]() $\mathcal {T}x$
. A subset
$\mathcal {T}x$
. A subset
![]() $A\subset X$
is called invariant if
$A\subset X$
is called invariant if
![]() $ta\in A$
for all
$ta\in A$
for all
![]() $a\in A$
and
$a\in A$
and
![]() $t\in \mathcal {T}$
. When
$t\in \mathcal {T}$
. When
![]() $Y\subset X$
is a closed and
$Y\subset X$
is a closed and
![]() $\mathcal {T}$
-invariant subset of the system
$\mathcal {T}$
-invariant subset of the system
![]() $(X,\mathcal {T}\hspace{2pt})$
we say that the system
$(X,\mathcal {T}\hspace{2pt})$
we say that the system
![]() $(Y,\mathcal {T}\hspace{2pt})$
is a subsystem of
$(Y,\mathcal {T}\hspace{2pt})$
is a subsystem of
![]() $(X,\mathcal {T}\hspace{2pt})$
. If
$(X,\mathcal {T}\hspace{2pt})$
. If
![]() $(X,\mathcal {T}\hspace{2pt})$
and
$(X,\mathcal {T}\hspace{2pt})$
and
![]() $(Y,\mathcal {T}\hspace{2pt})$
are two dynamical systems their product system is the system
$(Y,\mathcal {T}\hspace{2pt})$
are two dynamical systems their product system is the system
![]() $(X\times Y,\mathcal {T}\hspace{2pt})$
, where
$(X\times Y,\mathcal {T}\hspace{2pt})$
, where
![]() $t(x,y)=(tx,ty)$
. A system
$t(x,y)=(tx,ty)$
. A system
![]() $(X,\mathcal {T}\hspace{2pt})$
is called minimal if X contains no proper closed invariant subsets.
$(X,\mathcal {T}\hspace{2pt})$
is called minimal if X contains no proper closed invariant subsets.
A.2 Enveloping semigroups
Given a system
![]() $(X,\mathcal {T}\hspace{2pt})$
, its enveloping semigroup or Ellis semigroup
$(X,\mathcal {T}\hspace{2pt})$
, its enveloping semigroup or Ellis semigroup
![]() $E(X,\mathcal {T}\hspace{2pt})$
is defined as the closure of the set
$E(X,\mathcal {T}\hspace{2pt})$
is defined as the closure of the set
![]() $\{t:t\in \mathcal {T}\}$
in
$\{t:t\in \mathcal {T}\}$
in
![]() $X^{X}$
(with its compact, usually non-metrizable, pointwise convergence topology). The maps
$X^{X}$
(with its compact, usually non-metrizable, pointwise convergence topology). The maps
![]() $E\to E:p \mapsto pq$
and
$E\to E:p \mapsto pq$
and
![]() $p\mapsto tp$
are continuous for all
$p\mapsto tp$
are continuous for all
![]() $q\in E$
and
$q\in E$
and
![]() $t\in \mathcal {T}$
.
$t\in \mathcal {T}$
.
A.3 Idempotents and ideals
For a semigroup the element u with
![]() $u^{2} =u$
is called an idempotent. The Ellis–Numakura theorem says that for any enveloping semigroup E the set
$u^{2} =u$
is called an idempotent. The Ellis–Numakura theorem says that for any enveloping semigroup E the set
![]() $J(E)$
of idempotents of E is not empty [Reference Ellis6]. A non-empty subset
$J(E)$
of idempotents of E is not empty [Reference Ellis6]. A non-empty subset
![]() $I\subset E$
is a left ideal (respectively, right ideal) if it
$I\subset E$
is a left ideal (respectively, right ideal) if it
![]() $EI\subset I$
(respectively,
$EI\subset I$
(respectively,
![]() $IE\subset I$
). A minimal left ideal is the left ideal that does not contain any proper left ideal of E. Obviously every left ideal is a semigroup and every left ideal contains some minimal left ideal.
$IE\subset I$
). A minimal left ideal is the left ideal that does not contain any proper left ideal of E. Obviously every left ideal is a semigroup and every left ideal contains some minimal left ideal.
An idempotent
![]() $u \in J(E)$
is minimal if
$u \in J(E)$
is minimal if
![]() $v \in J(E)$
and
$v \in J(E)$
and
![]() $vu = v$
implies
$vu = v$
implies
![]() $uv = u$
. The following results are well known [Reference Ellis, Ellis and Nerurkar5, Reference Furstenberg and Katznelson7]. Let
$uv = u$
. The following results are well known [Reference Ellis, Ellis and Nerurkar5, Reference Furstenberg and Katznelson7]. Let
![]() $ L$
be a left ideal of enveloping semigroup E and
$ L$
be a left ideal of enveloping semigroup E and
![]() $u \in J(E)$
. Then there is some idempotent v in
$u \in J(E)$
. Then there is some idempotent v in
![]() $Lu$
such that
$Lu$
such that
![]() $uv = v$
and
$uv = v$
and
![]() $vu = v$
; an idempotent is minimal if and only if it is contained in some minimal left ideal.
$vu = v$
; an idempotent is minimal if and only if it is contained in some minimal left ideal.
A useful result about minimal points is the following proposition.
Proposition A.1. Let I be a minimal left ideal. A point
![]() $x\in X$
is minimal if and only if
$x\in X$
is minimal if and only if
![]() $ux=x$
for some
$ux=x$
for some
![]() $u\in I$
.
$u\in I$
.
A.4 Proximality
Two points
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
are called proximal if and only if
$x_{2}$
are called proximal if and only if
Let
![]() $\mathcal {U}_{X}$
be the unique uniform structure of X. Then the following assertions hold.
$\mathcal {U}_{X}$
be the unique uniform structure of X. Then the following assertions hold.
 $$ \begin{align*} \mathbf{ P}(X ) =\bigcap \{\mathcal{T}\alpha:\alpha\in \mathcal{U}_{X} \} \end{align*} $$
$$ \begin{align*} \mathbf{ P}(X ) =\bigcap \{\mathcal{T}\alpha:\alpha\in \mathcal{U}_{X} \} \end{align*} $$
is the collection of proximal pairs in X, the proximal relation.
Proposition A.2. Let
![]() $(X,\mathcal {T}\hspace{2pt})$
be a dynamical system. Then:
$(X,\mathcal {T}\hspace{2pt})$
be a dynamical system. Then:
-
(1) The points
 $x_{1},x_{2}$
are proximal in
$x_{1},x_{2}$
are proximal in
 $(X,\mathcal {T}\hspace{2pt})$
if and only if
$(X,\mathcal {T}\hspace{2pt})$
if and only if
 $px_{1}=px_{1}$
for some
$px_{1}=px_{1}$
for some
 $p\in E(X,\mathcal {T}\hspace{2pt})$
;
$p\in E(X,\mathcal {T}\hspace{2pt})$
; -
(2) If u is an idempotent in
 $E(X,\mathcal {T}\hspace{2pt})$
, then
$E(X,\mathcal {T}\hspace{2pt})$
, then
 $(x,ux)\in \mathbf {P}(X)$
for every
$(x,ux)\in \mathbf {P}(X)$
for every
 $x\in X$
;
$x\in X$
; -
(3) There is a minimal point
 $x^{\prime }\in \overline {\mathcal {O}(x,\mathcal {T} ) }$
such that
$x^{\prime }\in \overline {\mathcal {O}(x,\mathcal {T} ) }$
such that
 $(x,x^{\prime })\in \mathbf {P}(X)$
;
$(x,x^{\prime })\in \mathbf {P}(X)$
; -
(4) If
 $(X,T)$
is minimal, then
$(X,T)$
is minimal, then
 $(x, y) \in \mathbf {P}(X)$
if and only if there is some minimal idempotent
$(x, y) \in \mathbf {P}(X)$
if and only if there is some minimal idempotent
 $u\in E(X,\mathcal {T}\hspace{2pt})$
such that
$u\in E(X,\mathcal {T}\hspace{2pt})$
such that
 $y = ux$
.
$y = ux$
.