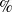Bayesian optimization for assist-as-needed controller in robot-assisted upper limb training based on energy information

Abstract

The assist-as-needed (AAN) controller is effective in robot-assisted rehabilitation. However, variations of the engagement of subjects with fixed controller often lead to unsatisfying results. Therefore, adaptive AAN that adjusts control parameters based on individualized engagement is essential to enhance the training effect further. Nevertheless, current approaches mainly focus on the within-trial real-time engagement estimation, and the presence of measurement noise may cause improper evaluation of engagement. In addition, most studies on human-in-loop optimization strategies modulate the controller by greedy strategies, which are prone to fall into local optima. These shortcomings in previous studies could significantly limit the efficacy of AAN. This paper proposes an adaptive AAN to promote engagement by providing subjects with a subject-adaptive assistance level based on trial-wise engagement estimation and performance. Firstly, the engagement is estimated from energy information, which assesses the work done by the subject during a full trial to reduce the influence of measurement outliers. Secondly, the AAN controller is adapted by Bayesian optimization (BO) to maximize the subject’s performance according to historical trial-wise performance. The BO algorithm is good at dealing with noisy signals within limited steps. Experiments with ten healthy subjects resulted in a decrease of 34.59$\%$ in their average trajectory error, accompanied by a reduction of 9.71$\%$ in their energy consumption, thus verifying the superiority of the proposed method to prior work. These results suggest that the proposed method could potentially improve the effect of upper limb rehabilitation.

1. Introduction

Stroke is a significant disease that seriously affects people’s physical and mental health globally [1]. Robot-aided rehabilitation is a novel solution to the increasing demand for stroke survivors with motor dysfunction [2–6]. However, continuous passive motion-based therapy does not generate significant improvement for post-stroke patients [7], and active movement is considered to be one of the most effective approaches to upper limb function restoration [8]. The patients’ engagement is a critical factor contributing to motor recovery [9]. Therefore, assist-as-needed (AAN) controllers have been developed to regulate assistive forces or task difficulty in recent years [10]. The AAN strategy emphasizes that robots exert minimum intervention to promote engagement. However, the training task, which is extremely easy or difficult, would lead the subject to get boring or frustrated [11]. Temporal variability in the subject’s engagement during the training is a challenge to the subject-adaptive controller to improve the training effect further [12]. A subject-adaptive controller is necessary to provide a subject-adaptive assistance level to improve performance and encourage engagement. Therefore, two key issues are essential to design a subject-adaptive AAN controller. The first is to estimate the subject’s engagement with the current assistance level in a task. The second is to develop the adaptation law for optimizing the AAN controller to provide subject-adaptive assistance.

The user’s engagement can be framed as a complex structure driven by motivation and executed through active participation. Many engagement estimation methods have been proposed [13]. Some approaches evaluate the user’s engagement with electromyography (EMG) but require additional EMG sensors [14–16]. On the other hand, some approaches fundamentally assume that the engagement is related to the interaction force, which is position dependent, and estimate the force from the Gaussian radial basis functions distribution across the workspace [17–19]. In ref. [20], a combination of the Kalman filter and Lyapunov stability analysis was proposed for subjects’ interaction force estimation. More recently, the estimation scheme was replaced by a nonlinear disturbance observer [21]. In these methods mentioned above, estimating subjects’ engagement is crucial for the controller adjustment. However, these approaches highly rely on the accurate modeling of the complex dynamics of a coupled human–robot interaction system, which is extremely difficult, and are prone to lead to noisy engagement estimations with measurement outliers especially during occasional poor movements.

Recent studies have employed human-in-loop optimization to adjust the controller’s parameter [22–26]. In refs. [27–29], subject’s task performance of recent 1–2 training trials was used to customize the difficulty level of movement task in the next training. Furthermore, the parameters of training tasks were iteratively optimized depending on the subjects’ current physiological state and task performance [30–32]. However, the controller parameter was defined and updated discretely, which may restrict the flexibility of the robotic system. In addition, these mentioned strategies try to adjust the parameter with greedy strategy. However, the greedy strategies could only obtain a locally optimal parameter of the controller [33].

To this end, we proposed an adaptive AAN controller for upper limb robotic training based on energy information (EI) to offer a subject-adaptive assistance level. Firstly, the subject’s engagement is estimated according to the subject’s energy contribution to the training task within a trial, which could be obtained by calculating the integral of the force contributed by the subject to the position, indicating the work done by the subject during the training trial [34]. Evaluating trial-wise engagement according to EI does not require complex modeling of the system and may be able to reduce the influence of measurement outliers. Moreover, the EI-based approach focuses more on the interactive forces of the training process and is barely affected by individual physiological differences. Secondly, the assistive force field was optimized trial by trial based on the subject’s performance and estimation of engagement to provide subject-adaptive assistance. In specific, the hyperparameter of the assistive force field is obtained with Bayesian optimization (BO), an efficient global optimization strategy that is well suited to find the maxima/minima of objective functions that are noisy and expensive to evaluate [35, 36]. By optimizing the AAN controller in a trial-by-trial and global way, it is expected to keep subjects engaged and improve the training effect.

All in all, the contributions of this study can be summarized as follows:

1. 1. In contrast to methods that rely on within-trial engagement estimation, the trail-wise estimation based on EI may be more robust to measurement outliers.

2. 2. Unlike the greedy strategy-based controller, the AAN controller optimized by BO can obtain the global optima with better adaptability and tolerance to objective function value noise.

The rest of this article is organized as follows: the architecture of the adaptive AAN controller is given in Section 2, followed by the experiment protocol provided in Section 3, experiment results in Section 4, discussions in Section 5, and finally, the conclusion is given in Section 6.

2. Method

2.1. System overview

The $ArmMotus^{TM}$ M2 robot (Fourier Intelligence Co., Ltd., Shanghai, China) was utilized in our work. It is an end-effector robot with two servo motors driving the handle in the horizontal plane. The handle connects to a force sensor to measure the two-dimensional force imposed by the subject, and it has a motion space in the horizontal plane of 0.55^*0.5 $\text{m}^{2}$ .

The schematic diagram of the proposed method is shown in Fig. 1, which is composed of several components. The roles of the main components are briefly listed below:

Figure 1. Schematic diagram of the adaptive AAN controller. Bayesian optimization is used to modulate the assisted robot’s hyperparameter ( $\lambda$ ) to maximize engagement and minimize the tracking error. The engagement is assessed with the EI-based approach. Based on the posterior at the current iteration, the parameter with the maximum probability of improvement is chosen and applied to the robot. This process repeats until it reaches a predetermined number of runs.

1. 1. AAN controller: it assists subjects in the trial by constructing a force field around a predefined trajectory.

2. 2. Friction compensation: it compensates for friction to ensure the robot’s back-drive capability so that the subject can better sense the assistive forces by the force field.

3. 3. Performance evaluation: it assesses the subject’s performance after each training trial in terms of trajectory tracking error (TE) and EI-based estimation of engagement (EG).

4. 4. BO: it suggests the optimal controller parameter for the next trial according to the subject’s performance in historical trials.

The subjects were asked to hold the handle to move according to the desired trajectory in every training trial. He/She made movement corrections in response to visual feedback and force feedback [37, 38]. After each trial, the posterior distribution of the subject’s performance to the hyperparameter was generated by the Gaussian process based on historical hyperparameters and performances. The hyperparameter for the next trial was obtained by maximizing the probability improvement (PI) function, which is designed to balance exploration and exploitation [39].

2.2. AAN controller

In order to activate the muscles of the upper limb, we adopted a commonly used reference trajectory composed of two semicircles of a 0.1 m radius [40]. The desired trajectory starts from P1 and gradually passes through P2–P5. Once the handle moves beyond P5 along the $x$ -axis, the current training trial ends. The AAN controller is featured by a force field to better achieve coordinated motion and keep the subject’s safety when the motion is instantaneously impeded [41, 42]. The assistive force field around the desired trajectory is given below and visualized in Fig. 2.

(1) \begin{equation} {\boldsymbol{f}_a} = \boldsymbol{f}_{\text{max}} \left[\left.1-\text{exp}\left(-\left(\frac{10*|{\Delta }d|}{\lambda }\right)^2\right)\right)\right]\end{equation}

where $\boldsymbol{f}_a$ and $\boldsymbol{f}_{\text{max}}$ denote the assistive force vector and the boundary vector of the force field, respectively, both pointing from the current position to the desired trajectory along the radial direction, ${\Delta }d$ indicates the trajectory deviation to the designed trajectory, and $\lambda$ is the hyperparameter that regulates the stiffness of force field. When the actual position deviates from the desired trajectory, the force field generates a force to push or pull the handle back to the desired trajectory. Moreover, the stiffness hyperparameter determines the profile of the resulting assistive force, as shown in Fig. 1.

Figure 2. Desired trajectory (from P1 to P5 flowing the arc), assistive force field (indicated by black arrow), and assistive force decomposition of example points on the handle (in the experiment, the arrows of a force field would not show to subjects) in the workspace.

As can be seen in Fig. 1, a higher value of $\lambda$ means the assistive force field is less rigid, and the operation is more compliant, which is helpful for subjects with stronger motor abilities. A lower value of $\lambda$ results in a stiffer assistive force field, which is good for people with limited motor skills.

The assistive force by the AAN controller is decomposed into two force vectors along the horizontal and vertical directions, respectively (as shown in Fig. 2). Then, such two force vectors are applied by actuators of the Fourier M2 robot.

2.3. Friction compensation

To deliver the AAN property by incorporating a force-free area along the reference trajectory/point, it is desired to realize a back-drivable robot system, so that it can be compliantly moved without resistive forces [43–45]. Therefore, it is necessary to incorporate feedforward control terms for compensating the robot’s dynamics.

Applying the dynamics of robot to the experimental robot system, the dynamics is interpreted as:

(2) \begin{equation}{{\boldsymbol{M}(\boldsymbol{p})}}{\ddot{\boldsymbol{p}}}+{\boldsymbol{C}}({\boldsymbol{p}},{\dot{\boldsymbol{p}}}){\dot{\boldsymbol{p}}}+{\boldsymbol{G}}({\boldsymbol{p}})+{\boldsymbol{F}}_f ={\boldsymbol{F}}_r+{\boldsymbol{F}}_h \end{equation}

where ${\boldsymbol{p}}=(x,y)^T$ , $\dot{\boldsymbol{p}}$ , $\ddot{\boldsymbol{p}}$ are the position vector, velocity vector, and acceleration vector, respectively. ${\boldsymbol{M}(\boldsymbol{p})}$ is the inertial matrix, ${\boldsymbol{C}}({\boldsymbol{p}},{\dot{\boldsymbol{p}}})$ denotes the centrifugal and Coriolis matrix, ${\boldsymbol{G}}({\boldsymbol{p}})$ is the gravity vector, ${\boldsymbol{F}}_f=(F_{fx},F_{fy})^T$ indicates the force induced by the robot’s friction, ${\boldsymbol{F}}_r=(F_{rx},F_{ry})^T$ is the force vector applied by actuators in the robot in the $x$ and $y$ axis, consisting of the force vector for compensating the friction and the assistive force vector ${\boldsymbol{f}}_a=(f_{ax},f_{ay})^T$ , and ${\boldsymbol{F}}_h=(f_{hx},f_{hy})^T$ is the force vector that subject applies to the end-effector.

There is a neglectable effect on the gravity caused by the end-effector movement since the robot platform is a planar robot, and a brace supports the subject’s forearm. The handle was required to be controlled at a low speed and low acceleration to allow the subject to feel the feedback force ( $||\dot{{\boldsymbol{p}}}||_2\le 0.025\,\text{m}/\text{s}$ and $||\ddot{{\boldsymbol{p}}}||_2\le 0.02\,\text{m}/\text{s}^2$ ), which made the influence of ${{\boldsymbol{M}(\boldsymbol{p})}}{\ddot{\boldsymbol{p}}}$ and ${\boldsymbol{C}}({\boldsymbol{p}},{\dot{\boldsymbol{p}}}){\dot{\boldsymbol{p}}}$ negligible. The current dynamic equation of the robot is simplified as follows:

(3) \begin{equation}{\boldsymbol{F}}_f ={\boldsymbol{F}}_r+{\boldsymbol{F}}_h \end{equation}

Although the handle was required to move slowly during the trial, there was still a high resistance to controlling the grip at speeds lower than the set speed. Therefore, the friction must be dynamically compensated to make the force field unaffected by friction. Based on the study of frictional models in [46], the frictional model of the robot in the $x$ or $y$ direction is given by:

(4) \begin{equation} F_f = \begin{cases} \ F(v), & \text{if} \enspace v\ne 0 \\ \ F_e, & \text{if} \enspace v=0 \; \text{and} \; |F_e|\lt F_S \\ \ F_Ssgn(F_e), & \text{otherwise} \\ \end{cases} \end{equation}

where $F_f$ is the friction in $x$ or $y$ direction, $F_e$ is the stiction related to the external force when $v=0$ , $F_S$ is the maximum of stiction proportional to the normal load, and $F(v)$ is the dynamic friction, which is described by:

(5) \begin{equation} F(v) = F_C + (F_S-F_C)\text{exp}\left(-(|v/v_s|)^{\delta _s}\right) \end{equation}

where $F_C$ is the Coulomb friction, $F_S$ is the stiction, $v_s$ denotes Stribeck velocity whose value is $0.1\,\text{m}/\text{s}$ , and $\delta _s$ is a constant which ranges from 0.5 to 1. In order to measure the static friction, we gradually increased the force exerted by the motor on the end-effector until it started to move and took its critical value as stiction. In addition, to mearsure the dynamic friction, the speed of the end-effector was controlled, ranging from $0.001$ to $0.2\,\text{m}/\text{s}$ automatically, and recorded the average output forces of the motors have maintained this speed. Finally, these data were fitted to the friction model $F(v)$ , and the fitting result is shown in Fig. 3.

Figure 3. Fitting model of the relationship between dynamic friction and velocity.

2.4. Performance metrics

Each training trial is assessed quantitatively by two metrics. The engagement demonstrates the subject’s contribution to the movement, and the trajectory error indicates the accuracy of the trajectory-tracking trial intuitively.

Based on the AAN-assisted control framework, we propose a new approach to estimate the subject’s engagement. The current working situation is that the position error caused by the subject’s operation will be corrected with the help of the assistive force, and the work done by the subject on the handle will be used exclusively to support the handle movement along the reference trajectory in the back-drivable system. Specifically, based on the deviation between the reference trajectory and the actual trajectory, the stiffness of the force field will determine the reduction of the energy consumed by the person in the case of the same error. In particular, we can estimate the trial-wise engagement from the EI and further improve the subject’s engagement in training by adjusting the hyperparameter of AAN [47].

As a sequence, the trial-wise energy contributed by the subject in each training trial is calculated as:

(6) \begin{equation} \text{EG} = \int _{\text{start}\_\text{point}}^{\text{finish}\_\text{point}}\boldsymbol{F}_h \textrm{d}\boldsymbol{L} \end{equation}

where $\boldsymbol{L}$ is the displacement vector from the current sample point to the next sample point. With reference to the coordinates of the guide points of the desired trajectory $(P1(0.1,0.2)$ , $P2(0.2,0.3)$ , $P3(0.3,0.2)$ , $P4(0.4,0.1)$ , $P5(0.5, 0.2))$ , Eq. (7) is calculated as:

(7) \begin{equation} \text{EG} = \int _{0.1}^{0.5}|\hat{f}_{hx}|\textrm{d}x+\int _{0.2}^{0.3}|\hat{f}_{hy}|\textrm{d}y+\int _{0.1}^{0.3}|\hat{f}_{hy}|\textrm{d}y+\int _{0.1}^{0.2}|\hat{f}_{hy}|\textrm{d}y \end{equation}

where $\hat{f}_{hx}$ and $\hat{f}_{hy}$ are the smoothed force to reduce the impact of outliers on the estimation during the training trial [48].

The mean absolute error is calculated to assess the trajectory error, which is the most intuitive to reflect the degree of deviation of the actual trajectory from the reference trajectory in each trial, which is described as:

(8) \begin{equation} \text{TE} = \frac{1}{2\pi r}\int _{\text{start}\_\text{point}}^{\text{finish}\_\text{point}}|y_s-y_d|\textrm{d} x \end{equation}

where $y_s$ and $y_d$ are the subject’s trajectory and the desired trajectory along the $y$ -axis, respectively. $r$ is the radius of the desired trajectory, and its value is $0.1\,\text{m}$ .

2.5. Adaptive AAN based on BO

As mentioned in Section 2.2, the assistive level relies on the hyperparameter. However, engagement and trajectory error varies with subjects, which makes the fixed hyperparameter formation the fixed assistive level, which cannot pair the subject’s performance, leading the training effect hard to effective improve. Therefore, we should optimize the hyperparameter of the controller adaptively according to the performance. Dealing with such an issue is formulated as solving the following optimization problem:

(9) \begin{equation} \lambda ^{*} = \underset{\text{min}\leq \lambda \leq \text{max}}{\text{argmax}}\,{J(\lambda )} \end{equation}

where $J(\lambda )$ denotes the relationship between the subject’s performance and the AAN controller’s hyperparameter. The hyperparameter ranges from $0.1$ (min value) to $1.0$ (max value). The minimum and maximum values are determined through preliminary experiments. Specifically, a value less than the lower limit will cause the force field to be unstable, making the task impossible to complete. A value above the upper limit will result in a force field in the workspace that is too weak for the subject to perceive the assistive force.

To optimize the robot actuation, we define a cost function to be maximized that weighs a metric of accuracy (the trajectory error) and a metric of engagement (the EI-based engagement), which can be described as:

(10) \begin{equation} J=\text{EG}-\beta *\text{TE} \end{equation}

where $\beta$ is the weight coefficient that expresses the tradeoff between the subject’s engagement and average trajectory error.

There are two characteristics for such an optimization problem. First, the objective function is expensive to evaluate since it can be assessed only after the subject finishes a training trial. Second, the subject’s performance could not be analytically expressed as a function of the hyperparameter of the AAN controller, and thus it also cannot be optimized by the gradient descent method. Employing greedy strategies is easily influenced by performance noise and can only acquire a locally optimal solution. To this end, we have adopted an effective method, that is, BO, to solve the problem in Eq. (9). BO is an efficient global optimization method that is particularly well suited to optimizing unknown objective functions that are expensive to evaluate [49]. It makes use of all the available historical information from the evaluation to compute a posterior distribution of cost as a function of the optimization variables and then uses acquisition functions computed on this posterior to select the next observation points to evaluate. In particular, it naturally balances exploitation with uncertainty reduction to guide exploration [50]; hence, global optimum could be reached with limited data.

In order to initial the Bayesian Optimization, some tests for stiffness parameter are necessary. In our study, six trials with different pseudo-randomly selected stiffness values from the pre-specified range to initialize the optimization, which was designed to avoid biased sampling that could lead to premature convergence [51]. The current hyperparameter and the corresponding objective function value were collected into the dataset $D=(\lambda _i,J_i)$ after $i\text{th}$ trial of training. Assuming that the cost function had an additive identically distributed and independent noise, the samples is expressed as:

(11) \begin{equation} J_i=J(\lambda )+\varepsilon, \varepsilon \sim N\left(0,{\sigma }^2 _{\text{noise}}\right) \end{equation}

where ${\sigma }^2 _{\text{noise}}$ is the variance of the noise. We take the approach of folding the noise into $k(\lambda,{\lambda }^{\prime})$ , which is expressed as:

(12) \begin{equation} k(\lambda,{\lambda }^{\prime})={\sigma }^2_{J}\text{exp}\left[-\frac{{(\lambda -{\lambda }^{\prime})}^2}{2l^2}\right]+{\sigma }^2 _{\text{noise}}\delta (\lambda,{\lambda }^{\prime}) \end{equation}

where $l$ is the hyperparameter of the characteristic length scale, and $\delta (\lambda,{\lambda }^{\prime})$ is the Kronecker delta function. In order to capture the uncertainty in the surrogate reconstruction of the objective function, and since the Gaussian process ( $\mathcal{GP}$ ) has become a standard surrogate for modeling objective function in BO [52], we construct the posterior distribution of $J(\lambda )$ with $\mathcal{GP}$ on $D$ as:

(13) \begin{equation} J(\lambda )=\mathcal{GP}\left(J;\mu (\lambda ),K_{J|D}\right) \end{equation}

where $\mu (\lambda )$ denotes the mean of the distribution, $K_{J|D}$ represents the covariance, and they are expressed as:

(14) \begin{equation} \mu (\lambda )=\textbf{k}_{*}(\lambda )\left(\textbf{K}+{\sigma }^2 _{\text{noise}}\textbf{I}\right)\textbf{K}^{-1}\textbf{J} \quad \textbf{J}=[J_1,J_2 \cdots J_n] \end{equation}

(15) \begin{equation} K_{J|D}=k(\lambda _{*},\lambda _{*})-\textbf{k}_{*}(\lambda )\left(\textbf{K}+{\sigma }^2 _{\text{noise}}\textbf{I}\right)^{-1}\textbf{k}_*(\lambda )^T \end{equation}

where $\textbf{K}$ and $\textbf{k}_{*}(\lambda )$ are expressed by:

(16) \begin{equation} \textbf{K}=\left [ \begin{matrix} k(\lambda _1,\lambda _1) & k(\lambda _1,\lambda _2) & \cdots & k(\lambda _1,\lambda _n) \\ k(\lambda _2,\lambda _1) & k(\lambda _2,\lambda _2) & \cdots & k(\lambda _2,\lambda _n) \\ \vdots & \vdots & \ddots & \vdots \\ k(\lambda _n,\lambda _1) & k(\lambda _n,\lambda _2) & \cdots & k(\lambda _n,\lambda _n) \end{matrix}\right ] \end{equation}

(17) \begin{equation} \textbf{k}_*(\lambda )=[k(\lambda _*,\lambda _1) \quad k(\lambda _*,\lambda _2) \enspace \cdots \enspace k(\lambda _*,\lambda _n)] \end{equation}

where ( $*$ ) is the predicted value of Bayesian linear regression. Collected data and Gaussian process prior induce a posterior distribution of objective function, and the acquisition function decides which point of $\lambda$ to observe in the next trial. The acquisition function of PI represents the maximum probability of improving over the best current value, which would take the form as:

(18) \begin{equation} \lambda _{n+1}=\underset{\text{min}\leq \lambda \leq \text{max}}{\text{argmax}}\,{\alpha _{PI}(\lambda )} \end{equation}

By evaluating $\lambda$ in the given range, the value which makes the PI function $\alpha _{PI}(\lambda )$ the maximum will be selected as the next observation point. The $\alpha _{PI}(\lambda )$ is expressed as:

(19) \begin{equation} \alpha _{PI}(\lambda )=\Phi (\mu (\lambda ),\sigma _J(\lambda ))=\Phi \left(\frac{\mu (\lambda )-J_{\text{max}|D}-\xi }{\sigma _J(\lambda )}\right) \end{equation}

where $\mu (\lambda )$ denotes the expectation obtained from the posterior distribution, $\Phi$ is the cumulative distribution function of the standard normal distribution, and $J_{\text{max}|D}$ is the max value of the cost function on $D$ . The $\xi$ is an adjustable parameter regulated to balance exploration and exploitation, which is set to 0 in our study.

This process was repeated for 15 trials. In total, there were 21 trials in the optimization process including 6 trials of initialization.

3. Experiments

Two experiments were conducted to evaluate the proposed methods. The first experiment aimed to validate the feasibility of the proposed engagement estimation method. In the second experiment, the proposed BO-based AAN training was compared to a greedy strategy-based training to demonstrate its advantages.

3.1. Subjects

In our study, we recruited 20 healthy adults, 10 males and 10 females, to participate in a comparison experiment. The age range of the subjects was 23–31 years, with an average age of 25.5. Ten participants, labeled as C1–C10, were assigned to the control group (CG) and were trained using a greedy strategy. The other 10 subjects, marked as E1–E10, were assigned to the experimental group (EXG) and were trained using the BO-based method. All experiments were approved by the Ethics Committee of Southeast University (2022ZDSYLL038-P01). Prior to the experiment, all subjects provided informed consent and received training to ensure safe operation.

3.2. Feasibility validation experiment of engagement estimation based on EI

An experiment was conducted to verify the feasibility of the proposed engagement estimation by evaluating the correlation between the proposed and the sEMG-based engagement estimation. Ten healthy adults (five males and five females, with an average age of 24.8) were recruited for the experiment consisting of 10 trials of trajectory tracking in the back-drivable system. The subjects were requested to control the robot’s handle along the reference trajectory in the absence of assistive force. Based on the characteristic of the movement, three Delsys sensors were placed on the brachioradialis, triceps brachii long and lateral head, and biceps brachii of the subject’s arm to record sEMG signals at 1000 Hz. In addition, the force sensor connected to the handle detected the interaction force at 300 $\text{Hz}$ . The sEMG-based engagement estimation of each trial was described as follows:

(20) \begin{equation} \text{EG}_{\text{sEMG}}=\frac{1}{4}\sum \limits _{n=1}^4 ||\textbf{S}_n||_2/\sqrt{N_n}, \quad n=1,2,3,4 \end{equation}

where $\textbf{S}_n$ is the amplitude vector of the collected $n\text{th}$ channel signals with length $N_n$ after rectification [53, 54]. The group’s average engagements in each trial were normalized first, and Pearson’s correlation coefficient was used to measure the correlation between the proposed and sEMG-based estimation method. The experiment results (as shown in Fig. 4) demonstrated a significant correlation between the two methods, with a Pearson’s coefficient of $r = 0.841$ and $p = 0.002$ . These findings support the feasibility of the proposed engagement estimation method.

3.3. Comparison experiment between BO-based and greedy strategy-based training

3.3.1. Experimental setup

The experimental setup is illustrated in Fig. 5, where the subject’s forearm was comfortably attached to the support frame, and the hand was gripping the handle. In each training trial, subjects were instructed to operate the handle and follow the desired trajectory until the grip reached $0.5\,\text{m}$ along the $x$ -axis. The desired and actual trajectories were displayed to the subjects during the training process. Additionally, the AAN controller generated force feedback based on the control law and provided feedback to the subject through the grip if the handle deviated from the preset trajectory. Although the desired trajectory for each trial remained constant, the stiffness of the assisted force field was regulated according to the subject’s performance.

Figure 4. The results of the experiments on engagement estimation.

Figure 5. Experimental setup of Fourier M2 robot for upper-limb training.

3.3.2. Experimental procedure

Experimental procedures for two groups were designed as shown in Fig. 6, which included the familiarization session (FR), the transparent session before training (TR1), the greedy strategy training session (GS)/BO training session, the transparent session after training (TR2), and the breaks therein. The FR aimed to familiarize subjects with the operation and trial. During the TR1 and TR2 sessions, subjects were instructed to complete the trial in the absence of the force field.

Figure 6. Experimental procedure of AAN optimized by greedy strategy and BO, respectively.

In the GS session for the CG, the hyperparameters of the force field were regulated using the greedy strategy. Specifically, the regulation approach was expressed as follows:

(21) \begin{equation} \lambda _{n+2}=\begin{cases} \ \lambda _{n+1}+0.1, & \text{if} \enspace J_{n+1}\gt J_n \; \text{and}\; J_{n+1}\gt J_n\\ \ \lambda _{n+1}-0.1, & \text{if} \enspace J_{n+1}\gt J_n \; \text{and}\; J_{n+1}\le J_n \\ \ \lambda _{n+1}-0.1, & \text{if} \enspace J_{n+1}\le J_n \; \text{and}\; J_{n+1}\gt J_n \\ \ \lambda _{n+1}+0.1, & \text{if} \enspace J_{n+1}\le J_n \; \text{and}\; J_{n+1}\le J_n \\ \end{cases} \quad n\in [1,19] \end{equation}

where $n$ denotes the serial number of training in the GS session. The current hyperparameter of the force field was regulated on the performance of the previous two trials in the GS session. To balance the tradeoff between the convergence speed and accuracy, we set the step size of the greedy algorithm to 0.1. A step size that is too small may result in a slower convergence, while a step size that is too large may hinder convergence.

In the BO session of the experimental group, the AAN controller initially selected random parameters within the given range for the first six trials. The subsequent 15 trials then optimized the hyperparameters based on the previous training results.

Each subject completed the training in approximately 40 min. Neither of the training methods imposed additional operational burden on the subjects as resting breaks were given between sessions.

3.3.3. Metrics

Since more engagement during training tends to lead to better training outcomes, the BO-based training aims to encourage more participant engagement by adjusting the assistance during training. Regulating the assistance in the training may increase the risk that subject will decrease engagement, as the human motor system tends to optimize engagement [55]. Therefore, monitoring the EG is beneficial for adjusting the assistance to encourage subject’s engagement in the training.

After the training, two metrics, TE and EG, were used to compare the subjects’ abilities. Smaller TE and EG in the absence of assistance suggested that subjects had better movement control capability with less energy consumption and error. The TE was calculated by Eq. (8), indicating the average trajectory error in the trajectory tracking trial. The EG was computed by Eq. (7), demonstrating the work done by the human on the handle during a training trial.

The pre- and post-training metrics were analyzed separately for each group to evaluate the impact of the training. Wilcoxon signed-rank tests were employed to determine the statistical significance of the observed differences.

4. Results

The comparison result for the TE and EG was shown in Fig. 7. The significance comparison analysis of the two metrics was as follows:

Figure 7. (a) Comparison of trajectory error between two groups before and after training. (b) Comparison of engagement between two groups before training and after training. The (ns) denotes $p\ge 0.05$ , (^*) $p\lt 0.05$ , (^**) $p\lt 0.01$ , (^***) $p\lt 0.001$ .

1. 1. Pre-training in CG vs. post-training in CG: The TE of the CG pre-training (5.85 $\pm$ 0.56 mm) and post-training (4.87 $\pm$ 0.46 mm) was significantly different (p = 0.005). The EG of the CG before (3.86 $\pm$ 0.17 J) and after training (3.67 $\pm$ 0.16 J) was not significantly different (p = 0.088), indicating that the training of the CG was able to the reduce trajectory error.

2. 2. Pre-training in EXG vs. post-training in EXG: There was a significant difference between pre-training (5.81 $\pm$ 0.45 mm) and post-training (3.80 $\pm$ 0.67 mm) in TE (p = 0.005). There was a significant difference between pre-training (3.71 $\pm$ 0.14 J) and post-training (3.34 $\pm$ 0.13 J) in EG (p = 0.000). It indicated that subjects’ energy expenditure decreased after optimized training.

Taken together, the results of 1 and 2 suggest that after training, participants were able to improve the accuracy of their movements without assistance and also reduce energy expenditure to complete the task.

The average TE and EG of the CG decreased by 16.65 $\%$ and 4.56 $\%$ after training, respectively. In comparison, the average TE and EG of the EXG decreased by 34.59 $\%$ and 9.71 $\%$ severally.

The significant differences in the metrics between the groups were compared as follows:

1. 1. TE of pre-training in CG (5.85 $\pm$ 0.56 mm) vs. pre-training in EXG (5.81 $\pm$ 0.45 mm): There was no significant difference between the errors of the two groups before training (p = 0.959), indicating that there was no difference in the control of movement between the two groups.

2. 2. EG of pre-training in CG (3.86 $\pm$ 0.17 J) vs. pre-training in EXG (3.71 $\pm$ 0.14 J): There was no significant difference in EG between the two groups before training (p = 0.376). The result suggested no difference in energy expenditure between the two groups performing the same trial under the same conditions.

3. 3. TE of post-training in CG (4.87 $\pm$ 0.46 mm) vs. post-training in EXG (3.80 $\pm$ 0.67 mm): The TE of the two groups possessed significant differences after training (p = 0.005), demonstrating that BO-based training improved motor control more than GS-based training.

4. 4. EG of post-training in CG (3.67 $\pm$ 0.16 J) vs. post-training in EXG (3.34 $\pm$ 0.13 J): The EG of the two groups possesses significant differences after training (p = 0.048), suggesting that the EXG was able to exhibit less energy expenditure in the same task.

Combining the results mentioned above, it was found that the BO-trained group exhibited greater accuracy and lower energy expenditure in completing the task under the same unassisted conditions compared to the CG.

In addition to comparing the pre- and post-training metrics of the two groups, we also analyzed the metrics during the training process. As the first six trials of the CG were used for optimization, we focused on the variation in performance from the $7\text{th}$ to the $21\text{th}$ training trails and compared the average TE and EG of the two groups per trial, as shown in Fig. 8. By fitting a linear regression to the TE and EG of $7\text{th}$ – $21\text{th}$ trials, we found that the slope of TE in CG is −0.016, while the slope of TE in EXG is −0.002, the slope of EG in CG is −0.0076, and the slope of EG in EXG is 0.0019. These results suggest that the TE gradually decreased during the training based on the greedy strategy, but the reduction of TE was smaller in the EXG. Moreover, the EG of CG decreased while the EG of EXG increased.

Figure 8. (a) Variation of trajectory error and fitted curves in optimization training. (b) Variation of engagement and fitted curves in optimization training (the $1\text{th}$ – $6\text{th}$ training trials of control group were used for optimization, while the $1\text{th}$ – $6\text{th}$ training trials of experimental group were used for initialization).

We further compared the TE and EG of the two groups during the training process using paired t-test and found a significant difference between the two groups in two metrics ( $p\lt 0.001$ ). The comparison results indicate that the BO-based training method encourages subjects to engage in the training, even though they make more trajectory errors. Our experimental results demonstrate that the proposed method can maintain a high level of engagement and even strengthen it over time.

In addition, a random subject from the EXG was selected to access the processed data and investigate the evolution of hyperparameter during the optimization process. This evaluation included the process of GP and the acquisition function used to select the optimal hyperparameters for the next trial.

Figure 9 displays the posterior distribution of the objective function with respect to the hyperparameter of AAN estimated by GP during the OP session. The PI function was then utilized to determine the minimum value that would maximize the likelihood of performance improvement within the given range, based on the posterior distribution. Despite subjects occasionally performing poorly near the optima, most of the sampled points were concentrated around $\lambda =0.58$ after 14 optimization training trials. This optimization process demonstrated that the global optimal point had been identified and that the noise of the objective function had minimal impact on adjusting the optima.

Figure 9. (a–c) denote the posterior distribution of the Gaussian process of the target function based on observations from $1\text{th}$ – $6\text{th}$ trials, $1\text{th}$ – $13\text{th}$ trials, and $1\text{th}$ – $20\text{th}$ trials in the OP session, respectively. (d–f) denote the probability of improvement that the value chosen by $\lambda$ for the next trial within a given range based on the historical performances respectively, and triangles denote the location of the participant-specific optimal hyperparameter.

5. Discussion

With BO-based optimization training, the average TE was reduced by 17.94 $\%$ , and the average EG was reduced by 5.15 $\%$ compared to the training based on the greedy algorithm. The study’s results have suggested a potential improvement in motor control of the upper limb through BO-based training. In line with optimization-assisted training based on greedy strategies [22–33], training based on BO not only optimized the parameters continuously but also did not fall in local optima, which highlights the importance of continuous and global optimization. In addition, BO-based training was more efficient than greedy strategy-based training, as demonstrated by the need for fewer trials to obtain the global optima in a high-performance noise environment.

It should be mentioned that while we have demonstrated in our investigations that short-term exercise training promotes subjects’ performance, the proposed controller has yet to be tested in clinical trials.

Future research will adaptively adjust the subject-specific search region by improving the optimization method to reduce the likelihood that the optimal value is on the boundary. In addition, more research will focus on the decay pattern of the subject’s improved performance after training. Moreover, applying the adaptive AAN to the patient’s recovery will be necessary.

6. Conclusion

This paper proposes an AAN training method based on EI for upper limb training. EI is validated to be a reliable metric of the subject’s level of engagement. Based on this, the hyperparameter of the controller is gradually optimized using BO. Through training in this way, the engagement in the training could be promoted with a subject-specific force field, thus leading to improved training effect. In a comparative experiment, the BO-based training method is found to reduce TE and energy consumption after training.

Future work will focus on carrying out the proposed method in the three-dimensional space, specifically for the purpose of upper limb rehabilitation in stroke patients. Additionally, the training experiments will include patients to validate the proposed training methods.