No CrossRef data available.
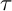 $\tau $-PERPENDICULAR WIDE SUBCATEGORIES
$\tau $-PERPENDICULAR WIDE SUBCATEGORIESPublished online by Cambridge University Press: 22 August 2023
Let 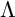 $\Lambda $ be a finite-dimensional algebra. A wide subcategory of
$\Lambda $ be a finite-dimensional algebra. A wide subcategory of 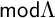 $\mathsf {mod}\Lambda $ is called left finite if the smallest torsion class containing it is functorially finite. In this article, we prove that the wide subcategories of
$\mathsf {mod}\Lambda $ is called left finite if the smallest torsion class containing it is functorially finite. In this article, we prove that the wide subcategories of  $\mathsf {mod}\Lambda $ arising from
$\mathsf {mod}\Lambda $ arising from 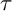 $\tau $-tilting reduction are precisely the Serre subcategories of left-finite wide subcategories. As a consequence, we show that the class of such subcategories is closed under further
$\tau $-tilting reduction are precisely the Serre subcategories of left-finite wide subcategories. As a consequence, we show that the class of such subcategories is closed under further 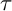 $\tau $-tilting reduction. This leads to a natural way to extend the definition of the “
$\tau $-tilting reduction. This leads to a natural way to extend the definition of the “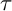 $\tau $-cluster morphism category” of
$\tau $-cluster morphism category” of 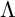 $\Lambda $ to arbitrary finite-dimensional algebras. This category was recently constructed by Buan–Marsh in the
$\Lambda $ to arbitrary finite-dimensional algebras. This category was recently constructed by Buan–Marsh in the 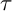 $\tau $-tilting finite case and by Igusa–Todorov in the hereditary case.
$\tau $-tilting finite case and by Igusa–Todorov in the hereditary case.
This work was supported by the Norwegian Research Council (Grant No. FRINAT 301375).