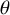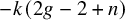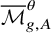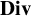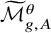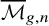Smooth Compactifications of the Abel-Jacobi Section

Abstract

For $\theta $ a small generic universal stability condition of degree $0$ and A a vector of integers adding up to $-k(2g-2+n)$, the spaces $\overline {\mathcal {M}}_{g,A}^\theta $ constructed in [AP21, HMP+22] are observed to lie inside the space $\textbf {Div}$ of [MW20], and their pullback under $\textbf {Rub} \to \textbf {Div}$ of loc. cit. to be smooth. This provides smooth and modular modifications $\widetilde {\mathcal {M}}_{g,A}^\theta $ of $\overline {\mathcal {M}}_{g,n}$ on which the logarithmic double ramification cycle can be calculated by several methods.

1 Introduction

The strata of multiscale differentials are the loci

$$ \begin{align*}\left\{(C,x_1,\cdots,x_n): (\omega^{\log})^{\otimes k}(\sum_{i=1}^n a_ix_i) \cong \mathcal{O}_C\right\} \end{align*} $$

in $\mathcal {M}_{g,n}$ for a vector $A = (a_1,\cdots ,a_n)$ of integers summing up to $-k(2g-2+n)$ . Extensions of these loci to the compactification $\overline {\mathcal {M}}_{g,n}$ have been the subject of a vast literature with different techniques and objectives. In its most algebraic incarnation, such an extension asks for a cycle

$$ \begin{align*}\mathsf{DR}^k_{g,A} \in \mathsf{CH}^g(\overline{\mathcal{M}}_{g,n}) \end{align*} $$

of the expected dimension supported on the ‘double ramification locus’

$$ \begin{align*}\mathsf{DRL}_{g,A}^k : = \left\{(C,x_1,\cdots,x_n): (\omega^{\log})^{\otimes k}(\sum a_ix_i) \cong \mathcal{O}_C\right\} \subset \overline{\mathcal{M}}_{g,n} \end{align*} $$

of multiscale differentials for the partition A. The cycle $\mathsf {DR}^k_{g,A}$ is called the double ramification cycle, as when $k=0$ , it parametrizes functions ramified over two points of $\mathbb {P}^1$ , namely zero and infinity. Even the definition of the cycle $\mathsf {DR}^k_{g,A}$ is subtle; the first rigorous definition was given in [GV05] for $k=0$ via the relative Gromov-Witten theory of $\mathbb {P}^1$ , and in [Hol21, MW20], in general, via Abel-Jacobi theory. Even subtler however is computing the class of $\mathsf {DR}^k_{g,A}$ in $\mathsf {CH}^g(\overline {\mathcal {M}}_{g,n})$ ; what is meant by computing here is finding an expression of $\mathsf {DR}^k_{g,A}$ in terms of generators of the tautological ring $\mathsf {R}^*(\overline {\mathcal {M}}_{g,n})$ . A remarkable such expression, known by now as Pixton’s formula, was discovered by Pixton and proven in [JPPZ17].

Perhaps surprisingly, the developments of [JPPZ17] are not the final word on the subject. For instance, if one adopts the Gromov-Witten theory perspective, it is natural to ask for a calculation of the virtual fundamental class for (rubber) relative stable maps to $\mathbb {P}^2$ instead of $\mathbb {P}^1$ , or in the multiscale language, for the corresponding classes and calculations of the ‘double double’ ramification loci

$$ \begin{align*}\{(C,x_1,\cdots,x_n): (\omega^{\log})^{\otimes k}(\sum a_ix_i) \cong \mathcal{O}_C \cong (\omega^{\log})^{\otimes k}(\sum b_ix_i)\} \end{align*} $$

for two partitions $A,B$ of $k(2g-2+n)$ . For these problems, the methods of [JPPZ17] have not been successfully adapted. To approach them, it has been understood ([HPS19], [Ran19], [HS22], [MR21], [Her19]) that one should study these problems in the context of logarithmic geometry. In this context, it is more natural to study instead the logarithmic double ramification cycle

$$ \begin{align*}\mathsf{logDR}^k_{g,A}. \end{align*} $$

This is a certain refinement of $\mathsf {DR}^k_{g,A}$ , but it does not live on $\overline {\mathcal {M}}_{g,n}$ – or, better, it does not lie in $\mathsf {CH}(\overline {\mathcal {M}}_{g,n})$ , but rather in the logarithmic Chow ring $\mathsf {logCH}(\overline {\mathcal {M}}_{g,n})$ ([Bar18], [MPS21]).

We will not define the $\mathsf {logDR}^k_{g,A}$ here (or the $\mathsf {DR}^k_{g,A}$ for that matter), but it is possible to explain the relevant aspects of the relationship between $\mathsf {logDR}^k_{g,A}$ and $\mathsf {DR}^k_{g,A}$ on general grounds. Let $(X,D)$ be a smooth Deligne-Mumford stack with a normal crossings divisor D; the case of primary interest is of course $X = \overline {\mathcal {M}}_{g,n}, D = \partial \overline {\mathcal {M}}_{g,n} = \overline {\mathcal {M}}_{g,n} - \mathcal {M}_{g,n}$ . The divisor D then stratifies X into the strata consisting of connected components of intersections $D_1 \cap \cdots \cap D_k$ of various irreducible components of D. ¹ A simple blowup is the blowup of X along a smooth stratum closure. Such a blowup $p:X' \to X$ produces a new pair $(X',D' = p^{-1}(D))$ . A blowup obtained by iterating this procedure a finite number of times is called an iterated blowup. A logarithmic modification of $(X,D)$ is any modification ² $p:X' \to X$ which can be dominated by an iterated blowup of $(X,D)$ . Logarithmic modifications form an inverse system, with a map $X" \to X'$ in the system if the modification $X" \to X$ factors through $X' \to X$ . In this case, we say that $X"$ is finer than $X'$ , or a refinement of it. The partial order determined by refinement yields a system of groups $\mathsf {CH}^{\text {op}}(X')$ indexed by Gysin pullback. Then

$$ \begin{align*}\mathsf{logCH}(X,D) := \varinjlim \mathsf{CH}^{\text{op}}(X'), \end{align*} $$

where $X' \to X$ ranges through logarithmic modifications of $(X,D)$ . ³ The ordinary Chow ring $\mathsf {CH}(X)$ is contained in $\mathsf {logCH}(X)$ as a subring, and there is a retraction (which is not a ring homomorphism) $\mathsf {logCH}(X) \to \mathsf {CH}(X)$ by pushforward. Thus, to say that $\mathsf {logDR}^k_{g,A}$ is a nontrivial refinement of $\mathsf {DR}^k_{g,A}$ in $\mathsf {logCH}(\overline {\mathcal {M}}_{g,n})$ is to say that $\mathsf {logDR}^k_{g,A} \notin \mathsf {CH}(\overline {\mathcal {M}}_{g,n}) \subset \mathsf {logCH}(\overline {\mathcal {M}}_{g,n})$ but its pushforward equals $\mathsf {DR}^k_{g,A}$ .

The ring $\mathsf {logCH}(X,D)$ is, apart from trivial cases, not finitely generated. However, any given element of it is determined by a finite amount of data: for each $x \in \mathsf {logCH}(X,D)$ , there exists some log modification $X' \to X$ and an element $x' \in \mathsf {CH}(X')$ so that $x = x'$ under the natural inclusion $\mathsf {CH}(X') \subset \mathsf {logCH}(X,D)$ . Such a pair $(X',x')$ is called a representative of x on $X'$ . It is often the case, however, that several such representatives $(X',x')$ exist, with none being preferable. For the sake of concreteness, one could have $(X_i',x_i'),i=1,2$ representing x, while by definition, there is a representative $(X",x")$ dominating both, meaning $p_i:X" \to X_i'$ is a modification and $x"=p_i^*(x_i)$ ; there may be no direct map $X_1 \to X_2$ or vice versa.

This is the case for $\mathsf {logDR}^k_{g,A}$ . Representatives of it can be found on any log modification $p: \overline {\mathcal {M}}_{g,n}' \to \overline {\mathcal {M}}_{g,n}$ which is sufficiently fine in some sense that we do not make precise here, but which intuitively means that the closure of $\mathsf {DRL}_{g,A}^k$ meets the boundary of $\overline {\mathcal {M}}_{g,n}'$ sufficiently transversely. The log modifications $\overline {\mathcal {M}}_{g,n}'$ are, however, neither unique nor canonical, and there is no coarsest or finest log modification supporting a representative. So, in a sense, the ambiguity of choosing a representative is built into the $\mathsf {logDR}^k_{g,A}$ problem.

While the ambiguity of a representative of a class in $\mathsf {logCH}$ causes few conceptual difficulties, it can cause substantial ones on more practical matters. For instance, if one is interested in writing a formula for the class, several hurdles have to be overcome: from the offset, one must decide which generating set for the various $\mathsf {CH}^{\text {op}}(X')$ to use. Fortunately, a good candidate for a generating set does exist, consisting of the Chow ring $\mathsf {CH}(X)$ and the algebra of boundary strata of the various $X'$ , which is captured by combinatorial data: the algebra of piecewise polynomial functions on the tropicalization of X [MPS21, MR21, Bri96, Pay06, FS97]. Even so, while this choice of generating set determines the form of the answer, to write down an explicit formula, one generally needs to have precise control over the additional generators adjoined. In practice, this means choosing a representative $(X',x')$ with some sort of special presentation.

Early approaches to the $\mathsf {logDR}^k_{g,A}$ focused on properties of the blowup $\overline {\mathcal {M}}_{g,n}' \to \overline {\mathcal {M}}_{g,n}$ supporting a representative. The idea here is that, since no best possible choice for $\overline {\mathcal {M}}_{g,n}'$ exists, one might as well choose one that is fine enough that avoids as many pathologies as possible: choose an $\overline {\mathcal {M}}_{g,n}'$ that is smooth, whose strata do not self-intersect, and so on. These approaches sufficed to prove soft properties of the $\mathsf {logDR}^k_{g,A}$ , which depend on the form of the class; it was proven, for instance, that it is tautological [MR21, HS22]. But choosing least pathological models $\overline {\mathcal {M}}_{g,n}'$ relies on abstract use of resolution of singularities, which makes the problem of finding an explicit formula essentially impossible.

In [HMP+22], Pixton’s formula was extended to $\mathsf {logDR}^k_{g,A}$ . The strategy adopted there was in the opposite direction: the compactifications $\overline {\mathcal {M}}_{g,n}'$ constructed were as closely tied with the geometry of the Abel-Jacobi section as possible. The reason for doing so was to connect the $\mathsf {logDR}^k_{g,A}$ with the DR cycle on the universal Picard stack, which had been calculated in [BHP+20] by a (rather elaborate) extension of the methods of [JPPZ17]. The end result was, for each ‘universal stability condition’ $\theta $ [KP19], which through works of [OS79, Cap94, KP19, Pan96, Mel19] produces a compactified Jacobian $\mathrm {Pic}^{\theta }$ , a log modification $\overline {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$ resolves the indeterminacies of the Abel-Jacobi section

$$ \begin{align*}\overline{\mathcal{M}}_{g,n} \dashrightarrow \mathrm{Pic}^{\theta}. \end{align*} $$

The study of such resolutions was initiated in [AP21] via tropical methods, at least in the presence of some mild assumptions on the stability condition, but studying the problem logarithmically allows one to go further, by endowing $\overline {\mathcal {M}}_{g,A}^\theta $ with an explicit functor of points. In other words, the nonpathological compactifications $\overline {\mathcal {M}}_{g,n}'$ were traded for modular ones. As the functor of points of $\overline {\mathcal {M}}_{g,A}^\theta $ can be understood completely explicitly when working logarithmically, this was sufficient to compute $\mathsf {logDR}^k_{g,A}$ on each $\overline {\mathcal {M}}_{g,A}^\theta $ .

However, the spaces $\overline {\mathcal {M}}_{g,A}^\theta $ are typically singular, and the calculation in [HMP+22] expresses $\mathsf {logDR}^k_{g,A}$ as an operational class. Nevertheless, there are significant advantages to working with a nonsingular space. For instance, in [MR21], the $\mathsf {logDR}^k_{g,A}$ is approached via strict transforms and Segre classes and requires as inputs [Ful98, Theorem 6.7] and [Alu16], which do not work for singular toroidal spaces such as $\overline {\mathcal {M}}_{g,A}^\theta $ . Furthermore, ongoing work of Abreu-Pagani and myself aims to calculate the $\mathsf {logDR}^k_{g,A}$ by Grothendieck-Riemann-Roch techniques, which require working with the class in the homological $\mathsf {CH}_*$ instead of the operational theory. For this approach, the singularities of $\overline {\mathcal {M}}_{g,A}^\theta $ cause difficulties.

The goal of this paper is to address these difficulties. For each universal stability condition $\theta $ , we construct a refinement

$$ \begin{align*}\widetilde{\mathcal{M}}_{g,A}^\theta \to \overline{\mathcal{M}}_{g,A}^\theta \end{align*} $$

and show the following:

Theorem 1.1. The stack $\widetilde {\mathcal {M}}_{g,A}^\theta $ is smooth. When $\theta $ is nondegenerate, the induced map $\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$ is a composition of a logarithmic modification with a root stack. Hence, it is proper, birational (an isomorphism over the compact type locus $\mathcal {M}_{g,n}^{\text {ct}})$ and of DM-type.

Furthermore, the refinement $\widetilde {\mathcal {M}}_{g,A}^\theta $ is modular:

Theorem 1.2. Let S be a logarithmic scheme, and $S \to \overline {\mathcal {M}}_{g,n}$ be a logarithmic map, corresponding to a family of curves $C \to S$ . Lifts of $S \to \widetilde {\mathcal {M}}_{g,A}^\theta $ correspond to pairs $(C' \to C,\alpha )$ consisting of

• • A destabilization $C' \to C$ ,

• • An equidimensional piecewise linear function $\alpha $ on $C'$ which twists $(\omega ^{\log })^{\otimes k}(\sum a_ix_i)$ to a $\theta $ -stable line bundle on $C'$ .

The notion of equidimensional piecewise linear function and twisting is explained in Section 4. Stability here is a minimality condition, also explained in 4, which ensures, among other things, finiteness of automorphisms groups. In particular, the strata of $\widetilde {\mathcal {M}}_{g,A}^\theta $ are entirely explicit and correspond to certain combinatorial/linear algebraic data, which we call $\theta $ -stable equidimensional flows. These are defined in 2.20.

In other words, the space $\widetilde {\mathcal {M}}_{g,A}^\theta $ is a ‘dream compactification’ of the double ramification problem: nonsingular and modular. In particular, $\widetilde {\mathcal {M}}_{g,A}^\theta $ carries a universal family $\widetilde {C}_{g,A}^\theta \to \widetilde {\mathcal {M}}_{g,A}^\theta $ and a universal line bundle $\mathcal {L}$ on $\widetilde {C}_{g,A}^\theta $ – that is, an Abel-Jacobi section

$$\begin{align*}\widetilde{\mathcal{M}}_{g,A}^\theta \to \mathrm{Pic}^\theta. \end{align*}$$

The line bundle $\mathcal {L}$ is simply the pullback of the universal line bundle on $\mathrm {Pic}^\theta $ . The universal family $\widetilde {C}_{g,A}^\theta $ is not the pullback but rather a blowup of the pullback of the universal family of $\mathrm {Pic}^\theta $ , which is also better behaved. Recall that a scheme is called quasi-smooth if every divisor is $\mathbb {Q}$ -Cartier. We have the following:

Theorem 1.3. The universal curve $\widetilde {C}_{g,A}^\theta $ is quasi-smooth.

From the perspective of the semistable reduction theorems, this result is surprising. The semistable reduction theorem ensures that given a family of curves $C \to S$ , we can find blowups $S' \to S$ and $C' \to C \times _S S'$ which are smooth; however, the blowup required on the base S depends on the family $C \to S$ , which makes constructing the semistable family $C' \to S'$ explicitly very difficult in practice.

The connection with the double ramification cycle is as follows: when $\theta $ is nondegenerate and sufficiently close to the $0$ stability condition, $\widetilde {\mathcal {M}}_{g,A}^\theta $ supports a representative of $\mathsf {logDR}^k_{g,A}$ , and the methods of [HMP+22] also apply.

Corollary 1.4. The universal $\mathsf {DR}$ formula for $\mathcal {L}$ computes the $\mathsf {logDR}^k_{g,A}$ on $\widetilde {\mathcal {M}}_{g,A}^\theta $ .

The smoothness of the spaces $\widetilde {\mathcal {M}}_{g,A}^\theta $ , however, also allows the use of alternative methods of calculation. This was, in fact, the main driver in writing the paper. Our motivations, ranked in order of confidence, can be listed as

• • Find a desingularization of $\overline {\mathcal {M}}_{g,A}^\theta $ in which one can calculate $\log \mathsf {DR}_{g,A}^k$ via traditional algebro-geometric techniques which avoid Gromov-Witten theory and localization.

• • Highlight the following phenomenon: $\widetilde {\mathcal {M}}_{g,A}^\theta $ is constructed by combining two faraway ideas. Stability conditions from the universal Jacobian provide a compact space $\overline {\mathcal {M}}_{g,A}^\theta $ . Techniques from stable maps then provide a desingularization relative to $\overline {\mathcal {M}}_{g,A}^\theta $ . We expect this phenomenon to be present in several moduli problems.

• • Optimize the computer calculations of $\log \mathsf {DR}_{g,A}^k$ . ⁴ Currently, the software deals with the singularities of $\overline {\mathcal {M}}_{g,n}^\theta $ by desingularizing using a general desingularization algorithm for cones.

The construction of the spaces $\widetilde {\mathcal {M}}_{g,A}^\theta $ itself is, in fact, very simple. In the brilliant work of Marcus and Wise [MW20], a modification

$$ \begin{align*}\mathbf{Div}_{g,A} \to \overline{\mathcal{M}}_{g,n} \end{align*} $$

is constructed. The modification is not of finite type and is highly nonseparated; it is the universal modification which resolves the Abel-Jacobi section to the universal Picard stack $\mathbf {Pic}_{g,n}$ . Along with it, a further modification

$$ \begin{align*}\mathbf{Rub}_{g,A} \to \mathbf{Div}_{g,A} \end{align*} $$

is given, which is, up to orbifold corrections, a log modification as above. We briefly review these constructions in Section 6. The motivation of [MW20] for these constructions is, in the case $k=0$ , to compare the double ramification locus

$$ \begin{align*}\mathsf{DRL}_{g,A}^k = \mathbf{Div}_{g,A} \times_{\mathbf{Pic}} \overline{\mathcal{M}}_{g,n} \end{align*} $$

with the space of relative rubber maps to $\mathbb {P}^1$ , which is identified as

$$ \begin{align*}\mathbf{Rub}_{g,A} \times_{\mathbf{Div}_{g,A}} \mathsf{DRL}_{g,A}^k. \end{align*} $$

Our observation is simply that the spaces $\overline {\mathcal {M}}_{g,A}^\theta $ constructed in [HMP+22] are open substacks of $\mathbf {Div}_{g,A}$ , and that $\mathbf {Rub}_{g,A}$ is smooth. Combining the two properties gives the spaces $\widetilde {\mathcal {M}}_{g,A}^\theta $ as

$$ \begin{align*}\mathbf{Rub}_{g,A} \times_{\mathbf{Div}_{g,A}} \overline{\mathcal{M}}_{g,A}^\theta. \end{align*} $$

Thus, the space $\widetilde {\mathcal {M}}_{g,A}^\theta $ is constructed by combining ideas from the theory of relative stable maps with universal stability conditions. Most of the work in the paper is devoted to understanding how this combination works – that is, what the functor of points of this fiber product is (a subtlety is that the fiber product is taken in the category of logarithmic schemes). The main technical tool that allows us to carry out this translation is the determination of a tropicalization of $\mathbf {Div}_{g,A}$ and the relevant auxiliary spaces. The tropicalization of $\mathbf {Div}_{g,A}$ is analogous to the tropicalization of the universal Jacobian, as discussed in [MMUV22], and is perhaps of independent interest to tropical geometers. The analogy with the tropicalization of the universal Jacobian can, in fact, be made precise by recognizing $\mathbf {Div}_{g,A}$ as the pullback of the universal Picard stack to $\overline {\mathcal {M}}_{g,n}$ via an Abel-Jacobi section, but we do not explore this direction here.

The paper is roughly organized into three parts: combinatorial (Section 2), tropical Sections 3 and 4), and logarithmic (Sections 5 and 6). The parts are of increasing complexity, with the concepts in each part building upon the concepts in the preceding ones by endowing them with additional structure: metric structures turn combinatorial objects into tropical ones, and logarithmic structures turn tropical objects into algebraic ones.

Regardless, in its purest form, the map $\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$ is built by constructing a cone stack $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$ , which is identified with a subdivision of the tropicalization $\mathcal {M}_{g,n}^{\text {trop}}$ of $\overline {\mathcal {M}}_{g,n}$ (with an integral structure that is a finite index substructure of the induced one). This is constructed in Section 4. The cone stack $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$ is, in fact, a moduli space of tropical objects – tropical curves with piecewise linear functions on them that satisfy certain properties, which are discussed in Sections 3 and 4. The cones in $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$ are indexed by the combinatorial data of Section 2. In fact, a cone in $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$ can be thought of as parametrizing all possible ways to enrich a given combinatorial type with a metric structure. The space $\widetilde {\mathcal {M}}_{g,A}^\theta $ is then built by algebraizing $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$ via general techniques of logarithmic geometry, explained in Section 5. Section 6 is devoted to the analysis of the resulting algebraization and contains the final form of the results. Section 7 explains how to compute $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$ algorithmically, and Section 8 is devoted to an example. The reader is encouraged to skip ahead to the corresponding part of Sections 7 and 8 when coming upon an unfamiliar notion in the main sections, to see how it works in practice.

2 Stable Flows

2.1 Graphs, divisors and flows

We begin with a short review of some essential notions from the theory of graphs. The notions are well-known, but we include them to avoid excessive referencing and to fix notation. We will follow the definitions of graphs and their morphisms from [MMUV22], although we will substitute oriented edges in the place of half-edges in our presentation. Let $\Gamma $ be a graph. We write $V(\Gamma )$ for the set of vertices of $\Gamma $ , $\mathcal {E}(\Gamma )$ for the set of oriented edges, $E(\Gamma )$ for the set of edges and $L(\Gamma )$ for the set of legs. A genus function on $\Gamma $ is a function

$$\begin{align*}h_\Gamma: V(\Gamma) \to \mathbb{N}. \end{align*}$$

The genus of $\Gamma $ is the natural number

$$\begin{align*}g = g(\Gamma) := \sum_{v \in V(\Gamma)} h_\Gamma(v) + \dim H_1(\Gamma). \end{align*}$$

When speaking about the genus of a graph, it is to be understood that a genus function has been specified. However, unless explicitly mentioned, our results do not require fixing the genus and apply equally well to graphs with or without a genus function. A marking on $\Gamma $ is a bijection between $\{1,\cdots ,n\}$ and $L(\Gamma )$ . A graph with a marking is called an n-marked graph.

Definition 2.2. A divisor on $\Gamma $ is a formal $\mathbb {Z}$ -linear combination of vertices of $\Gamma $ . The group of divisors on $\Gamma $ is denoted by $\mathsf {Div}(\Gamma )$ .

Of course, $\mathsf {Div}(\Gamma )$ is nothing but the free abelian group $\mathbb {Z}^{V(\Gamma )}$ on $V(\Gamma )$ , but we insist on the notation for clarity.

Example 2.2.1. Let $\Gamma $ be an n-marked genus g graph. Let $(a_1,\cdots ,a_n) \in \mathbb {Z}^n$ , $k \in \mathbb {Z}$ . Let

$$\begin{align*}A = \sum_{v \in V(\Gamma)} k(2h_\Gamma(v)-2 + \text{val}(v))v + \sum_{i=1}^n a_iv_i, \end{align*}$$

where $\text {val}(v)$ is the valence of v – the number of oriented edges $\vec {e}$ with $\mathfrak {r}(\vec {e})=v$ plus the number of legs on v – and $v_i$ is the vertex that contains the i-th leg. Then A is a divisor on $\Gamma $ . When the $a_i$ are all $0$ , A is called the log canonical divisor. When the $a_i$ are all $-1$ , it is called the canonical divisor.

There is an evident two-to-one cover $\mathcal {E}(\Gamma ) \to E(\Gamma )$ from the set of oriented edges to the set of edges, and every choice of orientation $\vec {\Gamma }$ on $\Gamma $ gives a section $E(\Gamma ) \to \mathcal {E}(\Gamma )$ , whose image we denote by $E(\vec {\Gamma })$ .

Definition 2.3. Given an oriented edge $\vec {e}$ , we write

• • e for the image of $\vec {e}$ in $E(\Gamma )$ .

• • for $\vec {e}$ with the opposite orientation.

• • $\mathfrak {r}(\vec {e})$ for the initial point of $\vec {e}$ .

• • for the terminal point of $\vec {e}$ .

Definition 2.4. A flow on $\Gamma $ is a function

$$ \begin{align*}s:\mathcal{E}(\Gamma) \to \mathbb{Z} \end{align*} $$

satisfying . We write $\mathsf {Flow}(\Gamma )$ for the group of flows on $\Gamma $ .

Of course, as above, $\mathsf {Flow}(\Gamma )$ can be identified with $\mathbb {Z}^{E(\vec {\Gamma })}$ after choosing an orientation on $\Gamma $ .

Any flow on s on $\Gamma $ determines a divisor $\mathsf {div}(s)$ on $\Gamma $ by setting

$$ \begin{align*}\mathsf{ord}_v(s) = \sum_{\{\vec{e} : \mathfrak{t}(\vec{e}) = v\}} s(\vec{e}) \end{align*} $$

and

$$ \begin{align*}\mathsf{div}(s) = \sum_{v \in V(\Gamma)} (\mathsf{ord}_v(s))v. \end{align*} $$

Here, the notation $\{\vec {e}: \mathfrak {t}(\vec {e})=v\}$ means the set of oriented edges whose terminal point is v. This procedure gives a homomorphism

$$ \begin{align*}\mathsf{div}:\mathsf{Flow}(\Gamma) \to \mathsf{Div}(\Gamma). \end{align*} $$

Definition 2.5. Let $\Gamma $ be a graph. A basic subdivision of $\Gamma $ is a graph $\Gamma '$ obtained from $\Gamma $ by replacing an oriented edge $\vec {e}$ ⁵ with two oriented edges $\vec {e_1},\vec {e_2}$ and a new vertex u, and setting

$$ \begin{align*} \mathfrak{r}(\vec{e_1}) = \mathfrak{r}(\vec{e})\\ \mathfrak{t}(\vec{e_1}) = \mathfrak{r}(\vec{e_2}) = u \\ \mathfrak{t}(\vec{e_2}) = \mathfrak{t}(\vec{e}). \end{align*} $$

There is an evident map $\Gamma ' \to \Gamma $ which sends $e_1,e_2,u$ to e and all other vertices and edges to themselves.

A subdivision of $\Gamma $ is a composition of basic subdivisions.

Let $\Gamma ' \to \Gamma $ be a subdivision. The additional vertices on $\Gamma '$ are called exceptional. A refinement of $\Gamma '$ is a further subdivision $\Gamma " \to \Gamma '$ .

Suppose $\Gamma ' \to \Gamma $ is a subdivision, and s is a flow on $\Gamma '$ . It is often desirable to find the minimal subdivision of $\Gamma $ on which s can be defined.

Definition 2.6. We say that $\Gamma '$ is minimal with respect to s if

$$ \begin{align*}\mathsf{ord}_v(s) \neq 0 \end{align*} $$

on all exceptional vertices v of $\Gamma '$ .

Lemma 2.7. Suppose $\Gamma '$ is a subdivision of $\Gamma $ , and s is a flow on $\Gamma '$ . There is a unique minimal subdivision $\Gamma _s \to \Gamma $ on which s can be defined.

Proof. Define $\Gamma _s$ as the subdivision of $\Gamma $ obtained by keeping only the exceptional vertices of $\Gamma '$ on which

$$ \begin{align*}\mathsf{ord}_v(s) \neq 0. \end{align*} $$

Since the slope of s changes on the vertices v, any subdivision that supports s must refine $\Gamma _s$ , whereby the uniqueness of $\Gamma _s$ follows.

2.8 Equidimensionality

Let $\Gamma $ be a graph, and s a flow on $\Gamma $ . Then s defines a partial orientation on $\Gamma $ , by orienting the edges so that $s(\vec {e})>0$ . The orientation is partial, as it is not defined on edges with $s(e) = 0$ . We call such edges contracted. The flow s defines an honest orientation on the graph $\overline {\Gamma }$ obtained from $\Gamma $ by contracting the contracted edges.

Definition 2.9. A flow s is called acyclic if the graph $\overline {\Gamma }$ has no oriented cycles for the orientation induced by s.

An acyclic flow s defines a partial order on the vertices of $\Gamma $ : the order is generated by the relation

$$ \begin{align*}v < w \end{align*} $$

if $v,w$ are the endpoints of an oriented edge $\vec {e}$ from v to w in the orientation determined by s. Endpoints of contracted edges are not comparable to one another.

Definition 2.10. Let $\Gamma $ be a graph. An ordering on $\Gamma $ is an acyclic flow s, together with the the choice of a total order among the vertices of the noncontracted edges of $\Gamma $ , extending the partial order determined by s. We say the ordering extends or is subordinate to s.

The flow s lifts to any subdivision $\Gamma ' \to \Gamma $ , by declaring $s(\vec {e}_i)=s(\vec {e})$ whenever $\vec {e} \in \mathcal {E}(\Gamma )$ is subdivided into $\vec {e}_1,\cdots ,\vec {e_n}$ in $\Gamma '$ , and an ordering extending s on $\Gamma $ lifts to an ordering extending s on $\Gamma '$ uniquely. We can rephrase the notion of ordering in the following convoluted way, which nevertheless will be meaningful in the next section:

Definition 2.11. A one-dimensional combinatorial target, or combinatorial line, is a graph X consisting of n-ordered vertices $v_1,\cdots ,v_n$ , with $v_{i+1}$ joined to $v_i$ by a single edge $f_i$ , along with two legs – one on $v_1$ and one on $v_n$ .

One-dimensional combinatorial targets X come with a canonical orientation, in which $f_i$ is oriented from $v_i$ to $v_{i+1}$ . We denote the canonical orientation by $E(\vec {X})$ .

We can then consider maps $\Gamma \to X$ . Morphisms for us take cells into cells (i.e. vertices or edges into vertices or edges). A morphism $\phi : \Gamma \to X$ also defines a partial order on $V(\Gamma )$ , by declaring $v<w$ if $\phi (v) = v_i$ , $\phi (w) = v_{j}$ , with $i < j$ . Vertices that map to the same vertex of X are incomparable with one another, and we do not define the order on vertices that map into edges of X. The following class of morphisms is then special:

Definition 2.12. A map $\Gamma \to X$ is equidimensional if it takes vertices to vertices.

Thus, an equidimensional morphism $\Gamma \to X$ defines a total order on the vertices of noncontracted edges (i.e., those edges which map to an edge instead of a vertex) of $\Gamma $ .

Definition 2.13. Let $\Gamma $ be a graph, and s an acyclic flow on $\Gamma $ . An equidimensional lift of s is the data of a subdivision $\Gamma ' \to \Gamma $ , a combinatorial line X and a morphism $\Gamma ' \to X$ compatible with the partial order on the vertices of $\Gamma '$ induced by (the lift of) s on $\Gamma '$ . This data is stable if all vertices of X are images of vertices of $\Gamma $ .

We note that stability is not an absolute notion, but it depends on the original graph $\Gamma $ on which s is defined.

Suppose $\Gamma ' \to X$ is an equidimensional lift of s. Then $\Gamma ' \to X$ defines an ordering $\kappa $ extending s, as it orders the vertices of $\Gamma '$ that lie on the noncontracted edges of $\Gamma '$ (i.e., those on which $s \neq 0$ , which are precisely the subdivisions of the noncontracted edges of $\Gamma $ ), and since $V(\Gamma ) \subset V(\Gamma ')$ , also the vertices of $\Gamma $ which lie on the noncontracted edges of $\Gamma $ . Conversely, given an ordering $\kappa $ extending s, we can define a combinatorial line $X_\kappa $ by taking one vertex $v_i$ for each vertex of a noncontracted edge of $\Gamma $ according to the order determined by $\kappa $ . This defines an evident function

$$ \begin{align*}\phi: \Gamma \to X_\kappa, \end{align*} $$

extending s. This is, however, not a morphism: edges of $\Gamma $ can map into unions of cells of $X_\kappa $ . There is a minimal subdivision $\Gamma _\kappa $ which turns $\Gamma \to X_\kappa $ into a morphism by adjoining the preimages of the vertices $\phi ^{-1}(v_i)$ to the noncontracted edges of $\Gamma _\kappa $ . The following lemma then follows:

Lemma 2.14. Orderings extending s are equivalent to stable equidimensional lifts of s, under the correspondence

$$ \begin{align*}\kappa \leftrightarrow \phi: \Gamma_\kappa \to X_\kappa. \end{align*} $$

2.15 Numerical stability conditions

Let $\Gamma $ be a graph.

Definition 2.16. A subdivision $\Gamma ' \to \Gamma $ is called a quasi-stable model of $\Gamma $ if every edge in $\Gamma $ is subdivided at most once.

In other words, the subdivision $\Gamma ' \to \Gamma $ introduces at most one exceptional vertex on each edge of $\Gamma $ .

Definition 2.17. A divisor D on a quasi-stable model $\Gamma '$ of $\Gamma $ is called admissible if its value on exceptional vertices is $1$ .

Finally, we recall that a stability condition $\theta $ on $\Gamma $ is simply a function

$$ \begin{align*}\theta: V(\Gamma) \to \mathbb{R}. \end{align*} $$

It is nondegenerate or generic if, for every $S \subset V(\Gamma )$ , we have

$$ \begin{align*}\theta(S) \pm \frac{E(S,S^c)}{2} \notin \mathbb{Z}, \end{align*} $$

where $\theta (S) = \sum _{v \in S} \theta (v)$ and $E(S,S^c)$ is the number of edges between S and its complement.

A stability condition determines a list of semistable divisors on $\Gamma $ : those D for which

$$ \begin{align*}\theta(S) - \frac{E(S,S^c)}{2} \le D(S) \le \theta(S) + \frac{E(S,S^c)}{2} \end{align*} $$

for all $S \subset V(\Gamma )$ . The divisor is stable if the inequalities are strict. Thus, a stability condition is nondegenerate if and only if all semistable divisors are stable.

A stability condition on $\Gamma $ lifts canonically to a quasi-stable model $\Gamma ' \to \Gamma $ by declaring its value on exceptional vertices to be $0$ .

Definition 2.18. Let $\theta $ be a stability condition on $\Gamma $ , and $\Gamma ' \to \Gamma $ a quasi-stable model. We call an admissible divisor D on $\Gamma '\ \theta $ -semistable if for every subgraph $S \subset \Gamma '$ , we have

$$ \begin{align*}\theta(S) - \frac{E(S,S^c)}{2} \le D(S) \le \theta(S) + \frac{E(S,S^c)}{2}. \end{align*} $$

We note that if $\theta $ is generic, the inequalities above are strict for every divisor supported on $V(\Gamma ) \subset V(\Gamma ')$ . However, equality can hold for divisors that have support on exceptional vertices. ⁶

We thus arrive at the key combinatorial notions of this paper. Let A denote a fixed divisor on $\Gamma $ , and $\theta $ a stability condition.

Definition 2.19. A $\theta $ -flow balancing A (or $\theta $ -flow for short) consists of a quasi-stable model $\Gamma ' \to \Gamma $ , a $\theta $ -semistable divisor D and an acyclic flow s with

$$ \begin{align*}\mathsf{div}(s) = A - D. \end{align*} $$

Definition 2.20. A $\theta $ -stable equidimensional flow (balancing A) consists of

• • A quasi-stable model $\Gamma ' \to \Gamma $ .

• • A $\theta $ -semistable divisor D on $\Gamma '$ .

• • An acyclic flow s on $\Gamma '$ balancing D:

  $$ \begin{align*}\mathsf{div(s)} = A-D. \end{align*} $$

• • A stable equidimensional lift $\Gamma " \to X$ of s.

2.21 Specialization

The data discussed above specializes with respect to edge contractions. Namely, if $\overline {\Gamma }$ is obtained from $\Gamma $ by contracting some edges, and $\phi : \Gamma \to \overline {\Gamma }$ denotes the contraction map,

1. (1) Divisors on $\Gamma $ specialize to divisors on $\overline {\Gamma }$ by $D \to \overline {D}$

   $$ \begin{align*}\overline{D}(v) = \sum_{w \in \phi^{-1}(v) \cap V(\Gamma)} D(w). \end{align*} $$

2. (2) Stability conditions specialize exactly analogously as $\overline {\theta }(v) = \sum \theta (w)$ .

3. (3) Flows specialize by $s \to \overline {s}$ , with

   $$ \begin{align*}\overline{s}(\vec{e}) = s(\vec{e}) \end{align*} $$

   under the natural inclusion $\mathcal {E}(\overline {\Gamma }) \subset \mathcal {E}(\Gamma )$ .

4. (4) The genus function $h_{\overline {\Gamma }}$ of $\overline {\Gamma }$ is defined by

   $$\begin{align*}h_{\overline{\Gamma}}(v) = g_{\Gamma}(\phi^{-1}(v)) = \sum_{w \in V(\Gamma) \cap \phi^{-1}(v)} h_\Gamma(w) + \dim H_1(\phi^{-1}(v)). \end{align*}$$

All notions discussed, starting with subdivisions and culminating with $\theta $ -stable equidimensional flows, specialize under these definitions.

Example 2.21.1. Let $\Gamma $ be an n-marked graph with a genus function $h_\Gamma $ . Let $(a_1,\cdots ,a_n) \in \mathbb {Z}^n$ , $k \in \mathbb {Z}$ and

$$\begin{align*}A = \sum_{v \in V(\Gamma)} k(2h_\Gamma(v)-2 + \text{val}(v))v + \sum_{i=1}^n a_iv_i \end{align*}$$

the divisor of example 2.2.1. Then A specializes to the analogous divisor

$$\begin{align*}\sum_{v \in V(\overline{\Gamma})} k(2h_{\overline{\Gamma}}(v)-2 +\text{val}(v))v + \sum_{i=1}^na_i\overline{v}_i \end{align*}$$

under any contraction $\Gamma \to \overline {\Gamma }$ , where $\overline {v}_i$ is the vertex of $\overline {\Gamma }$ that contains the i-th leg.

3 Abel-Jacobi Theory on Tropical Curves

The notions of the previous section are combinatorial. We extend them to tropical notions by introducing a metric on our graphs. We recall our convention: monoids M are sharp (they have no nontrivial units), finitely generated, integral and saturated. The category of monoids $\textbf {Mon}$ is dual to the category $\textbf {RPC}$ of cones, which means rational polyhedral cones together with an integral structure, under the correspondence

$$ \begin{align*} M \to M^{\vee}:= (\mathsf{Hom}(M,\mathbb{R}_{\ge 0}),\mathsf{Hom}(M,\mathbb{Z}))\\ \sigma^{\vee} = \{u \in \mathsf{Hom}(N,\mathbb{R}): u \ge 0 \text{ on }C\} \cap \mathsf{Hom}(N,\mathbb{Z}) \leftarrow \sigma = (C,N). \end{align*} $$

Let $\Gamma $ be a tropical curve metrized by a monoid M. In other words, $\Gamma $ is a graph together with a length function

$$ \begin{align*}\ell:E(\Gamma) \to M-0 \end{align*} $$

from its set of edges to the nonzero elements of M. We denote the length of the edge e by $\ell _e$ .

Divisors and flows are combinatorial data and do not take into account the metric structure of $\Gamma $ . Piecewise linear functions on $\Gamma $ , however, are honest tropical notions:

Definition 3.1. A piecewise linear function $\alpha $ is a function

$$ \begin{align*}\alpha: V(\Gamma) \to M^{\text{gp}} \end{align*} $$

from the vertices of $\Gamma $ to the associated group of M, which satisfies the following condition: for every oriented edge $\vec {e}$ in $\Gamma $ between $v,w \in \Gamma $ , there exists an integer $s(\vec {e}) \in \mathbf Z$ such that

$$ \begin{align*}\alpha(w) - \alpha(v) = s(\vec{e})\ell_e. \end{align*} $$

We write $\mathsf {PL}(\Gamma )$ for the group of piecewise linear functions on $\Gamma $ .

Every piecewise linear function $\alpha $ on $\Gamma $ determines a flow $s_\alpha $ by taking its underlying slopes:

$$ \begin{align*} \mathsf{PL}(\Gamma) \to \mathsf{Flow}(\Gamma)\\ \alpha \to s_{\alpha}, s_\alpha(\vec{e}) = \text{ slope of } \alpha \text{ on } \vec{e}. \end{align*} $$

In particular, we can talk about divisors of piecewise linear functions, orientations and so on, via the underlying flow. The flows that can arise from a piecewise linear function are constrained by the metric structure on $\Gamma $ .

Definition 3.2. We call a flow that arises as the underlying slopes of a piecewise linear function a twist on $\Gamma $ .

All flows that arise from piecewise linear functions are acyclic. The condition a flow must satisfy to be a twist, however, must involve the metric somehow. In short, we start with a flow s on $\Gamma $ and want to lift it to a function $\alpha $ . We can start at a vertex $v \in \Gamma $ and assign a value of $\alpha (v) \in M^{\text {gp}}$ arbitrarily. But then, the rest of the values $\alpha (w)$ are completely determined by the lengths of $\Gamma $ and the slopes of s (provided $\Gamma $ is connected). For any oriented path $P_{v \to w}$ from v to a vertex w, we must have

$$\begin{align*}\alpha(w) = \alpha(v) + \sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e, \end{align*}$$

and the function $\alpha $ is well-defined if and only if this expression is independent of path. This condition is most conveniently phrased in terms of the intersection pairing

$$ \begin{align*} \left \langle, \right \rangle : \mathsf{Flow}(\Gamma) \times \mathsf{Flow}(\Gamma) \to M^{\text{gp}} \\ \left \langle s, t \right \rangle = \frac{1}{2}\sum_{\vec{e} \in \mathcal{E}(\Gamma)} s(\vec{e})t(\vec{e})\ell_e. \end{align*} $$

In terms of the intersection pairing, the lifting problem amounts to the statement that for every $\gamma \in H_1(\Gamma )$ , we have

$$ \begin{align*}\left \langle s, \gamma \right \rangle = 0. \end{align*} $$

Here, $H_1(\Gamma )$ is considered as embedded in $\mathsf {Flow}(\Gamma ) \cong \mathbb {Z}^{E(\vec {\Gamma })}$ after choosing an orientation, by writing a cycle $\gamma $ as an oriented path

$$ \begin{align*}\gamma = \sum \vec{e} \end{align*} $$

and associating to $\gamma $ the flow defined by

if $\vec {e}$ appears in the path with the same orientation as in $\vec {\Gamma }$ , and $0$ if e is not in the path.

Remark 3.3. This inclusion identifies $H_1(\Gamma )$ with the kernel of

$$ \begin{align*}\mathsf{div}:\mathsf{Flow}(\Gamma) \to \mathsf{Div}(\Gamma). \end{align*} $$

This coincides with the usual identification of $H_1(\Gamma )$ with the kernel of

$$ \begin{align*}\mathbb{Z}^{E(\vec{\Gamma})} \to \mathbb{Z}^{V(\Gamma)} \end{align*} $$

coming from the CW-complex structure on $\Gamma $ .

3.4 Subdivisions of tropical curves

Let $\Gamma $ be a tropical curve. A subdivision of $\Gamma $ is a tropical curve $\Gamma '$ metrized by M, such that the underlying graph of $\Gamma '$ is a subdivision of the underlying graph of $\Gamma $ and such that the lengths of the edges $e' \in E(\Gamma ')$ that subdivide an edge $e \in E(\Gamma )$ add up to the length of e: if $\phi :E(\Gamma ') \to E(\Gamma )$ is the induced map of edges, we must have

$$ \begin{align*}\sum_{e' \in \phi^{-1}(e)} \ell_{e'} = \ell_e. \end{align*} $$

Subdivisions $\Gamma '$ come with an evident map $\Gamma ' \to \Gamma $ . The collection of vertices in $\Gamma '$ that are not in $\Gamma $ are called exceptional vertices. A refinenent of $\Gamma ' \to \Gamma $ is a further subdivision $\Gamma " \to \Gamma '$ .

Suppose $\Gamma ' \to \Gamma $ is a subdivision, and $\alpha $ is a piecewise linear function on $\Gamma '$ . It is often desirable to find the minimal subdivision of $\Gamma $ on which $\alpha $ can be defined.

Definition 3.5. We say that $\Gamma '$ is minimal with respect to $\alpha $ if

$$\begin{align*}\mathsf{div}(\alpha)(v) \neq 0 \end{align*}$$

on all exceptional vertices v of $\Gamma '$ .

Lemma 3.6. Suppose $\Gamma '$ is a subdivision of $\Gamma $ , and $\alpha $ is a piecewise linear function on $\Gamma '$ . There is a unique minimal subdivision $\Gamma _\alpha \to \Gamma $ on which $\alpha $ can be defined.

Proof. Define $\Gamma _\alpha $ as the subdivision of $\Gamma $ obtained by keeping only the exceptional vertices of $\Gamma '$ on which

$$ \begin{align*}\mathsf{div}(\alpha)(v) \neq 0. \end{align*} $$

Since the slope of $\alpha $ changes on the vertices v, any subdivision that supports $\alpha $ must refine $\Gamma _\alpha $ , whereby the uniqueness of $\Gamma _\alpha $ follows.

3.7 Equidimensional piecewise linear functions and twists

Any integral monoid $M \subset M^{\text {gp}}$ can be regarded as a partial order on $M^{\text {gp}}$ : for $x,y \in M^{\text {gp}}$ , we declare $x \le y$ if $y - x \in M$ . Thus, a piecewise linear function $\alpha $ on $\Gamma $ comes with a partial ordering of its values $\alpha (v) \in M^{\text {gp}}$ . This partial order is evidently compatible with the orientation on $\Gamma $ induced by the underlying twist of $\alpha $ .

Definition 3.8. Let $\Gamma $ be a tropical curve. A piecewise linear function is totally ordered if its values $\alpha (v)$ , $v \in V(\Gamma )$ , are totally ordered.

Remark 3.9. The condition that the values $\alpha (v)$ of the function $\alpha $ at the vertices v are totally ordered can be equivalently phrased in terms of the underlying flow s of $\alpha $ . Since for any $v,w$ we have that

$$\begin{align*}\alpha(w) = \alpha(v) + \sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \end{align*}$$

for any oriented path $P_{v \to w}$ , to say that $\alpha (w)$ comes after $\alpha (v)$ in a total order for $\alpha $ is to say that

$$\begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \in M \subset M^{\text{gp}} \end{align*}$$

for any oriented path $P_{v \to w}$ , or, equivalently, that the evaluation

$$\begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e(x) \ge 0 \end{align*}$$

for any $x \in \sigma = M^\vee $ .

Borrowing ideas from the theory of semistable reduction, we make the following definition.

Definition 3.10. A piecewise linear function $\alpha $ on $\Gamma $ is equidimensional if

• • The values $\alpha (v)$ are totally ordered.

• • For any edge e with endpoints $v,w$ that satisfy $\alpha (v)<\alpha (w)$ , and any vertex u with $\alpha (v) \leq \alpha (u) \leq \alpha (w)$ , we necessarily have $\alpha (u) = \alpha (v)$ or $\alpha (u) = \alpha (w)$ .

While on its face the definition of equidimensionality seems dependent on the values of $\alpha $ , the definition is, in fact, invariant under translation of the values $\alpha (v)$ by any common element $x \in M^{\text {gp}}$ . Thus, the definition descends to twists, and it makes sense to talk about equidimensional twists.

The definition of equidimensional piecewise linear function can perhaps be clarified by introducing its image, which is a one dimensional tropical target, also referred to as a tropical line.

Definition 3.11. A tropical line is the structure of a canonically oriented ⁷ one-dimensional polyhedral complex metrized by M on $\mathbb {R}$ .

We spell out the meaning of the definition: a tropical line is, thus, as a polyhedral complex, simply a combinatorial line X with a length assignment $\ell _{f_i} \in M-0$ for each of its edges. But to say that this polyhedral complex is a polyhedral complex structure on $\mathbb {R}$ over M means that it furthermore comes with a chosen piecewise linear embedding

$$ \begin{align*}\iota_X: X \subset \mathbb{R}. \end{align*} $$

This data is very similar to the definition of a piecewise linear function on a tropical curve: an element

$$ \begin{align*}\iota_X(v_i) := \gamma_i \in M^{\text{gp}} \end{align*} $$

for each vertex $v \in V(X)$ , such that

$$ \begin{align*}\gamma_{i+1}- \gamma_{i} = \ell_{f_i}. \end{align*} $$

In particular, the ordering on the vertices has been chosen so that $\gamma _{i+1}>\gamma _i$ by assumption, which means that the piecewise linear structure is compatible with the canonical orientation $E(\vec {X})$ of definition 2.11 on X. We will also consider the trivial polyhedral decomposition as an allowable tropical line, where $\mathbb {R}$ is considered as a single cell. In that case, we will simply write $\mathbb {R}$ for the tropical line.

Let $\Gamma $ be a tropical curve and X a tropical line metrized by M. By definition, a map of polyhedral complexes $\Gamma \to X$ is a piecewise linear map that respects the cell structure of the polyhedral decomposition: each cell (that is, vertex or edge) of $\Gamma $ maps into a cell of X (rather than a union of more than one cells). In particular, a piecewise linear function $\alpha $ on $\Gamma $ can be tautologically thought of as a map

$$ \begin{align*}\Gamma \to \mathbb{R} \end{align*} $$

to the trivial tropical line. The piecewise linear function $\alpha $ may or may not factor through X:

Since $\iota _X$ is a monomorphism, the arrow $\beta $ , if it exists, is unique.

Definition 3.12. A map of polyhedral complexes $P \to Q$ is called equidimensional if it takes cells onto cells.

As tropical curves and tropical lines are particularly simple examples of polyhedral complexes, the meaning of equidimensionality of a map

$$ \begin{align*}\beta: \Gamma \to X \end{align*} $$

is very simple to describe: it says that each vertex $v \in \Gamma $ must map to a vertex in X.

Lemma 3.13. Let $\Gamma $ be a tropical curve metrized by M, and let $\alpha $ be a piecewise linear function on $\Gamma $ . Then $\alpha $ is equidimensional if, and only if, there exist a tropical line X and a factorization of $\alpha $ through an equidimensional map $\beta : \Gamma \to X$ .

Proof. Suppose e is an edge of $\Gamma $ with endpoints $v,w$ , and $\alpha (w)> \alpha (v)$ . Suppose u is a vertex of $\Gamma $ with $\alpha (v) \le \alpha (u) \le \alpha (w)$ . If $\alpha $ factors through X, then $\beta (v)$ and $\beta (w)$ must be consecutive vertices $v_{i},v_{i+1}$ of X (otherwise, the edge e would map to a union of cells). But to say that $\beta $ is equidimensional is to say that $\beta (u)$ must be a vertex of X, and hence one of $v_{i},v_{i+1}$ . So either $\alpha (u)=\alpha (v)$ or $\alpha (u)=\alpha (w)$ . Conversely, given an equidimensional function $\alpha $ , we build X by taking one vertex $v_i$ for each distinct value in { $\alpha (v): v \in V(\Gamma )\}$ and define

$$ \begin{align*}\iota_X(v_i) = \alpha(v) \end{align*} $$

to be the corresponding value.

Remark 3.14. Note that while the definition of equidimensionality requires that vertices of $\Gamma $ must map to vertices of X, edges can map either onto edges or vertices of X. Edges that map onto vertices of X are precisely those on which the slope of $\alpha $ is $0$ (i.e., the contracted edges). We point out that in order for a given $\alpha $ to factor through X (i.e., in order for $\alpha = \iota _X \circ \beta $ to hold), strict constraints must hold between the lengths of the edges e of $\Gamma $ and the edges f of X. Suppose $\vec {f} \in E(\vec {X})$ is a canonically oriented edge of X (c.f. definition 2.11) between vertices $v_i$ and $v_{i+1}$ , and suppose an edge e of $\Gamma $ maps to f. Then, orienting e so that $s(\vec {e})> 0$ , we must have that $\beta $ maps the initial point $\mathfrak {r}(\vec {e}) = v$ to $v_i$ and the terminal point $\mathfrak {t}(\vec {e})=w$ to $v_{i+1}$ , and furthermore,

$$\begin{align*}s(\vec{e})\ell_e = \alpha(w) - \alpha(v) = \iota_X(v_{i+1})-\iota_X(v_i) = \ell_f. \end{align*}$$

Thus, in order for a given acyclic flow s to lift to an equidimensional twist with underlying combinatorial type $\Gamma \to X$ , the system of equations

$$\begin{align*}\text{ } s(\vec{e})\ell_e = \ell_f \text{ for all }\vec{e} \text{ that map to } \vec{f}, \vec{f} \in E(\vec{X}) \end{align*}$$

needs to be satisfied. We note that this system of equations is stronger than the equations $\left \langle \gamma , s \right \rangle = 0$ required for the flow to lift to a twist: since X is contractible, the image of any loop $\gamma \in H_1(\Gamma )$ in X is an oriented path $P=\sum \vec {f}$ where each edge appears an equal number of times with opposite orientations. But then

$$\begin{align*}\left \langle s, \gamma \right \rangle = \sum_{\vec{e} \in \gamma} s(\vec{e})\ell_e = \sum_{\vec{f} \in P} o(\vec{f}) \ell_f = 0, \end{align*}$$

where the $o(\vec {f})=1$ if $\vec {f}$ is canonically oriented and $-1$ otherwise.

Remark 3.15. The definition of equidimensionality may seem convoluted from the vantage of tropical curves metrized by monoids, but it is natural from the dual point of view of cone complexes and semistable reduction. We find the dual point of view more intuitive, but we stick with the tropical perspective as it is more ubiquitous in the literature. Namely, a tropical curve $\Gamma $ metrized by M is equivalent data to a map of cone complexes (with integral structure)

$$ \begin{align*}\Sigma_C \to \Sigma_S := M^{\vee}. \end{align*} $$

Plainly, one builds $\Sigma _C$ out of $\Gamma $ as a fibration over $\Sigma _S$ . The fiber over $x \in \Sigma _S$ is obtained by attaching a vertex $v_x$ for each $v \in V(\Gamma )$ and an edge of length $\ell _e(x) \in \mathbb {R}_{\ge 0}$ for each $e \in E(\Gamma )$ . Then, a piecewise linear function $\alpha $ on $\Gamma $ corresponds to a piecewise linear map $\tilde {\alpha }$

A tropical line X corresponds to a subdivision $\Sigma _X \to \Sigma _S \times \mathbb {R} \to \Sigma _S$ so that the composed map $\Sigma _X \to \Sigma _S$ is equidimensional (maps cells onto cells) and furthermore sends integral structures onto integral structures, and an equidimensional piecewise linear function that factors through X corresponds to a factorization of $\tilde {\alpha }$ through $\Sigma _X$ that sends cells of $\Sigma _C$ onto cells of $\Sigma _X$ . The name equidimensional comes from the fact that maps of fans which send cones onto cones are the ones that induce equidimensional maps of toric varieties.

Suppose $\alpha $ is a piecewise linear function or twist on $\Gamma $ , and $\Gamma ' \to \Gamma $ is a subdivision. Then $\alpha $ lifts to a piecewise linear function on $\Gamma '$ . Suppose $\alpha $ is equidimensional on $\Gamma '$ . We say that $\Gamma '$ is a minimal subdivision on which $\alpha $ is equidimensional if the following stability condition holds:

$(\star )$ For every exceptional vertex v of $\Gamma '$ , there exists a nonexceptional vertex w of $\Gamma $ such that $\alpha (v) = \alpha (w)$ .

We remark that the minimal $\Gamma '$ on which $\alpha $ is equidimensional is, in general, finer than the minimal model $\Gamma _\alpha $ on which $\alpha $ is defined. Furthermore, the model is unique if it exists. This is very similar to the combinatorial analogues in 2.14, but the tropical picture deviates here: a model where $\alpha $ becomes equidimensional may not exist, as the required combinatorial subdivisions may not lift with respect to the metric structure. Experts will recognize here that one can always find a minimal equidimensional model, but only after altering the base monoid M. However, one can say the following with relative ease:

Lemma 3.16. Suppose that $\Gamma $ is a tropical curve with piecewise linear function $\alpha $ , and $\Gamma '$ is a subdivision on $\Gamma $ on which $\alpha $ is equidimensional. Then a minimal model $\mathsf {Eq}_{\Gamma }(\alpha )$ on which $\alpha $ is equidimensional exists.

Proof. As in the construction of $\Gamma _\alpha $ , one obtains $\mathsf {Eq}_\Gamma (\alpha )$ from $\Gamma '$ by deleting all exceptional vertices in $\Gamma '$ that violate $(\star )$ .

Definition 3.17. Suppose $\alpha $ is a piecewise linear function on $\Gamma $ , and that $\alpha $ lifts to an equidimensional function

$$ \begin{align*}\Gamma' \to X \end{align*} $$

on some subdivision of $\Gamma $ . We call the lift stable if $\Gamma ' \to X$ is the minimal such lift (i.e., satisfies $(\star )$ ). We write

$$ \begin{align*}\alpha: \mathsf{Eq}_{\Gamma}(\alpha) \to X \end{align*} $$

for the minimal lift.

4 Tropical Moduli

This section closely follows [MW20] in spirit, but in the tropical world.

4.1 Cone complexes and cone stacks

Since we want to build tropical moduli spaces parametrizing our objects – tropical curves with various types of piecewise linear functions on them – and our objects come with automorphisms, the notion of a cone complex is inadequate. Rather, we will use the formalism of cone stacks, developed in [CCUW20]. We recall only the very basics of the theory that we will use from loc. cit and refer the interested reader there for a comprehensive treatment.

A face morphism or face map of cones $\tau \to \sigma $ is an isomorphism of $\tau $ with a face of $\sigma $ . Note that in the definition we consider $\sigma $ itself as a face, so arbitrary isomorphisms $\tau \to \sigma $ are considered face morphisms as well. A covering of a cone complex $\Sigma $ by face morphisms is a collection of face maps $\tau \to \Sigma $ that is jointly surjective. Such coverings generate a Grothendieck topology on the category of cone complexes. A cone stack is a stack on this site, with the (essentially straightforward) appropriate notion of algebraicity. Since face maps are, however, so simple, the notion of cone stack is, in fact, equivalent to the following much simpler definition [CCUW20][Proposition 2.19]:

Definition 4.2. A cone stack is a category fibered in groupoids

$$\begin{align*}\Sigma \to \textbf{RPC}^f,\end{align*}$$

where $\textbf {RPC}^f$ is the full subcategory of $\textbf {RPC}$ with face maps as morphisms.

Remark 4.3. Since the category of cones is equivalent to the category of monoids, we can consider $\Sigma $ equivalently as a category cofibered in groupoids over the category of monoids with morphisms being isomorphisms onto a quotient by a face. We will freely swap between conventions, as in our setup it is more convenient to work with the monoid M metrizing our tropical curves rather than its dual cone, but when writing $\Sigma (M)$ , we formally mean the groupoid $\Sigma (\sigma )$ , for $\sigma = M^\vee $ .

Most frequently, cone stacks natually arise as colimits. More precisely, suppose $\mathcal {D}$ is a category, and $F: \mathcal {D} \to \textbf {RPC}^f$ is a functor. Concretely, this amounts to the data of cones $\sigma _{\alpha }$ for $\alpha \in \text {Ob}(\mathcal {D})$ , and face morphisms $u_{\alpha \to \beta }: \sigma _\alpha \to \sigma _\beta $ for any morphism $\alpha \to \beta $ in $\mathcal {D}$ . Then one constructs a cone stack

$$\begin{align*}\varinjlim_{\mathcal{D}} \sigma_{\alpha} \to \textbf{RPC}^f \end{align*}$$

by taking the fiber over $\sigma $ to be the groupoid with objects

$$\begin{align*}\phi \in \coprod_{\alpha \in \text{Ob}(\mathcal{D})} \text{Hom}_{\textbf{RPC}}(\sigma,\sigma_{\alpha}) \end{align*}$$

(the notation here means all $\textbf {RPC}$ morphisms, not just face morphisms) and with an isomorphism from $\phi : \sigma \to \sigma _\alpha $ to $\psi :\sigma \to \sigma _\beta $ if there exists $\alpha \to \beta $ in $\mathcal {D}$ such that $u_{\alpha \to \beta } \circ \phi = \psi $ . We note that when all morphisms $u_{\alpha \to \beta }$ appearing in $F(\mathcal {D})$ are proper face morphisms (i.e., face morphisms to a proper face), the groupoid above is equivalent to a set. This way, one recovers the notion of generalized cone complexes of [ACP15] or cone spaces of [CCUW20]. Moreover, when there exists at most one morphism between any two $\sigma _\alpha \to \sigma _\beta $ , one gets an ordinary polyhedral complex. The following table, while simply an analogy, is perhaps helpful:

Example 4.3.1. Fix a genus g and a number of markings n. There is a cone stack $\mathcal {M}_{g,n}^{\text {trop}} \to \mathbf {RPC}^f$ which over a cone $\sigma $ parametrizes genus g, n-marked curves $\Gamma $ metrized by $M = \sigma ^\vee $ , defined by

$$\begin{align*}\mathcal{M}_{g,n}^{\text{trop}}(\sigma) = \{(\Gamma,\ell_e:E(\Gamma) \to M-0): g(\Gamma)=g, \{1,\cdots,n\} \cong L(\Gamma) \}. \end{align*}$$

For further details on the CFG structure, the interested reader is referred to [CCUW20].

4.4 Stacks of twists

We make the simplifying assumption that all graphs that appear have at least one leg.

Definition 4.5. We define cone stacks

$$ \begin{align*}\Sigma_{\textbf{Div}}, \Sigma_{\textbf{Ord}}, \Sigma_{\textbf{Rub}} \to \textbf{RPC}^f \end{align*} $$

by setting, for a cone $\sigma $ with dual monoid $M = \sigma ^\vee $

$$ \begin{align*} \Sigma_{\textbf{Div}}(\sigma) = \{\Gamma, \alpha \in \mathsf{PL}(\Gamma)\} \\ \Sigma_{\textbf{Ord}}(\sigma) = \{\Gamma, \alpha \in \mathsf{PL}(\Gamma) \text{ which is totally ordered} \}\\ \Sigma_{\textbf{Rub}}(\sigma) = \{\Gamma, \alpha \in \mathsf{PL}(\Gamma), \mathsf{Eq}_\Gamma(\alpha) \to X \}, \end{align*} $$

where

• • $\Gamma $ is metrized by M.

• • $\alpha $ vanishes on the vertex of $\Gamma $ containing the first leg.

Isomorphisms are isomorphism of graphs that respects the functions, orderings and equidimensional lifts.

Remark 4.6. The assumption that $\Gamma $ contains a leg is not serious, but we impose it to rigidify the problems above via the condition $\alpha =0$ on the vertex. Otherwise, we have to talk about tropical line torsors, which we would rather avoid as all applications we have in mind involve curves that already have a marking.

Let $\textbf {CombDiv}$ be the category whose objects consist of a graph $\Gamma $ and an acyclic flow s. A map $(\Gamma ,s) \to (\overline {\Gamma },\overline {s})$ in $\textbf {CombDiv}$ is given by a map $f: \Gamma \to \overline {\Gamma }$ , where $\overline {\Gamma }$ is an edge contraction of $\Gamma $ , such that $\overline {s} \circ f = s$ (in particular, automorphisms respecting the flow are allowed). Similarly, we define $\textbf {CombOrd}$ to consist of pairs $(\Gamma ,s)$ and a total ordering $\kappa $ on $\Gamma $ extending s, and $\textbf {CombRub}$ to consist of a pair $(\Gamma ,s)$ and a stable equidimensional lift $\Gamma ' \to X$ of s (2.13).

For each $(\Gamma ,s) \in \textbf {CombDiv}$ , define a cone

$$ \begin{align*}\sigma_{(\Gamma,s)} \subset \mathbb{R}_{\ge 0}^{E(\Gamma)} \end{align*} $$

consisting of the $\ell $ that satisfy the equations

$$ \begin{align*}\left \langle s,\gamma \right \rangle_{\ell} =0 \end{align*} $$

for all $\gamma \in H_1(\Gamma )$ . The pairing here is the intersection pairing of Section 3. By definition, the pairing requires a length on each edge of $\Gamma $ . The subscript $\ell $ here means that on the point $\ell = (\ell _{e})_{e \in E(\Gamma )}$ of $\mathbb {R}_{\ge 0}^{E(\Gamma )}$ , we give the tautological length $\ell _e$ to the edge e. Under a morphism $(\Gamma ,s) \to (\overline {\Gamma },\overline {s})$ , we get a face morphism

$$ \begin{align*}\sigma_{(\overline{\Gamma},\overline{s})} \to \sigma_{(\Gamma,s)} \end{align*} $$

and so we may glue the cones into a cone stack

$$ \begin{align*}\Sigma_{\textbf{Div}}' : = \varinjlim_{(\Gamma,s)} \sigma_{(\Gamma,s)}. \end{align*} $$

Similarly, as in the discussion in remark 3.14, for a triple $(\Gamma ,s,\Gamma ' \to X)$ in $\textbf {CombRub}$ , we take the cone

$$ \begin{align*}\sigma_{(\Gamma,s,\Gamma' \to X)} \subset \mathbb{R}_{\ge 0}^{E(\Gamma')} \times \mathbb{R}_{\ge 0}^{E(X)} \end{align*} $$

consisting of the $(\ell _{e},\ell _f)_{e \in E(\Gamma '),f \in E(X)}$ that satisfy

$$\begin{align*}s(\vec{e})\ell_e = \ell_f \end{align*}$$

whenever $\vec {e} \in \mathcal {E}(\Gamma ')$ maps to $\vec {f}$ in $E(\vec {X}) \subset \mathcal {E}(X)$ , and glue to a cone stack

$$ \begin{align*}\Sigma_{\textbf{Rub}}':=\varinjlim_{(\Gamma,s,\Gamma \to X)} \sigma_{(\Gamma,s,\Gamma' \to X)}. \end{align*} $$

Finally, as in remark 3.9, for $(\Gamma ,s,\kappa ) \in \mathbf {CombOrd}$ , we take the cone

$$ \begin{align*}\sigma_{(\Gamma,s,\kappa)} \subset \mathbb{R}_{\ge 0}^{E(\Gamma)} \end{align*} $$

defined by the equations

$$ \begin{align*}\left \langle s, \gamma \right \rangle_\ell = 0 \end{align*} $$

for $\gamma \in H_1(\Gamma )$ , and the additional condition: for any two vertices $v,w$ such that w comes later than v in the ordering $\kappa $ , and an oriented path $P_{v \to w}$ from v to w, we keep the lengths $\ell =(\ell _e)_{e \in E(\Gamma )} \subset \mathbb {R}_{\ge 0}^{E(\Gamma )}$ for which additionally,

$$\begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \ge 0. \end{align*}$$

⁸ Equivalently, we can fix a minimal vertex $v_0$ for $\kappa $ , and an oriented path $P_{v}$ from $v_0$ to v for each v, and keep the lengths $\ell $ such that

$$\begin{align*}\sum_{\vec{e} \in P_{v} } s(\vec{e})\ell_e \le \sum_{\vec{e} \in P_{w}} s(\vec{e})\ell_e \end{align*}$$

whenever $v \le w$ in the ordering $\kappa $ (the advantage of doing so is that one has to consider fewer paths: one for each vertex v instead of one for each pair of vertices $v,w$ ). We glue these cones to a cone stack

$$ \begin{align*}\Sigma_{\textbf{Ord}}' = \varinjlim_{(\Gamma,s,\kappa)} \sigma_{(\Gamma,s,\kappa)}. \end{align*} $$

Theorem 4.7. The cone stack $\Sigma _{\textbf {Div}}'$ represents the functor $\Sigma _{\textbf {Div}}$ , the cone stack $\Sigma _{\textbf {Ord}}'$ represents $\Sigma _{\textbf {Ord}}$ and the cone stack $\Sigma _{\textbf {Rub}}'$ represents $\Sigma _{\textbf {Rub}}$ .

Proof. Let M be a monoid, with $M^\vee = \sigma $ . An element $\Sigma _{\textbf {Div}}(M)$ is a tropical curve $\Gamma $ metrized by M, together with a piecewise linear function $\alpha $ vanishing on the vertex containing the first leg. This data defines a map

$$ \begin{align*} \sigma \to \mathbb{R}_{\ge 0}^{E(\Gamma)} \\ x \to (\ell_e(x)) \end{align*} $$

and an underlying flow $s_\alpha :=s$ . But the flow is a twist, and so

$$ \begin{align*}\left \langle s, \gamma \right \rangle \in M^{\text{gp}} \end{align*} $$

is $0$ . So the $\ell _e(x)$ map into $\sigma _{(\Gamma ,s)}$ . Conversely, a map $f: \sigma \to \sigma _{(\Gamma ,s)}$ defines a metric on $\Gamma $ , by taking $\ell _e \in M$ to be the composition

of f with the e-th projection. The acyclic flow s is a twist on $\Gamma $ , since the lengths have been chosen so that the equations $\left \langle s,\gamma \right \rangle = 0$ are satisfied. The twist only lifts to a piecewise linear function on $\Gamma $ up to translation by an element of $M^{\text {gp}}$ , but it lifts uniquely if we assume that its value is $0$ on the vertex containing the first leg. This shows

$$ \begin{align*}\Sigma_{\textbf{Div}} \cong \Sigma_{\textbf{Div}}'. \end{align*} $$

The proofs for $\textbf {Ord},\textbf {Rub}$ are similar, using the fact that the defining equations of the cones $\sigma _{(\Gamma ,s,\kappa )}$ and $\sigma _{(\Gamma ,s,\Gamma ' \to \Gamma )}$ are, according to remarks 3.9 and 3.14, precisely the conditions necessary for s to lift to a totally ordered or equidimensional twist, respectively.

There are evident maps $\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}} \to \Sigma _{\textbf {Div}}$ obtained by forgetting the additional structure at each step.

Lemma 4.8. The map $\Sigma _{\textbf {Ord}} \to \Sigma _{\textbf {Div}}$ is a subdivision. The map $\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}}$ is a finite index inclusion.

Proof. We first look at $\Sigma _{\textbf {Ord}} \to \Sigma _{\textbf {Div}}$ . It is clear that the map is a monomorphism, so it suffices to show that the map is bijective on $\mathbb {N}$ points. Given a tropical curve $\Gamma $ with integer lengths, and an $\alpha : \Gamma \to \mathbb {R}$ , the values of $\alpha $ are elements of $\mathbb {Z}$ , and so automatically totally ordered.

For the map $\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}}$ , it suffices to show that the map is bijective on $\mathbb {Q}_{\ge 0}$ points. We start with an $\alpha $ and an ordering $\kappa $ of its values and build a tropical line X by taking one vertex $v_i$ for each distinct value $\alpha (v)$ , with the ordering of $\kappa $ . We define an embedding $\iota _X: X \to \mathbb {R}$ by

$$ \begin{align*}\iota_X(v_i) = \text{ value of corresponding } \alpha(v). \end{align*} $$

There is a map of topological spaces $\Gamma \to X$ , but it does not respect cell structures, as interior points of edges of $\Gamma $ map to vertices of X. We refine $\Gamma $ to $\Gamma '$ obtained by subdividing along the preimages of the vertices of X. This gives a stable equidimensional PL function on $\alpha $ .

Remark 4.9. The argument in the proof essentially shows how the finite index inclusion in $\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}}$ arises. When subdividing $\Gamma $ to $\Gamma '$ , the new points may have rational coordinates; for instance, if an edge e from v to w has slope $s(e)$ , and $\alpha (u)$ is an intermediate value between $\alpha (v)$ and $\alpha (w)$ , the function $\alpha $ hits $\alpha (u)$ at the point

$$ \begin{align*}\frac{\alpha(u)-\alpha(v)}{s(e)} \end{align*} $$

of e, and thus e needs to be subdivided there. This point is in $M_{\mathbb {Q}}^{\text {gp}}$ , but not necessarily in $M^{\text {gp}}$ .

Lemma 4.10. The cone stack $\Sigma _{\textbf {Ord}}$ is simplicial and the cone stack $\Sigma _{\textbf {Rub}}$ is smooth.

Proof. It suffices to check that the cones $\sigma _{(\Gamma ,s,\Gamma ' \to X)}$ of $\Sigma _{\textbf {Rub}}$ are isomorphic to $\mathbb {N}^k$ for some k. But the equations

$$ \begin{align*}s(\vec{e})\ell_e = \ell_f \end{align*} $$

for $\vec {e}$ mapping to $\vec {f} \in E(\vec {X})$ show that the coordinates of the noncontracted edges in $E(\Gamma )$ are redundant, and the cone is, in fact, isomorphic to

$$ \begin{align*}\mathbb{N}^{E(X)} \times \mathbb{N}^{E^c(\Gamma)}, \end{align*} $$

where $E^c(\Gamma )$ denotes the set of contracted edges of $\Gamma $ . The fact that $\Sigma _{\textbf {Ord}}$ is simplicial follows from the fact that its cones are isomorphic to those of $\Sigma _{\textbf {Rub}}$ after tensoring with $\mathbb {Q}$ .

In fact, more can be said. From the isomorphism of the real points of a cone in $\Sigma _{\textbf {Ord}}$ with $\mathbb {R}_{\ge 0}^{E(X)} \times \mathbb {R}_{\ge 0}^{E^c(\Gamma )}$ , it follows that the rays (i.e., the one dimensional cones) in $\Sigma _{\mathbf {Ord}}$ are precisely those that parametrize maps $\alpha $ consisting of

• • Either a single contracted edge.

• • Or, maps without contracted components to a target with exactly one edge.

In either case, the map $\alpha $ automatically lifts to an equidimensional one. Thus, the sublattice structure of $\Sigma _{\textbf {Rub}}$ agrees with that of $\Sigma _{\textbf {Ord}}$ on rays. Since $\Sigma _{\textbf {Ord}}$ is simplicial, we obtain the following:

Corollary 4.11. Let $\sigma _{(\Gamma ,s,\kappa )}$ be a cone in $\Sigma _{\textbf {Ord}}$ , and $\sigma _{(\Gamma ,s,\Gamma ' \to X)}$ the corresponding cone in $\Sigma _{\textbf {Rub}}$ . The lattice of $\sigma _{(\Gamma ,s,\Gamma ' \to X)}$ is the lattice freely generated by the primitive vectors along the rays of $\sigma _{(\Gamma ,s,\kappa )}$ .

Proof. Since $\sigma _{(\Gamma ,s,\Gamma ' \to X)}$ is smooth (i.e., isomorphic to some $\mathbb {N}^k$ ), its lattice must be the lattice generated by the primitive vectors along its rays. Since those primitive vectors are the same as the primitive vectors of $\Sigma _{\textbf {Ord}}$ , the conclusion follows.

Thus, $\Sigma _{\textbf {Ord}}$ is in a certain sense a coarse moduli space of $\Sigma _{\textbf {Rub}}$ : see, for example, [GM15, Subsection 3.2].

4.12 Carving out small subcomplexes

The complexes $\Sigma _{\textbf {Div}}, \Sigma _{\textbf {Rub}}, \Sigma _{\textbf {Ord}}$ are very large: they are indexed by additional data over the category of all graphs, which is itself notoriously large. When algebraizing, as we will in the next section, the resulting schemes have infinitely many connected components and are highly nonseparated. Here, we want to impose several increasingly stringent conditions that carve out subcomplexes which algebraize to much more pleasant spaces.

First, we can, as usual, restrict our attention to genus g, n-marked graphs. We may then write

$$ \begin{align*}\Sigma_{\textbf{Div}_n} \end{align*} $$

which decomposes

$$ \begin{align*}\Sigma_{\textbf{Div}} = \coprod_{n \ge 1} \Sigma_{\textbf{Div}_{n}}. \end{align*} $$

Similar descriptions are available for the order and rubber versions.

Given an n-marked graph $\Gamma $ , we can consider $n+1$ -marked graphs $\Gamma _{c}$ , one for every cell c of $\Gamma $ (vertex or edge), obtained by attaching a leg $l_{n+1}$ on c when it is a vertex, and a bivalent vertex with a single leg $l_{n+1}$ on c when it is an edge. A map $\Gamma _{c} \to \Gamma $ is obtained by deleting the latter vertex. There is a map

$$ \begin{align*}\mathbb{R}_{\ge 0}^{E(\Gamma_c)} \to \mathbb{R}_{\ge 0}^{E(\Gamma)} \end{align*} $$

which is an isomorphism when $c=v$ is a vertex, and which is the fiber product

when e is an edge. Given a piecewise linear function $\alpha $ on $\Gamma $ , with underlying flow $s=s_\alpha $ , it lifts canonically to a piecewise linear function on $\Gamma _c$ by not changing the slopes if e has been subdivided. The union of the cones

$$\begin{align*}\sigma_{(\Gamma,s,n+1)} \subset \Sigma_{\mathbf{Div}_{n+1}} \end{align*}$$

forms a subcomplex with a forgetful map to $\sigma _{(\Gamma ,s,n)}$ .

Lemma 4.13. The universal family of $\Sigma _{\mathbf {Div}_{n}}$ restricts to

$$ \begin{align*}\varinjlim_{c \in V(\Gamma) \cup E(\Gamma)} \sigma_{(\Gamma_c,s,n+1)} \end{align*} $$

over $\sigma _{(\Gamma ,s,n)}$ .

Proof. Let $\mathcal {C} \to \Sigma _{\textbf {Div}_n}$ be the universal family, and $\sigma $ a cone. A map $\sigma \to \mathcal {C}$ is a map $\sigma \to \Sigma _{\textbf {Div}_n}$ , together with a section of

$$ \begin{align*}\mathcal{C} \times_{\Sigma_{\mathbf{Div}_n}} \sigma \to \sigma. \end{align*} $$

In other words, it consists of a tropical curve $\Gamma $ metrized by $M = \sigma ^\vee $ , a piecewise linear function $\alpha $ and a section of $\Gamma $ . The section is a point of $\Gamma $ , which is either a vertex or lies on an edge. Sections that land in e are in bijection with subdivisions $\Gamma '$ of $\Gamma $ whose underlying graph is $\Gamma _e$ , and are thus parametrized by the choice of lengths of the two pieces of e determined by the section. Since $\alpha $ lifts canonically to $\Gamma '$ by not altering the slopes, the triples $(\Gamma ,\alpha ,\text {section through } e)$ are in bijection with maps

$$ \begin{align*}\sigma \to \sigma_{(\Gamma_e,s,n+1)} \end{align*} $$

as claimed.

The analogous result does not hold for $\Sigma _{\textbf {Ord}}$ . The reason is that an ordering $\kappa $ does not lift canonically to an ordering on the universal curve. All that can be said is that the universal curve of $\Sigma _{\textbf {Ord}}$ is the pullback of the universal curve of $\Sigma _{\textbf {Div}}$ .

The result is also false for $\Sigma _{\textbf {Rub}}$ , but a curious intermediate statement can be obtained. Points of $\Sigma _{\textbf {Rub}}$ have more structure, contained in the map $\Gamma ' \to X$ . Suppose $\kappa $ is the induced ordering. The section of the universal curve in particular factors through some cell $\Gamma ^{\prime }_c$ of $\Gamma '$ now, and thus the ordering $\kappa $ lifts canonically to $\Gamma ^{\prime }_c$ : points in any cell of $\Gamma '$ are in a unique order relative to $\alpha $ . It follows that the universal curve of $\Sigma _{\textbf {Rub}_n}$ factors through $\Sigma _{\textbf {Ord}_{n+1}} \to \Sigma _{\textbf {Div}_{n+1}}$ . However, it does not necessarily factor through $\Sigma _{\textbf {Rub}_{n+1}}$ . The reason is that while $\alpha $ and the total ordering lift canonically to $\Gamma ^{\prime }_c$ , the equidimensional lift

$$ \begin{align*}\Gamma' \to X \end{align*} $$

does not. The induced map

$$ \begin{align*}\Gamma^{\prime}_{c} \to X \end{align*} $$

is no longer equidimensional. Further subdivision of X and consequently of $\Gamma ^{\prime }_c$ is required, which may require extracting additional roots, as in 4.9. Nevertheless, the argument suffices to show the following:

Lemma 4.14. The universal family of $\Sigma _{\textbf {Rub}}$ is simplicial.

Remark 4.15. To get a smooth universal family, one can work instead with an alternative stack $\Sigma _{\textbf {AF}}$ ⁹ parametrizing (a strenghtening of) equidimensional maps on orbifold tropical curves. We do not introduce this here as $\Sigma _{\textbf {Rub}}$ is good enough for our purposes.

We now continue our carving mission much more aggressively. As usual, we can fix the genus g of the graph, along with its n markings. This way, we obtain substacks

$$ \begin{align*}\Sigma_{?_{g,n}}. \end{align*} $$

Next, we fix a universal stability condition $\theta $ [KP19]. This means a stability condition for the universal family $\mathcal {C}_{g,n}^{\text {trop}} \to \mathcal {M}_{g,n}^{\text {trop}}$ of stable tropical curves: a numerical stability condition in the sense of Subsection 2.15 for each stable graph $\Gamma $ of genus g with n legs, which are compatible with respect to all contractions of edges and automorphisms. We restrict to stable graphs here for simplicity but, in fact, a similar procedure even works for the cone stack of all genus g, n-marked tropical curves $\mathfrak {M}_{g,n}^{\text {trop}}$ .

Let A be the divisor of example 2.2.1 associated to a vector $(a_1,\cdots ,a_n) \in \mathbb {Z}^n$ , $k \in \mathbb {Z}$ , which is compatible with contractions according to example 2.21.1.

Figure 1 Above, a point of $\Sigma _{\textbf {Ord}}$ , representing a piecewise linear function $\alpha $ with $\alpha (v)<\alpha (u)<\alpha (w)$ , and a lift to its universal family. The relation between $\alpha (u)$ and $\alpha (v_{n+1})$ on the universal family is undetermined. Below, an analogous point of $\Sigma _{\textbf {Rub}}$ . Here, the relation $\alpha (v_{n+1})<\alpha (u)=\alpha (u')$ is forced.

We write $\Sigma _{\mathbf {Div}_{g,A}^\theta } $ for the subcomplex of $\Sigma _{\mathbf {Div}_{g,n}}$ consisting of the cones $\sigma _{(\Gamma ,s)}$ such that the graph $\Gamma $ is quasi-stable, and $D = A - \mathsf {div}(s)$ is $\theta $ -stable. In other words, $(\Gamma ,s)$ is a $\theta $ -flow relative to the stabilization $\Gamma ^{\mathsf {st}}$ . We write

$$ \begin{align*}\Sigma_{\mathbf{Ord}_{g,A}^\theta} \end{align*} $$

for the subcomplex consisting of $(\Gamma ,s,\kappa )$ with $\Gamma $ quasi-stable and $D = A - \mathsf {div}(s)\ \theta $ -stable, and

$$ \begin{align*}\Sigma_{\mathbf{Rub}_{g,A}^\theta} \end{align*} $$

for the subcomplex consisting of $(\Gamma ,s,\Gamma ' \to X)$ with $\Gamma $ quasi-stable, $D = A - \mathsf {div}(s)\ \theta $ -stable and $\Gamma ' \to X$ a stable equidimensional lift. In other words, $(\Gamma ,s,\Gamma ' \to X)$ is a $\theta $ -stable equidimensional flow relative to the stable graph $\Gamma ^{\mathsf {st}}$ .

Lemma 4.16. The preimage of $\Sigma _{\mathbf {Div}_{g,A}^\theta }$ in $\Sigma _{\mathbf {Ord}_{g,n}}$ is $\Sigma _{\mathbf {Ord}_{g,A}^\theta } $ , and the preimage of $\Sigma _{\mathbf {Ord}_{g,A}^\theta }$ in $\Sigma _{\mathbf {Rub}_{g,n}}$ is $\Sigma _{\mathbf {Rub}_{g,A}^\theta } $ .

Proof. The proof is immediate from the definition of the morphisms.

The space $\Sigma _{\mathbf {Div}^\theta _{g,A}}$ has a stabilization map to $\mathcal {M}_{g,n}^{\text {trop}}$ . It is shown in theorem [HMP+22, Theorem 23] that for nondegenerate $\theta $ , this map factors isomorphically through a subdivision. We then get the following:

Corollary 4.17. Let $\theta $ be a nondegenerate stability condition. The map

$$ \begin{align*}\Sigma_{\mathbf{Rub}_{g,A}^\theta} \to \mathcal{M}_{g,n}^{\text{trop}}\end{align*} $$

factors isomorphically through the composition of a subdivision and a finite index sublattice inclusion.

5 Algebraizing and Globalizing

5.1 Tropicalization and tropical operations

In this paper, we use the language of logarithmic geometry as our main means to access algebro-geometric problems via combinatorial tools. We rapidly lay out our conventions. For a thorough treatment of logarithmic geometry, we refer the interested reader to [Kat89] and [Ogu18]. For a shallower treatment more adapted to our needs here, we refer to [HMP+22, MR21].

A log scheme (or log DM stack) is a pair $(S,M_S)$ consisting of a scheme (or DM stack) S with a log structure $M_S$ (i.e., a sheaf of monoids on the étale site of S with a homomorphism of monoids)

$$\begin{align*}\epsilon: M_S \to \mathcal{O}_S \end{align*}$$

to the structure sheaf of S with its multiplicative monoid structure, such that $\epsilon ^{-1}(\mathcal {O}_S^*) \cong \mathcal {O}_S^*$ . As is common, we drop $M_S$ from the notation; however, when speaking about a log scheme S, it it to be understood that a log structure $M_S$ is present.

The quotient

$$\begin{align*}\overline{M}_S := M_S/\mathcal{O}_S^* \end{align*}$$

is a constructible sheaf on S, called the characteristic monoid. The characteristic monoid stratifies S; the strata are the connected components of the loci of S on which $\overline {M}_S$ is locally constant. As with our conventions on monoids, we will assume throughout that $\overline {M}_S$ is a sheaf of finitely generated and saturated monoids.

The main example to keep in mind is a normal crossings pair – a smooth S with a normal crossings divisor D. This defines a log structure by setting, for an étale map $i: U \to S$ ,

$$\begin{align*}M_S(i:U \to S) = \{f \in \mathcal{O}_U: f|_{i^{-1}(S-D)} \in \mathcal{O}_U^*(i^{-1}(S-D))\}. \end{align*}$$

The characteristic monoid $\overline {M}_S$ is, in that case, at a point x of the étale site of S, equal to

$$\begin{align*}\overline{M}_{S,x} = \mathbb{N}^k, \end{align*}$$

where k is the number of distinct (in any sufficiently small étale neighborhood) branches of D that contain x.

The important point for us is that any cone stack, as in Section 4, can be given a functor of points in the category of log schemes: for a cone stack $\Sigma $ , one obtains a prestack

$$ \begin{align*}\Sigma \rightarrow \textbf{LogSch} \end{align*} $$

by defining

$$ \begin{align*}T \to \Sigma \rightsquigarrow \mathsf{Hom}(\overline{M}_T(T)^\vee, \Sigma). \end{align*} $$

The associated stack is representable by an algebraic stack with logarithmic structure, referred to as an Artin fan. Instead of introducing Artin fans here, we will simply understand morphisms from a log scheme to $\Sigma $ to mean maps to the associated stack.

Definition 5.2. Let S be a log DM stack. A tropicalization for S is a cone stack $\Sigma _S$ with a map $S \to \Sigma _S$ which is strict (i.e., induces an isomorphism on log structures) and has connected fibers.

In particular, under our definition, a tropicalization for S is not unique. For any log smooth DM stack S locally of finite type (for example, a normal crossings pair), one can construct a canonical tropicalization $\Sigma _S$ of S as follows. When S is sufficiently small – the technical term is atomic, meaning that S has a unique closed stratum and the restriction map $\overline {M}_S(S) \to \overline {M}_{S,x}$ is an isomorpism for any x in the closed stratum – it is easy to check that the rational polyhedral cone $\Sigma _S = \overline {M}_S(S)^{\vee }$ is a tropicalization. In general, we can find an étale cover U of S by atomic log schemes, and an étale cover V of $U \times _S U$ by atomic log schemes. Then, the coequalizer

considered as the cone stack associated to a colimit as in Section 4 is a tropicalization of S. It is straightforward to check that the composed map $U \to \Sigma _U \to \Sigma _S$ descends to a map $S \to \Sigma _S$ .

Example 5.2.1. Let $\overline {\mathcal {M}}_{g,n}$ be the moduli space of genus g, n-marked stable curves. The divisor of singular curves is a normal crossings divisor and so endows $\overline {\mathcal {M}}_{g,n}$ with a logarithmic structure. A tropicalization for $\overline {\mathcal {M}}_{g,n}$ is $\mathcal {M}_{g,n}^{\text {trop}}$ .

Let S be a log DM stack with a tropicalization $S \to \Sigma _S$ . Then, any map $\Sigma \to \Sigma _S$ induces a map

$$ \begin{align*}S \times_{\Sigma_S} \Sigma \to S. \end{align*} $$

The fiber product $S \times _{\Sigma _S} \Sigma $ is then an algebraic stack over S, and the map $S \times _{\Sigma _S} \Sigma \to \Sigma $ is a tropicalization of $S \times _{\Sigma _S} \Sigma $ . The importance of this observation for us is that, in this fashion, one can lift combinatorial operations one performs on $\Sigma _S$ to algebraic operations on S; often, they have clear geometric meaning. The ones we have encountered in Section 4 are:

• • Subdivisions $\Sigma \to \Sigma _S$ . These lift to log modifications $\widetilde {S} = S \times _{\Sigma _S} \Sigma \to S$ , which are proper, birational, surjective representable maps.

• • Roots $\Sigma _S' \to \Sigma _S$ , which are maps that replace the integral structure of $\Sigma _S$ with an integral structure coming from a finite index sublattice. These correspond to root stacks of S algebraically, which are proper, birational, nonrepresentable maps $S' \to S$ , which are bijective on geometric points – a generalization of roots along divisors of S. Details can be found in [BV12] and [GM15].

• • Inclusion of a subcomplex $\Sigma \subset \Sigma _S$ . These lift to open inclusions $V \subset S$ .

The three operations above are, furthermore, logarithmically étale and monomorphisms in the category of log schemes!

5.3 Logarithmic curves

Let $C \to S$ be a logarithmic curve (see [CCUW20, Section 7]). Applying the tropicalization construction of the previous subsection yields a map of cone stacks

$$ \begin{align*}\Sigma_C \to \Sigma_S. \end{align*} $$

Pulling back to S and unwinding the definitions, one arrives at the data of a family of tropical curves ¹⁰ over the scheme S, referred to as the tropicalization of $C \to S$ in the literature:

• • For each point $x \in S$ , an underlying graph $\Gamma _x$ : the dual graph of $C_x$ .

• • A tropical curve structure on $\Gamma _x$ metrized by $\overline {M}_{S,x}$ : for each edge $e \in E(\Gamma _x)$ , a length $\ell _e \in \overline {M}_{S,x}$ . The length $\ell _e$ is the ‘smoothing parameter’ of the corresponding node q in $C_x$ : there is a unique element $\ell _e$ in $\overline {M}_{S,x}$ such that

  $$ \begin{align*}\overline{M}_{C,q} \cong \overline{M}_{S,x} \oplus_{\mathbb{N}} {\mathbb{N}}^2\end{align*} $$
  under the map ${\mathbb {N}} \to \overline {M}_{S,x}$ sending $1 \to \ell _e$ , and the diagonal ${\mathbb {N}} \to {\mathbb {N}}^2$ .

• • Compatibility with étale specializations: for each étale specialization $\zeta : y \rightsquigarrow x$ , a map $f_\zeta :\Gamma _x \to \Gamma _y$ compatible with the induced map $\overline {M}_{S,x} \to \overline {M}_{S,y}$ .

The geometric notions on tropical curves discussed in the previous section globalize to logarithmic curves. The globalization works the same way for all concepts, by working fiber by fiber and demanding compatibility with étale specializations: a notion A on a tropical curve globalizes to the analogous notion on a logarithmic curve as a system of $A_x$ on $\Gamma _x/\overline {M}_{S,x}$ for each $x \in S$ , compatible with étale specializations. For example, a piecewise linear function on $C \to S$ is a collection of piecewise linear functions

$$ \begin{align*}\alpha_x \in \mathsf{PL}(\Gamma_x) \end{align*} $$

which are compatible with the maps $\Gamma _x \to \Gamma _y$ for each étale specialization $y \rightsquigarrow x$ . It is ordered, equidimensional, stable, etc. if all $\alpha _x$ are. For divisors, we use the term tropical divisor to avoid confusion with the traditional algebro-geometric notion. Thus, a tropical divisor on $C/S$ is a collection of divisors on each $\Gamma _x$ compatible with the contractions that arise from étale specializations.

Example 5.3.1. Let $C \to S$ be a logarithmic curve with n markings $x_1,\cdots ,x_n$ , and let $(a_1,\cdots ,a_n)$ be a vector of integers (for instance, one adding up to $-k(2g-2+n)$ ). The multidegree of $\omega _{C/S}^{\log }(\sum a_ix_i)$ defines a tropical divisor on $C/S$ : for each $x \in S$ , it is the divisor on $\Gamma _x/\overline {M}_{S,x}$ given by

$$ \begin{align*}A= \sum_{v \in V(\Gamma_x)} k\deg \omega^{\log}_{C_x}(v)+ \sum a_iv_i \end{align*} $$

for $v_i$ the vertex containing the marking $x_i$ , and where $\deg \omega _{C_x}^{\log }(v)$ is the degree of $\omega _{C_x}^{\log }$ on the component of $C_x$ corresponding to v. The divisor A is then precisely the divisor of example 2.2.1 and so is compatible with étale specializations by example 2.21.1. We warn the reader that our terminology here clashes with that of the introduction: the tropical divisor A does require the vector of integers $(a_1,\cdots ,a_n)$ as input but encodes more information.

Subdivisions deserve a special mention. A subdivision of the tropicalization of $C \to S$ is a subdivision of the fibers $\Gamma _x/\overline {M}_{S,x}$ compatible with étale specializations. These subdivisions certainly give rise to logarithmic modifications $C' \to C$ . However, the log modifications that arise this way are special, as the induced map $C' \to S$ remains a logarithmic curve.

Definition 5.4. We call a log modification $C' \to C$ that arises from a subdivision of the tropicalization a subdivision of $C \to S$ .

6 Algebraic Moduli

In this section, we will assume that all our curves come with at least one marking. This is analogous to the assumption in Section 4 that graphs have a leg and can be avoided. But nevertheless, we require it in order to simplify the presentation, as in our applications a marking is always present. We follow [MW20] and define the following:

Definition 6.1. The stack $\textbf {Div}$ on $\textbf {LogSch}$ parametrizing over S pairs $(C \to S,\alpha )$ , consisting of

• • A logarithmic curve $C \to S$ .

• • A piecewise linear function $\alpha $ on C, which is $0$ on the component containing the first marking.

Automorphisms are automorphisms of $\psi :C \to C$ fixing the underlying scheme of S, such that the induced automorphism $\overline {\psi }$ on the tropicalization of C respects $\alpha $ : $\overline {\psi } \circ \alpha = \alpha $ .

Definition 6.2. The stack $\textbf {Ord}$ parametrizing pairs $(C \to S, \alpha )$ of

• • A log curve $C \to S$ .

• • A piecewise linear function on C whose values are totally ordered and which is $0$ on the component containing the first marking.

Definition 6.3. The stack $\textbf {Rub}$ parametrizing pairs $(C \to S, \alpha , C' \to X)$ of

• • A log curve $C \to S$ .

• • A piecewise linear function $\alpha $ on C which is $0$ on the component containing the first marking.

• • A subdivision $C' \to C$ with a stable lift of $\alpha $ to an equidimensional map

  $$\begin{align*}C' \to X. \end{align*}$$

Automorphisms are defined as for $\mathbf {Div}$ .

Remark 6.4. The assumption that curves $C \to S$ carry a marking is put precisely in order to rigidify the stacks. We note, however, that in the case of $\textbf {Rub}$ , there is a canonical rigidification which does not depend on the presence of markings: the values of the function $\alpha $ are totally ordered, so we can always demand that $\alpha $ is $0$ on the minimal value.

There are evident forgetful maps $\mathbf {Rub} \to \mathbf {Ord} \to \mathbf {Div}$ , and forgetful-stabilization morphisms $\mathbf {Div} \to \overline {\mathcal {M}}_{g,n}$ . We note here that we are potentially in an uncomfortable situation; in Section 4, we introduced cone stacks $\Sigma _{\mathbf {Div}},\Sigma _{\mathbf {Ord}},\Sigma _{\mathbf {Rub}}$ , whereas we should have reserved the notation for tropicalizations of $\mathbf {Div},\mathbf {Rub},\mathbf {Ord}$ . However, we have the following:

Theorem 6.5. We have

$$ \begin{align*}\mathbf{Div} = \overline{\mathcal{M}}_{g,n} \times_{\mathcal{M}_{g,n}^{\text{trop}}} \Sigma_{\mathbf{Div}}. \end{align*} $$

Thus, $\textbf {Div} \to \Sigma _{\textbf {Div}}$ is a tropicalization for $\textbf {Div}$ . Analogous statements hold for $\mathbf {Ord},\mathbf {Rub}$ .

Proof. We construct a map $\mathbf {Div} \to \Sigma _{\mathbf {Div}}$ . Let S be a log scheme; we must construct a map $\mathbf {Div}(S) \to \Sigma _{\mathbf {Div}}(S)$ , which amounts to constructing a map locally around each $x \in S$ , compatibly with any étale specialization $\zeta : y \rightsquigarrow x$ . So we may replace S with a sufficiently small neighborhood of x. Then, we can assume that x is in the closed stratum of S and that $\overline {M}_{S,x} = \overline {M}_{S}(S)$ . Furthermore, $\overline {M}_{S,y}$ is a quotient of $\overline {M}_{S,x}$ by a face. Let $(C \to S,\alpha )$ be an element of $\mathbf {Div}(S)$ .

We write $\Gamma _x$ for the dual graph of $C_x$ , and $\Gamma _y$ for the dual graph of $C_y$ . These have the structure of tropical curves metrized by $\overline {M}_{S,x}$ and $\overline {M}_{S,y}$ , respectively. Furthermore, they carry piecewise linear functions $\alpha _x,\alpha _y$ .

The map $\overline {M}_{S,x} \to \overline {M}_{S,y}$ canonically induces a tropical curve $\overline {\Gamma }_x$ metrized by $\overline {M}_{S,y}$ , by contracting edges whose length is $0$ in $\overline {M}_{S,y}$ , and a piecewise linear function $\overline {\alpha }_x$ . We thus get two maps $\overline {M}_{S,y} \to \Sigma _{\mathbf {Div}}$ , corresponding to $(\overline {\Gamma }_x,\overline {\alpha }_x)$ and $(\Gamma _y,\alpha _y)$ .

The specialization $\zeta $ induces a map $\overline {\Gamma }_x \to \Gamma _y$ , which, by definition of a piecewise linear function on C, takes $\overline {\alpha }_x$ to $\alpha _y$ . This is precisely an isomorphism in $\Sigma _{\mathbf {Div}}$ , and so the map is compatible with specializations. Thus, we get the desired map $\mathbf {Div} \to \Sigma _{\mathbf {Div}}$ , and as a result, a map

$$ \begin{align*}\mathbf{Div} \to \overline{\mathcal{M}}_{g,n} \times_{\mathcal{M}_{g,n}^{\text{trop}}} \Sigma_{\mathbf{Div}}. \end{align*} $$

However, an element of the fiber product is a log curve $C \to S$ , together with a piecewise linear function on its tropicalization; and so the map $\mathbf {Div} \to \overline {\mathcal {M}}_{g,n} \times _{\mathcal {M}_{g,n}^{\text {trop}}} \Sigma _{\mathbf {Div}}$ is essentially surjective. Let S be the spectrum of an algebraically closed field, $C \to S$ a log curve, and $\Gamma $ its tropicalization, metrized by $M = \overline {M}_S(S)$ . The automorphism groups

$$ \begin{align*}\mathsf{Aut}(\overline{\mathcal{M}}_{g,n} \times_{\mathcal{M}_{g,n}^{\text{trop}}} \Sigma_{\mathbf{Div}})(S) \end{align*} $$

in the fiber product consist of pairs of an automorphism $\phi :\Gamma \to \Gamma $ with $\phi \circ \alpha = \alpha $ , together with an automorphism $\psi $ of C inducing $\phi $ (i.e., automorphisms $\psi $ of C with $\overline {\psi } \circ \alpha = \alpha $ ). These are exactly the automorphisms of $\mathbf {Div}$ .

The statements for $\textbf {Ord},\textbf {Rub}$ are proved precisely the same way.

Thus, $\textbf {Div},\textbf {Ord},\textbf {Rub}$ are obtained from $\overline {\mathcal {M}}_{g,n}$ by pulling back maps of cone stacks. Furthermore, the resulting maps $\textbf {Rub} \to \textbf {Ord} \to \textbf {Div}$ are either subdivisions or roots. As corollaries, we obtain several theorems by combining the tropical results of Section 4 with the algebraization discussion of Section 5.

Theorem 6.6 ([MW20, Corollary 5.3.5]).

The maps $\textbf {Rub} \to \mathbf {Ord} \to \mathbf {Div}$ are proper, log étale, birational log monomorphisms.

Theorem 6.7. The stack $\textbf {Rub}$ is nonsingular and its universal curve is quasi-smooth.

Theorem 6.8. The map $\textbf {Rub} \to \overline {\mathcal {M}}_{g,n}$ is of Deligne-Mumford type. The map $\textbf {Rub} \to \textbf {Ord}$ is a relative coarse moduli space over $\overline {\mathcal {M}}_{g,n}$ .

Proof. This follows from corollary 4.11 and [GM15, Proposition 3.2.6] by observing that the cones in $\Sigma _{\textbf {Ord}},\Sigma _{\textbf {Rub}}$ provide local charts for $\textbf {Ord},\textbf {Rub}$ .

Furthermore, if we fix a universal stability condition $\theta $ , $k \in \mathbb {Z}$ , and a vector of integers $(a_1,\cdots ,a_n)$ with $\sum a_i = -k(2g-2+n)$ , and let A be the divisor of example 5.3.1, we obtain:

Lemma 6.9. The stacks $\textbf {Div}_{g,A}^\theta $ , $\textbf {Ord}_{g,A}^\theta $ , $\textbf {Rub}_{g,A}^\theta $ are open substacks of $\mathbf {Div},\mathbf {Ord},\mathbf {Rub}$ .

However, we can restrict the natural map $\mathbf {Div}_{g,n} \to \overline {\mathcal {M}}_{g,n}$ to $\mathbf {Div}_{g,A}^\theta $ , and also the composition $\mathbf {Rub}_{g,A}^\theta \to \mathbf {Div}_{g,A}^\theta $ .

For the sake of completeness, we spell out the functor of points of $\textbf {Div}_{g,A}^\theta $ and $\textbf {Rub}_{g,A}^\theta $ . It is simpler to do so in the category $\textbf {LogSch}$ . For a log scheme S, the S points of $\mathbf {Div}_{g,A}^\theta $ consist of

• • A quasi-stable log curve $C \to S$ .

• • A piecewise linear function $\alpha $ , vanishing along the first marking, such that

  $$ \begin{align*}A-\mathsf{div}(\alpha) = D \end{align*} $$
  is $\theta $ -stable.

The S-points of $\textbf {Rub}_{g,A}^\theta $ are, in addition to the above,

• • A subdivision $C' \to C$ over S, a tropical target $X \to S$ and an equidimensional map

  $$ \begin{align*}C' \to X \end{align*} $$
  This data is required to be stable (i.e., $C',X$ are minimal with this property).

We can restrict the map $\mathbf {Div}_{g,n} \to \overline {\mathcal {M}}_{g,n}$ to its open substack $\mathbf {Div}_{g,A}^\theta $ . The content of 4.17 and the discussion preceeding it is then that the restriction $\mathbf {Div}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$ factors isomorphically through a log modification $\overline {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$ ; and the restriction of $\mathbf {Rub}_{g,n} \to \overline {\mathcal {M}}_{g,n}$ to $\mathbf {Rub}_{g,A}^\theta $ factors through a log modification followed by a root $\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$ . We summarize as follows:

Theorem 6.10. The stack $\widetilde {\mathcal {M}}_{g,A}^\theta $ is nonsingular. If $\theta $ is nondegenerate, the map $\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$ is proper, birational and of DM-type. The universal curve $\mathcal {C} \to \widetilde {\mathcal {M}}_{g,A}^\theta $ is quasi-smooth and carries a universal line bundle

$$ \begin{align*}\mathcal{L} = (\omega^{\log})^{\otimes k}(\sum a_ix_i) \otimes \mathcal{O}(\alpha) \end{align*} $$

which is $\theta $ -stable.

The line bundle $\mathcal {L}$ , in particular, gives an Abel-Jacobi section

$$ \begin{align*}\widetilde{\mathcal{M}}_{g,A}^\theta \to \text{Pic}^\theta \end{align*} $$

and can be used to compute the DR cycle: when $\theta $ is small and nondegenerate, the ‘universal DR formula’ of [BHP+20] applies, as in [HMP+22, Theorem A].

Remark 6.11. One can use the Abel-Jacobi section

$$ \begin{align*}\overline{\mathcal{M}}_{g,A}^\theta \to \text{Pic}^\theta \end{align*} $$

to pull back the universal Jacobian $\text {Jac}$ of multidegree $0$ line bundles. The resulting space

$$ \begin{align*}\overline{\mathcal{M}}_{g,n}^\theta \times_{\text{Pic}^\theta} \text{Jac} \end{align*} $$

is the space $M^{\diamond }$ of [Hol21]. Its pullback to $\widetilde {\mathcal {M}}_{g,A}^\theta $ is a desingularization, denoted by $\mathsf {tDR}$ in [MR21]. Pulling back further, replacing $\text {Jac}$ with its $0$ section $0$ gives

$$ \begin{align*}\mathsf{DRL} = \overline{\mathcal{M}}_{g,A}^\theta \times_{\text{Pic}^\theta}0. \end{align*} $$

This is a compact locus which supports the cycle $\mathsf {DR}_{g,A}^k$ . When $k=0$ , the further pullback

$$ \begin{align*}\widetilde{\mathcal{M}}_{g,A}^\theta \times_{\text{Pic}^\theta} 0 \end{align*} $$

can be identified with the rubber version of Bumsig Kim’s space of log stable maps to expansions of $\mathbb {P}^1$ . In fact, the tropical targets X are the cone stacks associated to expansions. But notice that in the definition of $\textbf {Rub}$ , we demand that curves map to tropical targets and not expansions. It is precisely the point that there a lot more maps to tropical targets than algebraic ones, and it is in this space that we carve out the smooth spaces $\widetilde {\mathcal {M}}_{g,A}^\theta $ . The space of maps to algebraic targets is of much smaller dimension.

7 Algorithms

Let $\theta $ be a non-degenerate stability condition, and A a divisor on the universal family of $\mathcal {M}_{g,n}^{\text {trop}}$ . We explain how to construct the cone stack of $\widetilde {\mathcal {M}}_{g,A}^\theta $ from that of $\overline {\mathcal {M}}_{g,n}$ algorithmically. The algorithm first constructs $\overline {\mathcal {M}}_{g,A}^\theta $ , precisely as in [HMP+22]. It then finds the cones in $\widetilde {\mathcal {M}}_{g,A}^\theta $ by unpacking the discussion of 4. It suffices to work cone by cone in $\mathcal {M}_{g,n}^{\text {trop}}$ . We thus fix a stable graph $\Gamma $ of type $g,n$ . We will write $\Sigma _{\Gamma }$ for the cone corresponding to $\Gamma $ in $\overline {\mathcal {M}}_{g,n}$ , $\Sigma _{\Gamma }^\theta $ for the cone in $\overline {\mathcal {M}}_{g,A}^\theta $ , and $\widetilde {\Sigma }_{\Gamma }^\theta $ for the cone in $\widetilde {\mathcal {M}}_{g,A}^\theta $ .

Algorithm:

1. 1. List all acyclic flows s on quasi-stable models of $\Gamma $ (without length assignments) with divisor $\mathsf {div}(s) = A -D$ . There is a finite number of possible such flows.

2. 2. For each such flow, find the $x \in \Sigma _\Gamma $ such that $\left \langle s, \gamma \right \rangle _x = 0$ for any $\gamma \in H_1(\Gamma )$ . The collection of such x for a specific flow is a cone of $\Sigma _{\Gamma }^\theta $ . In other words, $\Sigma _{\Gamma }^\theta $ is the subdivision of $\Sigma _\Gamma $ into the cones where the various acyclic flows lift to actual twists.

3. 3. Over a cone of $\Sigma _\Gamma ^\theta $ corresponding to $(\Gamma ',\alpha )$ , list all possible orderings $\kappa $ extending $\alpha $ . Equivalently, lift the data $\Gamma ',\alpha $ to stable equidimensional lifts $\Gamma " \to X$ of $\alpha $ . There is, again, only a finite number of such data.

4. 4. Find the vectors $x \in \Sigma _\Gamma ^\theta $ that realize a given order $\kappa $ . This means orienting the edges according to $\kappa $ this total order, ¹¹ choosing a minimal vertex v, and an oriented path $P_{v \to w}$ for every $w \in V(\Gamma ')$ ; for all given inequalities $\alpha (w) < \alpha (u)$ in the given order, find x such that

   $$ \begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \le \sum_{\vec{e} \in P_{v \to u}} s(\vec{e})\ell_e. \end{align*} $$

   This determines the cones $\sigma \in \widetilde {\Sigma }_{\Gamma }^\theta $ .

5. 5. For each cone $\sigma $ in $\widetilde {\Sigma _{\Gamma }}^\theta $ , take a generating set for $\sigma \cap N_{\Sigma _{\Gamma }^\theta }$ . For x in this generating set, find the minimal integral multiple $kx$ of x for which the quantities

   $$ \begin{align*}\frac{\alpha(u)-\alpha(v)}{s(f)},\frac{\alpha(w)-\alpha(v)}{s(f)} \end{align*} $$

   are integers when evaluated on $kx$ , where v ranges through all vertices of $\Gamma '$ , w is any vertex with $\alpha (w)$ the value consecutive to $\alpha (v)$ and f is any edge oriented away from v with other endpoint u. The sublattice generated by the $kx$ is the integral structure of $\widetilde {\Sigma }_{\Gamma }^\theta $ .

   Alternatively, the integral structure can be determined as the sublattice

   $$ \begin{align*}\oplus_{\rho \in \sigma(1)}{\mathbb{N}} x_{\rho} \subset {\mathbb{N}}^{E(\Gamma)} \end{align*} $$

   generated by the primitive vectors $x_\rho $ along the one dimensional faces $\rho $ of $\sigma $ .

Remark 7.1. Steps $2$ and $4$ are the hardest steps to carry out, as they involve solving a collection of linear inequalities. However, as is explained in [HMP+22], the difficulty of step $2$ is deceptive. In fact, it suffices to solve the equations $\left \langle s, \gamma \right \rangle _x = 0$ only for acyclic flows s supported on $\Gamma $ rather than a quasi-stable model. The system of inequalities then simplifies significantly, as it reduces to a linear system of equalities. These flows determine the minimal cones of $\Sigma _\Gamma ^\theta $ , and all other cones are determined by how twists specialize (i.e., via the combinatorics of specializations rather than the tropical geometry). The same is true for step $4$ : it suffices to solve the inequalities for total orders with the fewest possible strict inequalities. The other cones are determined by specializations. Thus, tropical geometry only enters to determine the shallowest strata. Afterwards, combinatorics takes over.

8 Example

We present an example of the construction. We use the ramification vector $A = (-4,3,1)$ on $\overline {\mathcal {M}}_{1,3}$ , and work out the subdivision of the cone $\mathbb {R}_{\ge 0}^3 = \left \langle \ell _1,\ell _2,\ell _3 \right \rangle $ corresponding to the triangular graph $\Gamma $ that consists of three vertices $v_1,v_2,v_3$ with three edges $e_1,e_2,e_3$ between them, depicted below:

We choose a small perturbation of $\theta = 0$ which is negative on the component containing the first marking and positive on the others. The acyclic flows balancing $A-D$ , as D ranges through $\theta $ -stable divisors on $\Gamma $ are then given in the following list (with slopes depicted in red):

The seven flows above contribute seven codimension $g=1$ cells in the subdivision $S^\theta $ of $\mathbb {R}_{\ge 0}^3$ . For example, the first listed flow contributes the wall

$$ \begin{align*}\ell_1 = 3\ell_2. \end{align*} $$

In general, to complete the subdivision, it is necessary to consider all $\theta $ -semistable divisors D on quasi-stable models of $\Gamma $ as well. There are eight such flows, but in this case, we do not need to list them; since $g=1$ , the $7$ codimension $1$ walls in fact determine the subdivision. ¹² The desired subdivision looks as follows (we present the induced subdivision of the triangle obtained by cutting $\mathbb {R}_{\ge 0}^3$ with the hyperplane $\ell _1+\ell _2+\ell _3 = 1$ ):

The shaded (slice of the) cone is special in $\Sigma _\Gamma ^\theta $ , as it is not simplicial. It is the region corresponding to the twist

The cone is subdivided further in $\widetilde {\Sigma }_\Gamma ^\theta $ , according to whether the piecewise linear function $\alpha $ is greater on the exceptional vertex u, or the vertex $v_2$ . This corresponds to the three ways to make $\alpha $ equidimensional, namely ¹³

or

or, the degenerate case (note that no subdivision of $\Gamma '$ is required here)

More concretely, if the edge $e_2$ has been subdivided as $\ell _2' + \ell _2"$ , with $\ell _2'$ the length of the edge connecting $v_1$ to the exceptional vertex, the cone is subdivided along the hyperplane

$$ \begin{align*}\ell_2' = 2\ell_1. \end{align*} $$

This yields the simplicial subdivision

Next, we determine the integral structure of the two maximal cones. In fact, the one corresponding to the second equidimensional twist has the induced integral structure, so we describe it only for the first twist

The three rays of the corresponding cone are obtained by specializing the values $\alpha (v_1),\alpha (u),\alpha (v_2),\alpha (v_3)$ so that only two of them are distinct. There are thus three ways to do so, respecting the given total order $\alpha (v_1) \le \alpha (u) \le \alpha (v_2) \le \alpha (v_3)$ :

$$ \begin{align*} \alpha(v_1) = \alpha(u) = \alpha(v_2) < \alpha(v_3)\\ \alpha(v_1) < \alpha(u) = \alpha(v_2) = \alpha(v_3)\\ \alpha(v_1) = \alpha(u) < \alpha(v_2) = \alpha(v_3) \end{align*} $$

The first of these is the specialization

Here, the subdivision demanded that

$$ \begin{align*}\ell_2 = \ell_2' + \ell_2" \end{align*} $$

and

$$ \begin{align*}\ell_2' \le 2 \ell_1. \end{align*} $$

Since $\ell _1$ is contracted, this leads to the relation

$$ \begin{align*}\ell_2 = \ell_2" \end{align*} $$

where the slope of $\alpha $ is $2$ , and so to the equation

$$ \begin{align*}2\ell_2 = \ell_3. \end{align*} $$

Thus, the specialization is the ray through the point

$$ \begin{align*}(0,1,2). \end{align*} $$

The other specializations are obtained similiarily, leading to the points $(1,2,0),(1,1,0)$ . The integral structure of the cone is then

$$ \begin{align*}{\mathbb{N}}(0,1,2) \oplus {\mathbb{N}}(1,2,0) \oplus {\mathbb{N}}(1,1,0) \subset {\mathbb{N}}^3. \end{align*} $$

Its index is computed as the determinant of the three vectors, and is found to be $2$ .