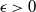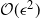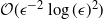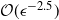1. Introduction
We are given a diffusion process
where
![]() $X_0=x_0\in\mathbb{R}^d$
is given,
$X_0=x_0\in\mathbb{R}^d$
is given,
![]() $\alpha\,:\,\mathbb{R}^d\rightarrow\mathbb{R}^d$
,
$\alpha\,:\,\mathbb{R}^d\rightarrow\mathbb{R}^d$
,
![]() $\beta\,:\,\mathbb{R}^d\rightarrow\mathbb{R}^{d\times d}$
, and
$\beta\,:\,\mathbb{R}^d\rightarrow\mathbb{R}^{d\times d}$
, and
![]() $\{W_t\}_{t\geq 0}$
is a standard d-dimensional Brownian motion. We consider the problem where this is a latent process and we observe it only through a sequence of data that are discrete and regular in time, and in particular where the structure of the observations is a special case of the structure in a state-space or hidden Markov model (HMM). More specifically, we suppose that data are observed at regular and unit times, forming a sequence of random variables
$\{W_t\}_{t\geq 0}$
is a standard d-dimensional Brownian motion. We consider the problem where this is a latent process and we observe it only through a sequence of data that are discrete and regular in time, and in particular where the structure of the observations is a special case of the structure in a state-space or hidden Markov model (HMM). More specifically, we suppose that data are observed at regular and unit times, forming a sequence of random variables
![]() $(Y_1,Y_2,\dots)$
. In particular, at time k we assume that, conditioning on all other random variables in the sequence and given the diffusion process
$(Y_1,Y_2,\dots)$
. In particular, at time k we assume that, conditioning on all other random variables in the sequence and given the diffusion process
![]() $\{X_t\}_{t\geq 0}$
,
$\{X_t\}_{t\geq 0}$
,
![]() $Y_k$
has a probability density function that depends on
$Y_k$
has a probability density function that depends on
![]() $x_k$
only and is denoted by
$x_k$
only and is denoted by
![]() $g(x_k,y_k)$
. These models have a wide class of applications from finance, econometrics, and engineering; see [Reference Beskos3, Reference Cappé, Moulines and Rydén5, Reference Del Moral6, Reference Golightly and Wilkinson12, Reference Ryder, Golightly, McGough and Prangle22] for some particular examples in various contexts.
$g(x_k,y_k)$
. These models have a wide class of applications from finance, econometrics, and engineering; see [Reference Beskos3, Reference Cappé, Moulines and Rydén5, Reference Del Moral6, Reference Golightly and Wilkinson12, Reference Ryder, Golightly, McGough and Prangle22] for some particular examples in various contexts.
In this paper we consider the problems of filtering and normalizing constant (marginal likelihood) estimation—that is, the recursive-in-time (k is the time index) computation of expectations with respect to the conditional distribution of
![]() $X_k|y_{1},\dots,y_k$
(filtering) and the calculation of the associated marginal likelihood of the data
$X_k|y_{1},\dots,y_k$
(filtering) and the calculation of the associated marginal likelihood of the data
![]() $(y_1,\dots,y_k)$
. For standard HMMs, that is, where the latent process is a discrete-time Markov chain, this is a notoriously challenging problem, requiring the application of advanced numerical (Monte Carlo) methods such as the particle filter; see e.g. [Reference Cappé, Moulines and Rydén5, Reference Del Moral6] for a survey. The particle filter simulates a collection of N samples in parallel, with the samples undergoing transitions such as sampling and resampling. The first of these uses the hidden Markov chain and the resampling samples with replacement amongst the collection samples using a weight (proportional to
$(y_1,\dots,y_k)$
. For standard HMMs, that is, where the latent process is a discrete-time Markov chain, this is a notoriously challenging problem, requiring the application of advanced numerical (Monte Carlo) methods such as the particle filter; see e.g. [Reference Cappé, Moulines and Rydén5, Reference Del Moral6] for a survey. The particle filter simulates a collection of N samples in parallel, with the samples undergoing transitions such as sampling and resampling. The first of these uses the hidden Markov chain and the resampling samples with replacement amongst the collection samples using a weight (proportional to
![]() $g(x_k,y_k)$
). The scenario which we consider is even more challenging, as typically the transition density associated to (1.1), assuming it exists, is intractable. This can limit the applicability of particle filters; although there are some exceptions [Reference Fearnhead, Papaspiliopoulos and Roberts8] and exact simulation methods [Reference Beskos and Roberts1, Reference Blanchet and Zhang4], these are often not general enough or too expensive to be of practical use in the filtering problem. As a result, we focus on the case where one discretizes the process (1.1) in time.
$g(x_k,y_k)$
). The scenario which we consider is even more challenging, as typically the transition density associated to (1.1), assuming it exists, is intractable. This can limit the applicability of particle filters; although there are some exceptions [Reference Fearnhead, Papaspiliopoulos and Roberts8] and exact simulation methods [Reference Beskos and Roberts1, Reference Blanchet and Zhang4], these are often not general enough or too expensive to be of practical use in the filtering problem. As a result, we focus on the case where one discretizes the process (1.1) in time.
In recent years, one of the most successful methods for improving Monte-Carlo-based estimators associated to probability laws under time-discretization has been the multilevel Monte Carlo (MLMC) method [Reference Giles9, Reference Giles10, Reference Heinrich13]. This is an approach that considers a collapsing-sum representation of an expectation with respect to a probability law at a given level of discretization. The collapsing element is associated to differences in expectations with increasingly coarse discretization levels, with a final (single) expectation at a course level. Then, if one can sample appropriate couplings of the probability laws at consecutive levels, it is possible to reduce the cost to achieve a certain mean squared error (MSE) in several examples, diffusions being one of them. This method has been combined with the particle filter in several articles, resulting in the multilevel particle filter (MLPF); see [Reference Jasra, Kamatani, Law and Zhou14, Reference Jasra, Kamatani, Osei and Zhou15, Reference Jasra, Law and Osei16], as well as [Reference Jasra, Law and Suciu17] for a review and [Reference Jasra, Law and Yu18] for extensions.
The method of [Reference Jasra, Kamatani, Law and Zhou14] is intrinsically based upon the ability to sample couplings of discretized diffusion processes. In almost all of the applications that we are aware of, this is based upon the synchronous coupling of Brownian motion for an Euler or Milstein scheme. These particular couplings inherit properties of the strong error of the associated time-discretization. The importance of the strong error rate is that it can help determine the efficiency gain of any MLMC approach, of which the MLPF is one. As is well known, in dimensions larger than two (
![]() $d> 2$
), the Milstein scheme, which is of higher (strong) order than the Euler method, can be difficult to implement numerically because of the need to simulate Lévy areas. Giles and Szpruch [Reference Giles and Szpruch11] consider computing expectations associated to the law of (1.1) at a given terminal time. They show that by eliminating the Lévy area and including an antithetic-type modification of the traditional MLMC estimator, one can maintain the strong error rate of the Milstein scheme even in a multidimensional setting. Moreover, the cost of the simulation is of the same order as for Euler discretizations, which are the ones most often used in multidimensional cases.
$d> 2$
), the Milstein scheme, which is of higher (strong) order than the Euler method, can be difficult to implement numerically because of the need to simulate Lévy areas. Giles and Szpruch [Reference Giles and Szpruch11] consider computing expectations associated to the law of (1.1) at a given terminal time. They show that by eliminating the Lévy area and including an antithetic-type modification of the traditional MLMC estimator, one can maintain the strong error rate of the Milstein scheme even in a multidimensional setting. Moreover, the cost of the simulation is of the same order as for Euler discretizations, which are the ones most often used in multidimensional cases.
We develop a new particle filter based upon the antithetic truncated Milstein scheme of [Reference Giles and Szpruch11]. We show empirically for a class of diffusion problems that, for
![]() $\epsilon>0$
given, the cost to produce an MSE of
$\epsilon>0$
given, the cost to produce an MSE of
![]() $\mathcal{O}(\epsilon^2)$
in the estimation of the filter is
$\mathcal{O}(\epsilon^2)$
in the estimation of the filter is
![]() $\mathcal{O}\big(\epsilon^{-2}\log(\epsilon)^2\big)$
. In the case of multidimensional diffusions with non-constant diffusion coefficient, the method of [Reference Jasra, Kamatani, Law and Zhou14] requires a cost of
$\mathcal{O}\big(\epsilon^{-2}\log(\epsilon)^2\big)$
. In the case of multidimensional diffusions with non-constant diffusion coefficient, the method of [Reference Jasra, Kamatani, Law and Zhou14] requires a cost of
![]() $\mathcal{O}\big(\epsilon^{-2.5}\big)$
to achieve the same MSE. We also show how this new particle filter can be used to compute the normalizing constant recursively in time, but we do not prove anything about the efficiency gains. Our theoretical results are not optimal and show only that the cost of the new method is
$\mathcal{O}\big(\epsilon^{-2.5}\big)$
to achieve the same MSE. We also show how this new particle filter can be used to compute the normalizing constant recursively in time, but we do not prove anything about the efficiency gains. Our theoretical results are not optimal and show only that the cost of the new method is
![]() $\mathcal{O}\big(\epsilon^{-2.5}\big)$
for the MSE of
$\mathcal{O}\big(\epsilon^{-2.5}\big)$
for the MSE of
![]() $\mathcal{O}(\epsilon^2)$
. We highlight exactly where the proof loses the rate needed.
$\mathcal{O}(\epsilon^2)$
. We highlight exactly where the proof loses the rate needed.
To provide a more detailed summary of the contribution of this paper, we state the following. First, the main point is to understand how the rather clever discretization scheme of [Reference Giles and Szpruch11] can be leveraged in the context of filtering and the multilevel method. Generally, for ordinary discretization schemes in MLMC, one has to simulate coupled samples at two levels of time-discretization, one that is fine and another that is coarse. Then this can be extended to the case of filtering diffusion processes, as was done in [Reference Jasra, Kamatani, Law and Zhou14] by constructing a coupling in the resampling mechanism of particle filters. In the method of [Reference Giles and Szpruch11], the authors sample a third ‘antithetic’ process at the finer level. We show how such a process can be incorporated into the context of particle filters with, to the best of our knowledge, a new resampling scheme. Second, there are significant technical challenges in showing that this new antithetic particle filter can provide the improvements in terms of cost and MSE that the approach of [Reference Giles and Szpruch11] does for ordinary diffusion processes. Unfortunately, we obtain a non-optimal rate; again, we highlight where the proof misses the extra rate.
The article is structured as follows. In Section 2 we give details on the model to be considered and the time-discretization associated to the process (1.1). In Section 3 we present our algorithm. Section 4 details our mathematical results and their algorithmic implications. In Section 5 we give numerical results that support our theory. Most of our mathematical proofs can be found in the appendices at the end of the article.
2. Model and discretization
2.1. State-space model
Our objective is to consider the filtering problem and normalizing constant estimation for a specific class of state-space models associated to the diffusion process (1.1). In particular, we will assume that (1.1) is subject to a certain assumption (A1) which is described in Section 4. This assumption is certainly strong enough to guarantee that (1.1) has a unique solution and in addition that the diffusion has a transition probability, which we denote, over one unit of time, by P(x, dx ′). We are then interested in filtering associated to the state-space model
where
![]() $y_{1:n}=(y_1,\dots,y_n)^{\top}\in\mathsf{Y}^n$
are observations, each with conditional density
$y_{1:n}=(y_1,\dots,y_n)^{\top}\in\mathsf{Y}^n$
are observations, each with conditional density
![]() $g(x_k,\cdot)$
. The filter associated to this measure is, for
$g(x_k,\cdot)$
. The filter associated to this measure is, for
![]() $k\in\mathbb{N}$
,
$k\in\mathbb{N}$
,
where
![]() $\mathsf{X}=\mathbb{R}^d$
. The denominator
$\mathsf{X}=\mathbb{R}^d$
. The denominator
is the normalizing constant or marginal likelihood. This latter object is often used in statistics for model selection.
In practice, we assume that working directly with P is not possible, because of either intractability or cost of simulation. We therefore propose to work with an alternative collection of filters based upon time-discretization, which is what we now describe.
2.2. Time-discretization
Typically one must time-discretize (1.1). We consider a time-discretization at equally spaced times, separated by
![]() $\Delta_l=2^{-l}$
. To continue with our exposition, we define the d-vector
$\Delta_l=2^{-l}$
. To continue with our exposition, we define the d-vector
![]() $H\,:\,\mathbb{R}^{2d}\times\mathbb{R}^+\rightarrow\mathbb{R}^d$
,
$H\,:\,\mathbb{R}^{2d}\times\mathbb{R}^+\rightarrow\mathbb{R}^d$
,
![]() $H_{\Delta}(x,z)=(H_{\Delta,1}(x,z),\dots,H_{\Delta,d}(x,z))^{\top}$
, where, for
$H_{\Delta}(x,z)=(H_{\Delta,1}(x,z),\dots,H_{\Delta,d}(x,z))^{\top}$
, where, for
![]() $i\in\{1,\dots,d\}$
,
$i\in\{1,\dots,d\}$
,
 \begin{eqnarray*}H_{\Delta,i}(x,z) & \,=\, & \sum_{(j,k)\in\{1,\dots,d\}^2} h_{ijk}(x)(z_jz_k-\Delta), \\h_{ijk}(x) & \,=\, & \frac{1}{2}\sum_{m\in\{1,\dots,d\}} \beta_{mk}(x)\frac{\partial \beta_{ij}(x)}{\partial x_m}.\end{eqnarray*}
\begin{eqnarray*}H_{\Delta,i}(x,z) & \,=\, & \sum_{(j,k)\in\{1,\dots,d\}^2} h_{ijk}(x)(z_jz_k-\Delta), \\h_{ijk}(x) & \,=\, & \frac{1}{2}\sum_{m\in\{1,\dots,d\}} \beta_{mk}(x)\frac{\partial \beta_{ij}(x)}{\partial x_m}.\end{eqnarray*}
We denote by
![]() $\mathcal{N}_d(\mu,\Sigma)$
the d-dimensional Gaussian distribution with mean vector
$\mathcal{N}_d(\mu,\Sigma)$
the d-dimensional Gaussian distribution with mean vector
![]() $\mu$
and covariance matrix
$\mu$
and covariance matrix
![]() $\Sigma$
; if
$\Sigma$
; if
![]() $d=1$
we drop the subscript d.
$d=1$
we drop the subscript d.
![]() $I_d$
is the
$I_d$
is the
![]() $d\times d$
identity matrix. A single-level version of the truncated Milstein scheme, which is the focus of this article, is presented in Algorithm 1. Ultimately, we will consider the antithetic truncated Milstein scheme in [Reference Giles and Szpruch11], which can be simulated as described in Algorithm 2. The method in Algorithm 2 is a means of approximating differences of expectations with respect to discretized laws at consecutive levels, as is used in MLMC; this latter approach will be detailed in Section 3.
$d\times d$
identity matrix. A single-level version of the truncated Milstein scheme, which is the focus of this article, is presented in Algorithm 1. Ultimately, we will consider the antithetic truncated Milstein scheme in [Reference Giles and Szpruch11], which can be simulated as described in Algorithm 2. The method in Algorithm 2 is a means of approximating differences of expectations with respect to discretized laws at consecutive levels, as is used in MLMC; this latter approach will be detailed in Section 3.
Algorithm 1 Truncated Milstein scheme on [0, 1].

Algorithm 2 Antithetic truncated Milstein scheme on [0, 1].

To understand the use of Algorithms 1 and 2, consider computing the expectation
which is generally approximated by considering
![]() $\int_{\mathsf{X}} x_1 P^l(x_0,dx_1)$
, where we denote the transition kernel induced by Algorithm 1 by
$\int_{\mathsf{X}} x_1 P^l(x_0,dx_1)$
, where we denote the transition kernel induced by Algorithm 1 by
![]() $P^l(x_0,dx_1)$
. This latter integral can certainly be approximated using Monte Carlo and Algorithm 1. However, there is an alternative using both Algorithms 1 and 2, which has been established by [Reference Giles and Szpruch11] as more efficient. Clearly one can write
$P^l(x_0,dx_1)$
. This latter integral can certainly be approximated using Monte Carlo and Algorithm 1. However, there is an alternative using both Algorithms 1 and 2, which has been established by [Reference Giles and Szpruch11] as more efficient. Clearly one can write
Now the rightmost term on the right-hand side of the above equation can be approximated by Monte Carlo and running Algorithm 1 at level
![]() $l-1$
. We then consider the difference on the right-hand side, independently, which can be approximated using Algorithm 2 N times:
$l-1$
. We then consider the difference on the right-hand side, independently, which can be approximated using Algorithm 2 N times:
 \begin{align*}\frac{1}{N}\sum_{i=1}^N\left(\tfrac{1}{2}\left\{X_1^{i,l}+X_1^{i,l,a}\right\}-X_1^{i,l-1}\right),\end{align*}
\begin{align*}\frac{1}{N}\sum_{i=1}^N\left(\tfrac{1}{2}\left\{X_1^{i,l}+X_1^{i,l,a}\right\}-X_1^{i,l-1}\right),\end{align*}
where the superscript i denotes the ith sample generated. The reason such an approximation works so well is that marginally
![]() $X_1^{i,l-1}$
has the same distribution as any sample generated by running Algorithm 1 at level
$X_1^{i,l-1}$
has the same distribution as any sample generated by running Algorithm 1 at level
![]() $l-1$
; similarly, both
$l-1$
; similarly, both
![]() $X_1^{i,l}$
and
$X_1^{i,l}$
and
![]() $X_1^{i,l,a}$
have the same distribution as any sample generated by running Algorithm 1 at level l. Moreover, the second moment of the term, which converges to zero as l increases,
$X_1^{i,l,a}$
have the same distribution as any sample generated by running Algorithm 1 at level l. Moreover, the second moment of the term, which converges to zero as l increases,
where
![]() $\|\cdot\|$
is the usual Euclidean norm, is of the same order (as a function of l) as if one considered a synchronous coupling of two discretizations of the exact Milstein scheme—that is, if one could sample an exact Milstein discretization at level l
$\|\cdot\|$
is the usual Euclidean norm, is of the same order (as a function of l) as if one considered a synchronous coupling of two discretizations of the exact Milstein scheme—that is, if one could sample an exact Milstein discretization at level l
![]() $\big(X_1^{l,M}\big)$
and using the same Brownian motion as at level
$\big(X_1^{l,M}\big)$
and using the same Brownian motion as at level
![]() $l-1$
$l-1$
![]() $\big(X_1^{l-1,M}\big)$
, and consider the second moment of
$\big(X_1^{l-1,M}\big)$
, and consider the second moment of
![]() $\big\|X_1^{l,M}-X_1^{l-1,M}\big\|$
. The reason why this is so important is that the rate of decrease of the aforementioned quantities is what enables MLMC (here we have described two levels) to improve over ordinary Monte Carlo. The key is that by using antithetic variates of the quantity (2.1) (in terms of square expectation) one has replicated the Milstein scheme without ever having to compute intractable Lévy areas.
$\big\|X_1^{l,M}-X_1^{l-1,M}\big\|$
. The reason why this is so important is that the rate of decrease of the aforementioned quantities is what enables MLMC (here we have described two levels) to improve over ordinary Monte Carlo. The key is that by using antithetic variates of the quantity (2.1) (in terms of square expectation) one has replicated the Milstein scheme without ever having to compute intractable Lévy areas.
For a given
![]() $l\in\mathbb{N}$
, we will be concerned with the filter induced by the following joint measure:
$l\in\mathbb{N}$
, we will be concerned with the filter induced by the following joint measure:
The filter associated to this measure is, for
![]() $k\in\mathbb{N}$
,
$k\in\mathbb{N}$
,
The associated normalizing constant is
Ultimately, we will seek to approximate expectations with respect to
![]() $\pi_k^l$
and to estimate
$\pi_k^l$
and to estimate
![]() $p^l(y_{1:k})$
as k increases, then study the MSE of a numerical approximation relative to considering the exact filter
$p^l(y_{1:k})$
as k increases, then study the MSE of a numerical approximation relative to considering the exact filter
![]() $\pi_k$
and associated normalizing constant
$\pi_k$
and associated normalizing constant
![]() $p(y_{1:k})$
.
$p(y_{1:k})$
.
3. Antithetic multilevel particle filters
3.1. Multilevel particle filter
Let
![]() $\varphi\in\mathcal{B}_b(\mathsf{X})$
, the latter denoting the collection of bounded and measurable real-valued functions; we write
$\varphi\in\mathcal{B}_b(\mathsf{X})$
, the latter denoting the collection of bounded and measurable real-valued functions; we write
![]() $\pi_k^l(\varphi)=\int_{\mathsf{X}}\varphi(x_k)\pi_k^l(dx_k)$
. Let
$\pi_k^l(\varphi)=\int_{\mathsf{X}}\varphi(x_k)\pi_k^l(dx_k)$
. Let
![]() $(\underline{L},\overline{L})\in\mathbb{N}_0\times\mathbb{N}$
, with
$(\underline{L},\overline{L})\in\mathbb{N}_0\times\mathbb{N}$
, with
![]() $\underline{L}<\overline{L}$
given. Our objective is the approximation of
$\underline{L}<\overline{L}$
given. Our objective is the approximation of
![]() $\pi_k^{\overline{L}}(\varphi)$
sequentially in time; this is the filtering problem. This can be achieved using the MLMC identity
$\pi_k^{\overline{L}}(\varphi)$
sequentially in time; this is the filtering problem. This can be achieved using the MLMC identity
 \begin{equation}\pi_k^{\overline{L}}(\varphi) = \pi_k^{\underline{L}}(\varphi) + \sum_{l=\underline{L}+1}^{\overline{L}} \big[\pi_{k}^l-\pi_{k}^{l-1}\big](\varphi).\end{equation}
\begin{equation}\pi_k^{\overline{L}}(\varphi) = \pi_k^{\underline{L}}(\varphi) + \sum_{l=\underline{L}+1}^{\overline{L}} \big[\pi_{k}^l-\pi_{k}^{l-1}\big](\varphi).\end{equation}
As noted in the introduction, the computational cost of approximating the right-hand side of (3.1) can be lower than that of approximating the left-hand side, when one is seeking to achieve a pre-specified MSE. The right-hand side of (3.1) can be approximated by the method in [Reference Jasra, Kamatani, Law and Zhou14], but we shall consider a modification which can improve on the computational effort to achieve a given MSE. Often
![]() $\overline{L}=1$
in the literature, but we have found in previous work that one needs to set it higher for the aforementioned improvement in computational effort.
$\overline{L}=1$
in the literature, but we have found in previous work that one needs to set it higher for the aforementioned improvement in computational effort.
We begin by approximating
![]() $\pi_k^{\underline{L}}(\varphi)$
, which can be done using the standard particle filter as described in Algorithm 3. Algorithm 3 generates
$\pi_k^{\underline{L}}(\varphi)$
, which can be done using the standard particle filter as described in Algorithm 3. Algorithm 3 generates
![]() $N_{\underline{L}}$
samples in parallel, and these samples undergo sampling operations (Steps 1 and 3) and resampling operations (Step 2). The sampling step uses Algorithm 1, and the resampling step is the well-known multinomial method. We refer the reader to e.g. [Reference Del Moral6] for an introduction to particle filter methods. It is by now standard in the literature that
$N_{\underline{L}}$
samples in parallel, and these samples undergo sampling operations (Steps 1 and 3) and resampling operations (Step 2). The sampling step uses Algorithm 1, and the resampling step is the well-known multinomial method. We refer the reader to e.g. [Reference Del Moral6] for an introduction to particle filter methods. It is by now standard in the literature that
 \begin{align*}\pi_k^{N_{\underline{L}},\underline{L}}(\varphi) \,:\!=\, \sum_{i=1}^{N_{\underline{L}}}\frac{g\big(X_k^{i,\underline{L}},y_k\big)}{\sum_{j=1}^{N_{l}} g\big(X_k^{j,\underline{L}},y_k\big)}\varphi\big(X_k^{i,\underline{L}}\big)\end{align*}
\begin{align*}\pi_k^{N_{\underline{L}},\underline{L}}(\varphi) \,:\!=\, \sum_{i=1}^{N_{\underline{L}}}\frac{g\big(X_k^{i,\underline{L}},y_k\big)}{\sum_{j=1}^{N_{l}} g\big(X_k^{j,\underline{L}},y_k\big)}\varphi\big(X_k^{i,\underline{L}}\big)\end{align*}
will converge almost surely to
![]() $\pi_k^{\underline{L}}(\varphi)$
, where the samples
$\pi_k^{\underline{L}}(\varphi)$
, where the samples
![]() $X_k^{i,\underline{L}}$
are after Step 1 or 3 of Algorithm 3. Therefore, recalling (3.1), at this stage we can approximate
$X_k^{i,\underline{L}}$
are after Step 1 or 3 of Algorithm 3. Therefore, recalling (3.1), at this stage we can approximate
![]() $\pi_k^{\underline{L}}(\varphi)$
recursively in time.
$\pi_k^{\underline{L}}(\varphi)$
recursively in time.
Algorithm 3 Particle filter at level
![]() $\underline{L}$
.
$\underline{L}$
.

In reference to (3.1), we will approximate the differences
![]() $\big[\pi_{k}^l-\pi_{k}^{l-1}\big](\varphi)$
sequentially in time and independently of using Algorithm 3 and for each l. As stated in the introduction, our objective is to leverage the work of [Reference Giles and Szpruch11] as described in Algorithm 2 and be able to insert this within a particle filter as given in Algorithm 3. The particle filter has two main operations, which are sampling and resampling. The sampling mechanism is to be achieved by using Algorithm 2. The problem is now the resampling approach. The main idea is to ensure that we resample the level-l coordinate just as if we had done so using the particle filter at level l; similarly, we want the same for the antithetic-level coordinate and finally we resample the level-
$\big[\pi_{k}^l-\pi_{k}^{l-1}\big](\varphi)$
sequentially in time and independently of using Algorithm 3 and for each l. As stated in the introduction, our objective is to leverage the work of [Reference Giles and Szpruch11] as described in Algorithm 2 and be able to insert this within a particle filter as given in Algorithm 3. The particle filter has two main operations, which are sampling and resampling. The sampling mechanism is to be achieved by using Algorithm 2. The problem is now the resampling approach. The main idea is to ensure that we resample the level-l coordinate just as if we had done so using the particle filter at level l; similarly, we want the same for the antithetic-level coordinate and finally we resample the level-
![]() $(l-1)$
coordinate just as if we had used the particle filter at level
$(l-1)$
coordinate just as if we had used the particle filter at level
![]() $l-1$
. Critically, the resampling for these three coordinates should be correlated, because if this is not the case, the effect of using Algorithm 2 is lost; see [Reference Jasra and Yu19] for a theoretical justification of this point. The reason we want to maintain the resampling as if the particle filter had been used is that we know this will produce consistent estimates of the filter. We seek to correlate the resampling because this can help ensure that we reduce the cost of achieving a pre-specified MSE, relative to using the particle filter.
$l-1$
. Critically, the resampling for these three coordinates should be correlated, because if this is not the case, the effect of using Algorithm 2 is lost; see [Reference Jasra and Yu19] for a theoretical justification of this point. The reason we want to maintain the resampling as if the particle filter had been used is that we know this will produce consistent estimates of the filter. We seek to correlate the resampling because this can help ensure that we reduce the cost of achieving a pre-specified MSE, relative to using the particle filter.
Algorithm 4 Maximal coupling-type resampling.

Algorithm 5 A new coupled particle filter for
![]() $l\in\mathbb{N}$
given.
$l\in\mathbb{N}$
given.

Algorithm 4 presents a new resampling method which we shall employ. This resampling method achieves the objectives discussed above and gives rise to the new coupled particle filter, which is described in Algorithm 5. Algorithm 5 consists of propagating
![]() $N_l$
samples of the three coordinates sequentially in time, using Algorithm 2 for the sampling and Algorithm 4 for the resampling. In this context one can define, for
$N_l$
samples of the three coordinates sequentially in time, using Algorithm 2 for the sampling and Algorithm 4 for the resampling. In this context one can define, for
![]() $(k,l,N_l,\varphi)\in\mathbb{N}^3\times\mathcal{B}_b(\mathsf{X})$
,
$(k,l,N_l,\varphi)\in\mathbb{N}^3\times\mathcal{B}_b(\mathsf{X})$
,
 \begin{eqnarray}\pi_k^{N_l,l}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} W_k^{i,l}\varphi\big(X_k^{i,l}\big), \\\bar{\pi}_k^{N_l,l-1}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} \bar{W}_k^{i,l-1}\varphi\big(X_k^{i,l-1}\big), \nonumber\\\pi_k^{N_l,l,a}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} W_k^{i,l,a}\varphi\big(X_k^{i,l,a}\big), \nonumber\end{eqnarray}
\begin{eqnarray}\pi_k^{N_l,l}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} W_k^{i,l}\varphi\big(X_k^{i,l}\big), \\\bar{\pi}_k^{N_l,l-1}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} \bar{W}_k^{i,l-1}\varphi\big(X_k^{i,l-1}\big), \nonumber\\\pi_k^{N_l,l,a}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} W_k^{i,l,a}\varphi\big(X_k^{i,l,a}\big), \nonumber\end{eqnarray}
and estimate
![]() $\big[\pi_{k}^l-\pi_{k}^{l-1}\big](\varphi)$
as
$\big[\pi_{k}^l-\pi_{k}^{l-1}\big](\varphi)$
as
The samples in
![]() $\Big(\pi_k^{N_l,l}(\varphi), \pi_k^{N_l,l,a}(\varphi),\bar{\pi}_k^{N_l,l-1}(\varphi)\Big)$
are obtained after Step 1 or Step 3 in Algorithm 5.
$\Big(\pi_k^{N_l,l}(\varphi), \pi_k^{N_l,l,a}(\varphi),\bar{\pi}_k^{N_l,l-1}(\varphi)\Big)$
are obtained after Step 1 or Step 3 in Algorithm 5.
3.2. Final algorithm
To conclude, the antithetic multilevel particle filter (AMLPF) is as follows:
-
1. At level
 $\underline{L}$
run Algorithm 3 sequentially in time.
$\underline{L}$
run Algorithm 3 sequentially in time. -
2. At level
 $l\in\{\underline{L}+1, \underline{L}+2,\dots,\overline{L}\}$
, independently of all other l and of Step 1, run Algorithm 3 sequentially in time.
$l\in\{\underline{L}+1, \underline{L}+2,\dots,\overline{L}\}$
, independently of all other l and of Step 1, run Algorithm 3 sequentially in time.
To approximate the right-hand side of (3.1) at any time k, one can use the estimator
 \begin{align*}\pi_k^{\overline{L},ML}(\varphi) \,:\!=\, \pi_k^{N_{\underline{L}},\underline{L}}(\varphi) + \sum_{l=\underline{L}+1}^{\overline{L}}\big[\pi_{k}^l-\pi_{k}^{l-1}\big]^{N_l}(\varphi),\end{align*}
\begin{align*}\pi_k^{\overline{L},ML}(\varphi) \,:\!=\, \pi_k^{N_{\underline{L}},\underline{L}}(\varphi) + \sum_{l=\underline{L}+1}^{\overline{L}}\big[\pi_{k}^l-\pi_{k}^{l-1}\big]^{N_l}(\varphi),\end{align*}
where
![]() $\pi_k^{N_{\underline{L}},\underline{L}}(\varphi)$
has the definition (3.3) when
$\pi_k^{N_{\underline{L}},\underline{L}}(\varphi)$
has the definition (3.3) when
![]() $l=\underline{L}$
and has been obtained using Algorithm 3.
$l=\underline{L}$
and has been obtained using Algorithm 3.
The normalizing constant
![]() $p^{\overline{L}}(y_{1:k})$
can also be approximated using the AMLPF. For any
$p^{\overline{L}}(y_{1:k})$
can also be approximated using the AMLPF. For any
![]() $(k,l,N_l,\varphi)\in\mathbb{N}^3\times\mathcal{B}_b(\mathsf{X})$
, we define
$(k,l,N_l,\varphi)\in\mathbb{N}^3\times\mathcal{B}_b(\mathsf{X})$
, we define
 \begin{eqnarray}\eta_k^{N_l,l}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} \varphi\big(X_k^{i,l}\big), \\\bar{\eta}_k^{N_l,l-1}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} \varphi\big(X_k^{i,l-1}\big), \nonumber\\\eta_k^{N_l,l,a}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} \varphi\big(X_k^{i,l,a}\big).\nonumber\end{eqnarray}
\begin{eqnarray}\eta_k^{N_l,l}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} \varphi\big(X_k^{i,l}\big), \\\bar{\eta}_k^{N_l,l-1}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} \varphi\big(X_k^{i,l-1}\big), \nonumber\\\eta_k^{N_l,l,a}(\varphi) & \,:\!=\, & \sum_{i=1}^{N_{l}} \varphi\big(X_k^{i,l,a}\big).\nonumber\end{eqnarray}
Then we have the following approximation:
 \begin{align*}p^{\overline{L},ML}(y_{1:k}) \,:\!=\, \prod_{j=1}^{k}\eta_j^{N_{\underline{L}},\underline{L}}(g_j) + \sum_{l=\underline{L}+1}^{\overline{L}}\Bigg\{\tfrac{1}{2}\prod_{j=1}^{k}\eta_j^{N_l,l,}(g_j) +\tfrac{1}{2}\prod_{j=1}^{k}\eta_j^{N_l,l,a}(g_j) -\prod_{j=1}^{k}\bar{\eta}_j^{N_{l-1},l-1,}(g_j)\Bigg\}\end{align*}
\begin{align*}p^{\overline{L},ML}(y_{1:k}) \,:\!=\, \prod_{j=1}^{k}\eta_j^{N_{\underline{L}},\underline{L}}(g_j) + \sum_{l=\underline{L}+1}^{\overline{L}}\Bigg\{\tfrac{1}{2}\prod_{j=1}^{k}\eta_j^{N_l,l,}(g_j) +\tfrac{1}{2}\prod_{j=1}^{k}\eta_j^{N_l,l,a}(g_j) -\prod_{j=1}^{k}\bar{\eta}_j^{N_{l-1},l-1,}(g_j)\Bigg\}\end{align*}
where
![]() $g_j(x)=g(x,y_j)$
is used as shorthand,
$g_j(x)=g(x,y_j)$
is used as shorthand,
![]() $g_j$
is assumed bounded and measurable for each
$g_j$
is assumed bounded and measurable for each
![]() $j\in\mathbb{N}$
, and
$j\in\mathbb{N}$
, and
![]() $\eta_k^{N_{\underline{L}},\underline{L}}(\varphi)$
has the definition (3.4) when
$\eta_k^{N_{\underline{L}},\underline{L}}(\varphi)$
has the definition (3.4) when
![]() $l=\underline{L}$
and has been obtained using Algorithm 3. This new estimator approximates the quantity
$l=\underline{L}$
and has been obtained using Algorithm 3. This new estimator approximates the quantity
 \begin{align*}p^{\underline{L}}(y_{1:k}) + \sum_{l=\underline{L}+1}^{\overline{L}}\big[p^{l}(y_{1:k})-p^{l-1}(y_{1:k})\big]\end{align*}
\begin{align*}p^{\underline{L}}(y_{1:k}) + \sum_{l=\underline{L}+1}^{\overline{L}}\big[p^{l}(y_{1:k})-p^{l-1}(y_{1:k})\big]\end{align*}
as was done in [Reference Jasra, Kamatani, Osei and Zhou15] and essentially uses the ordinary particle filter normalizing constant estimator to approximate
![]() $p^{\underline{L}}(y_{1:k})$
(see e.g. [Reference Del Moral6]). The approximation of the increment
$p^{\underline{L}}(y_{1:k})$
(see e.g. [Reference Del Moral6]). The approximation of the increment
![]() $\big[p^{l}(y_{1:k})-p^{l-1}(y_{1:k})\big]$
follows the approach used for the filter based upon the output from the AMLPF. This estimator is unbiased in terms of
$\big[p^{l}(y_{1:k})-p^{l-1}(y_{1:k})\big]$
follows the approach used for the filter based upon the output from the AMLPF. This estimator is unbiased in terms of
![]() $p^{\overline{L}}(y_{1:k})$
(see e.g. [Reference Del Moral6]) and is consistent as the number of samples used at each level grows. We note, however, that there is nothing in the estimator that ensures that it is almost surely positive, whereas it does approximate a positive quantity.
$p^{\overline{L}}(y_{1:k})$
(see e.g. [Reference Del Moral6]) and is consistent as the number of samples used at each level grows. We note, however, that there is nothing in the estimator that ensures that it is almost surely positive, whereas it does approximate a positive quantity.
4. Mathematical results
We now present our main mathematical result, which relates to the
![]() $\mathbb{L}_2$
-convergence of our estimator of the filter. We remark that we will consider the estimation of the normalizing constant in a sequel paper. The result is proved under two assumptions (A1) and (A2), which are stated below. We write
$\mathbb{L}_2$
-convergence of our estimator of the filter. We remark that we will consider the estimation of the normalizing constant in a sequel paper. The result is proved under two assumptions (A1) and (A2), which are stated below. We write
![]() $\mathsf{X}_2=\mathbb{R}^{d\times d}$
. By
$\mathsf{X}_2=\mathbb{R}^{d\times d}$
. By
![]() $\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
we denote the collection of twice continuously differentiable functions from
$\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
we denote the collection of twice continuously differentiable functions from
![]() $\mathsf{X}$
to
$\mathsf{X}$
to
![]() $\mathbb{R}$
(resp.
$\mathbb{R}$
(resp.
![]() $\mathsf{X}_2$
) with bounded derivatives of orders 1 and 2. Similarly,
$\mathsf{X}_2$
) with bounded derivatives of orders 1 and 2. Similarly,
![]() $\mathcal{C}^2(\mathsf{X},\mathsf{X})$
and
$\mathcal{C}^2(\mathsf{X},\mathsf{X})$
and
![]() $\mathcal{C}^2(\mathsf{X},\mathsf{X}_2)$
are respectively the collections of twice continuously differentiable functions from
$\mathcal{C}^2(\mathsf{X},\mathsf{X}_2)$
are respectively the collections of twice continuously differentiable functions from
![]() $\mathsf{X}$
to
$\mathsf{X}$
to
![]() $\mathsf{X}$
and from
$\mathsf{X}$
and from
![]() $\mathsf{X}$
to
$\mathsf{X}$
to
![]() $\mathsf{X}_2$
. For
$\mathsf{X}_2$
. For
![]() $\varphi\in\mathcal{B}_b(\mathsf{X})$
we use the notation
$\varphi\in\mathcal{B}_b(\mathsf{X})$
we use the notation
![]() $\pi_k^{\overline{L}}(\varphi)=\int_{\mathsf{X}}\varphi(x)\pi_k^{\overline{L}}(dx)$
. By
$\pi_k^{\overline{L}}(\varphi)=\int_{\mathsf{X}}\varphi(x)\pi_k^{\overline{L}}(dx)$
. By
![]() $\mathbb{E}$
we denote the expectation with respect to the law used to generate the AMLPF. We drop the dependence upon the data in
$\mathbb{E}$
we denote the expectation with respect to the law used to generate the AMLPF. We drop the dependence upon the data in
![]() $g(x_k,y_k)$
and simply write
$g(x_k,y_k)$
and simply write
![]() $g_k(x_k)$
in this section.
$g_k(x_k)$
in this section.
Our assumptions are as follows:
-
(A1)
-
• For each
 $(i,j)\in\{1,\dots,d\}$
,
$(i,j)\in\{1,\dots,d\}$
,
 $\alpha_i\in\mathcal{B}_b(\mathsf{X})$
,
$\alpha_i\in\mathcal{B}_b(\mathsf{X})$
,
 $\beta_{ij}\in\mathcal{B}_b(\mathsf{X})$
.
$\beta_{ij}\in\mathcal{B}_b(\mathsf{X})$
. -
• We have
 $\alpha\in\mathcal{C}^2(\mathsf{X},\mathsf{X})$
,
$\alpha\in\mathcal{C}^2(\mathsf{X},\mathsf{X})$
,
 $\beta\in\mathcal{C}^2(\mathsf{X},\mathsf{X}_2)$
.
$\beta\in\mathcal{C}^2(\mathsf{X},\mathsf{X}_2)$
. -
• We have that
 $\beta(x)\beta(x)^{\top}$
is uniformly positive definite.
$\beta(x)\beta(x)^{\top}$
is uniformly positive definite. -
• There exists a
 $C<+\infty$
such that for any
$C<+\infty$
such that for any
 $(x,i,j,k,m)\in\mathsf{X}\times\{1,\dots,d\}^{4}$
,
$(x,i,j,k,m)\in\mathsf{X}\times\{1,\dots,d\}^{4}$
,  \begin{align*}\max\left\{\left|\frac{\partial \alpha_i}{\partial x_m}(x)\right|,\left|\frac{\partial \beta_{ij}}{\partial x_m}(x)\right|,\left|\frac{\partial h_{ijk}}{\partial x_m}(x)\right|,\left|\frac{\partial^2 \alpha_i}{\partial x_{k}\partial x_m}(x)\right|,\left|\frac{\partial^2 \beta_{ij}}{\partial x_{k}\partial x_m}(x)\right|\right\} \leq C.\end{align*}
\begin{align*}\max\left\{\left|\frac{\partial \alpha_i}{\partial x_m}(x)\right|,\left|\frac{\partial \beta_{ij}}{\partial x_m}(x)\right|,\left|\frac{\partial h_{ijk}}{\partial x_m}(x)\right|,\left|\frac{\partial^2 \alpha_i}{\partial x_{k}\partial x_m}(x)\right|,\left|\frac{\partial^2 \beta_{ij}}{\partial x_{k}\partial x_m}(x)\right|\right\} \leq C.\end{align*}
-
-
(A2)
-
• For each
 $k\in\mathbb{N}$
,
$k\in\mathbb{N}$
,
 $g_k\in\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}^2(\mathsf{X},\mathbb{R})$
.
$g_k\in\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}^2(\mathsf{X},\mathbb{R})$
. -
• For each
 $k\in\mathbb{N}$
there exists a
$k\in\mathbb{N}$
there exists a
 $0<C<+\infty$
such that for any
$0<C<+\infty$
such that for any
 $x\in\mathsf{X}$
$x\in\mathsf{X}$
 $g_k(x)\geq C$
.
$g_k(x)\geq C$
. -
• For each
 $k\in\mathbb{N}$
there exists a
$k\in\mathbb{N}$
there exists a
 $0<C<+\infty$
such that for any
$0<C<+\infty$
such that for any
 $(x,j,m)\in\mathsf{X}\times\{1,\dots,d\}^2$
,
$(x,j,m)\in\mathsf{X}\times\{1,\dots,d\}^2$
,  \begin{align*}\max\left\{\bigg|\frac{\partial g_{k}}{\partial x_j}(x)\bigg|,\bigg|\frac{\partial^2 g_{k}}{\partial x_j\partial x_m}(x)\bigg|\right\} \leq C.\end{align*}
\begin{align*}\max\left\{\bigg|\frac{\partial g_{k}}{\partial x_j}(x)\bigg|,\bigg|\frac{\partial^2 g_{k}}{\partial x_j\partial x_m}(x)\bigg|\right\} \leq C.\end{align*}
-
Theorem 1. Assume (A1)–(A2). Then, for any
![]() $(k,\varphi)\in\mathbb{N}\times\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
, there exists a
$(k,\varphi)\in\mathbb{N}\times\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
, there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $\big(\underline{L},\overline{L},l,N_{\underline{L}},\dots,N_{\overline{L}}\big)\in\mathbb{N}_0^2\times\{\underline{L},\dots,\overline{L}\}\times\mathbb{N}^{\overline{L}-\underline{L}+1}$
with
$\big(\underline{L},\overline{L},l,N_{\underline{L}},\dots,N_{\overline{L}}\big)\in\mathbb{N}_0^2\times\{\underline{L},\dots,\overline{L}\}\times\mathbb{N}^{\overline{L}-\underline{L}+1}$
with
![]() $\underline{L}<\overline{L}$
,
$\underline{L}<\overline{L}$
,
 \begin{align*}\mathbb{E}\left[\left(\pi_k^{\overline{L},ML}(\varphi)-\pi_k^{\overline{L}}(\varphi)\right)^2\right] \leq C\Bigg(\frac{1}{N_{\underline{L}}} +\sum_{l=\underline{L}+1}^{\overline{L}}\frac{\Delta_l^{\tfrac{1}{2}}}{N_l}+ \sum_{(l,q)\in\mathsf{D}_{\underline{L},\overline{L}}}\frac{\Delta_l^{\tfrac{1}{2}}}{N_lN_q}\Bigg), \end{align*}
\begin{align*}\mathbb{E}\left[\left(\pi_k^{\overline{L},ML}(\varphi)-\pi_k^{\overline{L}}(\varphi)\right)^2\right] \leq C\Bigg(\frac{1}{N_{\underline{L}}} +\sum_{l=\underline{L}+1}^{\overline{L}}\frac{\Delta_l^{\tfrac{1}{2}}}{N_l}+ \sum_{(l,q)\in\mathsf{D}_{\underline{L},\overline{L}}}\frac{\Delta_l^{\tfrac{1}{2}}}{N_lN_q}\Bigg), \end{align*}
where
![]() $\mathsf{D}_{\underline{L},\overline{L}}=\{(l,q)\in\{\underline{L},\dots,\overline{L}\}\,:\,l\neq q\}$
.
$\mathsf{D}_{\underline{L},\overline{L}}=\{(l,q)\in\{\underline{L},\dots,\overline{L}\}\,:\,l\neq q\}$
.
Proof. This follows by using the
![]() $C_2$
-inequality to separate the terms
$C_2$
-inequality to separate the terms
![]() $\pi_k^{N_{\underline{L}},\underline{L}}(\varphi) -\pi_k^{\underline{L}}(\varphi)$
and
$\pi_k^{N_{\underline{L}},\underline{L}}(\varphi) -\pi_k^{\underline{L}}(\varphi)$
and
![]() $\sum_{l=\underline{L}+1}^{\overline{L}}\big[\pi_{k}^l-\pi_{k}^{l-1}\big]^{N_l}(\varphi)-\sum_{l=\underline{L}+1}^{\overline{L}}\big[\pi_{k}^l-\pi_{k}^{l-1}\big](\varphi)$
. Then one uses standard results for particle filters (see e.g. [Reference Beskos2, Lemma A.3]) for the
$\sum_{l=\underline{L}+1}^{\overline{L}}\big[\pi_{k}^l-\pi_{k}^{l-1}\big]^{N_l}(\varphi)-\sum_{l=\underline{L}+1}^{\overline{L}}\big[\pi_{k}^l-\pi_{k}^{l-1}\big](\varphi)$
. Then one uses standard results for particle filters (see e.g. [Reference Beskos2, Lemma A.3]) for the
![]() $\pi_k^{N_{\underline{L}},\underline{L}}(\varphi) -\pi_k^{\underline{L}}(\varphi)$
, and one multiplies out the brackets and uses Theorems 2 and 3 for the other term.
$\pi_k^{N_{\underline{L}},\underline{L}}(\varphi) -\pi_k^{\underline{L}}(\varphi)$
, and one multiplies out the brackets and uses Theorems 2 and 3 for the other term.
The implication of this result is as follows. We know that the bias
![]() $\big|\pi_k^{\underline{L}}(\varphi)-\pi_k(\varphi)\big|$
is
$\big|\pi_k^{\underline{L}}(\varphi)-\pi_k(\varphi)\big|$
is
![]() $\mathcal{O}(\Delta_{\overline{L}})$
. This can be proved in a similar manner to [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], using the fact that the truncated Milstein scheme is a first-order (weak) method. Therefore, for
$\mathcal{O}(\Delta_{\overline{L}})$
. This can be proved in a similar manner to [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], using the fact that the truncated Milstein scheme is a first-order (weak) method. Therefore, for
![]() $\epsilon>0$
given, one can choose
$\epsilon>0$
given, one can choose
![]() $\overline{L}$
such that
$\overline{L}$
such that
![]() $\Delta_{\overline{L}}=\mathcal{O}(\epsilon)$
(so that the squared bias is
$\Delta_{\overline{L}}=\mathcal{O}(\epsilon)$
(so that the squared bias is
![]() $\mathcal{O}(\epsilon^2)$
). Then, to choose
$\mathcal{O}(\epsilon^2)$
). Then, to choose
![]() $N_{\underline{L}},\dots,N_{\overline{L}}$
, one can set
$N_{\underline{L}},\dots,N_{\overline{L}}$
, one can set
![]() $N_{\underline{L}}=\mathcal{O}(\epsilon^{-2})$
and, just as in e.g. [Reference Giles9],
$N_{\underline{L}}=\mathcal{O}(\epsilon^{-2})$
and, just as in e.g. [Reference Giles9],
![]() $N_l=\mathcal{O}\big(\epsilon^{-2}\Delta_l^{3/4}\Delta_{\overline{L}}^{-1/4}\big)$
,
$N_l=\mathcal{O}\big(\epsilon^{-2}\Delta_l^{3/4}\Delta_{\overline{L}}^{-1/4}\big)$
,
![]() $l\in\{\underline{L}+1,\dots,\overline{L}\}$
. If one does this, one can verify that the upper bound in Theorem 1 is
$l\in\{\underline{L}+1,\dots,\overline{L}\}$
. If one does this, one can verify that the upper bound in Theorem 1 is
![]() $\mathcal{O}(\epsilon^2)$
, so the MSE is also
$\mathcal{O}(\epsilon^2)$
, so the MSE is also
![]() $\mathcal{O}(\epsilon^2)$
. The cost to run the algorithm per time step is
$\mathcal{O}(\epsilon^2)$
. The cost to run the algorithm per time step is
![]() $\mathcal{O}\big(\!\sum_{l=\underline{L}}^{\overline{L}}N_l\Delta_{l}^{-1}\big) = \mathcal{O}\big(\epsilon^{-2.5}\big)$
. However, as we see in our simulations, the cost should be lower, at
$\mathcal{O}\big(\!\sum_{l=\underline{L}}^{\overline{L}}N_l\Delta_{l}^{-1}\big) = \mathcal{O}\big(\epsilon^{-2.5}\big)$
. However, as we see in our simulations, the cost should be lower, at
![]() $\mathcal{O}\big(\epsilon^{-2}\log(\epsilon)^2\big)$
; this indicates that our proof is not optimal. In the case that (1.1) has a non-constant diffusion coefficient with
$\mathcal{O}\big(\epsilon^{-2}\log(\epsilon)^2\big)$
; this indicates that our proof is not optimal. In the case that (1.1) has a non-constant diffusion coefficient with
![]() $d> 2$
, the approach in [Reference Jasra, Kamatani, Law and Zhou14], based upon using Euler discretizations, would obtain an MSE of
$d> 2$
, the approach in [Reference Jasra, Kamatani, Law and Zhou14], based upon using Euler discretizations, would obtain an MSE of
![]() $\mathcal{O}(\epsilon^2)$
at a cost of
$\mathcal{O}(\epsilon^2)$
at a cost of
![]() $\mathcal{O}\big(\epsilon^{-2.5}\big)$
.
$\mathcal{O}\big(\epsilon^{-2.5}\big)$
.
5. Numerical results
5.1. Models
We consider three different models for our numerical experiments.
5.1.1. Model 1: geometric Brownian motion (GBM) process
The first model we use is
We set
![]() $Y_n|X_{n}=x \sim \mathcal{N}\big(\log(x),\tau^2\big)$
, where
$Y_n|X_{n}=x \sim \mathcal{N}\big(\log(x),\tau^2\big)$
, where
![]() $\tau^2=0.02$
and
$\tau^2=0.02$
and
![]() $\mathcal{N}(x,\tau^2)$
is the Gaussian distribution with mean x and variance
$\mathcal{N}(x,\tau^2)$
is the Gaussian distribution with mean x and variance
![]() $\tau^2$
. We choose
$\tau^2$
. We choose
![]() $x_0 = 1$
,
$x_0 = 1$
,
![]() $\mu = 0.02$
, and
$\mu = 0.02$
, and
![]() $\sigma = 0.2$
.
$\sigma = 0.2$
.
5.1.2. Model 2: Clark–Cameron SDE
The second model we consider is the Clark–Cameron stochastic differential equation (SDE) model (e.g. [Reference Giles and Szpruch11]) with initial conditions
![]() $x_0=(0,0)^{\top}$
:
$x_0=(0,0)^{\top}$
:
where
![]() $X_{j,t}$
denotes the jth dimension of
$X_{j,t}$
denotes the jth dimension of
![]() $X_t$
,
$X_t$
,
![]() $j\in\{1,\dots,d\}$
. In addition,
$j\in\{1,\dots,d\}$
. In addition,
![]() $Y_n|X_n=x\sim \mathcal{N}\big( \tfrac{X_{1} + X_{2}}{2},\tau^2\big)$
, where
$Y_n|X_n=x\sim \mathcal{N}\big( \tfrac{X_{1} + X_{2}}{2},\tau^2\big)$
, where
![]() $\tau^2=0.1$
.
$\tau^2=0.1$
.
5.1.3. Model 3: multidimensional SDEs with a nonlinear diffusion term (NLMs)
For our last model we use the following multidimensional SDEs, with
![]() $x_0=(0,0)^{\top}$
:
$x_0=(0,0)^{\top}$
:
 \begin{eqnarray*}dX_{1,t} & \,=\, & \theta_{1} (\mu_{1} - X_{1,t}) dt + \frac{\sigma_1}{\sqrt{1 + X_{1,t}^{2} }} dW_{1,t}, \\dX_{2,t} & \,=\, & \theta_{2} (\mu_{2} - X_{1,t}) dt + \frac{\sigma_2}{\sqrt{1 + X_{1,t}^{2}}} dW_{2,t}.\end{eqnarray*}
\begin{eqnarray*}dX_{1,t} & \,=\, & \theta_{1} (\mu_{1} - X_{1,t}) dt + \frac{\sigma_1}{\sqrt{1 + X_{1,t}^{2} }} dW_{1,t}, \\dX_{2,t} & \,=\, & \theta_{2} (\mu_{2} - X_{1,t}) dt + \frac{\sigma_2}{\sqrt{1 + X_{1,t}^{2}}} dW_{2,t}.\end{eqnarray*}
We set
![]() $Y_n|X_n=x\sim \mathcal{L}\left(\tfrac{X_{1} + X_{2}}{2},s\right)$
, where
$Y_n|X_n=x\sim \mathcal{L}\left(\tfrac{X_{1} + X_{2}}{2},s\right)$
, where
![]() $\mathcal{L}(m,s)$
is the Laplace distribution with location m and scale s. The values of the parameters that we choose are
$\mathcal{L}(m,s)$
is the Laplace distribution with location m and scale s. The values of the parameters that we choose are
![]() $(\theta_{1}, \theta_{2}) = (1,1)$
,
$(\theta_{1}, \theta_{2}) = (1,1)$
,
![]() $(\mu_{1}, \mu_{2}) = (0,0)$
,
$(\mu_{1}, \mu_{2}) = (0,0)$
,
![]() $(\sigma_{1}, \sigma_{2}) = (1,1)$
, and
$(\sigma_{1}, \sigma_{2}) = (1,1)$
, and
![]() $s= \sqrt{0.1}$
.
$s= \sqrt{0.1}$
.
5.2. Simulation settings
We will consider a comparison of the particle filter, MLPF (as in [Reference Jasra, Kamatani, Law and Zhou14]), and AMLPF. For our numerical experiments, we consider multilevel estimators at levels
![]() $l \in \{3,4,5,6,7\}$
. Resampling is performed adaptively. For the particle filters, resampling is done when the effective sample size (ESS) is less than
$l \in \{3,4,5,6,7\}$
. Resampling is performed adaptively. For the particle filters, resampling is done when the effective sample size (ESS) is less than
![]() $1/2$
of the particle numbers. Suppose that we have a collection of weights which sum to one,
$1/2$
of the particle numbers. Suppose that we have a collection of weights which sum to one,
![]() $(W^1,\dots,W^N)$
, for instance
$(W^1,\dots,W^N)$
, for instance
![]() $\big(W_k^{1,l},\dots,W_k^{N_l,l}\big)$
in Algorithm 5. Then the ESS can be calculated using the formula
$\big(W_k^{1,l},\dots,W_k^{N_l,l}\big)$
in Algorithm 5. Then the ESS can be calculated using the formula
This is a number between 1 and N and is a measure of the variability of the weights. Typically one would like this measure to be close to N. For the coupled filters, we use the ESS of the coarse filter as the measure of discrepancy, and resampling occurs at the same threshold as the particle filter. Each simulation is repeated 100 times.
5.3. Simulation results
We now present our numerical simulations to show the benefits of the AMLPF for the three models under consideration. In Figures 1 and 2 we present the rate of the cost and the MSE for the estimator for the filter and normalizing constant. The cost is computed using the CPU time, although we found similar results using the formula of Section 4. The figures show that as we increase the level from
![]() $l=3$
to
$l=3$
to
![]() $l=7$
, the difference between the costs of the two methods increases. In particular, the figures show the advantage and accuracy of using AMLPF. Table 1 presents the estimated rates of the MSE with respect to cost for the normalizing constant and filter. The results agree with the theory [Reference Jasra, Kamatani, Law and Zhou14] and the results of this article, which predicts a rate of
$l=7$
, the difference between the costs of the two methods increases. In particular, the figures show the advantage and accuracy of using AMLPF. Table 1 presents the estimated rates of the MSE with respect to cost for the normalizing constant and filter. The results agree with the theory [Reference Jasra, Kamatani, Law and Zhou14] and the results of this article, which predicts a rate of
![]() $-1.5$
for the particle filter,
$-1.5$
for the particle filter,
![]() $-1.25$
for the MLPF, and
$-1.25$
for the MLPF, and
![]() $-1$
for the AMLPF.
$-1$
for the AMLPF.

Figure 1. Cost rates as a function of the MSE. The results are for the filter.

Figure 2. Cost rates as a function of the MSE in our algorithms, with results for the normalizing constants.
Table 1. Estimated rates of MSE with respect to cost. ‘NC’ stands for normalizing constant.

Appendix A. Introduction and some notation
The purpose of this appendix is to provide the necessary technical results to prove Theorem 1. For a full understanding of the arguments, we advise the reader to read the proofs in order. It is possible to skip Section B and simply refer to the proofs, but the reader may miss some notation or nuances.
The structure of this appendix is as follows. We first consider some properties of the antithetic truncated Milstein scheme of [Reference Giles and Szpruch11]. We present several new results which are needed directly for the subsequent proofs. In Section C we consider the coupled particle filter as in Algorithm 5. This section is split into three subsections. The first of these, Section C.1, considers the application of the results in Section B to a coupled particle filter. These results feed into the final two subsections, which consider the convergence of
![]() $\big[\pi_{k}^l-\pi_{k}^{l-1}\big]^{N_l}(\varphi)$
in
$\big[\pi_{k}^l-\pi_{k}^{l-1}\big]^{N_l}(\varphi)$
in
![]() $\mathbb{L}_p$
(Section C.2) and the associated bias (Section C.3). This is the culmination of the work in this appendix and is summarized in Theorems 2 and 3. To prove our results we use two major assumptions, (A1) and (A2), which can be found in Section 4 of the main text.
$\mathbb{L}_p$
(Section C.2) and the associated bias (Section C.3). This is the culmination of the work in this appendix and is summarized in Theorems 2 and 3. To prove our results we use two major assumptions, (A1) and (A2), which can be found in Section 4 of the main text.
A.1. Some notation
Let
![]() $(\mathsf{V},\mathcal{V})$
be a measurable space. For
$(\mathsf{V},\mathcal{V})$
be a measurable space. For
![]() $\varphi\,:\,\mathsf{V}\rightarrow\mathbb{R}$
we write
$\varphi\,:\,\mathsf{V}\rightarrow\mathbb{R}$
we write
![]() $\mathcal{B}_b(\mathsf{V})$
for the collection of bounded measurable functions. Let
$\mathcal{B}_b(\mathsf{V})$
for the collection of bounded measurable functions. Let
![]() $\varphi\,:\,\mathbb{R}^d\rightarrow\mathbb{R}$
, and let
$\varphi\,:\,\mathbb{R}^d\rightarrow\mathbb{R}$
, and let
![]() $\textrm{Lip}(\mathbb{R}^{d})$
denote the collection of real-valued functions that are Lipschitz with respect to
$\textrm{Lip}(\mathbb{R}^{d})$
denote the collection of real-valued functions that are Lipschitz with respect to
![]() $\|\cdot\|$
(where
$\|\cdot\|$
(where
![]() $\|\cdot\|$
denotes the
$\|\cdot\|$
denotes the
![]() $\mathbb{L}_2$
-norm of a vector
$\mathbb{L}_2$
-norm of a vector
![]() $x\in\mathbb{R}^d$
). That is,
$x\in\mathbb{R}^d$
). That is,
![]() $\varphi\in\textrm{Lip}(\mathbb{R}^{d})$
if there exists a
$\varphi\in\textrm{Lip}(\mathbb{R}^{d})$
if there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(x,y)\in\mathbb{R}^{2d}$
,
$(x,y)\in\mathbb{R}^{2d}$
,
For
![]() $\varphi\in\mathcal{B}_b(\mathsf{V})$
, we write the supremum norm as
$\varphi\in\mathcal{B}_b(\mathsf{V})$
, we write the supremum norm as
![]() $\|\varphi\|_{\infty}=\sup_{x\in\mathsf{V}}|\varphi(x)|$
. For a measure
$\|\varphi\|_{\infty}=\sup_{x\in\mathsf{V}}|\varphi(x)|$
. For a measure
![]() $\mu$
on
$\mu$
on
![]() $(\mathsf{V},\mathcal{V})$
and a function
$(\mathsf{V},\mathcal{V})$
and a function
![]() $\varphi\in\mathcal{B}_b(\mathsf{V})$
, the notation
$\varphi\in\mathcal{B}_b(\mathsf{V})$
, the notation
![]() $\mu(\varphi)=\int_{\mathsf{V}}\varphi(x)\mu(dx)$
is used. For
$\mu(\varphi)=\int_{\mathsf{V}}\varphi(x)\mu(dx)$
is used. For
![]() $A\in\mathcal{V}$
, the indicator function is written as
$A\in\mathcal{V}$
, the indicator function is written as
![]() $\mathbb{I}_A(x)$
. If
$\mathbb{I}_A(x)$
. If
![]() $K\,:\,\mathsf{V}\times\mathcal{V}\rightarrow[0,\infty)$
is a non-negative operator and
$K\,:\,\mathsf{V}\times\mathcal{V}\rightarrow[0,\infty)$
is a non-negative operator and
![]() $\mu$
is a measure, we use the notation
$\mu$
is a measure, we use the notation
![]() $\mu K(dy) = \int_{\mathsf{V}}\mu(dx) K(x,dy),$
and for
$\mu K(dy) = \int_{\mathsf{V}}\mu(dx) K(x,dy),$
and for
![]() $\varphi\in\mathcal{B}_b(\mathsf{V})$
,
$\varphi\in\mathcal{B}_b(\mathsf{V})$
,
![]() $K(\varphi)(x) = \int_{\mathsf{V}} \varphi(y) K(x,dy).$
Throughout, we use C to denote a generic finite constant whose value may change at each appearance and whose dependencies (on model and simulation parameters) are clear from the context.
$K(\varphi)(x) = \int_{\mathsf{V}} \varphi(y) K(x,dy).$
Throughout, we use C to denote a generic finite constant whose value may change at each appearance and whose dependencies (on model and simulation parameters) are clear from the context.
Appendix B. Proofs for antithetic truncated Milstein scheme
The proofs of this section focus on the antithetic truncated Milstein discretization over a unit of time (i.e. as in Algorithm 2). The case we consider is almost identical to that in [Reference Giles and Szpruch11], except that we impose that our initial points
![]() $\big(x_0^l,x_0^{l-1},x_0^{l,a}\big)$
need not be equal. This constraint is important in our subsequent proofs for the coupled (and multilevel) particle filter. Our objective is to prove a result similar to [Reference Giles and Szpruch11, Theorem 4.10], and to that end we make the assumption (A1), which is stronger than [Reference Giles and Szpruch11, Assumption 4.1]. The stronger assumption is related to the boundedness of the drift and diffusion coefficients of (1.1). The reason we require this is that it greatly simplifies our (subsequent) proofs if the constants in the results below do not depend on the initial points
$\big(x_0^l,x_0^{l-1},x_0^{l,a}\big)$
need not be equal. This constraint is important in our subsequent proofs for the coupled (and multilevel) particle filter. Our objective is to prove a result similar to [Reference Giles and Szpruch11, Theorem 4.10], and to that end we make the assumption (A1), which is stronger than [Reference Giles and Szpruch11, Assumption 4.1]. The stronger assumption is related to the boundedness of the drift and diffusion coefficients of (1.1). The reason we require this is that it greatly simplifies our (subsequent) proofs if the constants in the results below do not depend on the initial points
![]() $\big(x_0^l,x_0^{l-1},x_0^{l,a}\big)$
; this would be the case otherwise. In this section,
$\big(x_0^l,x_0^{l-1},x_0^{l,a}\big)$
; this would be the case otherwise. In this section,
![]() $\mathbb{E}$
denotes the expectation with respect to the law associated to Algorithm 2.
$\mathbb{E}$
denotes the expectation with respect to the law associated to Algorithm 2.
The final result in this section, Proposition B.1, is our adaptation of [Reference Giles and Szpruch11, Theorem 4.10] and is proved using simple modifications of Lemmata 4.6, 4.7, and 4.9 and Corollary 4.8 in [Reference Giles and Szpruch11]. The proofs of Lemma 4.7 and Corollary 4.8 in [Reference Giles and Szpruch11] need not be modified, so we proceed to prove analogues of Lemmata 4.6 and 4.9.
Lemma B.1. Assume (A1). Then for any
![]() $p\in[1,\infty)$
there exists a
$p\in[1,\infty)$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $l\in\mathbb{N}$
,
$l\in\mathbb{N}$
,
 \begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{l,a}\big\|^p\right] \leq C\left(\Delta_l^{\tfrac{p}{2}}+\big\|x_0^{l}-x_0^{l-1}\big\|^p+\big\|x_0^{l,a}-x_0^{l-1}\big\|^p\right).\end{align*}
\begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{l,a}\big\|^p\right] \leq C\left(\Delta_l^{\tfrac{p}{2}}+\big\|x_0^{l}-x_0^{l-1}\big\|^p+\big\|x_0^{l,a}-x_0^{l-1}\big\|^p\right).\end{align*}
Proof. Using the
![]() $C_p$
-inequality, we have that
$C_p$
-inequality, we have that
 \begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{l,a}\big\|^p\right] \end{align*}
\begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{l,a}\big\|^p\right] \end{align*}
 \begin{align*} \leq C\left(\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{l-1}\big\|^p\right]+\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l,a}-X_{k\Delta_l}^{l-1}\big\|^p\right]\right).\end{align*}
\begin{align*} \leq C\left(\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{l-1}\big\|^p\right]+\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l,a}-X_{k\Delta_l}^{l-1}\big\|^p\right]\right).\end{align*}
Denoting by
![]() $X_t^x$
the solution of (1.1) with initial point x at time t, we have
$X_t^x$
the solution of (1.1) with initial point x at time t, we have
 \begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{l,a}\big\|^p\right] \end{align*}
\begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{l,a}\big\|^p\right] \end{align*}
 \begin{eqnarray*}& & \leq C\Bigg(\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{x_0^l}\Big\|^p\right] + \mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{x_0^l}-X_{k\Delta_l}^{x_0^{l-1}}\Big\|^p\right] \\ & & + \mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{l-1}-X_{k\Delta_l}^{x_0^{l-1}}\Big\|^p\right] +\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{l,a}-X_{k\Delta_l}^{x_0^{l,a}}\Big\|^p\right] \\ & & + \mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{x_0^{l,a}}-X_{k\Delta_l}^{x_0^{l-1}}\Big\|^p\right] +\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{l-1}-X_{k\Delta_l}^{x_0^{l-1}}\Big\|^p\right]\Bigg).\end{eqnarray*}
\begin{eqnarray*}& & \leq C\Bigg(\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{x_0^l}\Big\|^p\right] + \mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{x_0^l}-X_{k\Delta_l}^{x_0^{l-1}}\Big\|^p\right] \\ & & + \mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{l-1}-X_{k\Delta_l}^{x_0^{l-1}}\Big\|^p\right] +\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{l,a}-X_{k\Delta_l}^{x_0^{l,a}}\Big\|^p\right] \\ & & + \mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{x_0^{l,a}}-X_{k\Delta_l}^{x_0^{l-1}}\Big\|^p\right] +\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\Big\|X_{k\Delta_l}^{l-1}-X_{k\Delta_l}^{x_0^{l-1}}\Big\|^p\right]\Bigg).\end{eqnarray*}
The proof is then easily concluded via the strong convergence result [Reference Giles and Szpruch11, Lemma 4.2] and standard results for diffusion processes (e.g. via Gronwall and [Reference Rogers and Williams20, Corollary V.11.7]).
Remark B.1. Note that the proof also establishes the following: for any
![]() $p\in[1,\infty)$
there exists a
$p\in[1,\infty)$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $l\in\mathbb{N}$
,
$l\in\mathbb{N}$
,
 \begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{l-1}\big\|^p\right] \leq C\left(\Delta_l^{\tfrac{p}{2}}+\big\|x_0^{l}-x_0^{l-1}\big\|^p\right)\end{align*}
\begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l}-X_{k\Delta_l}^{l-1}\big\|^p\right] \leq C\left(\Delta_l^{\tfrac{p}{2}}+\big\|x_0^{l}-x_0^{l-1}\big\|^p\right)\end{align*}
and
 \begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l,a}-X_{k\Delta_l}^{l-1}\big\|^p\right] \leq C\left(\Delta_l^{\tfrac{p}{2}}+\big\|x_0^{l,a}-x_0^{l-1}\big\|^p\right).\end{align*}
\begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|X_{k\Delta_l}^{l,a}-X_{k\Delta_l}^{l-1}\big\|^p\right] \leq C\left(\Delta_l^{\tfrac{p}{2}}+\big\|x_0^{l,a}-x_0^{l-1}\big\|^p\right).\end{align*}
To state our next result, which mirrors [Reference Giles and Szpruch11, Lemma 4.9], we need to introduce a significant amount of notation directly from [Reference Giles and Szpruch11]. Below, we set
![]() $\overline{X}_{k\Delta_l}^l=\tfrac{1}{2}\big(X_{k\Delta_l}^l+X_{k\Delta_l}^{l,a}\big)$
,
$\overline{X}_{k\Delta_l}^l=\tfrac{1}{2}\big(X_{k\Delta_l}^l+X_{k\Delta_l}^{l,a}\big)$
,
![]() $k\in\big\{0,\dots,\Delta_l^{-1}\big\}$
. For
$k\in\big\{0,\dots,\Delta_l^{-1}\big\}$
. For
![]() $(i,k)\in\{1,\dots,d\}\times\big\{2,4,\dots,\Delta_l^{-1}\big\}$
we define
$(i,k)\in\{1,\dots,d\}\times\big\{2,4,\dots,\Delta_l^{-1}\big\}$
we define
 \begin{eqnarray*}R_{i,k}^{(1)} & \,=\, & \left\{\frac{1}{2}\left(\alpha_i\big(X_{k\Delta_l}^l\big)+\alpha_i\big(X_{k\Delta_l}^{l,a}\big)\right)-\alpha_i\big(\overline{X}_{k\Delta_l}^l\big)\right\}\Delta_{l-1}, \\M_{i,k}^{(1)} & \,=\, & \sum_{j=1}^d\left\{\frac{1}{2}\left(\beta_{ij}\big(X_{k\Delta_l}^l\big)+\beta_{ij}\big(X_{k\Delta_l}^{l,a}\big)\right)-\beta_{ij}\big(\overline{X}_{k\Delta_l}^l\big)\right\}\big[W_{j,(k+2)\Delta_l}-W_{j,k\Delta_l}\big], \\M_{i,k}^{(2)} & \,=\, & \sum_{(j,m)\in\{1,\dots,d\}^2}\left\{\frac{1}{2}\left(h_{ijm}\big(X_{k\Delta_l}^l\big)+h_{ijm}\big(X_{k\Delta_l}^{l,a}\big)\right)-h_{ijm}\big(\overline{X}_{k\Delta_l}^l\big)\right\}\Big(\big[W_{j,(k+2)\Delta_l}-W_{j,k\Delta_l}\big] \\ & & \times [W_{m,(k+2)\Delta_l}-W_{m,k\Delta_l}]-\Delta_{l-1}\Big),\\ M_{i,k}^{(3)} & \,=\, & \sum_{(j,m)\in\{1,\dots,d\}^2}\frac{1}{2}\left(h_{ijm}\big(X_{k\Delta_l}^l\big)-h_{ijm}\big(X_{k\Delta_l}^{l,a}\big)\right)\Big(\big[W_{j,(k+1)\Delta_l}-W_{j,k\Delta_l}\big]\big[W_{m,(k+2)\Delta_l}\\ & & -W_{m,(k+1)\Delta_l}\big] - \big[W_{m,(k+1)\Delta_l}-W_{m,k\Delta_l}\big]\big[W_{j,(k+2)\Delta_l}-W_{j,(k+1)\Delta_l}\big]\Big),\end{eqnarray*}
\begin{eqnarray*}R_{i,k}^{(1)} & \,=\, & \left\{\frac{1}{2}\left(\alpha_i\big(X_{k\Delta_l}^l\big)+\alpha_i\big(X_{k\Delta_l}^{l,a}\big)\right)-\alpha_i\big(\overline{X}_{k\Delta_l}^l\big)\right\}\Delta_{l-1}, \\M_{i,k}^{(1)} & \,=\, & \sum_{j=1}^d\left\{\frac{1}{2}\left(\beta_{ij}\big(X_{k\Delta_l}^l\big)+\beta_{ij}\big(X_{k\Delta_l}^{l,a}\big)\right)-\beta_{ij}\big(\overline{X}_{k\Delta_l}^l\big)\right\}\big[W_{j,(k+2)\Delta_l}-W_{j,k\Delta_l}\big], \\M_{i,k}^{(2)} & \,=\, & \sum_{(j,m)\in\{1,\dots,d\}^2}\left\{\frac{1}{2}\left(h_{ijm}\big(X_{k\Delta_l}^l\big)+h_{ijm}\big(X_{k\Delta_l}^{l,a}\big)\right)-h_{ijm}\big(\overline{X}_{k\Delta_l}^l\big)\right\}\Big(\big[W_{j,(k+2)\Delta_l}-W_{j,k\Delta_l}\big] \\ & & \times [W_{m,(k+2)\Delta_l}-W_{m,k\Delta_l}]-\Delta_{l-1}\Big),\\ M_{i,k}^{(3)} & \,=\, & \sum_{(j,m)\in\{1,\dots,d\}^2}\frac{1}{2}\left(h_{ijm}\big(X_{k\Delta_l}^l\big)-h_{ijm}\big(X_{k\Delta_l}^{l,a}\big)\right)\Big(\big[W_{j,(k+1)\Delta_l}-W_{j,k\Delta_l}\big]\big[W_{m,(k+2)\Delta_l}\\ & & -W_{m,(k+1)\Delta_l}\big] - \big[W_{m,(k+1)\Delta_l}-W_{m,k\Delta_l}\big]\big[W_{j,(k+2)\Delta_l}-W_{j,(k+1)\Delta_l}\big]\Big),\end{eqnarray*}
 \begin{eqnarray*}R_{i,k}^l & \,=\, & \sum_{j=1}^d\frac{\partial\alpha_i}{\partial x_j}\big(X_{k\Delta_l}^l\big)\Bigg(\alpha_{j}\big(X_{k\Delta_l}^l\big)\Delta_l+ \sum_{(m,n)\in\{1,\dots,d\}^2} h_{imn}\big(X_{k\Delta_l}^l\big)\Big(\big[W_{m,(k+1)\Delta_l}\\& & -W_{m,k\Delta_l}\big]\big[W_{n,(k+1)\Delta_l}- W_{n,k\Delta_l}\big]- \Delta_l\Big)\Bigg)\Delta_l + \frac{1}{2}\sum_{(j,m)\in\{1,\dots,d\}^2}\frac{\partial^2\alpha_i}{\partial x_j\partial x_m}\big(\xi_1^l\big)\big[X_{j,(k+1)\Delta_l}^l\\&& -X_{j,k\Delta_l}^l\big]\big[X_{m,(k+1)\Delta_l}^l-X_{m,k\Delta_l}^l\big]\Delta_l, \\ M_{i,k}^{(1,l)} & \,=\, & \sum_{(j,m)\in\{1,\dots,d\}^2}\frac{\partial\alpha_i}{\partial x_j}\big(X_{k\Delta_l}^l\big)\beta_{jm}\big(X_{k\Delta_l}^l\big)\big[W_{m,(k+1)\Delta_l}-W_{m,k\Delta_l}\big]\Delta_l,\end{eqnarray*}
\begin{eqnarray*}R_{i,k}^l & \,=\, & \sum_{j=1}^d\frac{\partial\alpha_i}{\partial x_j}\big(X_{k\Delta_l}^l\big)\Bigg(\alpha_{j}\big(X_{k\Delta_l}^l\big)\Delta_l+ \sum_{(m,n)\in\{1,\dots,d\}^2} h_{imn}\big(X_{k\Delta_l}^l\big)\Big(\big[W_{m,(k+1)\Delta_l}\\& & -W_{m,k\Delta_l}\big]\big[W_{n,(k+1)\Delta_l}- W_{n,k\Delta_l}\big]- \Delta_l\Big)\Bigg)\Delta_l + \frac{1}{2}\sum_{(j,m)\in\{1,\dots,d\}^2}\frac{\partial^2\alpha_i}{\partial x_j\partial x_m}\big(\xi_1^l\big)\big[X_{j,(k+1)\Delta_l}^l\\&& -X_{j,k\Delta_l}^l\big]\big[X_{m,(k+1)\Delta_l}^l-X_{m,k\Delta_l}^l\big]\Delta_l, \\ M_{i,k}^{(1,l)} & \,=\, & \sum_{(j,m)\in\{1,\dots,d\}^2}\frac{\partial\alpha_i}{\partial x_j}\big(X_{k\Delta_l}^l\big)\beta_{jm}\big(X_{k\Delta_l}^l\big)\big[W_{m,(k+1)\Delta_l}-W_{m,k\Delta_l}\big]\Delta_l,\end{eqnarray*}
 \begin{eqnarray*}M_{i,k}^{(2,l)} & \,=\, & \sum_{(j,m)\in\{1,\dots,d\}^2} \frac{\partial\beta_{ij}}{\partial x_m}\big(X_{k\Delta_l}^l\big)\Bigg(\alpha_m\big(X_{k\Delta_l}^l\big)\Delta_l +\sum_{(n,p)\in\{1,\dots,d\}^2}\!\!h_{mnp}\big(X_{k\Delta_l}^l\big)\big[\big[W_{n,(k+1)\Delta_l}-W_{n,k\Delta_l}\big] \\ & & \times\big[W_{p,(k+1)\Delta_l}-W_{p,k\Delta_l}\big]-\Delta_l\big]\Bigg)\big[W_{j,(k+2)\Delta_l}-W_{j,(k+1)\Delta_l}\big],\\ M_{i,k}^{(3,l)} & \,=\, & \sum_{(j,m)\in\{1,\dots,d\}^2}\left\{h_{ijm}\big(X_{(k+1)\Delta_l}^l\big)-h_{ijm}\big(X_{k\Delta_l}^l\big)\right\}\Big(\big[W_{j,(k+2)\Delta_l}-W_{j,(k+1)\Delta_l}\big]\big[W_{m,(k+2)\Delta_l}\\ & & - W_{m,(k+1)\Delta_l}\big]-\Delta_l\Big),\end{eqnarray*}
\begin{eqnarray*}M_{i,k}^{(2,l)} & \,=\, & \sum_{(j,m)\in\{1,\dots,d\}^2} \frac{\partial\beta_{ij}}{\partial x_m}\big(X_{k\Delta_l}^l\big)\Bigg(\alpha_m\big(X_{k\Delta_l}^l\big)\Delta_l +\sum_{(n,p)\in\{1,\dots,d\}^2}\!\!h_{mnp}\big(X_{k\Delta_l}^l\big)\big[\big[W_{n,(k+1)\Delta_l}-W_{n,k\Delta_l}\big] \\ & & \times\big[W_{p,(k+1)\Delta_l}-W_{p,k\Delta_l}\big]-\Delta_l\big]\Bigg)\big[W_{j,(k+2)\Delta_l}-W_{j,(k+1)\Delta_l}\big],\\ M_{i,k}^{(3,l)} & \,=\, & \sum_{(j,m)\in\{1,\dots,d\}^2}\left\{h_{ijm}\big(X_{(k+1)\Delta_l}^l\big)-h_{ijm}\big(X_{k\Delta_l}^l\big)\right\}\Big(\big[W_{j,(k+2)\Delta_l}-W_{j,(k+1)\Delta_l}\big]\big[W_{m,(k+2)\Delta_l}\\ & & - W_{m,(k+1)\Delta_l}\big]-\Delta_l\Big),\end{eqnarray*}
where, in
![]() $R_{i,k}^l$
,
$R_{i,k}^l$
,
![]() $\xi_1^l$
is some point which lies on the line between
$\xi_1^l$
is some point which lies on the line between
![]() $X_{k\Delta_l}^l$
and
$X_{k\Delta_l}^l$
and
![]() $X_{(k+1)\Delta_l}^l$
. In the case of
$X_{(k+1)\Delta_l}^l$
. In the case of
![]() $R_{i,k}^l$
and
$R_{i,k}^l$
and
![]() $M_{i,k}^{(j,l)}$
,
$M_{i,k}^{(j,l)}$
,
![]() $j\in\{1,2,3\}$
, one can substitute
$j\in\{1,2,3\}$
, one can substitute
![]() $X_{k\Delta_l}^l,\xi_1^{l},X_{(k+1)\Delta_l}^l$
for
$X_{k\Delta_l}^l,\xi_1^{l},X_{(k+1)\Delta_l}^l$
for
![]() $X_{k\Delta_l}^{l,a},\xi_1^{l,a},X_{(k+1)\Delta_l}^{l,a}$
$X_{k\Delta_l}^{l,a},\xi_1^{l,a},X_{(k+1)\Delta_l}^{l,a}$
![]() $\Big($
where
$\Big($
where
![]() $\xi_1^{l,a}$
is some point which lies on the line between
$\xi_1^{l,a}$
is some point which lies on the line between
![]() $X_{k\Delta_l}^{l,a}$
and
$X_{k\Delta_l}^{l,a}$
and
![]() $X_{(k+1)\Delta_l}^{l,a}\Big)$
; when we do so, we use the notation
$X_{(k+1)\Delta_l}^{l,a}\Big)$
; when we do so, we use the notation
![]() $R_{i,k}^{l,a}$
and
$R_{i,k}^{l,a}$
and
![]() $M_{i,k}^{(j,l,a)}$
,
$M_{i,k}^{(j,l,a)}$
,
![]() $j\in\{1,2,3\}$
. Finally we set
$j\in\{1,2,3\}$
. Finally we set
 \begin{eqnarray*}M_k & \,=\, & \sum_{j=1}^3 M_k^{(j)} + \frac{1}{2}\sum_{j=1}^3\Big\{M_k^{(j,l)} + M_k^{(j,l,a)}\Big\}, \\R_k & \,=\, & R_k^{(1)} + \frac{1}{2}\Big\{R_{i,k}^l+R_{i,k}^{l,a}\Big\}.\end{eqnarray*}
\begin{eqnarray*}M_k & \,=\, & \sum_{j=1}^3 M_k^{(j)} + \frac{1}{2}\sum_{j=1}^3\Big\{M_k^{(j,l)} + M_k^{(j,l,a)}\Big\}, \\R_k & \,=\, & R_k^{(1)} + \frac{1}{2}\Big\{R_{i,k}^l+R_{i,k}^{l,a}\Big\}.\end{eqnarray*}
We are now in a position to give our analogue of [Reference Giles and Szpruch11, Lemma 4.9].
Lemma B.2. Assume (A1). Then the following hold:
-
For any
 $p\in[1,\infty)$
there exists a
$p\in[1,\infty)$
there exists a
 $C<+\infty$
such that for any
$C<+\infty$
such that for any
 $l\in\mathbb{N}$
,
$l\in\mathbb{N}$
,  \begin{align*}\max_{k\in\{2,4,\dots,\Delta_l\}}\mathbb{E}[|R_k|^p] \leq C\Delta_l^p\left(\Delta_l^p + \big\|x_0^{l}-x_0^{l-1}\big\|^{2p}+\big\|x_0^{l,a}-x_0^{l-1}\big\|^{2p}\right).\end{align*}
\begin{align*}\max_{k\in\{2,4,\dots,\Delta_l\}}\mathbb{E}[|R_k|^p] \leq C\Delta_l^p\left(\Delta_l^p + \big\|x_0^{l}-x_0^{l-1}\big\|^{2p}+\big\|x_0^{l,a}-x_0^{l-1}\big\|^{2p}\right).\end{align*}
-
For any
 $p\in[1,\infty)$
there exists a
$p\in[1,\infty)$
there exists a
 $C<+\infty$
such that for any
$C<+\infty$
such that for any
 $l\in\mathbb{N}$
,
$l\in\mathbb{N}$
,  \begin{align*}\max_{k\in\{2,4,\dots,\Delta_l\}}\mathbb{E}[|M_k|^p] \end{align*}
\begin{align*}\max_{k\in\{2,4,\dots,\Delta_l\}}\mathbb{E}[|M_k|^p] \end{align*}
 \begin{align*}\!\!\!\!\!\!\!\leq C\!\left(\!\Delta_l^{\tfrac{3p}{2}}+\Delta_l^{\tfrac{p}{2}}\Big\{\big\|x_0^{l}-x_0^{l-1}\big\|^{2p}+\big\|x_0^{l,a}-x_0^{l-1}\big\|^{2p}\Big\} +\Delta_l^{p}\Big\{\big\|x_0^{l}-x_0^{l-1}\big\|^{p}+\big\|x_0^{l,a}-x_0^{l-1}\big\|^{p}\Big\}\!\right)\!.\end{align*}
\begin{align*}\!\!\!\!\!\!\!\leq C\!\left(\!\Delta_l^{\tfrac{3p}{2}}+\Delta_l^{\tfrac{p}{2}}\Big\{\big\|x_0^{l}-x_0^{l-1}\big\|^{2p}+\big\|x_0^{l,a}-x_0^{l-1}\big\|^{2p}\Big\} +\Delta_l^{p}\Big\{\big\|x_0^{l}-x_0^{l-1}\big\|^{p}+\big\|x_0^{l,a}-x_0^{l-1}\big\|^{p}\Big\}\!\right)\!.\end{align*}
Proof. The proof of this result essentially follows from [Reference Giles and Szpruch11] and controlling the terms (in
![]() $\mathbb{L}_p$
). The expressions
$\mathbb{L}_p$
). The expressions
![]() $\frac{1}{2}\sum_{j=1}^3\Big\{M_k^{(j,l)} + M_k^{(j,l,a)}\Big\}$
and
$\frac{1}{2}\sum_{j=1}^3\Big\{M_k^{(j,l)} + M_k^{(j,l,a)}\Big\}$
and
![]() $\frac{1}{2}\big\{R_{i,k}^l+R_{i,k}^{l,a}\big\}$
can be dealt with exactly as in [Reference Giles and Szpruch11, Lemma 4.7], so we need only consider the terms
$\frac{1}{2}\big\{R_{i,k}^l+R_{i,k}^{l,a}\big\}$
can be dealt with exactly as in [Reference Giles and Szpruch11, Lemma 4.7], so we need only consider the terms
![]() $\sum_{j=1}^3 M_k^{(j)}$
and
$\sum_{j=1}^3 M_k^{(j)}$
and
![]() $R_k^{(1)}$
. It will suffice to control in
$R_k^{(1)}$
. It will suffice to control in
![]() $\mathbb{L}_p$
any of the d coordinates of the aforementioned vectors, which is what we do below.
$\mathbb{L}_p$
any of the d coordinates of the aforementioned vectors, which is what we do below.
Beginning with
![]() $R_{i,k}^{(1)}$
, using the second-order Taylor expansion in [Reference Giles and Szpruch11], one has
$R_{i,k}^{(1)}$
, using the second-order Taylor expansion in [Reference Giles and Szpruch11], one has
 \begin{align*}R_{i,k}^{(1)} = \frac{1}{8}\sum_{(j,m)\in\{1,\dots,d\}^2}\left(\frac{\partial^2\alpha_i}{\partial x_j\partial x_m}\big(\xi_1^l\big)+\frac{\partial^2\alpha_i}{\partial x_j\partial x_m}\big(\xi_2^l\big)\right)\Big(X_{j,k\Delta_l}^l - X_{j,k\Delta_l}^{l,a}\Big)\Big(X_{m,k\Delta_l}^l - X_{m,k\Delta_l}^{l,a}\Big)\Delta_l,\end{align*}
\begin{align*}R_{i,k}^{(1)} = \frac{1}{8}\sum_{(j,m)\in\{1,\dots,d\}^2}\left(\frac{\partial^2\alpha_i}{\partial x_j\partial x_m}\big(\xi_1^l\big)+\frac{\partial^2\alpha_i}{\partial x_j\partial x_m}\big(\xi_2^l\big)\right)\Big(X_{j,k\Delta_l}^l - X_{j,k\Delta_l}^{l,a}\Big)\Big(X_{m,k\Delta_l}^l - X_{m,k\Delta_l}^{l,a}\Big)\Delta_l,\end{align*}
where
![]() $\xi_1^l$
is some point between
$\xi_1^l$
is some point between
![]() $\overline{X}^l_{k\Delta_l}$
and
$\overline{X}^l_{k\Delta_l}$
and
![]() $X^l_{k\Delta_l}$
and
$X^l_{k\Delta_l}$
and
![]() $\xi_2^l$
is some point between
$\xi_2^l$
is some point between
![]() $\overline{X}^l_{k\Delta_l}$
and
$\overline{X}^l_{k\Delta_l}$
and
![]() $X^{l,a}_{k\Delta_l}$
. Then it follows easily that
$X^{l,a}_{k\Delta_l}$
. Then it follows easily that
Application of Lemma B.1 yields that
which is the desired result.
For
![]() $M_{i,k}^{(1)}$
, again one has
$M_{i,k}^{(1)}$
, again one has
 \begin{eqnarray*}M_{i,k}^{(1)} & \,=\, & \frac{1}{16}\sum_{(j,m,n)\in\{1,\dots,d\}^3}\left\{\frac{\partial^2\beta_{ij}}{\partial x_m\partial x_n}\big(\xi_3^l\big) +\frac{\partial^2\beta_{ij}}{\partial x_m\partial x_n}\big(\xi_4^l\big)\right\}\Big(X_{m,k\Delta_l}^l - X_{m,k\Delta_l}^{l,a}\Big)\Big(X_{n,k\Delta_l}^l - X_{n,k\Delta_l}^{l,a}\Big) \\ & & \times\big[W_{j,(k+2)\Delta_l}-W_{j,k\Delta_l}\big],\end{eqnarray*}
\begin{eqnarray*}M_{i,k}^{(1)} & \,=\, & \frac{1}{16}\sum_{(j,m,n)\in\{1,\dots,d\}^3}\left\{\frac{\partial^2\beta_{ij}}{\partial x_m\partial x_n}\big(\xi_3^l\big) +\frac{\partial^2\beta_{ij}}{\partial x_m\partial x_n}\big(\xi_4^l\big)\right\}\Big(X_{m,k\Delta_l}^l - X_{m,k\Delta_l}^{l,a}\Big)\Big(X_{n,k\Delta_l}^l - X_{n,k\Delta_l}^{l,a}\Big) \\ & & \times\big[W_{j,(k+2)\Delta_l}-W_{j,k\Delta_l}\big],\end{eqnarray*}
where
![]() $\xi_3^l$
is some point between
$\xi_3^l$
is some point between
![]() $\overline{X}^l_{k\Delta_l}$
and
$\overline{X}^l_{k\Delta_l}$
and
![]() $X^l_{k\Delta_l}$
and
$X^l_{k\Delta_l}$
and
![]() $\xi_4^l$
is some point between
$\xi_4^l$
is some point between
![]() $\overline{X}^l_{k\Delta_l}$
and
$\overline{X}^l_{k\Delta_l}$
and
![]() $X^{l,a}_{k\Delta_l}$
. Then, using the independence of the Brownian increment (with the random variables
$X^{l,a}_{k\Delta_l}$
. Then, using the independence of the Brownian increment (with the random variables
![]() $\Big(X_{m,k\Delta_l}^l - X_{m,k\Delta_l}^{l,a}\Big)\Big(X_{n,k\Delta_l}^l - X_{n,k\Delta_l}^{l,a}\Big)\Big)$
and the same approach as above, one has
$\Big(X_{m,k\Delta_l}^l - X_{m,k\Delta_l}^{l,a}\Big)\Big(X_{n,k\Delta_l}^l - X_{n,k\Delta_l}^{l,a}\Big)\Big)$
and the same approach as above, one has
and applying Lemma B.1 yields
For
![]() $M_{i,k}^{(2)}$
one has
$M_{i,k}^{(2)}$
one has
 \begin{eqnarray*}M_{i,k}^{(2)} & \,=\, & \frac{1}{4}\sum_{(j,m,n)\in\{1,\dots,d\}^3}\left\{\frac{\partial h_{ijm}}{\partial x_n}\big(\xi_5^l\big) +\frac{\partial h_{ijm}}{\partial x_n}\big(\xi_6^l\big)\right\}\Big(X_{n,k\Delta_l}^l - X_{n,k\Delta_l}^{l,a}\Big) \\ & & \times \Big(\big[W_{j,(k+2)\Delta_l}-W_{j,k\Delta_l}\big]\big[W_{m,(k+2)\Delta_l}-W_{m,k\Delta_l}\big]-\Delta_{l-1}\Big),\end{eqnarray*}
\begin{eqnarray*}M_{i,k}^{(2)} & \,=\, & \frac{1}{4}\sum_{(j,m,n)\in\{1,\dots,d\}^3}\left\{\frac{\partial h_{ijm}}{\partial x_n}\big(\xi_5^l\big) +\frac{\partial h_{ijm}}{\partial x_n}\big(\xi_6^l\big)\right\}\Big(X_{n,k\Delta_l}^l - X_{n,k\Delta_l}^{l,a}\Big) \\ & & \times \Big(\big[W_{j,(k+2)\Delta_l}-W_{j,k\Delta_l}\big]\big[W_{m,(k+2)\Delta_l}-W_{m,k\Delta_l}\big]-\Delta_{l-1}\Big),\end{eqnarray*}
where
![]() $\xi_5^l$
is some point between
$\xi_5^l$
is some point between
![]() $\overline{X}^l_{k\Delta_l}$
and
$\overline{X}^l_{k\Delta_l}$
and
![]() $X^l_{k\Delta_l}$
and
$X^l_{k\Delta_l}$
and
![]() $\xi_6^l$
is some point between
$\xi_6^l$
is some point between
![]() $\overline{X}^l_{k\Delta_l}$
and
$\overline{X}^l_{k\Delta_l}$
and
![]() $X^{l,a}_{k\Delta_l}$
. As the Brownian increments are independent of
$X^{l,a}_{k\Delta_l}$
. As the Brownian increments are independent of
![]() $\Big(X_{n,k\Delta_l}^l - X_{n,k\Delta_l}^{l,a}\Big)$
and the dimensions are also independent of each other, one obtains
$\Big(X_{n,k\Delta_l}^l - X_{n,k\Delta_l}^{l,a}\Big)$
and the dimensions are also independent of each other, one obtains
Lemma B.1 gives
For
![]() $M_{i,k}^{(3)}$
, one has
$M_{i,k}^{(3)}$
, one has
 \begin{eqnarray*}M_{i,k}^{(3)} & \,=\, & \frac{1}{4}\sum_{(j,m,n)\in\{1,\dots,d\}^3}\left\{\frac{\partial h_{ijm}}{\partial x_n}\big(\xi_7^l\big) +\frac{\partial h_{ijm}}{\partial x_n}\big(\xi_8^l\big)\right\}\big(X_{k\Delta_l}^l-X_{k\Delta_l}^{l,a}\big)\Big(\big[W_{j,(k+1)\Delta_l}-W_{j,k\Delta_l}\big] \\ & & \times\big[W_{m,(k+2)\Delta_l}-W_{m,(k+1)\Delta_l}\big] -\big[W_{m,(k+1)\Delta_l}-W_{m,k\Delta_l}\big]\big[W_{j,(k+2)\Delta_l}-W_{j,(k+1)\Delta_l}\big]\Big),\end{eqnarray*}
\begin{eqnarray*}M_{i,k}^{(3)} & \,=\, & \frac{1}{4}\sum_{(j,m,n)\in\{1,\dots,d\}^3}\left\{\frac{\partial h_{ijm}}{\partial x_n}\big(\xi_7^l\big) +\frac{\partial h_{ijm}}{\partial x_n}\big(\xi_8^l\big)\right\}\big(X_{k\Delta_l}^l-X_{k\Delta_l}^{l,a}\big)\Big(\big[W_{j,(k+1)\Delta_l}-W_{j,k\Delta_l}\big] \\ & & \times\big[W_{m,(k+2)\Delta_l}-W_{m,(k+1)\Delta_l}\big] -\big[W_{m,(k+1)\Delta_l}-W_{m,k\Delta_l}\big]\big[W_{j,(k+2)\Delta_l}-W_{j,(k+1)\Delta_l}\big]\Big),\end{eqnarray*}
where
![]() $\xi_7^l$
is some point between
$\xi_7^l$
is some point between
![]() $\overline{X}^l_{k\Delta_l}$
and
$\overline{X}^l_{k\Delta_l}$
and
![]() $X^l_{k\Delta_l}$
and
$X^l_{k\Delta_l}$
and
![]() $\xi_8^l$
is some point between
$\xi_8^l$
is some point between
![]() $\overline{X}^l_{k\Delta_l}$
and
$\overline{X}^l_{k\Delta_l}$
and
![]() $X^{l,a}_{k\Delta_l}$
. Using essentially the same approach as for
$X^{l,a}_{k\Delta_l}$
. Using essentially the same approach as for
![]() $M_{i,k}^{(2)}$
, one obtains
$M_{i,k}^{(2)}$
, one obtains
which concludes the proof.
Proposition B.1. Assume (A1). Then for any
![]() $p\in[1,\infty)$
there exists a
$p\in[1,\infty)$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $l\in\mathbb{N}$
,
$l\in\mathbb{N}$
,
 \begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|\overline{X}_{k\Delta_l}^{l}-X_{k\Delta_l}^{l-1}\big\|^p\right]\end{align*}
\begin{align*}\mathbb{E}\left[\max_{k\in\big\{0,2,\dots,\Delta_l^{-1}\big\}}\big\|\overline{X}_{k\Delta_l}^{l}-X_{k\Delta_l}^{l-1}\big\|^p\right]\end{align*}
Proof. We omit the proof, because it is identical to that of [Reference Giles and Szpruch11, Theorem 4.10], except that one uses Lemma B.2 above instead of [Reference Giles and Szpruch11, Lemma 4.9].
Appendix C. Proofs for coupled particle filter
In this section,
![]() $\mathbb{E}$
denotes the expectation with respect to the law that generates the AMLPF.
$\mathbb{E}$
denotes the expectation with respect to the law that generates the AMLPF.
C.1. Rate proofs
Our analysis will apply to any coupling used in the second bullet point of Algorithm 4, Step 2. At any time point k of Algorithm 5, we will denote the resampled index of particle
![]() $i\in\{1,\dots,N_l\}$
by
$i\in\{1,\dots,N_l\}$
by
![]() $I_k^{i,l}$
(level l),
$I_k^{i,l}$
(level l),
![]() $I_k^{i,l-1}$
(level
$I_k^{i,l-1}$
(level
![]() $l-1$
), and
$l-1$
), and
![]() $I_k^{i,l,a}$
(level l antithetic). Now let
$I_k^{i,l,a}$
(level l antithetic). Now let
![]() $I_k^l(i)=I_k^{i,l}$
,
$I_k^l(i)=I_k^{i,l}$
,
![]() $I_k^{l-1}(i)=I_k^{i,l-1}$
,
$I_k^{l-1}(i)=I_k^{i,l-1}$
,
![]() $I_k^{l,a}(i)=I_k^{i,l,a}$
, and define
$I_k^{l,a}(i)=I_k^{i,l,a}$
, and define
![]() $\mathsf{S}_k^l$
as the collection of indices that choose the same ancestor at each resampling step, i.e.
$\mathsf{S}_k^l$
as the collection of indices that choose the same ancestor at each resampling step, i.e.
 \begin{eqnarray*}\mathsf{S}_k^l & \,=\, & \big\{i\in\{1,\dots,N_l\}\,:\,I_k^l(i)=I_k^{l-1}(i)=I_k^{l,a}(i),I_{k-1}^l\circ I_k^l(i)=I_{k-1}^{l-1}\circ I_k^{l-1}(i)=I_{k-1}^{l,a}\circ I_k^{l,a}(i),\dots,\\ & & I_{1}^l\circ I_2^l\circ\cdots\circ I_k^l(i) = I_{1}^{l-1}\circ I_2^{l-1}\circ\cdots\circ I_k^{l-1}(i)=I_{1}^{l,a}\circ I_2^{l,a}\circ\cdots\circ I_k^{l,a}(i)\big\}.\end{eqnarray*}
\begin{eqnarray*}\mathsf{S}_k^l & \,=\, & \big\{i\in\{1,\dots,N_l\}\,:\,I_k^l(i)=I_k^{l-1}(i)=I_k^{l,a}(i),I_{k-1}^l\circ I_k^l(i)=I_{k-1}^{l-1}\circ I_k^{l-1}(i)=I_{k-1}^{l,a}\circ I_k^{l,a}(i),\dots,\\ & & I_{1}^l\circ I_2^l\circ\cdots\circ I_k^l(i) = I_{1}^{l-1}\circ I_2^{l-1}\circ\cdots\circ I_k^{l-1}(i)=I_{1}^{l,a}\circ I_2^{l,a}\circ\cdots\circ I_k^{l,a}(i)\big\}.\end{eqnarray*}
We use the convention that
![]() $\mathsf{S}_0^l=\{1,\dots,N_l\}$
. Denote the
$\mathsf{S}_0^l=\{1,\dots,N_l\}$
. Denote the
![]() $\sigma$
-field generated by the simulated samples, resampled samples, and resampled indices up to time k by
$\sigma$
-field generated by the simulated samples, resampled samples, and resampled indices up to time k by
![]() $\hat{\mathcal{F}}_k^{l}$
, and denote the
$\hat{\mathcal{F}}_k^{l}$
, and denote the
![]() $\sigma$
-field which does the same, except excluding the resampled samples and indices, by
$\sigma$
-field which does the same, except excluding the resampled samples and indices, by
![]() $\mathcal{F}_k^{l}$
.
$\mathcal{F}_k^{l}$
.
Lemma C.1. Assume (A1)–(A2). Then for any
![]() $(p,k)\in[1,\infty)\times\mathbb{N}$
there exists a
$(p,k)\in[1,\infty)\times\mathbb{N}$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l)\in\mathbb{N}^2$
,
$(l,N_l)\in\mathbb{N}^2$
,
 \begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\left\{\Big\|X_k^{i,l}-X_k^{i,l-1}\Big\|^p +\Big\|X_k^{i,l,a}-X_k^{i,l-1}\Big\|^p +\Big\|X_k^{i,l}-X_k^{i,l,a}\Big\|^p\right\}\right] \leq C\Delta_l^{p/2}.\end{align*}
\begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\left\{\Big\|X_k^{i,l}-X_k^{i,l-1}\Big\|^p +\Big\|X_k^{i,l,a}-X_k^{i,l-1}\Big\|^p +\Big\|X_k^{i,l}-X_k^{i,l,a}\Big\|^p\right\}\right] \leq C\Delta_l^{p/2}.\end{align*}
Proof. The case
![]() $k=1$
follows from the work in [Reference Giles and Szpruch11] (the case
$k=1$
follows from the work in [Reference Giles and Szpruch11] (the case
![]() $p=[1,2)$
can be adapted from that paper), so we assume
$p=[1,2)$
can be adapted from that paper), so we assume
![]() $k\geq 2$
. By conditioning on
$k\geq 2$
. By conditioning on
![]() $\hat{\mathcal{F}}_{k-1}^{l}$
and applying Lemma B.1 (see also Remark B.1), we have
$\hat{\mathcal{F}}_{k-1}^{l}$
and applying Lemma B.1 (see also Remark B.1), we have
 \begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\left\{\Big\|X_k^{i,l}-X_k^{i,l-1}\Big\|^p +\Big\|X_k^{i,l,a}-X_k^{i,l-1}\Big\|^p +\Big\|X_k^{i,l}-X_k^{i,l,a}\Big\|^p\right\}\right]\end{align*}
\begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\left\{\Big\|X_k^{i,l}-X_k^{i,l-1}\Big\|^p +\Big\|X_k^{i,l,a}-X_k^{i,l-1}\Big\|^p +\Big\|X_k^{i,l}-X_k^{i,l,a}\Big\|^p\right\}\right]\end{align*}
 \begin{align*} \leq C\left(\Delta_l^{p/2} + \mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\left\{\Big\|\hat{X}_{k-1}^{i,l}-\hat{X}_{k-1}^{i,l-1}\Big\|^p +\Big\|\hat{X}_{k-1}^{i,l,a}-\hat{X}_{k-1}^{i,l-1}\Big\|^p +\Big\|\hat{X}_{k-1}^{i,l}-\hat{X}_{k-1}^{i,l,a}\Big\|^p\right\}\right] \right).\end{align*}
\begin{align*} \leq C\left(\Delta_l^{p/2} + \mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\left\{\Big\|\hat{X}_{k-1}^{i,l}-\hat{X}_{k-1}^{i,l-1}\Big\|^p +\Big\|\hat{X}_{k-1}^{i,l,a}-\hat{X}_{k-1}^{i,l-1}\Big\|^p +\Big\|\hat{X}_{k-1}^{i,l}-\hat{X}_{k-1}^{i,l,a}\Big\|^p\right\}\right] \right).\end{align*}
One can exchangeably write the expectation on the right-hand side as
 \begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\left\{\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l},l}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^p +\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l,a},l,a}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^p +\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l},l}-\hat{X}_{k-1}^{I_{k-1}^{i,l,a},l,a}\bigg\|^p\right\}\right].\end{align*}
\begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\left\{\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l},l}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^p +\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l,a},l,a}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^p +\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l},l}-\hat{X}_{k-1}^{I_{k-1}^{i,l,a},l,a}\bigg\|^p\right\}\right].\end{align*}
The proof from here is then essentially identical (up to the fact that one has three indices instead of two) to that of [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.3] and is hence omitted.
Lemma C.2. Assume (A1)–(A2). Then for any
![]() $(p,k)\in[1,\infty)\times\mathbb{N}$
there exists a
$(p,k)\in[1,\infty)\times\mathbb{N}$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l)\in\mathbb{N}^2$
,
$(l,N_l)\in\mathbb{N}^2$
,
 \begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\Big\|\overline{X}_k^{i,l}-X_k^{i,l-1}\Big\|^p\right] \leq C\Delta_l^{p}.\end{align*}
\begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\Big\|\overline{X}_k^{i,l}-X_k^{i,l-1}\Big\|^p\right] \leq C\Delta_l^{p}.\end{align*}
Proof. Following the start of the proof of Lemma C.1, except using Proposition B.1 instead of Lemma B.1, one can deduce that
 \begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\Big\|\overline{X}_k^{i,l}-X_k^{i,l-1}\Big\|^p\right] \leq\end{align*}
\begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\Big\|\overline{X}_k^{i,l}-X_k^{i,l-1}\Big\|^p\right] \leq\end{align*}
 \begin{align*}C\Bigg(\Delta_l^p + \mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\bigg\{\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l},l}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^{2p} +\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l,a},l,a}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^{2p}\bigg\}\right] \end{align*}
\begin{align*}C\Bigg(\Delta_l^p + \mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\bigg\{\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l},l}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^{2p} +\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l,a},l,a}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^{2p}\bigg\}\right] \end{align*}
 \begin{align*}+\Delta_l^{p/2}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\bigg\{\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l},l}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^{p} +\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l,a},l,a}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^{p}\bigg\}\right]\Bigg).\end{align*}
\begin{align*}+\Delta_l^{p/2}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\bigg\{\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l},l}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^{p} +\bigg\|\hat{X}_{k-1}^{I_{k-1}^{i,l,a},l,a}-\hat{X}_{k-1}^{I_{k-1}^{i,l-1},l-1}\bigg\|^{p}\bigg\}\right]\Bigg).\end{align*}
From here, one can follow the calculations in [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.3] to deduce that
 \begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\Big\|\overline{X}_k^{i,l}-X_k^{i,l-1}\Big\|^p\right] \leq\end{align*}
\begin{align*}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-1}^l}\Big\|\overline{X}_k^{i,l}-X_k^{i,l-1}\Big\|^p\right] \leq\end{align*}
 \begin{align*}C\Bigg(\Delta_l^p + \mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-2}^l}\left\{\Big\|X_{k-1}^{i,l}-X_{k-1}^{i,l-1}\Big\|^{2p} +\Big\|X_{k-1}^{i,l,a}-X_{k-1}^{i,l-1}\Big\|^{2p} +\Big\|X_{k-1}^{i,l}-X_{k-1}^{i,l,a}\Big\|^{2p}\right\}\right] \end{align*}
\begin{align*}C\Bigg(\Delta_l^p + \mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-2}^l}\left\{\Big\|X_{k-1}^{i,l}-X_{k-1}^{i,l-1}\Big\|^{2p} +\Big\|X_{k-1}^{i,l,a}-X_{k-1}^{i,l-1}\Big\|^{2p} +\Big\|X_{k-1}^{i,l}-X_{k-1}^{i,l,a}\Big\|^{2p}\right\}\right] \end{align*}
 \begin{align*}+\Delta_l^{p/2}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-2}^l}\left\{\Big\|X_{k-1}^{i,l}-X_{k-1}^{i,l-1}\Big\|^{p} +\Big\|X_{k-1}^{i,l,a}-X_{k-1}^{i,l-1}\Big\|^{p} +\Big\|X_{k-1}^{i,l}-X_{k-1}^{i,l,a}\Big\|^{p}\right\}\right]\Bigg).\end{align*}
\begin{align*}+\Delta_l^{p/2}\mathbb{E}\left[\frac{1}{N_l}\sum_{i\in\mathsf{S}_{k-2}^l}\left\{\Big\|X_{k-1}^{i,l}-X_{k-1}^{i,l-1}\Big\|^{p} +\Big\|X_{k-1}^{i,l,a}-X_{k-1}^{i,l-1}\Big\|^{p} +\Big\|X_{k-1}^{i,l}-X_{k-1}^{i,l,a}\Big\|^{p}\right\}\right]\Bigg).\end{align*}
Application of Lemma C.1 concludes the result.
Lemma C.3. Assume (A1)–(A2). Then for any
![]() $k\in\mathbb{N}$
there exists a
$k\in\mathbb{N}$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l)\in\mathbb{N}^2$
,
$(l,N_l)\in\mathbb{N}^2$
,
 \begin{align*} & \mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)\left|\left\{\frac{g_{k}\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}-\frac{g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)}\right\}\right|\right]\\[6pt]& \quad \leq C\left(\frac{\Delta_l^{1/2}}{N_l}+\frac{1}{N_l}\left\{1-\mathbb{E}\left[\frac{\textit{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\right\}\right).\end{align*}
\begin{align*} & \mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)\left|\left\{\frac{g_{k}\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}-\frac{g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)}\right\}\right|\right]\\[6pt]& \quad \leq C\left(\frac{\Delta_l^{1/2}}{N_l}+\frac{1}{N_l}\left\{1-\mathbb{E}\left[\frac{\textit{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\right\}\right).\end{align*}
Proof. We have the elementary decomposition
 \begin{align*} & \frac{g_{k}\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}-\frac{g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)} = \frac{g_{k}\big(X_k^{i,l}\big)-g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}\\[8pt]& \qquad + g_{k}\big(X_k^{i,l,a}\big)\left(\frac{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)-\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}\right).\end{align*}
\begin{align*} & \frac{g_{k}\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}-\frac{g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)} = \frac{g_{k}\big(X_k^{i,l}\big)-g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}\\[8pt]& \qquad + g_{k}\big(X_k^{i,l,a}\big)\left(\frac{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)-\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}\right).\end{align*}
So application of the triangle inequality along with the lower and upper bounds on
![]() $g_k$
(which are uniform in x) yields
$g_k$
(which are uniform in x) yields
 \begin{align*}\mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)\left|\left\{\frac{g_{k}\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}-\frac{g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)}\right\}\right|\right] \leq\\\end{align*}
\begin{align*}\mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)\left|\left\{\frac{g_{k}\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}-\frac{g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)}\right\}\right|\right] \leq\\\end{align*}
 \begin{align*} & \frac{C}{N_l}\Bigg(\mathbb{E}\Big[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)\Big|g_{k}\big(X_k^{i,l}\big)-g_{k}\big(X_k^{i,l,a}\big)\Big|\Big] +\frac{1}{N_l}\mathbb{E}\left[\sum_{j\in \mathsf{S}_{k-1}^l}\Big|g_{k}\Big(X_k^{j,l}\Big)-g_{k}\Big(X_k^{j,l,a}\Big)\Big|\right]\\& \qquad +1-\mathbb{E}\left[\frac{\textrm{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\Bigg).\end{align*}
\begin{align*} & \frac{C}{N_l}\Bigg(\mathbb{E}\Big[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)\Big|g_{k}\big(X_k^{i,l}\big)-g_{k}\big(X_k^{i,l,a}\big)\Big|\Big] +\frac{1}{N_l}\mathbb{E}\left[\sum_{j\in \mathsf{S}_{k-1}^l}\Big|g_{k}\Big(X_k^{j,l}\Big)-g_{k}\Big(X_k^{j,l,a}\Big)\Big|\right]\\& \qquad +1-\mathbb{E}\left[\frac{\textrm{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\Bigg).\end{align*}
Using the Lipschitz property of
![]() $g_k$
along with Lemma C.1 allows one to conclude the result.
$g_k$
along with Lemma C.1 allows one to conclude the result.
The following is a useful lemma that we will need below. Its proof is a matter of direct computation and is hence omitted.
Lemma C.4. Let
![]() $\big(G^l,f^l,G^a,f^a,G^{l-1},f^{l-1}\big)\in\mathbb{R}^6$
with
$\big(G^l,f^l,G^a,f^a,G^{l-1},f^{l-1}\big)\in\mathbb{R}^6$
with
![]() $\big(f^l,f^a,f^{l-1}\big)$
non-zero; then
$\big(f^l,f^a,f^{l-1}\big)$
non-zero; then
 \begin{eqnarray*}\frac{\tfrac{1}{2}G^l}{f^l} + \frac{\tfrac{1}{2}G^a}{f^a} - \frac{G^{l-1}}{f^{l-1}} & \,=\, & \frac{1}{f^{l-1}}\Big(\tfrac{1}{2}G^l+\tfrac{1}{2}G^a-G^{l-1}\Big) + \frac{1}{f^{a}f^{l}f^{l-1}}\Big(\tfrac{1}{2}(G^l-G^a)\big(f^{l-1}-f^l\big)f^a + \\ & &\tfrac{1}{2}G^a\Big[(f^a-f^l)\big(f^{l-1}-f^l\big) - 2f^l\Big\{\tfrac{1}{2}f^l + \tfrac{1}{2}f^a - f^{l-1}\Big\}\Big]\Big).\end{eqnarray*}
\begin{eqnarray*}\frac{\tfrac{1}{2}G^l}{f^l} + \frac{\tfrac{1}{2}G^a}{f^a} - \frac{G^{l-1}}{f^{l-1}} & \,=\, & \frac{1}{f^{l-1}}\Big(\tfrac{1}{2}G^l+\tfrac{1}{2}G^a-G^{l-1}\Big) + \frac{1}{f^{a}f^{l}f^{l-1}}\Big(\tfrac{1}{2}(G^l-G^a)\big(f^{l-1}-f^l\big)f^a + \\ & &\tfrac{1}{2}G^a\Big[(f^a-f^l)\big(f^{l-1}-f^l\big) - 2f^l\Big\{\tfrac{1}{2}f^l + \tfrac{1}{2}f^a - f^{l-1}\Big\}\Big]\Big).\end{eqnarray*}
Lemma C.5. Assume (A1)–(A2). Then for any
![]() $k\in\mathbb{N}$
there exists a
$k\in\mathbb{N}$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l)\in\mathbb{N}^2$
,
$(l,N_l)\in\mathbb{N}^2$
,
 \begin{align*}\mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)\left|\left\{\frac{\tfrac{1}{2}g_{k}\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}+\frac{\tfrac{1}{2}g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)}-\frac{g_{k}\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l-1}\big)}\right\}\right|\right] \end{align*}
\begin{align*}\mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)\left|\left\{\frac{\tfrac{1}{2}g_{k}\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}+\frac{\tfrac{1}{2}g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)}-\frac{g_{k}\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l-1}\big)}\right\}\right|\right] \end{align*}
 \begin{align*}\leq C\left(\frac{\Delta_l}{N_l}+\frac{1}{N_l}\left\{1-\mathbb{E}\left[\frac{\textit{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\right\}\right).\end{align*}
\begin{align*}\leq C\left(\frac{\Delta_l}{N_l}+\frac{1}{N_l}\left\{1-\mathbb{E}\left[\frac{\textit{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\right\}\right).\end{align*}
Proof. One can apply Lemma C.4 to see that
 \begin{align*}\frac{\tfrac{1}{2}g_{k}\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}+\frac{\tfrac{1}{2}g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)}-\frac{g_{k}\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l-1}\big)} = \sum_{j=1}^4 T_j,\end{align*}
\begin{align*}\frac{\tfrac{1}{2}g_{k}\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l}\big)}+\frac{\tfrac{1}{2}g_{k}\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l,a}\big)}-\frac{g_{k}\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_{k}\big(X_k^{j,l-1}\big)} = \sum_{j=1}^4 T_j,\end{align*}
where
 \begin{align*}T_1 & = \frac{1}{\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l-1}\Big)}\left\{\tfrac{1}{2}g_{k}\Big(X_k^{i,l}\Big)+\tfrac{1}{2}g_{k}\Big(X_k^{i,l,a}\Big)-g_{k}\Big(X_k^{i,l-1}\Big)\right\}, \\T_2 & = \frac{1}{2\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l}\Big)\Big]\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l-1}\Big)\Big]}\left(g_{k}\Big(X_k^{i,l}\Big)\right.\\& \qquad\qquad\qquad\qquad\qquad\left.-g_{k}\Big(X_k^{i,l,a}\Big)\right)\left(\sum_{j=1}^{N_l}\Big[g_{k}\Big(X_k^{j,l-1}\Big)-g_{k}\Big(X_k^{j,l}\Big)\Big]\right), \\T_3 & = \frac{g_{k}\Big(X_k^{i,l,a}\Big)}{2\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l,a}\Big)\Big]\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l}\Big)\Big]\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l-1}\Big)\Big]}\!\left(\sum_{j=1}^{N_l}\Big[g_{k}\Big(X_k^{j,l,a}\Big)-g_{k}\Big(X_k^{j,l}\Big)\Big]\right) \\[4pt]& \times \left(\sum_{j=1}^{N_l}\Big[g_{k}\Big(X_k^{j,l-1}\Big)-g_{k}\Big(X_k^{j,l}\Big)\Big]\right),\\ T_4 & = -\frac{g_{k}\Big(X_k^{i,l,a}\Big)}{\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l,a}\Big)\Big]\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l-1}\Big)\Big]}\left\{\sum_{j=1}^{N_l}\Big[\tfrac{1}{2}g_{k}\Big(X_k^{j,l}\Big) + \tfrac{1}{2}g_{k}\Big(X_k^{j,l,a}\Big) -g_{k}\Big(X_k^{j,l-1}\Big)\Big]\right\}\!.\end{align*}
\begin{align*}T_1 & = \frac{1}{\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l-1}\Big)}\left\{\tfrac{1}{2}g_{k}\Big(X_k^{i,l}\Big)+\tfrac{1}{2}g_{k}\Big(X_k^{i,l,a}\Big)-g_{k}\Big(X_k^{i,l-1}\Big)\right\}, \\T_2 & = \frac{1}{2\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l}\Big)\Big]\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l-1}\Big)\Big]}\left(g_{k}\Big(X_k^{i,l}\Big)\right.\\& \qquad\qquad\qquad\qquad\qquad\left.-g_{k}\Big(X_k^{i,l,a}\Big)\right)\left(\sum_{j=1}^{N_l}\Big[g_{k}\Big(X_k^{j,l-1}\Big)-g_{k}\Big(X_k^{j,l}\Big)\Big]\right), \\T_3 & = \frac{g_{k}\Big(X_k^{i,l,a}\Big)}{2\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l,a}\Big)\Big]\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l}\Big)\Big]\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l-1}\Big)\Big]}\!\left(\sum_{j=1}^{N_l}\Big[g_{k}\Big(X_k^{j,l,a}\Big)-g_{k}\Big(X_k^{j,l}\Big)\Big]\right) \\[4pt]& \times \left(\sum_{j=1}^{N_l}\Big[g_{k}\Big(X_k^{j,l-1}\Big)-g_{k}\Big(X_k^{j,l}\Big)\Big]\right),\\ T_4 & = -\frac{g_{k}\Big(X_k^{i,l,a}\Big)}{\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l,a}\Big)\Big]\Big[\sum_{j=1}^{N_l}g_{k}\Big(X_k^{j,l-1}\Big)\Big]}\left\{\sum_{j=1}^{N_l}\Big[\tfrac{1}{2}g_{k}\Big(X_k^{j,l}\Big) + \tfrac{1}{2}g_{k}\Big(X_k^{j,l,a}\Big) -g_{k}\Big(X_k^{j,l-1}\Big)\Big]\right\}\!.\end{align*}
The terms
![]() $T_1$
(resp.
$T_1$
(resp.
![]() $T_2$
) and
$T_2$
) and
![]() $T_4$
(resp.
$T_4$
(resp.
![]() $T_3$
) can be dealt with in a similar manner, so we only consider
$T_3$
) can be dealt with in a similar manner, so we only consider
![]() $T_1$
(resp.
$T_1$
(resp.
![]() $T_2$
).
$T_2$
).
For the case of
![]() $T_1$
we have the upper bound
$T_1$
we have the upper bound
Then one can apply [Reference Giles and Szpruch11, Lemma 2.2] along with Lemmata C.1 and C.2 to deduce that
For the case of
![]() $T_2$
we have the upper bound
$T_2$
we have the upper bound
 \begin{align*}& \mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)T_2\right]\leq \frac{C}{N_l^2}\Bigg(\mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)\big|g_{k}\big(X_k^{i,l,a}\big)-g_{k}\big(X_k^{i,l}\big)\big|\sum_{j\in\mathsf{S}_{k-1}^l}\big[g_{k}\big(X_k^{j,l-1}\big)-g_{k}\big(X_k^{j,l,a}\big)\big]\Big|\right]\\& \qquad + \mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)|g_{k}\big(X_k^{i,l,a}\big)-g_{k}\big(X_k^{i,l}\big)\Big|\Big(N_l - \textrm{Card}\big(\mathsf{S}_{k-1}^l\big)\Big)\right]\Bigg).\end{align*}
\begin{align*}& \mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)T_2\right]\leq \frac{C}{N_l^2}\Bigg(\mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)\big|g_{k}\big(X_k^{i,l,a}\big)-g_{k}\big(X_k^{i,l}\big)\big|\sum_{j\in\mathsf{S}_{k-1}^l}\big[g_{k}\big(X_k^{j,l-1}\big)-g_{k}\big(X_k^{j,l,a}\big)\big]\Big|\right]\\& \qquad + \mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)|g_{k}\big(X_k^{i,l,a}\big)-g_{k}\big(X_k^{i,l}\big)\Big|\Big(N_l - \textrm{Card}\big(\mathsf{S}_{k-1}^l\big)\Big)\right]\Bigg).\end{align*}
For the first term on the right-hand side one can use the Lipschitz property of
![]() $g_{k}$
, Cauchy–Schwarz, and Lemma C.1, and for the second term one can use the boundedness of
$g_{k}$
, Cauchy–Schwarz, and Lemma C.1, and for the second term one can use the boundedness of
![]() $g_k$
, to obtain
$g_k$
, to obtain
 \begin{align*}\mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)T_2\right] \leq C\left(\frac{\Delta_l}{N_l}+ \frac{1}{N_l}\left\{1-\mathbb{E}\left[\frac{\textrm{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\right\}\right),\end{align*}
\begin{align*}\mathbb{E}\left[\mathbb{I}_{\mathsf{S}_{k-1}^l}(i)T_2\right] \leq C\left(\frac{\Delta_l}{N_l}+ \frac{1}{N_l}\left\{1-\mathbb{E}\left[\frac{\textrm{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\right\}\right),\end{align*}
which concludes the proof.
Lemma C.6. Assume (A1)–(A2). Then for any
![]() $k\in\mathbb{N}_0$
there exists a
$k\in\mathbb{N}_0$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l)\in\mathbb{N}^2$
,
$(l,N_l)\in\mathbb{N}^2$
,
 \begin{align*}1-\mathbb{E}\left[\frac{\textit{Card}\big(\mathsf{S}_{k}^l\big)}{N_l}\right] \leq C\Delta_l^{1/2}.\end{align*}
\begin{align*}1-\mathbb{E}\left[\frac{\textit{Card}\big(\mathsf{S}_{k}^l\big)}{N_l}\right] \leq C\Delta_l^{1/2}.\end{align*}
Proof. We note that
 \begin{eqnarray}1-\mathbb{E}\left[\frac{\textrm{Card}\big(\mathsf{S}_{k}^l\big)}{N_l}\right] & \,=\, &1 - \mathbb{E}\left[\sum_{i=1}^{N_l} \min\!\left\{\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)}\frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)},\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}\right\}\right] \nonumber\\[3pt] & & + \mathbb{E}\!\left[\sum_{i\notin\mathsf{S}_{k-1}^l}\min\!\left\{\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)}\frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)},\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}\right\}\right]\nonumber\\[3pt] & \leq &1 - \mathbb{E}\!\left[\sum_{i=1}^{N_l} \min\!\left\{\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)}\frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)},\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}\right\}\right] \nonumber\\[3pt] & & + C\left(1-\mathbb{E}\!\left[\frac{\textrm{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\right).\end{eqnarray}
\begin{eqnarray}1-\mathbb{E}\left[\frac{\textrm{Card}\big(\mathsf{S}_{k}^l\big)}{N_l}\right] & \,=\, &1 - \mathbb{E}\left[\sum_{i=1}^{N_l} \min\!\left\{\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)}\frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)},\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}\right\}\right] \nonumber\\[3pt] & & + \mathbb{E}\!\left[\sum_{i\notin\mathsf{S}_{k-1}^l}\min\!\left\{\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)}\frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)},\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}\right\}\right]\nonumber\\[3pt] & \leq &1 - \mathbb{E}\!\left[\sum_{i=1}^{N_l} \min\!\left\{\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)}\frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)},\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}\right\}\right] \nonumber\\[3pt] & & + C\left(1-\mathbb{E}\!\left[\frac{\textrm{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\right).\end{eqnarray}
As our proof strategy is via induction (the initialization is trivially true since
![]() $\mathsf{S}_{0}^l=\{1,\dots,N_l\}$
), we need to focus on the first term on the right-hand side of (C.1).
$\mathsf{S}_{0}^l=\{1,\dots,N_l\}$
), we need to focus on the first term on the right-hand side of (C.1).
Now, applying twice the result that
![]() $\min\{a,b\} = \tfrac{1}{2}(a+b-|a-b|)$
for any
$\min\{a,b\} = \tfrac{1}{2}(a+b-|a-b|)$
for any
![]() $(a,b)\in\mathbb{R}^2$
, we easily obtain that
$(a,b)\in\mathbb{R}^2$
, we easily obtain that
 \begin{align*}1 - \sum_{i=1}^{N_l} \min\left\{\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)}\frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)},\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}\right\}\ \end{align*}
\begin{align*}1 - \sum_{i=1}^{N_l} \min\left\{\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)}\frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)},\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}\right\}\ \end{align*}
 \begin{align*}=\frac{1}{2}\sum_{i=1}^{N_l}\Bigg\{\frac{1}{2}\Bigg|\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)} - \frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)}\Bigg| +\Bigg|\frac{\tfrac{1}{2}g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)} +\frac{\tfrac{1}{2}g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)}\end{align*}
\begin{align*}=\frac{1}{2}\sum_{i=1}^{N_l}\Bigg\{\frac{1}{2}\Bigg|\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)} - \frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)}\Bigg| +\Bigg|\frac{\tfrac{1}{2}g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)} +\frac{\tfrac{1}{2}g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)}\end{align*}
 \begin{align*} -\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}-\frac{1}{2}\Bigg|\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)} - \frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)}\Bigg|\Bigg|\Bigg\}.\end{align*}
\begin{align*} -\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}-\frac{1}{2}\Bigg|\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)} - \frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)}\Bigg|\Bigg|\Bigg\}.\end{align*}
To shorten the subsequent notation, we set
 \begin{align*}\alpha_i & = \frac{1}{2}\Bigg|\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)} - \frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)}\Bigg| \\[3pt]\beta_i & = \frac{\tfrac{1}{2}g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)} +\frac{\tfrac{1}{2}g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)}-\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}.\end{align*}
\begin{align*}\alpha_i & = \frac{1}{2}\Bigg|\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)} - \frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)}\Bigg| \\[3pt]\beta_i & = \frac{\tfrac{1}{2}g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)} +\frac{\tfrac{1}{2}g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)}-\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}.\end{align*}
In this notation, we have that
 \begin{align} & 1 - \mathbb{E}\left[\sum_{i=1}^{N_l} \min\left\{\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)}\frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)},\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}\right\}\right]\nonumber\\& = \frac{1}{2}\mathbb{E}\left[\sum_{i=1}^{N_l}\{\alpha_i + |\beta_i-\alpha_i|\}\right]\end{align}
\begin{align} & 1 - \mathbb{E}\left[\sum_{i=1}^{N_l} \min\left\{\frac{g_k\big(X_k^{i,l}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l}\big)}\frac{g_k\big(X_k^{i,l,a}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l,a}\big)},\frac{g_k\big(X_k^{i,l-1}\big)}{\sum_{j=1}^{N_l}g_k\big(X_k^{j,l-1}\big)}\right\}\right]\nonumber\\& = \frac{1}{2}\mathbb{E}\left[\sum_{i=1}^{N_l}\{\alpha_i + |\beta_i-\alpha_i|\}\right]\end{align}
 \begin{align} \leq \frac{1}{2}\mathbb{E}\left[\sum_{i\in\mathsf{S}_{k-1}^l}\{\alpha_i + |\beta_i-\alpha_i|\}\right]+ C\left(1-\mathbb{E}\left[\frac{\textrm{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\right).\end{align}
\begin{align} \leq \frac{1}{2}\mathbb{E}\left[\sum_{i\in\mathsf{S}_{k-1}^l}\{\alpha_i + |\beta_i-\alpha_i|\}\right]+ C\left(1-\mathbb{E}\left[\frac{\textrm{Card}\big(\mathsf{S}_{k-1}^l\big)}{N_l}\right]\right).\end{align}
Then by induction, via Lemmata C.3 and C.5, it trivially follows that
 \begin{align*}1-\mathbb{E}\left[\frac{\textrm{Card}\big(\mathsf{S}_{k}^l\big)}{N_l}\right] \leq C\Delta_l^{1/2}.\end{align*}
\begin{align*}1-\mathbb{E}\left[\frac{\textrm{Card}\big(\mathsf{S}_{k}^l\big)}{N_l}\right] \leq C\Delta_l^{1/2}.\end{align*}
Remark C.1. Lemma C.6 is the place where the rate is lost. It is clear that this particular quantity cannot fall faster than
![]() $\mathcal{O}\big(\Delta_l^{1/2}\big)$
, as the right-hand side of (C.2) is exactly equal to
$\mathcal{O}\big(\Delta_l^{1/2}\big)$
, as the right-hand side of (C.2) is exactly equal to
 \begin{align*}\sum_{i=1}^{N_l}\max\{\alpha_i,\beta_i\}.\end{align*}
\begin{align*}\sum_{i=1}^{N_l}\max\{\alpha_i,\beta_i\}.\end{align*}
The expectation of this quantity falls exactly at
![]() $\mathcal{O}\big(\Delta_l^{1/2}\big)$
. We could not find a way to enhance the proof to deal with this point, so we leave it to future work.
$\mathcal{O}\big(\Delta_l^{1/2}\big)$
. We could not find a way to enhance the proof to deal with this point, so we leave it to future work.
Lemma C.7. Assume (A1)–(A2). Then for any
![]() $k\in\mathbb{N}$
there exists a
$k\in\mathbb{N}$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l,i)\in\mathbb{N}^2\times\{1,\dots,N_l\}$
,
$(l,N_l,i)\in\mathbb{N}^2\times\{1,\dots,N_l\}$
,
Proof. This follows from Lemmata C.2 and C.6; see e.g. the corresponding proof in [Reference Jasra, Kamatani, Law and Zhou14, Theorem D.5].
Remark C.2. In a similar manner to the proofs of Lemma C.7 and [Reference Jasra, Kamatani, Law and Zhou14, Theorem D.5], one can establish, assuming (A1)–(A2), that the following hold:
-
For any
 $k\in\mathbb{N}$
there exists a
$k\in\mathbb{N}$
there exists a
 $C<+\infty$
such that for any
$C<+\infty$
such that for any
 $(l,N_l,i)\in\mathbb{N}^2\times\{1,\dots,N_l\}$
,
$(l,N_l,i)\in\mathbb{N}^2\times\{1,\dots,N_l\}$
,  \begin{align*}\mathbb{E}\left[\min\Big\{\Big\|X_k^{i,l}-X_k^{i,l-1}\Big\|^p,1\Big\}\right] \leq C\Delta_l^{1/2}.\end{align*}
\begin{align*}\mathbb{E}\left[\min\Big\{\Big\|X_k^{i,l}-X_k^{i,l-1}\Big\|^p,1\Big\}\right] \leq C\Delta_l^{1/2}.\end{align*}
-
For any
 $k\in\mathbb{N}$
there exists a
$k\in\mathbb{N}$
there exists a
 $C<+\infty$
such that for any
$C<+\infty$
such that for any
 $(l,N_l,i)\in\mathbb{N}^2\times\{1,\dots,N_l\}$
,
$(l,N_l,i)\in\mathbb{N}^2\times\{1,\dots,N_l\}$
,  \begin{align*}\mathbb{E}\left[\min\Big\{\Big\|X_k^{i,l}-X_k^{i,l,a}\Big\|^p,1\Big\}\right] \leq C\Delta_l^{1/2}.\end{align*}
\begin{align*}\mathbb{E}\left[\min\Big\{\Big\|X_k^{i,l}-X_k^{i,l,a}\Big\|^p,1\Big\}\right] \leq C\Delta_l^{1/2}.\end{align*}
C.2. Particle convergence proofs:
 $\mathbb{L}_p$
-bounds
$\mathbb{L}_p$
-bounds
For a function
![]() $\varphi\in\mathcal{B}_b(\mathsf{X})\cap\textrm{Lip}(\mathsf{X})$
, we set
$\varphi\in\mathcal{B}_b(\mathsf{X})\cap\textrm{Lip}(\mathsf{X})$
, we set
![]() $\overline{\|\varphi\|}=\max\{\|\varphi\|_{\infty},\|\varphi\|_{\textrm{Lip}}\}$
, where
$\overline{\|\varphi\|}=\max\{\|\varphi\|_{\infty},\|\varphi\|_{\textrm{Lip}}\}$
, where
![]() $\|\cdot\|_{\textrm{Lip}}$
is the Lipschitz constant. We denote the
$\|\cdot\|_{\textrm{Lip}}$
is the Lipschitz constant. We denote the
![]() $N_l$
-empirical measures by
$N_l$
-empirical measures by
 \begin{align*}\eta_k^{N_l,l}(dx)&= \tfrac{1}{N}\sum_{i=1}^{N_l}\delta_{\{X_k^{i,l}\}}(dx),\\\eta_k^{N_l,l-1}(dx)&= \tfrac{1}{N}\sum_{i=1}^{N_l}\delta_{\{X_k^{i,l-1}\}}(dx),\\\eta_k^{N_l,l,a}(dx)&= \tfrac{1}{N}\sum_{i=1}^{N_l}\delta_{\{X_k^{i,l,a}\}}(dx),\end{align*}
\begin{align*}\eta_k^{N_l,l}(dx)&= \tfrac{1}{N}\sum_{i=1}^{N_l}\delta_{\{X_k^{i,l}\}}(dx),\\\eta_k^{N_l,l-1}(dx)&= \tfrac{1}{N}\sum_{i=1}^{N_l}\delta_{\{X_k^{i,l-1}\}}(dx),\\\eta_k^{N_l,l,a}(dx)&= \tfrac{1}{N}\sum_{i=1}^{N_l}\delta_{\{X_k^{i,l,a}\}}(dx),\end{align*}
where
![]() $k\in\mathbb{N}$
and
$k\in\mathbb{N}$
and
![]() $\delta_A(dx)$
is the Dirac mass on a set A. We define the predictors as follows: for
$\delta_A(dx)$
is the Dirac mass on a set A. We define the predictors as follows: for
![]() $l\in\mathbb{N}_0$
,
$l\in\mathbb{N}_0$
,
![]() $\eta_1^{l}(dx) = P^l(x_0,dx)$
, and for
$\eta_1^{l}(dx) = P^l(x_0,dx)$
, and for
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $\eta_k^{l}(dx) =\eta_{k-1}^l(g_{k-1}P^l(dx))/\eta_{k-1}^l(g_{k-1})$
.
$\eta_k^{l}(dx) =\eta_{k-1}^l(g_{k-1}P^l(dx))/\eta_{k-1}^l(g_{k-1})$
.
Lemma C.8. Assume (A1)–(A2). Then for any
![]() $(k,p)\in\mathbb{N}\times[1,\infty)$
there exists a
$(k,p)\in\mathbb{N}\times[1,\infty)$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l,\varphi)\in\mathbb{N}^2\times\mathcal{B}_b(\mathsf{X})\cap\textit{Lip}(\mathsf{X})$
,
$(l,N_l,\varphi)\in\mathbb{N}^2\times\mathcal{B}_b(\mathsf{X})\cap\textit{Lip}(\mathsf{X})$
,
 \begin{align*}\mathbb{E}\left[\Big|\Big[\eta_k^{N_l,l}-\eta_k^{N_l,l-1}\Big](\varphi)-\big[\eta_k^l-\eta_k^{l-1}\big](\varphi)\Big|^p\right] \leq \frac{C\overline{\|\varphi\|}^p\Delta_l^{\tfrac{1}{2}}}{N_l^{\tfrac{p}{2}}}.\end{align*}
\begin{align*}\mathbb{E}\left[\Big|\Big[\eta_k^{N_l,l}-\eta_k^{N_l,l-1}\Big](\varphi)-\big[\eta_k^l-\eta_k^{l-1}\big](\varphi)\Big|^p\right] \leq \frac{C\overline{\|\varphi\|}^p\Delta_l^{\tfrac{1}{2}}}{N_l^{\tfrac{p}{2}}}.\end{align*}
Proof. The proof is by induction, with initialization following easily from the Marcinkiewicz–Zygmund (MZ) inequality (the case
![]() $p\in[1,2)$
can be dealt with using the bound
$p\in[1,2)$
can be dealt with using the bound
![]() $p\in[2,\infty)$
and Jensen’s inequality) and strong convergence results for Euler discretizations. We therefore proceed to the induction step. We have that
$p\in[2,\infty)$
and Jensen’s inequality) and strong convergence results for Euler discretizations. We therefore proceed to the induction step. We have that
where
 \begin{eqnarray*}T_1 & \,=\, & \mathbb{E}\left[\Big|\Big[\eta_k^{N_l,l}-\eta_k^{N_l,l-1}\Big](\varphi) - \mathbb{E}\Big[\Big[\eta_k^{N_l,l}-\eta_k^{N_l,l-1}\Big](\varphi)|\mathcal{F}_{k-1}^l\Big]\Big|^p\right]^{1/p}, \\T_2 & \,=\, & \mathbb{E}\left[\Big|\mathbb{E}\Big[\Big[\eta_k^{N_l,l}-\eta_k^{N_l,l-1}\Big](\varphi)\Big|\mathcal{F}_{k-1}\Big]-\Big[\eta_k^l-\eta_k^{l-1}\Big](\varphi)\Big|^p\right]^{1/p}.\end{eqnarray*}
\begin{eqnarray*}T_1 & \,=\, & \mathbb{E}\left[\Big|\Big[\eta_k^{N_l,l}-\eta_k^{N_l,l-1}\Big](\varphi) - \mathbb{E}\Big[\Big[\eta_k^{N_l,l}-\eta_k^{N_l,l-1}\Big](\varphi)|\mathcal{F}_{k-1}^l\Big]\Big|^p\right]^{1/p}, \\T_2 & \,=\, & \mathbb{E}\left[\Big|\mathbb{E}\Big[\Big[\eta_k^{N_l,l}-\eta_k^{N_l,l-1}\Big](\varphi)\Big|\mathcal{F}_{k-1}\Big]-\Big[\eta_k^l-\eta_k^{l-1}\Big](\varphi)\Big|^p\right]^{1/p}.\end{eqnarray*}
We deal with the two terms in turn. For the case of
![]() $T_1$
, one can apply the (conditional) MZ inequality to obtain
$T_1$
, one can apply the (conditional) MZ inequality to obtain
Using
![]() $\varphi\in\mathcal{B}_b(\mathsf{X})\cap\textrm{Lip}(\mathsf{X})$
along with Remark C.2 yields
$\varphi\in\mathcal{B}_b(\mathsf{X})\cap\textrm{Lip}(\mathsf{X})$
along with Remark C.2 yields
 \begin{equation}T_1 \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{2p}}}{\sqrt{N_l}}.\end{equation}
\begin{equation}T_1 \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{2p}}}{\sqrt{N_l}}.\end{equation}
For
![]() $T_2$
, we first note that
$T_2$
, we first note that
 \begin{align*}=\left\{\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}P^l(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P^{l-1}(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\right\} -\left\{\frac{\eta_{k-1}^{l}\big(g_{k-1}P^l(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P^{l-1}(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right\},\end{align*}
\begin{align*}=\left\{\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}P^l(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P^{l-1}(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\right\} -\left\{\frac{\eta_{k-1}^{l}\big(g_{k-1}P^l(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P^{l-1}(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right\},\end{align*}
where we recall that
![]() $P^l$
(resp.
$P^l$
(resp.
![]() $P^{l-1}$
) represents the truncated Milstein kernel over unit time with discretization level
$P^{l-1}$
) represents the truncated Milstein kernel over unit time with discretization level
![]() $\Delta_l$
(resp.
$\Delta_l$
(resp.
![]() $\Delta_{l-1}$
). This can be further decomposed to
$\Delta_{l-1}$
). This can be further decomposed to
 \begin{align*}& =\Bigg\{\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})}\Bigg\}\\[5pt]& -\left\{\frac{\eta_{k-1}^{l}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right\} \end{align*}
\begin{align*}& =\Bigg\{\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})}\Bigg\}\\[5pt]& -\left\{\frac{\eta_{k-1}^{l}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right\} \end{align*}
 \begin{align*}+\left\{\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\right\} -\left\{\frac{\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right\}.\end{align*}
\begin{align*}+\left\{\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\right\} -\left\{\frac{\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right\}.\end{align*}
Therefore we have that
where
 \begin{eqnarray}T_3 & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})}\right|^{p}\right]^{1/p}, \\T_4 & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right|^{p}\right]^{1/p}, \nonumber\\T_5 & \,=\, & \mathbb{E}\Bigg[\Bigg|\left\{\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\right\} -\nonumber\\ & &\left\{\frac{\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right\}\Bigg|^{p}\Bigg]^{1/p}.\nonumber\end{eqnarray}
\begin{eqnarray}T_3 & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})}\right|^{p}\right]^{1/p}, \\T_4 & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right|^{p}\right]^{1/p}, \nonumber\\T_5 & \,=\, & \mathbb{E}\Bigg[\Bigg|\left\{\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\right\} -\nonumber\\ & &\left\{\frac{\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right\}\Bigg|^{p}\Bigg]^{1/p}.\nonumber\end{eqnarray}
The quantities
![]() $T_3$
and
$T_3$
and
![]() $T_4$
can be treated using similar calculations, so we only consider
$T_4$
can be treated using similar calculations, so we only consider
![]() $T_3$
. For the case of
$T_3$
. For the case of
![]() $T_3$
, clearly we have the upper bound
$T_3$
, clearly we have the upper bound
where
 \begin{eqnarray*}T_6 & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)-\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})}\right|^{p}\right]^{1/p}, \\T_7 & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})}\right|^{p}\right]^{1/p}.\end{eqnarray*}
\begin{eqnarray*}T_6 & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)-\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})}\right|^{p}\right]^{1/p}, \\T_7 & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})}\right|^{p}\right]^{1/p}.\end{eqnarray*}
For
![]() $T_6$
we have that
$T_6$
we have that
By using standard results for particle filters (e.g. [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6]) we have
Then, using standard results for weak errors (the truncated Milstein scheme is a first-order method), we have
For
![]() $T_7$
, again using weak errors, we have
$T_7$
, again using weak errors, we have
and again using standard results for particle filters, we obtain
Hence we have shown that
For
![]() $T_5$
, one can apply [Reference Jasra, Kamatani, Law and Zhou14, Lemma C.5] to show that
$T_5$
, one can apply [Reference Jasra, Kamatani, Law and Zhou14, Lemma C.5] to show that
 \begin{align*}T_5 \leq \sum_{j=1}^6 T_{j+7},\end{align*}
\begin{align*}T_5 \leq \sum_{j=1}^6 T_{j+7},\end{align*}
where
 \begin{eqnarray*}T_8 & \,=\, & \mathbb{E}\left[\left|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})}\left\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\right\}\right|^p\right]^{1/p}, \\T_9 & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\left\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1}) -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\right\}\right|^p\right]^{1/p},\\T_{10} & \,=\, & \mathbb{E}\left[\left|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\right|^p\right]^{1/p},\\T_{11} & \,=\, & \mathbb{E}\left[\left|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right|^p\right]^{1/p},\\T_{12} & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right|^p\right]^{1/p},\\T_{13} & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right|^p\right]^{1/p}.\end{eqnarray*}
\begin{eqnarray*}T_8 & \,=\, & \mathbb{E}\left[\left|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})}\left\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\right\}\right|^p\right]^{1/p}, \\T_9 & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\left\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1}) -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\right\}\right|^p\right]^{1/p},\\T_{10} & \,=\, & \mathbb{E}\left[\left|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\right|^p\right]^{1/p},\\T_{11} & \,=\, & \mathbb{E}\left[\left|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right|^p\right]^{1/p},\\T_{12} & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right|^p\right]^{1/p},\\T_{13} & \,=\, & \mathbb{E}\left[\left|\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right|^p\right]^{1/p}.\end{eqnarray*}
Since
![]() $T_8$
and
$T_8$
and
![]() $T_9$
can be bounded using similar approaches, we consider only
$T_9$
can be bounded using similar approaches, we consider only
![]() $T_8$
. Similarly,
$T_8$
. Similarly,
![]() $T_{10},\dots,T_{13}$
can be bounded in almost the same way, so we consider only
$T_{10},\dots,T_{13}$
can be bounded in almost the same way, so we consider only
![]() $T_{10}$
. For
$T_{10}$
. For
![]() $T_8$
we have the upper bound
$T_8$
we have the upper bound
Since
![]() $g_{k-1}P(\varphi)\in\mathcal{B}_b(\mathsf{X})\cap\textrm{Lip}(\mathsf{X})$
(see e.g. [Reference Del Moral, Jacod and Protter7, Equation (2.6)]), it follows by the induction hypothesis that
$g_{k-1}P(\varphi)\in\mathcal{B}_b(\mathsf{X})\cap\textrm{Lip}(\mathsf{X})$
(see e.g. [Reference Del Moral, Jacod and Protter7, Equation (2.6)]), it follows by the induction hypothesis that
 \begin{align*}T_8 \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{2p}}}{\sqrt{N_l}}.\end{align*}
\begin{align*}T_8 \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{2p}}}{\sqrt{N_l}}.\end{align*}
For
![]() $T_{10}$
, we have the upper bound
$T_{10}$
, we have the upper bound
Then, using [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2] and standard results for particle filters, we have
Therefore we deduce that
 \begin{equation}T_5 \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{2p}}}{\sqrt{N_l}}.\end{equation}
\begin{equation}T_5 \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{2p}}}{\sqrt{N_l}}.\end{equation}
The proof is then easily completed by combining (C.4), (C.6), and (C.7).
Remark C.3. One can also deduce the following result using an argument that is similar to (but simpler than) the proof of Lemma C.8. Assume (A1)–(A2). Then for any
![]() $(k,p)\in\mathbb{N}\times[1,\infty)$
there exists a
$(k,p)\in\mathbb{N}\times[1,\infty)$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l,\varphi)\in\mathbb{N}^2\times\mathcal{B}_b(\mathsf{X})\cap\textit{Lip}(\mathsf{X})$
,
$(l,N_l,\varphi)\in\mathbb{N}^2\times\mathcal{B}_b(\mathsf{X})\cap\textit{Lip}(\mathsf{X})$
,
 \begin{align*}\mathbb{E}\left[\big|\big[\eta_k^{N_l,l}-\eta_k^{N_l,l,a}\big](\varphi)\big|^p\right] \leq \frac{C\overline{\|\varphi\|}^p\Delta_l^{\tfrac{1}{2}}}{N_l^{\tfrac{p}{2}}}.\end{align*}
\begin{align*}\mathbb{E}\left[\big|\big[\eta_k^{N_l,l}-\eta_k^{N_l,l,a}\big](\varphi)\big|^p\right] \leq \frac{C\overline{\|\varphi\|}^p\Delta_l^{\tfrac{1}{2}}}{N_l^{\tfrac{p}{2}}}.\end{align*}
Below,
![]() $\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
denotes the collection of twice continuously differentiable functions from
$\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
denotes the collection of twice continuously differentiable functions from
![]() $\mathsf{X}$
to
$\mathsf{X}$
to
![]() $\mathbb{R}$
with bounded derivatives of orders 1 and 2.
$\mathbb{R}$
with bounded derivatives of orders 1 and 2.
Lemma C.9. Assume (A1)–(A2). Then for any
![]() $(k,p,\varphi)\in\mathbb{N}\times[1,\infty)\times\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
there exists a
$(k,p,\varphi)\in\mathbb{N}\times[1,\infty)\times\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l)\in\mathbb{N}^2$
,
$(l,N_l)\in\mathbb{N}^2$
,
 \begin{align*}\mathbb{E}\left[\big|\big[\tfrac{1}{2}\eta_k^{N_l,l}+\tfrac{1}{2}\eta_k^{N,l,a}-\eta_k^{N_l,l-1}\big](\varphi)-\big[\eta_k^l-\eta_k^{l-1}\big](\varphi)|^p\right] \leq C\left(\frac{\Delta_l^{\tfrac{1}{2}}}{N_l^{p/2}} +\frac{\Delta_l^{\tfrac{1}{2}}}{N_l^p}\right).\end{align*}
\begin{align*}\mathbb{E}\left[\big|\big[\tfrac{1}{2}\eta_k^{N_l,l}+\tfrac{1}{2}\eta_k^{N,l,a}-\eta_k^{N_l,l-1}\big](\varphi)-\big[\eta_k^l-\eta_k^{l-1}\big](\varphi)|^p\right] \leq C\left(\frac{\Delta_l^{\tfrac{1}{2}}}{N_l^{p/2}} +\frac{\Delta_l^{\tfrac{1}{2}}}{N_l^p}\right).\end{align*}
Proof. The proof is by induction. Initialization follows easily by the MZ inequality and [Reference Giles and Szpruch11, Lemma 2.2, Theorem 4.10] (the case
![]() $p\in[1,2)$
can also be covered with the theory of [Reference Giles and Szpruch11]), so we proceed immediately to the induction step.
$p\in[1,2)$
can also be covered with the theory of [Reference Giles and Szpruch11]), so we proceed immediately to the induction step.
As in the proof of Lemma C.8, one can add and subtract the conditional expectation to obtain an upper bound
where
 \begin{eqnarray*}T_1 & \,=\, & \mathbb{E}\left[|[\tfrac{1}{2}\eta_k^{N_l,l}+\tfrac{1}{2}\eta_k^{N,l,a}-\eta_k^{N_l,l-1}](\varphi)-\mathbb{E}[\tfrac{1}{2}\eta_k^{N_l,l}+\tfrac{1}{2}\eta_k^{N,l,a}-\eta_k^{N_l,l-1}](\varphi)|\mathcal{F}_{k-1}]|^p\right]^{1/p},\\T_2 & \,=\, & \mathbb{E}\left[|\mathbb{E}[\tfrac{1}{2}\eta_k^{N_l,l}+\tfrac{1}{2}\eta_k^{N,l,a}-\eta_k^{N_l,l-1}](\varphi)|\mathcal{F}_{k-1}]-[\eta_k^l-\eta_k^{l-1}](\varphi)|^p\right]^{1/p}.\end{eqnarray*}
\begin{eqnarray*}T_1 & \,=\, & \mathbb{E}\left[|[\tfrac{1}{2}\eta_k^{N_l,l}+\tfrac{1}{2}\eta_k^{N,l,a}-\eta_k^{N_l,l-1}](\varphi)-\mathbb{E}[\tfrac{1}{2}\eta_k^{N_l,l}+\tfrac{1}{2}\eta_k^{N,l,a}-\eta_k^{N_l,l-1}](\varphi)|\mathcal{F}_{k-1}]|^p\right]^{1/p},\\T_2 & \,=\, & \mathbb{E}\left[|\mathbb{E}[\tfrac{1}{2}\eta_k^{N_l,l}+\tfrac{1}{2}\eta_k^{N,l,a}-\eta_k^{N_l,l-1}](\varphi)|\mathcal{F}_{k-1}]-[\eta_k^l-\eta_k^{l-1}](\varphi)|^p\right]^{1/p}.\end{eqnarray*}
For
![]() $T_1$
one can use the conditional MZ inequality along with the boundedness of
$T_1$
one can use the conditional MZ inequality along with the boundedness of
![]() $\varphi$
, [Reference Giles and Szpruch11, Lemma 2.2], Lemma C.7, and Remark C.2 to deduce that
$\varphi$
, [Reference Giles and Szpruch11, Lemma 2.2], Lemma C.7, and Remark C.2 to deduce that
The case of
![]() $T_2$
is more challenging. We have the decomposition
$T_2$
is more challenging. We have the decomposition
where
 \begin{eqnarray}T_3 & \,=\, & \mathbb{E}\Bigg[\Bigg|\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Bigg\} \nonumber\\[3pt] & &-\Bigg\{\!\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\!\Bigg\}\Bigg|^p\Bigg]^{1/p}\!, \nonumber\\[3pt] T_4 & \,=\, & \mathbb{E}\Bigg[\Bigg|\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Bigg\} \nonumber\\[3pt] & & -\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Bigg|^p\Bigg]^{1/p}.\end{eqnarray}
\begin{eqnarray}T_3 & \,=\, & \mathbb{E}\Bigg[\Bigg|\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Bigg\} \nonumber\\[3pt] & &-\Bigg\{\!\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\!\Bigg\}\Bigg|^p\Bigg]^{1/p}\!, \nonumber\\[3pt] T_4 & \,=\, & \mathbb{E}\Bigg[\Bigg|\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Bigg\} \nonumber\\[3pt] & & -\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Bigg|^p\Bigg]^{1/p}.\end{eqnarray}
For
![]() $T_3$
one has the upper bound
$T_3$
one has the upper bound
 \begin{align*}T_3 \leq \sum_{j=1}^3 T_{j+4},\end{align*}
\begin{align*}T_3 \leq \sum_{j=1}^3 T_{j+4},\end{align*}
where
 \begin{eqnarray*}T_5 & \,=\, & \mathbb{E}\Bigg[\Bigg|\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})}\Bigg|^p\Bigg]^{1/p},\\[3pt]T_6 & \,=\, & \mathbb{E}\Bigg[\Bigg|\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})} -\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})}\Bigg|^p\Bigg]^{1/p},\\[3pt]T_7 & \,=\, &\mathbb{E}\Bigg[\Bigg|\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})} -\frac{\tfrac{1}{2}\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg|^p\Bigg]^{1/p}.\end{eqnarray*}
\begin{eqnarray*}T_5 & \,=\, & \mathbb{E}\Bigg[\Bigg|\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})}\Bigg|^p\Bigg]^{1/p},\\[3pt]T_6 & \,=\, & \mathbb{E}\Bigg[\Bigg|\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})} -\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})}\Bigg|^p\Bigg]^{1/p},\\[3pt]T_7 & \,=\, &\mathbb{E}\Bigg[\Bigg|\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})} -\frac{\tfrac{1}{2}\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg|^p\Bigg]^{1/p}.\end{eqnarray*}
Each of these terms can be controlled (almost) exactly as is done for (C.5) in the proof of Lemma C.8, so we do not give the proof; rather, we simply state that
For
![]() $T_4$
one can apply Lemma C.4 along with Minkowski to deduce that
$T_4$
one can apply Lemma C.4 along with Minkowski to deduce that
 \begin{align*}T_4 \leq \sum_{j=1}^4 T_{j+7},\end{align*}
\begin{align*}T_4 \leq \sum_{j=1}^4 T_{j+7},\end{align*}
where
 \begin{align*}T_8 & = \mathbb{E}\Bigg[\Bigg|\frac{1}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big)\\& \quad -\frac{1}{\eta_{k-1}^{l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{l}+ \tfrac{1}{2}\eta_{k-1}^{l} -\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Bigg|^p\Bigg]^{1/p},\\T_9 & = \mathbb{E}\Bigg[\Bigg|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{N_l,l-1}\\& \qquad -\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Bigg|^p\Bigg]^{1/p}, \\T_{10} & = \mathbb{E}\Bigg[\Bigg|\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}](g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{N_l,l-1}\\& \qquad -\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Bigg|^p\Bigg]^{1/p}, \\[3pt]T_{11} & = \mathbb{E}\Bigg[\Bigg|\frac{\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1})\\&\qquad -\frac{\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\times \Big[\tfrac{1}{2}\eta_{k-1}^{l}+\tfrac{1}{2}\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Bigg|^p\Bigg]^{1/p}.\end{align*}
\begin{align*}T_8 & = \mathbb{E}\Bigg[\Bigg|\frac{1}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big)\\& \quad -\frac{1}{\eta_{k-1}^{l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{l}+ \tfrac{1}{2}\eta_{k-1}^{l} -\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Bigg|^p\Bigg]^{1/p},\\T_9 & = \mathbb{E}\Bigg[\Bigg|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{N_l,l-1}\\& \qquad -\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Bigg|^p\Bigg]^{1/p}, \\T_{10} & = \mathbb{E}\Bigg[\Bigg|\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}](g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{N_l,l-1}\\& \qquad -\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Bigg|^p\Bigg]^{1/p}, \\[3pt]T_{11} & = \mathbb{E}\Bigg[\Bigg|\frac{\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1})\\&\qquad -\frac{\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\times \Big[\tfrac{1}{2}\eta_{k-1}^{l}+\tfrac{1}{2}\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Bigg|^p\Bigg]^{1/p}.\end{align*}
As the arguments for dealing with
![]() $T_8$
(resp.
$T_8$
(resp.
![]() $T_9$
) and
$T_9$
) and
![]() $T_{11}$
(resp.
$T_{11}$
(resp.
![]() $T_{10}$
) are similar, we only prove bounds for
$T_{10}$
) are similar, we only prove bounds for
![]() $T_8$
(resp.
$T_8$
(resp.
![]() $T_9$
). For
$T_9$
). For
![]() $T_8$
we have the upper bound
$T_8$
we have the upper bound
where
 \begin{align*}T_{12} & = \mathbb{E}\Bigg[\Bigg|\frac{1}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Bigg\{\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) -\Big[\tfrac{1}{2}\eta_{k-1}^{l}+\tfrac{1}{2}\eta_{k-1}^{l}\\ &-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Bigg\}\Bigg|^p\Bigg]^{1/p}, \\ T_{13} & = \mathbb{E}\Bigg[\Bigg|\frac{\Big[\tfrac{1}{2}\eta_{k-1}^{l}+\tfrac{1}{2}\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1})\Bigg|^p\Bigg]^{1/p}.\end{align*}
\begin{align*}T_{12} & = \mathbb{E}\Bigg[\Bigg|\frac{1}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Bigg\{\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) -\Big[\tfrac{1}{2}\eta_{k-1}^{l}+\tfrac{1}{2}\eta_{k-1}^{l}\\ &-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Bigg\}\Bigg|^p\Bigg]^{1/p}, \\ T_{13} & = \mathbb{E}\Bigg[\Bigg|\frac{\Big[\tfrac{1}{2}\eta_{k-1}^{l}+\tfrac{1}{2}\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1})\Bigg|^p\Bigg]^{1/p}.\end{align*}
For
![]() $T_{12}$
one can use the lower bound on
$T_{12}$
one can use the lower bound on
![]() $g_{k-1}$
along with
$g_{k-1}$
along with
![]() $g_{k-1}P(\varphi)\in\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
(see e.g. [Reference Stroock23, Corollary 2.2.8]) and the induction hypothesis to obtain
$g_{k-1}P(\varphi)\in\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
(see e.g. [Reference Stroock23, Corollary 2.2.8]) and the induction hypothesis to obtain
For
![]() $T_{13}$
we apply [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2] and standard results for particle filters to obtain
$T_{13}$
we apply [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2] and standard results for particle filters to obtain
Thus
For
![]() $T_9$
we have the upper bound
$T_9$
we have the upper bound
where
 \begin{eqnarray*}T_{14} & \,=\, & \mathbb{E}\Bigg[\Bigg|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\\& &-\Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{l}\Big](g_{k-1})\Big\}\Bigg|^p\Bigg]^{1/p}, \\T_{15} & \,=\, & \mathbb{E}\Bigg[\Bigg|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{l}\Big](g_{k-1})\Big\}\Bigg|^p\Bigg]^{1/p}.\end{eqnarray*}
\begin{eqnarray*}T_{14} & \,=\, & \mathbb{E}\Bigg[\Bigg|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\\& &-\Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{l}\Big](g_{k-1})\Big\}\Bigg|^p\Bigg]^{1/p}, \\T_{15} & \,=\, & \mathbb{E}\Bigg[\Bigg|\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{l}\Big](g_{k-1})\Big\}\Bigg|^p\Bigg]^{1/p}.\end{eqnarray*}
For
![]() $T_{14}$
one can use the lower bound on
$T_{14}$
one can use the lower bound on
![]() $g_{k-1}$
, Cauchy–Schwarz, Remark C.3, and Lemma C.8 to obtain
$g_{k-1}$
, Cauchy–Schwarz, Remark C.3, and Lemma C.8 to obtain
For
![]() $T_{15}$
one can use the lower bound on
$T_{15}$
one can use the lower bound on
![]() $g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], and Remark C.3 to obtain
$g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], and Remark C.3 to obtain
thus,
Therefore we have shown that
 \begin{equation}T_{4} \leq \frac{C}{\sqrt{N_l}}\left(\Delta_l^{1/2} + \frac{\Delta_l^{\tfrac{1}{2}}}{N_l^{p/2}}\right)^{1/p}.\end{equation}
\begin{equation}T_{4} \leq \frac{C}{\sqrt{N_l}}\left(\Delta_l^{1/2} + \frac{\Delta_l^{\tfrac{1}{2}}}{N_l^{p/2}}\right)^{1/p}.\end{equation}
The proof can be completed by combining the bounds (C.8), (C.10), and (C.11).
Theorem 2. Assume (A1)–(A2). Then for any
![]() $(k,p,\varphi)\in\mathbb{N}\times[1,\infty)\times\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
there exists a
$(k,p,\varphi)\in\mathbb{N}\times[1,\infty)\times\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l)\in\mathbb{N}^2$
,
$(l,N_l)\in\mathbb{N}^2$
,
 \begin{align*}\mathbb{E}\left[\big|\big[\pi_k^l-\pi_{k}^{l-1}\big]^{N_l}(\varphi) -\big[\pi_k^l-\pi_{k}^{l-1}\big](\varphi)\big|^p\right] \leq C\left(\frac{\Delta_l^{1/2}}{N_l^{p/2}} +\frac{\Delta_l^{\tfrac{1}{2}}}{N_l^p}\right).\end{align*}
\begin{align*}\mathbb{E}\left[\big|\big[\pi_k^l-\pi_{k}^{l-1}\big]^{N_l}(\varphi) -\big[\pi_k^l-\pi_{k}^{l-1}\big](\varphi)\big|^p\right] \leq C\left(\frac{\Delta_l^{1/2}}{N_l^{p/2}} +\frac{\Delta_l^{\tfrac{1}{2}}}{N_l^p}\right).\end{align*}
C.3. Particle convergence proofs: bias bounds
Lemma C.10. Assume (A1)–(A2). Then for any
![]() $k\in\mathbb{N}$
there exists a
$k\in\mathbb{N}$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l,\varphi)\in\mathbb{N}^2\times\mathcal{B}_b(\mathsf{X})\cap\textit{Lip}(\mathsf{X})$
,
$(l,N_l,\varphi)\in\mathbb{N}^2\times\mathcal{B}_b(\mathsf{X})\cap\textit{Lip}(\mathsf{X})$
,
 \begin{align*}\left|\mathbb{E}\left[\Big[\eta_k^{N_l,l}-\eta_k^{N_l,l-1}\Big](\varphi)-\big[\eta_k^l-\eta_k^{l-1}\big](\varphi)\right]\right| \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
\begin{align*}\left|\mathbb{E}\left[\Big[\eta_k^{N_l,l}-\eta_k^{N_l,l-1}\Big](\varphi)-\big[\eta_k^l-\eta_k^{l-1}\big](\varphi)\right]\right| \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
Proof. The proof is by induction. The case
![]() $k=1$
is trivial as there is no bias, so we proceed to the induction step. Following the proof of Lemma C.8, we have the decomposition
$k=1$
is trivial as there is no bias, so we proceed to the induction step. Following the proof of Lemma C.8, we have the decomposition
where
 \begin{align*}T_1 & = \left|\mathbb{E}\left[\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})}\right]\right|, \\[3pt]T_2 & = \left|\mathbb{E}\left[\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right]\right|, \\[3pt]T_3 & = \Bigg|\mathbb{E}\Bigg[\left\{\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\right\}\\& \qquad -\Bigg\{\frac{\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} - \frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Bigg]\Bigg|.\end{align*}
\begin{align*}T_1 & = \left|\mathbb{E}\left[\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})}\right]\right|, \\[3pt]T_2 & = \left|\mathbb{E}\left[\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\right]\right|, \\[3pt]T_3 & = \Bigg|\mathbb{E}\Bigg[\left\{\frac{\eta_{k-1}^{N_l,l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\right\}\\& \qquad -\Bigg\{\frac{\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} - \frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Bigg]\Bigg|.\end{align*}
![]() $T_1$
and
$T_1$
and
![]() $T_2$
can be bounded using almost the same calculations, so we consider only
$T_2$
can be bounded using almost the same calculations, so we consider only
![]() $T_1$
. The latter can easily be bounded above by
$T_1$
. The latter can easily be bounded above by
![]() $\sum_{j=1}^4 T_{j+3}$
, where
$\sum_{j=1}^4 T_{j+3}$
, where
 \begin{eqnarray*}T_4 & \,=\, & \left|\mathbb{E}\left[\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})}-\frac{1}{\eta_{k-1}^{l}(g_{k-1})}\Bigg\}\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{l}\Big]\big(g_{k-1}[P^l-P](\varphi)\big)\right]\right|,\\T_5 & \,=\, & \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{l}(g_{k-1})}\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{l}\Big]\big(g_{k-1}[P^l-P](\varphi)\big)\right]\right|,\\T_6 & \,=\, & \left|\mathbb{E}\left[\eta_{k-1}^{l}\big(g_{k-1}[P^l-P](\varphi)\big)\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})}-\frac{1}{\eta_{k-1}^{l}(g_{k-1})^2}\Bigg\}\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\right]\right|,\\T_7 & \,=\, & \left|\mathbb{E}\left[\frac{\eta_{k-1}^{l}\big(g_{k-1}[P^l-P](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})^2}\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\right]\right|.\end{eqnarray*}
\begin{eqnarray*}T_4 & \,=\, & \left|\mathbb{E}\left[\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})}-\frac{1}{\eta_{k-1}^{l}(g_{k-1})}\Bigg\}\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{l}\Big]\big(g_{k-1}[P^l-P](\varphi)\big)\right]\right|,\\T_5 & \,=\, & \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{l}(g_{k-1})}\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{l}\Big]\big(g_{k-1}[P^l-P](\varphi)\big)\right]\right|,\\T_6 & \,=\, & \left|\mathbb{E}\left[\eta_{k-1}^{l}\big(g_{k-1}[P^l-P](\varphi)\big)\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})}-\frac{1}{\eta_{k-1}^{l}(g_{k-1})^2}\Bigg\}\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\right]\right|,\\T_7 & \,=\, & \left|\mathbb{E}\left[\frac{\eta_{k-1}^{l}\big(g_{k-1}[P^l-P](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})^2}\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\right]\right|.\end{eqnarray*}
For both
![]() $T_4$
and
$T_4$
and
![]() $T_6$
, one can use the Cauchy–Schwarz inequality, along with [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6], the lower bound on
$T_6$
, one can use the Cauchy–Schwarz inequality, along with [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6], the lower bound on
![]() $g_{k-1}$
, and weak-error results for diffusions to show that
$g_{k-1}$
, and weak-error results for diffusions to show that
For
![]() $T_5$
and
$T_5$
and
![]() $T_7$
one can use standard bias bounds for particle filters (see e.g. the proof of [Reference Jasra, Kamatani, Law and Zhou14, Lemma C.3]), the lower bound on
$T_7$
one can use standard bias bounds for particle filters (see e.g. the proof of [Reference Jasra, Kamatani, Law and Zhou14, Lemma C.3]), the lower bound on
![]() $g_{k-1}$
, and weak-error results for diffusions to obtain
$g_{k-1}$
, and weak-error results for diffusions to obtain
hence
For
![]() $T_3$
, using [Reference Jasra, Kamatani, Law and Zhou14, Lemma C.5] we have the upper bound
$T_3$
, using [Reference Jasra, Kamatani, Law and Zhou14, Lemma C.5] we have the upper bound
![]() $T_3\leq\sum_{j=1}^6 T_{j+7}$
, where
$T_3\leq\sum_{j=1}^6 T_{j+7}$
, where
 \begin{align*}T_8 & = \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})}\left\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\right\}\right]\right|, \\[3pt]T_9 & = \left|\mathbb{E}\left[\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\left\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1}) -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\right\}\right]\right|,\\[3pt]T_{10} & = \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\}\right]\right|,\\[3pt]T_{11} & = \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right]\right|,\\[3pt]T_{12} & = \left|\mathbb{E}\left[\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right]\right|,\\[3pt]T_{13} & = \left|\mathbb{E}\left[\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right]\right|.\end{align*}
\begin{align*}T_8 & = \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})}\left\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\right\}\right]\right|, \\[3pt]T_9 & = \left|\mathbb{E}\left[\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\left\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1}) -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\right\}\right]\right|,\\[3pt]T_{10} & = \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\}\right]\right|,\\[3pt]T_{11} & = \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right]\right|,\\[3pt]T_{12} & = \left|\mathbb{E}\left[\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right]\right|,\\[3pt]T_{13} & = \left|\mathbb{E}\left[\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Big\}\right]\right|.\end{align*}
Since
![]() $T_8$
and
$T_8$
and
![]() $T_9$
can be bounded using similar approaches, we consider only
$T_9$
can be bounded using similar approaches, we consider only
![]() $T_8$
. Similarly,
$T_8$
. Similarly,
![]() $T_{10},\dots,T_{13}$
can be bounded in almost the same way, so we consider only
$T_{10},\dots,T_{13}$
can be bounded in almost the same way, so we consider only
![]() $T_{10}$
. For
$T_{10}$
. For
![]() $T_8$
one has
$T_8$
one has
![]() $T_8\leq T_{14}+T_{15}$
, where
$T_8\leq T_{14}+T_{15}$
, where
 \begin{align*}T_{14} & = \Bigg|\mathbb{E}\Bigg[\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})}-\frac{1}{\eta_{k-1}^{l}(g_{k-1})}\Bigg\}\Bigg\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big)\\& \qquad - \Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Bigg\}\Bigg]\Bigg|, \\T_{15} & = \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{l}(g_{k-1})}\left\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\right\}\right]\right|.\end{align*}
\begin{align*}T_{14} & = \Bigg|\mathbb{E}\Bigg[\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})}-\frac{1}{\eta_{k-1}^{l}(g_{k-1})}\Bigg\}\Bigg\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big)\\& \qquad - \Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Bigg\}\Bigg]\Bigg|, \\T_{15} & = \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{l}(g_{k-1})}\left\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\right\}\right]\right|.\end{align*}
For
![]() $T_{14}$
one can use Cauchy–Schwarz, the lower bound on
$T_{14}$
one can use Cauchy–Schwarz, the lower bound on
![]() $g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6], and Lemma C.8. For
$g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6], and Lemma C.8. For
![]() $T_{15}$
we can apply the lower bound on
$T_{15}$
we can apply the lower bound on
![]() $g_{k-1}$
and the induction hypothesis. These two arguments give that
$g_{k-1}$
and the induction hypothesis. These two arguments give that
 \begin{align*}\max\{T_{14},T_{15}\} \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{4}}}{N_l}\end{align*}
\begin{align*}\max\{T_{14},T_{15}\} \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{4}}}{N_l}\end{align*}
and hence that
 \begin{align*}T_8 \leq\frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
\begin{align*}T_8 \leq\frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
For
![]() $T_{10}$
we have the upper bound
$T_{10}$
we have the upper bound
![]() $T_{10}\leq T_{16}+T_{17}$
, where
$T_{10}\leq T_{16}+T_{17}$
, where
 \begin{eqnarray*}T_{16} & \,=\, & \Bigg|\mathbb{E}\Bigg[\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})}-\frac{1}{\eta_{k-1}^{l}(g_{k-1})^2}\Bigg\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\\ & &\times\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Bigg]\Bigg|,\\ T_{17} & \,=\, & \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{l}(g_{k-1})^2}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\right]\right|.\end{eqnarray*}
\begin{eqnarray*}T_{16} & \,=\, & \Bigg|\mathbb{E}\Bigg[\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{l}(g_{k-1})}-\frac{1}{\eta_{k-1}^{l}(g_{k-1})^2}\Bigg\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\\ & &\times\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Bigg]\Bigg|,\\ T_{17} & \,=\, & \left|\mathbb{E}\left[\frac{1}{\eta_{k-1}^{l}(g_{k-1})^2}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\right]\right|.\end{eqnarray*}
For
![]() $T_{15}$
one can use Cauchy–Schwarz, the lower bound on
$T_{15}$
one can use Cauchy–Schwarz, the lower bound on
![]() $g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6] (twice), and [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2]. For
$g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6] (twice), and [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2]. For
![]() $T_{16}$
we can apply the lower bound on
$T_{16}$
we can apply the lower bound on
![]() $g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], and bias results for particle filters. These two arguments give
$g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], and bias results for particle filters. These two arguments give
and thus
Thus we have proved that
 \begin{equation} T_2 \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{equation}
\begin{equation} T_2 \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{equation}
Remark C.4. Using the approach in the proof of Lemma C.10, one can also prove the following result. Assume (A1)–(A2). Then for any
![]() $k\in\mathbb{N}$
there exists a
$k\in\mathbb{N}$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l,\varphi)\in\mathbb{N}^2\times\mathcal{B}_b(\mathsf{X})\cap\textit{Lip}(\mathsf{X})$
,
$(l,N_l,\varphi)\in\mathbb{N}^2\times\mathcal{B}_b(\mathsf{X})\cap\textit{Lip}(\mathsf{X})$
,
 \begin{align*}\left|\mathbb{E}\left[\Big[\eta_k^{N_l,l}-\eta_k^{N_l,a}\Big](\varphi)\right]\right| \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
\begin{align*}\left|\mathbb{E}\left[\Big[\eta_k^{N_l,l}-\eta_k^{N_l,a}\Big](\varphi)\right]\right| \leq \frac{C\overline{\|\varphi\|}\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
Lemma C.11 . Assume (A1)–(A2). Then for any
![]() $(k,\varphi)\in\mathbb{N}\times\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
there exists a
$(k,\varphi)\in\mathbb{N}\times\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l,\varepsilon)\in\mathbb{N}^2\times(0,1/2)$
,
$(l,N_l,\varepsilon)\in\mathbb{N}^2\times(0,1/2)$
,
 \begin{align*}\left|\mathbb{E}\left[\Big[\tfrac{1}{2}\eta_k^{N_l,l}+\tfrac{1}{2}\eta_k^{N,l,a}-\eta_k^{N_l,l-1}\Big](\varphi)-\Big[\eta_k^l-\eta_k^{l-1}\Big](\varphi)\right]\right| \leq \frac{C\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
\begin{align*}\left|\mathbb{E}\left[\Big[\tfrac{1}{2}\eta_k^{N_l,l}+\tfrac{1}{2}\eta_k^{N,l,a}-\eta_k^{N_l,l-1}\Big](\varphi)-\Big[\eta_k^l-\eta_k^{l-1}\Big](\varphi)\right]\right| \leq \frac{C\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
Proof. The proof is by induction. The case
![]() $k=1$
is trivial as there is no bias, so we proceed to the induction step. Following the proof of Lemma C.9, we have the decomposition
$k=1$
is trivial as there is no bias, so we proceed to the induction step. Following the proof of Lemma C.9, we have the decomposition
where
 \begin{align}T_1 & = \Bigg|\mathbb{E}\Bigg[\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})}\nonumber\\& \qquad -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Bigg\}- \nonumber\\[3pt] &\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Bigg]\Bigg|, \nonumber\\[3pt] T_2 & = \Bigg|\mathbb{E}\Bigg[\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Bigg\} \nonumber\\[3pt] &-\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Bigg]\Bigg|.\end{align}
\begin{align}T_1 & = \Bigg|\mathbb{E}\Bigg[\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})}\nonumber\\& \qquad -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Bigg\}- \nonumber\\[3pt] &\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}\big[P^l-P\big](\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}\big[P^{l-1}-P\big](\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Bigg]\Bigg|, \nonumber\\[3pt] T_2 & = \Bigg|\mathbb{E}\Bigg[\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})} -\frac{\eta_{k-1}^{N_l,l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Bigg\} \nonumber\\[3pt] &-\Bigg\{\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} +\frac{\tfrac{1}{2}\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})} -\frac{\eta_{k-1}^{l-1}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Bigg]\Bigg|.\end{align}
For
![]() $T_1$
one can match the empirical and limit terms across the
$T_1$
one can match the empirical and limit terms across the
![]() $l,a,l-1$
and adopt the same proof approach as used for
$l,a,l-1$
and adopt the same proof approach as used for
![]() $T_1$
in the proof of Lemma C.10; since the proof would be repeated, we omit it and remark only that
$T_1$
in the proof of Lemma C.10; since the proof would be repeated, we omit it and remark only that
For
![]() $T_2$
, using Lemma C.4 and the triangle inequality, we have that
$T_2$
, using Lemma C.4 and the triangle inequality, we have that
![]() $T_2\leq\sum_{j=1}^4 T_{j+2}$
, where
$T_2\leq\sum_{j=1}^4 T_{j+2}$
, where
 \begin{align*}T_3 & = \Bigg|\mathbb{E}\Bigg[\frac{1}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) -\frac{1}{\eta_{k-1}^{l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{l}\\ & +\tfrac{1}{2}\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Bigg]\Bigg|,\\ T_4 & = \Bigg|\mathbb{E}\Bigg[\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\big\{\big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{N_l,l}\big](g_{k-1})\big\}\Bigg]\Bigg|,\end{align*}
\begin{align*}T_3 & = \Bigg|\mathbb{E}\Bigg[\frac{1}{\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) -\frac{1}{\eta_{k-1}^{l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{l}\\ & +\tfrac{1}{2}\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Bigg]\Bigg|,\\ T_4 & = \Bigg|\mathbb{E}\Bigg[\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\big\{\big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{N_l,l}\big](g_{k-1})\big\}\Bigg]\Bigg|,\end{align*}
 \begin{align*}T_{5} & = \Bigg|\mathbb{E}\Bigg[\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}](g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{N_l,l-1}\\& \qquad -\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Bigg]\Bigg|,\\T_{6} & = \Bigg|\mathbb{E}\Bigg[\frac{\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1})\\& -\frac{\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\times \Big[\tfrac{1}{2}\eta_{k-1}^{l}+\tfrac{1}{2}\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Bigg]\Bigg|.\end{align*}
\begin{align*}T_{5} & = \Bigg|\mathbb{E}\Bigg[\frac{\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}](g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Big\{\Big[\eta_{k-1}^{N_l,l-1}\\& \qquad -\eta_{k-1}^{N_l,l}\Big](g_{k-1})\Big\}\Bigg]\Bigg|,\\T_{6} & = \Bigg|\mathbb{E}\Bigg[\frac{\eta_{k-1}^{N_l,l,a}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{N_l,l,a}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1})\\& -\frac{\eta_{k-1}^{l}\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\times \Big[\tfrac{1}{2}\eta_{k-1}^{l}+\tfrac{1}{2}\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big](g_{k-1})\Bigg]\Bigg|.\end{align*}
As
![]() $T_3$
(resp.
$T_3$
(resp.
![]() $T_4$
) and
$T_4$
) and
![]() $T_{6}$
(resp.
$T_{6}$
(resp.
![]() $T_{5}$
) can be dealt with using similar arguments, we only prove bounds for
$T_{5}$
) can be dealt with using similar arguments, we only prove bounds for
![]() $T_3$
(resp.
$T_3$
(resp.
![]() $T_4$
). For
$T_4$
). For
![]() $T_3$
we have the upper bound
$T_3$
we have the upper bound
![]() $T_3\leq\sum_{j=1}^4 T_{j+6}$
, where
$T_3\leq\sum_{j=1}^4 T_{j+6}$
, where
 \begin{align*}T_7 & = \Bigg|\mathbb{E}\Bigg[\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l-1}(g_{k-1})} -\frac{1}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Big\{\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) \\ & \qquad \qquad -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Bigg]\Bigg|,\\ T_8 & = \Bigg|\mathbb{E}\Bigg[\frac{1}{\eta_{k-1}^{l-1}(g_{k-1})}\Big\{\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big)\\ & \qquad -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\} \Bigg]\Bigg|,\\ T_9 & = \Bigg|\mathbb{E}\Bigg[\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l-1}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})} -\frac{1}{\eta_{k-1}^{l-1}(g_{k-1})^2}\Bigg\}\\ & \qquad \times\big[\eta_{k-1}^{l-1}-\eta_{k-1}^{N_l,l-1}\big](g_{k-1})\Bigg]\Bigg|,\\ T_{10} & = \Bigg|\mathbb{E}\Bigg[\frac{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})^2}\Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1})\Bigg]\Bigg|.\end{align*}
\begin{align*}T_7 & = \Bigg|\mathbb{E}\Bigg[\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l-1}(g_{k-1})} -\frac{1}{\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Big\{\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big) \\ & \qquad \qquad -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Bigg]\Bigg|,\\ T_8 & = \Bigg|\mathbb{E}\Bigg[\frac{1}{\eta_{k-1}^{l-1}(g_{k-1})}\Big\{\Big[\tfrac{1}{2}\eta_{k-1}^{N_l,l}+\tfrac{1}{2}\eta_{k-1}^{N_l,l,a}-\eta_{k-1}^{N_l,l-1}\Big]\big(g_{k-1}P(\varphi)\big)\\ & \qquad -\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Big\} \Bigg]\Bigg|,\\ T_9 & = \Bigg|\mathbb{E}\Bigg[\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l-1}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})} -\frac{1}{\eta_{k-1}^{l-1}(g_{k-1})^2}\Bigg\}\\ & \qquad \times\big[\eta_{k-1}^{l-1}-\eta_{k-1}^{N_l,l-1}\big](g_{k-1})\Bigg]\Bigg|,\\ T_{10} & = \Bigg|\mathbb{E}\Bigg[\frac{\Big[\eta_{k-1}^{l}-\eta_{k-1}^{l-1}\Big]\big(g_{k-1}P(\varphi)\big)}{\eta_{k-1}^{l-1}(g_{k-1})^2}\Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{N_l,l-1}\Big](g_{k-1})\Bigg]\Bigg|.\end{align*}
For
![]() $T_7$
one can use Cauchy–Schwarz, the lower bound on
$T_7$
one can use Cauchy–Schwarz, the lower bound on
![]() $g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6], and Lemma C.9. For
$g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6], and Lemma C.9. For
![]() $T_8$
we can apply the lower bound on
$T_8$
we can apply the lower bound on
![]() $g_{k-1}$
and the induction hypothesis. These arguments yield
$g_{k-1}$
and the induction hypothesis. These arguments yield
 \begin{align*}\max\{T_7,T_8\} \leq \frac{C\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
\begin{align*}\max\{T_7,T_8\} \leq \frac{C\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
For
![]() $T_9$
we can use [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], Cauchy–Schwarz, the lower bound on
$T_9$
we can use [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], Cauchy–Schwarz, the lower bound on
![]() $g_{k-1}$
, and [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6] twice. For
$g_{k-1}$
, and [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6] twice. For
![]() $T_{10}$
we can use [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], the lower bound on
$T_{10}$
we can use [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], the lower bound on
![]() $g_{k-1}$
, and standard bias results for particle filters. This gives
$g_{k-1}$
, and standard bias results for particle filters. This gives
Collecting the above arguments, we have shown that
 \begin{align*}T_3 \leq \frac{C\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
\begin{align*}T_3 \leq \frac{C\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
For
![]() $T_4$
we have the upper bound
$T_4$
we have the upper bound
![]() $T_4\leq\sum_{j=1}^3 T_{j+10}$
, where
$T_4\leq\sum_{j=1}^3 T_{j+10}$
, where
 \begin{align*}T_{11} & = \Bigg|\mathbb{E}\Bigg[\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{N_l,l}\Big](g_{k-1}) \\ & \qquad\qquad - \Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{l}\Big](g_{k-1})\Big\}\Bigg]\Bigg|, \\ T_{12} & = \Bigg|\mathbb{E}\Bigg[\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{l}\Big](g_{k-1})\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\\ & \qquad \qquad - \frac{1}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Bigg]\Bigg|, \\[3pt] T_{13} & = \Bigg|\mathbb{E}\Bigg[\frac{[\eta_{k-1}^{l-1}-\eta_{k-1}^{l}](g_{k-1})}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Bigg]\Bigg|.\end{align*}
\begin{align*}T_{11} & = \Bigg|\mathbb{E}\Bigg[\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big\{\Big[\eta_{k-1}^{N_l,l-1}-\eta_{k-1}^{N_l,l}\Big](g_{k-1}) \\ & \qquad\qquad - \Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{l}\Big](g_{k-1})\Big\}\Bigg]\Bigg|, \\ T_{12} & = \Bigg|\mathbb{E}\Bigg[\tfrac{1}{2}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Big[\eta_{k-1}^{l-1}-\eta_{k-1}^{l}\Big](g_{k-1})\Bigg\{\frac{1}{\eta_{k-1}^{N_l,l}(g_{k-1})\eta_{k-1}^{N_l,l-1}(g_{k-1})}\\ & \qquad \qquad - \frac{1}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\Bigg\}\Bigg]\Bigg|, \\[3pt] T_{13} & = \Bigg|\mathbb{E}\Bigg[\frac{[\eta_{k-1}^{l-1}-\eta_{k-1}^{l}](g_{k-1})}{\eta_{k-1}^{l}(g_{k-1})\eta_{k-1}^{l-1}(g_{k-1})}\Big\{\Big[\eta_{k-1}^{N_l,l}-\eta_{k-1}^{N_l,l,a}\Big]\big(g_{k-1}P(\varphi)\big)\Big\}\Bigg]\Bigg|.\end{align*}
For
![]() $T_{11}$
one can use the lower bound on
$T_{11}$
one can use the lower bound on
![]() $g_{k-1}$
, Cauchy–Schwarz, Remark C.3, and Lemma C.9. For
$g_{k-1}$
, Cauchy–Schwarz, Remark C.3, and Lemma C.9. For
![]() $T_{12}$
we can apply [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], Cauchy–Schwarz, the lower bound on
$T_{12}$
we can apply [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2], Cauchy–Schwarz, the lower bound on
![]() $g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6], and Remark C.3. For
$g_{k-1}$
, [Reference Jasra, Kamatani, Law and Zhou14, Proposition C.6], and Remark C.3. For
![]() $T_{13}$
we can use the lower bound on
$T_{13}$
we can use the lower bound on
![]() $g_{k-1}$
, Remark C.4, and [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2]. Putting these results together, we have established that
$g_{k-1}$
, Remark C.4, and [Reference Jasra, Kamatani, Law and Zhou14, Lemma D.2]. Putting these results together, we have established that
 \begin{align*}\max\{T_{11},T_{12},T_{13}\} \leq\frac{C\Delta_l^{\tfrac{1}{4}}}{N_l},\end{align*}
\begin{align*}\max\{T_{11},T_{12},T_{13}\} \leq\frac{C\Delta_l^{\tfrac{1}{4}}}{N_l},\end{align*}
and thus we can deduce the same upper bound (up to a constant) for
![]() $T_4$
. As a result of the above arguments, we have established that
$T_4$
. As a result of the above arguments, we have established that
 \begin{equation}T_2 \leq \frac{C\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{equation}
\begin{equation}T_2 \leq \frac{C\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{equation}
Theorem 3. Assume (A1)–(A2). Then for any
![]() $(k,\varphi)\in\mathbb{N}\times\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
there exists a
$(k,\varphi)\in\mathbb{N}\times\mathcal{B}_b(\mathsf{X})\cap\mathcal{C}_b^2(\mathsf{X},\mathbb{R})$
there exists a
![]() $C<+\infty$
such that for any
$C<+\infty$
such that for any
![]() $(l,N_l)\in\mathbb{N}^2$
,
$(l,N_l)\in\mathbb{N}^2$
,
 \begin{align*}\left|\mathbb{E}\left[\big[\pi_k^l-\pi_{k}^{l-1}\big]^{N_l}(\varphi) -\big[\pi_k^l-\pi_{k}^{l-1}\big](\varphi)\right]\right| \leq\frac{C\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
\begin{align*}\left|\mathbb{E}\left[\big[\pi_k^l-\pi_{k}^{l-1}\big]^{N_l}(\varphi) -\big[\pi_k^l-\pi_{k}^{l-1}\big](\varphi)\right]\right| \leq\frac{C\Delta_l^{\tfrac{1}{4}}}{N_l}.\end{align*}
Acknowledgements
All of the authors were supported by KAUST baseline funding. We thank two referees and an editor for their valuable comments, which greatly improved the article.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.