Published online by Cambridge University Press: 12 April 2022
We examine the degree structure  $\operatorname {\mathrm {\mathbf {ER}}}$ of equivalence relations on
$\operatorname {\mathrm {\mathbf {ER}}}$ of equivalence relations on 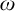 $\omega $ under computable reducibility. We examine when pairs of degrees have a least upper bound. In particular, we show that sufficiently incomparable pairs of degrees do not have a least upper bound but that some incomparable degrees do, and we characterize the degrees which have a least upper bound with every finite equivalence relation. We show that the natural classes of finite, light, and dark degrees are definable in
$\omega $ under computable reducibility. We examine when pairs of degrees have a least upper bound. In particular, we show that sufficiently incomparable pairs of degrees do not have a least upper bound but that some incomparable degrees do, and we characterize the degrees which have a least upper bound with every finite equivalence relation. We show that the natural classes of finite, light, and dark degrees are definable in  $\operatorname {\mathrm {\mathbf {ER}}}$. We show that every equivalence relation has continuum many self-full strong minimal covers, and that
$\operatorname {\mathrm {\mathbf {ER}}}$. We show that every equivalence relation has continuum many self-full strong minimal covers, and that 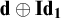 $\mathbf {d}\oplus \mathbf {\operatorname {\mathrm {\mathbf {Id}}}_1}$ needn’t be a strong minimal cover of a self-full degree
$\mathbf {d}\oplus \mathbf {\operatorname {\mathrm {\mathbf {Id}}}_1}$ needn’t be a strong minimal cover of a self-full degree 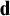 $\mathbf {d}$. Finally, we show that the theory of the degree structure
$\mathbf {d}$. Finally, we show that the theory of the degree structure  $\operatorname {\mathrm {\mathbf {ER}}}$ as well as the theories of the substructures of light degrees and of dark degrees are each computably isomorphic with second-order arithmetic.
$\operatorname {\mathrm {\mathbf {ER}}}$ as well as the theories of the substructures of light degrees and of dark degrees are each computably isomorphic with second-order arithmetic.