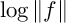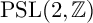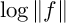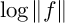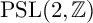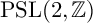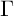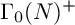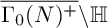KRONECKER LIMIT FUNCTIONS AND AN EXTENSION OF THE ROHRLICH–JENSEN FORMULA

Abstract

In [20], Rohrlich proved a modular analog of Jensen’s formula. Under certain conditions, the Rohrlich–Jensen formula expresses an integral of the log-norm $\log \Vert f \Vert $ of a ${\mathrm {PSL}}(2,{\mathbb {Z}})$ modular form f in terms of the Dedekind Delta function evaluated at the divisor of f. In [2], the authors re-interpreted the Rohrlich–Jensen formula as evaluating a regularized inner product of $\log \Vert f \Vert $ and extended the result to compute a regularized inner product of $\log \Vert f \Vert $ with what amounts to powers of the Hauptmodul of $\mathrm {PSL}(2,{\mathbb {Z}})$. In the present article, we revisit the Rohrlich–Jensen formula and prove that in the case of any Fuchsian group of the first kind with one cusp it can be viewed as a regularized inner product of special values of two Poincaré series, one of which is the Niebur–Poincaré series and the other is the resolvent kernel of the Laplacian. The regularized inner product can be seen as a type of Maass–Selberg relation. In this form, we develop a Rohrlich–Jensen formula associated with any Fuchsian group $\Gamma $ of the first kind with one cusp by employing a type of Kronecker limit formula associated with the resolvent kernel. We present two examples of our main result: First, when $\Gamma $ is the full modular group ${\mathrm {PSL}}(2,{\mathbb {Z}})$, thus reproving the theorems from [2]; and second when $\Gamma $ is an Atkin–Lehner group $\Gamma _{0}(N)^+$, where explicit computations of inner products are given for certain levels N when the quotient space $\overline {\Gamma _{0}(N)^+}\backslash \mathbb {H}$ has genus zero, one, and two.

1 Introduction and statement of results

1.1 The Poisson–Jensen formula

Let $D_{R} = \{z =x+iy\in {\mathbb C} : \vert z \vert < R\}$ be the disk of radius R centered at the origin in the complex plane ${\mathbb C}$ . Let F be a nonconstant meromorphic function on the closure $\overline {D_{R}}$ of $D_{R}$ . Denote by $c_{F}$ the leading nonzero coefficient of F at zero, meaning that for some integer m, we have that $F(z) = c_{F}z^{m} + O(z^{m+1})$ as z approaches zero. For any $a \in D_{R}$ , let $n_{F}(a)$ denote the order of F at a; there are a finite number of points a for which $n_{F}(a) \neq 0$ ; in this notation, $n_{F}(0) = m$ . Jensen’s formula, as stated on page 341 of [18], asserts that

(1) $$ \begin{align} \frac{1}{2\pi}\int\limits_{0}^{2\pi}\log\vert F(Re^{i\theta})\vert d\theta + \sum\limits_{a \in D_{R}} n_{F}(a) \log (\vert a \vert/R) + n_{F}(0) \log (1/R) = \log \vert c_{F}\vert. \end{align} $$

One can consider the action of a Möbius transformation which preserves $D_{R}$ and seek to compute the resulting expression from (1). Such a consideration leads to the Poisson–Jensen formula, and we refer the reader to page 161 of [17] for a statement and proof.

On their own, the Jensen formula and the Poisson–Jensen formula paved the way toward Nevanlinna theory, which in its most elementary interpretation establishes subtle growth estimates for meromorphic functions (see Chapter VI of [18]). Going further, Nevanlinna theory provided motivation for Vojta’s conjectures whose insight into arithmetic algebraic geometry is profound. In particular, page 34 of [23] contains a type of “dictionary” which translates between Nevalinna theory and number theory where Vojta proposes that Jensen’s formula should be viewed as analogous to the Artin–Whaples product formula from class field theory.

1.2 A modular generalization

In [20], Rohrlich proved what he aptly called a modular version of Jensen’s formula. We now shall describe Rohrlich’s result.

Let f be a meromorphic function on the upper half plane ${\mathbb H}$ which is invariant with respect to the action of the full modular group $\mathrm {PSL}(2,\mathbb {Z})$ . Set $\mathcal {F}$ to be the “usual” fundamental domain of the quotient $\mathrm {PSL}(2,\mathbb {Z})\backslash {\mathbb H}$ , and let $d\mu $ denote the area form of the hyperbolic metric. Assume that f does not have a pole at the cusp $\infty $ of $\mathcal {F}$ , and assume further that the Fourier expansion of f at $\infty $ has its constant term equal to one. Let $P(w)$ be the Kronecker limit function associated with the parabolic Eisenstein series associated with $\mathrm {PSL}(2,\mathbb {Z})$ ; below we will write $P(w)$ in terms of the Dedekind Delta function, but for now, we want to keep the concept of a Kronecker limit function in the conversation. With all this, the Rohrlich–Jensen formula is the statement that

(2) $$ \begin{align} \frac{1}{2\pi}\int\limits_{\mathrm{PSL}(2,\mathbb{Z})\backslash \mathbb{H}} \log|f(z)|d\mu(z) + \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}P(w) =0. \end{align} $$

In this expression, $\mathrm {ord}_w(f)$ denotes the order of f at w as a meromorphic function, and $\mathrm {ord}(w)$ denotes the order of the action of $\mathrm {PSL}(2,\mathbb {Z})$ on ${\mathbb H}$ . As a means by which one can see beyond the above setting, one can view (2) as evaluating the inner product

$$ \begin{align*}\langle 1,\log|f(z)| \rangle=\int\limits_{\mathrm{PSL}(2,\mathbb{Z})\backslash \mathbb{H}} 1\cdot \log|f(z)|d\mu(z) \end{align*} $$

within the Hilbert space of $L^{2}$ functions on $\mathrm {PSL}(2,\mathbb {Z})\backslash {\mathbb H}$ .

There are various directions in which (2) has been extended. In [20], Rohrlich described the analog of (2) for general Fuchsian groups of the first kind and for meromorphic modular forms f of nonzero weight (see page 19 of [20]). In [10], the authors studied the quotient of hyperbolic three space when acted upon by the discrete group $\mathrm {PSL}(2,\mathcal {O}_K)$ , where $\mathcal {O}_K$ denotes the ring of integers of an imaginary quadratic field K. In that setting, the function $\log \vert f \vert $ is replaced by a function which is harmonic at all but a finite number of points and at those points the function has prescribed singularities. As in [20], the analog of (2) involves a function P which is constructed from a type of Kronecker limit formula.

In [2], the authors returned to the setting of $\mathrm {PSL}(2,\mathbb {Z})$ acting on ${\mathbb H}$ . Let $q_{z}=e^{2\pi i z}$ be the standard local coordinate near $\infty $ of $\mathrm {PSL}(2,\mathbb {Z})\backslash {\mathbb H}$ . The Hauptmodul $j(z)$ is the unique $\mathrm {PSL}(2,\mathbb {Z})$ invariant holomorphic function on ${\mathbb H}$ whose expansion near $\infty $ is $j(z) = q_{z}^{-1} +744+ O(q_{z})$ as z approaches $\infty $ . Define $j_1(z)=j(z)-744$ . For integers $n\geq 2$ , let $T_{n}$ denote the nth Hecke operator, and set $j_{n}(z) = j|T_n (z)$ . The main results of [2] are the derivation of formulas for the regularized scalar product $\langle j_n(z),\log (({\mathrm {Im}} (z))^k|f(z)|) \rangle $ , where f is a weight $2k$ meromorphic modular form with respect to $\mathrm {PSL}(2,\mathbb {Z})$ . Below, we will discuss further the formulas from [2] and describe the way in which their results are natural extensions of (2).

1.3 Revisiting Rohrlich’s theorem

The purpose of this article is to extend the point of view that the Rohlrich–Jensen formula is the evaluation of a particular type of inner product and to prove the extension of this formula in the setting of an arbitrary, not necessarily arithmetic, Fuchsian group of the first kind with one cusp. To do so, we shall revisit the role of each of the two terms $j|T_n (z)$ and $\log (({\mathrm {Im}} (z))^k|f(z)|)$ .

The function $j|T_n (z)$ can be characterized as the unique holomorphic function, up to an additive constant, which is $\mathrm {PSL}(2,\mathbb {Z})$ invariant on ${\mathbb H}$ and whose expansion near $\infty $ is $q_{z}^{-n} + o(q_{z}^{-1})$ . These properties hold for the special value $s=1$ of the Niebur–Poincaré series $F_{-n}^{\Gamma }(z,s)$ , which is defined in [19] for any Fuchsian group $\Gamma $ of the first kind with one cusp (see §3.1). As proved in [19], for any $m\in \mathbb {Z} \setminus \{0\}$ , the Niebur–Poincaré series $F_{m}^{\Gamma }(z,s)$ is an eigenfunction of the hyperbolic Laplacian $\Delta _{\operatorname {\mathrm {hyp}}}$ ; specifically, we have that

$$ \begin{align*}\Delta_{\operatorname{\mathrm{hyp}}} F_{m}^{\Gamma}(z,s) = s(1-s)F_{m}^{\Gamma}(z,s). \end{align*} $$

Also, $F_{m}^{\Gamma }(z,s)$ is orthogonal to constant functions. Furthermore, if $\Gamma = \mathrm {PSL}(2,\mathbb {Z})$ , then for any positive integer n there is an explicitly computable constant $c_{n}$ such that

(3) $$ \begin{align} F_{-n}^{\mathrm{PSL}(2,\mathbb{Z})}(z,1) = \frac{1}{2\pi\sqrt{n}}j_{n}(z) + c_{n}. \end{align} $$

As a result, the Rohrlich–Jensen formula proved in [2], when combined with Rohrlich’s formula from [20], reduces to computing the regularized inner product of $F_{-n}^{\mathrm {PSL}(2,\mathbb {Z})}(z,1)$ with $\log (({\mathrm {Im}} (z))^k|f(z)|)$ .

As for the term $\log (({\mathrm {Im}} (z))^k|f(z)|)$ , we begin by recalling Proposition 12 from [16]. Let $\Gamma $ be a cofinite Fuchsian group with one cusp; the cusp is assumed to be at $\infty $ with the identity as its scaling matrix. Let $2k\geq 2$ be any even positive integer, and let f be a weight $2k$ holomorphic form which is $\Gamma $ invariant and with q-expansion at $\infty $ that is normalized so its constant term is equal to one. Set $\Vert f\Vert (z) = y^{k}\vert f(z) \vert $ , where $z=x+iy$ . Let $\mathcal {E}^{\mathrm {ell}}_{\Gamma ,w}(z,s)$ be the elliptic Eisenstein series associated with the aforementioned data; a summary of the relevant properties of $\mathcal {E}^{\mathrm {ell}}_{\Gamma ,w}(z,s)$ is given in §4.3. Then, in [16], it is proved that one has the asymptotic relation

(4) $$ \begin{align} \sum_{w\in \mathcal{F}_\Gamma} \mathrm{ord}_w(f) \mathcal{E}^{\mathrm{ell}}_{\Gamma,w}(z,s)= -s\log\left( |f(z)| |\eta_{\Gamma,\infty}^4(z)|^{-k}\right) + O(s^2) \,\,\,\,\, \mathrm{as }s \to 0, \end{align} $$

where $\mathcal {F}_\Gamma $ is the fundamental domain for the action of $\Gamma $ on $\mathbb {H}$ and $\eta _{\Gamma ,\infty }(z)$ is the analog of the classical eta function for the modular group (see (28) for the Kronecker limit formula for the non-holomorphic parabolic Eisenstein series). With this, formula (4) can be written as

(5) $$ \begin{align} \log\left( \Vert f\Vert (z) \right) = kP_{\Gamma}(z) - \sum_{w\in \mathcal{F}_\Gamma} \mathrm{ord}_w(f) \lim_{s\to 0} \frac{1}{s} \mathcal{E}^{\mathrm{ell}}_{\Gamma,w}(z,s),\end{align} $$

where $P_{\Gamma }(z)=\log (|\eta _{\Gamma ,\infty }^4(z)|{\mathrm {Im}} (z))$ is the Kronecker limit function associated with the non-holomorphic parabolic Eisenstein series $\mathcal {E}^{\mathrm {par}}_{\Gamma ,\infty }(z,s)$ ; the precise normalizations and expressions which define $\mathcal {E}^{\mathrm {par}}_{\Gamma ,\infty }(z,s)$ will be clarified below.

Following [3], one can recast (5) in terms of the resolvent kernel, which we now shall undertake.

The resolvent kernel, also called the automorphic Green’s function, $G_s^{\Gamma }(z,w)$ is the integral kernel which for almost all $s \in {\mathbb C}$ inverts the operator $\Delta _{\operatorname {\mathrm {hyp}}} + s(s-1)$ , meaning that for each $s\in {\mathbb C}$ for which $s(1-s)$ is not the eigenvalue of $\Delta _{\operatorname {\mathrm {hyp}}}$ , function $G_s^{\Gamma }(z,w)$ it is the integral kernel of the operator $(\Delta _{\operatorname {\mathrm {hyp}}} + s(s-1))^{-1}$ . Moreover,

$$ \begin{align*}\Delta_{\operatorname{\mathrm{hyp}}} G_s^{\Gamma}(z,w) = s(1-s) G_s^{\Gamma}(z,w). \end{align*} $$

The resolvent kernel is closely related to the elliptic Eisenstein series (see [25] as well as [3]). Specifically, from Corollary 7.4 of [25], after taking into account a sign difference in our normalization, we have that

(6) $$ \begin{align} \mathrm{ord}(w) \mathcal{E}^{\mathrm{ell}}_{\Gamma,w}(z,s) = -\frac{2^{s+1}\sqrt{\pi} \Gamma(s+1/2)}{\Gamma(s)}G_s^{\Gamma}(z,w) +O(s^2) \,\,\,\,\, \mathrm{as}\ s \to 0 \end{align} $$

for all $z,w \in \mathbb {H}$ with $z\neq \gamma w$ when $\gamma \in \Gamma $ . It is now evident that one can express $\log \left ( \Vert f \Vert (z) \right )$ as a type of Kronecker limit function. Indeed, upon using the functional equation for the Green’s function, we will prove below (§5.2) the following result.

Proposition 1. Let $\Gamma $ be a cofinite Fuchsian group with one cusp at $\infty $ with identity as its scaling matrix. Let $2k\geq 0$ be an even integer, and let f be a weight $2k$ meromorphic form which is $\Gamma $ invariant and with q-expansion at $\infty $ normalized so its constant term is equal to one. Then,

(7) $$ \begin{align} \log\left( \Vert f\Vert (z) \right)&=-2k + 2\pi \sum_{w\in \mathcal{F}_{\Gamma}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \lim_{s\to 1}\left(G_s^{\Gamma}(z,w) + \mathcal{E}_{\Gamma,\infty}^{\mathrm{par}}(z,s)\right)\notag \\ &= 2\pi \sum_{w\in \mathcal{F}_\Gamma} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \left[ \lim_{s\to 1}\left(G_s^{\Gamma}(z,w) + \mathcal{E}_{\Gamma,\infty}^{\mathrm{par}}(z,s)\right) - \frac{2}{\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(\Gamma \backslash {\mathbb H})} \right]. \end{align} $$

With all this, it is evident that one can view the inner product realization of the Rohrlich–Jensen formula as a special value of the inner product of the Niebur–Poincaré series $F_{m}^\Gamma (z,s)$ for $m\in \mathbb {Z}_{<0}$ and the resolvent kernel $G_{s}^{\Gamma }(z,w)$ plus the parabolic Eisenstein series $\mathcal {E}_{\Gamma ,\infty }^{\mathrm {par}}(z,s)$ .

Furthermore, because all terms are eigenfunctions of the Laplacian, one can seek to compute the inner product in hand in a manner similar to that which yields the Maass–Selberg formula.

1.4 Our main results

Unless otherwise explicitly stated, we will assume for the remainder of this article that $\Gamma $ is any Fuchsian group of the first kind with one cusp. By conjugating $\Gamma $ , if necessary, we may assume that the cusp is at $\infty $ , with the cuspidal width equal to one. The group $\Gamma $ will be arbitrary, but fixed, throughout this article, so, for the sake of brevity, in the sequel, we will suppress the index $\Gamma $ in the notation for Eisenstein series, the Niebur–Poincaré series, the Kronecker limit function, the fundamental domain, and the resolvent kernel. When $\Gamma $ is taken to be the modular group or the Atkin–Lehner group, that will be indicated in the notation.

With the above discussion, we have established that one manner in which the Rohrlich–Jensen formula can be understood is through the study of the regularized inner product

(8) $$ \begin{align} \langle F_{-n}(\cdot,1), \overline{\lim_{s\to 1} \left(G_s(\cdot,w) + \mathcal{E}_\infty^{\mathrm{par}}(\cdot,s)\right)} \rangle, \end{align} $$

which is defined as follows. Since $\Gamma $ has one cusp at $\infty $ , one can construct a (Ford) fundamental domain $\mathcal {F}$ of the action of $\Gamma $ on ${\mathbb H}$ . Let $M = \Gamma \backslash {\mathbb H}$ . A cuspidal neighborhood $\mathcal {F}_\infty (Y)$ of $\infty $ is given by $0 < x \leq 1$ and $y \geq Y$ , where $z=x+iy$ and some $Y \in {\mathbb R}$ sufficiently large. (We recall that we have normalized the cusp to be of width one.) Let $\mathcal {F}(Y) = \mathcal {F}\setminus \mathcal {F}_\infty (Y)$ . Then, we define (8) to be

$$ \begin{align*}\lim_{Y\to \infty} \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(z,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z), \end{align*} $$

where $d\mu _{\operatorname {\mathrm {hyp}}}(z)$ denotes the hyperbolic volume element. The function $G_s(z,w) + \mathcal {E}_\infty ^{\mathrm {par}}(z,s)$ is unbounded as $z \to w$ . However, the asymptotic growth of the function is logarithmic, thus integrable; hence, it is not necessary to regularize the integral in (8) in a neighborhood containing w. The need to regularize the inner product (8) stems solely from the exponential growth behavior of the factor $F_{-n}(z,1)$ as $z\to \infty $ .

Our first main result of this article is the following theorem.

Theorem 1. For any positive integer n and any point $w\in \mathcal {F}$ ,

(9) $$ \begin{align} \langle F_{-n}(\cdot,1), \overline{\lim_{s\to 1} \left(G_s(\cdot,w) + \mathcal{E}_\infty^{\mathrm{par}}(\cdot,s)\right)} \rangle = - \frac{\partial}{\partial s} F_{-n}(w,s) \Big|_{s=1}. \end{align} $$

We can combine Theorem 1 with the factorization formula (7) together with properties of $F_{-n}(z,1)$ , as proved in [19], in order to obtain the following extension of the Rohrlich–Jensen formula.

Corollary 1. In addition to the notation above, assume that the even weight $2k\geq 0$ meromorphic form f has been normalized so its q-expansion at $\infty $ has constant term equal to $1$ . Then we have that

(10) $$ \begin{align} \langle F_{-n}(\cdot ,1), \log\Vert f\Vert \rangle = - 2\pi \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}\frac{\partial}{\partial s} F_{-n}(w,s) \Big|_{s=1}. \end{align} $$

Let g be a $\Gamma $ invariant analytic function which has a pole at $\infty $ . As such, there is a positive integer K and set of complex numbers $\{a_{n}\}_{n=1}^{K}$ such that

$$ \begin{align*}g(z) = \sum_{n=1}^K a_n q_z^{-n} + O(1) \,\,\,\,\, \mathrm{as }z \rightarrow \infty. \end{align*} $$

It is proved in [19] that

(11) $$ \begin{align} g(z) = \sum_{n=1}^K 2\pi \sqrt{n}a_n F_{-n}(z,1) + c(g) \end{align} $$

for some constant depending only upon g. With this, we can combine Corollary 1 and the theorem on page 19 of [20] to obtain the following result.

Corollary 2. With notation as above, there is a constant $\beta $ , defined by the Laurent expansion of $\mathcal {E}_\infty ^{\mathrm {par}}(z,s)$ near $s=1$ , such that

(12) $$ \begin{align}\nonumber \langle g, \log\Vert f\Vert \rangle = - 2\pi \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} &\Bigg(2\pi \sum_{n=1}^K \sqrt{n}a_n\frac{\partial}{\partial s} F_{-n}(w,s) \Big|_{s=1} \\& \quad + c(g)(P(w) - \beta \operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M) +2) \Bigg). \end{align} $$

The constant $\beta $ is given in (28). We refer the reader to equation (28) for further details regarding the normalizations which define $\beta $ and the parabolic Kronecker limit function P.

Finally, we will consider the generating function of the normalized series constructed from the right-hand side of (9). Specifically, we will prove the following result.

Theorem 2. With notation as above, the generating series

$$ \begin{align*}\sum_{n\geq 1}2\pi \sqrt{n} \frac{\partial}{\partial s} F_{-n}(w,s) \Big|_{s=1}q_z^n \end{align*} $$

is, in the z variable, the holomorphic part of the weight two biharmonic Maass form

$$ \begin{align*}\mathcal{G}_w(z):=i\frac{\partial}{\partial z} \left( \frac{\partial}{\partial s} \left( G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right) \Big|_{s=1} \right). \end{align*} $$

Note that a weight two biharmonic Maass form is a function which satisfies the weight two modularity in z and which is annihilated by $\Delta _2^2=(\xi _0\circ \xi _2)^2$ , where, classically $\xi _\kappa := 2iy^\kappa \overline {\frac {\partial }{\partial \overline {z}}}$ . It is clear from the definition that $\mathcal {G}_w(z)$ satisfies the weight two modularity in the z variable. In §5.4, we will prove that $(\xi _0\circ \xi _2)^2\mathcal {G}_w(z)=0$ .

In the case $\Gamma = {\mathrm {PSL}}(2,{\mathbb {Z}})$ , our results yield the main theorems from [2], as we will discuss below.

1.5 Outline of the paper

In §2, we will establish notation and recall certain results from the literature. There are two specific examples of Poincaré series which are particularly important for our study, the Niebur–Poincaré series and the resolvent kernel. Both series are defined, and basic properties are summarized in §3. In §4, we state the Kronecker limit formulas associated with parabolic and elliptic Eisenstein series, and then prove Proposition 1. The proofs of the main results listed above will be given in §5.

To illustrate our results, various examples are given in §6. Our first example is when $\Gamma = {\mathrm {PSL}}(2,{\mathbb {Z}})$ , where, as claimed above, our results yield the main theorems of [2]. We then turn to the case when $\Gamma $ is an Atkin–Lehner group $\Gamma _0(N)^+$ for square-free level N. The first examples are when the genus of the quotient spaces $\overline {\Gamma _0(N)^+}\backslash {\mathbb H}$ are zero and when the function g in Corollary 2 is the Hauptmodul $j_N^+(z)$ . In somewhat common notation, we write $\overline {\Gamma _0(N)^+}$ to denote the projection of $\Gamma _0(N)^+$ onto $\mathrm {PSL}(2,\mathbb {R})$ . The next two examples we present are for levels $N=37$ and $N=103$ . For these levels, the genus of the quotients of ${\mathbb H}$ by $\overline {\Gamma _0(N)^+}$ are one and two, respectively. In these cases, certain generators of the corresponding function fields were constructed in [13]. Consequently, we are able to employ the results from [13] and fully develop Corollary 2.

2 Background material

2.1 Basic notation

Let $\Gamma \subset {\mathrm {PSL}}(2,\mathbb {R})$ denote a Fuchsian group of the first kind acting by fractional linear transformations on the hyperbolic upper half-plane $\mathbb {H}:=\{z=x+iy\in \mathbb {C}\, |\,x,y\in \mathbb {R};\,y>0\}$ . We let $M:=\Gamma \backslash \mathbb {H}$ , which is a finite volume hyperbolic Riemann surface, and denote by $p:\mathbb {H}\longrightarrow M$ the natural projection. We assume that M has $e_{\Gamma }$ elliptic fixed points and one cusp at $\infty $ of width one. By an abuse of notation, we also say that $\Gamma $ has a cusp at $\infty $ of width one, meaning that the stabilizer $\Gamma _\infty $ of $\infty $ is generated by the matrix $\bigl (\begin {smallmatrix} 1&1\\0&1\end {smallmatrix}\bigr )$ . We identify M locally with its universal cover $\mathbb {H}$ . By $\mathcal {F}$ we denote the “usual” (Ford) fundamental domain for $\Gamma $ acting on $\mathbb H$ .

We let $\mu _{\mathrm {hyp}}$ denote the hyperbolic metric on M which is compatible with the complex structure of M and has constant negative curvature equal to minus one. The hyperbolic line element $ds^{2}_{\operatorname {\mathrm {hyp}}}$ , respectively, the hyperbolic Laplacian $\Delta _{\operatorname {\mathrm {hyp}}}$ acting on functions, are given in the coordinate $z=x+iy$ on $\mathbb {H}$ by

$$ \begin{align*} ds^{2}_{\operatorname{\mathrm{hyp}}}:=\frac{dx^{2}+dy^{2}}{y^{2}},\quad\mathrm{respectively,} \quad\Delta_{\operatorname{\mathrm{hyp}}}:=-y^{2}\left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}\right). \end{align*} $$

By $d_{\mathrm {hyp}}(z,w)$ , we denote the hyperbolic distance between the two points $z\in \mathbb {H}$ and $w\in \mathbb {H}$ . Our normalization of the hyperbolic Laplacian is different from the one considered in [9] and [19] where the Laplacian is taken with the plus sign.

2.2 Modular forms

Following [21], we define a weakly modular form f of even weight $2k$ for $k \geq 0$ associated with $\Gamma $ to be a function f which is meromorphic on $\mathbb H$ , and at the cusps of $\Gamma $ , and satisfies the transformation property

(13) $$ \begin{align} f\left(\frac{az+b}{cz+d}\right) = (cz+d)^{2k}f(z), \quad\mathrm{for any }\begin{pmatrix}a&b\\c&d\end{pmatrix} \in \Gamma. \end{align} $$

In the setting of this paper, any weakly modular form f will satisfy the relation $f(z+1)=f(z)$ , so that for some positive integer N, we can write

$$ \begin{align*}f(z) = \sum\limits_{n=-N}^{\infty}a_{n}q_z^{n}, \quad\text{ where } q_z =e(z)= e^{2\pi iz}. \end{align*} $$

If $a_{n} = 0$ , for all $n < 0$ , then f is said to be holomorphic at the cusp at $\infty $ . A holomorphic modular form with respect to $\Gamma $ is a weakly modular form which is holomorphic on $\mathbb H$ and at all the cusps of $\Gamma $ .

When the weight k is zero, the transformation property (13) indicates that the function f is invariant with respect to the action of elements of the group $\Gamma $ , so it may be viewed as a meromorphic function on the surface $M=\Gamma \backslash \mathbb {H}$ . In other words, a meromorphic function on M is a weakly modular form of weight $0$ .

For any two weight $2k$ weakly modular forms f and g associated with $\Gamma $ , with integrable singularities at finitely many points in $\mathcal {F}$ , the generalized inner product $\langle \cdot ,\, \cdot \rangle $ is defined as

(14) $$ \begin{align} \langle f,g\rangle = \lim_{Y\to \infty} \int\limits_{\mathcal{F}(Y)}f(z) \overline{g(z)}(\mathrm{Im}(z))^{2k}d\mu_{\operatorname{\mathrm{hyp}}}(z), \end{align} $$

where the integration is taken over the portion $\mathcal {F}(Y)$ of the fundamental domain $\mathcal {F}$ equal to $\mathcal {F}\setminus \mathcal {F}_\infty (Y)$ .

2.3 Atkin–Lehner groups

Let $N=p_1\ldots p_r$ be a square-free, nonnegative integer including the case $N=1$ . The subset of $\mathrm {SL}(2,\mathbb {R})$ , defined by

$$ \begin{align*} \Gamma_0(N)^+: =\Big\{ \frac{1}{\sqrt{e}}\begin{pmatrix}a&b\\c&d\end{pmatrix}\in \mathrm{SL}(2,\mathbb{R}): & \, ad-bc=e, \, a,b,c,d,e\in\mathbb{Z}, \,e>0, \\& e\mid N,\ e\mid a, \ e\mid d,\ N\mid c \Big\} \end{align*} $$

is an arithmetic subgroup of $\mathrm {SL}(2,\mathbb {R})$ . We use the terminology Atkin–Lehner group of level N to describe $\Gamma _0(N)^+$ in part because the group is obtained by adding all Atkin–Lehner involutions to the congruence group $\Gamma _0(N)$ (see [1]). Let $\{\pm \mathrm {Id}\}$ denote the set of two elements, where $\mathrm {Id}$ is the identity matrix. In general, if $\Gamma $ is a subgroup of $\mathrm {SL}(2,\mathbb {R})$ , we let $\overline {\Gamma } := \Gamma /\{\pm \mathrm {Id}\}$ denote its projection into $\mathrm {PSL}(2,\mathbb {R})$ .

Set $Y_N^{+}:=\overline {\Gamma _0(N)^+} \backslash \mathbb {H}$ . According to [5], for any square-free N, the quotient space $Y_{N}^{+}$ has one cusp at $\infty $ with the cusp width equal to one. The spaces $Y_{N}^{+}$ will be used in the last section where we give examples of our results for generators of function fields of meromorphic functions on $Y_N^{+}$ .

2.4 Generators of function fields of Atkin–Lehner groups of small genus

An explicit construction of generators of function fields of all meromorphic functions on $Y_N^{+}$ with genus $g_{N,+}\leq 3$ was given in [13].

When $g_{N,+}=0$ , the function field of meromorphic functions on $Y_N^+$ is generated by a single function, the Hauptmodul $j_N^+(z)$ , which is normalized so that its q-expansion is of the form $q_z^{-1}+O(q_z)$ . The Hauptmodul $j_N^+(z)$ appears in the “Monstrous Moonshine” and was investigated in many papers, starting with Conway and Norton [4]. The action of the mth Hecke operator $T_m$ on $j_N^+(z)$ produces a meromorphic function on $Y_N^{+}$ with the q-expansion $j_N^+|T_{m}(z)= q_z^{-m} + O(q_z)$ .

When $g_{N,+}\geq 1$ , the function field of meromorphic functions on $Y_N^+$ is generated by two functions. For $g_{N,+}\leq 3$ , the results in [13] provided the explicit construction of certain generators $x_N^+(z)$ and $y_N^+(z)$ . Furthermore, it is shown that the q-expansions of these generators are of the form

$$ \begin{align*}x_N^+(z)=q_z^{-a}+\sum_{j=1}^{a-1}a_jq_z^{-j}+O(q_z) \quad \text{and} \quad y_N^+(z)=q_z^{-b}+\sum_{j=1}^{b-1}b_jq_z^{-j}+O(q_z), \end{align*} $$

where $a,b$ are positive integers with $a\leq 1+g_{N,+}$ , and $b\leq 2+g_{N,+}$ . Furthermore, for $g_{N,+} \leq 3$ , it is shown in [13] that all coefficients in the q-expansion for $x_N^+(z)$ and $y_N^+(z)$ are integers. For all such N, the precise values of these coefficients out to large order were computed, and the results are available at [15].

3 Two Poincaré series

In this section, we will define the Niebur–Poincaré series $F_{m}(z,s)$ and the resolvent kernel $G_s(z,w)$ ; one also refers to $G_s(z,w)$ as the automorphic Green’s function. We refer the reader to [19] for additional information regarding $F_{m}(z,s)$ and to [9] and [11] and references therein for further details regarding $G_s(z,w)$ . As said above, we will suppress the group $\Gamma $ from the notation.

3.1 Niebur–Poincaré series

We start with the definition and properties of the Niebur–Poincaré series $F_{m}(z,s)$ associated with a co-finite Fuchsian group with one cusp. We then will specialize results to the setting of Atkin–Lehner groups.

3.1.1 Niebur–Poincaré series associated with a co-finite Fuchsian group with one cusp

Let m be a nonzero integer, $z=x+iy\in \mathbb {H}$ , and $s\in \mathbb {C}$ with ${\mathrm {Re}}(s)>1$ . Recall the notation $e(x):=\exp (2\pi i x)$ , and let $I_{s-1/2}$ denote the modified I-Bessel function of the first kind (see (A.2)). The Niebur–Poincaré series $F_{m}(z,s)$ is defined formally by the series

(15) $$ \begin{align} F_m(z,s)=F_m^\Gamma(z,s):= \sum_{\gamma\in\Gamma_\infty \backslash \Gamma} e(m{\mathrm{Re}}(\gamma z))({\mathrm{Im}}(\gamma z))^{1/2}I_{s-1/2}(2\pi |m| {\mathrm{Im}}(\gamma z)). \end{align} $$

For fixed m and z, the series (15) converges absolutely and uniformly on any compact subset of the half plane ${\mathrm {Re}}(s)>1$ . Moreover, $\Delta _{\operatorname {\mathrm {hyp}}}F_m(z,s) = s(1-s) F_m(z,s)$ for all $s\in \mathbb {C}$ in the half plane ${\mathrm {Re}}(s)>1$ . From Theorem 5 of [19], we have that for any nonzero integer m, the function $F_m(z,s)$ admits a meromorphic continuation to the whole complex plane $s\in {\mathbb C}$ . Moreover, $F_m(z,s)$ is holomorphic at $s=1$ and, according to the spectral expansion given in Theorem 5 of [19], $F_m(z,1)$ is orthogonal to constant functions, meaning that

$$ \begin{align*}\langle F_m(z,1), 1 \rangle=0. \end{align*} $$

For our purposes, it is necessary to employ the Fourier expansion of $F_{m}(z,s)$ in the cusp $\infty $ . The Fourier expansion is proved in [19] and involves the Kloosterman sums $S(m,n;c)$ , which we now define. For any integers m and n, and real number $c\neq 0$ , define

$$ \begin{align*}S(m,n;c):= \sum_{\bigl(\begin{smallmatrix} a&\ast\\c&d\end{smallmatrix}\bigr)\in \Gamma_\infty \diagdown \Gamma \diagup \Gamma_\infty } e\left( \frac{ma + nd}{c}\right). \end{align*} $$

For ${\mathrm {Re}}(s)>1$ and $z=x+iy\in \mathbb {H}$ , the Fourier expansion of $F_m(z,s)$ is given by

(16) $$ \begin{align} F_m(z,s)=e(mx)y^{1/2}I_{s-1/2}(2\pi |m|y) + \sum_{k=-\infty}^{\infty}b_k(y,s;m)e(kx), \end{align} $$

where

$$ \begin{align*}b_0(y,s;m) = \frac{y^{1-s}}{(2s-1)\Gamma(s)}2\pi^s |m|^{s-1/2} \sum_{c>0} S(m,0;c)c^{-2s}=\frac{y^{1-s}}{(2s-1)}B_0(s;m). \end{align*} $$

The function $B_0(s;m)$ is denoted by $a_m(s)$ in [19]. For $k\neq 0$ , we have that

$$ \begin{align*}b_k(y,s;m)=B_k(s;m)y^{1/2}K_{s-1/2}(2\pi |k|y), \end{align*} $$

with

$$ \begin{align*}B_k(s;m)= 2 \sum_{c>0}S(m,k;c)c^{-1}\cdot \left\{ \begin{array}{ll} J_{2s-1}\left(\frac{4\pi}{c} \sqrt{mk}\right), & \mathrm{if \,}mk>0, \\ I_{2s-1}\left(\frac{4\pi}{c} \sqrt{|mk|}\right), & \mathrm{if \,} mk<0, \end{array} \right. \end{align*} $$

where we corrected certain typos in Theorem 1 of [19]. In the above expression, $J_{2s-1}$ denotes the J-Bessel function and $K_{s-1/2}$ is the modified Bessel function (see formulas (A.1) and (A.3)). According to the proof of Theorem 6 from [19], the Fourier expansion (16) extends by the principle of analytic continuation to the case when $s=1$ . Hence, by putting $B_k(1;m):= \lim _{s\downarrow 1} B_k(s;m)$ , and using the special values (A.5) of I-Bessel and K-Bessel functions of order $1/2$ , we have that

(17) $$ \begin{align} F_m(z,1)=\frac{\sinh(2\pi|m|y)}{\pi \sqrt{|m|}}e(mx) + B_0(1;m)+ \sum_{k\in\mathbb{Z}\setminus\{0\}}\frac{1}{2 \sqrt{|k|}} e^{-2\pi|k|y}B_k(1;m)e(kx). \end{align} $$

From page 75 of [11], one has the trivial bounds $I_1(y)\ll \min \{y,y^{-1/2}\}e^y$ and $J_1(y)\ll \min \{y,y^{-1/2}\}$ , which hold for any positive real number y. From this, we obtain the bound that

(18) $$ \begin{align} B_k(1;m) \ll \sqrt{|km|}\exp(4\pi \sqrt{|km|}/c_{\Gamma}). \end{align} $$

The constant $c_{\Gamma }>0$ is equal to the smallest left-lower entry $c>0$ of $\Gamma $ , and the implied constant is independent of $k,m$ .

It is clear from (17) that for $n>0$ one has that

$$ \begin{align*} F_{-n}(z,1) = \frac{1}{2\pi\sqrt{n}}q_{z}^{-n} + O(1) \,\,\,\,\,\mathrm{as }z \rightarrow \infty \end{align*} $$

(see also [19, Th. 6]). The Fourier expansion (17) combined with (18) also suffices to show that

(19) $$ \begin{align} F_n(z,1)\ll \exp(2\pi |n| {\mathrm{Im}}(z)), \quad \text{as } {\mathrm{Im}}(z) \to \infty \end{align} $$

for any nonzero integer n.

A similar bound holds true for the derivative of $F_{n}(z,s)$ in s, at $s=1$ . More precisely, we have the following lemma.

Lemma 3. Let n be a nonzero integer. Then

(20) $$ \begin{align} \left.\frac{\partial}{\partial s} F_{n}(z,s)\right|_{s=1} \ll \exp\left( 2\pi |n| {\mathrm{Im}}(z)\right) \,\,\,\,\, \mathrm{as Im}(z) \to \infty. \end{align} $$

Proof. The proof is similar to that of Lemma 4.3(1), page 19 of [2]. We begin by applying $\frac {\partial }{\partial s}$ to the Fourier expansion (16) and then take $s=1$ . Recall that the series in (16) converges uniformly in compact subsets of the half plane ${\mathrm {Re}}(s)>1$ . Also, $ F_{n}(z,s)$ is holomorphic at $s=1$ . Therefore, we can differentiate the series (16) termwise at $s=1$ to get that

(21) $$ \begin{align} \left.\frac{\partial}{\partial s} F_{n}(z,s)\right|_{s=1}= e(nx)y^{1/2} \left.\frac{\partial }{\partial \nu} I_{\nu}(2\pi |n|y)\right|_{\nu=1/2}+ \sum_{k=-\infty}^{\infty} \left.\frac{\partial}{\partial s} b_k(y,s;n)\right|_{s=1} e(kx). \end{align} $$

The bound (A.15) ensures that the first term on the right-hand side of (21) is of order $O(\exp \left ( 2\pi |n| y \right ))$ as $y={\mathrm {Im}}(z) \to \infty $ .

Next, we estimate $\left .\frac {\partial }{\partial s} b_k(y,s;n)\right |_{s=1}$ as $y \to \infty $ . When $k=0$ , it is immediate that

$$ \begin{align*}\left.\frac{\partial }{\partial s} b_0(y,s;n)\right|_{s=1}=O(\log (y)) \,\,\,\,\, \text{as } y \to \infty.\end{align*} $$

For $k\neq 0$ ,

(22) $$ \begin{align} \left.\frac{\partial }{\partial s} b_k(y,s;n)\right|_{s=1}= \sqrt{y}\left(\left.\frac{\partial }{\partial s} B_k(s;n)\right|_{s=1} K_{1/2}(2\pi |k|y) + B_k(1;n) \left.\frac{\partial }{\partial \nu} K_{\nu}(2\pi |k|y)\right|_{\nu=1/2} \right). \end{align} $$

The first term on the right-hand side of (22) can be estimated using the identity (A.5) combined with bounds (A.18) to deduce

$$ \begin{align*}\sqrt{y}\left.\frac{\partial }{\partial s} B_k(s;n)\right|_{s=1} K_{1/2}(2\pi |k|y)\ll \frac{e^{-2\pi |k|y}}{2\sqrt{k}}\cdot\frac{e^{4\pi\sqrt{|kn|}/c_{\Gamma}}}{\sqrt{|kn|}}. \end{align*} $$

Combining (18) with (A.15) yields that the second term on the right-hand side of (22) is $O\left (\exp \left (-2\pi |k|y + \frac {4\pi }{c_{\Gamma }}\sqrt {|nk|}\right )\right )$ as $y\to \infty $ .

This shows that the series on the right-hand side of (21) converges uniformly for y large enough and tends to zero as $y\to \infty $ . Since the first term is $O(\exp \left ( 2\pi |n| y \right ))$ as $y={\mathrm {Im}}(z) \to \infty $ , the proof is complete.

We note that the value of the derivative of the Niebur–Poincaré series at $s=1$ satisfies a differential equation, namely that

(23) $$ \begin{align} \notag \Delta_{\operatorname{\mathrm{hyp}}}\left(\frac{\partial}{\partial s}\left. F_{-n}(z,s) \right|_{s=1} \right) &=\lim_{s\to 1} \Delta_{\operatorname{\mathrm{hyp}}} \left(\frac{F_{-n}(z,s) - F_{-n}(z,1)}{(s-1)}\right)\\&=\lim_{s\to 1} \left(\frac{s(1-s)F_{-n}(z,s) -0}{(s-1)}\right) = -F_{-n}(z,1) \end{align} $$

for positive integers n.

3.1.2 Fourier expansion when $\Gamma $ is an Atkin–Lehner group

One can explicitly evaluate $B_0(1;m)$ for $m> 0$ when $\Gamma $ is an Atkin–Lehner group. Set $\Gamma =\overline {\Gamma _0(N)^+}$ where N is squarefree, which we express as $N=\prod \limits _{\nu =1}^r p_\nu $ . Let $B_{0,N}^+(1;m)$ denote the coefficient $B_0(1;m)$ for $\overline {\Gamma _0(N)^+}$ .

From Theorem 8 and Proposition 9 of [13], we get that

(24) $$ \begin{align} B_{0,N}^+(1;m)= \frac{12\sigma(m)}{\pi\sqrt{m}}\prod\limits_{\nu=1}^r \left(1- \frac{p_\nu^{\alpha_{p_\nu}(m)+1}(p_\nu -1) }{\left(p_\nu^{\alpha_{p_\nu}(m)+1} - 1\right)(p_\nu+1)}\right) , \end{align} $$

where $\sigma (m)$ denotes the sum of divisors of a positive integer m and $\alpha _p(m)$ is the largest integer such that $p^{\alpha _p(m)}$ divides m. These expressions will be used in our explicit examples in §6.

3.2 Automorphic Green’s function

The automorphic Green’s function, or resolvent kernel, $G_s(z,w)$ for the Laplacian on M is defined on page 31 of [9]. In the notation of [9], let $\chi $ be the identity character, $z,w\in \mathbb {H}$ with $w\neq \gamma z$ , for $\gamma \in \Gamma $ , and $s\in \mathbb {C}$ with ${\mathrm {Re}}(s)>1$ . Consider the series

$$ \begin{align*}G_s(z,w)= \sum_{\gamma\in\Gamma} k_s(\gamma z,w), \end{align*} $$

where

$$ \begin{align*}k_s(z,w):=-\frac{\Gamma(s)^2}{4\pi \Gamma(2s)}\left[1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right]^s F\left(s,s;2s;1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right) \end{align*} $$

with $F(\alpha ,\beta ;\gamma ;u)$ denoting the classical hypergeometric function. We should point out that the normalization we are using, which follows [9], differs from the normalization for the Green’s function in Chapter 5 of [11]; the two normalizations differ by a minus sign. With this said, it is proved in [9], Proposition 6.5 on page 33 that the series which defines $G_{s}(z,w)$ converges uniformly and absolutely on compact subsets of $(z,w,s) \in (\mathcal {F} \times \mathcal {F})'\times \{s\in \mathbb {C} :{\mathrm {Re}}(s)>1\}$ , where $(\mathcal {F} \times \mathcal {F})'= (\mathcal {F} \times \mathcal {F})\setminus \{(z,w)\in \mathcal {F}: z=w\}$ .

Furthermore, for all $s\in \mathbb {C}$ with ${\mathrm {Re}}(s)>1$ , and all $z,w \in \mathbb {H}$ with $z\neq \gamma w$ for $\gamma \in \Gamma $ , the function $G_s(z,w)$ is the eigenfunction of $\Delta _{\operatorname {\mathrm {hyp}}}$ associated with the eigenvalue $s(1-s)$ .

Combining formulas 9.134.1 and 8.703 from [8] and applying the identity

$$ \begin{align*}\cosh(d_{\operatorname{\mathrm{hyp}}}(z,w))=\left(2-\left[1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right]\right)\left(1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right)^{-1}, \end{align*} $$

we get that

$$ \begin{align*}k_s(z,w)=-\frac{1}{2\pi}Q^0_{s-1}(\cosh(d_{\operatorname{\mathrm{hyp}}}(z,w))), \end{align*} $$

where $Q_\nu ^{\mu }$ is the associated Legendre function, as defined by formula 8.703 in [8], with $\nu =s-1$ and $\mu =0$ .

Now, we can combine Theorem 4 of [19] with Theorem 5.3 of [11] to obtain the Fourier expansion of the automorphic Green’s function in terms of the Niebur–Poincaré series. Specifically, let $w\in \mathcal {F}$ be fixed. Assume $z \in \mathcal {F}$ with $y={\mathrm {Im}}(z)> \max \{{\mathrm {Im}}(\gamma w): \gamma \in \Gamma \}$ , and assume $s\in \mathbb {C}$ with ${\mathrm {Re}}(s)> 1$ . Then $G_{s}(z,w)$ admits the expansion

(25) $$ \begin{align} G_s(z,w)=-\frac{y^{1-s}}{2s-1}\mathcal{E}_\infty^{\mathrm{par}}(w,s)-\sum_{k\in\mathbb{Z}\smallsetminus \{0\}} y^{1/2}K_{s-1/2}(2\pi |k| y) F_{-k}(w,s)e(kx), \end{align} $$

where $\mathcal {E}_\infty ^{\mathrm {par}}(w,s)$ is the parabolic Eisenstein series associated with the cusp at $\infty $ of $\Gamma $ (see the next section for its full description).

The function $G_s(z,w)$ is unbounded as $z\to w$ and, according to Proposition 6.5 from [9], we have the asymptotic formula

$$ \begin{align*}G_s(z,w)=\frac{\mathrm{ord}(w)}{2\pi}\log|z-w|+O(1) \,\,\,\,\, \text{as}\quad z\to w. \end{align*} $$

4 Eisenstein series and their Kronecker limit formulas

The purpose of this section is twofold. First, we state the definitions of parabolic and elliptic Eisenstein series as well as their associated Kronecker limit formulas. Specific examples of the parabolic Kronecker limit formulas are recalled from [13]. Second, we prove the factorization theorem for meromorphic forms in terms of elliptic Kronecker limit functions, as stated in (5).

4.1 Parabolic Kronecker limit functions

Associated with the cusp at $\infty $ of $\Gamma $ one has a parabolic Eisenstein series ${\cal E}^{\mathrm {par}}_{\infty }(z,s)$ . Let $\Gamma _{\infty }$ denote the stabilizer subgroup within $\Gamma $ of $\infty $ . For $z\in \mathbb {H}$ and $s \in \mathbb {C}$ with $\mathrm {Re}(s)> 1$ , ${\cal E}^{\mathrm {par}}_{\infty }(z,s)$ is defined by the series

$$ \begin{align*} {\cal E}^{\mathrm{par}}_{\infty}(z,s) = \sum\limits_{\gamma \in \Gamma_{\infty}\backslash \Gamma}\mathrm{Im}(\gamma z)^{s}. \end{align*} $$

It is well known that ${\cal E}^{\mathrm {par}}_{\infty }(z,s)$ admits a meromorphic continuation to all $s\in {\mathbb C}$ and a functional equation in s.

For us, the Kronecker limit formula means the determination of the constant term in the Laurent expansion of ${\cal E}^{\mathrm {par}}_{\infty }(z,s)$ at $s=1$ . Classically, Kronecker’s limit formula is the assertion that for $\Gamma = \mathrm {PSL}(2,\mathbb {Z})$ one has that

(26) $$ \begin{align} \mathcal{E}^{\mathrm{par}}_{\infty}(z,s)= \frac{3}{\pi(s-1)} -\frac{1}{2\pi}\log\bigl(|\Delta(z)|{\mathrm{Im}}(z)^{6}\bigr)+C+O(s-1) \,\,\,\mathrm{as} \,\,\, s \rightarrow 1, \end{align} $$

where $C=6(1-12\,\zeta '(-1)-\log (4\pi ))/\pi $ and $\Delta (z)$ is Dedekind’s Delta function which is defined by

(27) $$ \begin{align} \Delta(z) = \left[q_{z}^{1/24}\prod\limits_{n=1}^{\infty}\left(1 - q_{z}^{n}\right)\right]^{24} = \eta(z)^{24}. \end{align} $$

We refer to [22] for a proof of (26), though the above formulation follows the normalization from [13].

For general Fuchsian groups of the first kind, Goldstein [7] studied analogs of the Kronecker’s limit formula associated with parabolic Eisenstein series. After a slight renormalization and trivial generalization, Theorem 3-1 from [7] asserts that the parabolic Eisenstein series $\mathcal {E}^{\mathrm {par}}_{\infty }(z,s)$ admits the Laurent expansion

(28) $$ \begin{align} \mathcal{E}^{\mathrm{par}}_{\infty}(z,s)= \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M) (s-1)} + \beta- \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \log (\vert\eta_{\infty}^4(z)\vert {\mathrm{Im}}(z)) + O(s-1), \end{align} $$

as $s \to 1$ and where $\beta =\beta _{\Gamma }$ is a certain real constant depending only on the group $\Gamma $ . As the notation suggests, the function $\eta _{\infty }(z)$ is a holomorphic form for $\Gamma $ and can be viewed as a generalization of the eta function $\eta (z)$ which is defined in (27) for the full modular group.

By employing the functional equation for the parabolic Eisenstein series, as stated in Theorem 6.5 of [11], one can re-write the Kronecker limit formula as stating that

(29) $$ \begin{align} \mathcal{E}^{\mathrm{par}}_{\infty}(z,s)= 1+ \log (\vert \eta_{\infty}^4(z)\vert {\mathrm{Im}}(z))\cdot s + O(s^2) \quad\text{ as } s \to 0 \end{align} $$

(see [16, Cor. 3]). In this formulation, we will call the function

$$ \begin{align*}P(z)=P_{\Gamma}(z):=\log (\vert \eta_{\infty}^4(z)\vert {\mathrm{Im}}(z)), \end{align*} $$

the parabolic Kronecker limit function of $\Gamma $ .

4.2 Atkin–Lehner groups

Let $N=p_1\ldots p_r$ be a positive square-free number, which includes the possibility that $N=1$ and set

$$ \begin{align*}\ell_N = 2^{1-r}\mathrm{lcm}\Big(4,\ 2^{r-1}\frac{24}{\mathrm{gcd}(24,\sigma(N))}\Big), \end{align*} $$

where $\mathrm {lcm}$ stands for the least common multiple of its argument and $\mathrm {gcd}$ denotes the greatest common divisor of its argument. In [13, Th. 16], it is proved that

(30) $$ \begin{align} \Delta_N(z):=\left( \prod_{v \mid N} \eta(v z) \right)^{\ell_N} \end{align} $$

is a weight $k_N=2^{r-1} \ell _N$ holomorphic form for $\Gamma _0(N)^+$ vanishing only at the cusp. By the valence formula, the order of vanishing of $\Delta _N(z)$ at the cusp is $\nu _N:=k_N \operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})/(4\pi )$ , where $\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})=\pi \sigma (N)/(3\cdot 2^r)$ is the hyperbolic volume of the surface $Y_N^{+}$ .

The Kronecker limit formula (28) for the parabolic Eisenstein series $\mathcal {E}^{\mathrm {par},N}_{\infty }(z,s)$ associated with $Y_N^{+}$ reads as

(31) $$ \begin{align} \mathcal{E}^{\mathrm{par},N}_{\infty}(z,s)= \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+}) (s-1)} + \beta_N - \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+})}P_N(z) + O((s-1)) \end{align} $$

as $s \to 1$ . From Examples 4 and 7 of [16], we have the explicit evaluations of $\beta _{N}$ and $P_{N}(z)$ . Namely,

(32) $$ \begin{align} \beta_N=- \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}} (Y_N^{+}) }\left( \sum_{j=1}^{r} \frac{(p_j -1)\log p_j}{2(p_j+1)}- \log N + 2\log (4\pi) + 24\zeta'(-1) - 2\right) \end{align} $$

and the parabolic Kronecker limit function $P_N(z)$ is given by

$$ \begin{align*}P_N(z)= \log\left( \sqrt[2^r]{\prod_{v \mid N} \vert \eta(vz)\vert ^4} \cdot {\mathrm{Im}}(z) \right). \end{align*} $$

4.3 Elliptic Kronecker limit functions

Elliptic subgroups of $\Gamma $ have finite order and a unique fixed point within $\mathbb H$ . For all but a finite number of $w \in \mathcal {F}$ , the order $\mathrm {ord}(w)$ of the elliptic subgroup $\Gamma _{w}$ which fixes w is one. For $z\in \mathbb {H}$ with $z\not =\gamma w$ , for $\gamma \in \Gamma $ and $s \in \mathbb {C}$ with $\mathrm {Re}(s)> 1$ , the elliptic Eisenstein series ${\cal E}^{\mathrm {ell}}_{w}(z,s)$ is defined by the series

(33) $$ \begin{align} {\cal E}^{\mathrm{ell}}_{w}(z,s) =\sum\limits_{\gamma \in \Gamma_{w}\backslash \Gamma} \sinh(d_{\mathrm{hyp}}(\gamma z, w))^{-s} = \sum\limits_{\gamma \in \Gamma_{w}\backslash \Gamma} \left( \frac{2\,\mathrm{Im}(w)\mathrm{Im}(\gamma z)}{|\gamma z-w|\,|\gamma z-\overline{w}|} \right)^s. \end{align} $$

It was first shown in [24] that (33) admits a meromorphic continuation to all $s \in {\mathbb C}$ .

The analog of the Kronecker limit formula for ${\cal E}^{\mathrm {ell}}_{w}(z,s)$ was first proved in [24] (see also [16, (4)], [25, Th. 5.2]). In the setting of this paper, it is shown in [24] that for any $w\in \mathcal {F}$ and $z\in \mathbb {H}$ with $z\not =\gamma w$ , the series (33) admits the Laurent expansion

(34) $$ \begin{align}\nonumber \mathcal{E}^{\mathrm{ell}}_{w}(z,s) &- \frac{2^{s}\sqrt{\pi}\,\Gamma(s-\frac{1}{2})}{\mathrm{ord}(w)\Gamma(s)}\mathcal{E}^{\mathrm{par}}_{\infty}(w,1-s) \,\mathcal{E}^{\mathrm{par}}_{\infty}(z,s) \\ & = -c_w -\log\bigl(|H_{\Gamma}(z,w)|{\mathrm{Im}}(z)^{c_w}\bigr)\cdot s+O(s^2)\quad\mathrm{as}\ s \rightarrow 0, \end{align} $$

where

$$ \begin{align*}c_w= \frac{2\pi}{\mathrm{ord}(w)\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}. \end{align*} $$

In the notation of [25], we are writing that $|H_{\Gamma }(z,w)|=|H_w(z)| {\mathrm {Im}}(w)^{c_w}$ .

Moreover, von Pippich proved that when viewed as a function of z, $H(z,w):=H_{\Gamma }(z,w)$ is holomorphic on $\mathbb {H}$ and uniquely determined up to multiplication by a complex constant of absolute value one. Additionally, $H(z,w)$ is an automorphic form with a nontrivial multiplier system with respect to $\Gamma $ acting on z and which depends on w.

In order to deduce behavior of $H(z,w)$ as $z\to \gamma w$ for $\gamma \in \Gamma $ , we apply Proposition 5.1 of [25]. In doing so, one gets that

$$ \begin{align*}\mathcal{E}^{\mathrm{ell}}_{w}(z,s)- \frac{2^{s}\sqrt{\pi}\,\Gamma(s-\frac{1}{2})}{\mathrm{ord}(w)\Gamma(s)}\mathcal{E}^{\mathrm{par}}_{\infty}(w,1-s) \,\mathcal{E}^{\mathrm{par}}_{\infty}(z,s)= -c_w+ \mathcal{K}_w(z)\cdot s +O(s^2) \,\,\, \mathrm{as} s \rightarrow 0, \end{align*} $$

and with $\mathcal {K}_w(z)=-\log |z-\gamma w| + O(1)$ as $z\to \gamma w$ for some $\gamma \in \Gamma $ . Combining this statement with (34), we immediately deduce that $H(z,w)$ , viewed as a function of variable $z\in \mathbb {H}$ , vanishes if and only if $z= \gamma w$ for some $\gamma \in \Gamma $ . Furthermore, the order of vanishing of $H(z,w)$ equals one.

4.4 A factorization theorem

In this section, we prove that equation (5) holds for meromorphic forms on $\Gamma $ of even weight $2k$ , suitably normalized at the cusp at $\infty $ . For meromorphic forms, we let $\mathrm {ord}_w(f)$ denote the order of f at w which is positive if w is a zero of f and negative if w is a pole of f. Let us start by proving that the factorization theorem holds for meromorphic forms.

Proposition 2. With notation as above, let f be an even weight $2k\geq 0$ meromorphic form on $\mathbb {H}$ with q-expansion at $\infty $ given by

(35) $$ \begin{align} f(z)= 1+ \sum_{n=1}^{\infty} b_{f}(n)q_z^n. \end{align} $$

Let $\mathrm {ord}_w(f)$ denote the order f at w and define the function

$$ \begin{align*}H_{f}(z):= \prod_{w \in \mathcal{F}} H(z,w)^{\mathrm{ord}_w(f)}, \end{align*} $$

where $H(z,w)=H_{\Gamma }(z,w)$ is given in (34). Then there exists a complex constant $c_{f}$ such that

(36) $$ \begin{align} f(z) = c_{f}H_{f}(z). \end{align} $$

Furthermore,

$$ \begin{align*}\left\vert c_{f}\right\vert = \exp \left(-\frac{2\pi}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \left( 2-\log 2 + P(w)- \beta\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)\right) \right ), \end{align*} $$

where $P(w)$ and $\beta $ are defined through the parabolic Kronecker limit function (28).

Proof. The proof closely follows the proof of Theorem 9 from [16]. Specifically, following the first part of the proof almost verbatim, we conclude that the quotient

$$ \begin{align*}F_f(z):=\frac{H_f(z)}{f(z)} \end{align*} $$

is a nonvanishing holomorphic function on M which is bounded and nonzero at the cusp at $\infty $ . The argument for this assertion is as follows. When viewed as a (multi-valued) function of $z\in M$ , $H(z,w)$ vanishes if and only if $z=w$ , and the order of vanishing is one. Therefore, we conclude that $F_f(z)$ is a quotient of two multi-valued meromorphic functions on M with the same divisors. By applying the Riemann–Roch theorem as in the proof of Theorem 9 from [16], we conclude that yields that $H_f(z)$ is a weight $2k$ meromorphic form on M, possibly twisted by a unitary character. Therefore, $F_f(z)$ is holomorphic on M.

From [16, Prop. 6], we have the asymptotic expansion in the cusp of $H(z,w)$ , namely that

(37) $$ \begin{align} H(z,w)=a_{w,\infty}\exp(-B_{w,\infty})+ O(\exp(-2\pi {\mathrm{Im}}(z))) \,\,\,\,\, \mathrm{as} {\mathrm{Im}}(z)\to \infty, \end{align} $$

where $a_{w,\infty }$ is a constant of modulus one and

$$ \begin{align*}B_{w,\infty}= - \frac{2\pi}{\mathrm{ord}(w)\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\left( 2-\log 2 + P(w)- \beta\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)\right). \end{align*} $$

When combining (37) with the q-expansion of f, as stated in (35), we obtain that $F_f(z)$ is bounded and nonzero at the cusp $\infty $ .

Since $F_{f}$ is holomorphic, nonvanishing and nonzero in the cusp, then the function $\log \vert F_{f}(z)\vert $ is $L^{2}$ and bounded on M. From its spectral expansion and the fact that $\log \vert F_{f}(z)\vert $ is harmonic, one concludes $\log \vert F_{f}(z)\vert $ is constant, hence so is $F_{f}(z)$ . The evaluation of the constant is obtained by considering the limiting behavior (37) as z approaches $\infty $ .

In summary, by following the proof of Proposition 12 from [16] verbatim, we obtain (4), and hence (5), for meromorphic forms f on $\mathbb {H}$ with q-expansion (35).

5 Proofs of main results

5.1 Proof of Theorem 1

Let $Y>1$ be sufficiently large so that the cuspidal neighborhood $\mathcal {F}_{\infty }(Y)$ of the cusp $\infty $ in $\mathcal {F}$ is of the form $\{z \in {\mathbb H} : 0 < x \leq 1, y> Y\}$ . For $s\in \mathbb {C}$ with ${\mathrm {Re}}(s)>1$ , and arbitrary, but fixed $w\in \mathcal {F}$ , we then have that

$$ \begin{align*} \int\limits_{\mathcal{F}(Y)}\Delta_{\operatorname{\mathrm{hyp}}}(F_{-n}(z,1))&\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \\ & -\int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\Delta_{\operatorname{\mathrm{hyp}}} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \\ &= -s(1-s)\int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z). \end{align*} $$

Actually, the first summand on the left-hand side is zero since $F_{-n}(z,1)$ is holomorphic; however, this judicious form of the number zero is significant since we will use the method behind the Maass–Selberg theorem to study the left-hand side of the above equation. Before this, note that the integrand on the right-hand side of the above equation is holomorphic at $s=1$ . As a result, we can write

$$ \begin{align*} \frac{\partial}{\partial s}&\left.\left(-s(1-s)\int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z)\right)\right|_{s=1}\\&= \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\lim_{s\to 1}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z). \end{align*} $$

When reversing the order of the above steps, we get that

(38) $$ \begin{align} \langle F_{-n}(z,1), &\overline{\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)} \rangle \notag \\&=\lim_{Y\to \infty} \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(z,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \notag \\&= \lim_{Y\to \infty} \left[\frac{\partial}{\partial s}\left( \int\limits_{\mathcal{F}(Y)}\Delta_{\operatorname{\mathrm{hyp}}}(F_{-n}(z,1))\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \right. \right.\notag \\&- \left.\left. \left. \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\Delta_{\operatorname{\mathrm{hyp}}} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \right) \right|_{s=1}\right]. \end{align} $$

The quantity on the right-hand side of (38) is setup for an application of Green’s theorem as in the proof of the Maass–Selberg relations for the Eisenstein series. As described on page 89 of [11], when applying Green’s theorem to each term on the right-side of (38) for fixed Y, the resulting boundary terms on the sides of the fundamental domain, which are identified by $\Gamma $ , will sum to zero. Therefore, we get that

(39) $$ \begin{align} \langle F_{-n}(z,1),& \overline{\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)} \rangle \notag \\&= \lim_{Y\to \infty} \left[\frac{\partial}{\partial s}\left( \int\limits_{0}^{1}\frac{\partial}{\partial y}F_{-n}(z,1)\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)dx \right. \right. \notag\\ &- \left.\left. \left. \int\limits_{0}^{1}F_{-n}(z,1)\frac{\partial}{\partial y} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)dx \right) \right|_{s=1}\right], \end{align} $$

where the functions of z and their derivatives with respect to $y={\mathrm {Im}}(z)$ are evaluated at $z=x+iY$ .

In order to compute the difference of the two integrals of the right-hand side of (39), we will use the Fourier expansions (17) and (25) of the series $F_{-n}(z,1)$ and $G_s(z,w)$ , respectively. It will be more convenient to write the first coefficient in the expansion (17) as $e(-nx)\sqrt {y}I_{\tfrac {1}{2}}(2\pi n y)$ , as in (16). As is well known, the various exponential functions $e(-nx)$ when integrated with respect to x are orthogonal to each other for different values of n. Using this observation, we can write the difference of two integrals on the right-hand side of (39) when evaluated at $z=x+iY$ as

$$ \begin{align*} &\quad -F_{-n}(w,s)\sqrt{Y} \bigg(\frac{\partial}{\partial y}\left(\sqrt{y}I_{\tfrac{1}{2}}(2\pi n y)\right)\bigg|_{y=Y}\cdot K_{s-\tfrac{1}{2}}(2\pi n Y) \\&\quad - I_{\tfrac{1}{2}}(2\pi n Y)\cdot \frac{\partial}{\partial y}\left(\sqrt{y}K_{s- \tfrac{1}{2}}(2\pi n y) \right)\bigg|_{y=Y}\bigg)\\&\quad + B_0(1;-n)(1-s)\frac{Y^{-s}}{2s-1}\mathcal{E}_\infty^{\mathrm{par}}(w,s) \\&\quad + \sum_{k\in\mathbb{Z}\smallsetminus\{0\}}F_k(w,s) \bigg( b_k(Y,1;-n)\cdot \frac{\partial}{\partial y}\left(\sqrt{y}K_{s- \tfrac{1}{2}}(2\pi |k| y) \right)\bigg|_{y=Y} \\&\quad -\frac{\partial}{\partial y}b_k(y,1;-n)\bigg|_{y=Y}\cdot \sqrt{Y} K_{s-\tfrac{1}{2}}(2\pi |k| Y) \bigg)\\& =T_1(Y,s;w) + T_2(Y,s;w)+T_3(Y,s;w), \end{align*} $$

where the last equality above provides the definitions of the functions $T_{1}$ , $T_{2}$ , and $T_{3}$ . Therefore, from (39), we have that

(40) $$ \begin{align} &\langle F_{-n}(z,1), \overline{\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)} \rangle \nonumber\\ & \quad = \lim_{Y\to \infty} \left[\left.\frac{\partial}{\partial s}\left( T_1(Y,s;w) + T_2(Y,s;w)+T_3(Y,s;w) \right)\right|_{s=1}\right]. \end{align} $$

We will study each of the three terms on the right-hand side of (40) separately.

To evaluate the term $T_{1}$ in (40), we apply formulas (A.19) and (A.20) in order to compute the derivatives of the Bessel functions in hand. In doing so, we conclude that

$$ \begin{align*} T_1(Y,s;w) &=-\frac{X}{2}F_{-n}(w,s)\bigg[K_{s-\tfrac{1}{2}}(X)(I_{-\tfrac{1}{2}}(X) \\& \qquad\qquad\qquad\qquad + I_{\tfrac{3}{2}}(X)) + I_{\tfrac{1}{2}}(X)(K_{s-\tfrac{3}{2}}(X) + K_{s+\tfrac{1}{2}}(X)) \bigg], \end{align*} $$

where we set $X=2\pi n Y$ . Next, we can express $K_{s+\tfrac {1}{2}} (X)$ in terms of $K_{s-\tfrac {1}{2}} (X)$ and $K_{s-\tfrac {3}{2}}(X)$ by using formula (A.6) with $\nu =s-1/2$ , which gives that

(41) $$ \begin{align} K_{s+\tfrac{1}{2}} (X)= K_{s-\tfrac{3}{2}} (X) + \frac{2s-1}{X}K_{s-\tfrac{1}{2}} (X). \end{align} $$

Therefore,

$$ \begin{align*} T_1(Y,s;w) &=-\frac{X}{2}F_{-n}(w,s)\bigg[K_{s-\tfrac{1}{2}}(X)\bigg(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X) + \frac{2s-1}{X}I_{\tfrac{1}{2}}(X)\bigg) \\& \qquad\qquad\qquad\qquad + 2 I_{\tfrac{1}{2}}(X)K_{s-\tfrac{3}{2}}(X) \bigg]. \end{align*} $$

Now, let us use formula (A.14) in order to differentiate $K_{s-\tfrac {1}{2}}(X)$ and $K_{s-\tfrac {3}{2}}(X)$ with respect to s at $s=1$ . When combined with the expression (A.5), for $I_{\tfrac {1}{2}}(X)$ , we deduce that

$$ \begin{align*} &\frac{\partial}{\partial s}\left.\left[K_{s-\tfrac{1}{2}}(X)\left(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X) + \frac{2s-1}{X}I_{\tfrac{1}{2}}(X)\right) +2 I_{\tfrac{1}{2}}(X)K_{s-\tfrac{3}{2}}(X) \right]\right|_{s=1}\\& \quad = \sqrt{\frac{\pi}{2X}}e^X\mathrm{Ei}(-2X)\left[ -(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X)) + \sqrt{\frac{2}{\pi X}} (2-1/X) \sinh (X) \right]\\& \qquad +\frac{2}{X^2}e^{-X}\sinh (X), \end{align*} $$

where $\mathrm {Ei}(x)$ denotes the exponential integral (see (A.7)).

Continuing, we now employ the bound (A.11) with $\nu =-1/2$ and when $\nu =3/2$ . This result, together with the bound (A.8) for the exponential integral yields that

$$ \begin{align*}\lim_{X\to\infty}\frac{X}{2}\frac{\partial}{\partial s}\left.\left[K_{s-\tfrac{1}{2}}(X)\left(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X) + \frac{2s-1}{X}I_{\tfrac{1}{2}}(X)\right) +2 I_{\tfrac{1}{2}}(X)K_{s-\tfrac{3}{2}}(X) \right]\right|_{s=1} =0. \end{align*} $$

Therefore,

$$ \begin{align*} &\lim_{Y\to \infty}\frac{\partial}{\partial s}\left. T_1(Y,s;w)\right|_{s=1}= - \frac{\partial}{\partial s}\left. F_{-n}(w,s)\right|_{s=1}\cdot \\& \quad \cdot\lim_{X\to \infty}\frac{X}{2}\left[K_{\tfrac{1}{2}}(X)(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X)) + I_{\tfrac{1}{2}}(X)(K_{-\tfrac{1}{2}}(X) + K_{\tfrac{3}{2}}(X)) \right]. \end{align*} $$

Finally, by applying (A.11) and (A.12) with $\nu =\pm 1/2$ and $\nu =3/2$ , we deduce that

$$ \begin{align*}\lim_{X\to \infty}\frac{X}{2}\left[K_{\tfrac{1}{2}}(X)(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X)) + I_{\tfrac{1}{2}}(X)(K_{-\tfrac{1}{2}}(X) + K_{\tfrac{3}{2}}(X)) \right]=1. \end{align*} $$

Therefore, we have proved that

(42) $$ \begin{align} \lim_{Y\to \infty}\frac{\partial}{\partial s}\left. T_1(Y,s;w)\right|_{s=1}= - \frac{\partial}{\partial s}\left. F_{-n}(w,s)\right|_{s=1}. \end{align} $$

As for the term $T_{2}$ in (40), let us use the Laurent series expansion (28) of $\mathcal {E}_\infty ^{\mathrm {par}}(w,s)$ , from which one easily deduces that

$$ \begin{align*}\frac{\partial}{\partial s}\left.(s-1)\frac{Y^{-s}}{2s-1}\mathcal{E}_\infty^{\mathrm{par}}(w,s)\right|_{s=1} = \frac{1}{Y}\left( \beta - \frac{P(w)+2+\log Y}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\right). \end{align*} $$

Therefore,

(43) $$ \begin{align} \lim_{Y\to \infty}\frac{\partial}{\partial s}\left. T_2(Y,s;w)\right|_{s=1}=0. \end{align} $$

It remains to study the term $T_{3}$ in (40). Let us set $g(s,y,\ell ):=\sqrt {y}K_{s-\tfrac {1}{2}}(2\pi \ell y)$ for some positive integer $\ell $ . Then $b_k(y,1;-n)=B_k(1;-n)g(1,y,|n|)$ and

(44) $$ \begin{align} T_3(Y,s;w)&=\sum_{k\in\mathbb{Z}\smallsetminus\{0\}} B_k(1;-n) F_k(w,s) \left( g(1,Y,|n|) \frac{\partial}{\partial y}\left.g(s,y,|k|)\right|_{y=Y} \right. \nonumber\\& \qquad\qquad\qquad\qquad\qquad\qquad\qquad - \left. g(s,Y,|k|)\frac{\partial}{\partial y}\left.g(1,y,|n|)\right|_{y=Y} \right). \end{align} $$

For positive integers m and $\ell $ , let us define, for notational convenience,

$$ \begin{align*}G(s,Y,m,\ell):=g(1,Y,m) \frac{\partial}{\partial y}\left.g(s,y,\ell)\right|_{y=Y}- g(s,Y,\ell)\frac{\partial}{\partial y}\left.g(1,y,m)\right|_{y=Y}; \end{align*} $$

observe that, according to (A.5),

$$ \begin{align*}g(1,y,m)=\frac{1}{2\sqrt{m}} e^{-2\pi my}. \end{align*} $$

In order to compute the derivative of the K-Bessel function with respect to the argument, we will use formula (A.20). When combining with equation (41), for $K_{s+\tfrac {1}{2}}(2\pi \ell Y)$ , we get that

(45) $$ \begin{align} G(s,Y,m,\ell) =\frac{e^{-2\pi m Y}}{2\sqrt{mY}}\left(( (1-s)+2\pi mY) K_{s-\tfrac{1}{2}}(2\pi \ell Y)-2\pi \ell Y K_{s-\tfrac{3}{2}}(2\pi\ell Y)\right). \end{align} $$

When $s=1$ , the bound (A.12) for the K-Bessel function immediately yields that

$$ \begin{align*}\left. G(s,Y,m,\ell)\right|_{s=1}\ll (m + \ell)\exp(-2\pi Y (m+\ell)) \,\,\,\,\, \mathrm{as} Y\to\infty \end{align*} $$

and for any two positive integers $m,\ell $ . Also, the implied constant is independent of $m, \ell , Y$ .

Observe that when differentiating the expression (45) for $G(s,Y,m,\ell )$ with respect to s and taking $s=1$ , the computations amount to computing various derivatives of the K-Bessel functions $K_\nu (z)$ with respect to the order $\nu $ at $\nu =\pm \frac {1}{2}$ which is easily done by applying formula (A.14). In doing so, and when combined with the bound (A.8) for the exponential integral, one immediately gets the bound that

(46) $$ \begin{align} \max\left\{G(s,Y,m,\ell), \left.\frac{\partial }{\partial s} G(s,Y,m,\ell)\right|_{s=1}\right\}\ll (m + \ell)\exp(-2\pi Y (m+\ell)) \,\,\, \mathrm{as} Y\to +\infty. \end{align} $$

As above, the implied constant is independent of $Y,m,\ell $ .

Notice that $G(s,Y,m,\ell )$ with $m=|n|$ and $\ell =|k|$ equals the expression inside the parenthesis in the sum (44) which defines $T_3(Y,s;w)$ . Therefore, in order to estimate $\left .\frac {\partial }{\partial s} T_3(Y,s;w)\right |_{s=1}$ as $Y\to \infty $ it suffices to combine the bound (46), with $m=|n|$ and $\ell =|k|$ , with the bounds (19) and (20) for $F_{k}(w,s)$ and $\frac {\partial }{\partial s} F_{k}(w,s)$ at $s=1$ . In doing so, we get that

$$ \begin{align*}\frac{\partial}{\partial s} T_3(Y,s;w)\Big|_{s=1}\ll \sum_{k\in\mathbb{Z}\smallsetminus\{0\}}(|n| + |k|) | B_k(1;-n)| \exp\left( -2\pi Y (|k|+|n|) + 2\pi|k| {\mathrm{Im}}(w)\right). \end{align*} $$

It remains to estimate the sum on the right-hand side of the above equation as $Y\to \infty $ . The bound (18) gives that

$$ \begin{align*} \frac{\partial}{\partial s}&\left. T_3(Y,s;w)\right|_{s=1} \\& \ll \sum_{k\in\mathbb{Z}\smallsetminus\{0\}} (|n| + |k| )\sqrt{|kn|}\exp\left( -2\pi \left( (|k|+|n|)Y - 2\sqrt{|kn|}/c_\Gamma -|k| {\mathrm{Im}}(w) \right) \right). \end{align*} $$

For $Y> 2{\mathrm {Im}}(w) + 2\sqrt {n}/c_\Gamma $ , this series over j is uniformly convergent and is $o(1)$ as $Y\to \infty $ . In other words,

(47) $$ \begin{align} \lim_{Y\to\infty}\frac{\partial}{\partial s}\left. T_3(Y,s;w)\right|_{s=1} =0. \end{align} $$

With all this, when combining (47) with (40), (42), and (43), we have that

$$ \begin{align*} \langle F_{-n}(z,1), \overline{\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)} \rangle =- \frac{\partial}{\partial s}\left. F_{-n}(w,s) \right|_{s=1}, \end{align*} $$

which completes the proof of (9).

5.2 Proof of Corollary 1

The proof of Corollary 1 is a combination of Theorem 1 and the factorization theorem as stated in Proposition 1. The details are as follows.

To begin, we shall prove Proposition 1. Starting with (5), which is written as

$$ \begin{align*}\log\left( y^k |f(z)| \right) = kP(z) - \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \lim_{s\to 0} \frac{1}{s} \mathrm{ord}(w)\mathcal{E}^{\mathrm{ell}}_{w}(z,s), \end{align*} $$

we can express $\lim _{s\to 0} \frac {1}{s}\mathrm {ord}(w) \mathcal {E}^{\mathrm {ell}}_{w}(z,s)$ in terms of the resolvent kernel. Specifically, using (6), we have that

(48) $$ \begin{align} \log\left( y^k |f(z)| \right)=kP(z) + \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \lim_{s\to 0} \left(\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w)\right). \end{align} $$

By applying the functional equation for the Green’s function, see Theorem 3.5 of [9] on pages 250–251, we get

$$ \begin{align*} \lim_{s\to 0}\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w) = \lim_{s\to 1} \frac{2^{1-s}\sqrt{\pi} \Gamma(1/2-s)}{\Gamma(2-s)}(1-2s)G_{1-s}(z,w)\\ =\lim_{s\to 1}\left(\frac{2^{1-s}\sqrt{\pi} \Gamma(1/2-s)}{\Gamma(2-s)}\left((1-2s)G_s(z,w)- \frac{}{}\mathcal{E}_\infty^{\mathrm{par}}(z,1-s)\mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)\right). \end{align*} $$

From the Kronecker limit formula (29), we know that

$$ \begin{align*}\mathcal{E}_\infty^{\mathrm{par}}(z,1-s)=1+P(z)(1-s)+O((1-s)^2) \,\,\,\,\, \mathrm{as} s\to 1. \end{align*} $$

When combined with the standard Taylor series expansion of the gamma function, we get that

$$ \begin{align*} \lim_{s\to 0}&\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w)= \lim_{s\to 1}\Big((2\pi (-1+(s-1)(2-\log 2))\cdot \\& \cdot \left[2(1-s)G_s(z,w) - (G_s(z,w)+\mathcal{E}_\infty^{\mathrm{par}}(w,s)) - P(z)(1-s)\mathcal{E}_\infty^{\mathrm{par}}(w,s)\right]\Big). \end{align*} $$

According to [11, p. 106], the point $s=1$ is the simple pole of $G_s(z,w)$ with the residue $-1/\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(M)$ . (Note: Our $G_s(z,w)$ differs from the automorphic Green’s function from [11] by a factor of $-1$ .) Therefore, the Kronecker limit formula (28) gives that

(49) $$ \begin{align} \lim_{s\to 0}\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w)&= -\frac{2\pi}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}P(z)- \frac{4\pi}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \\&\quad + 2\pi\lim_{s\to 1}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right).\notag \end{align} $$

Recall that the classical the Riemann–Roch theorem implies that

$$ \begin{align*}k\frac{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}{2\pi}=\sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}; \end{align*} $$

hence, after multiplying (49) by $\frac {\mathrm {ord}_w(f)}{\mathrm {ord}(w)} $ and taking the sum over all $w\in \mathcal {F}$ from (48), we arrive at (7), as claimed.

Having proved Proposition 1, observe that the left-hand side of (7) is real-valued. As proved in [19], $F_{-n}(z,1)$ is orthogonal to constant functions. Therefore, in order to prove (10) one simply applies (9), which was established above.

5.3 Proof of Corollary 2

In order to prove (12), it suffices to compute $\langle 1, \overline {\lim _{s\to 1}(G_s(z,w) + \mathcal {E}_{\infty }^{\mathrm {par}}(w,s))} \rangle $ , which we will write as

$$ \begin{align*}\int\limits_{\mathcal{F}}\lim_{s\to 1}\left(G_s(z,w) + \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)(s-1)}+ \mathcal{E}_{\infty}^{\mathrm{par}}(w,s)-\frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)(s-1)}\right)d\mu_{\operatorname{\mathrm{hyp}}}(z). \end{align*} $$

From its spectral expansion, the function $\lim _{s\to 1}\left (G_s(z,w) + \frac {1}{\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(M)(s-1)}\right )$ is $L^2$ on $\mathcal {F}$ and orthogonal to constant functions. Therefore, by using the Laurent series expansion (28), we get that

$$ \begin{align*}\langle 1, \overline{\lim_{s\to 1}(G_s(z,w) + \mathcal{E}_{\infty}^{\mathrm{par}}(w,s))} \rangle =\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)\left(\beta - \frac{P(w)}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\right), \end{align*} $$

which completes the proof.

5.4 Proof of Theorem 2

Our starting point is the Fourier expansion of the sum $G_s(z,w) + \mathcal {E}_\infty ^{\mathrm {par}}(w,s)$ . Namely, for ${\mathrm {Re}}(s)>1$ and ${\mathrm {Im}}(w)$ sufficiently large, we have that

(50) $$ \begin{align} G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)&=\left(1-\frac{y^{1-s}}{2s-1}\right)\mathcal{E}_\infty^{\mathrm{par}}(w,s) \notag \\& \quad -\sum_{k\in\mathbb{Z}\setminus\{0\}} \sqrt{y}K_{s-\tfrac{1}{2}}(2\pi |k| y)F_{-k}(w,s)e(kx). \end{align} $$

If ${\mathrm {Im}}(z)$ is sufficiently large, the exponential decay of $K_{s-\tfrac {1}{2}}(2\pi |k| y)$ is sufficient to ensure that the right-hand side of (50) is holomorphic at $s=1$ . The Laurent series expansion of $\mathcal {E}_\infty ^{\mathrm {par}}(w,s)$ , when combined with the expansions

$$ \begin{align*}y^{1-s}=1+(1-s)\log y + \tfrac{1}{2}(1-s)^2 \log^2y + O((1-s)^3)\end{align*} $$

and

$$ \begin{align*}(2s-1)^{-1}= (1-2(s-1))^{-1} = 1-2(s-1)+4(s-1)^2 + O((s-1)^3)\end{align*} $$

yields that

$$ \begin{align*} \frac{\partial}{\partial s}\bigg(1-\frac{y^{1-s}}{2s-1}\bigg)\mathcal{E}_\infty^{\mathrm{par}}(w,s) \bigg|_{s=1} &=\frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\bigg[ -4+2\beta\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)-2P(w) \\& \quad + \log y \bigg(\beta\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M) - P(w)-2\bigg) - \tfrac{1}{2}\log^2y \bigg]. \end{align*} $$

Additionally, for ${\mathrm {Im}}(z)$ sufficiently large, the series on the right-hand side of (50) is a uniformly convergent series of functions which are holomorphic at $s=1$ . As such, we may differentiate the series term by term. By employing (A.5) and (A.14), we deduce, for $k\neq 0$ , that

$$ \begin{align*} &\frac{\partial}{\partial s}\left. \left(\sqrt{y}K_{s-\tfrac{1}{2}}(2\pi |k| y)F_{-k}(w,s) \right) \right|_{s=1}=\frac{e^{-2\pi|k|y}}{2\sqrt{|k|}}\cdot \\& \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \cdot\left[ \frac{\partial}{\partial s}\left. F_{-k}(w,s) \right|_{s=1}- F_{-k}(w,1)e^{4\pi|k|y} \mathrm{Ei}(-4\pi |k|y)\right], \end{align*} $$

where $\mathrm {Ei}(x)$ denotes the exponential integral function. From this, we get the expression that

$$ \begin{align*} &\frac{\partial}{\partial s}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)\Big|_{s=1} = (\log y+2) \left(\beta - \frac{P(w)+2} {\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)}\right) - \frac{\log^2 y}{2\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)} \\& \quad - \sum_{k\in\mathbb{Z}\setminus\{0\}}\frac{1}{2\sqrt{|k|}}\left[ \frac{\partial}{\partial s} \left. F_{-k}(w,s) \right|_{s=1}- F_{-k}(w,1)e^{4\pi|k|y} \mathrm{Ei}(-4\pi |k|y)\right]e^{2\pi i kx - 2\pi|k|y}. \end{align*} $$

Let us now compute the derivative $\frac {\partial }{\partial z}$ of the above expression. After multiplying by $i=\sqrt {-1}$ , we get that

$$ \begin{align*} &\mathcal{G}_w(z)=\frac{1}{y}\left(\beta - \frac{P(w)+2}{\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)}\right) - \frac{\log y}{y \mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)} +\sum_{k\geq 1} 2\pi \sqrt{k} \frac{\partial}{\partial s}\left. F_{-k}(w,s) \right|_{s=1}q_z^k \\& \quad +\sum_{k\geq 1}\frac{F_{-k}(w,1)}{2\sqrt{k}y}q_z^k -\sum_{k\leq -1} 2\pi \sqrt{|k|} F_{-k}(w,1) \mathrm{Ei}(4\pi ky) q_z^k + \sum_{k\leq -1}\frac{F_{-k}(w,1)}{2\sqrt{|k|}y}e^{2\pi i k(x-iy)}. \end{align*} $$

The proof of the assertion that $\sum _{k\geq 1} 2\pi \sqrt {k} \frac {\partial }{\partial s}\left. F_{-k}(w,s) \right |_{s=1}q_z^k$ is the holomorphic part of $\mathcal {G}_w(z)$ follows by citing the uniqueness of the analytic continuation in z.

It is left to prove that $\mathcal {G}_w(z)$ is weight two biharmonic Maass form. Since $\mathcal {G}_w(z)$ is obtained by taking the derivative $\frac {\partial }{\partial z}$ of a $\Gamma $ -invariant function, it is obvious that $\mathcal {G}_w(z)$ is weight two in z. Moreover, the straightforward computation that

$$ \begin{align*}iy^2 \frac{\partial}{\partial \bar z}\mathcal{G}_w(z)=\Delta_{\operatorname{\mathrm{hyp}}}\left(\frac{\partial}{\partial s}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)\Big|_{s=1}\right)=- \lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right), \end{align*} $$

when combined with the fact that $\Delta _{\operatorname {\mathrm {hyp}}}\left ( \lim _{s\to 1} \left (G_s(z,w) + \mathcal {E}_\infty ^{\mathrm {par}}(w,s)\right )\right )=0$ , proves that $\mathcal {G}_w(z)$ is biharmonic.

6 Examples

6.1 The full modular group

Throughout this subsection, let $\Gamma =\mathrm {PSL}(2,\mathbb {Z})$ , in which case the parabolic Kronecker limit function, $P(w)$ can be expressed, in the notation of [2], as

where $\eta (w)$ is Dedekind’s eta function and the last equality follows from the definition of

given on page 1 of [2].

In this setting, Corollary 1, when combined with (3) and Rohrlich’s theorem (2) yields that

(51) $$ \begin{align} \langle j_n,\log||f||\rangle =2\pi\sqrt{n}\left( - 2\pi \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}\left(\frac{\partial}{\partial s} F_{-n}(w,s) \bigg|_{s=1} -c_nP(w)\right)\right). \end{align} $$

Moreover, equating the constant terms in the Fourier series expansions for $F_{-n}(z,1)$ and $j_n(z)$ , one easily deduces that $2\pi \sqrt {n}c_n=24\sigma (n)$ . This proves Theorem 1.2 of [2]. Furthermore, we have shown, in the notation of [2] one has that

(52)

This identity provides a description of

, for $n\geq 1$ different from the one given by formula (3.10) of [2]. Finally, from the identity (23), when combined with the fact that $ \Delta _{\operatorname {\mathrm {hyp}}}P(w)=1$ , which is a straightforward implication of the Kronecker limit formula (28), it follows that

which agrees with formula (3.10) of [2].

By reasoning as above, we easily see that Theorem 1.3 of [2] follows from Corollary 2 with $g(z)=j_n(z)$ .

Finally, in view of (51), Theorem 2 is closely related to the first part of Theorem 1.4 of [2]. Namely, for large enough ${\mathrm {Im}}(z)$ , in the notation of [2], we can write

Theorem 2 implies that the function $\mathbb {H}_w(z)$ is the holomorphic part of the weight two biharmonic Maass form

$$ \begin{align*}\widehat{\mathbb{H}}_w(z)=P(w)\widehat{E}_2(z)+\mathcal{G}_w(z),\end{align*} $$

where

$$ \begin{align*}\widehat{E}_2(z)=1-24\sum_{n\geq 1}\sigma(n)q_z^n - \frac{3}{\pi y} \end{align*} $$

is the weight two completed Eisenstein series for the full modular group.

Remark 4. The identity (52) also appears on page 99 of [12]. Furthermore, it is observed in [12] that $h^\ast _n(w)=\xi _0\left (\frac {\partial }{\partial s}\left. F_{-n}(w,s) \right |_{s=1} \right )$ is a harmonic weak Maass form of weight $2$ for which $\xi _2(h^\ast _n(w))=j_n(w)+24\sigma (n)$ and where $\xi _\kappa := 2iy^\kappa \overline {\frac {\partial }{\partial \overline {z}}}$ . Moreover, in Section 4 of [12], it is proved that each $h_n(w)$ is a harmonic Maass forms with bounded holomorphic parts. Additionally, it is shown in [12] that for each $n>0$ one has that $h^\ast _n(w)=4\pi h_n(w)$ , where the set $\{h_m(w)\}_{m\in \mathbb {Z}}$ is a basis for the space $\mathcal {V}$ of weight $2$ harmonic weak Maass forms; the basis was constructed in [6].

6.2 Genus zero Atkin–Lehner groups

Let $N=\prod _{\nu =1}^r p_\nu $ be a positive square-free integer which is one of the $44$ possible values for which the quotient space $Y_{N}^{+} =\overline { \Gamma _{0}^{+}(N)}\backslash {\mathbb H}$ has genus zero (see [5] for a list of such N as well as [14]). Let $\Delta _{N}(z)$ be the Kronecker limit function on $Y_{N}^{+}$ associated with the parabolic Eisenstein series; it is given by formula (30) above.

In the notation of §4.2, the function $\Delta _N(z)(j_N^+(z)-j_N^+(w))^{\nu _N}$ , is the weight $k_N=2^{r-1}\ell _N$ holomorphic modular form which possesses the constant term $1$ in its q-expansion. Furthermore, this function vanishes only at the point $z=w$ , and, by the Riemann–Roch formula, its order of vanishing is equal to $k_N \operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})\cdot \mathrm {ord}(w)/(4\pi )$ .

When $N=1$ , one has $k_1=12$ , $\ell _1=24$ , $\nu _1=1$ and $\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})=\pi /3$ , hence $\Delta _1(z)(j_1^+(z)-j_1^+(w))^{\nu _1}$ equals the prime form $(\Delta (z)(j(z)-j(w)))^{1/\mathrm {ord}(w)}$ taken to the power $\mathrm {ord}(w)$ (see page 3 of [2]).

For any integer $m>1$ , the q-expansion of the form $j_N^+|T_{m}(z)$ is $q_z^{-m}+O(q_z)$ ; hence there exists a constant $C_{m,N}$ such that $j_N^+|T_{m}(z)=2\pi \sqrt {m} F_{-m}(z,1) + C_{m,N}$ . The constant $C_{m,N}$ can be explicitly evaluated in terms of m and N by equating the constant terms in the q-expansions. Upon doing so, one obtains, using equation (24), that

$$ \begin{align*} C_{m,N}=-2\pi \sqrt{m} B_{0,N}^+(1;-m)&=-24\sigma(m)\prod\limits_{\nu=1}^r \left(1- \frac{p_\nu^{\alpha_{p_\nu}(m)+1}(p_\nu -1) }{\left(p_\nu^{\alpha_{p_\nu}(m)+1} - 1\right)(p_\nu+1)}\right)\\&=-24\sigma(m) \prod\limits_{\nu=1}^r \left(1- \kappa_{m}(p_\nu)\right), \end{align*} $$

where we simplified the notation by denoting the second term in the product over $\nu $ by $\kappa _m(p_\nu )$ . We now can apply Corollary 2 with

$$ \begin{align*}g(z)= j_N^+|T_{m}(z)=2\pi \sqrt{m} F_{-m}(z,1)-24\sigma(m)\prod\limits_{\nu=1}^r \left(1- \kappa_{m}(p_\nu)\right) \end{align*} $$

and $f(z)=\Delta _N(z)(j_N^+(z)-j_N^+(w))^{\nu _N}$ . Corollary 2 becomes the statement that

$$ \begin{align*} &\langle j_N^+|T_{m}(z), \log(y^{\tfrac{k_N}{2}} |\Delta_N(z)(j_N^+(z)-j_N^+(w))^{\nu_N}|) \rangle \\& \quad = -k_N \operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+})\bigg[\pi\sqrt{m}\frac{\partial}{\partial s}F_{-m}(w,s)\bigg|_{s=1} \\& \qquad +12\sigma(m)\prod\limits_{\nu=1}^r \left(1- \kappa_{m}(p_\nu)\right) \left(\beta_N\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+})-\log\left( |\Delta_N(w)|^{2/k_N} \cdot {\mathrm{Im}} (w)\right) -2\right)\bigg], \end{align*} $$

where $\beta _N$ is given by (32).

In this form, we have obtained an alternate proof and generalization of formula (1.2) from [2], which is the special case $N=1$ .

6.3 A genus one example

Let us consider the case when $\Gamma = \overline {\Gamma _{0}(37)^{+}}$ . The choice of $N=37$ is significant since this level corresponds to the smallest square-free integer N such that $Y_{N}^{+}$ is genus one. From Proposition 11 of [13], we have that $\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_{37}^{+})= 19\pi /3$ and

$$ \begin{align*}\beta_{37}=\frac{3}{19\pi}\left(\frac{10}{19}\log37+2-2\log(4\pi)-24\zeta'(-1)\right). \end{align*} $$

The function field generators are $x_{37}^+(z)=q_z^{-2} + 2q_z^{-1}+ O(q_z)$ and $y_{37}^+(z)=q_z^{-3} + 3q_z^{-1}+ O(q_z)$ , as displayed in Table 5 of [13]. The generators $x_{37}^+(z)$ and $y_{37}^+(z)$ satisfy the cubic relation $y^2 - x^3 + 6xy - 6x^2 + 41y + 49x + 300 = 0$ .

The functions $x_{37}^+(z)$ and $y_{37}^+(z)$ can be expressed in in terms of the Niebur–Poincaré series by comparing their q-expansions. The resulting expressions are that

$$ \begin{align*} x_{37}^+(z)&=2\pi[\sqrt{2}F_{-2}(z,1)+ 2F_{-1}(z,1)]-2\pi(\sqrt{2}B_{0,37}^+(1;-2)+2B_{0,37}^+(1;-1))\\&=2\pi[\sqrt{2}F_{-2}(z,1)+ 2F_{-1}(z,1)]-\frac{60}{19} \end{align*} $$

and

$$ \begin{align*} y_{37}^+(z)&=2\pi[\sqrt{3}F_{-3}(z,1)+ 3F_{-1}(z,1)]-2\pi(\sqrt{3}B_{0,37}^+(1;-3)+3B_{0,37}^+(1;-1))\\&=2\pi[\sqrt{3}F_{-3}(z,1)+ +3F_{-1}(z,1)]-\frac{84}{19}. \end{align*} $$

It is important to note that $x_{37}^+(z)$ has a pole of order two at $z=\infty $ , that is, its q-expansion begins with $q_z^{-2}$ . As such, $x_{37}^+(z)$ is a linear transformation of the Weierstrass $\wp $ -function, in the coordinates of the upper half plane, associated with the elliptic curve obtained by compactifying the space $Y_{37}^{+}$ . Hence, there are three distinct points $\{w\}$ on $Y_{37}^{+}$ , corresponding to the two torsion points under the group law, such that $x_{37}^+(z)-x_{37}^+(w)$ vanishes as a function of z only when $z=w$ . The order of vanishing necessarily is equal to two. The cusp form $\Delta _{37}(z)$ vanishes at $\infty $ to order $19$ . Therefore, for such w, the form

$$ \begin{align*}f_{37,w}(z)=\Delta_{37}^2(z)(x_{37}^+(z)-x_{37}^+(w))^{19} \end{align*} $$

is a weight $2k_{37}=24$ holomorphic form. The constant term in its q-expansion is equal to $1$ , and $f_{37,w}(z)$ vanishes for points $z \in \mathcal {F}$ only when $z=w$ . The order of vanishing of $f_{37,w}(z)$ at $z=w$ is $38\cdot \mathrm {ord}(w)$ .

With all this, we can apply Corollary 2. The resulting formulas are that

$$ \begin{align*} \langle x_{37}^+, \log(\Vert f_{37,w}\Vert ) \rangle &= -152\pi^2 \left(\frac{\partial}{\partial s} (\sqrt{2}F_{-2}(w,s) + 2F_{-1}(w,s))\bigg|_{s=1}\right)\\& \quad +240\pi\left(\log\left(|\eta(w)\eta(37w)|^2\cdot{\mathrm{Im}} (w)\right) -\frac{10}{19}\log37+2\log(4\pi) +24\zeta'(-1)\right) \end{align*} $$

and

$$ \begin{align*} \langle y_{37}^+, \log (\Vert f_{37,w}\Vert ) \rangle &= - 152\pi^2 \left(\frac{\partial}{\partial s} (\sqrt{3}F_{-3}(w,s) +3F_{-1}(w,s))\bigg|_{s=1}\right)\\& \quad + 336\pi\left(\!\log\left(|\eta(w)\eta(37w)|^2\cdot{\mathrm{Im}} (w)\right) -\frac{10}{19}\log37+2\log(4\pi) +24\zeta'(-1)\!\right). \end{align*} $$

Of course, one does not need to assume that w corresponds to a two torsion point. In general, Corollary 2 yields an expression where the right-hand side is a sum of two terms, and the corresponding factor in front would be one-half of the factors above.

6.4 A genus two example

Consider the level $N=103$ . In this case, $\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_{103}^{+})= 52\pi /3$ and the function field generators are $x_{103}^+(z)=q_z^{-3} + q_z^{-1} + O(q_z)$ and $y_{103}^+(z)=q_z^{-4} + 3q_z^{-2} + 3q_z^{-1} + O(q_z)$ , as displayed in Table 7 of [13]. The generators $x_{103}^+(z)$ and $y_{103}^+(z)$ satisfy the polynomial relation $y^3 - x^4 - 5yx^2 - 9x^3 + 16y^2 - 21yx - 60x^2 + 65y - 164x + 18 = 0$ . The surface $Y_{103}^{+}$ has genus two.

From Theorem 6 of [19], we can write $x_{103}^+(z)$ and $y_{103}^+(z)$ in terms of the Niebur–Poincaré series. Explicitly, we have that

$$ \begin{align*} x_{103}^+(z)&=2\pi[\sqrt{3}F_{-3}(z,1)+ F_{-1}(z,1)]-2\pi(\sqrt{3}B_{0,103}^+(1;-3)+B_{0,103}^+(1;-1))\\&=2\pi[\sqrt{3}F_{-3}(z,1)+ F_{-1}(z,1)]-\frac{15}{13} \end{align*} $$

and

$$ \begin{align*} y_{103}^+(z)&=2\pi[\sqrt{4}F_{-4}(z,1)+ 3\sqrt{2}F_{-2}(z,1) +3F_{-1}(z,1)]\\& \quad -2\pi(\sqrt{4}B_{0,103}^+(1;-4)+3\sqrt{2}B_{0,103}^+(1;-2)+3B_{0,103}^+(1;-1))\\&=2\pi[2F_{-4}(z,1)+ 3\sqrt{2}F_{-2}(z,1) +3F_{-1}(z,1)]-\frac{57}{13}. \end{align*} $$

The order of vanishing of $\Delta _{103}(z)$ at the cusp is $\nu _{103}=(12\cdot 52\pi /3)/(4\pi )=52$ . Therefore, for an arbitrary, fixed $w\in {\mathbb H}$ , the form

$$ \begin{align*}f_{103,w}(z)=\Delta_{103}^3(z)(x_{103}^+(z)-x_{103}^+(w))^{52}\end{align*} $$

is the weight $3k_{103}=36$ holomorphic form which has constant term in the q-expansion equal to $1$ . Let $\{w_{1}, w_{2}, w_{3}\}$ be the three, not necessarily distinct, points in the fundamental domain $\mathcal {F}$ where $(x_{103}^+(z)-x_{103}^+(w))$ vanishes. One of the points $w_{j}$ is equal to w. The form $f_{103,w_j}(z)$ vanishes at $z=w_{j}$ to order $52 \cdot \mathrm {ord}(w_j)$ , $j=1,2,3$ .

From §4.2, we have that

$$ \begin{align*}\beta_{103}=\frac{3}{52\pi}\left(\frac{53}{104}\log103+2-2\log(4\pi)-24\zeta'(-1)\right) \end{align*} $$

and $P_{103}(z)=\log \left (|\eta (z)\eta (103z)|^2\cdot {\mathrm {Im}} (z)\right )$ . Let us now apply Corollary 2 with $g(z)= x_{103}^+(z)$ , in which case $c(g)=-15/13$ . In doing so, we get that

$$ \begin{align*} \langle x_{103}^+, \log (\Vert f_{103,w}\Vert ) \rangle &= - 208\pi^2 \sum\limits_{j=1}^{3}\left(\frac{\partial}{\partial s}\left. (\sqrt{3}F_{-3}(w_j,s) +F_{-1}(w_j,s))\right|_{s=1}\right) \\& \quad +120\pi\sum\limits_{j=1}^{3}\left(\log\left(|\eta(w_j)\eta(103w_j)|^2\cdot{\mathrm{Im}} (w_{j})\right)\right) \\& \quad -360\pi\left(\frac{53}{104}\log103-2\log(4\pi) -24\zeta'(-1)\right). \end{align*} $$

Similarly, we can take $g(z)= y_{103}^+(z)$ , in which case $c(g)=-57/13$ and we get that

$$ \begin{align*} \langle y_{103}^+, \log (\Vert f_{103,w}\Vert ) \rangle &= - 208\pi^2 \sum\limits_{j=1}^{3} \left(\frac{\partial}{\partial s}\left. (2F_{-4}(w_{j},s)+ 3\sqrt{2}F_{-2}(w_{j},s) +3F_{-1}(w_{j},s))\right|_{s=1}\right) \\& \quad +456\pi\sum\limits_{j=1}^{3}\left(\log\left(|\eta(w_{j})\eta(103w_{j})|^2\cdot{\mathrm{Im}} (w_{j})\right)\right) \\& \quad -1368\pi\left(\frac{53}{104}\log103-2\log(4\pi) -24\zeta'(-1)\right). \end{align*} $$

6.5 An alternative formulation

In the above discussion, we have written the constant $\beta $ and the Kronecker limit function P separately. However, it should be pointed out that in all instances the appearance of these terms are in the combination $\beta \operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(M)- P(z)$ . From (28), we can write

$$ \begin{align*}\beta \operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)- P(z) = \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \mathrm{CT}_{s=1} \mathcal{E}^{\mathrm{par}}_{\infty}(z,s), \end{align*} $$

where $\mathrm {CT}_{s=1}$ denotes the constant term in the Laurent expansion at $s=1$ . It may be possible that such notational change can provide additional insight concerning the formulas presented above.

A Appendix: Special functions

For the sake of clarity, we define the special functions used throughout the paper and list some of their properties, such as asymptotic expansions, bounds, special values, and various relations.

A.1 The Bessel functions: Definitions and special values

The Bessel functions are solutions to a certain second-order differential equations. For a complex parameter $\nu $ , the J-Bessel function of order $\nu $ is given by the absolutely convergent power series

(A.1) $$ \begin{align} J_{\nu}(z)= \sum_{k=0}^{\infty}\frac{(-1)^k}{k! \Gamma(k+1+\nu)}\left(\frac{z}{2}\right)^{\nu + 2k}. \end{align} $$

The variable z is complex valued and lies in the cut complex plane $\mathbb {C}\setminus (-\infty ,0]$ . Also, $\Gamma $ denotes the classical gamma function. The I-Bessel function is given for the same range of variables $\nu $ and z by the absolutely convergent power series

(A.2) $$ \begin{align} I_{\nu}(z)= \sum_{k=0}^{\infty}\frac{1}{k! \Gamma(k+1+\nu)}\left(\frac{z}{2}\right)^{\nu + 2k}. \end{align} $$

For $\nu \in \mathbb {C}\setminus \mathbb {Z}$ and $z\in \mathbb {C}\setminus (-\infty ,0]$ , the K-Bessel function is defined as

(A.3) $$ \begin{align} K_{\nu}(z) = \frac{\pi}{2\sin(\pi \nu)}\left( I_{-\nu}(z) - I_{\nu}(z)\right), \end{align} $$

while Y-Bessel is defined by

(A.4) $$ \begin{align} Y_{\nu}(z) = \frac{1}{\sin(\pi \nu)}\left( \cos(\pi \nu)J_{\nu}(z) - J_{-\nu}(z)\right). \end{align} $$

To define $ K_{n}(z)$ and $Y_n(z)$ , for $n \in \mathbb {Z}$ , one simply takes the limit as $\nu \to n$ in (A.3) and (A.4).

For $\nu =1/2$ , the I-Bessel and K-Bessel functions reduce to hyperbolic and exponential function, respectively; from page 204 of [11], we quote the identities that

(A.5) $$ \begin{align} I_{1/2} (z) = \sqrt{\frac{2}{\pi z}}\sinh z \quad \text{and} \quad K_{1/2}(z) = \sqrt{\frac{\pi}{2 z}} e^{-z}, \end{align} $$

for $z\in \mathbb {C}\setminus (-\infty ,0]$ , where the square root is defined using the principal branch of the logarithm.

The I-Bessel and K-Bessel functions also satisfy recursion formulas. Quoting from [8], equations 8.486.1 and 8.486.10, we have that

(A.6) $$ \begin{align} z(I_{\nu-1}(z)-I_{\nu+1}(z))=2\nu I_{\nu}(z) \quad \text{and} \quad z(K_{\nu-1}(z)-K_{\nu+1}(z))=-2\nu K_{\nu}(z). \end{align} $$

A.2 Exponential integral

The exponential integral function is defined for a negative real number x as

$$ \begin{align*}\mathrm{Ei}(x)=\int\limits_{-\infty}^x \frac{e^t}{t}dt=\mathrm{li}(e^x) \end{align*} $$

(see [8, (8.211)]). For our purposes, we will use the following two representations of $\mathrm {Ei}(x)$ which we quote from [8], formulas 8.212.2 and 8.212.3. First, for $x>0$ , we have that

(A.7) $$ \begin{align} \mathrm{Ei}(\pm x)=e^{\pm x}\left(\pm \frac{ 1}{x} + \int\limits_{0}^{\infty}\frac{e^{-t}}{(\pm x-t)^2}\right). \end{align} $$

Second, $x>0$ , we have the series expansion

$$ \begin{align*}\mathrm{Ei}(x)=\gamma + \log x + \sum_{k=1}^{\infty}\frac{x^k}{k\cdot k!} \end{align*} $$

stated in [8], formula 8.214.2, where $\gamma $ denotes the Euler constant. The series expansion yields the coarse bound that $\mathrm {Ei}(x) \ll e^x$ as $x\to \infty $ . A bound for $\mathrm {Ei}(-x)$ as $x\to \infty $ can be obtained from the equation

$$ \begin{align*}\mathrm{Ei}(-x)=-e^{-x}\int\limits_{1}^{\infty}\frac{1}{x+\log t}\frac{dt}{t^2} \,\,\,\,\, \mathrm{for} x>0, \end{align*} $$

which we quote from [8], formula 8.212.10. From this expression, we get that

$$ \begin{align*}\left|\mathrm{Ei}(-x)\right|\leq e^{-x}\int\limits_{1}^{\infty}\frac{1}{x}\frac{dt}{t^2}=\frac{e^{-x}}{x} \,\,\,\,\, \mathrm{for} x>0. \end{align*} $$

In summary, we have the following bounds for $\mathrm {Ei}(\pm x)$ , as $x\to \infty $ :

(A.8) $$ \begin{align} \left|\mathrm{Ei}(- x)\right|\ll \frac{e^{-x}}{x} \quad \text{and} \quad \mathrm{Ei}(x)\ll e^x. \end{align} $$

A.3 Asymptotic behavior

We quote from [11], formulas (B.35) and (B.36), the asymptotic behavior of Bessel functions in the real positive variable y and for a fixed order $\nu $ . Namely, for $y>1+|\nu |^2$ , we have the following estimates:

(A.9) $$ \begin{align} J_{\nu}(y) = \sqrt{\frac{2}{\pi y}}\left( \cos\left(y-\frac{\pi}{2}\nu -\frac{\pi}{4}\right) + O\left(\frac{1+|\nu|^2}{y}\right)\right), \end{align} $$

(A.10) $$ \begin{align} Y_{\nu}(y) = \sqrt{\frac{2}{\pi y}}\left( \sin\left(y-\frac{\pi}{2}\nu -\frac{\pi}{4}\right) + O\left(\frac{1+|\nu|^2}{y}\right)\right), \end{align} $$

(A.11) $$ \begin{align} I_{\nu}(y) = \sqrt{\frac{1}{2\pi y}}e^y \left( 1 + O\left(\frac{1+|\nu|^2}{y}\right)\right), \end{align} $$

and

(A.12) $$ \begin{align} K_{\nu}(y) = \sqrt{\frac{\pi}{2 y}}e^{-y} \left( 1 + O\left(\frac{1+|\nu|^2}{y}\right)\right). \end{align} $$

For each of the stated bounds, the implied constant is absolute.

A.4 Bessel functions: Derivatives with respect to order and to argument

In this section, we quote results from [8] related to special values of derivatives of I-Bessel and K-Bessel functions with respect both to order and argument.

A.4.1 Derivatives with respect to the order

First, we quote formulas 8.486(1).20 and 8.486(1).21 for the derivative with respect to the order $\nu $ at $\nu =\pm 1/2$ :

(A.13) $$ \begin{align} \left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=\pm1/2} = \frac{1}{\sqrt{2\pi x}}\left(e^x \mathrm{Ei}(-2x) \mp e^{-x} \mathrm{Ei}(2x)\right) \,\,\,\,\, \mathrm{for} x>0 \end{align} $$

and

(A.14) $$ \begin{align} \left.\frac{\partial}{\partial\nu} K_{\nu}(x)\right|_{\nu=\pm 1/2} =\mp\sqrt{\frac{\pi}{2x}}e^x \mathrm{Ei}(-2x) \,\,\,\,\, \mathrm{for} x>0. \end{align} $$

Combining (A.13) and (A.14) with the bound (A.8) shows that for $x\to \infty $ , we have that

(A.15) $$ \begin{align} \left|\left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=\pm 1/2}\right|\ll\frac{e^x} {\sqrt{2\pi x}} \quad \text{and} \quad \left|\left.\frac{\partial}{\partial\nu}K_{\nu}(x)\right|_{\nu=\pm 1/2}\right|\ll \sqrt{\frac{\pi}{2x}}\frac{e^{-x}}{x}. \end{align} $$

Second, we quote formulas 8.486(1).8 and 8.486(1).6 with $n=1$ for the derivative with respect to the order $\nu $ at $\nu =1$ :

(A.16) $$ \begin{align} \left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=1} = K_1(x)-\frac{1}{x}I_0(x) \,\,\,\,\, \mathrm{for} x>0 \end{align} $$

and

(A.17) $$ \begin{align} \left.\frac{\partial}{\partial\nu} J_{\nu}(x)\right|_{\nu=1} = \frac{\pi}{2}Y_1(x) +\frac{1}{x} J_0(x) \,\,\,\,\, \mathrm{for} x>0. \end{align} $$

By combining the bounds (A.9)–(A.12), we immediately deduce the following bounds as $x\to \infty $ :

(A.18) $$ \begin{align} \left|\left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=1}\right|\ll\frac{e^x} {x\sqrt{2\pi x}} \quad \text{and} \quad \left|\left.\frac{\partial}{\partial\nu}J_{\nu}(x)\right|_{\nu=1}\right|\ll \sqrt{\frac{\pi}{2x}}. \end{align} $$

A.4.2 Derivatives with respect to the argument

We will quote formulas 8.486.2 and 8.486.11 of [8] expressing derivative of the I-Bessel and K-Bessel functions with respect to the argument in terms of a linear combination of the I-Bessel and K-Bessel functions with shifted orders:

(A.19) $$ \begin{align} \frac{d}{dz}I_{\nu}(z)=\frac{1}{2}\left(I_{\nu-1}(z) + I_{\nu+1}(z) \right) \end{align} $$

and

(A.20) $$ \begin{align} \frac{d}{dz}K_{\nu}(z)=-\frac{1}{2}\left(K_{\nu-1}(z) + K_{\nu+1}(z) \right). \end{align} $$