1 Introduction
Low-noise mode-locked lasers enable many applications such as precise frequency comb generation[Reference Newbury and Swann1, Reference Diddams and Opt2] optical communications[Reference Kawanishi3], timing synchronization[Reference Bergeron, Sinclair, Swann, Nelson, Deschênes, Baumann, Giorgetta, Coddington and Newbury4], and low-phase-noise microwave signal generation[Reference Xie, Bouchand, Nicolodi, Giunta, Hänsel, Lezius, Joshi, Datta, Alexandre, Lours, Tremblin, Santarelli, Holzwarth and Coq5]. Among the various ways to achieve low-noise femtosecond lasers, passively mode-locked fiber lasers are highly attractive, benefiting from compactness, robustness, high efficiency, and good beam quality[Reference Okhotnikov6]. Major pulse-shaping mechanisms include solitons[Reference Fermann and Hartl7], dispersion-managed (DM) solitons[Reference Tamura, Ippen, Haus and Nelson8], similaritons[Reference Nielsen, Ortaç, Schreiber, Limpert, Hohmuth, Richter and Tünnermann9], and dissipative solitons[Reference Grelu and Akhmediev10]. In particular, DM fiber lasers operating at near-zero net cavity dispersion (NCD) can achieve the lowest timing jitter and intensity noise[Reference Song, Kim, Jung, Kim and Kim11, Reference Nugent-Glandorf, Johnson, Kobayashi and Diddams12]. In our previous study, stable mode-locking can operate near-zero NCD by using saturable absorbers with a high modulation depth[Reference Yan, Liu, Guo, Zhang, Chu, Song and Hu13]. Higher pulse energy is favorable to further reduce the timing jitter[Reference Kim and Song14] and improve the performance of low-noise applications. However, with an increased pump power, the achievable pulse energy is limited by the intrinsic multi-pulsing phenomenon[Reference Kurtner, Der Au and Keller15, Reference Soto-Crespo, Grapinet, Grelu and Akhmediev16]. One possible origin of multi-pulsing is the overdriving of the saturable absorber[Reference Tang, Zhao, Zhao and Liu17, Reference Li, Wai and Kutz18], which is the case for saturable absorbers with non-monotonic response functions such as nonlinear polarization rotation and nonlinear optical loop mirrors. Another possible cause of multi-pulsing is the excessive amount of nonlinear phase accumulation induced by self-phase modulation (SPM)[Reference Renninger, Chong and Wise19].
A recent theoretical study has investigated the spectral filtering effect on the multi-pulsing dynamics in DM fiber lasers. With an increased pump power, the spectral width increases to a critical point before the onset of multi-pulsing. This critical spectral width (CSW) varies almost linearly with the spectral filter bandwidth. Thus, dissipative spectral filtering can also play a decisive role in the generation of multiple pulses[Reference Alsaleh, Uthayakumar, Felenou, Dinda, Grelu and Porsezian20]. In DM mode-locked Yb-doped fiber (YDF) lasers, chirped fiber Bragg gratings (CFBGs) have been utilized for dispersion compensation[Reference Hill, Bilodeau, Malo, Kitagawa, Thériault, Johnson, Albert and Takiguchi21, Reference Ortaç, Plötner, Schreiber, Limpert and Tünnermann22]. CFBGs are attractive because of their compactness, all-fiber configuration, and low splice loss. To obtain a smooth reflection spectrum, apodization is commonly used to suppress the oscillations and sidelobes[Reference Ennser, Zervas and Laming23]. Unfortunately, the reflection bandwidth of the apodized CFBG is much narrower than the gain bandwidth of the YDF, leading to a strong spectral filtering effect. This CFBG-induced spectral filtering effect potentially causes multi-pulsing in DM mode-locked YDF lasers.
In this paper, we experimentally investigate the effect of spectral filtering on multi-pulsing in DM mode-locked fiber lasers. The spectral width of a typical DM fiber laser varies monotonically with the NCD in the normal and anomalous dispersion regimes, respectively[Reference Baumgartl, Ortaç, Limpert and Tünnermann24, Reference Jeon, Lee, Lee and Opt25]. For a fixed spectral filter bandwidth, pulses with wider spectral widths experience more loss, and hence the pump power threshold for multi-pulsing is reduced. Consequently, the NCD has an impact on the multi-pulsing dynamics in DM mode-locked fiber lasers. In the experiment, we demonstrate that the pump power threshold for multi-pulsing decreases as the NCD approaches zero. The maximum single pulse energy can be increased to 0.42 nJ by operating the laser at a relatively large NCD[Reference Yan, Liu, Guo, Zhang, Chu, Song and Hu13]. We also observe that the CSW at the critical point is approximately constant, regardless of the NCD. The largest full-width at half-maximum (FWHM) spectral width obtained is 20.6 nm, which is limited by the 17-nm CFBG reflection bandwidth. The pulses are dechirped to 108 fs by using a hybrid grating-prism compressor. We also perform numerical simulations to investigate the spectral filtering effect on the multi-pulsing dynamics. The pump power threshold for multi-pulsing state decreases as the NCD approaches zero. The trend is similar when the spectral filtering bandwidth gets narrower. Hence, we demonstrate that the spectral filtering effect induced by the CFBG causes multi-pulsing. It is possible to further increase the single pulse energy by avoiding the strong spectral filtering effect.
2 Experimental setup and results
Figure 1 shows the experimental setup of a linear cavity configuration with polarization maintaining (PM) fibers. A piece of 60-cm long highly Yb-doped PM fiber (250 dB/m at 975 nm) is pumped by a 976-nm single-mode laser diode. A half-wave plate (HWP) in combination with a polarization beam splitter (PBS) is used to ensure the excitation along the slow axis of the PM fiber. The single-mode fibers (SMFs) used are PM980 fibers with a mode field diameter of 6.6 μm at 980 nm. A SESAM (Batop GMBH, SAM-1040-56-700fs) with a 34% modulation depth and a 70 μJ/cm2 saturation fluence is utilized for self-starting mode-locking. A PM-CFBG with −0.1-ps2 dispersion is employed for dispersion compensation. When the NCD is zero, the effective cavity length is 3.7 m, corresponding to a repetition rate of about 40.6 MHz. The CFBG also acts as a Gaussian spectral filter with a 17-nm bandwidth and a 13% peak reflectivity centered at 1030 nm. To compensate for third-order dispersion, a hybrid grating-prism compressor with 1200 lines/mm gratings and SF11 prisms is used to compress the output pulses.
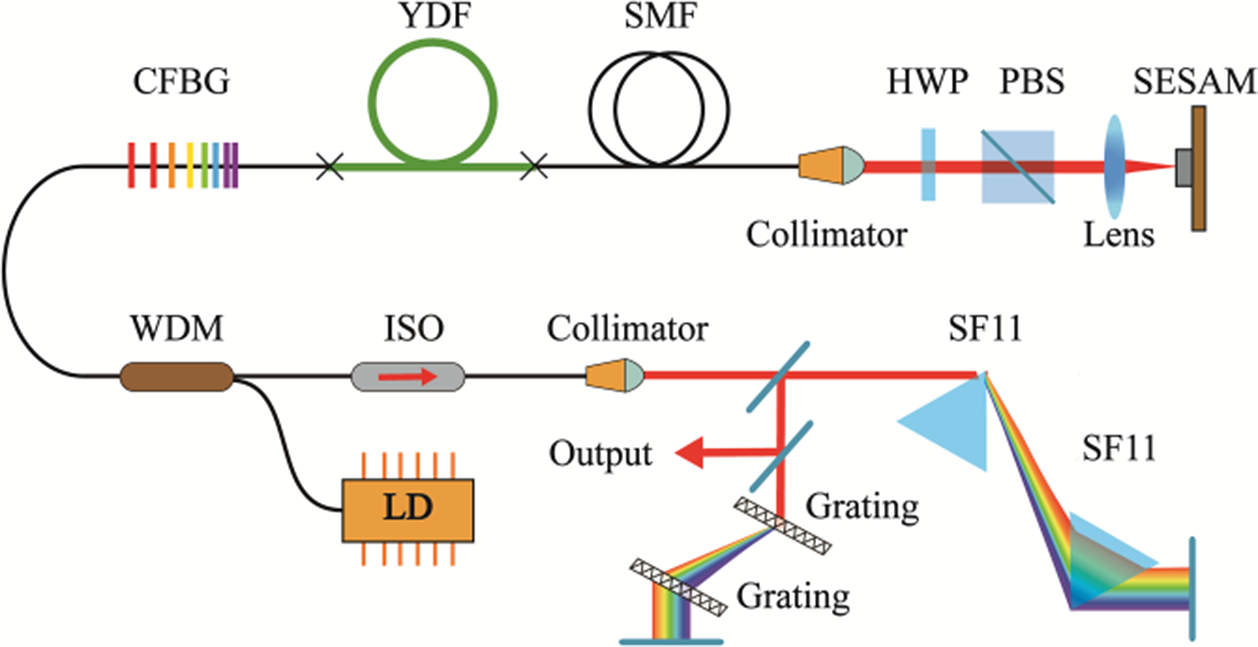
Figure 1 Experimental setup of the passively mode-locked all-PM fiber laser. LD, laser diode; WDM, wavelength division multiplexer; CFBG, chirped fiber Bragg grating; YDF, Yb-doped fiber; SMF, single-mode fiber; SESAM, semiconductor saturable absorber mirror; HWP, half-wave plate; PBS, polarization beam splitter; ISO, isolator.
The NCD of this fiber laser can be tuned from −0.03 ps2 to +0.025 ps2 by altering the length of the SMF between the collimator and the YDF. For each NCD, the pump power threshold for mode-locking is slightly different owing to the splice loss and other intra-cavity loss. To obtain stable mode-locking throughout the dispersion regime, the pump power is increased from 80 mW. Figure 2 shows an overview of the 10-dB spectral width and dechirped 3-dB pulse duration of the output pulses versus the NCD at different pump powers. At 80-mW pump power, the laser operates in the single-pulsing state with large normal and anomalous dispersion. As the NCD decreases, the spectral width gradually increases, which is typical of a DM fiber laser[Reference Baumgartl, Ortaç, Limpert and Tünnermann24]. However, a further decrease in the NCD leads to the generation of multiple pulses. The double-pulsing state is observed with the NCD ranging from −5.67 × 10−3 ps2 to +6.48 × 10−3 ps2 (Figure 2(a), gray area). Figure 3(a) shows the spectrum and the autocorrelation trace of soliton molecules for β net = +7.52 × 10−4 ps2. The spectral modulation period is 0.74 nm, corresponding to a pulse separation of 4.8 ps. We also measure the output spectra for two critical NCD values, as shown in Figure 3(b). For comparison, the measured CFBG reflection spectrum is also shown as the gray area. For β net = −5.67 × 10−3 ps2, the spectrum shows a Gaussian-like profile and fits well with the CFBG reflection spectrum. However, for β net = +6.48 × 10−3 ps2, the spectral edges fit with a parabolic-like profile. Furthermore, the output spectrum is restricted by the strong filtering effect compared with the typical self-similar spectrum with a parabolic top[Reference Ilday, Buckley, Clark and Wise26].

Figure 2 Spectral width at 10 dB (red solid squares) and dechirped pulse width at 3 dB (blue open circles) of the output pulses versus the NCD at a pump power of (a) 80 mW, (b) 90 mW, (c) 100 mW, (d) 110 mW, (e) 120 mW, and (f) 130 mW (gray area: multi-pulsing region).

Figure 3 (a) Spectrum and autocorrelation trace of soliton molecules at 80 mW pump power. (b) Spectra of single soliton states for two critical NCD values at 80 mW pump power (gray area: CFBG reflection spectrum).
With the pump power rising, the multi-pulsing region is enlarged, as shown in Figure 2. Thus, the DM fiber laser shows different pump power thresholds for the double-pulsing state with different NCD values. With close-to-zero NCD, the critical pump power of the double-pulsing state is slightly larger than the mode-locking threshold. With a larger NCD, the stable area for the single-pulsing regime extends towards a higher pump power. For β net ≤−1.56 × 10−2 ps2 and β net ≥+2 × 10−2 ps2, the laser can operate in the single-pulsing state at a maximum pump power of 130 mW. Note that, the CSW at the critical point is around 30 nm in the anomalous dispersion regime and 19 nm in the normal dispersion regime, regardless of the pump power. We attribute multi-pulsing generation to the spectral filtering effect. When the spectral width gets broader, the strong dissipative effect of the filter induces more loss. Once the pulse breaks up into two pulses, the energy of each pulse is reduced, resulting in wider pulse duration and narrower spectral width. Thus, the pulses can experience reduced loss induced by the spectral filtering effect. When the pump power exceeds 130 mW, the single-pulsing state cannot be obtained throughout the entire dispersion range due to excess nonlinear phase accumulation from SPM[Reference Haus, Tamura, Nelson and Ippen27].
The spectral width becomes broader either as the NCD approaches zero or as the pulse energy increases. However, the spectral filter inside the cavity limits the maximum spectral width and the shortest pulse duration that can be achieved. At 80 mW pump power, the maximum FWHM spectral width of 17.7 nm is obtained for β net = −5.67 × 10−3 ps2. The pulses are dechirped to 124 fs with the hybrid grating-prism compressor, as shown in Figure 4(a). At 100 mW pump power, the widest spectrum of 20.6 nm is obtained for β net = −6.71 × 10−3 ps2. The pulses can be compressed to 108 fs, as shown in Figure 4(b). When the pump power increases to 130 mW, the maximum spectral width is 19.4 nm with β net = −1.67 × 10−2 ps2. The output pulses can be compressed to 108 fs, as shown in Figure 4(c). The autocorrelation trace fits well with a Gaussian function, indicating high temporal quality. The laser produces 21 mW average power, corresponding to a 0.42 nJ pulse energy. An overview of the key parameters of the mode-locked YDF lasers using a CFBG for dispersion management is given in Table 1.

Figure 4 Autocorrelation traces of dechirped output pulses (blue solid lines) and Gaussian fitting curves (red dashed lines) at a pump power of (a) 80 mW, (b) 100 mW, and (c) 130 mW. Insets: corresponding spectra of output pulses.
Table 1 Overview of key parameters of mode-locked YDF lasers using a CFBG for dispersion management.

3 Numerical simulation and results
We consider a linear DM laser, as shown in Figure 5(a), with a piece of YDF, a piece of SMF, a SESAM, and a CFBG. The CFBG model is split into a short dispersion compensating fiber (DCF), a Gaussian bandpass filter, and an optical coupler (OC). Each fiber segment is modeled via the modified nonlinear Schördinger equation[Reference Agrawal31]:
 $$\begin{align}\frac{\partial A}{\partial z}+\frac{i}{2}\left({\beta}^{(2)}+ i g\frac{1}{\Omega_g^2}\right)\frac{\partial^2A}{\partial {\tau}^2}=\frac{g}{2}A+\frac{\beta^{(3)}}{6}\frac{\partial^3A}{\partial {\tau}^3}+ i\gamma {\left|A\right|}^2A,\end{align}$$
$$\begin{align}\frac{\partial A}{\partial z}+\frac{i}{2}\left({\beta}^{(2)}+ i g\frac{1}{\Omega_g^2}\right)\frac{\partial^2A}{\partial {\tau}^2}=\frac{g}{2}A+\frac{\beta^{(3)}}{6}\frac{\partial^3A}{\partial {\tau}^3}+ i\gamma {\left|A\right|}^2A,\end{align}$$
Figure 5 (a) Schematic of the numerical simulation model. Evolution of spectral width (red solid line) and temporal width (blue dotted line) when the NCD is for (b) β net = −1.1 × 10−3 ps2 and (c) β net = +1.5 × 10−2 ps2. YDF, Yb-doped fiber; SMF, single-mode fiber; SESAM, semiconductor saturable absorber mirror; DCF, dispersion compensating fiber; OC, optical coupler.
where A = A(z,τ) is the field envelope with z as the propagation coordinate and τ as the time-delay parameter, β (2) and β (3) are the group velocity dispersion (GVD) and third-order dispersion, respectively, γ is the nonlinear parameter, and Ωg is the gain bandwidth. The gain g is modeled by g = g 0/(1+E/E sat), where g 0 is the small-signal gain, E is the intracavity energy, and E sat is the saturation energy[Reference Yarutkina, Shtyrina, Fedoruk and Turitsyn32]. Here E is calculated by E = ∫|A|2dτ+E oppo, where E oppo is the energy of the pulses coming from the opposite direction of the gain fiber. The inclusion of E oppo is necessary when the pulses experience significantly different losses on the two sides of the gain fiber. The reflection of the SESAM is modeled by R = 1−ΔT/(1+P ave/P sat)−α ns, where ΔT is the modulation depth, P ave is the average power, P sat is the saturation power, and α ns is the nonsaturable loss. In the simulations, the parametric values of the YDF are L YDF = 0.6 m, Ωg = 40 nm, g 0 = 30 dB, and E sat = 0.2 nJ. For the SESAM, we set ΔT = 0.34, α ns = 0.22, and P sat = 40 W, consistent with the experimental values. We consider an OC with a 90% coupling ratio. For the DCF, we assume L DCF = 0.1 m with a GVD of −1 ps2/m. The spectral filter has a 17-nm (FWHM) Gaussian profile centered at 1030 nm. Before the SESAM (point F), an intracavity loss of 2.2 dB is applied to model the loss induced by the coupling process and the polarizer. In the simulations, we use 211 points, a 40-ps time span, and a 1-mm spatial step. The initial condition is a Gaussian pulse (10 ps, FWHM), injected at point D. The solution is assumed to be converged if the relative change of the pulse energy is lower than 10−9.
Figures 5(b) and 5(c) show the intra-cavity evolution of stable single pulses with β net = −1.1 × 10−3 ps2 and β net = +1.5 × 10−2 ps2, respectively. The CFBG shows an obvious dissipative effect, and the pulse width reaches the minimum in the CFBG. For an anomalous NCD, the pulses are negatively chirped after the CFBG, and thus the pulses and the spectrum are compressed in the latter fiber segments (YDF and SMF). Subsequently, the spectrum experiences nonlinear broadening through the SPM when the chirp becomes positive. For a normal NCD, the pulses are positively chirped along the cavity, and hence the SPM leads to spectral broadening after the CFBG (Figure 5(c)).
To study the multi-pulsing dynamics in the DM fiber laser, we vary the NCD and the saturation energy E sat to obtain different operation states. In Figure 6(a), white areas represent the stable multi-pulsing region. Near zero NCD, the laser generates multiple pulses with an extremely small E sat. With a stronger NCD, the threshold for multi-pulsing operation shifts towards a higher E sat, resulting in maximum spectral broadening through SPM. Therefore, pulses with the broadest spectrum are generated at the critical NCD. We observe that when E sat is larger than 0.25 nJ, single pulses cannot be obtained throughout the NCD regime. Thus, we set the maximum E sat at 0.25 nJ and, hence, the maximum spectral width of 19 nm is obtained for both β net = −1.1 × 10−3 ps2 and β net = +1.5 × 10−2 ps2. To achieve a low timing jitter, it is preferable to operate the DM laser with an anomalous NCD. For comparison, we fix the NCD at −1.1 × 10−3 ps2 and vary the spectral filter bandwidth and the saturation energy E sat. Figure 6(b) shows the spectral width of the pulses at point D in the cavity. With a narrow filter, the multi-pulsing state operates at a low E sat. A broadband spectral filter can support stable single pulses under a high E sat. This trend is similar to the results observed by varying the NCD in Figure 6(a). To further investigate the filtering effect on multi-pulsing, numerical simulation is carried out at the critical E sat for different filter bandwidths in the range of 1–40 nm. The spectral filtering exhibits different impacts depending on the filter bandwidth, as shown in Figure 6(c). For a filter bandwidth narrower than 9 nm, the laser operates in the multi-pulsing state when E sat is at the mode-locking threshold. The strongly dissipative action of the filtering induces extra loss, leading to a decreased multi-pulsing threshold. For a filter bandwidth in the 9–40 nm range, the spectral width of the pulses at point D gets wider with an increased filter bandwidth. The dissipative filtering effect is still present, and it restricts the spectral broadening through SPM. Both the spectral width of the output pulses and the corresponding E sat increase monotonically as the filter bandwidth gets wider. The spectral filtering results in multi-pulsing when the spectral width gets comparable with the filter bandwidth. The dissipative effect has a strong impact on the pulse-shaping mechanism, unlike in traditional DM fiber lasers where the pulses are only stabilized by a balance between GVD and SPM. Thus, the addition of the dissipative mechanism to DM cavities induces the generation of generalized dissipative solitons[Reference Renninger, Chong and Wise33]. The optimum condition where the shortest compressed pulses are obtained shifts from zero NCD to an anomalous NCD.

Figure 6 (a) FWHM spectral width of output pulses as a function of NCD and E sat. Linear scale: 4 nm ![]() 20 nm (white area: multi-pulsing region). (b) FWHM spectral width of pulses at point D as a function of filter bandwidth and E sat. Linear scale: 8 nm
20 nm (white area: multi-pulsing region). (b) FWHM spectral width of pulses at point D as a function of filter bandwidth and E sat. Linear scale: 8 nm ![]() 16 nm (white area: multi-pulsing region). (c) FWHM spectral width of pulses at the OC (red open squares) and at point D (red open-triangles) at critical pump power and corresponding E sat (blue solid circles).
16 nm (white area: multi-pulsing region). (c) FWHM spectral width of pulses at the OC (red open squares) and at point D (red open-triangles) at critical pump power and corresponding E sat (blue solid circles).
4 Conclusion
In this work, we experimentally demonstrate that the CFBG-induced spectral filtering effect can cause multi-pulsing in a DM mode-locked YDF laser. With an increased pump power, the spectral width keeps increasing until it reaches a critical point. And this CSW value is limited by the CFBG reflection bandwidth. By simulating this DM soliton laser with a split CFBG model, we demonstrate that the spectral filtering effect plays a decisive role in the multi-pulsing dynamics. The CSW at the critical point and the corresponding pump power are dependent on the spectral filtering bandwidth. Thus, CFBGs with broader reflection spectra can enable shorter compressed pulses and higher single-pulse energy. A recent work reports the management of the multi-pulsing state by using a fiber-based spectral filter in an all-normal dispersion fiber laser[Reference Khanolkar and Chong34], where the spectral filter plays an important role in stabilizing the pulses. Although a filter is not necessary for the DM soliton dynamics, the filtering effect still has a strong impact on the multi-pulsing process and hence a spectral filter with a tunable bandwidth can potentially control the multi-pulsing state.
Acknowledgements
This work was partially supported by the National Natural Science Foundation of China (NSFC) (Nos. U1730115, 61805174, and 61827821), the Tianjin Natural Science Foundation (No. 20JCQNJC01180), the Tianjin Research Program of Application Foundation and Advanced Technology of China (No. 17JCJQJC43500), and the Research and Development Program in Key Areas of Guangdong Province, China (No. 2020B090922004).









