The impact of the relaxation of the One-Child Policy on employment

Abstract

This paper examines how number of siblings affects employment under the relaxation of the One-Child Policy in China. We explore the One-and-A-Half-Child Policy in 1980s and examine its long-term impact on siblings and employment. With the data from 2010–2018 China Family Panel Studies, we find that individuals tend to have a larger number of siblings and have a higher probability of working in the places where the One-and-A-Half-Child Policy was implemented earlier. Using the degree of the impact of this policy as an instrumental variable for number of siblings, we find that one more sibling would increase the likelihood of working by 9.0 percentage points and increase the likelihood of working in the non-agricultural sector by 5.1 percentage points. Females are more affected by the relaxation than males. We also discuss the major mechanisms through which siblings affect employment. We find that the care-sharing effect of siblings increases labor supply and the social network effect of siblings brings more job opportunities and increases employment. The One-and-A-Half-Child Policy improves the labor market outcomes through both the channel of sharing care and the channel of social network.

1. Introduction

The One-Child Policy was gradually relaxed in recent years in China. The One-and-A-Half-Child Policy, which allowed rural couples to have a second child if the first one was a girl, was implements in rural areas in 1980s. The Two-Child Policy that allowed couples in both rural and urban areas to have a second child was implemented for couples that both husband and wife are the single child in 1990s, for couples that either husband or wife is the single child in 2014 and for all couples in 2016. These relaxation policies would have big impacts on individual development and economic growth. However, literature focuses on the impact of the One-Child Policy and lack the examination of the relaxation policy on individual outcomes. This paper explores the relaxation policy in 1980s and examines how siblings affect employment under the One-and-A-Half-Child Policy. The results of this paper would shed light on the long-term consequences of the relaxation of birth-control policies and provide important implications for the further reform in population policies.

The policy we examine is the One-and-A-Half-Child Policy enforced in the middle of 1980s in rural China. In 1979, the One-Child Policy was implemented and required a couple to have only one child. Due to the large demand of labor in agricultural production and the preference to have multiple children under the influence of traditional culture, the implementation of the One-Child Policy was difficult in villages. The One-and-A-Half-Child Policy was implemented in rural areas in the middle of 1980s. Under this policy, a rural couple can have a second child if the first one is a girl and other eligibility conditions are satisfied.¹ The time of the implementation of this policy varied across provinces.² Rural individuals who were in the places where the policy was implemented earlier tend to have more siblings. We use this variation in the years of implementation to identify the effect of siblings on employment.

The impact of the birth-control policy, especially the One-Child Policy, has been widely discussed in literature. The One-Child Policy lowers fertility rate, increases sex ratio, improves human capital accumulation and parental labor supply, and promotes economic growth [McElroy and Yang (2000), Li and Zhang (2007), Ebenstein (2010), Wu and Li (2014), He and Zhu (2016), Zhang (2017)]. The studies of the impact of the relaxation of the birth-control policy are few. Current studies related to the One-and-A-Half-Child Policy in the middle of 1980s mainly focus on children's human capital accumulation. For example, the investment in education and human capital level would be lower for the individuals in a family that is allowed to have a second child under the One-and-A-Half-Child Policy [Liu (2014), Qian (2009)]. Some studies investigate the relationships between fertility and parental labor supply under the relaxation population policy [Guo et al. (2018), Cao (2018)]. These studies generally focus on the short-term impact of population policies. We do not know much about the impact of population policies on the long-term outcomes.

In this paper, we explore the long-term impact of the One-and-A-Half-Child Policy on employment. Using data from the 2010–2018 China Family Panel Studies (CFPS), we first examine the policy effect on number of siblings and status of working. We find that an individual would have more siblings and have a higher probability of working if the One-and-A-Half-Child Policy was implemented earlier. In order to quantify the effect of siblings on working status, we exploit the regional variation in the time of the implementation of the One-and-A-Half-Child Policy and construct an instrumental variable for number of siblings. We find that having one more sibling increases the probability of working by 9.5 percentage points and increases the probability of working in the non-agricultural sector by 5.3 percentage points. In the heterogeneous analysis by gender, we find that these effects are larger for females than males. Then we discuss the major mechanisms of the impact of siblings on employment. We find that siblings share the responsibility of taking care of the elderly parents and increase labor supply. We also find that siblings extend family social network, provide help to each other in the labor market and facilitate employment. Finally, we investigate the effects of the gender of siblings and find that brothers have a larger impact on labor market outcomes and have a smaller role in supporting the elderly parents than sisters.

Our work contributes to the literature in the following way. First, being different from the existing literature that focuses on the short-term impact of population policies on children's human capital accumulation and parents' labor supply [Rosenzweig and Wolpin (1980), Angrist and Evans (1998), Li et al. (2008), Rosenzweig and Zhang (2009), Guo et al. (2018), Heath (2017)], we explore the long-term impact and examine the labor market outcomes after more than twenty years of the implementation of the relaxation policy. With data from 2010–2018 CFPS, we obtain rich information related to working and define the degree that one individual is affected by the One-and-A-Half-Child Policy based on the timing of the implementation of the policy in each province. Second, studies related to population policy in China mainly focus on the impact of the birth-control policies and lack the investigation of the relaxation policy [Zhang (2017)]. We exploit the One-and-A-Half-Child Policy and examine the long-term impact of this relaxation policy on employment. Third, current studies generally use ethnicity or monetary penalty associated with above-quota births as instruments to address the endogeneity of number of siblings [Li and Zhang (2007), Ebenstein (2010), Huang et al. (2016), Li and Wu (2018)]. Instead, we construct a policy variable that is based on the year when the relaxation policy was implemented as the instrumental variable for siblings. Forth, the existing studies generally use the risk-sharing effect of siblings and the relaxation of credit constraints to explain the effect of siblings [Li and Wu (2018), Wu and Zhao (2020)], we add to this literature by proposing the care-sharing effect and the social network effect of siblings.

Li and Wu (2018), Wu and Zhao (2020) and this paper all analyzes the impact of siblings on individual outcomes. This paper differs from Li and Wu (2018) and Wu and Zhao (2020) in the following ways. First, the outcomes and main mechanisms how siblings affect these outcomes are different. Li and Wu (2018) focus on how entrepreneurship is affected by siblings and find that the main channel through which siblings affect entrepreneurship is the relaxation of credit constraints. Wu and Zhao (2020) focus on how siblings affect household equity investment and find that the main channel through which siblings affect investment is risk sharing. This paper focus on how siblings affect labor market outcomes and the channels of care-sharing effect and social network effect of siblings. Second, Li and Wu (2018) and Wu and Zhao (2020) use the One-Child Policy as the source of identification. This paper exploits the relaxation of the One-Child Policy and use the One-and-A-Half-Child Policy as exogenous variation in siblings.

The rest of this paper is organized as follows. Section 2 introduces the background. Section 3 discusses our data and empirical strategy. Section 4 presents the main findings. Section 5 conducts mechanism analysis. Section 6 discusses the effect of the gender of siblings. Section 7 concludes.

2. Background

2.1 The relaxation of the One-Child Policy in rural China

In 1970s, the fertility rate in China was high. Couples had 5–6 children in average. The rapid population growth rate was expected to be harmful to individual development and overall economic growth. In 1979, the One-Child Policy was implemented and required a couple to have only one child. Due to the large demand of labor in agricultural production and the preference to have multiple children under the influence of traditional culture in rural China, the implementation of the One-Child Policy was difficult in villages. The One-and-A-Half-Child Policy was implemented in rural areas in 1984. Under this policy, a rural couple can have a second child if the first one was a girl. Figure 1 shows the trend of fertility rate in China. The fertility rate rebounded after the implementation of the relaxation policy in late 1980s.

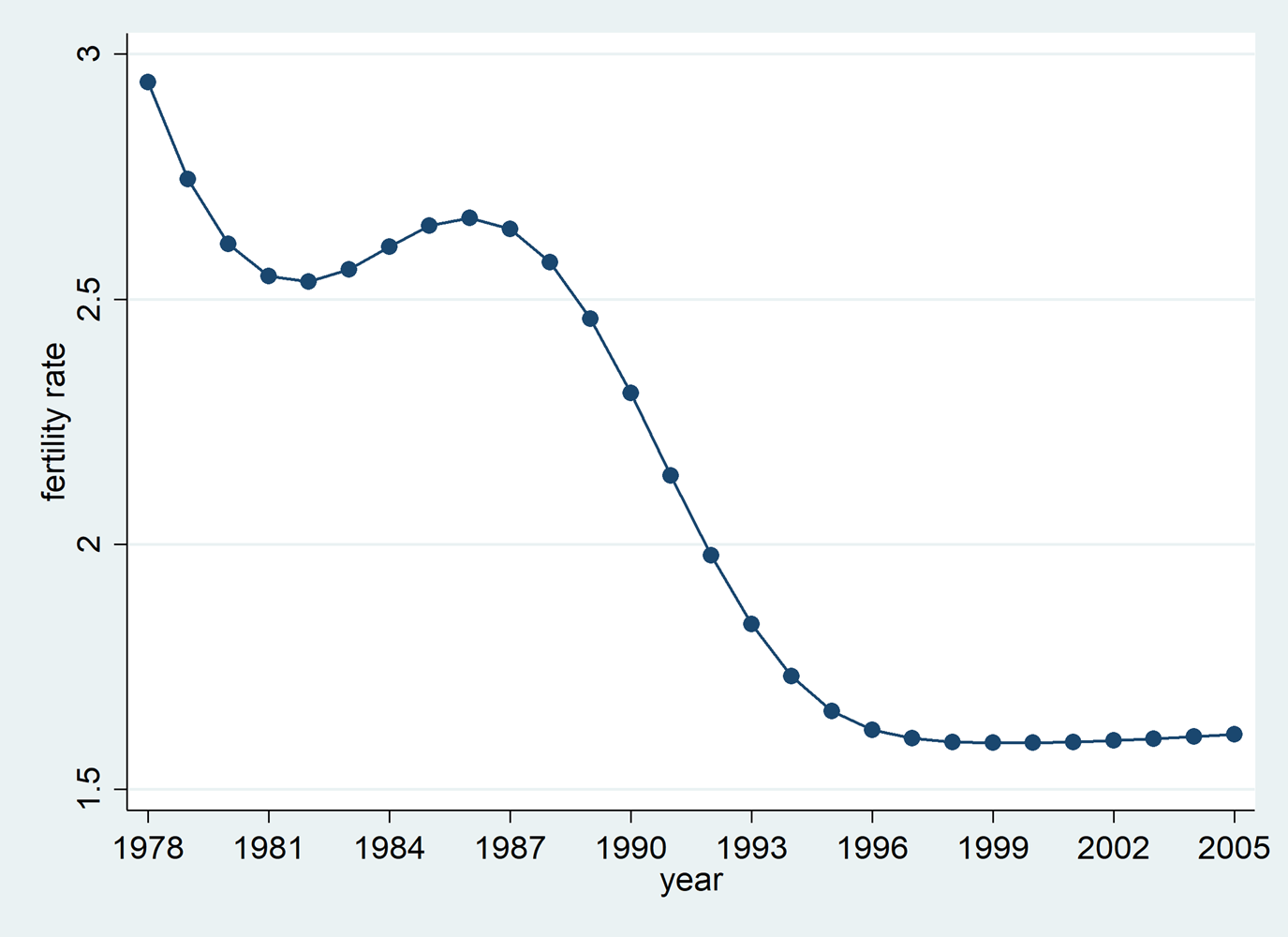
Figure 1. Fertility rate in China.

Note: Data are from the World Bank.

Local governments in China can determine their specific plans of implementation of the One-and-A-Half-Child Policy. We can classify provinces into three groups according to the variation in the implementation. The first group is the 19 provinces where rural couples can have a second child if the firstborn is a girl.³The second group is the provinces where the One-and-A-Half-Child Policy was implemented only in remote mountainous and special areas. These provinces include Beijing, Tianjin, Jiangsu, Sichuan and Chongqing. The third group is the provinces where the Two-Child Policy was implemented in rural areas. In these provinces, such as Hainan, Yunnan, Qinghai, Xinjiang and Ningxia, all couples in rural areas can have a second child [Gu et al. (2007)]. The implementation year also varied in different provinces. Figure 2 shows the years when provinces in each group implemented the relaxation policy in rural areas. Among the 19 provinces in the first group, the earliest province that implemented the policy was Guangdong (1986) and the latest province was Guizhou (1998). Most provinces implemented this policy between 1988 and 1990. In the second group where the One-and-A-Half-Child Policy was only implemented in remote mountainous and special areas, the earliest province was Sichuan and the latest one was Beijing. There are some additional requirements to have a second child under this policy. For example, the birth spacing between the first and the second birth is required to be more than four years and the mother's age is required to be more than 28 years old.⁴

Figure 2. Number of Provinces Implementing the One-and-A-Half-Child Policy.

Note: Data are from Population and Family Planning Regulation of each province.

Figure 3 shows the dynamic effects of the One-and-A-Half-Child Policy on number of siblings. We define the difference between birth year and policy year to be the years relative to policy implementation. The left panel shows the average number of siblings for people born before the policy. The right panel shows the average number of siblings for people born after the policy. There is a jump in the number of siblings after the implementation of the One-and-A-Half-Child Policy, which suggests that the number of siblings experience a discontinuous increase after the policy was implemented.

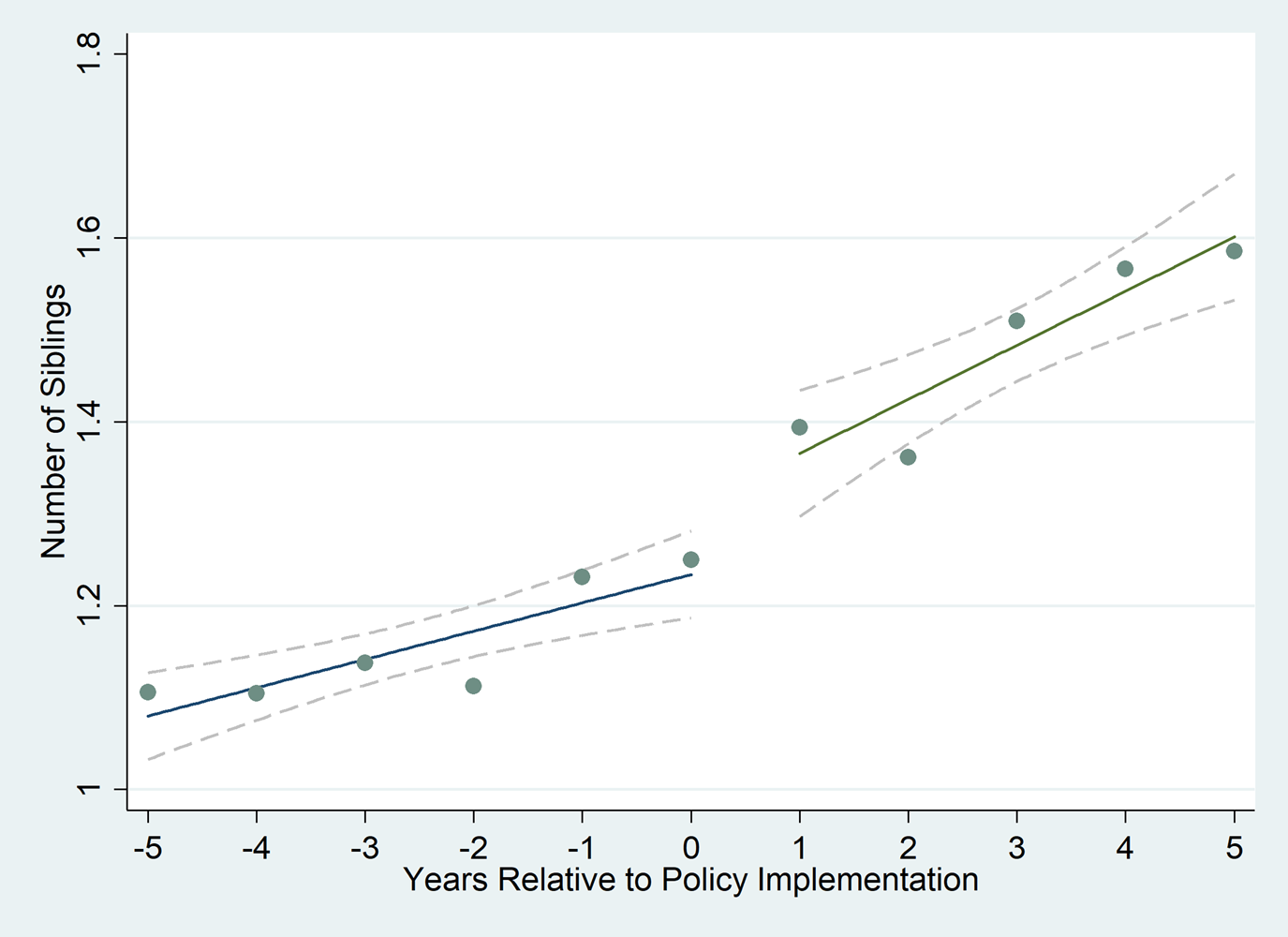
Figure 3. Dynamic effects of the One-and-A-Half-Child Policy on Number of Siblings.

Note: Data are from 2010–2018 CFPS. Years relative to policy implementation is defined based on the difference between birth year minus policy year, which is the year of the implementation of the One-and-A-Half-Child Policy.

2.2 The impact of the relaxation of the One-Child Policy

Current studies mainly focused on the impact of the One-and-A-Half-Child Policy on human capital accumulation. Qian (2009) and Liu (2014) use the data from the China Health and Nutrition Survey to analyze the impact of the fertility relaxation on children's health and education in the eight provinces covered by the data. Liu (2014) use fines as an instrumental variable for number of children, and find that children in families with higher fertility rates have lower heights. Qian (2009) use the ratio of those who are eligible to have a second child in the total population as an indicator of the policy and find that having a second child significantly increases the enrollment rate of the first child.

Some studies also examined how the relaxation policy in rural areas affects parental labor supply. Cao (2018) find that the opportunity to have a second child reduces female labor supply and income. For females whose husbands work in cities, it is difficult for them to balance agricultural production and childcare. Their labor supply would be more affected. Wang et al. (2017) investigate the determinants of having a second child and find that the rural females with lower education level, better health status and lower family wealth are more likely to have a second child.

In sum, the comprehensive analysis of the impact of One-and-A-Half-Child Policy on employment using nation-wide data is rare. This paper uses a survey data that cover most provinces in China and extends the literature in the examination of the long-term impact of the relaxation of birth-control policy on individual labor market outcomes.

3. Data and empirical strategy

3.1 Data

We use the data from 2010–2018 China Family Panel Study (CFPS), which is provided by the Institute of Social Science Survey of Peking University. This data contains rich information about individual employment and family member characteristics. Since the One-and-A-Half-Child Policy was only implemented in rural areas, our sample is restricted to the individuals born in rural areas. To eliminate the confounding effect of the One-Child Policy, we further restrict our sample to individuals who were born after 1979, the year of the implementation of the One-Child Policy.⁵ In the provinces where the One-and-A-Half-Child Policy was implemented only in remote mountainous and special areas, a small fraction of rural population was affected by the relaxation policy. We might underestimate the effect of the relaxation policy if samples in these provinces are included. In the provinces where the Two-Child Policy was implemented in rural areas, not only couples with a first daughter but also couples with a first son were affected by the policy. We might overestimate the effect of the One-and-A-Half-Child Policy if samples in these provinces are included. Thus, we exclude samples in the provinces that allow couples to have a second child only in the remote mountainous and special areas and samples in the provinces that allow all couples to have a second child.

Based on the year of the implementation of the One-and-A-Half-Child Policy in each province, we construct an indicator for the degree that a region is affected by the relaxation policy. We expect that the impact of the policy would be larger and individuals would be more likely to have a second child in the region where the policy was implemented earlier. Our policy indicator is defined as Policy _ij = (2010 − Relax _ij)/(2010 − min (Relax _ij)).⁶ Relax _ij is the year when province j, where individual i was born, implemented the relaxation policy. min (Relax _ij) is the earliest implementation year among all the provinces. For the places that do not implement the relaxation policy (such as Shanghai), the value of this indicator equals 0. The value of the policy indicator, Policy _ij, ranges between 0 and 1. The larger the value of the indicator, the greater an individual would be affected by this policy. Table 1 reports the descriptive statistics. The mean value of the policy indicator is 0.657. The average number of siblings is 1.3.

Table 1. Summary statistics

Note: Data are from 2010–2018 CFPS.

3.2 Empirical strategy

To estimate the effects of the One-and-A-Half-Child Policy, we use the following specification:

(1)$$Y_{ijt} = \beta _0 + \beta _1Policy_{ij} + \gamma X_{ijt} + t_i + p_j + \mu _{ijt}$$

where Y _ijt denotes a set of variables that are affected by the policy, such as number of siblings and whether the individual works or not. The control variable X _ijt includes gender, father's age at birth, and mother's age at birth in the estimation of the effect on number of children. We further include age, education level, marital status, and real GDP per capita at the prefecture level in the estimation of the effect on employment. t _i is birth year fixed effect. p _j is province fixed effect.

In order to quantify the effect of one additional sibling on employment, we then examine how number of siblings affects working status. To address the endogeneity problem in the estimation of the effect of number of siblings on employment, we use the variation in the number of siblings under the One-and-A-Half-Child Policy to conduct 2SLS estimation. Literature generally uses fines associated with above quota birth as instruments. We do not find strong correlation between fines and number of siblings for the individuals born after the One-Child Policy. What's more, the magnitude of fines is not exogenous and might be affected by the local economic development and fertility level. In this paper, we use the degree that an individual is affected by the One-and-A-Half-Child Policy to construct instruments for number of siblings. The empirical specification is the following:

(2)$$Y_{ijt} = \beta _0 + \beta _1Sibling\_Number_{ijt} + \gamma X_{ijt} + s_t + p_j + \mu _{ijt}$$

where Y _ijt denotes the variables related to working status. The control variable X _ijt include age, education level, marital status, and real GDP per capita at the prefecture level in the estimation of the effect on employment. s _t is survey year fixed effect. p _j is province fixed effect.

4. Results

4.1 Effect of the One-and-A-Half-Child Policy on number of siblings

Based on equation (1), we analyze how the One-and-A-Half-Child Policy affects number of siblings. Table 2 reports the results. The estimates in column 1 indicate that the policy indicator has a positive effect on number of siblings, suggesting that mothers would have a higher fertility rate if the policy was implemented earlier. Specifically, if the fertility relaxation policy was implemented one year earlier, number of siblings would increase by 0.053.⁷ In column 2, we add the variable of whether born after the implementation of the relaxation policy and its interaction term with policy indicator. The results indicate that individuals born after the implementation have more siblings and were more affected by the policy. Moreover, we add the gender of mother's first child and its interaction term with policy indicator in Column 3. The estimate of the intersection term is positive, suggesting that the mothers with firstborn girl would have higher fertility rate if the relaxation policy was implemented earlier. In sum, the results in Table 2 show that the One-and-A-Half-Child Policy in rural areas significantly increases number of siblings. The earlier the policy is implemented, the larger the number of siblings one individual would have.

Table 2. The impact of the One-and-A-Half-Child Policy on number of siblings

Note: Robust standard errors are in parentheses.

*Significant at 10%; **significant at 5%; ***significant at 1%.

4.2 Effect of the One-and-A-Half-Child Policy on employment

Then we examine the long-term effect of the fertility relaxation policy on labor market outcomes. Table 3 shows the effect on employment. Column 1 indicates that the One-and-A-Half-Child Policy significantly increases the probability of working. The development of non-agricultural sector provides more job opportunities and higher income. We also examine how the One-and-A-Half-Child Policy affects the probability of working in non-agricultural sector. In column 2, we find that the One-and-A-Half-Child Policy significantly increases the probability of working in the non-agricultural sector. The size of this impact is about half of the impact on the probability of working in the first column, which suggests that some individuals choose to work in the agricultural sector and the impact of the relaxation policy on the probability of working in the agricultural sector is similar to that in the non-agricultural sector. The main reason of the positive effect of the One-and-A-Half-Child Policy on employment may go through the increase in the number of siblings. The individuals in the region where the One-and-A-Half-Child Policy was implemented earlier, they would have more siblings, which could share the responsibility of taking care of the elderly parents and provide help in the labor market.

Table 3. The impact of the One-and-A-Half-Child Policy on employment

Note: Column 2 uses the working individuals. Robust standard errors are in parentheses.

*Significant at 10%; **significant at 5%; ***significant at 1%.

Columns 3–6 reports the heterogeneous results by gender. We find that the probability of working and the probability of working in non-agricultural sector is larger for females than males. In our sample, the probability of working is 53.6 percent for females and 70.1 percent for males. The space of the improvement in the probability of working is larger for females. With more siblings under the One-and-A-Half-Child Policy, females may benefit more from the care-sharing effect and social network effect of siblings.

4.3 Effect of number of siblings on employment

In order to quantify the effect of one additional sibling on labor market outcomes, we use the variation in the implementation of the One-and-A-Half-Child Policy to construct instruments for number of siblings. Table 4 reports the results in Two-Stage Least Square (2SLS) estimation. The OLS estimates are reported in column 1. We find number of sibling lowers the probability of working. Table 4 Column 2 reports the first-stage results in 2SLS estimation. The implementation of the One-and-A-Half-Child Policy significantly increases number of siblings. The first stage F statistic is 707.05 and the Anderson-Rubin weak identification test statistic is 81.76, suggesting that the instrument is valid.

Table 4. The impact of number of siblings on employment – 2SLS

Note: Robust standard errors are in parentheses.

*Significant at 10%; **significant at 5%; ***significant at 1%.

Column 3 and column 4 report the second stage results. Having one more sibling increases the probability of working by 9.0 percentage points and increases the probability of working in the non-agricultural sector by 5.1 percentage points. The estimate in 2SLS is larger than that in the OLS estimation, suggesting that we might under estimate the effect of siblings on employment without the use of instruments. Columns 5–6 also show the heterogeneous impact by gender. Similar to previous analysis, females are more affected than males.

The implementation of the One-and-A-Half-Child Policy may be correlated with local birth rate, which is also associated with mothers' fertility decisions. The One-and-A-Half-Child Policy might not be completely exogenous. We address this concern by regressing the implementation of the One-and-A-Half-Child Policy on lagged provincial birth rates. Using data from the Comprehensive Statistical Data and Materials on Sixty Years of New China, we find that that the birth rate did not have a significant effect on whether the local government implemented the fertility relaxation policy, which suggest that the implementation is exogenous in this study (Table 5).

Table 5. The impact of prior birth rate and economic development on policy implementation

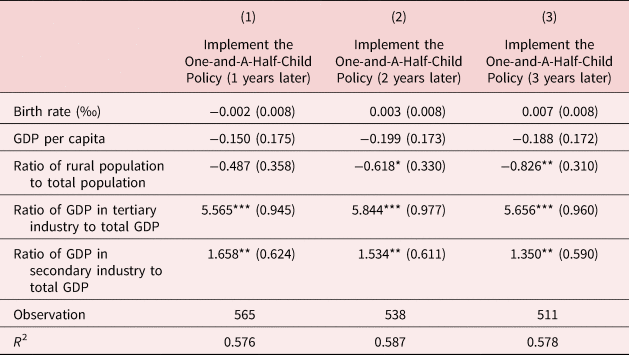
Note: Data are from China Compendium of Statistics 1949–2008. The results of fixed effect models are reported. Robust standard errors are in parentheses.

*Significant at 10%; **significant at 5%; ***significant at 1%.

5. How does siblings affect employment?

As we discussed before, number of siblings affects employment through two major channels. The first channel is care sharing. Siblings can reduce the burden of the responsibility to take care of the elderly parents. Individuals with more siblings could spend more time in the labor market. The second channel is social network. We expect individuals with more siblings have a larger network, which would help them in the labor market. In this section, we examine these two channels in the effect of siblings on employment.

5.1 The care-sharing effect of siblings

In 2019, the population aged 65 and above had reached 170 million, accounting for approximately 12.6% of the total population. The burden of taking care of elderly parents becomes a prominent problem for young couples, especially for those who were born after the One-Child Policy. Literature finds that caring the elderly significantly reduces the labor participation rate of the adult child [Ettner (1995), Carmichael and Charles (2003)]. Siblings could share the burden of caring the elderly parents. Having more siblings might alleviate the negative effect of caring the elderly on employment. In this section, we examine the care-sharing effect of siblings. We first investigate the relationship between number of siblings and labor supply. Then we use a series of variables associated with taking care of the elderly to analyze the influence of number of siblings on care sharing.

Table 6 reports the results on labor supply. The results from the 2nd stage in 2SLS are reported. We find that number of siblings significantly affects both the extensive margin (labor force participation) and the intensive margin (working hours per week) of labor supply. Having one more sibling increases the probability of participating in the labor market by 5.8 percentage points and increases working hours per week by 6.29 h. We also find number of siblings has a larger impact on females than males. Females tend to have a lower level of labor supply and bear larger responsibility in caring family members. Siblings reduce the burden of caring family members and increase labor supply for females (The reduced form results are listed in Appendix A1).

Table 6. The impact of number of siblings on labor supply

Note: The results from the 2nd stage in 2SLS are reported. The control variables are the same as that in Table 4. Robust standard errors are in parentheses.

*Significant at 10%; **significant at 5%; ***significant at 1%.

Panel A in Table 7 reports the results associated with several outcomes associated with caring the elderly parents. The results from the 2nd stage in 2SLS are reported (The reduced form results are listed in Appendix A2 Panel A). We find that number of siblings lowers the probability of taking care of parents and the frequency of taking care of parents.⁸ In the regression associated with financial support of children to their parents, we find that having one more sibling decreases the financial support to parents by 30.8%. These results suggest that having siblings significantly reduces the burden of taking care of parents.

Table 7. The care-sharing effect and social network effect of siblings

Note: The results from the 2nd stage in 2SLS are reported. The control variables are the same as that in Table 4. Since data related to caring parents is only available in 2016–2018 surveys, Columns 2–4 in Panel A use only 2016–2018 CFPS data. Since data of visits during Spring Festival is only available in 2010 survey, column 2 in Panel B uses only 2010 CFPS data. Robust standard errors are in parentheses.

*Significant at 10%; **significant at 5%; ***significant at 1%.

5.2 The social network effect of siblings

Siblings expand family's external communication boundaries. Having more siblings indicates a larger social network, which could provide information related to job opportunity and facilitate employment. Table 7 Panel B reports the results of the social network effect of siblings (The reduced form results are listed in Appendix A2 Panel B). Literature generally uses monetary gift and number of relatives visited during the Chinese New Year as a proxy for the size of social network [Knight and Yueh (2002), Wu and Zhao (2020)]. Following these studies, we find that number of siblings has positive effect on number of visits during the Chinese New Year. Having one more sibling increases the number of relatives and friends visited during the Chinese New Year by 2.4. In the analysis related to whether an individual receives help in job market, we find that individuals with more siblings have a higher probability of receiving help in finding a job, and particularly, a higher probability of receiving help from siblings.

Except for the mechanisms discussed above, siblings may affect human capital accumulation and have a negative effect on labor market outcomes. Literature finds that having more children lowers the education investment for each child in the family and has a negative impact on education, health and cognitive abilities of children [Rosenzweig and Zhang (2009), Zhang (2017), Li et al. (2018)]. Since we already have controlled education level in the main regression, the influence through the channel of human capital has been reflected by the coefficient of education level. The effect of siblings on labor market outcomes could be interpreted mainly through the channels of care-sharing effect and social network effect.

6. Does the gender of siblings matter?

The impact of brothers and sisters on employment could be quite different. First, males have higher employment rates and income, and therefore are more capable of providing employment-related assistance to family members [Chi and Li (2014)]. Second, males are more responsible for supporting the elder parents and helping other members in the family [Li and Wu (2018)]. We expect brothers would provide more help to their siblings in the job market. Third, females are more altruistic and might be more willing to help other family member than brothers [Wu and Li (2014)]. The overall effects of brothers and sisters on individual employment are not clear.

In this section, we examine the impact of gender of siblings on individual labor market outcomes. According to Zhou (2014), if total number of siblings is controlled in the regression, number of brothers is not related to the disturbance term, which indicates that number of brothers is exogenous. Following Zhou (2014) and Wu and Zhao (2020), we add number of brothers in the regression and control for number of siblings at the same time. Table 8 reports the results. Columns 1–2 show that number of brothers has no significant effect on whether an individual is working, but the probability of engaging in the non-agricultural sector increases with number of brothers. Columns 3–7 analyze the main mechanisms. We find that individual labor supply is not affected by the gender of siblings. However, number of brothers decreases the probability and frequency of caring parents, and lowers the financial support to parents. These results suggest that males play a larger role in supporting the elder parents. We do not find that brothers provide more help than sisters when an individual is searching a job, which indicates that the social network effect of brothers is not larger than that of sisters.

Table 8. Impacts of Gender of Siblings

Note: The results from OLS regression are reported, controlling number of siblings, male, age, years of education, married, prefectural real GDP per capita, survey year dummies and province dummies. Robust standard errors are in parentheses.

*Significant at 10%; **significant at 5%; ***significant at 1%.

7. Conclusion

The relaxation of birth-control policies may have a long-term impact on individual labor market outcomes. In this paper, we examine the impact of the relaxation of the One-Child Policy on number of siblings and employment. With the exogenous variation in the time of the implementation of the One-and-A-Half Policy in rural China in the 1980s, we find that an individual would have more siblings and be more likely to work and work in the non-agricultural job. Using the variation of number of siblings under the One-and-A-Half-Child Policy as instruments, we find that having one more sibling would increase the probability of working by 9.0 percentage points, and increases the probability of working in the non-agricultural sector by 5.1 percentage points. Furthermore, we show that number of siblings facilitates employment through sharing care for the elderly parents and through the larger social network that is helpful in searching for a job. Although the fertility relaxation policy may negatively affect human capital accumulation in the short term, the increasing number of siblings would improve labor market outcomes in the long term.

It is worth noting that females benefit more from the relaxation than males in the labor market. With more siblings, females not only have more time to participate in the labor market but also receive better outcomes with the assistance from their siblings. The relaxation of the population policy also contributes to the narrowing of the gender gap in the labor market.