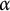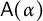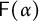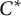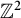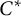1 Introduction
Given an action
![]() $\alpha $
of a group on the Cantor set X, the topological full group of
$\alpha $
of a group on the Cantor set X, the topological full group of
![]() $\alpha $
, denoted by
$\alpha $
, denoted by
![]() $\mathsf {F}(\alpha )$
, is the group of homeomorphisms on X which are locally given by
$\mathsf {F}(\alpha )$
, is the group of homeomorphisms on X which are locally given by
![]() $\alpha $
.
$\alpha $
.
In [Reference Juschenko and MonodJM13], Juschenko and Monod showed that topological full groups of Cantor minimal
![]() $\mathbb {Z}$
-systems are amenable. Together with results of Matui [Reference Matte BonMat06], this gave rise to the first examples of infinite, simple, finitely generated, amenable groups. On the other hand, in [Reference Elek and MonodEM13], Elek and Monod constructed an example of a free minimal
$\mathbb {Z}$
-systems are amenable. Together with results of Matui [Reference Matte BonMat06], this gave rise to the first examples of infinite, simple, finitely generated, amenable groups. On the other hand, in [Reference Elek and MonodEM13], Elek and Monod constructed an example of a free minimal
![]() $\mathbb {Z}^2$
-subshift whose topological full group contains a free group.
$\mathbb {Z}^2$
-subshift whose topological full group contains a free group.
A group
![]() $\Gamma $
is said to have the unique trace property if its reduced
$\Gamma $
is said to have the unique trace property if its reduced
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*_r(\Gamma )$
has a unique tracial state and to be
$C^*_r(\Gamma )$
has a unique tracial state and to be
![]() $C^*$
-simple if
$C^*$
-simple if
![]() $C^*_r(\Gamma )$
is simple. In [Reference Breuillard, Kalantar, Kennedy and OzawaBKKO17], Breuillard et al. showed that
$C^*_r(\Gamma )$
is simple. In [Reference Breuillard, Kalantar, Kennedy and OzawaBKKO17], Breuillard et al. showed that
![]() $\Gamma $
has the unique trace property if and only if it does not contain any non-trivial amenable normal subgroup, and in [Reference KennedyKen20], Kennedy showed that
$\Gamma $
has the unique trace property if and only if it does not contain any non-trivial amenable normal subgroup, and in [Reference KennedyKen20], Kennedy showed that
![]() $\Gamma $
is
$\Gamma $
is
![]() $C^*$
-simple if and only if it does not contain any nontrivial amenable uniformly recurrent subgroup (URS).
$C^*$
-simple if and only if it does not contain any nontrivial amenable uniformly recurrent subgroup (URS).
By using this new characterization of
![]() $C^*$
-simplicity, Le Boudec and Matte Bon showed in [Reference Le Boudec and Matte BonLBMB18] that the topological full group of a free minimal action of a countable non-amenable group on the Cantor set is
$C^*$
-simplicity, Le Boudec and Matte Bon showed in [Reference Le Boudec and Matte BonLBMB18] that the topological full group of a free minimal action of a countable non-amenable group on the Cantor set is
![]() $C^*$
-simple, and asked whether the same conclusion holds if one does not assume freeness. In [Reference Brix and ScarparoBS19], Brix and the author showed that it suffices to assume that the action is topologically free. In [Reference Kerr and Tucker-DrobKTD19], Kerr and Tucker-Drob obtained examples of
$C^*$
-simple, and asked whether the same conclusion holds if one does not assume freeness. In [Reference Brix and ScarparoBS19], Brix and the author showed that it suffices to assume that the action is topologically free. In [Reference Kerr and Tucker-DrobKTD19], Kerr and Tucker-Drob obtained examples of
![]() $C^*$
-simple topological full groups coming from actions of amenable groups.
$C^*$
-simple topological full groups coming from actions of amenable groups.
Given an action
![]() $\alpha $
of a group on the Cantor set, Nekrashevych introduced in [Reference NekrashevychNek19] the alternating full group of the action, which we denote by
$\alpha $
of a group on the Cantor set, Nekrashevych introduced in [Reference NekrashevychNek19] the alternating full group of the action, which we denote by
![]() $\mathsf {A}(\alpha )$
. This is a normal subgroup of
$\mathsf {A}(\alpha )$
. This is a normal subgroup of
![]() $\mathsf {F}(\alpha )$
generated by certain copies of finite alternating groups. It was shown in [Reference NekrashevychNek19] that if
$\mathsf {F}(\alpha )$
generated by certain copies of finite alternating groups. It was shown in [Reference NekrashevychNek19] that if
![]() $\alpha $
is minimal, then
$\alpha $
is minimal, then
![]() $\mathsf {A}(\alpha )$
is simple and is contained in every nontrivial normal subgroup of
$\mathsf {A}(\alpha )$
is simple and is contained in every nontrivial normal subgroup of
![]() $\mathsf {F}(\alpha )$
.
$\mathsf {F}(\alpha )$
.
In [Reference MatuiMB18], Matte Bon obtained a classification of URSs of topological full groups. By using this result, we show the following theorem.
Theorem (Theorem 3.5)
Let
![]() $\alpha $
be a minimal action of a countable group on the Cantor set. The following conditions are equivalent:
$\alpha $
be a minimal action of a countable group on the Cantor set. The following conditions are equivalent:
-
(i)
 $\mathsf {A}(\alpha )$
is non-amenable.
$\mathsf {A}(\alpha )$
is non-amenable. -
(ii) Any group H such that
 $\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
is
$\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
is
 $C^*$
-simple.
$C^*$
-simple. -
(iii) There exists a
 $C^*$
-simple group H such that
$C^*$
-simple group H such that
 $\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
.
$\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
.
As a consequence, we obtain the following corollary.
Corollary (Corollary 3.6)
Let
![]() $\alpha $
be a minimal action of a countable group on the Cantor set. Then
$\alpha $
be a minimal action of a countable group on the Cantor set. Then
![]() $\mathsf {F}(\alpha )$
has the unique trace property if and only if it is
$\mathsf {F}(\alpha )$
has the unique trace property if and only if it is
![]() $C^*$
-simple. If
$C^*$
-simple. If
![]() $\mathsf {A}(\alpha )=\mathsf {F}(\alpha )'$
, then
$\mathsf {A}(\alpha )=\mathsf {F}(\alpha )'$
, then
![]() $\mathsf {F}(\alpha )$
is non-amenable if and only if it is
$\mathsf {F}(\alpha )$
is non-amenable if and only if it is
![]() $C^*$
-simple.
$C^*$
-simple.
It is still an open problem whether
![]() $\mathsf {A}(\alpha )$
always coincides with
$\mathsf {A}(\alpha )$
always coincides with
![]() $\mathsf {F}(\alpha )'$
, but in many cases, this is known to be true. For example, it follows from results of Matui [Reference MatuiMat15] that this is the case for free Cantor minimal
$\mathsf {F}(\alpha )'$
, but in many cases, this is known to be true. For example, it follows from results of Matui [Reference MatuiMat15] that this is the case for free Cantor minimal
![]() $\mathbb {Z}^n$
-systems. This implies that the example of non-amenable topological full group coming from an action of
$\mathbb {Z}^n$
-systems. This implies that the example of non-amenable topological full group coming from an action of
![]() $\mathbb {Z}^2$
in [Reference Elek and MonodEM13] is
$\mathbb {Z}^2$
in [Reference Elek and MonodEM13] is
![]() $C^*$
-simple.
$C^*$
-simple.
2 Preliminaries
2.1 Topological dynamics
Given a locally compact Hausdorff space X, we denote by
![]() $\mathcal {B}(X)$
the Borel
$\mathcal {B}(X)$
the Borel
![]() $\sigma $
-algebra of X, and by
$\sigma $
-algebra of X, and by
![]() $\mathcal {P}(X)$
the space of regular probability measures on X.
$\mathcal {P}(X)$
the space of regular probability measures on X.
If
![]() $\Gamma $
is a group acting by homeomorphisms on X, we say that X is a locally compact
$\Gamma $
is a group acting by homeomorphisms on X, we say that X is a locally compact
![]() $\Gamma $
-space. If X admits no nontrivial
$\Gamma $
-space. If X admits no nontrivial
![]() $\Gamma $
-invariant closed subspaces, then we say that X (or the action) is minimal. Given
$\Gamma $
-invariant closed subspaces, then we say that X (or the action) is minimal. Given
![]() $U\subset X$
, let
$U\subset X$
, let
![]() $\operatorname {St}_{\Gamma} (U)$
consist of the elements of
$\operatorname {St}_{\Gamma} (U)$
consist of the elements of
![]() $\Gamma $
which fix pointwise U, and
$\Gamma $
which fix pointwise U, and
![]() $\operatorname {St}_{\Gamma} (U)^0$
consist of the elements of
$\operatorname {St}_{\Gamma} (U)^0$
consist of the elements of
![]() $\Gamma $
which fix pointwise a neighborhood of U. To ease the notation, given
$\Gamma $
which fix pointwise a neighborhood of U. To ease the notation, given
![]() $x\in X$
, we let
$x\in X$
, we let
![]() $\Gamma _x:=\operatorname {St}_{\Gamma} (\{x\})$
and
$\Gamma _x:=\operatorname {St}_{\Gamma} (\{x\})$
and
![]() $\Gamma _x^0:=\operatorname {St}_{\Gamma} (\{x\})^0$
.
$\Gamma _x^0:=\operatorname {St}_{\Gamma} (\{x\})^0$
.
Denote by
![]() $\operatorname {Sub}(\Gamma )$
the set of subgroups of
$\operatorname {Sub}(\Gamma )$
the set of subgroups of
![]() $\Gamma $
, endowed with the Chabauty topology; this is the restriction to
$\Gamma $
, endowed with the Chabauty topology; this is the restriction to
![]() $\operatorname {Sub}(\Gamma )$
of the product topology on
$\operatorname {Sub}(\Gamma )$
of the product topology on
![]() $\{0, 1\}^{\Gamma} $
, where every subgroup
$\{0, 1\}^{\Gamma} $
, where every subgroup
![]() $\Lambda \in \operatorname {Sub}(G)$
is identified with its characteristic function
$\Lambda \in \operatorname {Sub}(G)$
is identified with its characteristic function
![]() $\boldsymbol {1}_\Lambda \in \{0, 1\}^{\Gamma} $
. Notice that the space of amenable subgroups
$\boldsymbol {1}_\Lambda \in \{0, 1\}^{\Gamma} $
. Notice that the space of amenable subgroups
![]() $\operatorname {Sub}_{am}(\Gamma )$
is closed in
$\operatorname {Sub}_{am}(\Gamma )$
is closed in
![]() $\operatorname {Sub}(\Gamma )$
. We consider
$\operatorname {Sub}(\Gamma )$
. We consider
![]() $\operatorname {Sub}(\Gamma )$
as a compact
$\operatorname {Sub}(\Gamma )$
as a compact
![]() $\Gamma $
-space under the action by conjugation. A subgroup
$\Gamma $
-space under the action by conjugation. A subgroup
![]() $\Lambda \leq \Gamma $
is said to be confined if
$\Lambda \leq \Gamma $
is said to be confined if
![]() $\{e\}$
is not in the closure of the
$\{e\}$
is not in the closure of the
![]() $\Gamma $
-orbit of
$\Gamma $
-orbit of
![]() $\Lambda $
.
$\Lambda $
.
An invariant random subgroup (IRS) is a
![]() $\Gamma $
-invariant regular probability measure on
$\Gamma $
-invariant regular probability measure on
![]() $\operatorname {Sub}(\Gamma )$
. We say an IRS is amenable if its support is contained in
$\operatorname {Sub}(\Gamma )$
. We say an IRS is amenable if its support is contained in
![]() $\operatorname {Sub}_{am}(\Gamma )$
. By [Reference Breuillard, Kalantar, Kennedy and OzawaBKKO17, Corollary 4.3] and [Reference Bader, Duchesne and LécureuxBDL16, Corollary 1.5],
$\operatorname {Sub}_{am}(\Gamma )$
. By [Reference Breuillard, Kalantar, Kennedy and OzawaBKKO17, Corollary 4.3] and [Reference Bader, Duchesne and LécureuxBDL16, Corollary 1.5],
![]() $\Gamma $
has the unique trace property if and only if its unique amenable normal subgroup is
$\Gamma $
has the unique trace property if and only if its unique amenable normal subgroup is
![]() $\{e\}$
, if and only if its unique amenable IRS is
$\{e\}$
, if and only if its unique amenable IRS is
![]() $\delta _{\{e\}}$
.
$\delta _{\{e\}}$
.
A URS is a
![]() $\Gamma $
-invariant closed minimal subspace
$\Gamma $
-invariant closed minimal subspace
![]() $\mathcal {U}\subset \operatorname {Sub}(\Gamma )$
. We say
$\mathcal {U}\subset \operatorname {Sub}(\Gamma )$
. We say
![]() $\mathcal {U}$
is amenable if every element of
$\mathcal {U}$
is amenable if every element of
![]() $\mathcal {U}$
is amenable. By [Reference KennedyKen20, Theorem 4.1],
$\mathcal {U}$
is amenable. By [Reference KennedyKen20, Theorem 4.1],
![]() $\Gamma $
is
$\Gamma $
is
![]() $C^*$
-simple if and only if its only amenable URS is
$C^*$
-simple if and only if its only amenable URS is
![]() $\{\{e\}\}$
. Alternatively,
$\{\{e\}\}$
. Alternatively,
![]() $\Gamma $
is
$\Gamma $
is
![]() $C^*$
-simple if and only if it does not contain any confined amenable subgroup.
$C^*$
-simple if and only if it does not contain any confined amenable subgroup.
Suppose
![]() $\Gamma $
is countable and X is a minimal compact
$\Gamma $
is countable and X is a minimal compact
![]() $\Gamma $
-space. Let
$\Gamma $
-space. Let
![]() $\operatorname {Stab}_{\Gamma} \colon X\to \operatorname {Sub}(\Gamma )$
be the map given by
$\operatorname {Stab}_{\Gamma} \colon X\to \operatorname {Sub}(\Gamma )$
be the map given by
![]() $\operatorname {Stab}_{\Gamma} (x):=\Gamma _x$
and
$\operatorname {Stab}_{\Gamma} (x):=\Gamma _x$
and
![]() $\operatorname {Stab}_{\Gamma} ^0\colon X\to \operatorname {Sub}(\Gamma )$
be the map given by
$\operatorname {Stab}_{\Gamma} ^0\colon X\to \operatorname {Sub}(\Gamma )$
be the map given by
![]() $\operatorname {Stab}_{\Gamma} ^0(x):=\Gamma _x^0$
, for
$\operatorname {Stab}_{\Gamma} ^0(x):=\Gamma _x^0$
, for
![]() $x\in X$
. Notice that
$x\in X$
. Notice that
![]() $\operatorname {Stab}_{\Gamma} $
and
$\operatorname {Stab}_{\Gamma} $
and
![]() $\operatorname {Stab}_{\Gamma} ^0$
are Borel measurable and
$\operatorname {Stab}_{\Gamma} ^0$
are Borel measurable and
![]() $\Gamma $
-equivariant. Moreover, the set
$\Gamma $
-equivariant. Moreover, the set
![]() $Y:=\{x\in X:\Gamma _x=\Gamma _x^0\}$
is dense in X and
$Y:=\{x\in X:\Gamma _x=\Gamma _x^0\}$
is dense in X and
![]() $\operatorname {Stab}_{\Gamma} (Y)$
is a URS, the so-called stabilizer URS of the action
$\operatorname {Stab}_{\Gamma} (Y)$
is a URS, the so-called stabilizer URS of the action
![]() $\Gamma \!\curvearrowright \! X$
(for a proof of these last claims, see [Reference Le Boudec and Matte BonLBMB18, Section 2]).
$\Gamma \!\curvearrowright \! X$
(for a proof of these last claims, see [Reference Le Boudec and Matte BonLBMB18, Section 2]).
2.2 Topological full groups
Fix an action
![]() $\alpha $
of a group
$\alpha $
of a group
![]() $\Gamma $
on the Cantor set X. We say that a homeomorphism
$\Gamma $
on the Cantor set X. We say that a homeomorphism
![]() $h\colon U\to V$
between clopen subsets
$h\colon U\to V$
between clopen subsets
![]() $U,V\subset X$
is locally given by
$U,V\subset X$
is locally given by
![]() $\alpha $
if there exist
$\alpha $
if there exist
![]() $g_1,\dots ,g_n\in \Gamma $
and clopen sets
$g_1,\dots ,g_n\in \Gamma $
and clopen sets
![]() $A_1,\dots ,A_n\subset U$
such that
$A_1,\dots ,A_n\subset U$
such that
![]() $U=\bigsqcup _{i=1}^n A_i$
and
$U=\bigsqcup _{i=1}^n A_i$
and
![]() $h|_{A_i}=g_i|_{A_i}$
, for
$h|_{A_i}=g_i|_{A_i}$
, for
![]() $1\leq i \leq n$
. The topological full group of
$1\leq i \leq n$
. The topological full group of
![]() $\alpha $
, denoted by
$\alpha $
, denoted by
![]() $\mathsf {F}(\alpha )$
, is the group of homeomorphisms
$\mathsf {F}(\alpha )$
, is the group of homeomorphisms
![]() $h\colon X\to X$
which are locally given by
$h\colon X\to X$
which are locally given by
![]() $\alpha $
.
$\alpha $
.
Given
![]() $d\in \mathbb {N}$
, a d-multisection is a collection of d disjoint clopen sets
$d\in \mathbb {N}$
, a d-multisection is a collection of d disjoint clopen sets
![]() $(A_i)_{i=1}^d\subset X$
and
$(A_i)_{i=1}^d\subset X$
and
![]() $d^2$
homeomorphisms
$d^2$
homeomorphisms
![]() $(h_{i,j}\colon A_i\to A_j)_{i,j=1}^d$
which are locally given by
$(h_{i,j}\colon A_i\to A_j)_{i,j=1}^d$
which are locally given by
![]() $\alpha $
and such that, for
$\alpha $
and such that, for
![]() $1\leq i,j,k\leq d$
, it holds that
$1\leq i,j,k\leq d$
, it holds that
![]() $h_{j,k}h_{i,j}=h_{i,k}$
and
$h_{j,k}h_{i,j}=h_{i,k}$
and
![]() $h_{i,i}=\mathrm {Id}_{A_i}$
.
$h_{i,i}=\mathrm {Id}_{A_i}$
.
Given
![]() $d\in \mathbb {N}$
, let
$d\in \mathbb {N}$
, let
![]() $S_d$
and
$S_d$
and
![]() $A_d$
be the symmetric and alternating groups, respectively. Given a d-multisection
$A_d$
be the symmetric and alternating groups, respectively. Given a d-multisection
![]() $\mathcal {F}=((A_i)_{i=1}^d,(h_{i,j})_{i,j=1}^d)$
and
$\mathcal {F}=((A_i)_{i=1}^d,(h_{i,j})_{i,j=1}^d)$
and
![]() $\sigma \in S_d$
, let
$\sigma \in S_d$
, let
![]() $\mathcal {F}(\sigma )\in \mathsf {F}(\alpha )$
be given by
$\mathcal {F}(\sigma )\in \mathsf {F}(\alpha )$
be given by
![]() $\mathcal {F}(\sigma )|_{A_i}:=h_{\sigma (i),i}$
, for
$\mathcal {F}(\sigma )|_{A_i}:=h_{\sigma (i),i}$
, for
![]() $1\leq i \leq n$
and
$1\leq i \leq n$
and
![]() $\mathcal {F}(\sigma )(x)=x$
for
$\mathcal {F}(\sigma )(x)=x$
for
![]() $x\notin \bigsqcup _{i=1}^n A_i$
. The alternating full group
$x\notin \bigsqcup _{i=1}^n A_i$
. The alternating full group
![]() $\mathsf {A}(\alpha )$
is the subgroup of
$\mathsf {A}(\alpha )$
is the subgroup of
![]() $\mathsf {F}(\alpha )$
generated by
$\mathsf {F}(\alpha )$
generated by
Notice that
![]() $\mathsf {A}(\alpha )$
is normal in
$\mathsf {A}(\alpha )$
is normal in
![]() $\mathsf {F}(\alpha )$
and that
$\mathsf {F}(\alpha )$
and that
![]() $\mathsf {A}(\alpha )$
is contained in the derived subgroup
$\mathsf {A}(\alpha )$
is contained in the derived subgroup
![]() $\mathsf {F}(\alpha )'$
. If
$\mathsf {F}(\alpha )'$
. If
![]() $\alpha $
is a minimal action of a countable group on the Cantor set, then
$\alpha $
is a minimal action of a countable group on the Cantor set, then
![]() $\mathsf {A}(\alpha )$
is simple [Reference NekrashevychNek19, Theorem 4.1].
$\mathsf {A}(\alpha )$
is simple [Reference NekrashevychNek19, Theorem 4.1].
Remark 2.1 Alternatively,
![]() $\mathsf {F}(\alpha )$
and
$\mathsf {F}(\alpha )$
and
![]() $\mathsf {A}(\alpha )$
can be described as groups of bisections of the groupoid of germs of
$\mathsf {A}(\alpha )$
can be described as groups of bisections of the groupoid of germs of
![]() $\alpha $
. This is the point of view adopted in [Reference MatuiMB18, Reference NekrashevychNek19]. Conversely, given an effective groupoid G with unit space
$\alpha $
. This is the point of view adopted in [Reference MatuiMB18, Reference NekrashevychNek19]. Conversely, given an effective groupoid G with unit space
![]() $G^{(0)}$
homeomorphic to the Cantor set, denote by
$G^{(0)}$
homeomorphic to the Cantor set, denote by
![]() $\alpha $
the natural action of the topological full group of G on
$\alpha $
the natural action of the topological full group of G on
![]() $G^{(0)}$
. Then the topological and alternating full groups of G coincide with
$G^{(0)}$
. Then the topological and alternating full groups of G coincide with
![]() $\mathsf {F}(\alpha )$
and
$\mathsf {F}(\alpha )$
and
![]() $\mathsf {A}(\alpha )$
, respectively [Reference Nyland and OrtegaNO19, Corollary 4.7].
$\mathsf {A}(\alpha )$
, respectively [Reference Nyland and OrtegaNO19, Corollary 4.7].
3
 $\boldsymbol{C}^{\boldsymbol{*}}$
-simplicity of full groups
$\boldsymbol{C}^{\boldsymbol{*}}$
-simplicity of full groups
Given a locally compact
![]() $\Gamma $
-space X and
$\Gamma $
-space X and
![]() $U\subset X$
open not necessarily invariant, let
$U\subset X$
open not necessarily invariant, let
Alternatively, one can characterize
![]() $\mathcal {P}_{\Gamma} (U)$
as the measures
$\mathcal {P}_{\Gamma} (U)$
as the measures
![]() $\mu \in \mathcal {P}(U)$
such that
$\mu \in \mathcal {P}(U)$
such that
![]() $\mu (gA)=\mu (A)$
for every
$\mu (gA)=\mu (A)$
for every
![]() $g\in \Gamma $
and
$g\in \Gamma $
and
![]() $A\in \mathcal {B}(U)$
such that
$A\in \mathcal {B}(U)$
such that
![]() $gA\subset U$
.
$gA\subset U$
.
Proposition 3.1 Let X be a compact
![]() $\Gamma $
-space and
$\Gamma $
-space and
![]() $U\subset X$
open such that
$U\subset X$
open such that
![]() $X=\Gamma. U$
. Then the map
$X=\Gamma. U$
. Then the map
![]() $j\colon \mathcal {P}_{\Gamma} (X)\to \mathcal {P}_{\Gamma} (U)$
given by
$j\colon \mathcal {P}_{\Gamma} (X)\to \mathcal {P}_{\Gamma} (U)$
given by
![]() $j(\nu ):=\frac {\nu |_{\mathcal {B}(U)} }{\nu (U)}$
is a well-defined bijection.
$j(\nu ):=\frac {\nu |_{\mathcal {B}(U)} }{\nu (U)}$
is a well-defined bijection.
Proof Take
![]() $g_1,\dots ,g_n\in \Gamma $
such that
$g_1,\dots ,g_n\in \Gamma $
such that
![]() $X=\bigcup _{i=1}^n g_iU$
. For
$X=\bigcup _{i=1}^n g_iU$
. For
![]() $1\leq i \leq n$
, let
$1\leq i \leq n$
, let
 $$ \begin{align*}A_i:=U\setminus\bigcup_{j=1}^{i-1}g_i^{-1}g_j U.\end{align*} $$
$$ \begin{align*}A_i:=U\setminus\bigcup_{j=1}^{i-1}g_i^{-1}g_j U.\end{align*} $$
Then
![]() $X=\bigsqcup _{i=1}^n g_iA_i$
. Given
$X=\bigsqcup _{i=1}^n g_iA_i$
. Given
![]() $\nu \in \mathcal {P}_{\Gamma} (X)$
, obviously
$\nu \in \mathcal {P}_{\Gamma} (X)$
, obviously
![]() $\nu (U)\geq 1/n$
, so that j is a well-defined map. Moreover, given
$\nu (U)\geq 1/n$
, so that j is a well-defined map. Moreover, given
![]() $A\in \mathcal {B}(X)$
, we have
$A\in \mathcal {B}(X)$
, we have
 $$ \begin{align} \nu(A)=\sum_{i=1}^n\nu(g_i A_i\cap A)=\sum_{i=1}^n\nu(A_i\cap g_i^{-1} A). \end{align} $$
$$ \begin{align} \nu(A)=\sum_{i=1}^n\nu(g_i A_i\cap A)=\sum_{i=1}^n\nu(A_i\cap g_i^{-1} A). \end{align} $$
Since each
![]() $A_i$
is contained in U, this implies that
$A_i$
is contained in U, this implies that
![]() $\nu $
is determined by its restriction to
$\nu $
is determined by its restriction to
![]() $\mathcal {B}(U)$
.
$\mathcal {B}(U)$
.
If
![]() $\nu _1,\nu _2\in \mathcal {P}_{\Gamma} (X)$
are such that
$\nu _1,\nu _2\in \mathcal {P}_{\Gamma} (X)$
are such that
![]() $j(\nu _1)=j(\nu _2)$
, then
$j(\nu _1)=j(\nu _2)$
, then
![]() $\nu _1|_U=\frac {\nu _1(U)}{\nu _2(U)}\nu _2|_U$
. Furthermore, by (1), we have
$\nu _1|_U=\frac {\nu _1(U)}{\nu _2(U)}\nu _2|_U$
. Furthermore, by (1), we have
 $$ \begin{align*}1=\nu_1(X)=\sum_{i=1}^n\nu_1(A_i)=\sum_{i=1}^n\frac{\nu_1(U)}{\nu_2(U)}\nu_2(A_i)=\frac{\nu_1(U)}{\nu_2(U)}\nu_2(X)=\frac{\nu_1(U)}{\nu_2(U)},\end{align*} $$
$$ \begin{align*}1=\nu_1(X)=\sum_{i=1}^n\nu_1(A_i)=\sum_{i=1}^n\frac{\nu_1(U)}{\nu_2(U)}\nu_2(A_i)=\frac{\nu_1(U)}{\nu_2(U)}\nu_2(X)=\frac{\nu_1(U)}{\nu_2(U)},\end{align*} $$
and hence
![]() $\nu _1(U)=\nu _2(U)$
. Consequently,
$\nu _1(U)=\nu _2(U)$
. Consequently,
![]() $\nu _1=\nu _2$
and j is injective.
$\nu _1=\nu _2$
and j is injective.
Let us now show that j is surjective. Given
![]() $\mu \in \mathcal {P}_{\Gamma} (U)$
and
$\mu \in \mathcal {P}_{\Gamma} (U)$
and
![]() $A\in \mathcal {B}(X)$
, let
$A\in \mathcal {B}(X)$
, let
 $$ \begin{align*}\nu(A):=\sum_{i=1}^n\mu(A_i\cap g_i^{-1}A).\end{align*} $$
$$ \begin{align*}\nu(A):=\sum_{i=1}^n\mu(A_i\cap g_i^{-1}A).\end{align*} $$
Given
![]() $B\in \mathcal {B}(U)$
, we have
$B\in \mathcal {B}(U)$
, we have
 $$ \begin{align*}\nu(B)=\sum_{i=1}^n\mu(A_i\cap g_i^{-1}B)=\sum_{i=1}^n\mu(g_iA_i\cap B)=\mu(B),\end{align*} $$
$$ \begin{align*}\nu(B)=\sum_{i=1}^n\mu(A_i\cap g_i^{-1}B)=\sum_{i=1}^n\mu(g_iA_i\cap B)=\mu(B),\end{align*} $$
so that
![]() $\nu |_{\mathcal {B}(U)}=\mu $
.
$\nu |_{\mathcal {B}(U)}=\mu $
.
We claim that
![]() $\nu $
is
$\nu $
is
![]() $\Gamma $
-invariant. Fix
$\Gamma $
-invariant. Fix
![]() $A\in \mathcal {B}(X)$
and
$A\in \mathcal {B}(X)$
and
![]() $g\in \Gamma $
, and we will show that
$g\in \Gamma $
, and we will show that
![]() $\nu (A)=\nu (gA)$
.
$\nu (A)=\nu (gA)$
.
For
![]() $1\leq i\leq n$
, let
$1\leq i\leq n$
, let
![]() $h_i:=g^{-1}g_i$
,
$h_i:=g^{-1}g_i$
,
![]() $B_i:=A_i\cap g_i^{-1}A$
, and
$B_i:=A_i\cap g_i^{-1}A$
, and
![]() $C_i:=A_i\cap g_i^{-1}gA=A_i\cap h_i^{-1} A$
. By definition of
$C_i:=A_i\cap g_i^{-1}gA=A_i\cap h_i^{-1} A$
. By definition of
![]() $\nu $
, we have
$\nu $
, we have
![]() $\nu (A)=\sum _{i=1}^n\mu (B_i)$
and
$\nu (A)=\sum _{i=1}^n\mu (B_i)$
and
![]() $\nu (gA)=\sum _{i=1}^n\mu (C_i)$
.
$\nu (gA)=\sum _{i=1}^n\mu (C_i)$
.
Moreover, one can readily check that
![]() $A=\bigsqcup _{i=1}^n g_i B_i=\bigsqcup _{i=1}^n h_iC_i$
.
$A=\bigsqcup _{i=1}^n g_i B_i=\bigsqcup _{i=1}^n h_iC_i$
.
For
![]() $1\leq i,j\leq n$
, let
$1\leq i,j\leq n$
, let
![]() $B_{i,j}:=B_i\cap g_i^{-1}h_jC_j$
and
$B_{i,j}:=B_i\cap g_i^{-1}h_jC_j$
and
![]() $C_{i,j}:=h_j^{-1}g_iB_i\cap C_j$
.
$C_{i,j}:=h_j^{-1}g_iB_i\cap C_j$
.
Notice that, for
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $$ \begin{align*}\bigsqcup_{j=1}^n B_{i,j}=B_i\cap g_i^{-1}A=B_i\end{align*} $$
$$ \begin{align*}\bigsqcup_{j=1}^n B_{i,j}=B_i\cap g_i^{-1}A=B_i\end{align*} $$
and, for
![]() $1\leq j \leq n$
,
$1\leq j \leq n$
,
Furthermore,
![]() $g_i B_{i,j}=h_jC_{i,j}$
, and hence
$g_i B_{i,j}=h_jC_{i,j}$
, and hence
![]() $\mu (B_{i,j})=\mu (C_{i,j})$
, since
$\mu (B_{i,j})=\mu (C_{i,j})$
, since
![]() $B_{i,j}$
and
$B_{i,j}$
and
![]() $C_{i,j}$
are contained in U for every
$C_{i,j}$
are contained in U for every
![]() $i,j$
. Therefore,
$i,j$
. Therefore,
 $$ \begin{align*} \nu(A)=\sum_{i=1}^n\mu(B_i)=\sum_{i,j=1}^n \mu(B_{i,j})=\sum_{i,j=1}^n\mu(C_{i,j})=\sum_{j=1}^n\mu(C_j)=\nu(gA). \end{align*} $$
$$ \begin{align*} \nu(A)=\sum_{i=1}^n\mu(B_i)=\sum_{i,j=1}^n \mu(B_{i,j})=\sum_{i,j=1}^n\mu(C_{i,j})=\sum_{j=1}^n\mu(C_j)=\nu(gA). \end{align*} $$
Finally, we have that
![]() $j(\frac {\nu }{\nu (X)})=\frac {\nu |_{\mathcal {B}(U)}/\nu (X)}{\nu (U)/\nu (X)}=\nu |_{\mathcal {B}(U)}=\mu .$
$j(\frac {\nu }{\nu (X)})=\frac {\nu |_{\mathcal {B}(U)}/\nu (X)}{\nu (U)/\nu (X)}=\nu |_{\mathcal {B}(U)}=\mu .$
Remark 3.2 Let
![]() $\Gamma \!\curvearrowright \! X$
and
$\Gamma \!\curvearrowright \! X$
and
![]() $\Lambda \!\curvearrowright \! Y$
be actions on compact spaces. The actions are said to be Kakutani equivalent [Reference LiLi18, Definition 2.14] if there exist clopen sets
$\Lambda \!\curvearrowright \! Y$
be actions on compact spaces. The actions are said to be Kakutani equivalent [Reference LiLi18, Definition 2.14] if there exist clopen sets
![]() $A\subset X$
and
$A\subset X$
and
![]() $B\subset Y$
such that
$B\subset Y$
such that
![]() $X=\Gamma .A$
,
$X=\Gamma .A$
,
![]() $Y=\Lambda. B$
, and the partial transformation groupoids obtained by restriction to A and B are isomorphic. Proposition 3.1 implies that Kakutani equivalence induces a bijection between
$Y=\Lambda. B$
, and the partial transformation groupoids obtained by restriction to A and B are isomorphic. Proposition 3.1 implies that Kakutani equivalence induces a bijection between
![]() $\mathcal {P}_{\Gamma} (X)$
and
$\mathcal {P}_{\Gamma} (X)$
and
![]() $\mathcal {P}_\Lambda (X)$
.
$\mathcal {P}_\Lambda (X)$
.
The proof of the following result is analogous to [Reference Nyland and OrtegaNO19, Lemma 4.9(2)].
Lemma 3.3 Let
![]() $\alpha $
be a minimal action of a group
$\alpha $
be a minimal action of a group
![]() $\Gamma $
on the Cantor set X. Given
$\Gamma $
on the Cantor set X. Given
![]() $U\subset X$
clopen,
$U\subset X$
clopen,
![]() $x\in U$
, and
$x\in U$
, and
![]() $g\in \Gamma $
such that
$g\in \Gamma $
such that
![]() $g(x)\in U$
, there exists a neighborhood V of x and
$g(x)\in U$
, there exists a neighborhood V of x and
![]() $h\in \operatorname {St}_{\mathsf {A}(\alpha )}(U^{\mathsf {c}})$
such that
$h\in \operatorname {St}_{\mathsf {A}(\alpha )}(U^{\mathsf {c}})$
such that
![]() $g|_V=h|_V$
.
$g|_V=h|_V$
.
Proof Case 1:
![]() $g(x)\neq x$
. Take
$g(x)\neq x$
. Take
![]() $k\in \Gamma $
such that
$k\in \Gamma $
such that
![]() $k(g(x))\in U\setminus \{x,g(x)\}$
. Let V be a clopen neighborhood of x such that V,
$k(g(x))\in U\setminus \{x,g(x)\}$
. Let V be a clopen neighborhood of x such that V,
![]() $g(V)$
, and
$g(V)$
, and
![]() $kg(V)$
are disjoint subsets of U. Then the homeomorphisms
$kg(V)$
are disjoint subsets of U. Then the homeomorphisms
![]() $h_{2,1}:=g|_V$
and
$h_{2,1}:=g|_V$
and
![]() $h_{3,1}:=kg|_V$
give rise to a
$h_{3,1}:=kg|_V$
give rise to a
![]() $3$
-multisection
$3$
-multisection
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathcal {F}((123))|_V=g|_V$
and
$\mathcal {F}((123))|_V=g|_V$
and
![]() $\mathcal {F}((123))\in \operatorname {St}_{\mathsf {A}(\alpha )}(U^{\mathsf {c}})$
.
$\mathcal {F}((123))\in \operatorname {St}_{\mathsf {A}(\alpha )}(U^{\mathsf {c}})$
.
Case 2:
![]() $g(x)=x$
. Take
$g(x)=x$
. Take
![]() $k\in \Gamma $
such that
$k\in \Gamma $
such that
![]() $k(x)\in U\setminus \{ x\}$
. By Case 1, there are
$k(x)\in U\setminus \{ x\}$
. By Case 1, there are
![]() $h_1,h_2\in \operatorname {St}_{\mathsf {A}(\alpha )}(U^{\mathsf {c}})$
and
$h_1,h_2\in \operatorname {St}_{\mathsf {A}(\alpha )}(U^{\mathsf {c}})$
and
![]() $V_1,V_2$
neighborhoods of x and
$V_1,V_2$
neighborhoods of x and
![]() $k(x)$
, respectively, such that
$k(x)$
, respectively, such that
![]() $k|_{V_1}=h_1|_{V_1}$
and
$k|_{V_1}=h_1|_{V_1}$
and
![]() $gk^{-1}|_{V_2}=h_2|_{V_2}$
. Then
$gk^{-1}|_{V_2}=h_2|_{V_2}$
. Then
![]() $V:=V_1\cap k^{-1}(V_2)$
is a neighborhood of x such that
$V:=V_1\cap k^{-1}(V_2)$
is a neighborhood of x such that
![]() $h_2h_1|_V=g|_V$
.
$h_2h_1|_V=g|_V$
.
The next lemma uses the same idea of [Reference MatuiMB18, Corollary 6.5].
Lemma 3.4 Let
![]() $\alpha $
be a minimal action of a countable group
$\alpha $
be a minimal action of a countable group
![]() $\Gamma $
on the Cantor set X and H a group such that
$\Gamma $
on the Cantor set X and H a group such that
![]() $\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
. Then H is not
$\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
. Then H is not
![]() $C^*$
-simple if and only if
$C^*$
-simple if and only if
![]() $\mathsf {A}(\alpha )_x^0$
is amenable for all
$\mathsf {A}(\alpha )_x^0$
is amenable for all
![]() $x\in X$
.
$x\in X$
.
Proof Suppose H is not
![]() $C^*$
-simple. Then H contains a confined amenable subgroup. By [Reference MatuiMB18, Theorem 6.1], there exists
$C^*$
-simple. Then H contains a confined amenable subgroup. By [Reference MatuiMB18, Theorem 6.1], there exists
![]() $Q\subset X$
finite such that
$Q\subset X$
finite such that
![]() $\operatorname {St}_{\mathsf {A}(\alpha )}^0(Q)$
is amenable. Given
$\operatorname {St}_{\mathsf {A}(\alpha )}^0(Q)$
is amenable. Given
![]() $x\in X$
, take a net
$x\in X$
, take a net
![]() $(g_i)\subset \mathsf {F}(\alpha )$
such that
$(g_i)\subset \mathsf {F}(\alpha )$
such that
![]() $g_iq\to x$
for any
$g_iq\to x$
for any
![]() $q\in Q$
(existence of such a net
$q\in Q$
(existence of such a net
![]() $(g_i)$
follows from minimality and proximality of
$(g_i)$
follows from minimality and proximality of
![]() $\mathsf {F}(\alpha )\!\curvearrowright \! X$
; see [Reference MatuiMB18, Lemma 5.12]). Take K a limit point of
$\mathsf {F}(\alpha )\!\curvearrowright \! X$
; see [Reference MatuiMB18, Lemma 5.12]). Take K a limit point of
![]() $g_i\operatorname {St}_{\mathsf {A}(\alpha )}^0(Q)g_i^{-1}$
. One can readily check that
$g_i\operatorname {St}_{\mathsf {A}(\alpha )}^0(Q)g_i^{-1}$
. One can readily check that
![]() $\mathsf {A}(\alpha )_x^0\leq K$
, and hence
$\mathsf {A}(\alpha )_x^0\leq K$
, and hence
![]() $\mathsf {A}(\alpha )_x^0$
is amenable.
$\mathsf {A}(\alpha )_x^0$
is amenable.
Conversely, if
![]() $\mathsf {A}(\alpha )_x^0$
is amenable for all
$\mathsf {A}(\alpha )_x^0$
is amenable for all
![]() $x\in X$
, then since
$x\in X$
, then since
![]() $\mathsf {A}(\alpha )_x^0$
is nontrivial for every x, it follows that the stabilizer URS
$\mathsf {A}(\alpha )_x^0$
is nontrivial for every x, it follows that the stabilizer URS
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $\mathsf {A}(\alpha )\!\curvearrowright \! X$
is a nontrivial amenable URS of
$\mathsf {A}(\alpha )\!\curvearrowright \! X$
is a nontrivial amenable URS of
![]() $\mathsf {A}(\alpha )$
. By [Reference MatuiMB18, Theorem 6.1], any element of
$\mathsf {A}(\alpha )$
. By [Reference MatuiMB18, Theorem 6.1], any element of
![]() $\mathcal {U}$
is a confined subgroup of
$\mathcal {U}$
is a confined subgroup of
![]() $\mathsf {F}(\alpha )$
(hence of H as well). Therefore, H is not
$\mathsf {F}(\alpha )$
(hence of H as well). Therefore, H is not
![]() $C^*$
-simple.
$C^*$
-simple.
Theorem 3.5 Let
![]() $\alpha $
be a minimal action of a countable group
$\alpha $
be a minimal action of a countable group
![]() $\Gamma $
on the Cantor set X. The following conditions are equivalent:
$\Gamma $
on the Cantor set X. The following conditions are equivalent:
-
(i)
 $\mathsf {A}(\alpha )$
is non-amenable.
$\mathsf {A}(\alpha )$
is non-amenable. -
(ii) Any group H such that
 $\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
is
$\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
is
 $C^*$
-simple.
$C^*$
-simple. -
(iii) There exists a
 $C^*$
-simple group H such that
$C^*$
-simple group H such that
 $\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
.
$\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
.
Proof The implications (ii)
![]() $\implies $
(iii)
$\implies $
(iii)
![]() $\implies $
(i) are immediate.
$\implies $
(i) are immediate.
(i)
![]() $\implies $
(ii): Suppose that there exists H non-
$\implies $
(ii): Suppose that there exists H non-
![]() $C^*$
-simple such that
$C^*$
-simple such that
![]() $\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
. By Lemma 3.4,
$\mathsf {A}(\alpha )\leq H\leq \mathsf {F}(\alpha )$
. By Lemma 3.4,
![]() $\mathsf {A}(\alpha )_x^0$
is amenable for every
$\mathsf {A}(\alpha )_x^0$
is amenable for every
![]() $x\in X$
.
$x\in X$
.
Fix a clopen nonempty set U properly contained in X. Since, for any
![]() $x\in U^{\mathrm {c}}$
, we have
$x\in U^{\mathrm {c}}$
, we have
![]() $\Lambda :=\operatorname {St}_{\mathsf {A}(\alpha )}(U^{\mathsf {c}})\leq \mathsf {A}(\alpha )_x^0$
, it follows that
$\Lambda :=\operatorname {St}_{\mathsf {A}(\alpha )}(U^{\mathsf {c}})\leq \mathsf {A}(\alpha )_x^0$
, it follows that
![]() $\Lambda $
is amenable.
$\Lambda $
is amenable.
Let
![]() $\mu \in \mathcal {P}_\Lambda (U)$
, and we claim that
$\mu \in \mathcal {P}_\Lambda (U)$
, and we claim that
![]() $\mu \in \mathcal {P}_{\Gamma} (U)$
. By regularity, it suffices to show that, for any
$\mu \in \mathcal {P}_{\Gamma} (U)$
. By regularity, it suffices to show that, for any
![]() $K\subset U$
compact and
$K\subset U$
compact and
![]() $g\in \Gamma $
such that
$g\in \Gamma $
such that
![]() $g(K)\subset U$
, it holds that
$g(K)\subset U$
, it holds that
![]() $\mu (gK)=gK$
. By Lemma 3.3, there are
$\mu (gK)=gK$
. By Lemma 3.3, there are
![]() $h_1,\dots ,h_n\in \Lambda $
and a partition
$h_1,\dots ,h_n\in \Lambda $
and a partition
![]() $K=\bigsqcup _{i=1}^n K_i$
into compact sets such that
$K=\bigsqcup _{i=1}^n K_i$
into compact sets such that
![]() $g|_{K_i}=h_i|_{K_i}$
for
$g|_{K_i}=h_i|_{K_i}$
for
![]() $1\leq i\leq n$
. Therefore,
$1\leq i\leq n$
. Therefore,
 $$ \begin{align*}\mu(gK)=\sum_{i=1}^n\mu(gK_i)=\sum_{i=1}^n\mu(h_iK_i)=\sum_{i=1}^n\mu(K_i)=\mu(K)\end{align*} $$
$$ \begin{align*}\mu(gK)=\sum_{i=1}^n\mu(gK_i)=\sum_{i=1}^n\mu(h_iK_i)=\sum_{i=1}^n\mu(K_i)=\mu(K)\end{align*} $$
and
![]() $\mu \in \mathcal {P}_{\Gamma} (U)$
.
$\mu \in \mathcal {P}_{\Gamma} (U)$
.
We conclude from Proposition 3.1 that there is
![]() $\nu \in \mathcal {P}_{\Gamma} (X)=\mathcal {P}_{\mathsf {F}(\alpha )}(X)$
. Furthermore, by minimality of the action,
$\nu \in \mathcal {P}_{\Gamma} (X)=\mathcal {P}_{\mathsf {F}(\alpha )}(X)$
. Furthermore, by minimality of the action,
![]() $\nu $
has full support. Let
$\nu $
has full support. Let
![]() $\rho :=(\operatorname {Stab}_{\mathsf {A}(\alpha )}^0)_*\nu $
.
$\rho :=(\operatorname {Stab}_{\mathsf {A}(\alpha )}^0)_*\nu $
.
Given
![]() $g\in \Lambda \setminus \{e\}$
, we have
$g\in \Lambda \setminus \{e\}$
, we have
![]() $\rho (\{K\in \operatorname {Sub}(\mathsf {A}(\alpha )):g\in K\})\geq \nu (U^{\mathsf {c}})>0$
. Hence,
$\rho (\{K\in \operatorname {Sub}(\mathsf {A}(\alpha )):g\in K\})\geq \nu (U^{\mathsf {c}})>0$
. Hence,
![]() $\rho $
is a nontrivial amenable IRS on
$\rho $
is a nontrivial amenable IRS on
![]() $\mathsf {A}(\alpha )$
. Since
$\mathsf {A}(\alpha )$
. Since
![]() $\mathsf {A}(\alpha )$
is simple, this implies that
$\mathsf {A}(\alpha )$
is simple, this implies that
![]() $\mathsf {A}(\alpha )$
is amenable.
$\mathsf {A}(\alpha )$
is amenable.
The following is an immediate consequence of Theorem 3.5.
Corollary 3.6 Let
![]() $\alpha $
be a minimal action of a countable group on the Cantor set. Then
$\alpha $
be a minimal action of a countable group on the Cantor set. Then
![]() $\mathsf {F}(\alpha )$
has the unique trace property if and only if it is
$\mathsf {F}(\alpha )$
has the unique trace property if and only if it is
![]() $C^*$
-simple. If
$C^*$
-simple. If
![]() $\mathsf {A}(\alpha )=\mathsf {F}(\alpha )'$
, then
$\mathsf {A}(\alpha )=\mathsf {F}(\alpha )'$
, then
![]() $\mathsf {F}(\alpha )$
is non-amenable if and only if it is
$\mathsf {F}(\alpha )$
is non-amenable if and only if it is
![]() $C^*$
-simple.
$C^*$
-simple.
Remark 3.7 If
![]() $\alpha $
is an action of a group on the noncompact Cantor set X, then the topological full group
$\alpha $
is an action of a group on the noncompact Cantor set X, then the topological full group
![]() $\mathsf {F}(\alpha )$
is the group of homeomorphisms on X which are locally given by
$\mathsf {F}(\alpha )$
is the group of homeomorphisms on X which are locally given by
![]() $\alpha $
and have compact support. Moreover,
$\alpha $
and have compact support. Moreover,
![]() $\mathsf {A}(\alpha )$
is defined by requiring that the domains of the partial homeomorphisms of the multisections to be compact-open (as in [Reference MatuiMB18, Definition 5.1]). By arguing as in [Reference MatuiMB18, Corollary 6.5], the same conclusion of Theorem 3.5 and Corollary 3.6 holds in the noncompact case.
$\mathsf {A}(\alpha )$
is defined by requiring that the domains of the partial homeomorphisms of the multisections to be compact-open (as in [Reference MatuiMB18, Definition 5.1]). By arguing as in [Reference MatuiMB18, Corollary 6.5], the same conclusion of Theorem 3.5 and Corollary 3.6 holds in the noncompact case.
Example 3.8 It follows from [Reference MatuiMat12, Lemma 6.3] and [Reference MatuiMat15, Theorem 4.7] that, given a free minimal action
![]() $\alpha $
of
$\alpha $
of
![]() $\mathbb {Z}^n$
on the Cantor set, it holds that
$\mathbb {Z}^n$
on the Cantor set, it holds that
![]() $\mathsf {F}(\alpha )'=\mathsf {A}(\alpha )$
. Hence, the example of non-amenable topological full group coming from a Cantor minimal
$\mathsf {F}(\alpha )'=\mathsf {A}(\alpha )$
. Hence, the example of non-amenable topological full group coming from a Cantor minimal
![]() $\mathbb {Z}^2$
-system in [Reference Elek and MonodEM13] is
$\mathbb {Z}^2$
-system in [Reference Elek and MonodEM13] is
![]() $C^*$
-simple.
$C^*$
-simple.
Acknowledgment
I am grateful to Eduard Ortega and Nicolás Matte Bon for helpful comments. I also thank the anonymous referee for suggestions which helped to improve the presentation of this work and for pointing out an incorrection in the original formulation of Proposition 3.1.