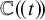The Ceresa class and tropical curves of hyperelliptic type

Abstract

We define a new algebraic invariant of a graph G called the Ceresa–Zharkov class and show that it is trivial if and only if G is of hyperelliptic type, equivalently, G does not have as a minor the complete graph on four vertices or the loop of three loops. After choosing edge lengths, this class specializes to an algebraic invariant of a tropical curve with underlying graph G that is closely related to the Ceresa cycle for an algebraic curve defined over $\mathbb {C}(\!(t)\!)$.

1 Introduction

Given a smooth genus $g\geq 2$ algebraic curve C together with a point $p \in C$ , there is a canonical null-homologous 1-cycle in its Jacobian $\operatorname {\mathrm {Jac}}(C)$ obtained by taking the difference of the images of C under the two Abel–Jacobi maps

$$ \begin{align*} C \hookrightarrow \operatorname{\mathrm{Jac}}(C) \hspace{10pt} x\mapsto [x] - [p] \hspace{10pt} \text{and} \hspace{10pt} x\mapsto [p] - [x]. \end{align*} $$

This is called the Ceresa cycle, and we denote it by $C - C^{-}$ . A landmark result of Ceresa in [6] is that this cycle, for a very general curve of genus $g\geq 3$ , is nontrivial in the Griffiths group of null-homologous cycles modulo algebraic equivalence. Nevertheless, it is always trivial for hyperelliptic curves, and it has long been conjectured that these are the only curves with trivial Ceresa cycle [13, Question 8.5], [4, Remark 1.2]. Although several recent results [1, 2, 4, 14] present nonhyperelliptic curves whose Ceresa cycles give rise to torsion classes in the Griffiths group, this problem remains open. The goal of this paper is to study hyperellipticity of tropical curves and graphs using cohomological invariants arising from the study of Ceresa triviality of algebraic curves defined over $\mathbb {C}(\!(t)\!)$ .

Degeneration techniques have long been used to study complex algebraic curves, both from the topological and algebraic/arithmetic perspectives. Tropical geometry provides a systematic framework for recording the combinatorial data of a stable degeneration as a tropical curve, that is, a graph with edge lengths and (possible) vertex weights. Topologically, stable degeneration is modeled by a family $\mathcal {C} \to D$ of Riemann surfaces over a small complex disc that is holomorphic over $D\setminus x$ and the fiber over x is a stable curve. Restricting to an infinitesimal neighborhood of x, we obtain a smooth algebraic curve C over $\mathbb {C}(\!(t)\!)$ that has stable reduction. The tropical curve corresponding to this degeneration is the (vertex-weighted) dual graph of the special fiber and its edge lengths record the speeds to which the nodes in the special fiber are formed.

In [10], the authors define a Ceresa class in the topological and tropical contexts that agrees with the $\ell $ -adic Ceresa class—the image of the Ceresa cycle of a curve defined over $\mathbb {C}(\!(t)\!)$ under the $\ell $ -adic Abel-Jacobi map—after applying a suitable comparison morphism. In this paper, we define the Ceresa–Zharkov class $\mathbf {w}(\Gamma )$ of a tropical curve $\Gamma $ ; this is a particular homomorphic image of the tropical Ceresa class, see §4 for the precise formulation. Notably, nontriviality of the Ceresa–Zharkov class implies nontriviality of the tropical Ceresa class.

In an effort to emulate the notion of generic real edge lengths, we define a graph-theoretic Ceresa–Zharkov class $\mathbf {w}_{\tau }(G)$ (depending on a hyperelliptic quasi-involution $\tau $ of the underlying genus-g surface $\Sigma _g$ , see §2.4), which lives in a module with coefficients in a polynomial ring whose variables correspond to the edges of G. Given a tropical curve $\Gamma $ with underlying graph G, (a representative of) the class $\mathbf {w}(\Gamma )$ is obtained by evaluating $\mathbf {w}_{\tau }(G)$ at the edge lengths of $\Gamma $ . We define what it means for $\mathbf {w}_{\tau }(G)$ to be trivial—whence we call G Ceresa–Zharkov trivial—so that triviality of $\mathbf {w}_{\tau }(G)$ implies triviality of $\mathbf {w}(\Gamma )$ for any tropical curve with underlying graph G. However, nontriviality of $\mathbf {w}_{\tau }(G)$ does not imply nontriviality of $\mathbf {w}(\Gamma )$ for a particular $\Gamma $ with underlying graph G, rather we view this as saying that $\mathbf {w}(\Gamma )$ is generically nontrivial.

Our main theorem completely determines when a graph is Ceresa–Zharkov trivial, and it is closely related to hyperellipticity as we now explain. According to the tropical Torelli theorem, it is possible for nonisomorphic tropical curves to have isomorphic Jacobians as principally polarized tropical abelian varieties. A tropical curve whose Jacobian is isomorphic to that of a hyperelliptic tropical curve is said to be of hyperelliptic type. These tropical curves are defined in [9], where it is shown that being of hyperelliptic type depends only on the underling graph, is preserved when taking connected minors and its forbidden minors are $K_4$ and $L_3$ , see Figure 1.

Theorem (Theorem 5.11).

A connected graph G of genus $g\geq 2$ is Ceresa–Zharkov trivial if and only if G is of hyperelliptic type, or equivalently, if and only if G has no $K_4$ or $L_3$ minor.

Figure 1 The graphs $K_4$ (left) and $L_3$ (right).

Our choice for the name “Ceresa–Zharkov” class comes from a related construction due to Zharkov in [17]. Independent of the tropical Ceresa class described above, Zharkov uses the tropical analogs of curves, Jacobians, the Abel-Jacobi map and algebraic equivalence, to define and study a purely tropical Ceresa cycle. The main result of his paper is that this “tropical Ceresa cycle” is not (tropically) algebraically equivalent to 0 for a generic tropical curve with a $K_4$ subgraph. As observed in [10, Remark 7.3], when the underlying graph of a tropical curve is $K_4$ , Zharkov’s Ceresa cycle and notion of triviality coincides with our Ceresa–Zharkov class. This suggests the following question.

Question. What is the precise relationship between the Ceresa–Zharkov class and the tropical Ceresa cycle defined by Zharkov in [17]?

Here is an outline of the paper. In §2, we recall the construction of the topological and tropical Ceresa class from [10], then define the Ceresa–Zharkov class for tropical curves. Next, in §3, we define and study the polynomial algebra in which the graph-theoretic Ceresa–Zharkov class is defined. We define the Ceresa–Zharkov class for graphs in §4, as well as study its elementary properties. Finally, we investigate the relationship between Ceresa–Zharkov triviality and being of hyperelliptic type in §5, where we prove the main theorem.

2 Background

2.1 Stable graphs, tropical curves and tropical Jacobians

Given a graph G, denote by $V(G)$ and $E(G)$ its set of vertices and edges, respectively. An edge of G is a loop if it is adjacent to a single vertex, and a pair of nonloop edges $(f,f')$ are parallel if they join the same pair of vertices. A (integral, unweighted) tropical curve $\Gamma $ consists of a finite connected graph G, possibly with loops and parallel edges, together with a positive integer-valued function $c: E(G) \to \mathbb {Z}$ on the edge set $E(G)$ . We view G as the underlying graph of $\Gamma $ and $c(e)$ as the length of the edge e. ¹ The genus of $\Gamma $ , written as $g(\Gamma )$ , is the first Betti number of G, that is,

$$ \begin{align*} g(\Gamma) = |E(G)| - |V(G)| + 1. \end{align*} $$

A tropical curve $\Gamma $ is said to be 2-connected if G has no cut-vertices; in particular, such a graph cannot have a loop or a bridge.

Let $\Gamma = (G,c)$ be a genus $g\geq 2$ tropical curve, and fix an orientation on G. The Jacobian of $\Gamma $ is the real g-dimensional torus

$$ \begin{align*} \operatorname{\mathrm{Jac}}(\Gamma) = H_1(G,\mathbb{R}) / H_1(G,\mathbb{Z}) \end{align*} $$

together with the positive definite symmetric quadratic form $Q_{\Gamma }$ on $H_1(G,\mathbb {R})$ given by

$$ \begin{align*} Q_{\Gamma}\left( \sum_{e\in E(G)} a_{e} \cdot e , \sum_{e\in E(G)} b_{e} \cdot e \right) = \sum_{e\in E(G)} a_e b_e \cdot c(e). \end{align*} $$

The valence of a vertex v is the number of half edges adjacent to it; in particular a loop edge contributes 2 to the valence. A connected graph is stable if every vertex has valence at least $3$ , and a tropical curve is stable if its underlying graph is stable. Two tropical curves are tropically equivalent if one can be obtained from the other by a sequence of the following moves:

• - adding or removing a 1-valent vertex and its incident edge, or

• - adding or removing a 2-valent vertex, preserving the underlying metric space.

Every tropical curve of genus $g\geq 2$ is tropically equivalent to a unique stable tropical curve.

A tropical curve is hyperelliptic if there is an involution $\sigma $ of $\Gamma $ such that the quotient $\Gamma /\sigma $ (in the sense of [8, § 2.2]) is a tree. A tropical curve is said to be of hyperelliptic type if its Jacobian is isomorphic to the Jacobian of a hyperelliptic tropical curve as a principally polarized tropical abelian variety. This notion is defined and studied in [9], where it is shown that $\Gamma $ is of hyperelliptic type if and only if its underlying graph has no $K_4$ or $L_3$ minor ([9, Theorem 1.1]); see Figure 1. Moreover, if $\Gamma $ is a 2-connected tropical curve of hyperelliptic type, then there is a hyperelliptic tropical curve $\Gamma '$ such that the underlying graph of $\Gamma $ is obtained from that of $\Gamma '$ by edge contractions.

2.2 Dual graphs and multitwists from tropical curves

We assume familiarity with surface topology and refer the reader to [12] for a comprehensive treatment. Given an orientable topological real surface S, possibly with boundary or punctures, denote by $\operatorname {\mathrm {Mod}}(S)$ its mapping class group. We write $\Sigma _g$ for a closed genus-g surface and $\Sigma _g^1$ a genus g surface with one boundary component. We always identify $\Sigma _g^1$ as the subsurface of $\Sigma _g$ obtained by removing a small open disc. Given a curve $\gamma $ on $\Sigma _g$ or $\Sigma _g^1$ , write $T_{\gamma }$ for the (left-handed) Dehn twist about $\gamma $ .

Let $\Lambda $ be a finite collection of pairwise disjoint isotopy classes of simple closed curves on $\Sigma _g$ . Its (unweighted) dual graph is the graph with

• - a vertex $v_S$ for every connected component S of $\Sigma _g\setminus \bigcup _{\ell \in \Lambda } \ell $ , and

• - an edge $e_{\ell }$ between $v_S$ and $v_{S'}$ for each $\ell $ in the boundary of S and $S'$ . The curve $\ell $ is said to be dual to $e_\ell $ .

Any connected genus-g graph is the dual graph of such a configuration. We are primarily interested in the case where $\Lambda $ is Lagrangian in the sense of [10], that is, each component S of $\Sigma _g\setminus \bigcup _{\ell \in \Lambda } \ell $ has genus $0$ .

Let $\Lambda _1$ and $\Lambda _2$ be two Lagrangian arrangements of curves on $\Sigma _g$ as above such that their dual graphs, $G_1$ and $G_2$ , respectively, are stable. Then $G_1$ is isomorphic to $G_2$ if and only if there is a mapping class of $\Sigma _g$ that takes $\Lambda _1$ to $\Lambda _2$ ; this follows from the well-known identification of the quotient of the curve complex of $\Sigma _g$ by $\operatorname {\mathrm {Mod}}(\Sigma _g)$ with the tropical moduli space of genus g tropical curves of total edge length 1; see [7, §1].

Given a genus-g tropical curve $\Gamma = (G,c)$ and $\Lambda $ an arrangement of curves on $\Sigma _g$ whose dual graph is G, define the multitwist

$$ \begin{align*} T_{\Gamma} = \prod_{e \in E(G)} T_{\ell_e}^{c(e)}. \end{align*} $$

(Recall that we only consider tropical curves with integer edge lengths.) By the previous paragraph and the fact that $\sigma T_{\ell }\sigma ^{-1} = T_{\sigma (\ell )}$ for any $\sigma \in \operatorname {\mathrm {Mod}}(\Sigma _g)$ , the mapping class $T_{\Gamma }$ is well defined up to conjugation in $\operatorname {\mathrm {Mod}}(\Sigma _g)$ . Furthermore, $T_{\Gamma } = T_{\Gamma '}$ where $\Gamma '$ is the unique stable tropical curve tropically equivalent to $\Gamma $ .

2.3 The Johnson homomorphism

Let $\mathcal {I}_g^1 \leq \operatorname {\mathrm {Mod}}(\Sigma _g^1)$ , resp. $\mathcal {I}_g \leq \operatorname {\mathrm {Mod}}(\Sigma _g)$ , denote the Torelli group. Set

$$ \begin{align*} H = H_1(\Sigma_g^1,\mathbb{Z}) \cong H_1(\Sigma_g,\mathbb{Z}), \hspace{10pt} \text{ and } \hspace{10pt} L=\wedge^3H. \end{align*} $$

The intersection product on H induces a $2$ -form $\omega \in \wedge ^2H$ , and taking the exterior product with $\omega $ yields an injection $H\hookrightarrow L$ . The Johnson homomorphism $J:\mathcal {I}_g^1 \to L$ , resp. $J:\mathcal {I}_g \to L/H$ , may be characterized in the following way. By [16, Theorem 2], the Torelli group is generated by separating twists (Dehn twists about separating curves) and bounding pair maps (a product $T_{\gamma }T_{\gamma '}^{-1}$ where $\gamma ,\gamma '$ form a separating pair). If $\gamma $ is a separating curve on $\Sigma _g^{1}$ , then $J(T_{\gamma }) = 0$ . Now, suppose that $\gamma ,\gamma '$ are a separating pair. The removal of $\gamma \cup \gamma '$ from $\Sigma _g^1$ separates $\Sigma _g^1$ into two surfaces S and $S'$ ; let S be the subsurface not containing the boundary component of $\Sigma _g^1$ . The form $\omega $ restricts to the intersection 2-form on S; denote this by $\omega _S$ . Then

$$ \begin{align*} J(T_{\gamma}T_{\gamma'}^{-1}) = \omega_{S} \wedge [\gamma], \end{align*} $$

where $[\gamma ]$ is oriented so that S appears on its right. The Johnson homomorphism on $\mathcal {I}_g$ is defined in a similar way, except that one can choose either surface S or $S'$ in the above formula; the two possible expressions are equivalent modulo H.

2.4 The tropical Ceresa class

Next, we briefly recall the definition of the Ceresa class of $\Gamma $ as was described in the Introduction; see [10] for more details. Fix a hyperelliptic quasi-involution $\tau $ , that is, a mapping class in $\operatorname {\mathrm {Mod}}(\Sigma _g)$ that acts as $-I$ on H. Consider the map

$$ \begin{align*} \nu_{\tau}: \operatorname{\mathrm{Mod}}(\Sigma_g) \to L/H \hspace{20pt} \gamma \mapsto J([\gamma,\tau]), \end{align*} $$

where $[\gamma ,\tau ] = \gamma \tau \gamma ^{-1}\tau ^{-1}$ is the commutator. This is a 1-cocycle, and its class in $H^1(\operatorname {\mathrm {Mod}}(\Sigma _g),L/H)$ is independent of the choice of $\tau $ [Ibid., Proposition 2.1]. The $\tau $ -Ceresa cocycle of $\Gamma $ , denoted by $\nu _{\tau }(\Gamma )$ , is the restriction of $\nu _{\tau }$ to $\langle T_{\Gamma }\rangle \cong \mathbb {Z}$ . Similarly, the Ceresa class of $\Gamma $ , denoted by $\nu (\Gamma )$ , is the class of $\nu _{\tau }(\Gamma )$ in $H^1(\mathbb {Z}, L/H)$ . Next, we will discuss several groups related to a filtration on L in which the Ceresa class lives and our computation will take place.

A subgroup Y of H is Lagrangian if $Y_{\mathbb {Q}}$ is a maximal isotropic subspace of the symplectic vector space $H_{\mathbb {Q}}$ (the symplectic form is induced by the intersection pairing on H) and $H/Y$ is torsion-free. Let $Y \leq H$ be the subgroup generated by the homology classes $\{[\ell ] \, : \, \ell \in \Lambda \}$ . This is a Lagrangian subgroup; see [Ibid., §6.1]. For values $q=0,1,2,3$ , define the following filtrations on L and $L/H$ :

$$ \begin{align*} F_q L = (\wedge^q Y) \wedge (\wedge^{3-q} H), \hspace{15pt} F_q (L/H) = \frac{F_{q}L + H}{H}, \hspace{15pt} \operatorname{\mathrm{gr}}_q^{F}(L/H) = \frac{F_q(L/H)}{F_{q-1}(L/H)}. \end{align*} $$

These filtrations and groups associated with them are discussed in detail in [Ibid., §5].

Since $H\subset F_1L$ and $F_3L \cap H = \{0\}$ , we have

(2.1) $$ \begin{align} F_0(L/H) = \frac{L}{H}, \hspace{10pt} F_1(L/H) = \frac{F_1L}{H}, \hspace{10pt} F_2(L/H) = \frac{F_2L+H}{H}, \hspace{10pt} F_3(L/H) \cong \frac{F_3L}{F_3L \cap H} \cong F_3L. \hspace{10pt} \end{align} $$

Denote by $\delta _{\Gamma }:H\to H$ the pushforward map on H induced by $T_{\Gamma }$ . Recall from [Ibid., Lemma 5.1] that $\delta _\Gamma (F_qL)\subset F_{q+1}L $ and $\delta _\Gamma $ preserves $\omega $ . Then the map $\delta _{\Gamma }-I$ restricts to the graded components

$$ \begin{align*} \delta_{\Gamma}-I : \operatorname{\mathrm{gr}}_{q}^F(L/H) \to \operatorname{\mathrm{gr}}_{q+1}^F(L/H). \end{align*} $$

Define groups

$$ \begin{align*} A(\delta_{\Gamma}) &= \operatorname{\mathrm{im}}( H^1(\langle \delta_{\Gamma} \rangle, F_2(L/H)) \to H^1(\langle \delta_{\Gamma} \rangle, L/H)) \cong \frac{F_2L + H}{(\delta_{\Gamma}-I)(F_1L) + H} \\ B(\delta_{\Gamma}) &= \operatorname{\mathrm{coker}}(\delta_{\Gamma} - I: \operatorname{\mathrm{gr}}_1^{F}(L/H) \to \operatorname{\mathrm{gr}}_2^{F}(L/H)) \cong \frac{F_2L + H}{(\delta_{\Gamma}-I)(F_1L) + F_3L + H} \\ C(\delta_{\Gamma}) &= \operatorname{\mathrm{coker}}\left( (\delta_{\Gamma} - I)^2: \operatorname{\mathrm{gr}}_1^{F}(L/H) \to \operatorname{\mathrm{gr}}_3^{F}(L/H)\right) \cong \frac{F_3L}{(\delta_{\Gamma}-I)^2(F_1L)}. \end{align*} $$

The isomorphisms for $A(\delta _{\Gamma })$ and $B(\delta _{\Gamma })$ follow from [Ibid., Proposition 5.4]. These three groups are finite since $(\delta _{\Gamma }-I): \operatorname {\mathrm {gr}}_{q}^F(L/H) \to \operatorname {\mathrm {gr}}_{q+1}^F(L/H)$ is rationally surjective for $q=1,2$ [Ibid.]. The identity map on $F_2L + H$ induces a homomorphism $A(\delta _{\Gamma }) \to B(\delta _{\Gamma })$ and we have an induced homomorphism $(\delta _{\Gamma } - I) : B(\delta _{\Gamma }) \to C(\delta _{\Gamma })$ . By [Ibid., Theorem 6.6], there is a hyperelliptic quasi-involution $\tau $ such that $\nu _{\tau }(\Gamma )$ lies in $F_2(L/H)$ . In practice, whenever we compute the tropical Ceresa class, we always use such a $\tau $ . In particular, the Ceresa class $\nu (\Gamma )$ lies in $A(\delta _{\Gamma }) \subset H^1(\langle \delta _\Gamma \rangle ,L/H)$ . This implies the main result of [Ibid.], that $\nu (\Gamma )$ is torsion. Now, we fix the following notation

$$ \begin{align*} \mathbf{v}(\Gamma) = \text{image of } \nu(\Gamma) \text{ in } B(\delta_{\Gamma}) \hspace{20pt} \mathbf{w}(\Gamma) = (\delta_{\Gamma}-I)(\mathbf{v}(\Gamma)) \in C(\delta_\Gamma). \end{align*} $$

If $\tau $ satisfies $\nu _\tau (\Gamma ) \in F_2(L/H)$ , by [Ibid., Proposition 6.7], the class $\mathbf {v}(\Gamma )$ has a particularly nice representative

(2.2) $$ \begin{align} \mathbf{v}_{\tau}(\Gamma) = \sum_{e\in E(G)} c(e)\, J([T_{\ell_e}, \tau]). \end{align} $$

The tropical curve $\Gamma $ is Ceresa trivial if $\nu (\Gamma )=0$ . If $\Gamma $ is Ceresa trivial, then $\mathbf {v}(\Gamma ) = 0$ . Given the above formula, $\mathbf {v}(\Gamma )$ is easier to compute than $\nu (\Gamma )$ , and therefore a good strategy to show that $\Gamma $ is Ceresa nontrivial is to show that $\mathbf {v}(\Gamma ) \neq 0$ in $B(\delta _{\Gamma })$ .

3 The action of a multitwist on some polynomial algebras

3.1 Multitwist on the homology of a surface

Throughout, given $\mathbb {Z}$ -modules A and R, we set $A_R = A\otimes _{\mathbb {Z}} R$ . Let $\Lambda $ be a collection of pairwise disjoint isotopy classes of simple closed curves on $\Sigma _{g}^{1}$ or $\Sigma _{g}$ . Define a polynomial ring

$$ \begin{align*} R[\Lambda] = \mathbb{Z}[x_{\ell} \, : \, \ell \in \Lambda] \end{align*} $$

which we denote by R when $\Lambda $ is clear from the context. Denote by $\langle a,b \rangle $ the intersection product of homology classes $a,b\in H = H_1(\Sigma _g,\mathbb {Z})$ . For any loop $\ell \in \Lambda $ , let $\delta _{\ell }: H_{R} \to H_{R}$ be the homomorphism defined on simple tensors by

(3.1) $$ \begin{align} \delta_{\ell}(h\otimes a) = h\otimes a + \langle h, [\ell] \rangle [\ell] \otimes x_{\ell} a. \end{align} $$

The map $\delta _{\ell }$ is an isomorphism with inverse

(3.2) $$ \begin{align} \delta_{\ell}^{-1}(h\otimes a) = h\otimes a - \langle h, [\ell] \rangle [\ell] \otimes x_{\ell} a. \end{align} $$

Because the loops in $\Lambda $ are pairwise disjoint, the $\delta _{\ell }$ ’s pairwise commute. The homomorphism $\delta _\ell $ is related to the pushforward $T_{\ell })_{*}:H\to H$ in the following way. Given a function $c:\Lambda \to \mathbb {Z}$ , let $R\to \mathbb {Z}$ be the evaluation ring homomorphism $x_{\ell }\mapsto c(\ell )$ . Then, under the identification $H \cong H\otimes _{\mathbb {Z}} R \otimes _{R} \mathbb {Z}$ , the map $\delta _{\ell } \otimes _{R} \operatorname {\mathrm {id}}_{\mathbb {Z}}$ is the pushforward of $T_{\ell }^{c(\ell )}$ on H by [12, Proposition 6.3].

Proposition 3.1. Given integers $\{a_{\ell } \, : \, \ell \in \Lambda \}$ , we have

$$ \begin{align*} \left(\prod_{\ell \in \Lambda} \delta_{\ell}^{a_{\ell}} \right) - I = \sum_{\ell\in \Lambda} a_{\ell} (\delta_{\ell}-I) \hspace{10pt} \text{ as maps } \hspace{10pt} H_R \to H_R. \end{align*} $$

Proof. It suffices to show

$$ \begin{align*} &\delta_{\ell}\delta_{\ell'} - I = (\delta_{\ell} - I) + (\delta_{\ell'} - I), \text{ and } \\ &\delta_{\ell}^{-1} - I = -(\delta_{\ell}-I). \end{align*} $$

The second formula follows readily from formulas (3.1) and (3.2). For the first formula, we have

$$ \begin{align*} (\delta_{\ell}\delta_{\ell'}-I)(h\otimes a) &= \delta_{\ell}(h \otimes a + \langle h, [\ell'] \rangle [\ell'] \otimes x_{\ell'} a)-h\otimes a \\ &= (\delta_{\ell}-I)(h\otimes a) + \langle h, [\ell'] \rangle \delta_{\ell}( [\ell'] \otimes x_{\ell'} a) \\ &= (\delta_{\ell}-I)(h\otimes a) + \langle h, [\ell'] \rangle ([\ell'] \otimes x_{\ell'} a + \langle [\ell'], [\ell] \rangle [\ell] \otimes x_{\ell}x_{\ell'} a) \\ &= (\delta_{\ell}-I)(h\otimes a) + \langle h, [\ell'] \rangle[\ell']\otimes x_{\ell'} a \\ &=(\delta_{\ell} - I)(h\otimes a) + (\delta_{\ell'} - I)(h\otimes a).\\[-34pt] \end{align*} $$

Next, define $\mathcal {B}=\langle \delta _{\ell } \, :\, \ell \in \Lambda \rangle $ , which is a free abelian subgroup of $\operatorname {\mathrm {Aut}}(H_R)$ whose rank is equal to the number of nonseparating loops in $\Lambda $ . Recall that $Y=\operatorname {\mathrm {span}}_{\mathbb {Z}}\{[\ell ] \, : \, \ell \in \Lambda \}$ , which is a Lagrangian subspace of H. The following is a straight-forward consequence of Equation (3.1) and Proposition 3.1.

Proposition 3.2. For any $f\in \mathcal {B}$ , we have

$$ \begin{align*} \mathrm{(1)} \;\; (f-I)(H_R) \subset Y_R, \hspace{20pt} \mathrm{(2)} \;\; (f-I)(Y_R) = 0, \hspace{20pt} \mathrm{(3)} \;\; (f-I)^2(H_R) = 0. \end{align*} $$

Denote by $\delta _{\Lambda }:H_R \to H_R$ the map

$$ \begin{align*} \delta_{\Lambda} = \prod_{\ell \in \Lambda} \delta_{\ell}. \end{align*} $$

By Proposition 3.1, as a map $H_R\to H_R$ , we have

$$ \begin{align*} \delta_{\Lambda}-I = \sum_{\ell \in \Lambda} (\delta_{\ell}-I). \end{align*} $$

3.2 The action of $\delta _{\Lambda }$ on $L_R$

The third exterior power of $\delta _{\Lambda }$ is a R-module homomorphism $\wedge ^3(H_R) \to \wedge ^3(H_R)$ . However, the natural R-module homomorphism

$$ \begin{align*} \wedge^3(H_R) \to L_R \hspace{20pt} (h_1\otimes f_1) \wedge (h_2\otimes f_2) \wedge (h_3\otimes f_3) \mapsto (h_1\wedge h_2 \wedge h_3) \otimes (f_1f_2f_3). \end{align*} $$

is an isomorphism; thus we may view the third exterior power of $\delta _{\Lambda }$ as an R-module endomorphism of $L_R$ which we still denote by $\delta _{\Lambda }$ . Next, we show that $\delta _{\Lambda }$ is an endomorphism of $L_R/H_R$ , but we need the following more general setup.

Let $\iota : S\hookrightarrow \Sigma _g$ be a subsurface (possibly with boundary) of $\Sigma _g$ . The homology of S splits as $H_{1}(S,\mathbb {Z}) \cong V \oplus W$ , where V is the subgroup of H generated by the boundary curves of S and W is a symplectic subspace of H whose symplectic form, which we denote by $\omega _S \in \wedge ^2W$ , is obtained by restricting the intersection of $\Sigma _g$ to S. Let $\mathcal {B}_S$ be the subgroup of $\mathcal {B}$ generated by the $\delta _{\ell }$ such that $\ell $ is isotopic to a curve in S.

Proposition 3.3. If $f\in \mathcal {B}_S$ , then

1. 1. $f(\omega _S) \equiv \omega _S \mod (V \wedge W)_R$ ;

2. 2. $(f-I)(h\wedge \omega _S) = (f-I)(h) \wedge \omega _S + f(h) \wedge \eta $ for some $\ \eta \in (V\wedge W)_R$ .

Remark 3.4. As a consequence, if $S=\Sigma _g$ and $f\in \mathcal {B}$ , then $(f-I)$ , as an endomorphism $L_R\to L_R$ , takes $H_R$ to $H_R$ (as an R-submodule of $L_R$ ). In particular, $\delta _\Lambda -I$ may be regarded as an R-module endomorphism of $L_R/H_R$ .

Proof of Proposition 3.3.

For (1), it suffices to show that

(3.3) $$ \begin{align} \delta_{\ell}(\omega_{S}) \equiv \omega_S\quad \mod (V\wedge W)_{R}. \end{align} $$

Choose a symplectic basis $\alpha _1,\ldots ,\alpha _g$ , $\beta _1,\ldots ,\beta _g$ of H such that $\alpha _1,\ldots ,\alpha _h,\beta _1,\ldots ,\beta _h$ is a symplectic basis of W. This means that

$$ \begin{align*} \omega_S = \sum_{i=1}^{h} \alpha_i \wedge \beta_i. \end{align*} $$

Write $[\ell ] = \mu + \lambda $ , where $\mu \in V$ and $\lambda \in W$ . We have

$$ \begin{align*} \lambda = \sum_{i=1}^h \left( - \langle \beta_i, [\ell] \rangle \alpha_i + \langle \alpha_i, [\ell] \rangle \beta_i \right). \end{align*} $$

We compute

$$ \begin{align*} \delta_{\ell}(\omega_S) &= \sum_{i=1}^{h} (\alpha_i + \langle \alpha_i, [\ell] \rangle [\ell] \otimes x_{\ell} ) \wedge (\beta_i + \langle \beta_i, [\ell] \rangle [\ell] \otimes x_{\ell} ) \\ &= \omega_S + \sum_{i=1}^{h}\left( \langle \beta_i, [\ell] \rangle \alpha_i\wedge [\ell] + \langle \alpha_i, [\ell] \rangle [\ell] \wedge \beta_i \right) \otimes x_{\ell} \\ &= \omega_S + [\ell] \wedge \sum_{i=1}^{h} \left( -\langle \beta_i, [\ell] \rangle \alpha_i + \langle \alpha_i, [\ell] \rangle \beta_i \right) \otimes x_{\ell} \\ & = \omega_S + \mu \wedge \lambda \otimes x_{\ell}, \end{align*} $$

from which formula (3.3) follows. For (2), we have

$$ \begin{align*} (f-I)(h\wedge \omega_{S}) = f(h) \wedge f(\omega_{S}) - h\wedge \omega_{S} = (f-I)(h) \wedge \omega_{S} + f(h) \wedge \eta \end{align*} $$

for some $\eta \in (V\wedge W)_R$ .

Similar to the integral setup in Section 2.4, we define a filtration on $ L_R$ and $L_R/H_R$ :

$$ \begin{align*} F_q L_R := (F_qL)_R \cong (\wedge^qY_R)\wedge (\wedge^{3-q}H_R) \hspace{20pt} \text{ and } \hspace{20pt} F_q (L_R/H_R) := (F_q(L/H))_R \end{align*} $$

and denote by $\operatorname {\mathrm {gr}}_{q}^{F}(L_R/H_R)$ the graded piece

$$ \begin{align*} \operatorname{\mathrm{gr}}_{q}^{F}(L_R/H_R) := \frac{F_{q}(L_R/H_R)}{F_{q+1}(L_R/H_R)}. \end{align*} $$

Proposition 3.5. Given $f\in \mathcal {B}$ and $h_1,h_2,h_3\in H$ , we have that

$$ \begin{align*} (f-I)(h_1\wedge h_2 \wedge h_3) & \; = \; (f - I)h_1 \wedge h_2 \wedge h_3 + h_1 \wedge (f-I) h_2 \wedge h_3 + h_1 \wedge h_2 \wedge (f - I) h_3 \\ &\quad + (f - I)h_1 \wedge (f - I) h_2 \wedge h_3 + (f - I) h_1 \wedge h_2 \wedge (f - I) h_3\\ &\quad + h_1 \wedge (f - I) h_2 \wedge (f - I) h_3 \\ &\quad + (f - I)h_1 \wedge (f - I) h_2 \wedge (f - I) h_3. \end{align*} $$

In particular, we have that $(f-I)(F_{q}(L_R)) \subset F_{q+1}(L_R)$ .

As a consequence of this proposition, the map $\delta _{\Lambda } -I$ on $L_R/H_R$ takes $F_{q}(L_R/H_R)$ to $F_{q+1}(L_R/H_R)$ and hence induces a map on graded components:

$$ \begin{align*} \delta_{\Lambda}-I:\operatorname{\mathrm{gr}}_{q}^{F}(L_R/H_R) \to \operatorname{\mathrm{gr}}_{q+1}^{F}(L_R/H_R). \end{align*} $$

Proposition 3.6. As maps $\operatorname {\mathrm {gr}}_{q}^{F}(L_R/H_R) \to \operatorname {\mathrm {gr}}_{q+1}^{F}(L_R/H_R)$ , we have

$$ \begin{align*} (\delta_{\Lambda}-I)(\alpha) = \sum_{\ell\in \Lambda} (\delta_{\ell}-I)(\alpha). \end{align*} $$

Proof. By Proposition 3.5, we have that

$$ \begin{align*} (\delta_{\Lambda}-I)(h_1\wedge h_2 \wedge h_3) \equiv (\delta_{\Lambda}-I)h_1 \wedge h_2 \wedge h_3 + h_1 \wedge (\delta_{\Lambda}-I) h_2 \wedge h_3 + h_1 \wedge h_2 \wedge (\delta_{\Lambda}-I) h_3\quad \mod F_{q}(L_R/H_R). \end{align*} $$

Now, apply Proposition 3.1.

In summary, the maps $\delta _{\Lambda }-I$ and $\sum _{\ell \in \Lambda }(\delta _{\ell }-I)$ coincide when viewed as maps on $H_R$ or the graded components $\operatorname {\mathrm {gr}}_{q}^F(L_R/H_R)$ but are different when viewed on the whole $L_R/H_R$ . This difference is important in the proof of Proposition 4.2.

3.3 Configuration of loops from graphs

Let G be a connected genus-g stable graph and $\Lambda = \{\ell _e \, : \, e\in E(G)\}$ a collection of pairwise disjoint isotopy classes of simple closed curves on $\Sigma _g$ whose dual graph is G, as in §2.2. The polynomial ring

$$ \begin{align*} R[G] = \mathbb{Z}[x_e \, : \, e\in E(G)] \end{align*} $$

is identified with $R[\Lambda ]$ by the relabeling $x_{e} = x_{\ell _e}$ . We simply write R when the graph G is clear from context. Define the endomorphism $\delta _{G}$ on $H_{R}$ (respectively, $L_R$ and $L_{R}/H_{R}$ ) by $\delta _{G} = \delta _{\Lambda }$ . The map $\delta _G$ is closely related to the polarization of the Jacobian of a tropical curve, as we see in the following construction.

Define the symmetric quadratic form $Q_{G}$ on $H_1(G,\mathbb {Z})\otimes R$

$$ \begin{align*} Q_{G}\left( \sum_{e\in E(G)} a_{e} \cdot e , \sum_{e\in E(G)} b_{e} \cdot e \right) = \sum_{e\in E(G)} a_e b_e \otimes x_{e}. \end{align*} $$

If $\Gamma = (G,c)$ is a tropical curve, then $Q_{\Gamma }$ is obtained from $Q_{G}$ by the substitution $x_e \mapsto c(e)$ . Let us give an explicit description of $Q_{G}$ . Enumerate the edges of G by $e_1,\ldots ,e_n$ so that $e_{g+1},\ldots ,e_{n}$ are the edges of a spanning tree T. Fix an arbitrary orientation on G. For $j=1,\ldots , g$ , the graph $T\cup \{e_j\}$ contains a unique cycle $\gamma _j$ ; orient $\gamma _j$ in the direction of $e_j$ . The cycles $\gamma _1,\ldots ,\gamma _g$ form a basis of $H_1(G,\mathbb {Z})$ . Let $x_i = x_{e_i}$ . The $(i,j)$ –entry of the matrix of $Q_{G}$ with respect to this basis is a linear form in the $x_k$ ’s: $x_k$ appears with coefficient $1$ if $\gamma _i$ and $\gamma _j$ traverse $e_k$ in the same direction, $-1$ if they traverse in the opposite direction and $0$ if they do not meet at $e_k$ . For details and examples, see [5, §4].

Now, we give the promised comparison to $\delta _{G}$ . Let $\ell _{k} = \ell _{e_k}$ . Orient $\ell _k$ so that the subsurface corresponding to the target of $e_k$ lies to the left of $\ell _k$ . Viewing G as a one-dimensional CW-complex, there is an embedding $\iota : G\hookrightarrow \Sigma _g$ so that $\iota (e_j) \cap \ell _j$ is a point. For $j=1,\ldots ,g$ , denote by $\alpha _j$ and $\beta _j$ the homology classes $-[\iota (\gamma _j)]$ and $[\ell _j]$ , respectively; the orientations are chosen so that the signed intersection number of $\alpha _i$ with $\beta _i$ is 1. Then $\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$ is a symplectic basis for H.

Since the $\ell \in \Lambda $ are pairwise nonintersecting, we have that $\delta _{G}(\beta _j) = \beta _j$ . For the $\alpha _j$ ’s, we have

$$ \begin{align*} \delta_{G}(\alpha_j) = \alpha_{j} + \sum_{k=1}^{n} \langle \alpha_j, [\ell_{k}] \rangle [\ell_{k}] \otimes x_{k}. \end{align*} $$

The $\beta _{i}$ –coefficient of $\delta _{G}(\alpha _j)$ is

$$ \begin{align*} \langle \alpha_i, \delta_{G}(\alpha_j) \rangle = \sum_{k=1}^{n} \langle \alpha_{i}, [\ell_k] \rangle \langle \alpha_j, [\ell_k] \rangle \otimes x_{k}. \end{align*} $$

This is a linear form in $x_{k}$ : $x_{k}$ appears with coefficient 1 if $\alpha _{i}$ and $\alpha _{j}$ have the same intersection pairing with $\ell _{k}$ , $-1$ if they have opposite intersection pairing and 0 otherwise. Thus, the matrix of $\delta _G:H_R\to H_R$ with respect to the ordered basis $\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$ is given by

(3.4) $$ \begin{align} \delta_{G} = \begin{pmatrix} I & 0 \\ Q_{G} & I \end{pmatrix}. \end{align} $$

This allows us to view $Q_G$ as a map $Y^{\perp }_{R} \to Y_R$ , where

$$ \begin{align*} Y=\operatorname{\mathrm{span}}_{\mathbb{Z}}\{[\ell] \, : \, \ell \in \Lambda\} = \operatorname{\mathrm{span}}_{\mathbb{Z}}\{\beta_1,\ldots,\beta_g\}, \hspace{10pt} \text{ and } \hspace{10pt} Y^{\perp}=\operatorname{\mathrm{span}}_{\mathbb{Z}}\{\alpha_1,\ldots,\alpha_g\}. \end{align*} $$

Example 3.7. Consider $G=K_4$ , the complete graph on $4$ vertices, with the orientation as in Figure 2. To its right is an arrangement of curves on $\Sigma _3$ whose dual graph is $K_4$ . Observe that each $\ell _i$ is oriented so that the subsurface corresponding to the target of $e_i$ lies to the left of $\ell _i$ . Also, observe that $\alpha _i$ is oriented so that the signed intersection product of $\alpha _i$ and $\beta _i:=[\ell _i]$ is 1. The matrix $Q_G$ is

(3.5) $$ \begin{align} Q_{G} = \begin{pmatrix} x_1 + x_5 + x_6 & -x_6 & -x_5 \\ -x_6 & x_2+x_4+x_6 & -x_4 \\ -x_5 & -x_4 & x_3+x_4+x_5 \end{pmatrix}. \end{align} $$

Figure 2 An arrangement of curves on $\Sigma _3$ with dual graph $K_4$ .

Combining the above connection between $\delta _{G}$ and $Q_{G}$ with Proposition 3.5, we deduce the following identities:

(3.6) $$ \begin{align} (\delta_G-I)(\alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} ) &= Q_G(\alpha_i) \wedge \alpha_j \wedge \beta_k + \alpha_i \wedge Q_G(\alpha_j) \wedge \beta_k + Q_G(\alpha_i) \wedge Q_G(\alpha_j) \wedge \beta_k,\notag \\ (\delta_G-I)(\alpha_{i} \wedge \beta_{j} \wedge \beta_{k} ) &= Q_G(\alpha_i) \wedge \beta_j \wedge \beta_k, \\ (\delta_G-I)^2(\alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} ) &= 2\, Q_G(\alpha_i) \wedge Q_G(\alpha_j) \wedge \beta_k. \notag \end{align} $$

Remark 3.8. Denote by $R_d \subset R$ the subspace of homogeneous degree d-forms in R. Because the entries of $Q_{G}$ are linear forms in R, the map $\delta _G-I$ may be viewed as a map $H_{R_d} \to H_{R_{d+1}}$ .

4 The Ceresa–Zharkov class

4.1 Ceresa–Zharkov triviality

Recall that we view $\Sigma _g^1$ as a subsurface of $\Sigma _g$ obtained by removing a small open disc D from $\Sigma _g$ . Recall that a hyperelliptic quasi-involution is an element of $\operatorname {\mathrm {Mod}}(\Sigma _g^1)$ or $\operatorname {\mathrm {Mod}}(\Sigma _g)$ whose action on $H = H_1(\Sigma _g^1,\mathbb {Z}) \cong H_{1}(\Sigma _g,\mathbb {Z})$ is $-I$ . Let $\tau '$ be a hyperelliptic quasi-involution on $\Sigma _g^{1}$ and $\tau $ its image under the natural map $\operatorname {\mathrm {Mod}}(\Sigma _g^1) \to \operatorname {\mathrm {Mod}}(\Sigma _g)$ . Let $\Lambda '$ be a finite collection of pairwise disjoint isotopy classes of simple closed curves on $\Sigma _g^1$ and $\Lambda $ the image of this collection under the inclusion $\Sigma _g^1\hookrightarrow \Sigma _g$ ; note that any finite collection of simple closed curves can be isotoped away from the disc D, so $\Lambda $ may represent any finite collection of isotopy classes of simple closed curves on $\Sigma _g$ .

The $\tau '$ -Ceresa cocycle of $\Lambda '$ , respectively the $\tau $ -Ceresa cocycle of $\Lambda $ , is defined as

$$ \begin{align*} \boldsymbol \mu_{\tau'}(\Lambda') = \sum_{\ell \in \Lambda'} J([T_{\ell},\tau']) \otimes x_{\ell} \in L_R, \hspace{5pt} \text{respectively,} \hspace{5pt} \mathbf{v}_{\tau}(\Lambda) = \sum_{\ell \in \Lambda} J([T_{\ell},\tau]) \otimes x_{\ell} \in L_R/H_R, \end{align*} $$

where J is the Johnson homomorphism; see §2.3. Define the $\tau $ -Ceresa–Zharkov cocycle as

$$ \begin{align*} \mathbf{w}_{\tau}(\Lambda) = (\delta_{\Lambda}-I)(\mathbf{v}_{\tau}(\Lambda)). \end{align*} $$

When G is a genus-g graph, we write $\mathbf {v}_{\tau }(G) = \mathbf {v}_{\tau }(\Lambda )$ and $\mathbf {w}_{\tau }(G) = \mathbf {w}_{\tau }(\Lambda )$ , where $\Lambda $ is an arrangement of curves whose dual graph is G. We say that G is Ceresa–Zharkov trivial if there is a $\tau $ such that $\mathbf {w}_{\tau }(G) = 0$ . In Lemma 4.3, we show that this notion is a well-defined property of the graph G. While our primary interest is in $\mathbf {w}_{\tau }(G)$ , we occasionally need the class $\boldsymbol \mu _{\tau '}(\Lambda ')$ in §5. Compare these to the definitions of the Ceresa–Zharkov class and Ceresa–Zharkov triviality of a tropical curve defined in §2.4. In practice, when we compute the tropical Ceresa class for a tropical curve $\Gamma $ , we use a hyperelliptic involution $\tau $ such that $\nu _{\tau }(\Gamma )$ lies in $F_2(L/H)$ as in §2.4. We do something similar in the graph-theoretic case. As before, $R_d\subset R$ denotes the linear subspace of degree d forms.

Proposition 4.1. There exists a hyperelliptic quasi-involution $\tau '$ of $\Sigma _g^1$ such that

$$ \begin{align*} \boldsymbol \mu_{\tau'}(\Lambda') \in F_2L \otimes R_1. \end{align*} $$

In particular, $\mathbf {v}_{\tau }(G)$ lies in $F_2(L/H) \otimes R_1$ and $\mathbf {w}_{\tau }(G)$ lies in $F_3L \otimes R_2$ , where $\tau $ is the image of $\tau '$ under $\operatorname {\mathrm {Mod}}(\Sigma _g^1) \to \operatorname {\mathrm {Mod}}(\Sigma _g)$ .

Proof. By [10, Theorem 6.6], there is a hyperelliptic quasi-involution $\tau '$ such that each $J([T_{\ell },\tau '])$ lies in $F_2L$ . The proposition now follows from Remark 3.8.

Here is a characterization for Ceresa–Zharkov triviality when we use such a $\tau $ .

Proposition 4.2. If G is Ceresa–Zharkov trivial and $\mathbf {v}_{\tau }(G) \in F_2(L/H) \otimes R_1$ , then

(4.1) $$ \begin{align} \mathbf{w}_{\tau}(G) \in (\delta_{G}-I)^2(F_1(L/H)). \end{align} $$

Conversely, if there exists a $\tau $ such that Equation (4.1) holds, then G is Ceresa–Zharkov trivial.

To prove this proposition, we first derive a characterization of Ceresa–Zharkov triviality that works for any $\tau $ but is more cumbersome to state due to the fact that the endomorphism $\delta _G-I$ of $L_R/H_R$ does not split as the sum $\sum _{e\in E(G)}(\delta _e-I)$ as discussed in §3.2.

Denote by $\psi _G:L_R/H_R \to L_R/H_R$ the composition

$$ \begin{align*} \psi_G = (\delta_G-I) \circ \left(\sum_{e\in E(G) }(\delta_e-1) \right). \end{align*} $$

Lemma 4.3. The following are equivalent.

1. 1. The graph G is Ceresa–Zharkov trivial;

2. 2. for every hyperelliptic quasi-involution $\tau $ , we have $\mathbf {w}_{\tau }(G) \in \psi _G(L/H)$ ;

3. 3. there is a hyperelliptic quasi-involution $\tau $ such that $\mathbf {w}_{\tau }(G) \in \psi _G(L/H)$ .

Proof. Given hyperelliptic quasi-involutions $\tau , \tilde {\tau }$ , we have

$$ \begin{align*} (J([T_{\ell_e},\tilde{\tau}]) - J([T_{\ell_e},\tau])) \otimes x_e = (T_{\ell_e}-I)_*(J(\tilde{\tau}^{-1} \tau)) \otimes x_e = (\delta_e-I)(J(\tilde{\tau}^{-1} \tau)) \end{align*} $$

and therefore

(4.2) $$ \begin{align} \mathbf{v}_{\tilde{\tau}}(G) - \mathbf{v}_{\tau}(G) = \sum_{e\in E(G)} (\delta_{e}-I)(J(\tilde{\tau}^{-1} \tau)). \end{align} $$

Suppose G is Ceresa–Zharkov trivial, say $\mathbf {w}_{\tau }(G)= 0$ for some $\tau $ . Applying $\delta _G-I$ to formula (4.2), we see that (1) $ \Rightarrow $ (2). The implication (2) $\Rightarrow $ (3) is trivial. Now, suppose (3) is true, say $\mathbf {w}_{\tau }(G) = \psi _G(\mathbf {u})$ for some $\mathbf {u} \in L/H$ . By surjectivity of the Johnson homomorphism, there is a $t\in \mathcal {I}_g$ such that $J(t)=\mathbf {u}$ . The function $\tilde {\tau } = \tau t$ is a hyperelliptic quasi-involution, and by the above equation, we have

$$ \begin{align*} \mathbf{v}_{\tilde{\tau}}(G) = \mathbf{v}_{\tau}(G) - \sum_{e\in E(G)} (\delta_{e}-I)(\mathbf{u}). \end{align*} $$

Applying $\delta _G-I$ , we get

$$ \begin{align*} \mathbf{w}_{\tilde{\tau}}(G) = \mathbf{w}_{\tau}(G) - \psi_G(\mathbf{u}) = 0, \end{align*} $$

as required.

Proof of Proposition 4.2.

Let $\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$ be the symplectic basis of H from §3.3. We first record the image of the simple wedges under the map $\psi _G$ using Proposition 3.5:

$$ \begin{align*} \psi_G(\alpha_{i} \wedge \alpha_{j} \wedge \alpha_{k} ) &= 2(Q_{G} \alpha_i \wedge Q_{G} \alpha_j \wedge \alpha_k + Q_{G} \alpha_i \wedge \alpha_j \wedge Q_{G} \alpha_k + \alpha_i \wedge Q_{G} \alpha_j \wedge Q_{G}\alpha_k) \\ &\quad +3 \, Q_G \alpha_i \wedge Q_{G} \alpha_j \wedge Q_{G} \alpha_k \\ \psi_G(\alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} ) &= 2\, Q_{G} \alpha_i \wedge Q_{G} \alpha_j \wedge \beta_k \\ \psi_G(\alpha_{i} \wedge \beta_{j} \wedge \beta_{k} ) &= \psi_G(\beta_{i} \wedge \beta_{j} \wedge \beta_{k} ) = 0. \end{align*} $$

By this computation, formula (3.6) and the fact that $(\delta _G-I)^2|_{F_2(L/H)} = 0$ , we deduce that $ (\delta _{G}-I)^2|_{F_1(L/H)} = \psi _{G} |_{F_1(L/H)}$ . Therefore,

(4.3) $$ \begin{align} (\delta_{G}-I)^2(F_1(L/H)) = \psi_G(F_1(L/H)) = \psi_G(L/H) \cap (F_3(L/H) \otimes R_2). \end{align} $$

Suppose G is Ceresa–Zharkov trivial and that $\mathbf {v}_{\tau }(G) \in F_2(L/H) \otimes R_1$ . Then the class $\mathbf {w}_{\tau }(G)$ lies in $\psi _G(L/H) \cap (F_3(L/H) \otimes R_2)$ by Lemma 4.3. So formula (4.1) follows from Equation (4.3), as required. Conversely, if there exists a $\tau $ such that formula (4.1) holds, then G is Ceresa–Zharkov trivial by Lemma 4.3 and formula (4.3).

4.2 Edge-contraction

In this section, we prove that Ceresa–Zharkov triviality is preserved under edge contraction. We prove in §5 that Ceresa–Zharkov triviality is a minor-closed property.

Suppose G is a connected graph, $f\in E(G)$ is a nonloop edge and $G/f$ the graph obtained from G by contracting f. Denote by $\zeta _f:R[G] \to R[G/f]$ the map that evaluates $x_f$ to 0; this is a retract of the natural inclusion $R[G/f] \subset R[G]$ .

Proposition 4.4. With G and f as above, we have an equality of maps $(L/H)_{R[G]} \to (L/H)_{R[G/f]} $ :

(4.4) $$ \begin{align} (1\otimes \zeta_f)\circ(\delta_{G}-I) = (\delta_{G/f}-I)\circ(1\otimes \zeta_f). \end{align} $$

Also,

$$ \begin{align*} (1\otimes \zeta_f) (\mathbf{v}_{\tau}(G)) = \mathbf{v}_{\tau}(G/f). \end{align*} $$

In particular, if G is Ceresa–Zharkov trivial, then so is $G/f$ .

Note that G and $G/f$ have the same genus g and both can be embedded into $\Sigma _g$ as described in §3.3. So the same $\tau \in \operatorname {\mathrm {Mod}}(\Sigma _g)$ gives Ceresa cocycles of G and $G/f$ .

Proof. First, consider the maps $1\otimes \zeta _f$ and $\delta _e-I$ on $H_R$ . We have

$$ \begin{align*} (1\otimes \zeta_f) (\delta_e-I) = (\delta_e-I) (1\otimes \zeta_f) \hspace{10pt} \text { when } e\neq f, \hspace{10pt} \text{ and } (1\otimes \zeta_f) (\delta_f-I) = 0. \end{align*} $$

As a map $H_R \to H_R$ , by Proposition 3.1, we have

$$ \begin{align*} (1\otimes \zeta_f) (\delta_G-I) = (1\otimes \zeta_f) \sum_{e\in E(G)}(\delta_e-I) = \sum_{e\in E(G/f)} (\delta_e-I) (1\otimes \zeta_f) = (\delta_{G/f}-I)(1\otimes \zeta_f). \end{align*} $$

Thus, the identity in formula (4.4) holds as maps $H_{R[G]} \to H_{R[G/f]}$ , and one readily extends this as an identity of morphisms $(L/H)_{R[G]} \to (L/H)_{R[G\setminus f]}$ using Proposition 3.5. Next, consider what happens for the Ceresa class. We have

$$ \begin{align*} (1\otimes \zeta_f)(\mathbf{v}_{\tau}(G)) = (1\otimes \zeta_f) \sum_{e\in E(G)} J([T_{\ell_e}, \tau]) \otimes x_e = \sum_{e\in E(G/f)} J([T_{\ell_e}, \tau]) \otimes x_e = \mathbf{v}_{\tau}(G/f). \end{align*} $$

Finally, suppose G is Ceresa–Zharkov trivial, say $\mathbf {w}_{\tau }(G) = 0$ for some $\tau $ . Then,

$$ \begin{align*} (\delta_{G/f}-I)(\mathbf{v}_{\tau}(G/f)) = (\delta_{G/f}-I)\circ (1\otimes \zeta_f)(\mathbf{v}_{\tau}(G)) = (1\otimes \zeta_f) \circ (\delta_{G}-I) (\mathbf{v}_{\tau}(G)) = 0, \end{align*} $$

and therefore $G/f$ is Ceresa–Zharkov trivial.

4.3 Tropical equivalence

Similar to the setting of tropical curves, two graphs are tropically equivalent if one can be obtained from the other via the following moves:

• - adding or removing a 1-valent vertex together with its adjacent edge,

• - subdividing a edge,

• - contracting exactly one edge adjacent to a 2-valent vertex.

In this section, we show Ceresa–Zharkov triviality is preserved under all these moves and thus is a property of tropical equivalence classes. This fact is analogous to [10, Lemma 4.4] which asserts that tropically equivalent tropical curves have the same Ceresa class.

Lemma 4.5. Let G be a connected graph and e a separating edge. Then

1. 1. $\delta _{G} = \delta _{G/e}$ ;

2. 2. $\mathbf {v}_{\tau }(G) = \mathbf {v}_{\tau }(G/e)$ ;

3. 3. $\mathbf {w}_{\tau }(G) = \mathbf {w}_{\tau }(G/e)$ .

In particular, the graph G is Ceresa–Zharkov trivial if and only if its 2-edge connectivization $G^2$ , which is obtained by contracting all separating edges of G, is Ceresa–Zharkov trivial.

Proof. Statement (1) follows from the fact that $\delta _{e} = I$ whenever e is a separating edge. Statement (2) follows from the fact that $[T_{\ell _e}, \tau ] = 1$ for any hyperelliptic quasi-involution $\tau $ . Finally, statement (3) is a consequence of (1) and (2).

Let G be a graph, and suppose $f \in E(G)$ is subdivided into two edges $e_1,e_2$ , producing the graph $G'$ . Consider the ring map $\phi _f:R[G] \to R[G']$ given by

$$ \begin{align*} \phi_f(x_e) = \left\{ \begin{array}{ll} x_e & \text{ if } e\neq f\\ x_{e_1} + x_{e_2} & \text{ if } e = f. \end{array} \right. \end{align*} $$

Lemma 4.6. With the above notation, we have

(4.5) $$ \begin{align} (1\otimes \phi_f) \circ (\delta_{G}-I) = (\delta_{G'}-I) \circ (1\otimes \phi_f) \end{align} $$

as morphisms $(L/H)_{R[G]} \to (L/H)_{R[G']}$ , and

$$ \begin{align*} (1 \otimes \phi_f) (\mathbf{v}_{\tau}(G)) = \mathbf{v}_{\tau}(G'). \end{align*} $$

Proof. First, observe that the loops $\ell _{f}$ , $\ell _{e_1}$ and $\ell _{e_2}$ are isotopic to each other, thus

$$ \begin{align*} T_{\ell_f} = T_{\ell_{e_1}} = T_{\ell_{e_2}} \end{align*} $$

as elements of $\operatorname {\mathrm {Mod}}(\Sigma _g)$ , and as a consequence,

$$ \begin{align*} \delta_{\ell_f} = \delta_{\ell_{e_1}} = \delta_{\ell_{e_2}}. \end{align*} $$

As morphisms $H_{R[G]} \to H_{R[G']}$ , we have

$$ \begin{align*} (1\otimes \phi_f) \circ (\delta_{e}-I) = \left\{ \begin{array}{ll} (\delta_{\ell_e}-I) \circ (1\otimes \phi_f) & \text{if } e \neq f \\ ((\delta_{\ell_{e_1}}-I) + (\delta_{\ell_{e_2}}-I) ) \circ (1\otimes \phi_f) & \text{if } e = f. \end{array} \right. \end{align*} $$

Therefore,

$$ \begin{align*} (1\otimes \phi_f) \circ (\delta_{G}-I) &= (1\otimes \phi_f) \circ \sum_{e\in E(G)} (\delta_{\ell_{e}}-I) \\ &= \left((\delta_{\ell_{e_1}}-I) + (\delta_{\ell_{e_2}}-I) + \sum_{e\in E(G)\setminus f} (\delta_{\ell_{e}}-I) \right) \circ (1\otimes \phi_f) \\ &= (\delta_{G'}-I) \circ (1\otimes \phi_f). \end{align*} $$

Thus, the identity in Formula 4.5 holds as morphisms $H_{R[G]} \to H_{R[G']}$ . One readily extends this as an identity of morphisms $(L/H)_{R[G]} \to (L/H)_{R[G']}$ using Proposition 3.5.

For the statement regarding the Ceresa class, we compute

$$ \begin{align*} (1\otimes \phi_f)(\mathbf{v}_{\tau}(G)) &= J([T_{\ell_f},\tau]) \otimes (x_{e_1} + x_{e_2}) + \sum_{e\in E(G) \setminus f} J([T_{\ell_e},\tau]) \otimes x_e \\ &= \sum_{e\in E(G')} J([T_{\ell_e},\tau]) \otimes x_e \\ &= \mathbf{v}_{\tau}(G').\\[-36pt] \end{align*} $$

Proposition 4.7. If G and $G'$ are tropically equivalent graphs, then G is Ceresa–Zharkov trivial if and only if $G'$ is Ceresa–Zharkov trivial.

Proof. If $G'$ is obtained from G by adding or contracting an edge adjacent to a 1-valent vertex, then the claim follows from Lemma 4.5. Now, suppose $G'$ is obtained from G by subdividing an edge $f \in E(G)$ into $e_1$ and $e_2$ . If $G'$ is Ceresa–Zharkov trivial, then G is Ceresa–Zharkov trivial by Proposition 4.4. Conversely, if G is Ceresa–Zharkov trivial, say $\mathbf {w}_{\tau }(G) = 0$ for some $\tau $ , then by Lemma 4.6 we have

$$ \begin{align*} \mathbf{w}_{\tau}(G') = (\delta_{G}-I) \circ (1\otimes \phi_f) (\mathbf{v}_{\tau}(G)) = (1\otimes \phi_f)(\mathbf{w}_{\tau}(G)) = 0 \end{align*} $$

and hence $G'$ is Ceresa–Zharkov trivial.

4.4 Relation to the tropical Ceresa class

Let $\Gamma = (G,c)$ be a tropical curve. Recall from Section 2.4 that $\mathbf {v}(\Gamma ) \in B(\delta _{\Gamma })$ is the image of the Ceresa class $\nu (\Gamma )$ under the map $A(\delta ) \to B(\delta )$ . Given $c:E(G) \to \mathbb {Z}_{>0}$ , define homomorphisms

$$ \begin{align*} \epsilon_{c}^{1}: F_2(L/H) \otimes R_1 \to B(\delta_{\Gamma}) \hspace{20pt} \epsilon_{c}^{2}: F_3(L/H) \otimes R_2 \to C(\delta_{\Gamma}) \end{align*} $$

by the compositions

$$ \begin{align*} &F_2(L/H)\otimes R_1 \to F_2(L/H) \to \operatorname{\mathrm{gr}}_2^F(L/H) \to B(\delta_{\Gamma}), \\ &F_3(L/H)\otimes R_2 \to F_3(L/H) \to \operatorname{\mathrm{gr}}_3^F(L/H) \to C(\delta_{\Gamma}), \end{align*} $$

respectively, where the first maps $ F_2(L/H)\otimes R_1 \to F_2(L/H)$ and $F_3(L/H)\otimes R_2 \to F_3(L/H)$ are given by the evaluation map $h\otimes f \mapsto h\otimes f(c)$ . We say that $\Gamma $ is Ceresa–Zharkov trivial if $\mathbf {w}(\Gamma ) = 0$ in $C(\delta _{\Gamma })$ .

Proposition 4.8. Let $\Gamma = (G,c)$ be a tropical curve, and let $\tau $ be a hyperelliptic quasi-involution such that $\mathbf {v}_{\tau }(G)$ lies in $F_2(L/H)\otimes R_1$ . Then

$$ \begin{align*} \epsilon_{c}^1(\mathbf{v}_{\tau}(G)) = \mathbf{v}(\Gamma), \hspace{15pt} \text{and} \hspace{15pt} \epsilon_{c}^{2}(\mathbf{w}_{\tau}(G)) = \mathbf{w}(\Gamma). \end{align*} $$

In particular, if G is Ceresa–Zharkov trivial, then so is $\Gamma $ .

Proof. This is a direct consequence of formula (2.2) and Proposition 4.2.

By [10, Proposition 4.6], if a tropical curve $\Gamma $ is hyperelliptic, then $\Gamma $ is Ceresa trivial. Assuming Theorem 5.11, we derive a similar statement for tropical curves of hyperelliptic type and Ceresa–Zharkov triviality.

Proposition 4.9. If a tropical curve $\Gamma $ is of hyperelliptic type, then $\Gamma $ is Ceresa–Zharkov trivial.

Proof. The statement follows from Proposition 4.8 and Theorem 5.11.

However, the converse to Proposition 4.9 is not true by Remark 5.8.

5 Ceresa–Zharkov trivial and tropical curves of hyperelliptic type

The main goal of this section is to prove Theorem 5.11, that a graph is Ceresa–Zharkov trivial if and only if it is of hyperelliptic type. Being of hyperelliptic type is a minor closed condition on graphs by [9, Proposition 3.8]. Because of this, Theorem 5.11 implies that Ceresa–Zharkov triviality is also a minor closed condition. Nevertheless, to prove this theorem, we need the fact that Ceresa–Zharkov triviality is preserved under edge contraction (Proposition 4.4) and under removal of a loop edge or an edge in a parallel pair (Proposition 5.1). The removal of these two types of edges are easier to handle for the following reason. Using Lemma 5.4, we may choose compatible homology bases and compatible hyperelliptic quasi-involutions of the Riemann surfaces corresponding to the original graph and the removal of such an edge. This allows for a direct comparison between the corresponding Ceresa–Zharkov classes.

Proposition 5.1. Consider either

1. 1. a connected graph $G_1$ with a loop edge a, or

2. 2. a 2-connected graph $G_2$ with a pair of parallel edges $(b,c)$ .

If $G_1$ , resp. $G_2$ , is Ceresa–Zharkov trivial, then so is $G_1\setminus a$ , resp. $G_2\setminus b$ .

We begin by describing, for any connected graph G, the images $(\delta _{G}-I)(F_2(L_R/H_R))$ and $(\delta _{G}-I)^2(F_1(L_R/H_R))$ . Order the edges of G by $e_1,\ldots ,e_n$ so that $e_{g+1},\ldots ,e_n$ are the edges of a spanning tree. Let $\alpha _1,\ldots ,\alpha _g,\beta _{1},\ldots ,\beta _{g}$ be the basis of $H_1(\Sigma _g,\mathbb {Z})$ from §3.3, so $\delta _{G}$ has the form in Equation (3.4). Write $q_{ij}$ for the entries of $Q_G$ .

Lemma 5.2. We have

$$ \begin{align*} (\delta_G-I) \left( \sum_{i; j<k} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} \right)= \sum_{r<s<t} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}, \end{align*} $$

where

$$ \begin{align*} c_{rst} = \sum_{i} (b_{irs}q_{ti} - b_{irt}q_{si} + b_{ist}q_{ri}). \end{align*} $$

Proof. By formula (3.6), we have that

$$ \begin{align*} (\delta_G-I) \sum_{i; j<k} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} = \sum_{i; j<k} Q_{G}(\alpha_i) \wedge \beta_j \wedge \beta_k \otimes b_{ijk} = \sum_{i; j<k; \ell} \beta_{\ell} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} q_{\ell i}. \end{align*} $$

Given $r<s<t$ one may extract the coefficient $c_{rst}$ for $\beta _{r} \wedge \beta _{s} \wedge \beta _{t} $ .

Lemma 5.3. We have

$$ \begin{align*} (\delta_G-I)^2 \sum_{i<j; k} \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} \otimes a_{ijk} = \sum_{r<s<t} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst} \hspace{10pt} \text{where} \hspace{5pt} c_{rst} = 2 \sum_{i<j} \, \begin{vmatrix} q_{ri} & q_{rj} & a_{ijr} \\ q_{si} & q_{sj} & a_{ijs} \\ q_{ti} & q_{tj} & a_{ijt} \end{vmatrix}. \end{align*} $$

Proof. By Formula 3.6, we have that

$$ \begin{align*} (\delta_G-I)^2 \left( \sum_{i<j; k} \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} \otimes a_{ijk} \right) &= \sum_{i<j; k} 2 Q_{G} \, \alpha_i \wedge Q_{G} \, \alpha_j \wedge \, \beta_k \otimes a_{ijk}\\ &= \sum_{i<j; k} \sum_{\ell<m} \beta_{\ell} \wedge \beta_{m} \wedge \beta_{k} \otimes 2a_{ijk} \begin{vmatrix} q_{\ell i} & q_{\ell j} \\ q_{m i} & q_{m j} \end{vmatrix}. \end{align*} $$

Given $r<s<t$ , the R-coefficient of $\beta _{r} \wedge \beta _{s} \wedge \beta _{t} $ is

$$ \begin{align*} c_{rst} = 2\sum_{i<j} \left( a_{ijr} \begin{vmatrix} q_{si} & q_{sj} \\ q_{ti} & q_{tj} \end{vmatrix} - a_{ijs} \begin{vmatrix} q_{ri} & q_{rj} \\ q_{ti} & q_{tj} \end{vmatrix} + a_{ijt} \begin{vmatrix} q_{ri} & q_{rj} \\ q_{si} & q_{sj} \end{vmatrix} \right) \end{align*} $$

and the summand is exactly the $3\times 3$ determinant appearing in the lemma.

Our next step is to show how the Ceresa classes of G and $G \setminus f$ are related. The two cases listed in Proposition 5.1 are similar, so we handle them in parallel. Let $G_1$ be a connected graph with a loop edge a and let $G_2$ be a 2-connected graph with a pair of parallel edges $b,c$ . Let $\Lambda _1 = \{\ell _e \, : \, e\in E(G_1)\}$ and $\Lambda _2 = \{\ell _e \, : \, e\in E(G_2)\}$ be two arrangements of isotopy classes of simple closed curves whose dual graphs are $G_1$ and $G_2$ , respectively. Suppose that $\ell _{a}$ , $\ell _{b}$ , $\ell _{c}$ are as in Figure 3, and every other $\ell _{e}$ lies in $\Sigma _{g}^1$ , the genus g subsurface with a boundary to the left of $\gamma $ . To emphasize the dependence on the genus g, we write

$$ \begin{align*} H(\Sigma_g^{n}) = H_1(\Sigma_{g}^{n},\mathbb{Z}), \hspace{10pt} L(\Sigma_{g}^{n}) = \wedge^3H_1(\Sigma_g^{n}), \end{align*} $$

where $n=0$ or $1$ . The inclusion $\Sigma _{g}^1\hookrightarrow \Sigma _{g+1}$ induces an inclusion on homology groups which we use to identify $H(\Sigma _g) \cong H(\Sigma _g^1)$ as a subgroup of $H(\Sigma _{g+1})$ . Now, recall that we obtain $\Sigma _{g}$ from $\Sigma _{g}^1$ by attaching a disc along $\gamma $ . Any two extensions of $\ell _{c}\cap \Sigma _{g}^1$ to $\Sigma _{g}$ are isotopic. Choose such an extension and denote it also by $\ell _{c}$ .

Figure 3 Arrangements of curves on $\Sigma _{g+1}$ with dual graphs $G_1$ and $G_2$ where (left) a is a loop edge and (right) $(b,c)$ are parallel edges. Here, we identify $\Sigma _{g}^1$ with the subsurface of $\Sigma _{g+1}$ to the left of $\gamma $ .

We may view $\Lambda _1\setminus \{\ell _a\}$ as an arrangement of curves on $\Sigma _g$ or $\Sigma _g^1$ . We may also view $\Lambda _2\setminus \{\ell _b\}$ as an arrangement of curves on $\Sigma _g$ , and $\Lambda _2\setminus \{\ell _b,\ell _{c}\}$ as an arrangement of curves on $\Sigma _g^1$ . Because $L(\Sigma _{g})/H(\Sigma _g)$ does not naturally embed into $L(\Sigma _{g+1})/H(\Sigma _{g+1})$ , we cannot directly compare $\mathbf {v}_{\tau }(\Lambda _1)$ with $\mathbf {v}_{\tau '}(\Lambda _1\setminus \{\ell _a\})$ , or $\mathbf {v}_{\tau }(\Lambda _2)$ with $\mathbf {v}_{\tau '}(\Lambda _2\setminus \{\ell _b\})$ . Instead, we compare these with Ceresa classes on $\Sigma _g^1$ in the following way.

Lemma 5.4. There are hyperelliptic quasi-involutions $\tau $ on $\Sigma _{g+1}$ , $\tau '$ on $\Sigma _{g}$ and $\tau "$ on $\Sigma _{g}^1$ , under the natural homomorphisms

$$ \begin{align*} &L(\Sigma_g^1)_{R[\Lambda_1 \setminus \{\ell_a\}]} \to L(\Sigma_g)_{R[\Lambda_1 \setminus \{\ell_a\}]} / H(\Sigma_g)_{R[\Lambda_1 \setminus \{\ell_a\}]} \\ &L(\Sigma_g^1)_{R[\Lambda_1 \setminus \{\ell_a\}]} \hookrightarrow L(\Sigma_{g+1}^1)_{R[\Lambda_1]} \to L(\Sigma_{g+1})_{R[\Lambda_1]} / H(\Sigma_{g+1})_{R[\Lambda_1]} \end{align*} $$

the class $\boldsymbol \mu _{\tau "}(\Lambda _1\setminus \{\ell _a\})$ maps to $\mathbf {v}_{\tau '}(\Lambda _1\setminus \{\ell _a\})$ and $\mathbf {v}_{\tau }(\Lambda _1)$ , respectively. Similarly, the natural homomorphisms

$$ \begin{align*} L(\Sigma_g)_{R[\Lambda_2\setminus \{\ell_{b},\ell_{c}\}]} &\to L(\Sigma_g)_{R[\Lambda_2 \setminus \{\ell_b\}]}/H(\Sigma_g)_{R[\Lambda_2 \setminus \{\ell_{b}\}]} \\ L(\Sigma_g^1)_{R[\Lambda_2\setminus \{\ell_b,\ell_{c}\}]} &\hookrightarrow L(\Sigma_{g+1})_{R[\Lambda_2]} \to L(\Sigma_{g+1})_{R[\Lambda_2]}/H(\Sigma_{g+1})_{R[\Lambda_2]} \end{align*} $$

take $\boldsymbol \mu _{\tau "}(\Lambda _2\setminus \{\ell _b,\ell _c\})$ to $\mathbf {v}_{\tau '}(\Lambda _2\setminus \{\ell _b\})$ and $\mathbf {v}_{\tau }(\Lambda _2)$ , respectively.

Furthermore, we may choose $\tau $ , $\tau '$ and $\tau "$ so that all classes defined above live in the $F_2$ part of the relevant filtration.

Proof. Consider the surfaces homeomorphic to $\Sigma _{g+1}$ in Figure 3. These depict $\Sigma _{g+1}$ embedded in $\mathbb {R}^3$ and bounding a handlebody V, the ‘inside’ of the surface. Assume that the curves in $\Lambda _1$ and $\Lambda _2$ are meridians, that is, they bound properly embedded discs in V. We use these assumptions in the next paragraph to show that the Ceresa classes all belong to $F_2$ .

Next, let $\tau $ be the hyperelliptic involution on $\Sigma _{g+1}$ given by rotation by $180^{\circ }$ about the axis illustrated in Figure 3; in particular, $\tau $ takes $\ell _f$ to $\ell _f$ (reversing its orientation) for $f=a$ , b, c. The map $\tau $ can be isotoped in a regular neighborhood of $\gamma $ so that it fixes $\gamma $ pointwise. Consequently, the mapping class $\tau \in \operatorname {\mathrm {Mod}}(\Sigma _{g+1})$ restricts to a hyperelliptic quasi-involution $\tau "$ on $\Sigma _{g}^{1}$ ; denote by $\tau '$ the image of $\tau "$ under the natural map $\operatorname {\mathrm {Mod}}(\Sigma _{g}^1) \to \operatorname {\mathrm {Mod}}(\Sigma _{g})$ . Because all the curves in $\Lambda _1$ and $\Lambda _2$ are meridians and the hyperelliptic quasi-involutions $\tau $ , $\tau '$ and $\tau "$ extend to homeomorphisms on the handlebodies, each $J([T_{\ell }, \tau "])$ , $J([T_{\ell }, \tau '])$ and $J([T_{\ell }, \tau ])$ lie in $F_2$ by [10, Theorem 6.6], and therefore $\boldsymbol \mu _{\tau "}$ , $\mathbf {v}_{\tau '}$ and $\mathbf {v}_{\tau '}$ lie in $F_2\otimes R_1$ .

Since $[T_{\ell _{f}},\tau ] = T_{\ell _{f}}T_{\tau (\ell _f)}^{-1}$ and $\tau (\ell _f)$ is isotopic to $\ell _f$ for $f=a,b,c$ , we have that $[T_{\ell _f},\tau ] = 1$ for $f=a,b,c$ . Similarly, we have $[T_{\ell _c},\tau '] = 1$ . Therefore,

$$ \begin{align*} \boldsymbol \mu_{\tau"}(\Lambda_1\setminus \{\ell_a\}) = \sum_{e\in E(G_1)\setminus \{a\}} J([T_{\ell_e}, \tau ]) \otimes x_e \hspace{10pt} \text{and} \hspace{10pt} \boldsymbol \mu_{\tau"}(\Lambda_2\setminus \{\ell_b,\ell_c\}) = \sum_{e\in E(G_1)\setminus \{b,c\}} J([T_{\ell_e}, \tau ]) \otimes x_e. \end{align*} $$

The lemma follows from these computations.

Proof of Proposition 5.1.

Suppose that the graph G and edge $f\in E(G)$ are either

1. 1. $G=G_1$ and $f=a$ is a loop edge, or

2. 2. $G=G_2$ , a 2-connected graph, and $f=b$ is parallel to another edge c.

Let $g+1$ be the genus of G. Order the edges of G by $e_0, \ldots , e_g, e_{g+1}, \ldots , e_n$ such that the last $n-(g+1)$ edges form a spanning tree of G and $e_0 = f$ . In the second case, assume that $e_1=c$ and orient $[\ell _{b}]$ and $[\ell _{c}]$ in the same direction. This is possible since $G_2$ is 2-connected, so $b,c$ are not a separating pair. Denote by $\alpha _{0},\ldots ,\alpha _g,\beta _0,\ldots ,\beta _g$ the basis described in Section 3.3. This identifies $Q_{G\setminus f}$ with the lower-right $g\times g$ submatrix of $Q_{G}$ . Let $q_{ij}$ denote the coordinates of $Q_{G}$ . When $G=G_1$ , we have

$$ \begin{align*} q_{00} = x_{0}, \hspace{10pt} \text{and} \hspace{10pt} q_{0j} = q_{j0} = 0 \hspace{10pt} \text{ for } \hspace{10pt} j\geq 1 \end{align*} $$

and when $G=G_2$ , we have

$$ \begin{align*} q_{00} = x_{0} + q_{01},\hspace{10pt} q_{11} = x_{1} + q_{01} \hspace{10pt} \text{and} \hspace{10pt} q_{0j} = q_{1j} \hspace{10pt} \text{ for } \hspace{10pt} j\geq 2. \end{align*} $$

By Lemma 5.4, there are hyperelliptic quasi-involutions $\tau $ on $\Sigma _{g+1}$ and $\tau '$ on $\Sigma _{g}$ such that

$$ \begin{align*} \mathbf{v}_{\tau}(G) = \sum_{ \substack{1\leq i\leq g \\ 1\leq j<k\leq g}} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} \hspace{10pt} \text{ in } \hspace{10pt} L(\Sigma_{g+1})_{R[G]}/H(\Sigma_{g+1})_{R[G]} \\ \mathbf{v}_{\tau'}(G\setminus f) = \sum_{\substack{1\leq i\leq g\\ 1\leq j<k\leq g}} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} \hspace{10pt} \text{ in } \hspace{10pt} L(\Sigma_{g})_{R[G\setminus f]}/H(\Sigma_{g})_{R[G\setminus f]}, \end{align*} $$

where $b_{ijk}$ ’s are linear forms in $R[G\setminus f]\subset R[G]$ . Implicit in this description is that $b_{0jk} = 0$ and $b_{i0k}=0$ . Because G is Ceresa–Zharkov trivial, by Proposition 4.2, there is a $\mathbf {u}\in F_1(L/H)$ , say

$$ \begin{align*} \mathbf{u}= \sum_{\substack{0\leq i<j \leq g \\ 0\leq k \leq g}} a_{ijk} \cdot \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} \end{align*} $$

with $a_{ijk} \in \mathbb {Z}$ such that $\mathbf {w}_{\tau }(G) = (\delta _G-I)^2(\mathbf {u})$ . We will show that $\mathbf {w}_{\tau '}(G\setminus f)$ lies in the image $(\delta _{G\setminus f}-I)^2(F_1(L(\Sigma _g)/H(\Sigma _g)))$ , whence $G\setminus f$ is Ceresa–Zharkov trivial by Proposition 4.2. Because $b_{0jk} = 0$ , we have

(5.1) $$ \begin{align} c_{rst} := \sum_{i=0}^{g} (b_{irs}q_{ti} - b_{irt}q_{si} + b_{ist}q_{ri}) = \sum_{i=1}^{g} (b_{irs}q_{ti} - b_{irt}q_{si} + b_{ist}q_{ri}) \end{align} $$

for $0\leq r<s<t \leq g$ . Therefore, by Lemma 5.2, we have

$$ \begin{align*} \mathbf{w}_{\tau}(G) &= (\delta_G-I)(\mathbf{v}_{\tau}(G)) = \sum_{0\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst} \hspace{15pt} \text{and} \\ \mathbf{w}_{\tau'}(G\setminus f) &= (\delta_{G\setminus f}-I)(\mathbf{v}_{\tau'}(G\setminus f)) = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}. \end{align*} $$

By the equality $\mathbf {w}_{\tau }(G) = (\delta _{G}-I)^2(\mathbf {u})$ and Lemma 5.3, we have

(5.2) $$ \begin{align} c_{rst} = 2\sum_{0\leq i<j \leq g} \begin{vmatrix} q_{ri} & q_{rj} & a_{ijr} \\ q_{si} & q_{sj} & a_{ijs} \\ q_{ti} & q_{tj} & a_{ijt} \end{vmatrix}. \end{align} $$

Set

$$ \begin{align*} \mathbf{u}'= \sum_{\substack{1\leq i<j \leq g \\ 1\leq k \leq g}} a_{ijk} \cdot \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k}. \end{align*} $$

Then

$$ \begin{align*} (\delta_{G\setminus f}-I)^2(\mathbf{u}') = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}' \hspace{15pt} \text{where} \hspace{15pt} c_{rst}' = 2\sum_{1\leq i<j \leq g} \begin{vmatrix} q_{ri} & q_{rj} & a_{ijr} \\ q_{si} & q_{sj} & a_{ijs} \\ q_{ti} & q_{tj} & a_{ijt} \end{vmatrix}. \end{align*} $$

Next, let’s compute the difference

$$ \begin{align*} &\mathbf{w}_{\tau'}(G\setminus f) - (\delta_{G\setminus f}-I)^2(\mathbf{u}') = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes (c_{rst} - c_{rst}'), \end{align*} $$

where

$$ \begin{align*} c_{rst} - c_{rst}' = 2\sum_{j=1}^g \begin{vmatrix} q_{r0} & q_{rj} & a_{0jr} \\ q_{s0} & q_{sj} & a_{0js} \\ q_{t0} & q_{tj} & a_{0jt} \end{vmatrix} \hspace{10pt} \text{for} \hspace{10pt} 1\leq r < s < t \leq g. \end{align*} $$

If we are in the first case, that is, $G=G_1$ and $f=a$ is a loop edge, then $q_{j0}=0$ for $j\geq 1$ , so the above formula implies $c_{rst}-c_{rst}' = 0$ , whence $\mathbf {w}_{\tau '}(G\setminus f) = (\delta _{G\setminus f}-I)^2(\mathbf {u}')$ .

For the rest of the proof, suppose we are in the second case, that is, $G=G_2$ and $f=b=e_0$ is parallel to the edge $c=e_1$ . Set

$$ \begin{align*} \mathbf{u}"= \sum_{\substack{2\leq j \leq g\\ 1\leq k \leq g}} a_{0jk} \cdot \alpha_{1} \wedge \alpha_{j} \wedge \beta_{k}. \end{align*} $$

We have

$$ \begin{align*} (\delta_{G\setminus f} -I)^2(\mathbf{u}") = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}" \hspace{15pt} \text{where} \hspace{15pt} c_{rst}" = 2 \sum_{j=2}^g \begin{vmatrix} q_{r1} & q_{rj} & a_{0jr} \\ q_{s1} & q_{sj} & a_{0js} \\ q_{t1} & q_{tj} & a_{0jt} \end{vmatrix}. \end{align*} $$

When $r\geq 2$ , we have that $q_{r0} = q_{r1}$ , and therefore $c_{rst} - c_{rst}' = c_{rst}"$ . Now, consider $r=1$ . Since $x_0$ only appears in $q_{00}$ , where $q_{00} = x_{0} + q_{01}$ , the coefficient of $x_0$ in $c_{rst}$ must equal 0 for all $0\leq r<s<t\leq g$ by formula (5.1). By extracting the coefficient of $x_0$ in the expression of $c_{0st}$ from formula (5.2), we see that

(5.3) $$ \begin{align} \sum_{j=1}^{g} \begin{vmatrix} q_{sj} & a_{0js} \\ q_{tj} & a_{0jt} \end{vmatrix} = 0. \end{align} $$

Therefore,

$$ \begin{align*} c_{1st}" - (c_{1st} - c_{1st}') = 2 (q_{11}-q_{10}) \sum_{j=1}^g \begin{vmatrix} q_{sj} & a_{0js} \\ q_{tj} & a_{0jt} \end{vmatrix} =0, \end{align*} $$

where the last equality follows from formula (5.3). So $c_{rst} = c_{rst}' + c_{rst}"$ and therefore

$$ \begin{align*} \mathbf{w}_{\tau'}(G\setminus f) &=\sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst} \\ &= \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes (c_{rst}' + c_{rst}") = (\delta_{G\setminus f}-I)^2(\mathbf{u}' + \mathbf{u}").\\[-44pt] \end{align*} $$

Next, we show that Ceresa–Zharkov triviality may be detected at the level of $2$ -connected components.

Proposition 5.5. A connected graph G is Ceresa–Zharkov trivial if and only if its 2-connected components are Ceresa–Zharkov trivial.

Proof. By induction, it suffices to consider the case where G has two 2-connected components $G_1$ and $G_2$ . Choose a separating curve $\gamma $ and an arrangement of simple closed curves $\Lambda = \{\ell _e \, : \, e\in E(G) \}$ such that

• - the dual graph of $\Lambda $ is G;

• - cutting along $\gamma $ separates $\Sigma _g$ into two subsurfaces $S_1\cong \Sigma _{g_1}^1$ and $S_2 \cong \Sigma _{g_2}^1$ ;

• - $\ell _e$ lies in $S_i$ whenever $e\in E(G_i)$ .

Denote by $H^{(i)} = H_1(\Sigma _{g_i}, \mathbb {Z})$ and $L^{(i)} = \wedge ^3H^{(i)}$ . The inclusion $S_i\subset \Sigma _g$ allows us to view $F_qL^{(i)} \otimes R$ as an R-submodule of $F_qL_R$ for $q=0,\ldots ,3$ . Choose hyperelliptic quasi-involutions $\tau _1'$ of $S_1$ and $\tau _2'$ of $S_2$ such that $\boldsymbol \mu _{\tau _i'}(\Lambda _i')$ lies in $F_2L^{(i)} \otimes R_1$ ; this is possible by Proposition 4.1. Let $\tau $ be the hyperelliptic quasi-involution of $\Sigma _g$ obtained that restricts to $\tau _i'$ on $S_i$ . Denote by $\tau _i\in \operatorname {\mathrm {Mod}}(\Sigma _{g_i})$ the image of $\tau '$ under the natural map $\operatorname {\mathrm {Mod}}(\Sigma _{g_i}^1) \to \operatorname {\mathrm {Mod}}(\Sigma _{g_i})$ ; thus $\tau _i$ is a hyperelliptic quasi-involution of $\Sigma _{g_i}$ . Then $\mathbf {v}_{\tau _1}(G_1), \mathbf {v}_{\tau _2}(G_2), \mathbf {v}_{\tau }(G)$ are in $F_2L\otimes R_1$ , and therefore $\mathbf {w}_{\tau _1}(G_1), \mathbf {w}_{\tau _2}(G_2), \mathbf {w}_{\tau }(G)$ are in $F_3L\otimes R_2$ .

Consider the following commutative diagram:

(5.4)

The right arrow on the bottom row is an isomorphism by formula (2.1). Consider $\boldsymbol \mu := \boldsymbol \mu _{\tau _1'}(\Lambda _1') + \boldsymbol \mu _{\tau _2'}(\Lambda _2')$ in $(F_2L^{(1)} \oplus F_2L^{(2)})_R$ . The composition of the top two arrows of the diagram in Equation (5.4) maps $\boldsymbol \mu $ to $\mathbf {v}_{\tau }(G)$ , which maps to $\mathbf {w}_{\tau }(G)$ by the right vertical arrow. The composition along the bottom takes $\boldsymbol \mu $ to $\mathbf {w}_{\tau _1}(G_1) + \mathbf {w}_{\tau _2}(G_2)$ . Thus,

(5.5) $$ \begin{align} \mathbf{w}_{\tau_1}(G_1) + \mathbf{w}_{\tau_2}(G_2) = \mathbf{w}_{\tau}(G). \end{align} $$

Suppose $G_1$ and $G_2$ are Ceresa–Zharkov trivial. By Proposition 4.2, there are elements $\mathbf {u}_i\in F_1(L^{(i)}/H^{(i)})$ such that $(\delta _{G_i}-I)^2(\mathbf {u}_i) = \mathbf {w}_{\tau _i}(G_i)$ . The restriction of $(\delta _G-I)^2$ to $F_1L^{(1)} \oplus F_1L^{(2)}$ is $(\delta _{G_1}-I)^2 \oplus (\delta _{G_2}-I)^2$ ; this follows from formula (3.6) and the fact that $Q_G = Q_{G_1}\oplus Q_{G_2}$ . So $(\delta _{G}-I)^2(\mathbf {u}_1+\mathbf {u}_2) = \mathbf {w}_{\tau }(G)$ , and therefore G is Ceresa–Zharkov trivial.

Conversely, suppose G is Ceresa–Zharkov trivial. Let T be a spanning tree of $G_1$ . Then $G/T$ is Ceresa–Zharkov trivial by Proposition 4.4. Observe that $G/T$ is obtained from $G_2$ by attaching $g_1$ loop edges to a single vertex of $G_2$ . So $G_2$ is Ceresa–Zharkov trivial by Proposition 5.1. Swapping the roles of $G_1$ and $G_2$ , we conclude that $G_1$ is also Ceresa–Zharkov trivial.

Recall from [9, §3] that a graph G is strongly of hyperelliptic type if there is a choice of edge lengths of G so that the resulting tropical curve is hyperelliptic. Such graphs are Ceresa–Zharkov trivial by the following proposition.

Proposition 5.6. Let G be a graph that has a separating pair of edges $(f,f')$ , and let $\Lambda = \{\ell _e \, : \, e\in E(G)\}$ be a collection of pairwise disjoint simple closed curves on $\Sigma _g$ with dual graph G. If $\tau $ is a hyperelliptic quasi-involution such that $\tau (\ell _{f}) = \ell _{f'}$ , then

$$ \begin{align*} (\delta_{G}-I)(J([T_{\ell_{f}}, \tau])\otimes 1) = 0. \end{align*} $$

In particular, if G is strongly of hyperelliptic type, then G is Ceresa–Zharkov trivial.

Proof. The removal of $\{f,f'\}$ from G separates this graph into two graphs $G_1$ and $G_2$ of gerena $g_1$ and $g_2$ , respectively. Order the edges of G by $e_1, \ldots , e_g, e_{g+1}, \ldots , e_{n}$ so that

• - $e_1,\ldots ,e_{g_1} \in E(G_1)$ , $e_{g_1+1},\ldots ,e_{g-1} \in E(G_2)$ , and $e_{g} = f$ ;

• - $e_{g+1}, \ldots , e_{n}$ are the edges of a spanning tree of G.

Necessarily, $f'$ must be among the edges of the spanning tree. Let $\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$ be the basis from §3.3. With respect to this basis, we have

$$ \begin{align*} Q_G = \begin{bmatrix} Q_{G_1} & 0 & * \\ 0 & Q_{G_2} & * \\ * & * & x_{f} \end{bmatrix}. \end{align*} $$

Cutting along $\ell _{f}$ and $\ell _{f'}$ separates the surface $\Sigma _g$ into two subsurfaces $S_1$ and $S_2$ . The homology of $S_i$ splits as a direct sum $V\oplus W_i$ , where $V = \mathbb {Z} \cdot [\ell _f]$ and $W_i$ is identified with a symplectic subspace of H under the map $H_1(S_i,\mathbb {Z}) \to H$ . The intersection 2-form $\omega _i$ of $W_i$ is the restriction of $\omega $ to $W_i$ , so

$$ \begin{align*} \omega_1 = \sum_{j=1}^{g_1} \alpha_j \wedge \beta_j \hspace{15pt} \text{and} \hspace{15pt} \omega_2 = \sum_{j=g_1+1}^{g-1} \alpha_j \wedge \beta_j. \end{align*} $$

Orient $[\ell _{f}]$ such that $S_1$ lies to its right. Because $\tau (\ell _{f}) = \ell _{f'}$ , we have that $\tau T_{\ell _{f}} \tau ^{-1} = T_{\ell _{f'}}$ , and hence

$$ \begin{align*} J([T_{\ell_{f}}, \tau]) = J(T_{\ell_{f}} T_{\ell_{f'}}^{-1}) = \omega_1\wedge [\ell_{f}] = - \omega_2 \wedge [\ell_{f'}]. \end{align*} $$

The expression $(\delta _{G}-I)(J(T_{\ell _{f}} T_{\ell _{f'}}^{-1}))$ is equal to

$$ \begin{align*} (\delta_{G}-I)(\omega_1\wedge [\ell_{f}]) = \sum_{j=1}^{g_1} (Q_{G} \, \alpha_j ) \wedge \beta_j \wedge \beta_g = \sum_{j=1}^{g_1} (Q_{G_1} \, \alpha_j ) \wedge \beta_j \wedge \beta_g = (\delta_{G_1}-I)(\omega_1\wedge [\ell_{f}]). \end{align*} $$

We use formula (3.6) in the first equality and $Q_{G}(\alpha _j) - Q_{G_1}(\alpha _j) \in \mathbb {Z}\cdot \beta _g$ for $j\leq g_1$ in the second. By Proposition 3.3 applied to V and $W=W_1$ , we have

$$ \begin{align*} (\delta_{G_1}-I)(\omega_1\wedge [\ell_{f}]) = \omega_1\wedge (\delta_{G_1}-I) ([\ell_{f}]) + \eta \wedge \delta_{G_1} ([\ell_f]) \end{align*} $$

for some $\eta \in V\wedge W_1$ . Since the curves in $\Lambda $ are disjoint, we have that $\delta _{G_1}([\ell _f]) = [\ell _{f}]$ . This implies that the first summand above is 0, and the second summand is in $V\wedge W_1\wedge V$ , which must also be 0 since $\dim V = 1$ . So we have $(\delta _{G}-I)(J([T_{\ell _{f}}, \tau ])) = 0$ , as required.

Now, suppose G is strongly of hyperelliptic type. By Proposition 4.7, we may assume that G is stable. Let $\Gamma $ be a hyperelliptic tropical curve with underlying graph G, and $\sigma $ be a hyperelliptic involution of $\Gamma $ . There is a hyperelliptic quasi-involution $\tau $ of $\Sigma _g$ such that $\tau (\ell _{e}) = \ell _{\sigma (e)}$ by [10, Lemma 4.5]. By [9, Proposition 2.5], for any edge $e\in E(G)$ , we have that $\sigma (e) = e$ or $\sigma (e) = f$ , where $(e,f)$ is a separating pair. In the first case, $[T_{\ell _e},\tau ] = 1$ . In the second case, $(\delta _G-I)(J([T_{\ell _e},\tau ])) = 0$ by the first part of this proposition. We conclude that $\mathbf {w}_{\tau }(G) = 0$ , that is, G is Ceresa–Zharkov trivial.

To prove Ceresa–Zharkov trivial implies hyperelliptic type, we use in an essential way the main theorem of [9], which states that a graph is of hyperelliptic type if and only if it has no $K_4$ or $L_3$ minor. We prove directly that these graphs are not Ceresa–Zharkov trivial, using Proposition 4.8.

Proposition 5.7. The graph $G=K_4$ is not Ceresa–Zharkov trivial.

Proof. By [10, Example 7.2], a Ceresa cocycle $\mathbf {v}_{\tau }(G)$ for the graph $K_4$ is given by

(5.6) $$ \begin{align} \mathbf{v}_{\tau}(G) = \alpha_{1} \wedge \beta_{1} \wedge \beta_{2} \otimes x_2 + (-\alpha_{2} \wedge \beta_{1} \wedge \beta_{2} - \alpha_{2} \wedge \beta_{2} \wedge \beta_{3} + \alpha_{2} \wedge \beta_{1} \wedge \beta_{3} ) \otimes x_5, \end{align} $$

which lies in $F_2(L/H) \otimes R_1$ . The matrix $Q_G$ is recorded in formula (3.5). We get

$$ \begin{align*} \mathbf{w}_{\tau}(G) = -2 \cdot \beta_{1} \wedge \beta_{2} \wedge \beta_{3} \otimes x_2x_5, \end{align*} $$

which lies in $F_3(L/H) \otimes R_2$ . By Proposition 4.8, it is sufficient to show that the tropical curve $\Gamma = (K_4,c)$ is not Ceresa–Zharkov trivial for some edge-length function $c:E(K_4) \to \mathbb {Z}_{>0}$ . Let c be the function that assigns the length 1 to each edge. Then $\mathbf {w}(\Gamma ) = -2 \, \beta _{1} \wedge \beta _{2} \wedge \beta _{3} $ , whereas $(\delta _{\Gamma }-I)^2(F_1(L/H))$ is spanned by $4\, \beta _{1} \wedge \beta _{2} \wedge \beta _{3} $ ; see [10, Remark 7.3]. So $\mathbf {w}(\Gamma ) \neq 0$ , as required.

Remark 5.8. Define $c:E(K_4) \to \mathbb {Z}_{>0}$ by $c(e_1) = 2$ and $c(e_i)=1$ for $i=2,\ldots ,6$ , and let $\Gamma =(K_4,c)$ . Then $(\delta _{\Gamma }-I)^2(F_1(L/H)) = F_3L$ , and hence $\mathbf {w}(\Gamma ) = 0$ . Therefore, $\Gamma $ is Ceresa–Zharkov trivial but clearly not of hyperelliptic type.

Proposition 5.9. The graph $G=L_3$ is not Ceresa–Zharkov trivial.

Proof. From [10, Example 7.6] by setting $c_7=c_8=c_9=0$ , we get

$$ \begin{align*} Q_G = \begin{pmatrix} x_1 + x_6 & 0 & x_6 & x_6 \\ 0 & x_2+x_5 & x_5 & x_5 \\ x_6 & x_5 & x_3+x_5+x_6 & x_5+x_6 \\ x_6 & x_5 & x_5+x_6 & x_4+x_5+x_6 \end{pmatrix}. \end{align*} $$

$$ \begin{align*} \mathbf{v}_{\tau}(G)= &(\alpha_{2} \wedge \beta_{2} \wedge \beta_{3} + \alpha_{2} \wedge \beta_{2} \wedge \beta_{4} -\alpha_{2} \wedge \beta_{1} \wedge \beta_{2} ) \otimes x_6 \\ -&(\alpha_{1} \wedge \beta_{1} \wedge \beta_{2} + \alpha_{1} \wedge \beta_{1} \wedge \beta_{3} + \alpha_{1} \wedge \beta_{1} \wedge \beta_{4} )\otimes x_5. \end{align*} $$

So we have

$$ \begin{align*} \mathbf{w}_{\tau}(G) = -2x_5x_6(\beta_1\wedge\beta_2\wedge\beta_3+\beta_1\wedge\beta_2\wedge\beta_4). \end{align*} $$

By Proposition 4.8, it is sufficient to show that the tropical curve $\Gamma = (L_3,c)$ is not Ceresa–Zharkov trivial for some edge-length function $c:E(L_3) \to \mathbb {Z}_{>0}$ . Let c be the function that assigns the length 1 to each edge. Using OSCAR [11, 15] (which runs in julia [3]), we show that $(\delta _{\Gamma }-I)^2(F_1(L/H))$ is spanned by

$$ \begin{align*} \begin{array}{ll} 2\beta_{1} \wedge \beta_{2} \wedge \beta_{3} + 2\beta_{1} \wedge \beta_{2} \wedge \beta_{4} + 2\beta_{2} \wedge \beta_{3} \wedge \beta_{4} , & \; 4\beta_{1} \wedge \beta_{2} \wedge \beta_{4} , \\ 2\beta_{1} \wedge \beta_{3} \wedge \beta_{4} +2\beta_{2} \wedge \beta_{3} \wedge \beta_{4} , & 4\beta_{2} \wedge \beta_{3} \wedge \beta_{4}. \end{array} \end{align*} $$

The code may be found in the github repositoryhttps://github.com/dcorey2814/ceresaZharkovClassOne readily verifies that $\mathbf {w}_{\tau }(\Gamma ) = -2\beta _{1} \wedge \beta _{2} \wedge \beta _{3} -2 \beta _{1} \wedge \beta _{2} \wedge \beta _{4} $ and $\mathbf {w}_{\tau }(\Gamma )$ is not in the $\mathbb {Z}$ -span of the vectors listed above. So $L_3$ is not Ceresa–Zharkov trivial.

Lemma 5.10. Suppose G is a graph with a minor $G'$ obtained by adding (parallel) edges to the complete graph $K_m$ . Then there are edges $S_1\subset E(G)$ and $S_2 \subset E(G/S_1)$ such that $(G/S_1) \setminus S_2$ is $G'$ , and every edge in $S_2$ is either a loop or parallel to another edge in $G/S_1$ .

Proof. The order in which edges are contracted or removed does not matter when forming a graph minor, so suppose $G' = (G/S_1) \setminus S_2$ . As contracting an edge drops the number of vertices by one and removing an edge preserves the number of vertices, we have that $V(G/S_1) = V(G')$ . As there is an edge between any two vertices in $G'$ , every edge in $S_1$ must be either a loop or parallel to some other edge.

Theorem 5.11. A connected graph G is Ceresa–Zharkov trivial if and only if it is of hyperelliptic type.

Proof. Suppose G is not of hyperelliptic type. By [9, Theorem 1.1], G has a $K_4$ or $L_3$ minor. By Lemma 5.10, there are subsets $S_1\subset E(G)$ and $S_2\subset E(G/S_1)$ such that $(G/S_1) \setminus S_2$ is $K_4$ or $L_3$ , and every edge of $S_2$ is a loop or parallel to another edge in $G/S_1$ . The graph $(G/S_1) \setminus S_2$ is not Ceresa–Zharkov trivial by Propositions 5.7 and 5.9. So $(G/S_1)$ is not Ceresa–Zharkov trivial by Propositions 5.1 and 5.5, and therefore G is not Ceresa–Zharkov trivial by Proposition 4.4.

For the converse, first suppose that G is of hyperelliptic type and 2-connected. By [9, Theorem 4.5], there is a $\tilde {G}$ that is strongly of hyperelliptic type such that $G = \tilde {G}/S$ for some subset $S\subset E(G)$ . The graph $\tilde {G}$ is Ceresa–Zharkov trivial by Proposition 5.6, and therefore so is G by Proposition 4.4.

In general, if G is of hyperelliptic type, then its 2-connected components are of hyperelliptic type, and hence Ceresa–Zharkov trivial. The graph G is Ceresa–Zharkov trivial by Proposition 5.5.

Corollary 5.12. The property of being Ceresa–Zharkov trivial is a minor closed condition on graphs.

Proof. This follows from Theorem 5.11 and the fact that being of hyperelliptic type is a minor closed condition on graphs [9, Proposition 3.8].