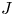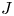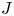1. Introduction
A basic requirement for magnetic fusion devices is the ability to confine collisionless particle orbits, a property which not all stellarators possess. Although the existence of nested magnetic surface is sufficient to confine circulating (untrapped) particle orbits to lowest order in the smallness of the gyroradius (Helander Reference Helander2014), particles that are trapped in local minima along the magnetic field tend to drift out of the plasma unless the field is carefully tailored to avoid this phenomenon.
If we write the magnetic field in Clebsch form (D'haeseleer et al. Reference D'haeseleer, Hitchon, Callen and Shohet2012), $\boldsymbol {B} = \boldsymbol {\nabla } \psi \times \boldsymbol {\nabla } \alpha$![]() , then the coordinates $(\psi,\alpha )$
, then the coordinates $(\psi,\alpha )$![]() are constant along $\boldsymbol {B}$
are constant along $\boldsymbol {B}$![]() and can thus be used to label field lines. In a field tracing out toroidal magnetic surfaces, we take $\psi$
and can thus be used to label field lines. In a field tracing out toroidal magnetic surfaces, we take $\psi$![]() to be the magnetic flux enclosed by such a surface divided by $2 {\rm \pi}$
to be the magnetic flux enclosed by such a surface divided by $2 {\rm \pi}$![]() , and $\alpha \in [0,2{\rm \pi} ]$
, and $\alpha \in [0,2{\rm \pi} ]$![]() thus labels the different field lines on each surface. In Boozer coordinates $\alpha = \theta - \iota \varphi$
thus labels the different field lines on each surface. In Boozer coordinates $\alpha = \theta - \iota \varphi$![]() , where $\theta$
, where $\theta$![]() denotes the poloidal angle, $\varphi$
denotes the poloidal angle, $\varphi$![]() the toroidal angle, and $\iota (\psi )$
the toroidal angle, and $\iota (\psi )$![]() the rotational transform (Boozer Reference Boozer1981).
the rotational transform (Boozer Reference Boozer1981).
As a trapped particle drifts across the field, the second adiabatic invariant (Hastie, Taylor & Haas Reference Hastie, Taylor and Haas1967)
is conserved to high accuracy if the gyroradius is small. Here, $m$![]() denotes the mass of the particle in question, $v_{\|} = v \sqrt {1-\lambda B}$
denotes the mass of the particle in question, $v_{\|} = v \sqrt {1-\lambda B}$![]() its speed along the magnetic-field line (if the electric field is sufficiently small) and $\ell$
its speed along the magnetic-field line (if the electric field is sufficiently small) and $\ell$![]() the arc length in this direction. The ratio of the magnetic moment to the kinetic energy is denoted by $\lambda = v_\perp ^2/(v^2 B)$
the arc length in this direction. The ratio of the magnetic moment to the kinetic energy is denoted by $\lambda = v_\perp ^2/(v^2 B)$![]() , where $B$
, where $B$![]() is the field strength, and the integration is carried out between two consecutive bounce points ($\ell _L$
is the field strength, and the integration is carried out between two consecutive bounce points ($\ell _L$![]() and $\ell _R$
and $\ell _R$![]() ) where $v_{\|}$
) where $v_{\|}$![]() vanishes.Footnote 1 Thus $\mathcal {J}_\|$
vanishes.Footnote 1 Thus $\mathcal {J}_\|$![]() is a function of the variables $(\psi,\alpha,v,\lambda )$
is a function of the variables $(\psi,\alpha,v,\lambda )$![]() .
.
The net cross-field magnetic drift of a magnetically trapped particle of charge $q$![]() travelling between two consecutive bounce points is given by the Hamiltonian equations (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1967; Helander Reference Helander2014)
travelling between two consecutive bounce points is given by the Hamiltonian equations (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1967; Helander Reference Helander2014)
In particular, the particle remains in the vicinity of one flux surface if $\partial \mathcal {J}_{\|}/\partial \alpha = 0$![]() . Magnetic fields in which this property holds for all orbits are called omnigenous (Hall & McNamara Reference Hall and McNamara1975; Cary & Shasharina Reference Cary and Shasharina1997). The direction and magnitude with which particles precess within the surface is governed by $\partial \mathcal {J}_\parallel /\partial \psi$
. Magnetic fields in which this property holds for all orbits are called omnigenous (Hall & McNamara Reference Hall and McNamara1975; Cary & Shasharina Reference Cary and Shasharina1997). The direction and magnitude with which particles precess within the surface is governed by $\partial \mathcal {J}_\parallel /\partial \psi$![]() . It is convenient to define a precession frequency $\omega _{\alpha}$
. It is convenient to define a precession frequency $\omega _{\alpha}$![]()
where the bounce time is
Fields in which the precession frequency is negative for electrons (that is, $q \omega _{\alpha} > 0$![]() ) and thus opposed to the diamagnetic drift ($q\omega _\star = p'(\psi )/n<0$
) and thus opposed to the diamagnetic drift ($q\omega _\star = p'(\psi )/n<0$![]() ), so-called maximum-$J$
), so-called maximum-$J$![]() -configurations, have long been known to possess favourable stability properties for trapped-particle modes (Rosenbluth Reference Rosenbluth1968; Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander, Proll & Plunk Reference Helander, Proll and Plunk2013).
-configurations, have long been known to possess favourable stability properties for trapped-particle modes (Rosenbluth Reference Rosenbluth1968; Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander, Proll & Plunk Reference Helander, Proll and Plunk2013).
The maximum-$J$![]() property is additionally correlated with, but not identical to (Helander Reference Helander2014), the existence of a magnetic well (Greene Reference Greene1997), which is beneficial for magnetohydrodynamic (MHD) stability. This circumstance has to do with its relation to magnetic curvature. If the magnetic curvature vector is decomposed into components in the direction of $\boldsymbol {\nabla } \psi$
property is additionally correlated with, but not identical to (Helander Reference Helander2014), the existence of a magnetic well (Greene Reference Greene1997), which is beneficial for magnetohydrodynamic (MHD) stability. This circumstance has to do with its relation to magnetic curvature. If the magnetic curvature vector is decomposed into components in the direction of $\boldsymbol {\nabla } \psi$![]() and $\boldsymbol {\nabla } \alpha$
and $\boldsymbol {\nabla } \alpha$![]()
then a positive value of $\kappa _\psi$![]() is referred to as favourable (or ‘good’) curvature. Since the guiding-centre curvature drift is in the direction $\boldsymbol {b} \times \boldsymbol {\kappa }$
is referred to as favourable (or ‘good’) curvature. Since the guiding-centre curvature drift is in the direction $\boldsymbol {b} \times \boldsymbol {\kappa }$![]() and
and
good curvature is clearly correlated with the maximum-$J$![]() property. Indeed, the latter can be interpreted as the condition that a certain average of the normal curvature should be favourable for all trapped-particle orbits.Footnote 2
property. Indeed, the latter can be interpreted as the condition that a certain average of the normal curvature should be favourable for all trapped-particle orbits.Footnote 2
The trapped particles in an omnigenous stellarator can precess in the poloidal, toroidal or helical directions, and if the precession is poloidal, the field is called quasi-isodynamic (QI) (Helander & Nührenberg Reference Helander and Nührenberg2009; Nührenberg Reference Nührenberg2010). This feature is determined by the topology of the contours of constant $|\boldsymbol {B}|$![]() . The aim of the present paper is to explore conditions under which a QI field may possess the maximum-$J$
. The aim of the present paper is to explore conditions under which a QI field may possess the maximum-$J$![]() -property. It has long been known that this can be the case at finite plasma $\beta$
-property. It has long been known that this can be the case at finite plasma $\beta$![]() (thermal pressure divided by magnetic pressure), very recently achieved at low values (Sánchez et al. Reference Sánchez, Velasco, Calvo and Mulas2023; Goodman et al. Reference Goodman2024) and, as we shall see, it is also possible (to a very good approximation) when $\beta$
(thermal pressure divided by magnetic pressure), very recently achieved at low values (Sánchez et al. Reference Sánchez, Velasco, Calvo and Mulas2023; Goodman et al. Reference Goodman2024) and, as we shall see, it is also possible (to a very good approximation) when $\beta$![]() vanishes. This is in stark contrast to quasisymmetric magnetic fields (including tokamaks), where the maximum-$J$
vanishes. This is in stark contrast to quasisymmetric magnetic fields (including tokamaks), where the maximum-$J$![]() -property is unattainable, at least in a region near the magnetic axis. If the maximum-$J$
-property is unattainable, at least in a region near the magnetic axis. If the maximum-$J$![]() condition is satisfied for some, but not all, particle orbits, then ${\partial \mathcal {J}_{\|}}/{\partial \psi }$
condition is satisfied for some, but not all, particle orbits, then ${\partial \mathcal {J}_{\|}}/{\partial \psi }$![]() must vanish for certain orbits, meaning they will not precess poloidally but drift in the radial direction, resulting in super-banana (Velasco et al. Reference Velasco, Calvo, Mulas, Sánchez, Parra and Cappa2021) or banana-drift convective (Paul et al. Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022) losses. It is clearly preferable that all orbits satisfy the maximum-$J$
must vanish for certain orbits, meaning they will not precess poloidally but drift in the radial direction, resulting in super-banana (Velasco et al. Reference Velasco, Calvo, Mulas, Sánchez, Parra and Cappa2021) or banana-drift convective (Paul et al. Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022) losses. It is clearly preferable that all orbits satisfy the maximum-$J$![]() condition.
condition.
Quasi-isodynamic stellarators are sometimes referred to as a system of linked mirrors (Boozer Reference Boozer1998). Following this analogy, the maximum-$J$![]() -condition can be seen to be closely related to the so-called minimum-$B$
-condition can be seen to be closely related to the so-called minimum-$B$![]() property in magnetic mirrors, which was proposed in the early 1960s (Taylor Reference Taylor1963). To see why, consider particles trapped in the vicinity of a local minimum, $B_{\rm min}(\psi )$
property in magnetic mirrors, which was proposed in the early 1960s (Taylor Reference Taylor1963). To see why, consider particles trapped in the vicinity of a local minimum, $B_{\rm min}(\psi )$![]() . Since
. Since

it follows that the maximum-$J$![]() -property requires
-property requires
at the field minimum. In other words, $B_{\rm min}$![]() increases with radius and the magnetic field strength assumes a global minimum on the magnetic axis of a maximum-$J$
increases with radius and the magnetic field strength assumes a global minimum on the magnetic axis of a maximum-$J$![]() stellarator (Helander Reference Helander2014). In the vicinity of this minimum, the surfaces of constant field strength are ellipsoids aligned with the magnetic field.
stellarator (Helander Reference Helander2014). In the vicinity of this minimum, the surfaces of constant field strength are ellipsoids aligned with the magnetic field.
In the following sections, we explore these ideas further and derive conditions for attaining the maximum-$J$![]() -condition, focusing particularly on deeply trapped particles close to the magnetic axis.
-condition, focusing particularly on deeply trapped particles close to the magnetic axis.
2. Trapped-particle precession
A derivation of the general expression for the precession frequency of trapped particles in an arbitrary stellarator is presented in Appendix A. The result is expressed as an integral along the magnetic field between two consecutive bounce points ($\varphi _L$![]() and $\varphi _R$
and $\varphi _R$![]() ), which in Boozer coordinates becomes
), which in Boozer coordinates becomes

For simplicity, we have assumed that the net toroidal plasma current enclosed by the magnetic surface under consideration vanishes, $I(\psi )=0$![]() .
.
In (2.1) there are two separate terms contributing to the precession: the radial derivative of $B=|\boldsymbol {B}|$![]() and the pressure gradient $p'$
and the pressure gradient $p'$![]() , which is negative for typical pressure profiles.Footnote 3 However, it would be wrong to conclude that a non-zero pressure gradient only affects the precession frequency through the explicit pressure term in (2.1). This naïve interpretation would imply that a negative pressure gradient tends to make $q\omega _{\alpha}$
, which is negative for typical pressure profiles.Footnote 3 However, it would be wrong to conclude that a non-zero pressure gradient only affects the precession frequency through the explicit pressure term in (2.1). This naïve interpretation would imply that a negative pressure gradient tends to make $q\omega _{\alpha}$![]() more negative and thus oppose the maximum-$J$
more negative and thus oppose the maximum-$J$![]() condition. However, the radial derivative of $|\boldsymbol {B}|$
condition. However, the radial derivative of $|\boldsymbol {B}|$![]() depends on the pressure profile in an equilibrium field, as the magnetic pressure responds to the change in thermal pressure. If the central plasma $\beta$
depends on the pressure profile in an equilibrium field, as the magnetic pressure responds to the change in thermal pressure. If the central plasma $\beta$![]() is increased, the magnetic-field strength usually drops in the centre of the plasma to hold the plasma in place, and $\partial _\psi B$
is increased, the magnetic-field strength usually drops in the centre of the plasma to hold the plasma in place, and $\partial _\psi B$![]() thus grows. The net result turns out, in practice, to make the maximum-$J$
thus grows. The net result turns out, in practice, to make the maximum-$J$![]() condition much easier to attain at high plasma beta compared with the case of a vacuum field. It is thus important to address the question of how $\partial _\psi B$
condition much easier to attain at high plasma beta compared with the case of a vacuum field. It is thus important to address the question of how $\partial _\psi B$![]() depends on the pressure, which we shall consider later.
depends on the pressure, which we shall consider later.
In general, $\omega _{\alpha}$![]() is a function, for each trapping well, of the pitch-angle parameter $\lambda$
is a function, for each trapping well, of the pitch-angle parameter $\lambda$![]() , the flux-surface label $\psi$
, the flux-surface label $\psi$![]() and the field-line label $\alpha$
and the field-line label $\alpha$![]() . The dependence on $\alpha$
. The dependence on $\alpha$![]() is present only when the field is not omnigeneous. Then the second adiabatic invariant depends on $\alpha$
is present only when the field is not omnigeneous. Then the second adiabatic invariant depends on $\alpha$![]() , and, as a result, the precession frequency of trapped particles varies as they drift from field line to field line. Numerical examples are shown in figure 1, where the normalised precession frequency
, and, as a result, the precession frequency of trapped particles varies as they drift from field line to field line. Numerical examples are shown in figure 1, where the normalised precession frequency
is displayed for three different numerically optimised QI fields (Goodman et al. Reference Goodman, Camacho Mata, Henneberg, Jorge, Landreman, Plunk, Smith, Mackenbach, Beidler and Helander2023). Here, $\psi _a$![]() denotes the value of $\psi$
denotes the value of $\psi$![]() at the plasma boundary and $\hat \omega _{\alpha}$
at the plasma boundary and $\hat \omega _{\alpha}$![]() has been plotted as a function of the trapping parameter (Roach, Connor & Janjua Reference Roach, Connor and Janjua1995)
has been plotted as a function of the trapping parameter (Roach, Connor & Janjua Reference Roach, Connor and Janjua1995)
As discussed below, the magnitude of $\hat {\omega }_{\alpha}$![]() can be interpreted as the precession frequency (for thermal particles) divided by the diamagnetic frequency (within a factor of order unity). The grey lines correspond to field lines on the same flux surface with different values of $\alpha$
can be interpreted as the precession frequency (for thermal particles) divided by the diamagnetic frequency (within a factor of order unity). The grey lines correspond to field lines on the same flux surface with different values of $\alpha$![]() . The fact that these lines are different from each other is an indication of departure from exact omnigeneity. For most of the discussion to follow, we shall assume, unless otherwise stated, that the field is omnigeneous. We may then choose any field line to compute the bounce average (1.7) of $\partial _\psi B$
. The fact that these lines are different from each other is an indication of departure from exact omnigeneity. For most of the discussion to follow, we shall assume, unless otherwise stated, that the field is omnigeneous. We may then choose any field line to compute the bounce average (1.7) of $\partial _\psi B$![]() , or alternatively its Boozer form in (2.1). In a vacuum field with $p'(\psi ) = 0$
, or alternatively its Boozer form in (2.1). In a vacuum field with $p'(\psi ) = 0$![]() , these integrals are weighted averages of $\partial _\psi B$
, these integrals are weighted averages of $\partial _\psi B$![]() , where the weight is positive for all trapped particles (i.e. all $\lambda$
, where the weight is positive for all trapped particles (i.e. all $\lambda$![]() ). It thus follows that the so-called minimum-$B$
). It thus follows that the so-called minimum-$B$![]() condition, $\partial _\psi B>0$
condition, $\partial _\psi B>0$![]() , is a sufficient condition for maximum-$J$
, is a sufficient condition for maximum-$J$![]() behaviour.
behaviour.

Figure 1. Example of precession in highly QI fields. Normalised precession frequency $\hat {\omega }_{\alpha}$![]() , (2.2), as a function of the trapping parameter $k^2$
, (2.2), as a function of the trapping parameter $k^2$![]() , (2.3), for three recently optimised QI configurations with different number of field periods $N$
, (2.3), for three recently optimised QI configurations with different number of field periods $N$![]() (Goodman et al. Reference Goodman, Camacho Mata, Henneberg, Jorge, Landreman, Plunk, Smith, Mackenbach, Beidler and Helander2023), in which omnigeneity is attained to a high degree. For each configuration, $\hat {\omega }_{\alpha}$
(Goodman et al. Reference Goodman, Camacho Mata, Henneberg, Jorge, Landreman, Plunk, Smith, Mackenbach, Beidler and Helander2023), in which omnigeneity is attained to a high degree. For each configuration, $\hat {\omega }_{\alpha}$![]() is displayed at two values of the normalised radial flux coordinate $\varrho$
is displayed at two values of the normalised radial flux coordinate $\varrho$![]() on a number of different field lines (grey curves), with the black curve representing $\alpha =0$
on a number of different field lines (grey curves), with the black curve representing $\alpha =0$![]() . A positive value of $\hat {\omega }_{\alpha}$
. A positive value of $\hat {\omega }_{\alpha}$![]() corresponds to the maximum-$J$
corresponds to the maximum-$J$![]() -property. Note that deeply trapped particles ($k^2 \rightarrow 0$
-property. Note that deeply trapped particles ($k^2 \rightarrow 0$![]() ) tend to behave worse than barely trapped ones, and the intermediate population can exhibit non-monotonic dependence on $k^2$
) tend to behave worse than barely trapped ones, and the intermediate population can exhibit non-monotonic dependence on $k^2$![]() .
.
2.1. Necessary conditions: special points
It is, however, not necessary to make $\partial _\psi B>0$![]() everywhere in order to attain the maximum-$J$
everywhere in order to attain the maximum-$J$![]() condition. Even if $\partial _\psi B < 0$
condition. Even if $\partial _\psi B < 0$![]() at certain positions along the field line, the average precession can still be favourable. The condition $\partial _\psi B>0$
at certain positions along the field line, the average precession can still be favourable. The condition $\partial _\psi B>0$![]() must nevertheless be satisfied at all local minima and maxima of $|\boldsymbol {B}|$
must nevertheless be satisfied at all local minima and maxima of $|\boldsymbol {B}|$![]() along the field line. At these points, deeply and barely trapped particles spend nearly all their time, other points along the orbit not contributing much to the average. It is therefore necessary, both at the bottom and top of every magnetic well, that $\partial _\psi B|_{\alpha,\varphi }>0$
along the field line. At these points, deeply and barely trapped particles spend nearly all their time, other points along the orbit not contributing much to the average. It is therefore necessary, both at the bottom and top of every magnetic well, that $\partial _\psi B|_{\alpha,\varphi }>0$![]() , even if $p'\neq 0$
, even if $p'\neq 0$![]() .
.
This result may be formally derived as the appropriate limits of (2.1), but a simpler argument has already been given in § 1: since the time required for a trapped particle to move from one bounce point to the next is equal to
the precession frequency for deeply trapped particles, for which $1-\lambda B \ll 1$![]() , becomes
, becomes
Since $\partial B/\partial \ell = 0$![]() at the point of minimum field strength, the derivative $\partial B / \partial \psi$
at the point of minimum field strength, the derivative $\partial B / \partial \psi$![]() can equally well be computed at constant Boozer angles $(\theta,\varphi )$
can equally well be computed at constant Boozer angles $(\theta,\varphi )$![]() for an omnigeneous stellarator. A similar argument holds for barely trapped particles. A more detailed discussion can be found in Appendix A, including a proof that the explicit pressure term does not contribute, (A10).
for an omnigeneous stellarator. A similar argument holds for barely trapped particles. A more detailed discussion can be found in Appendix A, including a proof that the explicit pressure term does not contribute, (A10).
Thus, if the minimum-$B$![]() -condition is satisfied at all local maxima and minima of $B$
-condition is satisfied at all local maxima and minima of $B$![]() along the field line, i.e. if
along the field line, i.e. if
then deeply and barely trapped particles are guaranteed to precess in the desired direction ($q \omega _{\alpha} > 0$![]() ). The recently proposed ‘flat-mirror’ criterion (Velasco et al. Reference Velasco, Calvo, Sánchez and Parra2023) can be re-interpreted as a condition like that in (2.6a,b). It would, however, be wrong to infer that all particles trapped at intermediate depths in the magnetic wells then precess in the same direction. Such a conclusion cannot be drawn by solely considering the radial gradient of $B$
). The recently proposed ‘flat-mirror’ criterion (Velasco et al. Reference Velasco, Calvo, Sánchez and Parra2023) can be re-interpreted as a condition like that in (2.6a,b). It would, however, be wrong to infer that all particles trapped at intermediate depths in the magnetic wells then precess in the same direction. Such a conclusion cannot be drawn by solely considering the radial gradient of $B$![]() at its extrema along the field. The conditions in (2.6a,b) are necessary for maximum-$J$
at its extrema along the field. The conditions in (2.6a,b) are necessary for maximum-$J$![]() , but not sufficient. Enforcing them as part of an optimisation effort may be helpful, but does not guarantee the maximum-$J$
, but not sufficient. Enforcing them as part of an optimisation effort may be helpful, but does not guarantee the maximum-$J$![]() behaviour everywhere.
behaviour everywhere.
This inference is, however, possible under additional assumptions about $|\boldsymbol {B}|$![]() . Obviously, if $\partial _\psi B$
. Obviously, if $\partial _\psi B$![]() were bounded from below by either of the local $|\boldsymbol {B}|$
were bounded from below by either of the local $|\boldsymbol {B}|$![]() gradients, then (2.6a,b) would become a necessary and sufficient criterion. One scenario in which this holds true is when the shape of the magnetic well along field lines behaves ‘rigidly.’ That is, in going from one surface to another, $|\boldsymbol {B}|=B_0(\psi )+\eta (\psi )f(\ell )$
gradients, then (2.6a,b) would become a necessary and sufficient criterion. One scenario in which this holds true is when the shape of the magnetic well along field lines behaves ‘rigidly.’ That is, in going from one surface to another, $|\boldsymbol {B}|=B_0(\psi )+\eta (\psi )f(\ell )$![]() along field lines. A particularly enlightening example is that of a sinusoidal variation along one field line, $|B|=B_{00}+B_M\cos \varphi$
along field lines. A particularly enlightening example is that of a sinusoidal variation along one field line, $|B|=B_{00}+B_M\cos \varphi$![]() , treated in Velasco et al. (Reference Velasco, Calvo, Sánchez and Parra2023). In general, however, the behaviour of $\partial _\psi B$
, treated in Velasco et al. (Reference Velasco, Calvo, Sánchez and Parra2023). In general, however, the behaviour of $\partial _\psi B$![]() , and thus $\omega _{\alpha}$
, and thus $\omega _{\alpha}$![]() , can be rather complicated. Figure 1 shows a recently published example of omnigeneity-optimised QI stellarators, where the behaviour at $k=(0,1)$
, can be rather complicated. Figure 1 shows a recently published example of omnigeneity-optimised QI stellarators, where the behaviour at $k=(0,1)$![]() (deeply and barely trapped particles respectively) are not always good indicators for intermediate particles. Nevertheless, given the simplicity and necessary nature of the condition in (2.6a,b), we shall use it as a representative feature of the maximum-$J$
(deeply and barely trapped particles respectively) are not always good indicators for intermediate particles. Nevertheless, given the simplicity and necessary nature of the condition in (2.6a,b), we shall use it as a representative feature of the maximum-$J$![]() -condition, and extend it to more global considerations.
-condition, and extend it to more global considerations.
2.2. Quasi-isodynamic fields
The treatment so far has considered little information about the magnetic field other than properties that follow directly from the requirements of the MHD equilibrium and omnigeneity. In the interest of describing the particulars of QI fields, however, we introduce to the discussion features unique to this class of stellarators. To do so, and to further simplify the discussion, we focus our attention to the vicinity of the magnetic axis.
By expansion in the minor-radius coordinate $r = \sqrt {2 \psi / \bar B}$![]() , where $\bar B$
, where $\bar B$![]() is some reference magnetic-field strength, which we choose to be equal to that at the minimum, to second order the magnetic-field magnitude may be written in the following form:
is some reference magnetic-field strength, which we choose to be equal to that at the minimum, to second order the magnetic-field magnitude may be written in the following form:
where, as shown in Appendix A, the coefficients satisfy the following relation in an exactly QI stellarator-symmetric field (Rodríguez & Plunk Reference Rodríguez and Plunk2023):
Here, $B_0(\varphi )$![]() and $B_{20}(\varphi )$
and $B_{20}(\varphi )$![]() are even in $\varphi$
are even in $\varphi$![]() whereas $d(\varphi )$
whereas $d(\varphi )$![]() and $B_{2s}(\varphi )$
and $B_{2s}(\varphi )$![]() are odd, if we choose the angle $\varphi$
are odd, if we choose the angle $\varphi$![]() to vanish at the point where $B_0(\varphi )$
to vanish at the point where $B_0(\varphi )$![]() attains its minimum. As a result, the first-order term $B_1$
attains its minimum. As a result, the first-order term $B_1$![]() vanishes at the minimum, and the precession frequency (2.5) for the most deeply trapped particles, being proportional to $\partial B/\partial \psi$
vanishes at the minimum, and the precession frequency (2.5) for the most deeply trapped particles, being proportional to $\partial B/\partial \psi$![]() , is determined by the second-order term $B_2$
, is determined by the second-order term $B_2$![]() . It becomes
. It becomes

where everything is evaluated at the minimum, $\varphi = 0$![]() , the primes denote a derivative with respect to the toroidal angle $\varphi$
, the primes denote a derivative with respect to the toroidal angle $\varphi$![]() , and $\omega _{\alpha }^{\text {non-QI}}$
, and $\omega _{\alpha }^{\text {non-QI}}$![]() represents the contribution from deviations from omnigeneity, which will be discussed later. To achieve $q\omega _{\alpha} >0$
represents the contribution from deviations from omnigeneity, which will be discussed later. To achieve $q\omega _{\alpha} >0$![]() , the magnetic field must be carefully tailored in such a way that for deeply trapped particles the quantity in the square brackets of (2.9) is positive. As we shall see, this is eminently possible but requires careful consideration of the terms within the square brackets.
, the magnetic field must be carefully tailored in such a way that for deeply trapped particles the quantity in the square brackets of (2.9) is positive. As we shall see, this is eminently possible but requires careful consideration of the terms within the square brackets.
As shown explicitly in Appendix B, (A25), departures from the condition of omnigeneity lead to additional terms in the expression for precession, here denoted by $\omega _{\alpha }^{\text {non-QI}}$![]() . These contributions may be interpreted as non-intrinsic contributions due to departures from QI. Breaking omnigeneity at first order in $r$
. These contributions may be interpreted as non-intrinsic contributions due to departures from QI. Breaking omnigeneity at first order in $r$![]() leads to a contribution that scales as $\omega _{\alpha,-1}^{\text {non-QI}}\propto \cos \alpha /r$
leads to a contribution that scales as $\omega _{\alpha,-1}^{\text {non-QI}}\propto \cos \alpha /r$![]() , (A24), while deviations at second order lead to $\omega _{\alpha,0}^{\text {non-QI}}\propto \cos 2\alpha$
, (A24), while deviations at second order lead to $\omega _{\alpha,0}^{\text {non-QI}}\propto \cos 2\alpha$![]() , (A25). Because of the dependence on $\alpha$
, (A25). Because of the dependence on $\alpha$![]() , there always exists a field line on which the non-omnigeneous contribution is $q\omega _{\alpha} ^{\text {non-QI}}<0$
, there always exists a field line on which the non-omnigeneous contribution is $q\omega _{\alpha} ^{\text {non-QI}}<0$![]() , i.e. detrimental to the maximum-$J$
, i.e. detrimental to the maximum-$J$![]() condition. The deviations that arise at first order are particularly worrying near the magnetic axis due to the $1/r$
condition. The deviations that arise at first order are particularly worrying near the magnetic axis due to the $1/r$![]() scaling. We explain the origin of this behaviour in the following subsection. From the forms above we may nevertheless conclude that omnigeneity is necessary for the maximum-$J$
scaling. We explain the origin of this behaviour in the following subsection. From the forms above we may nevertheless conclude that omnigeneity is necessary for the maximum-$J$![]() property.
property.
2.3. Comparison with quasisymmetric fields
Trapped-particle precession in a QI field is markedly different from that in quasisymmetric (QS) configurations, the other important class of optimised stellarators. Particle orbits in the latter are similar to those in tokamaks, and the maximum-$J$![]() property cannot be satisfied throughout the volume for all particle classes. In fact, close to the magnetic axis, the magnetic-field strength in any QS field (characterised by the helicity of the symmetry $N$
property cannot be satisfied throughout the volume for all particle classes. In fact, close to the magnetic axis, the magnetic-field strength in any QS field (characterised by the helicity of the symmetry $N$![]() ) is (Garren & Boozer Reference Garren and Boozer1991a; Landreman & Sengupta Reference Landreman and Sengupta2019)
) is (Garren & Boozer Reference Garren and Boozer1991a; Landreman & Sengupta Reference Landreman and Sengupta2019)
and the precession frequency of trapped particles becomes (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1967; Helander & Sigmar Reference Helander and Sigmar2005; Rodríguez & Mackenbach Reference Rodríguez and Mackenbach2023)
where $E$![]() and $K$
and $K$![]() denote elliptic integrals of the first and second kinds (Olver et al. Reference Olver, Daalhuis, Lozier, Schneider, Boisvert, Clark, Mille, Saunders, Cohl and McClain2020, § 19). Their argument is defined by $k=\sin (\chi _b/2)$
denote elliptic integrals of the first and second kinds (Olver et al. Reference Olver, Daalhuis, Lozier, Schneider, Boisvert, Clark, Mille, Saunders, Cohl and McClain2020, § 19). Their argument is defined by $k=\sin (\chi _b/2)$![]() , where $\chi _b$
, where $\chi _b$![]() is the bounce point in the well, so that $k=0$
is the bounce point in the well, so that $k=0$![]() refers to deeply trapped particles and $k=1$
refers to deeply trapped particles and $k=1$![]() to the trapped–passing boundary. This definition matches (2.3) to leading order. We present a plot of the behaviour in QS configurations in figure 2.
to the trapped–passing boundary. This definition matches (2.3) to leading order. We present a plot of the behaviour in QS configurations in figure 2.

Figure 2. Precession in zero-$\beta$![]() tokamaks and QS stellarators. Panel (a) shows the predicted dependence of the leading-order precession frequency in a tokamak or QS stellarator as a function of the trapping parameter, $k$
tokamaks and QS stellarators. Panel (a) shows the predicted dependence of the leading-order precession frequency in a tokamak or QS stellarator as a function of the trapping parameter, $k$![]() , (2.11). Panels (b,c) show the precession frequency on the boundary of actual QS vacuum configurations (Landreman & Paul Reference Landreman and Paul2022), normalised as in (2.2) (see Rodríguez & Mackenbach (Reference Rodríguez and Mackenbach2023) for more details and discussion). As in figure 1, the plots on the right show the variation with field line label $\alpha$
, (2.11). Panels (b,c) show the precession frequency on the boundary of actual QS vacuum configurations (Landreman & Paul Reference Landreman and Paul2022), normalised as in (2.2) (see Rodríguez & Mackenbach (Reference Rodríguez and Mackenbach2023) for more details and discussion). As in figure 1, the plots on the right show the variation with field line label $\alpha$![]() , which is difficult to discern due to the high degree of quasisymmetry in these configurations.
, which is difficult to discern due to the high degree of quasisymmetry in these configurations.
To make the comparison with the QI case more explicit, we turn to the general expression for the precession frequency close to the magnetic axis given in (A20) and consider the limit in which the magnetic-field strength only varies slightly along the magnetic axis. Then trapped particles have $1-\lambda B \ll 1$![]() and (A20) reduces to
and (A20) reduces to
where
The precession frequency is thus proportional to a bounce average of the function $f(\varphi )$![]() between the two turning points. This expression reveals several important differences between the precession frequency in QI and QS stellarators (including tokamaks):
between the two turning points. This expression reveals several important differences between the precession frequency in QI and QS stellarators (including tokamaks):
(i) In a QS field the particle precession becomes ‘infinite’ (${\sim }1/r$
 ) as the magnetic axis is approached, whereas it remains finite in QI fields. This $1/r$
) as the magnetic axis is approached, whereas it remains finite in QI fields. This $1/r$ behaviour comes from a finite poloidal component of the curvature drift as the axis is approached. In a QI configuration, the curvature of the magnetic field vanishes at the minimum on the axis, eliminating this behaviour. In the QS case, deeply trapped particles reside in the bad-curvature region, and the normal curvature is even about the minimum of $B$
behaviour comes from a finite poloidal component of the curvature drift as the axis is approached. In a QI configuration, the curvature of the magnetic field vanishes at the minimum on the axis, eliminating this behaviour. In the QS case, deeply trapped particles reside in the bad-curvature region, and the normal curvature is even about the minimum of $B$ (see figure 2.10). This difference in behaviour follows directly from the difference in the topology of $|\boldsymbol {B}|$
(see figure 2.10). This difference in behaviour follows directly from the difference in the topology of $|\boldsymbol {B}|$ contours, and its implications on the order-$r$
contours, and its implications on the order-$r$ correction to $B_0$
correction to $B_0$ , (2.8) and (2.10). Formally, this difference in parity explains the leading-order cancellation of the precession in QI fields and the elimination of the $1/r$
, (2.8) and (2.10). Formally, this difference in parity explains the leading-order cancellation of the precession in QI fields and the elimination of the $1/r$ contribution. The cancellation ceases to be exact, however, whenever the field deviates from omnigeneity. In that event, there will always exist some $r_a$
contribution. The cancellation ceases to be exact, however, whenever the field deviates from omnigeneity. In that event, there will always exist some $r_a$ such that, for $r< r_a$
such that, for $r< r_a$ , the field ceases to satisfy the maximum-$J$
, the field ceases to satisfy the maximum-$J$ condition (see figure 6 for example). It is known that omnigeneity must be broken at first order near the tops of the magnetic well (Plunk, Landreman & Helander Reference Plunk, Landreman and Helander2019; Rodríguez & Plunk Reference Rodríguez and Plunk2023), which unavoidably leads to a small, but finite, $r_a$
condition (see figure 6 for example). It is known that omnigeneity must be broken at first order near the tops of the magnetic well (Plunk, Landreman & Helander Reference Plunk, Landreman and Helander2019; Rodríguez & Plunk Reference Rodríguez and Plunk2023), which unavoidably leads to a small, but finite, $r_a$ below which some fraction of trapped particles near the magnetic well tops are not maximum-$J$
below which some fraction of trapped particles near the magnetic well tops are not maximum-$J$ . We discuss this issue further in Appendix A.4, but shall otherwise make the assumption of exact omnigeneity, so that this term may be neglected.
. We discuss this issue further in Appendix A.4, but shall otherwise make the assumption of exact omnigeneity, so that this term may be neglected.(ii) In QS stellarators, the fraction of trapped particles decreases as one approaches the magnetic axis, as it is the first-order poloidal variation of the field strength that defines the trapping well. In QI stellarators, this is not the case and there remains a finite trapped population on axis. This difference is important close to the axis, where there is a region with so-called potato orbits (Helander & Sigmar Reference Helander and Sigmar2005; Rodríguez & Mackenbach Reference Rodríguez and Mackenbach2023) in QS stellarators where the thin-orbit approximation to $\mathcal {J}_\parallel$
 breaks down.
breaks down.(iii) In QS, it is always the case that there are trapped particles precessing in opposite directions. Deeply trapped particles precess as in a minimum-$J$
 field ($q \omega _{\alpha} < 0$
field ($q \omega _{\alpha} < 0$ ), while barely trapped ones do so in the opposite way. This is generally not the case in QI, where the function $f$
), while barely trapped ones do so in the opposite way. This is generally not the case in QI, where the function $f$ , (2.13), has more freedom than in the QS case. This stems from differences in the distribution of good and bad curvature about the minimum of $|\boldsymbol {B}|$
, (2.13), has more freedom than in the QS case. This stems from differences in the distribution of good and bad curvature about the minimum of $|\boldsymbol {B}|$ .
.
These conclusions hold rigorously on the magnetic axis and, by continuity, also in its vicinity. The differences in the behaviour of curvature can be seen to hold approximately true in practice, as is shown through two examples in figure 3. In addition, in the QS case it has been shown that the near-axis description remains instructive as a model of QS configurations beyond its asymptotic regime (see figure 2 and Rodríguez & Mackenbach Reference Rodríguez and Mackenbach2023).

Figure 3. Curvature about the minimum in a QS and QI field. The plots show a comparison of the curvature ($\boldsymbol {B}\times \kappa \boldsymbol {\cdot }\boldsymbol {\nabla }\alpha$![]() ) in (a) a quasiaxisymmetric (the precise QA in Landreman & Paul Reference Landreman and Paul2022) and (b) a quasi-isodynamic (the $N=2$
) in (a) a quasiaxisymmetric (the precise QA in Landreman & Paul Reference Landreman and Paul2022) and (b) a quasi-isodynamic (the $N=2$![]() configuration in Goodman et al. Reference Goodman, Camacho Mata, Henneberg, Jorge, Landreman, Plunk, Smith, Mackenbach, Beidler and Helander2023) configurations. Panels (a i,b i) show a three-dimensional rendition of the boundary of the configurations, in which the colours display the quantity $\boldsymbol {B}\times \kappa \boldsymbol {\cdot }\boldsymbol {\nabla }\alpha$
configuration in Goodman et al. Reference Goodman, Camacho Mata, Henneberg, Jorge, Landreman, Plunk, Smith, Mackenbach, Beidler and Helander2023) configurations. Panels (a i,b i) show a three-dimensional rendition of the boundary of the configurations, in which the colours display the quantity $\boldsymbol {B}\times \kappa \boldsymbol {\cdot }\boldsymbol {\nabla }\alpha$![]() , with blue/red representing negative/positive values (good/bad curvatures) respectively. Panels (a ii,iii,b ii,iii) show the magnetic field $|\boldsymbol {B}|$
, with blue/red representing negative/positive values (good/bad curvatures) respectively. Panels (a ii,iii,b ii,iii) show the magnetic field $|\boldsymbol {B}|$![]() and the curvature along the field line, using the cylindrical coordinate $\phi$
and the curvature along the field line, using the cylindrical coordinate $\phi$![]() and the PEST poloidal angle $\vartheta$
and the PEST poloidal angle $\vartheta$![]() as coordinates along the field line. The scatter plot indicates the position of the minimum. These two examples illustrate the qualitative difference in the curvature parity between a QI and a QS field.
as coordinates along the field line. The scatter plot indicates the position of the minimum. These two examples illustrate the qualitative difference in the curvature parity between a QI and a QS field.
The most important observation is that, in the context of QI configurations, maximum-$J$![]() behaviour appears possible even in a vacuum field. Within the near-axis framework, whether this is the case depends on the sign of the bounce average of the function $f(\varphi )$
behaviour appears possible even in a vacuum field. Within the near-axis framework, whether this is the case depends on the sign of the bounce average of the function $f(\varphi )$![]() , which is analysed below.
, which is analysed below.
2.4. Shallowly and deeply trapped particles in QI
The special character of the bottom and top of the magnetic well provides us with a simple way to assess the possibility of maximum-$J$![]() behaviour in QI stellarators.
behaviour in QI stellarators.
Satisfying the maximum-$J$![]() -condition for the most shallowly trapped particles tends to be easy in practice. These particles spend most of their time close to the turning point where the field strength reaches its maximum along the field line, $B(\psi, \alpha, \varphi ) = B_{\rm max}(\psi )$
-condition for the most shallowly trapped particles tends to be easy in practice. These particles spend most of their time close to the turning point where the field strength reaches its maximum along the field line, $B(\psi, \alpha, \varphi ) = B_{\rm max}(\psi )$![]() , which is independent of the field-line label $\alpha$
, which is independent of the field-line label $\alpha$![]() in a QI stellarator. Moreover, the maximum is located at a constant value of the toroidal Boozer angle, $\varphi = \varphi _{\rm max}$
in a QI stellarator. Moreover, the maximum is located at a constant value of the toroidal Boozer angle, $\varphi = \varphi _{\rm max}$![]() , which is independent of $\alpha$
, which is independent of $\alpha$![]() (Cary & Shasharina Reference Cary and Shasharina1997; Landreman & Catto Reference Landreman and Catto2012; Helander Reference Helander2014). At the maximum, the Taylor expansion of the field strength in the coordinates $\alpha$
(Cary & Shasharina Reference Cary and Shasharina1997; Landreman & Catto Reference Landreman and Catto2012; Helander Reference Helander2014). At the maximum, the Taylor expansion of the field strength in the coordinates $\alpha$![]() and $\varphi$
and $\varphi$![]() is thus of the form
is thus of the form
since, at the toroidal angle of the maximum, the following derivatives all vanish:
Therefore $\nabla ^2 B=\nabla ^2 B_{\mathrm {max}}+B_{\varphi \varphi }|\boldsymbol {\nabla }\varphi |^2+\cdots$![]() , where the second term is negative at the top of the well. Now, in a vacuum field (zero plasma pressure), the quantity $B^2=B_x^2 + B_y^2 + B_z^2$
, where the second term is negative at the top of the well. Now, in a vacuum field (zero plasma pressure), the quantity $B^2=B_x^2 + B_y^2 + B_z^2$![]() is a subharmonic function since
is a subharmonic function since
where we have used $\nabla ^2 B_x = 0$![]() etc. for each Cartesian component of $\boldsymbol {B}$
etc. for each Cartesian component of $\boldsymbol {B}$![]() (Solov'ev & Shafranov Reference Solov'ev and Shafranov1970). Because of the maximum principle for subharmonic functions, the maximum of $B^2$
(Solov'ev & Shafranov Reference Solov'ev and Shafranov1970). Because of the maximum principle for subharmonic functions, the maximum of $B^2$![]() over any closed, bounded domain cannot be attained in its interior unless $B^2$
over any closed, bounded domain cannot be attained in its interior unless $B^2$![]() is constant (Evans Reference Evans2022, Theorem 1, Chapter 6.4.1). It thus follows that the function $B_{\rm max} (\psi )$
is constant (Evans Reference Evans2022, Theorem 1, Chapter 6.4.1). It thus follows that the function $B_{\rm max} (\psi )$![]() in (2.14) cannot have a local maximum at any value of $\psi$
in (2.14) cannot have a local maximum at any value of $\psi$![]() . Therefore, $B_{\rm max}'(\psi )\geq 0$
. Therefore, $B_{\rm max}'(\psi )\geq 0$![]() for all $\psi$
for all $\psi$![]() and, following (2.6a,b), then shallowly trapped particles must satisfy the maximum-$J$
and, following (2.6a,b), then shallowly trapped particles must satisfy the maximum-$J$![]() -condition, $q\omega _{\alpha} > 0$
-condition, $q\omega _{\alpha} > 0$![]() , throughout the plasma.Footnote 4 It should be clear that this argument holds for any omnigenous magnetic configuration, including a QS stellarator.
, throughout the plasma.Footnote 4 It should be clear that this argument holds for any omnigenous magnetic configuration, including a QS stellarator.
The situation is very different at the opposite end of the trapped population. The most deeply trapped particles at the bottom of the well tend to precess in the unfavourable direction. Indeed, these particles frequently (though not always, see figure 1), have the smallest value of $q\omega _{\alpha}$![]() . The relevant question here is then whether this tendency be reversed to make the system acquire the maximum-$J$
. The relevant question here is then whether this tendency be reversed to make the system acquire the maximum-$J$![]() property at the bottom of the trapping well.
property at the bottom of the trapping well.
In order to understand the maximum-$J$![]() condition on deeply trapped particles, we resort to (2.9), which provides an explicit expression for $\omega _{\alpha}$
condition on deeply trapped particles, we resort to (2.9), which provides an explicit expression for $\omega _{\alpha}$![]() in terms of $B_{20}$
in terms of $B_{20}$![]() , $B_0$
, $B_0$![]() and $d$
and $d$![]() . The expressions at this point may be further simplified by realising that the curvature of the magnetic axis vanishes at the point of minimum $|\boldsymbol {B}|$
. The expressions at this point may be further simplified by realising that the curvature of the magnetic axis vanishes at the point of minimum $|\boldsymbol {B}|$![]() , i.e. $\kappa (\varphi ) = 0$
, i.e. $\kappa (\varphi ) = 0$![]() when $\varphi = 0$
when $\varphi = 0$![]() . As a result, the behaviour of $|\boldsymbol {B}|$
. As a result, the behaviour of $|\boldsymbol {B}|$![]() is significantly constrained. The field around this point thus resembles a straight magnetic mirror, and thus we can gain some intuition about QI fields by analysing a straight magnetic mirror, which is done in Appendix C.
is significantly constrained. The field around this point thus resembles a straight magnetic mirror, and thus we can gain some intuition about QI fields by analysing a straight magnetic mirror, which is done in Appendix C.
With these remarks in mind, we proceed to consider the governing set of equations in the near-axis framework. Formally, we explore the properties of a magnetic field in MHD equilibrium that satisfies the solenoidal condition, and possess flux surfaces at $\varphi =0$![]() . The analysis is presented in Appendix B, assuming perfect QI at first order for simplicity, and leads to an explicit form for the average radial derivative of the magnetic pressure ($B_{20}$
. The analysis is presented in Appendix B, assuming perfect QI at first order for simplicity, and leads to an explicit form for the average radial derivative of the magnetic pressure ($B_{20}$![]() ), which is primary ingredient of (2.9), explicitly constructed in (B4) in Appendix B. When the condition of omnigeneity at second order is also imposed (that is, the choice of functions is made so that QI is satisfied at the bottom of the well at second order), the function $f$
), which is primary ingredient of (2.9), explicitly constructed in (B4) in Appendix B. When the condition of omnigeneity at second order is also imposed (that is, the choice of functions is made so that QI is satisfied at the bottom of the well at second order), the function $f$![]() in (2.12) can be written in the following form:
in (2.12) can be written in the following form:
with

where $\bar {d}=d/\kappa$![]() and $\bar {\alpha }=\bar {d}^4B_0^2/\bar {B}^2$
and $\bar {\alpha }=\bar {d}^4B_0^2/\bar {B}^2$![]() is directly related to the elongation (along the direction of curvature) of the cross-section at the toroidal position $\varphi =0$
is directly related to the elongation (along the direction of curvature) of the cross-section at the toroidal position $\varphi =0$![]() . There are thus five different terms contributing to $f$
. There are thus five different terms contributing to $f$![]() , which we proceed to analyse individually.
, which we proceed to analyse individually.
2.4.1. Role of pressure
As expected, increasing the pressure gradient supported by the field, $|p_2|=(\bar {B}/2)|\mathrm {d}p/\mathrm {d}\psi |$![]() , increases $f_0$
, increases $f_0$![]() . That is, it makes deeply trapped particles more likely to satisfy the maximum-$J$
. That is, it makes deeply trapped particles more likely to satisfy the maximum-$J$![]() condition $q\omega _{\alpha} >0$
condition $q\omega _{\alpha} >0$![]() . This is the well-known effect of finite $\beta$
. This is the well-known effect of finite $\beta$![]() improving the maximum-$J$
improving the maximum-$J$![]() property of QI fields, which is precisely the opposite to the naïve interpretation of the role of the pressure from the explicit term in (2.1), which vanishes at the extremal points. This effect of $p'$
property of QI fields, which is precisely the opposite to the naïve interpretation of the role of the pressure from the explicit term in (2.1), which vanishes at the extremal points. This effect of $p'$![]() is the same at both the bottom and top of the well, thus bringing both deeply and barely trapped particles towards $q\omega _{\alpha} >0$
is the same at both the bottom and top of the well, thus bringing both deeply and barely trapped particles towards $q\omega _{\alpha} >0$![]() . To a large extent, then, we would expect the rest of the trapped population to do likewise, and although we cannot prove it, it is convenient to think of this effect as an overall upshift of $q\omega _{\alpha}$
. To a large extent, then, we would expect the rest of the trapped population to do likewise, and although we cannot prove it, it is convenient to think of this effect as an overall upshift of $q\omega _{\alpha}$![]() . This diamagnetic behaviour turns out to be the same in the axisymmetric/QS limit (Rosenbluth & Sloan Reference Rosenbluth and Sloan1971; Rodríguez & Mackenbach Reference Rodríguez and Mackenbach2023, equation (3.6a)). The positive role of pressure gradients is well known (Wobig Reference Wobig1993).
. This diamagnetic behaviour turns out to be the same in the axisymmetric/QS limit (Rosenbluth & Sloan Reference Rosenbluth and Sloan1971; Rodríguez & Mackenbach Reference Rodríguez and Mackenbach2023, equation (3.6a)). The positive role of pressure gradients is well known (Wobig Reference Wobig1993).
Whether a non-zero pressure gradient is needed to ensure $f_0>0$![]() depends on the relative size of the other terms in (2.18). At a minimum, we need to overcome the detrimental effect of being located at the minimum of the magnetic field, $f_{B_0''}$
depends on the relative size of the other terms in (2.18). At a minimum, we need to overcome the detrimental effect of being located at the minimum of the magnetic field, $f_{B_0''}$![]() . The plasma beta, $\beta _0 = 2 \mu _0 p_0 / B_0^2$
. The plasma beta, $\beta _0 = 2 \mu _0 p_0 / B_0^2$![]() , that neutralises this term, $|\,f_p|=|\,f_{B_0''}|$
, that neutralises this term, $|\,f_p|=|\,f_{B_0''}|$![]() , we define to be $\beta _J$
, we define to be $\beta _J$![]() and provides an estimate of the critical $\beta$
and provides an estimate of the critical $\beta$![]() that leads to maximum-$J$
that leads to maximum-$J$![]() behaviour. If we consider a simple quadratic pressure profile for a field with minor radius (defined as in the near axis) $r=a$
behaviour. If we consider a simple quadratic pressure profile for a field with minor radius (defined as in the near axis) $r=a$![]() , then $\mathrm {d}p/\mathrm {d}\psi \approx -2p_0/B_0 a^2$
, then $\mathrm {d}p/\mathrm {d}\psi \approx -2p_0/B_0 a^2$![]() , and thus $f_0>0$
, and thus $f_0>0$![]() when
when
and $R_M/L_B^2=\partial _{\ell \ell } \ln B_0$![]() , $R_M=(B_{\mathrm {max}}-B_{\mathrm {min}})/B_{\mathrm {min}}$
, $R_M=(B_{\mathrm {max}}-B_{\mathrm {min}})/B_{\mathrm {min}}$![]() is the mirror ratio and $L_B$
is the mirror ratio and $L_B$![]() the characteristic parallel length scale of the bottom of the well. For typical field parameters (a moderately elongated cross-section with $\bar {\alpha }\sim 1$
the characteristic parallel length scale of the bottom of the well. For typical field parameters (a moderately elongated cross-section with $\bar {\alpha }\sim 1$![]() , a well of the scale of the major radius, and $R_M\sim 0.2$
, a well of the scale of the major radius, and $R_M\sim 0.2$![]() ), we get critical plasma betas around (or below) a per cent. This suggests that maximum-$J$
), we get critical plasma betas around (or below) a per cent. This suggests that maximum-$J$![]() behaviour is readily achievable at a moderate plasma $\beta$
behaviour is readily achievable at a moderate plasma $\beta$![]() .
.
2.4.2. Difficulties at the minimum
The special character of the bottom of the well is captured by the $f_{B_0''}$![]() term, which is negative (since $B_0''>0$
term, which is negative (since $B_0''>0$![]() ) and thus opposes maximum-$J$
) and thus opposes maximum-$J$![]() behaviour. The situation is, however, reversed at the maximum of $B$
behaviour. The situation is, however, reversed at the maximum of $B$![]() , where $B_0''<0$
, where $B_0''<0$![]() and $f_{B_0''} > 0$
and $f_{B_0''} > 0$![]() , implying an ‘intrinsic’ tendency for maximum-$J$
, implying an ‘intrinsic’ tendency for maximum-$J$![]() behaviour at this location. In fact, in a vacuum field, $f_0>0$
behaviour at this location. In fact, in a vacuum field, $f_0>0$![]() , in agreement with the general proof presented in the previous sections.
, in agreement with the general proof presented in the previous sections.
The detrimental contribution of $f_{B_0''}$![]() at the bottom of the well can be mitigated by reducing $B_0''$
at the bottom of the well can be mitigated by reducing $B_0''$![]() to a minimum, i.e. by flattening the bottom of the well (increasing $L_B$
to a minimum, i.e. by flattening the bottom of the well (increasing $L_B$![]() ) or reducing the mirror ratio $R_M$
) or reducing the mirror ratio $R_M$![]() . The elongation of the flux surfaces may also be tweaked to reduce $f_{B_0''}$
. The elongation of the flux surfaces may also be tweaked to reduce $f_{B_0''}$![]() , which is maximal for circular cross-sections ($\bar {\alpha }=1$
, which is maximal for circular cross-sections ($\bar {\alpha }=1$![]() ). However, note that the other geometric contributions to $f_0$
). However, note that the other geometric contributions to $f_0$![]() , (2.18) also depend on the elongation, and thus in relative terms this shaping may not be as effective although it does reduce $\beta _J$
, (2.18) also depend on the elongation, and thus in relative terms this shaping may not be as effective although it does reduce $\beta _J$![]() .
.
Flattening the bottom of the well comes with potential drawbacks in the form of sensitivity to deviations from omnigeneity. Having an extended region of small $\partial B_0 / \partial l$![]() makes the configuration more susceptible to error fields, as secondary shallow trapping wells may be created by small perturbations. Such wells can be seen in the near-axis description of $|\boldsymbol {B}|$
makes the configuration more susceptible to error fields, as secondary shallow trapping wells may be created by small perturbations. Such wells can be seen in the near-axis description of $|\boldsymbol {B}|$![]() , where the requirement of omnigeneity (and more particularly, that of poloidally closed $B$
, where the requirement of omnigeneity (and more particularly, that of poloidally closed $B$![]() -contours) limits the behaviour of $B_1$
-contours) limits the behaviour of $B_1$![]() depending on how flat $B_0$
depending on how flat $B_0$![]() is. As analysed in detail in Rodríguez & Plunk (Reference Rodríguez and Plunk2023), for a field near the minimum described by $B_1\sim \varphi ^v$
is. As analysed in detail in Rodríguez & Plunk (Reference Rodríguez and Plunk2023), for a field near the minimum described by $B_1\sim \varphi ^v$![]() and $B_0'\sim \varphi ^{u-1}$
and $B_0'\sim \varphi ^{u-1}$![]() , if $B_0$
, if $B_0$![]() is too flat, $u\geq 2v$
is too flat, $u\geq 2v$![]() (except $u=2,~v=1$
(except $u=2,~v=1$![]() ), this will introduce defects in $|\boldsymbol {B}|$
), this will introduce defects in $|\boldsymbol {B}|$![]() that lead to losses of deeply trapped particles. In fields where this situation is avoided, that is, for $u<2v$
that lead to losses of deeply trapped particles. In fields where this situation is avoided, that is, for $u<2v$![]() , the quantity $f_{\mathrm {QI}}$
, the quantity $f_{\mathrm {QI}}$![]() vanishes, (2.18e). Only in the special case of a first-order curvature zero ($v=1$
vanishes, (2.18e). Only in the special case of a first-order curvature zero ($v=1$![]() ) and a quadratic well ($u=2$
) and a quadratic well ($u=2$![]() ) is this contribution finite. Because $d^2/B_0'$
) is this contribution finite. Because $d^2/B_0'$![]() vanishes at $\varphi =0$
vanishes at $\varphi =0$![]() and is positive for $\varphi >0$
and is positive for $\varphi >0$![]() , its derivative must be greater than or equal to zero. Hence, $f_{\mathrm {QI}}\leq 0$
, its derivative must be greater than or equal to zero. Hence, $f_{\mathrm {QI}}\leq 0$![]() at the bottom of the well; that is, its contribution is detrimental. This makes the ‘standard’ first-order curvature zero and quadratic-well field (Camacho Mata, Plunk & Jorge Reference Camacho Mata, Plunk and Jorge2022) particularly unfavourable for maximum-$J$
at the bottom of the well; that is, its contribution is detrimental. This makes the ‘standard’ first-order curvature zero and quadratic-well field (Camacho Mata, Plunk & Jorge Reference Camacho Mata, Plunk and Jorge2022) particularly unfavourable for maximum-$J$![]() behaviour. Conversely, making the section of the field where minimum $|\boldsymbol {B}|$
behaviour. Conversely, making the section of the field where minimum $|\boldsymbol {B}|$![]() is located as straight as possible (larger $u$
is located as straight as possible (larger $u$![]() and $v$
and $v$![]() ) should be beneficial (see figure 4).
) should be beneficial (see figure 4).

Figure 4. Schematic depiction of trapping wells that favour maximum-$J$![]() behaviour. Certain magnetic field features make them more prone to maximum-$J$
behaviour. Certain magnetic field features make them more prone to maximum-$J$![]() behaviour than others. In particular, wide and flat magnetic trapping wells (a) at straighter sections (b) of the stellarator favour maximum-$J$
behaviour than others. In particular, wide and flat magnetic trapping wells (a) at straighter sections (b) of the stellarator favour maximum-$J$![]() . The diagram on the right is a schematic top-down view on an $N=2$
. The diagram on the right is a schematic top-down view on an $N=2$![]() stellarator, with the shading denoting $|\boldsymbol {B}|$
stellarator, with the shading denoting $|\boldsymbol {B}|$![]() .
.
2.4.3. Role of local shear, twist and elongation
The contribution of the torsion of the axis to $f_0$![]() is always beneficial since $f_{\tau _0^2} > 0$
is always beneficial since $f_{\tau _0^2} > 0$![]() . In fact, the larger the torsion, the larger $f_0$
. In fact, the larger the torsion, the larger $f_0$![]() and, thus, the closer the behaviour of deeply trapped particles will be to the maximum-$J$
and, thus, the closer the behaviour of deeply trapped particles will be to the maximum-$J$![]() requirement. The role of torsion may be surprising, but is understandable from the perspective of a straight magnetic mirror. At the bottom of a straight magnetic mirror, attaining maximum-$J$
requirement. The role of torsion may be surprising, but is understandable from the perspective of a straight magnetic mirror. At the bottom of a straight magnetic mirror, attaining maximum-$J$![]() is only possible if magnetic-field lines are locally twisted (see Appendix C and (C18a)–(C18b)), i.e. if they experience some form of left–right asymmetry, and in this way possess non-zero local magnetic shear. In the context of our QI stellarator, the appearance of the $\tau _0^2$
is only possible if magnetic-field lines are locally twisted (see Appendix C and (C18a)–(C18b)), i.e. if they experience some form of left–right asymmetry, and in this way possess non-zero local magnetic shear. In the context of our QI stellarator, the appearance of the $\tau _0^2$![]() term is simply a statement of the necessity of this twist about the magnetic axis, which is the geometric meaning of torsion.
term is simply a statement of the necessity of this twist about the magnetic axis, which is the geometric meaning of torsion.
The comparison with a straight magnetic mirror is also helpful for understanding the role of flux-surface elongation, which in a mirror needs to increase away from the bottom of the magnetic well (see figure 11). In the context of a stellarator-symmetric QI stellarator, the elongation of the cross-section at the minimum is given by $\bar {d}^2$![]() , as previously mentioned. Thus, a change in elongation would be expected to involve a term proportional to $\bar {d}''$
, as previously mentioned. Thus, a change in elongation would be expected to involve a term proportional to $\bar {d}''$![]() .Footnote 5 There is no term in $f_0$
.Footnote 5 There is no term in $f_0$![]() which involves $\bar {d}''$
which involves $\bar {d}''$![]() , but this is a result of the condition of omnigeneity at second order. In fact, upon relaxing the latter, $B_{20}$
, but this is a result of the condition of omnigeneity at second order. In fact, upon relaxing the latter, $B_{20}$![]() at the bottom of the well does depend on $\bar {d}''$
at the bottom of the well does depend on $\bar {d}''$![]() , (B5), and it is only through the omnigeneity condition of (B9) that this explicit dependence can be eliminated. From the omnigeneity condition it follows that $\bar {d}\bar {d}''(1+1/\bar {\alpha })=-(\tau _0\bar {d}l')^2(3+1/\bar {\alpha })+\dots$
, (B5), and it is only through the omnigeneity condition of (B9) that this explicit dependence can be eliminated. From the omnigeneity condition it follows that $\bar {d}\bar {d}''(1+1/\bar {\alpha })=-(\tau _0\bar {d}l')^2(3+1/\bar {\alpha })+\dots$![]() , meaning that increasing the torsion to favour $f_{\tau _0^2}$
, meaning that increasing the torsion to favour $f_{\tau _0^2}$![]() , requires one to modify $\bar {d}''$
, requires one to modify $\bar {d}''$![]() accordingly. The plasma cross-section must become elongated in the binormal direction away from the bottom of the well, which is a consequence purely of the omnigeneity condition. Looking at the contribution of the $\bar {d}''$
accordingly. The plasma cross-section must become elongated in the binormal direction away from the bottom of the well, which is a consequence purely of the omnigeneity condition. Looking at the contribution of the $\bar {d}''$![]() term to the equilibrium equation of $B_{20}$
term to the equilibrium equation of $B_{20}$![]() , (B5), we see that $\bar {d}\bar {d}''(1-1/\bar {\alpha })>0$
, (B5), we see that $\bar {d}\bar {d}''(1-1/\bar {\alpha })>0$![]() promotes maximum-$J$
promotes maximum-$J$![]() behaviour there. Shaping of elongation is once again vital, now for attaining maximum-$J$
behaviour there. Shaping of elongation is once again vital, now for attaining maximum-$J$![]() . For this shaping to be synergistic between the omnigeneity condition and maximum-$J$
. For this shaping to be synergistic between the omnigeneity condition and maximum-$J$![]() , we need a binormally elongated cross-section $\bar {\alpha }<1$
, we need a binormally elongated cross-section $\bar {\alpha }<1$![]() (i.e. binormal elongation at the minimum, $|\bar {d}|<1$
(i.e. binormal elongation at the minimum, $|\bar {d}|<1$![]() ). In practice, we seek shapes like the exaggerated schematic in figure 5, features that appear to be common in many QI configurations (Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022; Jorge et al. Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho Mata and Helander2022).
). In practice, we seek shapes like the exaggerated schematic in figure 5, features that appear to be common in many QI configurations (Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022; Jorge et al. Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho Mata and Helander2022).

Figure 5. Prototypical shape of flux surfaces of an omnigeneous, maximum-$J$![]() field near the point of minimum field strength. Three-dimensional illustration of features generally expected from maximum-$J$
field near the point of minimum field strength. Three-dimensional illustration of features generally expected from maximum-$J$![]() , QI magnetic fields. Note that field lines twist and that the elongation grows with increasing distance from the field-strength minimum.
, QI magnetic fields. Note that field lines twist and that the elongation grows with increasing distance from the field-strength minimum.
Given the central role played by the local field-line twist, a non-zero plasma current can be either beneficial or detrimental depending on its alignment with the torsion of the axis. As can be inferred from its contribution to the rotational transform (Mercier & Luc Reference Mercier and Luc1974), a negative current acts constructively with a positive torsion (and vice versa). The term $f_{I_2}$![]() reflects precisely this fact. In QI configurations, toroidal currents tend to be small and this contribution may then be disregarded.
reflects precisely this fact. In QI configurations, toroidal currents tend to be small and this contribution may then be disregarded.
All in all, we learn from this analysis that in a vacuum magnetic field there is only one way of possibly attaining maximum-$J$![]() behaviour for deeply trapped particles, which is to have a large torsion at the point of minimum $B$
behaviour for deeply trapped particles, which is to have a large torsion at the point of minimum $B$![]() , in the sense that $\tau _0 L_{B}>\sqrt {R_M/2}$
, in the sense that $\tau _0 L_{B}>\sqrt {R_M/2}$![]() , and thereby also a strong growth of binormal elongation. In other words, the binormal vector must rotate significantly within the magnetic well. From this analysis, it follows that it is possible to make deeply trapped particles precess in the favourable maximum-$J$
, and thereby also a strong growth of binormal elongation. In other words, the binormal vector must rotate significantly within the magnetic well. From this analysis, it follows that it is possible to make deeply trapped particles precess in the favourable maximum-$J$![]() direction, unlike the case in quasi-symmetric or tokamak fields. This result is robust even if we acknowledge the impossibility of exact QI at first order in the near-axis expansion, because the violation of omnigeneity is only necessary near the maximum of $|\boldsymbol {B}|$
direction, unlike the case in quasi-symmetric or tokamak fields. This result is robust even if we acknowledge the impossibility of exact QI at first order in the near-axis expansion, because the violation of omnigeneity is only necessary near the maximum of $|\boldsymbol {B}|$![]() .
.
The construction above poses some important practical difficulties. First of all, the field will generally tend to develop large shaping, both because the maximum-$J$![]() criterion requires significant torsion and omnigeneity also an increase in elongation (see the depiction in figure 5). Comparing the various contributions with $f_0$
criterion requires significant torsion and omnigeneity also an increase in elongation (see the depiction in figure 5). Comparing the various contributions with $f_0$![]() in (2.18) reveals that the shaping needs to be specific and substantial to endow the deeply trapped particles with the maximum-$J$
in (2.18) reveals that the shaping needs to be specific and substantial to endow the deeply trapped particles with the maximum-$J$![]() property. If the shaping is constrained by practical considerations, as is usually the case in stellarator optimisation studies, the opportunity for attaining the maximum-$J$
property. If the shaping is constrained by practical considerations, as is usually the case in stellarator optimisation studies, the opportunity for attaining the maximum-$J$![]() property is correspondingly limited. How much shaping is sufficient varies from case to case, and the competition between the various field and geometric quantities (we shall recall that the shaping arguments above are a simplified local view near the minimum). The second thing to bear in mind is that our considerations here are limited to deeply (and barely) trapped particles. Intermediate orbits could behave differently, which is something that needs to be checked by computing $\omega _{\alpha}$
property is correspondingly limited. How much shaping is sufficient varies from case to case, and the competition between the various field and geometric quantities (we shall recall that the shaping arguments above are a simplified local view near the minimum). The second thing to bear in mind is that our considerations here are limited to deeply (and barely) trapped particles. Intermediate orbits could behave differently, which is something that needs to be checked by computing $\omega _{\alpha}$![]() for all $k$
for all $k$![]() .
.
2.4.4. Beyond stellarator symmetry
The realisation that a certain level of asymmetry about the bottom of the magnetic well provides the means to enhance the precession of deeply trapped particles opens the door to several possibilities. In the case of a straight mirror, one needs to break left–right symmetry in order to achieve an omnigeneous, maximum-$J$![]() field (see Appendix C and Catto & Hazeltine (Reference Catto and Hazeltine1981)). In the case of a QI stellarator it is then natural to ask the question whether breaking stellarator symmetry can be exploited to further improve the behaviour of the deeply trapped particles.
field (see Appendix C and Catto & Hazeltine (Reference Catto and Hazeltine1981)). In the case of a QI stellarator it is then natural to ask the question whether breaking stellarator symmetry can be exploited to further improve the behaviour of the deeply trapped particles.
The procedure followed for the discussion above can be extended to the non-stellarator-symmetric case. The details of the derivation are presented in Appendix B. As a result of this extension, the expression for $f_0$![]() acquires a number of additional terms, and the stellarator-symmetric contributions are also modified. The additions are, however, limited if we specialise, for simplicity, to the case in which the elliptical cross-section at the bottom of the magnetic well remains up–down symmetric in the Frenet–Serret frame, i.e. if we choose $\sigma (\varphi =0)=0$
acquires a number of additional terms, and the stellarator-symmetric contributions are also modified. The additions are, however, limited if we specialise, for simplicity, to the case in which the elliptical cross-section at the bottom of the magnetic well remains up–down symmetric in the Frenet–Serret frame, i.e. if we choose $\sigma (\varphi =0)=0$![]() . In that case, there is only a single additional term that arises from stellarator symmetry, which is proportional to $(\bar {d}')^2$
. In that case, there is only a single additional term that arises from stellarator symmetry, which is proportional to $(\bar {d}')^2$![]()
It is clear that $f_{(\bar {d}')^2}\geq 0$![]() , and thus one can exploit stellarator-symmetry breaking to improve the maximum-$J$
, and thus one can exploit stellarator-symmetry breaking to improve the maximum-$J$![]() behaviour of deeply trapped particles. In this particular case, $f_{(\bar {d}')^2}>0$
behaviour of deeply trapped particles. In this particular case, $f_{(\bar {d}')^2}>0$![]() and thus any amount of symmetry breaking will help the precession of deeply trapped particles. When the level of asymmetry is such that it changes $\bar {d}$
and thus any amount of symmetry breaking will help the precession of deeply trapped particles. When the level of asymmetry is such that it changes $\bar {d}$![]() significantly within the well, $L_{\bar {d}}< L_{B_0}$
significantly within the well, $L_{\bar {d}}< L_{B_0}$![]() , where $L_{\bar {d}}^{-1}\sim \partial _\ell \ln \bar {d}$
, where $L_{\bar {d}}^{-1}\sim \partial _\ell \ln \bar {d}$![]() , this is capable of overturning the unfavourable contribution from $B_0''$
, this is capable of overturning the unfavourable contribution from $B_0''$![]() at the bottom of the well. This may be regarded as evidence that breaking stellarator symmetry might be beneficial.
at the bottom of the well. This may be regarded as evidence that breaking stellarator symmetry might be beneficial.
3. Some examples
We showed in the previous section that it is possible to achieve maximum-$J$![]() behaviour for deeply trapped particles in QI stellarators but not in QS ones. To attain this goal, the shaping of the magnetic field must, however, be carefully tailored and, in particular, significant shaping of the magnetic field is necessary to promote the correct precession behaviour. In this section, we construct concrete examples of QI fields and analyse their maximum-$J$
behaviour for deeply trapped particles in QI stellarators but not in QS ones. To attain this goal, the shaping of the magnetic field must, however, be carefully tailored and, in particular, significant shaping of the magnetic field is necessary to promote the correct precession behaviour. In this section, we construct concrete examples of QI fields and analyse their maximum-$J$![]() properties.
properties.
3.1. Near-axis constructions
We begin by considering configurations found through the near-axis expansion. To this end, we use the QI-specific developments of Plunk et al. (Reference Plunk, Landreman and Helander2019) and Rodríguez & Plunk (Reference Rodríguez and Plunk2023) as well as the general equilibrium framework of Landreman & Sengupta (Reference Landreman and Sengupta2019). To diagnose the resulting fields, we use the normalised precession frequency $\hat {\omega }_{\alpha}$![]() , (2.2), where we express $\psi _a$
, (2.2), where we express $\psi _a$![]() , the value of the flux at the boundary, in terms of an effective aspect ratio.
, the value of the flux at the boundary, in terms of an effective aspect ratio.
To this end, we denote the length of the magnetic axis by
where the integral is taken along the axis once around the torus. To lowest order in the distance from the magnetic axis, the volume enclosed by a flux surface $\psi = \psi _a$![]() is equal to (Helander Reference Helander2014)
is equal to (Helander Reference Helander2014)
where $B_0$![]() is the magnetic strength on axis. It is natural to define an ‘average’ minor radius $a$
is the magnetic strength on axis. It is natural to define an ‘average’ minor radius $a$![]() by setting $V = 2 {\rm \pi}R \cdot {\rm \pi}a^2$
by setting $V = 2 {\rm \pi}R \cdot {\rm \pi}a^2$![]() , and a logical definition of the aspect ratio is then
, and a logical definition of the aspect ratio is then

which may be expressed in terms of averages over the Boozer toroidal angle $\varphi$![]()

where the overline represents a toroidal average $\overline {(\ldots )}=\int _0^{2{\rm \pi} }(\ldots )\, \mathrm {d}\varphi /2{\rm \pi}$![]() . We shall use this form of the toroidal flux in the presentation of numerical results to follow (choosing the representative value of $A\sim 10$
. We shall use this form of the toroidal flux in the presentation of numerical results to follow (choosing the representative value of $A\sim 10$![]() ).
).
To illustrate the behaviour of the precession in some near-axis constructions, we first consider configurations recently constructed by Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022), which were designed to be QI to first order in the distance from the magnetic axis. This work emphasised the reduction of shaping and neoclassical transport losses when a global equilibrium was constructed using the near-axis field. Because only first-order considerations were taken into account, there is, in principle, not a unique precession frequency characterising these configurations since a certain degree of freedom exists at second order to complete the construction. Nevertheless, there is a ‘natural’ second-order extension of these configurations, which we refer to as the minimal-shaping construction, namely, the one that makes the $X_{2c}$![]() and $X_{2s}$
and $X_{2s}$![]() modulations in the near-axis vanish. The resulting field should be representative of the first-order construction, especially if one considers the construction of a global solution using the first-order fields. We construct the field following the equilibrium equations in Landreman & Sengupta (Reference Landreman and Sengupta2019) (see Appendix B), using the code pyQIC (Jorge, Agostinho & Rodríguez Reference Jorge, Agostinho and Rodríguez2023). With such a second-order field in place, we may calculate the precession frequency, which is plotted in figure 6 for the $N=2$
modulations in the near-axis vanish. The resulting field should be representative of the first-order construction, especially if one considers the construction of a global solution using the first-order fields. We construct the field following the equilibrium equations in Landreman & Sengupta (Reference Landreman and Sengupta2019) (see Appendix B), using the code pyQIC (Jorge, Agostinho & Rodríguez Reference Jorge, Agostinho and Rodríguez2023). With such a second-order field in place, we may calculate the precession frequency, which is plotted in figure 6 for the $N=2$![]() and $N=3$
and $N=3$![]() configurations of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022), where the necessary integrals were computed following (A24) and (A25). Some additional details are included in table 1.
configurations of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022), where the necessary integrals were computed following (A24) and (A25). Some additional details are included in table 1.

Figure 6. Precession of trapped electrons for two near-axis QI examples. Three-dimensional rendition of flux surfaces at $r=0.1$![]() (with the colour map representing the magnetic-field strength) and normalised precession frequency $\hat {\omega }_{\alpha}$
(with the colour map representing the magnetic-field strength) and normalised precession frequency $\hat {\omega }_{\alpha}$![]() at two different radii for near-axis fields with $N=2$
at two different radii for near-axis fields with $N=2$![]() and $N=3$
and $N=3$![]() of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022). The precession is computed using the analytical expressions derived in this paper. The near-axis fields have been constructed to second order, taking a ‘minimal-shaping’ construction $X_{2c}=0=X_{2s}$
of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022). The precession is computed using the analytical expressions derived in this paper. The near-axis fields have been constructed to second order, taking a ‘minimal-shaping’ construction $X_{2c}=0=X_{2s}$![]() . The grey curves denote the variation of precession between different field lines (with the black curve corresponding to the average over $\alpha$
. The grey curves denote the variation of precession between different field lines (with the black curve corresponding to the average over $\alpha$![]() ), reflecting the non-omnigeneous nature of the fields. Two different origins of the variability are apparent: a roughly $r$
), reflecting the non-omnigeneous nature of the fields. Two different origins of the variability are apparent: a roughly $r$![]() independent variation from the second-order contribution, and a variation proportional to $1/r$
independent variation from the second-order contribution, and a variation proportional to $1/r$![]() due to breaking omnigeneity at first order.
due to breaking omnigeneity at first order.
Table 1. Critical $\beta$![]() and geometric contributions. Geometric parameters and critical $\beta$
and geometric contributions. Geometric parameters and critical $\beta$![]() for the $N=2$
for the $N=2$![]() and $N=3$
and $N=3$![]() near-axis QI examples in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022). Here, $\beta ^\star$
near-axis QI examples in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022). Here, $\beta ^\star$![]() is a measure of the required plasma beta to prevent deeply trapped particles from precessing in the diamagnetic direction in an idealised omnigeneous field ($\beta _{\mathrm {tot}}^\star$
is a measure of the required plasma beta to prevent deeply trapped particles from precessing in the diamagnetic direction in an idealised omnigeneous field ($\beta _{\mathrm {tot}}^\star$![]() if the non-omnigeneous nature of the field is considered).
if the non-omnigeneous nature of the field is considered).

Similarly to the global QI-optimised stellarators in figure 1, these configurations do not have the maximum-$J$![]() property. Most of the trapped particles precess in the diamagnetic direction, but some particles with turning points close to the magnetic-field maxima behave as expected in a maximum-$J$
property. Most of the trapped particles precess in the diamagnetic direction, but some particles with turning points close to the magnetic-field maxima behave as expected in a maximum-$J$![]() field. This behaviour is similar to that in axisymmetric/QS fields: deeply trapped particles tend to co-precess with the diamagnetic frequency, while barely trapped ones do the opposite. The configurations importantly exhibit a significant field-line-to-field-line variation (see the different grey lines), as a result of deviations from omnigeneity. This should not come as a surprise given that the second-order construction is not QI. But in addition, as noted in the construction of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022), the tops of the wells deviate from QI already at first order. The result is a variability of $\hat {\omega }_{\alpha}$
field. This behaviour is similar to that in axisymmetric/QS fields: deeply trapped particles tend to co-precess with the diamagnetic frequency, while barely trapped ones do the opposite. The configurations importantly exhibit a significant field-line-to-field-line variation (see the different grey lines), as a result of deviations from omnigeneity. This should not come as a surprise given that the second-order construction is not QI. But in addition, as noted in the construction of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022), the tops of the wells deviate from QI already at first order. The result is a variability of $\hat {\omega }_{\alpha}$![]() that diverges as $r \rightarrow 0$
that diverges as $r \rightarrow 0$![]() and primarily affects shallowly trapped particles, see figure 6. Note, however, that this first-order effect is only noticeable very close to the axis. This is testimony to the quality of the QI optimisation performed by Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022).
and primarily affects shallowly trapped particles, see figure 6. Note, however, that this first-order effect is only noticeable very close to the axis. This is testimony to the quality of the QI optimisation performed by Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022).
Although the precise form of the curves in figure 6 depends on how the near-axis magnetic field has been completed at second order, the behaviour of deeply trapped particles is independent of this detail, as we learnt in previous sections. For these particles, it suffices to compute the various terms that make up $\omega _{\alpha}$![]() in (2.9) at the minimum of $B_0$
in (2.9) at the minimum of $B_0$![]() . For this calculation, however, one should not use the form of $f_0$
. For this calculation, however, one should not use the form of $f_0$![]() in (2.18) but instead relax the assumption of QI at second order. Setting the explicit non-QI contributions aside for now, we must use the expression for $B_{20}$
in (2.18) but instead relax the assumption of QI at second order. Setting the explicit non-QI contributions aside for now, we must use the expression for $B_{20}$![]() needed for (2.9). The necessary expressions are given in Appendix B, (B5), where we use the notation $\mathcal {P}_i$
needed for (2.9). The necessary expressions are given in Appendix B, (B5), where we use the notation $\mathcal {P}_i$![]() to denote the contribution of a quantity $i$
to denote the contribution of a quantity $i$![]() to $B_{20}$
to $B_{20}$![]() , in analogy to $f_i$
, in analogy to $f_i$![]() in $f_0$
in $f_0$![]() . These terms can be used to assess the near-axis construction at first order as in table 1. As $\bar {d}''=0$
. These terms can be used to assess the near-axis construction at first order as in table 1. As $\bar {d}''=0$![]() (and thus $\mathcal {P}_{\bar {d}\bar {d}''}=0$
(and thus $\mathcal {P}_{\bar {d}\bar {d}''}=0$![]() ) and $\bar {d}<1$
) and $\bar {d}<1$![]() in these examples, it is a priori clear that it is impossible for the deeply trapped particles to have the maximum-$J$
in these examples, it is a priori clear that it is impossible for the deeply trapped particles to have the maximum-$J$![]() property in these configurations. A finite plasma $\beta$
property in these configurations. A finite plasma $\beta$![]() would be necessary to attain this property. Much like the critical $\beta _J$
would be necessary to attain this property. Much like the critical $\beta _J$![]() in (2.19), we can define $\beta ^\star =a^2(\sum \mathcal {P}_i)/(2(\ell ')^2)$
in (2.19), we can define $\beta ^\star =a^2(\sum \mathcal {P}_i)/(2(\ell ')^2)$![]() , where $a$
, where $a$![]() is the value of $r$
is the value of $r$![]() at the plasma edge, which we take to be at roughly $a\sim R/10$
at the plasma edge, which we take to be at roughly $a\sim R/10$![]() . The quantity $\beta ^\star$
. The quantity $\beta ^\star$![]() represents the plasma $\beta$
represents the plasma $\beta$![]() necessary to make the vacuum QI configuration reverse the behaviour of deeply trapped particles. The key features for the equilibria in figure 6 are collected in table 1. We have at this point neglected the contribution of $\omega _{\alpha} ^{\text {non-QI}}$
necessary to make the vacuum QI configuration reverse the behaviour of deeply trapped particles. The key features for the equilibria in figure 6 are collected in table 1. We have at this point neglected the contribution of $\omega _{\alpha} ^{\text {non-QI}}$![]() to (2.9), and since the configurations listed in table 1 are not exactly omnigenous, it is actually necessary to increase $\beta$
to (2.9), and since the configurations listed in table 1 are not exactly omnigenous, it is actually necessary to increase $\beta$![]() further in order to overcome the $\alpha$
further in order to overcome the $\alpha$![]() -dependence. The requisite $\beta$
-dependence. The requisite $\beta$![]() can be estimated from (A26) and (B7), and we may thus define $\beta ^\star _{\mathrm {tot}}$
can be estimated from (A26) and (B7), and we may thus define $\beta ^\star _{\mathrm {tot}}$![]() as the total $\beta$
as the total $\beta$![]() needed to make the ‘least-maximum-$J$
needed to make the ‘least-maximum-$J$![]() ’ field line be so.
’ field line be so.
The analytical value of $\beta ^\star$![]() can be seen to be correct in the example of figure 7, where the plasma $\beta$
can be seen to be correct in the example of figure 7, where the plasma $\beta$![]() of the configuration in figure 6(a) increases. Here, the pressure gradient has been varied whilst the shape of the magnetic axis and the ellipticity of the flux surfaces in its vicinity is kept fixed to first order. Note that different authors and contexts mean different things by ‘increasing $\beta$
of the configuration in figure 6(a) increases. Here, the pressure gradient has been varied whilst the shape of the magnetic axis and the ellipticity of the flux surfaces in its vicinity is kept fixed to first order. Note that different authors and contexts mean different things by ‘increasing $\beta$![]() ’ (i.e. different features of the equilibrium are kept constant), making direct comparison difficult. Of course, reaching this $\beta$
’ (i.e. different features of the equilibrium are kept constant), making direct comparison difficult. Of course, reaching this $\beta$![]() is necessary but not sufficient for maximum-$J$
is necessary but not sufficient for maximum-$J$![]() of the whole trapped population. This is especially true in the examples in figure 6, where it is not the most deeply trapped particles that have the largest precession frequency. From the preceding analysis, we expect a non-zero plasma $\beta$
of the whole trapped population. This is especially true in the examples in figure 6, where it is not the most deeply trapped particles that have the largest precession frequency. From the preceding analysis, we expect a non-zero plasma $\beta$![]() to introduce an overall upshift of the precession $q\omega _{\alpha}$
to introduce an overall upshift of the precession $q\omega _{\alpha}$![]() , which is indeed seen numerically.
, which is indeed seen numerically.

Figure 7. Reversal of trapped-particle precession with increasing $\beta$![]() . Normalised precession frequency $\hat {\omega }_{\alpha}$
. Normalised precession frequency $\hat {\omega }_{\alpha}$![]() for three different values of plasma $\beta$
for three different values of plasma $\beta$![]() for the ‘minimally shaped’ near-axis field $N=2$
for the ‘minimally shaped’ near-axis field $N=2$![]() from Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022) at $r=0.01$
from Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022) at $r=0.01$![]() . The black lines correspond to the $\alpha ={\rm \pi} /4$
. The black lines correspond to the $\alpha ={\rm \pi} /4$![]() field line, and grey curves reflect the variation in precession frequency due to non-omnigeneity. The analytical estimate for the normalised pressure at which deeply trapped particles reverse their precession is $\beta ^\star = 5.5\,\%$
field line, and grey curves reflect the variation in precession frequency due to non-omnigeneity. The analytical estimate for the normalised pressure at which deeply trapped particles reverse their precession is $\beta ^\star = 5.5\,\%$![]() and corresponds to the middle set of curves. The legend on the right shows how the plasma cross-section at the radii $r=0.05, 0.1$
and corresponds to the middle set of curves. The legend on the right shows how the plasma cross-section at the radii $r=0.05, 0.1$![]() and toroidal angle $\phi =0$
and toroidal angle $\phi =0$![]() change with $\beta$
change with $\beta$![]() .
.
A central conclusion of our analysis thus far is the possibility of making deeply trapped particles acquire maximum-$J$![]() behaviour without the need of a non-zero plasma pressure. Accordingly, we now attempt to construct such a field first through optimisation within the near-axis framework. We construct an optimisation measure for maximum-$J$
behaviour without the need of a non-zero plasma pressure. Accordingly, we now attempt to construct such a field first through optimisation within the near-axis framework. We construct an optimisation measure for maximum-$J$![]() by summing $\omega _{\alpha} ^2$
by summing $\omega _{\alpha} ^2$![]() (which we have learnt how to compute) over values of $k$
(which we have learnt how to compute) over values of $k$![]() that satisfy $q \omega _{\alpha} <0$
that satisfy $q \omega _{\alpha} <0$![]() , call it $g_{\omega _{\alpha} }$
, call it $g_{\omega _{\alpha} }$![]() . We are also interested in imposing the condition of QI, especially at second order. At the maxima and minima of the field strength we learnt in this work that we must satisfy (B9), from which we may construct an additional cost function, call it $\check {g}_{\mathrm {QI}}$
. We are also interested in imposing the condition of QI, especially at second order. At the maxima and minima of the field strength we learnt in this work that we must satisfy (B9), from which we may construct an additional cost function, call it $\check {g}_{\mathrm {QI}}$![]() . Under the assumption of satisfying this condition, one can show that it is possible to choose the near-axis construction at second order in such a way that it guarantees the correct second-order QI behaviour elsewhere. We give the most essential elements of this in Appendix D, but leave a full exploration to a later publication. Note that this way of completing the solution is formally correct, but in practice (i.e. when taking into account shaping, QI breaking in buffer regions, etc.) it may not be the best choice. For our proof of principle, however, it should suffice. With this, then, we construct our near-axis cost function simply as the weighted sum of the negative $q\omega _{\alpha}$
. Under the assumption of satisfying this condition, one can show that it is possible to choose the near-axis construction at second order in such a way that it guarantees the correct second-order QI behaviour elsewhere. We give the most essential elements of this in Appendix D, but leave a full exploration to a later publication. Note that this way of completing the solution is formally correct, but in practice (i.e. when taking into account shaping, QI breaking in buffer regions, etc.) it may not be the best choice. For our proof of principle, however, it should suffice. With this, then, we construct our near-axis cost function simply as the weighted sum of the negative $q\omega _{\alpha}$![]() and the QI condition, (B9), at the $|\boldsymbol {B}|$
and the QI condition, (B9), at the $|\boldsymbol {B}|$![]() extrema, $g=g_{\omega _{\alpha} }+\check {g}_{\mathrm {QI}}$
extrema, $g=g_{\omega _{\alpha} }+\check {g}_{\mathrm {QI}}$![]() .
.
With the cost function thus defined, we must explicitly state which our minimal degrees of freedom are. We shall allow only the axis shape and the function $\bar {d}(\varphi )$![]() to vary, while keeping the field strength $B_0(\varphi )$
to vary, while keeping the field strength $B_0(\varphi )$![]() fixed. The idea is not to find a practical field, which would require limiting the shaping and other additional practical features (and unlocking other degrees of freedom such as $B_0$
fixed. The idea is not to find a practical field, which would require limiting the shaping and other additional practical features (and unlocking other degrees of freedom such as $B_0$![]() and the order of curvature zeroes). We are simply aiming at the construction of a proof-of-principle field that exhibits maximum-$J$
and the order of curvature zeroes). We are simply aiming at the construction of a proof-of-principle field that exhibits maximum-$J$![]() behaviour in vacuum, especially for the deeply trapped particles. Other details of the optimisation are left to Appendix D. In figure 8 we present the resulting optimised configuration for $N=1$
behaviour in vacuum, especially for the deeply trapped particles. Other details of the optimisation are left to Appendix D. In figure 8 we present the resulting optimised configuration for $N=1$![]() . The shaping is forbiddingly large, owing to the fact that no attention was paid to limit it. Flux surfaces are extremely shaped and limit the physical radius of the configuration ($r_c\approx 0.002$
. The shaping is forbiddingly large, owing to the fact that no attention was paid to limit it. Flux surfaces are extremely shaped and limit the physical radius of the configuration ($r_c\approx 0.002$![]() (Landreman Reference Landreman2021)). However, we may from this approach formally construct an asymptotic form of $B$
(Landreman Reference Landreman2021)). However, we may from this approach formally construct an asymptotic form of $B$![]() at any $r$
at any $r$![]() using its near-axis form as a model, and represent the geometry to first order to exhibit the features resulting from the optimisation.
using its near-axis form as a model, and represent the geometry to first order to exhibit the features resulting from the optimisation.

Figure 8. Proof of principle of a maximum-$J$![]() -optimised near-axis field. The panels show a near-axis field optimised so as to exhibit quasi-isodynamicity and maximum-$J$
-optimised near-axis field. The panels show a near-axis field optimised so as to exhibit quasi-isodynamicity and maximum-$J$![]() behaviour, especially near the minimum of the magnetic field on each flux surface. The shaping of the configuration is very large, and thus the resulting field impracticable, but shows that the optimisation criteria can be met. (a) A three-dimensional rendition of the field for $r=0.02$
behaviour, especially near the minimum of the magnetic field on each flux surface. The shaping of the configuration is very large, and thus the resulting field impracticable, but shows that the optimisation criteria can be met. (a) A three-dimensional rendition of the field for $r=0.02$![]() , using only the first-order description. (Second-order contributions are large and obscure the visualisation.) (b) First-order cross-sections near the minimum of $|\boldsymbol {B}|$
, using only the first-order description. (Second-order contributions are large and obscure the visualisation.) (b) First-order cross-sections near the minimum of $|\boldsymbol {B}|$![]() (in $(R,Z)$
(in $(R,Z)$![]() coordinates and between $\phi =3{\rm \pi} /4,5{\rm \pi} /4$
coordinates and between $\phi =3{\rm \pi} /4,5{\rm \pi} /4$![]() ). The dotted curve represents the position of the magnetic axis. (c) Precession $\hat {\omega }_{\alpha}$
). The dotted curve represents the position of the magnetic axis. (c) Precession $\hat {\omega }_{\alpha}$![]() computed numerically using $|\boldsymbol {B}|$
computed numerically using $|\boldsymbol {B}|$![]() from the near-axis expansion at two different radii on a number of field lines (grey curves, with the black representing the average). The increase in variability at low $r$
from the near-axis expansion at two different radii on a number of field lines (grey curves, with the black representing the average). The increase in variability at low $r$![]() is due to the buffer region in which omnigeneity is broken. For this example, this contribution was not minimised. Close to the magnetic axis, the field satisfies the maximum-$J$
is due to the buffer region in which omnigeneity is broken. For this example, this contribution was not minimised. Close to the magnetic axis, the field satisfies the maximum-$J$![]() criterion for almost every orbit, except those trapped in secondary minima (Rodríguez & Plunk Reference Rodríguez and Plunk2023).
criterion for almost every orbit, except those trapped in secondary minima (Rodríguez & Plunk Reference Rodríguez and Plunk2023).
The optimised field is one in which the deeply trapped particles exhibit maximum-$J$![]() behaviour (see figure 8c).Footnote 6 To achieve this, the optimiser has found a field with the features identified in the preceding section. Specifically, the flux surfaces are twisted in the necessary manner and elongated away from the region of low magnetic-field strength. Although maximum-$J$
behaviour (see figure 8c).Footnote 6 To achieve this, the optimiser has found a field with the features identified in the preceding section. Specifically, the flux surfaces are twisted in the necessary manner and elongated away from the region of low magnetic-field strength. Although maximum-$J$![]() behaviour has thus been achieved for deeply trapped particles, it is clear that the field is not exactly omnigenous especially at larger $k$
behaviour has thus been achieved for deeply trapped particles, it is clear that the field is not exactly omnigenous especially at larger $k$![]() . This is mainly due to the first-order deviations from omnigeneity which the optimisation target did not include (clearly seen by the growth of the variation going from the bottom to the top plot of figure 8). Reducing the ‘buffer region’ (the region where omnigeneity is violated at first order) would reduce number of trapped-particles that do not satisfy the maximum-$J$
. This is mainly due to the first-order deviations from omnigeneity which the optimisation target did not include (clearly seen by the growth of the variation going from the bottom to the top plot of figure 8). Reducing the ‘buffer region’ (the region where omnigeneity is violated at first order) would reduce number of trapped-particles that do not satisfy the maximum-$J$![]() condition.
condition.
3.2. Traditionally optimised equilibrium
Motivated by the theoretical possibility of a vacuum, QI, maximum-$J$![]() field and proceeding beyond the near-axis expansion, we now turn to more traditional, global, stellarator optimisation. From what we have learned, relaxing the requirements in shaping and pushing for QI and maximum-$J$
field and proceeding beyond the near-axis expansion, we now turn to more traditional, global, stellarator optimisation. From what we have learned, relaxing the requirements in shaping and pushing for QI and maximum-$J$![]() -behaviour should result in a valid equilibrium solution. We attempt this optimisation to verify these predictions. To this aim, we employ three target functions: $g_{QI}$
-behaviour should result in a valid equilibrium solution. We attempt this optimisation to verify these predictions. To this aim, we employ three target functions: $g_{QI}$![]() ensures that the field is QI, $g_{B_{\mathrm {min}}}$
ensures that the field is QI, $g_{B_{\mathrm {min}}}$![]() ensures that the most deeply trapped particles satisfy the maximum-$J$
ensures that the most deeply trapped particles satisfy the maximum-$J$![]() criterion, and $g_{J}$
criterion, and $g_{J}$![]() ensures that the other particles also do so. The total target function that we minimise is thus
ensures that the other particles also do so. The total target function that we minimise is thus
Both $g_{QI}$![]() and $g_{J}$
and $g_{J}$![]() are complicated targets, which are explained in greater detail by Goodman et al. (Reference Goodman2024), and so is the starting point for the optimisation. Broadly speaking, $g_{QI}$
are complicated targets, which are explained in greater detail by Goodman et al. (Reference Goodman2024), and so is the starting point for the optimisation. Broadly speaking, $g_{QI}$![]() penalises the difference between $J$
penalises the difference between $J$![]() -contours on a flux surface by computing the difference in the second adiabatic invariant and a closely related, artificially constructed, perfectly QI flux surface. From the calculation of $\mathcal {J}_\|$
-contours on a flux surface by computing the difference in the second adiabatic invariant and a closely related, artificially constructed, perfectly QI flux surface. From the calculation of $\mathcal {J}_\|$![]() , we also evaluate the term $g_{J}$
, we also evaluate the term $g_{J}$![]() , which imposes $\partial _\psi J < 0$
, which imposes $\partial _\psi J < 0$![]() in this constructed field. Thus, as $g_{QI}$
in this constructed field. Thus, as $g_{QI}$![]() and $g_J$
and $g_J$![]() decrease, the field becomes more QI and more maximum-$J$
decrease, the field becomes more QI and more maximum-$J$![]() .
.
The term $g_{B_{\mathrm {min}}}$![]() is a more straightforward target function. Using the fact that the maximum-$J$
is a more straightforward target function. Using the fact that the maximum-$J$![]() condition corresponds to minimum-$B$
condition corresponds to minimum-$B$![]() (for the most deeply and shallowly trapped particles), we simply designed this function to encourage the flux-surface's minimum field strength, $B_{\mathrm {min}}(s)$
(for the most deeply and shallowly trapped particles), we simply designed this function to encourage the flux-surface's minimum field strength, $B_{\mathrm {min}}(s)$![]() , to have a positive derivative, where $s = (r/a)^2$
, to have a positive derivative, where $s = (r/a)^2$![]() . To do this, for every consecutive pair of flux surface, the target calculates $B_{\mathrm {min}}$
. To do this, for every consecutive pair of flux surface, the target calculates $B_{\mathrm {min}}$![]() on $s_0$
on $s_0$![]() and $s_1=s_0 + \delta s$
and $s_1=s_0 + \delta s$![]() and then the fractional difference between the two
and then the fractional difference between the two
We can thus define the target as $f_{B_{\mathrm {min}}} = \max (0.01 - \delta _B, 0)^2$![]() , where the value of 0.01 has been chosen as an arbitrary positive number here.
, where the value of 0.01 has been chosen as an arbitrary positive number here.
We initialise optimisation from a near-axis construction with a flatter bottom of the magnetic well (which we know from the work above that should favour maximum-$J$![]() ), using techniques to be presented by Plunk et al. (Reference Plunk2024). The resulting optimised configuration is indeed (mostly) maximum-$J$
), using techniques to be presented by Plunk et al. (Reference Plunk2024). The resulting optimised configuration is indeed (mostly) maximum-$J$![]() and QI. This can be seen in the second adiabatic invariant contours of figure 10, which show that $\mathcal {J}$
and QI. This can be seen in the second adiabatic invariant contours of figure 10, which show that $\mathcal {J}$![]() decreases from the centre of the $(s,\alpha )$
decreases from the centre of the $(s,\alpha )$![]() plot radially outward, and the contours are approximately circular. It is evident, however, that for trapped particles sufficiently close to the bottom of the wells (see left-most plot), there is a fraction of the population that does not behave in a maximum-$J$
plot radially outward, and the contours are approximately circular. It is evident, however, that for trapped particles sufficiently close to the bottom of the wells (see left-most plot), there is a fraction of the population that does not behave in a maximum-$J$![]() fashion. This is signalled here by a relative shift of the approximately circular contours respect to the centre. As a result, there is a portion of field lines that are minimum-$J$
fashion. This is signalled here by a relative shift of the approximately circular contours respect to the centre. As a result, there is a portion of field lines that are minimum-$J$![]() (see also the top plot of figure 9c). In the spirit of a more quantitative measure, it would be convenient to come up with a single scalar that indicates what ‘fraction’ of the configuration truly behaves in a maximum-$J$
(see also the top plot of figure 9c). In the spirit of a more quantitative measure, it would be convenient to come up with a single scalar that indicates what ‘fraction’ of the configuration truly behaves in a maximum-$J$![]() fashion. For a Maxwellian distribution function, the fraction of the trapped-particle population whose rotation satisfies $q\omega _{\alpha} >0$
fashion. For a Maxwellian distribution function, the fraction of the trapped-particle population whose rotation satisfies $q\omega _{\alpha} >0$![]() is equal to
is equal to

where $\varTheta$![]() is the Heaviside step function, $\varrho =\sqrt {\psi /\psi _a}$
is the Heaviside step function, $\varrho =\sqrt {\psi /\psi _a}$![]()

and
is proportional to the bounce time of trapped particles. This way each flux surface is considered equally important (the Maxwellian distribution does not change from surface to surface). With this definition, for the optimised configuration above, $f_{\mathrm {max}\text -J}\approx 0.996$![]() . That is, a $99.6\,\%$
. That is, a $99.6\,\%$![]() of the volume is maximum-$J$
of the volume is maximum-$J$![]() ; i.e. for all intents and purposes, the configuration is maximum-$J$
; i.e. for all intents and purposes, the configuration is maximum-$J$![]() . The omnigeneous nature of the configuration can be quantified by the effective ripple (Nemov et al. Reference Nemov, Kasilov, Kernbichler and Heyn1999), which measures the $1/\nu$
. The omnigeneous nature of the configuration can be quantified by the effective ripple (Nemov et al. Reference Nemov, Kasilov, Kernbichler and Heyn1999), which measures the $1/\nu$![]() neoclassical transport and in the present case remains in the range $\epsilon _{\mathrm {eff}}\sim 0.15\,\%-0.45\,\%$
neoclassical transport and in the present case remains in the range $\epsilon _{\mathrm {eff}}\sim 0.15\,\%-0.45\,\%$![]() across the volume.
across the volume.

Figure 9. Example of a maximum-$J$![]() -optimised global equilibrium. The plots show a magnetic field optimised by minimising (3.5) so as to attain quasi-isodynamicity and maximum-$J$
-optimised global equilibrium. The plots show a magnetic field optimised by minimising (3.5) so as to attain quasi-isodynamicity and maximum-$J$![]() behaviour in a vacuum magnetic field. The configuration has an aspect ratio of $A_{\mathrm {VMEC}}\sim 7$
behaviour in a vacuum magnetic field. The configuration has an aspect ratio of $A_{\mathrm {VMEC}}\sim 7$![]() , three field periods and exhibits strong shaping, which was not constrained in this proof-of-principle example. (a) Three-dimensional rendition of the outermost surface of the field, where the colour map represents $|\boldsymbol {B}|$
, three field periods and exhibits strong shaping, which was not constrained in this proof-of-principle example. (a) Three-dimensional rendition of the outermost surface of the field, where the colour map represents $|\boldsymbol {B}|$![]() . (b) Detail of cross-sections near the core (at $\varrho =0.1$
. (b) Detail of cross-sections near the core (at $\varrho =0.1$![]() , and for reference to indicate the large shaping of surfaces $\varrho =0.5$
, and for reference to indicate the large shaping of surfaces $\varrho =0.5$![]() as broken contours) and about the minimum of $|\boldsymbol {B}|$
as broken contours) and about the minimum of $|\boldsymbol {B}|$![]() (in $(R,Z)$
(in $(R,Z)$![]() coordinates and between $\phi =3{\rm \pi} /4, 5{\rm \pi} /4$
coordinates and between $\phi =3{\rm \pi} /4, 5{\rm \pi} /4$![]() ), showing features of twist and shape studied analytically. The dotted curve represents the position of the magnetic axis. (c) Precession frequency at two radii on a number of field lines (grey curves, with the black $\alpha ={\rm \pi} /2$
), showing features of twist and shape studied analytically. The dotted curve represents the position of the magnetic axis. (c) Precession frequency at two radii on a number of field lines (grey curves, with the black $\alpha ={\rm \pi} /2$![]() ). The increase in variability at low $r$
). The increase in variability at low $r$![]() is a consequence of the breaking of omnigeneity. The overwhelming majority of all trapped particles satisfy the maximum-$J$
is a consequence of the breaking of omnigeneity. The overwhelming majority of all trapped particles satisfy the maximum-$J$![]() criterion, $\hat \omega _{\alpha} > 0$
criterion, $\hat \omega _{\alpha} > 0$![]() .
.

Figure 10. Contours of the second adiabatic invariant $\mathcal {J}_\parallel$![]() in polar coordinates $(s,\alpha )$
in polar coordinates $(s,\alpha )$![]() . Contours showing the second adiabatic invariant as a function of the polar coordinates $(s,\alpha )$
. Contours showing the second adiabatic invariant as a function of the polar coordinates $(s,\alpha )$![]() for three different trapped-particle classes. The values of $\lambda$
for three different trapped-particle classes. The values of $\lambda$![]() used are $\lambda =[(B_{\mathrm {max}}-B_{\mathrm {min}})\lambda _n+B_{{\rm min}}]^{-1}$
used are $\lambda =[(B_{\mathrm {max}}-B_{\mathrm {min}})\lambda _n+B_{{\rm min}}]^{-1}$![]() where $B_{\mathrm {max}}$
where $B_{\mathrm {max}}$![]() and $B_{\mathrm {min}}$
and $B_{\mathrm {min}}$![]() denote the maximum and minimum field strengths on the flux surface in question. An ideal omnigeneous field would have concentric circular contours. The wiggle in the contours is indicative of QI breaking, which is particularly prominent close to the trapped–passing boundary (small $\lambda$
denote the maximum and minimum field strengths on the flux surface in question. An ideal omnigeneous field would have concentric circular contours. The wiggle in the contours is indicative of QI breaking, which is particularly prominent close to the trapped–passing boundary (small $\lambda$![]() ). An ideally maximum-$J$
). An ideally maximum-$J$![]() field would show a monotonic decrease of $\mathcal {J}_\parallel$
field would show a monotonic decrease of $\mathcal {J}_\parallel$![]() along any ray emanating from the origin.
along any ray emanating from the origin.
To realise these features in a vacuum configuration, we see that the optimiser indeed found the extreme shaping that we expected in such a configuration. In particular, we observe extremely elongated flux surfaces towards the field maximum, and a dramatic, localised ‘twist’ of the flux surfaces near the field minimum. Such features can be seen in figure 9(b).
The resulting configuration also has a significant so-called ‘vacuum magnetic well’ of approximately 3.3 % (as defined in Landreman & Paul Reference Landreman and Paul2022), a property that is important for MHD stability (Landreman Reference Landreman2021). A field is said to have a vacuum magnetic well if $V''(\psi ) < 0$![]() (where $V$
(where $V$![]() is the volume enclosed by a flux surface). Generally, unless special care is taken, optimised configurations tend to have a ‘magnetic hill’, $i.e.$
is the volume enclosed by a flux surface). Generally, unless special care is taken, optimised configurations tend to have a ‘magnetic hill’, $i.e.$![]() $V''(\psi )>0$
$V''(\psi )>0$![]() , so it is notable that this configuration has such a substantial vacuum well.
, so it is notable that this configuration has such a substantial vacuum well.
The condition for a magnetic well means that, on a suitable average, the magnetic-field strength should increase with minor radius. This can be seen from the circumstance that the volume enclosed by a flux surface $\psi$![]() is
is
where the Jacobian in Boozer coordinates is $\mathcal {J} = (G + \iota I)/B^2$![]() . Since the flux-surface average is defined as
. Since the flux-surface average is defined as
it follows that $\langle B^2 \rangle = 4 {\rm \pi}^2 (G + \iota I) / V'$![]() and consequently
and consequently
where the last term vanishes in a vacuum field, where $G'(\psi )$![]() and $I(\psi )$
and $I(\psi )$![]() vanish. The magnetic well is sometimes defined without this term (Freidberg Reference Freidberg2014). Thus we see, as argued in § 1, that increasing the radial derivative of $B$
vanish. The magnetic well is sometimes defined without this term (Freidberg Reference Freidberg2014). Thus we see, as argued in § 1, that increasing the radial derivative of $B$![]() is directly related to MHD stability. Indeed, Helander (Reference Helander2014, p. 24) showed that there is a mathematical relation between maximum-$J$
is directly related to MHD stability. Indeed, Helander (Reference Helander2014, p. 24) showed that there is a mathematical relation between maximum-$J$![]() and magnetic-well criteria, but they are not identical. In the limit of large mirror ratio, where most particles are magnetically trapped, then the maximum-$J$
and magnetic-well criteria, but they are not identical. In the limit of large mirror ratio, where most particles are magnetically trapped, then the maximum-$J$![]() property rigorously implies a magnetic well. It is therefore not surprising that the particular configuration optimised here possesses a vacuum magnetic well.
property rigorously implies a magnetic well. It is therefore not surprising that the particular configuration optimised here possesses a vacuum magnetic well.
4. Discussion and conclusions
Before concluding the paper, we comment on the connection between the maximum-$J$![]() condition and the suppression of trapped-particle instabilities (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013) as well as the general reduction of curvature-driven instabilities and turbulence (Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). These phenomena are sensitive to the relative size of the drift frequency $\omega _d = k_{\alpha} \omega _{\alpha}$
condition and the suppression of trapped-particle instabilities (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander et al. Reference Helander, Proll and Plunk2013) as well as the general reduction of curvature-driven instabilities and turbulence (Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). These phenomena are sensitive to the relative size of the drift frequency $\omega _d = k_{\alpha} \omega _{\alpha}$![]() and the diamagnetic frequency
and the diamagnetic frequency
where $T$![]() denotes the plasma temperature in units of energy, $n$
denotes the plasma temperature in units of energy, $n$![]() the density and the wave vector has been taken to be $\boldsymbol {k} = k_{\alpha} \boldsymbol {\nabla } \alpha$
the density and the wave vector has been taken to be $\boldsymbol {k} = k_{\alpha} \boldsymbol {\nabla } \alpha$![]() . It is thus of interest to assess the magnitude of the ratio
. It is thus of interest to assess the magnitude of the ratio
which for a density profile $n = n_0(1-\psi /\psi _a)$![]() becomes $\omega _d / \omega _\ast = -\hat {\omega }_{\alpha} /2$
becomes $\omega _d / \omega _\ast = -\hat {\omega }_{\alpha} /2$![]() for particles moving at the thermal speed, $v = \sqrt {2T/m}$
for particles moving at the thermal speed, $v = \sqrt {2T/m}$![]() . In the QI cases studied numerically in the present paper, $\hat {\omega }_{\alpha}$
. In the QI cases studied numerically in the present paper, $\hat {\omega }_{\alpha}$![]() is of order $1/10$
is of order $1/10$![]() , making $\omega _d / \omega _\ast \ll 1$
, making $\omega _d / \omega _\ast \ll 1$![]() for most of the particles in a thermal distribution. This circumstance is stabilising to trapped-electron modes even if the absence of the maximum-$J$
for most of the particles in a thermal distribution. This circumstance is stabilising to trapped-electron modes even if the absence of the maximum-$J$![]() property. Relatively few electrons are able to satisfy the resonance condition in the limit $\omega _d/\omega _\ast \rightarrow 0$
property. Relatively few electrons are able to satisfy the resonance condition in the limit $\omega _d/\omega _\ast \rightarrow 0$![]() (Connor, Hastie & Helander Reference Connor, Hastie and Helander2006), and the nonlinear energy available to trapped electrons for driving instabilities is small (Mackenbach, Proll & Helander Reference Mackenbach, Proll and Helander2022; Mackenbach et al. Reference Mackenbach, Proll, Wakelkamp and Helander2023a). The latter was recently studied and labelled as the ‘strong’ regime (Rodríguez & Mackenbach Reference Rodríguez and Mackenbach2023), in which the available energy is only supplied by a small fraction of the trapped population proportional to $\omega _{\alpha} /\omega _\star$
(Connor, Hastie & Helander Reference Connor, Hastie and Helander2006), and the nonlinear energy available to trapped electrons for driving instabilities is small (Mackenbach, Proll & Helander Reference Mackenbach, Proll and Helander2022; Mackenbach et al. Reference Mackenbach, Proll, Wakelkamp and Helander2023a). The latter was recently studied and labelled as the ‘strong’ regime (Rodríguez & Mackenbach Reference Rodríguez and Mackenbach2023), in which the available energy is only supplied by a small fraction of the trapped population proportional to $\omega _{\alpha} /\omega _\star$![]() . From a practical point of view, it is true that as long as $|\hat \omega _{\alpha} | \ll 1$
. From a practical point of view, it is true that as long as $|\hat \omega _{\alpha} | \ll 1$![]() the magnetic field may not need to strictly satisfy the maximum-$J$
the magnetic field may not need to strictly satisfy the maximum-$J$![]() condition in order to substantially improve trapped-electron-mode stability. This condition is nevertheless helpful for MHD stability and fast-particle confinement, since particles with $\omega _{\alpha} = 0$
condition in order to substantially improve trapped-electron-mode stability. This condition is nevertheless helpful for MHD stability and fast-particle confinement, since particles with $\omega _{\alpha} = 0$![]() are less prone to collisionless losses (Velasco et al. Reference Velasco, Calvo, Mulas, Sánchez, Parra and Cappa2021; Paul et al. Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022). In any case, whenever the magnetic field of any concrete stellarator is optimised, a compromise will need to be found between the maximum-$J$
are less prone to collisionless losses (Velasco et al. Reference Velasco, Calvo, Mulas, Sánchez, Parra and Cappa2021; Paul et al. Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022). In any case, whenever the magnetic field of any concrete stellarator is optimised, a compromise will need to be found between the maximum-$J$![]() condition and other desirable properties.
condition and other desirable properties.
It is fortunate, although not merely a happy coincidence, that the maximum-$J$![]() property is related to both MHD stability, trapped-electron-mode suppression, and good fast-ion confinement: three very beneficial properties that are otherwise considered separate and independent of each other. Quasi-symmetric stellarators struggle to possess the maximum-$J$
property is related to both MHD stability, trapped-electron-mode suppression, and good fast-ion confinement: three very beneficial properties that are otherwise considered separate and independent of each other. Quasi-symmetric stellarators struggle to possess the maximum-$J$![]() property, but we show that QI ones are more amenable to it, and can be designed accordingly. Physically, this property is realised if all trapped particles experience average favourable magnetic curvature, and the precession frequency of these particles then has the opposite sign from the diamagnetic frequency. The behaviour of the most deep and the most shallow trapped-particle orbits can be examined analytically. It is found that the former usually precess in the wrong (i.e. diamagnetic) direction. This behaviour may be modified by appropriate twisting and flattening of the field near the bottom of the trapping well. Barely trapped particles always precess as desired, provided the magnetic field is perfectly omnigenous. Nevertheless, omnigeneity always fails for some of these particles, making them, too, precess in the wrong direction (as explicitly shown). As we have seen, despite this formal limitation, it is possible to design a vacuum QI field in which the vast majority of all particles satisfy the maximum-$J$
property, but we show that QI ones are more amenable to it, and can be designed accordingly. Physically, this property is realised if all trapped particles experience average favourable magnetic curvature, and the precession frequency of these particles then has the opposite sign from the diamagnetic frequency. The behaviour of the most deep and the most shallow trapped-particle orbits can be examined analytically. It is found that the former usually precess in the wrong (i.e. diamagnetic) direction. This behaviour may be modified by appropriate twisting and flattening of the field near the bottom of the trapping well. Barely trapped particles always precess as desired, provided the magnetic field is perfectly omnigenous. Nevertheless, omnigeneity always fails for some of these particles, making them, too, precess in the wrong direction (as explicitly shown). As we have seen, despite this formal limitation, it is possible to design a vacuum QI field in which the vast majority of all particles satisfy the maximum-$J$![]() condition.
condition.
Acknowledgements
Many of the numerical utilities to handle VMEC equilibria (Hirshman & Whitson Reference Hirshman and Whitson1983) are based on the stellarator package simsopt (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021). We gratefully acknowledge fruitful discussion with J.L. Velasco and R.J.J. Mackenbach.
Editor P. Catto thanks the referees for their advice in evaluating this article.
Funding
E.R. was supported by a grant by Alexander-von-Humboldt-Stiftung, Bonn, Germany, through a postdoctoral research fellowship, and A.G. was supported by a grant from the Simons Foundation (560651, PH). This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Declaration of interests
The authors report no conflict of interest.
Data availability
The data that support the findings of this study are openly available at the Zenodo repository with DOI/URL 10.5281/zenodo.10203417.
Appendix A. Precession frequency
A.1. General expressions
In accordance with the discussion in § 1, we first turn our attention to the derivatives of the adiabatic invariant $\mathcal {J}_\parallel$![]() . In Boozer coordinates, the magnetic field can be written as (Boozer Reference Boozer1981; Helander Reference Helander2014)
. In Boozer coordinates, the magnetic field can be written as (Boozer Reference Boozer1981; Helander Reference Helander2014)
the arc length element is ${\rm d}\ell = (G+\iota I) \,{\rm d} \varphi / B$![]() , so the adiabatic invariant becomes
, so the adiabatic invariant becomes
and its derivatives are

with
and the contribution from the boundary terms vanishing at the end points of the bounce integral. Equation (A4) can be simplified by using the MHD force balance equation. In particular, using (A1) to find the plasma current, computing $\boldsymbol {j}\times \boldsymbol {B}$![]() using the Boozer Jacobian and flux-surface averaging the $\boldsymbol {\nabla }\psi$
using the Boozer Jacobian and flux-surface averaging the $\boldsymbol {\nabla }\psi$![]() component of the equation (Kruskal & Kulsrud Reference Kruskal and Kulsrud1958; Helander Reference Helander2014)
component of the equation (Kruskal & Kulsrud Reference Kruskal and Kulsrud1958; Helander Reference Helander2014)
where $p(\psi )$![]() denotes the plasma pressure and angular brackets indicate the usual flux-surface average. Hence
denotes the plasma pressure and angular brackets indicate the usual flux-surface average. Hence

The bounce time is
and the precession frequency $\omega _{\alpha} = \Delta \alpha / \Delta t$![]() , using (1.2b), thus becomes
, using (1.2b), thus becomes

The same expressions may be reached by considering the bounce integral of the poloidal and radial drifts directly.
A.2. Precession for deeply trapped particles
The expression in (A9) is valid in any stellarator with flux surfaces, but becomes much simpler for deeply trapped particles. In this case $1-\lambda B \ll 1$![]() in the full integration domain, which also shrinks as $\lambda ^{-1}$
in the full integration domain, which also shrinks as $\lambda ^{-1}$![]() approaches the minimum of $|\boldsymbol {B}|$
approaches the minimum of $|\boldsymbol {B}|$![]() . This makes the first term in the square brackets dominate over the second one, and $F(\lambda,B) \approx 1/(2B^2 \sqrt {1-\lambda B})$
. This makes the first term in the square brackets dominate over the second one, and $F(\lambda,B) \approx 1/(2B^2 \sqrt {1-\lambda B})$![]() independently of the shape of the magnetic well. To show this, one can approximate the bottom of the well as $B\approx B_0(1+B^{(n)}\varphi ^n/n!)$
independently of the shape of the magnetic well. To show this, one can approximate the bottom of the well as $B\approx B_0(1+B^{(n)}\varphi ^n/n!)$![]() and evaluate for a deeply trapped particle with bounce point $\varphi _R$
and evaluate for a deeply trapped particle with bounce point $\varphi _R$![]()


The second term in the square bracket of (A9) thus yields a contribution that is ${\sim }(1-\lambda B_0)$![]() smaller than the first, and thus vanishes for deeply trapped particles regardless of the shape of the well.
smaller than the first, and thus vanishes for deeply trapped particles regardless of the shape of the well.
As a result, at the bottom of the magnetic well (i.e. at the point where ${\boldsymbol {B}} \boldsymbol {\cdot } \boldsymbol {\nabla } B = 0$![]() ) the precession frequency becomes simply
) the precession frequency becomes simply

This result regarding the local role of $\partial _\psi B$![]() also applies to the mostly shallowly trapped particles, which spend most of the time close to the turning point where the magnetic field strength reaches its maximum on the field line in question, $\lambda B_{\rm max} \simeq 1$
also applies to the mostly shallowly trapped particles, which spend most of the time close to the turning point where the magnetic field strength reaches its maximum on the field line in question, $\lambda B_{\rm max} \simeq 1$![]() .
.
The partial derivative of $B$![]() keeping $(\alpha,\varphi )$
keeping $(\alpha,\varphi )$![]() constant can be expressed in terms of common Boozer derivatives at fixed $(\theta,\varphi )$
constant can be expressed in terms of common Boozer derivatives at fixed $(\theta,\varphi )$![]() by using the chain rule
by using the chain rule
In this expression, the second term must vanish at the bottom of the magnetic well if the field is QI (in fact pseudosymmetry is sufficient Mikhailov et al. Reference Mikhailov, Shafranov, Subbotin, Isaev, Nührenberg, Zille and Cooper2002; Skovoroda Reference Skovoroda2005), as can be seen from the following argument. By definition, $(\iota \partial _\theta +\partial _\varphi )B=0$![]() at the bottom of the magnetic well. Moreover, in a QI field, the level contours of $B = |{\boldsymbol {B}}|$
at the bottom of the magnetic well. Moreover, in a QI field, the level contours of $B = |{\boldsymbol {B}}|$![]() are poloidally closed, which implies that $(c\partial _\theta +\partial _\varphi )B=0$
are poloidally closed, which implies that $(c\partial _\theta +\partial _\varphi )B=0$![]() for some $c(\psi,\theta,\varphi )\ne 0$
for some $c(\psi,\theta,\varphi )\ne 0$![]() that cannot equal $\iota$
that cannot equal $\iota$![]() , at least not at all minima of $B$
, at least not at all minima of $B$![]() . At the bottom of the well, then, the directional derivative of $B$
. At the bottom of the well, then, the directional derivative of $B$![]() vanishes in two independent directions tangential to the magnetic surface, which implies that it vanishes in any such direction including $\partial _\theta B = 0$
vanishes in two independent directions tangential to the magnetic surface, which implies that it vanishes in any such direction including $\partial _\theta B = 0$![]() . As a result, (A12) becomes
. As a result, (A12) becomes
A similar argument also applies to maxima of the field strength.
A.3. Near-axis expansion
We now consider the region close to the magnetic axis, expanding in the minor-radius variable $r = \sqrt {2 \psi / \bar B}$![]() , where $\bar B$
, where $\bar B$![]() is some reference magnetic-field strength. To second order, this expansion is (Garren & Boozer Reference Garren and Boozer1991b; Rodríguez & Plunk Reference Rodríguez and Plunk2023)
is some reference magnetic-field strength. To second order, this expansion is (Garren & Boozer Reference Garren and Boozer1991b; Rodríguez & Plunk Reference Rodríguez and Plunk2023)
with
To check for omnigeneity, let us write the integral in (A3) for $\partial _{\alpha} \mathcal {J}_\parallel$![]()
where $\partial F / \partial B = (\partial F(\lambda,B_0)) / \partial \varphi ) / B_0'(\varphi )$![]() and the integral is meant between bouncing points $\varphi _{R,L}$
and the integral is meant between bouncing points $\varphi _{R,L}$![]() . Expanding to second order in $r$
. Expanding to second order in $r$![]() and integrating by partsFootnote 7
and integrating by partsFootnote 7

where the integral is taken between bounce points of $B_0(\varphi )$![]() . If the field is to be omnigenous, $\partial _{\alpha} \mathcal {J}_\parallel = 0$
. If the field is to be omnigenous, $\partial _{\alpha} \mathcal {J}_\parallel = 0$![]() , this quantity must vanish for all $\lambda \in [B_{\rm max}^{-1},B_{\rm min}^{-1}]$
, this quantity must vanish for all $\lambda \in [B_{\rm max}^{-1},B_{\rm min}^{-1}]$![]() and all $\alpha \in [0,2{\rm \pi} ]$
and all $\alpha \in [0,2{\rm \pi} ]$![]() . For a stellarator-symmetric field, $B(r,\alpha,\varphi ) = B(r,-\alpha,-\varphi )$
. For a stellarator-symmetric field, $B(r,\alpha,\varphi ) = B(r,-\alpha,-\varphi )$![]() , we have the relations
, we have the relations
which are satisfied if $d$![]() is chosen to be odd in $\varphi$
is chosen to be odd in $\varphi$![]() , and $\nu = (n+1/2) {\rm \pi}$
, and $\nu = (n+1/2) {\rm \pi}$![]() . As a result of these constraints, the first-order contribution to (A17) in $r$
. As a result of these constraints, the first-order contribution to (A17) in $r$![]() vanishes. That at second order will also vanish if
vanishes. That at second order will also vanish if
These relations form the basic requirements for omnigeneity close to the magnetic axis and were recently derived by Rodríguez & Plunk (Reference Rodríguez and Plunk2023) by a different method that avoids the explicit integrals. We refer to that paper for further details and discussion.
Employing the same near-axis expansion to (A7) gives in analogy to (A17) for a general stellarator

where the integrals are, once again, taken between bounce points of $B_0(\varphi )$![]() . Substituting the omnigeneous forms of the magnetic-field functions into this integral, and noting that the enclosed toroidal current $I\sim r^2$
. Substituting the omnigeneous forms of the magnetic-field functions into this integral, and noting that the enclosed toroidal current $I\sim r^2$![]() (in the absence of an infinite current density on axis), one obtains $\omega _{\alpha} =\omega _{\alpha,\mathrm {vac}}+\omega _{\alpha,p}$
(in the absence of an infinite current density on axis), one obtains $\omega _{\alpha} =\omega _{\alpha,\mathrm {vac}}+\omega _{\alpha,p}$![]() with
with


where $p(r) = p_0 + p_2 r^2 + \cdots$![]() and ${\varphi _L}$
and ${\varphi _L}$![]() and $\varphi _R$
and $\varphi _R$![]() , to reiterate it, denote the toroidal locations of the bounce point to the left (L) and right (R) of the bottom of the well (for stellarator symmetry $\varphi _L=-\varphi _R$
, to reiterate it, denote the toroidal locations of the bounce point to the left (L) and right (R) of the bottom of the well (for stellarator symmetry $\varphi _L=-\varphi _R$![]() ). Although we have used the notation $\omega _{\alpha,\mathrm {vac}}$
). Although we have used the notation $\omega _{\alpha,\mathrm {vac}}$![]() and $\omega _{\alpha,p}$
and $\omega _{\alpha,p}$![]() , one should not forget that the former includes pressure effects through $B_{20}$
, one should not forget that the former includes pressure effects through $B_{20}$![]() . The flux average of $B_0^2$
. The flux average of $B_0^2$![]() appearing in this expression is equal to
appearing in this expression is equal to
A.4. Omnigeneity breaking
Because the expression in (A9) is valid for any stellarator, it provides an opportunity to learn how deviations from exact omnigeneity affect the precession frequency $\omega _{\alpha}$![]() . We consider this question from the near-axis perspective.
. We consider this question from the near-axis perspective.
A.4.1. First-order breaking
Let us start with the QI requirement at first order in $r$![]() . As we saw following (A17), the condition of omnigeneity requires the functions $d$
. As we saw following (A17), the condition of omnigeneity requires the functions $d$![]() and $\nu$
and $\nu$![]() to be odd and even, respectively, in $\varphi$
to be odd and even, respectively, in $\varphi$![]() (see Plunk & Helander Reference Plunk and Helander2018; Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022; Rodríguez & Plunk Reference Rodríguez and Plunk2023). This symmetry is crucial in a QI stellarator, as it causes the radial drift on either side of the magnetic well to cancel to leading order (as discussed in the main text). When the condition of omnigeneity is satisfied exactly, the $1/r$
(see Plunk & Helander Reference Plunk and Helander2018; Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022; Rodríguez & Plunk Reference Rodríguez and Plunk2023). This symmetry is crucial in a QI stellarator, as it causes the radial drift on either side of the magnetic well to cancel to leading order (as discussed in the main text). When the condition of omnigeneity is satisfied exactly, the $1/r$![]() contribution to $\omega _{\alpha}$
contribution to $\omega _{\alpha}$![]() in (A19) vanishes. This balance is delicate, however, as any small deviation can lead to a large precession, restoring the $O(1/r)$
in (A19) vanishes. This balance is delicate, however, as any small deviation can lead to a large precession, restoring the $O(1/r)$![]() dependence. This behaviour can be understood as the result of a finite poloidal drift occurring over an increasingly smaller flux surface as the magnetic axis is approached. The contribution may be written as
dependence. This behaviour can be understood as the result of a finite poloidal drift occurring over an increasingly smaller flux surface as the magnetic axis is approached. The contribution may be written as

following directly from (A19).
This term is, in principle, always present since omnigeneity can never be realised exactly except in trivial cases (Cary & Shasharina Reference Cary and Shasharina1997; Landreman & Catto Reference Landreman and Catto2012; Plunk et al. Reference Plunk, Landreman and Helander2019; Rodríguez & Plunk Reference Rodríguez and Plunk2023). In any non-axisymmetric torus, the requirements of omnigeneity clash with the required periodicity of the solution in $\theta$![]() and $\varphi$
and $\varphi$![]() . Formally, periodicity requires $\nu (-{\rm \pi} )=\nu ({\rm \pi} )+2{\rm \pi} (\iota -N)$
. Formally, periodicity requires $\nu (-{\rm \pi} )=\nu ({\rm \pi} )+2{\rm \pi} (\iota -N)$![]() in our near-axis description, which is incompatible with its even symmetry. This condition is necessarily broken at the points of maximum field strength, which we may write $\nu ={\rm \pi} /2+\tilde {\nu }$
in our near-axis description, which is incompatible with its even symmetry. This condition is necessarily broken at the points of maximum field strength, which we may write $\nu ={\rm \pi} /2+\tilde {\nu }$![]() and $\tilde {\nu }$
and $\tilde {\nu }$![]() is odd in $\varphi$
is odd in $\varphi$![]() . Barely trapped particles will always experience this lack of omnigeneity.
. Barely trapped particles will always experience this lack of omnigeneity.
Using this notation, we may rewrite the $O(1/r)$![]() contribution to the precession
contribution to the precession

to which contributions arise from any particles that venture into the region where omnigeneity is broken, i.e. $\sin \tilde {\nu }\neq 0$![]() . For these orbits, the non-omnigeneous part of the precession will always dominate for sufficiently small $r$
. For these orbits, the non-omnigeneous part of the precession will always dominate for sufficiently small $r$![]() . Because of the $\cos \alpha$
. Because of the $\cos \alpha$![]() dependence of the precession, these particles will precess in either poloidal direction depending on the field line considered. The immediate implication of this behaviour is that in a realistic magnetic field (one that allows for the necessary breaking of QI), the maximum-$J$
dependence of the precession, these particles will precess in either poloidal direction depending on the field line considered. The immediate implication of this behaviour is that in a realistic magnetic field (one that allows for the necessary breaking of QI), the maximum-$J$![]() property is technically not possible close to the magnetic axis, independently of plasma pressure.
property is technically not possible close to the magnetic axis, independently of plasma pressure.
This somewhat bleak result appears to rule out maximum-$J$![]() behaviour in QI configurations, much as in QS stellarators or tokamaks. It should, however, be noted that the factors that determine the size of the $1/r$
behaviour in QI configurations, much as in QS stellarators or tokamaks. It should, however, be noted that the factors that determine the size of the $1/r$![]() terms are naturally small. At the top of the magnetic well, where the conditions of exact omnigeneity need to be relaxed, it is by construction the case that the function $d$
terms are naturally small. At the top of the magnetic well, where the conditions of exact omnigeneity need to be relaxed, it is by construction the case that the function $d$![]() vanishes. That is, the magnetic-field perturbation $B_1$
vanishes. That is, the magnetic-field perturbation $B_1$![]() is small in the vicinity of the maximum, as is necessary for the consistency with a locally straight magnetic field (and for the contour of $B_{\mathrm {max}}$
is small in the vicinity of the maximum, as is necessary for the consistency with a locally straight magnetic field (and for the contour of $B_{\mathrm {max}}$![]() to be independent of the poloidal angle). By shrinking the region in which omnigeneity is broken, the number of particles for which the precession frequency diverges as $1/r$
to be independent of the poloidal angle). By shrinking the region in which omnigeneity is broken, the number of particles for which the precession frequency diverges as $1/r$![]() can be made arbitrarily small.Footnote 8 Only extremely close to the axis is the divergent behaviour of the precession frequency significant.
can be made arbitrarily small.Footnote 8 Only extremely close to the axis is the divergent behaviour of the precession frequency significant.
The size of this region can be gauged by estimating the minor radius $r_a$![]() below which the $1/r$
below which the $1/r$![]() behaviour, (A24), dominates over the second-order contributions, (A20). By way of example, we define and compute the critical radius $r_a=\sqrt {\sum _k w_{\alpha,-1}^2/\sum _k w_{\alpha,0}^2}$
behaviour, (A24), dominates over the second-order contributions, (A20). By way of example, we define and compute the critical radius $r_a=\sqrt {\sum _k w_{\alpha,-1}^2/\sum _k w_{\alpha,0}^2}$![]() (with the $-1$
(with the $-1$![]() and 0 indices referring to the respective $r$
and 0 indices referring to the respective $r$![]() scalings) for the near-axis fields in figure 6. The amplification of the precession and its variation from field line to field line is especially noticeable in figure 6(b) for which $r_a\sim 0.003$
scalings) for the near-axis fields in figure 6. The amplification of the precession and its variation from field line to field line is especially noticeable in figure 6(b) for which $r_a\sim 0.003$![]() , driven by the presence of ‘buffer’ regions (Plunk et al. Reference Plunk, Landreman and Helander2019; Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022). It may perhaps appear counterintuitive that close to the axis, where the field is most omnigeneous, the variation between field lines (an indicator of departure from omnigeneity) increases. However, the bounce-averaged radial drift $\omega _\psi$
, driven by the presence of ‘buffer’ regions (Plunk et al. Reference Plunk, Landreman and Helander2019; Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022). It may perhaps appear counterintuitive that close to the axis, where the field is most omnigeneous, the variation between field lines (an indicator of departure from omnigeneity) increases. However, the bounce-averaged radial drift $\omega _\psi$![]() does decrease linearly in $r$
does decrease linearly in $r$![]() as expected from (A17)), indicating that omnigeneity does become perfect in the limit $r \rightarrow 0$
as expected from (A17)), indicating that omnigeneity does become perfect in the limit $r \rightarrow 0$![]() . The existence of a region very close to the axis in which the maximum-$J$
. The existence of a region very close to the axis in which the maximum-$J$![]() condition cannot be satisfied is nevertheless unavoidable, but this region can, in principle, be made arbitrarily small.
condition cannot be satisfied is nevertheless unavoidable, but this region can, in principle, be made arbitrarily small.
A.4.2. Second-order breaking
From figure 6 it is clear that there are non-QI contributions even if the leading first-order field is precisely QI. In the exactly omnigenous limit, the contribution to $\omega _{\alpha}$![]() from second-order terms is $\alpha$
from second-order terms is $\alpha$![]() -independent, but one regains some $\alpha$
-independent, but one regains some $\alpha$![]() dependence when omnigeneity is broken. Taking into account the symmetry conditions on the various functions that constitute the near-axis description, we may write the non-QI contribution to the precession as
dependence when omnigeneity is broken. Taking into account the symmetry conditions on the various functions that constitute the near-axis description, we may write the non-QI contribution to the precession as

Two limits of this expression are of particular interest. The first limit concerns deeply trapped particles, which are relatively easily well confined and may therefore be omnigenous to second order. Then $\tilde \nu = 0$![]() and
and

The second limit of interest is realised when $B_{2c}$![]() has its QI form, (A18d). Then the first term in square brackets of the second integral vanishes, leaving a contribution that vanishes unless omnigeneity is broken at first order. The QI contribution $\omega _{\alpha,\mathrm {vac}}$
has its QI form, (A18d). Then the first term in square brackets of the second integral vanishes, leaving a contribution that vanishes unless omnigeneity is broken at first order. The QI contribution $\omega _{\alpha,\mathrm {vac}}$![]() in (A20) remains unchanged.
in (A20) remains unchanged.
A.5. Stellarator-symmetry breaking
The expressions above were derived under the assumption of stellarator symmetry. This is a convenient simplifying assumption, under which functions acquire a definite parity in $\varphi$![]() , which simplifies bounce integrals. If $B_0$
, which simplifies bounce integrals. If $B_0$![]() is not symmetric in $\varphi$
is not symmetric in $\varphi$![]() , the expressions need to be revisited although most of the considerations for symmetric fields continue to hold.
, the expressions need to be revisited although most of the considerations for symmetric fields continue to hold.
To deal with the stellarator asymmetric case, we employ the notation of Rodríguez & Plunk (Reference Rodríguez and Plunk2023) and denote the ‘bounce mapping’ by $\eta _0(\varphi )$![]() . This is the function that maps a point on one side of the magnetic well defined by $B_0$
. This is the function that maps a point on one side of the magnetic well defined by $B_0$![]() to the other side of the well, i.e. $B_0(\varphi ) = B_0[\eta _0(\varphi )]$
to the other side of the well, i.e. $B_0(\varphi ) = B_0[\eta _0(\varphi )]$![]() . Symmetry conditions on the functions $B_0$
. Symmetry conditions on the functions $B_0$![]() , $d$
, $d$![]() etc. then apply with respect to the mapping $\eta _0$
etc. then apply with respect to the mapping $\eta _0$![]() (Rodríguez & Plunk Reference Rodríguez and Plunk2023).
(Rodríguez & Plunk Reference Rodríguez and Plunk2023).
With this in mind, we proceed from (A19) without making any assumption of symmetry.Footnote 9 The first term, corresponding to the $1/r$![]() order, vanished due to the QI condition and the odd symmetry of $B_1$
order, vanished due to the QI condition and the odd symmetry of $B_1$![]() . It can be shown that this vanishing holds even when stellarator symmetry is abandoned
. It can be shown that this vanishing holds even when stellarator symmetry is abandoned

where we changed variables $\varphi =\eta _0(\bar {\varphi })$![]() for the first equality, applied the first-order QI condition in a generally non-symmetric QI field (equation (19) in Rodríguez & Plunk Reference Rodríguez and Plunk2023), and noted that the second integral is exactly the negative of the first one. This proves that the QI property is sufficient to make the integral vanish, without any stellarator-symmetry requirement being necessary. This should not come as a surprise.
for the first equality, applied the first-order QI condition in a generally non-symmetric QI field (equation (19) in Rodríguez & Plunk Reference Rodríguez and Plunk2023), and noted that the second integral is exactly the negative of the first one. This proves that the QI property is sufficient to make the integral vanish, without any stellarator-symmetry requirement being necessary. This should not come as a surprise.
The QI condition at second order may be succinctly written as an equation for the $\alpha$![]() -dependent part of $B_2$
-dependent part of $B_2$![]() as (equation (C12) in Rodríguez & Plunk Reference Rodríguez and Plunk2023)
as (equation (C12) in Rodríguez & Plunk Reference Rodríguez and Plunk2023)
where the subscript $b$![]() denotes the evaluation of the expression inside the brackets at $\eta _0$
denotes the evaluation of the expression inside the brackets at $\eta _0$![]() and the barred $\bar {B}_2$
and the barred $\bar {B}_2$![]() represents the poloidal average of $B_2$
represents the poloidal average of $B_2$![]() . Following the same substitution trick as for (A27), the $\theta$
. Following the same substitution trick as for (A27), the $\theta$![]() dependent part of the order $O(1)$
dependent part of the order $O(1)$![]() contribution to $\omega _{\alpha}$
contribution to $\omega _{\alpha}$![]() can be shown to vanish, only leaving the $\theta$
can be shown to vanish, only leaving the $\theta$![]() (or $\alpha$
(or $\alpha$![]() ) dependent piece. The conclusion is that the expression for the omnigeneous part of $\omega _{\alpha,0}$
) dependent piece. The conclusion is that the expression for the omnigeneous part of $\omega _{\alpha,0}$![]() is the same whether or not the field is stellarator symmetric, with the difference that in the asymmetric case usually $\varphi _L\neq -\varphi _R$
is the same whether or not the field is stellarator symmetric, with the difference that in the asymmetric case usually $\varphi _L\neq -\varphi _R$![]() . In addition, symmetry breaking will also affect the value of $B_{20}$
. In addition, symmetry breaking will also affect the value of $B_{20}$![]() .
.
Appendix B. Radial derivative of $B$ for deeply trapped particles in QI configurations
for deeply trapped particles in QI configurations
As we have seen in the main text, the average radial derivative of $B$![]() at the minimum along the field, $B_{20}=\bar {B}\partial _\psi B/2|_{\psi =0}$
at the minimum along the field, $B_{20}=\bar {B}\partial _\psi B/2|_{\psi =0}$![]() , is key in determining the tangential drift of trapped particles. This term is related to the magnetic well (3.12), which plays an important role for MHD stability (Freidberg Reference Freidberg2014; Landreman & Jorge Reference Landreman and Jorge2020; Rodríguez Reference Rodríguez2023).
, is key in determining the tangential drift of trapped particles. This term is related to the magnetic well (3.12), which plays an important role for MHD stability (Freidberg Reference Freidberg2014; Landreman & Jorge Reference Landreman and Jorge2020; Rodríguez Reference Rodríguez2023).
Regardless of whether the field is QI, the term $B_{20}$![]() must have a form that is consistent with the equilibrium and solenoidal properties of the magnetic field. That is, it must be consistent with $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}=0$
must have a form that is consistent with the equilibrium and solenoidal properties of the magnetic field. That is, it must be consistent with $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}=0$![]() and $\boldsymbol {j}\times \boldsymbol {B}=\boldsymbol {\nabla } p$
and $\boldsymbol {j}\times \boldsymbol {B}=\boldsymbol {\nabla } p$![]() . Within the asymptotic framework of the near-axis description of the field, the function $B_{20}$
. Within the asymptotic framework of the near-axis description of the field, the function $B_{20}$![]() is only partially constrained by the properties of the magnetic field on the axis and to first order. There is in general some freedom in its choice. However, at ‘straight’ sections where the curvature of the magnetic axis vanishes, the constraints of the equations become particularly stringent leaving no freedom. $B_{20}$
is only partially constrained by the properties of the magnetic field on the axis and to first order. There is in general some freedom in its choice. However, at ‘straight’ sections where the curvature of the magnetic axis vanishes, the constraints of the equations become particularly stringent leaving no freedom. $B_{20}$![]() becomes uniquely determined by lower-order choices and the plasma pressure. In this appendix we find determine its value and explore formal consequences of it.
becomes uniquely determined by lower-order choices and the plasma pressure. In this appendix we find determine its value and explore formal consequences of it.
For this purpose, we focus on the minimum of $|\boldsymbol {B}|$![]() along field, where deeply trapped particles reside and $\kappa =0$
along field, where deeply trapped particles reside and $\kappa =0$![]() . We are interested in relating the magnetic-field magnitude $B_{20}$
. We are interested in relating the magnetic-field magnitude $B_{20}$![]() to lower-order quantities in the near-axis expansion and to the flux-surface geometry. To do so, and as part of what is known as the inverse-coordinate approach to the near-axis expansion (Garren & Boozer Reference Garren and Boozer1991b), we describe flux surfaces in terms of Boozer coordinates (our independent set of coordinates) respect to a signed Frenet–Serret frame (Plunk et al. Reference Plunk, Landreman and Helander2019) $\{\hat {b},\hat {\kappa },\hat {\tau }\}$
to lower-order quantities in the near-axis expansion and to the flux-surface geometry. To do so, and as part of what is known as the inverse-coordinate approach to the near-axis expansion (Garren & Boozer Reference Garren and Boozer1991b), we describe flux surfaces in terms of Boozer coordinates (our independent set of coordinates) respect to a signed Frenet–Serret frame (Plunk et al. Reference Plunk, Landreman and Helander2019) $\{\hat {b},\hat {\kappa },\hat {\tau }\}$![]() as $\boldsymbol {x}-\boldsymbol {r}_0=X\hat {\kappa }+Y\hat {\tau }+Z\hat {b}$
as $\boldsymbol {x}-\boldsymbol {r}_0=X\hat {\kappa }+Y\hat {\tau }+Z\hat {b}$![]() . Here, $\boldsymbol {r}_0$
. Here, $\boldsymbol {r}_0$![]() represents the magnetic axis and $\{X,Y,Z\}$
represents the magnetic axis and $\{X,Y,Z\}$![]() are functions describing the flux-surface shape. The near-axis expansion framework is designed to uncover the connection between the $|\boldsymbol {B}|$
are functions describing the flux-surface shape. The near-axis expansion framework is designed to uncover the connection between the $|\boldsymbol {B}|$![]() and these features. The relevant equations and constructions can be found in Landreman & Sengupta (Reference Landreman and Sengupta2019), to which we refer for further details. We shall invoke results from this work, reproducing the necessary expressions. In what follows, the symbol $f_{ij}$
and these features. The relevant equations and constructions can be found in Landreman & Sengupta (Reference Landreman and Sengupta2019), to which we refer for further details. We shall invoke results from this work, reproducing the necessary expressions. In what follows, the symbol $f_{ij}$![]() represents the expansion coefficients of the function $f$
represents the expansion coefficients of the function $f$![]() , where the subscript $i$
, where the subscript $i$![]() corresponds to the power of $r$
corresponds to the power of $r$![]() in the expansion, and $j$
in the expansion, and $j$![]() equals $0,c$
equals $0,c$![]() or $s$
or $s$![]() depending on the $\theta$
depending on the $\theta$![]() harmonic it represents (constant, cosine or sine). At higher-order generalised notation can be devised (Rodríguez & Bhattacharjee Reference Rodríguez and Bhattacharjee2021).
harmonic it represents (constant, cosine or sine). At higher-order generalised notation can be devised (Rodríguez & Bhattacharjee Reference Rodríguez and Bhattacharjee2021).
We first consider the shape of flux surfaces in the direction normal to the magnetic axis and begin with the function $X_{20}$![]() , which describes a rigid shift of the flux surfaces relative to each other (akin to the Shafranov shift Landreman Reference Landreman2021; Rodríguez Reference Rodríguez2023). This function can be read off from equation (A34) of Landreman & Sengupta (Reference Landreman and Sengupta2019)
, which describes a rigid shift of the flux surfaces relative to each other (akin to the Shafranov shift Landreman Reference Landreman2021; Rodríguez Reference Rodríguez2023). This function can be read off from equation (A34) of Landreman & Sengupta (Reference Landreman and Sengupta2019)

where all the expressions on the right-hand side except $B_{20}, G_2$![]() and $I_2$
and $I_2$![]() are first-order quantities.
are first-order quantities.
Since $\kappa$![]() appears in the denominator of this expression, to avoid an unphysical diverging shift of flux surfaces at the point where $\kappa =0$
appears in the denominator of this expression, to avoid an unphysical diverging shift of flux surfaces at the point where $\kappa =0$![]() , $B_{20}$
, $B_{20}$![]() is highly constrained at this point. If the curvature has a zero of order $v$
is highly constrained at this point. If the curvature has a zero of order $v$![]() , then we expect the first $v-1$
, then we expect the first $v-1$![]() derivatives of $B_{20}$
derivatives of $B_{20}$![]() to be determined by (B1). Let us momentarily focus on $B_{20}(\varphi =0)$
to be determined by (B1). Let us momentarily focus on $B_{20}(\varphi =0)$![]() for $\kappa (\varphi =0)=0$
for $\kappa (\varphi =0)=0$![]() . We shall assume stellarator symmetry and the configuration to be QI to first order, so that $\bar {d}=d/\kappa$
. We shall assume stellarator symmetry and the configuration to be QI to first order, so that $\bar {d}=d/\kappa$![]() is even in $\varphi$
is even in $\varphi$![]() , the (signed) curvature is odd, the torsion even, $B_0$
, the (signed) curvature is odd, the torsion even, $B_0$![]() even, and $\sigma$
even, and $\sigma$![]() odd ($\sigma =(B_{1s}Y_{1s}+B_{1c}Y_{1c})/\bar {B}\kappa$
odd ($\sigma =(B_{1s}Y_{1s}+B_{1c}Y_{1c})/\bar {B}\kappa$![]() is a measure of up-down asymmetry). With this in mind, using the expression for $Z_{20}$
is a measure of up-down asymmetry). With this in mind, using the expression for $Z_{20}$![]() and $q_i$
and $q_i$![]() from equations (A24), (A27) and (A37–40) of Landreman & Sengupta (Reference Landreman and Sengupta2019), we findFootnote 10
from equations (A24), (A27) and (A37–40) of Landreman & Sengupta (Reference Landreman and Sengupta2019), we findFootnote 10

To further simplify this expression, we eliminate $\sigma '$![]() in favour of the properties of the axis and first-order quantities. Using the near-axis Riccati $\sigma$
in favour of the properties of the axis and first-order quantities. Using the near-axis Riccati $\sigma$![]() -equation (Landreman & Sengupta Reference Landreman and Sengupta2019, equation (A21)), assuming an exact QI magnetic field at first order $B_{1c}=-B_0 \,{\rm d}\sin \iota _0\varphi$
-equation (Landreman & Sengupta Reference Landreman and Sengupta2019, equation (A21)), assuming an exact QI magnetic field at first order $B_{1c}=-B_0 \,{\rm d}\sin \iota _0\varphi$![]() and $B_{1s}=B_0 \,{\rm d}\cos \iota _0\varphi$
and $B_{1s}=B_0 \,{\rm d}\cos \iota _0\varphi$![]() (Plunk et al. Reference Plunk, Landreman and Helander2019; Rodríguez & Plunk Reference Rodríguez and Plunk2023),
(Plunk et al. Reference Plunk, Landreman and Helander2019; Rodríguez & Plunk Reference Rodríguez and Plunk2023),
With this and the relation $\ell '=G_0/B_0$![]() (assuming $G_0>0$
(assuming $G_0>0$![]() ) (Landreman & Sengupta Reference Landreman and Sengupta2019, equation (A20)) we obtain
) (Landreman & Sengupta Reference Landreman and Sengupta2019, equation (A20)) we obtain
where
which are the forms used in the main text. It will be convenient to choose our reference field $\bar {B}$![]() to equal $B$
to equal $B$![]() at the bottom of the well, $B_0$
at the bottom of the well, $B_0$![]() , but we keep the expressions here general.
, but we keep the expressions here general.
An analogous approach to avoid divergence of $X_{2c}$![]() yields the consistent value of $B_{2c}$
yields the consistent value of $B_{2c}$![]() at the minimum of the magnetic field. In this case, we need equation (A36) from Landreman & Sengupta (Reference Landreman and Sengupta2019)
at the minimum of the magnetic field. In this case, we need equation (A36) from Landreman & Sengupta (Reference Landreman and Sengupta2019)

Then, as before, we may write for $B_{2c}$![]()

with all quantities evaluated at the point $\varphi =0$![]() . For a simple zero, the equivalent for $B_{2s}$
. For a simple zero, the equivalent for $B_{2s}$![]() yields that $B_{2s}(\varphi =0)=0$
yields that $B_{2s}(\varphi =0)=0$![]() . This is satisfied by the parity conditions derived from stellarator symmetry, and thus bring no additional information to the table. The expressions here presented may be found derived in a Mathematica script in the Zenodo repository associated with this paper. We re-emphasise that the form of these expressions assumes exact QI at first order in the near-axis expansion. For more general forms of the expressions see the comments in Appendix D.
. This is satisfied by the parity conditions derived from stellarator symmetry, and thus bring no additional information to the table. The expressions here presented may be found derived in a Mathematica script in the Zenodo repository associated with this paper. We re-emphasise that the form of these expressions assumes exact QI at first order in the near-axis expansion. For more general forms of the expressions see the comments in Appendix D.
B.1. Implications of the QI condition
We showed in Appendix A and learnt from Rodríguez & Plunk (Reference Rodríguez and Plunk2023) that, in an omnigeneous field, $B_{2c}$![]() must have a very particular form in a stellarator-symmetric field. At the same time, from the conditions of equilibrium, we have also found in (B7) that the value of $B_{2c}$
must have a very particular form in a stellarator-symmetric field. At the same time, from the conditions of equilibrium, we have also found in (B7) that the value of $B_{2c}$![]() is constrained at the bottom of the magnetic well. Thus, in principle, there are two different constraints that must be simultaneously satisfied in a QI field.
is constrained at the bottom of the magnetic well. Thus, in principle, there are two different constraints that must be simultaneously satisfied in a QI field.
To further look into this issue, we note that the $B_{2c}$![]() employed in this section is somewhat different from the QI form of $B_{2c}$
employed in this section is somewhat different from the QI form of $B_{2c}$![]() employed elsewhere in the text. In fact, $B_{2c}$
employed elsewhere in the text. In fact, $B_{2c}$![]() here (see Landreman & Sengupta Reference Landreman and Sengupta2019) is defined respect to the helical angle $\chi =\theta -N\varphi$
here (see Landreman & Sengupta Reference Landreman and Sengupta2019) is defined respect to the helical angle $\chi =\theta -N\varphi$![]() , where $N$
, where $N$![]() is related to the self-linking number of the signed Frenet frame of the axis (Rodríguez, Sengupta & Bhattacharjee Reference Rodríguez, Sengupta and Bhattacharjee2022). In contrast, the QI version of $B_{2c}$
is related to the self-linking number of the signed Frenet frame of the axis (Rodríguez, Sengupta & Bhattacharjee Reference Rodríguez, Sengupta and Bhattacharjee2022). In contrast, the QI version of $B_{2c}$![]() (which we may denote by $B_{2c}^{\mathrm {QI}}$
(which we may denote by $B_{2c}^{\mathrm {QI}}$![]() ) is defined in (A15) respect to the angle $\alpha +\nu$
) is defined in (A15) respect to the angle $\alpha +\nu$![]() . Therefore
. Therefore
where $\bar {\iota }=\iota -N$![]() . Now, for a stellarator-symmetric QI field at the bottom of the well, $\nu ={\rm \pi} /2$
. Now, for a stellarator-symmetric QI field at the bottom of the well, $\nu ={\rm \pi} /2$![]() and $\varphi =0$
and $\varphi =0$![]() , meaning that $B_{2c}=-B_{2c}^{\mathrm {QI}}$
, meaning that $B_{2c}=-B_{2c}^{\mathrm {QI}}$![]() . Due to the sign flip, the resulting constraint from (A18d) becomes
. Due to the sign flip, the resulting constraint from (A18d) becomes

The condition of omnigeneity at the bottom of the trapping well thus translates into an additional constraint on the zeroth- and first-order components that make up the magnetic field. In the limit of a vacuum field with no secondary minima of $|\boldsymbol {B}|$![]() , it follows that $\bar {d}\bar {d}''<0$
, it follows that $\bar {d}\bar {d}''<0$![]() : geometrically, flux surfaces must become more elongated in the binormal direction away from the minimum. This is a geometric consequence of the QI conditions.
: geometrically, flux surfaces must become more elongated in the binormal direction away from the minimum. This is a geometric consequence of the QI conditions.
With this constraint at hand, we may eliminate $\bar {d}''$![]() altogether from the expression we have for $B_{20}$
altogether from the expression we have for $B_{20}$![]() in (B4). Defining $f_0=B_{20}/B_0-(B_0^2d^2/B_0')'/4B_0=f_p+f_{B_0''}+f_{I_2}+f_{\tau _0^2}+f_{\mathrm {QI}}$
in (B4). Defining $f_0=B_{20}/B_0-(B_0^2d^2/B_0')'/4B_0=f_p+f_{B_0''}+f_{I_2}+f_{\tau _0^2}+f_{\mathrm {QI}}$![]() , the resulting expression is
, the resulting expression is

where $\bar {\alpha }=\bar {d}^4B_0^2/\bar {B}^2$![]() .
.
B.2. Stellarator-symmetry breaking
The derivation above may be extended to non-stellarator-symmetric fields, which leads to additional terms in various equations. For simplicity, we shall assume once again that the field is exactly omnigeneous to first order and that $\nu ={\rm \pi} /2$![]() . The latter condition is not necessary as one could add an even function $\tilde {\nu }$
. The latter condition is not necessary as one could add an even function $\tilde {\nu }$![]() while still satisfying the conditions of omnigeneity (Rodríguez & Plunk Reference Rodríguez and Plunk2023). In the interest of brevity, however, we only consider this simplest case.
while still satisfying the conditions of omnigeneity (Rodríguez & Plunk Reference Rodríguez and Plunk2023). In the interest of brevity, however, we only consider this simplest case.
As a result of the lack of symmetry, the expression for the magnetic well $B_{20}$![]() changes. Proceeding in an equivalent way to that above, it can be shown that, in the expression (B4), the coefficients of $B_{20}/B_0$
changes. Proceeding in an equivalent way to that above, it can be shown that, in the expression (B4), the coefficients of $B_{20}/B_0$![]() become (assuming $G_0>0$
become (assuming $G_0>0$![]() )
)

The main difference to the stellarator-symmetric case is the modification of terms through the breaking of up-down symmetry, $\sigma$![]() , and the appearance of three new terms. If the field is up-down symmetric at the minimum of $|\boldsymbol {B}|$
, and the appearance of three new terms. If the field is up-down symmetric at the minimum of $|\boldsymbol {B}|$![]() ($\sigma =0$
($\sigma =0$![]() ), the only new term compared with the stellarator-symmetric case is that proportional to $(\bar {d}')^2$
), the only new term compared with the stellarator-symmetric case is that proportional to $(\bar {d}')^2$![]() . This term is always positive, thus indicating a potential benefit of breaking stellarator symmetry to increase the depth of the radial well.
. This term is always positive, thus indicating a potential benefit of breaking stellarator symmetry to increase the depth of the radial well.
Proceeding similarly with $B_{2c}$![]() , we find
, we find

Now, when stellarator symmetry is broken, the condition of QI at second-order changes, and the self-consistency condition for $B_{2c}(0)$![]() will change accordingly. That is, we must check the implications of (A28), drawn from Rodríguez & Plunk (Reference Rodríguez and Plunk2023) (see (26b) there). At the bottom of the well it is always true that $\eta _0'\approx -1$
will change accordingly. That is, we must check the implications of (A28), drawn from Rodríguez & Plunk (Reference Rodríguez and Plunk2023) (see (26b) there). At the bottom of the well it is always true that $\eta _0'\approx -1$![]() , by virtue of having a minimum (and thus in a local Taylor expansion in $\varphi$
, by virtue of having a minimum (and thus in a local Taylor expansion in $\varphi$![]() , a leading even power of $\varphi$
, a leading even power of $\varphi$![]() ). Because $d$
). Because $d$![]() must vanish at this position rapidly enough to avoid the loss of confinement of deeply trapped particles (see the discussion on pseudosymmetry and the behaviour at the bottom of the well in Rodríguez & Plunk (Reference Rodríguez and Plunk2023)), $B_{2c}(0)$
must vanish at this position rapidly enough to avoid the loss of confinement of deeply trapped particles (see the discussion on pseudosymmetry and the behaviour at the bottom of the well in Rodríguez & Plunk (Reference Rodríguez and Plunk2023)), $B_{2c}(0)$![]() must be the same as in the stellarator-symmetric case, at least under the assumption made on the form of $\nu$
must be the same as in the stellarator-symmetric case, at least under the assumption made on the form of $\nu$![]() .
.
This way, we form the equivalent to (B10) when stellarator symmetry is broken, which becomes

Some of these expressions are used in the main text.
Appendix C. The magnetic mirror problem
There is an obvious analogy between magnetic mirrors and QI stellarators. Indeed, the latter are sometimes referred to as linked mirrors. This analogy is especially accurate near the maxima and minima of $|\boldsymbol {B}|$![]() along field lines, which tend to be located in places where the curvature is small (and vanishes on the magnetic axis) and where trapped particles thus have little sense of the toroidicity of the field. This analogy provides us with a practical tool to assess the behaviour of the QI field from the perspective of a straight magnetic mirror.
along field lines, which tend to be located in places where the curvature is small (and vanishes on the magnetic axis) and where trapped particles thus have little sense of the toroidicity of the field. This analogy provides us with a practical tool to assess the behaviour of the QI field from the perspective of a straight magnetic mirror.
C.1. Near-axis expansion procedure
The near-axis approximation (commonly referred to as the paraxial approximation in the context of magnetic mirrors) is common in the study of magnetic mirrors (Furth & Rosenbluth Reference Furth and Rosenbluth1964; Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1967; Catto, Tang & Baldwin Reference Catto, Tang and Baldwin1981; Savenko Reference Savenko2006). In this appendix, we adopt this approximation within the inverse-coordinate approach used for stellarators. We do so in an attempt to simplify the comparison and to clarify the quadrupole ansatz traditionally used in the analysis of magnetic mirrors.
We focus on the case of a vacuum field and describe the field lines as curves of constant $\psi$![]() and $\alpha$
and $\alpha$![]() , whose position is given by $\boldsymbol {x}(\psi,\alpha,z)=X\hat {\boldsymbol {x}}+Y\hat {\boldsymbol {y}}+(z+Z)\hat {\boldsymbol {z}}$
, whose position is given by $\boldsymbol {x}(\psi,\alpha,z)=X\hat {\boldsymbol {x}}+Y\hat {\boldsymbol {y}}+(z+Z)\hat {\boldsymbol {z}}$![]() in Cartesian coordinates. The $z$
in Cartesian coordinates. The $z$![]() -axis can be thought of as the ‘magnetic axis’, about which we will perform the expansion, and the function $Z$
-axis can be thought of as the ‘magnetic axis’, about which we will perform the expansion, and the function $Z$![]() can without loss of generality be chosen to vanish.
can without loss of generality be chosen to vanish.
In order to find the governing equations, we write the vacuum condition of the magnetic field and its Clebsch representation as (D'haeseleer et al. Reference D'haeseleer, Hitchon, Callen and Shohet2012)
or in the inverse-coordinate representation $\{\psi,\alpha,z\}$![]() ,
,
To relate it to the magnetic-field magnitude, we then write what we shall refer to as the Jacobian equation
which follows from taking the scalar product of (C1) with its right-hand-side, using the dual relation $\boldsymbol {\nabla }\psi \times \boldsymbol {\nabla }\alpha =\mathcal {J}^{-1}\partial _z\boldsymbol {x}=\boldsymbol {B}$![]() .
.
As usual, we need to expand these equations by expressing all functions as Taylor–Fourier expansions in the pseudo-radial coordinate $r=\sqrt {2\psi /\bar {B}}$![]() and $\alpha$
and $\alpha$![]() . The latter is a field-line label, and because we are in a straight, non-toroidal system, we may take it as our poloidal angle. (In the absence of toroidal flux surfaces, there is no need to introduce a toroidal or a helical angle.) The relevant functions in the expansion are $B,X$
. The latter is a field-line label, and because we are in a straight, non-toroidal system, we may take it as our poloidal angle. (In the absence of toroidal flux surfaces, there is no need to introduce a toroidal or a helical angle.) The relevant functions in the expansion are $B,X$![]() and $Y$
and $Y$![]() as well as the scalar potential $\varPhi$
as well as the scalar potential $\varPhi$![]() . We shall use the same index notation as in the regular stellarator near-axis expansion, so that, for instance,
. We shall use the same index notation as in the regular stellarator near-axis expansion, so that, for instance,

Here, the functions $X_{1c}(z)$![]() and $X_{1s}(z)$
and $X_{1s}(z)$![]() are considered to be first-order inputs to the problem alongside $B_0(z)$
are considered to be first-order inputs to the problem alongside $B_0(z)$![]() , the magnetic-field strength on axis.
, the magnetic-field strength on axis.
C.1.1. Zeroth order (C3)
To leading order $O(r^0)$![]() of (C3),
of (C3),
where $B_0$![]() is taken to be positive.
is taken to be positive.
C.1.2. Leading order (C2)
To leading order, $O(r^{-1})$![]() , there are three different equations we obtain from the three projections along the Cartesian basis of (C2). From the $\hat {z}$
, there are three different equations we obtain from the three projections along the Cartesian basis of (C2). From the $\hat {z}$![]() -projection we have
-projection we have
which is a statement of magnetic flux conservation along the flux tube labelled by $r$![]() . This is of course fully analogous to the situation in a stellarator, as it is a property inherent to any flux tube.
. This is of course fully analogous to the situation in a stellarator, as it is a property inherent to any flux tube.
For a non-vanishing magnetic field $B_0\neq 0$![]() , the other two components of (C2) to $O(r)$
, the other two components of (C2) to $O(r)$![]() can be combined linearly using $X_{1c}$
can be combined linearly using $X_{1c}$![]() and $X_{1s}$
and $X_{1s}$![]() . The result is that $\varPhi _{1,c} = \varPhi _{1,s}= 0$
. The result is that $\varPhi _{1,c} = \varPhi _{1,s}= 0$![]() . There is, in other words, no first-order contribution to the vacuum magnetic potential.
. There is, in other words, no first-order contribution to the vacuum magnetic potential.
Next, the first-order $O(r)$![]() form of (C3) yields the natural conclusion that $B_{1s}=0$
form of (C3) yields the natural conclusion that $B_{1s}=0$![]() and $B_{1c}=0$
and $B_{1c}=0$![]() , so that there is no $\alpha$
, so that there is no $\alpha$![]() -variation of the magnetic-field strength to first order. This is an expected result, as we well know that, in the absence of a pressure gradient, the perpendicular gradient of $|\boldsymbol {B}|$
-variation of the magnetic-field strength to first order. This is an expected result, as we well know that, in the absence of a pressure gradient, the perpendicular gradient of $|\boldsymbol {B}|$![]() is proportional to the curvature vector. In the vicinity of a straight axis, there is therefore no first-order variation of the magnetic-field strength. This circumstance sets the straight mirror apart from a typical QI stellarator, in which the toroidal nature of the field forces the field to exhibit such a variation in most places along the magnetic axis. The leading form of the field is then that at next order, which must be quadrupole-like.
is proportional to the curvature vector. In the vicinity of a straight axis, there is therefore no first-order variation of the magnetic-field strength. This circumstance sets the straight mirror apart from a typical QI stellarator, in which the toroidal nature of the field forces the field to exhibit such a variation in most places along the magnetic axis. The leading form of the field is then that at next order, which must be quadrupole-like.
C.1.3. Zeroth order (C2)
Let us now turn to the next order of (C2), which is $O(r^0)$![]() . At this order we have a total of six independent equations, as each of the projections has $\cos \alpha$
. At this order we have a total of six independent equations, as each of the projections has $\cos \alpha$![]() and $\sin \alpha$
and $\sin \alpha$![]() terms.
terms.
From the $\hat {z}$![]() projection, and constructing appropriate linear combinations of the equations, we may write the following equations for $Y_{2c}$
projection, and constructing appropriate linear combinations of the equations, we may write the following equations for $Y_{2c}$![]() and $Y_{2s}$
and $Y_{2s}$![]() :
:


which are thus explicitly related to the second-order quantities $X_2$![]() and $Y_{20}$
and $Y_{20}$![]() . This circumstance is reminiscent of the situation in a stellarator (equations (A32)–(A33) in Landreman & Sengupta Reference Landreman and Sengupta2019). In the interest of brevity, we shall not proceed to find expressions for these coefficients. Full expressions may be found in the Zenodo repository associated with this paper.
. This circumstance is reminiscent of the situation in a stellarator (equations (A32)–(A33) in Landreman & Sengupta Reference Landreman and Sengupta2019). In the interest of brevity, we shall not proceed to find expressions for these coefficients. Full expressions may be found in the Zenodo repository associated with this paper.
The remaining components of (C2) can also be combined to yield expressions for $\varPhi _2$![]() (i.e. three equations) and a consistency condition on first-order quantities. The former may be written as follows, using (C6):
(i.e. three equations) and a consistency condition on first-order quantities. The former may be written as follows, using (C6):
and the latter as
Because we have adopted an approach in which $X_{1s}$![]() and $X_{1c}$
and $X_{1c}$![]() are inputs to the near-axis construction, the second bracket must vanish. This is an ordinary differential equation for $Y_1$
are inputs to the near-axis construction, the second bracket must vanish. This is an ordinary differential equation for $Y_1$![]() , which together with (C6) give both $Y_{1s}$
, which together with (C6) give both $Y_{1s}$![]() and $Y_{1c}$
and $Y_{1c}$![]() in terms of $X_1$
in terms of $X_1$![]() and $B_0$
and $B_0$![]() . Introducing the definition $Y_{1c}=Y_{1s}\sigma$
. Introducing the definition $Y_{1c}=Y_{1s}\sigma$![]() , this equation can be cast, with (C6), into the form of a Riccati equation
, this equation can be cast, with (C6), into the form of a Riccati equation
while (C6) becomes
C.1.4. Second order (C3)
Having closed forms for the various terms in $\varPhi _2$![]() , we are in a position to evaluate the magnetic field $B_2$
, we are in a position to evaluate the magnetic field $B_2$![]() by considering the $O(r^2)$
by considering the $O(r^2)$![]() expansion of (C3). From each of its harmonics the following relations can be read off
expansion of (C3). From each of its harmonics the following relations can be read off
which uniquely describe the magnetic-field magnitude to second order in terms of first-order shaping. Note that the quadrupole nature of $|\boldsymbol {B}|$![]() arises naturally through the near-axis construction.
arises naturally through the near-axis construction.
C.2. Magnetic field at the bottom of the well
We now have all the tools we need to understand the behaviour of the field at the bottom of the magnetic well, which we define to be at $z=0$![]() . We choose to align our coordinate system with the leading elliptical shape at $z=0$
. We choose to align our coordinate system with the leading elliptical shape at $z=0$![]() and define the poloidal label $\alpha$
and define the poloidal label $\alpha$![]() in such a way that $\sigma (0)=0$
in such a way that $\sigma (0)=0$![]() and $X_{1s}(0)=0$
and $X_{1s}(0)=0$![]() , without any loss of generality.Footnote 11 By definition, ${B_0'(0)=0}$
, without any loss of generality.Footnote 11 By definition, ${B_0'(0)=0}$![]() and we shall choose our reference field as $B_0(0)=\bar {B}$
and we shall choose our reference field as $B_0(0)=\bar {B}$![]() .
.
With these definitions and choices, we may then evaluate the magnetic field at the bottom of the magnetic well for a general straight magnetic mirror. The result is


where all quantities are evaluated at $z=0$![]() .
.
C.3. Maximum-$J$ in a magnetic mirror
in a magnetic mirror
The analysis of the maximum-$J$![]() condition in a mirror closely follows that in a QI stellarator and proceeds from the general expression for the precession frequency (A9). In the context of a straight mirror, relaxing the conditions of omnigeneity and stellarator symmetry, but instead noting that there is no first-order variation in the field magnitude, $B_1$
condition in a mirror closely follows that in a QI stellarator and proceeds from the general expression for the precession frequency (A9). In the context of a straight mirror, relaxing the conditions of omnigeneity and stellarator symmetry, but instead noting that there is no first-order variation in the field magnitude, $B_1$![]() , we find in vacuum
, we find in vacuum

where $B_2=B_{20}+B_{2c}\cos 2\alpha +B_{2s}\sin 2\alpha$![]() , $z_{L,R}$
, $z_{L,R}$![]() are the bouncing points for given $\lambda$
are the bouncing points for given $\lambda$![]() and the magnetic-field functions are given in (C12). We may normalise $\omega _{\alpha}$
and the magnetic-field functions are given in (C12). We may normalise $\omega _{\alpha}$![]() following the prescription in (2.2), for which we need to define an edge flux $\psi _a$
following the prescription in (2.2), for which we need to define an edge flux $\psi _a$![]() . Following the same procedure as for the near-axis stellarator, defining the aspect ratio as $A=L/a$
. Following the same procedure as for the near-axis stellarator, defining the aspect ratio as $A=L/a$![]() , where $L$
, where $L$![]() is the length of the mirror
is the length of the mirror
At the bottom of the well, the expression for $\omega _{\alpha}$![]() for deeply trapped particles reduces to a form analogous to (2.9)
for deeply trapped particles reduces to a form analogous to (2.9)
For maximum-$J$![]() behaviour, i.e. $q\omega _{\alpha} >0$
behaviour, i.e. $q\omega _{\alpha} >0$![]() for all $\alpha$
for all $\alpha$![]() , it is thus necessary that
, it is thus necessary that
in addition to $B_{20}>0$![]() . Because the mirror has no first-order variation of $|\boldsymbol {B}|$
. Because the mirror has no first-order variation of $|\boldsymbol {B}|$![]() , the maximum-$J$
, the maximum-$J$![]() and minimum-$B$
and minimum-$B$![]() properties are equivalent, i.e. both require $\partial _\psi B>0$
properties are equivalent, i.e. both require $\partial _\psi B>0$![]() to leading order in the expansion in $r$
to leading order in the expansion in $r$![]() . This minimum-$B$
. This minimum-$B$![]() property is well known to endow the magnetic mirror with MHD stability at sufficiently low $\beta$
property is well known to endow the magnetic mirror with MHD stability at sufficiently low $\beta$![]() (Berkowitz, Grad & Rubin Reference Berkowitz, Grad and Rubin1958; Taylor Reference Taylor1963; Furth & Rosenbluth Reference Furth and Rosenbluth1964).
(Berkowitz, Grad & Rubin Reference Berkowitz, Grad and Rubin1958; Taylor Reference Taylor1963; Furth & Rosenbluth Reference Furth and Rosenbluth1964).
Using the expressions for $B_2$![]() at the bottom of the mirror, (C13), one may show that the maximum-$J$
at the bottom of the mirror, (C13), one may show that the maximum-$J$![]() condition is equivalent to
condition is equivalent to

These two conditions may qualitatively be interpreted as
Equation (C18a) is a statement about the elongation of flux surfaces having to grow away from the middle of the mirror, where $X_{1c}^2$![]() is the elongation of the elliptical cross-section in the $x$
is the elongation of the elliptical cross-section in the $x$![]() -direction. We are free to take $X_{1c}>1$
-direction. We are free to take $X_{1c}>1$![]() to make this direction coincide with the major axis of the ellipse. Then $X_{1c}''>0$
to make this direction coincide with the major axis of the ellipse. Then $X_{1c}''>0$![]() can be interpreted as a condition for growing elongation away from the minimum (in both directions). This property indeed constitutes a typical feature of optimised magnetic mirrors (see figure 11).
can be interpreted as a condition for growing elongation away from the minimum (in both directions). This property indeed constitutes a typical feature of optimised magnetic mirrors (see figure 11).

Figure 11. Example of an optimised ‘symmetric’ magnetic mirror. The figure shows a three-dimensional rendition of a near-axis magnetic mirror optimised for omnigeneity and the maximum-$J$![]() property. Panels (b,c) illustrate the elongation of flux surfaces, $\mathcal {E}$
property. Panels (b,c) illustrate the elongation of flux surfaces, $\mathcal {E}$![]() , and the normalised precession frequency (with $\hat {\omega }_{\alpha} >0$
, and the normalised precession frequency (with $\hat {\omega }_{\alpha} >0$![]() indicating maximum-$J$
indicating maximum-$J$![]() behaviour) as a function of $z$
behaviour) as a function of $z$![]() , where the black line represents the average over the field-line label $\alpha$
, where the black line represents the average over the field-line label $\alpha$![]() . The mirror was constructed assuming symmetry of $X_{1c}$
. The mirror was constructed assuming symmetry of $X_{1c}$![]() and $X_{1s}$
and $X_{1s}$![]() , and employs a simple quadratic magnetic field.
, and employs a simple quadratic magnetic field.
Equation (C18b) is more interesting than (C18a), as it involves more aspects of the field. Maximum-$J$![]() behaviour can only be attained if there is a sufficiently large ‘twist’ of field lines across the bottom of the magnetic well. By ‘twist’ we refer to the contribution from $X_{1c}'$
behaviour can only be attained if there is a sufficiently large ‘twist’ of field lines across the bottom of the magnetic well. By ‘twist’ we refer to the contribution from $X_{1c}'$![]() and $X_{1s}'$
and $X_{1s}'$![]() , which describes a left–right symmetry breaking of the field. This ‘local shearing’ of field lines and lack of symmetry about the minimum of the configuration is common in mirror designs. The twist of the field must be strong enough to overcome the effect of elongation and the natural tendency for a negative radial magnetic field derivative, indicated by the $B_0''$
, which describes a left–right symmetry breaking of the field. This ‘local shearing’ of field lines and lack of symmetry about the minimum of the configuration is common in mirror designs. The twist of the field must be strong enough to overcome the effect of elongation and the natural tendency for a negative radial magnetic field derivative, indicated by the $B_0''$![]() term.
term.
All in all, strong twist and large elongation are helpful for maximum-$J$![]() behaviour, but they must be balanced in a careful way. Making the minimum flat (reducing $B_0''$
behaviour, but they must be balanced in a careful way. Making the minimum flat (reducing $B_0''$![]() ) is also helpful. These features are visible in typically shaped mirrors such as the example shown in figure 11.
) is also helpful. These features are visible in typically shaped mirrors such as the example shown in figure 11.
C.4. Omnigeneity in a magnetic mirror
Magnetic mirrors can be made to be omnigenous by careful tailoring of the quadrupole magnetic field (Hall & McNamara Reference Hall and McNamara1975; Catto & Hazeltine Reference Catto and Hazeltine1981). What this means in an open ended device is that the surfaces of constant $\psi$![]() correspond to precession surfaces for all trapped species in the sense introduced by Hall & McNamara (Reference Hall and McNamara1975). In order to characterise this property, we measure of the ‘radial’ drift (normal to constant $\psi$
correspond to precession surfaces for all trapped species in the sense introduced by Hall & McNamara (Reference Hall and McNamara1975). In order to characterise this property, we measure of the ‘radial’ drift (normal to constant $\psi$![]() surfaces) by the quantity $Y_{\mathrm {omn}}=\boldsymbol {\nabla }\varPhi \times \boldsymbol {\nabla } B\boldsymbol {\cdot }\boldsymbol {\nabla }\psi /\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } B$
surfaces) by the quantity $Y_{\mathrm {omn}}=\boldsymbol {\nabla }\varPhi \times \boldsymbol {\nabla } B\boldsymbol {\cdot }\boldsymbol {\nabla }\psi /\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } B$![]() , which plays a key role in the analysis of stellarator omnigeneity and in our coordinates $(\psi,\alpha,z)$
, which plays a key role in the analysis of stellarator omnigeneity and in our coordinates $(\psi,\alpha,z)$![]() can be written as
can be written as
We follow the approach of Rodríguez & Plunk (Reference Rodríguez and Plunk2023) to obtain a near-axis expansion of the condition for omnigeneity, which requires that $Y_{\mathrm {omn}}$![]() is equal and opposite at bounce points.
is equal and opposite at bounce points.
Expanding this condition in powers of $r$![]() , we obtain $Y_{\mathrm {omn}}^{(1)}=0$
, we obtain $Y_{\mathrm {omn}}^{(1)}=0$![]() to first order by virtue of the straight axis: there is no leading curvature drift. It is only at the next order that there is a non-zero radial drift, so we may write $Y_{\mathrm {omn}}^{(2)}=Y_{\mathrm {omn},c}^{(2)}\cos 2\alpha +Y_{\mathrm {omn},s}^{(2)}\sin 2\alpha$
to first order by virtue of the straight axis: there is no leading curvature drift. It is only at the next order that there is a non-zero radial drift, so we may write $Y_{\mathrm {omn}}^{(2)}=Y_{\mathrm {omn},c}^{(2)}\cos 2\alpha +Y_{\mathrm {omn},s}^{(2)}\sin 2\alpha$![]() . The expansion gives
. The expansion gives


where
and we have made use of (C12). For omnigeneity, the expressions for $Y_{\mathrm {omn},c}^{(2)}$![]() and $Y_{\mathrm {omn},s}^{(2)}$
and $Y_{\mathrm {omn},s}^{(2)}$![]() must be even in $z$
must be even in $z$![]() (provided $B_0$
(provided $B_0$![]() is symmetric about its minimum). This imposes constraints on the choice of $X_{1c}$
is symmetric about its minimum). This imposes constraints on the choice of $X_{1c}$![]() and $X_{1s}$
and $X_{1s}$![]() .
.
It is natural to ask whether this condition is at all compatible with the maximum-$J$![]() requirements derived above. In other words, is it possible to design an omnigenous, maximum-$J$
requirements derived above. In other words, is it possible to design an omnigenous, maximum-$J$![]() magnetic mirror? Let us consider omnigeneity at the bottom of the mirror, in which the condition reduces to that of locally vanishing radial drift. Evaluating the square brackets in (C21) at the minimum, and requiring them to vanish (assuming a first-order zero of $B_0''\neq 0$
magnetic mirror? Let us consider omnigeneity at the bottom of the mirror, in which the condition reduces to that of locally vanishing radial drift. Evaluating the square brackets in (C21) at the minimum, and requiring them to vanish (assuming a first-order zero of $B_0''\neq 0$![]() )
)
which, incidentally, implies $B_{20}/B_0=X_{1c}''X_{1c}/2$![]() and $B_{2c}=0=B_{2s}$
and $B_{2c}=0=B_{2s}$![]() at the minimum. If we choose $X_{1c}''>0$
at the minimum. If we choose $X_{1c}''>0$![]() to comply by the first of the two maximum-$J$
to comply by the first of the two maximum-$J$![]() conditions, (C18a), the second maximum-$J$
conditions, (C18a), the second maximum-$J$![]() condition, (C18b), is satisfied by satisfying the condition of omnigeneity, (C23b). This suggests that it is possible to construct a mirror that is omnigeneous and satisfies the maximum-$J$
condition, (C18b), is satisfied by satisfying the condition of omnigeneity, (C23b). This suggests that it is possible to construct a mirror that is omnigeneous and satisfies the maximum-$J$![]() condition simultaneously, at least at the minimum. Indeed, Catto & Hazeltine (Reference Catto and Hazeltine1981) have shown that it is possible in a finite region around the minimum.
condition simultaneously, at least at the minimum. Indeed, Catto & Hazeltine (Reference Catto and Hazeltine1981) have shown that it is possible in a finite region around the minimum.
C.5. Example of approximately omnigeneous and maximum-$J$ mirror
mirror
To venture beyond the bottom of the well, we present a numerical example in which the maximum-$J$![]() and omnigeneity conditions are both satisfied over a non-zero interval in $z$
and omnigeneity conditions are both satisfied over a non-zero interval in $z$![]() . To construct such an example, we choose for simplicity a symmetric solution with well-defined parity (so that $X_{1s}$
. To construct such an example, we choose for simplicity a symmetric solution with well-defined parity (so that $X_{1s}$![]() and $X_{1c}$
and $X_{1c}$![]() are odd and even respectively). This guarantees the correct behaviour of (C21b), but leaves us free to find inputs such that $V_1+(\varPhi _{2c}/B_0)'=0$
are odd and even respectively). This guarantees the correct behaviour of (C21b), but leaves us free to find inputs such that $V_1+(\varPhi _{2c}/B_0)'=0$![]() . This task can be formulated as an optimisation problem in which $X_{1s}$
. This task can be formulated as an optimisation problem in which $X_{1s}$![]() and $X_{1c}$
and $X_{1c}$![]() are the degrees of freedom (fixing $B_0$
are the degrees of freedom (fixing $B_0$![]() ). We initialise the search with a configuration that satisfies the omnigeneity requirement at the bottom of the well (as we know in closed form what this choice should be). The result of the optimisation (with 6 scalar degrees of freedom) is presented in figure 11.
). We initialise the search with a configuration that satisfies the omnigeneity requirement at the bottom of the well (as we know in closed form what this choice should be). The result of the optimisation (with 6 scalar degrees of freedom) is presented in figure 11.
Appendix D. Details of near-axis optimisation for a vacuum QI field with the maximum-$J$ property
property
In this appendix, we document details of the optimisation approach to the near-axis field presented in figure 8 of the main text. A more in-depth discussion will be presented elsewhere.
The main goal of our optimisation effort is to construct a proof-of-concept near-axis field that exhibits the maximum-$J$![]() property in the omnigenous portion of the trapped-particle population. In that regard, we do not optimise for the particles in the so-called buffer region (Plunk et al. Reference Plunk, Landreman and Helander2019), the part of the domain where omnigeneity is violated in order to enforce periodicity of the magnetic field. In general, narrow buffer regions lead to large shaping gradients, and these regions are therefore often made relatively wide although omnigeneity then suffers. As far as the maximum-$J$
property in the omnigenous portion of the trapped-particle population. In that regard, we do not optimise for the particles in the so-called buffer region (Plunk et al. Reference Plunk, Landreman and Helander2019), the part of the domain where omnigeneity is violated in order to enforce periodicity of the magnetic field. In general, narrow buffer regions lead to large shaping gradients, and these regions are therefore often made relatively wide although omnigeneity then suffers. As far as the maximum-$J$![]() property is concerned, this will increase the number of particles with large (${\sim }1/r$
property is concerned, this will increase the number of particles with large (${\sim }1/r$![]() ) detrimental precession. We shall, however, not be concerned with this detail but argue that we could, in principle, shrink the buffer region to become arbitrarily small.
) detrimental precession. We shall, however, not be concerned with this detail but argue that we could, in principle, shrink the buffer region to become arbitrarily small.
Focusing, then, on the other contributions to the precession, we need to introduce a measure for maximum-$J$![]() behaviour that serves as a target function in the numerical optimisation. In order to exclude contributions from the buffer regions proportional to $1/r$
behaviour that serves as a target function in the numerical optimisation. In order to exclude contributions from the buffer regions proportional to $1/r$![]() , we evaluate the precession frequency as the sum of (A20) and (A25), and construct the target function as the sum
, we evaluate the precession frequency as the sum of (A20) and (A25), and construct the target function as the sum
taken over values of $k$![]() such that $\hat \omega _{\alpha} < 0$
such that $\hat \omega _{\alpha} < 0$![]() . The required integrals are evaluated using the help of the BAD library in python (Mackenbach et al. Reference Mackenbach, Duff, Gerard, Proll, Helander and Hegna2023b).
. The required integrals are evaluated using the help of the BAD library in python (Mackenbach et al. Reference Mackenbach, Duff, Gerard, Proll, Helander and Hegna2023b).
A second ingredient in the optimisation is the condition of omnigeneity (outside the buffer regions). Given first-order inputs, second-order choices necessary to enforce the correct form for $B_{2c}$![]() . Accordingly, we construct $X_{2c}$
. Accordingly, we construct $X_{2c}$![]() and $X_{2s}$
and $X_{2s}$![]() following (B6) and the equivalent for $X_{2s}$
following (B6) and the equivalent for $X_{2s}$![]() , assuming that $B_{2c}$
, assuming that $B_{2c}$![]() has the correct form for QI. Writing $X_{2c}=\tilde {X}_{2c}c_{2\alpha _1}+\tilde {X}_{2s}s_{2\alpha _1}$
has the correct form for QI. Writing $X_{2c}=\tilde {X}_{2c}c_{2\alpha _1}+\tilde {X}_{2s}s_{2\alpha _1}$![]() and $X_{2s}=\tilde {X}_{2c}s_{2\alpha _1}-\tilde {X}_{2s}c_{2\alpha _1}$
and $X_{2s}=\tilde {X}_{2c}s_{2\alpha _1}-\tilde {X}_{2s}c_{2\alpha _1}$![]() , we find
, we find

where $c_{2\alpha _1}=\cos 2\alpha _1$![]() and $s_{2\alpha _1}=\sin 2\alpha _1$
and $s_{2\alpha _1}=\sin 2\alpha _1$![]() , and
, and
and $\alpha _1=\nu -\iota \varphi$![]() in the notation of Appendix A, following Garren & Boozer (Reference Garren and Boozer1991b). This construction guarantees QI behaviour at second order for any odd $B_{2s}^{\mathrm {QI}}$
in the notation of Appendix A, following Garren & Boozer (Reference Garren and Boozer1991b). This construction guarantees QI behaviour at second order for any odd $B_{2s}^{\mathrm {QI}}$![]() , as can be checked by substitution. The only exceptions are points where the curvature vanishes, where we learnt in Appendix B, (B9), that the QI condition reduces to a condition on lower-order coefficients. An indication of the latter is that the construction will generally diverge wherever $\kappa =0$
, as can be checked by substitution. The only exceptions are points where the curvature vanishes, where we learnt in Appendix B, (B9), that the QI condition reduces to a condition on lower-order coefficients. An indication of the latter is that the construction will generally diverge wherever $\kappa =0$![]() , from which more general expressions than those of (B9) can be obtained which do not assume QI at first order (this is important for the tops of the well in practice). Thus, one must add to the optimisation a measure of the deviation from QI at the points of minimum and maximum field strength, which the optimiser should attempt to reduce. We denote the sum of this ‘residual’ at all extrema along the field by $\check {g}_{\mathrm {QI}}$
, from which more general expressions than those of (B9) can be obtained which do not assume QI at first order (this is important for the tops of the well in practice). Thus, one must add to the optimisation a measure of the deviation from QI at the points of minimum and maximum field strength, which the optimiser should attempt to reduce. We denote the sum of this ‘residual’ at all extrema along the field by $\check {g}_{\mathrm {QI}}$![]() . To simplify the available choices, we further take $p_2=0$
. To simplify the available choices, we further take $p_2=0$![]() and $\tilde {X}_{2s}=0$
and $\tilde {X}_{2s}=0$![]() , which is not the most general choice, and most likely not even the best, but suffices for our purposes. Although this approach enforces QI at second order exactly, it does not appear to be the best one in practice, as it leads to highly shaped configurations, and unnecessarily enforces QI at second order in regions where it is already violated at first order. However, it suffices for our purposes of proof-of-principle construction, and we leave further refinements for future work.
, which is not the most general choice, and most likely not even the best, but suffices for our purposes. Although this approach enforces QI at second order exactly, it does not appear to be the best one in practice, as it leads to highly shaped configurations, and unnecessarily enforces QI at second order in regions where it is already violated at first order. However, it suffices for our purposes of proof-of-principle construction, and we leave further refinements for future work.
The target function to be numerically is thus $g=g_{\omega _{\alpha} }+\check {g}_{\mathrm {QI}}$![]() , and we proceed to discuss the degrees of freedom over which the optimisation is to be carried out. At first order, there are many free functions, some of which will be fixed for simplicity. The magnetic-field strength is taken to vary along the axis as $B_0=1+0.16\cos \varphi$
, and we proceed to discuss the degrees of freedom over which the optimisation is to be carried out. At first order, there are many free functions, some of which will be fixed for simplicity. The magnetic-field strength is taken to vary along the axis as $B_0=1+0.16\cos \varphi$![]() , but the shape of the magnetic axis and the elongation measure $\bar {d}$
, but the shape of the magnetic axis and the elongation measure $\bar {d}$![]() are allowed to change. For the former, we vary three even Fourier harmonics (three for each $Z$
are allowed to change. For the former, we vary three even Fourier harmonics (three for each $Z$![]() and $R$
and $R$![]() describing the axis in cylindrical coordinates), a fourth one being chosen consistently to make the curvature vanish at $\phi =0,~{\rm \pi}$
describing the axis in cylindrical coordinates), a fourth one being chosen consistently to make the curvature vanish at $\phi =0,~{\rm \pi}$![]() (Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022; Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022). This restricts us to first-order zeroes of curvature (Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022; Camacho Mata & Plunk Reference Camacho Mata and Plunk2023). The function $\bar {d}$
(Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022; Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022). This restricts us to first-order zeroes of curvature (Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2022; Camacho Mata & Plunk Reference Camacho Mata and Plunk2023). The function $\bar {d}$![]() is allowed to have 7 degrees of freedom through collocation points of a symmetric spline, symmetry being necessary to preserve stellarator symmetry.
is allowed to have 7 degrees of freedom through collocation points of a symmetric spline, symmetry being necessary to preserve stellarator symmetry.
With the optimisation procedure defined this way, we finally need to specify a starting point, which we take to be a generic QI axis with $N=1$![]() and $\bar {d}=1$
and $\bar {d}=1$![]() . Other details, such as the buffer region size etc. can be found in the supplementary material, in which all the numerical tools are provided. The optimisation is performed using the near-axis code pyQIC (Jorge et al. Reference Jorge, Agostinho and Rodríguez2023) with appropriate upgrades (use of splines, second-order choice, etc.), and the optimisation libraries of scipy (the algorithms Nelder-Mead and BFGS are used, the latter as a refinement of the former). Broadly speaking, the optimisation proceeds in two stages: (i) Nelder–Mead optimisation for QI and maximum-$J$
. Other details, such as the buffer region size etc. can be found in the supplementary material, in which all the numerical tools are provided. The optimisation is performed using the near-axis code pyQIC (Jorge et al. Reference Jorge, Agostinho and Rodríguez2023) with appropriate upgrades (use of splines, second-order choice, etc.), and the optimisation libraries of scipy (the algorithms Nelder-Mead and BFGS are used, the latter as a refinement of the former). Broadly speaking, the optimisation proceeds in two stages: (i) Nelder–Mead optimisation for QI and maximum-$J$![]() behaviour at the minima and maxima of $B_0$
behaviour at the minima and maxima of $B_0$![]() ; (ii) full optimisation (on a few field lines) of the function $g$
; (ii) full optimisation (on a few field lines) of the function $g$![]() . Step (i) has the benefit of only requiring a first-order near-axis solution, thus being quite fast, while (ii) is slower as it needs to compute $\hat {\omega }_{\alpha}$
. Step (i) has the benefit of only requiring a first-order near-axis solution, thus being quite fast, while (ii) is slower as it needs to compute $\hat {\omega }_{\alpha}$![]() . Additional refinements are of course possible.
. Additional refinements are of course possible.
The results of the optimisation are presented in figure 8, and all the pertinent files and scripts are included in the Zenodo repository associated with this paper.