Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-13T14:46:03.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Liouville-type results for positive solutions of pseudo-relativistic Schrödinger system

Part of: Miscellaneous topics - Partial differential equations Partial differential equations

Published online by Cambridge University Press:  13 December 2021

Yuxia Guo  and
Shaolong Peng
Yuxia Guo
Affiliation:
Department of Mathematics, Tsinghua University, Beijing 100084, P. R. China (yguo@mail.tsinghua.edu.cn, psl20@mails.tsinghua.edu.cn)
Shaolong Peng
Affiliation:
Department of Mathematics, Tsinghua University, Beijing 100084, P. R. China (yguo@mail.tsinghua.edu.cn, psl20@mails.tsinghua.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we are concerned with the physically engaging pseudo-relativistic Schrödinger system:

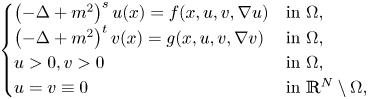
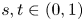\[ \begin{cases} \left(-\Delta+m^{2}\right)^{s}u(x)=f(x,u,v,\nabla u) & \hbox{in } \Omega,\\ \left(-\Delta+m^{2}\right)^{t}v(x)=g(x,u,v,\nabla v) & \hbox{in } \Omega,\\ u>0,v>0 & \hbox{in } \Omega, \\ u=v\equiv 0 & \hbox{in } \mathbb{R}^{N}\setminus\Omega, \end{cases} \]
where $s,t\in (0,1)$ and the mass $m>0.$ 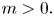By using the direct method of moving plane, we prove the strict monotonicity, symmetry and uniqueness for positive solutions to the above system in a bounded domain, unbounded domain, $\mathbb {R}^{N}$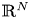, $\mathbb {R}^{N}_{+}$ 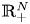and a coercive epigraph domain $\Omega$ 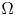in $\mathbb {R}^{N}$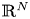, respectively.

Keywords

Pseudo-relativistic Schrödinger systemdirect methods of moving planesLiouville-type theoremsmonotonicitysymmetry

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 35B06: Symmetries, invariants, etc. 35B53: Liouville theorems, Phragmén-Lindelöf theorems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 1 , February 2023 , pp. 196 - 228
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosio, V.. Ground states solutions for a non-linear equation involving a pseudo-relativistic Schrödinger operator. J. Math. Phys. 57 (2016), 051502.CrossRefGoogle Scholar
Bertoin, J.. Lévy processes. Cambridge Tracts in Mathematics, vol. 121 (Cambridge: Cambridge University Press, 1996).Google Scholar
Brandle, C., Colorado, E., de Pablo, A. and Sanchez, U.. A concave-convex elliptic problem involving the fractional Laplacian. Proc. R. Soc. Edinburgh-A: Math. 143 (2013), 39–71.CrossRefGoogle Scholar
Cabré, X. and Tan, J.. Positive solutions of nonlinear problems involving the square root of the Laplacian. Adv. Math. 224 (2010), 2052–2093.CrossRefGoogle Scholar
Caffarelli, L. and Silvestre, L.. An extension problem related to the fractional Laplacian. Commun. PDEs 32 (2007), 1245–1260.CrossRefGoogle Scholar
Caffarelli, L. and Vasseur, L.. Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation. Ann. Math. 171 (2010), 1903–1930.CrossRefGoogle Scholar
Carmona, R., Masters, W. C. and Simon, B.. Relativistic Schrödinger operators: asymptotic behavior of the eigenfunctions. J. Funct. Anal. 91 (1990), 117–142.CrossRefGoogle Scholar
Chang, S.-Y. A. and Gonzàlez, M. d. M.. Fractional Laplacian in conformal geometry. Adv. Math. 226 (2011), 1410–1432.CrossRefGoogle Scholar
Chen, W. and Li, C.. Moving planes, moving spheres, and a priori estimates. J. Differ. Equ. 195 (2003), 1–13.CrossRefGoogle Scholar
Chen, W., Li, C. and Li, Y.. A direct method of moving planes for the fractional Laplacian. Adv. Math. 308 (2017), 404–437.CrossRefGoogle Scholar
Chen, W., Li, Y. and Ma, P.. The fractional Laplacian (Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd., 2020), 331.CrossRefGoogle Scholar
Chen, W., Li, C. and Ou, B.. Classification of solutions for an integral equation. Commun. Pure Appl. Math. 59 (2006), 330–343.CrossRefGoogle Scholar
Chen, W., Li, Y. and Zhang, R.. A direct method of moving spheres on fractional order equations. J. Funct. Anal. 272 (2017), 4131–4157.CrossRefGoogle Scholar
Chen, Y. and Liu, B.. Symmetry and non-existence of positive solutions for fractional p-Laplacian systems. Nonlinear Anal. 183 (2019), 303–322.CrossRefGoogle Scholar
Chen, W. and Qi, S.. Direct methods on fractional equations. Disc. Cont. Dyn. Syst. – A 39 (2019), 1269–1310.CrossRefGoogle Scholar
Chen, W. and Wu, L.. The sliding methods for the fractional $p$-Laplacian. Adv. Math. 361 (2020), 106933.Google Scholar
Cheng, T., Huang, G. and Li, C.. The maximum principles for fractional Laplacian equations and their applications. Commun. Contemp. Math. 19 (2017), 1750018.CrossRefGoogle Scholar
Constantin, P.. Euler equations, Navier–Stokes equations and turbulence. In Mathematical foundation of turbulent viscous flows. Lecture Notes in Mathematics, vol. 1871, pp. 1–43 (Berlin: Springer, 2006).CrossRefGoogle Scholar
Dai, W., Fang, Y., Huang, J., Qin, Y. and Wang, B.. Regularity and classification of solutions to static Hartree equations involving fractional Laplacians. Disc. Contin. Dyn. Syst. – A 39 (2019), 1389–1403.CrossRefGoogle Scholar
Dai, W. and Liu, Z.. Classification of nonnegative solutions to static Schrödinger-Hartree and Schrödinger-Maxwell equations with combined nonlinearities. Calc. Var. & PDEs 58 (2019), 156.CrossRefGoogle Scholar
Dai, W., Liu, Z. and Qin, G.. Classification of nonnegative solutions to static Schrödinger-Hartree-Maxwell type equations. SIAM J. Math. Anal. 53 (2021), 1379–1410.CrossRefGoogle Scholar
Dai, W. and Qin, G.. Classification of nonnegative classical solutions to third-order equations. Adv. Math. 328 (2018), 822–857.CrossRefGoogle Scholar
Dai, W., Qin, G. and Wu, D.. Direct methods for pseudo-relativistic Schrödinger operators. J. Geom. Anal. 31 (2021), 5555–5618.CrossRefGoogle Scholar
Dai, W. and Qin, G.. Liouville type theorems for fractional and higher order Hénon-Hardy equations via the method of scaling spheres, preprint, submitted for publication, arXiv:1810.02752.Google Scholar
Dipierro, S., Soave, N. and Valdinoci, E.. On fractional elliptic equations in Lipschitz sets and epigraphs: regularity, monotonicity and rigidity results. Math. Ann. 369 (2017), 1283–1326.CrossRefGoogle Scholar
Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.. Higher transcendental functions, vol. II (New York: McGraw-Hill, 1953).Google Scholar
Fall, M. M. and Felli, V.. Sharp essential self-adjointness of relativistic Schrödinger operators with a singular potential. J. Funct. Anal. 267 (2014), 1851–1877.CrossRefGoogle Scholar
Fall, M. M. and Felli, V.. Unique continuation properties for relativistic Schrödinger operators with a singular potential. Disc. Contin. Dyn. Syst. – A 35 (2015), 5827–5867.CrossRefGoogle Scholar
Frank, R. L., Lenzmann, E. and Silvestre, L.. Uniqueness of radial solutions for the fractional Laplacian. Commun. Pure Appl. Math. 69 (2013), 1671–1726.CrossRefGoogle Scholar
Guo, Y. and Liu, J.. Liouville type theorems for positive solutions of elliptic system in $R^{N}$. Commun. Partial Differ. Equ. 33 (2008), 263–284.CrossRefGoogle Scholar
Guo, Y. and Peng, S.. Symmetry and monotonicity of nonnegative solutions to pseudo-relativistic Choquard equations. Z. Angew. Math. Phys. 72 (2021), 20, Paper No. 120.CrossRefGoogle Scholar
Lieb, E. H. and Thirring, W. E.. Gravitational collapse in quantum mechanics with relativistic kinetic energy. Ann. Phys. 155 (1984), 494–512.CrossRefGoogle Scholar
Lieb, E. H. and Yau, H. T.. The Chandrasekhar theory of stellar collapse as the limit of quantum mechanics. Commun. Math. Phys., 112 (1987), 147–174.CrossRefGoogle Scholar
Liu, J., Guo, Y. and Zhang, Y.. Liouville-type theorems for polyharmonic systems in $R^{N}$. J. Differ. Equ. 225 (2006), 685–709.CrossRefGoogle Scholar
Liu, B. and Ma, L.. Radial symmetry results for fractional Laplacian systems. Nonlinear Anal. 146 (2016), 120–135.CrossRefGoogle Scholar
Peng, S.. Liouville theorems for fractional and higher order Hénon-Hardy systems on $\mathbb {R}^{n}$. Complex Variables Elliptic Equ. 66 (2021), 1839–1863.CrossRefGoogle Scholar
Silvestre, L.. Regularity of the obstacle problem for a fractional power of the Laplace operator. Commun. Pure Appl. Math. 60 (2007), 67–112.CrossRefGoogle Scholar