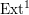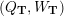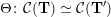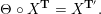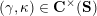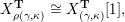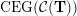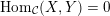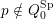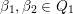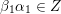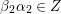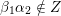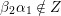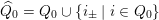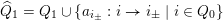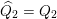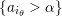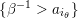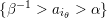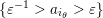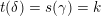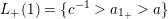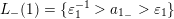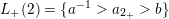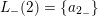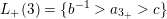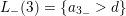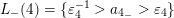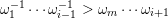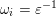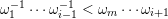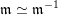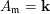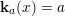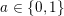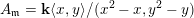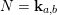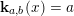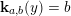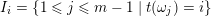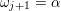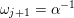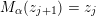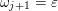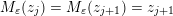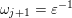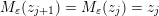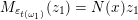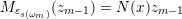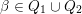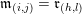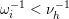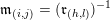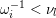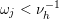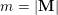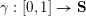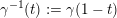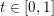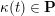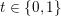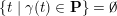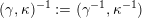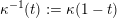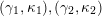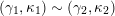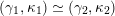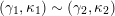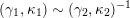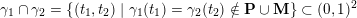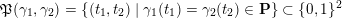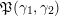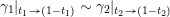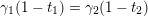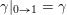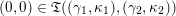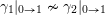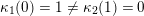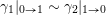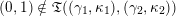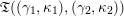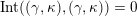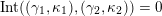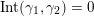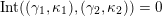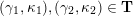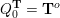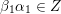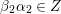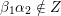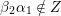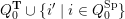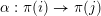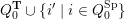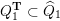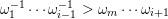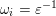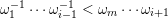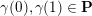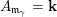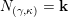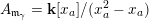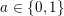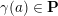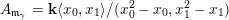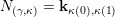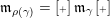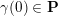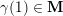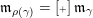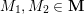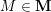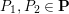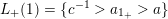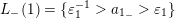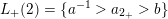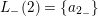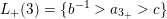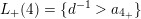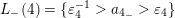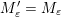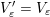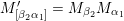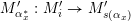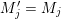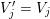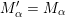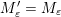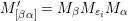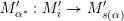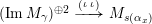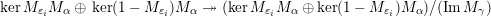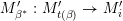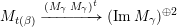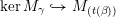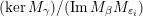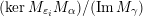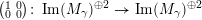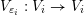1 Introduction
1.1 Overall
Cluster algebras were introduced by Fomin and Zelevinsky [Reference Fomin and ZelevinskyFZ02] around 2000, with quiver mutation as the combinatorial aspect. Derksen et al. [Reference Derksen, Weyman and ZelevinskyDWZ08] further developed quiver mutation to mutation of quivers with potential. During the last decade, the cluster phenomenon was spotted in various areas in mathematics, as well as in physics, including geometric topology and representation theory. On one hand, the geometric aspect of cluster theory was explored by Fomin et al. [Reference Fomin, Shapiro and ThurstonFST08] after the pioneering work of Fock and Goncharov [Reference Fock and GoncharovFG06, Reference Fock and GoncharovFG09]. They constructed a quiver
![]() $Q_{\mathbf{T}}$
(and later, Labardini-Fragoso [Reference Labardini-FragosoLab09a, Reference Irelli and Labardini-FragosoIL12] gave a corresponding potential
$Q_{\mathbf{T}}$
(and later, Labardini-Fragoso [Reference Labardini-FragosoLab09a, Reference Irelli and Labardini-FragosoIL12] gave a corresponding potential
![]() $W_{\mathbf{T}}$
) from any (tagged) triangulation
$W_{\mathbf{T}}$
) from any (tagged) triangulation
![]() $\mathbf{T}$
of a marked surface
$\mathbf{T}$
of a marked surface
![]() $\mathbf{S}$
. Moreover, they showed that mutation of quivers (with potential) is compatible with flip of triangulations. There are a lot of known results about cluster algebras in the surface case:
$\mathbf{S}$
. Moreover, they showed that mutation of quivers (with potential) is compatible with flip of triangulations. There are a lot of known results about cluster algebras in the surface case:
-
– Felikson et al. [Reference Felikson, Shapiro and TumarkinFST12] classified cluster algebras of finite mutation type, and established that they are all from marked surfaces except for a few cases;
-
– Musiker et al. [Reference Musiker, Schiffler and WilliamsMSW13] constructed two canonical bases by two types of collections of curves;
-
– Musiker et al. [Reference Musiker, Schiffler and WilliamsMSW11], Musiker and Williams [Reference Musiker and WilliamsMW13], and Canakci and Schiffler [Reference Canakci and SchifflerCS13, Reference Canakci and SchifflerCS15a, Reference Canakci and SchifflerCS15b] gave combinatorial formulae for cluster variables and relations;
-
– Mills [Reference MillsMil16] showed that there exist maximal green sequences for quivers with potential associated with triangulated marked surfaces except for once-punctured closed surfaces (cf. [Reference Alim, Cecotti, Córdova, Espahbodi, Rastogi and VafaACCERV13]).
On the other hand, the categorification of cluster algebras leads to representations of quivers, due to Buan et al. [Reference Buan, Marsh, Reineke, Reiten and TodorovBMRRT06]. Later, Amiot [Reference AmiotAmi09] introduced generalized cluster categories via Ginzburg dg algebras associated with quivers with potential. Then there is an associated cluster category
![]() ${\mathcal{C}}(\mathbf{T})$
for each triangulation
${\mathcal{C}}(\mathbf{T})$
for each triangulation
![]() $\mathbf{T}$
of
$\mathbf{T}$
of
![]() $\mathbf{S}$
.
$\mathbf{S}$
.
Several works have been done concerning the cluster categories associated with triangulations of surfaces. Namely, for some special cases:
-
– Caldero et al. [Reference Caldero, Chapoton and SchifflerCCS06] realized the cluster category of type
 $A_{n}$
by a regular polygon with
$A_{n}$
by a regular polygon with
 $n+3$
vertices (i.e. a disk with
$n+3$
vertices (i.e. a disk with
 $n+3$
vertices on its boundary);
$n+3$
vertices on its boundary); -
– Schiffler [Reference SchifflerSch08] realized the cluster category of type
 $D_{n}$
by a regular polygon with
$D_{n}$
by a regular polygon with
 $n$
vertices and one puncture in the center (i.e. a disk with
$n$
vertices and one puncture in the center (i.e. a disk with
 $n$
vertices on its boundary and one puncture in its interior).
$n$
vertices on its boundary and one puncture in its interior).
In the unpunctured case:
-
– Assem et al. [Reference Assem, Brüstle, Charbonneau-Jodoin and PlamondonABCP12] proved that the Jacobian algebra of such a quiver with potential is a gentle algebra and gave a bijection between arcs that are not in the triangulation and string modules of the associated gentle algebras;
-
– Brüstle and Zhang [Reference Brüstle and ZhangBZ11] generalized the bijection of [Reference Assem, Brüstle, Charbonneau-Jodoin and PlamondonABCP12] to a bijection between the set of curves and valued closed curves and the set of indecomposable objects in the associated cluster category. Under this bijection, they described irreducible morphisms, the Auslander–Reiten (AR) translation and AR-triangles in the cluster category by geometric terms in the surface. They also gave a bijection between triangulations of the surface and cluster tilting objects in the cluster category such that flip of an arc is compatible with mutation;
-
– based on Brüstle and Zhang’s work, Zhang et al. [Reference Zhang, Zhou and ZhuZZZ13] proved that the intersection number of two curves is equal to the dimension of
 $\operatorname{Ext}^{1}$
of the corresponding objects and gave a geometric model of torsion pairs and their mutations;
$\operatorname{Ext}^{1}$
of the corresponding objects and gave a geometric model of torsion pairs and their mutations; -
– Canakci and Schroll [Reference Canakci and SchrollCS14] described a basis for
 $\operatorname{Ext}^{1}$
in the cluster category and also computed a basis for
$\operatorname{Ext}^{1}$
in the cluster category and also computed a basis for
 $\operatorname{Ext}^{1}$
in the module category of the corresponding Jacobian algebra by distinguishing different types of crossings between curves;
$\operatorname{Ext}^{1}$
in the module category of the corresponding Jacobian algebra by distinguishing different types of crossings between curves; -
– Marsh and Palu [Reference Marsh and PaluMP14] showed that Calabi–Yau reduction (introduced in [Reference Iyama and YoshinoIY08]) can be interpreted as cutting along curves without self-intersections in the surface;
-
– the present authors [Reference QiuQiu16, Reference Qiu and ZhouQZ14] also investigated other categories, which are used to define cluster categories, see the formula (3.1), and obtained similar structures/formulae.
For general cases:
-
– for each ideal triangulation without self-folded triangles, Labardini-Fragoso [Reference Labardini-FragosoLab09b] associated a representation of the quiver with potential
 $(Q_{\mathbf{T}},W_{\mathbf{T}})$
to each curve without self-intersections and proved that mutation of representations is compatible with flip of triangulations;
$(Q_{\mathbf{T}},W_{\mathbf{T}})$
to each curve without self-intersections and proved that mutation of representations is compatible with flip of triangulations; -
– Brüstle and Qiu [Reference Brüstle and QiuBQ15] made an effort to understand a basic functor in the cluster category, i.e. the shift (or the AR-translation in this case), in terms of an element, the tagged rotation, in the tagged mapping class group of the marked surface. Their motivation lies in the study of the Seidel–Thomas braid group.
Notice that most of the above works deal only with the unpunctured case. This is because: (i) the usual flip does not work for self-folded triangles (cf. Figure 5) and (ii) the associated quivers with potential are much more complicated in the punctured case and their Jacobian algebras are not gentle (cf. [Reference Irelli and Labardini-FragosoIL12]). Fomin et al. solved (i) by introducing the notion of tagging.
In this paper, we aim to study the cluster categories associated to marked surfaces with punctures and with non-empty boundaries. The main tool is skewed-gentle algebras (a special kind of clannish algebras), which were developed in [Reference BondarenkoBon92, Reference Crawley-BoeveyCra89, Reference DengDen00, Reference GeißGei99, Reference Geiß and de la PeñaGdlP99]. The essential results are summarized as follows.
Theorem 1.1 (Theorems 4.16, 4.19, 5.2, 5.5 and 5.7).
Let
![]() $\mathbf{S}$
be a marked surface with punctures and with non-empty boundary. Given an admissible triangulation
$\mathbf{S}$
be a marked surface with punctures and with non-empty boundary. Given an admissible triangulation
![]() $\mathbf{T}$
of
$\mathbf{T}$
of
![]() $\mathbf{S}$
(see Definition 3.7), let
$\mathbf{S}$
(see Definition 3.7), let
![]() ${\mathcal{C}}(\mathbf{T})$
be the associated cluster category. Then there is a bijection
${\mathcal{C}}(\mathbf{T})$
be the associated cluster category. Then there is a bijection
 $$\begin{eqnarray}\begin{array}{@{}rccc@{}}X^{\mathbf{T}}: & \mathbf{C}^{\times }(\mathbf{S}) & \rightarrow & \mathfrak{S}(\mathbf{T})\\ & (\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705}) & \mapsto & X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rccc@{}}X^{\mathbf{T}}: & \mathbf{C}^{\times }(\mathbf{S}) & \rightarrow & \mathfrak{S}(\mathbf{T})\\ & (\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705}) & \mapsto & X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}\end{array}\end{eqnarray}$$
from the set
![]() $\mathbf{C}^{\times }(\mathbf{S})$
of tagged curves in the surface
$\mathbf{C}^{\times }(\mathbf{S})$
of tagged curves in the surface
![]() $\mathbf{S}$
to the set
$\mathbf{S}$
to the set
![]() $\mathfrak{S}(\mathbf{T})$
of string objects in the category
$\mathfrak{S}(\mathbf{T})$
of string objects in the category
![]() ${\mathcal{C}}(\mathbf{T})$
(see Definitions 3.1 and 4.6), satisfying the following.
${\mathcal{C}}(\mathbf{T})$
(see Definitions 3.1 and 4.6), satisfying the following.
-
(i) For every admissible triangulation
 $\mathbf{T}^{\prime }$
of
$\mathbf{T}^{\prime }$
of
 $\mathbf{S}$
, there is an equivalence
$\mathbf{S}$
, there is an equivalence
 $\unicode[STIX]{x1D6E9}:{\mathcal{C}}(\mathbf{T})\simeq {\mathcal{C}}(\mathbf{T}^{\prime })$
, such that
$\unicode[STIX]{x1D6E9}:{\mathcal{C}}(\mathbf{T})\simeq {\mathcal{C}}(\mathbf{T}^{\prime })$
, such that
 $\unicode[STIX]{x1D6E9}\circ X^{\mathbf{T}}=X^{\mathbf{T}^{\prime }}.$
$\unicode[STIX]{x1D6E9}\circ X^{\mathbf{T}}=X^{\mathbf{T}^{\prime }}.$
-
(ii) For any tagged curve
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
, we have
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
, we have
 $X_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}\cong X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}[1],$
where
$X_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}\cong X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}[1],$
where
 $\unicode[STIX]{x1D70C}$
is the tagged rotation (see Definition 3.2).
$\unicode[STIX]{x1D70C}$
is the tagged rotation (see Definition 3.2). -
(iii) For any two tagged curves
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
,
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
,
 $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
(not necessarily distinct), we have where
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
(not necessarily distinct), we have where $$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=\dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=\dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}}),\end{eqnarray}$$
 $\operatorname{Int}$
denotes the intersection number (see Definition 3.3).
$\operatorname{Int}$
denotes the intersection number (see Definition 3.3).
-
(iv) The exchange graph
 $\operatorname{CEG}({\mathcal{C}}(\mathbf{T}))$
of cluster tilting objects in
$\operatorname{CEG}({\mathcal{C}}(\mathbf{T}))$
of cluster tilting objects in
 ${\mathcal{C}}(\mathbf{T})$
is isomorphic to the exchange graph
${\mathcal{C}}(\mathbf{T})$
is isomorphic to the exchange graph
 $\operatorname{EG}^{\times }(\mathbf{S})$
of tagged triangulations of
$\operatorname{EG}^{\times }(\mathbf{S})$
of tagged triangulations of
 $\mathbf{S}$
and hence it is connected.
$\mathbf{S}$
and hence it is connected.
1.2 Context
In § 2 we recall notions and notation about skewed-gentle algebras that we will use throughout the paper. In § 3, we recall the background of cluster categories associated with triangulated marked surfaces. In § 4, we study the skewed-gentle algebra associated with an admissible triangulation and give a correspondence between tagged curves and string objects. The relation between such correspondences from different admissible triangulations is also studied. In § 5, we give homological interpretations of geometric objects from marked surfaces, namely tagged rotation, intersection numbers, and exchange graphs of tagged triangulations. An example is presented in § 6 to demonstrate some of the notions/results in the paper. The technical proof of the main theorem, Theorem 5.5, is given in § 7. In Appendix A we discuss some properties of admissible triangulations and in Appendix B we recall Derksen et al.’s mutation of decorated representations.
1.3 Conventions
Throughout this article,
![]() $\mathbf{k}$
denotes an algebraically closed field. For any
$\mathbf{k}$
denotes an algebraically closed field. For any
![]() $\mathbf{k}$
-algebra
$\mathbf{k}$
-algebra
![]() $A$
, an
$A$
, an
![]() $A$
-module means a finitely generated left
$A$
-module means a finitely generated left
![]() $A$
-module and we denote by
$A$
-module and we denote by
![]() $\mathsf{mod}\,A$
the category of all
$\mathsf{mod}\,A$
the category of all
![]() $A$
-modules. For a finite set
$A$
-modules. For a finite set
![]() $I$
, we denote by
$I$
, we denote by
![]() $|I|$
the number of elements in
$|I|$
the number of elements in
![]() $I$
. For an object
$I$
. For an object
![]() $X$
in a triangulated category
$X$
in a triangulated category
![]() ${\mathcal{C}}$
, we denote:
${\mathcal{C}}$
, we denote:
-
– by
 $\mathsf{add}\,X$
the full subcategory of
$\mathsf{add}\,X$
the full subcategory of
 ${\mathcal{C}}$
consisting of direct summands of direct sums of copies of
${\mathcal{C}}$
consisting of direct summands of direct sums of copies of
 $X$
;
$X$
; -
– by
 $X^{\bot }$
the full subcategory of
$X^{\bot }$
the full subcategory of
 ${\mathcal{C}}$
consisting of objects
${\mathcal{C}}$
consisting of objects
 $Y$
with
$Y$
with
 $\operatorname{Hom}_{{\mathcal{C}}}(X,Y)=0$
;
$\operatorname{Hom}_{{\mathcal{C}}}(X,Y)=0$
; -
– by
 ${\mathcal{C}}/(X)$
the additive quotient category of
${\mathcal{C}}/(X)$
the additive quotient category of
 ${\mathcal{C}}$
by
${\mathcal{C}}$
by
 $\mathsf{add}\,X$
.
$\mathsf{add}\,X$
.
2 Preliminaries on skewed-gentle algebras
We recall from [Reference BondarenkoBon92, Reference Crawley-BoeveyCra89, Reference DengDen00, Reference GeißGei99, Reference Geiß and de la PeñaGdlP99] some notions, notation and results about skewed-gentle algebras used in this paper.
2.1 Skewed-gentle algebras
A biquiver is a tuple
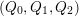 $(Q_{0},Q_{1},Q_{2})$
, where
$(Q_{0},Q_{1},Q_{2})$
, where
![]() $Q_{0}$
is the set of vertices,
$Q_{0}$
is the set of vertices,
![]() $Q_{1}$
is the set of solid arrows, and
$Q_{1}$
is the set of solid arrows, and
![]() $Q_{2}$
is the set of dashed arrows. Let
$Q_{2}$
is the set of dashed arrows. Let
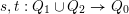 $s,t:Q_{1}\cup Q_{2}\rightarrow Q_{0}$
be the start/terminal functions of arrows. We call an arrow
$s,t:Q_{1}\cup Q_{2}\rightarrow Q_{0}$
be the start/terminal functions of arrows. We call an arrow
![]() $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
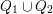 $Q_{1}\cup Q_{2}$
a loop if
$Q_{1}\cup Q_{2}$
a loop if
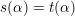 $s(\unicode[STIX]{x1D6FC})=t(\unicode[STIX]{x1D6FC})$
.
$s(\unicode[STIX]{x1D6FC})=t(\unicode[STIX]{x1D6FC})$
.
In this paper, we always assume that a biquiver
 $Q=(Q_{0},Q_{1},Q_{2})$
satisfies:
$Q=(Q_{0},Q_{1},Q_{2})$
satisfies:
-
– each arrow in
 $Q_{2}$
is a dashed loop;
$Q_{2}$
is a dashed loop; -
– there is at most one loop in
 $Q_{2}$
at each vertex;
$Q_{2}$
at each vertex; -
– there is no loop in
 $Q_{1}$
.
$Q_{1}$
.
Let
![]() $Q_{0}^{\operatorname{Sp}}$
be the subset of
$Q_{0}^{\operatorname{Sp}}$
be the subset of
![]() $Q_{0}$
consisting of vertices where there is a dashed loop in
$Q_{0}$
consisting of vertices where there is a dashed loop in
![]() $Q_{2}$
.
$Q_{2}$
.
Skewed-gentle algebras, modeled on gentle algebras, were introduced in [Reference Geiß and de la PeñaGdlP99] as a certain class of clannish algebras defined in [Reference Crawley-BoeveyCra89].
Definition 2.1. A pair
![]() $(Q,Z)$
of a biquiver
$(Q,Z)$
of a biquiver
![]() $Q$
and a set
$Q$
and a set
![]() $Z$
of compositions
$Z$
of compositions
![]() $ab$
of arrows
$ab$
of arrows
![]() $a,b$
in
$a,b$
in
![]() $Q_{1}$
is called skewed-gentle if the following conditions hold.
$Q_{1}$
is called skewed-gentle if the following conditions hold.
-
– For each vertex
 $p\in Q_{0}^{\operatorname{Sp}}$
, there is at most one arrow
$p\in Q_{0}^{\operatorname{Sp}}$
, there is at most one arrow
 $\unicode[STIX]{x1D6FC}\in Q_{1}$
ending at
$\unicode[STIX]{x1D6FC}\in Q_{1}$
ending at
 $p$
and at most one arrow
$p$
and at most one arrow
 $\unicode[STIX]{x1D6FD}\in Q_{1}$
starting at
$\unicode[STIX]{x1D6FD}\in Q_{1}$
starting at
 $p$
, with
$p$
, with
 $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\in Z$
(if both exist).
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\in Z$
(if both exist). -
– For each vertex
 $p\notin Q_{0}^{\operatorname{Sp}}$
, there are at most two arrows
$p\notin Q_{0}^{\operatorname{Sp}}$
, there are at most two arrows
 $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in Q_{1}$
ending at
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in Q_{1}$
ending at
 $p$
and at most two arrows
$p$
and at most two arrows
 $\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}\in Q_{1}$
starting at
$\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}\in Q_{1}$
starting at
 $p$
, and they can be labeled in such a way that
$p$
, and they can be labeled in such a way that
 $\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{1}\in Z$
,
$\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{1}\in Z$
,
 $\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{2}\in Z$
,
$\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{2}\in Z$
,
 $\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{2}\notin Z$
, and
$\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{2}\notin Z$
, and
 $\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{1}\notin Z$
.
$\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{1}\notin Z$
.
An algebra
![]() $\unicode[STIX]{x1D6EC}$
is called a skewed-gentle algebra if
$\unicode[STIX]{x1D6EC}$
is called a skewed-gentle algebra if
![]() $\unicode[STIX]{x1D6EC}$
is Morita equivalent to
$\unicode[STIX]{x1D6EC}$
is Morita equivalent to
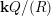 $\mathbf{k}Q/(R)$
for a skewed-gentle pair
$\mathbf{k}Q/(R)$
for a skewed-gentle pair
![]() $(Q,Z)$
, where
$(Q,Z)$
, where
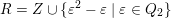 $R=Z\cup \{\unicode[STIX]{x1D700}^{2}-\unicode[STIX]{x1D700}\mid \unicode[STIX]{x1D700}\in Q_{2}\}$
.
$R=Z\cup \{\unicode[STIX]{x1D700}^{2}-\unicode[STIX]{x1D700}\mid \unicode[STIX]{x1D700}\in Q_{2}\}$
.
Example 2.2. Let
![]() $Q$
be the following biquiver with
$Q$
be the following biquiver with
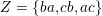 $Z=\{ba,cb,ac\}$
.
$Z=\{ba,cb,ac\}$
.

Then
![]() $(Q,Z)$
is a skewed-gentle pair and hence
$(Q,Z)$
is a skewed-gentle pair and hence
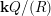 $\mathbf{k}Q/(R)$
is a skewed-gentle algebra, where
$\mathbf{k}Q/(R)$
is a skewed-gentle algebra, where
 $R=Z\cup \{\unicode[STIX]{x1D700}_{1}^{2}-\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{4}^{2}-\unicode[STIX]{x1D700}_{4}\}$
.
$R=Z\cup \{\unicode[STIX]{x1D700}_{1}^{2}-\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{4}^{2}-\unicode[STIX]{x1D700}_{4}\}$
.
2.2 Letters
Let
![]() $(Q,Z)$
be a skewed-gentle pair. Following [Reference Crawley-BoeveyCra89, Reference GeißGei99], we associate a new biquiver
$(Q,Z)$
be a skewed-gentle pair. Following [Reference Crawley-BoeveyCra89, Reference GeißGei99], we associate a new biquiver
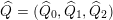 $\widehat{Q}=(\widehat{Q}_{0},\widehat{Q}_{1},\widehat{Q}_{2})$
with
$\widehat{Q}=(\widehat{Q}_{0},\widehat{Q}_{1},\widehat{Q}_{2})$
with
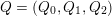 $Q=(Q_{0},Q_{1},Q_{2})$
by adding two new vertices
$Q=(Q_{0},Q_{1},Q_{2})$
by adding two new vertices
![]() $i_{+}$
and
$i_{+}$
and
![]() $i_{-}$
and two new solid arrows
$i_{-}$
and two new solid arrows
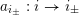 $a_{i_{\pm }}:i\rightarrow i_{\pm }$
for each vertex
$a_{i_{\pm }}:i\rightarrow i_{\pm }$
for each vertex
![]() $i\in Q_{0}$
. That is:
$i\in Q_{0}$
. That is:
-
–
 $\widehat{Q}_{0}=Q_{0}\cup \{i_{\pm }\mid i\in Q_{0}\}$
;
$\widehat{Q}_{0}=Q_{0}\cup \{i_{\pm }\mid i\in Q_{0}\}$
; -
–
 $\widehat{Q}_{1}=Q_{1}\cup \{a_{i_{\pm }}:i\rightarrow i_{\pm }\mid i\in Q_{0}\}$
;
$\widehat{Q}_{1}=Q_{1}\cup \{a_{i_{\pm }}:i\rightarrow i_{\pm }\mid i\in Q_{0}\}$
; -
–
 $\widehat{Q}_{2}=Q_{2}$
.
$\widehat{Q}_{2}=Q_{2}$
.
For example, the biquiver
![]() $\widehat{Q}$
associated with the biquiver
$\widehat{Q}$
associated with the biquiver
![]() $Q$
in Example 2.2 is as shown by the following diagram.
$Q$
in Example 2.2 is as shown by the following diagram.

For any arrow
![]() $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
![]() $\widehat{Q}$
, we define a direct letter
$\widehat{Q}$
, we define a direct letter
![]() $\unicode[STIX]{x1D6FC}$
and an inverse letter
$\unicode[STIX]{x1D6FC}$
and an inverse letter
![]() $\unicode[STIX]{x1D6FC}^{-1}$
, which are mutually inverse. Let
$\unicode[STIX]{x1D6FC}^{-1}$
, which are mutually inverse. Let
![]() $L$
be the set of all letters. The functions
$L$
be the set of all letters. The functions
![]() $s,t$
can be extended to
$s,t$
can be extended to
![]() $L$
by setting
$L$
by setting
 $s(\unicode[STIX]{x1D6FC}^{-1})=t(\unicode[STIX]{x1D6FC})$
and
$s(\unicode[STIX]{x1D6FC}^{-1})=t(\unicode[STIX]{x1D6FC})$
and
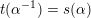 $t(\unicode[STIX]{x1D6FC}^{-1})=s(\unicode[STIX]{x1D6FC})$
. For each
$t(\unicode[STIX]{x1D6FC}^{-1})=s(\unicode[STIX]{x1D6FC})$
. For each
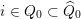 $i\in Q_{0}\subset \widehat{Q}_{0}$
, let
$i\in Q_{0}\subset \widehat{Q}_{0}$
, let
 $L(i):=\{l\in L\mid s(l)=i\}$
. We divide
$L(i):=\{l\in L\mid s(l)=i\}$
. We divide
![]() $L(i)$
into two disjoint subsets
$L(i)$
into two disjoint subsets
![]() $L_{+}(i)$
and
$L_{+}(i)$
and
![]() $L_{-}(i)$
with linear orders such that the subset
$L_{-}(i)$
with linear orders such that the subset
![]() $L_{\unicode[STIX]{x1D703}}(i)$
has one of the following forms:
$L_{\unicode[STIX]{x1D703}}(i)$
has one of the following forms:
-
–
 $\{a_{i_{\unicode[STIX]{x1D703}}}\}$
;
$\{a_{i_{\unicode[STIX]{x1D703}}}\}$
; -
–
 $\{a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D6FC}\}$
;
$\{a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D6FC}\}$
; -
–
 $\{\unicode[STIX]{x1D6FD}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}\}$
;
$\{\unicode[STIX]{x1D6FD}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}\}$
; -
–
 $\{\unicode[STIX]{x1D6FD}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D6FC}\}$
;
$\{\unicode[STIX]{x1D6FD}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D6FC}\}$
; -
–
 $\{\unicode[STIX]{x1D700}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D700}\}$
,
$\{\unicode[STIX]{x1D700}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D700}\}$
,
for
 $\unicode[STIX]{x1D703}\in \{\pm \}$
, some solid arrows
$\unicode[STIX]{x1D703}\in \{\pm \}$
, some solid arrows
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
in
$\unicode[STIX]{x1D6FD}$
in
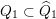 $Q_{1}\subset \widehat{Q}_{1}$
and some dashed arrow
$Q_{1}\subset \widehat{Q}_{1}$
and some dashed arrow
![]() $\unicode[STIX]{x1D700}$
in
$\unicode[STIX]{x1D700}$
in
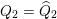 $Q_{2}=\widehat{Q}_{2}$
, satisfying that:
$Q_{2}=\widehat{Q}_{2}$
, satisfying that:
-
– for any two solid arrows
 $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
 $\unicode[STIX]{x1D6FF}$
in
$\unicode[STIX]{x1D6FF}$
in
 $Q_{1}\subset \widehat{Q}_{1}$
with
$Q_{1}\subset \widehat{Q}_{1}$
with
 $t(\unicode[STIX]{x1D6FF})=s(\unicode[STIX]{x1D6FE})=k$
, we have that
$t(\unicode[STIX]{x1D6FF})=s(\unicode[STIX]{x1D6FE})=k$
, we have that
 $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}\in Z$
if and only if
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}\in Z$
if and only if
 $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
 $\unicode[STIX]{x1D6FF}^{-1}$
are both in
$\unicode[STIX]{x1D6FF}^{-1}$
are both in
 $L_{+}(k)$
or
$L_{+}(k)$
or
 $L_{-}(k)$
.
$L_{-}(k)$
.
Observe that in the set
![]() $L_{\unicode[STIX]{x1D703}}(i)$
, the inverse of an arrow in
$L_{\unicode[STIX]{x1D703}}(i)$
, the inverse of an arrow in
![]() $Q$
is always greater than the arrow
$Q$
is always greater than the arrow
![]() $a_{i_{\unicode[STIX]{x1D703}}}$
, and an arrow in
$a_{i_{\unicode[STIX]{x1D703}}}$
, and an arrow in
![]() $Q$
is always smaller than the arrow
$Q$
is always smaller than the arrow
![]() $a_{i_{\unicode[STIX]{x1D703}}}$
. Notice that if
$a_{i_{\unicode[STIX]{x1D703}}}$
. Notice that if
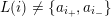 $L(i)\neq \{a_{i_{+}},a_{i_{-}}\}$
, then there are exactly two possible choices for the pair
$L(i)\neq \{a_{i_{+}},a_{i_{-}}\}$
, then there are exactly two possible choices for the pair
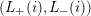 $(L_{+}(i),L_{-}(i))$
.
$(L_{+}(i),L_{-}(i))$
.
Example 2.3. In Example 2.2, one possible choice of the subsets
![]() $L_{\unicode[STIX]{x1D703}}(i)$
is:
$L_{\unicode[STIX]{x1D703}}(i)$
is:
-
–
 $L_{+}(1)=\{c^{-1}>a_{1_{+}}>a\}$
and
$L_{+}(1)=\{c^{-1}>a_{1_{+}}>a\}$
and
 $L_{-}(1)=\{\unicode[STIX]{x1D700}_{1}^{-1}>a_{1_{-}}>\unicode[STIX]{x1D700}_{1}\}$
;
$L_{-}(1)=\{\unicode[STIX]{x1D700}_{1}^{-1}>a_{1_{-}}>\unicode[STIX]{x1D700}_{1}\}$
; -
–
 $L_{+}(2)=\{a^{-1}>a_{2_{+}}>b\}$
and
$L_{+}(2)=\{a^{-1}>a_{2_{+}}>b\}$
and
 $L_{-}(2)=\{a_{2_{-}}\}$
;
$L_{-}(2)=\{a_{2_{-}}\}$
; -
–
 $L_{+}(3)=\{b^{-1}>a_{3_{+}}>c\}$
and
$L_{+}(3)=\{b^{-1}>a_{3_{+}}>c\}$
and
 $L_{-}(3)=\{a_{3_{-}}>d\}$
;
$L_{-}(3)=\{a_{3_{-}}>d\}$
; -
–
 $L_{+}(4)=\{d^{-1}>a_{4_{+}}\}$
and
$L_{+}(4)=\{d^{-1}>a_{4_{+}}\}$
and
 $L_{-}(4)=\{\unicode[STIX]{x1D700}_{4}^{-1}>a_{4_{-}}>\unicode[STIX]{x1D700}_{4}\}$
.
$L_{-}(4)=\{\unicode[STIX]{x1D700}_{4}^{-1}>a_{4_{-}}>\unicode[STIX]{x1D700}_{4}\}$
.
Note that the inverse letters
![]() $a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
are not listed here because they are not in any set
$a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
are not listed here because they are not in any set
![]() $L_{\unicode[STIX]{x1D703}}(i)$
. However they can still appear as first letters in words (see below).
$L_{\unicode[STIX]{x1D703}}(i)$
. However they can still appear as first letters in words (see below).
2.3 Words
A word
![]() $\mathfrak{m}$
is a sequence
$\mathfrak{m}$
is a sequence
 $\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
of letters in
$\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
of letters in
![]() $L$
satisfying that for any
$L$
satisfying that for any
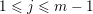 $1\leqslant j\leqslant m-1$
,
$1\leqslant j\leqslant m-1$
,
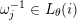 $\unicode[STIX]{x1D714}_{j}^{-1}\in L_{\unicode[STIX]{x1D703}}(i)$
and
$\unicode[STIX]{x1D714}_{j}^{-1}\in L_{\unicode[STIX]{x1D703}}(i)$
and
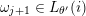 $\unicode[STIX]{x1D714}_{j+1}\in L_{\unicode[STIX]{x1D703}^{\prime }}(i)$
for different
$\unicode[STIX]{x1D714}_{j+1}\in L_{\unicode[STIX]{x1D703}^{\prime }}(i)$
for different
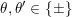 $\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\in \{\pm \}$
and some
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\in \{\pm \}$
and some
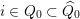 $i\in Q_{0}\subset \widehat{Q}_{0}$
. We call
$i\in Q_{0}\subset \widehat{Q}_{0}$
. We call
![]() $\unicode[STIX]{x1D714}_{1}$
the first letter of
$\unicode[STIX]{x1D714}_{1}$
the first letter of
![]() $\mathfrak{m}$
and
$\mathfrak{m}$
and
![]() $\unicode[STIX]{x1D714}_{m}$
the last letter of
$\unicode[STIX]{x1D714}_{m}$
the last letter of
![]() $\mathfrak{m}$
. Since both
$\mathfrak{m}$
. Since both
![]() $L_{\unicode[STIX]{x1D703}}(i)$
and
$L_{\unicode[STIX]{x1D703}}(i)$
and
![]() $L_{\unicode[STIX]{x1D703}^{\prime }}(i)$
are subsets of
$L_{\unicode[STIX]{x1D703}^{\prime }}(i)$
are subsets of
![]() $L(i)$
, we have
$L(i)$
, we have
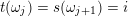 $t(\unicode[STIX]{x1D714}_{j})=s(\unicode[STIX]{x1D714}_{j+1})=i$
. The functions
$t(\unicode[STIX]{x1D714}_{j})=s(\unicode[STIX]{x1D714}_{j+1})=i$
. The functions
![]() $s,t$
can be generalized to the set of words by
$s,t$
can be generalized to the set of words by
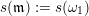 $s(\mathfrak{m}):=s(\unicode[STIX]{x1D714}_{1})$
and
$s(\mathfrak{m}):=s(\unicode[STIX]{x1D714}_{1})$
and
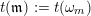 $t(\mathfrak{m}):=t(\unicode[STIX]{x1D714}_{m})$
. The inverse of a word
$t(\mathfrak{m}):=t(\unicode[STIX]{x1D714}_{m})$
. The inverse of a word
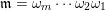 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
is defined as
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
is defined as
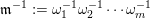 $\mathfrak{m}^{-1}:=\unicode[STIX]{x1D714}_{1}^{-1}\unicode[STIX]{x1D714}_{2}^{-1}\cdots \unicode[STIX]{x1D714}_{m}^{-1}$
. The product
$\mathfrak{m}^{-1}:=\unicode[STIX]{x1D714}_{1}^{-1}\unicode[STIX]{x1D714}_{2}^{-1}\cdots \unicode[STIX]{x1D714}_{m}^{-1}$
. The product
![]() $\mathfrak{n}\mathfrak{m}$
of two words
$\mathfrak{n}\mathfrak{m}$
of two words
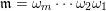 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
and
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
and
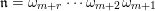 $\mathfrak{n}=\unicode[STIX]{x1D714}_{m+r}\cdots \unicode[STIX]{x1D714}_{m+2}\unicode[STIX]{x1D714}_{m+1}$
is defined to be
$\mathfrak{n}=\unicode[STIX]{x1D714}_{m+r}\cdots \unicode[STIX]{x1D714}_{m+2}\unicode[STIX]{x1D714}_{m+1}$
is defined to be
 $\unicode[STIX]{x1D714}_{m+r}\cdots \unicode[STIX]{x1D714}_{m+2}\unicode[STIX]{x1D714}_{m+1}\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
if this is again a word.
$\unicode[STIX]{x1D714}_{m+r}\cdots \unicode[STIX]{x1D714}_{m+2}\unicode[STIX]{x1D714}_{m+1}\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
if this is again a word.
A letter is called punctured if it is of the from
![]() $a_{i_{\unicode[STIX]{x1D703}}}$
or
$a_{i_{\unicode[STIX]{x1D703}}}$
or
![]() $a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
such that
$a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
such that
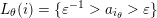 $L_{\unicode[STIX]{x1D703}}(i)=\{\unicode[STIX]{x1D700}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D700}\}$
for some dashed arrow
$L_{\unicode[STIX]{x1D703}}(i)=\{\unicode[STIX]{x1D700}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D700}\}$
for some dashed arrow
![]() $\unicode[STIX]{x1D700}$
. A word
$\unicode[STIX]{x1D700}$
. A word
![]() $\mathfrak{m}$
is called left inextensible (respectively right inextensible) if there is no letter
$\mathfrak{m}$
is called left inextensible (respectively right inextensible) if there is no letter
![]() $l$
such that
$l$
such that
![]() $l\mathfrak{m}$
(respectively
$l\mathfrak{m}$
(respectively
![]() $\mathfrak{m}l$
) is again a word. A word is called maximal if it is both left and right inextensible. It is obvious that a word
$\mathfrak{m}l$
) is again a word. A word is called maximal if it is both left and right inextensible. It is obvious that a word
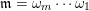 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
is right (respectively left) inextensible if and only if
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
is right (respectively left) inextensible if and only if
![]() $\unicode[STIX]{x1D714}_{1}$
(respectively
$\unicode[STIX]{x1D714}_{1}$
(respectively
![]() $\unicode[STIX]{x1D714}_{m}$
) is of the form
$\unicode[STIX]{x1D714}_{m}$
) is of the form
![]() $a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
(respectively
$a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
(respectively
![]() $a_{i_{\unicode[STIX]{x1D703}}}$
). In a word, except for its first letter (respectively last letter), there are no letters of the form
$a_{i_{\unicode[STIX]{x1D703}}}$
). In a word, except for its first letter (respectively last letter), there are no letters of the form
![]() $a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
(respectively
$a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
(respectively
![]() $a_{i_{\unicode[STIX]{x1D703}}}$
). In particular, each word contains at most two punctured letters.
$a_{i_{\unicode[STIX]{x1D703}}}$
). In particular, each word contains at most two punctured letters.
Example 2.4. In Example 2.2 with the disjoint subsets given in Example 2.3, the punctured letters are
![]() $a_{1_{-}}$
,
$a_{1_{-}}$
,
![]() $a_{1_{-}}^{-1}$
,
$a_{1_{-}}^{-1}$
,
![]() $a_{4_{-}}$
, and
$a_{4_{-}}$
, and
![]() $a_{4_{-}}^{-1}$
. The sequence
$a_{4_{-}}^{-1}$
. The sequence
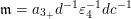 $\mathfrak{m}=a_{3_{+}}d^{-1}\unicode[STIX]{x1D700}_{4}^{-1}dc^{-1}$
is a word with
$\mathfrak{m}=a_{3_{+}}d^{-1}\unicode[STIX]{x1D700}_{4}^{-1}dc^{-1}$
is a word with
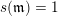 $s(\mathfrak{m})=1$
and
$s(\mathfrak{m})=1$
and
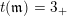 $t(\mathfrak{m})=3_{+}$
, which is left inextensible but not right inextensible.
$t(\mathfrak{m})=3_{+}$
, which is left inextensible but not right inextensible.
2.4 Orders
The linear orders in the sets
![]() $L_{\pm }(i),$
$L_{\pm }(i),$
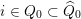 $i\in Q_{0}\subset \widehat{Q}_{0}$
, induce a partial order
$i\in Q_{0}\subset \widehat{Q}_{0}$
, induce a partial order
![]() ${\geqslant}$
on the set of words, such that
${\geqslant}$
on the set of words, such that
![]() $\mathfrak{m}>\mathfrak{r}$
if and only if
$\mathfrak{m}>\mathfrak{r}$
if and only if
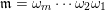 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
and
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
and
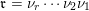 $\mathfrak{r}=\unicode[STIX]{x1D708}_{r}\cdots \unicode[STIX]{x1D708}_{2}\unicode[STIX]{x1D708}_{1}$
satisfy
$\mathfrak{r}=\unicode[STIX]{x1D708}_{r}\cdots \unicode[STIX]{x1D708}_{2}\unicode[STIX]{x1D708}_{1}$
satisfy
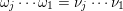 $\unicode[STIX]{x1D714}_{j}\cdots \unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D708}_{j}\cdots \unicode[STIX]{x1D708}_{1}$
and
$\unicode[STIX]{x1D714}_{j}\cdots \unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D708}_{j}\cdots \unicode[STIX]{x1D708}_{1}$
and
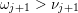 $\unicode[STIX]{x1D714}_{j+1}>\unicode[STIX]{x1D708}_{j+1}$
for some
$\unicode[STIX]{x1D714}_{j+1}>\unicode[STIX]{x1D708}_{j+1}$
for some
![]() $j\geqslant 0$
.
$j\geqslant 0$
.
For each vertex
![]() $i\in Q_{0}$
, let
$i\in Q_{0}$
, let
![]() $W_{\pm }(i)$
be the set of left inextensible words whose first letter is in
$W_{\pm }(i)$
be the set of left inextensible words whose first letter is in
![]() $L_{\pm }(i)$
. By construction,
$L_{\pm }(i)$
. By construction,
![]() $W_{\pm }(i)$
are linearly ordered. For each word
$W_{\pm }(i)$
are linearly ordered. For each word
![]() $\mathfrak{m}$
in
$\mathfrak{m}$
in
![]() $W_{\unicode[STIX]{x1D703}}(i)$
, we use
$W_{\unicode[STIX]{x1D703}}(i)$
, we use
![]() $\operatorname{[+]}\mathfrak{m}$
to denote its successor (if it exists) and use
$\operatorname{[+]}\mathfrak{m}$
to denote its successor (if it exists) and use
![]() $\operatorname{[-]}\mathfrak{m}$
to denote its predecessor (if it exists). So we have
$\operatorname{[-]}\mathfrak{m}$
to denote its predecessor (if it exists). So we have
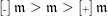 $\operatorname{[-]}\mathfrak{m}>\mathfrak{m}>\operatorname{[+]}\mathfrak{m}$
. In case
$\operatorname{[-]}\mathfrak{m}>\mathfrak{m}>\operatorname{[+]}\mathfrak{m}$
. In case
![]() $\mathfrak{m}$
is right inextensible, we set
$\mathfrak{m}$
is right inextensible, we set
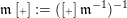 $\mathfrak{m}\operatorname{[+]}:=(\operatorname{[+]}\mathfrak{m}^{-1})^{-1}$
and
$\mathfrak{m}\operatorname{[+]}:=(\operatorname{[+]}\mathfrak{m}^{-1})^{-1}$
and
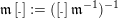 $\mathfrak{m}\operatorname{[-]}:=(\operatorname{[-]}\mathfrak{m}^{-1})^{-1}$
.
$\mathfrak{m}\operatorname{[-]}:=(\operatorname{[-]}\mathfrak{m}^{-1})^{-1}$
.
Let
![]() $\mathfrak{m}$
be a maximal word. By [Reference GeißGei99],
$\mathfrak{m}$
be a maximal word. By [Reference GeißGei99],
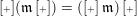 $\operatorname{[+]}(\mathfrak{m}\operatorname{[+]})=(\operatorname{[+]}\mathfrak{m})\operatorname{[+]}$
provided both of them exist; denote by
$\operatorname{[+]}(\mathfrak{m}\operatorname{[+]})=(\operatorname{[+]}\mathfrak{m})\operatorname{[+]}$
provided both of them exist; denote by
![]() $\operatorname{[+]}\mathfrak{m}\operatorname{[+]}$
one (or both) of them.
$\operatorname{[+]}\mathfrak{m}\operatorname{[+]}$
one (or both) of them.
Example 2.5. In Example 2.2 with the disjoint subsets given in Example 2.3, any word in the set
![]() $W_{+}(2)$
starts with one of the letters
$W_{+}(2)$
starts with one of the letters
![]() $b$
,
$b$
,
![]() $a^{-1}$
, or
$a^{-1}$
, or
![]() $a_{2_{+}}$
. A word in
$a_{2_{+}}$
. A word in
![]() $W_{+}(2)$
starting with
$W_{+}(2)$
starting with
![]() $a_{2_{+}}$
has to be
$a_{2_{+}}$
has to be
![]() $a_{2_{+}}$
since it is already left inextensible. Moreover, any word in
$a_{2_{+}}$
since it is already left inextensible. Moreover, any word in
![]() $W_{+}(2)$
that starts with
$W_{+}(2)$
that starts with
![]() $a^{-1}$
is bigger than
$a^{-1}$
is bigger than
![]() $a_{2_{+}}$
and any word that starts with
$a_{2_{+}}$
and any word that starts with
![]() $b$
is less than
$b$
is less than
![]() $a_{2_{+}}$
. Furthermore, we have
$a_{2_{+}}$
. Furthermore, we have
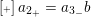 $\operatorname{[+]}a_{2_{+}}=a_{3_{-}}b$
and
$\operatorname{[+]}a_{2_{+}}=a_{3_{-}}b$
and
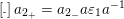 $\operatorname{[-]}a_{2_{+}}=a_{2_{-}}a\unicode[STIX]{x1D700}_{1}a^{-1}$
.
$\operatorname{[-]}a_{2_{+}}=a_{2_{-}}a\unicode[STIX]{x1D700}_{1}a^{-1}$
.
2.5 Admissible words
For technical reasons, we introduce a special letter
![]() $\unicode[STIX]{x1D700}^{\ast }$
for each dashed loop
$\unicode[STIX]{x1D700}^{\ast }$
for each dashed loop
![]() $\unicode[STIX]{x1D700}$
and a map
$\unicode[STIX]{x1D700}$
and a map
![]() $F$
on letters which sends the elements in
$F$
on letters which sends the elements in
 $\{\unicode[STIX]{x1D700}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D700}\}$
to
$\{\unicode[STIX]{x1D700}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D700}\}$
to
![]() $\unicode[STIX]{x1D700}^{\ast }$
and preserves the other letters.
$\unicode[STIX]{x1D700}^{\ast }$
and preserves the other letters.
A maximal word
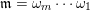 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
is called admissible if the following conditions hold.
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
is called admissible if the following conditions hold.
-
(A1) For each
 $\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}$
with
$\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}$
with
 $\unicode[STIX]{x1D700}$
a dashed loop, we have that
$\unicode[STIX]{x1D700}$
a dashed loop, we have that
 $\unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}>\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}$
, and for each
$\unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}>\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}$
, and for each
 $\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}^{-1}$
with
$\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}^{-1}$
with
 $\unicode[STIX]{x1D700}$
a dashed loop, we have that
$\unicode[STIX]{x1D700}$
a dashed loop, we have that
 $\unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}<\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}$
.
$\unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}<\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}$
. -
(A2) If
 $\mathfrak{m}$
contains two punctured letters, then
$\mathfrak{m}$
contains two punctured letters, then
 $F(\mathfrak{m})$
is not a proper power of
$F(\mathfrak{m})$
is not a proper power of
 $F(\mathfrak{m}^{\prime })$
for any maximal word
$F(\mathfrak{m}^{\prime })$
for any maximal word
 $\mathfrak{m}^{\prime }$
containing two punctured letters, where Let
$\mathfrak{m}^{\prime }$
containing two punctured letters, where Let $$\begin{eqnarray}F(\mathfrak{m}):=F(\unicode[STIX]{x1D714}_{m})\cdots F(\unicode[STIX]{x1D714}_{1})F(\unicode[STIX]{x1D714}_{2}^{-1})\cdots F(\unicode[STIX]{x1D714}_{m-1}^{-1}).\end{eqnarray}$$
$$\begin{eqnarray}F(\mathfrak{m}):=F(\unicode[STIX]{x1D714}_{m})\cdots F(\unicode[STIX]{x1D714}_{1})F(\unicode[STIX]{x1D714}_{2}^{-1})\cdots F(\unicode[STIX]{x1D714}_{m-1}^{-1}).\end{eqnarray}$$
 $\mathfrak{X}$
be the set of admissible words. Note that if
$\mathfrak{X}$
be the set of admissible words. Note that if
 $\mathfrak{m}$
is in
$\mathfrak{m}$
is in
 $\mathfrak{X}$
then so is its inverse
$\mathfrak{X}$
then so is its inverse
 $\mathfrak{m}^{-1}$
. Let
$\mathfrak{m}^{-1}$
. Let
 $\overline{\mathfrak{X}}$
be the set of all equivalence classes in
$\overline{\mathfrak{X}}$
be the set of all equivalence classes in
 $\mathfrak{X}$
with respect to
$\mathfrak{X}$
with respect to
 $\mathfrak{m}\simeq \mathfrak{m}^{-1}$
. But when we say an element
$\mathfrak{m}\simeq \mathfrak{m}^{-1}$
. But when we say an element
 $\mathfrak{m}$
in
$\mathfrak{m}$
in
 $\overline{\mathfrak{X}}$
, we always mean that
$\overline{\mathfrak{X}}$
, we always mean that
 $\mathfrak{m}$
is a representative in an equivalence class.
$\mathfrak{m}$
is a representative in an equivalence class.
Example 2.6. In Example 2.2 with the disjoint subsets given in Example 2.3, consider the word
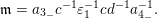 $\mathfrak{m}=a_{3_{-}}c^{-1}\unicode[STIX]{x1D700}_{1}^{-1}cd^{-1}a_{4_{-}}^{-1}.$
It is clear that
$\mathfrak{m}=a_{3_{-}}c^{-1}\unicode[STIX]{x1D700}_{1}^{-1}cd^{-1}a_{4_{-}}^{-1}.$
It is clear that
![]() $\mathfrak{m}$
is maximal. Since
$\mathfrak{m}$
is maximal. Since
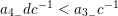 $a_{4_{-}}dc^{-1}<a_{3_{-}}c^{-1}$
,
$a_{4_{-}}dc^{-1}<a_{3_{-}}c^{-1}$
,
![]() $\mathfrak{m}$
satisfies (A1). Moreover,
$\mathfrak{m}$
satisfies (A1). Moreover,
![]() $\mathfrak{m}$
contains only one punctured letter
$\mathfrak{m}$
contains only one punctured letter
![]() $a_{4_{-}}^{-1}$
, so (A2) holds automatically. Hence
$a_{4_{-}}^{-1}$
, so (A2) holds automatically. Hence
![]() $\mathfrak{m}$
is admissible, i.e.
$\mathfrak{m}$
is admissible, i.e.
![]() $\mathfrak{m}\in \mathfrak{X}.$
$\mathfrak{m}\in \mathfrak{X}.$
2.6 Known results
In this subsection, we collect some results on indecomposable modules of skewed-gentle algebras and homomorphism spaces between them.
Let
![]() $\mathfrak{m}\in \overline{\mathfrak{X}}$
. Associate an indeterminate with each punctured letter in
$\mathfrak{m}\in \overline{\mathfrak{X}}$
. Associate an indeterminate with each punctured letter in
![]() $\mathfrak{m}$
and let
$\mathfrak{m}$
and let
![]() $A_{\mathfrak{m}}$
be the
$A_{\mathfrak{m}}$
be the
![]() $\mathbf{k}$
-algebra generated by these indeterminates
$\mathbf{k}$
-algebra generated by these indeterminates
![]() $x$
with relations
$x$
with relations
![]() $x^{2}=x$
. A one-dimensional module
$x^{2}=x$
. A one-dimensional module
![]() $N$
of
$N$
of
![]() $A_{\mathfrak{m}}$
is an algebra homomorphism
$A_{\mathfrak{m}}$
is an algebra homomorphism
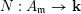 $N:A_{\mathfrak{m}}\rightarrow \mathbf{k}$
. It is determined (up to isomorphism) by the values
$N:A_{\mathfrak{m}}\rightarrow \mathbf{k}$
. It is determined (up to isomorphism) by the values
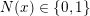 $N(x)\in \{0,1\}$
. More precisely:
$N(x)\in \{0,1\}$
. More precisely:
-
– if
 $\mathfrak{m}$
contains no punctured letters, then
$\mathfrak{m}$
contains no punctured letters, then
 $A_{\mathfrak{m}}=\mathbf{k}$
and there is one one-dimensional module
$A_{\mathfrak{m}}=\mathbf{k}$
and there is one one-dimensional module
 $N=\mathbf{k}$
;
$N=\mathbf{k}$
; -
– if
 $\mathfrak{m}$
contains one punctured letter, then
$\mathfrak{m}$
contains one punctured letter, then
 $A_{\mathfrak{m}}=\mathbf{k}[x]/(x^{2}-x)$
and there are two one-dimensional modules:
$A_{\mathfrak{m}}=\mathbf{k}[x]/(x^{2}-x)$
and there are two one-dimensional modules:
 $N=\mathbf{k}_{a}$
with
$N=\mathbf{k}_{a}$
with
 $\mathbf{k}_{a}(x)=a$
, for
$\mathbf{k}_{a}(x)=a$
, for
 $a\in \{0,1\}$
. Moreover, we have (2.1)
$a\in \{0,1\}$
. Moreover, we have (2.1) $$\begin{eqnarray}\displaystyle \dim _{\mathbf{k}}\operatorname{Hom}_{A_{\mathfrak{m}}}(\mathbf{k}_{u},\mathbf{k}_{v})=\unicode[STIX]{x1D6FF}_{u,v}\quad \forall u,v\in \{0,1\}; & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim _{\mathbf{k}}\operatorname{Hom}_{A_{\mathfrak{m}}}(\mathbf{k}_{u},\mathbf{k}_{v})=\unicode[STIX]{x1D6FF}_{u,v}\quad \forall u,v\in \{0,1\}; & & \displaystyle\end{eqnarray}$$
-
– if
 $\mathfrak{m}$
contains two punctured letters, then
$\mathfrak{m}$
contains two punctured letters, then
 $A_{\mathfrak{m}}=\mathbf{k}\langle x,y\rangle /(x^{2}-x,y^{2}-y)$
and there are four one-dimensional modules:
$A_{\mathfrak{m}}=\mathbf{k}\langle x,y\rangle /(x^{2}-x,y^{2}-y)$
and there are four one-dimensional modules:
 $N=\mathbf{k}_{a,b}$
with
$N=\mathbf{k}_{a,b}$
with
 $\mathbf{k}_{a,b}(x)=a$
and
$\mathbf{k}_{a,b}(x)=a$
and
 $\mathbf{k}_{a,b}(y)=b$
, for
$\mathbf{k}_{a,b}(y)=b$
, for
 $a,b\in \{0,1\}$
. Moreover, we have (2.2)
$a,b\in \{0,1\}$
. Moreover, we have (2.2) $$\begin{eqnarray}\displaystyle \dim _{\mathbf{k}}\operatorname{Hom}_{A_{\mathfrak{m}}}(\mathbf{k}_{u,u^{\prime }},\mathbf{k}_{v,v^{\prime }})=\unicode[STIX]{x1D6FF}_{u,v}\unicode[STIX]{x1D6FF}_{u^{\prime },v^{\prime }}\quad \forall u,v,u^{\prime },v^{\prime }\in \{0,1\}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim _{\mathbf{k}}\operatorname{Hom}_{A_{\mathfrak{m}}}(\mathbf{k}_{u,u^{\prime }},\mathbf{k}_{v,v^{\prime }})=\unicode[STIX]{x1D6FF}_{u,v}\unicode[STIX]{x1D6FF}_{u^{\prime },v^{\prime }}\quad \forall u,v,u^{\prime },v^{\prime }\in \{0,1\}. & & \displaystyle\end{eqnarray}$$
Construction 2.7. For each pair
![]() $(\mathfrak{m},N)$
with
$(\mathfrak{m},N)$
with
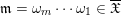 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}\in \overline{\mathfrak{X}}$
and a one-dimensional
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}\in \overline{\mathfrak{X}}$
and a one-dimensional
![]() $A_{\mathfrak{m}}$
-module
$A_{\mathfrak{m}}$
-module
![]() $N$
, the associated representation
$N$
, the associated representation
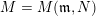 $M=M(\mathfrak{m},N)$
of
$M=M(\mathfrak{m},N)$
of
![]() $Q$
bounded by
$Q$
bounded by
![]() $R$
is constructed as follows.
$R$
is constructed as follows.
-
– For each vertex
 $i\in Q_{0}$
, let
$i\in Q_{0}$
, let
 $I_{i}=\{1\leqslant j\leqslant m-1\mid t(\unicode[STIX]{x1D714}_{j})=i\}$
.
$I_{i}=\{1\leqslant j\leqslant m-1\mid t(\unicode[STIX]{x1D714}_{j})=i\}$
. -
– Let
 $M_{i}$
be a vector space of dimension
$M_{i}$
be a vector space of dimension
 $|I_{i}|$
, say with base vectors
$|I_{i}|$
, say with base vectors
 $z_{j}$
,
$z_{j}$
,
 $j\in I_{i}$
.
$j\in I_{i}$
. -
– If
 $\unicode[STIX]{x1D714}_{j+1}=\unicode[STIX]{x1D6FC}$
an arrow in
$\unicode[STIX]{x1D714}_{j+1}=\unicode[STIX]{x1D6FC}$
an arrow in
 $Q_{1}$
, define
$Q_{1}$
, define
 $M_{\unicode[STIX]{x1D6FC}}(z_{j})=z_{j+1}$
, if
$M_{\unicode[STIX]{x1D6FC}}(z_{j})=z_{j+1}$
, if
 $\unicode[STIX]{x1D714}_{j+1}=\unicode[STIX]{x1D6FC}^{-1}$
, with
$\unicode[STIX]{x1D714}_{j+1}=\unicode[STIX]{x1D6FC}^{-1}$
, with
 $\unicode[STIX]{x1D6FC}$
an arrow in
$\unicode[STIX]{x1D6FC}$
an arrow in
 $Q_{1}$
, define
$Q_{1}$
, define
 $M_{\unicode[STIX]{x1D6FC}}(z_{j+1})=z_{j}$
.
$M_{\unicode[STIX]{x1D6FC}}(z_{j+1})=z_{j}$
. -
– If
 $\unicode[STIX]{x1D714}_{j+1}=\unicode[STIX]{x1D700}$
an arrow in
$\unicode[STIX]{x1D714}_{j+1}=\unicode[STIX]{x1D700}$
an arrow in
 $Q_{2}$
, define
$Q_{2}$
, define
 $M_{\unicode[STIX]{x1D700}}(z_{j})=M_{\unicode[STIX]{x1D700}}(z_{j+1})=z_{j+1}$
, if
$M_{\unicode[STIX]{x1D700}}(z_{j})=M_{\unicode[STIX]{x1D700}}(z_{j+1})=z_{j+1}$
, if
 $\unicode[STIX]{x1D714}_{j+1}=\unicode[STIX]{x1D700}^{-1}$
, with
$\unicode[STIX]{x1D714}_{j+1}=\unicode[STIX]{x1D700}^{-1}$
, with
 $\unicode[STIX]{x1D700}$
an arrow in
$\unicode[STIX]{x1D700}$
an arrow in
 $Q_{2}$
, define
$Q_{2}$
, define
 $M_{\unicode[STIX]{x1D700}}(z_{j+1})=M_{\unicode[STIX]{x1D700}}(z_{j})=z_{j}$
.
$M_{\unicode[STIX]{x1D700}}(z_{j+1})=M_{\unicode[STIX]{x1D700}}(z_{j})=z_{j}$
. -
– If
 $\unicode[STIX]{x1D714}_{1}$
(respectively
$\unicode[STIX]{x1D714}_{1}$
(respectively
 $\unicode[STIX]{x1D714}_{m}$
) is punctured with indeterminate
$\unicode[STIX]{x1D714}_{m}$
) is punctured with indeterminate
 $x$
, define
$x$
, define
 $M_{\unicode[STIX]{x1D700}_{t(\unicode[STIX]{x1D714}_{1})}}(z_{1})=N(x)z_{1}$
(respectively
$M_{\unicode[STIX]{x1D700}_{t(\unicode[STIX]{x1D714}_{1})}}(z_{1})=N(x)z_{1}$
(respectively
 $M_{\unicode[STIX]{x1D700}_{s(\unicode[STIX]{x1D714}_{m})}}(z_{m-1})=N(x)z_{m-1}$
), where
$M_{\unicode[STIX]{x1D700}_{s(\unicode[STIX]{x1D714}_{m})}}(z_{m-1})=N(x)z_{m-1}$
), where
 $\unicode[STIX]{x1D700}_{i}$
denotes the dashed loop at
$\unicode[STIX]{x1D700}_{i}$
denotes the dashed loop at
 $i$
.
$i$
. -
– All other components of
 $M_{\unicode[STIX]{x1D6FD}}$
are zero, for any
$M_{\unicode[STIX]{x1D6FD}}$
are zero, for any
 $\unicode[STIX]{x1D6FD}\in Q_{1}\cup Q_{2}$
.
$\unicode[STIX]{x1D6FD}\in Q_{1}\cup Q_{2}$
.
Example 2.8. Let
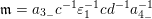 $\mathfrak{m}=a_{3_{-}}c^{-1}\unicode[STIX]{x1D700}_{1}^{-1}cd^{-1}a_{4_{-}}^{-1}$
be the admissible word in Example 2.6. Since
$\mathfrak{m}=a_{3_{-}}c^{-1}\unicode[STIX]{x1D700}_{1}^{-1}cd^{-1}a_{4_{-}}^{-1}$
be the admissible word in Example 2.6. Since
![]() $\mathfrak{m}$
contains one punctured letter
$\mathfrak{m}$
contains one punctured letter
![]() $a_{4_{-}}^{-1}$
, we have
$a_{4_{-}}^{-1}$
, we have
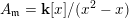 $A_{\mathfrak{m}}=\mathbf{k}[x]/(x^{2}-x)$
and there are two different one-dimensional
$A_{\mathfrak{m}}=\mathbf{k}[x]/(x^{2}-x)$
and there are two different one-dimensional
![]() $A_{\mathfrak{m}}$
-modules
$A_{\mathfrak{m}}$
-modules
![]() $\mathbf{k}_{u}$
for
$\mathbf{k}_{u}$
for
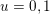 $u=0,1$
. By Construction 2.7, the associated representations
$u=0,1$
. By Construction 2.7, the associated representations
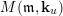 $M(\mathfrak{m},\mathbf{k}_{u})$
are as shown by the following diagram.
$M(\mathfrak{m},\mathbf{k}_{u})$
are as shown by the following diagram.

Theorem 2.9 [Reference BondarenkoBon92, Reference Crawley-BoeveyCra89, Reference DengDen00].
Let
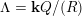 $\unicode[STIX]{x1D6EC}=\mathbf{k}Q/(R)$
be a skewed-gentle algebra. Then
$\unicode[STIX]{x1D6EC}=\mathbf{k}Q/(R)$
be a skewed-gentle algebra. Then
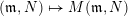 $(\mathfrak{m},N)\mapsto M(\mathfrak{m},N)$
is an injective map from the set of pairs
$(\mathfrak{m},N)\mapsto M(\mathfrak{m},N)$
is an injective map from the set of pairs
![]() $(\mathfrak{m},N)$
, with
$(\mathfrak{m},N)$
, with
![]() $\mathfrak{m}\in \bar{\mathfrak{X}}$
and
$\mathfrak{m}\in \bar{\mathfrak{X}}$
and
![]() $N$
a one-dimensional
$N$
a one-dimensional
![]() $A_{\mathfrak{m}}$
-module (up to isomorphism), to the set of indecomposable representations
$A_{\mathfrak{m}}$
-module (up to isomorphism), to the set of indecomposable representations
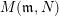 $M(\mathfrak{m},N)$
(up to isomorphism) of
$M(\mathfrak{m},N)$
(up to isomorphism) of
![]() $Q$
bounded by
$Q$
bounded by
![]() $R$
.
$R$
.
Remark 2.10. In fact, Bondarenko [Reference BondarenkoBon92], Crawley-Boevey [Reference Crawley-BoeveyCra89], and Deng [Reference DengDen00] proved the result above for general clannish algebras, where the map can be upgraded to a bijection by enlarging the set
![]() $\bar{\mathfrak{X}}$
and taking
$\bar{\mathfrak{X}}$
and taking
![]() $N$
to be an arbitrary indecomposable
$N$
to be an arbitrary indecomposable
![]() $A_{\mathfrak{m}}$
-module. Furthermore, any indecomposable module
$A_{\mathfrak{m}}$
-module. Furthermore, any indecomposable module
![]() $M$
, which is not in the image of the injective map in the above theorem, is in a homogeneous tube or in a tube of rank 2 and does not sit in the bottom of the tube. So in particular
$M$
, which is not in the image of the injective map in the above theorem, is in a homogeneous tube or in a tube of rank 2 and does not sit in the bottom of the tube. So in particular
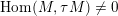 $\operatorname{Hom}(M,\unicode[STIX]{x1D70F}M)\neq 0$
for such an indecomposable module
$\operatorname{Hom}(M,\unicode[STIX]{x1D70F}M)\neq 0$
for such an indecomposable module
![]() $M$
.
$M$
.
The Auslander–Reiten translation
![]() $\unicode[STIX]{x1D70F}$
can be interpreted by the order of words.
$\unicode[STIX]{x1D70F}$
can be interpreted by the order of words.
Theorem 2.11 [Reference GeißGei99].
For any
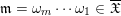 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}\in \overline{\mathfrak{X}}$
and any one-dimensional
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}\in \overline{\mathfrak{X}}$
and any one-dimensional
![]() $A_{\mathfrak{m}}$
-module
$A_{\mathfrak{m}}$
-module
![]() $N$
, if
$N$
, if
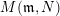 $M(\mathfrak{m},N)$
is not projective, then
$M(\mathfrak{m},N)$
is not projective, then
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}M(\mathfrak{m},N)=\left\{\begin{array}{@{}ll@{}}M(\operatorname{[+]}\mathfrak{m}\operatorname{[+]},\mathbf{k})\quad & \text{if }\mathfrak{m}\text{ contains no punctured letters and }N=\mathbf{k},\\ M(\operatorname{[+]}\mathfrak{m},\mathbf{k}_{1-a})\quad & \text{if only }\unicode[STIX]{x1D714}_{1}\text{ is punctured and }N=\mathbf{k}_{a},\\ M(\mathfrak{m},\mathbf{k}_{1-a,1-b})\quad & \text{if both }\unicode[STIX]{x1D714}_{1}\text{ and }\unicode[STIX]{x1D714}_{m}\text{ are punctured and }N=\mathbf{k}_{a,b}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}M(\mathfrak{m},N)=\left\{\begin{array}{@{}ll@{}}M(\operatorname{[+]}\mathfrak{m}\operatorname{[+]},\mathbf{k})\quad & \text{if }\mathfrak{m}\text{ contains no punctured letters and }N=\mathbf{k},\\ M(\operatorname{[+]}\mathfrak{m},\mathbf{k}_{1-a})\quad & \text{if only }\unicode[STIX]{x1D714}_{1}\text{ is punctured and }N=\mathbf{k}_{a},\\ M(\mathfrak{m},\mathbf{k}_{1-a,1-b})\quad & \text{if both }\unicode[STIX]{x1D714}_{1}\text{ and }\unicode[STIX]{x1D714}_{m}\text{ are punctured and }N=\mathbf{k}_{a,b}.\end{array}\right.\end{eqnarray}$$
For technical reasons, we also consider a trivial word
![]() $1_{i}$
corresponding to each vertex
$1_{i}$
corresponding to each vertex
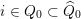 $i\in Q_{0}\subset \widehat{Q}_{0}$
. Let
$i\in Q_{0}\subset \widehat{Q}_{0}$
. Let
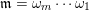 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
be a word in
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
be a word in
![]() $\overline{\mathfrak{X}}$
. For any integers
$\overline{\mathfrak{X}}$
. For any integers
![]() $i,j$
with
$i,j$
with
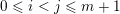 $0\leqslant i<j\leqslant m+1$
, we consider the subword
$0\leqslant i<j\leqslant m+1$
, we consider the subword
![]() $\mathfrak{m}_{(i,j)}$
of
$\mathfrak{m}_{(i,j)}$
of
![]() $\mathfrak{m}$
between
$\mathfrak{m}$
between
![]() $i$
and
$i$
and
![]() $j$
defined as
$j$
defined as
 $$\begin{eqnarray}\mathfrak{m}_{(i,j)}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D714}_{j-1}\cdots \unicode[STIX]{x1D714}_{i+1}\quad & \text{if }i<j-1,\\ 1_{t(\unicode[STIX]{x1D714}_{i})}\quad & \text{if }i=j-1,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}_{(i,j)}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D714}_{j-1}\cdots \unicode[STIX]{x1D714}_{i+1}\quad & \text{if }i<j-1,\\ 1_{t(\unicode[STIX]{x1D714}_{i})}\quad & \text{if }i=j-1,\end{array}\right.\end{eqnarray}$$
where
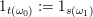 $1_{t(\unicode[STIX]{x1D714}_{0})}:=1_{s(\unicode[STIX]{x1D714}_{1})}$
.
$1_{t(\unicode[STIX]{x1D714}_{0})}:=1_{s(\unicode[STIX]{x1D714}_{1})}$
.
Let
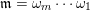 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
and
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
and
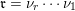 $\mathfrak{r}=\unicode[STIX]{x1D708}_{r}\cdots \unicode[STIX]{x1D708}_{1}$
be two words in
$\mathfrak{r}=\unicode[STIX]{x1D708}_{r}\cdots \unicode[STIX]{x1D708}_{1}$
be two words in
![]() $\bar{\mathfrak{X}}$
. A pair
$\bar{\mathfrak{X}}$
. A pair
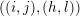 $((i,j),(h,l))$
of pairs of integers
$((i,j),(h,l))$
of pairs of integers
![]() $i,j,h,l$
with
$i,j,h,l$
with
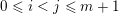 $0\leqslant i<j\leqslant m+1$
and
$0\leqslant i<j\leqslant m+1$
and
 $0\leqslant h<l\leqslant r+1$
is called an int-pair from
$0\leqslant h<l\leqslant r+1$
is called an int-pair from
![]() $\mathfrak{m}$
to
$\mathfrak{m}$
to
![]() $\mathfrak{r}$
if one of the following conditions holds:
$\mathfrak{r}$
if one of the following conditions holds:
-
–
 $\mathfrak{m}_{(i,j)}=\mathfrak{r}_{(h,l)}$
,
$\mathfrak{m}_{(i,j)}=\mathfrak{r}_{(h,l)}$
,
 $\unicode[STIX]{x1D714}_{i}^{-1}<\unicode[STIX]{x1D708}_{h}^{-1}$
and
$\unicode[STIX]{x1D714}_{i}^{-1}<\unicode[STIX]{x1D708}_{h}^{-1}$
and
 $\unicode[STIX]{x1D714}_{j}<\unicode[STIX]{x1D708}_{l}$
;
$\unicode[STIX]{x1D714}_{j}<\unicode[STIX]{x1D708}_{l}$
; -
–
 $\mathfrak{m}_{(i,j)}=(\mathfrak{r}_{(h,l)})^{-1}$
,
$\mathfrak{m}_{(i,j)}=(\mathfrak{r}_{(h,l)})^{-1}$
,
 $\unicode[STIX]{x1D714}_{i}^{-1}<\unicode[STIX]{x1D708}_{l}$
and
$\unicode[STIX]{x1D714}_{i}^{-1}<\unicode[STIX]{x1D708}_{l}$
and
 $\unicode[STIX]{x1D714}_{j}<\unicode[STIX]{x1D708}_{h}^{-1}$
;
$\unicode[STIX]{x1D714}_{j}<\unicode[STIX]{x1D708}_{h}^{-1}$
;
where if an inequality contains at least one of
![]() $\unicode[STIX]{x1D714}_{0}$
,
$\unicode[STIX]{x1D714}_{0}$
,
![]() $\unicode[STIX]{x1D714}_{m+1}$
,
$\unicode[STIX]{x1D714}_{m+1}$
,
![]() $\unicode[STIX]{x1D708}_{0}$
and
$\unicode[STIX]{x1D708}_{0}$
and
![]() $\unicode[STIX]{x1D708}_{r+1}$
then we assume that it holds automatically. Let
$\unicode[STIX]{x1D708}_{r+1}$
then we assume that it holds automatically. Let
![]() $H^{\mathfrak{m},\mathfrak{r}}$
be the set of int-pairs from
$H^{\mathfrak{m},\mathfrak{r}}$
be the set of int-pairs from
![]() $\mathfrak{m}$
and
$\mathfrak{m}$
and
![]() $\mathfrak{r}$
.
$\mathfrak{r}$
.
Example 2.12. Let
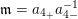 $\mathfrak{m}=a_{4_{+}}a_{4-}^{-1}$
and
$\mathfrak{m}=a_{4_{+}}a_{4-}^{-1}$
and
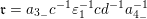 $\mathfrak{r}=a_{3_{-}}c^{-1}\unicode[STIX]{x1D700}_{1}^{-1}cd^{-1}a_{4_{-}}^{-1}$
be two admissible words for the skewed-gentle pair in Example 2.2 with the disjoint subsets given in Example 2.3. Then
$\mathfrak{r}=a_{3_{-}}c^{-1}\unicode[STIX]{x1D700}_{1}^{-1}cd^{-1}a_{4_{-}}^{-1}$
be two admissible words for the skewed-gentle pair in Example 2.2 with the disjoint subsets given in Example 2.3. Then
![]() $H^{\mathfrak{m},\mathfrak{r}}$
contains only one element
$H^{\mathfrak{m},\mathfrak{r}}$
contains only one element
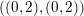 $((0,2),(0,2))$
for which
$((0,2),(0,2))$
for which
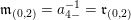 $\mathfrak{m}_{(0,2)}=a_{4-}^{-1}=\mathfrak{r}_{(0,2)}$
with
$\mathfrak{m}_{(0,2)}=a_{4-}^{-1}=\mathfrak{r}_{(0,2)}$
with
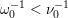 $\unicode[STIX]{x1D714}_{0}^{-1}<\unicode[STIX]{x1D708}_{0}^{-1}$
and
$\unicode[STIX]{x1D714}_{0}^{-1}<\unicode[STIX]{x1D708}_{0}^{-1}$
and
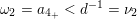 $\unicode[STIX]{x1D714}_{2}=a_{4_{+}}<d^{-1}=\unicode[STIX]{x1D708}_{2}$
.
$\unicode[STIX]{x1D714}_{2}=a_{4_{+}}<d^{-1}=\unicode[STIX]{x1D708}_{2}$
.
Notation 2.13. Let
![]() $(\mathfrak{m},N_{1})$
and
$(\mathfrak{m},N_{1})$
and
![]() $(\mathfrak{r},N_{2})$
be two pairs, where
$(\mathfrak{r},N_{2})$
be two pairs, where
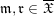 $\mathfrak{m},\mathfrak{r}\in \overline{\mathfrak{X}}$
and
$\mathfrak{m},\mathfrak{r}\in \overline{\mathfrak{X}}$
and
![]() $N_{1}$
(respectively
$N_{1}$
(respectively
![]() $N_{2}$
) is a one-dimensional module of
$N_{2}$
) is a one-dimensional module of
![]() $A_{\mathfrak{m}}$
(respectively
$A_{\mathfrak{m}}$
(respectively
![]() $A_{\mathfrak{r}}$
). For each int-pair
$A_{\mathfrak{r}}$
). For each int-pair
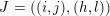 $J=((i,j),(h,l))$
in
$J=((i,j),(h,l))$
in
![]() $H^{\mathfrak{m},\mathfrak{r}}$
, denote by
$H^{\mathfrak{m},\mathfrak{r}}$
, denote by
![]() $A_{J}$
the
$A_{J}$
the
![]() $\mathbf{k}$
-algebra generated by the indeterminates associated with punctured letters contained in
$\mathbf{k}$
-algebra generated by the indeterminates associated with punctured letters contained in
![]() $\mathfrak{m}_{(i,j)}$
(or equivalently in
$\mathfrak{m}_{(i,j)}$
(or equivalently in
![]() $\mathfrak{r}_{(k,l)}$
). Then
$\mathfrak{r}_{(k,l)}$
). Then
![]() $A_{J}$
is a subalgebra of
$A_{J}$
is a subalgebra of
![]() $A_{\mathfrak{m}}$
and
$A_{\mathfrak{m}}$
and
![]() $A_{\mathfrak{r}}$
and hence both
$A_{\mathfrak{r}}$
and hence both
![]() $N_{1}$
and
$N_{1}$
and
![]() $N_{2}$
can be regarded as
$N_{2}$
can be regarded as
![]() $A_{J}$
-modules.
$A_{J}$
-modules.
Theorem 2.14 [Reference GeißGei99].
Under Notation 2.13, we have
 $$\begin{eqnarray}\dim _{\mathbf{k}}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(M(\mathfrak{m},N_{1}),M(\mathfrak{r},N_{2}))=\mathop{\sum }_{J\in H^{\mathfrak{m},\mathfrak{r}}}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(N_{1},N_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\mathbf{k}}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}}(M(\mathfrak{m},N_{1}),M(\mathfrak{r},N_{2}))=\mathop{\sum }_{J\in H^{\mathfrak{m},\mathfrak{r}}}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(N_{1},N_{2}).\end{eqnarray}$$
3 Background on cluster categories for marked surfaces
3.1 Jacobian algebras and Ginzburg dg algebras
Let
![]() $Q$
be a finite quiver and
$Q$
be a finite quiver and
![]() $W$
a potential on
$W$
a potential on
![]() $Q$
, that is, a sum of cycles in
$Q$
, that is, a sum of cycles in
![]() $Q$
. The Jacobian algebra of the quiver with potential
$Q$
. The Jacobian algebra of the quiver with potential
![]() $(Q,W)$
is the quotient
$(Q,W)$
is the quotient
 $$\begin{eqnarray}{\mathcal{P}}(Q,W):=\widehat{\mathbf{k}Q}/\overline{\unicode[STIX]{x2202}W},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}(Q,W):=\widehat{\mathbf{k}Q}/\overline{\unicode[STIX]{x2202}W},\end{eqnarray}$$
where
![]() $\widehat{\mathbf{k}Q}$
is the complete path algebra of
$\widehat{\mathbf{k}Q}$
is the complete path algebra of
![]() $Q$
,
$Q$
,
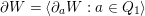 $\unicode[STIX]{x2202}W=\langle \unicode[STIX]{x2202}_{a}W:a\in Q_{1}\rangle$
and
$\unicode[STIX]{x2202}W=\langle \unicode[STIX]{x2202}_{a}W:a\in Q_{1}\rangle$
and
![]() $\overline{\unicode[STIX]{x2202}W}$
is the closure of
$\overline{\unicode[STIX]{x2202}W}$
is the closure of
![]() $\unicode[STIX]{x2202}W$
in
$\unicode[STIX]{x2202}W$
in
![]() $\widehat{\mathbf{k}Q}$
(cf. [Reference Derksen, Weyman and ZelevinskyDWZ08]).
$\widehat{\mathbf{k}Q}$
(cf. [Reference Derksen, Weyman and ZelevinskyDWZ08]).
The Jacobian algebra is the 0th cohomology of its refinement, the Ginzburg dg algebra
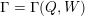 $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}(Q,W)$
of
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}(Q,W)$
of
![]() $(Q,W)$
(see the construction in [Reference KellerKel12, § 7.2]). There are three categories associated with
$(Q,W)$
(see the construction in [Reference KellerKel12, § 7.2]). There are three categories associated with
![]() $\unicode[STIX]{x1D6E4}$
, namely:
$\unicode[STIX]{x1D6E4}$
, namely:
-
– the finite dimensional derived category
 ${\mathcal{D}}_{fd}(\unicode[STIX]{x1D6E4})$
of
${\mathcal{D}}_{fd}(\unicode[STIX]{x1D6E4})$
of
 $\unicode[STIX]{x1D6E4}$
, which is a 3-Calabi–Yau category;
$\unicode[STIX]{x1D6E4}$
, which is a 3-Calabi–Yau category; -
– the perfect derived category
 $\operatorname{per}(\unicode[STIX]{x1D6E4})$
of
$\operatorname{per}(\unicode[STIX]{x1D6E4})$
of
 $\unicode[STIX]{x1D6E4}$
, which contains
$\unicode[STIX]{x1D6E4}$
, which contains
 ${\mathcal{D}}_{fd}(\unicode[STIX]{x1D6E4})$
;
${\mathcal{D}}_{fd}(\unicode[STIX]{x1D6E4})$
; -
– the cluster category
 ${\mathcal{C}}(\unicode[STIX]{x1D6E4})$
of
${\mathcal{C}}(\unicode[STIX]{x1D6E4})$
of
 $\unicode[STIX]{x1D6E4}$
, which is the (triangulated) 2-Calabi–Yau quotient category (3.1)
$\unicode[STIX]{x1D6E4}$
, which is the (triangulated) 2-Calabi–Yau quotient category (3.1) $$\begin{eqnarray}\displaystyle {\mathcal{C}}(\unicode[STIX]{x1D6E4}):=\operatorname{per}(\unicode[STIX]{x1D6E4})/{\mathcal{D}}_{fd}(\unicode[STIX]{x1D6E4}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{C}}(\unicode[STIX]{x1D6E4}):=\operatorname{per}(\unicode[STIX]{x1D6E4})/{\mathcal{D}}_{fd}(\unicode[STIX]{x1D6E4}). & & \displaystyle\end{eqnarray}$$
Furthermore there is a canonical cluster tilting object
![]() $T_{\unicode[STIX]{x1D6E4}}$
in
$T_{\unicode[STIX]{x1D6E4}}$
in
![]() ${\mathcal{C}}(\unicode[STIX]{x1D6E4})$
induced by the silting object
${\mathcal{C}}(\unicode[STIX]{x1D6E4})$
induced by the silting object
![]() $\unicode[STIX]{x1D6E4}$
in
$\unicode[STIX]{x1D6E4}$
in
![]() $\operatorname{per}\unicode[STIX]{x1D6E4}$
such that
$\operatorname{per}\unicode[STIX]{x1D6E4}$
such that
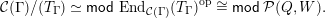 $$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6E4})/(T_{\unicode[STIX]{x1D6E4}})\simeq \mathsf{mod}\,\operatorname{End}_{{\mathcal{C}}(\unicode[STIX]{x1D6E4})}(T_{\unicode[STIX]{x1D6E4}})^{\text{op}}\cong \mathsf{mod}\,{\mathcal{P}}(Q,W).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}(\unicode[STIX]{x1D6E4})/(T_{\unicode[STIX]{x1D6E4}})\simeq \mathsf{mod}\,\operatorname{End}_{{\mathcal{C}}(\unicode[STIX]{x1D6E4})}(T_{\unicode[STIX]{x1D6E4}})^{\text{op}}\cong \mathsf{mod}\,{\mathcal{P}}(Q,W).\end{eqnarray}$$
See [Reference AmiotAmi09, Theorem 3.5] and [Reference Keller and ReitenKR07, § 2.1, Proposition (c)].
For a vertex
![]() $i$
of
$i$
of
![]() $Q$
, let
$Q$
, let
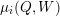 $\unicode[STIX]{x1D707}_{i}(Q,W)$
be the mutation of
$\unicode[STIX]{x1D707}_{i}(Q,W)$
be the mutation of
![]() $(Q,W)$
at
$(Q,W)$
at
![]() $i$
in the sense of [Reference Derksen, Weyman and ZelevinskyDWZ08], see also Appendix B. By [Reference Keller and YangKY11], there exists a canonical triangulated equivalence
$i$
in the sense of [Reference Derksen, Weyman and ZelevinskyDWZ08], see also Appendix B. By [Reference Keller and YangKY11], there exists a canonical triangulated equivalence
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D707}_{i}}:{\mathcal{C}}(\unicode[STIX]{x1D6E4}(Q,W))\simeq {\mathcal{C}}(\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D707}_{i}(Q,W))).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D707}_{i}}:{\mathcal{C}}(\unicode[STIX]{x1D6E4}(Q,W))\simeq {\mathcal{C}}(\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D707}_{i}(Q,W))).\end{eqnarray}$$
3.2 Quivers with potential from marked surfaces
Throughout the article,
![]() $\mathbf{S}$
denotes a marked surface with non-empty boundary in the sense of [Reference Fomin, Shapiro and ThurstonFST08], that is, a compact connected oriented surface
$\mathbf{S}$
denotes a marked surface with non-empty boundary in the sense of [Reference Fomin, Shapiro and ThurstonFST08], that is, a compact connected oriented surface
![]() $\mathbf{S}$
with a finite set
$\mathbf{S}$
with a finite set
![]() $\mathbf{M}$
of marked points on its boundary
$\mathbf{M}$
of marked points on its boundary
![]() $\unicode[STIX]{x2202}\mathbf{S}$
and a finite set
$\unicode[STIX]{x2202}\mathbf{S}$
and a finite set
![]() $\mathbf{P}$
of punctures in its interior
$\mathbf{P}$
of punctures in its interior
![]() $\mathbf{S}\setminus \unicode[STIX]{x2202}\mathbf{S}$
such that the following conditions hold:
$\mathbf{S}\setminus \unicode[STIX]{x2202}\mathbf{S}$
such that the following conditions hold:
-
– each connected component of
 $\unicode[STIX]{x2202}\mathbf{S}$
contains at least one marked point;
$\unicode[STIX]{x2202}\mathbf{S}$
contains at least one marked point; -
–
 $\mathbf{S}$
is not closed, i.e.
$\mathbf{S}$
is not closed, i.e.
 $\unicode[STIX]{x2202}\mathbf{S}\neq \emptyset$
;
$\unicode[STIX]{x2202}\mathbf{S}\neq \emptyset$
; -
– the rank
(3.4)of the surface is positive, where $$\begin{eqnarray}n=6g+3p+3b+m-6\end{eqnarray}$$
$$\begin{eqnarray}n=6g+3p+3b+m-6\end{eqnarray}$$
 $g$
is the genus of
$g$
is the genus of
 $\mathbf{S}$
,
$\mathbf{S}$
,
 $b$
the number of boundary components,
$b$
the number of boundary components,
 $m=|\mathbf{M}|$
the number of marked points and
$m=|\mathbf{M}|$
the number of marked points and
 $p=|\mathbf{P}|$
the number of punctures.
$p=|\mathbf{P}|$
the number of punctures.

Figure 1. The completions of curves.
Definition 3.1 (Curves and tagged curves).
Let
![]() $\mathbf{S}$
be a marked surface with non-empty boundary.
$\mathbf{S}$
be a marked surface with non-empty boundary.
-
– An (ordinary) curve in
 $\mathbf{S}$
is a continuous function
$\mathbf{S}$
is a continuous function
 $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow \mathbf{S}$
satisfying:
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow \mathbf{S}$
satisfying:-
∗ both
 $\unicode[STIX]{x1D6FE}(0)$
and
$\unicode[STIX]{x1D6FE}(0)$
and
 $\unicode[STIX]{x1D6FE}(1)$
are in
$\unicode[STIX]{x1D6FE}(1)$
are in
 $\mathbf{M}\cup \mathbf{P}$
;
$\mathbf{M}\cup \mathbf{P}$
; -
∗ for any
 $0<t<1$
,
$0<t<1$
,
 $\unicode[STIX]{x1D6FE}(t)$
is in
$\unicode[STIX]{x1D6FE}(t)$
is in
 $\mathbf{S}\setminus (\unicode[STIX]{x2202}\mathbf{S}\cup \mathbf{P})$
;
$\mathbf{S}\setminus (\unicode[STIX]{x2202}\mathbf{S}\cup \mathbf{P})$
; -
∗
 $\unicode[STIX]{x1D6FE}$
is not null-homotopic or homotopic to a boundary segment.
$\unicode[STIX]{x1D6FE}$
is not null-homotopic or homotopic to a boundary segment.
-
-
– The inverse of a curve
 $\unicode[STIX]{x1D6FE}$
is defined as
$\unicode[STIX]{x1D6FE}$
is defined as
 $\unicode[STIX]{x1D6FE}^{-1}(t):=\unicode[STIX]{x1D6FE}(1-t)$
for
$\unicode[STIX]{x1D6FE}^{-1}(t):=\unicode[STIX]{x1D6FE}(1-t)$
for
 $t\in [0,1]$
.
$t\in [0,1]$
. -
– For two curves
 $\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}$
,
$\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}$
,
 $\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
means that
$\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
means that
 $\unicode[STIX]{x1D6FE}_{1}$
is homotopic to
$\unicode[STIX]{x1D6FE}_{1}$
is homotopic to
 $\unicode[STIX]{x1D6FE}_{2}$
relative to
$\unicode[STIX]{x1D6FE}_{2}$
relative to
 $\{0,1\}$
(i.e. fixing the endpoints). Define an equivalence relation
$\{0,1\}$
(i.e. fixing the endpoints). Define an equivalence relation
 $\simeq$
on the set of curves in
$\simeq$
on the set of curves in
 $\mathbf{S}$
that
$\mathbf{S}$
that
 $\unicode[STIX]{x1D6FE}_{1}\simeq \unicode[STIX]{x1D6FE}_{2}$
if and only if either
$\unicode[STIX]{x1D6FE}_{1}\simeq \unicode[STIX]{x1D6FE}_{2}$
if and only if either
 $\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
or
$\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
or
 $\unicode[STIX]{x1D6FE}_{1}^{-1}\sim \unicode[STIX]{x1D6FE}_{2}$
. Denote by
$\unicode[STIX]{x1D6FE}_{1}^{-1}\sim \unicode[STIX]{x1D6FE}_{2}$
. Denote by
 $\mathbf{C}(\mathbf{S})$
the set of equivalence classes of curves in
$\mathbf{C}(\mathbf{S})$
the set of equivalence classes of curves in
 $\mathbf{S}$
with respect to
$\mathbf{S}$
with respect to
 $\simeq$
.
$\simeq$
. -
– Let
 $\unicode[STIX]{x1D6FE}$
be a curve in
$\unicode[STIX]{x1D6FE}$
be a curve in
 $\mathbf{C}(\mathbf{S})$
such that at least one of its endpoints is a puncture. Then define its completion
$\mathbf{C}(\mathbf{S})$
such that at least one of its endpoints is a puncture. Then define its completion
 $\bar{\unicode[STIX]{x1D6FE}}$
as in Figure 1.
$\bar{\unicode[STIX]{x1D6FE}}$
as in Figure 1. -
– A tagged curve is a pair
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
, where
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
, where
 $\unicode[STIX]{x1D6FE}$
is a curve in
$\unicode[STIX]{x1D6FE}$
is a curve in
 $\mathbf{S}$
and
$\mathbf{S}$
and
 $\unicode[STIX]{x1D705}:\{t\mid \unicode[STIX]{x1D6FE}(t)\in \mathbf{P}\}\rightarrow \{0,1\}$
is a map, satisfying the following conditions:
$\unicode[STIX]{x1D705}:\{t\mid \unicode[STIX]{x1D6FE}(t)\in \mathbf{P}\}\rightarrow \{0,1\}$
is a map, satisfying the following conditions:-
(T1)
 $\unicode[STIX]{x1D6FE}$
does not cut out a once-punctured monogon by a self-intersection (including endpoints), cf. Figure 2;
$\unicode[STIX]{x1D6FE}$
does not cut out a once-punctured monogon by a self-intersection (including endpoints), cf. Figure 2; -
(T2) if
 $\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(1)\in \mathbf{P}$
, then the completion
$\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(1)\in \mathbf{P}$
, then the completion
 $\bar{\unicode[STIX]{x1D6FE}}$
is not a proper power of a closed curve in the sense of the multiplication in the fundamental group of
$\bar{\unicode[STIX]{x1D6FE}}$
is not a proper power of a closed curve in the sense of the multiplication in the fundamental group of
 $\mathbf{S}$
.
$\mathbf{S}$
.
Note that
 $\unicode[STIX]{x1D705}(t)\in \mathbf{P}$
implies
$\unicode[STIX]{x1D705}(t)\in \mathbf{P}$
implies
 $t\in \{0,1\}$
. Moreover, write
$t\in \{0,1\}$
. Moreover, write
 $\unicode[STIX]{x1D705}=\emptyset$
when
$\unicode[STIX]{x1D705}=\emptyset$
when
 $\{t\mid \unicode[STIX]{x1D6FE}(t)\in \mathbf{P}\}=\emptyset$
by convention.
$\{t\mid \unicode[STIX]{x1D6FE}(t)\in \mathbf{P}\}=\emptyset$
by convention. -
-
– The inverse of a tagged curve
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
is defined as
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
is defined as
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})^{-1}:=(\unicode[STIX]{x1D6FE}^{-1},\unicode[STIX]{x1D705}^{-1})$
, where
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})^{-1}:=(\unicode[STIX]{x1D6FE}^{-1},\unicode[STIX]{x1D705}^{-1})$
, where
 $\unicode[STIX]{x1D705}^{-1}(t):=\unicode[STIX]{x1D705}(1-t)$
.
$\unicode[STIX]{x1D705}^{-1}(t):=\unicode[STIX]{x1D705}(1-t)$
. -
– For two tagged curves
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
,
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
,
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})\sim (\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
means that
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})\sim (\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
means that
 $\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
and
$\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
and
 $\unicode[STIX]{x1D705}_{1}=\unicode[STIX]{x1D705}_{2}$
. Define an equivalence relation
$\unicode[STIX]{x1D705}_{1}=\unicode[STIX]{x1D705}_{2}$
. Define an equivalence relation
 $\simeq$
on the set of tagged curves in
$\simeq$
on the set of tagged curves in
 $\mathbf{S}$
that
$\mathbf{S}$
that
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})\simeq (\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
if and only if either
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})\simeq (\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
if and only if either
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})\sim (\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
or
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})\sim (\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
or
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})\sim (\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})^{-1}$
. Denote by
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})\sim (\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})^{-1}$
. Denote by
 $\mathbf{C}^{\times }(\mathbf{S})$
the set of equivalence classes of tagged curves in
$\mathbf{C}^{\times }(\mathbf{S})$
the set of equivalence classes of tagged curves in
 $\mathbf{S}$
with respect to
$\mathbf{S}$
with respect to
 $\simeq$
.
$\simeq$
.

Figure 2. Once-punctured monogons.
Definition 3.2 (Tagged rotation [Reference Brüstle and QiuBQ15]).
The rotation
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})$
of a curve
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})$
of a curve
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\mathbf{C}(\mathbf{S})$
is the curve obtained from
$\mathbf{C}(\mathbf{S})$
is the curve obtained from
![]() $\unicode[STIX]{x1D6FE}$
by moving every endpoint of
$\unicode[STIX]{x1D6FE}$
by moving every endpoint of
![]() $\unicode[STIX]{x1D6FE}$
that is in
$\unicode[STIX]{x1D6FE}$
that is in
![]() $\mathbf{M}$
along the boundary anticlockwise to the next marked point. The tagged rotation
$\mathbf{M}$
along the boundary anticlockwise to the next marked point. The tagged rotation
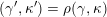 $(\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D705}^{\prime })=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
of a tagged curve
$(\unicode[STIX]{x1D6FE}^{\prime },\unicode[STIX]{x1D705}^{\prime })=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
of a tagged curve
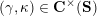 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
consists of the curve
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
consists of the curve
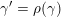 $\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})$
and the map
$\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})$
and the map
![]() $\unicode[STIX]{x1D705}^{\prime }$
defined by
$\unicode[STIX]{x1D705}^{\prime }$
defined by
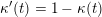 $\unicode[STIX]{x1D705}^{\prime }(t)=1-\unicode[STIX]{x1D705}(t)$
for
$\unicode[STIX]{x1D705}^{\prime }(t)=1-\unicode[STIX]{x1D705}(t)$
for
![]() $t$
with
$t$
with
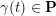 $\unicode[STIX]{x1D6FE}(t)\in \mathbf{P}$
, cf. Figure 3.
$\unicode[STIX]{x1D6FE}(t)\in \mathbf{P}$
, cf. Figure 3.

Figure 3. The tagged rotations of three tagged curves in
![]() $\mathbf{S}$
.
$\mathbf{S}$
.
Definition 3.3 (Intersection numbers).
For any two curves
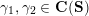 $\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\in \mathbf{C}(\mathbf{S})$
:
$\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\in \mathbf{C}(\mathbf{S})$
:
-
– let
 $\unicode[STIX]{x1D6FE}_{1}\cap \unicode[STIX]{x1D6FE}_{2}=\{(t_{1},t_{2})\mid \unicode[STIX]{x1D6FE}_{1}(t_{1})=\unicode[STIX]{x1D6FE}_{2}(t_{2})\notin \mathbf{P}\cup \mathbf{M}\}\subset (0,1)^{2}$
be the set of interior intersections between
$\unicode[STIX]{x1D6FE}_{1}\cap \unicode[STIX]{x1D6FE}_{2}=\{(t_{1},t_{2})\mid \unicode[STIX]{x1D6FE}_{1}(t_{1})=\unicode[STIX]{x1D6FE}_{2}(t_{2})\notin \mathbf{P}\cup \mathbf{M}\}\subset (0,1)^{2}$
be the set of interior intersections between
 $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
 $\unicode[STIX]{x1D6FE}_{2}$
;
$\unicode[STIX]{x1D6FE}_{2}$
; -
– the intersection number between them is defined to be
 $$\begin{eqnarray}\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}):=\min \{|\unicode[STIX]{x1D6FE}_{1}^{\prime }\cap \unicode[STIX]{x1D6FE}_{2}^{\prime }|\mid \unicode[STIX]{x1D6FE}_{1}^{\prime }\sim \unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}^{\prime }\sim \unicode[STIX]{x1D6FE}_{2}\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}):=\min \{|\unicode[STIX]{x1D6FE}_{1}^{\prime }\cap \unicode[STIX]{x1D6FE}_{2}^{\prime }|\mid \unicode[STIX]{x1D6FE}_{1}^{\prime }\sim \unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}^{\prime }\sim \unicode[STIX]{x1D6FE}_{2}\}.\end{eqnarray}$$
For any two tagged curves
![]() $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
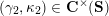 $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})\in \mathbf{C}^{\times }(\mathbf{S})$
:
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})\in \mathbf{C}^{\times }(\mathbf{S})$
:
-
– let
 $\mathfrak{P}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})=\{(t_{1},t_{2})\mid \unicode[STIX]{x1D6FE}_{1}(t_{1})=\unicode[STIX]{x1D6FE}_{2}(t_{2})\in \mathbf{P}\}\subset \{0,1\}^{2}$
be the set of intersections between
$\mathfrak{P}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})=\{(t_{1},t_{2})\mid \unicode[STIX]{x1D6FE}_{1}(t_{1})=\unicode[STIX]{x1D6FE}_{2}(t_{2})\in \mathbf{P}\}\subset \{0,1\}^{2}$
be the set of intersections between
 $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
 $\unicode[STIX]{x1D6FE}_{2}$
at
$\unicode[STIX]{x1D6FE}_{2}$
at
 $\mathbf{P}$
;
$\mathbf{P}$
; -
– A pair
 $(t_{1},t_{2})$
in
$(t_{1},t_{2})$
in
 $\mathfrak{P}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})$
is called a tagged intersection between
$\mathfrak{P}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})$
is called a tagged intersection between
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
 $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
if:
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
if:-
∗
 $\unicode[STIX]{x1D705}_{1}(t_{1})\neq \unicode[STIX]{x1D705}_{2}(t_{2})$
; and
$\unicode[STIX]{x1D705}_{1}(t_{1})\neq \unicode[STIX]{x1D705}_{2}(t_{2})$
; and -
∗ when
 $\unicode[STIX]{x1D6FE}_{1}|_{t_{1}\rightarrow (1-t_{1})}\sim \unicode[STIX]{x1D6FE}_{2}|_{t_{2}\rightarrow (1-t_{2})}$
, we have
$\unicode[STIX]{x1D6FE}_{1}|_{t_{1}\rightarrow (1-t_{1})}\sim \unicode[STIX]{x1D6FE}_{2}|_{t_{2}\rightarrow (1-t_{2})}$
, we have
 $\unicode[STIX]{x1D6FE}_{1}(1-t_{1})=\unicode[STIX]{x1D6FE}_{2}(1-t_{2})$
belongs to
$\unicode[STIX]{x1D6FE}_{1}(1-t_{1})=\unicode[STIX]{x1D6FE}_{2}(1-t_{2})$
belongs to
 $\mathbf{P}$
and
$\mathbf{P}$
and
 $\unicode[STIX]{x1D705}_{1}(1-t_{1})\neq \unicode[STIX]{x1D705}_{2}(1-t_{2})$
, where
$\unicode[STIX]{x1D705}_{1}(1-t_{1})\neq \unicode[STIX]{x1D705}_{2}(1-t_{2})$
, where
 $\unicode[STIX]{x1D6FE}|_{0\rightarrow 1}=\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}|_{0\rightarrow 1}=\unicode[STIX]{x1D6FE}$
and
 $\unicode[STIX]{x1D6FE}|_{1\rightarrow 0}=\unicode[STIX]{x1D6FE}^{-1}$
;
$\unicode[STIX]{x1D6FE}|_{1\rightarrow 0}=\unicode[STIX]{x1D6FE}^{-1}$
;
let
 $\mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))$
be the set of tagged intersections between
$\mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))$
be the set of tagged intersections between
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
 $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
;
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
; -
-
– the intersection number between them is defined to be
 $$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})):=\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})+|\mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))|.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})):=\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})+|\mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))|.\end{eqnarray}$$
We explain the intersection number of two tagged curves in some special cases.

Figure 4. The punctured intersections.
Example 3.4. Let
![]() $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
![]() $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
be two tagged curves in
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
be two tagged curves in
![]() $\mathbf{C}^{\times }(\mathbf{S})$
.
$\mathbf{C}^{\times }(\mathbf{S})$
.
-
– If all the endpoints of
 $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
 $\unicode[STIX]{x1D6FE}_{2}$
are in
$\unicode[STIX]{x1D6FE}_{2}$
are in
 $\mathbf{M}$
, then
$\mathbf{M}$
, then  $$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}).\end{eqnarray}$$
-
– If
 $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
 $\unicode[STIX]{x1D6FE}_{2}$
are not in the same equivalence class in
$\unicode[STIX]{x1D6FE}_{2}$
are not in the same equivalence class in
 $\mathbf{C}(\mathbf{S})$
(i.e.
$\mathbf{C}(\mathbf{S})$
(i.e.
 $\unicode[STIX]{x1D6FE}_{1}\nsim \unicode[STIX]{x1D6FE}_{2}$
and
$\unicode[STIX]{x1D6FE}_{1}\nsim \unicode[STIX]{x1D6FE}_{2}$
and
 $\unicode[STIX]{x1D6FE}_{1}\nsim \unicode[STIX]{x1D6FE}_{2}^{-1}$
), then
$\unicode[STIX]{x1D6FE}_{1}\nsim \unicode[STIX]{x1D6FE}_{2}^{-1}$
), then  $$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})+|\{(t_{1},t_{2})\mid \unicode[STIX]{x1D6FE}_{1}(t_{1})=\unicode[STIX]{x1D6FE}_{2}(t_{2})\in \mathbf{P},\unicode[STIX]{x1D705}_{1}(t_{1})\neq \unicode[STIX]{x1D705}_{2}(t_{2})\}|.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})+|\{(t_{1},t_{2})\mid \unicode[STIX]{x1D6FE}_{1}(t_{1})=\unicode[STIX]{x1D6FE}_{2}(t_{2})\in \mathbf{P},\unicode[STIX]{x1D705}_{1}(t_{1})\neq \unicode[STIX]{x1D705}_{2}(t_{2})\}|.\end{eqnarray}$$
-
– If
 $\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
whose endpoints are two different punctures, then
$\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
whose endpoints are two different punctures, then  $$\begin{eqnarray}|\mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))|=\left\{\begin{array}{@{}ll@{}}2\quad & \text{if }\unicode[STIX]{x1D705}_{1}(0)\neq \unicode[STIX]{x1D705}_{2}(0)\text{ and }\unicode[STIX]{x1D705}_{1}(1)\neq \unicode[STIX]{x1D705}_{2}(1),\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}|\mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))|=\left\{\begin{array}{@{}ll@{}}2\quad & \text{if }\unicode[STIX]{x1D705}_{1}(0)\neq \unicode[STIX]{x1D705}_{2}(0)\text{ and }\unicode[STIX]{x1D705}_{1}(1)\neq \unicode[STIX]{x1D705}_{2}(1),\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
-
– If the two tagged curves are as in Figure 4 where
 $\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}^{-1}$
and then
$\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}^{-1}$
and then $$\begin{eqnarray}\unicode[STIX]{x1D705}_{a}(t)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }a=1\text{ and }t=0,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}_{a}(t)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }a=1\text{ and }t=0,\\ 0\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
 $(0,0)\in \mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))$
. This is because
$(0,0)\in \mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))$
. This is because
 $\unicode[STIX]{x1D705}_{1}(0)=1\neq \unicode[STIX]{x1D705}_{2}(0)=0$
and
$\unicode[STIX]{x1D705}_{1}(0)=1\neq \unicode[STIX]{x1D705}_{2}(0)=0$
and
 $\unicode[STIX]{x1D6FE}_{1}|_{0\rightarrow 1}\nsim \unicode[STIX]{x1D6FE}_{2}|_{0\rightarrow 1}$
. For the pair
$\unicode[STIX]{x1D6FE}_{1}|_{0\rightarrow 1}\nsim \unicode[STIX]{x1D6FE}_{2}|_{0\rightarrow 1}$
. For the pair
 $(0,1)$
, we also have
$(0,1)$
, we also have
 $\unicode[STIX]{x1D705}_{1}(0)=1\neq \unicode[STIX]{x1D705}_{2}(1)=0$
. But since
$\unicode[STIX]{x1D705}_{1}(0)=1\neq \unicode[STIX]{x1D705}_{2}(1)=0$
. But since
 $\unicode[STIX]{x1D6FE}_{1}|_{0\rightarrow 1}\sim \unicode[STIX]{x1D6FE}_{2}|_{1\rightarrow 0}$
, we need to compare the values of
$\unicode[STIX]{x1D6FE}_{1}|_{0\rightarrow 1}\sim \unicode[STIX]{x1D6FE}_{2}|_{1\rightarrow 0}$
, we need to compare the values of
 $\unicode[STIX]{x1D705}_{1}(1)$
and
$\unicode[STIX]{x1D705}_{1}(1)$
and
 $\unicode[STIX]{x1D705}_{2}(0)$
. Because
$\unicode[STIX]{x1D705}_{2}(0)$
. Because
 $\unicode[STIX]{x1D705}_{1}(1)=0=\unicode[STIX]{x1D705}_{2}(0)$
, the pair
$\unicode[STIX]{x1D705}_{1}(1)=0=\unicode[STIX]{x1D705}_{2}(0)$
, the pair
 $(0,1)\notin \mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))$
. It is easy to see that neither
$(0,1)\notin \mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))$
. It is easy to see that neither
 $(1,0)$
nor
$(1,0)$
nor
 $(1,1)$
is in
$(1,1)$
is in
 $\mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))$
. Hence in this case we have We also mention that
$\mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))$
. Hence in this case we have We also mention that $$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=1.\end{eqnarray}$$
Since
$$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=1.\end{eqnarray}$$
Since $$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}))=2.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}))=2.\end{eqnarray}$$
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
has self-intersections, it is not a tagged arc in the sense of [Reference Fomin, Shapiro and ThurstonFST08] but it is in
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
has self-intersections, it is not a tagged arc in the sense of [Reference Fomin, Shapiro and ThurstonFST08] but it is in
 $\mathbf{C}^{\times }(\mathbf{S})$
.
$\mathbf{C}^{\times }(\mathbf{S})$
.
Remark 3.5. Note that we have less restriction for curves and tagged curves than Fomin et al., that is, we allow self-intersections. More precisely:
-
– the curves
 $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
 $\mathbf{C}(\mathbf{S})$
without self-intersections (i.e.
$\mathbf{C}(\mathbf{S})$
without self-intersections (i.e.
 $\operatorname{Int}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE})=0$
) are precisely the arcs in the sense of [Reference Fomin, Shapiro and ThurstonFST08, Definition 2.2];
$\operatorname{Int}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE})=0$
) are precisely the arcs in the sense of [Reference Fomin, Shapiro and ThurstonFST08, Definition 2.2]; -
– the tagged curves
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
in
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
in
 $\mathbf{C}^{\times }(\mathbf{S})$
without self-intersections (i.e.
$\mathbf{C}^{\times }(\mathbf{S})$
without self-intersections (i.e.
 $\operatorname{Int}((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705}),(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705}))=0$
) are precisely the tagged arcs in the sense of [Reference Fomin, Shapiro and ThurstonFST08, Definition 2.4];
$\operatorname{Int}((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705}),(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705}))=0$
) are precisely the tagged arcs in the sense of [Reference Fomin, Shapiro and ThurstonFST08, Definition 2.4]; -
– for two curves
 $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
 $\unicode[STIX]{x1D6FE}_{2}$
in
$\unicode[STIX]{x1D6FE}_{2}$
in
 $\mathbf{C}(\mathbf{S})$
without self-intersections, we have that
$\mathbf{C}(\mathbf{S})$
without self-intersections, we have that
 $\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})=0$
if and only if they are compatible in the sense of [Reference Fomin, Shapiro and ThurstonFST08, Definition 7.1];
$\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})=0$
if and only if they are compatible in the sense of [Reference Fomin, Shapiro and ThurstonFST08, Definition 7.1]; -
– for two tagged curves
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
 $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
in
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
in
 $\mathbf{C}^{\times }(\mathbf{S})$
without self-intersections, we have that
$\mathbf{C}^{\times }(\mathbf{S})$
without self-intersections, we have that
 $\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=0$
if and only if they are compatible in the sense of [Reference Fomin, Shapiro and ThurstonFST08, Definition 7.4].
$\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=0$
if and only if they are compatible in the sense of [Reference Fomin, Shapiro and ThurstonFST08, Definition 7.4].
By Remark 3.5, the following definitions of ideal triangulations and tagged triangulations are equivalent to the original ones in [Reference Fomin, Shapiro and ThurstonFST08].
Definition 3.6 (Ideal triangulations and tagged triangulations [Reference Fomin, Shapiro and ThurstonFST08]).
Let
![]() $\mathbf{S}$
be a marked surface with non-empty boundary.
$\mathbf{S}$
be a marked surface with non-empty boundary.
-
– An ideal triangulation is a maximal collection
 $\mathbf{T}$
of curves in
$\mathbf{T}$
of curves in
 $\mathbf{C}(\mathbf{S})$
such that
$\mathbf{C}(\mathbf{S})$
such that
 $\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})=0$
for any
$\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})=0$
for any
 $\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\in \mathbf{T}$
.
$\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\in \mathbf{T}$
. -
– A tagged triangulation is a maximal collection
 $\mathbf{T}$
of tagged curves in
$\mathbf{T}$
of tagged curves in
 $\mathbf{C}^{\times }(\mathbf{S})$
such that
$\mathbf{C}^{\times }(\mathbf{S})$
such that
 $\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=0$
for any
$\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=0$
for any
 $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})\in \mathbf{T}$
.
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})\in \mathbf{T}$
.
Any ideal/tagged triangulation
![]() $\mathbf{T}$
of
$\mathbf{T}$
of
![]() $\mathbf{S}$
consists of
$\mathbf{S}$
consists of
![]() $n$
ordinary/tagged curves (see [Reference Fomin, Shapiro and ThurstonFST08, Proposition 2.10, Theorem 7.9]), where
$n$
ordinary/tagged curves (see [Reference Fomin, Shapiro and ThurstonFST08, Proposition 2.10, Theorem 7.9]), where
![]() $n$
is the rank of
$n$
is the rank of
![]() $\mathbf{S}$
(cf. (3.4)). We require
$\mathbf{S}$
(cf. (3.4)). We require
![]() $n>0$
and exclude the case of a once-punctured monogon (where
$n>0$
and exclude the case of a once-punctured monogon (where
![]() $n=1$
) in the proofs. However, all the results hold in this case by direct checking and thus we will not exclude this case in the statements.
$n=1$
) in the proofs. However, all the results hold in this case by direct checking and thus we will not exclude this case in the statements.
A triangle in
![]() $\mathbf{T}$
has three distinct sides unless it is a self-folded triangle as in the left picture of Figure 5, where we call
$\mathbf{T}$
has three distinct sides unless it is a self-folded triangle as in the left picture of Figure 5, where we call
![]() $\unicode[STIX]{x1D6FC}$
the folded side and
$\unicode[STIX]{x1D6FC}$
the folded side and
![]() $\unicode[STIX]{x1D6FD}$
the remaining side.
$\unicode[STIX]{x1D6FD}$
the remaining side.

Figure 5. The self-folded triangle and the corresponding tagged version.
The flip of an ideal triangulation
![]() $\mathbf{T}$
, with respect to a curve
$\mathbf{T}$
, with respect to a curve
![]() $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
![]() $\mathbf{T}$
, is the unique ideal triangulation
$\mathbf{T}$
, is the unique ideal triangulation
![]() $\mathbf{T}^{\prime }$
(if it exists) that shares all curves in
$\mathbf{T}^{\prime }$
(if it exists) that shares all curves in
![]() $\mathbf{T}$
but
$\mathbf{T}$
but
![]() $\unicode[STIX]{x1D6FC}$
. One can always flip an ideal triangulation with respect to a curve unless it is the folded side of a self-folded triangle. To overcome this shortcoming, Fomin et al. [Reference Fomin, Shapiro and ThurstonFST08] introduced tagged triangulations, with tagged flips, so that every tagged triangulation can be flipped with respect to any tagged curve in it. The exchange graph of tagged triangulations with tagged flips is denoted by
$\unicode[STIX]{x1D6FC}$
. One can always flip an ideal triangulation with respect to a curve unless it is the folded side of a self-folded triangle. To overcome this shortcoming, Fomin et al. [Reference Fomin, Shapiro and ThurstonFST08] introduced tagged triangulations, with tagged flips, so that every tagged triangulation can be flipped with respect to any tagged curve in it. The exchange graph of tagged triangulations with tagged flips is denoted by
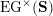 $\operatorname{EG}^{\times }(\mathbf{S})$
, that is, the graph whose vertices are tagged triangulations and whose edges are tagged flips.
$\operatorname{EG}^{\times }(\mathbf{S})$
, that is, the graph whose vertices are tagged triangulations and whose edges are tagged flips.
For each curve
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\mathbf{C}(\mathbf{S})$
with
$\mathbf{C}(\mathbf{S})$
with
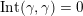 $\operatorname{Int}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE})=0$
, we define its tagged version
$\operatorname{Int}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE})=0$
, we define its tagged version
![]() $\unicode[STIX]{x1D6FE}^{\times }$
to be
$\unicode[STIX]{x1D6FE}^{\times }$
to be
![]() $(\unicode[STIX]{x1D6FE},\emptyset )$
unless
$(\unicode[STIX]{x1D6FE},\emptyset )$
unless
![]() $\unicode[STIX]{x1D6FE}$
is a loop enclosing a puncture, as
$\unicode[STIX]{x1D6FE}$
is a loop enclosing a puncture, as
![]() $\unicode[STIX]{x1D6FD}$
in the left picture of Figure 5. In that case
$\unicode[STIX]{x1D6FD}$
in the left picture of Figure 5. In that case
![]() $\unicode[STIX]{x1D6FD}^{\times }$
, as in the right picture of Figure 5, is defined to be
$\unicode[STIX]{x1D6FD}^{\times }$
, as in the right picture of Figure 5, is defined to be
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D705})$
, where
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D705})$
, where
![]() $\unicode[STIX]{x1D6FC}$
is the unique curve without self-intersections enclosed by
$\unicode[STIX]{x1D6FC}$
is the unique curve without self-intersections enclosed by
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
 $\unicode[STIX]{x1D705}(t)=1$
for
$\unicode[STIX]{x1D705}(t)=1$
for
![]() $t$
with
$t$
with
 $\unicode[STIX]{x1D6FC}(t)\in \mathbf{P}$
. In this way, each ideal triangulation
$\unicode[STIX]{x1D6FC}(t)\in \mathbf{P}$
. In this way, each ideal triangulation
![]() $\mathbf{T}$
induces a tagged triangulation
$\mathbf{T}$
induces a tagged triangulation
![]() $\mathbf{T}^{\times }$
consisting of the tagged versions of all curves in
$\mathbf{T}^{\times }$
consisting of the tagged versions of all curves in
![]() $\mathbf{T}$
.
$\mathbf{T}$
.
For each ideal triangulation
![]() $\mathbf{T}$
, there is an associated quiver with potential
$\mathbf{T}$
, there is an associated quiver with potential
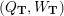 $(Q_{\mathbf{T}},W_{\mathbf{T}})$
(cf. [Reference Fomin, Shapiro and ThurstonFST08, Reference Irelli and Labardini-FragosoIL12]). In the paper, we only study
$(Q_{\mathbf{T}},W_{\mathbf{T}})$
(cf. [Reference Fomin, Shapiro and ThurstonFST08, Reference Irelli and Labardini-FragosoIL12]). In the paper, we only study
 $(Q_{\mathbf{T}},W_{\mathbf{T}})$
in the case when
$(Q_{\mathbf{T}},W_{\mathbf{T}})$
in the case when
![]() $\mathbf{T}$
is an admissible triangulation in the following sense (see Figure 14 for example).
$\mathbf{T}$
is an admissible triangulation in the following sense (see Figure 14 for example).
Definition 3.7. An ideal triangulation
![]() $\mathbf{T}$
is called admissible if every puncture in
$\mathbf{T}$
is called admissible if every puncture in
![]() $\mathbf{P}$
is contained in a self-folded triangle in
$\mathbf{P}$
is contained in a self-folded triangle in
![]() $\mathbf{T}$
.
$\mathbf{T}$
.
In particular, in such a triangulation, the folded side of each self-folded triangle connects a marked point in
![]() $\mathbf{M}$
and a puncture in
$\mathbf{M}$
and a puncture in
![]() $\mathbf{P}$
.
$\mathbf{P}$
.
In an admissible triangulation
![]() $\mathbf{T}$
, for a curve
$\mathbf{T}$
, for a curve
![]() $\unicode[STIX]{x1D6FC}\in \mathbf{T}$
, let
$\unicode[STIX]{x1D6FC}\in \mathbf{T}$
, let
![]() $\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FC})$
be the curve defined as follows: if
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FC})$
be the curve defined as follows: if
![]() $\unicode[STIX]{x1D6FC}$
is the folded side of a self-folded triangle in
$\unicode[STIX]{x1D6FC}$
is the folded side of a self-folded triangle in
![]() $\mathbf{T}$
(see the left picture of Figure 5), then
$\mathbf{T}$
(see the left picture of Figure 5), then
![]() $\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FC})$
is the corresponding remaining side (i.e.
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FC})$
is the corresponding remaining side (i.e.
![]() $\unicode[STIX]{x1D6FD}$
in the left picture of Figure 5); if there is no such triangle, set
$\unicode[STIX]{x1D6FD}$
in the left picture of Figure 5); if there is no such triangle, set
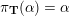 $\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D6FC}$
. The associated quiver with potential
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D6FC}$
. The associated quiver with potential
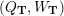 $(Q_{\mathbf{T}},W_{\mathbf{T}})$
is given by the following data (see Figure 6):
$(Q_{\mathbf{T}},W_{\mathbf{T}})$
is given by the following data (see Figure 6):
-
– the vertices of
 $Q_{\mathbf{T}}$
are labeled by the curves in
$Q_{\mathbf{T}}$
are labeled by the curves in
 $\mathbf{T}$
;
$\mathbf{T}$
; -
– there is an arrow from
 $i$
to
$i$
to
 $j$
whenever there is a non-self-folded triangle in
$j$
whenever there is a non-self-folded triangle in
 $\mathbf{T}$
having
$\mathbf{T}$
having
 $\unicode[STIX]{x1D70B}_{\mathbf{T}}(i)$
and
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(i)$
and
 $\unicode[STIX]{x1D70B}_{\mathbf{T}}(j)$
as edges with
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(j)$
as edges with
 $\unicode[STIX]{x1D70B}_{\mathbf{T}}(j)$
following
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(j)$
following
 $\unicode[STIX]{x1D70B}_{\mathbf{T}}(i)$
in the clockwise orientation (which is induced by the orientation of
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(i)$
in the clockwise orientation (which is induced by the orientation of
 $\mathbf{S}$
). For instance, the quiver for a non-self-folded triangle is shown in Figure 6;
$\mathbf{S}$
). For instance, the quiver for a non-self-folded triangle is shown in Figure 6; -
– each subset
 $\{i,j,k\}$
of
$\{i,j,k\}$
of
 $\mathbf{T}$
with
$\mathbf{T}$
with
 $\unicode[STIX]{x1D70B}_{\mathbf{T}}(i)$
,
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(i)$
,
 $\unicode[STIX]{x1D70B}_{\mathbf{T}}(j)$
,
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(j)$
,
 $\unicode[STIX]{x1D70B}_{\mathbf{T}}(k)$
forming an interior non-self-folded triangle in
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(k)$
forming an interior non-self-folded triangle in
 $\mathbf{T}$
yields a unique three-cycle up to cyclic permutation. The potential
$\mathbf{T}$
yields a unique three-cycle up to cyclic permutation. The potential
 $W_{\mathbf{T}}$
is the sum of all such three-cycles.
$W_{\mathbf{T}}$
is the sum of all such three-cycles.

Figure 6. The quiver associated with a non-self-folded triangle.
Then by § 3.1, there is an associated cluster category, denoted by
![]() ${\mathcal{C}}(\mathbf{T})$
.
${\mathcal{C}}(\mathbf{T})$
.
3.3 Correspondence
The objects and morphisms in
![]() ${\mathcal{C}}(\mathbf{T})$
are expected to correspond to curves and intersection numbers, respectively. A cluster tilting object
${\mathcal{C}}(\mathbf{T})$
are expected to correspond to curves and intersection numbers, respectively. A cluster tilting object
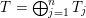 $T=\bigoplus _{j=1}^{n}T_{j}$
in a cluster category
$T=\bigoplus _{j=1}^{n}T_{j}$
in a cluster category
![]() ${\mathcal{C}}$
is an object satisfying
${\mathcal{C}}$
is an object satisfying
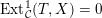 $\operatorname{Ext}_{{\mathcal{C}}}^{1}(T,X)=0$
if and only if
$\operatorname{Ext}_{{\mathcal{C}}}^{1}(T,X)=0$
if and only if
 $X\in \mathsf{add}\,T$
. The mutation
$X\in \mathsf{add}\,T$
. The mutation
![]() $\unicode[STIX]{x1D707}_{i}$
at the
$\unicode[STIX]{x1D707}_{i}$
at the
![]() $i$
th indecomposable direct summand acts on a cluster tilting object
$i$
th indecomposable direct summand acts on a cluster tilting object
 $T=\bigoplus _{j=1}^{n}T_{j}$
, by replacing
$T=\bigoplus _{j=1}^{n}T_{j}$
, by replacing
![]() $T_{i}$
with the unique indecomposable object
$T_{i}$
with the unique indecomposable object
![]() $T_{i}^{\prime }\ncong T_{i}$
satisfying that
$T_{i}^{\prime }\ncong T_{i}$
satisfying that
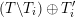 $(T\setminus T_{i})\oplus T_{i}^{\prime }$
is a cluster tilting object.
$(T\setminus T_{i})\oplus T_{i}^{\prime }$
is a cluster tilting object.
In the unpunctured case, we have the following known results.
Theorem 3.8 [Reference Brüstle and ZhangBZ11].
If
![]() $\mathbf{S}$
is unpunctured, then there is a bijection between the set of curves and valued closed curves in
$\mathbf{S}$
is unpunctured, then there is a bijection between the set of curves and valued closed curves in
![]() $\mathbf{S}$
and the set of indecomposable objects in
$\mathbf{S}$
and the set of indecomposable objects in
![]() ${\mathcal{C}}(\mathbf{T})$
. Under such a bijection:
${\mathcal{C}}(\mathbf{T})$
. Under such a bijection:
-
– rotation of curves is compatible with shift of objects;
-
– triangulations of
 $\mathbf{S}$
one-to-one correspond to cluster tilting objects in
$\mathbf{S}$
one-to-one correspond to cluster tilting objects in
 ${\mathcal{C}}(\mathbf{T})$
while flip of triangulations is compatible with mutation of cluster tilting objects.
${\mathcal{C}}(\mathbf{T})$
while flip of triangulations is compatible with mutation of cluster tilting objects.
Theorem 3.9 [Reference Zhang, Zhou and ZhuZZZ13].
If
![]() $\mathbf{S}$
is unpunctured, then for any two curves
$\mathbf{S}$
is unpunctured, then for any two curves
![]() $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$
, we have
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$
, we have
 $$\begin{eqnarray}\operatorname{Int}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF})=\dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{\unicode[STIX]{x1D6FE}},X_{\unicode[STIX]{x1D6FF}}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Int}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF})=\dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{\unicode[STIX]{x1D6FE}},X_{\unicode[STIX]{x1D6FF}}),\end{eqnarray}$$
where
 $X:\unicode[STIX]{x1D702}\mapsto X_{\unicode[STIX]{x1D702}}$
is the bijection in Theorem 3.8.
$X:\unicode[STIX]{x1D702}\mapsto X_{\unicode[STIX]{x1D702}}$
is the bijection in Theorem 3.8.
In the punctured case, we also know the following. Recall that a rigid indecomposable object in
![]() ${\mathcal{C}}(\mathbf{T})$
is reachable if it is a summand of some cluster tilting object, which is obtained from the canonical cluster tilting object by a sequence of mutations.
${\mathcal{C}}(\mathbf{T})$
is reachable if it is a summand of some cluster tilting object, which is obtained from the canonical cluster tilting object by a sequence of mutations.
Theorem 3.10 [Reference Brüstle and QiuBQ15].
Let
![]() $\mathbf{A}^{\times }(\mathbf{S})$
be the set of tagged curves in
$\mathbf{A}^{\times }(\mathbf{S})$
be the set of tagged curves in
![]() $\mathbf{C}^{\times }(\mathbf{S})$
without self-intersections and
$\mathbf{C}^{\times }(\mathbf{S})$
without self-intersections and
![]() ${\mathcal{I}}^{\times }(\mathbf{S})$
the set of reachable rigid indecomposable objects in
${\mathcal{I}}^{\times }(\mathbf{S})$
the set of reachable rigid indecomposable objects in
![]() ${\mathcal{C}}(\mathbf{T})$
. Under a canonical bijection
${\mathcal{C}}(\mathbf{T})$
. Under a canonical bijection
 $$\begin{eqnarray}\unicode[STIX]{x1D700}:\mathbf{A}^{\times }(\mathbf{S})\rightarrow {\mathcal{I}}^{\times }(\mathbf{S}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}:\mathbf{A}^{\times }(\mathbf{S})\rightarrow {\mathcal{I}}^{\times }(\mathbf{S}),\end{eqnarray}$$
the tagged rotation
![]() $\unicode[STIX]{x1D70C}$
on
$\unicode[STIX]{x1D70C}$
on
![]() $\mathbf{A}^{\times }(\mathbf{S})$
becomes the shift
$\mathbf{A}^{\times }(\mathbf{S})$
becomes the shift
![]() $[1]$
on
$[1]$
on
![]() ${\mathcal{I}}^{\times }(\mathbf{S})$
.
${\mathcal{I}}^{\times }(\mathbf{S})$
.
3.4 Cluster(-tilting) exchange graphs
The cluster(-tilting) exchange graph
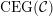 $\operatorname{CEG}({\mathcal{C}})$
of a cluster category
$\operatorname{CEG}({\mathcal{C}})$
of a cluster category
![]() ${\mathcal{C}}$
is the graph whose vertices are cluster tilting objects and whose edges are mutations. There are the following known results about connectedness of cluster exchange graphs.
${\mathcal{C}}$
is the graph whose vertices are cluster tilting objects and whose edges are mutations. There are the following known results about connectedness of cluster exchange graphs.
Theorem 3.11 [Reference Buan, Marsh, Reineke, Reiten and TodorovBMRRT06].
If
![]() ${\mathcal{C}}$
is the cluster category of an acyclic quiver, then
${\mathcal{C}}$
is the cluster category of an acyclic quiver, then
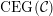 $\operatorname{CEG}({\mathcal{C}})$
is connected.
$\operatorname{CEG}({\mathcal{C}})$
is connected.
Theorem 3.12 [Reference Brüstle and ZhangBZ11].
If
![]() ${\mathcal{C}}$
is the cluster category from an unpunctured marked surface, then
${\mathcal{C}}$
is the cluster category from an unpunctured marked surface, then
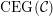 $\operatorname{CEG}({\mathcal{C}})$
is connected.
$\operatorname{CEG}({\mathcal{C}})$
is connected.
4 Strings and tagged curves
4.1 Skewed-gentle algebras from admissible triangulations
Let
![]() $\mathbf{T}$
be an admissible triangulation of
$\mathbf{T}$
be an admissible triangulation of
![]() $\mathbf{S}$
, i.e. every puncture is in a self-folded triangle (see Lemma A.1 for the existence of
$\mathbf{S}$
, i.e. every puncture is in a self-folded triangle (see Lemma A.1 for the existence of
![]() $\mathbf{T}$
), with the associated quiver with potential
$\mathbf{T}$
), with the associated quiver with potential
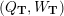 $(Q_{\mathbf{T}},W_{\mathbf{T}})$
and the cluster category
$(Q_{\mathbf{T}},W_{\mathbf{T}})$
and the cluster category
![]() ${\mathcal{C}}(\mathbf{T})$
.
${\mathcal{C}}(\mathbf{T})$
.
Let
![]() $\mathbf{T}^{o}$
be the subset of
$\mathbf{T}^{o}$
be the subset of
![]() $\mathbf{T}$
consisting of curves whose endpoints are in
$\mathbf{T}$
consisting of curves whose endpoints are in
![]() $\mathbf{M}$
. Now we associate a biquiver
$\mathbf{M}$
. Now we associate a biquiver
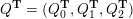 $Q^{\mathbf{T}}=(Q_{0}^{\mathbf{T}},Q_{1}^{\mathbf{T}},Q_{2}^{\mathbf{T}})$
with potential
$Q^{\mathbf{T}}=(Q_{0}^{\mathbf{T}},Q_{1}^{\mathbf{T}},Q_{2}^{\mathbf{T}})$
with potential
![]() $W^{\mathbf{T}}$
as follows:
$W^{\mathbf{T}}$
as follows:
-
–
 $Q_{0}^{\mathbf{T}}=\mathbf{T}^{o}$
, i.e. curves in
$Q_{0}^{\mathbf{T}}=\mathbf{T}^{o}$
, i.e. curves in
 $\mathbf{T}$
which are sides of non-self-folded triangles correspond to vertices in
$\mathbf{T}$
which are sides of non-self-folded triangles correspond to vertices in
 $Q_{0}^{\mathbf{T}}$
;
$Q_{0}^{\mathbf{T}}$
; -
– there is a solid arrow from
 $i$
to
$i$
to
 $j$
in
$j$
in
 $Q_{1}^{\mathbf{T}}$
whenever there is a non-self-folded triangle
$Q_{1}^{\mathbf{T}}$
whenever there is a non-self-folded triangle
 $\unicode[STIX]{x1D6E5}$
in
$\unicode[STIX]{x1D6E5}$
in
 $\mathbf{T}$
such that
$\mathbf{T}$
such that
 $\unicode[STIX]{x1D6E5}$
has sides
$\unicode[STIX]{x1D6E5}$
has sides
 $i$
and
$i$
and
 $j$
with
$j$
with
 $j$
following
$j$
following
 $i$
in the clockwise orientation;
$i$
in the clockwise orientation; -
– there is a dashed loop at
 $i$
in
$i$
in
 $Q_{2}^{\mathbf{T}}$
, denoted by
$Q_{2}^{\mathbf{T}}$
, denoted by
 $\unicode[STIX]{x1D700}_{i}$
, whenever
$\unicode[STIX]{x1D700}_{i}$
, whenever
 $i$
is the remaining side of a self-folded triangle;
$i$
is the remaining side of a self-folded triangle; -
– each non-self-folded triangle in
 $\mathbf{T}$
induces a unique three-cycle up to cyclic permutation. The potential
$\mathbf{T}$
induces a unique three-cycle up to cyclic permutation. The potential
 $W^{\mathbf{T}}$
is the sum of all such three-cycles.
$W^{\mathbf{T}}$
is the sum of all such three-cycles.
See the example in § 6. By construction, there are no loops in
![]() $Q_{1}^{\mathbf{T}}$
, any arrow in
$Q_{1}^{\mathbf{T}}$
, any arrow in
![]() $Q_{2}^{\mathbf{T}}$
is a loop and there is at most one loop in
$Q_{2}^{\mathbf{T}}$
is a loop and there is at most one loop in
![]() $Q_{2}^{\mathbf{T}}$
at each vertex. Hence the biquiver
$Q_{2}^{\mathbf{T}}$
at each vertex. Hence the biquiver
![]() $Q^{\mathbf{T}}$
satisfies the conditions on biquivers in § 2.1. Let
$Q^{\mathbf{T}}$
satisfies the conditions on biquivers in § 2.1. Let
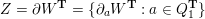 $Z=\unicode[STIX]{x2202}W^{\mathbf{T}}=\{\unicode[STIX]{x2202}_{a}W^{\mathbf{T}}:a\in Q_{1}^{\mathbf{T}}\}$
. We have the following straightforward observation.
$Z=\unicode[STIX]{x2202}W^{\mathbf{T}}=\{\unicode[STIX]{x2202}_{a}W^{\mathbf{T}}:a\in Q_{1}^{\mathbf{T}}\}$
. We have the following straightforward observation.
Lemma 4.1. The set
![]() $Z$
consists of
$Z$
consists of
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}$
for each pair
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}$
for each pair
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in Q_{1}^{\mathbf{T}}$
such that they are from the same non-self-folded triangle in
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in Q_{1}^{\mathbf{T}}$
such that they are from the same non-self-folded triangle in
![]() $\mathbf{T}$
.
$\mathbf{T}$
.
Proposition 4.2. The pair
 $(Q^{\mathbf{T}},Z)$
is skewed-gentle and the algebra
$(Q^{\mathbf{T}},Z)$
is skewed-gentle and the algebra
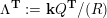 $\unicode[STIX]{x1D6EC}^{\mathbf{T}}:=\mathbf{k}Q^{\mathbf{T}}/(R)$
is a skewed-gentle algebra, where
$\unicode[STIX]{x1D6EC}^{\mathbf{T}}:=\mathbf{k}Q^{\mathbf{T}}/(R)$
is a skewed-gentle algebra, where
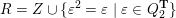 $R=Z\cup \{\unicode[STIX]{x1D700}^{2}=\unicode[STIX]{x1D700}\mid \unicode[STIX]{x1D700}\in Q_{2}^{\mathbf{T}}\}$
.
$R=Z\cup \{\unicode[STIX]{x1D700}^{2}=\unicode[STIX]{x1D700}\mid \unicode[STIX]{x1D700}\in Q_{2}^{\mathbf{T}}\}$
.
Proof. By Lemma 4.1, each element in
![]() $Z$
is of the form
$Z$
is of the form
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}$
for some
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}$
for some
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
in
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
in
![]() $Q_{1}^{\mathbf{T}}$
. Since every vertex
$Q_{1}^{\mathbf{T}}$
. Since every vertex
![]() $i\in Q_{0}^{\mathbf{T}}$
is a side of a non-self-folded triangle in
$i\in Q_{0}^{\mathbf{T}}$
is a side of a non-self-folded triangle in
![]() $\mathbf{T}$
, there are two possible cases.
$\mathbf{T}$
, there are two possible cases.
-
(1) The curve
 $i$
is a common side of two non-self-folded triangles in
$i$
is a common side of two non-self-folded triangles in
 $\mathbf{T}$
, see Figure 7. Then there is no dashed loop at
$\mathbf{T}$
, see Figure 7. Then there is no dashed loop at
 $i$
and there are at most two solid arrows
$i$
and there are at most two solid arrows
 $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}$
ending at
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}$
ending at
 $i$
and at most two solid arrows
$i$
and at most two solid arrows
 $\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}$
starting at
$\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}$
starting at
 $i$
. By Lemma 4.1,
$i$
. By Lemma 4.1,
 $\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{1}\in Z$
,
$\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{1}\in Z$
,
 $\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{2}\in Z$
,
$\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{2}\in Z$
,
 $\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{2}\notin Z$
and
$\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{2}\notin Z$
and
 $\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{1}\notin Z$
(if they exist).
$\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{1}\notin Z$
(if they exist). -
(2) The curve
 $i$
is a common side of a non-self-folded triangle and a self-folded triangle in
$i$
is a common side of a non-self-folded triangle and a self-folded triangle in
 $\mathbf{T}$
, see Figure 8. Then there is a dashed loop at
$\mathbf{T}$
, see Figure 8. Then there is a dashed loop at
 $i$
and there is at most one solid arrow
$i$
and there is at most one solid arrow
 $\unicode[STIX]{x1D6FC}$
ending at
$\unicode[STIX]{x1D6FC}$
ending at
 $i$
and at most one solid arrow
$i$
and at most one solid arrow
 $\unicode[STIX]{x1D6FD}$
starting at
$\unicode[STIX]{x1D6FD}$
starting at
 $i$
. By Lemma 4.1,
$i$
. By Lemma 4.1,
 $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\in Z$
(if they exist).
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\in Z$
(if they exist).
Hence by Definition 2.1,
 $(Q^{\mathbf{T}},Z)$
is skewed-gentle and the algebra
$(Q^{\mathbf{T}},Z)$
is skewed-gentle and the algebra
 $\unicode[STIX]{x1D6EC}^{\mathbf{T}}=\mathbf{k}Q^{\mathbf{T}}/(R)$
is a skewed-gentle algebra.◻
$\unicode[STIX]{x1D6EC}^{\mathbf{T}}=\mathbf{k}Q^{\mathbf{T}}/(R)$
is a skewed-gentle algebra.◻

Figure 7. Non-self-folded triangles with the corresponding quivers.

Figure 8. Self-folded triangles with the corresponding quivers.
Let
![]() $Q_{0}^{\operatorname{Sp}}$
be the subset of
$Q_{0}^{\operatorname{Sp}}$
be the subset of
![]() $Q_{0}^{\mathbf{T}}$
consisting of vertices where there are dashed loops.
$Q_{0}^{\mathbf{T}}$
consisting of vertices where there are dashed loops.
Remark 4.3. Comparing the constructions of
 $(Q_{\mathbf{T}},W_{\mathbf{T}})$
and
$(Q_{\mathbf{T}},W_{\mathbf{T}})$
and
 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
, one can obtain
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
, one can obtain
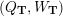 $(Q_{\mathbf{T}},W_{\mathbf{T}})$
(up to isomorphism) from
$(Q_{\mathbf{T}},W_{\mathbf{T}})$
(up to isomorphism) from
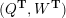 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
by splitting each vertex in
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
by splitting each vertex in
![]() $Q_{0}^{\operatorname{Sp}}$
into two vertices and removing all the dashed loops. More precisely:
$Q_{0}^{\operatorname{Sp}}$
into two vertices and removing all the dashed loops. More precisely:
-
– vertices in
 $Q_{\mathbf{T}}$
are indexed by elements in
$Q_{\mathbf{T}}$
are indexed by elements in
 $Q_{0}^{\mathbf{T}}\cup \{i^{\prime }\mid i\in Q_{0}^{\operatorname{Sp}}\}$
;
$Q_{0}^{\mathbf{T}}\cup \{i^{\prime }\mid i\in Q_{0}^{\operatorname{Sp}}\}$
; -
– arrows from
 $i$
to
$i$
to
 $j$
in
$j$
in
 $Q_{\mathbf{T}}$
are indexed by
$Q_{\mathbf{T}}$
are indexed by
 $^{j}\unicode[STIX]{x1D6FC}^{i}$
induced by arrows
$^{j}\unicode[STIX]{x1D6FC}^{i}$
induced by arrows
 $\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D70B}(i)\rightarrow \unicode[STIX]{x1D70B}(j)$
in
$\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D70B}(i)\rightarrow \unicode[STIX]{x1D70B}(j)$
in
 $Q_{1}^{\mathbf{T}}$
, where
$Q_{1}^{\mathbf{T}}$
, where
 $\unicode[STIX]{x1D70B}$
is the map on
$\unicode[STIX]{x1D70B}$
is the map on
 $Q_{0}^{\mathbf{T}}\cup \{i^{\prime }\mid i\in Q_{0}^{\operatorname{Sp}}\}$
sending
$Q_{0}^{\mathbf{T}}\cup \{i^{\prime }\mid i\in Q_{0}^{\operatorname{Sp}}\}$
sending
 $i^{\prime }$
to
$i^{\prime }$
to
 $i$
and being the identity on
$i$
and being the identity on
 $Q_{0}^{\mathbf{T}}$
;
$Q_{0}^{\mathbf{T}}$
; -
– the potential
 $W_{\mathbf{T}}$
is the sum of cycles that are obtained from cycles in
$W_{\mathbf{T}}$
is the sum of cycles that are obtained from cycles in
 $W^{\mathbf{T}}$
by replacing each
$W^{\mathbf{T}}$
by replacing each
 $\unicode[STIX]{x1D6FC}$
with
$\unicode[STIX]{x1D6FC}$
with
 $^{j}\unicode[STIX]{x1D6FC}^{i}$
for possible
$^{j}\unicode[STIX]{x1D6FC}^{i}$
for possible
 $i$
and
$i$
and
 $j$
.
$j$
.
See the example in § 6.
Now we prove that the Jacobian algebra
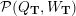 ${\mathcal{P}}(Q_{\mathbf{T}},W_{\mathbf{T}})$
is isomorphic to the skewed-gentle algebra
${\mathcal{P}}(Q_{\mathbf{T}},W_{\mathbf{T}})$
is isomorphic to the skewed-gentle algebra
![]() $\unicode[STIX]{x1D6EC}^{\mathbf{T}}$
.
$\unicode[STIX]{x1D6EC}^{\mathbf{T}}$
.
Proposition 4.4. There is an algebra isomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D711}:{\mathcal{P}}(Q_{\mathbf{T}},W_{\mathbf{T}})\cong \unicode[STIX]{x1D6EC}^{\mathbf{T}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}:{\mathcal{P}}(Q_{\mathbf{T}},W_{\mathbf{T}})\cong \unicode[STIX]{x1D6EC}^{\mathbf{T}}.\end{eqnarray}$$
Proof. For each quiver, denote by
![]() $e_{i}$
the trivial path associated with a vertex
$e_{i}$
the trivial path associated with a vertex
![]() $i$
. Noticing that
$i$
. Noticing that
 $\unicode[STIX]{x1D700}_{i}^{2}-\unicode[STIX]{x1D700}_{i}\in R$
for each
$\unicode[STIX]{x1D700}_{i}^{2}-\unicode[STIX]{x1D700}_{i}\in R$
for each
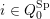 $i\in Q_{0}^{\operatorname{Sp}}$
, a complete set of primitive orthogonal idempotents of
$i\in Q_{0}^{\operatorname{Sp}}$
, a complete set of primitive orthogonal idempotents of
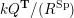 $kQ^{\mathbf{T}}/(R^{\operatorname{Sp}})$
is
$kQ^{\mathbf{T}}/(R^{\operatorname{Sp}})$
is
 $$\begin{eqnarray}\{e_{i}+(R^{\operatorname{Sp}})\mid i\in Q_{0}\setminus Q_{0}^{\operatorname{Sp}}\}\cup \{\unicode[STIX]{x1D700}_{i}+(R^{\operatorname{Sp}}),e_{i}-\unicode[STIX]{x1D700}_{i}+(R^{\operatorname{Sp}})\mid i\in Q_{0}^{\operatorname{Sp}}\},\end{eqnarray}$$
$$\begin{eqnarray}\{e_{i}+(R^{\operatorname{Sp}})\mid i\in Q_{0}\setminus Q_{0}^{\operatorname{Sp}}\}\cup \{\unicode[STIX]{x1D700}_{i}+(R^{\operatorname{Sp}}),e_{i}-\unicode[STIX]{x1D700}_{i}+(R^{\operatorname{Sp}})\mid i\in Q_{0}^{\operatorname{Sp}}\},\end{eqnarray}$$
where
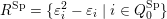 $R^{\operatorname{Sp}}=\{\unicode[STIX]{x1D700}_{i}^{2}-\unicode[STIX]{x1D700}_{i}\mid i\in Q_{0}^{\operatorname{Sp}}\}$
. Then using the recovery of
$R^{\operatorname{Sp}}=\{\unicode[STIX]{x1D700}_{i}^{2}-\unicode[STIX]{x1D700}_{i}\mid i\in Q_{0}^{\operatorname{Sp}}\}$
. Then using the recovery of
 $(Q_{\mathbf{T}},W_{\mathbf{T}})$
from
$(Q_{\mathbf{T}},W_{\mathbf{T}})$
from
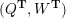 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
in Remark 4.3, there is an isomorphism
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
in Remark 4.3, there is an isomorphism
![]() $\unicode[STIX]{x1D711}$
of algebras from
$\unicode[STIX]{x1D711}$
of algebras from
![]() $kQ_{\mathbf{T}}$
to
$kQ_{\mathbf{T}}$
to
 $kQ^{\mathbf{T}}/(R^{\operatorname{Sp}})$
that sends
$kQ^{\mathbf{T}}/(R^{\operatorname{Sp}})$
that sends
![]() $^{j}\unicode[STIX]{x1D6FC}^{i}$
to
$^{j}\unicode[STIX]{x1D6FC}^{i}$
to
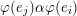 $\unicode[STIX]{x1D711}(e_{j})\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D711}(e_{i})$
, where
$\unicode[STIX]{x1D711}(e_{j})\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D711}(e_{i})$
, where
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(e_{i})=\left\{\begin{array}{@{}ll@{}}e_{i}+(R^{\operatorname{Sp}})\quad & \text{if }i\in Q_{0}^{\mathbf{T}}\setminus Q_{0}^{\operatorname{Sp}},\\ e_{i}-\unicode[STIX]{x1D700}_{i}+(R^{\operatorname{Sp}})\quad & \text{if }i\in Q_{0}^{\operatorname{Sp}},\\ \unicode[STIX]{x1D700}_{k}+(R^{\operatorname{Sp}})\quad & \text{if }i=k^{\prime }\text{for }k\in Q_{0}^{\operatorname{Sp}}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(e_{i})=\left\{\begin{array}{@{}ll@{}}e_{i}+(R^{\operatorname{Sp}})\quad & \text{if }i\in Q_{0}^{\mathbf{T}}\setminus Q_{0}^{\operatorname{Sp}},\\ e_{i}-\unicode[STIX]{x1D700}_{i}+(R^{\operatorname{Sp}})\quad & \text{if }i\in Q_{0}^{\operatorname{Sp}},\\ \unicode[STIX]{x1D700}_{k}+(R^{\operatorname{Sp}})\quad & \text{if }i=k^{\prime }\text{for }k\in Q_{0}^{\operatorname{Sp}}.\end{array}\right.\end{eqnarray}$$
By [Reference Irelli and Labardini-FragosoIL12, Theorem 5.7], the Jacobian algebra
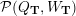 ${\mathcal{P}}(Q_{\mathbf{T}},W_{\mathbf{T}})$
is isomorphic to
${\mathcal{P}}(Q_{\mathbf{T}},W_{\mathbf{T}})$
is isomorphic to
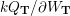 $kQ_{\mathbf{T}}/\unicode[STIX]{x2202}W_{\mathbf{T}}$
. Then what is left to show is that
$kQ_{\mathbf{T}}/\unicode[STIX]{x2202}W_{\mathbf{T}}$
. Then what is left to show is that
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}W_{\mathbf{T}})=\unicode[STIX]{x2202}W^{\mathbf{T}}$
, which follows directly from the recovery of
$\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}W_{\mathbf{T}})=\unicode[STIX]{x2202}W^{\mathbf{T}}$
, which follows directly from the recovery of
![]() $W_{\mathbf{T}}$
from
$W_{\mathbf{T}}$
from
![]() $W^{\mathbf{T}}$
in Remark 4.3.◻
$W^{\mathbf{T}}$
in Remark 4.3.◻
Remark 4.5. Note that Propositions 4.2 and 4.4 imply that the Jacobian algebra
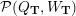 ${\mathcal{P}}(Q_{\mathbf{T}},W_{\mathbf{T}})$
is a skewed-gentle algebra for any admissible triangulation
${\mathcal{P}}(Q_{\mathbf{T}},W_{\mathbf{T}})$
is a skewed-gentle algebra for any admissible triangulation
![]() $\mathbf{T}$
of a marked surface. This result was first announced by Labardini-Fragoso (cf. [Reference Labardini-FragosoLab16]) and was first proved in [Reference Geiß, Labardini-Fragoso and SchröerGLS16].
$\mathbf{T}$
of a marked surface. This result was first announced by Labardini-Fragoso (cf. [Reference Labardini-FragosoLab16]) and was first proved in [Reference Geiß, Labardini-Fragoso and SchröerGLS16].
4.2 Correspondence
Denote by
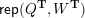 $\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
the category of finite dimensional
$\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
the category of finite dimensional
![]() $\mathbf{k}$
-linear representations of
$\mathbf{k}$
-linear representations of
![]() $Q$
bounded by
$Q$
bounded by
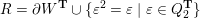 $R=\unicode[STIX]{x2202}W^{\mathbf{T}}\cup \{\unicode[STIX]{x1D700}^{2}=\unicode[STIX]{x1D700}\mid \unicode[STIX]{x1D700}\in Q_{2}^{\mathbf{T}}\}$
. By the equivalence (3.2) and Proposition 4.4, we have an equivalence
$R=\unicode[STIX]{x2202}W^{\mathbf{T}}\cup \{\unicode[STIX]{x1D700}^{2}=\unicode[STIX]{x1D700}\mid \unicode[STIX]{x1D700}\in Q_{2}^{\mathbf{T}}\}$
. By the equivalence (3.2) and Proposition 4.4, we have an equivalence
 $$\begin{eqnarray}F_{\mathbf{T}}:{\mathcal{C}}(\mathbf{T})/(T_{\mathbf{T}})\simeq \mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}}),\end{eqnarray}$$
$$\begin{eqnarray}F_{\mathbf{T}}:{\mathcal{C}}(\mathbf{T})/(T_{\mathbf{T}})\simeq \mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}}),\end{eqnarray}$$
where
![]() $T_{\mathbf{T}}$
denotes the canonical cluster tilting object in
$T_{\mathbf{T}}$
denotes the canonical cluster tilting object in
![]() ${\mathcal{C}}(\mathbf{T})$
(cf. § 3.1). So one can regard the set of indecomposable objects in
${\mathcal{C}}(\mathbf{T})$
(cf. § 3.1). So one can regard the set of indecomposable objects in
![]() ${\mathcal{C}}(\mathbf{T})$
as the union of the set of indecomposable representations in
${\mathcal{C}}(\mathbf{T})$
as the union of the set of indecomposable representations in
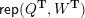 $\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
and the set of indecomposable direct summands of
$\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
and the set of indecomposable direct summands of
![]() $T_{\mathbf{T}}$
. Note that indecomposable direct summands of
$T_{\mathbf{T}}$
. Note that indecomposable direct summands of
![]() $T_{\mathbf{T}}$
are indexed by curves in
$T_{\mathbf{T}}$
are indexed by curves in
![]() $\mathbf{T}$
and hence also by tagged curves in
$\mathbf{T}$
and hence also by tagged curves in
![]() $\mathbf{T}^{\times }$
(which is the tagged version of
$\mathbf{T}^{\times }$
(which is the tagged version of
![]() $\mathbf{T}$
). Thus, we can write
$\mathbf{T}$
). Thus, we can write
 $$\begin{eqnarray}T_{\mathbf{T}}=\bigoplus _{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }}T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}.\end{eqnarray}$$
$$\begin{eqnarray}T_{\mathbf{T}}=\bigoplus _{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }}T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}.\end{eqnarray}$$
Definition 4.6. We call an indecomposable object
![]() $X$
in
$X$
in
![]() ${\mathcal{C}}(\mathbf{T})$
a string object if either
${\mathcal{C}}(\mathbf{T})$
a string object if either
![]() $X$
is a direct summand of the canonical cluster tilting object
$X$
is a direct summand of the canonical cluster tilting object
![]() $T_{\mathbf{T}}$
, or
$T_{\mathbf{T}}$
, or
![]() $F_{\mathbf{T}}(X)$
is an indecomposable representation in
$F_{\mathbf{T}}(X)$
is an indecomposable representation in
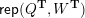 $\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
which is in the image of the injective map in Theorem 2.9. Denote the set of string objects in
$\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
which is in the image of the injective map in Theorem 2.9. Denote the set of string objects in
![]() ${\mathcal{C}}(\mathbf{T})$
by
${\mathcal{C}}(\mathbf{T})$
by
![]() $\mathfrak{S}(\mathbf{T})$
.
$\mathfrak{S}(\mathbf{T})$
.
To describe indecomposable representations in
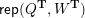 $\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
, we shall use notions and notation stated in § 2. Recall that from the biquiver
$\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
, we shall use notions and notation stated in § 2. Recall that from the biquiver
![]() $Q^{\mathbf{T}}$
, in § 2.2, we constructed a new biquiver
$Q^{\mathbf{T}}$
, in § 2.2, we constructed a new biquiver
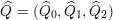 $\widehat{Q}=(\widehat{Q}_{0},\widehat{Q}_{1},\widehat{Q}_{2})$
by adding two new solid arrows
$\widehat{Q}=(\widehat{Q}_{0},\widehat{Q}_{1},\widehat{Q}_{2})$
by adding two new solid arrows
![]() $a_{i_{\pm }}$
(whose terminal vertices are also new vertices) for each vertex
$a_{i_{\pm }}$
(whose terminal vertices are also new vertices) for each vertex
![]() $i\in Q_{0}^{\mathbf{T}}$
. Recall that a letter is an arrow in
$i\in Q_{0}^{\mathbf{T}}$
. Recall that a letter is an arrow in
![]() $\widehat{Q}$
or its inverse. For each
$\widehat{Q}$
or its inverse. For each
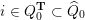 $i\in Q_{0}^{\mathbf{T}}\subset \widehat{Q}_{0}$
the set
$i\in Q_{0}^{\mathbf{T}}\subset \widehat{Q}_{0}$
the set
 $L(i)=\{l\in L\mid s(l)=i\}$
is divided into two disjoint subsets
$L(i)=\{l\in L\mid s(l)=i\}$
is divided into two disjoint subsets
![]() $L_{\unicode[STIX]{x1D703}}(i)$
,
$L_{\unicode[STIX]{x1D703}}(i)$
,
 $\unicode[STIX]{x1D703}\in \{\pm \}$
, with linear orders satisfying certain conditions.
$\unicode[STIX]{x1D703}\in \{\pm \}$
, with linear orders satisfying certain conditions.
Construction 4.7. We associate an arc segment
![]() $\mathfrak{a}(l)$
with each letter
$\mathfrak{a}(l)$
with each letter
![]() $l$
as follows.
$l$
as follows.
-
– For
 $l=\unicode[STIX]{x1D6FC}$
with
$l=\unicode[STIX]{x1D6FC}$
with
 $\unicode[STIX]{x1D6FC}$
an arrow from
$\unicode[STIX]{x1D6FC}$
an arrow from
 $i$
to
$i$
to
 $j$
in
$j$
in
 $Q_{1}^{\mathbf{T}}\subset \widehat{Q}_{1}$
,
$Q_{1}^{\mathbf{T}}\subset \widehat{Q}_{1}$
,
 $\unicode[STIX]{x1D6FC}$
is induced from a triangle
$\unicode[STIX]{x1D6FC}$
is induced from a triangle
 $\unicode[STIX]{x1D6E5}$
in
$\unicode[STIX]{x1D6E5}$
in
 $\mathbf{T}$
having
$\mathbf{T}$
having
 $i$
and
$i$
and
 $j$
as sides with
$j$
as sides with
 $j$
following
$j$
following
 $i$
in the clockwise orientation. Then we associate the arc segment (which is unique up to homotopy) in
$i$
in the clockwise orientation. Then we associate the arc segment (which is unique up to homotopy) in
 $\unicode[STIX]{x1D6E5}$
starting at (a point in)
$\unicode[STIX]{x1D6E5}$
starting at (a point in)
 $i$
and ending at (a point in)
$i$
and ending at (a point in)
 $j$
.
$j$
. -
– For
 $l=\unicode[STIX]{x1D700}$
with
$l=\unicode[STIX]{x1D700}$
with
 $\unicode[STIX]{x1D700}$
a dashed loop at
$\unicode[STIX]{x1D700}$
a dashed loop at
 $i$
, we associate the arc segment in the self-folded triangle whose remaining side is
$i$
, we associate the arc segment in the self-folded triangle whose remaining side is
 $i$
with the clockwise orientation.
$i$
with the clockwise orientation. -
– For
 $l=a_{i_{\unicode[STIX]{x1D703}}}$
with
$l=a_{i_{\unicode[STIX]{x1D703}}}$
with
 $a_{i_{\unicode[STIX]{x1D703}}}$
an arrow in
$a_{i_{\unicode[STIX]{x1D703}}}$
an arrow in
 $\widehat{Q}_{1}\setminus Q_{1}^{\mathbf{T}}$
, its associated segment is in the same triangle as the associated arc segments of other letters in
$\widehat{Q}_{1}\setminus Q_{1}^{\mathbf{T}}$
, its associated segment is in the same triangle as the associated arc segments of other letters in
 $L_{\unicode[STIX]{x1D703}}(i)$
. It starts at (a point in)
$L_{\unicode[STIX]{x1D703}}(i)$
. It starts at (a point in)
 $i$
and ends at a point in
$i$
and ends at a point in
 $\mathbf{M}\cup \mathbf{P}$
.
$\mathbf{M}\cup \mathbf{P}$
. -
– The arc segment
 $\mathfrak{a}(l^{-1})$
is the same as
$\mathfrak{a}(l^{-1})$
is the same as
 $\mathfrak{a}(l)$
but with the opposite orientation.
$\mathfrak{a}(l)$
but with the opposite orientation.
See Figure 9 (cf. Figures 7 and 8), where the disjoint subsets
![]() $L_{\unicode[STIX]{x1D703}}(i)$
are given by
$L_{\unicode[STIX]{x1D703}}(i)$
are given by
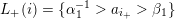 $L_{+}(i)=\{\unicode[STIX]{x1D6FC}_{1}^{-1}>a_{i_{+}}>\unicode[STIX]{x1D6FD}_{1}\}$
and
$L_{+}(i)=\{\unicode[STIX]{x1D6FC}_{1}^{-1}>a_{i_{+}}>\unicode[STIX]{x1D6FD}_{1}\}$
and
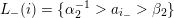 $L_{-}(i)=\{\unicode[STIX]{x1D6FC}_{2}^{-1}>a_{i_{-}}>\unicode[STIX]{x1D6FD}_{2}\}$
for the left picture and by
$L_{-}(i)=\{\unicode[STIX]{x1D6FC}_{2}^{-1}>a_{i_{-}}>\unicode[STIX]{x1D6FD}_{2}\}$
for the left picture and by
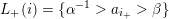 $L_{+}(i)=\{\unicode[STIX]{x1D6FC}^{-1}>a_{i_{+}}>\unicode[STIX]{x1D6FD}\}$
and
$L_{+}(i)=\{\unicode[STIX]{x1D6FC}^{-1}>a_{i_{+}}>\unicode[STIX]{x1D6FD}\}$
and
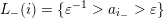 $L_{-}(i)=\{\unicode[STIX]{x1D700}^{-1}>a_{i_{-}}>\unicode[STIX]{x1D700}\}$
for the right picture. Note that
$L_{-}(i)=\{\unicode[STIX]{x1D700}^{-1}>a_{i_{-}}>\unicode[STIX]{x1D700}\}$
for the right picture. Note that
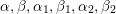 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{2}$
might not exist.
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{2}$
might not exist.

Figure 9. The arc segments associated with letters.
By Construction 4.7, any arc segment associated with a letter in
![]() $L(i)$
starts at
$L(i)$
starts at
![]() $i$
. The following lemma gives some basic topological interpretation of notions about letters.
$i$
. The following lemma gives some basic topological interpretation of notions about letters.
Lemma 4.8. For any two letters
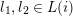 $l_{1},l_{2}\in L(i)$
:
$l_{1},l_{2}\in L(i)$
:
-
(1)
 $l_{1}$
and
$l_{1}$
and
 $l_{2}$
are in the same subset
$l_{2}$
are in the same subset
 $L_{\unicode[STIX]{x1D703}}(i)$
if and only if
$L_{\unicode[STIX]{x1D703}}(i)$
if and only if
 $\mathfrak{a}(l_{1})$
and
$\mathfrak{a}(l_{1})$
and
 $\mathfrak{a}(l_{2})$
are in the same triangle;
$\mathfrak{a}(l_{2})$
are in the same triangle; -
(2)
 $l_{1}>l_{2}$
if and only if they are of one of the forms in Figure 10(i) with
$l_{1}>l_{2}$
if and only if they are of one of the forms in Figure 10(i) with
 $\mathfrak{a}(l_{i})$
being the segment of
$\mathfrak{a}(l_{i})$
being the segment of
 $\unicode[STIX]{x1D6FE}_{i}$
cut out by the triangle;
$\unicode[STIX]{x1D6FE}_{i}$
cut out by the triangle; -
(3)
 $l=l_{i}$
is punctured if and only if one of the endpoints of
$l=l_{i}$
is punctured if and only if one of the endpoints of
 $\mathfrak{a}(l)$
is a puncture.
$\mathfrak{a}(l)$
is a puncture.

Figure 10. The orders.
Proof. For (1), recall that if
 $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}^{-1}\in L(i)$
for two solid arrows
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}^{-1}\in L(i)$
for two solid arrows
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FF}$
then
$\unicode[STIX]{x1D6FF}$
then
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FF}^{-1}$
are in the same subset
$\unicode[STIX]{x1D6FF}^{-1}$
are in the same subset
![]() $L_{\unicode[STIX]{x1D703}}(i)$
if and only if
$L_{\unicode[STIX]{x1D703}}(i)$
if and only if
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}\in Z$
. Then by Lemma 4.1,
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}\in Z$
. Then by Lemma 4.1,
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FF}$
are from the same triangle. By Construction 4.7,
$\unicode[STIX]{x1D6FF}$
are from the same triangle. By Construction 4.7,
![]() $\mathfrak{a}(\unicode[STIX]{x1D6FE})$
and
$\mathfrak{a}(\unicode[STIX]{x1D6FE})$
and
![]() $\mathfrak{a}(\unicode[STIX]{x1D6FF}^{-1})$
are in the same triangle. Also by Construction 4.7,
$\mathfrak{a}(\unicode[STIX]{x1D6FF}^{-1})$
are in the same triangle. Also by Construction 4.7,
![]() $\mathfrak{a}(\unicode[STIX]{x1D700})$
and
$\mathfrak{a}(\unicode[STIX]{x1D700})$
and
![]() $\mathfrak{a}(\unicode[STIX]{x1D700}^{-1})$
are in the same triangle for a dashed loop
$\mathfrak{a}(\unicode[STIX]{x1D700}^{-1})$
are in the same triangle for a dashed loop
![]() $\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}$
and
![]() $\mathfrak{a}(a_{i_{\unicode[STIX]{x1D703}}})$
is in the same triangle as the arc segments associated with other letters in
$\mathfrak{a}(a_{i_{\unicode[STIX]{x1D703}}})$
is in the same triangle as the arc segments associated with other letters in
![]() $L_{\unicode[STIX]{x1D703}}(i)$
. Hence we are done.
$L_{\unicode[STIX]{x1D703}}(i)$
. Hence we are done.
For (2), by definition we know two letters
![]() $l_{1}$
and
$l_{1}$
and
![]() $l_{2}$
are comparable if they are in the same subset
$l_{2}$
are comparable if they are in the same subset
![]() $L_{\unicode[STIX]{x1D703}}(i)$
. Then by (1) this is equivalent to
$L_{\unicode[STIX]{x1D703}}(i)$
. Then by (1) this is equivalent to
![]() $\mathfrak{a}(l_{1})$
and
$\mathfrak{a}(l_{1})$
and
![]() $\mathfrak{a}(l_{2})$
being in the same triangle and starting at the same curve
$\mathfrak{a}(l_{2})$
being in the same triangle and starting at the same curve
![]() $i$
. Note that the forms in Figure 10(i) correspond to
$i$
. Note that the forms in Figure 10(i) correspond to
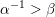 $\unicode[STIX]{x1D6FC}^{-1}>\unicode[STIX]{x1D6FD}$
for
$\unicode[STIX]{x1D6FC}^{-1}>\unicode[STIX]{x1D6FD}$
for
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\in Z$
,
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\in Z$
,
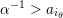 $\unicode[STIX]{x1D6FC}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}$
,
$\unicode[STIX]{x1D6FC}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}$
,
![]() $a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D6FD}$
,
$a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D6FD}$
,
 $\unicode[STIX]{x1D700}^{-1}>\unicode[STIX]{x1D700}$
,
$\unicode[STIX]{x1D700}^{-1}>\unicode[STIX]{x1D700}$
,
![]() $a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D700}$
, and
$a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D700}$
, and
 $\unicode[STIX]{x1D700}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}$
, respectively. These give all the possible cases for the order.
$\unicode[STIX]{x1D700}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}$
, respectively. These give all the possible cases for the order.
For (3),
![]() $l$
is punctured by definition if and only if
$l$
is punctured by definition if and only if
![]() $l$
is of the form
$l$
is of the form
![]() $a_{i_{\unicode[STIX]{x1D703}}}$
or
$a_{i_{\unicode[STIX]{x1D703}}}$
or
![]() $a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
such that
$a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
such that
 $L_{i_{\unicode[STIX]{x1D703}}}=\{\unicode[STIX]{x1D700}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D700}\}$
. Then by Construction 4.7,
$L_{i_{\unicode[STIX]{x1D703}}}=\{\unicode[STIX]{x1D700}^{-1}>a_{i_{\unicode[STIX]{x1D703}}}>\unicode[STIX]{x1D700}\}$
. Then by Construction 4.7,
![]() $\mathfrak{a}(l)$
is in a self-folded triangle and hence it has to connect the puncture in this triangle.◻
$\mathfrak{a}(l)$
is in a self-folded triangle and hence it has to connect the puncture in this triangle.◻
Recall that a word is a sequence
 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
of letters in
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
of letters in
![]() $L$
such that for any
$L$
such that for any
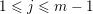 $1\leqslant j\leqslant m-1$
,
$1\leqslant j\leqslant m-1$
,
 $\unicode[STIX]{x1D714}_{j}^{-1}\in L_{\unicode[STIX]{x1D703}}(i)$
and
$\unicode[STIX]{x1D714}_{j}^{-1}\in L_{\unicode[STIX]{x1D703}}(i)$
and
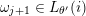 $\unicode[STIX]{x1D714}_{j+1}\in L_{\unicode[STIX]{x1D703}^{\prime }}(i)$
for different
$\unicode[STIX]{x1D714}_{j+1}\in L_{\unicode[STIX]{x1D703}^{\prime }}(i)$
for different
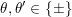 $\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\in \{\pm \}$
and some
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\in \{\pm \}$
and some
![]() $i\in Q_{0}^{\mathbf{T}}$
. By Lemma 4.8(1), this condition is equivalent to
$i\in Q_{0}^{\mathbf{T}}$
. By Lemma 4.8(1), this condition is equivalent to
![]() $\mathfrak{a}(\unicode[STIX]{x1D714}_{j}^{-1})$
and
$\mathfrak{a}(\unicode[STIX]{x1D714}_{j}^{-1})$
and
![]() $\mathfrak{a}(\unicode[STIX]{x1D714}_{j+1})$
starting at the same curve in
$\mathfrak{a}(\unicode[STIX]{x1D714}_{j+1})$
starting at the same curve in
![]() $\mathbf{T}$
, but being in the two triangles adjacent to this curve, respectively. Hence we can glue the two arc segments
$\mathbf{T}$
, but being in the two triangles adjacent to this curve, respectively. Hence we can glue the two arc segments
![]() $\mathfrak{a}(\unicode[STIX]{x1D714}_{j})$
and
$\mathfrak{a}(\unicode[STIX]{x1D714}_{j})$
and
![]() $\mathfrak{a}(\unicode[STIX]{x1D714}_{j+1})$
together to get a curve segment.
$\mathfrak{a}(\unicode[STIX]{x1D714}_{j+1})$
together to get a curve segment.
Construction 4.9. For each word
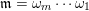 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
, we glue the corresponding arc segments
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
, we glue the corresponding arc segments
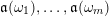 $\mathfrak{a}(\unicode[STIX]{x1D714}_{1}),\ldots ,\mathfrak{a}(\unicode[STIX]{x1D714}_{m})$
together in order to get a curve segment, denoted by
$\mathfrak{a}(\unicode[STIX]{x1D714}_{1}),\ldots ,\mathfrak{a}(\unicode[STIX]{x1D714}_{m})$
together in order to get a curve segment, denoted by
![]() $\mathfrak{a}(\mathfrak{m})$
.
$\mathfrak{a}(\mathfrak{m})$
.
Recall that for two words
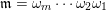 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
and
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{2}\unicode[STIX]{x1D714}_{1}$
and
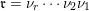 $\mathfrak{r}=\unicode[STIX]{x1D708}_{r}\cdots \unicode[STIX]{x1D708}_{2}\unicode[STIX]{x1D708}_{1}$
,
$\mathfrak{r}=\unicode[STIX]{x1D708}_{r}\cdots \unicode[STIX]{x1D708}_{2}\unicode[STIX]{x1D708}_{1}$
,
![]() $\mathfrak{m}>\mathfrak{r}$
if and only if there is
$\mathfrak{m}>\mathfrak{r}$
if and only if there is
![]() $j$
such that
$j$
such that
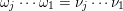 $\unicode[STIX]{x1D714}_{j}\cdots \unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D708}_{j}\cdots \unicode[STIX]{x1D708}_{1}$
and
$\unicode[STIX]{x1D714}_{j}\cdots \unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D708}_{j}\cdots \unicode[STIX]{x1D708}_{1}$
and
 $\unicode[STIX]{x1D714}_{j+1}>\unicode[STIX]{x1D708}_{j+1}$
.
$\unicode[STIX]{x1D714}_{j+1}>\unicode[STIX]{x1D708}_{j+1}$
.
Lemma 4.10. Let
![]() $\mathfrak{m}_{1}$
,
$\mathfrak{m}_{1}$
,
![]() $\mathfrak{m}_{2}$
be two words and
$\mathfrak{m}_{2}$
be two words and
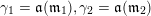 $\unicode[STIX]{x1D6FE}_{1}=\mathfrak{a}(\mathfrak{m}_{1}),\unicode[STIX]{x1D6FE}_{2}=\mathfrak{a}(\mathfrak{m}_{2})$
. Then
$\unicode[STIX]{x1D6FE}_{1}=\mathfrak{a}(\mathfrak{m}_{1}),\unicode[STIX]{x1D6FE}_{2}=\mathfrak{a}(\mathfrak{m}_{2})$
. Then
 $\mathfrak{m}_{1}\geqslant \mathfrak{m}_{2}$
if and only if
$\mathfrak{m}_{1}\geqslant \mathfrak{m}_{2}$
if and only if
![]() $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
![]() $\unicode[STIX]{x1D6FE}_{2}$
separate as in one of the forms in Figure 10 after they share the same curve segments from the start. The equality holds if and only if one of the forms in Figure 10(ii) occurs, and in this case
$\unicode[STIX]{x1D6FE}_{2}$
separate as in one of the forms in Figure 10 after they share the same curve segments from the start. The equality holds if and only if one of the forms in Figure 10(ii) occurs, and in this case
![]() $\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
.
$\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
.
Proof. By definition,
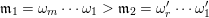 $\mathfrak{m}_{1}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}>\mathfrak{m}_{2}=\unicode[STIX]{x1D714}_{r}^{\prime }\cdots \unicode[STIX]{x1D714}_{1}^{\prime }$
if and only if there is a maximal integer
$\mathfrak{m}_{1}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}>\mathfrak{m}_{2}=\unicode[STIX]{x1D714}_{r}^{\prime }\cdots \unicode[STIX]{x1D714}_{1}^{\prime }$
if and only if there is a maximal integer
![]() $j\geqslant 0$
such that the first
$j\geqslant 0$
such that the first
![]() $j$
letters (from right to left) of
$j$
letters (from right to left) of
![]() $\mathfrak{m}_{1}$
and
$\mathfrak{m}_{1}$
and
![]() $\mathfrak{m}_{2}$
are the same pointwise and
$\mathfrak{m}_{2}$
are the same pointwise and
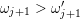 $\unicode[STIX]{x1D714}_{j+1}>\unicode[STIX]{x1D714}_{j+1}^{\prime }$
. By Lemma 4.8(2), this is equivalent to
$\unicode[STIX]{x1D714}_{j+1}>\unicode[STIX]{x1D714}_{j+1}^{\prime }$
. By Lemma 4.8(2), this is equivalent to
![]() $\mathfrak{a}(\mathfrak{m}_{1})$
and
$\mathfrak{a}(\mathfrak{m}_{1})$
and
![]() $\mathfrak{a}(\mathfrak{m}_{2})$
sharing the first
$\mathfrak{a}(\mathfrak{m}_{2})$
sharing the first
![]() $j$
arc segments and their
$j$
arc segments and their
![]() $(j+1)$
th arc segments having one of the forms in Figure 10(i). Clearly
$(j+1)$
th arc segments having one of the forms in Figure 10(i). Clearly
 $\mathfrak{m}_{1}=\mathfrak{m}_{2}$
if and only if one of the forms in Figure 10(ii) occurs and hence
$\mathfrak{m}_{1}=\mathfrak{m}_{2}$
if and only if one of the forms in Figure 10(ii) occurs and hence
![]() $\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
. Thus the lemma holds.◻
$\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
. Thus the lemma holds.◻
Recall that a word
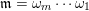 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
is maximal if and only if
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
is maximal if and only if
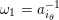 $\unicode[STIX]{x1D714}_{1}=a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
and
$\unicode[STIX]{x1D714}_{1}=a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
and
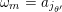 $\unicode[STIX]{x1D714}_{m}=a_{j_{\unicode[STIX]{x1D703}^{\prime }}}$
for some
$\unicode[STIX]{x1D714}_{m}=a_{j_{\unicode[STIX]{x1D703}^{\prime }}}$
for some
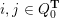 $i,j\in Q_{0}^{\mathbf{T}}$
and some
$i,j\in Q_{0}^{\mathbf{T}}$
and some
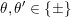 $\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\in \{\pm \}$
.
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\in \{\pm \}$
.
Lemma 4.11. The map
 $\mathfrak{m}\mapsto \mathfrak{a}(\mathfrak{m})$
is a bijection from the set of maximal words to the set of curves (up to homotopy) in
$\mathfrak{m}\mapsto \mathfrak{a}(\mathfrak{m})$
is a bijection from the set of maximal words to the set of curves (up to homotopy) in
![]() $\mathbf{S}$
that are not in
$\mathbf{S}$
that are not in
![]() $\mathbf{T}$
. Moreover,
$\mathbf{T}$
. Moreover,
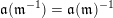 $\mathfrak{a}(\mathfrak{m}^{-1})=\mathfrak{a}(\mathfrak{m})^{-1}$
.
$\mathfrak{a}(\mathfrak{m}^{-1})=\mathfrak{a}(\mathfrak{m})^{-1}$
.
Proof. Let
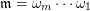 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
. Since
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
. Since
![]() $\mathfrak{m}$
is maximal, we have
$\mathfrak{m}$
is maximal, we have
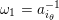 $\unicode[STIX]{x1D714}_{1}=a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
and
$\unicode[STIX]{x1D714}_{1}=a_{i_{\unicode[STIX]{x1D703}}}^{-1}$
and
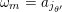 $\unicode[STIX]{x1D714}_{m}=a_{j_{\unicode[STIX]{x1D703}^{\prime }}}$
for some
$\unicode[STIX]{x1D714}_{m}=a_{j_{\unicode[STIX]{x1D703}^{\prime }}}$
for some
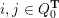 $i,j\in Q_{0}^{\mathbf{T}}$
and some
$i,j\in Q_{0}^{\mathbf{T}}$
and some
 $\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\in \{\pm \}$
. By Construction 4.7, the endpoints of
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\in \{\pm \}$
. By Construction 4.7, the endpoints of
![]() $\mathfrak{a}(\mathfrak{m})$
are in
$\mathfrak{a}(\mathfrak{m})$
are in
![]() $\mathbf{M}\cup \mathbf{P}$
. Because by Lemma 4.8(1), among the arc segments
$\mathbf{M}\cup \mathbf{P}$
. Because by Lemma 4.8(1), among the arc segments
 $\mathfrak{a}(\unicode[STIX]{x1D714}_{1}),\ldots ,\mathfrak{a}(\unicode[STIX]{x1D714}_{m})$
, no two adjacent arc segments are in the same triangle, the curve
$\mathfrak{a}(\unicode[STIX]{x1D714}_{1}),\ldots ,\mathfrak{a}(\unicode[STIX]{x1D714}_{m})$
, no two adjacent arc segments are in the same triangle, the curve
![]() $\mathfrak{a}(\mathfrak{m})$
has minimal intersections with the curves in
$\mathfrak{a}(\mathfrak{m})$
has minimal intersections with the curves in
![]() $\mathbf{T}^{o}$
. In particular, the intersection number of
$\mathbf{T}^{o}$
. In particular, the intersection number of
![]() $\mathfrak{a}(\mathfrak{m})$
with
$\mathfrak{a}(\mathfrak{m})$
with
![]() $\mathbf{T}$
is not zero. Hence
$\mathbf{T}$
is not zero. Hence
![]() $\mathfrak{a}(\mathfrak{m})$
is a curve in
$\mathfrak{a}(\mathfrak{m})$
is a curve in
![]() $\mathbf{S}$
which is not in
$\mathbf{S}$
which is not in
![]() $\mathbf{T}$
.
$\mathbf{T}$
.
On the other hand, for a curve
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
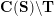 $\mathbf{C}(\mathbf{S})\setminus \mathbf{T}$
, since we consider it up to homotopy, we can assume
$\mathbf{C}(\mathbf{S})\setminus \mathbf{T}$
, since we consider it up to homotopy, we can assume
![]() $\unicode[STIX]{x1D6FE}$
has minimal intersections with the curves in
$\unicode[STIX]{x1D6FE}$
has minimal intersections with the curves in
![]() $\mathbf{T}$
. Take the product, denoted by
$\mathbf{T}$
. Take the product, denoted by
![]() $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
, of letters corresponding to the arc segments of
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
, of letters corresponding to the arc segments of
![]() $\unicode[STIX]{x1D6FE}$
divided by its intersections with
$\unicode[STIX]{x1D6FE}$
divided by its intersections with
![]() $\mathbf{T}^{o}$
in order. Then by Lemma 4.8(1),
$\mathbf{T}^{o}$
in order. Then by Lemma 4.8(1),
![]() $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
is a word and clearly it is maximal. Moreover, the correspondence between arc segments and letters implies that
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
is a word and clearly it is maximal. Moreover, the correspondence between arc segments and letters implies that
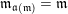 $\mathfrak{m}_{\mathfrak{a}(\mathfrak{m})}=\mathfrak{m}$
and
$\mathfrak{m}_{\mathfrak{a}(\mathfrak{m})}=\mathfrak{m}$
and
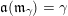 $\mathfrak{a}(\mathfrak{m}_{\unicode[STIX]{x1D6FE}})=\unicode[STIX]{x1D6FE}$
up to homotopy. Therefore,
$\mathfrak{a}(\mathfrak{m}_{\unicode[STIX]{x1D6FE}})=\unicode[STIX]{x1D6FE}$
up to homotopy. Therefore,
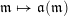 $\mathfrak{m}\mapsto \mathfrak{a}(\mathfrak{m})$
is the required bijection with
$\mathfrak{m}\mapsto \mathfrak{a}(\mathfrak{m})$
is the required bijection with
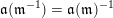 $\mathfrak{a}(\mathfrak{m}^{-1})=\mathfrak{a}(\mathfrak{m})^{-1}$
.◻
$\mathfrak{a}(\mathfrak{m}^{-1})=\mathfrak{a}(\mathfrak{m})^{-1}$
.◻
Recall from § 2.5 that a maximal word
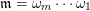 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
is called admissible if the following hold.
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
is called admissible if the following hold.
-
(A1) For each
 $\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}$
with
$\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}$
with
 $\unicode[STIX]{x1D700}$
a dashed loop, we have that
$\unicode[STIX]{x1D700}$
a dashed loop, we have that
 $\unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}>\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}$
, and for each
$\unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}>\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}$
, and for each
 $\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}^{-1}$
with
$\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}^{-1}$
with
 $\unicode[STIX]{x1D700}$
a dashed loop, we have that
$\unicode[STIX]{x1D700}$
a dashed loop, we have that
 $\unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}<\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}$
.
$\unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}<\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}$
. -
(A2) If
 $\mathfrak{m}$
contains two punctured letters then
$\mathfrak{m}$
contains two punctured letters then
 $F(\mathfrak{m})$
is not a proper power of
$F(\mathfrak{m})$
is not a proper power of
 $F(\mathfrak{m}^{\prime })$
for any maximal word
$F(\mathfrak{m}^{\prime })$
for any maximal word
 $\mathfrak{m}^{\prime }$
containing two punctured letters, where
$\mathfrak{m}^{\prime }$
containing two punctured letters, where  $$\begin{eqnarray}F(\mathfrak{m}):=F(\unicode[STIX]{x1D714}_{m})\cdots F(\unicode[STIX]{x1D714}_{1})F(\unicode[STIX]{x1D714}_{2}^{-1})\cdots F(\unicode[STIX]{x1D714}_{m-1}^{-1}).\end{eqnarray}$$
$$\begin{eqnarray}F(\mathfrak{m}):=F(\unicode[STIX]{x1D714}_{m})\cdots F(\unicode[STIX]{x1D714}_{1})F(\unicode[STIX]{x1D714}_{2}^{-1})\cdots F(\unicode[STIX]{x1D714}_{m-1}^{-1}).\end{eqnarray}$$
On the other hand, recall from Definition 3.1 that a pair
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
is called a tagged curve if the following hold.
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
is called a tagged curve if the following hold.
-
(T1) The curve
 $\unicode[STIX]{x1D6FE}$
does not cut out a once-punctured monogon by a self-intersection (including endpoints), cf. Figure 2.
$\unicode[STIX]{x1D6FE}$
does not cut out a once-punctured monogon by a self-intersection (including endpoints), cf. Figure 2. -
(T2) If
 $\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(1)\in \mathbf{P}$
, then the completion
$\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(1)\in \mathbf{P}$
, then the completion
 $\bar{\unicode[STIX]{x1D6FE}}$
is not a proper power of a closed curve in the sense of the multiplication in the fundamental group of
$\bar{\unicode[STIX]{x1D6FE}}$
is not a proper power of a closed curve in the sense of the multiplication in the fundamental group of
 $\mathbf{S}$
.
$\mathbf{S}$
.
Lemma 4.12. Let
![]() $\mathfrak{m}$
be a maximal word. Then
$\mathfrak{m}$
be a maximal word. Then
![]() $\mathfrak{m}$
satisfies (A1) if and only if
$\mathfrak{m}$
satisfies (A1) if and only if
![]() $\mathfrak{a}(\mathfrak{m})$
satisfies (T1);
$\mathfrak{a}(\mathfrak{m})$
satisfies (T1);
![]() $\mathfrak{m}$
satisfies (A2) if and only if
$\mathfrak{m}$
satisfies (A2) if and only if
![]() $\mathfrak{a}(\mathfrak{m})$
satisfies (T2).
$\mathfrak{a}(\mathfrak{m})$
satisfies (T2).
Proof. Let
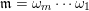 $\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
. Note that the curve
$\mathfrak{m}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}$
. Note that the curve
![]() $\mathfrak{a}(\mathfrak{m})$
does not satisfy (T1) if and only if it cuts out a once-punctured monogon as in Figure 2. This is equivalent to there being an arc segment
$\mathfrak{a}(\mathfrak{m})$
does not satisfy (T1) if and only if it cuts out a once-punctured monogon as in Figure 2. This is equivalent to there being an arc segment
![]() $\mathfrak{a}(\unicode[STIX]{x1D714}_{i})$
of
$\mathfrak{a}(\unicode[STIX]{x1D714}_{i})$
of
![]() $\mathfrak{a}(\mathfrak{m})$
with
$\mathfrak{a}(\mathfrak{m})$
with
![]() $\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}$
or
$\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}$
or
![]() $\unicode[STIX]{x1D700}^{-1}$
(for some dashed loop
$\unicode[STIX]{x1D700}^{-1}$
(for some dashed loop
![]() $\unicode[STIX]{x1D700}$
) which has the form as in Figure 11 with the right part being one of the forms in Figure 10. Let
$\unicode[STIX]{x1D700}$
) which has the form as in Figure 11 with the right part being one of the forms in Figure 10. Let
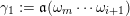 $\unicode[STIX]{x1D6FE}_{1}:=\mathfrak{a}(\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1})$
and
$\unicode[STIX]{x1D6FE}_{1}:=\mathfrak{a}(\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1})$
and
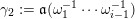 $\unicode[STIX]{x1D6FE}_{2}:=\mathfrak{a}(\unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1})$
. If
$\unicode[STIX]{x1D6FE}_{2}:=\mathfrak{a}(\unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1})$
. If
![]() $\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}$
, then the orientation of
$\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}$
, then the orientation of
![]() $\unicode[STIX]{x1D6FE}$
is as shown in Figure 11.
$\unicode[STIX]{x1D6FE}$
is as shown in Figure 11.
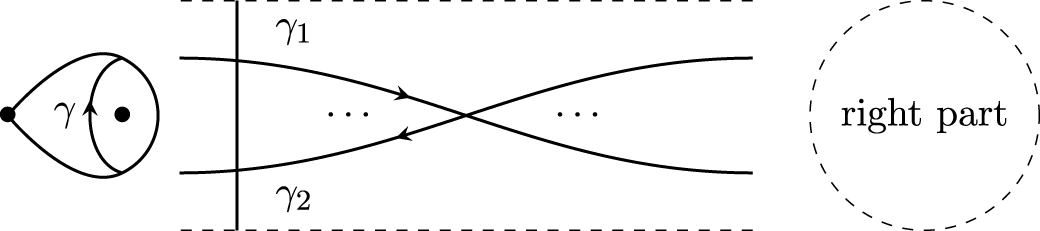
Figure 11. A once-punctured monogon from a curve.
By Lemma 4.10,
 $\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}\geqslant \unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}$
. Similarly, if
$\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}\geqslant \unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}$
. Similarly, if
 $\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}^{-1}$
then
$\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D700}^{-1}$
then
 $\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}\leqslant \unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}$
. This implies that (T1) does not hold for
$\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{i+1}\leqslant \unicode[STIX]{x1D714}_{1}^{-1}\cdots \unicode[STIX]{x1D714}_{i-1}^{-1}$
. This implies that (T1) does not hold for
![]() $\mathfrak{a}(\mathfrak{m})$
if and only if (A1) does not hold for
$\mathfrak{a}(\mathfrak{m})$
if and only if (A1) does not hold for
![]() $\mathfrak{m}$
.
$\mathfrak{m}$
.
Now consider the condition (A2). Note that by Lemma 4.8(3) both of the endpoints of
![]() $\mathfrak{a}(\mathfrak{m})$
are punctures if and only if
$\mathfrak{a}(\mathfrak{m})$
are punctures if and only if
![]() $\mathfrak{m}$
has two punctured letters
$\mathfrak{m}$
has two punctured letters
![]() $\unicode[STIX]{x1D714}_{1}$
and
$\unicode[STIX]{x1D714}_{1}$
and
![]() $\unicode[STIX]{x1D714}_{m}$
. In this case,
$\unicode[STIX]{x1D714}_{m}$
. In this case,
![]() $F(\mathfrak{m})$
(as a cycle) corresponds to the completion of
$F(\mathfrak{m})$
(as a cycle) corresponds to the completion of
![]() $\mathfrak{a}(\mathfrak{m})$
. Hence
$\mathfrak{a}(\mathfrak{m})$
. Hence
![]() $\mathfrak{a}(\mathfrak{m})$
satisfies (T2) if and only if
$\mathfrak{a}(\mathfrak{m})$
satisfies (T2) if and only if
![]() $\mathfrak{m}$
satisfies (A2).◻
$\mathfrak{m}$
satisfies (A2).◻
Let
![]() $\mathbf{C}_{0}(\mathbf{S})$
be the subset of
$\mathbf{C}_{0}(\mathbf{S})$
be the subset of
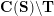 $\mathbf{C}(\mathbf{S})\setminus \mathbf{T}$
consisting of curves satisfying the conditions (T1) and (T2). That is,
$\mathbf{C}(\mathbf{S})\setminus \mathbf{T}$
consisting of curves satisfying the conditions (T1) and (T2). That is,
![]() $\mathbf{C}_{0}(\mathbf{S})$
consists of curves
$\mathbf{C}_{0}(\mathbf{S})$
consists of curves
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
 $\mathbf{C}(\mathbf{S})\setminus \mathbf{T}$
such that there exists a tagged curve
$\mathbf{C}(\mathbf{S})\setminus \mathbf{T}$
such that there exists a tagged curve
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
for some
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
for some
![]() $\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D705}$
.
By Lemmas 4.11 and 4.12, we have the following.
Lemma 4.13. The map
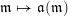 $\mathfrak{m}\mapsto \mathfrak{a}(\mathfrak{m})$
is a bijection
$\mathfrak{m}\mapsto \mathfrak{a}(\mathfrak{m})$
is a bijection
 $$\begin{eqnarray}\displaystyle \mathfrak{a}:\overline{\mathfrak{X}}\longrightarrow \mathbf{C}_{0}(\mathbf{S}), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{a}:\overline{\mathfrak{X}}\longrightarrow \mathbf{C}_{0}(\mathbf{S}), & & \displaystyle\end{eqnarray}$$
where
![]() $\overline{\mathfrak{X}}$
is the set of admissible words up to inverse.
$\overline{\mathfrak{X}}$
is the set of admissible words up to inverse.
For each
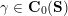 $\unicode[STIX]{x1D6FE}\in \mathbf{C}_{0}(\mathbf{S})$
, we denote by
$\unicode[STIX]{x1D6FE}\in \mathbf{C}_{0}(\mathbf{S})$
, we denote by
![]() $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
the preimage of
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
the preimage of
![]() $\unicode[STIX]{x1D6FE}$
under the bijection (4.3). Recall from § 2.6 that the algebra
$\unicode[STIX]{x1D6FE}$
under the bijection (4.3). Recall from § 2.6 that the algebra
![]() $A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}$
is generated by the indeterminates
$A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}$
is generated by the indeterminates
![]() $x$
associated with punctured letters in
$x$
associated with punctured letters in
![]() $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
with
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
with
![]() $x^{2}=x$
. So by Lemma 4.8(3) indeterminates of
$x^{2}=x$
. So by Lemma 4.8(3) indeterminates of
![]() $A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}$
are indexed by endpoints of
$A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}$
are indexed by endpoints of
![]() $\unicode[STIX]{x1D6FE}$
that are punctures.
$\unicode[STIX]{x1D6FE}$
that are punctures.
Construction 4.14. The one-dimensional
![]() $A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}$
-modules are classified in § 2.6. Using the notation there, each map
$A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}$
-modules are classified in § 2.6. Using the notation there, each map
![]() $\unicode[STIX]{x1D705}$
gives a one-dimensional
$\unicode[STIX]{x1D705}$
gives a one-dimensional
![]() $A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}$
-module
$A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}$
-module
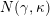 $N(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
as follows.
$N(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
as follows.
-
(i) If neither of the endpoints of
 $\unicode[STIX]{x1D6FE}$
is a puncture, then
$\unicode[STIX]{x1D6FE}$
is a puncture, then
 $A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}=\mathbf{k}$
. Let
$A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}=\mathbf{k}$
. Let
 $N_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}=\mathbf{k}$
.
$N_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}=\mathbf{k}$
. -
(ii) If exactly one endpoint of
 $\unicode[STIX]{x1D6FE}$
is a puncture, then
$\unicode[STIX]{x1D6FE}$
is a puncture, then
 $A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}=\mathbf{k}[x_{a}]/(x_{a}^{2}-x_{a})$
, where
$A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}=\mathbf{k}[x_{a}]/(x_{a}^{2}-x_{a})$
, where
 $a\in \{0,1\}$
with
$a\in \{0,1\}$
with
 $\unicode[STIX]{x1D6FE}(a)\in \mathbf{P}$
. Let
$\unicode[STIX]{x1D6FE}(a)\in \mathbf{P}$
. Let
 $N_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}=\mathbf{k}_{\unicode[STIX]{x1D705}(a)}$
.
$N_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}=\mathbf{k}_{\unicode[STIX]{x1D705}(a)}$
. -
(iii) If both of the endpoints of
 $\unicode[STIX]{x1D6FE}$
are punctures, then
$\unicode[STIX]{x1D6FE}$
are punctures, then
 $A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}=\mathbf{k}\langle x_{0},x_{1}\rangle /(x_{0}^{2}-x_{0},x_{1}^{2}-x_{1})$
. Let
$A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}=\mathbf{k}\langle x_{0},x_{1}\rangle /(x_{0}^{2}-x_{0},x_{1}^{2}-x_{1})$
. Let
 $N_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}=\mathbf{k}_{\unicode[STIX]{x1D705}(0),\unicode[STIX]{x1D705}(1)}$
.
$N_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}=\mathbf{k}_{\unicode[STIX]{x1D705}(0),\unicode[STIX]{x1D705}(1)}$
.
Thus, for each tagged curve
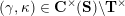 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})\setminus \mathbf{T}^{\times }$
, where
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})\setminus \mathbf{T}^{\times }$
, where
![]() $\mathbf{T}^{\times }$
is the tagged version of
$\mathbf{T}^{\times }$
is the tagged version of
![]() $\mathbf{T}$
(see § 3.2), there is an associated indecomposable representation
$\mathbf{T}$
(see § 3.2), there is an associated indecomposable representation
 $$\begin{eqnarray}\displaystyle M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}:=M^{\mathbf{T}}(\mathfrak{m}_{\unicode[STIX]{x1D6FE}},N_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}:=M^{\mathbf{T}}(\mathfrak{m}_{\unicode[STIX]{x1D6FE}},N_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}) & & \displaystyle\end{eqnarray}$$
in
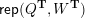 $\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
by Construction 2.7 and Theorem 2.9. For
$\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
by Construction 2.7 and Theorem 2.9. For
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }$
, let
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }$
, let
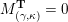 $M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=0$
.
$M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=0$
.
Definition 4.15. Define a map
![]() $X^{\mathbf{T}}$
from
$X^{\mathbf{T}}$
from
![]() $\mathbf{C}^{\times }(\mathbf{S})$
to the set
$\mathbf{C}^{\times }(\mathbf{S})$
to the set
![]() $\mathfrak{S}(\mathbf{T})$
of string objects in
$\mathfrak{S}(\mathbf{T})$
of string objects in
![]() ${\mathcal{C}}(\mathbf{T})$
by
${\mathcal{C}}(\mathbf{T})$
by
 $$\begin{eqnarray}X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=\left\{\begin{array}{@{}ll@{}}M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}\quad & \text{if }(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})\setminus \mathbf{T}^{\times },\\ T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}\quad & \text{if }(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=\left\{\begin{array}{@{}ll@{}}M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}\quad & \text{if }(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})\setminus \mathbf{T}^{\times },\\ T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}\quad & \text{if }(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }.\end{array}\right.\end{eqnarray}$$
Theorem 4.16. The map
![]() $X^{\mathbf{T}}$
is a bijection.
$X^{\mathbf{T}}$
is a bijection.
Proof. It is sufficient to prove that
![]() $X^{\mathbf{T}}$
is a bijection from the set
$X^{\mathbf{T}}$
is a bijection from the set
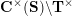 $\mathbf{C}^{\times }(\mathbf{S})\setminus \mathbf{T}^{\times }$
to the set of indecomposable representations
$\mathbf{C}^{\times }(\mathbf{S})\setminus \mathbf{T}^{\times }$
to the set of indecomposable representations
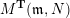 $M^{\mathbf{T}}(\mathfrak{m},N)$
with
$M^{\mathbf{T}}(\mathfrak{m},N)$
with
![]() $\mathfrak{m}\in \overline{\mathfrak{X}}$
and
$\mathfrak{m}\in \overline{\mathfrak{X}}$
and
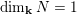 $\dim _{\mathbf{k}}N=1$
. This follows from the bijection (4.3) in Lemma 4.13 and the description of the one-dimensional
$\dim _{\mathbf{k}}N=1$
. This follows from the bijection (4.3) in Lemma 4.13 and the description of the one-dimensional
![]() $A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}$
-modules in Construction 4.14.◻
$A_{\mathfrak{m}_{\unicode[STIX]{x1D6FE}}}$
-modules in Construction 4.14.◻
4.3 Flips and mutations
We study
![]() $\diamondsuit$
-flips of an admissible triangulation
$\diamondsuit$
-flips of an admissible triangulation
![]() $\mathbf{T}$
in this subsection. Recall that the function
$\mathbf{T}$
in this subsection. Recall that the function
![]() $\unicode[STIX]{x1D70B}_{\mathbf{T}}$
on
$\unicode[STIX]{x1D70B}_{\mathbf{T}}$
on
![]() $\mathbf{T}$
is defined as follows: if
$\mathbf{T}$
is defined as follows: if
![]() $\unicode[STIX]{x1D6FE}$
is the folded side of a self-folded triangle in
$\unicode[STIX]{x1D6FE}$
is the folded side of a self-folded triangle in
![]() $\mathbf{T}$
, then
$\mathbf{T}$
, then
![]() $\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FE})$
is the corresponding remaining side; otherwise,
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FE})$
is the corresponding remaining side; otherwise,
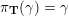 $\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}$
.
Definition 4.17 [Reference Fomin, Shapiro and ThurstonFST08, Definition 9.11].
Let
![]() $\mathbf{T}$
be an admissible triangulation of
$\mathbf{T}$
be an admissible triangulation of
![]() $\mathbf{S}$
. The
$\mathbf{S}$
. The
![]() $\diamondsuit$
-flip
$\diamondsuit$
-flip
![]() $f_{i}(\mathbf{T})$
associated with a curve
$f_{i}(\mathbf{T})$
associated with a curve
![]() $i\in \mathbf{T}^{o}$
is the unique admissible triangulation that shares all curves with
$i\in \mathbf{T}^{o}$
is the unique admissible triangulation that shares all curves with
![]() $\mathbf{T}$
except for the curves
$\mathbf{T}$
except for the curves
![]() $j$
satisfying
$j$
satisfying
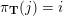 $\unicode[STIX]{x1D70B}_{\mathbf{T}}(j)=i$
.
$\unicode[STIX]{x1D70B}_{\mathbf{T}}(j)=i$
.
Note that there are two types of
![]() $\diamondsuit$
-flips: when
$\diamondsuit$
-flips: when
![]() $i$
is not a side of a self-folded triangle, the corresponding
$i$
is not a side of a self-folded triangle, the corresponding
![]() $\diamondsuit$
-flip is an ordinary flip, and when
$\diamondsuit$
-flip is an ordinary flip, and when
![]() $i$
is the remaining side of a self-folded triangle, the corresponding
$i$
is the remaining side of a self-folded triangle, the corresponding
![]() $\diamondsuit$
-flip is a combination of two ordinary flips occurring inside a once-punctured digon (see Figure A.1). Recall that an ordinary flip of a triangulation
$\diamondsuit$
-flip is a combination of two ordinary flips occurring inside a once-punctured digon (see Figure A.1). Recall that an ordinary flip of a triangulation
![]() $\mathbf{T}^{\prime }$
is a new triangulation
$\mathbf{T}^{\prime }$
is a new triangulation
![]() $\mathbf{T}^{\prime \prime }$
which shares all curves with
$\mathbf{T}^{\prime \prime }$
which shares all curves with
![]() $\mathbf{T}^{\prime }$
except for one.
$\mathbf{T}^{\prime }$
except for one.
The
![]() $\diamondsuit$
-flips of an admissible triangulation
$\diamondsuit$
-flips of an admissible triangulation
![]() $\mathbf{T}$
are indexed by the vertices of the quiver
$\mathbf{T}$
are indexed by the vertices of the quiver
![]() $Q^{\mathbf{T}}$
. Define the mutation
$Q^{\mathbf{T}}$
. Define the mutation
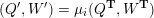 $(Q^{\prime },W^{\prime })=\unicode[STIX]{x1D707}_{i}(Q^{\mathbf{T}},W^{\mathbf{T}})$
at a vertex
$(Q^{\prime },W^{\prime })=\unicode[STIX]{x1D707}_{i}(Q^{\mathbf{T}},W^{\mathbf{T}})$
at a vertex
![]() $i\in Q_{0}^{\mathbf{T}}$
to be
$i\in Q_{0}^{\mathbf{T}}$
to be
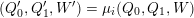 $(Q_{0}^{\prime },Q_{1}^{\prime },W^{\prime })=\unicode[STIX]{x1D707}_{i}(Q_{0},Q_{1},W)$
in the sense of [Reference Derksen, Weyman and ZelevinskyDWZ08] with
$(Q_{0}^{\prime },Q_{1}^{\prime },W^{\prime })=\unicode[STIX]{x1D707}_{i}(Q_{0},Q_{1},W)$
in the sense of [Reference Derksen, Weyman and ZelevinskyDWZ08] with
 $Q_{2}^{\prime }=Q_{2}$
. By [Reference Fomin, Shapiro and ThurstonFST08, Reference Labardini-FragosoLab09a],
$Q_{2}^{\prime }=Q_{2}$
. By [Reference Fomin, Shapiro and ThurstonFST08, Reference Labardini-FragosoLab09a],
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{i}(Q^{\mathbf{T}},W^{\mathbf{T}})\simeq (Q^{f_{i}(\mathbf{T})},W^{f_{i}(\mathbf{T})})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{i}(Q^{\mathbf{T}},W^{\mathbf{T}})\simeq (Q^{f_{i}(\mathbf{T})},W^{f_{i}(\mathbf{T})})\end{eqnarray}$$
for each
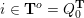 $i\in \mathbf{T}^{o}=Q_{0}^{\mathbf{T}}$
, where
$i\in \mathbf{T}^{o}=Q_{0}^{\mathbf{T}}$
, where
![]() $f_{i}$
is the
$f_{i}$
is the
![]() $\diamondsuit$
-flip associated with
$\diamondsuit$
-flip associated with
![]() $i$
. Then by [Reference Keller and YangKY11], there is an equivalence
$i$
. Then by [Reference Keller and YangKY11], there is an equivalence
 $\widetilde{\unicode[STIX]{x1D707}}_{i}:{\mathcal{C}}(\mathbf{T})\simeq {\mathcal{C}}(\mathbf{T}^{\prime })$
.
$\widetilde{\unicode[STIX]{x1D707}}_{i}:{\mathcal{C}}(\mathbf{T})\simeq {\mathcal{C}}(\mathbf{T}^{\prime })$
.
For each tagged curve
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
, the corresponding object
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
, the corresponding object
![]() $X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
in
$X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
in
![]() ${\mathcal{C}}(\mathbf{T})$
is given by the associated representation
${\mathcal{C}}(\mathbf{T})$
is given by the associated representation
![]() $M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
in
$M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
in
 $\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
through the equivalence
$\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
through the equivalence
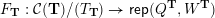 $F_{\mathbf{T}}:{\mathcal{C}}(\mathbf{T})/(T_{\mathbf{T}})\rightarrow \mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
. Then the equivalence
$F_{\mathbf{T}}:{\mathcal{C}}(\mathbf{T})/(T_{\mathbf{T}})\rightarrow \mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
. Then the equivalence
![]() $\widetilde{\unicode[STIX]{x1D707}}_{i}$
should be compatible with some mutation of representations. However, there is not a well-defined mutation on
$\widetilde{\unicode[STIX]{x1D707}}_{i}$
should be compatible with some mutation of representations. However, there is not a well-defined mutation on
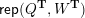 $\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
. Instead, we shall use decorated representations and their mutations introduced in [Reference Derksen, Weyman and ZelevinskyDWZ08]. A decorated representation of
$\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
. Instead, we shall use decorated representations and their mutations introduced in [Reference Derksen, Weyman and ZelevinskyDWZ08]. A decorated representation of
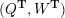 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
is a pair
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
is a pair
![]() $(M,V)$
, where
$(M,V)$
, where
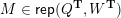 $M\in \mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
is a usual representation of
$M\in \mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
is a usual representation of
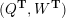 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
and
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
and
![]() $V$
is a representation of
$V$
is a representation of
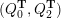 $(Q_{0}^{\mathbf{T}},Q_{2}^{\mathbf{T}})$
bounded by
$(Q_{0}^{\mathbf{T}},Q_{2}^{\mathbf{T}})$
bounded by
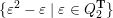 $\{\unicode[STIX]{x1D700}^{2}-\unicode[STIX]{x1D700}\mid \unicode[STIX]{x1D700}\in Q_{2}^{\mathbf{T}}\}$
.
$\{\unicode[STIX]{x1D700}^{2}-\unicode[STIX]{x1D700}\mid \unicode[STIX]{x1D700}\in Q_{2}^{\mathbf{T}}\}$
.
Construction 4.18. Let
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
be a tagged curve in
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
be a tagged curve in
![]() $\mathbf{C}^{\times }(\mathbf{S})$
. If
$\mathbf{C}^{\times }(\mathbf{S})$
. If
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\notin \mathbf{T}^{\times }$
, define
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\notin \mathbf{T}^{\times }$
, define
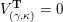 $V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=0$
; if
$V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=0$
; if
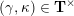 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }$
, define
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }$
, define
![]() $V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
by:
$V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
by:
-
–
 $V_{j}=0$
and
$V_{j}=0$
and
 $V_{\unicode[STIX]{x1D700}_{j}}=0$
, for
$V_{\unicode[STIX]{x1D700}_{j}}=0$
, for
 $j\neq \unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FE})$
;
$j\neq \unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FE})$
; -
–
 $V_{\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FE})}=\mathbf{k}$
;
$V_{\unicode[STIX]{x1D70B}_{\mathbf{T}}(\unicode[STIX]{x1D6FE})}=\mathbf{k}$
; -
–
 $V_{\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D70B}_{\boldsymbol{ T}}(\unicode[STIX]{x1D6FE})}}=1-\unicode[STIX]{x1D705}(a)$
if there exists a (unique)
$V_{\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D70B}_{\boldsymbol{ T}}(\unicode[STIX]{x1D6FE})}}=1-\unicode[STIX]{x1D705}(a)$
if there exists a (unique)
 $a$
with
$a$
with
 $\unicode[STIX]{x1D6FE}(a)\in \mathbf{P}$
.
$\unicode[STIX]{x1D6FE}(a)\in \mathbf{P}$
.
This construction, together with (4.4), gives a decorated representation
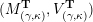 $(M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
associated with each tagged curve
$(M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
associated with each tagged curve
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
.
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
.
Let
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
be a tagged curve in
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
be a tagged curve in
![]() $\mathbf{C}^{\times }(\mathbf{S})$
and
$\mathbf{C}^{\times }(\mathbf{S})$
and
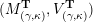 $(M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
the corresponding decorated representation. Construct
$(M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
the corresponding decorated representation. Construct
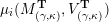 $\unicode[STIX]{x1D707}_{i}(M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
as in Appendix B. Now we prove that the map
$\unicode[STIX]{x1D707}_{i}(M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
as in Appendix B. Now we prove that the map
![]() $X^{\mathbf{T}}$
from tagged curves to string objects is independent of the choice of the admissible triangulation
$X^{\mathbf{T}}$
from tagged curves to string objects is independent of the choice of the admissible triangulation
![]() $\mathbf{T}$
.
$\mathbf{T}$
.
Theorem 4.19. For any two admissible triangulations
![]() $\mathbf{T}$
and
$\mathbf{T}$
and
![]() $\mathbf{T}^{\prime }$
, there is an equivalence
$\mathbf{T}^{\prime }$
, there is an equivalence
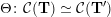 $\unicode[STIX]{x1D6E9}:{\mathcal{C}}(\mathbf{T})\simeq {\mathcal{C}}(\mathbf{T}^{\prime })$
such that
$\unicode[STIX]{x1D6E9}:{\mathcal{C}}(\mathbf{T})\simeq {\mathcal{C}}(\mathbf{T}^{\prime })$
such that
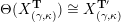 $\unicode[STIX]{x1D6E9}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})\cong X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}^{\prime }}$
, for every tagged curve
$\unicode[STIX]{x1D6E9}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})\cong X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}^{\prime }}$
, for every tagged curve
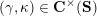 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
.
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
.
Proof. By Lemma A.2, any two admissible triangulations are connected by a sequence of
![]() $\diamondsuit$
-flips. Then using induction, it is sufficient to consider the case of
$\diamondsuit$
-flips. Then using induction, it is sufficient to consider the case of
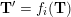 $\mathbf{T}^{\prime }=f_{i}(\mathbf{T})$
, a
$\mathbf{T}^{\prime }=f_{i}(\mathbf{T})$
, a
![]() $\diamondsuit$
-flip of
$\diamondsuit$
-flip of
![]() $\mathbf{T}$
. Recall that there is an equivalence
$\mathbf{T}$
. Recall that there is an equivalence
 $\widetilde{\unicode[STIX]{x1D707}}_{i}:{\mathcal{C}}(\mathbf{T})\simeq {\mathcal{C}}(\mathbf{T}^{\prime })$
.
$\widetilde{\unicode[STIX]{x1D707}}_{i}:{\mathcal{C}}(\mathbf{T})\simeq {\mathcal{C}}(\mathbf{T}^{\prime })$
.
We claim that for any tagged curve
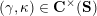 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
,
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
,
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{i}(M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})\cong (M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}^{\prime }},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}^{\prime }}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{i}(M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})\cong (M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}^{\prime }},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}^{\prime }}).\end{eqnarray}$$
Indeed, since
![]() $M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
and
$M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
and
![]() $V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
are constructed locally, we only need to prove that for each segment of
$V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
are constructed locally, we only need to prove that for each segment of
![]() $\unicode[STIX]{x1D6FE}$
crossing
$\unicode[STIX]{x1D6FE}$
crossing
![]() $i$
, the corresponding decorated representations
$i$
, the corresponding decorated representations
![]() $(M,V)$
of
$(M,V)$
of
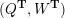 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
and
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
and
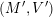 $(M^{\prime },V^{\prime })$
of
$(M^{\prime },V^{\prime })$
of
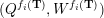 $(Q^{f_{i}(\mathbf{T})},W^{f_{i}(\mathbf{T})})$
satisfy
$(Q^{f_{i}(\mathbf{T})},W^{f_{i}(\mathbf{T})})$
satisfy
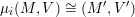 $\unicode[STIX]{x1D707}_{i}(M,V)\cong (M^{\prime },V^{\prime })$
. We list all the possible cases in Tables B.1 and B.2 in Appendix B for the first and second types of
$\unicode[STIX]{x1D707}_{i}(M,V)\cong (M^{\prime },V^{\prime })$
. We list all the possible cases in Tables B.1 and B.2 in Appendix B for the first and second types of
![]() $\diamondsuit$
-flips, respectively, up to symmetry. And in the same row of each case, we list the corresponding decorated representations, using Constructions 2.7 and 4.18. Then one can check (4.5) on a case by case basis.
$\diamondsuit$
-flips, respectively, up to symmetry. And in the same row of each case, we list the corresponding decorated representations, using Constructions 2.7 and 4.18. Then one can check (4.5) on a case by case basis.
Let
![]() $F^{\mathbf{T}}$
denote the equivalence (4.1). Consider the map
$F^{\mathbf{T}}$
denote the equivalence (4.1). Consider the map
![]() $\unicode[STIX]{x1D6F7}_{\mathbf{T}}$
from the set of (isoclasses of) objects in
$\unicode[STIX]{x1D6F7}_{\mathbf{T}}$
from the set of (isoclasses of) objects in
![]() ${\mathcal{C}}(\mathbf{T})$
to the set of (isoclasses of) decorated representations of
${\mathcal{C}}(\mathbf{T})$
to the set of (isoclasses of) decorated representations of
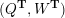 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
defined as follows. For any indecomposable object
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
defined as follows. For any indecomposable object
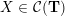 $X\in {\mathcal{C}}(\mathbf{T})$
which is not isomorphic to a direct summand of
$X\in {\mathcal{C}}(\mathbf{T})$
which is not isomorphic to a direct summand of
![]() $T_{\mathbf{T}}$
, define
$T_{\mathbf{T}}$
, define
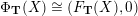 $\unicode[STIX]{x1D6F7}_{\mathbf{T}}(X)\cong (F_{\mathbf{T}}(X),0)$
; for any tagged curve
$\unicode[STIX]{x1D6F7}_{\mathbf{T}}(X)\cong (F_{\mathbf{T}}(X),0)$
; for any tagged curve
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }$
, define
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }$
, define
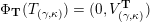 $\unicode[STIX]{x1D6F7}_{\mathbf{T}}(T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})})=(0,V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
. By definition, for any tagged curve
$\unicode[STIX]{x1D6F7}_{\mathbf{T}}(T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})})=(0,V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
. By definition, for any tagged curve
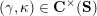 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
,
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
,
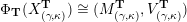 $\unicode[STIX]{x1D6F7}_{\mathbf{T}}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})\cong (M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
. Hence by (4.5), we have
$\unicode[STIX]{x1D6F7}_{\mathbf{T}}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})\cong (M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
. Hence by (4.5), we have
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{i}(\unicode[STIX]{x1D6F7}_{\mathbf{T}}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}))=\unicode[STIX]{x1D6F7}_{\boldsymbol{ T}^{\prime }}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}^{\prime }}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{i}(\unicode[STIX]{x1D6F7}_{\mathbf{T}}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}))=\unicode[STIX]{x1D6F7}_{\boldsymbol{ T}^{\prime }}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}^{\prime }}).\end{eqnarray}$$
By [Reference PlamondonPla11, Proposition 4.1],
![]() $\unicode[STIX]{x1D6F7}_{\mathbf{T}}$
is a bijection and
$\unicode[STIX]{x1D6F7}_{\mathbf{T}}$
is a bijection and
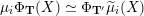 $\unicode[STIX]{x1D707}_{i}\unicode[STIX]{x1D6F7}_{\mathbf{T}}(X)\simeq \unicode[STIX]{x1D6F7}_{\mathbf{T}^{\prime }}\widetilde{\unicode[STIX]{x1D707}}_{i}(X)$
for any indecomposable object
$\unicode[STIX]{x1D707}_{i}\unicode[STIX]{x1D6F7}_{\mathbf{T}}(X)\simeq \unicode[STIX]{x1D6F7}_{\mathbf{T}^{\prime }}\widetilde{\unicode[STIX]{x1D707}}_{i}(X)$
for any indecomposable object
![]() $X$
in
$X$
in
![]() ${\mathcal{C}}(\mathbf{T})$
. Hence
${\mathcal{C}}(\mathbf{T})$
. Hence
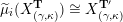 $\widetilde{\unicode[STIX]{x1D707}}_{i}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})\cong X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}^{\prime }}$
, as required.◻
$\widetilde{\unicode[STIX]{x1D707}}_{i}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})\cong X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}^{\prime }}$
, as required.◻
5 Homological interpretation of marked surfaces
5.1 AR-translation and AR-triangles
Note that we have chosen an admissible triangulation
![]() $\mathbf{T}$
and have a bijection
$\mathbf{T}$
and have a bijection
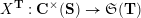 $X^{\mathbf{T}}:\mathbf{C}^{\times }(\mathbf{S})\rightarrow \mathfrak{S}(\mathbf{T})$
from the set of tagged curves to the set of string objects in the cluster category
$X^{\mathbf{T}}:\mathbf{C}^{\times }(\mathbf{S})\rightarrow \mathfrak{S}(\mathbf{T})$
from the set of tagged curves to the set of string objects in the cluster category
![]() ${\mathcal{C}}(\mathbf{T})$
. The tagged rotation (cf. Definition 3.2 and Figure 3)
${\mathcal{C}}(\mathbf{T})$
. The tagged rotation (cf. Definition 3.2 and Figure 3)
![]() $\unicode[STIX]{x1D70C}$
is a permutation on
$\unicode[STIX]{x1D70C}$
is a permutation on
![]() $\mathbf{C}^{\times }(\mathbf{S})$
while the shift functor
$\mathbf{C}^{\times }(\mathbf{S})$
while the shift functor
![]() $[1]$
in
$[1]$
in
![]() ${\mathcal{C}}(\mathbf{T})$
gives a permutation on the set
${\mathcal{C}}(\mathbf{T})$
gives a permutation on the set
![]() $\mathfrak{S}(\mathbf{T})$
. We will give a straightforward proof of Theorem 3.10, with a slight generalization to tagged curves.
$\mathfrak{S}(\mathbf{T})$
. We will give a straightforward proof of Theorem 3.10, with a slight generalization to tagged curves.
For a curve
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\mathbf{C}(\mathbf{S})$
with
$\mathbf{C}(\mathbf{S})$
with
 $\unicode[STIX]{x1D6FE}(1)\in \mathbf{M}$
, denote by
$\unicode[STIX]{x1D6FE}(1)\in \mathbf{M}$
, denote by
![]() $\operatorname{[+]}\unicode[STIX]{x1D6FE}$
the curve obtained from
$\operatorname{[+]}\unicode[STIX]{x1D6FE}$
the curve obtained from
![]() $\unicode[STIX]{x1D6FE}$
by moving
$\unicode[STIX]{x1D6FE}$
by moving
![]() $\unicode[STIX]{x1D6FE}(1)$
along the boundary anticlockwise to the next marked point; dually, for a curve
$\unicode[STIX]{x1D6FE}(1)$
along the boundary anticlockwise to the next marked point; dually, for a curve
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\mathbf{C}(\mathbf{S})$
with
$\mathbf{C}(\mathbf{S})$
with
 $\unicode[STIX]{x1D6FE}(0)\in \mathbf{M}$
, denote by
$\unicode[STIX]{x1D6FE}(0)\in \mathbf{M}$
, denote by
![]() $\unicode[STIX]{x1D6FE}\operatorname{[+]}$
the curve obtained from
$\unicode[STIX]{x1D6FE}\operatorname{[+]}$
the curve obtained from
![]() $\unicode[STIX]{x1D6FE}$
by moving
$\unicode[STIX]{x1D6FE}$
by moving
![]() $\unicode[STIX]{x1D6FE}(0)$
along the boundary anticlockwise to the next marked point. We first show the following lemma, where
$\unicode[STIX]{x1D6FE}(0)$
along the boundary anticlockwise to the next marked point. We first show the following lemma, where
![]() $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
is the word associated with
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
is the word associated with
![]() $\unicode[STIX]{x1D6FE}$
defined by the bijection (4.3) and
$\unicode[STIX]{x1D6FE}$
defined by the bijection (4.3) and
![]() $\operatorname{[+]}\mathfrak{m}$
and
$\operatorname{[+]}\mathfrak{m}$
and
![]() $\mathfrak{m}\operatorname{[+]}$
are defined in § 2.4. Recall that the set
$\mathfrak{m}\operatorname{[+]}$
are defined in § 2.4. Recall that the set
![]() $\mathbf{C}_{0}(\mathbf{S})$
consists of curves
$\mathbf{C}_{0}(\mathbf{S})$
consists of curves
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
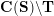 $\mathbf{C}(\mathbf{S})\setminus \mathbf{T}$
such that there exists a tagged curve
$\mathbf{C}(\mathbf{S})\setminus \mathbf{T}$
such that there exists a tagged curve
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
for some
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
for some
![]() $\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D705}$
.
Lemma 5.1. If
![]() $\unicode[STIX]{x1D6FE}$
is a curve in
$\unicode[STIX]{x1D6FE}$
is a curve in
![]() $\mathbf{C}_{0}(\mathbf{S})$
with
$\mathbf{C}_{0}(\mathbf{S})$
with
 $\unicode[STIX]{x1D6FE}(1)\in \mathbf{M}$
such that
$\unicode[STIX]{x1D6FE}(1)\in \mathbf{M}$
such that
![]() $\operatorname{[+]}\unicode[STIX]{x1D6FE}$
is in
$\operatorname{[+]}\unicode[STIX]{x1D6FE}$
is in
![]() $\mathbf{C}_{0}(\mathbf{S})$
, then
$\mathbf{C}_{0}(\mathbf{S})$
, then
![]() $\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
exists and
$\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
exists and
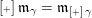 $\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}=\mathfrak{m}_{\operatorname{[+]}\unicode[STIX]{x1D6FE}}$
. Dually, if
$\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}=\mathfrak{m}_{\operatorname{[+]}\unicode[STIX]{x1D6FE}}$
. Dually, if
![]() $\unicode[STIX]{x1D6FE}$
is a curve in
$\unicode[STIX]{x1D6FE}$
is a curve in
![]() $\mathbf{C}_{0}(\mathbf{S})$
with
$\mathbf{C}_{0}(\mathbf{S})$
with
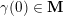 $\unicode[STIX]{x1D6FE}(0)\in \mathbf{M}$
such that
$\unicode[STIX]{x1D6FE}(0)\in \mathbf{M}$
such that
![]() $\unicode[STIX]{x1D6FE}\operatorname{[+]}$
is in
$\unicode[STIX]{x1D6FE}\operatorname{[+]}$
is in
![]() $\mathbf{C}_{0}(\mathbf{S})$
, then
$\mathbf{C}_{0}(\mathbf{S})$
, then
![]() $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}\operatorname{[+]}$
exists and
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}\operatorname{[+]}$
exists and
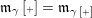 $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}\operatorname{[+]}=\mathfrak{m}_{\unicode[STIX]{x1D6FE}\operatorname{[+]}}$
.
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}\operatorname{[+]}=\mathfrak{m}_{\unicode[STIX]{x1D6FE}\operatorname{[+]}}$
.
Proof. We only prove the first assertion. By construction,
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\operatorname{[+]}\unicode[STIX]{x1D6FE}$
start at the same point, go through the same way at the beginning and then separate in a triangle as one of the following two forms, where
$\operatorname{[+]}\unicode[STIX]{x1D6FE}$
start at the same point, go through the same way at the beginning and then separate in a triangle as one of the following two forms, where
![]() $\unicode[STIX]{x1D6FF}$
is the boundary segment from
$\unicode[STIX]{x1D6FF}$
is the boundary segment from
![]() $\unicode[STIX]{x1D6FE}(1)$
to
$\unicode[STIX]{x1D6FE}(1)$
to
![]() $\operatorname{[+]}\unicode[STIX]{x1D6FE}(1)$
anticlockwise:
$\operatorname{[+]}\unicode[STIX]{x1D6FE}(1)$
anticlockwise:

By Lemma 4.10,
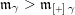 $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}>\mathfrak{m}_{\operatorname{[+]}\unicode[STIX]{x1D6FE}}$
. Moreover, since by construction
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}>\mathfrak{m}_{\operatorname{[+]}\unicode[STIX]{x1D6FE}}$
. Moreover, since by construction
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
![]() $\operatorname{[+]}\unicode[STIX]{x1D6FE}$
and
$\operatorname{[+]}\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FF}$
enclose a contractible triangle in the surface (i.e. a triangle which is homotopic to a point), by Lemma 4.10 again there is no curve
$\unicode[STIX]{x1D6FF}$
enclose a contractible triangle in the surface (i.e. a triangle which is homotopic to a point), by Lemma 4.10 again there is no curve
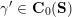 $\unicode[STIX]{x1D6FE}^{\prime }\in \mathbf{C}_{0}(\mathbf{S})$
starting at
$\unicode[STIX]{x1D6FE}^{\prime }\in \mathbf{C}_{0}(\mathbf{S})$
starting at
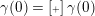 $\unicode[STIX]{x1D6FE}(0)=\operatorname{[+]}\unicode[STIX]{x1D6FE}(0)$
such that
$\unicode[STIX]{x1D6FE}(0)=\operatorname{[+]}\unicode[STIX]{x1D6FE}(0)$
such that
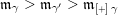 $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}>\mathfrak{m}_{\unicode[STIX]{x1D6FE}^{\prime }}>\mathfrak{m}_{\operatorname{[+]}\unicode[STIX]{x1D6FE}}$
. Therefore, the bijection (4.3) between curves in
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}>\mathfrak{m}_{\unicode[STIX]{x1D6FE}^{\prime }}>\mathfrak{m}_{\operatorname{[+]}\unicode[STIX]{x1D6FE}}$
. Therefore, the bijection (4.3) between curves in
![]() $\mathbf{C}_{0}(\mathbf{S})$
and words in
$\mathbf{C}_{0}(\mathbf{S})$
and words in
![]() $\overline{\mathfrak{X}}$
implies that
$\overline{\mathfrak{X}}$
implies that
![]() $\mathfrak{m}_{\operatorname{[+]}\unicode[STIX]{x1D6FE}}$
is the successor of
$\mathfrak{m}_{\operatorname{[+]}\unicode[STIX]{x1D6FE}}$
is the successor of
![]() $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
, i.e.
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
, i.e.
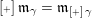 $\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}=\mathfrak{m}_{\operatorname{[+]}\unicode[STIX]{x1D6FE}}$
.◻
$\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}=\mathfrak{m}_{\operatorname{[+]}\unicode[STIX]{x1D6FE}}$
.◻
Theorem 5.2. Under the bijection
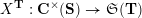 $X^{\mathbf{T}}:\mathbf{C}^{\times }(\mathbf{S})\rightarrow \mathfrak{S}(\mathbf{T})$
, the tagged rotation
$X^{\mathbf{T}}:\mathbf{C}^{\times }(\mathbf{S})\rightarrow \mathfrak{S}(\mathbf{T})$
, the tagged rotation
![]() $\unicode[STIX]{x1D70C}$
on
$\unicode[STIX]{x1D70C}$
on
![]() $\mathbf{C}^{\times }(\mathbf{S})$
becomes the shift
$\mathbf{C}^{\times }(\mathbf{S})$
becomes the shift
![]() $[1]$
on the set
$[1]$
on the set
![]() $\mathfrak{S}(\mathbf{T})$
, i.e. we have the following commutative diagram.
$\mathfrak{S}(\mathbf{T})$
, i.e. we have the following commutative diagram.

In particular, restricting to
![]() $\mathbf{A}^{\times }(\mathbf{S})$
, we get Theorem 3.10.
$\mathbf{A}^{\times }(\mathbf{S})$
, we get Theorem 3.10.
Proof. Let
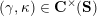 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
such that neither
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
such that neither
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
nor
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
nor
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
is in
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
is in
![]() $\mathbf{T}^{\times }$
. So both
$\mathbf{T}^{\times }$
. So both
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})$
are in
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})$
are in
![]() $\mathbf{C}_{0}(\mathbf{S})$
. Using Theorem 2.11, we show that
$\mathbf{C}_{0}(\mathbf{S})$
. Using Theorem 2.11, we show that
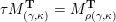 $\unicode[STIX]{x1D70F}M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
, where there are three cases, as follows.
$\unicode[STIX]{x1D70F}M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
, where there are three cases, as follows.
-
(1) If both
 $\unicode[STIX]{x1D6FE}(0)$
and
$\unicode[STIX]{x1D6FE}(0)$
and
 $\unicode[STIX]{x1D6FE}(1)$
are in
$\unicode[STIX]{x1D6FE}(1)$
are in
 $\mathbf{M}$
, then at least one of
$\mathbf{M}$
, then at least one of
 $\operatorname{[+]}\unicode[STIX]{x1D6FE}$
and
$\operatorname{[+]}\unicode[STIX]{x1D6FE}$
and
 $\unicode[STIX]{x1D6FE}\operatorname{[+]}$
is in
$\unicode[STIX]{x1D6FE}\operatorname{[+]}$
is in
 $\mathbf{C}_{0}(\mathbf{S})$
. This is because when they are both in
$\mathbf{C}_{0}(\mathbf{S})$
. This is because when they are both in
 $\mathbf{T}$
, one of
$\mathbf{T}$
, one of
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
and
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
and
 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
is forced to be in
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
is forced to be in
 $\mathbf{T}$
, which contradicts our assumption. Then we deduce that
$\mathbf{T}$
, which contradicts our assumption. Then we deduce that
 $\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})}=\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}\operatorname{[+]}$
by Lemma 5.1. On the other hand,
$\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})}=\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}\operatorname{[+]}$
by Lemma 5.1. On the other hand,
 $\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
contains no punctured letters by Lemma 4.8(3). Therefore, where
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
contains no punctured letters by Lemma 4.8(3). Therefore, where $$\begin{eqnarray}\unicode[STIX]{x1D70F}M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=M^{\mathbf{T}}(\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}\operatorname{[+]},\mathbf{k})=M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=M^{\mathbf{T}}(\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}\operatorname{[+]},\mathbf{k})=M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},\end{eqnarray}$$
 $\unicode[STIX]{x1D705}=\emptyset$
.
$\unicode[STIX]{x1D705}=\emptyset$
.
-
(2) If exactly one of
 $\unicode[STIX]{x1D6FE}(1)$
and
$\unicode[STIX]{x1D6FE}(1)$
and
 $\unicode[STIX]{x1D6FE}(0)$
is a puncture, assume that
$\unicode[STIX]{x1D6FE}(0)$
is a puncture, assume that
 $\unicode[STIX]{x1D6FE}(0)\in \mathbf{P}$
and
$\unicode[STIX]{x1D6FE}(0)\in \mathbf{P}$
and
 $\unicode[STIX]{x1D6FE}(1)\in \mathbf{M}$
without loss of generality. Then
$\unicode[STIX]{x1D6FE}(1)\in \mathbf{M}$
without loss of generality. Then
 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})=\operatorname{[+]}\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})=\operatorname{[+]}\unicode[STIX]{x1D6FE}$
,
 $\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})}=\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
, and Note that the part
$\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})}=\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}}$
, and Note that the part $$\begin{eqnarray}\unicode[STIX]{x1D70F}M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=M^{\mathbf{T}}(\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}},\mathbf{k}_{1-\unicode[STIX]{x1D705}(0)})=M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=M^{\mathbf{T}}(\operatorname{[+]}\mathfrak{m}_{\unicode[STIX]{x1D6FE}},\mathbf{k}_{1-\unicode[STIX]{x1D705}(0)})=M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}.\end{eqnarray}$$
 $\mathbf{k}_{1-\unicode[STIX]{x1D705}(0)}$
is constructed in Construction 4.14, which is determined by the tagging.
$\mathbf{k}_{1-\unicode[STIX]{x1D705}(0)}$
is constructed in Construction 4.14, which is determined by the tagging.
-
(3) If both
 $\unicode[STIX]{x1D6FE}(0)$
and
$\unicode[STIX]{x1D6FE}(0)$
and
 $\unicode[STIX]{x1D6FE}(1)$
are in
$\unicode[STIX]{x1D6FE}(1)$
are in
 $\mathbf{P}$
, then
$\mathbf{P}$
, then
 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}$
and  $$\begin{eqnarray}\unicode[STIX]{x1D70F}M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=M^{\mathbf{T}}(\mathfrak{m}_{\unicode[STIX]{x1D6FE}},\mathbf{k}_{1-\unicode[STIX]{x1D705}(0),1-\unicode[STIX]{x1D705}(1)})=M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=M^{\mathbf{T}}(\mathfrak{m}_{\unicode[STIX]{x1D6FE}},\mathbf{k}_{1-\unicode[STIX]{x1D705}(0),1-\unicode[STIX]{x1D705}(1)})=M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}.\end{eqnarray}$$
By [Reference Keller and ReitenKR07, Lemma in § 3.5], the shift
![]() $[1]$
in the triangulated category
$[1]$
in the triangulated category
![]() ${\mathcal{C}}(\mathbf{T})$
gives the AR-translation
${\mathcal{C}}(\mathbf{T})$
gives the AR-translation
![]() $\unicode[STIX]{x1D70F}$
in
$\unicode[STIX]{x1D70F}$
in
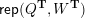 $\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
. Then we have
$\mathsf{rep}(Q^{\mathbf{T}},W^{\mathbf{T}})$
. Then we have
 $$\begin{eqnarray}\displaystyle X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}[1]=X_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}[1]=X_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}, & & \displaystyle\end{eqnarray}$$
for
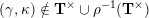 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\notin \mathbf{T}^{\times }\cup \unicode[STIX]{x1D70C}^{-1}(\mathbf{T}^{\times })$
. Furthermore,
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\notin \mathbf{T}^{\times }\cup \unicode[STIX]{x1D70C}^{-1}(\mathbf{T}^{\times })$
. Furthermore,
![]() $M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
is a projective representation for
$M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
is a projective representation for
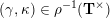 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \unicode[STIX]{x1D70C}^{-1}(\mathbf{T}^{\times })$
and
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \unicode[STIX]{x1D70C}^{-1}(\mathbf{T}^{\times })$
and
 $P_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}[1]=T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
for any
$P_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}[1]=T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
for any
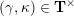 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }$
, where
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }$
, where
![]() $P_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
is the projective representation associated with the primitive idempotent indexed by
$P_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
is the projective representation associated with the primitive idempotent indexed by
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
. In particular,
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
. In particular,
 $$\begin{eqnarray}\{X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}[1]\mid (\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \unicode[STIX]{x1D70C}^{-1}(\mathbf{T}^{\times })\}=\{X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}\mid (\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }\}.\end{eqnarray}$$
$$\begin{eqnarray}\{X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}[1]\mid (\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \unicode[STIX]{x1D70C}^{-1}(\mathbf{T}^{\times })\}=\{X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}\mid (\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }\}.\end{eqnarray}$$
To finish the proof, we only need to show that
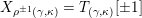 $X_{\unicode[STIX]{x1D70C}^{\pm 1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}=T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}[\pm 1]$
for
$X_{\unicode[STIX]{x1D70C}^{\pm 1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}=T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}[\pm 1]$
for
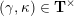 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }$
. There are two cases and we only deal with
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{T}^{\times }$
. There are two cases and we only deal with
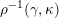 $\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
. Note that
$\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
. Note that
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
intersects
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
intersects
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
and the following diagrams show the local situation near this intersection.
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
and the following diagrams show the local situation near this intersection.

This enables us to deduce that
 $M_{\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
is not a projective presentation different from
$M_{\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
is not a projective presentation different from
![]() $P_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
. So
$P_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
. So
 $M_{\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=P_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
and
$M_{\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}=P_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
and
 $X_{\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}[1]=T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
.◻
$X_{\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}[1]=T_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
.◻
Remark 5.3. Using the description of AR-sequences in [Reference GeißGei99, § 5.4] and their relation with AR-triangles in [Reference Koenig and ZhuKZ08, Proposition 4.7], we can describe the AR-triangle ending at
![]() $X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
, where
$X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
, where
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
is a tagged curve in
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
is a tagged curve in
![]() $\mathbf{C}^{\times }(\mathbf{S})$
that does not connect two punctures. In the case when
$\mathbf{C}^{\times }(\mathbf{S})$
that does not connect two punctures. In the case when
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
does connect two punctures, the middle term of the AR-triangle is not a string object (and hence we do not have a description).
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
does connect two punctures, the middle term of the AR-triangle is not a string object (and hence we do not have a description).
In the following, let
![]() $\bar{\unicode[STIX]{x1D6FF}}$
be the completion of a curve
$\bar{\unicode[STIX]{x1D6FF}}$
be the completion of a curve
![]() $\unicode[STIX]{x1D6FF}$
which connects a marked point in
$\unicode[STIX]{x1D6FF}$
which connects a marked point in
![]() $\mathbf{M}$
and a puncture in
$\mathbf{M}$
and a puncture in
![]() $\mathbf{P}$
(see the top picture of Figure 1 for the induced orientation). Let
$\mathbf{P}$
(see the top picture of Figure 1 for the induced orientation). Let
 $X=X^{\mathbf{T}}$
and
$X=X^{\mathbf{T}}$
and
 $$\begin{eqnarray}X_{(\bar{\unicode[STIX]{x1D6FF}},\emptyset )}:=X_{(\unicode[STIX]{x1D6FF},\emptyset )}\oplus X_{(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D705}^{\prime })},\end{eqnarray}$$
$$\begin{eqnarray}X_{(\bar{\unicode[STIX]{x1D6FF}},\emptyset )}:=X_{(\unicode[STIX]{x1D6FF},\emptyset )}\oplus X_{(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D705}^{\prime })},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D705}^{\prime }(t)=1$
for
$\unicode[STIX]{x1D705}^{\prime }(t)=1$
for
![]() $t$
with
$t$
with
 $\unicode[STIX]{x1D6FF}(t)\in \mathbf{P}$
.
$\unicode[STIX]{x1D6FF}(t)\in \mathbf{P}$
.
-
– If both
 $\unicode[STIX]{x1D6FE}(0)$
and
$\unicode[STIX]{x1D6FE}(0)$
and
 $\unicode[STIX]{x1D6FE}(1)$
are in
$\unicode[STIX]{x1D6FE}(1)$
are in
 $\mathbf{M}$
(which implies
$\mathbf{M}$
(which implies
 $\unicode[STIX]{x1D705}=\emptyset$
), the AR-triangle ending at
$\unicode[STIX]{x1D705}=\emptyset$
), the AR-triangle ending at
 $X_{(\unicode[STIX]{x1D6FE},\emptyset )}$
is
$X_{(\unicode[STIX]{x1D6FE},\emptyset )}$
is  $$\begin{eqnarray}\displaystyle X_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\emptyset )}\rightarrow X_{(\unicode[STIX]{x1D6FE}\operatorname{[+]},\emptyset )}\oplus X_{(\operatorname{[+]}\unicode[STIX]{x1D6FE},\emptyset )}\rightarrow X_{(\unicode[STIX]{x1D6FE},\emptyset )}\;\rightarrow . & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\emptyset )}\rightarrow X_{(\unicode[STIX]{x1D6FE}\operatorname{[+]},\emptyset )}\oplus X_{(\operatorname{[+]}\unicode[STIX]{x1D6FE},\emptyset )}\rightarrow X_{(\unicode[STIX]{x1D6FE},\emptyset )}\;\rightarrow . & & \displaystyle \nonumber\end{eqnarray}$$
-
– If exactly one of
 $\unicode[STIX]{x1D6FE}(0)$
and
$\unicode[STIX]{x1D6FE}(0)$
and
 $\unicode[STIX]{x1D6FE}(1)$
is in
$\unicode[STIX]{x1D6FE}(1)$
is in
 $\mathbf{P}$
, the AR-triangle ending at
$\mathbf{P}$
, the AR-triangle ending at
 $X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
is
$X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}$
is  $$\begin{eqnarray}\displaystyle X_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}\rightarrow X_{(\operatorname{[+]}\bar{\unicode[STIX]{x1D6FE}},\emptyset )}\rightarrow X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}\;\rightarrow . & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}\rightarrow X_{(\operatorname{[+]}\bar{\unicode[STIX]{x1D6FE}},\emptyset )}\rightarrow X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}\;\rightarrow . & & \displaystyle \nonumber\end{eqnarray}$$

Figure 12. Cutting: five cases.
5.2 Cutting and Calabi–Yau reductions
Given a tagged curve
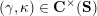 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
without self-intersections (i.e.
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})$
without self-intersections (i.e.
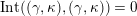 $\operatorname{Int}((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705}),(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705}))=0$
), let
$\operatorname{Int}((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705}),(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705}))=0$
), let
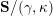 $\mathbf{S}/(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
be the marked surface obtained from
$\mathbf{S}/(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
be the marked surface obtained from
![]() $\mathbf{S}$
by cutting along
$\mathbf{S}$
by cutting along
![]() $\unicode[STIX]{x1D6FE}$
. More precisely, there are five cases as listed below.
$\unicode[STIX]{x1D6FE}$
. More precisely, there are five cases as listed below.
-
(1) If
 $\unicode[STIX]{x1D6FE}$
connects two different marked points
$\unicode[STIX]{x1D6FE}$
connects two different marked points
 $M_{1},M_{2}\in \mathbf{M}$
, then the resulting surface is shown as in the first column of Figure 12.
$M_{1},M_{2}\in \mathbf{M}$
, then the resulting surface is shown as in the first column of Figure 12. -
(2) If
 $\unicode[STIX]{x1D6FE}$
is a loop based on a marked point
$\unicode[STIX]{x1D6FE}$
is a loop based on a marked point
 $M\in \mathbf{M}$
, then the resulting surface is shown as in the second column of Figure 12.
$M\in \mathbf{M}$
, then the resulting surface is shown as in the second column of Figure 12. -
(3) If
 $\unicode[STIX]{x1D6FE}$
connects a marked point
$\unicode[STIX]{x1D6FE}$
connects a marked point
 $M\in \mathbf{M}$
and a puncture
$M\in \mathbf{M}$
and a puncture
 $P\in \mathbf{P}$
, then the resulting surface is shown as in the third column of Figure 12.
$P\in \mathbf{P}$
, then the resulting surface is shown as in the third column of Figure 12. -
(4) If
 $\unicode[STIX]{x1D6FE}$
connects two different punctures
$\unicode[STIX]{x1D6FE}$
connects two different punctures
 $P_{1},P_{2}\in \mathbf{P}$
, then the resulting surface is shown as in the fourth column of Figure 12.
$P_{1},P_{2}\in \mathbf{P}$
, then the resulting surface is shown as in the fourth column of Figure 12. -
(5) If
 $\unicode[STIX]{x1D6FE}$
is a loop based on a puncture
$\unicode[STIX]{x1D6FE}$
is a loop based on a puncture
 $P\in \mathbf{P}$
, then the resulting surface is shown as in the fifth column of Figure 12.
$P\in \mathbf{P}$
, then the resulting surface is shown as in the fifth column of Figure 12.
There is a canonical bijection between the tagged curves in
![]() $\mathbf{S}$
that do not intersect
$\mathbf{S}$
that do not intersect
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
and the tagged curves in
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
and the tagged curves in
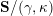 $\mathbf{S}/(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
. This bijection is straightforward to see for cases (1), (2), and (5), while there are several non-obvious correspondences between the tagged curves in the cases (3) and (4), which have been shown in Figure 13 (up to tagging). It is easy to check that this bijection preserves the intersection numbers.
$\mathbf{S}/(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
. This bijection is straightforward to see for cases (1), (2), and (5), while there are several non-obvious correspondences between the tagged curves in the cases (3) and (4), which have been shown in Figure 13 (up to tagging). It is easy to check that this bijection preserves the intersection numbers.

Figure 13. The non-trivial bijections for cutting.
Let
![]() $\mathbf{R}$
be a subset of an admissible triangulation
$\mathbf{R}$
be a subset of an admissible triangulation
![]() $\mathbf{T}$
. We define
$\mathbf{T}$
. We define
![]() $\mathbf{S}/\mathbf{R}$
to be the marked surface obtained from
$\mathbf{S}/\mathbf{R}$
to be the marked surface obtained from
![]() $\mathbf{S}$
by cutting successively along each tagged curve in
$\mathbf{S}$
by cutting successively along each tagged curve in
![]() $\mathbf{R}$
. Clearly the new marked surface is independent of the choice of orders of tagged curves in
$\mathbf{R}$
. Clearly the new marked surface is independent of the choice of orders of tagged curves in
![]() $\mathbf{R}$
and it inherits an admissible triangulation
$\mathbf{R}$
and it inherits an admissible triangulation
![]() $\mathbf{T}\setminus \mathbf{R}$
from
$\mathbf{T}\setminus \mathbf{R}$
from
![]() $\mathbf{S}$
. Denote by
$\mathbf{S}$
. Denote by
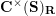 $\mathbf{C}^{\times }(\mathbf{S})_{\mathbf{R}}$
the set of tagged curves
$\mathbf{C}^{\times }(\mathbf{S})_{\mathbf{R}}$
the set of tagged curves
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
in
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
in
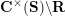 $\mathbf{C}^{\times }(\mathbf{S})\setminus \mathbf{R}$
that do not intersect the tagged curves in
$\mathbf{C}^{\times }(\mathbf{S})\setminus \mathbf{R}$
that do not intersect the tagged curves in
![]() $\mathbf{R}$
. By induction, there is a canonical bijection from
$\mathbf{R}$
. By induction, there is a canonical bijection from
 $\mathbf{C}^{\times }(\mathbf{S})_{\mathbf{R}}$
to
$\mathbf{C}^{\times }(\mathbf{S})_{\mathbf{R}}$
to
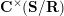 $\mathbf{C}^{\times }(\mathbf{S}/\mathbf{R})$
. For each tagged curve
$\mathbf{C}^{\times }(\mathbf{S}/\mathbf{R})$
. For each tagged curve
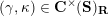 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})_{\mathbf{R}}$
, we still use the notation
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})_{\mathbf{R}}$
, we still use the notation
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
to denote its image under this bijection.
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
to denote its image under this bijection.
One the other hand, the object
 $R=\bigoplus _{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{R}}X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
is a direct summand of the canonical cluster tilting object
$R=\bigoplus _{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{R}}X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
is a direct summand of the canonical cluster tilting object
![]() $T_{\mathbf{T}}$
(cf. (4.2)) in
$T_{\mathbf{T}}$
(cf. (4.2)) in
![]() ${\mathcal{C}}(\mathbf{T})$
. Then the Calabi–Yau reduction
${\mathcal{C}}(\mathbf{T})$
. Then the Calabi–Yau reduction
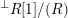 $^{\bot }R[1]/(R)$
is a
$^{\bot }R[1]/(R)$
is a
![]() $2$
-Calabi–Yau category with a cluster tilting object
$2$
-Calabi–Yau category with a cluster tilting object
![]() $T_{\mathbf{T}}\setminus R$
(see [Reference Iyama and YoshinoIY08, § 4]). The following lemma will be used in the proof of the main result in the next subsection. Indeed, this generalizes a result in [Reference Marsh and PaluMP14] on the relation between Calabi–Yau reduction and cutting to the punctured case.
$T_{\mathbf{T}}\setminus R$
(see [Reference Iyama and YoshinoIY08, § 4]). The following lemma will be used in the proof of the main result in the next subsection. Indeed, this generalizes a result in [Reference Marsh and PaluMP14] on the relation between Calabi–Yau reduction and cutting to the punctured case.
Lemma 5.4. Let
![]() $\mathbf{R}$
be a subset of an admissible triangulation
$\mathbf{R}$
be a subset of an admissible triangulation
![]() $\mathbf{T}$
and
$\mathbf{T}$
and
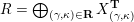 $R=\bigoplus _{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{R}}X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
. Then there is a canonical triangle equivalence
$R=\bigoplus _{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{R}}X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
. Then there is a canonical triangle equivalence
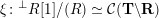 $\unicode[STIX]{x1D709}:^{\bot }R[1]/(R)\simeq {\mathcal{C}}(\mathbf{T}\setminus \mathbf{R})$
satisfying
$\unicode[STIX]{x1D709}:^{\bot }R[1]/(R)\simeq {\mathcal{C}}(\mathbf{T}\setminus \mathbf{R})$
satisfying
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})\cong X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}\setminus \mathbf{R}} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}(X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})\cong X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}\setminus \mathbf{R}} & & \displaystyle\end{eqnarray}$$
for each
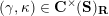 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})_{\mathbf{R}}$
.
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})_{\mathbf{R}}$
.
Proof. Notice that the corresponding biquiver with potential
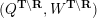 $(Q^{\mathbf{T}\setminus \mathbf{R}},W^{\mathbf{T}\setminus \mathbf{R}})$
can be obtained from the biquiver with potential
$(Q^{\mathbf{T}\setminus \mathbf{R}},W^{\mathbf{T}\setminus \mathbf{R}})$
can be obtained from the biquiver with potential
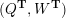 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
by deleting the vertices corresponding to the tagged curves in
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
by deleting the vertices corresponding to the tagged curves in
![]() $\mathbf{R}$
. By [Reference KellerKel13, Theorem 7.4], the canonical projection
$\mathbf{R}$
. By [Reference KellerKel13, Theorem 7.4], the canonical projection
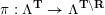 $\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D6EC}^{\mathbf{T}}\rightarrow \unicode[STIX]{x1D6EC}^{\mathbf{T}\setminus \mathbf{R}}$
induces the required equivalence
$\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D6EC}^{\mathbf{T}}\rightarrow \unicode[STIX]{x1D6EC}^{\mathbf{T}\setminus \mathbf{R}}$
induces the required equivalence
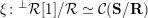 $\unicode[STIX]{x1D709}:^{\bot }{\mathcal{R}}[1]/{\mathcal{R}}\simeq {\mathcal{C}}(\mathbf{S}/\mathbf{R})$
. Furthermore, for each tagged curve
$\unicode[STIX]{x1D709}:^{\bot }{\mathcal{R}}[1]/{\mathcal{R}}\simeq {\mathcal{C}}(\mathbf{S}/\mathbf{R})$
. Furthermore, for each tagged curve
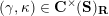 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})_{\mathbf{R}}$
, the support of the representation
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{C}^{\times }(\mathbf{S})_{\mathbf{R}}$
, the support of the representation
![]() $M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
does not contain the vertices corresponding to tagged curves in
$M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
does not contain the vertices corresponding to tagged curves in
![]() $\mathbf{R}$
. Hence it is preserved by the projection
$\mathbf{R}$
. Hence it is preserved by the projection
![]() $\unicode[STIX]{x1D70B}$
. Thus we deduce that (5.2) holds.◻
$\unicode[STIX]{x1D70B}$
. Thus we deduce that (5.2) holds.◻
5.3 Intersection numbers
Theorem 5.5. Let
![]() $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
![]() $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
be two tagged curves in
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
be two tagged curves in
![]() $\mathbf{C}^{\times }(\mathbf{S})$
. Then
$\mathbf{C}^{\times }(\mathbf{S})$
. Then
 $$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=\dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=\dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}})\end{eqnarray}$$
for any admissible triangulation
![]() $\mathbf{T}$
of
$\mathbf{T}$
of
![]() $\mathbf{S}$
.
$\mathbf{S}$
.
Proof. The proof is given in § 7. ◻
5.4 Connectedness of cluster exchange graphs
We apply our main result to study the exchange graph
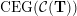 $\operatorname{CEG}({\mathcal{C}}(\mathbf{T}))$
of the cluster category
$\operatorname{CEG}({\mathcal{C}}(\mathbf{T}))$
of the cluster category
![]() ${\mathcal{C}}(\mathbf{T})$
.
${\mathcal{C}}(\mathbf{T})$
.
Corollary 5.6. The correspondence
![]() $X^{\mathbf{T}}$
in Theorem 4.16 induces bijections:
$X^{\mathbf{T}}$
in Theorem 4.16 induces bijections:
-
(i) between tagged curves without self-intersections in
 $\mathbf{S}$
and indecomposable rigid objects in
$\mathbf{S}$
and indecomposable rigid objects in
 ${\mathcal{C}}(\mathbf{T})$
;
${\mathcal{C}}(\mathbf{T})$
; -
(ii) between tagged triangulations of
 $\mathbf{S}$
and cluster tilting objects in
$\mathbf{S}$
and cluster tilting objects in
 ${\mathcal{C}}(\mathbf{T})$
.
${\mathcal{C}}(\mathbf{T})$
.
Moreover, under the last bijection, flip of tagged triangulations is compatible with mutation of cluster tilting objects.
Proof. By Remark 2.10, for any indecomposable representation
![]() $M$
of
$M$
of
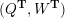 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
, if there is no tagged curve
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
, if there is no tagged curve
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
such that
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
such that
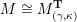 $M\cong M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
, then
$M\cong M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}}$
, then
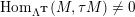 $\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}}}(M,\unicode[STIX]{x1D70F}M)\neq 0$
. This implies that
$\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}}}(M,\unicode[STIX]{x1D70F}M)\neq 0$
. This implies that
 $\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(M,M)\neq 0$
. Hence
$\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(M,M)\neq 0$
. Hence
![]() $M$
is not a rigid object in
$M$
is not a rigid object in
![]() ${\mathcal{C}}(\mathbf{T})$
. Thus, all rigid objects are string objects and hence the proposition follows from Theorem 5.5.◻
${\mathcal{C}}(\mathbf{T})$
. Thus, all rigid objects are string objects and hence the proposition follows from Theorem 5.5.◻
Theorem 5.7. The cluster exchange graph
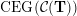 $\operatorname{CEG}({\mathcal{C}}(\mathbf{T}))$
is connected and
$\operatorname{CEG}({\mathcal{C}}(\mathbf{T}))$
is connected and
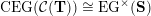 $\operatorname{CEG}({\mathcal{C}}(\mathbf{T}))\cong \operatorname{EG}^{\times }(\mathbf{S})$
. In particular, each rigid object in
$\operatorname{CEG}({\mathcal{C}}(\mathbf{T}))\cong \operatorname{EG}^{\times }(\mathbf{S})$
. In particular, each rigid object in
![]() ${\mathcal{C}}(\mathbf{T})$
is reachable.
${\mathcal{C}}(\mathbf{T})$
is reachable.
Proof. The isomorphism
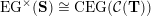 $\operatorname{EG}^{\times }(\mathbf{S})\cong \operatorname{CEG}({\mathcal{C}}(\mathbf{T}))$
of graphs follows directly from Corollary 5.6. The connectedness of
$\operatorname{EG}^{\times }(\mathbf{S})\cong \operatorname{CEG}({\mathcal{C}}(\mathbf{T}))$
of graphs follows directly from Corollary 5.6. The connectedness of
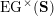 $\operatorname{EG}^{\times }(\mathbf{S})$
is proved in [Reference Fomin, Shapiro and ThurstonFST08, Proposition 7.10].◻
$\operatorname{EG}^{\times }(\mathbf{S})$
is proved in [Reference Fomin, Shapiro and ThurstonFST08, Proposition 7.10].◻
6 An example
Let
![]() $\mathbf{S}$
be a disk with three marked points on the boundary and two punctures in the interior. The corresponding cluster category
$\mathbf{S}$
be a disk with three marked points on the boundary and two punctures in the interior. The corresponding cluster category
![]() ${\mathcal{C}}(\mathbf{T})$
is the classical cluster category of type
${\mathcal{C}}(\mathbf{T})$
is the classical cluster category of type
![]() $\widetilde{D}_{5}$
. Let
$\widetilde{D}_{5}$
. Let
![]() $\mathbf{T}$
be the admissible triangulation shown in the top left picture of Figure 14.
$\mathbf{T}$
be the admissible triangulation shown in the top left picture of Figure 14.

Figure 14. An example.
Then the associated biquiver with potential
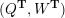 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
introduced in § 4.1 is as shown in the following diagram with
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
introduced in § 4.1 is as shown in the following diagram with
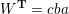 $W^{\mathbf{T}}=cba$
.
$W^{\mathbf{T}}=cba$
.

And the associated quiver with potential
 $(Q_{\mathbf{T}},W_{\mathbf{T}})$
introduced in § 3.2 is as shown in the following diagram with
$(Q_{\mathbf{T}},W_{\mathbf{T}})$
introduced in § 3.2 is as shown in the following diagram with
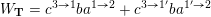 $W_{\mathbf{T}}=c^{3\rightarrow 1}ba^{1\rightarrow 2}+c^{3\rightarrow 1^{\prime }}ba^{1^{\prime }\rightarrow 2}$
(where the terms
$W_{\mathbf{T}}=c^{3\rightarrow 1}ba^{1\rightarrow 2}+c^{3\rightarrow 1^{\prime }}ba^{1^{\prime }\rightarrow 2}$
(where the terms
 $c^{3\rightarrow 1^{\prime }}ba^{1\rightarrow 2}$
and
$c^{3\rightarrow 1^{\prime }}ba^{1\rightarrow 2}$
and
 $c^{3\rightarrow 1}ba^{1\rightarrow 2}$
do not appear in
$c^{3\rightarrow 1}ba^{1\rightarrow 2}$
do not appear in
![]() $W_{\mathbf{T}}$
because they are not cycles).
$W_{\mathbf{T}}$
because they are not cycles).

We have
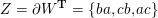 $Z=\unicode[STIX]{x2202}W^{\mathbf{T}}=\{ba,cb,ac\}$
. Then the biquiver
$Z=\unicode[STIX]{x2202}W^{\mathbf{T}}=\{ba,cb,ac\}$
. Then the biquiver
![]() $Q^{\mathbf{T}}$
with
$Q^{\mathbf{T}}$
with
![]() $Z$
is precisely the one in Example 2.2. Use the choice of disjoint subsets given in Example 2.3:
$Z$
is precisely the one in Example 2.2. Use the choice of disjoint subsets given in Example 2.3:
-
–
 $L_{+}(1)=\{c^{-1}>a_{1_{+}}>a\}$
and
$L_{+}(1)=\{c^{-1}>a_{1_{+}}>a\}$
and
 $L_{-}(1)=\{\unicode[STIX]{x1D700}_{1}^{-1}>a_{1_{-}}>\unicode[STIX]{x1D700}_{1}\}$
;
$L_{-}(1)=\{\unicode[STIX]{x1D700}_{1}^{-1}>a_{1_{-}}>\unicode[STIX]{x1D700}_{1}\}$
; -
–
 $L_{+}(2)=\{a^{-1}>a_{2_{+}}>b\}$
and
$L_{+}(2)=\{a^{-1}>a_{2_{+}}>b\}$
and
 $L_{-}(2)=\{a_{2_{-}}\}$
;
$L_{-}(2)=\{a_{2_{-}}\}$
; -
–
 $L_{+}(3)=\{b^{-1}>a_{3_{+}}>c\}$
and
$L_{+}(3)=\{b^{-1}>a_{3_{+}}>c\}$
and
 $L_{-}(3)=\{a_{3_{-}}>d\}$
;
$L_{-}(3)=\{a_{3_{-}}>d\}$
; -
–
 $L_{+}(4)=\{d^{-1}>a_{4_{+}}\}$
and
$L_{+}(4)=\{d^{-1}>a_{4_{+}}\}$
and
 $L_{-}(4)=\{\unicode[STIX]{x1D700}_{4}^{-1}>a_{4_{-}}>\unicode[STIX]{x1D700}_{4}\}$
.
$L_{-}(4)=\{\unicode[STIX]{x1D700}_{4}^{-1}>a_{4_{-}}>\unicode[STIX]{x1D700}_{4}\}$
.
Using Construction 4.7, the arc segments corresponding to direct letters are shown in the top pictures of Figure 14, and the inverse of letters corresponds to the reverse of direction of arc segments.
Consider the tagged curves
![]() $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
![]() $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
shown in the bottom left figure of Figure 14, where
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
shown in the bottom left figure of Figure 14, where
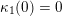 $\unicode[STIX]{x1D705}_{1}(0)=0$
and
$\unicode[STIX]{x1D705}_{1}(0)=0$
and
 $\unicode[STIX]{x1D705}_{2}(0)=1$
. The rotations
$\unicode[STIX]{x1D705}_{2}(0)=1$
. The rotations
 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
are shown in the bottom right picture of Figure 14. The intersection number between
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
are shown in the bottom right picture of Figure 14. The intersection number between
![]() $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
![]() $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
is
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
is
 $$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=1.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=1.\end{eqnarray}$$
On the representation side, since
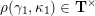 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})\in \mathbf{T}^{\times }$
, we have
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})\in \mathbf{T}^{\times }$
, we have
 $M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}}=0$
by Construction 4.14. Hence
$M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}}=0$
by Construction 4.14. Hence
 $$\begin{eqnarray}\displaystyle \dim \operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}}) & = & \displaystyle \dim \operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}}}(M_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}})\nonumber\\ \displaystyle & & \displaystyle +\dim \operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}}}(M_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}},M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}})\nonumber\\ \displaystyle & = & \displaystyle \dim \operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}}}(M_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim \operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}}) & = & \displaystyle \dim \operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}}}(M_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}})\nonumber\\ \displaystyle & & \displaystyle +\dim \operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}}}(M_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}},M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}})\nonumber\\ \displaystyle & = & \displaystyle \dim \operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}}}(M_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}}).\nonumber\end{eqnarray}$$
The words corresponding to
![]() $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})$
are
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})$
are
 $$\begin{eqnarray}\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}}=a_{4_{+}}a_{4-}^{-1}\quad \text{and}\quad \mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}=a_{3_{-}}c^{-1}\unicode[STIX]{x1D700}_{1}^{-1}cd^{-1}a_{4_{-}}^{-1},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}}=a_{4_{+}}a_{4-}^{-1}\quad \text{and}\quad \mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}=a_{3_{-}}c^{-1}\unicode[STIX]{x1D700}_{1}^{-1}cd^{-1}a_{4_{-}}^{-1},\end{eqnarray}$$
respectively. These two admissible words are precisely the two given in Example 2.12 and we have
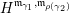 $H^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}$
contains only one element, which is
$H^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}$
contains only one element, which is
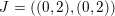 $J=((0,2),(0,2))$
containing one punctured letter
$J=((0,2),(0,2))$
containing one punctured letter
![]() $a_{4_{-}}^{-1}$
. Thus, we have
$a_{4_{-}}^{-1}$
. Thus, we have
 $$\begin{eqnarray}\displaystyle \dim \operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}}) & = & \displaystyle \dim _{\mathbf{k}}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}}}(M_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}})\nonumber\\ \displaystyle & = & \displaystyle \dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(\mathbf{k}_{\unicode[STIX]{x1D705}_{1}(0)},\mathbf{k}_{1-\unicode[STIX]{x1D705}_{2}(0)})\nonumber\\ \displaystyle & = & \displaystyle 1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim \operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}}) & = & \displaystyle \dim _{\mathbf{k}}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}}}(M_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}})\nonumber\\ \displaystyle & = & \displaystyle \dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(\mathbf{k}_{\unicode[STIX]{x1D705}_{1}(0)},\mathbf{k}_{1-\unicode[STIX]{x1D705}_{2}(0)})\nonumber\\ \displaystyle & = & \displaystyle 1.\nonumber\end{eqnarray}$$
7 Proof of Theorem 5.5
7.1 Adding marked points
Recall that we fix an admissible triangulation
![]() $\mathbf{T}$
of
$\mathbf{T}$
of
![]() $\mathbf{S}$
and two tagged curves
$\mathbf{S}$
and two tagged curves
![]() $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
![]() $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
in
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
in
![]() $\mathbf{C}^{\times }(\mathbf{S})$
.
$\mathbf{C}^{\times }(\mathbf{S})$
.
For technical reasons, we add some new marked points on the boundary of
![]() $\mathbf{S}$
as follows. Let
$\mathbf{S}$
as follows. Let
![]() $E$
be the set of marked points
$E$
be the set of marked points
![]() $P$
in
$P$
in
![]() $M$
that are endpoints of
$M$
that are endpoints of
![]() $\unicode[STIX]{x1D6FE}_{1}$
or
$\unicode[STIX]{x1D6FE}_{1}$
or
![]() $\unicode[STIX]{x1D6FE}_{2}$
. For each
$\unicode[STIX]{x1D6FE}_{2}$
. For each
![]() $P\in E$
, we add two marked points on each side of
$P\in E$
, we add two marked points on each side of
![]() $P$
on the boundary component containing
$P$
on the boundary component containing
![]() $P$
, denoted by
$P$
, denoted by
![]() $P_{l}^{\prime },P_{l}^{\prime \prime }$
, and
$P_{l}^{\prime },P_{l}^{\prime \prime }$
, and
![]() $P_{r}^{\prime },P_{r}^{\prime \prime }$
, respectively, see Figure 15.
$P_{r}^{\prime },P_{r}^{\prime \prime }$
, respectively, see Figure 15.

Figure 15. Adding marked points.
Let
![]() $\mathbf{S}^{\prime }$
be the new marked surface obtained from
$\mathbf{S}^{\prime }$
be the new marked surface obtained from
![]() $\mathbf{S}$
by adding these new marked points. For each
$\mathbf{S}$
by adding these new marked points. For each
![]() $P\in E$
, let
$P\in E$
, let
![]() $\mathbf{R}_{P}$
be the set of tagged curves as in Figure 15, where the right picture is for the case that
$\mathbf{R}_{P}$
be the set of tagged curves as in Figure 15, where the right picture is for the case that
![]() $P$
is a unique marked point on a boundary component. Take
$P$
is a unique marked point on a boundary component. Take
![]() $\mathbf{R}$
to be the disjoint union of
$\mathbf{R}$
to be the disjoint union of
![]() $\mathbf{R}_{P}$
for
$\mathbf{R}_{P}$
for
![]() $P\in E$
. Note that no two tagged curves in
$P\in E$
. Note that no two tagged curves in
![]() $\mathbf{R}$
cross each other and the cutting
$\mathbf{R}$
cross each other and the cutting
![]() $\mathbf{S}^{\prime }/\mathbf{R}$
is canonically homeomorphic to
$\mathbf{S}^{\prime }/\mathbf{R}$
is canonically homeomorphic to
![]() $\mathbf{S}$
. Hence
$\mathbf{S}$
. Hence
![]() $\mathbf{T}\cup \mathbf{R}$
is an admissible triangulation of
$\mathbf{T}\cup \mathbf{R}$
is an admissible triangulation of
![]() $\mathbf{S}^{\prime }$
.
$\mathbf{S}^{\prime }$
.
Lemma 7.1. Under the notation above, we have
 $$\begin{eqnarray}\dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}})=\dim _{\boldsymbol{ k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T}\cup \mathbf{R})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}\cup \mathbf{R}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}\cup \mathbf{R}}).\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}})=\dim _{\boldsymbol{ k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T}\cup \mathbf{R})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}\cup \mathbf{R}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}\cup \mathbf{R}}).\end{eqnarray}$$
Proof. Let
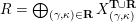 $R=\bigoplus _{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{R}}X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}\cup \mathbf{R}}$
, a direct summand of
$R=\bigoplus _{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})\in \mathbf{R}}X_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}\cup \mathbf{R}}$
, a direct summand of
![]() $T_{\mathbf{T}\cup \mathbf{R}}$
in
$T_{\mathbf{T}\cup \mathbf{R}}$
in
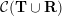 ${\mathcal{C}}(\mathbf{T}\cup \mathbf{R})$
. By Lemma 5.4, there is an equivalence
${\mathcal{C}}(\mathbf{T}\cup \mathbf{R})$
. By Lemma 5.4, there is an equivalence
 $\unicode[STIX]{x1D709}:^{\bot }R[1]/(R)\simeq {\mathcal{C}}(\mathbf{T})$
sending
$\unicode[STIX]{x1D709}:^{\bot }R[1]/(R)\simeq {\mathcal{C}}(\mathbf{T})$
sending
![]() $X_{(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})}^{\mathbf{T}\cup \mathbf{R}}$
to
$X_{(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})}^{\mathbf{T}\cup \mathbf{R}}$
to
![]() $X_{(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})}^{\mathbf{T}}$
,
$X_{(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})}^{\mathbf{T}}$
,
![]() $i=1,2$
(noting that any tagged curve in
$i=1,2$
(noting that any tagged curve in
![]() $\mathbf{R}$
does not cross
$\mathbf{R}$
does not cross
![]() $(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})$
). Hence,
$(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})$
). Hence,
 $$\begin{eqnarray}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}})\cong \operatorname{Ext}_{^{\bot }R[1]/(R)}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}\cup \mathbf{R}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}\cup \mathbf{R}}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T})}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}})\cong \operatorname{Ext}_{^{\bot }R[1]/(R)}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}\cup \mathbf{R}},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}\cup \mathbf{R}}).\end{eqnarray}$$
By [Reference Iyama and YoshinoIY08, Lemma 4.8], for any two objects
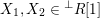 $X_{1},X_{2}\in ^{\bot }R[1]$
, there is an isomorphism
$X_{1},X_{2}\in ^{\bot }R[1]$
, there is an isomorphism
 $$\begin{eqnarray}\operatorname{Ext}_{^{\bot }R[1]/(R)}^{1}(X_{1},X_{2})\cong \operatorname{Ext}_{{\mathcal{C}}(\mathbf{T}\cup \mathbf{R})}^{1}(X_{1},X_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}_{^{\bot }R[1]/(R)}^{1}(X_{1},X_{2})\cong \operatorname{Ext}_{{\mathcal{C}}(\mathbf{T}\cup \mathbf{R})}^{1}(X_{1},X_{2}).\end{eqnarray}$$
Therefore, we get the equality, as required. ◻
Now we consider another admissible triangulation of
![]() $\mathbf{S}^{\prime }$
. For each
$\mathbf{S}^{\prime }$
. For each
![]() $P\in E$
, let
$P\in E$
, let
![]() $\mathbf{R}_{P}^{\prime }$
be the set of tagged curves as in Figure 16 and
$\mathbf{R}_{P}^{\prime }$
be the set of tagged curves as in Figure 16 and
![]() $\mathbf{R}^{\prime }$
the disjoint union of
$\mathbf{R}^{\prime }$
the disjoint union of
![]() $\mathbf{R}_{P}^{\prime }$
. By Lemma A.1, we can extend
$\mathbf{R}_{P}^{\prime }$
. By Lemma A.1, we can extend
![]() $\mathbf{R}^{\prime }$
to an admissible triangulation
$\mathbf{R}^{\prime }$
to an admissible triangulation
![]() $\mathbf{T}^{\prime }$
of
$\mathbf{T}^{\prime }$
of
![]() $\mathbf{S}^{\prime }$
. Due to Theorem 4.19, there is an equivalence
$\mathbf{S}^{\prime }$
. Due to Theorem 4.19, there is an equivalence
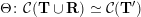 $\unicode[STIX]{x1D6E9}:{\mathcal{C}}(\mathbf{T}\cup \mathbf{R})\simeq {\mathcal{C}}(\mathbf{T}^{\prime })$
such that
$\unicode[STIX]{x1D6E9}:{\mathcal{C}}(\mathbf{T}\cup \mathbf{R})\simeq {\mathcal{C}}(\mathbf{T}^{\prime })$
such that
 $\unicode[STIX]{x1D6E9}(X_{(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})}^{\mathbf{T}\cup \mathbf{R}})\cong X_{(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})}^{\mathbf{T}^{\prime }}$
, for
$\unicode[STIX]{x1D6E9}(X_{(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})}^{\mathbf{T}\cup \mathbf{R}})\cong X_{(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})}^{\mathbf{T}^{\prime }}$
, for
![]() $i=1,2$
.
$i=1,2$
.
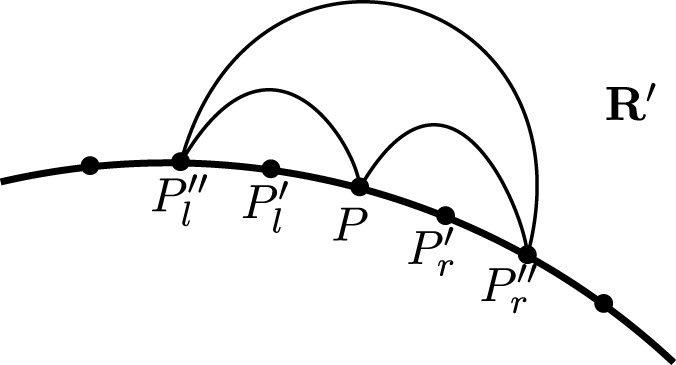
Figure 16. A partial triangulation associated with new marked points.
Therefore, this equivalence together with Lemma 7.1 implies that it is sufficient to prove
 $\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=\dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T}^{\prime })}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}^{\prime }},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}^{\prime }}).$
$\operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))=\dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T}^{\prime })}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}^{\prime }},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}^{\prime }}).$
Without loss of generality, fix representatives of
![]() $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
![]() $\unicode[STIX]{x1D6FE}_{2}$
with minimal intersections with
$\unicode[STIX]{x1D6FE}_{2}$
with minimal intersections with
![]() $\mathbf{T}^{\prime }$
and with each other. We further require that any intersection
$\mathbf{T}^{\prime }$
and with each other. We further require that any intersection
![]() $\unicode[STIX]{x1D6FE}_{1}\cap \unicode[STIX]{x1D6FE}_{2}$
does not intersect
$\unicode[STIX]{x1D6FE}_{1}\cap \unicode[STIX]{x1D6FE}_{2}$
does not intersect
![]() $\mathbf{T}^{\prime }$
.
$\mathbf{T}^{\prime }$
.
7.2 Normal intersections in the interior
We will use the notion of int-pairs from § 2.6. Recall that for any two admissible words
![]() $\mathfrak{m}$
and
$\mathfrak{m}$
and
![]() $\mathfrak{r}$
, we use
$\mathfrak{r}$
, we use
![]() $H^{\mathfrak{m},\mathfrak{r}}$
to denote the set of int-pairs from
$H^{\mathfrak{m},\mathfrak{r}}$
to denote the set of int-pairs from
![]() $\mathfrak{m}$
to
$\mathfrak{m}$
to
![]() $\mathfrak{r}$
. For
$\mathfrak{r}$
. For
 $v=0,1,2$
, let
$v=0,1,2$
, let
![]() $H_{v}^{\mathfrak{m},\mathfrak{r}}$
be the subset of
$H_{v}^{\mathfrak{m},\mathfrak{r}}$
be the subset of
![]() $H^{\mathfrak{m},\mathfrak{r}}$
consisting of int-pairs that contain
$H^{\mathfrak{m},\mathfrak{r}}$
consisting of int-pairs that contain
![]() $v$
punctured letters. Then
$v$
punctured letters. Then
 $H^{\mathfrak{m},\mathfrak{r}}=H_{0}^{\mathfrak{m},\mathfrak{r}}\cup H_{1}^{\mathfrak{m},\mathfrak{r}}\cup H_{2}^{\mathfrak{m},\mathfrak{r}}$
.
$H^{\mathfrak{m},\mathfrak{r}}=H_{0}^{\mathfrak{m},\mathfrak{r}}\cup H_{1}^{\mathfrak{m},\mathfrak{r}}\cup H_{2}^{\mathfrak{m},\mathfrak{r}}$
.
Lemma 7.2. Let
![]() $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})$
and
![]() $(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
be the two tagged curves in the theorem. There is a bijection between
$(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})$
be the two tagged curves in the theorem. There is a bijection between
![]() $\unicode[STIX]{x1D6FE}_{1}\cap \unicode[STIX]{x1D6FE}_{2}$
and the disjoint union
$\unicode[STIX]{x1D6FE}_{1}\cap \unicode[STIX]{x1D6FE}_{2}$
and the disjoint union
 $H_{0}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}\cup H_{0}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}}$
.
$H_{0}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}\cup H_{0}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}}$
.
Proof. Consider the triangle
![]() $\unicode[STIX]{x1D6E5}_{I}$
that contains an intersection
$\unicode[STIX]{x1D6E5}_{I}$
that contains an intersection
![]() $I$
in
$I$
in
![]() $\unicode[STIX]{x1D6FE}_{1}\cap \unicode[STIX]{x1D6FE}_{2}$
. Since the triangulation
$\unicode[STIX]{x1D6FE}_{1}\cap \unicode[STIX]{x1D6FE}_{2}$
. Since the triangulation
![]() $\mathbf{T}^{\prime }$
contains
$\mathbf{T}^{\prime }$
contains
![]() $\mathbf{R}^{\prime }$
which is constructed as in Figure 16, the following situations do not occur:
$\mathbf{R}^{\prime }$
which is constructed as in Figure 16, the following situations do not occur:

Therefore, we can deduce that
![]() $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
![]() $\unicode[STIX]{x1D6FE}_{2}$
share at least one curve in
$\unicode[STIX]{x1D6FE}_{2}$
share at least one curve in
![]() $\mathbf{T}^{\prime }$
. Hence the curve segments of
$\mathbf{T}^{\prime }$
. Hence the curve segments of
![]() $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
![]() $\unicode[STIX]{x1D6FE}_{2}$
near
$\unicode[STIX]{x1D6FE}_{2}$
near
![]() $I$
has the form in Figure 17 with four possible right (respectively left) parts, where
$I$
has the form in Figure 17 with four possible right (respectively left) parts, where
 $\{a,b\}=\{1,2\}$
.
$\{a,b\}=\{1,2\}$
.
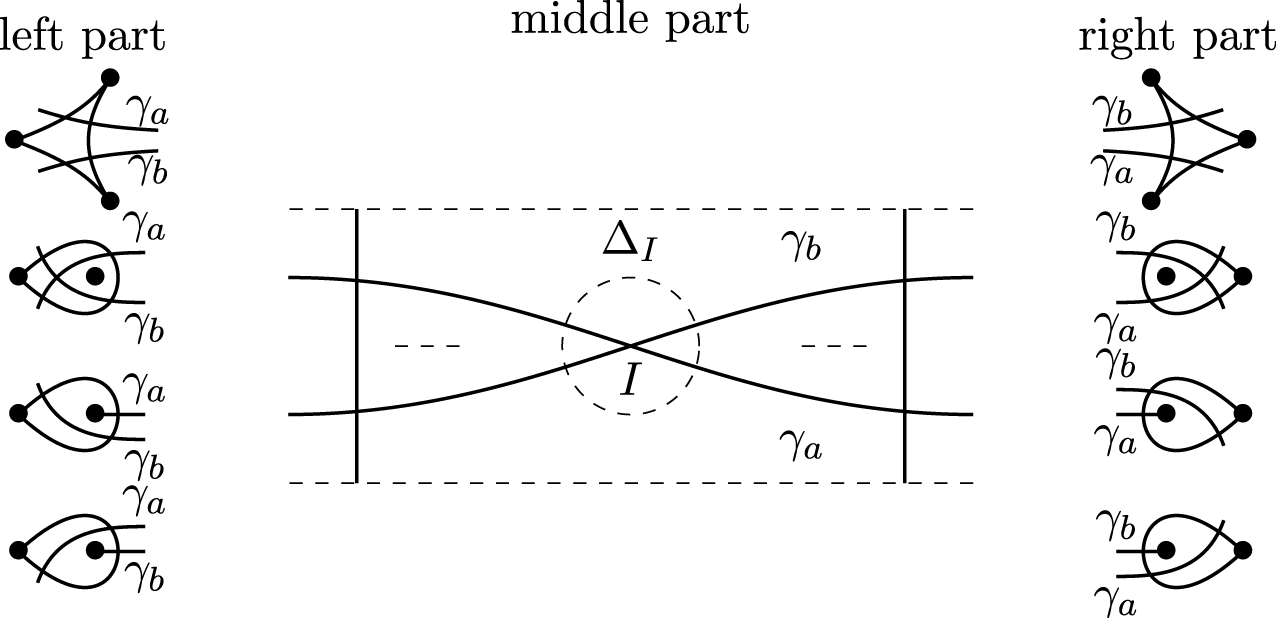
Figure 17. An interior intersection.
We will prove that such an intersection induces an int-pair in
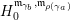 $H_{0}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{b}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{a})}}$
. Let
$H_{0}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{b}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{a})}}$
. Let
 $$\begin{eqnarray}\mathfrak{m}=\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{b}}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}\quad \text{and}\quad \mathfrak{r}=\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{a}}=\unicode[STIX]{x1D708}_{r}\cdots \unicode[STIX]{x1D708}_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}=\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{b}}=\unicode[STIX]{x1D714}_{m}\cdots \unicode[STIX]{x1D714}_{1}\quad \text{and}\quad \mathfrak{r}=\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{a}}=\unicode[STIX]{x1D708}_{r}\cdots \unicode[STIX]{x1D708}_{1}.\end{eqnarray}$$
Set
 $\mathfrak{r}^{\prime }=\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{a})}$
. We say that an arc segment is in
$\mathfrak{r}^{\prime }=\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{a})}$
. We say that an arc segment is in
![]() $\mathbf{R}^{\prime }$
if it is in a triangle formed by curves in
$\mathbf{R}^{\prime }$
if it is in a triangle formed by curves in
![]() $\mathbf{R}^{\prime }$
and boundary segments, and we say that a letter is from
$\mathbf{R}^{\prime }$
and boundary segments, and we say that a letter is from
![]() $\mathbf{R}^{\prime }$
if its corresponding arc segment is in
$\mathbf{R}^{\prime }$
if its corresponding arc segment is in
![]() $\mathbf{R}^{\prime }$
. Note that
$\mathbf{R}^{\prime }$
. Note that
![]() $\unicode[STIX]{x1D6FE}_{a}$
and
$\unicode[STIX]{x1D6FE}_{a}$
and
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{a})$
intersect the triangulation
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{a})$
intersect the triangulation
![]() $\mathbf{T}^{\prime }$
in the same way except for the parts near endpoints of
$\mathbf{T}^{\prime }$
in the same way except for the parts near endpoints of
![]() $\unicode[STIX]{x1D6FE}_{a}$
in
$\unicode[STIX]{x1D6FE}_{a}$
in
![]() $\mathbf{M}$
, where
$\mathbf{M}$
, where
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{a})$
intersects one more curve in
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{a})$
intersects one more curve in
![]() $\mathbf{R}^{\prime }$
than
$\mathbf{R}^{\prime }$
than
![]() $\unicode[STIX]{x1D6FE}_{a}$
as in Figure 18. Then
$\unicode[STIX]{x1D6FE}_{a}$
as in Figure 18. Then
 $\mathfrak{r}^{\prime }=x\unicode[STIX]{x1D708}_{r-1}\cdots \unicode[STIX]{x1D708}_{2}y$
, where
$\mathfrak{r}^{\prime }=x\unicode[STIX]{x1D708}_{r-1}\cdots \unicode[STIX]{x1D708}_{2}y$
, where
 $$\begin{eqnarray}x=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D708}_{r},\quad & \unicode[STIX]{x1D6FE}_{a}(1)\in \boldsymbol{ P}\\ \unicode[STIX]{x1D708}_{r+1}^{\prime }\unicode[STIX]{x1D708}_{r}^{\prime },\quad & \unicode[STIX]{x1D6FE}_{a}(1)\in \mathbf{M}\end{array}\right.\quad \text{and}\quad y=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D708}_{r},\quad & \unicode[STIX]{x1D6FE}_{a}(0)\in \mathbf{P}\\ \unicode[STIX]{x1D708}_{1}^{\prime }\unicode[STIX]{x1D708}_{0}^{\prime },\quad & \unicode[STIX]{x1D6FE}_{a}(0)\in \mathbf{M},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}x=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D708}_{r},\quad & \unicode[STIX]{x1D6FE}_{a}(1)\in \boldsymbol{ P}\\ \unicode[STIX]{x1D708}_{r+1}^{\prime }\unicode[STIX]{x1D708}_{r}^{\prime },\quad & \unicode[STIX]{x1D6FE}_{a}(1)\in \mathbf{M}\end{array}\right.\quad \text{and}\quad y=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D708}_{r},\quad & \unicode[STIX]{x1D6FE}_{a}(0)\in \mathbf{P}\\ \unicode[STIX]{x1D708}_{1}^{\prime }\unicode[STIX]{x1D708}_{0}^{\prime },\quad & \unicode[STIX]{x1D6FE}_{a}(0)\in \mathbf{M},\end{array}\right.\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D708}_{0}^{\prime }$
,
$\unicode[STIX]{x1D708}_{0}^{\prime }$
,
![]() $\unicode[STIX]{x1D708}_{1}^{\prime }$
,
$\unicode[STIX]{x1D708}_{1}^{\prime }$
,
![]() $\unicode[STIX]{x1D708}_{r}^{\prime }$
, and
$\unicode[STIX]{x1D708}_{r}^{\prime }$
, and
![]() $\unicode[STIX]{x1D708}_{r+1}^{\prime }$
are letters corresponding to arc segments of
$\unicode[STIX]{x1D708}_{r+1}^{\prime }$
are letters corresponding to arc segments of
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{a})$
in
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{a})$
in
![]() $\mathbf{R}^{\prime }$
. By Lemma 4.8(1) a letter in
$\mathbf{R}^{\prime }$
. By Lemma 4.8(1) a letter in
![]() $(\mathfrak{r}^{\prime })^{\pm 1}$
from
$(\mathfrak{r}^{\prime })^{\pm 1}$
from
![]() $\mathbf{R}^{\prime }$
is not smaller than any letter in
$\mathbf{R}^{\prime }$
is not smaller than any letter in
![]() $\mathfrak{m}^{\pm 1}$
or
$\mathfrak{m}^{\pm 1}$
or
![]() $\mathfrak{r}^{\pm 1}$
from
$\mathfrak{r}^{\pm 1}$
from
![]() $\mathbf{R}^{\prime }$
(cf. also Figure 18). In particular,
$\mathbf{R}^{\prime }$
(cf. also Figure 18). In particular,
![]() $(\mathfrak{r}^{\prime })^{\pm 1}$
and
$(\mathfrak{r}^{\prime })^{\pm 1}$
and
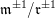 $\mathfrak{m}^{\pm 1}/\mathfrak{r}^{\pm 1}$
do not share letters from
$\mathfrak{m}^{\pm 1}/\mathfrak{r}^{\pm 1}$
do not share letters from
![]() $\mathbf{R}^{\prime }$
.
$\mathbf{R}^{\prime }$
.

Figure 18. The rotation of
![]() $\unicode[STIX]{x1D6FE}_{a}$
.
$\unicode[STIX]{x1D6FE}_{a}$
.
Without loss of generality, we assume that both of the orientations of
![]() $\unicode[STIX]{x1D6FE}_{a}$
and
$\unicode[STIX]{x1D6FE}_{a}$
and
![]() $\unicode[STIX]{x1D6FE}_{b}$
are from right to left in Figure 17. Then the curve segments in the middle part correspond to the subwords
$\unicode[STIX]{x1D6FE}_{b}$
are from right to left in Figure 17. Then the curve segments in the middle part correspond to the subwords
![]() $\mathfrak{m}_{(i,j)}$
and
$\mathfrak{m}_{(i,j)}$
and
![]() $\mathfrak{r}_{(h,l)}$
for some
$\mathfrak{r}_{(h,l)}$
for some
 $0<i<j<m$
,
$0<i<j<m$
,
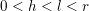 $0<h<l<r$
and the arc segments in the left (respectively right) part correspond to
$0<h<l<r$
and the arc segments in the left (respectively right) part correspond to
![]() $\unicode[STIX]{x1D714}_{j}$
and
$\unicode[STIX]{x1D714}_{j}$
and
![]() $\unicode[STIX]{x1D708}_{l}$
(respectively
$\unicode[STIX]{x1D708}_{l}$
(respectively
![]() $\unicode[STIX]{x1D714}_{i}$
and
$\unicode[STIX]{x1D714}_{i}$
and
![]() $\unicode[STIX]{x1D708}_{h}$
). By Lemma 4.8(2), we have
$\unicode[STIX]{x1D708}_{h}$
). By Lemma 4.8(2), we have
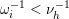 $\unicode[STIX]{x1D714}_{i}^{-1}<\unicode[STIX]{x1D708}_{h}^{-1}$
and
$\unicode[STIX]{x1D714}_{i}^{-1}<\unicode[STIX]{x1D708}_{h}^{-1}$
and
![]() $\unicode[STIX]{x1D714}_{j}<\unicode[STIX]{x1D708}_{l}$
. Thus
$\unicode[STIX]{x1D714}_{j}<\unicode[STIX]{x1D708}_{l}$
. Thus
 $J_{I}:=((i,j),(h,l))$
is an int-pair in
$J_{I}:=((i,j),(h,l))$
is an int-pair in
![]() $H_{0}^{\mathfrak{m},\mathfrak{r}}$
. Moreover, it is clear that any arc segment of
$H_{0}^{\mathfrak{m},\mathfrak{r}}$
. Moreover, it is clear that any arc segment of
![]() $\unicode[STIX]{x1D6FE}_{a}$
which connects a marked point in
$\unicode[STIX]{x1D6FE}_{a}$
which connects a marked point in
![]() $M$
does not appear in Figure 17. Therefore
$M$
does not appear in Figure 17. Therefore
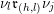 $\unicode[STIX]{x1D708}_{l}\mathfrak{r}_{(h,l)}\unicode[STIX]{x1D708}_{j}$
does not have letters from
$\unicode[STIX]{x1D708}_{l}\mathfrak{r}_{(h,l)}\unicode[STIX]{x1D708}_{j}$
does not have letters from
![]() $\mathbf{R}^{\prime }$
and thus it is also a subword of
$\mathbf{R}^{\prime }$
and thus it is also a subword of
![]() $\mathfrak{r}^{\prime }$
. Hence
$\mathfrak{r}^{\prime }$
. Hence
![]() $J_{I}$
is also an int-pair in
$J_{I}$
is also an int-pair in
![]() $H_{0}^{\mathfrak{m},\mathfrak{r}^{\prime }}$
and we obtain a map
$H_{0}^{\mathfrak{m},\mathfrak{r}^{\prime }}$
and we obtain a map
 $$\begin{eqnarray}\displaystyle J:\unicode[STIX]{x1D6FE}_{1}\cap \unicode[STIX]{x1D6FE}_{2} & \rightarrow & \displaystyle H_{0}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}\cup H_{0}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}}\nonumber\\ \displaystyle I & \mapsto & \displaystyle J_{I}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J:\unicode[STIX]{x1D6FE}_{1}\cap \unicode[STIX]{x1D6FE}_{2} & \rightarrow & \displaystyle H_{0}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}\cup H_{0}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}}\nonumber\\ \displaystyle I & \mapsto & \displaystyle J_{I}.\nonumber\end{eqnarray}$$
Clearly, different intersections correspond to different int-pairs. Hence the map
![]() $J$
is injective. So what is left to show is that the map
$J$
is injective. So what is left to show is that the map
![]() $J$
is surjective.
$J$
is surjective.
Let
 $J_{0}=((i,j),(h,l))$
be an int-pair in
$J_{0}=((i,j),(h,l))$
be an int-pair in
![]() $H_{0}^{\mathfrak{m},\mathfrak{r}^{\prime }}$
. Without loss of generality, we assume that
$H_{0}^{\mathfrak{m},\mathfrak{r}^{\prime }}$
. Without loss of generality, we assume that
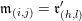 $\mathfrak{m}_{(i,j)}=\mathfrak{r}_{(h,l)}^{\prime }$
with
$\mathfrak{m}_{(i,j)}=\mathfrak{r}_{(h,l)}^{\prime }$
with
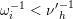 $\unicode[STIX]{x1D714}_{i}^{-1}<{\unicode[STIX]{x1D708}^{\prime }}_{h}^{-1}$
and
$\unicode[STIX]{x1D714}_{i}^{-1}<{\unicode[STIX]{x1D708}^{\prime }}_{h}^{-1}$
and
![]() $\unicode[STIX]{x1D714}_{j}<\unicode[STIX]{x1D708}_{l}^{\prime }$
, where
$\unicode[STIX]{x1D714}_{j}<\unicode[STIX]{x1D708}_{l}^{\prime }$
, where
![]() $\unicode[STIX]{x1D708}_{a}^{\prime }=\unicode[STIX]{x1D708}_{a}$
if
$\unicode[STIX]{x1D708}_{a}^{\prime }=\unicode[STIX]{x1D708}_{a}$
if
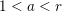 $1<a<r$
. Since
$1<a<r$
. Since
![]() $\mathfrak{m}$
and
$\mathfrak{m}$
and
![]() $\mathfrak{r}^{\prime }$
do not share letters from
$\mathfrak{r}^{\prime }$
do not share letters from
![]() $\mathbf{R}^{\prime }$
and
$\mathbf{R}^{\prime }$
and
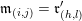 $\mathfrak{m}_{(i,j)}=\mathfrak{r}_{(h,l)}^{\prime }$
contains no punctured letters, we have
$\mathfrak{m}_{(i,j)}=\mathfrak{r}_{(h,l)}^{\prime }$
contains no punctured letters, we have
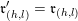 $\mathfrak{r}_{(h,l)}^{\prime }=\mathfrak{r}_{(h,l)}$
and the letters
$\mathfrak{r}_{(h,l)}^{\prime }=\mathfrak{r}_{(h,l)}$
and the letters
![]() $\unicode[STIX]{x1D714}_{i}$
,
$\unicode[STIX]{x1D714}_{i}$
,
![]() $\unicode[STIX]{x1D708}_{h}^{\prime }$
,
$\unicode[STIX]{x1D708}_{h}^{\prime }$
,
![]() $\unicode[STIX]{x1D714}_{j}$
, and
$\unicode[STIX]{x1D714}_{j}$
, and
![]() $\unicode[STIX]{x1D708}_{l}^{\prime }$
exist. Since
$\unicode[STIX]{x1D708}_{l}^{\prime }$
exist. Since
![]() $\unicode[STIX]{x1D714}_{i}^{-1}$
and
$\unicode[STIX]{x1D714}_{i}^{-1}$
and
![]() ${\unicode[STIX]{x1D708}^{\prime }}_{h}^{-1}$
are comparable, by Lemma 4.8(1) their corresponding arc segments are in the same triangle. Hence if
${\unicode[STIX]{x1D708}^{\prime }}_{h}^{-1}$
are comparable, by Lemma 4.8(1) their corresponding arc segments are in the same triangle. Hence if
![]() ${\unicode[STIX]{x1D708}_{h}^{\prime }}^{-1}$
is from
${\unicode[STIX]{x1D708}_{h}^{\prime }}^{-1}$
is from
![]() $\mathbf{R}^{\prime }$
, then so is
$\mathbf{R}^{\prime }$
, then so is
![]() $\unicode[STIX]{x1D714}_{i}^{-1}$
. This is a contradiction because
$\unicode[STIX]{x1D714}_{i}^{-1}$
. This is a contradiction because
![]() ${\unicode[STIX]{x1D708}_{h}^{\prime }}^{-1}$
is a letter in
${\unicode[STIX]{x1D708}_{h}^{\prime }}^{-1}$
is a letter in
![]() $(\mathfrak{r}^{\prime })^{-1}$
and
$(\mathfrak{r}^{\prime })^{-1}$
and
![]() $\unicode[STIX]{x1D714}_{i}^{-1}$
is in
$\unicode[STIX]{x1D714}_{i}^{-1}$
is in
![]() $\mathfrak{m}^{-1}$
. Hence neither
$\mathfrak{m}^{-1}$
. Hence neither
![]() $\unicode[STIX]{x1D708}_{h}^{\prime }$
nor
$\unicode[STIX]{x1D708}_{h}^{\prime }$
nor
![]() $\unicode[STIX]{x1D714}_{i}$
is from
$\unicode[STIX]{x1D714}_{i}$
is from
![]() $\mathbf{R}^{\prime }$
. Similarly, neither
$\mathbf{R}^{\prime }$
. Similarly, neither
![]() $\unicode[STIX]{x1D708}_{l}^{\prime }$
nor
$\unicode[STIX]{x1D708}_{l}^{\prime }$
nor
![]() $\unicode[STIX]{x1D714}_{j}$
is from
$\unicode[STIX]{x1D714}_{j}$
is from
![]() $\mathbf{R}^{\prime }$
. In particular, their corresponding arc segments do not connect to a marked point in
$\mathbf{R}^{\prime }$
. In particular, their corresponding arc segments do not connect to a marked point in
![]() $\mathbf{M}$
and we have
$\mathbf{M}$
and we have
![]() $\unicode[STIX]{x1D708}_{h}^{\prime }=\unicode[STIX]{x1D708}_{h}$
and
$\unicode[STIX]{x1D708}_{h}^{\prime }=\unicode[STIX]{x1D708}_{h}$
and
![]() $\unicode[STIX]{x1D708}_{l}^{\prime }=\unicode[STIX]{x1D708}_{l}$
. Then the curve segments corresponding to
$\unicode[STIX]{x1D708}_{l}^{\prime }=\unicode[STIX]{x1D708}_{l}$
. Then the curve segments corresponding to
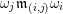 $\unicode[STIX]{x1D714}_{j}\mathfrak{m}_{(i,j)}\unicode[STIX]{x1D714}_{i}$
and
$\unicode[STIX]{x1D714}_{j}\mathfrak{m}_{(i,j)}\unicode[STIX]{x1D714}_{i}$
and
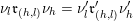 $\unicode[STIX]{x1D708}_{l}\mathfrak{r}_{(h,l)}\unicode[STIX]{x1D708}_{h}=\unicode[STIX]{x1D708}_{l}^{\prime }\mathfrak{r}_{(h,l)}^{\prime }\unicode[STIX]{x1D708}_{h}^{\prime }$
are of the form in Figure 17 (note that the left/right parts are the cases in Figure 10(1), where neither
$\unicode[STIX]{x1D708}_{l}\mathfrak{r}_{(h,l)}\unicode[STIX]{x1D708}_{h}=\unicode[STIX]{x1D708}_{l}^{\prime }\mathfrak{r}_{(h,l)}^{\prime }\unicode[STIX]{x1D708}_{h}^{\prime }$
are of the form in Figure 17 (note that the left/right parts are the cases in Figure 10(1), where neither
![]() $\unicode[STIX]{x1D6FE}_{i}$
connect to marked points in
$\unicode[STIX]{x1D6FE}_{i}$
connect to marked points in
![]() $\mathbf{M}$
). By construction, we see that
$\mathbf{M}$
). By construction, we see that
![]() $J_{0}$
is in the image of the map
$J_{0}$
is in the image of the map
![]() $J$
above, as required.◻
$J$
above, as required.◻
For an int-pair
![]() $J$
without punctured letters, since
$J$
without punctured letters, since
![]() $A_{J}\cong \mathbf{k}$
, the unique one-dimensional
$A_{J}\cong \mathbf{k}$
, the unique one-dimensional
![]() $A_{J}$
-module is
$A_{J}$
-module is
![]() $\mathbf{k}$
. Then
$\mathbf{k}$
. Then
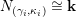 $N_{(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})}\cong \mathbf{k}$
as
$N_{(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D705}_{i})}\cong \mathbf{k}$
as
![]() $A_{J}$
-modules (cf. Notation 2.13). So we have the following consequence:
$A_{J}$
-modules (cf. Notation 2.13). So we have the following consequence:
 $$\begin{eqnarray}\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})=\mathop{\sum }_{\{a,b\}=\{1,2\}}\mathop{\sum }_{J\in H_{0}^{\mathfrak{ m}_{\unicode[STIX]{x1D6FE}_{a}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b})}}}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Int}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})=\mathop{\sum }_{\{a,b\}=\{1,2\}}\mathop{\sum }_{J\in H_{0}^{\mathfrak{ m}_{\unicode[STIX]{x1D6FE}_{a}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b})}}}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}).\end{eqnarray}$$
7.3 Tagged intersections at the ends
Recall that
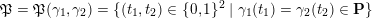 $\mathfrak{P}=\mathfrak{P}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})=\{(t_{1},t_{2})\in \{0,1\}^{2}\mid \unicode[STIX]{x1D6FE}_{1}(t_{1})=\unicode[STIX]{x1D6FE}_{2}(t_{2})\in \mathbf{P}\}$
is the set of intersections between
$\mathfrak{P}=\mathfrak{P}(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})=\{(t_{1},t_{2})\in \{0,1\}^{2}\mid \unicode[STIX]{x1D6FE}_{1}(t_{1})=\unicode[STIX]{x1D6FE}_{2}(t_{2})\in \mathbf{P}\}$
is the set of intersections between
![]() $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
![]() $\unicode[STIX]{x1D6FE}_{2}$
at
$\unicode[STIX]{x1D6FE}_{2}$
at
![]() $\mathbf{P}$
. Let
$\mathbf{P}$
. Let
 $$\begin{eqnarray}\mathfrak{P}_{1}=\{(t_{1},t_{2})\in \mathfrak{P}\mid \unicode[STIX]{x1D6FE}_{1}|_{t_{1}\rightarrow (1-t_{1})}\nsim \unicode[STIX]{x1D6FE}_{2}|_{t_{2}\rightarrow (1-t_{2})}\}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{P}_{1}=\{(t_{1},t_{2})\in \mathfrak{P}\mid \unicode[STIX]{x1D6FE}_{1}|_{t_{1}\rightarrow (1-t_{1})}\nsim \unicode[STIX]{x1D6FE}_{2}|_{t_{2}\rightarrow (1-t_{2})}\}\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathfrak{T}_{1}=\{(t_{1},t_{2})\in \mathfrak{P}_{1}\mid \unicode[STIX]{x1D705}_{1}(t_{1})\neq \unicode[STIX]{x1D705}_{2}(t_{2})\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{T}_{1}=\{(t_{1},t_{2})\in \mathfrak{P}_{1}\mid \unicode[STIX]{x1D705}_{1}(t_{1})\neq \unicode[STIX]{x1D705}_{2}(t_{2})\}.\end{eqnarray}$$
There is an analogue result of Lemma 7.2 for
![]() $\mathfrak{P}_{1}$
.
$\mathfrak{P}_{1}$
.
Lemma 7.3. There is a bijection between
![]() $\mathfrak{P}_{1}$
and the disjoint union
$\mathfrak{P}_{1}$
and the disjoint union
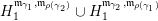 $H_{1}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}\cup H_{1}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}}$
.
$H_{1}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}\cup H_{1}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}}$
.
Proof. Each intersection in
![]() $\mathfrak{P}_{1}$
has the form in Figure 19 with four possible right parts and
$\mathfrak{P}_{1}$
has the form in Figure 19 with four possible right parts and
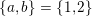 $\{a,b\}=\{1,2\}$
. Then the required bijection follows from a proof similar to that of Lemma 7.2.◻
$\{a,b\}=\{1,2\}$
. Then the required bijection follows from a proof similar to that of Lemma 7.2.◻

Figure 19. A punctured intersection.
For an intersection
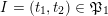 $I=(t_{1},t_{2})\in \mathfrak{P}_{1}$
, let
$I=(t_{1},t_{2})\in \mathfrak{P}_{1}$
, let
![]() $J_{I}$
be the corresponding int-pair in
$J_{I}$
be the corresponding int-pair in
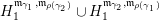 $H_{1}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}\cup H_{1}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}}$
. Then we have the associated algebra
$H_{1}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}\cup H_{1}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}}$
. Then we have the associated algebra
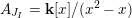 $A_{J_{I}}=\mathbf{k}[x]/(x^{2}-x)$
and
$A_{J_{I}}=\mathbf{k}[x]/(x^{2}-x)$
and
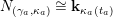 $N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})}\cong \mathbf{k}_{\unicode[STIX]{x1D705}_{a}(t_{a})}$
and
$N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})}\cong \mathbf{k}_{\unicode[STIX]{x1D705}_{a}(t_{a})}$
and
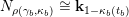 $N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}\cong \mathbf{k}_{1-\unicode[STIX]{x1D705}_{b}(t_{b})}$
as
$N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}\cong \mathbf{k}_{1-\unicode[STIX]{x1D705}_{b}(t_{b})}$
as
![]() $A_{J_{I}}$
-modules (cf. Notation 2.13), for
$A_{J_{I}}$
-modules (cf. Notation 2.13), for
 $\{a,b\}=\{1,2\}$
. Using the formula (2.1), we have
$\{a,b\}=\{1,2\}$
. Using the formula (2.1), we have
 $$\begin{eqnarray}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J_{I}}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{for }(t_{1},t_{2})\in \mathfrak{T}_{1},\\ 0\quad & \text{for }(t_{1},t_{2})\notin \mathfrak{T}_{1}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J_{I}}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{for }(t_{1},t_{2})\in \mathfrak{T}_{1},\\ 0\quad & \text{for }(t_{1},t_{2})\notin \mathfrak{T}_{1}.\end{array}\right.\end{eqnarray}$$
Hence, we obtain a consequence of Lemma 7.3:
 $$\begin{eqnarray}|\mathfrak{T}_{1}|=\mathop{\sum }_{\{a,b\}=\{1,2\}}\mathop{\sum }_{J\in H_{1}^{\mathfrak{ m}_{\unicode[STIX]{x1D6FE}_{a}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b})}}}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}).\end{eqnarray}$$
$$\begin{eqnarray}|\mathfrak{T}_{1}|=\mathop{\sum }_{\{a,b\}=\{1,2\}}\mathop{\sum }_{J\in H_{1}^{\mathfrak{ m}_{\unicode[STIX]{x1D6FE}_{a}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b})}}}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}).\end{eqnarray}$$
Let
 $$\begin{eqnarray}\mathfrak{P}_{2}=\{(t_{1},t_{2})\in \mathfrak{P}\mid \unicode[STIX]{x1D6FE}_{1}|_{t_{1}\rightarrow (1-t_{1})}\sim \unicode[STIX]{x1D6FE}_{2}|_{t_{2}\rightarrow (1-t_{2})},\unicode[STIX]{x1D6FE}_{1}(1-t_{1})=\unicode[STIX]{x1D6FE}_{2}(1-t_{2})\in \mathbf{P}\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{P}_{2}=\{(t_{1},t_{2})\in \mathfrak{P}\mid \unicode[STIX]{x1D6FE}_{1}|_{t_{1}\rightarrow (1-t_{1})}\sim \unicode[STIX]{x1D6FE}_{2}|_{t_{2}\rightarrow (1-t_{2})},\unicode[STIX]{x1D6FE}_{1}(1-t_{1})=\unicode[STIX]{x1D6FE}_{2}(1-t_{2})\in \mathbf{P}\}.\end{eqnarray}$$
Observe that for each
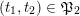 $(t_{1},t_{2})\in \mathfrak{P}_{2}$
,
$(t_{1},t_{2})\in \mathfrak{P}_{2}$
,
 $(1-t_{1},1-t_{2})$
is also in
$(1-t_{1},1-t_{2})$
is also in
![]() $\mathfrak{P}_{2}$
. We call them twin intersections (at punctures). Clearly, there is at most one pair of twin intersections in
$\mathfrak{P}_{2}$
. We call them twin intersections (at punctures). Clearly, there is at most one pair of twin intersections in
![]() $\mathfrak{P}_{2}$
. Let
$\mathfrak{P}_{2}$
. Let
 $$\begin{eqnarray}\mathfrak{T}_{2}=\{(t_{1},t_{2})\in \mathfrak{P}_{2}\mid \unicode[STIX]{x1D705}_{1}(t_{1})\neq \unicode[STIX]{x1D705}_{2}(t_{2}),\unicode[STIX]{x1D705}_{1}(1-t_{1})\neq \unicode[STIX]{x1D705}_{2}(1-t_{2})\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{T}_{2}=\{(t_{1},t_{2})\in \mathfrak{P}_{2}\mid \unicode[STIX]{x1D705}_{1}(t_{1})\neq \unicode[STIX]{x1D705}_{2}(t_{2}),\unicode[STIX]{x1D705}_{1}(1-t_{1})\neq \unicode[STIX]{x1D705}_{2}(1-t_{2})\}.\end{eqnarray}$$
Suppose that there is a (unique) pair of twin intersections
![]() $(t_{1},t_{2})$
and
$(t_{1},t_{2})$
and
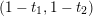 $(1-t_{1},1-t_{2})$
in
$(1-t_{1},1-t_{2})$
in
![]() $\mathfrak{P}_{2}$
. Then both the endpoints of
$\mathfrak{P}_{2}$
. Then both the endpoints of
![]() $\unicode[STIX]{x1D6FE}_{i}$
are in
$\unicode[STIX]{x1D6FE}_{i}$
are in
![]() $\mathbf{P}$
and thus
$\mathbf{P}$
and thus
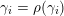 $\unicode[STIX]{x1D6FE}_{i}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{i})$
. Reversing one of
$\unicode[STIX]{x1D6FE}_{i}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{i})$
. Reversing one of
![]() $\unicode[STIX]{x1D6FE}_{i}$
if necessary, assume that
$\unicode[STIX]{x1D6FE}_{i}$
if necessary, assume that
![]() $\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
. So
$\unicode[STIX]{x1D6FE}_{1}\sim \unicode[STIX]{x1D6FE}_{2}$
. So
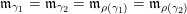 $\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}}=\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}}=\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}=\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}$
. Then this pair of twin intersections induces the int-pairs
$\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}}=\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}}=\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}=\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}$
. Then this pair of twin intersections induces the int-pairs
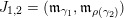 $J_{1,2}=(\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})})$
in
$J_{1,2}=(\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})})$
in
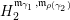 $H_{2}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}$
and
$H_{2}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{1}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{2})}}$
and
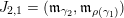 $J_{2,1}=(\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})})$
in
$J_{2,1}=(\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})})$
in
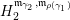 $H_{2}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}}$
, which are the only ones with two punctured letters. In this case, for any
$H_{2}^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{2}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{1})}}$
, which are the only ones with two punctured letters. In this case, for any
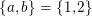 $\{a,b\}=\{1,2\}$
we have
$\{a,b\}=\{1,2\}$
we have
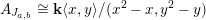 $A_{J_{a,b}}\cong \mathbf{k}\langle x,y\rangle /(x^{2}-x,y^{2}-y)$
and
$A_{J_{a,b}}\cong \mathbf{k}\langle x,y\rangle /(x^{2}-x,y^{2}-y)$
and
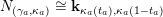 $N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})}\cong \mathbf{k}_{\unicode[STIX]{x1D705}_{a}(t_{a}),\unicode[STIX]{x1D705}_{a}(1-t_{a})}$
and
$N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})}\cong \mathbf{k}_{\unicode[STIX]{x1D705}_{a}(t_{a}),\unicode[STIX]{x1D705}_{a}(1-t_{a})}$
and
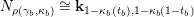 $N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}\cong \mathbf{k}_{1-\unicode[STIX]{x1D705}_{b}(t_{b}),1-\unicode[STIX]{x1D705}_{b}(1-t_{b})}$
as
$N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}\cong \mathbf{k}_{1-\unicode[STIX]{x1D705}_{b}(t_{b}),1-\unicode[STIX]{x1D705}_{b}(1-t_{b})}$
as
![]() $A_{J_{a,b}}$
-modules (cf. Notation 2.13). Using the formula (2.2), we have
$A_{J_{a,b}}$
-modules (cf. Notation 2.13). Using the formula (2.2), we have
 $$\begin{eqnarray}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J_{a,b}}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{for }(t_{1},t_{2})\in \mathfrak{T}_{2},\\ 0\quad & \text{for }(t_{1},t_{2})\notin \mathfrak{T}_{2},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J_{a,b}}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{for }(t_{1},t_{2})\in \mathfrak{T}_{2},\\ 0\quad & \text{for }(t_{1},t_{2})\notin \mathfrak{T}_{2},\end{array}\right.\end{eqnarray}$$
and hence
 $$\begin{eqnarray}|\mathfrak{T}_{2}|=\mathop{\sum }_{\{a,b\}=\{1,2\}}\mathop{\sum }_{J\in H_{2}^{\mathfrak{ m}_{\unicode[STIX]{x1D6FE}_{a}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b})}}}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}).\end{eqnarray}$$
$$\begin{eqnarray}|\mathfrak{T}_{2}|=\mathop{\sum }_{\{a,b\}=\{1,2\}}\mathop{\sum }_{J\in H_{2}^{\mathfrak{ m}_{\unicode[STIX]{x1D6FE}_{a}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b})}}}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}).\end{eqnarray}$$
7.4 Summary
By definition, we have
 $$\begin{eqnarray}|\mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))|=|\mathfrak{T}_{1}|+|\mathfrak{T}_{2}|.\end{eqnarray}$$
$$\begin{eqnarray}|\mathfrak{T}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2}))|=|\mathfrak{T}_{1}|+|\mathfrak{T}_{2}|.\end{eqnarray}$$
Combining (7.1), (7.2), (7.3), and (7.4), we have
 $$\begin{eqnarray}\displaystyle \operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})) & = & \displaystyle \mathop{\sum }_{\{a,b\}=\{1,2\}}\mathop{\sum }_{J\in H^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{a}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b})}}}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\{a,b\}=\{1,2\}}\dim _{\mathbf{k}}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}^{\prime }}}(M_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})}^{\mathbf{T}^{\prime }},M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}^{\mathbf{T}^{\prime }})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\{a,b\}=\{1,2\}}\dim _{\mathbf{k}}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}^{\prime }}}(M_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})}^{\mathbf{T}^{\prime }},\unicode[STIX]{x1D70F}M_{(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}^{\mathbf{T}^{\prime }})\nonumber\\ \displaystyle & = & \displaystyle \dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T}^{\prime })}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}^{\prime }},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}^{\prime }}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Int}((\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1}),(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})) & = & \displaystyle \mathop{\sum }_{\{a,b\}=\{1,2\}}\mathop{\sum }_{J\in H^{\mathfrak{m}_{\unicode[STIX]{x1D6FE}_{a}},\mathfrak{m}_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b})}}}\dim _{\mathbf{k}}\operatorname{Hom}_{A_{J}}(N_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})},N_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\{a,b\}=\{1,2\}}\dim _{\mathbf{k}}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}^{\prime }}}(M_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})}^{\mathbf{T}^{\prime }},M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}^{\mathbf{T}^{\prime }})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\{a,b\}=\{1,2\}}\dim _{\mathbf{k}}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}^{\mathbf{T}^{\prime }}}(M_{(\unicode[STIX]{x1D6FE}_{a},\unicode[STIX]{x1D705}_{a})}^{\mathbf{T}^{\prime }},\unicode[STIX]{x1D70F}M_{(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}^{\mathbf{T}^{\prime }})\nonumber\\ \displaystyle & = & \displaystyle \dim _{\mathbf{k}}\operatorname{Ext}_{{\mathcal{C}}(\mathbf{T}^{\prime })}^{1}(X_{(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D705}_{1})}^{\mathbf{T}^{\prime }},X_{(\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D705}_{2})}^{\mathbf{T}^{\prime }}).\nonumber\end{eqnarray}$$
Here, the second equality follows from Theorem 2.14, the third one follows from the fact that
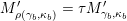 $M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}^{\prime }=\unicode[STIX]{x1D70F}M_{\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b}}^{\prime }$
(Theorem 5.2), and the last one follows from [Reference PaluPal08, Lemma 3.3]. This finishes the proof.◻
$M_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b})}^{\prime }=\unicode[STIX]{x1D70F}M_{\unicode[STIX]{x1D6FE}_{b},\unicode[STIX]{x1D705}_{b}}^{\prime }$
(Theorem 5.2), and the last one follows from [Reference PaluPal08, Lemma 3.3]. This finishes the proof.◻
Acknowledgements
The authors would like to thank the algebra group of NTNU, especially Aslak Bakke Buan and Idun Reiten, for their enthusiastic help. Further thanks are due to Daniel Labardini-Fragoso, Bangming Deng, Jie Xiao and Bin Zhu for their helpful discussions and comments. The authors would also like to thank the anonymous referees for many comments and suggestions that improved the presentation of the paper.
Appendix A Admissible triangulations
In this section, we give some results about admissible triangulations which will be used in the paper.
Lemma A.1. There is an admissible triangulation, i.e. every puncture is in a self-folded triangle, of any marked surface with non-empty boundary.
Proof. If the surface
![]() $\mathbf{S}$
does not admit any puncture, then any triangulation is admissible. Now let
$\mathbf{S}$
does not admit any puncture, then any triangulation is admissible. Now let
![]() $P$
be a puncture in
$P$
be a puncture in
![]() $\mathbf{S}$
. Use induction on the rank
$\mathbf{S}$
. Use induction on the rank
![]() $n$
, starting from the trivial case when
$n$
, starting from the trivial case when
![]() $n=1$
and
$n=1$
and
![]() $\mathbf{S}$
is a once-punctured monogon. Now suppose
$\mathbf{S}$
is a once-punctured monogon. Now suppose
![]() $n\geqslant 2$
. Consider the curve
$n\geqslant 2$
. Consider the curve
![]() $\unicode[STIX]{x1D6FC}$
with
$\unicode[STIX]{x1D6FC}$
with
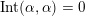 $\operatorname{Int}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})=0$
and
$\operatorname{Int}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})=0$
and
 $\unicode[STIX]{x1D6FC}(0)=\unicode[STIX]{x1D6FC}(1)=M$
, which encloses a disk with the puncture
$\unicode[STIX]{x1D6FC}(0)=\unicode[STIX]{x1D6FC}(1)=M$
, which encloses a disk with the puncture
![]() $P$
. Cutting along
$P$
. Cutting along
![]() $\unicode[STIX]{x1D6FC}$
we obtain a surface
$\unicode[STIX]{x1D6FC}$
we obtain a surface
![]() $\mathbf{S}/\unicode[STIX]{x1D6FC}$
(cf. the second column of Figure 12) whose rank is
$\mathbf{S}/\unicode[STIX]{x1D6FC}$
(cf. the second column of Figure 12) whose rank is
![]() $n-1$
. By inductive assumption we deduce that
$n-1$
. By inductive assumption we deduce that
![]() $\mathbf{S}/\unicode[STIX]{x1D6FC}$
, and hence
$\mathbf{S}/\unicode[STIX]{x1D6FC}$
, and hence
![]() $\mathbf{S}$
admits an admissible triangulation.◻
$\mathbf{S}$
admits an admissible triangulation.◻
Lemma A.2. Any two admissible triangulations are connected by a sequence of
![]() $\diamondsuit$
-flips.
$\diamondsuit$
-flips.
Proof. Let
![]() $\mathbf{T}_{i}$
,
$\mathbf{T}_{i}$
,
![]() $i=1,2$
, be two admissible triangulations. Use induction on the rank
$i=1,2$
, be two admissible triangulations. Use induction on the rank
![]() $n$
of the marked surface
$n$
of the marked surface
![]() $\mathbf{S}$
, starting with the trivial case when
$\mathbf{S}$
, starting with the trivial case when
![]() $n=1$
.
$n=1$
.
Consider a puncture
![]() $P$
, which is connected to exactly one marked point
$P$
, which is connected to exactly one marked point
![]() $M_{i}$
in
$M_{i}$
in
![]() $\mathbf{T}_{i}$
. If
$\mathbf{T}_{i}$
. If
 $PM_{1}\sim PM_{2}$
, we can delete the self-folded triangles containing
$PM_{1}\sim PM_{2}$
, we can delete the self-folded triangles containing
![]() $P$
from
$P$
from
![]() $\mathbf{T}_{i}$
and reduce to the case with a smaller rank.
$\mathbf{T}_{i}$
and reduce to the case with a smaller rank.
Now suppose that
 $PM_{1}\nsim PM_{2}$
. Freeze the self-folded triangle in
$PM_{1}\nsim PM_{2}$
. Freeze the self-folded triangle in
![]() $\mathbf{T}_{1}$
containing
$\mathbf{T}_{1}$
containing
![]() $PM_{1}$
. By inductive assumption for the remaining surface, we can flip
$PM_{1}$
. By inductive assumption for the remaining surface, we can flip
![]() $\mathbf{T}_{1}$
to a triangulation
$\mathbf{T}_{1}$
to a triangulation
![]() $\mathbf{T}_{1}^{\prime }$
, with local picture as in the left picture of Figure A.1 with
$\mathbf{T}_{1}^{\prime }$
, with local picture as in the left picture of Figure A.1 with
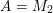 $A=M_{2}$
,
$A=M_{2}$
,
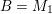 $B=M_{1}$
, and the curve
$B=M_{1}$
, and the curve
 $PA\sim PM_{2}$
. Then by one
$PA\sim PM_{2}$
. Then by one
![]() $\diamondsuit$
-flip we can locally flip
$\diamondsuit$
-flip we can locally flip
![]() $\mathbf{T}_{1}^{\prime }$
to another triangulation
$\mathbf{T}_{1}^{\prime }$
to another triangulation
![]() $\mathbf{T}_{1}^{\prime \prime }$
such that it contains the curve
$\mathbf{T}_{1}^{\prime \prime }$
such that it contains the curve
![]() $PM_{2}$
in
$PM_{2}$
in
![]() $\mathbf{T}_{2}$
, which becomes the
$\mathbf{T}_{2}$
, which becomes the
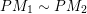 $PM_{1}\sim PM_{2}$
case above.◻
$PM_{1}\sim PM_{2}$
case above.◻

Figure A.1. A
![]() $\diamondsuit$
-flip.
$\diamondsuit$
-flip.
Appendix B Explicit version of Derksen et al.’s mutations of decorated representations for biquivers with potential
Let
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
be a tagged curve in
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})$
be a tagged curve in
![]() $\mathbf{C}^{\times }(\mathbf{S})$
and
$\mathbf{C}^{\times }(\mathbf{S})$
and
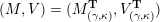 $(M,V)=(M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
be the corresponding decorated representation of
$(M,V)=(M_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}},V_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D705})}^{\mathbf{T}})$
be the corresponding decorated representation of
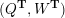 $(Q^{\mathbf{T}},W^{\mathbf{T}})$
, defined in Construction 4.18. For a vertex
$(Q^{\mathbf{T}},W^{\mathbf{T}})$
, defined in Construction 4.18. For a vertex
![]() $i\in Q_{0}^{\mathbf{T}}$
, construct
$i\in Q_{0}^{\mathbf{T}}$
, construct
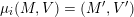 $\unicode[STIX]{x1D707}_{i}(M,V)=(M^{\prime },V^{\prime })$
as follows, where we use
$\unicode[STIX]{x1D707}_{i}(M,V)=(M^{\prime },V^{\prime })$
as follows, where we use
![]() ${\hookrightarrow}$
to denote the canonical inclusion and
${\hookrightarrow}$
to denote the canonical inclusion and
![]() ${\twoheadrightarrow}$
the canonical projection.
${\twoheadrightarrow}$
the canonical projection.
Table B.1. The first type of
![]() $\diamondsuit$
-flips.
$\diamondsuit$
-flips.

Table B.2. The second type of
![]() $\diamondsuit$
-flips.
$\diamondsuit$
-flips.

If there is no dashed loop at
![]() $i$
, the subquivers of
$i$
, the subquivers of
![]() $Q^{\mathbf{T}}$
and
$Q^{\mathbf{T}}$
and
![]() $\unicode[STIX]{x1D707}_{i}(Q^{\mathbf{T}})$
consisting of all arrows adjacent to
$\unicode[STIX]{x1D707}_{i}(Q^{\mathbf{T}})$
consisting of all arrows adjacent to
![]() $i$
are shown in the second row in Table B.1. Construct
$i$
are shown in the second row in Table B.1. Construct
 $\unicode[STIX]{x1D707}_{i}(M,V)=(M^{\prime },V^{\prime })$
as follows.
$\unicode[STIX]{x1D707}_{i}(M,V)=(M^{\prime },V^{\prime })$
as follows.
-
– For any
 $j\neq i$
, set
$j\neq i$
, set
 $M_{j}^{\prime }=M_{j}$
and
$M_{j}^{\prime }=M_{j}$
and
 $V_{j}^{\prime }=V_{j}$
.
$V_{j}^{\prime }=V_{j}$
. -
– Define
and $$\begin{eqnarray}M_{i}^{\prime }=\frac{\ker M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \ker M_{\unicode[STIX]{x1D6FE}_{2}}}{\operatorname{Im}\Bigl(\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FD}_{1}}\\ M_{\unicode[STIX]{x1D6FD}_{2}}\end{smallmatrix}\!\Bigr)}\oplus \operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{2}}\oplus \frac{\ker (\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FC}_{1}} & M_{\unicode[STIX]{x1D6FC}_{2}}\!\end{smallmatrix})}{\operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{2}}}\oplus V_{i}\end{eqnarray}$$
$$\begin{eqnarray}M_{i}^{\prime }=\frac{\ker M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \ker M_{\unicode[STIX]{x1D6FE}_{2}}}{\operatorname{Im}\Bigl(\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FD}_{1}}\\ M_{\unicode[STIX]{x1D6FD}_{2}}\end{smallmatrix}\!\Bigr)}\oplus \operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{2}}\oplus \frac{\ker (\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FC}_{1}} & M_{\unicode[STIX]{x1D6FC}_{2}}\!\end{smallmatrix})}{\operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{2}}}\oplus V_{i}\end{eqnarray}$$
 $$\begin{eqnarray}V_{i}^{\prime }=\frac{\ker M_{\unicode[STIX]{x1D6FD}_{1}}\cap \ker M_{\unicode[STIX]{x1D6FD}_{2}}}{\ker M_{\unicode[STIX]{x1D6FD}_{1}}\cap \ker M_{\unicode[STIX]{x1D6FD}_{2}}\cap (\operatorname{Im}M_{\unicode[STIX]{x1D6FC}_{1}}+\operatorname{Im}M_{\unicode[STIX]{x1D6FC}_{2}})}.\end{eqnarray}$$
$$\begin{eqnarray}V_{i}^{\prime }=\frac{\ker M_{\unicode[STIX]{x1D6FD}_{1}}\cap \ker M_{\unicode[STIX]{x1D6FD}_{2}}}{\ker M_{\unicode[STIX]{x1D6FD}_{1}}\cap \ker M_{\unicode[STIX]{x1D6FD}_{2}}\cap (\operatorname{Im}M_{\unicode[STIX]{x1D6FC}_{1}}+\operatorname{Im}M_{\unicode[STIX]{x1D6FC}_{2}})}.\end{eqnarray}$$
-
– For any arrow
 $a\in Q_{1}^{\mathbf{T}}$
not incident with
$a\in Q_{1}^{\mathbf{T}}$
not incident with
 $i$
, set
$i$
, set
 $M_{\unicode[STIX]{x1D6FC}}^{\prime }=M_{\unicode[STIX]{x1D6FC}}$
.
$M_{\unicode[STIX]{x1D6FC}}^{\prime }=M_{\unicode[STIX]{x1D6FC}}$
. -
– For any arrow
 $\unicode[STIX]{x1D700}\in Q_{2}^{\mathbf{T}}$
, set
$\unicode[STIX]{x1D700}\in Q_{2}^{\mathbf{T}}$
, set
 $M_{\unicode[STIX]{x1D700}}^{\prime }=M_{\unicode[STIX]{x1D700}}$
and
$M_{\unicode[STIX]{x1D700}}^{\prime }=M_{\unicode[STIX]{x1D700}}$
and
 $V_{\unicode[STIX]{x1D700}}^{\prime }=V_{\unicode[STIX]{x1D700}}$
.
$V_{\unicode[STIX]{x1D700}}^{\prime }=V_{\unicode[STIX]{x1D700}}$
. -
– Define
 $M_{[\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{1}]}^{\prime }=M_{\unicode[STIX]{x1D6FD}_{2}}M_{\unicode[STIX]{x1D6FC}_{1}}$
and
$M_{[\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{1}]}^{\prime }=M_{\unicode[STIX]{x1D6FD}_{2}}M_{\unicode[STIX]{x1D6FC}_{1}}$
and
 $M_{[\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{2}]}^{\prime }=M_{\unicode[STIX]{x1D6FD}_{1}}M_{\unicode[STIX]{x1D6FC}_{2}}$
.
$M_{[\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{2}]}^{\prime }=M_{\unicode[STIX]{x1D6FD}_{1}}M_{\unicode[STIX]{x1D6FC}_{2}}$
. -
– The map
 $M_{\unicode[STIX]{x1D6FC}_{x}^{\ast }}^{\prime }:M_{i}^{\prime }\rightarrow M_{s(\unicode[STIX]{x1D6FC}_{x})}^{\prime }$
, is given by the canonical inclusion
$M_{\unicode[STIX]{x1D6FC}_{x}^{\ast }}^{\prime }:M_{i}^{\prime }\rightarrow M_{s(\unicode[STIX]{x1D6FC}_{x})}^{\prime }$
, is given by the canonical inclusion
 $\operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{x}}{\hookrightarrow}M_{s(\unicode[STIX]{x1D6FC}_{x})}$
, and the composition where
$\operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{x}}{\hookrightarrow}M_{s(\unicode[STIX]{x1D6FC}_{x})}$
, and the composition where $$\begin{eqnarray}\frac{\ker (\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FC}_{1}} & M_{\unicode[STIX]{x1D6FC}_{2}}\end{smallmatrix}\!)}{\operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{2}}}\xrightarrow[{}]{a}\ker (\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FC}_{1}} & M_{\unicode[STIX]{x1D6FC}_{2}}\end{smallmatrix}\!){\hookrightarrow}M_{s(\unicode[STIX]{x1D6FC}_{1})}\oplus M_{s(\unicode[STIX]{x1D6FC}_{2})}{\twoheadrightarrow}M_{s(\unicode[STIX]{x1D6FC}_{x})},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\ker (\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FC}_{1}} & M_{\unicode[STIX]{x1D6FC}_{2}}\end{smallmatrix}\!)}{\operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{2}}}\xrightarrow[{}]{a}\ker (\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FC}_{1}} & M_{\unicode[STIX]{x1D6FC}_{2}}\end{smallmatrix}\!){\hookrightarrow}M_{s(\unicode[STIX]{x1D6FC}_{1})}\oplus M_{s(\unicode[STIX]{x1D6FC}_{2})}{\twoheadrightarrow}M_{s(\unicode[STIX]{x1D6FC}_{x})},\end{eqnarray}$$
 $a$
is a right inverse of the canonical projection
$a$
is a right inverse of the canonical projection  $$\begin{eqnarray}\ker (\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FC}_{1}} & M_{\unicode[STIX]{x1D6FC}_{2}}\end{smallmatrix}\!){\twoheadrightarrow}\frac{(\ker (\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FC}_{1}} & M_{\unicode[STIX]{x1D6FC}_{2}}\end{smallmatrix}\!))}{(\operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{2}})}.\end{eqnarray}$$
$$\begin{eqnarray}\ker (\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FC}_{1}} & M_{\unicode[STIX]{x1D6FC}_{2}}\end{smallmatrix}\!){\twoheadrightarrow}\frac{(\ker (\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FC}_{1}} & M_{\unicode[STIX]{x1D6FC}_{2}}\end{smallmatrix}\!))}{(\operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{2}})}.\end{eqnarray}$$
-
– The map
 $M_{\unicode[STIX]{x1D6FD}_{x}^{\ast }}^{\prime }:M_{t(\unicode[STIX]{x1D6FD}_{x})}^{\prime }\rightarrow M_{i}^{\prime }$
, is given by the map
$M_{\unicode[STIX]{x1D6FD}_{x}^{\ast }}^{\prime }:M_{t(\unicode[STIX]{x1D6FD}_{x})}^{\prime }\rightarrow M_{i}^{\prime }$
, is given by the map
 $M_{t(\unicode[STIX]{x1D6FD}_{x})}\xrightarrow[{}]{M_{\unicode[STIX]{x1D6FE}_{x}}}\operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{x}}$
and the composition where
$M_{t(\unicode[STIX]{x1D6FD}_{x})}\xrightarrow[{}]{M_{\unicode[STIX]{x1D6FE}_{x}}}\operatorname{Im}M_{\unicode[STIX]{x1D6FE}_{x}}$
and the composition where $$\begin{eqnarray}M_{t(\unicode[STIX]{x1D6FD}_{x})}{\hookrightarrow}M_{t(\unicode[STIX]{x1D6FD}_{1})}\oplus M_{t(\unicode[STIX]{x1D6FD}_{2})}\xrightarrow[{}]{b}\ker M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \ker M_{\unicode[STIX]{x1D6FE}_{2}}{\twoheadrightarrow}\frac{\ker M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \ker M_{\unicode[STIX]{x1D6FE}_{2}}}{\operatorname{Im}\Bigl(\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FD}_{1}}\\ M_{\unicode[STIX]{x1D6FD}_{2}}\end{smallmatrix}\!\Bigr)},\end{eqnarray}$$
$$\begin{eqnarray}M_{t(\unicode[STIX]{x1D6FD}_{x})}{\hookrightarrow}M_{t(\unicode[STIX]{x1D6FD}_{1})}\oplus M_{t(\unicode[STIX]{x1D6FD}_{2})}\xrightarrow[{}]{b}\ker M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \ker M_{\unicode[STIX]{x1D6FE}_{2}}{\twoheadrightarrow}\frac{\ker M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \ker M_{\unicode[STIX]{x1D6FE}_{2}}}{\operatorname{Im}\Bigl(\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FD}_{1}}\\ M_{\unicode[STIX]{x1D6FD}_{2}}\end{smallmatrix}\!\Bigr)},\end{eqnarray}$$
 $b$
is a left inverse of the inclusion
$b$
is a left inverse of the inclusion
 $\ker M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \ker M_{\unicode[STIX]{x1D6FE}_{2}}{\hookrightarrow}M_{t(\unicode[STIX]{x1D6FD}_{1})}\oplus M_{t(\unicode[STIX]{x1D6FD}_{2})}$
.
$\ker M_{\unicode[STIX]{x1D6FE}_{1}}\oplus \ker M_{\unicode[STIX]{x1D6FE}_{2}}{\hookrightarrow}M_{t(\unicode[STIX]{x1D6FD}_{1})}\oplus M_{t(\unicode[STIX]{x1D6FD}_{2})}$
.
If there is a dashed loop
![]() $\unicode[STIX]{x1D700}_{i}$
at
$\unicode[STIX]{x1D700}_{i}$
at
![]() $i$
, the subquivers of
$i$
, the subquivers of
![]() $Q^{\mathbf{T}}$
and
$Q^{\mathbf{T}}$
and
![]() $\unicode[STIX]{x1D707}_{i}(Q^{\mathbf{T}})$
consisting of all arrows adjacent to
$\unicode[STIX]{x1D707}_{i}(Q^{\mathbf{T}})$
consisting of all arrows adjacent to
![]() $i$
are shown in the second row in Table B.2. Construct
$i$
are shown in the second row in Table B.2. Construct
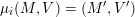 $\unicode[STIX]{x1D707}_{i}(M,V)=(M^{\prime },V^{\prime })$
as follows.
$\unicode[STIX]{x1D707}_{i}(M,V)=(M^{\prime },V^{\prime })$
as follows.
-
– For any
 $j\neq i$
, set
$j\neq i$
, set
 $M_{j}^{\prime }=M_{j}$
and
$M_{j}^{\prime }=M_{j}$
and
 $V_{j}^{\prime }=V_{j}$
.
$V_{j}^{\prime }=V_{j}$
. -
– Define
and $$\begin{eqnarray}M_{i}^{\prime }=\frac{\ker M_{\unicode[STIX]{x1D6FE}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}}}\oplus \frac{\ker M_{\unicode[STIX]{x1D6FE}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FD}}(1-M_{\unicode[STIX]{x1D700}_{i}})}\oplus \operatorname{Im}(M_{\unicode[STIX]{x1D6FE}})^{\oplus 2}\oplus \frac{\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}\oplus \ker (1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FE}}}\oplus V_{i}\end{eqnarray}$$
$$\begin{eqnarray}M_{i}^{\prime }=\frac{\ker M_{\unicode[STIX]{x1D6FE}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}}}\oplus \frac{\ker M_{\unicode[STIX]{x1D6FE}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FD}}(1-M_{\unicode[STIX]{x1D700}_{i}})}\oplus \operatorname{Im}(M_{\unicode[STIX]{x1D6FE}})^{\oplus 2}\oplus \frac{\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}\oplus \ker (1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FE}}}\oplus V_{i}\end{eqnarray}$$
 $$\begin{eqnarray}V_{i}^{\prime }=\frac{\ker M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}}}{\ker M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}}\cap \operatorname{Im}M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}}\oplus \frac{\ker M_{\unicode[STIX]{x1D6FD}}(1-M_{\unicode[STIX]{x1D700}_{i}})}{\ker M_{\unicode[STIX]{x1D6FD}}(1-M_{\unicode[STIX]{x1D700}_{i}})\cap \operatorname{Im}(1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$
$$\begin{eqnarray}V_{i}^{\prime }=\frac{\ker M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}}}{\ker M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}}\cap \operatorname{Im}M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}}\oplus \frac{\ker M_{\unicode[STIX]{x1D6FD}}(1-M_{\unicode[STIX]{x1D700}_{i}})}{\ker M_{\unicode[STIX]{x1D6FD}}(1-M_{\unicode[STIX]{x1D700}_{i}})\cap \operatorname{Im}(1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$
-
– The map
 $V_{\unicode[STIX]{x1D700}_{i}}^{\prime }$
is given by the identity on the first summand.
$V_{\unicode[STIX]{x1D700}_{i}}^{\prime }$
is given by the identity on the first summand. -
– For any arrow
 $a\in Q_{1}^{\mathbf{T}}$
not incident with
$a\in Q_{1}^{\mathbf{T}}$
not incident with
 $i$
, set
$i$
, set
 $M_{\unicode[STIX]{x1D6FC}}^{\prime }=M_{\unicode[STIX]{x1D6FC}}$
.
$M_{\unicode[STIX]{x1D6FC}}^{\prime }=M_{\unicode[STIX]{x1D6FC}}$
. -
– For any arrow
 $\unicode[STIX]{x1D700}\in Q_{2}^{\mathbf{T}}$
not incident with
$\unicode[STIX]{x1D700}\in Q_{2}^{\mathbf{T}}$
not incident with
 $i$
, set
$i$
, set
 $M_{\unicode[STIX]{x1D700}}^{\prime }=M_{\unicode[STIX]{x1D700}}$
and
$M_{\unicode[STIX]{x1D700}}^{\prime }=M_{\unicode[STIX]{x1D700}}$
and
 $V_{\unicode[STIX]{x1D700}}^{\prime }=V_{\unicode[STIX]{x1D700}}$
.
$V_{\unicode[STIX]{x1D700}}^{\prime }=V_{\unicode[STIX]{x1D700}}$
. -
– Define
 $M_{[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}]}^{\prime }=M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}$
.
$M_{[\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}]}^{\prime }=M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}$
. -
– The map
 $M_{\unicode[STIX]{x1D6FC}^{\ast }}^{\prime }:M_{i}^{\prime }\rightarrow M_{s(\unicode[STIX]{x1D6FC})}^{\prime }$
is given by the map
$M_{\unicode[STIX]{x1D6FC}^{\ast }}^{\prime }:M_{i}^{\prime }\rightarrow M_{s(\unicode[STIX]{x1D6FC})}^{\prime }$
is given by the map
 $(\operatorname{Im}M_{\unicode[STIX]{x1D6FE}})^{\oplus 2}\xrightarrow[{}]{(\!\begin{smallmatrix}\unicode[STIX]{x1D704} & \unicode[STIX]{x1D704}\end{smallmatrix}\!)}M_{s(\unicode[STIX]{x1D6FC}_{x})}$
and the composition where
$(\operatorname{Im}M_{\unicode[STIX]{x1D6FE}})^{\oplus 2}\xrightarrow[{}]{(\!\begin{smallmatrix}\unicode[STIX]{x1D704} & \unicode[STIX]{x1D704}\end{smallmatrix}\!)}M_{s(\unicode[STIX]{x1D6FC}_{x})}$
and the composition where $$\begin{eqnarray}\frac{\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}\oplus \ker (1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FE}}}\xrightarrow[{}]{a}\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}\oplus \ker (1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}}{\hookrightarrow}M_{s(\unicode[STIX]{x1D6FC})}\oplus M_{s(\unicode[STIX]{x1D6FC})},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}\oplus \ker (1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FE}}}\xrightarrow[{}]{a}\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}\oplus \ker (1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}}{\hookrightarrow}M_{s(\unicode[STIX]{x1D6FC})}\oplus M_{s(\unicode[STIX]{x1D6FC})},\end{eqnarray}$$
 $\unicode[STIX]{x1D704}$
is the inclusion and
$\unicode[STIX]{x1D704}$
is the inclusion and
 $a$
is a right inverse of the projections
$a$
is a right inverse of the projections
 $\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}\oplus \,\ker (1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}}{\twoheadrightarrow}(\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}\oplus \ker (1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}})/(\operatorname{Im}M_{\unicode[STIX]{x1D6FE}})$
.
$\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}\oplus \,\ker (1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}}{\twoheadrightarrow}(\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}}\oplus \ker (1-M_{\unicode[STIX]{x1D700}_{i}})M_{\unicode[STIX]{x1D6FC}})/(\operatorname{Im}M_{\unicode[STIX]{x1D6FE}})$
.
-
– The map
 $M_{\unicode[STIX]{x1D6FD}^{\ast }}^{\prime }:M_{t(\unicode[STIX]{x1D6FD})}^{\prime }\rightarrow M_{i}^{\prime }$
is given by the map
$M_{\unicode[STIX]{x1D6FD}^{\ast }}^{\prime }:M_{t(\unicode[STIX]{x1D6FD})}^{\prime }\rightarrow M_{i}^{\prime }$
is given by the map
 $M_{t(\unicode[STIX]{x1D6FD})}\xrightarrow[{}]{(\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FE}} & M_{\unicode[STIX]{x1D6FE}}\end{smallmatrix}\!)^{t}}(\operatorname{Im}M_{\unicode[STIX]{x1D6FE}})^{\oplus 2}$
and the composition where
$M_{t(\unicode[STIX]{x1D6FD})}\xrightarrow[{}]{(\!\begin{smallmatrix}M_{\unicode[STIX]{x1D6FE}} & M_{\unicode[STIX]{x1D6FE}}\end{smallmatrix}\!)^{t}}(\operatorname{Im}M_{\unicode[STIX]{x1D6FE}})^{\oplus 2}$
and the composition where $$\begin{eqnarray}M_{(t(\unicode[STIX]{x1D6FD}))}\xrightarrow[{}]{b}\ker M_{\unicode[STIX]{x1D6FE}}\xrightarrow[{}]{(\!\begin{smallmatrix}\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\prime }\end{smallmatrix}\!)}\frac{\ker M_{\unicode[STIX]{x1D6FE}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}}}\oplus \frac{\ker M_{\unicode[STIX]{x1D6FE}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FD}}(1-M_{\unicode[STIX]{x1D700}_{i}})},\end{eqnarray}$$
$$\begin{eqnarray}M_{(t(\unicode[STIX]{x1D6FD}))}\xrightarrow[{}]{b}\ker M_{\unicode[STIX]{x1D6FE}}\xrightarrow[{}]{(\!\begin{smallmatrix}\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\prime }\end{smallmatrix}\!)}\frac{\ker M_{\unicode[STIX]{x1D6FE}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}}}\oplus \frac{\ker M_{\unicode[STIX]{x1D6FE}}}{\operatorname{Im}M_{\unicode[STIX]{x1D6FD}}(1-M_{\unicode[STIX]{x1D700}_{i}})},\end{eqnarray}$$
 $b$
is a left inverse of the inclusion
$b$
is a left inverse of the inclusion
 $\ker M_{\unicode[STIX]{x1D6FE}}{\hookrightarrow}M_{(t(\unicode[STIX]{x1D6FD}))}$
and
$\ker M_{\unicode[STIX]{x1D6FE}}{\hookrightarrow}M_{(t(\unicode[STIX]{x1D6FD}))}$
and
 $\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\prime }$
are the projections.
$\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\prime }$
are the projections.
-
– The map
 $M_{\unicode[STIX]{x1D700}_{i}}^{\prime }$
is given by the identity on
$M_{\unicode[STIX]{x1D700}_{i}}^{\prime }$
is given by the identity on
 $(\ker M_{\unicode[STIX]{x1D6FE}})/(\operatorname{Im}M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}})$
, the identity on
$(\ker M_{\unicode[STIX]{x1D6FE}})/(\operatorname{Im}M_{\unicode[STIX]{x1D6FD}}M_{\unicode[STIX]{x1D700}_{i}})$
, the identity on
 $(\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}})/(\operatorname{Im}M_{\unicode[STIX]{x1D6FE}})$
, the map
$(\ker M_{\unicode[STIX]{x1D700}_{i}}M_{\unicode[STIX]{x1D6FC}})/(\operatorname{Im}M_{\unicode[STIX]{x1D6FE}})$
, the map
 $\big(\!\begin{smallmatrix}1 & 0\\ 0 & 0\end{smallmatrix}\!\big):\operatorname{Im}(M_{\unicode[STIX]{x1D6FE}})^{\oplus 2}\rightarrow \operatorname{Im}(M_{\unicode[STIX]{x1D6FE}})^{\oplus 2}$
, and
$\big(\!\begin{smallmatrix}1 & 0\\ 0 & 0\end{smallmatrix}\!\big):\operatorname{Im}(M_{\unicode[STIX]{x1D6FE}})^{\oplus 2}\rightarrow \operatorname{Im}(M_{\unicode[STIX]{x1D6FE}})^{\oplus 2}$
, and
 $V_{\unicode[STIX]{x1D700}_{i}}:V_{i}\rightarrow V_{i}$
.
$V_{\unicode[STIX]{x1D700}_{i}}:V_{i}\rightarrow V_{i}$
.
By [Reference Derksen, Weyman and ZelevinskyDWZ08, Corollary 10.12],
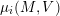 $\unicode[STIX]{x1D707}_{i}(M,V)$
is a decorated representation of
$\unicode[STIX]{x1D707}_{i}(M,V)$
is a decorated representation of
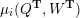 $\unicode[STIX]{x1D707}_{i}(Q^{\mathbf{T}},W^{\mathbf{T}})$
in both cases.
$\unicode[STIX]{x1D707}_{i}(Q^{\mathbf{T}},W^{\mathbf{T}})$
in both cases.
Remark B.1. The first mutation formula above for
![]() $(M,V)$
is an explicit version of Derksen et al.’s mutation of decorated representations [Reference Derksen, Weyman and ZelevinskyDWZ08]. The second mutation formula above is the composition of two Derksen et al.’s mutations of decorated representations.
$(M,V)$
is an explicit version of Derksen et al.’s mutation of decorated representations [Reference Derksen, Weyman and ZelevinskyDWZ08]. The second mutation formula above is the composition of two Derksen et al.’s mutations of decorated representations.