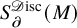1 Introduction
The classification of closed smooth d-manifolds and families thereof – smooth fibre bundles – is one of the guiding problems of geometric topology. From a homotopy-theoretic perspective, it is the study of the
![]() $\infty $
-groupoidFootnote
1
$\infty $
-groupoidFootnote
1
![]() $\mathscr {M}\mathrm {an}(d)^{\cong }$
of smooth closed d-manifolds and spaces of diffeomorphisms between them. A historically successful approach to relate – and partially reduce – the study of
$\mathscr {M}\mathrm {an}(d)^{\cong }$
of smooth closed d-manifolds and spaces of diffeomorphisms between them. A historically successful approach to relate – and partially reduce – the study of
![]() $\mathscr {M}\mathrm {an}(d)^{\cong }$
in high dimensions to more homotopy-theoretic and algebraic questions goes by comparison to the
$\mathscr {M}\mathrm {an}(d)^{\cong }$
in high dimensions to more homotopy-theoretic and algebraic questions goes by comparison to the
![]() $\infty $
-groupoid
$\infty $
-groupoid
![]() $\mathscr {S}^{\simeq }$
of spaces via the functor
$\mathscr {S}^{\simeq }$
of spaces via the functor
![]() $\mathscr {M}\mathrm {an}(d)^{\cong }\rightarrow \mathscr {S}^{\simeq }$
that assigns a manifold its homotopy type. For a given homotopy type X, one studies the fibre
$\mathscr {M}\mathrm {an}(d)^{\cong }\rightarrow \mathscr {S}^{\simeq }$
that assigns a manifold its homotopy type. For a given homotopy type X, one studies the fibre
which can be thought of as the space of manifold structures on X. The path components of this structure space are equivalence classes of manifolds with a homotopy equivalence to X,

and the path component of
![]() $S^{\mathscr {S}}(X)$
corresponding to such a pair
$S^{\mathscr {S}}(X)$
corresponding to such a pair
![]() $(M,\varphi )$
agrees with the identity component of the fibre
$(M,\varphi )$
agrees with the identity component of the fibre
![]() $\mathrm {hAut}(M)/\mathrm {Diff}(M)$
of the map
$\mathrm {hAut}(M)/\mathrm {Diff}(M)$
of the map
![]() $\mathrm {BDiff}(M)\rightarrow \mathrm {BhAut}(M)$
induced by considering diffeomorphisms as homotopy equivalences,
$\mathrm {BDiff}(M)\rightarrow \mathrm {BhAut}(M)$
induced by considering diffeomorphisms as homotopy equivalences,
Surgery theory and pseudoisotopy theory combine to provide an approximation to the structure space
![]() $S^{\mathscr {S}}(X)$
up to extensions in terms of three infinite loop spaces – one in the realm of each, algebraic K-theory, algebraic L-theory and stable homotopy theory (see [Reference Weiss and WilliamsWW01] for a survey). The unfortunate defect of this approach is that it really is only an approximation, in the sense that it can only capture a finite Postnikov truncation of
$S^{\mathscr {S}}(X)$
up to extensions in terms of three infinite loop spaces – one in the realm of each, algebraic K-theory, algebraic L-theory and stable homotopy theory (see [Reference Weiss and WilliamsWW01] for a survey). The unfortunate defect of this approach is that it really is only an approximation, in the sense that it can only capture a finite Postnikov truncation of
![]() $S^{\mathscr {S}}(X)$
depending on the dimension.
$S^{\mathscr {S}}(X)$
depending on the dimension.
Motivated by Goodwillie–Weiss’ embedding calculus and factorisation homology, we pursue a different approach to relate the study of
![]() $\mathscr {M}\mathrm {an}(d)^{\cong }$
to more homotopy-theoretic and algebraic questions, and we establish three fundamental properties of this alternative. Observing that the homotopy type of a manifold M can be viewed as that of the space of ordered configurations of k points in M for
$\mathscr {M}\mathrm {an}(d)^{\cong }$
to more homotopy-theoretic and algebraic questions, and we establish three fundamental properties of this alternative. Observing that the homotopy type of a manifold M can be viewed as that of the space of ordered configurations of k points in M for
![]() $k=1$
, this approach is motivated by the idea to remember the homotopy types of the configuration spaces for all values of k, together with the natural point-forgetting maps between them. It is, in fact, beneficial to consider configuration spaces of thickened points which admit more natural maps between them, by ‘splitting points’. To make this precise, one considers the
$k=1$
, this approach is motivated by the idea to remember the homotopy types of the configuration spaces for all values of k, together with the natural point-forgetting maps between them. It is, in fact, beneficial to consider configuration spaces of thickened points which admit more natural maps between them, by ‘splitting points’. To make this precise, one considers the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}\mathrm {isc}_d$
of finite disjoint unions of d-dimensional Euclidean spaces (i.e.,
$\mathscr {D}\mathrm {isc}_d$
of finite disjoint unions of d-dimensional Euclidean spaces (i.e.,
![]() $T\times \mathbf {R}^d$
for finite sets T) and spaces of smooth embeddings between them. A d-manifold M gives rise to a presheaf
$T\times \mathbf {R}^d$
for finite sets T) and spaces of smooth embeddings between them. A d-manifold M gives rise to a presheaf
![]() $E_M\colon \mathscr {D}\mathrm {isc}_d^{\mathrm {op}}\rightarrow \mathscr {S}$
on
$E_M\colon \mathscr {D}\mathrm {isc}_d^{\mathrm {op}}\rightarrow \mathscr {S}$
on
![]() $\mathscr {D}\mathrm {isc}_d$
with values in the
$\mathscr {D}\mathrm {isc}_d$
with values in the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {S}$
of spaces via
$\mathscr {S}$
of spaces via
By taking derivatives at the centres, the space
![]() $E_M(T\times \mathbf {R}^d)$
is equivalent to the ordered configuration space of
$E_M(T\times \mathbf {R}^d)$
is equivalent to the ordered configuration space of
![]() $k=|T|$
points in M together with framings of the tangent space of M at each of these points, and the homotopy type of the ordinary ordered configuration space of k points in M (in particular, that of M itself for
$k=|T|$
points in M together with framings of the tangent space of M at each of these points, and the homotopy type of the ordinary ordered configuration space of k points in M (in particular, that of M itself for
![]() $k=1$
) can be recovered as the quotient by the
$k=1$
) can be recovered as the quotient by the
![]() $\mathrm {Diff}(\mathbf {R}^d)^{T} \simeq \mathrm {O}(d)^T$
-action on
$\mathrm {Diff}(\mathbf {R}^d)^{T} \simeq \mathrm {O}(d)^T$
-action on
![]() $E_M(T\times \mathbf {R}^d)$
obtained by functoriality. The assignment
$E_M(T\times \mathbf {R}^d)$
obtained by functoriality. The assignment
![]() $M\mapsto E_M$
as in (1) is natural in embeddings of M, so it, in particular, defines a functor
$M\mapsto E_M$
as in (1) is natural in embeddings of M, so it, in particular, defines a functor
![]() $E\colon \mathscr {M}\mathrm {an}(d)^{\cong }\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)^\simeq $
to the
$E\colon \mathscr {M}\mathrm {an}(d)^{\cong }\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)^\simeq $
to the
![]() $\infty $
-groupoid of
$\infty $
-groupoid of
![]() $\mathscr {S}$
-valued presheaves on
$\mathscr {S}$
-valued presheaves on
![]() $\mathscr {D}\mathrm {isc}_d$
. The fibre of this functor at a presheaf
$\mathscr {D}\mathrm {isc}_d$
. The fibre of this functor at a presheaf
![]() $X \colon \mathscr {D}\mathrm {isc}^{\mathrm {op}}\rightarrow \mathscr {S}$
$X \colon \mathscr {D}\mathrm {isc}^{\mathrm {op}}\rightarrow \mathscr {S}$
is the eponymous
![]() $\mathscr {D}\mathrm {isc}$
-structure space of X. Analogous to the more traditional structure space
$\mathscr {D}\mathrm {isc}$
-structure space of X. Analogous to the more traditional structure space
![]() $S^{\mathscr {S}}(X)$
, the
$S^{\mathscr {S}}(X)$
, the
![]() $\mathscr {D}\mathrm {isc}$
-structure space
$\mathscr {D}\mathrm {isc}$
-structure space
![]() $S^{\mathscr {D}\mathrm {isc}}(X)$
can be thought as a space of manifold structures, this time on a presheaf as opposed to just a homotopy type. Similar to before, the path components
$S^{\mathscr {D}\mathrm {isc}}(X)$
can be thought as a space of manifold structures, this time on a presheaf as opposed to just a homotopy type. Similar to before, the path components
![]() $\pi _0\,S^{\mathscr {D}\mathrm {isc}}(X)$
are represented by pairs of a manifold with an equivalence of its presheaf to X,
$\pi _0\,S^{\mathscr {D}\mathrm {isc}}(X)$
are represented by pairs of a manifold with an equivalence of its presheaf to X,

and the path component of
![]() $S^{\mathscr {D}\mathrm {isc}}(X)$
corresponding to such a pair
$S^{\mathscr {D}\mathrm {isc}}(X)$
corresponding to such a pair
![]() $(M,\varphi )$
agrees with the identity component of the fibre
$(M,\varphi )$
agrees with the identity component of the fibre
![]() $\mathrm {Aut}(E_M)/\mathrm {Diff}(M)$
of the map
$\mathrm {Aut}(E_M)/\mathrm {Diff}(M)$
of the map
![]() $\mathrm {BDiff}(M)\rightarrow \mathrm {BAut}(E_M)$
induced by E,
$\mathrm {BDiff}(M)\rightarrow \mathrm {BAut}(E_M)$
induced by E,
In particular, the space
![]() $S^{\mathscr {D}\mathrm {isc}}(X)$
is nonempty if and only if
$S^{\mathscr {D}\mathrm {isc}}(X)$
is nonempty if and only if
![]() $X\simeq E_M$
for some closed smooth d-manifold M. If so, then
$X\simeq E_M$
for some closed smooth d-manifold M. If so, then
![]() $S^{\mathscr {D}\mathrm {isc}}(X)\simeq S^{\mathscr {D}\mathrm {isc}}(E_M)$
, so nothing is lost by assuming
$S^{\mathscr {D}\mathrm {isc}}(X)\simeq S^{\mathscr {D}\mathrm {isc}}(E_M)$
, so nothing is lost by assuming
![]() $X=E_M$
, in which case we abbreviate
$X=E_M$
, in which case we abbreviate ![]() . These are the spaces we focus on in this work. Informally speaking, they measure by how many manifolds the presheaf
. These are the spaces we focus on in this work. Informally speaking, they measure by how many manifolds the presheaf
![]() $X=E_M$
is realised, and how much their diffeomorphism groups differ from the automorphism group of X.
$X=E_M$
is realised, and how much their diffeomorphism groups differ from the automorphism group of X.
As the main results of this work, we establish three structural properties of
![]() $S^{\mathscr {D}\mathrm {isc}}(M)$
that one could summarise by saying that for most choices of M,
$S^{\mathscr {D}\mathrm {isc}}(M)$
that one could summarise by saying that for most choices of M,
-
A)
 $S^{\mathscr {D}\mathrm {isc}}(M)$
depends only little on the manifold M,
$S^{\mathscr {D}\mathrm {isc}}(M)$
depends only little on the manifold M, -
B)
 $S^{\mathscr {D}\mathrm {isc}}(M)$
is an infinite loop space, and
$S^{\mathscr {D}\mathrm {isc}}(M)$
is an infinite loop space, and -
C)
 $S^{\mathscr {D}\mathrm {isc}}(M)$
is nontrivial.
$S^{\mathscr {D}\mathrm {isc}}(M)$
is nontrivial.
We state these results in terms of a more general version
![]() $S_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
for manifolds that may have boundary, which is crucial for our methods. We postpone its definition to Section 1.2.1 below.
$S_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
for manifolds that may have boundary, which is crucial for our methods. We postpone its definition to Section 1.2.1 below.
A) Tangential
 $2$
-type invariance
$2$
-type invariance
To make the first property precise, recall that two manifolds M and N, possibly with boundary, have the same tangential
![]() $2$
-type if there is a map
$2$
-type if there is a map
![]() $B\rightarrow \mathrm {BO}$
so that the maps
$B\rightarrow \mathrm {BO}$
so that the maps
![]() $M\rightarrow \mathrm {BO}$
and
$M\rightarrow \mathrm {BO}$
and
![]() $N\rightarrow \mathrm {BO}$
classifying the stable tangent bundles of M and N admit lifts to maps
$N\rightarrow \mathrm {BO}$
classifying the stable tangent bundles of M and N admit lifts to maps
![]() $M\rightarrow B$
and
$M\rightarrow B$
and
![]() $N\rightarrow B$
that are
$N\rightarrow B$
that are
![]() $2$
-connected.
$2$
-connected.
Example. Choosing
![]() $B=\mathrm {BSpin} \times K(\pi ,1)$
, one sees that two spin manifolds M and N have the same tangential
$B=\mathrm {BSpin} \times K(\pi ,1)$
, one sees that two spin manifolds M and N have the same tangential
![]() $2$
-type if and only if their fundamental groupoids are equivalent. In particular, all simply connected spin manifolds have the same tangential
$2$
-type if and only if their fundamental groupoids are equivalent. In particular, all simply connected spin manifolds have the same tangential
![]() $2$
-type.
$2$
-type.
Our first main result is that in high dimensions, the
![]() $\mathscr {D}\mathrm {isc}$
-structure space
$\mathscr {D}\mathrm {isc}$
-structure space
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
depends only on the dimension d and the tangential
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
depends only on the dimension d and the tangential
![]() $2$
-type of M.
$2$
-type of M.
Theorem A. For compact d-manifolds M and N with
![]() $d\ge 5$
that have the same tangential
$d\ge 5$
that have the same tangential
![]() $2$
-type, there exists an equivalence
$2$
-type, there exists an equivalence
![]() $S_\partial ^{\mathscr {D}\mathrm {isc}}(M)\simeq S_\partial ^{\mathscr {D}\mathrm {isc}}(N)$
.
$S_\partial ^{\mathscr {D}\mathrm {isc}}(M)\simeq S_\partial ^{\mathscr {D}\mathrm {isc}}(N)$
.
In particular, the
![]() $\mathscr {D}\mathrm {isc}$
-structure space of a compact spin d-manifold M with
$\mathscr {D}\mathrm {isc}$
-structure space of a compact spin d-manifold M with
![]() $d\ge 5$
only depends on the fundamental groupoid, so we in particular have
$d\ge 5$
only depends on the fundamental groupoid, so we in particular have
![]() $\smash {S_\partial ^{\mathscr {D}\mathrm {isc}}(M) \simeq S_\partial ^{\mathscr {D}\mathrm {isc}}(D^d)}$
if M is simply connected. Theorem A also implies that
$\smash {S_\partial ^{\mathscr {D}\mathrm {isc}}(M) \simeq S_\partial ^{\mathscr {D}\mathrm {isc}}(D^d)}$
if M is simply connected. Theorem A also implies that
![]() $\smash {S_\partial ^{\mathscr {D}\mathrm {isc}}(M)}$
for a compact d-manifold M does not depend on the smooth structure of M, since homeomorphic manifolds have equivalent tangential
$\smash {S_\partial ^{\mathscr {D}\mathrm {isc}}(M)}$
for a compact d-manifold M does not depend on the smooth structure of M, since homeomorphic manifolds have equivalent tangential
![]() $2$
-types (see Example 5.2).
$2$
-types (see Example 5.2).
Remark. One ingredient in the above mentioned approximation to the conventional structure space
![]() $S^{\mathscr {S}}_\partial (M)$
has a similar invariance property (namely, the L-theory part depends only on the fundamental groupoid), but the others depend more substantially on the homotopy type of M.
$S^{\mathscr {S}}_\partial (M)$
has a similar invariance property (namely, the L-theory part depends only on the fundamental groupoid), but the others depend more substantially on the homotopy type of M.
Remark. Reformulated in terms of embedding calculus (see Section 1.1.1 for an outline of this relation), Theorem A is an extension of a result of Knudsen–Kupers [Reference Knudsen and KupersKK24a, 6.23] which applies to certain path components of
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
if M is
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
if M is
![]() $2$
-connected, of dimension
$2$
-connected, of dimension
![]() $d\ge 6$
, and
$d\ge 6$
, and
![]() $\partial M=S^{d-1}$
.
$\partial M=S^{d-1}$
.
B) Infinite loop space structure
As previously mentioned, the more traditional structure space
![]() $\smash {S^{\mathscr {S}}_\partial (M)}$
is an infinite loop space after a certain truncation and up to extensions. The
$\smash {S^{\mathscr {S}}_\partial (M)}$
is an infinite loop space after a certain truncation and up to extensions. The
![]() $\mathscr {D}\mathrm {isc}$
-structure space
$\mathscr {D}\mathrm {isc}$
-structure space
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
on the other hand is in high dimensions an actual infinite loop space – no truncations or extensions are necessary. This is our second main result.
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
on the other hand is in high dimensions an actual infinite loop space – no truncations or extensions are necessary. This is our second main result.
Theorem B. For a compact manifold M of dimension
![]() $d\ge 8$
, the space
$d\ge 8$
, the space
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
admits the structure of an infinite loop space.
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
admits the structure of an infinite loop space.
Remark.
-
(i) The bound
 $d\ge 8$
in Theorem B is not optimal. It can, for example, be improved to
$d\ge 8$
in Theorem B is not optimal. It can, for example, be improved to
 $d\ge 6$
if M is simply connected and spin (see Theorem 6.1). Further improvements are likely possible.
$d\ge 6$
if M is simply connected and spin (see Theorem 6.1). Further improvements are likely possible. -
(ii) The
 $\mathscr {D}\mathrm {isc}$
-structure space
$\mathscr {D}\mathrm {isc}$
-structure space
 $S_{\partial }^{\mathscr {D}\mathrm {isc}}(M)$
extends to a space-valued functor on an
$S_{\partial }^{\mathscr {D}\mathrm {isc}}(M)$
extends to a space-valued functor on an
 $\infty $
-category of compact d-manifolds and embeddings between them (see Section 4.5.2), but our construction of the infinite loop space structure on
$\infty $
-category of compact d-manifolds and embeddings between them (see Section 4.5.2), but our construction of the infinite loop space structure on
 $S_{\partial }^{\mathscr {D}\mathrm {isc}}(M)$
has less functoriality (see Remark 6.8).
$S_{\partial }^{\mathscr {D}\mathrm {isc}}(M)$
has less functoriality (see Remark 6.8).
C) Nontriviality
At this point, a very optimistic reader may wonder whether the
![]() $\mathscr {D}\mathrm {isc}$
-structure spaces
$\mathscr {D}\mathrm {isc}$
-structure spaces
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
are just contractible, which would in particular say that the diffeomorphism group
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
are just contractible, which would in particular say that the diffeomorphism group
![]() $\mathrm {Diff}(M)$
of a closed manifold M is equivalent to the automorphism group
$\mathrm {Diff}(M)$
of a closed manifold M is equivalent to the automorphism group
![]() $\mathrm {Aut}(E_M)$
of the associated presheaf. As our third main result, we show that this is never the case if one assumes the manifold to be spin and of dimension
$\mathrm {Aut}(E_M)$
of the associated presheaf. As our third main result, we show that this is never the case if one assumes the manifold to be spin and of dimension
![]() $d\ge 5$
.
$d\ge 5$
.
Theorem C. For a compact spin d-manifold
![]() $M\neq \varnothing $
with
$M\neq \varnothing $
with
![]() $d\ge 5$
, the space
$d\ge 5$
, the space
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
is not contractible.
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
is not contractible.
Remark. There are partial results in low dimensions that complement Theorem C.
-
(i) For
 $d\le 2$
, Theorem A of [Reference Krannich and KupersKK24b] implies
$d\le 2$
, Theorem A of [Reference Krannich and KupersKK24b] implies
 $\smash {S^{\mathscr {D}\mathrm {isc}}_\partial }(M)\simeq \ast $
(see Remark 1.1 (ii) loc.cit.).
$\smash {S^{\mathscr {D}\mathrm {isc}}_\partial }(M)\simeq \ast $
(see Remark 1.1 (ii) loc.cit.). -
(ii) For
 $d=3$
, we give several examples for which
$d=3$
, we give several examples for which
 $\smash {S^{\mathscr {D}\mathrm {isc}}_\partial }(M)$
is nontrivial, including
$\smash {S^{\mathscr {D}\mathrm {isc}}_\partial }(M)$
is nontrivial, including
 $M=D^3$
and
$M=D^3$
and
 $M=S^3$
(see Remark 8.16).
$M=S^3$
(see Remark 8.16). -
(iii) For
 $d=4$
, Theorem B of [Reference Knudsen and KupersKK24a] implies that
$d=4$
, Theorem B of [Reference Knudsen and KupersKK24a] implies that
 $\pi _0\,\smash {S^{\mathscr {D}\mathrm {isc}}_\partial }(M)$
surjects onto the set of isotopy classes of smooth structures on M as long as M is
$\pi _0\,\smash {S^{\mathscr {D}\mathrm {isc}}_\partial }(M)$
surjects onto the set of isotopy classes of smooth structures on M as long as M is
 $1$
-connected and closed, so
$1$
-connected and closed, so
 $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
is nontrivial for all such M that admit more than one smooth structure.
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
is nontrivial for all such M that admit more than one smooth structure.
This concludes the summary of our three main results. In the remainder of this introduction, we briefly indicate how
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
relates to embedding calculus, the little d-discs operad and factorisation homology, and then give a summary of the proofs of the main results, where we also make good for the omitted definition of
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
relates to embedding calculus, the little d-discs operad and factorisation homology, and then give a summary of the proofs of the main results, where we also make good for the omitted definition of
![]() $S_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
for manifolds with boundary.
$S_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
for manifolds with boundary.
1.1 Relation to embedding calculus, the
 $E_d$
-operad and factorisation homology
$E_d$
-operad and factorisation homology
1.1.1 Embedding calculus
Goodwillie and Weiss’ embedding calculus [Reference WeissWei99, Reference Goodwillie and WeissGW99] is a device to study embeddings via their restrictions to submanifolds of the source that are diffeomorphic to
![]() $T\times \mathbf {R}^d$
for finite sets T. It has the form of an approximation to the space of embeddings
$T\times \mathbf {R}^d$
for finite sets T. It has the form of an approximation to the space of embeddings
whose target is the limit of a tower of maps whose fibres admit a description in terms of the configurations spaces and frame bundles of W and
![]() $W'$
. The main result in this context, due to Goodwillie–Klein [Reference Goodwillie and KleinGK15], says that (2) is an equivalence if the handle codimension (dimension of
$W'$
. The main result in this context, due to Goodwillie–Klein [Reference Goodwillie and KleinGK15], says that (2) is an equivalence if the handle codimension (dimension of
![]() $W'$
minus handle dimension of W) is at least three. In general, the map (2) can fail to be an equivalence, and in a sense, the
$W'$
minus handle dimension of W) is at least three. In general, the map (2) can fail to be an equivalence, and in a sense, the
![]() $\mathscr {D}\mathrm {isc}$
-structure spaces may be seen as the ‘correction terms’ to (2) being an equivalence in codimension zero. Let us make this more precise.
$\mathscr {D}\mathrm {isc}$
-structure spaces may be seen as the ‘correction terms’ to (2) being an equivalence in codimension zero. Let us make this more precise.
The relation of the map (2) to
![]() $\mathscr {D}\mathrm {isc}$
-structure spaces is a reformulation of a result of Boavida de Brito–Weiss [Reference Boavida de Brito and WeissBdBW13], at least if M is closed (c.f. Remark 1.1). They show that (2) is equivalent to the map
$\mathscr {D}\mathrm {isc}$
-structure spaces is a reformulation of a result of Boavida de Brito–Weiss [Reference Boavida de Brito and WeissBdBW13], at least if M is closed (c.f. Remark 1.1). They show that (2) is equivalent to the map
![]() $\mathrm {Emb}(W,W')\rightarrow \mathrm {Map}_{\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)}(E_W,E_{W'})$
induced by the naturality of
$\mathrm {Emb}(W,W')\rightarrow \mathrm {Map}_{\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)}(E_W,E_{W'})$
induced by the naturality of
![]() $E_W$
in embeddings, which – for closed W and
$E_W$
in embeddings, which – for closed W and
![]() $W'$
and after discarding non-invertible components in source and target – is the map on mapping spaces induced by the functor
$W'$
and after discarding non-invertible components in source and target – is the map on mapping spaces induced by the functor
![]() $E\colon \mathscr {M}\mathrm {an}(d)^{\cong }\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)^{\simeq }$
used to define the
$E\colon \mathscr {M}\mathrm {an}(d)^{\cong }\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)^{\simeq }$
used to define the
![]() $\mathscr {D}\mathrm {isc}$
-structure space. Since the path space of a
$\mathscr {D}\mathrm {isc}$
-structure space. Since the path space of a
![]() $\infty $
-groupoid between two objects is naturally equivalent to the space of morphisms between the respective objects, this shows that the loop space of
$\infty $
-groupoid between two objects is naturally equivalent to the space of morphisms between the respective objects, this shows that the loop space of
![]() $S^{\mathscr {D}\mathrm {isc}}(M)$
at
$S^{\mathscr {D}\mathrm {isc}}(M)$
at
![]() $(M,\mathrm {id}_{E_M}) \in \pi _0\,S^{\mathscr {D}\mathrm {isc}}(M)$
is equivalent to the fibre at
$(M,\mathrm {id}_{E_M}) \in \pi _0\,S^{\mathscr {D}\mathrm {isc}}(M)$
is equivalent to the fibre at
![]() $\mathrm {id}$
of (2) for
$\mathrm {id}$
of (2) for
![]() $W=W'=M$
, so
$W=W'=M$
, so
Remark 1.1. A similar discussion applies if M has boundary, but this does not follow directly from [Reference Boavida de Brito and WeissBdBW13] since we deal with boundary conditions differently to loc.cit. (see Section 1.2.1).
Specialising Properties A–C to spin manifolds, they in particular imply the following:
Corollary D. For compact connected spin d-manifolds
![]() $M\neq \varnothing $
with
$M\neq \varnothing $
with
![]() $d\ge 5$
, the fibre
$d\ge 5$
, the fibre
is nontrivial and depends only on the fundamental group of M. It is an infinite loop space for
![]() $d\ge 8$
.
$d\ge 8$
.
1.1.2 The operad
 $E_d$
of little d-discs
$E_d$
of little d-discs
We continue by mentioning two connections between
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
and the operad
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
and the operad
![]() $E_d$
of little d-discs. The first is that
$E_d$
of little d-discs. The first is that
![]() $\mathscr {D}\mathrm {isc}_d$
agrees with the monoidal envelope (also known as the associated PROP) of the framed
$\mathscr {D}\mathrm {isc}_d$
agrees with the monoidal envelope (also known as the associated PROP) of the framed
![]() $E_d$
-operad, so
$E_d$
-operad, so
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
can be identified with the
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
can be identified with the
![]() $\infty $
-category of right-modules over this operad, and hence, the definition of
$\infty $
-category of right-modules over this operad, and hence, the definition of
![]() $S_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
for closed manifolds can be rephrased in these terms. There is a similar reformulation if M has boundary.
$S_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
for closed manifolds can be rephrased in these terms. There is a similar reformulation if M has boundary.
The second relation is less obvious and once more a result of work of Boavida de Brito and Weiss [Reference Boavida de Brito and WeissBdBW18]. To explain it, observe that the standard action of
![]() $\mathrm {O}(d)$
on the disc
$\mathrm {O}(d)$
on the disc
![]() $D^d$
induces an
$D^d$
induces an
![]() $\mathrm {O}(d)$
-action on the operad
$\mathrm {O}(d)$
-action on the operad
![]() $E_d$
of little d-discs. This action extends to the topological group
$E_d$
of little d-discs. This action extends to the topological group
![]() $\mathrm {Top}(d)$
of homeomorphisms of
$\mathrm {Top}(d)$
of homeomorphisms of
![]() $\mathbf {R}^d$
, so there is a map
$\mathbf {R}^d$
, so there is a map
with
![]() $\mathrm {Aut}(E_d)$
the automorphism group of the
$\mathrm {Aut}(E_d)$
the automorphism group of the
![]() $E_d$
-operad. Reformulated in our setting, their work (or alternatively work of Ducoulombier–Turchin [Reference Ducoulombier and TurchinDT22]) moreover implies that there is an equivalence
$E_d$
-operad. Reformulated in our setting, their work (or alternatively work of Ducoulombier–Turchin [Reference Ducoulombier and TurchinDT22]) moreover implies that there is an equivalence
In particular, Theorems B and C for
![]() $M=D^d$
(or rather certain refinements of them) imply the following:
$M=D^d$
(or rather certain refinements of them) imply the following:
Corollary E. The map
![]() $\mathrm {BTop}(d)\rightarrow \mathrm {BAut}(E_d)$
is an equivalence if and only if
$\mathrm {BTop}(d)\rightarrow \mathrm {BAut}(E_d)$
is an equivalence if and only if
![]() $d\le 2$
. Moreover, its fibre admits for
$d\le 2$
. Moreover, its fibre admits for
![]() $d\ge 6$
the structure of an infinite loop space after taking
$d\ge 6$
the structure of an infinite loop space after taking
![]() $(d+1)$
-fold loop spaces.
$(d+1)$
-fold loop spaces.
Remark 1.2. A couple of remarks on the equivalence (5) and Corollary E are in order.
-
(i) Dwyer and Hess asked whether the map (4) is an equivalence [Reference DwyerDwy14, 58 min]. The first part of Corollary E gives an answer.
-
(ii) The cases
 $d\le 2$
of the first part of Corollary E are not due to us: Horel [Reference HorelHor17] proved the case
$d\le 2$
of the first part of Corollary E are not due to us: Horel [Reference HorelHor17] proved the case
 $d=2$
. The case
$d=2$
. The case
 $d=1$
is folklore and can be proved via Horel’s approach.
$d=1$
is folklore and can be proved via Horel’s approach. -
(iii) The equivalence (5) can strictly speaking only be deduced from [Reference Boavida de Brito and WeissBdBW18] or [Reference Ducoulombier and TurchinDT22] after passing to certain components (see Theorem 8.1), but a different proof that does not require this was given as part of [Reference Krannich and KupersKK24c] (see Remark 8.2).
1.1.3 Factorisation homology
The final relation of
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
we would like to mention is one to factorisation homology (or topological chiral homology) [Reference SalvatoreSal01, Reference FrancisFra13, Reference AndradeAnd10, Reference Ayala and FrancisAF15, Reference LurieLur17]. In its simplest instance, this connection amounts to the (quite tautological) observation that for a framed
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
we would like to mention is one to factorisation homology (or topological chiral homology) [Reference SalvatoreSal01, Reference FrancisFra13, Reference AndradeAnd10, Reference Ayala and FrancisAF15, Reference LurieLur17]. In its simplest instance, this connection amounts to the (quite tautological) observation that for a framed
![]() $E_d$
-algebra A in a suitable
$E_d$
-algebra A in a suitable
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, there is a commutative diagram
$\mathscr {C}$
, there is a commutative diagram

of
![]() $\infty $
-categories in which the diagonal arrow is given by factorisation homology with coefficients in A and the vertical arrow by taking coends, using that A is in particular a functor
$\infty $
-categories in which the diagonal arrow is given by factorisation homology with coefficients in A and the vertical arrow by taking coends, using that A is in particular a functor
![]() $A\colon \mathscr {D}\mathrm {isc}_d\rightarrow \mathscr {C}$
. In fact, the functor E itself is an instance of factorisation homology – namely, with coefficients in the framed
$A\colon \mathscr {D}\mathrm {isc}_d\rightarrow \mathscr {C}$
. In fact, the functor E itself is an instance of factorisation homology – namely, with coefficients in the framed
![]() $E_d$
-algebra
$E_d$
-algebra
![]() $E_{D^d}\in \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
– so E may be viewed as the universal factorisation homology invariant on
$E_{D^d}\in \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
– so E may be viewed as the universal factorisation homology invariant on
![]() $\mathscr {M}\mathrm {an}(d)^{\cong }$
, and the study of
$\mathscr {M}\mathrm {an}(d)^{\cong }$
, and the study of
![]() $\mathscr {D}\mathrm {isc}$
-structure spaces as closely related to the question to which extent the theory of manifolds can be captured by factorisation homology.
$\mathscr {D}\mathrm {isc}$
-structure spaces as closely related to the question to which extent the theory of manifolds can be captured by factorisation homology.
1.2 Summary of proofs
We conclude with a summary of the proofs of Theorems A–C.
Some steps may be of independent interest. We highlight them with the Roman numerals (I)–(III).
1.2.1 The case with boundary
The more general
![]() $\mathscr {D}\mathrm {isc}$
-structure spaces
$\mathscr {D}\mathrm {isc}$
-structure spaces
![]() $\mathrm{S}_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
for manifolds M with boundary play a central role in the proofs of all main results of this work, even when specialised to closed manifolds, so we first make good on omitting its definition earlier.
$\mathrm{S}_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
for manifolds M with boundary play a central role in the proofs of all main results of this work, even when specialised to closed manifolds, so we first make good on omitting its definition earlier.
Fixing a closed
![]() $(d-1)$
-manifold Q, one replaces
$(d-1)$
-manifold Q, one replaces
![]() $\smash {\mathscr {M}\mathrm {an}(d)^{\cong }}$
with the
$\smash {\mathscr {M}\mathrm {an}(d)^{\cong }}$
with the
![]() $\infty $
-groupoid
$\infty $
-groupoid
![]() $\mathscr {M}\mathrm {an}(d)^{\cong }_Q$
of compact d-manifolds with an identification of their boundary with Q, and spaces of diffeomorphisms preserving these identifications. The definition (1) of the presheaf
$\mathscr {M}\mathrm {an}(d)^{\cong }_Q$
of compact d-manifolds with an identification of their boundary with Q, and spaces of diffeomorphisms preserving these identifications. The definition (1) of the presheaf
![]() $E_M$
still makes sense if M has boundary Q and thus yields a functor
$E_M$
still makes sense if M has boundary Q and thus yields a functor
![]() $\mathscr {M}\mathrm {an}(d)^{\cong }_Q\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)^\simeq $
, but if
$\mathscr {M}\mathrm {an}(d)^{\cong }_Q\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)^\simeq $
, but if
![]() $Q\neq \varnothing $
, then the presheaf
$Q\neq \varnothing $
, then the presheaf
![]() $E_M$
carries additional structure. Indeed, stacking cylinders induces an associative algebra structure on the presheaf
$E_M$
carries additional structure. Indeed, stacking cylinders induces an associative algebra structure on the presheaf
![]() $E_{Q\times I}\in \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
with respect to the symmetric monoidal structure on
$E_{Q\times I}\in \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
with respect to the symmetric monoidal structure on
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
given by Day convolution, induced by taking disjoint unions in
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
given by Day convolution, induced by taking disjoint unions in
![]() $\mathscr {D}\mathrm {isc}_d$
. Similarly, fixing a collar
$\mathscr {D}\mathrm {isc}_d$
. Similarly, fixing a collar
![]() $Q\times I\hookrightarrow M$
of the boundary of M, the presheaf
$Q\times I\hookrightarrow M$
of the boundary of M, the presheaf
![]() $E_{M}$
becomes a right-
$E_{M}$
becomes a right-
![]() $E_{Q\times I}$
-module. Made precise, this enhances the functor
$E_{Q\times I}$
-module. Made precise, this enhances the functor
![]() $E\colon \mathscr {M}\mathrm {an}(d)^{\cong }_Q\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)^\simeq $
to a functor
$E\colon \mathscr {M}\mathrm {an}(d)^{\cong }_Q\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)^\simeq $
to a functor
with target the
![]() $\infty $
-groupoid
$\infty $
-groupoid
![]() $\mathscr {M}\mathrm {od}(d)_{E_{Q\times I}}^\simeq $
of right-
$\mathscr {M}\mathrm {od}(d)_{E_{Q\times I}}^\simeq $
of right-
![]() $E_{Q\times I}$
-modules. The
$E_{Q\times I}$
-modules. The
![]() $\mathscr {D}\mathrm {isc}$
-structure space of a right-
$\mathscr {D}\mathrm {isc}$
-structure space of a right-
![]() $E_{Q\times I}$
-module X is then defined as the fibre
$E_{Q\times I}$
-module X is then defined as the fibre
that this recovers the previous definition in the case
![]() $Q=\varnothing $
follows by observing that
$Q=\varnothing $
follows by observing that
![]() $E_{\varnothing \times I}$
is the monoidal unit. As in the closed case, we abbreviate
$E_{\varnothing \times I}$
is the monoidal unit. As in the closed case, we abbreviate ![]() if the right-
if the right-
![]() $E_{Q \times I}$
-module
$E_{Q \times I}$
-module
![]() $X=E_M$
is induced by a manifold M with identified boundary
$X=E_M$
is induced by a manifold M with identified boundary
![]() $\partial M\cong Q$
. This is the generalisation of
$\partial M\cong Q$
. This is the generalisation of
![]() $S^{\mathscr {D}\mathrm {isc}}(M)$
for manifolds with boundary in terms of which we stated Theorems A–C above.
$S^{\mathscr {D}\mathrm {isc}}(M)$
for manifolds with boundary in terms of which we stated Theorems A–C above.
1.2.2 Extension to the bordism category
For the proofs of these results, we need to generalise the functor (6) further. Given another closed
![]() $(d-1)$
-manifold P, we write
$(d-1)$
-manifold P, we write
![]() $\mathscr {B}\mathrm {ord}(d)_{P,Q}$
for the
$\mathscr {B}\mathrm {ord}(d)_{P,Q}$
for the
![]() $\infty $
-groupoid of compact bordisms
$\infty $
-groupoid of compact bordisms
![]() $W\colon P\leadsto Q$
and spaces of diffeomorphisms preserving the identifications of the ends. For such a bordism, the associated presheaf
$W\colon P\leadsto Q$
and spaces of diffeomorphisms preserving the identifications of the ends. For such a bordism, the associated presheaf
![]() $E_W$
becomes a
$E_W$
becomes a
![]() $(E_{P\times I},E_{Q\times I})$
-bimodule in
$(E_{P\times I},E_{Q\times I})$
-bimodule in
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
, and we have a functor
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
, and we have a functor
to the
![]() $\infty $
-groupoid
$\infty $
-groupoid
![]() $\smash {\mathscr {M}\mathrm {od}(d)^\simeq _{E_{P\times I},E_{Q\times I}}}$
of
$\smash {\mathscr {M}\mathrm {od}(d)^\simeq _{E_{P\times I},E_{Q\times I}}}$
of
![]() $(E_{P\times I},E_{Q\times I})$
-bimodules, generalising the case
$(E_{P\times I},E_{Q\times I})$
-bimodules, generalising the case
![]() $P=\varnothing $
discussed in the previous subsection. Given another closed
$P=\varnothing $
discussed in the previous subsection. Given another closed
![]() $(d-1)$
-manifold R, one can show that there is a commutative square of
$(d-1)$
-manifold R, one can show that there is a commutative square of
![]() $\infty $
-groupoids
$\infty $
-groupoids

whose horizontal functors are induced by gluing bordisms and tensoring bimodules, respectively; this is essentially an instance of what is known as
![]() $\otimes $
-excision in the theory of factorisation homology. These squares suggest that the functors (7) might, in fact, arise as the maps induced on mapping spaces by a functor of
$\otimes $
-excision in the theory of factorisation homology. These squares suggest that the functors (7) might, in fact, arise as the maps induced on mapping spaces by a functor of
![]() $\infty $
-categories
$\infty $
-categories
from the d-dimensional bordism category to a Morita category whose objects are associative algebras in
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
and whose morphisms are bimodules. This turns out to be the case, but to prove our results, we need even more functoriality. For this, one notes that the presheaf
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
and whose morphisms are bimodules. This turns out to be the case, but to prove our results, we need even more functoriality. For this, one notes that the presheaf
![]() $E_M$
of a manifold makes equal sense if M is noncompact, so (8) ought to extend to a functor
$E_M$
of a manifold makes equal sense if M is noncompact, so (8) ought to extend to a functor
of
![]() $(\infty ,2)$
-categories from a larger bordism category of possibly noncompact manifolds that has codimension
$(\infty ,2)$
-categories from a larger bordism category of possibly noncompact manifolds that has codimension
![]() $0$
embeddings as
$0$
embeddings as
![]() $2$
-morphisms, not just diffeomorphisms, to a larger Morita category
$2$
-morphisms, not just diffeomorphisms, to a larger Morita category
![]() $\mathscr {M}\mathrm {od}(d)^{(\infty ,2)}$
that has morphisms of bimodules as
$\mathscr {M}\mathrm {od}(d)^{(\infty ,2)}$
that has morphisms of bimodules as
![]() $2$
-morphisms, not just invertible ones.
$2$
-morphisms, not just invertible ones.
In Section 3, relying on work of Haugseng [Reference HaugsengHau17], we carefully construct such a functor (9) of
![]() $(\infty ,2)$
-categories and show that it can be enhanced to a functor of symmetric monoidal
$(\infty ,2)$
-categories and show that it can be enhanced to a functor of symmetric monoidal
![]() $(\infty ,2)$
-categories. As part of Section 4, we show that for (possibly noncompact) bordisms
$(\infty ,2)$
-categories. As part of Section 4, we show that for (possibly noncompact) bordisms
![]() $W,W'\colon P\leadsto Q$
, one can identify the map between mapping spaces of
$W,W'\colon P\leadsto Q$
, one can identify the map between mapping spaces of
![]() $2$
-morphisms induced by (9)
$2$
-morphisms induced by (9)

with Goodwillie–Weiss’ embedding calculus approximation, so one might view the functor (9) as an enhancement of embedding calculus to the level of bordism categories. In particular,
-
(I) the functor (9) of symmetric monoidal
 $(\infty ,2)$
-categories equips the limit of the embedding calculus tower with homotopy coherent gluing, composition and disjoint union maps.
$(\infty ,2)$
-categories equips the limit of the embedding calculus tower with homotopy coherent gluing, composition and disjoint union maps.
The functor (9) and its relation to embedding calculus forms the technical backbone of the proofs of Theorems A–C in the later chapters, whose proof strategies we summarise now.
Remark 1.3. As part of [Reference Krannich and KupersKK24c], the functor (9) was generalised in several directions.
1.2.3 Theorem A: tangential
 $2$
-type invariance
$2$
-type invariance
The functor (8) in particular extends the
![]() $\mathscr {D}\mathrm {isc}$
-structure space of a manifold
$\mathscr {D}\mathrm {isc}$
-structure space of a manifold
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
to a space-valued functor of
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
to a space-valued functor of
![]() $\infty $
-categories
$\infty $
-categories
defined on the
![]() $\infty $
-category of null bordisms (i.e., the undercategory of
$\infty $
-category of null bordisms (i.e., the undercategory of
![]() $\varnothing \in \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}$
). Relying on the relation to embedding calculus via (9), a version of an isotopy extension theorem for embedding calculus due to Knudsen–Kupers [Reference Knudsen and KupersKK24a], and Goodwillie–Klein’s above mentioned convergence theorem, we show that the functor (10) sends a bordism
$\varnothing \in \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}$
). Relying on the relation to embedding calculus via (9), a version of an isotopy extension theorem for embedding calculus due to Knudsen–Kupers [Reference Knudsen and KupersKK24a], and Goodwillie–Klein’s above mentioned convergence theorem, we show that the functor (10) sends a bordism
![]() $W\colon P\leadsto Q$
to an equivalence if W can be built from a collar on P by attaching handles of index
$W\colon P\leadsto Q$
to an equivalence if W can be built from a collar on P by attaching handles of index
![]() $\ge 3$
. This leads to a proof of Theorem A, since it turns out that the value of any functor of the form (10) with this property depends up to equivalence only on the tangential
$\ge 3$
. This leads to a proof of Theorem A, since it turns out that the value of any functor of the form (10) with this property depends up to equivalence only on the tangential
![]() $2$
-type. This is an instance of
$2$
-type. This is an instance of
-
(II) a general tangential k-type invariance result for the values of certain functors on the category
 $\mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}_{\varnothing /}$
of null bordisms.
$\mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}_{\varnothing /}$
of null bordisms.
The proof of (II) amounts to a sequence of surgery arguments that we became aware of through the literature on the space of metrics of positive scalar curvature – in particular, [Reference Ebert and Randal-WilliamsERW22, Reference Ebert and WiemelerEW24].
1.2.4 Theorem B: infinite loop space
To construct an infinite loop space structure on
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
, we first use the tangential
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
, we first use the tangential
![]() $2$
-type invariance to show that it suffices to consider manifolds of the form
$2$
-type invariance to show that it suffices to consider manifolds of the form
![]() $M=P\times D^{2n}$
for P a closed manifold and
$M=P\times D^{2n}$
for P a closed manifold and
![]() $2n\ge 4$
. From the definition
$2n\ge 4$
. From the definition
it is clear that it suffices to prove that the right-hand map is a map of infinite loop spaces. After restriction to certain path-components that does not affect the fibre, this is what we do. More precisely, in the target, we restrict to modules equivalent to
![]() $\smash {E_{P\times W_{g,1}}}$
for
$\smash {E_{P\times W_{g,1}}}$
for
![]() $g\ge 0$
where
$g\ge 0$
where
![]() $W_{g,1}$
is short for the bordism
$W_{g,1}$
is short for the bordism
![]() $(S^n\times S^n)^{\sharp g}\backslash \mathrm {int}(D^{2n})\colon \varnothing \leadsto S^{2n-1}$
. In the source, we restrict to bordisms whose induced presheaf is equivalent to
$(S^n\times S^n)^{\sharp g}\backslash \mathrm {int}(D^{2n})\colon \varnothing \leadsto S^{2n-1}$
. In the source, we restrict to bordisms whose induced presheaf is equivalent to
![]() $E_{P\times W_{g,1}}$
for
$E_{P\times W_{g,1}}$
for
![]() $g\ge 0$
as a bimodule. We then use the full coherence provided by the functor (8) to enhance the restricted map to one of algebras over a certain higher-dimensional version
$g\ge 0$
as a bimodule. We then use the full coherence provided by the functor (8) to enhance the restricted map to one of algebras over a certain higher-dimensional version
![]() $\mathscr {W}$
of Tillmann’s surface operad [Reference TillmannTil00], constructed out of bordisms of the form
$\mathscr {W}$
of Tillmann’s surface operad [Reference TillmannTil00], constructed out of bordisms of the form
![]() $\sqcup ^{k} S^{2n-1}\leadsto \sqcup ^{l} S^{2n-1}$
for
$\sqcup ^{k} S^{2n-1}\leadsto \sqcup ^{l} S^{2n-1}$
for
![]() $k,l\ge 0$
that are obtained from the manifolds
$k,l\ge 0$
that are obtained from the manifolds
![]() $W_{g,1}$
by creating more boundary spheres. A variant of this operad has already appeared in work of Basterra–Bobkova–Ponto–Tillmann–Yaekel [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17] on operads with homological stability. They proved that algebras over this operad are
$W_{g,1}$
by creating more boundary spheres. A variant of this operad has already appeared in work of Basterra–Bobkova–Ponto–Tillmann–Yaekel [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17] on operads with homological stability. They proved that algebras over this operad are
![]() $E_1$
-spaces (via a ‘pair-of-pants’ product) which group-complete to infinite loop spaces, the main ingredient being a stable homological stability result of Galatius–Randal-Williams [Reference Galatius and Randal-WilliamsGRW17]. Translated to our setting, this implies that the fibre of the group completion of the restricted map is an infinite loop space. Using tangential
$E_1$
-spaces (via a ‘pair-of-pants’ product) which group-complete to infinite loop spaces, the main ingredient being a stable homological stability result of Galatius–Randal-Williams [Reference Galatius and Randal-WilliamsGRW17]. Translated to our setting, this implies that the fibre of the group completion of the restricted map is an infinite loop space. Using tangential
![]() $2$
-type invariance once more, we then show that in this case, group completion commutes with taking fibres. This only shows that
$2$
-type invariance once more, we then show that in this case, group completion commutes with taking fibres. This only shows that
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})$
is an infinite loop space after group completion, but we also show that this
$S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})$
is an infinite loop space after group completion, but we also show that this
![]() $E_1$
-space is already group-complete, using the s-cobordism theorem.
$E_1$
-space is already group-complete, using the s-cobordism theorem.
1.2.5 Theorem C: nontriviality
To show that
![]() $\smash {S^{\mathscr {D}\mathrm {isc}}_\partial }(M)$
is nontrivial for all compact spin manifolds M of dimension
$\smash {S^{\mathscr {D}\mathrm {isc}}_\partial }(M)$
is nontrivial for all compact spin manifolds M of dimension
![]() $d\ge 5$
, we first reduce to the case
$d\ge 5$
, we first reduce to the case
![]() $M=D^d$
using tangential
$M=D^d$
using tangential
![]() $2$
-type invariance. The equivalence (5) then further reduces this to showing that the fibre
$2$
-type invariance. The equivalence (5) then further reduces this to showing that the fibre
![]() $\mathrm {Aut}(E_d)/\mathrm {Top}(d)$
of (4) has a nontrivial homotopy group in sufficiently high degree, which we do by showing that the individual homotopy groups of
$\mathrm {Aut}(E_d)/\mathrm {Top}(d)$
of (4) has a nontrivial homotopy group in sufficiently high degree, which we do by showing that the individual homotopy groups of
![]() $\mathrm {Aut}(E_d)$
and
$\mathrm {Aut}(E_d)$
and
![]() $\mathrm {Top}(d)$
are sufficiently different. While quite a bit is known about the homotopy groups of
$\mathrm {Top}(d)$
are sufficiently different. While quite a bit is known about the homotopy groups of
![]() $\mathrm {Top}(d)$
, especially rationally, so far, almost nothing is known about the homotopy groups of
$\mathrm {Top}(d)$
, especially rationally, so far, almost nothing is known about the homotopy groups of
![]() $\mathrm {Aut}(E_d)$
besides for small values of d. This is in stark contrast to the automorphism group
$\mathrm {Aut}(E_d)$
besides for small values of d. This is in stark contrast to the automorphism group
![]() $\mathrm {Aut}((E_d)_{\mathbf {Q}})$
of the rationalised
$\mathrm {Aut}((E_d)_{\mathbf {Q}})$
of the rationalised
![]() $E_d$
-operad, whose homotopy groups have a complete description in terms of graph complexes à la Kontsevich due to work of Fresse–Turchin–Willwacher [Reference Fresse, Turchin and WillwacherFTW17]. Thus, to learn something about the homotopy groups of
$E_d$
-operad, whose homotopy groups have a complete description in terms of graph complexes à la Kontsevich due to work of Fresse–Turchin–Willwacher [Reference Fresse, Turchin and WillwacherFTW17]. Thus, to learn something about the homotopy groups of
![]() $\mathrm {Aut}(E_d)$
, one could try to study the comparison map
$\mathrm {Aut}(E_d)$
, one could try to study the comparison map
![]() $\mathrm {Aut}(E_d)\rightarrow \mathrm {Aut}((E_d)_{\mathbf {Q}})$
on homotopy groups. This is what we do. More generally,
$\mathrm {Aut}(E_d)\rightarrow \mathrm {Aut}((E_d)_{\mathbf {Q}})$
on homotopy groups. This is what we do. More generally,
-
(III) we study the effect on homotopy groups of the map
 $\mathrm {Map}(\mathscr {O},\mathscr {P})\rightarrow \mathrm {Map}(\mathscr {O}_{\mathbf {Q}},\mathscr {P}_{\mathbf {Q}})$
for operads
$\mathrm {Map}(\mathscr {O},\mathscr {P})\rightarrow \mathrm {Map}(\mathscr {O}_{\mathbf {Q}},\mathscr {P}_{\mathbf {Q}})$
for operads
 $\mathscr {O}$
and
$\mathscr {O}$
and
 $\mathscr {P}$
, induced by rationalisation.
$\mathscr {P}$
, induced by rationalisation.
For this, we first use work of Göppl and Weiss [Reference Göppl and WeissGW24] to decompose the mapping spaces as a limit of a tower of mapping spaces between truncated operads and show that under mild assumptions, the maps analogous to that in (III) between the stages of this tower are componentwise rationalisations. Rationalisation does not commute with sequential limits in general, so this does not imply that the map in (III) has the same property. However, we then show that this can only fail in an extreme way – namely, when some of the homotopy groups of
![]() $\mathrm {Map}(\mathscr {O},\mathscr {P})$
are uncountable. We also explain similar results for more general localisations and for more general towers of spaces.
$\mathrm {Map}(\mathscr {O},\mathscr {P})$
are uncountable. We also explain similar results for more general localisations and for more general towers of spaces.
Applied to
![]() $\mathscr {O}=\mathscr {P}=E_d$
, this shows that the homotopy groups of
$\mathscr {O}=\mathscr {P}=E_d$
, this shows that the homotopy groups of
![]() $\mathrm {Aut}(E_d)$
either agree rationally with those of
$\mathrm {Aut}(E_d)$
either agree rationally with those of
![]() $\mathrm {Aut}((E_d)_{\mathbf {Q}})$
, as described in Fresse–Turchin–Willwacher’s work, or some of them are uncountable. In either case, we can conclude that they are different from that of
$\mathrm {Aut}((E_d)_{\mathbf {Q}})$
, as described in Fresse–Turchin–Willwacher’s work, or some of them are uncountable. In either case, we can conclude that they are different from that of
![]() $\mathrm {Top}(d)$
: in the former by comparing them with known partial computations of the rational homotopy groups of
$\mathrm {Top}(d)$
: in the former by comparing them with known partial computations of the rational homotopy groups of
![]() $\mathrm {Top}(d)$
, and in the latter by using that
$\mathrm {Top}(d)$
, and in the latter by using that
![]() $\mathrm {Top}(d)$
has countable homotopy groups.
$\mathrm {Top}(d)$
has countable homotopy groups.
2
 $\infty $
-categorical preliminaries
$\infty $
-categorical preliminaries
Except for the final two sections (see Convention 7.1), we work in the setting of
![]() $\infty $
-categories. This section – which may be skipped on first reading and referred back to when necessary – serves to establish some notation and to recall definitions and facts used in later sections, as well as to prove a few technical results that we could not find in the literature. The topics are as follows:
$\infty $
-categories. This section – which may be skipped on first reading and referred back to when necessary – serves to establish some notation and to recall definitions and facts used in later sections, as well as to prove a few technical results that we could not find in the literature. The topics are as follows:
-
2.1 Conventions.
-
2.2 The coherent nerve.
-
2.3 Cocartesian fibrations.
-
2.4 The categories
 $\Delta $
,
$\Delta $
,
 $\mathsf {Gap}$
, and
$\mathsf {Gap}$
, and
 $\mathsf {Fin}_*$
.
$\mathsf {Fin}_*$
. -
2.5 Category and monoid objects.
-
2.6 Presheaves and the Yoneda embedding.
-
2.7
 $\infty $
-operads and generalised
$\infty $
-operads and generalised
 $\infty $
-operads.
$\infty $
-operads. -
2.8 Associative algebras and bimodules.
-
2.9 Haugseng’s Morita category.
-
2.10 Span and cospan categories.
2.1 Conventions
Unless mentioned otherwise, we follow the conventions and notation of [Reference LurieLur09a, Reference LurieLur17]. In particular,
-
• An
 $\infty $
-category is a quasi-category [Reference LurieLur09a, 1.1.2.4]. The
$\infty $
-category is a quasi-category [Reference LurieLur09a, 1.1.2.4]. The
 $\infty $
-category of
$\infty $
-category of
 $\infty $
-categories
$\infty $
-categories  is the coherent nerve
is the coherent nerve  of the
of the
 $\mathsf {Kan}$
-enriched category
$\mathsf {Kan}$
-enriched category
 $\mathsf {Cat}_\infty $
of small
$\mathsf {Cat}_\infty $
of small
 $\infty $
-categories [Reference LurieLur09a, 3.0.0.1]. We consider 1-categories as
$\infty $
-categories [Reference LurieLur09a, 3.0.0.1]. We consider 1-categories as
 $\infty $
-categories via their nerve.
$\infty $
-categories via their nerve. -
• A space is a Kan complex. If topological spaces appear, we implicitly replace them by their singular simplicial sets. The category of simplicial sets is denoted
 $\mathsf {S}$
and the full subcategory of Kan-complexes by
$\mathsf {S}$
and the full subcategory of Kan-complexes by
 $\mathsf {Kan} \subset \mathsf {S}$
. Both are enriched over themselves. The
$\mathsf {Kan} \subset \mathsf {S}$
. Both are enriched over themselves. The
 $\infty $
-category of spaces
$\infty $
-category of spaces  is the coherent nerve
is the coherent nerve  [Reference LurieLur09a, 1.2.16.1].
[Reference LurieLur09a, 1.2.16.1].
We use the following notational conventions:
-
• The letters
 $\mathscr {A}$
,
$\mathscr {A}$
,
 $\mathscr {B} $
,
$\mathscr {B} $
,
 $\mathscr {C}$
,
$\mathscr {C}$
,
 $\ldots $
typically stand for
$\ldots $
typically stand for
 $\infty $
-categories, whereas the letters
$\infty $
-categories, whereas the letters
 $\mathsf {A}$
,
$\mathsf {A}$
,
 $\mathsf {B}$
,
$\mathsf {B}$
,
 $\mathsf {C}$
,
$\mathsf {C}$
,
 $\ldots $
usually stand for
$\ldots $
usually stand for
 $\mathsf {S}$
-enriched,
$\mathsf {S}$
-enriched,
 $\mathsf {Kan}$
-enriched or 1-categories.
$\mathsf {Kan}$
-enriched or 1-categories. -
• Given an
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
and object c of
$\mathscr {C}$
and object c of
 $\mathscr {C}$
,
$\mathscr {C}$
,
 $\mathscr {C}_{c/}^{\mathrm {op}}$
is short for
$\mathscr {C}_{c/}^{\mathrm {op}}$
is short for
 $(\mathscr {C}_{c/})^{\mathrm {op}}$
and similarly
$(\mathscr {C}_{c/})^{\mathrm {op}}$
and similarly
 $\mathscr {C}^{\mathrm {op}}_{/c}$
is short for
$\mathscr {C}^{\mathrm {op}}_{/c}$
is short for
 $(\mathscr {C}_{/c})^{\mathrm {op}}$
. In other words, slices are taken before opposite categories.
$(\mathscr {C}_{/c})^{\mathrm {op}}$
. In other words, slices are taken before opposite categories.
2.2 The coherent nerve and the homotopy category
The coherent nerve ![]() is a functor from the
is a functor from the
![]() $1$
-category
$1$
-category
![]() $\mathsf {sCat}$
of
$\mathsf {sCat}$
of
![]() $\mathsf {S}$
-enriched categories to the
$\mathsf {S}$
-enriched categories to the
![]() $1$
-category of simplicial sets [Reference LurieLur09a, 1.1.5]. Some of its properties are as follows:
$1$
-category of simplicial sets [Reference LurieLur09a, 1.1.5]. Some of its properties are as follows:
-
(i) It is the right-adjoint in a Quillen equivalence [Reference LurieLur09a, 2.2.5.1], where
 $\mathsf {sCat}$
is equipped with the Bergner model structure whose
$\mathsf {sCat}$
is equipped with the Bergner model structure whose-
(a) fibrant objects are
 $\mathsf {Kan}$
-enriched categories [Reference LurieLur09a, A.3.2.24],
$\mathsf {Kan}$
-enriched categories [Reference LurieLur09a, A.3.2.24], -
(b) weak equivalences are Dwyer–Kan equivalences, so simplicial functors that induce weak homotopy equivalences on each mapping space and are an equivalence (of
 $1$
-categories) on homotopy categories [Reference LurieLur09a, A.3.2.4],
$1$
-categories) on homotopy categories [Reference LurieLur09a, A.3.2.4], -
(c) fibrations are simplicial functors that are Kan fibrations on each mapping space and isofibrations on homotopy categories [Reference LurieLur09a, A.3.2.24, A.3.2.25],
and
 $\mathsf {S}$
is equipped with the Joyal model structure of which we only need to know that its fibrant objects are precisely
$\mathsf {S}$
is equipped with the Joyal model structure of which we only need to know that its fibrant objects are precisely
 $\infty $
-categories [Reference LurieLur09a, 2.4.6.1]. In particular, the coherent nerve of a
$\infty $
-categories [Reference LurieLur09a, 2.4.6.1]. In particular, the coherent nerve of a
 $\mathsf {Kan}$
-enriched category is an
$\mathsf {Kan}$
-enriched category is an
 $\infty $
-category.
$\infty $
-category. -
-
(ii) Taking coherent nerves preserves objects and morphisms, in the sense that the
 $0$
- and
$0$
- and
 $1$
-simplices of
$1$
-simplices of
 $N_{\mathrm {coh}}(\mathsf {C})$
are the sets of objects and morphisms of
$N_{\mathrm {coh}}(\mathsf {C})$
are the sets of objects and morphisms of
 $\mathsf {C}$
[Reference LurieLur09a, p. 23].
$\mathsf {C}$
[Reference LurieLur09a, p. 23]. -
(iii) Taking coherent nerves preserves mapping spaces of
 $\mathsf {Kan}$
-enriched categories in that for a
$\mathsf {Kan}$
-enriched categories in that for a
 $\mathsf {Kan}$
-enriched category
$\mathsf {Kan}$
-enriched category
 $\mathsf {C}$
, we have
$\mathsf {C}$
, we have
 $\mathrm {Map}_{\mathsf {C}}(c,c')\simeq \mathrm {Map}_{N_{\mathrm {coh}}(\mathsf {C})}(c,c')$
[Reference LurieLur09a, 2.2].
$\mathrm {Map}_{\mathsf {C}}(c,c')\simeq \mathrm {Map}_{N_{\mathrm {coh}}(\mathsf {C})}(c,c')$
[Reference LurieLur09a, 2.2]. -
(iv) There is a natural equivalence
 $N_{\mathrm {coh}}(\mathsf {C}^{\mathrm {op}}) \simeq N_{\mathrm {coh}}(\mathsf {C})^{\mathrm {op}}$
. This is a consequence of the natural isomorphisms
$N_{\mathrm {coh}}(\mathsf {C}^{\mathrm {op}}) \simeq N_{\mathrm {coh}}(\mathsf {C})^{\mathrm {op}}$
. This is a consequence of the natural isomorphisms
 $\mathfrak {C}([n]^{\mathrm {op}}) \cong \mathfrak {C}([n])^{\mathrm {op}}$
, where
$\mathfrak {C}([n]^{\mathrm {op}}) \cong \mathfrak {C}([n])^{\mathrm {op}}$
, where
 $\mathfrak {C}(-)$
is the left adjoint to
$\mathfrak {C}(-)$
is the left adjoint to
 $N_{\mathrm {coh}}(-)$
.
$N_{\mathrm {coh}}(-)$
. -
(v) There is a canonical map
 $N_{\mathrm {coh}}(\mathrm {Fun}(\mathsf {C},\mathsf {D})) \to \mathrm {Fun}(N_{\mathrm {coh}}(\mathsf {C}),N_{\mathrm {coh}}(\mathsf {D}))$
obtained by appling
$N_{\mathrm {coh}}(\mathrm {Fun}(\mathsf {C},\mathsf {D})) \to \mathrm {Fun}(N_{\mathrm {coh}}(\mathsf {C}),N_{\mathrm {coh}}(\mathsf {D}))$
obtained by appling
 $N_{\mathrm {coh}}$
to the evaluation
$N_{\mathrm {coh}}$
to the evaluation
 $\mathrm {Fun}(\mathsf {C},\mathsf {D}) \times \mathsf {C} \rightarrow \mathsf {D}$
, using that as a right adjoint,
$\mathrm {Fun}(\mathsf {C},\mathsf {D}) \times \mathsf {C} \rightarrow \mathsf {D}$
, using that as a right adjoint,
 $N_{\mathrm {coh}}(-)$
preserves products to get
$N_{\mathrm {coh}}(-)$
preserves products to get
 $N_{\mathrm {coh}}(\mathrm {Fun}(\mathsf {C},\mathsf {D})) \times N_{\mathrm {coh}}(\mathsf {C}) \to N_{\mathrm {coh}}(\mathsf {D})$
, and adjoining over
$N_{\mathrm {coh}}(\mathrm {Fun}(\mathsf {C},\mathsf {D})) \times N_{\mathrm {coh}}(\mathsf {C}) \to N_{\mathrm {coh}}(\mathsf {D})$
, and adjoining over
 $N_{\mathrm {coh}}(\mathsf {C})$
.
$N_{\mathrm {coh}}(\mathsf {C})$
.
Restricting
![]() $N_{\mathrm {coh}}$
to
$N_{\mathrm {coh}}$
to
![]() $\mathsf {Cat} \subset \mathsf {sCat}$
gives a fully faithful functor of
$\mathsf {Cat} \subset \mathsf {sCat}$
gives a fully faithful functor of
![]() $1$
-categories from ordinary
$1$
-categories from ordinary
![]() $1$
-categories to
$1$
-categories to
![]() $\infty $
-categories. Applying
$\infty $
-categories. Applying
![]() $N_{\mathrm {coh}}$
, we obtain a functor
$N_{\mathrm {coh}}$
, we obtain a functor
![]() $\mathrm {Cat}\rightarrow \mathscr {C}\mathrm {at}_\infty $
of
$\mathrm {Cat}\rightarrow \mathscr {C}\mathrm {at}_\infty $
of
![]() $\infty $
-categories. This has a left-adjoint
$\infty $
-categories. This has a left-adjoint ![]() that assigns an
that assigns an
![]() $\infty $
-category its homotopy category. As described in [Reference LurieLur09a, 1.2.3],
$\infty $
-category its homotopy category. As described in [Reference LurieLur09a, 1.2.3],
![]() $h\mathscr {C}$
has the same objects as
$h\mathscr {C}$
has the same objects as
![]() $\mathscr {C}$
, morphism sets given by the path components of the respective mapping spaces in
$\mathscr {C}$
, morphism sets given by the path components of the respective mapping spaces in
![]() $\mathscr {C}$
, and composition is induced by the composition maps of mapping spaces. Some of its further properties are as follows:
$\mathscr {C}$
, and composition is induced by the composition maps of mapping spaces. Some of its further properties are as follows:
-
(i) The functor h preserves products.
-
(ii) The functor h preserves pullbacks if one of the maps is between 1-categories.
-
(iii) The functor h preserves cocartesian morphisms when the target is an 1-category.
These follow from the facts that taking mapping spaces in
![]() $\infty $
-categories preserves pullbacks, and that taking components preserves pullbacks in
$\infty $
-categories preserves pullbacks, and that taking components preserves pullbacks in
![]() $\mathscr {S}$
whose bottom right corner is discrete.
$\mathscr {S}$
whose bottom right corner is discrete.
2.3 Cocartesian fibrations
Lurie’s straightening equivalence [Reference LurieLur09a, 3.2]
identifies the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Fun}(\mathscr {C},\mathscr {C}\mathrm {at}_\infty )$
for an
$\mathrm {Fun}(\mathscr {C},\mathscr {C}\mathrm {at}_\infty )$
for an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
with the
$\mathscr {C}$
with the
![]() $\infty $
-category of cocartesian fibrations, which is the sub
$\infty $
-category of cocartesian fibrations, which is the sub
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Cocart}(\mathscr {C})\subset (\mathscr {C}\mathrm {at}_\infty )_{/\mathscr {C}}$
with objects cocartesian fibrations with target
$\mathrm {Cocart}(\mathscr {C})\subset (\mathscr {C}\mathrm {at}_\infty )_{/\mathscr {C}}$
with objects cocartesian fibrations with target
![]() $\mathscr {C}$
and whose morphisms are maps of cocartesian fibrations, in the following sense:
$\mathscr {C}$
and whose morphisms are maps of cocartesian fibrations, in the following sense:
Definition 2.1. Let
![]() $\varphi \colon \mathscr {E} \rightarrow \mathscr {B} $
be a functor between
$\varphi \colon \mathscr {E} \rightarrow \mathscr {B} $
be a functor between
![]() $\infty $
-categories.
$\infty $
-categories.
-
(i) A morphism
 $f\colon e\rightarrow e'$
in
$f\colon e\rightarrow e'$
in
 $\mathscr {E} $
is
$\mathscr {E} $
is
 $\varphi $
-cocartesian if for every
$\varphi $
-cocartesian if for every
 $x\in \mathscr {E} $
, the square
$x\in \mathscr {E} $
, the square 
is homotopy cartesian.
-
(ii) The functor
 $\varphi $
is a cocartesian fibration if for every object
$\varphi $
is a cocartesian fibration if for every object
 $e\in \mathscr {E} $
and morphism
$e\in \mathscr {E} $
and morphism
 $f\colon \varphi (e)\rightarrow b$
, there exists a cocartesian lift of f (i.e. a
$f\colon \varphi (e)\rightarrow b$
, there exists a cocartesian lift of f (i.e. a
 $\varphi $
-cocartesian morphism
$\varphi $
-cocartesian morphism
 $\tilde {f}\colon e\rightarrow \tilde {b}$
for some
$\tilde {f}\colon e\rightarrow \tilde {b}$
for some
 $\tilde {b}$
in
$\tilde {b}$
in
 $\mathscr {E} $
such that
$\mathscr {E} $
such that
 $\varphi (\tilde {f})=f$
).
$\varphi (\tilde {f})=f$
). -
(iii) A map of cocartesian fibrations from
 $\varphi \colon \mathscr {E} \rightarrow \mathscr {B} $
to
$\varphi \colon \mathscr {E} \rightarrow \mathscr {B} $
to
 $\varphi '\colon \mathscr {E} '\rightarrow \mathscr {B} $
is a functor
$\varphi '\colon \mathscr {E} '\rightarrow \mathscr {B} $
is a functor
 $\mathscr {E} \rightarrow \mathscr {E} '$
over
$\mathscr {E} \rightarrow \mathscr {E} '$
over
 $\mathscr {B} $
that sends
$\mathscr {B} $
that sends
 $\varphi $
-cocartesian morphisms to
$\varphi $
-cocartesian morphisms to
 $\varphi '$
-cocartesian morphisms.
$\varphi '$
-cocartesian morphisms.
Given a cocartesian fibration
![]() $\varphi \colon \mathscr {E} \rightarrow \mathscr {B} $
and an object
$\varphi \colon \mathscr {E} \rightarrow \mathscr {B} $
and an object
![]() $b\in \mathscr {B} $
, one writes
$b\in \mathscr {B} $
, one writes
![]() $\mathscr {E} _b\in \mathscr {C}\mathrm {at}_\infty $
for the fibre of
$\mathscr {E} _b\in \mathscr {C}\mathrm {at}_\infty $
for the fibre of
![]() $\varphi $
at b. Under the straightening equivalence (12), this corresponds to the value at b of the associated functor
$\varphi $
at b. Under the straightening equivalence (12), this corresponds to the value at b of the associated functor
![]() $\mathscr {B} \rightarrow \mathscr {C}\mathrm {at}_\infty $
. Moreover, the value of this functor on a morphism
$\mathscr {B} \rightarrow \mathscr {C}\mathrm {at}_\infty $
. Moreover, the value of this functor on a morphism
![]() $b\rightarrow b'$
in
$b\rightarrow b'$
in
![]() $\mathscr {B} $
corresponds to a functor
$\mathscr {B} $
corresponds to a functor
![]() $\mathscr {E}_b\rightarrow \mathscr {E}_b'$
induced by choosing cocartesian lifts of
$\mathscr {E}_b\rightarrow \mathscr {E}_b'$
induced by choosing cocartesian lifts of
![]() $b\rightarrow b'$
.
$b\rightarrow b'$
.
Remark 2.2. Definition 2.1 makes equal sense for a functor
![]() $\varphi \colon \mathsf {E}\rightarrow \mathsf {B}$
of
$\varphi \colon \mathsf {E}\rightarrow \mathsf {B}$
of
![]() $\mathsf {Kan}$
-enriched categories. In view of the natural equivalence
$\mathsf {Kan}$
-enriched categories. In view of the natural equivalence
![]() $\mathrm {Map}_{\mathsf {C}}(c,c')\simeq \mathrm {Map}_{N_{\mathrm {coh}}(\mathsf {C})}(c,c')$
, one sees that a morphism
$\mathrm {Map}_{\mathsf {C}}(c,c')\simeq \mathrm {Map}_{N_{\mathrm {coh}}(\mathsf {C})}(c,c')$
, one sees that a morphism
![]() $f\colon e\rightarrow e'$
in
$f\colon e\rightarrow e'$
in
![]() $\mathsf {E}$
is
$\mathsf {E}$
is
![]() $\varphi $
-cocartesian if and only if is
$\varphi $
-cocartesian if and only if is
![]() $N_{\mathrm {coh}}(\varphi )$
-cocartesian.
$N_{\mathrm {coh}}(\varphi )$
-cocartesian.
Given a cocartesian fibration
![]() $\varphi \colon \mathscr {E} \rightarrow \mathscr {B} $
and an
$\varphi \colon \mathscr {E} \rightarrow \mathscr {B} $
and an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, the functor
$\mathscr {C}$
, the functor
![]() $\varphi _{*}\colon \mathrm {Fun}(\mathscr {C},\mathscr {E}) \rightarrow \mathrm {Fun}(\mathscr {C},\mathscr {B} )$
is again a cocartesian fibration [Reference LurieLur09a, 3.1.2.1]. In particular, given a functor
$\varphi _{*}\colon \mathrm {Fun}(\mathscr {C},\mathscr {E}) \rightarrow \mathrm {Fun}(\mathscr {C},\mathscr {B} )$
is again a cocartesian fibration [Reference LurieLur09a, 3.1.2.1]. In particular, given a functor
![]() $f \colon \mathscr {C}\rightarrow \mathscr {E}$
and a natural transformation
$f \colon \mathscr {C}\rightarrow \mathscr {E}$
and a natural transformation
![]() $\eta \colon (\varphi \circ f)\rightarrow *_b$
to the constant functor
$\eta \colon (\varphi \circ f)\rightarrow *_b$
to the constant functor
![]() $*_b\colon \mathscr {C}\rightarrow \mathscr {B} $
with value
$*_b\colon \mathscr {C}\rightarrow \mathscr {B} $
with value
![]() $b\in B$
(equivalently, an extension of
$b\in B$
(equivalently, an extension of
![]() $(\varphi \circ f)$
to a functor
$(\varphi \circ f)$
to a functor
![]() $\mathscr {C}^\rhd \rightarrow \mathscr {B} $
on the right-cone whose value at the cone point is b), we can use that
$\mathscr {C}^\rhd \rightarrow \mathscr {B} $
on the right-cone whose value at the cone point is b), we can use that
![]() $\varphi _{*}$
is a cocartesian fibration to obtain a cocartesian lift to a functor
$\varphi _{*}$
is a cocartesian fibration to obtain a cocartesian lift to a functor
![]() $f_!\colon \mathscr {C}\rightarrow \mathscr {E}_b$
into the fibre over b. The functor
$f_!\colon \mathscr {C}\rightarrow \mathscr {E}_b$
into the fibre over b. The functor
![]() $f_!$
is called a cocartesian pushforward of f along
$f_!$
is called a cocartesian pushforward of f along
![]() $\eta $
.
$\eta $
.
2.4 The categories
 $\mathsf {Fin}_{*}$
,
$\mathsf {Fin}_{*}$
,
 $\Delta $
, and
$\Delta $
, and
 $\mathsf {Gap}$
$\mathsf {Gap}$
Recall the 1-category ![]() of pointed finite sets and pointed maps in between, with skeleton given by
of pointed finite sets and pointed maps in between, with skeleton given by ![]() for
for
![]() $p \geq 0$
. We write
$p \geq 0$
. We write ![]() for the interior of
for the interior of
![]() $\langle p \rangle $
. Three special types of morphisms are relevant for us: a morphism
$\langle p \rangle $
. Three special types of morphisms are relevant for us: a morphism
![]() $\alpha \colon \langle p \rangle \rightarrow \langle q \rangle $
is
$\alpha \colon \langle p \rangle \rightarrow \langle q \rangle $
is
-
(i) active if it satisfies
 $\alpha ^{-1}(\ast )=\{\ast \}$
,
$\alpha ^{-1}(\ast )=\{\ast \}$
, -
(ii) inert if
 $\alpha ^{-1}(i)$
consists of a single element for all
$\alpha ^{-1}(i)$
consists of a single element for all
 $i \in \langle \mathring {q} \rangle $
,
$i \in \langle \mathring {q} \rangle $
, -
(iii) Segal if it agrees with
 $\rho _i\colon \langle p \rangle \rightarrow \langle 1 \rangle $
for some
$\rho _i\colon \langle p \rangle \rightarrow \langle 1 \rangle $
for some
 $1\le i\le p$
where
$1\le i\le p$
where
 $\rho _i(i)=1$
and
$\rho _i(i)=1$
and
 $\rho (j)=\ast $
otherwise. Note this is equivalent to being inert with target
$\rho (j)=\ast $
otherwise. Note this is equivalent to being inert with target
 $\langle 1 \rangle $
.
$\langle 1 \rangle $
.
A closely related 1-category is the simplex category ![]() of nonempty finite totally ordered sets and weakly order-preserving maps between them. We mostly work with its skeleton given by
of nonempty finite totally ordered sets and weakly order-preserving maps between them. We mostly work with its skeleton given by ![]() for
for
![]() $p\ge 0$
. The wide subcategory of injective maps is denoted
$p\ge 0$
. The wide subcategory of injective maps is denoted ![]() . Four special types of morphisms are relevant for us: a morphism
. Four special types of morphisms are relevant for us: a morphism
![]() $\alpha \colon [p]\rightarrow [q]$
is
$\alpha \colon [p]\rightarrow [q]$
is
-
(i) active if it satisfies
 $\alpha (0)=0$
and
$\alpha (0)=0$
and
 $\alpha (p)=q$
,
$\alpha (p)=q$
, -
(ii) cellular if
 $\alpha (i+1)\le \alpha (i)+1$
for all i,
$\alpha (i+1)\le \alpha (i)+1$
for all i, -
(iii) inert if it is the inclusion of a subinterval, i.e.
 $\alpha (i)=\alpha (0)+i$
for all i, and
$\alpha (i)=\alpha (0)+i$
for all i, and -
(iv) Segal if it agrees with
 $\rho _i\colon [1]\rightarrow [q]$
for some
$\rho _i\colon [1]\rightarrow [q]$
for some
 $1\le i\le q$
where
$1\le i\le q$
where
 $\rho _i(0)=i-1$
and
$\rho _i(0)=i-1$
and
 $\rho (1)=i$
. Note this is equivalent to being inert with domain
$\rho (1)=i$
. Note this is equivalent to being inert with domain
 $[1]$
.
$[1]$
.
Occasionally, we work with a different model for
![]() $\Delta ^{\mathrm {op}}$
, given as follows. For
$\Delta ^{\mathrm {op}}$
, given as follows. For
![]() $p\ge 0$
, we write
$p\ge 0$
, we write ![]() for the totally ordered set
for the totally ordered set
![]() $(L<1<\ldots < p<R)$
and call L and R the left end and right end of
$(L<1<\ldots < p<R)$
and call L and R the left end and right end of ![]() , respectively. The sets
, respectively. The sets ![]() for
for
![]() $p\ge 0$
form the objects of the category
$p\ge 0$
form the objects of the category ![]() whose morphisms are weakly order-preserving maps that are the identity on ends. There is an isomorphism
whose morphisms are weakly order-preserving maps that are the identity on ends. There is an isomorphism
that sends
![]() $[p]$
to
$[p]$
to ![]() and a morphism
and a morphism
![]() $\alpha \colon [p]\rightarrow [q]$
to the morphism
$\alpha \colon [p]\rightarrow [q]$
to the morphism ![]() given by
given by
 $$ \begin{align*} {i}&\longmapsto \begin{cases}L& i\le \alpha(0),\\ j& \exists j\colon i\in [\alpha(j-1)+1,\alpha(j)],\\ R& i>\alpha(p).\end{cases} \end{align*} $$
$$ \begin{align*} {i}&\longmapsto \begin{cases}L& i\le \alpha(0),\\ j& \exists j\colon i\in [\alpha(j-1)+1,\alpha(j)],\\ R& i>\alpha(p).\end{cases} \end{align*} $$
This isomorphism maps
![]() $\smash {\Delta _{\mathrm {inj}}^{\mathrm {op}}}\subset \Delta ^{\mathrm {op}}$
isomorphically onto the wide subcategory
$\smash {\Delta _{\mathrm {inj}}^{\mathrm {op}}}\subset \Delta ^{\mathrm {op}}$
isomorphically onto the wide subcategory ![]() of surjective maps. Introducing the notation
of surjective maps. Introducing the notation ![]() for the interior of
for the interior of ![]() , a morphism
, a morphism ![]() , when considered as a morphism
, when considered as a morphism
![]() $c^{-1}(\alpha )\colon [p]\rightarrow [q]$
in
$c^{-1}(\alpha )\colon [p]\rightarrow [q]$
in
![]() $\Delta $
, is
$\Delta $
, is
-
(i) active if
 (we omit the parentheses in
(we omit the parentheses in  for legibility),
for legibility), -
(ii) cellular if the restriction
 is injective,
is injective, -
(iii) inert if the restriction
 is bijective,
is bijective, -
(iv) Segal if it agrees with
 for some
for some
 $1\le i\le q$
where
$1\le i\le q$
where
 $\rho _i'(j)=L$
if
$\rho _i'(j)=L$
if
 $j<i$
,
$j<i$
,
 $\rho _i'(j)=1$
if
$\rho _i'(j)=1$
if
 $j=i$
, and
$j=i$
, and
 $\rho _i'(j)=R$
if
$\rho _i'(j)=R$
if
 $j>i$
.
$j>i$
.
Remark 2.3.
-
(i) We think of
 as the ‘gap’ between
as the ‘gap’ between
 $i-1$
and i in
$i-1$
and i in
 $[p]$
, and observe that
$[p]$
, and observe that
 $\alpha \colon [p] \to [q]$
induces a map the other way between these gaps; see Figure 1 for an example.
$\alpha \colon [p] \to [q]$
induces a map the other way between these gaps; see Figure 1 for an example.
Figure 1 The isomorphism (13) between
 $\Delta ^{\mathrm {op}}$
(on the left) and
$\Delta ^{\mathrm {op}}$
(on the left) and
 $\mathsf {Gap}$
(on the right, but we omitted the elements that map to L or R). The morphism indicated is not active, cellular, inert or Segal.
$\mathsf {Gap}$
(on the right, but we omitted the elements that map to L or R). The morphism indicated is not active, cellular, inert or Segal. -
(ii) The functor
 $c\colon \Delta ^{\mathrm {op}}\rightarrow \mathsf {Gap}$
is related to the functor
$c\colon \Delta ^{\mathrm {op}}\rightarrow \mathsf {Gap}$
is related to the functor
 $\mathrm {Cut} \colon \Delta ^{\mathrm {op}} \to \mathscr {A}\mathrm {ssoc}^\otimes $
of [Reference LurieLur17, 4.1.2.9]: the pointed set
$\mathrm {Cut} \colon \Delta ^{\mathrm {op}} \to \mathscr {A}\mathrm {ssoc}^\otimes $
of [Reference LurieLur17, 4.1.2.9]: the pointed set
 $\mathrm {Cut}([n]) \cong \langle n \rangle $
can be obtained from the set
$\mathrm {Cut}([n]) \cong \langle n \rangle $
can be obtained from the set
 $c([n])$
by identifying L and R.
$c([n])$
by identifying L and R.
The three 1-categories
![]() $\mathsf {Fin}_{*}$
,
$\mathsf {Fin}_{*}$
,
![]() $\Delta $
and
$\Delta $
and
![]() $\mathsf {Gap}$
are related by a sequence of functors
$\mathsf {Gap}$
are related by a sequence of functors
where the first arrow is the isomorphism (13), and the second arrow is obtained by identifying the left and right ends L and R of objects in
![]() $\mathsf {Gap}$
and forgetting that morphisms are order-preserving.
$\mathsf {Gap}$
and forgetting that morphisms are order-preserving.
2.5 Category and monoid objects
Fix an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
with finite limits.
$\mathscr {C}$
with finite limits.
2.5.1 Category objects and monoid objects
A category object in
![]() $\mathscr {C}$
is a simplicial object
$\mathscr {C}$
is a simplicial object
![]() $X\in \mathrm {Fun}(\Delta ^{\mathrm {op}},\mathscr {C})$
satisfying the Segal condition, i.e., the map
$X\in \mathrm {Fun}(\Delta ^{\mathrm {op}},\mathscr {C})$
satisfying the Segal condition, i.e., the map
induced by the Segal maps
![]() $\rho _i\colon [1] \to [p]$
for
$\rho _i\colon [1] \to [p]$
for
![]() $1\le i\le p$
is an equivalence for all
$1\le i\le p$
is an equivalence for all
![]() $p\ge 0$
. We call
$p\ge 0$
. We call
![]() $X_{[1]}$
the underlying object of X. A monoid object is a category object X for which the map
$X_{[1]}$
the underlying object of X. A monoid object is a category object X for which the map
![]() $X_{[0]}\rightarrow *$
to the terminal object is an equivalence; equivalently, it is a simplicial object for which the analogues of the maps (15) with pullbacks replaced by products are equivalences. We write
$X_{[0]}\rightarrow *$
to the terminal object is an equivalence; equivalently, it is a simplicial object for which the analogues of the maps (15) with pullbacks replaced by products are equivalences. We write
for the full subcategories of category objects and monoid objects. Replacing simplicial by semisimplicial objects in this definition yields the categories
of non-unital category objects and non-unital monoid objects.
2.5.2 Commutative monoid objects
We may replace the role of the category
![]() $\Delta ^{\mathrm {op}}$
in the definition of a monoid object with
$\Delta ^{\mathrm {op}}$
in the definition of a monoid object with
![]() $\mathsf {Fin}_{*}$
to arrive at the notion of a commutative monoid object: a functor
$\mathsf {Fin}_{*}$
to arrive at the notion of a commutative monoid object: a functor
![]() $X\in \mathrm {Fun}(\mathsf {Fin}_{*},\mathscr {C})$
for which the maps
$X\in \mathrm {Fun}(\mathsf {Fin}_{*},\mathscr {C})$
for which the maps
![]() $X_{\langle p \rangle }\rightarrow X_{\langle 1 \rangle }\times \ldots \times X_{\langle 1 \rangle }$
induced by the Segal maps
$X_{\langle p \rangle }\rightarrow X_{\langle 1 \rangle }\times \ldots \times X_{\langle 1 \rangle }$
induced by the Segal maps
![]() $\rho _i\colon \langle p \rangle \rightarrow \langle 1 \rangle $
for
$\rho _i\colon \langle p \rangle \rightarrow \langle 1 \rangle $
for
![]() $1\le i\le p$
are equivalences for all
$1\le i\le p$
are equivalences for all
![]() $p\ge 0$
. These span the full subcategory
$p\ge 0$
. These span the full subcategory
of commutative monoid objects. Precomposition with the composition
![]() $\Delta ^{\mathrm {op}} \to \mathsf {Fin}_{*}$
of (14) induces a functor
$\Delta ^{\mathrm {op}} \to \mathsf {Fin}_{*}$
of (14) induces a functor
![]() $\mathrm {CMon}(\mathscr {C})\rightarrow \mathrm {Mon}(\mathscr {C})$
that ‘forgets commutativity’.
$\mathrm {CMon}(\mathscr {C})\rightarrow \mathrm {Mon}(\mathscr {C})$
that ‘forgets commutativity’.
Remark 2.4. There is a different perspective on commutative monoid objects in the form of an equivalence of
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathrm {Mon}_{\infty }(\mathscr {C})\simeq \mathrm {CMon}(\mathscr {C})$
where
$\mathrm {Mon}_{\infty }(\mathscr {C})\simeq \mathrm {CMon}(\mathscr {C})$
where
![]() $\mathrm {Mon}_{\infty }(\mathscr {C})$
is the limit in
$\mathrm {Mon}_{\infty }(\mathscr {C})$
is the limit in
![]() $\mathscr {C}\mathrm {at}_\infty $
$\mathscr {C}\mathrm {at}_\infty $
over the maps induced
![]() $\mathrm {ev}_{[1]}\colon \mathrm {Mon}(\mathscr {C})\rightarrow \mathscr {C}$
(combine [Reference HaugsengHau18, Proposition 10.11] with [Reference LurieLur17, 5.1.1.5, 2.4.2.5]). In particular, there is an equivalence
$\mathrm {ev}_{[1]}\colon \mathrm {Mon}(\mathscr {C})\rightarrow \mathscr {C}$
(combine [Reference HaugsengHau18, Proposition 10.11] with [Reference LurieLur17, 5.1.1.5, 2.4.2.5]). In particular, there is an equivalence
![]() $\mathrm {CMon}(\mathrm {Mon}(\mathscr {C}))\simeq \mathrm {CMon}(\mathscr {C})$
.
$\mathrm {CMon}(\mathrm {Mon}(\mathscr {C}))\simeq \mathrm {CMon}(\mathscr {C})$
.
2.5.3 Monoidal categories and double categories
For
![]() $\mathscr {C}=\mathscr {C}\mathrm {at}_\infty $
, (non-unital) monoid objects in
$\mathscr {C}=\mathscr {C}\mathrm {at}_\infty $
, (non-unital) monoid objects in
![]() $\mathscr {C}$
are also called (non-unital) monoidal
$\mathscr {C}$
are also called (non-unital) monoidal
![]() $\infty $
-categories, (non-unital) category objects in
$\infty $
-categories, (non-unital) category objects in
![]() $\mathscr {C}$
are called (non-unital) double
$\mathscr {C}$
are called (non-unital) double
![]() $\infty $
-categories, and (commutative) monoid objects in
$\infty $
-categories, and (commutative) monoid objects in
![]() $\mathscr {C}\mathrm {at}_\infty $
or
$\mathscr {C}\mathrm {at}_\infty $
or
![]() $\mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
are (symmetric) monoidal
$\mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
are (symmetric) monoidal
![]() $\infty $
- or double
$\infty $
- or double
![]() $\infty $
-categories. Via the straightening equivalence of Section 2.3, these can also be described as cocartesian fibrations
$\infty $
-categories. Via the straightening equivalence of Section 2.3, these can also be described as cocartesian fibrations
![]() $\mathscr {M}\rightarrow \Delta ^{\mathrm {op}}$
(or
$\mathscr {M}\rightarrow \Delta ^{\mathrm {op}}$
(or
![]() $\mathscr {M}\rightarrow \Delta ^{\mathrm {op}}_{\mathrm {inj}}$
in the non-unital case, or
$\mathscr {M}\rightarrow \Delta ^{\mathrm {op}}_{\mathrm {inj}}$
in the non-unital case, or
![]() $\mathscr {M}\rightarrow \mathsf {Fin}_{*}$
in the commutative case) such that the functors
$\mathscr {M}\rightarrow \mathsf {Fin}_{*}$
in the commutative case) such that the functors
induced by the cocartesian lifts of the Segal maps
![]() $\rho _i$
are equivalences.
$\rho _i$
are equivalences.
Example 2.5. For an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
with finite products, taking products induces a symmetric monoidal structure
$\mathscr {C}$
with finite products, taking products induces a symmetric monoidal structure
![]() $\mathscr {C}^{\times }\rightarrow \mathsf {Fin}_{*}$
on
$\mathscr {C}^{\times }\rightarrow \mathsf {Fin}_{*}$
on
![]() $\mathscr {C}$
, the cartesian structure [Reference LurieLur17, 2.4.1]. Dually, if
$\mathscr {C}$
, the cartesian structure [Reference LurieLur17, 2.4.1]. Dually, if
![]() $\mathscr {C}$
has finite coproducts, it carries a cocartesian symmetric monoidal structure
$\mathscr {C}$
has finite coproducts, it carries a cocartesian symmetric monoidal structure
![]() $\mathscr {C}^{\sqcup }\rightarrow \mathsf {Fin}_{*}$
[Reference LurieLur17, 2.4.3].
$\mathscr {C}^{\sqcup }\rightarrow \mathsf {Fin}_{*}$
[Reference LurieLur17, 2.4.3].
Remark 2.6. The definition of a monoidal
![]() $\infty $
-category given in [Reference LurieLur17, 4.1.1.10] is different from the one given above, but the resulting
$\infty $
-category given in [Reference LurieLur17, 4.1.1.10] is different from the one given above, but the resulting
![]() $\infty $
-categories turn out to be equivalent [Reference LurieLur17, 4.1.3].
$\infty $
-categories turn out to be equivalent [Reference LurieLur17, 4.1.3].
2.5.4 Mapping
 $\infty $
-categories
$\infty $
-categories
Given a double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
and objects
$\mathscr {C}\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
and objects
![]() $A,B\in \mathscr {C}_{[0]}$
, we define the mapping
$A,B\in \mathscr {C}_{[0]}$
, we define the mapping
![]() $\infty $
-category from A to B to be the
$\infty $
-category from A to B to be the
![]() $\infty $
-category given as the fibre in
$\infty $
-category given as the fibre in
![]() $\mathscr {C}\mathrm {at}_\infty $
$\mathscr {C}\mathrm {at}_\infty $
These mapping
![]() $\infty $
-categories come with composition functors
$\infty $
-categories come with composition functors
![]() $\mathscr {C}_{A,B}\times \mathscr {C}_{B,C}\rightarrow \mathscr {C}_{A,C}$
defined by taking vertical fibres in the commutative diagram in
$\mathscr {C}_{A,B}\times \mathscr {C}_{B,C}\rightarrow \mathscr {C}_{A,C}$
defined by taking vertical fibres in the commutative diagram in
![]() $\mathscr {C}\mathrm {at}_\infty $
$\mathscr {C}\mathrm {at}_\infty $

with top-left horizontal map induced by the Segal morphisms, top-right horizontal map by the unique active morphism
![]() $[2] \to [1]$
, and vertical map by the face maps.
$[2] \to [1]$
, and vertical map by the face maps.
2.5.5 Quasi-unital monoid and category objects
A non-unital category object
![]() $X\in \mathrm {Cat}_{\mathrm {nu}}(\mathscr {C})$
is quasi-unital if it admits a quasi-unit, which is by definition a morphism
$X\in \mathrm {Cat}_{\mathrm {nu}}(\mathscr {C})$
is quasi-unital if it admits a quasi-unit, which is by definition a morphism
![]() $u\colon X_{[0]}\rightarrow X_{[1]}$
together with a commutative diagram in
$u\colon X_{[0]}\rightarrow X_{[1]}$
together with a commutative diagram in
![]() $\mathscr {C}$
$\mathscr {C}$

such that the following two compositions are equivalent to the identity:
 $$ \begin{align} \begin{gathered}X_{[1]} \simeq X_{[0]}\times_{X_{[0]}}X_{[1]}\xrightarrow{(u,\mathrm{id})}X_{[1]}\times_{X_{[0]}}X_{[1]}\simeq X_{[2]}\overset{d_1}{\longrightarrow}X_{[1]}, \\ X_{[1]} \simeq X_{[1]}\times_{X_{[0]}}X_{[0]}\xrightarrow{(\mathrm{id},u)}X_{[1]}\times_{X_{[0]}}X_{[1]} \simeq X_{[2]}\overset{d_1}{\longrightarrow}X_{[1]}.\end{gathered} \end{align} $$
$$ \begin{align} \begin{gathered}X_{[1]} \simeq X_{[0]}\times_{X_{[0]}}X_{[1]}\xrightarrow{(u,\mathrm{id})}X_{[1]}\times_{X_{[0]}}X_{[1]}\simeq X_{[2]}\overset{d_1}{\longrightarrow}X_{[1]}, \\ X_{[1]} \simeq X_{[1]}\times_{X_{[0]}}X_{[0]}\xrightarrow{(\mathrm{id},u)}X_{[1]}\times_{X_{[0]}}X_{[1]} \simeq X_{[2]}\overset{d_1}{\longrightarrow}X_{[1]}.\end{gathered} \end{align} $$
Quasi-units are unique up to equivalence [Reference HaugsengHau21, Remark 4.8]. A morphism
![]() $\phi \colon X\rightarrow Y$
of non-unital category objects is quasi-unital if there exists a commutative diagram in
$\phi \colon X\rightarrow Y$
of non-unital category objects is quasi-unital if there exists a commutative diagram in
![]() $\mathscr {C}$
of the form
$\mathscr {C}$
of the form

such that the outer triangles are quasi-units for X and Y. As a result of the uniqueness of quasi-units, the composition of two quasi-unital morphisms is quasi-unital. We write ![]() for the subcategory of quasi-unital category objects in
for the subcategory of quasi-unital category objects in
![]() $\mathscr {C}$
, generated by quasi-unital objects and morphisms. Every category object is quasi-unital (
$\mathscr {C}$
, generated by quasi-unital objects and morphisms. Every category object is quasi-unital (
![]() $s_0\colon X_{[0]}\rightarrow X_{[1]}$
is a quasi-unit), and by [Reference HaugsengHau21, Theorem 4.14], the forgetful functor
$s_0\colon X_{[0]}\rightarrow X_{[1]}$
is a quasi-unit), and by [Reference HaugsengHau21, Theorem 4.14], the forgetful functor
![]() $\mathrm {Cat}(\mathscr {C})\rightarrow \mathrm {Cat}_{\mathrm {nu}}(\mathscr {C})$
induces an equivalence
$\mathrm {Cat}(\mathscr {C})\rightarrow \mathrm {Cat}_{\mathrm {nu}}(\mathscr {C})$
induces an equivalence
Remark 2.7. Note that if X a quasi-unital category object in
![]() $\mathscr {C}$
, Y a simplicial object in
$\mathscr {C}$
, Y a simplicial object in
![]() $\mathscr {C}$
(not necessarily a category object), and
$\mathscr {C}$
(not necessarily a category object), and
![]() $f\colon X\rightarrow Y$
a morphism of semisimplicial objects in
$f\colon X\rightarrow Y$
a morphism of semisimplicial objects in
![]() $\mathscr {C}$
, then
$\mathscr {C}$
, then
-
(i) it makes sense to ask for f to be quasi-unital (replace
 $u_Y$
in (17) by the
$u_Y$
in (17) by the
 $0$
th degeneracy map). This property is preserved by postcomposition with maps of simplicial objects,
$0$
th degeneracy map). This property is preserved by postcomposition with maps of simplicial objects, -
(ii) if
 $\mathscr {C}=\mathscr {C}\mathrm {at}_\infty $
and
$\mathscr {C}=\mathscr {C}\mathrm {at}_\infty $
and
 $Y'\subset Y$
is a levelwise full subcategory that is a quasi-unital category object, then a functor
$Y'\subset Y$
is a levelwise full subcategory that is a quasi-unital category object, then a functor
 $X\rightarrow Y'$
of non-unital category objects is quasi-unital if and only if the composition
$X\rightarrow Y'$
of non-unital category objects is quasi-unital if and only if the composition
 $X\rightarrow Y'\subset Y$
is quasi-unital in the sense of (i).
$X\rightarrow Y'\subset Y$
is quasi-unital in the sense of (i).
2.5.6 Double
 $\infty $
-,
$\infty $
-,
 $(\infty ,2)$
- and
$(\infty ,2)$
- and
 $(\infty ,1)$
-categories
$(\infty ,1)$
-categories
A double
![]() $\infty $
-category has an underlying
$\infty $
-category has an underlying
![]() $(\infty ,2)$
-category (in fact, two, but we will not need this) which in turn has an underlying
$(\infty ,2)$
-category (in fact, two, but we will not need this) which in turn has an underlying
![]() $\infty $
-category. More precisely, there are functors of
$\infty $
-category. More precisely, there are functors of
![]() $\infty $
-categories
$\infty $
-categories
where
![]() $\mathscr {C}\mathrm {at}_{(\infty ,2)}$
is the
$\mathscr {C}\mathrm {at}_{(\infty ,2)}$
is the
![]() $\infty $
-category of
$\infty $
-category of
![]() $(\infty ,2)$
-categories. We denote the composition by
$(\infty ,2)$
-categories. We denote the composition by
These functors have the following properties:
-
(i) The functors
 $(-)^{(\infty ,2)}$
and
$(-)^{(\infty ,2)}$
and
 $(-)^{\simeq _2}$
preserve finite products and hence (symmetric) monoidal structures, and so does their composition
$(-)^{\simeq _2}$
preserve finite products and hence (symmetric) monoidal structures, and so does their composition
 $(-)^{(\infty ,1)}$
.
$(-)^{(\infty ,1)}$
. -
(ii) For
 $\mathscr {C}\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
, the objects of
$\mathscr {C}\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
, the objects of
 $\mathscr {C}^{(\infty ,2)}$
can be identified with those of
$\mathscr {C}^{(\infty ,2)}$
can be identified with those of
 $\mathscr {C}$
. The analogous property holds for the functor
$\mathscr {C}$
. The analogous property holds for the functor
 $(-)^{\simeq _2}$
and thus also for their composition
$(-)^{\simeq _2}$
and thus also for their composition
 $(-)^{(\infty ,1)}$
.
$(-)^{(\infty ,1)}$
. -
(iii) For
 $\mathscr {C}\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
, the mapping
$\mathscr {C}\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
, the mapping
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}_{A,B}$
between two objects A and B in
$\mathscr {C}_{A,B}$
between two objects A and B in
 $\mathscr {C}$
can be identified with the corresponding mapping
$\mathscr {C}$
can be identified with the corresponding mapping
 $\infty $
-category in
$\infty $
-category in
 $\mathscr {C}^{(\infty ,2)}$
. The functor
$\mathscr {C}^{(\infty ,2)}$
. The functor
 $(-)^{\simeq _2}$
is on mapping
$(-)^{\simeq _2}$
is on mapping
 $\infty $
-categories given by taking cores (hence the notation), and thus, the same holds for
$\infty $
-categories given by taking cores (hence the notation), and thus, the same holds for
 $(-)^{(\infty ,1)}$
, so we have
$(-)^{(\infty ,1)}$
, so we have
 $\mathscr {C}_{A,B}^\simeq \simeq \mathrm {Map}_{\mathscr {C}^{(\infty ,1)}}(A,B)$
for objects A and B in
$\mathscr {C}_{A,B}^\simeq \simeq \mathrm {Map}_{\mathscr {C}^{(\infty ,1)}}(A,B)$
for objects A and B in
 $\mathscr {C}$
.
$\mathscr {C}$
.
One way to implement these
![]() $\infty $
-categories and functors between them is to use the equivalence
$\infty $
-categories and functors between them is to use the equivalence
![]() $\mathrm {Cat}_\infty \simeq \mathscr {C}\mathrm {SS}(\mathscr {S})$
to Rezk’s complete Segal spaces (a certain full subcategory of
$\mathrm {Cat}_\infty \simeq \mathscr {C}\mathrm {SS}(\mathscr {S})$
to Rezk’s complete Segal spaces (a certain full subcategory of
![]() $\mathrm {Cat}(\mathscr {S})$
[Reference HaugsengHau18, Section 3]) and model
$\mathrm {Cat}(\mathscr {S})$
[Reference HaugsengHau18, Section 3]) and model
![]() $\mathscr {C}\mathrm {at}_{(\infty ,2)}$
as the
$\mathscr {C}\mathrm {at}_{(\infty ,2)}$
as the
![]() $\infty $
-category of
$\infty $
-category of
![]() $2$
-fold complete Segal spaces
$2$
-fold complete Segal spaces
![]() $\mathscr {C}\mathrm {SS}_2(\mathscr {S})$
in the sense of Barwick (a certain full subcategory of
$\mathscr {C}\mathrm {SS}_2(\mathscr {S})$
in the sense of Barwick (a certain full subcategory of
![]() $\mathrm {Cat}(\mathrm {Cat}(\mathscr {S}))$
[Reference HaugsengHau18, Section 4]). In these models, the functor
$\mathrm {Cat}(\mathrm {Cat}(\mathscr {S}))$
[Reference HaugsengHau18, Section 4]). In these models, the functor
![]() $(-)^{(\infty ,2)}\colon \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )\rightarrow \mathscr {C}\mathrm {at}_{(\infty ,2)}$
is explained in [Reference HaugsengHau17, Remark 3.15], and the functor
$(-)^{(\infty ,2)}\colon \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )\rightarrow \mathscr {C}\mathrm {at}_{(\infty ,2)}$
is explained in [Reference HaugsengHau17, Remark 3.15], and the functor
![]() $(-)^{(\infty ,1)}\colon \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty ) \rightarrow \mathscr {C}\mathrm {at}_\infty $
can be constructed via the inductive description as 2-fold Segal spaces as
$(-)^{(\infty ,1)}\colon \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty ) \rightarrow \mathscr {C}\mathrm {at}_\infty $
can be constructed via the inductive description as 2-fold Segal spaces as
![]() $\mathscr {C}\mathrm {SS}_2(\mathscr {S})=\mathscr {C}\mathrm {SS}_{\mathscr {C}\mathrm {SS}(\mathscr {S})}(\mathscr {C}\mathrm {SS}(\mathscr {S}))$
[Reference HaugsengHau18, Section 7] by defining
$\mathscr {C}\mathrm {SS}_2(\mathscr {S})=\mathscr {C}\mathrm {SS}_{\mathscr {C}\mathrm {SS}(\mathscr {S})}(\mathscr {C}\mathrm {SS}(\mathscr {S}))$
[Reference HaugsengHau18, Section 7] by defining
![]() $(-)^{\simeq _2}$
as the right-adjoint
$(-)^{\simeq _2}$
as the right-adjoint
![]() $\mathscr {C}\mathrm {SS}_{\mathscr {C}\mathrm {SS}(\mathscr {S})}(\mathscr {C}\mathrm {SS}(\mathscr {S}))\rightarrow \mathscr {C}\mathrm {SS}_{\mathscr {S}}(\mathscr {S})=\mathscr {C}\mathrm {SS}(\mathscr {S})\simeq \mathscr {C}\mathrm {at}_\infty $
induced by the right-adjoint
$\mathscr {C}\mathrm {SS}_{\mathscr {C}\mathrm {SS}(\mathscr {S})}(\mathscr {C}\mathrm {SS}(\mathscr {S}))\rightarrow \mathscr {C}\mathrm {SS}_{\mathscr {S}}(\mathscr {S})=\mathscr {C}\mathrm {SS}(\mathscr {S})\simeq \mathscr {C}\mathrm {at}_\infty $
induced by the right-adjoint
![]() $\mathrm {ev}_{[0]}\colon \mathscr {C}\mathrm {SS}(\mathscr {S})\rightarrow \mathscr {S}$
to the inclusion
$\mathrm {ev}_{[0]}\colon \mathscr {C}\mathrm {SS}(\mathscr {S})\rightarrow \mathscr {S}$
to the inclusion
![]() $c\colon \mathscr {S}\rightarrow \mathscr {C}\mathrm {SS}(\mathscr {S})$
as constant simplicial spaces, using [Reference HaugsengHau18, Proposition 7.17].
$c\colon \mathscr {S}\rightarrow \mathscr {C}\mathrm {SS}(\mathscr {S})$
as constant simplicial spaces, using [Reference HaugsengHau18, Proposition 7.17].
It remains to justify properties (i)–(iii). That (i) holds for
![]() $(-)^{(\infty ,2)}$
is justified in [Reference HaugsengHau17, Remark 3.15] and for
$(-)^{(\infty ,2)}$
is justified in [Reference HaugsengHau17, Remark 3.15] and for
![]() $(-)^{\simeq _2}$
, it holds since it is a right adjoint. For (ii) and (iii), one uses [Reference HaugsengHau17, Lemma 5.50/5.51] and that
$(-)^{\simeq _2}$
, it holds since it is a right adjoint. For (ii) and (iii), one uses [Reference HaugsengHau17, Lemma 5.50/5.51] and that
![]() $\mathrm {ev}_{[0]}$
corresponds to taking cores under the equivalence
$\mathrm {ev}_{[0]}$
corresponds to taking cores under the equivalence
![]() $\mathscr {C}\mathrm {at}_\infty \simeq \mathscr {C}\mathrm {SS}(\mathscr {S})$
.
$\mathscr {C}\mathrm {at}_\infty \simeq \mathscr {C}\mathrm {SS}(\mathscr {S})$
.
2.6 Presheaves and the Yoneda embedding
Given an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, we write
$\mathscr {C}$
, we write ![]() for the
for the
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathscr {S}$
-valued presheaves. This admits all small limits and colimits [Reference LurieLur09a, 5.1.2.4], and there is a natural fully faithful Yoneda embedding
$\mathscr {S}$
-valued presheaves. This admits all small limits and colimits [Reference LurieLur09a, 5.1.2.4], and there is a natural fully faithful Yoneda embedding ![]() [Reference LurieLur09a, 5.1.3.1]. If
[Reference LurieLur09a, 5.1.3.1]. If
![]() $\mathscr {C}$
is (symmetric) monoidal, then its opposite
$\mathscr {C}$
is (symmetric) monoidal, then its opposite
![]() $\mathscr {C}^{\mathrm {op}}$
is (symmetric) monoidal [Reference LurieLur17, 2.4.2.7], and
$\mathscr {C}^{\mathrm {op}}$
is (symmetric) monoidal [Reference LurieLur17, 2.4.2.7], and
![]() $\mathrm {PSh}(\mathscr {C})$
carries a (symmetric) monoidal structure by Day convolution [Reference LurieLur17, 2.2.6.17] which, firstly, preserves small colimits in each variable, and, secondly, allows for an enhancement of the Yoneda embedding to a (symmetric) monoidal functor [Reference LurieLur17, 4.8.1.12, 4.8.1.13]. Explicitly, a formula for Day convolution is given by
$\mathrm {PSh}(\mathscr {C})$
carries a (symmetric) monoidal structure by Day convolution [Reference LurieLur17, 2.2.6.17] which, firstly, preserves small colimits in each variable, and, secondly, allows for an enhancement of the Yoneda embedding to a (symmetric) monoidal functor [Reference LurieLur17, 4.8.1.12, 4.8.1.13]. Explicitly, a formula for Day convolution is given by
![]() $(F \otimes G)(c") = \mathrm {colim}_{c" \to c \otimes c'} (F(c) \times G(c'))$
where the colimit is over the category of triples
$(F \otimes G)(c") = \mathrm {colim}_{c" \to c \otimes c'} (F(c) \times G(c'))$
where the colimit is over the category of triples
![]() $(c,c',u)$
with
$(c,c',u)$
with
![]() $c,c' \in \mathscr {C}$
and
$c,c' \in \mathscr {C}$
and
![]() $u \colon c" \to c \otimes c'$
[Reference LurieLur17, 2.2.6]. Moreover, from the construction, one sees that a lax (symmetric) monoidal functor
$u \colon c" \to c \otimes c'$
[Reference LurieLur17, 2.2.6]. Moreover, from the construction, one sees that a lax (symmetric) monoidal functor
![]() $\mathscr {C}\rightarrow \mathscr {D}$
(see Example 2.10) induces a lax (symmetric) monoidal functor
$\mathscr {C}\rightarrow \mathscr {D}$
(see Example 2.10) induces a lax (symmetric) monoidal functor
![]() $\mathrm {PSh}(\mathscr {D})\rightarrow \mathrm {PSh}(\mathscr {C})$
by precomposition.
$\mathrm {PSh}(\mathscr {D})\rightarrow \mathrm {PSh}(\mathscr {C})$
by precomposition.
Remark 2.8. Given a
![]() $\mathsf {Kan}$
-enriched category
$\mathsf {Kan}$
-enriched category
![]() $\mathsf {C}$
, there is a similar Yoneda embedding in
$\mathsf {C}$
, there is a similar Yoneda embedding in
![]() $\mathsf {Kan}$
-enriched categories
$\mathsf {Kan}$
-enriched categories
![]() $y_s\colon \mathsf {C}\rightarrow \mathrm {Fun}(\mathsf {C}^{\mathrm {op}},\mathsf {Kan})$
. Taking coherent nerves and postcomposing with the map
$y_s\colon \mathsf {C}\rightarrow \mathrm {Fun}(\mathsf {C}^{\mathrm {op}},\mathsf {Kan})$
. Taking coherent nerves and postcomposing with the map
![]() $N_{\mathrm {coh}}(\mathrm {Fun}(\mathsf {C}^{\mathrm {op}},\mathsf {Kan}))\rightarrow \mathrm {Fun}(N_{\mathrm {coh}}(\mathsf {C})^{\mathrm {op}},N_{\mathrm {coh}}(\mathsf {Kan}))=\mathrm {PSh}(N_{\mathrm {coh}}(\mathsf {C}))$
of Section 2.2 (v) yields a functor
$N_{\mathrm {coh}}(\mathrm {Fun}(\mathsf {C}^{\mathrm {op}},\mathsf {Kan}))\rightarrow \mathrm {Fun}(N_{\mathrm {coh}}(\mathsf {C})^{\mathrm {op}},N_{\mathrm {coh}}(\mathsf {Kan}))=\mathrm {PSh}(N_{\mathrm {coh}}(\mathsf {C}))$
of Section 2.2 (v) yields a functor
![]() $N_{\mathrm {coh}}(\mathsf {C})\rightarrow \mathrm {PSh}(N_{\mathrm {coh}}(\mathsf {C}))$
which turns out to agree with y up to equivalence, by the construction of y for
$N_{\mathrm {coh}}(\mathsf {C})\rightarrow \mathrm {PSh}(N_{\mathrm {coh}}(\mathsf {C}))$
which turns out to agree with y up to equivalence, by the construction of y for
![]() $\mathscr {C}=N_{\mathrm {coh}}(\mathsf {C})$
in [Reference LurieLur09a, 5.1.3.1].
$\mathscr {C}=N_{\mathrm {coh}}(\mathsf {C})$
in [Reference LurieLur09a, 5.1.3.1].
2.7
 $\infty $
-operads
$\infty $
-operads
Recall the following definition from [Reference LurieLur17, 2.1.1.10].
Definition 2.9. An
![]() $\infty $
-operad
$\infty $
-operad
![]() $\mathscr {O}$
is a functor
$\mathscr {O}$
is a functor
![]() $p \colon \mathscr {O}^\otimes \to \mathsf {Fin}_\ast $
with the following properties:
$p \colon \mathscr {O}^\otimes \to \mathsf {Fin}_\ast $
with the following properties:
-
(i)
 $\mathscr {O}^\otimes $
has cocartesian lifts for inert morphisms in
$\mathscr {O}^\otimes $
has cocartesian lifts for inert morphisms in
 $\mathsf {Fin}_\ast $
,
$\mathsf {Fin}_\ast $
, -
(ii) the map
 $\sqcap (\rho _i)_!\colon \mathscr {O}^\otimes _{\langle n \rangle } \rightarrow \sqcap _{i=1}^n \mathscr {O}^\otimes _{\langle 1 \rangle }$
induced by the Segal morphisms is an equivalence,
$\sqcap (\rho _i)_!\colon \mathscr {O}^\otimes _{\langle n \rangle } \rightarrow \sqcap _{i=1}^n \mathscr {O}^\otimes _{\langle 1 \rangle }$
induced by the Segal morphisms is an equivalence, -
(iii) given an object
 $x \in \mathscr {O}^\otimes _{\langle n \rangle }$
and cocartesian lifts
$x \in \mathscr {O}^\otimes _{\langle n \rangle }$
and cocartesian lifts
 $x \to x_i$
of the Segal morphisms
$x \to x_i$
of the Segal morphisms
 $\rho _i \colon \langle n \rangle \to \langle 1 \rangle $
, the following commutative diagram in
$\rho _i \colon \langle n \rangle \to \langle 1 \rangle $
, the following commutative diagram in
 $\mathscr {S}$
is cartesian:
$\mathscr {S}$
is cartesian: 
A map of
![]() $\infty $
-operads is a functor over
$\infty $
-operads is a functor over
![]() $\mathsf {Fin}_\ast $
that preserves cocartesian lifts over inert morphisms. Such a map
$\mathsf {Fin}_\ast $
that preserves cocartesian lifts over inert morphisms. Such a map
![]() $\mathscr {O}^{\otimes } \to \mathscr {P}^{\otimes }$
is also called an
$\mathscr {O}^{\otimes } \to \mathscr {P}^{\otimes }$
is also called an
![]() $\mathscr {O}$
-algebra in
$\mathscr {O}$
-algebra in
![]() $\mathscr {P}$
, and we write
$\mathscr {P}$
, and we write
for the full subcategory of such maps. Given an
![]() $\infty $
-operad
$\infty $
-operad
![]() $\mathscr {O}$
, we call the objects of
$\mathscr {O}$
, we call the objects of
![]() $\mathscr {O}^\otimes _{\langle 1 \rangle }$
the colours of
$\mathscr {O}^\otimes _{\langle 1 \rangle }$
the colours of
![]() $\mathscr {O}$
. Given colours
$\mathscr {O}$
. Given colours
![]() $x=(x_1,\ldots ,x_n) \in \sqcap ^n \smash {\mathscr {O}^\otimes _{\langle 1 \rangle }}\simeq \smash {\mathscr {O}^\otimes _{\langle n \rangle }}$
and
$x=(x_1,\ldots ,x_n) \in \sqcap ^n \smash {\mathscr {O}^\otimes _{\langle 1 \rangle }}\simeq \smash {\mathscr {O}^\otimes _{\langle n \rangle }}$
and
![]() $y \in \smash {\mathscr {O}^\otimes _{\langle 1 \rangle }}$
, the space of multi-operations is the subspace
$y \in \smash {\mathscr {O}^\otimes _{\langle 1 \rangle }}$
, the space of multi-operations is the subspace ![]() covering the unique active morphism
covering the unique active morphism
![]() $\langle n \rangle \to \langle 1 \rangle $
[Reference LurieLur17, 2.1.1.16]. If
$\langle n \rangle \to \langle 1 \rangle $
[Reference LurieLur17, 2.1.1.16]. If
![]() $\mathscr {O}^\otimes $
has a single colour
$\mathscr {O}^\otimes $
has a single colour
![]() $x\in \mathscr {O}^\otimes _{\langle 1 \rangle }$
, we abbreviate
$x\in \mathscr {O}^\otimes _{\langle 1 \rangle }$
, we abbreviate ![]() where x appears in the domain k times. These spaces of multi-operations can be composed using operadic composition maps, denoted
where x appears in the domain k times. These spaces of multi-operations can be composed using operadic composition maps, denoted ![]() , that satisfy the axioms of a coloured operad in the classical sense up to coherent homotopies [Reference LurieLur17, 2.1.1.17]. In particular, the homotopy operad
, that satisfy the axioms of a coloured operad in the classical sense up to coherent homotopies [Reference LurieLur17, 2.1.1.17]. In particular, the homotopy operad
![]() $h\mathscr {O}^\otimes \rightarrow \mathsf {Fin}_{*}$
(which is an operad as a result of the properties of h discussed in Section 2.2 and satisfies
$h\mathscr {O}^\otimes \rightarrow \mathsf {Fin}_{*}$
(which is an operad as a result of the properties of h discussed in Section 2.2 and satisfies
![]() $\mathrm {Mul}_{h\mathscr {O}}(x,y)=\pi _0\,\mathrm {Mul}_{\mathscr {O}}(x,y)$
) gives a coloured operad in the classical sense. By construction, there is a map of
$\mathrm {Mul}_{h\mathscr {O}}(x,y)=\pi _0\,\mathrm {Mul}_{\mathscr {O}}(x,y)$
) gives a coloured operad in the classical sense. By construction, there is a map of
![]() $\infty $
-operads
$\infty $
-operads
![]() $\mathscr {O}^\otimes \rightarrow h\mathscr {O}^\otimes $
.
$\mathscr {O}^\otimes \rightarrow h\mathscr {O}^\otimes $
.
Example 2.10. When viewed as a cocartesian fibration
![]() $\mathscr {C}^{\otimes }\rightarrow \mathsf {Fin}_\ast $
(see Section 2.5.3), every symmetric monoidal category
$\mathscr {C}^{\otimes }\rightarrow \mathsf {Fin}_\ast $
(see Section 2.5.3), every symmetric monoidal category
![]() $\mathscr {C}$
is an
$\mathscr {C}$
is an
![]() $\infty $
-operad. A map of
$\infty $
-operad. A map of
![]() $\infty $
-operads between symmetric monoidal categories is called a lax symmetric monoidal functor.
$\infty $
-operads between symmetric monoidal categories is called a lax symmetric monoidal functor.
Example 2.11. Every coloured operad in the category of
![]() $\mathsf {Kan}$
-complexes in the classical sense gives rise to an
$\mathsf {Kan}$
-complexes in the classical sense gives rise to an
![]() $\infty $
-operad via the operadic nerve [Reference LurieLur09a, 2.1.1.27]. For example, the associative
$\infty $
-operad via the operadic nerve [Reference LurieLur09a, 2.1.1.27]. For example, the associative
![]() $\infty $
-operad
$\infty $
-operad
![]() $\mathscr {A}\mathrm {ssoc}$
[Reference LurieLur17, 4.1.1.1, 4.1.1.3] is the operadic nerve of the ordinary operad with a single colour
$\mathscr {A}\mathrm {ssoc}$
[Reference LurieLur17, 4.1.1.1, 4.1.1.3] is the operadic nerve of the ordinary operad with a single colour
![]() $\ast $
, whose k-ary multi-operations
$\ast $
, whose k-ary multi-operations
![]() $\mathscr {A}\mathrm {ssoc}(k) = \mathrm {Mul}_{\mathscr {A}\mathrm {ssoc}}(*,\ldots ,*;*)$
is the set of linear orders of
$\mathscr {A}\mathrm {ssoc}(k) = \mathrm {Mul}_{\mathscr {A}\mathrm {ssoc}}(*,\ldots ,*;*)$
is the set of linear orders of
![]() $\underline {k} = \{1,2,\ldots ,k\}$
, and where operadic composition is concatenation of linear orders. An
$\underline {k} = \{1,2,\ldots ,k\}$
, and where operadic composition is concatenation of linear orders. An
![]() $\infty $
-operad
$\infty $
-operad
![]() $\mathscr {O}$
is equivalent to
$\mathscr {O}$
is equivalent to
![]() $\mathscr {A}\mathrm {ssoc}$
if and only if there is an isomorphism
$\mathscr {A}\mathrm {ssoc}$
if and only if there is an isomorphism
![]() $h\mathscr {O} \cong h\mathscr {A}\mathrm {ssoc}$
of operads in the
$h\mathscr {O} \cong h\mathscr {A}\mathrm {ssoc}$
of operads in the
![]() $1$
-category of sets and all spaces of operations in
$1$
-category of sets and all spaces of operations in
![]() $\mathscr {O}$
are homotopy discrete.
$\mathscr {O}$
are homotopy discrete.
2.7.1 Suboperads, endomorphism operads, and algebras over them
Let
![]() $\mathscr {O}$
be an
$\mathscr {O}$
be an
![]() $\infty $
-operad and
$\infty $
-operad and
![]() $\mathsf {O}_0 \subseteq h\mathscr {O}$
be a suboperad of the ordinary operad
$\mathsf {O}_0 \subseteq h\mathscr {O}$
be a suboperad of the ordinary operad
![]() $h\mathscr {O}$
in sets. The corresponding suboperad
$h\mathscr {O}$
in sets. The corresponding suboperad
![]() $\mathscr {O} \times _{h \mathscr {O}} \mathsf {O}_0$
of
$\mathscr {O} \times _{h \mathscr {O}} \mathsf {O}_0$
of
![]() $\mathscr {O}$
is defined as the pullback
$\mathscr {O}$
is defined as the pullback
![]() $\mathscr {O}^\otimes \times _{h\mathscr {O}^\otimes } \mathsf {O}_0^\otimes \rightarrow \mathsf {Fin}_\ast $
in the
$\mathscr {O}^\otimes \times _{h\mathscr {O}^\otimes } \mathsf {O}_0^\otimes \rightarrow \mathsf {Fin}_\ast $
in the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathscr {O}\mathrm {pd}_\infty }$
of
${\mathscr {O}\mathrm {pd}_\infty }$
of
![]() $\infty $
-operads, which has limits by [Reference LurieLur17, 2.1.4]. In particular, we may restrict
$\infty $
-operads, which has limits by [Reference LurieLur17, 2.1.4]. In particular, we may restrict
![]() $\mathscr {O}$
to a fixed collection of colours closed under equivalences to obtain a new
$\mathscr {O}$
to a fixed collection of colours closed under equivalences to obtain a new
![]() $\infty $
-operad. We call this a full suboperad.
$\infty $
-operad. We call this a full suboperad.
Remark 2.12. The forgetful functor
![]() ${\mathscr {O}\mathrm {pd}_\infty } \to (\mathscr {C}\mathrm {at}_\infty )_{/\mathsf {Fin}_\ast }$
creates limits by [Reference Ayala, Francis and TanakaAFT17, Lemma 1.13], so the pullback
${\mathscr {O}\mathrm {pd}_\infty } \to (\mathscr {C}\mathrm {at}_\infty )_{/\mathsf {Fin}_\ast }$
creates limits by [Reference Ayala, Francis and TanakaAFT17, Lemma 1.13], so the pullback
![]() $\mathscr {O} \times _{h \mathscr {O}} \mathsf {O}_0$
can be computes in
$\mathscr {O} \times _{h \mathscr {O}} \mathsf {O}_0$
can be computes in
![]() $\mathscr {C}\mathrm {at}_\infty $
.
$\mathscr {C}\mathrm {at}_\infty $
.
Example 2.13. For a symmetric
![]() $\infty $
-monoidal category
$\infty $
-monoidal category
![]() $\mathscr {C}$
viewed as an
$\mathscr {C}$
viewed as an
![]() $\infty $
-operad, its homotopy operad
$\infty $
-operad, its homotopy operad
![]() $h\mathscr {C}$
is a symmetric monoidal
$h\mathscr {C}$
is a symmetric monoidal
![]() $1$
-category in the classical sense. Given a sub symmetric monoidal category of
$1$
-category in the classical sense. Given a sub symmetric monoidal category of
![]() $\mathsf {C}_0\subset h\mathscr {C}$
in the
$\mathsf {C}_0\subset h\mathscr {C}$
in the
![]() $1$
-categorical sense, the associated sub
$1$
-categorical sense, the associated sub
![]() $\infty $
-operad
$\infty $
-operad
![]() $\mathscr {C} \times _{h \mathscr {C}} \mathsf {C}_0$
is again a symmetric
$\mathscr {C} \times _{h \mathscr {C}} \mathsf {C}_0$
is again a symmetric
![]() $\infty $
-monoidal category. Informally, this is given by restricting the objects and the components of the mapping spaces according to
$\infty $
-monoidal category. Informally, this is given by restricting the objects and the components of the mapping spaces according to
![]() $\mathsf {C}_0$
.
$\mathsf {C}_0$
.
Fix
![]() $\mathscr {C}$
a symmetric monoidal
$\mathscr {C}$
a symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, viewed as an
$\mathscr {C}$
, viewed as an
![]() $\infty $
-operad. The endomorphism operad of an object x in
$\infty $
-operad. The endomorphism operad of an object x in
![]() $\mathscr {C}$
is the full sub
$\mathscr {C}$
is the full sub
![]() $\infty $
-operad
$\infty $
-operad ![]() obtained by restricting to the colours equivalent to x. Writing
obtained by restricting to the colours equivalent to x. Writing ![]() for the unit in
for the unit in
![]() $\mathscr {C}$
, we can form the composition of maps of
$\mathscr {C}$
, we can form the composition of maps of
![]() $\infty $
-operads
$\infty $
-operads
to
![]() $\mathscr {S}$
equipped with the cartesian symmetric monoidal structure (see Example 2.5). The first map is induced by the inclusion, the second map the symmetric monoidal Yoneda embedding (see Section 2.6), and the third map the evaluation at the unit which is a map of
$\mathscr {S}$
equipped with the cartesian symmetric monoidal structure (see Example 2.5). The first map is induced by the inclusion, the second map the symmetric monoidal Yoneda embedding (see Section 2.6), and the third map the evaluation at the unit which is a map of
![]() $\infty $
-operads by naturality of the Day convolution in lax symmetric monoidal functors (see Section 2.6). The composition (19) enhances the mapping space
$\infty $
-operads by naturality of the Day convolution in lax symmetric monoidal functors (see Section 2.6). The composition (19) enhances the mapping space ![]() to an
to an
![]() $\mathrm {End}_{\mathscr {C}}(x)$
-algebra in
$\mathrm {End}_{\mathscr {C}}(x)$
-algebra in
![]() $\mathscr {S}$
.
$\mathscr {S}$
.
2.7.2 Generalised
 $\infty $
-operads
$\infty $
-operads
The condition (ii) in the definition of an
![]() $\infty $
-operad
$\infty $
-operad
![]() $\mathscr {O}$
in particular implies that
$\mathscr {O}$
in particular implies that
![]() $\smash {\mathscr {O}^{\otimes }_{\langle 0\rangle }}$
is trivial. Sometimes it it useful to relax the notion of an
$\smash {\mathscr {O}^{\otimes }_{\langle 0\rangle }}$
is trivial. Sometimes it it useful to relax the notion of an
![]() $\infty $
-operad to that of a generalised
$\infty $
-operad to that of a generalised
![]() $\infty $
-operad which need no longer satisfy
$\infty $
-operad which need no longer satisfy
![]() $\smash {\mathscr {O}^{\otimes }_{\langle 0\rangle }}\simeq \ast $
. The precise definition of a generalised
$\smash {\mathscr {O}^{\otimes }_{\langle 0\rangle }}\simeq \ast $
. The precise definition of a generalised
![]() $\infty $
-operad is not important for us, but it suffices to know that it is a functor
$\infty $
-operad is not important for us, but it suffices to know that it is a functor
![]() $\mathscr {O}^{\otimes }\rightarrow \mathsf {Fin}_\ast $
satisfying some weaker axioms than those for
$\mathscr {O}^{\otimes }\rightarrow \mathsf {Fin}_\ast $
satisfying some weaker axioms than those for
![]() $\infty $
-operads, but that the existence of cocartesian lifts for inert morphisms is still required. Maps of generalised operads
$\infty $
-operads, but that the existence of cocartesian lifts for inert morphisms is still required. Maps of generalised operads
![]() $\mathscr {O}\rightarrow \mathscr {P}$
are defined in the same way as for
$\mathscr {O}\rightarrow \mathscr {P}$
are defined in the same way as for
![]() $\infty $
-operads. Generalising the case of
$\infty $
-operads. Generalising the case of
![]() $\infty $
-operads, we denote the resulting subcategory by
$\infty $
-operads, we denote the resulting subcategory by
![]() $\mathrm {Alg}_{\mathscr {O}}(\mathscr {P})\subset \mathrm {Fun}_{\mathsf {Fin}_\ast }(\mathscr {O}^{\otimes },\mathscr {P}^{\otimes })$
and still call its objects
$\mathrm {Alg}_{\mathscr {O}}(\mathscr {P})\subset \mathrm {Fun}_{\mathsf {Fin}_\ast }(\mathscr {O}^{\otimes },\mathscr {P}^{\otimes })$
and still call its objects
![]() $\mathscr {O}$
-algebras in
$\mathscr {O}$
-algebras in
![]() $\mathscr {P}$
.
$\mathscr {P}$
.
2.7.3 (Generalised) nonsymmetric
 $\infty $
-operads
$\infty $
-operads
Replacing the category
![]() $\mathsf {Fin}_{*}$
by
$\mathsf {Fin}_{*}$
by
![]() $\Delta ^{\mathrm {op}}$
defines nonsymmetric variants of all of the above definitions and constructions (e.g. (generalised) nonsymmetric operads, maps between them, algebras in them, etc). We use the same notation for the symmetric and nonsymmetric constructions (e.g., for (generalised) nonsymmetric
$\Delta ^{\mathrm {op}}$
defines nonsymmetric variants of all of the above definitions and constructions (e.g. (generalised) nonsymmetric operads, maps between them, algebras in them, etc). We use the same notation for the symmetric and nonsymmetric constructions (e.g., for (generalised) nonsymmetric
![]() $\infty $
-operads
$\infty $
-operads
![]() $\mathscr {O}$
and
$\mathscr {O}$
and
![]() $\mathscr {P}$
, we write
$\mathscr {P}$
, we write
![]() $\mathrm {Alg}_{\mathscr {O}}(\mathscr {P})\subset \mathrm {Fun}_{\Delta ^{\mathrm {op}}}(\mathscr {O}^{\otimes },\mathscr {P}^{\otimes })$
for the
$\mathrm {Alg}_{\mathscr {O}}(\mathscr {P})\subset \mathrm {Fun}_{\Delta ^{\mathrm {op}}}(\mathscr {O}^{\otimes },\mathscr {P}^{\otimes })$
for the
![]() $\infty $
-category of maps of (generalised) nonsymmetric
$\infty $
-category of maps of (generalised) nonsymmetric
![]() $\infty $
-operads aka
$\infty $
-operads aka
![]() $\mathscr {O}$
-algebras in
$\mathscr {O}$
-algebras in
![]() $\mathscr {P}$
).
$\mathscr {P}$
).
Example 2.14. The following examples of generalised nonsymmetric
![]() $\infty $
-operads will be important:
$\infty $
-operads will be important:
-
(i) Cocartesian fibrations obtained by unstraightening double
 $\infty $
-categories.
$\infty $
-categories. -
(ii) The projection
 $\Delta ^{\mathrm {op}}_{/[p]}\rightarrow \Delta ^{\mathrm {op}}$
for all
$\Delta ^{\mathrm {op}}_{/[p]}\rightarrow \Delta ^{\mathrm {op}}$
for all
 $p\ge 0$
; see [Reference HaugsengHau17, Lemma 4.10].
$p\ge 0$
; see [Reference HaugsengHau17, Lemma 4.10]. -
(iii) The restriction
 $\Lambda ^{\mathrm {op}}_{/[p]}\rightarrow \Delta ^{\mathrm {op}}$
of the projection
$\Lambda ^{\mathrm {op}}_{/[p]}\rightarrow \Delta ^{\mathrm {op}}$
of the projection
 $\Delta ^{\mathrm {op}}_{/[p]}\rightarrow \Delta ^{\mathrm {op}}$
to the full subcategory
$\Delta ^{\mathrm {op}}_{/[p]}\rightarrow \Delta ^{\mathrm {op}}$
to the full subcategory  spanned by the cellular maps in
spanned by the cellular maps in
 $\Delta $
; see [Reference HaugsengHau17, Lemma 4.14].
$\Delta $
; see [Reference HaugsengHau17, Lemma 4.14].
Examples of maps between generalised nonsymmetric
![]() $\infty $
-operads that will be important are
$\infty $
-operads that will be important are
-
(i) The map
 $\Delta ^{\mathrm {op}}_{/[p]} \to \Delta ^{\mathrm {op}}_{/[q]}$
over
$\Delta ^{\mathrm {op}}_{/[p]} \to \Delta ^{\mathrm {op}}_{/[q]}$
over
 $\Delta ^{\mathrm {op}}$
induced by a morphism
$\Delta ^{\mathrm {op}}$
induced by a morphism
 $[p] \to [q]$
of
$[p] \to [q]$
of
 $\Delta $
.
$\Delta $
. -
(ii) The inclusion
 $\Lambda ^{\mathrm {op}}_{/[p]} \to \Delta ^{\mathrm {op}}_{[p]}$
over
$\Lambda ^{\mathrm {op}}_{/[p]} \to \Delta ^{\mathrm {op}}_{[p]}$
over
 $\Delta ^{\mathrm {op}}$
[Reference HaugsengHau17, Lemma 4.14].
$\Delta ^{\mathrm {op}}$
[Reference HaugsengHau17, Lemma 4.14].
2.8 Associative algebras and bimodules in the nonsymmetric setting
Given a monoidal
![]() $\infty $
-category viewed as a cocartesian fibration
$\infty $
-category viewed as a cocartesian fibration
![]() $\mathscr {C}^{\otimes }\rightarrow \Delta ^{\mathrm {op}}$
with underlying category
$\mathscr {C}^{\otimes }\rightarrow \Delta ^{\mathrm {op}}$
with underlying category ![]() , the
, the
![]() $\infty $
-categories
$\infty $
-categories ![]() and
and ![]() of associative algebras in
of associative algebras in
![]() $\mathscr {C}$
and bimodules in
$\mathscr {C}$
and bimodules in
![]() $\mathscr {C}$
are defined as
$\mathscr {C}$
are defined as
These are the
![]() $\infty $
-categories of
$\infty $
-categories of
![]() $\Delta ^{\mathrm {op}}$
- and
$\Delta ^{\mathrm {op}}$
- and
![]() $\Delta _{/[1]}^{\mathrm {op}}$
-algebras in
$\Delta _{/[1]}^{\mathrm {op}}$
-algebras in
![]() $\mathscr {C}$
as in Section 2.7.3. There is a functor
$\mathscr {C}$
as in Section 2.7.3. There is a functor
consisting of the projections to
![]() $\mathrm {Ass}(\mathscr {C})$
induced by precomposition with the functors
$\mathrm {Ass}(\mathscr {C})$
induced by precomposition with the functors
![]() $ \Delta =\Delta _{/[0]}\rightarrow \Delta _{/[1]}$
induced by the
$ \Delta =\Delta _{/[0]}\rightarrow \Delta _{/[1]}$
induced by the
![]() $0$
th and
$0$
th and
![]() $1$
st face map
$1$
st face map
![]() $[0]\rightarrow [1]$
, and the functor to
$[0]\rightarrow [1]$
, and the functor to
![]() $\smash {\mathscr {C}^{\otimes }_{[1]}}=\mathscr {C}$
given by evaluation at
$\smash {\mathscr {C}^{\otimes }_{[1]}}=\mathscr {C}$
given by evaluation at
![]() $\mathrm {id}_{[1]}\in \Delta _{/[1]}$
. The fibre in
$\mathrm {id}_{[1]}\in \Delta _{/[1]}$
. The fibre in
![]() $\mathscr {C}\mathrm {at}_\infty $
$\mathscr {C}\mathrm {at}_\infty $
at
![]() $(A,B)$
for associative algebras
$(A,B)$
for associative algebras
![]() $A,B\in \mathrm {Ass}(\mathscr {C})$
of the postcomposition
$A,B\in \mathrm {Ass}(\mathscr {C})$
of the postcomposition
![]() $\mathrm {BMod}(\mathscr {C})\rightarrow \mathrm {Ass}(\mathscr {C})\times \mathrm {Ass}(\mathscr {C})$
of (20) with the projection is the
$\mathrm {BMod}(\mathscr {C})\rightarrow \mathrm {Ass}(\mathscr {C})\times \mathrm {Ass}(\mathscr {C})$
of (20) with the projection is the
![]() $\infty $
-category of
$\infty $
-category of
![]() $(A,B)$
-bimodules.
$(A,B)$
-bimodules.
Remark 2.15. Associative algebras are closely related to monoid objects in the sense of Section 2.5: for a category
![]() $\mathscr {C}$
with finite products, equipped with the cartesian monoidal structure (see Example 2.5), we have an equivalence of
$\mathscr {C}$
with finite products, equipped with the cartesian monoidal structure (see Example 2.5), we have an equivalence of
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathrm {Ass}(\mathscr {C}^\times )\simeq \mathrm {Mon}(\mathscr {C})$
[Reference LurieLur17, 2.4.2.5].
$\mathrm {Ass}(\mathscr {C}^\times )\simeq \mathrm {Mon}(\mathscr {C})$
[Reference LurieLur17, 2.4.2.5].
Remark 2.16. Lurie uses different models for the
![]() $\infty $
-categories of associative algebras and bimodules in a monoidal
$\infty $
-categories of associative algebras and bimodules in a monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
(using the equivalent point of view on monoidal structures mentioned in Remark 2.6), but these turn out to be equivalent to
$\mathscr {C}$
(using the equivalent point of view on monoidal structures mentioned in Remark 2.6), but these turn out to be equivalent to
![]() $\mathrm {Ass}(\mathscr {C})$
and
$\mathrm {Ass}(\mathscr {C})$
and
![]() $\mathrm {BMod}(\mathscr {C})$
as defined above. For
$\mathrm {BMod}(\mathscr {C})$
as defined above. For
![]() $\mathrm {Ass}(\mathscr {C})$
, this is proved as [Reference LurieLur17, 4.1.3.19], and for
$\mathrm {Ass}(\mathscr {C})$
, this is proved as [Reference LurieLur17, 4.1.3.19], and for
![]() $\mathrm {BMod}(\mathscr {C})$
, it follows from an extension of that argument, or from Remark 2.18 below.
$\mathrm {BMod}(\mathscr {C})$
, it follows from an extension of that argument, or from Remark 2.18 below.
The following lemma on free
![]() $(A,B)$
-bimodules will be important later:
$(A,B)$
-bimodules will be important later:
Lemma 2.17. For a monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
and associative algebras
$\mathscr {C}$
and associative algebras
![]() $A,B\in \mathrm {Ass}(\mathscr {C})$
, the forgetful functor
$A,B\in \mathrm {Ass}(\mathscr {C})$
, the forgetful functor ![]() given as the composition of the inclusion into
given as the composition of the inclusion into
![]() $\mathrm {BMod}(\mathscr {C})$
followed by (20) and the projection to
$\mathrm {BMod}(\mathscr {C})$
followed by (20) and the projection to
![]() $\mathscr {C}$
has the following properties:
$\mathscr {C}$
has the following properties:
-
(i) For a fixed
 $\infty $
-category I such that
$\infty $
-category I such that
 $\mathscr {C}$
admits all I-indexed colimits, the functor
$\mathscr {C}$
admits all I-indexed colimits, the functor
 $U_{A,B}$
preserves and detects I-indexed colimits. The same holds for limits instead of colimits.
$U_{A,B}$
preserves and detects I-indexed colimits. The same holds for limits instead of colimits. -
(ii) The functor
 $U_{A,B}$
reflects equivalences.
$U_{A,B}$
reflects equivalences. -
(iii) The functor
 $U_{A,B}$
has a left-adjoint
$U_{A,B}$
has a left-adjoint  whose unit
whose unit
 $M\rightarrow U_{A,B}F_{A,B}(M)$
for
$M\rightarrow U_{A,B}F_{A,B}(M)$
for
 $M\in \mathscr {C}$
agrees with the map
$M\in \mathscr {C}$
agrees with the map
 $M\rightarrow A\otimes M\otimes B$
given by tensoring with the units of A and B.
$M\rightarrow A\otimes M\otimes B$
given by tensoring with the units of A and B. -
(iv) For a functor
 $\varphi \colon \mathscr {C}\rightarrow \mathscr {D}$
of monoidal
$\varphi \colon \mathscr {C}\rightarrow \mathscr {D}$
of monoidal
 $\infty $
-categories and
$\infty $
-categories and
 $M\in \mathscr {C}$
, the canonical morphism
$M\in \mathscr {C}$
, the canonical morphism
 $F_{\varphi (A),\varphi (B)}(\varphi (M))\rightarrow \varphi (F_{A,B}(M))$
is an equivalence.
$F_{\varphi (A),\varphi (B)}(\varphi (M))\rightarrow \varphi (F_{A,B}(M))$
is an equivalence.
Proof. Using 2.16, the first part follows from [Reference LurieLur17, 4.3.3.3, 4.3.3.9]. The remaining items follow from [Reference HaugsengHau17, Corollary 4.49]: The final part of this corollary in particular shows (ii) since right adjoints in monadic adjunctions reflect equivalences [Reference LurieLur17, 4.7.3.5] and the first part shows (iii). This leaves (iv). As a result of (ii), it suffices to show that
is an equivalence. Using the second part of (iii) this follows from the monoidality of
![]() $\varphi $
.
$\varphi $
.
2.9 Haugseng’s Morita category
In analogy with the classical Morita category of a ring, for a sufficiently nice monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, one would expect a double
$\mathscr {C}$
, one would expect a double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {ALG}(\mathscr {C})$
– the Morita category of
$\mathrm {ALG}(\mathscr {C})$
– the Morita category of
![]() $\mathscr {C}$
– whose
$\mathscr {C}$
– whose
![]() $\infty $
-category of objects
$\infty $
-category of objects
![]() $\mathrm {ALG}(\mathscr {C})_{[0]}$
is the
$\mathrm {ALG}(\mathscr {C})_{[0]}$
is the
![]() $\infty $
-category of associative algebras
$\infty $
-category of associative algebras
![]() $\mathrm {Ass}(\mathscr {C})$
, whose
$\mathrm {Ass}(\mathscr {C})$
, whose
![]() $\infty $
-category of morphisms
$\infty $
-category of morphisms
![]() $\mathrm {ALG}(\mathscr {C})_{[1]}$
is the category of bimodules
$\mathrm {ALG}(\mathscr {C})_{[1]}$
is the category of bimodules
![]() $\mathrm {BMod}(\mathscr {C})$
, and whose composition is given by ‘tensoring bimodules’. Haugseng constructed such a Morita category in [Reference HaugsengHau17] (denoted
$\mathrm {BMod}(\mathscr {C})$
, and whose composition is given by ‘tensoring bimodules’. Haugseng constructed such a Morita category in [Reference HaugsengHau17] (denoted
![]() $\mathrm {ALG}_1(\mathscr {C})$
therein) under mild assumptions on
$\mathrm {ALG}_1(\mathscr {C})$
therein) under mild assumptions on
![]() $\mathscr {C}$
. In what follows, we recall his construction and establish some properties not explicitly stated.
$\mathscr {C}$
. In what follows, we recall his construction and establish some properties not explicitly stated.
2.9.1 The pre-Morita category
For a monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}^{\otimes }\rightarrow \Delta ^{\mathrm {op}}$
, the pre-Morita simplicial
$\mathscr {C}^{\otimes }\rightarrow \Delta ^{\mathrm {op}}$
, the pre-Morita simplicial
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathscr {C}$
is the simplicial
$\mathscr {C}$
is the simplicial
![]() $\infty $
-category
$\infty $
-category ![]() with
with
The simplicial structure is given by precomposition with the functors
![]() $\smash {\Delta _{/[p]}\rightarrow \Delta _{/[q]}}$
induced by postcomposition with morphisms
$\smash {\Delta _{/[p]}\rightarrow \Delta _{/[q]}}$
induced by postcomposition with morphisms
![]() $[p]\rightarrow [q]$
in
$[p]\rightarrow [q]$
in
![]() $\Delta $
; this uses Example 2.14. By construction,
$\Delta $
; this uses Example 2.14. By construction,
![]() $\smash {\overline {\mathrm {ALG}}(-)}$
is natural in lax monoidal functors by postcomposition.
$\smash {\overline {\mathrm {ALG}}(-)}$
is natural in lax monoidal functors by postcomposition.
This definition extends the
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathrm {Ass}(\mathscr {C})=\overline {\mathrm {ALG}}(\mathscr {C} )_{[0]}$
and
$\mathrm {Ass}(\mathscr {C})=\overline {\mathrm {ALG}}(\mathscr {C} )_{[0]}$
and
![]() $\mathrm {BMod}(\mathscr {C})=\overline {\mathrm {ALG}}(\mathscr {C} )_{[1]}$
to a simplicial
$\mathrm {BMod}(\mathscr {C})=\overline {\mathrm {ALG}}(\mathscr {C} )_{[1]}$
to a simplicial
![]() $\infty $
-category
$\infty $
-category
![]() $\smash {\overline {\mathrm {ALG}}(\mathscr {C})}$
, but the result is not yet a double
$\smash {\overline {\mathrm {ALG}}(\mathscr {C})}$
, but the result is not yet a double
![]() $\infty $
-category: an object in
$\infty $
-category: an object in
![]() $\smash {\overline {\mathrm {ALG}}(\mathscr {C})_{[p]}}$
gives associative algebras
$\smash {\overline {\mathrm {ALG}}(\mathscr {C})_{[p]}}$
gives associative algebras
![]() $M(i)$
for
$M(i)$
for
![]() $0 \leq i \leq p$
and
$0 \leq i \leq p$
and
![]() $(M(i),M(j))$
-bimodules
$(M(i),M(j))$
-bimodules
![]() $M(i,j)$
for
$M(i,j)$
for
![]() $0 \leq i<j \leq p$
, and, informally speaking, we need to enforce that
$0 \leq i<j \leq p$
, and, informally speaking, we need to enforce that
![]() $M(i,j)$
is equivalent to the iterated tensor product
$M(i,j)$
is equivalent to the iterated tensor product
![]() $M(i,i+1) \otimes _{M(i+1)} M(i+1,i+2) \otimes _{M(i+2)} \cdots \otimes _{M(j-1)} M(j-1,j)$
.
$M(i,i+1) \otimes _{M(i+1)} M(i+1,i+2) \otimes _{M(i+2)} \cdots \otimes _{M(j-1)} M(j-1,j)$
.
2.9.2 Composite algebras and the Morita category
The condition on the
![]() $M(i,j)$
just mentioned can be made precise through the notion of a composite algebra from [Reference HaugsengHau17, Section 4.2]. It requires an assumption on
$M(i,j)$
just mentioned can be made precise through the notion of a composite algebra from [Reference HaugsengHau17, Section 4.2]. It requires an assumption on
![]() $\mathscr {C}$
that Haugseng calls having good relative tensor products [Reference HaugsengHau17, Definition 4.18], which is in particular satisfied if the underlying category
$\mathscr {C}$
that Haugseng calls having good relative tensor products [Reference HaugsengHau17, Definition 4.18], which is in particular satisfied if the underlying category
![]() $\mathscr {C}$
admits all geometric realisations (colimits indexed over
$\mathscr {C}$
admits all geometric realisations (colimits indexed over
![]() $\Delta ^{\mathrm {op}}$
) and if they are preserved by tensoring (on either side) with fixed objects of
$\Delta ^{\mathrm {op}}$
) and if they are preserved by tensoring (on either side) with fixed objects of
![]() $\mathscr {C}$
; this follows from [Reference HaugsengHau17, Lemma 4.19]. If
$\mathscr {C}$
; this follows from [Reference HaugsengHau17, Lemma 4.19]. If
![]() $\mathscr {C}$
has good relative tensor products, then the functor
$\mathscr {C}$
has good relative tensor products, then the functor
induced by the inclusion
![]() $\tau _p\colon \Lambda ^{\mathrm {op}}_{/[p]}\hookrightarrow \Delta ^{\mathrm {op}}_{/[p]}$
(see Example 2.14) admits a fully faithful left adjoint
$\tau _p\colon \Lambda ^{\mathrm {op}}_{/[p]}\hookrightarrow \Delta ^{\mathrm {op}}_{/[p]}$
(see Example 2.14) admits a fully faithful left adjoint
by [Reference HaugsengHau17, Corollary 4.20], and
![]() $M\in \overline {\mathrm {ALG}}(\mathscr {C} )_{[p]}$
is called composite if M is in the essential image of
$M\in \overline {\mathrm {ALG}}(\mathscr {C} )_{[p]}$
is called composite if M is in the essential image of
![]() $\tau _{p,!}$
, or equivalently if the counit
$\tau _{p,!}$
, or equivalently if the counit
![]() $\tau _{p,!}\tau _p^*M\rightarrow M$
is an equivalence [Reference HaugsengHau17, Definition 4.21]. By [Reference HaugsengHau17, Corollary 4.38], the simplicial structure on the pre-Morita category restricts to a simplicial structure on the full subcategories
$\tau _{p,!}\tau _p^*M\rightarrow M$
is an equivalence [Reference HaugsengHau17, Definition 4.21]. By [Reference HaugsengHau17, Corollary 4.38], the simplicial structure on the pre-Morita category restricts to a simplicial structure on the full subcategories
![]() $\smash {\mathrm {ALG}(\mathscr {C})_{[p]}\subset \overline {\mathrm {ALG}}(\mathscr {C} )_{[p]}}$
of composite objects, and by [Reference HaugsengHau17, Theorem 4.39], the result is a double
$\smash {\mathrm {ALG}(\mathscr {C})_{[p]}\subset \overline {\mathrm {ALG}}(\mathscr {C} )_{[p]}}$
of composite objects, and by [Reference HaugsengHau17, Theorem 4.39], the result is a double
![]() $\infty $
-category – the Morita double
$\infty $
-category – the Morita double
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathscr {C}$
$\mathscr {C}$
Note that
![]() $\Lambda _{/[p]}=\Delta _{/[p]}$
for
$\Lambda _{/[p]}=\Delta _{/[p]}$
for
![]() $p=0,1$
so
$p=0,1$
so
![]() $\mathrm {ALG}(\mathscr {C})_{[p]}\subseteq \overline {\mathrm {ALG}}(\mathscr {C})_{[p]}$
is an equality for
$\mathrm {ALG}(\mathscr {C})_{[p]}\subseteq \overline {\mathrm {ALG}}(\mathscr {C})_{[p]}$
is an equality for
![]() $p=0,1$
; that is,
$p=0,1$
; that is,
In particular, the mapping
![]() $\infty $
-categories between
$\infty $
-categories between
![]() $A,B\in \mathrm {ALG}(\mathscr {C})_{[0]}$
in the notation of Section 2.5.4 are given as
$A,B\in \mathrm {ALG}(\mathscr {C})_{[0]}$
in the notation of Section 2.5.4 are given as
![]() $\mathrm {ALG}(\mathscr {C})_{A,B}=\mathrm {BMod}_{A,B}(\mathscr {C})$
.
$\mathrm {ALG}(\mathscr {C})_{A,B}=\mathrm {BMod}_{A,B}(\mathscr {C})$
.
Remark 2.18. In [Reference LurieLur17, 4.4.3.10, 4.4.3.11], Lurie describes a Morita double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {BMod}(\mathscr {C})^\circledast $
for monoidal
$\mathrm {BMod}(\mathscr {C})^\circledast $
for monoidal
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathscr {C}$
that admit geometric realisations which are compatible with tensoring with a fixed object on either side (so they in particular admit good relative tensor products). One advantage of Lurie’s model is that it is functorial in all lax monoidal functors, whereas Haugseng’s is a priori only functorial in (strong) monoidal functors that are compatible with good relative tensor products (see Section 2.9.4 below). However, it turns out that Haugseng’s Morita double
$\mathscr {C}$
that admit geometric realisations which are compatible with tensoring with a fixed object on either side (so they in particular admit good relative tensor products). One advantage of Lurie’s model is that it is functorial in all lax monoidal functors, whereas Haugseng’s is a priori only functorial in (strong) monoidal functors that are compatible with good relative tensor products (see Section 2.9.4 below). However, it turns out that Haugseng’s Morita double
![]() $\infty $
-category
$\infty $
-category
![]() $ \mathrm {ALG}(\mathscr {C})$
is equivalent to Lurie’s
$ \mathrm {ALG}(\mathscr {C})$
is equivalent to Lurie’s
![]() $\mathrm {BMod}(\mathscr {C})^\circledast $
; see [Reference HaugsengHau23, Corollary 5.14]. In particular, on
$\mathrm {BMod}(\mathscr {C})^\circledast $
; see [Reference HaugsengHau23, Corollary 5.14]. In particular, on
![]() $0$
- and
$0$
- and
![]() $1$
-simplices, this comparison shows that Lurie’s and Haugseng’s models for the category of associative algebras and bimodules in a monoidal
$1$
-simplices, this comparison shows that Lurie’s and Haugseng’s models for the category of associative algebras and bimodules in a monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
are equivalent (cf. Remark 2.16), and on composition functors, it shows that Lurie’s and Haugseng’s models for relative tensor products of bimodules are equivalent.
$\mathscr {C}$
are equivalent (cf. Remark 2.16), and on composition functors, it shows that Lurie’s and Haugseng’s models for relative tensor products of bimodules are equivalent.
2.9.3 Composite algebras in terms of semisimplicial objects
We will now reformulate the condition on an object
![]() $M\in \overline {\mathrm {ALG}}(\mathscr {C} )_{[p]}$
to be composite in a form closer to the informal description mentioned at the end of Section 2.9.1, resulting in a convenient criterion for an object
$M\in \overline {\mathrm {ALG}}(\mathscr {C} )_{[p]}$
to be composite in a form closer to the informal description mentioned at the end of Section 2.9.1, resulting in a convenient criterion for an object
![]() $M \in \overline {\mathrm {ALG}}(\mathscr {C})_{[p]}$
to be composite. Before turning to the technical details, we describe this criterion informally. As mentioned before, the object M gives associative algebras
$M \in \overline {\mathrm {ALG}}(\mathscr {C})_{[p]}$
to be composite. Before turning to the technical details, we describe this criterion informally. As mentioned before, the object M gives associative algebras
![]() $M(i)$
for
$M(i)$
for
![]() $0 \leq i \leq p$
and
$0 \leq i \leq p$
and
![]() $(M(i),M(j))$
-bimodules
$(M(i),M(j))$
-bimodules
![]() $M(i,j)$
for
$M(i,j)$
for
![]() $0 \leq i<j\leq p$
. For each such bimodule, there is an ‘iterated bar-construction’ semisimplicial object
$0 \leq i<j\leq p$
. For each such bimodule, there is an ‘iterated bar-construction’ semisimplicial object
![]() $M(i,j)_\bullet $
in
$M(i,j)_\bullet $
in
![]() $\mathscr {C}$
augmented over
$\mathscr {C}$
augmented over
![]() $M(i,j)$
, with k-simplices
$M(i,j)$
, with k-simplices
The criterion is then equivalent to requiring that the augmentation geometrically realises to an equivalence for all
![]() $0 \leq i<j\leq p$
. In fact, for bookkeeping reasons, it is convenient to rephrase this criterion slightly: For each
$0 \leq i<j\leq p$
. In fact, for bookkeeping reasons, it is convenient to rephrase this criterion slightly: For each
![]() $q\ge 0$
and each sequence
$q\ge 0$
and each sequence
![]() $\alpha =(0\le i_0 \leq \ldots \leq i_q\le p)$
of integers, we have an augmented semisimplicial object over
$\alpha =(0\le i_0 \leq \ldots \leq i_q\le p)$
of integers, we have an augmented semisimplicial object over
![]() $M(i_0,i_1)\otimes M(i_1,i_2)\otimes \ldots \otimes M(i_{q-1},i_q)$
given by the diagonal of the q-fold semisimplicial object
$M(i_0,i_1)\otimes M(i_1,i_2)\otimes \ldots \otimes M(i_{q-1},i_q)$
given by the diagonal of the q-fold semisimplicial object
![]() $M(i_0,i_1)_\bullet \otimes M(i_1,i_2)_\bullet \otimes \ldots \otimes M(i_{q-1},i_q)_\bullet $
. The criterion is that its augmentation has to realise to an equivalence (see Corollary 2.25).
$M(i_0,i_1)_\bullet \otimes M(i_1,i_2)_\bullet \otimes \ldots \otimes M(i_{q-1},i_q)_\bullet $
. The criterion is that its augmentation has to realise to an equivalence (see Corollary 2.25).
To make this precise, we denote by
![]() $\Delta ^{\mathrm {act}}$
the wide subcategory of
$\Delta ^{\mathrm {act}}$
the wide subcategory of
![]() $\Delta $
given by the active maps and by
$\Delta $
given by the active maps and by
![]() $\mathscr {C}^{\otimes ,\mathrm {act}}$
the pullback of
$\mathscr {C}^{\otimes ,\mathrm {act}}$
the pullback of
![]() $\mathscr {C}^{\otimes }\rightarrow \Delta ^{\mathrm {op}}$
along the inclusion
$\mathscr {C}^{\otimes }\rightarrow \Delta ^{\mathrm {op}}$
along the inclusion
![]() $\Delta ^{\mathrm {act},\mathrm {op}}\rightarrow \Delta ^{\mathrm {op}}$
. The unique active maps
$\Delta ^{\mathrm {act},\mathrm {op}}\rightarrow \Delta ^{\mathrm {op}}$
. The unique active maps
![]() $[1]\rightarrow [p]$
define a natural transformation from the inclusion
$[1]\rightarrow [p]$
define a natural transformation from the inclusion
![]() $\Delta ^{\mathrm {act},\mathrm {op}}\rightarrow \Delta ^{\mathrm {op}}$
to the constant functor at
$\Delta ^{\mathrm {act},\mathrm {op}}\rightarrow \Delta ^{\mathrm {op}}$
to the constant functor at
![]() $[1]\in \Delta ^{\mathrm {op}}$
, which we can precompose with the projection
$[1]\in \Delta ^{\mathrm {op}}$
, which we can precompose with the projection
![]() $\mathscr {C}^{\otimes ,\mathrm {act}}\rightarrow \Delta ^{\mathrm {act},\mathrm {op}}$
. Taking a cocartesian pushforward (see Section 2.3) of the canonical map
$\mathscr {C}^{\otimes ,\mathrm {act}}\rightarrow \Delta ^{\mathrm {act},\mathrm {op}}$
. Taking a cocartesian pushforward (see Section 2.3) of the canonical map
![]() $\mathscr {C}^{\otimes ,\mathrm {act}}\rightarrow \mathscr {C}^{\otimes }$
along this natural transformation gives a functor
$\mathscr {C}^{\otimes ,\mathrm {act}}\rightarrow \mathscr {C}^{\otimes }$
along this natural transformation gives a functor
Now write
![]() $\Delta ^{\mathrm {act}}_{/[p]}$
for the wide subcategory of
$\Delta ^{\mathrm {act}}_{/[p]}$
for the wide subcategory of
![]() $\Delta _{/[p]}$
of those morphisms that map to
$\Delta _{/[p]}$
of those morphisms that map to
![]() $\Delta ^{\mathrm {act}}$
under the projection and
$\Delta ^{\mathrm {act}}$
under the projection and
![]() $ \Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]}\subset \Delta ^{\mathrm {act},\mathrm {op}}_{/[p]}$
for the full subcategory of cellular maps. For
$ \Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]}\subset \Delta ^{\mathrm {act},\mathrm {op}}_{/[p]}$
for the full subcategory of cellular maps. For
![]() $M\in \overline {\mathrm {ALG}}(\mathscr {C})_{[p]}\subset \mathrm {Fun}_{\Delta ^{\mathrm {op}}}(\Delta ^{\mathrm {op}}_{/[p]},\mathscr {C}^{\otimes })$
and an object
$M\in \overline {\mathrm {ALG}}(\mathscr {C})_{[p]}\subset \mathrm {Fun}_{\Delta ^{\mathrm {op}}}(\Delta ^{\mathrm {op}}_{/[p]},\mathscr {C}^{\otimes })$
and an object
![]() $\alpha \colon [q]\rightarrow [p]$
of
$\alpha \colon [q]\rightarrow [p]$
of
![]() $\Delta ^{\mathrm {act},\mathrm {op}}_{/[p]}$
, we consider the composition
$\Delta ^{\mathrm {act},\mathrm {op}}_{/[p]}$
, we consider the composition
where
![]() $\mathrm {pr}$
is the projection,
$\mathrm {pr}$
is the projection, ![]() is the right-cone (this freely adds a terminal object and can be modelled by the join
is the right-cone (this freely adds a terminal object and can be modelled by the join
![]() $(-) \ast \Delta ^0$
), and
$(-) \ast \Delta ^0$
), and
![]() $\mathrm {can}$
is the extension of the inclusion
$\mathrm {can}$
is the extension of the inclusion
![]() $\smash {(\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha } \subset (\Delta ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha }}$
to the cone
$\smash {(\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha } \subset (\Delta ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha }}$
to the cone
![]() $((\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha })^{\rhd }$
by sending the terminal object to
$((\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha })^{\rhd }$
by sending the terminal object to
![]() $\mathrm {id}_\alpha $
.
$\mathrm {id}_\alpha $
.
Lemma 2.19. For a monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
with good relative tensor products, an object
$\mathscr {C}$
with good relative tensor products, an object
![]() $M\in \overline {\mathrm {ALG}}(\mathscr {C} )_{[p]}$
is composite if and only if the composition (23) is a colimit diagram for all
$M\in \overline {\mathrm {ALG}}(\mathscr {C} )_{[p]}$
is composite if and only if the composition (23) is a colimit diagram for all
![]() $\alpha $
.
$\alpha $
.
Proof. By definition, M is composite if the counit
![]() $\tau _{p,!}\tau _p^*M\rightarrow M$
is an equivalence. Using Proposition 4.16 and Corollary A.60 of [Reference HaugsengHau17], this is equivalent to asking whether the identity
$\tau _{p,!}\tau _p^*M\rightarrow M$
is an equivalence. Using Proposition 4.16 and Corollary A.60 of [Reference HaugsengHau17], this is equivalent to asking whether the identity
![]() $\tau _p^*M\rightarrow \tau _p^*M$
exhibits M as the operadic left Kan extension of
$\tau _p^*M\rightarrow \tau _p^*M$
exhibits M as the operadic left Kan extension of
![]() $\tau _p^*M$
along
$\tau _p^*M$
along
![]() $\tau _p$
in the sense of Definition A.56 loc.cit. By Lemma A.53 loc.cit., this is in turn equivalent to the condition that the functor
$\tau _p$
in the sense of Definition A.56 loc.cit. By Lemma A.53 loc.cit., this is in turn equivalent to the condition that the functor
![]() $(\smash {(\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})}\times \Delta ^1)\sqcup _{(\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})\times \{0\}}(\Delta ^{\mathrm {act},\mathrm {op}}_{/[p]})\times \{0\}\rightarrow \mathscr {C}$
induced by the restriction of
$(\smash {(\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})}\times \Delta ^1)\sqcup _{(\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})\times \{0\}}(\Delta ^{\mathrm {act},\mathrm {op}}_{/[p]})\times \{0\}\rightarrow \mathscr {C}$
induced by the restriction of
to
![]() $\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]}\times \Delta ^1$
is a left Kan extension in the sense of [Reference LurieLur09a, 4.3.3.2]. As
$\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]}\times \Delta ^1$
is a left Kan extension in the sense of [Reference LurieLur09a, 4.3.3.2]. As
![]() $\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]}\subset \Delta ^{\mathrm {act},\mathrm {op}}_{/[p]}$
is a full subcategory inclusion, we can use the simpler characterisation of left Kan extensions from [Reference LurieLur09a, 4.3.2.2], which is exactly the condition of the statement.
$\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]}\subset \Delta ^{\mathrm {act},\mathrm {op}}_{/[p]}$
is a full subcategory inclusion, we can use the simpler characterisation of left Kan extensions from [Reference LurieLur09a, 4.3.2.2], which is exactly the condition of the statement.
Unravelling the definitions, the category
![]() $(\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha }$
for
$(\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha }$
for
![]() $\alpha \colon [q] \to [p]$
is the 1-category whose objects are factorisations of
$\alpha \colon [q] \to [p]$
is the 1-category whose objects are factorisations of
![]() $\alpha $
into an active map followed by a cellular map,
$\alpha $
into an active map followed by a cellular map,

Note that if
![]() $\alpha $
is active, then so must be
$\alpha $
is active, then so must be
![]() $[r] \to [p]$
. Given another such factorisation, with middle object
$[r] \to [p]$
. Given another such factorisation, with middle object
![]() $[r']$
, a morphism from the factorisation involving
$[r']$
, a morphism from the factorisation involving
![]() $[r]$
to that involving
$[r]$
to that involving
![]() $[r']$
is an active map
$[r']$
is an active map
![]() $[r']\rightarrow [r]$
that makes everything commute:
$[r']\rightarrow [r]$
that makes everything commute:

Colimits over this category – as appearing in Lemma 2.19 – can be rephrased in terms of semisimplicial objects that are easier to handle. Making this precise involves the following construction:
Construction 2.20. Let
![]() $\alpha \colon [q] \to [p]$
be an object of
$\alpha \colon [q] \to [p]$
be an object of
![]() $\Delta ^{\mathrm {op}}_{/[p]}$
considered as a sequence
$\Delta ^{\mathrm {op}}_{/[p]}$
considered as a sequence
![]() $(i_0\leq \ldots \leq i_q) \subseteq [p]$
. Let
$(i_0\leq \ldots \leq i_q) \subseteq [p]$
. Let
![]() $J \subseteq [q-1]$
be the set of indices j for which
$J \subseteq [q-1]$
be the set of indices j for which
![]() $i_j < i_{j+1}$
and set
$i_j < i_{j+1}$
and set ![]() . Enumerating the indices in the interval
. Enumerating the indices in the interval
![]() $[i_0,i_q]$
that do not lie in
$[i_0,i_q]$
that do not lie in
![]() $(i_0,\ldots ,i_q)$
in order as
$(i_0,\ldots ,i_q)$
in order as
![]() $m_1,\ldots ,m_{k_{\alpha }}$
, there is a functor
$m_1,\ldots ,m_{k_{\alpha }}$
, there is a functor
given as follows: writing ![]() , it sends an object
, it sends an object
![]() $([a_1],\ldots ,[a_q])\in (\Delta ^{\mathrm {op}})^{k_{\alpha }}$
to
$([a_1],\ldots ,[a_q])\in (\Delta ^{\mathrm {op}})^{k_{\alpha }}$
to

where
![]() $\alpha _1^{\vec {a}}$
is given by the weakly increasing sequence that contains
$\alpha _1^{\vec {a}}$
is given by the weakly increasing sequence that contains
![]() $(i_0\le \ldots \le i_q)$
as well as each
$(i_0\le \ldots \le i_q)$
as well as each
![]() $m_j$
repeated
$m_j$
repeated
![]() $a_j+1$
times. The map
$a_j+1$
times. The map
![]() $\alpha _0^{\vec {a}}$
is the unique injective map such that
$\alpha _0^{\vec {a}}$
is the unique injective map such that
![]() $\alpha ^{\vec {a}}_1\circ \alpha ^{\vec {a}}_0=\alpha $
.
$\alpha ^{\vec {a}}_1\circ \alpha ^{\vec {a}}_0=\alpha $
.
Example 2.21. If
![]() $\alpha \colon [2] \to [p]$
is given by the sequence
$\alpha \colon [2] \to [p]$
is given by the sequence
![]() $(i\le i+2\le i+4)$
, then
$(i\le i+2\le i+4)$
, then
![]() $k_{\alpha }=2$
, the map
$k_{\alpha }=2$
, the map
![]() $\alpha ^{\vec {a}}_1$
is given by the sequence
$\alpha ^{\vec {a}}_1$
is given by the sequence
![]() $(i\le i+1\le \ldots \le i+1\le i+2\le i+3\le \ldots \le i+3\le i+4)$
where
$(i\le i+1\le \ldots \le i+1\le i+2\le i+3\le \ldots \le i+3\le i+4)$
where
![]() $i+1$
appears
$i+1$
appears
![]() $a_1+1$
times and
$a_1+1$
times and
![]() $i+3$
appears
$i+3$
appears
![]() $a_2+1$
times, and the map
$a_2+1$
times, and the map
![]() $\alpha ^{\vec {a}}_0$
is given by the inclusion of
$\alpha ^{\vec {a}}_0$
is given by the inclusion of
![]() $(i\le i+2\le i+4)$
into this sequence.
$(i\le i+2\le i+4)$
into this sequence.
For later reference, we spell out how
![]() $\rho _\alpha $
translates under the isomorphism
$\rho _\alpha $
translates under the isomorphism
![]() $\Delta \cong \mathsf {Gap}$
.
$\Delta \cong \mathsf {Gap}$
.
Construction 2.22. Let ![]() be an object of
be an object of ![]() considered as a sequence
considered as a sequence
![]() $(i_1\leq \ldots \leq i_p)$
with
$(i_1\leq \ldots \leq i_p)$
with ![]() . The quantity
. The quantity
![]() $k_\alpha $
is then given by
$k_\alpha $
is then given by ![]() . We enumerate this set in order by
. We enumerate this set in order by
![]() $n_1<\ldots <n_{k_\alpha }$
. The functor
$n_1<\ldots <n_{k_\alpha }$
. The functor
![]() $\rho _\alpha $
takes the form
$\rho _\alpha $
takes the form
and can be described as follows: abbreviating ![]() as in the
as in the
![]() $\Delta ^{\mathrm {op}}$
-case, for an object
$\Delta ^{\mathrm {op}}$
-case, for an object ![]() , it sends
, it sends ![]() to the factorisation
to the factorisation

where ![]() is given by the sequence obtained from the sequence
is given by the sequence obtained from the sequence
![]() $(i_1\leq \ldots \leq i_p)$
by inserting a gap of length
$(i_1\leq \ldots \leq i_p)$
by inserting a gap of length
![]() $a_i$
between
$a_i$
between
![]() $i_{n_j}$
and
$i_{n_j}$
and
![]() $i_{n_j+1}$
for
$i_{n_j+1}$
for
![]() $j=1,\ldots , k_\alpha $
, and
$j=1,\ldots , k_\alpha $
, and ![]() is the unique surjective map such that
is the unique surjective map such that
![]() $\alpha _0^{\vec {a}}\circ \alpha _1^{\vec {a}}=\alpha $
.
$\alpha _0^{\vec {a}}\circ \alpha _1^{\vec {a}}=\alpha $
.
The following lemma is a generalisation of [Reference HaugsengHau17, Lemma 4.17].
Lemma 2.23. The functor
![]() $\rho _\alpha $
from Construction 2.20 is cofinal.
$\rho _\alpha $
from Construction 2.20 is cofinal.
Proof. By [Reference LurieLur09a, Theorem 4.1.3.1], it suffices to prove that
![]() $((\Delta ^{\mathrm {op}})^{k_{\alpha }})_{X/}$
has an initial object for all objects X of
$((\Delta ^{\mathrm {op}})^{k_{\alpha }})_{X/}$
has an initial object for all objects X of
![]() $(\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha }$
, i.e., for all factorisations X
$(\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha }$
, i.e., for all factorisations X
of
![]() $\alpha $
into an active
$\alpha $
into an active
![]() $\beta $
followed by a cellular
$\beta $
followed by a cellular
![]() $\alpha '$
. The category
$\alpha '$
. The category
![]() $((\Delta ^{\mathrm {op}})^{k_{\alpha }})_{X/}$
then has objects given by active maps
$((\Delta ^{\mathrm {op}})^{k_{\alpha }})_{X/}$
then has objects given by active maps
![]() $\delta \colon [k_\alpha ^{\vec {a}}]\rightarrow [r]$
such that in
$\delta \colon [k_\alpha ^{\vec {a}}]\rightarrow [r]$
such that in
the full composition agrees with
![]() $\alpha $
, the composition of the first two arrows with
$\alpha $
, the composition of the first two arrows with
![]() $\beta $
, and the composition of the final two arrows with
$\beta $
, and the composition of the final two arrows with
![]() $\alpha _1^{\vec {a}}$
. The morphisms are induced by those of
$\alpha _1^{\vec {a}}$
. The morphisms are induced by those of
![]() $(\Delta ^{\mathrm {op}})^{{k_{\alpha }}}$
via
$(\Delta ^{\mathrm {op}})^{{k_{\alpha }}}$
via
![]() $[k_\alpha ^{\vec {a}}]$
. We now describe an object of this category: define the number
$[k_\alpha ^{\vec {a}}]$
. We now describe an object of this category: define the number
![]() $b_j$
by letting
$b_j$
by letting
![]() $b_j+1$
be the number of times
$b_j+1$
be the number of times
![]() $m_j$
in Construction 2.20 appears in
$m_j$
in Construction 2.20 appears in
![]() $\alpha '$
(
$\alpha '$
(
![]() $b_j\ge 1$
since
$b_j\ge 1$
since
![]() $\alpha '$
is cellular and
$\alpha '$
is cellular and
![]() $\beta $
is active). Then there is a unique map
$\beta $
is active). Then there is a unique map
![]() $\smash {[k_\alpha ^{\vec {b}}]\rightarrow [r]}$
that fits in a factorisation as above, and this map is active because
$\smash {[k_\alpha ^{\vec {b}}]\rightarrow [r]}$
that fits in a factorisation as above, and this map is active because
![]() $[q] \to [r]$
is active. For another factorisation (24), one checks there is unique morphism
$[q] \to [r]$
is active. For another factorisation (24), one checks there is unique morphism
![]() $([a_1],\ldots ,[a_{k_{\alpha }}]) \to ([b_1],\ldots ,[b_{k_{\alpha }}])$
in
$([a_1],\ldots ,[a_{k_{\alpha }}]) \to ([b_1],\ldots ,[b_{k_{\alpha }}])$
in
![]() $\Delta ^{k_{\alpha }}$
that induces a morphism of factorisations, so the factorisation we described provides an initial object in
$\Delta ^{k_{\alpha }}$
that induces a morphism of factorisations, so the factorisation we described provides an initial object in
![]() $((\Delta ^{\mathrm {op}})^{{k_{\alpha }}})_{X/}$
as wished.
$((\Delta ^{\mathrm {op}})^{{k_{\alpha }}})_{X/}$
as wished.
Example 2.24. In the case of Example 2.21 and X given by
![]() $[2] \to [6] \to [p]$
with
$[2] \to [6] \to [p]$
with
![]() $[6] \to [p]$
given by
$[6] \to [p]$
given by
![]() $(i \leq i \leq i+1 \leq i+1 \leq i+2 \leq i+3 \leq i+4)$
(which determines the active morphism
$(i \leq i \leq i+1 \leq i+1 \leq i+2 \leq i+3 \leq i+4)$
(which determines the active morphism
![]() $[2] \to [6]$
uniquely), the initial object in
$[2] \to [6]$
uniquely), the initial object in
![]() $((\Delta ^{\mathrm {op}})^{{k_{\alpha }}})_{X/}$
is given as follows: we get
$((\Delta ^{\mathrm {op}})^{{k_{\alpha }}})_{X/}$
is given as follows: we get
![]() $k_\alpha =2$
,
$k_\alpha =2$
,
![]() $([b_1],[b_2]) = ([1],[0])$
,
$([b_1],[b_2]) = ([1],[0])$
,
![]() $\smash {k^{\vec {b}}_\alpha } = 5$
, and
$\smash {k^{\vec {b}}_\alpha } = 5$
, and
![]() $\delta \colon [5] \to [6]$
is
$\delta \colon [5] \to [6]$
is
![]() $(0 \leq 2 \leq 3 \leq 4 \leq 5 \leq 6)$
. To see it is initial, note that equivalently it is terminal among pairs
$(0 \leq 2 \leq 3 \leq 4 \leq 5 \leq 6)$
. To see it is initial, note that equivalently it is terminal among pairs
![]() $([a_1],[a_2])$
with factorisations
$([a_1],[a_2])$
with factorisations
![]() $[2] \to [k^{\vec {a}}_\alpha ] \to [6] \to [p]$
, which is true since
$[2] \to [k^{\vec {a}}_\alpha ] \to [6] \to [p]$
, which is true since
![]() $\delta \colon [5] \to [6]$
is bijective onto those elements in
$\delta \colon [5] \to [6]$
is bijective onto those elements in
![]() $[6]$
which do not get mapped to the image of
$[6]$
which do not get mapped to the image of
![]() $\alpha $
.
$\alpha $
.
We now consider the composition

which we abbreviate as
![]() $\eta ^\alpha $
; similar for
$\eta ^\alpha $
; similar for
![]() $\mathsf {Gap}$
instead of
$\mathsf {Gap}$
instead of
![]() $\Delta ^{\mathrm {op}}$
. Unravelling the definitions, one checks that
$\Delta ^{\mathrm {op}}$
. Unravelling the definitions, one checks that
![]() $\eta ^{\alpha }$
maps an object
$\eta ^{\alpha }$
maps an object
![]() $[a]\in \Delta ^{\mathrm {op}}_{\mathrm {inj}}$
to
$[a]\in \Delta ^{\mathrm {op}}_{\mathrm {inj}}$
to
![]() $\alpha _1^{\vec {a}}\colon [k_\alpha ^{\vec {a}}]\rightarrow [p]$
with
$\alpha _1^{\vec {a}}\colon [k_\alpha ^{\vec {a}}]\rightarrow [p]$
with
![]() $\vec {a}=(a,\ldots ,a)$
and the cone point to
$\vec {a}=(a,\ldots ,a)$
and the cone point to
![]() $\alpha \colon [q]\rightarrow [p]$
. The unique map from
$\alpha \colon [q]\rightarrow [p]$
. The unique map from
![]() $[a]$
to the cone point is mapped to
$[a]$
to the cone point is mapped to
![]() $\smash {\alpha _0^{\vec {a}}\colon [q]\rightarrow [k_\alpha ^{\vec {a}}]}$
. Since the inclusion
$\smash {\alpha _0^{\vec {a}}\colon [q]\rightarrow [k_\alpha ^{\vec {a}}]}$
. Since the inclusion
![]() $\smash {\Delta ^{\mathrm {op}}_{\mathrm {inj}}\subset \Delta ^{\mathrm {op}}}$
is cofinal [Reference LurieLur09a, 4.1.1.8], the category
$\smash {\Delta ^{\mathrm {op}}_{\mathrm {inj}}\subset \Delta ^{\mathrm {op}}}$
is cofinal [Reference LurieLur09a, 4.1.1.8], the category
![]() $\Delta ^{\mathrm {op}}$
is sifted, and hence, the diagonal
$\Delta ^{\mathrm {op}}$
is sifted, and hence, the diagonal
![]() $\Delta ^{\mathrm {op}}\rightarrow (\Delta ^{\mathrm {op}})^2$
is cofinal [Reference LurieLur09a, 5.5.8.1, 5.5.8.4], the functor
$\Delta ^{\mathrm {op}}\rightarrow (\Delta ^{\mathrm {op}})^2$
is cofinal [Reference LurieLur09a, 5.5.8.1, 5.5.8.4], the functor
![]() $\rho _\alpha $
is cofinal by the previous lemma, and cofinal functors are closed under composition [Reference LurieLur09a, 4.1.1.3 (2)], the composition
$\rho _\alpha $
is cofinal by the previous lemma, and cofinal functors are closed under composition [Reference LurieLur09a, 4.1.1.3 (2)], the composition
![]() $\smash {\Delta ^{\mathrm {op}}_{\mathrm {inj}}\rightarrow (\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha }}$
is cofinal. As colimits in
$\smash {\Delta ^{\mathrm {op}}_{\mathrm {inj}}\rightarrow (\Lambda ^{\mathrm {act},\mathrm {op}}_{/[p]})_{/\alpha }}$
is cofinal. As colimits in
![]() $\infty $
-categories are unaffected by precomposition with cofinal functors [Reference LurieLur09a, 4.1.1.8], we can simplify the condition in Lemma 2.19 further to:
$\infty $
-categories are unaffected by precomposition with cofinal functors [Reference LurieLur09a, 4.1.1.8], we can simplify the condition in Lemma 2.19 further to:
Corollary 2.25. For a monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
with good relative tensor products, an object
$\mathscr {C}$
with good relative tensor products, an object
![]() $M\in \overline {\mathrm {ALG}}(\mathscr {C} )_{[p]}$
is composite if and only if for all
$M\in \overline {\mathrm {ALG}}(\mathscr {C} )_{[p]}$
is composite if and only if for all
![]() $\alpha \in \Delta ^{\mathrm {op}}_{/[p]}$
, the following is a colimit diagram:
$\alpha \in \Delta ^{\mathrm {op}}_{/[p]}$
, the following is a colimit diagram:
Example 2.26. We spell out two exemplary cases of Corollary 2.25 and relate them to the informal description of Corollary 2.25 from the beginning of this subsection, involving the augmented semisimplicial objects
![]() $M(i,j)_\bullet $
. First, for
$M(i,j)_\bullet $
. First, for
![]() $\alpha =(0\le 2) \colon [1] \to [2]$
, we have
$\alpha =(0\le 2) \colon [1] \to [2]$
, we have
![]() $k_\alpha = 1$
, and the functor
$k_\alpha = 1$
, and the functor
![]() $\smash {(\Delta _{\mathrm {inj}}^{\mathrm {op}})^\rhd \to \Delta ^{\mathrm {act},\mathrm {op}}_{/[2]}}$
sends
$\smash {(\Delta _{\mathrm {inj}}^{\mathrm {op}})^\rhd \to \Delta ^{\mathrm {act},\mathrm {op}}_{/[2]}}$
sends
![]() $[a]$
to the sequence
$[a]$
to the sequence
![]() $(0 \leq 1 \leq \ldots \leq 1 \leq 2)$
where
$(0 \leq 1 \leq \ldots \leq 1 \leq 2)$
where
![]() $1$
appears
$1$
appears
![]() $a+1$
times, and it sends the cone point to
$a+1$
times, and it sends the cone point to
![]() $(0 \leq 2)$
. Applying M and
$(0 \leq 2)$
. Applying M and
![]() $(-)_!$
, we obtain the augmented semisimplicial object corresponding to
$(-)_!$
, we obtain the augmented semisimplicial object corresponding to
![]() $M(0,2)_\bullet $
. For
$M(0,2)_\bullet $
. For
![]() $\alpha \colon [q] \to [p]$
given by a sequence
$\alpha \colon [q] \to [p]$
given by a sequence
![]() $(i_0 \leq \cdots \leq i_q) \subseteq [p]$
so that
$(i_0 \leq \cdots \leq i_q) \subseteq [p]$
so that
![]() $i_{j+1} = i_j+1$
, we have
$i_{j+1} = i_j+1$
, we have
![]() $k_\alpha = 0$
, so the composition in the statement is a constant augmented semisimplicial object; this fits with the informal description since
$k_\alpha = 0$
, so the composition in the statement is a constant augmented semisimplicial object; this fits with the informal description since
![]() $M(i,j)_\bullet $
is constant if
$M(i,j)_\bullet $
is constant if
![]() $j=i+1$
.
$j=i+1$
.
2.9.4 Functoriality and monoidality
Postcomposition induces a functor
which is on p-simplices given by
![]() $\mathrm {Alg}_{{\Delta ^{\mathrm {op}}}_{/[p]}}(-)$
. The latter preserves limits [Reference HaugsengHau17, p. 1701], so (25) does as well and in particular induces a functor between commutative monoid objects
$\mathrm {Alg}_{{\Delta ^{\mathrm {op}}}_{/[p]}}(-)$
. The latter preserves limits [Reference HaugsengHau17, p. 1701], so (25) does as well and in particular induces a functor between commutative monoid objects
The situation for
![]() $\mathrm {ALG}(-)$
is only slightly more complicated. Let
$\mathrm {ALG}(-)$
is only slightly more complicated. Let
![]() $\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )^{\mathrm {grtp}}\subset \mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )$
the (non-full) subcategory of monoidal categories that admit good relative tensor products and functors that are compatible with them. The latter is made precise in [Reference HaugsengHau17, Definition 4.18], but all we need is that (i) monoidal categories admit good relative tensor products if their underlying categories admit all geometric realisations and these are compatible with tensoring with a fixed object on either side, and that (ii) functors of monoidal categories that preserve geometric realisations are compatible with good relative tensor products. Then
$\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )^{\mathrm {grtp}}\subset \mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )$
the (non-full) subcategory of monoidal categories that admit good relative tensor products and functors that are compatible with them. The latter is made precise in [Reference HaugsengHau17, Definition 4.18], but all we need is that (i) monoidal categories admit good relative tensor products if their underlying categories admit all geometric realisations and these are compatible with tensoring with a fixed object on either side, and that (ii) functors of monoidal categories that preserve geometric realisations are compatible with good relative tensor products. Then
![]() $\mathrm {ALG}(-)$
gives rise to a functor
$\mathrm {ALG}(-)$
gives rise to a functor
![]() $\mathrm {ALG}(-)\colon \mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )^{\mathrm {grtp}}\longrightarrow \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
(see [Reference HaugsengHau17, Corollary 5.41]). By [Reference HaugsengHau17, Lemma 5.38 (iii)], the category
$\mathrm {ALG}(-)\colon \mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )^{\mathrm {grtp}}\longrightarrow \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
(see [Reference HaugsengHau17, Corollary 5.41]). By [Reference HaugsengHau17, Lemma 5.38 (iii)], the category
![]() $\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )^{\mathrm {grtp}}$
admits products, and these are preserved by the forgetful functor
$\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )^{\mathrm {grtp}}$
admits products, and these are preserved by the forgetful functor
![]() $\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )^{\mathrm {grtp}}\rightarrow \mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )$
. Moreover,
$\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )^{\mathrm {grtp}}\rightarrow \mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )$
. Moreover,
![]() $\mathrm {ALG}(-)$
is product-preserving: we may test this on p-simplices for
$\mathrm {ALG}(-)$
is product-preserving: we may test this on p-simplices for
![]() $p\ge 0$
, and since it has values in double
$p\ge 0$
, and since it has values in double
![]() $\infty $
-categories, it suffices to check this for
$\infty $
-categories, it suffices to check this for
![]() $p=0,1$
where it follows from (21) and the corresponding fact for
$p=0,1$
where it follows from (21) and the corresponding fact for
![]() $\overline {\mathrm {ALG}}(-)$
.
$\overline {\mathrm {ALG}}(-)$
.
![]() $\mathrm {ALG}(-)$
thus induces a functor on commutative monoid objects:
$\mathrm {ALG}(-)$
thus induces a functor on commutative monoid objects:
2.10 Span and cospan categories
We summarise the construction of a double
![]() $\infty $
-category of cospans from [Reference HaugsengHau18, Section 5].
$\infty $
-category of cospans from [Reference HaugsengHau18, Section 5].
2.10.1 Categories of (co)spans
For an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, the pre-span simplicial
$\mathscr {C}$
, the pre-span simplicial
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathscr {C}$
is
$\mathscr {C}$
is
where
![]() $\Sigma ^\bullet \colon \Delta \rightarrow \mathrm {Cat}$
is defined as follows: on objects, it sends
$\Sigma ^\bullet \colon \Delta \rightarrow \mathrm {Cat}$
is defined as follows: on objects, it sends
![]() $[n] \in \Delta $
the poset
$[n] \in \Delta $
the poset
![]() $\Sigma ^n$
of pairs
$\Sigma ^n$
of pairs
![]() $(i,j)$
with
$(i,j)$
with
![]() $0 \leq i \leq j \leq n$
, and
$0 \leq i \leq j \leq n$
, and
![]() $(i,j) \preceq (i',j')$
if and only if
$(i,j) \preceq (i',j')$
if and only if
![]() $i \leq i'$
and
$i \leq i'$
and
![]() $j' \leq j$
, and on morphisms sends
$j' \leq j$
, and on morphisms sends
![]() $\phi \colon [n] \to [m]$
to the functor
$\phi \colon [n] \to [m]$
to the functor
![]() $\Sigma ^n \to \Sigma ^m$
given by
$\Sigma ^n \to \Sigma ^m$
given by
![]() $(i,j) \mapsto (\phi (i),\phi (j))$
.
$(i,j) \mapsto (\phi (i),\phi (j))$
.
If
![]() $\mathscr {C}$
has finite limits, then the span double
$\mathscr {C}$
has finite limits, then the span double
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathscr {C}$
$\mathscr {C}$
is the levelwise full subcategory
![]() $\mathrm {SPAN}^+(\mathscr {C})\subset \overline {\mathrm {SPAN}}^+(\mathscr {C})$
of cartesian functors, where
$\mathrm {SPAN}^+(\mathscr {C})\subset \overline {\mathrm {SPAN}}^+(\mathscr {C})$
of cartesian functors, where
![]() $(\Sigma ^p \to \mathscr {C})\in \overline {\mathrm {SPAN}}^+(\mathscr {C})_{[p]}$
is cartesian if the natural map from it to the right Kan extension of its restriction to the full subcategory
$(\Sigma ^p \to \mathscr {C})\in \overline {\mathrm {SPAN}}^+(\mathscr {C})_{[p]}$
is cartesian if the natural map from it to the right Kan extension of its restriction to the full subcategory
![]() $\Lambda ^p\subset \Sigma ^p$
on
$\Lambda ^p\subset \Sigma ^p$
on
![]() $(i,j)$
with
$(i,j)$
with
![]() $j-i \leq 1$
is an equivalence. By [Reference HaugsengHau18, Proposition 5.14],
$j-i \leq 1$
is an equivalence. By [Reference HaugsengHau18, Proposition 5.14],
![]() $\mathrm {SPAN}^+(\mathscr {C})$
is indeed a double
$\mathrm {SPAN}^+(\mathscr {C})$
is indeed a double
![]() $\infty $
-category. We have
$\infty $
-category. We have
![]() $\mathrm {SPAN}^+(\mathscr {C})_{[0]} = \mathscr {C}$
, and arguing as in [Reference HaugsengHau18, Proposition 8.3], one sees that the mapping
$\mathrm {SPAN}^+(\mathscr {C})_{[0]} = \mathscr {C}$
, and arguing as in [Reference HaugsengHau18, Proposition 8.3], one sees that the mapping
![]() $\infty $
-categories are
$\infty $
-categories are
![]() $\mathrm {SPAN}^+(\mathscr {C})_{A,B} \simeq \mathscr {C}_{/A \times B}$
.
$\mathrm {SPAN}^+(\mathscr {C})_{A,B} \simeq \mathscr {C}_{/A \times B}$
.
Dually, one defines the cospan double
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathscr {C}$
and its pre-version as
$\mathscr {C}$
and its pre-version as
where the outer
![]() $(-)^{\mathrm {op}}$
denotes taking levelwise opposites, and the second definition requires
$(-)^{\mathrm {op}}$
denotes taking levelwise opposites, and the second definition requires
![]() $\mathscr {C}$
to have finite colimits. The mapping
$\mathscr {C}$
to have finite colimits. The mapping
![]() $\infty $
-categories are then given by
$\infty $
-categories are then given by
![]() $\mathrm {COSPAN}^+(\mathscr {C})_{A,B}\simeq \mathscr {C}_{A\sqcup B/}$
.
$\mathrm {COSPAN}^+(\mathscr {C})_{A,B}\simeq \mathscr {C}_{A\sqcup B/}$
.
2.10.2 Relation to Morita categories
Cospan categories and Morita categories are not unrelated: if
![]() $\mathscr {C}$
has finite colimits, then it has good relative tensor products as in Section 2.9.2 when equipped with the cocartesian symmetric monoidal structure
$\mathscr {C}$
has finite colimits, then it has good relative tensor products as in Section 2.9.2 when equipped with the cocartesian symmetric monoidal structure
![]() $\mathscr {C}^{\sqcup }$
[Reference Haugseng, Melani and SafronovHMS20, Remark 2.5.14]. By Corollaries 2.6.8 and 2.6.10 loc.cit., there is an equivalence of double
$\mathscr {C}^{\sqcup }$
[Reference Haugseng, Melani and SafronovHMS20, Remark 2.5.14]. By Corollaries 2.6.8 and 2.6.10 loc.cit., there is an equivalence of double
![]() $\infty $
-categories
$\infty $
-categories
Moreover, functors that preserve finite colimits are compatible with good relative tensor products, so
![]() $\mathrm {COSPAN}^+(\mathscr {C})$
inherits the functoriality and monoidality properties from
$\mathrm {COSPAN}^+(\mathscr {C})$
inherits the functoriality and monoidality properties from
![]() $\mathrm {ALG}(\mathscr {C}^{\sqcup })$
as discussed in Section 2.9.4 for monoidal categories with finite colimits and functors that preserve those (there is also an a priori description, but we will not need it). Tracing through the proof, one sees that under the equivalence (27), an object
$\mathrm {ALG}(\mathscr {C}^{\sqcup })$
as discussed in Section 2.9.4 for monoidal categories with finite colimits and functors that preserve those (there is also an a priori description, but we will not need it). Tracing through the proof, one sees that under the equivalence (27), an object
![]() $M \in \mathrm {ALG}(\mathscr {C})_{[p]}$
is sent to the sequence of cospans
$M \in \mathrm {ALG}(\mathscr {C})_{[p]}$
is sent to the sequence of cospans

where the map
![]() $M(i) \to M(i,i+1)$
is given by
$M(i) \to M(i,i+1)$
is given by
![]() $M(i) \xrightarrow {\mathrm {inc}} M(i) \sqcup M(i,i+1) \xrightarrow {\text {act}} M(i,i+1)$
, and similarly for
$M(i) \xrightarrow {\mathrm {inc}} M(i) \sqcup M(i,i+1) \xrightarrow {\text {act}} M(i,i+1)$
, and similarly for
![]() $M(i+1) \to M(i,i+1)$
. Here we used the notation from Section 2.9.1.
$M(i+1) \to M(i,i+1)$
. Here we used the notation from Section 2.9.1.
3 From the bordism to the Morita category
As part of the introduction, we announced in Section 1.2.2 the construction of a functor
of symmetric monoidal
![]() $(\infty ,2)$
-categories where the domain is an
$(\infty ,2)$
-categories where the domain is an
![]() $(\infty ,2)$
-category of possibly non-compact
$(\infty ,2)$
-category of possibly non-compact
![]() $(d-1)$
-dimensional manifolds with bordisms as
$(d-1)$
-dimensional manifolds with bordisms as
![]() $1$
-morphisms and embeddings as
$1$
-morphisms and embeddings as
![]() $2$
-morphisms, and the target is a Morita
$2$
-morphisms, and the target is a Morita
![]() $(\infty ,2)$
-category of the symmetric monoidal
$(\infty ,2)$
-category of the symmetric monoidal
![]() $\infty $
-category of presheaves on an
$\infty $
-category of presheaves on an
![]() $\infty $
-category of disjoint unions of d-dimensional open discs with embeddings as morphisms and disjoint union as monoidal structure. What we will actually do is to construct (28) as a functor between symmetric monoidal double
$\infty $
-category of disjoint unions of d-dimensional open discs with embeddings as morphisms and disjoint union as monoidal structure. What we will actually do is to construct (28) as a functor between symmetric monoidal double
![]() $\infty $
-categories, which is more general by the discussion in Section 2.5.6.
$\infty $
-categories, which is more general by the discussion in Section 2.5.6.
For most of the arguments in the proofs of Theorems A–C, the precise construction of (28) does not play a role. We summarise the key features in Section 4, so readers who mainly care about Theorems A–C may skip this technical section on a first reading.
The steps we take in this section to construct the functor (28) are as follows:
-
Step ① Construct a non-unital double
 $\infty $
-category
$\infty $
-category
 $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\in \mathrm {Cat}_{\mathrm {nu}}(\mathscr {C}\mathrm {at}_\infty )$
of possibly non-compact
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\in \mathrm {Cat}_{\mathrm {nu}}(\mathscr {C}\mathrm {at}_\infty )$
of possibly non-compact
 $(d-1)$
-manifolds with embeddings and bordisms between them.
$(d-1)$
-manifolds with embeddings and bordisms between them. -
Step ② Construct a monoidal
 $\infty $
-category
$\infty $
-category
 $\mathscr {M}\mathrm {an}_d\in \mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )$
of possibly non-compact d-manifolds and embeddings between them, monoidal via disjoint union.
$\mathscr {M}\mathrm {an}_d\in \mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty )$
of possibly non-compact d-manifolds and embeddings between them, monoidal via disjoint union. -
Step ③ Construct a morphism
 $E^{\mathrm {geo}} \colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\rightarrow \overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d)$
of semisimplicial
$E^{\mathrm {geo}} \colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\rightarrow \overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d)$
of semisimplicial
 $\infty $
-categories to the pre-Morita category of
$\infty $
-categories to the pre-Morita category of
 $\mathscr {M}\mathrm {an}_d$
from Section 2.9, viewed as a semisimplicial object.
$\mathscr {M}\mathrm {an}_d$
from Section 2.9, viewed as a semisimplicial object. -
Step ④ Show that the composition
lands in the Morita category $$\begin{align*}\qquad \quad \overline{E} \colon \mathrm{nc}\mathscr{B}\mathrm{ord}(d)^{\mathrm{nu}} \rightarrow \overline{\mathrm{ALG}}(\mathscr{M}\mathrm{an}_d)\rightarrow \overline{\mathrm{ALG}}(\mathrm{PSh}(\mathscr{M}\mathrm{an}_d))\rightarrow\overline{\mathrm{ALG}}(\mathrm{PSh}(\mathscr{D}\mathrm{isc}_d)) \end{align*}$$
$$\begin{align*}\qquad \quad \overline{E} \colon \mathrm{nc}\mathscr{B}\mathrm{ord}(d)^{\mathrm{nu}} \rightarrow \overline{\mathrm{ALG}}(\mathscr{M}\mathrm{an}_d)\rightarrow \overline{\mathrm{ALG}}(\mathrm{PSh}(\mathscr{M}\mathrm{an}_d))\rightarrow\overline{\mathrm{ALG}}(\mathrm{PSh}(\mathscr{D}\mathrm{isc}_d)) \end{align*}$$
 . The second map is induced by the Yoneda embedding and the third map by the full subcategory
. The second map is induced by the Yoneda embedding and the third map by the full subcategory
 $\mathscr {D}\mathrm {isc}_d\subset \mathscr {M}\mathrm {an}_d$
on manifolds diffeomorphic to
$\mathscr {D}\mathrm {isc}_d\subset \mathscr {M}\mathrm {an}_d$
on manifolds diffeomorphic to
 $T\times \mathbf {R}^d$
for finite sets T.
$T\times \mathbf {R}^d$
for finite sets T.
-
Step ⑤ Argue that
 $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}$
can be enhanced to a (unital) double
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}$
can be enhanced to a (unital) double
 $\infty $
-category
$\infty $
-category
 $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
, and that
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
, and that
 $\overline {E}$
can be enhanced to a functor of double
$\overline {E}$
can be enhanced to a functor of double
 $\infty $
-categories as in (28).
$\infty $
-categories as in (28). -
Step ⑥ Argue that the resulting functor
 $E \colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d) \to \mathscr {M}\mathrm {od}(d)$
can be enhanced to a functor of symmetric monoidal double
$E \colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d) \to \mathscr {M}\mathrm {od}(d)$
can be enhanced to a functor of symmetric monoidal double
 $\infty $
-categories.
$\infty $
-categories.
We will conclude the section with some enhancements of the bordism category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
:
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
:
-
Step ⑦ Construct variants
 $\mathscr {B}\mathrm {ord}(d)$
,
$\mathscr {B}\mathrm {ord}(d)$
,
 $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^\partial $
and
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^\partial $
and
 $\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)$
of
$\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)$
of
 $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
by restricting to compact manifolds and diffeomorphisms instead of embeddings, allowing manifolds with boundary, and adding tangential structures.
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
by restricting to compact manifolds and diffeomorphisms instead of embeddings, allowing manifolds with boundary, and adding tangential structures. -
Step ⑧ Construct for a closed p-manifold P a map of symmetric monoidal double
 $\infty $
-categories
$\infty $
-categories
 $P \times (-) \colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d) \to \mathrm {nc}\mathscr {B}\mathrm {ord}(d+p)$
induced by taking cartesian product with P, and extend this construction to the variants from
Step ⑦.
$P \times (-) \colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d) \to \mathrm {nc}\mathscr {B}\mathrm {ord}(d+p)$
induced by taking cartesian product with P, and extend this construction to the variants from
Step ⑦.
Remark 3.1. Some remarks on the construction of the functor (28):
-
(i) One may ask whether this construction can be ‘fully extended’; that is, whether one can upgrade
 $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
to a symmetric monoidal
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
to a symmetric monoidal
 $(d+1)$
-fold
$(d+1)$
-fold
 $\infty $
-category and the functor E to a map of such objects with target the symmetric monoidal
$\infty $
-category and the functor E to a map of such objects with target the symmetric monoidal
 $(d+1)$
-fold Morita
$(d+1)$
-fold Morita
 $\infty $
-category of
$\infty $
-category of
 $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
from [Reference HaugsengHau17, Section 5], which would in particular give a functor of symmetric monoidal
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
from [Reference HaugsengHau17, Section 5], which would in particular give a functor of symmetric monoidal
 $(\infty ,d+1)$
-categories. There are no conceptual issues in doing so, but it would involve additional bookkeeping and make our construction less transparent. Since we do not need it to prove the main results, we did not include it.
$(\infty ,d+1)$
-categories. There are no conceptual issues in doing so, but it would involve additional bookkeeping and make our construction less transparent. Since we do not need it to prove the main results, we did not include it. -
(ii) We construct (28) as a functor of symmetric monoidal double
 $\infty $
-categories, but all later arguments only use the underlying functor of symmetric monoidal
$\infty $
-categories, but all later arguments only use the underlying functor of symmetric monoidal
 $(\infty ,2)$
-categories.
$(\infty ,2)$
-categories. -
(iii) There are at least three constructions of a Morita
 $(\infty ,2)$
-category of a sufficiently nice monoidal
$(\infty ,2)$
-category of a sufficiently nice monoidal
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
that for
$\mathscr {C}$
that for
 $\mathscr {C}=\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
might serve as potential targets for (28):
$\mathscr {C}=\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
might serve as potential targets for (28):-
(a) Lurie’s model
 $\mathrm {BMod}(\mathscr {C})$
from [Reference LurieLur17, 4.4.3.11],
$\mathrm {BMod}(\mathscr {C})$
from [Reference LurieLur17, 4.4.3.11], -
(b) Haugseng’s model
 $\mathrm {ALG}_1(\mathscr {C})$
from [Reference HaugsengHau17, Section 4], denoted
$\mathrm {ALG}_1(\mathscr {C})$
from [Reference HaugsengHau17, Section 4], denoted
 $\mathrm {ALG}(\mathscr {C})$
in Section 2.9,
$\mathrm {ALG}(\mathscr {C})$
in Section 2.9, -
(c) Scheimbauer’s model
 $\mathrm {Alg}_1(\mathscr {C})$
from [Reference ScheimbauerSch14, Section 3].
$\mathrm {Alg}_1(\mathscr {C})$
from [Reference ScheimbauerSch14, Section 3].
Haugseng’s and Lurie’s model are known to be equivalent (see Remark 2.18). For our purposes, Haugseng’s model turned out to be the most convenient choice.
-
-
(iv) For some of our later arguments, it is crucial that E is defined on the bordism category
 $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
that involves noncompact manifolds; the restriction to the typically considered subcategory
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
that involves noncompact manifolds; the restriction to the typically considered subcategory
 $\mathscr {B}\mathrm {ord}(d)$
that only involves compact manifolds is not sufficient. If one is mainly interested in a functor from the compact variant
$\mathscr {B}\mathrm {ord}(d)$
that only involves compact manifolds is not sufficient. If one is mainly interested in a functor from the compact variant
 $\mathscr {B}\mathrm {ord}(d)$
to a Morita category of
$\mathscr {B}\mathrm {ord}(d)$
to a Morita category of
 $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
, then there are other potential routes to a construction (e.g., by modifying a construction of Scheimbauer [Reference ScheimbauerSch14] or relying on the cobordism hypothesis [Reference LurieLur09b]).
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
, then there are other potential routes to a construction (e.g., by modifying a construction of Scheimbauer [Reference ScheimbauerSch14] or relying on the cobordism hypothesis [Reference LurieLur09b]).
Throughout the following subsections corresponding to the steps above, we generically refer to Section 2 for a recollection of the
![]() $\infty $
-categorical concepts and facts involved.
$\infty $
-categorical concepts and facts involved.
Step ① The bordism category via manifolds with walls
We will construct the non-unital double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\in \mathrm {Cat}_{\mathrm {nu}}(\mathscr {C}\mathrm {at}_\infty )$
as the levelwise coherent nerve of a semisimplicial object in
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\in \mathrm {Cat}_{\mathrm {nu}}(\mathscr {C}\mathrm {at}_\infty )$
as the levelwise coherent nerve of a semisimplicial object in
![]() $\mathsf {Kan}$
-enriched categories
$\mathsf {Kan}$
-enriched categories
Convention 3.2. Throughout this section, we fix a constant
![]() $0<\epsilon <\tfrac {1}{2}$
. We write
$0<\epsilon <\tfrac {1}{2}$
. We write
![]() $\mathrm {tr}_\lambda \colon \mathbf {R}\rightarrow \mathbf {R}$
for the translation by
$\mathrm {tr}_\lambda \colon \mathbf {R}\rightarrow \mathbf {R}$
for the translation by
![]() $\lambda \in \mathbf {R}$
. For a subset
$\lambda \in \mathbf {R}$
. For a subset
![]() $W\subset \mathbf {R}\times \mathbf {R}^\infty $
, we write
$W\subset \mathbf {R}\times \mathbf {R}^\infty $
, we write
for subsets
![]() $A\subset \mathbf {R}$
. If
$A\subset \mathbf {R}$
. If
![]() $A=\{a\}$
is a singleton, we abbreviate
$A=\{a\}$
is a singleton, we abbreviate ![]() .
.
We first set up some language. A
![]() $[p]$
-walled d-manifold for
$[p]$
-walled d-manifold for
![]() $[p]\in \Delta $
is a pair
$[p]\in \Delta $
is a pair ![]() of a d-dimensional smooth submanifold
of a d-dimensional smooth submanifold
![]() $W\subset \mathbf {R}\times \mathbf {R}^\infty $
without boundary and an order-preserving map
$W\subset \mathbf {R}\times \mathbf {R}^\infty $
without boundary and an order-preserving map
![]() $\mu \colon [p]\rightarrow \mathbf {R}$
such that the following is satisfied
$\mu \colon [p]\rightarrow \mathbf {R}$
such that the following is satisfied
-
(i)
 $\mu (i)+\epsilon <\mu (i+1)-\epsilon $
for all i,
$\mu (i)+\epsilon <\mu (i+1)-\epsilon $
for all i, -
(ii) the projection
 $\mathrm {pr}\colon W\rightarrow \mathbf {R}$
to the first coordinate is transverse to
$\mathrm {pr}\colon W\rightarrow \mathbf {R}$
to the first coordinate is transverse to
 $\mu \colon [p]\rightarrow \mathbf {R}$
,
$\mu \colon [p]\rightarrow \mathbf {R}$
, -
(iii)
 $W|_{[\mu (i)-\epsilon ,\mu (i)+\epsilon ]}=\mathrm {tr}_{\mu (i)}[-\epsilon ,+\epsilon ]\times W|_{\mu (i)}$
for all i;
$W|_{[\mu (i)-\epsilon ,\mu (i)+\epsilon ]}=\mathrm {tr}_{\mu (i)}[-\epsilon ,+\epsilon ]\times W|_{\mu (i)}$
for all i;
see Figure 2 for an example. The space
of embeddings between
![]() $[p]$
-walled d-manifolds
$[p]$
-walled d-manifolds
![]() $(W,\mu )$
and
$(W,\mu )$
and
![]() $(W,\mu ')$
is the subspace of those embeddings
$(W,\mu ')$
is the subspace of those embeddings
![]() $\varphi $
that satisfy the following properties for all i:
$\varphi $
that satisfy the following properties for all i:
-
(i) they satisfy the equality
 $\varphi ^{-1}(W'|_{[\mu '(i)+\epsilon ,\mu '(i+1)-\epsilon ]})=W|_{[\mu (i)+\epsilon ,\mu (i+1)-\epsilon ]}$
as well as the equality
$\varphi ^{-1}(W'|_{[\mu '(i)+\epsilon ,\mu '(i+1)-\epsilon ]})=W|_{[\mu (i)+\epsilon ,\mu (i+1)-\epsilon ]}$
as well as the equality
 $\varphi ^{-1}(W'|_{[\mu '(i)-\epsilon ,\mu '(i)+\epsilon ]})=W|_{[\mu (i)-\epsilon ,\mu (i)+\epsilon ]}$
, and
$\varphi ^{-1}(W'|_{[\mu '(i)-\epsilon ,\mu '(i)+\epsilon ]})=W|_{[\mu (i)-\epsilon ,\mu (i)+\epsilon ]}$
, and -
(ii) they restrict on
 $W|_{[\mu (i)-\epsilon ,\mu (i)+\epsilon ]}$
to an embedding of the form for some embedding
$W|_{[\mu (i)-\epsilon ,\mu (i)+\epsilon ]}$
to an embedding of the form for some embedding
 $\varphi _i\in \mathrm {Emb}(W|_{\mu (i)}, W'|_{\mu '(i)})$
.
$\varphi _i\in \mathrm {Emb}(W|_{\mu (i)}, W'|_{\mu '(i)})$
.
Using this terminology,
![]() $\mathsf {ncBord}(d)^{\mathrm {nu}}$
is defined as the semisimplicial
$\mathsf {ncBord}(d)^{\mathrm {nu}}$
is defined as the semisimplicial
![]() $\mathsf {Kan}$
-enriched category whose
$\mathsf {Kan}$
-enriched category whose
![]() $\mathsf {Kan}$
-enriched category
$\mathsf {Kan}$
-enriched category
![]() $\smash {\mathsf {ncBord}(d)^{\mathrm {nu}}_{[p]}}$
of p-simplices has possibly non-compact
$\smash {\mathsf {ncBord}(d)^{\mathrm {nu}}_{[p]}}$
of p-simplices has possibly non-compact
![]() $[p]$
-walled d-manifolds
$[p]$
-walled d-manifolds
![]() $(W,\mu )$
as its objects, spaces of embeddings between
$(W,\mu )$
as its objects, spaces of embeddings between
![]() $[p]$
-walled d-manifolds as morphisms, and composition given by composition of embeddings. The semisimplicial structure is given by ‘forgetting walls’ (i.e., by precomposition of
$[p]$
-walled d-manifolds as morphisms, and composition given by composition of embeddings. The semisimplicial structure is given by ‘forgetting walls’ (i.e., by precomposition of
![]() $\mu \colon [p]\rightarrow \mathbf {R}$
with morphisms in
$\mu \colon [p]\rightarrow \mathbf {R}$
with morphisms in
![]() $\Delta _{\mathrm {inj}}$
).
$\Delta _{\mathrm {inj}}$
).

Figure 2 A
![]() $[3]$
-walled
$[3]$
-walled
![]() $1$
-manifold. The vertical projection is
$1$
-manifold. The vertical projection is
![]() $\mu $
and the intervals in
$\mu $
and the intervals in
![]() $\mathbf {R}$
are the
$\mathbf {R}$
are the
![]() $[\mu (i)-\epsilon ,\mu (i)+\epsilon ]$
’s, which are disjoint in accordance with (i). The dashed lines indicate the hyperplanes
$[\mu (i)-\epsilon ,\mu (i)+\epsilon ]$
’s, which are disjoint in accordance with (i). The dashed lines indicate the hyperplanes
![]() $\{\mu (i)\} \times \mathbf {R}^\infty $
. Note that W is transverse to these and a product near them, as imposed in (ii) and (iii).
$\{\mu (i)\} \times \mathbf {R}^\infty $
. Note that W is transverse to these and a product near them, as imposed in (ii) and (iii).
The non-unital double
![]() $\infty $
-category
$\infty $
-category
is now defined as the levelwise coherent nerve of
![]() $\mathsf {ncBord}(d)^{\mathrm {nu}}$
(i.e., we have
$\mathsf {ncBord}(d)^{\mathrm {nu}}$
(i.e., we have ![]() ). This implicitly claims that the semisimplicial object
). This implicitly claims that the semisimplicial object
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\in \mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathscr {C}\mathrm {at}_\infty )$
is indeed a double
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\in \mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathscr {C}\mathrm {at}_\infty )$
is indeed a double
![]() $\infty $
-category (i.e., that it satisfies the Segal condition).
$\infty $
-category (i.e., that it satisfies the Segal condition).
Lemma 3.3.
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}$
is a non-unital double
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}$
is a non-unital double
![]() $\infty $
-category.
$\infty $
-category.
Proof. This is straightforward, so we will only sketch the proof. One first observes that the Segal maps
![]() $\mathsf {ncBord}(d)^{\mathrm {nu}}_{[p]}\rightarrow \mathsf {ncBord}(d)^{\mathrm {nu}}_{[1]}\times _{\mathsf {ncBord}(d)^{\mathrm {nu}}_{[0]}}\ldots \times _{\mathsf {ncBord}(d)^{\mathrm {nu}}_{[0]}}\mathsf {ncBord}(d)^{\mathrm {nu}}_{[1]}$
before taking coherent nerves are Dwyer–Kan equivalences, so weak equivalences in the Bergner model structure from Section 2.2 (i). Since the
$\mathsf {ncBord}(d)^{\mathrm {nu}}_{[p]}\rightarrow \mathsf {ncBord}(d)^{\mathrm {nu}}_{[1]}\times _{\mathsf {ncBord}(d)^{\mathrm {nu}}_{[0]}}\ldots \times _{\mathsf {ncBord}(d)^{\mathrm {nu}}_{[0]}}\mathsf {ncBord}(d)^{\mathrm {nu}}_{[1]}$
before taking coherent nerves are Dwyer–Kan equivalences, so weak equivalences in the Bergner model structure from Section 2.2 (i). Since the
![]() $\mathsf {ncBord}(d)^{\mathrm {nu}}_{[p]}$
are
$\mathsf {ncBord}(d)^{\mathrm {nu}}_{[p]}$
are
![]() $\mathsf {Kan}$
-enriched, they are fibrant in this model structure. Next, one shows that source and target maps
$\mathsf {Kan}$
-enriched, they are fibrant in this model structure. Next, one shows that source and target maps
![]() $\mathsf {ncBord}(d)^{\mathrm {nu}}_{[1]}\rightarrow \mathsf {ncBord}(d)^{\mathrm {nu}}_{[0]}$
are Kan fibrations on morphism spaces and isofibrations on homotopy categories, so they are fibrations in the model structure and the pullbacks appearing in the above maps are homotopy pullbacks. Using that the coherent nerve is the right Quillen functor in the Quillen equivalence between the Joyal and the Bergner model structure (see Section 2.2 (i)) and therefore preserves homotopy pullbacks and weak equivalences between fibrant objects, it follows that the Segal maps
$\mathsf {ncBord}(d)^{\mathrm {nu}}_{[1]}\rightarrow \mathsf {ncBord}(d)^{\mathrm {nu}}_{[0]}$
are Kan fibrations on morphism spaces and isofibrations on homotopy categories, so they are fibrations in the model structure and the pullbacks appearing in the above maps are homotopy pullbacks. Using that the coherent nerve is the right Quillen functor in the Quillen equivalence between the Joyal and the Bergner model structure (see Section 2.2 (i)) and therefore preserves homotopy pullbacks and weak equivalences between fibrant objects, it follows that the Segal maps
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[p]}\rightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[1]}\times _{\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[0]}}\ldots \times _{\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[0]}}\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[1]}$
in
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[p]}\rightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[1]}\times _{\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[0]}}\ldots \times _{\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[0]}}\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[1]}$
in
![]() $\mathrm {Cat}_\infty $
are equivalences.
$\mathrm {Cat}_\infty $
are equivalences.
Step ② The monoidal category of manifolds and embeddings
We construct the monoidal
![]() $\infty $
-category of (possibly noncompact) d-manifolds and embeddings between them as a cocartesian fibration
$\infty $
-category of (possibly noncompact) d-manifolds and embeddings between them as a cocartesian fibration ![]() obtained as the coherent nerve of a functor
obtained as the coherent nerve of a functor
of
![]() $\mathsf {Kan}$
-enriched categories. Objects of
$\mathsf {Kan}$
-enriched categories. Objects of
![]() $\mathsf {Man}_d^{\otimes }$
are pairs
$\mathsf {Man}_d^{\otimes }$
are pairs ![]() of
of ![]() and a smooth submanifold
and a smooth submanifold ![]() without boundary; the distinguished
without boundary; the distinguished
![]() $\mathbf {R}$
-coordinate is not necessary but comes in handy later. To define the space of morphisms, given
$\mathbf {R}$
-coordinate is not necessary but comes in handy later. To define the space of morphisms, given ![]() , we write
, we write
to distinguish it from the notation
![]() $W|_A$
for
$W|_A$
for
![]() $A\subset \mathbf {R}$
from Convention 3.2. Using this, we set
$A\subset \mathbf {R}$
from Convention 3.2. Using this, we set
where the subscript
![]() $(-)_\varphi $
indicates that we restrict to embeddings that cover
$(-)_\varphi $
indicates that we restrict to embeddings that cover
![]() $\varphi $
(i.e., that make
$\varphi $
(i.e., that make

commute). The composition in
![]() $\mathsf {Man}_d^\otimes $
is induced by the composition in
$\mathsf {Man}_d^\otimes $
is induced by the composition in
![]() $\mathsf {Gap}$
and composition of embeddings. The functor (30) sends
$\mathsf {Gap}$
and composition of embeddings. The functor (30) sends ![]() to
to ![]() . Taking coherent nerves defines
. Taking coherent nerves defines
![]() $\mathscr {M}\mathrm {an}_d^{\otimes }\rightarrow \mathsf {Gap}\cong \Delta ^{\mathrm {op}}$
, which one easily checks to be a monoidal
$\mathscr {M}\mathrm {an}_d^{\otimes }\rightarrow \mathsf {Gap}\cong \Delta ^{\mathrm {op}}$
, which one easily checks to be a monoidal
![]() $\infty $
-category using the description in terms of cocartesian fibrations from Section 2.5.3.
$\infty $
-category using the description in terms of cocartesian fibrations from Section 2.5.3.
Remark 3.4. By construction, the underlying category
![]() $\mathscr {M}\mathrm {an}_d$
of the monoidal
$\mathscr {M}\mathrm {an}_d$
of the monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {M}\mathrm {an}_d^{\otimes }\rightarrow \Delta ^{\mathrm {op}}$
(the fibre over
$\mathscr {M}\mathrm {an}_d^{\otimes }\rightarrow \Delta ^{\mathrm {op}}$
(the fibre over
![]() $[1]\in \Delta ^{\mathrm {op}}$
) agrees with the coherent nerve of the
$[1]\in \Delta ^{\mathrm {op}}$
) agrees with the coherent nerve of the
![]() $\mathsf {Kan}$
-enriched category whose objects are smooth submanifolds
$\mathsf {Kan}$
-enriched category whose objects are smooth submanifolds
![]() $W\subset \mathbf {R}^\infty $
without boundary and spaces of embeddings between them. Informally speaking, the monoidal structure is given by taking disjoint unions. Note that this monoidal structure is not cocartesian, since typically
$W\subset \mathbf {R}^\infty $
without boundary and spaces of embeddings between them. Informally speaking, the monoidal structure is given by taking disjoint unions. Note that this monoidal structure is not cocartesian, since typically
![]() $\mathrm {Emb}(M\sqcup N,W)\not \simeq \mathrm {Emb}(M,W)\times \mathrm {Emb}(N,W)$
.
$\mathrm {Emb}(M\sqcup N,W)\not \simeq \mathrm {Emb}(M,W)\times \mathrm {Emb}(N,W)$
.
Step ②.1 Cocartesian pushforward along active maps
For later reference, we spell out a model of the cocartesian pushforward
from Section 2.9.3 in the case
![]() $\mathscr {C}^{\otimes }=\mathscr {M}\mathrm {an}_d^{\otimes }$
. It is the coherent nerve of a simplicially enriched functor
$\mathscr {C}^{\otimes }=\mathscr {M}\mathrm {an}_d^{\otimes }$
. It is the coherent nerve of a simplicially enriched functor
defined on the pullback of
![]() $\mathsf {Man}^{\otimes }_d$
along the inclusion
$\mathsf {Man}^{\otimes }_d$
along the inclusion
![]() $\mathsf {Gap}^{\mathrm {act}}\rightarrow \mathsf {Gap}$
of the wide subcategory of active maps as in Section 2.4. The functor (32) is given by taking ‘taking disjoint unions’, using that the restriction to active maps in
$\mathsf {Gap}^{\mathrm {act}}\rightarrow \mathsf {Gap}$
of the wide subcategory of active maps as in Section 2.4. The functor (32) is given by taking ‘taking disjoint unions’, using that the restriction to active maps in
![]() $\mathsf {Man}_d^{\otimes ,\mathrm {act}}$
means precisely that the embeddings appearing in (31) are defined on the whole manifold W, not just on a subset depending on the maps
$\mathsf {Man}_d^{\otimes ,\mathrm {act}}$
means precisely that the embeddings appearing in (31) are defined on the whole manifold W, not just on a subset depending on the maps
![]() $\varphi $
. As a point-set implementation, one can model this ‘disjoint unions’-functor induced by viewing a submanifold
$\varphi $
. As a point-set implementation, one can model this ‘disjoint unions’-functor induced by viewing a submanifold ![]() as a submanifold of
as a submanifold of
![]() $\mathbf {R}\times \mathbf {R}\times \mathbf {R}^\infty $
using the inclusion
$\mathbf {R}\times \mathbf {R}\times \mathbf {R}^\infty $
using the inclusion ![]() and sending a submanifold
and sending a submanifold ![]() to its image under the diffeomorphism
to its image under the diffeomorphism
with ![]() and
and ![]() . Said differently, the functor (32) is a composition of functors of
. Said differently, the functor (32) is a composition of functors of
![]() $\mathsf {Kan}$
-enriched categories
$\mathsf {Kan}$
-enriched categories
where
![]() $\smash {\widetilde {\mathsf {Man}_d^{\otimes }}}$
has submanifolds
$\smash {\widetilde {\mathsf {Man}_d^{\otimes }}}$
has submanifolds
![]() $W\subset \mathbf {R}\times \mathbf {R}\times \mathbf {R}^\infty $
without boundary as objects and all embeddings between them as morphisms. The second functor sends W to
$W\subset \mathbf {R}\times \mathbf {R}\times \mathbf {R}^\infty $
without boundary as objects and all embeddings between them as morphisms. The second functor sends W to
![]() $s(W)$
on objects and is on morphisms induced by conjugating embeddings
$s(W)$
on objects and is on morphisms induced by conjugating embeddings
![]() $W\hookrightarrow W'$
with the diffeomorphisms
$W\hookrightarrow W'$
with the diffeomorphisms
![]() $W\cong s(W)$
and
$W\cong s(W)$
and
![]() $W'\cong s(W')$
induced by s. The first functor sends an object
$W'\cong s(W')$
induced by s. The first functor sends an object ![]() to
to ![]() and is on morphism spaces (31) induced by the inclusion
and is on morphism spaces (31) induced by the inclusion
![]() $\mathrm {Emb}(W, W')_\varphi \subset \mathrm {Emb}(W, W')$
of components.
$\mathrm {Emb}(W, W')_\varphi \subset \mathrm {Emb}(W, W')$
of components.
Step ③ From
 $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}$
to the pre-Morita category of manifolds
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}$
to the pre-Morita category of manifolds
The construction of the morphism
![]() $E^{\mathrm {geo}} \colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\rightarrow \overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d)$
goes via the following substeps:
$E^{\mathrm {geo}} \colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\rightarrow \overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d)$
goes via the following substeps:
-
(a) Set up preparatory language.
-
(b) Replace the undercategories
 by a simplicial thickening
by a simplicial thickening  .
. -
(c) Construct a functor of semisimplicial objects in
 $\mathsf {Kan}$
-enriched categories (34)
$\mathsf {Kan}$
-enriched categories (34)
-
(d) Argue that the resulting functor of semisimplicial
 $\infty $
-categories (35)lands in the levelwise full subcategory
$\infty $
-categories (35)lands in the levelwise full subcategory
 .
.
Substep (a) I: walls and chambers
For a
![]() $[p]$
-walled d-manifold
$[p]$
-walled d-manifold
![]() $(W,\mu )$
as in
Step ①, we define
$(W,\mu )$
as in
Step ①, we define
the submanifolds of walls, chambers and thickened chambers of
![]() $(W,\mu )$
, as
$(W,\mu )$
, as

There is an inclusion
![]() $\mathrm {ch}(W,\mu )\subset \mathrm {tch}(W,\mu )$
whose complement of the interior we abbreviate as
$\mathrm {ch}(W,\mu )\subset \mathrm {tch}(W,\mu )$
whose complement of the interior we abbreviate as
We call this the collars of
![]() $(W,\mu )$
. Informally,
$(W,\mu )$
. Informally,
![]() $\mu $
prescribes hyperplanes
$\mu $
prescribes hyperplanes
![]() $\{\mu (i)\} \times \mathbf {R}^\infty $
intersecting W in the walls, the (thickened) chambers are (thickened) regions between the walls, and the collars are collar neighbourhoods in the thickened chambers; see Figure 3 for an example.
$\{\mu (i)\} \times \mathbf {R}^\infty $
intersecting W in the walls, the (thickened) chambers are (thickened) regions between the walls, and the collars are collar neighbourhoods in the thickened chambers; see Figure 3 for an example.

Figure 3 A
![]() $[1]$
-walled
$[1]$
-walled
![]() $1$
-manifold. Its walls
$1$
-manifold. Its walls
![]() $\mathrm {wall}(W,\mu )$
are the
$\mathrm {wall}(W,\mu )$
are the
![]() $0$
-manifold indicated by the squares, its chambers
$0$
-manifold indicated by the squares, its chambers
![]() $\mathrm {ch}(W,\mu )$
are the thick region, its collars
$\mathrm {ch}(W,\mu )$
are the thick region, its collars
![]() $\mathrm {coll}(W,\mu )$
are the dotted regions, and its thickened chambers
$\mathrm {coll}(W,\mu )$
are the dotted regions, and its thickened chambers
![]() $\mathrm {tch}(W,\mu )$
are the union of the chambers and the collars.
$\mathrm {tch}(W,\mu )$
are the union of the chambers and the collars.

Figure 4 Given the
![]() $[3]$
-walled
$[3]$
-walled
![]() $1$
-manifold
$1$
-manifold
![]() $(W,\mu )$
of Figure 2 and the indicated morphism
$(W,\mu )$
of Figure 2 and the indicated morphism ![]() , this shows the resulting
, this shows the resulting
![]() $\mathrm {lab}_\alpha (W,\mu )$
. The following informal description may help:
$\mathrm {lab}_\alpha (W,\mu )$
. The following informal description may help:
![]() $\alpha $
tells which ‘parts’ of
$\alpha $
tells which ‘parts’ of ![]() to put in which ‘box’ of
to put in which ‘box’ of ![]() , and if a box is not hit by
, and if a box is not hit by
![]() $\alpha $
, it contains a ‘connecting part’.
$\alpha $
, it contains a ‘connecting part’.
Given in addition a morphism ![]() , we define the submanifold
, we define the submanifold
of pieces labelled by
![]() $\alpha $
as the union
$\alpha $
as the union ![]() , where we set
, where we set ![]() using the isomorphism (13) and thinking of
using the isomorphism (13) and thinking of ![]() as a subset of
as a subset of
![]() $[q]=\{0<\ldots <q\}$
. Informally,
$[q]=\{0<\ldots <q\}$
. Informally,
![]() $\mathrm {lab}_\alpha (W,\mu )$
is the set
$\mathrm {lab}_\alpha (W,\mu )$
is the set ![]() labelled by chambers and thickened walls of W as prescribed by
labelled by chambers and thickened walls of W as prescribed by
![]() $\alpha $
; see Figure 4 for an example.
$\alpha $
; see Figure 4 for an example.
Constructing the functor (34) will require us to describe embeddings out of
![]() $\mathrm {lab}_\alpha (W,\mu )$
, for which it is helpful to decompose this manifold into two parts as follows: the map
$\mathrm {lab}_\alpha (W,\mu )$
, for which it is helpful to decompose this manifold into two parts as follows: the map ![]() restricts to an embedding
restricts to an embedding
using which we define a submanifold
of thickened walls labelled by
![]() $\alpha $
; see Figure 5 for an example. We have a preferred decomposition
$\alpha $
; see Figure 5 for an example. We have a preferred decomposition
where the gluing uses the identification ![]() induced by the restriction of (36) to the boundary
induced by the restriction of (36) to the boundary ![]() . The restriction
. The restriction
of (36) to ![]() provides a collar of this boundary.
provides a collar of this boundary.

Figure 5 The submanifold
![]() $\mathrm {wlab}_\alpha (W,\mu )$
for
$\mathrm {wlab}_\alpha (W,\mu )$
for
![]() $\mathrm {lab}_\alpha (W,\mu )$
as in Figure 4.
$\mathrm {lab}_\alpha (W,\mu )$
as in Figure 4.
Substep (a) II:
 $\mathrm {wlab}_\alpha (-)$
as a pullback
$\mathrm {wlab}_\alpha (-)$
as a pullback
Unwrapping the definitions, one sees that ![]() is a disjoint union of products of
is a disjoint union of products of
![]() $W|_{\mu (i)}$
for some i with a (open, half-open or closed) interval of length
$W|_{\mu (i)}$
for some i with a (open, half-open or closed) interval of length
![]() $2\cdot \epsilon $
. More precisely, for
$2\cdot \epsilon $
. More precisely, for ![]() , the components
, the components
![]() $\mathrm {wlab}_\alpha (W,\mu )|^{\{i\}}$
of
$\mathrm {wlab}_\alpha (W,\mu )|^{\{i\}}$
of
![]() $\mathrm {wlab}_\alpha (W,\mu )$
lying over i are
$\mathrm {wlab}_\alpha (W,\mu )$
lying over i are
![]() $\mathrm {tr}_{\mu (t^\alpha _i)}(-\epsilon ,+\epsilon )\times W|_{\mu (t_i^\alpha )}$
for
$\mathrm {tr}_{\mu (t^\alpha _i)}(-\epsilon ,+\epsilon )\times W|_{\mu (t_i^\alpha )}$
for
![]() $i\not \in \mathrm {im}(\alpha )$
, and they are
$i\not \in \mathrm {im}(\alpha )$
, and they are
for
![]() $i\in \mathrm {im}(\alpha )$
. From this description, we see in particular that there are preferred maps
$i\in \mathrm {im}(\alpha )$
. From this description, we see in particular that there are preferred maps
where we view
![]() $(\mathbf {R},\mu )$
as a
$(\mathbf {R},\mu )$
as a
![]() $[p]$
-walled
$[p]$
-walled
![]() $1$
-manifold. Indeed, the first map is given by sending the components of
$1$
-manifold. Indeed, the first map is given by sending the components of
![]() $\mathrm {wlab}_\alpha (W,\mu )$
whose first factor is an interval around
$\mathrm {wlab}_\alpha (W,\mu )$
whose first factor is an interval around
![]() $\mu (t_i^{\alpha })\in \mathbf {R}$
to
$\mu (t_i^{\alpha })\in \mathbf {R}$
to
![]() $t_i^{\alpha }\in [p]$
, the second map is induced by the first map and the projection to
$t_i^{\alpha }\in [p]$
, the second map is induced by the first map and the projection to
![]() $\mathbf {R}^\infty $
, and the final map is given by the projection to
$\mathbf {R}^\infty $
, and the final map is given by the projection to ![]() . In particular, this exhibits
. In particular, this exhibits
![]() $\mathrm {wlab}_\alpha (W,\mu )$
as the pullback
$\mathrm {wlab}_\alpha (W,\mu )$
as the pullback
which will be useful to construct embeddings out of
![]() $\mathrm {wlab}_\alpha (W,\mu )$
; see Figure 6 for an example.
$\mathrm {wlab}_\alpha (W,\mu )$
; see Figure 6 for an example.
It will also be useful to observe that
![]() $\mathrm {wlab}_\alpha (\mathbf {R},\mu )$
is related to
$\mathrm {wlab}_\alpha (\mathbf {R},\mu )$
is related to
![]() $\mathrm {wlab}_\alpha (\mathbf {R},\mu ')$
for possibly different
$\mathrm {wlab}_\alpha (\mathbf {R},\mu ')$
for possibly different
![]() $\mu '\colon [p]\rightarrow \mathbf {R}$
by a preferred diffeomorphism
$\mu '\colon [p]\rightarrow \mathbf {R}$
by a preferred diffeomorphism
uniquely characterised by requiring it to (i) preserve the order induced by the lexicographical order on ![]() and (ii) agree with translation on each component. For convenience, we fix a particular choice of
and (ii) agree with translation on each component. For convenience, we fix a particular choice of
![]() $\mu $
– namely, the inclusion
$\mu $
– namely, the inclusion
![]() $[p]=\{0,1,\ldots ,p\}\subset \mathbf {R}$
in which case we omit
$[p]=\{0,1,\ldots ,p\}\subset \mathbf {R}$
in which case we omit
![]() $\mu $
from the notation, so for instance, we abbreviate
$\mu $
from the notation, so for instance, we abbreviate
![]() $\mathrm {wlab}_\alpha (\mathbf {R})=\mathrm {wlab}_\alpha (\mathbf {R},\mathrm {inc})$
.
$\mathrm {wlab}_\alpha (\mathbf {R})=\mathrm {wlab}_\alpha (\mathbf {R},\mathrm {inc})$
.
Substep (b): Thickening
As a next step, we replace the undercategory functor
by a simplicial thickening after precomposition with the inclusion
![]() $\mathsf {Gap}_{\mathrm {sur}}^{\mathrm {op}}\rightarrow \mathsf {Gap}^{\mathrm {op}}$
of (the opposite of) the wide subcategory of surjective morphisms. By ‘simplicial thickening’, we mean a functor whose values need no longer be discrete categories and which comes with a natural transformation to
$\mathsf {Gap}_{\mathrm {sur}}^{\mathrm {op}}\rightarrow \mathsf {Gap}^{\mathrm {op}}$
of (the opposite of) the wide subcategory of surjective morphisms. By ‘simplicial thickening’, we mean a functor whose values need no longer be discrete categories and which comes with a natural transformation to ![]() that is a levelwise Dwyer–Kan equivalence.
that is a levelwise Dwyer–Kan equivalence.
We first define a
![]() $\mathsf {Kan}$
-enriched category
$\mathsf {Kan}$
-enriched category ![]() that is Dwyer–Kan equivalent to
that is Dwyer–Kan equivalent to ![]() . Its objects are the same as those of
. Its objects are the same as those of ![]() – that is, morphisms
– that is, morphisms ![]() in
in
![]() $\mathsf {Gap}$
. The space of morphisms from the object
$\mathsf {Gap}$
. The space of morphisms from the object ![]() to the object
to the object ![]() is
is
where the subscript
![]() $\gamma $
indicates that we restrict to embeddings
$\gamma $
indicates that we restrict to embeddings
![]() $\overline {\gamma }$
that
$\overline {\gamma }$
that
-
(i) make the diagrams
commute (i.e., they cover
 $\gamma $
and preserve the collars (38)), and
$\gamma $
and preserve the collars (38)), and
-
(ii) are order-preserving with respect to lexicographical order on
 and
and  .
.
The composition in ![]() is induced by the composition in
is induced by the composition in ![]() , forgetting components, and composition of embeddings. By construction, there is a forgetful functor
, forgetting components, and composition of embeddings. By construction, there is a forgetful functor ![]() which is a Dwyer–Kan equivalence as a result of the contractibility of the space of monotonous embeddings between connected intervals. Postcomposing this functor with the projection
which is a Dwyer–Kan equivalence as a result of the contractibility of the space of monotonous embeddings between connected intervals. Postcomposing this functor with the projection ![]() and varying p, we obtain a functor
and varying p, we obtain a functor
with a natural transformation to (41) that consists of the Dwyer–Kan equivalences just discussed.
Substep (c):
 $E^{\mathrm {geo}}$
on the level of
$E^{\mathrm {geo}}$
on the level of
 $\mathsf {Kan}$
-enriched categories
$\mathsf {Kan}$
-enriched categories
We now turn towards the construction of a functor of semisimplicial
![]() $\mathsf {Kan}$
-enriched categories
$\mathsf {Kan}$
-enriched categories
The value of
![]() $E^{\mathrm {geo}}_{[p]}$
at
$E^{\mathrm {geo}}_{[p]}$
at
![]() $(W,\mu )\in (\mathsf {ncBord}(d)^{\mathrm {nu}})_{[p]}$
is the functor
$(W,\mu )\in (\mathsf {ncBord}(d)^{\mathrm {nu}})_{[p]}$
is the functor
over
![]() $\mathsf {Gap}$
defined as follows: on objects, it maps
$\mathsf {Gap}$
defined as follows: on objects, it maps ![]() to
to ![]() . On a morphism given by a pair
. On a morphism given by a pair
![]() $(\gamma ,\overline {\gamma })$
of a morphism
$(\gamma ,\overline {\gamma })$
of a morphism ![]() under
under ![]() in
in
![]() $\mathsf {Gap}$
and an embedding
$\mathsf {Gap}$
and an embedding ![]() , it is given by the embedding
, it is given by the embedding
over
![]() $\gamma $
constructed via the following recipe: using the decomposition (37) and
$\gamma $
constructed via the following recipe: using the decomposition (37) and ![]() , the embedding
, the embedding
![]() $E^{\mathrm {geo}}_{[p]}(W,\mu )(\overline {\gamma })$
is of the form
$E^{\mathrm {geo}}_{[p]}(W,\mu )(\overline {\gamma })$
is of the form
On ![]() , we declare it to be the identity, and on the complement, we use the pullback description (39) and the translations (40) to define it via the commutative diagram
, we declare it to be the identity, and on the complement, we use the pullback description (39) and the translations (40) to define it via the commutative diagram

This finishes the construction of the functor ![]() . Note that it commutes with the functors to
. Note that it commutes with the functors to
![]() $\mathsf {Gap}$
by construction.
$\mathsf {Gap}$
by construction.
Having defined
![]() $E^{\mathrm {geo}}_{[p]}$
on objects, defining it on morphisms amounts to specifying maps
$E^{\mathrm {geo}}_{[p]}$
on objects, defining it on morphisms amounts to specifying maps

where
![]() $\mathsf {Nat}_{\mathsf {Gap}}(-,-)$
is the hom-functor in the
$\mathsf {Nat}_{\mathsf {Gap}}(-,-)$
is the hom-functor in the
![]() $\mathsf {Kan}$
-enriched category
$\mathsf {Kan}$
-enriched category ![]() (i.e., the space of natural transformations covering the identity on
(i.e., the space of natural transformations covering the identity on
![]() $\mathsf {Gap}$
). These maps are induced by the evident naturality of the
$\mathsf {Gap}$
). These maps are induced by the evident naturality of the
![]() $\mathrm {lab}_\alpha (-)$
-construction in embeddings of
$\mathrm {lab}_\alpha (-)$
-construction in embeddings of
![]() $[p]$
-walled d-manifolds.
$[p]$
-walled d-manifolds.
To finish the construction of (42), we have to argue that the
![]() $E^{\mathrm {geo}}_{[p]}$
’s assemble to a morphism of semisimplicial objects in
$E^{\mathrm {geo}}_{[p]}$
’s assemble to a morphism of semisimplicial objects in
![]() $\mathsf {Kan}$
-enriched categories as in (42). But this is merely a case of going through the definitions; ultimately, it amounts to the identity
$\mathsf {Kan}$
-enriched categories as in (42). But this is merely a case of going through the definitions; ultimately, it amounts to the identity
![]() $\mathrm {lab}_{\beta \circ c(\delta )}(W,\mu )=\mathrm {lab}_\beta (W,\mu \circ \delta )$
.
$\mathrm {lab}_{\beta \circ c(\delta )}(W,\mu )=\mathrm {lab}_\beta (W,\mu \circ \delta )$
.
Substep (d):
 $E^{\mathrm {geo}}$
on the level of
$E^{\mathrm {geo}}$
on the level of
 $\infty $
-categories
$\infty $
-categories
Taking coherent nerves, we obtain
which comes with an equivalence to ![]() induced by the equivalence
induced by the equivalence ![]() from Substep (b). From
from Substep (b). From
![]() $E^{\mathrm {geo}} _{[\bullet ]}$
, we obtain a morphism of semisimplicial objects in
$E^{\mathrm {geo}} _{[\bullet ]}$
, we obtain a morphism of semisimplicial objects in
![]() $\mathscr {C}\mathrm {at}_\infty $
$\mathscr {C}\mathrm {at}_\infty $
given by postcomposing the coherent nerve applied to (42) with the canonical map
from Property (v) of Section 2.2.
Lemma 3.5. The image of the functor (44) lies in the levelwise full subcategory
![]() $\overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d) \subset \mathrm {Fun}_{\Delta ^{\mathrm {op}}}(\Delta _{/[\bullet ]}^{\mathrm {op}},\mathscr {M}\mathrm {an}_d^{\otimes })$
from Section 2.9.1.
$\overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d) \subset \mathrm {Fun}_{\Delta ^{\mathrm {op}}}(\Delta _{/[\bullet ]}^{\mathrm {op}},\mathscr {M}\mathrm {an}_d^{\otimes })$
from Section 2.9.1.
Proof. In view of Remark 2.2, it suffices to show that for a
![]() $[p]$
-walled manifold
$[p]$
-walled manifold
![]() $(W,\mu )$
, and objects
$(W,\mu )$
, and objects ![]() and
and ![]() , the functor
, the functor ![]() of
of
![]() $\mathsf {Kan}$
-enriched categories sends embeddings
$\mathsf {Kan}$
-enriched categories sends embeddings ![]() whose underlying map
whose underlying map ![]() is inert to cocartesian morphisms in
is inert to cocartesian morphisms in
![]() $\mathsf {Man}_d^{\otimes }$
with respect to the projection
$\mathsf {Man}_d^{\otimes }$
with respect to the projection
![]() $\mathsf {Man}_d^{\otimes }\rightarrow \mathsf {Gap}$
. In other words, for objects
$\mathsf {Man}_d^{\otimes }\rightarrow \mathsf {Gap}$
. In other words, for objects ![]() , we need to check that the square of Kan-complexes
, we need to check that the square of Kan-complexes

is homotopy cartesian. Taking vertical homotopy fibres, it suffices to show that the maps
are weak equivalences. Since
![]() $\gamma $
is inert, the restricted map
$\gamma $
is inert, the restricted map ![]() is bijective, so it suffices to show that the embedding
is bijective, so it suffices to show that the embedding ![]() is an isotopy equivalence over
is an isotopy equivalence over
![]() $\gamma $
. To see this, note that since
$\gamma $
. To see this, note that since ![]() is bijective, the embedding
is bijective, the embedding ![]() is an isotopy equivalence over
is an isotopy equivalence over
![]() $\gamma $
and under
$\gamma $
and under ![]() , from which it follows that
, from which it follows that
![]() $E^{\mathrm {geo}}_{[p]}(W,\mu )(\overline {\gamma })$
is an isotopy equivalence over
$E^{\mathrm {geo}}_{[p]}(W,\mu )(\overline {\gamma })$
is an isotopy equivalence over
![]() $\gamma $
as claimed.
$\gamma $
as claimed.
By the previous lemma, (44) restricts to a morphism ![]() of semisimplicial
of semisimplicial
![]() $\infty $
-categories. This completes
Step ③.
$\infty $
-categories. This completes
Step ③.
Step ④ Composite algebras
We now consider the composition
Here,
![]() $E^{\mathrm {geo}}$
is the functor from the previous step,
$E^{\mathrm {geo}}$
is the functor from the previous step,
![]() $y_{*}$
is induced by the (monoidal) Yoneda embedding
$y_{*}$
is induced by the (monoidal) Yoneda embedding
![]() $y\colon \mathscr {M}\mathrm {an}_d\rightarrow \mathrm {PSh}(\mathscr {M}\mathrm {an}_d)$
(see Section 2.6), and
$y\colon \mathscr {M}\mathrm {an}_d\rightarrow \mathrm {PSh}(\mathscr {M}\mathrm {an}_d)$
(see Section 2.6), and
![]() $\iota ^*$
is the functor induced by the lax monoidal functor
$\iota ^*$
is the functor induced by the lax monoidal functor
![]() $\mathrm {PSh}(\mathscr {M}\mathrm {an}_d)\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
which is itself induced by the inclusion
$\mathrm {PSh}(\mathscr {M}\mathrm {an}_d)\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
which is itself induced by the inclusion
![]() $\iota \colon \mathscr {D}\mathrm {isc}_d\hookrightarrow \mathscr {M}\mathrm {an}_d$
of the full subcategory spanned by manifolds diffeomorphic to
$\iota \colon \mathscr {D}\mathrm {isc}_d\hookrightarrow \mathscr {M}\mathrm {an}_d$
of the full subcategory spanned by manifolds diffeomorphic to
![]() $T \times \mathbf {R}^d$
for finite sets T with monoidal structure inherited from
$T \times \mathbf {R}^d$
for finite sets T with monoidal structure inherited from
![]() $\mathscr {M}\mathrm {an}$
. By the properties of presheaf categories discussed in Section 2.6, the monoidal category
$\mathscr {M}\mathrm {an}$
. By the properties of presheaf categories discussed in Section 2.6, the monoidal category
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
has good relative tensor products in the sense of Section 2.9.2, so it makes sense to ask whether (45) lands in the levelwise full subcategory
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
has good relative tensor products in the sense of Section 2.9.2, so it makes sense to ask whether (45) lands in the levelwise full subcategory
![]() $\mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))\subset \overline {\mathrm {ALG}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
of Section 2.9.2. This section serves to prove this:
$\mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))\subset \overline {\mathrm {ALG}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
of Section 2.9.2. This section serves to prove this:
Proposition 3.6. The functor
![]() $\smash {\overline {E}}$
from (45) factors through
$\smash {\overline {E}}$
from (45) factors through
![]() $\mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))\subset \overline {\mathrm {ALG}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
.
$\mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))\subset \overline {\mathrm {ALG}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
.
We will first explain how Proposition 3.6 follows from a seemingly different result and then prove that other result. The argument involves a simplicial thickening
of the right-cone
![]() $\mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
of the category
$\mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
of the category
![]() $\mathsf {Gap}_{\mathrm {sur}}$
(the category obtained by freely adding a terminal object
$\mathsf {Gap}_{\mathrm {sur}}$
(the category obtained by freely adding a terminal object
![]() $\infty \in \mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
) in terms of the manifolds
$\infty \in \mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
) in terms of the manifolds
where
![]() $a\ge 0$
. The objects of
$a\ge 0$
. The objects of
![]() $\underline {\mathsf {Gap}_{\mathrm {sur}}^{\rhd }}$
are the same as those of
$\underline {\mathsf {Gap}_{\mathrm {sur}}^{\rhd }}$
are the same as those of
![]() $\mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
. The space of morphisms
$\mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
. The space of morphisms ![]() between objects of
between objects of
![]() $\mathsf {Gap}_{\mathrm {sur}}\subset \mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
is defined as
$\mathsf {Gap}_{\mathrm {sur}}\subset \mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
is defined as
where the subscript
![]() $(-)_{\gamma }$
indicates we restrict to embeddings
$(-)_{\gamma }$
indicates we restrict to embeddings
![]() $\overline {\gamma }$
that cover
$\overline {\gamma }$
that cover
![]() $\gamma $
, are the identity on
$\gamma $
, are the identity on
![]() $L \times [-\epsilon ,-\tfrac {\epsilon }{2}) \cup R \times (\tfrac {\epsilon }{2},\epsilon ]$
and preserve the lexicographic order inherited from
$L \times [-\epsilon ,-\tfrac {\epsilon }{2}) \cup R \times (\tfrac {\epsilon }{2},\epsilon ]$
and preserve the lexicographic order inherited from ![]() and
and ![]() . Finally, the space of morphisms
. Finally, the space of morphisms ![]() is defined as
is defined as
where the subscript
![]() $(-)_\infty $
indicates that we restrict to embeddings
$(-)_\infty $
indicates that we restrict to embeddings
![]() $\overline {\gamma }$
that agree on
$\overline {\gamma }$
that agree on
![]() $L \times [-\epsilon ,-\tfrac {\epsilon }{2}) \cup R \times (\tfrac {\epsilon }{2},\epsilon ]$
with the projection to the second coordinate and preserve the lexicographical order inherited from
$L \times [-\epsilon ,-\tfrac {\epsilon }{2}) \cup R \times (\tfrac {\epsilon }{2},\epsilon ]$
with the projection to the second coordinate and preserve the lexicographical order inherited from ![]() and
and
![]() $\mathbf {R}$
. The space of morphisms
$\mathbf {R}$
. The space of morphisms ![]() is the space of self-embeddings of
is the space of self-embeddings of ![]() that agree with the identity on the complement of
that agree with the identity on the complement of
![]() $[-\tfrac {\epsilon }{2},\tfrac {\epsilon }{2}]$
. This category admits an evident functor to
$[-\tfrac {\epsilon }{2},\tfrac {\epsilon }{2}]$
. This category admits an evident functor to
![]() $\mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
which is an equivalence as a result of the contractibility of the space of order-preserving embeddings between intervals.
$\mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
which is an equivalence as a result of the contractibility of the space of order-preserving embeddings between intervals.
Convention. In what follows, we occasionally omit the choices of embeddings of manifolds into Euclidean spaces for brevity. For instance, we treat
![]() $\mathsf {Man}_d=(\mathsf {Man}_d^{\otimes })_{[1]}$
from Section
Step ② as the
$\mathsf {Man}_d=(\mathsf {Man}_d^{\otimes })_{[1]}$
from Section
Step ② as the
![]() $\mathsf {Kan}$
-enriched category of abstract smooth d-manifolds and codimension
$\mathsf {Kan}$
-enriched category of abstract smooth d-manifolds and codimension
![]() $0$
embeddings.
$0$
embeddings.
Given a (possibly noncompact) d-manifold without boundary V equipped with k disjoint codimension
![]() $1$
submanifolds
$1$
submanifolds
![]() $V_i\subset V$
that are topologically closed in V as a subspace, equipped with disjoint bicollars
$V_i\subset V$
that are topologically closed in V as a subspace, equipped with disjoint bicollars
![]() $[-\epsilon ,\epsilon ]\times V_i\subset V$
, we construct a simplicially enriched functor
$[-\epsilon ,\epsilon ]\times V_i\subset V$
, we construct a simplicially enriched functor
which on objects, sends ![]() to
to ![]() and
and ![]() to
to
where
![]() $V^\ast $
is the manifold obtained from V by cutting out
$V^\ast $
is the manifold obtained from V by cutting out
![]() $\cup _{i=1}^k[-\tfrac {\epsilon }{2},\tfrac {\epsilon }{2}]\times V_i$
and extending the resulting collars
$\cup _{i=1}^k[-\tfrac {\epsilon }{2},\tfrac {\epsilon }{2}]\times V_i$
and extending the resulting collars
![]() $[-\epsilon ,-\tfrac {\epsilon }{2})\times V_i\sqcup (\tfrac {\epsilon }{2},\epsilon ]\times V_i$
to collars
$[-\epsilon ,-\tfrac {\epsilon }{2})\times V_i\sqcup (\tfrac {\epsilon }{2},\epsilon ]\times V_i$
to collars
![]() $[-\epsilon ,\epsilon )\times V_i\sqcup (-\epsilon ,\epsilon ]\times V_i$
. Given a morphism
$[-\epsilon ,\epsilon )\times V_i\sqcup (-\epsilon ,\epsilon ]\times V_i$
. Given a morphism ![]() , there is an embedding
, there is an embedding ![]() that is the identity of
that is the identity of
![]() $V^\ast $
outside the extended collars and agrees on the remaining part with
$V^\ast $
outside the extended collars and agrees on the remaining part with
![]() $\overline {\gamma } \times \mathrm {id}_{V_i}$
. Finally, for
$\overline {\gamma } \times \mathrm {id}_{V_i}$
. Finally, for ![]() or
or ![]() , one defines embeddings
, one defines embeddings ![]() or
or ![]() in the same manner.
in the same manner.
Writing
![]() $\underline {\mathsf {Gap}_{\mathrm {sur}}}\subset \underline {\mathsf {Gap}^\rhd _{\mathrm {sur}}}$
for the full subcategory covering the inclusion
$\underline {\mathsf {Gap}_{\mathrm {sur}}}\subset \underline {\mathsf {Gap}^\rhd _{\mathrm {sur}}}$
for the full subcategory covering the inclusion
![]() $\mathsf {Gap}_{\mathrm {sur}}\subset \mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
, Proposition 3.6 will be a consequence of the following proposition involving homotopy colimits in the Kan–Quillen model structure on
$\mathsf {Gap}_{\mathrm {sur}}\subset \mathsf {Gap}_{\mathrm {sur}}^{\rhd }$
, Proposition 3.6 will be a consequence of the following proposition involving homotopy colimits in the Kan–Quillen model structure on
![]() $\mathsf {S}$
.
$\mathsf {S}$
.
Proposition 3.7. For a manifold D diffeomorphic to
![]() $T\times \mathbf {R}^d$
for a finite set T, the map
$T\times \mathbf {R}^d$
for a finite set T, the map
induced by the inclusion
![]() $\underline {\mathsf {Gap}_{\mathrm {sur}}} \subset \underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd }$
is an equivalence.
$\underline {\mathsf {Gap}_{\mathrm {sur}}} \subset \underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd }$
is an equivalence.
We postpone the proof to the next subsection and first explain how it implies Proposition 3.6.
Proof Proof of Proposition 3.6.
Consulting the definition of the Morita category, we have to show that the image of any object
![]() $\smash {(W,\mu )\in \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[p]}}$
in
$\smash {(W,\mu )\in \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}_{[p]}}$
in
![]() $\smash {\overline {\mathrm {ALG}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))_{[p]}}$
is composite in the sense of Section 2.9.2. By Corollary 2.25, this is equivalent to proving that for each
$\smash {\overline {\mathrm {ALG}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))_{[p]}}$
is composite in the sense of Section 2.9.2. By Corollary 2.25, this is equivalent to proving that for each
![]() $\alpha \in \Delta ^{\mathrm {op}}_{/[p]}$
,
$\alpha \in \Delta ^{\mathrm {op}}_{/[p]}$
,
becomes a colimit diagram when postcomposed with
![]() $(\iota ^*\circ y)\colon \mathscr {M}\mathrm {an}_d\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
. We first make the composition (46) more explicit. Recall from
Step ③ (c) that
$(\iota ^*\circ y)\colon \mathscr {M}\mathrm {an}_d\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
. We first make the composition (46) more explicit. Recall from
Step ③ (c) that
was obtained from a functor between simplicially enriched categories
by taking coherent nerves and using the equivalence ![]() from
Step ③ (b). We now give a similar description of the composition (46) as a simplicially enriched functor using a simplicial functor to the full subcategory
from
Step ③ (b). We now give a similar description of the composition (46) as a simplicially enriched functor using a simplicial functor to the full subcategory ![]() covering
covering ![]()
to the pullback ![]() of
of ![]() along
along ![]() . The functor
. The functor
![]() $\underline {\eta ^\alpha }$
will make
$\underline {\eta ^\alpha }$
will make

commutative where
![]() $\eta ^\alpha $
is the functor from Section 2.9.3. The construction involves the notation of Construction 2.22 (
$\eta ^\alpha $
is the functor from Section 2.9.3. The construction involves the notation of Construction 2.22 (
![]() $k_\alpha $
,
$k_\alpha $
,
![]() $\alpha _1^{\vec {a}}$
,
$\alpha _1^{\vec {a}}$
,
![]() $n_i$
, etc.) and the discussion preceding Corollary 2.25. On objects,
$n_i$
, etc.) and the discussion preceding Corollary 2.25. On objects,
![]() $\smash {\underline {\eta ^\alpha }}$
is determined by
$\smash {\underline {\eta ^\alpha }}$
is determined by
![]() $\eta ^\alpha $
. On morphisms, it sends
$\eta ^\alpha $
. On morphisms, it sends ![]() to the right-hand embedding in a commutative square of embeddings (here
to the right-hand embedding in a commutative square of embeddings (here
![]() $\vec {a}=(a,\ldots ,a)$
and
$\vec {a}=(a,\ldots ,a)$
and
![]() $\vec {b}=(b,\ldots ,b)$
)
$\vec {b}=(b,\ldots ,b)$
)

The ith component of the upper horizontal map is the embedding
that is the unique inclusion of components that preserves the lexicographic order inherited from ![]() and
and ![]() and covers the map
and covers the map ![]() given by the sequence
given by the sequence
![]() $\alpha _1^{\vec {a}}(n_i)<\alpha _1^{\vec {a}}(n_i)+1<\ldots <\alpha _1^{\vec {a}}(n_i)+a<\alpha _1^{\vec {a}}(n_i+1)$
(note that this is not a morphism in
$\alpha _1^{\vec {a}}(n_i)<\alpha _1^{\vec {a}}(n_i)+1<\ldots <\alpha _1^{\vec {a}}(n_i)+a<\alpha _1^{\vec {a}}(n_i+1)$
(note that this is not a morphism in
![]() $\mathsf {Gap}$
as it does not preserve the endpoints). The bottom horizontal embedding is defined in the same way, and the right-hand embedding is defined to agree with
$\mathsf {Gap}$
as it does not preserve the endpoints). The bottom horizontal embedding is defined in the same way, and the right-hand embedding is defined to agree with
![]() $\overline {\gamma }$
on the components hit by the horizontal embedding and on the complement as the unique inclusion of components that covers the map
$\overline {\gamma }$
on the components hit by the horizontal embedding and on the complement as the unique inclusion of components that covers the map ![]() and preserves the lexicographic order. Similarly,
and preserves the lexicographic order. Similarly,
![]() $\underline {\eta }^\alpha $
sends a morphism in
$\underline {\eta }^\alpha $
sends a morphism in
![]() $\underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd }$
given by an embedding
$\underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd }$
given by an embedding ![]() to the right-hand embedding in the square
to the right-hand embedding in the square

where the top horizontal embedding is the same as before, and the bottom embedding includes the ith copy of ![]() as the unique
as the unique
![]() $[-\epsilon ,\epsilon ]$
-component in
$[-\epsilon ,\epsilon ]$
-component in
![]() $\mathrm {wlab}_{\alpha }(\mathbf {R})$
that maps to
$\mathrm {wlab}_{\alpha }(\mathbf {R})$
that maps to ![]() under the projection (using the notation from Construction 2.22) and to
under the projection (using the notation from Construction 2.22) and to ![]() under the map
under the map
![]() $\mathrm {wlab}_{\alpha }(\mathbf {R})\rightarrow [p]$
from
Step ③ (a) II. The right vertical embedding is defined via the left vertical one on the components hit by the horizontal map and as the unique inclusion of components that cover the map
$\mathrm {wlab}_{\alpha }(\mathbf {R})\rightarrow [p]$
from
Step ③ (a) II. The right vertical embedding is defined via the left vertical one on the components hit by the horizontal map and as the unique inclusion of components that cover the map ![]() and preserve the lexicographic order on
and preserve the lexicographic order on ![]() and
and ![]() .
.
By construction, the composition (46) is equivalent to the coherent nerve of the composition
where
![]() $(-)_!$
is the simplicial ‘disjoint unions’-functor of (32). Tracing through the definitions, one checks that this functor agrees up to equivalence with the functor
$(-)_!$
is the simplicial ‘disjoint unions’-functor of (32). Tracing through the definitions, one checks that this functor agrees up to equivalence with the functor ![]() for the manifold
for the manifold
![]() $V=\mathrm {lab}_\alpha (W,\mu )_!$
with the
$V=\mathrm {lab}_\alpha (W,\mu )_!$
with the
![]() $k_\alpha $
different bicollared submanifolds
$k_\alpha $
different bicollared submanifolds
![]() $[-\epsilon ,\epsilon ]\times W_{\mu (j)}\cong W_{[\mu (j)-\epsilon ,\mu (j)+\epsilon ]}\subset \mathrm {lab}_\alpha (W,\mu )_!$
for
$[-\epsilon ,\epsilon ]\times W_{\mu (j)}\cong W_{[\mu (j)-\epsilon ,\mu (j)+\epsilon ]}\subset \mathrm {lab}_\alpha (W,\mu )_!$
for ![]() with
with ![]() and
and
![]() $ \alpha (j)=\alpha (j+1)$
. Using that a diagram
$ \alpha (j)=\alpha (j+1)$
. Using that a diagram
![]() $A\colon K^{\rhd }\rightarrow \mathscr {C}$
is a colimit diagram if and only if the natural map
$A\colon K^{\rhd }\rightarrow \mathscr {C}$
is a colimit diagram if and only if the natural map
![]() $\mathrm {colim}_{K}A\rightarrow \mathrm {colim}_{K^{\rhd }}A$
is an equivalence, this implies that it suffices to show that the colimit
$\mathrm {colim}_{K}A\rightarrow \mathrm {colim}_{K^{\rhd }}A$
is an equivalence, this implies that it suffices to show that the colimit
is unaffected by precomposing the diagram with the functor
![]() $N_{\mathrm {coh}}(\underline {\mathsf {Gap}_{\mathrm {sur}}})\rightarrow N_{\mathrm {coh}}(\underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd })$
induced by inclusion. Using that (i) equivalences in functor categories are detected objectwise, (ii) colimits in functor categories commute with evaluation at a fixed object
$N_{\mathrm {coh}}(\underline {\mathsf {Gap}_{\mathrm {sur}}})\rightarrow N_{\mathrm {coh}}(\underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd })$
induced by inclusion. Using that (i) equivalences in functor categories are detected objectwise, (ii) colimits in functor categories commute with evaluation at a fixed object
![]() $D\in \mathscr {D}\mathrm {isc}_d$
[Reference LurieLur09a, 5.1.2.3], and (iii) the compatibility of the simplicial and
$D\in \mathscr {D}\mathrm {isc}_d$
[Reference LurieLur09a, 5.1.2.3], and (iii) the compatibility of the simplicial and
![]() $\infty $
-categorical Yoneda embedding (see Remark 2.8), we see that it is enough to show that the colimit
$\infty $
-categorical Yoneda embedding (see Remark 2.8), we see that it is enough to show that the colimit
is unaffected by precomposing the diagram with
![]() $N_{\mathrm {coh}}(\underline {\mathsf {Gap}_{\mathrm {sur}}})\rightarrow N_{\mathrm {coh}}(\underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd })$
for each object
$N_{\mathrm {coh}}(\underline {\mathsf {Gap}_{\mathrm {sur}}})\rightarrow N_{\mathrm {coh}}(\underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd })$
for each object
![]() $D\in \mathscr {D}\mathrm {isc}_d$
where
$D\in \mathscr {D}\mathrm {isc}_d$
where
![]() $y_s\colon \mathsf {Man}_d\rightarrow \mathrm {Fun}(\mathsf {Man}_d,\mathsf {Kan})$
is the simplicial Yoneda embedding of the
$y_s\colon \mathsf {Man}_d\rightarrow \mathrm {Fun}(\mathsf {Man}_d,\mathsf {Kan})$
is the simplicial Yoneda embedding of the
![]() $\mathsf {Kan}$
-enriched category
$\mathsf {Kan}$
-enriched category
![]() $\mathsf {Man}_d$
. Using that model category-theoretic homotopy colimits are compatible with
$\mathsf {Man}_d$
. Using that model category-theoretic homotopy colimits are compatible with
![]() $\infty $
-categorical colimits [Reference LurieLur09a, 4.2.4.1], the claim reduces to showing that the natural map between homotopy colimits in the Kan–Quillen model structure
$\infty $
-categorical colimits [Reference LurieLur09a, 4.2.4.1], the claim reduces to showing that the natural map between homotopy colimits in the Kan–Quillen model structure
is an equivalence. This is Proposition 3.7.
Proof Proof of Proposition 3.7.
This proof will eventually rely on a microfibration argument, which is why we phrase the argument in the category of topological spaces
![]() $\mathsf {Top}$
as opposed to simplicial sets
$\mathsf {Top}$
as opposed to simplicial sets
![]() $\mathsf {S}$
. Relying on the usual Quillen equivalence between the category of simplicial sets
$\mathsf {S}$
. Relying on the usual Quillen equivalence between the category of simplicial sets
![]() $\mathsf {S}$
and that of topological spaces
$\mathsf {S}$
and that of topological spaces
![]() $\mathsf {Top}$
, the claim has an evident reformulation in terms of homotopy colimits of
$\mathsf {Top}$
, the claim has an evident reformulation in terms of homotopy colimits of
![]() $\mathsf {Top}$
-enriched
$\mathsf {Top}$
-enriched
![]() $\mathsf {Top}$
-valued functors, and it is this reformulation that we shall prove.
$\mathsf {Top}$
-valued functors, and it is this reformulation that we shall prove.
To begin with, we note that it suffices to show the claim for
![]() $D=\underline {n}\times \mathbf {R}^d$
for
$D=\underline {n}\times \mathbf {R}^d$
for
![]() $n\ge 0$
. Next, we simplify the functor
$n\ge 0$
. Next, we simplify the functor
![]() $\mathrm {Emb}(\underline {n}\times \mathbf {R}^d,-)\colon \mathsf {Man}_d\rightarrow \mathsf {Top}$
in terms of the functor
$\mathrm {Emb}(\underline {n}\times \mathbf {R}^d,-)\colon \mathsf {Man}_d\rightarrow \mathsf {Top}$
in terms of the functor
![]() $C_n^{\mathrm {fr}}\colon \mathsf {Man}_d\rightarrow \mathsf {Top}$
given by taking framed configurations (i.e., the pullback of functors
$C_n^{\mathrm {fr}}\colon \mathsf {Man}_d\rightarrow \mathsf {Top}$
given by taking framed configurations (i.e., the pullback of functors

whose right vertical map is induced by the projection
![]() $\mathrm {Fr}(W)\rightarrow W$
of the frame bundle of manifolds
$\mathrm {Fr}(W)\rightarrow W$
of the frame bundle of manifolds
![]() $W\in \mathsf {Man}_d$
). Taking derivatives at the centres
$W\in \mathsf {Man}_d$
). Taking derivatives at the centres
![]() $\underline {n}\times \{0\}\subset \underline {n}\times \mathbf {R}^d$
gives a natural transformation
$\underline {n}\times \{0\}\subset \underline {n}\times \mathbf {R}^d$
gives a natural transformation
![]() $\mathrm {Emb}(\underline {n}\times \mathbf {R},-)\rightarrow C^{\mathrm {fr}}_n(-)$
which is a componentwise weak equivalence, so we conclude that in order to prove Proposition 3.7, it suffices to show that the map
$\mathrm {Emb}(\underline {n}\times \mathbf {R},-)\rightarrow C^{\mathrm {fr}}_n(-)$
which is a componentwise weak equivalence, so we conclude that in order to prove Proposition 3.7, it suffices to show that the map
is a weak equivalence. This is a map between homotopy colimits in spaces, which we model by a bar construction. In general, given a
![]() $\mathsf {Top}$
-enriched category
$\mathsf {Top}$
-enriched category
![]() $\mathsf {C}$
and
$\mathsf {C}$
and
![]() $\mathsf {Top}$
-enriched functors
$\mathsf {Top}$
-enriched functors
![]() $F \colon \mathsf {C} \to \mathsf {Top}$
and
$F \colon \mathsf {C} \to \mathsf {Top}$
and
![]() $G \colon \mathsf {C}^{\mathrm {op}} \to \mathsf {Top}$
, the bar-construction
$G \colon \mathsf {C}^{\mathrm {op}} \to \mathsf {Top}$
, the bar-construction
![]() $B_\bullet (F,\mathsf {C},G) \colon \Delta ^{\mathrm {op}} \rightarrow \mathsf {Top}$
is the simplicial space
$B_\bullet (F,\mathsf {C},G) \colon \Delta ^{\mathrm {op}} \rightarrow \mathsf {Top}$
is the simplicial space
![]() $\textstyle {[r] \longmapsto \bigsqcup _{(c_0,\ldots ,c_r)} F(c_0) \times \mathsf {C}(c_0,c_1) \times \cdots \times \mathsf {C}(c_{r-1},c_r) \times G(c_r)}$
where
$\textstyle {[r] \longmapsto \bigsqcup _{(c_0,\ldots ,c_r)} F(c_0) \times \mathsf {C}(c_0,c_1) \times \cdots \times \mathsf {C}(c_{r-1},c_r) \times G(c_r)}$
where
![]() $(c_0,\ldots ,c_r)$
runs through ordered sequences of
$(c_0,\ldots ,c_r)$
runs through ordered sequences of
![]() $(r+1)$
objects in
$(r+1)$
objects in
![]() $\mathsf {C}$
. If G has weakly contractible values, the thick geometric realisation
$\mathsf {C}$
. If G has weakly contractible values, the thick geometric realisation ![]() is a model for
is a model for
![]() $\mathrm {hocolim}_{\mathsf {C}} F$
(see, for example, [Reference RiehlRie14, Corollary 9.2.7]; since we take thick geometric realisations, we do not need to worry about cofibrancy issues). Choosing
$\mathrm {hocolim}_{\mathsf {C}} F$
(see, for example, [Reference RiehlRie14, Corollary 9.2.7]; since we take thick geometric realisations, we do not need to worry about cofibrancy issues). Choosing
![]() $\mathsf {C}=\underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd }$
and
$\mathsf {C}=\underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd }$
and ![]() , it therefore suffices to show that
, it therefore suffices to show that
induced by
![]() $\underline {\mathsf {Gap}_{\mathrm {sur}}}\subset \underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd }$
is a weak equivalence on thick realisations. There is an augmentation
$\underline {\mathsf {Gap}_{\mathrm {sur}}}\subset \underline {\mathsf {Gap}_{\mathrm {sur}}^\rhd }$
is a weak equivalence on thick realisations. There is an augmentation
induced by composition of embeddings and evaluation of
![]() $C_n^{\mathrm {fr}}(-)$
. This admits an extra degeneracy, so it induces an equivalence on (thick) realisation (see, for example, [Reference RiehlRie14, Example 4.5.7]). This leaves us with showing that the composition of (49) and (50)
$C_n^{\mathrm {fr}}(-)$
. This admits an extra degeneracy, so it induces an equivalence on (thick) realisation (see, for example, [Reference RiehlRie14, Example 4.5.7]). This leaves us with showing that the composition of (49) and (50)
is an equivalence on thick realisations. To prove this, we consider a semisimplicial space
![]() $\mathrm {wall}_\bullet $
whose space of p-simplices is the space of order-preserving functions
$\mathrm {wall}_\bullet $
whose space of p-simplices is the space of order-preserving functions
![]() $\tau \colon [p] \to (-\epsilon ,\epsilon )$
with simplicial structure by precomposition, and we define an augmented semisimplicial space
$\tau \colon [p] \to (-\epsilon ,\epsilon )$
with simplicial structure by precomposition, and we define an augmented semisimplicial space
for
![]() $a\ge 0$
whose space of p-simplices
$a\ge 0$
whose space of p-simplices
is the subspace of pairs of a function
![]() $\tau \colon [p]\rightarrow (\epsilon ,\epsilon )$
and an embedding
$\tau \colon [p]\rightarrow (\epsilon ,\epsilon )$
and an embedding ![]() that is disjoint from the image of
that is disjoint from the image of
![]() $\tau $
. Varying a, this defines a functor
$\tau $
. Varying a, this defines a functor
![]() $(\underline {\mathsf {Gap}_{\mathrm {sur}}})^{\mathrm {op}}\times \Delta _{\mathrm {inj}}^{\mathrm {op}}\longrightarrow \mathsf {Top}$
that is compatible with (52), so we obtain an augmentation of semisimplicial spaces
$(\underline {\mathsf {Gap}_{\mathrm {sur}}})^{\mathrm {op}}\times \Delta _{\mathrm {inj}}^{\mathrm {op}}\longrightarrow \mathsf {Top}$
that is compatible with (52), so we obtain an augmentation of semisimplicial spaces
where we have geometrically realised the semisimplicial direction of the bar-construction. In Lemma 3.8 below, we will show that (52) realises to a weak equivalence. Together with the fact that, up to weak equivalence, it does not matter in which direction one realises a bisemisimplicial space first (so we may realise the ![]() -direction before the bar-direction) and that the geometric realisation of a levelwise weak equivalence is a weak equivalence, this implies that the map in (54) realises to a weak equivalence. It thus remains to show that the augmented semisimplicial space
-direction before the bar-direction) and that the geometric realisation of a levelwise weak equivalence is a weak equivalence, this implies that the map in (54) realises to a weak equivalence. It thus remains to show that the augmented semisimplicial space
obtained by combining (54) and (51) realises to a weak equivalence. To prove this remaining claim, we consider the sub-simplicial space ![]() consisting of pairs of an order-preserving function
consisting of pairs of an order-preserving function
![]() $\tau \colon [p]\rightarrow (-\epsilon ,\epsilon )$
and a framed configurations
$\tau \colon [p]\rightarrow (-\epsilon ,\epsilon )$
and a framed configurations
![]() $\vec {x}\in C_n(V)$
that is disjoint from the submanifolds
$\vec {x}\in C_n(V)$
that is disjoint from the submanifolds
![]() $\{\tau (j)\}\times V_i\subset V$
for all
$\{\tau (j)\}\times V_i\subset V$
for all
![]() $j=0,\ldots ,p$
and
$j=0,\ldots ,p$
and
![]() $i=1,\ldots ,k$
(here, we used the collars
$i=1,\ldots ,k$
(here, we used the collars
![]() $[-\epsilon ,\epsilon ]\times V_i\subset V$
; see Figure 7 for an example). The projection to
$[-\epsilon ,\epsilon ]\times V_i\subset V$
; see Figure 7 for an example). The projection to
![]() $\mathrm {wall}_p$
in (53) and the augmentation to
$\mathrm {wall}_p$
in (53) and the augmentation to
![]() $C_n^{\mathrm {fr}}(V)$
assemble to a semisimplicial map over
$C_n^{\mathrm {fr}}(V)$
assemble to a semisimplicial map over
![]() $C_n^{\mathrm {fr}}(V)$
$C_n^{\mathrm {fr}}(V)$
which we show to be a levelwise weak equivalence in Lemma 3.8 3.8 (levelwise with respect to the ![]() -direction, in which we did not realise yet). This leaves us with showing that the augmentation
-direction, in which we did not realise yet). This leaves us with showing that the augmentation ![]() realises to a weak equivalence. This is Lemma 3.8 3.8.
realises to a weak equivalence. This is Lemma 3.8 3.8.

Figure 7 An example of an element of
![]() $\mathrm {wall}_2^V$
. We suppressed the framings at the points in the configuration indicated by the black points.
$\mathrm {wall}_2^V$
. We suppressed the framings at the points in the configuration indicated by the black points.
We now supply the postponed ingredients to the proof of Proposition 3.7. This finishes the proof of that proposition and thus also that of Proposition 3.6.
Lemma 3.8.
Proof. We begin with a general observation. Let X be a nonempty totally ordered topological poset (by which we mean topological space X with a total order on its underlying set). If the function
![]() $\max (x_0,-)\colon X\rightarrow X$
is continuous for some
$\max (x_0,-)\colon X\rightarrow X$
is continuous for some
![]() $x_0\in X$
, then the nerve of X is weakly contractible, since the sequence of inequalities
$x_0\in X$
, then the nerve of X is weakly contractible, since the sequence of inequalities
![]() $x\le \max (x_0,x)\ge x_0$
induces a zig-zag of natural transformations from the identity on X to the constant functor with values
$x\le \max (x_0,x)\ge x_0$
induces a zig-zag of natural transformations from the identity on X to the constant functor with values
![]() $x_0$
, so we obtain a homotopy between the identity map of the nerve of X and the constant map.
$x_0$
, so we obtain a homotopy between the identity map of the nerve of X and the constant map.
Replacing the (half-)open intervals in the definition of ![]() with closed intervals, we get a weakly equivalent semisimplicial space. Doing so, it follows from a version of the parametrised isotopy extension theorem on restricting embeddings to compact submanifolds (c.f. [Reference PalaisPal60]) that the augmentation (52) is a levelwise fibration. Hence, to prove 3.8, it suffices to show that the semisimplicial space given by the fibres over an embedding
with closed intervals, we get a weakly equivalent semisimplicial space. Doing so, it follows from a version of the parametrised isotopy extension theorem on restricting embeddings to compact submanifolds (c.f. [Reference PalaisPal60]) that the augmentation (52) is a levelwise fibration. Hence, to prove 3.8, it suffices to show that the semisimplicial space given by the fibres over an embedding ![]() realises to a weakly contractible space. This agrees with the nerve of the nonempty totally ordered poset of real numbers
realises to a weakly contractible space. This agrees with the nerve of the nonempty totally ordered poset of real numbers
![]() $t\in (-\epsilon ,\epsilon )$
disjoint from the image of e, so the claim follows from the observation.
$t\in (-\epsilon ,\epsilon )$
disjoint from the image of e, so the claim follows from the observation.
To show part 3.8, we choose for all
![]() $p\ge 0$
an order-preserving function
$p\ge 0$
an order-preserving function
![]() $\tau \colon [p]\rightarrow (\epsilon ,\epsilon )$
and an embedding
$\tau \colon [p]\rightarrow (\epsilon ,\epsilon )$
and an embedding ![]() such that
such that
![]() $\tau $
hits every component of the complement of e. This induces an equivalence
$\tau $
hits every component of the complement of e. This induces an equivalence
which in turn induces the left vertical equivalence in the commutative diagram

whose top horizontal map is induced by composition and evaluation. The latter is a weak equivalence for the same reason as (50). The right vertical map is induced by the function
![]() $\tau \colon [p]\rightarrow (-\epsilon ,\epsilon )$
and the embedding e, and is easily seen to be an equivalence as well: use that it lands in the deformation retract of
$\tau \colon [p]\rightarrow (-\epsilon ,\epsilon )$
and the embedding e, and is easily seen to be an equivalence as well: use that it lands in the deformation retract of
![]() $\mathrm {wall}_p^V\subset \mathrm {wall}_p\times C_n^{\mathrm {fr}}(V)$
given by those pairs whose first coordinate agrees with
$\mathrm {wall}_p^V\subset \mathrm {wall}_p\times C_n^{\mathrm {fr}}(V)$
given by those pairs whose first coordinate agrees with
![]() $\tau $
(i.e., the space of framed configurations in the complement
$\tau $
(i.e., the space of framed configurations in the complement
![]() $V\backslash \cup _{j,i}\tau (j)\times V_i$
) and that the vertical map is induced by the embedding
$V\backslash \cup _{j,i}\tau (j)\times V_i$
) and that the vertical map is induced by the embedding ![]() obtained from e which is an isotopy equivalence, so induces an equivalence on framed configuration spaces. It follows that the bottom horizontal map is an equivalence.
obtained from e which is an isotopy equivalence, so induces an equivalence on framed configuration spaces. It follows that the bottom horizontal map is an equivalence.
To show that
![]() $\|\varepsilon \|$
is a weak equivalence, note that its fibre at a framed configuration
$\|\varepsilon \|$
is a weak equivalence, note that its fibre at a framed configuration
![]() $\vec {x}\in C_n^{\mathrm {fr}}(X)$
is the realisation of the nerve of the nonempty totally ordered topological poset of real numbers
$\vec {x}\in C_n^{\mathrm {fr}}(X)$
is the realisation of the nerve of the nonempty totally ordered topological poset of real numbers
![]() $t\in (\epsilon ,\epsilon )$
such that
$t\in (\epsilon ,\epsilon )$
such that
![]() $\{t\}\times V_i\subset V$
is disjoint from
$\{t\}\times V_i\subset V$
is disjoint from
![]() $\vec {x}$
for all
$\vec {x}$
for all
![]() $i=1,\ldots k$
, so it is weakly contractible by the above observation. We now show that
$i=1,\ldots k$
, so it is weakly contractible by the above observation. We now show that
![]() $\|\varepsilon \|$
is a microfibration, which will finish the proof because any microfibration with weakly contractible fibres is a weak equivalence by [Reference WeissWei05, Lemma 2]. The remaining task is thus to show that given commutative solid arrows as in
$\|\varepsilon \|$
is a microfibration, which will finish the proof because any microfibration with weakly contractible fibres is a weak equivalence by [Reference WeissWei05, Lemma 2]. The remaining task is thus to show that given commutative solid arrows as in

there is an
![]() $0<\delta \le 1$
for which a dashed lift as indicated exists. For this, we note that the necessary data to lift a framed configuration
$0<\delta \le 1$
for which a dashed lift as indicated exists. For this, we note that the necessary data to lift a framed configuration
![]() $\vec {x}\in C^{\mathrm {fr}}_n(V)$
to
$\vec {x}\in C^{\mathrm {fr}}_n(V)$
to ![]() is a point
is a point
![]() $z\in \mathrm {int}(\Delta ^p)$
for some number
$z\in \mathrm {int}(\Delta ^p)$
for some number
![]() $p\ge 0$
, a function
$p\ge 0$
, a function
![]() $\tau \colon [p]\rightarrow (-\epsilon ,\epsilon )$
such that
$\tau \colon [p]\rightarrow (-\epsilon ,\epsilon )$
such that
![]() $\vec {x}$
is disjoint from
$\vec {x}$
is disjoint from
![]() $\{\tau (i)\}\times V_j\subset V$
for all i and j. For any
$\{\tau (i)\}\times V_j\subset V$
for all i and j. For any
![]() $\vec {x}'$
close enough to
$\vec {x}'$
close enough to
![]() $\vec {x}$
, the same data works, so for each
$\vec {x}$
, the same data works, so for each
![]() $x\in D^i$
, we get lifts
$x\in D^i$
, we get lifts
![]() $\psi (x,t)$
for
$\psi (x,t)$
for
![]() $t\in [0,\delta _x]$
for some
$t\in [0,\delta _x]$
for some
![]() $0<\delta _x\le 1$
, uses that the subspaces
$0<\delta _x\le 1$
, uses that the subspaces
![]() $V_i\subset V$
are closed. By compactness, we can find a uniform choice of
$V_i\subset V$
are closed. By compactness, we can find a uniform choice of
![]() $\delta _x$
for
$\delta _x$
for
![]() $x\in D^i$
. This gives the lift.
$x\in D^i$
. This gives the lift.
Step ⑤ Unitality
The goal of this step is to prove the following proposition, which uses the terminology of Section 2.5.5 and its variation from Remark 2.7 (i).
Proposition 3.9. The non-unital bordism category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\in \mathrm {Cat}_{\mathrm {nu}}(\mathscr {C}\mathrm {at}_\infty )$
is quasi-unital and the following morphism of semisimplicial objects in
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\in \mathrm {Cat}_{\mathrm {nu}}(\mathscr {C}\mathrm {at}_\infty )$
is quasi-unital and the following morphism of semisimplicial objects in
![]() $\mathscr {C}\mathrm {at}_\infty $
is quasi-unital
$\mathscr {C}\mathrm {at}_\infty $
is quasi-unital
By the equivalence (18), the non-unital double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}$
thus extends to a (unital) double
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}$
thus extends to a (unital) double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
. The second part of the proposition together with Remark 2.7 (ii) and Lemma 3.5 implies that the composition (45) is quasi-unital in the sense of Remark 2.7 (i), so using the second part of this remark once more, together with Proposition 3.6, we conclude that the functor of double
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
. The second part of the proposition together with Remark 2.7 (ii) and Lemma 3.5 implies that the composition (45) is quasi-unital in the sense of Remark 2.7 (i), so using the second part of this remark once more, together with Proposition 3.6, we conclude that the functor of double
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\rightarrow \mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
is quasi-unital and thus extends by the equivalence (18) essentially uniquely to a functor of double
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\rightarrow \mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
is quasi-unital and thus extends by the equivalence (18) essentially uniquely to a functor of double
![]() $\infty $
-categories
$\infty $
-categories
Proof Proof of Proposition 3.9.
This is tedious but straightforward, so do not spell out all details. Recalling that
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}$
is the levelwise coherent nerve of a semisimplicial
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}$
is the levelwise coherent nerve of a semisimplicial
![]() $\mathsf {Kan}$
-enriched category
$\mathsf {Kan}$
-enriched category
![]() $\mathsf {ncBord}(d)^{\mathrm {nu}}$
, the quasi-unit is given by the coherent nerve of the simplicial functor
$\mathsf {ncBord}(d)^{\mathrm {nu}}$
, the quasi-unit is given by the coherent nerve of the simplicial functor
![]() $u\colon \mathsf {ncBord}(d)^{\mathrm {nu}}_{[0]}\rightarrow \mathsf {ncBord}(d)^{\mathrm {nu}})_{[1]}$
which sends a
$u\colon \mathsf {ncBord}(d)^{\mathrm {nu}}_{[0]}\rightarrow \mathsf {ncBord}(d)^{\mathrm {nu}})_{[1]}$
which sends a
![]() $[0]$
-walled d-manifold
$[0]$
-walled d-manifold
![]() $(W,\mu )$
to
$(W,\mu )$
to
![]() $(\mathbf {R}\times W|_{\mu (0)},\mu ')$
with
$(\mathbf {R}\times W|_{\mu (0)},\mu ')$
with
![]() $\mu '(0)=\mu (0)$
and
$\mu '(0)=\mu (0)$
and
![]() $\mu '(1)=\mu (0)+1$
. On morphisms, it is induced by sending
$\mu '(1)=\mu (0)+1$
. On morphisms, it is induced by sending
![]() $\varphi \colon W|_{[\mu (0)-\epsilon ,\mu (0)+\epsilon ]}\rightarrow W'|_{[\mu '(0)-\epsilon ,\mu '(0)+\epsilon ]}$
to
$\varphi \colon W|_{[\mu (0)-\epsilon ,\mu (0)+\epsilon ]}\rightarrow W'|_{[\mu '(0)-\epsilon ,\mu '(0)+\epsilon ]}$
to
![]() $\mathrm {id}_{\mathbf {R}}\times \varphi _{0}$
.
$\mathrm {id}_{\mathbf {R}}\times \varphi _{0}$
.
To prove that the functor
![]() $E^{\mathrm {geo}}\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\rightarrow \mathrm {Fun}_{\Delta ^{\mathrm {op}}}({\Delta ^{\mathrm {op}}}_{/[\bullet ]},\mathscr {M}\mathrm {an}_d^{\otimes })$
is quasi-unital, recall that it was constructed as the coherent nerve of the zig-zag
$E^{\mathrm {geo}}\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\rightarrow \mathrm {Fun}_{\Delta ^{\mathrm {op}}}({\Delta ^{\mathrm {op}}}_{/[\bullet ]},\mathscr {M}\mathrm {an}_d^{\otimes })$
is quasi-unital, recall that it was constructed as the coherent nerve of the zig-zag
of semisimplicial objects in
![]() $\mathsf {Kan}$
-enriched categories. We first construct the top horizontal functor in a commutative diagram of
$\mathsf {Kan}$
-enriched categories. We first construct the top horizontal functor in a commutative diagram of
![]() $\mathsf {Kan}$
-enriched categories
$\mathsf {Kan}$
-enriched categories

where ![]() is the unique morphism. On objects, the top arrow agrees with the bottom one. On morphisms, the top arrow is given by sending an embedding
is the unique morphism. On objects, the top arrow agrees with the bottom one. On morphisms, the top arrow is given by sending an embedding ![]() to the unique dashed embedding that makes the diagram
to the unique dashed embedding that makes the diagram

commute where the bottom surjection is the identity if
![]() $\alpha '(1)\in \{L,R\}$
and otherwise the union of the identity over
$\alpha '(1)\in \{L,R\}$
and otherwise the union of the identity over ![]() with the map
with the map
over
![]() $\alpha '(1)$
; the top arrow is defined in the same way by replacing
$\alpha '(1)$
; the top arrow is defined in the same way by replacing
![]() $\alpha '$
by
$\alpha '$
by
![]() $\alpha $
. Applying
$\alpha $
. Applying
![]() $\mathrm {Fun}_{\mathsf {Gap}}(-,\mathsf {Man}_d^\otimes )$
to (56) results in a commutative diagram of
$\mathrm {Fun}_{\mathsf {Gap}}(-,\mathsf {Man}_d^\otimes )$
to (56) results in a commutative diagram of
![]() $\mathsf {Kan}$
-enriched categories
$\mathsf {Kan}$
-enriched categories

so
![]() $N_{\mathrm {coh}}(-)$
applied to the top arrow models the
$N_{\mathrm {coh}}(-)$
applied to the top arrow models the
![]() $0$
th degeneracy map of
$0$
th degeneracy map of
![]() $\mathrm {Fun}_{\Delta ^{\mathrm {op}}}(\Delta ^{\mathrm {op}}_{/[\bullet ]},\mathscr {M}\mathrm {an}_d^\sqcup )$
. Using this model for the degeneracy and the above quasi-unit for
$\mathrm {Fun}_{\Delta ^{\mathrm {op}}}(\Delta ^{\mathrm {op}}_{/[\bullet ]},\mathscr {M}\mathrm {an}_d^\sqcup )$
. Using this model for the degeneracy and the above quasi-unit for
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}=N_{\mathrm {coh}}(\mathsf {ncBord}(d)^{\mathrm {nu}})$
, it is tedious but straightforward to check that
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}=N_{\mathrm {coh}}(\mathsf {ncBord}(d)^{\mathrm {nu}})$
, it is tedious but straightforward to check that
![]() $N_{\mathrm {coh}}(E^{\mathrm {geo}}_\bullet )$
, and thus,
$N_{\mathrm {coh}}(E^{\mathrm {geo}}_\bullet )$
, and thus,
![]() $E^{\mathrm {geo}}$
is quasi-unital.
$E^{\mathrm {geo}}$
is quasi-unital.
Step ⑥ Symmetric monoidal structure
In this step, we promote the functor of double
![]() $\infty $
-categories
$\infty $
-categories
![]() $E\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d) \rightarrow \mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
to a functor of symmetric monoidal double
$E\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d) \rightarrow \mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
to a functor of symmetric monoidal double
![]() $\infty $
-categories (modelled as commutative monoid objects in
$\infty $
-categories (modelled as commutative monoid objects in
![]() $\mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
; see Section 2.5.3). This is not difficult and essentially amounts to adding an index by a finite pointed set
$\mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
; see Section 2.5.3). This is not difficult and essentially amounts to adding an index by a finite pointed set
![]() $\langle s\rangle \in \mathsf {Fin}_{*}$
to the previous steps. To avoid being too repetitive, we will not spell out all details.
$\langle s\rangle \in \mathsf {Fin}_{*}$
to the previous steps. To avoid being too repetitive, we will not spell out all details.
Convention. Given a space X, a map
![]() $\lambda \colon X\rightarrow \langle s\rangle $
to
$\lambda \colon X\rightarrow \langle s\rangle $
to
![]() $\langle s\rangle $
, and a subset
$\langle s\rangle $
, and a subset
![]() $A\subset \langle s\rangle $
, we denote the preimage of A by
$A\subset \langle s\rangle $
, we denote the preimage of A by ![]() in order to distinguish it from the notation
in order to distinguish it from the notation
![]() $X|_A$
and
$X|_A$
and
![]() $X|^A$
introduced in Convention 3.2 and
Step ②.
$X|^A$
introduced in Convention 3.2 and
Step ②.
Step ①’: the bordism category
We start by extending
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
to a symmetric monoidal non-unital double
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)\in \mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty )$
to a symmetric monoidal non-unital double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\in \mathrm {CMon}(\mathrm {Cat}_{\mathrm {nu}}(\mathscr {C}\mathrm {at}_\infty ))$
as follows: first, we extend the semisimplicial object
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\in \mathrm {CMon}(\mathrm {Cat}_{\mathrm {nu}}(\mathscr {C}\mathrm {at}_\infty ))$
as follows: first, we extend the semisimplicial object
![]() $\mathsf {ncBord}(d)^{\mathrm {nu}}\in \mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathsf {sCat})$
in
$\mathsf {ncBord}(d)^{\mathrm {nu}}\in \mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathsf {sCat})$
in
![]() $\mathsf {Kan}$
-enriched categories to an object
$\mathsf {Kan}$
-enriched categories to an object
![]() $\mathsf {ncBord}(d)^{\mathrm {nu}}\in \mathrm {Fun}(\mathsf {Fin}_{*},\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathsf {sCat}))=\mathrm {Fun}(\mathsf {Fin}_{*}\times \Delta _{\mathrm {inj}}^{\mathrm {op}},\mathsf {sCat})$
; evaluation at
$\mathsf {ncBord}(d)^{\mathrm {nu}}\in \mathrm {Fun}(\mathsf {Fin}_{*},\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathsf {sCat}))=\mathrm {Fun}(\mathsf {Fin}_{*}\times \Delta _{\mathrm {inj}}^{\mathrm {op}},\mathsf {sCat})$
; evaluation at
![]() $\langle 1\rangle \in \mathsf {Fin}_{*}$
recovers the previous construction. The value of
$\langle 1\rangle \in \mathsf {Fin}_{*}$
recovers the previous construction. The value of
![]() $\mathsf {ncBord}(d)^{\mathrm {nu}}$
at
$\mathsf {ncBord}(d)^{\mathrm {nu}}$
at
![]() $([p],\langle s\rangle )$
for
$([p],\langle s\rangle )$
for
![]() $\langle s\rangle \in \mathsf {Fin}_{*}$
is the
$\langle s\rangle \in \mathsf {Fin}_{*}$
is the
![]() $\mathsf {Kan}$
-enriched category
$\mathsf {Kan}$
-enriched category
![]() ${\mathsf {ncBord}(d)^{\mathrm {nu}}}_{[p],\langle s\rangle }$
whose objects are
${\mathsf {ncBord}(d)^{\mathrm {nu}}}_{[p],\langle s\rangle }$
whose objects are
![]() $[p]$
-walled d-manifolds
$[p]$
-walled d-manifolds
![]() $(W,\mu )$
together with a map
$(W,\mu )$
together with a map
![]() $\lambda \colon W\rightarrow \langle \mathring {s}\rangle $
, which we think of as a way to decompose W into disjoint summands indexed by
$\lambda \colon W\rightarrow \langle \mathring {s}\rangle $
, which we think of as a way to decompose W into disjoint summands indexed by
![]() $\langle \mathring {s}\rangle $
. Morphisms from
$\langle \mathring {s}\rangle $
. Morphisms from
![]() $(W,\mu ,\lambda )$
to
$(W,\mu ,\lambda )$
to
![]() $(W',\mu ',\lambda ')$
are embeddings of
$(W',\mu ',\lambda ')$
are embeddings of
![]() $[p]$
-walled manifolds that are additionally assumed to commute with the maps to
$[p]$
-walled manifolds that are additionally assumed to commute with the maps to
![]() $\langle \mathring {s}\rangle $
. The functoriality of
$\langle \mathring {s}\rangle $
. The functoriality of
![]() ${\mathsf {ncBord}(d)^{\mathrm {nu}}}_{[p],\langle s\rangle }$
in p is defined as for
${\mathsf {ncBord}(d)^{\mathrm {nu}}}_{[p],\langle s\rangle }$
in p is defined as for
![]() ${\mathsf {ncBord}(d)^{\mathrm {nu}}}_{[p]}$
, and that in
${\mathsf {ncBord}(d)^{\mathrm {nu}}}_{[p]}$
, and that in
![]() $\langle s\rangle $
is for
$\langle s\rangle $
is for
![]() $\varphi \in \mathsf {Fin}_{*}(\langle s\rangle , \langle s'\rangle )$
on objects given by
$\varphi \in \mathsf {Fin}_{*}(\langle s\rangle , \langle s'\rangle )$
on objects given by
![]() $\smash {(W,\mu ,\lambda )\mapsto ({}^{\varphi ^{-1}\langle \mathring {s}\rangle }|W,\mu ,\varphi \circ \lambda )}$
and on morphisms by restricting embeddings. A mild extension of the proof of Lemma 3.3 then shows that taking coherent nerves yields a commutative monoid object in double
$\smash {(W,\mu ,\lambda )\mapsto ({}^{\varphi ^{-1}\langle \mathring {s}\rangle }|W,\mu ,\varphi \circ \lambda )}$
and on morphisms by restricting embeddings. A mild extension of the proof of Lemma 3.3 then shows that taking coherent nerves yields a commutative monoid object in double
![]() $\infty $
-categories, as wished.
$\infty $
-categories, as wished.
Step ②’: the manifold category
Next, we extend the monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {M}\mathrm {an}_d$
(thought of as a cocartesian fibration
$\mathscr {M}\mathrm {an}_d$
(thought of as a cocartesian fibration
![]() $\mathscr {M}\mathrm {an}^{\otimes }_d\rightarrow \mathsf {Gap}$
) to an symmetric monoidal
$\mathscr {M}\mathrm {an}^{\otimes }_d\rightarrow \mathsf {Gap}$
) to an symmetric monoidal
![]() $\infty $
-category. It will be convenient to view it as a commutative monoid object in monoidal
$\infty $
-category. It will be convenient to view it as a commutative monoid object in monoidal
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathscr {M}\mathrm {an}_d\in \mathrm {CMon}(\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty ))\subset \mathrm {Fun}(\mathsf {Fin}_{*},\mathrm {Fun}(\mathsf {Gap},\mathscr {C}\mathrm {at}_\infty ))$
. To this end, we extend the construction of the functor
$\mathscr {M}\mathrm {an}_d\in \mathrm {CMon}(\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty ))\subset \mathrm {Fun}(\mathsf {Fin}_{*},\mathrm {Fun}(\mathsf {Gap},\mathscr {C}\mathrm {at}_\infty ))$
. To this end, we extend the construction of the functor
![]() $\mathsf {Man}^{\otimes }_d\rightarrow \mathsf {Gap}$
of
$\mathsf {Man}^{\otimes }_d\rightarrow \mathsf {Gap}$
of
![]() $\mathsf {Kan}$
-enriched categories to yield
$\mathsf {Kan}$
-enriched categories to yield
![]() $\mathsf {Kan}$
-enriched functors
$\mathsf {Kan}$
-enriched functors
![]() ${\mathsf {Man}_d}^{\sqcup ,\langle s\rangle }\rightarrow \mathsf {Gap}$
, one for each pointed set
${\mathsf {Man}_d}^{\sqcup ,\langle s\rangle }\rightarrow \mathsf {Gap}$
, one for each pointed set
![]() $\langle s\rangle \in \mathsf {Fin}_{*}$
. Objects of
$\langle s\rangle \in \mathsf {Fin}_{*}$
. Objects of
![]() $\smash {\mathsf {Man}^{\otimes ,\langle s\rangle }_d}$
are now triples
$\smash {\mathsf {Man}^{\otimes ,\langle s\rangle }_d}$
are now triples ![]() of
of ![]() , a smooth submanifold
, a smooth submanifold ![]() and a map
and a map
![]() $\lambda \colon W\rightarrow \langle \mathring {s}\rangle $
. The space of morphisms is defined as before, with the additional requirement that the embeddings have to commute with the reference maps to
$\lambda \colon W\rightarrow \langle \mathring {s}\rangle $
. The space of morphisms is defined as before, with the additional requirement that the embeddings have to commute with the reference maps to
![]() $\langle \mathring {s}\rangle $
. Given a map
$\langle \mathring {s}\rangle $
. Given a map
![]() $\varphi \colon \langle s\rangle \rightarrow \langle s'\rangle $
in
$\varphi \colon \langle s\rangle \rightarrow \langle s'\rangle $
in
![]() $\mathsf {Fin}_{*}$
, there is a functor
$\mathsf {Fin}_{*}$
, there is a functor
![]() ${\mathsf {Man}_d}^{\sqcup ,\langle s\rangle }\rightarrow {\mathsf {Man}_d}^{\sqcup ,\langle s'\rangle }$
over
${\mathsf {Man}_d}^{\sqcup ,\langle s\rangle }\rightarrow {\mathsf {Man}_d}^{\sqcup ,\langle s'\rangle }$
over
![]() $\mathsf {Gap}$
which on objects is given by
$\mathsf {Gap}$
which on objects is given by ![]() and on morphisms is induced by restriction. This yields a functor from
and on morphisms is induced by restriction. This yields a functor from
![]() $\mathsf {Fin}_{*}$
to cocartesian fibrations over
$\mathsf {Fin}_{*}$
to cocartesian fibrations over
![]() $\mathsf {Gap}$
. Using straightening and taking coherent nerves then gives the desired commutative monoid object in monoidal
$\mathsf {Gap}$
. Using straightening and taking coherent nerves then gives the desired commutative monoid object in monoidal
![]() $\infty $
-categories.
$\infty $
-categories.
Step ③’: from the bordism category to the pre-Morita category of manifolds
By the discussion in Section 2.9.4, taking pre-Morita categories of
![]() $\mathscr {M}\mathrm {an}_d\in \mathrm {CMon}(\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty ))$
yields a commutative monoid object
$\mathscr {M}\mathrm {an}_d\in \mathrm {CMon}(\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty ))$
yields a commutative monoid object
![]() $\smash {\overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d)\in \mathrm {CMon}(\mathrm {Fun}(\Delta ^{\mathrm {op}},\mathscr {C}\mathrm {at}_\infty ))}$
, and our next task is to upgrade the morphism
$\smash {\overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d)\in \mathrm {CMon}(\mathrm {Fun}(\Delta ^{\mathrm {op}},\mathscr {C}\mathrm {at}_\infty ))}$
, and our next task is to upgrade the morphism
![]() $E^{\mathrm {geo}}\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\rightarrow \overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d)$
in
$E^{\mathrm {geo}}\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}}\rightarrow \overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d)$
in
![]() $\smash {\mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathscr {C}\mathrm {at}_\infty )}$
from
Step ③ to a morphism in
$\smash {\mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathscr {C}\mathrm {at}_\infty )}$
from
Step ③ to a morphism in
![]() $\mathrm {CMon}(\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathscr {C}\mathrm {at}_\infty ))$
. To do this, we first define for each
$\mathrm {CMon}(\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathscr {C}\mathrm {at}_\infty ))$
. To do this, we first define for each
![]() $\langle s\rangle \in \mathsf {Fin}_{*}$
a variant
$\langle s\rangle \in \mathsf {Fin}_{*}$
a variant ![]() in
in
![]() $\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathsf {sCat})$
of (42). For this, note that in the notation of Substep (a) I, projection on
$\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathsf {sCat})$
of (42). For this, note that in the notation of Substep (a) I, projection on
![]() $\mathbf {R}\times \mathbf {R}^\infty $
gives a map
$\mathbf {R}\times \mathbf {R}^\infty $
gives a map
![]() $\mathrm {lab}_\alpha (W,\mu )\rightarrow W$
for any
$\mathrm {lab}_\alpha (W,\mu )\rightarrow W$
for any
![]() $[p]$
-walled manifold, so if W comes with a map to
$[p]$
-walled manifold, so if W comes with a map to
![]() $\langle \mathring {s}\rangle $
, then so does
$\langle \mathring {s}\rangle $
, then so does
![]() $\mathrm {lab}_\alpha (W,\mu )$
. Based on this observation, the construction of
$\mathrm {lab}_\alpha (W,\mu )$
. Based on this observation, the construction of
![]() $\smash {E^{\mathrm {geo}}_{[\bullet ]}}$
from (42) directly generalises to a functor
$\smash {E^{\mathrm {geo}}_{[\bullet ]}}$
from (42) directly generalises to a functor
![]() $\smash {E^{\mathrm {geo}}_{[\bullet ],\langle s\rangle }}$
as desired by incorporating the maps to
$\smash {E^{\mathrm {geo}}_{[\bullet ],\langle s\rangle }}$
as desired by incorporating the maps to
![]() $\langle s\rangle $
. Varying s, the maps
$\langle s\rangle $
. Varying s, the maps
![]() $\smash {E^{\mathrm {geo}}_{[\bullet ],\langle s\rangle }}$
define a morphism in
$\smash {E^{\mathrm {geo}}_{[\bullet ],\langle s\rangle }}$
define a morphism in
![]() $\mathrm {Fun}(\mathsf {Fin}_{*},\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathsf {sCat}))$
. Taking coherent nerves gives desired extension of
$\mathrm {Fun}(\mathsf {Fin}_{*},\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathsf {sCat}))$
. Taking coherent nerves gives desired extension of
![]() $E^{\mathrm {geo}}$
to a morphism in the full subcategory
$E^{\mathrm {geo}}$
to a morphism in the full subcategory
![]() $\mathrm {CMon}(\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathscr {C}\mathrm {at}_\infty ))\subset \mathrm {Fun}(\mathsf {Fin}_{*},\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathscr {C}\mathrm {at}_\infty ))$
,
$\mathrm {CMon}(\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathscr {C}\mathrm {at}_\infty ))\subset \mathrm {Fun}(\mathsf {Fin}_{*},\mathrm {Fun}(\Delta _{\mathrm {inj}}^{\mathrm {op}},\mathscr {C}\mathrm {at}_\infty ))$
,
Step ④’: composite algebras
We claim that the two functors
extend to morphisms in
![]() $\mathrm {CMon}(\mathscr {C}\mathrm {at}_\infty )\simeq \mathrm {CMon}(\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty ))$
(see Remark 2.4). For the first map, we discussed this in Section 2.6. A restriction map on presheaves such as the second map in (58) is only lax symmetric monoidal in general, but turns out to be actually monoidal in our case:
$\mathrm {CMon}(\mathscr {C}\mathrm {at}_\infty )\simeq \mathrm {CMon}(\mathrm {Mon}(\mathscr {C}\mathrm {at}_\infty ))$
(see Remark 2.4). For the first map, we discussed this in Section 2.6. A restriction map on presheaves such as the second map in (58) is only lax symmetric monoidal in general, but turns out to be actually monoidal in our case:
Lemma 3.10. The lax symmetric monoidal functor
![]() $\mathrm {PSh}(\mathscr {M}\mathrm {an}_d) \to \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
induced by restriction along the inclusion
$\mathrm {PSh}(\mathscr {M}\mathrm {an}_d) \to \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
induced by restriction along the inclusion
![]() $\iota ^* \colon \mathscr {D}\mathrm {isc}_d\hookrightarrow \mathscr {M}\mathrm {an}_d$
is strong monoidal.
$\iota ^* \colon \mathscr {D}\mathrm {isc}_d\hookrightarrow \mathscr {M}\mathrm {an}_d$
is strong monoidal.
Proof. By the formula for Day convolution, it suffices to verify that for finite sets S, the inclusion
![]() $\smash {(\mathscr {D}\mathrm {isc}_d \times \mathscr {D}\mathrm {isc}_d)^{\mathrm {op}}_{S \times \mathbf {R}^d/} \subset (\mathscr {M}\mathrm {an}_d \times \mathscr {M}\mathrm {an}_d)^{\mathrm {op}}_{S \times \mathbf {R}^d/}}$
is cofinal (recall the convention to take slices before opposition). By [Reference LurieLur09a, 4.1.3.1], it suffices to prove that
$\smash {(\mathscr {D}\mathrm {isc}_d \times \mathscr {D}\mathrm {isc}_d)^{\mathrm {op}}_{S \times \mathbf {R}^d/} \subset (\mathscr {M}\mathrm {an}_d \times \mathscr {M}\mathrm {an}_d)^{\mathrm {op}}_{S \times \mathbf {R}^d/}}$
is cofinal (recall the convention to take slices before opposition). By [Reference LurieLur09a, 4.1.3.1], it suffices to prove that
![]() $\smash {((\mathscr {D}\mathrm {isc}_d \times \mathscr {D}\mathrm {isc}_d)^{\mathrm {op}}_{S \times \mathbf {R}^d/})_{/u}}$
has a terminal object for all triples
$\smash {((\mathscr {D}\mathrm {isc}_d \times \mathscr {D}\mathrm {isc}_d)^{\mathrm {op}}_{S \times \mathbf {R}^d/})_{/u}}$
has a terminal object for all triples
![]() $(M,M',u)$
of
$(M,M',u)$
of
![]() $M,M' \in \mathscr {M}\mathrm {an}_d$
and
$M,M' \in \mathscr {M}\mathrm {an}_d$
and
![]() $u \colon S \times \mathbf {R}^d \hookrightarrow M \sqcup M'$
. Such a terminal object is given by the factorisation
$u \colon S \times \mathbf {R}^d \hookrightarrow M \sqcup M'$
. Such a terminal object is given by the factorisation
![]() $\smash {S \times \mathbf {R}^d=T \times \mathbf {R}^d\sqcup T' \times \mathbf {R}^d\xrightarrow {u} M}$
where the decomposition
$\smash {S \times \mathbf {R}^d=T \times \mathbf {R}^d\sqcup T' \times \mathbf {R}^d\xrightarrow {u} M}$
where the decomposition
![]() $S=T\sqcup T'$
is so that
$S=T\sqcup T'$
is so that
![]() $T \times \mathbf {R}^d = u^{-1}(M)$
and
$T \times \mathbf {R}^d = u^{-1}(M)$
and
![]() $T' \times \mathbf {R}^d = u^{-1}(M')$
.
$T' \times \mathbf {R}^d = u^{-1}(M')$
.
After applying
![]() $\overline {\mathrm {ALG}}(-)$
to (58), this gives a composition of morphisms in
$\overline {\mathrm {ALG}}(-)$
to (58), this gives a composition of morphisms in
![]() $\mathrm {CMon}(\mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathscr {C}\mathrm {at}_\infty ))$
(see Section 2.9.4) which we may precompose with (57) to arrive at an enhancement of (45) to
$\mathrm {CMon}(\mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathscr {C}\mathrm {at}_\infty ))$
(see Section 2.9.4) which we may precompose with (57) to arrive at an enhancement of (45) to
in
![]() $\mathrm {CMon}(\mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathscr {C}\mathrm {at}_\infty ))\subset \mathrm {Fun}(\mathsf {Fin}_{*}\times \Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathscr {C}\mathrm {at}_\infty ))$
. To show that this composition lands in the levelwise full subcategory
$\mathrm {CMon}(\mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathscr {C}\mathrm {at}_\infty ))\subset \mathrm {Fun}(\mathsf {Fin}_{*}\times \Delta ^{\mathrm {op}}_{\mathrm {inj}},\mathscr {C}\mathrm {at}_\infty ))$
. To show that this composition lands in the levelwise full subcategory
![]() $\mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))\subset \overline {\mathrm {ALG}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
(which lies in the full subcategory
$\mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))\subset \overline {\mathrm {ALG}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
(which lies in the full subcategory
![]() $\mathrm {CMon}(\mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty ))\subset \mathrm {CMon}(\smash {\mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}}},\mathscr {C}\mathrm {at}_\infty ))$
; see Section 2.9.4), by the Segal property it suffices to show this after evaluation at
$\mathrm {CMon}(\mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty ))\subset \mathrm {CMon}(\smash {\mathrm {Fun}(\Delta ^{\mathrm {op}}_{\mathrm {inj}}},\mathscr {C}\mathrm {at}_\infty ))$
; see Section 2.9.4), by the Segal property it suffices to show this after evaluation at
![]() $\langle 1\rangle \in \mathsf {Fin}_{*}$
where it agrees with the previously variant without symmetric monoidal structures for which we have already checked this property in
Step ④, so we obtain a map
$\langle 1\rangle \in \mathsf {Fin}_{*}$
where it agrees with the previously variant without symmetric monoidal structures for which we have already checked this property in
Step ④, so we obtain a map
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}} \rightarrow \mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
in
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\mathrm {nu}} \rightarrow \mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
in
![]() $\mathrm {CMon}(\mathrm {Cat}_{\mathrm {nu}}(\mathscr {C}\mathrm {at}_\infty ))$
. Finally, a minor extension of the arguments of
Step ⑤ to incorporate indexing maps to finite sets enhances this to a functor of symmetric monoidal double
$\mathrm {CMon}(\mathrm {Cat}_{\mathrm {nu}}(\mathscr {C}\mathrm {at}_\infty ))$
. Finally, a minor extension of the arguments of
Step ⑤ to incorporate indexing maps to finite sets enhances this to a functor of symmetric monoidal double
![]() $\infty $
-categories
$\infty $
-categories
![]() $E\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)\rightarrow \mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
.
$E\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)\rightarrow \mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
.
Step ⑦ Variants
We now define several variants of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, related by a diagram
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, related by a diagram

of symmetric monoidal double
![]() $\infty $
-categories. Informally speaking,
$\infty $
-categories. Informally speaking,
![]() $\mathscr {B}\mathrm {ord}(d)$
is obtained from
$\mathscr {B}\mathrm {ord}(d)$
is obtained from
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
by restricting to compact bordisms between closed manifolds and diffeomorphisms between them; the versions with a
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
by restricting to compact bordisms between closed manifolds and diffeomorphisms between them; the versions with a
![]() $(-)^{\partial }$
-subscript allow manifolds to have boundary, all vertical maps and the left horizontal maps are induced by inclusion, and the right horizontal maps are induced by taking boundaries.
$(-)^{\partial }$
-subscript allow manifolds to have boundary, all vertical maps and the left horizontal maps are induced by inclusion, and the right horizontal maps are induced by taking boundaries.
Step ⑦.1 Compact variant
To define the compact variant
![]() $\mathscr {B}\mathrm {ord}(d)$
, we say that a
$\mathscr {B}\mathrm {ord}(d)$
, we say that a
![]() $[p]$
-walled d-manifold
$[p]$
-walled d-manifold
![]() $(W,\mu )$
is of of compact type if the subspace
$(W,\mu )$
is of of compact type if the subspace
![]() $W|_{[\mu (0)-\epsilon ,\mu (p)+\epsilon ]} \subseteq W$
is compact. Restricting to
$W|_{[\mu (0)-\epsilon ,\mu (p)+\epsilon ]} \subseteq W$
is compact. Restricting to
![]() $[p]$
-walled d-manifolds of compact type in the construction of
$[p]$
-walled d-manifolds of compact type in the construction of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
and to spaces of diffeomorphisms instead of embeddings defines the symmetric monoidal double
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
and to spaces of diffeomorphisms instead of embeddings defines the symmetric monoidal double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {B}\mathrm {ord}(d)$
. By construction, it comes with a levelwise subcategory inclusion into
$\mathscr {B}\mathrm {ord}(d)$
. By construction, it comes with a levelwise subcategory inclusion into
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
. This is the leftmost vertical map in (60).
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
. This is the leftmost vertical map in (60).
Step ⑦.2 Variants with boundary
To define the variant
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\partial }$
of
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\partial }$
of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
involving manifolds with boundary, we replace
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
involving manifolds with boundary, we replace
![]() $[p]$
-walled d-manifolds
$[p]$
-walled d-manifolds
![]() $(W,\mu )$
, where
$(W,\mu )$
, where
![]() $W\subset \mathbf {R}\times \mathbf {R}^{\infty }$
is required to have no boundary, by
$W\subset \mathbf {R}\times \mathbf {R}^{\infty }$
is required to have no boundary, by
![]() $[p]$
-walled d-manifolds with boundary: these are pairs
$[p]$
-walled d-manifolds with boundary: these are pairs
![]() $(W,\mu )$
of a smooth submanifold
$(W,\mu )$
of a smooth submanifold
![]() $W\subset \mathbf {R}\times [0,\infty )\times \mathbf {R}^{\infty }$
, possibly with boundary, together with an order-perserving function
$W\subset \mathbf {R}\times [0,\infty )\times \mathbf {R}^{\infty }$
, possibly with boundary, together with an order-perserving function
![]() $\mu \colon [p]\rightarrow \mathbf {R}$
such that
$\mu \colon [p]\rightarrow \mathbf {R}$
such that
-
(i)
 $(W,\mu )$
satisfies the conditions in the definition of
$(W,\mu )$
satisfies the conditions in the definition of
 $[p]$
-walled d-manifolds (see
Step ①),
$[p]$
-walled d-manifolds (see
Step ①), -
(ii)
 $\partial W=W\cap (\mathbf {R}\times \{0\}\times \mathbf {R}^{\infty })$
such that
$\partial W=W\cap (\mathbf {R}\times \{0\}\times \mathbf {R}^{\infty })$
such that
 $W\cap (\mathbf {R}\times [0,\epsilon ]\times \mathbf {R}^{\infty })=\partial W\times [0,\epsilon ]$
under the appropriate identifications.
$W\cap (\mathbf {R}\times [0,\epsilon ]\times \mathbf {R}^{\infty })=\partial W\times [0,\epsilon ]$
under the appropriate identifications.
The space
![]() $\mathrm {Emb}((W,\mu ),(W',\mu '))$
of embeddings of
$\mathrm {Emb}((W,\mu ),(W',\mu '))$
of embeddings of
![]() $[p]$
-walled d-manifolds with boundary is defined in the same way as in the case without boundary, except that we demand in addition that the embedding
$[p]$
-walled d-manifolds with boundary is defined in the same way as in the case without boundary, except that we demand in addition that the embedding
![]() $\varphi \colon W|_{[\mu (0)-\epsilon ,\mu (p)+\epsilon ]}\hookrightarrow W'|_{[\mu '(0)-\epsilon ,\mu '(p)+\epsilon ]}$
also satisfies
$\varphi \colon W|_{[\mu (0)-\epsilon ,\mu (p)+\epsilon ]}\hookrightarrow W'|_{[\mu '(0)-\epsilon ,\mu '(p)+\epsilon ]}$
also satisfies
-
(i)
 $\varphi ^{-1}(\mathbf {R}\times [0,\epsilon ]\times \mathbf {R}^{\infty })=(W|_{[\mu (0)-\epsilon ,\mu (p)+\epsilon ]})\cap (\mathbf {R}\times [0,\epsilon ]\times \mathbf {R}^{\infty })$
,
$\varphi ^{-1}(\mathbf {R}\times [0,\epsilon ]\times \mathbf {R}^{\infty })=(W|_{[\mu (0)-\epsilon ,\mu (p)+\epsilon ]})\cap (\mathbf {R}\times [0,\epsilon ]\times \mathbf {R}^{\infty })$
, -
(ii) under the appropriate identifications,
 $\varphi $
restricts to an embedding of the form for some embedding
$\varphi $
restricts to an embedding of the form for some embedding
 $\partial \varphi \colon \partial W|_{[\mu (0)-\epsilon ,\mu (p)+\epsilon ]}\hookrightarrow \partial W'|_{[\mu (0)-\epsilon ,\mu (p)+\epsilon ]}$
.
$\partial \varphi \colon \partial W|_{[\mu (0)-\epsilon ,\mu (p)+\epsilon ]}\hookrightarrow \partial W'|_{[\mu (0)-\epsilon ,\mu (p)+\epsilon ]}$
.
Replacing the
![]() $[p]$
-walled d-manifolds in the construction of
$[p]$
-walled d-manifolds in the construction of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
by
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
by
![]() $[p]$
-walled d-manifolds with boundaries in the sense just described gives rise to a symmetric monoidal double
$[p]$
-walled d-manifolds with boundaries in the sense just described gives rise to a symmetric monoidal double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\partial }$
which receives a levelwise full subcategory inclusion from
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\partial }$
which receives a levelwise full subcategory inclusion from
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, induced by the inclusion
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, induced by the inclusion
![]() $\mathbf {R}\times \mathbf {R}^{\infty } \cong \mathbf {R}\times \{1\}\times \mathbf {R}^{\infty }\subset \mathbf {R}\times [0,\infty )\times \mathbf {R}^{\infty }$
. This inclusion restricts to a functor
$\mathbf {R}\times \mathbf {R}^{\infty } \cong \mathbf {R}\times \{1\}\times \mathbf {R}^{\infty }\subset \mathbf {R}\times [0,\infty )\times \mathbf {R}^{\infty }$
. This inclusion restricts to a functor
![]() $\mathscr {B}\mathrm {ord}(d)\rightarrow \mathscr {B}\mathrm {ord}(d)^{\partial }$
where
$\mathscr {B}\mathrm {ord}(d)\rightarrow \mathscr {B}\mathrm {ord}(d)^{\partial }$
where
![]() $\mathscr {B}\mathrm {ord}(d)^{\partial }$
is the symmetric monoidal double
$\mathscr {B}\mathrm {ord}(d)^{\partial }$
is the symmetric monoidal double
![]() $\infty $
-category given as the levelwise subcategory of
$\infty $
-category given as the levelwise subcategory of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\partial }$
obtained by restricting to
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\partial }$
obtained by restricting to
![]() $[p]$
-walled d-manifolds with boundary of compact type, defined by the same condition as for the variant without boundary, and to diffeomorphisms between them instead of embeddings. This explains (60), except for the horizontal functor of the right square which is induced by sending a
$[p]$
-walled d-manifolds with boundary of compact type, defined by the same condition as for the variant without boundary, and to diffeomorphisms between them instead of embeddings. This explains (60), except for the horizontal functor of the right square which is induced by sending a
![]() $[p]$
-walled d-manifold with boundary
$[p]$
-walled d-manifold with boundary
![]() $W\subset \mathbf {R}\times [0,\infty )\times \mathbf {R}^\infty $
to its boundary
$W\subset \mathbf {R}\times [0,\infty )\times \mathbf {R}^\infty $
to its boundary
![]() $\partial W=W\cap (\mathbf {R}\times \{0\}\times \mathbf {R}^\infty )$
, with the same walls, and restricting embeddings to the boundary.
$\partial W=W\cap (\mathbf {R}\times \{0\}\times \mathbf {R}^\infty )$
, with the same walls, and restricting embeddings to the boundary.
Step ⑦.3 Tangential structures without boundary
Associating to a smooth manifold M its frame bundle
![]() $\mathrm {Fr}(M)$
with its canonical right
$\mathrm {Fr}(M)$
with its canonical right
![]() $\mathrm {GL}_d(\mathbf {R})$
-action induces a functor of
$\mathrm {GL}_d(\mathbf {R})$
-action induces a functor of
![]() $\mathsf {Kan}$
-enriched categories
$\mathsf {Kan}$
-enriched categories
where
![]() $\mathsf {Man}_d^{\otimes }$
is the symmetric monoidal
$\mathsf {Man}_d^{\otimes }$
is the symmetric monoidal
![]() $\infty $
-category from
Step ② and
Step ⑥, and
$\infty $
-category from
Step ② and
Step ⑥, and
![]() $\mathrm {GL}_d$
is the (singular simplicial set of) the topological group
$\mathrm {GL}_d$
is the (singular simplicial set of) the topological group
![]() $\mathrm {GL}_d(\mathbf {R})$
viewed as a
$\mathrm {GL}_d(\mathbf {R})$
viewed as a
![]() $\mathsf {Kan}$
-enriched groupoid with one object. The superscript
$\mathsf {Kan}$
-enriched groupoid with one object. The superscript
![]() $(-)^\circ $
indicates that we pass to the full subcategory on the fibrant-cofibrant objects in the projective model structure on
$(-)^\circ $
indicates that we pass to the full subcategory on the fibrant-cofibrant objects in the projective model structure on
![]() $\mathrm {Fun}(\mathrm {GL}^{\mathrm {op}}_d,\mathsf {S})$
, as in [Reference LurieLur17, A.3.3.2]. Let us explain why functor
$\mathrm {Fun}(\mathrm {GL}^{\mathrm {op}}_d,\mathsf {S})$
, as in [Reference LurieLur17, A.3.3.2]. Let us explain why functor
![]() $\mathrm {Fr}(-)$
takes values in this subcategory. First,
$\mathrm {Fr}(-)$
takes values in this subcategory. First,
![]() $\mathrm {Fr}(M)$
is fibrant: in the projective model structure, an object is fibrant if its underlying simplicial set is a Kan complex, and this is the case for
$\mathrm {Fr}(M)$
is fibrant: in the projective model structure, an object is fibrant if its underlying simplicial set is a Kan complex, and this is the case for
![]() $\mathrm {Fr}(M)$
as a singular simplicial set of a topological space. Second,
$\mathrm {Fr}(M)$
as a singular simplicial set of a topological space. Second,
![]() $\mathrm {Fr}(M)$
is cofibrant: because the map
$\mathrm {Fr}(M)$
is cofibrant: because the map
![]() $\mathrm {Fun}(\mathrm {GL}_d^{\mathrm {op}},\mathsf {S}) \to \mathsf {S}$
that forgets the action is the right adjoint in a Quillen adjunction, each map
$\mathrm {Fun}(\mathrm {GL}_d^{\mathrm {op}},\mathsf {S}) \to \mathsf {S}$
that forgets the action is the right adjoint in a Quillen adjunction, each map
![]() $\mathrm {GL}_d(\mathbf {R}) \times S \to \mathrm {GL}_d(\mathbf {R}) \times S'$
with canonical right
$\mathrm {GL}_d(\mathbf {R}) \times S \to \mathrm {GL}_d(\mathbf {R}) \times S'$
with canonical right
![]() $\mathrm {GL}_d(\mathbf {R})$
-action and
$\mathrm {GL}_d(\mathbf {R})$
-action and
![]() $S \to S'$
a monomorphism is a cofibration, and
$S \to S'$
a monomorphism is a cofibration, and
![]() $\mathrm {Fr}(M)$
– being locally trivial – is isomorphic to a (possibly transfinite) composition of pushouts against such maps.
$\mathrm {Fr}(M)$
– being locally trivial – is isomorphic to a (possibly transfinite) composition of pushouts against such maps.
Applying coherent nerves to the map (61) and viewing
![]() $\mathrm {GL}_d$
as an
$\mathrm {GL}_d$
as an
![]() $\infty $
-category via the coherent nerve gives a functor of
$\infty $
-category via the coherent nerve gives a functor of
![]() $\infty $
-categories
$\infty $
-categories
where the second equivalence is an instance of [Reference LurieLur09a, 4.2.4.4]. Since the unit
![]() $\varnothing \in (\mathscr {M}\mathrm {an}_d^{\otimes })_{[1]}$
is initial and so
$\varnothing \in (\mathscr {M}\mathrm {an}_d^{\otimes })_{[1]}$
is initial and so
![]() $\mathscr {M}\mathrm {an}_d^\sqcup $
is unital as an
$\mathscr {M}\mathrm {an}_d^\sqcup $
is unital as an
![]() $\infty $
-operad [Reference LurieLur17, 2.3.1.1], this functor extends uniquely to a lax symmetric monoidal functor
$\infty $
-operad [Reference LurieLur17, 2.3.1.1], this functor extends uniquely to a lax symmetric monoidal functor
![]() $\mathrm {Fr}(-)\colon \mathscr {M}\mathrm {an}^{\otimes }\rightarrow \mathrm {PSh}(\mathrm {GL}_d)^\sqcup $
, where
$\mathrm {Fr}(-)\colon \mathscr {M}\mathrm {an}^{\otimes }\rightarrow \mathrm {PSh}(\mathrm {GL}_d)^\sqcup $
, where
![]() $\mathrm {PSh}(\mathrm {GL}_d)$
carries the cocartesian symmetric monoidal structure [Reference LurieLur17, 2.4.3.9]. Note that
$\mathrm {PSh}(\mathrm {GL}_d)$
carries the cocartesian symmetric monoidal structure [Reference LurieLur17, 2.4.3.9]. Note that
![]() $\mathrm {Fr}(M)\sqcup \mathrm {Fr}(N)\rightarrow \mathrm {Fr}(M\sqcup N)$
is an equivalence for manifolds M and N, so this is actually (strong) symmetric monoidal.
$\mathrm {Fr}(M)\sqcup \mathrm {Fr}(N)\rightarrow \mathrm {Fr}(M\sqcup N)$
is an equivalence for manifolds M and N, so this is actually (strong) symmetric monoidal.
By an easier version of the argument in Step ④, the composition
lands in the Morita double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {ALG}(\mathrm {PSh}(\mathrm {GL}_d))\subset \overline {\mathrm {ALG}}(\mathrm {PSh}(\mathrm {GL}_d))$
, which is equivalent to
$\mathrm {ALG}(\mathrm {PSh}(\mathrm {GL}_d))\subset \overline {\mathrm {ALG}}(\mathrm {PSh}(\mathrm {GL}_d))$
, which is equivalent to
![]() $\mathrm {COSPAN}^+(\mathrm {PSh}(\mathrm {GL}_d))$
(see Section 2.10.2). We thus arrive at a functor of symmetric monoidal double
$\mathrm {COSPAN}^+(\mathrm {PSh}(\mathrm {GL}_d))$
(see Section 2.10.2). We thus arrive at a functor of symmetric monoidal double
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathrm {Fr}(-)\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)\rightarrow \mathrm {COSPAN}^+(\mathrm {PSh}(\mathrm {GL}_d))$
. Informally, this is given by sending a bordism
$\mathrm {Fr}(-)\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)\rightarrow \mathrm {COSPAN}^+(\mathrm {PSh}(\mathrm {GL}_d))$
. Informally, this is given by sending a bordism
![]() $W\colon P \leadsto Q$
to the cospan
$W\colon P \leadsto Q$
to the cospan
![]() $\mathrm {Fr}(c(P))\rightarrow \mathrm {Fr}(W)\leftarrow \mathrm {Fr}(c(Q))$
, where
$\mathrm {Fr}(c(P))\rightarrow \mathrm {Fr}(W)\leftarrow \mathrm {Fr}(c(Q))$
, where
![]() $c(P),c(Q)\subset W$
are collar neighbourhoods of the boundary components.
$c(P),c(Q)\subset W$
are collar neighbourhoods of the boundary components.
Definition 3.11. Given a tangential structure ![]() , we define
, we define
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)$
and
$\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)$
and
![]() $\mathscr {B}\mathrm {ord}^\theta (d)$
by the following pullbacks in symmetric monoidal double
$\mathscr {B}\mathrm {ord}^\theta (d)$
by the following pullbacks in symmetric monoidal double
![]() $\infty $
-categories:
$\infty $
-categories:

here, the rightmost vertical map is induced by the forgetful functor
![]() $\mathrm {PSh}(\mathrm {GL}_d)_{/\theta }\rightarrow \mathrm {PSh}(\mathrm {GL}_d)$
which preserves colimits [Reference LurieLur17, 1.2.13.8] and thus induces a functor on cospan categories.
$\mathrm {PSh}(\mathrm {GL}_d)_{/\theta }\rightarrow \mathrm {PSh}(\mathrm {GL}_d)$
which preserves colimits [Reference LurieLur17, 1.2.13.8] and thus induces a functor on cospan categories.
Varying
![]() $\theta $
induces functors
$\theta $
induces functors
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}^{(-)}(d),\mathscr {B}\mathrm {ord}^{(-)}(d)\colon \mathrm {PSh}(\mathrm {GL}_d)\rightarrow \mathrm {CMon}(\mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty ))$
. In particular, for a map
$\mathrm {nc}\mathscr {B}\mathrm {ord}^{(-)}(d),\mathscr {B}\mathrm {ord}^{(-)}(d)\colon \mathrm {PSh}(\mathrm {GL}_d)\rightarrow \mathrm {CMon}(\mathrm {Cat}(\mathscr {C}\mathrm {at}_\infty ))$
. In particular, for a map
![]() $\theta \rightarrow \theta '$
in
$\theta \rightarrow \theta '$
in
![]() $\mathrm {PSh}(\mathrm {GL}_d)$
, we have functors
$\mathrm {PSh}(\mathrm {GL}_d)$
, we have functors
Step ⑦.4 Tangential structures with boundary
To define the version
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^\partial $
that includes tangential structure, one uses a variant
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^\partial $
that includes tangential structure, one uses a variant
of the map
![]() $E^{\mathrm {geo}}\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)\rightarrow \overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d)$
between commutative monoid objects in simplicial
$E^{\mathrm {geo}}\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)\rightarrow \overline {\mathrm {ALG}}(\mathscr {M}\mathrm {an}_d)$
between commutative monoid objects in simplicial
![]() $\infty $
-categories. The symmetric monoidal
$\infty $
-categories. The symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {M}\mathrm {an}^\partial _d$
is defined in the same way as
$\mathscr {M}\mathrm {an}^\partial _d$
is defined in the same way as
![]() $\mathscr {M}\mathrm {an}_d$
except that we use submanifolds
$\mathscr {M}\mathrm {an}_d$
except that we use submanifolds ![]() that may have boundary, but have to satisfy the evident analogue of (ii) in the definition of a
that may have boundary, but have to satisfy the evident analogue of (ii) in the definition of a
![]() $[p]$
-walled d-manifold with boundary. With this modification, the construction in
Step ③ and its extensions in
Step ⑤ and
Step ⑥ extend almost verbatim to give the map (63) in
$[p]$
-walled d-manifold with boundary. With this modification, the construction in
Step ③ and its extensions in
Step ⑤ and
Step ⑥ extend almost verbatim to give the map (63) in
![]() $\smash {\mathrm {CMon}(\mathrm {Fun}(\Delta ^{\mathrm {op}},\mathscr {C}\mathrm {at}_\infty ))}$
.
$\smash {\mathrm {CMon}(\mathrm {Fun}(\Delta ^{\mathrm {op}},\mathscr {C}\mathrm {at}_\infty ))}$
.
Assigning to a manifold
![]() $W\in (\mathscr {M}\mathrm {an}^{\partial ,\otimes }_d)_{[1]}$
the map
$W\in (\mathscr {M}\mathrm {an}^{\partial ,\otimes }_d)_{[1]}$
the map
![]() $\mathrm {Fr}(\partial W\times [0,\epsilon ])\rightarrow \mathrm {Fr}(W)$
induced by the inclusion, induces an extension of the functor
$\mathrm {Fr}(\partial W\times [0,\epsilon ])\rightarrow \mathrm {Fr}(W)$
induced by the inclusion, induces an extension of the functor
![]() $(\mathscr {M}\mathrm {an}_d^\sqcup )_{[1]}\rightarrow \mathrm {PSh}(\mathrm {GL}_d)$
to a functor of
$(\mathscr {M}\mathrm {an}_d^\sqcup )_{[1]}\rightarrow \mathrm {PSh}(\mathrm {GL}_d)$
to a functor of
![]() $\infty $
-categories
$\infty $
-categories
which, by the same argument as in the case without boundary, extends to a symmetric monoidal functor
![]() $\mathrm {Fr}(-)\colon \mathscr {M}\mathrm {an}^{\partial ,\otimes }_d\rightarrow \mathrm {PSh}([1]\times \mathrm {GL}_d)^\sqcup $
, where the target is equipped with the cocartesian symmetric monoidal structure. This functor allows us to extend Definition 3.11 to define symmetric monoidal double
$\mathrm {Fr}(-)\colon \mathscr {M}\mathrm {an}^{\partial ,\otimes }_d\rightarrow \mathrm {PSh}([1]\times \mathrm {GL}_d)^\sqcup $
, where the target is equipped with the cocartesian symmetric monoidal structure. This functor allows us to extend Definition 3.11 to define symmetric monoidal double
![]() $\infty $
-categories
$\infty $
-categories
for any tangential structure
![]() $\theta $
with boundary by which mean a map
$\theta $
with boundary by which mean a map
![]() $\theta =(\theta ^\partial {\rightarrow }\theta ^\circ )\in \mathrm {PSh}([1]\times \mathrm {GL}_d)$
.
$\theta =(\theta ^\partial {\rightarrow }\theta ^\circ )\in \mathrm {PSh}([1]\times \mathrm {GL}_d)$
.
Step ⑦.5 Taking boundaries with tangential structures
Next, we extend the ‘taking-boundaries functors’
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\partial }\rightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}(d-1)$
and
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^{\partial }\rightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}(d-1)$
and
![]() $\mathscr {B}\mathrm {ord}(d)^{\partial }\rightarrow \mathscr {B}\mathrm {ord}(d-1)$
from (60) to include tangential structures. This involves the commutative diagram
$\mathscr {B}\mathrm {ord}(d)^{\partial }\rightarrow \mathscr {B}\mathrm {ord}(d-1)$
from (60) to include tangential structures. This involves the commutative diagram

of
![]() $\infty $
-categories where the leftmost vertical map is induced by sending a submanifold
$\infty $
-categories where the leftmost vertical map is induced by sending a submanifold ![]() to its boundary (i.e., the intersection with
to its boundary (i.e., the intersection with ![]() ). The arrow labelled
). The arrow labelled
![]() $\mathrm {res}$
is induced by precomposition with the inclusion
$\mathrm {res}$
is induced by precomposition with the inclusion
![]() $\{1\}\times \mathrm {GL}_d\subset [1]\times \mathrm {GL}_d$
, and the arrow labelled
$\{1\}\times \mathrm {GL}_d\subset [1]\times \mathrm {GL}_d$
, and the arrow labelled
![]() $\mathrm {ind}_{d-1}^d$
is the left adjoint to the functor
$\mathrm {ind}_{d-1}^d$
is the left adjoint to the functor
![]() $\mathrm {res}_{d-1}^d\colon \mathrm {PSh}(\mathrm {GL}_{d})\rightarrow \mathrm {PSh}(\mathrm {GL}_{d-1})$
induced by precomposition with the inclusion
$\mathrm {res}_{d-1}^d\colon \mathrm {PSh}(\mathrm {GL}_{d})\rightarrow \mathrm {PSh}(\mathrm {GL}_{d-1})$
induced by precomposition with the inclusion
![]() $\mathrm {GL}_{d-1}(\mathbf {R})\subset \mathrm {GL}_{d}(\mathbf {R})$
using the first
$\mathrm {GL}_{d-1}(\mathbf {R})\subset \mathrm {GL}_{d}(\mathbf {R})$
using the first
![]() $(d-1)$
-coordinates. One way to provide the commutativity of (64) is to recognise this diagram as the coherent nerve of a diagram of
$(d-1)$
-coordinates. One way to provide the commutativity of (64) is to recognise this diagram as the coherent nerve of a diagram of
![]() $\mathsf {Kan}$
-enriched categories (using [Reference LurieLur09a, 5.2.4.6] for
$\mathsf {Kan}$
-enriched categories (using [Reference LurieLur09a, 5.2.4.6] for
![]() $\mathrm {ind}_{d-1}^d$
) and then use the fact that the extension
$\mathrm {ind}_{d-1}^d$
) and then use the fact that the extension
![]() $\mathrm {ind}_{d-1}^d(\mathrm {Fr}(\partial W))\rightarrow \mathrm {Fr}(\partial W\times [0,\epsilon ])$
of the
$\mathrm {ind}_{d-1}^d(\mathrm {Fr}(\partial W))\rightarrow \mathrm {Fr}(\partial W\times [0,\epsilon ])$
of the
![]() $\mathrm {GL}_{d-1}(\mathbf {R})$
-equivariant map
$\mathrm {GL}_{d-1}(\mathbf {R})$
-equivariant map
![]() $\mathrm {Fr}(\partial W)\rightarrow \mathrm {Fr}(\partial W\times [0,\epsilon ])$
induced by the inclusion
$\mathrm {Fr}(\partial W)\rightarrow \mathrm {Fr}(\partial W\times [0,\epsilon ])$
induced by the inclusion
![]() $\partial W\times \{0\}\subset \partial W\times [0,\epsilon ]$
and the canonical non-zero vector field on
$\partial W\times \{0\}\subset \partial W\times [0,\epsilon ]$
and the canonical non-zero vector field on
![]() $[0,\epsilon ]$
is a natural equivalence of
$[0,\epsilon ]$
is a natural equivalence of
![]() $\mathrm {GL}_d(\mathbf {R})$
-spaces.
$\mathrm {GL}_d(\mathbf {R})$
-spaces.
Equipping all categories of presheaves with the cocartesian symmetric monoidal structure and using the universality property as in
Step ⑦.3, we can extend (64) to a commutative diagram of symmetric monoidal
![]() $\infty $
-categories. Applying
$\infty $
-categories. Applying
![]() $\overline {\mathrm {ALG}}(-)$
, using the
$\overline {\mathrm {ALG}}(-)$
, using the
![]() $E^{\mathrm {geo}}$
-functors, and the equivalence
$E^{\mathrm {geo}}$
-functors, and the equivalence
![]() $\mathrm {ALG}(\mathscr {C})\simeq \mathrm {COSPAN}^+(\mathscr {C})$
for cocartesian
$\mathrm {ALG}(\mathscr {C})\simeq \mathrm {COSPAN}^+(\mathscr {C})$
for cocartesian
![]() $\mathscr {C}$
, this leads to a commutative diagram of symmetric monoidal double
$\mathscr {C}$
, this leads to a commutative diagram of symmetric monoidal double
![]() $\infty $
-categories
$\infty $
-categories

For a tangential structure with boundary
![]() $\theta =(\theta ^\partial {\rightarrow }\theta ^\circ )\in \mathrm {PSh}([1]\times \mathrm {GL}_d)$
, this induces extensions
$\theta =(\theta ^\partial {\rightarrow }\theta ^\circ )\in \mathrm {PSh}([1]\times \mathrm {GL}_d)$
, this induces extensions
of the ‘taking boundaries’ functors from (60).
Example 3.12. The tangential structure with boundary encoding framings is ![]() , so the above in particular gives a functor of symmetric monoidal double
, so the above in particular gives a functor of symmetric monoidal double
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(d)^{\partial }\rightarrow \mathscr {B}\mathrm {ord}^{\mathrm {1{-}fr}}(d-1)^{\partial }$
from the compact framed d-dimensional bordism category with boundary to the d-dimensional bordism category with boundary, and the tangential structure
$\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(d)^{\partial }\rightarrow \mathscr {B}\mathrm {ord}^{\mathrm {1{-}fr}}(d-1)^{\partial }$
from the compact framed d-dimensional bordism category with boundary to the d-dimensional bordism category with boundary, and the tangential structure ![]() encodes framings of the once-stablised tangent bundle.
encodes framings of the once-stablised tangent bundle.
Step ⑧ Product functors
Given a smooth p-manifold P, possibly with boundary, we now explain the construction of a ‘taking products’ functor of symmetric monoidal double
![]() $\infty $
-categories
$\infty $
-categories
which restricts to product functors of the form
if P has no boundary, is compact or is closed, respectively. This will involve smoothing corners.
We fix an embedding
![]() $P\subset [0,\infty )\times \mathbf {R}^N$
for some
$P\subset [0,\infty )\times \mathbf {R}^N$
for some
![]() $N\ge 0$
which satisfies the condition (ii) in the definition of a
$N\ge 0$
which satisfies the condition (ii) in the definition of a
![]() $[p]$
-walled d-manifolds with boundary (ignoring the first
$[p]$
-walled d-manifolds with boundary (ignoring the first
![]() $\mathbf {R}$
-factor). Furthermore, we fix once and for all a homeomorphism
$\mathbf {R}$
-factor). Furthermore, we fix once and for all a homeomorphism
![]() $\psi \colon [0,\infty )\times [0,\infty )\rightarrow [0,\infty )\times \mathbf {R}$
such that
$\psi \colon [0,\infty )\times [0,\infty )\rightarrow [0,\infty )\times \mathbf {R}$
such that
-
(i)
 $\psi $
agrees with the identity on
$\psi $
agrees with the identity on
 $[0,\infty )\times \{0\}$
and with the clockwise rotation by
$[0,\infty )\times \{0\}$
and with the clockwise rotation by
 $\pi /2$
on
$\pi /2$
on
 $\{0\}\times [0,\infty )$
. In particular, it fixes the origin.
$\{0\}\times [0,\infty )$
. In particular, it fixes the origin. -
(ii)
 $\psi $
is a diffeomorphism away from the origin.
$\psi $
is a diffeomorphism away from the origin. -
(iii)
 $\psi ^{-1}([0,\epsilon ]\times \mathbf {R})\subset \big ([0,\epsilon ]\times [0,\infty )\cup [0,\infty )\times [0,\epsilon ]\big )$
,
$\psi ^{-1}([0,\epsilon ]\times \mathbf {R})\subset \big ([0,\epsilon ]\times [0,\infty )\cup [0,\infty )\times [0,\epsilon ]\big )$
, -
(iv)
 $\psi ([0,\delta ]\times [0,\infty )\cup [0,\infty )\times [0,\delta ])\subset [0,\epsilon ]\times \mathbf {R}$
for some fixed
$\psi ([0,\delta ]\times [0,\infty )\cup [0,\infty )\times [0,\delta ])\subset [0,\epsilon ]\times \mathbf {R}$
for some fixed
 $0<\delta \le \epsilon $
$0<\delta \le \epsilon $
-
(v)
 $\psi $
fixes the point
$\psi $
fixes the point
 $(1,1)$
.
$(1,1)$
.
Using
![]() $\psi $
and its properties (i)–(iii), given a
$\psi $
and its properties (i)–(iii), given a
![]() $[p]$
-walled d-manifold with boundary
$[p]$
-walled d-manifold with boundary
![]() $(W,\mu )$
, we obtain a
$(W,\mu )$
, we obtain a
![]() $[p]$
-walled
$[p]$
-walled
![]() $(d+p)$
-manifold with boundary
$(d+p)$
-manifold with boundary
![]() $(\Psi (P\times W),\mu )$
with
$(\Psi (P\times W),\mu )$
with
![]() $\Psi (P\times W)$
the image of
$\Psi (P\times W)$
the image of
![]() $P\times W$
under
$P\times W$
under
 $$ \begin{align*} &[0,\infty)\times\mathbf{R}^N\times \mathbf{R}\times[0,\infty)\times\mathbf{R}^\infty \xrightarrow{\text{swap}}\mathbf{R}\times [0,\infty)\times [0,\infty)\times\mathbf{R}^N\times \mathbf{R}^\infty\\ &\qquad \xrightarrow{\mathrm{id}_{\mathbf{R}}\times \psi\times \mathrm{id}_{\mathbf{R}^N \times \mathbf{R}^\infty}} \mathbf{R}\times [0,\infty)\times \mathbf{R} \times\mathbf{R}^N\times \mathbf{R}^\infty \xrightarrow{\mathrm{id}_{\mathbf{R} \times [0,\infty)} \times \text{shift}}\mathbf{R}\times [0,\infty)\times\mathbf{R}^\infty, \end{align*} $$
$$ \begin{align*} &[0,\infty)\times\mathbf{R}^N\times \mathbf{R}\times[0,\infty)\times\mathbf{R}^\infty \xrightarrow{\text{swap}}\mathbf{R}\times [0,\infty)\times [0,\infty)\times\mathbf{R}^N\times \mathbf{R}^\infty\\ &\qquad \xrightarrow{\mathrm{id}_{\mathbf{R}}\times \psi\times \mathrm{id}_{\mathbf{R}^N \times \mathbf{R}^\infty}} \mathbf{R}\times [0,\infty)\times \mathbf{R} \times\mathbf{R}^N\times \mathbf{R}^\infty \xrightarrow{\mathrm{id}_{\mathbf{R} \times [0,\infty)} \times \text{shift}}\mathbf{R}\times [0,\infty)\times\mathbf{R}^\infty, \end{align*} $$
where the first map swaps the right
![]() $[0,\infty ) \times \mathbf {R}^N$
-factor with the middle
$[0,\infty ) \times \mathbf {R}^N$
-factor with the middle
![]() $\mathbf {R}\times [0,\infty )$
-factor. For instance, condition (iii) is used to ensure the condition
$\mathbf {R}\times [0,\infty )$
-factor. For instance, condition (iii) is used to ensure the condition
![]() $\Psi (P\times W)\cap (\mathbf {R}\times [0,\epsilon ]\times \mathbf {R}^\infty )=\partial (\Psi (P\times W))\times [0,\epsilon ]$
in the definition of a
$\Psi (P\times W)\cap (\mathbf {R}\times [0,\epsilon ]\times \mathbf {R}^\infty )=\partial (\Psi (P\times W))\times [0,\epsilon ]$
in the definition of a
![]() $[p]$
-walled manifold with boundary. Note that
$[p]$
-walled manifold with boundary. Note that
![]() $\Psi (P\times W)$
comes with a preferred homeomorphism
$\Psi (P\times W)$
comes with a preferred homeomorphism
![]() $P\times W\cong \Psi (P\times W)$
which is a diffeomorphism away from
$P\times W\cong \Psi (P\times W)$
which is a diffeomorphism away from
![]() $\partial P\times \partial W$
as a consequence of condition (ii). Taking products with P and conjugating with
$\partial P\times \partial W$
as a consequence of condition (ii). Taking products with P and conjugating with
![]() $\psi $
induces a map
$\psi $
induces a map
which is well-defined due to the collaring condition (ii) on embeddings between
![]() $[p]$
-walled d-manifolds with boundaries. Going through the construction of
$[p]$
-walled d-manifolds with boundaries. Going through the construction of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^\partial $
, one checks that the assignment
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^\partial $
, one checks that the assignment
![]() $(W,\mu )\mapsto (\Psi (P\times W),\mu )$
together with the maps between embedding spaces just discussed leads to functors as desired.
$(W,\mu )\mapsto (\Psi (P\times W),\mu )$
together with the maps between embedding spaces just discussed leads to functors as desired.
These product functors can be extended to include tangential structures. To this end, one notes that there is a functor of symmetric monoidal categories
![]() $(P\times -)\colon \mathscr {M}\mathrm {an}_d^\partial \rightarrow \mathscr {M}\mathrm {an}_{p+d}^\partial $
defined as for (65). On underlying
$(P\times -)\colon \mathscr {M}\mathrm {an}_d^\partial \rightarrow \mathscr {M}\mathrm {an}_{p+d}^\partial $
defined as for (65). On underlying
![]() $\infty $
-categories, this participates in a diagram of
$\infty $
-categories, this participates in a diagram of
![]() $\infty $
-categories
$\infty $
-categories

where the upper right vertical arrow is the functor that sends a map
![]() $X\rightarrow Y$
of
$X\rightarrow Y$
of
![]() $\mathrm {GL}_d(\mathbf {R})$
-spaces to
$\mathrm {GL}_d(\mathbf {R})$
-spaces to
viewed as a map of
![]() $(\mathrm {GL}_{p}(\mathbf {R})\times \mathrm {GL}_d(\mathbf {R}))$
-spaces, and the functor
$(\mathrm {GL}_{p}(\mathbf {R})\times \mathrm {GL}_d(\mathbf {R}))$
-spaces, and the functor
![]() $\mathrm {ind}_{p,d}^{p+d}$
is the left adjoint to the restriction along the inclusion
$\mathrm {ind}_{p,d}^{p+d}$
is the left adjoint to the restriction along the inclusion
![]() $\mathrm {GL}_p(\mathbf {R})\times \mathrm {GL}_d(\mathbf {R})\subset \mathrm {GL}_{p+d}(\mathbf {R})$
. (66) can be extended to a commutative square of
$\mathrm {GL}_p(\mathbf {R})\times \mathrm {GL}_d(\mathbf {R})\subset \mathrm {GL}_{p+d}(\mathbf {R})$
. (66) can be extended to a commutative square of
![]() $\infty $
-categories in a way similar to what we did for (64): recognise it as the coherent nerve of a diagram of
$\infty $
-categories in a way similar to what we did for (64): recognise it as the coherent nerve of a diagram of
![]() $\mathsf {Kan}$
-enriched categories and then use that the two compositions are related by a zig-zag of natural equivalences. In this case, the zig-zag is provided by the commutative diagram
$\mathsf {Kan}$
-enriched categories and then use that the two compositions are related by a zig-zag of natural equivalences. In this case, the zig-zag is provided by the commutative diagram

of
![]() $(\mathrm {GL}_{p}(\mathbf {R})\times \mathrm {GL}_{d}(\mathbf {R}))$
-spaces which is natural in W and consists of vertical equivalences when taking adjoints with respect to the
$(\mathrm {GL}_{p}(\mathbf {R})\times \mathrm {GL}_{d}(\mathbf {R}))$
-spaces which is natural in W and consists of vertical equivalences when taking adjoints with respect to the
![]() $(\smash {\mathrm {ind}_{p,d}^{p+d}},\smash {\mathrm {res}_{p,d}^{p+d}})$
-adjunction. Here,
$(\smash {\mathrm {ind}_{p,d}^{p+d}},\smash {\mathrm {res}_{p,d}^{p+d}})$
-adjunction. Here, ![]() and
and ![]() , the lower vertical arrows are induced by the inclusions
, the lower vertical arrows are induced by the inclusions
![]() $\mathrm {int}(P)\subset P$
and
$\mathrm {int}(P)\subset P$
and
![]() $\mathrm {int}(W)\subset W$
, and the upper vertical arrows by the preferred embedding
$\mathrm {int}(W)\subset W$
, and the upper vertical arrows by the preferred embedding
![]() $\mathrm {int}(P)\times \mathrm {int}(W)\hookrightarrow \Psi (P\times W)$
induced by
$\mathrm {int}(P)\times \mathrm {int}(W)\hookrightarrow \Psi (P\times W)$
induced by
![]() $\psi $
; this uses property (iv) of
$\psi $
; this uses property (iv) of
![]() $\psi $
. Similarly to the final paragraph of
Step ⑦.5, (66) yields a commutative diagram of symmetric monoidal double
$\psi $
. Similarly to the final paragraph of
Step ⑦.5, (66) yields a commutative diagram of symmetric monoidal double
![]() $\infty $
-categories
$\infty $
-categories

Now given a tangential structure with boundary
![]() $\lambda =(\lambda ^\partial \rightarrow \lambda ^\circ )\in \mathrm {PSh}([1]\times \mathrm {GL}_p)$
, and a
$\lambda =(\lambda ^\partial \rightarrow \lambda ^\circ )\in \mathrm {PSh}([1]\times \mathrm {GL}_p)$
, and a
![]() $\lambda $
-structure on P in the form of a map
$\lambda $
-structure on P in the form of a map
![]() $\ell _P\colon (\mathrm {Fr}(P),\mathrm {Fr}(\partial P\times [0,\epsilon ]))\rightarrow (\lambda ^\circ ,\lambda ^{\partial })$
in
$\ell _P\colon (\mathrm {Fr}(P),\mathrm {Fr}(\partial P\times [0,\epsilon ]))\rightarrow (\lambda ^\circ ,\lambda ^{\partial })$
in
![]() $\mathrm {PSh}([1]\times \mathrm {GL}_p)$
, then (67) induces a functor of symmetric monoidal double
$\mathrm {PSh}([1]\times \mathrm {GL}_p)$
, then (67) induces a functor of symmetric monoidal double
![]() $\infty $
-categories
$\infty $
-categories
where ![]() .This also extends the variants of the product functors mentioned below (65), where property (v) of
.This also extends the variants of the product functors mentioned below (65), where property (v) of
![]() $\psi $
is used for the variants without boundary.
$\psi $
is used for the variants without boundary.
Example 3.13. In the case of framings
![]() $\mathrm {fr}_p=\lambda =(\mathrm {id}\colon \mathrm {GL}_p(\mathbf {R})\rightarrow \mathrm {GL}_p(\mathbf {R}))$
and
$\mathrm {fr}_p=\lambda =(\mathrm {id}\colon \mathrm {GL}_p(\mathbf {R})\rightarrow \mathrm {GL}_p(\mathbf {R}))$
and
![]() $\mathrm {fr}_d=\theta =(\mathrm {id}\colon \mathrm {GL}_d(\mathbf {R})\rightarrow \mathrm {GL}_d(\mathbf {R}))$
, we have
$\mathrm {fr}_d=\theta =(\mathrm {id}\colon \mathrm {GL}_d(\mathbf {R})\rightarrow \mathrm {GL}_d(\mathbf {R}))$
, we have
![]() $\mathrm {glue}(\mathrm {fr}_p,\mathrm {fr}_d)\simeq \mathrm {fr}_{d+p}$
, so omitting the subscripts, we have a product functor of symmetric monoidal double
$\mathrm {glue}(\mathrm {fr}_p,\mathrm {fr}_d)\simeq \mathrm {fr}_{d+p}$
, so omitting the subscripts, we have a product functor of symmetric monoidal double
![]() $\infty $
-categories
$\infty $
-categories
![]() $((P,\ell _P)\times (-))\colon \mathrm {nc}\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(d)^\partial \rightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(p+d)^\partial $
for framed p-manifolds P, and similarly for the compact variants.
$((P,\ell _P)\times (-))\colon \mathrm {nc}\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(d)^\partial \rightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(p+d)^\partial $
for framed p-manifolds P, and similarly for the compact variants.
4 Properties of E, embedding calculus and
 $\mathscr {D}\mathrm {isc}$
-structure spaces
$\mathscr {D}\mathrm {isc}$
-structure spaces
The main outcome of the previous section is the construction of a functor
of symmetric monoidal double
![]() $\infty $
-categories, in the sense of Section 2.5.3, from a bordism category of (possible noncompact)
$\infty $
-categories, in the sense of Section 2.5.3, from a bordism category of (possible noncompact)
![]() $(d-1)$
-manifolds to a Morita category on the category
$(d-1)$
-manifolds to a Morita category on the category
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
of presheaves on a category
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
of presheaves on a category
![]() $\mathscr {D}\mathrm {isc}_d$
of finite disjoint unions of d-dimensional Euclidean spaces and codimension
$\mathscr {D}\mathrm {isc}_d$
of finite disjoint unions of d-dimensional Euclidean spaces and codimension
![]() $0$
embeddings between them. We also constructed variants
$0$
embeddings between them. We also constructed variants
![]() $\mathscr {B}\mathrm {ord}(d)$
,
$\mathscr {B}\mathrm {ord}(d)$
,
![]() $\mathscr {B}\mathrm {ord}(d)^\partial $
and
$\mathscr {B}\mathrm {ord}(d)^\partial $
and
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^\partial $
of
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^\partial $
of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, related by a diagram of symmetric monoidal double
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, related by a diagram of symmetric monoidal double
![]() $\infty $
-categories (60), as well as enhancements with tangential structures of all of these bordism categories.
$\infty $
-categories (60), as well as enhancements with tangential structures of all of these bordism categories.
This section has several purposes: first, in Section 4.1, we give more practical descriptions of these double
![]() $\infty $
-categories by describing their objects and mapping
$\infty $
-categories by describing their objects and mapping
![]() $\infty $
-categories in a model-independent and more intuitive manner, and we explain the functor E in these terms. For most of the arguments in the later sections, this discussion is sufficient, and there is no need to know the specifics of the construction in Section 3. Second, we establish three properties of the functor E:
$\infty $
-categories in a model-independent and more intuitive manner, and we explain the functor E in these terms. For most of the arguments in the later sections, this discussion is sufficient, and there is no need to know the specifics of the construction in Section 3. Second, we establish three properties of the functor E:
-
• a descent property in Section 4.2,
-
• a close relationship to Goodwillie–Weiss’ embedding calculus in Section 4.3, and
-
• an isotopy extension property in Section 4.4.
Finally, in Section 4.5, we give the precise definition of the
![]() $\mathscr {D}\mathrm {isc}$
-structure spaces.
$\mathscr {D}\mathrm {isc}$
-structure spaces.
4.1 Mapping
 $\infty $
-categories
$\infty $
-categories
Recall from Section 2.5.4 that a double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
has mapping
$\mathscr {C}$
has mapping
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathscr {C}_{A,B}$
for objects
$\mathscr {C}_{A,B}$
for objects
![]() $A,B\in \mathscr {C}_{[0]}$
, and these feature in composition functors
$A,B\in \mathscr {C}_{[0]}$
, and these feature in composition functors
![]() $\mathscr {C}_{A,B}\times \mathscr {C}_{B,C}\rightarrow \mathscr {C}_{A,C}$
. We now spell these out for some of the double
$\mathscr {C}_{A,B}\times \mathscr {C}_{B,C}\rightarrow \mathscr {C}_{A,C}$
. We now spell these out for some of the double
![]() $\infty $
-categories of the previous section.
$\infty $
-categories of the previous section.
4.1.1
 $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
In short: objects of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
are (possibly noncompact)
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
are (possibly noncompact)
![]() $(d-1)$
-manifolds P without boundary, and given two such manifolds P and Q, the objects of the mapping
$(d-1)$
-manifolds P without boundary, and given two such manifolds P and Q, the objects of the mapping
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
are bordisms
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
are bordisms
![]() $W\colon P\leadsto Q$
and the mapping spaces in
$W\colon P\leadsto Q$
and the mapping spaces in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
are given by embedding spaces relative to the boundary. The composition in these mapping
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
are given by embedding spaces relative to the boundary. The composition in these mapping
![]() $\infty $
-categories is by composing embeddings, the composition functor
$\infty $
-categories is by composing embeddings, the composition functor
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q} \times \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{Q,R} \rightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,R}$
by gluing bordisms, and the symmetric monoidal structure by disjoint union.
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q} \times \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{Q,R} \rightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,R}$
by gluing bordisms, and the symmetric monoidal structure by disjoint union.
More precisely, given a
![]() $(d-1)$
-manifold P, we may use the weak Whitney embedding theorem to choose an embedding
$(d-1)$
-manifold P, we may use the weak Whitney embedding theorem to choose an embedding
![]() $P\subset \mathbf {R}^{\infty }$
and can thus view P as a
$P\subset \mathbf {R}^{\infty }$
and can thus view P as a
![]() $[0]$
-walled manifold
$[0]$
-walled manifold
![]() $(\mathbf {R}\times P,\mu )$
in the sense of
Step ① of Section 3 (and hence as an object in
$(\mathbf {R}\times P,\mu )$
in the sense of
Step ① of Section 3 (and hence as an object in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{[0]}$
) by setting
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{[0]}$
) by setting
![]() $\mu (0)=0$
. Moreover, it is easy to see that each object in
$\mu (0)=0$
. Moreover, it is easy to see that each object in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{[0]}$
is equivalent to one of this form, so we will no longer distinguish between abstract
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{[0]}$
is equivalent to one of this form, so we will no longer distinguish between abstract
![]() $(d-1)$
-manifolds and objects in
$(d-1)$
-manifolds and objects in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{[0]}$
. Similarly, given a bordism
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{[0]}$
. Similarly, given a bordism ![]() between
between
![]() $(d-1)$
-manifolds, we may embed it suitably collared in
$(d-1)$
-manifolds, we may embed it suitably collared in
![]() $[0,1]\times \mathbf {R}^\infty $
so that
$[0,1]\times \mathbf {R}^\infty $
so that
![]() $((\infty ,0]\times P\cup W\cup [1,\infty )\times Q,\mu )$
with
$((\infty ,0]\times P\cup W\cup [1,\infty )\times Q,\mu )$
with
![]() $\mu (i)=i$
for
$\mu (i)=i$
for
![]() $i=0,1$
is a
$i=0,1$
is a
![]() $[1]$
-walled manifold and thus an object in the mapping
$[1]$
-walled manifold and thus an object in the mapping
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
. Again, any object is equivalent to one of this form, so we will also no longer distinguish between abstract bordisms
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
. Again, any object is equivalent to one of this form, so we will also no longer distinguish between abstract bordisms
![]() $P\leadsto Q$
and objects in
$P\leadsto Q$
and objects in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
. The identification of the mapping spaces in
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
. The identification of the mapping spaces in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
is justified by the following:
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
is justified by the following:
Lemma 4.1. Given possibly noncompact bordisms
![]() $W,W'\colon P\leadsto Q$
between
$W,W'\colon P\leadsto Q$
between
![]() $(d-1)$
-manifolds
$(d-1)$
-manifolds
![]() $P,Q$
without boundary, there is a natural equivalence
$P,Q$
without boundary, there is a natural equivalence
![]() $ \mathrm {Map}_{\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}}(W,W')\simeq \mathrm {Emb}_\partial (W,W')$
in
$ \mathrm {Map}_{\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}}(W,W')\simeq \mathrm {Emb}_\partial (W,W')$
in
![]() $\mathscr {S}$
.
$\mathscr {S}$
.
Proof. Using that mapping spaces in a pullback of
![]() $\infty $
-categories are pullbacks of the mapping spaces, and that coherent nerves of
$\infty $
-categories are pullbacks of the mapping spaces, and that coherent nerves of
![]() $\mathsf {Kan}$
-enriched categories preserve mapping spaces, we see
$\mathsf {Kan}$
-enriched categories preserve mapping spaces, we see
![]() $\mathrm {Map}_{\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}}(W,W')$
is the fibre (i.e., pullback along the indicated inclusion of a point) in
$\mathrm {Map}_{\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}}(W,W')$
is the fibre (i.e., pullback along the indicated inclusion of a point) in
![]() $\mathscr {S}$
$\mathscr {S}$
where the subscript
![]() $(-)_w$
indicates that we restrict to the subspace of embeddings e that in some fixed collars,
$(-)_w$
indicates that we restrict to the subspace of embeddings e that in some fixed collars,
![]() $P \times [0,1] \hookrightarrow W$
and
$P \times [0,1] \hookrightarrow W$
and
![]() $Q \times [-1,0] \hookrightarrow W$
have the form
$Q \times [-1,0] \hookrightarrow W$
have the form
![]() $\mathrm {id}\times e_P$
and
$\mathrm {id}\times e_P$
and
![]() $\mathrm {id}\times e_Q$
for self-embeddings
$\mathrm {id}\times e_Q$
for self-embeddings
![]() $e_P$
and
$e_P$
and
![]() $e_Q$
of P and Q, respectively. The map
$e_Q$
of P and Q, respectively. The map
![]() $\mathrm {res}$
is induced by restriction to
$\mathrm {res}$
is induced by restriction to
![]() $e_P$
and
$e_P$
and
![]() $e_Q$
. It is not hard to see that this is a Kan fibration, so the fibre in
$e_Q$
. It is not hard to see that this is a Kan fibration, so the fibre in
![]() $\mathscr {S}$
agrees with the point-set fibre over
$\mathscr {S}$
agrees with the point-set fibre over
![]() $(\mathrm {id},\mathrm {id})$
. The latter is
$(\mathrm {id},\mathrm {id})$
. The latter is
![]() $\mathrm {Emb}_{\partial }(W,W')$
, so we obtain an equivalence as claimed.
$\mathrm {Emb}_{\partial }(W,W')$
, so we obtain an equivalence as claimed.
4.1.2
 $\mathscr {B}\mathrm {ord}(d)$
$\mathscr {B}\mathrm {ord}(d)$
Under the identification of the objects in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{[0]}$
as
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{[0]}$
as
![]() $(d-1)$
-manifolds P without boundary, those in the subcategory
$(d-1)$
-manifolds P without boundary, those in the subcategory
![]() $\mathscr {B}\mathrm {ord}(d)_{[0]}$
correspond to
$\mathscr {B}\mathrm {ord}(d)_{[0]}$
correspond to
![]() $(d-1)$
-manifolds P without boundary that are also compact. Similarly, the objects in the mapping
$(d-1)$
-manifolds P without boundary that are also compact. Similarly, the objects in the mapping
![]() $\infty $
-categories of the levelwise subcategory
$\infty $
-categories of the levelwise subcategory
![]() $\mathscr {B}\mathrm {ord}(d)\subset \mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
correspond to compact bordisms between closed manifolds. The morphism spaces in the mapping
$\mathscr {B}\mathrm {ord}(d)\subset \mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
correspond to compact bordisms between closed manifolds. The morphism spaces in the mapping
![]() $\infty $
-categories are given by spaces of diffeomorphisms fixing the boundary. Hence, unlike for
$\infty $
-categories are given by spaces of diffeomorphisms fixing the boundary. Hence, unlike for
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, all mapping
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, all mapping
![]() $\infty $
-categories of
$\infty $
-categories of
![]() $\mathscr {B}\mathrm {ord}(d)$
are
$\mathscr {B}\mathrm {ord}(d)$
are
![]() $\infty $
-groupoids and can be regarded as spaces. Thus, by the discussion of Section 2.5.6, not much is lost by applying
$\infty $
-groupoids and can be regarded as spaces. Thus, by the discussion of Section 2.5.6, not much is lost by applying
![]() $(-)^{(\infty ,1)}$
and considering the symmetric monoidal
$(-)^{(\infty ,1)}$
and considering the symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}$
with objects closed
$\mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}$
with objects closed
![]() $(d-1)$
-manifolds and mapping spaces
$(d-1)$
-manifolds and mapping spaces
where
![]() $[W]$
ranges over compact bordisms
$[W]$
ranges over compact bordisms
![]() $W \colon P \leadsto Q$
up to diffeomorphism relative to the ends. Composition is by gluing bordisms and the symmetric monoidal structure by disjoint union.
$W \colon P \leadsto Q$
up to diffeomorphism relative to the ends. Composition is by gluing bordisms and the symmetric monoidal structure by disjoint union.
4.1.3
 $\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)$
$\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)$
In short: given a tangential structure
![]() $\theta $
in the form of a
$\theta $
in the form of a
![]() $\mathrm {GL}_d(\mathbf {R})$
-space
$\mathrm {GL}_d(\mathbf {R})$
-space
![]() $\theta $
, the objects of
$\theta $
, the objects of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)$
are (possibly noncompact)
$\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)$
are (possibly noncompact)
![]() $(d-1)$
-manifolds P with a
$(d-1)$
-manifolds P with a
![]() $\theta $
-structure on their once-stabilised tangent bundle (i.e., a
$\theta $
-structure on their once-stabilised tangent bundle (i.e., a
![]() $\mathrm {GL}_d(\mathbf {R})$
-equivariant map
$\mathrm {GL}_d(\mathbf {R})$
-equivariant map
![]() $\theta _P\colon \mathrm {Fr}(I\times N) \rightarrow \theta $
where
$\theta _P\colon \mathrm {Fr}(I\times N) \rightarrow \theta $
where
![]() $\mathrm {Fr}(-)$
denotes the frame bundle and
$\mathrm {Fr}(-)$
denotes the frame bundle and
![]() $I=[0,1]$
). The objects of the mapping category
$I=[0,1]$
). The objects of the mapping category
![]() $\smash {\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta }(d)_{(P,\theta _P),(Q,\theta _Q)}$
are bordisms with
$\smash {\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta }(d)_{(P,\theta _P),(Q,\theta _Q)}$
are bordisms with
![]() $\theta $
-structures and the morphisms are
$\theta $
-structures and the morphisms are
![]() $\theta $
-embeddings, fixed on the boundary. The composition and monoidal structure is as in
$\theta $
-embeddings, fixed on the boundary. The composition and monoidal structure is as in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, but with the addition of
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, but with the addition of
![]() $\theta $
-structures.
$\theta $
-structures.
To justify this, recall from Section
Step ⑦.3 that the noncompact bordism category with
![]() $\theta $
-structures is defined as the pullback of symmetric monoidal double
$\theta $
-structures is defined as the pullback of symmetric monoidal double
![]() $\infty $
-categories
$\infty $
-categories
so the claimed description of the objects follows by using that forgetting symmetric monoidal structures preserves pullbacks and that pullbacks of double
![]() $\infty $
-categories are computed levelwise. This also shows that the mapping
$\infty $
-categories are computed levelwise. This also shows that the mapping
![]() $\infty $
-categories are given by pullbacks of
$\infty $
-categories are given by pullbacks of
![]() $\infty $
-categories
$\infty $
-categories

which justifies the description of the objects in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)_{(P,\theta _P),(Q,\theta _Q)}$
when combined with the equivalence
$\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)_{(P,\theta _P),(Q,\theta _Q)}$
when combined with the equivalence
![]() $\mathrm {COSPAN}^+(\mathscr {C})_{A,B}\simeq \mathscr {C}_{A\sqcup B/}$
mentioned in Section 2.10. Combining this discussion with the fact that mapping spaces in a pullback of
$\mathrm {COSPAN}^+(\mathscr {C})_{A,B}\simeq \mathscr {C}_{A\sqcup B/}$
mentioned in Section 2.10. Combining this discussion with the fact that mapping spaces in a pullback of
![]() $\infty $
-categories agree with the pullback of the mapping spaces, we arrive at the following precise version of the description of the mapping spaces in the mapping
$\infty $
-categories agree with the pullback of the mapping spaces, we arrive at the following precise version of the description of the mapping spaces in the mapping
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)_{(P,\theta _P),(Q,\theta _Q)}$
.
$\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)_{(P,\theta _P),(Q,\theta _Q)}$
.
Lemma 4.2. Given
![]() $(d-1)$
-manifolds
$(d-1)$
-manifolds
![]() $(P,\theta _P),(Q,\theta _Q)$
without boundary together with
$(P,\theta _P),(Q,\theta _Q)$
without boundary together with
![]() $\theta $
-structures on their once-stabilised tangent bundle, and
$\theta $
-structures on their once-stabilised tangent bundle, and
![]() $\theta $
-bordisms
$\theta $
-bordisms
![]() $(W,\theta _W),(W',\theta _{W'})\colon (P,\theta _P)\leadsto (Q,\theta _Q)$
, there is a natural pullback diagram in
$(W,\theta _W),(W',\theta _{W'})\colon (P,\theta _P)\leadsto (Q,\theta _Q)$
, there is a natural pullback diagram in
![]() $\mathscr {S}$
.
$\mathscr {S}$
.

4.1.4
 $\mathscr {B}\mathrm {ord}^\theta (d)$
$\mathscr {B}\mathrm {ord}^\theta (d)$
The previous discussion of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)$
applies also to the levelwise subcategory
$\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)$
applies also to the levelwise subcategory
![]() $\mathscr {B}\mathrm {ord}^\theta (d)$
when restricting to compact manifolds throughout. By a minor enhancement of the argument in Section 4.1.2, the mapping
$\mathscr {B}\mathrm {ord}^\theta (d)$
when restricting to compact manifolds throughout. By a minor enhancement of the argument in Section 4.1.2, the mapping
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathscr {B}\mathrm {ord}^\theta (d)$
are
$\mathscr {B}\mathrm {ord}^\theta (d)$
are
![]() $\infty $
-groupoids, so as for
$\infty $
-groupoids, so as for
![]() $\mathscr {B}\mathrm {ord}(d)$
, not much is lost by applying
$\mathscr {B}\mathrm {ord}(d)$
, not much is lost by applying
![]() $(-)^{(\infty ,1)}$
and considering the symmetric monoidal
$(-)^{(\infty ,1)}$
and considering the symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {B}\mathrm {ord}^\theta (d)^{(\infty ,1)}$
with closed
$\mathscr {B}\mathrm {ord}^\theta (d)^{(\infty ,1)}$
with closed
![]() $(d-1)$
-manifolds with
$(d-1)$
-manifolds with
![]() $\theta $
-structure on their once-stabilised tangent bundle as objects and as mapping spaces
$\theta $
-structure on their once-stabilised tangent bundle as objects and as mapping spaces
where
![]() $[W]$
ranges over compact bordisms
$[W]$
ranges over compact bordisms
![]() $W \colon P \leadsto Q$
up to diffeomorphism relative to the ends and
$W \colon P \leadsto Q$
up to diffeomorphism relative to the ends and
![]() $\mathrm {BDiff}^\theta _\partial (W,\theta _P \sqcup \theta _Q)$
is the quotient
$\mathrm {BDiff}^\theta _\partial (W,\theta _P \sqcup \theta _Q)$
is the quotient
![]() $\mathrm {Map}_{\mathrm {PSh}(\mathrm {GL}_d)_{\mathrm {Fr}(I \times P) \sqcup \mathrm {Fr}(I \sqcup Q)/}}(\mathrm {Fr}(W),\theta ) / \mathrm {Diff}_\partial (W)$
where the action is induced by precomposition (by standard bundle theory, this agrees with other definitions of
$\mathrm {Map}_{\mathrm {PSh}(\mathrm {GL}_d)_{\mathrm {Fr}(I \times P) \sqcup \mathrm {Fr}(I \sqcup Q)/}}(\mathrm {Fr}(W),\theta ) / \mathrm {Diff}_\partial (W)$
where the action is induced by precomposition (by standard bundle theory, this agrees with other definitions of
![]() $\mathrm {BDiff}^\theta _\partial (-)$
in the literature such as that in [Reference Galatius and Randal-WilliamsGRW14, Definition 1.5]). Composition is given by gluing
$\mathrm {BDiff}^\theta _\partial (-)$
in the literature such as that in [Reference Galatius and Randal-WilliamsGRW14, Definition 1.5]). Composition is given by gluing
![]() $\theta $
-bordisms and the symmetric monoidal structure by disjoint union.
$\theta $
-bordisms and the symmetric monoidal structure by disjoint union.
4.1.5 Variants with boundary
The discussion for the variants
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^\partial $
and
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)^\partial $
and
![]() $\mathscr {B}\mathrm {ord}(d)^\partial $
with boundary and their enhancements with tangential structures
$\mathscr {B}\mathrm {ord}(d)^\partial $
with boundary and their enhancements with tangential structures
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)^\partial $
and
$\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)^\partial $
and
![]() $\mathscr {B}\mathrm {ord}^\theta (d)^\partial $
is the same as that for the version without boundary, except that we allow the
$\mathscr {B}\mathrm {ord}^\theta (d)^\partial $
is the same as that for the version without boundary, except that we allow the
![]() $(d-1)$
-manifolds that appear as objects to have boundary and the bordisms
$(d-1)$
-manifolds that appear as objects to have boundary and the bordisms
![]() $W\colon P\leadsto Q$
to be bordisms of manifolds with boundary. The bordisms thus come with a decomposition
$W\colon P\leadsto Q$
to be bordisms of manifolds with boundary. The bordisms thus come with a decomposition
![]() $\partial W= \partial _0W \cup \partial ^hW\cup \partial _1W$
into codimension
$\partial W= \partial _0W \cup \partial ^hW\cup \partial _1W$
into codimension
![]() $0$
submanifolds where the ends
$0$
submanifolds where the ends
![]() $\partial _iW$
s are disjoint and come with identifications
$\partial _iW$
s are disjoint and come with identifications
![]() $P\cong \partial _0W$
and
$P\cong \partial _0W$
and
![]() $Q\cong \partial _1W$
, and the horizontal boundary
$Q\cong \partial _1W$
, and the horizontal boundary
![]() $\partial ^hW$
meets the ends in a corner. Embeddings between such manifolds are required to preserve this decomposition, map the interior to the interior, and be the identity near the ends, but they are allowed to move the horizontal boundary. The discussion for the variants
$\partial ^hW$
meets the ends in a corner. Embeddings between such manifolds are required to preserve this decomposition, map the interior to the interior, and be the identity near the ends, but they are allowed to move the horizontal boundary. The discussion for the variants
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)^\partial $
and
$\mathrm {nc}\mathscr {B}\mathrm {ord}^\theta (d)^\partial $
and
![]() $\mathscr {B}\mathrm {ord}^\theta (d)^\partial $
with tangential structures is similar; on the ends, the tangential structures are fixed, but not on the horizontal boundary.
$\mathscr {B}\mathrm {ord}^\theta (d)^\partial $
with tangential structures is similar; on the ends, the tangential structures are fixed, but not on the horizontal boundary.
4.1.6
 $\mathscr {D}\mathrm {isc}_d$
and
$\mathscr {D}\mathrm {isc}_d$
and
 $\mathscr {M}\mathrm {od}(d)$
$\mathscr {M}\mathrm {od}(d)$
The objects of the symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}\mathrm {isc}_d$
can be identified with d-manifolds without boundary that are diffeomorphic to a finite disjoint union of
$\mathscr {D}\mathrm {isc}_d$
can be identified with d-manifolds without boundary that are diffeomorphic to a finite disjoint union of
![]() $\mathbf {R}^d$
’s. The mapping spaces are given by codimension
$\mathbf {R}^d$
’s. The mapping spaces are given by codimension
![]() $0$
embeddings and the symmetric monoidal structure by disjoint union. Day convolution equips the
$0$
embeddings and the symmetric monoidal structure by disjoint union. Day convolution equips the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
of
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
of
![]() $\mathscr {S}$
-valued presheaves with a symmetric monoidal structure, and the objects of
$\mathscr {S}$
-valued presheaves with a symmetric monoidal structure, and the objects of
![]() $\mathscr {M}\mathrm {od}(d)=\mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
are associative algebras in
$\mathscr {M}\mathrm {od}(d)=\mathrm {ALG}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
are associative algebras in
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
(see Section 2.9). The mapping
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
(see Section 2.9). The mapping
![]() $\infty $
-category between two associative algebras
$\infty $
-category between two associative algebras
![]() $A,B \in \mathscr {M}\mathrm {od}(d)$
is the
$A,B \in \mathscr {M}\mathrm {od}(d)$
is the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {M}\mathrm {od}(d)_{A,B}$
of
$\mathscr {M}\mathrm {od}(d)_{A,B}$
of
![]() $(A,B)$
-bimodules and bimodule maps between these (see Section 2.8 where this category is denoted
$(A,B)$
-bimodules and bimodule maps between these (see Section 2.8 where this category is denoted
![]() $\mathrm {BMod}_{A,B}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
)). The composition functors
$\mathrm {BMod}_{A,B}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
)). The composition functors
![]() $\mathscr {M}\mathrm {od}(d)_{A,B} \times \mathscr {M}\mathrm {od}(d)_{B,C} \rightarrow \mathscr {M}\mathrm {od}(d)_{A,C}$
are given taking tensor products over B, which we denote by
$\mathscr {M}\mathrm {od}(d)_{A,B} \times \mathscr {M}\mathrm {od}(d)_{B,C} \rightarrow \mathscr {M}\mathrm {od}(d)_{A,C}$
are given taking tensor products over B, which we denote by
![]() $(-)\cup _{B}(-)$
to emphasise the similarity with the bordism category. The symmetric monoidal structure is given by external tensor product.
$(-)\cup _{B}(-)$
to emphasise the similarity with the bordism category. The symmetric monoidal structure is given by external tensor product.
4.1.7 The functor E
In terms of the identifications of the objects and mapping categories of source and target explained in Sections 4.1.1 and 4.1.6, the functor
![]() $E \colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d) \rightarrow \mathscr {M}\mathrm {od}(d)$
of symmetric monoidal double
$E \colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d) \rightarrow \mathscr {M}\mathrm {od}(d)$
of symmetric monoidal double
![]() $\infty $
-categories is on objects given by sending a
$\infty $
-categories is on objects given by sending a
![]() $(d-1)$
-manifold P to the presheaf
$(d-1)$
-manifold P to the presheaf
![]() $E_{P\times I}=\mathrm {Emb}(-,P\times I)$
where
$E_{P\times I}=\mathrm {Emb}(-,P\times I)$
where
![]() $I=[0,1]$
is equipped with the algebra structure induced by ‘stacking’. On mapping
$I=[0,1]$
is equipped with the algebra structure induced by ‘stacking’. On mapping
![]() $\infty $
-categories, it is given by the functor
$\infty $
-categories, it is given by the functor
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q} \rightarrow \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}$
which sends a bordism
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q} \rightarrow \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}$
which sends a bordism
![]() $W \colon M \leadsto N$
to the presheaf
$W \colon M \leadsto N$
to the presheaf
![]() $E_W=\mathrm {Emb}(-,W)$
with its
$E_W=\mathrm {Emb}(-,W)$
with its
![]() $(E_{P \times I},E_{Q \times I})$
-bimodule structure by ‘stacking’, using fixed collars
$(E_{P \times I},E_{Q \times I})$
-bimodule structure by ‘stacking’, using fixed collars
![]() $P\times I\hookrightarrow W$
and
$P\times I\hookrightarrow W$
and
![]() $Q\times I\hookrightarrow W$
of both ends, where the convention is that the canonical vector field on
$Q\times I\hookrightarrow W$
of both ends, where the convention is that the canonical vector field on
![]() $P \times I$
is inwards pointing and that of
$P \times I$
is inwards pointing and that of
![]() $Q\times I$
is outwards pointing. On morphisms, it sends an embedding
$Q\times I$
is outwards pointing. On morphisms, it sends an embedding
![]() $W \hookrightarrow W'$
that is fixed on the boundary to the map
$W \hookrightarrow W'$
that is fixed on the boundary to the map
![]() $E_W\rightarrow E_{W'}$
induced by postcomposition. That E is a functor of double
$E_W\rightarrow E_{W'}$
induced by postcomposition. That E is a functor of double
![]() $\infty $
-categories in particular says that, given bordisms
$\infty $
-categories in particular says that, given bordisms
![]() $W\colon P\leadsto Q$
and
$W\colon P\leadsto Q$
and
![]() $W'\colon Q\leadsto R$
, we have a preferred equivalence
$W'\colon Q\leadsto R$
, we have a preferred equivalence
![]() $E_{W\cup _QW'}\simeq E_W\cup _{E_{Q\times I}}E_{W'}$
of
$E_{W\cup _QW'}\simeq E_W\cup _{E_{Q\times I}}E_{W'}$
of
![]() $(E_{P\times I},E_{R\times I})$
-bimodules.
$(E_{P\times I},E_{R\times I})$
-bimodules.
We will often restrict the functor E to the levelwise subcategory
![]() $\mathscr {B}\mathrm {ord}(d)$
of
$\mathscr {B}\mathrm {ord}(d)$
of
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
and pass to underlying symmetric monoidal
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
and pass to underlying symmetric monoidal
![]() $\infty $
-categories (i.e., apply the functor
$\infty $
-categories (i.e., apply the functor
![]() $(-)^{(\infty ,1)}$
from Section 2.5.6, which has little effect on
$(-)^{(\infty ,1)}$
from Section 2.5.6, which has little effect on
![]() $\mathscr {B}\mathrm {ord}(d)$
; see Section 4.1.2) to obtain a functor of symmetric monoidal
$\mathscr {B}\mathrm {ord}(d)$
; see Section 4.1.2) to obtain a functor of symmetric monoidal
![]() $\infty $
-categories
$\infty $
-categories
![]() $E\colon \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}\rightarrow \mathscr {M}\mathrm {od}(d)^{(\infty ,1)}$
. Recall from Section 2.5.6 that the mapping spaces of
$E\colon \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}\rightarrow \mathscr {M}\mathrm {od}(d)^{(\infty ,1)}$
. Recall from Section 2.5.6 that the mapping spaces of
![]() $\mathscr {M}\mathrm {od}(d)^{(\infty ,1)}$
are given as
$\mathscr {M}\mathrm {od}(d)^{(\infty ,1)}$
are given as
![]() $\mathrm {Map}_{\mathscr {M}\mathrm {od}(d)^{(\infty ,1)}}(A,B)\simeq \mathscr {M}\mathrm {od}(d)^{\simeq }_{A,B}$
.
$\mathrm {Map}_{\mathscr {M}\mathrm {od}(d)^{(\infty ,1)}}(A,B)\simeq \mathscr {M}\mathrm {od}(d)^{\simeq }_{A,B}$
.
4.2 Descent with respect to Weiss
 $\infty $
-covers
$\infty $
-covers
We now prove a descent property for the mapping spaces in
![]() $\mathscr {M}\mathrm {od}(d)_{E_{P\times I},E_{Q\times I}}$
for (possibly noncompact)
$\mathscr {M}\mathrm {od}(d)_{E_{P\times I},E_{Q\times I}}$
for (possibly noncompact)
![]() $(d-1)$
-manifolds P and Q without boundary. To state it, given a bordism
$(d-1)$
-manifolds P and Q without boundary. To state it, given a bordism
![]() $W\colon P\leadsto Q$
, we write
$W\colon P\leadsto Q$
, we write
![]() $\mathscr {O}(W)$
for the poset of open subsets of W containing a neighbourhood of the boundary, ordered by inclusion. A subposet
$\mathscr {O}(W)$
for the poset of open subsets of W containing a neighbourhood of the boundary, ordered by inclusion. A subposet
![]() $\mathscr {U}\subset \mathscr {O}(M)$
is a Weiss
$\mathscr {U}\subset \mathscr {O}(M)$
is a Weiss
![]() $\infty $
-cover of M if any finite subset of M is contained in some
$\infty $
-cover of M if any finite subset of M is contained in some
![]() $O\in \mathscr {U}$
. Such a cover is complete if it contains a Weiss
$O\in \mathscr {U}$
. Such a cover is complete if it contains a Weiss
![]() $\infty $
-cover for
$\infty $
-cover for
![]() $\bigcap _{O\in \mathscr {U}'} O$
for any finite subset
$\bigcap _{O\in \mathscr {U}'} O$
for any finite subset
![]() $\mathscr {U}'\subset \mathscr {U}$
. A functor
$\mathscr {U}'\subset \mathscr {U}$
. A functor
![]() $F\colon \mathscr {O}(W)^{\mathrm {op}}\rightarrow \mathscr {C}$
to an
$F\colon \mathscr {O}(W)^{\mathrm {op}}\rightarrow \mathscr {C}$
to an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
satisfies descent for Weiss
$\mathscr {C}$
satisfies descent for Weiss
![]() $\infty $
-covers if for every nonempty
$\infty $
-covers if for every nonempty
![]() $O\in \mathscr {O}(W)$
and every complete Weiss
$O\in \mathscr {O}(W)$
and every complete Weiss
![]() $\infty $
-cover
$\infty $
-cover
![]() $\mathscr {U}\subset \mathscr {O}(O)$
, the diagram
$\mathscr {U}\subset \mathscr {O}(O)$
, the diagram
![]() $F(O)\rightarrow \{F(U)\}_{U\in \mathscr {U}}$
is a limit.
$F(O)\rightarrow \{F(U)\}_{U\in \mathscr {U}}$
is a limit.
Proposition 4.3. For a nonempty bordism
![]() $W\in \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
and a bimodule
$W\in \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
and a bimodule
![]() $X\in \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}$
, the functor
$X\in \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}$
, the functor
![]() $\mathrm {Map}_{\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}}(E_{(-)},X)\colon \mathscr {O}(W)^{\mathrm {op}}\rightarrow \mathscr {S}$
satisfies descent for Weiss
$\mathrm {Map}_{\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}}(E_{(-)},X)\colon \mathscr {O}(W)^{\mathrm {op}}\rightarrow \mathscr {S}$
satisfies descent for Weiss
![]() $\infty $
-covers.
$\infty $
-covers.
Proof. It suffices to show that for a given complete Weiss
![]() $\infty $
-cover
$\infty $
-cover
![]() $\mathscr {U}\subset \mathscr {O}(O)$
of nonempty open subset
$\mathscr {U}\subset \mathscr {O}(O)$
of nonempty open subset
![]() $O\in \mathscr {O}(W)$
, the diagram
$O\in \mathscr {O}(W)$
, the diagram
![]() $\{E_U\}_{U\in \mathscr {U}}\rightarrow E_O$
is a colimit diagram in
$\{E_U\}_{U\in \mathscr {U}}\rightarrow E_O$
is a colimit diagram in
![]() $\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}=\mathrm {BMod}_{E_{P \times I},E_{Q \times I}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
. Since
$\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}=\mathrm {BMod}_{E_{P \times I},E_{Q \times I}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
. Since
![]() $\mathscr {U}$
is cofiltered, its nerve is weakly contractible, so by Lemma 2.17 (i), it suffices to show that the diagram is a colimit diagram after applying the forgetful functor to
$\mathscr {U}$
is cofiltered, its nerve is weakly contractible, so by Lemma 2.17 (i), it suffices to show that the diagram is a colimit diagram after applying the forgetful functor to
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
. The result is is the diagram
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
. The result is is the diagram
![]() $\{\mathrm {Emb}(-,U)\}_{U\in \mathscr {U}}\rightarrow \mathrm {Emb}(-,O)$
in
$\{\mathrm {Emb}(-,U)\}_{U\in \mathscr {U}}\rightarrow \mathrm {Emb}(-,O)$
in
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
, so as colimits in functor categories are computed objectwise [Reference LurieLur09a, 5.1.2.3], it suffices to show that
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
, so as colimits in functor categories are computed objectwise [Reference LurieLur09a, 5.1.2.3], it suffices to show that
![]() $\{\mathrm {Emb}(T\times \mathbf {R}^d,U)\}_{U\in \mathscr {U}}\rightarrow \mathrm {Emb}(T\times \mathbf {R}^d ,O)$
is a colimit diagram in
$\{\mathrm {Emb}(T\times \mathbf {R}^d,U)\}_{U\in \mathscr {U}}\rightarrow \mathrm {Emb}(T\times \mathbf {R}^d ,O)$
is a colimit diagram in
![]() $\mathscr {S}$
for all finite sets T, or equivalently, that it is a homotopy colimit diagram in the Kan–Quillen model structure on simplicial sets. This holds by a well-known argument; see the proof of [Reference Knudsen and KupersKK24a, Lemma 6.4].
$\mathscr {S}$
for all finite sets T, or equivalently, that it is a homotopy colimit diagram in the Kan–Quillen model structure on simplicial sets. This holds by a well-known argument; see the proof of [Reference Knudsen and KupersKK24a, Lemma 6.4].
Remark 4.4. The assumption that W is nonempty is necessary: for
![]() $W=\varnothing $
, the empty cover
$W=\varnothing $
, the empty cover
![]() $\mathscr {U} = \varnothing $
is a cover of W, but
$\mathscr {U} = \varnothing $
is a cover of W, but
![]() $E_W$
is not the colimit of the empty diagram as
$E_W$
is not the colimit of the empty diagram as
![]() $E_W(\varnothing ) \simeq \ast $
.
$E_W(\varnothing ) \simeq \ast $
.
4.3 Relationship to embedding calculus
Using Proposition 4.3, we now relate the functor
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}_{P,Q}\rightarrow \mathscr {M}\mathrm {od}(d)_{P\times I,Q\times I}$
induced by E on mapping
$\mathrm {nc}\mathscr {B}\mathrm {ord}_{P,Q}\rightarrow \mathscr {M}\mathrm {od}(d)_{P\times I,Q\times I}$
induced by E on mapping
![]() $\infty $
-categories to the map
$\infty $
-categories to the map
![]() $\mathrm {Emb}_\partial (W,W')\rightarrow T_\infty \mathrm {Emb}_\partial (W,W')$
provided by embedding calculus as introduced in [Reference WeissWei99, Reference WeissWei11].
$\mathrm {Emb}_\partial (W,W')\rightarrow T_\infty \mathrm {Emb}_\partial (W,W')$
provided by embedding calculus as introduced in [Reference WeissWei99, Reference WeissWei11].
Theorem 4.5. Given bordisms
![]() $W,W'\in \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
, the map
$W,W'\in \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
, the map
agrees up to equivalence with the map
![]() $\mathrm {Emb}_\partial (W,W') \to T_\infty \mathrm {Emb}_\partial (W,W')$
from [Reference WeissWei99].
$\mathrm {Emb}_\partial (W,W') \to T_\infty \mathrm {Emb}_\partial (W,W')$
from [Reference WeissWei99].
Proof. We consider the poset
![]() $\mathscr {U}$
of open subsets
$\mathscr {U}$
of open subsets
![]() $U\subset W$
that are unions
$U\subset W$
that are unions
![]() $U=c(P) \cup D\cup c(Q)$
of three disjoint open subsets of W where
$U=c(P) \cup D\cup c(Q)$
of three disjoint open subsets of W where
![]() $c(P)$
and
$c(P)$
and
![]() $c(Q)$
are open collars of the boundary components P and Q and D is diffeomorphic to
$c(Q)$
are open collars of the boundary components P and Q and D is diffeomorphic to
![]() $T\times \mathbf {R}^d$
for some finite set T, ordered by inclusion. Considering
$T\times \mathbf {R}^d$
for some finite set T, ordered by inclusion. Considering
![]() $U\in \mathscr {U}$
as an object in
$U\in \mathscr {U}$
as an object in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
, we obtain a commutative square in
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
, we obtain a commutative square in
![]() $\mathscr {S}$
$\mathscr {S}$

whose vertical arrows are induced by restriction. By Lemma 4.1, the map ![]() agrees with the restriction map
agrees with the restriction map
![]() $\mathrm {Emb}_\partial (W,W')\rightarrow \lim _{U\in \mathscr {U}}\mathrm {Emb}_\partial (U,W')$
which in turn agrees with the map
$\mathrm {Emb}_\partial (W,W')\rightarrow \lim _{U\in \mathscr {U}}\mathrm {Emb}_\partial (U,W')$
which in turn agrees with the map
![]() $\mathrm {Emb}_\partial (W,W')\rightarrow T_\infty \mathrm {Emb}_\partial (W,W')$
by the discussion in [Reference WeissWei99, Sections 5, 10], so the claim follows once we show that
$\mathrm {Emb}_\partial (W,W')\rightarrow T_\infty \mathrm {Emb}_\partial (W,W')$
by the discussion in [Reference WeissWei99, Sections 5, 10], so the claim follows once we show that ![]() and
and ![]() are equivalences. As
are equivalences. As
![]() $\mathscr {U}\subset \mathscr {O}(W)$
is a complete Weiss
$\mathscr {U}\subset \mathscr {O}(W)$
is a complete Weiss
![]() $\infty $
-cover, the map
$\infty $
-cover, the map ![]() is an equivalence by Proposition 4.3. To prove that the map
is an equivalence by Proposition 4.3. To prove that the map ![]() is an equivalence, we show that for all
is an equivalence, we show that for all
![]() $U\in \mathscr {U}$
, the individual maps
$U\in \mathscr {U}$
, the individual maps
before taking limits are equivalences. To give a convincing proof of this, we rely on the specific construction of E from Section 3 and refer to that section for the notation. Recall that the functor E arose from restricting the codomain of the composition of simplicial objects in
![]() $\infty $
-categories
$\infty $
-categories
where
![]() $(\iota ^*\circ y)\colon \mathscr {M}\mathrm {an}_d\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
is the Yoneda embedding followed by restriction along the inclusion
$(\iota ^*\circ y)\colon \mathscr {M}\mathrm {an}_d\rightarrow \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
is the Yoneda embedding followed by restriction along the inclusion
![]() $\iota \colon \mathscr {D}\mathrm {isc}_d \hookrightarrow \mathscr {M}\mathrm {an}_d$
. This factorisation induces a commutative diagram
$\iota \colon \mathscr {D}\mathrm {isc}_d \hookrightarrow \mathscr {M}\mathrm {an}_d$
. This factorisation induces a commutative diagram

where the top composition is obtained from (71) by evaluation at
![]() $[1]$
and taking fibres of the face maps
$[1]$
and taking fibres of the face maps
![]() $(d_0,d_1)$
, the middle and rightmost vertical map are the forgetful maps from Lemma 2.17 and the bottom left horizontal map is the coherent nerve of the functor
$(d_0,d_1)$
, the middle and rightmost vertical map are the forgetful maps from Lemma 2.17 and the bottom left horizontal map is the coherent nerve of the functor
![]() $\mathsf {ncBord}(d)_{[1]}\rightarrow \mathsf {Man}_d$
of
$\mathsf {ncBord}(d)_{[1]}\rightarrow \mathsf {Man}_d$
of
![]() $\mathsf {Kan}$
-enriched categories that sends a
$\mathsf {Kan}$
-enriched categories that sends a
![]() $[1]$
-walled manifold
$[1]$
-walled manifold
![]() $(W,\mu )$
to
$(W,\mu )$
to
![]() $W|_{(\mu (0)-\epsilon ,\mu (1)+\epsilon )}$
. In particular, for
$W|_{(\mu (0)-\epsilon ,\mu (1)+\epsilon )}$
. In particular, for
![]() $U=c(P)\cup D \cup c(Q)\in \mathscr {U}$
considered as an object in
$U=c(P)\cup D \cup c(Q)\in \mathscr {U}$
considered as an object in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
, the inclusion
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
, the inclusion
![]() $D\subset U$
viewed as a morphism in
$D\subset U$
viewed as a morphism in
![]() $\mathscr {M}\mathrm {an}_d$
gives a morphism
$\mathscr {M}\mathrm {an}_d$
gives a morphism
![]() $D\rightarrow U_{E^{\mathrm {geo}}(P),E^{\mathrm {geo}}(Q)}(E^{\mathrm {geo}}(U))$
in
$D\rightarrow U_{E^{\mathrm {geo}}(P),E^{\mathrm {geo}}(Q)}(E^{\mathrm {geo}}(U))$
in
![]() $\mathscr {M}\mathrm {an}_d$
, so by adjunction, a morphism
$\mathscr {M}\mathrm {an}_d$
, so by adjunction, a morphism
![]() $F_{E^{\mathrm {geo}}(P),E^{\mathrm {geo}}(Q)}(D)\rightarrow E^{\mathrm {geo}}(U)$
in
$F_{E^{\mathrm {geo}}(P),E^{\mathrm {geo}}(Q)}(D)\rightarrow E^{\mathrm {geo}}(U)$
in
![]() $\mathrm {BMod}_{E^{\mathrm {geo}}(P),E^{\mathrm {geo}}(Q)}(\mathscr {M}\mathrm {an}_d)$
which we claim to be an equivalence. By Lemma 2.17 (ii), it suffices to show that the image
$\mathrm {BMod}_{E^{\mathrm {geo}}(P),E^{\mathrm {geo}}(Q)}(\mathscr {M}\mathrm {an}_d)$
which we claim to be an equivalence. By Lemma 2.17 (ii), it suffices to show that the image
under
![]() $U_{E^{\mathrm {geo}}(M),E^{\mathrm {geo}}(N)}$
is an equivalence. This is a consequence of the second part of Lemma 2.17 (iii). Applying
$U_{E^{\mathrm {geo}}(M),E^{\mathrm {geo}}(N)}$
is an equivalence. This is a consequence of the second part of Lemma 2.17 (iii). Applying
![]() $(\iota ^*\circ y)$
and using Lemma 2.17 (iv), it follows that the natural map
$(\iota ^*\circ y)$
and using Lemma 2.17 (iv), it follows that the natural map
![]() $F_{E_{P \times I},E_{Q \times I}}(E_D)\rightarrow E_U$
in
$F_{E_{P \times I},E_{Q \times I}}(E_D)\rightarrow E_U$
in
![]() $\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}$
is an equivalence. As
$\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}$
is an equivalence. As
![]() $F_{E_{P \times I},E_{Q \times I}}$
is left-adjoint to the forgetful functor
$F_{E_{P \times I},E_{Q \times I}}$
is left-adjoint to the forgetful functor
![]() $U_{E_{P \times I},E_{Q \times I}}$
, the map (70) thus has the form
$U_{E_{P \times I},E_{Q \times I}}$
, the map (70) thus has the form
and is given by the restriction map
![]() $\mathrm {Emb}_\partial (c(M)\cup D\cup c(N),W')\rightarrow \mathrm {Emb}_\partial (D,W')$
followed by the map induced by the Yoneda embedding. The former is an equivalence by the contractibility of the space of collars, and the latter is an equivalence by the Yoneda lemma since D lies in the full subcategory
$\mathrm {Emb}_\partial (c(M)\cup D\cup c(N),W')\rightarrow \mathrm {Emb}_\partial (D,W')$
followed by the map induced by the Yoneda embedding. The former is an equivalence by the contractibility of the space of collars, and the latter is an equivalence by the Yoneda lemma since D lies in the full subcategory
![]() $\mathscr {D}\mathrm {isc}_d\subset \mathscr {M}\mathrm {an}_d$
, so the composition is an equivalence.
$\mathscr {D}\mathrm {isc}_d\subset \mathscr {M}\mathrm {an}_d$
, so the composition is an equivalence.
Remark 4.6. The first part of the previous proof in particular shows that for bordisms
![]() $W\in \mathrm {nc}\mathscr {B}\mathrm {ord}_{P,Q}$
that are diffeomorphic, relative to the ends, to
$W\in \mathrm {nc}\mathscr {B}\mathrm {ord}_{P,Q}$
that are diffeomorphic, relative to the ends, to
![]() $[0,1)\times P\sqcup T\times \mathbf {R}^d \sqcup (-1,0]\times Q$
for some finite set T, the map (69) is an equivalence for all bordisms
$[0,1)\times P\sqcup T\times \mathbf {R}^d \sqcup (-1,0]\times Q$
for some finite set T, the map (69) is an equivalence for all bordisms
![]() $W'\in \mathrm {nc}\mathscr {B}\mathrm {ord}_{P,Q}$
. In particular, for
$W'\in \mathrm {nc}\mathscr {B}\mathrm {ord}_{P,Q}$
. In particular, for
![]() $T=\varnothing $
, we see from the contractibility of the space of collars that both the source and target of this map are both contractible.
$T=\varnothing $
, we see from the contractibility of the space of collars that both the source and target of this map are both contractible.
Combining Theorem 4.5 with the convergence of embedding calculus in handle codimension
![]() $\ge 3$
due to Goodwillie, Klein and Weiss (see [Reference Goodwillie and WeissGW99, Fact 5.1] and [Reference Goodwillie and KleinGK15]), we conclude the following:
$\ge 3$
due to Goodwillie, Klein and Weiss (see [Reference Goodwillie and WeissGW99, Fact 5.1] and [Reference Goodwillie and KleinGK15]), we conclude the following:
Corollary 4.7. Fix bordisms
![]() $W,W'\in \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
. If W can be obtained from a closed collar of
$W,W'\in \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
. If W can be obtained from a closed collar of
![]() $P\sqcup Q\cong \partial W$
by attaching handles of index
$P\sqcup Q\cong \partial W$
by attaching handles of index
![]() $\le d-3$
, then the map
$\le d-3$
, then the map
induced by E is an equivalence.
4.3.1 Comparison with the model of Boavida de Brito–Weiss
Theorem 4.5 shows that the map (69) is a model for embedding calculus, so agrees up to weak equivalence with any other model. Among the previously established models, that of Boavida de Brito–Weiss [Reference Boavida de Brito and WeissBdBW13] is closest to ours. Like ours, their model enhances the embedding calculus approximation
![]() $\mathrm {Emb}_\partial (W,W')\rightarrow T_\infty \mathrm {Emb}_\partial (W,W')$
to a functor on
$\mathrm {Emb}_\partial (W,W')\rightarrow T_\infty \mathrm {Emb}_\partial (W,W')$
to a functor on
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
. This section serves to extend Theorem 4.5 to a comparison of the functors as opposed to just the individual maps on mapping spaces. This will in particular show that the monoid structures on
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
. This section serves to extend Theorem 4.5 to a comparison of the functors as opposed to just the individual maps on mapping spaces. This will in particular show that the monoid structures on
![]() $T_\infty \mathrm {Emb}_\partial (W,W)$
induced by composition in our and their model agree, which we will use in Section 8.1.
$T_\infty \mathrm {Emb}_\partial (W,W)$
induced by composition in our and their model agree, which we will use in Section 8.1.
For this, we write
![]() $(\mathscr {D}\mathrm {isc}_d)_{P,Q}\subset \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
for the full subcategory of those bordisms that are diffeomorphic relative to the boundary to
$(\mathscr {D}\mathrm {isc}_d)_{P,Q}\subset \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
for the full subcategory of those bordisms that are diffeomorphic relative to the boundary to
![]() $P\times [0,1)\sqcup T\times \mathbf {R}^d\sqcup (-1,0]\times Q$
for some finite set T. When translated from
$P\times [0,1)\sqcup T\times \mathbf {R}^d\sqcup (-1,0]\times Q$
for some finite set T. When translated from
![]() $\mathsf {Kan}$
-enriched categories to
$\mathsf {Kan}$
-enriched categories to
![]() $\infty $
-categories, Boavida de Brito–Weiss’s model for the embedding calculus approximation
$\infty $
-categories, Boavida de Brito–Weiss’s model for the embedding calculus approximation
![]() $\mathrm {Emb}_\partial (W,W')\rightarrow T_\infty \mathrm {Emb}_\partial (W,W')$
is the map on mapping spaces between W and
$\mathrm {Emb}_\partial (W,W')\rightarrow T_\infty \mathrm {Emb}_\partial (W,W')$
is the map on mapping spaces between W and
![]() $W'$
induced by the composition
$W'$
induced by the composition
of the Yoneda embedding with the inclusion
![]() $\iota \colon (\mathscr {D}\mathrm {isc}_d)_{P,Q}\hookrightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
(cf. Section 9 loc.cit.).
$\iota \colon (\mathscr {D}\mathrm {isc}_d)_{P,Q}\hookrightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
(cf. Section 9 loc.cit.).
Proposition 4.8. There is an equivalence of
![]() $\infty $
-categories
$\infty $
-categories
which fits into a commutative diagram of
![]() $\infty $
-categories
$\infty $
-categories

Proof. The functor
![]() $\varphi $
is defined as the composition
$\varphi $
is defined as the composition
With this choice, the canonical natural transformation
![]() $y\rightarrow E^*\circ y \circ E$
induces a natural transformation from the right-hand diagonal functor
$y\rightarrow E^*\circ y \circ E$
induces a natural transformation from the right-hand diagonal functor
![]() $(\iota ^*\circ y)$
in the claimed triangle to
$(\iota ^*\circ y)$
in the claimed triangle to
![]() $(\varphi \circ E)$
, and we will first show that this is an equivalence to obtain commutativity of the triangle. On a bordism
$(\varphi \circ E)$
, and we will first show that this is an equivalence to obtain commutativity of the triangle. On a bordism
![]() $W\in \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
, this natural transformation is the map in
$W\in \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
, this natural transformation is the map in
![]() $\mathrm {PSh}((\mathscr {D}\mathrm {isc}_d)_{P,Q})$
induced by E
$\mathrm {PSh}((\mathscr {D}\mathrm {isc}_d)_{P,Q})$
induced by E
which is an equivalence by Remark 4.6. Note that this in particular shows that
![]() $E\circ \iota $
is fully faithful.
$E\circ \iota $
is fully faithful.
It remains to show that
![]() $\varphi $
is an equivalence. We will use that for
$\varphi $
is an equivalence. We will use that for
![]() $U\in (\mathscr {D}\mathrm {isc}_d)_{P,Q}$
, we have
$U\in (\mathscr {D}\mathrm {isc}_d)_{P,Q}$
, we have
![]() $E_{U}\simeq F_{E_{P \times I},E_{Q \times I}}(E_{T_U\times \mathbf {R}^d})\in \mathscr {M}\mathrm {od}(d)_{E_{P \times I}}$
as a result of the final part of the proof of Theorem 4.5; here,
$E_{U}\simeq F_{E_{P \times I},E_{Q \times I}}(E_{T_U\times \mathbf {R}^d})\in \mathscr {M}\mathrm {od}(d)_{E_{P \times I}}$
as a result of the final part of the proof of Theorem 4.5; here,
![]() $T_U$
is the finite set such that
$T_U$
is the finite set such that
![]() $U\cong P\times [0,1)\sqcup T_U\times \mathbf {R}^d\sqcup (-1,0]\times Q$
. This property in particular implies that
$U\cong P\times [0,1)\sqcup T_U\times \mathbf {R}^d\sqcup (-1,0]\times Q$
. This property in particular implies that
![]() $\varphi $
is conservative, using that
$\varphi $
is conservative, using that
![]() $U_{E_{P \times I},E_{Q \times I}}$
is conservative by Lemma 2.17 (ii), and that a map of presheaves is an equivalence if it is one objectwise. To show that
$U_{E_{P \times I},E_{Q \times I}}$
is conservative by Lemma 2.17 (ii), and that a map of presheaves is an equivalence if it is one objectwise. To show that
![]() $\varphi $
is an equivalence, it thus suffices to prove that it has a fully faithful left adjoint. This left adjoint is given by the colimit preserving extension
$\varphi $
is an equivalence, it thus suffices to prove that it has a fully faithful left adjoint. This left adjoint is given by the colimit preserving extension
![]() $\smash {\overline {E\circ \iota }\colon \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)_{P,Q})\rightarrow \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}}$
along the Yoneda embedding of the fully faithful functor
$\smash {\overline {E\circ \iota }\colon \mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)_{P,Q})\rightarrow \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}}$
along the Yoneda embedding of the fully faithful functor
![]() $E\circ \iota $
, using that
$E\circ \iota $
, using that
![]() $\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}\simeq \mathrm {BMod}_{E_{P \times I},E_{Q \times I}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
has colimits as a result of Lemma 2.17. By [Reference LurieLur09a, 5.1.6.10], this left adjoint
$\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}\simeq \mathrm {BMod}_{E_{P \times I},E_{Q \times I}}(\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d))$
has colimits as a result of Lemma 2.17. By [Reference LurieLur09a, 5.1.6.10], this left adjoint
![]() $\overline {E\circ \iota }$
is fully faithful if
$\overline {E\circ \iota }$
is fully faithful if
![]() $E_{U}\in \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}$
is completely compact for all
$E_{U}\in \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}$
is completely compact for all
![]() $U\in (\mathscr {D}\mathrm {isc}_d)_{P,Q}$
, i.e. if
$U\in (\mathscr {D}\mathrm {isc}_d)_{P,Q}$
, i.e. if
![]() ${\mathrm {Map}_{\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}}(E_U,-)\colon \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}\rightarrow \mathscr {S}}$
preserves small colimits. Since
${\mathrm {Map}_{\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}}(E_U,-)\colon \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}\rightarrow \mathscr {S}}$
preserves small colimits. Since
![]() $E_{U}\simeq F_{E_{P \times I},E_{Q \times I}}(E_{T_U\times \mathbf {R}^d})$
, this condition is by adjunction equivalent to
$E_{U}\simeq F_{E_{P \times I},E_{Q \times I}}(E_{T_U\times \mathbf {R}^d})$
, this condition is by adjunction equivalent to
![]() $\smash {\mathrm {Map}_{\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)}(E_{T_U\times \mathbf {R}^d},U_{E_{P \times I},E_{Q \times I}}(-))}$
preserving small colimits which indeed holds, by the Yoneda lemma and the fact that
$\smash {\mathrm {Map}_{\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)}(E_{T_U\times \mathbf {R}^d},U_{E_{P \times I},E_{Q \times I}}(-))}$
preserving small colimits which indeed holds, by the Yoneda lemma and the fact that
![]() $U_{E_{P \times I},E_{Q \times I}}$
preserves colimits by Lemma 2.17 (i).
$U_{E_{P \times I},E_{Q \times I}}$
preserves colimits by Lemma 2.17 (i).
Remark 4.9. Considering bordisms
![]() $W\colon P\leadsto Q$
as bordisms
$W\colon P\leadsto Q$
as bordisms
![]() $\varnothing \leadsto P\sqcup Q$
or
$\varnothing \leadsto P\sqcup Q$
or
![]() $P\sqcup Q\leadsto \varnothing $
leads to equivalences between
$P\sqcup Q\leadsto \varnothing $
leads to equivalences between
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
,
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}$
,
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{\varnothing ,P\sqcup Q},$
and
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{\varnothing ,P\sqcup Q},$
and
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P\sqcup Q,\varnothing }$
, and similarly for
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P\sqcup Q,\varnothing }$
, and similarly for
![]() $(\mathscr {D}\mathrm {isc}_d)_{P\sqcup Q}$
– compatible with the functor
$(\mathscr {D}\mathrm {isc}_d)_{P\sqcup Q}$
– compatible with the functor
![]() $(\iota ^*\circ y)$
. It thus follows from Proposition 4.8 that
$(\iota ^*\circ y)$
. It thus follows from Proposition 4.8 that
![]() $E\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}\rightarrow \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}$
agrees up to equivalences with the analogous functors involving
$E\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P,Q}\rightarrow \mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{Q \times I}}$
agrees up to equivalences with the analogous functors involving
![]() $\mathscr {M}\mathrm {od}(d)_{E_{\varnothing },E_{P\times I\sqcup Q \times I}}$
or
$\mathscr {M}\mathrm {od}(d)_{E_{\varnothing },E_{P\times I\sqcup Q \times I}}$
or
![]() $\mathscr {M}\mathrm {od}(d)_{E_{P\times I\sqcup Q \times I,E_{\varnothing }}}$
. That the latter two categories are equivalent can also be deduced from Remark 2.16 and [Reference LurieLur17, 4.6.3.11] (no
$\mathscr {M}\mathrm {od}(d)_{E_{P\times I\sqcup Q \times I,E_{\varnothing }}}$
. That the latter two categories are equivalent can also be deduced from Remark 2.16 and [Reference LurieLur17, 4.6.3.11] (no
![]() $(-)^{\mathrm {rev}}$
appears since we implicitly used the anti-homomorphism of
$(-)^{\mathrm {rev}}$
appears since we implicitly used the anti-homomorphism of
![]() $E_{P \times I}$
or
$E_{P \times I}$
or
![]() $E_{Q \times I}$
by reflection in I).
$E_{Q \times I}$
by reflection in I).
4.4 Isotopy extension for E
A key input in the proof of Theorem A in Section 5.3 will be a version of the isotopy extension theorem for the mapping spaces in
![]() $\mathscr {M}\mathrm {od}(d)_{P,Q}$
. In view of Theorem 4.5, this amounts to an isotopy extension theorem for embedding calculus. Such a theorem has been proved by Knudsen–Kupers [Reference Knudsen and KupersKK24a, Theorem 6.1], but instead of reducing the version we need from theirs, it is more convenient to give a direct proof based on their strategy.
$\mathscr {M}\mathrm {od}(d)_{P,Q}$
. In view of Theorem 4.5, this amounts to an isotopy extension theorem for embedding calculus. Such a theorem has been proved by Knudsen–Kupers [Reference Knudsen and KupersKK24a, Theorem 6.1], but instead of reducing the version we need from theirs, it is more convenient to give a direct proof based on their strategy.
The setting is as follows. We fix two compact bordisms
![]() $W\colon P\leadsto Q$
,
$W\colon P\leadsto Q$
,
![]() $W'\colon R\leadsto S$
, two possibly noncompact bordisms
$W'\colon R\leadsto S$
, two possibly noncompact bordisms
![]() $M,N\colon Q\leadsto R$
, and an open collar neighbourhood
$M,N\colon Q\leadsto R$
, and an open collar neighbourhood
![]() $c(M)\subset M$
viewed as a bordism
$c(M)\subset M$
viewed as a bordism
![]() $Q\leadsto R$
. Writing c for the inclusion
$Q\leadsto R$
. Writing c for the inclusion
![]() $c(M)\subset M$
viewed as a morphism in
$c(M)\subset M$
viewed as a morphism in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{Q,R}$
, we have a commutative diagram
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{Q,R}$
, we have a commutative diagram

which maps via the functor
![]() $E\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)\rightarrow \mathscr {M}\mathrm {od}(d)$
to the corresponding square for
$E\colon \mathrm {nc}\mathscr {B}\mathrm {ord}(d)\rightarrow \mathscr {M}\mathrm {od}(d)$
to the corresponding square for
![]() $\mathscr {M}\mathrm {od}(d)$
$\mathscr {M}\mathrm {od}(d)$

Note that the bottom left corners in both squares are contractible by Remark 4.6. Moreover, in view of Lemma 4.1, the square ![]() has up to equivalence the form
has up to equivalence the form

As the restriction map
![]() $\mathrm {Emb}_\partial (W\cup _Qc(M)\cup _RW',W \cup _Q N\cup _R W')\rightarrow \mathrm {Emb}_{P\sqcup S}(W\sqcup W',W\cup _Q N\cup _R W')$
is an equivalence and
$\mathrm {Emb}_\partial (W\cup _Qc(M)\cup _RW',W \cup _Q N\cup _R W')\rightarrow \mathrm {Emb}_{P\sqcup S}(W\sqcup W',W\cup _Q N\cup _R W')$
is an equivalence and
![]() $W\sqcup W'$
is compact, it follows from the parametrised isotopy extension theorem that this square is cartesian, so the same holds for the square
$W\sqcup W'$
is compact, it follows from the parametrised isotopy extension theorem that this square is cartesian, so the same holds for the square ![]() .
.
The isotopy extension result we will prove says that the same holds for ![]() under a certain condition on the convergence of embedding calculus – namely, that the map from the bottom right of
under a certain condition on the convergence of embedding calculus – namely, that the map from the bottom right of ![]() to the bottom right corner of
to the bottom right corner of ![]() is an equivalence if M is replaced by
is an equivalence if M is replaced by ![]() for
for
![]() $\underline {k} = \{1,2,\ldots ,k\}$
and all
$\underline {k} = \{1,2,\ldots ,k\}$
and all
![]() $k\ge 0$
. We denote by
$k\ge 0$
. We denote by ![]() the square obtained from
the square obtained from ![]() by replacing the categories
by replacing the categories
![]() $\mathscr {M}\mathrm {od}(d)_{E_{Q \times I},E_{R \times I}}$
and
$\mathscr {M}\mathrm {od}(d)_{E_{Q \times I},E_{R \times I}}$
and
![]() $\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{S\times I}}$
in the top row by their cores.
$\mathscr {M}\mathrm {od}(d)_{E_{P \times I},E_{S\times I}}$
in the top row by their cores.
Theorem 4.10. If the map induced by E
 $$\begin{align*}& \mathrm{Map}_{\mathrm{nc}\mathscr{B}\mathrm{ord}(d)_{P,S}} \big(W\cup_QC_k\cup_RW',W\cup_QN\cup_RW'\big)\\ &\quad \rightarrow\mathrm{Map}_{\mathscr{M}\mathrm{od}(d)_{E_{P \times I},E_{S\times I}}}\big(E_{W\cup_QC_k\cup_RW'},E_{W\cup_QN\cup_RW'}\big) \end{align*}$$
$$\begin{align*}& \mathrm{Map}_{\mathrm{nc}\mathscr{B}\mathrm{ord}(d)_{P,S}} \big(W\cup_QC_k\cup_RW',W\cup_QN\cup_RW'\big)\\ &\quad \rightarrow\mathrm{Map}_{\mathscr{M}\mathrm{od}(d)_{E_{P \times I},E_{S\times I}}}\big(E_{W\cup_QC_k\cup_RW'},E_{W\cup_QN\cup_RW'}\big) \end{align*}$$
is an equivalence for all
![]() $k\ge 0$
, then the square
$k\ge 0$
, then the square ![]() is cartesian. If this assumption in addition holds for M in place of N, then the square
is cartesian. If this assumption in addition holds for M in place of N, then the square ![]() is also cartesian.
is also cartesian.
Proof. We first show the claim for ![]() . We write
. We write
![]() $\mathscr {U}$
for the poset of open subsets of M that are unions
$\mathscr {U}$
for the poset of open subsets of M that are unions
![]() $U=D\cup c'(M)$
such that
$U=D\cup c'(M)$
such that
![]() $c(M)\subset M$
is an open collar of the boundary that contains the chosen collar
$c(M)\subset M$
is an open collar of the boundary that contains the chosen collar
![]() $c(M)\subset M$
and
$c(M)\subset M$
and
![]() $D\subset M$
is diffeomorphic to
$D\subset M$
is diffeomorphic to
![]() $T\times \mathbf {R}^d$
for some finite set T. Considering U as an object in
$T\times \mathbf {R}^d$
for some finite set T. Considering U as an object in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{Q,R}$
, we have a functor
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{Q,R}$
, we have a functor
![]() $\mathscr {U}\rightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{Q,R}$
. Since the square
$\mathscr {U}\rightarrow \mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{Q,R}$
. Since the square ![]() is natural in M, it maps to the limit of the same squares for M replaced by
is natural in M, it maps to the limit of the same squares for M replaced by
![]() $U\in \mathscr {U}$
$U\in \mathscr {U}$

We claim that it suffices to show this square of limits is cartesian. To justify this, we show that the maps from ![]() to the square of limits are all equivalences. For the maps between the bottom left corners and between the bottom right corners, this follows from the fact that the diagram is constant and the category
to the square of limits are all equivalences. For the maps between the bottom left corners and between the bottom right corners, this follows from the fact that the diagram is constant and the category
![]() $\mathscr {U}$
is weakly contractible since it is cofiltered. For the top-right corner and top-left corner, it follows from Proposition 4.3 since the posets
$\mathscr {U}$
is weakly contractible since it is cofiltered. For the top-right corner and top-left corner, it follows from Proposition 4.3 since the posets
![]() $\mathscr {U}$
and
$\mathscr {U}$
and
![]() $\{W\cup _QU\cup _RW'\,|\,U\in \mathscr {U}\}$
are complete Weiss
$\{W\cup _QU\cup _RW'\,|\,U\in \mathscr {U}\}$
are complete Weiss
![]() $\infty $
-covers of M and
$\infty $
-covers of M and
![]() $W\cup _QM\cup _RW'$
.
$W\cup _QM\cup _RW'$
.
To show that the previous square of limits is cartesian, note that it receives a map from the analogous square using
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
instead of
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
instead of
![]() $\mathscr {M}\mathrm {od}(d)$
, and this map of squares consists of equivalences: for the top right and bottom right corner, it holds by assumption, and for the top left and bottom left corner, it holds by Remark 4.6. The square using
$\mathscr {M}\mathrm {od}(d)$
, and this map of squares consists of equivalences: for the top right and bottom right corner, it holds by assumption, and for the top left and bottom left corner, it holds by Remark 4.6. The square using
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
is a limit of squares of the form
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
is a limit of squares of the form ![]() , with M replaced by
, with M replaced by
![]() $U\in \mathscr {U}$
, so it is cartesian since we have already explained that
$U\in \mathscr {U}$
, so it is cartesian since we have already explained that ![]() is cartesian and limits of cartesian squares remain cartesian.
is cartesian and limits of cartesian squares remain cartesian.
To show the claim for ![]() , we first assume
, we first assume
![]() $M=N$
, in which case, the claim follows from the following fact: given a monoid A in
$M=N$
, in which case, the claim follows from the following fact: given a monoid A in
![]() $\mathscr {S}$
acting on a space X and
$\mathscr {S}$
acting on a space X and
![]() $x\in X$
, consider the fibre sequence
$x\in X$
, consider the fibre sequence
whose fibre inherits the structure of a monoid in
![]() $\mathscr {S}$
from that of A and the A-action on X. Then one checks that the sequence obtained by passing to group-like components in fibre and total space remains a fibre sequence.
$\mathscr {S}$
from that of A and the A-action on X. Then one checks that the sequence obtained by passing to group-like components in fibre and total space remains a fibre sequence.
To deduce the general case of ![]() from that of
from that of ![]() , it suffices to prove that if
, it suffices to prove that if
![]() $\varphi \colon E_M \to E_N$
has the property that
$\varphi \colon E_M \to E_N$
has the property that ![]() is an equivalence, then
is an equivalence, then
![]() $\varphi $
is also an equivalence. To prove this, we pick an inverse
$\varphi $
is also an equivalence. To prove this, we pick an inverse
![]() $\psi ' \colon E_{W \cup _Q N \cup _R W'} \to E_{W \cup _Q M \cup _R W'}$
to
$\psi ' \colon E_{W \cup _Q N \cup _R W'} \to E_{W \cup _Q M \cup _R W'}$
to
![]() $\varphi '$
and claim that the image of
$\varphi '$
and claim that the image of
![]() $\psi '$
under the right-vertical map in the square
$\psi '$
under the right-vertical map in the square ![]() with the role of M and N reversed lies in the component of the bottom horizontal map. To see this, we extend this square to the bottom by
with the role of M and N reversed lies in the component of the bottom horizontal map. To see this, we extend this square to the bottom by

where the left vertical map is an equivalence as both source and target are contractible, and the right vertical map is an equivalence because
![]() $\varphi '$
is one by assumption. To see whether the image of
$\varphi '$
is one by assumption. To see whether the image of
![]() $\psi '$
in the upper right corner is in the component hit by the upper horizontal map, it thus suffices to show that the image of
$\psi '$
in the upper right corner is in the component hit by the upper horizontal map, it thus suffices to show that the image of
![]() $\psi '$
in the bottom horizontal corner is in the component hit by the bottom horizontal map. But this follows from the relation
$\psi '$
in the bottom horizontal corner is in the component hit by the bottom horizontal map. But this follows from the relation
![]() $[\varphi '\circ \psi ']=[\mathrm {id}]$
in the set of components, which holds by the choice of
$[\varphi '\circ \psi ']=[\mathrm {id}]$
in the set of components, which holds by the choice of
![]() $\psi '$
. Using that the square
$\psi '$
. Using that the square ![]() with the role of M and N reverse is a pullback (this is where we use the additional hypothesis for M), we conclude that there exists
with the role of M and N reverse is a pullback (this is where we use the additional hypothesis for M), we conclude that there exists
![]() $\psi \colon E_N \to E_M$
such that
$\psi \colon E_N \to E_M$
such that
![]() $[\psi ']= [W\cup _Q\psi \cup _RW']$
. To finish the proof, it suffices to show that
$[\psi ']= [W\cup _Q\psi \cup _RW']$
. To finish the proof, it suffices to show that
![]() $\varphi \circ \psi $
and
$\varphi \circ \psi $
and
![]() $\psi \circ \varphi $
are both equivalences, since then
$\psi \circ \varphi $
are both equivalences, since then
![]() $\varphi $
has to be an equivalence. But this follows from the case
$\varphi $
has to be an equivalence. But this follows from the case
![]() $M=N$
treated above, using that both compositions become equivalences after applying
$M=N$
treated above, using that both compositions become equivalences after applying
![]() $W\cup _Q(-)\cup _RW'$
since this even holds for
$W\cup _Q(-)\cup _RW'$
since this even holds for
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
individually.
$\varphi $
individually.
Remark 4.11. The proof of Theorem 4.10 in particular shows that if the assumption in the statement holds for M and N, then the following map detects equivalences:
4.5
 $\mathscr {D}\mathrm {isc}$
-structure spaces
$\mathscr {D}\mathrm {isc}$
-structure spaces
We conclude this section with the definition of the
![]() $\mathscr {D}\mathrm {isc}$
-structure spaces and a discussion some of their functoriality. Given objects
$\mathscr {D}\mathrm {isc}$
-structure spaces and a discussion some of their functoriality. Given objects
![]() $P\in \mathscr {B}\mathrm {ord}(d)$
and
$P\in \mathscr {B}\mathrm {ord}(d)$
and
![]() $A\in \mathscr {M}\mathrm {od}(d)$
(i.e., a closed
$A\in \mathscr {M}\mathrm {od}(d)$
(i.e., a closed
![]() $(d-1)$
-manifold P and an associative algebra A in
$(d-1)$
-manifold P and an associative algebra A in
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
), we abbreviate the
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
), we abbreviate the
![]() $\infty $
-category of nullbordisms of P and the analogue for right A-modules by
$\infty $
-category of nullbordisms of P and the analogue for right A-modules by
Remark 4.12. Note that
![]() $E_\varnothing $
is the monoidal unit in
$E_\varnothing $
is the monoidal unit in
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
, so
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
, so
![]() $\mathscr {M}\mathrm {od}(d)_{E_\varnothing ,A}$
may be viewed as an
$\mathscr {M}\mathrm {od}(d)_{E_\varnothing ,A}$
may be viewed as an
![]() $\infty $
-category of right-A-modules. Using Remark 2.16 and [Reference LurieLur17, 4.3.2.8], one sees that this agrees with Lurie’s model of the
$\infty $
-category of right-A-modules. Using Remark 2.16 and [Reference LurieLur17, 4.3.2.8], one sees that this agrees with Lurie’s model of the
![]() $\infty $
-category of right-A-modules, but we will not use this.
$\infty $
-category of right-A-modules, but we will not use this.
4.5.1
 $\mathscr {D}\mathrm {isc}$
-structure spaces of modules
$\mathscr {D}\mathrm {isc}$
-structure spaces of modules
For
![]() $A=E_{P\times I}$
for a closed
$A=E_{P\times I}$
for a closed
![]() $(d-1)$
-manifold P, the functor E induces a functor
$(d-1)$
-manifold P, the functor E induces a functor
![]() $\mathscr {B}\mathrm {ord}(d)_{P}\rightarrow \mathscr {M}\mathrm {od}(d)_{P\times I}$
. As the source is an
$\mathscr {B}\mathrm {ord}(d)_{P}\rightarrow \mathscr {M}\mathrm {od}(d)_{P\times I}$
. As the source is an
![]() $\infty $
-groupoid by the discussion Section 4.1.2, it lands in the core
$\infty $
-groupoid by the discussion Section 4.1.2, it lands in the core
![]() $\mathscr {M}\mathrm {od}(d)^\simeq _{P\times I}\subset \mathscr {M}\mathrm {od}(d)_{P\times I}$
. The
$\mathscr {M}\mathrm {od}(d)^\simeq _{P\times I}\subset \mathscr {M}\mathrm {od}(d)_{P\times I}$
. The
![]() $\mathscr {D}\mathrm {isc}$
-structure spaces are the fibres of this functor of
$\mathscr {D}\mathrm {isc}$
-structure spaces are the fibres of this functor of
![]() $\infty $
-groupoids:
$\infty $
-groupoids:
Definition 4.13. The
![]() $\mathscr {D}\mathrm {isc}$
-structure space of a right-
$\mathscr {D}\mathrm {isc}$
-structure space of a right-
![]() $E_{P \times I}$
-module
$E_{P \times I}$
-module
![]() $X\in \mathscr {M}\mathrm {od}(d)_{E_{P\times I}}$
is the fibre
$X\in \mathscr {M}\mathrm {od}(d)_{E_{P\times I}}$
is the fibre
From the description of the object and mapping spaces of
![]() $\mathscr {B}\mathrm {ord}(d)$
and
$\mathscr {B}\mathrm {ord}(d)$
and
![]() $\mathscr {M}\mathrm {od}(d)$
in Section 2.5.4, we see that the path components of
$\mathscr {M}\mathrm {od}(d)$
in Section 2.5.4, we see that the path components of
![]() $S^{\mathscr {D}\mathrm {isc}}_P(X)$
are given by
$S^{\mathscr {D}\mathrm {isc}}_P(X)$
are given by

and that the component of a pair
![]() $(M,\varphi )$
agrees with the identity component
$(M,\varphi )$
agrees with the identity component
of the fibre
![]() $\mathrm {Aut}_{\mathscr {M}\mathrm {od}(d)_P}(E_M)/\mathrm {Diff}_\partial (M)$
of the map
$\mathrm {Aut}_{\mathscr {M}\mathrm {od}(d)_P}(E_M)/\mathrm {Diff}_\partial (M)$
of the map
![]() $\mathrm {BDiff}_\partial (M)\rightarrow \mathrm {BAut}_{\mathscr {M}\mathrm {od}(d)_P}(E_M)$
induced by E. This can also be rephrased in the form of an equivalence
$\mathrm {BDiff}_\partial (M)\rightarrow \mathrm {BAut}_{\mathscr {M}\mathrm {od}(d)_P}(E_M)$
induced by E. This can also be rephrased in the form of an equivalence
where
![]() $[M]$
runs through diffeomorphism classes of compact manifolds M with identified boundary
$[M]$
runs through diffeomorphism classes of compact manifolds M with identified boundary
![]() $\partial M\cong P$
for which there exists an equivalence
$\partial M\cong P$
for which there exists an equivalence
![]() $E_M\rightarrow X$
of right
$E_M\rightarrow X$
of right
![]() $E_{P\times I}$
-modules.
$E_{P\times I}$
-modules.
4.5.2
 $\mathscr {D}\mathrm {isc}$
-structure spaces of manifolds
$\mathscr {D}\mathrm {isc}$
-structure spaces of manifolds
Given a compact d-manifold W with identified boundary
![]() $\partial W\cong P$
, considered as an object in
$\partial W\cong P$
, considered as an object in
![]() $\mathscr {B}\mathrm {ord}(d)_{P}$
, we abbreviate
$\mathscr {B}\mathrm {ord}(d)_{P}$
, we abbreviate
This is natural in
![]() $\smash {W \in \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}_{\varnothing /}}$
in that it gives a functor
$\smash {W \in \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}_{\varnothing /}}$
in that it gives a functor
![]() $\smash {S^{\mathscr {D}\mathrm {isc}}_\partial (-) \colon \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}_{\varnothing /} \rightarrow \mathscr {S}}$
from the
$\smash {S^{\mathscr {D}\mathrm {isc}}_\partial (-) \colon \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}_{\varnothing /} \rightarrow \mathscr {S}}$
from the
![]() $\infty $
-category of nullbordisms to the
$\infty $
-category of nullbordisms to the
![]() $\infty $
-category of spaces. In particular, for bordisms
$\infty $
-category of spaces. In particular, for bordisms
![]() $W\colon \varnothing \leadsto P$
and
$W\colon \varnothing \leadsto P$
and
![]() $W' \in \mathscr {B}\mathrm {ord}(d)_{P,Q}$
, we have a gluing map
$W' \in \mathscr {B}\mathrm {ord}(d)_{P,Q}$
, we have a gluing map
![]() $(- \cup _P W) \colon S^{\mathscr {D}\mathrm {isc}}_\partial (W) \rightarrow S^{\mathscr {D}\mathrm {isc}}_\partial (W \cup _P W')$
.
$(- \cup _P W) \colon S^{\mathscr {D}\mathrm {isc}}_\partial (W) \rightarrow S^{\mathscr {D}\mathrm {isc}}_\partial (W \cup _P W')$
.
5 Theorem A:
 $2$
-type invariance
$2$
-type invariance
The goal of this section is to prove Theorem A, which says that the
![]() $\mathscr {D}\mathrm {isc}$
-structure space of a compact d-manifold depends for
$\mathscr {D}\mathrm {isc}$
-structure space of a compact d-manifold depends for
![]() $d\ge 5$
only on the tangential 2-type, a notion that we recall in Section 5.1. As outlined in Section 1.2.3, this will be an application of a general tangential k-type invariance result, proved in Section 5.2, about the values of certain functors on a category of compact null bordisms. That
$d\ge 5$
only on the tangential 2-type, a notion that we recall in Section 5.1. As outlined in Section 1.2.3, this will be an application of a general tangential k-type invariance result, proved in Section 5.2, about the values of certain functors on a category of compact null bordisms. That
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (-)$
satisfies its hypotheses is verified in Section 5.3.
$S^{\mathscr {D}\mathrm {isc}}_\partial (-)$
satisfies its hypotheses is verified in Section 5.3.
Convention.
-
(i) In contrast to the previous sections, all manifolds – which were already assumed to be smooth – are now also assumed to be compact. Nonempty boundaries are allowed.
-
(ii) In this section, we adopt the point of view on
 $\theta $
-structures in terms of bundle maps (always required to be fibrewise injective), which is different but by basic bundle theory equivalent to that in terms of
$\theta $
-structures in terms of bundle maps (always required to be fibrewise injective), which is different but by basic bundle theory equivalent to that in terms of
 $\mathrm {GL}_d(\mathbf {R})$
-spaces from Section 4.1.3. For the convenience of the reader, we recall the necessary definitions from scratch in Section 5.1.2.
$\mathrm {GL}_d(\mathbf {R})$
-spaces from Section 4.1.3. For the convenience of the reader, we recall the necessary definitions from scratch in Section 5.1.2.
5.1 Tangential k-types
We start with some manifold-theoretic preliminaries.
5.1.1
 $\theta $
-manifolds and tangential k-types
$\theta $
-manifolds and tangential k-types
Given a map
![]() $\theta \colon B\rightarrow \mathrm {BO}$
, a
$\theta \colon B\rightarrow \mathrm {BO}$
, a
![]() $\theta $
-manifold M is a manifold with a
$\theta $
-manifold M is a manifold with a
![]() $\theta $
-structure on its stable tangent bundle, by which we mean in this section a stable bundle map
$\theta $
-structure on its stable tangent bundle, by which we mean in this section a stable bundle map
![]() $\ell _M\colon \tau _M^s\rightarrow \theta ^*\gamma $
from the stable tangent bundle of M to the pullback of the universal stable vector bundle
$\ell _M\colon \tau _M^s\rightarrow \theta ^*\gamma $
from the stable tangent bundle of M to the pullback of the universal stable vector bundle
![]() $\gamma $
over
$\gamma $
over
![]() $\mathrm {BO}$
along
$\mathrm {BO}$
along
![]() $\theta $
. A tangential structure is k-connected if the underlying map
$\theta $
. A tangential structure is k-connected if the underlying map
![]() $\bar {\ell }_M\colon M\rightarrow B$
is k-connected in the usual sense.
$\bar {\ell }_M\colon M\rightarrow B$
is k-connected in the usual sense.
Given a codimension
![]() $0$
embedding
$0$
embedding
![]() $e\colon M\hookrightarrow N$
and a
$e\colon M\hookrightarrow N$
and a
![]() $\theta $
-structure
$\theta $
-structure
![]() $\ell _N$
on N, we obtain a
$\ell _N$
on N, we obtain a
![]() $\theta $
-structure
$\theta $
-structure
![]() $e^*\ell _N$
on M by precomposition with the stable derivative of e. Two
$e^*\ell _N$
on M by precomposition with the stable derivative of e. Two
![]() $\theta $
-manifolds M and N are
$\theta $
-manifolds M and N are
![]() $\theta $
-diffeomorphic if there exists a diffeomorphism
$\theta $
-diffeomorphic if there exists a diffeomorphism
![]() $\phi \colon M\rightarrow N$
of the underlying manifolds such that
$\phi \colon M\rightarrow N$
of the underlying manifolds such that
![]() $\phi ^*\ell _N$
and
$\phi ^*\ell _N$
and
![]() $\ell _M$
are homotopic as bundle maps. A codimension
$\ell _M$
are homotopic as bundle maps. A codimension
![]() $0$
embedding
$0$
embedding
![]() $e\colon M\hookrightarrow N$
is an equivalence on tangential k-types if N admits a k-connected
$e\colon M\hookrightarrow N$
is an equivalence on tangential k-types if N admits a k-connected
![]() $\theta $
-structure
$\theta $
-structure
![]() $\ell _N$
for some
$\ell _N$
for some
![]() $\theta $
such that
$\theta $
such that
![]() $e^*\ell _N$
is again k-connected. Two manifolds M and N have the same tangential k-type if there is a
$e^*\ell _N$
is again k-connected. Two manifolds M and N have the same tangential k-type if there is a
![]() $\theta \colon B\rightarrow \mathrm {BO}$
such that M and N admit k-connected
$\theta \colon B\rightarrow \mathrm {BO}$
such that M and N admit k-connected
![]() $\theta $
-structures
$\theta $
-structures
![]() $\ell _M$
and
$\ell _M$
and
![]() $\ell _N$
(for the same
$\ell _N$
(for the same
![]() $\theta $
).
$\theta $
).
Example 5.1. Any codimension
![]() $0$
embedding
$0$
embedding
![]() $M\hookrightarrow N$
that is k-connected is an equivalence on tangential k-types. This is clear from the definition as long as N admits a k-connected
$M\hookrightarrow N$
that is k-connected is an equivalence on tangential k-types. This is clear from the definition as long as N admits a k-connected
![]() $\theta $
-structure with respect to some
$\theta $
-structure with respect to some
![]() $\theta $
, and there is indeed always such a choice: pick a Moore-Postnikov factorisation
$\theta $
, and there is indeed always such a choice: pick a Moore-Postnikov factorisation
![]() $N\rightarrow B\rightarrow \mathrm {BO}$
of a classifying map for the stable tangent bundle of N into a k-connected map followed by a k-coconnected map
$N\rightarrow B\rightarrow \mathrm {BO}$
of a classifying map for the stable tangent bundle of N into a k-connected map followed by a k-coconnected map
![]() $\theta \colon B\rightarrow \mathrm {BO}$
.
$\theta \colon B\rightarrow \mathrm {BO}$
.
Example 5.2. The case of most interest to us is
![]() $k=2$
, where there is a simple recipe to decide whether two d-manifolds
$k=2$
, where there is a simple recipe to decide whether two d-manifolds
![]() $M_0$
and
$M_0$
and
![]() $M_1$
have the same tangential k-types. If the
$M_1$
have the same tangential k-types. If the
![]() $M_i$
are disconnected, then they have the same tangential
$M_i$
are disconnected, then they have the same tangential
![]() $2$
-type if and only if there exists a bijection between their components such that the corresponding components have the same tangential
$2$
-type if and only if there exists a bijection between their components such that the corresponding components have the same tangential
![]() $2$
-type. For connected manifolds
$2$
-type. For connected manifolds
![]() $M_0$
and
$M_0$
and
![]() $M_1$
, one can decide whether they have the same tangential
$M_1$
, one can decide whether they have the same tangential
![]() $2$
-type as follows (cf. [Reference KreckKre99, p. 712–713]; Kreck deals with normal k-types as opposed to tangential k-types and has a different indexing convention, but neither of this makes a difference):
$2$
-type as follows (cf. [Reference KreckKre99, p. 712–713]; Kreck deals with normal k-types as opposed to tangential k-types and has a different indexing convention, but neither of this makes a difference):
-
(i) The functionals
 $w_2(M_i) \colon \pi _2(M_i)\rightarrow \mathbf {Z}/2$
for
$w_2(M_i) \colon \pi _2(M_i)\rightarrow \mathbf {Z}/2$
for
 $i=0,1$
induced by the second Stiefel–Whitney classes need to be both trivial or nontrivial.
$i=0,1$
induced by the second Stiefel–Whitney classes need to be both trivial or nontrivial. -
(ii) If they are both nontrivial, then
 $M_0$
and
$M_0$
and
 $M_1$
have the same tangential
$M_1$
have the same tangential
 $2$
-type if and only if there exists an abstract isomorphism
$2$
-type if and only if there exists an abstract isomorphism
 $\varphi \colon \pi _1(M_0)\rightarrow \pi _1(M_1)$
such that
$\varphi \colon \pi _1(M_0)\rightarrow \pi _1(M_1)$
such that
 $\varphi ^*w_1(M_1)=w_1(M_0)$
, where
$\varphi ^*w_1(M_1)=w_1(M_0)$
, where
 $w_1(M_i) \in \mathrm {H}^1(M_i;\mathbf {Z}/2)\cong \mathrm {H}^1(K(\pi _1M_i,1);\mathbf {Z}/2)$
is the first Stiefel–Whitney class.
$w_1(M_i) \in \mathrm {H}^1(M_i;\mathbf {Z}/2)\cong \mathrm {H}^1(K(\pi _1M_i,1);\mathbf {Z}/2)$
is the first Stiefel–Whitney class. -
(iii) If they are both trivial, then there are unique classes
 $w_2(M_i) \in \mathrm {H}^2(K(\pi _1(M_i),1);\mathbf {Z}/2)$
that pull back to the second Stiefel–Whitney classes along the canonical maps
$w_2(M_i) \in \mathrm {H}^2(K(\pi _1(M_i),1);\mathbf {Z}/2)$
that pull back to the second Stiefel–Whitney classes along the canonical maps
 $M_i\rightarrow K(\pi _1(M_i),1)$
. Then
$M_i\rightarrow K(\pi _1(M_i),1)$
. Then
 $M_0$
and
$M_0$
and
 $M_1$
have the same tangential
$M_1$
have the same tangential
 $2$
-type if and only if there exists an abstract isomorphism
$2$
-type if and only if there exists an abstract isomorphism
 $\varphi \colon \pi _1(M_0)\rightarrow \pi _1(M_1)$
with
$\varphi \colon \pi _1(M_0)\rightarrow \pi _1(M_1)$
with
 $\varphi ^*w_j(M_1)=w_j(M_0)$
for
$\varphi ^*w_j(M_1)=w_j(M_0)$
for
 $j=1,2$
.
$j=1,2$
.
In particular, if
![]() $M_0$
and
$M_0$
and
![]() $M_1$
are spin,
$M_1$
are spin,
![]() $w_i(M)$
and
$w_i(M)$
and
![]() $w_i(N)$
vanish for
$w_i(N)$
vanish for
![]() $i\le 2$
, so the recipe shows that they have the same tangential
$i\le 2$
, so the recipe shows that they have the same tangential
![]() $2$
-types if and only if their fundamental groupoids are equivalent. It also implies that the tangential
$2$
-types if and only if their fundamental groupoids are equivalent. It also implies that the tangential
![]() $2$
-type of a smooth manifold does not depend on the smooth structure, since Stiefel–Whitney classes are defined for topological manifolds.
$2$
-type of a smooth manifold does not depend on the smooth structure, since Stiefel–Whitney classes are defined for topological manifolds.
Lemma 5.3. Let M be an m-manifold and
![]() $k\ge 0$
a number. For any
$k\ge 0$
a number. For any
![]() $d\ge 4$
with
$d\ge 4$
with
![]() $k\le \lfloor \tfrac {d}{2}\rfloor $
, there exists a closed d-manifold P with the same tangential k-type as M.
$k\le \lfloor \tfrac {d}{2}\rfloor $
, there exists a closed d-manifold P with the same tangential k-type as M.
Proof. We may assume
![]() $k\ge 1$
and that M is connected; apply the claim to each connected component otherwise. Choose a Moore–Postnikov k-factorisation
$k\ge 1$
and that M is connected; apply the claim to each connected component otherwise. Choose a Moore–Postnikov k-factorisation
![]() $M\rightarrow B\rightarrow \mathrm {BO}$
of the stable tangent bundle into a k-connected map followed by a k-coconnected map
$M\rightarrow B\rightarrow \mathrm {BO}$
of the stable tangent bundle into a k-connected map followed by a k-coconnected map
![]() $\theta \colon B\rightarrow \mathrm {BO}$
. The condition
$\theta \colon B\rightarrow \mathrm {BO}$
. The condition
![]() $k\le \lfloor \tfrac {d}{2}\rfloor $
in particular implies that
$k\le \lfloor \tfrac {d}{2}\rfloor $
in particular implies that
![]() $d \ge k+1$
, so the d-sphere
$d \ge k+1$
, so the d-sphere
![]() $S^d$
admits a
$S^d$
admits a
![]() $\theta $
-structure by obstruction theory. Doing surgeries compatible with the
$\theta $
-structure by obstruction theory. Doing surgeries compatible with the
![]() $\theta $
-structure (see [Reference KreckKre99, Proposition 4]), we obtain a closed d-manifold P with a k-connected
$\theta $
-structure (see [Reference KreckKre99, Proposition 4]), we obtain a closed d-manifold P with a k-connected
![]() $\theta $
-structure.
$\theta $
-structure.
5.1.2
 $\theta $
-bordism
$\theta $
-bordism
Given a
![]() $\theta $
-manifold M, a choice of inwards pointing vector field induces a
$\theta $
-manifold M, a choice of inwards pointing vector field induces a
![]() $\theta $
-structure on the boundary
$\theta $
-structure on the boundary
![]() $\partial M$
. Using the canonical vector field
$\partial M$
. Using the canonical vector field
![]() $\smash {\frac {\partial }{\partial x}}$
on
$\smash {\frac {\partial }{\partial x}}$
on
![]() $[0,1]$
, we moreover obtain a
$[0,1]$
, we moreover obtain a
![]() $\theta $
-structure on
$\theta $
-structure on
![]() $M\times [0,1]$
, which restricts to a
$M\times [0,1]$
, which restricts to a
![]() $\theta $
-structure on the double
$\theta $
-structure on the double
![]() $M\cup _{\partial M}\overline {M} \cong \partial (M\times [0,1])$
of M. Here,
$M\cup _{\partial M}\overline {M} \cong \partial (M\times [0,1])$
of M. Here,
![]() $\overline {M}$
is the
$\overline {M}$
is the
![]() $\theta $
-manifold whose underlying manifold is M but which is equipped with the opposite
$\theta $
-manifold whose underlying manifold is M but which is equipped with the opposite
![]() $\theta $
-structure obtained by restricting the induced
$\theta $
-structure obtained by restricting the induced
![]() $\theta $
-structure on
$\theta $
-structure on
![]() $M\times [0,1]$
to
$M\times [0,1]$
to
![]() $M\times \{1\}\subset \partial (M\times [0,1])$
. A
$M\times \{1\}\subset \partial (M\times [0,1])$
. A
![]() $\theta $
-bordism from a d-dimensional
$\theta $
-bordism from a d-dimensional
![]() $\theta $
-manifold P to another d-dimensional
$\theta $
-manifold P to another d-dimensional
![]() $\theta $
-manifold Q is a
$\theta $
-manifold Q is a
![]() $(d+1)$
-dimensional
$(d+1)$
-dimensional
![]() $\theta $
-manifold W together with a
$\theta $
-manifold W together with a
![]() $\theta $
-diffeomorphism
$\theta $
-diffeomorphism
![]() $\partial W\cong P\sqcup \smash {\overline {Q}}$
; we denote this
$\partial W\cong P\sqcup \smash {\overline {Q}}$
; we denote this ![]() . A
. A
![]() $\theta $
-manifold P is
$\theta $
-manifold P is
![]() $\theta $
-null bordant if there is a
$\theta $
-null bordant if there is a
![]() $\theta $
-bordism
$\theta $
-bordism
![]() $P \leadsto \varnothing $
. By construction, the double
$P \leadsto \varnothing $
. By construction, the double
![]() $M\cup _{\partial M} \overline {M}$
of any
$M\cup _{\partial M} \overline {M}$
of any
![]() $\theta $
-manifold M is
$\theta $
-manifold M is
![]() $\theta $
-nullbordant.
$\theta $
-nullbordant.
5.1.3 Handle decompositions
Given a compact d-dimensional bordism
![]() $W\colon P\leadsto Q$
between closed
$W\colon P\leadsto Q$
between closed
![]() $(d-1)$
-manifolds, a handle decomposition of the bordism W is a decomposition
$(d-1)$
-manifolds, a handle decomposition of the bordism W is a decomposition
of W as a union of bordisms between closed
![]() $(d-1)$
-manifolds
$(d-1)$
-manifolds
![]() $W_i$
such that
$W_i$
such that
![]() $W(k-1,k]$
is obtained from a collar on
$W(k-1,k]$
is obtained from a collar on
![]() $W_{k-1}$
by attaching finitely many handles of index k. Such a decomposition always exists – for instance, by choosing a self-indexing Morse function. By construction,
$W_{k-1}$
by attaching finitely many handles of index k. Such a decomposition always exists – for instance, by choosing a self-indexing Morse function. By construction,
![]() $W_{k+1}$
is obtained from
$W_{k+1}$
is obtained from
![]() $W_{k}$
by finitely many k-surgeries. We abbreviate
$W_{k}$
by finitely many k-surgeries. We abbreviate
and consider these as bordisms from
![]() $W_m$
to
$W_m$
to
![]() $W_k$
and from
$W_k$
and from
![]() $W_{m-1}$
to
$W_{m-1}$
to
![]() $W_k$
, respectively. The idea behind the notation is that the half-open or closed interval indicates which handles the submanifold contains. Given
$W_k$
, respectively. The idea behind the notation is that the half-open or closed interval indicates which handles the submanifold contains. Given
![]() $m\le k$
, we say that W has handle type
$m\le k$
, we say that W has handle type
![]() $[m,k]$
if there is a handle decomposition with
$[m,k]$
if there is a handle decomposition with
![]() $W=W[m,k]$
. A d-manifold M has handle type
$W=W[m,k]$
. A d-manifold M has handle type
![]() $[m,k]$
if it has that property when viewed as a bordism
$[m,k]$
if it has that property when viewed as a bordism
![]() $M\colon \varnothing \leadsto \partial M$
. It is said to have handle dimension
$M\colon \varnothing \leadsto \partial M$
. It is said to have handle dimension
![]() $\le k$
if it has handle type
$\le k$
if it has handle type
![]() $[0,k]$
. A codimension
$[0,k]$
. A codimension
![]() $0$
submanifold inclusion
$0$
submanifold inclusion
![]() $N \subset \mathrm {int}(M)$
has relative handle type
$N \subset \mathrm {int}(M)$
has relative handle type
![]() $[m,k]$
if the bordism
$[m,k]$
if the bordism
![]() $M\backslash \mathrm {int}(N)\colon \partial N\leadsto \partial M$
has handle type
$M\backslash \mathrm {int}(N)\colon \partial N\leadsto \partial M$
has handle type
![]() $[m,k]$
, and
$[m,k]$
, and
![]() $N\subset \mathrm {int}(M)$
has relative handle dimension
$N\subset \mathrm {int}(M)$
has relative handle dimension
![]() $\le k$
if this bordism has handle type
$\le k$
if this bordism has handle type
![]() $[0,k]$
.
$[0,k]$
.
5.1.4 Handle trading and connectivity
The following two lemmas are certainly standard, but we could not find references for them in the generality we needed.
Lemma 5.4. Let
![]() $W\colon P\leadsto Q$
be a bordism between closed d-manifolds P and Q with
$W\colon P\leadsto Q$
be a bordism between closed d-manifolds P and Q with
![]() $d\ge 4$
. If both boundary inclusions
$d\ge 4$
. If both boundary inclusions
![]() $P\subset W\supset Q$
are k-connected for some
$P\subset W\supset Q$
are k-connected for some
![]() $k\ge 0$
, then the following holds:
$k\ge 0$
, then the following holds:
-
(i) If
 $2k<d-1$
, then
$2k<d-1$
, then
 $W\colon P\leadsto Q$
has handle type
$W\colon P\leadsto Q$
has handle type
 $[k+1,d-k]$
and
$[k+1,d-k]$
and -
(ii) If
 $2k=d-1$
, then
$2k=d-1$
, then
 $W\sharp (S^{k+1}\times S^{k+1})^{\sharp r}\colon P\leadsto Q$
has type
$W\sharp (S^{k+1}\times S^{k+1})^{\sharp r}\colon P\leadsto Q$
has type
 $[k+1,d-k]$
for some
$[k+1,d-k]$
for some
 $r\ge 0$
.
$r\ge 0$
.
Proof. We begin with the first case. Starting from a handle decomposition of the bordism
![]() $W\colon P\leadsto Q$
, we obtain a potentially different handle decomposition of W of type
$W\colon P\leadsto Q$
, we obtain a potentially different handle decomposition of W of type
![]() $[k+1,d+1]$
by handle trading, without changing the number of i-handles for
$[k+1,d+1]$
by handle trading, without changing the number of i-handles for
![]() $i\ge k+3$
(see, for example, the proof of [Reference WallWal71, Theorem 3]). Now we apply the same procedure to the dual of this new handle decomposition to obtain yet another handle decomposition, this time of type
$i\ge k+3$
(see, for example, the proof of [Reference WallWal71, Theorem 3]). Now we apply the same procedure to the dual of this new handle decomposition to obtain yet another handle decomposition, this time of type
![]() $[0,d-k]$
and with the same number of i-handles for
$[0,d-k]$
and with the same number of i-handles for
![]() $i\le d-k-2$
. Since
$i\le d-k-2$
. Since
![]() $k\le d-k-2$
and we previously arranged that there are no i-handles for
$k\le d-k-2$
and we previously arranged that there are no i-handles for
![]() $i\le k$
, the resulting decomposition has type
$i\le k$
, the resulting decomposition has type
![]() $[k+1,d-k]$
.
$[k+1,d-k]$
.
In the case
![]() $2k=d-1$
, we may reindex so that the claim reads as follows (set
$2k=d-1$
, we may reindex so that the claim reads as follows (set
![]() $n=k+1$
): given a
$n=k+1$
): given a
![]() $2n$
-dimensional bordism
$2n$
-dimensional bordism
![]() $W\colon P\leadsto Q$
with
$W\colon P\leadsto Q$
with
![]() $2n\ge 6$
such that the inclusions
$2n\ge 6$
such that the inclusions
![]() $P\subset W\supset Q$
are
$P\subset W\supset Q$
are
![]() $(n-1)$
-connected, there exists an
$(n-1)$
-connected, there exists an
![]() $r\ge 0$
such that the bordism
$r\ge 0$
such that the bordism
![]() $(W\sharp (S^n\times S^n)^{\sharp r})\colon P\leadsto Q$
admits a handle decomposition with only n-handles. We are not aware of a classical reference for this fact; we learned it from the proof of [Reference Galatius and Randal-WilliamsGRW14, Lemma 6.21].
$(W\sharp (S^n\times S^n)^{\sharp r})\colon P\leadsto Q$
admits a handle decomposition with only n-handles. We are not aware of a classical reference for this fact; we learned it from the proof of [Reference Galatius and Randal-WilliamsGRW14, Lemma 6.21].
Lemma 5.5. Let
![]() $\theta \colon B\rightarrow \mathrm {BO}$
be a map and
$\theta \colon B\rightarrow \mathrm {BO}$
be a map and
![]() $(P,\ell _P)$
and
$(P,\ell _P)$
and
![]() $(Q,\ell _Q)$
two closed d-dimensional
$(Q,\ell _Q)$
two closed d-dimensional
![]() $\theta $
-manifolds that are
$\theta $
-manifolds that are
![]() $\theta $
-bordant. Assume
$\theta $
-bordant. Assume
![]() $d\ge 4$
and fix
$d\ge 4$
and fix
![]() $k\ge 0$
with
$k\ge 0$
with
![]() $2k<d$
.
$2k<d$
.
-
(i) If
 $\ell _P$
is k-connected, then there is a
$\ell _P$
is k-connected, then there is a
 $\theta $
-bordism
$\theta $
-bordism
 $W\colon P\leadsto Q$
such that
$W\colon P\leadsto Q$
such that
 $P\subset W$
is k-connected.
$P\subset W$
is k-connected. -
(ii) If also
 $\ell _Q$
is k-connected, then we may assume that
$\ell _Q$
is k-connected, then we may assume that
 $W\supset Q$
is k-connected as well.
$W\supset Q$
is k-connected as well.
Proof. For part (i), we refer to the proof of the correction [Reference Hebestreit and JoachimHJ20, Proposition p. 48] to a part of [Reference KreckKre99, Proposition 4]. The proof of part (ii) is a minor extension of their argument which we spell out for the convenience of the reader in the case
![]() $k\ge 1$
, leaving
$k\ge 1$
, leaving
![]() $k=0$
as an easy exercise.
$k=0$
as an easy exercise.
Starting from a
![]() $\theta $
-bordism
$\theta $
-bordism
![]() $(W,\ell _W)\colon (P,\ell _P)\leadsto (Q,\ell _Q)$
, we can assume that
$(W,\ell _W)\colon (P,\ell _P)\leadsto (Q,\ell _Q)$
, we can assume that
![]() $\ell _W$
is k-connected by performing surgery in the interior of W. As
$\ell _W$
is k-connected by performing surgery in the interior of W. As
![]() $\ell _P$
and
$\ell _P$
and
![]() $\ell _Q$
are k-connected, this ensures that the inclusions
$\ell _Q$
are k-connected, this ensures that the inclusions
![]() $P\subset W\supset Q$
induce an isomorphism on homotopy groups at all basepoints in degrees
$P\subset W\supset Q$
induce an isomorphism on homotopy groups at all basepoints in degrees
![]() $\le k-1$
. By considering each component in
$\le k-1$
. By considering each component in
![]() $\pi _0(P)\cong \pi _0(W)\cong \pi _0(Q)\cong \pi _0(B)$
separately, we may assume that each of
$\pi _0(P)\cong \pi _0(W)\cong \pi _0(Q)\cong \pi _0(B)$
separately, we may assume that each of
![]() $P,W,Q,B$
is connected. We now consider the long exact sequences
$P,W,Q,B$
is connected. We now consider the long exact sequences

of the pairs
![]() $(W,P)$
and
$(W,P)$
and
![]() $(W,Q)$
. We first assume
$(W,Q)$
. We first assume
![]() $k\ge 2$
. By the relative Hurewicz theorem, we have
$k\ge 2$
. By the relative Hurewicz theorem, we have
![]() $\pi _k(W,P)\cong \mathrm {H}_k(\widetilde {W},\widetilde {P})$
and similarly for
$\pi _k(W,P)\cong \mathrm {H}_k(\widetilde {W},\widetilde {P})$
and similarly for
![]() $\pi _k(W,Q)$
, where
$\pi _k(W,Q)$
, where
![]() $\smash {\widetilde {(-)}}$
denotes the universal covers, so these groups are in particular finitely generated as
$\smash {\widetilde {(-)}}$
denotes the universal covers, so these groups are in particular finitely generated as
![]() $\pi _1(W)$
-modules. Contemplating the diagram shows that there are finite sets of elements
$\pi _1(W)$
-modules. Contemplating the diagram shows that there are finite sets of elements
![]() $\{p_i\}$
and
$\{p_i\}$
and
![]() $\{q_i\}$
of
$\{q_i\}$
of
![]() $\pi _k(W)$
that (i) map trivially to
$\pi _k(W)$
that (i) map trivially to
![]() $\pi _k(B)$
(and thus trivially to
$\pi _k(B)$
(and thus trivially to
![]() $\pi _k(\mathrm {BO})$
) and (ii) map to sets of generators of
$\pi _k(\mathrm {BO})$
) and (ii) map to sets of generators of
![]() $\pi _k(W,P)$
and
$\pi _k(W,P)$
and
![]() $\pi _k(W,Q)$
as
$\pi _k(W,Q)$
as
![]() $\pi _1(W)$
-modules, respectively. As
$\pi _1(W)$
-modules, respectively. As
![]() $2k<d$
, we may represent these elements by two disjoint embeddings
$2k<d$
, we may represent these elements by two disjoint embeddings
![]() $\overline {p}\colon {\sqcup ^i} S^k\times D^{d+1-k}\hookrightarrow \mathrm {int}(W)$
and
$\overline {p}\colon {\sqcup ^i} S^k\times D^{d+1-k}\hookrightarrow \mathrm {int}(W)$
and
![]() $\overline {q}\colon {\sqcup ^i} S^k\times D^{d+1-k}\hookrightarrow \mathrm {int}(W)$
. Doing
$\overline {q}\colon {\sqcup ^i} S^k\times D^{d+1-k}\hookrightarrow \mathrm {int}(W)$
. Doing
![]() $\theta $
-surgery on these embeddings (see [Reference KreckKre99, Lemma 2]) yields a
$\theta $
-surgery on these embeddings (see [Reference KreckKre99, Lemma 2]) yields a
![]() $\theta $
-bordism
$\theta $
-bordism
![]() $W'\colon P\leadsto Q$
which we claim to satisfy the requirements of the statement; that is,
$W'\colon P\leadsto Q$
which we claim to satisfy the requirements of the statement; that is,
![]() $\pi _i(W',P)=0$
and
$\pi _i(W',P)=0$
and
![]() $\pi _i(W',Q)=0$
for
$\pi _i(W',Q)=0$
for
![]() $i\le k$
– the reason being that (i)
$i\le k$
– the reason being that (i)
![]() $\pi _i(W',P)$
vanishes for
$\pi _i(W',P)$
vanishes for
![]() $i\le k-1$
since it is isomorphic to
$i\le k-1$
since it is isomorphic to
![]() $\pi _i(W,P)=0$
, and (ii)
$\pi _i(W,P)=0$
, and (ii)
![]() $\pi _k(W',Q)$
vanishes since it is a quotient of
$\pi _k(W',Q)$
vanishes since it is a quotient of
![]() $\pi _k(W,Q)$
by a subgroup that contains the
$\pi _k(W,Q)$
by a subgroup that contains the
![]() $\pi _1(W)$
-orbit of the images of
$\pi _1(W)$
-orbit of the images of
![]() $\{p_i\}$
and
$\{p_i\}$
and
![]() $\{q_i\}$
, and we chose the
$\{q_i\}$
, and we chose the
![]() $\{p_i\}$
so that their images generate
$\{p_i\}$
so that their images generate
![]() $\pi _k(W',P)$
as
$\pi _k(W',P)$
as
![]() $\pi _1(W)$
-modules. The same argument applies to the groups
$\pi _1(W)$
-modules. The same argument applies to the groups
![]() $\pi _i(W',Q)$
, so the claim in the case
$\pi _i(W',Q)$
, so the claim in the case
![]() $k\ge 2$
follows. For
$k\ge 2$
follows. For
![]() $k=1$
, the same argument applies even though
$k=1$
, the same argument applies even though
![]() $\pi _1(W,P)$
and
$\pi _1(W,P)$
and
![]() $\pi _1(W,Q)$
need no longer be groups: instead of the relative Hurewicz theorem, one uses that
$\pi _1(W,Q)$
need no longer be groups: instead of the relative Hurewicz theorem, one uses that
![]() $\pi _1(W)$
is finitely generated, being the fundamental group of a compact manifold.
$\pi _1(W)$
is finitely generated, being the fundamental group of a compact manifold.
Combining the previous two lemmas we get the following:
Corollary 5.6. Let
![]() $\theta \colon B\rightarrow \mathrm {BO}$
be a map and
$\theta \colon B\rightarrow \mathrm {BO}$
be a map and
![]() $(P,\ell _P)$
and
$(P,\ell _P)$
and
![]() $(Q,\ell _Q)$
two closed
$(Q,\ell _Q)$
two closed
![]() $\theta $
-manifolds of dimension
$\theta $
-manifolds of dimension
![]() $d\ge 4$
that are
$d\ge 4$
that are
![]() $\theta $
-bordant. If
$\theta $
-bordant. If
![]() $\ell _P$
and
$\ell _P$
and
![]() $\ell _Q$
are k-connected for some
$\ell _Q$
are k-connected for some
![]() $k\ge 0$
with
$k\ge 0$
with
![]() $2k<d$
, then Q can be obtained from P by a finite sequence of p-surgeries with
$2k<d$
, then Q can be obtained from P by a finite sequence of p-surgeries with
![]() $k\le p\le d-k-1$
.
$k\le p\le d-k-1$
.
5.2 k-type invariance
To state the announced tangential k-type result, we denote by ![]() the
the
![]() $1$
-category whose objects are smooth compact d-manifolds (potentially with boundary) and whose morphisms are isotopy classes of codimension
$1$
-category whose objects are smooth compact d-manifolds (potentially with boundary) and whose morphisms are isotopy classes of codimension
![]() $0$
embeddings. Fixing another
$0$
embeddings. Fixing another
![]() $1$
-category
$1$
-category
![]() $\mathsf {C}$
, we prove the following result for functors of the form
$\mathsf {C}$
, we prove the following result for functors of the form
![]() $F\colon h\mathsf {Man}^{\mathrm {c}}_d\rightarrow \mathsf {C}$
.
$F\colon h\mathsf {Man}^{\mathrm {c}}_d\rightarrow \mathsf {C}$
.
Theorem 5.7. Let
![]() $d\ge 4$
and
$d\ge 4$
and
![]() $F\colon h\mathsf {Man}^{\mathrm {c}}_d\rightarrow \mathsf {C}$
be a functor such that F maps codimension
$F\colon h\mathsf {Man}^{\mathrm {c}}_d\rightarrow \mathsf {C}$
be a functor such that F maps codimension
![]() $0$
submanifold inclusions of relative handle type
$0$
submanifold inclusions of relative handle type
![]() $[k+1,d]$
to isomorphisms for some fixed
$[k+1,d]$
to isomorphisms for some fixed
![]() $0\le k<d/2$
. Then for any compact d-manifolds M and N of the same tangential k-type, the following holds:
$0\le k<d/2$
. Then for any compact d-manifolds M and N of the same tangential k-type, the following holds:
-
(i) There exists an isomorphism
 $F(M)\cong F(N)$
.
$F(M)\cong F(N)$
. -
(ii) For any codimension
 $0$
embedding
$0$
embedding
 $e\colon L\hookrightarrow M$
where L has handle dimension
$e\colon L\hookrightarrow M$
where L has handle dimension
 $\le k$
, there is an embedding
$\le k$
, there is an embedding
 $e'\colon L\hookrightarrow N$
for which the isomorphism (i) can be chosen so that the diagram is commutative.
$e'\colon L\hookrightarrow N$
for which the isomorphism (i) can be chosen so that the diagram is commutative.
-
(iii) Any embedding
 $e\colon M\hookrightarrow N$
that is an equivalence on tangential k-types induces an isomorphism
$e\colon M\hookrightarrow N$
that is an equivalence on tangential k-types induces an isomorphism
 $F(M)\cong F(N)$
as in (i).
$F(M)\cong F(N)$
as in (i).
Remark 5.8. Theorem 5.7 is based on arguments we learned from the literature on the space of positive scalar curvature metrics on a manifold M – in particular, [Reference Ebert and Randal-WilliamsERW22, Reference Ebert and WiemelerEW24]. This space shares strong formal properties with the
![]() $\mathscr {D}\mathrm {isc}$
-structure space: it is often an infinite loop space [Reference Ebert and Randal-WilliamsERW22, Theorems A-B], depends conjecturally only on the tangential
$\mathscr {D}\mathrm {isc}$
-structure space: it is often an infinite loop space [Reference Ebert and Randal-WilliamsERW22, Theorems A-B], depends conjecturally only on the tangential
![]() $2$
-type (see [Reference Ebert and WiemelerEW24, Conjecture C] and [Reference Ebert and Randal-WilliamsERW22, Section 9]), and is often nontrivial (see, for example, [Reference Ebert and Randal-WilliamsERW22, Remark 1.1.1]).
$2$
-type (see [Reference Ebert and WiemelerEW24, Conjecture C] and [Reference Ebert and Randal-WilliamsERW22, Section 9]), and is often nontrivial (see, for example, [Reference Ebert and Randal-WilliamsERW22, Remark 1.1.1]).
Remark 5.9. Taking complements,
![]() $h\mathsf {Man}^{\mathrm {c}}_d$
can be viewed equivalently as the ‘homotopy category of null bordisms’, by which we mean the undercategory
$h\mathsf {Man}^{\mathrm {c}}_d$
can be viewed equivalently as the ‘homotopy category of null bordisms’, by which we mean the undercategory
![]() $\smash {h\mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}_{\varnothing /}}$
of the empty manifold
$\smash {h\mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}_{\varnothing /}}$
of the empty manifold
![]() $\varnothing $
viewed as an object in the homotopy category
$\varnothing $
viewed as an object in the homotopy category
![]() $h\mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}$
, whose objects are closed
$h\mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}$
, whose objects are closed
![]() $(d-1)$
-manifolds and whose morphisms are diffeomorphism classes of compact bordisms.
$(d-1)$
-manifolds and whose morphisms are diffeomorphism classes of compact bordisms.
As preparation to the proof of Theorem 5.7, we show that the values of the functor are invariant under certain surgeries.
Lemma 5.10. Let F be as in Theorem 5.7. If two compact d-manifolds M and N differ by p-surgeries in the interior with
![]() $k\le p\le d-k-1$
, then there exists an isomorphism
$k\le p\le d-k-1$
, then there exists an isomorphism
![]() $F(M)\cong F(N)$
.
$F(M)\cong F(N)$
.
Proof. It suffices to show the claim in the case where N is obtained from M by a single p-surgery along an embedding
![]() $S^p\times D^{d-p}\hookrightarrow \mathrm {int}(M)$
. We consider the zig-zag
$S^p\times D^{d-p}\hookrightarrow \mathrm {int}(M)$
. We consider the zig-zag
induced by the inclusions
![]() $M\backslash \mathrm {int}(S^p\times D^{d-p})\subset M$
and
$M\backslash \mathrm {int}(S^p\times D^{d-p})\subset M$
and
![]() $M\backslash \mathrm {int}(S^p\times D^{d-p}) \subset N$
. The former has relative handle type
$M\backslash \mathrm {int}(S^p\times D^{d-p}) \subset N$
. The former has relative handle type
![]() $[d-p,d]$
, and the latter has relative handle type
$[d-p,d]$
, and the latter has relative handle type
![]() $[p+1,d]$
. As
$[p+1,d]$
. As
![]() $d-p\ge k+1$
and
$d-p\ge k+1$
and
![]() $p+1\ge k+1$
, and F sends inclusions of submanifolds of relative handle type
$p+1\ge k+1$
, and F sends inclusions of submanifolds of relative handle type
![]() $[k+1,d]$
to isomorphisms by assumption, we conclude the claim.
$[k+1,d]$
to isomorphisms by assumption, we conclude the claim.
Proof Proof of Theorem 5.7.
Recall that two d-manifolds M and N have the same tangential k-type if there exists a map
![]() $\theta \colon B\rightarrow \mathrm {BO}$
and k-connected
$\theta \colon B\rightarrow \mathrm {BO}$
and k-connected
![]() $\theta $
-structures
$\theta $
-structures
![]() $\ell _M$
and
$\ell _M$
and
![]() $\ell _N$
on M and N.
$\ell _N$
on M and N.
Part (i) of the claim asserts an isomorphism
![]() $F(M)\cong F(N)$
. In the case that
$F(M)\cong F(N)$
. In the case that
![]() $(M,\ell _M)$
and
$(M,\ell _M)$
and
![]() $(N,\ell _N)$
are closed manifolds that are
$(N,\ell _N)$
are closed manifolds that are
![]() $\theta $
-bordant, this follows directly from Corollary 5.6 and Lemma 5.10. To show the general case, we pick a handle decomposition of M viewed as a bordism
$\theta $
-bordant, this follows directly from Corollary 5.6 and Lemma 5.10. To show the general case, we pick a handle decomposition of M viewed as a bordism
![]() $M\colon \varnothing \leadsto \partial M$
and consider the zig-zag (using the notation from Section 5.1.3)
$M\colon \varnothing \leadsto \partial M$
and consider the zig-zag (using the notation from Section 5.1.3)
whose arrows are induced by
![]() $M[k+1,d]\colon M_k\leadsto \partial M$
and
$M[k+1,d]\colon M_k\leadsto \partial M$
and
![]() $\overline {M{[0,k]}}\colon M_k\leadsto \varnothing $
. The former is of handle type
$\overline {M{[0,k]}}\colon M_k\leadsto \varnothing $
. The former is of handle type
![]() $[k+1,d]$
and the latter of handle type
$[k+1,d]$
and the latter of handle type
![]() $[d-k,d]$
, so using that
$[d-k,d]$
, so using that
![]() $d-k>k$
, the two submanifold inclusions inducing the maps in the zig-zag have relative handle type
$d-k>k$
, the two submanifold inclusions inducing the maps in the zig-zag have relative handle type
![]() $[k+1,d]$
, so the zig-zag consists of isomorphisms. Applying the same reasoning for N, we see that the claim follows once we provide an isomorphism between the values of F at the two doubles
$[k+1,d]$
, so the zig-zag consists of isomorphisms. Applying the same reasoning for N, we see that the claim follows once we provide an isomorphism between the values of F at the two doubles
![]() $M[0,k]\cup _{M_k}\overline {M[0,k]}$
and
$M[0,k]\cup _{M_k}\overline {M[0,k]}$
and
![]() $N[0,k]\cup _{N_k}\overline {N[0,k]}$
. Both of these doubles are closed manifolds that are
$N[0,k]\cup _{N_k}\overline {N[0,k]}$
. Both of these doubles are closed manifolds that are
![]() $\theta $
-nullbordant (see Section 5.1.2), so they are in particular
$\theta $
-nullbordant (see Section 5.1.2), so they are in particular
![]() $\theta $
-bordant to each other. This implies the claim by the first part as long as we make sure that the induced
$\theta $
-bordant to each other. This implies the claim by the first part as long as we make sure that the induced
![]() $\theta $
-structures on these doubles are k-connected. But this is the case, since it holds for M and N by assumptions, and the above handle considerations in particular imply that all inclusions in
$\theta $
-structures on these doubles are k-connected. But this is the case, since it holds for M and N by assumptions, and the above handle considerations in particular imply that all inclusions in
![]() $M\supset M[0,k]\subset M[0,k]\cup _{M_k}\overline {M[0,k]}$
and
$M\supset M[0,k]\subset M[0,k]\cup _{M_k}\overline {M[0,k]}$
and
![]() $N\supset N[0,k]\subset N[0,k]\cup _{N_k}\overline {N[0,k]}$
are k-connected.
$N\supset N[0,k]\subset N[0,k]\cup _{N_k}\overline {N[0,k]}$
are k-connected.
To prove part (ii), we fix an embedding
![]() $L\hookrightarrow M$
as in the claim which we may assume by transversality to be contained in
$L\hookrightarrow M$
as in the claim which we may assume by transversality to be contained in
![]() $M[0,k]\subset M$
, as the complement
$M[0,k]\subset M$
, as the complement
![]() $M[k+1,d]\supset \partial M$
has relative handle dimension
$M[k+1,d]\supset \partial M$
has relative handle dimension
![]() $\le d-(k+1)$
and L has handle dimension
$\le d-(k+1)$
and L has handle dimension
![]() $\le k$
by assumption. The zig-zag (74) is then compatible with the maps from
$\le k$
by assumption. The zig-zag (74) is then compatible with the maps from
![]() $F(L)$
induced by inclusion. Now
$F(L)$
induced by inclusion. Now
![]() $M[0,k]\cup _{M_k}\overline {M[0,k]}$
differs from
$M[0,k]\cup _{M_k}\overline {M[0,k]}$
differs from
![]() $N[0,k]\cup _{N_k}\overline {N[0,k]}$
by surgeries of index
$N[0,k]\cup _{N_k}\overline {N[0,k]}$
by surgeries of index
![]() $k\le p\le d-k-1$
, which we may assume (again by transversality) to be done away from L, so there is an embedding
$k\le p\le d-k-1$
, which we may assume (again by transversality) to be done away from L, so there is an embedding
![]() $L\hookrightarrow N[0,k]\cup _{N_k}\overline {N[0,k]}$
, such that the induced isomorphism
$L\hookrightarrow N[0,k]\cup _{N_k}\overline {N[0,k]}$
, such that the induced isomorphism
![]() $F(M[0,k]\cup _{M_k}\overline {M[0,k]})\cong F(N[0,k]\cup _{N_k}\overline {N[0,k]})$
is compatible with the maps from
$F(M[0,k]\cup _{M_k}\overline {M[0,k]})\cong F(N[0,k]\cup _{N_k}\overline {N[0,k]})$
is compatible with the maps from
![]() $F(L)$
. Using transversality one last time, we see that we may isotope the embedding
$F(L)$
. Using transversality one last time, we see that we may isotope the embedding
![]() $L\hookrightarrow N[0,k]\cup _{N_k}\overline {N[0,k]}$
to land in
$L\hookrightarrow N[0,k]\cup _{N_k}\overline {N[0,k]}$
to land in
![]() $N[0,k]$
since
$N[0,k]$
since
![]() $\overline {N[0,k]}\subset $
has handle dimension
$\overline {N[0,k]}\subset $
has handle dimension
![]() $\le k$
and
$\le k$
and
![]() $2k< d$
. With respect to the isotoped embedding, the zig-zag (74) is compatible with the maps from
$2k< d$
. With respect to the isotoped embedding, the zig-zag (74) is compatible with the maps from
![]() $F(N)$
, and this concludes the proof.
$F(N)$
, and this concludes the proof.
For part (iii), we may assume without loss of generality that the embedding is a submanifold inclusion of the form
![]() $M\subset M\cup _{\partial M} W$
for
$M\subset M\cup _{\partial M} W$
for
![]() $W\colon \partial M\leadsto \partial N$
a bordism. We now consider the commutative square of codimension
$W\colon \partial M\leadsto \partial N$
a bordism. We now consider the commutative square of codimension
![]() $0$
submanifold inclusions
$0$
submanifold inclusions

where
![]() $c(M_k)\subset M$
is a closed bicollar of
$c(M_k)\subset M$
is a closed bicollar of
![]() $M_k\subset M$
. The vertical inclusions are of relative handle type
$M_k\subset M$
. The vertical inclusions are of relative handle type
![]() $[k+1,d]$
(this uses
$[k+1,d]$
(this uses
![]() $d-k\ge k+1$
), so we conclude that they map to isomorphisms under F. It thus suffices to show that F maps the top horizontal inclusion to an isomorphism. Since the vertical inclusions and the
$d-k\ge k+1$
), so we conclude that they map to isomorphisms under F. It thus suffices to show that F maps the top horizontal inclusion to an isomorphism. Since the vertical inclusions and the
![]() $\theta $
-structures
$\theta $
-structures
![]() $\ell _M$
and
$\ell _M$
and
![]() $\ell _N$
are k-connected, it follows that the top horizontal inclusion is an equivalence on tangential k-type equivalence. Since
$\ell _N$
are k-connected, it follows that the top horizontal inclusion is an equivalence on tangential k-type equivalence. Since
![]() $d\ge 4$
, we have
$d\ge 4$
, we have
![]() $d/2\le d-2$
, so
$d/2\le d-2$
, so
![]() $k<\min (d/2,d-2)$
. Abbreviating
$k<\min (d/2,d-2)$
. Abbreviating
![]() $V=M[k,d] \cup _{\partial M} W$
, an application of [Reference Krannich and KupersKK24c, Lemma 6.10] shows that we can factor the top horizontal inclusion as a composition of the form
$V=M[k,d] \cup _{\partial M} W$
, an application of [Reference Krannich and KupersKK24c, Lemma 6.10] shows that we can factor the top horizontal inclusion as a composition of the form
![]() $c(M_k)\subset c(M_k)\cup _{M_k}V[k,k]\subset c(M_k)\cup _{M_k}V$
, where the first inclusion is obtained by attaching trivial k-handles and the second by attaching
$c(M_k)\subset c(M_k)\cup _{M_k}V[k,k]\subset c(M_k)\cup _{M_k}V$
, where the first inclusion is obtained by attaching trivial k-handles and the second by attaching
![]() $\ge k+1$
-handles. By assumption, F sends the second inclusion to an isomorphism, so it suffices to show that the same holds for the first inclusion. By attaching cancelling
$\ge k+1$
-handles. By assumption, F sends the second inclusion to an isomorphism, so it suffices to show that the same holds for the first inclusion. By attaching cancelling
![]() $(k+1)$
-handles, the first inclusion fits into a sequence of inclusions
$(k+1)$
-handles, the first inclusion fits into a sequence of inclusions
![]() $c(M_k)\subset c(M_k)\cup _{M_k}V[k,k]\subset c'(M_k)$
whose composition is given by attaching a collar (so is an isotopy equivalence), and the second inclusion is obtained by attaching
$c(M_k)\subset c(M_k)\cup _{M_k}V[k,k]\subset c'(M_k)$
whose composition is given by attaching a collar (so is an isotopy equivalence), and the second inclusion is obtained by attaching
![]() $(k+1)$
-handles. Now F sends the second inclusion and the composition to isomorphisms, and so also the first.
$(k+1)$
-handles. Now F sends the second inclusion and the composition to isomorphisms, and so also the first.
5.3
 $2$
-type invariance of the
$2$
-type invariance of the
 $\mathscr {D}\mathrm {isc}$
-structure space
$\mathscr {D}\mathrm {isc}$
-structure space
By Section 4.5.2, the
![]() $\mathscr {D}\mathrm {isc}$
-structure spaces of compact manifolds form the values of a functor
$\mathscr {D}\mathrm {isc}$
-structure spaces of compact manifolds form the values of a functor
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (-)\colon \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}_{\varnothing /}\rightarrow \mathscr {S}$
of
$S^{\mathscr {D}\mathrm {isc}}_\partial (-)\colon \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}_{\varnothing /}\rightarrow \mathscr {S}$
of
![]() $\infty $
-categories, which induces on homotopy categories in view of Remark 5.9 a functor
$\infty $
-categories, which induces on homotopy categories in view of Remark 5.9 a functor
The goal of this section is to show that this functor satisfies the assumptions of Theorem 5.7 for
![]() $k=2$
. This can be rephrased as follows:
$k=2$
. This can be rephrased as follows:
Proposition 5.11. Let ![]() and
and
![]() $W\colon P \leadsto Q$
be d-dimensional bordisms. If W is of handle type
$W\colon P \leadsto Q$
be d-dimensional bordisms. If W is of handle type
![]() $[3,d]$
, then the gluing map
$[3,d]$
, then the gluing map
![]() $(-\cup _P W)\colon S^{\mathscr {D}\mathrm {isc}}_\partial (M)\rightarrow S^{\mathscr {D}\mathrm {isc}}_\partial (M\cup _PW)$
is an equivalence.
$(-\cup _P W)\colon S^{\mathscr {D}\mathrm {isc}}_\partial (M)\rightarrow S^{\mathscr {D}\mathrm {isc}}_\partial (M\cup _PW)$
is an equivalence.
Once this is proved, Theorem 5.7 implies the following refined version of Theorem A.
Theorem 5.12. Let
![]() $d\ge 5$
, and M, N be two compact d-manifolds of the same tangential
$d\ge 5$
, and M, N be two compact d-manifolds of the same tangential
![]() $2$
-type.
$2$
-type.
-
(i) There exists an equivalence
 $S^{\mathscr {D}\mathrm {isc}}_\partial (M)\simeq S^{\mathscr {D}\mathrm {isc}}_\partial (N)$
.
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)\simeq S^{\mathscr {D}\mathrm {isc}}_\partial (N)$
. -
(ii) For any embedding
 $e\colon L\hookrightarrow M$
of a d-manifold L with handle dimension
$e\colon L\hookrightarrow M$
of a d-manifold L with handle dimension
 $\le 2$
, there is an embedding
$\le 2$
, there is an embedding
 $e'\colon L\hookrightarrow N$
so that the equivalence of 5.12 can be chosen to be compatible with
$e'\colon L\hookrightarrow N$
so that the equivalence of 5.12 can be chosen to be compatible with  $$\begin{align*}e_{*}\colon S^{\mathscr{D}\mathrm{isc}}_\partial(L)\rightarrow S^{\mathscr{D}\mathrm{isc}}_\partial(M)\quad\text{and}\quad e^{\prime}_{*}\colon S^{\mathscr{D}\mathrm{isc}}_\partial(L)\rightarrow S^{\mathscr{D}\mathrm{isc}}_\partial(N). \end{align*}$$
$$\begin{align*}e_{*}\colon S^{\mathscr{D}\mathrm{isc}}_\partial(L)\rightarrow S^{\mathscr{D}\mathrm{isc}}_\partial(M)\quad\text{and}\quad e^{\prime}_{*}\colon S^{\mathscr{D}\mathrm{isc}}_\partial(L)\rightarrow S^{\mathscr{D}\mathrm{isc}}_\partial(N). \end{align*}$$
-
(iii) Any embedding
 $e\colon M\hookrightarrow N$
that induces an equivalence on tangential
$e\colon M\hookrightarrow N$
that induces an equivalence on tangential
 $2$
-types induces an equivalence
$2$
-types induces an equivalence
 $S^{\mathscr {D}\mathrm {isc}}_\partial (M)\simeq S^{\mathscr {D}\mathrm {isc}}_\partial (N)$
as in 5.12.
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)\simeq S^{\mathscr {D}\mathrm {isc}}_\partial (N)$
as in 5.12.
Proof Proof of Proposition 5.11.
Unravelling the statement using Definition 4.13, the task is to show that

is a pullback in
![]() $\mathscr {S}$
, where
$\mathscr {S}$
, where
![]() $\smash {\mathscr {M}\mathrm {od}(d)^{\mathrm {rep},\simeq }_{E_{P \times I}}\subset \mathscr {M}\mathrm {od}(d)^{\simeq }_{E_{P \times I}}}$
and
$\smash {\mathscr {M}\mathrm {od}(d)^{\mathrm {rep},\simeq }_{E_{P \times I}}\subset \mathscr {M}\mathrm {od}(d)^{\simeq }_{E_{P \times I}}}$
and
![]() $\smash {\mathscr {M}\mathrm {od}(d)^{\mathrm {rep},\simeq }_{E_{Q \times I}}\subset \mathscr {M}\mathrm {od}(d)^{\simeq }_{E_{Q \times I}}}$
are the
$\smash {\mathscr {M}\mathrm {od}(d)^{\mathrm {rep},\simeq }_{E_{Q \times I}}\subset \mathscr {M}\mathrm {od}(d)^{\simeq }_{E_{Q \times I}}}$
are the
![]() $\infty $
-groupoids given as the full subcategories of those objects in the image of the functor
$\infty $
-groupoids given as the full subcategories of those objects in the image of the functor
![]() $E\colon \mathscr {B}\mathrm {ord}(d)_{P}\rightarrow \mathscr {M}\mathrm {od}(d)^{\simeq }_{E_{P \times I}}$
and in the image of its analogue for P replaced by Q, respectively. We prove that it is a pullback by showing that the map on horizontal fibres are equivalences, for which we use that for any map
$E\colon \mathscr {B}\mathrm {ord}(d)_{P}\rightarrow \mathscr {M}\mathrm {od}(d)^{\simeq }_{E_{P \times I}}$
and in the image of its analogue for P replaced by Q, respectively. We prove that it is a pullback by showing that the map on horizontal fibres are equivalences, for which we use that for any map
![]() $f\colon E\rightarrow B$
in
$f\colon E\rightarrow B$
in
![]() $\mathscr {S}$
(thought of as a full subcategory of
$\mathscr {S}$
(thought of as a full subcategory of
![]() $\mathscr {C}\mathrm {at}_\infty $
) and a point
$\mathscr {C}\mathrm {at}_\infty $
) and a point
![]() $b\in B$
, the fibre of f over b agrees with the colimit
$b\in B$
, the fibre of f over b agrees with the colimit
![]() $\mathrm {colim}_{E}\,\mathrm {Map}_B(f(-),b)$
. This follows from [Reference LurieLur09a, 3.3.4.6] combined with the fact that the fibre over b is the total space of the unstraightening of the functor
$\mathrm {colim}_{E}\,\mathrm {Map}_B(f(-),b)$
. This follows from [Reference LurieLur09a, 3.3.4.6] combined with the fact that the fibre over b is the total space of the unstraightening of the functor
![]() $\mathrm {Map}_B(f(-),b)\colon E\rightarrow \mathscr {S}$
, which in turn follows from [Reference LurieLur09a, 3.3.2.8].
$\mathrm {Map}_B(f(-),b)\colon E\rightarrow \mathscr {S}$
, which in turn follows from [Reference LurieLur09a, 3.3.2.8].
Applying this to the situation at hand and using the description of E on mapping spaces from Section 4.1.7, the claim follows once we show that for each nullbordism
![]() $N\in \mathscr {B}\mathrm {ord}(d)_{Q}$
, the map
$N\in \mathscr {B}\mathrm {ord}(d)_{Q}$
, the map
is an equivalence. Using the factorisation
![]() $E\colon \mathscr {B}\mathrm {ord}(d)\to \mathscr {M}\mathrm {od}(d)$
through the noncompact version of the bordism double
$E\colon \mathscr {B}\mathrm {ord}(d)\to \mathscr {M}\mathrm {od}(d)$
through the noncompact version of the bordism double
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, this map fits into a commutative diagram
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)$
, this map fits into a commutative diagram

where the bottom vertical equivalences result from the fact that the bordism
![]() $(P\times (-1,0])\colon \varnothing \leadsto P$
is initial in
$(P\times (-1,0])\colon \varnothing \leadsto P$
is initial in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P}$
and its image under E is initial in
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P}$
and its image under E is initial in
![]() $\mathscr {M}\mathrm {od}(d)^{\mathrm {rep}}_{E_{P \times I}}$
, by Remark 4.6. By Corollary 4.7, the bottom map is an equivalence as the handle dimension of
$\mathscr {M}\mathrm {od}(d)^{\mathrm {rep}}_{E_{P \times I}}$
, by Remark 4.6. By Corollary 4.7, the bottom map is an equivalence as the handle dimension of
![]() $P\times (-1,0]\cup _P W$
relative to Q is
$P\times (-1,0]\cup _P W$
relative to Q is
![]() $\le d-3$
by assumption. It thus suffices to show that
$\le d-3$
by assumption. It thus suffices to show that ![]() and
and ![]() are equivalences.
are equivalences.
We begin with ![]() . Since the mapping spaces in
. Since the mapping spaces in
![]() $\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P}$
are given by spaces of embeddings fixing the boundary and composition is given by composition of embeddings (see Section 4.1.1) and the same holds for
$\mathrm {nc}\mathscr {B}\mathrm {ord}(d)_{P}$
are given by spaces of embeddings fixing the boundary and composition is given by composition of embeddings (see Section 4.1.1) and the same holds for
![]() $\mathscr {B}\mathrm {ord}(d)_{P}$
with embeddings replaced by diffeomorphisms (see Section 4.1.2), the map
$\mathscr {B}\mathrm {ord}(d)_{P}$
with embeddings replaced by diffeomorphisms (see Section 4.1.2), the map ![]() is the map induced by restriction
is the map induced by restriction
Using the decomposition
![]() $\mathscr {B}\mathrm {ord}(d)_{P}=\bigsqcup _{M\in \pi _0\,\mathscr {B}\mathrm {ord}(d)_{P}}\mathrm {BDiff}_\partial (M)$
into path components (see Section 4.1.2), this can further be simplified as
$\mathscr {B}\mathrm {ord}(d)_{P}=\bigsqcup _{M\in \pi _0\,\mathscr {B}\mathrm {ord}(d)_{P}}\mathrm {BDiff}_\partial (M)$
into path components (see Section 4.1.2), this can further be simplified as
 $$ \begin{align} \underset{M\in \pi_0\,\mathscr{B}\mathrm{ord}(d)_{P}}\bigsqcup \mathrm{Diff}_\partial(M\cup_P W,N)/ \mathrm{Diff}_\partial(M) \longrightarrow \mathrm{Emb}_Q(W,N). \end{align} $$
$$ \begin{align} \underset{M\in \pi_0\,\mathscr{B}\mathrm{ord}(d)_{P}}\bigsqcup \mathrm{Diff}_\partial(M\cup_P W,N)/ \mathrm{Diff}_\partial(M) \longrightarrow \mathrm{Emb}_Q(W,N). \end{align} $$
To show that the map (76) is an equivalence, we show separately that it induces a bijection on components and that it is an equivalence on each component. To see that it is surjective on components, pick an embedding
![]() $e\in \mathrm {Emb}_Q(W,N)$
. Up to changing e within its isotopy class, we can assume that
$e\in \mathrm {Emb}_Q(W,N)$
. Up to changing e within its isotopy class, we can assume that
![]() $P\subset W$
is mapped to the interior of N and that the complement of
$P\subset W$
is mapped to the interior of N and that the complement of
![]() $e(W\backslash P)\subset N$
defines a bordism
$e(W\backslash P)\subset N$
defines a bordism
![]() $(N\backslash e(W\backslash P))\colon P\leadsto Q$
. In this case, the class in
$(N\backslash e(W\backslash P))\colon P\leadsto Q$
. In this case, the class in
![]() $\pi _0\,\mathrm {Diff}_\partial (M\cup _P W,N)/ \pi _0\,\mathrm {Diff}_\partial (M)=\pi _0(\mathrm {Diff}_\partial (M\cup _P W,N)/ \mathrm {Diff}_\partial (M))$
of the diffeomorphism
$\pi _0\,\mathrm {Diff}_\partial (M\cup _P W,N)/ \pi _0\,\mathrm {Diff}_\partial (M)=\pi _0(\mathrm {Diff}_\partial (M\cup _P W,N)/ \mathrm {Diff}_\partial (M))$
of the diffeomorphism
![]() $(N\backslash e(W\backslash P))\cup _P W\cong N$
obtained by extending e by the identity provides a preimage of
$(N\backslash e(W\backslash P))\cup _P W\cong N$
obtained by extending e by the identity provides a preimage of
![]() $[e]\in \pi _0\,\mathrm {Emb}_Q(W,N)$
. Injectivity of (76) on
$[e]\in \pi _0\,\mathrm {Emb}_Q(W,N)$
. Injectivity of (76) on
![]() $\pi _0$
follows from the isotopy extension theorem in the form of the homotopy fibre sequence
$\pi _0$
follows from the isotopy extension theorem in the form of the homotopy fibre sequence
with fibre taken over the image of a diffeomorphism
![]() $\phi \colon M\cup _PW\cong N$
. This sequence also implies that (76) is an equivalence on components, which finishes the proof for
$\phi \colon M\cup _PW\cong N$
. This sequence also implies that (76) is an equivalence on components, which finishes the proof for ![]() .
.
The argument for ![]() is similar. Using Sections 4.1.6 and 4.1.7, the reduction to showing that (76) is an equivalence applies also to the map
is similar. Using Sections 4.1.6 and 4.1.7, the reduction to showing that (76) is an equivalence applies also to the map ![]() and shows that it agrees with the map
and shows that it agrees with the map

induced by the inclusion
![]() $P\times (-1,0]\cup _PW\subset M\cup _PW$
. From the commutativity of the big diagram above and the fact that
$P\times (-1,0]\cup _PW\subset M\cup _PW$
. From the commutativity of the big diagram above and the fact that ![]() and the bottom horizontal map are equivalences, we see that
and the bottom horizontal map are equivalences, we see that ![]() is surjective on
is surjective on
![]() $\pi _0(-)$
, so we must show it is injective on
$\pi _0(-)$
, so we must show it is injective on
![]() $\pi _0(-)$
and induces an equivalence on components. This follows as for
$\pi _0(-)$
and induces an equivalence on components. This follows as for ![]() once we show that for
once we show that for
![]() $E_M\in \mathscr {M}\mathrm {od}(d)^{\mathrm {rep},\simeq }_{E_{P \times I}}$
and
$E_M\in \mathscr {M}\mathrm {od}(d)^{\mathrm {rep},\simeq }_{E_{P \times I}}$
and
![]() $\phi \in \mathrm {Map}_{\mathscr {M}\mathrm {od}(d)_{E_{Q \times I}}^{\simeq }}(E_M\cup _{E_P} E_W,E_N)$
, the sequence
$\phi \in \mathrm {Map}_{\mathscr {M}\mathrm {od}(d)_{E_{Q \times I}}^{\simeq }}(E_M\cup _{E_P} E_W,E_N)$
, the sequence
whose left map is given by
![]() $\phi \circ ((-)\cup _{E_{P \times I}}{\mathrm {id}_{E_W}})$
, is a homotopy fibre sequence when taking homotopy fibres over the image of
$\phi \circ ((-)\cup _{E_{P \times I}}{\mathrm {id}_{E_W}})$
, is a homotopy fibre sequence when taking homotopy fibres over the image of
![]() $\phi $
. By postcomposition with an inverse of
$\phi $
. By postcomposition with an inverse of
![]() $\phi $
, it suffices to show this in the case
$\phi $
, it suffices to show this in the case
![]() $\phi =\mathrm {id}$
. This follows from the second part of Theorem 4.10 (set
$\phi =\mathrm {id}$
. This follows from the second part of Theorem 4.10 (set
![]() $P=\varnothing $
,
$P=\varnothing $
,
![]() $Q=P$
,
$Q=P$
,
![]() $R=Q$
,
$R=Q$
,
![]() $W=\varnothing $
,
$W=\varnothing $
,
![]() $W'=W$
,
$W'=W$
,
![]() $M=M$
, and
$M=M$
, and
![]() $N=M$
). The hypothesis to apply this result holds by Corollary 4.7, since it follows from the assumption that
$N=M$
). The hypothesis to apply this result holds by Corollary 4.7, since it follows from the assumption that
![]() $\underline {k}\times \mathbf {R}^d\sqcup P\times (-1,0]\cup _PW$
is the interior of a manifold obtained from a closed collar on Q by attaching
$\underline {k}\times \mathbf {R}^d\sqcup P\times (-1,0]\cup _PW$
is the interior of a manifold obtained from a closed collar on Q by attaching
![]() $(\le d-3)$
-handles for all k.
$(\le d-3)$
-handles for all k.
We conclude this section with a first application of the tangential
![]() $2$
-type invariance. We will later use it to reduce the proof of the nontriviality result for
$2$
-type invariance. We will later use it to reduce the proof of the nontriviality result for
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
to the case of
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
to the case of
![]() $M=D^d$
.
$M=D^d$
.
Corollary 5.13. For a compact spin d-manifold
![]() $M\neq \varnothing $
with
$M\neq \varnothing $
with
![]() $d\ge 5$
, the space
$d\ge 5$
, the space
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
contains
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
contains
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
as a homotopy retract.
$S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
as a homotopy retract.
Proof. This essentially follows from the fact that any finitely presented group arises as the fundamental group of a compact connected codimension
![]() $0$
-submanifold
$0$
-submanifold
![]() $N\subset D^k$
as long as
$N\subset D^k$
as long as
![]() $k\ge 5$
(in fact,
$k\ge 5$
(in fact,
![]() $k \geq 4$
is known to suffice, but we will not need this harder result). Indeed, apply this to
$k \geq 4$
is known to suffice, but we will not need this harder result). Indeed, apply this to
![]() $k=d$
and the fundamental group of each path component of M to obtain a compact d-manifold
$k=d$
and the fundamental group of each path component of M to obtain a compact d-manifold
![]() $N\subset D^d$
whose fundamental groupoid is equivalent to that of M. Since N admits an embedding into
$N\subset D^d$
whose fundamental groupoid is equivalent to that of M. Since N admits an embedding into
![]() $D^d$
, it is in particular spin, so the final discussion in Example 5.2 shows that M and N have the same tangential
$D^d$
, it is in particular spin, so the final discussion in Example 5.2 shows that M and N have the same tangential
![]() $2$
-type. Using the tangential
$2$
-type. Using the tangential
![]() $2$
-type invariance of
$2$
-type invariance of
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (-)$
from Theorem 5.12, it thus suffices to show the claim for N. The latter follows by choosing an embedded disc
$S^{\mathscr {D}\mathrm {isc}}_\partial (-)$
from Theorem 5.12, it thus suffices to show the claim for N. The latter follows by choosing an embedded disc
![]() $D^d\subset N$
so that the composition
$D^d\subset N$
so that the composition
![]() $D^d\subset N\subset D^d$
is isotopic to the identity and applying
$D^d\subset N\subset D^d$
is isotopic to the identity and applying
![]() $S_\partial ^{\mathscr {D}\mathrm {isc}}(-)$
.
$S_\partial ^{\mathscr {D}\mathrm {isc}}(-)$
.
6 Theorem B: infinite loop space
The goal of this section is the proof of Theorem B, or rather the following strengthening of it:
Theorem 6.1. For a compact manifold M of dimension
![]() $d \geq 8$
,
$d \geq 8$
,
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
admits the structure of an infinite loop space. If M is
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
admits the structure of an infinite loop space. If M is
![]() $1$
-connected spin, then the bound
$1$
-connected spin, then the bound
![]() $d\ge 8$
can be improved to
$d\ge 8$
can be improved to
![]() $d\ge 6$
.
$d\ge 6$
.
In Section 1.2.4, we already gave an informal overview of the proof. We now make it precise.
6.1 Operads with homological stability
The proof of Theorem 6.1 relies on work of Basterra–Bobkova–Ponto–Tillmann–Yaekel [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17] on operads with homological stability which generalises earlier work of Tillmann [Reference TillmannTil00]. We summarise their main result in this subsection.
Remark 6.2. [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17] is written in the setting of classical operads in topological spaces and algebras over them. To make it fit in our framework, we will rephrase their result in terms of (symmetric)
![]() $\infty $
-operads and algebras over them (see Section 2.7). This translation is justified by the fact that there is an equivalence of
$\infty $
-operads and algebras over them (see Section 2.7). This translation is justified by the fact that there is an equivalence of
![]() $\infty $
-categories between the
$\infty $
-categories between the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathscr {O}\mathrm {pd}_\infty }$
of
${\mathscr {O}\mathrm {pd}_\infty }$
of
![]() $\infty $
-operads, and the
$\infty $
-operads, and the
![]() $\infty $
-category underlying the model category
$\infty $
-category underlying the model category
![]() ${s\mathscr {O}\mathrm {p}}$
of classical coloured operads in simplicial sets (see [Reference Chu, Haugseng and HeutsCHH18, p. 858]), which is in turn Quillen equivalent to that of classical coloured operads in topological spaces; these equivalences do not affect the induced operad in the homotopy category. These equivalences extend to corresponding equivalences between categories of algebras over operads: [Reference Pavlov and ScholbachPS18, Theorem 7.11] shows that (under mild conditions) the comparison functor from the
${s\mathscr {O}\mathrm {p}}$
of classical coloured operads in simplicial sets (see [Reference Chu, Haugseng and HeutsCHH18, p. 858]), which is in turn Quillen equivalent to that of classical coloured operads in topological spaces; these equivalences do not affect the induced operad in the homotopy category. These equivalences extend to corresponding equivalences between categories of algebras over operads: [Reference Pavlov and ScholbachPS18, Theorem 7.11] shows that (under mild conditions) the comparison functor from the
![]() $\infty $
-category underlying the model category of algebras over a simplicial operad to the
$\infty $
-category underlying the model category of algebras over a simplicial operad to the
![]() $\infty $
-category of algebras over the associated
$\infty $
-category of algebras over the associated
![]() $\infty $
-operad is an equivalence, and applying
$\infty $
-operad is an equivalence, and applying
![]() $\mathrm {Sing}(-)$
, induces (under mild conditions) a Quillen equivalence from the model category of algebras over a topological operad to the model category of algebras over the corresponding simplicial operad. The ‘mild conditions’ in both steps are satisfied for all operads appearing in this section.
$\mathrm {Sing}(-)$
, induces (under mild conditions) a Quillen equivalence from the model category of algebras over a topological operad to the model category of algebras over the corresponding simplicial operad. The ‘mild conditions’ in both steps are satisfied for all operads appearing in this section.
Let
![]() $\mathbf {N}_0$
denote the set of nonnegative integers. To state the main result of [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17], we consider
$\mathbf {N}_0$
denote the set of nonnegative integers. To state the main result of [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17], we consider
![]() $\mathbf {N}_0$
-graded
$\mathbf {N}_0$
-graded
![]() $\infty $
-operads, by which we mean (symmetric)
$\infty $
-operads, by which we mean (symmetric)
![]() $\infty $
-operads
$\infty $
-operads
![]() $\mathscr {P}$
, together with a map of
$\mathscr {P}$
, together with a map of
![]() $\infty $
-operads
$\infty $
-operads ![]() to the
to the
![]() $\infty $
-operad
$\infty $
-operad
![]() $\mathsf {Fin}^{\mathbf {N}_0}_\ast $
that is induced (via the operadic nerve [Reference LurieLur17, 2.1.1.27]) by
$\mathsf {Fin}^{\mathbf {N}_0}_\ast $
that is induced (via the operadic nerve [Reference LurieLur17, 2.1.1.27]) by
![]() $\mathbf {N}_0$
under addition, considered as a symmetric monoidal category with a single object. Unpacking the definition, this amounts to an
$\mathbf {N}_0$
under addition, considered as a symmetric monoidal category with a single object. Unpacking the definition, this amounts to an
![]() $\mathbf {N}_0$
-indexed disjoint union decomposition
$\mathbf {N}_0$
-indexed disjoint union decomposition
![]() $\mathrm {Mul}_{\mathscr {P}}(x_1,\ldots ,x_n;y)=\sqcup _{g\ge 0}\mathrm {Mul}_{\mathscr {P}}(x_1,\ldots ,x_n;y)_g$
of all spaces of multi-operations that is additive under operadic composition. Every
$\mathrm {Mul}_{\mathscr {P}}(x_1,\ldots ,x_n;y)=\sqcup _{g\ge 0}\mathrm {Mul}_{\mathscr {P}}(x_1,\ldots ,x_n;y)_g$
of all spaces of multi-operations that is additive under operadic composition. Every
![]() $\infty $
-operad
$\infty $
-operad
![]() $\mathscr {O}$
can be viewed as an
$\mathscr {O}$
can be viewed as an
![]() $\mathbf {N}_0$
-graded operad in grading
$\mathbf {N}_0$
-graded operad in grading
![]() $0$
; formally, this amounts to considering the composition
$0$
; formally, this amounts to considering the composition
![]() $\mathscr {O}^{\otimes }\rightarrow \mathsf {Fin}_\ast \rightarrow \mathsf {Fin}^{\mathbf {N}_0}_\ast $
, where the second arrow is induced by
$\mathscr {O}^{\otimes }\rightarrow \mathsf {Fin}_\ast \rightarrow \mathsf {Fin}^{\mathbf {N}_0}_\ast $
, where the second arrow is induced by
![]() $\{0\}\subset \mathbf {N}_0$
.
$\{0\}\subset \mathbf {N}_0$
.
Definition 6.3. An operad with homological stability is an
![]() $\mathbf {N}_0$
-graded
$\mathbf {N}_0$
-graded
![]() $\infty $
-operad
$\infty $
-operad
![]() $\mathscr {P}$
with a single colour (whose space of k-ary operations we write as
$\mathscr {P}$
with a single colour (whose space of k-ary operations we write as
![]() $\mathrm {Mul}_{\mathscr {P}}(\ast ,\ldots ,\ast ;\ast )=\mathscr {P}(k)=\sqcup _{g\ge 0}\mathscr {P}_g(k)$
), together with
$\mathrm {Mul}_{\mathscr {P}}(\ast ,\ldots ,\ast ;\ast )=\mathscr {P}(k)=\sqcup _{g\ge 0}\mathscr {P}_g(k)$
), together with
-
(i) a map of
 $\mathbf {N}_0$
-graded
$\mathbf {N}_0$
-graded
 $\infty $
-operads
$\infty $
-operads
 $\mathscr {A}\mathrm {ssoc} \rightarrow \mathscr {P}$
from the associative operad
$\mathscr {A}\mathrm {ssoc} \rightarrow \mathscr {P}$
from the associative operad
 $\mathscr {A}\mathrm {ssoc}$
(see Example 2.11) concentrated in degree
$\mathscr {A}\mathrm {ssoc}$
(see Example 2.11) concentrated in degree
 $0$
, and
$0$
, and -
(ii) a distinguished element
 $s\in \mathscr {P}_1(1)$
, called the stabilising element,
$s\in \mathscr {P}_1(1)$
, called the stabilising element,
such that
-
(a) the map on
 $2$
-ary operations
$2$
-ary operations
 $\mathscr {A}\mathrm {ssoc}(2)\rightarrow \mathscr {P}_0(2)$
lands in a single path component, and
$\mathscr {A}\mathrm {ssoc}(2)\rightarrow \mathscr {P}_0(2)$
lands in a single path component, and -
(b) the map
 induced by taking horizontal colimits in the commutative diagram in
induced by taking horizontal colimits in the commutative diagram in
 $\mathscr {S}$
is an integral homology isomorphism for all
$\mathscr {S}$
is an integral homology isomorphism for all
 $k\ge 0$
; here,
$k\ge 0$
; here,
 $\circ _P(-;-)$
is the operadic composition, and
$\circ _P(-;-)$
is the operadic composition, and
 $*\in \mathscr {P}_0(0)$
is the image of
$*\in \mathscr {P}_0(0)$
is the image of
 $\ast \simeq \mathscr {A}\mathrm {ssoc}(0) \rightarrow \mathscr {P}_0(0)$
.
$\ast \simeq \mathscr {A}\mathrm {ssoc}(0) \rightarrow \mathscr {P}_0(0)$
.
Given
![]() $\mathscr {P}$
as in Definition 6.3, we may forget the grading and consider the composition
$\mathscr {P}$
as in Definition 6.3, we may forget the grading and consider the composition
where the first arrow is the functor between
![]() $\infty $
-categories of algebras in
$\infty $
-categories of algebras in
![]() $\mathscr {S}$
with its cartesian symmetric monoidal structure, induced by the morphism
$\mathscr {S}$
with its cartesian symmetric monoidal structure, induced by the morphism
![]() $\mathscr {A}\mathrm {ssoc} \rightarrow \mathscr {P}$
of
$\mathscr {A}\mathrm {ssoc} \rightarrow \mathscr {P}$
of
![]() $\infty $
-operads (see Section 2.7), the second arrow is given by group completion (i.e., the left adjoint of the full subcategory inclusion
$\infty $
-operads (see Section 2.7), the second arrow is given by group completion (i.e., the left adjoint of the full subcategory inclusion
![]() $\mathrm {Mon}^{\mathrm {grp}}(\mathscr {S})\subset \mathrm {Mon}(\mathscr {S})$
of group-like objects – that is, those monoid objects
$\mathrm {Mon}^{\mathrm {grp}}(\mathscr {S})\subset \mathrm {Mon}(\mathscr {S})$
of group-like objects – that is, those monoid objects
![]() $M\in \mathrm {Mon}(\mathscr {S})\subset \mathrm {Fun}(\Delta ^{\mathrm {op}},\mathscr {S})$
in the sense of Section 2.5 for which the induced monoid of path components
$M\in \mathrm {Mon}(\mathscr {S})\subset \mathrm {Fun}(\Delta ^{\mathrm {op}},\mathscr {S})$
in the sense of Section 2.5 for which the induced monoid of path components
![]() $\pi _0(M_{[1]})$
is a group), and the final arrow is the forgetful functor, given by evaluation at
$\pi _0(M_{[1]})$
is a group), and the final arrow is the forgetful functor, given by evaluation at
![]() $[1]\in \Delta $
. Recall (see, for example, [Reference LurieLur17, 5.2.6]) that the composition of the final two arrows sends
$[1]\in \Delta $
. Recall (see, for example, [Reference LurieLur17, 5.2.6]) that the composition of the final two arrows sends
![]() $M\in \mathrm {Mon}(\mathscr {S})$
to the pullback in
$M\in \mathrm {Mon}(\mathscr {S})$
to the pullback in
![]() $\mathscr {S}$
$\mathscr {S}$

Writing
![]() $\mathrm {Alg}^{\mathrm {grp}}_{E_\infty }(\mathscr {S})\subset \mathrm {Alg}_{E_\infty }(\mathscr {S})$
for the full subcategory of group-like algebras in
$\mathrm {Alg}^{\mathrm {grp}}_{E_\infty }(\mathscr {S})\subset \mathrm {Alg}_{E_\infty }(\mathscr {S})$
for the full subcategory of group-like algebras in
![]() $\mathscr {S}$
over the
$\mathscr {S}$
over the
![]() $E_\infty $
-operad [Reference LurieLur17, 5.1.1.6], the main result of [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17] reads as follows:
$E_\infty $
-operad [Reference LurieLur17, 5.1.1.6], the main result of [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17] reads as follows:
Theorem 6.4 (Basterra–Bobkova–Ponto–Tillmann–Yeakel).
For an operad with homological stability
![]() $\mathscr {P}$
, there exists a dashed functor fitting into a commutative diagram of
$\mathscr {P}$
, there exists a dashed functor fitting into a commutative diagram of
![]() $\infty $
-categories
$\infty $
-categories

where U is the forgetful functor.
In other words, the underlying space of the group completion of an algebra over an operad with homological stability (viewed as an ungraded operad) admits functorially the structure of a group-like
![]() $E_\infty $
-algebra, or equivalently – by the recognition principle [Reference LurieLur17, 5.2.6.26] – of an infinite loop space.
$E_\infty $
-algebra, or equivalently – by the recognition principle [Reference LurieLur17, 5.2.6.26] – of an infinite loop space.
6.2 A manifold operad with homological stability
The main example of an operad with homological stability considered in [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17] is constructed out of the manifolds
for
![]() $k,l\ge 0$
and
$k,l\ge 0$
and
![]() $n\ge 1$
, considered as bordisms of the form
$n\ge 1$
, considered as bordisms of the form
![]() $\sqcup ^kS^{2n-1}\leadsto \sqcup ^lS^{2n-1}$
. Here,
$\sqcup ^kS^{2n-1}\leadsto \sqcup ^lS^{2n-1}$
. Here,
![]() $\smash {\sharp }$
denotes the connected sum operation. This is also the operad that is relevant for the proof of Theorem 6.1, so we recall its construction in our setting. We omit the
$\smash {\sharp }$
denotes the connected sum operation. This is also the operad that is relevant for the proof of Theorem 6.1, so we recall its construction in our setting. We omit the
![]() $2n$
-superscripts for brevity.
$2n$
-superscripts for brevity.
Consider the tangential structure
![]() $\theta =\tau ^*\mathrm {Fr}(\gamma )$
in the sense of Section 4.1.3 given as the
$\theta =\tau ^*\mathrm {Fr}(\gamma )$
in the sense of Section 4.1.3 given as the
![]() $\mathrm {GL}_{2n}(\mathbf {R})$
-space, which is the pullback of the frame bundle of the universal bundle
$\mathrm {GL}_{2n}(\mathbf {R})$
-space, which is the pullback of the frame bundle of the universal bundle
![]() $\gamma \rightarrow \mathrm {BO}(2n)$
along the n-connected cover map
$\gamma \rightarrow \mathrm {BO}(2n)$
along the n-connected cover map
![]() $\tau \colon \tau _{> n}\mathrm {BO}(2n)\rightarrow \mathrm {BO}(2n)$
. Since
$\tau \colon \tau _{> n}\mathrm {BO}(2n)\rightarrow \mathrm {BO}(2n)$
. Since
![]() $S^{2n-1}$
is stably parallelisable, its once-stabilised tangent bundle admits a
$S^{2n-1}$
is stably parallelisable, its once-stabilised tangent bundle admits a
![]() $\theta $
-structure
$\theta $
-structure
![]() $\ell _0$
compatible its canonical orientation, unique up to equivalence of
$\ell _0$
compatible its canonical orientation, unique up to equivalence of
![]() $\theta $
-structures. We consider the symmetric monoidal
$\theta $
-structures. We consider the symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {B}\mathrm {ord}^{\theta }(2n)^{(\infty ,1)}$
from Section 4.1.3 and write
$\mathscr {B}\mathrm {ord}^{\theta }(2n)^{(\infty ,1)}$
from Section 4.1.3 and write
![]() $\mathscr {B}\mathrm {ord}^{\theta }(2n)^{(\infty ,1),W}$
for the sub symmetric monoidal
$\mathscr {B}\mathrm {ord}^{\theta }(2n)^{(\infty ,1),W}$
for the sub symmetric monoidal
![]() $\infty $
-category (see Example 2.13) obtained by restricting objects to those equivalent to
$\infty $
-category (see Example 2.13) obtained by restricting objects to those equivalent to
![]() $\sqcup ^k(S^{2n-1},\ell _0)$
for
$\sqcup ^k(S^{2n-1},\ell _0)$
for
![]() $k\ge 0$
and restricting morphisms to those
$k\ge 0$
and restricting morphisms to those
![]() $\theta $
-bordisms whose underlying bordism without
$\theta $
-bordisms whose underlying bordism without
![]() $\theta $
-structure is equivalent to a disjoint union of
$\theta $
-structure is equivalent to a disjoint union of
![]() $W_{g,k+1}$
’s for some
$W_{g,k+1}$
’s for some
![]() $g,k\ge 0$
. Up to issues with components and different models, [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17, Theorem 1.3] shows that the endomorphism operad
$g,k\ge 0$
. Up to issues with components and different models, [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17, Theorem 1.3] shows that the endomorphism operad
of
![]() $(S^{2n-1},\ell _0)$
in this category (see Section 2.7.1) can be enhanced to an operad with homological stability for all
$(S^{2n-1},\ell _0)$
in this category (see Section 2.7.1) can be enhanced to an operad with homological stability for all
![]() $2n\ge 2$
. For completeness and to deal with these issues, we give a proof in our setting by adapting their argument. As in [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17], the main ingredient is a stable homological stability result of Galatius–Randal-Williams [Reference Galatius and Randal-WilliamsGRW17] (for the case
$2n\ge 2$
. For completeness and to deal with these issues, we give a proof in our setting by adapting their argument. As in [Reference Basterra, Bobkova, Ponto, Tillmann and YeakelBBP+17], the main ingredient is a stable homological stability result of Galatius–Randal-Williams [Reference Galatius and Randal-WilliamsGRW17] (for the case
![]() $2n=2$
, one can use [Reference HarerHar85]).
$2n=2$
, one can use [Reference HarerHar85]).
Proposition 6.5.
![]() $\mathscr {W}$
admits the structure of an operad with homological stability for all
$\mathscr {W}$
admits the structure of an operad with homological stability for all
![]() $2n\ge 2$
.
$2n\ge 2$
.
Proof. By definition and (68), the space of k-ary operations
is the
![]() $\infty $
-groupoid of
$\infty $
-groupoid of
![]() $\theta $
-bordisms
$\theta $
-bordisms
![]() $\sqcup ^k (S^{2n-1},\ell _0)\leadsto (S^{2n-1},\ell _0)$
that are, after forgetting
$\sqcup ^k (S^{2n-1},\ell _0)\leadsto (S^{2n-1},\ell _0)$
that are, after forgetting
![]() $\theta $
-structures, equivalent to
$\theta $
-structures, equivalent to
![]() $W_{g,k+1}$
for some
$W_{g,k+1}$
for some
![]() $g \geq 0$
. As the manifolds
$g \geq 0$
. As the manifolds
![]() $W_{g,k+1}$
are pairwise non-diffeomorphic for
$W_{g,k+1}$
are pairwise non-diffeomorphic for
![]() $g\ge 0$
, this induces a decomposition
$g\ge 0$
, this induces a decomposition
![]() $\mathscr {W}(k)=\sqcup _{g\ge 0}\mathscr {W}(k)_g$
which is compatible with the operad structure given by gluing bordisms with
$\mathscr {W}(k)=\sqcup _{g\ge 0}\mathscr {W}(k)_g$
which is compatible with the operad structure given by gluing bordisms with
![]() $\theta $
-structures, so it gives rise to an
$\theta $
-structures, so it gives rise to an
![]() $\mathbf {N}_0$
-grading on
$\mathbf {N}_0$
-grading on
![]() $\mathscr {W}$
.
$\mathscr {W}$
.
To construct a map
![]() $\mathscr {A}\mathrm {ssoc}\rightarrow \mathscr {W}$
from the associative operad (put in degree
$\mathscr {A}\mathrm {ssoc}\rightarrow \mathscr {W}$
from the associative operad (put in degree
![]() $0$
), we first use Example 2.11 to recognise
$0$
), we first use Example 2.11 to recognise
![]() $\mathscr {A}\mathrm {ssoc}$
as a suboperad in the sense of Section 2.7.1 of the endomorphism operad
$\mathscr {A}\mathrm {ssoc}$
as a suboperad in the sense of Section 2.7.1 of the endomorphism operad
![]() $\mathrm {End}_{\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(2)^{\partial ,(\infty ,1)}}(D^1,\mathrm {st})$
of the
$\mathrm {End}_{\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(2)^{\partial ,(\infty ,1)}}(D^1,\mathrm {st})$
of the
![]() $1$
-disc with the standard
$1$
-disc with the standard
![]() $1$
-framing (that is, framing of its once-stabilised tangent bundle) considered as an object of the
$1$
-framing (that is, framing of its once-stabilised tangent bundle) considered as an object of the
![]() $2$
-dimensional framed bordism category with boundary from Section 4.1.3 (formally, the tangential structure involved is
$2$
-dimensional framed bordism category with boundary from Section 4.1.3 (formally, the tangential structure involved is
![]() $\mathrm {fr}=(\mathrm {id}\colon \mathrm {GL}_{2}(\mathbf {R})\rightarrow \mathrm {GL}_{2}(\mathbf {R})$
). Namely, we restrict to those bordisms
$\mathrm {fr}=(\mathrm {id}\colon \mathrm {GL}_{2}(\mathbf {R})\rightarrow \mathrm {GL}_{2}(\mathbf {R})$
). Namely, we restrict to those bordisms
![]() $(N,\ell )\colon {\sqcup ^k}(D^1,\mathrm {st})\leadsto (D^1,\mathrm {st})$
for which
$(N,\ell )\colon {\sqcup ^k}(D^1,\mathrm {st})\leadsto (D^1,\mathrm {st})$
for which
![]() $(N,\ell )$
is diffeomorphic (after smoothing corners) to
$(N,\ell )$
is diffeomorphic (after smoothing corners) to
![]() $D^2$
with its standard framing such that
$D^2$
with its standard framing such that
![]() ${\sqcup ^k}(D^1,\mathrm {st})\subset \partial D^2$
is orientation-preserving,
${\sqcup ^k}(D^1,\mathrm {st})\subset \partial D^2$
is orientation-preserving,
![]() $(D^1,\mathrm {st})\subset \partial D^2$
is orientation-reversing (see Figure 8 for an example). From Example 2.11, one sees that this suboperad is equivalent to
$(D^1,\mathrm {st})\subset \partial D^2$
is orientation-reversing (see Figure 8 for an example). From Example 2.11, one sees that this suboperad is equivalent to
![]() $\mathscr {A}\mathrm {ssoc}$
since its space of k-ary operations is homotopy discrete with components
$\mathscr {A}\mathrm {ssoc}$
since its space of k-ary operations is homotopy discrete with components
![]() $\Sigma _k$
(with the regular
$\Sigma _k$
(with the regular
![]() $\Sigma _k$
-action) as a consequence of the facts that (i) the diffeomorphism group of
$\Sigma _k$
-action) as a consequence of the facts that (i) the diffeomorphism group of
![]() $D^2$
fixing some boundary intervals is contractible as a result of the equivalences
$D^2$
fixing some boundary intervals is contractible as a result of the equivalences
![]() $\mathrm {Diff}_\partial (D^1)\simeq \ast $
and
$\mathrm {Diff}_\partial (D^1)\simeq \ast $
and
![]() $\mathrm {Diff}_\partial (D^2)\simeq \ast $
(the first is folklore, the latter is [Reference SmaleSma59, Theorem B]) and that (ii) the space of framings of
$\mathrm {Diff}_\partial (D^2)\simeq \ast $
(the first is folklore, the latter is [Reference SmaleSma59, Theorem B]) and that (ii) the space of framings of
![]() $D^2$
relative to fixed
$D^2$
relative to fixed
![]() $1$
-framings on collared intervals in the boundary is homotopy discrete (as
$1$
-framings on collared intervals in the boundary is homotopy discrete (as
![]() $\Omega \mathrm {GL}_2(\mathbf {R})$
is).
$\Omega \mathrm {GL}_2(\mathbf {R})$
is).

Figure 8 A
![]() $5$
-ary operation in the
$5$
-ary operation in the
![]() $\infty $
-operad
$\infty $
-operad
![]() $\mathscr {W}$
.
$\mathscr {W}$
.
Now we consider the composition of symmetric monoidal
![]() $\infty $
-categories
$\infty $
-categories
where the first arrow takes the product with
![]() $D^{2n-1}$
equipped with the standard framing and smooths corners (see Example 3.13), the second arrow takes boundaries and lands in the bordism category with
$D^{2n-1}$
equipped with the standard framing and smooths corners (see Example 3.13), the second arrow takes boundaries and lands in the bordism category with
![]() $1$
-stabilised framings (see Example 3.12), and the final arrow is induced by the naturality (62) in the tangential structure and the fact that there is a map of tangential structures
$1$
-stabilised framings (see Example 3.12), and the final arrow is induced by the naturality (62) in the tangential structure and the fact that there is a map of tangential structures
![]() $(\mathrm {1{-}fr}) \to \theta $
since
$(\mathrm {1{-}fr}) \to \theta $
since
![]() $\tau \colon \tau _{>n}\mathrm {BO}(2n)\rightarrow \mathrm {BO}(2n)$
arises as the pullback of
$\tau \colon \tau _{>n}\mathrm {BO}(2n)\rightarrow \mathrm {BO}(2n)$
arises as the pullback of
![]() $\tau _{>n}\mathrm {BO}(2n+1)\rightarrow \mathrm {BO}(2n+1)$
along
$\tau _{>n}\mathrm {BO}(2n+1)\rightarrow \mathrm {BO}(2n+1)$
along
![]() $\mathrm {BO}(2n)\rightarrow \mathrm {BO}(2n+1)$
and thus receives a map from the pullback of
$\mathrm {BO}(2n)\rightarrow \mathrm {BO}(2n+1)$
and thus receives a map from the pullback of
![]() $* \to \mathrm {BO}(2n+1)$
. Taking endomorphism operads and precomposing with the map from
$* \to \mathrm {BO}(2n+1)$
. Taking endomorphism operads and precomposing with the map from
![]() $\mathscr {A}\mathrm {ssoc}$
, we have a composition
$\mathscr {A}\mathrm {ssoc}$
, we have a composition
which lands in the suboperad of
![]() $\smash {\mathrm {End}_{\mathscr {B}\mathrm {ord}^{\theta }(2n)^{(\infty ,1)}}(S^{2n-1},\ell _0)}$
whose underlying bordisms are equivalent to
$\smash {\mathrm {End}_{\mathscr {B}\mathrm {ord}^{\theta }(2n)^{(\infty ,1)}}(S^{2n-1},\ell _0)}$
whose underlying bordisms are equivalent to
![]() $W_{0,k+1}$
, using that
$W_{0,k+1}$
, using that
![]() $\partial (D^2\times D^{2n-1})\backslash \mathrm {int}(\sqcup ^{k+1}D^1\times D^{2n-1})\cong W_{0,k+1}$
after smoothing corners. In other words, it lands in the degree
$\partial (D^2\times D^{2n-1})\backslash \mathrm {int}(\sqcup ^{k+1}D^1\times D^{2n-1})\cong W_{0,k+1}$
after smoothing corners. In other words, it lands in the degree
![]() $0$
-part of the operad
$0$
-part of the operad
![]() $\mathscr {W}$
and thus gives a map
$\mathscr {W}$
and thus gives a map
![]() $\mathscr {A}\mathrm {ssoc} \rightarrow \mathscr {W}$
as in part (i) of Definition 6.3. As
$\mathscr {A}\mathrm {ssoc} \rightarrow \mathscr {W}$
as in part (i) of Definition 6.3. As
![]() $s\in \mathscr {W}_1(1)$
in part (ii), we choose the bordism
$s\in \mathscr {W}_1(1)$
in part (ii), we choose the bordism
![]() $W_{1,1}\colon S^{2n-1}\leadsto S^{2n-1}$
with an admissible
$W_{1,1}\colon S^{2n-1}\leadsto S^{2n-1}$
with an admissible
![]() $\theta $
-structure as in [Reference Galatius and Randal-WilliamsGRW17, p. 130] that extends
$\theta $
-structure as in [Reference Galatius and Randal-WilliamsGRW17, p. 130] that extends
![]() $\ell _0$
on the boundary spheres.
$\ell _0$
on the boundary spheres.
It remains to check conditions (a) and (b) of Definition 6.3. For (a), one observes that already the composition
![]() $\smash {\mathscr {A}\mathrm {ssoc}(2)\rightarrow \mathrm {End}_{\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(2)^{\partial ,(\infty ,1)}}(D^1,\mathrm {st})(2) \rightarrow \mathrm {End}_{\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(2n+1)^{\partial ,(\infty ,1)}}(D^{2n},\mathrm {st})(2)}$
lands in a single path component, since the bordism
$\smash {\mathscr {A}\mathrm {ssoc}(2)\rightarrow \mathrm {End}_{\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(2)^{\partial ,(\infty ,1)}}(D^1,\mathrm {st})(2) \rightarrow \mathrm {End}_{\mathscr {B}\mathrm {ord}^{\mathrm {fr}}(2n+1)^{\partial ,(\infty ,1)}}(D^{2n},\mathrm {st})(2)}$
lands in a single path component, since the bordism
![]() $(D^{2n+1},\mathrm {st})\colon {\sqcup ^2}(D^{2n},\mathrm {st})\leadsto (D^{2n},\mathrm {st})$
is for
$(D^{2n+1},\mathrm {st})\colon {\sqcup ^2}(D^{2n},\mathrm {st})\leadsto (D^{2n},\mathrm {st})$
is for
![]() $n\ge 1$
framed diffeomorphic to the same bordism with the two source components permuted using the isotopy extension theorem and the fact that the space of framed embeddings
$n\ge 1$
framed diffeomorphic to the same bordism with the two source components permuted using the isotopy extension theorem and the fact that the space of framed embeddings
![]() $\sqcup ^2 D^{d}\hookrightarrow D^{d}$
is connected for
$\sqcup ^2 D^{d}\hookrightarrow D^{d}$
is connected for
![]() $d\ge 2$
.
$d\ge 2$
.
Finally, to verify (b), we note that the image of
![]() $\ast \simeq \mathscr {A}\mathrm {ssoc}(0)\rightarrow \mathscr {W}$
is the bordism
$\ast \simeq \mathscr {A}\mathrm {ssoc}(0)\rightarrow \mathscr {W}$
is the bordism
![]() $D^{2n}\colon S^{2n-1}\leadsto \varnothing $
, equipped with some
$D^{2n}\colon S^{2n-1}\leadsto \varnothing $
, equipped with some
![]() $\theta $
-structure, so the map
$\theta $
-structure, so the map
![]() $\mathscr {W}_\infty (k)\rightarrow \mathscr {W}_{\infty }(0)$
is a homology equivalence as a result of applying [Reference Galatius and Randal-WilliamsGRW17, Theorem 1.3] to the bordism (with some
$\mathscr {W}_\infty (k)\rightarrow \mathscr {W}_{\infty }(0)$
is a homology equivalence as a result of applying [Reference Galatius and Randal-WilliamsGRW17, Theorem 1.3] to the bordism (with some
![]() $\theta $
-structure)
$\theta $
-structure)
which, being
![]() $(n-1)$
-connected relative to its source, satisfies the condition of that theorem.
$(n-1)$
-connected relative to its source, satisfies the condition of that theorem.
6.3 Group completion and
 $\mathscr {D}\mathrm {isc}$
-structure spaces
$\mathscr {D}\mathrm {isc}$
-structure spaces
Fixing numbers
![]() $2\le 2n\le d$
and a closed
$2\le 2n\le d$
and a closed
![]() $(d-2n)$
-manifold P, we consider the sequence of symmetric monoidal
$(d-2n)$
-manifold P, we consider the sequence of symmetric monoidal
![]() $\infty $
-categories
$\infty $
-categories
where U forgets tangential structures,
![]() $P\times (-)$
takes products (see
Step ⑧ in Section 3), and the final functor is discussed in Section 4.1.7. (78) lands in the sub symmetric monoidal
$P\times (-)$
takes products (see
Step ⑧ in Section 3), and the final functor is discussed in Section 4.1.7. (78) lands in the sub symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
which is obtained by the restricting the objects to those equivalent to
![]() $E_{\sqcup ^k P\times S^{2n-1}\times I}$
for
$E_{\sqcup ^k P\times S^{2n-1}\times I}$
for
![]() $k\ge 0$
and the morphisms to those bimodules equivalent to
$k\ge 0$
and the morphisms to those bimodules equivalent to
![]() $E_{\sqcup ^m P\times W_{g,k+1}}$
for some
$E_{\sqcup ^m P\times W_{g,k+1}}$
for some
![]() $m,k,g\ge 0$
. We write
$m,k,g\ge 0$
. We write
for the symmetric monoidal sub
![]() $\infty $
-category obtained by restricting objects and morphisms to those that land in
$\infty $
-category obtained by restricting objects and morphisms to those that land in
![]() $\mathscr {M}\mathrm {od}(d)^{(\infty ,1),W}\subset \mathscr {M}\mathrm {od}(d)^{(\infty ,1)}$
. Taking endomorphism operads, we obtain a composition
$\mathscr {M}\mathrm {od}(d)^{(\infty ,1),W}\subset \mathscr {M}\mathrm {od}(d)^{(\infty ,1)}$
. Taking endomorphism operads, we obtain a composition
 $$\begin{align*}\mathscr{A}\mathrm{ssoc} \rightarrow \mathscr{W} &=\mathrm{End}_{\mathscr{B}\mathrm{ord}^\theta(2n)^{(\infty,1),W}}(S^{2n-1},\ell_0)\\ &\rightarrow \mathrm{End}_{\mathscr{B}\mathrm{ord}(d)^{(\infty,1),\overline{W}}}(P\times S^{2n-1})\rightarrow \mathrm{End}_{\mathscr{M}\mathrm{od}(d)^{(\infty,1),W}}(P\times S^{2n-1}) \end{align*}$$
$$\begin{align*}\mathscr{A}\mathrm{ssoc} \rightarrow \mathscr{W} &=\mathrm{End}_{\mathscr{B}\mathrm{ord}^\theta(2n)^{(\infty,1),W}}(S^{2n-1},\ell_0)\\ &\rightarrow \mathrm{End}_{\mathscr{B}\mathrm{ord}(d)^{(\infty,1),\overline{W}}}(P\times S^{2n-1})\rightarrow \mathrm{End}_{\mathscr{M}\mathrm{od}(d)^{(\infty,1),W}}(P\times S^{2n-1}) \end{align*}$$
of maps of
![]() $\infty $
-operads. On
$\infty $
-operads. On
![]() $0$
-ary operations, this induces a map of
$0$
-ary operations, this induces a map of
![]() $\mathscr {W}$
-algebras (see Section 2.7.1)
$\mathscr {W}$
-algebras (see Section 2.7.1)
which we can also view as a map of
![]() $\mathscr {A}\mathrm {ssoc}$
-algebras in
$\mathscr {A}\mathrm {ssoc}$
-algebras in
![]() $\mathscr {S}$
, or equivalently, one of monoid objects in
$\mathscr {S}$
, or equivalently, one of monoid objects in
![]() $\mathscr {S}$
. Going through the construction, the unit in
$\mathscr {S}$
. Going through the construction, the unit in
![]() $\mathrm {Map}_{\mathscr {M}\mathrm {od}(d)^{(\infty ,1),W}}(\varnothing , E_{P\times S^{2n-1}\times I})$
is given by the bimodule
$\mathrm {Map}_{\mathscr {M}\mathrm {od}(d)^{(\infty ,1),W}}(\varnothing , E_{P\times S^{2n-1}\times I})$
is given by the bimodule
![]() $E_{P\times D^{2n}}$
, and the fibre at that object of (79), viewed as a map in
$E_{P\times D^{2n}}$
, and the fibre at that object of (79), viewed as a map in
![]() $\mathscr {S}$
, is exactly
$\mathscr {S}$
, is exactly
![]() $S^{\mathscr {D}\mathrm {isc}}(P\times D^{2n})$
from Section 4.5.2. Since the forgetful functor
$S^{\mathscr {D}\mathrm {isc}}(P\times D^{2n})$
from Section 4.5.2. Since the forgetful functor
![]() $\mathrm {Mon}(\mathscr {S})\rightarrow \mathscr {S}$
preserves limits,
$\mathrm {Mon}(\mathscr {S})\rightarrow \mathscr {S}$
preserves limits,
![]() $S^{\mathscr {D}\mathrm {isc}}(P\times D^{2n})$
inherits a monoid structure which fits into a pullback diagram in
$S^{\mathscr {D}\mathrm {isc}}(P\times D^{2n})$
inherits a monoid structure which fits into a pullback diagram in
![]() $\mathrm {Mon}(\mathscr {S})$
$\mathrm {Mon}(\mathscr {S})$

Under mild conditions, this square remains a pullback after group completion. We show this as the first part of the following proposition.
Proposition 6.6. Fix
![]() $2\le 2n\le d$
with
$2\le 2n\le d$
with
![]() $d\ge 6$
and a closed
$d\ge 6$
and a closed
![]() $(d-2n)$
-manifold P.
$(d-2n)$
-manifold P.
-
(i) If also
 $2n\ge 4$
, then the pullback (80) in
$2n\ge 4$
, then the pullback (80) in
 $\mathrm {Mon}(\mathscr {S})$
remains a pullback after group completion.
$\mathrm {Mon}(\mathscr {S})$
remains a pullback after group completion. -
(ii)
 $S_\partial ^{\mathscr {D}\mathrm {isc}}(P\times D^{2n})$
is group-like when considered as a monoid object in
$S_\partial ^{\mathscr {D}\mathrm {isc}}(P\times D^{2n})$
is group-like when considered as a monoid object in
 $\mathscr {S}$
.
$\mathscr {S}$
.
Proof. The first part is an application of the following fact, which can be deduced from [Reference SteimleSte21, Theorem 2.11]: if a map
![]() $\varphi \colon X\rightarrow Y$
of monoid objects in
$\varphi \colon X\rightarrow Y$
of monoid objects in
![]() $\mathscr {S}$
has the property that for all
$\mathscr {S}$
has the property that for all
![]() $y\in Y$
there is an
$y\in Y$
there is an
![]() $x\in X$
such that
$x\in X$
such that
![]() $\varphi (x)=y$
and the following squares are pullbacks in
$\varphi (x)=y$
and the following squares are pullbacks in
![]() $\mathscr {S}$
$\mathscr {S}$

then group completion preserves pullbacks of monoid objects in
![]() $\mathscr {S}$
along the map
$\mathscr {S}$
along the map
![]() $\varphi \colon X\rightarrow Y$
.
$\varphi \colon X\rightarrow Y$
.
To conclude 6.6, it thus suffices to check the condition for the right vertical map in (80) which amounts to showing that the square in
![]() $\mathscr {S}$
$\mathscr {S}$

is cartesian for all
![]() $g\ge 0$
, where
$g\ge 0$
, where ![]() denotes the monoid structure of the monoid objects in (80), and that the same holds for the square where we take products from the left. We focus on the former; the latter is proved in the same way.
denotes the monoid structure of the monoid objects in (80), and that the same holds for the square where we take products from the left. We focus on the former; the latter is proved in the same way.
Going through the construction of the map
![]() $\mathscr {A}\mathrm {ssoc}\rightarrow \mathscr {W}$
in the proof of Proposition 6.5, we see that
$\mathscr {A}\mathrm {ssoc}\rightarrow \mathscr {W}$
in the proof of Proposition 6.5, we see that ![]() is given a ‘pair of pants-product’: it sends a bordism
is given a ‘pair of pants-product’: it sends a bordism
![]() $M\colon \varnothing \leadsto P\times S^{2n-1}$
to the disjoint union
$M\colon \varnothing \leadsto P\times S^{2n-1}$
to the disjoint union
![]() $(M\sqcup P\times W_{g,1})\colon \varnothing \leadsto \sqcup ^2P\times S^{2n-1}$
and then takes composition with
$(M\sqcup P\times W_{g,1})\colon \varnothing \leadsto \sqcup ^2P\times S^{2n-1}$
and then takes composition with
![]() $(P\times W_{0,2+1})\colon \sqcup ^2P\times S^{2n-1}\leadsto P\times S^{2n-1}$
. By monoidality, this agrees with the map that sends
$(P\times W_{0,2+1})\colon \sqcup ^2P\times S^{2n-1}\leadsto P\times S^{2n-1}$
. By monoidality, this agrees with the map that sends
![]() $M\colon \varnothing \leadsto P\times S^{2n-1}$
first to its composition with
$M\colon \varnothing \leadsto P\times S^{2n-1}$
first to its composition with
![]() $([0,1]\times P\times S^{2n-1}\sqcup P\times W_{g,1})\colon P\times S^{2n-1}\leadsto \sqcup ^2 P\times S^{2n-1}$
and then takes composition with
$([0,1]\times P\times S^{2n-1}\sqcup P\times W_{g,1})\colon P\times S^{2n-1}\leadsto \sqcup ^2 P\times S^{2n-1}$
and then takes composition with
![]() $P\times W_{0,2+1}\colon \sqcup ^2P\times S^{2n-1}\leadsto P\times S^{2n-1}$
. The composition of the latter two bordisms is diffeomorphic, as a self-bordism of
$P\times W_{0,2+1}\colon \sqcup ^2P\times S^{2n-1}\leadsto P\times S^{2n-1}$
. The composition of the latter two bordisms is diffeomorphic, as a self-bordism of
![]() $P\times S^{2n-1}$
, to
$P\times S^{2n-1}$
, to
![]() $ P\times W_{g,1+1}$
. The same argument applies to
$ P\times W_{g,1+1}$
. The same argument applies to ![]() , so using monoidality of the functor
, so using monoidality of the functor
![]() $E\colon \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}\rightarrow \mathscr {M}\mathrm {od}(d)^{(\infty ,1)}$
, we may replace the top and bottom maps in the previous square by the gluing maps
$E\colon \mathscr {B}\mathrm {ord}(d)^{(\infty ,1)}\rightarrow \mathscr {M}\mathrm {od}(d)^{(\infty ,1)}$
, we may replace the top and bottom maps in the previous square by the gluing maps
![]() $(-)\cup _{P\times S^{2n-1}}(P\times W_{g,1+1})$
and
$(-)\cup _{P\times S^{2n-1}}(P\times W_{g,1+1})$
and
![]() $(-)\cup _{E_{P\times S^{2n-1}\times I}}E_{P\times W_{g,1+1}}$
, respectively. Taking vertical homotopy fibres, it thus suffices to show that for
$(-)\cup _{E_{P\times S^{2n-1}\times I}}E_{P\times W_{g,1+1}}$
, respectively. Taking vertical homotopy fibres, it thus suffices to show that for
![]() $h\ge 0$
, the gluing map
$h\ge 0$
, the gluing map
is an equivalence. In the setting of Theorem 5.12, this map is induced by the inclusion
![]() $(\mathrm {id}_P\times \mathrm {inc})\colon P\times W_{h,1}\hookrightarrow P\times W_{h+g,1}$
, so it is an equivalence by part (iii) of the theorem because the latter inclusion is an equivalence on tangential
$(\mathrm {id}_P\times \mathrm {inc})\colon P\times W_{h,1}\hookrightarrow P\times W_{h+g,1}$
, so it is an equivalence by part (iii) of the theorem because the latter inclusion is an equivalence on tangential
![]() $2$
-types as a result of
$2$
-types as a result of
![]() $W_{h,1}$
for all
$W_{h,1}$
for all
![]() $h\ge 0$
being parallelisable and
$h\ge 0$
being parallelisable and
![]() $1$
-connected since we assumed
$1$
-connected since we assumed
![]() $2n\ge 4$
.
$2n\ge 4$
.
To show (ii), we first recall from Section 4.5 that
![]() $\pi _0\, S_\partial ^{\mathscr {D}\mathrm {isc}}(P\times D^{2n})$
is the set of equivalence classes of pairs
$\pi _0\, S_\partial ^{\mathscr {D}\mathrm {isc}}(P\times D^{2n})$
is the set of equivalence classes of pairs
![]() $(W,\phi )$
of a compact manifold W whose boundary is identified with
$(W,\phi )$
of a compact manifold W whose boundary is identified with
![]() $P\times S^{2n-1}$
, together with an equivalence
$P\times S^{2n-1}$
, together with an equivalence
![]() $\phi \colon E_M\rightarrow E_{P\times D^{2n}}$
in
$\phi \colon E_M\rightarrow E_{P\times D^{2n}}$
in
![]() $\mathscr {M}\mathrm {od}(d)^{\simeq }_{P\times S^{2n-1}}$
, and two such pairs are equivalent if there exists a diffeomorphism between the manifolds that makes the evident triangle in
$\mathscr {M}\mathrm {od}(d)^{\simeq }_{P\times S^{2n-1}}$
, and two such pairs are equivalent if there exists a diffeomorphism between the manifolds that makes the evident triangle in
![]() $\mathscr {M}\mathrm {od}(d)^{\simeq }_{P\times S^{2n-1}}$
homotopy commute. Forgetting
$\mathscr {M}\mathrm {od}(d)^{\simeq }_{P\times S^{2n-1}}$
homotopy commute. Forgetting
![]() $\phi $
induces an exact sequence of pointed sets
$\phi $
induces an exact sequence of pointed sets
where
![]() $M_\partial (P \times D^{2n})$
is the pointed set of compact d-manifolds W with boundary identified with
$M_\partial (P \times D^{2n})$
is the pointed set of compact d-manifolds W with boundary identified with
![]() $P \times S^{2n-1}$
such that there exists an unspecified equivalence
$P \times S^{2n-1}$
such that there exists an unspecified equivalence
![]() $E_W \simeq E_{P \times D^{2n}}$
in
$E_W \simeq E_{P \times D^{2n}}$
in
![]() $\mathscr {M}\mathrm {od}(d)_{E_{P \times D^{2n}}}$
, up to diffeomorphism relative to the boundary, and based at
$\mathscr {M}\mathrm {od}(d)_{E_{P \times D^{2n}}}$
, up to diffeomorphism relative to the boundary, and based at
![]() $P \times D^{2n}$
. The monoid structure on
$P \times D^{2n}$
. The monoid structure on
![]() $\pi _0\,S^{\mathscr {D}\mathrm {isc}}_\partial (P \times D^{2n})$
given by the ‘pair of pants product’ induces a compatible monoid structure on
$\pi _0\,S^{\mathscr {D}\mathrm {isc}}_\partial (P \times D^{2n})$
given by the ‘pair of pants product’ induces a compatible monoid structure on
![]() $M_\partial (P \times D^{2n})$
, concretely given by
$M_\partial (P \times D^{2n})$
, concretely given by
A priori, the leftmost pointed set in (81) carries two monoid structures – one induced by the ‘pair of pants product’ ![]() and one by composition – but these agree by the Eckmann–Hilton argument. Thus, (81) is an exact sequence of monoids whose leftmost term is a group. Monoid-extensions of groups are groups, so it suffices to show that
and one by composition – but these agree by the Eckmann–Hilton argument. Thus, (81) is an exact sequence of monoids whose leftmost term is a group. Monoid-extensions of groups are groups, so it suffices to show that
![]() $M_\partial (P \times D^{2n})$
is a group. We do so by showing that every element has a right- and a left-inverse; since the two constructions are essentially identical, we will only explain the right-inverse.
$M_\partial (P \times D^{2n})$
is a group. We do so by showing that every element has a right- and a left-inverse; since the two constructions are essentially identical, we will only explain the right-inverse.
For this, it is convenient to use the notion of relative bordism
![]() $V \colon N_0 \leadsto N_1$
between two compact manifolds
$V \colon N_0 \leadsto N_1$
between two compact manifolds
![]() $N_0$
and
$N_0$
and
![]() $N_1$
with identified boundary
$N_1$
with identified boundary
![]() $\partial N_0\cong \partial N_1$
, by which we mean a compact manifold V with a division of its boundary into three codimension zero submanifolds
$\partial N_0\cong \partial N_1$
, by which we mean a compact manifold V with a division of its boundary into three codimension zero submanifolds
![]() $\partial V = N_0 \cup (\partial N_0 \times I) \cup N_1$
that intersect at corners. Up to creating some corners, we can regard an element
$\partial V = N_0 \cup (\partial N_0 \times I) \cup N_1$
that intersect at corners. Up to creating some corners, we can regard an element
![]() $W\in M_\partial (P\times D^{2n})$
as a relative bordism of the form
$W\in M_\partial (P\times D^{2n})$
as a relative bordism of the form
![]() $P \times D^{2n-1} \leadsto P \times D^{2n-1}$
by dividing the identified boundary
$P \times D^{2n-1} \leadsto P \times D^{2n-1}$
by dividing the identified boundary
![]() $\partial W\cong P\times S^{2n-1}$
into
$\partial W\cong P\times S^{2n-1}$
into
![]() $(P \times D^{2n-1}\times \{0\}) \cup (P \times \partial D^{2n-1}\times [0,1]) \cup (P \times D^{2n-1}\times \{1\})$
. In these terms, the monoid structure is given by composition of relative bordisms. By definition of
$(P \times D^{2n-1}\times \{0\}) \cup (P \times \partial D^{2n-1}\times [0,1]) \cup (P \times D^{2n-1}\times \{1\})$
. In these terms, the monoid structure is given by composition of relative bordisms. By definition of
![]() $M_\partial (P\times D^{2n})$
, the manifold W admits an equivalence
$M_\partial (P\times D^{2n})$
, the manifold W admits an equivalence
![]() $\phi \colon E_W \to E_{P \times D^{2n}}$
in
$\phi \colon E_W \to E_{P \times D^{2n}}$
in
![]() $\mathscr {M}\mathrm {od}(d)_{E_{P\times S^{2n-1}\times I}}$
. In general, for manifold N viewed as a nullbordism
$\mathscr {M}\mathrm {od}(d)_{E_{P\times S^{2n-1}\times I}}$
. In general, for manifold N viewed as a nullbordism
![]() $N\colon \varnothing \leadsto \partial N$
, we can consider the composition
$N\colon \varnothing \leadsto \partial N$
, we can consider the composition
in
![]() $\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
using the Day convolution product
$\mathrm {PSh}(\mathscr {D}\mathrm {isc}_d)$
using the Day convolution product
![]() $\otimes $
, the unique embedding
$\otimes $
, the unique embedding
![]() $\varnothing \rightarrow N$
and the fact that
$\varnothing \rightarrow N$
and the fact that
![]() $E_{\varnothing }$
is the monoidal unit. Evaluating this composition at
$E_{\varnothing }$
is the monoidal unit. Evaluating this composition at
![]() $\mathbf {R}^d$
and taking quotients by the
$\mathbf {R}^d$
and taking quotients by the
![]() $\mathrm {Diff}(\mathbf {R}^d)\simeq \mathrm {Emb}(\mathbf {R}^d,\mathbf {R}^d)$
-action by functoriality recovers the homotopy class of the boundary inclusion
$\mathrm {Diff}(\mathbf {R}^d)\simeq \mathrm {Emb}(\mathbf {R}^d,\mathbf {R}^d)$
-action by functoriality recovers the homotopy class of the boundary inclusion
![]() $\partial N\subset N$
. Applying this principle to the equivalence
$\partial N\subset N$
. Applying this principle to the equivalence
![]() $\phi $
above, we obtain a homotopy equivalence
$\phi $
above, we obtain a homotopy equivalence
![]() $W \simeq P \times D^{2n}$
under
$W \simeq P \times D^{2n}$
under
![]() $P \times S^{2n-1}$
. In terms of relative bordisms, this says that W is a strongly inertial relative h-cobordism: that is, not only are the inclusions of the incoming and outgoing boundary homotopy equivalences, but the induced homotopy equivalence between them is homotopic to a diffeomorphism relative to the boundary. Since we assumed
$P \times S^{2n-1}$
. In terms of relative bordisms, this says that W is a strongly inertial relative h-cobordism: that is, not only are the inclusions of the incoming and outgoing boundary homotopy equivalences, but the induced homotopy equivalence between them is homotopic to a diffeomorphism relative to the boundary. Since we assumed
![]() $d \geq 6$
, relative h-cobordisms
$d \geq 6$
, relative h-cobordisms
![]() $W \colon W_0 = P \times D^{2n-1} \leadsto W_1$
, up to diffeomorphism relative to the incoming boundary
$W \colon W_0 = P \times D^{2n-1} \leadsto W_1$
, up to diffeomorphism relative to the incoming boundary
![]() $P \times D^{2n-1}$
, are classified by their Whitehead torsion
$P \times D^{2n-1}$
, are classified by their Whitehead torsion
![]() $\tau (W) \in \mathrm {Wh}_1(\pi _1\,P)$
, and the Whitehead torsions of strongly inertial relative h-cobordisms form a subgroup (cf. the discussion in [Reference Jahren and KwasikJK15, Section 3]). Thus, we may find another strongly relative h-cobordism
$\tau (W) \in \mathrm {Wh}_1(\pi _1\,P)$
, and the Whitehead torsions of strongly inertial relative h-cobordisms form a subgroup (cf. the discussion in [Reference Jahren and KwasikJK15, Section 3]). Thus, we may find another strongly relative h-cobordism
![]() $W' \colon P \times D^{2n-1} \leadsto P \times D^{2n-1}$
with a diffeomorphism
$W' \colon P \times D^{2n-1} \leadsto P \times D^{2n-1}$
with a diffeomorphism
![]() $W \cup _{P \times D^{2n-1}} W' \cong P \times D^{2n}$
that respects part of the boundary identification – namely,
$W \cup _{P \times D^{2n-1}} W' \cong P \times D^{2n}$
that respects part of the boundary identification – namely,
![]() $P \times D^{2n-1} \{0\}\cup (P \times \partial D^{2n-1} \times [0,1])$
. By changing the identification of the outgoing boundary of
$P \times D^{2n-1} \{0\}\cup (P \times \partial D^{2n-1} \times [0,1])$
. By changing the identification of the outgoing boundary of
![]() $W'$
if necessary, we may assume that this diffeomorphism respects the full boundary identification. Smoothing corners, this gives a diffeomorphism
$W'$
if necessary, we may assume that this diffeomorphism respects the full boundary identification. Smoothing corners, this gives a diffeomorphism ![]() relative to
relative to
![]() $P \times S^{2n-1}$
. To show that
$P \times S^{2n-1}$
. To show that
![]() $W'$
is a right inverse to W in
$W'$
is a right inverse to W in
![]() $M_\partial (P\times D^{2n})$
, it thus suffices to produce an equivalence
$M_\partial (P\times D^{2n})$
, it thus suffices to produce an equivalence
![]() $E_{W'}\simeq E_{P \times D^{2n}}$
in
$E_{W'}\simeq E_{P \times D^{2n}}$
in
![]() $\mathscr {M}\mathrm {od}_{E_{P \times S^{2n-1} \times I}}$
. This is given by
$\mathscr {M}\mathrm {od}_{E_{P \times S^{2n-1} \times I}}$
. This is given by
Corollary 6.7. For
![]() $4\le 2n\le d$
with
$4\le 2n\le d$
with
![]() $d\ge 6$
and a closed
$d\ge 6$
and a closed
![]() $(d-2n)$
-manifold P, the
$(d-2n)$
-manifold P, the
![]() $\mathscr {D}\mathrm {isc}$
-structure space
$\mathscr {D}\mathrm {isc}$
-structure space
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})$
admits the structure of an infinite loop space.
$S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})$
admits the structure of an infinite loop space.
Proof. Combining both parts of Proposition 6.6,
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})$
agrees with the fibre of the group completion of the right vertical map in (80). As the group completion of a map of
$S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})$
agrees with the fibre of the group completion of the right vertical map in (80). As the group completion of a map of
![]() $\mathscr {W}$
-algebras, this map can be enhanced to a map of infinite loop spaces by Theorem 6.4 and Proposition 6.5. Fibres of infinite loop maps carry infinite loop space structures, so the claim follows.
$\mathscr {W}$
-algebras, this map can be enhanced to a map of infinite loop spaces by Theorem 6.4 and Proposition 6.5. Fibres of infinite loop maps carry infinite loop space structures, so the claim follows.
Combining Corollary 6.7 with the invariance under the tangential
![]() $2$
-type from Theorem 5.12, we can complete the goal of this section:
$2$
-type from Theorem 5.12, we can complete the goal of this section:
Proof Proof of Theorem 6.1.
For M a compact d-manifold with
![]() $d\ge 8$
, we pick an
$d\ge 8$
, we pick an
![]() $2n\ge 4$
such that
$2n\ge 4$
such that
![]() $2n-d\ge 4$
(the choice
$2n-d\ge 4$
(the choice
![]() $2n=4$
always works) and use the case
$2n=4$
always works) and use the case
![]() $k=2$
of Lemma 5.3 to pick a closed
$k=2$
of Lemma 5.3 to pick a closed
![]() $(d-2n)$
-manifold P of the same tangential
$(d-2n)$
-manifold P of the same tangential
![]() $2$
-type as M. Both
$2$
-type as M. Both
![]() $P\times D^{2n}$
and M are d-dimensional and have the same tangential
$P\times D^{2n}$
and M are d-dimensional and have the same tangential
![]() $2$
-type, so
$2$
-type, so
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})\simeq S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
by Theorem 5.12 5.12. As
$S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})\simeq S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
by Theorem 5.12 5.12. As
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})$
admits the structure of an infinite loop space by Corollary 6.7, the first part follows. For the claimed improvement, one can replace the role of P in the argument with
$S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})$
admits the structure of an infinite loop space by Corollary 6.7, the first part follows. For the claimed improvement, one can replace the role of P in the argument with
![]() $P=S^{d-2n}$
for any
$P=S^{d-2n}$
for any
![]() $2n\ge 4$
with
$2n\ge 4$
with
![]() $d-2n\ge 2$
, using that any two
$d-2n\ge 2$
, using that any two
![]() $1$
-connected spin manifolds have the same tangential
$1$
-connected spin manifolds have the same tangential
![]() $2$
-type (see Example 5.2).
$2$
-type (see Example 5.2).
Remark 6.8. The construction of the infinite loop space structure on
![]() $\mathrm{S}_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
as presented in this section comes with several drawbacks:
$\mathrm{S}_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
as presented in this section comes with several drawbacks:
-
(i) It depends on several choices, most notably: (a) the choice of
 $2n\ge 4$
with
$2n\ge 4$
with
 $2n-d\ge 4$
and (b) the choice of a closed
$2n-d\ge 4$
and (b) the choice of a closed
 $(d-2n)$
-manifold P of the same tangential
$(d-2n)$
-manifold P of the same tangential
 $2$
-type as M. In particular, the construction does not lift the functor
$2$
-type as M. In particular, the construction does not lift the functor
 $\smash {S_\partial ^{\mathscr {D}\mathrm {isc}}(-)\colon \mathscr {B}\mathrm {ord}(d)_{/\varnothing }^{(\infty ,1)}\rightarrow \mathscr {S}}$
to a functor with values in
$\smash {S_\partial ^{\mathscr {D}\mathrm {isc}}(-)\colon \mathscr {B}\mathrm {ord}(d)_{/\varnothing }^{(\infty ,1)}\rightarrow \mathscr {S}}$
to a functor with values in
 $\smash {\mathrm {Alg}_{E_\infty }^{\mathrm {grp}}(\mathscr {S})}$
, but it does enhances the
$\smash {\mathrm {Alg}_{E_\infty }^{\mathrm {grp}}(\mathscr {S})}$
, but it does enhances the
 $\mathrm {Diff}(P)$
-action on the space
$\mathrm {Diff}(P)$
-action on the space
 $\mathrm{S}_\partial ^{\mathscr {D}\mathrm {isc}}(D^{2n}\times P)$
for fixed
$\mathrm{S}_\partial ^{\mathscr {D}\mathrm {isc}}(D^{2n}\times P)$
for fixed
 $2n\ge 4$
and a closed manifold P to an action in
$2n\ge 4$
and a closed manifold P to an action in
 $\smash {\mathrm {Alg}_{E_\infty }^{\mathrm {grp}}(\mathscr {S})}$
.
$\smash {\mathrm {Alg}_{E_\infty }^{\mathrm {grp}}(\mathscr {S})}$
. -
(ii) The restrictions on the dimension are likely not optimal.
-
(iii) The space
 $S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})$
ought to carry the structure of an
$S^{\mathscr {D}\mathrm {isc}}_\partial (P\times D^{2n})$
ought to carry the structure of an
 $E_{2n}$
-algebra, and the infinite loop space structure we give ought to extend this
$E_{2n}$
-algebra, and the infinite loop space structure we give ought to extend this
 $E_{2n}$
-structure.
$E_{2n}$
-structure.
We expect that there is a better construction of the infinite loop space structure on
![]() $\mathrm{S}_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
that does not suffer from these shortcomings.
$\mathrm{S}_\partial ^{\mathscr {D}\mathrm {isc}}(M)$
that does not suffer from these shortcomings.
7 Localisations of mapping spaces between operads
This section serves to prove general results on mapping spaces between (truncated) operads and their localisations at collections of primes. In particular, given
![]() $\infty $
-operads
$\infty $
-operads
![]() $\mathscr {O}$
and
$\mathscr {O}$
and
![]() $\mathscr {P}$
, we rely on work of Göppl–Weiss [Reference Göppl and WeissGW24] to study the effect on homotopy groups of a map
$\mathscr {P}$
, we rely on work of Göppl–Weiss [Reference Göppl and WeissGW24] to study the effect on homotopy groups of a map
from the rationalisation of the mapping space between
![]() $\mathscr {O}$
and
$\mathscr {O}$
and
![]() $\mathscr {P}$
to the mapping space between the respective rationalisations. In Section 8, we use these results to prove Theorems C and E.
$\mathscr {P}$
to the mapping space between the respective rationalisations. In Section 8, we use these results to prove Theorems C and E.
Convention 7.1. Up to this point, we phrased our results and arguments in the language of
![]() $\infty $
-categories. In this and the following section, we will use several intermediate results from various sources, none of which are written in this language. To stay close to these sources, we switch language for the remainder of this paper and work in the category of simplicial sets or the category of compactly generated weak Hausdorff spaces. We denote either of these categories by
$\infty $
-categories. In this and the following section, we will use several intermediate results from various sources, none of which are written in this language. To stay close to these sources, we switch language for the remainder of this paper and work in the category of simplicial sets or the category of compactly generated weak Hausdorff spaces. We denote either of these categories by
![]() $\mathsf {S}$
and leave the necessary transitions based on the usual Quillen equivalence between the standard model structures on these categories to the reader. As a result of not working
$\mathsf {S}$
and leave the necessary transitions based on the usual Quillen equivalence between the standard model structures on these categories to the reader. As a result of not working
![]() $\infty $
-categorically, we have to derive all mapping spaces in various categories that appear (spaces, operads, etc.) with respect to a class of weak equivalences for example, using Dwyer–Kan’s functorial simplicial localisation [Reference Dwyer and KanDK80a, Reference Dwyer and KanDK80b]. We indicate various derived mapping spaces by adding an h-subscript, so write
$\infty $
-categorically, we have to derive all mapping spaces in various categories that appear (spaces, operads, etc.) with respect to a class of weak equivalences for example, using Dwyer–Kan’s functorial simplicial localisation [Reference Dwyer and KanDK80a, Reference Dwyer and KanDK80b]. We indicate various derived mapping spaces by adding an h-subscript, so write
![]() $\mathrm {Map}^h(-,-)$
, and we will mention the class of weak equivalences with respect we derive whenever a new type of derived mapping space is considered.
$\mathrm {Map}^h(-,-)$
, and we will mention the class of weak equivalences with respect we derive whenever a new type of derived mapping space is considered.
7.1 Localisation of spaces and groups at a set of primes
We first recall some facts about T-localisations of spaces for a set of primes T. Recall that a space Z is T-local if the map
![]() $(- \circ g) \colon \mathrm {Map}^h_{\mathsf {S}}(Y,Z) \to \mathrm {Map}^h_{\mathsf {S}}(X,Z)$
is a weak equivalence for any map
$(- \circ g) \colon \mathrm {Map}^h_{\mathsf {S}}(Y,Z) \to \mathrm {Map}^h_{\mathsf {S}}(X,Z)$
is a weak equivalence for any map
![]() $g \colon X \to Y$
that is an isomorphism on
$g \colon X \to Y$
that is an isomorphism on
![]() $\mathrm {H}_{*}(-;\mathbf {Z}_T)$
. Here, the mapping spaces are derived with respect to weak homotopy equivalences, and
$\mathrm {H}_{*}(-;\mathbf {Z}_T)$
. Here, the mapping spaces are derived with respect to weak homotopy equivalences, and
![]() $\mathbf {Z}_T$
is the localisation of
$\mathbf {Z}_T$
is the localisation of
![]() $\mathbf {Z}$
obtained by inverting all primes in T. Immediately from the definition, we see that the class of T-local spaces is closed under
$\mathbf {Z}$
obtained by inverting all primes in T. Immediately from the definition, we see that the class of T-local spaces is closed under
-
(i) taking homotopy limits,
-
(ii) passing to collections of path components,
-
(iii) applying
 $\mathrm {Map}^h_{\mathsf {S}}(X,-)$
for any space X.
$\mathrm {Map}^h_{\mathsf {S}}(X,-)$
for any space X.
A map
![]() $f \colon X \to Y$
is a T-localisation if Y is T-local and f is a
$f \colon X \to Y$
is a T-localisation if Y is T-local and f is a
![]() $\mathbf {Z}_T$
-homology isomorphism. Any space admits a T-localisation, and, suitably modelled, this yields an
$\mathbf {Z}_T$
-homology isomorphism. Any space admits a T-localisation, and, suitably modelled, this yields an
![]() $\mathsf {S}$
-enriched functor
$\mathsf {S}$
-enriched functor
together with a natural transformation
![]() $r_T \colon \mathrm {id} \to (-)_T$
which enjoys the following properties (see, for example, [Reference FarjounFar96, 1.A.3, 1.A.8, 1.B.2, 1.B.7, 1.C.9, 1.C.13, 1.E.4]):
$r_T \colon \mathrm {id} \to (-)_T$
which enjoys the following properties (see, for example, [Reference FarjounFar96, 1.A.3, 1.A.8, 1.B.2, 1.B.7, 1.C.9, 1.C.13, 1.E.4]):
-
(a) the map
 $r_T \colon X \to X_T$
is a T-localisation, so a weak equivalence if X is T-local,
$r_T \colon X \to X_T$
is a T-localisation, so a weak equivalence if X is T-local, -
(b)
 $(-)_T$
preserves weak equivalences,
$(-)_T$
preserves weak equivalences, -
(c) the canonical map
 $(X\times Y)_T\rightarrow X_T\times Y_T$
is a weak equivalence,
$(X\times Y)_T\rightarrow X_T\times Y_T$
is a weak equivalence, -
(d) the map
 $(-)\circ r_T\colon \mathrm {Map}^h_{\mathsf {S}}(X_T,Y)\rightarrow \mathrm {Map}^h_{\mathsf {S}}(X,Y)$
is a weak equivalence if Y is T-local.
$(-)\circ r_T\colon \mathrm {Map}^h_{\mathsf {S}}(X_T,Y)\rightarrow \mathrm {Map}^h_{\mathsf {S}}(X,Y)$
is a weak equivalence if Y is T-local.
If T is the set of all primes, T-localisation is rationalisation, which we denote as ![]() .
.
7.1.1 Localisation of groups
Recall that a group G is T-local if the map
![]() $(- \circ g) \colon \mathrm {Hom}(H,G) \to \mathrm {Hom}(K,G)$
is an isomorphism for all
$(- \circ g) \colon \mathrm {Hom}(H,G) \to \mathrm {Hom}(K,G)$
is an isomorphism for all
![]() $g \colon K \to H$
such that
$g \colon K \to H$
such that
![]() $\mathrm {H}_1(g;\mathbf {Z}_T)$
is an isomorphism and
$\mathrm {H}_1(g;\mathbf {Z}_T)$
is an isomorphism and
![]() $\mathrm {H}_2(g;\mathbf {Z}_T)$
is surjective. The homotopy groups of a T-local space at any basepoint are T-local groups [Reference BousfieldBou75, Theorem 5.5]. A morphism of groups
$\mathrm {H}_2(g;\mathbf {Z}_T)$
is surjective. The homotopy groups of a T-local space at any basepoint are T-local groups [Reference BousfieldBou75, Theorem 5.5]. A morphism of groups
![]() $f\colon H\rightarrow G$
is a T-localisation if G is T-local and f has the property on
$f\colon H\rightarrow G$
is a T-localisation if G is T-local and f has the property on
![]() $\mathrm {H}_{*}(-;\mathbf {Z}_T)$
for
$\mathrm {H}_{*}(-;\mathbf {Z}_T)$
for
![]() $*=1,2$
just described. One way to construct T-localisations of groups is as follows: the functor (84) has an analogue
$*=1,2$
just described. One way to construct T-localisations of groups is as follows: the functor (84) has an analogue
![]() $(-)_T \colon \mathsf {S}_{*} \rightarrow \mathsf {S}_{*}$
in the pointed setting, which agrees with (84) on connected spaces [Reference FarjounFar96, A.7]. Defining
$(-)_T \colon \mathsf {S}_{*} \rightarrow \mathsf {S}_{*}$
in the pointed setting, which agrees with (84) on connected spaces [Reference FarjounFar96, A.7]. Defining ![]() , we obtain a functor
, we obtain a functor
![]() $(-)_T \colon \mathsf {Grp} \rightarrow \mathsf {Grp}$
on the category of groups with a natural transformation
$(-)_T \colon \mathsf {Grp} \rightarrow \mathsf {Grp}$
on the category of groups with a natural transformation
![]() $\mathrm {id}\rightarrow (-)_T$
which is a T-localisation [Reference BousfieldBou75, Lemma 7.3]. Note that we have
$\mathrm {id}\rightarrow (-)_T$
which is a T-localisation [Reference BousfieldBou75, Lemma 7.3]. Note that we have
![]() $(G)^{\mathrm {ab}}\otimes \mathbf {Z}_T\cong (G_T)^{\mathrm {ab}}\otimes \mathbf {Z}_T$
by construction and the Hurewicz theorem. On nilpotent groups,
$(G)^{\mathrm {ab}}\otimes \mathbf {Z}_T\cong (G_T)^{\mathrm {ab}}\otimes \mathbf {Z}_T$
by construction and the Hurewicz theorem. On nilpotent groups,
![]() $(-)_T$
agrees with the usual T-localisation of nilpotent groups in the algebraic sense.
$(-)_T$
agrees with the usual T-localisation of nilpotent groups in the algebraic sense.
7.1.2 Localisation of nilpotent spaces
Recall that a space X is nilpotent if it is connected, has nilpotent fundamental group, and its
![]() $\pi _1(X)$
-action on
$\pi _1(X)$
-action on
![]() $\pi _i(X)$
for
$\pi _i(X)$
for
![]() $i\ge 2$
is nilpotent. T-localisation preserves nilpotent spaces and can be characterised as follows (see, for example, [Reference May and PontoMP12, 6.1.2]):
$i\ge 2$
is nilpotent. T-localisation preserves nilpotent spaces and can be characterised as follows (see, for example, [Reference May and PontoMP12, 6.1.2]):
Lemma 7.2. Let
![]() $f \colon X \to Y$
be a map from a nilpotent space X to a T-local space Y. Then the following are equivalent:
$f \colon X \to Y$
be a map from a nilpotent space X to a T-local space Y. Then the following are equivalent:
-
(i)
 $f \colon X \to Y$
is a T-localisation of spaces,
$f \colon X \to Y$
is a T-localisation of spaces, -
(ii)
 $f_{*} \colon \widetilde {\mathrm {H}}_k(X;\mathbf {Z}) \to \widetilde {\mathrm {H}}_k(Y;\mathbf {Z})$
is a T-localisation of abelian groups for all
$f_{*} \colon \widetilde {\mathrm {H}}_k(X;\mathbf {Z}) \to \widetilde {\mathrm {H}}_k(Y;\mathbf {Z})$
is a T-localisation of abelian groups for all
 $k\ge 1$
,
$k\ge 1$
, -
(iii)
 $f_{*} \colon \pi _k(X) \to \pi _k(Y)$
is a T-localisation of abelian and nilpotent groups for all
$f_{*} \colon \pi _k(X) \to \pi _k(Y)$
is a T-localisation of abelian and nilpotent groups for all
 $k\ge 1$
.
$k\ge 1$
.
Localisations of nilpotent spaces behave well with respect to many constructions, such as the following:
Lemma 7.3. Let
![]() $f \colon X \to A$
and
$f \colon X \to A$
and
![]() $g \colon Y \to A$
be based maps between spaces with nilpotent basepoint component. Then
$g \colon Y \to A$
be based maps between spaces with nilpotent basepoint component. Then
-
(i) the basepoint component
 $(X\times ^h_AY)_0\subseteq X\times ^h_AY$
of the homotopy pullback is nilpotent,
$(X\times ^h_AY)_0\subseteq X\times ^h_AY$
of the homotopy pullback is nilpotent, -
(ii) the natural map
 $(X\times ^h_AY)_0 \to (X_T\times ^h_{A_T}Y_T)_0$
is a T-localisation of nilpotent spaces, and
$(X\times ^h_AY)_0 \to (X_T\times ^h_{A_T}Y_T)_0$
is a T-localisation of nilpotent spaces, and -
(iii) if
 $X_0$
,
$X_0$
,
 $Y_0$
and
$Y_0$
and
 $A_0$
have finitely generated homotopy groups, then so does
$A_0$
have finitely generated homotopy groups, then so does
 $(X\times ^h_AY)_0$
.
$(X\times ^h_AY)_0$
.
Proof. Since
![]() $(X_0\times ^h_{A_0}Y_0)_0=(X\times ^h_AY)_0$
, and similarly for the localised version, we may assume that X, Y and A are connected. In this case, (i) and (ii) are [Reference May and PontoMP12, 6.2.5]. For (iii), we use the long exact sequence for the homotopy groups of a homotopy pullback which exhibits
$(X_0\times ^h_{A_0}Y_0)_0=(X\times ^h_AY)_0$
, and similarly for the localised version, we may assume that X, Y and A are connected. In this case, (i) and (ii) are [Reference May and PontoMP12, 6.2.5]. For (iii), we use the long exact sequence for the homotopy groups of a homotopy pullback which exhibits
![]() $\pi _i(X\times ^h_AY)$
for
$\pi _i(X\times ^h_AY)$
for
![]() $i\ge 1$
as a central extension of subquotients of finitely generated nilpotent groups. As the latter are closed under taking subgroups, quotients and extensions, the statement follows.
$i\ge 1$
as a central extension of subquotients of finitely generated nilpotent groups. As the latter are closed under taking subgroups, quotients and extensions, the statement follows.
The next lemma involves equivariant mapping spaces ![]() between G-spaces for finite groups G, which we derive with respect to the G-equivariant maps whose underlying maps of spaces are weak homotopy equivalences.
between G-spaces for finite groups G, which we derive with respect to the G-equivariant maps whose underlying maps of spaces are weak homotopy equivalences.
Lemma 7.4. Let X and Y be G-spaces for G a finite group. If
-
•
 $X_{hG}$
is weakly equivalent to a finite CW complex and
$X_{hG}$
is weakly equivalent to a finite CW complex and -
• Y has nilpotent path components,
then for any
![]() $f\in \mathrm {Map}^h_G(X,Y)$
, the following holds:
$f\in \mathrm {Map}^h_G(X,Y)$
, the following holds:
-
(i) the path component
 $\mathrm {Map}^h_G(X,Y)_f\subseteq \mathrm {Map}^h_G(X,Y) $
is nilpotent,
$\mathrm {Map}^h_G(X,Y)_f\subseteq \mathrm {Map}^h_G(X,Y) $
is nilpotent, -
(ii) the postcomposition map
 $(r_T \circ (-))\colon \mathrm {Map}^h_G(X,Y)_f\rightarrow \mathrm {Map}^h_G(X,Y_T)_{(r_T\circ f)}$
is a T-localisation,
$(r_T \circ (-))\colon \mathrm {Map}^h_G(X,Y)_f\rightarrow \mathrm {Map}^h_G(X,Y_T)_{(r_T\circ f)}$
is a T-localisation, -
(iii) if Y has finitely generated homotopy groups at all basepoints, then so does
 $\mathrm {Map}^h_G(X,Y)_f$
.
$\mathrm {Map}^h_G(X,Y)_f$
.
Proof. By the assumption on
![]() $X_{hG}$
, we may assume that X is a finite G-CW complex consisting of free G-cells. This allows us to argue by induction on the number of cells: if X is obtained from
$X_{hG}$
, we may assume that X is a finite G-CW complex consisting of free G-cells. This allows us to argue by induction on the number of cells: if X is obtained from
![]() $X'$
by attaching a single free G-cell, there are commutative squares
$X'$
by attaching a single free G-cell, there are commutative squares

The left square is a homotopy pushout of G-spaces, and the right square is obtained from it by applying
![]() $\mathrm {Map} ^h_G(-,Y)$
, so it is a homotopy pullback. By an induction over a principal Postnikov tower of the path components of Y, one sees that the conclusions hold for all components of the right-hand terms of the right-hand diagram. By induction, we may assume they hold for the bottom-left corner in the right diagram, so using Lemma 7.3 and that subgroups of (finitely generated) nilpotent groups are (finitely generated) nilpotent, they also hold for all components of the top-left corner in the right diagram.
$\mathrm {Map} ^h_G(-,Y)$
, so it is a homotopy pullback. By an induction over a principal Postnikov tower of the path components of Y, one sees that the conclusions hold for all components of the right-hand terms of the right-hand diagram. By induction, we may assume they hold for the bottom-left corner in the right diagram, so using Lemma 7.3 and that subgroups of (finitely generated) nilpotent groups are (finitely generated) nilpotent, they also hold for all components of the top-left corner in the right diagram.
Recall that a
![]() $\underline {k}$
-cubical diagram is a functor on the poset of subsets of
$\underline {k}$
-cubical diagram is a functor on the poset of subsets of ![]() .
.
Lemma 7.5. Let X be a
![]() $\underline {k}$
-cubical diagram of spaces with nilpotent path components.
$\underline {k}$
-cubical diagram of spaces with nilpotent path components.
-
(i)
 $\mathrm {holim}_{\varnothing \neq I\subseteq \underline {r}}X(I)$
has nilpotent components, and the map
$\mathrm {holim}_{\varnothing \neq I\subseteq \underline {r}}X(I)$
has nilpotent components, and the map
 $\mathrm {holim}_{\varnothing \neq I\subseteq \underline {k}}X(I)\rightarrow \mathrm {holim}_{\varnothing \neq I\subseteq \underline {k}}(X(I)_T)$
induced by the T-localisations of the
$\mathrm {holim}_{\varnothing \neq I\subseteq \underline {k}}X(I)\rightarrow \mathrm {holim}_{\varnothing \neq I\subseteq \underline {k}}(X(I)_T)$
induced by the T-localisations of the
 $X(I)$
’s, is a T-localisation when restricted to any component of the source and the corresponding component of the target.
$X(I)$
’s, is a T-localisation when restricted to any component of the source and the corresponding component of the target. -
(ii) If
 $X(I)$
has finitely generated homotopy groups at all basepoints for all
$X(I)$
has finitely generated homotopy groups at all basepoints for all
 $\varnothing \neq I\subseteq \underline {k}$
, then
$\varnothing \neq I\subseteq \underline {k}$
, then
 $\mathrm {holim}_{\varnothing \neq I\subseteq \underline {k}}X(I)$
has finitely generated homotopy groups at all basepoints.
$\mathrm {holim}_{\varnothing \neq I\subseteq \underline {k}}X(I)$
has finitely generated homotopy groups at all basepoints.
Proof. We prove the claim by induction on k. For
![]() $k=1$
, the claim is vacuous as
$k=1$
, the claim is vacuous as
![]() $\mathrm {holim}_{\varnothing \neq I\subseteq \underline {1}}X(I)\simeq X(\underline {1})$
. For larger k, we use that the homotopy limit fits into a homotopy cartesian square
$\mathrm {holim}_{\varnothing \neq I\subseteq \underline {1}}X(I)\simeq X(\underline {1})$
. For larger k, we use that the homotopy limit fits into a homotopy cartesian square

By induction, the conclusion of the statement holds for two diagrams defining the bottom row, and by assumption also for
![]() $X(\underline {k})$
, so Lemma 7.3 gives the induction step.
$X(\underline {k})$
, so Lemma 7.3 gives the induction step.
7.2 Operads and dendroidal spaces
In this and the following sections, operads
![]() $\mathsf {O}, \mathsf {P},\ldots $
are understood as single-coloured operads in
$\mathsf {O}, \mathsf {P},\ldots $
are understood as single-coloured operads in
![]() $\mathbf {S}$
in the classical sense. Declaring a weak equivalence to be a levelwise weak equivalence gives rise to derived mapping spaces
$\mathbf {S}$
in the classical sense. Declaring a weak equivalence to be a levelwise weak equivalence gives rise to derived mapping spaces
![]() $\smash {\mathrm {Map}_{\mathsf {Opd}}^h(\mathsf {O},\mathsf {P})}$
between such operads. We will be mostly interested in
$\smash {\mathrm {Map}_{\mathsf {Opd}}^h(\mathsf {O},\mathsf {P})}$
between such operads. We will be mostly interested in
![]() $1$
-reduced operads which are operads
$1$
-reduced operads which are operads
![]() $\mathsf {O}$
whose space of
$\mathsf {O}$
whose space of
![]() $0$
- and
$0$
- and
![]() $1$
-ary operations
$1$
-ary operations
![]() $\mathsf {O}(0)$
and
$\mathsf {O}(0)$
and
![]() $\mathsf {O}(1)$
are weakly contractible. For such operads, there are equivalent point of views on their mapping spaces that we will make us of, related by natural maps
$\mathsf {O}(1)$
are weakly contractible. For such operads, there are equivalent point of views on their mapping spaces that we will make us of, related by natural maps
which we explain in the following two subsections. Part of our discussion in this and the following subsection is similar to that in [Reference WeissWei21, Section 3.4].
7.2.1 Dendroidal spaces and the map 
The two alternative points of view stem from Moerdijk–Weiss’ dendroidal spaces. Briefly (see [Reference Heuts and MoerdijkHM22] for details), the category of dendroidal spaces is the category of presheaves
![]() $\mathscr {O} \colon {\Omega }^{\mathrm {op}} \to \mathsf {S}$
on a certain category
$\mathscr {O} \colon {\Omega }^{\mathrm {op}} \to \mathsf {S}$
on a certain category ![]() of finite rooted trees with specified subsets of leaves. More formally, an object
of finite rooted trees with specified subsets of leaves. More formally, an object
![]() $(t,\le ,\ell (t))$
in
$(t,\le ,\ell (t))$
in
![]() $\Omega $
is a finite partially ordered set
$\Omega $
is a finite partially ordered set
![]() $(t,\le )$
of edges together with a specified subset
$(t,\le )$
of edges together with a specified subset
![]() $\ell (t)\subset t$
of maximal elements (the leaves) such that (a)
$\ell (t)\subset t$
of maximal elements (the leaves) such that (a)
![]() $\{v\in t\,|\,w\le v\}$
is totally ordered for all
$\{v\in t\,|\,w\le v\}$
is totally ordered for all
![]() $w\in T$
and (b) there is a unique maximal element
$w\in T$
and (b) there is a unique maximal element
![]() $v\in T$
with respect to the partial order, the root (see Section 3.2 loc.cit.). The subset
$v\in T$
with respect to the partial order, the root (see Section 3.2 loc.cit.). The subset ![]() is the set of vertices of the tree. The incoming edges
is the set of vertices of the tree. The incoming edges
![]() $\mathrm {in}(v)\subset t$
of a vertex v is the set of maximal elements in
$\mathrm {in}(v)\subset t$
of a vertex v is the set of maximal elements in
![]() $\{w\in t\,|\,w<v\}$
. We refer to Section 3.2–3.3 loc.cit. for a description of the morphisms in
$\{w\in t\,|\,w<v\}$
. We refer to Section 3.2–3.3 loc.cit. for a description of the morphisms in
![]() $\Omega $
. There is a functor
$\Omega $
. There is a functor
![]() $N_d(-)$
from operads to dendroidal spaces, the dendroidal nerve (see Example 12.11 loc.cit.), given by
$N_d(-)$
from operads to dendroidal spaces, the dendroidal nerve (see Example 12.11 loc.cit.), given by ![]() . Declaring weak equivalences between dendroidal spaces to be levelwise weak equivalences gives rise to derived mapping spaces
. Declaring weak equivalences between dendroidal spaces to be levelwise weak equivalences gives rise to derived mapping spaces ![]() of dendroidal spaces, and as
of dendroidal spaces, and as
![]() $N_d(-)$
preserves weak equivalence, we obtain the map
$N_d(-)$
preserves weak equivalence, we obtain the map ![]() .
.
7.2.2 (
 $1$
-reduced) dendroidal Segal spaces and the map
$1$
-reduced) dendroidal Segal spaces and the map 
There is a convenient class of dendroidal spaces that includes dendroidal nerves of
![]() $1$
-reduced operads but is homotopically more flexible. To define it, we consider the k-corolla which is the unique (up to isomorphism) tree in
$1$
-reduced operads but is homotopically more flexible. To define it, we consider the k-corolla which is the unique (up to isomorphism) tree in
![]() ${\Omega }$
with one vertex and k leaves, denoted by
${\Omega }$
with one vertex and k leaves, denoted by
![]() $t_k$
. The unique (up to isomorphism) tree in
$t_k$
. The unique (up to isomorphism) tree in
![]() ${\Omega }$
with no vertices is denoted
${\Omega }$
with no vertices is denoted
![]() $\eta $
. For each vertex v in a tree t, there is a morphism
$\eta $
. For each vertex v in a tree t, there is a morphism
![]() $t_k\rightarrow t$
(unique up to automorphism of
$t_k\rightarrow t$
(unique up to automorphism of
![]() $t_k$
) that takes the root to v and the leaves to
$t_k$
) that takes the root to v and the leaves to
![]() $\mathrm {in}(v)$
. Given a dendroidal space
$\mathrm {in}(v)$
. Given a dendroidal space
![]() $\mathscr {O}$
and a tree t, these morphisms assemble to a map
$\mathscr {O}$
and a tree t, these morphisms assemble to a map
The following definition mimics the definition of a
![]() $1$
-reduced operad on the level of dendroidal Segal spaces. The examples to keep in mind are dendroidal nerves
$1$
-reduced operad on the level of dendroidal Segal spaces. The examples to keep in mind are dendroidal nerves
![]() $N_{d}\mathsf {O}$
of
$N_{d}\mathsf {O}$
of
![]() $1$
-reduced operads.
$1$
-reduced operads.
Definition 7.6. A
![]() $1$
-reduced dendroidal Segal space
$1$
-reduced dendroidal Segal space
![]() $\mathscr {O}$
is a dendroidal space such that the values
$\mathscr {O}$
is a dendroidal space such that the values
![]() $\mathscr {O}(t_0)$
and
$\mathscr {O}(t_0)$
and
![]() $\mathscr {O}(t_1)$
at the
$\mathscr {O}(t_1)$
at the
![]() $0$
- and
$0$
- and
![]() $1$
-corollas are weakly contractible and such that (86) is a weak equivalences for all trees
$1$
-corollas are weakly contractible and such that (86) is a weak equivalences for all trees
![]() $t\in \Omega $
(this says in particular that
$t\in \Omega $
(this says in particular that
![]() $\mathscr {O}(\eta )$
is weakly contractible).
$\mathscr {O}(\eta )$
is weakly contractible).
The full subcategory ![]() of closed trees (i.e., trees t with
of closed trees (i.e., trees t with
![]() $\ell (v)=\varnothing $
) (see [Reference Heuts and MoerdijkHM22, p. 92, 97], is often easier to work with. Presheaves
$\ell (v)=\varnothing $
) (see [Reference Heuts and MoerdijkHM22, p. 92, 97], is often easier to work with. Presheaves
![]() $\mathscr {O} \colon {\smash {\overline {\Omega }}}^{\mathrm {op}} \to \mathsf {S}$
are called closed dendroidal spaces. Morphisms between those are still natural transformations and weak equivalences are levelwise; we denote the resulting derived mapping spaces by
$\mathscr {O} \colon {\smash {\overline {\Omega }}}^{\mathrm {op}} \to \mathsf {S}$
are called closed dendroidal spaces. Morphisms between those are still natural transformations and weak equivalences are levelwise; we denote the resulting derived mapping spaces by ![]() . Restriction along
. Restriction along
![]() ${\smash {\overline {\Omega }}}\subset {\Omega }$
induces a map
${\smash {\overline {\Omega }}}\subset {\Omega }$
induces a map
of which ![]() is a special case. For
is a special case. For
![]() $1$
-reduced operads
$1$
-reduced operads
![]() $\mathsf {O}$
and
$\mathsf {O}$
and
![]() $\mathsf {P}$
, both maps
$\mathsf {P}$
, both maps ![]() and
and ![]() turn out to be weak equivalences (see [Reference Heuts and MoerdijkHM22, Corollary 14.42] for
turn out to be weak equivalences (see [Reference Heuts and MoerdijkHM22, Corollary 14.42] for ![]() and [Reference Göppl and WeissGW24, Lemma 3.2.4] for
and [Reference Göppl and WeissGW24, Lemma 3.2.4] for ![]() ):
):
Proposition 7.7. For
![]() $1$
-reduced operads
$1$
-reduced operads
![]() $\mathsf {O}$
and
$\mathsf {O}$
and
![]() $\mathsf {P}$
, the maps
$\mathsf {P}$
, the maps ![]() and
and ![]() are weak equivalences.
are weak equivalences.
7.3 A tower of derived mapping spaces
The category
![]() ${\smash {\overline {\Omega }}}$
of closed trees admits a filtration
${\smash {\overline {\Omega }}}$
of closed trees admits a filtration
by the full subcategories ![]() on those trees whose vertices v have at most k incoming edges. Denoting the restriction of a closed dendroidal space
on those trees whose vertices v have at most k incoming edges. Denoting the restriction of a closed dendroidal space
![]() $\mathscr {O}$
along
$\mathscr {O}$
along
![]() ${\smash {\overline {\Omega }}}_{\leq k}\subset {\smash {\overline {\Omega }}}$
by the same symbol, we obtain a natural tower of derived mapping spaces
${\smash {\overline {\Omega }}}_{\leq k}\subset {\smash {\overline {\Omega }}}$
by the same symbol, we obtain a natural tower of derived mapping spaces

all derived with respect to the levelwise weak equivalences. For simplicity, we write
This tower was studied by Göppl and Weiss [Reference Göppl and WeissGW24]. In Lemma 3.1.1 loc.cit. they note that it converges; that is, we have a weak equivalence
To identify its layers (i.e., the homotopy fibres of the vertical maps), they consider the kth matching and latching object of a
![]() $1$
-reduced dendroidal space
$1$
-reduced dendroidal space
![]() $\mathscr {O}$
$\mathscr {O}$
Here,
![]() $\overline {t}_k\in \smash {\overline {\Omega }}$
is the closed k-corolla, the unique (up to isomorphism) closed tree with
$\overline {t}_k\in \smash {\overline {\Omega }}$
is the closed k-corolla, the unique (up to isomorphism) closed tree with
![]() $k+1$
vertices of which one has k incoming edges and the others have none. Permuting incoming edges defines an action of the symmetric group
$k+1$
vertices of which one has k incoming edges and the others have none. Permuting incoming edges defines an action of the symmetric group
![]() $\Sigma _k$
on
$\Sigma _k$
on
![]() $\overline {t}_k$
in
$\overline {t}_k$
in
![]() $\smash {\overline {\Omega }}$
which induces a natural
$\smash {\overline {\Omega }}$
which induces a natural
![]() $\Sigma _k$
-action on
$\Sigma _k$
-action on
![]() $\mathrm {Match}_k(\mathscr {P})$
and
$\mathrm {Match}_k(\mathscr {P})$
and
![]() $\mathrm {Latch}_k(\mathscr {P})$
. These are related by
$\mathrm {Latch}_k(\mathscr {P})$
. These are related by
![]() $\Sigma _k$
-equivariant maps
$\Sigma _k$
-equivariant maps
Göppl and Weiss used these maps to identify the vertical homotopy fibres in the above tower in terms of the matching and latching objects and spaces of derived maps between
![]() $\Sigma _k$
-spaces; see Theorem 3.2.7 and Remark 3.2.15 loc.cit.:
$\Sigma _k$
-spaces; see Theorem 3.2.7 and Remark 3.2.15 loc.cit.:
Theorem 7.8 (Göppl–Weiss).
For
![]() $k\ge 1$
and
$k\ge 1$
and
![]() $1$
-reduced dendroidal Segal spaces
$1$
-reduced dendroidal Segal spaces
![]() $\mathscr {O}$
and
$\mathscr {O}$
and
![]() $\mathscr {P}$
, there is a natural homotopy cartesian square whose left and top arrow is induced by restriction
$\mathscr {P}$
, there is a natural homotopy cartesian square whose left and top arrow is induced by restriction

The corner
![]() $P_k(\mathscr {O},\mathscr {P})$
fits into a natural homotopy cartesian square
$P_k(\mathscr {O},\mathscr {P})$
fits into a natural homotopy cartesian square

whose bottom and right maps are induced by (90).
7.4 Localisations of dendroidal spaces
Given a dendroidal space
![]() $\mathscr {O}$
, its T-localisation
$\mathscr {O}$
, its T-localisation
![]() $\mathscr {O}_T$
for a set of primes T is the dendroidal space given as the composition of
$\mathscr {O}_T$
for a set of primes T is the dendroidal space given as the composition of
![]() $\mathscr {O}\colon {\Omega }^{\mathrm {op}} \rightarrow \mathsf {S}$
with the localisation functor
$\mathscr {O}\colon {\Omega }^{\mathrm {op}} \rightarrow \mathsf {S}$
with the localisation functor
![]() $(-)_T\colon \mathsf {S}\rightarrow \mathsf {S}$
. The natural transformation
$(-)_T\colon \mathsf {S}\rightarrow \mathsf {S}$
. The natural transformation
![]() $\mathrm {id}_{\mathsf {S}}\rightarrow (-)_T$
induces a map
$\mathrm {id}_{\mathsf {S}}\rightarrow (-)_T$
induces a map
![]() $r_T\colon \mathscr {O}\rightarrow \mathscr {O}_T$
of dendroidal Segal spaces. It follows from properties (b) and (c) from Section 7.1 that if
$r_T\colon \mathscr {O}\rightarrow \mathscr {O}_T$
of dendroidal Segal spaces. It follows from properties (b) and (c) from Section 7.1 that if
![]() $\mathscr {O}$
is a
$\mathscr {O}$
is a
![]() $1$
-reduced dendroidal Segal space, then so is
$1$
-reduced dendroidal Segal space, then so is
![]() $\mathscr {O}_T$
.
$\mathscr {O}_T$
.
Lemma 7.9. For dendroidal spaces
![]() $\mathscr {O}$
and
$\mathscr {O}$
and
![]() $\mathscr {P}$
such that
$\mathscr {P}$
such that
![]() $\mathscr {P}$
is levelwise T-local,
$\mathscr {P}$
is levelwise T-local,
![]() $\mathrm {Map}^h_{\mathrm {PSh}(\Omega )}(\mathscr {O},\mathscr {P})$
is T-local and the natural zig-zag
$\mathrm {Map}^h_{\mathrm {PSh}(\Omega )}(\mathscr {O},\mathscr {P})$
is T-local and the natural zig-zag
consists of weak equivalences. The same holds when replacing
![]() $\Omega $
by
$\Omega $
by
![]() $\smash {\overline {\Omega }}$
or
$\smash {\overline {\Omega }}$
or
![]() $\smash {\overline {\Omega }}_{\le k}$
.
$\smash {\overline {\Omega }}_{\le k}$
.
Proof. The derived mapping spaces appearing in the statement are formed in a category of space-valued presheaves with levelwise weak equivalences, so they can be computed as homotopy limits of a diagram of levelwise mapping spaces. We saw in Section 7.1 that T-local spaces are closed under taking homotopy limits and applying
![]() $\mathrm {Map}^h_{\mathsf {S}}(X,-)$
for any space X, so this implies the first part of the claim. Moreover, this argument reduces the second part to proving that the zigzag of derived mapping spaces in the category of spaces
$\mathrm {Map}^h_{\mathsf {S}}(X,-)$
for any space X, so this implies the first part of the claim. Moreover, this argument reduces the second part to proving that the zigzag of derived mapping spaces in the category of spaces
consists of weak equivalences for all trees
![]() $t\in \Omega $
. For the second map, this follows follows the fact that
$t\in \Omega $
. For the second map, this follows follows the fact that
![]() $r_T\colon \mathscr {P}(t)\rightarrow \mathscr {P}(t)_T$
is a weak equivalence by property (a) of T-localisation. For the first map, we note
$r_T\colon \mathscr {P}(t)\rightarrow \mathscr {P}(t)_T$
is a weak equivalence by property (a) of T-localisation. For the first map, we note
agrees with postcomposition with
![]() $r_T\colon \mathscr {P}(t)\rightarrow \mathscr {P}(t)_T$
, and so is a weak equivalence. The second map is a weak equivalence by property (d), so the first map is one too.
$r_T\colon \mathscr {P}(t)\rightarrow \mathscr {P}(t)_T$
, and so is a weak equivalence. The second map is a weak equivalence by property (d), so the first map is one too.
7.4.1 Localisations of derived mapping spaces
Recalling the abbreviations of (88), denoting the path component of
![]() $f\in \mathrm {Map}^h_{\leq k}(\mathscr {O},\mathscr {P})$
by
$f\in \mathrm {Map}^h_{\leq k}(\mathscr {O},\mathscr {P})$
by
and abbreviating
![]() $\mathscr {O}(\overline {t}_k)$
to
$\mathscr {O}(\overline {t}_k)$
to
![]() $\mathscr {O}(k)$
, we can now state the following result:
$\mathscr {O}(k)$
, we can now state the following result:
Theorem 7.10. Let
![]() $\mathscr {P}$
and
$\mathscr {P}$
and
![]() $\mathscr {O}$
be
$\mathscr {O}$
be
![]() $1$
-reduced dendroidal Segal spaces such that for all
$1$
-reduced dendroidal Segal spaces such that for all
![]() $k\ge 0$
,
$k\ge 0$
,
-
•
 $\mathscr {P}(k)$
has nilpotent path components and
$\mathscr {P}(k)$
has nilpotent path components and -
•
 $\mathscr {O}(k)_{h\Sigma _k}$
and
$\mathscr {O}(k)_{h\Sigma _k}$
and
 $\mathrm {Latch}_k(\mathscr {O})_{h\Sigma _k}$
are weakly equivalent to finite CW complexes.
$\mathrm {Latch}_k(\mathscr {O})_{h\Sigma _k}$
are weakly equivalent to finite CW complexes.
Then the following holds for all
![]() $k\ge 0$
and any map
$k\ge 0$
and any map
![]() $f\in \mathrm {Map}^h_{\le k}(\mathscr {O},\mathscr {P})$
:
$f\in \mathrm {Map}^h_{\le k}(\mathscr {O},\mathscr {P})$
:
-
(i) the path component
 $\mathrm {Map}^h_{\le k}(\mathscr {O},\mathscr {P})_f$
is nilpotent,
$\mathrm {Map}^h_{\le k}(\mathscr {O},\mathscr {P})_f$
is nilpotent, -
(ii) for a set of primes T, the natural map induced by T-localisation
 $r_T\colon \mathscr {P}\rightarrow \mathscr {P}_T$
is a T-localisation of nilpotent spaces, and
$r_T\colon \mathscr {P}\rightarrow \mathscr {P}_T$
is a T-localisation of nilpotent spaces, and $$\begin{align*}\mathrm{Map}^h_{\leq k}(\mathscr{O},\mathscr{P})_f \longrightarrow \mathrm{Map}^h_{\leq k}(\mathscr{O},\mathscr{P}_{T})_{r_T\circ f} \end{align*}$$
$$\begin{align*}\mathrm{Map}^h_{\leq k}(\mathscr{O},\mathscr{P})_f \longrightarrow \mathrm{Map}^h_{\leq k}(\mathscr{O},\mathscr{P}_{T})_{r_T\circ f} \end{align*}$$
-
(iii) if the spaces
 $\mathscr {P}(k')$
have finitely generated homotopy groups at all basepoints for all
$\mathscr {P}(k')$
have finitely generated homotopy groups at all basepoints for all
 $k'\ge 0$
, then so does
$k'\ge 0$
, then so does
 $\mathrm {Map}^h_{\leq k}(\mathscr {O},\mathscr {P})_f$
.
$\mathrm {Map}^h_{\leq k}(\mathscr {O},\mathscr {P})_f$
.
The first part of this result (and the strategy of proof) is similar to [Reference WeissWei21, Proposition 5.2.4]. We start the proof with an auxiliary lemma:
Lemma 7.11. Let T be a set of primes and
![]() $\mathscr {P}$
a
$\mathscr {P}$
a
![]() $1$
-reduced dendroidal Segal space such that
$1$
-reduced dendroidal Segal space such that
![]() $\mathscr {P}(k)$
has nilpotent path components for all
$\mathscr {P}(k)$
has nilpotent path components for all
![]() $k\ge 0$
. The following holds for all
$k\ge 0$
. The following holds for all
![]() $k\ge 0$
:
$k\ge 0$
:
-
(i)
 $\mathrm {Match}_k(\mathscr {P})$
has nilpotent path components,
$\mathrm {Match}_k(\mathscr {P})$
has nilpotent path components, -
(ii) the natural map
 $\mathrm {Match}_k(\mathscr {P})\rightarrow \mathrm {Match}_k(\mathscr {P}_T)$
is a T-localisation when restricted to a path component of the source and the corresponding path component of the target,
$\mathrm {Match}_k(\mathscr {P})\rightarrow \mathrm {Match}_k(\mathscr {P}_T)$
is a T-localisation when restricted to a path component of the source and the corresponding path component of the target, -
(iii) if the space
 $\mathscr {P}(k')$
has finitely generated homotopy groups at all basepoints for
$\mathscr {P}(k')$
has finitely generated homotopy groups at all basepoints for
 $0 \leq k' \leq k$
, then so does
$0 \leq k' \leq k$
, then so does
 $\mathrm {Match}_k(\mathscr {P})$
.
$\mathrm {Match}_k(\mathscr {P})$
.
Proof. Identifying the vertices of
![]() $\overline {t}_k$
with no incoming edges with
$\overline {t}_k$
with no incoming edges with
![]() $\underline {k} = \{1,2,\ldots ,k\}$
, every subset
$\underline {k} = \{1,2,\ldots ,k\}$
, every subset
![]() $I\subseteq \underline {k}$
defines a closed subcorolla
$I\subseteq \underline {k}$
defines a closed subcorolla
![]() $\overline {t}_I\subseteq \overline {t}_k$
. This gives rise to an
$\overline {t}_I\subseteq \overline {t}_k$
. This gives rise to an
![]() $\underline {k}$
-cubical diagram
$\underline {k}$
-cubical diagram
![]() $\underline {k} \supseteq I \mapsto \mathscr {P}(\overline {t}_{\underline {k} \setminus I})$
. By the argument above Theorem 3.4.7 in [Reference WeissWei21], there is a natural equivalence
$\underline {k} \supseteq I \mapsto \mathscr {P}(\overline {t}_{\underline {k} \setminus I})$
. By the argument above Theorem 3.4.7 in [Reference WeissWei21], there is a natural equivalence
![]() $\mathrm {Match}_k(\mathscr {P})\simeq \mathrm {holim}_{\varnothing \neq I\subseteq \underline {k}}\mathscr {P}(\overline {t}_{\underline {k} \setminus I})$
, so the claim follows from an application of Lemma 7.5.
$\mathrm {Match}_k(\mathscr {P})\simeq \mathrm {holim}_{\varnothing \neq I\subseteq \underline {k}}\mathscr {P}(\overline {t}_{\underline {k} \setminus I})$
, so the claim follows from an application of Lemma 7.5.
Proof Proof of Theorem 7.10.
We prove the claim by induction on k. The initial case
![]() $k=0$
is trivial since
$k=0$
is trivial since
![]() $\mathscr {P}$
is assumed to be
$\mathscr {P}$
is assumed to be
![]() $1$
-reduced, so the mapping spaces appearing in the statement are contractible. For the induction step, we assume the claim for
$1$
-reduced, so the mapping spaces appearing in the statement are contractible. For the induction step, we assume the claim for
![]() $k-1$
and prove it for k. To do so, we consider the homotopy cartesian squares of Theorem 7.8. A choice of
$k-1$
and prove it for k. To do so, we consider the homotopy cartesian squares of Theorem 7.8. A choice of
![]() $f\in \mathrm {Map}^h_{\le k}(\mathscr {O},\mathscr {P})$
induces basepoints in all spaces participating in these squares; we denote these also by f. Now consider the maps
$f\in \mathrm {Map}^h_{\le k}(\mathscr {O},\mathscr {P})$
induces basepoints in all spaces participating in these squares; we denote these also by f. Now consider the maps
 $$ \begin{align} \begin{aligned}\mathrm{Map}^h_{\Sigma_k}(\mathscr{O}(k),\mathscr{P}(k))_f &\longrightarrow \mathrm{Map}^h_{\Sigma_k}(\mathscr{O}(k),\mathscr{P}(k)_T)_{f} \\ \mathrm{Map}^h_{\Sigma_k}(\mathscr{O}(k),\mathrm{Match}_k(\mathscr{P}))_f &\longrightarrow \mathrm{Map}^h_{\Sigma_k}(\mathscr{O}(k),\mathrm{Match}_k(\mathscr{P})_T)_{f}\\ \mathrm{Map}^h_{\Sigma_k}(\mathrm{Latch}_k(\mathscr{O}),\mathscr{P}(k))_f &\longrightarrow \mathrm{Map}^h_{\Sigma_k}(\mathrm{Latch}_k(\mathscr{O}),\mathscr{P}(k)_T)_{ f} \\ \mathrm{Map}^h_{\Sigma_k}(\mathrm{Latch}_k(\mathscr{O}),\mathrm{Match}_k(\mathscr{P}))_f &\longrightarrow \mathrm{Map}^h_{\Sigma_k}(\mathrm{Latch}_k(\mathscr{O}),\mathrm{Match}_k(\mathscr{P})_T)_{f} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned}\mathrm{Map}^h_{\Sigma_k}(\mathscr{O}(k),\mathscr{P}(k))_f &\longrightarrow \mathrm{Map}^h_{\Sigma_k}(\mathscr{O}(k),\mathscr{P}(k)_T)_{f} \\ \mathrm{Map}^h_{\Sigma_k}(\mathscr{O}(k),\mathrm{Match}_k(\mathscr{P}))_f &\longrightarrow \mathrm{Map}^h_{\Sigma_k}(\mathscr{O}(k),\mathrm{Match}_k(\mathscr{P})_T)_{f}\\ \mathrm{Map}^h_{\Sigma_k}(\mathrm{Latch}_k(\mathscr{O}),\mathscr{P}(k))_f &\longrightarrow \mathrm{Map}^h_{\Sigma_k}(\mathrm{Latch}_k(\mathscr{O}),\mathscr{P}(k)_T)_{ f} \\ \mathrm{Map}^h_{\Sigma_k}(\mathrm{Latch}_k(\mathscr{O}),\mathrm{Match}_k(\mathscr{P}))_f &\longrightarrow \mathrm{Map}^h_{\Sigma_k}(\mathrm{Latch}_k(\mathscr{O}),\mathrm{Match}_k(\mathscr{P})_T)_{f} \end{aligned} \end{align} $$
induced by postcomposition with the T-localisations of the codomains. Combining Lemma 7.4 with Lemma 7.11, all four maps are T-localisations of nilpotent spaces. Moreover, by the first part of Lemma 7.11, we may replace
![]() $\mathrm {Match}_k(\mathscr {P})_T$
in the codomain of the second and fourth map by
$\mathrm {Match}_k(\mathscr {P})_T$
in the codomain of the second and fourth map by
![]() $\mathrm {Match}_k(\mathscr {P}_T)$
. An application of Lemma 7.3 to the second square in Theorem 7.8 shows that the map
$\mathrm {Match}_k(\mathscr {P}_T)$
. An application of Lemma 7.3 to the second square in Theorem 7.8 shows that the map
![]() $P_k(\mathscr {O},\mathscr {P})_f\rightarrow P_k(\mathscr {O},\mathscr {P}_T)_{f}$
between the components induced by f is a T-localisation of nilpotent spaces. Combining this with the induction hypothesis, another application of Lemma 7.3 – this time to the first square – shows that the natural map
$P_k(\mathscr {O},\mathscr {P})_f\rightarrow P_k(\mathscr {O},\mathscr {P}_T)_{f}$
between the components induced by f is a T-localisation of nilpotent spaces. Combining this with the induction hypothesis, another application of Lemma 7.3 – this time to the first square – shows that the natural map
![]() $\smash {\mathrm {Map}^h_{\leq k}}(\mathscr {O},\mathscr {P})_f \rightarrow \smash {\mathrm {Map}^h_{\leq k}}(\mathscr {O},\mathscr {P}_{T})_{f}$
is a T-localisation between nilpotent spaces, so (i) and (ii) hold.
$\smash {\mathrm {Map}^h_{\leq k}}(\mathscr {O},\mathscr {P})_f \rightarrow \smash {\mathrm {Map}^h_{\leq k}}(\mathscr {O},\mathscr {P}_{T})_{f}$
is a T-localisation between nilpotent spaces, so (i) and (ii) hold.
We argue similarly for (iii): if the spaces
![]() $\mathscr {P}(k)$
have finitely generated homotopy groups at all basepoints, then so does
$\mathscr {P}(k)$
have finitely generated homotopy groups at all basepoints, then so does
![]() $\mathrm {Match}_k(\mathscr {P})$
by the second part of Lemma 7.11. By the second part of Lemma 7.4, we conclude that the domains of the four maps have finitely generated homotopy groups, so the same holds for
$\mathrm {Match}_k(\mathscr {P})$
by the second part of Lemma 7.11. By the second part of Lemma 7.4, we conclude that the domains of the four maps have finitely generated homotopy groups, so the same holds for
![]() $P_k(\mathscr {O},\mathscr {P})_f$
by an application of the final part of Lemma 7.3 and thus also for
$P_k(\mathscr {O},\mathscr {P})_f$
by an application of the final part of Lemma 7.3 and thus also for
![]() $\smash {\mathrm {Map}^h_{\le k}}(\mathscr {O},\mathscr {P})_f$
by another application of that lemma and the induction hypothesis.
$\smash {\mathrm {Map}^h_{\le k}}(\mathscr {O},\mathscr {P})_f$
by another application of that lemma and the induction hypothesis.
This finishes the first part of this section as outlined in Section 1.2.5 after (III).
7.5 Inverse limits and countability
The second part of this section begins with general results on the behaviour of homotopy groups of homotopy limits of towers of spaces.
7.5.1 Towers of groups
Following [Reference Bousfield and KanBK72, IX.2], we call a sequence of groups
![]() $G_0\leftarrow G_1\leftarrow G_2\leftarrow \cdots $
a tower of groups and abbreviate it by
$G_0\leftarrow G_1\leftarrow G_2\leftarrow \cdots $
a tower of groups and abbreviate it by ![]() . Such a tower has a limit group
. Such a tower has a limit group
![]() $\lim _kG_k$
and a pointed
$\lim _kG_k$
and a pointed
![]() $\lim ^1$
-set
$\lim ^1$
-set
![]() $\lim ^1_kG_k$
[Reference Bousfield and KanBK72, IX.2.1]. If the tower consists of abelian groups, then
$\lim ^1_kG_k$
[Reference Bousfield and KanBK72, IX.2.1]. If the tower consists of abelian groups, then
![]() $\lim ^1_k G_k$
inherits an abelian group structure. A short exact sequence of towers of groups induces a long exact sequence as follows [Reference Bousfield and KanBK72, IX.2.3]:
$\lim ^1_k G_k$
inherits an abelian group structure. A short exact sequence of towers of groups induces a long exact sequence as follows [Reference Bousfield and KanBK72, IX.2.3]:
Lemma 7.12. A levelwise short exact sequence of towers of groups
induces a natural exact sequence of groups and pointed sets
Recall that a map
![]() $\{f_k\} \colon \{G_k\} \to \{H_k\}$
of towers of groups is called a pro-isomorphism if for all
$\{f_k\} \colon \{G_k\} \to \{H_k\}$
of towers of groups is called a pro-isomorphism if for all
![]() $s \geq 0$
, there exists a
$s \geq 0$
, there exists a
![]() $t \geq s$
and a homomorphism
$t \geq s$
and a homomorphism
![]() $H_{t} \to G_s$
such that the diagram
$H_{t} \to G_s$
such that the diagram

commutes. Pro-isomorphisms have the following property [Reference Bousfield and KanBK72, Proposition III.2.6]:
Lemma 7.13. For a pro-isomorphism
![]() $\{f_k\} \colon \{G_k\} \to \{H_k\}$
, the induced map
$\{f_k\} \colon \{G_k\} \to \{H_k\}$
, the induced map
![]() $\lim _kG_k \to \lim _kH_k$
is an isomorphism, and the induced map
$\lim _kG_k \to \lim _kH_k$
is an isomorphism, and the induced map
![]() $\lim ^1_kG_k \to \lim ^1_kH_k$
is a pointed bijection.
$\lim ^1_kG_k \to \lim ^1_kH_k$
is a pointed bijection.
For a tower of groups
![]() $\{G_k\}$
and
$\{G_k\}$
and
![]() $r\ge 1$
, the rth derived tower
$r\ge 1$
, the rth derived tower
![]() $(G^{(r)}_k)$
is defined by
$(G^{(r)}_k)$
is defined by
For each fixed k, this defines a tower
![]() $\{G^{(r)}_k\}_{r \in \mathbf {N}}$
of inclusions of subgroups. The tower
$\{G^{(r)}_k\}_{r \in \mathbf {N}}$
of inclusions of subgroups. The tower
![]() $(G_k)$
is called Mittag–Leffler if for each k, there is an
$(G_k)$
is called Mittag–Leffler if for each k, there is an
![]() $m<\infty $
so that
$m<\infty $
so that
![]() $\lim _{m' \geq m} \smash {G_k^{(m')}}\rightarrow \smash {G_k^{(m)}}$
is an isomorphism. Examples of Mittag–Leffler towers include towers of finite groups or finite dimensional vector spaces. Mittag–Leffler towers have the following property [Reference Bousfield and KanBK72, Corollary IX.3.5]:
$\lim _{m' \geq m} \smash {G_k^{(m')}}\rightarrow \smash {G_k^{(m)}}$
is an isomorphism. Examples of Mittag–Leffler towers include towers of finite groups or finite dimensional vector spaces. Mittag–Leffler towers have the following property [Reference Bousfield and KanBK72, Corollary IX.3.5]:
Lemma 7.14. If a tower of groups
![]() $\{G_k\}$
is Mittag–Leffler, then
$\{G_k\}$
is Mittag–Leffler, then
![]() $\lim ^1_kG_k=*$
.
$\lim ^1_kG_k=*$
.
To recognise Mittag–Leffler towers, we use the following result from [Reference McGibbon and MøllerMM92, Theorem 2]:
Lemma 7.15 (McGibbon–Møller).
For a tower
![]() $\{G_k\}$
of countable groups, the following statements are equivalent:
$\{G_k\}$
of countable groups, the following statements are equivalent:
-
(i)
 $\lim ^1_k G_k$
is countable,
$\lim ^1_k G_k$
is countable, -
(ii)
 $\lim ^1_k G_k$
vanishes,
$\lim ^1_k G_k$
vanishes, -
(iii) the tower
 $\{G_k\}$
is Mittag–Leffler.
$\{G_k\}$
is Mittag–Leffler.
The following lemma appears in [Reference Dydak and SegalDS78, Corollary 6.1.9], but we include a proof for the convenience of the reader. For a group G, we denote the constant tower with value G by
![]() $\{c\,G\}$
.
$\{c\,G\}$
.
Lemma 7.16 (Dydak–Segal).
If a tower of groups
![]() $\{G_k\}$
is Mittag–Leffler and
$\{G_k\}$
is Mittag–Leffler and
![]() $\lim _k G_k$
is countable, then the canonical map
$\lim _k G_k$
is countable, then the canonical map
![]() $\{c\lim _k G_k\} \to \{G_k\}$
is a pro-isomorphism.
$\{c\lim _k G_k\} \to \{G_k\}$
is a pro-isomorphism.
Proof. Any Mittag–Leffler tower of groups
![]() $\{G_k\}$
is pro-isomorphic to one with surjective transition maps (consider the tower
$\{G_k\}$
is pro-isomorphic to one with surjective transition maps (consider the tower
![]() $\{G_k'\}$
of stable images
$\{G_k'\}$
of stable images
![]() $G_k'\subset G_k$
(i.e.,
$G_k'\subset G_k$
(i.e.,
![]() $G_k'=\mathrm {im}(G_{k+m}\rightarrow G_k)$
for
$G_k'=\mathrm {im}(G_{k+m}\rightarrow G_k)$
for
![]() $m\gg 0$
)), so we may assume this is the case. This in particular ensures that the maps
$m\gg 0$
)), so we may assume this is the case. This in particular ensures that the maps
![]() $\lim _k G_k\rightarrow G_k$
are surjective, so
$\lim _k G_k\rightarrow G_k$
are surjective, so
![]() $G_k$
is countable for all
$G_k$
is countable for all
![]() $k\ge 0$
, and it also shows that the claim is true if
$k\ge 0$
, and it also shows that the claim is true if
![]() $\lim _k G_k = 0$
. and thus,
$\lim _k G_k = 0$
. and thus,
![]() $G_k=0$
for all k. We use this special case to prove the following claim, which implies the general statement when applied to the map
$G_k=0$
for all k. We use this special case to prove the following claim, which implies the general statement when applied to the map
![]() $\{c\lim _k G_k\} \to \{G_k\}$
:
$\{c\lim _k G_k\} \to \{G_k\}$
:
Claim. Let
![]() $\{G_k\}$
be a Mittag–Leffler tower of countable groups and
$\{G_k\}$
be a Mittag–Leffler tower of countable groups and
![]() $\{f_k\} \colon \{G_k\} \to \{H_k\}$
a levelwise surjective map of towers of groups. If
$\{f_k\} \colon \{G_k\} \to \{H_k\}$
a levelwise surjective map of towers of groups. If
![]() $\lim _k f_k \colon \lim _k G_k \to \lim _k H_k$
is an isomorphism, then
$\lim _k f_k \colon \lim _k G_k \to \lim _k H_k$
is an isomorphism, then
![]() $\{f_k\}$
is a pro-isomorphism.
$\{f_k\}$
is a pro-isomorphism.
Proof of claim.
Consider the short exact sequence of towers
![]() $1 \rightarrow \{\ker (f_k)\} \rightarrow \{G_k\} \rightarrow \{H_k\} \rightarrow 1$
and the associated long exact sequence of Lemma 7.12. Since (a) the map
$1 \rightarrow \{\ker (f_k)\} \rightarrow \{G_k\} \rightarrow \{H_k\} \rightarrow 1$
and the associated long exact sequence of Lemma 7.12. Since (a) the map
![]() $\lim _k f_k \colon \lim _k G_k \to \lim _k H_k$
is an isomorphism, (b)
$\lim _k f_k \colon \lim _k G_k \to \lim _k H_k$
is an isomorphism, (b)
![]() $\{G_k\}$
is Mittag–Leffler, and (c) Lemma 7.14, it follows that
$\{G_k\}$
is Mittag–Leffler, and (c) Lemma 7.14, it follows that
![]() $\lim _k \ker (f_k)$
and
$\lim _k \ker (f_k)$
and
![]() $\lim ^1_k \ker (f_k) $
both vanish. Invoking Lemma 7.15, we see that
$\lim ^1_k \ker (f_k) $
both vanish. Invoking Lemma 7.15, we see that
![]() $\{\ker (f_k)\}$
is Mittag–Leffler, so by the first part of the proof,
$\{\ker (f_k)\}$
is Mittag–Leffler, so by the first part of the proof,
![]() $\{\ker (f_k)\}$
is pro-isomorphic to
$\{\ker (f_k)\}$
is pro-isomorphic to
![]() $\{c\,0\}$
. The result follows since a levelwise surjective map of towers of groups is a pro-isomorphism if its towers of levelwise kernels are pro-isomorphic to
$\{c\,0\}$
. The result follows since a levelwise surjective map of towers of groups is a pro-isomorphism if its towers of levelwise kernels are pro-isomorphic to
![]() $\{c\,0\}$
[Reference Bousfield and KanBK72, Proposition III.2.2].
$\{c\,0\}$
[Reference Bousfield and KanBK72, Proposition III.2.2].
This completes the proof of the lemma.
Mittag–Leffler towers often behave well with T-localisation in the sense of Section 7.1.1:
Lemma 7.17. Let
![]() $\{G_k\}$
be Mittag–Leffler. If
$\{G_k\}$
be Mittag–Leffler. If
![]() $\lim _k G_k$
is countable, then the canonical map
$\lim _k G_k$
is countable, then the canonical map
is an isomorphism for any set of primes T.
Proof. By Lemma 7.16, the canonical map of towers
![]() $\{c\, \lim _kG_k\} \rightarrow \{G_k\}$
is a pro-isomorphism, as
$\{c\, \lim _kG_k\} \rightarrow \{G_k\}$
is a pro-isomorphism, as
![]() $\lim _kG_k$
is countable. As
$\lim _kG_k$
is countable. As
![]() $(-)_T$
preserves pro-isomorphisms and limits of constant towers, the canonical map from the constant tower on
$(-)_T$
preserves pro-isomorphisms and limits of constant towers, the canonical map from the constant tower on
![]() $\{\lim _kG_k\}_T$
to
$\{\lim _kG_k\}_T$
to
![]() $\{(G_k)_T\}$
is a pro-isomorphism, and the result follows from Lemma 7.13.
$\{(G_k)_T\}$
is a pro-isomorphism, and the result follows from Lemma 7.13.
Remark 7.18. We stated Lemma 7.17 in terms of T-localisation since this is what we will use, but the same proof applied to
![]() $(-)_T$
replaces by any endofunctor on the category of groups.
$(-)_T$
replaces by any endofunctor on the category of groups.
7.5.2 Towers of spaces
Given a tower
![]() $X_0 \leftarrow X_1 \leftarrow \cdots $
of based spaces, taking homotopy groups results in a tower of pointed sets
$X_0 \leftarrow X_1 \leftarrow \cdots $
of based spaces, taking homotopy groups results in a tower of pointed sets
![]() $\{\pi _i(X_k)\}$
(of groups for
$\{\pi _i(X_k)\}$
(of groups for
![]() $i \geq 1$
). The limits of these towers fit into the following Milnor exact sequence [Reference Bousfield and KanBK72, Theorem IX.3.1].
$i \geq 1$
). The limits of these towers fit into the following Milnor exact sequence [Reference Bousfield and KanBK72, Theorem IX.3.1].
Lemma 7.19. For a tower
![]() $X_0 \leftarrow X_1 \leftarrow \cdots $
of based spaces and
$X_0 \leftarrow X_1 \leftarrow \cdots $
of based spaces and
![]() $i\ge 0$
, there is a natural short exact sequence of pointed sets (of groups for
$i\ge 0$
, there is a natural short exact sequence of pointed sets (of groups for
![]() $i\ge 1$
)
$i\ge 1$
)
Together with Lemma 7.15, this has the following consequence.
Proposition 7.20. Fix
![]() $i\ge 1$
. For a tower of based spaces
$i\ge 1$
. For a tower of based spaces
![]() $X_0 \leftarrow X_1 \leftarrow \cdots $
such that
$X_0 \leftarrow X_1 \leftarrow \cdots $
such that
![]() $\pi _i(X_k)$
is countable for all
$\pi _i(X_k)$
is countable for all
![]() $k\ge 0$
, at least one of the following statements holds:
$k\ge 0$
, at least one of the following statements holds:
-
(i)
 $\pi _{*}(\mathrm {holim}_k X_k)$
is uncountable in degree
$\pi _{*}(\mathrm {holim}_k X_k)$
is uncountable in degree
 $i-1$
or i,
$i-1$
or i, -
(ii)
 $({\lim }_k \pi _i(X_k))_T \rightarrow {\lim }_k(\pi _i(X_k)_T)$
is an isomorphism for all sets of primes T.
$({\lim }_k \pi _i(X_k))_T \rightarrow {\lim }_k(\pi _i(X_k)_T)$
is an isomorphism for all sets of primes T.
Moreover, if
![]() $\pi _{i+1}(X_k)$
is countable for all
$\pi _{i+1}(X_k)$
is countable for all
![]() $k\ge 0$
, then at least one of the following is the case:
$k\ge 0$
, then at least one of the following is the case:
-
(i’)
 $\pi _i(\mathrm {holim}_k X_k)$
is uncountable,
$\pi _i(\mathrm {holim}_k X_k)$
is uncountable, -
(ii’) the natural surjection
 $\pi _i(\mathrm {holim}_k X_k) \rightarrow {\lim }_k \pi _i(X_k)$
is an isomorphism.
$\pi _i(\mathrm {holim}_k X_k) \rightarrow {\lim }_k \pi _i(X_k)$
is an isomorphism.
Proof. By Lemma 7.15, the assumption that
![]() $\pi _i(X_k)$
is countable for
$\pi _i(X_k)$
is countable for
![]() $k\ge 0$
implies that either (a)
$k\ge 0$
implies that either (a)
![]() $\lim ^1_k(\pi _i(X_k))$
is uncountable or (b) the tower is Mittag–Leffler. In case (a), we apply Lemma 7.19 in degree
$\lim ^1_k(\pi _i(X_k))$
is uncountable or (b) the tower is Mittag–Leffler. In case (a), we apply Lemma 7.19 in degree
![]() $i-1$
to conclude that
$i-1$
to conclude that
![]() $\pi _{i-1}(\mathrm {holim}_k X_k)$
is uncountable, so (i) holds. In case (b), either
$\pi _{i-1}(\mathrm {holim}_k X_k)$
is uncountable, so (i) holds. In case (b), either
![]() $\pi _i(\mathrm {holim}_k X_k)$
is uncountable and (i) holds, or it is countable and Lemma 7.19 in degree i implies that
$\pi _i(\mathrm {holim}_k X_k)$
is uncountable and (i) holds, or it is countable and Lemma 7.19 in degree i implies that
![]() ${\lim _k}\, \pi _{i}(X_k)$
is countable, so (ii) holds by Lemma 7.17. Similarly, if
${\lim _k}\, \pi _{i}(X_k)$
is countable, so (ii) holds by Lemma 7.17. Similarly, if
![]() $\pi _{i+1}(X_k)$
is countable for
$\pi _{i+1}(X_k)$
is countable for
![]() $k\ge 0$
, then either
$k\ge 0$
, then either
![]() $\pi _i(\mathrm {holim}_k X_k)$
is uncountable and (i
$\pi _i(\mathrm {holim}_k X_k)$
is uncountable and (i
![]() $'$
) holds, or it is countable and so
$'$
) holds, or it is countable and so
![]() $\lim _k^1\pi _{i+1}(X_k)$
is countable by Lemma 7.19 and thus vanishes by Lemma 7.15, so the claim follows from the Milnor exact sequence.
$\lim _k^1\pi _{i+1}(X_k)$
is countable by Lemma 7.19 and thus vanishes by Lemma 7.15, so the claim follows from the Milnor exact sequence.
7.6 Applications to maps between operads
Together with Theorem 7.10, we use Proposition 7.20 to prove the following result about the map
for
![]() $1$
-reduced dendroidal Segal spaces
$1$
-reduced dendroidal Segal spaces
![]() $\mathscr {O}$
and
$\mathscr {O}$
and
![]() $\mathscr {P}$
in the sense of Section 7.2.
$\mathscr {P}$
in the sense of Section 7.2.
Theorem 7.21. Let
![]() $\mathscr {O}$
and
$\mathscr {O}$
and
![]() $\mathscr {P}$
be
$\mathscr {P}$
be
![]() $1$
-reduced dendroidal Segal spaces such that for all
$1$
-reduced dendroidal Segal spaces such that for all
![]() $k\ge 0$
,
$k\ge 0$
,
-
• all components of
 $\mathscr {P}(k)$
are nilpotent and have finitely generated homotopy groups,
$\mathscr {P}(k)$
are nilpotent and have finitely generated homotopy groups, -
•
 $\mathscr {O}(k)$
and
$\mathscr {O}(k)$
and
 $\mathrm {Latch}_k(\mathscr {O})_{h\Sigma _k}$
are weakly equivalent to finite CW complexes.
$\mathrm {Latch}_k(\mathscr {O})_{h\Sigma _k}$
are weakly equivalent to finite CW complexes.
Then for all
![]() $i\ge 1$
and all basepoints
$i\ge 1$
and all basepoints
![]() $f\in \mathrm {Map}^h(\mathscr {O},\mathscr {P})$
, at least one of the following is the case:
$f\in \mathrm {Map}^h(\mathscr {O},\mathscr {P})$
, at least one of the following is the case:
-
(i)
 $\pi _{*}(\mathrm {Map}^h(\mathscr {O},\mathscr {P}))$
is uncountable in degree
$\pi _{*}(\mathrm {Map}^h(\mathscr {O},\mathscr {P}))$
is uncountable in degree
 $i-1$
or i,
$i-1$
or i, -
(ii) the canonical map
 $\pi _{i}(\mathrm {Map}^h(\mathscr {O},\mathscr {P}))_{\mathbf {Q}} \to \pi _i(\mathrm {Map}^h(\mathscr {O}_{\mathbf {Q}},\mathscr {P}_{\mathbf {Q}}))$
is an isomorphism.
$\pi _{i}(\mathrm {Map}^h(\mathscr {O},\mathscr {P}))_{\mathbf {Q}} \to \pi _i(\mathrm {Map}^h(\mathscr {O}_{\mathbf {Q}},\mathscr {P}_{\mathbf {Q}}))$
is an isomorphism.
Proof. During the proof, we implicitly use the equivalence
![]() $\mathrm {Map}^h(\mathscr {O},\mathscr {P}_{\mathbf {Q}})\simeq \mathrm {Map}^h(\mathscr {O}_{\mathbf {Q}},\mathscr {P}_{\mathbf {Q}})$
and its truncated analogue (see Lemma 7.9). Then (89) gives
$\mathrm {Map}^h(\mathscr {O},\mathscr {P}_{\mathbf {Q}})\simeq \mathrm {Map}^h(\mathscr {O}_{\mathbf {Q}},\mathscr {P}_{\mathbf {Q}})$
and its truncated analogue (see Lemma 7.9). Then (89) gives
so from the two Milnor sequences (see Lemma 7.19) together with the fact that
![]() $\pi _i(\mathrm {Map}^h(\mathscr {O}_{\mathbf {Q}},\mathscr {P}_{\mathbf {Q}}))$
is
$\pi _i(\mathrm {Map}^h(\mathscr {O}_{\mathbf {Q}},\mathscr {P}_{\mathbf {Q}}))$
is
![]() $\mathbf {Q}$
-local as the homotopy group of a
$\mathbf {Q}$
-local as the homotopy group of a
![]() $\mathbf {Q}$
-local space (see Lemma 7.9), we obtain a square
$\mathbf {Q}$
-local space (see Lemma 7.9), we obtain a square

Assuming that
![]() $\pi _{*}(\mathrm {Map}^h(\mathscr {O},\mathscr {P}))$
is countable in degrees
$\pi _{*}(\mathrm {Map}^h(\mathscr {O},\mathscr {P}))$
is countable in degrees
![]() $i-1$
and i, we need to show that the left vertical map is an isomorphism, which we do proving that this holds for the three circled maps. By Theorem 7.10 (iii), the homotopy groups of
$i-1$
and i, we need to show that the left vertical map is an isomorphism, which we do proving that this holds for the three circled maps. By Theorem 7.10 (iii), the homotopy groups of
![]() $\mathrm {Map}^h_{\le k}(\mathscr {O},\mathscr {P})$
are finitely generated for all k, so they are in particular countable. By Proposition 7.20 (ii
$\mathrm {Map}^h_{\le k}(\mathscr {O},\mathscr {P})$
are finitely generated for all k, so they are in particular countable. By Proposition 7.20 (ii
![]() $'$
), this implies that
$'$
), this implies that ![]() is an isomorphism, even before rationalisation. By Theorem 7.10 (ii), we have
is an isomorphism, even before rationalisation. By Theorem 7.10 (ii), we have
![]() $\pi _{k}(\mathrm {Map}^h_{\le k}(\mathscr {O},\mathscr {P}))_{\mathbf {Q}} \cong \pi _{k}(\mathrm {Map}^h_{\le k}(\mathscr {O}_{\mathbf {Q}},\mathscr {P}_{\mathbf {Q}}))$
for all
$\pi _{k}(\mathrm {Map}^h_{\le k}(\mathscr {O},\mathscr {P}))_{\mathbf {Q}} \cong \pi _{k}(\mathrm {Map}^h_{\le k}(\mathscr {O}_{\mathbf {Q}},\mathscr {P}_{\mathbf {Q}}))$
for all
![]() $k\ge 1$
, so
$k\ge 1$
, so ![]() is an isomorphism by Proposition 7.20 (ii). Finally, by the Milnor sequence (see Lemma 7.19),
is an isomorphism by Proposition 7.20 (ii). Finally, by the Milnor sequence (see Lemma 7.19), ![]() is surjective and its kernel agrees with
is surjective and its kernel agrees with
![]() $\lim ^1_k\pi _{i+1}(\mathrm {Map}^h_{\le k}(\mathscr {P}_{\mathbf {Q}},\mathscr {O}_{\mathbf {Q}}))$
, so it is an isomorphism if
$\lim ^1_k\pi _{i+1}(\mathrm {Map}^h_{\le k}(\mathscr {P}_{\mathbf {Q}},\mathscr {O}_{\mathbf {Q}}))$
, so it is an isomorphism if
![]() $\{\pi _{i+1}(\mathrm {Map}^h_{\le k}(\mathscr {P}_{\mathbf {Q}},\mathscr {O}_{\mathbf {Q}}))\}$
is Mittag–Leffler. For this it suffices that it is a tower of finite-dimensional vector spaces, which is indeed the case by Theorem 7.10 (ii) and (iii).
$\{\pi _{i+1}(\mathrm {Map}^h_{\le k}(\mathscr {P}_{\mathbf {Q}},\mathscr {O}_{\mathbf {Q}}))\}$
is Mittag–Leffler. For this it suffices that it is a tower of finite-dimensional vector spaces, which is indeed the case by Theorem 7.10 (ii) and (iii).
7.6.1 Applications to maps between
 $E_n$
-operads
$E_n$
-operads
Here and henceforth, we write
![]() $E_n$
for any operad weakly equivalent to the operad of little n-discs (the unital version, so
$E_n$
for any operad weakly equivalent to the operad of little n-discs (the unital version, so
![]() $E_n(0)\simeq *$
). As
$E_n(0)\simeq *$
). As
![]() $E_n(1)\simeq \ast $
, we can consider
$E_n(1)\simeq \ast $
, we can consider
![]() $E_n$
via the dendroidal nerve as a
$E_n$
via the dendroidal nerve as a
![]() $1$
-reduced dendroidal Segal space, denoted by the same symbol, and abbreviate its T-localisation (see Section 7.4) by
$1$
-reduced dendroidal Segal space, denoted by the same symbol, and abbreviate its T-localisation (see Section 7.4) by
![]() $E_n^T$
. Proposition 7.7 says that the derived mapping spaces between
$E_n^T$
. Proposition 7.7 says that the derived mapping spaces between
![]() $E_n$
-operads do not depend on whether we consider them as operads or as
$E_n$
-operads do not depend on whether we consider them as operads or as
![]() $1$
-reduced dendroidal Segal spaces. Keeping this in mind, we use Theorems 7.10 and 7.21 to prove the following two results:
$1$
-reduced dendroidal Segal spaces. Keeping this in mind, we use Theorems 7.10 and 7.21 to prove the following two results:
Theorem 7.22. Fix
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $m\ge 3$
, and a set of primes T. For
$m\ge 3$
, and a set of primes T. For
![]() $f\in \mathrm {Map}^h_{\le r}(E_n,E_{m})$
and
$f\in \mathrm {Map}^h_{\le r}(E_n,E_{m})$
and
![]() $k\ge 0$
, the following holds:
$k\ge 0$
, the following holds:
-
(i) the path component
 $\mathrm {Map}^h_{\le k}(E_n,E_{m})_f$
is nilpotent,
$\mathrm {Map}^h_{\le k}(E_n,E_{m})_f$
is nilpotent, -
(ii) the map
 $(r_T\circ (-))\colon \mathrm {Map}^h_{\le k}(E_n,E_{m})_f\rightarrow \mathrm {Map}^h_{\le k}(E_n,E_{m}^T)_{r_T\circ f}$
is a T-localisation,
$(r_T\circ (-))\colon \mathrm {Map}^h_{\le k}(E_n,E_{m})_f\rightarrow \mathrm {Map}^h_{\le k}(E_n,E_{m}^T)_{r_T\circ f}$
is a T-localisation, -
(iii) the homotopy groups of
 $\mathrm {Map}^h_{\le k}(E_n,E_{m})_f$
are finitely generated.
$\mathrm {Map}^h_{\le k}(E_n,E_{m})_f$
are finitely generated.
The case of Theorem 7.22 that will be relevant to the proof of Theorem C and Corollary E in the next section is
![]() $n=m$
. For
$n=m$
. For
![]() $m-n\ge 2$
and
$m-n\ge 2$
and
![]() $(-)_T$
being rationalisation, this result appears also in Section 10.2 of [Reference Fresse, Turchin and WillwacherFTW17] (see Remark 10.9 and Proposition 10.10 loc.ċit.).
$(-)_T$
being rationalisation, this result appears also in Section 10.2 of [Reference Fresse, Turchin and WillwacherFTW17] (see Remark 10.9 and Proposition 10.10 loc.ċit.).
Theorem 7.23. Fix
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $m\ge 3$
. For all
$m\ge 3$
. For all
![]() $i\ge 1$
and any basepoint in
$i\ge 1$
and any basepoint in
![]() $\mathrm {Map}^h(E_n,E_m)$
, at least one of the following statements holds:
$\mathrm {Map}^h(E_n,E_m)$
, at least one of the following statements holds:
-
(i)
 $\pi _{*}(\mathrm {Map}^h(E_n,E_m))$
is uncountable in degrees
$\pi _{*}(\mathrm {Map}^h(E_n,E_m))$
is uncountable in degrees
 $i-1$
or i,
$i-1$
or i, -
(ii) the canonical map
 $\pi _{i}(\mathrm {Map}^h(E_n,E_m))_{\mathbf {Q}} \to \pi _{i}(\mathrm {Map}^h(E_n^{\mathbf {Q}},E^{\mathbf {Q}}_m))$
is an isomorphism.
$\pi _{i}(\mathrm {Map}^h(E_n,E_m))_{\mathbf {Q}} \to \pi _{i}(\mathrm {Map}^h(E_n^{\mathbf {Q}},E^{\mathbf {Q}}_m))$
is an isomorphism.
Proof Proof of Theorems 7.22 and 7.23.
This follows from Theorems 7.10 and 7.21 once we checked the hypothesis. The space of k-ary operations
![]() $E_n(k)$
is weakly equivalent to the space of ordered configurations
$E_n(k)$
is weakly equivalent to the space of ordered configurations
![]() $F_k(\mathbf {R}^n)$
, so
$F_k(\mathbf {R}^n)$
, so
![]() $E_n$
is
$E_n$
is
![]() $1$
-reduced for all
$1$
-reduced for all
![]() $n\ge 1$
. Moreover, by transversality,
$n\ge 1$
. Moreover, by transversality,
![]() $E_n(k)$
is
$E_n(k)$
is
![]() $1$
-connected (so in particular, nilpotent) as long as
$1$
-connected (so in particular, nilpotent) as long as
![]() $n\ge 3$
, so its homotopy groups are finitely generated if its homology groups are. We are thus left to show that
$n\ge 3$
, so its homotopy groups are finitely generated if its homology groups are. We are thus left to show that
![]() $E_n(k)_{h\Sigma _k}$
and
$E_n(k)_{h\Sigma _k}$
and
![]() $\mathrm {Latch}_k(E_n)_{h\Sigma _k}$
have the weak homotopy type of finite CW complexes for all
$\mathrm {Latch}_k(E_n)_{h\Sigma _k}$
have the weak homotopy type of finite CW complexes for all
![]() $n\ge 1$
and that
$n\ge 1$
and that
![]() $E_n(k)$
has degreewise finitely generated homology groups for
$E_n(k)$
has degreewise finitely generated homology groups for
![]() $n\ge 3$
. By [Reference Göppl and WeissGW24, Examples 1.1.6, 2.1.13] (see also [Reference WeissWei21, Proposition 3.4.6]), the map
$n\ge 3$
. By [Reference Göppl and WeissGW24, Examples 1.1.6, 2.1.13] (see also [Reference WeissWei21, Proposition 3.4.6]), the map
![]() $\mathrm {Latch}_n(E_n)\rightarrow E_n(k)$
agrees up to weak equivalence of
$\mathrm {Latch}_n(E_n)\rightarrow E_n(k)$
agrees up to weak equivalence of
![]() $\Sigma _k$
-spaces with the boundary inclusion
$\Sigma _k$
-spaces with the boundary inclusion
![]() $\partial \mathrm {FM}_n(k)\subset \mathrm {FM}_n(k)$
of the Fulton–MacPherson compactification of
$\partial \mathrm {FM}_n(k)\subset \mathrm {FM}_n(k)$
of the Fulton–MacPherson compactification of
![]() $F_k(\mathbf {R}^n)$
. This is a compact manifold with corners and free
$F_k(\mathbf {R}^n)$
. This is a compact manifold with corners and free
![]() $\Sigma _k$
-action [Reference SinhaSin04], so we conclude (i) that
$\Sigma _k$
-action [Reference SinhaSin04], so we conclude (i) that
![]() $(E_n(k))_{h\Sigma _k}\simeq FM_n/\Sigma _k$
and
$(E_n(k))_{h\Sigma _k}\simeq FM_n/\Sigma _k$
and
![]() $(\mathrm {Latch}_k(E_n))_{h\Sigma _k}\simeq \partial FM_n/\Sigma _k$
have the weak homotopy type of smooth compact manifolds with corners and so are weakly equivalent to finite CW complexes, and (ii) that
$(\mathrm {Latch}_k(E_n))_{h\Sigma _k}\simeq \partial FM_n/\Sigma _k$
have the weak homotopy type of smooth compact manifolds with corners and so are weakly equivalent to finite CW complexes, and (ii) that
![]() $E_n(k)\simeq \mathrm {FM}_n(k)$
has degreewise finitely generated homology.
$E_n(k)\simeq \mathrm {FM}_n(k)$
has degreewise finitely generated homology.
8 Theorem C: nontriviality
In this section, we prove results on the homotopy groups of the homotopy fibre
![]() $\mathrm {Aut}^h(E_d)/\mathrm {Top}(d)$
of the map
$\mathrm {Aut}^h(E_d)/\mathrm {Top}(d)$
of the map
![]() $\mathrm {BTop}(d)\rightarrow \mathrm {BAut}^h(E_d)$
mentioned as (4) in the introduction (and explained below), and deduce results on the homotopy groups of
$\mathrm {BTop}(d)\rightarrow \mathrm {BAut}^h(E_d)$
mentioned as (4) in the introduction (and explained below), and deduce results on the homotopy groups of
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
; Theorem C and Corollary E will follow as special cases. As explained in the outline in Section 1.2.5, the main ingredient besides Theorem 7.23 is work of Boavida de Brito–Weiss [Reference Boavida de Brito and WeissBdBW18] and work of Fresse–Turchin–Willwacher [Reference Fresse, Turchin and WillwacherFTW17]. We also make use of results of Krannich, Kupers, Randal-Williams and Watanabe [Reference Krannich and Randal-WilliamsKrRW21, Reference Kupers and Randal-WilliamsKuRW25, Reference WatanabeWat09], though this can be avoided in most cases (see Remark 8.15).
$S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
; Theorem C and Corollary E will follow as special cases. As explained in the outline in Section 1.2.5, the main ingredient besides Theorem 7.23 is work of Boavida de Brito–Weiss [Reference Boavida de Brito and WeissBdBW18] and work of Fresse–Turchin–Willwacher [Reference Fresse, Turchin and WillwacherFTW17]. We also make use of results of Krannich, Kupers, Randal-Williams and Watanabe [Reference Krannich and Randal-WilliamsKrRW21, Reference Kupers and Randal-WilliamsKuRW25, Reference WatanabeWat09], though this can be avoided in most cases (see Remark 8.15).
8.1 A theorem of Boavida de Brito–Weiss
We first extract the relevant parts of [Reference Boavida de Brito and WeissBdBW18]. By Theorem 1.2 loc.cit., the space
![]() $\mathrm {Map}^h(E_d,E_d) = \smash {\mathrm {Map}^h_{\mathsf {Opd}}}(E_d,E_d)$
of derived operad maps is equivalent to a mapping space between certain
$\mathrm {Map}^h(E_d,E_d) = \smash {\mathrm {Map}^h_{\mathsf {Opd}}}(E_d,E_d)$
of derived operad maps is equivalent to a mapping space between certain
![]() $\infty $
-categories of configurations spaces associated to
$\infty $
-categories of configurations spaces associated to
![]() $\mathbf {R}^d$
. These configuration categories only depend on the underlying topological manifold, so this in particular shows that the standard action of
$\mathbf {R}^d$
. These configuration categories only depend on the underlying topological manifold, so this in particular shows that the standard action of
![]() $\mathrm {O}(d)$
on
$\mathrm {O}(d)$
on
![]() $E_d$
factors through an action of
$E_d$
factors through an action of
![]() $\mathrm {Top}(d)$
and thus gives a map
$\mathrm {Top}(d)$
and thus gives a map
We will explain below how a reformulation of further results of Boavida de Brito–Weiss relates the homotopy fibre
![]() $\mathrm {Aut}^h(E_d)/\mathrm {Top}(d)$
of this map to the
$\mathrm {Aut}^h(E_d)/\mathrm {Top}(d)$
of this map to the
![]() $\mathscr {D}\mathrm {isc}$
-structure space
$\mathscr {D}\mathrm {isc}$
-structure space
![]() $S_\partial ^{\mathscr {D}\mathrm {isc}}(D^d)$
of a disc. To state the precise result, we denote by
$S_\partial ^{\mathscr {D}\mathrm {isc}}(D^d)$
of a disc. To state the precise result, we denote by
the collection of those path components that are sent to classes in the image of the map
![]() $\pi _{d+1}(\mathrm {BO}(d))\rightarrow \pi _{d+1}(\mathrm {BTop}(d))$
under the map
$\pi _{d+1}(\mathrm {BO}(d))\rightarrow \pi _{d+1}(\mathrm {BTop}(d))$
under the map
Theorem 8.1 (Boavida de Brito–Weiss).
For
![]() $d \neq 4$
, there exists a
$d \neq 4$
, there exists a
![]() $0$
-coconnected map of the form
$0$
-coconnected map of the form
Recall that being
![]() $0$
-coconnected amounts to being an ‘inclusion of path components’, meaning a map that induces an injection on
$0$
-coconnected amounts to being an ‘inclusion of path components’, meaning a map that induces an injection on
![]() $\pi _0(-)$
and an isomorphism on
$\pi _0(-)$
and an isomorphism on
![]() $\pi _i(-)$
for
$\pi _i(-)$
for
![]() $i\ge 1$
. After taking loop spaces, Theorem 8.1 can also be deduced from work of Ducoulombier–Turchin [Reference Ducoulombier and TurchinDT22, (13)].
$i\ge 1$
. After taking loop spaces, Theorem 8.1 can also be deduced from work of Ducoulombier–Turchin [Reference Ducoulombier and TurchinDT22, (13)].
Remark 8.2. After this work was finalised, a different proof of Theorem 8.1 was given in [Reference Krannich and KupersKK24c, Section 5.9.4]. This proof is independent of [Reference Boavida de Brito and WeissBdBW18] and [Reference Ducoulombier and TurchinDT22] and shows the slightly stronger statement
![]() $\Omega ^{d+1} ({\mathrm {Aut}^h(E_d)}/{\mathrm {Top}(d)})\simeq S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
.
$\Omega ^{d+1} ({\mathrm {Aut}^h(E_d)}/{\mathrm {Top}(d)})\simeq S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
.
Proof Proof of Theorem 8.1.
This can be deduced from [Reference Boavida de Brito and WeissBdBW18] as follows: combining their Theorems 1.2 and 1.4 with their Section 6 (see also Equation (1.3)), there is contractible space
![]() $\mathrm {C}(D^d,D^d)$
(a certain mapping space of configuration categories) which fits into a homotopy cartesian square
$\mathrm {C}(D^d,D^d)$
(a certain mapping space of configuration categories) which fits into a homotopy cartesian square

where
![]() $\mathrm {Bun}_\partial (TD^d,TD^d)$
is the space of vector bundle maps of
$\mathrm {Bun}_\partial (TD^d,TD^d)$
is the space of vector bundle maps of
![]() $TD^d$
that are fixed on the boundary and
$TD^d$
that are fixed on the boundary and
![]() $T_\infty \mathrm {Emb}_\partial (D^d,D^d)$
is the embedding calculus approximation to
$T_\infty \mathrm {Emb}_\partial (D^d,D^d)$
is the embedding calculus approximation to
![]() $\mathrm {Emb}_\partial (D^d,D^d)$
. The bottom horizontal map admits a factorisation
$\mathrm {Emb}_\partial (D^d,D^d)$
. The bottom horizontal map admits a factorisation
through the space of topological microbundle maps (compare the proof of Theorem 1.6 loc.cit.). Under the equivalences
![]() $\mathrm {Bun}_\partial (TD^d,TD^d)\simeq \Omega ^d\mathrm {O}(d)$
and
$\mathrm {Bun}_\partial (TD^d,TD^d)\simeq \Omega ^d\mathrm {O}(d)$
and
![]() $\mathrm {Bun}_\partial (TD^d,TD^d)^{\mathrm {Top}}\simeq \Omega ^d\mathrm {Top}(d)$
, this agrees with the d-fold looping of the composition
$\mathrm {Bun}_\partial (TD^d,TD^d)^{\mathrm {Top}}\simeq \Omega ^d\mathrm {Top}(d)$
, this agrees with the d-fold looping of the composition
![]() $\mathrm {O}(d)\rightarrow \mathrm {Top}(d)\rightarrow \mathrm {Aut}^h(E_d)$
.
$\mathrm {O}(d)\rightarrow \mathrm {Top}(d)\rightarrow \mathrm {Aut}^h(E_d)$
.
Now the factorisation (93) allows us to form the commutative diagram

whose front and back face are homotopy cartesian; the former by what was said above and the latter by smoothing theory (see [Reference Kirby and SiebenmannKS77, Essay V]; this uses
![]() $d\neq 4$
). Note that
$d\neq 4$
). Note that
![]() $\mathrm {Emb}_\partial (D^d,D^d) = \mathrm {Diff}_\partial (D^d)$
and
$\mathrm {Emb}_\partial (D^d,D^d) = \mathrm {Diff}_\partial (D^d)$
and
![]() $\mathrm {Emb}_\partial (D^d,D^d)^{\mathrm {Top}} = \mathrm {Homeo}_\partial (D^d)$
. From the constructions in [Reference Boavida de Brito and WeissBdBW18], one sees that this diagram is in fact a diagram of
$\mathrm {Emb}_\partial (D^d,D^d)^{\mathrm {Top}} = \mathrm {Homeo}_\partial (D^d)$
. From the constructions in [Reference Boavida de Brito and WeissBdBW18], one sees that this diagram is in fact a diagram of
![]() $A_\infty $
-spaces if one uses the
$A_\infty $
-spaces if one uses the
![]() $A_\infty $
-structure on
$A_\infty $
-structure on
![]() $T_\infty \mathrm {Emb}_\partial (D^d,D^d)$
by composition induced by the model for embedding calculus with boundary condition from [Reference Boavida de Brito and WeissBdBW13, p. 379] which agrees with the
$T_\infty \mathrm {Emb}_\partial (D^d,D^d)$
by composition induced by the model for embedding calculus with boundary condition from [Reference Boavida de Brito and WeissBdBW13, p. 379] which agrees with the
![]() $A_\infty $
-structure provided by our model as a result of Proposition 4.8 (see the discussion at the beginning of Section 4.3.1). Using contractibility of
$A_\infty $
-structure provided by our model as a result of Proposition 4.8 (see the discussion at the beginning of Section 4.3.1). Using contractibility of
![]() $\mathrm {C}(D^d,D^d)$
and of
$\mathrm {C}(D^d,D^d)$
and of
![]() $\mathrm {Homeo}_\partial (D^d)$
(using the Alexander trick) and Theorem 4.5, the diagram becomes a map of homotopy fibre sequences
$\mathrm {Homeo}_\partial (D^d)$
(using the Alexander trick) and Theorem 4.5, the diagram becomes a map of homotopy fibre sequences

of
![]() $A_\infty $
-spaces. Here, we used the abbreviation from (72). Aside from the bottom left fibre, all spaces in this diagram are visibly group-like, so this fibre is as well; that is,
$A_\infty $
-spaces. Here, we used the abbreviation from (72). Aside from the bottom left fibre, all spaces in this diagram are visibly group-like, so this fibre is as well; that is,
using the notation from Section 4.5. We may thus deloop the diagram once (after restricting the components of the rightmost spaces to those in the image of the maps from
![]() $\Omega ^d\mathrm {O}(d)$
) and take vertical homotopy fibres to get
$\Omega ^d\mathrm {O}(d)$
) and take vertical homotopy fibres to get
The right-hand space is a collection of components of
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
by (73), so the claim follows.
$S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
by (73), so the claim follows.
8.2 Some results of Fresse–Turchin–Willwacher
Next, we recall part of work of Fresse–Turchin–Willwacher [Reference Fresse, Turchin and WillwacherFTW17], who gave a complete description of the rational homotopy groups of
![]() $\mathrm {Map}^h(E_n,\smash {E_{m}^{\mathbf {Q}}})$
in terms of certain graph complexes. We collect the parts of their results that are relevant to us below, after explaining why they are applicable in our setting.
$\mathrm {Map}^h(E_n,\smash {E_{m}^{\mathbf {Q}}})$
in terms of certain graph complexes. We collect the parts of their results that are relevant to us below, after explaining why they are applicable in our setting.
8.2.1 A comparison
The derived mapping spaces
![]() $\mathrm {Map}^h(E_n,E^{\mathbf {Q}}_{m})$
considered in [Reference Fresse, Turchin and WillwacherFTW17] differ a priori from those we considered in Section 7.6.1 in two ways:
$\mathrm {Map}^h(E_n,E^{\mathbf {Q}}_{m})$
considered in [Reference Fresse, Turchin and WillwacherFTW17] differ a priori from those we considered in Section 7.6.1 in two ways:
First, the derived mapping spaces between operads considered in [Reference Fresse, Turchin and WillwacherFTW17] are formed not in the usual category
![]() $\mathrm {s}\mathrm {Op}$
of simplicial operads as we did in Section 7.2, but instead in a certain category
$\mathrm {s}\mathrm {Op}$
of simplicial operads as we did in Section 7.2, but instead in a certain category
![]() $\mathrm {s}\Lambda \mathrm {Op}_{\varnothing *}$
of connected simplicial
$\mathrm {s}\Lambda \mathrm {Op}_{\varnothing *}$
of connected simplicial
![]() $\Lambda $
-operads, equipped with levelwise weak equivalences. This category is isomorphic to the full subcategory
$\Lambda $
-operads, equipped with levelwise weak equivalences. This category is isomorphic to the full subcategory
![]() $\mathrm {s}\mathrm {Op}_{*1}\subset \mathrm {s}\mathrm {Op}$
of the category of simplicial operads such that
$\mathrm {s}\mathrm {Op}_{*1}\subset \mathrm {s}\mathrm {Op}$
of the category of simplicial operads such that
![]() $\mathsf {P}(0)$
and
$\mathsf {P}(0)$
and
![]() $\mathsf {P}(1)$
are singletons (see the discussion following Proposition 4.4. loc.cit.). The inclusion functor
$\mathsf {P}(1)$
are singletons (see the discussion following Proposition 4.4. loc.cit.). The inclusion functor
![]() $\mathrm {s}\Lambda \mathrm {Op}_{\varnothing *}\cong \mathrm {s}\mathrm {Op}_{*1}\to \mathrm {s}\mathrm {Op}$
induces weak equivalences on derived mapping spaces: by [Reference Fresse, Turchin and WillwacherFTW18, Theorem 1], the inclusion
$\mathrm {s}\Lambda \mathrm {Op}_{\varnothing *}\cong \mathrm {s}\mathrm {Op}_{*1}\to \mathrm {s}\mathrm {Op}$
induces weak equivalences on derived mapping spaces: by [Reference Fresse, Turchin and WillwacherFTW18, Theorem 1], the inclusion
![]() $\mathrm {s}\mathrm {Op}_{*} \to \mathrm {s}\mathrm {Op}$
induces weak equivalences on derived mapping spaces, and the same holds for
$\mathrm {s}\mathrm {Op}_{*} \to \mathrm {s}\mathrm {Op}$
induces weak equivalences on derived mapping spaces, and the same holds for
![]() $\mathrm {s}\mathrm {Op}_{*1} \to \mathrm {s}\mathrm {Op}_{*}$
since this full subcategory inclusion preserves fibrant and cofibrant objects in suitable model categories on these categories with levelwise weak equivalences (see [Reference FresseFre17, p. 369] where this is explained in terms of the isomorphic categories
$\mathrm {s}\mathrm {Op}_{*1} \to \mathrm {s}\mathrm {Op}_{*}$
since this full subcategory inclusion preserves fibrant and cofibrant objects in suitable model categories on these categories with levelwise weak equivalences (see [Reference FresseFre17, p. 369] where this is explained in terms of the isomorphic categories
![]() $\mathrm {s}\Lambda \mathrm {Op}_{\varnothing *}\subset \mathrm {s}\Lambda \mathrm {Op}_{\varnothing }$
). Hence, the mapping spaces
$\mathrm {s}\Lambda \mathrm {Op}_{\varnothing *}\subset \mathrm {s}\Lambda \mathrm {Op}_{\varnothing }$
). Hence, the mapping spaces
![]() $\mathrm {Map}^h(E_n,E_m)$
considered in [Reference Fresse, Turchin and WillwacherFTW17] agree with any of the variants of mapping space we discussed in (85) as a result of Proposition 7.7, using that the space of
$\mathrm {Map}^h(E_n,E_m)$
considered in [Reference Fresse, Turchin and WillwacherFTW17] agree with any of the variants of mapping space we discussed in (85) as a result of Proposition 7.7, using that the space of
![]() $0$
- and
$0$
- and
![]() $1$
-operations of
$1$
-operations of
![]() $E_n$
are weakly contractible.
$E_n$
are weakly contractible.
Second, the authors in [Reference Fresse, Turchin and WillwacherFTW17] rationalise operads differently than we do – namely, via a rationalisation functor of Fresse [Reference FresseFre17, Section 12.2] (therein denoted
![]() $\smash {LG_\bullet \Omega _\sharp ^*}(-)$
and phrased in terms of the isomorphism
$\smash {LG_\bullet \Omega _\sharp ^*}(-)$
and phrased in terms of the isomorphism
![]() $\mathrm {s}\Lambda \mathrm {Op}_{\varnothing *}\cong \mathrm {s}\mathrm {Op}_{*1}$
mentioned above) that we denote
$\mathrm {s}\Lambda \mathrm {Op}_{\varnothing *}\cong \mathrm {s}\mathrm {Op}_{*1}$
mentioned above) that we denote
This functor comes with a natural transformation
![]() $r_{\mathrm {F}\mathbf {Q}}\colon \mathrm {id}\rightarrow (-)_{\mathrm {F}\mathbf {Q}}$
and has the property that any operad
$r_{\mathrm {F}\mathbf {Q}}\colon \mathrm {id}\rightarrow (-)_{\mathrm {F}\mathbf {Q}}$
and has the property that any operad
![]() $\mathsf {P}\in \mathrm {s}\mathrm {Op}_{*1}$
, the induced maps
$\mathsf {P}\in \mathrm {s}\mathrm {Op}_{*1}$
, the induced maps
![]() $r_{\mathrm {F}\mathbf {Q}}\colon \mathsf {P}(k)\rightarrow \mathsf {P}_{\mathrm {F}\mathbf {Q}}(k)$
agree up to weak equivalence with the Sullivan rationalisation as long as
$r_{\mathrm {F}\mathbf {Q}}\colon \mathsf {P}(k)\rightarrow \mathsf {P}_{\mathrm {F}\mathbf {Q}}(k)$
agree up to weak equivalence with the Sullivan rationalisation as long as
![]() $\mathrm {H}^*(\mathsf {P}(k);\mathbf {Q})$
is degreewise finite dimensional for all
$\mathrm {H}^*(\mathsf {P}(k);\mathbf {Q})$
is degreewise finite dimensional for all
![]() $k\ge 1$
(see Theorem 2.2.1 loc.cit.). We can compare this to the rationalisation
$k\ge 1$
(see Theorem 2.2.1 loc.cit.). We can compare this to the rationalisation
![]() $(-)_{\mathbf {Q}}$
we use (that is, levelwise T-localisation for T the set of all primes) as follows:
$(-)_{\mathbf {Q}}$
we use (that is, levelwise T-localisation for T the set of all primes) as follows:
Lemma 8.3. If
![]() $\mathsf {P}\in \mathrm {s}\mathrm {Op}_{*1}$
is levelwise connected nilpotent such that
$\mathsf {P}\in \mathrm {s}\mathrm {Op}_{*1}$
is levelwise connected nilpotent such that
![]() $\mathrm {H}^*(\mathsf {P}(k);\mathbf {Q})$
is degreewise finite dimensional for all
$\mathrm {H}^*(\mathsf {P}(k);\mathbf {Q})$
is degreewise finite dimensional for all
![]() $k\ge 1$
, then there exists a natural zig-zag of weak equivalences
$k\ge 1$
, then there exists a natural zig-zag of weak equivalences
between the dendroidal nerve of Fresse’s rationalisation and the rationalisation of the dendroidal nerve in the sense of Section 7.4.
Proof. Consider the zigzag
![]() $N_d(\mathsf {P}_{\mathrm {F}\mathbf {Q}})\overset {r_{\mathbf {Q}}}{\longrightarrow } (N_d (\mathsf {P}_{\mathrm {F}\mathbf {Q}}))_{\mathbf {Q}} \xleftarrow {N_d(r_{\mathrm {F}\mathbf {Q}})_{\mathbf {Q}}} (N_d (\mathsf {P}))_{\mathbf {Q}}$
. To check both these maps are weak equivalences, it suffices to do so levelwise. Using the dendroidal Segal condition and the fact that rationalisation commutes with products of connected nilpotent spaces by Lemma 7.3 (ii), we may verify this on corollas. For those, the zig-zag becomes
$N_d(\mathsf {P}_{\mathrm {F}\mathbf {Q}})\overset {r_{\mathbf {Q}}}{\longrightarrow } (N_d (\mathsf {P}_{\mathrm {F}\mathbf {Q}}))_{\mathbf {Q}} \xleftarrow {N_d(r_{\mathrm {F}\mathbf {Q}})_{\mathbf {Q}}} (N_d (\mathsf {P}))_{\mathbf {Q}}$
. To check both these maps are weak equivalences, it suffices to do so levelwise. Using the dendroidal Segal condition and the fact that rationalisation commutes with products of connected nilpotent spaces by Lemma 7.3 (ii), we may verify this on corollas. For those, the zig-zag becomes
Under the assumption on
![]() $\mathsf {P}(k)$
, Sullivan rationalisation agrees with the rationalisation in Section 7.1, so all three spaces in the zig-zag are
$\mathsf {P}(k)$
, Sullivan rationalisation agrees with the rationalisation in Section 7.1, so all three spaces in the zig-zag are
![]() $\mathbf {Q}$
-local and the two maps are weak equivalences.
$\mathbf {Q}$
-local and the two maps are weak equivalences.
8.2.2 Homotopy groups of spaces of maps between rationalised
 $E_n$
-operads
$E_n$
-operads
The ingredient from [Reference Fresse, Turchin and WillwacherFTW17] required for the proofs of Theorem C and Corollary E is a computation of the homotopy groups of the derived mapping space
![]() $\smash {\mathrm {Map}^h(E_d,E^{\mathbf {Q}}_d)}$
based at the rationalisation map
$\smash {\mathrm {Map}^h(E_d,E^{\mathbf {Q}}_d)}$
based at the rationalisation map
![]() $\smash {r_{\mathbf {Q}}\colon E_d\rightarrow E_d^{\mathbf {Q}}}$
in a range of degrees, which we summarise as the first two items in the following theorem. In its statement, we write
$\smash {r_{\mathbf {Q}}\colon E_d\rightarrow E_d^{\mathbf {Q}}}$
in a range of degrees, which we summarise as the first two items in the following theorem. In its statement, we write
![]() $\mathbf {Q}[k]$
for the
$\mathbf {Q}[k]$
for the
![]() $\mathbf {Z}$
-graded
$\mathbf {Z}$
-graded
![]() $1$
-dimensional vector space concentrated in degree k, and we write
$1$
-dimensional vector space concentrated in degree k, and we write
![]() $\iota \colon E_d\rightarrow E_{d+k}$
for the standard inclusion.
$\iota \colon E_d\rightarrow E_{d+k}$
for the standard inclusion.
Theorem 8.4 (Fresse–Turchin–Willwacher).
-
(i) For
 $2n\ge 4$
, we have an inclusion of graded rational vector spaces This inclusion is an equality in degrees
$2n\ge 4$
, we have an inclusion of graded rational vector spaces This inclusion is an equality in degrees $$ \begin{align*} \pi_{*>0}(\mathrm{Map}^h(E_{2n},E^{\mathbf{Q}}_{2n}), r_{\mathbf{Q}})\supset&\textstyle{\Big(\bigoplus_{i\ge0}\mathbf{Q}[2n-4i-1]\Big)}\oplus\\ &\mathbf{Q}[6n-6]\oplus\mathbf{Q}[10n-10]\oplus\mathbf{Q}[12n-15]\oplus\\ &\mathbf{Q}[14n-14]\oplus \mathbf{Q}[16n-16]\oplus \mathbf{Q}[16n-19]\oplus \\ & \mathbf{Q}[18n-18]\oplus\mathbf{Q}[18n-21]. \end{align*} $$
$$ \begin{align*} \pi_{*>0}(\mathrm{Map}^h(E_{2n},E^{\mathbf{Q}}_{2n}), r_{\mathbf{Q}})\supset&\textstyle{\Big(\bigoplus_{i\ge0}\mathbf{Q}[2n-4i-1]\Big)}\oplus\\ &\mathbf{Q}[6n-6]\oplus\mathbf{Q}[10n-10]\oplus\mathbf{Q}[12n-15]\oplus\\ &\mathbf{Q}[14n-14]\oplus \mathbf{Q}[16n-16]\oplus \mathbf{Q}[16n-19]\oplus \\ & \mathbf{Q}[18n-18]\oplus\mathbf{Q}[18n-21]. \end{align*} $$
 $*\le 20n-28$
.
$*\le 20n-28$
.
-
(ii) For
 $2n+1\ge 3$
, we have an inclusion of graded rational vector spaces This inclusion is an equality in degrees
$2n+1\ge 3$
, we have an inclusion of graded rational vector spaces This inclusion is an equality in degrees $$ \begin{align*} \pi_{*>0}(\mathrm{Map}^h(E_{2n+1},E^{\mathbf{Q}}_{2n+1}),r_{\mathbf{Q}}) \supset&\textstyle{\Big(\bigoplus_{i\ge0}\mathbf{Q}[2n-4i-2]\Big)}\oplus\\ &\mathbf{Q}[4n-1]\oplus\mathbf{Q}[6n-3]\oplus\mathbf{Q}[8n-5]\oplus\\ &\mathbf{Q}^2[10n-7]\oplus\mathbf{Q}^2[12n-9]\oplus \mathbf{Q}[12n-6]\oplus \\ & \mathbf{Q}^3[14n-11]\oplus\mathbf{Q}[14n-8]. \end{align*} $$
$$ \begin{align*} \pi_{*>0}(\mathrm{Map}^h(E_{2n+1},E^{\mathbf{Q}}_{2n+1}),r_{\mathbf{Q}}) \supset&\textstyle{\Big(\bigoplus_{i\ge0}\mathbf{Q}[2n-4i-2]\Big)}\oplus\\ &\mathbf{Q}[4n-1]\oplus\mathbf{Q}[6n-3]\oplus\mathbf{Q}[8n-5]\oplus\\ &\mathbf{Q}^2[10n-7]\oplus\mathbf{Q}^2[12n-9]\oplus \mathbf{Q}[12n-6]\oplus \\ & \mathbf{Q}^3[14n-11]\oplus\mathbf{Q}[14n-8]. \end{align*} $$
 $*\le 16n-14$
.
$*\le 16n-14$
.
-
(iii) For
 $d \ge 2$
,
$d \ge 2$
,
 $(-)\circ \iota \colon \mathrm {Map}^h(E_d,E^{\mathbf {Q}}_{d})_{r_{\mathbf {Q}}}\rightarrow \mathrm {Map}^h(E_{d-1},E^{\mathbf {Q}}_{d})_{r_{\mathbf {Q}}\circ \iota }$
is a weak equivalence.
$(-)\circ \iota \colon \mathrm {Map}^h(E_d,E^{\mathbf {Q}}_{d})_{r_{\mathbf {Q}}}\rightarrow \mathrm {Map}^h(E_{d-1},E^{\mathbf {Q}}_{d})_{r_{\mathbf {Q}}\circ \iota }$
is a weak equivalence. -
(iv) For
 $d \ge 1$
,
$d \ge 1$
,
 $\pi _{d+1}(\mathrm {Map}^h(E_d,E^{\mathbf {Q}}_{d+2}),r_{\mathbf {Q}} \circ \iota )$
is an infinite-dimensional
$\pi _{d+1}(\mathrm {Map}^h(E_d,E^{\mathbf {Q}}_{d+2}),r_{\mathbf {Q}} \circ \iota )$
is an infinite-dimensional
 $\mathbf {Q}$
-vector space.
$\mathbf {Q}$
-vector space.
Proof. By [Reference Fresse, Turchin and WillwacherFTW17, Corollary 5], there is an isomorphism of graded vector spaces of the form
![]() $\pi _{*>0}(\mathrm {Map}^h(E_{d},E^{\mathbf {Q}}_{d}),r_{\mathbf {Q}})\cong H_{*>0}(\mathrm {GC}_d^2)$
for
$\pi _{*>0}(\mathrm {Map}^h(E_{d},E^{\mathbf {Q}}_{d}),r_{\mathbf {Q}})\cong H_{*>0}(\mathrm {GC}_d^2)$
for
![]() $d\ge 3$
, where
$d\ge 3$
, where
![]() $\mathrm {GC}_d^2$
is a certain graph complex introduced by Kontsevich (see loc.cit. for details). This complex splits into subcomplexes according to the number of loops of the graphs. The subspaces in (i) and (ii) are the homologies of the subcomplexes of loop order
$\mathrm {GC}_d^2$
is a certain graph complex introduced by Kontsevich (see loc.cit. for details). This complex splits into subcomplexes according to the number of loops of the graphs. The subspaces in (i) and (ii) are the homologies of the subcomplexes of loop order
![]() $\le 9$
and
$\le 9$
and
![]() $\le 7$
depending on the parity of d (see Equation (4) loc.cit.). The fact that this subspace spans the full homology in the claimed ranges appears as Corollary 6 loc.cit., which proves (i) and (ii) (see also [Reference Brun and WillwacherBW24] for more computations in this direction). Part (iii) is [Reference Fresse, Turchin and WillwacherFTW17, Equation (12)]. Part (iv) follows from the isomorphism
$\le 7$
depending on the parity of d (see Equation (4) loc.cit.). The fact that this subspace spans the full homology in the claimed ranges appears as Corollary 6 loc.cit., which proves (i) and (ii) (see also [Reference Brun and WillwacherBW24] for more computations in this direction). Part (iii) is [Reference Fresse, Turchin and WillwacherFTW17, Equation (12)]. Part (iv) follows from the isomorphism
![]() $\smash {\pi _k(\mathrm {Map}^h(E_d,E^{\mathbf {Q}}_{d+2}),r_{\mathbf {Q}} \circ \mathrm {inc})\cong H_{k-1}(\mathrm {HCG}_{d,d+2})}$
of Corollary 3 loc.cit. by considering the
$\smash {\pi _k(\mathrm {Map}^h(E_d,E^{\mathbf {Q}}_{d+2}),r_{\mathbf {Q}} \circ \mathrm {inc})\cong H_{k-1}(\mathrm {HCG}_{d,d+2})}$
of Corollary 3 loc.cit. by considering the
![]() $1$
-loop contribution to degree n of
$1$
-loop contribution to degree n of
![]() $\mathrm {HCG}_{d,d+2}$
explained in Equation (2) loc.cit. and noting that the graph
$\mathrm {HCG}_{d,d+2}$
explained in Equation (2) loc.cit. and noting that the graph
![]() $H_k$
in that equation has degree d for all k.
$H_k$
in that equation has degree d for all k.
Remark 8.5. Note that we have
![]() $\mathrm {Map}^h(E_{n},E^{\mathbf {Q}}_{m})_{r_{\mathbf {Q}}\circ \iota }\simeq \mathrm {Map}^h(E^{\mathbf {Q}}_{n},E^{\mathbf {Q}}_{m})_{\iota ^{\mathbf {Q}}}$
by Lemma 7.9.
$\mathrm {Map}^h(E_{n},E^{\mathbf {Q}}_{m})_{r_{\mathbf {Q}}\circ \iota }\simeq \mathrm {Map}^h(E^{\mathbf {Q}}_{n},E^{\mathbf {Q}}_{m})_{\iota ^{\mathbf {Q}}}$
by Lemma 7.9.
8.3 Homotopy groups of
 $\mathrm {Aut}^h(E_d)/\mathrm {Top}(d)$
$\mathrm {Aut}^h(E_d)/\mathrm {Top}(d)$
We now state our main technical result on the homotopy groups of the fibre
![]() $\mathrm {Aut}^h(E_d)/\mathrm {Top}(d)$
of the map
$\mathrm {Aut}^h(E_d)/\mathrm {Top}(d)$
of the map
![]() $\mathrm {BTop}(d)\rightarrow \mathrm {BAut}^h(E_d)$
from (92). We phrase the result in terms of the following statement that we will refer to as
$\mathrm {BTop}(d)\rightarrow \mathrm {BAut}^h(E_d)$
from (92). We phrase the result in terms of the following statement that we will refer to as
![]() $(\operatorname {\mathbf {H}}^d_{k,m})$
. It depends on a choice of dimension
$(\operatorname {\mathbf {H}}^d_{k,m})$
. It depends on a choice of dimension
![]() $d\ge 1$
and degrees
$d\ge 1$
and degrees
![]() $k,m\ge 2$
.
$k,m\ge 2$
.
At least one of the following two scenarios is the case:
-
(i)
 $\pi _{*}(\mathrm {Aut}^h(E_d)/\mathrm {Top}(d))$
is uncountable in degree
$\pi _{*}(\mathrm {Aut}^h(E_d)/\mathrm {Top}(d))$
is uncountable in degree
 $k-2$
or
$k-2$
or
 $k-1$
, or
$k-1$
, or
 $(\operatorname {\mathbf {H}}^d_{k,m})$
$(\operatorname {\mathbf {H}}^d_{k,m})$
-
(ii)
 $\pi _{m}(\mathrm {Aut}^h(E_d)/\mathrm {Top}(d))_{\mathbf {Q}}$
is nontrivial.
$\pi _{m}(\mathrm {Aut}^h(E_d)/\mathrm {Top}(d))_{\mathbf {Q}}$
is nontrivial.
Theorem 8.6. The statement
![]() $(\operatorname {\mathbf {H}}^d_{k,m})$
holds in the following cases:
$(\operatorname {\mathbf {H}}^d_{k,m})$
holds in the following cases:
-
(i) dimension
 $d=3$
and degrees
$d=3$
and degrees
 $k=7$
and
$k=7$
and
 $m=6$
,
$m=6$
, -
(ii) dimension
 $d=4$
and degrees
$d=4$
and degrees
 $k=4$
and
$k=4$
and
 $m=4$
,
$m=4$
, -
(iii) dimension
 $d=2n+1\ge 5$
, degrees
$d=2n+1\ge 5$
, degrees
 $k\le 8n-12$
with
$k\le 8n-12$
with
 $k\equiv 0\ (\mathrm {mod}\ 4)$
and
$k\equiv 0\ (\mathrm {mod}\ 4)$
and
 $k\neq 6n-2$
, and
$k\neq 6n-2$
, and
 $m=k$
. For
$m=k$
. For
 $2n+1=5$
, the bound
$2n+1=5$
, the bound
 $k\le 8n-12$
can be weakened to
$k\le 8n-12$
can be weakened to
 $k\le 8n-8$
,
$k\le 8n-8$
, -
(iv) dimension
 $d=2n\ge 6$
, degrees
$d=2n\ge 6$
, degrees
 $2n\le k\le 8n-12$
with
$2n\le k\le 8n-12$
with
 $k\equiv 0\ (\mathrm {mod}\ 4)$
, and
$k\equiv 0\ (\mathrm {mod}\ 4)$
, and
 $m=k$
. If n is odd, then the condition
$m=k$
. If n is odd, then the condition
 $2n\le k$
can be removed.
$2n\le k$
can be removed.
This in particular shows that the map
![]() $\mathrm {BTop}(d)\rightarrow \mathrm{BAut}^h(E_d)$
is not a weak equivalence for
$\mathrm {BTop}(d)\rightarrow \mathrm{BAut}^h(E_d)$
is not a weak equivalence for
![]() $d\ge 3$
, so proves the first part of Corollary E in these cases (the second part follows by combining Theorems 6.1 and 8.1). In the low-dimensional case
$d\ge 3$
, so proves the first part of Corollary E in these cases (the second part follows by combining Theorems 6.1 and 8.1). In the low-dimensional case
![]() $d\le 2$
, the map is an equivalence which one can see by combining the facts that in these dimensions,
$d\le 2$
, the map is an equivalence which one can see by combining the facts that in these dimensions,
![]() $\mathrm {BO}(d)\rightarrow \mathrm {BTop}(d)$
and
$\mathrm {BO}(d)\rightarrow \mathrm {BTop}(d)$
and
![]() $\mathrm {BO}(d)\rightarrow \mathrm {BAut}^h(E_d)$
are weak equivalences, the first by [Reference Kirby and SiebenmannKS77, Essay V.§5.0(7)] and the latter by work of Horel for
$\mathrm {BO}(d)\rightarrow \mathrm {BAut}^h(E_d)$
are weak equivalences, the first by [Reference Kirby and SiebenmannKS77, Essay V.§5.0(7)] and the latter by work of Horel for
![]() $d=2$
[Reference HorelHor17, Theorem 8.5] and a folklore result for
$d=2$
[Reference HorelHor17, Theorem 8.5] and a folklore result for
![]() $d=1$
.
$d=1$
.
To prepare the proof of Theorem 8.6, we extract two results on the homotopy groups of the space
![]() $\mathrm {BTop}(d)$
from the literature. The first says they are countable, and its proof requires the following lemma which is likely known to experts but for which we do not know a reference.
$\mathrm {BTop}(d)$
from the literature. The first says they are countable, and its proof requires the following lemma which is likely known to experts but for which we do not know a reference.
Lemma 8.7. For a compact topological manifold M, possible with boundary, or the interior of such a manifold, the homotopy groups of
![]() $\mathrm {BHomeo}_\partial (M)$
are countable.
$\mathrm {BHomeo}_\partial (M)$
are countable.
Lemma 8.7 will be a consequence of the following point-set topological fact. Recall that a topological space is second countable if its topology has a countable basis, and locally weakly-contractible if for every neighbourhood U of a point p, there exists a weakly-contractible open neighbourhood
![]() $V \subseteq U$
of p.
$V \subseteq U$
of p.
Lemma 8.8. If X is a locally weakly-contractible second countable space, then the homotopy groups of X based at any basepoint are countable.
Proof. Recall (for instance, from [Reference DugundjiDug78, VIII.6.3]) that every second countable space X is Lindelöf (i.e., every open cover has a countable subcover). For locally weakly contractible X, we apply this to the collection of all weakly-contractible open subsets to see that X admits a countable open cover by weakly-contractible subsets. As being a locally weakly-contractible second countable space is preserved by passing to an open subset, the same is true for open subsets of X. This allows one to inductively construct an open hypercover
![]() $U_\bullet \to X$
such that each
$U_\bullet \to X$
such that each
![]() $U_\bullet $
has countable many components, each of which is weakly-contractible. Now consider the zigzag
$U_\bullet $
has countable many components, each of which is weakly-contractible. Now consider the zigzag
![]() $X \leftarrow \mathrm {hocolim}\,U_\bullet \rightarrow \mathrm {hocolim}\,\pi _0(U_\bullet )$
whose left map is the weak homotopy equivalence of [Reference Dugger and IsaksenDI04, Theorem 1.3] and whose right map is induced by taking path components, so it is also a weak homotopy equivalence since homotopy colimits take objectwise weak homotopy equivalences to weak homotopy equivalences. Now observe that the right term is equivalent to a countable CW complex – for example, using the formula in [Reference Dugger and IsaksenDI04, Proposition 3.2] exhibiting the homotopy colimit as the geometric realisation of a simplicial set with countable sets of k-simplices for all k – and hence has countable homotopy groups.
$X \leftarrow \mathrm {hocolim}\,U_\bullet \rightarrow \mathrm {hocolim}\,\pi _0(U_\bullet )$
whose left map is the weak homotopy equivalence of [Reference Dugger and IsaksenDI04, Theorem 1.3] and whose right map is induced by taking path components, so it is also a weak homotopy equivalence since homotopy colimits take objectwise weak homotopy equivalences to weak homotopy equivalences. Now observe that the right term is equivalent to a countable CW complex – for example, using the formula in [Reference Dugger and IsaksenDI04, Proposition 3.2] exhibiting the homotopy colimit as the geometric realisation of a simplicial set with countable sets of k-simplices for all k – and hence has countable homotopy groups.
Proof Proof of Lemma 8.7.
For M compact, restriction to the boundary induces a fibration sequence
![]() $\mathrm {Homeo}_\partial (M) \rightarrow \mathrm {Homeo}(M) \rightarrow \mathrm {Homeo}(\partial M)$
as a result of the existence of collars. Hence, it suffices to prove the result for the topological group of homeomorphisms of a compact manifold with boundary or the interior of such a manifold, with no boundary condition. This space is second countable in the compact-open topology [Reference Gleason and PalaisGP57, Proposition 5.4] and locally contractible by [Reference ČernavskiĭČer69, Theorem 1, Theorem 2] (or [Reference ChernavskiĭChe08, Corollary] for the case
$\mathrm {Homeo}_\partial (M) \rightarrow \mathrm {Homeo}(M) \rightarrow \mathrm {Homeo}(\partial M)$
as a result of the existence of collars. Hence, it suffices to prove the result for the topological group of homeomorphisms of a compact manifold with boundary or the interior of such a manifold, with no boundary condition. This space is second countable in the compact-open topology [Reference Gleason and PalaisGP57, Proposition 5.4] and locally contractible by [Reference ČernavskiĭČer69, Theorem 1, Theorem 2] (or [Reference ChernavskiĭChe08, Corollary] for the case
![]() $\mathbf {R}^d$
, which also serves an erratum for the previous reference) or [Reference Edwards and KirbyEK71, Corollary 1.1, Corollary 6.1] (or [Reference KirbyKir69, Theorem 4] for the case
$\mathbf {R}^d$
, which also serves an erratum for the previous reference) or [Reference Edwards and KirbyEK71, Corollary 1.1, Corollary 6.1] (or [Reference KirbyKir69, Theorem 4] for the case
![]() $\mathbf {R}^d$
), so the claim follows from Lemma 8.8.
$\mathbf {R}^d$
), so the claim follows from Lemma 8.8.
Applying Lemma 8.7 to
![]() $\mathbf {R}^d=\mathrm {int}(D^d)$
, we conclude the following:
$\mathbf {R}^d=\mathrm {int}(D^d)$
, we conclude the following:
Corollary 8.9. The homotopy groups of
![]() $\mathrm {BTop}(d)$
are countable.
$\mathrm {BTop}(d)$
are countable.
Remark 8.10. For
![]() $d \neq 4$
, Corollary 8.9 also follows by combining [Reference Milnor and McClearyMil09, Lemma 10, p. 188] with [Reference Kirby and SiebenmannKS77, Essay V.§5.0(1)]. The advantage of the proof above is that it applies to
$d \neq 4$
, Corollary 8.9 also follows by combining [Reference Milnor and McClearyMil09, Lemma 10, p. 188] with [Reference Kirby and SiebenmannKS77, Essay V.§5.0(1)]. The advantage of the proof above is that it applies to
![]() $d=4$
.
$d=4$
.
The second result on
![]() $\mathrm {BTop}(d)$
we will use follows from works of Krannich, Kupers, Randal-Williams and Watanabe [Reference Krannich and Randal-WilliamsKrRW21, Reference Kupers and Randal-WilliamsKuRW25, Reference WatanabeWat09]. It concerns two commutative squares
$\mathrm {BTop}(d)$
we will use follows from works of Krannich, Kupers, Randal-Williams and Watanabe [Reference Krannich and Randal-WilliamsKrRW21, Reference Kupers and Randal-WilliamsKuRW25, Reference WatanabeWat09]. It concerns two commutative squares

where the vertical arrows are induced by the inclusion
![]() $\mathrm {O}(d)\subset \mathrm {Top}(d)$
and the horizontal arrows by the stabilisation map, the Euler class
$\mathrm {O}(d)\subset \mathrm {Top}(d)$
and the horizontal arrows by the stabilisation map, the Euler class
![]() $e\in \mathrm {H}^{2n}(\mathrm {BTop}(2n);\mathbf {Q})$
, and the odd-dimensional analogue of its square
$e\in \mathrm {H}^{2n}(\mathrm {BTop}(2n);\mathbf {Q})$
, and the odd-dimensional analogue of its square
![]() $E\in \mathrm {H}^{2n+1}(\mathrm {BTop}(2n+1);\mathbf {Q})$
(see [Reference Krannich and Randal-WilliamsKrRW21, Sections 1.2.2 and 8.1.1] for further information on this class). That the right vertical maps are rational equivalences follows from the finiteness of the groups
$E\in \mathrm {H}^{2n+1}(\mathrm {BTop}(2n+1);\mathbf {Q})$
(see [Reference Krannich and Randal-WilliamsKrRW21, Sections 1.2.2 and 8.1.1] for further information on this class). That the right vertical maps are rational equivalences follows from the finiteness of the groups
![]() $\pi _{*}(\mathrm {Top}/\mathrm {O})$
[Reference Kirby and SiebenmannKS77, Essay V.§5.0(5)].
$\pi _{*}(\mathrm {Top}/\mathrm {O})$
[Reference Kirby and SiebenmannKS77, Essay V.§5.0(5)].
Theorem 8.11. The maps induced by the bottom horizontal arrows
are surjective in degrees
![]() $k\le 4n-1$
for all n, and in degrees
$k\le 4n-1$
for all n, and in degrees
![]() $k\le 8n-12$
as long as
$k\le 8n-12$
as long as
![]() $n\ge 3$
. Moreover, the right-hand map for
$n\ge 3$
. Moreover, the right-hand map for
![]() $n=2$
is also surjective in degree
$n=2$
is also surjective in degree
![]() $4n$
.
$4n$
.
Proof. In degrees
![]() $*\le 4n-1$
, the claimed surjectivity follows from the classical fact that the upper horizontal arrows are rationally surjective in exactly this range.
$*\le 4n-1$
, the claimed surjectivity follows from the classical fact that the upper horizontal arrows are rationally surjective in exactly this range.
In order to show the claim for the bottom horizontal map in the left square of (94) for
![]() $n\ge 3$
in the range
$n\ge 3$
in the range
![]() $*\le 8n-12$
, it thus suffices to show that the map
$*\le 8n-12$
, it thus suffices to show that the map
![]() $\Omega ^{2n}_0\mathrm {BTop}(2n)\rightarrow \Omega ^{2n}_0\mathrm {BTop}$
is surjective on
$\Omega ^{2n}_0\mathrm {BTop}(2n)\rightarrow \Omega ^{2n}_0\mathrm {BTop}$
is surjective on
![]() $\pi _{*}(-)_{\mathbf {Q}}$
for
$\pi _{*}(-)_{\mathbf {Q}}$
for
![]() $*\le 6n-12$
, which can be further reduced to showing that the map
$*\le 6n-12$
, which can be further reduced to showing that the map
![]() $\mathrm {BDiff}_\partial (D^{2n})\simeq \Omega ^{2n}_0\mathrm {Top}(2n)/\mathrm {O}(2n)\rightarrow \Omega ^{2n}_0\mathrm {Top}/\mathrm {O}(2n)$
is surjective on
$\mathrm {BDiff}_\partial (D^{2n})\simeq \Omega ^{2n}_0\mathrm {Top}(2n)/\mathrm {O}(2n)\rightarrow \Omega ^{2n}_0\mathrm {Top}/\mathrm {O}(2n)$
is surjective on
![]() $\pi _{*}(-)_{\mathbf {Q}}$
for
$\pi _{*}(-)_{\mathbf {Q}}$
for
![]() $*\le 6n-13$
; here, we have used Morlet’s smoothing theory equivalence [Reference Kirby and SiebenmannKS77, p 241]. This surjectivity was proved in [Reference Kupers and Randal-WilliamsKuRW25, Corollary 6.7]. By precomposing the map
$*\le 6n-13$
; here, we have used Morlet’s smoothing theory equivalence [Reference Kirby and SiebenmannKS77, p 241]. This surjectivity was proved in [Reference Kupers and Randal-WilliamsKuRW25, Corollary 6.7]. By precomposing the map
![]() $\mathrm {BTop}(2n+1)\rightarrow \mathrm {BTop}$
with
$\mathrm {BTop}(2n+1)\rightarrow \mathrm {BTop}$
with
![]() $\mathrm {BTop}(2n)\rightarrow \mathrm {BTop}(2n+1)$
, this argument also shows that the bottom horizontal map in the right square of (94) for
$\mathrm {BTop}(2n)\rightarrow \mathrm {BTop}(2n+1)$
, this argument also shows that the bottom horizontal map in the right square of (94) for
![]() $n\ge 3$
is surjective on
$n\ge 3$
is surjective on
![]() $\pi _{*}(-)_{\mathbf {Q}}$
for
$\pi _{*}(-)_{\mathbf {Q}}$
for
![]() $*\le 6n-12$
as long as
$*\le 6n-12$
as long as
![]() $*\neq 4n$
.
$*\neq 4n$
.
This leaves us with showing that for all
![]() $n\ge 2$
, the bottom horizontal map of the right square of (94) is surjective on
$n\ge 2$
, the bottom horizontal map of the right square of (94) is surjective on
![]() $\pi _{4n}(-)_{\mathbf {Q}}$
. Since the pullback of the class
$\pi _{4n}(-)_{\mathbf {Q}}$
. Since the pullback of the class
![]() $E\in \mathrm {H}^{4n}(\mathrm {BTop}(2n+1);\mathbf {Q})$
to
$E\in \mathrm {H}^{4n}(\mathrm {BTop}(2n+1);\mathbf {Q})$
to
![]() $\mathrm {BO}(2n)$
agrees with
$\mathrm {BO}(2n)$
agrees with
![]() $e^2$
by definition of E and hence is decomposable, evaluation of the pullback of E on the image of the Hurewicz map
$e^2$
by definition of E and hence is decomposable, evaluation of the pullback of E on the image of the Hurewicz map
![]() $\pi _{4n}(\mathrm {BO}(2n))_{\mathbf {Q}} \to H_{4n}(\mathrm {BO}(2n);\mathbf {Q})$
is trivial. Hence, the fact that the map
$\pi _{4n}(\mathrm {BO}(2n))_{\mathbf {Q}} \to H_{4n}(\mathrm {BO}(2n);\mathbf {Q})$
is trivial. Hence, the fact that the map
![]() $\mathrm {BO}(2n)\rightarrow \mathrm {BTop}$
is surjective on
$\mathrm {BO}(2n)\rightarrow \mathrm {BTop}$
is surjective on
![]() $\pi _{4n}(-)_{\mathbf {Q}}$
implies that the direct summand
$\pi _{4n}(-)_{\mathbf {Q}}$
implies that the direct summand
![]() $\pi _{4n}(\mathrm {BTop})_{\mathbf {Q}}\subset \pi _{4n}(K(\mathbf {Q},4n)\times \mathrm {BTop})_{\mathbf {Q}}$
is in the image. So we are left with showing that the map
$\pi _{4n}(\mathrm {BTop})_{\mathbf {Q}}\subset \pi _{4n}(K(\mathbf {Q},4n)\times \mathrm {BTop})_{\mathbf {Q}}$
is in the image. So we are left with showing that the map
![]() $E\colon \mathrm {BTop}(2n+1)\rightarrow K(\mathbf {Q},4n)$
is nontrivial for all
$E\colon \mathrm {BTop}(2n+1)\rightarrow K(\mathbf {Q},4n)$
is nontrivial for all
![]() $n\ge 2$
. Using the smoothing theory equivalence
$n\ge 2$
. Using the smoothing theory equivalence
![]() $\mathrm {BDiff}^{\mathrm {fr}}_\partial (D^{2n+1})_0\simeq \Omega ^{2n+1}_0\mathrm {Top}(2n+1)$
involving the framed diffeomorphism group, the composition
$\mathrm {BDiff}^{\mathrm {fr}}_\partial (D^{2n+1})_0\simeq \Omega ^{2n+1}_0\mathrm {Top}(2n+1)$
involving the framed diffeomorphism group, the composition
agrees by [Reference Krannich and Randal-WilliamsKrRW21, Theorem B.4, Remark B.5] up to a constant with the ‘Kontsevich class’
![]() $\zeta _{2,3}$
from [Reference WatanabeWat09, p. 631], so it is nontrivial for
$\zeta _{2,3}$
from [Reference WatanabeWat09, p. 631], so it is nontrivial for
![]() $n\ge 2$
by Theorem 3.1 loc.cit and [Reference WatanabeWat22].
$n\ge 2$
by Theorem 3.1 loc.cit and [Reference WatanabeWat22].
Proof Proof of Theorem 8.6.
Throughout the proof, we use the fact that
![]() $\pi _{k>0}(\mathrm {BTop})_{\mathbf {Q}}$
is
$\pi _{k>0}(\mathrm {BTop})_{\mathbf {Q}}$
is
![]() $1$
-dimensional for
$1$
-dimensional for
![]() $k\equiv 0\ (\mathrm {mod}\ 4)$
and trivial otherwise, and that
$k\equiv 0\ (\mathrm {mod}\ 4)$
and trivial otherwise, and that
![]() $\mathrm {BTop}(d)$
has countable homotopy groups by Corollary 8.9. We divide the proof into three cases.
$\mathrm {BTop}(d)$
has countable homotopy groups by Corollary 8.9. We divide the proof into three cases.
-
 $d=3$
Applying Theorem 7.23 for
$d=3$
Applying Theorem 7.23 for
 $n=m=3$
and
$n=m=3$
and
 $i=6$
, we see that either
$i=6$
, we see that either-
(a)
 $\pi _{*}(\mathrm {BAut}^h(E_3))$
is uncountable in degrees
$\pi _{*}(\mathrm {BAut}^h(E_3))$
is uncountable in degrees
 $6$
or
$6$
or
 $7$
, or
$7$
, or -
(b)
 $\pi _7(\mathrm {BAut}^h(E_3))_{\mathbf {Q}} \cong \pi _7(\mathrm {BAut}^h(E_3^{\mathbf {Q}}))$
.
$\pi _7(\mathrm {BAut}^h(E_3))_{\mathbf {Q}} \cong \pi _7(\mathrm {BAut}^h(E_3^{\mathbf {Q}}))$
.-
By the long exact sequence of
 $\mathrm {Aut}^h(E_3)/\mathrm {Top}(3)\rightarrow \mathrm {BTop}(3)\rightarrow \mathrm {BAut}^h(E_3)$
, there is nothing left to show in the first case since
$\mathrm {Aut}^h(E_3)/\mathrm {Top}(3)\rightarrow \mathrm {BTop}(3)\rightarrow \mathrm {BAut}^h(E_3)$
, there is nothing left to show in the first case since
 $\mathrm {BTop}(d)$
has countable homotopy groups. In the second case, we use that first, the map
$\mathrm {BTop}(d)$
has countable homotopy groups. In the second case, we use that first, the map
 $\mathrm {BO}(3)\rightarrow \mathrm {BTop}(3)$
is a weak equivalence by [Reference HatcherHat83, p. 605], and thus,
$\mathrm {BO}(3)\rightarrow \mathrm {BTop}(3)$
is a weak equivalence by [Reference HatcherHat83, p. 605], and thus,
 $\pi _7(\mathrm {BTop}(3))_{\mathbf {Q}} \cong \pi _7(\mathrm {BO}(3))_{\mathbf {Q}}$
vanishes, and that second, Theorem 8.4 (ii) combined with Remark 8.5 shows that
$\pi _7(\mathrm {BTop}(3))_{\mathbf {Q}} \cong \pi _7(\mathrm {BO}(3))_{\mathbf {Q}}$
vanishes, and that second, Theorem 8.4 (ii) combined with Remark 8.5 shows that
 $\pi _7(\mathrm {BAut}^h(\smash {E_3^{\mathbf {Q}}}))\cong \pi _6(\mathrm {Map}^h(\smash {E_3^{\mathbf {Q}}},\smash {E_3^{\mathbf {Q}}});\mathrm {id})$
is nontrivial – in fact, at least
$\pi _7(\mathrm {BAut}^h(\smash {E_3^{\mathbf {Q}}}))\cong \pi _6(\mathrm {Map}^h(\smash {E_3^{\mathbf {Q}}},\smash {E_3^{\mathbf {Q}}});\mathrm {id})$
is nontrivial – in fact, at least
 $3$
-dimensional (since
$3$
-dimensional (since
 $12n-6=14n-8$
for
$12n-6=14n-8$
for
 $n=3$
). Using the same long exact sequence as before, this shows the claim in the second case.
$n=3$
). Using the same long exact sequence as before, this shows the claim in the second case.
-
-
-
 $d=4$
The logic is the same as in the case
$d=4$
The logic is the same as in the case
 $d=3$
: we again apply Theorem 7.23, this time for
$d=3$
: we again apply Theorem 7.23, this time for
 $n=m=4$
and
$n=m=4$
and
 $i=3$
, to see that either
$i=3$
, to see that either-
(a)
 $\pi _{*}(\mathrm {BAut}^h(E_4))$
is uncountable in degrees
$\pi _{*}(\mathrm {BAut}^h(E_4))$
is uncountable in degrees
 $3$
or
$3$
or
 $4$
, or
$4$
, or -
(b)
 $\pi _4(\mathrm {BAut}^h(E_4))_{\mathbf {Q}} \cong \pi _4(\mathrm {BAut}^h(E_4^{\mathbf {Q}}))$
.
$\pi _4(\mathrm {BAut}^h(E_4))_{\mathbf {Q}} \cong \pi _4(\mathrm {BAut}^h(E_4^{\mathbf {Q}}))$
.-
As before, there is nothing left to show in the first case. In the second case, we use that first,
 $\pi _4(\mathrm {BTop}(4))_{\mathbf {Q}}$
is at least
$\pi _4(\mathrm {BTop}(4))_{\mathbf {Q}}$
is at least
 $2$
-dimensional as a result of Theorem 8.11, and that second,
$2$
-dimensional as a result of Theorem 8.11, and that second,
 $\pi _4(\mathrm {BAut}^h({E_4}^{\mathbf {Q}}))$
is
$\pi _4(\mathrm {BAut}^h({E_4}^{\mathbf {Q}}))$
is
 $1$
-dimensional as a result of Theorem 8.4 (i) (since
$1$
-dimensional as a result of Theorem 8.4 (i) (since
 $2n-4i-1 = 3$
for
$2n-4i-1 = 3$
for
 $i=0$
, and all other terms are in degree
$i=0$
, and all other terms are in degree
 $\geq 7$
).
$\geq 7$
).
-
-
-
 $d\ge 5$
Theorem 7.23 for
$d\ge 5$
Theorem 7.23 for
 $n=m=d$
and
$n=m=d$
and
 $i=k-1$
shows that either
$i=k-1$
shows that either-
(a)
 $\pi _{*}(\mathrm {BAut}^h(E_{d}))$
is uncountable in degrees k or
$\pi _{*}(\mathrm {BAut}^h(E_{d}))$
is uncountable in degrees k or
 $k-1$
, or
$k-1$
, or -
(b)
 $\pi _{k}(\mathrm {BAut}^h(E_{d}))_{\mathbf {Q}} \cong \pi _{k}(\mathrm {BAut}^h(E_{d}^{\mathbf {Q}}))$
.
$\pi _{k}(\mathrm {BAut}^h(E_{d}))_{\mathbf {Q}} \cong \pi _{k}(\mathrm {BAut}^h(E_{d}^{\mathbf {Q}}))$
.-
As previously, nothing is left to show in the first case. In the second case, we first consider odd d. If
 $d=2n+1\ge 5$
and
$d=2n+1\ge 5$
and
 $1\le k\le 8n-12$
(or
$1\le k\le 8n-12$
(or
 $1\le k\le 8n-8$
if
$1\le k\le 8n-8$
if
 $n=2$
) such that
$n=2$
) such that
 $k\neq 6n-2$
and
$k\neq 6n-2$
and
 $k\equiv 0\ (\mathrm {mod}\ 4)$
, then we use first, that
$k\equiv 0\ (\mathrm {mod}\ 4)$
, then we use first, that
 $\pi _{k}(\mathrm {BTop}(2n+1))_{\mathbf {Q}}$
is at least
$\pi _{k}(\mathrm {BTop}(2n+1))_{\mathbf {Q}}$
is at least
 $2$
-dimensional if
$2$
-dimensional if
 $k=4n$
and otherwise at least
$k=4n$
and otherwise at least
 $1$
-dimensional by Theorem 8.11, and second, that Theorem 8.4 (ii) shows that
$1$
-dimensional by Theorem 8.11, and second, that Theorem 8.4 (ii) shows that
 $\pi _k(\mathrm {BAut}^h(E_{2n+1}^{\mathbf {Q}}))$
is trivial for
$\pi _k(\mathrm {BAut}^h(E_{2n+1}^{\mathbf {Q}}))$
is trivial for
 $k\neq 4n$
and
$k\neq 4n$
and
 $1$
-dimensional for
$1$
-dimensional for
 $k=4n$
. Finally, for even
$k=4n$
. Finally, for even
 $d=2n\ge 6$
and
$d=2n\ge 6$
and
 $k\equiv 0\ (\mathrm {mod}\ 4)$
with
$k\equiv 0\ (\mathrm {mod}\ 4)$
with
 $2n\le k\le 8n-2$
for n even and
$2n\le k\le 8n-2$
for n even and
 $k\le 8n-2$
for n odd, we use a) that
$k\le 8n-2$
for n odd, we use a) that
 $\pi _{k}(\mathrm {BTop}(2n))_{\mathbf {Q}}$
is at least
$\pi _{k}(\mathrm {BTop}(2n))_{\mathbf {Q}}$
is at least
 $1$
-dimensional and at least
$1$
-dimensional and at least
 $2$
-dimensional for
$2$
-dimensional for
 $k=2n$
if n is even by Theorem 8.11, and b) that Theorem 8.4 (i) shows that
$k=2n$
if n is even by Theorem 8.11, and b) that Theorem 8.4 (i) shows that
 $\pi _{k}(\mathrm {BAut}^h(E_{2n}^{\mathbf {Q}}))$
is trivial for
$\pi _{k}(\mathrm {BAut}^h(E_{2n}^{\mathbf {Q}}))$
is trivial for
 $k\neq 2n$
and
$k\neq 2n$
and
 $1$
-dimensional for
$1$
-dimensional for
 $k=2n$
.
$k=2n$
.
-
-
Remark 8.12. The proof of Theorem 8.6 simply compares the homotopy groups of
![]() $\mathrm {Top}(d)$
and
$\mathrm {Top}(d)$
and
![]() $\mathrm {Aut}^h(E_d)$
abstractly. It does not use anything about the specific map
$\mathrm {Aut}^h(E_d)$
abstractly. It does not use anything about the specific map
![]() $\mathrm {Top}(d)\rightarrow \mathrm {Aut}^h(E_d)$
.
$\mathrm {Top}(d)\rightarrow \mathrm {Aut}^h(E_d)$
.
8.3.1 Applications to
 $S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
$S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
In view of the
![]() $0$
-coconnected map of Theorem 8.1
$0$
-coconnected map of Theorem 8.1
as long as
![]() $k-d-3\ge 0$
, the statement
$k-d-3\ge 0$
, the statement
![]() $(\operatorname {\mathbf {H}}^d_{k,m})$
implies the following variant for
$(\operatorname {\mathbf {H}}^d_{k,m})$
implies the following variant for
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
:
$S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
:
At least one of the following two scenarios is the case:
-
(i)
 $\pi _{*}(S^{\mathscr {D}\mathrm {isc}}_\partial (D^d))$
is uncountable in degree
$\pi _{*}(S^{\mathscr {D}\mathrm {isc}}_\partial (D^d))$
is uncountable in degree
 $k-d-3$
or
$k-d-3$
or
 $k-d-2$
, or
$k-d-2$
, or
 $(\operatorname {\mathbf {H}}^{d,\mathscr {D}\mathrm {isc}}_{k,m})$
$(\operatorname {\mathbf {H}}^{d,\mathscr {D}\mathrm {isc}}_{k,m})$
-
(ii)
 $\pi _{m-d-1}(S^{\mathscr {D}\mathrm {isc}}_\partial (D^d))_{\mathbf {Q}}$
is nontrivial.
$\pi _{m-d-1}(S^{\mathscr {D}\mathrm {isc}}_\partial (D^d))_{\mathbf {Q}}$
is nontrivial.
For
![]() $k-d-3=0$
, this implication uses that if
$k-d-3=0$
, this implication uses that if
![]() $\pi _{0}(\Omega ^{d+1}\mathrm {Aut}^h(E_d)/\mathrm {Top}(d))$
is uncountable, then so is
$\pi _{0}(\Omega ^{d+1}\mathrm {Aut}^h(E_d)/\mathrm {Top}(d))$
is uncountable, then so is
![]() $\pi _{0}(\Omega ^{d+1}_{\mathrm {O}(d)}\mathrm {Aut}^h(E_d)/\mathrm {Top}(d))$
. This is because
$\pi _{0}(\Omega ^{d+1}_{\mathrm {O}(d)}\mathrm {Aut}^h(E_d)/\mathrm {Top}(d))$
. This is because
![]() $\pi _{d+1}(\mathrm {BTop}(d))$
is countable, so if the domain of the map
$\pi _{d+1}(\mathrm {BTop}(d))$
is countable, so if the domain of the map
![]() $\pi _{d+1}(\mathrm {Aut}(E_d)/\mathrm {Top}(d))\rightarrow \pi _{d+1}(\mathrm {BTop}(d))$
is uncountable, then so is its kernel. Combined with Theorem 8.6, we therefore obtain the following:
$\pi _{d+1}(\mathrm {Aut}(E_d)/\mathrm {Top}(d))\rightarrow \pi _{d+1}(\mathrm {BTop}(d))$
is uncountable, then so is its kernel. Combined with Theorem 8.6, we therefore obtain the following:
Corollary 8.13. Under the additional assumption
![]() $k-d-3\ge 0$
, the statement
$k-d-3\ge 0$
, the statement
![]() $(\operatorname {\mathbf {H}}^{d,\mathscr {D}\mathrm {isc}}_{k,m})$
holds for all choices of triples
$(\operatorname {\mathbf {H}}^{d,\mathscr {D}\mathrm {isc}}_{k,m})$
holds for all choices of triples
![]() $(d,k,m)$
to which Theorem 8.6 applies.
$(d,k,m)$
to which Theorem 8.6 applies.
We now use Corollary 8.13 to prove that
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
is not contractible for all
$S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
is not contractible for all
![]() $d\ge 5$
with
$d\ge 5$
with
![]() $d\neq 3$
.
$d\neq 3$
.
Theorem 8.14. For
![]() $d=3$
or
$d=3$
or
![]() $d\ge 5$
, the space
$d\ge 5$
, the space
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
is not contractible.
$S^{\mathscr {D}\mathrm {isc}}_\partial (D^d)$
is not contractible.
Proof. For
![]() $d=3$
, the claim follows from
$d=3$
, the claim follows from
![]() $(\operatorname {\mathbf {H}}^{d,\mathscr {D}\mathrm {isc}}_{k,m})$
for the triple
$(\operatorname {\mathbf {H}}^{d,\mathscr {D}\mathrm {isc}}_{k,m})$
for the triple
![]() $(d,k,m)=(3,7,6)$
since this statement holds true in this case
$(d,k,m)=(3,7,6)$
since this statement holds true in this case
![]() $k-d-3\ge 0$
and Theorem 8.6 applies to this triple. In the case
$k-d-3\ge 0$
and Theorem 8.6 applies to this triple. In the case
![]() $d\ge 5$
, the claim follows similarly as long as we ensure that there exists a k such that
$d\ge 5$
, the claim follows similarly as long as we ensure that there exists a k such that
![]() $k-d-3\ge 0$
and Theorem 8.6 applies to the triple
$k-d-3\ge 0$
and Theorem 8.6 applies to the triple
![]() $(d,k,k)$
. For
$(d,k,k)$
. For
![]() $d=2n+1$
with
$d=2n+1$
with
![]() $n\ge 4$
, we pick the unique
$n\ge 4$
, we pick the unique
![]() $k\equiv 0\ (\mathrm {mod}\ 4)$
with
$k\equiv 0\ (\mathrm {mod}\ 4)$
with
![]() $2n+5\le k\le 2n+8$
. This satisfies the requirements because
$2n+5\le k\le 2n+8$
. This satisfies the requirements because
![]() $k-d-3\ge 0$
and
$k-d-3\ge 0$
and
![]() $k\neq 6n-2$
as
$k\neq 6n-2$
as
![]() $2n+8<6n-2$
and
$2n+8<6n-2$
and
![]() $2n+8\le 8n-12$
. For
$2n+8\le 8n-12$
. For
![]() $d=2n+1$
with
$d=2n+1$
with
![]() $n=3$
, we choose
$n=3$
, we choose
![]() $k=12$
. This works because
$k=12$
. This works because
![]() $k-d-3=2\ge 0$
and
$k-d-3=2\ge 0$
and
![]() $12\le 8n-12=12$
. For
$12\le 8n-12=12$
. For
![]() $d=2n+1$
with
$d=2n+1$
with
![]() $n=2$
, we choose
$n=2$
, we choose
![]() $k=8$
, which works using the improvement of the bound since
$k=8$
, which works using the improvement of the bound since
![]() $k-d-3=0\ge 0$
and
$k-d-3=0\ge 0$
and
![]() $k\le 8n-8=8$
. For
$k\le 8n-8=8$
. For
![]() $d=2n$
with
$d=2n$
with
![]() $n\ge 4$
, we can pick the unique
$n\ge 4$
, we can pick the unique
![]() $k\equiv 0\ (\mathrm {mod}\ 4)$
with
$k\equiv 0\ (\mathrm {mod}\ 4)$
with
![]() $2n+4\le k\le 2n+7$
, which is valid since
$2n+4\le k\le 2n+7$
, which is valid since
![]() $k-d-3\ge 0$
and
$k-d-3\ge 0$
and
![]() $k\le 2n+7\le 8n-12$
. Finally, for
$k\le 2n+7\le 8n-12$
. Finally, for
![]() $d=2n$
with
$d=2n$
with
![]() $n=3$
, we pick
$n=3$
, we pick
![]() $k=12$
, which works because
$k=12$
, which works because
![]() $k-d-3=3\ge 0$
and
$k-d-3=3\ge 0$
and
![]() $k\le 8n-12=12$
.
$k\le 8n-12=12$
.
Remark 8.15. If one relaxes the range
![]() $k\le 8n-12$
in Theorem 8.6 (iii) and (iv) to
$k\le 8n-12$
in Theorem 8.6 (iii) and (iv) to
![]() $k\le 4n-1$
, then the proof we gave does not rely on the recent works [Reference Krannich and Randal-WilliamsKrRW21, Reference Kupers and Randal-WilliamsKuRW25, Reference WatanabeWat09], since the proof of Theorem 8.11 does not use them in this range. This is sufficient to deduce Corollary E. It also gives a weaker version of Corollary 8.13 that does not rely on these works. The latter is good enough to conclude Theorem 8.14 except in dimensions
$k\le 4n-1$
, then the proof we gave does not rely on the recent works [Reference Krannich and Randal-WilliamsKrRW21, Reference Kupers and Randal-WilliamsKuRW25, Reference WatanabeWat09], since the proof of Theorem 8.11 does not use them in this range. This is sufficient to deduce Corollary E. It also gives a weaker version of Corollary 8.13 that does not rely on these works. The latter is good enough to conclude Theorem 8.14 except in dimensions
![]() $d=5,6,7$
.
$d=5,6,7$
.
Combining Theorem 8.14 with Corollary 5.13 implies Theorem C.
Remark 8.16. Even though Theorem 8.14 applies to
![]() $d=3$
and all orientable
$d=3$
and all orientable
![]() $3$
-manifolds M are spin, we cannot conclude that
$3$
-manifolds M are spin, we cannot conclude that
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
is nontrivial in this case, because our tangential
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
is nontrivial in this case, because our tangential
![]() $2$
-type invariance result does not apply if
$2$
-type invariance result does not apply if
![]() $d=3$
, so Corollary 5.13 is not available. Nonetheless,
$d=3$
, so Corollary 5.13 is not available. Nonetheless,
![]() $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
is nontrivial if M embeds into
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
is nontrivial if M embeds into
![]() $D^3$
after removing finitely many codimension
$D^3$
after removing finitely many codimension
![]() $0$
discs, since
$0$
discs, since
-
(i) removing discs does not change the homotopy type of
 $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
by Proposition 5.11,
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
by Proposition 5.11, -
(ii)
 $S^{\mathscr {D}\mathrm {isc}}_\partial (D^3)$
is a homotopy retract of
$S^{\mathscr {D}\mathrm {isc}}_\partial (D^3)$
is a homotopy retract of
 $S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
if M embeds into
$S^{\mathscr {D}\mathrm {isc}}_\partial (M)$
if M embeds into
 $D^3$
by the same argument as in the second part of proof of Corollary 5.13, and
$D^3$
by the same argument as in the second part of proof of Corollary 5.13, and -
(iii)
 $S^{\mathscr {D}\mathrm {isc}}_\partial (D^3)$
is nontrivial by Theorem 8.14.
$S^{\mathscr {D}\mathrm {isc}}_\partial (D^3)$
is nontrivial by Theorem 8.14.
This applies in particular to
![]() $S^3$
or to the handlebodies
$S^3$
or to the handlebodies
![]() $(S^1\times D^2)^{\natural g}\natural (S^2\times D^1)^{\natural g}$
for
$(S^1\times D^2)^{\natural g}\natural (S^2\times D^1)^{\natural g}$
for
![]() $g,h\ge 0$
, with
$g,h\ge 0$
, with
![]() $\natural $
denoting the boundary connected sum operation.
$\natural $
denoting the boundary connected sum operation.
8.4 Positive codimension
We conclude this section with a brief discussion of an analogue of the nontriviality results of the previous section in positive codimension, by which we mean the following: the subgroup
![]() $\mathrm {O}(c)\subset \mathrm {O}(d)$
acting on the last c coordinates stabilises the standard inclusion
$\mathrm {O}(c)\subset \mathrm {O}(d)$
acting on the last c coordinates stabilises the standard inclusion
![]() $E_{d-c}\rightarrow E_d$
for
$E_{d-c}\rightarrow E_d$
for
![]() $c\ge 0$
under the
$c\ge 0$
under the
![]() $\mathrm {O}(d)$
-action on
$\mathrm {O}(d)$
-action on
![]() $\mathrm {Map}^h(E_{d-c},E_d)$
, so we have a map
$\mathrm {Map}^h(E_{d-c},E_d)$
, so we have a map
![]() $\mathrm {O}(d)/\mathrm {O}(c)\rightarrow \mathrm {Map}^h(E_{d-c},E_d)$
. In the same way as in the case
$\mathrm {O}(d)/\mathrm {O}(c)\rightarrow \mathrm {Map}^h(E_{d-c},E_d)$
. In the same way as in the case
![]() $c=d$
discussed in Section 8.1, Boavida de Brito–Weiss’ work [Reference Boavida de Brito and WeissBdBW18] shows that this action factors as a composition
$c=d$
discussed in Section 8.1, Boavida de Brito–Weiss’ work [Reference Boavida de Brito and WeissBdBW18] shows that this action factors as a composition
where
![]() $\mathrm {Top}(d,d-c)\subset \mathrm {Top}(d)$
is the subgroup of those homeomorphisms that fix
$\mathrm {Top}(d,d-c)\subset \mathrm {Top}(d)$
is the subgroup of those homeomorphisms that fix
![]() $\{0\}\times \mathbf {R}^{d-c}\subset \mathbf {R}^d$
. Generalising from the codimension
$\{0\}\times \mathbf {R}^{d-c}\subset \mathbf {R}^d$
. Generalising from the codimension
![]() $c=0$
case of Corollary E, one might wonder whether
$c=0$
case of Corollary E, one might wonder whether
is a weak equivalence. In codimension
![]() $c\ge 3$
, this was shown by Boavida de Brito–Weiss [Reference Boavida de Brito and WeissBdBW18, Theorem 1.6] after taking
$c\ge 3$
, this was shown by Boavida de Brito–Weiss [Reference Boavida de Brito and WeissBdBW18, Theorem 1.6] after taking
![]() $(d-c+1)$
-fold loop spaces. Adapting the methods of the previous subsection, we consider the remaining cases
$(d-c+1)$
-fold loop spaces. Adapting the methods of the previous subsection, we consider the remaining cases
![]() $c=1,2$
. As before, we phrase the result in terms of the following placeholder statement involving dimension
$c=1,2$
. As before, we phrase the result in terms of the following placeholder statement involving dimension
![]() $d\ge 1$
, codimension
$d\ge 1$
, codimension
![]() $c\in \{1,2\}$
, degrees
$c\in \{1,2\}$
, degrees
![]() $k\ge 3$
and
$k\ge 3$
and
![]() $m\ge 1$
.
$m\ge 1$
.
At least one of the following two scenarios is the case:
-
(i) The homotopy groups
are uncountable in degree $$\begin{align*}\pi_{*}\Big(\mathrm{hofib}_\iota\big(\mathrm{Top}(d)/\mathrm{Top}(d,d-c) \rightarrow \mathrm{Map}^h(E_{d-c},E_{d})\big)\Big)\end{align*}$$
$$\begin{align*}\pi_{*}\Big(\mathrm{hofib}_\iota\big(\mathrm{Top}(d)/\mathrm{Top}(d,d-c) \rightarrow \mathrm{Map}^h(E_{d-c},E_{d})\big)\Big)\end{align*}$$
 $k-3$
or
$k-3$
or
 $k-2$
, or
$k-2$
, or
 $(\operatorname {\mathbf {H}}^{d,c}_{k,m})$
$(\operatorname {\mathbf {H}}^{d,c}_{k,m})$
-
(ii) The homotopy group
is nontrivial. $$\begin{align*}\pi_{m-1}\Big(\mathrm{hofib}_\iota\big(\mathrm{Top}(d)/\mathrm{Top}(d,d-c) \rightarrow \mathrm{Map}^h(E_{d-c},E_{d})\big)\Big)_{\mathbf{Q}}\end{align*}$$
$$\begin{align*}\pi_{m-1}\Big(\mathrm{hofib}_\iota\big(\mathrm{Top}(d)/\mathrm{Top}(d,d-c) \rightarrow \mathrm{Map}^h(E_{d-c},E_{d})\big)\Big)_{\mathbf{Q}}\end{align*}$$
The proof requires some results about the homotopy groups of the spaces
![]() $\mathrm {Top}(d,d-c)$
:
$\mathrm {Top}(d,d-c)$
:
Lemma 8.17.
-
(i) The map
 $(-) \times \mathbf {R}^{d-1} \colon \mathrm {O}(1) \simeq \mathrm {Top}(1) \to \mathrm {Top}(d,d-1)$
is a homotopy equivalence.
$(-) \times \mathbf {R}^{d-1} \colon \mathrm {O}(1) \simeq \mathrm {Top}(1) \to \mathrm {Top}(d,d-1)$
is a homotopy equivalence. -
(ii) The map
 $(-) \times \mathbf {R}^{d-2} \colon \mathrm {O}(2) \simeq \mathrm {Top}(2) \to \mathrm {Top}(d,d-2)$
is
$(-) \times \mathbf {R}^{d-2} \colon \mathrm {O}(2) \simeq \mathrm {Top}(2) \to \mathrm {Top}(d,d-2)$
is
 $(d-2)$
-connected.
$(d-2)$
-connected.
Proof. Part (i) admits an elementary argument: if
![]() $f(-,-) \colon \mathbf {R}^{d-1}\times \mathbf {R}=\mathbf {R}^d \to \mathbf {R}^d$
is an orientation-preserving homeomorphism fixing
$f(-,-) \colon \mathbf {R}^{d-1}\times \mathbf {R}=\mathbf {R}^d \to \mathbf {R}^d$
is an orientation-preserving homeomorphism fixing
![]() $\mathbf {R}^{d-1}\times \{0\}$
pointwise, then
$\mathbf {R}^{d-1}\times \{0\}$
pointwise, then

gives an isotopy of homeomorphisms that extends continuously to
![]() $t=\infty $
with value
$t=\infty $
with value
![]() $\mathrm {id}_{\mathbf {R}^d}$
and depends continuously on f. If f is orientation-reversing, a similar formula works. Part (ii) is due to Kirby–Siebenmann [Reference Kirby and SiebenmannKS75, Theorem B] for
$\mathrm {id}_{\mathbf {R}^d}$
and depends continuously on f. If f is orientation-reversing, a similar formula works. Part (ii) is due to Kirby–Siebenmann [Reference Kirby and SiebenmannKS75, Theorem B] for
![]() $d\neq 4$
, who deduce it using immersion theory from an existence and uniqueness result for normal bundles of codimension
$d\neq 4$
, who deduce it using immersion theory from an existence and uniqueness result for normal bundles of codimension
![]() $2$
locally flat embeddings into d-manifolds. In the remaining case
$2$
locally flat embeddings into d-manifolds. In the remaining case
![]() $d=4$
, the necessary results on normal bundles of locally flat embeddings of surfaces into
$d=4$
, the necessary results on normal bundles of locally flat embeddings of surfaces into
![]() $4$
-manifolds were established later by Freedman–Quinn [Reference Freedman and QuinnFQ90, Section 9.4].
$4$
-manifolds were established later by Freedman–Quinn [Reference Freedman and QuinnFQ90, Section 9.4].
Remark 8.18. The proof of Corollary 8.9 extends to show that
![]() $\mathrm {Top}(d,d-c)$
has countable homotopy groups: use Lemma 8.8, that it is second countable being a subspace of
$\mathrm {Top}(d,d-c)$
has countable homotopy groups: use Lemma 8.8, that it is second countable being a subspace of
![]() $\mathrm {Top}(d)$
, and that it is locally weakly-contractible by the variant of [Reference Edwards and KirbyEK71, Corollary 7.3] for this group.
$\mathrm {Top}(d)$
, and that it is locally weakly-contractible by the variant of [Reference Edwards and KirbyEK71, Corollary 7.3] for this group.
Theorem 8.19. The statement
![]() $(\operatorname {\mathbf {H}}^{d,c}_{k,m})$
holds in the following cases.
$(\operatorname {\mathbf {H}}^{d,c}_{k,m})$
holds in the following cases.
-
(i) For
 $c=1$
, it holds for all choices of
$c=1$
, it holds for all choices of
 $(d,k,m)$
to which Theorem 8.6 applies.
$(d,k,m)$
to which Theorem 8.6 applies. -
(ii) For
 $c=2$
, it holds for
$c=2$
, it holds for
 $d\ge 3$
,
$d\ge 3$
,
 $k=d$
and
$k=d$
and
 $m=d-1$
.
$m=d-1$
.
Proof. For 8.19, we consider the following zig-zag of maps:
 $$\begin{align*}\mathrm{Top}(d) &\rightarrow \mathrm{Top}(d)/\mathrm{Top}(d,d-1)\\ & \rightarrow \mathrm{Map}^h(E_{d-1},E_d)\xrightarrow{r_{\mathbf{Q}}\circ(-)} \mathrm{Map}^h(E_{d-1},E_d^{\mathbf{Q}})\xleftarrow{(-)\circ \iota}\mathrm{Map}^h(E_{d},E_d^{\mathbf{Q}}). \end{align*}$$
$$\begin{align*}\mathrm{Top}(d) &\rightarrow \mathrm{Top}(d)/\mathrm{Top}(d,d-1)\\ & \rightarrow \mathrm{Map}^h(E_{d-1},E_d)\xrightarrow{r_{\mathbf{Q}}\circ(-)} \mathrm{Map}^h(E_{d-1},E_d^{\mathbf{Q}})\xleftarrow{(-)\circ \iota}\mathrm{Map}^h(E_{d},E_d^{\mathbf{Q}}). \end{align*}$$
After taking loop spaces, the leftmost and the rightmost arrow become weak equivalences – the former by Lemma 8.17 (i) and the latter by Theorem 8.4 (iii). Since the homotopy groups of
![]() $\mathrm {Top}(d)$
are countable by Corollary 8.9, it thus suffices to prove that for choices
$\mathrm {Top}(d)$
are countable by Corollary 8.9, it thus suffices to prove that for choices
![]() $k\ge 3$
and
$k\ge 3$
and
![]() $m\ge 1$
as in the claim, either
$m\ge 1$
as in the claim, either
-
(a)
 $\pi _{*}(\mathrm {Map}(E_d,E_d);\mathrm {id})$
is uncountable in degrees
$\pi _{*}(\mathrm {Map}(E_d,E_d);\mathrm {id})$
is uncountable in degrees
 $k-2$
or
$k-2$
or
 $k-1$
, or
$k-1$
, or -
(b) the dimension of
 $\pi _{m-1}(\mathrm {Top}(d);\mathrm {id})_{\mathbf {Q}}$
is larger than that of
$\pi _{m-1}(\mathrm {Top}(d);\mathrm {id})_{\mathbf {Q}}$
is larger than that of
 $\pi _{m-1}(\mathrm {Map}(E_d,E_d);\mathrm {id})_{\mathbf {Q}}$
.
$\pi _{m-1}(\mathrm {Map}(E_d,E_d);\mathrm {id})_{\mathbf {Q}}$
.
But we already showed this, as part of the proof of Theorem 8.6. To establish 8.19, we apply Theorem 7.23 to degree
![]() $i=d-1$
to conclude that either
$i=d-1$
to conclude that either
-
(a)
 $\pi _{*}(\mathrm {Map}^h(E_{d-c},E_{d}),\iota )$
is uncountable in degrees
$\pi _{*}(\mathrm {Map}^h(E_{d-c},E_{d}),\iota )$
is uncountable in degrees
 $d-2$
or
$d-2$
or
 $d-1$
, or
$d-1$
, or -
(b)
 $\pi _{d-1}(\mathrm {Map}^h(E_{d-c},E_{d}),\iota )_{\mathbf {Q}} \cong \pi _{d-1}(\mathrm {Map}^h(E_{d-c},E^{\mathbf {Q}}_{d}),r_{\mathbf {Q}}\circ \iota )$
.
$\pi _{d-1}(\mathrm {Map}^h(E_{d-c},E_{d}),\iota )_{\mathbf {Q}} \cong \pi _{d-1}(\mathrm {Map}^h(E_{d-c},E^{\mathbf {Q}}_{d}),r_{\mathbf {Q}}\circ \iota )$
.
Since
![]() $\pi _{d-1}(\mathrm {Map}^h(E_{d-2},E^{\mathbf {Q}}_{d}),r_{\mathbf {Q}}\circ \iota )$
is infinite-dimensional by Theorem 8.4 (iv), it suffices to show that the groups
$\pi _{d-1}(\mathrm {Map}^h(E_{d-2},E^{\mathbf {Q}}_{d}),r_{\mathbf {Q}}\circ \iota )$
is infinite-dimensional by Theorem 8.4 (iv), it suffices to show that the groups
![]() $\pi _{*}(\mathrm {Top}(d)/\mathrm {Top}(d,d-2))$
are finitely generated in degrees
$\pi _{*}(\mathrm {Top}(d)/\mathrm {Top}(d,d-2))$
are finitely generated in degrees
![]() $*\le d-1$
. The latter follows from a combination of the following facts:
$*\le d-1$
. The latter follows from a combination of the following facts:
-
(i)
 $\pi _{*}(\mathrm {Top}(d))$
is finitely generated in degrees
$\pi _{*}(\mathrm {Top}(d))$
is finitely generated in degrees
 $*\le d-1$
for all d.
$*\le d-1$
for all d. -
(ii) The map
 $(-)\times \mathbf {R}^{d-2}\colon \mathrm {O}(2)\simeq \mathrm {Top}(2)\rightarrow \mathrm {Top}(d,d-2)$
is
$(-)\times \mathbf {R}^{d-2}\colon \mathrm {O}(2)\simeq \mathrm {Top}(2)\rightarrow \mathrm {Top}(d,d-2)$
is
 $(d-2)$
-connected, so in particular,
$(d-2)$
-connected, so in particular,
 $\pi _{*}(\mathrm {Top}(d,d-2))$
is finitely generated in degrees
$\pi _{*}(\mathrm {Top}(d,d-2))$
is finitely generated in degrees
 $*\le d-2$
.
$*\le d-2$
.
The first statement follows from [Reference Kirby and SiebenmannKS77, Essay V.§5.0] for
![]() $d\neq 4$
and from [Reference Freedman and QuinnFQ90, Theorem 8.7A] for
$d\neq 4$
and from [Reference Freedman and QuinnFQ90, Theorem 8.7A] for
![]() $d=4$
, and the second is Lemma 8.17 (ii).
$d=4$
, and the second is Lemma 8.17 (ii).
Unwrapping the statement, Theorem 8.19 in particular implies the following:
Corollary 8.20. The map (95) is not an equivalence if
![]() $d \geq 3$
and
$d \geq 3$
and
![]() $c=\{1,2\}$
.
$c=\{1,2\}$
.
Remark 8.21. There are no maps of the form
![]() $E_{d-c} \to E_d$
for
$E_{d-c} \to E_d$
for
![]() $c<0$
. Indeed, by restricting to
$c<0$
. Indeed, by restricting to
![]() $2$
-ary operations, such a map would induce an equivariant map
$2$
-ary operations, such a map would induce an equivariant map
![]() $\smash {S^{d-c-1}} \to \smash {S^{d-1}}$
with respect to the antipodal action, which implies
$\smash {S^{d-c-1}} \to \smash {S^{d-1}}$
with respect to the antipodal action, which implies
![]() $c\ge 0$
by the Borsuk–Ulam theorem.
$c\ge 0$
by the Borsuk–Ulam theorem.
List of Symbols

Acknowledgements
Our thanks go to Fabian Hebestreit and Markus Land for answering several questions on
![]() $\infty $
-categories, to Rune Haugseng and Claudia Scheimbauer for helpful conversations on their work, to Calista Bernard for sharing her view on manifold calculus and bordism categories, and to Oscar Randal-Williams for general discussions.
$\infty $
-categories, to Rune Haugseng and Claudia Scheimbauer for helpful conversations on their work, to Calista Bernard for sharing her view on manifold calculus and bordism categories, and to Oscar Randal-Williams for general discussions.
Competing interest
The authors have no competing interest to declare.
Financial support
MK was partially funded by the ERC under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 756444), and partially by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2044 –390685587, Mathematics Münster: Dynamics–Geometry–Structure. AK acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC) [funding reference number 512156 and 512250], as well as the Research Competitiveness Fund of the University of Toronto at Scarborough. This material is partially based on work supported by the Swedish Research Council under grant no. 2016-06596 while the authors were in residence at Institut Mittag-Leffler in Djursholm, Sweden, during the semester Higher algebraic structures in algebra, topology and geometry.