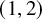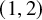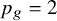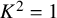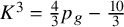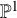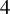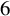Introduction
A
![]() $(1,2)$
-surface S is a minimal surface of general type with invariants
$(1,2)$
-surface S is a minimal surface of general type with invariants
![]() $p_g=2$
,
$p_g=2$
,
![]() $q=0$
,
$q=0$
,
![]() $K^2=1$
. These surfaces are classified in [Reference HorikawaHor76b, Theorem 2.1] as double covers of the weighted projective space
$K^2=1$
. These surfaces are classified in [Reference HorikawaHor76b, Theorem 2.1] as double covers of the weighted projective space
![]() ${\mathbb {P}}(1,1,2)$
(equivalently the quadric cone), branched over a curve of weighted degree ten and also over the singular point
${\mathbb {P}}(1,1,2)$
(equivalently the quadric cone), branched over a curve of weighted degree ten and also over the singular point
![]() $(0,0,1)$
. Their canonical model is a hypersurface of weighted degree ten in
$(0,0,1)$
. Their canonical model is a hypersurface of weighted degree ten in
![]() ${\mathbb {P}}(1,1,2,5)$
, with at worst rational double points as singularities (compare [Reference Franciosi, Pardini and RollenskeFPR17, Theorem 3.3], where this known result is generalized to Gorenstein stable surfaces).
${\mathbb {P}}(1,1,2,5)$
, with at worst rational double points as singularities (compare [Reference Franciosi, Pardini and RollenskeFPR17, Theorem 3.3], where this known result is generalized to Gorenstein stable surfaces).
These surfaces lie at the heart of the recent progress in the study of threefolds of general type (see, for example, [Reference Chen, Chen and JiangCCJ20, Reference Catanese, Chen and ZhangCCZ06, Reference Hu and ZhangHZ22a]). Namely, it seems that the threefolds that are fibred in
![]() $(1,2)$
-surfaces are somewhat analogous to the genus
$(1,2)$
-surfaces are somewhat analogous to the genus
![]() $2$
fibrations in the theory of surfaces of general type.
$2$
fibrations in the theory of surfaces of general type.
There is now a satisfactory theory of surfaces with a genus
![]() $2$
fibration (e.g., [Reference Horikawa, Baily and ShiodaHor77, Reference XiaoXia85, Reference ReidRei90, Reference Catanese and PignatelliCP06, Reference PignatelliPig09]). A key feature of genus
$2$
fibration (e.g., [Reference Horikawa, Baily and ShiodaHor77, Reference XiaoXia85, Reference ReidRei90, Reference Catanese and PignatelliCP06, Reference PignatelliPig09]). A key feature of genus
![]() $2$
fibrations is that the singular fibres may have several different topological types (see [Reference OggOgg66]), but despite this, they fit ‘algebraically’ into just two classes: the canonical ring of a genus
$2$
fibrations is that the singular fibres may have several different topological types (see [Reference OggOgg66]), but despite this, they fit ‘algebraically’ into just two classes: the canonical ring of a genus
![]() $2$
fibre is generated by three or four elements, according to whether the fibre is
$2$
fibre is generated by three or four elements, according to whether the fibre is
![]() $2$
-connected or not. It would be nice to have a similar theory for threefolds fibred in
$2$
-connected or not. It would be nice to have a similar theory for threefolds fibred in
![]() $(1,2)$
-surfaces, but the reality is much more complicated. Indeed, the study of surfaces fibred in curves of genus
$(1,2)$
-surfaces, but the reality is much more complicated. Indeed, the study of surfaces fibred in curves of genus
![]() $g\geq 3$
is already much more difficult (see [Reference Ashikaga and KonnoAK02, Reference ReidRei90]).
$g\geq 3$
is already much more difficult (see [Reference Ashikaga and KonnoAK02, Reference ReidRei90]).
This paper originated from the observation ([Reference HorikawaHor76a, Reference Catanese and PignatelliCP06]) that the minimal surfaces of general type fulfilling the Noether equality
![]() $K_S^2=2p_g-4$
are exactly those with a genus
$K_S^2=2p_g-4$
are exactly those with a genus
![]() $2$
fibration
$2$
fibration
![]() $f \colon S \rightarrow {\mathbb {P}}^1$
such that all fibres are
$f \colon S \rightarrow {\mathbb {P}}^1$
such that all fibres are
![]() $2$
-connected – in other words, such that all fibres look like smooth fibres from the point of view of the generation of the canonical ring. This motivates the concept of simple fibrations in
$2$
-connected – in other words, such that all fibres look like smooth fibres from the point of view of the generation of the canonical ring. This motivates the concept of simple fibrations in
![]() $(1,2)$
-surfaces (see Definition 4.1); these are threefolds X with canonical singularities and a morphism
$(1,2)$
-surfaces (see Definition 4.1); these are threefolds X with canonical singularities and a morphism
![]() $\pi \colon X \rightarrow B$
, where the relative canonical class is ample and B is a smooth curve such that the canonical ring of each fibre is algebraically like the ring of a
$\pi \colon X \rightarrow B$
, where the relative canonical class is ample and B is a smooth curve such that the canonical ring of each fibre is algebraically like the ring of a
![]() $(1,2)$
-surface.
$(1,2)$
-surface.
In this paper, we develop a systematic theory of these simple fibrations. They have a natural description as hypersurfaces in
![]() ${\mathbb {P}}(1,1,2,5)$
-bundles over the base curve B; in particular, we have a classification of all simple fibrations over
${\mathbb {P}}(1,1,2,5)$
-bundles over the base curve B; in particular, we have a classification of all simple fibrations over
![]() ${\mathbb {P}}^1$
as Cartier divisors in some toric
${\mathbb {P}}^1$
as Cartier divisors in some toric
![]() $4$
-fold (Theorem 1.11). They are denoted by
$4$
-fold (Theorem 1.11). They are denoted by
![]() $X(d;d_0)$
in the following, and they have geometric genus
$X(d;d_0)$
in the following, and they have geometric genus
![]() $p_g=3d-2$
and canonical volume
$p_g=3d-2$
and canonical volume
![]() $K^3=4d-6$
; in particular,
$K^3=4d-6$
; in particular,
The toric
![]() $4$
-fold depends on two nonnegative integers: d, that is related to
$4$
-fold depends on two nonnegative integers: d, that is related to
![]() $p_g$
by the formula above, and
$p_g$
by the formula above, and
![]() $d_0$
, that may be any integer from
$d_0$
, that may be any integer from
![]() $\frac {d}4$
to
$\frac {d}4$
to
![]() $\frac 32d$
.
$\frac 32d$
.
Indeed, the Noether inequality
![]() $K_X^3\geq \frac 43 p_g-\frac {10}3$
has recently been proven [Reference Chen, Chen and JiangCCJ20], except possibly threefolds with
$K_X^3\geq \frac 43 p_g-\frac {10}3$
has recently been proven [Reference Chen, Chen and JiangCCJ20], except possibly threefolds with
![]() $5\le p_g\le 10$
. It is not known if these exceptions exist. The threefolds for which the equality holds are said to be on the Noether line, so our
$5\le p_g\le 10$
. It is not known if these exceptions exist. The threefolds for which the equality holds are said to be on the Noether line, so our
![]() $X(d;d_0)$
are canonical models of threefolds on the Noether line.
$X(d;d_0)$
are canonical models of threefolds on the Noether line.
There are other works about threefolds on the Noether line, some of which appeared during the development of this project, which started in 2015. Kobayashi [Reference KobayashiKob92] discovered infinitely many families of threefolds on the Noether line. These are constructed by taking the minimal model of a certain genus two fibration over a Hirzebruch surface. Kobayashi’s construction was generalised by Chen and Hu [Reference Chen and HuCH17], who claimed a classification of smooth canonical threefolds on the Noether line for
![]() $p_g \geq 7$
. Their threefolds correspond to our
$p_g \geq 7$
. Their threefolds correspond to our
![]() $X(d;d_0)$
with
$X(d;d_0)$
with
![]() $d \leq d_0$
. In fact, those
$d \leq d_0$
. In fact, those
![]() $X(d;d_0)$
with
$X(d;d_0)$
with
![]() $d>d_0$
are singular unless d is divisible by
$d>d_0$
are singular unless d is divisible by
![]() $8$
and
$8$
and
![]() $7d=8d_0$
, in which case the general
$7d=8d_0$
, in which case the general
![]() $X\left ( d; \frac 78 d\right )$
is (rather surprisingly) smooth!
$X\left ( d; \frac 78 d\right )$
is (rather surprisingly) smooth!
Using our description as divisors in a toric variety, we could prove, among other things,
Theorem 0.1.
-
1. The canonical
 $3$
-folds constructed by Kobayashi–Chen–Hu form an open subset of a unirational component of the moduli space of canonical
$3$
-folds constructed by Kobayashi–Chen–Hu form an open subset of a unirational component of the moduli space of canonical
 $3$
-folds with
$3$
-folds with
 $K_X^3=\frac 43 p_g-\frac {10}3$
for all
$K_X^3=\frac 43 p_g-\frac {10}3$
for all
 $p_g\geq 7$
(Propositions 2.2 and 2.4).
$p_g\geq 7$
(Propositions 2.2 and 2.4). -
2. The general
 $3$
-fold in this component is a Mori Dream Space (Theorem 1.16).
$3$
-fold in this component is a Mori Dream Space (Theorem 1.16). -
3. Suppose that
 $p_g \geq 22$
is of the form
$p_g \geq 22$
is of the form
 $3d-2$
with d divisible by
$3d-2$
with d divisible by
 $8$
. Then, the moduli space of canonical
$8$
. Then, the moduli space of canonical
 $3$
-folds with
$3$
-folds with
 $K_X^3=\frac 43 p_g-\frac {10}3$
contains a second component whose general element is smooth and which includes our threefolds
$K_X^3=\frac 43 p_g-\frac {10}3$
contains a second component whose general element is smooth and which includes our threefolds
 $X\left (d;\frac 78 d\right )$
(Theorem 5.4).
$X\left (d;\frac 78 d\right )$
(Theorem 5.4).
Parts 1 and 3 of this theorem look very similar to Horikawa’s famous classification of the minimal surfaces of general type on the Noether line [Reference HorikawaHor76a, Theorems 3.3 and 7.1]. The moduli space of Horikawa surfaces with
![]() $K^2$
divisible by
$K^2$
divisible by
![]() $8$
has two unirational, irreducible, connected components while that of surfaces with
$8$
has two unirational, irreducible, connected components while that of surfaces with
![]() $K^2$
not divisible by
$K^2$
not divisible by
![]() $8$
has just one. For threefolds, when the two components arise, they actually do intersect; more precisely, we produce a canonical threefold with a curve of singularities, which lies in the intersection of both irreducible components.
$8$
has just one. For threefolds, when the two components arise, they actually do intersect; more precisely, we produce a canonical threefold with a curve of singularities, which lies in the intersection of both irreducible components.
By analogy with Horikawa’s mentioned results, we conjecture that all threefolds on the Noether line are in our list for
![]() $p_g$
sufficiently large. Then, we would have, as in Horikawa’s case, one or two irreducible components with a smooth element in it, and a complete description of the moduli space should be obtained exploiting our classification in Theorem 1.11.
$p_g$
sufficiently large. Then, we would have, as in Horikawa’s case, one or two irreducible components with a smooth element in it, and a complete description of the moduli space should be obtained exploiting our classification in Theorem 1.11.
This conjecture is supported by the recent results of [Reference Hu and ZhangHZ22b], where it has been proven that all canonical threefolds on the Noether line are Gorenstein. Moreover, [Reference Hu and ZhangHZ22b] also determine two further lines which lie above but parallel to the Noether line, which they call the second and third Noether lines. If
![]() $p_g\geq 11$
, then all canonical threefolds which do not lie on the Noether line lie on or above the second Noether line, and analogously, threefolds above the second line lie on or above the third one. In fact, simple fibrations in
$p_g\geq 11$
, then all canonical threefolds which do not lie on the Noether line lie on or above the second Noether line, and analogously, threefolds above the second line lie on or above the third one. In fact, simple fibrations in
![]() $(1,2)$
-surfaces over
$(1,2)$
-surfaces over
![]() ${\mathbb {P}}^1$
may be non-Gorenstein, in which case (for the sake of simplicity, we suppose that
${\mathbb {P}}^1$
may be non-Gorenstein, in which case (for the sake of simplicity, we suppose that
![]() $B={\mathbb {P}}^1$
, see Proposition 4.21 for the full statement) the general simple fibration has N isolated quotient
$B={\mathbb {P}}^1$
, see Proposition 4.21 for the full statement) the general simple fibration has N isolated quotient
![]() $\frac 12(1,1,1)$
singularities and
$\frac 12(1,1,1)$
singularities and
![]() $K^3=\frac 43p_g-\frac {10}3+\frac {N}6$
. When
$K^3=\frac 43p_g-\frac {10}3+\frac {N}6$
. When
![]() $N=1$
and
$N=1$
and
![]() $2$
, we get the two lines in [Reference Hu and ZhangHZ22b]. So, an explanation for their result could be that for
$2$
, we get the two lines in [Reference Hu and ZhangHZ22b]. So, an explanation for their result could be that for
![]() $p_g$
big enough and
$p_g$
big enough and
![]() $K^3 \leq \frac 43p_g-\frac {10}3+\epsilon $
(for some positive
$K^3 \leq \frac 43p_g-\frac {10}3+\epsilon $
(for some positive
![]() $\epsilon $
), all canonical threefolds are simple fibrations in
$\epsilon $
), all canonical threefolds are simple fibrations in
![]() $(1,2)$
-surfaces.
$(1,2)$
-surfaces.
We also mention that [Reference Hu and ZhangHZ22b] proved that the canonical image of a canonical threefold on the Noether line is smooth for
![]() $p_g\geq 23$
but could not determine if their bound is sharp. Our construction shows that their result is sharp because
$p_g\geq 23$
but could not determine if their bound is sharp. Our construction shows that their result is sharp because
![]() $X(8;2)$
has
$X(8;2)$
has
![]() $p_g=22$
and canonical image a cone (see Example 1.13).
$p_g=22$
and canonical image a cone (see Example 1.13).
The paper is organized as follows.
Section 1 is devoted to the production of canonical threefolds on the Noether line. For the convenience of the reader, we describe them directly as Cartier divisors in a suitable linear system in a specific toric
![]() $4$
-fold. The construction is then very explicit, depending on two integers d,
$4$
-fold. The construction is then very explicit, depending on two integers d,
![]() $d_0$
. The main result is the already mentioned Theorem 1.11 giving a complete classification of Gorenstein simple fibrations in
$d_0$
. The main result is the already mentioned Theorem 1.11 giving a complete classification of Gorenstein simple fibrations in
![]() $(1,2)$
-surfaces. We determine their singularities and numerical invariants according to the values of
$(1,2)$
-surfaces. We determine their singularities and numerical invariants according to the values of
![]() $d,d_0$
. The canonical image is the Hirzebruch surface
$d,d_0$
. The canonical image is the Hirzebruch surface
![]() ${\mathbb {F}}_e$
with
${\mathbb {F}}_e$
with
![]() $e=3d-2d_0$
. The dichotomy of Theorem 0.1 emerges here, as we find smooth examples with
$e=3d-2d_0$
. The dichotomy of Theorem 0.1 emerges here, as we find smooth examples with
![]() $e \leq d$
and with
$e \leq d$
and with
![]() $e=\frac 54 d$
. Finally, we show that, in the first case, the general
$e=\frac 54 d$
. Finally, we show that, in the first case, the general
![]() $X(d;d_0)$
is a Mori Dream Space.
$X(d;d_0)$
is a Mori Dream Space.
In Section 2, we study the deformation theory of those
![]() $X(d;d_0)$
with
$X(d;d_0)$
with
![]() $e \leq d$
, showing that they form a single unirational family, whose general element has
$e \leq d$
, showing that they form a single unirational family, whose general element has
![]() $e=0$
or
$e=0$
or
![]() $1$
, according to the parity of
$1$
, according to the parity of
![]() $p_g$
. This family covers an open dense subset of one irreducible component of the moduli space.
$p_g$
. This family covers an open dense subset of one irreducible component of the moduli space.
In Section 3, we develop the basics of the theory of weighted projective bundles over a nonsingular base B. This is a natural generalization of the standard theory of
![]() ${\mathbb {P}}^n$
-bundles
${\mathbb {P}}^n$
-bundles
![]() ${\mathbb {P}}({\mathcal {E}})\to B$
, where
${\mathbb {P}}({\mathcal {E}})\to B$
, where
![]() ${\mathcal {E}}$
is a vector bundle over B. In particular, Proposition 3.19 provides a relative Euler sequence for weighted projective bundles and a formula for the relative canonical sheaf.
${\mathcal {E}}$
is a vector bundle over B. In particular, Proposition 3.19 provides a relative Euler sequence for weighted projective bundles and a formula for the relative canonical sheaf.
In Section 4, we finally give a definition of simple fibrations in
![]() $(1,2)$
-surfaces, showing that their relative canonical algebra embeds them as a divisor in a bundle in weighted projective spaces
$(1,2)$
-surfaces, showing that their relative canonical algebra embeds them as a divisor in a bundle in weighted projective spaces
![]() ${\mathbb {P}}(1,1,2,5)$
. Then, we compute their invariants and show that if they are regular and Gorenstein, then they can be embedded in a toric
${\mathbb {P}}(1,1,2,5)$
. Then, we compute their invariants and show that if they are regular and Gorenstein, then they can be embedded in a toric
![]() $4$
-fold, giving the threefolds considered in section 1.
$4$
-fold, giving the threefolds considered in section 1.
We complete the proof of Theorem 0.1 in Section 5. Here, we first compare our simple fibrations in
![]() $(1,2)$
-surfaces with the Kobayashi–Chen–Hu construction, in the cases where the two coincide. Essentially, the Kobayashi–Chen–Hu model is the blowup of the base curve in
$(1,2)$
-surfaces with the Kobayashi–Chen–Hu construction, in the cases where the two coincide. Essentially, the Kobayashi–Chen–Hu model is the blowup of the base curve in
![]() $|K_X|$
. Then, we consider the case
$|K_X|$
. Then, we consider the case
![]() $7d=8d_0$
and show that these threefolds are not degenerations of threefolds given by the Kobayashi–Chen–Hu construction, although we do find a common singular degeneration with canonical singularities.
$7d=8d_0$
and show that these threefolds are not degenerations of threefolds given by the Kobayashi–Chen–Hu construction, although we do find a common singular degeneration with canonical singularities.
In Section 6, we finish our classification of simple fibrations over
![]() ${\mathbb {P}}^1$
by studying a handful of special cases whose canonical class is not ample. After applying the minimal model program, we find three canonical threefolds with
${\mathbb {P}}^1$
by studying a handful of special cases whose canonical class is not ample. After applying the minimal model program, we find three canonical threefolds with
![]() $p_g=4,7,10$
, respectively, which lie above the Noether line but extremely close to it; the last two appeared already recently in the literature in [Reference Chen, Jiang and LiCJL20] by a totally different construction, whereas the first one appears to be new.
$p_g=4,7,10$
, respectively, which lie above the Noether line but extremely close to it; the last two appeared already recently in the literature in [Reference Chen, Jiang and LiCJL20] by a totally different construction, whereas the first one appears to be new.
1 Threefolds on the Noether line
In this section, we introduce and classify the simple fibrations in
![]() $(1,2)$
-surfaces that are regular and Gorenstein, and we show that (apart from a few exceptions) they are canonical threefolds on the Noether line.
$(1,2)$
-surfaces that are regular and Gorenstein, and we show that (apart from a few exceptions) they are canonical threefolds on the Noether line.
1.1 Toric bundles
Choose integers
![]() $d,d_0$
and define
$d,d_0$
and define
![]() ${\mathbb {F}}={\mathbb {F}}(d;d_0)$
to be the toric 4-fold with weight matrix
${\mathbb {F}}={\mathbb {F}}(d;d_0)$
to be the toric 4-fold with weight matrix
 $$ \begin{align} \begin{pmatrix} t_0 & t_1 & x_0 & x_1 & y & z\\ 1 & 1 & d-d_0 & d_0-2d & 0 & 0\\ 0 & 0 & 1 & 1 & 2 & 5 \end{pmatrix} \end{align} $$
$$ \begin{align} \begin{pmatrix} t_0 & t_1 & x_0 & x_1 & y & z\\ 1 & 1 & d-d_0 & d_0-2d & 0 & 0\\ 0 & 0 & 1 & 1 & 2 & 5 \end{pmatrix} \end{align} $$
and irrelevant ideal
![]() $I=(t_0,t_1)\cap (x_0,x_1,y,z)$
. In other words,
$I=(t_0,t_1)\cap (x_0,x_1,y,z)$
. In other words,
![]() $({\mathbb {C}}^*)^2$
acts on
$({\mathbb {C}}^*)^2$
acts on
![]() ${\mathbb {C}}^6$
with coordinates
${\mathbb {C}}^6$
with coordinates
![]() $t_0,t_1,x_0,x_1,y,z$
via (1.1):
$t_0,t_1,x_0,x_1,y,z$
via (1.1):
and
![]() ${\mathbb {F}}$
is the quotient
${\mathbb {F}}$
is the quotient
![]() $({\mathbb {C}}^6\smallsetminus V(I))/({\mathbb {C}}^*)^2$
.
$({\mathbb {C}}^6\smallsetminus V(I))/({\mathbb {C}}^*)^2$
.
Up to exchanging the
![]() $x_j$
, we may and do assume without loss of generality any of the following equivalent conditions:
$x_j$
, we may and do assume without loss of generality any of the following equivalent conditions:
The divisor class group
![]() $\operatorname {\mathrm {Cl}}({\mathbb {F}})$
is isomorphic to
$\operatorname {\mathrm {Cl}}({\mathbb {F}})$
is isomorphic to
![]() ${\mathbb {Z}}^2$
([Reference Cox, Little and SchenckCLS11, §5.1]). We choose generators
${\mathbb {Z}}^2$
([Reference Cox, Little and SchenckCLS11, §5.1]). We choose generators
![]() $F,H$
defined by
$F,H$
defined by
![]() $t_0$
and
$t_0$
and
![]() $t_0^{d_0}x_0$
, respectively. With this choice, the tautological sheaf
$t_0^{d_0}x_0$
, respectively. With this choice, the tautological sheaf
![]() ${\mathcal {O}}_{\mathbb {F}}(1)$
has class
${\mathcal {O}}_{\mathbb {F}}(1)$
has class
![]() $H-dF$
.
$H-dF$
.
Each of the coordinates
![]() $\rho \in \{t_0,t_1,x_0,x_1,y,z\}$
corresponds to a torus invariant irreducible Weil divisor
$\rho \in \{t_0,t_1,x_0,x_1,y,z\}$
corresponds to a torus invariant irreducible Weil divisor
![]() $D_\rho $
in
$D_\rho $
in
![]() ${\mathbb {F}}$
whose class is as follows:
${\mathbb {F}}$
whose class is as follows:
 $$ \begin{gather*} [D_{t_0}]=[D_{t_1}]=F,\quad \quad [D_{x_0}]=H-d_0F,\quad \quad [D_{x_1}]=H+(d_0-3d)F,\\ [D_y]=2(H-dF),\quad \quad [D_z]=5(H-dF). \end{gather*} $$
$$ \begin{gather*} [D_{t_0}]=[D_{t_1}]=F,\quad \quad [D_{x_0}]=H-d_0F,\quad \quad [D_{x_1}]=H+(d_0-3d)F,\\ [D_y]=2(H-dF),\quad \quad [D_z]=5(H-dF). \end{gather*} $$
Note that
![]() $D_y\cap D_z$
is a Hirzebruch surface
$D_y\cap D_z$
is a Hirzebruch surface
![]() ${\mathbb {F}}_e$
.
${\mathbb {F}}_e$
.
Proposition 1.1.
![]() $\omega _{{\mathbb {F}}(d;d_0)} \cong {\mathcal {O}}_{{\mathbb {F}}(d;d_0)} (-9H+(10d-2)F)$
.
$\omega _{{\mathbb {F}}(d;d_0)} \cong {\mathcal {O}}_{{\mathbb {F}}(d;d_0)} (-9H+(10d-2)F)$
.
Proof. We have
![]() $[K_{{\mathbb {F}}}]=-[D_{t_0} + D_{t_1}+D_{x_0} + D_{x_1} + D_y + D_z]$
by [Reference Cox, Little and SchenckCLS11, Thm 8.2.3].
$[K_{{\mathbb {F}}}]=-[D_{t_0} + D_{t_1}+D_{x_0} + D_{x_1} + D_y + D_z]$
by [Reference Cox, Little and SchenckCLS11, Thm 8.2.3].
Lemma 1.2. The intersection numbers on
![]() ${\mathbb {F}}(d;d_0)$
are
${\mathbb {F}}(d;d_0)$
are
Proof. Clearly,
![]() $F^2=0$
because any two distinct fibres are disjoint. Since the intersection
$F^2=0$
because any two distinct fibres are disjoint. Since the intersection
![]() $D_{t_0}\cap D_{x_0} \cap D_y \cap D_z$
is a reduced smooth point,
$D_{t_0}\cap D_{x_0} \cap D_y \cap D_z$
is a reduced smooth point,
![]() $D_{t_0} D_{x_0} D_y D_z=10H^3F=1$
. Similarly,
$D_{t_0} D_{x_0} D_y D_z=10H^3F=1$
. Similarly,
![]() $D_{x_0} \cap D_{x_1} \cap D_y \cap D_z$
is empty, so
$D_{x_0} \cap D_{x_1} \cap D_y \cap D_z$
is empty, so
Rearranging and substituting
![]() $H^3F=\frac 1{10}$
gives
$H^3F=\frac 1{10}$
gives
![]() $H^4=\frac d2$
.
$H^4=\frac d2$
.
Proposition 1.3. The numerical divisor class
![]() $aH+bF$
is
$aH+bF$
is
-
1. nef if and only if
 $a \geq 0$
and
$a \geq 0$
and
 $b\geq -a\min (d,d_0)$
;
$b\geq -a\min (d,d_0)$
; -
2. ample if and only if
 $a> 0$
and
$a> 0$
and
 $b> -a\min (d,d_0)$
.
$b> -a\min (d,d_0)$
.
Proof. By [Reference Cox, Little and SchenckCLS11, Thms 6.3.12 and 6.3.13],
![]() $aH+bF$
is nef (resp. ample) if and only if its restriction to any torus invariant irreducible curve is nonnegative (resp. positive). Torus invariant irreducible curves on
$aH+bF$
is nef (resp. ample) if and only if its restriction to any torus invariant irreducible curve is nonnegative (resp. positive). Torus invariant irreducible curves on
![]() ${\mathbb {F}}$
are intersections of three of the divisors
${\mathbb {F}}$
are intersections of three of the divisors
![]() $D_{\rho }$
.
$D_{\rho }$
.
The Proposition then follows from
 $$ \begin{align*} (aH+bF)D_{t_0}D_yD_z&=10aH^3F=a,\\ (aH+bF)D_{x_1}D_yD_z&=10(aH^4+(b-a(5d-d_0)))H^3F=b+ad_0,\\ (aH+bF)D_{x_0}D_{x_1}D_y&=2aH^4+2(b-4ad)H^3F=\tfrac15(b+ad). \end{align*} $$
$$ \begin{align*} (aH+bF)D_{t_0}D_yD_z&=10aH^3F=a,\\ (aH+bF)D_{x_1}D_yD_z&=10(aH^4+(b-a(5d-d_0)))H^3F=b+ad_0,\\ (aH+bF)D_{x_0}D_{x_1}D_y&=2aH^4+2(b-4ad)H^3F=\tfrac15(b+ad). \end{align*} $$
The other triples do not add any extra conditions.
The complete linear system
![]() $|F|$
defines a toric fibration
$|F|$
defines a toric fibration
![]() $f\colon {\mathbb {F}}\to {\mathbb {P}}^1$
whose fibre is the weighted projective space
$f\colon {\mathbb {F}}\to {\mathbb {P}}^1$
whose fibre is the weighted projective space
![]() ${\mathbb {P}}(1,1,2,5)$
. The singular locus of
${\mathbb {P}}(1,1,2,5)$
. The singular locus of
![]() ${\mathbb {F}}$
is the disjoint union of two torus invariant rational curves, corresponding to the two isolated singularities of
${\mathbb {F}}$
is the disjoint union of two torus invariant rational curves, corresponding to the two isolated singularities of
![]() ${\mathbb {P}}(1,1,2,5)$
. These are the two sections:
${\mathbb {P}}(1,1,2,5)$
. These are the two sections:
Indeed, in a neighbourhood of every point of
![]() $\mathfrak {s}_2$
resp.
$\mathfrak {s}_2$
resp.
![]() $\mathfrak {s}_5$
,
$\mathfrak {s}_5$
,
![]() ${\mathbb {F}}$
is analytically isomorphic to the product of a smooth
${\mathbb {F}}$
is analytically isomorphic to the product of a smooth
![]() $1$
-dimensional disc with the corresponding singularity of
$1$
-dimensional disc with the corresponding singularity of
![]() ${\mathbb {P}}(1,1,2,5)$
: a quotient singularity of type
${\mathbb {P}}(1,1,2,5)$
: a quotient singularity of type
![]() $\frac 12(1,1,1)$
resp.
$\frac 12(1,1,1)$
resp.
![]() $\frac 15(1,1,2)$
.
$\frac 15(1,1,2)$
.
In particular,
![]() ${\mathbb {F}}$
is
${\mathbb {F}}$
is
![]() ${\mathbb Q}$
-Gorenstein of index
${\mathbb Q}$
-Gorenstein of index
![]() $\operatorname {\mathrm {lcm}}(2,5)=10$
. Since F and
$\operatorname {\mathrm {lcm}}(2,5)=10$
. Since F and
![]() $10H$
are Cartier, we may consider the complete linear system
$10H$
are Cartier, we may consider the complete linear system
![]() $|10(H-dF)|$
.
$|10(H-dF)|$
.
1.2 Gorenstein regular simple fibrations
Definition 1.4. A Gorenstein regular simple fibration in
![]() $(1,2)$
-surfaces of type
$(1,2)$
-surfaces of type
![]() $(d,d_0)$
is an element
$(d,d_0)$
is an element
![]() $X \in |10(H-dF)|$
on
$X \in |10(H-dF)|$
on
![]() ${\mathbb {F}}(d;d_0)$
with at worst canonical singularities. We sometimes denote
${\mathbb {F}}(d;d_0)$
with at worst canonical singularities. We sometimes denote
![]() $X\subset {\mathbb {F}}(d;d_0)$
by
$X\subset {\mathbb {F}}(d;d_0)$
by
![]() $X(d;d_0)$
.
$X(d;d_0)$
.
We abuse notation and write
![]() $f:=f|_X\colon X\to {\mathbb {P}}^1$
. Each fibre of f is a hypersurface in a weighted projective
$f:=f|_X\colon X\to {\mathbb {P}}^1$
. Each fibre of f is a hypersurface in a weighted projective
![]() $3$
-space and therefore,
$3$
-space and therefore,
![]() $R^1f_*{\mathcal {O}}_X=0$
. By the Leray spectral sequence, this implies that
$R^1f_*{\mathcal {O}}_X=0$
. By the Leray spectral sequence, this implies that
![]() $q_1(X)=h^1(f_*{\mathcal {O}}_{X})=h^1({\mathcal {O}}_{{\mathbb {P}}^1})=0$
. Therefore, X is regular.
$q_1(X)=h^1(f_*{\mathcal {O}}_{X})=h^1({\mathcal {O}}_{{\mathbb {P}}^1})=0$
. Therefore, X is regular.
The hypersurface X is defined by a polynomial of the form
 $$\begin{align*}\sum_{a_0+a_1+2a_2+5a_5 = 10} c_{a_0,a_1,a_2}(t_0,t_1)x_0^{a_0}x_1^{a_1}y^{a_2}z^{a_5}, \end{align*}$$
$$\begin{align*}\sum_{a_0+a_1+2a_2+5a_5 = 10} c_{a_0,a_1,a_2}(t_0,t_1)x_0^{a_0}x_1^{a_1}y^{a_2}z^{a_5}, \end{align*}$$
where
![]() $c_{a_0,a_1,a_2}(t_0,t_1)$
is a homogeneous polynomial whose degree is
$c_{a_0,a_1,a_2}(t_0,t_1)$
is a homogeneous polynomial whose degree is
The choices we made in defining
![]() ${\mathbb {F}}$
and X imply that
${\mathbb {F}}$
and X imply that
![]() $\deg c_{0,0,0}=\deg c_{0,0,5} =0$
. That is, the coefficients of
$\deg c_{0,0,0}=\deg c_{0,0,5} =0$
. That is, the coefficients of
![]() $z^2$
and
$z^2$
and
![]() $y^5$
are constant. After scaling z, we may assume that
$y^5$
are constant. After scaling z, we may assume that
![]() $c_{0,0,0}=1$
since otherwise, X would contain
$c_{0,0,0}=1$
since otherwise, X would contain
![]() $\mathfrak {s}_5$
. The singular locus of X would then be noncanonical, a contradiction. Similarly we may scale y to ensure
$\mathfrak {s}_5$
. The singular locus of X would then be noncanonical, a contradiction. Similarly we may scale y to ensure
![]() $c_{0,0,5}=1$
since otherwise, X would have
$c_{0,0,5}=1$
since otherwise, X would have
![]() $\mathfrak {s}_2$
as a noncanonical singular curve. Then, by a coordinate change (completing the square), we make the coefficients of all monomials
$\mathfrak {s}_2$
as a noncanonical singular curve. Then, by a coordinate change (completing the square), we make the coefficients of all monomials
![]() $x_0^{a_0}x_1^{a_1}y^{a_2}z$
equal to zero. We are left with a polynomial of the form
$x_0^{a_0}x_1^{a_1}y^{a_2}z$
equal to zero. We are left with a polynomial of the form
 $$ \begin{align} z^2+y^5+\sum_{\substack{a_0+a_1+2a_2 = 10\\a_2\ne5}} c_{a_0,a_1,a_2}(t_0,t_1)x_0^{a_0}x_1^{a_1}y^{a_2}. \end{align} $$
$$ \begin{align} z^2+y^5+\sum_{\substack{a_0+a_1+2a_2 = 10\\a_2\ne5}} c_{a_0,a_1,a_2}(t_0,t_1)x_0^{a_0}x_1^{a_1}y^{a_2}. \end{align} $$
We proved that
![]() $X \cap {\mathfrak s}_2=X \cap {\mathfrak s}_5=\emptyset $
. In particular, X is contained in the smooth locus of
$X \cap {\mathfrak s}_2=X \cap {\mathfrak s}_5=\emptyset $
. In particular, X is contained in the smooth locus of
![]() ${\mathbb {F}}$
, and therefore, it is Gorenstein.
${\mathbb {F}}$
, and therefore, it is Gorenstein.
Remark 1.5. Note that
![]() $X(d;d_0)$
has an involution obtained by changing the sign of the variable z, describing X as double cover of
$X(d;d_0)$
has an involution obtained by changing the sign of the variable z, describing X as double cover of
![]() $D_z$
. The branch locus is the surface determined by the restriction of the polynomial (1.4) to
$D_z$
. The branch locus is the surface determined by the restriction of the polynomial (1.4) to
![]() $D_z$
and the index 2 rational curve
$D_z$
and the index 2 rational curve
![]() ${\mathfrak {s}}_2$
considered as a subscheme of
${\mathfrak {s}}_2$
considered as a subscheme of
![]() $D_z$
. Indeed,
$D_z$
. Indeed,
![]() $D_z$
is a
$D_z$
is a
![]() ${\mathbb {P}}(1,1,2)$
-bundle over
${\mathbb {P}}(1,1,2)$
-bundle over
![]() ${\mathbb {P}}^1$
(see §4.2).
${\mathbb {P}}^1$
(see §4.2).
For fixed
![]() $d,d_0$
, the varieties
$d,d_0$
, the varieties
![]() $X(d;d_0)$
form a unirational family. The next result determines when this family is not empty and the type of singularities of the general element in it. The proof is an exercise in Newton polytopes that we postpone to §1.4.
$X(d;d_0)$
form a unirational family. The next result determines when this family is not empty and the type of singularities of the general element in it. The proof is an exercise in Newton polytopes that we postpone to §1.4.
Proposition 1.6. Gorenstein regular simple fibrations in
![]() $(1,2)$
-surfaces of type
$(1,2)$
-surfaces of type
![]() $(d,d_0)$
exist if and only if
$(d,d_0)$
exist if and only if
![]() $d_0 \geq \frac 14 d$
. The singular locus of the general
$d_0 \geq \frac 14 d$
. The singular locus of the general
![]() $X(d;d_0)$
is contained in the torus invariant section
$X(d;d_0)$
is contained in the torus invariant section
![]() $\mathfrak {s}_0:= D_{x_1} \cap D_y \cap D_z$
. More precisely,
$\mathfrak {s}_0:= D_{x_1} \cap D_y \cap D_z$
. More precisely,
-
(a) X is nonsingular iff
 $d \leq d_0 \leq \frac 32 d$
or
$d \leq d_0 \leq \frac 32 d$
or
 $d_0 = \frac 78 d$
;
$d_0 = \frac 78 d$
; -
(b) X has
 $8d_0-7d$
terminal singularities iff
$8d_0-7d$
terminal singularities iff
 $\frac 78 d< d_0< d$
;
$\frac 78 d< d_0< d$
; -
(c) X has canonical singularities along
 $\mathfrak {s}_0$
iff
$\mathfrak {s}_0$
iff
 $\frac 14d \leq d_0 < \frac 78 d$
.
$\frac 14d \leq d_0 < \frac 78 d$
.
 $\Box $
$\Box $
Remark 1.7. Since
![]() $\frac 14 d \leq d_0 \leq \frac 32 d$
, we see that neither d nor
$\frac 14 d \leq d_0 \leq \frac 32 d$
, we see that neither d nor
![]() $d_0$
may be negative.
$d_0$
may be negative.
By Proposition 1.1 and the adjunction formula, the canonical divisor class of
![]() $X(d;d_0)$
is
$X(d;d_0)$
is
Lemma 1.8. Suppose
![]() $X(d;d_0)$
satisfies the conditions of Proposition 1.6. Then,
$X(d;d_0)$
satisfies the conditions of Proposition 1.6. Then,
-
1.
 $K_X$
is ample if and only if
$K_X$
is ample if and only if
 $\min (d,d_0) \geq 3$
;
$\min (d,d_0) \geq 3$
; -
2.
 $K_X$
is nef if and only if
$K_X$
is nef if and only if
 $\min (d,d_0)\geq 2$
.
$\min (d,d_0)\geq 2$
.
Proof. We prove part 1 since part 2 is similar. By (1.5),
![]() $K_X=(H-2F)|_X$
. By Proposition 1.3, if
$K_X=(H-2F)|_X$
. By Proposition 1.3, if
![]() $\min (d,d_0)\geq 3$
, then
$\min (d,d_0)\geq 3$
, then
![]() $H-2F$
is ample on
$H-2F$
is ample on
![]() ${\mathbb {F}}(d;d_0)$
, and therefore, its restriction to X is ample too.
${\mathbb {F}}(d;d_0)$
, and therefore, its restriction to X is ample too.
Conversely, consider the curve
![]() $\Gamma :=X \cap D_{x_0} \cap D_{x_1}$
which is contained in X. Then,
$\Gamma :=X \cap D_{x_0} \cap D_{x_1}$
which is contained in X. Then,
![]() $K_X\Gamma =d-2$
, so
$K_X\Gamma =d-2$
, so
![]() $d\leq 2$
implies that
$d\leq 2$
implies that
![]() $K_X$
is not ample. Finally, if
$K_X$
is not ample. Finally, if
![]() $d_0\leq 2$
and
$d_0\leq 2$
and
![]() $d\geq 3$
, then
$d\geq 3$
, then
![]() $d_0 < \frac 78 d$
, and so
$d_0 < \frac 78 d$
, and so
![]() ${\mathfrak {s}}_0 \subset X$
by Proposition 1.6. Since
${\mathfrak {s}}_0 \subset X$
by Proposition 1.6. Since
![]() $(H-2F){\mathfrak {s}}_0=d_0-2$
, we are done.
$(H-2F){\mathfrak {s}}_0=d_0-2$
, we are done.
We now examine the canonical map of X. Let
![]() ${\mathbb {F}}_e$
be the Hirzebruch surface with fibre l and positive section
${\mathbb {F}}_e$
be the Hirzebruch surface with fibre l and positive section
![]() $\delta $
with
$\delta $
with
![]() $\delta ^2=e$
. The class of the negative section is
$\delta ^2=e$
. The class of the negative section is
![]() $\delta -el$
.
$\delta -el$
.
Proposition 1.9. Suppose
![]() $\min (d,d_0)\ge 3$
. Then, the canonical map of
$\min (d,d_0)\ge 3$
. Then, the canonical map of
![]() $X(d,d_0)$
is a rational map whose image is the embedding of the Hirzebruch surface
$X(d,d_0)$
is a rational map whose image is the embedding of the Hirzebruch surface
![]() ${\mathbb {F}}_e$
,
${\mathbb {F}}_e$
,
![]() $e=3d-2d_0$
via the linear system
$e=3d-2d_0$
via the linear system
![]() $|(d_0-2)l+\delta |$
.
$|(d_0-2)l+\delta |$
.
Proof. By (1.5) and the vanishing of
![]() $H^1({\mathbb {F}},{\mathcal {O}}_{{\mathbb {F}}}(-X+H-2F)) = H^1({\mathbb {F}},K_{{\mathbb {F}}})$
, the canonical system of X is spanned by the following
$H^1({\mathbb {F}},{\mathcal {O}}_{{\mathbb {F}}}(-X+H-2F)) = H^1({\mathbb {F}},K_{{\mathbb {F}}})$
, the canonical system of X is spanned by the following
![]() $3d-2$
monomials:
$3d-2$
monomials:
Thus, X is mapped to the image of the toric variety
![]() $D_y \cap D_z \cong {\mathbb {F}}_{e}$
in
$D_y \cap D_z \cong {\mathbb {F}}_{e}$
in
![]() ${\mathbb {P}}^{3d-3}$
. This is an embedding of
${\mathbb {P}}^{3d-3}$
. This is an embedding of
![]() ${\mathbb {F}}_e$
because
${\mathbb {F}}_e$
because
![]() $d_0\ge 3$
.
$d_0\ge 3$
.
Remark 1.10. The base locus of
![]() $|K_X|$
is the rational curve
$|K_X|$
is the rational curve
![]() $\Gamma :=X\cap D_{x_0}\cap D_{x_1}$
.
$\Gamma :=X\cap D_{x_0}\cap D_{x_1}$
.
Thus, almost all (excluding a few degenerate cases with d,
![]() $d_0$
small, see Remark 1.3) Gorenstein regular simple fibrations in
$d_0$
small, see Remark 1.3) Gorenstein regular simple fibrations in
![]() $(1,2)$
-surfaces are canonical threefolds with canonical image a Hirzebruch surface. For each admissible pair
$(1,2)$
-surfaces are canonical threefolds with canonical image a Hirzebruch surface. For each admissible pair
![]() $d,d_0$
, we have a unirational family of canonical threefolds that are all on the Noether line, as follows.
$d,d_0$
, we have a unirational family of canonical threefolds that are all on the Noether line, as follows.
Theorem 1.11. Gorenstein regular simple fibrations in
![]() $(1,2)$
-surfaces of type
$(1,2)$
-surfaces of type
![]() $(d,d_0)$
are canonical 3-folds if and only if
$(d,d_0)$
are canonical 3-folds if and only if
![]() $\min (d,d_0) \geq 3$
. In these cases,
$\min (d,d_0) \geq 3$
. In these cases,
Their canonical image is the Hirzebruch surface
![]() ${\mathbb {F}}_e$
,
${\mathbb {F}}_e$
,
![]() $e=3d-2d_0$
. They form a unirational family that is not empty if and only if
$e=3d-2d_0$
. They form a unirational family that is not empty if and only if
![]() $e \leq \frac 52 d$
.
$e \leq \frac 52 d$
.
The singular locus of the general
![]() $X(d;d_0)$
is contained in the torus invariant section
$X(d;d_0)$
is contained in the torus invariant section
![]() $\mathfrak {s}_0:= D_{x_1} \cap D_y \cap D_z$
and more precisely it is
$\mathfrak {s}_0:= D_{x_1} \cap D_y \cap D_z$
and more precisely it is
-
1. empty if
 $e \leq d$
or
$e \leq d$
or
 $e = \frac 54 d$
;
$e = \frac 54 d$
; -
2.
 $5d-4e$
terminal singular points if
$5d-4e$
terminal singular points if
 $d<e < \frac 54d$
;
$d<e < \frac 54d$
; -
3.
 $\mathfrak {s}_0$
if
$\mathfrak {s}_0$
if
 $\frac 54d < e \leq \frac 52d$
.
$\frac 54d < e \leq \frac 52d$
.
Proof. Most of the statement follows by Lemma 1.8, Proposition 1.9 and Proposition 1.6, reformulating the inequalities in Proposition 1.6 in terms of e (instead of
![]() $d_0$
) and d. It remains to prove the given formulas for the invariants.
$d_0$
) and d. It remains to prove the given formulas for the invariants.
We already showed that
![]() $p_g=3d-2$
and
$p_g=3d-2$
and
![]() $q_1=0$
. Since the Leray spectral sequence of the direct image of
$q_1=0$
. Since the Leray spectral sequence of the direct image of
![]() ${\mathcal {O}}_{X}$
degenerates at page
${\mathcal {O}}_{X}$
degenerates at page
![]() $2$
, we have
$2$
, we have
![]() $h^2({\mathcal {O}}_{X})=h^0(R^2f_*{\mathcal {O}}_{X})$
. By Grothendieck duality,
$h^2({\mathcal {O}}_{X})=h^0(R^2f_*{\mathcal {O}}_{X})$
. By Grothendieck duality,
and since
![]() $3d>d_0>0$
, we get
$3d>d_0>0$
, we get
![]() $q_2=0$
. Finally,
$q_2=0$
. Finally,
![]() $K_{X}^3=X(H-2F)^3=10(H^4-(d+6)H^3F)=4d-6$
.
$K_{X}^3=X(H-2F)^3=10(H^4-(d+6)H^3F)=4d-6$
.
1.3 Simple fibrations with
 $K_X$
nef but not ample
$K_X$
nef but not ample
By Proposition 1.6, there are a small number of
![]() $X(d;d_0)$
with
$X(d;d_0)$
with
![]() $\min (d_0,d)=2$
which still have at worst canonical singularities. The complete list is
$\min (d_0,d)=2$
which still have at worst canonical singularities. The complete list is
![]() $X(2;3)$
and
$X(2;3)$
and
![]() $X(d;2)$
for
$X(d;2)$
for
![]() $d=2,\dots ,8$
. In all of these cases,
$d=2,\dots ,8$
. In all of these cases,
![]() $K_X$
is nef and big (big because
$K_X$
is nef and big (big because
![]() $K_X^3>0$
) and the invariants are the same as those of Theorem 1.11, so these also lie on the Noether line. Below, we discuss these cases in more detail, first the case
$K_X^3>0$
) and the invariants are the same as those of Theorem 1.11, so these also lie on the Noether line. Below, we discuss these cases in more detail, first the case
![]() $d=2$
and then the cases
$d=2$
and then the cases
![]() $d\ge 3$
.
$d\ge 3$
.
Example 1.12 (see [Reference Chen and HuCH17, Remark 2.3]).
The canonical image of
![]() $X(2;3)$
is
$X(2;3)$
is
![]() ${\mathbb {F}}_0$
(i.e.,
${\mathbb {F}}_0$
(i.e.,
![]() ${\mathbb {P}}^1\times {\mathbb {P}}^1$
), and the canonical model is the complete intersection
${\mathbb {P}}^1\times {\mathbb {P}}^1$
), and the canonical model is the complete intersection
![]() $X_{2,10}\subset {\mathbb {P}}(1^4,2,5)$
, where the quadric equation does not contain the variable of weight 2. We see that
$X_{2,10}\subset {\mathbb {P}}(1^4,2,5)$
, where the quadric equation does not contain the variable of weight 2. We see that
![]() $X(2;3)\to X_{2,10}$
contracts the base curve
$X(2;3)\to X_{2,10}$
contracts the base curve
![]() $\Gamma =X\cap D_{x_0}\cap D_{x_1}$
of
$\Gamma =X\cap D_{x_0}\cap D_{x_1}$
of
![]() $|K_X|$
to a 3-fold ordinary double point at
$|K_X|$
to a 3-fold ordinary double point at
![]() $(0,0,0,0,-1,1)$
. The other small resolution gives a second simple fibration in
$(0,0,0,0,-1,1)$
. The other small resolution gives a second simple fibration in
![]() $(1,2)$
-surfaces, corresponding to the other ruling on
$(1,2)$
-surfaces, corresponding to the other ruling on
![]() ${\mathbb {F}}_0$
. The two fibrations are related by the Atiyah flop. The canonical model of
${\mathbb {F}}_0$
. The two fibrations are related by the Atiyah flop. The canonical model of
![]() $X(2;2)$
is still
$X(2;2)$
is still
![]() $X_{2,10}$
, but now the rank of the quadric has dropped to three, and X has a curve of singularities.
$X_{2,10}$
, but now the rank of the quadric has dropped to three, and X has a curve of singularities.
Example 1.13. For each
![]() $X(d;2)$
with
$X(d;2)$
with
![]() $d=3,\dots ,8$
, the image of the canonical map is the cone
$d=3,\dots ,8$
, the image of the canonical map is the cone
![]() $\bar {\mathbb {F}}_e$
over a rational normal curve of degree
$\bar {\mathbb {F}}_e$
over a rational normal curve of degree
![]() $e=3d-4$
. Indeed, the canonical model of
$e=3d-4$
. Indeed, the canonical model of
![]() $X(d;2)$
is obtained by contracting the curve
$X(d;2)$
is obtained by contracting the curve
![]() ${\mathfrak {s}}_0$
to an isolated canonical singularity lying over the vertex of
${\mathfrak {s}}_0$
to an isolated canonical singularity lying over the vertex of
![]() $\bar {\mathbb {F}}_e$
.
$\bar {\mathbb {F}}_e$
.
The varieties
![]() $X(2;2)$
and
$X(2;2)$
and
![]() $X(7;2)$
appeared recently in the literature. More precisely, a hypersurface in a weighted projective space birational to them is in [Reference Chen, Jiang and LiCJL20, Table 10], respectively in line 7 and line 11. The other examples seem to be new. The variety
$X(7;2)$
appeared recently in the literature. More precisely, a hypersurface in a weighted projective space birational to them is in [Reference Chen, Jiang and LiCJL20, Table 10], respectively in line 7 and line 11. The other examples seem to be new. The variety
![]() $X(8;2)$
is a canonical
$X(8;2)$
is a canonical
![]() $3$
-fold with
$3$
-fold with
![]() $p_g=22$
and
$p_g=22$
and
![]() $K^3=26$
with singular canonical image. This shows that the bound
$K^3=26$
with singular canonical image. This shows that the bound
![]() $p_g \geq 23$
in [Reference Hu and ZhangHZ22b, Theorem 1.2, (3)] is optimal, a question left open there.
$p_g \geq 23$
in [Reference Hu and ZhangHZ22b, Theorem 1.2, (3)] is optimal, a question left open there.
1.4 Proof of Proposition 1.6
We assume throughout that X is general. If
![]() $d_0 \geq d$
, by (1.3), all
$d_0 \geq d$
, by (1.3), all
![]() $c_{a_0,a_1,a_2}$
have nonnegative degree. Thus, X is a general element of a base point free linear system contained in the smooth part of
$c_{a_0,a_1,a_2}$
have nonnegative degree. Thus, X is a general element of a base point free linear system contained in the smooth part of
![]() ${\mathbb {F}}$
, and therefore, X is smooth by the classical Bertini Theorem.
${\mathbb {F}}$
, and therefore, X is smooth by the classical Bertini Theorem.
From now on, we assume that
![]() $d_0<d$
and examine the Newton polytope of X. The base locus of
$d_0<d$
and examine the Newton polytope of X. The base locus of
![]() $|X|$
is
$|X|$
is
![]() ${\mathfrak {s}}_0$
. Indeed, it follows from (1.3) that
${\mathfrak {s}}_0$
. Indeed, it follows from (1.3) that
![]() $\deg c_{10,0,0}<0$
and
$\deg c_{10,0,0}<0$
and
![]() $\deg c_{0,10,0}\ge 0$
. In particular, any singularities of X lie on
$\deg c_{0,10,0}\ge 0$
. In particular, any singularities of X lie on
![]() ${\mathfrak {s}}_0$
. In fact, by (1.3), we have
${\mathfrak {s}}_0$
. In fact, by (1.3), we have
![]() $\deg c_{a_0,0,a_2}<0$
for all
$\deg c_{a_0,0,a_2}<0$
for all
![]() $a_0,a_2$
. Thus, the polynomial (1.4) has the form
$a_0,a_2$
. Thus, the polynomial (1.4) has the form
where g vanishes along
![]() $\mathfrak {s}_0$
.
$\mathfrak {s}_0$
.
First, suppose that
![]() $d_0\ge \frac 78d$
, or equivalently,
$d_0\ge \frac 78d$
, or equivalently,
![]() $\deg c_{9,1,0}\ge 0$
. By generality,
$\deg c_{9,1,0}\ge 0$
. By generality,
![]() $c_{9,1,0}$
has distinct roots, and X has
$c_{9,1,0}$
has distinct roots, and X has
![]() $\deg c_{9,1,0}=8d_0-7d \geq 0$
isolated singular points on
$\deg c_{9,1,0}=8d_0-7d \geq 0$
isolated singular points on
![]() $\mathfrak {s}_0$
that are local analytically of the form
$\mathfrak {s}_0$
that are local analytically of the form
![]() $(tx_1 + z^2 + y^5 = 0)$
. These are terminal singularities (cf. [Reference Kollár, Mori, Clemens and CortiKM98, Corollary 5.38]). Notice that if
$(tx_1 + z^2 + y^5 = 0)$
. These are terminal singularities (cf. [Reference Kollár, Mori, Clemens and CortiKM98, Corollary 5.38]). Notice that if
![]() $d_0 = \frac 78 d$
, then by generality,
$d_0 = \frac 78 d$
, then by generality,
![]() $c_{9,1,0}$
is a nonzero constant, and X is smooth.
$c_{9,1,0}$
is a nonzero constant, and X is smooth.
Assume now that
![]() $d_0<\frac 78d$
. Then, the polynomial (1.4) has the form
$d_0<\frac 78d$
. Then, the polynomial (1.4) has the form
where g vanishes at
![]() $\mathfrak {s}_0$
with multiplicity at least
$\mathfrak {s}_0$
with multiplicity at least
![]() $3$
. So, X is singular along
$3$
. So, X is singular along
![]() $\mathfrak {s}_0$
.
$\mathfrak {s}_0$
.
By [Reference Reid, de Géometrie and d’AngersRei80, §1.14], if the nonisolated singularities are canonical, then the general fibre
![]() $X_t$
of
$X_t$
of
![]() $X\to {\mathbb {P}}^1$
has Du Val singularities, and the special fibres have at worst elliptic singularities (dissident points). Conversely, if the general fibre has Du Val singularities, then X has cDV singularities there and therefore is canonical (see e.g., [Reference Kollár, Mori, Clemens and CortiKM98, §5.3]). For the dissident points, we will show directly that there is a crepant blowup
$X\to {\mathbb {P}}^1$
has Du Val singularities, and the special fibres have at worst elliptic singularities (dissident points). Conversely, if the general fibre has Du Val singularities, then X has cDV singularities there and therefore is canonical (see e.g., [Reference Kollár, Mori, Clemens and CortiKM98, §5.3]). For the dissident points, we will show directly that there is a crepant blowup
![]() $X'\to X$
which has cDV singularities [Reference ReidRei87, §3].
$X'\to X$
which has cDV singularities [Reference ReidRei87, §3].
The following Lemma gives a necessary and sufficient condition for
![]() $X_t$
to have at worst Du Val singularities.
$X_t$
to have at worst Du Val singularities.
Lemma 1.14. [Reference ReidRei87, §4.6, §4.9] Let
![]() $0\in S\colon (F=0)\subset \mathbb {A}^3$
be an isolated hypersurface singularity. Then,
$0\in S\colon (F=0)\subset \mathbb {A}^3$
be an isolated hypersurface singularity. Then,
![]() $0\in S$
is Du Val if and only if in any analytic coordinate system, F has monomials of weight
$0\in S$
is Du Val if and only if in any analytic coordinate system, F has monomials of weight
![]() $<1$
with respect to each of the weights
$<1$
with respect to each of the weights
![]() $\frac 12(1,1,0)$
,
$\frac 12(1,1,0)$
,
![]() $\frac 13(1,1,1)$
,
$\frac 13(1,1,1)$
,
![]() $\frac 14(2,1,1)$
,
$\frac 14(2,1,1)$
,
![]() $\frac 16(3,2,1)$
.
$\frac 16(3,2,1)$
.
We next prove that
![]() $d_0\geq \frac {d}4$
. Let
$d_0\geq \frac {d}4$
. Let
![]() $\mathbf {x}=x_1/x_0$
,
$\mathbf {x}=x_1/x_0$
,
![]() $\mathbf {y}=y/x_0^2$
and
$\mathbf {y}=y/x_0^2$
and
![]() $\mathbf {z}=z/x_0^5$
be local fibre coordinates near the point
$\mathbf {z}=z/x_0^5$
be local fibre coordinates near the point
![]() ${\mathfrak {s}}_0\cap X_t$
. Considering
${\mathfrak {s}}_0\cap X_t$
. Considering
![]() $\mathbf {x},\mathbf {y},\mathbf {z}$
as an analytic coordinate system with weights
$\mathbf {x},\mathbf {y},\mathbf {z}$
as an analytic coordinate system with weights
![]() $\frac 14(1,1,2)$
, we see that Lemma 1.14 ensures there is a nonvanishing
$\frac 14(1,1,2)$
, we see that Lemma 1.14 ensures there is a nonvanishing
![]() $c_{a_0,a_1,a_2}$
with
$c_{a_0,a_1,a_2}$
with
![]() $a_1+a_2 < 4$
. Since
$a_1+a_2 < 4$
. Since
![]() $a_0+a_1+2a_2=10$
, that is equivalent to
$a_0+a_1+2a_2=10$
, that is equivalent to
![]() $a_0-a_1>2$
and then, by a parity argument, to
$a_0-a_1>2$
and then, by a parity argument, to
![]() $a_0-a_1 \geq 4$
. Since
$a_0-a_1 \geq 4$
. Since
![]() $a_0+a_1\le 10$
, it follows from (1.3) that
$a_0+a_1\le 10$
, it follows from (1.3) that
![]() $4d_0-d=\frac {10d-4e}2 \geq \deg c_{a_0,a_1,a_2} \geq 0$
.
$4d_0-d=\frac {10d-4e}2 \geq \deg c_{a_0,a_1,a_2} \geq 0$
.
Finally, we prove that if
![]() $d_0\geq \frac {d}4$
, then the general X has canonical singularities. To do this, we apply Lemma 1.14 with all permutations of the weights on the local fibre coordinates. We note that for general
$d_0\geq \frac {d}4$
, then the general X has canonical singularities. To do this, we apply Lemma 1.14 with all permutations of the weights on the local fibre coordinates. We note that for general
![]() $X_t$
, the local equation always contains the monomials
$X_t$
, the local equation always contains the monomials
![]() $\mathbf {z}^2$
,
$\mathbf {z}^2$
,
![]() $\mathbf {y}^5$
and
$\mathbf {y}^5$
and
![]() $\mathbf {x}^3$
, the latter because
$\mathbf {x}^3$
, the latter because
![]() $\deg c_{7,3,0}=4d_0-d\geq 0$
. The reader can easily check that for all the prescribed weights, at least one of these three monomials has weight
$\deg c_{7,3,0}=4d_0-d\geq 0$
. The reader can easily check that for all the prescribed weights, at least one of these three monomials has weight
![]() $<1$
. Thus, if
$<1$
. Thus, if
![]() $c_{7,3,0}$
does not vanish at t, then X has cDV singularities there.
$c_{7,3,0}$
does not vanish at t, then X has cDV singularities there.
By generality,
![]() $c_{7,3,0}$
has
$c_{7,3,0}$
has
![]() $4d_0-d$
distinct zeros. Over each of these, X possibly has a dissident point, locally given by at worst
$4d_0-d$
distinct zeros. Over each of these, X possibly has a dissident point, locally given by at worst
![]() $\mathbf {z}^2+\mathbf {y}^5+t\mathbf {x}^3=0$
. This is not cDV, but the relevant affine chart of the crepant blowup is given by
$\mathbf {z}^2+\mathbf {y}^5+t\mathbf {x}^3=0$
. This is not cDV, but the relevant affine chart of the crepant blowup is given by
The blown-up variety
![]() $X'$
is defined locally by
$X'$
is defined locally by
![]() $\mathbf {z}^{\prime 2}+\mathbf {y}^{\prime 5}+\mathbf {x}^{\prime 3}=0$
, which is then cDV. Hence, the dissident points of X are also canonical.
$\mathbf {z}^{\prime 2}+\mathbf {y}^{\prime 5}+\mathbf {x}^{\prime 3}=0$
, which is then cDV. Hence, the dissident points of X are also canonical.
![]() $\Box $
$\Box $
1.5 Mori Dream Spaces
In this section, we prove that the general
![]() $X(d;d_0)$
is a Mori Dream Space when
$X(d;d_0)$
is a Mori Dream Space when
![]() $d\leq d_0$
. Here, by ‘general’, we mean that
$d\leq d_0$
. Here, by ‘general’, we mean that
![]() $X(d;d_0)$
is an element of a suitable dense open subset of the linear system
$X(d;d_0)$
is an element of a suitable dense open subset of the linear system
![]() $|10(H-dF)|$
.
$|10(H-dF)|$
.
By definition [Reference Arzhantsev, Derenthal, Hausen and LafaceAD+15, Definition 3.3.4.1], a Mori Dream Space is an irreducible normal projective variety with finitely generated divisor class group and finitely generated Cox ring. The divisor class group
![]() $\operatorname {\mathrm {Cl}}(\cdot )$
is the group of linear equivalence classes of Weil divisors on the variety. In particular, it coincides with the Picard group
$\operatorname {\mathrm {Cl}}(\cdot )$
is the group of linear equivalence classes of Weil divisors on the variety. In particular, it coincides with the Picard group
![]() $\operatorname {\mathrm {Pic}}(\cdot )$
when the variety is smooth.
$\operatorname {\mathrm {Pic}}(\cdot )$
when the variety is smooth.
The main point is proving the following.
Proposition 1.15. If
![]() $d\leq d_0$
and X is general, then the natural map
$d\leq d_0$
and X is general, then the natural map
is an isomorphism.
Proof. Note that
![]() $ |10(H-dF)|$
is nef but not ample by Proposition 1.3. In particular, we cannot apply directly [Reference Ravindra and SrinivasRS06, Theorem 1].
$ |10(H-dF)|$
is nef but not ample by Proposition 1.3. In particular, we cannot apply directly [Reference Ravindra and SrinivasRS06, Theorem 1].
We consider a desingularisation
![]() $\tilde {{\mathbb {F}}} \rightarrow {\mathbb {F}}$
of the singular locus, the curves
$\tilde {{\mathbb {F}}} \rightarrow {\mathbb {F}}$
of the singular locus, the curves
![]() $\mathfrak {s}_2$
and
$\mathfrak {s}_2$
and
![]() $\mathfrak {s}_5$
, of
$\mathfrak {s}_5$
, of
![]() ${\mathbb {F}}$
. Let E be the exceptional locus.
${\mathbb {F}}$
. Let E be the exceptional locus.
The general X is a smooth
![]() $3$
-fold that does not intersect
$3$
-fold that does not intersect
![]() $\mathfrak {s}_2$
or
$\mathfrak {s}_2$
or
![]() $\mathfrak {s}_5$
, so its pull-back is a divisor
$\mathfrak {s}_5$
, so its pull-back is a divisor
![]() $\tilde {X}$
in
$\tilde {X}$
in
![]() $\tilde {{\mathbb {F}}}$
mapped isomorphically to X. The divisor
$\tilde {{\mathbb {F}}}$
mapped isomorphically to X. The divisor
![]() $\tilde {X}$
is big since
$\tilde {X}$
is big since
![]() $\tilde {X}^4=X^4=10^4(H^4-4dH^3F)=10^3 d>0$
. By the first lines of the proof of Proposition 1.6, since we assumed
$\tilde {X}^4=X^4=10^4(H^4-4dH^3F)=10^3 d>0$
. By the first lines of the proof of Proposition 1.6, since we assumed
![]() $d\geq d_0$
, the linear system
$d\geq d_0$
, the linear system
![]() $|10(H-dF)|$
is base point free and therefore
$|10(H-dF)|$
is base point free and therefore
![]() $|\tilde {X}|$
is base point free as well.
$|\tilde {X}|$
is base point free as well.
We factor the restriction map
![]() $\rho \colon \operatorname {\mathrm {Pic}}(\tilde {{\mathbb {F}}}) \rightarrow \operatorname {\mathrm {Pic}}(\tilde {X})$
through
$\rho \colon \operatorname {\mathrm {Pic}}(\tilde {{\mathbb {F}}}) \rightarrow \operatorname {\mathrm {Pic}}(\tilde {X})$
through
![]() $\operatorname {\mathrm {Pic}}(\tilde {{\mathbb {F}}}\setminus E)$
as follows:
$\operatorname {\mathrm {Pic}}(\tilde {{\mathbb {F}}}\setminus E)$
as follows:
Following [Reference Ravindra and SrinivasRS06, Section 1], we have isomorphisms
so our claim is that
![]() $\rho _2$
is an isomorphism.
$\rho _2$
is an isomorphism.
By a standard argument (detailed in [Reference Ravindra and SrinivasRS06, Section 1]),
![]() $\rho _1$
is surjective with kernel isomorphic to the free abelian group generated by the classes of the irreducible divisorial components of E.
$\rho _1$
is surjective with kernel isomorphic to the free abelian group generated by the classes of the irreducible divisorial components of E.
Since
![]() $\tilde {X}$
is big and base point free (and
$\tilde {X}$
is big and base point free (and
![]() $\dim \tilde {{\mathbb {F}}}=4\geq 3$
), we can apply the Grothendieck–Lefschetz Theorem for big linear systems [Reference Ravindra and SrinivasRS06, Theorem 2].
$\dim \tilde {{\mathbb {F}}}=4\geq 3$
), we can apply the Grothendieck–Lefschetz Theorem for big linear systems [Reference Ravindra and SrinivasRS06, Theorem 2].
Part a) of the G–L Theorem shows that the kernel of
![]() $\rho $
is generated by the classes of the irreducible divisors of
$\rho $
is generated by the classes of the irreducible divisors of
![]() $\tilde {{\mathbb {F}}}$
contracted to a point by the map induced by the linear system
$\tilde {{\mathbb {F}}}$
contracted to a point by the map induced by the linear system
![]() $|\tilde {X}|$
. They are exactly the divisors supported on E, since no irreducible Weil divisor of
$|\tilde {X}|$
. They are exactly the divisors supported on E, since no irreducible Weil divisor of
![]() ${\mathbb {F}}$
is contracted to a point by
${\mathbb {F}}$
is contracted to a point by
![]() $|10(H-dF)|$
. So,
$|10(H-dF)|$
. So,
![]() $\ker \rho =\ker \rho _1$
which, since
$\ker \rho =\ker \rho _1$
which, since
![]() $\rho _1$
is surjective, implies that
$\rho _1$
is surjective, implies that
![]() $\rho _2$
is injective.
$\rho _2$
is injective.
Finally, since
![]() $\dim \tilde {{\mathbb {F}}}=4$
, part c) of the G–L Theorem shows that in our situation,
$\dim \tilde {{\mathbb {F}}}=4$
, part c) of the G–L Theorem shows that in our situation,
![]() $\rho $
is surjective, and therefore
$\rho $
is surjective, and therefore
![]() $\rho _2$
is surjective too.
$\rho _2$
is surjective too.
When the pull-back map
![]() $\operatorname {\mathrm {Cl}}({\mathbb {F}}(d;d_0)) \rightarrow \operatorname {\mathrm {Cl}}(X(d;d_0))$
is an isomorphism, [Reference Arzhantsev, Derenthal, Hausen and LafaceAD+15, Corollary 4.1.1.5] (see also [Reference Artebani and LafaceAL12]) can be applied, giving directly the following.
$\operatorname {\mathrm {Cl}}({\mathbb {F}}(d;d_0)) \rightarrow \operatorname {\mathrm {Cl}}(X(d;d_0))$
is an isomorphism, [Reference Arzhantsev, Derenthal, Hausen and LafaceAD+15, Corollary 4.1.1.5] (see also [Reference Artebani and LafaceAL12]) can be applied, giving directly the following.
Theorem 1.16. If
![]() $d \leq d_0$
and X is general, defined by a polynomial f as in (1.4), then the Cox ring of X is
$d \leq d_0$
and X is general, defined by a polynomial f as in (1.4), then the Cox ring of X is
In particular, X is a Mori Dream Space.
Proof. Using the notation of [Reference Arzhantsev, Derenthal, Hausen and LafaceAD+15], let
![]() $\bar X$
be the affine hypersurface
$\bar X$
be the affine hypersurface
![]() $\{f=0\}$
in
$\{f=0\}$
in
![]() ${\mathbb {C}}^6$
and let
${\mathbb {C}}^6$
and let
![]() $\hat X = \bar X\smallsetminus \{t_0=t_1=0\}\cup \{x_0=x_1=y=z=0\}$
be the subset of
$\hat X = \bar X\smallsetminus \{t_0=t_1=0\}\cup \{x_0=x_1=y=z=0\}$
be the subset of
![]() $\bar X$
obtained by removing the irrelevant locus. The only relevant component of
$\bar X$
obtained by removing the irrelevant locus. The only relevant component of
![]() $\bar X \smallsetminus \hat X$
is
$\bar X \smallsetminus \hat X$
is
![]() $\{z^2+y^5=t_0=t_1=0\}$
, which has codimension
$\{z^2+y^5=t_0=t_1=0\}$
, which has codimension
![]() $2$
in
$2$
in
![]() $\bar X$
. Hence, the last assumption of [Reference Arzhantsev, Derenthal, Hausen and LafaceAD+15, Corollary 4.1.1.5] is fulfilled.
$\bar X$
. Hence, the last assumption of [Reference Arzhantsev, Derenthal, Hausen and LafaceAD+15, Corollary 4.1.1.5] is fulfilled.
2 Deformations of threefolds on the Noether line
In this section, we study deformations of the canonical threefolds constructed in §1. By Theorem 1.11, we have canonical threefolds
![]() $X(d;d_0)$
on the Noether line for every
$X(d;d_0)$
on the Noether line for every
![]() $d,d_0$
with
$d,d_0$
with
![]() $d,d_0 \geq 3$
,
$d,d_0 \geq 3$
,
![]() $0\leq e \leq \frac 52 d$
. Since
$0\leq e \leq \frac 52 d$
. Since
![]() $p_g=3d-2$
is invariant under deformation, in the rest of this section we will consider
$p_g=3d-2$
is invariant under deformation, in the rest of this section we will consider
![]() $d\geq 3$
fixed.
$d\geq 3$
fixed.
The projection onto coordinates
![]() $(t_0,t_1;x_0,x_1)$
defines a rational map
$(t_0,t_1;x_0,x_1)$
defines a rational map
![]() ${\mathbb {F}}(d;d_0) \dashrightarrow {\mathbb {F}}_e$
whose restriction to X is the canonical map. The standard degeneration
${\mathbb {F}}(d;d_0) \dashrightarrow {\mathbb {F}}_e$
whose restriction to X is the canonical map. The standard degeneration
![]() ${\mathbb {F}}_{e} \leadsto {\mathbb {F}}_{e+2}$
lifts easily to degenerations
${\mathbb {F}}_{e} \leadsto {\mathbb {F}}_{e+2}$
lifts easily to degenerations
![]() ${\mathbb {F}}(d;d_0+1)\leadsto {\mathbb {F}}(d;d_0)$
.
${\mathbb {F}}(d;d_0+1)\leadsto {\mathbb {F}}(d;d_0)$
.
We start by showing that the threefolds with minimal
![]() $e \leq 1$
, that is
$e \leq 1$
, that is
![]() $X\left ( d; \left \lfloor \frac {3d}2 \right \rfloor \right )$
, form a dense subset of an irreducible component of the moduli space.
$X\left ( d; \left \lfloor \frac {3d}2 \right \rfloor \right )$
, form a dense subset of an irreducible component of the moduli space.
We collect some preliminary vanishing results in the following.
Lemma 2.1. For every integer
![]() $n \geq 0$
, we have
$n \geq 0$
, we have
-
1. for all
 $q \neq 0$
,
$q \neq 0$
,
 $h^q({\mathcal {O}}_{\mathbb {F}}(nF))=0$
;
$h^q({\mathcal {O}}_{\mathbb {F}}(nF))=0$
; -
2. for all
 $n \leq d_0+1$
,
$n \leq d_0+1$
,
 $h^1({\mathcal {O}}_{\mathbb {F}}(H-nF))=0$
;
$h^1({\mathcal {O}}_{\mathbb {F}}(H-nF))=0$
; -
3. if
 $e\leq d$
, then
$e\leq d$
, then
 $h^q({\mathcal {O}}_{\mathbb {F}}(n(H-dF)))=0$
for all
$h^q({\mathcal {O}}_{\mathbb {F}}(n(H-dF)))=0$
for all
 $q\ne 0$
;
$q\ne 0$
; -
4. if
 $e\leq d$
, then
$e\leq d$
, then
 $n'> 0$
implies
$n'> 0$
implies
 $h^q({\mathcal {O}}_{\mathbb {F}}(-n'(H-dF)-nF))=0$
for all
$h^q({\mathcal {O}}_{\mathbb {F}}(-n'(H-dF)-nF))=0$
for all
 $q\ne 4$
.
$q\ne 4$
.
Proof. (1) This follows directly from the Demazure Vanishing Theorem [Reference Cox, Little and SchenckCLS11, Thm 9.2.3] since F is nef.
(2) If
![]() $n \leq d_0+1$
, then
$n \leq d_0+1$
, then
![]() $n-1 \leq d_0 \leq 3d-d_0$
. Thus,
$n-1 \leq d_0 \leq 3d-d_0$
. Thus,
![]() $H^0({\mathcal {O}}_{\mathbb {F}}(H-(n-1)F))$
contains multiples of both
$H^0({\mathcal {O}}_{\mathbb {F}}(H-(n-1)F))$
contains multiples of both
![]() $x_0$
and
$x_0$
and
![]() $x_1$
. Hence, the restriction to a fibre
$x_1$
. Hence, the restriction to a fibre
![]() $H^0({\mathcal {O}}_{\mathbb {F}}(H-(n-1)F)) \rightarrow H^0({\mathcal {O}}_ {{\mathbb {P}}(1,1,2,5)}(1))\cong {\mathbb {C}}^2$
is surjective. Suppose that
$H^0({\mathcal {O}}_{\mathbb {F}}(H-(n-1)F)) \rightarrow H^0({\mathcal {O}}_ {{\mathbb {P}}(1,1,2,5)}(1))\cong {\mathbb {C}}^2$
is surjective. Suppose that
![]() $H^1({\mathcal {O}}_{\mathbb {F}}(H-n_0F))$
vanishes for some
$H^1({\mathcal {O}}_{\mathbb {F}}(H-n_0F))$
vanishes for some
![]() $n_0\geq n$
. Then, the claim follows by recursively applying the cohomology exact sequence associated to the exact sequence
$n_0\geq n$
. Then, the claim follows by recursively applying the cohomology exact sequence associated to the exact sequence
Indeed, for
![]() $n\leq \min (d,d_0)$
, we have
$n\leq \min (d,d_0)$
, we have
![]() $H-nF$
is nef by Proposition 1.3, and then
$H-nF$
is nef by Proposition 1.3, and then
![]() $h^1({\mathcal {O}}_{\mathbb {F}}(H-nF))=0$
by the Demazure Vanishing Theorem.
$h^1({\mathcal {O}}_{\mathbb {F}}(H-nF))=0$
by the Demazure Vanishing Theorem.
(3) By Proposition 1.3, if
![]() $e\leq d$
, then
$e\leq d$
, then
![]() $H-dF$
is nef. The statement follows again by the Demazure Vanishing Theorem.
$H-dF$
is nef. The statement follows again by the Demazure Vanishing Theorem.
(4) This follows by Batyrev–Borisov vanishing [Reference Cox, Little and SchenckCLS11, Thm 9.2.7]. Indeed, since
![]() $e\leq d$
, the divisor
$e\leq d$
, the divisor
![]() $N:=n'(H-dF)+nF$
is a sum of nef divisors and therefore nef. We only need then to show that, for a divisor
$N:=n'(H-dF)+nF$
is a sum of nef divisors and therefore nef. We only need then to show that, for a divisor
![]() $D=\sum a_\rho D_\rho $
in the class of N, the polytope
$D=\sum a_\rho D_\rho $
in the class of N, the polytope
has an internal point. We choose
![]() $D=\frac {n'}2 D_y+nD_{t_1}$
. Recall that
$D=\frac {n'}2 D_y+nD_{t_1}$
. Recall that
![]() $M_{\mathbb {R}} \subset {\mathbb {R}}^6$
is the orthogonal of the two bottom rows of (1.1) and choose
$M_{\mathbb {R}} \subset {\mathbb {R}}^6$
is the orthogonal of the two bottom rows of (1.1) and choose
![]() $0 < \epsilon \ll 1$
. A direct computation shows that
$0 < \epsilon \ll 1$
. A direct computation shows that
![]() $\epsilon (d,d,1,1,-6,2)$
is an internal point of
$\epsilon (d,d,1,1,-6,2)$
is an internal point of
![]() $P_D$
.
$P_D$
.
Now, we can prove the announced result.
Proposition 2.2. The threefolds
![]() $X\!\left ( d; \left \lfloor \frac {3d}2 \right \rfloor \right )$
form a dense open subset of an irreducible component of the moduli space.
$X\!\left ( d; \left \lfloor \frac {3d}2 \right \rfloor \right )$
form a dense open subset of an irreducible component of the moduli space.
We need to prove that every small deformation of a smooth
![]() $X\left ( d; \left \lfloor \frac {3d}2 \right \rfloor \right )$
is still an
$X\left ( d; \left \lfloor \frac {3d}2 \right \rfloor \right )$
is still an
![]() $X\left ( d; \left \lfloor \frac {3d}2 \right \rfloor \right )$
. Looking at the exact sequence defining the normal bundle of X in
$X\left ( d; \left \lfloor \frac {3d}2 \right \rfloor \right )$
. Looking at the exact sequence defining the normal bundle of X in
![]() ${\mathbb {F}}$
${\mathbb {F}}$
we see that it suffices to prove
![]() $H^1(T_{{\mathbb {F}}|X})=0$
, since then the induced map
$H^1(T_{{\mathbb {F}}|X})=0$
, since then the induced map
![]() $H^0 (N_{X|{\mathbb {F}}}) \rightarrow H^1 (T_X)$
is surjective. So, Proposition 2.2 is a consequence of the following.
$H^0 (N_{X|{\mathbb {F}}}) \rightarrow H^1 (T_X)$
is surjective. So, Proposition 2.2 is a consequence of the following.
Lemma 2.3. If
![]() $d_0=\left \lfloor \frac {3d}2 \right \rfloor $
, then
$d_0=\left \lfloor \frac {3d}2 \right \rfloor $
, then
![]() $H^1(T_{{\mathbb {F}}|X})=0$
.
$H^1(T_{{\mathbb {F}}|X})=0$
.
Proof. By the restriction exact sequence
we need only prove that
![]() $H^1(T_{\mathbb {F}} )$
and
$H^1(T_{\mathbb {F}} )$
and
![]() $H^2( T_{\mathbb {F}}(-X) )$
vanish.
$H^2( T_{\mathbb {F}}(-X) )$
vanish.
Consider the cohomology exact sequence associated to the dual of the Euler sequence (see [Reference Cox, Little and SchenckCLS11, Thm 8.1.6])
We use Lemma 2.1. By part (1),
![]() $h^2({\mathcal {O}}_{\mathbb {F}})=h^1({\mathcal {O}}_{\mathbb {F}}(D_{t_j}))=0$
; by part (3),
$h^2({\mathcal {O}}_{\mathbb {F}})=h^1({\mathcal {O}}_{\mathbb {F}}(D_{t_j}))=0$
; by part (3),
![]() $h^1({\mathcal {O}}_{\mathbb {F}}({D_{y}})= h^1({\mathcal {O}}_{\mathbb {F}}(D_{z}))=0$
; by part (2),
$h^1({\mathcal {O}}_{\mathbb {F}}({D_{y}})= h^1({\mathcal {O}}_{\mathbb {F}}(D_{z}))=0$
; by part (2),
![]() $h^1({\mathcal {O}}_{\mathbb {F}}(D_{x_0}))=0$
and, since
$h^1({\mathcal {O}}_{\mathbb {F}}(D_{x_0}))=0$
and, since
![]() $d_0=\left \lfloor \frac {3d}2 \right \rfloor \Rightarrow 3d-d_0\leq d_0+1$
, also
$d_0=\left \lfloor \frac {3d}2 \right \rfloor \Rightarrow 3d-d_0\leq d_0+1$
, also
![]() $h^1({\mathcal {O}}_{\mathbb {F}}(D_{x_1}))=0$
. Then,
$h^1({\mathcal {O}}_{\mathbb {F}}(D_{x_1}))=0$
. Then,
![]() $h^1(T_{\mathbb {F}} )=0$
.
$h^1(T_{\mathbb {F}} )=0$
.
Consider now the tensor product of the sequence (2.1) by
![]() ${\mathcal {O}}_{\mathbb {F}}(-X)$
. By Lemma 2.1, part (4),
${\mathcal {O}}_{\mathbb {F}}(-X)$
. By Lemma 2.1, part (4),
![]() $h^3({\mathcal {O}}_{\mathbb {F}}(-X))=h^2({\mathcal {O}}_{\mathbb {F}}({D_{x_0}}-X)=h^2({\mathcal {O}}_{\mathbb {F}}(D_{x_1}-X))=h^2({\mathcal {O}}_{\mathbb {F}}({D_{y}}-X)=h^2({\mathcal {O}}_{\mathbb {F}}(D_{z}-X))=0$
; moreover, also
$h^3({\mathcal {O}}_{\mathbb {F}}(-X))=h^2({\mathcal {O}}_{\mathbb {F}}({D_{x_0}}-X)=h^2({\mathcal {O}}_{\mathbb {F}}(D_{x_1}-X))=h^2({\mathcal {O}}_{\mathbb {F}}({D_{y}}-X)=h^2({\mathcal {O}}_{\mathbb {F}}(D_{z}-X))=0$
; moreover, also
![]() $h^2({\mathcal {O}}_{\mathbb {F}}(-X))=0$
, and then by
$h^2({\mathcal {O}}_{\mathbb {F}}(-X))=0$
, and then by
since ([Reference DolgachevDol82, 1.4.1])
![]() $h^2({\mathcal {O}}_{{\mathbb {P}}(1,1,2,5)}(-10) )=0$
also
$h^2({\mathcal {O}}_{{\mathbb {P}}(1,1,2,5)}(-10) )=0$
also
![]() $h^2({\mathcal {O}}_{\mathbb {F}}(D_{t_j}-X))=0$
. Then,
$h^2({\mathcal {O}}_{\mathbb {F}}(D_{t_j}-X))=0$
. Then,
![]() $h^2(T_{\mathbb {F}}(-X) )=0$
.
$h^2(T_{\mathbb {F}}(-X) )=0$
.
Now we try to lift the degenerations
![]() ${\mathbb {F}}_{e-2} \leadsto {\mathbb {F}}_{e}$
to degenerations
${\mathbb {F}}_{e-2} \leadsto {\mathbb {F}}_{e}$
to degenerations
![]() $X(d;d_0+1)\leadsto X(d;d_0)$
by the argument of [Reference PignatelliPig12, Remark 1.3]. We first construct a degeneration
$X(d;d_0+1)\leadsto X(d;d_0)$
by the argument of [Reference PignatelliPig12, Remark 1.3]. We first construct a degeneration
![]() ${\mathbb {F}}(d;d_0+1)\leadsto {\mathbb {F}}(d;d_0)$
. Assume then
${\mathbb {F}}(d;d_0+1)\leadsto {\mathbb {F}}(d;d_0)$
. Assume then
![]() $d < \left \lfloor \frac {3d}{2} \right \rfloor $
(
$d < \left \lfloor \frac {3d}{2} \right \rfloor $
(
![]() $e \geq 2$
) and let
$e \geq 2$
) and let
![]() $\tilde {\mathbb {F}}$
be the toric variety with weight matrix
$\tilde {\mathbb {F}}$
be the toric variety with weight matrix
 $$\begin{align*}\renewcommand{\arraystretch}{1.2} \begin{pmatrix} t_0 & t_1 & \tilde x_0 & x_0 & x_1 & y & z\\ 1 & 1 & d-d_0 & d-d_0-1 & d_0-2d+1 & 0 & 0\\ 0 & 0 & 1 & 1 & 1 & 2 & 5 \end{pmatrix}\end{align*}$$
$$\begin{align*}\renewcommand{\arraystretch}{1.2} \begin{pmatrix} t_0 & t_1 & \tilde x_0 & x_0 & x_1 & y & z\\ 1 & 1 & d-d_0 & d-d_0-1 & d_0-2d+1 & 0 & 0\\ 0 & 0 & 1 & 1 & 1 & 2 & 5 \end{pmatrix}\end{align*}$$
and irrelevant ideal
![]() $(t_0,t_1)\cap (\tilde x_0,x_0,x_1,y,z)$
.
$(t_0,t_1)\cap (\tilde x_0,x_0,x_1,y,z)$
.
Consider the family
![]() $\tilde {\mathbb {F}} \times \Lambda \supset {\mathcal {F}}\to \Lambda $
defined by
$\tilde {\mathbb {F}} \times \Lambda \supset {\mathcal {F}}\to \Lambda $
defined by
with parameter
![]() $\lambda \in \Lambda $
, where
$\lambda \in \Lambda $
, where
![]() $\Lambda $
is a disc around
$\Lambda $
is a disc around
![]() $0\in {\mathbb {C}}$
.
$0\in {\mathbb {C}}$
.
Set as usual
![]() ${\mathcal {F}}_\lambda $
for the fibre over
${\mathcal {F}}_\lambda $
for the fibre over
![]() $\lambda \in \Lambda $
. Then, for
$\lambda \in \Lambda $
. Then, for
![]() $\lambda \neq 0$
, the equation (2.2) eliminates
$\lambda \neq 0$
, the equation (2.2) eliminates
![]() $\tilde x_0$
, and thus, the fibre
$\tilde x_0$
, and thus, the fibre
![]() ${\mathcal {F}}_\lambda $
is isomorphic to
${\mathcal {F}}_\lambda $
is isomorphic to
![]() ${\mathbb {F}}(d;d_0+1)$
. On the contrary,
${\mathbb {F}}(d;d_0+1)$
. On the contrary,
![]() ${\mathcal {F}}_0 \cong {\mathbb {F}}(d;d_0)$
with ‘coordinates’
${\mathcal {F}}_0 \cong {\mathbb {F}}(d;d_0)$
with ‘coordinates’
![]() $t_0,t_1,\tilde x_0,\tilde x_1:=\frac {x_1}{t_0}=\frac {x_0}{t_1^{e-1}},y,z$
.
$t_0,t_1,\tilde x_0,\tilde x_1:=\frac {x_1}{t_0}=\frac {x_0}{t_1^{e-1}},y,z$
.
We choose generators
![]() $\tilde {F}$
and
$\tilde {F}$
and
![]() $\tilde {H}$
of
$\tilde {H}$
of
![]() $\operatorname {\mathrm {Cl}}(\tilde {\mathbb {F}})$
defined, respectively, by
$\operatorname {\mathrm {Cl}}(\tilde {\mathbb {F}})$
defined, respectively, by
![]() $t_0$
and
$t_0$
and
![]() $t_0^{d_0+1}x_0$
. Notice that the restrictions of
$t_0^{d_0+1}x_0$
. Notice that the restrictions of
![]() $\tilde {H}$
and
$\tilde {H}$
and
![]() $\tilde {F}$
to
$\tilde {F}$
to
![]() ${\mathcal {F}}_\lambda \cong {\mathbb {F}}(d;*)$
give, respectively, the classes H and F. This is obvious for
${\mathcal {F}}_\lambda \cong {\mathbb {F}}(d;*)$
give, respectively, the classes H and F. This is obvious for
![]() $\tilde {F}$
and for
$\tilde {F}$
and for
![]() $\lambda \neq 0$
. For the restriction of
$\lambda \neq 0$
. For the restriction of
![]() $\tilde {H}$
to
$\tilde {H}$
to
![]() ${\mathcal {F}}_0 \cong {\mathbb {F}}(d;d_0)$
, it follows since the divisors of
${\mathcal {F}}_0 \cong {\mathbb {F}}(d;d_0)$
, it follows since the divisors of
![]() $t_0^{d}\tilde x_0$
and
$t_0^{d}\tilde x_0$
and
![]() $t_0^{d+1}x_0$
belong to the same class.
$t_0^{d+1}x_0$
belong to the same class.
Then, for every
![]() $\tilde X\in |10(\tilde {H}-d\tilde {F})|$
on
$\tilde X\in |10(\tilde {H}-d\tilde {F})|$
on
![]() $\tilde {\mathbb {F}}$
, the flat family
$\tilde {\mathbb {F}}$
, the flat family
defines a degeneration
![]() $X(d;d_0+1)\leadsto X(d;d_0)$
if all fibres have canonical singularities. This works very well when
$X(d;d_0+1)\leadsto X(d;d_0)$
if all fibres have canonical singularities. This works very well when
![]() $d_0$
is big enough (i.e., when e is small enough).
$d_0$
is big enough (i.e., when e is small enough).
Proposition 2.4. If
![]() $e\leq d$
, then every
$e\leq d$
, then every
![]() $X(d;d_0)$
lies in the closure of the family of the
$X(d;d_0)$
lies in the closure of the family of the
![]() $X(d;\left \lfloor \frac {3d}2 \right \rfloor )$
.
$X(d;\left \lfloor \frac {3d}2 \right \rfloor )$
.
Proof. Arguing as in the previous section, we may assume that
![]() $\tilde X$
is defined by a polynomial of the form
$\tilde X$
is defined by a polynomial of the form
analogous to (1.4). Intersecting with
![]() ${\mathcal {F}}_0\cong {\mathbb {F}}(d;d_0)$
, we can substitute
${\mathcal {F}}_0\cong {\mathbb {F}}(d;d_0)$
, we can substitute
![]() $x_0=t_1^{e-1}\tilde x_1$
and
$x_0=t_1^{e-1}\tilde x_1$
and
![]() $x_1=t_0\tilde x_1$
to get a polynomial of the form
$x_1=t_0\tilde x_1$
to get a polynomial of the form
![]() $z^2+\sum _{\tilde a_0+\tilde a_1+2a_2 = 10} c_{\tilde a_0,\tilde a_1,a_2}(\tilde x_0)^{\tilde a_0}(\tilde x_1)^{\tilde a_1}y^{a_2}$
with
$z^2+\sum _{\tilde a_0+\tilde a_1+2a_2 = 10} c_{\tilde a_0,\tilde a_1,a_2}(\tilde x_0)^{\tilde a_0}(\tilde x_1)^{\tilde a_1}y^{a_2}$
with
Recall that, by (1.3),
![]() $\deg c_{\tilde a_0,\tilde a_1,a_2}=\tilde a_1\left (\frac {d+e}2 \right )+\tilde a_0\left (\frac {d-e}2 \right )$
, so
$\deg c_{\tilde a_0,\tilde a_1,a_2}=\tilde a_1\left (\frac {d+e}2 \right )+\tilde a_0\left (\frac {d-e}2 \right )$
, so
Then, by the assumption
![]() $e\leq d$
, it follows that
$e\leq d$
, it follows that
![]() $\deg c_{\tilde a_0,\tilde a_1,a_2} \geq \tilde a_1 e$
. Since every homogeneous polynomial in
$\deg c_{\tilde a_0,\tilde a_1,a_2} \geq \tilde a_1 e$
. Since every homogeneous polynomial in
![]() ${\mathbb {C}}[t_0,t_1]$
of degree
${\mathbb {C}}[t_0,t_1]$
of degree
![]() $\ge \tilde a_1e$
belongs to the ideal
$\ge \tilde a_1e$
belongs to the ideal
![]() $(t_0,t_1^{e-1})^{\tilde a_1}$
, it follows that the polynomial of
$(t_0,t_1^{e-1})^{\tilde a_1}$
, it follows that the polynomial of
![]() ${\mathcal {X}}_0$
in
${\mathcal {X}}_0$
in
![]() ${\mathbb {F}}(d;d_0)$
may assume every possible value of (1.4). Hence, every
${\mathbb {F}}(d;d_0)$
may assume every possible value of (1.4). Hence, every
![]() $X(d;d_0)$
can be deformed to a
$X(d;d_0)$
can be deformed to a
![]() $X(d;d_0+1)$
.
$X(d;d_0+1)$
.
The condition
![]() $e \leq d$
is necessary in the previous proof to ensure that the scrollar deformations deform every
$e \leq d$
is necessary in the previous proof to ensure that the scrollar deformations deform every
![]() $X(d,d_0)$
(
$X(d,d_0)$
(
![]() $d_0 \neq \lfloor \frac {3d}2 \rfloor $
) to some
$d_0 \neq \lfloor \frac {3d}2 \rfloor $
) to some
![]() $X(d,d_0+1)$
. For
$X(d,d_0+1)$
. For
![]() $e>d$
, the situation looks more tricky, and it seems that we have more components.
$e>d$
, the situation looks more tricky, and it seems that we have more components.
This, however, includes almost all smooth threefolds; by Proposition 1.6, we only miss those with
![]() $5d=4e$
– that is,
$5d=4e$
– that is,
![]() $7d=8d_0$
. In fact, they belong to a different component (see the forthcoming Theorem 5.4).
$7d=8d_0$
. In fact, they belong to a different component (see the forthcoming Theorem 5.4).
3 On
 ${\mathbb {P}}(a_1,\ldots ,a_r)$
-bundles
${\mathbb {P}}(a_1,\ldots ,a_r)$
-bundles
We develop some foundations for weighted
![]() ${\mathbb {P}}^r$
-bundles over a nonsingular base B, generalizing the work of Mullet ([Reference MulletMul09]). Such bundles can be constructed by taking relative Proj of a sheaf
${\mathbb {P}}^r$
-bundles over a nonsingular base B, generalizing the work of Mullet ([Reference MulletMul09]). Such bundles can be constructed by taking relative Proj of a sheaf
![]() ${\mathcal {S}}$
of graded
${\mathcal {S}}$
of graded
![]() ${\mathcal {O}}_B$
-algebras. We do not assume that
${\mathcal {O}}_B$
-algebras. We do not assume that
![]() ${\mathcal {S}}$
is generated in degree 1.
${\mathcal {S}}$
is generated in degree 1.
3.1 Weighted symmetric algebras
Definition 3.1. Let B be an algebraic variety,
![]() $a_i$
positive integers. A weighted symmetric algebra
$a_i$
positive integers. A weighted symmetric algebra
![]() ${\mathcal {S}}$
on B with weights
${\mathcal {S}}$
on B with weights
![]() $(a_1,\ldots ,a_n)$
is a sheaf of graded
$(a_1,\ldots ,a_n)$
is a sheaf of graded
![]() ${\mathcal {O}}_B$
-algebras
${\mathcal {O}}_B$
-algebras
![]() ${\mathcal {S}}:=\bigoplus _{d \geq 0}{\mathcal {S}}_d$
such that
${\mathcal {S}}:=\bigoplus _{d \geq 0}{\mathcal {S}}_d$
such that
![]() ${\mathcal {S}}_0 \cong {\mathcal {O}}_B$
and B is covered by open sets U with the property
${\mathcal {S}}_0 \cong {\mathcal {O}}_B$
and B is covered by open sets U with the property
where
![]() ${\mathcal {O}}_U[x_1,\ldots ,x_n]$
is graded by
${\mathcal {O}}_U[x_1,\ldots ,x_n]$
is graded by
![]() $\deg x_i=a_i$
. We sometimes use the shorthand notation
$\deg x_i=a_i$
. We sometimes use the shorthand notation
![]() $a^r$
to denote a repeated r times.
$a^r$
to denote a repeated r times.
Example 3.2. If
![]() ${\mathcal {E}}$
is a locally free sheaf on B of rank r, then
${\mathcal {E}}$
is a locally free sheaf on B of rank r, then
![]() $\operatorname {\mathrm {Sym}}({\mathcal {E}})$
is a weighted symmetric algebra with weights
$\operatorname {\mathrm {Sym}}({\mathcal {E}})$
is a weighted symmetric algebra with weights
![]() $(1^r)$
.
$(1^r)$
.
The inclusion
![]() ${\mathcal {S}}_1 \subset {\mathcal {S}}$
induces an injective morphism of sheaves of algebras
${\mathcal {S}}_1 \subset {\mathcal {S}}$
induces an injective morphism of sheaves of algebras
![]() $\operatorname {\mathrm {Sym}} ({\mathcal {S}}_1) \rightarrow {\mathcal {S}}$
, which is an isomorphism if and only if
$\operatorname {\mathrm {Sym}} ({\mathcal {S}}_1) \rightarrow {\mathcal {S}}$
, which is an isomorphism if and only if
![]() $a_i=1$
for all i. Therefore, the weighted symmetric algebras with weights
$a_i=1$
for all i. Therefore, the weighted symmetric algebras with weights
![]() $(1^r)$
are exactly the usual symmetric algebras
$(1^r)$
are exactly the usual symmetric algebras
![]() $\operatorname {\mathrm {Sym}}({\mathcal {E}})$
, where
$\operatorname {\mathrm {Sym}}({\mathcal {E}})$
, where
![]() ${\mathcal {E}}$
is a locally free sheaf of rank r on B. Similarly, all weighted symmetric algebras with weights
${\mathcal {E}}$
is a locally free sheaf of rank r on B. Similarly, all weighted symmetric algebras with weights
![]() $(a^r)$
are isomorphic to some
$(a^r)$
are isomorphic to some
![]() $\operatorname {\mathrm {Sym}}({\mathcal {E}})$
up to changing the grading as follows.
$\operatorname {\mathrm {Sym}}({\mathcal {E}})$
up to changing the grading as follows.
Example 3.3. Let a be a positive integer. We define
![]() $\operatorname {\mathrm {Sym}}^{(a)}({\mathcal {E}})=\bigoplus _{d\ge 0}\operatorname {\mathrm {Sym}}^{(a)}({\mathcal {E}})_d$
, where
$\operatorname {\mathrm {Sym}}^{(a)}({\mathcal {E}})=\bigoplus _{d\ge 0}\operatorname {\mathrm {Sym}}^{(a)}({\mathcal {E}})_d$
, where
 $$\begin{align*}\operatorname{\mathrm{Sym}}^{(a)}({\mathcal{E}})_{d} \cong \begin{cases} \operatorname{\mathrm{Sym}}({\mathcal{E}})_k & \text{if }d=ka \\ 0 & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Sym}}^{(a)}({\mathcal{E}})_{d} \cong \begin{cases} \operatorname{\mathrm{Sym}}({\mathcal{E}})_k & \text{if }d=ka \\ 0 & \text{otherwise}. \end{cases} \end{align*}$$
The algebra structure is inherited from the natural isomorphism with
![]() $\operatorname {\mathrm {Sym}}({\mathcal {E}})$
.
$\operatorname {\mathrm {Sym}}({\mathcal {E}})$
.
If we take two weighted symmetric algebras
![]() ${\mathcal {S}}$
and
${\mathcal {S}}$
and
![]() ${\mathcal {S}}'$
with respective weights
${\mathcal {S}}'$
with respective weights
![]() $(a_1,\ldots ,a_m)$
and
$(a_1,\ldots ,a_m)$
and
![]() $(a^{\prime }_1, \ldots , a^{\prime }_n)$
, then
$(a^{\prime }_1, \ldots , a^{\prime }_n)$
, then
![]() ${\mathcal {S}} \otimes _{{\mathcal {O}}_B} {\mathcal {S}}'$
has a natural structure of weighted symmetric algebra with weights
${\mathcal {S}} \otimes _{{\mathcal {O}}_B} {\mathcal {S}}'$
has a natural structure of weighted symmetric algebra with weights
![]() $(a_1,\ldots a_m,a^{\prime }_1,\ldots ,a^{\prime }_n)$
. This leads us to the following definition.
$(a_1,\ldots a_m,a^{\prime }_1,\ldots ,a^{\prime }_n)$
. This leads us to the following definition.
Definition 3.4. Choose positive integers
![]() $a_1<a_2<\cdots < a_n$
and locally free sheaves
$a_1<a_2<\cdots < a_n$
and locally free sheaves
![]() ${\mathcal {E}}_{a_1},\ldots ,{\mathcal {E}}_{a_n}$
over B. Then, we define the associated free weighted symmetric algebra
${\mathcal {E}}_{a_1},\ldots ,{\mathcal {E}}_{a_n}$
over B. Then, we define the associated free weighted symmetric algebra
whose weights are
![]() $(a_1^{r_{a_1}},\dots ,a_n^{r_{a_n}})$
, where
$(a_1^{r_{a_1}},\dots ,a_n^{r_{a_n}})$
, where
![]() $r_{a_i}=\operatorname {\mathrm {rank}} {\mathcal {E}}_{a_i}$
.
$r_{a_i}=\operatorname {\mathrm {rank}} {\mathcal {E}}_{a_i}$
.
To consider more general weighted symmetric algebras, we will need the following
Definition 3.5. Let
![]() ${\mathcal {S}}$
be a weighted symmetric algebra. For a nonnegative integer
${\mathcal {S}}$
be a weighted symmetric algebra. For a nonnegative integer
![]() $\tau $
, we define the truncated subalgebra
$\tau $
, we define the truncated subalgebra
![]() ${\mathcal {S}}[\tau ]$
as the sheaf of subalgebras locally generated by
${\mathcal {S}}[\tau ]$
as the sheaf of subalgebras locally generated by
![]() $1$
and
$1$
and
![]() $\{x_j \mid \deg x_j \leq \tau \}$
as an
$\{x_j \mid \deg x_j \leq \tau \}$
as an
![]() ${\mathcal {O}}_U$
-algebra (see Definition 3.1 for notation).
${\mathcal {O}}_U$
-algebra (see Definition 3.1 for notation).
Example 3.6. If
![]() ${\mathcal {S}}$
is a weighted symmetric algebra with weights
${\mathcal {S}}$
is a weighted symmetric algebra with weights
![]() $a_1<a_2<\ldots <a_n$
, then
$a_1<a_2<\ldots <a_n$
, then
![]() ${\mathcal {S}}[0]={\mathcal {O}}_B$
,
${\mathcal {S}}[0]={\mathcal {O}}_B$
,
![]() ${\mathcal {S}}[\tau ]={\mathcal {S}}$
if and only if
${\mathcal {S}}[\tau ]={\mathcal {S}}$
if and only if
![]() $\tau \geq a_n$
.
$\tau \geq a_n$
.
Example 3.7. If
![]() ${\mathcal {S}}$
is a weighted symmetric algebra with weights
${\mathcal {S}}$
is a weighted symmetric algebra with weights
![]() $(a^r)$
, then
$(a^r)$
, then
![]() ${\mathcal {S}}[\tau ]={\mathcal {S}}$
if
${\mathcal {S}}[\tau ]={\mathcal {S}}$
if
![]() $\tau \geq a$
, whereas
$\tau \geq a$
, whereas
![]() ${\mathcal {S}}[\tau ]={\mathcal {S}}_0\cong {\mathcal {O}}_B$
if
${\mathcal {S}}[\tau ]={\mathcal {S}}_0\cong {\mathcal {O}}_B$
if
![]() $\tau < a$
.
$\tau < a$
.
Example 3.8. Since we assumed that
![]() $a_i<a_{i+1}$
in Def. 3.4, we have
$a_i<a_{i+1}$
in Def. 3.4, we have
More generally, if
![]() ${\mathcal {S}}$
is a weighted symmetric algebra with weights
${\mathcal {S}}$
is a weighted symmetric algebra with weights
![]() $(a_1^{r_1}, \ldots , a_n^{r_n})$
, where
$(a_1^{r_1}, \ldots , a_n^{r_n})$
, where
![]() $a_1<\cdots <a_n$
, then
$a_1<\cdots <a_n$
, then
![]() ${\mathcal {S}}[\tau ]$
is a weighted symmetric algebra with weights
${\mathcal {S}}[\tau ]$
is a weighted symmetric algebra with weights
![]() $(a_1^{r_1}, \ldots , a_t^{r_t})$
, where
$(a_1^{r_1}, \ldots , a_t^{r_t})$
, where
![]() $a_t=\max \{ a_j\mid a_j \leq \tau \}$
.
$a_t=\max \{ a_j\mid a_j \leq \tau \}$
.
Truncation enables us to define an analogue of the sheaves
![]() ${\mathcal {E}}_{a_j}$
for any weighted symmetric algebra.
${\mathcal {E}}_{a_j}$
for any weighted symmetric algebra.
Definition 3.9. Let
![]() ${\mathcal {S}}$
be a weighted symmetric algebra with weights
${\mathcal {S}}$
be a weighted symmetric algebra with weights
![]() $(a_1^{r_1}, \ldots , a_n^{r_n})$
, where
$(a_1^{r_1}, \ldots , a_n^{r_n})$
, where
![]() $a_1<\cdots <a_n$
. For every
$a_1<\cdots <a_n$
. For every
![]() $1\le j\le n$
, the characteristic sheaf of degree
$1\le j\le n$
, the characteristic sheaf of degree
![]() $a_j$
is the cokernel
$a_j$
is the cokernel
![]() ${\mathcal {E}}_{a_j}({\mathcal {S}})$
of the natural inclusion
${\mathcal {E}}_{a_j}({\mathcal {S}})$
of the natural inclusion
Since
![]() ${\mathcal {S}}_{|U}\cong {\mathcal {O}}_U[x_1,\dots ,x_r]$
, this is a locally free sheaf of rank
${\mathcal {S}}_{|U}\cong {\mathcal {O}}_U[x_1,\dots ,x_r]$
, this is a locally free sheaf of rank
![]() $r_j$
. We denote the projection maps by
$r_j$
. We denote the projection maps by
![]() $\epsilon _{a_j} \colon {\mathcal {S}}_{a_j} \rightarrow {\mathcal {E}}_{a_j}({\mathcal {S}})$
.
$\epsilon _{a_j} \colon {\mathcal {S}}_{a_j} \rightarrow {\mathcal {E}}_{a_j}({\mathcal {S}})$
.
Remark 3.10. A weighted symmetric algebra with weights
![]() $(a_1^{r_1}, \ldots , a_n^{r_n})$
is free (see Definition 3.4) of the form
$(a_1^{r_1}, \ldots , a_n^{r_n})$
is free (see Definition 3.4) of the form
![]() $\operatorname {\mathrm {wSym}}_{a_1,\ldots ,a_n} ({\mathcal {E}}_{a_1} , \cdots , {\mathcal {E}}_{a_n})$
if and only if all
$\operatorname {\mathrm {wSym}}_{a_1,\ldots ,a_n} ({\mathcal {E}}_{a_1} , \cdots , {\mathcal {E}}_{a_n})$
if and only if all
![]() $\epsilon _{a_j}$
have a right inverse.
$\epsilon _{a_j}$
have a right inverse.
The proof of the following Proposition is left as an exercise.
Proposition 3.11. Let
![]() ${\mathcal {S}}$
be a weighted symmetric algebra with weights
${\mathcal {S}}$
be a weighted symmetric algebra with weights
![]() $(a_1^{r_1}, \ldots , a_n^{r_n})$
, with
$(a_1^{r_1}, \ldots , a_n^{r_n})$
, with
![]() $a_1<\cdots <a_n$
. The natural map
$a_1<\cdots <a_n$
. The natural map
is surjective, and its kernel is the ideal sheaf locally generated by the elements of the form
![]() $u \otimes 1 - 1 \otimes \sigma _{a_n}(u)$
.
$u \otimes 1 - 1 \otimes \sigma _{a_n}(u)$
.
The maps
![]() $\sigma _{a_j}$
determine
$\sigma _{a_j}$
determine
![]() ${\mathcal {S}}$
recursively. Indeed, we can use the above Proposition to construct every weighted symmetric algebra with weights
${\mathcal {S}}$
recursively. Indeed, we can use the above Proposition to construct every weighted symmetric algebra with weights
![]() $(a_1^{r_1}, \ldots , a_n^{r_n})$
, where
$(a_1^{r_1}, \ldots , a_n^{r_n})$
, where
![]() $a_1<\cdots <a_n$
according to the following algorithm:
$a_1<\cdots <a_n$
according to the following algorithm:
-
Step 1 Set
 ${\mathcal {S}}[a_1-1]={\mathcal {S}}[0]={\mathcal {O}}_B$
, the symmetric algebra which is zero in degrees
${\mathcal {S}}[a_1-1]={\mathcal {S}}[0]={\mathcal {O}}_B$
, the symmetric algebra which is zero in degrees
 $>0$
.
$>0$
. -
Step 2 Given
 ${\mathcal {S}}[a_j-1]$
, choose a locally free sheaf
${\mathcal {S}}[a_j-1]$
, choose a locally free sheaf
 ${\mathcal {S}}_{a_j}$
and an inclusion
${\mathcal {S}}_{a_j}$
and an inclusion
 $\sigma _{a_j}\colon {\mathcal {S}}[a_j-1]_{a_j} \rightarrow {\mathcal {S}}_{a_j}$
with locally free cokernel
$\sigma _{a_j}\colon {\mathcal {S}}[a_j-1]_{a_j} \rightarrow {\mathcal {S}}_{a_j}$
with locally free cokernel
 ${\mathcal {E}}_{a_j}$
. Then, by Proposition 3.11, we define
${\mathcal {E}}_{a_j}$
. Then, by Proposition 3.11, we define
 ${\mathcal {S}}[a_{j}]={\mathcal {S}}[a_{j+1}-1]$
to be the quotient of
${\mathcal {S}}[a_{j}]={\mathcal {S}}[a_{j+1}-1]$
to be the quotient of
 ${\mathcal {S}}[a_j-1] \otimes _{{\mathcal {O}}_B} \operatorname {\mathrm {Sym}}^{(a_j)} \left ( {\mathcal {S}}_{a_j} \right )$
by the ideal sheaf locally generated by the elements of the form
${\mathcal {S}}[a_j-1] \otimes _{{\mathcal {O}}_B} \operatorname {\mathrm {Sym}}^{(a_j)} \left ( {\mathcal {S}}_{a_j} \right )$
by the ideal sheaf locally generated by the elements of the form
 $u \otimes 1 - 1 \otimes \sigma _{a_n}(u)$
.
$u \otimes 1 - 1 \otimes \sigma _{a_n}(u)$
. -
Step 3 Finally, set
 ${\mathcal {S}}:={\mathcal {S}}[a_n]$
.
${\mathcal {S}}:={\mathcal {S}}[a_n]$
.
It is helpful to work out the specific case of weighted symmetric algebras
![]() ${\mathcal {S}}$
with weights
${\mathcal {S}}$
with weights
![]() $(1,1,2,5)$
in detail. The primary example to have in mind is
$(1,1,2,5)$
in detail. The primary example to have in mind is
![]() $\operatorname {\mathrm {wSym}}_{1,2,5}({\mathcal {E}}_1, {\mathcal {E}}_2, {\mathcal {E}}_5)$
, in which case the maps
$\operatorname {\mathrm {wSym}}_{1,2,5}({\mathcal {E}}_1, {\mathcal {E}}_2, {\mathcal {E}}_5)$
, in which case the maps
![]() $\epsilon _2$
,
$\epsilon _2$
,
![]() $\epsilon _5$
below have a right inverse.
$\epsilon _5$
below have a right inverse.
The characteristic sheaves of
![]() ${\mathcal {S}}$
are three vector bundles
${\mathcal {S}}$
are three vector bundles
![]() ${\mathcal {E}}_1$
,
${\mathcal {E}}_1$
,
![]() ${\mathcal {E}}_2$
and
${\mathcal {E}}_2$
and
![]() ${\mathcal {E}}_5$
of respective ranks
${\mathcal {E}}_5$
of respective ranks
![]() $2,1,1$
. Set
$2,1,1$
. Set
![]() ${\mathcal {S}}_1:={\mathcal {E}}_1$
and
${\mathcal {S}}_1:={\mathcal {E}}_1$
and
![]() ${\mathcal {S}}[1]=\operatorname {\mathrm {Sym}}{\mathcal {S}}_1$
. We get the short exact sequence
${\mathcal {S}}[1]=\operatorname {\mathrm {Sym}}{\mathcal {S}}_1$
. We get the short exact sequence
where
![]() $\sigma _2$
is locally the inclusion
$\sigma _2$
is locally the inclusion
![]() ${\mathcal {O}}_U[x_0,x_1]_2\to {\mathcal {O}}_U[x_0,x_1,y]_2$
. In this case,
${\mathcal {O}}_U[x_0,x_1]_2\to {\mathcal {O}}_U[x_0,x_1,y]_2$
. In this case,
![]() ${\mathcal {S}}[2]_5$
can be written down explicitly as cokernel of the injective map
${\mathcal {S}}[2]_5$
can be written down explicitly as cokernel of the injective map
given by
The map
![]() $\sigma _5$
is locally the inclusion
$\sigma _5$
is locally the inclusion
![]() ${\mathcal {O}}_U[x_0,x_1,y]_5\to {\mathcal {O}}_U[x_0,x_1,y,z]_5$
, giving the exact sequence
${\mathcal {O}}_U[x_0,x_1,y]_5\to {\mathcal {O}}_U[x_0,x_1,y,z]_5$
, giving the exact sequence
Since the highest weight is
![]() $5$
, we have constructed
$5$
, we have constructed
![]() ${\mathcal {S}}$
.
${\mathcal {S}}$
.
3.2 Bundles in weighted projective spaces
Definition 3.12. Let
![]() ${\mathcal {S}}$
be a weighted symmetric algebra with weights
${\mathcal {S}}$
be a weighted symmetric algebra with weights
![]() $(a_1,\ldots ,a_n)$
. Then,
$(a_1,\ldots ,a_n)$
. Then,
![]() ${\mathbb {F}}:={\mathbf {P}\mathrm{roj}}_B({\mathcal {S}})$
is called a
${\mathbb {F}}:={\mathbf {P}\mathrm{roj}}_B({\mathcal {S}})$
is called a
![]() ${\mathbb {P}}(a_1,\ldots ,a_n)$
-bundle over B.
${\mathbb {P}}(a_1,\ldots ,a_n)$
-bundle over B.
By definition,
![]() ${\mathbb {F}}$
comes with a natural projection
${\mathbb {F}}$
comes with a natural projection
![]() $\pi \colon {\mathbb {F}} \rightarrow B$
whose fibres are all isomorphic to the weighted projective space
$\pi \colon {\mathbb {F}} \rightarrow B$
whose fibres are all isomorphic to the weighted projective space
![]() ${\mathbb {P}}(a_1,\ldots ,a_n)$
. There are also sheaves
${\mathbb {P}}(a_1,\ldots ,a_n)$
. There are also sheaves
![]() ${\mathcal {O}}_{{\mathbb {F}}}(d)$
([Reference GrothendieckGro61, (3.2.5.1)]) for all
${\mathcal {O}}_{{\mathbb {F}}}(d)$
([Reference GrothendieckGro61, (3.2.5.1)]) for all
![]() $d \in {\mathbb {Z}}$
whose restriction on each fibre is isomorphic to the sheaf
$d \in {\mathbb {Z}}$
whose restriction on each fibre is isomorphic to the sheaf
![]() ${\mathcal {O}}_{{\mathbb {P}}(a_1,\ldots ,a_n)}(d)$
. For every coherent sheaf
${\mathcal {O}}_{{\mathbb {P}}(a_1,\ldots ,a_n)}(d)$
. For every coherent sheaf
![]() ${\mathcal {F}}$
on
${\mathcal {F}}$
on
![]() ${\mathbb {F}}$
, we write as usual
${\mathbb {F}}$
, we write as usual
![]() ${\mathcal {F}}(d)$
for
${\mathcal {F}}(d)$
for
![]() ${\mathcal {F}} \otimes {\mathcal {O}}_{\mathbb {F}}(d)$
.
${\mathcal {F}} \otimes {\mathcal {O}}_{\mathbb {F}}(d)$
.
Remark 3.13. By definition for all
![]() $d \geq 0$
,
$d \geq 0$
,
![]() $\pi _* {\mathcal {O}}_{\mathbb {F}}(d) \cong {\mathcal {S}}_d$
, and for all
$\pi _* {\mathcal {O}}_{\mathbb {F}}(d) \cong {\mathcal {S}}_d$
, and for all
![]() $d < 0$
,
$d < 0$
,
![]() $\pi _* {\mathcal {O}}_{\mathbb {F}}(d) =0$
.
$\pi _* {\mathcal {O}}_{\mathbb {F}}(d) =0$
.
Remark 3.14. If L is a line bundle on B, then
![]() ${\mathbf {P}\mathrm{roj}}_B({\mathcal {S}})\cong {\mathbf {P}\mathrm{roj}}_B({\mathcal {S}}\widehat \otimes L)$
, where
${\mathbf {P}\mathrm{roj}}_B({\mathcal {S}})\cong {\mathbf {P}\mathrm{roj}}_B({\mathcal {S}}\widehat \otimes L)$
, where
![]() ${\mathcal {S}}\widehat \otimes L$
is the weighted symmetric algebra with
${\mathcal {S}}\widehat \otimes L$
is the weighted symmetric algebra with
![]() $({\mathcal {S}}\widehat \otimes L)_d={\mathcal {S}}_d\otimes L^d$
.
$({\mathcal {S}}\widehat \otimes L)_d={\mathcal {S}}_d\otimes L^d$
.
Remark 3.15. If
![]() $B={\mathbb {P}}^k$
,
$B={\mathbb {P}}^k$
,
![]() ${\mathcal {S}}=\operatorname {\mathrm {wSym}}_{a_1,\ldots ,a_n} ({\mathcal {E}}_{a_1} , \cdots , {\mathcal {E}}_{a_n})$
and all
${\mathcal {S}}=\operatorname {\mathrm {wSym}}_{a_1,\ldots ,a_n} ({\mathcal {E}}_{a_1} , \cdots , {\mathcal {E}}_{a_n})$
and all
![]() ${\mathcal {E}}_j$
split as sums of line bundles, then
${\mathcal {E}}_j$
split as sums of line bundles, then
![]() ${\mathbb {F}}$
is the toric variety in [Reference MulletMul09, Construction 3.2].
${\mathbb {F}}$
is the toric variety in [Reference MulletMul09, Construction 3.2].
Example 3.16. Suppose
![]() ${\mathcal {E}}_1$
is locally free of rank
${\mathcal {E}}_1$
is locally free of rank
![]() $2$
and
$2$
and
![]() ${\mathcal {E}}_2$
,
${\mathcal {E}}_2$
,
![]() ${\mathcal {E}}_5$
are line bundles on
${\mathcal {E}}_5$
are line bundles on
![]() $B={\mathbb {P}}^1$
. Then,
$B={\mathbb {P}}^1$
. Then,
![]() ${\mathcal {S}}:=\operatorname {\mathrm {wSym}}_{1,2,5}({\mathcal {E}}_1, {\mathcal {E}}_2, {\mathcal {E}}_5)$
is a weighted symmetric algebra with weights
${\mathcal {S}}:=\operatorname {\mathrm {wSym}}_{1,2,5}({\mathcal {E}}_1, {\mathcal {E}}_2, {\mathcal {E}}_5)$
is a weighted symmetric algebra with weights
![]() $(1,1,2,5)$
. Since every vector bundle on
$(1,1,2,5)$
. Since every vector bundle on
![]() ${\mathbb {P}}^1$
splits as a direct sum of line bundles, we may write
${\mathbb {P}}^1$
splits as a direct sum of line bundles, we may write
![]() ${\mathcal {E}}_1={\mathcal {O}}(d_0)\oplus {\mathcal {O}}(d_1)$
,
${\mathcal {E}}_1={\mathcal {O}}(d_0)\oplus {\mathcal {O}}(d_1)$
,
![]() ${\mathcal {E}}_2={\mathcal {O}}(d_2)$
,
${\mathcal {E}}_2={\mathcal {O}}(d_2)$
,
![]() ${\mathcal {E}}_5={\mathcal {O}}(d_5)$
.
${\mathcal {E}}_5={\mathcal {O}}(d_5)$
.
The relative Proj of
![]() ${\mathcal {S}}$
over B is naturally isomorphic to the toric variety
${\mathcal {S}}$
over B is naturally isomorphic to the toric variety
![]() ${\mathbb {C}}^6/\!/({\mathbb {C}}^*)^2$
with weight matrix
${\mathbb {C}}^6/\!/({\mathbb {C}}^*)^2$
with weight matrix
 $$\begin{align*}\begin{pmatrix} t_0 & t_1 & x_0 & x_1 & y & z\\ 1 & 1 & -d_0 & -d_1 & -d_2 & -d_5\\ 0 & 0 & 1 & 1 & 2 & 5 \end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} t_0 & t_1 & x_0 & x_1 & y & z\\ 1 & 1 & -d_0 & -d_1 & -d_2 & -d_5\\ 0 & 0 & 1 & 1 & 2 & 5 \end{pmatrix} \end{align*}$$
and irrelevant ideal
![]() $(t_0,t_1)\cap (x_0,x_1,y,z)$
. If there exists
$(t_0,t_1)\cap (x_0,x_1,y,z)$
. If there exists
![]() $d\in {\mathbb {Z}}$
such that
$d\in {\mathbb {Z}}$
such that
![]() $d_1=3d-d_0$
,
$d_1=3d-d_0$
,
![]() $d_2=2d$
,
$d_2=2d$
,
![]() $d_5=5d$
, then
$d_5=5d$
, then
![]() ${{\mathbf{P}\mathrm{roj}}_B} ({\mathcal {S}})$
is isomorphic to
${{\mathbf{P}\mathrm{roj}}_B} ({\mathcal {S}})$
is isomorphic to
![]() ${\mathbb {F}}(d;d_0)$
, the toric variety with weight matrix (1.1) of §1; indeed, the reader can check that the latter is isomorphic to
${\mathbb {F}}(d;d_0)$
, the toric variety with weight matrix (1.1) of §1; indeed, the reader can check that the latter is isomorphic to
![]() ${\mathbf {P}\mathrm{roj}}_B({\mathcal {S}}\otimes {\mathcal {O}}_{{\mathbb {P}}^1}(-d))$
.
${\mathbf {P}\mathrm{roj}}_B({\mathcal {S}}\otimes {\mathcal {O}}_{{\mathbb {P}}^1}(-d))$
.
Remark 3.17. Not every
![]() ${\mathbb {P}}^n$
-bundle is relative Proj of a symmetric algebra. There is an obstruction which is a torsion element in
${\mathbb {P}}^n$
-bundle is relative Proj of a symmetric algebra. There is an obstruction which is a torsion element in
![]() $H^2({\mathcal {O}}_B^*)$
. Examples are known where B is a 2-dimensional complex torus [Reference Elencwajg and NarasimhanEN83].
$H^2({\mathcal {O}}_B^*)$
. Examples are known where B is a 2-dimensional complex torus [Reference Elencwajg and NarasimhanEN83].
3.3 Relative dualising sheaf
Definition 3.18. We say that a
![]() ${\mathbb {P}}(a_1,\dots ,a_n)$
-bundle over B is well-formed if the fibre
${\mathbb {P}}(a_1,\dots ,a_n)$
-bundle over B is well-formed if the fibre
![]() ${\mathbb {P}}(a_1,\dots ,a_n)$
is well-formed – in other words, if
${\mathbb {P}}(a_1,\dots ,a_n)$
is well-formed – in other words, if
![]() $\operatorname {\mathrm {hcf}}(a_1,\dots ,a_n)=1$
and
$\operatorname {\mathrm {hcf}}(a_1,\dots ,a_n)=1$
and
![]() $\operatorname {\mathrm {hcf}}(a_1,\dots ,\widehat {a_i},\dots ,a_n)=1$
for all i.
$\operatorname {\mathrm {hcf}}(a_1,\dots ,\widehat {a_i},\dots ,a_n)=1$
for all i.
Let
![]() ${\mathbb {F}}$
be a well-formed
${\mathbb {F}}$
be a well-formed
![]() ${\mathbb {P}}(a_1,\dots ,a_n)$
-bundle. Then,
${\mathbb {P}}(a_1,\dots ,a_n)$
-bundle. Then,
![]() ${\mathbb {F}}$
is singular in codimension
${\mathbb {F}}$
is singular in codimension
![]() $\ge 2$
, and we denote by
$\ge 2$
, and we denote by
![]() $j\colon W\to {\mathbb {F}}$
the inclusion of the nonsingular locus W inside
$j\colon W\to {\mathbb {F}}$
the inclusion of the nonsingular locus W inside
![]() ${\mathbb {F}}$
. Recall that
${\mathbb {F}}$
. Recall that
![]() $\omega _{{\mathbb {F}}/B}=j_*\omega _{W/B}$
.
$\omega _{{\mathbb {F}}/B}=j_*\omega _{W/B}$
.
Proposition 3.19. Let
![]() ${\mathbb {F}}={\mathbf {P}\mathrm{roj}}_B({\mathcal {S}})$
be a well-formed
${\mathbb {F}}={\mathbf {P}\mathrm{roj}}_B({\mathcal {S}})$
be a well-formed
![]() ${\mathbb {P}}(a_1^{r_1},\dots ,a_n^{r_n})$
-bundle,
${\mathbb {P}}(a_1^{r_1},\dots ,a_n^{r_n})$
-bundle,
![]() $a_1<a_2<\cdots < a_n$
. There is a sheaf
$a_1<a_2<\cdots < a_n$
. There is a sheaf
![]() ${\mathcal {V}}$
on
${\mathcal {V}}$
on
![]() ${\mathbb {F}}$
and an exact sequence:
${\mathbb {F}}$
and an exact sequence:
This is the relative Euler sequence in the sense that its restriction to a fibre of
![]() $\pi \colon {\mathbb {F}}\to B$
gives the Euler sequence for
$\pi \colon {\mathbb {F}}\to B$
gives the Euler sequence for
![]() ${\mathbb {P}}(a_1^{r_1},\dots ,a_n^{r_n})$
([Reference DolgachevDol82, §2]).
${\mathbb {P}}(a_1^{r_1},\dots ,a_n^{r_n})$
([Reference DolgachevDol82, §2]).
Then, we have
-
1. There is an exact sequence
 $$\begin{align*}0\to\bigoplus_k\pi^*{\mathcal{S}}[a_k-1]_{a_k}\otimes{\mathcal{O}}_{{\mathbb{F}}}(-a_k)\to\bigoplus_k\pi^*{\mathcal{S}}_{a_k}\otimes{\mathcal{O}}_{{\mathbb{F}}}(-a_k)\to{\mathcal{V}}\to0.\end{align*}$$
$$\begin{align*}0\to\bigoplus_k\pi^*{\mathcal{S}}[a_k-1]_{a_k}\otimes{\mathcal{O}}_{{\mathbb{F}}}(-a_k)\to\bigoplus_k\pi^*{\mathcal{S}}_{a_k}\otimes{\mathcal{O}}_{{\mathbb{F}}}(-a_k)\to{\mathcal{V}}\to0.\end{align*}$$
-
2. The relative dualising sheaf of
 ${\mathbb {F}}$
is where
${\mathbb {F}}$
is where $$\begin{align*}\textstyle{\omega_{{{\mathbb{F}}}/B}\cong\pi^*\left( \bigotimes_k \det {\mathcal{E}}_{a_k} \right) \left( -\sum_k r_k a_k \right)}, \end{align*}$$
$$\begin{align*}\textstyle{\omega_{{{\mathbb{F}}}/B}\cong\pi^*\left( \bigotimes_k \det {\mathcal{E}}_{a_k} \right) \left( -\sum_k r_k a_k \right)}, \end{align*}$$
 ${\mathcal {E}}_{a_k}$
is the characteristic sheaf of
${\mathcal {E}}_{a_k}$
is the characteristic sheaf of
 ${\mathcal {S}}$
in degree
${\mathcal {S}}$
in degree
 $a_k$
.
$a_k$
.
Proof. First, consider the following natural map of
![]() ${\mathcal {S}}$
-modules:
${\mathcal {S}}$
-modules:
 $$\begin{align*}\tilde\varphi\colon\bigoplus_{k=1}^n{\mathcal{S}}_{a_k}\otimes{\mathcal{S}}(-a_k)\to{\mathcal{S}},\end{align*}$$
$$\begin{align*}\tilde\varphi\colon\bigoplus_{k=1}^n{\mathcal{S}}_{a_k}\otimes{\mathcal{S}}(-a_k)\to{\mathcal{S}},\end{align*}$$
which is defined on each direct summand by multiplication of sections
![]() $s\otimes t\mapsto \deg s\cdot st$
and then extending by linearity. If we choose local isomorphisms
$s\otimes t\mapsto \deg s\cdot st$
and then extending by linearity. If we choose local isomorphisms
 $$\begin{align*}{\mathcal{S}}_{a_k}|_U\cong{\mathcal{O}}_U[x_1,\dots,x_r]_{a_k}\cong\bigoplus_{i=1}^{N}{\mathcal{O}}_U\cdot \textrm{d} m_{k_i},\end{align*}$$
$$\begin{align*}{\mathcal{S}}_{a_k}|_U\cong{\mathcal{O}}_U[x_1,\dots,x_r]_{a_k}\cong\bigoplus_{i=1}^{N}{\mathcal{O}}_U\cdot \textrm{d} m_{k_i},\end{align*}$$
where
![]() $\textrm {d} m_{k_i}$
,
$\textrm {d} m_{k_i}$
,
![]() $i=1,\dots ,N$
are the free generators corresponding to the monomials
$i=1,\dots ,N$
are the free generators corresponding to the monomials
![]() $m_{k_i}$
in
$m_{k_i}$
in
![]() ${\mathcal {S}}_{a_k}|_U$
of degree
${\mathcal {S}}_{a_k}|_U$
of degree
![]() $a_{k}$
, then
$a_{k}$
, then
![]() $\tilde \varphi $
maps
$\tilde \varphi $
maps
![]() $\textrm {d} m_{k_i}$
to
$\textrm {d} m_{k_i}$
to
![]() $a_k m_{k_i}$
. The degree shift ensures that
$a_k m_{k_i}$
. The degree shift ensures that
![]() $\deg \textrm {d} m_{k_i}=\deg m_{k_i}=a_k$
.
$\deg \textrm {d} m_{k_i}=\deg m_{k_i}=a_k$
.
Let
![]() $\tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
be the kernel of
$\tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
be the kernel of
![]() $\tilde \varphi $
and
$\tilde \varphi $
and
![]() $\tilde \Omega _{{\mathbb {F}}/B}$
its associated sheaf on
$\tilde \Omega _{{\mathbb {F}}/B}$
its associated sheaf on
![]() ${\mathbb {F}}$
. Then, the induced maps of associated sheaves on
${\mathbb {F}}$
. Then, the induced maps of associated sheaves on
![]() ${\mathbb {F}}$
form a short exact sequence
${\mathbb {F}}$
form a short exact sequence
 $$\begin{align*}0\to\tilde\Omega_{{\mathbb{F}}/B}\to\bigoplus_{k=1}^n\pi^*{\mathcal{S}}_{a_k}\otimes{\mathcal{O}}_{{\mathbb{F}}}(-a_k)\to{\mathcal{O}}_{{\mathbb{F}}}\to0,\end{align*}$$
$$\begin{align*}0\to\tilde\Omega_{{\mathbb{F}}/B}\to\bigoplus_{k=1}^n\pi^*{\mathcal{S}}_{a_k}\otimes{\mathcal{O}}_{{\mathbb{F}}}(-a_k)\to{\mathcal{O}}_{{\mathbb{F}}}\to0,\end{align*}$$
where the exactness on the right follows because
![]() $\tilde \varphi $
is surjective in degrees
$\tilde \varphi $
is surjective in degrees
![]() $\ge 1$
.
$\ge 1$
.
Note that
![]() $\tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
is a locally free
$\tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
is a locally free
![]() ${\mathcal {S}}$
-module and using the isomorphism
${\mathcal {S}}$
-module and using the isomorphism
![]() ${\mathcal {S}}|_U\cong {\mathcal {O}}_U[x_1,\dots ,x_r]$
, it has local generators
${\mathcal {S}}|_U\cong {\mathcal {O}}_U[x_1,\dots ,x_r]$
, it has local generators
 $$\begin{align*}a_i \cdot x_i\textrm{d} x_j-a_j\cdot x_j\textrm{d} x_i \ \ \text{ and }\ \ \textrm{d} m_k-\sum_{i=1}^r\dfrac{\partial m_k}{\partial x_i}\textrm{d} x_i,\end{align*}$$
$$\begin{align*}a_i \cdot x_i\textrm{d} x_j-a_j\cdot x_j\textrm{d} x_i \ \ \text{ and }\ \ \textrm{d} m_k-\sum_{i=1}^r\dfrac{\partial m_k}{\partial x_i}\textrm{d} x_i,\end{align*}$$
where here we write
![]() $a_i$
for the degree of
$a_i$
for the degree of
![]() $x_i$
. However,
$x_i$
. However,
![]() $\Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
is locally generated as an
$\Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
is locally generated as an
![]() ${\mathcal {S}}|_U$
-module by the generators of the first type – that is,
${\mathcal {S}}|_U$
-module by the generators of the first type – that is,
![]() $a_i \cdot x_i\textrm {d} x_j-a_j\cdot x_j\textrm {d} x_i$
.
$a_i \cdot x_i\textrm {d} x_j-a_j\cdot x_j\textrm {d} x_i$
.
Let
![]() ${\mathcal {K}}:=\bigoplus _{k=1}^n{\mathcal {S}}[a_k-1]_{a_k}\otimes {\mathcal {S}}(-a_k)$
. We construct a map
${\mathcal {K}}:=\bigoplus _{k=1}^n{\mathcal {S}}[a_k-1]_{a_k}\otimes {\mathcal {S}}(-a_k)$
. We construct a map
![]() $\alpha \colon {\mathcal {K}}\to \tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
whose cokernel is
$\alpha \colon {\mathcal {K}}\to \tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
whose cokernel is
![]() $\Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
. Locally, we define
$\Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
. Locally, we define
![]() $\alpha _U\colon {\mathcal {K}}|_U\to \tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}|_U$
by
$\alpha _U\colon {\mathcal {K}}|_U\to \tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}|_U$
by
 $$\begin{align*}m\otimes 1\mapsto\textrm{d} m-\sum_{i=1}^r\tfrac{\partial m}{\partial x_i}\textrm{d} x_i,\end{align*}$$
$$\begin{align*}m\otimes 1\mapsto\textrm{d} m-\sum_{i=1}^r\tfrac{\partial m}{\partial x_i}\textrm{d} x_i,\end{align*}$$
where
![]() $m=m(x_1,\dots ,x_r)$
is a section of
$m=m(x_1,\dots ,x_r)$
is a section of
![]() ${\mathcal {S}}|_U[a_k-1]_{a_k}$
. Next, we show that
${\mathcal {S}}|_U[a_k-1]_{a_k}$
. Next, we show that
![]() $\alpha $
is well-defined. Suppose that
$\alpha $
is well-defined. Suppose that
![]() ${\mathcal {S}}|_V\cong {\mathcal {O}}_V[x_1',\dots ,x_r']$
. The transition function on
${\mathcal {S}}|_V\cong {\mathcal {O}}_V[x_1',\dots ,x_r']$
. The transition function on
![]() $U\cap V$
is an isomorphism
$U\cap V$
is an isomorphism
![]() $v\colon {\mathcal {O}}_{U\cap V}[x_1',\dots ,x_r']\to {\mathcal {O}}_{U\cap V}[x_1,\dots ,x_r]$
,
$v\colon {\mathcal {O}}_{U\cap V}[x_1',\dots ,x_r']\to {\mathcal {O}}_{U\cap V}[x_1,\dots ,x_r]$
,
![]() $x_i=v_i(x^{\prime }_1,\dots ,x^{\prime }_r)$
. We denote the induced isomorphisms on
$x_i=v_i(x^{\prime }_1,\dots ,x^{\prime }_r)$
. We denote the induced isomorphisms on
![]() ${\mathcal {K}}$
and
${\mathcal {K}}$
and
![]() $\tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
by v as well. Then,
$\tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
by v as well. Then,
 $$\begin{align*}\alpha_U(m(x))=\alpha_U(m(v(x')))=\textrm{d} m(v(x')))-\sum_{i=1}^r \dfrac{\partial m(v(x'))}{\partial v_i}\textrm{d} v_i(x'). \end{align*}$$
$$\begin{align*}\alpha_U(m(x))=\alpha_U(m(v(x')))=\textrm{d} m(v(x')))-\sum_{i=1}^r \dfrac{\partial m(v(x'))}{\partial v_i}\textrm{d} v_i(x'). \end{align*}$$
Now, by the chain rule, we have
 $$ \begin{align*} \left(\tfrac{\partial m(v(x'))}{\partial x_1'},\dots,\tfrac{\partial m(v(x'))}{\partial x_r'}\right)&=\left(\tfrac{\partial m(v)}{\partial v_1},\dots,\tfrac{\partial m(v)}{\partial v_r}\right)\cdot D_{x'}v(x')\ \ \text{and }\\ (\textrm{d} v_1,\dots,\textrm{d} v_r)^t&=D_{x'}v(x')\cdot(\textrm{d} x_1',\dots,\textrm{d} x_r')^t. \end{align*} $$
$$ \begin{align*} \left(\tfrac{\partial m(v(x'))}{\partial x_1'},\dots,\tfrac{\partial m(v(x'))}{\partial x_r'}\right)&=\left(\tfrac{\partial m(v)}{\partial v_1},\dots,\tfrac{\partial m(v)}{\partial v_r}\right)\cdot D_{x'}v(x')\ \ \text{and }\\ (\textrm{d} v_1,\dots,\textrm{d} v_r)^t&=D_{x'}v(x')\cdot(\textrm{d} x_1',\dots,\textrm{d} x_r')^t. \end{align*} $$
Multiplying the first equation on the right by
![]() $D_{x'}v(x')^{-1}$
and combining them, we get
$D_{x'}v(x')^{-1}$
and combining them, we get
 $$\begin{align*}\sum_{i=1}^r \dfrac{\partial m(v(x'))}{\partial v_i}\textrm{d} v_i(x')=\left(\tfrac{\partial m(v(x'))}{\partial x_1'},\dots,\tfrac{\partial m(v(x'))}{\partial x_r'}\right)\cdot(\textrm{d} x_1',\dots,\textrm{d} x_r')^t.\end{align*}$$
$$\begin{align*}\sum_{i=1}^r \dfrac{\partial m(v(x'))}{\partial v_i}\textrm{d} v_i(x')=\left(\tfrac{\partial m(v(x'))}{\partial x_1'},\dots,\tfrac{\partial m(v(x'))}{\partial x_r'}\right)\cdot(\textrm{d} x_1',\dots,\textrm{d} x_r')^t.\end{align*}$$
It follows that
 $$\begin{align*}\alpha_U(m(x))=\textrm{d} m(v(x'))-\sum_{i=1}^r \dfrac{\partial m(v(x'))}{\partial x^{\prime}_i}\textrm{d} x_i'=\alpha_V(m(v(x'))), \end{align*}$$
$$\begin{align*}\alpha_U(m(x))=\textrm{d} m(v(x'))-\sum_{i=1}^r \dfrac{\partial m(v(x'))}{\partial x^{\prime}_i}\textrm{d} x_i'=\alpha_V(m(v(x'))), \end{align*}$$
and thus,
![]() $\alpha $
is well-defined. Hence, we have a short exact sequence
$\alpha $
is well-defined. Hence, we have a short exact sequence
The two short exact sequences involving
![]() $\tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
fit together as the middle row respectively first column of the following commutative diagram:
$\tilde \Omega _{{\mathcal {S}}/{\mathcal {O}}_B}$
fit together as the middle row respectively first column of the following commutative diagram:

The composition
![]() $\tilde \iota \circ \alpha \colon {\mathcal {K}}\to \bigoplus _{k=1}^n{\mathcal {S}}_{a_k}\otimes {\mathcal {S}}(-a_k)$
is injective. We call the cokernel
$\tilde \iota \circ \alpha \colon {\mathcal {K}}\to \bigoplus _{k=1}^n{\mathcal {S}}_{a_k}\otimes {\mathcal {S}}(-a_k)$
is injective. We call the cokernel
![]() ${\mathcal {V}}_{{\mathcal {S}}}$
and fill in the third row using a diagram chasing argument. Since
${\mathcal {V}}_{{\mathcal {S}}}$
and fill in the third row using a diagram chasing argument. Since
![]() $\tilde \varphi $
is surjective in degrees
$\tilde \varphi $
is surjective in degrees
![]() $\ge 1$
,
$\ge 1$
,
![]() $\tilde \varphi =\varphi \circ \beta $
and
$\tilde \varphi =\varphi \circ \beta $
and
![]() $\beta $
is surjective, it follows that
$\beta $
is surjective, it follows that
![]() $\varphi $
is surjective in degrees
$\varphi $
is surjective in degrees
![]() $\ge 1$
. Thus, the sequence of sheaves of
$\ge 1$
. Thus, the sequence of sheaves of
![]() ${\mathcal {O}}_{{\mathbb {F}}}$
-modules associated to the bottom row is the relative Euler sequence (3.2) on
${\mathcal {O}}_{{\mathbb {F}}}$
-modules associated to the bottom row is the relative Euler sequence (3.2) on
![]() ${\mathbb {F}}$
.
${\mathbb {F}}$
.
We can now prove statements (1) and (2).
(1) is proved by taking the exact sequence of sheaves associated to the middle column of the above diagram.
(2) Since
![]() ${\mathbb {F}}$
is well-formed, the singular locus of
${\mathbb {F}}$
is well-formed, the singular locus of
![]() ${\mathbb {F}}$
has codimension
${\mathbb {F}}$
has codimension
![]() $\ge 2$
. Hence, it suffices to prove that the two sheaves are isomorphic on the nonsingular locus
$\ge 2$
. Hence, it suffices to prove that the two sheaves are isomorphic on the nonsingular locus
![]() $W\subset {\mathbb {F}}$
. We restrict the relative Euler sequence (3.2) to W. Then, this is an exact sequence of vector bundles and since
$W\subset {\mathbb {F}}$
. We restrict the relative Euler sequence (3.2) to W. Then, this is an exact sequence of vector bundles and since
![]() $\omega _{W/B}=\det \Omega _{W/B}$
, we deduce that
$\omega _{W/B}=\det \Omega _{W/B}$
, we deduce that
![]() $\omega _{W/B}=\det {\mathcal {V}}$
. By part (1), we conclude that
$\omega _{W/B}=\det {\mathcal {V}}$
. By part (1), we conclude that
![]() $\omega _{W/B}$
is the restriction of
$\omega _{W/B}$
is the restriction of
![]() $\det \left (\bigoplus _{k}\pi ^*{\mathcal {E}}_{a_k}(-a_k)\right )\cong \pi ^*\left ( \bigotimes _k \det {\mathcal {E}}_{a_k} \right )(-\sum _k r_ka_k)$
to W.
$\det \left (\bigoplus _{k}\pi ^*{\mathcal {E}}_{a_k}(-a_k)\right )\cong \pi ^*\left ( \bigotimes _k \det {\mathcal {E}}_{a_k} \right )(-\sum _k r_ka_k)$
to W.
Example 3.20. Let
![]() ${\mathbb {F}}={\mathbb {P}}_B({\mathcal {E}})$
, where
${\mathbb {F}}={\mathbb {P}}_B({\mathcal {E}})$
, where
![]() ${\mathcal {E}}$
is a vector bundle of rank r over B. Then,
${\mathcal {E}}$
is a vector bundle of rank r over B. Then,
![]() $\varphi \colon {\mathcal {E}}\otimes \operatorname {\mathrm {Sym}}{\mathcal {E}}\to (\operatorname {\mathrm {Sym}}{\mathcal {E}})(1)$
is the canonical surjection ([Reference GrothendieckGro61, §4.1]). The cotangent sequence reads
$\varphi \colon {\mathcal {E}}\otimes \operatorname {\mathrm {Sym}}{\mathcal {E}}\to (\operatorname {\mathrm {Sym}}{\mathcal {E}})(1)$
is the canonical surjection ([Reference GrothendieckGro61, §4.1]). The cotangent sequence reads
and the relative dualising sheaf is
![]() $\omega _{{\mathbb {F}}/B}=\pi ^*(\det {\mathcal {E}})(-r)$
.
$\omega _{{\mathbb {F}}/B}=\pi ^*(\det {\mathcal {E}})(-r)$
.
4 Simple fibrations in (1,2)-surfaces
Definition 4.1. A simple fibration in
![]() $(1,2)$
-surfaces is a morphism
$(1,2)$
-surfaces is a morphism
![]() $\pi \colon X \rightarrow B$
between compact varieties of respective dimension
$\pi \colon X \rightarrow B$
between compact varieties of respective dimension
![]() $3$
and
$3$
and
![]() $1$
such that
$1$
such that
-
1. B is smooth;
-
2. X has canonical singularities;
-
3.
 $K_X$
is
$K_X$
is
 $\pi $
-ample;
$\pi $
-ample; -
4. for all
 $p \in B$
, the canonical ring
$p \in B$
, the canonical ring
 $R(X_p, K_{X_p}):=\bigoplus _d H^0(X_p,K_{X_p})$
of the surface
$R(X_p, K_{X_p}):=\bigoplus _d H^0(X_p,K_{X_p})$
of the surface
 $X_p:=\pi ^{*}(p)$
is generated by four elements of respective degree
$X_p:=\pi ^{*}(p)$
is generated by four elements of respective degree
 $1,1,2$
and
$1,1,2$
and
 $5$
and related by a single equation of degree
$5$
and related by a single equation of degree
 $10$
.
$10$
.
The fibres
![]() $X_p$
of
$X_p$
of
![]() $\pi \colon X\to B$
with at worst Du Val singularities are
$\pi \colon X\to B$
with at worst Du Val singularities are
![]() $(1,2)$
-surfaces.
$(1,2)$
-surfaces.
Remark 4.2. In applications, we are interested in
![]() $X,B$
compact. The first part of the forthcoming discussion can be generalized to
$X,B$
compact. The first part of the forthcoming discussion can be generalized to
![]() $\pi \colon X\to B$
proper.
$\pi \colon X\to B$
proper.
Remark 4.3. Suppose that
![]() $X\to B$
is a fibration all of whose fibres
$X\to B$
is a fibration all of whose fibres
![]() $X_b$
are stable Gorenstein surfaces with
$X_b$
are stable Gorenstein surfaces with
![]() $p_g(X_b)=2$
,
$p_g(X_b)=2$
,
![]() $K_{X_b}^2=1$
. Then, X is simple by [Reference Franciosi, Pardini and RollenskeFPR17, Thm 3.3, part 1] and Theorem 4.6 below.
$K_{X_b}^2=1$
. Then, X is simple by [Reference Franciosi, Pardini and RollenskeFPR17, Thm 3.3, part 1] and Theorem 4.6 below.
Nonsimple fibrations
![]() $X \rightarrow B$
whose general fibre is a
$X \rightarrow B$
whose general fibre is a
![]() $(1,2)$
-surface do exist; see [Reference Franciosi, Pardini and RollenskeFPR17, Ex. 4.7] or Example 4.13.
$(1,2)$
-surface do exist; see [Reference Franciosi, Pardini and RollenskeFPR17, Ex. 4.7] or Example 4.13.
Remark 4.4. Theorem 4.23 below proves that all the Gorenstein regular simple fibrations with
![]() $K_X^3=\tfrac {4p_g-10}3$
appear in Section 1. That is, under the above assumptions,
$K_X^3=\tfrac {4p_g-10}3$
appear in Section 1. That is, under the above assumptions,
![]() $\epsilon _2\colon {\mathcal {S}}_2\to {\mathcal {E}}_2$
always has a right inverse.
$\epsilon _2\colon {\mathcal {S}}_2\to {\mathcal {E}}_2$
always has a right inverse.
Example 4.5. Simple fibrations need not be Gorenstein nor stable. For example, consider
where, for simplicity, B is a small disc with coordinate t (it is not difficult to construct an example with B compact). Then, X has nonreduced central fibre a weighted projective space
![]() ${\mathbb {P}}(1,1,2)$
with multiplicity
${\mathbb {P}}(1,1,2)$
with multiplicity
![]() $2$
. Despite this, if
$2$
. Despite this, if
![]() $f|_{t=0}$
is general, then X has only (nonisolated) canonical singularities.
$f|_{t=0}$
is general, then X has only (nonisolated) canonical singularities.
4.1 Relative canonical model
Recall that the relative canonical sheaf of
![]() $\pi \colon X\to B$
is
$\pi \colon X\to B$
is
and the relative canonical algebra of
![]() $\pi $
is the sheaf of
$\pi $
is the sheaf of
![]() ${\mathcal {O}}_B$
-algebras
${\mathcal {O}}_B$
-algebras
Since we assumed that
![]() $K_X$
is
$K_X$
is
![]() $\pi $
-ample, X and
$\pi $
-ample, X and
![]() ${\mathbf {P}\mathrm{roj}}_B{\mathcal {R}}$
are isomorphic.
${\mathbf {P}\mathrm{roj}}_B{\mathcal {R}}$
are isomorphic.
Theorem 4.6. Let
![]() $\pi \colon X\to B$
be a simple fibration in
$\pi \colon X\to B$
be a simple fibration in
![]() $(1,2)$
-surfaces. Then, there is a weighted symmetric algebra
$(1,2)$
-surfaces. Then, there is a weighted symmetric algebra
![]() ${\mathcal {S}}(X)$
with weights
${\mathcal {S}}(X)$
with weights
![]() $(1^2,2,5)$
such that X is isomorphic to a hypersurface of relative degree
$(1^2,2,5)$
such that X is isomorphic to a hypersurface of relative degree
![]() $10$
in the
$10$
in the
![]() ${\mathbb {P}}(1,1,2,5)$
-bundle
${\mathbb {P}}(1,1,2,5)$
-bundle
![]() ${\mathbb {F}}(X):={\mathbf {P}\mathrm{roj}}_B({\mathcal {S}}) \to B$
.
${\mathbb {F}}(X):={\mathbf {P}\mathrm{roj}}_B({\mathcal {S}}) \to B$
.
Proof. Throughout this proof, we use implicitly the formula
![]() $\operatorname {\mathrm {rank}} {\mathcal {R}}_n=h^0(S,K_S)$
, where S is a
$\operatorname {\mathrm {rank}} {\mathcal {R}}_n=h^0(S,K_S)$
, where S is a
![]() $(1,2)$
-surface. Hence,
$(1,2)$
-surface. Hence,
![]() $\operatorname {\mathrm {rank}} {\mathcal {R}}_1=2$
and
$\operatorname {\mathrm {rank}} {\mathcal {R}}_1=2$
and
![]() $\operatorname {\mathrm {rank}}{\mathcal {R}}_n=3+\frac 12n(n-1)$
for
$\operatorname {\mathrm {rank}}{\mathcal {R}}_n=3+\frac 12n(n-1)$
for
![]() $n\ge 2$
.
$n\ge 2$
.
We construct
![]() ${\mathcal {S}}(X)$
as follows: First, consider the weighted symmetric algebra
${\mathcal {S}}(X)$
as follows: First, consider the weighted symmetric algebra
![]() $\operatorname {\mathrm {Sym}} {\mathcal {R}}_1$
with weights
$\operatorname {\mathrm {Sym}} {\mathcal {R}}_1$
with weights
![]() $(1^2)$
. Since any fibre S is mapped to
$(1^2)$
. Since any fibre S is mapped to
![]() ${\mathbb {P}}^1$
by
${\mathbb {P}}^1$
by
![]() $|K_S|$
, there are no relations involving only variables of degree
$|K_S|$
, there are no relations involving only variables of degree
![]() $1$
. Hence, the natural map
$1$
. Hence, the natural map
![]() $\operatorname {\mathrm {Sym}} {\mathcal {R}}_1 \to {\mathcal {R}}$
is injective and an isomorphism in degree
$\operatorname {\mathrm {Sym}} {\mathcal {R}}_1 \to {\mathcal {R}}$
is injective and an isomorphism in degree
![]() $1$
.
$1$
.
The multiplication map
![]() $\sigma _2 \colon \operatorname {\mathrm {Sym}}({\mathcal {R}}_1)_2 \rightarrow {\mathcal {R}}_2$
has cokernel
$\sigma _2 \colon \operatorname {\mathrm {Sym}}({\mathcal {R}}_1)_2 \rightarrow {\mathcal {R}}_2$
has cokernel
![]() ${\mathcal {E}}_2$
which is locally free of rank
${\mathcal {E}}_2$
which is locally free of rank
![]() $1$
because S is mapped onto
$1$
because S is mapped onto
![]() ${\mathbb {P}}(1,1,2)$
by
${\mathbb {P}}(1,1,2)$
by
![]() $|2K_S|$
. Hence, we can construct (cf. §3.1) a weighted symmetric algebra
$|2K_S|$
. Hence, we can construct (cf. §3.1) a weighted symmetric algebra
![]() ${\mathcal {S}}'$
with weights
${\mathcal {S}}'$
with weights
![]() $(1^2,2)$
with an injective morphism
$(1^2,2)$
with an injective morphism
![]() ${\mathcal {S}}'\hookrightarrow {\mathcal {R}}$
, which is an isomorphism in degrees
${\mathcal {S}}'\hookrightarrow {\mathcal {R}}$
, which is an isomorphism in degrees
![]() $1$
,
$1$
,
![]() $2$
,
$2$
,
![]() $3$
and
$3$
and
![]() $4$
.
$4$
.
The cokernel
![]() ${\mathcal {E}}_5$
of the inclusion
${\mathcal {E}}_5$
of the inclusion
![]() ${\mathcal {S}}_5'\hookrightarrow {\mathcal {R}}_5$
is locally free of rank
${\mathcal {S}}_5'\hookrightarrow {\mathcal {R}}_5$
is locally free of rank
![]() $1$
, so we get a weighted symmetric algebra
$1$
, so we get a weighted symmetric algebra
![]() ${\mathcal {S}} \supset {\mathcal {S}}'$
with weights
${\mathcal {S}} \supset {\mathcal {S}}'$
with weights
![]() $(1^2,2,5)$
such that
$(1^2,2,5)$
such that
![]() ${\mathcal {S}}' \cong {\mathcal {S}}[2]$
. There is a morphism
${\mathcal {S}}' \cong {\mathcal {S}}[2]$
. There is a morphism
![]() ${\mathcal {S}} \rightarrow {\mathcal {R}}$
that is an isomorphism in degrees
${\mathcal {S}} \rightarrow {\mathcal {R}}$
that is an isomorphism in degrees
![]() $\le 9$
and thereafter surjective, so inducing an inclusion
$\le 9$
and thereafter surjective, so inducing an inclusion
of X as divisor in a
![]() ${\mathbb {P}}(1,1,2,5)$
-bundle over B. The relative degree of X is then
${\mathbb {P}}(1,1,2,5)$
-bundle over B. The relative degree of X is then
![]() $10$
, the degree of the single equation defining its general fibre.
$10$
, the degree of the single equation defining its general fibre.
Remark 4.7. Conversely, any divisor X of relative degree
![]() $10$
in a
$10$
in a
![]() ${\mathbb {P}}(1^2,2,5)$
-bundle over a smooth curve B and with at worst canonical singularities is a simple fibration in
${\mathbb {P}}(1^2,2,5)$
-bundle over a smooth curve B and with at worst canonical singularities is a simple fibration in
![]() $(1,2)$
-surfaces. Thus, from now on, we assume that a simple fibration is a hypersurface of relative degree
$(1,2)$
-surfaces. Thus, from now on, we assume that a simple fibration is a hypersurface of relative degree
![]() $10$
in a
$10$
in a
![]() ${\mathbb {P}}(1,1,2,5)$
-bundle with
${\mathbb {P}}(1,1,2,5)$
-bundle with
![]() $\omega _{X/B}={\mathcal {O}}_{{\mathbb {F}}}(1)_{|X}$
.
$\omega _{X/B}={\mathcal {O}}_{{\mathbb {F}}}(1)_{|X}$
.
4.2
X as double cover of a
 ${\mathbb {P}}(1,1,2)$
-bundle
${\mathbb {P}}(1,1,2)$
-bundle
We first describe the singular locus of
![]() ${\mathbb {F}}$
as in §1.
${\mathbb {F}}$
as in §1.
Definition 4.8. The singular locus of a
![]() ${\mathbb {P}}(1,1,2,5)$
-bundle over B is the disjoint union of two sections
${\mathbb {P}}(1,1,2,5)$
-bundle over B is the disjoint union of two sections
![]() ${\mathfrak s}_2$
and
${\mathfrak s}_2$
and
![]() ${\mathfrak s}_5$
, where
${\mathfrak s}_5$
, where
![]() ${\mathfrak s}_k$
has Gorenstein index k.
${\mathfrak s}_k$
has Gorenstein index k.
Since X has at worst canonical singularities, we get some constraints on the intersections
![]() $X \cap {\mathfrak {s}}_k$
.
$X \cap {\mathfrak {s}}_k$
.
Proposition 4.9. Let
![]() $\pi \colon X\to B$
be a simple fibration in
$\pi \colon X\to B$
be a simple fibration in
![]() $(1,2)$
-surfaces and suppose that
$(1,2)$
-surfaces and suppose that
![]() $X\subset {\mathbb {F}}(X)$
, where
$X\subset {\mathbb {F}}(X)$
, where
![]() ${\mathbb {F}}(X)$
is the
${\mathbb {F}}(X)$
is the
![]() ${\mathbb {P}}(1,1,2,5)$
-bundle constructed in Theorem 4.6. Then,
${\mathbb {P}}(1,1,2,5)$
-bundle constructed in Theorem 4.6. Then,
-
1.
 $X \cap {\mathfrak {s}}_5=\emptyset $
;
$X \cap {\mathfrak {s}}_5=\emptyset $
; -
2.
 ${\mathfrak {s}}_2 \not \subset X$
.
${\mathfrak {s}}_2 \not \subset X$
.
Proof. (1) Suppose
![]() $p\in X\cap {\mathfrak s}_5$
. Then, in a neighbourhood of p,
$p\in X\cap {\mathfrak s}_5$
. Then, in a neighbourhood of p,
![]() ${\mathbb {F}}(X)$
has a singular point that is a quotient singularity of type
${\mathbb {F}}(X)$
has a singular point that is a quotient singularity of type
![]() $\frac 15(1,1,2,0)$
. Since X is a Cartier divisor, P is a noncanonical singular point of X, at best a
$\frac 15(1,1,2,0)$
. Since X is a Cartier divisor, P is a noncanonical singular point of X, at best a
![]() $\frac 15(1,1,2)$
point, which is a contradiction (see also [Reference Franciosi, Pardini and RollenskeFPR17, Rmk 4.6]).
$\frac 15(1,1,2)$
point, which is a contradiction (see also [Reference Franciosi, Pardini and RollenskeFPR17, Rmk 4.6]).
(2) Suppose
![]() ${\mathfrak {s}}_2\subset X$
. For a general point p in B, there is a local analytic neighbourhood
${\mathfrak {s}}_2\subset X$
. For a general point p in B, there is a local analytic neighbourhood
![]() $p\in V\subset B$
such that the equation of X has the form
$p\in V\subset B$
such that the equation of X has the form
![]() $z^2=q(x_0,x_1)y^4+\dots $
, where q is (at best) a relative quadratic form over V. Thus, in a neighbourhood of
$z^2=q(x_0,x_1)y^4+\dots $
, where q is (at best) a relative quadratic form over V. Thus, in a neighbourhood of
![]() ${\mathfrak {s}}_2$
, X looks like
${\mathfrak {s}}_2$
, X looks like
![]() $V\times \{(z^2=q)\subset \frac 12(1,1,1)\}$
. This is at best a curve of singularities
$V\times \{(z^2=q)\subset \frac 12(1,1,1)\}$
. This is at best a curve of singularities
![]() $V\times \frac 14(1,1)$
[Reference HackingHac16], which is not canonical, a contradiction.
$V\times \frac 14(1,1)$
[Reference HackingHac16], which is not canonical, a contradiction.
We now show that X is a double cover of a
![]() ${\mathbb {P}}(1,1,2)$
-bundle.
${\mathbb {P}}(1,1,2)$
-bundle.
Definition 4.10. We define the truncated subalgebra
![]() ${\mathcal Q}(X):={\mathcal {S}}(X)[2]$
and let
${\mathcal Q}(X):={\mathcal {S}}(X)[2]$
and let
![]() $g \colon {\mathbb {F}}(X) \dashrightarrow {\mathbb {Q}}(X):={\mathbf {P}\mathrm{roj}}_B{\mathcal Q}(X)$
be the natural map corresponding to the inclusion
$g \colon {\mathbb {F}}(X) \dashrightarrow {\mathbb {Q}}(X):={\mathbf {P}\mathrm{roj}}_B{\mathcal Q}(X)$
be the natural map corresponding to the inclusion
![]() $\mathcal {Q}(X)\subset {\mathcal {S}}(X)$
.
$\mathcal {Q}(X)\subset {\mathcal {S}}(X)$
.
In the toric case of §1 or Example 3.16,
![]() ${\mathbb {Q}}(X)$
is naturally isomorphic to the torus invariant divisor
${\mathbb {Q}}(X)$
is naturally isomorphic to the torus invariant divisor
![]() $D_z$
.
$D_z$
.
Lemma 4.11. The restriction
![]() $g_{|X}\colon X\to {\mathbb {Q}}(X)$
is a finite morphism of degree 2. The double-cover involution on X lifts to
$g_{|X}\colon X\to {\mathbb {Q}}(X)$
is a finite morphism of degree 2. The double-cover involution on X lifts to
![]() ${\mathcal {S}}$
(and
${\mathcal {S}}$
(and
![]() $\mathcal R$
) in such a way that the invariant part of
$\mathcal R$
) in such a way that the invariant part of
![]() $\mathcal R$
is
$\mathcal R$
is
![]() $\mathcal Q$
.
$\mathcal Q$
.
Proof. The indeterminacy locus of g is
![]() ${\mathfrak {s}}_5$
, so by Proposition 4.9(1), the restriction
${\mathfrak {s}}_5$
, so by Proposition 4.9(1), the restriction
![]() $g_{|X} \colon X \to {{\mathbb {Q}}(X)}$
is a finite morphism of degree
$g_{|X} \colon X \to {{\mathbb {Q}}(X)}$
is a finite morphism of degree
![]() $2$
. The involution on X which swaps the two sheets of this covering can be lifted to
$2$
. The involution on X which swaps the two sheets of this covering can be lifted to
![]() ${\mathcal {S}}$
.
${\mathcal {S}}$
.
Indeed, on an open subset
![]() $U\subset B$
, we have
$U\subset B$
, we have
![]() ${\mathcal {S}}_{|U}\cong {\mathcal {O}}_U[x_0,x_1,y,z]$
with
${\mathcal {S}}_{|U}\cong {\mathcal {O}}_U[x_0,x_1,y,z]$
with
![]() $\deg x_j=1$
,
$\deg x_j=1$
,
![]() $\deg y=2$
,
$\deg y=2$
,
![]() $\deg z=5$
. Proposition 4.9(1), implies that the coefficient of
$\deg z=5$
. Proposition 4.9(1), implies that the coefficient of
![]() $z^2$
in the equation of X never vanishes; completing the square, we may assume that the equation has the form
$z^2$
in the equation of X never vanishes; completing the square, we may assume that the equation has the form
![]() $z^2=f(x_0,x_1,y)$
. Then, the involution may be lifted to
$z^2=f(x_0,x_1,y)$
. Then, the involution may be lifted to
![]() ${\mathcal {S}}_{|U}$
as the involution fixing
${\mathcal {S}}_{|U}$
as the involution fixing
![]() $x_0,x_1,y$
and mapping
$x_0,x_1,y$
and mapping
![]() $z \mapsto -z$
. These glue in the obvious way to give an involution on
$z \mapsto -z$
. These glue in the obvious way to give an involution on
![]() ${\mathcal {S}}$
and a splitting into invariant and anti-invariant parts:
${\mathcal {S}}$
and a splitting into invariant and anti-invariant parts:
![]() ${\mathcal {S}}={\mathcal {S}}^+ \oplus {\mathcal {S}}^-$
. By construction, the involution preserves X, so we get a splitting
${\mathcal {S}}={\mathcal {S}}^+ \oplus {\mathcal {S}}^-$
. By construction, the involution preserves X, so we get a splitting
![]() ${\mathcal {R}}={\mathcal {R}}^+ \oplus {\mathcal {R}}^-$
, and clearly,
${\mathcal {R}}={\mathcal {R}}^+ \oplus {\mathcal {R}}^-$
, and clearly,
![]() ${\mathcal {R}}^+={\mathcal Q}$
.
${\mathcal {R}}^+={\mathcal Q}$
.
Remark 4.12. Notice the analogy with the splitting of the relative canonical algebra of a genus
![]() $2$
fibration induced by the hyperelliptic involution of the fibres [Reference Catanese and PignatelliCP06, Lem. 4.3].
$2$
fibration induced by the hyperelliptic involution of the fibres [Reference Catanese and PignatelliCP06, Lem. 4.3].
Example 4.13. If we allow the quadric cone to degenerate to a quadric of rank two over a finite number of points of B, then we obtain a fibration in
![]() $(1,2)$
-surfaces that is not simple. For example, consider the complete intersection
$(1,2)$
-surfaces that is not simple. For example, consider the complete intersection
where, for simplicity, B is a small disc with coordinate t. When t is invertible, the fibre
![]() $X_t$
is just a hypersurface of degree
$X_t$
is just a hypersurface of degree
![]() $10$
in
$10$
in
![]() ${\mathbb {P}}(1,1,2,5)$
because
${\mathbb {P}}(1,1,2,5)$
because
![]() $y_0$
is eliminated using
$y_0$
is eliminated using
![]() $\frac 1t x_0x_1$
. However, when t is not invertible, the fibre
$\frac 1t x_0x_1$
. However, when t is not invertible, the fibre
![]() $X_0$
is a reducible surface with two components
$X_0$
is a reducible surface with two components
![]() $(x_i=0)$
. In fact,
$(x_i=0)$
. In fact,
![]() $X_0$
consists of two singular K3 surfaces glued along a line (see [Reference Franciosi, Pardini and RollenskeFPR17, Ex. 4.7]).
$X_0$
consists of two singular K3 surfaces glued along a line (see [Reference Franciosi, Pardini and RollenskeFPR17, Ex. 4.7]).
We describe
![]() ${\mathcal {R}}^-$
as a
${\mathcal {R}}^-$
as a
![]() $\mathcal Q$
-module.
$\mathcal Q$
-module.
Proposition 4.14. The map
![]() $\epsilon _5 \colon {\mathcal {S}}_5(X) \rightarrow {\mathcal {E}}_5$
has a right inverse. Moreover,
$\epsilon _5 \colon {\mathcal {S}}_5(X) \rightarrow {\mathcal {E}}_5$
has a right inverse. Moreover,
Proof. For all
![]() $d\le 4$
, we get
$d\le 4$
, we get
![]() ${\mathcal {S}}_d^+={\mathcal Q}_d$
and thus,
${\mathcal {S}}_d^+={\mathcal Q}_d$
and thus,
![]() ${\mathcal {S}}_d^-=0$
. In degree
${\mathcal {S}}_d^-=0$
. In degree
![]() $5$
,
$5$
,
![]() ${\mathcal {S}}_5^+={\mathcal Q}_5=\ker \epsilon _5$
so that
${\mathcal {S}}_5^+={\mathcal Q}_5=\ker \epsilon _5$
so that
![]() $(\epsilon _5)_{|{\mathcal {S}}_5^-}$
is an isomorphism, whose inverse is a right inverse for
$(\epsilon _5)_{|{\mathcal {S}}_5^-}$
is an isomorphism, whose inverse is a right inverse for
![]() $\epsilon _5$
. Hence,
$\epsilon _5$
. Hence,
![]() ${\mathcal {R}}_5^- \cong {\mathcal {S}}_5^- \cong {\mathcal {E}}_5$
.
${\mathcal {R}}_5^- \cong {\mathcal {S}}_5^- \cong {\mathcal {E}}_5$
.
Now as locally free
![]() ${\mathcal {O}}_B$
-modules,
${\mathcal {O}}_B$
-modules,
![]() ${\mathcal {R}}_d^+$
and
${\mathcal {R}}_d^+$
and
![]() ${\mathcal {R}}_d^-$
are generated by the monomials
${\mathcal {R}}_d^-$
are generated by the monomials
![]() $x_0^ax_1^by^c$
with
$x_0^ax_1^by^c$
with
![]() $a+b+2c=d$
(resp.
$a+b+2c=d$
(resp.
![]() $x_0^ax_1^by^cz$
with
$x_0^ax_1^by^cz$
with
![]() $a+b+2c=d-5$
). Thus, all multiplication maps
$a+b+2c=d-5$
). Thus, all multiplication maps
are isomorphisms, completing the proof.
Now, we describe the ‘equation’ of X in
![]() ${\mathbb {F}}={\mathbf {P}\mathrm{roj}}_B({\mathcal {S}})\xrightarrow {\pi }B$
. For any line bundle
${\mathbb {F}}={\mathbf {P}\mathrm{roj}}_B({\mathcal {S}})\xrightarrow {\pi }B$
. For any line bundle
![]() ${\mathcal {L}}$
on B, there are natural isomorphisms
${\mathcal {L}}$
on B, there are natural isomorphisms
![]() $H^0({\mathbb {F}},{\mathcal {O}}_{{\mathbb {F}}}(d)\otimes \pi _{\mathbb {F}}^* {\mathcal {L}}^{-1}) \cong \operatorname {\mathrm {Hom}}_{{\mathcal {O}}_B}({\mathcal {L}}, {\mathcal {S}}_d)$
. So, X is defined by a map
$H^0({\mathbb {F}},{\mathcal {O}}_{{\mathbb {F}}}(d)\otimes \pi _{\mathbb {F}}^* {\mathcal {L}}^{-1}) \cong \operatorname {\mathrm {Hom}}_{{\mathcal {O}}_B}({\mathcal {L}}, {\mathcal {S}}_d)$
. So, X is defined by a map
![]() $ {\mathcal {L}} \hookrightarrow {\mathcal {S}}_{10}$
for a suitable line bundle
$ {\mathcal {L}} \hookrightarrow {\mathcal {S}}_{10}$
for a suitable line bundle
![]() ${\mathcal {L}}$
. The line bundle can be determined precisely
${\mathcal {L}}$
. The line bundle can be determined precisely
Corollary 4.15. The hypersurface
![]() $X\subset {\mathbb {F}}$
is defined by an injective homomorphism
$X\subset {\mathbb {F}}$
is defined by an injective homomorphism
![]() $ {\mathcal {E}}_5^2 \hookrightarrow {\mathcal {S}}^+_{10}. $
$ {\mathcal {E}}_5^2 \hookrightarrow {\mathcal {S}}^+_{10}. $
Proof. Since the involution of
![]() ${\mathbb {F}}(X)$
preserves X, the image of
${\mathbb {F}}(X)$
preserves X, the image of
![]() ${\mathcal {L}}$
is contained in the invariant part
${\mathcal {L}}$
is contained in the invariant part
![]() ${\mathcal {S}}^+_{10}$
(or in
${\mathcal {S}}^+_{10}$
(or in
![]() ${\mathcal {S}}^-_{10}$
, but this would contradict Proposition 4.9(1)). By Proposition 4.14,
${\mathcal {S}}^-_{10}$
, but this would contradict Proposition 4.9(1)). By Proposition 4.14,
![]() ${\mathcal {E}}_5 \cong {\mathcal {R}}_5^- \cong {\mathcal {S}}_5^-$
. Then,
${\mathcal {E}}_5 \cong {\mathcal {R}}_5^- \cong {\mathcal {S}}_5^-$
. Then,
![]() ${\mathcal {S}}_{10}^+$
splits as
${\mathcal {S}}_{10}^+$
splits as
![]() ${\mathcal Q}_{10} \oplus {\mathcal {E}}_5^2$
. This corresponds locally to separating the polynomials in
${\mathcal Q}_{10} \oplus {\mathcal {E}}_5^2$
. This corresponds locally to separating the polynomials in
![]() $x_0,x_1,y$
from those involving
$x_0,x_1,y$
from those involving
![]() $z^2$
.
$z^2$
.
Consider the induced projection
![]() ${\mathcal {S}}_{10}^+ \to {\mathcal {E}}_5^2$
. Then, Proposition 4.9(1) says that the composition of maps
${\mathcal {S}}_{10}^+ \to {\mathcal {E}}_5^2$
. Then, Proposition 4.9(1) says that the composition of maps
![]() $ {\mathcal {L}} \to {\mathcal {S}}_{10}^+ \to {\mathcal {E}}_5^2 $
is surjective. Therefore, since both
$ {\mathcal {L}} \to {\mathcal {S}}_{10}^+ \to {\mathcal {E}}_5^2 $
is surjective. Therefore, since both
![]() ${\mathcal {L}}$
and
${\mathcal {L}}$
and
![]() ${\mathcal {E}}_5$
are line bundles,
${\mathcal {E}}_5$
are line bundles,
![]() ${\mathcal {L}} \cong {\mathcal {E}}_5^2$
.
${\mathcal {L}} \cong {\mathcal {E}}_5^2$
.
We can now translate the conditions of Proposition 4.9 coming from the canonical singularities of X in terms of the characteristic sheaves
![]() ${\mathcal {E}}_1$
,
${\mathcal {E}}_1$
,
![]() ${\mathcal {E}}_2$
and
${\mathcal {E}}_2$
and
![]() ${\mathcal {E}}_5$
.
${\mathcal {E}}_5$
.
Corollary 4.16.
-
1.
 ${\mathcal {E}}_5 \cong (\det {\mathcal {E}}_1) \otimes {\mathcal {E}}_2$
.
${\mathcal {E}}_5 \cong (\det {\mathcal {E}}_1) \otimes {\mathcal {E}}_2$
. -
2.
 $h^0({\mathcal {E}}_2^3 \otimes (\det {\mathcal {E}}_1)^{-2}) \neq 0$
.
$h^0({\mathcal {E}}_2^3 \otimes (\det {\mathcal {E}}_1)^{-2}) \neq 0$
.
Remark 4.17. Note that (1) together with Proposition 4.14 shows that
![]() ${\mathcal {R}}$
is determined as a
${\mathcal {R}}$
is determined as a
![]() ${\mathcal Q}$
-module by
${\mathcal Q}$
-module by
![]() ${\mathcal Q}$
itself:
${\mathcal Q}$
itself:
Proof. (1) By Proposition 3.19,
and since
![]() $X \in |{\mathcal {O}}_{\mathbb {F}}(10) \otimes \pi ^* {\mathcal {E}}_5^{-2}|$
, the adjunction formula gives
$X \in |{\mathcal {O}}_{\mathbb {F}}(10) \otimes \pi ^* {\mathcal {E}}_5^{-2}|$
, the adjunction formula gives
Finally, by Remark 4.7, we have
![]() $\omega _{X/B}\cong {\mathcal {O}}_{X}(1)$
, so the thesis follows immediately.
$\omega _{X/B}\cong {\mathcal {O}}_{X}(1)$
, so the thesis follows immediately.
(2) This proof is inspired by [Reference PignatelliPig12, Definition 2.4 and Proposition 2.5]). The map
![]() $\operatorname {\mathrm {Sym}}^5(\epsilon _2) \colon \operatorname {\mathrm {Sym}}^5 ({\mathcal {S}}_2) \to {\mathcal {E}}_2^5$
induced by
$\operatorname {\mathrm {Sym}}^5(\epsilon _2) \colon \operatorname {\mathrm {Sym}}^5 ({\mathcal {S}}_2) \to {\mathcal {E}}_2^5$
induced by
![]() $\epsilon _2 \colon {\mathcal {S}}_2 \to {\mathcal {E}}_2$
factors through
$\epsilon _2 \colon {\mathcal {S}}_2 \to {\mathcal {E}}_2$
factors through
![]() ${\mathcal Q}_{10}$
giving a map
${\mathcal Q}_{10}$
giving a map
![]() $\alpha \colon {\mathcal Q}_{10}\to {\mathcal {E}}_2^5$
whose kernel consists of those elements of
$\alpha \colon {\mathcal Q}_{10}\to {\mathcal {E}}_2^5$
whose kernel consists of those elements of
![]() ${\mathcal Q_{10}}$
vanishing along
${\mathcal Q_{10}}$
vanishing along
![]() ${\mathfrak {s}}_2$
.
${\mathfrak {s}}_2$
.
By Corollary 4.15, X is defined by a map
![]() ${\mathcal {E}}_5^2 \rightarrow {\mathcal {S}}_{10}^+\cong {\mathcal Q}_{10} \oplus {\mathcal {E}}_5^2$
, where locally, the factor
${\mathcal {E}}_5^2 \rightarrow {\mathcal {S}}_{10}^+\cong {\mathcal Q}_{10} \oplus {\mathcal {E}}_5^2$
, where locally, the factor
![]() ${\mathcal {E}}_5^2$
gives the multiples of
${\mathcal {E}}_5^2$
gives the multiples of
![]() $z^2$
, and therefore,
$z^2$
, and therefore,
![]() ${\mathcal {E}}_5^2$
is in the ideal sheaf of
${\mathcal {E}}_5^2$
is in the ideal sheaf of
![]() ${\mathfrak {s}}_2$
. Hence,
${\mathfrak {s}}_2$
. Hence,
![]() ${\mathfrak {s}}_2 \not \subset X$
if and only if the composition of the first component of this map
${\mathfrak {s}}_2 \not \subset X$
if and only if the composition of the first component of this map
![]() ${\mathcal {E}}_5^2 \to {\mathcal Q}_{10}$
with
${\mathcal {E}}_5^2 \to {\mathcal Q}_{10}$
with
![]() $\alpha \colon {\mathcal Q}_{10}\to {\mathcal {E}}_2^5$
is not the zero map. Thus,
$\alpha \colon {\mathcal Q}_{10}\to {\mathcal {E}}_2^5$
is not the zero map. Thus,
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {O}}_B}({\mathcal {E}}_5^2,{\mathcal {E}}_2^5)\neq 0$
. Substituting
$\operatorname {\mathrm {Hom}}_{{\mathcal {O}}_B}({\mathcal {E}}_5^2,{\mathcal {E}}_2^5)\neq 0$
. Substituting
![]() ${\mathcal {E}}_5 \cong (\det {\mathcal {E}}_1) \otimes {\mathcal {E}}_2$
, we obtain the result.
${\mathcal {E}}_5 \cong (\det {\mathcal {E}}_1) \otimes {\mathcal {E}}_2$
, we obtain the result.
The corollary suggests the following definition
Definition 4.18. Let
![]() $\pi \colon X\to B$
be a simple fibration in
$\pi \colon X\to B$
be a simple fibration in
![]() $(1,2)$
-surfaces. Then,
$(1,2)$
-surfaces. Then,
Geometrically, N is the expected number of
![]() $\frac 12(1,1,1)$
singularities on X. In fact, by the proof of Corollary 4.16(2), if the divisor in
$\frac 12(1,1,1)$
singularities on X. In fact, by the proof of Corollary 4.16(2), if the divisor in
![]() $|{\mathcal {E}}_2^3 \otimes (\det {\mathcal {E}}_1)^{-2}|$
corresponding to the homomorphism in that proof is reduced, then X intersects
$|{\mathcal {E}}_2^3 \otimes (\det {\mathcal {E}}_1)^{-2}|$
corresponding to the homomorphism in that proof is reduced, then X intersects
![]() ${\mathfrak {s}}_2$
in N quasismooth points of X, of type
${\mathfrak {s}}_2$
in N quasismooth points of X, of type
![]() $\frac 12(1,1,1)$
.
$\frac 12(1,1,1)$
.
4.3 The invariants of a simple fibration in
 $(1,2)$
-surfaces
$(1,2)$
-surfaces
To compute the invariants of a simple fibration in
![]() $(1,2)$
-surfaces, we need the following lemma.
$(1,2)$
-surfaces, we need the following lemma.
Lemma 4.19. Let
![]() $\pi \colon X \rightarrow B$
be a simple fibration in
$\pi \colon X \rightarrow B$
be a simple fibration in
![]() $(1,2)$
-surfaces and suppose
$(1,2)$
-surfaces and suppose
![]() ${\mathcal {L}}$
is any line bundle on B. Then, for
${\mathcal {L}}$
is any line bundle on B. Then, for
![]() $i=0,1$
, we have
$i=0,1$
, we have
and for
![]() $i=2,3$
, we have
$i=2,3$
, we have
 $$\begin{align*}h^i({\mathcal{O}}_{X}(dK_{X/B})\otimes \pi^*{\mathcal{L}})= \left\{\begin{array}{ll} h^{i-2}({\mathcal{L}}) & \text{ for } d=1\\ 0 & \text{ for } d \geq 2. \end{array} \right.\end{align*}$$
$$\begin{align*}h^i({\mathcal{O}}_{X}(dK_{X/B})\otimes \pi^*{\mathcal{L}})= \left\{\begin{array}{ll} h^{i-2}({\mathcal{L}}) & \text{ for } d=1\\ 0 & \text{ for } d \geq 2. \end{array} \right.\end{align*}$$
Proof. Since the fibres are hypersurfaces in weighted projective space, we have
Thus, in combination with the projection formula
we see that the Leray spectral sequence of the direct image of
![]() ${\mathcal {O}}_{X}(dK_{X/B}) \otimes \pi ^*{\mathcal {L}}$
degenerates at page
${\mathcal {O}}_{X}(dK_{X/B}) \otimes \pi ^*{\mathcal {L}}$
degenerates at page
![]() $2$
for each d and
$2$
for each d and
![]() ${\mathcal {L}}$
.
${\mathcal {L}}$
.
Whence for
![]() $i=0,1$
and any
$i=0,1$
and any
![]() $d\ge 1$
, we have
$d\ge 1$
, we have
When
![]() $i=2,3$
, we get
$i=2,3$
, we get
If
![]() $d\geq 2$
, then
$d\geq 2$
, then
![]() $R^2\pi _* {\mathcal {O}}_{X}(dK_{X/B})=0$
by the base change theorem because the fibres are canonically polarised. Thus,
$R^2\pi _* {\mathcal {O}}_{X}(dK_{X/B})=0$
by the base change theorem because the fibres are canonically polarised. Thus,
![]() $h^i({\mathcal {O}}_X(dK_{X/B})\otimes \pi ^*{\mathcal {L}})=0$
for
$h^i({\mathcal {O}}_X(dK_{X/B})\otimes \pi ^*{\mathcal {L}})=0$
for
![]() $d\ge 2$
. When
$d\ge 2$
. When
![]() $d=1$
,
$d=1$
,
![]() $R^2\pi _*{\mathcal {O}}_X(K_{X/B})\cong (\pi _*{\mathcal {O}}_X)^{\vee }$
by Grothendieck duality, so
$R^2\pi _*{\mathcal {O}}_X(K_{X/B})\cong (\pi _*{\mathcal {O}}_X)^{\vee }$
by Grothendieck duality, so
![]() $h^i({\mathcal {O}}_X(K_{X/B})\otimes \pi ^*{\mathcal {L}})=h^{i-2}(\pi _*{\mathcal {O}}_X\otimes {\mathcal {L}})=h^{i-2}({\mathcal {L}})$
.
$h^i({\mathcal {O}}_X(K_{X/B})\otimes \pi ^*{\mathcal {L}})=h^{i-2}(\pi _*{\mathcal {O}}_X\otimes {\mathcal {L}})=h^{i-2}({\mathcal {L}})$
.
Now we compute the birational invariants of X.
Proposition 4.20. Let
![]() $\pi \colon X \rightarrow B$
be a simple projective fibration in
$\pi \colon X \rightarrow B$
be a simple projective fibration in
![]() $(1,2)$
-surfaces. Then,
$(1,2)$
-surfaces. Then,
 $$ \begin{align*} p_g(X)&=h^0({\mathcal{E}}_1 \otimes \omega_B),& q_1(X)&=g(B)=:b,\\ q_2(X)&=h^1({\mathcal{E}}_1 \otimes \omega_B)\leq 2,& \chi(\omega_X)&=\chi({\mathcal{E}}_1)-5\chi({\mathcal{O}}_B). \end{align*} $$
$$ \begin{align*} p_g(X)&=h^0({\mathcal{E}}_1 \otimes \omega_B),& q_1(X)&=g(B)=:b,\\ q_2(X)&=h^1({\mathcal{E}}_1 \otimes \omega_B)\leq 2,& \chi(\omega_X)&=\chi({\mathcal{E}}_1)-5\chi({\mathcal{O}}_B). \end{align*} $$
Proof. The first three equalities follow from Lemma 4.19 with
![]() ${\mathcal {L}}=\omega _B$
. For the last, note that
${\mathcal {L}}=\omega _B$
. For the last, note that
![]() $\chi (\omega _X)=p_g-q_2+q_1-1=\chi ({\mathcal {E}}_1\otimes \omega _B)-\chi ({\mathcal {O}}_B)$
. Then, by the Riemann–Roch Theorem for curves,
$\chi (\omega _X)=p_g-q_2+q_1-1=\chi ({\mathcal {E}}_1\otimes \omega _B)-\chi ({\mathcal {O}}_B)$
. Then, by the Riemann–Roch Theorem for curves,
![]() $\chi ({\mathcal {E}}_1\otimes \omega _B)=\chi ({\mathcal {E}}_1)+2\deg (\omega _B)$
, and the result follows.
$\chi ({\mathcal {E}}_1\otimes \omega _B)=\chi ({\mathcal {E}}_1)+2\deg (\omega _B)$
, and the result follows.
The inequality
![]() $q_2 \leq \operatorname {\mathrm {rank}}({\mathcal {E}}_1)= 2$
follows then by the semipositivity of
$q_2 \leq \operatorname {\mathrm {rank}}({\mathcal {E}}_1)= 2$
follows then by the semipositivity of
![]() ${\mathcal {E}}_1$
([Reference ViehwegVie83, Thm III]).
${\mathcal {E}}_1$
([Reference ViehwegVie83, Thm III]).
Then, we compute the top selfintersection of the canonical divisor of X.
Proposition 4.21. Let
![]() $\pi \colon X \rightarrow B$
be a simple fibration in (1,2)-surfaces. Then,
$\pi \colon X \rightarrow B$
be a simple fibration in (1,2)-surfaces. Then,
Proof. By Lemma 4.19,
![]() $\chi (\omega _X^2)=\chi ({\mathcal {R}}_2\otimes \omega _B^2)$
; twisting the exact sequence
$\chi (\omega _X^2)=\chi ({\mathcal {R}}_2\otimes \omega _B^2)$
; twisting the exact sequence
![]() $ 0\to \operatorname {\mathrm {Sym}}^2({\mathcal {R}}_1)\to {\mathcal {R}}_2 \to {\mathcal {E}}_2 \to 0$
by
$ 0\to \operatorname {\mathrm {Sym}}^2({\mathcal {R}}_1)\to {\mathcal {R}}_2 \to {\mathcal {E}}_2 \to 0$
by
![]() $\omega _B^2$
, we get
$\omega _B^2$
, we get
 $$ \begin{align*} \chi(\omega_X^2)&=\chi({\mathcal{R}}_2\otimes\omega_B^2)\\ &=\chi(S^2({\mathcal{R}}_1\otimes\omega_B))+\chi({\mathcal{E}}_2\otimes\omega_B^2)\\ &=3\chi({\mathcal{R}}_1\otimes\omega_B)-3\chi({\mathcal{O}}_B)+\chi({\mathcal{E}}_2)+\deg\omega_B^2. \end{align*} $$
$$ \begin{align*} \chi(\omega_X^2)&=\chi({\mathcal{R}}_2\otimes\omega_B^2)\\ &=\chi(S^2({\mathcal{R}}_1\otimes\omega_B))+\chi({\mathcal{E}}_2\otimes\omega_B^2)\\ &=3\chi({\mathcal{R}}_1\otimes\omega_B)-3\chi({\mathcal{O}}_B)+\chi({\mathcal{E}}_2)+\deg\omega_B^2. \end{align*} $$
By Proposition 4.20, this last line is equivalent to
However, the Riemann–Roch formula [Reference ReidRei87, Cor. 10.3] gives
Combining these two expressions to eliminate
![]() $\chi (\omega _X^2)$
and simplifying gives
$\chi (\omega _X^2)$
and simplifying gives
![]() $K^3_{X} =2\chi ({\mathcal {E}}_2)-8\chi ({\mathcal {O}}_B)-\frac {N}2$
. Finally, substituting
$K^3_{X} =2\chi ({\mathcal {E}}_2)-8\chi ({\mathcal {O}}_B)-\frac {N}2$
. Finally, substituting
![]() $\chi ({\mathcal {E}}_2)= \frac 13 \left ( N + 2 \chi ({\mathcal {E}}_1)-\chi ({\mathcal {O}}_B) \right ) $
and then
$\chi ({\mathcal {E}}_2)= \frac 13 \left ( N + 2 \chi ({\mathcal {E}}_1)-\chi ({\mathcal {O}}_B) \right ) $
and then
![]() $\chi ({\mathcal {E}}_1)=\chi (\omega _X)+5\chi ({\mathcal {O}}_B)$
, we obtain the result.
$\chi ({\mathcal {E}}_1)=\chi (\omega _X)+5\chi ({\mathcal {O}}_B)$
, we obtain the result.
As a corollary, we get a Noether type inequality for simple fibrations in
![]() $(1,2)$
-surfaces.
$(1,2)$
-surfaces.
Corollary 4.22. Let
![]() $\pi \colon X \rightarrow B$
be a simple fibration in
$\pi \colon X \rightarrow B$
be a simple fibration in
![]() $(1,2)$
-surfaces. Then,
$(1,2)$
-surfaces. Then,
![]() $K^3_{X}\geq \frac 13{(4(p_g-q_2)-10(1-q_1))}$
with equality holding if and only if X is Gorenstein.
$K^3_{X}\geq \frac 13{(4(p_g-q_2)-10(1-q_1))}$
with equality holding if and only if X is Gorenstein.
We conclude this section with the following Theorem, which shows that the results of Section 1 are complete.
Theorem 4.23. Let
![]() $\pi \colon X\to B$
be a Gorenstein regular simple fibration with
$\pi \colon X\to B$
be a Gorenstein regular simple fibration with
![]() $K_X^3=\frac {4p_g-10}3$
. Then, X appears in Section 1.
$K_X^3=\frac {4p_g-10}3$
. Then, X appears in Section 1.
Proof. Since X is regular, we know that
![]() $B={\mathbb {P}}^1$
. Moreover, X is Gorenstein, so
$B={\mathbb {P}}^1$
. Moreover, X is Gorenstein, so
![]() $N=q_2=0$
. By definition of N and Corollary 4.16, there is a d such that
$N=q_2=0$
. By definition of N and Corollary 4.16, there is a d such that
![]() $\det {\mathcal {E}}_1={\mathcal {O}}_{{\mathbb {P}}^1}(3d)$
,
$\det {\mathcal {E}}_1={\mathcal {O}}_{{\mathbb {P}}^1}(3d)$
,
![]() ${\mathcal {E}}_2={\mathcal {O}}_{{\mathbb {P}}^1}(2d)y$
,
${\mathcal {E}}_2={\mathcal {O}}_{{\mathbb {P}}^1}(2d)y$
,
![]() ${\mathcal {E}}_5={\mathcal {O}}_{{\mathbb {P}}^1}(5d)z$
. Moreover, there is a unique
${\mathcal {E}}_5={\mathcal {O}}_{{\mathbb {P}}^1}(5d)z$
. Moreover, there is a unique
![]() $d_0\le 3d-d_0$
such that
$d_0\le 3d-d_0$
such that
![]() ${\mathcal {E}}_1={\mathcal {O}}_{{\mathbb {P}}^1}(d_0)x_0\oplus {\mathcal {O}}_{{\mathbb {P}}^1}(3d-d_0)x_1$
.
${\mathcal {E}}_1={\mathcal {O}}_{{\mathbb {P}}^1}(d_0)x_0\oplus {\mathcal {O}}_{{\mathbb {P}}^1}(3d-d_0)x_1$
.
Now consider the short exact sequence
The main point of the proof is to show that
![]() $\epsilon _2$
has a right inverse.
$\epsilon _2$
has a right inverse.
We have
![]() $\operatorname {\mathrm {Sym}}^2{\mathcal {E}}_1={\mathcal {O}}(2d_0)x_0^2\oplus {\mathcal {O}}(3d)x_0x_1\oplus {\mathcal {O}}(6d-2d_0)x_1^2$
and
$\operatorname {\mathrm {Sym}}^2{\mathcal {E}}_1={\mathcal {O}}(2d_0)x_0^2\oplus {\mathcal {O}}(3d)x_0x_1\oplus {\mathcal {O}}(6d-2d_0)x_1^2$
and
![]() $d,d_0\ge 0$
by Fujita semipositivity. In this case,
$d,d_0\ge 0$
by Fujita semipositivity. In this case,
because
![]() $3d\ge 2d$
and
$3d\ge 2d$
and
![]() $6d-2d_0\ge 2d$
. Standard cohomological arguments allow us to deduce the existence of an inverse when
$6d-2d_0\ge 2d$
. Standard cohomological arguments allow us to deduce the existence of an inverse when
![]() $d_0\ge d$
, so we assume that
$d_0\ge d$
, so we assume that
![]() $d_0\le d-1$
.
$d_0\le d-1$
.
We complete the proof arguing by contradiction. We show that if the extension class in (4.1) corresponding to the above short exact sequence is nontrivial, then
![]() $\operatorname {\mathrm {Hom}}_{{\mathcal {O}}_{{\mathbb {P}}^1}}({\mathcal {E}}_5^2,\mathcal {Q}_{10})$
is zero. Arguing as in the proof of 4.16(2), this implies that
$\operatorname {\mathrm {Hom}}_{{\mathcal {O}}_{{\mathbb {P}}^1}}({\mathcal {E}}_5^2,\mathcal {Q}_{10})$
is zero. Arguing as in the proof of 4.16(2), this implies that
![]() ${\mathfrak {s}}_2\subset X$
, which is a contradiction.
${\mathfrak {s}}_2\subset X$
, which is a contradiction.
Motivated by this, we define
![]() $\mathcal {I}=x_1\mathcal {Q}$
, the sheaf of ideals locally principally generated by
$\mathcal {I}=x_1\mathcal {Q}$
, the sheaf of ideals locally principally generated by
![]() ${\mathcal {O}}(3d-d_0)x_1$
. Then, define
${\mathcal {O}}(3d-d_0)x_1$
. Then, define
![]() $\mathcal {T}=\mathcal {Q}/\mathcal {I}$
and note that
$\mathcal {T}=\mathcal {Q}/\mathcal {I}$
and note that
![]() ${\mathbf {P}\mathrm{roj}}_{{\mathbb {P}}^1}(\mathcal {T})$
is the divisor
${\mathbf {P}\mathrm{roj}}_{{\mathbb {P}}^1}(\mathcal {T})$
is the divisor
![]() $(x_1=0)$
in the
$(x_1=0)$
in the
![]() ${\mathbb {P}}(1,1,2)$
-bundle
${\mathbb {P}}(1,1,2)$
-bundle
![]() ${\mathbb {Q}}(X)$
over
${\mathbb {Q}}(X)$
over
![]() ${\mathbb {P}}^1$
.
${\mathbb {P}}^1$
.
Replacing
![]() ${\mathcal {E}}_1$
with
${\mathcal {E}}_1$
with
![]() $\mathcal {Q}_1$
and
$\mathcal {Q}_1$
and
![]() ${\mathcal {S}}_2$
with
${\mathcal {S}}_2$
with
![]() $\mathcal {Q}_2$
in the above short exact sequence and quotienting by
$\mathcal {Q}_2$
in the above short exact sequence and quotienting by
![]() $\mathcal {I}$
, the multiplication maps in
$\mathcal {I}$
, the multiplication maps in
![]() $\mathcal {T}$
give the following exact sequence
$\mathcal {T}$
give the following exact sequence
and
![]() $\tilde \epsilon _2$
has a right inverse if and only if
$\tilde \epsilon _2$
has a right inverse if and only if
![]() $\epsilon _2$
has, because of (4.1).
$\epsilon _2$
has, because of (4.1).
Since
![]() $\mathcal {T}$
is generated in degree 2, and
$\mathcal {T}$
is generated in degree 2, and
![]() $\mathcal {T}_1$
has rank 1, the multiplication map
$\mathcal {T}_1$
has rank 1, the multiplication map
![]() $\operatorname {\mathrm {Sym}}^{k}\mathcal {T}_2\to \mathcal {T}_{2k}$
is an isomorphism. Note that
$\operatorname {\mathrm {Sym}}^{k}\mathcal {T}_2\to \mathcal {T}_{2k}$
is an isomorphism. Note that
![]() $\mathcal {T}_2$
is a direct sum of two line bundles on
$\mathcal {T}_2$
is a direct sum of two line bundles on
![]() ${\mathbb {P}}^1$
. Thus, if (4.2) does not split, then the maximal degree in
${\mathbb {P}}^1$
. Thus, if (4.2) does not split, then the maximal degree in
![]() $\mathcal {T}_2$
is
$\mathcal {T}_2$
is
![]() $<2d$
, and hence, the maximal degree in
$<2d$
, and hence, the maximal degree in
![]() $\mathcal {T}_{2k}$
is
$\mathcal {T}_{2k}$
is
![]() $<2kd$
.
$<2kd$
.
Since
![]() $\mathcal {T}$
is a quotient of
$\mathcal {T}$
is a quotient of
![]() $\mathcal {Q}$
, we get a surjective map
$\mathcal {Q}$
, we get a surjective map
![]() $\mathcal {Q}_{10}\to \mathcal {T}_{10}$
. Thus, all summands of
$\mathcal {Q}_{10}\to \mathcal {T}_{10}$
. Thus, all summands of
![]() $\mathcal {Q}_{10}$
are line bundles of degree
$\mathcal {Q}_{10}$
are line bundles of degree
![]() $<10d$
. Since
$<10d$
. Since
![]() ${\mathcal {E}}_5^2\cong {\mathcal {O}}(10d)$
, it follows that
${\mathcal {E}}_5^2\cong {\mathcal {O}}(10d)$
, it follows that
![]() $\operatorname {\mathrm {Hom}}({\mathcal {E}}_5^2,\mathcal {Q}_{10})$
is zero. Hence,
$\operatorname {\mathrm {Hom}}({\mathcal {E}}_5^2,\mathcal {Q}_{10})$
is zero. Hence,
![]() $\epsilon _2$
has a right inverse.
$\epsilon _2$
has a right inverse.
We already know that
![]() $\epsilon _5$
has a right inverse by Proposition 4.14. Thus,
$\epsilon _5$
has a right inverse by Proposition 4.14. Thus,
![]() ${\mathcal {S}}(X)\cong \operatorname {\mathrm {wSym}}_{1,2,5}({\mathcal {E}}_1,{\mathcal {E}}_2,{\mathcal {E}}_5)$
, and hence,
${\mathcal {S}}(X)\cong \operatorname {\mathrm {wSym}}_{1,2,5}({\mathcal {E}}_1,{\mathcal {E}}_2,{\mathcal {E}}_5)$
, and hence,
![]() ${\mathbb {F}}$
is a toric variety as in Example 3.16. This finishes the proof.
${\mathbb {F}}$
is a toric variety as in Example 3.16. This finishes the proof.
5 More on threefolds on the Noether line
5.1 Kobayashi’s construction
We relate our simple fibrations with the threefolds on the Noether line constructed by Kobayashi [Reference KobayashiKob92] and generalised by Chen–Hu [Reference Chen and HuCH17].
Proposition 5.1. The smooth threefolds in [Reference Chen and HuCH17, Thm 1.1] are exactly those of Theorem 1.11 part (1) with
![]() $e \leq d$
.
$e \leq d$
.
Proof. In [Reference Chen and HuCH17, Thm 1.1], the authors generalise Kobayashi’s construction to exhibit threefolds
![]() $Y(a,e)$
on the Noether line with canonical image
$Y(a,e)$
on the Noether line with canonical image
![]() ${\mathbb {F}}_{e}$
and
${\mathbb {F}}_{e}$
and
![]() $p_g(Y)=6a-3e-2$
for all pairs of integers
$p_g(Y)=6a-3e-2$
for all pairs of integers
![]() $a,e$
with
$a,e$
with
![]() $a\geq e\geq 0$
excepting
$a\geq e\geq 0$
excepting
![]() $(a,e)=(2,2)$
,
$(a,e)=(2,2)$
,
![]() $(1,1)$
,
$(1,1)$
,
![]() $(1,0)$
,
$(1,0)$
,
![]() $(0,0)$
.
$(0,0)$
.
We show that
![]() $Y(a,e)$
is the same as our
$Y(a,e)$
is the same as our
![]() $X(d;d_0)$
with
$X(d;d_0)$
with
![]() $d=2a-e$
,
$d=2a-e$
,
![]() $d_0=2d-a$
.
$d_0=2d-a$
.
Recall that there is a double cover
![]() $X(d;d_0)\to D_z$
, where
$X(d;d_0)\to D_z$
, where
![]() $D_z$
is a bundle in quadric cones over
$D_z$
is a bundle in quadric cones over
![]() ${\mathbb {P}}^1$
(see Remark 1.5). We perform a weighted blowup
${\mathbb {P}}^1$
(see Remark 1.5). We perform a weighted blowup
![]() $D^{\prime }_z\to D_z$
of the index 2 section
$D^{\prime }_z\to D_z$
of the index 2 section
![]() ${\mathfrak {s}}_2=D_{x_0}\cap D_{x_1}\cap D_z$
and a corresponding blowup
${\mathfrak {s}}_2=D_{x_0}\cap D_{x_1}\cap D_z$
and a corresponding blowup
![]() $X'\to X$
of the preimage of
$X'\to X$
of the preimage of
![]() ${\mathfrak {s}}_2$
in X, to obtain the following diagram:
${\mathfrak {s}}_2$
in X, to obtain the following diagram:

Recall from §1 that
![]() $\delta $
is the positive section and l is the fibre on
$\delta $
is the positive section and l is the fibre on
![]() ${\mathbb {F}}_e$
. We claim that
${\mathbb {F}}_e$
. We claim that
![]() $D^{\prime }_z$
is the following
$D^{\prime }_z$
is the following
![]() ${\mathbb {P}}^1$
-bundle over
${\mathbb {P}}^1$
-bundle over
![]() ${\mathbb {F}}_e$
:
${\mathbb {F}}_e$
:
Indeed, in coordinates, the blowup
![]() $D_z'\to D_z$
is given by
$D_z'\to D_z$
is given by
where u is the section defining the exceptional divisor E. Note that
![]() $s=t_0^{2(d_0-d)}x_0^2$
is a section of
$s=t_0^{2(d_0-d)}x_0^2$
is a section of
![]() ${\mathcal {O}}_{{\mathbb {F}}_e}(2\delta +(d+e)l)$
because
${\mathcal {O}}_{{\mathbb {F}}_e}(2\delta +(d+e)l)$
because
![]() $2(d_0-d)=d+e$
. The rational function
$2(d_0-d)=d+e$
. The rational function
![]() $s/y$
on
$s/y$
on
![]() $D_z$
pulls back to
$D_z$
pulls back to
![]() $su^2/y$
on
$su^2/y$
on
![]() $D_z'$
. Since y,
$D_z'$
. Since y,
![]() $u^2$
are the fibre coordinates of
$u^2$
are the fibre coordinates of
![]() $D_z'\to {\mathbb {F}}_e$
, we get the claimed
$D_z'\to {\mathbb {F}}_e$
, we get the claimed
![]() ${\mathbb {P}}^1$
-bundle over
${\mathbb {P}}^1$
-bundle over
![]() ${\mathbb {F}}_e$
.
${\mathbb {F}}_e$
.
Moreover,
![]() $X'\to D^{\prime }_z$
is a double cover with branch locus
$X'\to D^{\prime }_z$
is a double cover with branch locus
![]() $B+E$
, where
$B+E$
, where
![]() $B\in |{\mathcal {O}}_{D_z'}(5)|$
is the strict transform of the branch divisor of
$B\in |{\mathcal {O}}_{D_z'}(5)|$
is the strict transform of the branch divisor of
![]() $X\to D_z$
and E is the exceptional divisor of
$X\to D_z$
and E is the exceptional divisor of
![]() $D_z'\to D_z$
. This is the Kobayashi–Chen–Hu construction with
$D_z'\to D_z$
. This is the Kobayashi–Chen–Hu construction with
![]() $d+e=2a$
. The condition
$d+e=2a$
. The condition
![]() $a\geq e$
is equivalent to the condition
$a\geq e$
is equivalent to the condition
![]() $e\leq d$
.
$e\leq d$
.
The short list of exclusions
![]() $(a,e)=(2,2),\dots $
mentioned above are just the
$(a,e)=(2,2),\dots $
mentioned above are just the
![]() $X(d;d_0)$
, which violate
$X(d;d_0)$
, which violate
![]() $\min (d,d_0)\geq 3$
(i.e., those with
$\min (d,d_0)\geq 3$
(i.e., those with
![]() $K_X$
nonample).
$K_X$
nonample).
We thus have more smooth examples than [Reference Chen and HuCH17], namely the general Gorenstein regular simple fibration in
![]() $(1,2)$
-surfaces with
$(1,2)$
-surfaces with
![]() $e=\frac 54d$
; that is,
$e=\frac 54d$
; that is,
![]() $8d_0=7d$
. The simplest possible example is
$8d_0=7d$
. The simplest possible example is
![]() $X(8;7)$
:
$X(8;7)$
:
Example 5.2. Choose
![]() $d=8$
,
$d=8$
,
![]() $d_0=7$
, so
$d_0=7$
, so
![]() $e=10$
. The polynomial
$e=10$
. The polynomial
defines a smooth 3-fold
![]() $X(8;7)\subset {\mathbb {F}}(8;7)$
. By Theorem 1.11, this is a canonical 3-fold with
$X(8;7)\subset {\mathbb {F}}(8;7)$
. By Theorem 1.11, this is a canonical 3-fold with
![]() $p_g=22$
and
$p_g=22$
and
![]() $K_X^3=26$
, not belonging to the examples in [Reference Chen and HuCH17, Thm 1.1], since in this case,
$K_X^3=26$
, not belonging to the examples in [Reference Chen and HuCH17, Thm 1.1], since in this case,
![]() $e=10$
,
$e=10$
,
![]() $a=9$
. Therefore, it contradicts [Reference Chen and HuCH17, Prop. 4.6.(b)] and consequently the last assertion in [Reference Chen and HuCH17, Thm 1.3].
$a=9$
. Therefore, it contradicts [Reference Chen and HuCH17, Prop. 4.6.(b)] and consequently the last assertion in [Reference Chen and HuCH17, Thm 1.3].
Remark 5.3 (The discriminant can be disconnected).
If
![]() $e=\frac 54d$
, then we can still blow up the curve
$e=\frac 54d$
, then we can still blow up the curve
![]() ${\mathfrak {s}}_2$
in
${\mathfrak {s}}_2$
in
![]() $D_z$
to obtain a construction in the style of Kobayashi as explained above. Thus,
$D_z$
to obtain a construction in the style of Kobayashi as explained above. Thus,
![]() $X'\to D^{\prime }_z$
is a double cover branched over E and the surface B defined by
$X'\to D^{\prime }_z$
is a double cover branched over E and the surface B defined by
 $$\begin{align*}u^{10}(\underbrace{x_0^{\prime 9}x_1'+\dots+c_{0,10,0}x_1^{\prime 10}}_{a_0})+ u^8y(\underbrace{c_{7,1,1}x_0^{\prime 7}x_1'+\dots}_{a_1})+\dots+y^5.\end{align*}$$
$$\begin{align*}u^{10}(\underbrace{x_0^{\prime 9}x_1'+\dots+c_{0,10,0}x_1^{\prime 10}}_{a_0})+ u^8y(\underbrace{c_{7,1,1}x_0^{\prime 7}x_1'+\dots}_{a_1})+\dots+y^5.\end{align*}$$
The blowup resolves the base locus of
![]() $|K_X|$
, and the projection
$|K_X|$
, and the projection
![]() $X'\to {\mathbb {F}}_e$
onto coordinates
$X'\to {\mathbb {F}}_e$
onto coordinates
![]() $t_0,t_1,x_0',x_1'$
is a genus 2 fibration over
$t_0,t_1,x_0',x_1'$
is a genus 2 fibration over
![]() ${\mathbb {F}}_e$
with fibre
${\mathbb {F}}_e$
with fibre
![]() $(z^2=\sum _i a_i(p)u^{10-2i}y^i)\subset {\mathbb {P}}(1_u,2_y,5_z)$
, where p is a point of
$(z^2=\sum _i a_i(p)u^{10-2i}y^i)\subset {\mathbb {P}}(1_u,2_y,5_z)$
, where p is a point of
![]() ${\mathbb {F}}_e$
and
${\mathbb {F}}_e$
and
![]() $a_i(t_0,t_1,x^{\prime }_0,x^{\prime }_1)$
are the coefficients as in the above displayed formula.
$a_i(t_0,t_1,x^{\prime }_0,x^{\prime }_1)$
are the coefficients as in the above displayed formula.
The discriminant
![]() $\Delta \subset {\mathbb {F}}_e$
of the genus two fibration
$\Delta \subset {\mathbb {F}}_e$
of the genus two fibration
![]() $X'\to {\mathbb {F}}_e$
is reducible because all
$X'\to {\mathbb {F}}_e$
is reducible because all
![]() $a_i$
are divisible by
$a_i$
are divisible by
![]() $x_1'$
. Moreover, the two components of
$x_1'$
. Moreover, the two components of
![]() $\Delta $
are disjoint because the monomial
$\Delta $
are disjoint because the monomial
![]() $x_0^{\prime 9}x_1'$
appears in
$x_0^{\prime 9}x_1'$
appears in
![]() $a_0$
with constant nonzero coefficient.
$a_0$
with constant nonzero coefficient.
5.2 A second component of the moduli space
Theorem 5.4. For every
![]() $p_g\geq 7$
of the form
$p_g\geq 7$
of the form
![]() $3d-2$
, let
$3d-2$
, let
![]() ${\mathcal {N}}_{p_g}^0$
be the subset of the moduli space of canonical threefolds with geometric genus
${\mathcal {N}}_{p_g}^0$
be the subset of the moduli space of canonical threefolds with geometric genus
![]() $p_g$
and
$p_g$
and
![]() $K^3=\frac 43p_g-\frac {10}3$
given by smooth simple fibrations in
$K^3=\frac 43p_g-\frac {10}3$
given by smooth simple fibrations in
![]() $(1,2)$
-surfaces. Then,
$(1,2)$
-surfaces. Then,
![]() ${\mathcal {N}}_{p_g}^0$
has
${\mathcal {N}}_{p_g}^0$
has
-
• one connected component if d is not divisible by
 $8$
,
$8$
, -
• two connected components if d is divisible by
 $8$
.
$8$
.
All these components are unirational.
One component is formed by those 3-folds with canonical image
![]() ${\mathbb {F}}_e$
,
${\mathbb {F}}_e$
,
![]() $0 \leq e \leq d$
. This is an open subset of the moduli space of canonical
$0 \leq e \leq d$
. This is an open subset of the moduli space of canonical
![]() $3$
-folds.
$3$
-folds.
When d is divisible by
![]() $8$
, there is a second component of the moduli space of canonical
$8$
, there is a second component of the moduli space of canonical
![]() $3$
-folds, including smooth
$3$
-folds, including smooth
![]() $3$
-folds whose canonical image is
$3$
-folds whose canonical image is
![]() ${\mathbb {F}}_{\frac 54 d}$
. The intersection of the closures of the components in the moduli space of canonical
${\mathbb {F}}_{\frac 54 d}$
. The intersection of the closures of the components in the moduli space of canonical
![]() $3$
-folds is not empty.
$3$
-folds is not empty.
In particular, the moduli space of canonical
![]() $3$
-folds with given
$3$
-folds with given
![]() $p_g=3d-2$
,
$p_g=3d-2$
,
![]() $K^3=\frac 43p_g-\frac {10}3$
is reducible when d is divisible by
$K^3=\frac 43p_g-\frac {10}3$
is reducible when d is divisible by
![]() $8$
.
$8$
.
Proof. By Propositions 1.6, 2.2, 2.4 and 4.22, all smooth simple fibrations with
![]() $e\neq \frac 54d$
are Gorenstein regular of the form
$e\neq \frac 54d$
are Gorenstein regular of the form
![]() $X(d;d_0)$
with
$X(d;d_0)$
with
![]() $d_0\geq d$
. Moreover, they belong to the same irreducible component of the moduli space of canonical
$d_0\geq d$
. Moreover, they belong to the same irreducible component of the moduli space of canonical
![]() $3$
-folds, whose general element is a
$3$
-folds, whose general element is a
![]() $X\left (d;\left \lfloor \frac 32d \right \rfloor \right )$
.
$X\left (d;\left \lfloor \frac 32d \right \rfloor \right )$
.
Now, assume d divisible by
![]() $8$
and choose
$8$
and choose
![]() $d_0=\frac 78 d$
so that
$d_0=\frac 78 d$
so that
![]() $e=\frac 54d$
. A general scrollar deformation
$e=\frac 54d$
. A general scrollar deformation
![]() ${\mathcal {X}}$
as in §2 gives a degeneration
${\mathcal {X}}$
as in §2 gives a degeneration
![]() $X(d;d_0+1)\leadsto X(d;d_0)$
with singular central fibre
$X(d;d_0+1)\leadsto X(d;d_0)$
with singular central fibre
![]() ${\mathcal {X}}_0$
. Indeed, in the notation of the proofs of Propositions 1.6 and 2.4 in this case, we get first of all
${\mathcal {X}}_0$
. Indeed, in the notation of the proofs of Propositions 1.6 and 2.4 in this case, we get first of all
-
•
 $\deg c_{10,0,0} <0 \Rightarrow \mathfrak {s}_0\subset X(d;d_0)$
.
$\deg c_{10,0,0} <0 \Rightarrow \mathfrak {s}_0\subset X(d;d_0)$
. -
•
 $\deg c_{9,1,0} =0$
and
$\deg c_{9,1,0} =0$
and
 $c_{9,1,0} \in (t_0,t_1)^{e-1} \Rightarrow c_{9,1,0}=0$
that implies
$c_{9,1,0} \in (t_0,t_1)^{e-1} \Rightarrow c_{9,1,0}=0$
that implies
 $\mathfrak {s}_0\subset \operatorname {\mathrm {Sing}} X(d;d_0)$
and then the degeneration
$\mathfrak {s}_0\subset \operatorname {\mathrm {Sing}} X(d;d_0)$
and then the degeneration
 ${\mathcal {X}}_0$
can not be smooth.
${\mathcal {X}}_0$
can not be smooth.
However, for general
![]() ${\mathcal {X}}$
,
${\mathcal {X}}$
,
![]() ${\mathcal {X}}_0$
is canonical. Indeed,
${\mathcal {X}}_0$
is canonical. Indeed,
![]() $\deg c_{7,3,0} =2e$
. Then, following the argument of the proof of Proposition 2.4, we may get any
$\deg c_{7,3,0} =2e$
. Then, following the argument of the proof of Proposition 2.4, we may get any
![]() $c_{7,3,0} \in (t_0,t_1^{e-1})^3$
of degree
$c_{7,3,0} \in (t_0,t_1^{e-1})^3$
of degree
![]() $2e$
: these are all the multiples of
$2e$
: these are all the multiples of
![]() $t_0$
, and, in particular, we may get
$t_0$
, and, in particular, we may get
![]() $c_{7,3,0} $
with distinct roots – that is, the condition we used in Proposition 1.6 to ensure that the general element has canonical singularities. In particular, near
$c_{7,3,0} $
with distinct roots – that is, the condition we used in Proposition 1.6 to ensure that the general element has canonical singularities. In particular, near
![]() $t_0=0$
,
$t_0=0$
,
![]() ${\mathcal {X}}_0$
looks like
${\mathcal {X}}_0$
looks like
![]() $(z^2+y^5+t_0x_1^3=0)$
, which is canonical by §1.4.
$(z^2+y^5+t_0x_1^3=0)$
, which is canonical by §1.4.
We now show that there is no degeneration
![]() $X(d;d_0)\leadsto X\left ( d; \frac 78 d \right )$
with
$X(d;d_0)\leadsto X\left ( d; \frac 78 d \right )$
with
![]() $d_0 \ge d$
and all fibres nonsingular. The argument is inspired by Horikawa [Reference HorikawaHor76a, Lemma 7.3], although it is more complicated to set up in our situation. Suppose, by contradiction, that
$d_0 \ge d$
and all fibres nonsingular. The argument is inspired by Horikawa [Reference HorikawaHor76a, Lemma 7.3], although it is more complicated to set up in our situation. Suppose, by contradiction, that
![]() ${\mathcal {X}}\to \Lambda $
is such a degeneration. The relative canonical linear system
${\mathcal {X}}\to \Lambda $
is such a degeneration. The relative canonical linear system
![]() $|K_{{\mathcal {X}}/\Lambda }|$
gives a rational map
$|K_{{\mathcal {X}}/\Lambda }|$
gives a rational map
![]() ${\mathcal {X}}/\Lambda \to {\mathcal {F}}/\Lambda $
, where
${\mathcal {X}}/\Lambda \to {\mathcal {F}}/\Lambda $
, where
![]() ${\mathcal {F}}$
is a degeneration of surfaces
${\mathcal {F}}$
is a degeneration of surfaces
![]() ${\mathbb {F}}_{3d-2d_0}\leadsto {\mathbb {F}}_{\frac 54d}$
. If
${\mathbb {F}}_{3d-2d_0}\leadsto {\mathbb {F}}_{\frac 54d}$
. If
![]() $3d-2d_0\ne 0$
, then the Hirzebruch surface
$3d-2d_0\ne 0$
, then the Hirzebruch surface
![]() ${\mathbb {F}}_{3d-2d_0}$
admits a unique fibration to
${\mathbb {F}}_{3d-2d_0}$
admits a unique fibration to
![]() ${\mathbb {P}}^1$
. However, if
${\mathbb {P}}^1$
. However, if
![]() $3d-2d_0=0$
, then
$3d-2d_0=0$
, then
![]() $d\ge 3$
and by §1.9, one of the two fibrations
$d\ge 3$
and by §1.9, one of the two fibrations
![]() ${\mathbb {F}}_0\to {\mathbb {P}}^1$
is distinguished by the canonical linear system of X. Thus, each fibre of
${\mathbb {F}}_0\to {\mathbb {P}}^1$
is distinguished by the canonical linear system of X. Thus, each fibre of
![]() ${\mathcal {F}}/\Lambda $
has a unique distinguished fibration to
${\mathcal {F}}/\Lambda $
has a unique distinguished fibration to
![]() ${\mathbb {P}}^1$
, and hence,
${\mathbb {P}}^1$
, and hence,
![]() ${\mathcal {X}}/\Lambda $
admits a map to
${\mathcal {X}}/\Lambda $
admits a map to
![]() ${\mathbb {P}}^1_{\Lambda }={\mathbb {P}}^1\times \Lambda $
factoring through
${\mathbb {P}}^1_{\Lambda }={\mathbb {P}}^1\times \Lambda $
factoring through
![]() ${\mathcal {F}}/\Lambda $
. Moreover, this map induces the fibration in
${\mathcal {F}}/\Lambda $
. Moreover, this map induces the fibration in
![]() $(1,2)$
-surfaces
$(1,2)$
-surfaces
![]() ${\mathcal {X}}_\lambda \to {\mathbb {P}}^1$
on each fibre.
${\mathcal {X}}_\lambda \to {\mathbb {P}}^1$
on each fibre.
Now, the relative bicanonical linear system
![]() $|2K_{{\mathcal {X}}/{\mathbb {P}}^1_\Lambda }|$
endows
$|2K_{{\mathcal {X}}/{\mathbb {P}}^1_\Lambda }|$
endows
![]() ${\mathcal {X}}$
with a double cover structure of the quadric cone bundle
${\mathcal {X}}$
with a double cover structure of the quadric cone bundle
![]() $\mathcal {Q}\to {\mathbb {P}}^1_{\Lambda }$
. This is the relative version of the double cover
$\mathcal {Q}\to {\mathbb {P}}^1_{\Lambda }$
. This is the relative version of the double cover
![]() $X\to {\mathbb {Q}}(X)$
on each fibre as defined in 4.10. The branch locus consists of a divisor
$X\to {\mathbb {Q}}(X)$
on each fibre as defined in 4.10. The branch locus consists of a divisor
![]() $\mathcal {B}\subset \mathcal {Q}$
and the special section
$\mathcal {B}\subset \mathcal {Q}$
and the special section
![]() ${\mathfrak {s}}_2\colon {\mathbb {P}}^1_{\Lambda }\to \mathcal {Q}/\Lambda $
corresponding to the vertex on each fibre of
${\mathfrak {s}}_2\colon {\mathbb {P}}^1_{\Lambda }\to \mathcal {Q}/\Lambda $
corresponding to the vertex on each fibre of
![]() $\mathcal {Q}/{\mathbb {P}}^1_{\Lambda }$
. In particular, we have a distinguished element y which cuts out a divisor in
$\mathcal {Q}/{\mathbb {P}}^1_{\Lambda }$
. In particular, we have a distinguished element y which cuts out a divisor in
![]() $\mathcal {Q}$
which is isomorphic to
$\mathcal {Q}$
which is isomorphic to
![]() ${\mathcal {F}}$
. Thus, the family
${\mathcal {F}}$
. Thus, the family
![]() $({\mathcal {F}},\mathcal {B}|_{y=0})$
is a degeneration of pairs
$({\mathcal {F}},\mathcal {B}|_{y=0})$
is a degeneration of pairs
where the general B is irreducible, but the central
![]() $B_0$
is disconnected. This is impossible since, as observed by Horikawa [Reference HorikawaHor76a, Lemma 7.3, p. 382], if t is sufficiently close to
$B_0$
is disconnected. This is impossible since, as observed by Horikawa [Reference HorikawaHor76a, Lemma 7.3, p. 382], if t is sufficiently close to
![]() $0$
, then
$0$
, then
![]() $\mathcal {B}_t$
must be disconnected.
$\mathcal {B}_t$
must be disconnected.
6 Threefolds with
 $K_X$
big but not nef
$K_X$
big but not nef
In this section, we analyse those
![]() $X(d;d_0)$
with
$X(d;d_0)$
with
![]() $\min (d,d_0)=0,1$
and at worst canonical singularities. First, by Proposition 1.6, we have
$\min (d,d_0)=0,1$
and at worst canonical singularities. First, by Proposition 1.6, we have
![]() $0\le \frac 14d\le d_0 \le \frac 32d$
. Hence, if
$0\le \frac 14d\le d_0 \le \frac 32d$
. Hence, if
![]() $\min (d,d_0)=0$
, then
$\min (d,d_0)=0$
, then
![]() $d=d_0=0$
and
$d=d_0=0$
and
![]() $X(0;0)$
is a product
$X(0;0)$
is a product
![]() ${\mathbb {P}}^1\times (S_{10}\subset {\mathbb {P}}(1,1,2,5))$
. Second, if
${\mathbb {P}}^1\times (S_{10}\subset {\mathbb {P}}(1,1,2,5))$
. Second, if
![]() $\min (d,d_0)=1$
, then
$\min (d,d_0)=1$
, then
![]() $d_0=1$
and there are four possibilities, the first of which is
$d_0=1$
and there are four possibilities, the first of which is
![]() $X(1;1)$
, which has Kodaira dimension
$X(1;1)$
, which has Kodaira dimension
![]() $0$
. The other three are more interesting to us.
$0$
. The other three are more interesting to us.
Proposition 6.1. Consider
![]() $X=X(d;1)$
with
$X=X(d;1)$
with
![]() $d=2,3,4$
. Then, X has canonical singularities along
$d=2,3,4$
. Then, X has canonical singularities along
![]() ${\mathfrak {s}}_0$
, and
${\mathfrak {s}}_0$
, and
![]() $K_X$
is big but not nef. After flipping the negative curve
$K_X$
is big but not nef. After flipping the negative curve
![]() ${\mathfrak {s}}_0$
, we get a quasismooth variety
${\mathfrak {s}}_0$
, we get a quasismooth variety
![]() $X^+(d;1)$
in
$X^+(d;1)$
in
![]() ${\mathbb {F}}^+(d;1)$
with
${\mathbb {F}}^+(d;1)$
with
![]() $K_{X^+}$
nef and big. The invariants of
$K_{X^+}$
nef and big. The invariants of
![]() $X^+$
are listed in Table 1.
$X^+$
are listed in Table 1.
Table 1 Threefolds with
![]() $K_X$
not nef.
$K_X$
not nef.

Since
![]() $X(2;1)$
has a model as a hypersurface in weighted projective space (see Remark 6.3), it can be found using the methods of [Reference Brown, Kasprzyk and ZhuBKZ19], [Reference Brown and KasprzykBK16]. The
$X(2;1)$
has a model as a hypersurface in weighted projective space (see Remark 6.3), it can be found using the methods of [Reference Brown, Kasprzyk and ZhuBKZ19], [Reference Brown and KasprzykBK16]. The
![]() $3$
-folds
$3$
-folds
![]() $X(3;1)$
and
$X(3;1)$
and
![]() $X(4;1)$
are in [Reference Chen, Jiang and LiCJL20, Table 10], respectively in lines
$X(4;1)$
are in [Reference Chen, Jiang and LiCJL20, Table 10], respectively in lines
![]() $8$
and
$8$
and
![]() $10$
.
$10$
.
Proof. Since
![]() $d_0=1$
and
$d_0=1$
and
![]() $d\ge 2$
, we know that X is singular along
$d\ge 2$
, we know that X is singular along
![]() ${\mathfrak {s}}_0$
by Proposition 1.6. Moreover, by Lemma 1.8 and its proof, we have
${\mathfrak {s}}_0$
by Proposition 1.6. Moreover, by Lemma 1.8 and its proof, we have
![]() $K_X\cdot {\mathfrak {s}}_0=(-2F+H)\cdot {\mathfrak {s}}_0=d_0-2=-1<0$
; hence,
$K_X\cdot {\mathfrak {s}}_0=(-2F+H)\cdot {\mathfrak {s}}_0=d_0-2=-1<0$
; hence,
![]() $K_X$
is not nef.
$K_X$
is not nef.
We determine a minimal model for X by applying the toric minimal model program to
![]() ${\mathbb {F}}(d;1)$
(see [Reference Cox, Little and SchenckCLS11, §15]). The ray spanned by the class of the curve
${\mathbb {F}}(d;1)$
(see [Reference Cox, Little and SchenckCLS11, §15]). The ray spanned by the class of the curve
![]() ${\mathfrak {s}}_0$
is extremal in
${\mathfrak {s}}_0$
is extremal in
![]() $\operatorname {\mathrm {\overline {NE}}}({\mathbb {F}})$
, and there is a birational map
$\operatorname {\mathrm {\overline {NE}}}({\mathbb {F}})$
, and there is a birational map
![]() ${\mathbb {F}}\dashrightarrow {\mathbb {F}}^+$
which flips
${\mathbb {F}}\dashrightarrow {\mathbb {F}}^+$
which flips
![]() ${\mathfrak {s}}_0$
to a weighted projective plane
${\mathfrak {s}}_0$
to a weighted projective plane
![]() $S^+$
. The flipped variety
$S^+$
. The flipped variety
![]() ${\mathbb {F}}^+$
is toric with the same weight matrix as
${\mathbb {F}}^+$
is toric with the same weight matrix as
![]() ${\mathbb {F}}$
, but the irrelevant ideal is changed to
${\mathbb {F}}$
, but the irrelevant ideal is changed to
![]() $(t_0,t_1,x_0)\cap (x_1,y,z)$
. The nef cone of
$(t_0,t_1,x_0)\cap (x_1,y,z)$
. The nef cone of
![]() ${\mathbb {F}}^+$
is
${\mathbb {F}}^+$
is
![]() ${\mathbb {R}}_+(H-F)+{\mathbb {R}}_+(H-dF)$
. Hence,
${\mathbb {R}}_+(H-F)+{\mathbb {R}}_+(H-dF)$
. Hence,
![]() $H-2F$
is (at least) nef on
$H-2F$
is (at least) nef on
![]() ${\mathbb {F}}^+$
.
${\mathbb {F}}^+$
.
The birational transform
![]() $X^+$
is defined by the same element of
$X^+$
is defined by the same element of
![]() $|{10(H-dF)}|$
as X was, but we consider
$|{10(H-dF)}|$
as X was, but we consider
![]() $X^+$
as a subvariety of
$X^+$
as a subvariety of
![]() ${\mathbb {F}}^+$
. By the above discussion,
${\mathbb {F}}^+$
. By the above discussion,
![]() $K_{X^+}=(H-2F)_{X^+}$
is nef.
$K_{X^+}=(H-2F)_{X^+}$
is nef.
The rest of the proof is a case by case computation, showing that
![]() $X^+$
is quasismooth, determining the quotient singularities of
$X^+$
is quasismooth, determining the quotient singularities of
![]() $X^+$
and the invariants
$X^+$
and the invariants
![]() $p_g$
and
$p_g$
and
![]() $K^3$
(see the following example for
$K^3$
(see the following example for
![]() $X^+(2;1)$
).
$X^+(2;1)$
).
Example 6.2. Consider the toric variety
![]() ${\mathbb {F}}^+(2;1)$
with weight matrix
${\mathbb {F}}^+(2;1)$
with weight matrix
![]() $\left (\begin {smallmatrix} 1 & 1 & 1 & -3 & 0 & 0 \\ 0 & 0 & 1 & 1 & 2 & 5 \end {smallmatrix}\right )$
and irrelevant ideal
$\left (\begin {smallmatrix} 1 & 1 & 1 & -3 & 0 & 0 \\ 0 & 0 & 1 & 1 & 2 & 5 \end {smallmatrix}\right )$
and irrelevant ideal
![]() $(t_0,t_1,x_0)\cap (x_1,y,z)$
. Let
$(t_0,t_1,x_0)\cap (x_1,y,z)$
. Let
![]() $X^+(2;1)$
be a general element of the linear system
$X^+(2;1)$
be a general element of the linear system
![]() $|{10(H-2F)}|$
. After the usual coordinate changes (see §1), the equation of
$|{10(H-2F)}|$
. After the usual coordinate changes (see §1), the equation of
![]() $X^+$
can be written as
$X^+$
can be written as
where g is contained in the ideal
![]() $(t_0,t_1)$
and for simplicity, we set all coefficients to be 1. More precisely, a Newton polygon computation shows that
$(t_0,t_1)$
and for simplicity, we set all coefficients to be 1. More precisely, a Newton polygon computation shows that
![]() $x_1g(1,1,1,x_1,y)$
does not contain any monomials
$x_1g(1,1,1,x_1,y)$
does not contain any monomials
![]() $x_1^\alpha y^\beta $
with
$x_1^\alpha y^\beta $
with
![]() $\beta <5-2\alpha $
, and thus,
$\beta <5-2\alpha $
, and thus,
![]() $X(2;1)$
has a curve of
$X(2;1)$
has a curve of
![]() $D_6$
singularities along
$D_6$
singularities along
![]() ${\mathfrak {s}}_0$
.
${\mathfrak {s}}_0$
.
Taking the irrelevant ideal into account, we see that the base locus of
![]() $|{10(H-2F)}|$
in
$|{10(H-2F)}|$
in
![]() ${\mathbb {F}}^+(2;1)$
is the single point
${\mathbb {F}}^+(2;1)$
is the single point
![]() $P\colon (t_0=t_1=y=z=0)$
. Moreover,
$P\colon (t_0=t_1=y=z=0)$
. Moreover,
![]() $X^+$
is quasismooth at P because the equation contains the monomial
$X^+$
is quasismooth at P because the equation contains the monomial
![]() $x_0^6x_1^2y$
, so the affine cone over
$x_0^6x_1^2y$
, so the affine cone over
![]() $X^+$
is nonsingular at P.
$X^+$
is nonsingular at P.
The flipped locus on
![]() ${\mathbb {F}}^+$
is
${\mathbb {F}}^+$
is
![]() $S^+$
defined by
$S^+$
defined by
![]() $t_0=t_1=0$
, which implies that
$t_0=t_1=0$
, which implies that
![]() $x_0\ne 0$
because of the irrelevant ideal. Hence, we can rescale
$x_0\ne 0$
because of the irrelevant ideal. Hence, we can rescale
![]() $x_0$
to eliminate one of the
$x_0$
to eliminate one of the
![]() ${\mathbb {C}}^*$
-actions on
${\mathbb {C}}^*$
-actions on
![]() ${\mathbb {F}}^+$
. Row operations on the weight matrix show that the remaining
${\mathbb {F}}^+$
. Row operations on the weight matrix show that the remaining
![]() ${\mathbb {C}}^*$
-action reduces to
${\mathbb {C}}^*$
-action reduces to
 $$\begin{align*}\begin{pmatrix} t_0 & t_1 & x_1 & y & z \\ -1 & -1 & 4 & 2 & 5 \end{pmatrix}.\end{align*}$$
$$\begin{align*}\begin{pmatrix} t_0 & t_1 & x_1 & y & z \\ -1 & -1 & 4 & 2 & 5 \end{pmatrix}.\end{align*}$$
Thus,
![]() $S^+\cong {\mathbb {P}}(4,2,5)$
and the flipped curve
$S^+\cong {\mathbb {P}}(4,2,5)$
and the flipped curve
![]() ${\mathfrak {s}}_0^+=X^+\cap S^+$
is defined by
${\mathfrak {s}}_0^+=X^+\cap S^+$
is defined by
![]() $z^2+y^5+x_1y^3+x_1^2y=0$
in
$z^2+y^5+x_1y^3+x_1^2y=0$
in
![]() $S^+$
.
$S^+$
.
Next we determine the quotient singularities of
![]() $X^+$
. Using the row-reduced weight matrix, we may identify the orbifold charts on
$X^+$
. Using the row-reduced weight matrix, we may identify the orbifold charts on
![]() ${\mathbb {F}}^+$
covering
${\mathbb {F}}^+$
covering
![]() ${\mathfrak {s}}_0^+$
; they are
${\mathfrak {s}}_0^+$
; they are
![]() $U_{x_0,x_1}\cong \frac 14(3,3,2,1)$
,
$U_{x_0,x_1}\cong \frac 14(3,3,2,1)$
,
![]() $U_{x_0,y}\cong \frac 12(1,1,2,1)$
and
$U_{x_0,y}\cong \frac 12(1,1,2,1)$
and
![]() $U_{x_0,z}\cong \frac 15(4,4,4,2)$
. Note that
$U_{x_0,z}\cong \frac 15(4,4,4,2)$
. Note that
![]() $U_{x_0,x_1}$
and
$U_{x_0,x_1}$
and
![]() $U_{x_0,y}$
cover a curve
$U_{x_0,y}$
cover a curve
![]() $\Gamma \cong {\mathbb {P}}(4,2)$
of
$\Gamma \cong {\mathbb {P}}(4,2)$
of
![]() $\frac 12(1,1,1)$
singularities containing a dissident
$\frac 12(1,1,1)$
singularities containing a dissident
![]() $\frac 14(3,3,1)$
point. Since
$\frac 14(3,3,1)$
point. Since
![]() $X^+\cap \Gamma $
is defined by
$X^+\cap \Gamma $
is defined by
![]() $y^5+x_1y^3+x_1^2y=0$
, we see that
$y^5+x_1y^3+x_1^2y=0$
, we see that
![]() $X^+$
contains two
$X^+$
contains two
![]() $\frac 12(1,1,1)$
points and the
$\frac 12(1,1,1)$
points and the
![]() $\frac 14(3,3,1)$
point. The other chart
$\frac 14(3,3,1)$
point. The other chart
![]() $U_{x_0,z}$
has an isolated index 5 singularity which is not contained in
$U_{x_0,z}$
has an isolated index 5 singularity which is not contained in
![]() $X^+$
because of the monomial
$X^+$
because of the monomial
![]() $z^2$
.
$z^2$
.
Thus, the basket of singularities of
![]() $X^+$
is
$X^+$
is
![]() $\{2\times \frac 12(1,1,1),\frac 14(3,3,1)\}$
. Moreover,
$\{2\times \frac 12(1,1,1),\frac 14(3,3,1)\}$
. Moreover,
![]() $\chi ({\mathcal {O}}_X)=1-0+0-4=-3$
and
$\chi ({\mathcal {O}}_X)=1-0+0-4=-3$
and
![]() $P_2(X)=11$
. Next, we apply the orbifold Riemann–Roch formula [Reference ReidRei87] for
$P_2(X)=11$
. Next, we apply the orbifold Riemann–Roch formula [Reference ReidRei87] for
![]() $\chi (2K_X)$
:
$\chi (2K_X)$
:
 $$\begin{align*}\frac12K_{X^+}^3=P_2(X)+3\chi({\mathcal{O}}_X)-\sum_{Q\in{\mathcal{B}}}\frac{b(r-b)}{2r}, \end{align*}$$
$$\begin{align*}\frac12K_{X^+}^3=P_2(X)+3\chi({\mathcal{O}}_X)-\sum_{Q\in{\mathcal{B}}}\frac{b(r-b)}{2r}, \end{align*}$$
where
![]() $Q\cong \frac 1r(1,-1,b)$
, to get
$Q\cong \frac 1r(1,-1,b)$
, to get
Remark 6.3 (Hypersurface model of
 $X^+(2;1)$
).
$X^+(2;1)$
).
Recall that
![]() $K_{X^+(2;1)}$
is nef but not ample. In this case, there is a model of
$K_{X^+(2;1)}$
is nef but not ample. In this case, there is a model of
![]() $X^+(2;1)$
as a hypersurface in weighted projective space:
$X^+(2;1)$
as a hypersurface in weighted projective space:
This has
![]() $3$
-divisible canonical class, an additional Gorenstein canonical singularity
$3$
-divisible canonical class, an additional Gorenstein canonical singularity
![]() $\frac 13(1,1,1)$
on the line
$\frac 13(1,1,1)$
on the line
![]() ${\mathbb {P}}(6,15)$
. Let
${\mathbb {P}}(6,15)$
. Let
![]() $a_0,a_1,b,c,d$
denote the coordinates on
$a_0,a_1,b,c,d$
denote the coordinates on
![]() ${\mathbb {P}}(1,1,4,6,15)$
. The contraction
${\mathbb {P}}(1,1,4,6,15)$
. The contraction
![]() $X^+(2;1)\to X_{30}$
is given by
$X^+(2;1)\to X_{30}$
is given by
which is the crepant resolution of the
![]() $\frac 13(1,1,1)$
point. The pencil
$\frac 13(1,1,1)$
point. The pencil
![]() $|{\mathcal {O}}(1)|$
are surfaces with
$|{\mathcal {O}}(1)|$
are surfaces with
![]() $p_g=2$
,
$p_g=2$
,
![]() $K^2=\frac 43$
,
$K^2=\frac 43$
,
![]() $2\times A_1$
,
$2\times A_1$
,
![]() $A_3$
and a
$A_3$
and a
![]() $\frac 13(1,1)$
singularity, the minimal resolution being a
$\frac 13(1,1)$
singularity, the minimal resolution being a
![]() $(1,2)$
-surface.
$(1,2)$
-surface.
6.1 Nonterminal flips
The birational map
![]() $X\dashrightarrow X^+$
is a nonterminal flip because X is singular along
$X\dashrightarrow X^+$
is a nonterminal flip because X is singular along
![]() ${\mathfrak {s}}_0$
. One approach to describing this map would be to resolve the singularities along
${\mathfrak {s}}_0$
. One approach to describing this map would be to resolve the singularities along
![]() ${\mathfrak {s}}_0$
and then run the MMP to get a minimal model. See Figure 1 for a schematic picture of this for
${\mathfrak {s}}_0$
and then run the MMP to get a minimal model. See Figure 1 for a schematic picture of this for
![]() $X(2;1)$
.
$X(2;1)$
.

Figure 1 Schematic picture of the flip
![]() $X(2;1)$
to
$X(2;1)$
to
![]() $X^+(2;1)$
.
$X^+(2;1)$
.
Unlike in Proposition 1.9, the canonical linear system of
![]() $X(2;1)$
has a fixed part
$X(2;1)$
has a fixed part
![]() $D_{x_1}$
, and
$D_{x_1}$
, and
![]() $|K_X-D_{x_1}|$
is a basepoint free pencil of
$|K_X-D_{x_1}|$
is a basepoint free pencil of
![]() $(1,2)$
-surfaces. Every fibre has a
$(1,2)$
-surfaces. Every fibre has a
![]() $D_6$
-singularity along the section
$D_6$
-singularity along the section
![]() ${\mathfrak {s}}_0$
. On
${\mathfrak {s}}_0$
. On
![]() $X^+$
,
$X^+$
,
![]() $|K_{X^+}|$
is a pencil with base curve
$|K_{X^+}|$
is a pencil with base curve
![]() ${\mathfrak {s}}_0^+$
. Each element of
${\mathfrak {s}}_0^+$
. Each element of
![]() $|K_X|$
is a
$|K_X|$
is a
![]() $(1,2)$
-surface with a
$(1,2)$
-surface with a
![]() $D_6$
-singularity where it meets
$D_6$
-singularity where it meets
![]() ${\mathfrak {s}}_0$
. The flip extracts the central curve
${\mathfrak {s}}_0$
. The flip extracts the central curve
![]() ${\mathfrak {s}}_0^+$
giving a partial resolution of the
${\mathfrak {s}}_0^+$
giving a partial resolution of the
![]() $D_6$
-singularity, so each element of
$D_6$
-singularity, so each element of
![]() $|K_{X^+}|$
has two
$|K_{X^+}|$
has two
![]() $A_1$
-singularities and one
$A_1$
-singularities and one
![]() $A_3$
-singularity, lying on the base curve
$A_3$
-singularity, lying on the base curve
![]() ${\mathfrak {s}}_0^+$
.
${\mathfrak {s}}_0^+$
.
The other two cases have a similar description:
-
• After a crepant blowup,
 $X(3;1)$
has a curve of
$X(3;1)$
has a curve of
 $E_8$
-singularities along
$E_8$
-singularities along
 ${\mathfrak {s}}_0$
, and the flip extracts the curve marked with a square in Figure 2 below, so the pencil
${\mathfrak {s}}_0$
, and the flip extracts the curve marked with a square in Figure 2 below, so the pencil
 $|K_{X^+}|$
consists of
$|K_{X^+}|$
consists of
 $(1,2)$
-surfaces with one
$(1,2)$
-surfaces with one
 $A_1$
-singularity and one
$A_1$
-singularity and one
 $A_6$
-singularity on the base curve
$A_6$
-singularity on the base curve
 ${\mathfrak {s}}_0^+$
.
${\mathfrak {s}}_0^+$
. -
• There is also a curve of
 $E_8$
-singularities along
$E_8$
-singularities along
 ${\mathfrak {s}}_0$
in
${\mathfrak {s}}_0$
in
 $X(4;1)$
. This time, the partial resolution extracts the curve marked with a triangle in Figure 2, and the elements of
$X(4;1)$
. This time, the partial resolution extracts the curve marked with a triangle in Figure 2, and the elements of
 $|K_{X^+}|$
have
$|K_{X^+}|$
have
 $A_1$
,
$A_1$
,
 $A_2$
and
$A_2$
and
 $A_4$
-singularities.
$A_4$
-singularities.

Figure 2 Partial resolutions of
![]() $X(3;1)$
and
$X(3;1)$
and
![]() $X(4;1)$
.
$X(4;1)$
.
Acknowledgements
We started this project many years ago, in 2015, at a conference in Bayreuth celebrating Fabrizio Catanese’s 65th birthday. We find it appropriate to mention him here. In fact, several of the techniques used here may be traced back to his work and his teaching. For example, as is evident from the frequent references to [Reference Catanese and PignatelliCP06], we were inspired by the study of the relative canonical algebra of fibrations of surfaces to curves, which was developed by Catanese and many other people, and taught by him to the second author during his doctoral studies. We thank him for the enthusiasm, guidance and support that he has provided to us and to the mathematical community.
The second author would like to thank Alex Massarenti for inspiring discussions on Mori Dream Spaces (in particular, pointing him to the beautiful result [Reference Arzhantsev, Derenthal, Hausen and LafaceAD+15, Corollary 4.1.1.5]) without which we would not have obtained Theorem 1.16. Moreover, we thank Balázs Szendrői for his comments on the proof.
We also thank Gavin Brown, Meng Chen, Yifan Chen, Yong Hu, Chen Jiang and Tong Zhang for helpful comments on a previous draft of this paper.
Competing interests
The authors have no competing interest to declare.
Funding statement
The second author was partially supported by INdAM (GNSAGA) and by MIUR PRIN 2017 ‘Moduli Theory and Birational Classification’.