Published online by Cambridge University Press: 08 November 2022
For a graph G, let 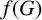 $f(G)$ denote the maximum number of edges in a bipartite subgraph of G. Given a positive integer m and a fixed graph H, let
$f(G)$ denote the maximum number of edges in a bipartite subgraph of G. Given a positive integer m and a fixed graph H, let 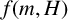 $f(m,H)$ denote the minimum possible cardinality of
$f(m,H)$ denote the minimum possible cardinality of 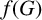 $f(G)$, as G ranges over all graphs on m edges that contain no copy of H. We prove bounds on
$f(G)$, as G ranges over all graphs on m edges that contain no copy of H. We prove bounds on 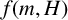 $f(m,H)$ for some bipartite graphs H and give a bound for a conjecture of Alon et al. [‘MaxCut in H-free graphs’, Combin. Probab. Comput. 14 (2005), 629–647] concerning
$f(m,H)$ for some bipartite graphs H and give a bound for a conjecture of Alon et al. [‘MaxCut in H-free graphs’, Combin. Probab. Comput. 14 (2005), 629–647] concerning 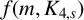 $f(m,K_{4,s})$.
$f(m,K_{4,s})$.
Supported by the National Natural Science Foundation of China (No. 11801149).