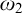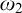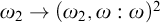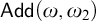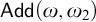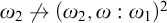1 Introduction
Since Ramsey’s result [Reference Ramsey10] that every infinite graph contains an infinite clique or an infinite independent set the area of partition relations has been very active. However, any straightforward generalizations of his result are bound to fail; the classical result of Sierpiński [Reference Sierpiński11] states that:
![]() ${2^\kappa } \not \to ({\kappa ^+})^2$
. Nevertheless there are ways to generalize Ramsey’s result.
${2^\kappa } \not \to ({\kappa ^+})^2$
. Nevertheless there are ways to generalize Ramsey’s result.
Dushnik and Miller showed in [Reference Dushnik and Miller2] that the relation
![]() ${\kappa } \to ({\kappa }, {\omega })^2$
always holds. Our notation for partition relations is standard; the reader unfamiliar with the arrow notation can find definitions in Section 1.1.
${\kappa } \to ({\kappa }, {\omega })^2$
always holds. Our notation for partition relations is standard; the reader unfamiliar with the arrow notation can find definitions in Section 1.1.
Most questions concerning partition relations on
![]() ${\omega _1}$
have been answered. Considering the order type of the clique Erdős and Rado [Reference Erdős and Rado3] improved the previous result to
${\omega _1}$
have been answered. Considering the order type of the clique Erdős and Rado [Reference Erdős and Rado3] improved the previous result to
![]() ${{\omega _1}} \to ({{\omega _1}}, {\omega +1})^2$
. By a result of Hajnal [Reference Hajnal4] their result is optimal as
${{\omega _1}} \to ({{\omega _1}}, {\omega +1})^2$
. By a result of Hajnal [Reference Hajnal4] their result is optimal as
![]() $\mathsf {CH}$
implies
$\mathsf {CH}$
implies
![]() ${{\omega _1}} \not \to ({{\omega _1}}, {\omega +2})^2$
. The best possible relation
${{\omega _1}} \not \to ({{\omega _1}}, {\omega +2})^2$
. The best possible relation
![]() ${{\omega _1}} \to ({{\omega _1}}, {\alpha })^2$
for any countable ordinal
${{\omega _1}} \to ({{\omega _1}}, {\alpha })^2$
for any countable ordinal
![]() $\alpha $
may consistently hold as shown by Todorčević in [Reference Todorčević12].
$\alpha $
may consistently hold as shown by Todorčević in [Reference Todorčević12].
The case of
![]() ${\omega _2}$
is far from being resolved. Erdős and Rado’s previous result extends also to
${\omega _2}$
is far from being resolved. Erdős and Rado’s previous result extends also to
![]() ${\omega _2}$
, i.e.,
${\omega _2}$
, i.e.,
![]() ${{\omega _2}} \to ({{\omega _2}}, {\omega + 1})^2$
in
${{\omega _2}} \to ({{\omega _2}}, {\omega + 1})^2$
in
![]() $\mathsf {ZFC}$
, but they also showed [Reference Erdős and Rado3] that
$\mathsf {ZFC}$
, but they also showed [Reference Erdős and Rado3] that
![]() $\mathsf {CH}$
implies
$\mathsf {CH}$
implies
![]() ${{\omega _2}} \to ({{\omega _2}}, {\omega _1 + 1})^2$
; on the other hand
${{\omega _2}} \to ({{\omega _2}}, {\omega _1 + 1})^2$
; on the other hand
![]() ${{\omega _2}} \to ({{\omega _2}}, {\omega _1})^2$
already implies
${{\omega _2}} \to ({{\omega _2}}, {\omega _1})^2$
already implies
![]() $\mathsf {CH}$
. If on top of
$\mathsf {CH}$
. If on top of
![]() $\mathsf {CH}$
we further assume
$\mathsf {CH}$
we further assume
![]() $2^{\omega _1}={\omega _2}$
, we are limited by
$2^{\omega _1}={\omega _2}$
, we are limited by
![]() $\omega _1 + 1$
, i.e.,
$\omega _1 + 1$
, i.e.,
![]() ${{\omega _2}} \not \to ({{\omega _2}}, {\omega _1 + 2})^2$
holds. Rather surprisingly Laver [Reference Laver8] showed that
${{\omega _2}} \not \to ({{\omega _2}}, {\omega _1 + 2})^2$
holds. Rather surprisingly Laver [Reference Laver8] showed that
![]() $\mathsf {MA} + 2^\omega = {\omega _2}$
implies
$\mathsf {MA} + 2^\omega = {\omega _2}$
implies
![]() ${{\omega _2}} \not \to ({{\omega _2}}, {\omega + 2})^2$
.
${{\omega _2}} \not \to ({{\omega _2}}, {\omega + 2})^2$
.
If we weaken the assumption on the homogeneous set there are further results. Baumgartner [Reference Baumgartner1] showed that after adding
![]() ${\omega _2}$
Silver reals via countable support product to a model of
${\omega _2}$
Silver reals via countable support product to a model of
![]() $\mathsf {CH}$
we obtain a model where
$\mathsf {CH}$
we obtain a model where
![]() ${{\omega _2}} \to ({{\omega _2}}, {\omega : {\omega _2}})^2$
.
${{\omega _2}} \to ({{\omega _2}}, {\omega : {\omega _2}})^2$
.
Our results are in a similar vein as Baumgartner’s, instead of looking for a clique in a graph with no cofinal independent set we will be searching only for bipartite graphs. Our results can be seen as showing how much of the partition relation
![]() ${{\omega _2}} \to ({{\omega _2}}, {\omega _1})^2$
remains after adding Cohen reals. We will prove that
${{\omega _2}} \to ({{\omega _2}}, {\omega _1})^2$
remains after adding Cohen reals. We will prove that
![]() ${{\omega _2}} \to ({{\omega _2}}, {\omega : \omega })^2$
holds after forcing with
${{\omega _2}} \to ({{\omega _2}}, {\omega : \omega })^2$
holds after forcing with
![]() $\mathsf {Add}(\omega , {{\omega _2}})$
in a model of
$\mathsf {Add}(\omega , {{\omega _2}})$
in a model of
![]() $\mathsf {CH}$
. On the other hand the same conclusion as in the Silver model cannot hold after adding Cohen reals as
$\mathsf {CH}$
. On the other hand the same conclusion as in the Silver model cannot hold after adding Cohen reals as
![]() $\mathsf {Add}(\omega , {{\omega _2}}) \Vdash {\omega _2} \not \to ({\omega : \omega _1})^2$
.
$\mathsf {Add}(\omega , {{\omega _2}}) \Vdash {\omega _2} \not \to ({\omega : \omega _1})^2$
.
Our main results are in a more general setting covering also the case of adding
![]() $\lambda ^+$
many Cohen subsets of
$\lambda ^+$
many Cohen subsets of
![]() $\kappa $
for
$\kappa $
for
![]() $\kappa , \lambda $
regular and its effect on the analogous partition relations. In particular we also get that
$\kappa , \lambda $
regular and its effect on the analogous partition relations. In particular we also get that
![]() ${\omega _3} \to ({\omega _3}, {\omega _1 : \omega _1})^2$
holds after adding
${\omega _3} \to ({\omega _3}, {\omega _1 : \omega _1})^2$
holds after adding
![]() $\omega _3$
Cohen subsets of
$\omega _3$
Cohen subsets of
![]() ${\omega _1}$
to a model of
${\omega _1}$
to a model of
![]() $\mathsf {GCH}$
.
$\mathsf {GCH}$
.
Notation
We use standard set theoretic notation. If X is a set and
![]() $\mu $
a cardinal, then
$\mu $
a cardinal, then
![]() $[X]^\mu := \left \{ {Y \subseteq X \mid |Y| = \mu } \right \}$
. For two sets
$[X]^\mu := \left \{ {Y \subseteq X \mid |Y| = \mu } \right \}$
. For two sets
![]() $X,Y$
we define
$X,Y$
we define
![]() $X \otimes Y := \left \{ {\{x,y\} \mid x \in X \land y \in Y} \right \}$
. If
$X \otimes Y := \left \{ {\{x,y\} \mid x \in X \land y \in Y} \right \}$
. If
![]() $X,Y$
are subsets of some ordered set, then
$X,Y$
are subsets of some ordered set, then
![]() $X<Y$
means that each element of X lies below each element of Y.
$X<Y$
means that each element of X lies below each element of Y.
![]() $\mathsf {H}(\kappa )$
denotes the collection of all sets hereditarily of cardinality less than
$\mathsf {H}(\kappa )$
denotes the collection of all sets hereditarily of cardinality less than
![]() $\kappa $
; these sets will be used for constructing suitable elementary submodels; for more on this subject we refer the reader to [Reference Just and Weese5, Chapter 24]. A collection of sets forms a
$\kappa $
; these sets will be used for constructing suitable elementary submodels; for more on this subject we refer the reader to [Reference Just and Weese5, Chapter 24]. A collection of sets forms a
![]() $\Delta $
-system if there is a fixed set r such that the intersection of any two sets in the collection is exactly r. By
$\Delta $
-system if there is a fixed set r such that the intersection of any two sets in the collection is exactly r. By
![]() $\mathrm {ot}(X)$
we mean the order type of a well-ordered set X.
$\mathrm {ot}(X)$
we mean the order type of a well-ordered set X.
A graph G is a pair
![]() $(V,E)$
, where V is an arbitrary set and
$(V,E)$
, where V is an arbitrary set and
![]() $E \subseteq [V]^2$
. A subset
$E \subseteq [V]^2$
. A subset
![]() $X \subseteq V$
is complete if
$X \subseteq V$
is complete if
![]() $[X]^2 \subseteq E$
. An independent set in G is a subset X of V such that
$[X]^2 \subseteq E$
. An independent set in G is a subset X of V such that
![]() $[X]^2 \cap E$
is empty. If the vertex set of the graph is well-ordered and
$[X]^2 \cap E$
is empty. If the vertex set of the graph is well-ordered and
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are ordinals, then a subgraph (sometimes referred to as configuration) of type
$\beta $
are ordinals, then a subgraph (sometimes referred to as configuration) of type
![]() $(\alpha : \beta )$
is one whose vertex set is
$(\alpha : \beta )$
is one whose vertex set is
![]() $A \cup B$
, where A has order type
$A \cup B$
, where A has order type
![]() $\alpha $
and B has order type
$\alpha $
and B has order type
![]() $\beta $
,
$\beta $
,
![]() $A<B$
and
$A<B$
and
![]() $A \otimes B \subseteq E$
.
$A \otimes B \subseteq E$
.
Given ordinals
![]() $\alpha , \beta , \gamma $
the partition relation
$\alpha , \beta , \gamma $
the partition relation
![]() ${\alpha } \to ({\beta }, {\gamma })^2$
is the statement that given a function
${\alpha } \to ({\beta }, {\gamma })^2$
is the statement that given a function
![]() $c: [\alpha ]^2 \to 2$
there is a subset X of
$c: [\alpha ]^2 \to 2$
there is a subset X of
![]() $\alpha $
such that either the order type of X is
$\alpha $
such that either the order type of X is
![]() $\beta $
and
$\beta $
and
![]() $c"[X]^2 = \{0\}$
or the order type of X is
$c"[X]^2 = \{0\}$
or the order type of X is
![]() $\gamma $
and
$\gamma $
and
![]() $c"[X]^2 = \{1\}$
. The weaker relation
$c"[X]^2 = \{1\}$
. The weaker relation
![]() ${\alpha } \to ({\beta }, {\gamma : \delta })^2$
says that for every function
${\alpha } \to ({\beta }, {\gamma : \delta })^2$
says that for every function
![]() $c: [\alpha ]^2 \to 2$
either there is an
$c: [\alpha ]^2 \to 2$
either there is an
![]() $X \subseteq \alpha $
such that the order type of X is
$X \subseteq \alpha $
such that the order type of X is
![]() $\beta $
and
$\beta $
and
![]() $c"[X]^2 = \{0\}$
or there are sets
$c"[X]^2 = \{0\}$
or there are sets
![]() $X,Y \subseteq \alpha $
such that
$X,Y \subseteq \alpha $
such that
![]() $X<Y$
, the order type of X is
$X<Y$
, the order type of X is
![]() $\gamma $
, the order type of Y is
$\gamma $
, the order type of Y is
![]() $\delta $
, and
$\delta $
, and
![]() $c"[X \otimes Y] = \{1\}$
.
$c"[X \otimes Y] = \{1\}$
.
By a slight abuse of notation we will write
![]() $c(\alpha , \beta )$
instead of
$c(\alpha , \beta )$
instead of
![]() $c(\{\alpha , \beta \})$
and when writing
$c(\{\alpha , \beta \})$
and when writing
![]() $c(\alpha , \beta )$
we also tacitly assume that
$c(\alpha , \beta )$
we also tacitly assume that
![]() $\alpha < \beta $
if a natural ordering is present. The notation
$\alpha < \beta $
if a natural ordering is present. The notation
![]() ${\alpha } \to ({\beta }, {\gamma })^2$
is shortened to
${\alpha } \to ({\beta }, {\gamma })^2$
is shortened to
![]() ${\alpha } \to ({\beta })^2$
, when
${\alpha } \to ({\beta })^2$
, when
![]() $\beta = \gamma $
.
$\beta = \gamma $
.
Each function
![]() $c : [\alpha ]^2 \to 2$
defines a graph on
$c : [\alpha ]^2 \to 2$
defines a graph on
![]() $\alpha $
, namely
$\alpha $
, namely
![]() $(\alpha , c^{-1}[\{1\}])$
. Thus it will sometimes be convenient to talk about arbitrary functions on
$(\alpha , c^{-1}[\{1\}])$
. Thus it will sometimes be convenient to talk about arbitrary functions on
![]() $\alpha $
and instead of looking for homogeneous sets for the coloring we can consider independent sets and cliques, i.e., we can rephrase the notion of partition relations as follows: for ordinals
$\alpha $
and instead of looking for homogeneous sets for the coloring we can consider independent sets and cliques, i.e., we can rephrase the notion of partition relations as follows: for ordinals
![]() $\alpha , \beta , \gamma $
the partition relation
$\alpha , \beta , \gamma $
the partition relation
![]() ${\alpha } \to ({\beta }, {\gamma })^2$
says that given any graph whose vertex set is
${\alpha } \to ({\beta }, {\gamma })^2$
says that given any graph whose vertex set is
![]() $\alpha $
and there is no independent set of order type
$\alpha $
and there is no independent set of order type
![]() $\beta $
we can find a complete subgraph of order type
$\beta $
we can find a complete subgraph of order type
![]() $\gamma $
. The relation
$\gamma $
. The relation
![]() ${\alpha } \to ({\beta }, {\gamma : \delta })^2$
says that every graph on
${\alpha } \to ({\beta }, {\gamma : \delta })^2$
says that every graph on
![]() $\alpha $
either has an independent set of order type
$\alpha $
either has an independent set of order type
![]() $\beta $
or a subgraph of type
$\beta $
or a subgraph of type
![]() $(\gamma : \delta )$
.
$(\gamma : \delta )$
.
Suppose
![]() $\kappa \le \lambda $
are cardinals, the forcing for adding
$\kappa \le \lambda $
are cardinals, the forcing for adding
![]() $\lambda $
many Cohen subsets of
$\lambda $
many Cohen subsets of
![]() $\kappa $
will be denoted
$\kappa $
will be denoted
![]() $\mathsf {Add}({\kappa }, {\lambda })$
, its underlying set is
$\mathsf {Add}({\kappa }, {\lambda })$
, its underlying set is
![]() $\left \{ {p : \lambda \to 2 \mid |p|<\kappa } \right \}$
, and the ordering is reverse inclusion (see [Reference Kunen6] for an introduction to independence proofs in set theory).
$\left \{ {p : \lambda \to 2 \mid |p|<\kappa } \right \}$
, and the ordering is reverse inclusion (see [Reference Kunen6] for an introduction to independence proofs in set theory).
2 Positive result
As the central tool of this section will be double
![]() $\Delta $
-systems let us review a classical result about the existence of
$\Delta $
-systems let us review a classical result about the existence of
![]() $\Delta $
-systems. The proof can be found in [Reference Kunen6].
$\Delta $
-systems. The proof can be found in [Reference Kunen6].
Theorem 2.1 (
 $\Delta $
-system lemma).
$\Delta $
-system lemma).
Suppose
![]() $\kappa $
is an infinite cardinal,
$\kappa $
is an infinite cardinal,
![]() $\lambda> \kappa $
is regular, for each
$\lambda> \kappa $
is regular, for each
![]() $\alpha < \lambda $
we have
$\alpha < \lambda $
we have
![]() $|\alpha ^{<\kappa }| < \lambda $
, and
$|\alpha ^{<\kappa }| < \lambda $
, and
![]() $\mathcal {A}$
is a collection of sets such that
$\mathcal {A}$
is a collection of sets such that
![]() $|\mathcal {A}| \ge \lambda $
. If for all
$|\mathcal {A}| \ge \lambda $
. If for all
![]() $x \in \mathcal {A}$
we have
$x \in \mathcal {A}$
we have
![]() $|x|<\kappa $
, then there is a
$|x|<\kappa $
, then there is a
![]() $\mathcal {B} \subseteq \mathcal {A}$
, such that
$\mathcal {B} \subseteq \mathcal {A}$
, such that
![]() $|\mathcal {B}| = \lambda $
and
$|\mathcal {B}| = \lambda $
and
![]() $\mathcal {B}$
forms a
$\mathcal {B}$
forms a
![]() $\Delta $
-system.
$\Delta $
-system.
Double
![]() $\Delta $
-systems were introduced by Todorčević in [Reference Todorčević13] and utilized also in other papers. For an application in a similar context see [Reference Todorčević14, Theorem 3.3]. A nice exposition on double
$\Delta $
-systems were introduced by Todorčević in [Reference Todorčević13] and utilized also in other papers. For an application in a similar context see [Reference Todorčević14, Theorem 3.3]. A nice exposition on double
![]() $\Delta $
-systems and their higher analogues can be found in [Reference Lambie-Hanson7].
$\Delta $
-systems and their higher analogues can be found in [Reference Lambie-Hanson7].
Definition 2.2. Let
![]() $\Gamma $
be a set of ordinals and
$\Gamma $
be a set of ordinals and
![]() $D := \left \{ {p_{\alpha \beta } \mid \left \{ {\alpha , \beta } \right \} \in [\Gamma ]^2} \right \}$
a collection of sets. We say that D is a double
$D := \left \{ {p_{\alpha \beta } \mid \left \{ {\alpha , \beta } \right \} \in [\Gamma ]^2} \right \}$
a collection of sets. We say that D is a double
![]() $\Delta $
-system with root
$\Delta $
-system with root
![]() $p^0 \cup p^1$
if the following holds:
$p^0 \cup p^1$
if the following holds:
-
(1) For every
 $\alpha \in \Gamma \left \{ {p_{\alpha \beta } \mid \beta \in \Gamma \setminus (\alpha + 1)} \right \}$
is a
$\alpha \in \Gamma \left \{ {p_{\alpha \beta } \mid \beta \in \Gamma \setminus (\alpha + 1)} \right \}$
is a
 $\Delta $
-system with root
$\Delta $
-system with root
 $p^0_\alpha $
.
$p^0_\alpha $
. -
(2) For every
 $\beta \in \Gamma \left \{ {p_{\alpha \beta } \mid \alpha \in \Gamma \cap \beta } \right \}$
is a
$\beta \in \Gamma \left \{ {p_{\alpha \beta } \mid \alpha \in \Gamma \cap \beta } \right \}$
is a
 $\Delta $
-system with root
$\Delta $
-system with root
 $p^1_\beta $
.
$p^1_\beta $
. -
(3)
 $\{p^0_\alpha \mid \alpha \in \Gamma \}$
is a
$\{p^0_\alpha \mid \alpha \in \Gamma \}$
is a
 $\Delta $
-system with root
$\Delta $
-system with root
 $p^0$
.
$p^0$
. -
(4)
 $\{p^1_\beta \mid \beta \in \Gamma \}$
is a
$\{p^1_\beta \mid \beta \in \Gamma \}$
is a
 $\Delta $
-system with root
$\Delta $
-system with root
 $p^1$
.
$p^1$
.
Remark. In our case the sets
![]() $p_{\alpha \beta }$
will be conditions in the Cohen forcing. The notation
$p_{\alpha \beta }$
will be conditions in the Cohen forcing. The notation
![]() $p_{\alpha \beta }$
implicitly assumes that
$p_{\alpha \beta }$
implicitly assumes that
![]() $\alpha < \beta $
. Note also that the conditions on the double
$\alpha < \beta $
. Note also that the conditions on the double
![]() $\Delta $
-system ensure that
$\Delta $
-system ensure that
![]() $\bigcap \{p_{\alpha \beta } \mid \{\alpha ,\beta \} \in [\Gamma ]^2\} = p^0 = p^1$
.
$\bigcap \{p_{\alpha \beta } \mid \{\alpha ,\beta \} \in [\Gamma ]^2\} = p^0 = p^1$
.
We will define the notion of isomorphism between forcing conditions.
Definition 2.3. Given
![]() $p,q \in \mathsf {Add}({\kappa }, {\lambda })$
we define the set
$p,q \in \mathsf {Add}({\kappa }, {\lambda })$
we define the set
![]() $\mathrm {type}(p)$
as the sequence
$\mathrm {type}(p)$
as the sequence
![]() $(p_i)_{i < \mu }$
, where
$(p_i)_{i < \mu }$
, where
![]() $\mu = \mathrm {ot}(\mathrm {dom}(p))$
and
$\mu = \mathrm {ot}(\mathrm {dom}(p))$
and
![]() $(p_i)_{i < \mu }$
is an enumeration of the values of p as a sequence respecting the ordering of its domain. Conditions
$(p_i)_{i < \mu }$
is an enumeration of the values of p as a sequence respecting the ordering of its domain. Conditions
![]() $p,q$
are isomorphic,
$p,q$
are isomorphic,
![]() $p \simeq q$
, if
$p \simeq q$
, if
![]() $\mathrm {type}(p) = \mathrm {type}(q)$
.
$\mathrm {type}(p) = \mathrm {type}(q)$
.
The type of a pair,
![]() $\mathrm {type}(p,q)$
, is defined again as a sequence
$\mathrm {type}(p,q)$
, is defined again as a sequence
![]() $(s_i)_{i < \eta }$
, where
$(s_i)_{i < \eta }$
, where
![]() $\eta = \mathrm {ot}(\mathrm {dom}(p) \cup \mathrm {dom}(q))$
and if
$\eta = \mathrm {ot}(\mathrm {dom}(p) \cup \mathrm {dom}(q))$
and if
![]() $(r_i)_{i < \eta }$
is an enumeration of
$(r_i)_{i < \eta }$
is an enumeration of
![]() $\mathrm {dom}(p) \cup \mathrm {dom}(q)$
respecting the ordering, then
$\mathrm {dom}(p) \cup \mathrm {dom}(q)$
respecting the ordering, then
![]() $s_i = (v_p^i, v_q^i)$
, where if
$s_i = (v_p^i, v_q^i)$
, where if
![]() $r_i \in \mathrm {dom}(p)$
, then
$r_i \in \mathrm {dom}(p)$
, then
![]() $v_p^i = p(r_i)$
, else
$v_p^i = p(r_i)$
, else
![]() $v_p^i = 2$
; analogously for
$v_p^i = 2$
; analogously for
![]() $v_q^i$
. Two pairs of conditions
$v_q^i$
. Two pairs of conditions
![]() $(p,q), (r,s)$
are isomorphic,
$(p,q), (r,s)$
are isomorphic,
![]() $(p,q) \simeq (r,s)$
, if
$(p,q) \simeq (r,s)$
, if
![]() $\mathrm {type}(p,q) = \mathrm {type}(r,s)$
.
$\mathrm {type}(p,q) = \mathrm {type}(r,s)$
.
Remark. The sets
![]() $\mathrm {type}(p)$
and
$\mathrm {type}(p)$
and
![]() $\mathrm {type}(p,q)$
just record all information about a condition (a pair of conditions). In other words it codes them as structures. Also note that
$\mathrm {type}(p,q)$
just record all information about a condition (a pair of conditions). In other words it codes them as structures. Also note that
![]() $\mathrm {type}(p,q) = \mathrm {type}(r,s)$
implies the equality of types coordinate-wise, i.e.,
$\mathrm {type}(p,q) = \mathrm {type}(r,s)$
implies the equality of types coordinate-wise, i.e.,
![]() $\mathrm {type}(p) = \mathrm {type}(r)$
and
$\mathrm {type}(p) = \mathrm {type}(r)$
and
![]() $\mathrm {type}(q) = \mathrm {type}(s)$
.
$\mathrm {type}(q) = \mathrm {type}(s)$
.
In further applications we will need a more uniform version of
![]() $\Delta $
-systems of conditions.
$\Delta $
-systems of conditions.
Lemma 2.4. Suppose
![]() $\kappa < \lambda $
are regular cardinals,
$\kappa < \lambda $
are regular cardinals,
![]() $|2^\mu | < \lambda $
for all
$|2^\mu | < \lambda $
for all
![]() $\mu < \kappa $
, and
$\mu < \kappa $
, and
![]() $\left \{ {p_\alpha \mid \alpha < \lambda } \right \}$
is a set of conditions in
$\left \{ {p_\alpha \mid \alpha < \lambda } \right \}$
is a set of conditions in
![]() $\mathsf {Add}({\kappa }, {\lambda ^+})$
forming a
$\mathsf {Add}({\kappa }, {\lambda ^+})$
forming a
![]() $\Delta $
-system. There are an
$\Delta $
-system. There are an
![]() $X \in [\lambda ]^\lambda $
and an
$X \in [\lambda ]^\lambda $
and an
![]() $s \subseteq \mathrm {ot}(\mathrm {dom}(p_0))$
such that
$s \subseteq \mathrm {ot}(\mathrm {dom}(p_0))$
such that
![]() $:$
$:$
-
(1) for all
 $\alpha , \beta \in X$
we have
$\alpha , \beta \in X$
we have
 $\mathrm {type}(p_\alpha ) = \mathrm {type}(p_\beta )$
, and
$\mathrm {type}(p_\alpha ) = \mathrm {type}(p_\beta )$
, and -
(2) for all
 $\alpha \in X$
if
$\alpha \in X$
if
 $(d_i \mid i < \mathrm {ot}(\mathrm {dom}(p_\alpha )))$
is an increasing enumeration of the domain of
$(d_i \mid i < \mathrm {ot}(\mathrm {dom}(p_\alpha )))$
is an increasing enumeration of the domain of
 $p_\alpha $
, then
$p_\alpha $
, then
 $\{ (d_i, p_\alpha (d_i)) \mid i \in s \}$
is exactly the root of the original
$\{ (d_i, p_\alpha (d_i)) \mid i \in s \}$
is exactly the root of the original
 $\Delta $
-system.
$\Delta $
-system.
Proof The proof is a routine counting argument.
To ensure that the types of all the conditions are the same note that the order type of the domain of any condition from
![]() $\mathsf {Add}({\kappa }, {\lambda ^+})$
is an ordinal below
$\mathsf {Add}({\kappa }, {\lambda ^+})$
is an ordinal below
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $f:\lambda \to \kappa $
be a function such that
$f:\lambda \to \kappa $
be a function such that
![]() $f(\alpha )=\mathrm {ot}(\mathrm {dom}(p_\alpha ))$
. As
$f(\alpha )=\mathrm {ot}(\mathrm {dom}(p_\alpha ))$
. As
![]() $\kappa < \lambda $
and
$\kappa < \lambda $
and
![]() $\lambda $
is regular we get a
$\lambda $
is regular we get a
![]() $\gamma _0 < \kappa $
and an
$\gamma _0 < \kappa $
and an
![]() $A \in [\lambda ]^\lambda $
such that the order type of the domain of
$A \in [\lambda ]^\lambda $
such that the order type of the domain of
![]() $p_\alpha $
is
$p_\alpha $
is
![]() $\gamma _0$
for all
$\gamma _0$
for all
![]() $\alpha \in A$
. Next consider each function from
$\alpha \in A$
. Next consider each function from
![]() $\gamma _0$
to
$\gamma _0$
to
![]() $2$
. As
$2$
. As
![]() $2^{\gamma _0} < \lambda $
, there is less than
$2^{\gamma _0} < \lambda $
, there is less than
![]() $\lambda $
many such functions. Given a condition
$\lambda $
many such functions. Given a condition
![]() $p_\alpha $
for
$p_\alpha $
for
![]() $\alpha \in A$
let
$\alpha \in A$
let
![]() $\varphi _{\alpha }: \gamma _0 \to \mathrm {dom}(p_\alpha )$
be the unique increasing bijection and define a function
$\varphi _{\alpha }: \gamma _0 \to \mathrm {dom}(p_\alpha )$
be the unique increasing bijection and define a function
![]() $g: \lambda \to 2^{\gamma _0}$
such that
$g: \lambda \to 2^{\gamma _0}$
such that
![]() $g(\alpha ) = p_\alpha \circ \varphi _\alpha $
. As before there are an
$g(\alpha ) = p_\alpha \circ \varphi _\alpha $
. As before there are an
![]() $A' \in [A]^\lambda $
and a fixed function
$A' \in [A]^\lambda $
and a fixed function
![]() $q: \gamma _0 \to 2$
such that
$q: \gamma _0 \to 2$
such that
![]() $\mathrm {type}(p_\alpha ) = q$
for each
$\mathrm {type}(p_\alpha ) = q$
for each
![]() $\alpha \in A'$
.
$\alpha \in A'$
.
To make sure that the relative position of the root of the
![]() $\Delta $
-system stays the same across all conditions define another function
$\Delta $
-system stays the same across all conditions define another function
![]() $h: \lambda \to 2^{\gamma _0}$
such that
$h: \lambda \to 2^{\gamma _0}$
such that
![]() $h(\alpha )(\beta ) = 1$
if and only if
$h(\alpha )(\beta ) = 1$
if and only if
![]() $(\varphi _\alpha (\beta ), p_\alpha (\varphi _\alpha (\beta ))$
is in the root of the
$(\varphi _\alpha (\beta ), p_\alpha (\varphi _\alpha (\beta ))$
is in the root of the
![]() $\Delta $
-system. Analogously as before we find a function
$\Delta $
-system. Analogously as before we find a function
![]() $r: \gamma _0 \to 2$
such that for
$r: \gamma _0 \to 2$
such that for
![]() $\lambda $
many
$\lambda $
many
![]() $\alpha $
we have
$\alpha $
we have
![]() $h(\alpha ) = r$
, and this ensures the second condition.
$h(\alpha ) = r$
, and this ensures the second condition.
Lemma 2.5. Suppose
![]() $\gamma _0 \le \gamma _1$
are ordinals and
$\gamma _0 \le \gamma _1$
are ordinals and
![]() $\left \{ {p_\alpha \mid \alpha < \gamma _0} \right \}$
,
$\left \{ {p_\alpha \mid \alpha < \gamma _0} \right \}$
,
![]() $\left \{ {q_\alpha \mid \alpha < \gamma _1} \right \}$
are sets of conditions in
$\left \{ {q_\alpha \mid \alpha < \gamma _1} \right \}$
are sets of conditions in
![]() $\mathsf {Add}({\kappa }, {\lambda })$
. If
$\mathsf {Add}({\kappa }, {\lambda })$
. If
![]() $\left \{ {q_\alpha \mid \alpha < \gamma _1} \right \}$
forms a
$\left \{ {q_\alpha \mid \alpha < \gamma _1} \right \}$
forms a
![]() $\Delta $
-system and for each
$\Delta $
-system and for each
![]() $\alpha < \beta < \gamma _0$
we have
$\alpha < \beta < \gamma _0$
we have
![]() $(p_\alpha , p_\beta ) \simeq (q_\alpha , q_\beta )$
, then
$(p_\alpha , p_\beta ) \simeq (q_\alpha , q_\beta )$
, then
![]() $\left \{ {p_\alpha \mid \alpha < \gamma _0} \right \}$
also forms a
$\left \{ {p_\alpha \mid \alpha < \gamma _0} \right \}$
also forms a
![]() $\Delta $
-system.
$\Delta $
-system.
Proof First enumerate in increasing order the domain of
![]() $q_0$
as
$q_0$
as
![]() $(d_i \mid i < \mathrm {ot}(\mathrm {dom}(q_0)))$
. As the conditions
$(d_i \mid i < \mathrm {ot}(\mathrm {dom}(q_0)))$
. As the conditions
![]() $\left \{ {q_\alpha \mid \alpha < \gamma _1} \right \}$
are isomorphic and form a
$\left \{ {q_\alpha \mid \alpha < \gamma _1} \right \}$
are isomorphic and form a
![]() $\Delta $
-system let s be the set of indices
$\Delta $
-system let s be the set of indices
![]() $i < \mathrm {ot}(\mathrm {dom}(q_0))$
such that
$i < \mathrm {ot}(\mathrm {dom}(q_0))$
such that
![]() $\left \{ {(d_i, q_0(d_i)) \mid i \in s} \right \}$
is exactly the root.
$\left \{ {(d_i, q_0(d_i)) \mid i \in s} \right \}$
is exactly the root.
If we similarly enumerate the domain of
![]() $p_0$
as
$p_0$
as
![]() $(e_i \mid i < \mathrm {ot}(\mathrm {dom}(p_0)))$
(note that
$(e_i \mid i < \mathrm {ot}(\mathrm {dom}(p_0)))$
(note that
![]() $\mathrm {ot}(\mathrm {dom}(q_0)) = \mathrm {ot}(\mathrm {dom}(p_0))$
), we claim that
$\mathrm {ot}(\mathrm {dom}(q_0)) = \mathrm {ot}(\mathrm {dom}(p_0))$
), we claim that
![]() $\left \{ {(e_i, p_0(e_i)) \mid i \in s} \right \}$
is the root of the
$\left \{ {(e_i, p_0(e_i)) \mid i \in s} \right \}$
is the root of the
![]() $\Delta $
-system formed by the conditions
$\Delta $
-system formed by the conditions
![]() $\left \{ {p_\alpha \mid \alpha < \gamma _0} \right \}$
.
$\left \{ {p_\alpha \mid \alpha < \gamma _0} \right \}$
.
Given any
![]() $p_\alpha $
and
$p_\alpha $
and
![]() $p_\beta $
as this pair is isomorphic to the pair
$p_\beta $
as this pair is isomorphic to the pair
![]() $(q_\alpha , q_\beta )$
we have that
$(q_\alpha , q_\beta )$
we have that
![]() $d_i \in \mathrm {dom}(q_\alpha ) \cap \mathrm {dom}(q_\beta )$
if and only if
$d_i \in \mathrm {dom}(q_\alpha ) \cap \mathrm {dom}(q_\beta )$
if and only if
![]() $e_i \in \mathrm {dom}(p_\alpha ) \cap \mathrm {dom}(p_\beta )$
and this happens exactly when
$e_i \in \mathrm {dom}(p_\alpha ) \cap \mathrm {dom}(p_\beta )$
and this happens exactly when
![]() $i \in s$
, also when
$i \in s$
, also when
![]() $d_i \in \mathrm {dom}(q_\alpha ) \cap \mathrm {dom}(q_\beta )$
then
$d_i \in \mathrm {dom}(q_\alpha ) \cap \mathrm {dom}(q_\beta )$
then
![]() $d_i$
is also the i-th element of the domain of both
$d_i$
is also the i-th element of the domain of both
![]() $q_\alpha $
and
$q_\alpha $
and
![]() $q_\beta $
and the same holds for
$q_\beta $
and the same holds for
![]() $e_i$
and any
$e_i$
and any
![]() $p_\alpha $
and
$p_\alpha $
and
![]() $p_\beta $
. Finally as the conditions
$p_\beta $
. Finally as the conditions
![]() $\left \{ {q_\alpha \mid \alpha < \gamma _1} \right \}$
are isomorphic so are
$\left \{ {q_\alpha \mid \alpha < \gamma _1} \right \}$
are isomorphic so are
![]() $\left \{ {p_\alpha \mid \alpha < \gamma _0} \right \}$
so in particular
$\left \{ {p_\alpha \mid \alpha < \gamma _0} \right \}$
so in particular
![]() $p_\alpha \simeq p_0 \simeq p_\beta $
and we are done.
$p_\alpha \simeq p_0 \simeq p_\beta $
and we are done.
The main theorem follows.
Theorem 2.6. Suppose
![]() $\kappa < \lambda $
are regular cardinals. If
$\kappa < \lambda $
are regular cardinals. If
![]() $\lambda ^{<\lambda } = \lambda $
and for each
$\lambda ^{<\lambda } = \lambda $
and for each
![]() $\alpha < \lambda $
we have
$\alpha < \lambda $
we have
![]() $|\alpha ^{<\kappa }| < \lambda $
, then
$|\alpha ^{<\kappa }| < \lambda $
, then
![]() $\mathsf {Add}({\kappa }, {\lambda ^+})$
forces the relation
$\mathsf {Add}({\kappa }, {\lambda ^+})$
forces the relation
![]() ${\lambda ^+} \to ({\lambda ^+}, {\mu : \mu })^2$
for any
${\lambda ^+} \to ({\lambda ^+}, {\mu : \mu })^2$
for any
![]() $\mu < \kappa ^+$
.
$\mu < \kappa ^+$
.
Proof Consider the extension by the Cohen forcing adding
![]() $\lambda ^+$
subsets of
$\lambda ^+$
subsets of
![]() $\kappa $
. Fix a condition q and a name
$\kappa $
. Fix a condition q and a name
![]() $\dot {c}$
such that q forces that in the extension c is a function from
$\dot {c}$
such that q forces that in the extension c is a function from
![]() $[\lambda ^+]^2$
to
$[\lambda ^+]^2$
to
![]() $2$
. Without loss of generality we will assume that
$2$
. Without loss of generality we will assume that
![]() $q=\emptyset $
. If it is the case that
$q=\emptyset $
. If it is the case that
we are done, so suppose this is not the case. Now an improved double
![]() $\Delta $
-system can be found.
$\Delta $
-system can be found.
The proof of the following claim closely resembles the argument in [Reference Todorčević14, Theorem 3.3], where Todorčević constructs a double
![]() $\Delta $
-system of Cohen conditions with analogous properties but he considers colorings with range
$\Delta $
-system of Cohen conditions with analogous properties but he considers colorings with range
![]() $\omega $
. Todorčević used this technique already in [Reference Todorčević13].
$\omega $
. Todorčević used this technique already in [Reference Todorčević13].
Claim 1. There are a set
![]() $X \in [\lambda ^+]^{\lambda }$
of order type
$X \in [\lambda ^+]^{\lambda }$
of order type
![]() $\lambda $
and a set of conditions
$\lambda $
and a set of conditions
![]() $D := \left \{ {p_{\alpha \beta } \in \mathsf {Add}({\kappa }, {\lambda ^+}) \mid \left \{ {\alpha , \beta } \right \} \in [X]^2} \right \}$
such that the following holds
$D := \left \{ {p_{\alpha \beta } \in \mathsf {Add}({\kappa }, {\lambda ^+}) \mid \left \{ {\alpha , \beta } \right \} \in [X]^2} \right \}$
such that the following holds
![]() $:$
$:$
-
(1)
 $p_{\alpha \beta } \Vdash \dot {c}(\alpha , \beta ) = 1$
.
$p_{\alpha \beta } \Vdash \dot {c}(\alpha , \beta ) = 1$
. -
(2) D forms a double
 $\Delta $
-system.
$\Delta $
-system.
Proof In the ground model for every
![]() $\alpha < \beta $
in
$\alpha < \beta $
in
![]() $\lambda ^+$
either
$\lambda ^+$
either
![]() $\emptyset \Vdash \dot {c}(\alpha , \beta ) = 0$
or there is a condition p such that
$\emptyset \Vdash \dot {c}(\alpha , \beta ) = 0$
or there is a condition p such that
![]() $p \Vdash \dot {c}(\alpha , \beta ) = 1$
. For every pair fulfilling the second option fix such a condition
$p \Vdash \dot {c}(\alpha , \beta ) = 1$
. For every pair fulfilling the second option fix such a condition
![]() $p_{\alpha \beta }$
, otherwise put
$p_{\alpha \beta }$
, otherwise put
![]() $p_{\alpha \beta } := \emptyset $
. Consider a regular cardinal
$p_{\alpha \beta } := \emptyset $
. Consider a regular cardinal
![]() $\theta $
large enough so that
$\theta $
large enough so that
![]() $\mathsf {H}(\theta )$
contains all the relevant objects we have considered so far. Choose an elementary submodel M of
$\mathsf {H}(\theta )$
contains all the relevant objects we have considered so far. Choose an elementary submodel M of
![]() $\mathsf {H}(\theta )$
of size
$\mathsf {H}(\theta )$
of size
![]() $\lambda $
such that
$\lambda $
such that
![]() $M^{<\lambda } \subseteq M$
(we assume
$M^{<\lambda } \subseteq M$
(we assume
![]() $\lambda ^{<\lambda } = \lambda $
in the ground model) and
$\lambda ^{<\lambda } = \lambda $
in the ground model) and
![]() $\delta := M \cap \lambda ^+$
has cofinality
$\delta := M \cap \lambda ^+$
has cofinality
![]() $\lambda $
. Fix also a
$\lambda $
. Fix also a
![]() $\lambda $
-sequence converging to
$\lambda $
-sequence converging to
![]() $\delta $
, say
$\delta $
, say
![]() $(d_\alpha \mid \alpha < \lambda )$
.
$(d_\alpha \mid \alpha < \lambda )$
.
Subclaim 1. There is a set, B, cofinal in
![]() $\delta $
of order type
$\delta $
of order type
![]() $\lambda $
with the following properties for every
$\lambda $
with the following properties for every
![]() $\alpha < \beta < \gamma $
in
$\alpha < \beta < \gamma $
in
![]() $B:$
$B:$
-
(1)
 $p_{\alpha \beta } \simeq p_{\alpha \delta }$
.
$p_{\alpha \beta } \simeq p_{\alpha \delta }$
. -
(2)
 $p_{\alpha \beta }\restriction \beta = {p_{\alpha \delta }}\restriction {\delta }$
.
$p_{\alpha \beta }\restriction \beta = {p_{\alpha \delta }}\restriction {\delta }$
. -
(3)
 $(p_{\alpha \gamma }, p_{\beta \gamma }) \simeq (p_{\alpha \delta }, p_{\beta \delta })$
.
$(p_{\alpha \gamma }, p_{\beta \gamma }) \simeq (p_{\alpha \delta }, p_{\beta \delta })$
. -
(4)
 $\mathrm {dom}({p_{\alpha \beta }}) \subseteq \gamma $
.
$\mathrm {dom}({p_{\alpha \beta }}) \subseteq \gamma $
. -
(5)
 $p_{\alpha \beta } \Vdash \dot {c}(\alpha , \beta ) = 1$
.
$p_{\alpha \beta } \Vdash \dot {c}(\alpha , \beta ) = 1$
. -
(6)
 $p_{\alpha \delta } \Vdash \dot {c}(\alpha , \delta ) = 1$
.
$p_{\alpha \delta } \Vdash \dot {c}(\alpha , \delta ) = 1$
.
Proof The set B cannot be an element of M, but any initial segment of such a set B belongs to M because M is closed under sequences of length
![]() $<\lambda $
, and this will be used in the inductive construction. Suppose we have constructed an initial segment of B, a sequence
$<\lambda $
, and this will be used in the inductive construction. Suppose we have constructed an initial segment of B, a sequence
![]() $b := (b_\xi \mid \xi < \beta )$
for some ordinal
$b := (b_\xi \mid \xi < \beta )$
for some ordinal
![]() $\beta < \lambda $
satisfying all the conditions, and
$\beta < \lambda $
satisfying all the conditions, and
![]() $b_\alpha \ge d_\alpha $
for all
$b_\alpha \ge d_\alpha $
for all
![]() $\alpha < \beta $
. We want to construct
$\alpha < \beta $
. We want to construct
![]() $b_\beta $
above
$b_\beta $
above
![]() $d_\beta $
. Note that
$d_\beta $
. Note that
![]() $b \in M$
as the sequence has length
$b \in M$
as the sequence has length
![]() $<\lambda $
, and also
$<\lambda $
, and also
![]() $d_\beta \in M$
. Consider the following sequences/matrices for every
$d_\beta \in M$
. Consider the following sequences/matrices for every
![]() $\eta \in \lambda ^+ \setminus d_\beta $
:
$\eta \in \lambda ^+ \setminus d_\beta $
:
 $$ \begin{align*} S_1^\eta &:= (\mathrm{type}(p_{\alpha \eta}) \mid \alpha \in b), \\ S_2^\eta &:= ({p_{\alpha \eta}}\restriction{\eta} \mid \alpha \in b), \\ S_3^\eta &:= (\mathrm{type}(p_{\alpha \eta}, p_{\beta \eta}) \mid \alpha < \beta \in b). \end{align*} $$
$$ \begin{align*} S_1^\eta &:= (\mathrm{type}(p_{\alpha \eta}) \mid \alpha \in b), \\ S_2^\eta &:= ({p_{\alpha \eta}}\restriction{\eta} \mid \alpha \in b), \\ S_3^\eta &:= (\mathrm{type}(p_{\alpha \eta}, p_{\beta \eta}) \mid \alpha < \beta \in b). \end{align*} $$
For any
![]() $\eta \in M$
all three sets
$\eta \in M$
all three sets
![]() $S_1^\eta , S_2^\eta $
, and
$S_1^\eta , S_2^\eta $
, and
![]() $S_3^\eta $
are definable in M and moreover the entire sequence
$S_3^\eta $
are definable in M and moreover the entire sequence
![]() $(S^\eta _i \mid \eta < \lambda ^+)$
is in M for each i in
$(S^\eta _i \mid \eta < \lambda ^+)$
is in M for each i in
![]() $\{1,2,3\}$
. Note also that
$\{1,2,3\}$
. Note also that
![]() $S_i^\delta $
is an element of M for
$S_i^\delta $
is an element of M for
![]() $i\in \left \{ {1,2,3} \right \}$
even though
$i\in \left \{ {1,2,3} \right \}$
even though
![]() $\delta \not \in M$
; this follows from M being closed under sequences of length
$\delta \not \in M$
; this follows from M being closed under sequences of length
![]() $<\lambda $
. Now define the set:
$<\lambda $
. Now define the set:
 $$ \begin{align*} S := \{ \eta < &\ \lambda^+ \mid \eta \ge d_\beta \land S_1^\eta = S_1^\delta \land S_2^\eta = S_2^\delta \land S_3^\eta = S_3^\delta \land \\& \land \eta> \sup\left\{ {\sup\mathrm{dom}(p_{\alpha \beta}) \mid \alpha < \beta \in b} \right\} \land \forall \alpha \in b : p_{\alpha \eta} \Vdash \dot{c}(\alpha, \eta) = 1 \}. \end{align*} $$
$$ \begin{align*} S := \{ \eta < &\ \lambda^+ \mid \eta \ge d_\beta \land S_1^\eta = S_1^\delta \land S_2^\eta = S_2^\delta \land S_3^\eta = S_3^\delta \land \\& \land \eta> \sup\left\{ {\sup\mathrm{dom}(p_{\alpha \beta}) \mid \alpha < \beta \in b} \right\} \land \forall \alpha \in b : p_{\alpha \eta} \Vdash \dot{c}(\alpha, \eta) = 1 \}. \end{align*} $$
It is obvious that S is definable in M and
![]() $\delta \in S$
; thus S is a stationary subset of
$\delta \in S$
; thus S is a stationary subset of
![]() $\lambda ^+$
.
$\lambda ^+$
.
Finally consider the set
If
![]() $\delta $
is not an element of T, then there is some
$\delta $
is not an element of T, then there is some
![]() $\xi \in S \cap \delta $
for which
$\xi \in S \cap \delta $
for which
![]() $\emptyset \not \Vdash \dot {c}(\xi , \delta ) = 0$
so
$\emptyset \not \Vdash \dot {c}(\xi , \delta ) = 0$
so
![]() $p_{\xi \delta }$
was defined as some condition p such that
$p_{\xi \delta }$
was defined as some condition p such that
![]() $p \Vdash \dot {c}(\xi , \delta ) = 1$
, as
$p \Vdash \dot {c}(\xi , \delta ) = 1$
, as
![]() $\xi $
is also an element of S we can put
$\xi $
is also an element of S we can put
![]() $b_\beta := \xi $
. Now each condition of the claim is satisfied as witnessed by
$b_\beta := \xi $
. Now each condition of the claim is satisfied as witnessed by
![]() $\xi $
belonging to S and the fact that
$\xi $
belonging to S and the fact that
![]() $\xi $
witnesses that
$\xi $
witnesses that
![]() $\delta \not \in T$
.
$\delta \not \in T$
.
On the other hand if
![]() $\delta \in T$
, then T is unbounded in
$\delta \in T$
, then T is unbounded in
![]() $\lambda ^+$
and clearly
$\lambda ^+$
and clearly
![]() $\emptyset \Vdash \dot {c}"[T]^2 = \{0\}$
, a contradiction.
$\emptyset \Vdash \dot {c}"[T]^2 = \{0\}$
, a contradiction.
Let B be the set constructed in the previous subclaim. We can also assume that
![]() $\left \{ {p_{\alpha \delta } \mid \alpha \in B} \right \}$
is a
$\left \{ {p_{\alpha \delta } \mid \alpha \in B} \right \}$
is a
![]() $\Delta $
-system (we assume that for each
$\Delta $
-system (we assume that for each
![]() $\alpha < \lambda $
we have
$\alpha < \lambda $
we have
![]() $|\alpha ^{<\kappa }| < \lambda $
) so in particular
$|\alpha ^{<\kappa }| < \lambda $
) so in particular
![]() $p_{\alpha \delta } \simeq p_{\beta \delta }$
for
$p_{\alpha \delta } \simeq p_{\beta \delta }$
for
![]() $\alpha , \beta \in B$
. We now show that the set B can be refined so that the set of conditions
$\alpha , \beta \in B$
. We now show that the set B can be refined so that the set of conditions
![]() $\left \{ {p_{\alpha \beta } \mid \left \{ {\alpha , \beta } \right \} \in [B]^2} \right \}$
will form a double
$\left \{ {p_{\alpha \beta } \mid \left \{ {\alpha , \beta } \right \} \in [B]^2} \right \}$
will form a double
![]() $\Delta $
-system.
$\Delta $
-system.
The previous paragraph, condition (3), and Lemma 2.5 imply that for each
![]() $\gamma $
also the set
$\gamma $
also the set
![]() $\left \{ {p_{\alpha \gamma } \mid \alpha \in B \cap \gamma } \right \}$
is a
$\left \{ {p_{\alpha \gamma } \mid \alpha \in B \cap \gamma } \right \}$
is a
![]() $\Delta $
-system with root
$\Delta $
-system with root
![]() $p^1_\gamma $
. We can now assume that
$p^1_\gamma $
. We can now assume that
![]() $\left \{ {p^1_\gamma \mid \gamma \in B} \right \}$
also forms a
$\left \{ {p^1_\gamma \mid \gamma \in B} \right \}$
also forms a
![]() $\Delta $
-system with root
$\Delta $
-system with root
![]() $p^1$
.
$p^1$
.
Conditions (1), (2), and (4) imply that for each
![]() $\alpha \in B$
the set of conditions
$\alpha \in B$
the set of conditions
![]() $\left \{ {p_{\alpha \beta } \mid \beta \in B \setminus (\alpha + 1)} \right \}$
is a
$\left \{ {p_{\alpha \beta } \mid \beta \in B \setminus (\alpha + 1)} \right \}$
is a
![]() $\Delta $
-system with root
$\Delta $
-system with root
![]() $p^0_\alpha := {p_{\alpha \delta }}\restriction {\delta }$
. Given any
$p^0_\alpha := {p_{\alpha \delta }}\restriction {\delta }$
. Given any
![]() $p_{\alpha \beta }$
and
$p_{\alpha \beta }$
and
![]() $p_{\alpha \gamma }$
for
$p_{\alpha \gamma }$
for
![]() $\alpha < \beta < \gamma $
in B consider the intersection
$\alpha < \beta < \gamma $
in B consider the intersection
![]() $p_{\alpha \beta } \cap p_{\alpha \gamma }$
, and clearly
$p_{\alpha \beta } \cap p_{\alpha \gamma }$
, and clearly
![]() ${p_{\alpha \delta }}\restriction {\delta } \subseteq p_{\alpha \beta } \cap p_{\alpha \gamma }$
by condition (2). For the other direction if
${p_{\alpha \delta }}\restriction {\delta } \subseteq p_{\alpha \beta } \cap p_{\alpha \gamma }$
by condition (2). For the other direction if
![]() $(d,v) \in p_{\alpha \beta } \cap p_{\alpha \gamma }$
, then
$(d,v) \in p_{\alpha \beta } \cap p_{\alpha \gamma }$
, then
![]() $d < \gamma $
by condition (4), thus
$d < \gamma $
by condition (4), thus
![]() $(d,v) \in p_{\alpha \gamma }\restriction \gamma $
and again by condition (2)
$(d,v) \in p_{\alpha \gamma }\restriction \gamma $
and again by condition (2)
![]() $(d,v) \in p_{\alpha \delta }\restriction {\delta }$
. Finally we can also assume that
$(d,v) \in p_{\alpha \delta }\restriction {\delta }$
. Finally we can also assume that
![]() $\left \{ {p^0_\alpha \mid \alpha \in B} \right \}$
forms a
$\left \{ {p^0_\alpha \mid \alpha \in B} \right \}$
forms a
![]() $\Delta $
-system with root
$\Delta $
-system with root
![]() $p^0$
. Let X be the refined set B; this is our desired set.
$p^0$
. Let X be the refined set B; this is our desired set.
We will denote the root
![]() $p^0 = p^1$
of the double
$p^0 = p^1$
of the double
![]() $\Delta $
-system simply as p.
$\Delta $
-system simply as p.
Before we proceed fix an ordinal
![]() $\kappa \le \mu < \kappa ^+$
. Choose two sets:
$\kappa \le \mu < \kappa ^+$
. Choose two sets:
![]() $X_0$
and
$X_0$
and
![]() $X_1$
, subsets of X such that
$X_1$
, subsets of X such that
![]() $X_0 < X_1$
and the order type of both sets is
$X_0 < X_1$
and the order type of both sets is
![]() $\kappa \cdot \mu $
. Fix also a bijection
$\kappa \cdot \mu $
. Fix also a bijection
![]() $g: \kappa \to \mu $
.
$g: \kappa \to \mu $
.
Claim 2.
p forces a
![]() $(\mu : \mu )$
configuration in color
$(\mu : \mu )$
configuration in color
![]() $1$
.
$1$
.
Proof Let G be a generic set containing p, by induction we will construct sequences
![]() $(s_\alpha \mid \alpha < \kappa )$
in
$(s_\alpha \mid \alpha < \kappa )$
in
![]() $X_0$
and
$X_0$
and
![]() $(t_\alpha \mid \alpha < \kappa )$
in
$(t_\alpha \mid \alpha < \kappa )$
in
![]() $X_1$
such that
$X_1$
such that
![]() $s_\alpha $
is in the
$s_\alpha $
is in the
![]() $g(\alpha )$
-th section of
$g(\alpha )$
-th section of
![]() $X_0$
, i.e., if
$X_0$
, i.e., if
![]() $f: \kappa \cdot \mu \to X_0$
is the unique increasing bijection then
$f: \kappa \cdot \mu \to X_0$
is the unique increasing bijection then
and denote this subset of
![]() $X_0$
as
$X_0$
as
![]() $X_0^\alpha $
, analogously for
$X_0^\alpha $
, analogously for
![]() $t_\alpha $
and
$t_\alpha $
and
![]() $X_1$
. We will make sure that for all
$X_1$
. We will make sure that for all
![]() $\alpha , \beta \in \kappa $
we have
$\alpha , \beta \in \kappa $
we have
![]() $p_{s_\alpha t_\beta } \in G$
; as
$p_{s_\alpha t_\beta } \in G$
; as
![]() $p_{s_\alpha t_\beta }$
forces the color of the pair
$p_{s_\alpha t_\beta }$
forces the color of the pair
![]() $\{s_\alpha , t_\beta \}$
to be
$\{s_\alpha , t_\beta \}$
to be
![]() $1$
this will ensure the conclusion of the claim.
$1$
this will ensure the conclusion of the claim.
To start the induction note that by genericity for some
![]() $\alpha \in X_0^0$
we have
$\alpha \in X_0^0$
we have
![]() $p^0_\alpha \in G$
, this is because
$p^0_\alpha \in G$
, this is because
![]() $\left \{ {p^0_\alpha \mid \alpha \in X_0^0} \right \}$
is a
$\left \{ {p^0_\alpha \mid \alpha \in X_0^0} \right \}$
is a
![]() $\Delta $
-system of size
$\Delta $
-system of size
![]() $\kappa $
with root
$\kappa $
with root
![]() $p^0 \ge p$
and thus this set is predense below p. By the same argument there is some
$p^0 \ge p$
and thus this set is predense below p. By the same argument there is some
![]() $\beta \in X_1^0$
such that
$\beta \in X_1^0$
such that
![]() $p_{\alpha \beta }$
is in G, so put
$p_{\alpha \beta }$
is in G, so put
![]() $s_0 := \alpha $
and
$s_0 := \alpha $
and
![]() $t_0 := \beta $
.
$t_0 := \beta $
.
Suppose we have already constructed
![]() $(s_\alpha \mid \alpha < \gamma )$
and
$(s_\alpha \mid \alpha < \gamma )$
and
![]() $(t_\alpha \mid \alpha < \gamma )$
such that
$(t_\alpha \mid \alpha < \gamma )$
such that
![]() $p_{s_\alpha t_\beta } \in G$
for all
$p_{s_\alpha t_\beta } \in G$
for all
![]() $\alpha , \beta < \gamma $
. We will now find
$\alpha , \beta < \gamma $
. We will now find
![]() $\sigma \in X_0^\gamma $
such that
$\sigma \in X_0^\gamma $
such that
![]() $\left \{ {p_{\sigma t_\alpha } \mid \alpha < \gamma } \right \} \subseteq G$
and this will be our
$\left \{ {p_{\sigma t_\alpha } \mid \alpha < \gamma } \right \} \subseteq G$
and this will be our
![]() $s_\gamma $
.
$s_\gamma $
.
Suppose that no
![]() $\sigma $
satisfies our requirements, i.e., there is no
$\sigma $
satisfies our requirements, i.e., there is no
![]() $\sigma $
in
$\sigma $
in
![]() $X_0^\gamma $
such that
$X_0^\gamma $
such that
![]() $\left \{ {p_{\sigma t_\alpha } \mid \alpha < \gamma } \right \} \subseteq G$
. Then there must exist a condition
$\left \{ {p_{\sigma t_\alpha } \mid \alpha < \gamma } \right \} \subseteq G$
. Then there must exist a condition
![]() $r \le p$
forcing this (note that
$r \le p$
forcing this (note that
![]() $\left \{ {p_{\sigma t_\alpha } \mid \alpha < \gamma } \right \}$
is an element of the ground model because our forcing is
$\left \{ {p_{\sigma t_\alpha } \mid \alpha < \gamma } \right \}$
is an element of the ground model because our forcing is
![]() $\kappa $
-closed):
$\kappa $
-closed):
This means that for all
![]() $\sigma \in X_0^\gamma $
there exists a
$\sigma \in X_0^\gamma $
there exists a
![]() $\beta < \gamma $
such that
$\beta < \gamma $
such that
![]() $r \bot p_{\sigma t_\beta }$
. By going to a refinement we can assume that for
$r \bot p_{\sigma t_\beta }$
. By going to a refinement we can assume that for
![]() $\kappa $
many
$\kappa $
many
![]() $\sigma $
there is a fixed
$\sigma $
there is a fixed
![]() $\beta ' < \gamma $
such that
$\beta ' < \gamma $
such that
![]() $r \bot p_{\sigma t_{\beta '}}$
; call this set C. However note that the set
$r \bot p_{\sigma t_{\beta '}}$
; call this set C. However note that the set
![]() $\{p_{\sigma t_{\beta '}} \mid \sigma \in C\}$
is a
$\{p_{\sigma t_{\beta '}} \mid \sigma \in C\}$
is a
![]() $\Delta $
-system with root
$\Delta $
-system with root
![]() $p^1_{t_{\beta '}}$
which is contained in the generic set G because
$p^1_{t_{\beta '}}$
which is contained in the generic set G because
![]() $p_{s_0 t_{\beta '}} \le p^1_{t_{\beta '}}$
and
$p_{s_0 t_{\beta '}} \le p^1_{t_{\beta '}}$
and
![]() $p_{s_0 t_{\beta '}} \in G$
. Since r has size
$p_{s_0 t_{\beta '}} \in G$
. Since r has size
![]() $<\kappa $
and
$<\kappa $
and
![]() $r \parallel p^1_{t_{\beta '}}$
, it cannot be incompatible with every condition from
$r \parallel p^1_{t_{\beta '}}$
, it cannot be incompatible with every condition from
![]() $\{p_{\sigma t_{\beta '}} \mid \sigma \in C\}$
, a contradiction.
$\{p_{\sigma t_{\beta '}} \mid \sigma \in C\}$
, a contradiction.
The construction of
![]() $t_\gamma $
is almost verbatim.
$t_\gamma $
is almost verbatim.
This concludes the proof.⊣
3 A negative partition relation from Cohen forcing
The result of the previous section cannot be strengthened so that the second partition of the bipartite graph has size
![]() $\kappa ^+$
.
$\kappa ^+$
.
Proposition 3.1. If
![]() $\kappa < \lambda $
are regular cardinals, then
$\kappa < \lambda $
are regular cardinals, then
![]() $\mathsf {Add}({\kappa }, {\lambda }) \Vdash {\lambda } \not \to ({\kappa : \kappa ^+})^2$
.
$\mathsf {Add}({\kappa }, {\lambda }) \Vdash {\lambda } \not \to ({\kappa : \kappa ^+})^2$
.
Proof Consider an equivalent form of the forcing notion, specifically the poset
![]() $C_{S} : = \left \{ {p : S \to 2 \mid |p| < \kappa } \right \}$
, where
$C_{S} : = \left \{ {p : S \to 2 \mid |p| < \kappa } \right \}$
, where
![]() $S := [\lambda ]^2$
and the ordering is reverse inclusion. We will prove that the generic graph, the union over the generic set G, added this way does not contain a homogeneous
$S := [\lambda ]^2$
and the ordering is reverse inclusion. We will prove that the generic graph, the union over the generic set G, added this way does not contain a homogeneous
![]() $(\kappa : \kappa ^+)$
configuration.
$(\kappa : \kappa ^+)$
configuration.
Suppose, for contradiction, that in the extension there are a set X of size
![]() $\kappa $
and a set Y of size
$\kappa $
and a set Y of size
![]() $\kappa ^+$
above it so that all edges between them are monochromatic. Use the fact that when forcing with
$\kappa ^+$
above it so that all edges between them are monochromatic. Use the fact that when forcing with
![]() $\mathsf {Add}({\kappa }, {\lambda })$
any set of size
$\mathsf {Add}({\kappa }, {\lambda })$
any set of size
![]() $\kappa $
can be decided already when forcing over a domain of size
$\kappa $
can be decided already when forcing over a domain of size
![]() $\kappa $
[Reference Kunen6, Lemma VIII.2.2]. To be more precise denote by M the ground model; there is a set
$\kappa $
[Reference Kunen6, Lemma VIII.2.2]. To be more precise denote by M the ground model; there is a set
![]() $I \subseteq [\lambda ]^2$
of size
$I \subseteq [\lambda ]^2$
of size
![]() $\kappa $
so that
$\kappa $
so that
![]() $X \in M[G \cap C_{I}]$
(note that
$X \in M[G \cap C_{I}]$
(note that
![]() $C_{[\lambda ]^2} \cong C_{I} \times C_{[\lambda ]^2 \setminus I}$
). Now working in the extension by
$C_{[\lambda ]^2} \cong C_{I} \times C_{[\lambda ]^2 \setminus I}$
). Now working in the extension by
![]() $C_I$
, there must exist a condition p in
$C_I$
, there must exist a condition p in
![]() $ C_{[\lambda ]^2 \setminus I}$
so that
$ C_{[\lambda ]^2 \setminus I}$
so that
![]() $p \Vdash y \in \dot {Y}$
for some
$p \Vdash y \in \dot {Y}$
for some
![]() $y \not \in \bigcup I$
, otherwise
$y \not \in \bigcup I$
, otherwise
![]() $C_{[\lambda ]^2 \setminus I} \Vdash \dot {Y} \subseteq \bigcup I$
, which is not possible. Now p has size
$C_{[\lambda ]^2 \setminus I} \Vdash \dot {Y} \subseteq \bigcup I$
, which is not possible. Now p has size
![]() $<\kappa $
and
$<\kappa $
and
![]() $|X|=\kappa $
; hence there must be an
$|X|=\kappa $
; hence there must be an
![]() $x \in X \setminus \bigcup \mathrm {dom}(p)$
. Now p can be extended by the pair
$x \in X \setminus \bigcup \mathrm {dom}(p)$
. Now p can be extended by the pair
![]() $(\left \{ {x, y} \right \}, i)$
for both
$(\left \{ {x, y} \right \}, i)$
for both
![]() $i \in \left \{ {0, 1} \right \}$
, which is a contradiction.
$i \in \left \{ {0, 1} \right \}$
, which is a contradiction.
4 Possible strengthening of our result
The consistency of the relation
![]() ${{\omega _2}} \to ({{\omega _2}}, {\omega + 2})^2$
with
${{\omega _2}} \to ({{\omega _2}}, {\omega + 2})^2$
with
![]() $\neg \mathsf {CH}$
is unknown and seems to be substantially more involved than our result. By a result of Raghavan and Todorčević [Reference Raghavan and Todorčević9] this relation implies the non-existence of
$\neg \mathsf {CH}$
is unknown and seems to be substantially more involved than our result. By a result of Raghavan and Todorčević [Reference Raghavan and Todorčević9] this relation implies the non-existence of
![]() ${\omega _2}$
-Suslin trees. Laver showed [Reference Laver8] that in a model where
${\omega _2}$
-Suslin trees. Laver showed [Reference Laver8] that in a model where
![]() $\mathsf {MA}$
holds and
$\mathsf {MA}$
holds and
![]() $2^\omega = {\omega _2}$
we have
$2^\omega = {\omega _2}$
we have
![]() ${{\omega _2}} \not \to ({{\omega _2}}, {\omega : 2})^2$
.
${{\omega _2}} \not \to ({{\omega _2}}, {\omega : 2})^2$
.
Question 4.1. Is the relation
![]() ${{\omega _2}} \to ({{\omega _2}}, {\omega + 2})^2$
consistent with
${{\omega _2}} \to ({{\omega _2}}, {\omega + 2})^2$
consistent with
![]() $\neg \mathsf {CH}$
?
$\neg \mathsf {CH}$
?
Acknowledgement
The author is grateful to David Chodounský, Chris Lambie-Hanson, and Stevo Todorčević for helpful discussions on the topic which greatly improved the exposition of this paper.
Funding
This work was supported by Charles University Research Center Program No. UNCE/SCI/022 and by the Academy of Sciences of the Czech Republic (RVO 67985840).