1. Introduction
Townsend’s classical self-preserving approach to characterising the behaviour of turbulent shear flows rests on the hypothesis that, at sufficiently large Reynolds numbers, the flow will eventually (i.e. sufficiently far downstream) ‘forget’ anything about how it was created and thus have a universal form determined solely by the necessary integral constraints. Analysis then leads to the well-known scaling laws for the mean velocity and turbulence stress fields, whose details depend only on the type of flow. For an axisymmetric wake, the analysis leads to a wake width governed by
 ${\it\delta}\sim (x-x_{o})^{{\it\lambda}}$
and a decay in centreline velocity deficit governed by
${\it\delta}\sim (x-x_{o})^{{\it\lambda}}$
and a decay in centreline velocity deficit governed by
 $u_{o}\sim (x-x_{o})^{-2{\it\lambda}}$
(with
$u_{o}\sim (x-x_{o})^{-2{\it\lambda}}$
(with
 ${\it\lambda}=1/3$
), where
${\it\lambda}=1/3$
), where
 $x$
is the distance downstream from the wake-generating object and
$x$
is the distance downstream from the wake-generating object and
 $x_{o}$
is a virtual origin. The turbulence statistics follow corresponding self-similar behaviour. Over the 60 years or so since Townsend’s early work, there have been many, largely experimental, studies of all the possible flow types, which have assessed the adequacy of the classical scaling laws. Such studies are never very straightforward, and this is particularly true for the axisymmetric wake. To be confident about both
$x_{o}$
is a virtual origin. The turbulence statistics follow corresponding self-similar behaviour. Over the 60 years or so since Townsend’s early work, there have been many, largely experimental, studies of all the possible flow types, which have assessed the adequacy of the classical scaling laws. Such studies are never very straightforward, and this is particularly true for the axisymmetric wake. To be confident about both
 ${\it\lambda}$
and
${\it\lambda}$
and
 $x_{o}$
, it is necessary that the Reynolds numbers (both initial – set by the body geometry and upstream velocity – and local – set by
$x_{o}$
, it is necessary that the Reynolds numbers (both initial – set by the body geometry and upstream velocity – and local – set by
 $\sqrt{k}$
and
$\sqrt{k}$
and
 ${\it\delta}$
, say) are large enough to ensure that Townsend’s ‘memory’ hypothesis and the Kolmogorov dissipation hypothesis are reasonable. In addition, there should be a sufficiently large range in
${\it\delta}$
, say) are large enough to ensure that Townsend’s ‘memory’ hypothesis and the Kolmogorov dissipation hypothesis are reasonable. In addition, there should be a sufficiently large range in
 $x$
downstream of the initial development region (a priori of unknown length). It is not easy to satisfy both requirements simultaneously.
$x$
downstream of the initial development region (a priori of unknown length). It is not easy to satisfy both requirements simultaneously.
There has thus been some controversy over whether the Townsend scalings hold. In fact, starting with the work of Bevilaqua & Lykoudis (Reference Bevilaqua and Lykoudis1978) over 35 years ago, there is mounting evidence that the geometry of the wake-generating body has a marked influence on the far-wake growth rate and turbulence even in regions where self-similarity is present, which leads to questions about whether the initial conditions really are ever forgotten. Much later, a similar result was found for plane wakes by Zhou & Antonia (Reference Zhou and Antonia1995). Johansson, George & Gourlay (Reference Johansson, George and Gourlay2003) undertook a more complete analysis and showed that, for small Reynolds number, an additional scaling was possible (for which
 ${\it\lambda}=1/2$
) and that both solutions can indeed be dependent on initial conditions. A numerical study was first done for a high-Reynolds-number case by Gourlay et al. (Reference Gourlay, Arendt, Fritts and Werne2001). Both they and Redford, Castro & Coleman (Reference Redford, Castro and Coleman2012) studied the spatially homogeneous but time-developing equivalent of axisymmetric wakes using direct numerical simulation (DNS). The latter showed apparently unequivocally that, for late enough times (corresponding to very far downstream in the spatially developing case), the classical
${\it\lambda}=1/2$
) and that both solutions can indeed be dependent on initial conditions. A numerical study was first done for a high-Reynolds-number case by Gourlay et al. (Reference Gourlay, Arendt, Fritts and Werne2001). Both they and Redford, Castro & Coleman (Reference Redford, Castro and Coleman2012) studied the spatially homogeneous but time-developing equivalent of axisymmetric wakes using direct numerical simulation (DNS). The latter showed apparently unequivocally that, for late enough times (corresponding to very far downstream in the spatially developing case), the classical
 ${\it\lambda}=1/3$
universal behaviour occurs, in which the multiplying constants (e.g. in the growth-rate relation for
${\it\lambda}=1/3$
universal behaviour occurs, in which the multiplying constants (e.g. in the growth-rate relation for
 ${\it\delta}$
) are truly independent of the initial conditions and
${\it\delta}$
) are truly independent of the initial conditions and
 $C_{{\it\epsilon}}$
is essentially constant.
$C_{{\it\epsilon}}$
is essentially constant.
It is especially crucial to recognise that all the extant work has assumed the adequacy of Kolmogorov’s hypothesis (that the small-scale motions evolve much more rapidly than the time scale of the evolution of the whole flow), which led, with additional assumptions, to the famous equilibrium dissipation law,
 ${\it\epsilon}=C_{{\it\epsilon}}k^{3/2}/L$
(with
${\it\epsilon}=C_{{\it\epsilon}}k^{3/2}/L$
(with
 $C_{{\it\epsilon}}=\text{const}.$
). The major objective of Dairay, Obligado & Vassilicos (Reference Dairay, Obligado and Vassilicos2015) is to ‘establish the existence of a new non-equilibrium dissipation law’, which assumes that, given a global Reynolds number set by the initial conditions,
$C_{{\it\epsilon}}=\text{const}.$
). The major objective of Dairay, Obligado & Vassilicos (Reference Dairay, Obligado and Vassilicos2015) is to ‘establish the existence of a new non-equilibrium dissipation law’, which assumes that, given a global Reynolds number set by the initial conditions,
 $C_{{\it\epsilon}}\sim \mathit{Re}_{l}^{-n}$
, where
$C_{{\it\epsilon}}\sim \mathit{Re}_{l}^{-n}$
, where
 $\mathit{Re}_{l}$
is a local Reynolds number. They do this for an axisymmetric wake, comparing their data with the scaling-law exponents that arise on the basis of this new dissipation law.
$\mathit{Re}_{l}$
is a local Reynolds number. They do this for an axisymmetric wake, comparing their data with the scaling-law exponents that arise on the basis of this new dissipation law.
2. Overview
After a brief introduction to the arguments leading to the classical axisymmetric wake scalings in which
 ${\it\lambda}=1/3$
, not least their reliance on the assumption that
${\it\lambda}=1/3$
, not least their reliance on the assumption that
 $C_{{\it\epsilon}}=\text{const}.$
, Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) introduce their alternative non-equilibrium dissipation law (discussed more fully by Vassilicos (Reference Vassilicos2015)), which states that
$C_{{\it\epsilon}}=\text{const}.$
, Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) introduce their alternative non-equilibrium dissipation law (discussed more fully by Vassilicos (Reference Vassilicos2015)), which states that
 $C_{{\it\epsilon}}\sim \mathit{Re}_{G}^{m}/\mathit{Re}_{l}^{n}$
, where
$C_{{\it\epsilon}}\sim \mathit{Re}_{G}^{m}/\mathit{Re}_{l}^{n}$
, where
 $\mathit{Re}_{G}$
is a global Reynolds number set by the initial conditions and
$\mathit{Re}_{G}$
is a global Reynolds number set by the initial conditions and
 $\mathit{Re}_{l}$
is a local one, which for an axisymmetric wake (as for grid turbulence) falls with distance downstream. From the equations of motion and on the basis of the similarity arguments by George (Reference George, George and Arndt1989) (and see also Johansson et al. (Reference Johansson, George and Gourlay2003)), this leads to the wake scaling laws derived by Nedić, Vassilicos & Ganapathisubramani (Reference Nedić, Vassilicos and Ganapathisubramani2013), which can essentially be expressed as
$\mathit{Re}_{l}$
is a local one, which for an axisymmetric wake (as for grid turbulence) falls with distance downstream. From the equations of motion and on the basis of the similarity arguments by George (Reference George, George and Arndt1989) (and see also Johansson et al. (Reference Johansson, George and Gourlay2003)), this leads to the wake scaling laws derived by Nedić, Vassilicos & Ganapathisubramani (Reference Nedić, Vassilicos and Ganapathisubramani2013), which can essentially be expressed as
 ${\it\delta}\sim (x-x_{o})^{1/(3-n)}$
and
${\it\delta}\sim (x-x_{o})^{1/(3-n)}$
and
 $u_{o}\sim (x-x_{o})^{-2/(3-n)}$
, with
$u_{o}\sim (x-x_{o})^{-2/(3-n)}$
, with
 $n=m=1$
(cf.
$n=m=1$
(cf.
 $n=m=0$
for
$n=m=0$
for
 ${\it\lambda}=1/3$
). Note that this value of
${\it\lambda}=1/3$
). Note that this value of
 $n$
and
$n$
and
 $m$
is the same as for a laminar wake (
$m$
is the same as for a laminar wake (
 ${\it\lambda}=1/2$
), although it arises for different reasons. However, it can also arise (and does) when the classical Kolmogorov law is assumed for a fully turbulent, high-Reynolds-number wake characterised by large ratios of turbulence to viscous stress, provided only that the eddy viscosity is constant (Redford et al.
Reference Redford, Castro and Coleman2012). The presence of
${\it\lambda}=1/2$
), although it arises for different reasons. However, it can also arise (and does) when the classical Kolmogorov law is assumed for a fully turbulent, high-Reynolds-number wake characterised by large ratios of turbulence to viscous stress, provided only that the eddy viscosity is constant (Redford et al.
Reference Redford, Castro and Coleman2012). The presence of
 $n=1$
scaling is thus not necessarily associated with low Reynolds number.
$n=1$
scaling is thus not necessarily associated with low Reynolds number.
Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) examine their scalings by exploring the wake of an irregular (fractal-type) bluff plate with sharp edges, using both a wind tunnel experiment and a matching DNS. This is unusual, not only in that both approaches are used in the same work but also because the DNS is of a spatially developing wake (as in the experiment), rather than a time-developing one, with the generating body included in the computational domain. Whilst this allows capture of the near wake it has the inevitable consequence that the available downstream extent of the wake is somewhat limited. It is also unusual because of the use of a fractal-type wake-generating plate, which leads, in the very near field, to a (‘multi-scale’) flow having a mixture of wake-like and jet-like character. For the DNS, great care is taken to ensure that there is sufficient domain size, grid resolution and statistical convergence. For the experiments, the plate is placed in a low-turbulence wind tunnel at
 $\mathit{Re}_{G}=U_{\infty }L_{b}/{\it\nu}=40\,000$
, where
$\mathit{Re}_{G}=U_{\infty }L_{b}/{\it\nu}=40\,000$
, where
 $L_{b}=\sqrt{A}$
, with
$L_{b}=\sqrt{A}$
, with
 $A$
the plate area. The measurements are made using hot-wire anemometry and extend to
$A$
the plate area. The measurements are made using hot-wire anemometry and extend to
 $x\approx 50L_{b}$
, whereas the DNS has
$x\approx 50L_{b}$
, whereas the DNS has
 $\mathit{Re}_{G}=5000$
and reaches approximately
$\mathit{Re}_{G}=5000$
and reaches approximately
 $x=100L_{b}$
.
$x=100L_{b}$
.
The results suggest that, over most of the extent of the wind tunnel wake (
 $15\leqslant x/L_{b}\leqslant 50$
),
$15\leqslant x/L_{b}\leqslant 50$
),
 $C_{{\it\epsilon}}\mathit{Re}_{l}^{n}$
with
$C_{{\it\epsilon}}\mathit{Re}_{l}^{n}$
with
 $n=1$
is more closely constant than is
$n=1$
is more closely constant than is
 $C_{{\it\epsilon}}$
. Actually, they show that a better fit requires
$C_{{\it\epsilon}}$
. Actually, they show that a better fit requires
 $n\approx 0.77$
. Further downstream (
$n\approx 0.77$
. Further downstream (
 $55\leqslant x/L_{b}\leqslant 100$
) the DNS data suggest a change to
$55\leqslant x/L_{b}\leqslant 100$
) the DNS data suggest a change to
 $n\approx 0.5$
. To derive theoretical scalings for wake width and velocity deficit that have
$n\approx 0.5$
. To derive theoretical scalings for wake width and velocity deficit that have
 $n\neq 1$
, the authors make a ‘constant anisotropy’ assumption – that the Reynolds shear stress and the turbulent kinetic energy profiles scale in the same way (but not with
$n\neq 1$
, the authors make a ‘constant anisotropy’ assumption – that the Reynolds shear stress and the turbulent kinetic energy profiles scale in the same way (but not with
 $u_{o}^{2}$
). This is essentially a revised Townsend–George theory (Townsend Reference Townsend1976; George Reference George, George and Arndt1989), but includes the new ‘non-equilibrium dissipation’ law. (Note that only the latter is necessary for
$u_{o}^{2}$
). This is essentially a revised Townsend–George theory (Townsend Reference Townsend1976; George Reference George, George and Arndt1989), but includes the new ‘non-equilibrium dissipation’ law. (Note that only the latter is necessary for
 $n=1$
.) The variations of
$n=1$
.) The variations of
 $u_{o}$
and
$u_{o}$
and
 ${\it\delta}$
along the wake are shown to conform quite well to the new scalings,
${\it\delta}$
along the wake are shown to conform quite well to the new scalings,
 $u_{o}\sim (x-x_{o})^{{\it\alpha}}$
and
$u_{o}\sim (x-x_{o})^{{\it\alpha}}$
and
 ${\it\delta}\sim (x-x_{o})^{{\it\beta}}$
, with
${\it\delta}\sim (x-x_{o})^{{\it\beta}}$
, with
 ${\it\alpha}=-2{\it\beta}=-2(1+n)/(3+n)$
, albeit with different
${\it\alpha}=-2{\it\beta}=-2(1+n)/(3+n)$
, albeit with different
 $n$
(
$n$
(
 ${<}1$
) for the upstream and downstream halves of the
${<}1$
) for the upstream and downstream halves of the
 $x$
region studied. Given that the local Reynolds number (
$x$
region studied. Given that the local Reynolds number (
 $\sqrt{k}{\it\delta}/{\it\nu}$
) only falls to around 230 by
$\sqrt{k}{\it\delta}/{\it\nu}$
) only falls to around 230 by
 $x=100L_{b}$
in the DNS, and is very much higher in the wind tunnel, it is arguably difficult to claim that it is too small to expect the classical scaling to hold.
$x=100L_{b}$
in the DNS, and is very much higher in the wind tunnel, it is arguably difficult to claim that it is too small to expect the classical scaling to hold.
In addition to the increasing body of evidence that the value of
 $C_{{\it\epsilon}}$
can depend on initial conditions, Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) (following Nedić et al. (Reference Nedić, Vassilicos and Ganapathisubramani2013), along with the same group’s work on grid turbulence) thus go much further and question the universality of Reynolds-number independence of
$C_{{\it\epsilon}}$
can depend on initial conditions, Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) (following Nedić et al. (Reference Nedić, Vassilicos and Ganapathisubramani2013), along with the same group’s work on grid turbulence) thus go much further and question the universality of Reynolds-number independence of
 $C_{{\it\epsilon}}$
. No physical explanation is offered for why the
$C_{{\it\epsilon}}$
. No physical explanation is offered for why the
 $C_{{\it\epsilon}}\mathit{Re}_{l}^{n}=\text{const}.$
dissipation law might apply, but it does provide revised scaling laws for axisymmetric wakes that fit the present data.
$C_{{\it\epsilon}}\mathit{Re}_{l}^{n}=\text{const}.$
dissipation law might apply, but it does provide revised scaling laws for axisymmetric wakes that fit the present data.
3. Future
Although there is considerable evidence for the adequacy of the classical dissipation relation, it is apparent that it may be too simplistic, at more than one level. (Actually, it has long been recognised that
 $C_{{\it\epsilon}}$
is unlikely to be universal (Taylor Reference Taylor1935).) It is already clear that, whilst at sufficiently large Reynolds number
$C_{{\it\epsilon}}$
is unlikely to be universal (Taylor Reference Taylor1935).) It is already clear that, whilst at sufficiently large Reynolds number
 $C_{{\it\epsilon}}$
may become constant, its precise value can depend on initial conditions (e.g. Sreenivasan Reference Sreenivasan1998; Antonia & Pearson Reference Antonia and Pearson2000). Dairay et al.’s data seem even more revealing, in that, using only one wake-generating body, they show that
$C_{{\it\epsilon}}$
may become constant, its precise value can depend on initial conditions (e.g. Sreenivasan Reference Sreenivasan1998; Antonia & Pearson Reference Antonia and Pearson2000). Dairay et al.’s data seem even more revealing, in that, using only one wake-generating body, they show that
 $C_{{\it\epsilon}}$
is not even constant, but rather varies with local Reynolds number. The Kolmogorov law
$C_{{\it\epsilon}}$
is not even constant, but rather varies with local Reynolds number. The Kolmogorov law
 ${\it\epsilon}=C_{{\it\epsilon}}k^{3/2}/L$
, with
${\it\epsilon}=C_{{\it\epsilon}}k^{3/2}/L$
, with
 $C_{{\it\epsilon}}=\text{const}.$
, is often seen as ‘one of the cornerstone assumptions of turbulence theory’ but Lumley (Reference Lumley1992) remarked that the ‘mechanism that sets the level of dissipation in a turbulent flow, particularly in changing circumstances’, is worthy of further study. If the results of the Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) study can be shown to be typical of other high-Reynolds-number turbulent shear flows ‘in changing circumstances’, or indeed in axisymmetric wakes at significantly higher
$C_{{\it\epsilon}}=\text{const}.$
, is often seen as ‘one of the cornerstone assumptions of turbulence theory’ but Lumley (Reference Lumley1992) remarked that the ‘mechanism that sets the level of dissipation in a turbulent flow, particularly in changing circumstances’, is worthy of further study. If the results of the Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) study can be shown to be typical of other high-Reynolds-number turbulent shear flows ‘in changing circumstances’, or indeed in axisymmetric wakes at significantly higher
 $\mathit{Re}_{l}$
than they could reach, the premonition implied by Lumley’s remark will prove to have been prophetic. The matter is certainly worthy of more extensive study, not least because the non-equilibrium dissipation law seems to break the link between the presence of
$\mathit{Re}_{l}$
than they could reach, the premonition implied by Lumley’s remark will prove to have been prophetic. The matter is certainly worthy of more extensive study, not least because the non-equilibrium dissipation law seems to break the link between the presence of
 $-5/3$
spectra and classical cascade arguments. This new law seems to hold over much of any wake region that is likely to exist in real applications, so, even without any physical explanation, it would seem to be important. One can expect further experiments exploring the issue, aimed not least at finding whether (and if so, why) there is a final transition to a more classical scaling at some greater distance downstream, as Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) suggest, even though
$-5/3$
spectra and classical cascade arguments. This new law seems to hold over much of any wake region that is likely to exist in real applications, so, even without any physical explanation, it would seem to be important. One can expect further experiments exploring the issue, aimed not least at finding whether (and if so, why) there is a final transition to a more classical scaling at some greater distance downstream, as Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) suggest, even though
 $\mathit{Re}_{l}$
must continue to fall.
$\mathit{Re}_{l}$
must continue to fall.
Finally, note that little is known about how the very-near-wake flow transitions to the region explored by Dairay et al. (Reference Dairay, Obligado and Vassilicos2015). The process must surely be very dependent on the geometry of the generating body. The near-wake usually contains interesting and complex dynamics (e.g. the recent work of Rigas et al. (Reference Rigas, Morgans, Brackston and Morrison2015) and references therein). There would seem to be much scope for exploration of the various transition regions. And there remains the need for a physical explanation for the new non-equilibrium dissipation relation.
 ${\it\epsilon}$, of turbulence kinetic energy,
${\it\epsilon}$, of turbulence kinetic energy, 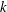 $k$. It has usually been assumed (sometimes implicitly) that this is governed by the famous Kolmogorov relation
$k$. It has usually been assumed (sometimes implicitly) that this is governed by the famous Kolmogorov relation 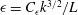 ${\it\epsilon}=C_{{\it\epsilon}}k^{3/2}/L$, where
${\it\epsilon}=C_{{\it\epsilon}}k^{3/2}/L$, where 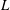 $L$ is a length scale of the energy-containing eddies and
$L$ is a length scale of the energy-containing eddies and 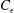 $C_{{\it\epsilon}}$ is a constant. The paper by Dairay et al. (J. Fluid Mech. vol. 781, 2015, pp. 166–195) demonstrates, however, that, in the specific context of an axisymmetric wake, there can be regions where
$C_{{\it\epsilon}}$ is a constant. The paper by Dairay et al. (J. Fluid Mech. vol. 781, 2015, pp. 166–195) demonstrates, however, that, in the specific context of an axisymmetric wake, there can be regions where  ${\it\epsilon}$ has a different behaviour, characterised by a
${\it\epsilon}$ has a different behaviour, characterised by a 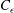 $C_{{\it\epsilon}}$ that is not constant but depends on a varying local Reynolds number (despite the existence of a
$C_{{\it\epsilon}}$ that is not constant but depends on a varying local Reynolds number (despite the existence of a 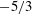 $-5/3$ region in the spectra). This leads to fundamentally different scaling laws for the wake.
$-5/3$ region in the spectra). This leads to fundamentally different scaling laws for the wake.



1. Introduction
Townsend’s classical self-preserving approach to characterising the behaviour of turbulent shear flows rests on the hypothesis that, at sufficiently large Reynolds numbers, the flow will eventually (i.e. sufficiently far downstream) ‘forget’ anything about how it was created and thus have a universal form determined solely by the necessary integral constraints. Analysis then leads to the well-known scaling laws for the mean velocity and turbulence stress fields, whose details depend only on the type of flow. For an axisymmetric wake, the analysis leads to a wake width governed by ${\it\delta}\sim (x-x_{o})^{{\it\lambda}}$
and a decay in centreline velocity deficit governed by
${\it\delta}\sim (x-x_{o})^{{\it\lambda}}$
and a decay in centreline velocity deficit governed by
 $u_{o}\sim (x-x_{o})^{-2{\it\lambda}}$
(with
$u_{o}\sim (x-x_{o})^{-2{\it\lambda}}$
(with
 ${\it\lambda}=1/3$
), where
${\it\lambda}=1/3$
), where
 $x$
is the distance downstream from the wake-generating object and
$x$
is the distance downstream from the wake-generating object and
 $x_{o}$
is a virtual origin. The turbulence statistics follow corresponding self-similar behaviour. Over the 60 years or so since Townsend’s early work, there have been many, largely experimental, studies of all the possible flow types, which have assessed the adequacy of the classical scaling laws. Such studies are never very straightforward, and this is particularly true for the axisymmetric wake. To be confident about both
$x_{o}$
is a virtual origin. The turbulence statistics follow corresponding self-similar behaviour. Over the 60 years or so since Townsend’s early work, there have been many, largely experimental, studies of all the possible flow types, which have assessed the adequacy of the classical scaling laws. Such studies are never very straightforward, and this is particularly true for the axisymmetric wake. To be confident about both
 ${\it\lambda}$
and
${\it\lambda}$
and
 $x_{o}$
, it is necessary that the Reynolds numbers (both initial – set by the body geometry and upstream velocity – and local – set by
$x_{o}$
, it is necessary that the Reynolds numbers (both initial – set by the body geometry and upstream velocity – and local – set by
 $\sqrt{k}$
and
$\sqrt{k}$
and
 ${\it\delta}$
, say) are large enough to ensure that Townsend’s ‘memory’ hypothesis and the Kolmogorov dissipation hypothesis are reasonable. In addition, there should be a sufficiently large range in
${\it\delta}$
, say) are large enough to ensure that Townsend’s ‘memory’ hypothesis and the Kolmogorov dissipation hypothesis are reasonable. In addition, there should be a sufficiently large range in
 $x$
downstream of the initial development region (a priori of unknown length). It is not easy to satisfy both requirements simultaneously.
$x$
downstream of the initial development region (a priori of unknown length). It is not easy to satisfy both requirements simultaneously.
There has thus been some controversy over whether the Townsend scalings hold. In fact, starting with the work of Bevilaqua & Lykoudis (Reference Bevilaqua and Lykoudis1978) over 35 years ago, there is mounting evidence that the geometry of the wake-generating body has a marked influence on the far-wake growth rate and turbulence even in regions where self-similarity is present, which leads to questions about whether the initial conditions really are ever forgotten. Much later, a similar result was found for plane wakes by Zhou & Antonia (Reference Zhou and Antonia1995). Johansson, George & Gourlay (Reference Johansson, George and Gourlay2003) undertook a more complete analysis and showed that, for small Reynolds number, an additional scaling was possible (for which ${\it\lambda}=1/2$
) and that both solutions can indeed be dependent on initial conditions. A numerical study was first done for a high-Reynolds-number case by Gourlay et al. (Reference Gourlay, Arendt, Fritts and Werne2001). Both they and Redford, Castro & Coleman (Reference Redford, Castro and Coleman2012) studied the spatially homogeneous but time-developing equivalent of axisymmetric wakes using direct numerical simulation (DNS). The latter showed apparently unequivocally that, for late enough times (corresponding to very far downstream in the spatially developing case), the classical
${\it\lambda}=1/2$
) and that both solutions can indeed be dependent on initial conditions. A numerical study was first done for a high-Reynolds-number case by Gourlay et al. (Reference Gourlay, Arendt, Fritts and Werne2001). Both they and Redford, Castro & Coleman (Reference Redford, Castro and Coleman2012) studied the spatially homogeneous but time-developing equivalent of axisymmetric wakes using direct numerical simulation (DNS). The latter showed apparently unequivocally that, for late enough times (corresponding to very far downstream in the spatially developing case), the classical
 ${\it\lambda}=1/3$
universal behaviour occurs, in which the multiplying constants (e.g. in the growth-rate relation for
${\it\lambda}=1/3$
universal behaviour occurs, in which the multiplying constants (e.g. in the growth-rate relation for
 ${\it\delta}$
) are truly independent of the initial conditions and
${\it\delta}$
) are truly independent of the initial conditions and
 $C_{{\it\epsilon}}$
is essentially constant.
$C_{{\it\epsilon}}$
is essentially constant.
It is especially crucial to recognise that all the extant work has assumed the adequacy of Kolmogorov’s hypothesis (that the small-scale motions evolve much more rapidly than the time scale of the evolution of the whole flow), which led, with additional assumptions, to the famous equilibrium dissipation law, ${\it\epsilon}=C_{{\it\epsilon}}k^{3/2}/L$
(with
${\it\epsilon}=C_{{\it\epsilon}}k^{3/2}/L$
(with
 $C_{{\it\epsilon}}=\text{const}.$
). The major objective of Dairay, Obligado & Vassilicos (Reference Dairay, Obligado and Vassilicos2015) is to ‘establish the existence of a new non-equilibrium dissipation law’, which assumes that, given a global Reynolds number set by the initial conditions,
$C_{{\it\epsilon}}=\text{const}.$
). The major objective of Dairay, Obligado & Vassilicos (Reference Dairay, Obligado and Vassilicos2015) is to ‘establish the existence of a new non-equilibrium dissipation law’, which assumes that, given a global Reynolds number set by the initial conditions,
 $C_{{\it\epsilon}}\sim \mathit{Re}_{l}^{-n}$
, where
$C_{{\it\epsilon}}\sim \mathit{Re}_{l}^{-n}$
, where
 $\mathit{Re}_{l}$
is a local Reynolds number. They do this for an axisymmetric wake, comparing their data with the scaling-law exponents that arise on the basis of this new dissipation law.
$\mathit{Re}_{l}$
is a local Reynolds number. They do this for an axisymmetric wake, comparing their data with the scaling-law exponents that arise on the basis of this new dissipation law.
2. Overview
After a brief introduction to the arguments leading to the classical axisymmetric wake scalings in which ${\it\lambda}=1/3$
, not least their reliance on the assumption that
${\it\lambda}=1/3$
, not least their reliance on the assumption that
 $C_{{\it\epsilon}}=\text{const}.$
, Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) introduce their alternative non-equilibrium dissipation law (discussed more fully by Vassilicos (Reference Vassilicos2015)), which states that
$C_{{\it\epsilon}}=\text{const}.$
, Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) introduce their alternative non-equilibrium dissipation law (discussed more fully by Vassilicos (Reference Vassilicos2015)), which states that
 $C_{{\it\epsilon}}\sim \mathit{Re}_{G}^{m}/\mathit{Re}_{l}^{n}$
, where
$C_{{\it\epsilon}}\sim \mathit{Re}_{G}^{m}/\mathit{Re}_{l}^{n}$
, where
 $\mathit{Re}_{G}$
is a global Reynolds number set by the initial conditions and
$\mathit{Re}_{G}$
is a global Reynolds number set by the initial conditions and
 $\mathit{Re}_{l}$
is a local one, which for an axisymmetric wake (as for grid turbulence) falls with distance downstream. From the equations of motion and on the basis of the similarity arguments by George (Reference George, George and Arndt1989) (and see also Johansson et al. (Reference Johansson, George and Gourlay2003)), this leads to the wake scaling laws derived by Nedić, Vassilicos & Ganapathisubramani (Reference Nedić, Vassilicos and Ganapathisubramani2013), which can essentially be expressed as
$\mathit{Re}_{l}$
is a local one, which for an axisymmetric wake (as for grid turbulence) falls with distance downstream. From the equations of motion and on the basis of the similarity arguments by George (Reference George, George and Arndt1989) (and see also Johansson et al. (Reference Johansson, George and Gourlay2003)), this leads to the wake scaling laws derived by Nedić, Vassilicos & Ganapathisubramani (Reference Nedić, Vassilicos and Ganapathisubramani2013), which can essentially be expressed as
 ${\it\delta}\sim (x-x_{o})^{1/(3-n)}$
and
${\it\delta}\sim (x-x_{o})^{1/(3-n)}$
and
 $u_{o}\sim (x-x_{o})^{-2/(3-n)}$
, with
$u_{o}\sim (x-x_{o})^{-2/(3-n)}$
, with
 $n=m=1$
(cf.
$n=m=1$
(cf.
 $n=m=0$
for
$n=m=0$
for
 ${\it\lambda}=1/3$
). Note that this value of
${\it\lambda}=1/3$
). Note that this value of
 $n$
and
$n$
and
 $m$
is the same as for a laminar wake (
$m$
is the same as for a laminar wake (
 ${\it\lambda}=1/2$
), although it arises for different reasons. However, it can also arise (and does) when the classical Kolmogorov law is assumed for a fully turbulent, high-Reynolds-number wake characterised by large ratios of turbulence to viscous stress, provided only that the eddy viscosity is constant (Redford et al.
Reference Redford, Castro and Coleman2012). The presence of
${\it\lambda}=1/2$
), although it arises for different reasons. However, it can also arise (and does) when the classical Kolmogorov law is assumed for a fully turbulent, high-Reynolds-number wake characterised by large ratios of turbulence to viscous stress, provided only that the eddy viscosity is constant (Redford et al.
Reference Redford, Castro and Coleman2012). The presence of
 $n=1$
scaling is thus not necessarily associated with low Reynolds number.
$n=1$
scaling is thus not necessarily associated with low Reynolds number.
Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) examine their scalings by exploring the wake of an irregular (fractal-type) bluff plate with sharp edges, using both a wind tunnel experiment and a matching DNS. This is unusual, not only in that both approaches are used in the same work but also because the DNS is of a spatially developing wake (as in the experiment), rather than a time-developing one, with the generating body included in the computational domain. Whilst this allows capture of the near wake it has the inevitable consequence that the available downstream extent of the wake is somewhat limited. It is also unusual because of the use of a fractal-type wake-generating plate, which leads, in the very near field, to a (‘multi-scale’) flow having a mixture of wake-like and jet-like character. For the DNS, great care is taken to ensure that there is sufficient domain size, grid resolution and statistical convergence. For the experiments, the plate is placed in a low-turbulence wind tunnel at $\mathit{Re}_{G}=U_{\infty }L_{b}/{\it\nu}=40\,000$
, where
$\mathit{Re}_{G}=U_{\infty }L_{b}/{\it\nu}=40\,000$
, where
 $L_{b}=\sqrt{A}$
, with
$L_{b}=\sqrt{A}$
, with
 $A$
the plate area. The measurements are made using hot-wire anemometry and extend to
$A$
the plate area. The measurements are made using hot-wire anemometry and extend to
 $x\approx 50L_{b}$
, whereas the DNS has
$x\approx 50L_{b}$
, whereas the DNS has
 $\mathit{Re}_{G}=5000$
and reaches approximately
$\mathit{Re}_{G}=5000$
and reaches approximately
 $x=100L_{b}$
.
$x=100L_{b}$
.
The results suggest that, over most of the extent of the wind tunnel wake ( $15\leqslant x/L_{b}\leqslant 50$
),
$15\leqslant x/L_{b}\leqslant 50$
),
 $C_{{\it\epsilon}}\mathit{Re}_{l}^{n}$
with
$C_{{\it\epsilon}}\mathit{Re}_{l}^{n}$
with
 $n=1$
is more closely constant than is
$n=1$
is more closely constant than is
 $C_{{\it\epsilon}}$
. Actually, they show that a better fit requires
$C_{{\it\epsilon}}$
. Actually, they show that a better fit requires
 $n\approx 0.77$
. Further downstream (
$n\approx 0.77$
. Further downstream (
 $55\leqslant x/L_{b}\leqslant 100$
) the DNS data suggest a change to
$55\leqslant x/L_{b}\leqslant 100$
) the DNS data suggest a change to
 $n\approx 0.5$
. To derive theoretical scalings for wake width and velocity deficit that have
$n\approx 0.5$
. To derive theoretical scalings for wake width and velocity deficit that have
 $n\neq 1$
, the authors make a ‘constant anisotropy’ assumption – that the Reynolds shear stress and the turbulent kinetic energy profiles scale in the same way (but not with
$n\neq 1$
, the authors make a ‘constant anisotropy’ assumption – that the Reynolds shear stress and the turbulent kinetic energy profiles scale in the same way (but not with
 $u_{o}^{2}$
). This is essentially a revised Townsend–George theory (Townsend Reference Townsend1976; George Reference George, George and Arndt1989), but includes the new ‘non-equilibrium dissipation’ law. (Note that only the latter is necessary for
$u_{o}^{2}$
). This is essentially a revised Townsend–George theory (Townsend Reference Townsend1976; George Reference George, George and Arndt1989), but includes the new ‘non-equilibrium dissipation’ law. (Note that only the latter is necessary for
 $n=1$
.) The variations of
$n=1$
.) The variations of
 $u_{o}$
and
$u_{o}$
and
 ${\it\delta}$
along the wake are shown to conform quite well to the new scalings,
${\it\delta}$
along the wake are shown to conform quite well to the new scalings,
 $u_{o}\sim (x-x_{o})^{{\it\alpha}}$
and
$u_{o}\sim (x-x_{o})^{{\it\alpha}}$
and
 ${\it\delta}\sim (x-x_{o})^{{\it\beta}}$
, with
${\it\delta}\sim (x-x_{o})^{{\it\beta}}$
, with
 ${\it\alpha}=-2{\it\beta}=-2(1+n)/(3+n)$
, albeit with different
${\it\alpha}=-2{\it\beta}=-2(1+n)/(3+n)$
, albeit with different
 $n$
(
$n$
(
 ${<}1$
) for the upstream and downstream halves of the
${<}1$
) for the upstream and downstream halves of the
 $x$
region studied. Given that the local Reynolds number (
$x$
region studied. Given that the local Reynolds number (
 $\sqrt{k}{\it\delta}/{\it\nu}$
) only falls to around 230 by
$\sqrt{k}{\it\delta}/{\it\nu}$
) only falls to around 230 by
 $x=100L_{b}$
in the DNS, and is very much higher in the wind tunnel, it is arguably difficult to claim that it is too small to expect the classical scaling to hold.
$x=100L_{b}$
in the DNS, and is very much higher in the wind tunnel, it is arguably difficult to claim that it is too small to expect the classical scaling to hold.
In addition to the increasing body of evidence that the value of $C_{{\it\epsilon}}$
can depend on initial conditions, Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) (following Nedić et al. (Reference Nedić, Vassilicos and Ganapathisubramani2013), along with the same group’s work on grid turbulence) thus go much further and question the universality of Reynolds-number independence of
$C_{{\it\epsilon}}$
can depend on initial conditions, Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) (following Nedić et al. (Reference Nedić, Vassilicos and Ganapathisubramani2013), along with the same group’s work on grid turbulence) thus go much further and question the universality of Reynolds-number independence of
 $C_{{\it\epsilon}}$
. No physical explanation is offered for why the
$C_{{\it\epsilon}}$
. No physical explanation is offered for why the
 $C_{{\it\epsilon}}\mathit{Re}_{l}^{n}=\text{const}.$
dissipation law might apply, but it does provide revised scaling laws for axisymmetric wakes that fit the present data.
$C_{{\it\epsilon}}\mathit{Re}_{l}^{n}=\text{const}.$
dissipation law might apply, but it does provide revised scaling laws for axisymmetric wakes that fit the present data.
3. Future
Although there is considerable evidence for the adequacy of the classical dissipation relation, it is apparent that it may be too simplistic, at more than one level. (Actually, it has long been recognised that $C_{{\it\epsilon}}$
is unlikely to be universal (Taylor Reference Taylor1935).) It is already clear that, whilst at sufficiently large Reynolds number
$C_{{\it\epsilon}}$
is unlikely to be universal (Taylor Reference Taylor1935).) It is already clear that, whilst at sufficiently large Reynolds number
 $C_{{\it\epsilon}}$
may become constant, its precise value can depend on initial conditions (e.g. Sreenivasan Reference Sreenivasan1998; Antonia & Pearson Reference Antonia and Pearson2000). Dairay et al.’s data seem even more revealing, in that, using only one wake-generating body, they show that
$C_{{\it\epsilon}}$
may become constant, its precise value can depend on initial conditions (e.g. Sreenivasan Reference Sreenivasan1998; Antonia & Pearson Reference Antonia and Pearson2000). Dairay et al.’s data seem even more revealing, in that, using only one wake-generating body, they show that
 $C_{{\it\epsilon}}$
is not even constant, but rather varies with local Reynolds number. The Kolmogorov law
$C_{{\it\epsilon}}$
is not even constant, but rather varies with local Reynolds number. The Kolmogorov law
 ${\it\epsilon}=C_{{\it\epsilon}}k^{3/2}/L$
, with
${\it\epsilon}=C_{{\it\epsilon}}k^{3/2}/L$
, with
 $C_{{\it\epsilon}}=\text{const}.$
, is often seen as ‘one of the cornerstone assumptions of turbulence theory’ but Lumley (Reference Lumley1992) remarked that the ‘mechanism that sets the level of dissipation in a turbulent flow, particularly in changing circumstances’, is worthy of further study. If the results of the Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) study can be shown to be typical of other high-Reynolds-number turbulent shear flows ‘in changing circumstances’, or indeed in axisymmetric wakes at significantly higher
$C_{{\it\epsilon}}=\text{const}.$
, is often seen as ‘one of the cornerstone assumptions of turbulence theory’ but Lumley (Reference Lumley1992) remarked that the ‘mechanism that sets the level of dissipation in a turbulent flow, particularly in changing circumstances’, is worthy of further study. If the results of the Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) study can be shown to be typical of other high-Reynolds-number turbulent shear flows ‘in changing circumstances’, or indeed in axisymmetric wakes at significantly higher
 $\mathit{Re}_{l}$
than they could reach, the premonition implied by Lumley’s remark will prove to have been prophetic. The matter is certainly worthy of more extensive study, not least because the non-equilibrium dissipation law seems to break the link between the presence of
$\mathit{Re}_{l}$
than they could reach, the premonition implied by Lumley’s remark will prove to have been prophetic. The matter is certainly worthy of more extensive study, not least because the non-equilibrium dissipation law seems to break the link between the presence of
 $-5/3$
spectra and classical cascade arguments. This new law seems to hold over much of any wake region that is likely to exist in real applications, so, even without any physical explanation, it would seem to be important. One can expect further experiments exploring the issue, aimed not least at finding whether (and if so, why) there is a final transition to a more classical scaling at some greater distance downstream, as Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) suggest, even though
$-5/3$
spectra and classical cascade arguments. This new law seems to hold over much of any wake region that is likely to exist in real applications, so, even without any physical explanation, it would seem to be important. One can expect further experiments exploring the issue, aimed not least at finding whether (and if so, why) there is a final transition to a more classical scaling at some greater distance downstream, as Dairay et al. (Reference Dairay, Obligado and Vassilicos2015) suggest, even though
 $\mathit{Re}_{l}$
must continue to fall.
$\mathit{Re}_{l}$
must continue to fall.
Finally, note that little is known about how the very-near-wake flow transitions to the region explored by Dairay et al. (Reference Dairay, Obligado and Vassilicos2015). The process must surely be very dependent on the geometry of the generating body. The near-wake usually contains interesting and complex dynamics (e.g. the recent work of Rigas et al. (Reference Rigas, Morgans, Brackston and Morrison2015) and references therein). There would seem to be much scope for exploration of the various transition regions. And there remains the need for a physical explanation for the new non-equilibrium dissipation relation.