Determination of wind-fed model parameters of neutron stars in high-mass X-ray binaries

Abstract

We have studied several neutron star high-mass X-ray binaries (HMXBs) with super-giant (SG) companions using a wind-fed binary model associated with the magnetic field. By using the concept of torque balance, the magnetic field parameter determines the mass accretion rate. This would help us to consider the relationship between wind velocity and mass-loss rate. These parameters significantly improve our understanding of the accretion mechanism. The wind velocity is critical in determining the X-ray features. This can be used to identify the ejection process and the stochastic variations in their accretion regimes. However, even in systems with a long orbital period, an accretion disk can be created when the wind velocity is slow. This will allow the HMXB of both types, SG and Be, to be better characterised by deriving accurate properties from these binaries. In addition, we have performed segmentation in the parameter space of donors intended for several SG-HMXB listed in our sample set. The parameter space can be categorised into five regimes, depending on the possibility of disk formation associated with accretion from the stellar wind. This can give a quantitative clarification of the observed variability and the properties of these objects. For most of the systems, we show that the derived system parameters are consistent with the assumption that the system is emitting X-rays through direct accretion. However, there are some sources (LMC X-4, Cen X-3 and OAO1657-415) that are not in the direct accretion regime, although they share similar donor parameters. This may indicate that these systems are transitioning from a normal wind accretion phase to partial RLOF regimes.

1. Introduction

The detection of Cyclotron Resonance Scattering Features (CRSFs) in spectra of many accreting neutron stars (NSs) with high magnetic field ( $\textrm{B} \geq 10^{12} \textrm{G}$ ) provides valuable insights into the physics of emitting regions and the evolution of these systems. They form due to resonant scattering processes with electrons, protons, and other ions in the plane and perpendicular to the magnetic field (Voges et al. 1982; Wilson, Finger, & Camero-Arranz 2008; Ye et al. 2020). The cyclotron line features provide the only direct estimate of the magnetic field strength of NSs in X-ray binary systems. In High-Mass X-ray Binaries (HMXBs), a NS accretes matter from a companion star via stellar wind. The accreted matter is channeled along field lines of the strong magnetic field of the NS onto the magnetic poles. X-ray emission from the NS is produced in regions around the magnetic poles (see Podsiadlowski et al. 2004; van den Heuvel 2009; Cai et al. 2012). It is noteworthy to mention here that most observed cyclotron lines have been detected above 10 keV and are interpreted as electron features, with inferred magnetic fields $B\sim 10^{12}$ G (Heindl et al. 2003). The combined effects of poor statistics, photoelectric absorption and the lack of evidence for a remnant accretion disk have made these energy sources elusive.

Most efforts to calculate theoretical cyclotron lines have been performed in a line-forming region with a constant temperature and density of an electron-proton plasma permeated by a uniform magnetic field (Wheaton et al. 1979; Orlandini et al. 1999; Yamamoto et al. 2011; Ye et al. 2019). Nishimura (2005) calculated cyclotron lines assuming a strong variation in field strength with distance from an emission region. However, no model generating such high flux and high temperature at a layer deeper than absorbing heavy atoms has been proposed.

According to recent studies, several pulsars show changes in luminosity dependence in the cyclotron resonance energy (Coburn et al. 2002; Pottschmidt et al. 2011; Reig et al. 2016; El Mellah et al. 2019a). The first aim of this paper is to derive magnetic field strengths, which is crucial for these systems, and obtain clues about the evolution of HMXBs, which can be understood in terms of the conservative evolution of normal massive binary systems.

The second aim of this study is to derive unknown parameters of HMXBs without uncertainty in the strength of the NS magnetic field. With robust data on the NS magnetic field, combined with spin period ( $P_{\mathrm{spin}}$ ) and orbital period ( $P_{\mathrm{orb}}$ ), we can fix several hitherto-unknown parameters, such as wind velocity and wind mass-loss rate. These parameters influence significantly the model of wind-fed binary systems and can constrain the effects of binary evolution (Taani & Khasawneh 2017; Dai et al. 2017; Taani et al. 2019a, b; Karino et al. 2019; El Mellah et al. 2019a, b; Karino 2020). From this standpoint, with observations of NS magnetic fields, we could constrain the end products of HMXBs, such as a NS-NS merger, (Taani 2016; Kasen et al. 2017) and core-collapse supernovae (see Frebel & Norris 2015; Mardini et al. 2019a, b, 2020), which is considered to be one of the most powerful gravitational wave sources and also the most probable site for heavy element creation (Postnov & Yungelson 2006; Taani 2015).

In the next section, we introduce the recent results of NS magnetic field given by the CRSF observations to find the wind equation solution. In Section 3, we discuss the method to obtain hitherto-unknown binary parameters from robust data on the NS magnetic field in SG-HMXBs. In Section 4, we discuss our findings. The last section is devoted to conclusions.

Table 1. List of some observational parameters of all known persistent sources with supergiant companions.

References.– These references are to period measurements in the literature. Some have errors originating from applied analysis, designated with a dagger, or from the supplied data, designated with an asterisk. (1) Cusumano et al. (1998); (2) Coburn et al. (2002); (3) Rivers et al. (2010); (4) Clark et al. (1990); (5) Rodes-Roca et al. (2009); (6) Robba et al. (2001); (7) Kreykenbohm et al. (2005); (8) Makishima et al. (1999); (9) Kreykenbohm et al. (2002); (10) Schanne et al. (2007); (11) Santangelo et al. (1998); (12) Barbera et al. (2001); (13) Orlandini et al. (1999); (14) Denis, Bulik, & Marcinkowski (2010); (15) Pottschmidt et al. (2011); (16) Nespoli, Fabregat, & Mennickent (2010); (17) D’Ai et al. (2011); (18) Reynolds et al. (1999); (19) Bonning & Falanga (2005); (20) den Hartog et al. (2006); (21) Bodaghee et al. (2016); (22) Lutovinov, Tsygankov, & Postnov (2017).

2. Cyclotron lines

Since the physical conditions are expected to vary over the emission region, the X-ray spectrum is expected to change with the viewing angle and therefore with pulse phase. This variation can be because during one rotation phase different parts of the surface are exposed and also due to change in local field structure due to accretion dynamics, e.g. change in accretion rate, as is seen for sources like Her X-1 and V0332+53. The difference in time scales of variation for cyclotron line energy $E_{\mathrm{cyc}}$ and luminosity will allow researchers to distinguish between these two distinct cases. (Nagase et al. 1991; Wilson et al. 2008). In this work, we have selected 11 persistent sources with SG companions known to have at least one cyclotron line (see Table 1). Here, our analysis of all pointing observations provides an opportunity to infer the values of magnetic field strength according to their spectra. The gravitational redshift z that at the NS surface is approximately

(1) \begin{equation}z\simeq\frac{1}{\sqrt{1-\frac{2GM_{\mathrm{NS}}}{R_{\mathrm{NS}}c^{2}}}}-1\simeq0.3,\end{equation}

where $M_{\mathrm{NS}}, R_{\mathrm{NS}}$ , G, and c are the NS mass, radius, gravitational constant and speed of light, respectively. Assuming canonical values for $M_{\mathrm{NS}}$ and $R_{\mathrm{NS}}$ of 1.4 $\mathrm{M}_{\odot}$ and 10 km, thus z = 0.3. As such, the line energy changes the fundamental cyclotron line (keV) to become related to the magnetic field strength and its configuration (Trüemper et al. 1978) by the equation

(2) \begin{equation}\begin{array}{rcl} E_{\mathrm{cyc}}=11.6 keV B_{12} (1+z)^{-1} .\end{array}\end{equation}

Here B $_{12}$ is the magnetic field strength in units of 1012 G, and the higher harmonics have an energy n times the fundamental energy $E_{\mathrm{cyc}}$ (see, e.g. Wilson et al. 2008, and references therein). The effect of NS rotation on the variation in the shape of the cyclotron line features is considered. This could be correlated to the accretion geometry and other mechanisms (Bachetti et al. 2014).

In general, the magnetic field of NSs spans a range from $10^{8}\mathrm{G}$ or less (LMXBs) to $10^{15} \mathrm{G}$ (magnetars). We list the computed magnetic strengths along with other system parameters for selected SG-HMXBs in Table 2. These values show no correlation with the spin period of wind-fed systems (see Figure 1).

Table 2. List of derived parameters for SG HMXBs.

The data on mass and radius of donor are taken from Falanga et al. (2015), Reig et al. (2016), Chaty et al. (2008), Rawls et al. (2011), Cusumano et al. (2010), Mason et al. (2012). The luminosity and effective temperature are computed by their approximated stellar evolution track given by Hurley et al. (2000). From these donor data, the terminal velocity of the wind and the wind mass-loss rate from SG stars are derived by polynomial approximation given by Vink et al. (2001).

Figure 1. The magnetic field as a function of the spin period of SG-HMXBs.

It should be noticed that, of course, we need to consider some observational biases, such as: too strong of a magnetic field prevents accretion onto the NS and we could not observe such systems as bright X-ray sources (Taani et al. 2020; Karino 2020). Besides such possibility of biases, this concentration around $B \approx 10^{12} \mathrm{G}$ will draw a lot of interest and promote further studies on the NS magnetic field (Taani et al. 2019a, b). The fundamental energy covers a wide range, starting at 10 keV for Swift J1626.6-5156 (DeCesar, Pottschmidt, & Wilms 2009) to 100 keV for LMC X-4 (la Barbera et al. 2001).

The strong energy variation of the cyclotron lines (for example, in V0332+53, GRO J1008-57 and GX301-2) can be used to argue that during different phases of the X-ray pulses, regions with different magnetic fields are observed.

It is noteworthy to mention here that 4U 0115+634 is one of the pulsars whose CRSFs have been studied in great detail (see, e.g., Wheaton et al. 1979; Nagase et al. 1991; Nishimura 2005). In previous outbursts, CRSFs have been detected up to the fifth harmonic (Heindl et al. 2003; Ferrigno et al. 2011). This high number of detected CRSFs in 4U 0115+634 makes this system an outstanding laboratory to study the physics of cyclotron lines in X-ray pulsars.

3. Investigating wind parameters in SG HMXB systems

Under the assumption that the spin period of a NS is nearly in torque equilibrium at a steady mass accretion rate, the magnetic radius (where the magnetic pressure balances with the accretion ram pressure) and corotation radius $r_{\mathrm{co}}$ (the radius where the Keplerian angular velocity equals the NS spin angular velocity) have similar values (Donati et al. 2011), and enough amount of angular momentum could be received via wind accretion (Karino et al. 2019), one estimates the magnetic field strength as

(3) \begin{equation}B_{\mathrm{NS}} = 2.2 \times 10^{12} \mathrm{G} \times \zeta^{1/2}\left( \frac{\dot{\textit{M}}}{10^{18} \mathrm{g\, s}^{-1}} \right)^{1/2}\left( \frac{\textit{P}_{\mathrm{s}}}{1 \mathrm{s}} \right)^{7/6} ,\end{equation}

assuming that the mass of the NS is 1.4 M $_\odot $ and its radius is 10 km (Ghosh & Lamb 1979; Campana et al. 2002; Tsygankov et al. 2016). The parameter $\zeta$ is the ratio of accretion velocity to the free-fall velocity, and hereafter we fix this value as 0.5. However, we should note here that, the effect of the accretion flow geometry (spherical, disk-like or planar) must be taken into account (Karino et al. 2019).

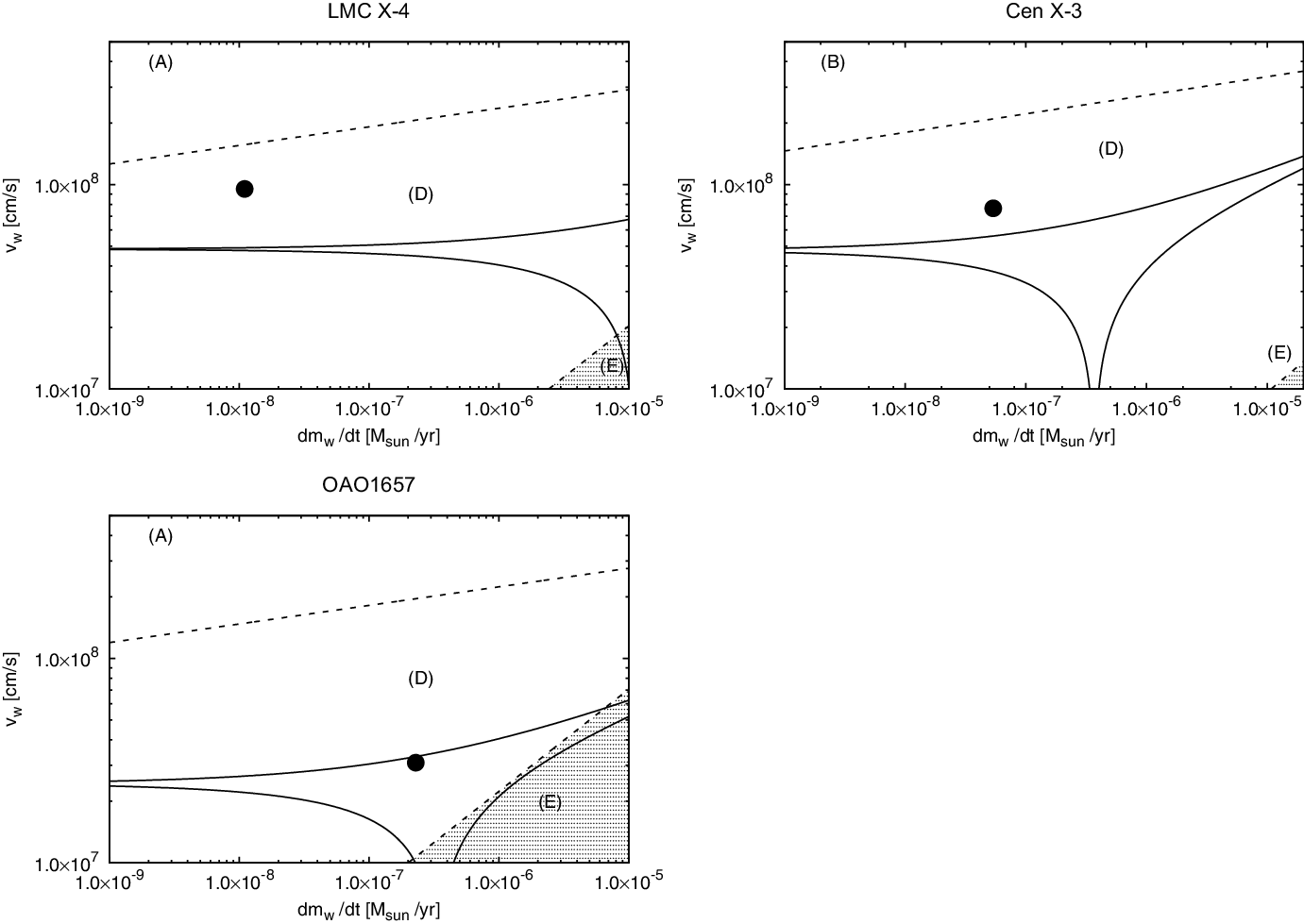
Figure 2. Plots of the wind velocity vs mass-loss rate, in various accretion regimes. The position of each source is shown by a black filled circle. As shown clearly, the parameter space can be categorised into (A) supersonic inhibition regime, (B) subsonic inhibition regime, (C) supersonic propeller regime, (D) subsonic propeller regime, and (E) direct accretion regime indicated by the shaded region, and the solution of the wind equation is represented by solid curves.

The mass accretion rate $\dot{M}$ can be obtained as the following, if we assume the Hoyle–Lyttleton accretion scenario using the local density at the position of the NS (see, e.g. Bondi & Hoyle 1944 and references therein).

(4) \begin{equation}\dot{M} = \rho_{\mathrm{w}} v_{\mathrm{rel}} \pi R_{\mathrm{acc}}^{2} .\end{equation}

Under the condition of the spherical stellar wind (Walter, Lutovinov, & Bozzo 2015), the local density of the wind matter becomes

(5) \begin{equation}\rho_{\mathrm{w}} = \frac{ \dot{m}_{\mathrm{w}} }{ 4 \pi a^{2} v_{\mathrm{w}} },\end{equation}

where $\dot{m}_{\mathrm{w}}$ is the wind mass-loss rate from the donor. The estimation depends on the empirical stellar-evolution model. Here, orbital radius a can be obtained from the orbital period of the system and donor mass. Note that we assume here that, the systems are in circular orbits. Combining them, we have

(6) \begin{equation}\dot{M} = \dot{m}_{\mathrm{w}} \times\frac{ G^{2} M^{2}_{\mathrm{NS}} }{ a^{2} v_{\mathrm{w}} v^{3}_{\mathrm{rel}} } .\end{equation}

We can deduce the mass accretion rate from the observed X-ray luminosity. The relative velocity of the wind to the NS is

(7) \begin{equation}v_{\mathrm{rel}} = \left( v^{2}_{\mathrm{orb}} + v^{2}_{\mathrm{w}} \right)^{1/2}\end{equation}

and the velocity of the line-driven wind is usually prescribed in the model by so-called $\beta-$ low:

(8) \begin{equation}v_{\mathrm{w}} = v_{\infty}\left( 1 - \frac{R_{\mathrm{d}}}{a} \right)^{\beta} .\end{equation}

In this study, we assume $\beta$ to be in the range of around 0.6–1.5 based on models of the donor (Puls, Vink, & Najarro 2008), $v_{\infty}$ denotes the terminal velocity of the wind.

On the other hand, unless the orbital radius is very small, the ratio of mass accretion rate to mass-loss due to stellar wind, can be approximated as the ratio of the accretion region $\left(4 \pi G^{2} M^{2}_{\mathrm{NS}} / v^{2}_{\mathrm{rel}}\right)$ to the sphere whose radius is the orbital radius ( $4 \pi a^{2}$ ). This is equivalent to replacing the stellar wind velocity by the relative velocity in Equation (6). Then, with the help of this equation, we get

(9) \begin{equation}v^{2}_{\mathrm{w}} = -v^{2}_{\mathrm{orb}} \pm \sqrt{ \frac{ G^{2} M^{2}_{\mathrm{NS}} }{ a^{2} \dot{M} } \dot{m}_{\mathrm{w}} }.\end{equation}

The wind parameters such as $\dot{m}_{\mathrm{w}}$ and $v_{\infty}$ contain large uncertainties. The observational biases should be considered, as the opacity reduction and the unknowns in the geometry and emission mechanisms of the system (see, e.g., Mushtukov et al. 2015). Combining above wind equations with CRSF data introduced in the previous section, a single relationship between $\dot{m}_{\mathrm{w}}$ and $v_{\infty}$ can be obtained as a solution. In addition, the CRSF data help us to make a concentration on the estimation of the stellar wind parameters. The orbital semi-major axis a is obtained from the orbital period if the mass of the donor is known. In Table 2, we show the values of donor mass and donor radius, which has appeared in Equation (8).

Figure 3. The same as previous, for the wind mass-loss rate, accretion mass-loss rate and accretion regimes. The position of each source is shown by a black filled circle.

Figure 4. The same initial conditions in terms of the stellar wind parameters as in Figures 2–3, but these sources show different features and different distributions. These systems show that, the accretion stage can go from wind accretion to partial RLOF.

If we choose the mass-loss rate from the donor $\dot{m}_{\mathrm{w}}$ as a fundamental variable, then Equation (9) becomes a biquadratic equation and has four solutions. Two of them are physically nonsense, so we consider the other two solutions since they have a clear correlation between wind velocity and the mass loss rate of donors in SG-HMXBs. These solutions of the wind velocity are shown in Figures 2–4 by solid curves, as functions of mass-loss rate in SG-HMXBs. Note that, the uncertainty caused by the strength of the NS magnetic field is negligible, since this uncertainty is determined fairly accurately from CRSF data, and is also much smaller than the uncertainty of all other considered parameters such as in $\dot{m}_{\mathrm{w}}$ and $v_{\infty}$ . In these figures, the wind parameters given by the frequently used wind model by Vink, de Koter, & Lamers (2001) are shown at the same time. The approximated wind mass-loss rates from SG stars are given by the complex functions of mass, radius (escape velocity) and luminosity (effective temperature) of SG stars. To derive the mass-loss rate of the HMXB donors, we use the mass and radius data which are derived and introduced in previous papers (Chaty et al. 2008; Cusumano et al. 2010; Rawls et al. 2011; Mason et al. 2012; Falanga et al. 2015; Reig et al. 2016) based on the observations and the stellar-evolution model. The estimation depends on the empirical stellar-evolution model. From these data, we derive the effective temperature and corresponding luminosity using approximated stellar evolution scheme. We compile Equations (1)–(30) in Hurley, Pols, & Tout (2000) and find the evolution stage of each donors in SG-HMXBs listed in Table 2. Then, we derive the effective temperature at this evolutionary stage.

The wind parameters ( $v_{\infty}$ and $\dot{m}_{\mathrm{w}}$ ) we obtained are reported in Table 2. From these results, we could confirm that terminal velocities of the wind from donors in SG HMXBs are rather slow. In seven systems, the terminal velocities of donors dip from the typical wind velocity of galactic single SG stars $\left(1000-2000\, \mathrm{km\,s}^{-1}\right)$ . This result is consistent with recent result given by Giménez-García et al. (2016) who argued that the stellar wind of donors in persistent HMXBs is systematically slow.a For instance, from recent observations, it is suggested that the wind velocity in persistent SG HMXBs, Vela X-1, is relatively slow $\left(v_{\infty} = 700\,\mathrm{km\,s}^{-1}\right)$ , this might be due to the ionisation of the stellar wind by the radiation from NS, and thus prevents the acceleration of the stellar wind (Kretschmar et al. 2021). In our samples, even for systems with higher $v_{\infty}$ , the wind velocities at the NS positions are typically $v_{\mathrm{w}} \approx 500\,\mathrm{km\,s}^{-1}$ , and still show very slow wind. However, in some tight binaries, the tidal effects could reduce stellar wind velocity towards the accretor (Hirai & Mandel 2021).

It is broadly considered that in wind-fed HMXBs, the wind matter is captured by the NS magnetic field at a certain radius, and transported onto the polar regions of the NS. In this process, around the polar region, the accretion column is formed, and the potential energy of the accretion matter is converted into strong X-ray radiation.

However, it is believed that, when the NS (and consequently NS magnetic field lines) rotates rapidly, the accretion matter cannot fall onto the NS surface and in some conditions it could be expelled out (Pfahl et al. 2002; Podsiadlowski et al. 2004). This rotational inhibition of the accretion matter is called the propeller effect (see Reig and Zezas 2018). The propeller/accretion limit could be defined by three typical radii (accretion radius $R_{\mathrm{acc}}$ , is the distance at which inflowing matter is gravitationally concentrated toward the NS. Magnetic radius $r_{\mathrm{m}}$ , is the distance at which the pressure of the NS magnetic field balances the ram pressure of inflowing materials. Corotation radius $r_{\mathrm{co}}$ is the radius where the Keplerian angular velocity equals the NS spin angular velocity.

The parameter space could divided into five accretion regimes based on their magnitude relation (Stella, White, & Rosner 1986; Bozzo, Falanga, & Stella 2008). That is, the parameter space can be categorised into

• (A) supersonic inhibition regime ( $r_{\mathrm{m}} > r_{\mathrm{a}}, r_{\mathrm{co}}$ ),

• (B) subsonic inhibition regime ( $r_{\mathrm{co}} > r_{\mathrm{m}} > r_{\mathrm{a}}$ ),

• (C) supersonic propeller regime ( $r_{\mathrm{a}} > r_{\mathrm{m}} > r_{\mathrm{co}}$ ),

• (D) subsonic propeller regime ( $r_{\mathrm{co}} , r_{\mathrm{a}} > r_{\mathrm{m}}$ , $\dot{M} < \dot{M}_{\mathrm{c}}$ ),

• (E) direct accretion regime ( $r_{\mathrm{m}} < r_{\mathrm{a}}, r_{\mathrm{co}}$ ).

Here, $\dot{M}_{\mathrm{c}}$ $\left(\sim 10^{-7} \mathrm{M}_{\odot} \mathrm{yr}^{-1}\right)$ denotes the critical limit where radiative cooling starts working (see Bozzo et al. 2008).

In the figures shown below (Figures 2–4), the different accretion regimes (A) to (E) are divided by dashed lines. The propeller regime is defined when the accretion radius of the accretion disk is larger than the magnetic radius. In contrast, in the supersonic inhibition regime, the magnetic radius is larger than the accretion radius and corotation radius, so it rotates more slowly than the inner regions of the disk (Frank, King, & Raine 2002). The shaded region denotes the direct accretion regime such that only systems in this region can be observed as a persistent HMXB. The efficiency of the propeller depends weakly on the magnetic moment of the star (Ustyugova et al. 2006). Since if the angular velocity of the star is larger, then the efficiency of the propeller becomes higher (Tsygankov et al. 2016). In contrast, the magnetic gate (or magnetic barrier), which refers to the effect of magnetic pressure, will prevent the material from accreting in the inhibition regime. Thus, the centrifugal gate (or centrifugal barrier), which refers to the propeller effect, will also propel away material along the magnetospheric boundary of the NS. The two gates are closed, preventing accretion onto the NS. In addition, the subsonic propeller regime becomes clearer as the strength of the propeller increases. As the strength increases there is a sharp decrease in the accretion rate to the star.

It is noteworthy to mention here that the CRSF data allow us to better identify the propeller region and the accretion region as shown clearly in the Figures 2–4. In particular, the solid curves in these figures represent the wind equation solution for the theoretical relations between $\dot{m}_{\mathrm{w}}$ and $v_{\mathrm{w}}$ as given by Equation (9) with the CRSF data. In addition, the CRSF data make us concentrate on the estimation of the stellar wind parameters. We show that when these curves come into the direct accretion region (shaded region) created in the figures, the systems with corresponding parameters can lead to X-ray emission.

4. Discussion

4.1. Wind parameters

In this work, the orbits of binary systems have consistently been assumed to be circular. As in HMXB, the orbital eccentricity becomes smaller due to the tidal effects, as well as the wind-NS interaction (Zahn 1977). Therefore, when dealing with wind-fed SG-HMXBs, the semi-major axis is often used as a representative value of the binary separation (e.g. Bozzo et al. 2008; Shakura et al. 2012). However, HMXB is a young system and some systems are not yet fully circularised. Indeed, 4U1907 has non-zero eccentricity ( $e \sim 0.3$ ). Here, assuming an eccentricity of 0.3, we examined how much the results would be affected. For systems with a $P_{\mathrm{orb}}\sim 10\,\rm$ d, the wind is already sufficiently accelerated that no significant change is expected. On the other hand, the binary separation varies from $(1-e)a$ to $(1+e)a$ with semi-major axis a. This leads to variations in the mass accretion rate, roughly between a factor of 0.5 and 2, for $e = 0.3$ . The values obtained here are considered to be average values within this range, for the system with the largest orbital eccentricity.

In the Figures 2–4, we show the direct accretion region where the systems with corresponding parameters can emit strong X-rays. In the same figures, we plot the wind parameters given by the standard wind model combined with the stellar evolution track; furthermore we show the theoretical relations between the $\dot{m}_{\mathrm{w}}$ and $v_{\mathrm{w}}$ given by Equation (9) with the CRSF data. The position of each source is based on the results reported in Table 2. In systems shown in Figures 2 and 3, these plots show good consistency: the plots are located in the direct accretion region (shaded region) and roughly follow the theoretical curves (obtained with CRSF data). These results partly explain the slow wind tendencies in SG-HMXBs. Namely, when the wind velocity becomes too high, the wind plots might go outside of the accretion regime from the upper boundary of the shaded region. For typical mass-loss rate in SG stars (say, $10^{-7} \mathrm{M}_{\odot} \mathrm{yr}^{-1}$ ), the upper bound of the accretion regime is ${\approx}800\,\mathrm{km \, s}^{-1}$ . Then, the systems with fast-wind donors cannot be observed as bright persistent X-ray sources.

On the other hand, our model cannot be applied for three binaries, such as LMC X-4, Cen X-3 and OAO1657 (see Figure 4) although they share similar donor parameters. Since in systems with shortest orbital periods (LMC X-4 and Cen X-3) the Roche-lobe filling factors approach quite near to 1, their accretion mode may not be typical wind accretion any more. Their accretion mode could enter in the regime of RLOF, or quasi RLOF (Shakura et al. 2012; Shakura, Postnov, & Hjalmarsdotter 2013). In this case, it is little wonder that we cannot obtain consistent wind parameters for these sources. Additionally, OAO1657 shows an inconsistent parameter set. Note that, the Roche lobe filling factor is much smaller and RLOF cannot be realised. On the other hand, it is suggested that the donor in this system is a Wolf-Rayet star (Mason et al. 2009; Mason et al. 2012). In this case, it might be an ill choice to adopt to the line-driven wind for typical SG stars. It is also argued that the system parameters of OAO1657 cannot be reproduced with standard binary evolution theory: a lot of mysteries remained in the understanding of this system (Jenke et al. 2012; Walter et al. 2015). Recently, it has been shown that wind-RLOF accretion, a process that connects from wind accretion to RLOF, occurs in systems with short orbital periods (El Mellah et al. 2019b).

4.2. NS magnetic field

The question of where exactly the magnetic field is measured still remains unanswered. This depends on the accretion geometry and flow and other mechanisms (Wei et al. 2010; Coburn et al. 2002; Kreykenbohm et al. 2005), since their line profiles reflect the geometrical and physical properties of the accretion column near the magnetic poles of the NS, and therefore constitute a diagnostic tool for accessing the physics of accretion.

It is noteworthy to mention here that the NS magnetic fields in Table 2 are surprisingly concentrated in a narrow range ${\sim}10^{12} \mathrm{G}$ . Despite the fact that their physical properties, in particular their energy band (10–100 keV) which governs the evolution, are different, they strongly depend on the assumed parameters, and these parameters dominate their evolutionary stages. Thus, the magnetic field itself is of fundamental significance to having a thorough insight into the physics of the emitting region structure and could also be imperative to assisting us in improving our understanding of binary evolution. Otherwise, the implementation of known stellar evolution and observational statistics in population synthesis codes will remain a major issue in our understanding of the processes occurring in binaries or in the treatment of selection effects (Postnov & Yungelson 2006; Taani & Khasawneh 2017; Taani, Vallejo, & Abu-Saleem 2022). A note should be made concerning the validity of the torque equilibrium assumption, it was qualitatively interpreted that it is most likely that the NSs considered in this work reached torque equilibrium. Karino et al. (2019) considered the wind accretion mechanisms associated with angular momentum transport in an asymmetric wind model. They found that large amount of angular momentum can be transported to form an accretion disk, just because enough wind-inhomogeneity occurs at a small separation distance in binary and/or if the stellar wind is slow.

Finally, our results shown in Figures 2–4 clearly demonstrate the variety of SG-HMXBs based on the different types of interactions between the wind mass-loss rate and the characteristic of three NS radii (accretion, and corotation radius). This diversity of X-ray binary systems is important in principle, and could be used to demonstrate the properties of wind-fed systems such as SG-HMXBs, and the parameters entirely control their evolution. We should note that in Figures 2 and 3, 7, objects are located in the direct accretion regimes, and their evolutionary stages can be manifested as wind-fed HMXBs, while 3 objects in Figure 4 (LMC X-4, Cen X-3, and OAO1657) are clearly moving from the normal wind accretion phase to a partial RLOF.

5. Summary and conclusions

The following conclusions and implications are obtained:

We have investigated some physical quantities for several HMXBs with supergiant companions. The magnetic field, which is generated by the cyclotron lines- gives the mass accretion rate, based on the assumption of torque balance. The mass accretion rate allows us to derive a relation between the terminal wind velocity and the mass-loss rate of the donor. Furthermore, for all systems, our analysis (direct accretion condition shown by shaded region, and wind equation solution with CRSF data shown by solid curves) indicates that the wind velocity must be systematically slow.

By adopting the accretion regime model by Bozzo et al. (2008), we have explored the parameter space in several regimes to support the intrinsic variabilities of mass accretion rate and wind velocity. This may allow us to study an evolutionary path for several SG-HMXBs in these diagrams. Different regimes are sufficient to distinguish the bright X-ray sources spatially, and the magnetic field-wind velocity can be probed. As a result, the persistent SG HMXBs within the shaded region can be observed through the direct accretion regime. This interpretation is predicated on its emission of accretion in high-energy X-rays.

It is seen that the wind velocity causes a significant effect on the results of their X-ray features and it could be used to determine the ejection mechanism of mass. When the wind velocity is slow, the accretion disk is often formed even in systems with large orbital period. This will allow us to better characterise the HMXB of both types, SG and Be, hosting NS, by deriving accurate properties of those compact binaries.

From the updated measurement of HMXB cyclotron lines, the derived magnetic fields given by the CRSF data are all concentrated around ${\sim}10^{12} \mathrm{G}$ . Note that, the fundamental energy during X-ray observation, spin and other physical parameters property diverges and varies. The existence of a high magnetic field has the potential to regulate their formation and evolution.

The accretion mechanism for the fast spinning NSs ( $P_{\mathrm{spin}} \leq 40$ s) with a short orbital period ( $P_{\mathrm{orb}} \leq 10$ d), like in LMC X-4, Cen X-3 and OAO1657 (see Figure 4) can not be constrained by our model. In LMC X-4 and Cen X-3, these two binary systems are extremely tight systems. Thus, the accretion mechanism can therefore not be approximated by spherical wind, because in such tight systems the concentrated asymmetric wind or RLOF accretion should be considered (El Mellah et al. 2019a, b). Although OAO 1657 is a further evolved star with a long orbit, the donor of this system can be detected throughout its evolution as a Wolf-Rayet star. On the contrary, it can be seen from Figures 2 and 3, that the results are good for systems with long orbital periods, and we can successfully apply the stellar evolution code directly to these systems.

Finally, one would hope that the results of this work will be improved with data from INTEGRAL, ${eRosita}$ and ${HXMT}$ , which can provide significant increase in the observational sensitivity of a few cyclotron sources as well as population synthesis studies.