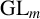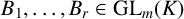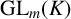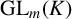A MORDELL–LANG-TYPE PROBLEM FOR $\mathrm{GL}_{m}$

Abstract

We prove a nonabelian variant of the classical Mordell–Lang conjecture in the context of finite- dimensional central simple algebras. We obtain the following result as a particular case of a more general statement. Let K be an algebraically closed field of characteristic zero, let $B_1,\dots ,B_r\in \mathrm {GL}_m(K)$ be matrices with multiplicatively independent eigenvalues and let V be a closed subvariety of $\mathrm {GL}_m(K)$ not passing through zero. Then there exist only finitely many elements of $\mathrm {GL}_m(K)$ of the form $B_1^{n_1}\cdots B_r^{n_r}$ (as we vary $n_1,\dots ,n_r$ in $\mathbb {Z}$) lying on the subvariety V.

1. Introduction

Many important classes of Diophantine problems can be formulated by starting with a set of invertible matrices $B_1,\ldots ,B_r\in \mathrm {GL}_m$ (over some algebraically closed field K) and studying the set

(1.1) $$ \begin{align} \{(n_1,\ldots ,n_r)\in \mathbb{Z}^r\colon B_1^{n_1}\cdots B_r^{n_r}\in V\} \end{align} $$

for a given subvariety $V\subseteq \mathrm {GL}_m(K)$ . We mention just a small sample of questions that fall under this framework. When $r=1$ , $K=\mathbb {Q}$ and V is the set of matrices whose $(1,1)$ -entry is zero then this question is equivalent to Skolem’s problem, which asks whether there is a decision procedure to determine if an integer linear recurrence has a zero. By increasing r and using block diagonal matrices, we can similarly study solutions $(n_1,\ldots ,n_r)\in \mathbb {N}^r$ to $f_1(n_1)+\cdots +f_r(n_r)=0$ , where $f_1,\ldots ,f_r$ are sequences satisfying linear recurrences. This problem was considered by Cerlienco et al. [2] and it was later shown by Derksen and Masser [3] that determining whether there is a solution is undecidable.

The above construction can be further generalised by considering some ambient algebraic variety G endowed with finitely many self-maps $\varphi _1,\dots , \varphi _r$ , and a given starting point $\alpha \in G$ and a subvariety $V\subset G$ . Then one studies the structure of the set

(1.2) $$ \begin{align} \{(n_1,\dots,n_r)\in{\mathbb N}^r\colon (\varphi_1^{\circ n_1}\circ \varphi_2^{\circ n_2}\circ \cdots \circ \varphi_r^{\circ n_r})(\alpha)\in V\}. \end{align} $$

The Mordell–Lang conjecture (proven by Laurent [8] in the case of algebraic tori, by Faltings [4] in the case of abelian varieties and by Vojta [12] for arbitrary semiabelian varieties) asserts that if G is a semiabelian variety (defined over an algebraically closed field K of characteristic $0$ ), then the intersection of any finitely generated subgroup $\Gamma $ of $G(K)$ with a subvariety $V\subset G$ is a finite union of cosets of subgroups of $\Gamma $ . This famed conjecture can easily be translated into a question of type (1.2) by taking the self-maps $\varphi _i$ on G to be translations by elements from a finite set of generators for $\Gamma $ . This alternative interpretation of the classical Mordell–Lang question led to the formulation of the dynamical Mordell–Lang conjecture. (See [1] for a comprehensive treatment of this problem.)

Recently, two of the authors (see [7] and Ghioca and Huang, ‘A non-abelian variant of the classical Mordell–Lang conjecture’, submitted for publication) have investigated S-unit equations in finite-dimensional division rings. By embedding these rings into matrix rings, one can phrase many of these ‘noncommutative S-unit questions’ in the above general framework.

As it turns out, there is a natural dichotomy that arises when studying the original problem (1.1) inside $\mathrm {GL}_m$ . When the matrices are diagonalisable, then the solution sets are well behaved and a version of the Mordell–Lang conjecture holds in this context (see [6, Theorem 1.3]). Even though the result from [6] is stated in the context of endomorphisms of semiabelian varieties, the problem translates immediately to a question regarding finitely generated subgroups of $\mathrm {GL}_m$ of diagonalisable matrices. Indeed, given diagonalisable matrices $B_i$ , that is,

$$ \begin{align*}B_i=C_i^{-1}\cdot D_i\cdot C_i \quad\text{for some } C_i\in \mathrm{GL}_m \text{ and some diagonalisable matrix } D_i,\end{align*} $$

then the question of finding all r-tuples $(n_1,\dots , n_r)\in {\mathbb Z}^r$ with the property that

$$ \begin{align*}B_1^{n_1}\cdots B_r^{n_r}\in V \quad\text{(for some given subvariety } V \text{ of } \mathrm{GL}_m)\end{align*} $$

reduces to the classical Mordell–Lang problem for algebraic tori, solved by Laurent [8]. However, when one allows arbitrary matrices $B_i$ , the above general question becomes undecidable and work of Scanlon and Yasufuku [10] shows that any Diophantine subset of $\mathbb {N}^r$ can be realised as the set of solutions to an equation $B_1^{n_1}\cdots B_r^{n_r}\in V$ for a subvariety V of $\mathrm {GL}_m(K)$ . The fundamental difference between these two situations is that in the diagonalisable case, the analysis reduces to the study of equations

$$ \begin{align*}P(\lambda_{1,1}^{n_1},\ldots ,\lambda_{1,m}^{n_1},\ldots , \lambda_{r,1}^{n_r},\ldots ,\lambda_{r,m}^{n_r})=0\end{align*} $$

(with P a polynomial and $\lambda _{i,j}$ eigenvalues of the matrices), which, although difficult, can be greatly aided with the help of theorems on S-unit equations (see [8, 11]).

In the nondiagnonalisable case, however, one must now contend with polynomial- exponential equations and the famed DPRM theorem (see [9]) shows that every recursively enumerable subset of $\mathbb {N}^r$ (that is, every subset that can be enumerated by a Turing machine) can be realised as the zero set of such an equation.

Somewhat surprisingly, we are able to show that the pathologies that arise in the nondiagonalisable case can be handled when one imposes conditions on the eigenvalues of the matrix generators and only considers subvarieties V of $M_n(K)$ that do not pass through the origin. Given a field K, we recall that a collection of elements $s_1,\dots ,s_r\in \overline {K}^\times $ is multiplicatively independent if $n_1,\dots ,n_r\in {\mathbb Z}$ and $s_1^{n_1} \cdots s_r^{n_r}=1$ imply that $n_1=\cdots =n_r=0$ . We say a collection of elements $B_1,\dots ,B_r\in M_r(K)$ has multiplicatively independent eigenvalues if the set of eigenvalues (counted without multiplicity) of $B_1,\ldots ,B_r$ are pairwise disjoint and their union is multiplicatively independent. Our main result is the following general Mordell–Lang variant.

Theorem 1.1. Let K be an algebraically closed field of characteristic zero, let $B_1,\dots ,B_r\in \mathrm {GL}_m(K)$ be matrices with multiplicatively independent eigenvalues and let V be a closed subvariety of $\mathrm {GL}_m(K)$ not passing through zero. If

$$ \begin{align*} \Gamma:=\{{B_1^{n_1} \cdots B_r^{n_r}: n_1,\dots,n_r\in {\mathbb Z}}\}, \end{align*} $$

then $\lvert {V(K)\cap \Gamma \rvert } < \infty $ .

In fact, we prove a slightly more general (although equivalent) version of Theorem 1.1 for central simple algebras (see Theorem 2.2), which has the advantage of being immediately applicable to recent ‘noncommutative’ variants of the Mordell–Lang problem.

We note that the finiteness we obtain can be viewed as the ‘generic’ situation of the Mordell–Lang conjecture; that is, one generally expects the intersection of a finitely generated group in a semiabelian variety with a subvariety to be finite unless there is some additional geometric structure that explains the infinite intersection. One cannot expect to get a general finiteness result of the form given in Theorem 2.2 without some mild constraints. We give examples in Section 2.3 which show that attempts to weaken the hypotheses can give rise to pathological intersection sets.

The outline of this paper is as follows. In Section 2, we state a couple of technical results, which are both variants of the classical Mordell–Lang problem in two different settings. Theorem 2.2 is an equivalent formulation of Theorem 1.1 in the context of finite-dimensional central simple algebras, while Theorem 2.7 is a variant of the classical Mordell–Lang theorem in the context of commutative linear algebraic groups. Theorem 2.7 is also a key ingredient in our proof of Theorem 2.2. We prove Theorem 2.7 in Section 3 and we conclude our proof of Theorem 2.2 in Section 4.

2. A couple of variants of the classical Mordell–Lang conjecture

We start by setting the notation for our paper.

2.1. Notation

Throughout this paper, let ${\mathbb N}$ denote the set of nonnegative integers, K be a field of characteristic $0$ and A be a finite-dimensional central simple algebra over K. We let $\ell :=[A:K]$ . Geometrically, A can be identified with the K-points of the $\ell $ -dimensional affine space $\mathbb {A}^\ell (K)$ . Moreover, since the multiplicative group $A^\times $ embeds into $\operatorname {\mathrm {GL}}_\ell (K)$ by $f\mapsto L_f$ , where $L_f:A\to A$ is the left-multiplication map by f, we see that $A^\times $ can be identified with the K-points of a linear algebraic group. For $f\in A$ , we define $\Lambda _f$ to be the set of eigenvalues of $L_f$ over the algebraic closure $\overline {K}$ , not counting multiplicities.

Definition 2.1. We say a collection of elements $f_1,\dots ,f_r\in A^\times $ has multiplicatively independent eigenvalues if $\Lambda _{f_1},\dots ,\Lambda _{f_r}$ are disjoint and their union is multiplicatively independent.

In this paper, unless otherwise noted, each algebraic group is connected.

2.2. A variant of the Mordell–Lang problem for central simple algebras

The following result is an equivalent re-statement of Theorem 1.1 in the setting of finite-dimensional central simple algebras.

Theorem 2.2. Let $K,A$ be as above, V be a closed K-subvariety of A not passing through zero, $f_1,\dots ,f_r\in A^\times $ , and $\Gamma $ be the set

$$ \begin{align*} \Gamma=\{{f_1^{n_1} \cdots f_r^{n_r}: n_1,\dots,n_r\in {\mathbb Z}}\}\subseteq A^\times. \end{align*} $$

If $f_1,\dots , f_r$ have multiplicatively independent eigenvalues, then $\lvert {V(K)\cap \Gamma \rvert } < \infty $ .

Next, we present various examples showing the relevance of the hypotheses from Theorem 2.2.

2.3. Examples

We first recall that for any nilpotent matrix x in $\operatorname {\mathrm {Mat}}_n(K)$ (so that $x^n=0$ ), there is a well-defined unipotent matrix

$$ \begin{align*} \exp(x):=\sum_{k=0}^\infty \frac{x^k}{k!} = \sum_{k=0}^{n-1} \frac{x^k}{k!}. \end{align*} $$

Moreover, $\exp (x+y)=\exp (x)\exp (y)$ if $xy=yx$ .

We denote by $\varepsilon _n$ the nilpotent matrix

$$ \begin{align*} \varepsilon_n:=\begin{bmatrix} 0 & 1 & & \\ & 0 & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{bmatrix} \in \operatorname{\mathrm{Mat}}_n(K). \end{align*} $$

The following example shows the necessity of the assumption of Theorem 2.2 that V does not pass through $0$ .

Example 2.3. Let $A=\operatorname {\mathrm {Mat}}_3(K)$ , $\varepsilon :=\varepsilon _3$ , $f_1=2\exp (\varepsilon )$ and $f_2=3\exp (-\varepsilon ^2)$ . Then for $n_1,n_2\in {\mathbb Z}$ ,

$$ \begin{align*} f_1^{n_1}f_2^{n_2}=2^{n_1}3^{n_2}\exp(n_1 \varepsilon-n_2 \varepsilon^2) = 2^{n_1} 3^{n_2} \bigg(1+n_1 \varepsilon + \bigg(-n_2+\frac{n_1^2}{2}\bigg) \varepsilon^2\bigg). \end{align*} $$

Hence, if $V\subseteq A$ is cut out by the condition that the top-right entry is zero, then $f_1^{n_1} f_2^{n_2}\in V$ if and only if $n_2={n_1^2}/{2}$ . The corresponding subset in ${\mathbb Z}^2$ is not only infinite, but also not a finite union of cosets of subgroups of ${\mathbb Z}^2$ .

In this example, $f_1,f_2$ have multiplicatively independent eigenvalues, but $0\in V$ .

In view of Ghioca and Huang (‘A non-abelian variant of the classical Mordell–Lang conjecture’, submitted for publication), it is tempting to replace the assumption of Theorem 2.2 that $f_1,\dots ,f_r$ have multiplicatively independent eigenvalues by the assumption that $\det (f_1)$ , $\dots ,\det (f_r)$ are multiplicatively independent. The following example shows we cannot do so.

Example 2.4. Let $A=\operatorname {\mathrm {Mat}}_4(K)$ , $\varepsilon :=\varepsilon _3$ , $f_1=\mathrm {diag}(2\exp (\varepsilon ),1)\in \operatorname {\mathrm {Mat}}_{3+1}(K)$ and $f_2=\mathrm {diag}(3\exp (-\varepsilon ^2),1)$ . Let $V\subseteq A$ be cut out by the condition that the $(3,1)$ -entry is zero and the $(4,4)$ -entry is $1$ . Then by the same argument as the preceding example, $f_1^{n_1}f_2^{n_2}\in V$ if and only if $n_2={n_1^2}/{2}$ .

In this example, $0\notin V$ , and $\det (f_1)=2^3, \det (f_2)=3^3$ are multiplicatively independent. However, $f_1$ has eigenvalues $\{2,1\}$ , and the presence of $1$ implies that $f_1,f_2$ do not have multiplicatively independent eigenvalues.

Finally, the next example shows that if one were to replace the set $\Gamma $ from Theorem 2.2 with the subgroup generated by $f_1,\dots , f_r$ , then the conclusion would fail.

Example 2.5. Let $A=\operatorname {\mathrm {Mat}}_2(K)$ , $f_1=\mathrm {diag}(2,3)$ and $f_2=\mathrm {diag}(5,7)+\varepsilon $ , where $\varepsilon =\big [\begin {smallmatrix} 0 & 1 \\ 0 & 0 \end {smallmatrix}\big ]$ . Then the subgroup $\Gamma $ generated by $f_1, f_2$ contains $u:=f_1 f_2 f_1^{-1} f_2^{-1}=I_2 - \varepsilon /21$ . In particular, $u^n$ for $n\in {\mathbb N}$ gives infinitely many elements in $V(K)\cap \Gamma $ , where

$$ \begin{align*} V=\left\{{\begin{bmatrix} a & b\\c & d \end{bmatrix}: a=d=1, c=0}\right\}. \end{align*} $$

2.4. A variant of the Mordell–Lang problem in an arbitrary commutative algebraic group

Theorem 2.7 is our key ingredient for proving Theorem 2.2 and it is itself another variant of the classical Mordell–Lang problem (this time in the context of the commutative linear algebraic groups).

One of the most important special cases of the classical Mordell–Lang conjecture says that given a semiabelian variety G (defined over an algebraically closed field K of characteristic $0$ ) and given a finitely generated subgroup $\Gamma \subset G(K)$ , if

(2.1) $$ \begin{align} V\ \text{contains no translate of a nontrivial algebraic subgroup of}\ G, \end{align} $$

then $|V(K)\cap \Gamma |<\infty $ . It is natural to consider extensions of the classical Mordell–Lang conjecture to arbitrary commutative algebraic groups G. The first such case to consider would be for affine groups, that is, when G is isomorphic to $\mathbb {G}_m^\ell \times \mathbb {G}_a^k$ for some $k,\ell \in {\mathbb N}$ , and once again study this problem under the assumption (2.1). However, [5, Examples 1.1 and 1.2] show that the presence of multiple copies of $\mathbb {G}_a$ will generate counterexamples of the Mordell–Lang principle. Our next Theorem 2.7 provides a setting where the aforementioned variant of the Mordell–Lang conjecture holds even in the presence of arbitrarily many copies of $\mathbb {G}_a$ in the linear algebraic group G.

To state Theorem 2.7, we need the following definition.

Definition 2.6. Let G be a commutative linear algebraic group over a field K of characteristic $0$ , and $\Gamma $ be a finitely generated subgroup of $G(K)$ . We say $\Gamma \subseteq G(K)$ is strongly independent if there are $r,\,u,\,\ell _1,\dots ,\ell _r\in {\mathbb Z}_{\geq 0}$ and an isomorphism $G\simeq \mathbb {G}_m^{\ell _1+\cdots +\ell _r}\times \mathbb {G}_a^u$ , under which a generating set $g_1,\dots ,g_r$ of $\Gamma $ takes the form

(2.2) $$ \begin{align} \begin{aligned} g_1 &= (\lambda_{1,1},\dots,\lambda_{1,\ell_1})\times (1,\dots,1) \times \cdots \times (1,\dots,1) \times \overline{b}_1,\\ g_2 &= (1,\dots,1) \times (\lambda_{2,1},\dots,\lambda_{2,\ell_2}) \times \cdots \times (1,\dots,1) \times \overline{b}_2, \\ &\vdots \\ g_r &= (1,\dots,1) \times (1,\dots,1) \times \cdots \times (\lambda_{r,1},\dots,\lambda_{r,\ell_r}) \times \overline{b}_r, \end{aligned} \end{align} $$

where $\lambda _{i,j}\in K^\times $ are multiplicatively independent and $\overline {b}_1,\dots ,\overline {b}_r\in K^u$ (that is, they are K-vectors with u entries). In this case, we let $T_i:=\mathbb {G}_m^{\ell _i}$ and $U=\mathbb {G}_a^u$ , and we say $\Gamma \subseteq G(K)$ is strongly independent with respect to the decomposition $G=T_1\times \dots \times T_r\times U$ .

Theorem 2.7. Let G be a commutative linear algebraic group over a field K of characteristic zero, $V\subseteq G$ be a closed subvariety and $\Gamma $ be a finitely generated subgroup of $G(K)$ . Assume:

1. (i) The subgroup $\Gamma $ is strongly independent in $G(K)$ with respect to some decomposition $G=T_1\times \dots \times T_r\times U$ ; and

2. (ii) there is no $i\in \{1,\dots , r\}$ and no geometric point $v\in (\prod _{j\ne i} T_j)\times U$ such that

   (2.3) $$ \begin{align} T_i\times \{{v}\} \subseteq V. \end{align} $$

Then $\lvert {V(K)\cap \Gamma \rvert } < \infty $ .

2.5. Remarks regarding Theorem 2.7

We show next that the conclusion in Theorem 2.7 fails if one removes the hypotheses regarding V and $\Gamma $ .

First of all, condition (2.3) is a weaker version of condition (2.1) and in its absence, Theorem 2.7 would fail as the next example shows.

Example 2.8. Consider $G=\mathbb {G}_m^2$ and let $\Gamma $ be generated by $(2,1)$ and $(1,3)$ , while $V=\{2\}\times \mathbb {G}_m$ . Then clearly, $V\cap \Gamma $ is infinite. Note that in this example, $\Gamma $ is strongly independent, but V does not satisfy hypothesis (2.3) from Theorem 2.7.

The relevance of the hypothesis that $\Gamma $ is strongly independent is more subtle. On one hand, the next example shows that in its absence, one would definitely have to strengthen the hypothesis (2.3) to the original hypothesis (2.1) from the classical Mordell–Lang problem.

Example 2.9. Consider the case when $G=\mathbb {G}_m^2$ and $\Gamma \subset G(K)$ is spanned by $(2,1)$ and $(1,4)$ . Then $\Gamma $ is contained in the subvariety V given by the equation $x_2=x_1^2$ . We note that V meets the hypothesis (2.3) from Theorem 2.7, but since $\Gamma $ is not strongly independent, the intersection $V\cap \Gamma $ is infinite in this case.

However, the following example shows that even if we were to strengthen the hypothesis (2.3) to (2.1), one would still not obtain the desired conclusion in Theorem 2.7 in the absence of the hypothesis that $\Gamma $ is strongly independent.

Example 2.10. Consider the case when $G=\mathbb {G}_m\times \mathbb {G}_a$ , and $\Gamma $ is generated by $(2,1)$ and $(2,0)$ . Then $\Gamma $ has infinite intersection with the diagonal subvariety $V\subset G$ given by the equation $x_1=x_2$ . Indeed, $\Gamma $ consists of all points of the form

$$ \begin{align*}\{(2^{m+n},m)\colon m,n\in{\mathbb Z}\}\end{align*} $$

and so, $V\cap \Gamma $ consists of the set

$$ \begin{align*}\{(2^s,2^s)\colon s\in{\mathbb N}\},\end{align*} $$

which is not a finite union of cosets of subgroups of $\Gamma $ . In this case, V is a curve, which is not a coset of a subgroup of $\Gamma $ , but nevertheless, the intersection $V\cap \Gamma $ is infinite. Note that $\Gamma $ is not strongly independent in this example.

3. Proof of Theorem 2.7

In this section, we work with the notation and hypotheses from Theorem 2.7 to prove it.

It suffices to prove Theorem 2.7 assuming K is algebraically closed. Therefore, we may assume $G=\mathbb {G}_m^\ell \times \mathbb {G}_a^k$ for some $\ell ,k\in \mathbb {N}$ . Furthermore, we can write

$$ \begin{align*}\ell:=\ell_1+\ell_2+\cdots +\ell_r,\end{align*} $$

where the group $\Gamma $ is generated by

(3.1) $$ \begin{align} \begin{aligned} g_1 &= (\lambda_{1,1},\dots,\lambda_{1,\ell_1})\times (1,\dots,1) \times \dots \times (1,\dots,1) \times \overline{b}_1,\\ g_2 &= (1,\dots,1) \times (\lambda_{2,1},\dots,\lambda_{2,\ell_2}) \times \dots \times (1,\dots,1) \times \overline{b}_2, \\ &\vdots \\ g_r &= (1,\dots,1) \times (1,\dots,1) \times \dots \times (\lambda_{r,1},\dots,\lambda_{r,\ell_r}) \times \overline{b}_r \end{aligned} \end{align} $$

for some $\overline {b}_1,\dots , \overline {b}_r\in \mathbb {G}_a^k(K)$ ; moreover, the elements $\lambda _{i,j}\in K^\times $ are multiplicatively independent. We write

(3.2) $$ \begin{align} \overline{b}_i:=(b_{i,1},\dots, b_{i,k}) \quad\text{for }i=1,\dots, r, \end{align} $$

where each $b_{i,j}\in K$ (for $1\le i\le r$ and $1\le j\le k$ ).

Taking into account that $\ell =\ell _1+\cdots +\ell _r$ , we represent each polynomial f in the vanishing ideal $\mathcal {I}(V)$ of V as a polynomial in

$$ \begin{align*}K[x_{1,1},\dots, x_{1,\ell_1},x_{2,1},\dots, x_{2,\ell_2},\dots, x_{r,1},\dots, x_{r,\ell_r},y_1,\dots, y_k].\end{align*} $$

So, we let $f_1,\dots , f_m$ be a given set of generators for $\mathcal {I}(V)$ and we consider next $f_s$ for some s with $1\le s\le m$ . Then we can write $f_s$ as

(3.3) $$ \begin{align} f_s:=\sum_{\overline{j}=(j_{i,u})_{\tiny\substack{{1\le i\le r}\\ 1\le u\le \ell_i}}} \prod_{i=1}^r\prod_{u=1}^{\ell_i} x_{i,u}^{j_{i,u}}\cdot P_{s,\overline{j}}(y_1,\dots, y_k), \end{align} $$

where the sum in (3.3) runs over a finite set $J_s$ of tuples

$$ \begin{align*}\overline{j}:=(j_{1,1},\dots, j_{1,\ell_1},j_{2,1},\dots, j_{2,\ell_2},\dots, j_{r,1},\dots, j_{r,\ell_r})\in\mathbb{N}^\ell, \end{align*} $$

while $P_{s,\overline {j}}\in K[y_1,\dots , y_k]$ is some nonzero polynomial.

For each $\overline {j}\in J_s$ , there is a polynomial $Q_{s,\overline {j}}\in K[z_1,\dots , z_r]$ (depending on the $\overline {b}_i$ terms, according to (3.2)) with the property that

(3.4) $$ \begin{align} Q_{s,\overline{j}}(n_1,\dots, n_r):=P_{s,\overline{j}}\bigg(\sum_{i=1}^r n_i\cdot \overline{b}_i\bigg) \quad\text{for each }n_1,\dots, n_r\in\mathbb{Z}. \end{align} $$

Using (3.1), (3.2) and (3.4), we see that $f_s$ vanishes at the point $g_1^{n_1}\cdots g_r^{n_r}\in \mathbb {G}_m^\ell \times \mathbb {G}_a^k$ (for some integers $n_1,\dots , n_r$ ) if and only if

(3.5) $$ \begin{align} \sum_{\overline{j}\in J_s} \prod_{i=1}^r\prod_{u=1}^{\ell_i} \lambda_{i,u}^{j_{i,u}\cdot n_i}\cdot Q_{s,\overline{j}}(n_1,\dots, n_r)=0. \end{align} $$

So, $\prod _{i=1}^r g_i^{n_i}\in V$ if and only if $\overline {n}:=(n_1,\dots , n_r)$ satisfies the system of equations (3.5) for $s=1,\dots ,m$ . We argue by contradiction and assume there exists an infinite set of solutions $\mathcal {S}:=\{\overline {n}^{(i)}\}_{i\ge 1}$ to the above system of polynomial-exponential equations (3.5). To simplify the index notation from (3.5), we re-write that equation as

(3.6) $$ \begin{align} \sum_{\overline{j}\in J_s} \left(\overline{\lambda}^{\overline{j}}\right)^{\overline{n}}\cdot Q_{s,\overline{j}}(\overline{n})=0, \end{align} $$

where $\overline {\lambda }:=(\lambda _{i,u})_{\substack {1\le i\le r\\ 1\le u\le \ell _i}}$ and

$$ \begin{align*}\bigg(\overline{\lambda}^{\overline{j}}\bigg)^{\overline{n}}:=\prod_{i=1}^r \prod_{u=1}^{\ell_i} \lambda_{i,u}^{j_{i,u}\cdot n_i}.\end{align*} $$

To analyse the system of m polynomial-exponential equations (3.5), we will apply the method from [8, Section 8]. Since there are finitely many partitions for each set of indices $J_s$ , there exists a given collection of partitions

(3.7) $$ \begin{align} \mathcal{P}:=(\mathcal{P}_s)_{1\le s\le m}, \end{align} $$

where $\mathcal {P}_s$ is a partition of $J_s$ for each $s=1,\dots , m$ , which is maximally compatible (as defined in [8, page 320]) for infinitely many solutions $\overline {n}\in \mathcal {S}$ for the system of polynomial-exponential equations (3.5). At the expense of replacing $\mathcal {S}$ by a suitable infinite subset, we may assume that each of the solutions $\overline {n}\in \mathcal {S}$ is maximally compatible with the given partition (3.7). The compatibility of the collection of partitions $\mathcal {P}$ with respect to each solution $\overline {n}\in \mathcal {S}$ refers to the fact that for each $s=1,\dots , m$ , considering the partition $\mathcal {P}_s$ of $J_s$ given by

(3.8) $$ \begin{align} J_s:=J_{s,1}\cup \cdots \cup J_{s,v_s} \quad\text{(for some positive integer } v_s), \end{align} $$

we have, for each $s=1,\dots , m$ ,

(3.9) $$ \begin{align} \sum_{\overline{j}\in J_{s,i}} \bigg(\overline{\lambda}^{\overline{j}}\bigg)^{\overline{n}} Q_{s,\overline{j}}(\overline{n})=0 \quad\text{for each }i=1,\dots,v_s. \end{align} $$

The maximality of the collection $\mathcal {P}$ refers to the fact that there is no further refined collection of partitions (3.8) such that equations (3.9) hold for each subpart of each corresponding partition of $J_s$ for $s=1,\dots , m$ .

We let $H_{\mathcal {P}}$ be the subgroup of ${\mathbb Z}^r$ defined as in [8, page 319], that is, $H_{\mathcal {P}}$ consists of all $\overline {n}\in {\mathbb Z}^r$ with the property that for each $s=1,\dots , m$ and for each $i=1,\dots , v_s$ ,

(3.10) $$ \begin{align} \bigg(\overline{\lambda}^{\overline{j_1}}\bigg)^{\overline{n}} = \bigg(\overline{\lambda}^{\overline{j_2}}\bigg)^{\overline{n}} \quad\text{for each }\,\overline{j}_1,\overline{j}_2\in J_{s,i}. \end{align} $$

According to [8, Theorem 6], $H_{\mathcal {P}}$ cannot be the trivial subgroup of ${\mathbb Z}^r$ since we assumed there exists an infinite set $\mathcal {S}$ of solutions $\overline {n}$ maximally compatible with respect to $\mathcal {P}$ . So, from now on, we assume there exists some nontrivial $\overline {n}^{(0)}\in H_{\mathcal {P}}$ (that is, not all the entries of $\overline {n}^{(0)}$ are equal to $0$ ). Without loss of generality, we assume that

$$ \begin{align*} \overline{n}^{(0)}:=(n^{(0)}_1,\dots, n^{(0)}_r) \quad\text{with }n^{(0)}_1\ne 0. \end{align*} $$

Equation (3.10) says that for each $s=1,\dots ,m$ and for each $i=1,\dots , v_s$ ,

(3.11) $$ \begin{align} \bigg(\overline{\lambda}^{\overline{j}}\bigg)^{\overline{n}^{(0)}} \text{ is the same as we vary }\overline{j}\in J_{s,i}. \end{align} $$

We fix some $s\in \{1,\dots , m\}$ and also some $i\in \{1,\dots , v_s\}$ ; then we write each $\overline {j}\in J_{s,i}$ as we did before: $\overline {j}:=(j_{1,1},j_{1,2},\dots ,j_{1,\ell _1},j_{2,1},j_{2,2}, \dots , j_{2,\ell _2},\dots ,j_{r,1},j_{r,2},\dots , j_{r,\ell _r})$ . Re-writing (3.11) using the index notation as in (3.5), we see that

(3.12) $$ \begin{align} \prod_{p=1}^r \prod_{u=1}^{\ell_p} \lambda_{p,u}^{j_{p,u}\cdot n^{(0)}_p}\text{ is constant as we vary}\ \overline{j}\in J_{s,i}. \end{align} $$

Since the $\lambda _{p,u}$ are multiplicatively independent and also, $n^{(0)}_1\ne 0$ , it follows from (3.12) that for each $s=1,\dots , m$ and for each $i=1,\dots , v_s$ , the vector

(3.13) $$ \begin{align} \overline{j}^{(1)}:=(j_{1,1},j_{1,2},\dots, j_{1,\ell_1})\ \text{is constant as we vary}\ \overline{j}\in J_{s,i}. \end{align} $$

We let $\overline {n}^{(1)}\in \mathcal {S}$ and write (3.9) for $\overline {n}:=\overline {n}^{(1)}$ . It follows that, for each $s\in \{1,\dots , m\}$ and for each $i\in \{1,\dots , v_s\}$ ,

$$ \begin{align*} \sum_{\overline{j}\in J_{s,i}}\prod_{p=1}^r\prod_{u=1}^{\ell_p} \lambda_{p,u}^{j_{p,u}\cdot n_p^{(1)}} Q_{s,\overline{j}}(\overline{n}^{(1)})=0, \end{align*} $$

where $\overline {n}^{(1)}:=(n_1^{(1)},\dots , n_r^{(1)})$ . Using (3.13), we divide (3.9) by

$$ \begin{align*}\prod_{u=1}^{\ell_1} \lambda_{1,u}^{j_{1,u}\cdot n^{(1)}_1}\end{align*} $$

and therefore,

(3.14) $$ \begin{align} \sum_{\overline{j}\in J_{s,i}} \prod_{p=2}^r \prod_{u=1}^{\ell_p} \lambda_{p,u}^{j_{p,u}\cdot n^{(1)}_p} \cdot Q_{s,\overline{j}}(\overline{n}^{(1)})=0. \end{align} $$

We write $\overline {y}^{(1)}:=\sum _{i=1}^r n^{(1)}_i\cdot \overline {b}_i\in \mathbb {G}_a^k(K)$ . Specialising $\overline {y}$ to $\overline {y}^{(1)}$ in (3.3), we re-write that equation (for each $s=1,\dots , m$ ) according to the given partition $\mathcal {P}_s$ of $J_s$ as follows (see also the way we re-wrote (3.5) as (3.6)):

(3.15) $$ \begin{align} f_s(\overline{x},\overline{y}^{(1)})=\sum_{i=1}^{v_s} \sum_{\overline{j}\in J_{s,i}} (\overline{x})^{\overline{j}}\cdot P_{s,\overline{j}}(\overline{y}^{(1)}). \end{align} $$

In (3.15), we have (as before) $(\overline {x})^{\overline {j}}:=\prod _{p=1}^r\prod _{u=1}^{\ell _p} x_{p,u}^{j_{p,u}}$ . Using (3.13) and (3.14) (for each $s=1,\dots , m$ and each $i=1,\dots , v_s$ ), and specialising further in (3.15) each

$$ \begin{align*}x_{p,j}:=\lambda_{p,j}^{n^{(1)}_p} \quad\text{for}\ p=2,\dots, r\ \text{and}\ j=1,\dots, \ell_p,\end{align*} $$

we see that

(3.16) $$ \begin{align} f_s\bigg(x_{1,1},\dots, x_{1,\ell_1}, \lambda_{2,1}^{n^{(1)}_2}, \lambda_{2,2}^{n^{(1)}_2},\dots, \lambda_{2,\ell_2}^{n^{(1)}_2}, \dots, \lambda_{r,1}^{n^{(1)}_r},\dots, \lambda_{r,\ell_r}^{n^{(1)}_r},\overline{y}^{(1)}\bigg)=0 \end{align} $$

for any $x_{1,1},\dots , x_{1,\ell _1}$ . Thus, (3.16) tells us that V contains the entire subvariety of $\mathbb {G}_m^\ell \times \mathbb {G}_a^k=T_1\times \cdots T_r\times \mathbb {G}_a^k$ given by

$$ \begin{align*}T_1\times \bigg\{\bigg(\lambda_{2,1}^{n^{(1)}_2}, \lambda_{2,2}^{n^{(1)}_2},\dots, \lambda_{2,\ell_2}^{n^{(1)}_2}, \dots, \lambda_{r,1}^{n^{(1)}_r},\dots, \lambda_{r,\ell_r}^{n^{(1)}_r},\overline{y}^{(1)}\bigg)\bigg\},\end{align*} $$

thus contradicting the hypothesis from Theorem 2.7. Therefore, indeed, we only have finitely many solutions to the system of polynomial-exponential equations (3.6). This concludes our proof of Theorem 2.7.

4. Proof of Theorem 2.2

In this section, we work with the notation and the hypotheses from Theorem 2.2 to prove it.

By base-changing from K to the algebraic closure $\overline {K}$ , we may assume K is algebraically closed and $A=\operatorname {\mathrm {Mat}}_n(K)$ is the matrix algebra for some $n\geq 1$ , so that $f_1,\dots ,f_r\in \operatorname {\mathrm {GL}}_n(K)$ . Note that the eigenvalues of $L_{f_i}$ are just the eigenvalues of $f_i$ repeated n times, so $\Lambda _{f_i}$ is simply the set of eigenvalues of $f_i$ (not counting multiplicities).

Consider the commutative K-subalgebra $K[f_i]$ of $\operatorname {\mathrm {Mat}}_n(K)$ generated by $f_i$ . We have commutative linear algebraic groups $G_i:=K[f_i]^\times $ and $G:=G_1\times \dots \times G_r$ . Let $g_i$ be the element $(1,\dots ,f_i,\dots ,1)$ in G and let $\Gamma '$ be the subgroup of G generated by $g_1,\dots ,g_r$ .

Over an algebraically closed field K, any commutative linear algebraic group is necessarily of the form $\mathbb {G}_m^\ell \times \mathbb {G}_a^u$ with $\ell ,u\geq 0$ . Indeed, one has a direct product decomposition into the semisimple part (which gives a torus) and the unipotent part. For a commutative unipotent group, the exponential map is an isomorphism of algebraic groups, so the unipotent part is of the form $\mathbb {G}_a^u$ .

Next, we will be more explicit regarding each algebraic group $G_i$ . Let $\Lambda _{f_i}=\{{\lambda _{i,1},\dots ,\lambda _{i,\ell _i}}\}$ and let $G_i=T_i\times U_i$ , where $T_i$ is the semisimple part and $U_i$ is the unipotent part. Using the Jordan canonical form of $f_i$ , we have an isomorphism $T_i\simeq (K^\times )^{\ell _i}$ , such that the image of $f_i$ projected onto $T_i$ is identified with $(\lambda _{i,1},\dots ,\lambda _{i,\ell _i})$ .

Let $U:=U_1\times \dots \times U_r\simeq \mathbb {G}_a^u$ and $T:=T_1\times \dots \times T_r$ . From the above discussion, we get an isomorphism $G= T\times U\simeq \mathbb {G}_m^{\ell _1+\dots +\ell _r} \times \mathbb {G}_a^u$ under which $g_1,\dots ,g_r$ takes the form of (2.2) for some $v_1,\dots ,v_r\in K^u$ . Since $f_1,\dots ,f_r$ have multiplicatively independent eigenvalues, $\lambda _{i,j}$ are multiplicatively independent. Thus, $\Gamma '\subseteq G$ is strongly independent in the sense of Definition 2.6.

Define an algebraic map (not necessarily a group homomorphism)

$$ \begin{align*} \mu: G=G_1\times \dots \times G_r\to \operatorname{\mathrm{GL}}_n(K), \quad (z_1,\dots,z_r)\to z_1\cdots z_r, \end{align*} $$

where the multiplication takes place in $\operatorname {\mathrm {GL}}_n(K)$ , and let $W:=\mu ^{-1}(V)$ , which is a closed subvariety of G. We claim that W does not contain a subvariety of the form $T_i\times \{{v}\}$ for some $i\in \{1,\dots , r\}$ and some $v\in (\prod _{j\ne i}T_j)\times U$ .

We argue by contradiction. Without loss of generality, assume that $T_1\times \{{v}\}\subseteq W$ for some $v\in (\prod _{i=2}^rT_i)\times U$ . Consider the canonical map $\tau _1:K^\times \hookrightarrow G_1\subseteq \operatorname {\mathrm {GL}}_n(K)$ given by the scalar matrices. Then, $\tau _1$ in fact maps into $T_1=(K^\times )^{\ell _1}$ and takes the form $\tau _1(c)=(c,\dots ,c)$ . A crucial property of $\mu $ is that it behaves well with scalar multiplication: for $c\in K^\times $ and $(z_1,\dots ,z_r)\in G=G_1\times \dots \times G_r$ ,

$$ \begin{align*} \mu(\tau_1(c)\cdot (z_1,\dots,z_r))=\mu(cz_1,\dots,z_r)=c\mu(z_1,\dots,z_r). \end{align*} $$

Now we pick $(z_1,\dots ,z_r)\in G$ that lies in $T_1\times \{{v}\}$ under the identification $G= T\times U$ . For all $c\in K^\times $ , since $T_1\times \{{v}\}$ is a $T_1$ -coset of G and $\tau _1(c)\in T_1\subseteq T$ , it follows that $\tau _1(c)\cdot (z_1,\dots ,z_r)\in T_1\times \{{v}\}$ . Since $T_1\times \{{v}\}\subseteq W$ , applying $\mu $ gives

$$ \begin{align*} c\mu(z_1,\dots,z_r)\in V \quad\text{for all }c\in K^\times. \end{align*} $$

As V is Zariski closed in $\operatorname {\mathrm {Mat}}_n(K)$ , we have $0\in V$ , contradicting the hypothesis from Theorem 2.2. This proves the claim.

Finally, since the assumptions of Theorem 2.7 are verified, $\lvert {W(K)\cap \Gamma '\rvert }<\infty $ . Applying $\mu $ , this means $f_1^{n_1}\cdots f_r^{n_r}\in V$ for only finitely many $(n_1,\dots ,n_r)\in {\mathbb Z}^r$ , so the conclusion of Theorem 2.2 is proved.