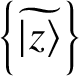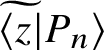1 Introduction
In a commentary included in his edition of Szegő’s collected works, Askey [Reference Askey2] introduced sets of biorthogonal polynomials on the unit circle. These polynomials are defined as follows in terms of the standard Gauss hypergeometric series:
 $$ \begin{align} P_n(z; \alpha, \beta) = \frac{(\beta)_n}{(\alpha+1)_n} {}{_2}F_1 \left( {-n, \alpha+1 \atop 1-\beta-n } ;z\right), \end{align} $$
$$ \begin{align} P_n(z; \alpha, \beta) = \frac{(\beta)_n}{(\alpha+1)_n} {}{_2}F_1 \left( {-n, \alpha+1 \atop 1-\beta-n } ;z\right), \end{align} $$
where
![]() $(a)_k = a(a+1)\dotsm (a+k-1), k=1, 2, \dotsc $
and
$(a)_k = a(a+1)\dotsm (a+k-1), k=1, 2, \dotsc $
and
![]() $(a)_0=1$
, are the Pochhammer symbols. The normalisation is chosen so that
$(a)_0=1$
, are the Pochhammer symbols. The normalisation is chosen so that
![]() $P_n(z)$
and
$P_n(z)$
and
![]() $Q_n(z)$
are monic. The biorthogonality of these polynomials was proven in [Reference Askey3] using slightly different conventions; it here reads:
$Q_n(z)$
are monic. The biorthogonality of these polynomials was proven in [Reference Askey3] using slightly different conventions; it here reads:
 $$ \begin{align} - \frac{1}{2\pi i}\oint_{\lvert z\rvert=1} dz {(-z)}^{-1-\beta} ( 1-z ) ^{\alpha+\beta} P_m(z; \alpha, \beta) Q_n\left(\frac{1}{z}; \alpha, \beta\right) = \frac{m!\Gamma(m+\alpha +\beta +1)}{\Gamma(\alpha +1) \Gamma(\beta +1)} \delta_{mn}, \end{align} $$
$$ \begin{align} - \frac{1}{2\pi i}\oint_{\lvert z\rvert=1} dz {(-z)}^{-1-\beta} ( 1-z ) ^{\alpha+\beta} P_m(z; \alpha, \beta) Q_n\left(\frac{1}{z}; \alpha, \beta\right) = \frac{m!\Gamma(m+\alpha +\beta +1)}{\Gamma(\alpha +1) \Gamma(\beta +1)} \delta_{mn}, \end{align} $$
where
![]() $\Gamma (x)$
is the standard gamma function. Remember that
$\Gamma (x)$
is the standard gamma function. Remember that
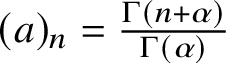 $ (a)_n = \frac {\Gamma (n+ \alpha )}{\Gamma (\alpha )}$
. The branch of
$ (a)_n = \frac {\Gamma (n+ \alpha )}{\Gamma (\alpha )}$
. The branch of
![]() ${(-z)}^{-1-\beta }$
is chosen such that
${(-z)}^{-1-\beta }$
is chosen such that
![]() ${(-z)}^{-1-\beta }= \lvert z\rvert ^{-1-\beta }$
if
${(-z)}^{-1-\beta }= \lvert z\rvert ^{-1-\beta }$
if
![]() $\arg z=\pi $
[Reference Hendriksen and van Rossum14]; this is reflected in [Reference Askey2], [Reference Askey3] by making the polar variable run from
$\arg z=\pi $
[Reference Hendriksen and van Rossum14]; this is reflected in [Reference Askey2], [Reference Askey3] by making the polar variable run from
![]() $-\pi $
to
$-\pi $
to
![]() $\pi $
. For the connection with the spherical harmonics of the Heisenberg group, see [Reference Greiner and Koornwinder10]. Let us also record that special cases of the Askey polynomials were obtained in [Reference Shen22] as Fourier transforms of Laguerre polynomials (with weights attached). We refer to [Reference Temme23] for historical remarks regarding these polynomials (see also [Reference Borrego-Morell and Rafaeli4]).
$\pi $
. For the connection with the spherical harmonics of the Heisenberg group, see [Reference Greiner and Koornwinder10]. Let us also record that special cases of the Askey polynomials were obtained in [Reference Shen22] as Fourier transforms of Laguerre polynomials (with weights attached). We refer to [Reference Temme23] for historical remarks regarding these polynomials (see also [Reference Borrego-Morell and Rafaeli4]).
In his comments, Askey expressed the opinion that the
![]() $P_n(z; \alpha , \beta )$
are the natural analogues of the Jacobi polynomials on the unit circle. We here reinforce this viewpoint by offering a unified algebraic description of these Askey polynomials on
$P_n(z; \alpha , \beta )$
are the natural analogues of the Jacobi polynomials on the unit circle. We here reinforce this viewpoint by offering a unified algebraic description of these Askey polynomials on
![]() $S^1$
and of the Jacobi polynomials. This will involve the introduction of an algebra to be called meta-Jacobi that will be seen to account for the bispectrality of both classes of functions.
$S^1$
and of the Jacobi polynomials. This will involve the introduction of an algebra to be called meta-Jacobi that will be seen to account for the bispectrality of both classes of functions.
Let us register for reference the definition and key properties of the monic Jacobi polynomials
 $\hat {P}_n^{\left (\alpha , \beta \right )}(x)$
defined on the interval
$\hat {P}_n^{\left (\alpha , \beta \right )}(x)$
defined on the interval
![]() $[0,1]$
:
$[0,1]$
:
 $$ \begin{align} \hat{P}_n ^{\left(\alpha, \beta\right)}(x) = \frac{(-1)^n(1-\beta)_n} {(1 + \alpha + n)_n} {_2}F_1 \left( {-n, n + \alpha + 1 \atop 1 - \beta} ;x\right). \end{align} $$
$$ \begin{align} \hat{P}_n ^{\left(\alpha, \beta\right)}(x) = \frac{(-1)^n(1-\beta)_n} {(1 + \alpha + n)_n} {_2}F_1 \left( {-n, n + \alpha + 1 \atop 1 - \beta} ;x\right). \end{align} $$
Please note that for convenience an unconventional choice has been made for the parameters. These polynomials possess the following orthogonality property:
 $$ \begin{align} \int_0^1 \hat{P}_m ^{\left(\alpha, \beta\right)}(x) \hat{P}_n ^{\left(\alpha, \beta\right)}(x) {x}^{-\beta} ( 1-x ) ^{\alpha+\beta} dx = h_n \delta_{mn}, \qquad \alpha + \beta> -1, \ \beta < 1, \end{align} $$
$$ \begin{align} \int_0^1 \hat{P}_m ^{\left(\alpha, \beta\right)}(x) \hat{P}_n ^{\left(\alpha, \beta\right)}(x) {x}^{-\beta} ( 1-x ) ^{\alpha+\beta} dx = h_n \delta_{mn}, \qquad \alpha + \beta> -1, \ \beta < 1, \end{align} $$
with the normalisation factor
![]() $h_n$
given by
$h_n$
given by
 $$ \begin{align} h_n= n! \frac{\Gamma(n - \beta +1) \Gamma(n + \alpha + 1) \Gamma(n + \alpha + \beta + 1)}{\Gamma (2n + \alpha + 1) \Gamma (2n + \alpha + 2)}. \end{align} $$
$$ \begin{align} h_n= n! \frac{\Gamma(n - \beta +1) \Gamma(n + \alpha + 1) \Gamma(n + \alpha + \beta + 1)}{\Gamma (2n + \alpha + 1) \Gamma (2n + \alpha + 2)}. \end{align} $$
As is well known, in addition to satisfying a three-term recurrence relation, the polynomials
 $\hat {P}_n^{\left (\alpha , \beta \right )}(x)$
are eigenfunctions of the hypergeometric operator
$\hat {P}_n^{\left (\alpha , \beta \right )}(x)$
are eigenfunctions of the hypergeometric operator
 $$ \begin{align} \mathcal{M} = x(x-1) \partial_x^2 + [ (\alpha+2)x + \beta-1 ] \partial_x ,\end{align} $$
$$ \begin{align} \mathcal{M} = x(x-1) \partial_x^2 + [ (\alpha+2)x + \beta-1 ] \partial_x ,\end{align} $$
with eigenvalue
![]() $n(n + \alpha +1)$
. These bispectral properties are encoded in the Jacobi algebra
$n(n + \alpha +1)$
. These bispectral properties are encoded in the Jacobi algebra
![]() $\mathfrak {J}$
[Reference Genest, Ismail, Vinet and Zhedanov9] defined in terms of three generators
$\mathfrak {J}$
[Reference Genest, Ismail, Vinet and Zhedanov9] defined in terms of three generators
![]() $K_1$
,
$K_1$
,
![]() $K_2$
and
$K_2$
and
![]() $K_3$
verifying the relations
$K_3$
verifying the relations
 $$ \begin{align} [K_2, K_3] &=aK_2^2 + bK_2, \end{align} $$
$$ \begin{align} [K_2, K_3] &=aK_2^2 + bK_2, \end{align} $$
where
![]() $[A, B]=AB-BA$
,
$[A, B]=AB-BA$
,
![]() $\{A,B\}=AB+BA$
and
$\{A,B\}=AB+BA$
and
![]() $a, b, c, d$
are structure constants. Indeed,
$a, b, c, d$
are structure constants. Indeed,
![]() $\mathfrak {J}$
is realised by taking
$\mathfrak {J}$
is realised by taking
In this model where the generators
![]() $K_1$
and
$K_1$
and
![]() $K_2$
are the bispectral operators, we have
$K_2$
are the bispectral operators, we have
 $$ \begin{align} K_3= 2x(x-1) \partial_x^2 + [ (\alpha+2)x + \beta-1 ] \partial_x, \end{align} $$
$$ \begin{align} K_3= 2x(x-1) \partial_x^2 + [ (\alpha+2)x + \beta-1 ] \partial_x, \end{align} $$
and the parameters
![]() $a, b, c, d$
are
$a, b, c, d$
are
Headway in the algebraic description of bispectral biorthogonal functions was achieved recently by studying polynomial and rational functions of Hahn type [Reference Tsujimoto, Vinet and Zhedanov27], [Reference Vinet and Zhedanov29]. (Related Hahn rational functions also appear in [Reference Koepf and Masjed-Jamei19], [Reference Masjed-Jamei and Koepf20].) In broad strokes, the general picture that emerges is as follows. Recall that generalised eigenvalue problems (GEVPs) of the form
![]() $Md_n=\lambda _n Ld_n$
, where M and L are two operators and
$Md_n=\lambda _n Ld_n$
, where M and L are two operators and
![]() $\lambda $
is the eigenvalue, naturally lead to biorthogonal functions which are rational (or polynomial) when M and L act tridiagonally in associated bases [Reference Zhedanov30]. Assume this to be the case. In the context mentioned before, it proved possible to adjoin a third operator X to M and L such that the biorthogonal special functions are the overlaps between the relevant GEVP basis
$\lambda $
is the eigenvalue, naturally lead to biorthogonal functions which are rational (or polynomial) when M and L act tridiagonally in associated bases [Reference Zhedanov30]. Assume this to be the case. In the context mentioned before, it proved possible to adjoin a third operator X to M and L such that the biorthogonal special functions are the overlaps between the relevant GEVP basis
![]() $\{d_n\}$
and the eigenbasis
$\{d_n\}$
and the eigenbasis
 $\left \{e^*_z\right \}$
of the adjoint
$\left \{e^*_z\right \}$
of the adjoint
![]() $X^T$
of X. As for the biorthogonal partners, they are given reciprocally in terms of the bases for the corresponding adjoint problems. This offers a picture which is parallel to the description of hypergeometric (finite) polynomials using Leonard pairs [Reference Terwilliger24]. The differential/difference equation of the biorthogonal functions follows readily from the fact that
$X^T$
of X. As for the biorthogonal partners, they are given reciprocally in terms of the bases for the corresponding adjoint problems. This offers a picture which is parallel to the description of hypergeometric (finite) polynomials using Leonard pairs [Reference Terwilliger24]. The differential/difference equation of the biorthogonal functions follows readily from the fact that
![]() $M-\lambda _n L$
, which annihilates
$M-\lambda _n L$
, which annihilates
![]() $d_n$
, acts tridiagonally in the basis
$d_n$
, acts tridiagonally in the basis
 $\left \{e^*_z\right \}$
. The second spectral equation stems from the observation that the operator
$\left \{e^*_z\right \}$
. The second spectral equation stems from the observation that the operator
![]() $R^T=L^T X^T$
is such that
$R^T=L^T X^T$
is such that
![]() $R^Te^*_{z} -z L^Te^*_{z} =0$
and that
$R^Te^*_{z} -z L^Te^*_{z} =0$
and that
![]() $R = XL$
acts tridiagonally on the basis
$R = XL$
acts tridiagonally on the basis
![]() $\{d_n\}$
. The algebra generated by the triplet of operators
$\{d_n\}$
. The algebra generated by the triplet of operators
![]() $(M, L, R)$
– which we have called the rational Hahn algebra (
$(M, L, R)$
– which we have called the rational Hahn algebra (
![]() $r\mathfrak {h}$
) in the particular case treated in [Reference Tsujimoto, Vinet and Zhedanov27], [Reference Vinet and Zhedanov29] – thus accounts for the two GEVPs that embody the bispectrality of the biorthogonal functions. Since R factorises as
$r\mathfrak {h}$
) in the particular case treated in [Reference Tsujimoto, Vinet and Zhedanov27], [Reference Vinet and Zhedanov29] – thus accounts for the two GEVPs that embody the bispectrality of the biorthogonal functions. Since R factorises as
![]() $XL$
, the algebra generated by
$XL$
, the algebra generated by
![]() $(M, L, R)$
can be embedded in the meta-algebra generated by
$(M, L, R)$
can be embedded in the meta-algebra generated by
![]() $(M, L, X)$
. The associated family of orthogonal polynomials also arises in this context as the overlaps between the eigenfunctions of the linear pencil
$(M, L, X)$
. The associated family of orthogonal polynomials also arises in this context as the overlaps between the eigenfunctions of the linear pencil
![]() $W=M + \mu L$
and the vectors
$W=M + \mu L$
and the vectors
 $\left \{e^*_z\right \}$
(or equivalently as the scalar product of the eigenbases of the adjoint problems). The bispectrality of these polynomial functions is accounted for by the algebra generated by
$\left \{e^*_z\right \}$
(or equivalently as the scalar product of the eigenbases of the adjoint problems). The bispectrality of these polynomial functions is accounted for by the algebra generated by
![]() $(X, W)$
. In our paradigm study, they are the Hahn polynomials, with W and X seen to generate the known Hahn algebra
$(X, W)$
. In our paradigm study, they are the Hahn polynomials, with W and X seen to generate the known Hahn algebra
![]() $\mathfrak {h}$
. In summary, for functions of the Hahn type, we have observed that the meta-algebra
$\mathfrak {h}$
. In summary, for functions of the Hahn type, we have observed that the meta-algebra
![]() $m\mathfrak {h}$
subsumes both
$m\mathfrak {h}$
subsumes both
![]() $r\mathfrak {h}$
and
$r\mathfrak {h}$
and
![]() $\mathfrak {h}$
and thus provides a unified description of both the biorthogonal and orthogonal families of functions. The two-dimensional subalgebra of
$\mathfrak {h}$
and thus provides a unified description of both the biorthogonal and orthogonal families of functions. The two-dimensional subalgebra of
![]() $m\mathfrak {h}$
generated by M and L is on its own remarkable, since its three-diagonal representations lead alone to the corresponding orthogonal polynomials, the Hahn ones in this instance. The adjunction of X to form the three-generated algebra has in fact the effect of constraining the representations of M and L to be three-diagonal in the eigenbasis of X.
$m\mathfrak {h}$
generated by M and L is on its own remarkable, since its three-diagonal representations lead alone to the corresponding orthogonal polynomials, the Hahn ones in this instance. The adjunction of X to form the three-generated algebra has in fact the effect of constraining the representations of M and L to be three-diagonal in the eigenbasis of X.
We contend that this approach, which allows the simultaneous description of hypergeometric orthogonal polynomials and associated families of biorthogonal functions, extends beyond the Hahn-functions case from which it is drawn. We shall add support to this suggestion by showing that the biorthogonal Askey polynomials on the unit circle together with the Jacobi polynomials are amenable to a unified treatment that follows the lines already sketched. In so doing we will provide an algebraic interpretation of the bispectral properties of the Askey polynomials which is of interest in its own right. We might point out that it has been shown in [Reference Grünbaum, Vinet and Zhedanov12] that the recurrence relation of these polynomials can be obtained from a linear pencil in
![]() $\mathfrak {su}(1,1)$
– but without providing a full account of the bispectrality.
$\mathfrak {su}(1,1)$
– but without providing a full account of the bispectrality.
The rest of the paper is organised as follows. The meta-Jacobi algebra
![]() $m\mathfrak {J}$
is introduced and discussed in the next section. It is shown to be isomorphic to the universal enveloping algebra of
$m\mathfrak {J}$
is introduced and discussed in the next section. It is shown to be isomorphic to the universal enveloping algebra of
![]() $\mathfrak {su}(1, 1)$
. The GEVPs and eigenvalue problems (EVPs) are solved on an
$\mathfrak {su}(1, 1)$
. The GEVPs and eigenvalue problems (EVPs) are solved on an
![]() $m\mathfrak {J}$
module, and the appropriate overlaps are shown to yield the special functions of interest. The orthogonality relations are seen to follow from the completeness and orthogonality of the GEVP and EVP bases. The algebraic setup is used in Section 4 to derive and interpret various properties of the Askey polynomials
$m\mathfrak {J}$
module, and the appropriate overlaps are shown to yield the special functions of interest. The orthogonality relations are seen to follow from the completeness and orthogonality of the GEVP and EVP bases. The algebraic setup is used in Section 4 to derive and interpret various properties of the Askey polynomials
![]() $ P_n(z; \alpha , \beta )$
, and in particular their bispectrality. A differential model of
$ P_n(z; \alpha , \beta )$
, and in particular their bispectrality. A differential model of
![]() $m\mathfrak {J}$
is obtained and used to obtain the differential equation and recurrence relation of the polynomials
$m\mathfrak {J}$
is obtained and used to obtain the differential equation and recurrence relation of the polynomials
![]() $ P_n(z; \alpha , \beta )$
, as well as some contiguity formulas. Perspectives are offered in the last section to conclude. Computational details are included in three appendices for completeness and for the convenience of the reader.
$ P_n(z; \alpha , \beta )$
, as well as some contiguity formulas. Perspectives are offered in the last section to conclude. Computational details are included in three appendices for completeness and for the convenience of the reader.
2 The meta-Jacobi algebra
 $m\mathfrak {J}$
$m\mathfrak {J}$
The fundamental algebraic structure upon which the subsequent analysis hinges is introduced next.
Definition 2.1. The meta-Jacobi algebra
![]() $m\mathfrak {J}$
has generators L, M and X (and the central
$m\mathfrak {J}$
has generators L, M and X (and the central
![]() $1$
) verifying the commutation relations
$1$
) verifying the commutation relations
It is taken to be defined over the real numbers, with the parameters
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
in
$\beta $
in
![]() $\mathbb {R}$
unless specified otherwise.
$\mathbb {R}$
unless specified otherwise.
The Casimir element is checked to be
 $$ \begin{align} Q= \left\{L^2,X\right\} -(\alpha + 1) \{L,X\} - \{M,X\} + 2 M + 2 \beta L. \end{align} $$
$$ \begin{align} Q= \left\{L^2,X\right\} -(\alpha + 1) \{L,X\} - \{M,X\} + 2 M + 2 \beta L. \end{align} $$
We shall now observe that
![]() $m\mathfrak {J}$
is isomorphic to the universal algebra of a Lie algebra. Recall that
$m\mathfrak {J}$
is isomorphic to the universal algebra of a Lie algebra. Recall that
![]() $\mathfrak {su}(1,1)$
viewed as a Lie algebra over
$\mathfrak {su}(1,1)$
viewed as a Lie algebra over
![]() $\mathbb {R}$
has the commutation relations
$\mathbb {R}$
has the commutation relations
and the standard Casimir operator
 $$ \begin{align} J^2 = J_0^2 - J_0 -J_+J_-. \end{align} $$
$$ \begin{align} J^2 = J_0^2 - J_0 -J_+J_-. \end{align} $$
Proposition 2.1. The meta-Jacobi algebra
![]() $m\mathfrak {J}$
is isomorphic to the universal enveloping algebra of
$m\mathfrak {J}$
is isomorphic to the universal enveloping algebra of
![]() $\mathfrak {su}(1,1)$
.
$\mathfrak {su}(1,1)$
.
This is confirmed by first observing that the commutation relations (2.5) of
![]() $\mathfrak {su}(1,1)$
are recovered by using the commutation relations (2.1), (2.2) and (2.3) of
$\mathfrak {su}(1,1)$
are recovered by using the commutation relations (2.1), (2.2) and (2.3) of
![]() $m\mathfrak {J}$
and setting
$m\mathfrak {J}$
and setting
 $$ \begin{align} J_0&=L - \frac{1}{2}(\alpha - \beta +1), \end{align} $$
$$ \begin{align} J_0&=L - \frac{1}{2}(\alpha - \beta +1), \end{align} $$
That we have an isomorphism is established by noting that this map is invertible and provides the following expressions of L, M and X in terms of the
![]() $\mathfrak {su}(1,1)$
generators:
$\mathfrak {su}(1,1)$
generators:
 $$ \begin{align} &L= J_0 +\frac{1}{2}(\alpha -\beta+1), \end{align} $$
$$ \begin{align} &L= J_0 +\frac{1}{2}(\alpha -\beta+1), \end{align} $$
 $$ \begin{align} &M= {J_0}^{2}+J_- - \beta \,J_0 -\frac{1}{4}(\alpha-\beta +1)(\alpha+\beta +1), \end{align} $$
$$ \begin{align} &M= {J_0}^{2}+J_- - \beta \,J_0 -\frac{1}{4}(\alpha-\beta +1)(\alpha+\beta +1), \end{align} $$
The isomorphism between the two-generated subalgebras spanned by
![]() $\{L, M\}$
and
$\{L, M\}$
and
![]() $\{J_0, J_-\}$
was observed in [Reference Gaddis7]. In light of the foregoing formulas, the Casimir operator (2.4) of the meta-Jacobi algebra can be expressed as
$\{J_0, J_-\}$
was observed in [Reference Gaddis7]. In light of the foregoing formulas, the Casimir operator (2.4) of the meta-Jacobi algebra can be expressed as
 $$ \begin{align} Q = 2 J^2 - \frac{1}{2} (\alpha - \beta +1)^2. \end{align} $$
$$ \begin{align} Q = 2 J^2 - \frac{1}{2} (\alpha - \beta +1)^2. \end{align} $$
Remark 2.1. It will be clear in the following that the
![]() $m\mathfrak {J}$
presentation is best suited for the algebraic interpretation of the Askey polynomials. The terminology recalls the parallel with the treatment of the biorthogonal rational functions of Hahn type [Reference Tsujimoto, Vinet and Zhedanov27] that uses the meta-Hahn algebra.
$m\mathfrak {J}$
presentation is best suited for the algebraic interpretation of the Askey polynomials. The terminology recalls the parallel with the treatment of the biorthogonal rational functions of Hahn type [Reference Tsujimoto, Vinet and Zhedanov27] that uses the meta-Hahn algebra.
Proposition 2.2. The Jacobi algebra
![]() $\mathfrak {J}$
defined in equations (1.8), (1.9) and (1.10) admits a simple embedding in the meta-Jacobi algebra
$\mathfrak {J}$
defined in equations (1.8), (1.9) and (1.10) admits a simple embedding in the meta-Jacobi algebra
![]() $m\mathfrak {J}$
.
$m\mathfrak {J}$
.
This is seen by setting
and consequently
Using the commutation relations (2.1), (2.2) and (2.3) of
![]() $m\mathfrak {J}$
, it is straightforwardly verified that
$m\mathfrak {J}$
, it is straightforwardly verified that
![]() $K_1, K_2, K_3$
thus defined obey those of
$K_1, K_2, K_3$
thus defined obey those of
![]() $\mathfrak {J}$
with the parameters given by
$\mathfrak {J}$
with the parameters given by
Note the dependence of the parameter d on the Casimir element Q. The distinctive feature of the meta-Jacobi algebra lies, as we see, in the fact that
![]() $K_3$
is resolved as a quadratic expression in terms of the fundamental generators X and L.
$K_3$
is resolved as a quadratic expression in terms of the fundamental generators X and L.
Remark 2.2. In the following section we shall call upon representations of
![]() $\mathfrak {su}(1,1)$
and hence of
$\mathfrak {su}(1,1)$
and hence of
![]() $m\mathfrak {J}$
to interpret the Askey and Jacobi polynomials. In an irreducible representation, the Casimir element
$m\mathfrak {J}$
to interpret the Askey and Jacobi polynomials. In an irreducible representation, the Casimir element
![]() $J^2$
of
$J^2$
of
![]() $\mathfrak {su}(1,1)$
takes the form
$\mathfrak {su}(1,1)$
takes the form
![]() $\tau (\tau -1)$
. Hereafter, we shall consider representations with
$\tau (\tau -1)$
. Hereafter, we shall consider representations with
 $$ \begin{align} \tau=\frac{1}{2}(\alpha + \beta +1). \end{align} $$
$$ \begin{align} \tau=\frac{1}{2}(\alpha + \beta +1). \end{align} $$
Equation (2.13), which establishes the relation between the Casimir operator Q of
![]() $m\mathfrak {J}$
and the one of
$m\mathfrak {J}$
and the one of
![]() $\mathfrak {su}(1,1)$
, then yields for the value of Q:
$\mathfrak {su}(1,1)$
, then yields for the value of Q:
Let us stress the coherence of the particular realisation of the Jacobi algebra
![]() $\mathfrak {J}$
in terms of the bispectral operators of the Jacobi polynomials given in the introduction with the embedding of
$\mathfrak {J}$
in terms of the bispectral operators of the Jacobi polynomials given in the introduction with the embedding of
![]() $\mathfrak {J}$
in
$\mathfrak {J}$
in
![]() $m\mathfrak {J}$
given in Proposition 2.2. Indeed, we see that with these choices for the Casimir elements, the parameter d of the Jacobi algebra as given in equation (2.16) takes the proper value:
$m\mathfrak {J}$
given in Proposition 2.2. Indeed, we see that with these choices for the Casimir elements, the parameter d of the Jacobi algebra as given in equation (2.16) takes the proper value:
![]() $d=(\alpha +1)\beta -Q-1=\alpha (1-\beta )$
.
$d=(\alpha +1)\beta -Q-1=\alpha (1-\beta )$
.
3 Representations of the meta-Jacobi algebra and special functions
In this section we shall establish the connection between the meta-Jacobi algebra
![]() $m\mathfrak {J}$
, the Askey polynomials
$m\mathfrak {J}$
, the Askey polynomials
![]() $P_n(z; \alpha , \beta )$
, their biorthogonal partners
$P_n(z; \alpha , \beta )$
, their biorthogonal partners
![]() $Q_n(z; \alpha , \beta )$
and the Jacobi polynomials
$Q_n(z; \alpha , \beta )$
and the Jacobi polynomials
 $\hat {P}_n^{\left (\alpha , \beta \right )}(x)$
. To that end, we shall consider an
$\hat {P}_n^{\left (\alpha , \beta \right )}(x)$
. To that end, we shall consider an
![]() $m\mathfrak {J}$
representation space inferred from the isomorphism of this algebra with
$m\mathfrak {J}$
representation space inferred from the isomorphism of this algebra with
![]() $\mathfrak {su}(1,1)$
. We shall obtain the bases associated to the various EVPs and GEVPs defined on the chosen module to show that their overlaps are essentially the special functions already mentioned. This will cast these functions in their proper algebraic framework and readily lead to their (bi)orthogonality relations. We shall be working on a real infinite-dimensional space equipped with a scalar product denoted by
$\mathfrak {su}(1,1)$
. We shall obtain the bases associated to the various EVPs and GEVPs defined on the chosen module to show that their overlaps are essentially the special functions already mentioned. This will cast these functions in their proper algebraic framework and readily lead to their (bi)orthogonality relations. We shall be working on a real infinite-dimensional space equipped with a scalar product denoted by
![]() $\langle | \rangle $
.
$\langle | \rangle $
.
![]() $A^T$
will stand for the transpose of A:
$A^T$
will stand for the transpose of A:
 $\left (\left \langle u | A^T\right ) | v\right \rangle = \langle u| ( A | v\rangle )$
.
$\left (\left \langle u | A^T\right ) | v\right \rangle = \langle u| ( A | v\rangle )$
.
Consider the infinite-dimensional module
![]() $\mathfrak {V}(\tau )$
, with
$\mathfrak {V}(\tau )$
, with
![]() $\tau \in \mathbb {R}$
defined as follows by the action of the generators on the basis vectors
$\tau \in \mathbb {R}$
defined as follows by the action of the generators on the basis vectors
![]() $| \tau , k \rangle , k \in \mathbb {Z}$
:
$| \tau , k \rangle , k \in \mathbb {Z}$
:
(See in this connection [Reference Howe and Tan15].) It is readily checked that the Casimir element
 $J^2=J_0^2 - J_0 - J_+J_- = \tau (\tau - 1)$
on this representation space. The basis vectors are taken to be orthonormalised:
$J^2=J_0^2 - J_0 - J_+J_- = \tau (\tau - 1)$
on this representation space. The basis vectors are taken to be orthonormalised:
Remark 3.1. Let us note the following:
-
1. The representation defined in the foregoing is not unitarisable [Reference Tomasini and Ørsted25].
-
2. It is reducible with the action of the Casimir element given overall by the same constant, meaning that the representations involved are all of the same kind. It contains the unitary positive discrete series [Reference Groenevelt and Koelink11], [Reference Howe and Tan15], [Reference Masson and Repka21], [Reference Vilenkin and Klimyk28] as an irreducible component. This submodule is spanned by the basis vectors with
 $k \in \mathbb {Z}_+$
.
$k \in \mathbb {Z}_+$
.
Use now formulas (2.10), (2.11) and (2.12) of Proposition 2.2, that define the isomorphism between
![]() $m\mathfrak {J}$
and
$m\mathfrak {J}$
and
![]() $\mathfrak {su}(1,1)$
, and take as already indicated
$\mathfrak {su}(1,1)$
, and take as already indicated
 $\tau =\frac {1}{2}(\alpha + \beta +1)$
; the following actions of
$\tau =\frac {1}{2}(\alpha + \beta +1)$
; the following actions of
![]() $L, M, X$
on the basis states
$L, M, X$
on the basis states
![]() $|\tau , k \rangle $
are readily found:
$|\tau , k \rangle $
are readily found:
 $$ \begin{align} M |\tau, k \rangle&= k \big[(k + \alpha + 1) |\tau, k \rangle + ( k + \alpha + \beta) |\tau, k - 1\rangle \big], \end{align} $$
$$ \begin{align} M |\tau, k \rangle&= k \big[(k + \alpha + 1) |\tau, k \rangle + ( k + \alpha + \beta) |\tau, k - 1\rangle \big], \end{align} $$
The adjoint actions can be read off directly:
Let us introduce the operator
![]() $\mathcal {T}_{\pm }$
on
$\mathcal {T}_{\pm }$
on
![]() $\mathfrak {V}(\tau )$
such that
$\mathfrak {V}(\tau )$
such that
Consider a vector
![]() $| f\rangle = \sum _{k=-\infty }^{\infty } f(k) |\tau , k \rangle $
in
$| f\rangle = \sum _{k=-\infty }^{\infty } f(k) |\tau , k \rangle $
in
![]() $\mathfrak {V}(\tau )$
. We have
$\mathfrak {V}(\tau )$
. We have
 $$ \begin{align} \mathcal{T}_{\pm}| f\rangle = \sum _{k=-\infty}^{\infty} f(k) \mathcal{T}_{\pm}|\tau, k \rangle = \sum _{k=-\infty}^{\infty} \left(T_{\mp}f(k)\right)|\tau, k \rangle, \end{align} $$
$$ \begin{align} \mathcal{T}_{\pm}| f\rangle = \sum _{k=-\infty}^{\infty} f(k) \mathcal{T}_{\pm}|\tau, k \rangle = \sum _{k=-\infty}^{\infty} \left(T_{\mp}f(k)\right)|\tau, k \rangle, \end{align} $$
where
![]() $T_{\pm }$
stands for the shift operators acting on functions of k:
$T_{\pm }$
stands for the shift operators acting on functions of k:
![]() $T_{\pm }f(k)=f(k\pm 1)$
.
$T_{\pm }f(k)=f(k\pm 1)$
.
Remark 3.2. A realisation of
![]() $m\mathfrak {J}$
in terms of shift operators can hence be inferred from the (dual) transformations of the components of a vector
$m\mathfrak {J}$
in terms of shift operators can hence be inferred from the (dual) transformations of the components of a vector
![]() $| f\rangle $
in the basis
$| f\rangle $
in the basis
![]() $\{|\tau , k \rangle \}$
defined through
$\{|\tau , k \rangle \}$
defined through
![]() $V| f\rangle = \sum _{k=-\infty }^{\infty } f(k) V|\tau , k \rangle = \sum _{k=-\infty }^{\infty } \left (\mathrm {V}^Tf(k)\right ) |\tau , k \rangle $
. Equations (3.8), (3.9) and (3.10) thus yield the following representation in terms of unbounded operators on
$V| f\rangle = \sum _{k=-\infty }^{\infty } f(k) V|\tau , k \rangle = \sum _{k=-\infty }^{\infty } \left (\mathrm {V}^Tf(k)\right ) |\tau , k \rangle $
. Equations (3.8), (3.9) and (3.10) thus yield the following representation in terms of unbounded operators on
![]() $\ell ^2 (\mathbb {Z)}$
:
$\ell ^2 (\mathbb {Z)}$
:
The adjoints in this model are readily computed using
![]() $T_{\pm }^T=T_{\mp }$
.
$T_{\pm }^T=T_{\mp }$
.
We are now ready to construct the bases of
![]() $\mathfrak {V}(\tau )$
coming in adjoint pairs, whose overlaps will provide the algebraic interpretation we are looking for. (They will be in part the
$\mathfrak {V}(\tau )$
coming in adjoint pairs, whose overlaps will provide the algebraic interpretation we are looking for. (They will be in part the
![]() $d_n, d^*_n, e_z, e^*_z $
of the introduction.) The bases that will intervene are the following:
$d_n, d^*_n, e_z, e^*_z $
of the introduction.) The bases that will intervene are the following:
-
1. The GEVP bases
 $\{| P_n\rangle \}$
and
$\{| P_n\rangle \}$
and
 $\{| Q_n\rangle \}$
: (3.16)It will be recalled [Reference Vinet and Zhedanov29], [Reference Zhedanov30] that the sets
$\{| Q_n\rangle \}$
: (3.16)It will be recalled [Reference Vinet and Zhedanov29], [Reference Zhedanov30] that the sets $$ \begin{align} M| P_n\rangle = \nu _n L| P_n\rangle, \qquad M^T | Q_n\rangle = \nu _n L^T | Q_n\rangle. \end{align} $$
$$ \begin{align} M| P_n\rangle = \nu _n L| P_n\rangle, \qquad M^T | Q_n\rangle = \nu _n L^T | Q_n\rangle. \end{align} $$
 $\{| P_n\rangle \}$
and
$\{| P_n\rangle \}$
and
 $\left \{L^T | Q_n\rangle \right \}$
form by construction two biorthogonal ensembles of vectors: (3.17)
$\left \{L^T | Q_n\rangle \right \}$
form by construction two biorthogonal ensembles of vectors: (3.17) $$ \begin{align} \left\langle P_m | L^T | Q_n\right\rangle = 0,\qquad m\neq n. \end{align} $$
$$ \begin{align} \left\langle P_m | L^T | Q_n\right\rangle = 0,\qquad m\neq n. \end{align} $$
-
2. The EVP bases
 $\{| z\rangle \}$
and
$\{| z\rangle \}$
and
 $\left \{\widetilde {| z\rangle }\right \}$
: (3.18)
$\left \{\widetilde {| z\rangle }\right \}$
: (3.18) $$ \begin{align} X| z\rangle=z| z\rangle, \qquad X^T\widetilde{| z\rangle} =z\widetilde{| z\rangle}. \end{align} $$
$$ \begin{align} X| z\rangle=z| z\rangle, \qquad X^T\widetilde{| z\rangle} =z\widetilde{| z\rangle}. \end{align} $$
-
3. The EVP bases
 $\{| J_n\rangle \}$
and
$\{| J_n\rangle \}$
and
 $\left \{\widetilde {| J_n\rangle }\right \}$
: (3.19)
$\left \{\widetilde {| J_n\rangle }\right \}$
: (3.19) $$ \begin{align} M | J_n\rangle=\mu_n | J_n\rangle, \qquad M^T\widetilde{| J_n\rangle}=\mu_n \widetilde{| J_n\rangle}. \end{align} $$
$$ \begin{align} M | J_n\rangle=\mu_n | J_n\rangle, \qquad M^T\widetilde{| J_n\rangle}=\mu_n \widetilde{| J_n\rangle}. \end{align} $$
3.1 Eigenvectors of X and
 $X^T$
$X^T$
It is directly checked that the EVP (3.18) is satisfied by
 $$ \begin{align} | z\rangle &= \gamma \sum_{k=-\infty}^{\infty} (z-1)^{-k-a}|\tau, k\rangle, \end{align} $$
$$ \begin{align} | z\rangle &= \gamma \sum_{k=-\infty}^{\infty} (z-1)^{-k-a}|\tau, k\rangle, \end{align} $$
 $$ \begin{align} \widetilde{| z\rangle} &= \tilde{\gamma} \sum_{k=-\infty}^{\infty} (z-1)^{k+\tilde{a}}|\tau, k\rangle, \end{align} $$
$$ \begin{align} \widetilde{| z\rangle} &= \tilde{\gamma} \sum_{k=-\infty}^{\infty} (z-1)^{k+\tilde{a}}|\tau, k\rangle, \end{align} $$
with
![]() $a, \tilde {a} \in \mathbb {R}$
and where
$a, \tilde {a} \in \mathbb {R}$
and where
![]() $\gamma , \tilde {\gamma } \in \mathbb {C}$
are normalisation constants. That
$\gamma , \tilde {\gamma } \in \mathbb {C}$
are normalisation constants. That
![]() $| z\rangle $
and
$| z\rangle $
and
 $\widetilde {| z'\rangle }$
are orthogonal can be seen as follows. We have
$\widetilde {| z'\rangle }$
are orthogonal can be seen as follows. We have
 $$ \begin{align} \widetilde{\langle z' |}z\rangle= \gamma \tilde{\gamma}\sum_{k, l=-\infty}^{\infty} (z'-1)^{-k-a}(z-1)^{l+\tilde{a}}\langle \tau, k | \tau, l\rangle. \end{align} $$
$$ \begin{align} \widetilde{\langle z' |}z\rangle= \gamma \tilde{\gamma}\sum_{k, l=-\infty}^{\infty} (z'-1)^{-k-a}(z-1)^{l+\tilde{a}}\langle \tau, k | \tau, l\rangle. \end{align} $$
Now let
![]() $z=1+e^{i\phi }$
,
$z=1+e^{i\phi }$
,
![]() $z'=1+e^{i\phi '}$
, so that equation (3.22) becomes
$z'=1+e^{i\phi '}$
, so that equation (3.22) becomes
 $$ \begin{align} \widetilde{\langle z' |}z\rangle=\gamma \tilde{\gamma}e^{i\left(\tilde{a}\phi - a \phi '\right)}\sum_{k=-\infty} ^{\infty} e^{i\left(\phi - \phi '\right)k}. \end{align} $$
$$ \begin{align} \widetilde{\langle z' |}z\rangle=\gamma \tilde{\gamma}e^{i\left(\tilde{a}\phi - a \phi '\right)}\sum_{k=-\infty} ^{\infty} e^{i\left(\phi - \phi '\right)k}. \end{align} $$
We then see that upon imposing
we find
 $$ \begin{align} \widetilde{\langle z' |}z\rangle=-2\pi i \gamma \tilde{\gamma} \delta(z-z') \end{align} $$
$$ \begin{align} \widetilde{\langle z' |}z\rangle=-2\pi i \gamma \tilde{\gamma} \delta(z-z') \end{align} $$
with the help of the Fourier series of Dirac’s delta function and of a standard property of this distribution. Since
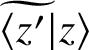 $ \widetilde {\langle z' |}z\rangle $
is manifestly translation-invariant, equation (3.25) is preserved when the variable z lies on the unit circle centred at
$ \widetilde {\langle z' |}z\rangle $
is manifestly translation-invariant, equation (3.25) is preserved when the variable z lies on the unit circle centred at
![]() $z=0$
.
$z=0$
.
We also have the completeness relation
 $$ \begin{align} \frac{1}{2\pi i \gamma \tilde{\gamma}} \oint _C dz \widetilde{| z \rangle} \langle z | = 1, \end{align} $$
$$ \begin{align} \frac{1}{2\pi i \gamma \tilde{\gamma}} \oint _C dz \widetilde{| z \rangle} \langle z | = 1, \end{align} $$
where the contour C consists in the unit circle infinitesimally deformed so that the singularity at
![]() $z=1$
lies inside C. Indeed,
$z=1$
lies inside C. Indeed,
 $$ \begin{align} \frac{1}{2\pi i \gamma \tilde{\gamma}} \oint _C dz \widetilde{| z \rangle} \langle z | = \frac{1}{2\pi i} \oint _C dz (z-1)^{k-l-a +\tilde{a}} \sum_{k, l = -\infty} ^{\infty}|\tau, k \rangle \langle \tau, l|. \end{align} $$
$$ \begin{align} \frac{1}{2\pi i \gamma \tilde{\gamma}} \oint _C dz \widetilde{| z \rangle} \langle z | = \frac{1}{2\pi i} \oint _C dz (z-1)^{k-l-a +\tilde{a}} \sum_{k, l = -\infty} ^{\infty}|\tau, k \rangle \langle \tau, l|. \end{align} $$
Again the choice (3.24) for the integration constants a and
![]() $\tilde {a}$
consistently ensures that the integral over z becomes
$\tilde {a}$
consistently ensures that the integral over z becomes
 $\frac {1}{2\pi i} \oint _C dz (z-1)^{k-l-1} = \delta _{kl}$
and hence
$\frac {1}{2\pi i} \oint _C dz (z-1)^{k-l-1} = \delta _{kl}$
and hence
 $$ \begin{align} \frac{1}{2\pi i \gamma \tilde{\gamma}} \oint _C dz \widetilde{| z \rangle}\langle z |= \sum _{k=-\infty}^{\infty} |\tau, k \rangle \langle \tau, k| =1. \end{align} $$
$$ \begin{align} \frac{1}{2\pi i \gamma \tilde{\gamma}} \oint _C dz \widetilde{| z \rangle}\langle z |= \sum _{k=-\infty}^{\infty} |\tau, k \rangle \langle \tau, k| =1. \end{align} $$
This will play a key role in the derivation of the orthogonality relations.
3.2 GEVP bases
We shall now obtain the bases
![]() $\{| P_n\rangle \}$
and
$\{| P_n\rangle \}$
and
![]() $\{| Q_n\rangle \}$
of
$\{| Q_n\rangle \}$
of
![]() $\mathfrak {V}(\tau )$
that satisfy the GEVP (3.16). First we need to determine the set of eigenvalues
$\mathfrak {V}(\tau )$
that satisfy the GEVP (3.16). First we need to determine the set of eigenvalues
![]() $\nu $
. From the explicit two-diagonal actions (3.5) and (3.6) of L and M on the basis vectors
$\nu $
. From the explicit two-diagonal actions (3.5) and (3.6) of L and M on the basis vectors
![]() $\{|\tau , k\rangle \}$
, it is readily seen that the (formal) determinantal condition is
$\{|\tau , k\rangle \}$
, it is readily seen that the (formal) determinantal condition is
 $$ \begin{align} \det(M-\nu L) =\prod_{k=-\infty} ^{\infty} \left[ k(k + \alpha +1) - \nu ( k + \alpha + 1)\right] = 0, \end{align} $$
$$ \begin{align} \det(M-\nu L) =\prod_{k=-\infty} ^{\infty} \left[ k(k + \alpha +1) - \nu ( k + \alpha + 1)\right] = 0, \end{align} $$
and hence (disregarding the degenerate case where
![]() $\alpha \in \mathbb {Z}$
) that the spectrum consists in the following values:
$\alpha \in \mathbb {Z}$
) that the spectrum consists in the following values:
Remark 3.3. In the following, as we consider GEVPs and EVPs, we shall limit ourselves to eigenvalues corresponding to nonnegative n – that is,
![]() $n \in \mathbb {Z}^\geq $
. This will not restrain the breadth of the algebraic description, since the same results would be obtained with other choices. For completeness, indications of how the equations are handled for negative values of n are given in Appendix C.
$n \in \mathbb {Z}^\geq $
. This will not restrain the breadth of the algebraic description, since the same results would be obtained with other choices. For completeness, indications of how the equations are handled for negative values of n are given in Appendix C.
Let
 $$ \begin{align} | P_n\rangle = \sum_{k=-\infty} ^{\infty} d_n(k) |\tau, k\rangle. \end{align} $$
$$ \begin{align} | P_n\rangle = \sum_{k=-\infty} ^{\infty} d_n(k) |\tau, k\rangle. \end{align} $$
The generalised eigenvalue equation
![]() $M| P_n\rangle = n L | P_n\rangle $
implies the following recurrence relation for the expansion coefficients
$M| P_n\rangle = n L | P_n\rangle $
implies the following recurrence relation for the expansion coefficients
![]() $d_n(k)$
:
$d_n(k)$
:
From equation (3.32), it is immediately seen that for
![]() $n\geq 0$
,
$n\geq 0$
,
The explicit expression of the nonzero coefficients
![]() $d_n(k)$
reads
$d_n(k)$
reads
 $$ \begin{align} d_n(k)= d_n(0) \frac{(-1)^k(-n)_k(\alpha +1)_k}{k!(\alpha + \beta +1)_k}, \qquad k=0, 1, 2, \dotsc, n. \end{align} $$
$$ \begin{align} d_n(k)= d_n(0) \frac{(-1)^k(-n)_k(\alpha +1)_k}{k!(\alpha + \beta +1)_k}, \qquad k=0, 1, 2, \dotsc, n. \end{align} $$
Turn now to the adjoint GEVP
![]() $M^T | Q_m\rangle = m L^T | Q_m\rangle $
, which imposes on the coefficients
$M^T | Q_m\rangle = m L^T | Q_m\rangle $
, which imposes on the coefficients
![]() $d_m^*(k)$
in
$d_m^*(k)$
in
 $$ \begin{align} | Q_m\rangle = \sum_{k=-\infty} ^{\infty} d_m^*(k) |\tau, k\rangle \end{align} $$
$$ \begin{align} | Q_m\rangle = \sum_{k=-\infty} ^{\infty} d_m^*(k) |\tau, k\rangle \end{align} $$
the recurrence relation
Assuming
![]() $m\geq 0$
as previously indicated, one immediately notices that equation (3.36) implies
$m\geq 0$
as previously indicated, one immediately notices that equation (3.36) implies
In view of this fact, let
the relation (3.36) then becomes
It is found to have for its solution
 $$ \begin{align} d_m^*(m+l)= \frac{(-1)^l (m + 1)_l (m + \alpha + \beta + 1)_l}{l! (m + \alpha + 2)_l} d_m^*(m), \qquad l=0, 1, \dotsc. \end{align} $$
$$ \begin{align} d_m^*(m+l)= \frac{(-1)^l (m + 1)_l (m + \alpha + \beta + 1)_l}{l! (m + \alpha + 2)_l} d_m^*(m), \qquad l=0, 1, \dotsc. \end{align} $$
Apart from the initial condition
![]() $d_m^*(m)$
, equation (3.40) fully determines
$d_m^*(m)$
, equation (3.40) fully determines
 $$ \begin{align} | Q_m\rangle = \sum_{l=0} ^{\infty} d_m^*(m+l) |\tau, m + l\rangle. \end{align} $$
$$ \begin{align} | Q_m\rangle = \sum_{l=0} ^{\infty} d_m^*(m+l) |\tau, m + l\rangle. \end{align} $$
From general linear algebra considerations [Reference Tsujimoto, Vinet and Zhedanov27], [Reference Vinet and Zhedanov29], [Reference Zhedanov30], we know that the vectors
![]() $| P_n\rangle $
and
$| P_n\rangle $
and
![]() $L^T | Q_m \rangle $
are biorthogonal for
$L^T | Q_m \rangle $
are biorthogonal for
![]() $n\neq m$
. We have
$n\neq m$
. We have
 $$ \begin{align} &(\langle P_n | M) | Q_m\rangle =n (\langle P_n | L) | Q_m\rangle \nonumber \\ &=\left\langle P_n | \left(M^T | Q_m\right\rangle\right)= m\left\langle P_m | \left(L^T | Q_m\right\rangle\right)= m (\langle P_n | L) | Q_m\rangle. \end{align} $$
$$ \begin{align} &(\langle P_n | M) | Q_m\rangle =n (\langle P_n | L) | Q_m\rangle \nonumber \\ &=\left\langle P_n | \left(M^T | Q_m\right\rangle\right)= m\left\langle P_m | \left(L^T | Q_m\right\rangle\right)= m (\langle P_n | L) | Q_m\rangle. \end{align} $$
It follows that
 $$ \begin{align} (n-m)(\langle P_n | L) | Q_m\rangle = (n-m)\left\langle P_n | \left(L^T | Q_m\right\rangle\right) = 0, \end{align} $$
$$ \begin{align} (n-m)(\langle P_n | L) | Q_m\rangle = (n-m)\left\langle P_n | \left(L^T | Q_m\right\rangle\right) = 0, \end{align} $$
which implies the asserted biorthogonality if
![]() $m \neq n$
. Since the derivation we shall provide of the biorthogonality of the Askey polynomials will rest on this property obtained formally, we shall next directly verify that it holds in the case at hand and determine the norm.
$m \neq n$
. Since the derivation we shall provide of the biorthogonality of the Askey polynomials will rest on this property obtained formally, we shall next directly verify that it holds in the case at hand and determine the norm.
From the observations already made, we see that
 $$ \begin{align} \left\langle P_n | L^T | Q_m \right\rangle &= \sum_{k=-\infty}^n \sum_{l=0}^{\infty} d_n(k) d_m^*(l+m) \left\langle \tau, k | L^T | \tau, l+m\right\rangle \nonumber \\ &=\sum_{k=-\infty}^n \sum_{l=0}^{\infty} d_n(k) d_m^*(l+m)(m + l + \alpha + 1) \delta _{k, l+m}. \end{align} $$
$$ \begin{align} \left\langle P_n | L^T | Q_m \right\rangle &= \sum_{k=-\infty}^n \sum_{l=0}^{\infty} d_n(k) d_m^*(l+m) \left\langle \tau, k | L^T | \tau, l+m\right\rangle \nonumber \\ &=\sum_{k=-\infty}^n \sum_{l=0}^{\infty} d_n(k) d_m^*(l+m)(m + l + \alpha + 1) \delta _{k, l+m}. \end{align} $$
We readily find that
 $$ \begin{align} \left\langle P_n | L^T | Q_m \right\rangle = 0 \qquad \text{if}\ m>n. \end{align} $$
$$ \begin{align} \left\langle P_n | L^T | Q_m \right\rangle = 0 \qquad \text{if}\ m>n. \end{align} $$
It remains to consider the situation when
![]() $m \leq n$
. Substituting into equation (3.44) expressions (3.34) and (3.40) for
$m \leq n$
. Substituting into equation (3.44) expressions (3.34) and (3.40) for
![]() $d_n(k)$
and
$d_n(k)$
and
![]() $d_m^*(m+l)$
, using a few properties of the Pochhammer symbols such as
$d_m^*(m+l)$
, using a few properties of the Pochhammer symbols such as
![]() $x(x+1)_{l-1}=(x)_l$
and
$x(x+1)_{l-1}=(x)_l$
and
![]() $(x)_{m+l}=(x)_m(x+m)_l$
, and performing one of the sums, we arrive at
$(x)_{m+l}=(x)_m(x+m)_l$
, and performing one of the sums, we arrive at
 $$ \begin{align} \left\langle P_n | L^T | Q_m \right\rangle = d_n(0) d_m^*(m) (-1)^m \frac{(-n)_m (\alpha + 1)_{m+1} }{m!(\alpha + \beta + 1)_m } \sum_{l=0} ^{n-m} \frac{(-n+m)_l}{l!}. \end{align} $$
$$ \begin{align} \left\langle P_n | L^T | Q_m \right\rangle = d_n(0) d_m^*(m) (-1)^m \frac{(-n)_m (\alpha + 1)_{m+1} }{m!(\alpha + \beta + 1)_m } \sum_{l=0} ^{n-m} \frac{(-n+m)_l}{l!}. \end{align} $$
We then recall the binomial formula
 $$ \begin{align} (1-x)^{\xi} = \sum _{k=0} ^{\infty} \frac{(-\xi)_k}{k!} x^k \end{align} $$
$$ \begin{align} (1-x)^{\xi} = \sum _{k=0} ^{\infty} \frac{(-\xi)_k}{k!} x^k \end{align} $$
to conclude that
 $$ \begin{align} \left\langle P_n | L^T | Q_m \right\rangle = N_n \delta _{m,n}, \end{align} $$
$$ \begin{align} \left\langle P_n | L^T | Q_m \right\rangle = N_n \delta _{m,n}, \end{align} $$
with
 $$ \begin{align} N_n = d_n(0) d_n^*(n) \frac{( \alpha + 1)_{n+1}}{(\alpha + \beta + 1)_n}. \end{align} $$
$$ \begin{align} N_n = d_n(0) d_n^*(n) \frac{( \alpha + 1)_{n+1}}{(\alpha + \beta + 1)_n}. \end{align} $$
3.3 Askey polynomials and their biorthogonal partners
Let us now identify some of the special functions that arise from this representation theoretic setting. In light of the completeness relation (3.26) and the orthogonality relation (3.48), we see that
 $\widetilde {\langle z |} P_n \rangle $
and
$\widetilde {\langle z |} P_n \rangle $
and
 $\left \langle z | L^T | Q_n \right \rangle $
provide two families of biorthogonal functions on the unit circle, since
$\left \langle z | L^T | Q_n \right \rangle $
provide two families of biorthogonal functions on the unit circle, since
 $$ \begin{align} \frac{1}{2\pi i \gamma \tilde{\gamma}} \oint _{\lvert z\rvert=1} dz \langle P_n \widetilde{| z\rangle}\left\langle z | L^T | Q_m \right\rangle = \left\langle P_n | L^T | Q_m\right\rangle = N_n \delta_{m,n}. \end{align} $$
$$ \begin{align} \frac{1}{2\pi i \gamma \tilde{\gamma}} \oint _{\lvert z\rvert=1} dz \langle P_n \widetilde{| z\rangle}\left\langle z | L^T | Q_m \right\rangle = \left\langle P_n | L^T | Q_m\right\rangle = N_n \delta_{m,n}. \end{align} $$
These are explicitly obtained in the following.
3.3.1 The overlaps
 $\widetilde {\langle z |} P_n \rangle $
$\widetilde {\langle z |} P_n \rangle $
From the expansions (3.21) and (3.31) of
![]() $ \widetilde {| z\rangle }$
and
$ \widetilde {| z\rangle }$
and
![]() $| P_n \rangle $
over the orthonormal basis vectors
$| P_n \rangle $
over the orthonormal basis vectors
![]() $|\tau , k \rangle $
, we have
$|\tau , k \rangle $
, we have
 $$ \begin{align} \widetilde{\langle z |}P_n \rangle = \tilde{\gamma} \sum_{l=-\infty} ^n (z-1)^{l+\tilde{a}} d_n(l). \end{align} $$
$$ \begin{align} \widetilde{\langle z |}P_n \rangle = \tilde{\gamma} \sum_{l=-\infty} ^n (z-1)^{l+\tilde{a}} d_n(l). \end{align} $$
Upon inserting equation (3.34) for
![]() $d_n(l)$
, we observe that
$d_n(l)$
, we observe that
 $\widetilde {\langle z |}P_n \rangle $
is the
$\widetilde {\langle z |}P_n \rangle $
is the
![]() ${_2}F_1$
polynomial
${_2}F_1$
polynomial
 $$ \begin{align} \widetilde{\langle z |}P_n \rangle = \tilde{\gamma}d_n(0) (z - 1)^{\tilde{a}} {}_{2}F_{1}\left({-n, \alpha + 1 \atop \alpha + \beta + 1}; 1 - z \right ). \end{align} $$
$$ \begin{align} \widetilde{\langle z |}P_n \rangle = \tilde{\gamma}d_n(0) (z - 1)^{\tilde{a}} {}_{2}F_{1}\left({-n, \alpha + 1 \atop \alpha + \beta + 1}; 1 - z \right ). \end{align} $$
The Askey polynomials are then recognised with the help of the Pfaff formula [Reference Andrews, Askey and Roy1]:
 $$ \begin{align} {_2}F_1\left({-n, b \atop c}; z \right ) = \frac{(c-b)_n}{(c)_n}{_2}F_1\left({-n, b \atop -n + b + 1 - c}; 1 - z \right ). \end{align} $$
$$ \begin{align} {_2}F_1\left({-n, b \atop c}; z \right ) = \frac{(c-b)_n}{(c)_n}{_2}F_1\left({-n, b \atop -n + b + 1 - c}; 1 - z \right ). \end{align} $$
We find
 $$ \begin{align} \widetilde{\langle z |}P_n \rangle = \tilde{\gamma} d_n(0) \frac{(\alpha +1)_n}{(\alpha + \beta +1)_n}(z - 1)^{\tilde{a}} P_n(z; \alpha, \beta), \end{align} $$
$$ \begin{align} \widetilde{\langle z |}P_n \rangle = \tilde{\gamma} d_n(0) \frac{(\alpha +1)_n}{(\alpha + \beta +1)_n}(z - 1)^{\tilde{a}} P_n(z; \alpha, \beta), \end{align} $$
where the polynomials
![]() $P_n(z; \alpha , \beta )$
are as defined in equation (1.1).
$P_n(z; \alpha , \beta )$
are as defined in equation (1.1).
Proposition 3.1. The Askey polynomials
![]() $P_n(z; \alpha , \beta )$
have a natural interpretation in the representation theory of the meta-Jacobi algebra. They occur according to equation (3.54) as the overlaps between two bases of the module
$P_n(z; \alpha , \beta )$
have a natural interpretation in the representation theory of the meta-Jacobi algebra. They occur according to equation (3.54) as the overlaps between two bases of the module
 $\mathfrak {V}\left (\tau =\frac {1}{2} (\alpha + \beta + 1)\right )$
satisfying, respectively, equations defined in terms of the generators
$\mathfrak {V}\left (\tau =\frac {1}{2} (\alpha + \beta + 1)\right )$
satisfying, respectively, equations defined in terms of the generators
![]() $X, L, M$
of
$X, L, M$
of
![]() $m\mathfrak {J}$
. The first basis consists in the eigenvectors of
$m\mathfrak {J}$
. The first basis consists in the eigenvectors of
![]() $X^T$
(the transpose of X) and the second is formed by the vectors solving the GEVP defined by L and M.
$X^T$
(the transpose of X) and the second is formed by the vectors solving the GEVP defined by L and M.
One may remark that the reducible module allows us to posit the eigenvalue problem for X.
3.3.2 The overlaps
 $\left \langle z |L^T |Q_m \right \rangle $
$\left \langle z |L^T |Q_m \right \rangle $
The biorthogonal partners to the Askey polynomials are obtained in a similar fashion. From equations (3.8), (3.40) and (3.41) we have
 $$ \begin{align} L^T |Q_m\rangle = d_m^*(m) (m+\alpha +1)\sum _{l=0}^{\infty} \frac{(-1)^l (m+1)_l (m+\alpha + \beta +1)_l}{l! (m+ \alpha + 1)_l} |\tau , l+m\rangle. \end{align} $$
$$ \begin{align} L^T |Q_m\rangle = d_m^*(m) (m+\alpha +1)\sum _{l=0}^{\infty} \frac{(-1)^l (m+1)_l (m+\alpha + \beta +1)_l}{l! (m+ \alpha + 1)_l} |\tau , l+m\rangle. \end{align} $$
Combining with equation (3.20) and using the orthonormality of the basis vectors
![]() $|\tau , k\rangle $
, we find
$|\tau , k\rangle $
, we find
 $$ \begin{align} \left\langle z | L^{T} | Q_{m} \right\rangle = \gamma d_m^*(m) (m + \alpha + 1) (z-1)^{-m-a} {}_{2}F_{1}\left({m+1, m+\alpha + \beta + 1 \atop m +\alpha + 1}; \frac{1}{1-z} \right ). \end{align} $$
$$ \begin{align} \left\langle z | L^{T} | Q_{m} \right\rangle = \gamma d_m^*(m) (m + \alpha + 1) (z-1)^{-m-a} {}_{2}F_{1}\left({m+1, m+\alpha + \beta + 1 \atop m +\alpha + 1}; \frac{1}{1-z} \right ). \end{align} $$
We may now use the fact that any three solutions of the hypergeometric equation are related by linear relations and call upon transformation formulas of
![]() ${_2}F_1$
series under homographic transformations to make the biorthogonal partners of the Askey polynomials appear in this overlap. Indeed, following the steps described in Appendix A, we arrive at the following expression:
${_2}F_1$
series under homographic transformations to make the biorthogonal partners of the Askey polynomials appear in this overlap. Indeed, following the steps described in Appendix A, we arrive at the following expression:
 $$ \begin{align} \left\langle z| L^T| Q_m\right\rangle & = \gamma d_m^*(m) (m + \alpha + 1) (z - 1)^{1-a} \nonumber \\ & \quad \times \Bigg[ \frac{\Gamma (m + \alpha +1 )\Gamma (\beta + 1)}{\Gamma (m + \beta + 2)\Gamma (\alpha)}{_2}F_1\left( {m + 1, 1 - \alpha \atop m + \beta + 2}; z \right ) \nonumber \\ &\quad - \frac{\Gamma (m + \alpha + 1) \Gamma (m + \beta + 1)}{m! \Gamma (m + \alpha + \beta + 1)} (-z)^{-1-\beta} (1 - z)^{\alpha + \beta} Q_m \left(\frac{1}{z}, \alpha, \beta\right) \Bigg], \end{align} $$
$$ \begin{align} \left\langle z| L^T| Q_m\right\rangle & = \gamma d_m^*(m) (m + \alpha + 1) (z - 1)^{1-a} \nonumber \\ & \quad \times \Bigg[ \frac{\Gamma (m + \alpha +1 )\Gamma (\beta + 1)}{\Gamma (m + \beta + 2)\Gamma (\alpha)}{_2}F_1\left( {m + 1, 1 - \alpha \atop m + \beta + 2}; z \right ) \nonumber \\ &\quad - \frac{\Gamma (m + \alpha + 1) \Gamma (m + \beta + 1)}{m! \Gamma (m + \alpha + \beta + 1)} (-z)^{-1-\beta} (1 - z)^{\alpha + \beta} Q_m \left(\frac{1}{z}, \alpha, \beta\right) \Bigg], \end{align} $$
where
![]() $Q_m(z)$
is defined as in equation (1.2).
$Q_m(z)$
is defined as in equation (1.2).
Remark 3.4. Note that the first term in this expression for
 $\left \langle z| L^T| Q_m\right \rangle $
is a power series, while the second one, which contains the polynomial
$\left \langle z| L^T| Q_m\right \rangle $
is a power series, while the second one, which contains the polynomial
![]() $Q_n$
in the variable
$Q_n$
in the variable
![]() $\frac {1}{z}$
, has the transcendental factor
$\frac {1}{z}$
, has the transcendental factor
![]() $z^{-\beta }$
. Restrictions on z could be imposed with regard to the convergence of the power series, or it could be treated formally, as the focus is on the polynomial partner
$z^{-\beta }$
. Restrictions on z could be imposed with regard to the convergence of the power series, or it could be treated formally, as the focus is on the polynomial partner
![]() $Q_n(z, \alpha , \beta )$
.
$Q_n(z, \alpha , \beta )$
.
The following proposition summarises the main results of this subsection.
Proposition 3.2. The biorthogonal partners
![]() $Q_n(z, \alpha , \beta )$
of the Askey polynomials
$Q_n(z, \alpha , \beta )$
of the Askey polynomials
![]() $P_n(z; \alpha , \beta )$
arise in the representation theory of the meta-Jacobi algebra in the overlaps (see equation (3.57)), between the eigenbasis vectors of the generator X and the basis vectors that obey the GEVP defined by the operators
$P_n(z; \alpha , \beta )$
arise in the representation theory of the meta-Jacobi algebra in the overlaps (see equation (3.57)), between the eigenbasis vectors of the generator X and the basis vectors that obey the GEVP defined by the operators
![]() $M^T$
and
$M^T$
and
![]() $L^T$
.
$L^T$
.
3.3.3 Biorthogonality relation
The interpretation of the Askey polynomials in the framework of the meta-Jacobi algebra leads to a natural derivation of their biorthogonality. Recall equation (3.50). First observe that in multiplying the expressions of the overlaps
 $\widetilde {\langle z|}P_n \rangle $
and
$\widetilde {\langle z|}P_n \rangle $
and
 $\left \langle z | L^T |Q_m\right \rangle $
, as they are given by formulas (3.54) and (3.57), the factor
$\left \langle z | L^T |Q_m\right \rangle $
, as they are given by formulas (3.54) and (3.57), the factor
![]() $(z-1)^{1-a + \tilde {a}}$
reduces to
$(z-1)^{1-a + \tilde {a}}$
reduces to
![]() $1$
because of equation (3.24). Furthermore, one observes that the product of the first term in equation (3.57) – a power series – with the polynomial
$1$
because of equation (3.24). Furthermore, one observes that the product of the first term in equation (3.57) – a power series – with the polynomial
![]() $P_n(z, \alpha , \beta )$
will give a vanishing contribution when integrated over the circle
$P_n(z, \alpha , \beta )$
will give a vanishing contribution when integrated over the circle
![]() $\lvert z\rvert =1$
. Equation (3.50) thus yields
$\lvert z\rvert =1$
. Equation (3.50) thus yields
 $$ \begin{align} d_n(0) d_m^*(m) &\frac{(m + \alpha + 1) (\alpha + 1)_n}{(\alpha + \beta + 1)_n} \frac{\Gamma (m + \alpha + 1) \Gamma (m + \beta + 1)}{m! \Gamma (m + \alpha + \beta + 1)} \nonumber\\ &\times \frac{-1}{2 \pi i} \oint_{\lvert z\rvert=1} dz (-z)^{-1 - \beta} (1-z)^{\alpha + \beta}P_n(z, \alpha, \beta) Q_m \left(\frac{1}{z}, \alpha, \beta\right) = N_n \delta_{m,n}. \end{align} $$
$$ \begin{align} d_n(0) d_m^*(m) &\frac{(m + \alpha + 1) (\alpha + 1)_n}{(\alpha + \beta + 1)_n} \frac{\Gamma (m + \alpha + 1) \Gamma (m + \beta + 1)}{m! \Gamma (m + \alpha + \beta + 1)} \nonumber\\ &\times \frac{-1}{2 \pi i} \oint_{\lvert z\rvert=1} dz (-z)^{-1 - \beta} (1-z)^{\alpha + \beta}P_n(z, \alpha, \beta) Q_m \left(\frac{1}{z}, \alpha, \beta\right) = N_n \delta_{m,n}. \end{align} $$
Recalling that
![]() $N_n$
is given by equation (3.49), we thus recover precisely the biorthogonality relation (1.3).
$N_n$
is given by equation (3.49), we thus recover precisely the biorthogonality relation (1.3).
3.4 Eigenbases of M and
 $M^T$
$M^T$
We now undertake to show that the Jacobi polynomials can be described within the same algebraic framework. We already noted in Proposition 2.2 that the elements X and M generate the Jacobi algebra
![]() $\mathfrak {J}$
, which is thus embedded in
$\mathfrak {J}$
, which is thus embedded in
![]() $m\mathfrak {J}$
. We therefore expect to see the Jacobi polynomials occur in the overlaps between the eigenvectors of X,
$m\mathfrak {J}$
. We therefore expect to see the Jacobi polynomials occur in the overlaps between the eigenvectors of X,
![]() $X^T$
and
$X^T$
and
![]() $M^T$
, M, respectively. We shall hence first determine the eigenbases of
$M^T$
, M, respectively. We shall hence first determine the eigenbases of
![]() $\mathfrak {V}(\tau )$
associated to M and
$\mathfrak {V}(\tau )$
associated to M and
![]() $M^T$
.
$M^T$
.
From the two-diagonal action (3.6) of M, we see that the spectrum
![]() $\{\mu _n \}$
of this operator is of the form
$\{\mu _n \}$
of this operator is of the form
Consider the EVPs (3.19). Set
 $$ \begin{align} |J_n\rangle = \sum_{k=-\infty}^{\infty} f_n (k) |\tau, k\rangle. \end{align} $$
$$ \begin{align} |J_n\rangle = \sum_{k=-\infty}^{\infty} f_n (k) |\tau, k\rangle. \end{align} $$
The eigenvalue equation
![]() $M |J_n\rangle = n(n + \alpha + 1) |J_n\rangle $
yields the following two-term recurrence relation for the coefficients
$M |J_n\rangle = n(n + \alpha + 1) |J_n\rangle $
yields the following two-term recurrence relation for the coefficients
![]() $f_n(k)$
:
$f_n(k)$
:
which can be rewritten as
Here again, we shall focus on the case
![]() $n \geq 0$
. This equation is then found to imply that
$n \geq 0$
. This equation is then found to imply that
and is solved by
 $$ \begin{align} f_n(k) = f_n (0) (-1)^k\frac{(-n)_k (n + \alpha + 1)_k}{k! (\alpha + \beta + 1)_k}, \qquad k = 0, 1, \dotsc, n. \end{align} $$
$$ \begin{align} f_n(k) = f_n (0) (-1)^k\frac{(-n)_k (n + \alpha + 1)_k}{k! (\alpha + \beta + 1)_k}, \qquad k = 0, 1, \dotsc, n. \end{align} $$
Similarly, let
 $$ \begin{align} \widetilde{|J_n\rangle} = \sum_{k=-\infty}^{\infty} \tilde{f}_n (k) |\tau, k\rangle. \end{align} $$
$$ \begin{align} \widetilde{|J_n\rangle} = \sum_{k=-\infty}^{\infty} \tilde{f}_n (k) |\tau, k\rangle. \end{align} $$
The EVP
 $M^T \widetilde {|J_n \rangle } = n (n + \alpha + 1) \widetilde {|J_n \rangle } $
is readily seen to give
$M^T \widetilde {|J_n \rangle } = n (n + \alpha + 1) \widetilde {|J_n \rangle } $
is readily seen to give
In this instance, for
![]() $m \geq 0$
, we observe that
$m \geq 0$
, we observe that
We set
![]() $k = n + l , l = 0, 1, 2, \dotsc ,$
and convert equation (3.66) into
$k = n + l , l = 0, 1, 2, \dotsc ,$
and convert equation (3.66) into
to find
 $$ \begin{align} \tilde{f}_n (n + l) = \tilde{f}_n (n) (-1)^l \frac{(n + 1)_l (n +1 + \alpha + \beta)_l}{l! (2n + \alpha + 2)_l}. \end{align} $$
$$ \begin{align} \tilde{f}_n (n + l) = \tilde{f}_n (n) (-1)^l \frac{(n + 1)_l (n +1 + \alpha + \beta)_l}{l! (2n + \alpha + 2)_l}. \end{align} $$
We can now verify that
![]() $|J_n\rangle $
and
$|J_n\rangle $
and
 $\widetilde {|J_m \rangle }$
are orthogonal when
$\widetilde {|J_m \rangle }$
are orthogonal when
![]() $m \neq n$
. This proceeds in a way similar to the computation of
$m \neq n$
. This proceeds in a way similar to the computation of
 $\left \langle P_n | L^T | Q_m \right \rangle $
carried out before. Clearly,
$\left \langle P_n | L^T | Q_m \right \rangle $
carried out before. Clearly,
 $\langle J_n \widetilde {| J_m \rangle } = 0$
if
$\langle J_n \widetilde {| J_m \rangle } = 0$
if
![]() $m> n$
. If
$m> n$
. If
![]() $m \leq n$
, after some algebraic simplifications we see that
$m \leq n$
, after some algebraic simplifications we see that
 $$ \begin{align} \langle J_n \widetilde{| J_m \rangle} = f_n(0) \tilde{f}_m(n) (-1)^m\frac{(-n)_m (n + \alpha + 1)_m}{m! (\alpha + \beta + 1)_m } {_2}F_1\left({m - n, n + m + \alpha + 1 \atop 2m + \alpha + 2}; 1 \right ). \end{align} $$
$$ \begin{align} \langle J_n \widetilde{| J_m \rangle} = f_n(0) \tilde{f}_m(n) (-1)^m\frac{(-n)_m (n + \alpha + 1)_m}{m! (\alpha + \beta + 1)_m } {_2}F_1\left({m - n, n + m + \alpha + 1 \atop 2m + \alpha + 2}; 1 \right ). \end{align} $$
From the Vandermonde formula [Reference Gasper and Rahman8]
 $$ \begin{align} {_2}F_1\left({-n, b \atop c}; 1 \right ) = \frac{(c-b)_n}{(c)_n}, \end{align} $$
$$ \begin{align} {_2}F_1\left({-n, b \atop c}; 1 \right ) = \frac{(c-b)_n}{(c)_n}, \end{align} $$
we may then conclude that because of the factor
![]() $(m - n +1)_{n-m}$
that appears,
$(m - n +1)_{n-m}$
that appears,
 $\langle J_n \widetilde {| J_m \rangle } = 0$
unless
$\langle J_n \widetilde {| J_m \rangle } = 0$
unless
![]() $n=m$
, in which case
$n=m$
, in which case
 $$ \begin{align} \langle J_n \widetilde{| J_m \rangle} = \mathcal{N}_n \delta_{m,n}, \end{align} $$
$$ \begin{align} \langle J_n \widetilde{| J_m \rangle} = \mathcal{N}_n \delta_{m,n}, \end{align} $$
with
 $$ \begin{align} \mathcal{N}_n = f_n(0) \tilde{f}_n(n) \frac{(n + \alpha + 1)_n}{(\alpha + \beta + 1)_n}. \end{align} $$
$$ \begin{align} \mathcal{N}_n = f_n(0) \tilde{f}_n(n) \frac{(n + \alpha + 1)_n}{(\alpha + \beta + 1)_n}. \end{align} $$
3.5 Jacobi polynomials
We will now observe how the Jacobi polynomials emerge in this framework and indicate how this allows for another derivation of their orthogonality relation.
3.5.1 The overlaps
Let us now look at the overlaps
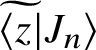 $\widetilde {\langle z |} J_n \rangle $
and
$\widetilde {\langle z |} J_n \rangle $
and
 $\langle z \widetilde {| J_m \rangle }$
. From equations (3.21), (3.60) and (3.64) we obtain
$\langle z \widetilde {| J_m \rangle }$
. From equations (3.21), (3.60) and (3.64) we obtain
 $$ \begin{align} \widetilde{\langle z |} J_n \rangle = \tilde{\gamma} f_n(0) (z - 1 )^{\tilde{a}} {}_{2}F_1\left({-n, n + \alpha + 1 \atop \alpha + \beta + 1}; 1-z \right ). \end{align} $$
$$ \begin{align} \widetilde{\langle z |} J_n \rangle = \tilde{\gamma} f_n(0) (z - 1 )^{\tilde{a}} {}_{2}F_1\left({-n, n + \alpha + 1 \atop \alpha + \beta + 1}; 1-z \right ). \end{align} $$
Using equation (A.1) – or equivalently equation (3.53) – we arrive at
 $$ \begin{align} \widetilde{\langle z |} J_n \rangle = \tilde{\gamma} (z - 1)^{\tilde{a}} \frac{(-1)^n \Gamma (1 + \alpha + \beta) \Gamma (\beta) \Gamma (2n + \alpha + 1) \Gamma (1 - \beta)}{\Gamma (-n + \beta) \Gamma (n + \alpha + \beta + 1)\Gamma (n + \alpha + 1) \Gamma (n + 1 - \beta)} \hat{P}_n^{\left(\alpha, \beta\right)}(z), \end{align} $$
$$ \begin{align} \widetilde{\langle z |} J_n \rangle = \tilde{\gamma} (z - 1)^{\tilde{a}} \frac{(-1)^n \Gamma (1 + \alpha + \beta) \Gamma (\beta) \Gamma (2n + \alpha + 1) \Gamma (1 - \beta)}{\Gamma (-n + \beta) \Gamma (n + \alpha + \beta + 1)\Gamma (n + \alpha + 1) \Gamma (n + 1 - \beta)} \hat{P}_n^{\left(\alpha, \beta\right)}(z), \end{align} $$
where
 $\hat {P}_n^{\left (\alpha , \beta \right )}(z)$
are the Jacobi polynomials defined in equation (1.4) extended to the complex plane.
$\hat {P}_n^{\left (\alpha , \beta \right )}(z)$
are the Jacobi polynomials defined in equation (1.4) extended to the complex plane.
The second overlap is recovered from equations (3.20), (3.65) and (3.69). We find
 $$ \begin{align} \langle z \widetilde{| J_m \rangle} = \gamma {\tilde{f}}_m(m) {(z-1)^{-m - a}}{} {_2}{F_1}\left({m + 1, m + \alpha + \beta + 1 \atop 2m +\alpha + 2}; \frac{1}{1-z} \right ). \end{align} $$
$$ \begin{align} \langle z \widetilde{| J_m \rangle} = \gamma {\tilde{f}}_m(m) {(z-1)^{-m - a}}{} {_2}{F_1}\left({m + 1, m + \alpha + \beta + 1 \atop 2m +\alpha + 2}; \frac{1}{1-z} \right ). \end{align} $$
At this point, by performing the transformations described in Appendix B that make use of identities involving gamma functions and solutions of the hypergeometric equation, the following formula is discovered:
 $$ \begin{align} \langle z \widetilde{| J_m \rangle} & = (-1)^{m + 1}\gamma {\tilde{f}}_m(m) (z-1)^{1 - a}\nonumber \\ & \quad \times\Bigg[ \frac{\Gamma (2m + \alpha +2 )\Gamma (-\beta)}{\Gamma (m + \alpha + 1)\Gamma (m -\beta +1)} {}{_2}F_1\left( {m + 1, -m - \alpha \atop 1 + \beta}; z \right ) \nonumber \\ & \quad + \frac{(-1)^m \Gamma (2m + \alpha + 2) \Gamma (\beta) \Gamma (2m + \alpha + 1)\Gamma (1 - \beta)}{m! \Gamma (m + \alpha + \beta + 1) \Gamma (m + \alpha + 1) \Gamma (m + 1 - \beta)} (-z)^{-\beta} (1 - z)^{\alpha + \beta} \hat{P}_m^{\left(\alpha, \beta\right)}(z) \Bigg]. \end{align} $$
$$ \begin{align} \langle z \widetilde{| J_m \rangle} & = (-1)^{m + 1}\gamma {\tilde{f}}_m(m) (z-1)^{1 - a}\nonumber \\ & \quad \times\Bigg[ \frac{\Gamma (2m + \alpha +2 )\Gamma (-\beta)}{\Gamma (m + \alpha + 1)\Gamma (m -\beta +1)} {}{_2}F_1\left( {m + 1, -m - \alpha \atop 1 + \beta}; z \right ) \nonumber \\ & \quad + \frac{(-1)^m \Gamma (2m + \alpha + 2) \Gamma (\beta) \Gamma (2m + \alpha + 1)\Gamma (1 - \beta)}{m! \Gamma (m + \alpha + \beta + 1) \Gamma (m + \alpha + 1) \Gamma (m + 1 - \beta)} (-z)^{-\beta} (1 - z)^{\alpha + \beta} \hat{P}_m^{\left(\alpha, \beta\right)}(z) \Bigg]. \end{align} $$
Remark 3.5. As already encountered in expression (3.57) of
![]() $\langle z| L^T| Q_m\rangle $
, we see that the first term in equation (3.77) is a power series, and the second, which involves the Jacobi polynomials, contains the transcendental term
$\langle z| L^T| Q_m\rangle $
, we see that the first term in equation (3.77) is a power series, and the second, which involves the Jacobi polynomials, contains the transcendental term
![]() $z^{-\beta }$
.
$z^{-\beta }$
.
Proposition 3.3. The Jacobi polynomials
 $\hat {P}_m^{\left (\alpha , \beta \right )}(z)$
over
$\hat {P}_m^{\left (\alpha , \beta \right )}(z)$
over
![]() $\mathbb {C}$
also arise in the context of the meta-Jacobi algebra
$\mathbb {C}$
also arise in the context of the meta-Jacobi algebra
![]() $m\mathfrak {J}$
. They occur as per equations (3.75) and (3.77) in two overlaps between eigenbases of the module
$m\mathfrak {J}$
. They occur as per equations (3.75) and (3.77) in two overlaps between eigenbases of the module
 $\mathfrak {V}\left (\frac {1}{2} (\alpha + \beta + 1)\right )$
: on the one hand between the eigenstates of M and
$\mathfrak {V}\left (\frac {1}{2} (\alpha + \beta + 1)\right )$
: on the one hand between the eigenstates of M and
![]() $X^T$
and on the other hand between those of
$X^T$
and on the other hand between those of
![]() $M^T$
and X.
$M^T$
and X.
3.5.2 Orthogonality
This interpretation of the Jacobi polynomials in the framework of the algebra
![]() $m\mathfrak {J}$
entails a derivation of their orthogonality. Owing to the completeness relation (3.28), we have
$m\mathfrak {J}$
entails a derivation of their orthogonality. Owing to the completeness relation (3.28), we have
 $$ \begin{align} \frac{1}{2 \pi i \gamma \tilde{\gamma}} \oint _{C_{\lvert z\rvert=1} }\langle J_n \widetilde{| z \rangle} \langle z \widetilde{| J_m \rangle} = \langle J_n \widetilde{| J_m \rangle} = \mathcal{N}_n \delta_{m,n}, \end{align} $$
$$ \begin{align} \frac{1}{2 \pi i \gamma \tilde{\gamma}} \oint _{C_{\lvert z\rvert=1} }\langle J_n \widetilde{| z \rangle} \langle z \widetilde{| J_m \rangle} = \langle J_n \widetilde{| J_m \rangle} = \mathcal{N}_n \delta_{m,n}, \end{align} $$
where
![]() $\mathcal {N}_n$
is given by equation (3.73). When substituting expressions (3.75) and (3.77) for
$\mathcal {N}_n$
is given by equation (3.73). When substituting expressions (3.75) and (3.77) for
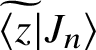 $\widetilde {\langle z |} J_n \rangle $
and
$\widetilde {\langle z |} J_n \rangle $
and
 $\langle z \widetilde {| J_m \rangle }$
, we first observe anew that the resulting factor
$\langle z \widetilde {| J_m \rangle }$
, we first observe anew that the resulting factor
![]() $(z-1)^{1-a + \tilde {a}} = 1$
, since
$(z-1)^{1-a + \tilde {a}} = 1$
, since
![]() $1 - a + \tilde {a} = 0$
. Then we note that the product of
$1 - a + \tilde {a} = 0$
. Then we note that the product of
 $\widetilde {\langle z |} J_n \rangle $
with the first term of equation (3.77) is a power series that will integrate to
$\widetilde {\langle z |} J_n \rangle $
with the first term of equation (3.77) is a power series that will integrate to
![]() $0$
over the unit circle. Taking into account formula (3.73) for
$0$
over the unit circle. Taking into account formula (3.73) for
![]() $\mathcal {N}_n$
and after some simplifications, equation (3.78) thus amounts to
$\mathcal {N}_n$
and after some simplifications, equation (3.78) thus amounts to
 $$ \begin{align} - \frac{1}{2 \pi i} \left(\frac{\pi}{\sin \pi \beta}\right) \oint _{C_{\lvert z\rvert=1}} dz (-z)^{-\beta} (1 - z) ^{\alpha + \beta} \hat{P}_n^{\left(\alpha, \beta\right)}(z)\hat{P}_m^{\left(\alpha, \beta\right)}(z) = h_n \delta _{m,n}, \end{align} $$
$$ \begin{align} - \frac{1}{2 \pi i} \left(\frac{\pi}{\sin \pi \beta}\right) \oint _{C_{\lvert z\rvert=1}} dz (-z)^{-\beta} (1 - z) ^{\alpha + \beta} \hat{P}_n^{\left(\alpha, \beta\right)}(z)\hat{P}_m^{\left(\alpha, \beta\right)}(z) = h_n \delta _{m,n}, \end{align} $$
with
![]() $h_n$
given in equation (1.6). In obtaining equation (3.79) we have used the identity
$h_n$
given in equation (1.6). In obtaining equation (3.79) we have used the identity
![]() $\Gamma (x) \Gamma (1-x) = \frac {\pi }{\sin \pi x}$
, and in particular
$\Gamma (x) \Gamma (1-x) = \frac {\pi }{\sin \pi x}$
, and in particular
 $$ \begin{align} \Gamma (-n + \beta) \Gamma (n + 1 - \beta) = \frac{\pi}{\sin \pi (-n + \beta)} = (-1)^n \dfrac{\pi}{\sin \pi \beta}. \end{align} $$
$$ \begin{align} \Gamma (-n + \beta) \Gamma (n + 1 - \beta) = \frac{\pi}{\sin \pi (-n + \beta)} = (-1)^n \dfrac{\pi}{\sin \pi \beta}. \end{align} $$
Finally, the orthogonality of the Jacobi polynomials on the interval
![]() $[0, 1]$
is recovered by using the contour depicted in Figure 1 and computations carried out in [Reference Hendriksen and van Rossum14]. Schematically the contour
$[0, 1]$
is recovered by using the contour depicted in Figure 1 and computations carried out in [Reference Hendriksen and van Rossum14]. Schematically the contour
![]() $\Xi = C_{\lvert z\rvert =1} + [1, 0] + C_{\epsilon } + [0, 1]$
, it is composed of the unit circle (short of crossing the branch cut), the segment from
$\Xi = C_{\lvert z\rvert =1} + [1, 0] + C_{\epsilon } + [0, 1]$
, it is composed of the unit circle (short of crossing the branch cut), the segment from
![]() $x=1$
to
$x=1$
to
![]() $x=0$
below the branch cut, a circle of radius
$x=0$
below the branch cut, a circle of radius
![]() $\epsilon $
around
$\epsilon $
around
![]() $z=0$
and the segment from
$z=0$
and the segment from
![]() $x=0$
to
$x=0$
to
![]() $x=1$
above the branch cut. Consider the integral in equation (3.79) with the contour
$x=1$
above the branch cut. Consider the integral in equation (3.79) with the contour
![]() $C_{\lvert z\rvert =1}$
replaced by the contour
$C_{\lvert z\rvert =1}$
replaced by the contour
![]() $\Xi $
of Figure 1. Since no singularities are enclosed by
$\Xi $
of Figure 1. Since no singularities are enclosed by
![]() $\Xi $
, that integral is equal to
$\Xi $
, that integral is equal to
![]() $0$
.
$0$
.

Figure 1 The contour
![]() $\Xi $
.
$\Xi $
.
If we restrict
![]() $\beta $
to be smaller than
$\beta $
to be smaller than
![]() $1$
– that is, if we take
$1$
– that is, if we take
![]() $\beta < 1$
as in the standard definition of the Jacobi polynomials – it is readily seen that
$\beta < 1$
as in the standard definition of the Jacobi polynomials – it is readily seen that
 $$ \begin{align} \lim_{\epsilon \to 0} \frac{1}{2 \pi i} \oint _{C_{\epsilon}}dz (-z)^{-\beta} (1 - z) ^{\alpha + \beta} \hat{P}_n^{\left(\alpha, \beta\right)}(z)\hat{P}_m^{\left(\alpha, \beta\right)}(z) = 0, \qquad \text{for}\ \beta < 1. \end{align} $$
$$ \begin{align} \lim_{\epsilon \to 0} \frac{1}{2 \pi i} \oint _{C_{\epsilon}}dz (-z)^{-\beta} (1 - z) ^{\alpha + \beta} \hat{P}_n^{\left(\alpha, \beta\right)}(z)\hat{P}_m^{\left(\alpha, \beta\right)}(z) = 0, \qquad \text{for}\ \beta < 1. \end{align} $$
It follows that the integral over
![]() $C_{\lvert z\rvert =1}$
must be the negative of the sum of the integrals over and above the real axis. Hence, recalling the choice of branch
$C_{\lvert z\rvert =1}$
must be the negative of the sum of the integrals over and above the real axis. Hence, recalling the choice of branch
![]() $(-z)^{-\beta } = \lvert z\rvert ^{-\beta }$
when
$(-z)^{-\beta } = \lvert z\rvert ^{-\beta }$
when
![]() $\arg z = \pi $
, we have
$\arg z = \pi $
, we have
 $$ \begin{align} &- \frac{1}{2 \pi i} \left(\frac{\pi}{\sin \pi \beta}\right) \oint _{C_{\lvert z\rvert=1}} dz (-z)^{-\beta} (1 - z) ^{\alpha + \beta} \hat{P}_n^{\left(\alpha, \beta\right)}(z)\hat{P}_m^{\left(\alpha, \beta\right)}(z) = \nonumber \\ & \frac{1}{2i} \left(\frac{1}{\sin \pi \beta}\right) e^{i\pi \beta} \left(1 - e^{-2 \pi i \beta}\right) \int_0^1 x^{-\beta} (1 - x) ^{\alpha + \beta} \hat{P}_n^{\left(\alpha, \beta\right)}(x)\hat{P}_m^{\left(\alpha, \beta\right)}(x) dx. \end{align} $$
$$ \begin{align} &- \frac{1}{2 \pi i} \left(\frac{\pi}{\sin \pi \beta}\right) \oint _{C_{\lvert z\rvert=1}} dz (-z)^{-\beta} (1 - z) ^{\alpha + \beta} \hat{P}_n^{\left(\alpha, \beta\right)}(z)\hat{P}_m^{\left(\alpha, \beta\right)}(z) = \nonumber \\ & \frac{1}{2i} \left(\frac{1}{\sin \pi \beta}\right) e^{i\pi \beta} \left(1 - e^{-2 \pi i \beta}\right) \int_0^1 x^{-\beta} (1 - x) ^{\alpha + \beta} \hat{P}_n^{\left(\alpha, \beta\right)}(x)\hat{P}_m^{\left(\alpha, \beta\right)}(x) dx. \end{align} $$
The factors before the integral sign in the last expression cancel, and this gives the orthogonality relation (1.5) of the Jacobi polynomials in view of equation (3.79).
4 Algebraic derivation of the properties of the Askey polynomials
We shall indicate in this section how various properties of the biorthogonal Askey polynomials on the circle naturally follow from their interpretation based on the meta-Jacobi algebra. Recall that
 $$ \begin{align} |P_n\rangle = d_n(0) \sum_{k=0}^n (-1)^k \frac{(-n)_k (\alpha + 1)_k}{k! (\alpha + \beta + 1)_k} |\tau, k\rangle. \end{align} $$
$$ \begin{align} |P_n\rangle = d_n(0) \sum_{k=0}^n (-1)^k \frac{(-n)_k (\alpha + 1)_k}{k! (\alpha + \beta + 1)_k} |\tau, k\rangle. \end{align} $$
Looking at the overlap
 $\widetilde {\langle z|} P_n\rangle $
given in equation (3.54), without loss of generality we can set from now on
$\widetilde {\langle z|} P_n\rangle $
given in equation (3.54), without loss of generality we can set from now on
It is moreover natural to take the initial values
![]() $d_n(0)$
of the recurrence relation (3.32) to be
$d_n(0)$
of the recurrence relation (3.32) to be
 $$ \begin{align} d_n(0; \alpha, \beta) = \frac{(\alpha + \beta + 1)_n}{(\alpha + 1)_n}, \end{align} $$
$$ \begin{align} d_n(0; \alpha, \beta) = \frac{(\alpha + \beta + 1)_n}{(\alpha + 1)_n}, \end{align} $$
so that
 $$ \begin{align} \widetilde{\langle z|} P_n\rangle = P_n(z; \alpha, \beta), \end{align} $$
$$ \begin{align} \widetilde{\langle z|} P_n\rangle = P_n(z; \alpha, \beta), \end{align} $$
identifying
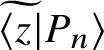 $\widetilde {\langle z|} P_n\rangle $
precisely with the Askey polynomials. This also means that
$\widetilde {\langle z|} P_n\rangle $
precisely with the Askey polynomials. This also means that
![]() $|\tau , n\rangle $
has coefficient
$|\tau , n\rangle $
has coefficient
![]() $1$
in
$1$
in
![]() $|P_n\rangle $
:
$|P_n\rangle $
:
 $$ \begin{align} |P_n\rangle = \frac{(\alpha + \beta + 1)_n}{(\alpha + 1)_n} |\tau, 0\rangle + \dotsb + |\tau, n\rangle. \end{align} $$
$$ \begin{align} |P_n\rangle = \frac{(\alpha + \beta + 1)_n}{(\alpha + 1)_n} |\tau, 0\rangle + \dotsb + |\tau, n\rangle. \end{align} $$
4.1 Action of L and
 $R=XL$
in the basis
$R=XL$
in the basis
 $\{|P_n\rangle \}$
$\{|P_n\rangle \}$
We shall now show that the generator L and the product
![]() $XL$
act in a two-diagonal fashion in the basis
$XL$
act in a two-diagonal fashion in the basis
![]() $\{|P_n\rangle , n=0, 1, \dots \}$
. We have
$\{|P_n\rangle , n=0, 1, \dots \}$
. We have
 $$ \begin{align} L |P_n(\alpha, \beta)\rangle = \frac{(\alpha + \beta + 1)_n}{(\alpha + 1)_n} \sum_{k=0}^n (-1)^k \frac{(-n)_k (\alpha + 1)_k}{k! (\alpha + \beta + 1)_k} L|\tau, k\rangle. \end{align} $$
$$ \begin{align} L |P_n(\alpha, \beta)\rangle = \frac{(\alpha + \beta + 1)_n}{(\alpha + 1)_n} \sum_{k=0}^n (-1)^k \frac{(-n)_k (\alpha + 1)_k}{k! (\alpha + \beta + 1)_k} L|\tau, k\rangle. \end{align} $$
From equation (3.5) and the identity
 $$ \begin{align} (-n)_k (k + \alpha + 1) &= (-n)_k [n + \alpha + 1 + (-n + k) ]\nonumber \\ &= (n + \alpha + 1) (-n)_k - n(-n + 1)_k, \end{align} $$
$$ \begin{align} (-n)_k (k + \alpha + 1) &= (-n)_k [n + \alpha + 1 + (-n + k) ]\nonumber \\ &= (n + \alpha + 1) (-n)_k - n(-n + 1)_k, \end{align} $$
we see that
 $$ \begin{align} L |P_n(\alpha, \beta)\rangle = (n + \alpha + 1) |P_n(\alpha, \beta)\rangle - \frac{n (n + \alpha + \beta)}{(n + \alpha)} |P_{n-1} (\alpha, \beta) \rangle. \end{align} $$
$$ \begin{align} L |P_n(\alpha, \beta)\rangle = (n + \alpha + 1) |P_n(\alpha, \beta)\rangle - \frac{n (n + \alpha + \beta)}{(n + \alpha)} |P_{n-1} (\alpha, \beta) \rangle. \end{align} $$
Alternatively, using
we note that L also has the effect of shifting the parameters:
Consider now the action of the operator
![]() $R=XL$
. Knowing that L acts diagonally as per equation (3.5) on the basis vectors
$R=XL$
. Knowing that L acts diagonally as per equation (3.5) on the basis vectors
![]() $|\tau , k\rangle $
, and according to equation (3.7), we have
$|\tau , k\rangle $
, and according to equation (3.7), we have
 $$ \begin{align} R |P_n(\alpha, \beta)\rangle = \frac{(\alpha + \beta + 1)_n}{(\alpha + 1)_n} \sum_{k=0}^n (-1)^k \frac{(-n)_k (\alpha + 1)_k (k + \alpha + 1)}{k! (\alpha + \beta + 1)_k} [|\tau, k\rangle + |\tau, k + 1\rangle]. \end{align} $$
$$ \begin{align} R |P_n(\alpha, \beta)\rangle = \frac{(\alpha + \beta + 1)_n}{(\alpha + 1)_n} \sum_{k=0}^n (-1)^k \frac{(-n)_k (\alpha + 1)_k (k + \alpha + 1)}{k! (\alpha + \beta + 1)_k} [|\tau, k\rangle + |\tau, k + 1\rangle]. \end{align} $$
Collecting the factors of the vectors
![]() $|\tau , k\rangle $
,
$|\tau , k\rangle $
,
![]() $k=0, \dotsc , n+1$
, we find
$k=0, \dotsc , n+1$
, we find
 $$ \begin{align} R |P_n(\alpha, \beta)\rangle &= \frac{(\alpha + \beta + 1)_n}{(\alpha + 1)_n} \Bigg[ (\alpha + 1) |\tau, 0\rangle \nonumber\\ &\quad + \sum_{k=1}^n \frac{(-1)^k (\alpha + 1)_k}{k! (\alpha + \beta + 1)_k} [ (-n)_k (k + \alpha + 1) - (-n)_{k-1} k(k + \alpha + \beta) ] |\tau,k \rangle \nonumber\\ & \quad + \frac{(\alpha + 1)_{n+1}}{(\alpha + \beta + 1)_n} |\tau, n + 1 \rangle \Bigg]. \end{align} $$
$$ \begin{align} R |P_n(\alpha, \beta)\rangle &= \frac{(\alpha + \beta + 1)_n}{(\alpha + 1)_n} \Bigg[ (\alpha + 1) |\tau, 0\rangle \nonumber\\ &\quad + \sum_{k=1}^n \frac{(-1)^k (\alpha + 1)_k}{k! (\alpha + \beta + 1)_k} [ (-n)_k (k + \alpha + 1) - (-n)_{k-1} k(k + \alpha + \beta) ] |\tau,k \rangle \nonumber\\ & \quad + \frac{(\alpha + 1)_{n+1}}{(\alpha + \beta + 1)_n} |\tau, n + 1 \rangle \Bigg]. \end{align} $$
The two relations
come in handy in deriving the following identity:
 $$ \begin{align} &(-n)_k (k + \alpha + 1) - k (-n)_{k-1} (k + \alpha + \beta) \nonumber \\ &\quad = (-n)_k (k + \alpha + 1) - [ (-n)_k - (-n-1)_k ] (k + \alpha + \beta) \nonumber \\ & \quad = (-n)_k (1 - \beta) + (-n - 1)_k (k + \alpha + \beta) \nonumber \\ &\quad = (-n)_k (-n - \beta) + (-n-1)_k ( n + \alpha + \beta + 1). \end{align} $$
$$ \begin{align} &(-n)_k (k + \alpha + 1) - k (-n)_{k-1} (k + \alpha + \beta) \nonumber \\ &\quad = (-n)_k (k + \alpha + 1) - [ (-n)_k - (-n-1)_k ] (k + \alpha + \beta) \nonumber \\ & \quad = (-n)_k (1 - \beta) + (-n - 1)_k (k + \alpha + \beta) \nonumber \\ &\quad = (-n)_k (-n - \beta) + (-n-1)_k ( n + \alpha + \beta + 1). \end{align} $$
Clearly, equation (4.13) has been used in getting the second line and equation (4.14) has been added to the third line to obtain the end result. Upon inserting this relation (4.15) into equation (4.12), we recognise easily that R is a two-diagonal raising operator:
In the following we shall also consider the element
4.2 A differential realisation
A differential model of the meta-Jacobi algebra is directly obtained. With the choices in equation (4.2), we have
 $$ \begin{align} \widetilde{\langle z |} \tau, k\rangle \equiv f(z, k) = (z - 1)^k. \end{align} $$
$$ \begin{align} \widetilde{\langle z |} \tau, k\rangle \equiv f(z, k) = (z - 1)^k. \end{align} $$
We can dually define an operator acting on the variable z as follows:
 $$ \begin{align} \mathcal{O}_z \widetilde{\langle z |} \tau, k\rangle = \widetilde{\langle z |} O |\tau, k\rangle = \mathrm{O}_k f(z, k), \end{align} $$
$$ \begin{align} \mathcal{O}_z \widetilde{\langle z |} \tau, k\rangle = \widetilde{\langle z |} O |\tau, k\rangle = \mathrm{O}_k f(z, k), \end{align} $$
where
![]() $\mathcal {O}_z$
corresponds to the operator O acting on the module
$\mathcal {O}_z$
corresponds to the operator O acting on the module
 $\mathfrak {V}\left (\frac {1}{2} (\alpha + \beta + 1)\right )$
and
$\mathfrak {V}\left (\frac {1}{2} (\alpha + \beta + 1)\right )$
and
![]() $\mathrm {O}_k$
as in Remark 3.2, acts on the components
$\mathrm {O}_k$
as in Remark 3.2, acts on the components
![]() $f(z,k)$
of the vector
$f(z,k)$
of the vector
![]() $\widetilde {|z\rangle }$
. With
$\widetilde {|z\rangle }$
. With
![]() $O = L, M, X$
we find the following:
$O = L, M, X$
we find the following:
Proposition 4.1. The differential operators
![]() $\mathcal {L}$
,
$\mathcal {L}$
,
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {X}$
provide a realisation of the commutation relations (2.1), (2.2) and (2.3) of the meta-Jacobi algebra:
$\mathcal {X}$
provide a realisation of the commutation relations (2.1), (2.2) and (2.3) of the meta-Jacobi algebra:
 $$ \begin{align}\begin{aligned} \mathcal{M}= z(z-1) \partial_z^2 + \left[ (\alpha+2)z + \beta-1 \right] \partial_z; \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathcal{M}= z(z-1) \partial_z^2 + \left[ (\alpha+2)z + \beta-1 \right] \partial_z; \end{aligned}\end{align} $$
It follows that
![]() $R=XL$
and
$R=XL$
and
![]() $\tilde {R}=XM$
are realised by
$\tilde {R}=XM$
are realised by
 $$ \begin{align}\tilde{\mathcal{R}} = z^2 (z-1) \partial _z ^2 + z[(\alpha+2)z+\beta-1 ] \partial_z. \end{align} $$
$$ \begin{align}\tilde{\mathcal{R}} = z^2 (z-1) \partial _z ^2 + z[(\alpha+2)z+\beta-1 ] \partial_z. \end{align} $$
Remark 4.2. One may also take X acting on the left on
![]() $\widetilde {\langle z |}$
and giving the eigenvalue z so that
$\widetilde {\langle z |}$
and giving the eigenvalue z so that
 $$ \begin{align} \mathcal{R} \widetilde{\langle z |}P_n(\alpha, \beta)\rangle = \widetilde{\langle z |}XL |P_n(\alpha, \beta)\rangle= z \widetilde{\langle z |}L |P_n(\alpha, \beta)\rangle = z\mathcal{L} \widetilde{\langle z |}P_n(\alpha, \beta)\rangle, \end{align} $$
$$ \begin{align} \mathcal{R} \widetilde{\langle z |}P_n(\alpha, \beta)\rangle = \widetilde{\langle z |}XL |P_n(\alpha, \beta)\rangle= z \widetilde{\langle z |}L |P_n(\alpha, \beta)\rangle = z\mathcal{L} \widetilde{\langle z |}P_n(\alpha, \beta)\rangle, \end{align} $$
and similarly for
![]() $\tilde {R} = XM$
.
$\tilde {R} = XM$
.
Remark 4.3. Note that
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {M}$
have the property of stabilising spaces of polynomials of given degrees, whereas
$\mathcal {M}$
have the property of stabilising spaces of polynomials of given degrees, whereas
![]() $\mathcal {X}$
,
$\mathcal {X}$
,
![]() $\mathcal {R}$
,
$\mathcal {R}$
,
![]() $\tilde {\mathcal {R}}$
raise the degree by
$\tilde {\mathcal {R}}$
raise the degree by
![]() $1$
. In the spirit of [Reference Gaboriaud, Tsujimoto, Vinet and Zhedanov6], [Reference Grünbaum, Vinet and Zhedanov13], [Reference Tsujimoto, Vinet and Zhedanov26], for example,
$1$
. In the spirit of [Reference Gaboriaud, Tsujimoto, Vinet and Zhedanov6], [Reference Grünbaum, Vinet and Zhedanov13], [Reference Tsujimoto, Vinet and Zhedanov26], for example,
![]() $\mathcal {X}$
,
$\mathcal {X}$
,
![]() $\mathcal {R}$
,
$\mathcal {R}$
,
![]() $\tilde {\mathcal {R}}$
are operators of Heun type.
$\tilde {\mathcal {R}}$
are operators of Heun type.
Remark 4.4. Observe that
![]() $\mathcal {M}$
precisely coincides with the hypergeometric operator (1.7), albeit in the variable z.
$\mathcal {M}$
precisely coincides with the hypergeometric operator (1.7), albeit in the variable z.
Remark 4.5. This differential model for
![]() $m\mathfrak {J}$
can also be retrieved by using the Barut–Ghirardello realisation of
$m\mathfrak {J}$
can also be retrieved by using the Barut–Ghirardello realisation of
![]() $\mathfrak {su}(1,1)$
,
$\mathfrak {su}(1,1)$
,
 $$ \begin{align} J_0&=(z-1)\frac{d}{dz} + \tau, \nonumber \\ J_+&=(z-1),\nonumber \\ J_-&=(z-1)\frac{d^2}{dz^2}+2\tau\frac{d}{dz}, \qquad \tau = \frac{1}{2}(\alpha + \beta + 1), \end{align} $$
$$ \begin{align} J_0&=(z-1)\frac{d}{dz} + \tau, \nonumber \\ J_+&=(z-1),\nonumber \\ J_-&=(z-1)\frac{d^2}{dz^2}+2\tau\frac{d}{dz}, \qquad \tau = \frac{1}{2}(\alpha + \beta + 1), \end{align} $$
in formulas (2.10), (2.11) and (2.12), giving L, M and X in terms of the
![]() $\mathfrak {su}(1,1)$
generators. Note that the variable z is here translated by
$\mathfrak {su}(1,1)$
generators. Note that the variable z is here translated by
![]() $1$
with respect to the usual Barut–Ghirardello formulas.
$1$
with respect to the usual Barut–Ghirardello formulas.
Given expression (4.4) of
![]() $P_n(z; \alpha , \beta )$
as
$P_n(z; \alpha , \beta )$
as
 $\widetilde {\langle z |}P_n(\alpha , \beta ) \rangle $
, in view of the actions (4.8) and (4.16) of L and R on the vectors
$\widetilde {\langle z |}P_n(\alpha , \beta ) \rangle $
, in view of the actions (4.8) and (4.16) of L and R on the vectors
![]() $|P_n\rangle $
, of Remark 4.1 and of the realisations of these operators already given (equations (4.20)–(4.24)), we have the following:
$|P_n\rangle $
, of Remark 4.1 and of the realisations of these operators already given (equations (4.20)–(4.24)), we have the following:
Proposition 4.2. The biorthogonal Askey polynomials
![]() $P_n(z; \alpha , \beta )$
on the unit circle satisfy the following differential identities:
$P_n(z; \alpha , \beta )$
on the unit circle satisfy the following differential identities:
 $$ \begin{align} \mathcal{L} P_n(z; \alpha, \beta) &= (n+\alpha+1) P_n(z; \alpha, \beta) - \frac{n (\alpha+\beta+n)}{\alpha+n} P_{n-1}(z; \alpha, \beta), \end{align} $$
$$ \begin{align} \mathcal{L} P_n(z; \alpha, \beta) &= (n+\alpha+1) P_n(z; \alpha, \beta) - \frac{n (\alpha+\beta+n)}{\alpha+n} P_{n-1}(z; \alpha, \beta), \end{align} $$
 $$ \begin{align} \mathcal{M} P_n(z; \alpha, \beta) &= n(n+\alpha+1) P_n(z; \alpha, \beta) - \frac{n^2 (\alpha+\beta+n)}{\alpha+n} P_{n-1}(z; \alpha, \beta), \end{align} $$
$$ \begin{align} \mathcal{M} P_n(z; \alpha, \beta) &= n(n+\alpha+1) P_n(z; \alpha, \beta) - \frac{n^2 (\alpha+\beta+n)}{\alpha+n} P_{n-1}(z; \alpha, \beta), \end{align} $$
4.3 Bispectrality
The bispectral equations of the Askey polynomials can now easily be identified and interpreted in terms of generalised eigenvalue problems.
4.3.1 The differential equation
The GEVP
![]() $M |P_n(\alpha , \beta )\rangle = n L |P_n(\alpha , \beta )\rangle $
translates after projection on
$M |P_n(\alpha , \beta )\rangle = n L |P_n(\alpha , \beta )\rangle $
translates after projection on
![]() $\widetilde {\langle z |}$
into the second-order differential equation
$\widetilde {\langle z |}$
into the second-order differential equation
with eigenvalue n and where the operators
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {L}$
are respectively given by equations (4.28) and (4.27).
$\mathcal {L}$
are respectively given by equations (4.28) and (4.27).
4.3.2 The recurrence relation
The recurrence relation is obtained by considering the GEVP
which is satisfied by construction (see equation (4.25) in Remark 4.2). Expressing in equation (4.32) the two-diagonal actions (4.27) and (4.29) of
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {R}$
, one arrives at the recurrence relation
$\mathcal {R}$
, one arrives at the recurrence relation
where
 $$ \begin{align} b_n = -\frac{\beta+n}{\alpha+n+1}, \qquad g_n = -\frac{n(n+\alpha+\beta)}{(\alpha+n)(\alpha+n+1)}. \end{align} $$
$$ \begin{align} b_n = -\frac{\beta+n}{\alpha+n+1}, \qquad g_n = -\frac{n(n+\alpha+\beta)}{(\alpha+n)(\alpha+n+1)}. \end{align} $$
This recurrence relation was obtained by Hendriksen and van Rossum in [Reference Hendriksen and van Rossum14]. It was derived in [Reference Grünbaum, Vinet and Zhedanov12] by considering linear pencils in
![]() $\mathfrak {sl}_2$
. It is also constructed through a gluing procedure by Kim and Stanton in their recent study of
$\mathfrak {sl}_2$
. It is also constructed through a gluing procedure by Kim and Stanton in their recent study of
![]() $R_I$
polynomials [Reference Kim and Stanton17].
$R_I$
polynomials [Reference Kim and Stanton17].
Remark 4.6. It is manifest from this recurrence relation of
![]() $R_I$
-type [Reference Ismail and Masson16] that z (resp., X) is a lower Hessenberg matrix on the space of Askey polynomials (resp., in the basis
$R_I$
-type [Reference Ismail and Masson16] that z (resp., X) is a lower Hessenberg matrix on the space of Askey polynomials (resp., in the basis
![]() $\{|P_n(\alpha , \beta )\rangle \}$
). This feature of the representation theory of
$\{|P_n(\alpha , \beta )\rangle \}$
). This feature of the representation theory of
![]() $m\mathfrak {J}$
was also observed in a study of the meta-Hahn algebra [Reference Vinet and Zhedanov29].
$m\mathfrak {J}$
was also observed in a study of the meta-Hahn algebra [Reference Vinet and Zhedanov29].
4.4 Contiguity relations
Some contiguity relations for the Askey polynomials also arise naturally in the meta-Jacobi algebra framework. Indeed, we already observed in equation (4.10) that the generator L has the effect of performing the shifts
![]() $\alpha \rightarrow \alpha + 1$
,
$\alpha \rightarrow \alpha + 1$
,
![]() $\beta \rightarrow \beta - 1$
when acting on
$\beta \rightarrow \beta - 1$
when acting on
![]() $|P_n (\alpha , \beta ) \rangle $
. That M has a similar effect follows from the fact that
$|P_n (\alpha , \beta ) \rangle $
. That M has a similar effect follows from the fact that
![]() $M=nL$
in the GEVP basis
$M=nL$
in the GEVP basis
![]() $|P_n (\alpha , \beta ) \rangle $
. This translates into the following for the polynomials
$|P_n (\alpha , \beta ) \rangle $
. This translates into the following for the polynomials
 $P_n(\alpha , \beta ) = \widetilde {\langle z |} P_n (\alpha , \beta )\rangle $
:
$P_n(\alpha , \beta ) = \widetilde {\langle z |} P_n (\alpha , \beta )\rangle $
:
Proposition 4.4. The Askey polynomials
![]() $P_n(\alpha , \beta )$
verify the following contiguity equations:
$P_n(\alpha , \beta )$
verify the following contiguity equations:
where
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {M}$
are the differential operators (4.20) and (4.21), respectively.
$\mathcal {M}$
are the differential operators (4.20) and (4.21), respectively.
Remark 4.7. Given the explicit form (1.1) of the Askey polynomials, these relations can be checked directly on
![]() $P_n(z;\alpha ,\beta )$
with the differential operators
$P_n(z;\alpha ,\beta )$
with the differential operators
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {M}$
. Having done this, comparing equations (4.35) and (4.36) offers a way to show that the Askey polynomials are solutions of the GEVP (4.31).
$\mathcal {M}$
. Having done this, comparing equations (4.35) and (4.36) offers a way to show that the Askey polynomials are solutions of the GEVP (4.31).
4.5 Solutions of the generalised eigenvalue problems in the differential realisation
We shall finally examine how solving the GEVP
![]() $\mathcal {M}f(z) = n \mathcal {L} f(z)$
and the adjoint problem compares to the representation-theoretic computations that were performed for the overlaps
$\mathcal {M}f(z) = n \mathcal {L} f(z)$
and the adjoint problem compares to the representation-theoretic computations that were performed for the overlaps
 $\widetilde {\langle z|}P_n(\alpha , \beta )\rangle $
and
$\widetilde {\langle z|}P_n(\alpha , \beta )\rangle $
and
 $\left \langle z |L^T |Q_m(\alpha , \beta )\right \rangle $
. A first look shows that the GEVPs in the differential model will be of hypergeometric nature, as is confirmed by the expressions of the overlaps. Let us focus on this more closely.
$\left \langle z |L^T |Q_m(\alpha , \beta )\right \rangle $
. A first look shows that the GEVPs in the differential model will be of hypergeometric nature, as is confirmed by the expressions of the overlaps. Let us focus on this more closely.
Given expressions (4.20) and (4.21) for
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {M}$
, we see that
$\mathcal {M}$
, we see that
![]() $\mathcal {M}f(z) = n \mathcal {L} f(z)$
takes the form of the hypergeometric equation [Reference Erdelyi, Magnus, Oberhettinger and Tricomi5]
$\mathcal {M}f(z) = n \mathcal {L} f(z)$
takes the form of the hypergeometric equation [Reference Erdelyi, Magnus, Oberhettinger and Tricomi5]
 $$ \begin{align} z (1-z) \frac{d^2 f}{dz^2} + [c - (a + b + 1)z] \frac{df}{dz} - ab f = 0, \end{align} $$
$$ \begin{align} z (1-z) \frac{d^2 f}{dz^2} + [c - (a + b + 1)z] \frac{df}{dz} - ab f = 0, \end{align} $$
with parameters
In the following we shall use Bateman’s nomenclature [Reference Erdelyi, Magnus, Oberhettinger and Tricomi5] for the
![]() $24$
Kummer solutions; these are arranged in six sets such that the four elements in each set represent the same function. The representatives
$24$
Kummer solutions; these are arranged in six sets such that the four elements in each set represent the same function. The representatives
![]() $u_1, u_2, \dotsc , u_6$
of the sets are in general different, although equation (3.53) is a case where
$u_1, u_2, \dotsc , u_6$
of the sets are in general different, although equation (3.53) is a case where
![]() $u_1 \propto u_2$
. With the parameters given by equation (4.38), it is immediate to see that the solution
$u_1 \propto u_2$
. With the parameters given by equation (4.38), it is immediate to see that the solution
 $$ \begin{align} u_1 = {_2}F_1 \left( {a, b\atop c}; z\right) \end{align} $$
$$ \begin{align} u_1 = {_2}F_1 \left( {a, b\atop c}; z\right) \end{align} $$
will yield directly (up to a constant) the Askey polynomials
![]() $P_n(z; \alpha , \beta )$
.
$P_n(z; \alpha , \beta )$
.
Consider now the adjoint operators
 $$ \begin{align}\begin{aligned} \mathcal{M}^T = z(z-1) \partial_z^2 + [(2-\alpha)z -\beta-1 ] \partial_z - \alpha \mathcal{I}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathcal{M}^T = z(z-1) \partial_z^2 + [(2-\alpha)z -\beta-1 ] \partial_z - \alpha \mathcal{I}. \end{aligned}\end{align} $$
The adjoint GEVP
![]() $\mathcal {M}^T f^*(z) = m \mathcal {L} f^*(z)$
also turns out to yield the hypergeometric equation (4.37), but this time with parameters
$\mathcal {M}^T f^*(z) = m \mathcal {L} f^*(z)$
also turns out to yield the hypergeometric equation (4.37), but this time with parameters
Recall that
![]() $\mathcal {L}^T f^*(z)$
will provide a solution orthogonal to
$\mathcal {L}^T f^*(z)$
will provide a solution orthogonal to
![]() $f(z)$
. Selecting
$f(z)$
. Selecting
![]() $u_1$
for
$u_1$
for
![]() $f^*$
also will lead to functions trivially orthogonal over the unit circle. Consider instead
$f^*$
also will lead to functions trivially orthogonal over the unit circle. Consider instead
 $$ \begin{align} f^*(z) = u_3 = {(1 - z)^{-a}}{}{_2}F_1 \left( {a, c - b\atop a + 1 - b}; \frac{1}{1 - z}\right). \end{align} $$
$$ \begin{align} f^*(z) = u_3 = {(1 - z)^{-a}}{}{_2}F_1 \left( {a, c - b\atop a + 1 - b}; \frac{1}{1 - z}\right). \end{align} $$
Using
 $$ \begin{align} \frac{(k + m + \alpha + 1)}{(m + \alpha + 2)_k} = \frac{(m + \alpha + 1)}{(m + \alpha + 1)_k}, \end{align} $$
$$ \begin{align} \frac{(k + m + \alpha + 1)}{(m + \alpha + 2)_k} = \frac{(m + \alpha + 1)}{(m + \alpha + 1)_k}, \end{align} $$
it is easy to find that in that case,
 $$ \begin{align} \mathcal{L}^T f^*(z) = ( m + \alpha + 1){(1-z)^{-m - 1}}{} {_2}F_1 \left( {m + 1, m + \alpha + \beta + 1\atop m + \alpha + 1}; \frac{1}{1 - z}\right). \end{align} $$
$$ \begin{align} \mathcal{L}^T f^*(z) = ( m + \alpha + 1){(1-z)^{-m - 1}}{} {_2}F_1 \left( {m + 1, m + \alpha + \beta + 1\atop m + \alpha + 1}; \frac{1}{1 - z}\right). \end{align} $$
We thus see that choosing the solution
![]() $u_3$
yields the result (3.56) obtained algebraically for
$u_3$
yields the result (3.56) obtained algebraically for
 $\left \langle z |L^T |P_m (\alpha , \beta ) \right \rangle $
. (Recall that the constant a in this expression is here set equal to
$\left \langle z |L^T |P_m (\alpha , \beta ) \right \rangle $
. (Recall that the constant a in this expression is here set equal to
![]() $1$
.) The reader is reminded of equation (3.57), where this function is seen to be composed of two parts: one a power series in z and the other the function orthogonal to the Askey polynomial dressed with the hypergeometric weight.
$1$
.) The reader is reminded of equation (3.57), where this function is seen to be composed of two parts: one a power series in z and the other the function orthogonal to the Askey polynomial dressed with the hypergeometric weight.
Let us point out that within the differential realisation, it is possible to pick a solution of
![]() $\mathcal {M}^T f^*(z) = m \mathcal {L} f^*(z)$
that will solely give the biorthogonal partner
$\mathcal {M}^T f^*(z) = m \mathcal {L} f^*(z)$
that will solely give the biorthogonal partner
 $Q_m\left (\frac {1}{z}, \alpha , \beta \right )$
multiplied by the weight. Indeed, take
$Q_m\left (\frac {1}{z}, \alpha , \beta \right )$
multiplied by the weight. Indeed, take
![]() $f^*(z)$
to be given by the solution
$f^*(z)$
to be given by the solution
 $$ \begin{align} u_4 = {(1 - z)^{-b}}{} {_2}F_1 \left( {b, c - a\atop b + 1 - a}; \frac{1}{1 - z}\right). \end{align} $$
$$ \begin{align} u_4 = {(1 - z)^{-b}}{} {_2}F_1 \left( {b, c - a\atop b + 1 - a}; \frac{1}{1 - z}\right). \end{align} $$
Substituting the parameters (4.42), we have in this instance
 $$ \begin{align} f^*(z) &= {(1 - z)^{\alpha}}{} {_2}F_1 \left( {-\alpha, \beta\atop -\alpha - m}; \frac{1}{1 - z}\right) \nonumber\\ &= \sum_{k=0}^{\infty} \frac{(-\alpha)_k (\beta)_k}{(-\alpha - m)_k} \frac{(1 - z) ^{-k + \alpha}}{k!}. \end{align} $$
$$ \begin{align} f^*(z) &= {(1 - z)^{\alpha}}{} {_2}F_1 \left( {-\alpha, \beta\atop -\alpha - m}; \frac{1}{1 - z}\right) \nonumber\\ &= \sum_{k=0}^{\infty} \frac{(-\alpha)_k (\beta)_k}{(-\alpha - m)_k} \frac{(1 - z) ^{-k + \alpha}}{k!}. \end{align} $$
The action of
![]() $\mathcal {L}^T$
is again readily computed when the argument is a function of
$\mathcal {L}^T$
is again readily computed when the argument is a function of
![]() $(1 - z)$
:
$(1 - z)$
:
 $$ \begin{align} \mathcal{L}^Tf^*(z) &= \sum_{k=1}^{\infty} \frac{(-\alpha)_k (\beta)_k}{(-\alpha - m)_k} \frac{(1 - z) ^{-k + \alpha}}{(k-1)!} \nonumber \\ &=\sum_{l=0}^{\infty} \frac{(-\alpha)_{l+1} (\beta)_{l+1}}{(-\alpha - m)_{l+1}} \frac{(1 - z) ^{-l + \alpha -1}}{l!} \nonumber \\ & = \frac{\alpha \beta}{(\alpha +m)} {(1 - z)^{\alpha -1}}{} {_2}F_1 \left( {-\alpha + 1, \beta + 1 \atop 1 -\alpha - m}; \frac{1}{1 - z}\right), \end{align} $$
$$ \begin{align} \mathcal{L}^Tf^*(z) &= \sum_{k=1}^{\infty} \frac{(-\alpha)_k (\beta)_k}{(-\alpha - m)_k} \frac{(1 - z) ^{-k + \alpha}}{(k-1)!} \nonumber \\ &=\sum_{l=0}^{\infty} \frac{(-\alpha)_{l+1} (\beta)_{l+1}}{(-\alpha - m)_{l+1}} \frac{(1 - z) ^{-l + \alpha -1}}{l!} \nonumber \\ & = \frac{\alpha \beta}{(\alpha +m)} {(1 - z)^{\alpha -1}}{} {_2}F_1 \left( {-\alpha + 1, \beta + 1 \atop 1 -\alpha - m}; \frac{1}{1 - z}\right), \end{align} $$
where we have used
![]() $(x)_{l+1} = x (x + 1)_l$
. We thus observe that the action of
$(x)_{l+1} = x (x + 1)_l$
. We thus observe that the action of
![]() $\mathcal {L}^T$
is to effect
$\mathcal {L}^T$
is to effect
![]() $ \alpha \rightarrow \alpha - 1, \; \beta \rightarrow \beta + 1$
; in view of the parameter identification (4.42), the action of
$ \alpha \rightarrow \alpha - 1, \; \beta \rightarrow \beta + 1$
; in view of the parameter identification (4.42), the action of
![]() $\mathcal {L}^T$
on
$\mathcal {L}^T$
on
![]() $u_4$
yields again
$u_4$
yields again
![]() $u_4$
, with the following parameters:
$u_4$
, with the following parameters:
Now another expression for
![]() $u_4$
is
$u_4$
is
 $$ \begin{align} u_4 = (-z)^{a - c} {(1 - z)^{c-a-b}}{} {_2}F_1 \left( {1 - a, c - a\atop b + 1 - a}; \frac{1}{z}\right). \end{align} $$
$$ \begin{align} u_4 = (-z)^{a - c} {(1 - z)^{c-a-b}}{} {_2}F_1 \left( {1 - a, c - a\atop b + 1 - a}; \frac{1}{z}\right). \end{align} $$
Using the parameters (4.49), we then find that choosing
![]() $u_4$
as solution of the hypergeometric equation stemming from the adjoint GEVP
$u_4$
as solution of the hypergeometric equation stemming from the adjoint GEVP
![]() $\mathcal {M}^T f^*(z) = m \mathcal {L} f^*(z)$
leads to
$\mathcal {M}^T f^*(z) = m \mathcal {L} f^*(z)$
leads to
 $$ \begin{align} \mathcal{L}^Tf^*(z) \propto (-z) ^{-1 - \beta} (1 - z)^{\alpha + \beta} Q_m\left(\frac{1}{z}, \alpha, \beta\right). \end{align} $$
$$ \begin{align} \mathcal{L}^Tf^*(z) \propto (-z) ^{-1 - \beta} (1 - z)^{\alpha + \beta} Q_m\left(\frac{1}{z}, \alpha, \beta\right). \end{align} $$
That is, we obtain as unique term, up to a factor, the orthogonal partner of
![]() $P_n(z; \alpha , \beta )$
multiplied by the weight.
$P_n(z; \alpha , \beta )$
multiplied by the weight.
5 Conclusion
It is now time to wrap up and offer perspectives. We have presented a unified algebraic interpretation of the biorthogonal Askey polynomials on the circle and of the Jacobi polynomials on the interval
![]() $[0, 1]$
. It is based on an algebra with three generators
$[0, 1]$
. It is based on an algebra with three generators
![]() $L, M, X$
verifying quadratic relations, which we have called the meta-Jacobi algebra and denoted by
$L, M, X$
verifying quadratic relations, which we have called the meta-Jacobi algebra and denoted by
![]() $m\mathfrak {J}$
. The Askey polynomials
$m\mathfrak {J}$
. The Askey polynomials
![]() $P_n(z; \alpha , \beta )$
arise as overlaps between the basis elements that are on the one hand the solutions, on an infinite-dimensional module, of the generalised eigenvalue problem defined by the generators L and M, and on the other hand, the eigenvectors of the adjoint of X. The biorthogonal partners
$P_n(z; \alpha , \beta )$
arise as overlaps between the basis elements that are on the one hand the solutions, on an infinite-dimensional module, of the generalised eigenvalue problem defined by the generators L and M, and on the other hand, the eigenvectors of the adjoint of X. The biorthogonal partners
![]() $Q_n(z; \alpha , \beta )$
are obtained similarly from the reciprocal adjoints. The same framework is seen to provide an algebraic picture for the Jacobi polynomials as overlaps between the eigenbases of M and of
$Q_n(z; \alpha , \beta )$
are obtained similarly from the reciprocal adjoints. The same framework is seen to provide an algebraic picture for the Jacobi polynomials as overlaps between the eigenbases of M and of
![]() $X^T$
(or of
$X^T$
(or of
![]() $M^T$
and X). Proofs of the orthogonality relations were found to follow. With the introduction of a differential model for the meta-Jacobi algebra, the bispectrality of the Askey polynomials
$M^T$
and X). Proofs of the orthogonality relations were found to follow. With the introduction of a differential model for the meta-Jacobi algebra, the bispectrality of the Askey polynomials
![]() $P_n(z; \alpha , \beta )$
was accounted for in particular; their differential equation and the recurrence relation were explicitly obtained and found to be of GEVP form.
$P_n(z; \alpha , \beta )$
was accounted for in particular; their differential equation and the recurrence relation were explicitly obtained and found to be of GEVP form.
The meta-Jacobi algebra is actually isomorphic to the universal algebra of the Lie algebra
![]() $\mathfrak {su}(1, 1)$
. We nevertheless kept with the (possibly redundant) terminology because the relevant presentation is parallel to that of the meta-Hahn algebra previously introduced [Reference Tsujimoto, Vinet and Zhedanov27], [Reference Vinet and Zhedanov29] to treat in a unified way orthogonal polynomials and biorthogonal rational functions of Hahn type. Both algebras involve a noncommutative generalisation of the plane which is supplemented by the addition of a third generator that brings to the fore significant representation-theoretic features. The use of GEVPs proved to be a key aspect. As said already in the introduction, we see a pattern develop and we suspect that it might be possible to associate meta-algebras to most entries of the Askey scheme, so as to simultaneously describe the bispectrality of the hypergeometric polynomials and of associated biorthogonal (rational) functions. This most likely relates to the forays by Kim and Stanton [Reference Kim and Stanton17] toward the development of a scheme for orthogonal polynomials of type
$\mathfrak {su}(1, 1)$
. We nevertheless kept with the (possibly redundant) terminology because the relevant presentation is parallel to that of the meta-Hahn algebra previously introduced [Reference Tsujimoto, Vinet and Zhedanov27], [Reference Vinet and Zhedanov29] to treat in a unified way orthogonal polynomials and biorthogonal rational functions of Hahn type. Both algebras involve a noncommutative generalisation of the plane which is supplemented by the addition of a third generator that brings to the fore significant representation-theoretic features. The use of GEVPs proved to be a key aspect. As said already in the introduction, we see a pattern develop and we suspect that it might be possible to associate meta-algebras to most entries of the Askey scheme, so as to simultaneously describe the bispectrality of the hypergeometric polynomials and of associated biorthogonal (rational) functions. This most likely relates to the forays by Kim and Stanton [Reference Kim and Stanton17] toward the development of a scheme for orthogonal polynomials of type
![]() $R_I$
. To be sure, it is with enthusiasm that we plan to pursue investigations of meta-algebras and their relations to special functions. Looking at further generalisations, it is known that there are elliptic biorthogonal rational functions that have an interpretation in terms of structures related to elliptic quantum groups (see, e.g., [Reference Koelink, Van Norden and Rosengren18]); it would of course be of interest to see if the analysis presented here could arise as a limit from these connections.
$R_I$
. To be sure, it is with enthusiasm that we plan to pursue investigations of meta-algebras and their relations to special functions. Looking at further generalisations, it is known that there are elliptic biorthogonal rational functions that have an interpretation in terms of structures related to elliptic quantum groups (see, e.g., [Reference Koelink, Van Norden and Rosengren18]); it would of course be of interest to see if the analysis presented here could arise as a limit from these connections.
Appendix A The computation of
 $\left \langle z | L^T | Q_m\right \rangle $
$\left \langle z | L^T | Q_m\right \rangle $
We provide in this appendix the details on how the result of Proposition 3.2 is obtained.
Given expression (3.56) for
 $\left \langle z | L^T | Q_m\right \rangle $
, we use the following linear relation between Kummer solutions of the hypergeometric equation [Reference Erdelyi, Magnus, Oberhettinger and Tricomi5]:
$\left \langle z | L^T | Q_m\right \rangle $
, we use the following linear relation between Kummer solutions of the hypergeometric equation [Reference Erdelyi, Magnus, Oberhettinger and Tricomi5]:
 $$ \begin{align} {_2}F_1\left({a, b \atop c }; z \right) &= \frac{\Gamma (a + 1 -c) \Gamma (b + 1 - c)}{\Gamma (a + b + 1 - c) \Gamma (1 - c)}{} {_2}F_1\left({a, b \atop a + b + 1 - c }; 1- z \right) \nonumber \\ & \quad - \frac{\Gamma (a + 1 - c) \Gamma (b + 1 - c) \Gamma ( c - 1)}{\Gamma (a) \Gamma (b) \Gamma (1 - c)} z^{1-c} {(1-z)^{c - a - b}} {} {_2}F_1\left({1 - a, 1 - b \atop 2 - c }; z \right). \end{align} $$
$$ \begin{align} {_2}F_1\left({a, b \atop c }; z \right) &= \frac{\Gamma (a + 1 -c) \Gamma (b + 1 - c)}{\Gamma (a + b + 1 - c) \Gamma (1 - c)}{} {_2}F_1\left({a, b \atop a + b + 1 - c }; 1- z \right) \nonumber \\ & \quad - \frac{\Gamma (a + 1 - c) \Gamma (b + 1 - c) \Gamma ( c - 1)}{\Gamma (a) \Gamma (b) \Gamma (1 - c)} z^{1-c} {(1-z)^{c - a - b}} {} {_2}F_1\left({1 - a, 1 - b \atop 2 - c }; z \right). \end{align} $$
This yields
 $$ \begin{align} &{_2}F_1\left({m+1, m + \alpha + \beta + 1 \atop m + \alpha + 1 }; \frac{1}{1-z} \right) \nonumber \\ &\quad =\frac{\Gamma (1 - \alpha) \Gamma (\beta + 1)}{\Gamma (m + \beta + 2) \Gamma (- m - \alpha)}{} {_2}F_1\left({m + 1, m + \alpha + \beta + 1 \atop m + \beta + 2 }; \frac{z}{z-1} \right) \nonumber\\ &\qquad - \frac{\Gamma (1 - \alpha) \Gamma (\beta + 1) \Gamma (m + \alpha)}{m! \Gamma (m + \alpha + \beta + 1) \Gamma (-m - \alpha)} (-z)^{-m - \beta - 1} {(1-z)^{2m + \alpha + \beta + 1}}{} {_2}F_1\left({-m, - m - \alpha - \beta \atop 1 - m - \alpha }; \frac{1}{1-z} \right). \end{align} $$
$$ \begin{align} &{_2}F_1\left({m+1, m + \alpha + \beta + 1 \atop m + \alpha + 1 }; \frac{1}{1-z} \right) \nonumber \\ &\quad =\frac{\Gamma (1 - \alpha) \Gamma (\beta + 1)}{\Gamma (m + \beta + 2) \Gamma (- m - \alpha)}{} {_2}F_1\left({m + 1, m + \alpha + \beta + 1 \atop m + \beta + 2 }; \frac{z}{z-1} \right) \nonumber\\ &\qquad - \frac{\Gamma (1 - \alpha) \Gamma (\beta + 1) \Gamma (m + \alpha)}{m! \Gamma (m + \alpha + \beta + 1) \Gamma (-m - \alpha)} (-z)^{-m - \beta - 1} {(1-z)^{2m + \alpha + \beta + 1}}{} {_2}F_1\left({-m, - m - \alpha - \beta \atop 1 - m - \alpha }; \frac{1}{1-z} \right). \end{align} $$
Now use [Reference Erdelyi, Magnus, Oberhettinger and Tricomi5],
 $$ \begin{align} {_2}F_1\left({a, c - b \atop c }; \frac{z}{z - 1} \right) = {(1 - z)^{a}}{} {_2}F_1\left({a, b \atop c }; z \right) \end{align} $$
$$ \begin{align} {_2}F_1\left({a, c - b \atop c }; \frac{z}{z - 1} \right) = {(1 - z)^{a}}{} {_2}F_1\left({a, b \atop c }; z \right) \end{align} $$
and
 $$ \begin{align} {_2}F_1\left({a, c - b \atop a + 1 - b }; \frac{1}{1-z} \right) = (1 - z)^{a} {(-z)^{- a}} {} {_2}F_1\left({a,\; a + 1 - c \atop a + 1 - b }; \frac{1}{z} \right), \end{align} $$
$$ \begin{align} {_2}F_1\left({a, c - b \atop a + 1 - b }; \frac{1}{1-z} \right) = (1 - z)^{a} {(-z)^{- a}} {} {_2}F_1\left({a,\; a + 1 - c \atop a + 1 - b }; \frac{1}{z} \right), \end{align} $$
to re-express the two
![]() ${_2}F_1$
s on the right-hand side of equation (A.2) as functions of z and
${_2}F_1$
s on the right-hand side of equation (A.2) as functions of z and
![]() $\frac {1}{z}$
, respectively. Recalling then the definition (1.2) of the biorthogonal partner
$\frac {1}{z}$
, respectively. Recalling then the definition (1.2) of the biorthogonal partner
![]() $Q_m(z, \alpha , \beta )$
of the Askey polynomials, one arrives at equation (3.57) with the help of the relation
$Q_m(z, \alpha , \beta )$
of the Askey polynomials, one arrives at equation (3.57) with the help of the relation
which is a consequence of the identity
 $$ \begin{align} \Gamma(x) \Gamma (1-x) = \frac{\pi}{\sin \pi x}. \end{align} $$
$$ \begin{align} \Gamma(x) \Gamma (1-x) = \frac{\pi}{\sin \pi x}. \end{align} $$
Appendix B The determination of
 $\langle z \widetilde {| J_n \rangle }$
$\langle z \widetilde {| J_n \rangle }$
Details on how formula (3.77) for
 $\langle z \widetilde {| J_m \rangle }$
is obtained are given here. We need to transform the
$\langle z \widetilde {| J_m \rangle }$
is obtained are given here. We need to transform the
![]() ${_2}F_1$
that occurs in expression (3.76) of this overlap. First we use the following relation between three solutions of the hypergeometric equation [Reference Erdelyi, Magnus, Oberhettinger and Tricomi5]:
${_2}F_1$
that occurs in expression (3.76) of this overlap. First we use the following relation between three solutions of the hypergeometric equation [Reference Erdelyi, Magnus, Oberhettinger and Tricomi5]:
 $$ \begin{align} {_2}F_1\left({a, b \atop c }; z \right) &= \frac{\Gamma (c) \Gamma (b - a)}{\Gamma (c - a) \Gamma (b)} {(-z)^{-a}}{} {_2}F_1\left({a, a + 1 - c \atop a + 1 - b }; \frac{1}{z} \right) \nonumber \\[6pt] & \quad + \frac{\Gamma (c) \Gamma (a - b)}{\Gamma (c-b) \Gamma (a)} (-z)^{a-c} {(1-z)^{c - a - b}} {} {_2}F_1\left({1 - a, c - a \atop b + 1 - a }; \frac{1}{z} \right). \end{align} $$
$$ \begin{align} {_2}F_1\left({a, b \atop c }; z \right) &= \frac{\Gamma (c) \Gamma (b - a)}{\Gamma (c - a) \Gamma (b)} {(-z)^{-a}}{} {_2}F_1\left({a, a + 1 - c \atop a + 1 - b }; \frac{1}{z} \right) \nonumber \\[6pt] & \quad + \frac{\Gamma (c) \Gamma (a - b)}{\Gamma (c-b) \Gamma (a)} (-z)^{a-c} {(1-z)^{c - a - b}} {} {_2}F_1\left({1 - a, c - a \atop b + 1 - a }; \frac{1}{z} \right). \end{align} $$
From this identity we find
 $$ \begin{align} &{_2}F_1\left({m+1, m + \alpha + \beta + 1 \atop 2m + \alpha + 2 }; \frac{1}{1-z} \right) \nonumber \\[6pt] &\quad = (z - 1 )^{m+1} \Bigg[\frac{\Gamma (2m + \alpha + 2) \Gamma (\alpha + \beta)}{\Gamma (m + \alpha + 1) \Gamma (m + \alpha + \beta + 1)} {} {_2}F_1\left({m + 1, -m - \alpha \atop 1 - \alpha - \beta }; 1 - z \right) \nonumber \\[6pt] &\qquad + \frac{\Gamma (2m + \alpha + 2) \Gamma (- \alpha - \beta)}{m! \Gamma (m + 1 - \beta)} z^{-\beta}{(z - 1)^{\alpha + \beta}} {} {_2}F_1\left({-m, m + \alpha + 1 \atop \alpha + \beta + 1}; 1-z \right)\Bigg]. \end{align} $$
$$ \begin{align} &{_2}F_1\left({m+1, m + \alpha + \beta + 1 \atop 2m + \alpha + 2 }; \frac{1}{1-z} \right) \nonumber \\[6pt] &\quad = (z - 1 )^{m+1} \Bigg[\frac{\Gamma (2m + \alpha + 2) \Gamma (\alpha + \beta)}{\Gamma (m + \alpha + 1) \Gamma (m + \alpha + \beta + 1)} {} {_2}F_1\left({m + 1, -m - \alpha \atop 1 - \alpha - \beta }; 1 - z \right) \nonumber \\[6pt] &\qquad + \frac{\Gamma (2m + \alpha + 2) \Gamma (- \alpha - \beta)}{m! \Gamma (m + 1 - \beta)} z^{-\beta}{(z - 1)^{\alpha + \beta}} {} {_2}F_1\left({-m, m + \alpha + 1 \atop \alpha + \beta + 1}; 1-z \right)\Bigg]. \end{align} $$
We now apply relation (A.1) to convert each of the two
![]() ${_2}F_1$
s on the right-hand side of equation (B.2) that are functions of
${_2}F_1$
s on the right-hand side of equation (B.2) that are functions of
![]() $(1-z)$
into combinations of
$(1-z)$
into combinations of
![]() ${_2}F_1$
s that are functions of z. This leads to
${_2}F_1$
s that are functions of z. This leads to
 $$ \begin{align} &{_2}F_1\left({m+1, m + \alpha + \beta + 1 \atop 2m + \alpha + 2 }; \frac{1}{1-z} \right) \nonumber \\[6pt] &\quad = \frac{\Gamma (2m + \alpha + 2) \Gamma(\alpha + \beta)\Gamma (1 - \alpha - \beta) \Gamma(-\beta) }{\Gamma (m + \alpha + 1) \Gamma (m + \alpha + \beta + 1) \Gamma (1 +m - \beta) \Gamma (-m - \alpha - \beta) } {(z-1)^{m + 1}}{} {_2}F_1\left({m + 1, -m - \alpha \atop 1 + \beta }; z \right) \nonumber\\[6pt] & \qquad + \Bigg[(-1)^{\left(\alpha + \beta\right)}\frac{\Gamma (2m + \alpha + 2) \Gamma (\alpha +\beta)\Gamma (1 - \alpha - \beta) \Gamma (\beta)}{m! \Gamma (m + \alpha + 1) \Gamma (-m - \alpha) \Gamma (m + \alpha + \beta +1)} \nonumber \\[6pt] &\qquad + \frac{\Gamma( 2m + \alpha + 2) \Gamma (- \alpha - \beta) \Gamma (\alpha + \beta + 1) \Gamma (\beta)}{m! \Gamma (m + 1 - \beta)\Gamma (-m + \beta) \Gamma (m + \alpha + \beta + 1)}\Bigg] z^{-\beta}{(z - 1)^{m + 1 +\alpha + \beta}} {} {_2}F_1\left({-m, m + \alpha + 1 \atop 1 - \beta}; z \right). \end{align} $$
$$ \begin{align} &{_2}F_1\left({m+1, m + \alpha + \beta + 1 \atop 2m + \alpha + 2 }; \frac{1}{1-z} \right) \nonumber \\[6pt] &\quad = \frac{\Gamma (2m + \alpha + 2) \Gamma(\alpha + \beta)\Gamma (1 - \alpha - \beta) \Gamma(-\beta) }{\Gamma (m + \alpha + 1) \Gamma (m + \alpha + \beta + 1) \Gamma (1 +m - \beta) \Gamma (-m - \alpha - \beta) } {(z-1)^{m + 1}}{} {_2}F_1\left({m + 1, -m - \alpha \atop 1 + \beta }; z \right) \nonumber\\[6pt] & \qquad + \Bigg[(-1)^{\left(\alpha + \beta\right)}\frac{\Gamma (2m + \alpha + 2) \Gamma (\alpha +\beta)\Gamma (1 - \alpha - \beta) \Gamma (\beta)}{m! \Gamma (m + \alpha + 1) \Gamma (-m - \alpha) \Gamma (m + \alpha + \beta +1)} \nonumber \\[6pt] &\qquad + \frac{\Gamma( 2m + \alpha + 2) \Gamma (- \alpha - \beta) \Gamma (\alpha + \beta + 1) \Gamma (\beta)}{m! \Gamma (m + 1 - \beta)\Gamma (-m + \beta) \Gamma (m + \alpha + \beta + 1)}\Bigg] z^{-\beta}{(z - 1)^{m + 1 +\alpha + \beta}} {} {_2}F_1\left({-m, m + \alpha + 1 \atop 1 - \beta}; z \right). \end{align} $$
Simplifications are carried out through repeated use of identity (A.6) and various implications, such as equation (A.5), and by observing that
 $$ \begin{align} &\frac{1}{\sin \pi(\alpha + \beta)} \left((-1)^{\alpha + \beta} \sin \pi \alpha + \sin \pi \beta \right) \nonumber \\[3pt] &\quad = \frac{e^{i \pi \alpha}}{\sin \pi (\alpha + \beta)} \left(e^{i \pi \beta} \sin \pi \alpha + e^{-i \pi \alpha} \sin \pi \beta\right) = e^{i \pi \alpha} = (-1)^{\alpha}. \end{align} $$
$$ \begin{align} &\frac{1}{\sin \pi(\alpha + \beta)} \left((-1)^{\alpha + \beta} \sin \pi \alpha + \sin \pi \beta \right) \nonumber \\[3pt] &\quad = \frac{e^{i \pi \alpha}}{\sin \pi (\alpha + \beta)} \left(e^{i \pi \beta} \sin \pi \alpha + e^{-i \pi \alpha} \sin \pi \beta\right) = e^{i \pi \alpha} = (-1)^{\alpha}. \end{align} $$
One finally obtains
 $$ \begin{align} &{_2}F_1\left({m+1, m + \alpha + \beta + 1 \atop 2m + \alpha + 2 }; \frac{1}{1-z} \right) \nonumber \\[5pt] &\quad = (1 - z )^{m+1} \Bigg[\frac{\Gamma (2m + \alpha + 2) \Gamma(-\beta)}{\Gamma (m + \alpha + 1) \Gamma (m - \beta + 1)} {} {_2}F_1\left({m + 1, -m - \alpha \atop 1 + \beta }; z \right) \nonumber\\[5pt] &\qquad + \frac{\Gamma (2m + \alpha + 2) \Gamma (\beta)}{m! \Gamma (m + \alpha + \beta +1)} (-z)^{-\beta}{(1-z)^{\alpha + \beta}} {} {_2}F_1\left({-m, m + \alpha + 1 \atop 1 - \beta}; z \right)\Bigg], \end{align} $$
$$ \begin{align} &{_2}F_1\left({m+1, m + \alpha + \beta + 1 \atop 2m + \alpha + 2 }; \frac{1}{1-z} \right) \nonumber \\[5pt] &\quad = (1 - z )^{m+1} \Bigg[\frac{\Gamma (2m + \alpha + 2) \Gamma(-\beta)}{\Gamma (m + \alpha + 1) \Gamma (m - \beta + 1)} {} {_2}F_1\left({m + 1, -m - \alpha \atop 1 + \beta }; z \right) \nonumber\\[5pt] &\qquad + \frac{\Gamma (2m + \alpha + 2) \Gamma (\beta)}{m! \Gamma (m + \alpha + \beta +1)} (-z)^{-\beta}{(1-z)^{\alpha + \beta}} {} {_2}F_1\left({-m, m + \alpha + 1 \atop 1 - \beta}; z \right)\Bigg], \end{align} $$
which readily gives equation (3.77).
Appendix C Negative eigenvalues
In the main part of the paper, it sufficed for the purpose of interpreting the Askey polynomials and their biorthogonal partners to focus on GEVP and EVP solutions with nonnegative (integer) eigenvalues. For completeness, we briefly indicate in this appendix how situations with negative integers can be treated and seen to lead to redundant information.
C.1
Consider equation (3.32) and assume that
![]() $n < 0$
. Let
$n < 0$
. Let
In this case, the recursion relation still implies
![]() $d_n(k) = 0$
for
$d_n(k) = 0$
for
![]() $k> n$
but no longer bounds k from below. Write k in the form
$k> n$
but no longer bounds k from below. Write k in the form
Upon substituting in equations (C.1) and (C.2) and taking
![]() $d_n(k) \equiv \tilde {d}_s(s+l)$
, equation (3.32) becomes
$d_n(k) \equiv \tilde {d}_s(s+l)$
, equation (3.32) becomes
We observe that this last relation coincides with condition (3.36), which was obtained from the adjoint GEVP with a positive eigenvalue under the substitutions
Hence,
 $$ \begin{align} d_n(k)= d_{-s-1}(-s-1-l)=(-1)^l \frac{(s+1)_l (s-\alpha - \beta + 1)_l}{l! (s - \alpha + 1)_l} d_n(n), \qquad s, l = 0, 1, 2, \dotsc. \end{align} $$
$$ \begin{align} d_n(k)= d_{-s-1}(-s-1-l)=(-1)^l \frac{(s+1)_l (s-\alpha - \beta + 1)_l}{l! (s - \alpha + 1)_l} d_n(n), \qquad s, l = 0, 1, 2, \dotsc. \end{align} $$
C.2
Examine now equation (3.36) when
![]() $m < 0$
. Set
$m < 0$
. Set
![]() $m=-s-1, s=0, 1, \dotsc $
. In this case, the recursion equation implies that
$m=-s-1, s=0, 1, \dotsc $
. In this case, the recursion equation implies that
![]() $d^*_m (k)=0$
for
$d^*_m (k)=0$
for
![]() $k<m$
and also truncates at
$k<m$
and also truncates at
![]() $k=0$
. The nonzero values of
$k=0$
. The nonzero values of
![]() $d_n^*(k)$
therefore only occur for
$d_n^*(k)$
therefore only occur for
Incorporating the previous redefinitions in equation (3.36) and taking
 $d^*_m(k)=d_{-s-1}^*(-l-1) \equiv \tilde {d}_m^*(l)$
, we get
$d^*_m(k)=d_{-s-1}^*(-l-1) \equiv \tilde {d}_m^*(l)$
, we get
and we see that this equation can be retrieved from equation (3.32) under the substitutions
It follows that for negative m that
 $$ \begin{align} d_m^*(k)=d_{-s-1}^*(-l - 1) = (-1)^l \frac{(-s)_l(-\alpha)_l}{l! (-\alpha -\beta + 1)_l} d^*_n(-1), \qquad l=0, \dotsc, s. \end{align} $$
$$ \begin{align} d_m^*(k)=d_{-s-1}^*(-l - 1) = (-1)^l \frac{(-s)_l(-\alpha)_l}{l! (-\alpha -\beta + 1)_l} d^*_n(-1), \qquad l=0, \dotsc, s. \end{align} $$
C.3
We may check the orthogonality of
![]() $|P_n\rangle $
and
$|P_n\rangle $
and
![]() $L^T|Q_m\rangle $
,
$L^T|Q_m\rangle $
,
![]() $m \neq n$
, for various possibilities regarding the sign of the indices m and n. In summary, the summation ranges are as follows:
$m \neq n$
, for various possibilities regarding the sign of the indices m and n. In summary, the summation ranges are as follows:
-
• For
 $n \geq 0, m\geq 0$
, (C.10)
$n \geq 0, m\geq 0$
, (C.10) $$ \begin{align} &|P_n\rangle = \sum_{k=0} ^{n} d_n(k) |\tau, k\rangle, \end{align} $$
(C.11)
$$ \begin{align} &|P_n\rangle = \sum_{k=0} ^{n} d_n(k) |\tau, k\rangle, \end{align} $$
(C.11) $$ \begin{align} &|Q_m\rangle = \sum_{k=m} ^{\infty} d_m(k) |\tau, k\rangle. \end{align} $$
$$ \begin{align} &|Q_m\rangle = \sum_{k=m} ^{\infty} d_m(k) |\tau, k\rangle. \end{align} $$
-
• For
 $n < 0, m < 0$
, (C.12)
$n < 0, m < 0$
, (C.12) $$ \begin{align} &|P_n\rangle = \sum_{k=-\infty} ^{n} d_n(k) |\tau, k\rangle, \end{align} $$
(C.13)
$$ \begin{align} &|P_n\rangle = \sum_{k=-\infty} ^{n} d_n(k) |\tau, k\rangle, \end{align} $$
(C.13) $$ \begin{align} &|Q_m\rangle = \sum_{k=m} ^{-1} d_m(k) |\tau, k\rangle. \end{align} $$
$$ \begin{align} &|Q_m\rangle = \sum_{k=m} ^{-1} d_m(k) |\tau, k\rangle. \end{align} $$
It is manifest that orthogonality prevails when one index is nonnegative and the other is negative. When the two indices are negative, the proof of orthogonality follows the one given for two nonnegative indices, since as we observed, the change of signs basically flips the coefficients d and
![]() $d^*$
.
$d^*$
.
C.4
Regarding the special functions, in light of this exchange of the expansion coefficients, the roles of
![]() $|P_n\rangle $
and
$|P_n\rangle $
and
![]() $L^T|Q_m\rangle $
are inverted when the indices are negative. For instance, we have
$L^T|Q_m\rangle $
are inverted when the indices are negative. For instance, we have
 $$ \begin{align} |Q_{-s-1}\rangle = \sum_{l=0}^s (-1)^l \frac{(-s)_l(-\alpha)_l}{l! (-\alpha - \beta + 1)_l} |\tau, -l-1\rangle. \end{align} $$
$$ \begin{align} |Q_{-s-1}\rangle = \sum_{l=0}^s (-1)^l \frac{(-s)_l(-\alpha)_l}{l! (-\alpha - \beta + 1)_l} |\tau, -l-1\rangle. \end{align} $$
The overlap of
![]() $L^T|Q_{-s-1}\rangle $
with the state
$L^T|Q_{-s-1}\rangle $
with the state
![]() $|z\rangle $
given in equation (3.20) is then found to be
$|z\rangle $
given in equation (3.20) is then found to be
 $$ \begin{align} \left\langle z |L^T|Q_{-s-1}\right\rangle = \alpha d_{-s-1}(-1) {(z-1)^{\tilde{a}-1}}{} {_2}F_1\left({-s, 1-\alpha \atop 1-\alpha -\beta }; 1- z \right). \end{align} $$
$$ \begin{align} \left\langle z |L^T|Q_{-s-1}\right\rangle = \alpha d_{-s-1}(-1) {(z-1)^{\tilde{a}-1}}{} {_2}F_1\left({-s, 1-\alpha \atop 1-\alpha -\beta }; 1- z \right). \end{align} $$
Owing again to equation (3.53), we see that the Askey polynomials arise in this case in the overlap
 $ \left \langle z |L^T|Q_{-s-1}\right \rangle $
with a change of parameters.
$ \left \langle z |L^T|Q_{-s-1}\right \rangle $
with a change of parameters.
Again, when nonterminating series are encountered, the proper convergence restrictions can be imposed so that the full overlaps are defined or one may take a formal approach to get at the polynomials.
C.5
Things can be seen to proceed similarly in the treatment of the Jacobi polynomials if negative indices are considered.
Acknowledgments
The authors are grateful to Tom Koornwinder for correspondence and for bringing some references to their attention. They have much appreciated Erik Koelink’s comments on the manuscript and are thankful to Julien Gaboriaud for kind assistance. The second author acknowledges the hospitality of the CRM over an extended period and the award of a Simons CRM professorship.
Funding statement
The work of the first author is supported in part by a Discovery Grant from the Natural Sciences and Engineering Research Council (NSERC) of Canada. The second author is funded by the National Foundation of China (grant 11771015).
Conflicts of Interest
None.