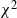1. Introduction
Markov Chain Monte Carlo (MCMC) is one of the main sampling methods in Bayesian statistics. Given a target density
![]() $\pi$
with respect to Lebsegue measure on
$\pi$
with respect to Lebsegue measure on
![]() $\mathbb{R}^d$
, an MCMC algorithm often simulates a Markov chain
$\mathbb{R}^d$
, an MCMC algorithm often simulates a Markov chain
![]() $(X_n)_{n\geq 0}$
, with transition kernel
$(X_n)_{n\geq 0}$
, with transition kernel
![]() $P$
, such that
$P$
, such that
![]() $\pi$
is its corresponding invariant measure. Under some generic conditions, the distribution of
$\pi$
is its corresponding invariant measure. Under some generic conditions, the distribution of
![]() $X_n$
converges to
$X_n$
converges to
![]() $\pi$
geometrically quickly. This indicates the existence of some mixing time
$\pi$
geometrically quickly. This indicates the existence of some mixing time
![]() $n_0$
, such that the distribution of
$n_0$
, such that the distribution of
![]() $X_n$
is close to
$X_n$
is close to
![]() $\pi$
when
$\pi$
when
![]() $n>n_0$
. In other words, given a test function
$n>n_0$
. In other words, given a test function
![]() $f\;:\;\mathbb{R}^d\to \mathbb{R}$
, we can use the following approximation:
$f\;:\;\mathbb{R}^d\to \mathbb{R}$
, we can use the following approximation:
In practice, this allows us to approximate the average of a test function
![]() $\mathbb{E}^\pi f(X)$
using the temporal average of the Markov chain:
$\mathbb{E}^\pi f(X)$
using the temporal average of the Markov chain:
The efficiency of the approximation scheme (2) is largely determined by the convergence speed of the Markov Chain
![]() $(X_n)_{n\geq 0}$
to
$(X_n)_{n\geq 0}$
to
![]() $\pi$
or the mixing time
$\pi$
or the mixing time
![]() $n_0$
. In particular, it will take
$n_0$
. In particular, it will take
![]() $O(n_0)$
iterations to produce an approximately independent sample. In this context, convergence analysis has been a key component in the MCMC literature (see, for example, Section 4.1 of [Reference Andrieu, De Freitas, Doucet and Jordan1, Reference Joulin and Ollivier27]).
$O(n_0)$
iterations to produce an approximately independent sample. In this context, convergence analysis has been a key component in the MCMC literature (see, for example, Section 4.1 of [Reference Andrieu, De Freitas, Doucet and Jordan1, Reference Joulin and Ollivier27]).
When implementing MCMC on complicated target densities, it is often the case that we can simulate only a perturbed Markov chain
![]() $(\widehat{X}_n)_{n\geq 0}$
with transition kernel
$(\widehat{X}_n)_{n\geq 0}$
with transition kernel
![]() $\widehat{P}$
. This is mainly due to two reasons:
$\widehat{P}$
. This is mainly due to two reasons:
-
(i) The transition kernel
 $P$
cannot be simulated directly. For example, if
$P$
cannot be simulated directly. For example, if
 $(X_n)_{n\geq 0}$
is described by a stochastic differential equation (SDE) evaluated at a countable set of time points, using numerical schemes like the Euler–Maruyama method will induce discretization errors.
$(X_n)_{n\geq 0}$
is described by a stochastic differential equation (SDE) evaluated at a countable set of time points, using numerical schemes like the Euler–Maruyama method will induce discretization errors. -
(ii) We do not have direct access to
 $\pi(x)$
or its derivatives. This is quite common in Bayesian inverse problems [Reference Stuart40], where the target density can be written as(3)In (3),
$\pi(x)$
or its derivatives. This is quite common in Bayesian inverse problems [Reference Stuart40], where the target density can be written as(3)In (3), \begin{equation}\pi(x)\propto p_0(x)\exp\left(-\tfrac12 \|G(x)-y\|^2\right).\end{equation}
\begin{equation}\pi(x)\propto p_0(x)\exp\left(-\tfrac12 \|G(x)-y\|^2\right).\end{equation}
 $p_0$
is the prior density of the unknown parameter
$p_0$
is the prior density of the unknown parameter
 $x$
,
$x$
,
 $G$
describes the data-generating process, and
$G$
describes the data-generating process, and
 $y$
is the observed data. In many cases,
$y$
is the observed data. In many cases,
 $G$
is formulated through an involved partial differential equation, and we can compute only an approximation of it,
$G$
is formulated through an involved partial differential equation, and we can compute only an approximation of it,
 $\widehat{G}$
[Reference Beskos, Jasra, Law, Marzouk and Zhou5, Reference Bui-Thanh, Ghattas, Martin and Stadler7, Reference Hairer, Stuart and Vollmer21]. The corresponding “numerical” density becomes(4)In other settings, we may have access to
$\widehat{G}$
[Reference Beskos, Jasra, Law, Marzouk and Zhou5, Reference Bui-Thanh, Ghattas, Martin and Stadler7, Reference Hairer, Stuart and Vollmer21]. The corresponding “numerical” density becomes(4)In other settings, we may have access to \begin{equation}\widehat{\pi}(x)\propto p_0(x)\exp\left(-\tfrac12 \|\widehat{G}(x)-y\|^2\right).\end{equation}
\begin{equation}\widehat{\pi}(x)\propto p_0(x)\exp\left(-\tfrac12 \|\widehat{G}(x)-y\|^2\right).\end{equation}
 $\pi(x)$
, but accurate evaluation of its gradient
$\pi(x)$
, but accurate evaluation of its gradient
 $\nabla \pi(x)$
may not be accessible since it often involves highly dimensional adjoint models. If we want to use gradient-based MCMC, e.g. Metropolis Adjusted Langevin Algorithm (MALA), we can use only an approximately correct proposal. However, the Metropolis–Hastings step can guarantee that the target density remains the same, i.e.
$\nabla \pi(x)$
may not be accessible since it often involves highly dimensional adjoint models. If we want to use gradient-based MCMC, e.g. Metropolis Adjusted Langevin Algorithm (MALA), we can use only an approximately correct proposal. However, the Metropolis–Hastings step can guarantee that the target density remains the same, i.e.
 $\widehat{\pi}=\pi$
.
$\widehat{\pi}=\pi$
.
In the above-mentioned scenarios, we run an MCMC
![]() $(\widehat{X}_n)_{n\geq 0}$
with transition kernel
$(\widehat{X}_n)_{n\geq 0}$
with transition kernel
![]() $\widehat{P}$
and target density
$\widehat{P}$
and target density
![]() $\widehat{\pi}$
, which is the invariant measure of
$\widehat{\pi}$
, which is the invariant measure of
![]() $(\widehat{X}_n)_{n\geq 0}$
. In both scenarios (1) and (2) listed above, we would like to approximate
$(\widehat{X}_n)_{n\geq 0}$
. In both scenarios (1) and (2) listed above, we would like to approximate
![]() $\mathbb{E}^{\pi} f(X)$
using
$\mathbb{E}^{\pi} f(X)$
using
There are two key questions to address when using estimators of the form (5): The first question concerens the convergence speed of
![]() $(\widehat{X}_n)_{n\geq 0}$
toward its invariant measure
$(\widehat{X}_n)_{n\geq 0}$
toward its invariant measure
![]() $\widehat{\pi}$
, which determines the efficiency of the estimators in (5). In particular, if we use
$\widehat{\pi}$
, which determines the efficiency of the estimators in (5). In particular, if we use
![]() $D$
to denote some metric between two distributions and use
$D$
to denote some metric between two distributions and use
![]() $\nu$
to denote the distribution of
$\nu$
to denote the distribution of
![]() $\widehat{X}_0$
, we are interested in how quickly
$\widehat{X}_0$
, we are interested in how quickly
![]() $D(\nu\widehat{P}^n, \widehat{\pi})$
converges to zero. The second question concerns approximation accuracy, which can be measured by either the distance between the two invariant measures,
$D(\nu\widehat{P}^n, \widehat{\pi})$
converges to zero. The second question concerns approximation accuracy, which can be measured by either the distance between the two invariant measures,
![]() $D(\widehat{\pi}, \pi)$
or the distance between the distribution of
$D(\widehat{\pi}, \pi)$
or the distance between the distribution of
![]() $\widehat{X}_n$
and
$\widehat{X}_n$
and
![]() $\pi$
,
$\pi$
,
![]() $D(\nu\widehat{P}^n, \pi)$
. For MCMC based on
$D(\nu\widehat{P}^n, \pi)$
. For MCMC based on
![]() $(\widehat{X}_n)_{n\geq 0}$
to achieve fast convergence and high approximation accuracy, we need to impose the following two high-level conditions (these conditions will be made more precise in our subsequent development) [Reference Andrieu, De Freitas, Doucet and Jordan1]:
$(\widehat{X}_n)_{n\geq 0}$
to achieve fast convergence and high approximation accuracy, we need to impose the following two high-level conditions (these conditions will be made more precise in our subsequent development) [Reference Andrieu, De Freitas, Doucet and Jordan1]:
-
(1)
 $\widehat{P}$
is a good approximation of
$\widehat{P}$
is a good approximation of
 $P$
.
$P$
. -
(2)
 $(X_n)_{n\geq 0}$
converges to its invariant measure
$(X_n)_{n\geq 0}$
converges to its invariant measure
 $\pi$
quickly enough.
$\pi$
quickly enough.
Condition 1 is necessary because if
![]() $\widehat{P}$
is not a good approximation of
$\widehat{P}$
is not a good approximation of
![]() $P$
,
$P$
,
![]() $\widehat{\pi}$
is unlikely to be close to
$\widehat{\pi}$
is unlikely to be close to
![]() $\pi$
, and the convergence property of
$\pi$
, and the convergence property of
![]() $(X_n)_{n\geq 0}$
will not be useful in inferring the convergence property of
$(X_n)_{n\geq 0}$
will not be useful in inferring the convergence property of
![]() $(\widehat{X}_n)_{n\geq 0}$
. Condition 2 is also necessary. Otherwise, the approximation error may increase with the number of iterations. For example, one can think of an unstable autoregressive sequence in which numerical errors often increase exponentially with the number of iterations. Since Condition 1 involves only the one-step transition kernels, it is easier to fulfill. Hence, it is reasonable to study Condition 2 first and then formulate a version of Condition 1 that is compatible with the corresponding Condition 2.
$(\widehat{X}_n)_{n\geq 0}$
. Condition 2 is also necessary. Otherwise, the approximation error may increase with the number of iterations. For example, one can think of an unstable autoregressive sequence in which numerical errors often increase exponentially with the number of iterations. Since Condition 1 involves only the one-step transition kernels, it is easier to fulfill. Hence, it is reasonable to study Condition 2 first and then formulate a version of Condition 1 that is compatible with the corresponding Condition 2.
In the literature on Markov chains, convergence to stationarity is often studied using one of two frameworks. The main differences between the two frameworks are the metrics and the analytical tools involved. The first type of metric are the Wasserstein metrics [Reference Meyn and Tweedie31]. The associated convergence results are often termed “geometric ergodicity.” Establishing convergence under the Wasserstein metrics often involves finding an appropriate Lyapunov function
![]() $V$
and constructing an appropriate coupling [Reference Lindvall28]. For simplicity, we will call this framework Wasserstein convergence. The second framework uses the
$V$
and constructing an appropriate coupling [Reference Lindvall28]. For simplicity, we will call this framework Wasserstein convergence. The second framework uses the
![]() $\chi^2$
distance [Reference Bakry, Gentil and Ledoux3] (or KL-divergence as in [Reference Vempala and Wibisono45]). Establishing convergence under the
$\chi^2$
distance [Reference Bakry, Gentil and Ledoux3] (or KL-divergence as in [Reference Vempala and Wibisono45]). Establishing convergence under the
![]() $\chi^2$
distance often involves functional analysis or other partial differential equation (PDE) tools such as Poincaré inequality and log Sobolev inequality. For simplicity, we will refer to this framework as the “
$\chi^2$
distance often involves functional analysis or other partial differential equation (PDE) tools such as Poincaré inequality and log Sobolev inequality. For simplicity, we will refer to this framework as the “
![]() $\chi^2$
convergence”.
$\chi^2$
convergence”.
Establishing Wasserstein convergence is often viewed as being more intuitive, as it involves a standard Lyapunov function and coupling construction. Establishing
![]() $\chi^2$
convergence can be weaker, but it often provides tighter quantification, especially in high-dimensional settings. For example, for the unadjusted Langevin algorithm, [Reference Chen, Du and Tong9] uses Wasserstein convergence, and the analysis works only for a fixed dimension; [Reference Dong and Tong11, Reference Vempala and Wibisono45] use
$\chi^2$
convergence can be weaker, but it often provides tighter quantification, especially in high-dimensional settings. For example, for the unadjusted Langevin algorithm, [Reference Chen, Du and Tong9] uses Wasserstein convergence, and the analysis works only for a fixed dimension; [Reference Dong and Tong11, Reference Vempala and Wibisono45] use
![]() $\chi^2$
convergence, and the analysis works in high-dimensional settings. We also note that these two frameworks are related: In particular, on one hand, under suitable regularity conditions, geometric ergodicity leads to the existence of a spectral gap and, hence,
$\chi^2$
convergence, and the analysis works in high-dimensional settings. We also note that these two frameworks are related: In particular, on one hand, under suitable regularity conditions, geometric ergodicity leads to the existence of a spectral gap and, hence,
![]() $\chi^2$
convergence (see, for example, Proposition 2.8 in [Reference Hairer, Stuart and Vollmer21]; see also [Reference Gallegos-Herrada, Ledvinka and Rosenthal19] for a more complete discussion of the connection). On the other hand, under proper regularity conditions, convergence under the
$\chi^2$
convergence (see, for example, Proposition 2.8 in [Reference Hairer, Stuart and Vollmer21]; see also [Reference Gallegos-Herrada, Ledvinka and Rosenthal19] for a more complete discussion of the connection). On the other hand, under proper regularity conditions, convergence under the
![]() $\chi^2$
distance leads to convergence under the total variation distance.
$\chi^2$
distance leads to convergence under the total variation distance.
We discuss both frameworks in this paper because for some Markov chains, we may have knowledge of only one form of convergence. For example, to the best of our knowledge, the parallel tempering methods are studied only under the
![]() $\chi^2$
distance [Reference Dong and Tong12, Reference Woodard, Schmidler and Huber46]. Preconditioned Crank–Nicolson algorithms are studied only under the Wasserstein distance [Reference Hairer, Stuart and Vollmer21]. The unadjusted Langevin algorithm was first studied under the Wasserstein distance [Reference Durmus and Moulines14, Reference Dwivedi, Chen, Wainwright and Yu16] and was later studied under the KL divergence [Reference Vempala and Wibisono45]. While there might be theoretical value to establishing convergence in both metrics, doing so is practically unnecessary. In this paper, we assume the convergence of
$\chi^2$
distance [Reference Dong and Tong12, Reference Woodard, Schmidler and Huber46]. Preconditioned Crank–Nicolson algorithms are studied only under the Wasserstein distance [Reference Hairer, Stuart and Vollmer21]. The unadjusted Langevin algorithm was first studied under the Wasserstein distance [Reference Durmus and Moulines14, Reference Dwivedi, Chen, Wainwright and Yu16] and was later studied under the KL divergence [Reference Vempala and Wibisono45]. While there might be theoretical value to establishing convergence in both metrics, doing so is practically unnecessary. In this paper, we assume the convergence of
![]() $(X_n)_{n\geq 0}$
under either the Wasserstein distance or the
$(X_n)_{n\geq 0}$
under either the Wasserstein distance or the
![]() $\chi^2$
distance, and we then study the convergence of
$\chi^2$
distance, and we then study the convergence of
![]() $(\widehat{X}_n)_{n\geq 0}$
under one of the two metrics accordingly. We address the question not only qualitatively but also quantitatively in order to establish bounds for the convergence speed and the approximation accuracy of
$(\widehat{X}_n)_{n\geq 0}$
under one of the two metrics accordingly. We address the question not only qualitatively but also quantitatively in order to establish bounds for the convergence speed and the approximation accuracy of
![]() $(\widehat{X}_n)_{n\geq 0}$
.
$(\widehat{X}_n)_{n\geq 0}$
.
1.1. Related literature
The approximation and convergence questions we study here are fundamental for MCMC and have been studied in various settings before. Most existing works focus on specific approximation schemes. For example, [Reference Breyer, Roberts and Rosenthal6, Reference Roberts, Rosenthal and Schwartz35] study ergodicity of
![]() $\widehat{P}$
if
$\widehat{P}$
if
![]() $\widehat{P}(x,A)=P(x,h^{-1}(A))$
for some round-off function
$\widehat{P}(x,A)=P(x,h^{-1}(A))$
for some round-off function
![]() $h$
. [Reference Hervé and Ledoux22] studies the ergodicity property of finite-rank, nonnegative, sub-Markov kernels in relation to the ergodicity property of the original Markov kernel. [Reference Bardenet, Doucet and Holmes4] studies the convergence and approximation problems of an adaptive subsampling approach under the assumption of uniform ergodicity. [Reference Medina-Aguayo, Rudolf and Schweizer30] studies the approximation problem for Monte Carlo within Metropolis algorithms. In general, there is a lack of a unified framework.
$h$
. [Reference Hervé and Ledoux22] studies the ergodicity property of finite-rank, nonnegative, sub-Markov kernels in relation to the ergodicity property of the original Markov kernel. [Reference Bardenet, Doucet and Holmes4] studies the convergence and approximation problems of an adaptive subsampling approach under the assumption of uniform ergodicity. [Reference Medina-Aguayo, Rudolf and Schweizer30] studies the approximation problem for Monte Carlo within Metropolis algorithms. In general, there is a lack of a unified framework.
To provide a comprehensive overview of how perturbation of MCMC affects the approximation accuracy and convergence speed, we put together four sets of results. First, we study the approximation problem under the Wasserstein distance, i.e. the ergodicity framework. The corresponding result (Theorem 1) is taken directly from [Reference Rudolf and Schweizer38]. Approximation accuracy—i.e. bounds for the difference between the
![]() $n$
th step distributions of the perturbed chain and the original chain, under the Wasserstein distance—has also been studied in [Reference Johndrow and Mattingly25, Reference Pillai and Smith34, Reference Shardlow and Stuart39] under similar but arguably stronger assumptions. For example, [Reference Shardlow and Stuart39] requires the perturbed chain to remain close to the original Markov chain uniformly over a bounded number of iterations, while we require controlling the errors of only one-step transition kernels. [Reference Pillai and Smith34] focuses on MCMC algorithms with the subsampling type of errors. It requires the existence of a subset
$n$
th step distributions of the perturbed chain and the original chain, under the Wasserstein distance—has also been studied in [Reference Johndrow and Mattingly25, Reference Pillai and Smith34, Reference Shardlow and Stuart39] under similar but arguably stronger assumptions. For example, [Reference Shardlow and Stuart39] requires the perturbed chain to remain close to the original Markov chain uniformly over a bounded number of iterations, while we require controlling the errors of only one-step transition kernels. [Reference Pillai and Smith34] focuses on MCMC algorithms with the subsampling type of errors. It requires the existence of a subset
![]() $\hat G$
in which both the unperturbed and the perturbed chains remain with a high probability and there is a uniform bound on the errors of one-step transition kernels on
$\hat G$
in which both the unperturbed and the perturbed chains remain with a high probability and there is a uniform bound on the errors of one-step transition kernels on
![]() $\hat G$
. [Reference Johndrow and Mattingly25] requires the Markov chains to be uniformly ergodic, which limits the applicability of the results to non-compact-state spaces. Second, we study the convergence problem under the Wasserstein distance. The corresponding result (Theorem 2) is new but follows from similar lines of analysis as in [Reference Rudolf and Schweizer38]. The papers [Reference Johndrow and Mattingly24, Reference Pillai and Smith34] also analyze the convergence of the perturbed chain, under only the total variation distance, however (and thus requires uniform ergodicity rather than geometric ergodicity). The convergence problem has also been studied in [Reference Ferré, Hervé and Ledoux18], but [Reference Ferré, Hervé and Ledoux18] does not quantify how the convergence rate depends on the perturbation size. Third and fourth, we study the convergence and the approximation problems under the
$\hat G$
. [Reference Johndrow and Mattingly25] requires the Markov chains to be uniformly ergodic, which limits the applicability of the results to non-compact-state spaces. Second, we study the convergence problem under the Wasserstein distance. The corresponding result (Theorem 2) is new but follows from similar lines of analysis as in [Reference Rudolf and Schweizer38]. The papers [Reference Johndrow and Mattingly24, Reference Pillai and Smith34] also analyze the convergence of the perturbed chain, under only the total variation distance, however (and thus requires uniform ergodicity rather than geometric ergodicity). The convergence problem has also been studied in [Reference Ferré, Hervé and Ledoux18], but [Reference Ferré, Hervé and Ledoux18] does not quantify how the convergence rate depends on the perturbation size. Third and fourth, we study the convergence and the approximation problems under the
![]() $\chi^2$
distance. The recent work [Reference Negrea and Rosenthal32] studies the approximation accuracy and the convergence rate of
$\chi^2$
distance. The recent work [Reference Negrea and Rosenthal32] studies the approximation accuracy and the convergence rate of
![]() $\widehat{P}$
under the
$\widehat{P}$
under the
![]() $\chi^2$
distance. Compared to our work, [Reference Negrea and Rosenthal32] requires stronger assumptions. For example, [Reference Negrea and Rosenthal32] requires
$\chi^2$
distance. Compared to our work, [Reference Negrea and Rosenthal32] requires stronger assumptions. For example, [Reference Negrea and Rosenthal32] requires
![]() $\widehat{P}$
to be
$\widehat{P}$
to be
![]() $L_2(\pi) \rightarrow L_2(\pi)$
, which can be difficult to verify in practice.
$L_2(\pi) \rightarrow L_2(\pi)$
, which can be difficult to verify in practice.
As just reviewed, many existing works focus on studying the approximation problem. The convergence problem is less studied. However, it is worth pointing out that most of these approximation results show only
where
![]() $\rho$
is the convergence rate of
$\rho$
is the convergence rate of
![]() $P$
and
$P$
and
![]() $\epsilon$
is the difference between
$\epsilon$
is the difference between
![]() $P$
and
$P$
and
![]() $\widehat{P}$
. Because
$\widehat{P}$
. Because
![]() $\epsilon$
is nonzero, this does not directly imply the convergence of
$\epsilon$
is nonzero, this does not directly imply the convergence of
![]() $D(\nu \widehat{P}^n, \widehat{\pi})$
to zero. Moreover, if one has a convergence result, e.g.
$D(\nu \widehat{P}^n, \widehat{\pi})$
to zero. Moreover, if one has a convergence result, e.g.
![]() $D(\nu \widehat{P}^n, \widehat{\pi})=O(\hat{\rho}^n)$
for some
$D(\nu \widehat{P}^n, \widehat{\pi})=O(\hat{\rho}^n)$
for some
![]() $\hat{\rho}\in (0,1)$
, and if
$\hat{\rho}\in (0,1)$
, and if
![]() $\widehat{\pi}$
has an explicit smaller approximation error
$\widehat{\pi}$
has an explicit smaller approximation error
![]() $D(\pi, \widehat{\pi})=o(\epsilon)$
, using triangular inequality, we can establish a tighter upper bound for
$D(\pi, \widehat{\pi})=o(\epsilon)$
, using triangular inequality, we can establish a tighter upper bound for
![]() $D(\nu \widehat{P}^n, \pi)$
.
$D(\nu \widehat{P}^n, \pi)$
.
Lastly, while the connection between the Wasserstein convergence and the MCMC sampling error is well known, most results are asymptotic, i.e. in the form of the central limit theorem [Reference Jones26]. Non-asymptotic error bounds are more useful in practice [Reference Joulin and Ollivier27]. Our work provides a comprehensive list of finite-sample performance quantifications for numerical MCMC samplers. We demonstrate that our results can be easily applied to the analysis of various algorithms in Sections 4 and 5.
1.2. Notations
For a probability measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{R}^d$
, we define
$\mathbb{R}^d$
, we define
We also use
![]() $\mu(dx)$
to denote the corresponding density function. For
$\mu(dx)$
to denote the corresponding density function. For
![]() $\mu$
-squared integrable functions
$\mu$
-squared integrable functions
![]() $f,g\;:\; \Omega \rightarrow \mathbb{R}$
, we define the inner product with respect to
$f,g\;:\; \Omega \rightarrow \mathbb{R}$
, we define the inner product with respect to
![]() $\mu$
as
$\mu$
as
Then,
![]() $\|\,f\|_{\mu}^2 =\langle f,f\rangle_{\mu}=\int_{\mathbb{R}^d} f(x)^2\mu(dx)$
. In what follows, we omit
$\|\,f\|_{\mu}^2 =\langle f,f\rangle_{\mu}=\int_{\mathbb{R}^d} f(x)^2\mu(dx)$
. In what follows, we omit
![]() $\mathbb{R}^d$
from the integral notation when it is clear from the context. For a transition kernel
$\mathbb{R}^d$
from the integral notation when it is clear from the context. For a transition kernel
![]() $P$
, we define
$P$
, we define
For a measurable function
![]() $f$
, we define
$f$
, we define
![]() $\delta_xPf=Pf(x)=\int f(y)P(x,dy)$
. We say that
$\delta_xPf=Pf(x)=\int f(y)P(x,dy)$
. We say that
![]() $P$
is symmetric with respect to
$P$
is symmetric with respect to
![]() $\pi$
if for any measurable functions
$\pi$
if for any measurable functions
![]() $f,g$
,
$f,g$
,
Lastly, we denote
![]() $C$
as a generic constant whose value can change from line to line.
$C$
as a generic constant whose value can change from line to line.
1.3. Organization
We start by developing general results for the Wasserstein convergence in Section 2 and the
![]() $\chi^2$
convergence in Section 3. We demonstrate how to apply these frameworks on two popular Metropolis–Hastings–MCMC algorithms in Section 4 and on the more involved parallel tempering algorithm in Section 5. Finally, in Section 6, we verify our claims numerically on a Bayesian inverse problem, which tries to infer the initial condition and the model parameters in the predator–prey system.
$\chi^2$
convergence in Section 3. We demonstrate how to apply these frameworks on two popular Metropolis–Hastings–MCMC algorithms in Section 4 and on the more involved parallel tempering algorithm in Section 5. Finally, in Section 6, we verify our claims numerically on a Bayesian inverse problem, which tries to infer the initial condition and the model parameters in the predator–prey system.
2. Wasserstein Convergence
We start our discussion with the Wasserstein convergence. Following [Reference Rudolf and Schweizer38], we first introduce the metric we use and the notion of ergodicity. For a lower semi-continuous function
![]() $V\;:\;\mathbb{R}^d \rightarrow [1,\infty]$
, we define
$V\;:\;\mathbb{R}^d \rightarrow [1,\infty]$
, we define
For two probability measures
![]() $\mu$
and
$\mu$
and
![]() $\nu$
on
$\nu$
on
![]() $\mathbb{R}^d$
, we define
$\mathbb{R}^d$
, we define
It can be shown that
![]() $\|\mu-\nu\|_V=W_{d_V}(\mu,\nu)$
where
$\|\mu-\nu\|_V=W_{d_V}(\mu,\nu)$
where
![]() $W$
denotes the Wasserstein distance (Lemma 3.1 in [Reference Rudolf and Schweizer38]). If we use the constant function
$W$
denotes the Wasserstein distance (Lemma 3.1 in [Reference Rudolf and Schweizer38]). If we use the constant function
![]() $V(x)=1$
, this gives the well-known total variation distance, i.e.
$V(x)=1$
, this gives the well-known total variation distance, i.e.
Note that using
![]() $V(x)=1$
neglects the location information of
$V(x)=1$
neglects the location information of
![]() $x$
. This location information can be crucial for problems with unbounded domains.
$x$
. This location information can be crucial for problems with unbounded domains.
In general, for problems with unbounded domains, one often chooses
![]() $V$
to be a Lyapunov function. Given a Markov chain
$V$
to be a Lyapunov function. Given a Markov chain
![]() $X_n$
with transition kernel
$X_n$
with transition kernel
![]() $P$
, which we will write together as
$P$
, which we will write together as
![]() $(X_n, P)$
for short, we say
$(X_n, P)$
for short, we say
![]() $V\;:\;\mathbb{R}^d\to [1,\infty)$
is a Lyapunov function if there exist
$V\;:\;\mathbb{R}^d\to [1,\infty)$
is a Lyapunov function if there exist
![]() $\lambda\in(0,1)$
and
$\lambda\in(0,1)$
and
![]() $L>0$
such that
$L>0$
such that
and the sublevel sets of
![]() $V$
are compact. The choice of
$V$
are compact. The choice of
![]() $V$
depends on the Markov chain and the target density. It can often be chosen as
$V$
depends on the Markov chain and the target density. It can often be chosen as
![]() $\|x\|^2$
or
$\|x\|^2$
or
![]() $-\log \pi(x)$
or as functions of certain moments; see, for example, [Reference Hairer and Mattingly20, Reference Hairer, Stuart and Vollmer21, Reference Rudolf and Schweizer38].
$-\log \pi(x)$
or as functions of certain moments; see, for example, [Reference Hairer and Mattingly20, Reference Hairer, Stuart and Vollmer21, Reference Rudolf and Schweizer38].
If
![]() $\pi$
is the invariant measure of
$\pi$
is the invariant measure of
![]() $X_n$
, we say
$X_n$
, we say
![]() $X_n$
is geometrically ergodic under
$X_n$
is geometrically ergodic under
![]() $\|\,\cdot\,\|_V$
(see Theorem 16.1 in [Reference Meyn and Tweedie31]) if there are constants
$\|\,\cdot\,\|_V$
(see Theorem 16.1 in [Reference Meyn and Tweedie31]) if there are constants
![]() $\rho\in(0,1)$
and
$\rho\in(0,1)$
and
![]() $C_0\in(0,\infty)$
, such that for any
$C_0\in(0,\infty)$
, such that for any
![]() $n\in \mathbb{Z}^+$
,
$n\in \mathbb{Z}^+$
,
We refer to
![]() $\rho$
as the ergodicity coefficient. Note that the smaller the value of
$\rho$
as the ergodicity coefficient. Note that the smaller the value of
![]() $\rho$
, the faster the convergence to stationarity. From (8), using the triangle inequality, we obtain an equivalent definition of geometric ergodicity, which requires that for any
$\rho$
, the faster the convergence to stationarity. From (8), using the triangle inequality, we obtain an equivalent definition of geometric ergodicity, which requires that for any
![]() $x$
and
$x$
and
![]() $y$
,
$y$
,
The equivalence can be seen from
where
![]() $C_0=C_0^{\prime}(1+ \pi V )$
.
$C_0=C_0^{\prime}(1+ \pi V )$
.
The approximation problem under Wasserstein distance has been studied in [Reference Rudolf and Schweizer38]. We present one of their main results here, which is related to our subsequent development. Interested readers can find more general discussion in the original work.
Theorem 1. (Corollary 3.3 in [Reference Rudolf and Schweizer38]) Suppose
![]() $(X_n, P)$
is geometrically ergodic, i.e., as in (9). Suppose
$(X_n, P)$
is geometrically ergodic, i.e., as in (9). Suppose
![]() $\widehat{V}$
is a Lyapunov function for
$\widehat{V}$
is a Lyapunov function for
![]() $(\widehat{X}_n,\widehat{P})$
in the sense of (7) and that
$(\widehat{X}_n,\widehat{P})$
in the sense of (7) and that
Then, for some constant
![]() $C$
, we have
$C$
, we have
The bound in (12) and the triangular inequality give us an approximation error bound
for some constant
![]() $C'$
.
$C'$
.
Remark 1. By restricting our attention to distance functions of the form (6), we focus on a specific form of Wasserstein distance due to its connection to geometric ergodicity. The work [Reference Rudolf and Schweizer38] also studies the approximation problem under a more general form of Wasserstein ergodicity (see Theorem 3.1 in [Reference Rudolf and Schweizer38]).
Note that the right-hand side of (12) is not converging to zero as
![]() $n\to 0$
. Thus, it cannot help us learn the ergodicity of
$n\to 0$
. Thus, it cannot help us learn the ergodicity of
![]() $\widehat{X}_n$
or whether
$\widehat{X}_n$
or whether
![]() $\widehat{X}_n$
has a unique invariant measure. The next result shows that ergodicity can be obtained with essentially the same conditions as Theorem 1 (note that condition (8) leads to (13) through (10)).
$\widehat{X}_n$
has a unique invariant measure. The next result shows that ergodicity can be obtained with essentially the same conditions as Theorem 1 (note that condition (8) leads to (13) through (10)).
Theorem 2.
Suppose
![]() $V$
is a Lyapunov function for
$V$
is a Lyapunov function for
![]() $P$
in the sense of (7). In addition, assume there exist
$P$
in the sense of (7). In addition, assume there exist
![]() $N\in \mathbb{Z}^+$
and
$N\in \mathbb{Z}^+$
and
![]() $\rho\in(0,1)$
, such that for any
$\rho\in(0,1)$
, such that for any
![]() $n\geq N$
,
$n\geq N$
,
Lastly, there is an
![]() $\epsilon_0>0$
, and the following holds for some
$\epsilon_0>0$
, and the following holds for some
![]() $\epsilon\in(0,\epsilon_0]$
,
$\epsilon\in(0,\epsilon_0]$
,
Then,
![]() $V$
is a Lyapunov function for
$V$
is a Lyapunov function for
![]() $\widehat{P}$
as well with
$\widehat{P}$
as well with
Moreover,
![]() $\widehat{X}_n$
has a unique invariant measure
$\widehat{X}_n$
has a unique invariant measure
![]() $\widehat{\pi}$
and there exist
$\widehat{\pi}$
and there exist
![]() $C_1,D_1\in(0,\infty)$
independent of
$C_1,D_1\in(0,\infty)$
independent of
![]() $\epsilon$
, such that
$\epsilon$
, such that
In Theorem 2,
![]() $\epsilon_0$
is chosen such that
$\epsilon_0$
is chosen such that
![]() $\lambda+\epsilon_0<1$
and
$\lambda+\epsilon_0<1$
and
![]() $\rho+D_1\epsilon_0<1$
. Theorem 2 indicates that if
$\rho+D_1\epsilon_0<1$
. Theorem 2 indicates that if
![]() $P$
is geometrically ergodic with ergodicity coefficient
$P$
is geometrically ergodic with ergodicity coefficient
![]() $\rho$
and if
$\rho$
and if
![]() $\widehat{P}$
is
$\widehat{P}$
is
![]() $\epsilon$
-close to
$\epsilon$
-close to
![]() $P$
as characterized by (14),
$P$
as characterized by (14),
![]() $\widehat{P}$
is also geometrically ergodic. Moreover, the ergodicity coefficient of
$\widehat{P}$
is also geometrically ergodic. Moreover, the ergodicity coefficient of
![]() $\widehat{P}$
is bounded above by
$\widehat{P}$
is bounded above by
![]() $\rho+D_1\epsilon$
.
$\rho+D_1\epsilon$
.
In statistical applications, we are more interested in turning convergence results into error bounds for the Monte Carlo estimators. The central limit theorem of ergodic Markov chains was studied in [Reference Jones26, Reference Tierney44], which provide asymptotic error quantifications. In practice, non-asymptotic bounds for finite values of
![]() $n$
may be more desirable. The following proposition appeared in [Reference Joulin and Ollivier27, Reference Rudolf37]. We provide an explicit statement here to show the variance bound along with a simple proof for self-completeness. For simplicity, we assume the Markov chain is initialized with the invariant measure, i.e.
$n$
may be more desirable. The following proposition appeared in [Reference Joulin and Ollivier27, Reference Rudolf37]. We provide an explicit statement here to show the variance bound along with a simple proof for self-completeness. For simplicity, we assume the Markov chain is initialized with the invariant measure, i.e.
![]() $\widehat{X}_0\sim\widehat{\pi}$
, so a burn-in period is not necessary.
$\widehat{X}_0\sim\widehat{\pi}$
, so a burn-in period is not necessary.
Proposition 1.
Suppose
![]() $\|\delta_x\widehat{P}^n-\delta_y \widehat{P}^n\|_V\leq \widehat{\rho}^n d_V(x,y)$
for some
$\|\delta_x\widehat{P}^n-\delta_y \widehat{P}^n\|_V\leq \widehat{\rho}^n d_V(x,y)$
for some
![]() $\widehat{\rho}\in (0,1)$
. Then, for any
$\widehat{\rho}\in (0,1)$
. Then, for any
![]() $f$
that is 1-Lipschitz under
$f$
that is 1-Lipschitz under
![]() $\|\,\cdot\,\|_V$
,
$\|\,\cdot\,\|_V$
,
In addition, if we use
![]() $\hat{f}_M=\frac{1}{M}\sum_{k=1}^M f(\widehat{X}_k)$
as an estimator of
$\hat{f}_M=\frac{1}{M}\sum_{k=1}^M f(\widehat{X}_k)$
as an estimator of
![]() $\widehat{\pi} f$
starting from
$\widehat{\pi} f$
starting from
![]() $\widehat{X}_0\sim \widehat{\pi}$
,
$\widehat{X}_0\sim \widehat{\pi}$
,
In many applications, we are interested in the properties of
![]() $\widehat{\pi}$
on compact regions. In these scenarios, the associated test functions will be bounded, and
$\widehat{\pi}$
on compact regions. In these scenarios, the associated test functions will be bounded, and
![]() $1$
-Lipschitz will be under
$1$
-Lipschitz will be under
![]() $\|\,\cdot\,\|_V$
. To learn tail properties of
$\|\,\cdot\,\|_V$
. To learn tail properties of
![]() $\widehat{\pi}$
such as intermittency, the test functions often need to grow with
$\widehat{\pi}$
such as intermittency, the test functions often need to grow with
![]() $\|x\|$
. In order to apply Proposition 2, we would need the Lyapunov function
$\|x\|$
. In order to apply Proposition 2, we would need the Lyapunov function
![]() $V$
to grow at a similar scale.
$V$
to grow at a similar scale.
3.
 $\chi^2$
convergence
$\chi^2$
convergence
In this section, we discuss convergence under the
![]() $\chi^2$
divergence. We first introduce some notations. For a transition kernel
$\chi^2$
divergence. We first introduce some notations. For a transition kernel
![]() $P$
and density
$P$
and density
![]() $\mu$
, we define
$\mu$
, we define
where
![]() $\|\,f\|_{\mu}^2=\langle f, f\rangle_{\mu}$
. For two probability measures
$\|\,f\|_{\mu}^2=\langle f, f\rangle_{\mu}$
. For two probability measures
![]() $\mu$
and
$\mu$
and
![]() $\nu$
on
$\nu$
on
![]() $\mathbb{R}^d$
, where
$\mathbb{R}^d$
, where
![]() $\nu$
is absolutely continuous with respect to
$\nu$
is absolutely continuous with respect to
![]() $\mu$
, we define the
$\mu$
, we define the
![]() $\chi^2$
divergence of
$\chi^2$
divergence of
![]() $\nu$
from
$\nu$
from
![]() $\mu$
as:
$\mu$
as:
For a transition kernel
![]() $P$
that is reversible with respect to
$P$
that is reversible with respect to
![]() $\pi$
, the spectral gap of
$\pi$
, the spectral gap of
![]() $P$
is defined as [Reference Hairer, Stuart and Vollmer21]
$P$
is defined as [Reference Hairer, Stuart and Vollmer21]
Note that by repeatedly applying (15), we have for any
![]() $f\in L^2(\pi)$
$f\in L^2(\pi)$
Thus, the larger the spectral gap, the more quickly
![]() $X_n$
converges to its invariant measure.
$X_n$
converges to its invariant measure.
Remark 2. An alternative definition of the spectral gap takes the form [Reference Andrieu and Vihola2, Reference Bakry, Gentil and Ledoux3]
Note that these two spectral gaps are related through
![]() $1-\kappa(P)=(1-\kappa_a(P))^2$
.
$1-\kappa(P)=(1-\kappa_a(P))^2$
.
3.1. General
 $\chi^2$
approximation and convergence
$\chi^2$
approximation and convergence
Theorem 3.
Our first result assumes that
![]() $(X_n,P)$
has a spectral gap and that
$(X_n,P)$
has a spectral gap and that
![]() $\widehat{P}$
is a close approximation of
$\widehat{P}$
is a close approximation of
![]() $P$
: Suppose
$P$
: Suppose
![]() $P$
is a reversible transition kernel with invariant measure
$P$
is a reversible transition kernel with invariant measure
![]() $\pi$
and a spectral gap
$\pi$
and a spectral gap
![]() $\kappa(P)>0$
in the sense of (15). There is an
$\kappa(P)>0$
in the sense of (15). There is an
![]() $\epsilon_0>0$
such that for any transition kernel
$\epsilon_0>0$
such that for any transition kernel
![]() $\widehat{P}$
satisfying
$\widehat{P}$
satisfying
![]() $\|P-\widehat{P}\|_\pi\leq \epsilon<\epsilon_0$
and any
$\|P-\widehat{P}\|_\pi\leq \epsilon<\epsilon_0$
and any
![]() $a\in(0,1)$
, there exists a constant
$a\in(0,1)$
, there exists a constant
![]() $C$
that may depend on
$C$
that may depend on
![]() $\kappa(P)$
such that the following holds with
$\kappa(P)$
such that the following holds with
![]() $\widehat{\kappa}=(1-a)\kappa(P)-\frac{C\epsilon^2}{a}\in(0,1)$
:
$\widehat{\kappa}=(1-a)\kappa(P)-\frac{C\epsilon^2}{a}\in(0,1)$
:
-
(i) For any
 $f\in L^2(\pi)$
,
$f\in L^2(\pi)$
, \begin{align*}\|\widehat{P}^nf-\pi\widehat{P}^nf\|_{\pi}^2 \leq (1-\widehat{\kappa})^{n}\textrm{var}_\pi f \end{align*}
\begin{align*}\|\widehat{P}^nf-\pi\widehat{P}^nf\|_{\pi}^2 \leq (1-\widehat{\kappa})^{n}\textrm{var}_\pi f \end{align*}
-
(ii)
 $\widehat{P}$
has an invariant measure
$\widehat{P}$
has an invariant measure
 $\widehat{\pi}$
, which satisfies
$\widehat{\pi}$
, which satisfies
 \begin{align*}|(\widehat{\pi}-\pi \widehat{P}^n)f|^2 \leq C\epsilon^2(1-\widehat{\kappa})^{n}\textrm{var}_\pi f.\end{align*}
\begin{align*}|(\widehat{\pi}-\pi \widehat{P}^n)f|^2 \leq C\epsilon^2(1-\widehat{\kappa})^{n}\textrm{var}_\pi f.\end{align*}
Moreover,
 $D_{\chi^2}(\widehat{\pi}\|\pi)\leq C\epsilon^2$
.
$D_{\chi^2}(\widehat{\pi}\|\pi)\leq C\epsilon^2$
.
In Theorem 3,
![]() $\epsilon_0$
is chosen such that
$\epsilon_0$
is chosen such that
![]() $\hat\kappa\in(0,1)$
. Theorem 3 indicates that if
$\hat\kappa\in(0,1)$
. Theorem 3 indicates that if
![]() $\widehat{P}$
and
$\widehat{P}$
and
![]() $P$
are
$P$
are
![]() $\epsilon$
-close to each other as quantified by
$\epsilon$
-close to each other as quantified by
![]() $\|\widehat{P}-P\|_{\pi}\leq \epsilon$
, then
$\|\widehat{P}-P\|_{\pi}\leq \epsilon$
, then
![]() $\widehat{P}$
has a stationary distribution
$\widehat{P}$
has a stationary distribution
![]() $\widehat{\pi}$
. Moreover,
$\widehat{\pi}$
. Moreover,
![]() $\widehat{\pi}$
and
$\widehat{\pi}$
and
![]() $\pi$
are
$\pi$
are
![]() $\epsilon$
-close to each other as quantified by
$\epsilon$
-close to each other as quantified by
![]() $D_{\chi^2}(\widehat{\pi}\|\pi)\leq C\epsilon^2$
. We also note that showing that
$D_{\chi^2}(\widehat{\pi}\|\pi)\leq C\epsilon^2$
. We also note that showing that
![]() $\|\widehat{P}^nf-\pi\widehat{P}^nf\|_{\pi}^2 \leq (1-\widehat{\kappa})^{n} \textrm{var}_\pi f$
is different than finding the spectral gap of
$\|\widehat{P}^nf-\pi\widehat{P}^nf\|_{\pi}^2 \leq (1-\widehat{\kappa})^{n} \textrm{var}_\pi f$
is different than finding the spectral gap of
![]() $\widehat{P}$
, since the latter would need a similar inequality but with
$\widehat{P}$
, since the latter would need a similar inequality but with
![]() $\pi$
replaced by
$\pi$
replaced by
![]() $\widehat{\pi}$
. In other words, Theorem 3 does not provide a spectral gap for
$\widehat{\pi}$
. In other words, Theorem 3 does not provide a spectral gap for
![]() $\widehat{P}$
. On the other hand, we can obtain error bounds for Monte Carlo estimators using the bounds established in Theorem 3:
$\widehat{P}$
. On the other hand, we can obtain error bounds for Monte Carlo estimators using the bounds established in Theorem 3:
Proposition 2.
Under the same conditions as those in Theorem 3, for any
![]() $f\in L^2(\pi)$
and any initial distribution
$f\in L^2(\pi)$
and any initial distribution
![]() $\widehat{X}_0\sim \nu\ll\pi$
, there exists a constant
$\widehat{X}_0\sim \nu\ll\pi$
, there exists a constant
![]() $C$
such that
$C$
such that
In addition, if
![]() $f$
is bounded, there exists a constant
$f$
is bounded, there exists a constant
![]() $C$
such that
$C$
such that
where
![]() $\hat{f}_M=\frac{1}{M}\sum_{k=1}^M f(\widehat{X}_k)$
.
$\hat{f}_M=\frac{1}{M}\sum_{k=1}^M f(\widehat{X}_k)$
.
Remark 3. [Reference Negrea and Rosenthal32] provides a result similar to the first claim in Theorem 3 (see Lemma A.6 in [Reference Negrea and Rosenthal32]). But it requires stronger assumptions on
![]() $\widehat{P}$
, namely, it requires that
$\widehat{P}$
, namely, it requires that
![]() $\widehat{P}$
is ergodic and aperiodic and that it is a mapping from
$\widehat{P}$
is ergodic and aperiodic and that it is a mapping from
![]() $L_2(\pi)$
to
$L_2(\pi)$
to
![]() $L_2(\pi)$
. Our result does not require these assumptions.
$L_2(\pi)$
. Our result does not require these assumptions.
3.2. Spectral gap with density ratio bounds
In this section, we show that stronger results can be established if we can bound the ratio between the invariant densities
![]() $\pi$
and
$\pi$
and
![]() $\widehat{\pi}$
. Such a bound is assessable if we have an explicit characterization of
$\widehat{\pi}$
. Such a bound is assessable if we have an explicit characterization of
![]() $\widehat{\pi}$
. For example, in Bayesian inverse problems,
$\widehat{\pi}$
. For example, in Bayesian inverse problems,
![]() $\pi(x)\propto p_0(x)\exp\!({-}\frac12\|G(x)-y\|^2)$
, while
$\pi(x)\propto p_0(x)\exp\!({-}\frac12\|G(x)-y\|^2)$
, while
![]() $\widehat{\pi}(x)\propto p_0(x)\exp\!({-}\frac12\|\widehat{G}(x)-y\|^2)$
. In this case, a density ratio bound can be obtained if
$\widehat{\pi}(x)\propto p_0(x)\exp\!({-}\frac12\|\widehat{G}(x)-y\|^2)$
. In this case, a density ratio bound can be obtained if
![]() $\|G(x)-\widehat{G}(x)\|$
is bounded. This is practically feasible by using an accurate numerical approximation of
$\|G(x)-\widehat{G}(x)\|$
is bounded. This is practically feasible by using an accurate numerical approximation of
![]() $G$
; and the approximation error can be estimated by the grid size or Galerkin truncation used in the numerical scheme (see, for example, [Reference Hoang, Schwab and Stuart23]). Similar assumptions have also been imposed in existing Bayesian computation literature; see, for example, [Reference Beskos, Jasra, Law, Marzouk and Zhou5].
$G$
; and the approximation error can be estimated by the grid size or Galerkin truncation used in the numerical scheme (see, for example, [Reference Hoang, Schwab and Stuart23]). Similar assumptions have also been imposed in existing Bayesian computation literature; see, for example, [Reference Beskos, Jasra, Law, Marzouk and Zhou5].
Theorem 4.
Suppose
![]() $P$
and
$P$
and
![]() $\widehat{P}$
are two reversible transition kernels with invariant densities
$\widehat{P}$
are two reversible transition kernels with invariant densities
![]() $\pi$
and
$\pi$
and
![]() $\widehat{\pi}$
respectively. We further assume that
$\widehat{\pi}$
respectively. We further assume that
![]() $\pi(x)/\widehat{\pi}(x)\in [(1+\epsilon)^{-1}, 1+\epsilon]$
, and that
$\pi(x)/\widehat{\pi}(x)\in [(1+\epsilon)^{-1}, 1+\epsilon]$
, and that
![]() $\|P-\widehat{P}\|_{\pi}\leq\epsilon$
. Then there exists a universal constant
$\|P-\widehat{P}\|_{\pi}\leq\epsilon$
. Then there exists a universal constant
![]() $C$
such that
$C$
such that
Note that for
![]() $\epsilon$
small enough,
$\epsilon$
small enough,
![]() $\kappa(P)-C\epsilon>0$
. Based on the spectral gap, we have the following non-asymptotic Monte Carlo error bound:
$\kappa(P)-C\epsilon>0$
. Based on the spectral gap, we have the following non-asymptotic Monte Carlo error bound:
Proposition 3.
Suppose
![]() $(\widehat{X}_n,\widehat{P})$
has a spectral gap
$(\widehat{X}_n,\widehat{P})$
has a spectral gap
![]() $\widehat{\kappa}$
. Suppose the initial distribution is
$\widehat{\kappa}$
. Suppose the initial distribution is
![]() $\nu$
, i.e.
$\nu$
, i.e.
![]() $\widehat{X}_0\sim \nu$
. Then
$\widehat{X}_0\sim \nu$
. Then
In addition, if
![]() $\nu=\widehat{\pi}$
, then for
$\nu=\widehat{\pi}$
, then for
![]() $\hat{f}_M=\frac{1}{M}\sum_{k=1}^M$
, we have
$\hat{f}_M=\frac{1}{M}\sum_{k=1}^M$
, we have
Note that Proposition 3 is not a new result. A more delicate central limit theorem version of it can be found as Theorem 4.4 of [Reference Hairer, Stuart and Vollmer21]. We provide a short proof of the proposition in the Appendix B for self-completeness.
Before we conclude our discussion of the
![]() $\chi^2$
convergence, we remark that even though the condition
$\chi^2$
convergence, we remark that even though the condition
![]() $\|P-\widehat{P}\|_\pi\leq \epsilon$
is reasonable for the spectral gap analysis, it can be hard to verify directly in some applications. To remedy this issue, the next proposition shows that we can bound
$\|P-\widehat{P}\|_\pi\leq \epsilon$
is reasonable for the spectral gap analysis, it can be hard to verify directly in some applications. To remedy this issue, the next proposition shows that we can bound
![]() $\|P-\widehat{P}\|_\pi$
through a bound for
$\|P-\widehat{P}\|_\pi$
through a bound for
![]() $\|\delta_x P - \delta_x\widehat{P}\|_{TV}$
, which can be easier to obtain using coupling techniques.
$\|\delta_x P - \delta_x\widehat{P}\|_{TV}$
, which can be easier to obtain using coupling techniques.
Proposition 4.
Suppose there exists a
![]() $\pi$
-measurable function
$\pi$
-measurable function
![]() $V\;:\;\mathbb{R}^d\rightarrow[1,\infty)$
such that
$V\;:\;\mathbb{R}^d\rightarrow[1,\infty)$
such that
![]() $\|\delta_x P - \delta_x\widehat{P}\|_{TV}\leq \epsilon V(x)$
. In addition, suppose
$\|\delta_x P - \delta_x\widehat{P}\|_{TV}\leq \epsilon V(x)$
. In addition, suppose
![]() $\frac1a\leq \pi(x)/\hat\pi(x)\leq a$
for some constant
$\frac1a\leq \pi(x)/\hat\pi(x)\leq a$
for some constant
![]() $a>0$
. Then
$a>0$
. Then
4. Application: Metropolis–Hastings MCMC on perturbed densities
Random walk Metropolis (RWM) and Metropolis adjusted Langevin algorithm (MALA) are two popular MCMC samplers when it comes to sampling a generic density
![]() $\pi$
. Many existing works have already studied their spectral gap under suitable conditions on
$\pi$
. Many existing works have already studied their spectral gap under suitable conditions on
![]() $\pi$
[Reference Dwivedi, Chen, Wainwright and Yu15, Reference Hairer, Stuart and Vollmer21, Reference Roberts and Tweedie36]. When implementing these samplers, it is often the case that we have access only to an approximation of
$\pi$
[Reference Dwivedi, Chen, Wainwright and Yu15, Reference Hairer, Stuart and Vollmer21, Reference Roberts and Tweedie36]. When implementing these samplers, it is often the case that we have access only to an approximation of
![]() $\pi$
, which we denote as
$\pi$
, which we denote as
![]() $\widehat{\pi}$
. In this section, we will demonstrate how to apply our analysis framework to establish proper bounds for the spectral gap of the “numerical” RWM and MALA.
$\widehat{\pi}$
. In this section, we will demonstrate how to apply our analysis framework to establish proper bounds for the spectral gap of the “numerical” RWM and MALA.
In fact, we can develop some general results for the Metropolis–Hastings (MH) type of Monte Carlo algorithm. Assume the proposals are given by some smooth transition density
![]() $R(x,x^{\prime})$
. Due to the possibility of rejection, MH Monte Carlo transition densities w.r.t. Lebesgue measure can be written as
$R(x,x^{\prime})$
. Due to the possibility of rejection, MH Monte Carlo transition densities w.r.t. Lebesgue measure can be written as
![]() $P(x,x^{\prime})=\gamma(x)\delta_x(x^{\prime})+\beta(x,x^{\prime})$
with
$P(x,x^{\prime})=\gamma(x)\delta_x(x^{\prime})+\beta(x,x^{\prime})$
with
The perturbed transition density can be written as
![]() $\widehat{P}(x,x^{\prime})=\hat{\gamma}(x)\delta_x(x^{\prime})+\widehat{\beta}(x,x^{\prime})$
. We provide some sufficient conditions under which the difference between
$\widehat{P}(x,x^{\prime})=\hat{\gamma}(x)\delta_x(x^{\prime})+\widehat{\beta}(x,x^{\prime})$
. We provide some sufficient conditions under which the difference between
![]() $P$
and
$P$
and
![]() $\widehat{P}$
is of order
$\widehat{P}$
is of order
![]() $\epsilon$
.
$\epsilon$
.
Lemma 1.
If the transition density is of the form
![]() $P(x,x^{\prime})=\gamma(x)\delta_x(x^{\prime})+\beta(x,x^{\prime}) $
with
$P(x,x^{\prime})=\gamma(x)\delta_x(x^{\prime})+\beta(x,x^{\prime}) $
with
![]() $\nu(x) P(x,x^{\prime})=\nu(x^{\prime}) P(x^{\prime},x)$
, suppose that
$\nu(x) P(x,x^{\prime})=\nu(x^{\prime}) P(x^{\prime},x)$
, suppose that
![]() $\widehat{P}(x,x^{\prime})=\hat{\gamma}(x)\delta_x(x^{\prime})+\hat{\beta}(x,x^{\prime})$
with
$\widehat{P}(x,x^{\prime})=\hat{\gamma}(x)\delta_x(x^{\prime})+\hat{\beta}(x,x^{\prime})$
with
for some constant
![]() $C\in(0,\infty)$
. Then there exists a constant
$C\in(0,\infty)$
. Then there exists a constant
![]() $C_1\in(0,\infty)$
such that
$C_1\in(0,\infty)$
such that
![]() $\|P-\widehat{P}\|_\nu\leq C_1\epsilon.$
$\|P-\widehat{P}\|_\nu\leq C_1\epsilon.$
4.1. Random walk Metropolis
RWM considers implementing the MH procedure on random walk proposals. That is, we use
in (16). It is worth noting that using a perturbed density
![]() $\widehat{\pi}$
does not affect this proposal.
$\widehat{\pi}$
does not affect this proposal.
Proposition 5.
For RWM, there is an
![]() $\epsilon_0 > 0$
so that for any
$\epsilon_0 > 0$
so that for any
![]() $\epsilon<\epsilon_0$
and
$\epsilon<\epsilon_0$
and
![]() $\sup_x|\log\pi(x)-\log\hat\pi (x)|\leq C\epsilon$
, there is a constant
$\sup_x|\log\pi(x)-\log\hat\pi (x)|\leq C\epsilon$
, there is a constant
![]() $C_1$
so that
$C_1$
so that
If the original RWM has a spectral gap and if
![]() $\sup_x|\log\pi(x)-\log\hat\pi (x)|\leq C\epsilon$
, then Proposition 5, together with Theorem 4, implies that the perturbed RWM has a proper spectral gap as well. In practice, an estimate of
$\sup_x|\log\pi(x)-\log\hat\pi (x)|\leq C\epsilon$
, then Proposition 5, together with Theorem 4, implies that the perturbed RWM has a proper spectral gap as well. In practice, an estimate of
![]() $\epsilon$
can be obtained by analyzing the numerical scheme used; see Section 3.2 for more details.
$\epsilon$
can be obtained by analyzing the numerical scheme used; see Section 3.2 for more details.
4.2. Metropolis adjusted Langevin algorithm
MALA considers implementing the MH procedure on proposals following the Langevin diffusion. That is, we use
in (16). Using a perturbed density
![]() $\widehat{\pi}$
does change this proposal. We discuss the perturbation in two separate cases. In particular, we shall verify that the condition
$\widehat{\pi}$
does change this proposal. We discuss the perturbation in two separate cases. In particular, we shall verify that the condition
![]() $\|P_{MALA}-\widehat{P}_{MALA}\|_{\pi}\leq \epsilon$
holds under appropriate assumptions on
$\|P_{MALA}-\widehat{P}_{MALA}\|_{\pi}\leq \epsilon$
holds under appropriate assumptions on
![]() $\widehat{\pi}$
in the two cases. Then, if
$\widehat{\pi}$
in the two cases. Then, if
![]() $P_{MALA}$
has a spectral gap, the numerical sampler
$P_{MALA}$
has a spectral gap, the numerical sampler
![]() $\widehat{P}_{MALA}$
has a proper spectral gap as well.
$\widehat{P}_{MALA}$
has a proper spectral gap as well.
4.2.1. Bounded domain
When the support of
![]() $\pi$
and
$\pi$
and
![]() $\widehat{\pi}$
is bounded, the analysis is quite straightforward with Lemma 1.
$\widehat{\pi}$
is bounded, the analysis is quite straightforward with Lemma 1.
Proposition 6.
For MALA, there is an
![]() $\epsilon_0>0$
so that for any
$\epsilon_0>0$
so that for any
![]() $\epsilon<\epsilon_0$
, if
$\epsilon<\epsilon_0$
, if
![]() $\sup_x|\log\pi(x)-\log\hat\pi(x)|\leq C\epsilon$
,
$\sup_x|\log\pi(x)-\log\hat\pi(x)|\leq C\epsilon$
,
![]() $\sup_x\|\nabla\log\pi(x)-\nabla\log\hat\pi(x)\|\leq C\epsilon$
and if the support of
$\sup_x\|\nabla\log\pi(x)-\nabla\log\hat\pi(x)\|\leq C\epsilon$
and if the support of
![]() $\pi$
and
$\pi$
and
![]() $\widehat{\pi}$
is bounded, then
$\widehat{\pi}$
is bounded, then
4.2.2. Unbounded support
When the support of the density is unbounded, directly bounding
![]() $\|P_{MALA}-\widehat{P}_{MALA}\|_{\pi}$
becomes difficult. Instead, we consider establishing
$\|P_{MALA}-\widehat{P}_{MALA}\|_{\pi}$
becomes difficult. Instead, we consider establishing
![]() $\| \delta_xP- \delta_x\widehat{P}\|_{TV}=O(\epsilon)$
.
$\| \delta_xP- \delta_x\widehat{P}\|_{TV}=O(\epsilon)$
.
Proposition 7.
For MALA, if
![]() $\log \pi$
is Lipschitz,
$\log \pi$
is Lipschitz,
![]() $\sup_x|\log\pi(x)-\log\hat\pi(x)|\leq L_\pi\epsilon$
and, moreover,
$\sup_x|\log\pi(x)-\log\hat\pi(x)|\leq L_\pi\epsilon$
and, moreover,
![]() $\sup_x\|\nabla\log\pi(x)-\nabla\log\widehat{\pi}(x)\|\leq L_\pi\epsilon$
, for any
$\sup_x\|\nabla\log\pi(x)-\nabla\log\widehat{\pi}(x)\|\leq L_\pi\epsilon$
, for any
![]() $\delta>0$
, there exists
$\delta>0$
, there exists
![]() $C_{\delta}\in(0,\infty)$
such that for
$C_{\delta}\in(0,\infty)$
such that for
![]() $h<(\frac{5L_{\pi}}{\delta} + 20L_{\pi})^{-1}$
,
$h<(\frac{5L_{\pi}}{\delta} + 20L_{\pi})^{-1}$
,
When
![]() $\pi(x)$
is sub-Gaussian, we can find a
$\pi(x)$
is sub-Gaussian, we can find a
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $V(x)=\exp\!(\delta \|x\|^2)$
is
$V(x)=\exp\!(\delta \|x\|^2)$
is
![]() $L_2$
-integrable under
$L_2$
-integrable under
![]() $\pi$
. Then Proposition 4 indicates that
$\pi$
. Then Proposition 4 indicates that
![]() $\|P- \widehat{P}\|_{\pi}=O(\sqrt{\epsilon})$
.
$\|P- \widehat{P}\|_{\pi}=O(\sqrt{\epsilon})$
.
5. Application: Parallel Tempering with Perturbed Densities
In this section, we demonstrate how to apply our framework to parallel tempering (PT) algorithms [Reference Earl and Deem17, Reference Tawn and Roberts42, Reference Tawn, Roberts and Rosenthal43]. These algorithms are also referred to as the replica exchange methods [Reference Dong and Tong11, Reference Dupuis, Liu, Plattner and Doll13, Reference Sugita and Okamoto41]. Compared with regular MCMC samplers like RWM and MALA, PT tries to sample a multiple-tempered version of the target density. Such a design can improve the convergence rate on densities with multiple isolated modes.
To implement PT, a sequence of distributions
![]() $\pi_0,\ldots, \pi_K$
is considered, where the last one is the target density
$\pi_0,\ldots, \pi_K$
is considered, where the last one is the target density
![]() $\pi_K =\pi$
. The first density,
$\pi_K =\pi$
. The first density,
![]() $\pi_0$
, is usually a distribution that is easy to draw samples from. The intermediate distributions,
$\pi_0$
, is usually a distribution that is easy to draw samples from. The intermediate distributions,
![]() $\pi_k$
’s
$\pi_k$
’s
![]() $1\leq k\leq K-1$
, are set up so that the two neighboring densities are similar to each other. A common choice for the intermediate distributions is to consider interpolations between
$1\leq k\leq K-1$
, are set up so that the two neighboring densities are similar to each other. A common choice for the intermediate distributions is to consider interpolations between
![]() $\pi_K$
and
$\pi_K$
and
![]() $\pi_0$
:
$\pi_0$
:
where
![]() $0=\beta_0<\beta_1<\ldots <\beta_K=1$
is a sequence of parameters. PT intends to generate samples from the product density
$0=\beta_0<\beta_1<\ldots <\beta_K=1$
is a sequence of parameters. PT intends to generate samples from the product density
To do so, its iterations consist of
![]() $K+1$
parts, i.e.
$K+1$
parts, i.e.
![]() $X_n=(X^0_{n},\ldots,X^K_{n})$
, and the updating rule is given by the following two steps:
$X_n=(X^0_{n},\ldots,X^K_{n})$
, and the updating rule is given by the following two steps:
-
(i) Update each
 $X^k_{n}$
to
$X^k_{n}$
to
 $X^{k}_{n+1}$
according to a transition kernel
$X^{k}_{n+1}$
according to a transition kernel
 $M_k$
, whose stationary distribution is
$M_k$
, whose stationary distribution is
 $\pi_k$
. In practice,
$\pi_k$
. In practice,
 $M_k$
is often taken as the transition kernel obtained by repeating the RWM or MALA update for
$M_k$
is often taken as the transition kernel obtained by repeating the RWM or MALA update for
 $t_k$
steps. That is,
$t_k$
steps. That is,
 $M_k=P_{RWM}^{t_k}$
or
$M_k=P_{RWM}^{t_k}$
or
 $M_k=P_{MALA}^{t_k}$
.
$M_k=P_{MALA}^{t_k}$
. -
(ii) Pick an index
 $k\in \{0,\ldots,K-1\}$
uniformly at random, and swap the values of
$k\in \{0,\ldots,K-1\}$
uniformly at random, and swap the values of
 $X^k_{n+1}$
and
$X^k_{n+1}$
and
 $X^{k+1}_{n+1}$
with probability
$X^{k+1}_{n+1}$
with probability
 $\alpha_k(X_{n+1}^k,X^{k+1}_{n+1})$
, where
$\alpha_k(X_{n+1}^k,X^{k+1}_{n+1})$
, where
The pseudo-code of PT is given in Algorithm 1.
The exchange procedure can be described by the transition probability on
![]() $R^{(K+1)d}\times R^{(K+1)d}$
:
$R^{(K+1)d}\times R^{(K+1)d}$
:
where
![]() $S_k(x)=(x^0,\ldots, x^{k-1},x^{k+1},x^k, x^{k+2},\ldots, x^K)$
. With a little change of notation, we write the transition kernel as
$S_k(x)=(x^0,\ldots, x^{k-1},x^{k+1},x^k, x^{k+2},\ldots, x^K)$
. With a little change of notation, we write the transition kernel as
![]() $Q_k$
as well; i.e.
$Q_k$
as well; i.e.
![]() $Q_kf(x)=Q_k(x,x)f(x)+Q_k(x,S_k(x))f(S_k(x))$
. The transition kernel of PT can then be written as
$Q_kf(x)=Q_k(x,x)f(x)+Q_k(x,S_k(x))f(S_k(x))$
. The transition kernel of PT can then be written as
 \begin{equation}P=\left(M_{0}\otimes \cdots \otimes M_K\right) \left(\frac{1}{K}\sum_{\mathbf{k}\in \{0,\ldots,K-1\}} Q_{k}\right),\end{equation}
\begin{equation}P=\left(M_{0}\otimes \cdots \otimes M_K\right) \left(\frac{1}{K}\sum_{\mathbf{k}\in \{0,\ldots,K-1\}} Q_{k}\right),\end{equation}
where the direct product of two transition kernels is given by
Algorithm 1 Parallel Tempering

The spectral gap of
![]() $P$
in (17) has been studied in [Reference Woodard, Schmidler and Huber46]. Assuming the state space can be partitioned into
$P$
in (17) has been studied in [Reference Woodard, Schmidler and Huber46]. Assuming the state space can be partitioned into
![]() $\mathbb{R}^d=\cup_{i=1}^J A_j$
, it is shown that
$\mathbb{R}^d=\cup_{i=1}^J A_j$
, it is shown that
![]() $\kappa(P)$
can be seen as the product of three elements: (1) the maximal spectral gap when sampling
$\kappa(P)$
can be seen as the product of three elements: (1) the maximal spectral gap when sampling
![]() $\pi_k$
,
$\pi_k$
,
![]() $k\geq 1$
, constrained on one piece,
$k\geq 1$
, constrained on one piece,
![]() $A_j$
; (2) the spectral gap when sampling
$A_j$
; (2) the spectral gap when sampling
![]() $\pi_0$
using
$\pi_0$
using
![]() $M_0$
; and (3) the density ratio
$M_0$
; and (3) the density ratio
![]() $\pi_k(A_j)/\pi_{k+1}(A_j)$
. In particular, if
$\pi_k(A_j)/\pi_{k+1}(A_j)$
. In particular, if
![]() $\pi_0$
is easy to sample,
$\pi_0$
is easy to sample,
![]() $\pi_k$
is not very different from
$\pi_k$
is not very different from
![]() $\pi_{k+1}$
, and the sampling of
$\pi_{k+1}$
, and the sampling of
![]() $\pi_k$
constrained on
$\pi_k$
constrained on
![]() $A_j$
is efficient, then PT can be highly efficient. When implementing PT numerically, we may not have access to the exact values of
$A_j$
is efficient, then PT can be highly efficient. When implementing PT numerically, we may not have access to the exact values of
![]() $\pi_k$
but only an
$\pi_k$
but only an
![]() $\epsilon$
-approximation, which we denote as
$\epsilon$
-approximation, which we denote as
![]() $\widehat{\pi}_k$
. Then the corresponding PT uses a sampler
$\widehat{\pi}_k$
. Then the corresponding PT uses a sampler
![]() $\widehat{M}_k$
, with invariant measure
$\widehat{M}_k$
, with invariant measure
![]() $\widehat{\pi}_k$
at each replica, while the exchange probability is given by
$\widehat{\pi}_k$
at each replica, while the exchange probability is given by
The corresponding transition kernel can be written as
 \begin{align*}\widehat{P}=\left(\widehat{M}_{0}\otimes \cdots \otimes \widehat{M}_K\right) \left(\frac{1}{K}\sum_{\mathbf{k}\in \{0,\ldots,K-1\}} \widehat{Q}_{k}\right).\end{align*}
\begin{align*}\widehat{P}=\left(\widehat{M}_{0}\otimes \cdots \otimes \widehat{M}_K\right) \left(\frac{1}{K}\sum_{\mathbf{k}\in \{0,\ldots,K-1\}} \widehat{Q}_{k}\right).\end{align*}
It is natural to ask whether this numerical PT will inherit the spectral gap of
![]() $P$
. The next result, together with Theorem 4, indicate that under appropriate regularity conditions on
$P$
. The next result, together with Theorem 4, indicate that under appropriate regularity conditions on
![]() $\widehat{\pi}_k$
’s, the numerical PT also has a proper spectral gap.
$\widehat{\pi}_k$
’s, the numerical PT also has a proper spectral gap.
Proposition 8.
Suppose that for each replica, if the target distribution satisfies
![]() $\sup_x|\log\widehat{\pi}_k(x)-\log\pi_k(x)|\leq \epsilon$
and the transition kernel satisfies
$\sup_x|\log\widehat{\pi}_k(x)-\log\pi_k(x)|\leq \epsilon$
and the transition kernel satisfies
![]() $\|P_k-\widehat{P}_k\|_{\pi_k}\leq \epsilon$
, then the transition kernel of PT satisfies the following for some constant
$\|P_k-\widehat{P}_k\|_{\pi_k}\leq \epsilon$
, then the transition kernel of PT satisfies the following for some constant
![]() $C$
:
$C$
:
Before we prove Proposition 8, we first prove two auxiliary lemmas. The first lemma shows that different compositions of approximated transition kernels yield approximation kernels of similar accuracy. In particular, it helps us establish the condition
![]() $\|P_k-\widehat{P}_k\|_{\pi_k}\leq \epsilon$
in Proposition 8 if we use
$\|P_k-\widehat{P}_k\|_{\pi_k}\leq \epsilon$
in Proposition 8 if we use
![]() $M_k=P_{RWM}^{t_k}$
or
$M_k=P_{RWM}^{t_k}$
or
![]() $M_k=P_{MALA}^{t_k}$
.
$M_k=P_{MALA}^{t_k}$
.
Lemma 2
-
(i) For two transition kernels
 $R$
and
$R$
and
 $S$
, both with invariant measure
$S$
, both with invariant measure
 $\nu$
, if
$\nu$
, if
 $\|R-\widehat{R}\|_\nu\leq C\epsilon$
and if
$\|R-\widehat{R}\|_\nu\leq C\epsilon$
and if
 $\|S-\widehat{S}\|_\nu\leq C\epsilon$
, then there is a constant
$\|S-\widehat{S}\|_\nu\leq C\epsilon$
, then there is a constant
 $C'$
so that
$C'$
so that
 \begin{align*}\|RS-\widehat{R}\widehat{S}\|_{\nu}\leq C'\epsilon.\end{align*}
\begin{align*}\|RS-\widehat{R}\widehat{S}\|_{\nu}\leq C'\epsilon.\end{align*}
-
(ii) For two transition kernels
 $R_1$
and
$R_1$
and
 $R_2$
, with invariant measure
$R_2$
, with invariant measure
 $\nu_1$
and
$\nu_1$
and
 $\nu_2$
respectively, if
$\nu_2$
respectively, if
 $\|R_1-\hat R_1\|_{\nu_1}\leq C\epsilon$
and if
$\|R_1-\hat R_1\|_{\nu_1}\leq C\epsilon$
and if
 $\| R_2-\hat R_2\|_{\nu_2}\leq C\epsilon$
, then there is a constant
$\| R_2-\hat R_2\|_{\nu_2}\leq C\epsilon$
, then there is a constant
 $C'$
so that
where
$C'$
so that
where \begin{align*}\|R_1\otimes R_2 -\widehat{R}_1\otimes \widehat{R}_2\|_\nu \leq C'\epsilon,\end{align*}
\begin{align*}\|R_1\otimes R_2 -\widehat{R}_1\otimes \widehat{R}_2\|_\nu \leq C'\epsilon,\end{align*}
 $\nu=\nu_1\times\nu_2$
is the joint invariance distribution.
$\nu=\nu_1\times\nu_2$
is the joint invariance distribution.
-
(iii) For
 $n$
transition kernels
$n$
transition kernels
 $S_1, S_2, \dots, S_n$
, all with invariant measure
$S_1, S_2, \dots, S_n$
, all with invariant measure
 $\nu$
, if
$\nu$
, if
 $\|S_i-\widehat{S}_i\|_\nu\leq C\epsilon$
for
$\|S_i-\widehat{S}_i\|_\nu\leq C\epsilon$
for
 $i=1,\dots, n$
, then for
$i=1,\dots, n$
, then for
 $U=\frac1n\sum_{i=1}^n S_i$
and
$U=\frac1n\sum_{i=1}^n S_i$
and
 $\widehat{U}=\frac1n\sum_{i=1}^{s} \widehat{S}_i$
, there is a constant
$\widehat{U}=\frac1n\sum_{i=1}^{s} \widehat{S}_i$
, there is a constant
 $C'$
so that
$C'$
so that
 \begin{align*}\|U - \widehat{U}\|_\nu\leq C'\epsilon.\end{align*}
\begin{align*}\|U - \widehat{U}\|_\nu\leq C'\epsilon.\end{align*}
The second lemma establishes proper bounds for the swapping transition.
Lemma 3.
Let
![]() $Q$
be a transition probability of form
$Q$
be a transition probability of form
where
![]() $S(x)$
is some given map. Suppose
$S(x)$
is some given map. Suppose
![]() $Q$
is reversible with a density
$Q$
is reversible with a density
![]() $\nu$
, i.e.
$\nu$
, i.e.
Similarly, let
![]() $\widehat{Q}$
denote the transition probability of the form
$\widehat{Q}$
denote the transition probability of the form
reversible with
![]() $\widehat{\nu}$
. If for some constant
$\widehat{\nu}$
. If for some constant
![]() $C$
,
$C$
,
![]() $(1-C\epsilon)a(x,S(x))\leq \widehat{a}(x,S(x))\leq (1+C\epsilon)a(x,S(x))$
, then
$(1-C\epsilon)a(x,S(x))\leq \widehat{a}(x,S(x))\leq (1+C\epsilon)a(x,S(x))$
, then
6. Numerical examples
In this section, we present some numerical examples based on the predator–prey system to illustrate the theoretical results developed in the preceding sections.
6.1. Predator–prey system
We consider inferring the parameters of a system of ordinary differential equations (ODEs) that models the predator–prey system [Reference Lotka29]. Denoting the populations of prey and predator by
![]() $( \gamma_p, \gamma_q )$
, the populations change over time according to the pair of coupled ODEs is
$( \gamma_p, \gamma_q )$
, the populations change over time according to the pair of coupled ODEs is
 \begin{align}\frac{d \gamma_p}{dt} & = r \gamma_p \left(1 - \frac{\gamma_p}{K}\right) - s \left(\frac{\gamma_p \,\gamma_q }{w + \gamma_p}\right), \nonumber \\\frac{d \gamma_q}{dt} & = u \left(\frac{\gamma_p \,\gamma_q }{w + \gamma_p}\right) - v \gamma_q, \end{align}
\begin{align}\frac{d \gamma_p}{dt} & = r \gamma_p \left(1 - \frac{\gamma_p}{K}\right) - s \left(\frac{\gamma_p \,\gamma_q }{w + \gamma_p}\right), \nonumber \\\frac{d \gamma_q}{dt} & = u \left(\frac{\gamma_p \,\gamma_q }{w + \gamma_p}\right) - v \gamma_q, \end{align}
with initial conditions
![]() $\gamma_p(0)$
and
$\gamma_p(0)$
and
![]() $\gamma_q(0)$
.
$\gamma_q(0)$
.
![]() $r$
,
$r$
,
![]() $K$
,
$K$
,
![]() $a$
,
$a$
,
![]() $s$
,
$s$
,
![]() $u$
, and
$u$
, and
![]() $v$
are model parameters that control the dynamics of the populations of prey and predator. In the absence of the predator, the population of prey evolves according to the logistic equation, which is characterized by
$v$
are model parameters that control the dynamics of the populations of prey and predator. In the absence of the predator, the population of prey evolves according to the logistic equation, which is characterized by
![]() $r$
and
$r$
and
![]() $K$
. In the absence of the prey, the population of the predator has an exponential decay rate
$K$
. In the absence of the prey, the population of the predator has an exponential decay rate
![]() $v$
. The additional parameters
$v$
. The additional parameters
![]() $s,w$
, and
$s,w$
, and
![]() $u$
characterize the interaction between the predator population and the prey population.
$u$
characterize the interaction between the predator population and the prey population.
In the inference problem, we want to estimate both the model parameters and the initial conditions. In this case, we have
![]() $d = 8$
and denote
$d = 8$
and denote
A commonly used prior for this problem is a uniform distribution over a hypercube
![]() $(a_1,b_1) \times \cdots \times (a_d,b_d) $
(see e.g. [Reference Parno and Marzouk33]). Here we set
$(a_1,b_1) \times \cdots \times (a_d,b_d) $
(see e.g. [Reference Parno and Marzouk33]). Here we set
![]() $a_i = 10^{-3}$
and
$a_i = 10^{-3}$
and
![]() $b_i = 2\times 10^2$
for all
$b_i = 2\times 10^2$
for all
![]() $i$
. Noisy observations of both
$i$
. Noisy observations of both
![]() $\gamma_p(t;\; \theta)$
and
$\gamma_p(t;\; \theta)$
and
![]() $\gamma_q(t;\; \theta)$
at times regularly spaced at
$\gamma_q(t;\; \theta)$
at times regularly spaced at
![]() $m = 20$
time points in
$m = 20$
time points in
![]() $t \in [2, 40]$
are used to infer
$t \in [2, 40]$
are used to infer
![]() $\theta$
. This defines a so-called forward model,
$\theta$
. This defines a so-called forward model,
that maps a given parameter
![]() $\theta$
to the observables. The observables are perturbed with independent Gaussian observational errors with mean zero and variance
$\theta$
to the observables. The observables are perturbed with independent Gaussian observational errors with mean zero and variance
![]() $4$
. A “true” parameter
$4$
. A “true” parameter
is used to generate the synthetic observed data set, which is denoted by
![]() $y$
. The trajectories of
$y$
. The trajectories of
![]() $\gamma_p(t;\; \theta_{\rm true})$
and
$\gamma_p(t;\; \theta_{\rm true})$
and
![]() $\gamma_q(t;\; \theta_{\rm true})$
together with the synthetic data set are shown in Figure 1.
$\gamma_q(t;\; \theta_{\rm true})$
together with the synthetic data set are shown in Figure 1.

Figure 1. Left and middle: the trajectories of
![]() $\gamma_p(t;\; \theta_{\rm true})$
and
$\gamma_p(t;\; \theta_{\rm true})$
and
![]() $\gamma_q(t;\; \theta_{\rm true})$
computed using the second-order Runge–Kutta method, with different time step size
$\gamma_q(t;\; \theta_{\rm true})$
computed using the second-order Runge–Kutta method, with different time step size
![]() $\eta$
. Right: the
$\eta$
. Right: the
![]() $L_2$
error of the model outputs with different time step sizes
$L_2$
error of the model outputs with different time step sizes
![]() $\eta$
. Here
$\eta$
. Here
![]() $G(\theta_{\rm true})$
is computed using
$G(\theta_{\rm true})$
is computed using
![]() $\eta = \eta_0 \times 2^{-6}$
. The trajectories computed by the time step size
$\eta = \eta_0 \times 2^{-6}$
. The trajectories computed by the time step size
![]() $\eta = \eta_0 \times 2^{-6}$
are used to generate a synthetic data set. The observed data sets of the prey and the predator are shown as circles and squares, respectively.
$\eta = \eta_0 \times 2^{-6}$
are used to generate a synthetic data set. The observed data sets of the prey and the predator are shown as circles and squares, respectively.
To prevent rejections caused by proposal samples that fall outside of the hypercube, we further consider the prior distribution as the pushforward of the standard Gaussian measure, with the probability density function
under a diffeomorphic transformation
![]() $T\; :\; \mathbb{R}^d \rightarrow \mathbb{R}^d$
that maps each coordinate
$T\; :\; \mathbb{R}^d \rightarrow \mathbb{R}^d$
that maps each coordinate
In other words,
![]() $p_0(x)$
is the prior distribution for the transformed parameter
$p_0(x)$
is the prior distribution for the transformed parameter
![]() $x = T^{-1}(\theta)$
. Writing
$x = T^{-1}(\theta)$
. Writing
![]() $G(x) = F(T(x))$
, our goal is to characterize the posterior distribution
$G(x) = F(T(x))$
, our goal is to characterize the posterior distribution
The system of ODEs in (18), and hence the function
![]() $G(x)$
, has to be numerically solved by some ODE solvers. Here we use the second-order explicit Runge–Kutta method, with time step size
$G(x)$
, has to be numerically solved by some ODE solvers. Here we use the second-order explicit Runge–Kutta method, with time step size
![]() $\eta$
, to solve (18). As shown in Figure 1, the trajectories of
$\eta$
, to solve (18). As shown in Figure 1, the trajectories of
![]() $\gamma_p(t;\; \theta_{\rm true})$
and
$\gamma_p(t;\; \theta_{\rm true})$
and
![]() $\gamma_q(t;\; \theta_{\rm true})$
converge as
$\gamma_q(t;\; \theta_{\rm true})$
converge as
![]() $\eta \rightarrow 0$
at a rate of
$\eta \rightarrow 0$
at a rate of
![]() $O(\eta^2)$
(see [Reference Butcher8] for a detailed analysis). The numerical solver, which is characterized by the step size
$O(\eta^2)$
(see [Reference Butcher8] for a detailed analysis). The numerical solver, which is characterized by the step size
![]() $\eta$
, defines the approximate model
$\eta$
, defines the approximate model
![]() $\widehat{G}(x)$
and the approximate posterior density
$\widehat{G}(x)$
and the approximate posterior density
![]() $\widehat{\pi}(x)$
. Figure 2 shows the estimated marginal distributions (using Algorithm 1) of perturbed posteriors defined by various time step sizes. Here we observe that as
$\widehat{\pi}(x)$
. Figure 2 shows the estimated marginal distributions (using Algorithm 1) of perturbed posteriors defined by various time step sizes. Here we observe that as
![]() $h$
decreases, the estimated marginal distributions almost overlap each other, which suggests that the perturbed distributions converge as the discretized model
$h$
decreases, the estimated marginal distributions almost overlap each other, which suggests that the perturbed distributions converge as the discretized model
![]() $\widehat{G}$
converges.
$\widehat{G}$
converges.

Figure 2. Marginal distributions of perturbed posteriors defined by various time step sizes.
6.2. MCMC results
To validate the theoretical results of Metropolis–Hasting MCMC on perturbed densities in Section 4, we first simulate the RWM algorithm with invariant densities
![]() $\widehat{\pi}(x)$
defined by various time step sizes, as shown in Figure 1. All the Markov chains in this set of simulation experiments are generated using the same Gaussian random walk proposal distribution. The box plots of the integrated autocorrelation times (IACTs) of the resulting Markov chains are shown in Figure 3. Then we simulate MALA with invariant densities
$\widehat{\pi}(x)$
defined by various time step sizes, as shown in Figure 1. All the Markov chains in this set of simulation experiments are generated using the same Gaussian random walk proposal distribution. The box plots of the integrated autocorrelation times (IACTs) of the resulting Markov chains are shown in Figure 3. Then we simulate MALA with invariant densities
![]() $\widehat{\pi}(x)$
defined by the same set of time step sizes. The box plots of the resulting IACTs are shown in Figure 4. Again, all the Markov chains are generated using the same proposal distribution. For both algorithms, we simulate each Markov chain for
$\widehat{\pi}(x)$
defined by the same set of time step sizes. The box plots of the resulting IACTs are shown in Figure 4. Again, all the Markov chains are generated using the same proposal distribution. For both algorithms, we simulate each Markov chain for
![]() $10^{6}$
iterations after discarding burn-in samples and repeat the simulation for
$10^{6}$
iterations after discarding burn-in samples and repeat the simulation for
![]() $20$
times with different initial states to produce the box plots. As established in our theoretical analysis, for both algorithms the resulting Markov chains targeting various approximate posterior densities produce similar IACTs.
$20$
times with different initial states to produce the box plots. As established in our theoretical analysis, for both algorithms the resulting Markov chains targeting various approximate posterior densities produce similar IACTs.

Figure 3. Box plots of integrated autocorrelation times (IACTs) of the first four parameter Markov chains simulated by the RWM algorithm. Here,
![]() $20$
realizations of Markov chains are used to estimate the IACT.
$20$
realizations of Markov chains are used to estimate the IACT.

Figure 4. Box plots of integrated autocorrelation times (IACTs) of the first four parameter Markov chains simulated by the MALA algorithm. Here,
![]() $20$
realizations of Markov chains are used to estimate the IACT.
$20$
realizations of Markov chains are used to estimate the IACT.
To validate the theoretical results on the parallel tempering with perturbed densities in Section 5, we simulate Algorithm 1 with the same Gaussian random walk as in RWM. For each of the invariant densities
![]() $\widehat{\pi}(x)$
defined by various time step sizes, we set
$\widehat{\pi}(x)$
defined by various time step sizes, we set
![]() $K=4$
, and the intermediate distributions take the form
$K=4$
, and the intermediate distributions take the form
where
![]() $\beta_k = 1 + \alpha^{-K} - \alpha^{-k}$
with
$\beta_k = 1 + \alpha^{-K} - \alpha^{-k}$
with
![]() $\alpha = 1.3$
and
$\alpha = 1.3$
and
![]() $k = \{0,1,2,3,4\}$
. Here
$k = \{0,1,2,3,4\}$
. Here
![]() $\beta_k$
is an increasing sequence such that
$\beta_k$
is an increasing sequence such that
![]() $\beta_K = 1$
. The same Gaussian random walk is used across all replicas to simulate the Markov chain. The box plots of the IACTs of resulting Markov chains are shown in Figure 5. Similar to the previous experiments, the resulting Markov chains targeting various approximate posterior densities produce similar IACTs. Furthermore, we noticed that the IACTs of Algorithm 1 are smaller than those of the RMW and MALA algorithm, which suggests that Algorithm 1 has a better mixing rate.
$\beta_K = 1$
. The same Gaussian random walk is used across all replicas to simulate the Markov chain. The box plots of the IACTs of resulting Markov chains are shown in Figure 5. Similar to the previous experiments, the resulting Markov chains targeting various approximate posterior densities produce similar IACTs. Furthermore, we noticed that the IACTs of Algorithm 1 are smaller than those of the RMW and MALA algorithm, which suggests that Algorithm 1 has a better mixing rate.

Figure 5. Box plots of integrated autocorrelation times (IACTs) of the first four parameters of Markov chains simulated by Algorithm 1. Here,
![]() $20$
realizations of Markov chains are used to estimate the IACT.
$20$
realizations of Markov chains are used to estimate the IACT.
7. Conclusion
In this paper, we quantify the convergence speed and the approximation accuracy of numerical MCMC samplers under two general frameworks: ergodicity and spectral gap. Our results can be easily applied to study the efficiency and accuracy of various sampling algorithms. In particular, we demonstrate how to apply our framework to study Metropolis–Hasting MCMC algorithms and parallel tempering Monte Carlo algorithms. These results are validated by numerical simulations on a Bayesian inverse problem based on the predator–prey model.
In the applications in Sections 4 and 5, we assume that we can approximate the target transition kernels with some uniform accuracy guarantees. In some problems with unbounded domains, this can be difficult to achieve. It would be interesting to relax such requirements to the ones assumed in [Reference Cotter, Dashti and Stuart10].
Appendix A. Proof for the Wasserstein convergence
Proof of Theorem
2. Let
![]() $Q$
be the optimal coupled measure between
$Q$
be the optimal coupled measure between
![]() $\delta_xP$
and
$\delta_xP$
and
![]() $\delta_x\widehat{P}$
from the Kantorovich–Rubinstein theorem. Then
$\delta_x\widehat{P}$
from the Kantorovich–Rubinstein theorem. Then
 \begin{equation*}\begin{split}|PV(x)-\widehat{P} V(x)|&=\left|\int Q_{x}(dx^{\prime},dy^{\prime}) (V(x^{\prime})-V(y^{\prime}))\right|\\&\leq \left|\int Q_{x}(dx^{\prime},dy^{\prime}) (V(x^{\prime})+V(y^{\prime}))1_{x^{\prime}\neq y^{\prime}}\right|=\|\delta_x P- \delta_x \widehat{P}\|_V.\end{split}\end{equation*}
\begin{equation*}\begin{split}|PV(x)-\widehat{P} V(x)|&=\left|\int Q_{x}(dx^{\prime},dy^{\prime}) (V(x^{\prime})-V(y^{\prime}))\right|\\&\leq \left|\int Q_{x}(dx^{\prime},dy^{\prime}) (V(x^{\prime})+V(y^{\prime}))1_{x^{\prime}\neq y^{\prime}}\right|=\|\delta_x P- \delta_x \widehat{P}\|_V.\end{split}\end{equation*}
Next, as
![]() $\|\delta_x P-\delta_x \widehat{P}\|_V\leq \epsilon V (x)$
, we have
$\|\delta_x P-\delta_x \widehat{P}\|_V\leq \epsilon V (x)$
, we have
In addition, because
![]() $V$
is a Lyapunov function under
$V$
is a Lyapunov function under
![]() $P$
,
$P$
,
As
![]() $(\lambda+\epsilon)\in(0,1)$
for
$(\lambda+\epsilon)\in(0,1)$
for
![]() $\epsilon$
small enough,
$\epsilon$
small enough,
![]() $V$
is a Lyapunov function under
$V$
is a Lyapunov function under
![]() $\widehat{P}$
with parameters
$\widehat{P}$
with parameters
![]() $\lambda+\epsilon$
and
$\lambda+\epsilon$
and
![]() $L$
.
$L$
.
We next establish a bound for
![]() $\|\delta_x\widehat{P}^n - \delta_y \widehat{P}^n\|_V$
,
$\|\delta_x\widehat{P}^n - \delta_y \widehat{P}^n\|_V$
,
![]() $x\neq y$
using
$x\neq y$
using
For
![]() $\|\delta_x\widehat{P}^n-\delta_x P^n\|_V$
, by Theorem 1, we have
$\|\delta_x\widehat{P}^n-\delta_x P^n\|_V$
, by Theorem 1, we have
for some
![]() $C$
because
$C$
because
![]() $V(x)\geq 1$
. A similar bound holds for
$V(x)\geq 1$
. A similar bound holds for
![]() $\|\delta_yP^n-\delta_y \widehat{P}^n\|_V$
as well—i.e.
$\|\delta_yP^n-\delta_y \widehat{P}^n\|_V$
as well—i.e.
For any
![]() $l\leq N$
, Let
$l\leq N$
, Let
![]() $D_1=\frac{C}{N\rho^{2N-1}}$
. Then (19) leads to
$D_1=\frac{C}{N\rho^{2N-1}}$
. Then (19) leads to
 \begin{equation}\begin{split}\|\delta_x\widehat{P}^{l+N} - \delta_y \widehat{P}^{l+N}\|_V &\leq\rho^{l+N} d_V(x,y)+C\epsilon (V(x)+V(y))\\&= \left(\rho^{l+N} + C\epsilon\right)d_V(x,y)\leq (\rho+D_1\epsilon)^{l+N} d_V(x,y),\end{split}\end{equation}
\begin{equation}\begin{split}\|\delta_x\widehat{P}^{l+N} - \delta_y \widehat{P}^{l+N}\|_V &\leq\rho^{l+N} d_V(x,y)+C\epsilon (V(x)+V(y))\\&= \left(\rho^{l+N} + C\epsilon\right)d_V(x,y)\leq (\rho+D_1\epsilon)^{l+N} d_V(x,y),\end{split}\end{equation}
where the last inequality follows from
![]() $(a+b)^N>a^N+Na^{N-1}b$
for all
$(a+b)^N>a^N+Na^{N-1}b$
for all
![]() $a,b>0,$
which comes from Taylor expansion.
$a,b>0,$
which comes from Taylor expansion.
Next, let
![]() $\widehat{Q}^{k}_{x,y}$
be the optimal coupled measure between
$\widehat{Q}^{k}_{x,y}$
be the optimal coupled measure between
![]() $\delta_x \widehat{P}^{kN}$
and
$\delta_x \widehat{P}^{kN}$
and
![]() $\delta_y \widehat{P}^{kN}$
. Then
$\delta_y \widehat{P}^{kN}$
. Then
 \begin{equation} \begin{split}\|\delta_x \widehat{P}^{kN}-\delta_y \widehat{P}^{kN}\|_V&\leq \int \widehat{Q}_{x,y}^{k-1}(dx^{\prime},dy^{\prime}) \|\delta_{x^{\prime}} \hat P^N - \delta_{y^{\prime}} \hat P^N\|_V\\&\leq \int \widehat{Q}_{x,y}^{k-1}(dx^{\prime},dy^{\prime}) (\rho+D_1\epsilon)^N d_V(x^{\prime},y^{\prime})\\&\leq (\rho+D_1\epsilon)^{kN} d_V(x,y).\end{split}\end{equation}
\begin{equation} \begin{split}\|\delta_x \widehat{P}^{kN}-\delta_y \widehat{P}^{kN}\|_V&\leq \int \widehat{Q}_{x,y}^{k-1}(dx^{\prime},dy^{\prime}) \|\delta_{x^{\prime}} \hat P^N - \delta_{y^{\prime}} \hat P^N\|_V\\&\leq \int \widehat{Q}_{x,y}^{k-1}(dx^{\prime},dy^{\prime}) (\rho+D_1\epsilon)^N d_V(x^{\prime},y^{\prime})\\&\leq (\rho+D_1\epsilon)^{kN} d_V(x,y).\end{split}\end{equation}
For any
![]() $n\geq N$
, we can write
$n\geq N$
, we can write
![]() $n=kN+N+l$
, for
$n=kN+N+l$
, for
![]() $k,l\in \mathbb{Z}_0^+$
, and
$k,l\in \mathbb{Z}_0^+$
, and
 \begin{equation*}\begin{split}\|\delta_x \widehat{P}^{n}-\delta_y \widehat{P}^{n}\|_V&\leq \int \widehat{Q}^k_{x,y}(dx^{\prime},dy^{\prime})\|\delta_{x^{\prime}} \hat P^{N+l} - \delta_{y^{\prime}} \hat P^{N+l}\|_V\\&\leq C_1(\rho+D_1\epsilon)^{N+l} \int \widehat{Q}^k_{x,y}(dx^{\prime},dy^{\prime})d_V(x^{\prime},y^{\prime}) \mbox{ by (20)}\\&\leq C_1(\rho+D_1\epsilon)^{l+kN+N}d_V(x,y) \mbox{ by (21)}\\&=C_1(\rho+D_1\epsilon)^{n}d_V(x,y).\end{split}\end{equation*}
\begin{equation*}\begin{split}\|\delta_x \widehat{P}^{n}-\delta_y \widehat{P}^{n}\|_V&\leq \int \widehat{Q}^k_{x,y}(dx^{\prime},dy^{\prime})\|\delta_{x^{\prime}} \hat P^{N+l} - \delta_{y^{\prime}} \hat P^{N+l}\|_V\\&\leq C_1(\rho+D_1\epsilon)^{N+l} \int \widehat{Q}^k_{x,y}(dx^{\prime},dy^{\prime})d_V(x^{\prime},y^{\prime}) \mbox{ by (20)}\\&\leq C_1(\rho+D_1\epsilon)^{l+kN+N}d_V(x,y) \mbox{ by (21)}\\&=C_1(\rho+D_1\epsilon)^{n}d_V(x,y).\end{split}\end{equation*}
Lastly, we show that
![]() $\widehat{P}$
has a unique invariant measure
$\widehat{P}$
has a unique invariant measure
![]() $\widehat{\pi}$
. Fix a point
$\widehat{\pi}$
. Fix a point
![]() $x$
, considering a sequence
$x$
, considering a sequence
![]() $\{\delta_x\widehat{P}^n, n=1,2,\ldots\}$
. Note that
$\{\delta_x\widehat{P}^n, n=1,2,\ldots\}$
. Note that
 \begin{align*}\|\delta_x\widehat{P}^n-\delta_x\widehat{P}^{n+1}\|_V&\leq \int \|\delta_x\widehat{P}^n-\delta_y\widehat{P}^{n}\|_V\widehat{P}(x,dy)\\\&\leq C_1(\rho+D_1\epsilon)^{n}\mathbb{E}[d_V(x,\widehat{X}_1)]\\&\leq C_1 (\rho+D_1\epsilon)^n[ (\lambda+1+\epsilon)V(x)+L].\end{align*}
\begin{align*}\|\delta_x\widehat{P}^n-\delta_x\widehat{P}^{n+1}\|_V&\leq \int \|\delta_x\widehat{P}^n-\delta_y\widehat{P}^{n}\|_V\widehat{P}(x,dy)\\\&\leq C_1(\rho+D_1\epsilon)^{n}\mathbb{E}[d_V(x,\widehat{X}_1)]\\&\leq C_1 (\rho+D_1\epsilon)^n[ (\lambda+1+\epsilon)V(x)+L].\end{align*}
This implies that
![]() $\delta_x\widehat{P}^n$
is a Cauchy sequence in
$\delta_x\widehat{P}^n$
is a Cauchy sequence in
![]() $d_V$
as well as the total variation distance. Since the sublevel sets of
$d_V$
as well as the total variation distance. Since the sublevel sets of
![]() $V$
are compact and
$V$
are compact and
![]() $\delta_x\widehat{P}^n V$
remains bounded, it is a tight sequence. Therefore, the sequence has a limit, which we denote by
$\delta_x\widehat{P}^n V$
remains bounded, it is a tight sequence. Therefore, the sequence has a limit, which we denote by
![]() $\pi_x$
. Next, we show that
$\pi_x$
. Next, we show that
![]() $\pi_x=\pi_y$
:
$\pi_x=\pi_y$
:
Proof of Proposition
1. For the first claim, let
![]() $Q_{x,y}^n$
be the the optimal coupled measure between
$Q_{x,y}^n$
be the the optimal coupled measure between
![]() $\delta_{x}\widehat{P}^n $
and
$\delta_{x}\widehat{P}^n $
and
![]() $\delta_{y}\widehat{P}^n $
for any
$\delta_{y}\widehat{P}^n $
for any
![]() $x,y\in\mathbb{R}^d$
. Then
$x,y\in\mathbb{R}^d$
. Then
 \begin{equation}\begin{split}|\delta_x \widehat{P}^n f -\widehat{\pi} f|&=|\delta_{x}\widehat{P}^n f-\widehat{\pi} \widehat{P}^n f|\\&\leq \int |\delta_{x}\widehat{P}^n f-\delta_y\widehat{P}^n f|\widehat{\pi}(dy)\\&\leq \int \int Q^n_{x,y}(dx^{\prime},dy^{\prime})|\,f(x^{\prime})-f(y^{\prime})|\widehat{\pi}(dy)\\&\leq \int \|\delta_{x}\widehat{P}^n - \delta_y\widehat{P}^n\|_V \widehat{\pi}(dy)\\&\leq \widehat{\rho}^n \int d_V(x,y)\widehat{\pi}(dy)\leq \widehat{\rho}^n(V(x)+\widehat{\pi} V).\end{split}\end{equation}
\begin{equation}\begin{split}|\delta_x \widehat{P}^n f -\widehat{\pi} f|&=|\delta_{x}\widehat{P}^n f-\widehat{\pi} \widehat{P}^n f|\\&\leq \int |\delta_{x}\widehat{P}^n f-\delta_y\widehat{P}^n f|\widehat{\pi}(dy)\\&\leq \int \int Q^n_{x,y}(dx^{\prime},dy^{\prime})|\,f(x^{\prime})-f(y^{\prime})|\widehat{\pi}(dy)\\&\leq \int \|\delta_{x}\widehat{P}^n - \delta_y\widehat{P}^n\|_V \widehat{\pi}(dy)\\&\leq \widehat{\rho}^n \int d_V(x,y)\widehat{\pi}(dy)\leq \widehat{\rho}^n(V(x)+\widehat{\pi} V).\end{split}\end{equation}
For the second claim, note that for any
![]() $f$
with
$f$
with
![]() $\widehat{\pi} f=0$
, we have
$\widehat{\pi} f=0$
, we have
 \begin{align*}\mathbb{E}_{\widehat{\pi}}[(\hat{f}_M-\widehat{\pi} f)^2]&=\frac{1}{M^2}\mathbb{E}_{\widehat{\pi}} \left[\sum_{j,k=1}^M f(\widehat{X}_j) f(\widehat{X}_{k})\right]\\&\leq \frac{2}{M^2}\mathbb{E}_{\widehat{\pi}} \left[\sum_{j=1}^M |\,f(\widehat{X}_j)| \sum_{k=0}^\infty |\,f(\widehat{X}_{j+k})|\right]\\&= \frac{2}{M}\mathbb{E}_{\widehat{\pi}} \left[|\,f(\widehat{X}_0)|\mathbb{E}\left[\sum_{k=0}^\infty |\,f(\widehat{X}_{k})|\Big|\widehat{X}_0\right]\right]\mbox{ since $\widehat{X}_j\sim \widehat{\pi}$}\end{align*}
\begin{align*}\mathbb{E}_{\widehat{\pi}}[(\hat{f}_M-\widehat{\pi} f)^2]&=\frac{1}{M^2}\mathbb{E}_{\widehat{\pi}} \left[\sum_{j,k=1}^M f(\widehat{X}_j) f(\widehat{X}_{k})\right]\\&\leq \frac{2}{M^2}\mathbb{E}_{\widehat{\pi}} \left[\sum_{j=1}^M |\,f(\widehat{X}_j)| \sum_{k=0}^\infty |\,f(\widehat{X}_{j+k})|\right]\\&= \frac{2}{M}\mathbb{E}_{\widehat{\pi}} \left[|\,f(\widehat{X}_0)|\mathbb{E}\left[\sum_{k=0}^\infty |\,f(\widehat{X}_{k})|\Big|\widehat{X}_0\right]\right]\mbox{ since $\widehat{X}_j\sim \widehat{\pi}$}\end{align*}
 \begin{align*}&\leq \frac{2}{M}\mathbb{E}_{\widehat{\pi}} \left[|\,f(\widehat{X}_0)| \sum_{k=0}^\infty \widehat{\rho}^k(V(\widehat{X}_0)+\widehat{\pi} V)\right] \mbox{ from (22)}\\&\leq \frac{2}{ (1-\widehat{\rho})M}\mathbb{E}_{\widehat{\pi}}\Big[|\,f(\widehat{X}_0)|(V(\widehat{X}_0)+\widehat{\pi} V)\Big].\end{align*}
\begin{align*}&\leq \frac{2}{M}\mathbb{E}_{\widehat{\pi}} \left[|\,f(\widehat{X}_0)| \sum_{k=0}^\infty \widehat{\rho}^k(V(\widehat{X}_0)+\widehat{\pi} V)\right] \mbox{ from (22)}\\&\leq \frac{2}{ (1-\widehat{\rho})M}\mathbb{E}_{\widehat{\pi}}\Big[|\,f(\widehat{X}_0)|(V(\widehat{X}_0)+\widehat{\pi} V)\Big].\end{align*}
Appendix B. Proof for the
 $\chi^2$
convergence
$\chi^2$
convergence
Proof of Theorem
3. We will write
![]() $\kappa=\kappa(P)$
for short.
$\kappa=\kappa(P)$
for short.
For Claim 1, first note that
 \begin{equation}\begin{split}\textrm{var}_\pi (\widehat{P} f)=&\, \frac12\int\left(\widehat{P} f(x)-\widehat{P} f(y)\right)^2\pi(dx)\pi(dy)\\=&\, \frac12\int\left(Pf(x)-Pf(y)+(P-\widehat{P})f(y)-(P-\widehat{P})\, f(x)\right)^2\pi(dx)\pi(dy)\\\leq& \left(\frac12+\frac{a\kappa}{2}\right)\int\left(Pf(x)-Pf(y)\right)^2\pi(dx)\pi(dy)\\&+\left(\frac12+\frac{1}{2a\kappa}\right)\int\left((P-\widehat{P})\, f(x)-(P-\widehat{P})\, f(y)\right)^2\pi(dx)\pi(dy)\\\leq&\, (1+a \kappa) \textrm{var}_\pi(P f)+\left(2+\frac{2}{a\kappa}\right)\int((P-\widehat{P})f(x))^2\pi(dx).\end{split}\end{equation}
\begin{equation}\begin{split}\textrm{var}_\pi (\widehat{P} f)=&\, \frac12\int\left(\widehat{P} f(x)-\widehat{P} f(y)\right)^2\pi(dx)\pi(dy)\\=&\, \frac12\int\left(Pf(x)-Pf(y)+(P-\widehat{P})f(y)-(P-\widehat{P})\, f(x)\right)^2\pi(dx)\pi(dy)\\\leq& \left(\frac12+\frac{a\kappa}{2}\right)\int\left(Pf(x)-Pf(y)\right)^2\pi(dx)\pi(dy)\\&+\left(\frac12+\frac{1}{2a\kappa}\right)\int\left((P-\widehat{P})\, f(x)-(P-\widehat{P})\, f(y)\right)^2\pi(dx)\pi(dy)\\\leq&\, (1+a \kappa) \textrm{var}_\pi(P f)+\left(2+\frac{2}{a\kappa}\right)\int((P-\widehat{P})f(x))^2\pi(dx).\end{split}\end{equation}
Here we used
![]() $AB\leq \frac{a\kappa}{2} A^2+ \frac{2}{a\kappa}B^2$
to get the first inequality.
$AB\leq \frac{a\kappa}{2} A^2+ \frac{2}{a\kappa}B^2$
to get the first inequality.
Next, note that
Let
![]() $\Delta f(x)=f(x)-\pi f$
. Then,
$\Delta f(x)=f(x)-\pi f$
. Then,
Plugging the bounds (24) and (25) into (23), we have
Using induction with
![]() $C=2+2/\kappa$
, we find
$C=2+2/\kappa$
, we find
For Claim 2, first note that
 \begin{equation*}\begin{split}\left|\int \widehat{P} f(x)\pi(dx) - \pi f \right| &= \left|\int (\widehat{P}-P)f(x)\pi(dx) \right|\\&=\left|\int (\widehat{P}-P)\Delta f(x)\pi(dx) \right| \mbox{ recall that $\Delta f(x)=f(x)-\pi f$}\\&\leq \left(\int \left((\widehat{P}-P)\Delta f(x)\right)^2\pi(dx) \right)^{1/2}\\&=\|(P-\widehat{P}) \Delta f\|_\pi\leq \epsilon\sqrt{\textrm{var}_\pi f}.\end{split}\end{equation*}
\begin{equation*}\begin{split}\left|\int \widehat{P} f(x)\pi(dx) - \pi f \right| &= \left|\int (\widehat{P}-P)f(x)\pi(dx) \right|\\&=\left|\int (\widehat{P}-P)\Delta f(x)\pi(dx) \right| \mbox{ recall that $\Delta f(x)=f(x)-\pi f$}\\&\leq \left(\int \left((\widehat{P}-P)\Delta f(x)\right)^2\pi(dx) \right)^{1/2}\\&=\|(P-\widehat{P}) \Delta f\|_\pi\leq \epsilon\sqrt{\textrm{var}_\pi f}.\end{split}\end{equation*}
Then, because
![]() $\int P g(x)\pi(dx)=\int g(x)\pi(dx)$
for any function
$\int P g(x)\pi(dx)=\int g(x)\pi(dx)$
for any function
![]() $g$
,
$g$
,
 \begin{equation*}\begin{split}\left|\int (\widehat{P}^{n+1}-\widehat{P}^n)f(x)\pi(dx)\right|&=\left|\int (\widehat{P}-P)(\widehat{P}^nf)(x)\pi(dx)\right|\\&\leq \epsilon \sqrt{\textrm{var}_\pi (\widehat{P}^n f)}\leq \epsilon (1-\widehat{\kappa})^{n/2}\sqrt{ \textrm{var}_\pi\; f},\end{split}\end{equation*}
\begin{equation*}\begin{split}\left|\int (\widehat{P}^{n+1}-\widehat{P}^n)f(x)\pi(dx)\right|&=\left|\int (\widehat{P}-P)(\widehat{P}^nf)(x)\pi(dx)\right|\\&\leq \epsilon \sqrt{\textrm{var}_\pi (\widehat{P}^n f)}\leq \epsilon (1-\widehat{\kappa})^{n/2}\sqrt{ \textrm{var}_\pi\; f},\end{split}\end{equation*}
from Claim 1. Let
![]() $\mu_n=\pi \widehat{P}^n$
and
$\mu_n=\pi \widehat{P}^n$
and
![]() $f=\text{sgn}(\mu_{n+1}-\mu_n)$
. Because
$f=\text{sgn}(\mu_{n+1}-\mu_n)$
. Because
![]() $\textrm{var}_\pi f\leq \mathbb{E}_\pi |\,f|^2=1$
,
$\textrm{var}_\pi f\leq \mathbb{E}_\pi |\,f|^2=1$
,
Thus,
![]() $\mu_n$
is a Cauchy sequence under the total variation metric, which implies that the sequence has a limit
$\mu_n$
is a Cauchy sequence under the total variation metric, which implies that the sequence has a limit
![]() $\widehat{\pi}$
and that
$\widehat{\pi}$
and that
When letting
![]() $n=0$
, we have
$n=0$
, we have
Consider
![]() $f=\widehat{\pi}/\pi$
.
$f=\widehat{\pi}/\pi$
.
![]() $D_{\chi^2}(\widehat{\pi}\|\pi)=|\widehat{\pi} f -\pi f|=\textrm{var}_\pi f$
. Combining this with (26), we have
$D_{\chi^2}(\widehat{\pi}\|\pi)=|\widehat{\pi} f -\pi f|=\textrm{var}_\pi f$
. Combining this with (26), we have
Proof of Proposition 2. For the first claim, we note that
 \begin{align*}|\nu\widehat{P}^n f-\pi \widehat{P}^n f|&\leq \int \frac{\nu(x)}{\pi(x)}\pi(dx)|\widehat{P}^n f(x)-\pi \widehat{P}^n f|\\&\leq \sqrt{\int \Big(\frac{\nu(x)}{\pi(x)}\Big)^2 \pi(dx)} \sqrt{\int |\widehat{P}^n f(x)-\pi \widehat{P}^nf |^2\pi(dx)}\\&\leq \sqrt{D_{\chi^2}(\nu\|\pi)+1}\times (1- \hat{\kappa})^{n/2}\sqrt{\textrm{var}_\pi f} \mbox{ by Theorem 3.}\end{align*}
\begin{align*}|\nu\widehat{P}^n f-\pi \widehat{P}^n f|&\leq \int \frac{\nu(x)}{\pi(x)}\pi(dx)|\widehat{P}^n f(x)-\pi \widehat{P}^n f|\\&\leq \sqrt{\int \Big(\frac{\nu(x)}{\pi(x)}\Big)^2 \pi(dx)} \sqrt{\int |\widehat{P}^n f(x)-\pi \widehat{P}^nf |^2\pi(dx)}\\&\leq \sqrt{D_{\chi^2}(\nu\|\pi)+1}\times (1- \hat{\kappa})^{n/2}\sqrt{\textrm{var}_\pi f} \mbox{ by Theorem 3.}\end{align*}
Meanwhile,
By triangular inequality,
 \begin{equation*}\begin{split}|\nu\widehat{P}^n f-\widehat{\pi} f|&\leq |\nu\widehat{P}^n f-\pi \widehat{P}^n f|+|\pi \widehat{P}^nf-\widehat{\pi} f|\\&\leq (1-\widehat{\kappa})^{n/2}\sqrt{\textrm{var}_\pi f}\left(\sqrt{D_{\chi^2}(\nu\|\pi)+1}+C\epsilon\right).\end{split}\end{equation*}
\begin{equation*}\begin{split}|\nu\widehat{P}^n f-\widehat{\pi} f|&\leq |\nu\widehat{P}^n f-\pi \widehat{P}^n f|+|\pi \widehat{P}^nf-\widehat{\pi} f|\\&\leq (1-\widehat{\kappa})^{n/2}\sqrt{\textrm{var}_\pi f}\left(\sqrt{D_{\chi^2}(\nu\|\pi)+1}+C\epsilon\right).\end{split}\end{equation*}
For the second part, we first note that for any
![]() $f$
with
$f$
with
![]() $\widehat{\pi} f=0$
, we have
$\widehat{\pi} f=0$
, we have
 \begin{align*}\mathbb{E}_{\widehat{\pi}}[(\hat{f}_M-\widehat{\pi} f)^2]&=\frac{1}{M^2}\mathbb{E}_{\widehat{\pi}}\left[\sum_{j,k=1}^M f(\widehat{X}_j) f(\widehat{X}_{k})\right]\\&\leq \frac{2}{M^2}\mathbb{E}_{\widehat{\pi}}\left[\sum_{j=1}^M |\,f(\widehat{X}_j)| \sum_{k=0}^\infty |\,f(\widehat{X}_{j+k})|\right]\\&= \frac{2}{M}\sum_{k=0}^\infty \mathbb{E}_{\widehat{\pi}}\left[|\,f(\widehat{X}_0)||\,f(\widehat{X}_{k})|\right]\\&\leq \frac{2}{M}\sqrt{\mathbb{E}_{\widehat{\pi}}[f(\widehat{X}_0)^2]} \sum_{k=0}^\infty \sqrt{\mathbb{E}_{\widehat{\pi}}[(\widehat{P}^k f(\widehat{X}_0))^2]}.\end{align*}
\begin{align*}\mathbb{E}_{\widehat{\pi}}[(\hat{f}_M-\widehat{\pi} f)^2]&=\frac{1}{M^2}\mathbb{E}_{\widehat{\pi}}\left[\sum_{j,k=1}^M f(\widehat{X}_j) f(\widehat{X}_{k})\right]\\&\leq \frac{2}{M^2}\mathbb{E}_{\widehat{\pi}}\left[\sum_{j=1}^M |\,f(\widehat{X}_j)| \sum_{k=0}^\infty |\,f(\widehat{X}_{j+k})|\right]\\&= \frac{2}{M}\sum_{k=0}^\infty \mathbb{E}_{\widehat{\pi}}\left[|\,f(\widehat{X}_0)||\,f(\widehat{X}_{k})|\right]\\&\leq \frac{2}{M}\sqrt{\mathbb{E}_{\widehat{\pi}}[f(\widehat{X}_0)^2]} \sum_{k=0}^\infty \sqrt{\mathbb{E}_{\widehat{\pi}}[(\widehat{P}^k f(\widehat{X}_0))^2]}.\end{align*}
Next,

Because
![]() $\sup_x|\,f(x)|\leq C$
for some
$\sup_x|\,f(x)|\leq C$
for some
![]() $C\in(0,\infty)$
,
$C\in(0,\infty)$
,
![]() $\sup_x|\widehat{P}^k f(x)|\leq C$
and
$\sup_x|\widehat{P}^k f(x)|\leq C$
and
![]() $\sup_x|(\widehat{P}^k-\pi \widehat{P}^k)f(x)|\leq 2C$
. Then
$\sup_x|(\widehat{P}^k-\pi \widehat{P}^k)f(x)|\leq 2C$
. Then
Thus,
and we can further find a constant
![]() $C'$
such that
$C'$
such that
Proof of Theorem
4. To simplify the notation, let
![]() $\kappa$
denote the spectral gap of
$\kappa$
denote the spectral gap of
![]() $P$
and let
$P$
and let
![]() $\widehat{\kappa}$
denote the spectral gap of
$\widehat{\kappa}$
denote the spectral gap of
![]() $\widehat{P}$
. By the definition of spectral gap, i.e. (15), we have
$\widehat{P}$
. By the definition of spectral gap, i.e. (15), we have
First, note that
 \begin{equation}\begin{split}\textrm{var}_{\widehat{\pi}}\, f&=\mathbb{E}_{\widehat{\pi}} [(f-\widehat{\pi} f)^2]\\&\leq \mathbb{E}_{\widehat{\pi}} [(f-\pi f)^2]\\&\leq (1+\epsilon)\mathbb{E}_{\pi}[(f-\pi f)^2] \\ &=(1+\epsilon)\textrm{var}_\pi f.\end{split}\end{equation}
\begin{equation}\begin{split}\textrm{var}_{\widehat{\pi}}\, f&=\mathbb{E}_{\widehat{\pi}} [(f-\widehat{\pi} f)^2]\\&\leq \mathbb{E}_{\widehat{\pi}} [(f-\pi f)^2]\\&\leq (1+\epsilon)\mathbb{E}_{\pi}[(f-\pi f)^2] \\ &=(1+\epsilon)\textrm{var}_\pi f.\end{split}\end{equation}
We next establish two useful bounds:
 \begin{equation}\begin{split}|\langle f, (I-P^2)f\rangle_{\widehat{\pi}}-\langle f, (I-P^2)f\rangle_{\pi}|&\leq \int |\,f(x)(I-P^2)f(x) |\epsilon \pi(dx) \\&\leq \epsilon\|\,f\|_\pi \|(I-P^2)f\|_\pi\leq \epsilon\|\,f\|_\pi^2,\end{split}\end{equation}
\begin{equation}\begin{split}|\langle f, (I-P^2)f\rangle_{\widehat{\pi}}-\langle f, (I-P^2)f\rangle_{\pi}|&\leq \int |\,f(x)(I-P^2)f(x) |\epsilon \pi(dx) \\&\leq \epsilon\|\,f\|_\pi \|(I-P^2)f\|_\pi\leq \epsilon\|\,f\|_\pi^2,\end{split}\end{equation}
and
 \begin{equation}\begin{split}|\langle f, (\widehat{P}^2-P^2)f\rangle_{\widehat{\pi}}|&\leq \|\,f\|_{\widehat{\pi}} \|(\widehat{P}^2-P^2)f\|_{\widehat{\pi}}\\&\leq (1+\epsilon)^2\|\,f\|_\pi \|(\widehat{P}^2-P^2)f\|_{\pi} \\ &\leq (1+\epsilon)^2\|\,f\|_\pi (2\|(\widehat{P}-P)Pf\|_{\pi}+\|(\widehat{P}-P)^2f\|_{\pi}) \\&\leq (1+\epsilon)^2\|\,f\|_\pi (2\epsilon\|Pf\|_{\pi}+\epsilon\|(\widehat{P}-P)f\|_{\pi}) \\&\leq (1+\epsilon)^2\|\,f\|_\pi (2\epsilon\|\,f\|_{\pi}+\epsilon^2\|\,f\|_{\pi}) \\&\leq 3(1+\epsilon)^2\epsilon\|\,f\|_\pi^2\\&\leq C\epsilon\|\,f\|_\pi^2.\end{split}\end{equation}
\begin{equation}\begin{split}|\langle f, (\widehat{P}^2-P^2)f\rangle_{\widehat{\pi}}|&\leq \|\,f\|_{\widehat{\pi}} \|(\widehat{P}^2-P^2)f\|_{\widehat{\pi}}\\&\leq (1+\epsilon)^2\|\,f\|_\pi \|(\widehat{P}^2-P^2)f\|_{\pi} \\ &\leq (1+\epsilon)^2\|\,f\|_\pi (2\|(\widehat{P}-P)Pf\|_{\pi}+\|(\widehat{P}-P)^2f\|_{\pi}) \\&\leq (1+\epsilon)^2\|\,f\|_\pi (2\epsilon\|Pf\|_{\pi}+\epsilon\|(\widehat{P}-P)f\|_{\pi}) \\&\leq (1+\epsilon)^2\|\,f\|_\pi (2\epsilon\|\,f\|_{\pi}+\epsilon^2\|\,f\|_{\pi}) \\&\leq 3(1+\epsilon)^2\epsilon\|\,f\|_\pi^2\\&\leq C\epsilon\|\,f\|_\pi^2.\end{split}\end{equation}
Then
 \begin{equation}\begin{split}|\langle f, (I-\widehat{P}^2) f\rangle_{\widehat{\pi}}|&\geq|\langle f, (I-P^2) f\rangle_{\widehat{\pi}}| - |\langle f, (\widehat{P}^2-P^2)f\rangle_{\widehat{\pi}}| \mbox{ by triangular inequality}\\&\geq |\langle f, (I-P^2) f\rangle_{\widehat{\pi}}|-C\epsilon\|\,f\|_\pi^2 \mbox{ by the bound in (29)}\\&\geq |\langle f, (I-P^2) f\rangle_{\pi}| - |\langle f, (I-P^2) f\rangle_{\pi}-\langle f, (I-P^2) f\rangle_{\widehat{\pi}}|-C\epsilon\|\,f\|_\pi^2\\&\geq |\langle f, (I-P^2) f\rangle_{\pi}|-C\epsilon\|\,f\|_\pi^2 -C\epsilon\|\,f\|_\pi^2 \mbox{ by the bound in (28)}\\&\geq \langle f, (I-P^2) f\rangle_{\pi} - C\epsilon \textrm{var}_\pi f.\end{split}\end{equation}
\begin{equation}\begin{split}|\langle f, (I-\widehat{P}^2) f\rangle_{\widehat{\pi}}|&\geq|\langle f, (I-P^2) f\rangle_{\widehat{\pi}}| - |\langle f, (\widehat{P}^2-P^2)f\rangle_{\widehat{\pi}}| \mbox{ by triangular inequality}\\&\geq |\langle f, (I-P^2) f\rangle_{\widehat{\pi}}|-C\epsilon\|\,f\|_\pi^2 \mbox{ by the bound in (29)}\\&\geq |\langle f, (I-P^2) f\rangle_{\pi}| - |\langle f, (I-P^2) f\rangle_{\pi}-\langle f, (I-P^2) f\rangle_{\widehat{\pi}}|-C\epsilon\|\,f\|_\pi^2\\&\geq |\langle f, (I-P^2) f\rangle_{\pi}|-C\epsilon\|\,f\|_\pi^2 -C\epsilon\|\,f\|_\pi^2 \mbox{ by the bound in (28)}\\&\geq \langle f, (I-P^2) f\rangle_{\pi} - C\epsilon \textrm{var}_\pi f.\end{split}\end{equation}
Combining (27) and (30), we have
![]() $\widehat{\kappa} \geq \kappa -C\epsilon. $
$\widehat{\kappa} \geq \kappa -C\epsilon. $
Proof of Proposition 3. For the first claim,
 \begin{align*}|\nu\widehat{P}^n f-\widehat{\pi} f|&=|\nu\widehat{P}^n f-\widehat{\pi} \widehat{P}^n f|\\&\leq \int \frac{\nu(x)}{\widehat{\pi}(x)}\widehat{\pi}(x)|\widehat{P}^n f(x)-\widehat{\pi} \widehat{P}^n f|dx\\&\leq \sqrt{\int \Big(\frac{\nu(x)}{\widehat{\pi}(x)}\Big)^2 \widehat{\pi}(x)dx} \sqrt{\int |\widehat{P}^n f(x)-\widehat{\pi} \widehat{P}^nf |^2\widehat{\pi}(x)dx}\\&\leq \sqrt{D_{\chi^2}(\nu\|\widehat{\pi})+1}\times (1- \hat{\kappa})^{n/2}\sqrt{\textrm{var}_{\widehat{\pi}}\, f}.\end{align*}
\begin{align*}|\nu\widehat{P}^n f-\widehat{\pi} f|&=|\nu\widehat{P}^n f-\widehat{\pi} \widehat{P}^n f|\\&\leq \int \frac{\nu(x)}{\widehat{\pi}(x)}\widehat{\pi}(x)|\widehat{P}^n f(x)-\widehat{\pi} \widehat{P}^n f|dx\\&\leq \sqrt{\int \Big(\frac{\nu(x)}{\widehat{\pi}(x)}\Big)^2 \widehat{\pi}(x)dx} \sqrt{\int |\widehat{P}^n f(x)-\widehat{\pi} \widehat{P}^nf |^2\widehat{\pi}(x)dx}\\&\leq \sqrt{D_{\chi^2}(\nu\|\widehat{\pi})+1}\times (1- \hat{\kappa})^{n/2}\sqrt{\textrm{var}_{\widehat{\pi}}\, f}.\end{align*}
For the second part, we first note that if we replace
![]() $f$
with
$f$
with
![]() $f-\widehat{\pi} f$
, with a little change in notation, we have
$f-\widehat{\pi} f$
, with a little change in notation, we have
 \begin{equation*}\begin{split}\mathbb{E}_{\widehat{\pi}}[(\hat{f}_M-\widehat{\pi} f)^2]&=\frac{1}{M^2}\mathbb{E}_{\widehat{\pi}}\left[\sum_{j,k=1}^M f(\widehat{X}_j) f(\widehat{X}_{k})\right]\\&\leq \frac{2}{M^2}\mathbb{E}_{\widehat{\pi}}\left[\sum_{j=1}^M |\,f(\widehat{X}_j)| \sum_{k=0}^\infty |\,f(\widehat{X}_{j+k})|\right]\\&= \frac{2}{M}\sum_{k=0}^\infty \mathbb{E}_{\widehat{\pi}}\left[|\,f(\widehat{X}_0)| |\,f(\widehat{X}_{k})|\right]\end{split}\end{equation*}
\begin{equation*}\begin{split}\mathbb{E}_{\widehat{\pi}}[(\hat{f}_M-\widehat{\pi} f)^2]&=\frac{1}{M^2}\mathbb{E}_{\widehat{\pi}}\left[\sum_{j,k=1}^M f(\widehat{X}_j) f(\widehat{X}_{k})\right]\\&\leq \frac{2}{M^2}\mathbb{E}_{\widehat{\pi}}\left[\sum_{j=1}^M |\,f(\widehat{X}_j)| \sum_{k=0}^\infty |\,f(\widehat{X}_{j+k})|\right]\\&= \frac{2}{M}\sum_{k=0}^\infty \mathbb{E}_{\widehat{\pi}}\left[|\,f(\widehat{X}_0)| |\,f(\widehat{X}_{k})|\right]\end{split}\end{equation*}
 \begin{equation*}\begin{split}&\leq \frac{2}{M}\sqrt{\mathbb{E}_{\widehat{\pi}}[f(\widehat{X}_0)^2]} \sum_{k=0}^\infty \sqrt{\mathbb{E}_{\widehat{\pi}}[(\widehat{P}^k f(\widehat{X}_0))^2]}\\&\leq \frac{2}{M}\sqrt{\mathbb{E}_{\widehat{\pi}}[f(\widehat{X}_0)^2]} \sum_{k=0}^\infty (1-\widehat{\kappa})^{k/2}\sqrt{\textrm{var}_{\widehat{\pi}}\, f}\\&=\frac{2}{M(1-(1-\widehat{\kappa})^{1/2})}\textrm{var}_{\widehat{\pi}}\, f\end{split}\end{equation*}
\begin{equation*}\begin{split}&\leq \frac{2}{M}\sqrt{\mathbb{E}_{\widehat{\pi}}[f(\widehat{X}_0)^2]} \sum_{k=0}^\infty \sqrt{\mathbb{E}_{\widehat{\pi}}[(\widehat{P}^k f(\widehat{X}_0))^2]}\\&\leq \frac{2}{M}\sqrt{\mathbb{E}_{\widehat{\pi}}[f(\widehat{X}_0)^2]} \sum_{k=0}^\infty (1-\widehat{\kappa})^{k/2}\sqrt{\textrm{var}_{\widehat{\pi}}\, f}\\&=\frac{2}{M(1-(1-\widehat{\kappa})^{1/2})}\textrm{var}_{\widehat{\pi}}\, f\end{split}\end{equation*}
Proof of Proposition
4. Let
![]() $Q_x$
be the optimal coupled measure between
$Q_x$
be the optimal coupled measure between
![]() $\delta_x P$
and
$\delta_x P$
and
![]() $\delta_x\widehat{P}$
. Then
$\delta_x\widehat{P}$
. Then
 \begin{align*}|(\delta_xP-\delta_x\widehat{P})\, f|&\leq \int Q_x(dx^{\prime},dy^{\prime}) |\,f(x^{\prime})-f(y^{\prime})|\\&= \int Q_x(dx^{\prime},dy^{\prime}) (|\,f(x^{\prime})-f(y^{\prime})|)1_{x^{\prime}\neq y^{\prime}}.\end{align*}
\begin{align*}|(\delta_xP-\delta_x\widehat{P})\, f|&\leq \int Q_x(dx^{\prime},dy^{\prime}) |\,f(x^{\prime})-f(y^{\prime})|\\&= \int Q_x(dx^{\prime},dy^{\prime}) (|\,f(x^{\prime})-f(y^{\prime})|)1_{x^{\prime}\neq y^{\prime}}.\end{align*}
Next
 \begin{align*}\|(P-\hat P)f\|_\pi^2=&\int \pi(dx)|(\delta_xP-\delta_x\widehat{P})\, f|^2\\\leq& \int \pi (dx) \left(\int Q_x(dx^{\prime},dy^{\prime}) (|\,f(x^{\prime})-f(y^{\prime})|)1_{x^{\prime}\neq y^{\prime}}\right)^2\\\leq& \left(\int \pi (dx)Q_x(dx^{\prime},dy^{\prime}) \left(2f(x^{\prime})^2+2f(y^{\prime})^2\right)\right)\left(\int \pi (dx) Q_x(dx^{\prime},dy^{\prime}) 1_{x^{\prime}\neq y^{\prime}}\right)\\\leq&\, 2 \left(\langle \pi P, f^2\rangle+\langle \pi \widehat{P}, f^2\rangle\right) \left(\epsilon \int \pi(dx)V(x) \right)\\\leq&\, 2\epsilon\left(\langle \pi, f^2\rangle+a\langle \widehat{\pi} \widehat{P}, f^2\rangle\right)(\pi V)\\\leq&\, 2\epsilon\left(1+a^2\right)\|\,f\|_{\pi}^2\|V\|_\pi. \end{align*}
\begin{align*}\|(P-\hat P)f\|_\pi^2=&\int \pi(dx)|(\delta_xP-\delta_x\widehat{P})\, f|^2\\\leq& \int \pi (dx) \left(\int Q_x(dx^{\prime},dy^{\prime}) (|\,f(x^{\prime})-f(y^{\prime})|)1_{x^{\prime}\neq y^{\prime}}\right)^2\\\leq& \left(\int \pi (dx)Q_x(dx^{\prime},dy^{\prime}) \left(2f(x^{\prime})^2+2f(y^{\prime})^2\right)\right)\left(\int \pi (dx) Q_x(dx^{\prime},dy^{\prime}) 1_{x^{\prime}\neq y^{\prime}}\right)\\\leq&\, 2 \left(\langle \pi P, f^2\rangle+\langle \pi \widehat{P}, f^2\rangle\right) \left(\epsilon \int \pi(dx)V(x) \right)\\\leq&\, 2\epsilon\left(\langle \pi, f^2\rangle+a\langle \widehat{\pi} \widehat{P}, f^2\rangle\right)(\pi V)\\\leq&\, 2\epsilon\left(1+a^2\right)\|\,f\|_{\pi}^2\|V\|_\pi. \end{align*}
Appendix C. Verification for Metropolis–Hastings MCMC
We first present an auxiliary lemma, which is well known:
Lemma 4.
Suppose a transition kernel
![]() $P$
is reversible with invariant measure
$P$
is reversible with invariant measure
![]() $\pi$
. Then
$\pi$
. Then
![]() $\|P\|_\pi\leq 1$
.
$\|P\|_\pi\leq 1$
.
Proof We first note that
 \begin{equation*}\begin{split}&\int f(x)^2\pi(dx) - \int \pi(dx)f(x)f(y)P^2(x,dy)\\=&\, \frac{1}{2}\int \pi(dx)f(x)^2P^2(x,dy)+\frac{1}{2}\int\pi(dx)f(y)^2P^2(x,dy) -\int \pi(dx)f(x)f(y)P^2(x,dy)\\=&\, \frac{1}{2}\int \pi(dx)(f(x)-f(y))^2P^2(x,dy)\geq 0.\end{split}\end{equation*}
\begin{equation*}\begin{split}&\int f(x)^2\pi(dx) - \int \pi(dx)f(x)f(y)P^2(x,dy)\\=&\, \frac{1}{2}\int \pi(dx)f(x)^2P^2(x,dy)+\frac{1}{2}\int\pi(dx)f(y)^2P^2(x,dy) -\int \pi(dx)f(x)f(y)P^2(x,dy)\\=&\, \frac{1}{2}\int \pi(dx)(f(x)-f(y))^2P^2(x,dy)\geq 0.\end{split}\end{equation*}
Thus,
Proof of Lemma
1. For any density of the form
![]() $\mu(x)=\nu(x)s(x)$
, we have
$\mu(x)=\nu(x)s(x)$
, we have
 \begin{align*}| \mu (P-\widehat{P})\, f|&\leq \int \mu(x) |\alpha(x)-\hat{\alpha}(x)| |\,f(x)|dx+\int \mu(x) |\beta(x,x^{\prime})-\hat{\beta}(x,x^{\prime})| |\,f(x^{\prime})|dx^{\prime}dx\\&\leq C\epsilon \int \mu(x) |\,f(x)|dx+C\epsilon \int \mu(x) \beta(x,x^{\prime}) |\,f(x^{\prime})|dx^{\prime}dx\\&\leq C\epsilon \int \mu(x) |\,f(x)|dx+C\epsilon \int \mu(x) P(x,x^{\prime}) |\,f(x^{\prime})|dx^{\prime}dx\\&=C\epsilon \int \nu(x)s(x) |\,f(x)|dx+C\epsilon \int \nu(x)s(x) P(x,x^{\prime}) |\,f(x^{\prime})|dx^{\prime}dx\\&\leq C\epsilon \| s \|_\nu \|\,f\|_\nu+C\epsilon \| s \|_\nu \|P f\|_\nu\\&\leq 2C\epsilon \| s \|_\nu \|\,f\|_\nu \mbox{ by Lemma 4.}\end{align*}
\begin{align*}| \mu (P-\widehat{P})\, f|&\leq \int \mu(x) |\alpha(x)-\hat{\alpha}(x)| |\,f(x)|dx+\int \mu(x) |\beta(x,x^{\prime})-\hat{\beta}(x,x^{\prime})| |\,f(x^{\prime})|dx^{\prime}dx\\&\leq C\epsilon \int \mu(x) |\,f(x)|dx+C\epsilon \int \mu(x) \beta(x,x^{\prime}) |\,f(x^{\prime})|dx^{\prime}dx\\&\leq C\epsilon \int \mu(x) |\,f(x)|dx+C\epsilon \int \mu(x) P(x,x^{\prime}) |\,f(x^{\prime})|dx^{\prime}dx\\&=C\epsilon \int \nu(x)s(x) |\,f(x)|dx+C\epsilon \int \nu(x)s(x) P(x,x^{\prime}) |\,f(x^{\prime})|dx^{\prime}dx\\&\leq C\epsilon \| s \|_\nu \|\,f\|_\nu+C\epsilon \| s \|_\nu \|P f\|_\nu\\&\leq 2C\epsilon \| s \|_\nu \|\,f\|_\nu \mbox{ by Lemma 4.}\end{align*}
Next, taking
![]() $\mu\propto |(P-\widehat{P})f|\nu$
, we have
$\mu\propto |(P-\widehat{P})f|\nu$
, we have
which further implies that there is a
![]() $C_1$
such that
$C_1$
such that
![]() $\|P-\widehat{P}\|_\nu\leq C_1\epsilon.$
$\|P-\widehat{P}\|_\nu\leq C_1\epsilon.$
Proof of Proposition 5. We denote the acceptance probabilities for the original process and the perturbed process as
respectively. Since for any positive numbers
![]() $a,b,c,d$
,
$a,b,c,d$
,
and since
![]() $\exp\!({-}C\epsilon)\leq \pi(x)/\hat\pi(x)\leq \exp\!(C\epsilon)$
, we have
$\exp\!({-}C\epsilon)\leq \pi(x)/\hat\pi(x)\leq \exp\!(C\epsilon)$
, we have
Using the fact that
![]() $\beta(x,x^{\prime})=R(x,x^{\prime})b(x,x^{\prime})$
and
$\beta(x,x^{\prime})=R(x,x^{\prime})b(x,x^{\prime})$
and
![]() $\hat\beta(x,x^{\prime})=R(x,x^{\prime})\hat b(x,x^{\prime})$
, we have
$\hat\beta(x,x^{\prime})=R(x,x^{\prime})\hat b(x,x^{\prime})$
, we have
In addition, for
![]() $\alpha(x)=\int R(x,x^{\prime})(1-b(x,x^{\prime}))dx^{\prime}$
and
$\alpha(x)=\int R(x,x^{\prime})(1-b(x,x^{\prime}))dx^{\prime}$
and
![]() $\hat \alpha(x)=\int R(x,x^{\prime})(1-\hat b(x,x^{\prime}))dx^{\prime}$
,
$\hat \alpha(x)=\int R(x,x^{\prime})(1-\hat b(x,x^{\prime}))dx^{\prime}$
,
By Lemma 1, we can find a
![]() $C_1$
such that
$C_1$
such that
Proof of Proposition 6. Note that
and
As
![]() $|\nabla\log \widehat{\pi}(x)- \nabla\log \pi(x)|\leq C\epsilon$
and the support is bounded, we can enlarge the value of
$|\nabla\log \widehat{\pi}(x)- \nabla\log \pi(x)|\leq C\epsilon$
and the support is bounded, we can enlarge the value of
![]() $C$
so that
$C$
so that
Let the acceptance probability be
 \begin{equation*}\begin{split}b(x,x^{\prime})=&\frac{\pi(x^{\prime})\exp\left(-\frac1{4h}\|x-x^{\prime}+\nabla \log \pi(x^{\prime})h \|^2\right)}{\pi(x) \exp\left(-\frac1{4h}\|x^{\prime}-x+\nabla \log \pi(x)h\|^2\right)}\wedge 1\\=&\left\{\exp\left(\log \pi(x^{\prime})-\log \pi(x)-\frac1{2}\langle x-x^{\prime},\nabla \log \pi(x^{\prime})-\nabla \log\pi(x)\rangle\right)\right.\\&\left.\times \exp\left(\frac{h}{4} \left[\|\nabla \log \pi(x^{\prime})\|^2-\|\nabla \log \pi(x)\|^2\right]\right)\right\}\wedge 1\end{split}\end{equation*}
\begin{equation*}\begin{split}b(x,x^{\prime})=&\frac{\pi(x^{\prime})\exp\left(-\frac1{4h}\|x-x^{\prime}+\nabla \log \pi(x^{\prime})h \|^2\right)}{\pi(x) \exp\left(-\frac1{4h}\|x^{\prime}-x+\nabla \log \pi(x)h\|^2\right)}\wedge 1\\=&\left\{\exp\left(\log \pi(x^{\prime})-\log \pi(x)-\frac1{2}\langle x-x^{\prime},\nabla \log \pi(x^{\prime})-\nabla \log\pi(x)\rangle\right)\right.\\&\left.\times \exp\left(\frac{h}{4} \left[\|\nabla \log \pi(x^{\prime})\|^2-\|\nabla \log \pi(x)\|^2\right]\right)\right\}\wedge 1\end{split}\end{equation*}
Similarly, we define
 \begin{equation*}\begin{split}\hat b(x,x^{\prime}) =& \frac{\hat\pi(x^{\prime})\exp\left(-\frac1{4h}\|x-x^{\prime}+\nabla \log \hat \pi(x^{\prime})h \|^2\right)}{\hat\pi(x) \exp\left(-\frac1{4h}\| x^{\prime}-x+\nabla \log \hat\pi(x)h\|^2\right)}\wedge 1 \\=&\left\{\exp\left(\log \hat\pi(x^{\prime})-\log \hat\pi(x)-\frac1{2}\langle x-x^{\prime},\nabla \log \hat\pi(x^{\prime})-\nabla \log\hat\pi(x)\rangle\right)\right.\\&\left.\times \exp\left(\frac{h}{4} \left[\|\nabla \log \hat\pi(x^{\prime})\|^2-\|\nabla \log \hat\pi(x)\|^2\right]\right)\right\}\wedge 1\end{split}\end{equation*}
\begin{equation*}\begin{split}\hat b(x,x^{\prime}) =& \frac{\hat\pi(x^{\prime})\exp\left(-\frac1{4h}\|x-x^{\prime}+\nabla \log \hat \pi(x^{\prime})h \|^2\right)}{\hat\pi(x) \exp\left(-\frac1{4h}\| x^{\prime}-x+\nabla \log \hat\pi(x)h\|^2\right)}\wedge 1 \\=&\left\{\exp\left(\log \hat\pi(x^{\prime})-\log \hat\pi(x)-\frac1{2}\langle x-x^{\prime},\nabla \log \hat\pi(x^{\prime})-\nabla \log\hat\pi(x)\rangle\right)\right.\\&\left.\times \exp\left(\frac{h}{4} \left[\|\nabla \log \hat\pi(x^{\prime})\|^2-\|\nabla \log \hat\pi(x)\|^2\right]\right)\right\}\wedge 1\end{split}\end{equation*}
Since
![]() $|\log \pi(x)-\log \widehat{\pi}_k(x)|\leq C\epsilon, \|\nabla\log \pi(x)-\nabla\log \widehat{\pi}_k(x)\|\leq C\epsilon$
, and the support is bounded, we can further enlarge
$|\log \pi(x)-\log \widehat{\pi}_k(x)|\leq C\epsilon, \|\nabla\log \pi(x)-\nabla\log \widehat{\pi}_k(x)\|\leq C\epsilon$
, and the support is bounded, we can further enlarge
![]() $C$
such that
$C$
such that
Lastly, for
![]() $\beta(x,x^{\prime})=R(x,x^{\prime})b(x,x^{\prime})$
and
$\beta(x,x^{\prime})=R(x,x^{\prime})b(x,x^{\prime})$
and
![]() $\hat\beta(x,x^{\prime})=\hat R(x,x^{\prime})\hat b(x,x^{\prime})$
,
$\hat\beta(x,x^{\prime})=\hat R(x,x^{\prime})\hat b(x,x^{\prime})$
,
In addition, for
![]() $\alpha(x)=\int R(x,x^{\prime})(1-b(x,x^{\prime}))dx^{\prime}$
and
$\alpha(x)=\int R(x,x^{\prime})(1-b(x,x^{\prime}))dx^{\prime}$
and
![]() $\hat \alpha(x)=\int \hat R(x,x^{\prime})(1-\hat b(x,x^{\prime}))dx^{\prime}$
,
$\hat \alpha(x)=\int \hat R(x,x^{\prime})(1-\hat b(x,x^{\prime}))dx^{\prime}$
,
 \begin{equation*}\begin{split}|\alpha(x) - \hat \alpha(x)| \leq & \int |R(x,x^{\prime})-\hat R(x,x^{\prime})|(1-b(x,x^{\prime}))dx^{\prime}\\& + \int \hat R(x, x^{\prime})|b(x,x^{\prime})-\hat b(x,x^{\prime})|dx^{\prime}\\\leq&\, C\epsilon \int R(x,x^{\prime})dx^{\prime} + C\epsilon \int \hat R(x,x^{\prime})dx^{\prime}=2C\epsilon\end{split}\end{equation*}
\begin{equation*}\begin{split}|\alpha(x) - \hat \alpha(x)| \leq & \int |R(x,x^{\prime})-\hat R(x,x^{\prime})|(1-b(x,x^{\prime}))dx^{\prime}\\& + \int \hat R(x, x^{\prime})|b(x,x^{\prime})-\hat b(x,x^{\prime})|dx^{\prime}\\\leq&\, C\epsilon \int R(x,x^{\prime})dx^{\prime} + C\epsilon \int \hat R(x,x^{\prime})dx^{\prime}=2C\epsilon\end{split}\end{equation*}
By Lemma 1, we have a constant
![]() $C_1$
such that
$C_1$
such that
Proof of Proposition 7. The transition kernel of MALA takes the form
where
with
and
![]() $\alpha(x)=1-\int \beta(x,dy)$
. Similarly, we can write
$\alpha(x)=1-\int \beta(x,dy)$
. Similarly, we can write
![]() $\widehat{P}(x,y)=\widehat{\alpha}(x)\delta_x(y) + \widehat{\beta}(x,y)$
when using the perturbed target density
$\widehat{P}(x,y)=\widehat{\alpha}(x)\delta_x(y) + \widehat{\beta}(x,y)$
when using the perturbed target density
![]() $\widehat{\pi}$
.
$\widehat{\pi}$
.
We prove the proposition by showing that
In particular, note that
![]() $a\wedge q-\widehat{a}\wedge \widehat{q}\in \{a-\hat{a}, q-\hat{q}, a-\hat{q},\hat{a}-q\}$
, which further implies that
$a\wedge q-\widehat{a}\wedge \widehat{q}\in \{a-\hat{a}, q-\hat{q}, a-\hat{q},\hat{a}-q\}$
, which further implies that
Thus, if the bounds in (31) hold, then
 \begin{align*}\|\delta_xP-\delta_x\widehat{P}\|_{TV}&=\int |\beta(x,y)-\widehat{\beta}(x,y)|dy+|\alpha(x)-\widehat{\alpha}(x)|\\&\leq 2\int |\beta(x,y)-\widehat{\beta}(x,y)|dy\\&\leq 2\int |a(x,y)-\widehat{a}(x,y)|dy+2\int |q(x,y)-\widehat{q}(x,y)|dy\\&\leq 2C\epsilon (1+\exp\!(\delta x^2)).\end{align*}
\begin{align*}\|\delta_xP-\delta_x\widehat{P}\|_{TV}&=\int |\beta(x,y)-\widehat{\beta}(x,y)|dy+|\alpha(x)-\widehat{\alpha}(x)|\\&\leq 2\int |\beta(x,y)-\widehat{\beta}(x,y)|dy\\&\leq 2\int |a(x,y)-\widehat{a}(x,y)|dy+2\int |q(x,y)-\widehat{q}(x,y)|dy\\&\leq 2C\epsilon (1+\exp\!(\delta x^2)).\end{align*}
In order to obtain the first part of (31), note that by the intermediate value theorem,
![]() $|\exp\!(a)-\exp\!(b)|\leq |\exp\!(a)+\exp\!(b)||a-b|$
holds for any
$|\exp\!(a)-\exp\!(b)|\leq |\exp\!(a)+\exp\!(b)||a-b|$
holds for any
![]() $a,b$
, so we can bound
$a,b$
, so we can bound
 \begin{align}\notag|q(x,y)-\hat{q}(x,y)|\leq& \frac1{4}|q(x,y)+\hat{q}(x,y)|\|\nabla\log \pi(x)-\nabla\log \widehat{\pi}(x)\|\\\notag&\left(\|y-x-h\nabla\log \pi(x)\|+\|y-x-h\nabla\log \widehat{\pi}(x)\|\right)\\\leq& \frac{C\epsilon}4|q(x,y)+\hat{q}(x,y)|\left(\|y-x-h\nabla\log \pi(x)\|+\|y-x-h\nabla\log \widehat{\pi}(x)\|\right).\end{align}
\begin{align}\notag|q(x,y)-\hat{q}(x,y)|\leq& \frac1{4}|q(x,y)+\hat{q}(x,y)|\|\nabla\log \pi(x)-\nabla\log \widehat{\pi}(x)\|\\\notag&\left(\|y-x-h\nabla\log \pi(x)\|+\|y-x-h\nabla\log \widehat{\pi}(x)\|\right)\\\leq& \frac{C\epsilon}4|q(x,y)+\hat{q}(x,y)|\left(\|y-x-h\nabla\log \pi(x)\|+\|y-x-h\nabla\log \widehat{\pi}(x)\|\right).\end{align}
Note that
![]() $q(x,y)$
is the proposal density of
$q(x,y)$
is the proposal density of
![]() $y$
. Thus,
$y$
. Thus,

Similarly,
Therefore, we use (32) and find a larger
![]() $C$
such that
$C$
such that
To handle the second part of (31), we use
![]() $|\exp\!(a)-\exp\!(b)|\leq |\exp\!(a)+\exp\!(b)||a-b|$
again and find
$|\exp\!(a)-\exp\!(b)|\leq |\exp\!(a)+\exp\!(b)||a-b|$
again and find
 \begin{align*}&|a(x,y)-\widehat{a}(x,y)|\\=&\left|\frac{\pi(y)}{\pi(x)}q(y,x)-\frac{\widehat{\pi}(y)}{\widehat{\pi}(x)}\hat{q}(y,x)\right|\\\leq& \frac14\left|\frac{\pi(y)}{\pi(x)}q(y,x)+\frac{\widehat{\pi}(y)}{\widehat{\pi}(x)}\hat{q}(y,x)\right|\bigg(|\log \pi(x)-\log \widehat{\pi}(x)|+|\log \pi(y)-\log \widehat{\pi}(y)|\\&+\|\nabla\log \pi(y)-\nabla\log \widehat{\pi}(y)\|\left(\|y+h\nabla\log \pi(y)-x\|+\|y+h\nabla\log \widehat{\pi}(y)-x\|\right)\bigg)\\\leq& \frac{C\epsilon}{4}\left|\frac{\pi(y)}{\pi(x)}q(y,x)+\frac{\widehat{\pi}(y)}{\widehat{\pi}(x)}\hat{q}(y,x)\right|\left(2+\left(\|y+h\nabla\log \pi(y)-x\|+\|y+h\nabla\log \widehat{\pi}(y)-x\|\right)\right).\end{align*}
\begin{align*}&|a(x,y)-\widehat{a}(x,y)|\\=&\left|\frac{\pi(y)}{\pi(x)}q(y,x)-\frac{\widehat{\pi}(y)}{\widehat{\pi}(x)}\hat{q}(y,x)\right|\\\leq& \frac14\left|\frac{\pi(y)}{\pi(x)}q(y,x)+\frac{\widehat{\pi}(y)}{\widehat{\pi}(x)}\hat{q}(y,x)\right|\bigg(|\log \pi(x)-\log \widehat{\pi}(x)|+|\log \pi(y)-\log \widehat{\pi}(y)|\\&+\|\nabla\log \pi(y)-\nabla\log \widehat{\pi}(y)\|\left(\|y+h\nabla\log \pi(y)-x\|+\|y+h\nabla\log \widehat{\pi}(y)-x\|\right)\bigg)\\\leq& \frac{C\epsilon}{4}\left|\frac{\pi(y)}{\pi(x)}q(y,x)+\frac{\widehat{\pi}(y)}{\widehat{\pi}(x)}\hat{q}(y,x)\right|\left(2+\left(\|y+h\nabla\log \pi(y)-x\|+\|y+h\nabla\log \widehat{\pi}(y)-x\|\right)\right).\end{align*}
Note that the first part can be bounded by
 \begin{align*}&\int \frac{\pi(y)}{\pi(x)}q(y,x)\left(C+(\|y+h\nabla\log \pi(y)-x\|+\|y+h\nabla\log \widehat{\pi}(y)-x\|\right)dx\\\leq& \int \frac{\pi(y)}{\pi(x)}q(y,x)\left(C+h\epsilon+2\|y+h\nabla\log \pi(y)-x\|\right)dx\\=& \int \frac{\pi(y)}{(2\pi h)^{d/4}\pi(x)}\sqrt{q(y,x)}\,\cdot\, (2\pi h)^{d/4}\sqrt{q(y,x)}\left(C+h\epsilon+2\|y+h\nabla\log \pi(y)-x\|\right)dx\end{align*}
\begin{align*}&\int \frac{\pi(y)}{\pi(x)}q(y,x)\left(C+(\|y+h\nabla\log \pi(y)-x\|+\|y+h\nabla\log \widehat{\pi}(y)-x\|\right)dx\\\leq& \int \frac{\pi(y)}{\pi(x)}q(y,x)\left(C+h\epsilon+2\|y+h\nabla\log \pi(y)-x\|\right)dx\\=& \int \frac{\pi(y)}{(2\pi h)^{d/4}\pi(x)}\sqrt{q(y,x)}\,\cdot\, (2\pi h)^{d/4}\sqrt{q(y,x)}\left(C+h\epsilon+2\|y+h\nabla\log \pi(y)-x\|\right)dx\end{align*}
For
![]() $\tfrac{\pi(y)}{\pi(x)}(2\pi h)^{-d/4}\sqrt{q(y,x)}$
, we can bound it by
$\tfrac{\pi(y)}{\pi(x)}(2\pi h)^{-d/4}\sqrt{q(y,x)}$
, we can bound it by
 \begin{equation*}\begin{split}&\frac{1}{(2\pi h)^{d/4}}\frac{\pi(y)}{\pi(x)}\sqrt{q(y,x)}\\=&\, \frac{1}{(2\pi h)^{d/2}}\exp\left(\log\pi(y)-\log\pi(x)-\frac1{8h}\|y+h\nabla\log \pi(y)-x\|^2\right)\\\leq&\, \frac{1}{(2\pi h)^{d/2}}\exp\left(\langle\nabla\log\pi(w), y-x\rangle-\frac1{8h}\|y-x\|^2-\frac{1}{4}\langle\nabla\log \pi(y), y-x\rangle\right)\mbox{ for some $w$}\\\leq&\, \frac{1}{(2\pi h)^{d/2}} \exp\left(\frac{5L_\pi}{4}\|y-x\|(\|x\|+\|y-x\|+C)-\frac1{8h}\|y-x\|^2\right)\mbox{ by Lipschitzness of $\nabla \log \pi$}\\\leq&\, \frac{1}{(2\pi h)^{d/2}} \exp\left(\left(\frac{5L_\pi}{16\delta} + \frac{5L_{\pi}}{4} - \frac{1}{8h}\right)\|y-x\|^2 + \delta \|x\|^2+10L_\pi^2 C^2\right)\\\leq&\, \frac{1}{(2\pi h)^{d/2}} \exp\left( - \frac{1}{16h}\|y-x\|^2 + \delta \|x\|^2+10L_\pi^2 C^2\right) \mbox{ as $h<\big(\frac{5L_{\pi}}{\delta} + 20L_{\pi}\big)^{-1}$.}\end{split}\end{equation*}
\begin{equation*}\begin{split}&\frac{1}{(2\pi h)^{d/4}}\frac{\pi(y)}{\pi(x)}\sqrt{q(y,x)}\\=&\, \frac{1}{(2\pi h)^{d/2}}\exp\left(\log\pi(y)-\log\pi(x)-\frac1{8h}\|y+h\nabla\log \pi(y)-x\|^2\right)\\\leq&\, \frac{1}{(2\pi h)^{d/2}}\exp\left(\langle\nabla\log\pi(w), y-x\rangle-\frac1{8h}\|y-x\|^2-\frac{1}{4}\langle\nabla\log \pi(y), y-x\rangle\right)\mbox{ for some $w$}\\\leq&\, \frac{1}{(2\pi h)^{d/2}} \exp\left(\frac{5L_\pi}{4}\|y-x\|(\|x\|+\|y-x\|+C)-\frac1{8h}\|y-x\|^2\right)\mbox{ by Lipschitzness of $\nabla \log \pi$}\\\leq&\, \frac{1}{(2\pi h)^{d/2}} \exp\left(\left(\frac{5L_\pi}{16\delta} + \frac{5L_{\pi}}{4} - \frac{1}{8h}\right)\|y-x\|^2 + \delta \|x\|^2+10L_\pi^2 C^2\right)\\\leq&\, \frac{1}{(2\pi h)^{d/2}} \exp\left( - \frac{1}{16h}\|y-x\|^2 + \delta \|x\|^2+10L_\pi^2 C^2\right) \mbox{ as $h<\big(\frac{5L_{\pi}}{\delta} + 20L_{\pi}\big)^{-1}$.}\end{split}\end{equation*}
For
![]() $(2\pi h)^{d/4}\sqrt{q(y,x)}\left(C+h\epsilon+2\|y+h\nabla\log \pi(y)-x\|\right)$
, first note that we can find a larger
$(2\pi h)^{d/4}\sqrt{q(y,x)}\left(C+h\epsilon+2\|y+h\nabla\log \pi(y)-x\|\right)$
, first note that we can find a larger
![]() $C$
such that
$C$
such that
 \begin{align*}&(2\pi h)^{d/4}\sqrt{q(y,x)}\|y+h\nabla\log \pi(y)-x\|\\=&\exp\left(-\frac1{8h}\|y+h\nabla\log \pi(y)-x\|^2\right)\|y+h\nabla\log \pi(y)-x\|\leq C.\end{align*}
\begin{align*}&(2\pi h)^{d/4}\sqrt{q(y,x)}\|y+h\nabla\log \pi(y)-x\|\\=&\exp\left(-\frac1{8h}\|y+h\nabla\log \pi(y)-x\|^2\right)\|y+h\nabla\log \pi(y)-x\|\leq C.\end{align*}
Combining these two upper bounds, we can find a
![]() $C_1$
such that
$C_1$
such that
Similarly, we can show that
 \begin{align*}&\int \frac{\widehat{\pi}(y)}{\widehat{\pi}(x)}\hat{q}(y,dx)\left(C+(\|y+h\nabla\log \pi(y)-x\|+\|y+h\nabla\log \widehat{\pi}(y)-x\|\right)\\\leq& \int \frac{\widehat{\pi}(y)}{\widehat{\pi}(x)}\hat{q}(y,dx)\left(C+h\epsilon+2\|y+h\nabla\log \widehat{\pi}(y)-x\|\right)\leq C\exp\!(\delta \|x\|^2).\end{align*}
\begin{align*}&\int \frac{\widehat{\pi}(y)}{\widehat{\pi}(x)}\hat{q}(y,dx)\left(C+(\|y+h\nabla\log \pi(y)-x\|+\|y+h\nabla\log \widehat{\pi}(y)-x\|\right)\\\leq& \int \frac{\widehat{\pi}(y)}{\widehat{\pi}(x)}\hat{q}(y,dx)\left(C+h\epsilon+2\|y+h\nabla\log \widehat{\pi}(y)-x\|\right)\leq C\exp\!(\delta \|x\|^2).\end{align*}
Thus,
![]() $\int |a(x,y)-\widehat{a}(x,y)|dy\leq C\epsilon\exp\!(\delta x^2)$
for some
$\int |a(x,y)-\widehat{a}(x,y)|dy\leq C\epsilon\exp\!(\delta x^2)$
for some
![]() $C$
. This concludes the proof of (35) and our claim.
$C$
. This concludes the proof of (35) and our claim.
Appendix D. Verification for the parallel tempering algorithm
Proof of Lemma
2. For claim 1, note that for any
![]() $\|\,f\|_\nu\leq 1$
,
$\|\,f\|_\nu\leq 1$
,
 \begin{equation*}\begin{split}\|RSf-\widehat{R}\widehat{S} f\|_\nu&\leq \|R(S-\widehat{S})f\|_\nu+\|(R-\widehat{R})\widehat{S} f\|_\nu\\&\leq \|(S-\widehat{S})f\|_\nu+C\epsilon\|\widehat{S} f\|_\nu \mbox{ by Lemma 4}\\&\leq C\epsilon \|\,f\|_\nu+C\epsilon\| (\widehat{S} - S) f\|_\nu + C\epsilon\|S f\|_{\nu} \\&\leq (2C+C^2\epsilon)\epsilon \|\,f\|_\nu \mbox{ by Lemma 4.}\end{split}\end{equation*}
\begin{equation*}\begin{split}\|RSf-\widehat{R}\widehat{S} f\|_\nu&\leq \|R(S-\widehat{S})f\|_\nu+\|(R-\widehat{R})\widehat{S} f\|_\nu\\&\leq \|(S-\widehat{S})f\|_\nu+C\epsilon\|\widehat{S} f\|_\nu \mbox{ by Lemma 4}\\&\leq C\epsilon \|\,f\|_\nu+C\epsilon\| (\widehat{S} - S) f\|_\nu + C\epsilon\|S f\|_{\nu} \\&\leq (2C+C^2\epsilon)\epsilon \|\,f\|_\nu \mbox{ by Lemma 4.}\end{split}\end{equation*}
For claim 2, we first note that
We will show that
For any
![]() $f(x,y)$
, we define
$f(x,y)$
, we define
Then for each fixed
![]() $y$
, since
$y$
, since
![]() $\|R_1-\widehat{R}_1\|_{\nu_1}\leq C \epsilon$
,
$\|R_1-\widehat{R}_1\|_{\nu_1}\leq C \epsilon$
,
Thus,
Similarly, we can show that
From claim 1, we can find a
![]() $C'$
so that
$C'$
so that
For claim 3, by triangular inequality, we have
Proof of Lemma
3. Denote
![]() $x^{\prime}=S(x)$
. For any density of form
$x^{\prime}=S(x)$
. For any density of form
![]() $\mu(x)=s(x)\nu(x)$
, we have
$\mu(x)=s(x)\nu(x)$
, we have
 \begin{align*}|\mu (Q-\widehat{Q}) f|&\leq \int \mu(x) |a(x,x^{\prime})-\widehat{a}(x,x^{\prime})| |\,f(x)|dx+\int \mu(x) |a(x,x^{\prime})-\widehat{a}(x,x^{\prime})| |\,f(x^{\prime})|dx\\&\leq C\epsilon \int \mu(x) |\,f(x)|dx+C\epsilon \int \mu(x) a(x,x^{\prime}) |\,f(x^{\prime})|dx\\&\leq C\epsilon \int s(x)\nu(x) |\,f(x)|dx+C\epsilon \int s(x)\nu(x) (Q(x,x)|\,f(x)|+Q(x,x^{\prime}) |\,f(x^{\prime})|)dx\\&\leq C\epsilon \| s \|_\nu \|\,f\|_\nu+C\epsilon \| s \|_\nu \|Q |\,f|\|_\nu\\&\leq 2C\epsilon \| s \|_\nu \|\,f\|_\nu.\end{align*}
\begin{align*}|\mu (Q-\widehat{Q}) f|&\leq \int \mu(x) |a(x,x^{\prime})-\widehat{a}(x,x^{\prime})| |\,f(x)|dx+\int \mu(x) |a(x,x^{\prime})-\widehat{a}(x,x^{\prime})| |\,f(x^{\prime})|dx\\&\leq C\epsilon \int \mu(x) |\,f(x)|dx+C\epsilon \int \mu(x) a(x,x^{\prime}) |\,f(x^{\prime})|dx\\&\leq C\epsilon \int s(x)\nu(x) |\,f(x)|dx+C\epsilon \int s(x)\nu(x) (Q(x,x)|\,f(x)|+Q(x,x^{\prime}) |\,f(x^{\prime})|)dx\\&\leq C\epsilon \| s \|_\nu \|\,f\|_\nu+C\epsilon \| s \|_\nu \|Q |\,f|\|_\nu\\&\leq 2C\epsilon \| s \|_\nu \|\,f\|_\nu.\end{align*}
Taking
![]() $\mu(x)\propto |(Q-\widehat{Q})f(x)|\nu(x)$
, we have the result.
$\mu(x)\propto |(Q-\widehat{Q})f(x)|\nu(x)$
, we have the result.
Proof of Proposition 8. Recall that
 \begin{align*}P=MQ,\quad M=\left(M_{0}\otimes \cdots \otimes M_K\right),\quad Q= \left(\frac{1}{K}\sum_{k\in \{0,\ldots,K-1\}} Q_{k,k+1}\right).\end{align*}
\begin{align*}P=MQ,\quad M=\left(M_{0}\otimes \cdots \otimes M_K\right),\quad Q= \left(\frac{1}{K}\sum_{k\in \{0,\ldots,K-1\}} Q_{k,k+1}\right).\end{align*}
and
 \begin{align*}\widehat{P}=\widehat{M}\widehat{Q},\quad \widehat{M}=\left(\widehat{M}_{0}\otimes \cdots \otimes \widehat{M}_K\right),\quad \widehat{Q}=\left(\frac{1}{K}\sum_{k\in \{0,\ldots,K-1\}} \widehat{Q}_{k,k+1}\right).\end{align*}
\begin{align*}\widehat{P}=\widehat{M}\widehat{Q},\quad \widehat{M}=\left(\widehat{M}_{0}\otimes \cdots \otimes \widehat{M}_K\right),\quad \widehat{Q}=\left(\frac{1}{K}\sum_{k\in \{0,\ldots,K-1\}} \widehat{Q}_{k,k+1}\right).\end{align*}
Since
![]() $M$
is a product of
$M$
is a product of
![]() $M_k$
, Lemma 2 claim 2 indicates that
$M_k$
, Lemma 2 claim 2 indicates that
![]() $\|M-\widehat{M}\|_\Pi\leq C_1\epsilon$
for some
$\|M-\widehat{M}\|_\Pi\leq C_1\epsilon$
for some
![]() $C_1$
. Then note that if
$C_1$
. Then note that if
![]() $a\leq C A, b\leq CB$
, then
$a\leq C A, b\leq CB$
, then
![]() $\min \{a,b\}\leq C\min\{A,B\}$
so the acceptance probability of
$\min \{a,b\}\leq C\min\{A,B\}$
so the acceptance probability of
![]() $Q_{k,k+1}$
and
$Q_{k,k+1}$
and
![]() $\widehat{Q}_{k,k+1}$
satisfies
$\widehat{Q}_{k,k+1}$
satisfies
for some constant
![]() $D$
. Then Lemma 3 indicates that
$D$
. Then Lemma 3 indicates that
![]() $\|Q_{k,k+1}-\widehat{Q}_{k,k+1}\|_\Pi\leq C_2\epsilon$
for some
$\|Q_{k,k+1}-\widehat{Q}_{k,k+1}\|_\Pi\leq C_2\epsilon$
for some
![]() $C_2$
and Lemma 2 claim 3 indicates that for some
$C_2$
and Lemma 2 claim 3 indicates that for some
![]() $C_3$
,
$C_3$
,
Finally, we use claim 1 from Lemma 2 and find that
![]() $\|P-\widehat{P}\|_\Pi\leq C'\epsilon$
for some
$\|P-\widehat{P}\|_\Pi\leq C'\epsilon$
for some
![]() $C'$
.
$C'$
.
Acknowledgement
We thank Daniel Rudolf for discussing of some the results and providing us with some references.
Funding information
TC is supported by the Australian Research Council grant DP210103092. JD is supported by NSF grant DMS-1720433. AJ is supported by KAUST baseline funding. XT is supported by the Singapore Ministry of Education (MOE) grant Tier-1-A-8000459-00-00.
Competing interests
There were no competing interests that arose during the preparation or publication process of this article to declare.