Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T17:18:06.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional instabilities over a rectangular open cavity: from linear stability analysis to experimentation

Published online by Cambridge University Press:  28 April 2014

J. de Vicente ,
J. Basley ,
F. Meseguer-Garrido ,
J. Soria  and
V. Theofilis
J. de Vicente*
Affiliation:
School of Aerospace Engineering, Universidad Politécnica de Madrid, Pza. Cardenal Cisneros 3, E-28040 Madrid, Spain
J. Basley
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton 3800, Australia CNRS, Laboratoire d’Informatique pour la Mécanique et les Sciences de l’Ingénieur, F-91403 Orsay, France Université Paris-Sud, F-91405 Orsay, France
F. Meseguer-Garrido
Affiliation:
School of Aerospace Engineering, Universidad Politécnica de Madrid, Pza. Cardenal Cisneros 3, E-28040 Madrid, Spain
J. Soria
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton 3800, Australia
V. Theofilis
Affiliation:
School of Aerospace Engineering, Universidad Politécnica de Madrid, Pza. Cardenal Cisneros 3, E-28040 Madrid, Spain
*
†Email address for correspondence: fj.devicente@upm.es
Get access Rights & Permissions [Opens in a new window]

Abstract

Three-dimensional instabilities arising in open cavity flows are responsible for complex broad-banded dynamics. Existing studies either focus on theoretical properties of ideal simplified flows or observe the final state of experimental flows. This paper aims to establish a connection between the onset of the centrifugal instabilities and their final expression within the fully saturated flow. 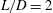To that end, a linear three-dimensional modal instability analysis of steady two-dimensional states developing in an open cavity of aspect ratio $L/D=2$ (length over depth) is conducted. This analysis is performed together with an experimental study in the same geometry adding spanwise endwalls. Two different Reynolds numbers are investigated through spectral analyses and modal decomposition. The physics of the flow is thoroughly described exploiting the strengths of each methodology. The main flow structures are identified and salient space and time scales are characterised. Results indicate that the structures obtained from linear analysis are mainly consistent with the fully saturated experimental flow. The analysis also brings to light the selection and alteration of certain wave properties, which could be caused by nonlinearities or the change of spanwise boundary conditions.

JFM classification

Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 189 - 220
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albensoeder, S. & Kuhlmann, H. C. 2006 Nonlinear three-dimensional flow in the lid-driven square cavity. J. Fluid Mech. 569, 465–480.CrossRefGoogle Scholar
Albensoeder, S., Kuhlmann, H. C. & Rath, H. J. 2001 Three-dimensional centrifugal-flow instabilities in the lid-driven-cavity problem. Phys. Fluids 13, 121–135.CrossRefGoogle Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.CrossRefGoogle Scholar
Basley, J.2012 An experimental investigation on waves and coherent structures in a three-dimensional open cavity flow. PhD thesis, Université Paris-Sud, Nash University.Google Scholar
Basley, J., Pastur, L. R., Lusseyran, F., Faure, T. M. & Delprat, N. 2011 Experimental investigation of global structures in an incompressible cavity flow using time-resolved PIV. Exp. Fluids 50 (4), 905–918.CrossRefGoogle Scholar
Basley, J., Pastur, L. R., Delprat, N. & Lusseyran, F. 2013 Space–time aspects of a three-dimensional multi-modulated open cavity flow. Phys. Fluids 25 (6), 064105.CrossRefGoogle Scholar
Brès, G. A. & Colonius, T. 2008 Three-dimensional instabilities in compressible flow over open cavities. J. Fluid Mech. 599, 309–339.CrossRefGoogle Scholar
Cattafesta III, L. N., Garg, S., Kegerise, M. S. & Jones, G. S. 1998 Experiments on compressible flow-induced cavity oscillations. Proceedings of the 29th Fluid Dynamics Conference, AIAA Paper 98-2912 .Google Scholar
Chiang, T., Sheu, W. & Hwang, R. 1998 Effects of the Reynolds number on the eddy structure in a lid-driven cavity. Intl J. Numer. Meth. Fluids 26, 557–579.3.0.CO;2-R>CrossRefGoogle Scholar
Douay, C. L., Guéniat, F., Pastur, L., Lusseyran, F. & Faure, T. M. 2011 Instabilités centrifuges dans un écoulement de cavité: décomposition en modes dynamiques, Comptes-Rendus des Rencontres du Non-linéaire, vol. 14, pp. 47–52. Non-Linéaire Publications.Google Scholar
von Ellenrieder, K., Kostas, J. & Soria, J. 2001 Measurements of a wall-bounded turbulent, separated flow using HPIV. J. Turbul. 2, 1–15.CrossRefGoogle Scholar
Faure, T. M., Adrianos, P., Lusseyran, F. & Pastur, L. R. 2007 Visualizations of the flow inside an open cavity at medium range Reynolds numbers. Exp. Fluids 42 (2), 169–184.CrossRefGoogle Scholar
Faure, T. M., Pastur, L. R., Lusseyran, F., Fraigneau, Y. & Bisch, D. 2009 Three-dimensional centrifugal instabilities development inside a parallelepipedic open cavity of various shape. Exp. Fluids 47 (3), 395–410.CrossRefGoogle Scholar
Gonzalez, L. M., Ahmed, M., Kühnen, J., Kuhlmann, H. C. & Theofilis, V. 2011 Three-dimensional flow instability in a lid-driven isosceles triangular cavity. J. Fluid Mech. 675, 369–396.CrossRefGoogle Scholar
Guermond, J.-L., Migeon, C., Pineau, G. & Quartapelle, L. 2002 Start-up flows in a three-dimensional rectangular driven cavity of aspect ratio 1:1:2 at $Re=1000$ . J. Fluid Mech. 450, 169–199.CrossRefGoogle Scholar
Huang, N. E., Shen, Z. & Long, S. R. 1999 A new view of nonlinear water waves: the Hilbert spectrum. Annu. Rev. Fluid Mech. 31, 417–457.CrossRefGoogle Scholar
Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., Yen, N.-C., Tung, C. C. & Liu, H. H. 1998 The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time-series analysis. Proc. R. Soc. Lond. A 454, 903–995.CrossRefGoogle Scholar
Kegerise, M. A., Spina, E. F., Garg, S. & Cattafesta III, L. N. 2004 Mode-switching and nonlinear effects in compressible flow over a cavity. Phys. Fluids 16, 678–687.CrossRefGoogle Scholar
Knisely, C. & Rockwell, D. 1982 Self-sustained low-frequency components in an impinging shear layer. J. Fluid Mech. 116, 157–186.CrossRefGoogle Scholar
Koseff, J. R. & Street, R. L. 1984a Visualization studies of a shear driven three-dimensional recirculating flow. Trans. ASME: J. Fluids Engng 106, 21–29.Google Scholar
Koseff, J. R. & Street, R. L. 1984b On endwall effects in a lid-driven cavity flow. Trans. ASME: J. Fluids Engng 106, 385–389.Google Scholar
Koseff, J. R. & Street, R. L. 1984c The lid-driven cavity flow: a synthesis of qualitative and quantitative observations. Trans. ASME: J. Fluids Engng 106, 390–398.Google Scholar
Meseguer-Garrido, F., de Vicente, J., Valero, E. & Theofilis, V. 2011 Effect of aspect ratio on the three-dimensional global instability analysis of incompressible open cavity flows In 6th AIAA Theoretical Fluid Mechanics Conference, Honolulu, Hawaii, vol. 3605. AIAA.CrossRefGoogle Scholar
Meseguer-Garrido, F., de Vicente, J., Valero, E. & Theofilis, V.2014 Three-dimensional global instability analysis of incompressible open cavity flows. J. Fluid Mech. (submitted).CrossRefGoogle Scholar
Migeon, C. 2002 Details on the start-up development of the Taylor–Görtler-like vortices inside a square-section lid-driven cavity for $1000 < Re < 3200$ . Exp. Fluids 33, 594–602.CrossRefGoogle Scholar
Migeon, C., Pineau, G. & Texier, A. 2003 Three-dimensionality development inside standard parallelepipedic lid-driven cavities at $Re=1000$ . J. Fluids Struct. 17, 717–738.CrossRefGoogle Scholar
Neary, M. D. & Stephanoff, K. D. 1987 Shear-layer-driven transition in a rectangular cavity. Phys. Fluids 30 (10), 2936–2946.CrossRefGoogle Scholar
Parker, K., von Ellenrieder, K. D. & Soria, J. 2007 Morphology of the forced oscillatory flow past a finite-span wing at low Reynolds number. J. Fluid Mech. 571, 327–357.CrossRefGoogle Scholar
Piot, E., Casalis, G., Muller, F. & Bailly, C. 2006 Investigation of the pse approach for subsonic and supersonic hot jets. detailed comparisons with LES and Linearized Euler Equation results. Intl J. Aeroacoust. 5 (4), 361–393.CrossRefGoogle Scholar
Powell, A. 1953 On edge tones and associated phenomena. Acustica 3, 233–243.Google Scholar
Rockwell, D. 1977 Prediction of oscillation frequencies for unstable flow past cavities. Trans. ASME: J. Fluids Engng 99, 294–300.Google Scholar
Rockwell, D. & Knisely, C. 1980 Observations of the three dimensional nature of unstable flow past a cavity. Phys. Fluids 23, 425–431.CrossRefGoogle Scholar
Rockwell, D. & Naudascher, E. 1979 Self-sustained oscillations of impinging free shear layers. Annu. Rev. Fluid Mech. 11, 67–94.CrossRefGoogle Scholar
Rossiter, J. E.1964 Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. Aeronaut. Res. Counc. R & M 3438.Google Scholar
Rowley, C. W., Colonius, T. & Basu, A. J. 2002 On self-sustained oscillations in two-dimensional compressible flow over rectangular cavities. J. Fluid Mech. 455, 315–346.CrossRefGoogle Scholar
Shankar, P. N. & Deshpande, M. D. 2000 Fluid mechanics in the driven cavity. Annu. Rev. Fluid Mech. 32, 93–136.CrossRefGoogle Scholar
Soria, J. 1996a An adaptative cross-correlation digital PIV technique for unsteady flow investigations. In Proc. Australian Conf. on Laser Diagnostics in Fluid Mechanics and Combustion, Sydney, Australia (ed. Masri, A. & Honnery, D.), vol. 1, pp. 29–48. University of Sydney, Sydney, Australia.Google Scholar
Soria, J. 1996b An investigation of the near wake of a circular cylinder using a video-based digital cross-correlation particle image velocimetry technique. Exp. Therm. Fluid Sci. 12, 221–233.CrossRefGoogle Scholar
Soria, J.1998 Multigrid approach to cross-correlation digital PIV and HPIV analysis. In 13th Australasian Fluid Mechanics Conference, Melbourne, Australia.Google Scholar
Soria, J., Cater, J. & Kostas, J. 1999 High resolution multigrid cross-correlation digital PIV measurements of a turbulent starting jet using half frame image shift ®lm recording. Opt. Laser Technol. 31, 3–12.CrossRefGoogle Scholar
Theofilis, V.2000 Globally unstable basic flows in open cavities. In AIAA Paper 2000-1965.CrossRefGoogle Scholar
Theofilis, V. & Colonius, T.2003 An algorithm for the recovery of 2- and 3-D BiGlobal instabilities of compressible flow over 2-d open cavities. AIAA Paper 2003-4143.CrossRefGoogle Scholar
Theofilis, V. & Colonius, T.2004 Three-dimensional instabilities of compressible flow over open cavities: direct solution of the biglobal eigenvalue problem. AIAA Paper 2004-2544.CrossRefGoogle Scholar
Theofilis, V., Colonius, T. & Seifert, A.(ed.) 2001 Proceedings of the “AFOSR/EOARD/ERCOFTAC SIG-33 Global Flow Instability Control Symposium I”, 23–25 September 2001, Creta Maris, Hersonissos, Greece.Google Scholar
de Vicente, J.2010 Spectral multi-domain method for the global instability analysis of complex cavity flows. PhD thesis, Universidad Politécnica de Madrid.Google Scholar
de Vicente, J., Paredes, P., Valero, E. & Theofilis, V. 2011 Wave-like disturbances on the downstream wall of an open cavity In 6th AIAA Theoretical Fluid Mechanics Conference, Honolulu, Hawaii, vol. 3754. AIAA.CrossRefGoogle Scholar
de Vicente, J., Rodriguez, D., Theofilis, V. & Valero, E. 2010 Stability analysis in spanwise-periodic double-sided lid-driven cavity flows with complex cross-sectional profiles. Comput. Fluids 43 (1), 143–153.CrossRefGoogle Scholar